f) cotg 300 ctg 60 2 d) cos 5 cos 6 Al ser un ángulo del primer cuadrante, todas las razones son positivas. Así, tenemos: tg α 3
|
|
|
- Ἀνδρομάχη Κοντολέων
- 6 χρόνια πριν
- Προβολές:
Transcript
1 .9. Calcula el valor de las siguientes razones trigonométricas reduciéndolas al primer cuadrante. a) sen 0 c) tg 0 e) sec 0 b) cos d) cosec f) cotg 00 Solucionario a) sen 0 sen 0 d) cosec sen sen b) cos cos c) tg 0 tg 0 e) sec 0 sec 60 cos 60 f) cotg 00 ctg 60 tg Calcula el valor eacto de las siguientes razones trigonométricas. a) sen b) cosec c) tg d) cos 6 6 a) sen sen c) tg tg b) cosec cosec 6 6 d) cos cos 6 6 sen 6.. Sabiendo que la cotangente de un ángulo del primer cuadrante vale, calcula el resto de las razones de dicho ángulo. Al ser un ángulo del primer cuadrante, todas las razones son positivas. Así, tenemos: tg tg sec sec tg sen cos tg ( cosec ) cos.. Calcula las restantes razones de sabiendo que: sec y que 90 < < 80. Al ser un ángulo del segundo cuadrante, el seno y la cosecante son positivos y el resto de razones son negativas. sec cos sen cos sen sen cosec tg s en cotg cos sen.. Halla todas las razones trigonométricas de si se sabe que cotg y que < <. Al ser un ángulo del tercer cuadrante, la tangente y la cotangente son positivas, y el resto de razones, negativas. tg ;tg sec sec tg cos sen cos tg cosec
2 .. Calcula la razón pedida en cada caso: a) sen, si tg y II b) tg, si cos y IV 9 9 a) cotg sen sen. Como II, sen c otg b) tg tg co s 9 tg, ya que IV Calcula las razones trigonométricas de 7 y rad. a) sen 7 sen (0 ) sen 0 cos cos 0 sen cos 7 cos (0 ) cos 0 cos sen 0 sen tg 7 s en cos7 b) sen cos sen sen cos cos sen cos cos cos sen sen tg Demuestra que sen cos. sen sen cos cos sen cos () cos.7. Desarrolla las epresiones de cos y de tg en función de las razones trigonométricas del ángulo. cos cos ( ) cos cos sen sen cos (cos sen ) sen sen cos cos cos sen sen cos cos cos sen cos cos tg tg tg tg tg tg tg tg tg tg tg ( ) tg tg tg tg tg tg t g tg tg tg tg tg ( tg ) tg.8. Si es un ángulo del segundo cuadrante y sen, calcula las razones de. Como es del. cuadrante, sen sen c cos c es del primero y todas sus razones son positivas. cos 9 os os y, por último, tg
3 .9. Transforma las siguientes sumas en productos. Solucionario a) sen sen b) sen 7 sen c) cos cos 8 d) cos 0 cos 0 a) sen sen sen cos sen cos 0 b) sen 7 sen cos 7 sen 7 cos sen 0 c) cos cos 8 cos 8 cos 8 cos 0 cos 0 d) cos 0 cos 0 sen 0 0 sen 0 0 sen 0 sen Transforma los siguientes productos en sumas. a) sen 80 sen 0 b) cos cos 0 a) A B 80, A B 0 A 0, B 0 sen 80 sen 0 (cos 0 cos 0) b) A B, A B 0 A, B cos cos 0 (cos cos ).. Comprueba que cos 7 cos = cos. cos 7 cos cos 7 cos 7 cos 60 cos cos cos.. Simplifica la siguiente epresión: c os cos sen sen cos cos cos cos cos cotg s en sen sen sen cos.. Resuelve las siguientes ecuaciones y da los resultados en grados y en radianes. a) sen c) cos 0 b) tg 0 d) tg 0 a) sen El seno de un ángulo vale únicamente en 90, 0, 80, etc. Por tanto: k con k Z o k con k Z b) tg 0 La tangente vale 0 en los ángulos 0, 80, 60, 0, etc. Por tanto: 80 k con k Z o k con k Z c) cos El coseno es negativo para los ángulos de los cuadrantes. y. Por tanto: 0 60 k, 0 60 k con k Z o k, k con k Z d) tg La tangente es positiva para los ángulos de los cuadrantes. y. Por tanto: 0 60 k, 0 60 k con k Z o 6 k 7 k con k Z 6.. Resuelve los siguientes sistemas de ecuaciones en el intervalo [0, ]. tg ( y) y a) b) sen sen y sen sen y
4 tg ( y) a) tg y cotg y tg y y Solución: 6, y 6 sen sen y sen sen y tg ( y) y y b) ; y 6 ; y 6 ; y 6 ; y 6 sen sen sen y sen y y 6, y Calcula la longitud del lado c de un triángulo ABC sabiendo que a 0 cm, Ap y Bp 00. a c Cp c a sen Cp 0 sen 8, cm sen Ap sen Cp sen Ap sen.6. Calcula la longitud del lado c de un triángulo ABC sabiendo que a = cm, b = cm y Cp =. c a b ab cos Cp cos 7,0 c 8,6 cm.7. Resuelve los siguientes triángulos rectángulos y calcula sus áreas. a) Ap 90, b cm, a 0 cm b) Bp 90, Cp, b 0 m c) Cp 90, b 0 mm, a 8 mm a) c 0,; sen Bp b a 0,7 Bp 8, Cp '. Área: b c 99, cm 0 b) A 906; a b cos Cp 0 cos 9,06 m; c b sen Cp 0 sen, m. Área: a c 9,6 m c) c 0 8 0,9 mm; tg Bp b a 0 0,6 Bp 9, Ap Área: b a 90 mm 8.8. Resuelve los siguientes triángulos y calcula sus áreas. a) Ap 80, Bp 0, a 8 dm c) a 0 cm, b cm, c 0 cm b) *Ap 80, a 0 m, b m d) *Ap 7, b 8 mm, c mm a) Ap Bp Cp 80 Cp Aplicando el teorema del seno: a b b a sen Bp 8 sen 0, dm sen Ap sen Bp sen Ap sen 80 a c c a sen Cp 8 sen 60 7,0 dm sen Ap sen Cp sen Ap sen 80 Área: S a b sen Cp 8, dm b) Aplicando el teorema del seno: sen Bp bse nap se n 80 0,9 Bp 9 9 a 0 Cp Por el teorema del coseno: c a b ab cos Cp 0 0 cos 70 9,6 c 9,7 m Área: S a c sen Bp,6 m
5 Solucionario c) Por el teorema del coseno: cos Ap b c a bc cos Bp a c b ac cos Cp a b c ab Área: S a c sen Bp 7,6 cm d) Por el teorema del coseno: 0,87 Ap 8 7 0,687 Bp 6 0, Cp 0 9 a b c bc cos Ap 8 8 cos 7 8, a,8 mm Aplicando el teorema del seno: sen Bp b se n Ap 8s en 7 0,6 Bp 7,88 7 a,8 Cp ,88 67, 67 7 Área: S b c sen Ap 6,6 mm EJERCICIOS Medida de ángulos.9. Copia y completa las siguientes tablas. Grados 0 60 Radianes Grados 0 0 Radianes Grados 80 Radianes 6 Grados 60 Radianes 6 Grados Radianes 6 Grados Radianes 6 Grados Radianes 7 6 Grados Radianes Pasa de grados a radianes. a) 8 b) 0 c) 76 0 d) 8 0 a) rad c) ,87 80 rad 96 b) rad d) 8 0 8, 80 7 rad 8.. Pasa de radianes a grados. a) rad b) rad c) rad d) rad a) rad c) rad b) rad d) rad Indica los siguientes ángulos como suma de un número entero de vueltas completas más el ángulo restante. a) b) 00 c) 6 rad d) rad 7 a) vueltas 8 c) vueltas rad b) vueltas 60 d) 0 vueltas 0 rad 7 7 7
6 Razones trigonométricas.. Halla los valores eactos de las razones trigonométricas de los ángulos agudos del triángulo de la figura. B Bp Cp a b b sen b b cos, y tg b b c = b A b a C.. En un triángulo isósceles, el lado mayor es el triple del lado menor. Calcula las razones trigonométricas. Llamando al lado menor, el lado mayor será 6. Altura: h (6) Si el ángulo mayor es, sen, cos ytg. Para hallar las razones del ángulo menor,, teniendo en cuenta que, podemos aplicar las fórmulas correspondientes. sen = sen () sen sen cos,coscos ( ) cos sen cos tg = s en = cos 7.. (TIC) Utiliza la calculadora para hallar el valor de las siguientes razones trigonométricas. Aproima los resultados a las milésimas. a) sen 6 e) cotg i) sec 6 b) cos f) sec j) tg c) tg g) sen 0 k) tg d) cosec 7 h) cos l) cotg a) sen 6 0,88 e) cotg 0,8 i) sen 6,679 b) cos 0,9 f) sec,0 j) tg 0, c) tg 0, g) sen 0 0, k) tg 0,667 d) cosec 7,0 h) cos 0,97 l) cotg 0,6.6. (TIC) Utiliza la calculadora para hallar el valor de las siguientes razones trigonométricas. Aproima los resultados a las milésimas y ten en cuenta que todos los ángulos están dados en radianes. a) sen b) cosec c) cos d) sec e) tg f) cotg,7 7 a) sen 0,9 c) cos 0, e) tg 0,77 7 b) cosec, d) sec,0 f) cotg,7,.7. (TIC) Con ayuda de la calculadora, halla la medida en grados del ángulo del primer cuadrante tal que: a) sen 0, c) tg 0, e) sec 0, b) cosec 0, d) cos 0, f) cotg 0,0 a) sen 0, 0 d) sec 0, No eiste ningún ángulo. b) cosec 0, No eiste ningún ángulo. e) cos 0, 6 6 c) tg 0, f) cotg 0,0 89 6
7 .8. Calcula, de forma eacta, el valor de las siguientes razones trigonométricas. a) sen 0 d) cosec 0 g) sec 0 b) cos e) tg 00 h) cotg c) sen 7 7 f) tg i) sec Solucionario a) sen 0 sen 60 d) cosec 0 cosec 0 g) sec 0sec 60 b) cos cos e) tg 00 tg 60 h) cotg cotg c) sen 7 sen f) tg 7 tg 60 i) sec sec.9. Halla el valor eacto de las siguientes razones trigonométricas. a) sen b) cos (600) c) cosec d) cotg 80 e) tg () f) sec a) sen sen sen d) cotg 80 cotg 0 b) cos (600) cos 600 cos 0 cos 60 e) tg () tg tg 0 c) cosec cosec f) sec sec sec sen.0. Calcula todas las razones trigonométricas del ángulo sabiendo que: a) Es un ángulo del primer cuadrante y cos. d) < < y sec b) Pertenece al segundo cuadrante y sen 0,. e) 90 < < 80 y cotg c) 80 < < 70 y tg f) < < y cosec a) Al ser un ángulo del primer cuadrante, todas las razones trigonométricas son positivas. sen cos sen sen 9 9 sen 9 sec co s,cosec sen,tg s en, cotg cos tg b) Al ser un ángulo del segundo cuadrante, el seno y la cosecante son positivos y el resto de razones son negativas. sen cos cos cos 6 cos 6 tg s en cos, cotg tg, cosec, se n sec co s c) Al ser un ángulo del tercer cuadrante, la tangente y la cotangente son positivas y el resto de razones son negativas. tg cotg cos sen cos tg, tg sec sec g t 6 cosec
8 d) Al ser un ángulo del cuarto cuadrante, el coseno y la cosecante son positivos y el resto de razones son negativas. sec cos,sen cos sen sen sen tg s en cotg cosec cos tg se n e) Al ser un ángulo del segundo cuadrante, el seno y la cosecante son positivos y el resto de razones son negativas. cotg tg tg sec sec tg sen cos tg cos cosec f) Al ser un ángulo del tercer cuadrante, la tangente y la cotangente son positivas y el resto de razones son negativas. cosec sen sen cos cos cos cos tg s en cos cotg, sec co tg s.. Calcula en función de h el valor de cada una de las siguientes razones trigonométricas. a) sen, siendo sen 7 h. f) cosec 70, siendo cotg 99 h. b) cos 0, siendo tg 0 h. g) tg 90, siendo sen 0 h. c) tg 60, siendo sen 80 h. h) sen 8, siendo cos 7 h. d) cos 0, siendo sen 0 h. i) sec 0, siendo cotg 67 h. e) cos 7, siendo sen h. j) sec, siendo sen h. a) sen sen 7 h b) cos 0 g t 0 g t 0 s c) tg 60 cos 60 en 60 h tg 60 h h h h ( d) cos 0 cos 0 en s0 h e) cos 7 en s7 en s 67 s 80) en h f) cosec 70 cosec cosec 9 otg c9 h g) tg 90 tg 0 h h) sen 8 cos 7 h i) sec 0 sec cosec 67 c cos sen 67 otg 7 6 h j) sec sec cos h s en h
9 Solucionario Relaciones entre las razones trigonométricas.. Calcula, en función de h, la razón trigonométrica que se indica en cada caso. a) cosec, sabiendo que cotg h. b) sec 0, sabiendo que cotg h. c) tg 8, sabiendo que cos 9 h. a) cosec cosec cotg h b) sec 0 cos 0 cos h c) tg 8 8 cos g t cotg cos (cos ) 9 h / h h h h.. Sabiendo que sen h y que es un ángulo del primer cuadrante, calcula en función de h: a) sen (90 ) b) tg (080 ) a) 90 es también un ángulo del primer cuadrante; sen (90 ) cos h. h b) ; tg (080 ) tg () tg h.. Si tg h y es un ángulo del primer cuadrante, calcula en función de h: a) sen (90 ) b) cotg (080 ) tg sec cos tg h ; sen cos tg h h a) 90 es también un ángulo del primer cuadrante; sen (90 ) cos h b) ; cotg (080 ) cotg () cotg h.. Sabiendo que cosec 7, calcula: a) sen (80 ) b) sec 7 está en el tercer cuadrante o en el cuarto. Por tanto, 80 y 7 están en el. o. er cuadrantes. No se puede saber el signo de cos, por lo que no se puede saber el signo de sen (80 ). a) sen (80 ) sen (90 ) cos s en b) sec 7 sec se cos c ose c cosec 7 n Demuestra que tg (70 ) cotg. tg(70 ) s en ( 70 ) cos ( 70 ) sen 70 cos cos 70 sen cos 70 cos sen 70 sen cos se n cotg
10 .7. Desarrolla en función de sen y cos la epresión de sen. sen sen ( ) sen cos cos sen sen (cos sen ) cos (sen cos ) sen cos sen sen cos sen cos sen.8. Sabiendo que sen 0, y cos 0,, y que y son ángulos del primer cuadrante, calcula: a) sen ( ) b) cos ( ) c) sec ( ) d) cotg ( ) sen 0,; cos 0,968; sen 0,866; cos 0, a) sen ( ) 0, 0, 0,968 0,866 0,96 b) cos ( ) 0,968 0, 0, 0,866 0,7 c) sec ( ),7 cos ( ) 0,968 0, 0, 0,866 d) cotg ( ) tg tg tg ( ) tg tg 0, 0,9 68 0, 866 0, 0, 0,9 68 0, 866 0, 0,98.9. Si sen 0, y cos 0,, siendo < < y < <, calcula: a) sen ( ) b) cos ( ) c) tg ( ) sen 0, ; cos 0,97 ; sen 0,866 ; cos 0, a) sen ( ) 0, 0, 0,97 0,866 0,99 b) cos ( ) 0,97 0, 0, 0,866 0,80 0, tg tg 0,9 7 0, 866 c) tg ( ) 0, 0,7 tg tg 0, 0,9 7 0, 866 0,.0. Sabiendo que tg, calcula las razones trigonométricas del ángulo en cada caso. a) Si es un ángulo del primer cuadrante. b) Si es un ángulo del tercer cuadrante. a) El ángulo pertenece al segundo cuadrante. Al ser tg, 90. tg cos tg ; sen sen sen cos , cos cos sen 9 0 0, 0,9 0, ,6 tg 0,7 0,8 b) Los mismos valores del apartado anterior, ya que el ángulo también pertenece en este caso al segundo cuadrante... Calcula el valor de la tangente de sabiendo que es un ángulo del primer cuadrante y que sen. cos sen 8 cos sen cos 8 7 cos 8 sen ; tg tg ( ) sen cos
11 Solucionario.. Calcula, de forma eacta, las razones trigonométricas de los siguientes ángulos. a) b) 7 0 a) sen sen 0 cos cos 0 c tg o s co 0 s 0 b) sen 7 0 sen cos 7 0 cos cos 0 cos 0 cos cos sen 7 tg 7 0 ' c os 7 ( ) ( )( ).. Si cos y 90 < < 80, calcula las razones trigonométricas de. Si el ángulo pertenece al segundo cuadrante, el ángulo sen c o s s pertenece al primero. 6 ;cos c o ; tg Transforma en producto de razones trigonométricas las siguientes sumas. a) sen 8 sen d) sen 0 sen b) cos 00 cos 0 e) cos cos 7 c) sen sen f) cos cos 9 a) sen 8 sen sen 8 cos 8 sen 0 cos 8 b) cos 00 cos 0 cos 00 0 cos 00 0 cos 0 cos 80 c) sen sen sen cos sen cos d) sen 0 sen cos 0 sen 0 cos 6 sen 0 e) cos cos 7 sen 7 sen 7 sen 0 sen (7) sen 0 sen 7 f) cos cos 9 sen 9 sen 9 sen sen 9 9
12 .. Transforma en suma de razones trigonométricas los siguientes productos. a) sen cos c) sen 0 cos 7 b) cos 9 cos 8 d) sen 9 sen a) sen cos sen sen b) cos 9 cos 8 (cos cos 7) c) sen 0 cos 7 (sen sen ()) (sen sen ) d) sen 9 sen (cos cos 9).6. Transforma en productos las siguientes sumas. a) sen sen c) cos 6 cos b) sen sen d) cos 8 cos a) sen sen sen cos sen cos b) sen sen cos sen cos sen c) cos 6 cos cos 6 cos 6 cos cos d) cos 8 cos sen 8 sen 8 sen sen.7. Simplifica la epresión sen π sen. sen π π sen sen cos sen π cos π π π π sen cos cos sen π cos sen cos sen cos.8. Desarrolla las siguientes epresiones. a) sen ( β γ) c) sen ( β) b) cos ( β γ) d) cos ( β) a) sen ( β γ) sen ( (β γ)) sen cos (β γ) cos sen (β γ) sen cos β cos γ sen sen β sen γ cos sen β cos γ cos cos β sen γ sen cos β cos γ cos sen β cos γ cos cos β sen γ sen sen β sen γ b) cos ( β γ) cos ( (β γ)) cos cos (β γ) sen sen (β γ) cos cos β cos γ cos sen β sen γ sen sen β cos γ sen cos β sen γ cos cos β cos γ cos sen β sen γ sen cos β sen γ sen sen β cos γ c) sen ( β) sen cos β cos sen β sen cos cos β cos sen β sen sen β d) cos ( β) cos cos β sen sen β cos (cos β sen β) sen sen β cos β cos cos β cos sen β sen sen β cos β
13 Solucionario.9. Demuestra las siguientes identidades trigonométricas. a) sen cos sen cos g) tg tg cos cot b) se n cos cosec h) tg π tg π tg c) tg sen tg sen i) sen sen β sen ( β) sen ( β) tg d) tg tg j) (cos cos β) (sen sen β) sen β co s e) tg cotg sec cosec k) tg f) cos sen sen tg sen cos a) sen cos sen cos sen cos (sen cos ) cos cos tg sen cos s en sen cos cos cos sen cos c os cotg sen sen b) cosec se n cos sen cos sen cos se n c) tg sen s en sen cos e) tg cotg s en cos se n cos sec cosec cos s en sen cos sen ( cos ) cos s en sen cos tg sen tg d) tg tg tg tg tg tg tg s en tg cos tg tg s en cos sen cos cos tg tg tg cos sen c os cos sen cos f) cos sen cos sen sencos sen sen cos se n se n cos cos sen tg sen cos sen sen g) cos sen cos s en os cos c s en tg cos sen cos h) tg tg tg tgtg tg tg tg tg tg i) sen ( β) sen ( β) (sen cos β cos sen β) (sen cos β cos sen β) sen cos β cos sen β sen cos β ( sen ) sen β sen cos β sen sen β sen β sen (cos β sen β) sen β sen sen β j) (cos cos β) (sen sen β) cos cos β cos cos β sen sen β sen sen β (cos ( β) cos ( β)) (cos ( β) cos ( β)) cos ( β) cos ( β) cos ( β) cos ( β) cos ( β) cos β sen β sen β sen β k) Equivale a la identidad del apartado h. sen sen cos cos tg π a tg π tg tg tg tg tg tg tg tg tg tg g tg
14 .60. Simplifica las siguientes epresiones trigonométricas. a) (sen cos ) (sen cos ) e) sen (tg cotg ) cos sen b) tg tg β (cotg cotg β) f) cos sen c) tg sen cos g) tg c os tg sen tg cos d) sen a) (sen cos ) (sen cos ) sen cos sen cos sen cos sen cos b) tg tg β (cotg cot β) tg tg β tg tg β tg tg β t g β tg tg tg β tg tg β sen c) tg c os cos sen cos tg sen cos sen cos sen c os cos d) sen sen sen sen e) sen (tg cotg ) sen cos s en cos cos s en cos sen f) cos sen sen cos ( sen )( sen ) sen sen cos cos sen cos sen (sen ) (sen )(cos )(cos ) (sen )(cos ) ( cos ) ( sen ) g) tg tg se sen sen cos n cos c tg os cos sen tg cos tg tg tg.6. Simplifica las siguientes epresiones utilizando las fórmulas de transformación de sumas en productos. sen 8 sen a) b) co s cos β sen c) d) cos sen( β) sen sen cos cos sen sen sen 8 sen sen cos sen sen a) sen c) cos cos sen sen co s sen cos b) co cos cos β cos β cos β cos s cos β sen( β) d) cos cos cotg sen sen sen sen β sen β cos β cos Ecuaciones y sistemas de ecuaciones.6. (TIC) Resuelve las siguientes ecuaciones trigonométricas indicando todas sus soluciones en grados. a) sen c) tg e) cos g) sen 0 b) cos d) sen f) tg h) cos 0 a) sen 060 k d) sen 60 k f) sen 0 80 k 060 k 60 k b) cos 060 k 060 k e) cos g) cos 0 60 k c) tg 60 k f) tg 60 k 060 k 060 k 060 k 060 k
15 .6. (TIC) Resuelve las siguientes ecuaciones trigonométricas indicando todas sus soluciones en radianes. a) sen c) tg e) cos b) cos d) sen 0 f) tg a) sen b) cos k d) sen 0 k k k k 7 π k e) cos k k c) tg f) tg k 7 k k k k 8 7 k 8 7 k k Solucionario 6k 6k 0 8 k k k k (TIC) Halla todas las soluciones de las siguientes ecuaciones trigonométricas. a) sen cos b) sen sen 0 c) sen cos 0 d) sen cos a) sen cos tg 60 k 60 k sen 0 80 k b) sen sen 0 sencos sen 0 sen ( cos ) k cos 0060 k c) sen cos 0 tg 6060 k 060 k d) sen cos sen sen sen sen sen sen sen 0 sen 60 k.6. (TIC) Resuelve las siguientes ecuaciones trigonométricas en el intervalo [0, 60]. a) tg cotg b) 8cos 8cos 9 c) tg cotg d) sen cos cos a) tg cot g tg tg tg tg tg tg 0 tg 6 tg tg b) 8 cos 8cos 9 8cos 8sen 8cos 9 0 8cos 8 8cos 8cos cos 8cos 0 cos ; 8 9 tg tg c) tg cot g tg tg tg tg tg tg tg 0, 0 0, 0 d) sen cos cos sen cos sen cos sen cos cos cos cos cos 60, 00 0, 0
16 .66. (TIC) Halla las soluciones de las siguientes ecuaciones trigonométricas comprendidas en el intervalo [0, π]. a) sen tg 0 b) sen tg 0 c) cos sen sen cos a) sen tg 0 sen co s b) sen tg 0 sen s c 0 0 sen c en os 0 c) cos sen sen cos cos cos sen sen cos cos sen cos cos cos sen 0 sen 0 sen 0 0,, 0 no aporta soluciones co s os cos 0 ;, tg : 6, 6 sen 0 0,, cos 7, (TIC) Resuelve las siguientes ecuaciones trigonométricas en el intervalo [, ]. a) sen sen 6 0 b) cos cos cos c) cos sen a) sen sen 6 0 sen 9 cos sen ,, 9 9 cos 0,, b) cos cos cos cos cos cos cos ( cos ) 0 cos 0, cos,, c) cos sen cos sen sen 6
17 Solucionario.68. (TIC) Resuelve los siguientes sistemas de ecuaciones trigonométricas en el intervalo [0, 60]. sen cos y a) b) cos cos y c) d) sen cos y y 90 sen cos y cos sen y tg tg y y 90 cos y sen a) sen cos y sen sen cos y 70 cos y sen cos y b) sen ( y) cos sen y (sen ( y) sen ( y)) (sen ( y) sen ( y)) sen ( y) sen ( y) sen ( y) sen ( y) 90, y 60 90, y 0 90, y 0 90, y 00 70, y 60 70, y 0 70, y 0 70, y 00 sen ( y) sen ( y) sen ( y) sen ( y) sen ( y) Soluciones: y 0, y 0 sen ( y) 0 y 0, y 80 (, y )( 7, y 7)( 8, y 0)( 0, y 8)( 6, y )(, y 6) c) cos cos y cos y cos y cos y cos y y 90 y y 90 y y 60 y 90 y 90 90, y 0 d) tg tg y tg tg( ) tg tg tg, y Solución:, y Resolución de triángulos.69. Resuelve los siguientes triángulos rectángulos. a) Ap 90, a mm, c mm c) Cp 90, Ap 0, a dm b) Bp 90, a 8 cm, c cm d) Bp 90, Ap, b m a) b 0,7 mm, sen Cp Cp Bp 7 b) b 8 cm; tg Cp Cp 8 7 Ap 8 c) Bp 70; c a,09 dm; b a sen Ap se n 0,97 dm tg Ap tg 0 d) Cp 7; a b sen Ap sen,88 m; c b cos Ap cos,9 m
18 .70. Calcula el área de cada uno de estos triángulos rectángulos. a) Ap 90, a 7 mm, c mm b) A c) B C 0 m 90 B A dm C a) b 7 8 S 8 0 mm b) a 0 sen m; c m; S m c) b a 6 9,07 dm; S 6 9,07,6 dm tg 0 tg Ap.7. Resuelve los siguientes triángulos. a) b 0 cm, c 8 cm, Cp 0 c) a cm, Bp 0, c cm e) a 0 cm, Bp 0, Cp 0 b) a cm, b 9 cm, c 0 cm d) a cm, b cm, Cp f) b cm, Bp, C 6 b c a) sen Bp b s en Cp 0 s en0 0,9 Bp 7 0, Ap 0 sen Bp sen Cp c 8 a sen Ap c c sen Ap a 8 s en 0 0, cm sen Cp sen Cp sen 0 b) cos Ap b c a bc cos Bp a c b ac cos Cp a b c ab Ap 90 0,976 Bp 0,9 Ap 77 9 c) b a c ac cos Bp 9 0 cos 0 8,09 b,88 cm b sen Bp c sen Cp sen Cp c s en Bp sen 0 8,888 Dos soluciones b,88 Cp 6 9, Ap 88 Cp 8, Ap 9 d) c a b ab cos Cp 60 cos 7,0 c 8,608 cm b sen Bp c sen Cp sen Bp b s en Cp c e) Ap sen 8 0,999 Dos soluciones, 608 Cp 88, Ap 6 Cp 9, Ap 6 a sen Ap a sen Ap c a sen Cp c 0 sen 0, cm sen Cp sen Ap sen 00 b a sen B b 0 sen 0, cm sen Bp sen Ap sen 00 f) Ap b sen Bp b sen Bp a a sen Cp c sen 6 7,66 sen Cp sen Bp sen a b sen Ap a sen 60 6, cm sen Ap sen Bp sen
19 Solucionario.7. Calcula el área de cada uno de estos triángulos. a) Ap 80, b cm, c 6 cm d) Ap 66, a cm, c 0 cm b) Ap 70, Bp 0, c 0 cm e) a 0 cm, b cm, Cp c) a 6 cm, b cm, c cm a) S bc senap 96,96 cm b) Cp 70, a 0 S ac senbp 8,6 cm c) cosap b c a 0,79 senap 0,60 bc a c c sen Ap 0 sen 66 d) sen Cp. No hay triángulo. sen Ap sen Cp a e) S ab sen Cp,0 cm PROBLEMAS.7. Un globo está sujeto a una cuerda de 0 m de longitud. Por la acción del viento, el globo se encuentra a una altura de 8 m. Calcula la inclinación de la cuerda respecto de la línea de tierra. 8 Sea la inclinación buscada. Entonces, sea En cierta ciudad, en el mediodía del solsticio de verano, los rayos solares tienen una inclinación de 7. Calcula la longitud de la sombra de un edificio de m de altura. tg 7,8 m.7. Una señal de tráfico indica que la inclinación de un tramo de carretera es del 8%, lo cual quiere decir que en un desplazamiento horizontal de 00 m se realiza un ascenso de 8 m de altura. a) Qué ángulo forma la carretera con la horizontal? b) Cuántos metros hay que recorrer para ascender? a) tg 0,08 b) Sea el recorrido pedido: sen sen 70 m.76. Desde un punto del suelo se ve la copa de un pino bajo un ángulo de. Si nos alejamos, m hacia otro punto del suelo, alineado con el anterior y con el pie del pino, vemos la copa bajo un ángulo de º. Calcula la altura del pino. Sea h la altura del pino y la distancia del pie del pino al primer punto. tg h h tg 0,9 0,9, 0, 0,9, h, m h 0, tg,,.77. Calcula la altura de los dos edificios de la figura. Sea la altura del primer edificio e y la del segundo. tg tg 6 m tg 6 6 y y tg 6 6 m y 6 8 m
20 .78. Dos coches, con velocidades constantes respectivas de 90 y 80 km por hora, toman dos carreteras que se bifurcan con un ángulo de 8. Qué distancia habrá entre ellos cuando lleven minutos de viaje? El ángulo que forman las dos carreteras es 8. Sean e y e los espacios recorridos por los dos coches: e 90 0,, km d, 0, 08 cos 7,9 km e 80 0, 0 km.79. Dos coches parten a la vez de un cruce del que salen dos carreteras: una en dirección norte y otra en dirección nornordeste. Uno de los coches toma la primera de ellas con una velocidad uniforme de 70 km por hora, y el otro la segunda con una velocidad constante de 90 km por hora. A qué distancia se encontrarán al cabo de 0 minutos? El ángulo que forman las dos carreteras es 0. Sean e y e los espacios recorridos por los dos coches: e 70 0, km d os c 8, km e 90 0, km.80. Dos ciudades A y B están situadas sobre el mismo meridiano de la esfera terrestre, mientras que la ciudad C se encuentra en el mismo paralelo que A. La latitud de A es de 0 Norte. a) Si la ciudad B está 0 km al norte de A, calcula su latitud sabiendo que el radio de la Tierra es de unos 670 km. b) Si la ciudad C está situada en un meridiano a 0 al oeste de A, qué distancia separa estas dos ciudades? a) Recordando que la longitud de un arco de amplitud grados y de una circunferencia de radio r es L π r : β π L 80 π r π 670 b) Se calcula en primer lugar el radio del paralelo correspondiente. r sen 0 r 879,7 km; L 6 70 π r 80 km.8. Un avión vuela entre dos ciudades, A y B, que distan entre sí 7 km. Las visuales desde A y B hasta el avión forman con la horizontal ángulos de 6 y de amplitud, respectivamente. Calcula la altura a la que vuela el avión y las distancias a las que se encuentra de A y de B, suponiendo que el avión y las ciudades están sobre el mismo plano vertical. VB sen 6 7 sen VB 9 km VA 7 A 6º B VA km h VB sen, km 7 sen sen V º.8. Calcula el ángulo de tiro del jugador que está situado en el punto B del campo. 60 tg CBA p 7, 0,687 CBA p BA 0 tg DBA p, BA, 0,8 DBA p
21 Solucionario.8. Calcula la distancia entre los puntos A y B. A AD sen 0 7, AD,77 sen 7 B BD sen 8 9, BD 7,7 sen 7 7, m, m AB,77 7,7,,77 7,7 cos(8077) 8,7 AB,7 m E D C.8. Calcula el área de un pentágono regular si su perímetro coincide con el de un cuadrado que tiene cm de área. El lado del cuadrado mide cm. El perímetro del pentágono 8 cm. Cada lado del pentágono mide 9,6 cm. tg 6, 8,8 Ap 6,6 cm A Ap tg 6 pentágono períme tro Ap 8 6,6 8,6 cm 6º Ap,8 cm.8. Calcula los radios y las áreas de las circunferencias inscrita y circunscrita a un octógono regular de cm de lado. tg 60 / / R 6, cm Sc πr cm 6 R sen 0 cm 60 tg / / r 6 r tg 0 6,0 cm S c πr cm,º R r.86. Calcula el área del paralelogramo cuyos lados miden 0 y cm, respectivamente, si uno de sus ángulos mide. El paralelogramo se puede dividir en dos triángulos iguales. S t 0 sen S p 0 sen 86,0 cm º 0 cm cm.87. a) Halla una fórmula que permita calcular el área de un rombo conociendo las medidas de su lado y de uno de sus ángulos. b) Cuál es el área de un rombo de cm de lado si uno de sus ángulos mide 0? a) El rombo se puede dividir en dos triángulos isósceles iguales. S t sen S R sen b) S R sen 0,6 cm.88. Dado el triángulo de la figura. a) Calcula las razones trigonométricas de los ángulos agudos. b) Halla la medida de los segmentos BH y CH. C cm A H 8 cm B a) BC 7 cm sen Bp 8 cos Bp tg Bp sen Cp cos Cp 8 tg Cp 7 7 b) CH cos Cp, cm BH 8 cos Bp,76 cm
22 .89. Calcula el ángulo que forman la diagonal del cubo y la diagonal de una cara del mismo. Sea a la arista del cubo. Diagonal del cubo: D a a a a a. Diagonal de una cara: d a a a a d a cos 6 D D d.90. Calcula la amplitud del ángulo de la figura. La figura se puede dividir en dos triángulos iguales, ya que tienen los tres lados iguales. tg a a 6 8 a a π rad a.9. Calcula la altura, el perímetro y el área del trapecio de la figura. cm a Altura: h 6 tg 0,0 cm Lado restante: b 6 cos 0,6 cm Perímetro:,6 cm Área: 0,0, cm 0 cm 0.9. Las bases de un trapecio isósceles miden 0 y cm, respectivamente. El ángulo que forma la base mayor con cada uno de los lados no paralelos es de. Calcula la altura, el perímetro y el área del trapecio. tg h 0 h,7 cm º h 0 cos,, co,0 cm s P, cm ; A (0 ) h, cm.9. Se ha colocado un poste sujeto al suelo mediante dos anclajes como aparece en la figura. Determina si las medidas son correctas. CB 6 sen 0 sen(8008),86 AB,86 tg,8 m BD 6 sen 8 sen(8008),6 AB,6 tg 0,7 m Los datos no son correctos..9. Un hombre que está situado al oeste de una emisora de radio observa que su ángulo de elevación es de. Camina 0 m hacia el sur y observa que el ángulo de elevación es ahora de 0. Halla la altura de la antena. La distancia inicial a la torre será igual a la altura de la antena (ángulo de ). h Desde el segundo punto, la distancia a la torre será h. tg 0 Al ser el triángulo del suelo rectángulo, h 0 (h) h,6 m.
23 .9. Dos personas que están separadas por km de distancia, sobre su plano vertical y en el mismo momento, una nube bajo ángulos respectivos de 7 8 y 8 7. Calcula la altura de la nube y la distancia de la misma a cada uno de los observadores. Solucionario Hay dos posibles interpretaciones del problema. N A B km N 7º km A B Si la nube está situada entre los dos observadores: NB NB,0 km sen 7 8 sen NA NA, km sen 8 7 sen h NB sen 8 7 km Si la nube está situada a un mismo lado de los dos observadores: NB NB 0,0 km sen 7 8 sen 0 9 NA NA 0, km sen 9 sen 0 9 h NB sen km.96 Determina, en función del número de lados, las áreas de los polígonos regulares de n lados inscritos y circunscritos, respectivamente, a una circunferencia de 0 cm de radio. Polígono de n lados inscrito en una circunferencia de radio 0 cm: S n S t n 0 sen 6 0 0n sen 6 0 n n Siendo S t la superficie de un triángulo cuyos lados son un lado del polígono y dos radios de la circunferencia circunscrita. Polígono de n lados circunscrito en una circunferencia de radio 0 cm: S perímetro apotema n 0 tg n tg 8 0 n n.97. a) Demuestra que en cualquier triángulo ABC, rectángulo en A, se verifica que: sen Bp sen Cp b) Demuestra que cualquier triángulo ABC que verifique la igualdad anterior es isósceles o rectángulo. a) Bp Cp 90 Bp 80 Cp sen Bp sen (80 Cp) sen Cp b) sen Bp sen Cp Bp Cp Bp Cp es isósceles Bp 80Cp Bp Cp 80 Bp Cp 90 Ap 90 es restángulo.98. Si Ap, Bp y Cp son los tres ángulos de un triángulo cualquiera, calcula el valor de la epresión: cotg Ap cotg Bp cotg Ap cotg Cp cotg Bp cotg Cp tg Ap tg Bp cotg(ap Bp) cotg Ap cotg Bp cotg (80Cp) cotg Cp tg (Ap Bp) tg Ap tg Bp cotg Ap cotg Bp Por tanto: cotg Ap cotg Bp cotg Ap cotg Cp cotg Bp cotg Cp La epresión vale.
ACTIVIDADES INICIALES
 Solucionario Trigonometría ACTIVIDADES INICIALES.I. En una recta r hay tres puntos: A, B y C, que distan, sucesivamente, y cm. Por esos puntos se trazan rectas paralelas que cortan otra, s, en M, N y P.
Solucionario Trigonometría ACTIVIDADES INICIALES.I. En una recta r hay tres puntos: A, B y C, que distan, sucesivamente, y cm. Por esos puntos se trazan rectas paralelas que cortan otra, s, en M, N y P.
TRIGONOMETRIA. hipotenusa L 2. hipotenusa
 TRIGONOMETRIA. Calcular las razones trigonométricas de 0º, º y 60º. Para calcular las razones trigonométricas de º, nos ayudamos de un triángulo rectángulo isósceles como el de la figura. cateto opuesto
TRIGONOMETRIA. Calcular las razones trigonométricas de 0º, º y 60º. Para calcular las razones trigonométricas de º, nos ayudamos de un triángulo rectángulo isósceles como el de la figura. cateto opuesto
SOLUCIONES DE LAS ACTIVIDADES Págs. 101 a 119
 Página 0. a) b) π 4 π x 0 4 π π / 0 π / x 0º 0 x π π. 0 rad 0 π π rad 0 4 π 0 π rad 0 π 0 π / 4. rad 4º 4 π π 0 π / rad 0º π π 0 π / rad 0º π 4. De izquierda a derecha: 4 80 π rad π / rad 0 Página 0. tg
Página 0. a) b) π 4 π x 0 4 π π / 0 π / x 0º 0 x π π. 0 rad 0 π π rad 0 4 π 0 π rad 0 π 0 π / 4. rad 4º 4 π π 0 π / rad 0º π π 0 π / rad 0º π 4. De izquierda a derecha: 4 80 π rad π / rad 0 Página 0. tg
PÁGINA 106 PÁGINA a) sen 30 = 1/2 b) cos 120 = 1/2. c) tg 135 = 1 d) cos 45 = PÁGINA 109
 PÁGINA 0. La altura del árbol es de 8,5 cm.. BC m. CA 70 m. a) x b) y PÁGINA 0. tg a 0, Con calculadora: sß 0,9 t{ ««}. cos a 0, Con calculadora: st,8 { \ \ } PÁGINA 05. cos a 0,78 tg a 0,79. sen a 0,5
PÁGINA 0. La altura del árbol es de 8,5 cm.. BC m. CA 70 m. a) x b) y PÁGINA 0. tg a 0, Con calculadora: sß 0,9 t{ ««}. cos a 0, Con calculadora: st,8 { \ \ } PÁGINA 05. cos a 0,78 tg a 0,79. sen a 0,5
FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS
 5 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Página PARA EMPEZAR, REFLEXIONA Y RESUELVE. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora:
5 FUNCIONES Y FÓRMULAS TRIGONOMÉTRICAS Página PARA EMPEZAR, REFLEXIONA Y RESUELVE. Aunque el método para resolver las siguientes preguntas se sistematiza en la página siguiente, puedes resolverlas ahora:
Métodos Matemáticos en Física L4F. CONDICIONES de CONTORNO+Fuerzas Externas (Cap. 3, libro APL)
 L4F. CONDICIONES de CONTORNO+Fuerzas Externas (Cap. 3, libro Condiciones de contorno. Fuerzas externas aplicadas sobre una cuerda. condición que nos describe un extremo libre en una cuerda tensa. Ecuación
L4F. CONDICIONES de CONTORNO+Fuerzas Externas (Cap. 3, libro Condiciones de contorno. Fuerzas externas aplicadas sobre una cuerda. condición que nos describe un extremo libre en una cuerda tensa. Ecuación
Las Funciones Trigonométricas
 Caítulo 3 Las Funciones Trigonométricas 3.. El círculo trigonométrico Vamos a suoner conocido el sistema cartesiano en lo que se refiere a concetos fundamentales como son los de abscisa y ordenada de un
Caítulo 3 Las Funciones Trigonométricas 3.. El círculo trigonométrico Vamos a suoner conocido el sistema cartesiano en lo que se refiere a concetos fundamentales como son los de abscisa y ordenada de un
EXERCICIOS DE REFORZO: RECTAS E PLANOS
 EXERCICIOS DE REFORZO RECTAS E PLANOS Dada a recta r z a) Determna a ecuacón mplícta do plano π que pasa polo punto P(,, ) e é perpendcular a r Calcula o punto de nterseccón de r a π b) Calcula o punto
EXERCICIOS DE REFORZO RECTAS E PLANOS Dada a recta r z a) Determna a ecuacón mplícta do plano π que pasa polo punto P(,, ) e é perpendcular a r Calcula o punto de nterseccón de r a π b) Calcula o punto
1 La teoría de Jeans. t + (n v) = 0 (1) b) Navier-Stokes (conservación del impulso) c) Poisson
 1 La teoría de Jeans El caso ás siple de evolución de fluctuaciones es el de un fluído no relativista. las ecuaciones básicas son: a conservación del núero de partículas n t + (n v = 0 (1 b Navier-Stokes
1 La teoría de Jeans El caso ás siple de evolución de fluctuaciones es el de un fluído no relativista. las ecuaciones básicas son: a conservación del núero de partículas n t + (n v = 0 (1 b Navier-Stokes
την..., επειδή... Se usa cuando se cree que el punto de vista del otro es válido, pero no se concuerda completamente
 - Concordar En términos generales, coincido con X por Se usa cuando se concuerda con el punto de vista de otro Uno tiende a concordar con X ya Se usa cuando se concuerda con el punto de vista de otro Comprendo
- Concordar En términos generales, coincido con X por Se usa cuando se concuerda con el punto de vista de otro Uno tiende a concordar con X ya Se usa cuando se concuerda con el punto de vista de otro Comprendo
NÚMEROS COMPLEXOS. Páxina 147 REFLEXIONA E RESOLVE. Extraer fóra da raíz. Potencias de. Como se manexa k 1? Saca fóra da raíz:
 NÚMEROS COMPLEXOS Páxina 7 REFLEXIONA E RESOLVE Extraer fóra da raíz Saca fóra da raíz: a) b) 00 a) b) 00 0 Potencias de Calcula as sucesivas potencias de : a) ( ) ( ) ( ) b) ( ) c) ( ) 5 a) ( ) ( ) (
NÚMEROS COMPLEXOS Páxina 7 REFLEXIONA E RESOLVE Extraer fóra da raíz Saca fóra da raíz: a) b) 00 a) b) 00 0 Potencias de Calcula as sucesivas potencias de : a) ( ) ( ) ( ) b) ( ) c) ( ) 5 a) ( ) ( ) (
Problemas xeométricos
 Problemas xeométricos Contidos 1. Figuras planas Triángulos Paralelogramos Trapecios Trapezoides Polígonos regulares Círculos, sectores e segmentos 2. Corpos xeométricos Prismas Pirámides Troncos de pirámides
Problemas xeométricos Contidos 1. Figuras planas Triángulos Paralelogramos Trapecios Trapezoides Polígonos regulares Círculos, sectores e segmentos 2. Corpos xeométricos Prismas Pirámides Troncos de pirámides
LUGARES XEOMÉTRICOS. CÓNICAS
 LUGARES XEOMÉTRICOS. CÓNICAS Páxina REFLEXIONA E RESOLVE Cónicas abertas: parábolas e hipérboles Completa a seguinte táboa, na que a é o ángulo que forman as xeratrices co eixe, e, da cónica e b o ángulo
LUGARES XEOMÉTRICOS. CÓNICAS Páxina REFLEXIONA E RESOLVE Cónicas abertas: parábolas e hipérboles Completa a seguinte táboa, na que a é o ángulo que forman as xeratrices co eixe, e, da cónica e b o ángulo
Escenas de episodios anteriores
 Clase 09/10/2013 Tomado y editado de los apuntes de Pedro Sánchez Terraf Escenas de episodios anteriores objetivo: estudiar formalmente el concepto de demostración matemática. caso de estudio: lenguaje
Clase 09/10/2013 Tomado y editado de los apuntes de Pedro Sánchez Terraf Escenas de episodios anteriores objetivo: estudiar formalmente el concepto de demostración matemática. caso de estudio: lenguaje
EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS. 3. Cal é o vector de posición da orixe de coordenadas O? Cales son as coordenadas do punto O?
 EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS Representa en R os puntos S(2, 2, 2) e T(,, ) 2 Debuxa os puntos M (, 0, 0), M 2 (0,, 0) e M (0, 0, ) e logo traza o vector OM sendo M(,, ) Cal é o vector de
EXERCICIOS AUTOAVALIABLES: RECTAS E PLANOS Representa en R os puntos S(2, 2, 2) e T(,, ) 2 Debuxa os puntos M (, 0, 0), M 2 (0,, 0) e M (0, 0, ) e logo traza o vector OM sendo M(,, ) Cal é o vector de
Lógica Proposicional. Justificación de la validez del razonamiento?
 Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento? os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento? os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Trigonometría. Obxectivos. Antes de empezar.
 7 Trigonometría Obxectivos Nesta quincena aprenderás a: Calcular as razóns trigonométricas dun ángulo. Calcular todas as razóns trigonométricas dun ángulo a partir dunha delas. Resolver triángulos rectángulos
7 Trigonometría Obxectivos Nesta quincena aprenderás a: Calcular as razóns trigonométricas dun ángulo. Calcular todas as razóns trigonométricas dun ángulo a partir dunha delas. Resolver triángulos rectángulos
Lógica Proposicional
 Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Proposicional educción Natural Proposicional - 1 Justificación de la validez del razonamiento os maneras diferentes de justificar Justificar que la veracidad de las hipótesis implica la veracidad de la
Áreas de corpos xeométricos
 9 Áreas de corpos xeométricos Obxectivos Nesta quincena aprenderás a: Antes de empezar 1.Área dos prismas....... páx.164 Área dos prismas Calcular a área de prismas rectos de calquera número de caras.
9 Áreas de corpos xeométricos Obxectivos Nesta quincena aprenderás a: Antes de empezar 1.Área dos prismas....... páx.164 Área dos prismas Calcular a área de prismas rectos de calquera número de caras.
Filipenses 2:5-11. Filipenses
 Filipenses 2:5-11 Filipenses La ciudad de Filipos fue nombrada en honor de Felipe II de Macedonia, padre de Alejandro. Con una pequeña colonia judía aparentemente no tenía una sinagoga. El apóstol fundó
Filipenses 2:5-11 Filipenses La ciudad de Filipos fue nombrada en honor de Felipe II de Macedonia, padre de Alejandro. Con una pequeña colonia judía aparentemente no tenía una sinagoga. El apóstol fundó
A proba constará de vinte cuestións tipo test. As cuestións tipo test teñen tres posibles respostas, das que soamente unha é correcta.
 Páxina 1 de 9 1. Formato da proba Formato proba constará de vinte cuestións tipo test. s cuestións tipo test teñen tres posibles respostas, das que soamente unha é correcta. Puntuación Puntuación: 0.5
Páxina 1 de 9 1. Formato da proba Formato proba constará de vinte cuestións tipo test. s cuestións tipo test teñen tres posibles respostas, das que soamente unha é correcta. Puntuación Puntuación: 0.5
ln x, d) y = (3x 5 5x 2 + 7) 8 x
 EXERCICIOS AUTOAVALIABLES: CÁLCULO DIFERENCIAL. Deriva: a) y 7 6 + 5, b) y e, c) y e) y 7 ( 5 ), f) y ln, d) y ( 5 5 + 7) 8 n e ln, g) y, h) y n. Usando a derivada da función inversa, demostra que: a)
EXERCICIOS AUTOAVALIABLES: CÁLCULO DIFERENCIAL. Deriva: a) y 7 6 + 5, b) y e, c) y e) y 7 ( 5 ), f) y ln, d) y ( 5 5 + 7) 8 n e ln, g) y, h) y n. Usando a derivada da función inversa, demostra que: a)
Semellanza e trigonometría
 7 Semellanza e trigonometría Obxectivos Nesta quincena aprenderás a: Recoñecer triángulos semellantes. Calcular distancias inaccesibles, aplicando a semellanza de triángulos. Nocións básicas de trigonometría.
7 Semellanza e trigonometría Obxectivos Nesta quincena aprenderás a: Recoñecer triángulos semellantes. Calcular distancias inaccesibles, aplicando a semellanza de triángulos. Nocións básicas de trigonometría.
PAU XUÑO 2011 MATEMÁTICAS II
 PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
Ventiladores helicoidales murales o tubulares, versión PL equipados con hélice de plástico y versión AL equipados con hélice de aluminio.
 HCH HCT HCH HCT Ventiladores helicoidales murales o tubulares, de gran robustez Ventiladores helicoidales murales o tubulares, versión PL equipados con hélice de plástico y versión AL equipados con hélice
HCH HCT HCH HCT Ventiladores helicoidales murales o tubulares, de gran robustez Ventiladores helicoidales murales o tubulares, versión PL equipados con hélice de plástico y versión AL equipados con hélice
Problemas resueltos del teorema de Bolzano
 Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
Problemas resueltos del teorema de Bolzano 1 S e a la fun ción: S e puede af irm a r que f (x) está acotada en el interva lo [1, 4 ]? P or no se r c ont i nua f (x ) e n x = 1, la f unció n no e s c ont
Tema: Enerxía 01/02/06 DEPARTAMENTO DE FÍSICA E QUÍMICA
 Tema: Enerxía 01/0/06 DEPARTAMENTO DE FÍSICA E QUÍMICA Nome: 1. Unha caixa de 150 kg descende dende o repouso por un plano inclinado por acción do seu peso. Se a compoñente tanxencial do peso é de 735
Tema: Enerxía 01/0/06 DEPARTAMENTO DE FÍSICA E QUÍMICA Nome: 1. Unha caixa de 150 kg descende dende o repouso por un plano inclinado por acción do seu peso. Se a compoñente tanxencial do peso é de 735
Inmigración Estudiar. Estudiar - Universidad. Indicar que quieres matricularte. Indicar que quieres matricularte en una asignatura.
 - Universidad Me gustaría matricularme en la universidad. Indicar que quieres matricularte Me quiero matricular. Indicar que quieres matricularte en una asignatura en un grado en un posgrado en un doctorado
- Universidad Me gustaría matricularme en la universidad. Indicar que quieres matricularte Me quiero matricular. Indicar que quieres matricularte en una asignatura en un grado en un posgrado en un doctorado
TEMA IV: FUNCIONES HIPERGEOMETRICAS
 TEMA IV: FUNCIONES HIPERGEOMETRICAS 1. La ecuación hipergeométrica x R y α, β, γ parámetros reales. x(1 x)y + [γ (α + β + 1)x]y αβy 0 (1.1) Dividiendo en (1.1) por x(1 x) obtenemos (x 0, x 1) y + γ (α
TEMA IV: FUNCIONES HIPERGEOMETRICAS 1. La ecuación hipergeométrica x R y α, β, γ parámetros reales. x(1 x)y + [γ (α + β + 1)x]y αβy 0 (1.1) Dividiendo en (1.1) por x(1 x) obtenemos (x 0, x 1) y + γ (α
Académico Introducción
 - Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... general para un ensayo/tesis Για να απαντήσουμε αυτή την ερώτηση, θα επικεντρωθούμε πρώτα... Para introducir un área específica
- Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... general para un ensayo/tesis Για να απαντήσουμε αυτή την ερώτηση, θα επικεντρωθούμε πρώτα... Para introducir un área específica
TEMA 6.- BIOMOLÉCULAS ORGÁNICAS IV: ÁCIDOS NUCLEICOS
 TEMA 6.- BIMLÉCULAS RGÁNICAS IV: ÁCIDS NUCLEICS A.- Características generales de los Ácidos Nucleicos B.- Nucleótidos y derivados nucleotídicos El esqueleto covalente de los ácidos nucleicos: el enlace
TEMA 6.- BIMLÉCULAS RGÁNICAS IV: ÁCIDS NUCLEICS A.- Características generales de los Ácidos Nucleicos B.- Nucleótidos y derivados nucleotídicos El esqueleto covalente de los ácidos nucleicos: el enlace
FORMULARIO DE ELASTICIDAD
 U. D. Resistencia de Mateiales, Elasticidad Plasticidad Depatamento de Mecánica de Medios Continuos Teoía de Estuctuas E.T.S. Ingenieos de Caminos, Canales Puetos Univesidad Politécnica de Madid FORMULARIO
U. D. Resistencia de Mateiales, Elasticidad Plasticidad Depatamento de Mecánica de Medios Continuos Teoía de Estuctuas E.T.S. Ingenieos de Caminos, Canales Puetos Univesidad Politécnica de Madid FORMULARIO
Tema 3. Espazos métricos. Topoloxía Xeral,
 Tema 3. Espazos métricos Topoloxía Xeral, 2017-18 Índice Métricas en R n Métricas no espazo de funcións Bólas e relacións métricas Definición Unha métrica nun conxunto M é unha aplicación d con valores
Tema 3. Espazos métricos Topoloxía Xeral, 2017-18 Índice Métricas en R n Métricas no espazo de funcións Bólas e relacións métricas Definición Unha métrica nun conxunto M é unha aplicación d con valores
Catálogodegrandespotencias
 www.dimotor.com Catálogogranspotencias Índice Motores grans potencias 3 Motores asíncronos trifásicos Baja Tensión y Alta tensión.... 3 Serie Y2 Baja tensión 4 Motores asíncronos trifásicos Baja Tensión
www.dimotor.com Catálogogranspotencias Índice Motores grans potencias 3 Motores asíncronos trifásicos Baja Tensión y Alta tensión.... 3 Serie Y2 Baja tensión 4 Motores asíncronos trifásicos Baja Tensión
IX. ESPAZO EUCLÍDEO TRIDIMENSIONAL: Aplicacións ao cálculo de distancias, áreas e volumes
 IX. ESPAZO EUCLÍDEO TRIDIMENSIONAL: Aplicacións ao cálculo de distancias, áreas e volumes 1.- Distancia entre dous puntos Se A e B son dous puntos do espazo, defínese a distancia entre A e B como o módulo
IX. ESPAZO EUCLÍDEO TRIDIMENSIONAL: Aplicacións ao cálculo de distancias, áreas e volumes 1.- Distancia entre dous puntos Se A e B son dous puntos do espazo, defínese a distancia entre A e B como o módulo
Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
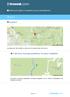 Ruta por Epiro: Ioannina y sus alrededores Día 1 Kostitsi La población de Kostitsi se ubica en la región Epiro de Grecia. Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
Ruta por Epiro: Ioannina y sus alrededores Día 1 Kostitsi La población de Kostitsi se ubica en la región Epiro de Grecia. Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου Ευρύτερη περιοχή χαράδρας ποταμού Αράχθου
Caderno de traballo. Proxecto EDA 2009 Descartes na aula. Departamento de Matemáticas CPI A Xunqueira Fene
 Departamento de Matemáticas CPI A Xunqueira Fene Nome: 4º ESO Nº Páx. 1 de 36 FIGURAS SEMELLANTES 1. CONCEPTO DE SEMELLANZA Intuitivamente: Dúas figuras son SEMELLANTES se teñen a mesma forma pero distinto
Departamento de Matemáticas CPI A Xunqueira Fene Nome: 4º ESO Nº Páx. 1 de 36 FIGURAS SEMELLANTES 1. CONCEPTO DE SEMELLANZA Intuitivamente: Dúas figuras son SEMELLANTES se teñen a mesma forma pero distinto
1. Formato da proba [CM.PM.001.Z]
![1. Formato da proba [CM.PM.001.Z] 1. Formato da proba [CM.PM.001.Z]](/thumbs/87/95733869.jpg) [CM.PM.00.Z]. Formato da proba Formato! A proba consta de vinte cuestións tipo test.! As cuestións tipo test teñen tres posibles respostas das que soamente unha é correcta. Puntuación! Puntuación: 0,50
[CM.PM.00.Z]. Formato da proba Formato! A proba consta de vinte cuestións tipo test.! As cuestións tipo test teñen tres posibles respostas das que soamente unha é correcta. Puntuación! Puntuación: 0,50
INICIACIÓN AO CÁLCULO DE DERIVADAS. APLICACIÓNS
 INICIACIÓN AO CÁLCULO DE DERIVADAS. APLICACIÓNS Páina 0 REFLEXIONA E RESOLVE Coller un autobús en marca Na gráfica seguinte, a liña vermella representa o movemento dun autobús que arranca da parada e vai,
INICIACIÓN AO CÁLCULO DE DERIVADAS. APLICACIÓNS Páina 0 REFLEXIONA E RESOLVE Coller un autobús en marca Na gráfica seguinte, a liña vermella representa o movemento dun autobús que arranca da parada e vai,
I.E.S. CADERNO Nº 6 NOME: DATA: / / Semellanza
 Semellanza Contidos 1. Semellanza Figuras semellantes Teorema de Tales Triángulos semellantes 2. Triángulos rectángulos. Teoremas Teorema do cateto Teorema da altura Teorema de Pitágoras xeneralizado 3.
Semellanza Contidos 1. Semellanza Figuras semellantes Teorema de Tales Triángulos semellantes 2. Triángulos rectángulos. Teoremas Teorema do cateto Teorema da altura Teorema de Pitágoras xeneralizado 3.
TEORÍA DE XEOMETRÍA. 1º ESO
 TEORÍA DE XEOMETRÍA. 1º ESO 1. CORPOS XEOMÉTRICOS No noso entorno observamos continuamente obxectos de diversas formas: pelotas, botes, caixas, pirámides, etc. Todos estes obxectos son corpos xeométricos.
TEORÍA DE XEOMETRÍA. 1º ESO 1. CORPOS XEOMÉTRICOS No noso entorno observamos continuamente obxectos de diversas formas: pelotas, botes, caixas, pirámides, etc. Todos estes obxectos son corpos xeométricos.
ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΑΡΑΣΚΕΥΗ 24 ΙΟΥΝΙΟΥ 2005 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ
 ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΑΡΑΣΚΕΥΗ 24 ΙΟΥΝΙΟΥ 2005 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ Α. Να αποδώσετε στο τετράδιό σας στην ελληνική γλώσσα το παρακάτω κείμενο,
ΑΡΧΗ 1 ης ΣΕΛΙΔΑΣ KΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΑΡΑΣΚΕΥΗ 24 ΙΟΥΝΙΟΥ 2005 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΑ ΙΣΠΑΝΙΚΑ Α. Να αποδώσετε στο τετράδιό σας στην ελληνική γλώσσα το παρακάτω κείμενο,
Una visión alberiana del tema. Abstract *** El marco teórico. democracia, república y emprendedores; alberdiano
 Abstract Una visión alberiana del tema - democracia, república y emprendedores; - - alberdiano El marco teórico *** - 26 LIBERTAS SEGUNDA ÉPOCA - - - - - - - - revolución industrial EMPRENDEDORES, REPÚBLICA
Abstract Una visión alberiana del tema - democracia, república y emprendedores; - - alberdiano El marco teórico *** - 26 LIBERTAS SEGUNDA ÉPOCA - - - - - - - - revolución industrial EMPRENDEDORES, REPÚBLICA
PAU XUÑO 2010 MATEMÁTICAS II
 PAU XUÑO 010 MATEMÁTICAS II Código: 6 (O alumno/a deber responder só aos eercicios dunha das opcións. Punuación máima dos eercicios de cada opción: eercicio 1= 3 punos, eercicio = 3 punos, eercicio 3 =
PAU XUÑO 010 MATEMÁTICAS II Código: 6 (O alumno/a deber responder só aos eercicios dunha das opcións. Punuación máima dos eercicios de cada opción: eercicio 1= 3 punos, eercicio = 3 punos, eercicio 3 =
Procedementos operatorios de unións non soldadas
 Procedementos operatorios de unións non soldadas Técnicas de montaxe de instalacións Ciclo medio de montaxe e mantemento de instalacións frigoríficas 1 de 28 Técnicas de roscado Unha rosca é unha hélice
Procedementos operatorios de unións non soldadas Técnicas de montaxe de instalacións Ciclo medio de montaxe e mantemento de instalacións frigoríficas 1 de 28 Técnicas de roscado Unha rosca é unha hélice
Física P.A.U. ELECTROMAGNETISMO 1 ELECTROMAGNETISMO. F = m a
 Física P.A.U. ELECTOMAGNETISMO 1 ELECTOMAGNETISMO INTODUCIÓN MÉTODO 1. En xeral: Debúxanse as forzas que actúan sobre o sistema. Calcúlase a resultante polo principio de superposición. Aplícase a 2ª lei
Física P.A.U. ELECTOMAGNETISMO 1 ELECTOMAGNETISMO INTODUCIÓN MÉTODO 1. En xeral: Debúxanse as forzas que actúan sobre o sistema. Calcúlase a resultante polo principio de superposición. Aplícase a 2ª lei
Corpos xeométricos. Obxectivos. Antes de empezar. 1. Poliedros... páx. 4 Definición Elementos dun poliedro
 9 Corpos xeométricos Obxectivos Nesta quincena aprenderás a: Identificar que é un poliedro. Determinar os elementos dun poliedro: Caras, arestas e vértices. Clasificar os poliedros. Especificar cando un
9 Corpos xeométricos Obxectivos Nesta quincena aprenderás a: Identificar que é un poliedro. Determinar os elementos dun poliedro: Caras, arestas e vértices. Clasificar os poliedros. Especificar cando un
Exercicios de Física 02a. Campo Eléctrico
 Exercicios de Física 02a. Campo Eléctrico Problemas 1. Dúas cargas eléctricas de 3 mc están situadas en A(4,0) e B( 4,0) (en metros). Caalcula: a) o campo eléctrico en C(0,5) e en D(0,0) b) o potencial
Exercicios de Física 02a. Campo Eléctrico Problemas 1. Dúas cargas eléctricas de 3 mc están situadas en A(4,0) e B( 4,0) (en metros). Caalcula: a) o campo eléctrico en C(0,5) e en D(0,0) b) o potencial
Ámbito científico tecnolóxico. Xeometría. Unidade didáctica 2. Módulo 3. Educación a distancia semipresencial
 Educación secundaria para persoas adultas Ámbito científico tecnolóxico Educación a distancia semipresencial Módulo 3 Unidade didáctica 2 Xeometría Índice 1. Introdución... 3 1.1 Descrición da unidade
Educación secundaria para persoas adultas Ámbito científico tecnolóxico Educación a distancia semipresencial Módulo 3 Unidade didáctica 2 Xeometría Índice 1. Introdución... 3 1.1 Descrición da unidade
Probas de acceso a ciclos formativos de grao medio CMPM001. Proba de. Código. Matemáticas. Parte matemática. Matemáticas.
 Probas de acceso a ciclos formativos de grao medio Proba de Matemáticas Código CMPM001 Páxina 1 de 9 Parte matemática. Matemáticas 1. Formato da proba Formato A proba consta de vinte cuestións tipo test.
Probas de acceso a ciclos formativos de grao medio Proba de Matemáticas Código CMPM001 Páxina 1 de 9 Parte matemática. Matemáticas 1. Formato da proba Formato A proba consta de vinte cuestións tipo test.
PRUEBA INICIAL DE CLASIFICACIÓN CURSO Documento para adjuntar a la Solicitud de plaza
 PRUEBA INICIAL DE CLASIFICACIÓN CURSO 2017-18 Documento para adjuntar a la Solicitud de plaza Yo con DNI, número de teléfono y dirección de correo electrónico, solicitante del idioma, nivel, declaro bajo
PRUEBA INICIAL DE CLASIFICACIÓN CURSO 2017-18 Documento para adjuntar a la Solicitud de plaza Yo con DNI, número de teléfono y dirección de correo electrónico, solicitante del idioma, nivel, declaro bajo
La transformada de ondícula continua y algunas clases de operadores de localización
 La transformada de ondícula continua y algunas clases de operadores de localización Gerardo Ramos Vázquez Dr. Egor Maximenko Instituto Politécnico Nacional, ESFM diciembre 2016 Contenido El grupo afín
La transformada de ondícula continua y algunas clases de operadores de localización Gerardo Ramos Vázquez Dr. Egor Maximenko Instituto Politécnico Nacional, ESFM diciembre 2016 Contenido El grupo afín
MATEMÁTICAS. (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 puntos)
 21 MATEMÁTICAS (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 Dada a matriz a) Calcula os valores do parámetro m para os que A ten inversa.
21 MATEMÁTICAS (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 Dada a matriz a) Calcula os valores do parámetro m para os que A ten inversa.
μέλλων τελευτᾶν 0,25 puntos καὶ βουλόμενος 0,25 puntos τοὺς αὐτοῦ παῖδας ἐμπείρους εἶναι τῆς γεωργίας, 0,5 puntos
 Materia: GRIEGO II. EvAU CURSO 17/18 CRITERIOS ESPECÍFICOS DE CORRECCIÓN PROPUESTA A: EL LABRADOR Y SUS HIJOS 1.- Traducción íntegra del texto: (4 puntos). Se ponderará, ante todo: - La recta adecuación
Materia: GRIEGO II. EvAU CURSO 17/18 CRITERIOS ESPECÍFICOS DE CORRECCIÓN PROPUESTA A: EL LABRADOR Y SUS HIJOS 1.- Traducción íntegra del texto: (4 puntos). Se ponderará, ante todo: - La recta adecuación
PAU XUÑO 2012 MATEMÁTICAS II
 PAU Código: 6 XUÑO 01 MATEMÁTICAS II (Responder só aos exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio = 3 puntos, exercicio 3= puntos, exercicio
PAU Código: 6 XUÑO 01 MATEMÁTICAS II (Responder só aos exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio = 3 puntos, exercicio 3= puntos, exercicio
A circunferencia e o círculo
 10 A circunferencia e o círculo Obxectivos Nesta quincena aprenderás a: Identificar os diferentes elementos presentes na circunferencia e o círculo. Coñecer as posicións relativas de puntos, rectas e circunferencias.
10 A circunferencia e o círculo Obxectivos Nesta quincena aprenderás a: Identificar os diferentes elementos presentes na circunferencia e o círculo. Coñecer as posicións relativas de puntos, rectas e circunferencias.
Για να ρωτήσετε αν κάποιος μπορεί να σας βοηθήσει να γεμίσετε μια φόρμα
 - Γενικά Dónde tengo que pedir el formulario/impreso para? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα Dónde tengo que pedir el formulario/impreso para? Cuál es la fecha de expedición de su (documento)?
- Γενικά Dónde tengo que pedir el formulario/impreso para? Για να ρωτήσετε που μπορείτε να βρείτε μια φόρμα Dónde tengo que pedir el formulario/impreso para? Cuál es la fecha de expedición de su (documento)?
Ταξίδι Τρώγοντας έξω. Τρώγοντας έξω - Στην είσοδο. Τρώγοντας έξω - Παραγγελία φαγητού
 - Στην είσοδο Me gustaría reservar una mesa para _[número de personas]_ a las _[hora]_. Για να κάνετε κράτηση Una mesa para _[número de personas]_, por favor. Για να ζητήσετε τραπέζι Aceptan tarjetas de
- Στην είσοδο Me gustaría reservar una mesa para _[número de personas]_ a las _[hora]_. Για να κάνετε κράτηση Una mesa para _[número de personas]_, por favor. Για να ζητήσετε τραπέζι Aceptan tarjetas de
90 LIBERTAS SEGUNDA ÉPOCA. Introducción: La necesidad de una Reforma Institucional
 1 3 - - Abstract - - - 90 LIBERTAS SEGUNDA ÉPOCA Introducción: La necesidad de una Reforma Institucional - - - - - - - - - UNA PROPUESTA DE REFORMA MONETARIA PARA ARGENTINA 91 1 políticas establecidas
1 3 - - Abstract - - - 90 LIBERTAS SEGUNDA ÉPOCA Introducción: La necesidad de una Reforma Institucional - - - - - - - - - UNA PROPUESTA DE REFORMA MONETARIA PARA ARGENTINA 91 1 políticas establecidas
NÚMEROS REAIS. Páxina 27 REFLEXIONA E RESOLVE. O paso de Z a Q. O paso de Q a Á
 NÚMEROS REAIS Páxina 7 REFLEXIONA E RESOLVE O paso de Z a Q Di cales das seguintes ecuacións se poden resolver en Z e para cales é necesario o conxunto dos números racionais, Q. a) x 0 b) 7x c) x + d)
NÚMEROS REAIS Páxina 7 REFLEXIONA E RESOLVE O paso de Z a Q Di cales das seguintes ecuacións se poden resolver en Z e para cales é necesario o conxunto dos números racionais, Q. a) x 0 b) 7x c) x + d)
TEST DE INDEPENDENCIA EN SERIES TEMPORALES
 TEST DE INDEPENDENCIA EN SERIES TEMPORALES Titulación: Doctorado en Tecnologías Industriales Alumno/a: Salvador Vera Nieto Director/a/s: José Salvador Cánovas Peña Antonio Guillamón Frutos Cartagena, 10
TEST DE INDEPENDENCIA EN SERIES TEMPORALES Titulación: Doctorado en Tecnologías Industriales Alumno/a: Salvador Vera Nieto Director/a/s: José Salvador Cánovas Peña Antonio Guillamón Frutos Cartagena, 10
PAU XUÑO 2011 MATEMÁTICAS II
 PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
PAU XUÑO 2011 MATEMÁTICAS II Código: 26 (O alumno/a debe responder só os exercicios dunha das opcións. Puntuación máxima dos exercicios de cada opción: exercicio 1= 3 puntos, exercicio 2= 3 puntos, exercicio
La experiencia de la Mesa contra el Racismo
 La experiencia de la Mesa contra el Racismo Informe Di icultad para identi icarse como discriminado Subsistencia de mecanismos individuales para enfrentar el racismo Las propuestas de las organizaciones
La experiencia de la Mesa contra el Racismo Informe Di icultad para identi icarse como discriminado Subsistencia de mecanismos individuales para enfrentar el racismo Las propuestas de las organizaciones
XEOMETRÍA NO ESPAZO. - Se dun vector se coñecen a orixe, o módulo, a dirección e o sentido, este está perfectamente determinado no espazo.
 XEOMETRÍA NO ESPAZO Vectores fixos Dos puntos do espazo, A e B, determinan o vector fixo AB, sendo o punto A a orixe e o punto B o extremo, é dicir, un vector no espazo é calquera segmento orientado que
XEOMETRÍA NO ESPAZO Vectores fixos Dos puntos do espazo, A e B, determinan o vector fixo AB, sendo o punto A a orixe e o punto B o extremo, é dicir, un vector no espazo é calquera segmento orientado que
ΕΙΣΑΓΩΓΗ INTRODUCCIÓN
 ΕΝΗΜΕΡΩΣΗ ΚΑΙ ΔΙΑΒΟΥΛΕΥΣΗ ΣΤΑ ΕΥΡΩΠΑΙΚΑ ΣΥΜΒΟΥΛΙΑ ΕΡΓΑΖΟΜΕΝΩΝ (ΕΣΕ) KAI Η ΚΟΙΝΟΤΙΚΗ ΟΔΗΓΙΑ 2009/38 INFORMACIÓN Y CONSULTA EN LOS COMITÉS DE EMPRESA EUROPEOS (CEE) Y LA DIRECTIVA COMUNITARIA 2009/38 Αθανάσιος
ΕΝΗΜΕΡΩΣΗ ΚΑΙ ΔΙΑΒΟΥΛΕΥΣΗ ΣΤΑ ΕΥΡΩΠΑΙΚΑ ΣΥΜΒΟΥΛΙΑ ΕΡΓΑΖΟΜΕΝΩΝ (ΕΣΕ) KAI Η ΚΟΙΝΟΤΙΚΗ ΟΔΗΓΙΑ 2009/38 INFORMACIÓN Y CONSULTA EN LOS COMITÉS DE EMPRESA EUROPEOS (CEE) Y LA DIRECTIVA COMUNITARIA 2009/38 Αθανάσιος
Κυρ. Ιωάννου Οδ. Δωριέων 34 Τ.Κ 8068, Λάρνακα. Adam Smith 8 Crossfield Road Selly Oak Birmingham West Midlands B29 1WQ
 - Dirección Κυρ. Ιωάννου Οδ. Δωριέων 34 Τ.Κ 8068, Λάρνακα Formato de dirección de México: Colonia Código postal + Estado, Ciudad. Jeremy Rhodes 212 Silverback Drive California Springs CA 92926 Formato
- Dirección Κυρ. Ιωάννου Οδ. Δωριέων 34 Τ.Κ 8068, Λάρνακα Formato de dirección de México: Colonia Código postal + Estado, Ciudad. Jeremy Rhodes 212 Silverback Drive California Springs CA 92926 Formato
Το ίκτυο Βιβλιοθηκών του Τµήµατος Κοινωνικού Έργου της Caja Madrid. La Red de Bibliotecas de Obra Social Caja Madrid
 Το ίκτυο Βιβλιοθηκών του Τµήµατος Κοινωνικού Έργου της Caja Madrid La Red de Bibliotecas de Obra Social Caja Madrid Το ίκτυο Βιβλιοθηκών αποτελεί τµήµα ενός Χρηµατοπιστωτικού Φορέα που προορίζει ποσοστό
Το ίκτυο Βιβλιοθηκών του Τµήµατος Κοινωνικού Έργου της Caja Madrid La Red de Bibliotecas de Obra Social Caja Madrid Το ίκτυο Βιβλιοθηκών αποτελεί τµήµα ενός Χρηµατοπιστωτικού Φορέα που προορίζει ποσοστό
5.1. Relaciones elementales. Dado el triángulo ABC, que se muestra en la figura
 Cpítulo 5 Triángulos Hemos trbjdo on el triángulo retángulo en generl hor estudiremos un triángulo ulquier y sus reliones más importntes. 5.1. Reliones elementles Ddo el triángulo ABC, que se muestr en
Cpítulo 5 Triángulos Hemos trbjdo on el triángulo retángulo en generl hor estudiremos un triángulo ulquier y sus reliones más importntes. 5.1. Reliones elementles Ddo el triángulo ABC, que se muestr en
Tema 1 : TENSIONES. Problemas resueltos F 1 S. n S. O τ F 4 F 2. Prof.: Jaime Santo Domingo Santillana E.P.S.-Zamora (U.SAL.
 Tea : TENSIONES S S u n S 4 O Probleas resuelos Prof: Jae Sano Dongo Sanllana EPS-Zaora (USL) - 8 -Las coponenes del esado de ensones en un puno son: N/ -5 N/ 8 N/ 4 N/ - N/ N/ Se pde deernar: ) Las ensones
Tea : TENSIONES S S u n S 4 O Probleas resuelos Prof: Jae Sano Dongo Sanllana EPS-Zaora (USL) - 8 -Las coponenes del esado de ensones en un puno son: N/ -5 N/ 8 N/ 4 N/ - N/ N/ Se pde deernar: ) Las ensones
Digestión de los lípidos
 Digestión de los lípidos El 90% de los lípidos de la dieta está conformado por triacilglicéridos. El 10% restante está compuesto por fosfolípidos, colesterol, ésteres de colesterol y ácidos grasos libres
Digestión de los lípidos El 90% de los lípidos de la dieta está conformado por triacilglicéridos. El 10% restante está compuesto por fosfolípidos, colesterol, ésteres de colesterol y ácidos grasos libres
VII. RECTAS E PLANOS NO ESPAZO
 VII. RETS E PLNOS NO ESPZO.- Ecuacións da recta Unha recta r no espao queda determinada por un punto, punto base, e un vector v non nulo que se chama vector director ou direccional da recta; r, v é a determinación
VII. RETS E PLNOS NO ESPZO.- Ecuacións da recta Unha recta r no espao queda determinada por un punto, punto base, e un vector v non nulo que se chama vector director ou direccional da recta; r, v é a determinación
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΥΛΙΚΟ ΓΙΑ ΤΑ ΚΕΝΤΡΑ ΔΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΥΛΙΚΟ ΓΙΑ ΤΑ ΚΕΝΤΡΑ ΔΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ ΘΕΜΑΤΙΚΟΣ ΑΞΟΝΑΣ: ΓΛΩΣΣΑ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: Ισπανικά για τον τουρισμό(α1-α2) Συγγραφέας: Δημήτρης Ε. Φιλιππής
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΥΛΙΚΟ ΓΙΑ ΤΑ ΚΕΝΤΡΑ ΔΙΑ ΒΙΟΥ ΜΑΘΗΣΗΣ ΘΕΜΑΤΙΚΟΣ ΑΞΟΝΑΣ: ΓΛΩΣΣΑ ΚΑΙ ΕΠΙΚΟΙΝΩΝΙΑ ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: Ισπανικά για τον τουρισμό(α1-α2) Συγγραφέας: Δημήτρης Ε. Φιλιππής
CENTRIFUGAL AIR COOLED CONDENSERS CONDENSADORES DE AIRE CENTRÍFUGOS. GPC, GMC and GSC Series. Series GPC, GMC y GSC
 CENTRIFUGAL AIR COOLED CONDENSERS GPC, GMC and GSC Series CONDENSADORES DE AIRE CENTRÍFUGOS Series GPC, GMC y GSC Key Example / Ejemplo de nomenclatura de modelos GP Direct Drive 900/100 rpm / Transmisión
CENTRIFUGAL AIR COOLED CONDENSERS GPC, GMC and GSC Series CONDENSADORES DE AIRE CENTRÍFUGOS Series GPC, GMC y GSC Key Example / Ejemplo de nomenclatura de modelos GP Direct Drive 900/100 rpm / Transmisión
Problemas y cuestiones de electromagnetismo
 Problemas y cuestiones de electromagnetismo 1.- Dúas cargas eléctricas puntuais de 2 e -2 µc cada unha están situadas respectivamente en (2,0) e en (-2,0) (en metros). Calcule: a) campo eléctrico en (0,0)
Problemas y cuestiones de electromagnetismo 1.- Dúas cargas eléctricas puntuais de 2 e -2 µc cada unha están situadas respectivamente en (2,0) e en (-2,0) (en metros). Calcule: a) campo eléctrico en (0,0)
Το παρόν σχέδιο μαθήματος δημιουργήθηκε από την κα. Radost Mazganova, καθηγήτρια Ισπανικών και την κα. Yordanka Yordanova, καθηγήτρια χημείας
 Μάθημα (τίτλος) Καθαρές ουσίες και μείγματα Επίπεδο γλωσσικής επάρκειας Α1 Α2 Β1 Β2 C1 Τάξη/βαθμίδα: πέμπτη Αριθμός μαθητών στην τάξη: 15 Θέμα: Άνθρωπος και φύση / Ουσίες και οι ιδιότητές τους Προϋποθέσεις
Μάθημα (τίτλος) Καθαρές ουσίες και μείγματα Επίπεδο γλωσσικής επάρκειας Α1 Α2 Β1 Β2 C1 Τάξη/βαθμίδα: πέμπτη Αριθμός μαθητών στην τάξη: 15 Θέμα: Άνθρωπος και φύση / Ουσίες και οι ιδιότητές τους Προϋποθέσεις
Nro. 01 Septiembre de 2011
 SOL Cultura La Tolita, de 400 ac. a 600 dc. En su representación se sintetiza toda la mitología ancestral del Ecuador. Trabajado en oro laminado y repujado. Museo Nacional Banco Central del Ecuador Dirección
SOL Cultura La Tolita, de 400 ac. a 600 dc. En su representación se sintetiza toda la mitología ancestral del Ecuador. Trabajado en oro laminado y repujado. Museo Nacional Banco Central del Ecuador Dirección
MATEMÁTICAS. (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 puntos)
 1 MATEMÁTICAS (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 puntos) Opción 1. Dada a matriz a) Calcula os valores do parámetro m para os
1 MATEMÁTICAS (Responder soamente a unha das opcións de cada bloque temático). BLOQUE 1 (ÁLXEBRA LINEAL) (Puntuación máxima 3 puntos) Opción 1. Dada a matriz a) Calcula os valores do parámetro m para os
EXERCICIOS DE REFORZO: SISTEMAS DE ECUACIÓNS LINEAIS
 EXERCICIOS DE REFORZO: SISTEMAS DE ECUACIÓNS LINEAIS. ) Clul os posiles vlores de,, pr que triz A verifique relión (A I), sendo I triz identidde de orde e triz nul de orde. ) Cl é soluión dun siste hooéneo
EXERCICIOS DE REFORZO: SISTEMAS DE ECUACIÓNS LINEAIS. ) Clul os posiles vlores de,, pr que triz A verifique relión (A I), sendo I triz identidde de orde e triz nul de orde. ) Cl é soluión dun siste hooéneo
EJERCICIOS DE VIBRACIONES Y ONDAS
 EJERCICIOS DE VIBRACIONES Y ONDAS 1.- Cando un movemento ondulatorio se atopa na súa propagación cunha fenda de dimensións pequenas comparables as da súa lonxitude de onda prodúcese: a) polarización; b)
EJERCICIOS DE VIBRACIONES Y ONDAS 1.- Cando un movemento ondulatorio se atopa na súa propagación cunha fenda de dimensións pequenas comparables as da súa lonxitude de onda prodúcese: a) polarización; b)
δικαιοσύνης διδασκαλεῖα. ἀλλ οἱ µὲν δυνάµενοι τρέφειν τοὺς παῖδας
 Instrucciones: a) Duración: 1 hora y 30 minutos. b) Se podrá hacer uso del diccionario y de su apéndice gramatical. c) El alumno elegirá y desarrollará en su totalidad una de las dos opciones propuestas,
Instrucciones: a) Duración: 1 hora y 30 minutos. b) Se podrá hacer uso del diccionario y de su apéndice gramatical. c) El alumno elegirá y desarrollará en su totalidad una de las dos opciones propuestas,
ε x = du dx ε(x) = ds ds = du(x) dx
 Capítulo 8 ECUCIONES DIFERENCIES Cálculo de desplazamientos Dr. Fernando Flores 8.. INTRODUCCIÓN En este capítulo se sistematizan las ecuaciones que gobiernan el comportamiento de vigas. En general se
Capítulo 8 ECUCIONES DIFERENCIES Cálculo de desplazamientos Dr. Fernando Flores 8.. INTRODUCCIÓN En este capítulo se sistematizan las ecuaciones que gobiernan el comportamiento de vigas. En general se
FL/STEM Σχεδιασμός/Πρότυπο μαθήματος (χημεία) 2015/2016. Μάθημα (τίτλος) Οξυγόνο. Παραγωγή οξυγόνου Επίπεδο επάρκειας γλώσσας < Α1 Α2 Β1 Β2 C1
 Μάθημα (τίτλος) Οξυγόνο. Παραγωγή οξυγόνου Επίπεδο επάρκειας γλώσσας < Α1 Α2 Β1 Β2 C1 Τάξη/βαθμίδα: 6η Αριθμός μαθητών στην τάξη: 8 Περιεχόμενο μαθήματος: Οξυγόνο. Θέμα: Άνθρωπος και φύση Ουσίες Προϋποθέσεις
Μάθημα (τίτλος) Οξυγόνο. Παραγωγή οξυγόνου Επίπεδο επάρκειας γλώσσας < Α1 Α2 Β1 Β2 C1 Τάξη/βαθμίδα: 6η Αριθμός μαθητών στην τάξη: 8 Περιεχόμενο μαθήματος: Οξυγόνο. Θέμα: Άνθρωπος και φύση Ουσίες Προϋποθέσεις
Código: 25 XUÑO 2016 PAU FÍSICA OPCIÓN A OPCIÓN B
 PAU Código: 5 XUÑO 016 FÍSICA Puntuación máxima: Cuestiones 4 puntos (1 cada cuestión, teórica o práctica). Problemas 6 puntos (1 cada apartado). No se valorará la simple anotación de un ítem cómo solución
PAU Código: 5 XUÑO 016 FÍSICA Puntuación máxima: Cuestiones 4 puntos (1 cada cuestión, teórica o práctica). Problemas 6 puntos (1 cada apartado). No se valorará la simple anotación de un ítem cómo solución
1. A INTEGRAL INDEFINIDA 1.1. DEFINICIÓN DE INTEGRAL INDEFINIDA 1.2. PROPRIEDADES
 TEMA / CÁLCULO INTEGRAL MATEMÁTICA II 07 Eames e Tetos de Matemática de Pepe Sacau ten unha licenza Creative Commons Atriución Compartir igual.0 Internacional. A INTEGRAL INDEFINIDA.. DEFINICIÓN DE INTEGRAL
TEMA / CÁLCULO INTEGRAL MATEMÁTICA II 07 Eames e Tetos de Matemática de Pepe Sacau ten unha licenza Creative Commons Atriución Compartir igual.0 Internacional. A INTEGRAL INDEFINIDA.. DEFINICIÓN DE INTEGRAL
Academic Opening Opening - Introduction Greek Spanish En este ensayo/tesis analizaré/investigaré/evaluaré...
 - Introduction Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... General opening for an essay/thesis En este ensayo/tesis analizaré/investigaré/evaluaré... Για να απαντήσουμε αυτή
- Introduction Σε αυτήν την εργασία/διατριβή θα αναλύσω/εξετάσω/διερευνήσω/αξιολογήσω... General opening for an essay/thesis En este ensayo/tesis analizaré/investigaré/evaluaré... Για να απαντήσουμε αυτή
Física P.A.U. VIBRACIÓNS E ONDAS 1 VIBRACIÓNS E ONDAS
 Física P.A.U. VIBRACIÓNS E ONDAS 1 VIBRACIÓNS E ONDAS PROBLEMAS M.H.S.. 1. Dun resorte elástico de constante k = 500 N m -1 colga unha masa puntual de 5 kg. Estando o conxunto en equilibrio, desprázase
Física P.A.U. VIBRACIÓNS E ONDAS 1 VIBRACIÓNS E ONDAS PROBLEMAS M.H.S.. 1. Dun resorte elástico de constante k = 500 N m -1 colga unha masa puntual de 5 kg. Estando o conxunto en equilibrio, desprázase
Ταξίδι Γενικά. Γενικά - Τα απαραίτητα. Γενικά - Συνομιλία. Παράκληση για βοήθεια. Ερώτηση σε πρόσωπο αν μιλά αγγλικά
 - Τα απαραίτητα Podría ayudarme? Παράκληση για βοήθεια Habla inglés? Ερώτηση σε πρόσωπο αν μιλά αγγλικά Habla_[idioma]_? Ερώτηση σε πρόσωπο αν μιλά ορισμένη γλώσσα No hablo_[idioma]_. Διασαφήνιση ότι δεν
- Τα απαραίτητα Podría ayudarme? Παράκληση για βοήθεια Habla inglés? Ερώτηση σε πρόσωπο αν μιλά αγγλικά Habla_[idioma]_? Ερώτηση σε πρόσωπο αν μιλά ορισμένη γλώσσα No hablo_[idioma]_. Διασαφήνιση ότι δεν
Análisis de las Enneadas de Plotino. Gonzalo Hernández Sanjorge A Parte Rei 20
 Análisis de las Enneadas de Plotino, Tratado Cuarto de la Enneada Primera Acerca de la felicidad1 Gonzalo Hernández Sanjorge La felicidad vinculada al vivir bien: la sensación y la razón. Identificar qué
Análisis de las Enneadas de Plotino, Tratado Cuarto de la Enneada Primera Acerca de la felicidad1 Gonzalo Hernández Sanjorge La felicidad vinculada al vivir bien: la sensación y la razón. Identificar qué
ÁCIDOS ORGÁNICOS MAS COMUNES
 ÁCIDOS ORGÁNICOS MAS COMUNES Los nombres triviales de los ácidos carboxílicos se designan según la fuente natural de la que inicialmente se aislaron. Se clasificaron así: Nombres de los ácidos carboxílicos
ÁCIDOS ORGÁNICOS MAS COMUNES Los nombres triviales de los ácidos carboxílicos se designan según la fuente natural de la que inicialmente se aislaron. Se clasificaron así: Nombres de los ácidos carboxílicos
EXERCICIOS DE ÁLXEBRA. PAU GALICIA
 Maemáicas II EXERCICIOS DE ÁLXEBRA PAU GALICIA a) (Xuño ) Propiedades do produo de marices (só enuncialas) b) (Xuño ) Sexan M e N M + I, onde I denoa a mariz idenidade de orde n, calcule N e M 3 Son M
Maemáicas II EXERCICIOS DE ÁLXEBRA PAU GALICIA a) (Xuño ) Propiedades do produo de marices (só enuncialas) b) (Xuño ) Sexan M e N M + I, onde I denoa a mariz idenidade de orde n, calcule N e M 3 Son M
Metrología Cuántica e Información Cuántica de Fisher.
 Metrología Cuántica e Información Cuántica de Fisher. Entrelazamiento y Distinguibilidad en Interferometría Atómica. Diego Alejandro Lancheros Seminario de Óptica Cuántica. Universidad de Los Andes. Table
Metrología Cuántica e Información Cuántica de Fisher. Entrelazamiento y Distinguibilidad en Interferometría Atómica. Diego Alejandro Lancheros Seminario de Óptica Cuántica. Universidad de Los Andes. Table
Física P.A.U. ELECTROMAGNETISMO 1 ELECTROMAGNETISMO
 Física P.A.U. ELECTROMAGNETISMO 1 ELECTROMAGNETISMO PROBLEMAS CAMPO ELECTROSTÁTICO 1. Dúas cargas eléctricas de 3 mc están situadas en A(4, 0) e B(-4, 0) (en metros). Calcula: a) O campo eléctrico en C(0,
Física P.A.U. ELECTROMAGNETISMO 1 ELECTROMAGNETISMO PROBLEMAS CAMPO ELECTROSTÁTICO 1. Dúas cargas eléctricas de 3 mc están situadas en A(4, 0) e B(-4, 0) (en metros). Calcula: a) O campo eléctrico en C(0,
Diseño y cálculo de un hangar para Grado en Ingeniería. aviones. E.T.S. de Ingeniería Industrial, Informática y de Telecomunicación
 E.T.S. de ngeniería ndustrial, nformática y de Telecomunicación Diseño y cálculo de un hangar para Grado en ngeniería aviones en Tecnologías de Telecomunicación Trabajo Fin de Grado Nombre y apellidos
E.T.S. de ngeniería ndustrial, nformática y de Telecomunicación Diseño y cálculo de un hangar para Grado en ngeniería aviones en Tecnologías de Telecomunicación Trabajo Fin de Grado Nombre y apellidos
Inmigración Documentos
 - General Πού μπορώ να βρω τη φόρμα για ; Pedir un formulario Πότε εκδόθηκε το [έγγραφο] σας; Pedir la fecha de expedición de un documento Πού εκδόθηκε το [έγγραφο] σας; Pedir el lugar de expedición de
- General Πού μπορώ να βρω τη φόρμα για ; Pedir un formulario Πότε εκδόθηκε το [έγγραφο] σας; Pedir la fecha de expedición de un documento Πού εκδόθηκε το [έγγραφο] σας; Pedir el lugar de expedición de
Los Determinantes y los Pronombres
 Los Determinantes y los Pronombres Englobamos dentro de los determinantes al artículo y a todos los adjetivos determinativos (demostrativos, posesivos, numerales, indefinidos, interrogativos y exclamativos).
Los Determinantes y los Pronombres Englobamos dentro de los determinantes al artículo y a todos los adjetivos determinativos (demostrativos, posesivos, numerales, indefinidos, interrogativos y exclamativos).
Inmigración Documentos
 - General Dónde tengo que pedir el formulario/impreso para? Pedir un formulario Cuál es la fecha de expedición de su (documento)? Pedir la fecha de expedición de un documento Cuál es el lugar de expedición
- General Dónde tengo que pedir el formulario/impreso para? Pedir un formulario Cuál es la fecha de expedición de su (documento)? Pedir la fecha de expedición de un documento Cuál es el lugar de expedición
Profr. Efraín Soto Apolinar.
 1 Identidades Trigonométrias No te preoupes por tus difiultades en matemátias. todavía mayores. Alert Einstein. Te puedo asegurar que las mías son Funiones trigonométrias Las funiones trigonométrias son
1 Identidades Trigonométrias No te preoupes por tus difiultades en matemátias. todavía mayores. Alert Einstein. Te puedo asegurar que las mías son Funiones trigonométrias Las funiones trigonométrias son
IV FESTIVAL LEA. Concurso entre escuelas de aprendizaje del español
 IV FESTIVAL LEA El IV Festival Iberoamericano Literatura En Atenas, organizado por la revista Cultural Sol Latino, el Instituto Cervantes de Atenas y la Fundación María Tsakos, dura este año dos semanas:
IV FESTIVAL LEA El IV Festival Iberoamericano Literatura En Atenas, organizado por la revista Cultural Sol Latino, el Instituto Cervantes de Atenas y la Fundación María Tsakos, dura este año dos semanas:
Obxectivos. Resumo. titor. corpos xeométricos. Calcular as. súas áreas volumes. Terra. deles.
 8 Corpos xeométricos Obxectivos Nesta quincena aprenderás a: Distinguir as clases de corpos xeométricos. Construíloss a partir do seu desenvolvemento plano. Calcular as súas áreas e volumes. Localizar
8 Corpos xeométricos Obxectivos Nesta quincena aprenderás a: Distinguir as clases de corpos xeométricos. Construíloss a partir do seu desenvolvemento plano. Calcular as súas áreas e volumes. Localizar
dr 1...dp N exp [ βh ({p}, {r})], (1) p 2 i 2m +Φ(r 1,..., r N ). (2) Z id = N!Λ 3N Z = Q(N,V,T). (6) Z = Z id
![dr 1...dp N exp [ βh ({p}, {r})], (1) p 2 i 2m +Φ(r 1,..., r N ). (2) Z id = N!Λ 3N Z = Q(N,V,T). (6) Z = Z id dr 1...dp N exp [ βh ({p}, {r})], (1) p 2 i 2m +Φ(r 1,..., r N ). (2) Z id = N!Λ 3N Z = Q(N,V,T). (6) Z = Z id](/thumbs/70/63026255.jpg) Física de Líquidos L. Mederos Instituto de Ciencia de Materiales de Madrid Consejo Superior de Investigaciones Científicas 5 de abril de 2004 Índice. Descripción microscópica de un líquido. 2.. Conceptos
Física de Líquidos L. Mederos Instituto de Ciencia de Materiales de Madrid Consejo Superior de Investigaciones Científicas 5 de abril de 2004 Índice. Descripción microscópica de un líquido. 2.. Conceptos
