Tehnici de imbunatatire si restaurare a imaginilor
|
|
|
- Πρίαμ Εὐκλείδης Λύκος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Tehnici de imbunatatire si restaurare a imaginilor Tehnici de imbunatatire si restaurare a imaginilor... 1 I. Tehnici de imbunatatire si restaurare in domeniul spatial Conversia nivelelor de gri Prelucrari folosind histograma imaginii Corectia distorsiunilor geometrice Reducerea zgomotului din imagini Estimarea zgomotului dintr-o imagine Modelarea zgomotelor Filtre spatiale Filtre de mediere Filtre ordonate (filtre rang) II. Tehnici de imbunatatire si restaurare in domeniul frecventei Transformata Fourier Transformata Fourier discreta (Discrete Fourier Transform) II. Tehnici de prelucrare a imaginilor color Transformari de culoare Evidentierea culorilor de interes Egalizarea histogramei Netezirea si marirea contrastului Imbunatatirea unei imagini (Image enhancement) - cresterea calitatii imaginii la un nivel care usureaza interpretarea sa sau extragerea caracteristicilor existente in imagine. Operatii tipice de imbunatatire a imaginilor: Conversia nivelelor de gri Conversia histogramei Conversia culorilor Netezirea zgomotului Evidentierea caracteristicilor
2 Restaurarea unei imagini (Image restoration) reconstruirea unei imagini degradate prin defectele introduse de sistemul de achizitie, cunoscand natura defectelor. Cauzele degradarii pot fi: Defecte ale lentilelor optice Neliniaritati ale senzorului (care transforma semnalul optic in semnal electric) Miscarea relativa dintre obiect si camera Focalizare gresita Turbulenta atmosferica etc. Unele degradari sunt de natura geometrica altele se manifesta prin aparitia unor intensitati (culori ) in imagine care nu redau puncte ale imaginii reale (zgomote). Operatiile tipice de restaurare sunt: Corectia distorsiunilor geometrice Reducerea zgomotului din imagine O imagine este un semnal electric bidimensional. Tehnicile de imbunatatire si restaurare folosesc transformari care se aplica pe reprezentarea imaginii: o in domeniul spatial (x,y): asupra pixelilor imaginii o in domeniul frecventei (amplitudinea si frecventa semnalelor care produc imaginea): asupra Transformatei Fourier a imaginii Operatiile de imbunatatire sunt, in general, transformari in domeniul spatial. Pentru restaurarea imaginilor se folosesc in special transformari in domeniul frecventei. In cele ce urmeaza consideram imagini in mai multe nivele de gri. Multe dintre operatiile aplicate acestor imagini se extind asupra imaginilor color. 2
3 I. Tehnici de imbunatatire si restaurare in domeniul spatial O imagine in mai multe nivele de gri se reprezinta in domeniul spatial printr-o functie bidimensionala, f(x, y), unde: - (x,y) este o adresa de pixel imagine - f(x,y) este intensitatea (nivelul de gri al) pixelului Vom considera imaginea reprezentata printr-o matrice bi-dimensionala, img, astfel incat img[y][x] = f(x,y). Notam cu T transformarea aplicata unei imagini f(x,y) imaginea de intrare, care se doreste a fi imbunatatita- si cu g(x,y) imaginea rezultata prin aplicarea transformarii: g(x,y) = T(f(x,y)). Transformarea T este definita pe o vecinatate a pixelului (x,y), de forma unei ferestre dreptunghiulare centrata in pixelul (x,y). Vecinatea poate fi redusa la pixelul (x,y). Notam cu: 0, 1, 2, 3,., L-1, nivelele de gri din imagine, Lmax = L-1. In exemplele de implementare a diferitelor operatii este utilizat limbajul C. Matricea imagine este de tipul imagine, definit astfel: typedef unsigned char ** imagine; 1. Conversia nivelelor de gri Imbunatatirea contrastului (Contrast stretching) Fiind date 2 nivele de intensitate, Lval si Hval, Lval < Hval, transformarea este: 3
4 g(x,y) = 0 daca f(x,y) < =Lval Lmax daca f(x,y) > = Hval s * ( f(x,y) Lval) Lval < f(x,y) < Hval unde s = Lmax/(Hval Lval), deci, intensitatile pixelilor Lval < f(x,y) < Hval sunt scalate a.i. sa fie uniform distribuite in imagine. Aplicarea unui prag (thresholding): g(x,y) = 0 daca f(x,y) < P Lmax daca f(x,y) > = P unde P este numita valoare de prag. Aceste doua transformari pot fi definite si printr-o functie de transformare a nivelului de gri: T: 0.. (L-1) 0.. (L-1) Domeniul de definitie reprezinta nivelele de gri din imaginea de intrare iar domeniul rezultatului nivelele de gri din imaginea de iesire. In acest caz, T este o functie liniara definita pe portiuni. Cazul general in care T este o functie liniara definita pe portiuni poate fi reprezentat astfel: 4
5 Evidentierea caracteristicilor Se evidentiaza un domeniu specific de nivele de gri din imagine, reducand totodata nivelele din afara domeniului la un nivel constant: g(x, y) = v1 daca f(x,y) < =Lval sau f(x,y) >= Hval v2 altfel 5
6 unde, in general, v1 este mic iar v2 este mare. Se evidentiaza un domeniu specific de nivele de gri din imagine, lasand nemodificate nivelele din afara domeniului: g(x, y) = f(x,y) daca f(x,y) < =Lval sau f(x,y) >= Hval v2 altfel Corectia Gamma Pentru majoritatea monitoarelor, curba de raspuns intensitate putere semnal (voltaj) este o functie, I = voltaj 2.5. Deci, daca cerem afisarea unui pixel in intensitatea k, pixelul va fi afisat cu intensitatea k 2.5. Deoarece nivelele de voltaj 6
7 trimise monitorului sunt intre 0 si 1, intensitatea afisata va fi mai mica decat aceea dorita. Monitoarele au gama = 2.5 Corectia gamma consta in ridicarea la putere a semnalului de intrare cu (1/2.5 = 0.4). Deci, pentru imaginile afisate pe un monitor corectia gama este: g(x,y) = f(x,y) 0.4 Solutia nu este generala, deoarece anumite sisteme au corectia gama inclusa in hardware. Asfel sunt Macintosh si Silicon Graphics. Calculatoarele Sun si PC nu au corectia gama inclusa in mod standard dar anumite placi grafice instalate pe aceste calculatoare pot face aceasta corectie. O corectie asemanatoare ar trebui facuta unei imagini care este afisata pe ecran si se doreste tiparirea sa la o imprimanta. Imaginea imprimata poate aparea mai luminata. Valoarea lui gama depinde de echipament. 2. Prelucrari folosind histograma imaginii Histograma unei imagini cu nivelele de gri k= 0, 1,...L-1 este o functie discreta, h(k) = n k, unde n k este numarul de pixeli din imagine, cu intensitatea k. Histograma normalizata este definita prin functia: h(k) = n k / n, unde n este numarul total de pixeli din imagine. 7
8 Histograma imaginii da informatii importante asupra continutului imaginii. Astfel: daca valorile mari ale histogramei sunt concentrate in zona de intensitati mici, imaginea este intunecata. daca valorile mari ale histogramei sunt concentrate in zona de intensitati mari, imaginea este luminoasa. H h 0 L-1 0 Imagine intunecata imagine luminoasa L-1 0 L-1 8
9 daca imaginea contine 2 obiecte cu intensitati diferite sau un obiect care se distinge clar de fond, histograma prezinta doi lobi (varfuri de maxim local, respectiv un varf de minim local). Daca histograma este concentrata intr-o zona ingusta de intensitati, contrastul imaginii este slab si calitatea imaginii (in privinta perceperii) este slaba. Calitatea imaginii poate fi imbunatatita modificandu-i histograma, printr-o transformare numita egalizarea histogramei sau liniarizarea histogramei. H g g = T h ) k ( k egalizarea histogramei L-1 Probabilitatea de aparitie in imagine a nivelului de intensitate k este aproximata prin: pr(k) = nk / n, k=0,..l-1 Transformarea de egalizare a histogramei este definita astfel: g k = k j = 0 n j n = k j= 0 h j Intensitatea k din imaginea de intrare se va inlocui cu intensitatea g k * (L-1) in imaginea de iesire. Calculul histogramei normalizate: 9
10 typedef unsigned char **imagine; } void histo(imagine a, int H, int W, int L, float *h) {unsigned long*lh,n; * alocare lh for (i=0;i<l;i++) lh[i]=0; for (i=0; i<h; I++) for (j=0; j<w;j++) lh[ (unsigned int) a[i][j]]++; n=(float) H*W; for (i=0; i<l; i++) h[i]=lh[i]/n; * dealocare lh; Functia pentru calculul imaginii pe baza histogramei transformate: void histegal (imagine In, imagine Out, int H, int W, int L) { int i, j; int *f = ( ) malloc( ); float * h = ( ) malloc(l*sizeof( )); float *g =. // Calcul histograma imagine de intrare histo( In, H, W, L, h); // transforma histograma g[0] = h[0]; for ( I=1; I<L; I++ ) g[i] = g[i-1] + h[i] // Calculeaza intensitatile din imaginea de iesire for(i = 0; i<l; ++ ) 10
11 f[i] = g[i]* (L-1); for(i = 0; i<h; I++ ) for(j = 0; j<w; j++ ) Out[i][j] = ((unsigned char) f[(unsigned int)in[i][j]]; * dealocare f, h, g } Imaginea de iesire are un contrast mult mai bun decat imaginea de intrare deoarece intensitatile din imaginea de intrare sunt scalate a.i. sa fie relativ uniform distribuite in imagine. Egalizarea histogramei tinde sa amplifice zgomotul. Alte prelucrari pe baza de histograma au drept scop: reducerea numarului de nivele de gri din imaginea initiala transforma histogramei intr-una specificata. 3. Corectia distorsiunilor geometrice Corectia se bazeaza pe cunoasterea modelului matematic al distorsiunilor. Astfel, distorsiunea geometrica este definita printr-un set de ecuatii de transformare a pozitiilor pixelilor, din pozitiile reale (x,y) in pozitiile distorsionate (x',y'): x' = h x (x,y) y' = h y (x,y) h x si h y sunt de obicei liniare pentru distorsiunile perspectiva sau cuadrice pentru distorsiunile produse de camere video. Fie f(x,y) imaginea distorsionata si g(x,y) imaginea corectata. Corectia poate fi descrisa astfel: 11
12 Pentru fiecare pixel (x, y) al imaginii f(x,y) Calculeaza x = h x (x,y) si y = h y (x,y) g(x,y) = f ( x, y ) (x',y') poate sa nu fie o adresa de pixel x, y sunt numere reale. In acest caz valoarea g(x,y) se calculeaza prin interpolarea valorilor pixelilor intre care se afla pozitia (x',y'). De exemplu: x1 < x '< x2, y1 < y' < y2 g(x,y) = f(x',y') se va aproxima astfel: a = (y2 - y') * g(x1,y1) + (y'-y1) * g(x1,y2) b = (y2 - y') * g(x2,y1) + (y'-y1) * g(x2,y2) g(x,y) = (x2-x') * a + (x'-x1) * b 4. Reducerea zgomotului ( noise ) din imagini Sistemele optice si electronice folosite la producerea imaginilor introduc zgomote a caror intensitate depinde de calitatea aparaturii. Zgomotul este o informatie nedorita 12
13 care deterioreaza calitatea unei imagini. Reducerea zgomotului are ca scop imbunatatirea calitatii imaginii Estimarea zgomotului dintr-o imagine Fie n imagini ale aceleiasi scene, obtinuta cu acelasi sistem de achizitie si in aceleasi conditii de achizitie: E 0,... E n-1 de N*N pixeli Pentru fiecare pixel (i,j) se calculeaza, media: σ(i,j) este o estimare a deviatiei standard a zgomotului de achizitie in pixelul (i,j); E 1 n n 1 k =0 ( i, j) = E ( i j) σ k, 1 = n 1 k= ( ) n 1 2, ( i j) E ( i, j) E ( i, j) N 1 N 1 i= 0 j= 0 σ N N ( i, j) media zgomotului pentru intreaga imagine, zgomotul maxim. max ( σ ( i, j) ) 0 i N 1 0 j N 1 13
14 Camera video introduce si un alt tip de zgomot: valorile pixelilor nu sunt complet independente una de alta, fotosenzorii de pe acelasi rand nu produc valori independente. Se poate verifica folosind autocovarianti C EE (i,j) imaginii unui sablon uniform spatial paralel cu planul imaginii si iluminat de lumina difuza: C N N i j = ( ) ( E ( i + i', j + j' ) E ( i + i', j j' )) ' ' ( i', j' ) c E ( i, j) E ( i, j) EE + i= 0 j= 0 1 c =, N ' = N i' 1, N ' = N j' 1 2 i j N 4.2. Modelarea zgomotelor Zgomotul din imaginile digitale poate proveni dintr-o multitudine de surse. Procesul de achizitie al imaginilor digitale, care converteste o imagine optica intr-un semnal electric continuu este un proces primar generator de zgomote. La fiecare pas din procesul de achizitie exista fluctuatii cauzate de fenomene naturale si acestea aduaga o valoare aleatoare la extragerea fiecarei valori a luminozitatii pentru un pixel dat. Exista doua tipuri de zgomote: Independente de continutul imaginii Dependente de continutul imaginii O imagine cu zgomot independent de continutul imaginii poate fi modelata prin: unde: g(x,y) = f(x,y) + n(x,y) f(x,y) este imaginea de intrare pentru dispozitivul de formare a imaginii (imaginea reala) 14
15 n(x,y) reprezinta zgomotul independent de continutul imaginii, numit si zgomot aditiv In cazul in care zgomotul depinde de continutul imaginii (de exemplu, radiatii monocromatice produse de o suprafata, care produc interferente de unde), zgomotul poate fi reprezentat printr-un model ne-liniar. Deoarece aceste modele matematice sunt mai complicate, zgomotul este considerat, daca este posibil, ca fiind independent de date (continutul imaginii). Modelarea matematica a zgomotelor este utila nu numai pentru reducerea lor ci si pentru sinteza unor imagini cu zgomote tipice, in scopul analizei algoritmilor de filtrare a zgomotelor. Astfel, tipurile uzuale de zgomot sunt: zgomotul gaussian, zgomotul uniform si cel de tip salt-and peper (sare si piper / impuls). Ele sunt modelate prin caracteristicile lor de probabilitate. Zgomotul gaussian Distributia Gaussiana 1-D are forma: G(x) = (1 /(2πσ)) 1/2 exp( -(x m) 2 / 2 σ 2 ) unde x este o variabila aleatoare, m este media distributiei iar σ reprezinta deviatia standard a distributiei. Figura urmatoare reda distributia Gaussiana 1-D cu media zero (centrata in x = 0) si σ = 1: 15
16 Zgomotul Gaussian este modelat prin functia de densitate a probabilitatii, FDP(g) = (1 /(2πσ) 1/2 ) exp( -(g-m) 2 / 2 σ 2 ) unde: g este nivelul de gri; m = media zgomotului; σ = deviatia standard a zgomotului; 16
17 Aproximativ 70% din valori sunt incadrate intre medie ± σ (deviatia standard) si 95% dintre valori sunt cuprinse intre medie ± 2σ. Se poate considera ca valoarea acestei FDP este nula la aproximativ 3σ de valoarea medie. Fiecare pixel din imaginea cu zgomot Gaussian are o valoare rezultata din insumarea valorii reale a pixelului cu o valoare aleatoare cu distributie Gaussiana. n(x,y) = FDP(f(x,y)) Modelul gausian este cel mai des folosit pentru modelarea proceselor cu zgomot natural, cum ar fi cele care provin din zgomotul electronic in sistemul de achizitie al imaginilor. 17
18 Zgomotul uniform Functia de distributie este: FDP(g) = 1/(b-a), a<=g<=b FDP(g) = 0, altfel Zgomot sare si piper (salt-and-peper) Functia de distributie este: 18
19 FDP(g) =A, pentru g=a FDP(g) =B, pentru g=b FDP(g) =0, altfel In modelul de zgomot de tip salt-and-peper exista doar doua valori posibile, A si B. Din aceasta cauza se mai numeste si zgomot de tip impuls (speckle). Probabilitatea de aparitie a fiecaruia este mai mica de 0.1; la valori mai mari decat acestea, zgomotul va domina imaginea. Pentru o imagine de 8 biti, valoarea de intensitate tipica pentru zgomotul peper este 0 si pentru zgomotul salt este 255. Zgomotul salt-and-peper este in general cauzat de functionarea proasta a celulelor din senzorii camerelor, greseli ale locatiilor de memorie, erori de sincronizare in procesul de digitizare sau erori (pierderi de biti) pe canalul de comunicatie in cazul transmisilor imaginilor. Alte tipuri de zgomote sunt cele avand FDP de urmatoarele tipuri: - zgomot exponential negativ - zgomot gamma - zgomot Rayleigh Nota: a se consulta fisierul image processing.zip de pe site Filtre spatiale Filtrarea spatiala a imaginilor digitale este o operatie care se aplica local, la nivelul fiecarui pixel din imagine, inlocuind valoarea pixelului curent cu o valoare ce depinde de valorile pixelilor vecini (de aici si denumirea lor de filtre spatiale se considera o vecinatate spatiala in sistemul de coordonate asociat imaginii). Aceste filtre opereaza pe vecinatati mici, intre 3x3 si 11x11. 19
20 Principalele categorii de filtre spatiale folosite la inlaturarea zgomotelor sunt filtrele de mediere si filtrele ordonate(filtre rang). Filtrele de mediere sunt in general filtre liniare aplicate printr-o operatie de convolutie a imaginii cu un nucleu (masca) de convolutie. Ele determina o mediere ponderata a vecinilor. Sunt mai eficiente pentru imagini cu zgomot uniform sau zgomot gaussian. Filtrele ordonate sunt filtre neliniare implementate prin ordonarea crescatoare a valorilor pixelilor din vecinatatea pixelului curent. Aceasta ordonare se foloseste pentru a selecta una dintre valori. Filtrele ordonate (in special filtrul median) sunt mai eficiente pentru imaginile cu zgomote salt-and-peper, zgomote exponential negative si zgomote Reyleigh. Un filtru care isi schimba comportamentul bazandu-se pe caracteristicile nivelelor de gri ale vecinilor este numit filtru adaptativ, si aceste filtre sunt des folosite in multe aplicatii practice Filtre de mediere Filtrele de mediere sunt filtre spatiale liniare. Ele modifica valoarea fiecarui pixel calculand o medie ponderata a valorilor pixelilor dintr-o vecinatate a sa (fereastra de filtrare). Ponderile sunt definite intr-o matrice de forma vecinatatii, numita masca de convolutie sau kernel. Aplicarea filtrului peste intreaga imagine este numita adesea convolutia imaginii cu masca de convolutie. Fie f(x,y) imaginea pe care se aplica filtrul si w masca de convolutie, un dreptunghi cu laturile de 2*a, 2*b. Imaginea filtrata in pixelul (x,y) este data de convolutia discreta: a b g(x,y) = Σ Σ w(i,j) * f( x+i, y+j) i= -a j= -b 20
21 Diferitele tipuri de filtre de mediere se deosebesc prin valorile w(i,j). Daca toate valorile din w(i,j) sunt pozitive, filtrul realizeaza o netezire medie (average smoothing) a imaginii. Filtrul medie Cel mai simplu filtru de mediere este filtrul medie, care inlocuieste valoarea fiecarui pixel cu media aritmetica a valorilor pixelilor din fereastra de filtrare. De exemplu, pentru a=1, b=1 (fereastra de filtrare 3x3 pixeli), filtrul medie este definit astfel: 1 1 g(x,y) = 1/9 Σ Σ f( x+i, y+j) i= -1 j= -1 Filtrul medie este un filtru de netezire (FTJ- filtru trece jos ). Tot un FTJ este si filtrul cu urmatoarea masca: Un FTJ atenueaza componentele de inalta frecventa din imagine, care pot reprezenta zgomote. Imaginea rezultata din aplicarea unui FTJ este mai incetostata (neclara) decat imaginea originala. Filtrul atenueaza tranzitiile bruste de intensitate lasand impresia ca imaginea are mai putine detalii. 21
22 Un filtru trece sus (FTS) accentueaza componentele de inalta frecventa, avand un efect mic asupra celor de joasa frecventa. In imaginea rezultata din aplicarea unui FTS sunt accentuate diferentele de intensitate (detaliile) in zonele de tranzitie de intensitate. Un exemplu de FTS este filtrul cu urmatoarea masca: W(0,0) = 9 w(i,j) = -1, pentru toate celelalte elemente De asemenea, filtrul Laplacian cu masca: Functia prezentata in continuare aplica filtrul medie pe un dreptunghi din imaginea a, reprezentat prin colturile sale (N1, M1), (N2, M2), rezultatul fiind memorat in matricea b. Masca de filtrare are w x h pixeli. void f_net (imagine a, imagine b, int w, int h, int N1, int M1, int N2, int M2) { float wh, s; wh= (float)(w*h); w2 = w/2; h2 = h/2; for ( k = N1 + w2; k < N2 w2; k++) for ( l = M1 + h2; l < M2 h2; l++) 22
23 } { } s=0; for ( i = -h2; i <= h2; i++) for ( j = -w2; j < w2; j++) s + = a[l+i][k+j]; b[k][l] = (unsigned char) (s/wh); Filtrul gaussian Functia de distributie Gaussiana 2D, cu m=0, are forma: g(x,y) = (1 /(2πσ 2 )) exp( -(x 2 + y 2 )/ (2 σ 2 )) Figura urmatoare ilustreaza distributia cu media (0,0) si σ = 1: 23
24 Ideea netezirii Gaussiene este de a folosi aceasta distributie spatiala ca o functie de acoperire a pixelilor imaginii si aceasta se realizeaza prin convolutie. Masca filtrului este o aproximare discreta a acestei functii. Cu toate ca teoretic functia este diferita de zero in orice punct, in practica ea poate fi considerata nula la o distanta de aproximativ 3σ fata de medie. Deci, masca de convolutie poate fi limitata la aceasta valoare. Urmatoarea masca de convolutie cu valori intregi aproximeaza distributia Gaussiana cu deviatia standard (σ ) = 1.0 O alta masca de convolutie, care aproximeaza distributia Gaussana cu σ = 1.4, este: 24
25 Filtrul Gaussian este un filtru de netezire, ca si filtrul medie. Gradul de netezire este determinat de valoarea deviatiei standard. Cu cat valoarea deviatiei este mai mare cu atat nucleul (masca) de convolutie este mai mare. Netezirea este cu atat mai puternica cu cat valoarea σ si dimensiunea nucleului de convolutie gaussian sunt mai mari. In general valoarea σ a filtrului trebuie corelata cu nivelul zgomotului din imagine: un zgomot gaussian puternic se va filtra cu un nucleu gaussian si σ mai mari. Filtrul Gaussian se deosebeste de filtrul medie ( care acorda ponderi egale pixelilor din fereastra de filtrare) prin faptul ca efectueaza o medie ponderata a pixelilor din fereastra, cu ponderile crescatoare spre pixelul din centru. Din aceasta cauza, filtrul Gaussian produce o netezire mai fina si conserva frontierele mai bine decat un filtru medie de aceeasi dimensiune. Filtrul gaussian poate fi folosit pentru eliminarea zgomotului gaussian si a zgomotului uniform. O masca de 3x3 care aproximeaza convolutia Gaussiana este urmatoarea: Filtre ordonate (filtre rang) In general, zgomotele din imagine apar in domeniul frecventelor inalte din spectrul imaginii. De aceea, pentru inlaturarea lor se folosesc filtre trece-jos (filtre de 25
26 netezire). Filtrele liniare trece-jos tind sa reduca detaliile din imagini (frontiere, colturi), care sunt reprezentate prin frecvente inalte. Ele diminueaza punctele de front, degradand in acest fel imaginea. Filtrele neliniare reduc zgomotele, pastrand totodata fronturile si detaliile din imagine. O clasa de filtre neliniare este aceea a filtrelor ordonate, numite si filtre rang. Ele se bazeaza pe o ordonare a intensitatilor pixelilor din fereastra de filtrare. Fie P=(x,y) un punct al imaginii si Vp= rxs o vecinatate a sa. Fie f 1, f 2,.., f N intensitatile pixelilor din vecinatatea Vp si R Vp ordonarea lor crescatoare (vectorul ordonat al intensitatlor) R Vp = { f 1, f 2,, f N }, f i f i+1 Aplicarea unui filtru rang este definita astfel: g(p) = Rang j (R Vp ) adica, intensitatea pixelului P in imaginea filtrata va fi aceea memorata in pozitia j a vectorului R Vp. Pentru j = 1 se obtine filtrul min: g (p) = min (R Vp ) = min { f(p) p V} Pentru j = N se obtine filtrul max: g (p) = max (R Vp ) = max { f(p) p V} Filtrul median Este definit pentru N impar. El corespunde pozitiei de mijloc in vectorul R, deci: g (p) = Rang (N+1)/2 (R Vp ) g (p) este intensitatea mediana dintre cele N intensitati. 26
27 Filtrul max poate elimina impulsurile negative (spoturi negre). Filtrul min elimina impulsurile pozitive (spoturi albe). Filtrul median inlatura zgomotele fara a degrada imaginea deci fara a atenua punctele de front. Filtrele liniare de netezire tind sa distribuie zgomotele in punctele inconjuratoare acelora care reprezinta zgomot. Exemplu: N=5, R Vp = { 100, 110, 120, 130, 250}. Intensitatea 250 poate fi un zgomot (impuls) sau un punct caracteristic in imagine. Iesirea filtrului median va fi 120, in timp ce a filtrului medie 710/5 = 142. Alegerea vecinatatii (fereastra de filtrare) Forma vecinatatii in care se calculeaza cele N intensitati influenteaza efectul filtrului. In general, vecinatatea se alege mica pentru a se evita efortul de calcul presupus de sortarea unui vector mare de intensitati. Alegerea formei ferestrei se poate baza pe o cunoastere a caracteristicilor de zgomot din imagine, de ex. orientarea orizontala sau verticala. Fereastra de filtrare pentru filtrul median poate fi de forma patrata (ex. 3x3), dreptunghiulara sau cruce. Imaginea poate fi filtrata de mai multe ori folosind aceeasi fereastra. Proprietatile filtrului median 1. Reduce variatia intensitatilor din imagine, producand regiuni de intensitate constanta sau aproape constanta. Forma regiunilor depinde de geometria ferestrei de filtrare, aspect neplacut deoarece sunt introduse in imaginea filtrata regiuni care nu existau. 2. Netezeste oscilatiile de intensitate cu o perioada mai mica decat latimea ferestrei. 27
28 3. Modifica valoarea medie a intensitatilor din imagine daca distributia spatiala a zgomotului nu este simetrica in fereastra. 4. Conserva anumite forme de frontiere. 5. Nu genereaza noi nivele de gri. Aplicarea filtrului median La aplicarea filtrelor liniare se efectueaza calcule de inmultire si adunare. Aplicarea filtrului median presupune sortarea unui vector de numere intregi. Acest calcul poate fi eficientizat in mai multe moduri. Astfel, vectorul corespunzator pozitiei (x+1, y) se poate obtine prin modificarea vectorului sortat corespunzator pozitiei (x, y): se elimina din vector pixelii de pe prima coloana a ferestrei, ramanand (n x m 2n) pixeli din vechiul vector. Algoritmul Huang (pentru aplicarea filtrului median) Fereastra de NxM pixeli este deplasata pe randuri, de la stanga la dreapta. Ferestrele centrate in pixelii (i, j) si (i+1, j) au in comun (M x N - 2N) pixeli. Calculul valorii mediane din fereastra curenta se bazeaza pe valoarea mediana a ferestrei anterioare si pe histograma imaginii din fereastra. Astfel, valoarea mediana poate fi determinata stiind ca N/2 pixeli ai imaginii din fereastra au intensitati mai mici decat ea. Ex: 4, 6, 8, 10, 11, 12, 14 (N=7) Valoarea mediana este 10; pozitia (N+1)/2 = 4 In vectorul sortat al intensitatilor, N/2 intensitati sunt mai mici decat valoarea mediana. 28
29 Daca valoarea mediana corespunde pozitiei i in histograma (nivelul i de intensitate), atunci numarul total de pixeli cu intensitatea mai mica decat i este i-1 Σ h(j) j=0 unde h este vectorul histograma ( l(k)=numarul de pixeli cu intensitatea k ). Algoritmul Huang in pseudocod: Pentru fiecare rand al imaginii Pentru prima fereastra de pe rand calculeaza histograma construieste si sorteaza vectorul pixelilor din fereastra determina valoarea mediana Pentru celelalte ferestre de pe rand actualizeaza histograma: - scazand contributiile pixelilor de pe coloana din stanga a ferestrei - adaugand contributiile pixelilor de pe coloana din dreapta a ferestrei determina valoarea mediana a ferestrei folosind valoarea mediana a ferestrei anterioare, care se ajusteaza impunand conditia: (nr.pixeli cu intensitate < med ) = N/2 Implementarea in C a algoritmului: void Huang-median (imagine a, imagine b, int N, int M, //laturile ferestrei int Nmax, int Mmax )//dim. Imagine { int k, l, i, j, NM, *t; unsigned long hist[256]; t = (int*) malloc ( (unsigned int) (N*M) * sizeof (int) ); 29
30 NM = N*M; NM2 = NM/2; N2 = N/2; M2 = M/2; for ( k = N2; k < Nmax - N2; k++ ) { /*initializarea histogramei*/ for ( i = 0; i < 256; i++) hist[i]=0; // calc. histograma si val. mediana pt. prima fereastra for ( i = 0; i < N; i++ ) for ( j = 0; j < M; j++ ) { g = t [M * i + j] = a[k + i N2 ][j]; hist [g]++; } sortare (t, NM); med = t [NM2]; //val mediana b[k][m2] = med; //calculeaza nr. de pixeli cu intensitatea < med ltmed = 0; for ( i = 0; i < med; i++) ltmed+=hist[i]; //calculeaza val mediana pt celelalte ferestre de pe linia k for ( l = M2+1; l < Mmax M2; l++) { //calculeaza histograma si ltmed for ( i =0; i < N; i++) { g = a [k+i-n2][l-m2-1]; hist [g]--; if (g < med) ltmed--; g = a [k+i-n2][l+m2]; hist [g] ++; if (g<med) ltmed++; } //calculeaza valoarea mediana a ferestrei l if (ltmed > NM2) 30
31 } //for k free (t); } do{ med --; ltmed- = hist [med]; } while (lmed > NM2); else while (ltmed + hist [med] <= NM2) { ltmed += hist [med]; med ++; } b [k][l] = med; } //for l Algoritmul este mai rapid decat in cazul folosirii sortarii in fiecare fereastra, chiar daca se foloseste un algoritm de sortare rapid. Observatie: Filtrul nu se aplica pe marginea de latime N/2, repectiv M/2 a imaginii. Pentru filtrarea acestor margini se foloseste o fereastra trunchiata. O alta metoda de reducere a timpului de calcul la aplicarea filtrului median consta in calculul iterativ al valorii mediane din R Vp, bit cu bit, incepand cu bitul cel mai semnificativ. Metoda este ilustrata de urmatorul exemplu: Fie { 3,9,4,7,5} intensitatile pixelilor din fereastra. 31
32 1. Se determina bitul valoare medie de pe pozitia cea mai semnificativa. Acesta va fi bitul cel mai semnificativ al valorii mediane. b3 b2 b1 b med = 0 2. Se continua numai cu valorile care au b3 = 0 Se determina bitul valoare medie din pozitia b med = 1 3. Se procedeaza la fel pentru a obtine bitii b1 si b0 ai valorii mediane med = 0 med = 1 Valoarea mediana ar putea fi 4 (alegand b0 = 0) sau 5 (b0 =1). Dar, valoarea mediana trebuie sa fie mai mare decat doua elemente ale vectorului ( N= 5, N/2 = 2), deci se alege b0 =1. Atunci cand pe o pozitie numarul de biti = 0 este egal cu numarul de biti = 1, sunt necesare teste suplimentare pentru alegerea valorii bitului median. Testul foloseste conditia ca N/2 elemente ale vectorului sa fie mai mici ca valoarea mediana. 32
33 II. Tehnici de imbunatatire si restaurare in domeniul frecventei 1. Transformata Fourier Exista mai multe tipuri de transformari ale imaginilor care produc reprezentari in care apar proprietati ale imaginilor nedisponibile in spatiul imaginii. Astfel, transformata Fourier a unei imagini este o reprezentare in domeniul frecventei. Multe prelucrari de imagine presupun eliminarea din imagine a componentelor de o anumita frecventa, de exemplu cele de nivel coborat sau cele de nivel inalt. Aceste operatii sunt usor de realizat pe transformata Fourier a imaginii. O prelucrare de imagine bazata pe transformata Fourier are loc in trei pasi: Se calculeaza transformata Fourier a imaginii Se proceseaza reprezentarea in domeniul Fourier Se calculeaza transformata Fourier inversa, obtinandu-se imaginea prelucrata Transformata Fourier a unei imagini I(x,y) este definita astfel: F(u,v)= I(x,y) exp[-j2π(ux + vy)]dxdy iar inversa transformarii: I(x,y)= F(u,v) exp[j2π(ux+vy)]dudv Domeniul Fourier este complex si poate fi reprezentat ca: F(u,v)=Real(u,v) + j Imag(u,v) In prelucrarea imaginilor se folosesc amplitudinea si faza: 33
34 F(u,v) = (Real(u,v) 2 + Imag(u,v) 2 ) 1/2 Φ(u,v) = tan -1 ( Imag(u,v) / Real(u,v)) Fie I(x) un semnal 1D. Transformata Fourier a functiei I(x) este: unde j= 1 iar u reprezinta frecventa. Semnalul F(u) poate fi transformat din domeniul frecventei in domeniul spatial prin transformata Fourier inversa: [ cos2 ( π ux) j sin( 2π ux) ] dx = F ( u) = I ( x) I ( x )exp( j 2π ux) dx I(x)= F u) [ cos( 2πux) + j sin( 2πux) ] du = ( F ( u)exp( j2π ux) du F(u) reprezinta spectrul amplitudinii semnalului. I(x) se descompune intr-un set de componente de unda sinusoidale,f(x). Fiecare punct in F(u) specifica amplitudinea si frecventa unei singure componente sinusoidale de unda: f(x) F(u) x -u 0 u 34
35 O functie bi-dimensionala, I(x,y) ( o functie imagine), se decompune intr-un set de frecvente spatiale F(u,v). Un punct F(u,v) este o masura a frecventei spatiale (u,v) in imagine. O frecventa spatiala, F(u,v), este o suprafata cu ondulatii sinusoidale a caror rata de ondulatie este data de distanta punctului (u,v) fata de origine: (u 2 + v 2 ) 1/2 Deci, toate frecventele spatiale cu aceeasi rata de ondulatie se reprezinta prin puncte aflate pe circumferinta unui cerc: r = (u 2 + v 2 ) 1/2 Orientarea suprafetei (unghiul fata de axa OX) este data de tan -1 (u/v). Un singur punct, F(u,v), ne spune cat de mult dintr-o anumita frecventa este continut intr-o imagine. 2. Transformata Fourier discreta (Discrete Fourier Transform) Fie I(x), 0 x N 1, o secventa discreta reprezentand un semnal 1D esantionat. Transformata Fourier a semnalului astfel reprezentat se numeste transformata Fourier discreta: F ( u) = 0 x N 1 I ( x )exp( j 2πux / N ) O imagine, I(x,y), este un semnal discret bi-dimensional 0 x N 1, 0 y N Transformata Fourier a imaginii I(x,y) este: 35
36 F ( u, v ) = N 1 1 N 2 1 iar transformata Fourier discreta inversa: I ( x, y ) 2π ux 2π vy I ( x, y ) exp( j j ) N x = 0 y = 0 1 N 2 1 N * N N 1 1 N 2 1 = 2π ux F ( u, v ) exp( j + N 2π vy j ) 1 2 u = 0 v = 0 1 N 2 O prelucrare de imagine bazata pe transformata Fourier inseamna: Calculul transformatei F(u,v) Procesarea transformatei prin aplicarea unui filtru H(u,v) - H(u,v)*F(u,v) Calculul transformatei Fourier inverse a produsului H(u,v)*F(u,v) Deci, imaginea prelucrata este: I ( x, y ) = T ' 1 ( H(u,v)* F(u,v)) unde F(u,v)=T(I(x,y)) Partea imaginara a functiei I (x,y) se neglijeaza, fiind de regula foarte mica. Definitie: Un filtru trece jos, H(u,v) este definit astfel: H(u,v) = 1 daca H(u,v) = 0 daca 2 2 u + v < 2 2 u + v 2 r r 2 ceea ce inseamna eliminarea frecventelor cu rata de ondulatie mai mare ca r din F(u,v) (care corespund la raze mai mari ca r): daca u 2 + v 2 > r atunci H(u,v)*F(u,v) = 0 Adesea, frecventele inalte reprezinta semnal fals in imagine (zgomot), indus de echipamentele electronice de producere a imaginilor discrete. Zgomotul se reprezinta prin puncte negre in zone de imagine albe sau puncte albe in zone de imagine negre. 36
37 Definitie: Un filtru trece sus, H(u,v) este definit astfel: H(u,v) = 0 daca H(u,v) = 1 daca 2 2 u + v < 2 2 u + v 2 r r 2 Prin aplicarea unui filtru trece sus sunt eliminate frecvantele joase din F(u,v) (mai mici ca r ): daca u 2 + v 2 < r atunci H(u,v)*F(u,v) = 0 Scopul aplicarii unui filtru trece sus este evidentierea detaliilor din imagine. Pot fi folosite si alte filtre: Pentru a rejecta o anumita banda de frecventa, r1 r r2 Pentru a retine doar o banda de frecvente Pentru a retine sau elimina structuri coerente cu anumite orientari. II. Tehnici de prelucrare a imaginilor color Exista mai multe modele (sisteme) in care pot fi reprezentate culorile pixelilor: RGB, HSL sau HSV (Hue -nuanta, Saturation - saturatie, Value intensitate), YIQ si altele. Doua categorii de metode: Se proceseaza separat fiecare componenta a culorii si se compune rezultatul; in unele cazuri prelucrarea se aplica numai uneia dintre componente, de exemplu, intensitatea; Se lucreaza cu vectori de culoare (fiecare culoare are trei componente, fiind reprezentata printr-un vector in spatiul culorilor). De exemplu, culoarea unui pixel p(x,y) se reprezinta in spatiul (R,G,B) prin vectorul (Cr(x,y), Cg(x,y), Cb(x,y)). 37
38 1. Transformari de culoare Fie o transformare de intensitate definita printr-o functie, g(x,y) = k* f(x,y), 0< k < 1, sau s = T(r), unde r este o culoare in imaginea de intrare iar s este culoarea in care este transformata r (in imaginea de iesire) sau (s1, s2, s3 ) = T( r1, r2, r3), unde ri si si sunt componentele celor 2 culori (ex. R,G,B). Transformarea poate fi efectuata astfel: In HSV : s3 = k* r3 In RGB : s1 = k*r1, s2 = k*r2, s3 = k*r3 Cu toate ca transformarea este mult mai simpla in HSV, conversia din RGB in HSV este mult mai costisitoare decat efectuarea transformarii in RGB. Complementul unei imagini color Fiecare culoare are o culoare complementara asa dupa cum un nivel de gri are un negativ (Neg(g) = Lmax g). Aceasta proprietate este importanata in imbunatatirea detaliilor din zonele intunecate ale unei imagini color. Culorile complementare culorilor R, G, B sunt, respectiv, C(Cyan), M(Magenta) si Y(Yellow). Calculul complementului unei imagini color inseamna inlocuirea fiecarei culori cu complementul sau. 2. Evidentierea culorilor de interes 38
39 Este utila pentru evidentierea obiectelor din imagine. Spatiul culorilor de interes dintr-o imagine poate fi reprezentat printr-un cub sau printr-o sfera. De exemplu: 1. Cubul cu latura w si centrul in (a1,a2,a3) 2. Sfera de raza R si centrul in (a1,a2,a3) (a1,a2,a3) poate fi media culorilor din subspatiul culorilor de interes. Pixelii a caror culoare nu se incadreaza in volumul de interes sunt setati la o culoare neutrala, pe care o notam cu n. Atunci, transformarea si = T (ri) este: 1. si = n, daca ( rj aj > w/2), j=1 sau j=2 sau j=3 ri, altfel ( i=0,1,.,lmax) 2. si = n, daca (r1-a1) 2 + (r2 a2) 2 + (r3 a3) 2 > R 2 ri, altfel ( i=0,1,.,lmax) 3. Egalizarea histogramei Poate fi efectuata ca si pentru imagini cu nivele de gri: Separat asupra fiecarei componente de culoare. Asupra componentei V (intensitate) din reprezentarea HSV a culorii, lasand culorile (componentele H si S) neschimbate. 39
40 4. Netezirea si marirea contrastului Ca si in cazul imaginilor in nivele de gri, operatiile de netezire (smoothing) si marire a contrastului (sharpening) se implementeaza folosind filtre spatiale definite prin diferite masti de convolutie. De exemplu, netezirea folosind filtrul medie aplicat fiecarei componente a culorii, pe o fereastra de 3x3 pixeli, este definita astfel : 1 1 g λ (x,y) = 1/9 Σ Σ f λ ( x+i, y+j) i= -1 j= -1 40
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
prin egalizarea histogramei
 Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
Zgomotul se poate suprapune informaţiei utile în două moduri: g(x, y) = f(x, y) n(x, y) (6.2)
 Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Lucrarea 6 Zgomotul în imagini BREVIAR TEORETIC Zgomotul este un semnal aleator, care afectează informaţia utilă conţinută într-o imagine. El poate apare de-alungul unui lanţ de transmisiune, sau prin
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Captura imaginilor. este necesară o sursă de lumină (λ: lungimea de undă a sursei)
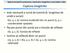 Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
Captura imaginilor este necesară o sursă de lumină (λ: lungimea de undă a sursei) E(x, y, z, λ): lumina incidentă într-un punct (x, y, z coordonatele spațiale) fiecare punct din scenă are o funcție de
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
LIMITARILE FILTRARII LINIARE A IMAGINILOR
 La ce folosea filtrarea liniara de netezire? LIMITARILE FILTRARII LINIARE A IMAGINILOR Reducerea efectelor zgomotului aditiv, de tip Gaussian suprapus imaginii. ZAGA : f ( l, = f0( l, + z( l, z( l, N(
La ce folosea filtrarea liniara de netezire? LIMITARILE FILTRARII LINIARE A IMAGINILOR Reducerea efectelor zgomotului aditiv, de tip Gaussian suprapus imaginii. ZAGA : f ( l, = f0( l, + z( l, z( l, N(
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
prin operaţii punctuale
 Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Lucrarea 3 Îmbunătăţirea imaginilor prin operaţii punctuale BREVIAR TEORETIC Termenul general de îmbunătăţire a imaginilor se referă la o clasă largă de operaţii, ce au ca scop mărirea detectabilităţii
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
LIMITARILE FILTRARII LINIARE A IMAGINILOR C. VERTAN
 LIMITARILE FILTRARII LINIARE A IMAGINILOR La ce folosea filtrarea liniara de netezire? Reducerea efectelor zgomotului aditiv, de tip Gaussian suprapus imaginii. ZAGA : f ( l, c) = f0( l, c) + z( l, c)
LIMITARILE FILTRARII LINIARE A IMAGINILOR La ce folosea filtrarea liniara de netezire? Reducerea efectelor zgomotului aditiv, de tip Gaussian suprapus imaginii. ZAGA : f ( l, c) = f0( l, c) + z( l, c)
OPERATII DE PRELUCRARE A IMAGINILOR C. VERTAN
 OPERATII DE PRELUCRARE A IMAGINILOR Prelucrare = Black Box Image In, Image Out Analiza imaginilor este Image In, Description Out Tipuri de operatii de prelucrare Clasificare dupa numarul de pixeli din
OPERATII DE PRELUCRARE A IMAGINILOR Prelucrare = Black Box Image In, Image Out Analiza imaginilor este Image In, Description Out Tipuri de operatii de prelucrare Clasificare dupa numarul de pixeli din
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
III. Reprezentarea informaţiei în sistemele de calcul
 Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
2 Transformări liniare între spaţii finit dimensionale
 Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane
 Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Tratarea numerică a semnalelor
 LUCRAREA 5 Tratarea numerică a semnalelor Filtre numerice cu răspuns finit la impuls (filtre RFI) Filtrele numerice sunt sisteme discrete liniare invariante în timp care au rolul de a modifica spectrul
LUCRAREA 5 Tratarea numerică a semnalelor Filtre numerice cu răspuns finit la impuls (filtre RFI) Filtrele numerice sunt sisteme discrete liniare invariante în timp care au rolul de a modifica spectrul
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Transformate pentru semnale multidimensionale
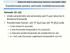 Transformate pentru semnale multidimensionale Semnale 1D: s(t) Unele caracteristici ale semnalului pot fi ușor descrise în domeniul frecvență Transformata Fourier: s(t) S(ω) (sau s(t) S(f t )) unde t este
Transformate pentru semnale multidimensionale Semnale 1D: s(t) Unele caracteristici ale semnalului pot fi ușor descrise în domeniul frecvență Transformata Fourier: s(t) S(ω) (sau s(t) S(f t )) unde t este
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
4. Măsurarea tensiunilor şi a curenţilor electrici. Voltmetre electronice analogice
 4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Componente şi Circuite Electronice Pasive. Laborator 4. Măsurarea parametrilor mărimilor electrice
 Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Laborator 4 Măsurarea parametrilor mărimilor electrice Obiective: o Semnalul sinusoidal, o Semnalul dreptunghiular, o Semnalul triunghiular, o Generarea diferitelor semnale folosind placa multifuncţională
Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism. (Y = f(x)).
 Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Laborator 1: INTRODUCERE ÎN ALGORITMI. Întocmit de: Claudia Pârloagă. Îndrumător: Asist. Drd. Gabriel Danciu
 INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
Transformări de frecvenţă
 Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Lucrarea 22 Tranformări de frecvenţă Scopul lucrării: prezentarea metodei de inteză bazate pe utilizarea tranformărilor de frecvenţă şi exemplificarea aceteia cu ajutorul unui filtru trece-jo de tip Sallen-Key.
Transformata Laplace
 Tranformata Laplace Tranformata Laplace generalizează ideea tranformatei Fourier in tot planul complex Pt un emnal x(t) pectrul au tranformata Fourier ete t ( ω) X = xte dt Pt acelaşi emnal x(t) e poate
Tranformata Laplace Tranformata Laplace generalizează ideea tranformatei Fourier in tot planul complex Pt un emnal x(t) pectrul au tranformata Fourier ete t ( ω) X = xte dt Pt acelaşi emnal x(t) e poate
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
Toate subiectele sunt obligatorii. Timpul de lucru efectiv este de 3 ore. Se acordă din oficiu 10 puncte. SUBIECTUL I.
 Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Erori si incertitudini de măsurare. Modele matematice Instrument: proiectare, fabricaţie, Interacţiune măsurand instrument:
 Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
Erori i incertitudini de măurare Sure: Modele matematice Intrument: proiectare, fabricaţie, Interacţiune măurandintrument: (tranfer informaţie tranfer energie) Influente externe: temperatura, preiune,
8 Intervale de încredere
 8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
z a + c 0 + c 1 (z a)
 1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Analiza și Prelucrarea Digitală a Semnalelor Video
 Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Analiza și Prelucrarea Digitală a Semnalelor Video Conf. dr. ing. Radu Ovidiu Preda radu@comm.pub.ro Ș.l. dr. ing. Ionuţ Pirnog ionut@comm.pub.ro Site disciplină: www.comm.pub.ro/preda/apdsv Analiza și
Aparate de măsurat. Măsurări electronice Rezumatul cursului 2. MEE - prof. dr. ing. Ioan D. Oltean 1
 Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
Aparate de măsurat Măsurări electronice Rezumatul cursului 2 MEE - prof. dr. ing. Ioan D. Oltean 1 1. Aparate cu instrument magnetoelectric 2. Ampermetre şi voltmetre 3. Ohmetre cu instrument magnetoelectric
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Concurs MATE-INFO UBB, 1 aprilie 2017 Proba scrisă la MATEMATICĂ
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
Sisteme liniare - metode directe
 Sisteme liniare - metode directe Radu T. Trîmbiţaş 27 martie 2016 1 Eliminare gaussiană Să considerăm sistemul liniar cu n ecuaţii şi n necunoscute Ax = b, (1) unde A K n n, b K n 1 sunt date, iar x K
Sisteme liniare - metode directe Radu T. Trîmbiţaş 27 martie 2016 1 Eliminare gaussiană Să considerăm sistemul liniar cu n ecuaţii şi n necunoscute Ax = b, (1) unde A K n n, b K n 1 sunt date, iar x K
CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE. MMIC Monolithic Microwave Integrated Circuit
 CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE MMIC Monolithic Microwave Integrated Circuit CUPRINS 1. Avantajele si limitarile MMIC 2. Modelarea dispozitivelor active 3. Calculul timpului de viata al MMIC
CIRCUITE INTEGRATE MONOLITICE DE MICROUNDE MMIC Monolithic Microwave Integrated Circuit CUPRINS 1. Avantajele si limitarile MMIC 2. Modelarea dispozitivelor active 3. Calculul timpului de viata al MMIC
* K. toate K. circuitului. portile. Considerând această sumă pentru toate rezistoarele 2. = sl I K I K. toate rez. Pentru o bobină: U * toate I K K 1
 FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
FNCȚ DE ENERGE Fie un n-port care conține numai elemente paive de circuit: rezitoare dipolare, condenatoare dipolare și bobine cuplate. Conform teoremei lui Tellegen n * = * toate toate laturile portile
Geometrie computationala 2. Preliminarii geometrice
 Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Matrice. Determinanti. Sisteme liniare
 Matrice 1 Matrice Adunarea matricelor Înmulţirea cu scalar. Produsul 2 Proprietăţi ale determinanţilor Rangul unei matrice 3 neomogene omogene Metoda lui Gauss (Metoda eliminării) Notiunea de matrice Matrice
Matrice 1 Matrice Adunarea matricelor Înmulţirea cu scalar. Produsul 2 Proprietăţi ale determinanţilor Rangul unei matrice 3 neomogene omogene Metoda lui Gauss (Metoda eliminării) Notiunea de matrice Matrice
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
Tranzistoare bipolare cu joncţiuni
 Tranzistoare bipolare cu joncţiuni 1. Noţiuni introductive Tranzistorul bipolar cu joncţiuni, pe scurt, tranzistorul bipolar, este un dispozitiv semiconductor cu trei terminale, furnizat de către producători
Tranzistoare bipolare cu joncţiuni 1. Noţiuni introductive Tranzistorul bipolar cu joncţiuni, pe scurt, tranzistorul bipolar, este un dispozitiv semiconductor cu trei terminale, furnizat de către producători
Scoruri standard Curba normală (Gauss) M. Popa
 Scoruri standard Curba normală (Gauss) M. Popa Scoruri standard cunoaştere evaluare, măsurare evaluare comparare (Gh. Zapan) comparare raportare la un sistem de referință Povestea Scufiței Roşii... 70
Scoruri standard Curba normală (Gauss) M. Popa Scoruri standard cunoaştere evaluare, măsurare evaluare comparare (Gh. Zapan) comparare raportare la un sistem de referință Povestea Scufiței Roşii... 70
Functii Breviar teoretic 8 ianuarie ianuarie 2011
 Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Laborator 6. Integrarea ecuaţiilor diferenţiale
 Laborator 6 Integrarea ecuaţiilor diferenţiale Responsabili: 1. Surdu Cristina(anacristinasurdu@gmail.com) 2. Ştirbăţ Bogdan(bogdanstirbat@yahoo.com) Obiective În urma parcurgerii acestui laborator elevul
Laborator 6 Integrarea ecuaţiilor diferenţiale Responsabili: 1. Surdu Cristina(anacristinasurdu@gmail.com) 2. Ştirbăţ Bogdan(bogdanstirbat@yahoo.com) Obiective În urma parcurgerii acestui laborator elevul
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R. 4.1 Proprietăţi topologice ale lui R Puncte de acumulare
 Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Să se arate că n este număr par. Dan Nedeianu
 Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
2. Circuite logice 2.4. Decodoare. Multiplexoare. Copyright Paul GASNER
 2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
Metode Runge-Kutta. 18 ianuarie Probleme scalare, pas constant. Dorim să aproximăm soluţia problemei Cauchy
 Metode Runge-Kutta Radu T. Trîmbiţaş 8 ianuarie 7 Probleme scalare, pas constant Dorim să aproximăm soluţia problemei Cauchy y (t) = f(t, y), a t b, y(a) = α. pe o grilă uniformă de (N + )-puncte din [a,
Metode Runge-Kutta Radu T. Trîmbiţaş 8 ianuarie 7 Probleme scalare, pas constant Dorim să aproximăm soluţia problemei Cauchy y (t) = f(t, y), a t b, y(a) = α. pe o grilă uniformă de (N + )-puncte din [a,
Curs 2 Şiruri de numere reale
 Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener
 Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener 1 Caracteristica statică a unei diode Zener În cadranul, dioda Zener (DZ) se comportă ca o diodă redresoare
Analiza funcționării și proiectarea unui stabilizator de tensiune continuă realizat cu o diodă Zener 1 Caracteristica statică a unei diode Zener În cadranul, dioda Zener (DZ) se comportă ca o diodă redresoare
Câmp de probabilitate II
 1 Sistem complet de evenimente 2 Schema lui Poisson Schema lui Bernoulli (a bilei revenite) Schema hipergeometrică (a bilei neîntoarsă) 3 4 Sistem complet de evenimente Definiţia 1.1 O familie de evenimente
1 Sistem complet de evenimente 2 Schema lui Poisson Schema lui Bernoulli (a bilei revenite) Schema hipergeometrică (a bilei neîntoarsă) 3 4 Sistem complet de evenimente Definiţia 1.1 O familie de evenimente
Vectori liberi Produs scalar Produs vectorial Produsul mixt. 1 Vectori liberi. 2 Produs scalar. 3 Produs vectorial. 4 Produsul mixt.
 liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
Algebra si Geometrie Seminar 9
 Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Conice - Câteva proprietǎţi elementare
 Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Electronică STUDIUL FENOMENULUI DE REDRESARE FILTRE ELECTRICE DE NETEZIRE
 STDIL FENOMENLI DE REDRESARE FILTRE ELECTRICE DE NETEZIRE Energia electrică este transportată şi distribuită la consumatori sub formă de tensiune alternativă. În multe aplicaţii este însă necesară utilizarea
STDIL FENOMENLI DE REDRESARE FILTRE ELECTRICE DE NETEZIRE Energia electrică este transportată şi distribuită la consumatori sub formă de tensiune alternativă. În multe aplicaţii este însă necesară utilizarea
Spatii liniare. Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară. Mulţime infinită liniar independentă
 Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 21.2 - Sistemul de criptare ElGamal Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Scurt istoric
riptografie şi Securitate - Prelegerea 21.2 - Sistemul de criptare ElGamal Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Scurt istoric
