1. Structura internă. Categorii de comenzi MAPLE.
|
|
|
- ÔΠρωτεύς Ανδρέου
- 5 χρόνια πριν
- Προβολές:
Transcript
1 Metode de optimizare Noţiuni recapitulative - MAPLE 1. Structura internă. Categorii de comenzi MAPLE. MAPLE este un mediu de programare pentru calcule numerice şi simbolice. Calculul simbolic este calculul cu variabile şi constante care respectă regulile algebrice, ale analizei şi ale altor ramuri ale matematicii. MAPLE-ul permite manipularea formulelor care utilizează simboluri, necunoscute şi operaţii formale, în comparaţie cu limbajele de programare tradiţionale care utilizează doar date numerice, caractere şi şiruri de caractere. Se încadrează în aceeaşi clasă de produse software ca şi Mathematica, MathCAD, MATLAB şi TKSolver. MAPLE are trei componente de bază: nucleul (kernel), biblioteca standard (library) şi interfaţă cu utilizatorul (interface). Nucleul este scris în C şi realizează cea mai mare parte a calculelor făcute de sistem. Biblioteca standard este automat încărcată în memorie la deschidere unei sesiuni MAPLE. În afara acestei biblioteci există o bibliotecă extinsă cu rutine destinate rezolvării unor probleme mai complicate, ca de exemplu, rezolvarea sistemelor de ecuaţii, probleme de statistică sau algebră liniară. Această bibliotecă nu este încărcată automat în memorie, ci trebuie accesată, atunci când este necesar. Interfaţa cu utilizatorul este scrisă în C. Interfaţa pentru sistemul de operare Windows este bazată pe ferestre. O foaie (formular) de programare MAPLE (fişier MAPLE, fişier cu extensia.mws) existentă poate fi încărcată selectând Open din meniul File, iar o foaie nouă de programare MAPLE poate fi creată selectând New din meniul File. Salvarea foii de programare MAPLE se realizează selectând Save sau Save as (pentru salvarea sub un alt nume) din meniul File. Foia de programare se poate salva sub forma unui fişier text sau latex dacă se selectează Export as din meniu File. Încheierea sesiunii MAPLE se face selectând Exit din meniul File, sau prin clic pe butonul de închidere X. Foile de programare MAPLE constau în cinci tipuri de zone: text, input (intrare), ouput (ieşire), 2D graphics (grafică 2D), 3D graphics (grafică 3D), şi animation (animaţie). În zona text se introduce textul necesar documentării. Zona input este zona în care se introduc comenzile MAPLE şi este recunoscută după 1
2 Mădălina Roxana Buneci Metode de Optimizare Laborator promptul > prezent în marginea din stânga. Întinderea zonei input sau a zonei text este arătată printr-o bară verticală în partea stângă. Comutarea între cele două zone se poate face cu ajutorul tastei funcţionale F5 sau din bara de meniu. Zona output este generată automat la furnizarea răspunsului. Colecţia de butoane şi informaţia afişată în bara de context (sub bara de instrumente) depind de conţinutul curent definit tipul de zonă în care se găseşte cursorul. Informaţia despre foia de programare curentă este afişată în bara de stare, în partea de jos a ecranului. MAPLE este un mediu interpretat. Explicăm în continuare ce înseamnă aceasta. Pentru ca un program (indiferent de limbajul în care este scris) să poată fi executat de calculator este necesar să fi tradus în limbaj maşină. Există trei modalităţi principale pentru a obţine această traducere: interpretarea, asamblarea şi compilarea. Programele asamblate şi cele compilate sunt traduse în limbaj maşină înainte ca să fie utilizate. Interpretarea este un tip special de traducere, în care programul este tradus în instrucţiuni în limbaj maşină din mers, adică în timpul execuţiei sale. Mai precis, programul care trebuie interpretat (să-l numim P) este preluat de un program de interpretare (interpretorul I). Când se utilizează programul P, calculatorul rulează de fapt interpretorul I, iar interpretorul I execută paşii programului P. Interpretorul verifică textul programului P şi îndeplineşte instrucţiunile acestuia pas cu pas. Interpretarea este flexibilă deoarece ce un program interpretat poate fi adaptat, schimbat sau revizuit din mers. Sigur interpretarea are şi dezavantaje asupra cărora nu insistăm aici (de exemplu, programele interpretate nu pot fi executate dacă nu există şi un interpretor corespunzător). Fiind un mediu interpretat MAPLE permite realizare de rutine interactive. Apariţia promptului > în fereastra MAPLE semnifică faptul că se poate introduce o comandă. Fiecare comandă (cu excepţia comenzii?) trebuie încheiată cu punct şi virgulă (;) sau două puncte (:). Omiterea acestora generează o eroare de sintaxă. Rectificarea se face prin tipărind ; sau : pe o linie nouă. Fiecare comanda este executată după apăsarea tastei ENTER. Dacă s-a utilizat : pentru încheierea comenzii, comanda este executată fără a se afişa rezultatele, iar cazul utilizării ; se afişează şi rezultatele. 2
3 Metode de optimizare Noţiuni recapitulative - MAPLE MAPLE dispune de peste 2000 de funcţii predefinite şi comenzi. Fiecare comandă este introdusă, în zona input, în felul următor: > nume_comanda(param1,param2,...); Numele comenzilor a fost ales astfel încât pe de o parte să fie apropiat de funcţionalitatea comenzii şi pe de altă parte să fie cât mai scurt posibil. MAPLE este un mediu case-sensitive (se face distincţie între literele mari şi literele mici). Cele mai multe comenzi încep cu literă mică şi au în corespondenţă o aceeaşi comandă care începe cu literă mare. Aceasta din urmă poartă denumirea de comandă inertă şi rolul ei este doar de afişare matematică a unei expresii. Cele mai multe comenzi MAPLE necesită o listă de parametri la intrare. Această listă poate conţine de exemplu, numere, expresii, mulţimi, etc., sau poate să nu conţină nici un parametru. Indiferent de numărul de parametri specificaţi, ei trebuie incluşi între paranteze rotunde (). Toate comenzile au număr minim de parametri de tip precizat, de cele mai multe ori într-o ordine precizată. Multe comenzi pot fi utilizate cu un număr de parametri mai mare strict decât acest număr minim de parametri. Aceşti extra parametri reprezintă de obicei opţiuni de control al funcţionării comenzii respective. Comenzi MAPLE pot fi folosite ca parametri. Acestea sunt evaluate şi rezultatele lor sunt inserate în lista de parametri. Comenzile MAPLE se pot clasifica în trei categorii: 1. Comenzi care se încarcă automat la deschiderea unei se încarcă automat la deschiderea unei sesiuni MAPLE. Acestea pot fi apelate direct aşa cum s-a precizat mai sus. 2. Comenzi din biblioteca extinsă. Înainte de a le folosi acestea trebuie mai întâi încărcate în memorie cu ajutorul comenzii readlib sub forma > readlib(nume_comanda); 3. Comenzi care aparţin unor pachete specializate. Există două modalităţi de utilizare a acestor comenzi: prin specificarea pachetului sub forma: > nume_pachet[nume_comanda](param1,param2,...); cu ajutorul comenzii with. Un apel de forma >with(nume_pachet); 3
4 Mădălina Roxana Buneci Metode de Optimizare Laborator are ca urmare încărcarea în memorie şi afişarea în zona ouput a tuturor comenzilor din pachet. Până la încheierea sesiunii MAPLE acestea pot utilizate ca şi cele din prima categorie. Din cele de mai sus rezultă că nu este întotdeauna suficient să se cunoască numele unei comenzii. Uneori ea trebuie încărcată din bibliotecă sau dintr-un pachet. Dacă nu s-a făcut acest lucru şi s-a introdus comanda, MAPLE nu generează un mesaj de eroare, ci afişează în zona output, comanda introdusă în zona input. În acest caz trebuie verificat dacă este scrisă corect comanda (inclusiv dacă literele mari şi mici se potrivesc), sau trebuie încărcată în memorie. Informaţii asupra modului corect de introducere a unei comenzi se pot obţine cu ajutorul comenzii help. Există mai mute modalităţi de utilizare a acestei comenzi. Este recomdabilă, următoarea formă: >? nume_comanda O comandă de forma: >? afişează informaţii generale despre structura help-ului. Altă variantă presupune un apel de forma > help(`nume_comanda`); De remarcat faptul că numele comenzii este inclus între apostrofuri întoarse (backquotes). 2. Operatori, constante şi funcţii predefinite în MAPLE. Expresii. O expresie este o combinaţie validă de operatori şi variabile, constante, şi apeluri de funcţii. Operaţie Operator Exemple Adunare + x+y Scădere - x-y Opus - -x 4
5 Metode de optimizare Noţiuni recapitulative - MAPLE Înmulţire * x*y Împărţire / x/y Ridicare la putere (x y ) ** sau ^ x**y sau x^y Tabelul precedent conţine operatorii aritmetici de bază din MAPLE. Precedenţa operatorilor este aceeaşi ca în majoritatea limbajelor de programare. Mai întâi sunt evaluate expresiile din paranteze. În lista următoare prioritatea cade de sus în jos: 1. (operator unar) 2. **, ^ 3. *, / 4. +, -(scădere) De remarcat faptul că exponenţierea succesivă nu e validă. Astfel MAPLE nu poate evalua x^y^z. O expresie de acest fel trebuie introdusă sub forma x^(y^z). Ori de câte ori există ambiguităţi trebuie utilizate ( ). Următorul tabel prezintă funcţiile de bază din MAPLE ce pot interveni în expresiile aritmetice. Notaţie MAPLE Semnificaţie abs(x) x (modulul) iquo(x,y) partea întreagă a împărţirii x/y irem(x,y) restul împărţirii lui x la y trunc(x) cel mai mare număr întreg x, dacă x 0, sau cel mai mic frac(x) round(x) floor(x) ceil(x) sqrt(x) sau x^(1/2) număr întreg x, dacă x < 0 x-trunc(x) rotunjeşte pe x la cel mai apropiat întreg cel mai mare număr întreg x cel mai mic număr întreg x x 5
6 Mădălina Roxana Buneci Metode de Optimizare Laborator exp(x) ln(x) sau log(x) sin(x) cos(x) tan(x) e x lnx (logaritm natural) sinx cosx tgx Facem câteva remarci asupra funcţiilor irem şi iqou (deoarece nu respectă întocmai teorema împărţirii cu rest). Asfel dacă m şi n sunt două numere întregi, n este nenul şi r este numărul întreg returnat de irem, atunci este satisfăcută relaţia: m = n*q + r, abs(r) < abs(n) şi m*r 0. Dacă m şi n nu sunt amândouă numere întregi, atunci irem rămâne neevaluată. Ambele funcţii pot fi utilizate şi cu câte trei parametri. Dacă al treilea parametru este prezent în funcţia irem, atunci lui i se asignează câtul, iar în cazul funcţiei iquo i se asignează restul împărţirii. > irem(29,4,'q'); > q; > iquo(29,4,'r'); > r; > irem(-29,4); > irem(29,-4); > irem(-29,-4); > iquo(-29,4); > iquo(29,-4); > iquo(-29,-4); Funcţiile rem şi quo se aplică polinoamelor şi reprezintă analoagele funcţiilor irem şi iquo. Acestea cer obligatoriu al treilea parametru ce indică nedeterminata în raport cu care se consideră polinomul. Opţional admit al patrulea parametru, cu acelaşi rol ca parametru 3 din funcţiile irem şi iquo. Asfel dacă a şi b sunt două 6
7 Metode de optimizare Noţiuni recapitulative - MAPLE polinoame, b este nenul, r restul returnat de rem şi q este câtul returnat de quo, atunci este satisfăcută relaţia: > rem(x^5+2*x+1, x^2+x+1, x, 'q'); > q; > quo(x^5+2*x+1, x^2+x+1, x); > quo(x^5+2*y+z, x^2+x+1, x,'r'); > r; a = b*q + r, grad(r) < grad(n) x x 3 - x x 3 - x x 3 - x y + z x Funcţia factorial(k) calculează k! (k factorial, 12 k). Acelaşi efect în are şi k!, după cum rezultă din exemplele de mai jos: > factorial(4); > 4!; > 6!; > factorial(factorial(3))=3!!; = 720 Tabelul de mai jos conţine câteva constante MAPLE: Constantă Pi infinity Notaţia matematică π I i, i 2 = -1 gamma true false constanta lui Euler adevăr, în cazul evaluării booleene fals, în cazul evaluării booleene 7
8 Mădălina Roxana Buneci Metode de Optimizare Laborator De reţinut că pi (scris cu literă mică) se referă la litera grecească π. Tipul booleean în MAPLE are două valori: true şi false. Expresiile booleene (logice) pot fi formate cu ajutorul operatorilor de comparaţie şi operatorilor logici. Următoarele două tabele conţin aceşti operatori. Operator Simbol Exemple egal = x=y diferit <> x<>y mai mare > x>y mai mare egal >= x>=y mai mic < x<y mai mic egal <= x<=y Operator Simbol Exemple Negaţie (non) unar not not x Conjuncţie (şi) and x and y disjuncţie (sau) or x or y Ordinea de efectuare a operaţiilor este: not, and, or. În MAPLE există expresii similare cu expresiile din C formate cu operatorul virgulă. Astfel o secvenţă de expresii în MAPLE este un şir de expresii separate între ele prin virgulă. Cele mai multe funcţii din MAPLE cer la intrare o secvenţă de expresii, şi întorc un rezultat ce conţine o secvenţă de instrucţiuni. Cel mai simplu mod de a crea o secvenţă de instrucţiuni este: > 1,2,3,4,5; > a=1,b=a+2,c+2; 1, 2, 3, 4, 5 a = 1, b = a + 2, c + 2 Alternativ, există alte două moduri de a crea secvenţe de instrucţiuni în MAPLE: cu ajutorul operatorului $ sau cu ajutorul comenzii seq. Următoarele exemple sunt edificatoare: > a$5; > $2..7; a, a, a, a, a 8
9 Metode de optimizare Noţiuni recapitulative - MAPLE > i^2$i=1..3; > seq(i!,i=1..4); > seq(i!!,i=1..4); 2, 3, 4, 5, 6, 7 1, 4, 9 1, 2, 6, 24 1, 2, 720, Secvenţă vidă este desemnată prin NULL. 3. Comenzi de calcul în MAPLE. Tabelul de mai jos conţine comenzile din MAPLE pentru diferenţiere, integrare şi însumare. Notaţie MAPLE Semnificaţie diff(f(x),x) derivată parţială Notaţie matematică f x int(f(x),x) integrală indefinită f ( x) sum(f(n),n) suma seriei dx =1 n f ( n) int(f(x),x=a..b) integrală definită b f ( x) sum(f(k),k=a..b) sumă de la a la b a b k= a f ( k) dx Diff, Int, Sum, reprezintă comenzile inerte corespunzătoare. > diff(sin(x),x); > diff(cox(x),y); > diff(x*sin(cos(x)),x); > diff(ln(x),x); cos(x) 0 sin(cos(x)) - x cos(cos(x)) sin(x) 1 x 9
10 Mădălina Roxana Buneci Metode de Optimizare Laborator > Diff(ln(x),x); > Diff(ln(x),x) = diff(ln(x),x); x > Diff(sin(x)*tan(y),x,y)= diff(sin(x)*tan(y),x,y); > int( sin(x), x ); > Int( sin(x), x ); > int( sin(x), x=0..pi ); 2 yx sin(x) tan(y) > Int( x^2*ln(x), x=1..3 )=int( x^2*ln(x), x=1..3 ); 3 1 x ln(x) ln(x) = x 1 sin(x) tan(y) = cos(x) (1 + tan(y) 2 ) -cos(x) sin(x) dx 2 26 x ln(x) dx = 9 ln(3) - 9 >Int( Int(exp(-x^2-y^2), x=0..infinity ), y=0..infinity) = int(int( exp(-x^2-y^2), x=0..infinity ), y=0..infinity); 2 2 ( x y e ) dxdy > sum(k^2,k=1..4); > Sum(k^2,k=1..4); 30 > Sum(k^2,k=1..n)=sum(k^2,k=1..n); k= > sum(1/k^2,k=1..infinity); 1 π 6 > Sum(1/k!,k=0..infinity)=sum(1/k!,k=0..infinity); n 4 k= 1 k 2 1 = π k = (n+1) (n+1) n = e k =0 k! Prezentăm în continuare câteva exemple cu comenzile expand, factor şi simplify. Principalul rol al comenzii expand este aplicarea distributivităţii produsului faţă de adunare. Comanda factor se aplică pentru descompunerea în factori ireductibili a polinoamelor de mai multe variabile. Iar comanda simplify aplică regulile de simplificare într-o expresie. > expand((x^2-y^2)^2*(x^2+y^2)^2); X 8-2 X 4 Y 4 + Y 8 10
11 Metode de optimizare Noţiuni recapitulative - MAPLE > factor(x^6-y^6); (X - Y) (X + Y) (X 2 + X Y + Y 2 ) (X 2 - X Y + Y 2 ) > simplify((x^6-y^6)/(x^2+x*y+y^2)); X 4 - Y X 3 + Y 3 X Y 4 4. Reprezentări grafice în MAPLE. Comenzile destinate reprezentărilor grafice sunt incluse în pachetul plots. Numele pachetului trebuie să preceadă fiecare comandă. Altă variantă presupune încărcarea întregului pachet în memorie cu ajutorul comenzii with: > with(plots); [animate, animate3d, changecoords, complexplot, complexplot3d, conformal, contourplot, contourplot3d, coordplot, coordplot3d, cylinderplot, densityplot, display, display3d, fieldplot, fieldplot3d, gradplot, gradplot3d, implicitplot, implicitplot3d, inequal, listcontplot, listcontplot3d, listdensityplot, listplot, listplot3d, loglogplot, logplot, matrixplot, odeplot, pareto, pointplot, pointplot3d, polarplot, polygonplot, polygonplot3d, polyhedraplot, replot, rootlocus, semilogplot, setoptions, setoptions3d, spacecurve, sparsematrixplot, sphereplot, surfdata, textplot, textplot3d, tubeplot] Prezentăm câteva exemple cu comenzile plot, plot3d şi animate3d. Plot este destinată reprezentărilor grafice în plan şi poate fi folosită sub mai multe forme. Prezentăm de fiecare dată numărul minim de parametri ceruţi. Notaţie MAPLE plot(f(x),x = a..b) plot([f(x),g(x), ],x = a..b) Curba/Curbele reprezentate y = f(x), x [a,b] plot([f(t),g(t),t = a..b]) x = f ( t) y = g( t) y = f(x),y = g(x), x [a,b] t [ a, b] Reprezentarea grafică se face conform cu opţiunile (de stil, culoare, axe, coordonate, rezoluţie ) indicate în comandă sau în raport cu cele implicite. Unele din aceste opţiuni se pot stabili şi din meniul contextual: se introduce comanda de reprezentare grafică a curbei, iar apoi se selectează din bara de context, sau prin clic cu butonul drept al mouse-ului pe grafic, opţiunile dorite. 11
12 Mădălina Roxana Buneci Metode de Optimizare Laborator Implicit se folosesc coordonatele carteziene. Dacă se doreşte utilizarea altor coordonate, acestea trebuie specificate, prin introducerea în lista de opţiuni sub forma coords = nume_coordonate. O opţiune de forma discont=true, determină apelul comenzii Discont pentru determinarea punctelor de discontinuitate a funcţiei ce se reprezintă grafic. > plot(sin(x)*ln(x), x=pi..8*pi); > plot([sin(x),cos(x)],x=0..2*pi,title=`sinus si cosinus`); >plot([sin(t),cos(t),t=0..2*pi],title=`cerc`); > plot(sin(2*t),t=0..2*pi,coords=polar, color=black); 12
13 Metode de optimizare Noţiuni recapitulative - MAPLE >plot(sin(x)/x, x=-3*pi..3*pi,discont=true); Comanda plot3d este destinată reprezentării grafice a suprafeţelor în spaţiu tridimensional. Ca şi în cazul comenzii plot reprezentarea grafică se face conform cu opţiunile indicate în comandă sau în raport cu cele implicite. Unele din aceste opţiuni se pot stabili şi din meniul contextual. Comanda plot3d poate fi folosită sub mai multe forme. Prezentăm de fiecare dată numărul minim de parametri ceruţi. Notaţie MAPLE Suprafaţa/Suprafe ţele reprezentate plot3d(f(x,y),x = a..b,y=c..d) z = f(x,y), (x,y) [a,b] [c,d] plot({f(x,y),g(x,y)},x = a..b,y=c..d) z = f(x,y),z=g(x,y) (x,y) [a,b] [c,d] plot([f(u,v),g(u,v),h(u,v)],u=a..b,v=c.. d) x = f y = g z = h ( u, v) ( u, v) ( u, v) 13
14 Mădălina Roxana Buneci Metode de Optimizare Laborator Exemple >plot3d(cos(x)*sin(y),x=-2*pi..2*pi,y=-2*pi..2*pi); >plot3d([v*cos(u),v*sin(u),v*ln(u)],u=pi..4*pi,v=0..1); Comenzile animate şi animate3d sunt destinate animaţiei în plan şi spaţiu. Comanda animate3d(f(x,y,t),x=a..b,y=b..c,t=t1..t2) creează animaţie cu ajutorul cadrelor obţinute prin reprezentarea grafică a suprafeţelor z t = f(x,y,t), (x,y) [a,b] [c,d] pentru valori ale lui t în intervalul [t1,t2]. Numărul de cadre poate fi stabilit cu ajutorul opţiunii frames (implicit sunt 8). Exemplu: >animate3d(cos(x)*sin(t*y),x=-pi..pi,y=-pi..pi,t=1..2); 14
15 Metode de optimizare Noţiuni recapitulative - MAPLE 5. Numere, şiruri şi identificatori. Constantele numerice din MAPLE sunt de trei tipuri: întregi raţionale în virgulă mobilă Constantele întregi sunt şiruri de cifre zecimale (0..9) eventual precedate de un semn (+,-) reprezentând un număr întreg. Numărul maxim de cifre permise este dependent de sistem, dar în general este mai mare de Exemple de constante întregi: > 0; > 123; > -6789; > ; Constantele raţionale utilizează operatorul de împărţire / pentru a separa numărătorul de numitor. Astfel m/n cu m şi n constante întregi reprezintă numărul raţional n m. Exemple de constante raţionale: > 2/3; > -6/7; > 4/6; > 4/2; > -39/13; următoare: Se observă că MAPLE face automat simplificarea fracţiilor. Reprezentarea unei constante în virgulă mobilă conţine în general câmpurile 15
16 Mădălina Roxana Buneci Metode de Optimizare Laborator partea întreagă punctul zecimal partea fracţionară e sau E şi un exponent cu semn (opţional); Se poate omite partea întreagă sau partea fracţionară, dar nu amândouă. De asemenea, se poate omite punctul zecimal sau litera e(e) şi exponentul, dar nu amândouă. Exemple de constante în virgulă mobilă: > 2.3; 2.3 > e-9 >.1234; > 123E56; > 1.; 1. Constante în virgulă mobilă pot fi obţinute şi cu comanda Float. Această comandă are forma şi întoarce mantisa*10 ^exponent. > Float(123,56); Float(mantisa,exponent); Expresiile aritmetice cu operanzi constante întregi sau raţionale sunt evaluate exact în MAPLE (rezultatul este o constantă raţională sau o constantă întreagă). > 1/3+4/5; > 1/3+8; > 1/3+2/3; În cazul în care expresia conţine constante în virgulă mobilă, atunci constantele întregi şi cele raţionale (care apar eventual în expresie) sunt convertite în 16
17 Metode de optimizare Noţiuni recapitulative - MAPLE virgulă mobilă (sunt aproximate cu constante în virgulă mobilă). Rezultatul expresiei este în acest caz o constantă în virgulă mobilă. > 1/3.+4/5; > 1./3+8; > 1/3+2/3.; > e-2; Orice număr real nenul x poate fi scris sub formă normalizată, în baza 10: x = ±m 10 p cu 0,1 m<1, (m = mantisa). În calcule se reţin de obicei un număr finit de cifre zecimale ale mantisei. Numărul de cifre care se reţin se numeşte număr de cifre semnificative. Numărul de cifre semnificative poate fi controlat în MAPLE cu ajutorul variabilei globale Digits. Valoarea implicită pentru pentru digits este 10. > 1./7; > Digits:=20; > 1./7; Digits := Deci MAPLE poate lucra în virgulă mobilă cu o precizie teoretic infinită. Pentru a determina evaluarea unei expresii în virgulă mobilă (chiar dacă toţi operanzii din expresie sunt întregi sau raţionali) se poate folosi comanda evalf. evalf(expresie) determină evaluarea expresiei la o valoare în virgulă mobilă, cu numărul de cifre semnificative stabilit de variabila Digits. evalf(expresie,n) determină evaluarea expresiei la o valoare în virgulă mobilă, utilizând n de cifre semnificative (valoarea variabilei Digits nu este afectată). > evalf(1/7); > evalf(1/7,20); > evalf(pi);
18 Mădălina Roxana Buneci Metode de Optimizare Laborator > evalf(pi,30); Există o întreagă familie de funcţii de evaluare numerică şi algebrică a expresiilor: eval evaluează în întregime o expresie evala evaluează algebric o expresie evalf evaluează numeric o expresie evalb evaluează boolean o expresie evalm evaluează matriceal o expresie evalc evaluează în mulţimea numerelor complexe o expresie În MAPLE un şir de caractere (string) constă dintr-o succesiune de caractere cuprinse între apostrofuri întoarse (backquote) (`). Punctul (.) reprezintă operatorul de concatenare pentru şirurile de caractere în MAPLE. > `Acesta este un string in MAPLE`; Acesta este un string in MAPLE > `1+2=?`; 1+2=? > `acesta este. un string`; acesta este. un string > `acesta este`.` un string`; acesta este un string Un identificator în MAPLE este un şir de caractere alfabetice (A-Z, a-z), cifre (0-9) şi caracterul _ (liniuţa de subliniere, underline), şir în care primul caracter este un caracter alfabetic (A-Z, a-z). Un identificator nu poate conţine mai mult de 499 de caractere. MAPLE este case-sensitive, ceea ce însemnă că identificatorul nume este diferit de identificatorul Nume. Identificatorii nu trebuie incluşi între (`). MAPLE conţine un număr de identificatori predefiniţi (identificatori rezervaţi). O listă a acestora poate fi obţinută cu comanda sau >? ininame > help (`ininame`); 6. Structuri de date Listele (lists) în MAPLE sunt şiruri ordonate de expresii, separate între ele prin virgulă şi incluse între paranteze drepte []. Ordinea expresiilor este dată de 18
19 Metode de optimizare Noţiuni recapitulative - MAPLE poziţia în care apar în listă. Dacă L este o listă L[i] desemnează elementul de pe poziţia i. Lista vidă este desemnată prin []. Se pot efectua următoarele operaţii cu liste: extragerea din lista L a elementelor de poziţia i până la poziţia j: L(i..j) sau op(i..j,l).; adăugarea unui element x la lista L: [x,op(l)] (adaugă elementul pe prima poziţie), [op(l),x] (adaugă elementul pe ultima poziţie); modificarea elementului de pe poziţia i: subsop(i=x,l) sau L[i]:=x; eliminarea elementului de pe poziţia i: subsop(i=null,l); > L:=[1,2,3,4]; > L[2]; > L[2]:=5; > L; > L[2..4]; > op(2..4,l); > L1:=[6,op(L)]; > L2:=[op(L),6]; > subsop(4=7,l2); > L2; > subsop(4=null,l2); > L2; L := [1, 2, 3, 4] 2 L[2] := 5 [1, 5, 3, 4] [5, 3, 4] 5, 3, 4 L1 := [6, 1, 5, 3, 4] L2 := [1, 5, 3, 4, 6] [1, 5, 3, 7, 6] [1, 5, 3, 4, 6] [1, 5, 3, 6] [1, 5, 3, 4, 6] Mulţimile (sets) în MAPLE sunt şiruri neordonate de expresii, separate între ele prin virgulă şi incluse între acolade {}. Duplicatele sunt eliminate. Mulţimea vidă este desemnată prin {}. Se pot efectua următoarele operaţii cu mulţimi: reuniune: operatorul union intersecţie: operatorul intersect diferenţă: operatorul minus 19
20 Mădălina Roxana Buneci Metode de Optimizare Laborator indexaţi. > M:={red, green, blue}; > S:={1,2,1,3,2}; > M union S; > S minus {2}; > S intersect {2,3,7}; M := {red, green, blue} S := {1, 2, 3} {1, 2, 3, red, green, blue} {1, 3} {2, 3} Tablourile (tables) în MAPLE sunt structuri de date ai căror membri sunt > t:=table([(culoare1)=red,(culoare2)=green, (culoare3)=blue]); t := table([ culoare1 = red culoare2 = green culoare3 = blue ]) >t[culoare2]; green Un tablou cu zero sau mai multe dimensiuni, pentru care fiecare dimensiune are domeniu întreg se numeşte în MAPLE array. Pentru a crea un array se poate apela funcţia array sub forma: array( domeniile de indexare, listă de iniţializare) Parametrii sunt opţionali şi pot apărea în orice ordine. >v := array(1..4); >v[2]; >v[2]:=3; v := array(1.. 4, []) v[2] v[2] := 3 >evalm(v); >A := array(1..2,1..2); >A[1,2] := x; >A[1,1]; [v[1], 3, v[3], v[4]] A := array(1.. 2, 1.. 2, []) A[1, 2] := x 20
21 Metode de optimizare Noţiuni recapitulative - MAPLE >A[1,2]; >evalm(a); A[1, 1] x A[1, 1] x A[2, 1] A[2, 2] >A := array(1..2,1..2, [ [1,x], [x,x^2] ] ); 1 x A := x x 2 Matricele (matrix) în MAPLE sunt tablouri bidimensionale cu indexate de la 1. Cu alte cuvinte un apel matrix(m,n, listă de iniţializare) este echivalent cu array(1..m,1..n, listă de iniţializare). > M:=matrix(3,2,[[1,2],[3,4],[5,6]]); 1 2 M := > M[1,2]; 2 Pachetul linalg conţine comenzi pentru multe operaţii cu matrice. 7. Atribuirea. Decizia. Structuri repetitive. Atribuirea are forma x:=v: Efectul acestei instrucţiuni constă în evaluarea expresiei v pentru valorile curente ale variabilelor pe care le conţine şi înscrierea rezultatului în locaţia de memorie rezervată variabilei x Decizia are forma: if condiţie then instrucţiuni1 else instrucţiuni2 fi; 21
22 Mădălina Roxana Buneci Metode de Optimizare Laborator Da condiţie Nu instrucţiuni1 instrucţiuni2 Condiţia este o expresie logică (formată cu operatori logici sau relaţionali). Modul de execuţie al deciziei (precum rezultă din subschema logică de mai sus) este următorul: 1. se evaluează condiţia 2. dacă rezultatul este adevărat se execută instrucţiuni1, în caz contrar se execută instrucţiuni2. 3. se trece la comanda care urmează după decizie În cazul în care else lipseşte se foloseşte forma simplificată: if condiţie then instrucţiuni fi; Da condiţie instrucţiuni Nu 1. se evaluează condiţia 2. dacă rezultatul este adevărat se execută instrucţiuni 3. se trece la comanda care urmează după decizie Un extra element elif (ţinând loc de else+if) poate fi adăugat în decizie, obţinând: > a := 3; b := 7; > if (a > b) then a else b fi; > if (a > b) then c:=7 fi; if/then/elif/then /else/fi a := 3 b :=
23 Metode de optimizare Noţiuni recapitulative - MAPLE > c; > if (a > b) then c:=7 elif (a<b) then c:=9 fi; forme: 4 c := 9 Există două instrucţiuni repetitive în MAPLE: for şi while. For are mai multe (1) for i from ei by p to ef do instrucţiuni od; unde i este variabila de contorizare, p este pasul cu care se face incrementarea (decrementarea), iar ei (respectiv ef ) este o expresie care determină valoarea iniţială (respectiv finală) a contorului. Modul de execuţie al acestei instrucţiuni este următorul: 1. se execută atribuirea i : = ei 2. se evaluează condiţia i ef dacă p > 0 (sau i ef dacă p < 0), şi dacă este îndeplinită această condiţie se trece la pasul 3, altfel se trece la pasul 5 3. se execută instrucţiuni 4. se execută atribuirea i := i + p 5. se execută comanda care urmează după for Comanda este echivalentă cu următoarea subschemă logică (pentru p >0): i := ei Nu i ef Da instrucţiuni i:=i + p Construcţiile from ei şi by p poate lipsi, caz în care ei se ia 1 şi pasul se consideră egal cu 1. (2) for i from ei by p while condiţie do instrucţiuni od; Modul de execuţie al acestei instrucţiuni este următorul: 1. se execută atribuirea i : = ei 2. se evaluează condiţia trecută după while, şi dacă este îndeplinită, se trece la pasul 3, altfel se trece la pasul 5 23
24 Mădălina Roxana Buneci Metode de Optimizare Laborator se execută instrucţiuni 4. se execută atribuirea i := i + p 5. se execută comanda care urmează după for Comanda este echivalentă cu următoarea subschemă logică: i := ei Nu condiţie Da instrucţiuni i:=i + p Ca şi înainte construcţiile from ei şi by p poate lipsi, caz în care ei se ia 1, iar pasul se consideră egal cu 1. Condiţia este dată printr-o expresie booleană. Ambele clause to şi while pot fi prezente în instrucţiunea for: În acest caz 1. se execută atribuirea i : = ei (3) for i from ei by p to ef while condiţie do instrucţiuni od; 2. se evaluează condiţia i ef dacă p > 0 (sau i ef dacă p < 0), şi condiţia trecută după while; dacă amândouă sunt îndeplinite se trece la pasul 3, altfel se trece la pasul 5 3. se execută instrucţiuni 4. se execută atribuirea i := i + p 5. se execută comanda care urmează după for În cazul următoarei instrucţiuni for contorul i parcurge toate elementele unei liste sau unei mulţimi (expr): > for i from 6 by 2 to 10 do print(i) od; > suma := 0; > for i from 11 by 2 while i < 15 do (4) for i in expr while condiţie do instrucţiuni od;
25 Metode de optimizare Noţiuni recapitulative - MAPLE > suma := suma + i > od; > L:=[1,5,3]; > suma:=0; > for z in L do > suma:=suma+z > od; Ciclu cu test iniţial are forma: suma := 0 suma := 11 suma := 24 L := [1, 5, 3] suma := 0 suma := 1 suma := 6 suma := 9 while condiţie do instrucţiuni od; Testul pentru repetarea calculelor se face înaintea execuţiei grupului de comenzi care trebuie repetate. Dacă este îndeplinită condiţia, se execută instrucţiunile după care se reevaluează condiţia. În caz contrar, se trece la comanda care urmează după ciclul cu test iniţial. Subschema logică echivalentă este următoarea: Nu condiţie Da instrucţiuni Condiţie reprezintă o expresie booleană. > x:=234; x := 234 > while x>0 do x:=iquo(x,10,'r');print(r); od; x := 23 4 x := 2 3 x := 0 8. Proceduri în MAPLE. În principal, necesitatea subprogramelor se datorează faptului că de multe ori algoritmul prevede executarea aceloraşi instrucţiuni pentru date diferite. Grupul de 25
26 Mădălina Roxana Buneci Metode de Optimizare Laborator instrucţiuni care se repetă poate constitui o unitate distinctă căreia i se dă un nume şi un set de parametri. Ori de câte ori va fi necesară execuţia acestui grup de instrucţiuni se specifică numele şi parametrii care actualizează grupul de instrucţiuni (astfel se scurtează dimensiunea şi creşte claritate programului). Grupul de instrucţiuni se numeşte procedură (procedure) în MAPLE. Forma unei proceduri este: nume:=proc (param1, param2, ) local lista declaraţii locale; global lista declaraţii globale; options listă opţiuni; description descriere; instrucţiuni end Nu toate elementele de mai sus sunt obligatorii. Dacă este necesar ca procedura să întoarcă o valoare, se poate folosi apelul RETURN(v) în şirul de instrucţiuni din corpul procedurii. Parametrii care apar în scrierea unei proceduri se numesc parametrii formali, ei având un rol descriptiv (un parametru formal este o variabilă al cărei nume este cunoscut, dar al cărei conţinut nu este precizat decât în momentul execuţiei). În cadrul listei parametrii formali sunt separaţi prin virgulă. Numele procedurii (nume) este un identificator MAPLE Apelul unei proceduri se face cu comanda: nume (listă parametrii actuali) parametrii actuali fiind expresii despărţite între ele prin virgulă în cadrul listei. În momentul execuţiei parametrii actuali substituie parametrii formali. Un apel de procedură determină următoarele acţiuni: se stabileşte corespondenţa între argumente şi parametrii se execută instrucţiunile subprogramului, până când se ajunge la end sau la o instrucţiune RETURN. Efectul acestor instrucţiuni (end şi RETURN) este întoarcerea în unitatea de program în care a avut loc apelul, şi anume la instrucţiunea ce urmează imediat acestui apel (precizăm că o procedură poate 26
27 Metode de optimizare Noţiuni recapitulative - MAPLE apela la rândul său o altă procedură). Un apel de procedură este corect dacă între parametrii actuali şi cei formali există o corespondenţă atât ca număr, cât şi ca tip şi organizare. Exemplu: Să presupunem că se dă un număr întreg pozitiv x, şi se cere lista cifrelor corespunzând reprezentării binare a lui x. Procedura următoare rezolvă această problemă. > lbinar:=proc(x) local y,l; y:=x; L:=[]; while y>0 do L:=[irem(y,2,'c'),op(L)];y:=c; od; RETURN(L); end; > lbinar(27); > lbinar(32); [1, 1, 0, 1, 1,1] [1, 0, 0, 0, 0, 0] Procedura lbinarfr de mai jos întoarce lista primelor n cifre ale reprezentării binare a unui număr x, cu proprietatea 0 x<1. > lbinarfr:=proc(x,n) local y,i,l; y:=x;l:=[]; for i from 1 to n do y:=y*2; L:=[op(L),floor(y)];y:=frac(y)od; RETURN(L); end; > lbinarfr(0.15,10); [0, 0, 1, 0, 0, 1, 1, 0, 0, 1] Procedura lbin întoarce lista cifrelor binare corespunzătoare unui număr real x. Pentru partea fracţionară a numărului se reţin n cifre. Procedura lbin apelează procedurile precedente. > lbin:=proc(x,n) local y,l1,l2,l; y:=abs(x); L1:=lbinar(floor(y)); 27
28 Mădălina Roxana Buneci Metode de Optimizare Laborator L2:=lbinarfr(frac(y),n); L:=[L1,L2]; RETURN(L); end; > lbin(23.15,10); [[1, 0, 1, 1, 1], [0, 0, 1, 0, 0, 1, 1, 0, 0, 1]] 28
Lucrarea de laborator nr. 1
 Metode Numerice - Lucrarea de laborator 1 Lucrarea de laborator nr. 1 I. Scopul lucrării Introducere în MAPLE II. Conţinutul lucrării 1. Structura internă. Categorii de comenzi MAPLE. 2. Operatori, constante
Metode Numerice - Lucrarea de laborator 1 Lucrarea de laborator nr. 1 I. Scopul lucrării Introducere în MAPLE II. Conţinutul lucrării 1. Structura internă. Categorii de comenzi MAPLE. 2. Operatori, constante
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
III. Reprezentarea informaţiei în sistemele de calcul
 Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Metode Numerice Curs 3 III. Reprezentarea informaţiei în sistemele de calcul III.1. Reprezentarea internă a numerelor întregi III. 1.1. Reprezentarea internă a numerelor întregi fără semn (pozitive) Reprezentarea
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
ComputerMath Explorarea matematicii folosind calculatorul și sofware-ul educațional
 ComputerMath Explorarea matematicii folosind calculatorul și sofware-ul educațional Prof. Drd. Octavia-Maria Nica Universitatea Babeș-Bolyai, Catedra de Matematică Aplicată, Loc. Cluj-Napoca, Jud. Cluj
ComputerMath Explorarea matematicii folosind calculatorul și sofware-ul educațional Prof. Drd. Octavia-Maria Nica Universitatea Babeș-Bolyai, Catedra de Matematică Aplicată, Loc. Cluj-Napoca, Jud. Cluj
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Limbaje de Programare Curs 3 Iteraţia. Reprezentare internă. Operatori pe biţi
 Limbaje de Programare Curs 3 Iteraţia. Reprezentare internă. Operatori pe biţi Dr. Casandra Holotescu Universitatea Politehnica Timişoara Ce discutăm azi... 1 Iteraţia 2 Reprezentare internă 3 Operaţii
Limbaje de Programare Curs 3 Iteraţia. Reprezentare internă. Operatori pe biţi Dr. Casandra Holotescu Universitatea Politehnica Timişoara Ce discutăm azi... 1 Iteraţia 2 Reprezentare internă 3 Operaţii
EDITURA PARALELA 45 MATEMATICĂ DE EXCELENŢĂ. Clasa a X-a Ediţia a II-a, revizuită. pentru concursuri, olimpiade şi centre de excelenţă
 Coordonatori DANA HEUBERGER NICOLAE MUŞUROIA Nicolae Muşuroia Gheorghe Boroica Vasile Pop Dana Heuberger Florin Bojor MATEMATICĂ DE EXCELENŢĂ pentru concursuri, olimpiade şi centre de excelenţă Clasa a
Coordonatori DANA HEUBERGER NICOLAE MUŞUROIA Nicolae Muşuroia Gheorghe Boroica Vasile Pop Dana Heuberger Florin Bojor MATEMATICĂ DE EXCELENŢĂ pentru concursuri, olimpiade şi centre de excelenţă Clasa a
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
III.2.2. Reprezentarea în virgulă mobilă
 III... Reprezentarea în virgulă mobilă Una dintre cele mai răspândite reprezentări internă (în PC-uri) a numerelor reale este reprezentarea în virgulă mobilă. Reprezentarea în virgulă mobilă presupune
III... Reprezentarea în virgulă mobilă Una dintre cele mai răspândite reprezentări internă (în PC-uri) a numerelor reale este reprezentarea în virgulă mobilă. Reprezentarea în virgulă mobilă presupune
2. Circuite logice 2.2. Diagrame Karnaugh. Copyright Paul GASNER 1
 2. Circuite logice 2.2. Diagrame Karnaugh Copyright Paul GASNER Diagrame Karnaugh Tehnică de simplificare a unei expresii în sumă minimă de produse (minimal sum of products MSP): Există un număr minim
2. Circuite logice 2.2. Diagrame Karnaugh Copyright Paul GASNER Diagrame Karnaugh Tehnică de simplificare a unei expresii în sumă minimă de produse (minimal sum of products MSP): Există un număr minim
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
Ecuatii exponentiale. Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. a x = b, (1)
 Ecuatii exponentiale Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. Cea mai simpla ecuatie exponentiala este de forma a x = b, () unde a >, a. Afirmatia.
Ecuatii exponentiale Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. Cea mai simpla ecuatie exponentiala este de forma a x = b, () unde a >, a. Afirmatia.
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R. 4.1 Proprietăţi topologice ale lui R Puncte de acumulare
 Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
 4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
4. CIRCUITE LOGICE ELEMENTRE 4.. CIRCUITE LOGICE CU COMPONENTE DISCRETE 4.. PORŢI LOGICE ELEMENTRE CU COMPONENTE PSIVE Componente electronice pasive sunt componente care nu au capacitatea de a amplifica
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
Laborator 1: INTRODUCERE ÎN ALGORITMI. Întocmit de: Claudia Pârloagă. Îndrumător: Asist. Drd. Gabriel Danciu
 INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
INTRODUCERE Laborator 1: ÎN ALGORITMI Întocmit de: Claudia Pârloagă Îndrumător: Asist. Drd. Gabriel Danciu I. NOŢIUNI TEORETICE A. Sortarea prin selecţie Date de intrare: un şir A, de date Date de ieşire:
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Teme de implementare in Matlab pentru Laboratorul de Metode Numerice
 Teme de implementare in Matlab pentru Laboratorul de Metode Numerice As. Ruxandra Barbulescu Septembrie 2017 Orice nelamurire asupra enunturilor/implementarilor se rezolva in cadrul laboratorului de MN,
Teme de implementare in Matlab pentru Laboratorul de Metode Numerice As. Ruxandra Barbulescu Septembrie 2017 Orice nelamurire asupra enunturilor/implementarilor se rezolva in cadrul laboratorului de MN,
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Lucrarea de laborator nr. 2
 Metode Numerice Lucrarea de laborator nr. I. Scopul lucrării Reprezentarea numerelor reale în calculator. Erori de rotunjire. II. III. Conţinutul lucrării. Reprezentarea numerelor reale sub formă normalizată..
Metode Numerice Lucrarea de laborator nr. I. Scopul lucrării Reprezentarea numerelor reale în calculator. Erori de rotunjire. II. III. Conţinutul lucrării. Reprezentarea numerelor reale sub formă normalizată..
Curs 2 Şiruri de numere reale
 Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Laborator 11. Mulţimi Julia. Temă
 Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Laborator 11 Mulţimi Julia. Temă 1. Clasa JuliaGreen. Să considerăm clasa JuliaGreen dată de exemplu la curs pentru metoda locului final şi să schimbăm numărul de iteraţii nriter = 100 în nriter = 101.
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Toate subiectele sunt obligatorii. Timpul de lucru efectiv este de 3 ore. Se acordă din oficiu 10 puncte. SUBIECTUL I.
 Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Laborator 4 suport teoretic Tipuri de date utilizate în limbajul de programare C.
 Laborator 4 suport teoretic Tipuri de date utilizate în limbajul de programare C. Toate valorile parametrilor unei probleme, adică datele cu care operează un program, sunt reprezentate în MO sub formă
Laborator 4 suport teoretic Tipuri de date utilizate în limbajul de programare C. Toate valorile parametrilor unei probleme, adică datele cu care operează un program, sunt reprezentate în MO sub formă
Taylor Polynomials. 2 x2 6 x3 24 x4
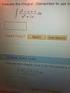 > Taylor Polynomials > Taylor Polynomials about x = 0. A primary use of Taylor polynomials is to find good polynomial approximations to a function near a specified value. As a first example, we use a fourth
> Taylor Polynomials > Taylor Polynomials about x = 0. A primary use of Taylor polynomials is to find good polynomial approximations to a function near a specified value. As a first example, we use a fourth
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
Ecuatii trigonometrice
 Ecuatii trigonometrice Ecuatiile ce contin necunoscute sub semnul functiilor trigonometrice se numesc ecuatii trigonometrice. Cele mai simple ecuatii trigonometrice sunt ecuatiile de tipul sin x = a, cos
Ecuatii trigonometrice Ecuatiile ce contin necunoscute sub semnul functiilor trigonometrice se numesc ecuatii trigonometrice. Cele mai simple ecuatii trigonometrice sunt ecuatiile de tipul sin x = a, cos
Lucrare. Varianta aprilie I 1 Definiţi noţiunile de număr prim şi număr ireductibil. Soluţie. Vezi Curs 6 Definiţiile 1 şi 2. sau p b.
 Lucrare Soluţii 28 aprilie 2015 Varianta 1 I 1 Definiţi noţiunile de număr prim şi număr ireductibil. Soluţie. Vezi Curs 6 Definiţiile 1 şi 2 Definiţie. Numărul întreg p se numeşte număr prim dacă p 0,
Lucrare Soluţii 28 aprilie 2015 Varianta 1 I 1 Definiţi noţiunile de număr prim şi număr ireductibil. Soluţie. Vezi Curs 6 Definiţiile 1 şi 2 Definiţie. Numărul întreg p se numeşte număr prim dacă p 0,
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Subiecte Clasa a V-a
 (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
(40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
1.3 Baza a unui spaţiu vectorial. Dimensiune
 .3 Baza a unui spaţiu vectorial. Dimensiune Definiţia.3. Se numeşte bază a spaţiului vectorial V o familie de vectori B care îndeplineşte condiţiile de mai jos: a) B este liniar independentă; b) B este
.3 Baza a unui spaţiu vectorial. Dimensiune Definiţia.3. Se numeşte bază a spaţiului vectorial V o familie de vectori B care îndeplineşte condiţiile de mai jos: a) B este liniar independentă; b) B este
Spatii liniare. Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară. Mulţime infinită liniar independentă
 Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
Noţiunea de spaţiu liniar 1 Noţiunea de spaţiu liniar Exemple Subspaţiu liniar Acoperire (înfăşurătoare) liniară 2 Mulţime infinită liniar independentă 3 Schimbarea coordonatelor unui vector la o schimbare
2. Circuite logice 2.5. Sumatoare şi multiplicatoare. Copyright Paul GASNER
 2. Circuite logice 2.5. Sumatoare şi multiplicatoare Copyright Paul GASNER Adunarea în sistemul binar Adunarea se poate efectua în mod identic ca la adunarea obişnuită cu cifre arabe în sistemul zecimal
2. Circuite logice 2.5. Sumatoare şi multiplicatoare Copyright Paul GASNER Adunarea în sistemul binar Adunarea se poate efectua în mod identic ca la adunarea obişnuită cu cifre arabe în sistemul zecimal
Laborator 6. Integrarea ecuaţiilor diferenţiale
 Laborator 6 Integrarea ecuaţiilor diferenţiale Responsabili: 1. Surdu Cristina(anacristinasurdu@gmail.com) 2. Ştirbăţ Bogdan(bogdanstirbat@yahoo.com) Obiective În urma parcurgerii acestui laborator elevul
Laborator 6 Integrarea ecuaţiilor diferenţiale Responsabili: 1. Surdu Cristina(anacristinasurdu@gmail.com) 2. Ştirbăţ Bogdan(bogdanstirbat@yahoo.com) Obiective În urma parcurgerii acestui laborator elevul
INTRODUCERE ÎN PROGRAMAREA MATLAB
 LUCRAREA Nr. 2 INTRODUCERE ÎN PROGRAMAREA MATLAB. Obiective Lucrarea are ca scop însuşirea modului de lucru cu produsul program Matlab pentru calcul numeric, utilizând funcńii matematice uzuale. 2. NoŃiuni
LUCRAREA Nr. 2 INTRODUCERE ÎN PROGRAMAREA MATLAB. Obiective Lucrarea are ca scop însuşirea modului de lucru cu produsul program Matlab pentru calcul numeric, utilizând funcńii matematice uzuale. 2. NoŃiuni
Instructiunea while. Forma generala: while (expresie) instructiune;
 Instructiunea while while (expresie) instructiune; Modul de executie: 1) Se evalueaza expresie, daca expresie = 0 (fals) se iese din instructiunea while, altfel (expresie 0, deci adevarat) se trece la
Instructiunea while while (expresie) instructiune; Modul de executie: 1) Se evalueaza expresie, daca expresie = 0 (fals) se iese din instructiunea while, altfel (expresie 0, deci adevarat) se trece la
Concurs MATE-INFO UBB, 1 aprilie 2017 Proba scrisă la MATEMATICĂ
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
2. Circuite logice 2.4. Decodoare. Multiplexoare. Copyright Paul GASNER
 2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
2. Circuite logice 2.4. Decodoare. Multiplexoare Copyright Paul GASNER Definiţii Un decodor pe n bits are n intrări şi 2 n ieşiri; cele n intrări reprezintă un număr binar care determină în mod unic care
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
Să se arate că n este număr par. Dan Nedeianu
 Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Progresii aritmetice si geometrice. Progresia aritmetica.
 Progresii aritmetice si geometrice Progresia aritmetica. Definitia 1. Sirul numeric (a n ) n N se numeste progresie aritmetica, daca exista un numar real d, numit ratia progresia, astfel incat a n+1 a
Progresii aritmetice si geometrice Progresia aritmetica. Definitia 1. Sirul numeric (a n ) n N se numeste progresie aritmetica, daca exista un numar real d, numit ratia progresia, astfel incat a n+1 a
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Examen AG. Student:... Grupa: ianuarie 2016
 16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
16-17 ianuarie 2016 Problema 1. Se consideră graful G = pk n (p, n N, p 2, n 3). Unul din vârfurile lui G se uneşte cu câte un vârf din fiecare graf complet care nu-l conţine, obţinându-se un graf conex
Universitatea din Bucureşti Facultatea de Matematică şi Informatică. Algebră (1)
 Universitatea din ucureşti.7.4 Facultatea de Matematică şi Informatică oncursul de admitere iulie 4 omeniul de licenţă alculatoare şi Tehnologia Informaţiei lgebră (). Fie x,y astfel încât x+y = şi x +
Universitatea din ucureşti.7.4 Facultatea de Matematică şi Informatică oncursul de admitere iulie 4 omeniul de licenţă alculatoare şi Tehnologia Informaţiei lgebră (). Fie x,y astfel încât x+y = şi x +
Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism. (Y = f(x)).
 Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Teoremă. (Y = f(x)). Orice izometrie f : (X, d 1 ) (Y, d 2 ) este un homeomorfism Demonstraţie. f este continuă pe X: x 0 X, S Y (f(x 0 ), ε), S X (x 0, ε) aşa ca f(s X (x 0, ε)) = S Y (f(x 0 ), ε) : y
Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane
 Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
IV. CUADRIPOLI SI FILTRE ELECTRICE CAP. 13. CUADRIPOLI ELECTRICI
 V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
Exemple de probleme rezolvate pentru cursurile DEEA Tranzistoare bipolare cu joncţiuni
 Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Arhitectura Calculatoarelor. Fizică - Informatică an II. 2. Circuite logice. Copyright Paul GASNER 1
 Arhitectura Calculatoarelor Fizică - Informatică an II gasner@uaic.ro 2. Circuite logice Copyright Paul GASNER 1 Funcţii booleene Porţi logice Circuite combinaţionale codoare şi decodoare Cuprins multiplexoare
Arhitectura Calculatoarelor Fizică - Informatică an II gasner@uaic.ro 2. Circuite logice Copyright Paul GASNER 1 Funcţii booleene Porţi logice Circuite combinaţionale codoare şi decodoare Cuprins multiplexoare
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
f(x) = l 0. Atunci f are local semnul lui l, adică, U 0 V(x 0 ) astfel încât sgnf(x) = sgnl, x U 0 D\{x 0 }. < f(x) < l +
 Semnul local al unei funcţii care are limită. Propoziţie. Fie f : D (, d) R, x 0 D. Presupunem că lim x x 0 f(x) = l 0. Atunci f are local semnul lui l, adică, U 0 V(x 0 ) astfel încât sgnf(x) = sgnl,
Semnul local al unei funcţii care are limită. Propoziţie. Fie f : D (, d) R, x 0 D. Presupunem că lim x x 0 f(x) = l 0. Atunci f are local semnul lui l, adică, U 0 V(x 0 ) astfel încât sgnf(x) = sgnl,
Metode Runge-Kutta. 18 ianuarie Probleme scalare, pas constant. Dorim să aproximăm soluţia problemei Cauchy
 Metode Runge-Kutta Radu T. Trîmbiţaş 8 ianuarie 7 Probleme scalare, pas constant Dorim să aproximăm soluţia problemei Cauchy y (t) = f(t, y), a t b, y(a) = α. pe o grilă uniformă de (N + )-puncte din [a,
Metode Runge-Kutta Radu T. Trîmbiţaş 8 ianuarie 7 Probleme scalare, pas constant Dorim să aproximăm soluţia problemei Cauchy y (t) = f(t, y), a t b, y(a) = α. pe o grilă uniformă de (N + )-puncte din [a,
Noţiuni introductive
 Metode Numerice Noţiuni introductive Erori. Condiţionare numerică. Stabilitatea algoritmilor. Complexitatea algoritmilor. Metodele numerice reprezintă tehnici prin care problemele matematice sunt reformulate
Metode Numerice Noţiuni introductive Erori. Condiţionare numerică. Stabilitatea algoritmilor. Complexitatea algoritmilor. Metodele numerice reprezintă tehnici prin care problemele matematice sunt reformulate
Matrice. Determinanti. Sisteme liniare
 Matrice 1 Matrice Adunarea matricelor Înmulţirea cu scalar. Produsul 2 Proprietăţi ale determinanţilor Rangul unei matrice 3 neomogene omogene Metoda lui Gauss (Metoda eliminării) Notiunea de matrice Matrice
Matrice 1 Matrice Adunarea matricelor Înmulţirea cu scalar. Produsul 2 Proprietăţi ale determinanţilor Rangul unei matrice 3 neomogene omogene Metoda lui Gauss (Metoda eliminării) Notiunea de matrice Matrice
Examen AG. Student:... Grupa:... ianuarie 2011
 Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
Problema 1. Pentru ce valori ale lui n,m N (n,m 1) graful K n,m este eulerian? Problema 2. Să se construiască o funcţie care să recunoască un graf P 3 -free. La intrare aceasta va primi un graf G = ({1,...,n},E)
28. SUPRADEFINIREA OPERATORILOR
 28. SUPRADEFINIREA OPERATORILOR Pentru un tip clasă se poate defini un set de operatori asociaţi prin supradefinirea operatorilor existenţi, ceea ce permite realizarea de operaţii specifice cu noul tip
28. SUPRADEFINIREA OPERATORILOR Pentru un tip clasă se poate defini un set de operatori asociaţi prin supradefinirea operatorilor existenţi, ceea ce permite realizarea de operaţii specifice cu noul tip
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
4. Măsurarea tensiunilor şi a curenţilor electrici. Voltmetre electronice analogice
 4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
4. Măsurarea tensiunilor şi a curenţilor electrici oltmetre electronice analogice oltmetre de curent continuu Ampl.c.c. x FTJ Protectie Atenuator calibrat Atenuatorul calibrat divizor rezistiv R in const.
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 21.2 - Sistemul de criptare ElGamal Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Scurt istoric
riptografie şi Securitate - Prelegerea 21.2 - Sistemul de criptare ElGamal Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Scurt istoric
Functii Breviar teoretic 8 ianuarie ianuarie 2011
 Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Programarea Calculatoarelor
 Programarea Calculatoarelor Modul 1: Rezolvarea algoritmică a problemelor Introducere în programare Algoritm Obiectele unui algoritm Date Constante Variabile Expresii Operaţii specifice unui algoritm şi
Programarea Calculatoarelor Modul 1: Rezolvarea algoritmică a problemelor Introducere în programare Algoritm Obiectele unui algoritm Date Constante Variabile Expresii Operaţii specifice unui algoritm şi
Conice - Câteva proprietǎţi elementare
 Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
INTERPOLARE. y i L i (x). L(x) = i=0
 INTERPOLARE Se dau punctele P 0, P 1,..., P n in plan sau in spatiu, numite noduri si avand vectorii de pozitie r 0, r 1,..., r n. Problemă. Să se găsească o curbă (dintr-o anumită familie) care să treacă
INTERPOLARE Se dau punctele P 0, P 1,..., P n in plan sau in spatiu, numite noduri si avand vectorii de pozitie r 0, r 1,..., r n. Problemă. Să se găsească o curbă (dintr-o anumită familie) care să treacă
prin egalizarea histogramei
 Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
Lucrarea 4 Îmbunătăţirea imaginilor prin egalizarea histogramei BREVIAR TEORETIC Tehnicile de îmbunătăţire a imaginilor bazate pe calculul histogramei modifică histograma astfel încât aceasta să aibă o
2 Transformări liniare între spaţii finit dimensionale
 Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
