Partikula kargatua: m = 1/2. m = + 1/2
|
|
|
- Σπύρο Πυλαρινός
- 7 χρόνια πριν
- Προβολές:
Transcript
1 2 Ikasgaia. E.M..ERREATZIA MAGETIK UKLEARRA ETA MAA EPEKTRMETRIA (EM) ERREATZIA MAGETIK UKLEARRA ukleoen popietate magnetikoak. Lamo-en ekuaioa. Ppm eskala. Integaioa. eta 3 nukleoen leakunta kimikoa pin-spin akoplamendua. einaleen anikoitasuna Potoi baliokideak eta e-baliokideak 2.. UKLEE PRPIETATE MAGETIKAK ukleo atomiko gutiek spin ( bia egin ) deituiko popietate kuantikoa dute. Potoia eta neutoia e dia patikula elementalak, baiik eta kuak-e osatuikoak. Potoi batek 3 kuak ditu. Edoein patikula baten I spin-enbakiak patikula hoek hasiean uen iudi bebea bei iateko eman beha duen bia-kopuua adieaten du. (ME) MAA-EPEKTRMETRIA Ioniaioa; fagmentaioa; ioi-banaketa Masa/kaga elaioa (m/) Fagmentaioa Konposatu oganiko batuen masa-espektuak I = I = I = /2 I = /2 Potoiaen kasuan, /2 bia eman beha da, eta I = /2 da. ukleido baten I spin-enbakia, bee potoi (p) eta neutoi (n) kopuuaekin lotua dago. a) Σ(p + n) = paea denean I = edo I =, 2, 3... nukleido hauek e dute eemu magnetikoekin inteakionaten b) Σ(p + n) = epaea denean I = /2 edo I = 3/2, 5/2,... nukleido hauek (bate ee I = /2 dutenak) eemu magnetikoekiko sentikoak dia eta EM teknikaako apoposak: F P UKLEE PRPIETATE MAGETIKAK I spin-enbakia duen nukleoai kanpotik eemu magnetikoa eaten baaio, (2I + ) spin-egoea soten dia, bakoitak m enbaki kuantiko magnetikoa duelaik: m = +I, I-,... I. m Zenbaki magnetikoak, eta 3 -en kasuan, +/2 eta /2 balioak ha ditake kanpotik eemu magnetiko bat eaitakoan. Egoea hauetako bakoitai enegia ebedina dagokione, batetik bestea igaoteko, E langa gainditu beha da, hν iati-fekuentia kuanto baten inteakioa. m = Egonkotua m = Desegonkotua E = E m = m = 2.3. PRTIARE MMETU MAGETIKA Patikula kagatugabea: L : momentu angeluaa Patikula kagatua: L: momentu angeluaa µ : momentu magnetikoa L = p (eemu gabitatoioik gabe) G o µ = γ L ( γ : konstante giomagnetikoa) m : enbaki kuantiko magnetikoa L h = m 2π = m h µ γ (eemu magnetikoik gabe) Kanpo-eemuak peesioa sotaaten du p: momentu lineala 2π ω ω L µ L G o eemu gabitatoioan µ θ eemu magnetikoan
2 2.4. ERREATZIA: LARMR-E EKUAZIA E-en balioa kalkulateko, potoi batek spin-egoea egonkoenean ( m = +/2) eta eegonkoenean (m = /2) duen enegia kalkulatu beha da. Enegia hoi momentu magnetikoa (µ) eta kanpo-eemu magnetikoaen ( ) ateko bidekadua eskalaak ematen du, een eta geo eta handiagoa bihuten denean, E ee handiagoa bihuten baita (Zeeman efektua): h E(m egoean) = µ Bo cos θ = µ Bo = γ 2 m Bo π E E B B 2 B 3 E (m= ) = + γh/4π E 2 E 3 E (m= ) = γh/4π µ (m= ) Lamo-en ekuaioak, nukleo batek bee momentu magnetikoa ( m = +/2) egoeatik (m = /2) egoeaa aldateko beha den ν fekuentia ematen du. Aldaketa hau eesonantia da. µ µ µ (m= ) γ h γ h γ h E = h ν = E ( m= -/2) E (m= +/2) = Bo = Bo 4π 4π 2π ν 2.6. PATAILA-EFEKTUA γ = 2 π 2.5. E.M.. (MR) EXPERIMETUA ETA APARATUA Pila bat potoiak dituen molekula-lagina (konposatu oganiko baten disoluioa) Bo eemu magnetikopean ipinten denean, potoi gehienak ( m = +/2) egoean daude. Kanpotik fekuentia aldakoeko tansmisoe bate iadiatu, eesonantia getatuko da ν Lamo-en fekuentia ediesten den unean eta oduan, enegia xugatuko du laginak potoiak ( m = /2) egoeaa eamane. Eeeptoe batek enegia-absotio hoi neutu, seinalea (espektua emango du) µ = E=hv Tansmisoea v 2.7. LERRAKUTZA KIMIKA µ µ Eeeptoea µ = - /2 Absotioa ν Potoiak e daude isolatuak molekuletan, baiik eta elektoie inguatuak. Elektoiak ee kagatuik daudene, been mugimenduak kanpotik eaitako eemuaen kontako B i eemu induitua soten dute. ndoio, hidogeno-atomoen nukleoek jasaten duten eemu efektiboa B f da. B = B B B = σ B B f B i e f o i i i o B i kanpotik eaitako -en funtio dene (σ pantaila-konstanteaen bitate uenki popotionala), Lamo-en ekuaio uendua honela idat daiteke: γ γ νi = B f = ( σi ) = νo( σi ) (ν 2π 2 π o : potoiaen Lamo-en fekuentia) B i = B f = E o ν ο < > > > B i B f < E i = cte ν i Fekuentia: Enegía: Apantailaketa Eemua E o E i B i, σ i ν o ν i idogeno-atomo mota bakoitak molekula oganiko baten bauan elektoi-dentsitate ebedina duene,eesonantia emateko behako duen ν i fekuentia efektiboa ee ebedina iango da bakoitaentat. ndoio, E.M..-ai eske, molekula bakoitak dituen hidogeno ebedinak espeimentalki beeitu ahal iango ditugu. Munduan eha dauden ekipoek eemu magnetiko ebedinak ditutene, eta ν i fekuentia -ekin aldaten dene, leakunta kimikoa asmatu da (ppm, milioiko atitan adieaia). oetaako, tetametilsilanoa () hatu da eefeentia intenaioala beala, bee hidogeno-atomoen eesonantia-fekuentia eaguten dien beste molekula oganikoena baino handiagoa delako. Gau egun, funtio-talde nagusietako hidogeno-atomo gutien leakunta kimikoak eaguten dia (tauletan daude) eta beaien balioak molekula eeagunenekin konpaatu, aken hauen iaea kimikoa deduitu daiteke i 3 ν ( ppm) = i ν i ν ν i o ν 6 ν ef ppm ppm
3 2.8. IDRGE EZBERDIE E.M.. LERRAKUTZAK 2.9.,4-DIMETILBETZEARE -EM EPEKTRUA Funtio-Taldea () ppm Funtio-Taldea () ppm idokabuoak Alkoholak, aminak (mugikoak) R 2 R Alilikoak, bentilikoak Esteen α-posiioak = R 2 2 R Kaboniloen α-posiioak Binilikoak = Amidak R R R Alkinoak Aminen α-posiioak R Alkohol edo eteen α-posiioak R alogenuoen α-posiioak l 2 B Aomatikoak Aldehidoak Aido kaboxilikoak Molekula honetan 2 motatako potoiak daude: alde batetik 3 taldeei dagokien 6 potoiak (2.3 ppm) eta bestaldetik 4 aomatikak (7. ppm). einale bakoitaen apiko aalea potoi-kopuuaekiko popotionala da ppm 2.. KARB EZBERDIE 3 E.M.. LERRAKUTZAK 2.. METIL METAKRILATARE 3 -EM EPEKTRUA Kabonoaen isotopoak 2 / 3 : 98.9/. popotioan aukiten dia atuan. 2 -en I = da eta ein da EM egiteko eabili. 3 -EMespektuak egiteko, laginak -EM baino kontentatuagoak ian beha dia 3 -EM-ko leakunta kimiko txikienetan sp3 kabonoak ematen dute eesonantia, altuenetan sp2 eta sp kabonoak. TALDEAK 3 (ppm) Alkilo Alkilo Alkilo 2-6 Aminak Alkoholak/eteak X (X: l, B,I) 25-8 R R X -= (X:, R, R, R) EM espektuan 5 kabono ebaliokide ageten dia. Espektu hauetan e dago elaio uenik seinaleen aalea eta kabono-kopuuaen atean = 6 = 4 = 2 2 Dl 3 (disolbatailea) ppm
4 2.2. PI-PI AKPLAMEDUA: n J AB KTATEA 2.3. EIALE AKPLATUE AIZKITAUA Molekula oganiko bateko bi potoi magnetikoki ebaliokide ( A eta X ) elkaengandik hubil badaude (n lotuako distantiaa n = 2 edo 3), oduan bi seinale eman behaean, 4 seinale ageten dia -EM espektuan: A eta X akoplatuta daudela esaten da. Itxaotakoa: m ( A ) m ( X ) A spin-egoea X Benetakoa: ν A ν X Σ m + A R R X 2 J AB = 4 6 A X J AX ν A2 ν A ν X2 ν X onen aaoia ea da: potoi bakaak dituen 2 spin-egoea posibleetatik, potoi-bikotean 4 lau spin-egoeaa pasaten da. Potoi bakoitean bi tantsiio dia posible eta, ondoio, 4 eesonantia-seinale ebedin ikusten dia, bakoita enegia ebedinea ( A potoiaentat ν A eta ν A2 eta X potoiaentat ν X eta ν X2. ν X eta ν X2 fekuentia-difeentiai (-tan) akopamendu-konstantea ( n J AX ) deito. A X 3 J AX = - 8 -EM espektuetan A motako potoia beste mota bateko, 2, 3,..x potoiekin akoplaten bada, aken hauek ( m = ±/2) enbaki magnetikoaen, 2, 3,...x elementuko konbinaioak eman ditakete, M anikoitasuneko seinaleak emane (x = : singletea; x = : dobletea; x = 2: tipletea; x = 3: kuadupletea; x = 4: kintupletea; x = 5: sextupletea; etab...) istema pin-egoea m A ( 3 J ) einalea A A A + + 3/2 3/2 : : 2 : : 3 : 3 : dobletea tipletea M = x + kuadupletea 2.4.,,2-TRIKLRETAARE -EM EPEKTRUA Molekula honetan bi motatako potoiak daude: l 2 (desapantailatuenak, tipletea), 2 l (apantailatuenak, dobletea). l l l ETIL KLRAZETATARE -EM EPEKTRUA Molekula honetan 3 motatako potoiak daude: 2 l (singletea), 2 (kuadupletea), 3 (tipletea) Espektu hau 6M-ko EM apaatu bate eegistatu da. ν () 6 l ppm ( ppm ) ( ppm )
5 2.6. MAA EPEKTRMETRIARE IARRIAK 2.7. MAA EPEKTRMETRIARE IARRIAK Ioniaioa: Enegia handiko patikulak (> 8Kcal/mol-eko elektoiak) molekula oganikotan talka egiten dutenean, M obitaleko elektoia infinitoa bultaten da. oela, molekula katioi-eadikala beala ioniaten da, ioi molekulaa emane. Teknika honi Inpaktu Elektonikoko Masa Espektometia (E.I.M.) deito (ikus 8.8. atala). M e M 2 e Molekula Enegia handiko elektoia Katioi-eadikala (ioi molekulaa) Fagmentaioa: Elektoi bonbadataileen enegia M molekulaen ioniaio-potentiala doidoi jadesteko adinakoa balit, ioi molekulaa sotu amaituko litateke poesua. Baina elektoien enegia asko ee handiagoa da (7 ev) ( ev = 95KJ.mol ), eta ioi molekulaa, fagmentatu egiten da, beste katioi-eadikal txikiagoak, katioiak, eadikalak eta patikula neutoak emane. Masa espektometoak positiboki kagatuiko espeieak detektaten ditu. M + xif i x j j + xkr k + xl l i j k l (Katioi - eadikalak) (Katioiak) (Eadikalak) (eutoak) Espeie kagatuak Ioi-banaketa eta m/ elaioa: Molekula baten ioniaio eta fagmentaioan sotutako patikula positiboak banateko, V potential elektiko bate aeleaten dia, eta geo B eemu magnetiko baten eha pasa aaten dia. oela, fagmentu bakoitaen masa-kaga (m/) elaioaen aabea, patikulek eadio ebedineko tajektoia ikulaak egiten ditute. Fagmentu baten m/ elaio enbat eta handiagoa ian, bee kubatua-eadioa ee handiagoa da. Eaitako V eta B potentialak jakine V eta kubatua eadioak neutu, patikula bakoitaen m/ elaioa atea M m/ Fagmentua V potential elektikoa aeleatu B = f (m/) daiteke. m = 2 B 2 2 V Kontutan ianik ia beti fagmentuen kaga = iaten dela, patikulen masa uenean jakin daiteke. einaleen intentsitatea: Fagmentuen egonkotasuna handiagoa ian ala, been biia lueagoa iango da eta detektoean saiago aalduko dia; bea, been seinaleak handiagoak iango dia. einale handienai oinai seinalea (base-peak) esaten aio GA-KRMATGRAFA-MAA EPEKTRMETRA (G M) 2.9. E.M. EPEKTRUE AALIIA M.E. ekipo modenotan gas-komatogafoa (G.K.) akoplaten aio espektometoai, molekula ebedinen nahasteak txanda baka batean analisatu ahal iateko. Lagina ( µl) Injektoea (3º) Banataile kapilaa (Labea: 2 3 ) Gas-komatogafoa (molekula-banaketa) M 7 ev utsunea: 6 -To M M 2 M + M M M M V Ioniaioganbaa Aeleaioganbaa % = f (m/e) Detektagailua (Ioi-banaketa) M Espektua m/e denagailua E.M. espektu baten itxua ookoa apikoa da. Betan, fagmentu bakoitaen intentsitate elatibo nomaliatua (I) adieaten da m/ balioaen auean (dalton-etan edo m.a.u.-tan neutua). I 5 B Bi motatako espektuak daude: eesoluio txikikoak eta eesoluio handikoak. ahi eta bigaenaen infomaioa asko ee ehatagoa ian, lehendabiikoa ee oso paktikoa da. Fagmentuak Eesoluio txikia (m/) Eesoluio handia (m/) M m/ inaiko seinalea (base peak) Ioi molekulaa
6 2.2. ITPE ERAGIA Masa espektometoan elementu atomiko bakoitaen isotopoak ea beeiten dia. ndoio, kontutan hatu beha da detektatuiko molekula eeal bakoita isotopokonbinaioa dela eta konbinaio bakoitak m/ ebedina emango duela. Molekula oganiko gehienen isotopo nagusiak taula honetan bildutakoak dia. Elementua l B I Isotopoa (%)* [Masa] ()[,78] 2 ()[2,] 4 ()[4,3] 6 ()[5,9949] 35 l ()[34,9689] 79 B ()[78,983] 27 I ()[26,945] Isotopoa (%)**[Masa] 2 (,5)[2,4] 3 (,8)[3,34] 5 (,38)[5,] 8 (,2)[7,9992] 37 l (32.5)[36,9659] 8 B (98.)[8,963] * Isotopo nagusiak %-a doituak. ** Beste isotopo adieagaien popotio elatiboak ITPE ERAGIA 3 isotopoaen eagine, M ioi molekulaaen gainetik M+ seinalea ageten da. M eta M+ -en ateko intentsitate elatiboa molekulak dituen - atomo kopuua handiten da. (% - atomo bakoiteko). alogenoak dituten molekuletan, M ioi molekulaen gainetik M+2 seinalea ageten da. l deibatuek M eta M+2 %/%33 popotioan ematen ditute, B deibatuek %: % popotioan l 3 -B l 37 l M M B 79 B M M+ 2 3 M M E.M. FRAGMETUE ITERPRETAZIA E.M. FRAGMETUE ITERPRETAZIA Molekula oganikoen lotuek enegia ebedinak ditutene, lehendabii eten egingo dien lotuak ahulenak iango dia. Adibide, G ( ) < G ( ) ( 5 5 ) a b a b m/ : 77 (43%) m/: 57 (.6%) ( 6 5 ) M: 34 m/ : 5 (%) m/: 29 (2%) einalen intentsitate handiena fagmentu egonkoenak ematen ditute; hots, eesonantia, eagin induktibo eta eagopen esteiko egonkotutako espeie kationikoak = < (º) + < (2)º + < (3º) + < Me= 2 + < Ph I
7 2.24. ZEBAIT M.. EPEKTRU ADIERAZGARRI ZEBAIT M.. EPEKTRU ADIERAZGARRI idokabuotan, lotuak lotuak baino eaago eten egiten dia eta katioi sekundaio edo tetiaioak soten badia, seinale handiak ematen ditute. Teknika honen bitate, isomeo konstituionalak oso ongi beeiten dia. 3 3 n-ktanoa Etil-3-metil-pentanoa idokabuo aomatikotan, bentilo ( )(m/= 9) saitan osaten da eta bee seinalea oso handia da katioia egonkoa delako. alogenoak (l) daudenean, M eta M+2 isotopoak 3: popotioan aalten dia. 3 n-butilbentenoa 3 l 4-Kloometil-toluenoa ZEBAIT M.. EPEKTRU ADIERAZGARRI Alkoholetan, lotua beehala eten egiten da (M ) emane eta geo, 2 galten da. Alkohol 3º-ek kabokatioi oso egonkoak ematen ditute eta seinale handiak. 3 n-butanola 3 s-butanola t-butanola ZEBAIT M.. EPEKTRU ADIERAZGARRI Aldehido eta etonetan kabonilo taldeaen alde bakoiteko atiak ematen ditu seinaleak. Aldehidotan M seinalea aalten da eta etonetan, ailio ioiak (R- + ) Metil-pentanala Metil-pentanona 6 2
ANGELUAK. 1. Bi zuzenen arteko angeluak. Paralelotasuna eta perpendikulartasuna
 Metika espazioan ANGELUAK 1. Bi zuzenen ateko angeluak. Paalelotasuna eta pependikulatasuna eta s bi zuzenek eatzen duten angelua, beaiek mugatzen duten planoan osatzen duten angeluik txikiena da. A(x
Metika espazioan ANGELUAK 1. Bi zuzenen ateko angeluak. Paalelotasuna eta pependikulatasuna eta s bi zuzenek eatzen duten angelua, beaiek mugatzen duten planoan osatzen duten angeluik txikiena da. A(x
3. Ikasgaia. MOLEKULA ORGANIKOEN GEOMETRIA: ORBITALEN HIBRIDAZIOA ISOMERIA ESPAZIALA:
 3. Ikasgaia. MLEKULA RGAIKE GEMETRIA: RBITALE IBRIDAZIA KARB DERIBATUE ISMERIA ESPAZIALA Vant off eta LeBel-en proposamena RBITAL ATMIKE IBRIDAZIA ibridaio tetragonala ibridaio digonala Beste hibridaioak
3. Ikasgaia. MLEKULA RGAIKE GEMETRIA: RBITALE IBRIDAZIA KARB DERIBATUE ISMERIA ESPAZIALA Vant off eta LeBel-en proposamena RBITAL ATMIKE IBRIDAZIA ibridaio tetragonala ibridaio digonala Beste hibridaioak
7.GAIA. ESTATISTIKA DESKRIBATZAILEA. x i n i N i f i
 7.GAIA. ESTATISTIKA DESKRIBATZAILEA 1. Osatu ondorengo maiztasun-taula: x i N i f i 1 4 0.08 2 4 3 16 0.16 4 7 0.14 5 5 28 6 38 7 7 45 0.14 8 2. Ondorengo banaketaren batezbesteko aritmetikoa 11.5 dela
7.GAIA. ESTATISTIKA DESKRIBATZAILEA 1. Osatu ondorengo maiztasun-taula: x i N i f i 1 4 0.08 2 4 3 16 0.16 4 7 0.14 5 5 28 6 38 7 7 45 0.14 8 2. Ondorengo banaketaren batezbesteko aritmetikoa 11.5 dela
1. Gaia: Mekanika Kuantikoaren Aurrekoak
 1) Kimika Teorikoko Laborategia 2012.eko irailaren 12 Laburpena 1 Uhin-Partikula Dualtasuna 2 Trantsizio Atomikoak eta Espektroskopia Hidrogeno Atomoaren Espektroa Bohr-en Eredua 3 Argia: Partikula (Newton)
1) Kimika Teorikoko Laborategia 2012.eko irailaren 12 Laburpena 1 Uhin-Partikula Dualtasuna 2 Trantsizio Atomikoak eta Espektroskopia Hidrogeno Atomoaren Espektroa Bohr-en Eredua 3 Argia: Partikula (Newton)
9. Gaia: Espektroskopiaren Oinarriak eta Espektro Atomiko
 9. Gaia: Espektroskopiaren Oinarriak eta Espektro Atomikoak 1) Kimika Teorikoko Laborategia 2012.eko irailaren 21 Laburpena 1 Espektroskopiaren Oinarriak 2 Hidrogeno Atomoa Espektroskopia Esperimentua
9. Gaia: Espektroskopiaren Oinarriak eta Espektro Atomikoak 1) Kimika Teorikoko Laborategia 2012.eko irailaren 21 Laburpena 1 Espektroskopiaren Oinarriak 2 Hidrogeno Atomoa Espektroskopia Esperimentua
Banaketa normala eta limitearen teorema zentrala
 eta limitearen teorema zentrala Josemari Sarasola Estatistika enpresara aplikatua Josemari Sarasola Banaketa normala eta limitearen teorema zentrala 1 / 13 Estatistikan gehien erabiltzen den banakuntza
eta limitearen teorema zentrala Josemari Sarasola Estatistika enpresara aplikatua Josemari Sarasola Banaketa normala eta limitearen teorema zentrala 1 / 13 Estatistikan gehien erabiltzen den banakuntza
= 32 eta β : z = 0 planoek osatzen duten angelua.
 1 ARIKETA Kalkulatu α : 4x+ 3y+ 10z = 32 eta β : z = 0 planoek osatzen duten angelua. Aurki ezazu α planoak eta PH-k osatzen duten angelua. A'' A' 27 A''1 Ariketa hau plano-aldaketa baten bidez ebatzi
1 ARIKETA Kalkulatu α : 4x+ 3y+ 10z = 32 eta β : z = 0 planoek osatzen duten angelua. Aurki ezazu α planoak eta PH-k osatzen duten angelua. A'' A' 27 A''1 Ariketa hau plano-aldaketa baten bidez ebatzi
LOTURA KIMIKOA :LOTURA KOBALENTEA
 Lotura kobalenteetan ez-metalen atomoen arteko elektroiak konpartitu egiten dira. Atomo bat beste batengana hurbiltzen denean erakarpen-indar berriak sortzen dira elektroiak eta bere inguruko beste atomo
Lotura kobalenteetan ez-metalen atomoen arteko elektroiak konpartitu egiten dira. Atomo bat beste batengana hurbiltzen denean erakarpen-indar berriak sortzen dira elektroiak eta bere inguruko beste atomo
Batxilergo Zientifiko-Teknikoa MATEMATIKA II GEOMETRIA. Ignazio Zuloaga B.H.I. (Eibar)
 atilego Zientifiko-Teknikoa MTEMTIK II GEOMETRI Ignaio Zloaga.H.I. (Eiba) URKIIDE Geometia EKTOREK ESPZION... EKTOREK ESPZION... V EKTORE-ESPZIO. DEFINIZIOK... E V eta R MULTZOEN RTEKO ERLZIO... ERREFERENTZI
atilego Zientifiko-Teknikoa MTEMTIK II GEOMETRI Ignaio Zloaga.H.I. (Eiba) URKIIDE Geometia EKTOREK ESPZION... EKTOREK ESPZION... V EKTORE-ESPZIO. DEFINIZIOK... E V eta R MULTZOEN RTEKO ERLZIO... ERREFERENTZI
DERIBAZIO-ERREGELAK 1.- ALDAGAI ERREALEKO FUNTZIO ERREALAREN DERIBATUA. ( ) ( )
 DERIBAZIO-ERREGELAK.- ALDAGAI ERREALEKO FUNTZIO ERREALAREN DERIBATUA. Izan bitez D multzo irekian definituriko f funtzio erreala eta puntuan deribagarria dela esaten da baldin f ( f ( D puntua. f zatidurak
DERIBAZIO-ERREGELAK.- ALDAGAI ERREALEKO FUNTZIO ERREALAREN DERIBATUA. Izan bitez D multzo irekian definituriko f funtzio erreala eta puntuan deribagarria dela esaten da baldin f ( f ( D puntua. f zatidurak
C, H, O, N, (S, P, Cl, Br...)
 1. Ikasgaia. KIMIKA RGAIKA SARRERA KIMIKA RGAIKA ZER DA ETA ZERTARAK BALI DU? Kimika rganikoaren definizioa Zer du karbonoak Taula Periodikoko beste elementu kimikoek ez dutena? Zertarako balio du Kimika
1. Ikasgaia. KIMIKA RGAIKA SARRERA KIMIKA RGAIKA ZER DA ETA ZERTARAK BALI DU? Kimika rganikoaren definizioa Zer du karbonoak Taula Periodikoko beste elementu kimikoek ez dutena? Zertarako balio du Kimika
Hirukiak,1. Inskribatutako zirkunferentzia. Zirkunskribatutako zirkunferentzia. Aldekidea. Isoszelea. Marraztu 53mm-ko aldedun hiruki aldekidea
 Hirukiak, Poligonoa: elkar ebakitzen diren zuzenen bidez mugatutako planoaren zatia da. Hirukia: hiru aldeko poligonoa da. Hiruki baten zuzen bakoitza beste biren batuketa baino txiakiago da eta beste
Hirukiak, Poligonoa: elkar ebakitzen diren zuzenen bidez mugatutako planoaren zatia da. Hirukia: hiru aldeko poligonoa da. Hiruki baten zuzen bakoitza beste biren batuketa baino txiakiago da eta beste
Mikel Lizeaga 1 XII/12/06
 0. Sarrera 1. X izpiak eta erradiazioa 2. Nukleoaren osaketa. Isotopoak 3. Nukleoaren egonkortasuna. Naturako oinarrizko interakzioak 4. Masa-defektua eta lotura-energia 5. Erradioaktibitatea 6. Zergatik
0. Sarrera 1. X izpiak eta erradiazioa 2. Nukleoaren osaketa. Isotopoak 3. Nukleoaren egonkortasuna. Naturako oinarrizko interakzioak 4. Masa-defektua eta lotura-energia 5. Erradioaktibitatea 6. Zergatik
MATEMATIKAKO ARIKETAK 2. DBH 3. KOADERNOA IZENA:
 MATEMATIKAKO ARIKETAK 2. DBH 3. KOADERNOA IZENA: Koaderno hau erabiltzeko oharrak: Koaderno hau egin bazaizu ere, liburuan ezer ere idatz ez dezazun izan da, Gogora ezazu, orain zure liburua den hori,
MATEMATIKAKO ARIKETAK 2. DBH 3. KOADERNOA IZENA: Koaderno hau erabiltzeko oharrak: Koaderno hau egin bazaizu ere, liburuan ezer ere idatz ez dezazun izan da, Gogora ezazu, orain zure liburua den hori,
Hidrogeno atomoaren energi mailen banatzea eremu kubiko batean
 Hidrogeno atomoaren energi mailen banatzea eremu kubiko batean Pablo Mínguez Elektrika eta Elektronika Saila Euskal Herriko Unibertsitatea/Zientzi Fakultatea 644 P.K., 48080 BILBAO Laburpena: Atomo baten
Hidrogeno atomoaren energi mailen banatzea eremu kubiko batean Pablo Mínguez Elektrika eta Elektronika Saila Euskal Herriko Unibertsitatea/Zientzi Fakultatea 644 P.K., 48080 BILBAO Laburpena: Atomo baten
Trigonometria ANGELU BATEN ARRAZOI TRIGONOMETRIKOAK ANGELU BATEN ARRAZOI TRIGONOMETRIKOEN ARTEKO ERLAZIOAK
 Trigonometria ANGELU BATEN ARRAZOI TRIGONOMETRIKOAK SINUA KOSINUA TANGENTEA ANGELU BATEN ARRAZOI TRIGONOMETRIKOEN ARTEKO ERLAZIOAK sin α + cos α = sin α cos α = tg α 0º, º ETA 60º-KO ANGELUEN ARRAZOI TRIGONOMETRIKOAK
Trigonometria ANGELU BATEN ARRAZOI TRIGONOMETRIKOAK SINUA KOSINUA TANGENTEA ANGELU BATEN ARRAZOI TRIGONOMETRIKOEN ARTEKO ERLAZIOAK sin α + cos α = sin α cos α = tg α 0º, º ETA 60º-KO ANGELUEN ARRAZOI TRIGONOMETRIKOAK
EREDU ATOMIKOAK.- ZENBAKI KUANTIKOAK.- KONFIGURAZIO ELEKTRONIKOA EREDU ATOMIKOAK
 EREDU ATOMIKOAK Historian zehar, atomoari buruzko eredu desberdinak sortu dira. Teknologia hobetzen duen neurrian datu gehiago lortzen ziren atomoaren izaera ezagutzeko, Beraz, beharrezkoa da aztertzea,
EREDU ATOMIKOAK Historian zehar, atomoari buruzko eredu desberdinak sortu dira. Teknologia hobetzen duen neurrian datu gehiago lortzen ziren atomoaren izaera ezagutzeko, Beraz, beharrezkoa da aztertzea,
MARRAZKETA TEKNIKOA. Batxilergoa 1. Rafael Ciriza Roberto Galarraga Mª Angeles García José Antonio Oriozabala. erein
 MRRZKET TEKNIKO atxilegoa 1 Rafael Ciiza Robeto Galaaga Mª ngeles Gacía José ntonio Oiozabala eein Eusko Jaulaitzako Hezkuntza, Unibetsitate eta Ikeketa sailak onetsia (2003-09-25) zalaen diseinua: Itui
MRRZKET TEKNIKO atxilegoa 1 Rafael Ciiza Robeto Galaaga Mª ngeles Gacía José ntonio Oiozabala eein Eusko Jaulaitzako Hezkuntza, Unibetsitate eta Ikeketa sailak onetsia (2003-09-25) zalaen diseinua: Itui
ARIKETAK (1) : KONPOSATU ORGANIKOEN EGITURA KIMIKOA [1 3. IKASGAIAK]
![ARIKETAK (1) : KONPOSATU ORGANIKOEN EGITURA KIMIKOA [1 3. IKASGAIAK] ARIKETAK (1) : KONPOSATU ORGANIKOEN EGITURA KIMIKOA [1 3. IKASGAIAK]](/thumbs/71/66032020.jpg) 1. Partzialeko ariketak 1 ARIKETAK (1) : KNPSATU RGANIKEN EGITURA KIMIKA [1 3. IKASGAIAK] 1.- ndorengo konposatuak kontutan hartuta, adierazi: Markatutako atomoen hibridazioa. Zein lotura diren kobalenteak,
1. Partzialeko ariketak 1 ARIKETAK (1) : KNPSATU RGANIKEN EGITURA KIMIKA [1 3. IKASGAIAK] 1.- ndorengo konposatuak kontutan hartuta, adierazi: Markatutako atomoen hibridazioa. Zein lotura diren kobalenteak,
Solido zurruna 2: dinamika eta estatika
 Solido zurruna 2: dinamika eta estatika Gaien Aurkibidea 1 Solido zurrunaren dinamikaren ekuazioak 1 1.1 Masa-zentroarekiko ekuazioak.................... 3 2 Solido zurrunaren biraketaren dinamika 4 2.1
Solido zurruna 2: dinamika eta estatika Gaien Aurkibidea 1 Solido zurrunaren dinamikaren ekuazioak 1 1.1 Masa-zentroarekiko ekuazioak.................... 3 2 Solido zurrunaren biraketaren dinamika 4 2.1
UNIBERTSITATERA SARTZEKO HAUTAPROBAK ATOMOAREN EGITURA ETA SISTEMA PERIODIKOA. LOTURA KIMIKOA
 UNIBERTSITATERA SARTZEKO HAUTAPROBAK ATOMOAREN EGITURA ETA SISTEMA PERIODIKOA. LOTURA KIMIKOA 1. (98 Ekaina) Demagun Cl - eta K + ioiak. a) Beraien konfigurazio elektronikoak idatz itzazu, eta elektroi
UNIBERTSITATERA SARTZEKO HAUTAPROBAK ATOMOAREN EGITURA ETA SISTEMA PERIODIKOA. LOTURA KIMIKOA 1. (98 Ekaina) Demagun Cl - eta K + ioiak. a) Beraien konfigurazio elektronikoak idatz itzazu, eta elektroi
(1)σ (2)σ (3)σ (a)σ n
 5 Gaia 5 Determinanteak 1 51 Talde Simetrikoa Gogoratu, X = {1,, n} bada, X-tik X-rako aplikazio bijektiboen multzoa taldea dela konposizioarekiko Talde hau, n mailako talde simetrikoa deitzen da eta S
5 Gaia 5 Determinanteak 1 51 Talde Simetrikoa Gogoratu, X = {1,, n} bada, X-tik X-rako aplikazio bijektiboen multzoa taldea dela konposizioarekiko Talde hau, n mailako talde simetrikoa deitzen da eta S
PROGRAMA LABURRA (gutxiengoa)
 PROGRAMA LABURRA gutiengoa Batilergo Zientiiko-Teknikoa MATEMATIKA I Ignacio Zuloaga BHI Eibar IGNACIO ZULOAGA B.I. EIBAR Gutiengo programa Zientiiko-Teknikoa. maila Ekuaio esponentialak Ariketa ebatiak:
PROGRAMA LABURRA gutiengoa Batilergo Zientiiko-Teknikoa MATEMATIKA I Ignacio Zuloaga BHI Eibar IGNACIO ZULOAGA B.I. EIBAR Gutiengo programa Zientiiko-Teknikoa. maila Ekuaio esponentialak Ariketa ebatiak:
1. jarduera. Zer eragin du erresistentzia batek zirkuitu batean?
 1. jarduera Zer eragin du erresistentzia batek zirkuitu batean? 1. Hastapeneko intentsitatearen neurketa Egin dezagun muntaia bat, generadore bat, anperemetro bat eta lanpa bat seriean lotuz. 2. Erresistentzia
1. jarduera Zer eragin du erresistentzia batek zirkuitu batean? 1. Hastapeneko intentsitatearen neurketa Egin dezagun muntaia bat, generadore bat, anperemetro bat eta lanpa bat seriean lotuz. 2. Erresistentzia
1 Aljebra trukakorraren oinarriak
 1 Aljebra trukakorraren oinarriak 1.1. Eraztunak eta gorputzak Geometria aljebraikoa ikasten hasi aurretik, hainbat egitura aljebraiko ezagutu behar ditu irakurleak: espazio bektorialak, taldeak, gorputzak,
1 Aljebra trukakorraren oinarriak 1.1. Eraztunak eta gorputzak Geometria aljebraikoa ikasten hasi aurretik, hainbat egitura aljebraiko ezagutu behar ditu irakurleak: espazio bektorialak, taldeak, gorputzak,
1. Higidura periodikoak. Higidura oszilakorra. Higidura bibrakorra.
 1. Higidura periodikoak. Higidura oszilakorra. Higidura bibrakorra. 2. Higidura harmoniko sinplearen ekuazioa. Grafikoak. 3. Abiadura eta azelerazioa hhs-an. Grafikoak. 4. Malguki baten oszilazioa. Osziladore
1. Higidura periodikoak. Higidura oszilakorra. Higidura bibrakorra. 2. Higidura harmoniko sinplearen ekuazioa. Grafikoak. 3. Abiadura eta azelerazioa hhs-an. Grafikoak. 4. Malguki baten oszilazioa. Osziladore
ELASTIKOTASUNAREN TEORIA ETA MATERIALEN ERRESISTENTZIA. Ruben Ansola Loyola
 ELSTIKOTSUNREN TEORI ET MTERILEN ERRESISTENTZI Ruben nsola Loyola Udako Euskal Unibertsitatea Bilbo, 005 HEZKUNTZ, UNIBERTSITTE ET IKERKET SIL DERTMENTO DE EDUCCIÓN UNIVERSIDDES E INVESTIGCIÓN «Liburu
ELSTIKOTSUNREN TEORI ET MTERILEN ERRESISTENTZI Ruben nsola Loyola Udako Euskal Unibertsitatea Bilbo, 005 HEZKUNTZ, UNIBERTSITTE ET IKERKET SIL DERTMENTO DE EDUCCIÓN UNIVERSIDDES E INVESTIGCIÓN «Liburu
MATEMATIKAKO ARIKETAK 2. DBH 3. KOADERNOA IZENA:
 MATEMATIKAKO ARIKETAK. DBH 3. KOADERNOA IZENA: Koaderno hau erabiltzeko oharrak: Koaderno hau egin bazaizu ere, liburuan ezer ere idatz ez dezazun izan da, Gogora ezazu, orain zure liburua den hori, datorren
MATEMATIKAKO ARIKETAK. DBH 3. KOADERNOA IZENA: Koaderno hau erabiltzeko oharrak: Koaderno hau egin bazaizu ere, liburuan ezer ere idatz ez dezazun izan da, Gogora ezazu, orain zure liburua den hori, datorren
Aldehido eta Zetonak(II). Enolatoak eta Karbonilodun α,β-asegabeak
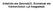 Aldehido eta Zetonak(II). Enolatoak eta Karbonilodun α,β-asegabeak Konposatu Karbonilikoen α Hidrogenoen Azidotasuna: Enolatoak Karboniloarekiko α hidrogenoak ohi baino azidoagoak dira Sortzen den anioia
Aldehido eta Zetonak(II). Enolatoak eta Karbonilodun α,β-asegabeak Konposatu Karbonilikoen α Hidrogenoen Azidotasuna: Enolatoak Karboniloarekiko α hidrogenoak ohi baino azidoagoak dira Sortzen den anioia
1.1 Sarrera: telekomunikazio-sistemak
 1 TELEKOMUNIKAZIOAK 1.1 Sarrera: telekomunikazio-sistemak Telekomunikazio komertzialetan bi sistema nagusi bereiz ditzakegu: irratia eta telebista. Telekomunikazio-sistema horiek, oraingoz, noranzko bakarrekoak
1 TELEKOMUNIKAZIOAK 1.1 Sarrera: telekomunikazio-sistemak Telekomunikazio komertzialetan bi sistema nagusi bereiz ditzakegu: irratia eta telebista. Telekomunikazio-sistema horiek, oraingoz, noranzko bakarrekoak
Makina elektrikoetan sortzen diren energi aldaketak eremu magnetikoaren barnean egiten dira: M A K I N A. Sorgailua. Motorea.
 Magnetismoa M1. MGNETISMO M1.1. Unitate magnetikoak Makina elektrikoetan sortzen diren energi aldaketak eremu magnetikoaren barnean egiten dira: M K I N Energia Mekanikoa Sorgailua Energia Elektrikoa Energia
Magnetismoa M1. MGNETISMO M1.1. Unitate magnetikoak Makina elektrikoetan sortzen diren energi aldaketak eremu magnetikoaren barnean egiten dira: M K I N Energia Mekanikoa Sorgailua Energia Elektrikoa Energia
ERREAKZIOAK. Adizio elektrozaleak Erredukzio erreakzioak Karbenoen adizioa Adizio oxidatzaileak Alkenoen hausketa oxidatzailea
 ERREAKZIAK Adizio elektrozaleak Erredukzio erreakzioak Karbenoen adizioa Adizio oxidatzaileak Alkenoen hausketa oxidatzailea ADIZI ELEKTRZALEK ERREAKZIAK idrogeno halurozko adizioak Alkenoen hidratazioa
ERREAKZIAK Adizio elektrozaleak Erredukzio erreakzioak Karbenoen adizioa Adizio oxidatzaileak Alkenoen hausketa oxidatzailea ADIZI ELEKTRZALEK ERREAKZIAK idrogeno halurozko adizioak Alkenoen hidratazioa
BIZIDUNEN OSAERA ETA EGITURA
 BIZIDUNEN OSAERA ETA EGITURA 1 1.1. EREDU ATOMIKO KLASIKOAK 1.2. SISTEMA PERIODIKOA 1.3. LOTURA KIMIKOA 1.3.1. LOTURA IONIKOA 1.3.2. LOTURA KOBALENTEA 1.4. LOTUREN POLARITATEA 1.5. MOLEKULEN ARTEKO INDARRAK
BIZIDUNEN OSAERA ETA EGITURA 1 1.1. EREDU ATOMIKO KLASIKOAK 1.2. SISTEMA PERIODIKOA 1.3. LOTURA KIMIKOA 1.3.1. LOTURA IONIKOA 1.3.2. LOTURA KOBALENTEA 1.4. LOTUREN POLARITATEA 1.5. MOLEKULEN ARTEKO INDARRAK
Teknika Interbaloa λ E (Kcal) Eragina ME (MS) < 10nm > 800 Ionizazioa. UM (UV) Ikuskorra. 1 Ikasgaia. METODO ESPEKTROSKOPIKOAK
 1 Ikasgaia. TD SPKTRSKPIKAK 1.1. ATRIA-NRGIA INTRAKZIA SARRRA spektro elektromagetikoa Tratsizio elektroikoak molekula orgaikota SPKTRU ULTRARA (U..) TA IKUSKRRA Talde kromoforoak Sistema kojokatuak SPKTRSKPIA
1 Ikasgaia. TD SPKTRSKPIKAK 1.1. ATRIA-NRGIA INTRAKZIA SARRRA spektro elektromagetikoa Tratsizio elektroikoak molekula orgaikota SPKTRU ULTRARA (U..) TA IKUSKRRA Talde kromoforoak Sistema kojokatuak SPKTRSKPIA
Emaitzak: a) 0,148 mol; 6,35 atm; b) 0,35; 0,32; 0,32; 2,2 atm; 2,03 atm; 2.03 atm c) 1,86; 0,043
 KIMIKA OREKA KIMIKOA UZTAILA 2017 AP1 Emaitzak: a) 0,618; b) 0,029; 1,2 EKAINA 2017 AP1 Emaitzak:a) 0,165; 0,165; 1,17 mol b) 50 c) 8,89 atm UZTAILA 2016 BP1 Emaitzak: a) 0,148 mol; 6,35 atm; b) 0,35;
KIMIKA OREKA KIMIKOA UZTAILA 2017 AP1 Emaitzak: a) 0,618; b) 0,029; 1,2 EKAINA 2017 AP1 Emaitzak:a) 0,165; 0,165; 1,17 mol b) 50 c) 8,89 atm UZTAILA 2016 BP1 Emaitzak: a) 0,148 mol; 6,35 atm; b) 0,35;
Bentzeno eta konposatu aromatikoen ordezkapen elektrozalea
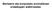 Bentzeno eta konposatu aromatikoen ordezkapen elektrozalea Ordezkapen Elektrozale Aromatikoa Areno (Ar-H) hidrokarburu aromatikoen izen orokorra da Aril taldea (Ar) arenoak hidrogenoa galdu ondoren sortzen
Bentzeno eta konposatu aromatikoen ordezkapen elektrozalea Ordezkapen Elektrozale Aromatikoa Areno (Ar-H) hidrokarburu aromatikoen izen orokorra da Aril taldea (Ar) arenoak hidrogenoa galdu ondoren sortzen
5. Ikasgaia. ALKOHOLAK
 5. Ikasgaia. ALKLAK EGITUA ETA EZAUGAIAK Egitura, adibide adierazgarriak eta propietate fisikoak Propietate espektroskopikoak ALKLEN LBIDE INDUSTIALA ALKLEN SINTESIA Alkenoen hidratazioa (oximerkuriazioa/desmerkuriazioa)
5. Ikasgaia. ALKLAK EGITUA ETA EZAUGAIAK Egitura, adibide adierazgarriak eta propietate fisikoak Propietate espektroskopikoak ALKLEN LBIDE INDUSTIALA ALKLEN SINTESIA Alkenoen hidratazioa (oximerkuriazioa/desmerkuriazioa)
ESTATISTIKA ENPRESARA APLIKATUA (Bigarren zatia: praktika). Irakaslea: Josemari Sarasola Data: 2016ko maiatzaren 12a - Iraupena: Ordu t erdi
 ESTATISTIKA ENPRESARA APLIKATUA (Bigarren zatia: praktika). Irakaslea: Josemari Sarasola Data: 2016ko maiatzaren 12a - Iraupena: Ordu t erdi I. ebazkizuna (2.25 puntu) Poisson, esponentziala, LTZ Zentral
ESTATISTIKA ENPRESARA APLIKATUA (Bigarren zatia: praktika). Irakaslea: Josemari Sarasola Data: 2016ko maiatzaren 12a - Iraupena: Ordu t erdi I. ebazkizuna (2.25 puntu) Poisson, esponentziala, LTZ Zentral
SELEKTIBITATEKO ARIKETAK: EREMU ELEKTRIKOA
 SELEKTIBITATEKO ARIKETAK: EREMU ELEKTRIKOA 95i 10 cm-ko aldea duen karratu baten lau erpinetako hirutan, 5 μc-eko karga bat dago. Kalkula itzazu: a) Eremuaren intentsitatea laugarren erpinean. 8,63.10
SELEKTIBITATEKO ARIKETAK: EREMU ELEKTRIKOA 95i 10 cm-ko aldea duen karratu baten lau erpinetako hirutan, 5 μc-eko karga bat dago. Kalkula itzazu: a) Eremuaren intentsitatea laugarren erpinean. 8,63.10
2. ERDIEROALEEN EZAUGARRIAK
 2. ERDIEROALEEN EZAUGARRIAK Gaur egun, dispositibo elektroniko gehienak erdieroale izeneko materialez fabrikatzen dira eta horien ezaugarri elektrikoak dispositiboen funtzionamenduaren oinarriak dira.
2. ERDIEROALEEN EZAUGARRIAK Gaur egun, dispositibo elektroniko gehienak erdieroale izeneko materialez fabrikatzen dira eta horien ezaugarri elektrikoak dispositiboen funtzionamenduaren oinarriak dira.
Proba parametrikoak. Josemari Sarasola. Gizapedia. Josemari Sarasola Proba parametrikoak 1 / 20
 Josemari Sarasola Gizapedia Josemari Sarasola Proba parametrikoak 1 / 20 Zer den proba parametrikoa Proba parametrikoak hipotesi parametrikoak (hau da parametro batek hartzen duen balioari buruzkoak) frogatzen
Josemari Sarasola Gizapedia Josemari Sarasola Proba parametrikoak 1 / 20 Zer den proba parametrikoa Proba parametrikoak hipotesi parametrikoak (hau da parametro batek hartzen duen balioari buruzkoak) frogatzen
Antzekotasuna ANTZEKOTASUNA ANTZEKOTASUN- ARRAZOIA TALESEN TEOREMA TRIANGELUEN ANTZEKOTASUN-IRIZPIDEAK BIGARREN IRIZPIDEA. a b c
 ntzekotasuna NTZEKOTSUN IRUI NTZEKOK NTZEKOTSUN- RRZOI NTZEKO IRUIK EGITE TLESEN TEOREM TRINGELUEN NTZEKOTSUN-IRIZPIEK LEHEN IRIZPIE $ = $' ; $ = $' IGRREN IRIZPIE a b c = = a' b' c' HIRUGRREN IRIZPIE
ntzekotasuna NTZEKOTSUN IRUI NTZEKOK NTZEKOTSUN- RRZOI NTZEKO IRUIK EGITE TLESEN TEOREM TRINGELUEN NTZEKOTSUN-IRIZPIEK LEHEN IRIZPIE $ = $' ; $ = $' IGRREN IRIZPIE a b c = = a' b' c' HIRUGRREN IRIZPIE
Magnetismoa. Ferromagnetikoak... 7 Paramagnetikoak... 7 Diamagnetikoak Elektroimana... 8 Unitate magnetikoak... 9
 Magnetismoa manak eta imanen teoriak... 2 manaren definizioa:... 2 manen arteko interakzioak (elkarrekintzak)... 4 manen teoria molekularra... 4 man artifizialak... 6 Material ferromagnetikoak, paramagnetikoak
Magnetismoa manak eta imanen teoriak... 2 manaren definizioa:... 2 manen arteko interakzioak (elkarrekintzak)... 4 manen teoria molekularra... 4 man artifizialak... 6 Material ferromagnetikoak, paramagnetikoak
Konposatu Organikoak
 6. Ikasgaia. HIDRKARBURE MEKLATURA ETA FRMULAZIA ERRADIKALAK ETA FUTZI-TALDEAK Konposatu organikoen sailkapena Kate karbonoduna eta funtzio-taldeak Segida homologoak I.U.P.A.C. MEKLATURA-SISTEMA Izen arruntak,
6. Ikasgaia. HIDRKARBURE MEKLATURA ETA FRMULAZIA ERRADIKALAK ETA FUTZI-TALDEAK Konposatu organikoen sailkapena Kate karbonoduna eta funtzio-taldeak Segida homologoak I.U.P.A.C. MEKLATURA-SISTEMA Izen arruntak,
Zirkunferentzia eta zirkulua
 10 Zirkunferentzia eta zirkulua Helburuak Hamabostaldi honetan, hau ikasiko duzu: Zirkunferentzian eta zirkuluan agertzen diren elementuak identifikatzen. Puntu, zuzen eta zirkunferentzien posizio erlatiboak
10 Zirkunferentzia eta zirkulua Helburuak Hamabostaldi honetan, hau ikasiko duzu: Zirkunferentzian eta zirkuluan agertzen diren elementuak identifikatzen. Puntu, zuzen eta zirkunferentzien posizio erlatiboak
0.Gaia: Fisikarako sarrera. ARIKETAK
 1. Zein da A gorputzaren gainean egin behar dugun indarraren balioa pausagunean dagoen B-gorputza eskuinalderantz 2 m desplazatzeko 4 s-tan. Kalkula itzazu 1 eta 2 soken tentsioak. (Iturria: IES Nicolas
1. Zein da A gorputzaren gainean egin behar dugun indarraren balioa pausagunean dagoen B-gorputza eskuinalderantz 2 m desplazatzeko 4 s-tan. Kalkula itzazu 1 eta 2 soken tentsioak. (Iturria: IES Nicolas
Amina primarioak izendatzerakoan alkonaren O atzizkia kendu eta AMINA eransten da" Izenda daitezke baita ere alkil amina bezela"
 Aminak t Nomenklatura Amina primarioak izendatzerakoan alkonaren O atzizkia kendu eta AMINA eransten da Izenda daitezke baita ere alkil amina bezela Amina sekundario eta tertziarioetan erradikal organikoari
Aminak t Nomenklatura Amina primarioak izendatzerakoan alkonaren O atzizkia kendu eta AMINA eransten da Izenda daitezke baita ere alkil amina bezela Amina sekundario eta tertziarioetan erradikal organikoari
Elementu baten ezaugarriak mantentzen dituen partikularik txikiena da atomoa.
 Atomoa 1 1.1. MATERIAREN EGITURA Elektrizitatea eta elektronika ulertzeko gorputzen egitura ezagutu behar da; hau da, gorputz bakun guztiak hainbat partikula txikik osatzen dituztela kontuan hartu behar
Atomoa 1 1.1. MATERIAREN EGITURA Elektrizitatea eta elektronika ulertzeko gorputzen egitura ezagutu behar da; hau da, gorputz bakun guztiak hainbat partikula txikik osatzen dituztela kontuan hartu behar
15 Ikasgaia. ALKANOAK ETA ZIKLOALKANOAK
 15 kasgaia. ALKANAK ETA ZKLALKANAK 15.1. ALKANAK: EGTUA ALKANEN EZAUGA FSKAK Egitura eta nomenklatura Propietate fisikoak ALKANEN LBDEAK Lorbide industrialak Laborategi-sintesiak ALKANEN EEAKZAK rdezkapen
15 kasgaia. ALKANAK ETA ZKLALKANAK 15.1. ALKANAK: EGTUA ALKANEN EZAUGA FSKAK Egitura eta nomenklatura Propietate fisikoak ALKANEN LBDEAK Lorbide industrialak Laborategi-sintesiak ALKANEN EEAKZAK rdezkapen
EREMU GRABITATORIOA ETA UNIBERTSOKO GRABITAZIOA
 AIXERROTA BHI EREMU GRABITATORIOA ETA UNIBERTSOKO GRABITAZIOA 2012 uztaila P1. Urtebete behar du Lurrak Eguzkiaren inguruko bira oso bat emateko, eta 149 milioi km ditu orbita horren batez besteko erradioak.
AIXERROTA BHI EREMU GRABITATORIOA ETA UNIBERTSOKO GRABITAZIOA 2012 uztaila P1. Urtebete behar du Lurrak Eguzkiaren inguruko bira oso bat emateko, eta 149 milioi km ditu orbita horren batez besteko erradioak.
ESTATISTIKA ENPRESARA APLIKATUA (Praktika: Bigarren zatia) Irakaslea: JOSEMARI SARASOLA Data: 2013ko maiatzaren 31a. Iraupena: 90 minutu
 ESTATISTIKA ENPRESARA APLIKATUA (Praktika: Bigarren zatia) Irakaslea: JOSEMARI SARASOLA Data: 2013ko maiatzaren 31a. Iraupena: 90 minutu I. ebazkizuna Ekoizpen-prozesu batean pieza bakoitza akastuna edo
ESTATISTIKA ENPRESARA APLIKATUA (Praktika: Bigarren zatia) Irakaslea: JOSEMARI SARASOLA Data: 2013ko maiatzaren 31a. Iraupena: 90 minutu I. ebazkizuna Ekoizpen-prozesu batean pieza bakoitza akastuna edo
1. Oinarrizko kontzeptuak
 1. Oinarrizko kontzeptuak Sarrera Ingeniaritza Termikoa deritzen ikasketetan hasi berri den edozein ikaslerentzat, funtsezkoa suertatzen da lehenik eta behin, seguru aski sarritan entzun edota erabili
1. Oinarrizko kontzeptuak Sarrera Ingeniaritza Termikoa deritzen ikasketetan hasi berri den edozein ikaslerentzat, funtsezkoa suertatzen da lehenik eta behin, seguru aski sarritan entzun edota erabili
DBH3 MATEMATIKA ikasturtea Errepaso. Soluzioak 1. Aixerrota BHI MATEMATIKA SAILA
 DBH MATEMATIKA 009-010 ikasturtea Errepaso. Soluzioak 1 ALJEBRA EKUAZIOAK ETA EKUAZIO SISTEMAK. EBAZPENAK 1. Ebazpena: ( ) ( x + 1) ( )( ) x x 1 x+ 1 x 1 + 6 x + x+ 1 x x x 1+ 6 6x 6x x x 1 x + 1 6x x
DBH MATEMATIKA 009-010 ikasturtea Errepaso. Soluzioak 1 ALJEBRA EKUAZIOAK ETA EKUAZIO SISTEMAK. EBAZPENAK 1. Ebazpena: ( ) ( x + 1) ( )( ) x x 1 x+ 1 x 1 + 6 x + x+ 1 x x x 1+ 6 6x 6x x x 1 x + 1 6x x
I. ikasgaia: Probabilitateen kalkulua
 I. ikasgaia: Probabilitateen kalkulua 1 Eranskina: Konbinatoria 2 Probabilitate kontzeptua 2.1 Laplaceren erregela 2.2 Maiztasun-ikuspuntua 2.3 Ikuspuntu subjektiboa 3 Gertakizunen aljebra 3.1 Aurkako
I. ikasgaia: Probabilitateen kalkulua 1 Eranskina: Konbinatoria 2 Probabilitate kontzeptua 2.1 Laplaceren erregela 2.2 Maiztasun-ikuspuntua 2.3 Ikuspuntu subjektiboa 3 Gertakizunen aljebra 3.1 Aurkako
1 GEOMETRIA DESKRIBATZAILEA...
 Aurkibidea 1 GEOMETRIA DESKRIBATZAILEA... 1 1.1 Proiekzioa. Proiekzio motak... 3 1.2 Sistema diedrikoaren oinarriak... 5 1.3 Marrazketarako hitzarmenak. Notazioak... 10 1.4 Puntuaren, zuzenaren eta planoaren
Aurkibidea 1 GEOMETRIA DESKRIBATZAILEA... 1 1.1 Proiekzioa. Proiekzio motak... 3 1.2 Sistema diedrikoaren oinarriak... 5 1.3 Marrazketarako hitzarmenak. Notazioak... 10 1.4 Puntuaren, zuzenaren eta planoaren
LANBIDE EKIMENA. Proiektuaren bultzatzaileak. Laguntzaileak. Hizkuntz koordinazioa
 Analisia eta Kontrola Materialak eta entsegu fisikoak LANBIDE EKIMENA LANBIDE EKIMENA LANBIDE EKIMENA Proiektuaren bultzatzaileak Laguntzaileak Hizkuntz koordinazioa Egilea(k): HOSTEINS UNZUETA, Ana Zuzenketak:
Analisia eta Kontrola Materialak eta entsegu fisikoak LANBIDE EKIMENA LANBIDE EKIMENA LANBIDE EKIMENA Proiektuaren bultzatzaileak Laguntzaileak Hizkuntz koordinazioa Egilea(k): HOSTEINS UNZUETA, Ana Zuzenketak:
Energia-metaketa: erredox orekatik baterietara
 Energia-metaketa: erredox orekatik baterietara Paula Serras Verónica Palomares ISBN: 978-84-9082-038-4 EUSKARAREN ARLOKO ERREKTOREORDETZAREN SARE ARGITALPENA Liburu honek UPV/EHUko Euskararen Arloko Errektoreordetzaren
Energia-metaketa: erredox orekatik baterietara Paula Serras Verónica Palomares ISBN: 978-84-9082-038-4 EUSKARAREN ARLOKO ERREKTOREORDETZAREN SARE ARGITALPENA Liburu honek UPV/EHUko Euskararen Arloko Errektoreordetzaren
Ekuazioak eta sistemak
 4 Ekuazioak eta sistemak Helburuak Hamabostaldi honetan hauxe ikasiko duzu: Bigarren mailako ekuazio osoak eta osatugabeak ebazten. Ekuazio bikarratuak eta bigarren mailako batera murriztu daitezkeen beste
4 Ekuazioak eta sistemak Helburuak Hamabostaldi honetan hauxe ikasiko duzu: Bigarren mailako ekuazio osoak eta osatugabeak ebazten. Ekuazio bikarratuak eta bigarren mailako batera murriztu daitezkeen beste
SELEKTIBITATEKO ARIKETAK: EREMU ELEKTRIKOA
 SELEKTIBITATEKO ARIKETAK: EREMU ELEKTRIKOA 1. (2015/2016) 20 cm-ko tarteak bereizten ditu bi karga puntual q 1 eta q 2. Bi kargek sortzen duten eremu elektrikoa q 1 kargatik 5 cm-ra dagoen A puntuan deuseztatu
SELEKTIBITATEKO ARIKETAK: EREMU ELEKTRIKOA 1. (2015/2016) 20 cm-ko tarteak bereizten ditu bi karga puntual q 1 eta q 2. Bi kargek sortzen duten eremu elektrikoa q 1 kargatik 5 cm-ra dagoen A puntuan deuseztatu
1.- KIMIKA ORGANIKOA SARRERA. 1.- Kimika organikoa Bilakaera historikoa eta definizioa Kimika organikoaren garrantzia
 SAEA 1.- Kimika organikoa. 1.1.- Bilakaera historikoa eta definizioa 1.2.- Kimika organikoaren garrantzia 1.- KIMIKA GANIKA 1.1.- Bilakaera historikoa eta definizioa. Konposatu organikoak antzinatik ezagutzen
SAEA 1.- Kimika organikoa. 1.1.- Bilakaera historikoa eta definizioa 1.2.- Kimika organikoaren garrantzia 1.- KIMIKA GANIKA 1.1.- Bilakaera historikoa eta definizioa. Konposatu organikoak antzinatik ezagutzen
4. GAIA MASAREN IRAUPENAREN LEGEA: MASA BALANTZEAK
 4. GAIA MASAREN IRAUPENAREN LEGEA: MASA BALANTZEAK GAI HAU IKASTEAN GAITASUN HAUEK LORTU BEHARKO DITUZU:. Sistema ireki eta itxien artea bereiztea. 2. Masa balantze sinpleak egitea.. Taula estekiometrikoa
4. GAIA MASAREN IRAUPENAREN LEGEA: MASA BALANTZEAK GAI HAU IKASTEAN GAITASUN HAUEK LORTU BEHARKO DITUZU:. Sistema ireki eta itxien artea bereiztea. 2. Masa balantze sinpleak egitea.. Taula estekiometrikoa
Fisika BATXILERGOA 2. Jenaro Guisasola Ane Leniz Oier Azula
 Fisika BATXILERGOA 2 Jenaro Guisasola Ane Leniz Oier Azula Obra honen edozein erreprodukzio modu, banaketa, komunikazio publiko edo aldaketa egiteko, nahitaezkoa da jabeen baimena, legeak aurrez ikusitako
Fisika BATXILERGOA 2 Jenaro Guisasola Ane Leniz Oier Azula Obra honen edozein erreprodukzio modu, banaketa, komunikazio publiko edo aldaketa egiteko, nahitaezkoa da jabeen baimena, legeak aurrez ikusitako
Agoitz DBHI Unitatea: JOKU ELEKTRIKOA Orria: 1 AGOITZ. Lan Proposamena
 Agoitz DBHI Unitatea: JOKU ELEKTRIKOA Orria: 1 1. AKTIBITATEA Lan Proposamena ARAZOA Zurezko oinarri baten gainean joko elektriko bat eraiki. Modu honetan jokoan asmatzen dugunean eta ukitzen dugunean
Agoitz DBHI Unitatea: JOKU ELEKTRIKOA Orria: 1 1. AKTIBITATEA Lan Proposamena ARAZOA Zurezko oinarri baten gainean joko elektriko bat eraiki. Modu honetan jokoan asmatzen dugunean eta ukitzen dugunean
KANTEN ETIKA. Etika unibertsal baten bila. Gizaki guztientzat balioko zuen etika bat.
 EN ETIKA Etika unibertsal baten bila. Gizaki guztientzat balioko zuen etika bat. Kantek esan zuen bera baino lehenagoko etikak etika materialak zirela 1 etika materialak Etika haiei material esaten zaie,
EN ETIKA Etika unibertsal baten bila. Gizaki guztientzat balioko zuen etika bat. Kantek esan zuen bera baino lehenagoko etikak etika materialak zirela 1 etika materialak Etika haiei material esaten zaie,
ALKENOAK (I) EGITURA ETA SINTESIA
 ALKENOAK (I) EGITURA ETA SINTESIA SARRERA Karbono-karbono lotura bikoitza agertzen duten konposatuak dira alkenoak. Olefina ere deitzen zaiete, izen hori olefiant-ik dator eta olioa ekoizten duen gasa
ALKENOAK (I) EGITURA ETA SINTESIA SARRERA Karbono-karbono lotura bikoitza agertzen duten konposatuak dira alkenoak. Olefina ere deitzen zaiete, izen hori olefiant-ik dator eta olioa ekoizten duen gasa
4.GAIA. ESPAZIO BEKTORIALAK
 4.GAIA. ESPAZIO BEKTORIALAK. Defiizioa. Propietateak 3. Azpiespazio bektorialak 4. Kobiazio liealak 5. Depedetzia eta idepedetzia lieala 6. Oiarria eta dimetsioa 7. Oiarri-aldaketa 8. Azpiespazio bektoriale
4.GAIA. ESPAZIO BEKTORIALAK. Defiizioa. Propietateak 3. Azpiespazio bektorialak 4. Kobiazio liealak 5. Depedetzia eta idepedetzia lieala 6. Oiarria eta dimetsioa 7. Oiarri-aldaketa 8. Azpiespazio bektoriale
OREKA KIMIKOA GAIEN ZERRENDA
 GAIEN ZERRENDA Nola lortzen da oreka kimikoa? Oreka konstantearen formulazioa Kc eta Kp-ren arteko erlazioa Disoziazio-gradua Frakzio molarrak eta presio partzialak Oreka kimikoaren noranzkoa Le Chatelier-en
GAIEN ZERRENDA Nola lortzen da oreka kimikoa? Oreka konstantearen formulazioa Kc eta Kp-ren arteko erlazioa Disoziazio-gradua Frakzio molarrak eta presio partzialak Oreka kimikoaren noranzkoa Le Chatelier-en
Jakintza-arloa: Kimika
 Jakintza-arloa: Kimika Diodo-laser bidezko espektroskopia infragorria espantsio supertsonikoan: bentzenoaren eta C6H5X (X=F, C1, NH2) deribatu monoordezkatuen bibrazioerrotazioko espektroak Egilea: ARAITZ
Jakintza-arloa: Kimika Diodo-laser bidezko espektroskopia infragorria espantsio supertsonikoan: bentzenoaren eta C6H5X (X=F, C1, NH2) deribatu monoordezkatuen bibrazioerrotazioko espektroak Egilea: ARAITZ
Gaiari lotutako EDUKIAK (127/2016 Dekretua, Batxilergoko curriculuma)
 Termodinamika Gaiari lotutako EDUKIAK (127/2016 Dekretua, Batxilergoko curriculuma) Erreakzio kimikoetako transformazio energetikoak. Espontaneotasuna 1. Energia eta erreakzio kimikoa. Prozesu exotermikoak
Termodinamika Gaiari lotutako EDUKIAK (127/2016 Dekretua, Batxilergoko curriculuma) Erreakzio kimikoetako transformazio energetikoak. Espontaneotasuna 1. Energia eta erreakzio kimikoa. Prozesu exotermikoak
EREMU NAGNETIKOA ETA INDUKZIO ELEKTROMAGNETIKOA
 EREMU NAGNETIKOA ETA INDUKZIO ELEKTROMAGNETIKOA Datu orokorrak: Elektroiaren masa: 9,10 10-31 Kg, Protoiaren masa: 1,67 x 10-27 Kg Elektroiaren karga e = - 1,60 x 10-19 C µ ο = 4π 10-7 T m/ampere edo 4π
EREMU NAGNETIKOA ETA INDUKZIO ELEKTROMAGNETIKOA Datu orokorrak: Elektroiaren masa: 9,10 10-31 Kg, Protoiaren masa: 1,67 x 10-27 Kg Elektroiaren karga e = - 1,60 x 10-19 C µ ο = 4π 10-7 T m/ampere edo 4π
Poisson prozesuak eta loturiko banaketak
 Gizapedia Poisson banaketa Poisson banaketak epe batean (minutu batean, ordu batean, egun batean) gertaera puntualen kopuru bat (matxura kopurua, istripu kopurua, igarotzen den ibilgailu kopurua, webgune
Gizapedia Poisson banaketa Poisson banaketak epe batean (minutu batean, ordu batean, egun batean) gertaera puntualen kopuru bat (matxura kopurua, istripu kopurua, igarotzen den ibilgailu kopurua, webgune
Atal honetan, laborategiko zirkuituetan oinarrizkoak diren osagai pasibo nagusiak analizatuko ditugu: erresistentziak, kondentsadoreak eta harilak.
 1. SARRERA Atal honetan, laborategiko zirkuituetan oinarrizkoak diren osagai pasibo nagusiak analizatuko ditugu: erresistentziak, kondentsadoreak eta harilak. Horien artean interesgarrienak diren erresistentziak
1. SARRERA Atal honetan, laborategiko zirkuituetan oinarrizkoak diren osagai pasibo nagusiak analizatuko ditugu: erresistentziak, kondentsadoreak eta harilak. Horien artean interesgarrienak diren erresistentziak
UNITATE DIDAKTIKOA ELEKTRIZITATEA D.B.H JARDUERA. KORRONTE ELEKTRIKOA. Helio atomoa ASKATASUNA BHI 1.- ATOMOAK ETA KORRONTE ELEKTRIKOA
 1. JARDUERA. KORRONTE ELEKTRIKOA. 1 1.- ATOMOAK ETA KORRONTE ELEKTRIKOA Material guztiak atomo deitzen diegun partikula oso ttipiez osatzen dira. Atomoen erdigunea positiboki kargatua egon ohi da eta tinkoa
1. JARDUERA. KORRONTE ELEKTRIKOA. 1 1.- ATOMOAK ETA KORRONTE ELEKTRIKOA Material guztiak atomo deitzen diegun partikula oso ttipiez osatzen dira. Atomoen erdigunea positiboki kargatua egon ohi da eta tinkoa
Zenbait fenolen eutsitako mintz likidoen zeharreko garraioaren azterketa
 Jakintza-arloa: Kimika Zenbait fenolen eutsitako mintz likidoen zeharreko garraioaren azterketa Egilea: GORKA ARANA MOMOITIO Urtea: 1996 Zuzendaria: Unibertsitatea: NESTOR ETXEBARRIA LOIZATE UPV-EHU ISBN:
Jakintza-arloa: Kimika Zenbait fenolen eutsitako mintz likidoen zeharreko garraioaren azterketa Egilea: GORKA ARANA MOMOITIO Urtea: 1996 Zuzendaria: Unibertsitatea: NESTOR ETXEBARRIA LOIZATE UPV-EHU ISBN:
AURKIBIDEA I. KORRONTE ZUZENARI BURUZKO LABURPENA... 7
 AURKIBIDEA Or. I. KORRONTE ZUZENARI BURUZKO LABURPENA... 7 1.1. MAGNITUDEAK... 7 1.1.1. Karga elektrikoa (Q)... 7 1.1.2. Intentsitatea (I)... 7 1.1.3. Tentsioa ()... 8 1.1.4. Erresistentzia elektrikoa
AURKIBIDEA Or. I. KORRONTE ZUZENARI BURUZKO LABURPENA... 7 1.1. MAGNITUDEAK... 7 1.1.1. Karga elektrikoa (Q)... 7 1.1.2. Intentsitatea (I)... 7 1.1.3. Tentsioa ()... 8 1.1.4. Erresistentzia elektrikoa
2011 Kimikako Euskal Olinpiada
 2011 Kimikako Euskal Olinpiada ARAUAK (Arretaz irakurri): Zuzena den erantzunaren inguruan zirkunferentzia bat egin. Ordu bete eta erdiko denbora epean ahalik eta erantzun zuzen gehien eman behar dituzu
2011 Kimikako Euskal Olinpiada ARAUAK (Arretaz irakurri): Zuzena den erantzunaren inguruan zirkunferentzia bat egin. Ordu bete eta erdiko denbora epean ahalik eta erantzun zuzen gehien eman behar dituzu
Solido zurruna 1: biraketa, inertzia-momentua eta momentu angeluarra
 Solido zurruna 1: biraketa, inertzia-momentua eta momentu angeluarra Gaien Aurkibidea 1 Definizioa 1 2 Solido zurrunaren zinematika: translazioa eta biraketa 3 2.1 Translazio hutsa...........................
Solido zurruna 1: biraketa, inertzia-momentua eta momentu angeluarra Gaien Aurkibidea 1 Definizioa 1 2 Solido zurrunaren zinematika: translazioa eta biraketa 3 2.1 Translazio hutsa...........................
Oxidazio-erredukzio erreakzioak
 Oxidazio-erredukzio erreakzioak Lan hau Creative Commons-en Nazioarteko 3.0 lizentziaren mendeko Azterketa-Ez komertzial-partekatu lizentziaren mende dago. Lizentzia horren kopia ikusteko, sartu http://creativecommons.org/licenses/by-ncsa/3.0/es/
Oxidazio-erredukzio erreakzioak Lan hau Creative Commons-en Nazioarteko 3.0 lizentziaren mendeko Azterketa-Ez komertzial-partekatu lizentziaren mende dago. Lizentzia horren kopia ikusteko, sartu http://creativecommons.org/licenses/by-ncsa/3.0/es/
1. MATERIALEN EZAUGARRIAK
 1. MATERIALEN EZAUGARRIAK Materialek dituzten ezaugarri kimiko, fisiko eta mekanikoek oso eragin handia dute edozein soldadura-lanetan. Hori guztia, hainbat prozesu erabiliz, metal desberdinen soldadura
1. MATERIALEN EZAUGARRIAK Materialek dituzten ezaugarri kimiko, fisiko eta mekanikoek oso eragin handia dute edozein soldadura-lanetan. Hori guztia, hainbat prozesu erabiliz, metal desberdinen soldadura
Funtzioak FUNTZIO KONTZEPTUA FUNTZIO BATEN ADIERAZPENAK ENUNTZIATUA TAULA FORMULA GRAFIKOA JARRAITUTASUNA EREMUA ETA IBILTARTEA EBAKIDURA-PUNTUAK
 Funtzioak FUNTZIO KONTZEPTUA FUNTZIO BATEN ADIERAZPENAK ENUNTZIATUA TAULA FORMULA GRAFIKOA JARRAITUTASUNA EREMUA ETA IBILTARTEA EBAKIDURA-PUNTUAK GORAKORTASUNA ETA BEHERAKORTASUNA MAIMOAK ETA MINIMOAK
Funtzioak FUNTZIO KONTZEPTUA FUNTZIO BATEN ADIERAZPENAK ENUNTZIATUA TAULA FORMULA GRAFIKOA JARRAITUTASUNA EREMUA ETA IBILTARTEA EBAKIDURA-PUNTUAK GORAKORTASUNA ETA BEHERAKORTASUNA MAIMOAK ETA MINIMOAK
Aldagai Anitzeko Funtzioak
 Aldagai Anitzeko Funtzioak Bi aldagaiko funtzioak Funtzio hauen balioak bi aldagai independenteen menpekoak dira: 1. Adibidea: x eta y aldeetako laukizuzenaren azalera, S, honela kalkulatzen da: S = x
Aldagai Anitzeko Funtzioak Bi aldagaiko funtzioak Funtzio hauen balioak bi aldagai independenteen menpekoak dira: 1. Adibidea: x eta y aldeetako laukizuzenaren azalera, S, honela kalkulatzen da: S = x
1. Ur-ponpa batek 200 W-eko potentzia badu, kalkulatu zenbat ZP dira [0,27 ZP]
![1. Ur-ponpa batek 200 W-eko potentzia badu, kalkulatu zenbat ZP dira [0,27 ZP] 1. Ur-ponpa batek 200 W-eko potentzia badu, kalkulatu zenbat ZP dira [0,27 ZP]](/thumbs/76/73146936.jpg) Ariketak Liburukoak (78-79 or): 1,2,3,4,7,8,9,10,11 Osagarriak 1. Ur-ponpa batek 200 W-eko potentzia badu, kalkulatu zenbat ZP dira [0,27 ZP] 2. Gorputz bat altxatzeko behar izan den energia 1,3 kwh-koa
Ariketak Liburukoak (78-79 or): 1,2,3,4,7,8,9,10,11 Osagarriak 1. Ur-ponpa batek 200 W-eko potentzia badu, kalkulatu zenbat ZP dira [0,27 ZP] 2. Gorputz bat altxatzeko behar izan den energia 1,3 kwh-koa
GIZA GIZARTE ZIENTZIEI APLIKATUTAKO MATEMATIKA I BINOMIALA ETA NORMALA 1
 BINOMIALA ETA NORMALA 1 PROBABILITATEA Maiztasu erlatiboa: fr i = f i haditze bada, maiztasuak egokortzera joko dira, p zebaki batera hurbilduz. Probabilitatea p zebakia da. Probabilitateak maiztasue idealizazioak
BINOMIALA ETA NORMALA 1 PROBABILITATEA Maiztasu erlatiboa: fr i = f i haditze bada, maiztasuak egokortzera joko dira, p zebaki batera hurbilduz. Probabilitatea p zebakia da. Probabilitateak maiztasue idealizazioak
9. K a p itu lu a. Ekuazio d iferen tzial arrun tak
 9. K a p itu lu a Ekuazio d iferen tzial arrun tak 27 28 9. K A P IT U L U A E K U A Z IO D IF E R E N T Z IA L A R R U N T A K UEP D o n o stia M ate m atik a A p lik atu a S aila 29 Oharra: iku rra rekin
9. K a p itu lu a Ekuazio d iferen tzial arrun tak 27 28 9. K A P IT U L U A E K U A Z IO D IF E R E N T Z IA L A R R U N T A K UEP D o n o stia M ate m atik a A p lik atu a S aila 29 Oharra: iku rra rekin
ARIKETAK (I) : KONPOSATU ORGANIKOEN LOTURAK [1 5. IKASGAIAK]
![ARIKETAK (I) : KONPOSATU ORGANIKOEN LOTURAK [1 5. IKASGAIAK] ARIKETAK (I) : KONPOSATU ORGANIKOEN LOTURAK [1 5. IKASGAIAK]](/thumbs/91/106132187.jpg) Arikk-I (1-5 Ikasgaiak) 1 ARIKETAK (I) : KPSATU RGAIKE LTURAK [1 5. IKASGAIAK] 1.- 3 6 formula molekularreko 8 egitur-formula marraztu. 2.- Azido bentzoiko solidoararen disolbagarritasuna urn honako hau
Arikk-I (1-5 Ikasgaiak) 1 ARIKETAK (I) : KPSATU RGAIKE LTURAK [1 5. IKASGAIAK] 1.- 3 6 formula molekularreko 8 egitur-formula marraztu. 2.- Azido bentzoiko solidoararen disolbagarritasuna urn honako hau
1. MATERIAREN PROPIETATE OROKORRAK
 http://thales.cica.es/rd/recursos/rd98/fisica/01/fisica-01.html 1. MATERIAREN PROPIETATE OROKORRAK 1.1. BOLUMENA Nazioarteko Sisteman bolumen unitatea metro kubikoa da (m 3 ). Hala ere, likido eta gasen
http://thales.cica.es/rd/recursos/rd98/fisica/01/fisica-01.html 1. MATERIAREN PROPIETATE OROKORRAK 1.1. BOLUMENA Nazioarteko Sisteman bolumen unitatea metro kubikoa da (m 3 ). Hala ere, likido eta gasen
2. PROGRAMEN ESPEZIFIKAZIOA
 2. PROGRAMEN ESPEZIFIKAZIOA 2.1. Asertzioak: egoera-multzoak adierazteko formulak. 2.2. Aurre-ondoetako espezifikazio formala. - 1 - 2.1. Asertzioak: egoera-multzoak adierazteko formulak. Programa baten
2. PROGRAMEN ESPEZIFIKAZIOA 2.1. Asertzioak: egoera-multzoak adierazteko formulak. 2.2. Aurre-ondoetako espezifikazio formala. - 1 - 2.1. Asertzioak: egoera-multzoak adierazteko formulak. Programa baten
1-A eta 1-8 ariketen artean bat aukeratu (2.5 puntu)
 UNIBERTSITATERA SARTZEKO HAUTAPROBAK 2004ko EKAINA ELEKTROTEKNIA PRUEBAS DE ACCESO A LA UNIVERSIDAD JUNIO 2004 ELECTROTECNIA 1-A eta 1-8 ariketen artean bat aukeratu (2.5 1-A ARIKETA Zirkuitu elektriko
UNIBERTSITATERA SARTZEKO HAUTAPROBAK 2004ko EKAINA ELEKTROTEKNIA PRUEBAS DE ACCESO A LA UNIVERSIDAD JUNIO 2004 ELECTROTECNIA 1-A eta 1-8 ariketen artean bat aukeratu (2.5 1-A ARIKETA Zirkuitu elektriko
I. KAPITULUA Zenbakia. Aldagaia. Funtzioa
 I. KAPITULUA Zenbakia. Aldagaia. Funtzioa 1. ZENBAKI ERREALAK. ZENBAKI ERREALEN ADIERAZPENA ZENBAKIZKO ARDATZEKO PUNTUEN BIDEZ Matematikaren oinarrizko kontzeptuetariko bat zenbakia da. Zenbakiaren kontzeptua
I. KAPITULUA Zenbakia. Aldagaia. Funtzioa 1. ZENBAKI ERREALAK. ZENBAKI ERREALEN ADIERAZPENA ZENBAKIZKO ARDATZEKO PUNTUEN BIDEZ Matematikaren oinarrizko kontzeptuetariko bat zenbakia da. Zenbakiaren kontzeptua
KONPUTAGAILUEN TEKNOLOGIAKO LABORATEGIA
 eman ta zabal zazu Euskal Herriko Unibertsitatea Informatika Fakultatea Konputagailuen rkitektura eta Teknologia saila KONPUTGILUEN TEKNOLOGIKO LBORTEGI KTL'000-00 Bigarren parteko dokumentazioa: Sistema
eman ta zabal zazu Euskal Herriko Unibertsitatea Informatika Fakultatea Konputagailuen rkitektura eta Teknologia saila KONPUTGILUEN TEKNOLOGIKO LBORTEGI KTL'000-00 Bigarren parteko dokumentazioa: Sistema
Jose Miguel Campillo Robles. Ur-erlojuak
 HIDRODINAMIKA Hidrodinamikako zenbait kontzeptu garrantzitsu Fluidoen garraioa Fluxua 3 Lerroak eta hodiak Jarraitasunaren ekuazioa 3 Momentuaren ekuazioa 4 Bernouilli-ren ekuazioa 4 Dedukzioa 4 Aplikazioak
HIDRODINAMIKA Hidrodinamikako zenbait kontzeptu garrantzitsu Fluidoen garraioa Fluxua 3 Lerroak eta hodiak Jarraitasunaren ekuazioa 3 Momentuaren ekuazioa 4 Bernouilli-ren ekuazioa 4 Dedukzioa 4 Aplikazioak
Elementu honek elektrizitatea sortzen du, hau da, bi punturen artean potentzial-diferentzia mantentzen du.
 Korronte zuzena 1 1.1. ZIRKUITU ELEKTRIKOA Instalazio elektrikoetan, elektroiak sorgailuaren borne batetik irten eta beste bornera joaten dira. Beraz, elektroiek desplazatzeko egiten duten bidea da zirkuitu
Korronte zuzena 1 1.1. ZIRKUITU ELEKTRIKOA Instalazio elektrikoetan, elektroiak sorgailuaren borne batetik irten eta beste bornera joaten dira. Beraz, elektroiek desplazatzeko egiten duten bidea da zirkuitu
DINAMIKA. c Ugutz Garitaonaindia Antsoategi Ingeniaritza Mekanikoa Saila Gasteizko I.I.T. eta T.I.T.U.E. Euskal Herriko Unibertsitatea
 DINAMIKA c Ugutz Gartaonanda Antsoateg Ingenartza Mekankoa Sala Gastezko I.I.T. eta T.I.T.U.E. Euskal Herrko Unbertstatea 2000/2001 kasturtea Índce 1. SARRERA 3 2. INDARRAK 3 3. ERREFERENTZIA SISTEMA DINAMIKAN.
DINAMIKA c Ugutz Gartaonanda Antsoateg Ingenartza Mekankoa Sala Gastezko I.I.T. eta T.I.T.U.E. Euskal Herrko Unbertstatea 2000/2001 kasturtea Índce 1. SARRERA 3 2. INDARRAK 3 3. ERREFERENTZIA SISTEMA DINAMIKAN.
ARIKETAK (7) : ALKENOAK ETA ALKINOAK [ IKASGAIAK]
![ARIKETAK (7) : ALKENOAK ETA ALKINOAK [ IKASGAIAK] ARIKETAK (7) : ALKENOAK ETA ALKINOAK [ IKASGAIAK]](/thumbs/92/110485094.jpg) 2. Partzialeko ariketak 1 ARIKETAK (7) : ALKEAK ETA ALKIAK [22-25. IKASGAIAK] 1.- ndorengo konposatuen IUPAC izenak eman: b ) 3 C 3 C 2 C e) f) g) 2 C 2.- ndorengo erreakzioa kontutan harturik: C3 Marraztu
2. Partzialeko ariketak 1 ARIKETAK (7) : ALKEAK ETA ALKIAK [22-25. IKASGAIAK] 1.- ndorengo konposatuen IUPAC izenak eman: b ) 3 C 3 C 2 C e) f) g) 2 C 2.- ndorengo erreakzioa kontutan harturik: C3 Marraztu
Inekuazioak. Helburuak. 1. Ezezagun bateko lehen orria 74 mailako inekuazioak Definizioak Inekuazio baliokideak Ebazpena Inekuazio-sistemak
 5 Inekuazioak Helburuak Hamabostaldi honetan hauxe ikasiko duzu: Ezezagun bateko lehen eta bigarren mailako inekuazioak ebazten. Ezezagun bateko ekuaziosistemak ebazten. Modu grafikoan bi ezezaguneko lehen
5 Inekuazioak Helburuak Hamabostaldi honetan hauxe ikasiko duzu: Ezezagun bateko lehen eta bigarren mailako inekuazioak ebazten. Ezezagun bateko ekuaziosistemak ebazten. Modu grafikoan bi ezezaguneko lehen
MOTOR ASINKRONOAK TRIFASIKOAK Osaera Funtzionamendua Bornen kaxa: Konexio motak (Izar moduan edo triangelu moduan):...
 Makina Elektrikoak MAKINA ELEKTRIKOAK... 3 Motak:... 3 Henry-Faradayren legea... 3 ALTERNADOREA:... 6 DINAMOA:... 7 Ariketak generadoreak (2010eko selektibitatekoa):... 8 TRANSFORMADOREAK:... 9 Ikurrak...
Makina Elektrikoak MAKINA ELEKTRIKOAK... 3 Motak:... 3 Henry-Faradayren legea... 3 ALTERNADOREA:... 6 DINAMOA:... 7 Ariketak generadoreak (2010eko selektibitatekoa):... 8 TRANSFORMADOREAK:... 9 Ikurrak...
4. Hipotesiak eta kontraste probak.
 1 4. Hipotesiak eta kontraste probak. GAITASUNAK Gai hau bukatzerako ikaslea gai izango da ikerketa baten: - Helburua adierazteko. - Hipotesia adierazteko - Hipotesi nulua adierazteko - Hipotesi nulu estatistikoa
1 4. Hipotesiak eta kontraste probak. GAITASUNAK Gai hau bukatzerako ikaslea gai izango da ikerketa baten: - Helburua adierazteko. - Hipotesia adierazteko - Hipotesi nulua adierazteko - Hipotesi nulu estatistikoa
7. Gaia: Alkenoak 1.- Alkenoen ezaugarriak 2.- Alkenoen erreaktibitatea.
 7. Gaia: Alkenoak 1.- Alkenoen ezaugarriak 1.1.- Funtzio-taldearen ezaugarriak 1.1.1.- Alkenoen egonkortasun erlatiboa. 1.2.- Alkenoen ezaugarri fisikoak. 2.- Alkenoen erreaktibitatea. 2.1.- idrogenazio
7. Gaia: Alkenoak 1.- Alkenoen ezaugarriak 1.1.- Funtzio-taldearen ezaugarriak 1.1.1.- Alkenoen egonkortasun erlatiboa. 1.2.- Alkenoen ezaugarri fisikoak. 2.- Alkenoen erreaktibitatea. 2.1.- idrogenazio
Bilboko Ingeniarien Goi Eskolan ematen den ikasgaiaren apunteak.
 2006-2007 kurtsoa Seinale eta Sistemak I Bilboko Ingeniarien Goi Eskolan ematen den ikasgaiaren apunteak. Joseba Imanol Madariaga Longarai 2000-2006 Apunte hauek kopiatu, banatu eta aldatu ditzakezu ohar
2006-2007 kurtsoa Seinale eta Sistemak I Bilboko Ingeniarien Goi Eskolan ematen den ikasgaiaren apunteak. Joseba Imanol Madariaga Longarai 2000-2006 Apunte hauek kopiatu, banatu eta aldatu ditzakezu ohar
MATEMATIKARAKO SARRERA OCW 2015
 MATEMATIKARAKO SARRERA OCW 2015 Mathieu Jarry iturria: Flickr CC-BY-NC-ND-2.0 https://www.flickr.com/photos/impactmatt/4581758027 Leire Legarreta Solaguren EHU-ko Zientzia eta Teknologia Fakultatea Matematika
MATEMATIKARAKO SARRERA OCW 2015 Mathieu Jarry iturria: Flickr CC-BY-NC-ND-2.0 https://www.flickr.com/photos/impactmatt/4581758027 Leire Legarreta Solaguren EHU-ko Zientzia eta Teknologia Fakultatea Matematika
