# % # & & ( ) +,. /! , ), %, 0 ) 1,2 / % ) (,2 / 3 % ) 7,2 / # % & (
|
|
|
- Αδώνια Δασκαλόπουλος
- 6 χρόνια πριν
- Προβολές:
Transcript
1
2 ! # % #&& () +,. /!,), %,0) 1,/ # % %) (,/ & ( %456 0 ) 7,/ )!
3 SET-1, 8 9 Choose the correct option :, ; <,= If roots of are equal then which of the following is Correct? >: ;,= If then value of will be which of the following? (Integers)? (fractional No) ) (Irrational ) ( (, (non real) : 0(Α 0(#4ΒΧ Χ, (Α 4,= If the perimeter and area of circle are equal then radius of circle will be? >4( units) 4(Pie units) 4(4 units)!4(7 units) : >ΕΕ ΕΕΦ Γ,= Median of,, 4, 5, 6 is? : (Α ΧΧΗ6Ι(,,= Longest chord of circle is? 9(arc) ϑ(diameter) 9(cord),(None of these)
4 Φ: X- )# %,,=!: Co-ordinate of X-axis is? ( x, 0) (0, y ) (0,0) ( x, y ),= The value of 1 > Κ: ) ),= The sum of Probabilities of events will be? Λ > Μ: 09 ϑνο,= The standard form of one variable linear equation is? :,= If then will be? &, 8 Λ Λ Fill up the blank with correct answers : - : Ν 4 Ι#4Β) Ι)::::::::::::) Χ Χ,,=
5 The ratio of areas of two similar triangles are equal to the ratio of the of corresponding sides? >: Ε>ΕΕ ΕΓ::::::::::::,= The median of 1,,, 4, 5 is : sin 50 + cos 40 = cos... : tan(90 θ) =... : (Α % :::::::::::::::::::: Χ? %,/ The tangent of circle touches at..point. Φ: A.p(? Γ<ΕΠ<::::::::::::::::::::,,= Common defference of A.p. are +ve, -ve or!: )::::::::::::::::::::::,,/ The Graph of linear equation is.. Κ: b 4ac:::::::::::::::::::::::,Ι,/ b 4ac is clled Μ: (, Ι,,:::::::::::::::::::::::::::,,/ The equations which has no any solution is called. >: )Γ;Α1Θ#4Β::::::::::::::::::::::::::::::::,,/ The total surface area of hemisphere is >: Ρ Χ, Σ Ι? Τ0( Λ,/ > Find quadratic polynomial which roots are Τ and Λ: a b c 1 1 >>:, ) 1 Χ 0Υ )! a b c,) / > a b c 1 1 Comparing, a b and 1 the linear pair of equations and c! are consistent or inconsistent. >: ς Γ<Β>,/ Ρ Ν / > Product of two consecutive positive integers is 40. Write it in the form of quadratic Equation.
6 > : ; Χ? P(ΦΕΛΦ) / > Find the distance of point P(ΦΕΛΦ) from the origin. >: Ω (Prove that) θ tanθ 1 tan 1 = sec + tan θ >Φ: Φ) 7Η ( Ι0Ξ & ( Γ / > Find HFC of 6 and 54 from Euclids division algorithm. >!: <) 64 cm,ψβ Γ Χ, Ο Γ Α1Θ#4Β / > Two cubes of each volume 64 cm added adjoining edges to form cuboid. Find surface area of cubiod. >Κ: Χ 94PA ) PB(Α % 0Υ, & APO=0 AOB=? In the given figure PA and PB are tangents of the circle and APO=0 θ > >Μ: a ( a, ) ) (, 4) Χ9 Κ,/ > Find the value of a if distance between ( a, ) and (, 4) is 8 units. : α ) β Ρ Χ, ( ) f x = ax + bx + c f ( x) ax bx c = + +?, α + β / > If α and β is Zeroes of f ( x) = ax + bx + c. find α + β : : >ΕΕ!ΕΜΕΕΓ / > Find mean of, 5, 7, 9, 10, 15. >: Ω + 50),/ Prove that + 5 is an irrational number. : Ρ x 7x + = 0 / Find the roots of the quadratic equation x 7x + = 0 : 0A.P. a = 5, d =, a n = 50 n 0( S n /
7 Find and A.P. n and S n if a = 5, d =, a n = 50 : 7 Χ? ( 5, ),( 6, 4) ) ( 7, ) ΡΧ, %1,= Are the points ( 5, ),( 6, 4) and ( 7, ) vertices of isoceles? Φ: 4 Ι Ι)BC, CA) ABς%D, E, F Γ Χ?, ar( DEF) ar( ABC) / Σ D, E, F are mid points of the sides BC, CA and AB respectively of ABC Determine ar( DEF) ar( ABC).!: Ω (prove that) 1 secθ tanθ secθ tanθ = + Κ: tan A = cot( A 18 ) Ι,Υ A?,/ A / If tan A = cot( A 18 ) where A is an acute angle Find the value of A. Μ: ΧΓ) Γς%>Φ:Κ) >!:Μ, Χ, / If mean and median of symmetric distribution is 6.8 and 7.9 then find mode. : 0.6 Νϑ7 / Express 0.6 as rational number in simplest form : 0( ϑ<ς 10,/Σ / Sum of number and its reciprocal is 10 Find the number. >: Χ Χ ΧΧ,Σ / Calculate the mode of the given frequency distribution. ()? C.I
8 (Ζ & No. of students : Β ( Γ, (Solve graphically) :- 5 x y = 1 x + y = 8 : )Υ Γ)0Η6Ι,),) Η6Ι, Η6 % Ι[,) &0 Χ,/Η6 Χ? Ι,ΥΗ6 % Ι[,Κ,Ε Η6 Υ9 / A tree break due to storm and the broken part bends so that the top of the tree touches the ground making an angle of 0 with ground. The distance between the Foot of the tree to the point where the top touches the ground is 8 m. find the height of the tree, : Ω 4 Ι()? Ι)(Χ Χ,,/ In an right triangle, the square of hypotenuse is equal to the sum of the squares of other two sides. Φ: 0Η6, Ρ #4Β / The lengths of minute hand of a clock is 14 cm. Find the area in 5 minutes covered by minute hand.!: AB=1 cm.9) :5 ) Χ/ Draw a line AB=1 cm. and divide it in the ratio :5.
9 8 (ANSWERS) ( cotθ Χ? 16.? ( (7 19. ) 0. #
10 >: Β = α + β = = Β = αβ = ( + 1)( 1) ( ) (1) 1 = = = Ρ Χ, x x x ( α + β) x + αβ ( ) x + x + >>: x y = 8 a1 x b1 y c = 4x 6y = 9 ax b y c 0 Comparing we get 8 = = 4 9 a1 b1 c1 = a b c 0 Ψ),/ + + = >: ς 0 x) x + 1,/ Ε ( 1) 40 x x + = x x + x = 40 + x 40 = 0 > : Χ? ( 0,0) p( 6, 6) ( 6 0) ( 6 0) = + ( D ( x ) x1 ) ( y y1) = = + = 7 = 6 4
11 >: L.H.S = tan θ 1 tanθ 1 = θ θ θ (tanθ 1) (tan 1)(tan + tan 1+ 1 ) { a b = ( a b)( a + ab + b ) = θ + + θ (tan 1 tan ) = sec θ + tanθ = R.H.S L.H.S=R.H.S >Φ: 54)6(6 7Η ( Ι ( Γ 4 6 = )54(4 54 = = )1( 1 >!: 0 Ι = a cm. v = a 64 = a a = 64 = 4 cm. Ε0 Χ,/ 9Η = 4cm + 4cm = 8 cm. Α1Θ#4 = ( lb + bh + lh) cm ( ) ( cm 16cm cm) 80cm 160cm >Κ:,), APO = 0 = + + = + + = = OA APΓ OAP = 90 AOP = 180 ( ) = = 60 AOB = 60 = 10
12 >Μ:, (, ), (, 4) A a B = 84 A) BΧ9 ( a) (4 ) = + 8 ( a) = + { D ( x x ) ( y y ) = ( a) 4 = ( a) = 60 ( a) = a 60 = 60 a ± = a = ( ± 60) : 9Υ α 0( β Ρ Χ, ax + bx + c?,/ b c α + β =, a αβ = a α + β = α + β β ( ) b c =. a a b c b ac = = a a a : b ac a α + β =,5,7,9,10,15 ;Γ ( ) x =
13 = x = 8 48 = = 8 6 >: + 50,/ 5 : + = a b 5 a b = a 5 = b,,? 50),/,Υ ( Γ,/) + 5 0,/ 0() )),,/ Ρ x x + = 7 0 a =, b = 7, c = D b ac = 4 = ( 7) 4 = 49 4 = 5 b ± D x = a ( 7) ± 5 7 ± 5 = = =, =, =, =, : A. P,), a = 5, d =, a n = 50 a = a + ( n 1) d n 50 = 5 + ( n 1) = ( n 1) 45 ( n 1) =
14 45 = ( n 1) n 1 = 15 n = = 16 n = 16 n Sn = { a + ( n 1) d} 16 { 5 + (16 1) } = 8( ) = 8 55 = 440 n = 16, S = 440. : n 4 Ι %1) AB = (5 6) + ( + 4) = + = (6 7) ( 4 ) BC = = + = AB BC = Φ: ABC ΡΧ,,/ 9Υ D) Eς BC ) AC Γ Χ?,/ DE AB DE FA:::::::::::::::::::::: (i) D) F ς BC ) ABΓ Χ?,/ DF AE ::::::::::::::::::::::::(ii) (i) ) (ii) AFDE ) BDEF 0? 9 Ι,/ DF AC EDF = A, DEF = B DEFABC 1 AB ar DEF DB = = = = ar ABC AB AB =1:4 ( ) ( ) 1 1 ( ) ( ) 4
15 !: 1 L. H. S = secθ tanθ 1 secθ + tanθ = secθ tanθ secθ + tanθ secθ + tanθ secθ + tanθ = = sec θ tan θ 1 = secθ + tan θ = R. H. S L. H. S = R. H. S. θ θ ( sec tan = 1) Κ:,), tan A = cot( A 180 )?,/ cot(90 A) = cot( A 18 ) 90 A = A 18 Μ: { tan θ = cot(90 θ ) = A + A 108 = A 108 A = = 6 A = 6,), ;Γ = 6.8 ; Γ 7.9 = Χ, = ;Γ ;Γ = = = 0.1 Χ, 0.1 = :
16 x = 0.6 x = ( i) 10x = ( ii) ( ii) ( i) : >: 9x = 6 6 x = = 9 x = x,/ ϑ<ς = 1 x % Ε 10 x + = 1 10 x + = x x( x ) 1( x ) = 0 x x x + = x x x + = ( x )(x 1) = 0 x = 0 x = ) 1 : 0( x 1 = 0 x = 1 x = 1 ()? (Ζ & f Λ> > >Λ Λ! Λ! Φ!ΛΚ Φ ΚΛ Φ,Υ( ΓΧ Χ!Ι Λ(,/) Χ,( Λ,/ l = 40, f = 7, f 1 =, f = 6, i =
17 : f f 1 0 f0 f 1 f1 7 = = = = 4 0 Χ, ( M ) = l + M = 4 0 x y 1 = y = x 1 x y Λ > 0( x y 8 + = y 8 x = x y Κ > Β,, 0Υ(, ) 0,/) x, y : Η6 Υ9 AB, P C Χ? [,/ AP PC x = = & PCB = 0 Χ,/ BC 8 m. PBC = = =
18 cos0 = 8 = x BC PC x = 8 16 x = m. 16 AP = m. Β tan 0 PC = BC 1 PB = 8 8 PB = AB = AP = PB = + = 4 8 = m. = m = 8 m. Η6 Υ9 = 8 m. : ABC 0, Ι ABC = 90 )& B,/, Ω, AC = AB + BC Χ(Λ BD AC 9/ ΛADB 0(ABC ADB = ABC = 90 A = A ADBABC AA
19 AD AB = AB AC AD AC = AB i....( ) BDC ABC CD BC = BC AC CD AC = BC ii....( ) ( i) ) ( ii) ΙΗ6 AD. AC + CD. AC = AB + BC AC( AD + CD) = AB + BC Ε AC. AC = AB + BC ( AD + CD = AC) AC = AB + BC, Ω &/ Φ: Χ,/ 1 5 ]]]] = ]]]] ]]]]5 6 = 0 ]]]] ;Χ( r) 14 cm. = Ρ # τ r θ = 60!: ( ) = cm = cm 616 = cm = 05. cm. i AB 1 cm. = 9/ ( ii) BAX = ABY 9/
20 ( iii) AB + 5 = 8Χ Χ ( A1... A8 ) ( 7 / 9 BY 8Χ Χ ( B1, B... B8 ) ( 7 / ( iv) A B 5 /, AB P Χ?,/ AP 4.5 = cm 0( PB = 7.5 cm.
21 ! # % #&& () +,. /!,), %,0) 1,/ # % %) (,/ & ( %456 0 ) 7,/ )!
22 +,% ).,/ #,// Λ Λ, 8 0 &1 :π,/ 01 0!1) 01 ) ) 01 π 01!0!1!01! 01 >: ; ), 4! 010!1!0101Μ : Ρ Χ,,) 56?,/ 47 (,) ,%8 10!10,8, 1010%8, 1010%8 1 Χ,, 5?α 8 β, ,/ α β 7 (, 5α 8 β 1 α 56 1 β 01,0!101/01 ) 4 Ι&9;& :&9 59 9, &&9& :& ! 0!1Φ 01 01Μ
23 Φ: ) Γ,,/!! ( 010!1>0101, Χ? 08, 1) 0681 ( ΗΓΛ Χ?,Λ,,, ;08, 10681! 010)8%10!10)81010)8 1010,8 1 <.0=/ /,&1Χ Χ,,/.0=/ /,&1 01.&0!1,.&01,&01& =(ΑΑ Γ0(ϑ),,/! 01π 0!1 01π 01 /&Υ9 ( )Γ,Λ! 0160!101)01< Ψ:::::::::::::::::,,,/!,>/ 5! 5:::::::::::::::::,/!,>/ 5! 5 %)ΩΛ(ΑΑ :::::::::::::::::::::::::::::,,/
24 9Χ Χ (ς:::::::::::::::::::::::,ι,/ ( ) /,. % / ::::::::::::::::::::,/ /,. % / 6(Α Ω,&.::::::::::::::::::::,,/.?!: :)) )#::::::::::::::::::,,/ Α :) < & & ) (?,.:::::::::::::::::::::,/ &!.: Μ: Χ, 4 Ι,,/:::::::::::::::::::::::::: & >: ) ) )Β:::::::::::::::::::::::::,,/! Ρ Χ,?Λ>0(Λ, Χ, Σ / > # ( Β,,) Ρ Β) Βς_ 0(_, Ρ / > _ Χ (# % 0 5 (:)) % 5(:,) Ρ,/ >
25 # 5 (:)% 5(: Ρ,6 5%:/ΑΑ / > #,6 5%:/ ) 4 Ι&9&:6 8&9:6 89:6 ::::::::::9 / &9&:6 8&9:6 89:6 9 6 Χ? 0 8, 1) 0, 8 1 ( ΗΓ Χ? / > #,, ; 0 8, 10, 8 1,), &9 +# Βς6 ),/ +#:), 9Σ / > Α &9 +# 6 (+#:) 9 >Κ: 4 Ι? Ι 0%8,)180,81) 0/8, 1,/ > # 0%8,)180,810/8, 1 = &:%Χ &0( & / > &:%Χ & & %/ ) / 5 %/ / 5. 6/ / / > # ) / 5 %/ / 5. 6/ / :& %8<8%8<8,,,,,,,,,,,,,,,,,!Κ, 4 & %8<8%8<,,,,,,,,,,,,< % Ω Λ %0),/ Λ %!
26 %%Η ( ΓΚΕΜ) > / # #<8= )!(# Β % )) ς>), &,, / Ε #! /) (!)! %) 0,0,/ # %,) 5 :/ %6)Α Φ&Φ9:ΦΦ Ω &: ) 9: % Φ&Φ9:ΦΦ &:? 9: %0 4 Ι#4Β Ι 0%8180,8%1) 0<861,/ # 0%8180,8%10<861 %<.0=/ /,1 4 ) ( Γ / #.0=/ /,1!(
27 %=0Χ ΒΙ,/ [ Χ Χ Ο, / & #!! (! / Ω , 1 : 1 Sin Q % 1+ SinQ ( ΕΕΕΚΕ>>Ε>ΜΕ Ε>( &>ΜΓ> 5( /% # 5(&! /8)8<8 8 =8 8% 8( = ) Γ 0# 1 ()? /,) ),)/ )/,)) )),6/ 6/,6) 6),/ /,) Χ Χ > Κ Φ Φ > :Β ( Γ, /0.!( 1 ) 5(:6,(: 0 4 %) (0),Ι 4 (0 )Ω )Γ,/ Υ9)), ΑΑ Θ #4Β / & (! %)!( ()) (
28 :0 Ι Η6 [ ) Γ;Χ,Ι,ΙΧ?Φ,Ι,/ Υ9 /!/.Γ Φ # 6 4 Ι0 4 Ι0Χ Χ,), 4 ΙΝ,/ Ω / 8!:0 4 Ι&9Χ( Ι9: 8&9:% 4 ΙΝ 4 ΙΧ( Ι Ι0 4 Ι Ι))Χ%,/ &99: 8&9:% )Χ%
29 8 8! 0!1 0!1%010!1)016010!1<01=01/010>:( () ): n π : : :?Φ:(Α Ω!:? Κ. : : 50,1 ΗΜ:Ν >:)?Β:α 5 β :, 50,)1:,6?Β:α β :, 0,)1:/ Ρ Χ,,0α 5 β 1 5α β,0, >>:Β: 1 4 Β: 1 4 Ρ,0Β1 5Β:/, Χ:/ 4x x :/, 5:/ % 5 (5) 5! (5 :/ % 5(: 5! (5 :/
30 ,) Ρ,ΙΧ a a = b b 1 1 P = 1 P = 6 > :,6 5%:/ : 8!:,68:% :!,:0,61, %:%6, : >/( () ),/ >: 4 Ι&9 &9 :06 1:%6 9 :06 1:%6 & : 06 1 : &9 5 9 :%6 5%6 : : & & : &9 59 ) &90,/ 9:=/ / 6 0 Χ? 0 8, 1) 0, ( ΗΓ Χ?
31 + ( ) =, =, = (0,0), &9 +# ( ) ( ) ar ABC BC = ar DEF EF 64cm BC = = 11cm 15.4 ( cm ) BC ( ) 64cm X 15.4 cm = 11cm ( ) 64cm X 15.4 cm BC = 11cm 8X15.4 = cm = 8X1.4cm 11 : < 4 Ι 0%8,)180,81) 0/8, 1? 0 8(1 x x + x + x 1 = ( ) y y + y + y 1 = = = 6 = = = = 1 ( )? :0 81 =& = 4.&: 1 Cos A : 1 4 : :
32 .&: 7 4 Cos A &: 4 Sin A = 7 : 7 4 %/ ) / 5 %/ /,. 6/ / : ( 1) + : 1 + = 4 4 %& %8<8%8,,,,,,,,,,,,,,,,,,,, :%8:<,%:)8 :<8: :50,1 <:%50,1 ) <,%:0,1 ) ):0,1 ) 0,1: 75 5 :),:) :)5:6 :6 % Λ : p 0, ),/ q ),Υ ( Γ,/
33 ) ) ) ),,/ ), 0),/ %%<: =:% % ):) ) #0<8=8 )1: %, :,: : : / %)x 5x + p = 0 :%8!:,)8: :!,:0,)1, % : ), 9Υ,,/ :/ ), :/ : ) : 5 1 %6,Φ&Φ9:ΦΦ
34 OA OD : OC OB &Φ Φ9 &Φ : Φ90;,1 & OA OD : OC OB 0,1 &Φ Φ9 &: 0( : 9 % 4 Ι 0%8180,8%10(0<861,/ 1 4 Ι#4Β: 1( y y ) + ( y y ) + ( y y ) x x x ( 6) + ( 4)(6 4) + 8(4 ) : [ ] 1 = [ ( ) ) ] 1 1 = [ ) ] = 9 :)( Κ: &90,/
35 9:=/ / :01 &:=/ /,.: AB AC : BC AC 01.0=/ /,1: BC AC 01 01) 01.0=/ /,1: %=ΙΧ0Χ ΒΙ, [:8 8%8,/ Ο :Φ [Ο, : 4 6 : 1 Sin q = = Cos q Cos q / L. H. S. ( sec q tan q) ( ) ( ) 1 Sin q 1 Sin q 1 Sin q = = = Cos q Cos q 1 Sin q ( ) ( ) ( ) ( ) 1 Sin q 1 Sin q 1 Sin q = = = R. H. S. 1+ Sin q 1 Sin q 1+ Cos q
36 Ε.:. Γ:) ):/Ι5)5<5 5 =5 5% 5(5 = Μ ) =:<)5 5( ),<): 5( /: 5( 5(:/ ()? 01 Χ Χ 0#1 9Χ Χ 01 /,) ),)/ % ) )/,)) < % )),6/ 6 = 6/,6) 6 ) 6),/ % < /,) %/ :%/
37 N 0 : :)8,9Χ Χ Μ)? ), Ι(Λ)? ΛΦ,/ ) Γ(ΛΦ,/ :))8:%8:68:) N c. f Γ = l + i f 15 1 = = = = = : 5(:6, (: (:6, (:, (:x- > ( Φ > / (, /
38 Β,, 0Υ0 Χ? >Ε>,/ ) : 8(: : Υ9:)
39 4 :%) Υ9:)),%) : = + = [ Υ9 1 + (.5 ) h r cm = cm = 156.5cm = 1.5cm ΑΑ Θ#=)Ω(ςΑΑ Θ# 65(ςΑ Θ# :>π 5π : π 0 51 : 7 %)0 %)5 )1: /)05 )1 : =) : ) ) &9, Ι Υ9,/
40 9 [,/9: 9 :0 5/1 &9 6/ / : AB BC : p b : h x : h x = 6 4 Ι&90( 4 Ι +#, &: 0( AB AC : DE DF
41 Ω, &9 +# Χ(Λ &9&9&: + &&: +0( & /, &0( +#/ 94 &: +0Χ(1 &: # &: 0,1 & +#0.&.1 &: +8 &+: #01, AB AC : DE DF AB AM : AC AN 0 +:&8 #:&1 ϑϑ9 : 90( : 01 : +0( : # 9: + & : # )Χ &90( +# &: 0,1 9: +8 : #0 1 &90( +#,0/
42 & +#0&&&1 <!:9Υ 4 Ι Ι0Υ% 0(,,/),,/ 0ΧΙ,/ 9 ΛΛΛΛ 019: 9/ 01 Χ? 9 Μ Χ/&9:% /& /&90 Χ/ 019 & ) 0?Χ,0 9Κ9/
43 01)0 5 ) ΧΗ6 Χ? % 89 80(9 ) 89Κ ) 99 8:9 9 8:9 9 %: 9 % 9 : 9 9 ),/ 019 % 0 Χ? 5 ) [ 0(9 ), Ι(9 %? 0 0Χ56 Η 9Γ α[,9/ 01Γ, Ι(&? 0 Χ56 Η9&&Γ α[,9/ &ΓΓ / &Γ9ΓΟ,)/ &9 &Γ9Γ
44 ! # % #&& () +,. /!,), %,0) 1,/ # % %) (,/ & ( %456 0 ) 7,/ )!
45 Λ Λ Λ, 8 9(Choose the correct answer) : Ρ,Ε Β,/ Sum of the roots of the quadratic equation will be (a) b c (b) b (c) a b c (d) a a >:,/ The roots of the equation will be a p (a) q a (b) ap (c) p aq ± (d) aq p : 0Α1Θ#4Β,,/ Total surface area of a sphere is (a) r sq unit (b) r sq unit (c) 4r sq unit (d) r sq unit : ; ),= Which of the following is a prime number? (a) 6 (b) 9 (c) 15 (d) 11 : Χβ Χ? (Α ) Γ % 0Υ9Ι,/ The maximum no. of tangents drawn from a external point to a circle is (a) (b) (c) 1 (d) 4 Φ: Χ? )A(,-4) ) B(4,-) ( ΗΓ Χ?, The mid point of the line-segment joining the points A(,-4) andb(4,-) is (a) (6,-6) (b) (-1,-) (c) (,-) (d) (-,)
46 !: ) (,, The probability of an impossible event is Κ: (a) zero (b) 1 (c) -1 (d) 1+ tan θ, 1+ tan θ is equal to (a) sec θ (b) cos ec θ (c) tan θ (d) cot θ Μ: 4cos ec θ 4cot θ Χ Χ, 4cos ec θ 4cot θ is equal to (a) 1 (b) 0 (c) (d) 4 : )χη:) Γ 0(?8),Ι, (a) (b) ()? (c) Γ (d), The difference of maximum value and minimum value of a data is called (a) Range (b) Class Inverval (c) Mid Point (d) None of these 7 &, 8 Ρ /(Fill up the blanks with correct answer) : (Χ, ::::::::::::::::::::::::::::::::::::::,,/ The polynomial of power two is called. >: (Α (, ::::::::::::::::::::::::::::::::::::::Χ Χ,/ Two circles are angruent if their.. are equal. : Χ? (-4, ) ::::::::::::::::::::::::::::::::::::::9 &%Η:/ Point (-4, ) lies in the..quadrant. : )# Χ? % ::::::::::::::::::::::::::::::::::::::,,/ The Co-ordinate of any point an y-axis is... : Χ? ::::::::::::::::::::::::::::::::::::::,/
47 Distance of P(x,-y) from the origin will be... Φ: sinθ = 1, ::::::::::::::::: sinθ = 1, then : 0 0!: sin 5 + cos 5 ::::::::::::::::,,/ 0 0 sin 5 + cos 5 is Κ: ΕΕΦΕ!ΕΜΓ::::::::::::::::,/ Μ: %8)8688= 0::::::::::::::::,/ is an number. >: 4 Ι, 4 Ι:::::::::::::::::::::::::::::::,,/ If two triangles are equiangulars then triangles will be. >: Ρ Χ, Σ Ι?Λ) Β>,/ Sum and product of zeros are - and find the quadratic polynomial. >>: x / If then find the value of x. >: 0 ΡΧ, 4 ΙABC B=90 0 Ω AC =AB In Isocels triangle ABC, B=90 0 then to prove that AC =AB > : Χ? Ψ(,) &(4,1)Χ9 Σ Ι0 Find the distance between the pair of points (,) and (4,1) >: 0Φcm 4 ( 4 Η 4 ΗΦ,/ Find the perimeter of sector whose radius is 6 cm and angle of sector is >Φ: ΕΚΕΕΚ::::::::::: Κ,/ Which term of A.P. is,8,1,18 is 8. >!: If 5 tan = 1 θ sin θ + cosθ / 5 tan θ = sin θ + cosθ 1
48 >Κ: SinA = CosB & A) B? Ω A + B = 90 0 If SinA = CosB&89 A + B = >Μ: 0)Ω(Α ΓΦcm, ϑ / If circumference of semi circle is 6 find its diameter. : 4 ΙΝ, 0 Χ?Γ / Write the condition for similarity of two triangles. : 0(Α #4Β) Γ, (Α 4 7,= If the Values of area and circumference of a circle are equal, what is the value of radius of the circle. >: Ω 0),/ % Prove that! : Ρ x x + 1 = 0 Find the roots of quadratic equation x x + 1 = 0 : 7Η ( Ι0Ξ & &>> / Using Eaclids division algorithm find H.C.F. of 15 and 5. : (ΞΧ, 4 4cm) 4 cm #4Β / The inner and outer radius of ring are cm and 4cm find its area. Φ: 4 Ι? Σ Ι 1(,-5) (-7, 4)) (10,-),/ Find centroid of triangle whose co-ordinates of vertices are (,-5) % % % % (-7, 4)(10,-). 4 x!:, + y = 8 6 Solve 4y = 5 x Κ: Φ Υ9(0 Γ(Γ [4m, 0 [8m, 9 / The shadow of 6m vertical pilar is 4m, just then the shadow of tower is 8m % % find height of tower.
49 Μ: Ω (Prove it) 1+ sinθ cosθ + = secθ cosθ 1+ sinθ : sin θ = cosθ sin θ + cosθ / If sin θ = cosθ then find sin θ + cosθ. : 0APλΕ 0( Μ, & / In an AP λ, and total terms be 9 then find first term. >: ; ΧΓ, / If mean of the following distribution is 50 find the value of ()? 01 Χ Χ (f) : Υ9) ϑ(0θχ Υ9) ϑ (0 7δ( Ι, 1Χ9Θδ1Θ#4Β / From a solid cylinder of height.4cm and diameter 1.4cm, a conical cavity of same height and same diameter is cut of. Find the surface area of the remaining solid. : Β ( Γ, Λ Solve from graphical method. x + y = x+5y = 1 : Ω Ν 4 Ι#4Β) Ι)( ) Χ Χ,,/ The ratio of area of two similar triangles is equal to the ratio of the squares of corresponding sides. Φ: )Γ 0 0(Μ & Χ? ) %?, Υ9 / The angle of elevations of the top of tower from two points an the ground at distance of 4m and 9m from the base of tower in the same straight line are complementary find height of tower. % % % % ) ) ) )
50 Answer ( 8 8 )of Set b c c d a c a a d a Ρ 4 0Υ Ρ () x + y Φ ) Ν >:?Β?Β Ρ Χ,?Β?Β >>: 9x 5 = 0 9x = 5 x 5 = 9 x = 5 5 = ± 9 >: ΡΧ, AB = BC & AC = AB + BC = AB + AB ( BC = AB) = AB = AC = AB
51 > : Χ? )Χ9 & Χ9 = ( 4 ) + ( 1 ) ( ) = = = 8 = >: 4 Η πrθ = r = = 1 cm + cm 7 = 1 cm cm = 18.5cm >Φ: a=, d=8 = 5, an =8, n=? 4 a n = a + (n - 1)d 8= + (n - 1)x5 8 - = (n - 1)x5 5 = (n - 1)x5 (n - 1) = 7 n = 8 >!: 5k tanθ = = 1 k AB BC AB = 5 K, BC = 1K AC + = AB + BC = ( 5K) (1K ) = 5K + 144K = 169K = 1K
52 >Κ: AB 5K sin θ = = = AC 1K BC 1K cos θ = = = AC 1K sin θ + cosθ = + = 1 1 sin A = cos B sin A = sin(90 B) A = 90 B A + B = 90 >Μ: )Ω(Α Γ πr + r = 6cm r( π + ) = 6cm r = 6cm = πr + r! r = 6cm 6 cm r = 6cm 7 r = r 7cm : 4 ΙΝΟ,, (i) Χ Χ, & = (ii) Ι0Υ0,),/ : (Α #4Β = πr ( (Α Γ = πr,(α #4Βε(Α Γ πr πr = r =
53 >:,, 0, r = ( s 0) s ; r ) sε) 7 1ΘΗ,/ a = b Ο,Ι,Υ a) b,),/ b = a ) b = a ( Ι,/ ( Ι /,Ι,Υ,/ ) ) 0 1ΘΗ>,/,Υ ( Γ Ο,)/) 0),/ : x x + 1 = 0 D = ( ) 4 1 = 8 8 = 0 b ± a D 0 ± ± 0 1 1, 1 4 : 7Η ( Ι
54 : (Ξ# ( R r ) = π = π 4 cm ( ) = π 16 9 cm ( ) Φ:? ( x, y),/ = 7πcm 4 Ι 1(, 5),( 7,4) ) ( 10, ),/ x1 + x + x x = y = y + y + 1 y x = y = x = y = x = y = 1? %(, 1),/ 4 x!: + y = 8 6 4y = 5 x Φ0( 4 x + 18y = y = 0 x # # 4y
55 68 y = = = 8 x 4 = 8 6 = x 4 x = 4 x = = x =, y = Κ: Υ9,/ ABC ~ DEF AB = DE BC EF 6 = h h = 6 8 h = 6 8 = θ θ θ θ 1+ sin cos Μ: # = + cos 1+ sin = ( 1+ sinθ ) + cos cosθ ( 1+ sinθ ) θ 1+ sin θ + sinθ + cos θ cosθ = ( 1+ sinθ ) 1+ sin θ + cos θ + sinθ = cosθ + sinθ = cosθ ( 1+ sinθ ) ( 1+ sinθ ) + sinθ = cosθ sinθ cosθ = ( 1+ sinθ ) ( 1+ sinθ ) 1 cos ( + sinθ ) θ ( 1+ sinθ ) =
56 = = secθ % cosθ
57 : sin θ = cosθ sin = cos θ θ AB tan θ = = = K ( let) BC AB = K BC = K AC AB + BC = ( ) = K + K = K + K = 4K = K sinθ = AB AC K K = = cosθ = BC AC K 1 = = K sin + cos θ θ :,Υ & n = s n ( a + l) 9 a 144 = ( + 8) 144 = a = + = + 8 = a a = 4
58 >: c. i f x fx fx x = N f = 96 + x fx = 70 x x = 96 + x ( 96 + x) = 70x x = 70x x 50x = x = x = = 4 0 x = 4 : ΧΑ1Θ#εΧΑ1Θ#Τ)Γ #Τ (ςα1θ# = π rh + πr + πrl = πr ( h + r + l) ( ) = cm 7 7 = cm 7 10 ( )
59 176 = 8.0 cm = cm = 17.6cm ( ) l + = h r = ( ) ( ) = = 6.5 =.5cm : y 1 x 5 = : 4 ΙABC) PQR,/, ABC ~ PQR < Ω, ar ar ( ABC) ( PQR) = AB PQ = BC QR = [ 4 Ι#4ΒΣ 0 CA RP
60 1;Χ() )α φ 1 ar ( ABC) = BC AM 1 ar ( PQR) = QR PN ar ar 1 BC AM ( ABC) BC AM = = ( PQR) 1 QR PN QR PN )Χ +(0(,) +, +.,% ( ) <Μ +(.,) AM = PN AB PQ 0( +.,% AB BC CA = = PQ QR RP ar( ABC) ar( PQR) = AB PQ AM PN ) AB AB = > PQ PQ AB = PQ Θ Ω,
61 ar( ABC) ar( PQR) = AB PQ = BC QR Φ: Υ9,/ /, & = CA RP ABC 0 tan(90 θ ) = AB BC tan(90 θ ) = 4 0 h h cotθ = 4 ABC tanθ = AB BD h tanθ = 9 cot θ tan θ = h h 4 9 h 1= h = 6 6 h = 6 m = 6m!: 4 (Α 9/ (Α? 0 Ρ Ι / Ρ Ι Χ? (? (Α 9/,,(Α 0(+ Χ?,/ Χ? ) + % 9Σ
62 ! # % #&& () +,. /!,), %,0) 1,/ # % %) (,/ & ( %456 0 ) 7,/ 15 Minutes of extra time have been allotted for Candidates to read the Questions.
63 xf.kr (lsv&4) Lke; %?kavk 15 feuv MATH (SET-4) Time : Hrs 15 Min. Full Marks : 100 lgh mùkj pqus %& Choose the correct answer :-,d f}?kkr lehdj.k dk?kkr gksxka 1 (d) ([k) 0 (x) 1 (?k) buesa ls dksbz ugha The degree of a quadratic equation will be (a) (b) 0 (c) 1 (d) None of these - ;fn sin θ = cos θ rks θ dk eku gksxka 1 (d) 0 ([k) 45 (x) 60 (?k) 90 If sin θ = cos θthen the value of θwill be (a) 0 (b) 45 (c) 60 (d) 90 - pøh; prqhkzqt ds leeq[k dks.kksa dks ;ksx gksxka 1 (d) 60 ([k) 180 (x) 90 (?k) 0 The sum of either pair of the opposite angles of a cyclic quadrilateral will be (a) 60 (b) 180 (c) 90 (d) 0 4- fcunq (µ5] µ4) fdl prqfkkza'k esa flfkr gs \ 1 (d) izfke ([k) f}rkh; (x) r`rh; (?k) prqfkz In which quadrant does the point ( 5, 4) lie? (a) 1 st (b) nd (c) rd (d) 4 th rfkk BAC = ABCesa BCdks D fcunq rd c<+k;k x;k gs ftlls ACD =110 rks ABCdk eku gksxka 1 (d) 5 ([k) 57 (x) (?k) 1 In ABC, side BC is extended up to D such that ACD =110 and BAC = 57 then the value of ABCwill be (a) 5 (b) 57 (c) (d) 1 6- ;fn 6, 8, 9, xrfkk 1 dk ekè; 10 gks rks xdk eku gksxka 1 (d) ([k) % (x) (?k) ) If the mean of 6, 8, 9, x, 1 is 10 then the value of x will be,))
64 (a) (b) % (c) (d) ) 7-,d iklk dks mnkyus ij,d vhkkt; la[;k vkus dh izkfkfedrk gksxha 1 (d) 1 ([k) 1 (x) 1 4 (?k) buesa ls dksbz ugha In a throw of dice, the probability of getting a prime number will be (a) 1 (b) 1 (c) 1 4 (d) None of these 8- A.P. 40, 15,10, 5,...dk 10oka in gasa 1 In A.P. 40, 15,10, 5,...10 th term is... (d) 184 ([k) 186 (x) 18 (?k) ABCesa AB = ACrFkk < BAC = 50 rks < ABCdk eku gksxk 1 (d) 60 ([k) 65 (x) 70 (?k) 75 In ABC, AB = AC and < BAC = 50 then the value of < ABCwill be (a) 60 (b) 65 (c) 70 (d) 75 sin dk eku gksxka 1 cos1 (d) 0 ([k) µ1 (x) 1 (?k) buesa ls dksbz ugha The value of sin 59 will be cos1 (a) 0 (b) 1 (c) 1 (d) None of these fjdr LFkkuksa dh iwfrz djs %& Fill in the blanks :- 11- f}?kkr lehj.k ax + bx + c = 0ds ewy oklrfod vksj vlkeu gsa rks foospd 'kwu; ls gksxka 1 If the roots of the quadratic equation value of discriminant will be... than zero. ax + bx + c = 0is real and unequal then the 1- cosec θ 1dk eku gksrk gsa 1 The value of cosec θ 1 is... 1-?kukHk esa fdukjs gksrs gsaa 1 The number of edges in a cuboid is x v{k ij flfkr fdlh fcunq dk y fu;ked gksrk gsa 1 The ordinate of any point situated upon x-axis is izfke ik p fo"ke la[;kvksa dk ekè; gksxka 1 The mean of first five odd numbers will be...
65 16- fdlh vo';ahkkoh ;k fuf'pr?kvuk Edh izk;f;drk P(E) =... 1 The probability P(E) of an sure event or certainly E = fdlh ckg~; fcunq ls o`r ij vf/dre [khaph tkusokyh Li'kZ js[kkvksa dh la[;k gksrh gsa 1 The number of maximum tangents from an external point is a circle is fdlh laekrj Js.kh esa nks Øfed inksa dk cjkcj gksrk gsa 1 In a arithmetic progression... between two consecutive terms are equal. (, ) 19- nks fcunqvksa ( 1, 1 ) x y vksj x y ds chp dh nwjh gksxh The distance between two points ( x1, y1 ) and ( x, y) will be ifjes; la[;k esa gj ds cjkcj dhkh ugha gksrk gsa 1 Denominator of a rational number never equal to... vfr y?kq mùkjh; iz'u%& Very Short Questions 1- f}?kkr cgqin x + 8x + 15ds 'kwu;d Kkr dhft,a Find the zeroes of quadratic polynomial x + 8x k dk eku fudkysa ftlds fy, x = 1 f}?kkr lehdj.k x + kx + = 0 dk,d ewy gksa Find the value of k for which x = 1 is a root of the quadratic equation x + kx + = 0 - ABC dh Hkqtk AB vksj AC ij D vksj E fcunq Øe'k% bl izdkj gs fd DE BC vksj AD =.6 cm, AB = 10 cm, AE = 4.5 cm rks AC dk eku fudkysaa If D and E are the points on the sides AB and AC of ABCsuch that DE BCand AD =.6 cm, AB = 10 cm, AE = 4.5 cm then find the value of AC. 4- fl¼ djsa fd o`r dh leku thok, dsuæ ij leku dks.k cukrh gsaa Prove that equal chords of a circle subtend equal angles at the centre. 5- fcunqvksa (µ4] 7) vksj (1] µ5) ds chp dh nwjh Kkr dhft,a Find out the distance between the points ( 4, 7) and (1, 5). 6- ;fn fdlh o`r ds thok dh yeckbz 4 lsehú gks vksj o`r ds dsuæ ij thok Mkyk x;ka yec dh yackbz 5 lsehú gks rks o`r dh f=kt;k fudkysaa If the length of the chord of circle is 4 cm and the perpendicular drawn from the centre is 5 cm then find the radius of the circle. 7- nks?kuksa ds vk;ruksa esa 1 % 8 dk vuqikr gs rks mudh dksjksa esa D;k vuqikr gksxk \ The ratio in volumes between two cubes is 1 : 8 then find the ratio between their edges. 8- tanθ dk eku sinθ ds :i esa O;Dr djsaa
66 Express tanθ in terms of sinθ. cos cos 59 cosec1 dk eku fudkysaa sin10 Evaluate cos80 + cos59 cosec1. sin10 0- fcunq (µ5] 4) vksj (7] µ8) dks feykusokyh js[kk[kam ds eè; fcunq dk fu;ked fudkysaa Find the co-ordinates of the midpoint of the line segment joining ( 5, 4) and (7, 8). 1- lekraj Js.kh 6] 9] 1] 15] dk 5oka in fudkysaa Find out the 5 th term of the AP 6, 9, 1, 15,... y?kq mùkjh; iz'u %& Short Questions: 4 - ( x 1) vksj ( x + x + 1) dk eúlú fudkysaa Find HCF of ( x 1) and 4 ( x + x + 1). - ;fn nks la[;kvksa dk ;ksxiqy 15 gs vksj muds O;qRØeksa dk ;ksxiqy gks rks nksuksa la[;kvksa 10 dks Kkr djsaa The sum of two numbers is 15 and the sum of their reciprocals is then find both 10 the numbers. 4- ABCds 'kh"kz A(1, 1)vkSj B(5,1) gsaa ;fn f=khkqt ds xq:rodsuæ ds fu;ked ( 5,1) gksa rks fcunq C ds fu;ked fy[ksaa Two vertices of ABCare A(1, 1)and B(5,1). If the co-ordinates of the centroid be 5 (,1) then find the co-ordinates of the vertex C ls 00 ds chp lhkh fo"ke la[;kvksa dk ;ksxiqy Kkr djsaa Find the sum of all odd numbers between 100 and ;fn fdlh ds dks.kksa dh ekiksa dk vuqikr :: 4gks rks lcls cm+s dks.k dh eki Kkr djsaa If the ratio of measurements of angles of a triangle are :: 4then find the measure of the greatest angle. 7- ABCds 'kh"kksz A(, 0), B(5, )vksj C( 8, 5)gSa rks ds xq:rodsuæ ds fu;ked fy[ksaa Find the centroid of the triangle whose vertices are A(, 0), B(5, )and C( 8, 5). 8-,d FkSys esa mtyh rfkk dkyh xksfy;k gsaa ;n`pn;k,d mtyh xksyh fudkyus dh izkf;drk fudkysaa A bag contains white and black balls. Find the probability of drawing a white ball at random.
67 + θ θ + = θ 1 cosθ 1+ cosθ 9- fl¼ djsa fd 1 cos 1 cos cosec Proove that 1+ cosθ 1 cos θ + = cosecθ. 1 cosθ 1+ cosθ 40- ;fn m = a cos θ + bsin θ vksj n = asin θ bcos θrks fl¼ djsa fd m n a b + = fueu lkj.kkh dk ekè; fudkysaa oxz varjky 0&10 10&0 0&0 0&40 40&50 ckjackjrk Find the mean of the following data. Class Interval Frequency fueu lkj.kkh dk cgqyd fudkysaa vk;q o"kksz esa 4µ6 6µ8 8µ10 10µ1 1µ14 cppksa dh la[;k Find the mode of the following data. Age Years in Frequency nh?kz mùkjh; iz'u %& Long Question : 4-,d oxz dk {ks=kiqy fudkysa ftldk?ksjk ml vk;r ds?ksjs ds cjkcj gs ftldh,d Hkqtk 48 ehvj gs rfkk mldh pksm+kbz dh rhu xquh gsa 5 Find the area of the square whose boundary is equal to the boundary of a rectangle whose one side is 48 m and three times its breadth. 44- fueufyf[kr lehdj.k dk xzkiq [khaps rfkk bldk izfrpnsn fcunq Kkr djsaa 5 y = x and x 4y = 6 Draw a graph for the following equations and find their intersecting point. y = x and x 4y = 6
68 45-,d LrEHk ds Nk;k dh yeckbz] LrEHk dh mq pkbz ls 1 xquh gsa lw;z dk muu;u dks.k Kkr djsaa 5 The shadow of a vertical pillar is the angle of elevation of the sun. 1 times of the height of the vertical pillar. Find vfkok OR,d irax ftldh Mksjh {ksfrt ry ds lkfk 45 dk dks.k cukrh gs] 75 ehvj dh mq pkbz ij mm+ jgh gsa ;fn Mksjh esa <hy u gks rks bldh yeckbz fu/kzfjr djsaa A Kite whose thread is inclined at an angle 45 with horizontal layer, is flying at the height of 75 m. Being considered that the thread is fully straight then find its length. 46- ;fn ABC dk dks.k B U;wudks.k gks vksj AD, BC vfkok BC ds c<+k, gq, Hkkx ij yac gks] rks AC = AB + BC BC BD 5 If the angles B of a AC AB BC BC BD ABCbe acute and AD is perpendicular to BC produced then = lsehú yacs js[kk[kam dks : ds vuqikr esa var% fohkkftr djsaa 5 Divide a line segment of 10 cm in the ratio : internally. vfkok OR ;fn,d js[kk fdlh f=khkqt dh nks Hkqtkvksa dks,d gh vuqikr esa fohkkftr djs] rks og rhljh Hkqtk ds lekukarj gksrh gsa fl¼ djsaa If a line divides only two sides of a triangle in the same ratio, then the line is parallel to the third side, prove it.
69 SOLUTION (1) (d) () ([k) () ([k) (4) (x) (5) (d) (6) (x) (7) (d) (8) (?k) (9) ([k) (10) (x) (11) cm+k (1) cot θ (1) 1 (14) 0 ('kwu;) (15) 5 (16) 1 (17) (18) varj (19) ( x x ) ( y y ) (0) 0 (1) f}?kkr cgqir x = + 8x + 15 = x + (5 + ) x + 15 = x + 5x + x + 15 = x( x + 5) + ( x + 5) = ( x + )( x + 5) x + 8x + 5 = 0 or, ( x + )( x + 5) = 0 either x + = 0 or, x + 5 = 0 x = x = 5 vhkh"v 'kwu;d =, 5 () f}?kkr lehdj.k x kx = mi;qzdr lehdj.k esa x = 1j[kus ij (1) + k 1 + = 0 or, 1 + k + = 0 or, k = 4Ans. () iz'ukuqlkj] DE BCvkSj AD =.6cm, AB = 10cm, AE = 4.5cm, AC =? DB = AB AD = 10.6 = 6.4cm pwfd ge tkursa gsa fd ;fn fdlh f=khkqt dh fdlh,d Hkqtk ds lekurj dksbz js[kk [khaph tk; rks vu; nks Hkqtk,,d gh vuqikr esa fohkkftr gksrh gsaa AD AE = DB EC or, = 6.4 EC or, EC = = 8cm.6 10
70 AC = AE + EC = = 1.5cm Ans. (4) eku fy;k fd vksj o`r dh nks leku thok, gsa ftudk dsuæ O gsa fl¼ djuk gs fdµ D AB = CDiz'ukuqlkj AOB COD (SSS) AOB = COD (CPCT) AOB = COD izek.k%µ AOBvkSj COD esa] OA = OC, OB = ODo`r dh lhkh f=kt;k, leku gksrh gsaa vr% o`r dh leku thok, dsuæ ij leku dks.k cukrh gsa (5) fcunqvksa (µ4] 7) vksj (1] µ5) ds chp dh nwjh = (1 + 4) + ( 5 7) = = 169 = 1bdkbZ (6) eku fy;k fd OdsUæ okyk o`r dh thok AB dh yackbz 4 lsehú gs vksj o`r dsuæ O ls thok AB ij Mkyk x;k yac OPdh yackbz 5 lsehú gsa OPBesa] OA OP i. e., AB = 4cm, OP = 5cm OAP vksj OBPesa] OPA = OPB = 90 (iz'ukuqlkj) = OB (o`r dh f=kt;k, cjkcj gksrh gs) = OP (Common) OAP OBP(RHS) 4 AP BP = = 1cm OPB = 90 (OB) = (OP) + (PB) = = = 169 OB = 169 = 1cm Ans.
71 (7) eku fy;k fd igys vksj nwljs?kuksa ds dksjksa dh yackbz Øe'k% xvksj ybdkbz gsa iz'ukuqlkj] ifz ke?ku dk vk;ru 1 = nlw js?ku dk vk;ru 8 x 1/ 1/ or, x or, x = y 8 y = = = = 8 y 8 dksjksa dk vhkh"v vuqikr = x : y = 1: Ans. (8) sin θ tan θ = = cos θ sin θ 1 sin θ Ans. (9) cos80 + cos59 cosec sin10 cos(90 10 ) = + cos(90 1 ) cosec1 sin10 sin10 = + sin 1 cosec1 sin10 = = Ans. (0) fcunq (µ5] 4) vksj (7] µ8) dks feykusokyh js[kk[kam ds eè; fcunq ds fu;ked (1) lekurj Js.kh 6] 9] 1] 15] ( 8) =, 4 8 =, ;gk a = 6, d = t t1 = 9 6 = t = a + ( n 1) d n t 5 = 6 + (5 1) = 6 + (4 ) = = 108 Ans. () x 1 ( x) (1) = 4 = 1, = (1, ) Ans. = ( x 1)( x + x + 1) 4 x + x + 1 = ( x ) + x 1 + (1) x
72 = ( x + 1) x = ( x + 1 x)( x x) = ( x x + 1)( x + x + 1) vhkh"v eúlú = x + x + 1 Ans. () eku fy;k fd izfke la[;k = x iz'ukuqlkj] iz'ukuqlkj] or, or, or, or, or, or, or, f}rh; la[;k = 15 x 1 1 x + 15 x = x + x = x(15 x) x x = 150 x 45x = 0 ( x 15x + 50) = 0 x 15x + 50 = 0 ( 0 ) x (10 + 5) x + 50 = 0 x 10 x 5x + 50 = 0 or, x( x 10) 5( x 10) = 0 or, ( x 5)( x 10) = 0 x 5 = 0 or, x 10 = 0 x = 5 x = 10 vhkh"v la[;k x = 5, 10 Ans. (4) eku fy;k fd fcunq C ds fu;ked ( x, y) f=khkqt ds xq:ro dsuæ ds fu;ked x y =, 6 + x y =, gsaa rks iz'ukuqlkj] xq:rodsuæ dk xfu;ked 5 =
73 i. e., 6 + x 5 = or, 6 + x = 5 or, x = 5 6 = 1 iqu%] xq:ro dsuæ dk y fu;ked = 1 y or, = 1 or, y = vr% fcu C dk fu;ked = ( 1, ) Ans. (5) vr% 100 ls 00 ds chp lhkh fo"ke la[;kvksa dk ;ksxiqy ;gk ] a = t n = d = t t = = a + ( n 1) d = 199 or, ( n 1) = 199 or, ( n 1) = = 98 or, 98 n 1 = = 49 n = = 50 n Sn = { a + ( n 1) d} 50 = { (50 1)} = 5{0 + 98} = 5 00 = 7500 Ans. (6) eku fy;k fd vuqikr dh jkf'k xgsa Rkks] dk izfke dks.k = x f}rh; dks.k = x r`rh; dks.k = 4x pwafd ds rhuksa dks.kksa dk ;ksxiqy 180 gksrk gsa x + x + 4x = 180 or, 9x = 180
74 180 or, x = = 0 9 lcls cm+k dks.k = 4x = 4 0 = 80 Ans. (7) p wfd ge tkurs gsa fd] ( x 1, y 1 ), ( x, y ) vksj ( x, y) ls cus 'kh"kksza okys ds xq:ro dsuæ ds fu;ked x 1 + x + x, y 1 + y + y = = , 6 =, = (,1) Ans. (8) ekuk fd S = dqy Ifj.kkeksa dk lewg = {W, W, W, B, B} ;gk W = mtyh xksyh vksj B = dkyh xksyh n(s) = 5 Ekku fy;k E mtyh xksyh fudkyus dh?kvuk dks iznf'kzr djrk gsa vfkkzr~ n(e) = i. e., E = {W, W, W} n(e) P(E) = = Ans. n(s) 5 (9) L.H.S. = 1 + cosθ 1 cosθ + 1 cosθ 1 + cosθ 1 + cosθ 1 + cosθ 1 cosθ 1 cosθ = + 1 cosθ 1 + cosθ 1 + cosθ 1 cosθ (1 + cos θ) (1 cos θ) = + 1 cos θ 1 + cos θ 1 + cosθ 1 cosθ = + sin θ sin θ 1 + cosθ 1 cosθ = + sin θ sin θ 1 + cos θ + 1 cosθ = sin θ = sin θ = cosecθ = R.H.S. Proved (40) iz'ukuqlkj] m = a cosθ + bsin θ
75 vksj n = asin θ bcos θ L.H.S. = m + n = ( a cosθ + b sin θ) + ( a sin θ b cos θ) = a cos θ + b sin θ + absin θcosθ + a sin θ + b cos θ absin θcosθ = a (cos θ + sin θ) + b (sin θ + cos θ) = a 1 + b 1 = a + b = R.H.S. Proved (41) oxz vurjky ckjeckjrk ( f ) eè; fcunq ( x ) f x 0 µ µ µ µ µ Σ f = 50 Σ fx = 1100 (4) Ekkè; vk;q o"kz esa Σfx 1100 = = = Ans. Σf 50 cppksa dh la[;k 4 µ 6 6 µ µ µ µ 14 7 cgqyd (Mode) M o = l + i fo f 1 fo f 1 f1
76 tgk ] l = Modal class vfkkzr~ vf/dre ckjeckjrk okyk oxz dh fueu lhek fo = Modal class dh ckjeckjrk f 1 = Modal class ds Bhd igys okyk oxz dh ckjeckjrk f 1 = Modal classds Bhd ckn okyk oxz dh ckjeckjrk i =oxz vurjky dh yackbz iz'ukuqlkj]] vf/dre ckjeckjrk okyk oxz vurjky (8 µ 10) ftldh ckjeckjrk 0 gsa vfkkzr~ l = 8, fo = 0, f 1 = 8, f1 = 1, i = 6 4 = 0 8 vhkh"v cgqyd = 8 + ( 0) = 8 + = = 8 + = = 9.o"kZ Ans. 10 (4) eku fy;k fd vk;r dh pksm+kbz = xehú iz'ukuqlkj] x = or, x = = 16 ehú vk;r dk?ksjk vfkkzr~ ifjfefr = (yeckbz $ pksm+kbz) = ( ) = 64 = 18 ehú iz'ukuqlkj] oxz dk?ksjk vfkkzr~ ifjfefr = vk;r dk?ksjk vfkkzr ifjfefr 4 Hkqtk = 18 or, Hkqtk = 18 = ehú 4 oxz dh {ks=kiqy = (Hkqtk) = () 104 y = x...(1) (44) and x 4y = 6...() lehú (1) y x = = oxz ehvj Ans. x 1 1 y 1 5 (x, y) (1, 1) (, ) ( 1, 5)
77 lehú () x 4y = 6 x 6 y 0 (x, y) (, 0) (6, ) (, )
78 (45) eku fy;k fd AB,d h ehvj mq pk LrEHk gsa lw;z ds izdk'k esa LrEHk dh Nk;k BC gs ftlls lw;z dk muu;u dks.k /jkry ds C fcunq ij θ dks.k cukrk gsa iz'ukuqlkj] LrEHk Nk;k BCdh yeckbz ABCesa] ABC = 90 vksj ACB = θ AB tan ACB = BC h or, tan θ = h / 1 = h h = = h = h = tan 60 θ = 60 Ans. ^vfkok* or AB sin ACB = sin45 = AC eku fy;k fd,d irax i`foh ds /jkry B ls 75 ehvj dh mq pkbz ij AfcUnq ij mm+ jgh gs ftldh Mksjh ACdh yeckbz Kkr djuh gs] {ksfrt ry C fcunq ij 45 dk dks.k cukrh gsa vfkkzr~ ACB = 45 ABCesa ABC = = AC or, AC = 75 ehvj Ans. = = ehVj Ans.
79 (46) ledks.k f=khkqt ADB esa D =,d ledks.k ikfkkxksjl izes; ls AB = AD + BD --- (1) fiqj ledks.k f=khkqt ADCesa D =,d ledks.k ikfkkxksjl izes; ls AC = AD + DC --- () fp=k ( I ) ls DC = BC BD DC = (BC BD) = BC BC BD BD fp=k ( II ) ls DC = DB CB DC = (DB CB) = DB DB CB + CB = BD BC BD + BC = BC BC BD + BD nksuksa fp=k esa] DC = BC BC BD + BD nksuksa vksj AD tksm+us ij AD + DC BC BC BD + AD BD (1) vksj () dks iz;ksx esa ykus ij AC = BC BC BD + AB AC = AB + BC BC BD Proved (47) jpuk ds pj.k %& (i ) AB = 10cm,d js[kk[kam [khapka fp=k ( I ) = + (ii ) ABds lkfk fcunq Aij dksbz U;wudks.k cukrh gqbz js[kk AD [khapka fp=k ( II ) (iii ) ADij 5 ($) cjkcj pki AL, LM, MN, NQ, QC dkvdj L, M, N, Q, Cvafdr djsaxsa (iv)cvksj Bdks feyk nsaxsa ( v ) rhljs fcunq (va'k = ) Nls NP BC[khapk tks AB dks Pij dkvrh gsaa bl izdkj PfcUnq ABdks : ds vuqikr esa var% fohkkftr djrk gsa
80 (48) eku fy;k fd ABC,d f=khkqt gsa blesa,d js[kk DEtks Øe'k% AB,AC ij flfkr gsa bl izdkj AD AE = DB EC Rkks fl¼ djuk gs fd DE BC cukov µ eku fy;k fd DE, BCds lekurj ugha gs rks BCds lekurj,d vu; js[kk DE [khapka izek.k µ cukov ds vuqlkj DE BC FkSYl izes; ls] AD AE = DB E C IjUrq fn;k gqvk gs AD AE = DB EC AE AE = EC E C nksuksa rjiq 1 tksm+us ij AE AE + 1 = +1 EC E C AE + EC AE + E C = EC E C AC AC = EC E C EC = E C ;g rhkh lahko gs tc E,oa E,d gh fcunq ij gksa vr% BC ds lekurj js[kk DE gh gs] DE ugha gsa DE BC Proved
81 ! # % #&& () +,. /!,), %,0) 1,/ # % %) (,/ & ( %456 0 ) 7,/ )!
82 Lke; %?kavk 15 feuv xf.kr (lsv&5) MATH (SET-5) Time : Hrs 15 Min. Full Marks : 100 lgh mùkj pqus %& Choose the correct answer :- pøh; prqhkzqt ds pkjks dks.kksa dks ;ksx gksxka 1 (d) 180 ([k) 540 (x) 60 (?k) lhkh Sum of four angles of quadrilateral will be? (a) 180 (b) 540 (c) 60 (d) All - cot 60 dk eku gksxka 1 (d) ([k) 1 (x) 1 (?k) 0 Value of cot 60 will be 1 (a) (b) (c) 1 (d) 0 - fuf'pr?kvuk dk izkf;drk gksrh gsa 1 (d) 1 ([k) 0 (x) 1 (?k) 1 Probability of sure event is? 1 (a) (b) 0 (c) 1 (d) 1 4- sin(90 A) fueu esa fdlds fdlds cjkcj gs \ 1 (d) cos A ([k) tan A (x) sec A (?k) coseca sin(90 A) is equal to which of the following? (a) cos A (b) tan A (c) sec A (d) coseca 5- izfke ik p le izkd`r la[;kvksa dk ekè; gksxkµ 1 (d) 8 ([k) 10 (x) 4 (?k) 6 Mean of the first five even natural number will be (a) 8 (b) 10 (c) 4 (d) 6 6- nks o`rksa dh f=kt;kvksa dk vuqikr 1 % gs rks {ks=kiqyksa dk vuqikr D;k gksxk \ 1 (d) 1 % 9 ([k) % 9 (x) % (?k) %
83 If the ratio of radius of two circles is : then the ratio of their area will be (a) 1 : 9 (b) : 9 (c) : (d) : 7- ;fn lw;z dh muufr dks.k 60 gs] rc 0 ehú yach Nk;k cukus okyh mæx ehukj dh mq pkbz gs \ 1 (d) m ([k) 0 m (x) 5 m (?k) 0 m If the altitude of the sun is 60 then what is the height of the vertical tower making the 0 metre long shadow (a) m (b) 0 m (c) 5 m (d) 0 m 8-,d v¼zxksys dk vk;ru lsehú gs] rks v¼zxksys dk oø i`"b {ks=kiqy D;k gksxk\ 1 (d) 77 lsehú ([k) 696 lsehú (x) 6 lsehú (?k) 16 lsehú What will curved surface area of Hemisphere whose volume is cm (d) 77 cm ([k) 696 cm (x) 6 cm (?k) 16 cm 9- fcunq Pls fdlh o`r dh Li'kZ js[kk dh yeckbz 4 lsehú gs vksj dsuæ ls Pdh nwjh 5 lsehú gs] rks o`r dh f=kt;k gsµ 1 (d) 1 lsehú ([k) 8 lsehú (x) 1-5 lsehú (?k) 7 lsehú If length of the tangent of a circle from point P is 4 cm and distance from centre of P is 5 cm then the radius of the circle is (a) 1cm (b) 8 cm (c) 1.5 cm (d) 7 cm 10- (µ] µ) fdl ikn esa gksxk \ 1 (d) r`rh; ikn ([k) prqfkz ikn (x) izfke ikn (?k) f}rh; ikn Which quadrant will the point (, ) lie? (a) Third quadrant (b) Fourth quadrant (c) First quadrant (d) Second quadrant fjdr LFkkuksa dh iwfrz djs %& Fill in the blanks :- 11- ax + bx + c = 0ds ewy oklrfod vksj vlkeu gsa ;fn gksa 1 ax + bx + c = 0is real and unequal if... The roots of 1- cosec(90 A) = ] 8] 9] 7] 8] 9] 9] ] 5] 4 dk cgqyd gs A What s mode of 7, 8, 9, 7, 8, 9, 9,, 5, dk n'keyo izlkj gksrk gsa 1 5 Decimal expansions of 17 is... 5
84 15- fn;s x;s fp=k esa x dk eku gksxka 1 What will be the value of x in the given figure (triangle)? 16- nks cgqhkqt le:i gksrs gsaa ;fn muds laxr dks.k cjkcj gks rfkk laxr Hkqtk, gksaa 1 Two regular polygon will be similar if their corresonding angle are equal and corresponding sides be dkrhz; ry esa flfkr fdlh fcunq (µ4] 5) esa dksfv dk eku gksxk A 1 The value of ordinate of point ( 4, 5) in cartesian plan A.P 5, 9,1,17,... dk lkozarj gksxka 1 The common difference of A.P. 5, 9, 1, 17 is sin 60 cos0 sin0 cos60 dk eku gksrk gsa 1 The value of sin 60 cos0 sin0 cos60 is D;k x x + = 0dk,d ewy gs \ Is a root in x x + = 0... vfr y?kq mùkjh; iz'u%& Very Short Questions : 1- fn;s x, A.P 16,, 8, 4,...dk igyk in vksj lkoz varj Kkr djsaa Find the first term and common difference in the given A.P 16,, 8, 4, fl¼ djsa fd cot 48 cot cot 4 cot 57 = 1 - ;fn Prove that cot 48 cot cot 4 cot 57 = 1 If cos A = 4 rks sin AvkSj tan A dk eku fudkysaa cos A = 4 then find the value of sin Aand tan A. 4- vkd`fr esa DE BC gsa rks ECKkr dhft,a In the figure DE BCthen find EC?
85 5- cxy ds fp=k esa PAvkSj PBo`r dh Li'kZ js[kk gsa rfkk APO = 0 rks AOB D;k gksxk\ In the figure PA and PB is tangent line of circle and APO = 0 then what is the value of AOB. 6- f}?kkr lehdj.k 6 x x = 0 ds izd`fr Kkr djsaa Find the nature of the quadratic equation a b c a b c 6 x x = vuqikrksa 1, 1, 1 dh rqyuk dj Kkr dhft, fd fn;s x;s jsf[kd lehdj.k dk ;qxe laxr gs ;k vlaxra a On comparing the ratios 1 b, 1 c, 1 a b c x y = 8rFkk 4 x 6y = 9 of the given linear equations x y = 8 and 4 x 6y = 9, find out whether the given pair of linear equations consistent or in consistent. 8- fn, x, ds fp=k esa ;fn PR CBvkSj PS CDgks rks fl¼ djsa fd OR = OS OB OD In the given figure if PR CBand PS CDthen prove that OR = OS OB OD. 9-,d lef}ckgq ABCesa <C = 90 rks fl¼ djsa fd AB = AC Angle (<C) = 90 in a isosceles triangle then prove that AB = AC. 0- ml xksys dk i`"b {ks=kiqy fudkysa ftldk O;kl 14 lsehú gsa Find the surface area of sphere where diameter is 14 cm. 1- ;fn fcunq P(, )dh nwjh Q(10, y)ls 10 bdkbz gks rks ydk eku Kkr djsaa If the distance from Q(10, y) to point P(, ) is 10 unit then find the value of y.
86 y?kq mùkjh; iz'u %& Short Questions: - fl¼ djsa fd 5,d vifjes; la[;k gsa Prove that 5 is irrational. - 1 lsehú O;kl] okyh 8 lsehú yach rk cs dh,d NM+ dks,d leku pksm+kbz okys 18 ehú yacs,d rkj ds :i esa [khapk tkrk gsa rkj dh eksvkbz Kkr djsa A copper rod of diameter 1 cm and lenth 8 cm is drawn into a wire of length 18 m of uniform thickness. Find the thickness of the wire? 4- fl¼ dhft, fd (1 sina)(seca + tana) =1 Prove that (1 sina)(seca + tana) =1 5- vuqikrksa cosa, tanavksj seca dks sinads inksa esa O;Dr dhft,a Express the ratios cosa, tanaand seca in terms of sina. 6- fdlh fhkuu ds va'k vksj gj dk ;ksx 10 gsa ;fn gj esa tksm+ fn;k tk; rks fhkuu 1 gks tkrk gsa fhkuu Kkr djsaa The sum of numerator and denominator of any fraction is 10. If is added to denominator the fraction becomes 1. Find the fraction. 7- nks vadksa okyh fdruh la[;k, ls fohkkt; gsa \ How many number of two digit is divisible by? 8-,d FkSys esa yky vksj 5 dkyh xsan gs bl FkSys ls,d xsan ;kn`pn;k fudkyh tkrh gsa bldh izkf;drk D;k gksxh fd xsan (d) yky gs] ([k) yky ugha gsa In a bag there is red and 5 black balls. One ball is taking out atrandom. What will be probability of ball in (a) is it red? (b) is it not red? cot A cos A coseca 1 = cot A + cos A coseca fl¼ dhft, fd Prove that cot A cos A coseca 1 = cot A + cos A coseca fueufyf[kr ckjackjrk forj.k dk cgqyd Kkr djsaa Find the Mode of following frequency distribution. oxz varjky 6µ10 11µ15 16µ0 1µ5 6µ0 ckjackjrk f}?kkr lehdj.k x 6x + = 0 ds ewy Kkr dhft,a Find the roots of the quadratic equation x 6x + = ;fn sina = cos(a 6 ) gks tgk ] A,d U;wudks.k gs rks Adk eku Kkr dhft,a If sina = cos(a 6 ) where A is an acute angle. Find the value of A.
87 nh?kz mùkjh; iz'u %& Long Question : 4- xzkiqh; fof/ ls lehdj.k gy djsaa 5 Solve the equation by graphically. x 4y + 14 = 0 x + y 14 = 0 44-,d lery tehu ij [km+h ehukj dh Nk;k ml flfkr esa 0 ehú vf/d yach gks tkrh gs tc fd lw;z dk muurka'k 60 ls?kvdj 0 gks tkrk gsa ehukj dh mq pkbz Kkr dhft,a 5 The shadow of a towar standing on a level ground is found to be 0m longer when the sun s altitude is 0 then what it is 60. Find the height of the towar. 45- ikuh ls iwjh Hkjh gqbz,d v¼zxksykdkj Vadh dks,d ikbi }kjk 4 7 yhvj izfr lsdsam dh nj ls [kkyh fd;k tkrk gsa ;fn Vadh dk O;kl ehú gs rks og fdrus le; esa vk/h [kkyh gks tk;sxh \ ( π = ) A hemispherical tank full of water is emptied by a pipe at the rate of ltr/sec. How 7 much time will it take to empty half of the tank, if it is m in diameter?(take π = ) ABC esa C ledks.k gsa ;fn Cls ABij [khaps x;s yac dh yackbz P gks vksj AB = c, BC = a8 CA = bvksj CD = p rks fl¼ djsa fd = P a + b 5 ABC is a right triangle in which C = 90, CD AB. If AB = c, BC = a, CA = b and CD = pthen prove that = +. P a b vfkok ^OR 46- cxy ds fp=k esa PDC PBA, BPC = 15 ] CDP = 70 rks DPC, DCP,oa PAB Kkr djsaa In side by figure PDC PBA, BPC = 15 <BPC =15 and CDP = 70 then find DPC, DCF and PAB? 47- lsehú f=kt;k okys o`r ds ckgj flfkr,d fcunq ls ml ij Li'kZ js[kkvksa dh jpuk djsaa 5 To construct the tangents to a circle of radius cm from a point outside it?
88 SOLUTION (1) (x) () ([k) () (x) (4) (d) (5) (?k) (6) (d) (7) (?k) (8) (d) (9) (?k) (10) (d) (11) b 4ac > 0 (1) sec A (1) 9 (14) 0-68 (15) 10 (16) lekuqikrh (17) 4 (18) 1 (19) 1 (0) gk (1) igyk in ( a ) = 16 lkoz varj ( d ) =nwljk in µ igyk in = 16 = 6 Ans. () L.H.S. = cot 48 cot cot 4 cot 57 = cot(90 4)cot(90 57 )cot 4 cot 57 = tan 4 tan 57 cot 4 cot = tan 4 tan 57 = 1 R.H.S. Proved tan 4 tan 57 () Given cos A = sina = 1 cos A = 1 = 1 = = sin A tana = = = = Ans. cos A 4 4 (4) fn;k x;k gs ABCesa DE BC AD AE BD = EC 1.5 = 1 EC = EC BC = = BC = cm Ans. 15 (5) APO = 0 OA APij OAP = 90 AOP =180 ( ) = = 60 Ans. (6) fn;k gqvk gsµ 6 x x = 0 ;gk a = 6, b = 1, c =
89 D = b 4ac = ( 1) 4 6 = = 49 > 0 D > 0 (7) x y = 8 4 x 6y = 9 ewy oklrfod vksj vleku gsa a 1 =, b1 =, c 1 = 8 a = 4, b = 6, c = 9 b = = = vfkkzr~ 1 b 1 c = 1 a b c a 1 b 1 c =, =, =, a 4 b 6 c vr% jsf[kd lehdj.kksa dk ;qxe laxr gsa (8) fp=kkuqlkj OBCesa] PR CB FksYl izes; ls OR OP = --- (1) OB OC iqu% OCD esa] PS CD FksYl izes; ls OP OS = --- () OC OD vr% (1) vksj () ls OR OS = lr;kfira OB OD (9) fn;k x;k gs iz'u ls ABC,d lef}ckgq f=khkqt gs ftldk dks.k C ledks.k gsa fl¼ djuk gsµ AB = AC ACBesa] Rkks AB (0) ge tkurs gsa fd iz'u ls C = 90, AC = BC(fn;k gs) AB = AC + BC (ikbfkksxksjl izes; ls) d =14cm, = AC + AC [BC = AC] = AC fl¼ gqvk d 14 r = = = 7cm
90 Xkksys dk i`"b {ks=kiqy = πr (1) PQ = ( 10) + ( y) PQ 8 ( y) = (7) = = 46cm Ans. = + + iz'u ls PQ =10 10 = y + y or, y + 6 y 7 = 0 or, y + 9 y y 7 = 0 or, y( y + 9) ( y + 9) = 0 or, ( y + 9)( y ) = 0 y = 9, Ans. () ekuk fd 5,d ifjes; la[;k gsa a 5 =, b tgk a vksj b ( b 0) lgvhkkt; la[;k, gsa a vr% 5 b = gsa blh lehdj.k esa iquo;zoflfkr djus ij gesa izkir gksrk gsa = 5 a b pw fd a vksj b iw.kkzad la[;k, gs] blfy, 5 a b la[;k gsa,d ifjes; la[;k gs vfkkzr~ ifjes; ijarq blls bl rf; dk fojks/khkkl izkir gksrk gs fd,d vifjes; la[;k gsa gesa ;g fojks/khkkl viuh xyr dyiuk ds dkj.k izkir gqvk gs fd 5,d ifjes; la[;k gsa vr% ge fu"d"kz fudkyrs gsa fd 5,d vifjes; la[;k gsa () NM+ dk vk;ru 1 = π 8 cm = π cm leku vk;ru okys rkj dh yackbz = 18m =1800cm ;fn rkj ds vuqizlfk dh f=kt;k r gs rks] rkj dk vk;ru = π r 1800 cm vr% π r 1800 = π π 1 r = = π r = 900
91 1 1 r = = cm vr% rkj ds vuqizlfk rkj dk O;kl] rkj dh pksm+kbz 1 cm 15 (4) L.H.S. = seca(1 sina)(seca + tana) 1 1 sina = (1 sina) + cos A cosa cosa (1 sina)(1+ sina) = cos A 1 sin A cos A = = 1 R.H.S Proved cos A cos A = = (5) ge tkurs gsa fd cos A + sin A = 1 So, cos A = 1 sin A vfkkzr~] cos A = 1 sin A ± blls ;g izkir gksrk gs cos A = sina vr% tan A = = cosa sina 1 sin A 1 1 vksj seca = = cos A 1 sin A (6) ekuk fd fhkuu x = y 1 sin A iz'ukuqlkj] x + y = 10 (i) x 1 = y + ;k] x = y + x y = (ii) lehú (i) rfkk (ii) dks tksm+us Ikj x + y = 10 x y = 1 x = = 4 x = 1 x = 4 lehú (i) j[kus ij 4 + y = 10 y = 6 x 4 vr% vhkh"v fhkuu = = y 6. ;kfu 0.67mm (yxhkx)
92 (7) 10,11,1,1,..., 99esa vadksa okyh mls fohkkt; la[;k, 1,15,18, 1, 4,..., 99 ;gk ls lú{ksú ds fy, a = 1, d = 15 1 =, l = 99 l = a + ( n 1) d 99 = 1 + ( n 1) = n 1 = n 1 ;k n 1= 9, n = 0 Ans. (8) FkSys esa dqy xsan = + 5 = 8 dqy lahkkfor ifj.kkeksa dh la[;k = 8 (9) (d) P (yky xsan) = 8 5 ([k) P (yky xsan ugha) = 1 = Ans. 8 8 cos A cos A cota cos A L.H.S. = = sina cota + cos A cos A + cos A sina 1 1 cos A 1 1 sina sina coseca 1 = = = = R.H.S 1 1 coseca + 1 cos A sina sina (40) ;gk cgqyd oxz 16µ0 gsa D;ksafd bldh ckjackjrk lokzf/d gsa 16µ0 esa viorhz cukus ij ;g oxz = bl izdkj] l = 15.5, f0 = 50, f 1 = 0, fi = 40, i = 5 f 0 f Mode = l + 1 ils f0 f 1 f i M 0 = = = = 18.8 (41) x 6x + = x 6 x 6x + = x( x ) ( x ) = ( x )( x ) vr% lehdj.k ds ewy x ds os eku gsa] ftuds fy, ( x )( x ) = 0 x = x = 0
93 iqu% ] vr% x = 0 x = 6 0 x x + = ds ewy, gsaa (4) ;gk fn;k gqvk gs fd sina = cos(a 6 ) --- (1) sin A = cos(90 A) blfy, ge (1) dks bl :i esa fy[k ldrs gsaa cos(90 A) = cos(a 6 ) D;ksafd 90 AvkSj A 6 nksuksa U;wudks.k gs rks 90 A = A 6 A A = 6 90 izkir gksrk gsa (4) 116 4A = 116 A= A = 9 4 x 4y + 14 = 0...(1) and x + y 14 = 0...() lehú (1) x 4y + 14 = 0 lehú () x + y 14 = 0 x 4 y = 14 x + y = 14 x + 14 = 4y x = 14 y x y = y x = 4 x 0 y 4.5 nksuksa vkys[kksa dk dvku fcunq (] 4) gsa vr% gy & x = y = 4 x 4 0 y 1 7 4
94 (44) eku fyft, fd ABehukj dh yackbz h ehvj gsa vksj BC, x ehvj gsa DC = 0ehVj DB = DC + CB = (0 + x) ehú vr% DB = (0 + x) ehú vc ;gk nks ledks.k f=khkqt ABCvkSj ABDgSA ledks.k ABCesa AB tan 60 = BC h x AB ABDesa] tan 0 = BD 1 h or, = x + 0 (1) ls gesa izkir gksrk gsa h x = ---(1) ---() = ---() bl eku dks () esa izfrlfkkfir djus ij gesa ;g izkir gksrk gs ( x ) = x + 0;kfu fd x = x + 0 x x = 0 blfy, () ls x = 15 0 x = 0 x = = 15 vr% ehukj dh mq pkbz 15 gsa (45) v¼zxksykdkj Vadh dh f=kt;k vr% Vadh dk vk;ru = m = m 7 m = 7 99 m = 14 ml ikuh dk vk;ru] ftls [kkyh fd;k tkuk gsa 1 99 m = 14
95 = 1000 = yhvj 8 8 vc 5 yhvj ikuh [kkyh gksrk gs 1 lsdsam esaaa 7 blfy, yhvj ikuh [kkyh gksxk = = = 990 second = feuv Ans. (46) ABC esa ABdks vk/kj ysrs gq, dk {ks=kiqy 1 = AB CD 1 = C p iqu% BCdks vk/kj ekurs gq, 1 1 ABCdk {ks=kiqy = BC AC= ab 1 1 C p = ab C p = a b 1 C 1 c = = p ab p a b 1 b + a = p a b ikbfkkxksjl izes; ls] ABCesa c a b b a = + a b a b = + Proved p a b DPC + BPC =180 DPC +15 =180 DPC = = 55 CPD esa] = + vfkok (jsf[kd ;qxe vfhkx`ghr) o CDP + DPC + DCP =180 (f=khkqt ds rhuksa ;ksx dk ;ksx 180 gksrk gsa)
96 DCP =180 ;k DCP =180 ( ) = DCP = 55 iqu% PDC PBA (fn;k gs) PAB = PCD PAB = 55 ( PCD = 55 ) blh izdkj DPC = 55 DCP = 55, PAB = 55 (47) jpuk ds pj.kµ (1) dksbz fcanq 0 dks dsunzekudj lsehú f=kt;k dk,d o`ùk [khpsaxsa () o`ùk ds ckgj dksbz fcanq fcanq P ysaxsa () PO dks feyk,sxs vksj bls lef}hkkftr djsaxs eku fd POdk eè; fcunq M gsa (4) Mdks dsunz eku dj rfkk MOf=kT;k ysdj,d o`ùk [khpsaxsaa ;g fn, x, o`ùk dks Q vksj R Ikj izfrpnsn djrk gsa (5) Mdks Q rfkk R ls feyk,saxs rc PQvkSj PRvHkh"V Li'kZ js[kk, feyrh gsa
97 ! # % #&& () +,. /!,), %,0) 1,/ # % %) (,/ & ( %456 0 ) 7,/ )!
98 Lke; %?kavk 15 feuv xf.kr (lsv&6) MATH (SET-6) Time : Hrs 15 Min. Full Marks : 100 lgh mùkj pqus %& Choose the correct answer :- fueu esa ls dksu f}?kkr lehdj.k x + x 6 = 0 dk,d gy gs \ 1 (d) x = ([k) x = (x) x = (?k) x = Which of the following is a solution of the quadratic equation x + x 6 = 0? (a) x = (b) x = (c) x = (d) x = - nksa la[;kvksa dk e-l- 5 rfkk y-l- 50 gsa rks budk xq.kuiqy fueu esa ls dksu gksxk \ 1 (d) 1050 ([k) 1150 (x) 150 (?k) 150 H.C.F. and L.C.M. of two numbers are 5 and 50 respectively. Which of the following is the product of the numbers? (a) 1050 (b) 1150 (c) 150 (d) fueu esa ls dksu ifjes; la[;k gs \ 1 (d) 1 ([k) 16 Which of the following is a rational number. (a) 1 (b) 16 (x) (c) (?k) fdlh ABC esa A = 90, BC =1cm, AB =1cm rks fueu esa ls dk eku dksu gs \ 1 (d) (d) lsehú ([k) 4 lsehú (x) 5 lsehú (?k) 6 lsehú In AC? ABC 8 A = 90, BC =1cm, AB =1cm 8 which of the following is the value of (a) cm (b) 4 cm (c) 5 cm (d) 6 cm 5- lekarj Js.kh 11, 8, 5,...dk izfke /ukred in fueu esa ls dksu gksxk \ 1 (d) 1 ([k) µ (x) (?k) Which of the following is the first positive term of the given A.P. 11, 8, 5,...? (a) 1 (b) (c) (d)
99 6- fdlh fcunq P( x, y) dk ewy fcunq ls nwjh fueu esa ls dksu gksxk \ 1 (d) x + y ([k) x y (x) x + y (?k) x y Which of the following is the distance of a point P( x, y ) from the origin? (a) x + y (b) x y (c) x + y (d) x y 7- f=khkqt dk xq:ro dsuæ mldh ekfè;dk dks fueu esa ls fdl vuqikr esa fohkkftr djrk gs \ 1 (d) 1 % ([k) % 1 (x) 1 % (?k) % 1 Centroid of a triangle divides its median in which of the following ratio? (a) 1 : (b) : 1 (c) 1 : (d) : 1 8- cosec60 dk eku fueu esa dksu gs \ 1 (d) ([k) (x) Which of the following is the value of cosec60? (a) (b) 9- cosec cot (c) (d) (?k) θ θdk eku fueu esa dksu gs \ 1 (d) 1 ([k) (x) (?k) 1 Which of the following is the value of cosec θ cot θ (a) 1 (b) (c) (d) o`r dk {ks=kiqy dk lw=k fueu esa dksu gs \ 1 (d) π r ([k) π r (x) π r (?k) π r Which of the following is the formula for area of a circle? (a) π r fjdr LFkkuksa dh iwfrz djs %& Fill in the blanks : (b) π r (c) π r (d) πr dk n'keyo izlkj gksxka 1 Decimal expansion of 5 is f}?kkr lehdj.k ax + bx + c = 0 ds ewyksa dk xq.kuiqy gksrk gsa 1 Product of the roots of a quadratic equation ax + bx + c = 0 is...
100 1- ABC,d ledks.k f=khkqt gs ftldk B = 90, C = 0 rks A = ABC is a right angle triangle in which B = 90, C = 0 then A = dksbz ljy js[kk fdlh f=khkqt dh nks Hkqtkvksa dks leku vuqikr esa dkvrh gs rks og js[kk rhljh Hkqtk ds gksrh gsa 1 If a line divides any two sides of a triangle in the same ratio, the line must be... to the third side. 15- ;fn lekraj Js.kh dk izfke in a rfkk bldk lokzarj dgks rks n oka in = a + (...) d 1 If the first term of an A.P. is a and its common difference is d then n th term = a + (...) d 16- o`r dh Li'kZ js[kk o`r dks ftl fcunq ij Li'kZ djrk gs mls dgk tkrk gsa 1 The tangent line touches the circle on a point is called ;fn lekarj Js.kh dk n th If th n in t n }kjk lwfpr gks rks tn tn 1 =... lwfpr gksrk gsa 1 term of an A.P. is denoted by t n then tn tn 1 is denoted by cos θ cjkcj gksrk gsa 1 1 cos θ s equal to tan0 dk eku gksrk gsa 1 The value of tan0 = ekè; µ cgqyd =... (ekè; µ ekfè;dk) 1 Mean Mode =... (Mean Median) vfr y?kq mùkjh; iz'u%& Very Short Questions : 1- fn[kk, fd fn;k x;k lehdj.k ;qxe vfojks/h] fojks/h ;k vkfjr gsa x + y = 7vkSj 6x + 5y = 11 Show that the given simultaneous equations are consistent, inconsistent or dependent. x + y = 7and 6x + 5y = 11-1 x ds fy, gy djsaa 10 x = x 1 Solve for x, 10 x = x - ABC,d ledks.k f=khkqt gs ftldk A = 90 ] AM BC. ABM rfkk CAM esa laca/ crk, A ABC is a right triangle in which A = 90, AM BC. Show the relation between ABMand CAM.
101 4- fn;s x;s fp=k esa Oo`r dk dsuæ gsa APvkSj AQckg~; fcunq Als nks Li'kZ js[kk;sa gsaa ;fn OPQ = 0 rks dk PAQ eku fudkysa In the adjoin figure, O is the centre of a circle. From external point A, two tangents AP and AQ drawn on the circle. If OPQ = 0 then find measure of PAQ. 5- fcunq (] ) rfkk (4] 1) ds chp dh nwjh Kkr dhft,a Find the distance between the points (, ) and (4, 1). 6-7 lsehú f=kt;k okys o`r ds f=kt;[kam dh ifjfefr Kkr djsa ftldk dsuæh; dks.k 90 gsa Find the perimeter of a sector of a circle whose central angle is 90 and radius 7 cm. 7-8 lsehú Hkqtk okys oxz ds vanj cus egùke oxz dk {ks=kiqy Kkr djsaa Find the area of the circle that can be inscribed in a square of side 8 cm. 8- fn[kk, fd fcunq A(0,1), B(, ), C(, 4)lajs[k gsaa Show that the points A(0,1), B(, ), C(, 4)are collinear. 9- ;fn 5sin θ = 4rks cosθvksj cotθdk eku fudkysaa If 5sin θ = 4then find cosθand cotθ. 0- fl¼ djsa fd sin 40 + sin 75 = cos15 + cos50 Prove that sin 40 + sin 75 = cos15 + cos fn;s x;s lekarj Js.kh ] 8] 1] 18] ds 15oka in dk eku fy[ksaa Write a 15 th term of the given A.P., 8, 1, 18,... y?kq mùkjh; iz'u %& Short Questions: - fl¼ djsa fd,d vifjes; la[;k gsa Prove that is an irrational number. - nksa la[;k, 96,oa 404 dk eúlú rfkk yúlú vhkkt; xq.ku[kam fof/ ls Kkr djsaa Find the HCF and LCM of 96 and 404 by prime factorization method.
102 4- gy djsa%& 6x + y 6xy = 0vkSj x + 4 y 5xy = 0 Solve the equation : 6x + y 6xy = 0and x + 4 y 5xy = 0 5- f}?kkr lehdj.k x 5x + 1 = 0ds ewyksa dh izd`fr Kkr djsaa Find the nature of roots for the quadratic equation 6- fdlh ABC esa AD BC] ;fn In any triangle triangle. ABC, AD BC. If x 5x + 1 = 0. BD DA = rks fl¼ djsa fd ABC ledks.k f=khkqt gsaa DA DC BD DA = then prove that ABC is right DA DC 7- fcunq A(5,1) dh y &v{k ls yacor nwjh Kkr djsaa Find the perpendicular distance of point A(5, 1) from y-axis. 8-,d csx esa 6 yky,oa 5 uhyk xsan gsa ;fn csx ls,d xsan dks ;n`pn;k fudkyh tk, rks blds yky ugha gksus dh izkf;drk Kkr djsaa A bag contains 6 red and 5 blue balls. If a ball is drawn at random. Find the probability the ball is not red fl¼ djsa fd cos A sin A = cos A 1 Prove that 4 4 cos A sin A = cos A tan 45 + cos 0 sin 60 dk eku fudkysaa Find the value of tan 45 + cos 0 sin fdlh Ldwy dh d{kk IXdh 51 ym+ds dh mq pkbz;ksa (lsehú esa) dk,d losz{k.k fd;k x;k vksj fueufyf[kr vkadm+s izkir fd, x,a ekè;d mq pkbz Kkr dhft,a mq pkbz (lsehú esa) ym+dksa dh la[;k 140 ls de ls de ls de ls de ls de ls de 51
103 A survey regarding the heights (in cm) of 51 boys of class IX of a school was conducted and the following data was obtained. Find the median height. Height (in cm.) Numbers of Boys less than less than less than less than less than less than fueufyf[kr vkadm+ksa dk cgqyd Kkr dhft,a izkirkad 10 ls de 0 ls de 0 ls de 40 ls de 50 ls de 60 ls de 70 ls de 80 ls de ckjackjrk Find the mode of the following data. Marks less less less less less less less less than than than than than than than than Frequency nh?kz mùkjh; iz'u %& Long Question : 4-,d vk;rkdkj dkxt dk VqdM+k ftldk eki 44cm 18cmgSA bls yackbz ds vuq:i eksm+dj csyukdkj cuk fn;k tkrk gsa csyu dk vk;ru fudkysaa 5 A rectangular sheet of paper of dimension 44cm 18cm is rolled along its length and a cylinder is formed. Find volume of cylinder.
104 44-,d VkWoj ds ikn ls,d edku ds 'kh"kz dk muu;u dks.k 0 rfkk edku ds ikn ls VkWoj ds 'kh"kz dk muu;u dks.k 45 gsa VkWoj dh mq pkbz 0 ehvj gs rks edku dh mq pkbz Kkr djsaa 5 The angle of elevation of the top of a building from foot of the tower is 0 and the angle of elevation of top of the tower from the foot of the building is 45. If the tower is 0m high, find the height of the building. vfkok OR lw;z ds muu;.k dks.k 0 ds fy, VkWoj dh Nk;k dh yackbz 0 ehvj gs rks lw;z ds 60 ds muu;u dks.k ds fy, Nk;k dh yackbz Kkr djsaa If the shadow of a tower is 0m long when sun s elevation is 0. What is the length of the shadow when sun s elevation is 60? 45- xzkiqh; fof/ ls lehdj.k ;qxe dk gy djsaa 5 x y + 1 = 0 x + y 1 = 0 Graphically solve the simultaneous equation. x y + 1 = 0 x + y 1 = fl¼ djsa fd o`r ds O;kl ds Nksj fcunqvksa ij [khaph x;h Li'kZ js[kk, lekarj gksrh gsaa 5 Prove that the tangents drawn at the ends of a diameter of a circle are parallel. vfkok OR fl¼ djsa fd ledks.k f=khkqt ds d.kz dk oxz vu; nks Hkqtkvksa ds oxksz ds ;ksx ds cjkcj gksrk gsa Prove that in a right triangle, the square on the hypotenuse is equal to the sum of the squares on the other two sides. 47-,d f=khkqt ABCdh jpuk djsa tcfd AB = 4cm, BC = 5cm, AC = 6cm A blesa ml nwljs f=khkqt dh jpuk djsa ftudh Øekuqlkj Hkqtk, ABC dh Hkqtkvksa dk xq.kk gksa 5 Construct a triangle ABC in which AB = 4cm, BC = 5cm, AC = 6cm. Then construct another triangle whose sides are times the corresponding sides of ABC. vfkok OR 7 lsehú dh,d ljy js[kk [khapdj mls % 5 ds vuqikr esa var% fohkkftr djsaa Draw a line segment of length 7cm. Find a point on it which divides internally it in the ratio :5.
105 SOLUTION (1) ([k) () (x) () (?k) (4) (x) (5) (d) (6) (x) (7) ([k) (8) (?k) (9) (d) (10) (x) (11) lkr (1) c a (1) 60 (14) lekarj (15) n 1 (16) Li'kZ fcunq (17) lkoz&varj ( d ) (18) sinθ (19) (0) 1 (1) fn;s x;s lehdj.k x + y = 7, 6x + 5y = 11esa a 1 b1 =, = a 6 b 5 a 1 b 1 a b () lehdj.k ;qxe vfojks/h gsa 1 10 x = x x x 10 1 = 10 x x 1 = 0 10 x 5x + x 1 = 0 ( x 1)(5 x + 1) = x =, 5 () fp=k esa] BAC = 90 vksj AM BC AMB = AMC = 90 <ABM CAM nksuksa f=khkqt le:i gksaxsa
106 (4) fn;s x;s fp=k esa OPQ = 0 PAQ = OPQ = 0 = 40 (5) fcunq (] ) vksj (4] 1) ds chp dh nwjh (6) f=kt;[kam dh ifjfefr (Perimeter of sector) = ( x x ) ( y y ) = ( 4) + ( 1) = 8 = bdkbz πrθ = r + r = = = 5cm (7) oxz dh Hkqtk (side of square) = 8cm o`r dh f=kt;k = 4cm o`r dk {ks=kiqy = πr 5 = 16 = cm 7 7 (8) rhu fcunqvksa A(0] 1)] B(] ) vksj C(] 4) ls cus ABC dk {ks=kiqy 1 = [0( 4) + (4 1) + (1 )] 1 = [ ] = 0
107 pwafd ABC dk {ks=kiqy = 0 vr% rhuksa fcunq lajs[k gsaa (9) 4 5sin θ = p 4 sin θ = 5 = h ;gk ] vr% p = 4, h = 5, b =? b = h p = (5) (4) = 5 16 = 9 = cos θ = rfkk 5 cot θ = 4 (0) sin 40 + sin 75 = sin(90 50) + sin(90 15) = cos50 + cos15 = cos15 + cos50 (1) lekurj Js.kh ] 8] 1] 18] ;gk a =, d = t t1 = 8 = 5, n = 15 t = a + ( n 1) d n t 15 = + (15 1) 5 = + 70 = 7 () ekuk fd,d ifjes; la[;k gsa rc = p, p,oa q/u iw.kkzad rfkk mhk;fu"b xq.ku[kam ugha gsa q oxz djus ij p = or p = q q (le la[;k) --- (1) phkh le la[;k gsa --- () iqu% ekuk fd p = m, miw.kkzad gsa p = 4m or, = m or, q (lehú1 ls) q = m qhkh le la[;k gsa --- () () vksj () ls p, q le la[;k gs blfy, p vksj q esa mhk;fu"b xq.ku[kam gksxka tks dyiuk ds foijhr gsa vr% ifjes; la[;k] ;g ekuuk xyr gsa vfkkzr~ vifjes; la[;k gsa
108 () 96 = 404 = 101 eúlú = = 4 yúlú = 101 = 9696 (4) 6x + y 6xy = 0 or, 6x + y = 6xy xyls Hkkx nsus ij 6 + = 6 y x iqu% x + 4y = 5xy xyls Hkkx nsus ij eqn.() 4 + = 5 y x eqn.(1) --- (1) --- () = 15 y x 6 + = 6 y x 9 = 9 x x = 1 lehú (1) esa x = 1 j[kus ij] 6 6 y = = y = 6 y = gy % x = 1, y = (5) x 5x + 1 = 0 a = b = c = ;gk, 5, 1 D = b 4 ac = ( 5) 4 1 = = 5 8 = < 0 vr% ewy oklrfod ugha gksxka (6) BDA rfkk CDA esa] BDA = CDA = 90 iz'u ls] BD DA = DA DC BDA CDA
109 BAD = ACD o 90 ABD = ACD vfkkzr~ ABD + ACD = 90 BAC = 90 vr% ABC,d ledks.k f=khkqt gsa (7) y- v{k ij fcunq dk fu;ked (0] 1) gsa (5] 1) ls yecor nwjh (0] 1) dk = (0 5) + (1 1) = = 5 (8) csx esa dqy xsanks dh la[;k = =11 lahko dqy ifj.kkeksa dh la[;k =11 yky xsnkas dh lúa 6 P(yky xsan) = = lha ko dqy ifj.kkekas dh lúa 11 bdkbz P (yky xsan ugha) = = 1 = = (9) cos A sin A = (cos A) (sin A) = (cos A + sin A)(cos A sin A) = cos A sin A cos A + sin A = 1 = cos A (1 cos A) = cos A 1 (40) tan 45 + cos 0 sin 60 = (1) + = 1 + = 4 4
110 (41) oxz vurjky ( c. i.) ckjeckjrk ( f ) lap;h ckjackjrk ( c f ) 140 ls de µ µ µ µ µ vc N = 51gSA N = 51 rks N = 51 = 5.5gSA N cf lw=k ls] ekè;d = l + h f varjky 145 µ 150 ekè;d oxz varjky esa vkrk gsa l (fueu lhek) = 145 ekè;d oxz 145 µ 150 tks Bhd igys oxz dh lap;h ckjackjrk ( cf ) = 11 eè;e oxz 145 µ 150 dh ckjackjrk f = 18rFkk oxz eki ( h ) = 5 gsa (4) ekè;d = = = rks ym+dksa dh ekè;d mq pkbz = 149.0cm gsa izkirkad lap;h ckajckjrk ckjackjrk 10 ls de µ (¾40 µ 5) 0 µ (¾60 µ 40) 0 µ (¾75 µ 60) 40 µ (¾95 µ 75) 50 µ (¾10 µ 95) 60 µ (¾195 µ 10) 70 µ (¾45µ 195)
111 cgqyd oxz 60 µ 70 gs D;ksafd bldh ckjackjrk lokzf/d gsa fo f (Mode) M 1 o = l + i fo f f tgk ] 1 1 l = Modal class vfkkzr~ vf/dre ckjeckjrk okyk oxz dh fueu lhek fo = Modal class dh ckjeckjrk f 1 = Modal class ds Bhd igys okyk oxz dh ckjeckjrk f 1 = Modal classds Bhd ckn okyk oxz dh ckjeckjrk i =oxz vurjky dh yackbz ;gk ] l = 60, fo = 65, f 1 = 5, f1 = 50, i = 10 vhkh"v cgqyd 65 5 = ( 65) = 60 + = = 60 + = = 66.7Ans. (4) vk;rkdkj dkxt dks yackbz ls eksm+k x;k gsa csyu dh ifjf/ = π r = 44cm or, 44 7 r = = 7cm csyu dh mq pkbz ( h) = 18cm csyu dh vk;ru = πr h 7 = 7 18 = 77cm Ans.
112 (44) ekuk fd edku dh mq ú h m gs rfkk BD = x cm ABD esa] 0 tan 45 = x or, x = 0 m CBD esa] tan 0 = h 0 1 or, = h 0 0 or, h = 0 or, h = = 10 m = m edku dh mq ú = 17. m ABC esa] vfkok OR tan 0 = h 0 1 or, = h 0 or, h = 10 iqu% ABD esa] tan 60 = h x 10 or, = x or, x = 10m
113 Nk;k dh yackbz = 10m (45) lehdj.k x y + 1= 0ls y = x (1) lehdj.k x + y 1 = 0ls lehú(1) dk eku lkj.kh 1 x y = --- () x 0 1 y 1 0 lehú() dk eku lkj.kh x 0 4 y 6 0 lehdj.kksa ds vkys[k (] ) ij izfrpnsn djrs gsaa vr% gy x =, y = (46) ekuk fd,d o`r ftldk dsuæ OgSA ABo`r dk O;kl gsa CDrFkk EF nks Li'kZ js[kk;sa gsaa AB CDrFkk AB EF CAB = 90 rfkk ABF = 90 CAB = ABF rfkk ;s,dkarj dks.k gsaa CD EF Proved ekuk fd ABC,d ledks.k f=khkqt gsa ftldk B = 90 ACd.kZ gsa BD ACMkyk ADB rfkk ABC esa vfkok OR
114 BAD = BAC (mhk;fu"v dks.k) ADB = ABC = 90 ADB ABC AB AD or AB AC AD AC = AB = --- (1) blh izdkj BDC rfkk ABC Hkh le:i gsaa BC DC or BC AC DC AC = BC = --- () (1)$() djus ij AB + BC = AC(AD + DC) = AC AC = AC or, AC = AB + BC Proved. (47) cukov ds pj.k%µ BC = 5cm BdsUæ ls AB = 4cm pki [khapk C dsuæ ls AC = 6cm pki [khapka dvku fcanq feyk;ka ABC BX ij BB 1 = B1B = BBfpUg yxk;saa cuk B,oa Cdks feyk;saa B ls B C B C[khapsaA C ls C A CA[khapsaA vhkh"v f=khkqt A BC cuka
115 cukov ds pj.k%µ vfkok OR (i) AB = 7cm[khapkA (ii) A fcunq ls U;wudks.k ysdj AX [khapka A X ij AA 1 = A1A = AA,... = A7A 8, 5 + = 8 cjkcj pki [khapka (iii) BA8dks feyk;saa A P BA [khapka fcunq P, ABdks :5esa ck Vrh gsa (iv) 8 AP : PB = :5 bl izdkj P fcunq ABdks %5 ds vuqikr esa var% fohkkftr djrk gsa
116 ! # % #&& () +,. /!,), %,0) 1,/ # % %) (,/ & ( %456 0 ) 7,/ )!
117 Lke; %?kavk 15 feuv xf.kr (lsv&7) MATH (SET-7) Time : Hrs 15 Min. Full Marks : 100 lgh mùkj pqus %& Choose the correct answer :- fueufyf[kr esa dksu vifjes; gs \ 1 (d) 64 6 ([k) 81 (x) 15 (?k) 49 9 Which of the following number is irrational? (a) 64 6 (b) 81 (c) 15 (d) - fueukafdr esa dksu cgqin ugha gs \ 1 (d) 7x ([k) y + (x) x + x + 7(?k) Which of the following is not polynomials. (a) 7x (b) - ;fn y + (c) x + x + 7 (d) x x x x + 7 sin θ = gks rks cosθeku gksxkµ 1 5 (d) 4 5 ([k) 4 (x) 5 6 (?k) 5 If sin θ = then value of cosθ 5 (a) 4 5 (b) 4 (c) 5 6 (d) 5 4- ;fn cosθ = gks rks θdk eku gsµ 1 (d) 45 o ([k) 60 o (x) 0 o (?k) 90 o If cosθ = then the value of θ. (a) 45 o (b) 60 o (c) 0 o (d) 90 o 5- fueufyf[kr esa dksu&lh?kvuk dh izkf;drk ugha gks ldrk gsa 1 (d) ([k) 15 (x) 15% (?k) 0.7% In the following which is not the probability of an event? (a) (b) 15 (c) 15% (d) 0.7%
118 6- ;fn fdlh o`r dh f=kt;k nqxquh dj nh tk; rks iqjkus,ao u;s o`rksa ds {ks=kiqyksa dk vuqikr D;k gksxka 1 (d) ([k) (x) (?k) If the radius of a circle becomes twice then the ratio of any of the old and new circle will be (a) (b) (c) (d) 7- fcunqvksa (µ5] 7) vksj (µ1] ) ds chp dh nwjh gsµ 1 (d) ([k) (x) 4 (?k) 5 Find the distance between the point ( 5, 7) and ( 1, ) (a) (b) (c) 4 (d) 5 8- ckg~; Li'kZ djus okys nks o`rksa ds mhk;fu"v Li'kZ js[kkvksa dh la[;k fdruh gsa 1 (d) 1 ([k) (x) (?k) 4 How many are common tangents if two circle are touched externally each other? (a) 1 (b) (c) (d) 4 9- f}?kkr cgqin ds 'kwu;kad dh la[;k fdruh gksrh gs \ 1 (d) ([k) (x) 1 (?k) 4 How many are numbers of zeroes in quadratic polynomial? (a) (b) (c) 1 (d) ;fn cgqin P( x) = x x + 5esa 'kwu;kad α, β gks rks α + βdk eku gksxkµ 1 (d) 5 ([k) µ5 (x) (?k) µ If α, β are the zeroes of the polynomial P( ) = + 5 x x x then value of α + βwill be (a) 5 (b) 5 (c) (d) fjdr LFkkuksa dh iwfrz djs %& Fill in the blanks :- 11- forj.k esa vf/dre ckjackjrk okyk oxz oxz dgykrk gsa 1 In a frequency distribution the class having maximum frequency is said to be tc fdlh vuqøe ds in fdlh fu;e ds rgr fy[ks tkrs gsa mls dgrs gsa 1 When the terms of a sequence has written in a difinite pattern than it is called π la[;k gsaa 1 π is an... number. 14- rhu?kkr okys cgqin dgykrs gsa 1 The polynomial having three degree is called...
119 15- fn;s x;s fp=k esa ABC esa A = 90 vksj AD BC A ;fn BD = 9 lsehú rfkk CD = 4 lsehú] rks AD = In the given figure A = 90 and AD BCif BD = 9cm and CD = 4cm then what will be of AD = ewy fcunq ls P( x, y) dh nwjh gksxha 1 The distance of a point P( x, y) from the origin is dkrhz; ry esa flfkr fdlh fcunq (µ4] 0) ds Hkqt dk eku gksxka 1 The value of abscissa of point ( 4, 0) situated at Cartesian plane sec θ 7 tan θ = ;fn θ = 90, rks tan θ =... 1 If θ = 90, then the value of tan θ is.. 0- ads eku ds fy, d m gksxka 1 d mfor the value of a... vfr y?kq mùkjh; iz'u%& Very Short Questions : 1- f}?kkr cgqin Kkr djsa] ftuds 'kwu;dksa dk ;ksx,oa xq.kuiqy Øe'k% µ vksj gsa Find the quadratic polynomial. If sum and product of zeroes are and respectively. - ewyksa dh izd`fr crkb, ;fn f}?kkr lehdj.k x 6x + = 0gksA If quadratic equation is 6 + = 0 x x then find the nature of its roots. - ABC,d leckgq f=khkqt gs] ftldh izr;sd Hkqtk a lsehú gks rks fl¼ dhft, fd f=khkqt dk 'kh"kzyec alsehú gksxka ABC is an equilateral triangle whose each sides are a cm then prove that altitude of the triangle will be a?
120 4- fdlh o`r ds dsuæ ls 5 lsehú nwj flfkr fcunq A ls [khaph xbz Li'kZ js[kk dh yackbz 4 lsehú gs] rks o`r dh f=kt;k fudkysaa From a point A which is at the distance 5 cm from the centre of the circle. The length of the tangent drawn on the circle is 4 cm. Find its radius. θ 5- fcunqvksa ( a cos, 0) rfkk ( 0, a sin θ ) ds chp dh nwjh fudkysaa Find out the distance between the points ( a cos θ, 0 ) and ( 0, a sin θ ). 6- ;fn,d o`r ds {ks=kiqy vksj ifjf/ dk la[;kred eku leku gs] rks o`r dh f=kt;k D;k gksxh \ What will be the radius of the circle if the area of a circle and circumferences are numerically same? 7- 'kadq dk vk;ru fudkysa] ftldh mq pkbz 8 lsehú vksj vk/kj dh f=kt;k 1 lsehú gsa Find the volume of the cone whose height 8 cm and base of radius is 1cm. k rfkk B( k, 5) 8- ;fn fcunq A(, ) ls fcunq P(0, )dh nwfj;k leku gks rks k dk eku Kkr djsaa If the point P(0, ) is equidistant from the points A(, k) and B(k, 5). Find the value of k. θ = rks fl¼ djsa fd 4 cos θ cosθ = 0 9- ;fn 0 If θ = 0 then prove that 4 cos θ cosθ = vhkkt; xq.ku[kam fof/ }kjk 7] 11] 19 dk egùke lekorzd vksj y?kqre lekorzd Kkr dhft,a Find the HCF and LCM of 7, 11, 19 by prime factorisation method. 1- laekrj Js.kh 0-6] 1-7] -8] -9] ds izfke 100 inksa dk ;ksx Kkr djsaa Find the sum of first 100 terms of the A.P. 0.6, 1.7,.8,.9,... y?kq mùkjh; iz'u %& Short Questions: - fl¼ djsa fd 7,d vifjes; la[;k gsa Prove that 7 is an irrational number. - fueufyf[kr ckjackjrk cavu fdlh eksgyys ds 68 mihkksdrkvksa dh fctyh dh ekfld [kir n'kkzrk gsa budk ekè; Kkr fdft,a Following are the frequency distribution of a colony where monthly electric consumption of 68 consumers shows then, what will be their mean? ekfld [kir (;wfuv esa) Monthly Consumption (Unit) mihkksdrkvksa dh la[;k No. of Consumers 5µ5 5µ45 45µ65 65µ85 85µ µ15 15µ
121 4- gy djsa%µ = rfkk 6 x 1 y 5 1 Solve it:- x 1 + y = and 1 x 1 y = 6 1 x 1 y =. 5- f}?kkr lehdj.k x x + 4 = 0 dk fofodrdj vksj ewyksa dh izd`fr Kkr dhft,a Find the discriminant and nature of the roots of the quadratic equation x x + 4 = ;fn ABCesa AD BCgS rks fl¼ djsa fd AB AC BD CD If in ABC8 AD BCprove that AB AC = BD CD. = 7- k dk eku Kkr dhft, ;fn rhuksa fcunq, (16, )] ( k, 8) rfkk (4, 10) lajs[kh gksa Find the value of k if three points (16, ), (k, 8) and (4, 10) are collinear. 8- fdlh dkj.k ls 10 [kjkc isu 10 vpns isuksa ls fey x;s gsaa dsoy ns[kdj ;g ugha crk;k tk ldrk gs fd dksu isu [kjkc isu gs ;k vpnk gsa bl fej.k esa ls,d isu ;kn`pn;k fudkyk tkrk gsa fudkys x;s isu dh vpnh gksus dh izkf;drk Kkr dhft,a Due to some reason 10 damage pen and 10 good pens has mix. It can not be seen only by searching which is damage or which is good. From this mix. the pens is taken out at random. Find the probability of pen which is good after taking out. 9- fl¼ dhft, fd 1 cot A = cot A 1 tan A 1 cot A Prove that = cot A 1 tan A. 40- fl¼ dhft, fd 1 cos A 1 cos A = coseca cot A, Prove that = coseca cot A 1 + cos A 1 + cos A 41- Hkwfe ds,d fcunq ls tks ehukj ds ikn fcunq ls 60 ehvj dh nwjh ij gsa ehukj ds f'k[kj dk muu;u dks.k 60 gsa ehukj dh mq pkbz Kkr dhft,a A point from a land where base of tower point s distance is 60 meter. Tower s angles of elevation is 60 then find the height of tower dk f=kdks.kferh; vuqikr fudkysaa Find the trigonometrical ratios of 45.
122 nh?kz mùkjh; iz'u %& Long Question : 4-,d f[kyksus dh f=kt;k 6 lsehú okys,d 'kadq ds vkdkj dk gs] tks mlh f=kt;k okys,d v¼zxksys ij vè;kjksfir gsa bl f[kyksus dh laiw.kz mq pkbz 11 lsehú gsa bl f[kyksus dk laiw.kz i`"bh; {ks=kiqy Kkr dhft,a 5 A toy is in the form of a cone of radius 6 cm. mounted on a hemisphere of same radius. The total height of the toy is 11 cm. Find the total surface area of the toy. 44- xzkiqh; fof/ ls gy djsa%µ 5 x + y = 6rFkk x 4y = 1 Solve graphically: x + y = 6and x 4y = ;fn uhps fn;s gq, cavu dk ekè;d 8-5 gks rks xvksj ydk eku Kkr dhft,a oxz varjky 0&10 10&0 0&0 0&40 40&50 50µ60 ;ksx ckjackjrk 4 x 1 15 y 5 60 If following are the frequency distribution of median then find the value of x and y? Class Interval Total Frequency 4 x 1 1 y ;fn OdsUæ okys o`r ij okg~; fcunq T ls nks Li'kZ js[kk, TP rfkk TQ [khaph xbz gs] rks fl¼ dhft, fd PTQ = OPQ 5 If two tangents TP and TQ are drawn to a circle with centre O from a external point T then prove that PTQ = OPQ lsehú yeck,d js[kk[kam [khafp, vksj bls % ds vuqikr esa fohkkftr dhft,a izr;sd Hkkxksa dks ekfi,a 5 Draw a line segment which is 5.6 cm long divided into : then measure each parts? OR -5 lsehú f=kt;k dk o`r [khapsa blds ifjxr,d leckgq f=khkqt cuk;saa Draw a circle whose radius is.5 cm and form circumscribe equilateral triangle.
123 SOLUTION (1) (x) () (x) () (d) (4) (x) (5) ([k) (6) (x) (7) (x) (8) (x) (9) (d) (10) (x) (11) cgqyd (1) Js<+h (1) vifjes; (14) f=k?kkrh (15) 6 lsehú (16) x + y (17) µ4 (18) 7 (19) 1 (0) 0 (1) α =, β = f}?kkr cgqin x ( ) x. = α + β + α β = x ( + ) x + ( ) = x + x 6 () f}?kkr lehdj.k x 6x + = 0 ax + bx + c = 0 ls rqyuk djus ij a =, b = 6, c = D = b 4 ac = ( 6) 4 = 6 4 = 1 1 > 0 f}?kkr lehdj.k ds oklrfod vksj fhkuu ewy gksaxsaa () ABCesa AB = BC = CA = arfkk AD BC ADB esa] a a AD = ( a) = a 4 = f=khkqt ds 'kh"kzyac a = alsehú 4 = a lsehú (lr;kfir) (4),d o`r ftldk dsuæ lsehú O gsa ckg~; fcunq A ls Li'kZ js[kk PA dh yackbz 4 lsehú gs rfkk A dh dsuæ O ls nwjh 5 lsehú gsa <APO = 90 vc ledks.k OPAesa] ;k] ;k] OA = PA + OP (5) = (4) + OP 5 16 = OP ;k] 9 = OP OP = cm
124 (5) fcunqvksa ( a cos θ, 0) rfkk (0, a sin θ ) ds chp dh nwjh (6) o`r dh ifjf/ ¾ o`r dk {ks=kiqy π R = πr R = R R = ek=kd 1 (7) 'kadq dk vk;ru ¾ πr hesa] 1 = = 1 8 cm = 196 cm (8) iz'ukuqlkj] fn;k gs%µ PA = PB ( a ) ( a ) = ( cos θ ) (0) + (0) ( sin θ) = a cos θ + a sin θ ;kfu fd] PA = PB... (1) PA = (0 ) + ( k) vc] lehdj.k (1) ls PB = (0 k ) + ( 5) (0 ) + ( k) = (0 ) + ( k ) ;k] k k k = + 9 ;k] 4k = 4 k = 1 (9) LHS = 4 cos θ cos θ = 4cos 0 cos0 = 4 4 = 8 = 0 RHS Proved = = a (cos θ + sin θ ) = a 1 = a (0) lozizfke gesa nh gqbz la[;kvksa ds vhkkt; xq.ku[kam fy[krs gsaa 7 = 7 1, 11 = 11 1vkSj 19 = 19 1 yúlú = = 146, eúlú = 1 Ans. (1) ekuk fd A.Pdk igyk in arfkk lkoz&varj d gs rks
125 a = 0.6, d = = 1.1 gesa A.P.ds 100 inksa dk ;ksx Kkr djuk gsa n Sn = [ a + ( n 1) d] esa a = 0.6, d = 1.1, n = 100j[kus ij 100 S 100 = [ (100 1) 1.1] = 50( ) = 50( ) = = 5505 Ans. () ekuk fd 7,d ifjes; la[;k gsa vfkkzr ge nks iw.kkzad a vksj b( b 0) izkir dj ldrs gsa a fd 7 = gsa b ;fn avksj b esa 1 ds vfrfjdr dksbz mhk;fu"v xq.ku[kam gksa rks ge ml mhk;fu"v xq.ku[kam ls Hkkx ysdj avksj b dks lgvhkkt; cuk ldrs gsaa vr% b 7 = agsa () nksuksa i{kksa dks oxz djus ij gesa 7b a = --- (1) izkir gksrk gsa vr% a, 7ls fohkkftr gsa blfy, 7, a dks Hkh fohkkftr djsxka ekuk fd a = 7 c, tgk,d iw.kkzad gsa adk eku lehdj.k (1) esa j[kus ij] 7 b = (7 c), 7b = 49 c, b = 7c b, 7ls fohkkftr gsa blfy, 7, bdks fohkkftr djsxka vr% avksj b esa de ls de,d mhk;fu"v xq.k[kam 7 gsa ijurq blls rf; dk fojks/khkkl izkir gksrk gs fd a vksj b lgvhkkt; gsa gesa ;g fojks/khkkl viuh =kqfviw.kz dyiuk ds dkj.k izkir gqvk fd 7,d ifjes; la[;k gsa vr% fu"d"kz izkir gqvk fd 7,d vifjes; la[;k gsa ekfld [kir oxz fpug `ckjackjrk ( x ) ( f ) f x 5µ µ µ µ µ µ µ f = 68 fx = 5400
126 Ekkè; fx 5400 = = = Ans. f 68 (4) = --- (1) x 1 y 6 1 x 1 y = --- () lehú(1) dks ls xq.kk dj lehú() ds lkfk tksm+us ij] x 1 + y + x 1 y = + or, 1 = 7 or, = 1 x 1 x 1 or, x 1 = or, x = + 1 = 4 x = 4 lehú(1) esa x dk eku gksus ij y = + y = = = = y = y 1 y = + = 5 x = 4, y = 5 Ans. (5) x x + 4 = 0 a =, b =, c = 4 D = b 4 ac = ( ) 4 4 = 9 = D < 0, dksbz oklrfod ewy ugha gsa (6) ledks.k ABD esa BD = AB AD...(1) iqu% ledks.k ADCesa CD = AC AD...() lehú(1) esa () dks j[kus ij BD CD = (AB AD ) (AC AD ) = AB AD AC + AD = AB AC Proved
127 (7) eku fy;k fd A( x1, y1 ) = (16, ) B( x, y) = ( k, 8) vksj C( x, y) = (4, 10) ;fn ABCdk {ksú ¾ 0 rks fcanq A,B, C lajs[kh gksxha 1 [ ( ) + ( ) + ( )] = x y y x y y x y y 1 16( ) + k( 10 ) + 4( + 8) = 0 [ 0] 16 + k = 0 1k + 40 = 0 1k + 7 = k = 7 k = = 6 1 vr% fn;s x, fcunq k = 6 ds lajs[kh gsa (8) isuksa dh dqy la[;k ¾ 10 $ 10 ¾ 10 P (,d vpnk isu) (9) L.H.S. = 10 1 = = Ans cos A 1 1 cot A sin A = 1 tan A sin A 1 cos A sin A cos A sin A sin A cos A cos A = cos A sin A = sin A cos A sin A cos A sin A cos A cos A cos A = = = cot A = R.H.S Proved sin A (sin A cos A) sina (40) L.H.S. = 1 cos A 1 cos A 1 cos A = 1 + cos A 1 + cos A 1 cos A (1 cos A) (1 cos A) 1 cos A = = = 1 cos A sin A sin A sin A = (coseca cota) = coseca cot A = R.H.S Proved
128 (41) ekuk fd ABehukj gs ftldh mq pkbz h ehú gsa Hkwfe ds,d fcunq C tks ehukj ds ikn Bls 60 ehú dh nwjh ij gs ;kfu BC =60 ehú ledks.k ABCesa AB h tan 60 = = BC 60 h = 60 h = 60 = = ehú 10.9 (4) ekuk fd ABC,d ledks.k lef}ckgq gsa ftldh izr;sd Hkqtk x gsa A = C = 45, B = 90, Ekuk fd AB = BC = x ikbfkksxksjl izes; ls] ledks.k ABCesa] d.kz ¾ yac $ vk/kj AC = AB + BC = x + x = x AC = x = x AB x 1 BC x 1 vr% sin 45 = = =, cos 45 = = = AC x AC x AB BC tan 45 = x x 1, cot 45 1 BC = x = = AB = x = AC AC sec 45 = x x, co sec45 BC = x = = AB = x = (4) 'kadq dh f=kt;k ¾ v¼zxksys dh f=kt;k R = 6 cm ehú f[kyksus dh dqy mq pkbz ¾ 11 lsehú 'kadq dh mq pkbz ¾ (11 µ 6) ¾ 5 lsehú 'kadq dh fr;zd mq pkbz R h = + = = = 65 = 7.81lsehú crzu dh dqy i`"bh; {ks=kiqy ¾ 'kadq dk i`"bh; {ks=kiqy $ v¼zxksys dk i`"bh; {ks=kiqy = π rl + π R = π R( l + R) = 6 ( ) = = 7.56 Ans. 7 7
129 (44) x + y = 6...(1) vksj x 4y = 1...() lehú(1) ls x + y = 6 or, x = 6 6y x 6 0 y 0 1 (x, y) (6, 0) (, 1) (0, ) lehú() ls x 4 y = 1 or, x = 1 + 4y or, 1 + 4y x = x y 0 1 (x, y) (6, 0) (8, 1) (0, ) nksuksa vkys[kksa dk dvku fcunq (6] 0) gsa vr% gy x = 6, y = 0gksxkA
130 (45) 45 + x + y = 60 oxz varjky ckjackjrk ( f ) lap;hckjackjrk ( c f ) 0µ µ0 x 4 + x 0µ x 0µ x 40µ50 y 40 + x + y 50µ x + y dqy N = 60 x + y = = 15 y = 15 x...(1) Ekkè;d ¾ 8-5 (fn;k gqvk gs) N = = 0 ekè;d oxz ¾ 0 µ 0 ;gk ] l = 0, h = 10, N = 60, C = 4 + x, f = 1 Ekkè;d N l + C = h; f 60 (4 + x ) 8.5 = (6 x) 8.5 = = x 81.5 = 10x 81.5 x = = lehú (1) ls y = = 6.85 vr% x = 8.15, y = 6.85 (46) fn;k x;k gs fd %µo dsuæ okys o`r ds okg~; fcunq Tls TPvkSj TQLi'kZ js[kk, [khaph xbz gsa tks o`r dks Øe'k% PvkSj QfcUnqvksa ij Li'kZ djrh gsaa fl¼ djuk gs fd PTQ = OPQ izek.k%µ ekuk fd PTQ = x rc TQP + TPQ + PTQ = 180
131 ds rhuksa dks.kksa dk ;ksx ¾ 180 TQP + TPQ = 180 x --- (1) pwafd o`r ds ckg~; fcunq ls [khaph xbz Li'kZ js[kkvksa dh yackbz leku gksrh gsa TP = TQ TQP = TPQ fdurq TQP + TPQ = 180 x TQP + TQP = 180 x vr% TPQ,d lef}ckgq gsa 180 x x TQP = = 90 x x = vc OPQ = OPT TPQ = QPQ = PTQ PTQ = OPQ Proved (47) jpuk ds pj.k%µ (d) AB = 5.6 cmdk,d js[kk[kam [khapka ([k) A ls mqij dh vksj U;wudks.k BAX = 60 ABY = 60 cuk;ka (x) 5 fcunqvksa dks AXvkSj BYij leku eki dk vafdr fd;ka cuk;k vksj B i uhps dh vksj leku (?k) AvkSj B 5 ] A vksj B vksj A 5, Bdks feyk;ka (M+) A, B js[kk[kam ABdks Pij % ds vuqikr esa fohkdr djrk gsa PA vksj PBdks eki dj ge ikrs gsa fd PA =.4cmvkSj PB =.cm
132 vfkok (d).5cmdh f=kt;k ls,d o`r [khapka ([k) o`r dks dsuæ Odks o`r ds fdlh fcunq Als feyk;ka (x) Oij AOB = 10 vafdr fd;k] tgk Bo`r ij gsa (?k) fiqj Oij BOC = 10 vafdr fd;k tgk ij C o`r ij gsa (M+) Aij <OAR = 90 cukdj Aij Li'khZ AQ [khapka (p) blh izdkj o`r ds fcunq B vksj Cij Hkh Li'khZ [khapka (N) rhuksa Li'kZ js[kkvksa dks c<+kdj PQR gqvka vafdr fd;ka bl izdkj PQR vhkh"v f=khkqt
133 ! # % #&& () +,. /!,), %,0) 1,/ # % %) (,/ & ( %456 0 ) 7,/ )!
134 xf.kr (lsv& 8) Maths (Set- 8) le; %?kavk 15 feuv lgh mùkj pqus%& Choose the correct answer :- 1- sin 45º dk eku gksxk A 1 1 (d) ([k) ½ (x) (?k) ¼ The value of sin 45º will be (a) (b) ½ (c) 1 (d) ¼ - fueufyf[kr esa dksu ifjes; la[;k gs \ 1 49 (d) 101 ([k) (x) (?k) 18 Which of the following is rational Number? (a) (b) 64 (c) (d) sin θ + cos θ cjkcj gs& 1 (d) ([k)&1 (x) 1 (?k) sin θ + cos θ is equal to (a) (b) -1 (c) 1 (d) 4- founq (&] ) fdl ikn esa gksxk A 1 (d) izfke ([k) f}rh; (x) r`rh; (?k) prqfkz Point (-, ) lies in which quadrant (a) First (b) Second (c) Third (d) Fourth
135 5- csyu dk oø i`"b dk {ks=kiqy gksxk 1 (d) rh ([k) πrh (x) πrh (?k) πrh The Curved Surface area of cylinder is (a) rh (b) πrh (c) πrh (d) πrh 6- fueufyf[kr esa dksu f}?kkr lehdj.k ugha gs \ 1 (d) (x + ) = x(x - 1) ([k) (x + 1) = (x - ) (x) (x - ) (x + ) = 6 (?k) x 1 + x = Which of the following is not quadratic equation (a) (x + ) = x(x - 1) (b) (x + 1) = (x - ) (c) (x - ) (x + ) = 6 (d) x 1 + x = 7- ;fn ABC esa AC = AB + BC rks B dh eki gs 1 (d) 60º ([k) 75º (x) 90º (?k) 45º What is measurement of B in triangle ABC if AC = AB + BC (a) 60º (b) 75º (c) 90º (d) 45º 8-7] ] 5] 8] 6] 10] 9] 1 dh ekfè;dk D;k gs \ 1 (d) 8 ([k) 7 (x) 6 (?k) 7-5 What is the median of 7,, 5, 8, 6, 10, 9, 1 (a) 8 (b) 7 (c) 6 (d) nks iklksa dks,d lkfk iqsadk tkrk gs A nksuksa ij 6 vkus dh izkf;drk gsa 1 (d) 6 1 ([k) (x) 6 (?k) 4 1 The probability of six on both if two dice will throw at once. (a) 1 6 (b) 1 6 (c) 5 6 (d) 1 4
136 10-4 ds fdrus xq.kt 10 vksj 50 ds chp im+rs gsa \ 1 (d) 60 ([k) 50 (x) 55 (?k) 5 How many multiples between 10 and 50. (a) 60 (b) 50 (c) 55 (d) 5 fjdr LFkkuksa dh iwfrz djsa %& Fill in the blanks : , -6, -,,..., 4 esa inksa dh la[;k gs A 1 The number of term in -10, -6, -,,..., 4 is ;fn nks la[;kvksa dk e- l-¾5 vksj y- l-¾50 rks la[;kvksa dk xq.kuiqy gksxk If H.C.F. of two numbers are 5 and L.C.M. is 50 then what will the multiplication oxz vurjky ds eè;&founq dks dgrs gsa A (Mid point of class Interval is... ) 14- f=khkqt dk {ks=kiqy = ½ x... x... 1 Area of triangle = ½ x... x ;fn tan 5º cot 5º = sina rks A dk eku gs A 1 If tan 5º cot 5º = sin A then value of A ,d la[;k gs A is a... number. 17- og lehdj.k ;qxe ftldk dksbz gy u gks lehdj.k dgykrk gs A 1 Such equation which has no solution is called... equation. 18- ;fn f}?kkr lehdj.k 7x - 5x + 1 = 0 ds 'kwu;d α] β gks] rks α + β = 1 If α] β be zeros of quadratic equation 7x - 5x + 1 = 0 then α + β =
137 19- nks cgqhkqt le:i gksrs gsa ;fn muds laxr dks.k cjkcj gks rfkk laxr Hkqtk, gksa Two polygon will be similar if their corresponding angle are equal and corresponding sides are lehdj.k px + qx + r = 0 ds fy, q - 4pr dks dgk tkrk gs A 1 For the equation px + qx + r = 0, q - 4pr is said to be fn[kk, fd x = - lehdj.k x + 5x + = 0 dk gy gs A Show that x = - is a solution of equation x + 5x + = ifjes; la[;k 4 5 ds 1 Find the decimal expansion of rational number is ter rminating or non terminating reccuring. n'keyo izlkj lkr ;k vlkar vkorhz gs] Kkr djsa A - nh xbz vkd`fr esa ;fn PQ RS gs rks fl¼ dhft, fd POQ SOR gs A 4 5 In the figures if PQ RS then prove that POQ SOR 4- ;fn fdlh vuqøe dk n ok in 4n + 5 gks rks blds izfke rhu in If nth term of sequence is 4n + 5 find first three term? 5- tk p dhft, fd fueu lehdj.k f}?kkr lehdj.k gs ;k ugha \ Kkr djsa A x x + = x, x 0 Examine following equation is quadric equation or not x ls0 eh0 f=kt;k okys fdlh o`r dh ifjf/ crkosa A Find the circumference of circle whose radius is 4.9 cm. x = x, x 0
138 7- eku Kkr djsa& Find the value of cos 0º (1 + tan 0º) 8- fdlh o`r dh ifjf/ ls0 eh0 gs A mlds prqfkkz'k dk {ks=kiqy fudkysa A Find the area of quadrant of circle if circumference of circle is cm. 9- ;fn?ku dk dqy i`"b {ks=kiqy 150 eh0 gks rks mldk vk;ru D;k gksxk A What will be volum if total surfaces Area of cube is 150 m 0- ewy foanq ls founq (4] &) dh nwjh Kkr dhft, A Find distance from origin and point (4, -). 1- ;fn cgqin x - x - (k - ) dk,d 'kwu;d &4 gks rks K dk eku fudkysa \ If one zero of the polynomial x - x - (k - ) is -4 then find the value of K. 1 - fl¼ dhft, fd,d vifjes; la[;k gs A Prove that 1 is an irrational number. - nks yxkrkj?kukred iw.kkzd Kkr djs ftuds oxks± dk ;ksx 65 gks A Find two consecutive positives no whose sum of squares is ;fn A = 60º vksj B = 0º rks fl¼ djsa If A = 60º and B = 0º then prove that tan (A - B) = tan A tan B 1 + tan A.tan B tan A tan B 1 + tan A.tan B 5- fueu lkj.kh 400 fu;kwu ysiksa dk thou dky n'kkzrk gs A thou dky (?kavks esa) ysiksa dh la[;k 1500& & & &500 86
139 500& & & ,d ysai dk ekè;d thou dky Kkr dhft,a In the following table represent the time period of 400 neon Lamp.! 1500& & & & & & & Find the median life time of a lamp. 6- fl¼ djsa 1 + cot θ = cosecθ 1+ cosecθ Prove that 1 + cot θ = cosecθ 1+ cosecθ 7- fueufyf[kr okjackjrk cavu (lkj.kh) ds fy, ekè; ifjdfyr djsa A oxz vurjky 0&8 8&16 16&4 4& &40 40&48 ckjackjrk The following frequency distribution (table) is # % 0&8 8&16 16&4 4& &40 40&48 & (
140 Find the mean. 8- f}?kkr cnqin x - 8 ds 'kwu;d Kkr dhft, A Find the zeros of quadratic polynomial x gy djsa & (x + 4) (x - 4) = 0 Solve - (x + 4) (x - 4) = jke vksj ';ke nkslr gsa A D;k izk;fdrk gs fd mu nksuksa dk tue fnu (1) fhkuu gks (),d gh gks \ (vf/o"kz dh mis{kk djsa) \ Ram and Shyam is a friend. What will be probability of both birthday is (i) different (ii) same (ignore leep year) 41- ;fn ledks.k f=khkqt ABC esa B = 90º, AB = 1 ls0 eh0] BC = 16 ls0 eh0 rks AC dk eku fudkfy, A If right angle in ABC B = 90º, AB = 1 cm, BC = 16 cm then find the value of AC? 4- ;fn fcanq (1] )] (4, y), (x, 6) vksj (] 5) blh Øe esa ysus ij,d lekarj prqhkqzt ds 'kh"kz gks rks x vksj y Kkr dhft, A If point (1, ), (4, y), (x, 6) and (,5) are the vertices of a parallelogram taken in order find x and y. 4- xzkiqhd fof/ ls gy dhft, A 5 Solve graphically. 5x + 7y = 50 7x + 5y = eh0 Å ps,d Hkou ds 'kh"kz ls fdlh ehukj ds 'kh"kz ij muu;u dks.k 60º gs vksj ehukj ds pj.k dk voufr dks.k 0º gs A ehukj dh Å pkbz Kkr djsa A 5
141 The angle of elevation on the top to 7m height a building to the top of the tower is 60º and fort of the tower angle of depression is 0º. Then find the height of the tower. vfkok (or) tehu ij flfkr fdlh founq ls 0 eh0 Å ps,d Hkou ij [km+k,d >ams ds tm+ vksj 'kh"kz ds muu;u dks.k Øe'k% 45º vksj 60º gs A >ams dh Å pkbz Kkr dhft, A The angle of elevation from a point at the ground to 0 meter height building on which a flag top and root is respectively 45º and 60º then find the height of a flag ls0 eh0 f=kt;k dk,d /krq dk xksyk fi?kykdj 6 ls0 eh0 f=kt;k okys csyu ds :i esa <kyk tkrk gs A csyu dh Å pkbz fudkysa A 5 A metal sphere of 4. cm radius is melted and form cylinder with radius 6 cm. Find the height of the cylinder? 46- ;fn,d f=khkqt ds nks dks.k nwljs f=khkqt ds laxr ds nks dks.kksa ds cjkcj gks rks os nks f=khkqt le:i gksxsa A 5 If two angles of a triangle is equal to another corresponding angles are similar then prove it? 47-5 ls0eh0 f=kt;k dk,d o`r [khaps A o`r dh nks Li'kZ js[kk,a [khaps tks vkils esa,d&nwljs ls 60º dks.k ij >qds gsa A 5 Draw a circle of radius 5 cm. draw a pair of tangents to this circle which are inclined to each other at an angle of 60º. vfkok (or) 8 ls0 eh0 yeck,d js[kk[kam AB [khfp, vksj bls fcunq P bl izdkj var% fohkkftr djsa fd AP PB = gks A
142 Draw a line segment AB of length 8cm and divide its internally at P such that AP = PB
143 ! [k )!?k! SOLUTION x 7! [k! x 1!?k /! x!?k +! d!! d! ) )! )! oxz&fpug 14-, vk0 Å º 16. vifjes; 17- fojks/h 18-./ fn;k x;k lehdj.k gs A lekuqikrh 0- foospd ) ) 0 0 leh0 esa ck, i{k esa j[kus ij ) ) 0 0 ) 0 0 ) vr% fn;s x;s lehdj.k dh gy ugha gs A - 1 x 5 1 x x 5 = = 4 65 (10) 65 = = nh xbz ifjes; la[;k lkar vkoùkhz gs A - nh xbz vkd`fr esa ;fn 54 gs] rks fl¼ dhft, fd gs A iz'u ds vuqlkj fd 54 4 (,dkarj dks.k) 5 (,dkarj dks.k) rfkk ('kh"kzfhkeq[k dks.k) vr% le:irk ds vuqlkj ;gk
144 ) 7 ) / izfke rhu in Øe'k% 9] 1] 17 gs A 5- fn;k x;k lehdj.k 0 ) ;k] = x x x + x ;k] ) izkir lehdj.k esa leh0 dk?kkr gs vr% ;g f}?kkr lehdj.k ugha gs A 6- o`r dh ifjf/ )π ) 7!+ 7 ) ))!/ 77!/!! 7- ) º 0 ) º ) º ) º ) 1 º cos 0º 8- ifjf/ )π ) )) ifjf/ )) 7 ;k] ) )) / )) / )). ) )) /.) 1 prqfkkz'k dk {ks=kiqy π ) !1) ) ?ku dk dqy i`"b {ks0¾ 1 (fdukjk) ;k] 1 )
145 ;k].1 ) ;k] ) ) 5 (dsoy?kukred eku)?ku dk vk;ru ) eh! nwjh 6 ( 4 0) + ( 0) ( ) vr% vhkh"v nwjh 6 bdkb;k (0] 0) 1- fn;k x;k cgqin ) ) 0 ) cgqin dk,d 'wku;d &4 gs A 7 7 ) 7 ) 0 ) ) ) ) + vr% dk eku + gksxk A! - ekuk fd 1,d ifjes; la[;k gs ifjes; la[;k dh ifjhkk"kk ds vuqlkj 1 p eku fy;k fd!!!!!!!!!!!!!!!!!!!!!!!!!!!!! q tgk rfkk & iw.kkzd gs rfkk & 8 vksj rfkk & esa 1 ds vfrfjdr dksbz xq.ku [kam mhk;fu"b ugha gs A ;kfu fd rfkk & lg vhkkt; la[;k, gs A
146 1 p vc (1) ls q & ) ) & ) (nksuksa rjiq oxz djus ij) () )9 & ) dks fohkkftr djrk gs A )9 & dks fohkkftr djrk gs (izes; ls) () vr% eku fy;k fd & ) vc ) ls & ) ) ) ) ) ) ) 7 ) ) ) ) ) ) )9 ) dks fohkkftr djrk gs A )9 dks fohkkftr djrk gs (izes; ls) (4) bl izdkj () rfkk (4) ls ;g fu"d"kz fudyrk (4) gs fd,oa & esa A vfrfjdr vu; mhk;fu"b xq.ku[kam gs A bl izdkj gesa,d fojks/khkkl feyrk gs A 1 vr% gekjk ;g ekuuk fd ifjes; la[;k gs xyr gs A 1 vr%,d vifjes; la[;k gs A - ekuk fd nks yxkrkj /u iw.kkzd vksj 0 gs A iz'ukuqlkj ) 0 0 ) 1 ;k] ) 0 ) 0 ) 0 1 ;k] ) ) 0 ) 17 ;k] ) 0 )
147 ;k] ) 0 7 ) ;k] ;k] (vlahko) ;k 0 7 pw fd /ukred iw.kkzd gs vr% vhkh"v la[;k, 1 vksj 14 gs A 4-!!4! 60º - 0º) = tan 0º = 1 tan A tan B R.H.S. = = 1+ tan A.tan B = tan 60º tan 0º 1+ tan 60º.tan 0º =. =. : 1+ 1 L.H.S. = R.H.S. Proved 5- ;gk ge fueu lkj.kh cukrs gsa A thou dky (?kavs esa) okjaokjrk lap;h okjaokjrk 1500& & & & & & & N 400 ;gk = = 00 N = f = 400 blds Bhd cm+h lap;h ckjeckjrk 16 okyk oxz
148 000&500 gs A rks ekè;d oxz 000&500 gs A ekè;d M = l + N f F x i N = 00 l = 00, f = 86, F = 10, i = = x = x = = vr% ekè;d thou dky ¾ ?kaVs A 6- L.H.S. = 1 + cot θ 1+ cosec θ = 1 + cosec θ 1 1+ cosecθ (cot θ = cosec θ - 1) = 1 + (cos ecθ + 1)(cos ecθ 1) cos ecθ ekè; dh x.kuk fueu lkj.kh cukdj djrs gsa A = 1 + cosecθ - 1 = cosecθ = R.H.S. Proved oxz vurjky #!! oxz fpug okjackjrk (f) ckjackjrk x oxz fpug! ) ) )7 1)7 ) 7 ) )7) ) 1 77 ) )) +1 f = 100, fx = 64
149 64 ekè; x = = 6.4 Ans ekuk fd fn;k x;k cgqin p(x) = x - 8 vc p(x) = 0 x - 8 = 0 x - ( ) = 0 (x + ) (x - ) = 0 x + = 0 ;k] x - = 0 x = - ;k] x = vr% fn, x, cgqin ds 'kwu;d gs - rfkk 9- (x + 4) (x - 4) = 0 ;k] x - 4 = 0 ;k] x - 16 = 0 ;k] x = 6 x = + 6 = + 6 x = 6, jke vksj ';ke nkslr gs A lahko ifj.kkeksa dh dqy la[;k ¾ 65 jke ds tue fnu dks vyx djrs gq, fnuksa dh la[;k 65&1 ¾ 64 bu 64 fnuksa esa fdlh fnu ;fn ';ke dk tue fnu gks rks nksuksa ds tue fnu fhkuu gksxsa A (1) fhkuu tue fnu gksus dh?kvuk E ds vuqdqy ifjek.kksa dh la[;kk ¾ P(E) = 65 () tue fnu,d gh gksus dh?kvuk dh izkf;drk 1 - P(E) = 1-64 =
150 41- ledks.k ABC esa B = 90º, AB = 1 cm, BC = 16 cm, AC =? AC = AB + BC = 1) (16) ( + A = = 400 = 0 cm 1cm B 90º 16 cm 4- ekuk fd lekarj prqhkqzt ds 'kh"kz A (1,), B (4, y), C (x, 6) rfkk C D (, 5) gs A ge tkurs gs fd lekarj prqhkqzt ds fod.kz ijlij lef}hkkftr djrs gsa A vr% fod.kz AC ds eè; fcanq ds funs'kkad ¾ fod.kz BD ds eè; fcanq ds funsz'kkad 1+ x y + 5, =, ;k] 1+ x, 4 ¾ 7 + 5, y 1+ x = (i) y + 5 rfkk 4 ¾ (ii) leh0 (i) ls + x = x 7 = 14 ;k] x = 14 - = 1 1 x = = 6 lehdj.k (ii) ls] y + 5 = 4 x = 8 ;k] y = 8-5 =
151 vr% x = 6 vksj y = 4-5x + 7y = (i) 7x + 5y = 46...(ii) 5x = 50-7y 50 7y x = 5 x y x = 46-5y 46 5y x = 7 7. x y 0 5 fcanqvksa(10]0)](]5)]( (4-4]4)](7-]) fcanqvksa(6-57]0)](]5)] (5-14])(7-]) dks xzkiq isij ij n'kkzdj feykus ij dks xzkiq isij ij n'kkzdj feykus ij leh0 (i) dk vkys[k feysxk A leh0 (ii) dk vkys[k feysxk A nksuksa vkys[kksa dk dvku fcanq (] 5) gs vr% gy x =, y = 5
152 44- ekuk fd ehukj dh Å pkbz AB gsa PR AB [khapk iz'u ls APR = 60º, RPB = 0º = PBQ edku dk Å pkbz PQ = 7 eh0 vc ledks.k PQB ls tan 0º = PQ 7 m = QB QB 1 = 7m QB QB = 7 vc ledks.k ARP ls AR tan 60º = PR = AR PQ = QB =7 7 AR = 7 x m = 1 m vr% ehukj dh Å pkbz = AB = AR + RB = AR + PQ (RB = PQ) = 1 m + 7 m = 8 m vfkok ekuk fd >ams dh Å pkbz AC = x eh0 gs A BC ledks.k CBP ls tan 45º = BP 0 1 = or BP = BP 0 m ledks.k ABP ls tan60º = BP AB BC + = BPAC ;gk BC= 0 eh0 AC ¾ x eh0] BP ¾ 0 eh0 = ( 0+ x) 0 or 0 = 0 + x
153 x = 0-1 = 0 x (1.7-1) = vr% vhkh"v >ams dh Å pkbz ¾ eh xksys dk vk;ru = 4 π r = x π x (4.) cm ;fn csyu dh Å pkbz h cm gks rks csyu dk vk;ru = πr h = π x (6) x h cm iz'ukuqlkj] csyu dk vk;ru ¾ xksys dk vk;ru 4 π x 6 x h = π x 4. x 4. x 4. 4 π x 4. x 4. x4. 4. x4. x4. h = x = =.74 cm π x fo'ks"k izfrkk& eku ysa fd ABC vksj DEF esa B = E rfkk C = F fl¼ djuk gs ABCC DEF mrifr ABC DEF ge tkurs gs fd A + B + C = 180º rfkk D + E + F = 180º A + B + C = D + E + F ;k A + B + CC = D + E + F (fn;s x, laca/ksa ls) ;k A = D bl izdkj nksuksa ABCC vksj DEF ledksf.kd gq, vfkkzr~ A = D, B = E, C = F vr% dks.k&dks.k&dks.k le:irk ls DEF DEF 47- jpuk ds pj.k%& pj.k&1 fcunq O dks dsuæ ysdj 5 ls0 eh0 f=kt;k dk,d o`r [khpsaxs A
154 pj.k& o`r dk dksbz O;kl POQ [khapsxs A pj.k& QOC = 60º bl izdkj cuk;sxsa fd OC o`r ls founq C ij feys A pj.k& 4 PA PQ vksj CB OC [khpsaxsa A bl izdkj PA vksj CB,d nwljs dks fcunq D ij izfrpnsn djsaxs A rks DP vksj DC o`r dh vhkh"v Li'kZ js[kk, gs tks 60º ds dks.kk ij >qds gs A
155 vfkok jpuk ds pj.k&1 AB = 8 cm [khpsaxs A pj.k& fcunq ij U;wu dks.k cukrs gq, js[kk : [khapsxs A pj.k& : ij 0 ) ) cjkcj pk; ysrs gq, # dkvsxsa rfkk # fy[ksaxs A pj.k& 4 # dks feyk;saxs A pj.k& 5 rhljs fcanq ls # dks [khpsxsa tks AB dks P ij dkvrh gs A bl izdkj fcunq dks ) ds vuqikr esa vr% fohkkftr djrk gs A
156 ! # % #&& () +,. /!,), %,0) 1,/ # % %) (,/ & ( %456 0 ) 7,/ )!
157 Set - 9 Λ Λ Λ,. 90 &1 % %(,/ & % & !1) 0, 01)( ,0 1 () ΡΓ Χ,?, + ),,/ ()! ( + ), 01, 0!1 01= 01/ % ΡΓ Χ,?,/ Β ( 010,8, 1 0!10 8, 1 010, , 1,.( 08!1 Γ.( 08!1Χ Χ,/ #08!1ΚΕ08! ! / 01! ) 6 % &: &,/ % &: Λ.&! ! Ν 4 Ι Ι0Υ>),/#4Β),/ % 01= 0!1% 01= 01 % Χ? &0%810(9061Χ9,/! &0% !1! < ΕΕ>ΕΕΕ>ΕΧ,,/ 8 8)8 8/8%8 8% 01 0!1% 01 01) = (Α ΓΥ>), 4 )),/
158 % 01= 0!1% 01 % 01% / Χ,Ο 0()?,9,0/ ) ΧΗ6, (, 01+ 0!1Μ 01Ε 01 % ) 6 < = / Χ?, 4 Ι#4Β:::::::::::::::::::::::::,/ ΝΝΝΝΝΝ 0::::::::::::::::::::::::::::,/ ΝΝΝΝΝΝΝΝ! > Λ :/::::::::::::::::::::::::::,/ > Λ :/./ / :0ΝΝΝΝΝΝ1 (:::::::::::::::::::::::::,,/ &.ΝΝΝΝΝΝΝΝ 678 8::::::::::::::::::::::::::::::::::::: Ι Ι0Υ, 4 Ι:::::::::::::::::::::::::::::::::::,/ ΝΝΝΝΝΝ Γ;Χ89Η6! & 9, 0 (;Χ:::::::::::::,/ 8! (!8! (!ΝΝ 0+1://) 80+ 1:ΝΝΝΝΝΝΝ 0+1://) 80+ 1:ΝΝΝΝΝΝΝ (Α Γ, (Α #4Β:::::::::::::::::::::,/ ΝΝΝΝΝΝΝ 0 ΡΓ Χ, Σ Ι? &Β,/ # ( Β Β
159 % ) 6 < = %/ % ΡΓ Ο%,/:/Σ / # Ο%,/:/ Ι 0 Χ? 0 8,%1) 0,68 1Χ9 4,/ # (! 0 8,%10,68(1/ (Α 4 ),) Γ)? ΚΚ,/ 4 0Υ / / << # & :%8:), (Υ / & :%8:)8 / Λ6/ / %/ / 56/ / %/ / # 6/ / %/ / 56/ / %/ / Χ? Ψ08!1 &0,8,!1Χ9 / #! 08!10,8,!1 ΕΕ>ΕΕ!Ε ΕΜ)ΥΗ6 Γ / # 8%8 8)888= 00Χ ΒΙ,/0) Ο Σ / & #!! (! 8: &.80(8 / 8: & Ι Ι0Υ% 8 0(),/ Ω Ι0,0 4 Ι,/. % 8 ) Ω Ι00),/ %! %% % ΡΓ 5 5%:/ΠΣ ΕΙΧ Χ Χ,/ # Π 5 5%:/ << / % / / 6 / :
160 %) %6 % %< %= / % Ω Ι00 1 &9:; : = <:; &>? = & ) ( ς% ) ΛΚ,?,/ % = &,< (4 & Β Κ,)# (, Χ? Σ Ι0Ι>ΕΛ) Λ>ΕΜ &,/ #, 0 8,)10, 8=1 0Χ, 4 Ι Ι,/< 1;Χ;ΧΣ / &9 # 0 Χ ΒΙ,/7, 0Χ )0/ &!! ( ) (Α Γ) 4 )?!, (Α #4Β /! % # 8 ( Α) Α Γ>, / # Λ 8 ( ΑΑ Χ, Λ0#1 ()? F /, / /,/ /,6/ 6/,</ </,// //, / / %) ) 6/ %) %/ Β ( Γ, Λ0. ( 1 : : ) 4 0(Α 0 % 0Υ 90ΕΙ Φ γ,/ % 6/ / Ω Ι0 (Α? 9 Ι9 Ι,,/!!
161 6! χ9 ( % 0(( %?Φ,) )(,/χ( χ9σ Ι0/ #!! 6/ / ) /! Φ9Η6) :, 0, / Χ9Χ,,,/ (,, #4Β 9 0ΙΧ 9 0<, )(%,,/ 4 6 ) /Π Χ %/ <
162 .. %& %01 01 )0! <01 =01 /01?0/1 :( () ) :> :Ν Φ:!:Ν Κ:Β Χ =0/=)1 /0%<) 1?Β: ):?Β: ): Ρ Χ,,0 ), ),0,,,% :8!:,%8 :,/8 : Ο:0,%1 Ο 0,/1:=5/:= >.Ε : :>+>,0Φ Γ& : 9 8> :&Η 8>0 :Α( Ι Α( % ϑ+(, 0,68(1 Χ9 1+, +, Κ 1+!, +, Κ:0,<1 50(5%1 Κ:650(5%1 Κ,6:0(5%1 Κ6:0(5%1 Κ(5%:!:6 (5%:6 Κ(5%:6 (5%:6 (:6,%:% (:,6,%:,= Ι(:%8,=,(Α 4Ι5 & (Α 4 5,/,5 & 5 :/,(Α Γ: Λ5 (Α Γ: Λ5 % Λ5, Λ5 :<< Κ Λ05 & 5 1:<<
163 ) 5 & 5 :?Μ Λ : Ν Γ 5 & 5 :0 1 : 5 & 5 : Ο01 Ι5 5 :/ 5 & 5 : 5 & :) ΙΗ6 Ι 5 & : Α : Ι5 :/, :6% 5 & : 85 :6% & :%8!:):/Ο &Η : :50Ο1 Ο &Η :%50/Ο1 ):%5= ):%5):< (χ :< 6 6/ / %/ / 56/ / %/ / : 5 : : : &08!10(90,8,!1Χ9 Π+, +, :1+Ο Ο, +Θ Θ, : Ο Θ :1+Ο Θ,:1Ο Θ < )χη6εε>εε!ε ΕΜΧ56 ςι Ε>ΕΕ ΕΕ!ΕΜ9Υ :8 ;Γ:0 9& 1Χχ :0 1(χ :(χ : ;Γ: = 00Χ ΒΙ,/ Ε>ΕΕ ΕΕΦ ) >ΕΕΕ Ι) Ο : % :& %/ 8: & :;Ρ &9: Π 9:)Π &:1+Υ, +ΑΥ, :Υ ΑΥ ΣΤ & :! Υ :%Π9
164 678: ;Ρ ;ς :&Ω % &Ω :& & Ξ8: Ρς Ω : : ;ς &Ω & 4 Ι Ι0Υ,/ &:% 89: 8&9:) & :0% 1 :6= &9 :0) 1 : ) 9 :0 1 : &9 59 : ) 5 :6= :& Ι&9 59 :& % ) Ψ0 Ι()? Ι)(Χ Χ,/ Ι,0Ψ,/ 0,/ Ι: ; Ρ Κ : Ο Θ Κ :!,,,,,,,,,,01 )& Η>,),/ ΚΟ,/::::::::::::::::::01 Ι01 :! Κ! : Ι!,Κ Θ01) 01)!,/) 1Θ Η>,/,,? ( Γ,/Ι0),/ %% ΡΓ 5 5%:/,Υ&: 8!: 8:% :,:0Π1 Ο %:Π, 9Υ, Χ Χ,/ Ι :/ ΚΠ : Π: Π:!
165 % Ε.: << / % / / 6 / : << / % / 0=/ /,<< / 10=/ /, % / 1 : << / % / << / % / 0 0=/ /,1: 1 :0 << / << / 10 % / % / 1 :Κ:0 8ΞΖ8:1 ::. ΙΕ.:. %) : &9 [ Ε.: &9:; :; ] _ [ _ : &9 [ _ [ _ 0&: _α[ : _ [ _ & 1 ; : &9; ; ; & :& : &9; &>; & χδε ; ; &>; :&>βχ &>; : &>; :. ΙΕ.:. %6 & % :8 = :,< % :5 :,010 :50,1 = :5<:,<Ο01 5 : > φγ> >%φγ& 01:5:< Ι: & :, >% (χ?,/ Ι :/ & :50,1 Κ/:<50Ο10, 1 Κ/,<:0Ο10, 1 Κ,<:0Ο10, 1 Κ0Ο1: > :5:) > : Ι:)χ9(?,/
166 % )# Χ? 081Ι&0 8,)1) 0, 8=1 &,/ 0 818&0 8,)1 & : & 1+, +Α, :1+, Α Ι & :0,1 5 ) 08/1890, 8=1 9 : 9:1+, +, 1+,, & 9 Ι & :ϑη Κ0,1 5 ):05 1 5< ΚΟ5 5 ): 555< Κ,5 =:55<) Κ,Ο:<)Ο = Κ,<:)6 Κ: % :, > Ι:, Ι,)# Χ? 0,8/1,/ %< &90Χ,Ψ, Ι< Ι,/ 1&9 & 9Η/9Υ & 89 Ρ Ι,/ Ι9 : :( Ψ&9 & 1+Ο, ηι & 1+Ο, Ο :Ο Ο :Ο :Ο Ι& : 9 ) < 1;Χ Ψ,/ %= 0 Χ ΒΙ,), ; Ο,,/ ΝΝΝΝΝΝΝΝΝΝΝΝΝ0861 / ΝΝΝΝΝΝΝΝΝΝΝΝΝ %8180%8, 1ΝΝΝΝΝΝΝΝΝΝΝΝΝ0% ΝΝΝΝΝΝΝΝΝΝΝΝΝ0861 0)8180)8 1ΝΝΝΝΝΝΝΝΝΝΝΝΝ0) ΝΝΝΝΝΝΝΝΝΝΝΝΝ06861 Β ( :Φ( Ι0Χ ),/ ) 0Χ ) : && 9Υ, (Α Γ0( 4 )? %,/ Ι #55:% Κ5+#,:% %
167 Κ5+,:% Κ5+,:% Κ5+,:% Κ ϕ :% Κ%5:% 5: κ : 5: Ι(Α #:#5: 0 1 : :) (Α #:) 5 8 5%85)8)5 ;Γ: >: +9,9+9,9+09,9+9, 0 Κ>: &9& 0 : &+>&, :%051:%5% 0 Κ%5%: : %:,%Κ%:,%Κ: :%:% ()? /, / /,/ /,6/ Χ Χ / %) ) 6/,</ 6/ </,// //, / %) %/,ΥΧ Χ Χ Φ,ΙΦ6ΛΚ()? ),/) Χ,(ΦΛΚ,/ Ιλ:6/8µ Η :6/8µ, :) 8µ :%)8δ: / / :5 µ >µ µ µ µ Οδ %Η> :6/5 ν%η>> / :6/5 &Η> /:6/5 &Η> /:6/5&%Η :6/5<:6< % Κ Κ
168 / = / ) / =, / ) 0/81 / < 6 0=8)1 08/1 08/1,, Φ 6</ Κ,, 0/81 Β,, 0Υ Χ? ΜΕ,/), ( Α 9 Λ & 01? 4 0(Α 9/ + 01(Α ϑ&φ9 / Φ 01Φ οπθρ:6/ / Χ/,0Φ(Α,/ 9 01 Χ? & οθστ:=/ / Χ & οθρυ:=/ / Χ/στ ϖ θσ &ρυϖφ 01 & ) + α[,/ &0( (Α %,Ι )Φ γ,/οσωρ:6/ / ) 0(Α Ι? Φ,/(Α? 9 Ι&9 9 Ι)ς% 88 0(. Χ? ) %,/9Υ Χ, Χ? (Α % 0ΥΧ Χ,,/ Ι& : &. 9 : 9 +<4 +Β 7 + :. Κ σω πω ρξ τξ σψ πζ ρζ τψ Κ +σψ τψ, +πζ ρζ, +σω πω, +ρξ τξ,. Κ στ πρ σπ ρτ Κ στ σπ+{στ πρ, Ισπ πρ+σπ ρτ, & 9
169 6 Ισπ πρ ρτ τσ {σπρτ09 Ι,/ &9 ( Υ9!,/ (( Υ9,/ οωσξ:6/ / οξσω:) / Ιοσζπ:) / 09&1 &9:: 6/ / &9 ) / : ;Ρ Ρ : Ρ )/ & Κ πζ Ν}πζ σξ Ν} Ψ & 6/ / : ; : Κ ϑ Κ : Ν} 9 ( Υ9: :5 :Ν}5 Ν} Ν} Ν}, 9:Φ, ::9:/ Χ/ ://// {Φ,/ Ι Θ Θ Ι%/ Θ Θ &ΗΗΗΗ %Η &ΗΗΗΗ %/:)/// %Η Ι, Ρ Χ,) :Κ9Κ, :ΚΦΚ: : 9 0<, )(%,/ ) Ι, Ρ 9 #:, : 0ΗΗΗ [ : 0ΗΗΗν&ΗΗ :)6 )//
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
1 Adda247 No. 1 APP for Banking & SSC Preparation Website:store.adda247.com
 Adda47 No. APP for Banking & SSC Preparation Website:store.adda47.com Email:ebooks@adda47.com S. Ans.(d) Given, x + x = 5 3x x + 5x = 3x x [(x + x ) 5] 3 (x + ) 5 = 3 0 5 = 3 5 x S. Ans.(c) (a + a ) =
Adda47 No. APP for Banking & SSC Preparation Website:store.adda47.com Email:ebooks@adda47.com S. Ans.(d) Given, x + x = 5 3x x + 5x = 3x x [(x + x ) 5] 3 (x + ) 5 = 3 0 5 = 3 5 x S. Ans.(c) (a + a ) =
Trigonometry 1.TRIGONOMETRIC RATIOS
 Trigonometry.TRIGONOMETRIC RATIOS. If a ray OP makes an angle with the positive direction of X-axis then y x i) Sin ii) cos r r iii) tan x y (x 0) iv) cot y x (y 0) y P v) sec x r (x 0) vi) cosec y r (y
Trigonometry.TRIGONOMETRIC RATIOS. If a ray OP makes an angle with the positive direction of X-axis then y x i) Sin ii) cos r r iii) tan x y (x 0) iv) cot y x (y 0) y P v) sec x r (x 0) vi) cosec y r (y
Matrices and Determinants
 Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Matrices and Determinants SUBJECTIVE PROBLEMS: Q 1. For what value of k do the following system of equations possess a non-trivial (i.e., not all zero) solution over the set of rationals Q? x + ky + 3z
Section 8.3 Trigonometric Equations
 99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
99 Section 8. Trigonometric Equations Objective 1: Solve Equations Involving One Trigonometric Function. In this section and the next, we will exple how to solving equations involving trigonometric functions.
Inverse trigonometric functions & General Solution of Trigonometric Equations. ------------------ ----------------------------- -----------------
 Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Inverse trigonometric functions & General Solution of Trigonometric Equations. 1. Sin ( ) = a) b) c) d) Ans b. Solution : Method 1. Ans a: 17 > 1 a) is rejected. w.k.t Sin ( sin ) = d is rejected. If sin
Quadratic Expressions
 Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Quadratic Expressions. The standard form of a quadratic equation is ax + bx + c = 0 where a, b, c R and a 0. The roots of ax + bx + c = 0 are b ± b a 4ac. 3. For the equation ax +bx+c = 0, sum of the roots
Trigonometric Formula Sheet
 Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
Trigonometric Formula Sheet Definition of the Trig Functions Right Triangle Definition Assume that: 0 < θ < or 0 < θ < 90 Unit Circle Definition Assume θ can be any angle. y x, y hypotenuse opposite θ
3.4 SUM AND DIFFERENCE FORMULAS. NOTE: cos(α+β) cos α + cos β cos(α-β) cos α -cos β
 3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
3.4 SUM AND DIFFERENCE FORMULAS Page Theorem cos(αβ cos α cos β -sin α cos(α-β cos α cos β sin α NOTE: cos(αβ cos α cos β cos(α-β cos α -cos β Proof of cos(α-β cos α cos β sin α Let s use a unit circle
2. THEORY OF EQUATIONS. PREVIOUS EAMCET Bits.
 EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
EAMCET-. THEORY OF EQUATIONS PREVIOUS EAMCET Bits. Each of the roots of the equation x 6x + 6x 5= are increased by k so that the new transformed equation does not contain term. Then k =... - 4. - Sol.
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
 f=hkqt ds lokzaxle gksus ds fy, 'krsz ज य म त 3 le:irk vksj lokzaxlerk जब द आक त य सम न आक र और सम न आक त क ह ह, व आक त य सव गसम कहल ह द न आक त य क ब च क इस घटन क सव न ग सम कह ह f=hkqt ds lokzaxle gksus
f=hkqt ds lokzaxle gksus ds fy, 'krsz ज य म त 3 le:irk vksj lokzaxlerk जब द आक त य सम न आक र और सम न आक त क ह ह, व आक त य सव गसम कहल ह द न आक त य क ब च क इस घटन क सव न ग सम कह ह f=hkqt ds lokzaxle gksus
CRASH COURSE IN PRECALCULUS
 CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
CRASH COURSE IN PRECALCULUS Shiah-Sen Wang The graphs are prepared by Chien-Lun Lai Based on : Precalculus: Mathematics for Calculus by J. Stuwart, L. Redin & S. Watson, 6th edition, 01, Brooks/Cole Chapter
Homework 8 Model Solution Section
 MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
MATH 004 Homework Solution Homework 8 Model Solution Section 14.5 14.6. 14.5. Use the Chain Rule to find dz where z cosx + 4y), x 5t 4, y 1 t. dz dx + dy y sinx + 4y)0t + 4) sinx + 4y) 1t ) 0t + 4t ) sinx
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΔ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2013 21 ΑΠΡΙΛΙΟΥ 2013 Β & Γ ΛΥΚΕΙΟΥ. www.cms.org.cy
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΔ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2013 21 ΑΠΡΙΛΙΟΥ 2013 Β & Γ ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΔ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2013 21 ΑΠΡΙΛΙΟΥ 2013 Β & Γ ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ
Pg The perimeter is P = 3x The area of a triangle is. where b is the base, h is the height. In our case b = x, then the area is
 Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Pg. 9. The perimeter is P = The area of a triangle is A = bh where b is the base, h is the height 0 h= btan 60 = b = b In our case b =, then the area is A = = 0. By Pythagorean theorem a + a = d a a =
Section 7.6 Double and Half Angle Formulas
 09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
09 Section 7. Double and Half Angle Fmulas To derive the double-angles fmulas, we will use the sum of two angles fmulas that we developed in the last section. We will let α θ and β θ: cos(θ) cos(θ + θ)
Review Test 3. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Review Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the exact value of the expression. 1) sin - 11π 1 1) + - + - - ) sin 11π 1 ) ( -
Review Test MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the exact value of the expression. 1) sin - 11π 1 1) + - + - - ) sin 11π 1 ) ( -
Practice Exam 2. Conceptual Questions. 1. State a Basic identity and then verify it. (a) Identity: Solution: One identity is csc(θ) = 1
 Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Conceptual Questions. State a Basic identity and then verify it. a) Identity: Solution: One identity is cscθ) = sinθ) Practice Exam b) Verification: Solution: Given the point of intersection x, y) of the
Areas and Lengths in Polar Coordinates
 Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
Kiryl Tsishchanka Areas and Lengths in Polar Coordinates In this section we develop the formula for the area of a region whose boundary is given by a polar equation. We need to use the formula for the
CHAPTER 12: PERIMETER, AREA, CIRCUMFERENCE, AND 12.1 INTRODUCTION TO GEOMETRIC 12.2 PERIMETER: SQUARES, RECTANGLES,
 CHAPTER : PERIMETER, AREA, CIRCUMFERENCE, AND SIGNED FRACTIONS. INTRODUCTION TO GEOMETRIC MEASUREMENTS p. -3. PERIMETER: SQUARES, RECTANGLES, TRIANGLES p. 4-5.3 AREA: SQUARES, RECTANGLES, TRIANGLES p.
CHAPTER : PERIMETER, AREA, CIRCUMFERENCE, AND SIGNED FRACTIONS. INTRODUCTION TO GEOMETRIC MEASUREMENTS p. -3. PERIMETER: SQUARES, RECTANGLES, TRIANGLES p. 4-5.3 AREA: SQUARES, RECTANGLES, TRIANGLES p.
If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2
![If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2 If we restrict the domain of y = sin x to [ π, π ], the restrict function. y = sin x, π 2 x π 2](/thumbs/53/31933086.jpg) Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
CBC MATHEMATICS DIVISION MATH 2412-PreCalculus Exam Formula Sheets
 System of Equations and Matrices 3 Matrix Row Operations: MATH 41-PreCalculus Switch any two rows. Multiply any row by a nonzero constant. Add any constant-multiple row to another Even and Odd functions
System of Equations and Matrices 3 Matrix Row Operations: MATH 41-PreCalculus Switch any two rows. Multiply any row by a nonzero constant. Add any constant-multiple row to another Even and Odd functions
Solutions to Exercise Sheet 5
 Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
Solutions to Eercise Sheet 5 jacques@ucsd.edu. Let X and Y be random variables with joint pdf f(, y) = 3y( + y) where and y. Determine each of the following probabilities. Solutions. a. P (X ). b. P (X
TRIGONOMETRIC FUNCTIONS
 Chapter TRIGONOMETRIC FUNCTIONS. Overview.. The word trigonometry is derived from the Greek words trigon and metron which means measuring the sides of a triangle. An angle is the amount of rotation of
Chapter TRIGONOMETRIC FUNCTIONS. Overview.. The word trigonometry is derived from the Greek words trigon and metron which means measuring the sides of a triangle. An angle is the amount of rotation of
If we restrict the domain of y = sin x to [ π 2, π 2
 Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Chapter 3. Analytic Trigonometry 3.1 The inverse sine, cosine, and tangent functions 1. Review: Inverse function (1) f 1 (f(x)) = x for every x in the domain of f and f(f 1 (x)) = x for every x in the
Math 6 SL Probability Distributions Practice Test Mark Scheme
 Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Math 6 SL Probability Distributions Practice Test Mark Scheme. (a) Note: Award A for vertical line to right of mean, A for shading to right of their vertical line. AA N (b) evidence of recognizing symmetry
Volume of a Cuboid. Volume = length x breadth x height. V = l x b x h. The formula for the volume of a cuboid is
 Volume of a Cuboid The formula for the volume of a cuboid is Volume = length x breadth x height V = l x b x h Example Work out the volume of this cuboid 10 cm 15 cm V = l x b x h V = 15 x 6 x 10 V = 900cm³
Volume of a Cuboid The formula for the volume of a cuboid is Volume = length x breadth x height V = l x b x h Example Work out the volume of this cuboid 10 cm 15 cm V = l x b x h V = 15 x 6 x 10 V = 900cm³
Answers - Worksheet A ALGEBRA PMT. 1 a = 7 b = 11 c = 1 3. e = 0.1 f = 0.3 g = 2 h = 10 i = 3 j = d = k = 3 1. = 1 or 0.5 l =
 C ALGEBRA Answers - Worksheet A a 7 b c d e 0. f 0. g h 0 i j k 6 8 or 0. l or 8 a 7 b 0 c 7 d 6 e f g 6 h 8 8 i 6 j k 6 l a 9 b c d 9 7 e 00 0 f 8 9 a b 7 7 c 6 d 9 e 6 6 f 6 8 g 9 h 0 0 i j 6 7 7 k 9
C ALGEBRA Answers - Worksheet A a 7 b c d e 0. f 0. g h 0 i j k 6 8 or 0. l or 8 a 7 b 0 c 7 d 6 e f g 6 h 8 8 i 6 j k 6 l a 9 b c d 9 7 e 00 0 f 8 9 a b 7 7 c 6 d 9 e 6 6 f 6 8 g 9 h 0 0 i j 6 7 7 k 9
Mock Exam 7. 1 Hong Kong Educational Publishing Company. Section A 1. Reference: HKDSE Math M Q2 (a) (1 + kx) n 1M + 1A = (1) =
 Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
Mock Eam 7 Mock Eam 7 Section A. Reference: HKDSE Math M 0 Q (a) ( + k) n nn ( )( k) + nk ( ) + + nn ( ) k + nk + + + A nk... () nn ( ) k... () From (), k...() n Substituting () into (), nn ( ) n 76n 76n
PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY
 GRADE TRIALS EXAMINATION AUGUST 05 MATHEMATICS PAPER Time: 3 hours Examiners: Miss Eastes, Mrs. Jacobsz, Mrs. Dwyer 50 marks PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY. Read the questions carefully.
GRADE TRIALS EXAMINATION AUGUST 05 MATHEMATICS PAPER Time: 3 hours Examiners: Miss Eastes, Mrs. Jacobsz, Mrs. Dwyer 50 marks PLEASE READ THE FOLLOWING INSTRUCTIONS CAREFULLY. Read the questions carefully.
10/3/ revolution = 360 = 2 π radians = = x. 2π = x = 360 = : Measures of Angles and Rotations
 //.: Measures of Angles and Rotations I. Vocabulary A A. Angle the union of two rays with a common endpoint B. BA and BC C. B is the vertex. B C D. You can think of BA as the rotation of (clockwise) with
//.: Measures of Angles and Rotations I. Vocabulary A A. Angle the union of two rays with a common endpoint B. BA and BC C. B is the vertex. B C D. You can think of BA as the rotation of (clockwise) with
çfrykse f=dks.kferh; Qyu (Inverse trigonometric functions)
 Download FREE Stud Package from www.tekoclasses.com & Learn on Video www.mathsbsuhag.com Phone : 9 9 7779, 989 888 fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksMs rqjar e/;e eu dj ';kea iq#"k flag
Download FREE Stud Package from www.tekoclasses.com & Learn on Video www.mathsbsuhag.com Phone : 9 9 7779, 989 888 fo/u fopkjr Hkh# tu] ugha vkjehks dke] foifr ns[k NksMs rqjar e/;e eu dj ';kea iq#"k flag
Section 9.2 Polar Equations and Graphs
 180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
180 Section 9. Polar Equations and Graphs In this section, we will be graphing polar equations on a polar grid. In the first few examples, we will write the polar equation in rectangular form to help identify
UNIT-1 SQUARE ROOT EXERCISE 1.1.1
 UNIT-1 SQUARE ROOT EXERCISE 1.1.1 1. Find the square root of the following numbers by the factorization method (i) 82944 2 10 x 3 4 = (2 5 ) 2 x (3 2 ) 2 2 82944 2 41472 2 20736 2 10368 2 5184 2 2592 2
UNIT-1 SQUARE ROOT EXERCISE 1.1.1 1. Find the square root of the following numbers by the factorization method (i) 82944 2 10 x 3 4 = (2 5 ) 2 x (3 2 ) 2 2 82944 2 41472 2 20736 2 10368 2 5184 2 2592 2
PARTIAL NOTES for 6.1 Trigonometric Identities
 PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
PARTIAL NOTES for 6.1 Trigonometric Identities tanθ = sinθ cosθ cotθ = cosθ sinθ BASIC IDENTITIES cscθ = 1 sinθ secθ = 1 cosθ cotθ = 1 tanθ PYTHAGOREAN IDENTITIES sin θ + cos θ =1 tan θ +1= sec θ 1 + cot
ANSWERSHEET (TOPIC = DIFFERENTIAL CALCULUS) COLLECTION #2. h 0 h h 0 h h 0 ( ) g k = g 0 + g 1 + g g 2009 =?
 Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
Teko Classes IITJEE/AIEEE Maths by SUHAAG SIR, Bhopal, Ph (0755) 3 00 000 www.tekoclasses.com ANSWERSHEET (TOPIC DIFFERENTIAL CALCULUS) COLLECTION # Question Type A.Single Correct Type Q. (A) Sol least
ikb~;øe l= ek/;fed f'k{kk e.my] e/;izns'k] Hkksiky d{kk 12oha xf.kr ikb~;øe vk/kkfjr v/;kiu izf'k{k.k funszf'kdk
![ikb~;øe l= ek/;fed f'k{kk e.my] e/;izns'k] Hkksiky d{kk 12oha xf.kr ikb~;øe vk/kkfjr v/;kiu izf'k{k.k funszf'kdk ikb~;øe l= ek/;fed f'k{kk e.my] e/;izns'k] Hkksiky d{kk 12oha xf.kr ikb~;øe vk/kkfjr v/;kiu izf'k{k.k funszf'kdk](/thumbs/81/84469134.jpg) ikb~;øe l= 008-09 ikb~;øe vk/kkfjr v/;kiu if'k{k.k funszf'kdk d{kk oha f.kr ek/;fed f'k{kk e.my] e/;ins'k] Hkksiky lokzf/kdkj lqjf{kr ek/;fed f'k{kk e.my] e/;ins'k] Hkksiky i'u&i= CywfiUV BLUE PRINT OF
ikb~;øe l= 008-09 ikb~;øe vk/kkfjr v/;kiu if'k{k.k funszf'kdk d{kk oha f.kr ek/;fed f'k{kk e.my] e/;ins'k] Hkksiky lokzf/kdkj lqjf{kr ek/;fed f'k{kk e.my] e/;ins'k] Hkksiky i'u&i= CywfiUV BLUE PRINT OF
MathCity.org Merging man and maths
 MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
MathCity.org Merging man and maths Exercise 10. (s) Page Textbook of Algebra and Trigonometry for Class XI Available online @, Version:.0 Question # 1 Find the values of sin, and tan when: 1 π (i) (ii)
CHAPTER 25 SOLVING EQUATIONS BY ITERATIVE METHODS
 CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
CHAPTER 5 SOLVING EQUATIONS BY ITERATIVE METHODS EXERCISE 104 Page 8 1. Find the positive root of the equation x + 3x 5 = 0, correct to 3 significant figures, using the method of bisection. Let f(x) =
EE512: Error Control Coding
 EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
EE512: Error Control Coding Solution for Assignment on Finite Fields February 16, 2007 1. (a) Addition and Multiplication tables for GF (5) and GF (7) are shown in Tables 1 and 2. + 0 1 2 3 4 0 0 1 2 3
Rectangular Polar Parametric
 Harold s Precalculus Rectangular Polar Parametric Cheat Sheet 15 October 2017 Point Line Rectangular Polar Parametric f(x) = y (x, y) (a, b) Slope-Intercept Form: y = mx + b Point-Slope Form: y y 0 = m
Harold s Precalculus Rectangular Polar Parametric Cheat Sheet 15 October 2017 Point Line Rectangular Polar Parametric f(x) = y (x, y) (a, b) Slope-Intercept Form: y = mx + b Point-Slope Form: y y 0 = m
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 19/5/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Αν κάπου κάνετε κάποιες υποθέσεις να αναφερθούν στη σχετική ερώτηση. Όλα τα αρχεία που αναφέρονται στα προβλήματα βρίσκονται στον ίδιο φάκελο με το εκτελέσιμο
MATHEMATICS. 1. If A and B are square matrices of order 3 such that A = -1, B =3, then 3AB = 1) -9 2) -27 3) -81 4) 81
 1. If A and B are square matrices of order 3 such that A = -1, B =3, then 3AB = 1) -9 2) -27 3) -81 4) 81 We know that KA = A If A is n th Order 3AB =3 3 A. B = 27 1 3 = 81 3 2. If A= 2 1 0 0 2 1 then
1. If A and B are square matrices of order 3 such that A = -1, B =3, then 3AB = 1) -9 2) -27 3) -81 4) 81 We know that KA = A If A is n th Order 3AB =3 3 A. B = 27 1 3 = 81 3 2. If A= 2 1 0 0 2 1 then
k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +
[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R + k A = [k, k]( )[a 1, a 2 ] = [ka 1,ka 2 ] 4For the division of two intervals of confidence in R +](/thumbs/73/69566903.jpg) Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Chapter 3. Fuzzy Arithmetic 3- Fuzzy arithmetic: ~Addition(+) and subtraction (-): Let A = [a and B = [b, b in R If x [a and y [b, b than x+y [a +b +b Symbolically,we write A(+)B = [a (+)[b, b = [a +b
Aquinas College. Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET
 Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
Aquinas College Edexcel Mathematical formulae and statistics tables DO NOT WRITE ON THIS BOOKLET Pearson Edexcel Level 3 Advanced Subsidiary and Advanced GCE in Mathematics and Further Mathematics Mathematical
is like multiplying by the conversion factor of. Dividing by 2π gives you the
 Chapter Graphs of Trigonometric Functions Answer Ke. Radian Measure Answers. π. π. π. π. 7π. π 7. 70 8. 9. 0 0. 0. 00. 80. Multipling b π π is like multipling b the conversion factor of. Dividing b 0 gives
Chapter Graphs of Trigonometric Functions Answer Ke. Radian Measure Answers. π. π. π. π. 7π. π 7. 70 8. 9. 0 0. 0. 00. 80. Multipling b π π is like multipling b the conversion factor of. Dividing b 0 gives
Second Order Partial Differential Equations
 Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
Chapter 7 Second Order Partial Differential Equations 7.1 Introduction A second order linear PDE in two independent variables (x, y Ω can be written as A(x, y u x + B(x, y u xy + C(x, y u u u + D(x, y
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΣΤ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2015 26 ΑΠΡΙΛΙΟΥ 2015 Β & Γ ΛΥΚΕΙΟΥ. www.cms.org.cy
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΣΤ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2015 26 ΑΠΡΙΛΙΟΥ 2015 Β & Γ ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΣΤ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2015 26 ΑΠΡΙΛΙΟΥ 2015 Β & Γ ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ
COMPLEX NUMBERS. 1. A number of the form.
 COMPLEX NUMBERS SYNOPSIS 1. A number of the form. z = x + iy is said to be complex number x,yєr and i= -1 imaginary number. 2. i 4n =1, n is an integer. 3. In z= x +iy, x is called real part and y is called
COMPLEX NUMBERS SYNOPSIS 1. A number of the form. z = x + iy is said to be complex number x,yєr and i= -1 imaginary number. 2. i 4n =1, n is an integer. 3. In z= x +iy, x is called real part and y is called
Homework 3 Solutions
 Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Homework 3 Solutions Igor Yanovsky (Math 151A TA) Problem 1: Compute the absolute error and relative error in approximations of p by p. (Use calculator!) a) p π, p 22/7; b) p π, p 3.141. Solution: For
Spherical Coordinates
 Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
Spherical Coordinates MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Spherical Coordinates Another means of locating points in three-dimensional space is known as the spherical
Chapter 5. Exercise 5A. Chapter minor arc AB = θ = 90 π = major arc AB = minor arc AB =
 Chapter 5 Chapter 5 Exercise 5. minor arc = 50 60.4 0.8cm. major arc = 5 60 4.7 60.cm. minor arc = 60 90 60 6.7 8.cm 4. major arc = 60 0 60 8 = 6 = cm 5. minor arc = 50 5 60 0 = cm 6. major arc = 80 8
Chapter 5 Chapter 5 Exercise 5. minor arc = 50 60.4 0.8cm. major arc = 5 60 4.7 60.cm. minor arc = 60 90 60 6.7 8.cm 4. major arc = 60 0 60 8 = 6 = cm 5. minor arc = 50 5 60 0 = cm 6. major arc = 80 8
AREAS AND LENGTHS IN POLAR COORDINATES. 25. Find the area inside the larger loop and outside the smaller loop
 SECTIN 9. AREAS AND LENGTHS IN PLAR CRDINATES 9. AREAS AND LENGTHS IN PLAR CRDINATES A Click here for answers. S Click here for solutions. 8 Find the area of the region that is bounded by the given curve
SECTIN 9. AREAS AND LENGTHS IN PLAR CRDINATES 9. AREAS AND LENGTHS IN PLAR CRDINATES A Click here for answers. S Click here for solutions. 8 Find the area of the region that is bounded by the given curve
Core Mathematics C12
 Write your name here Surname Other names Pearson Edexcel International Advanced Level Centre Number Candidate Number Core Mathematics C12 Advanced Subsidiary Wednesday 25 May 2016 Morning Time: 2 hours
Write your name here Surname Other names Pearson Edexcel International Advanced Level Centre Number Candidate Number Core Mathematics C12 Advanced Subsidiary Wednesday 25 May 2016 Morning Time: 2 hours
Example Sheet 3 Solutions
 Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
Example Sheet 3 Solutions. i Regular Sturm-Liouville. ii Singular Sturm-Liouville mixed boundary conditions. iii Not Sturm-Liouville ODE is not in Sturm-Liouville form. iv Regular Sturm-Liouville note
SOLUTIONS & ANSWERS FOR KERALA ENGINEERING ENTRANCE EXAMINATION-2018 PAPER II VERSION B1
 SOLUTIONS & ANSWERS FOR KERALA ENGINEERING ENTRANCE EXAMINATION-8 PAPER II VERSION B [MATHEMATICS]. Ans: ( i) It is (cs5 isin5 ) ( i). Ans: i z. Ans: i i i The epressin ( i) ( ). Ans: cs i sin cs i sin
SOLUTIONS & ANSWERS FOR KERALA ENGINEERING ENTRANCE EXAMINATION-8 PAPER II VERSION B [MATHEMATICS]. Ans: ( i) It is (cs5 isin5 ) ( i). Ans: i z. Ans: i i i The epressin ( i) ( ). Ans: cs i sin cs i sin
IIT JEE (2013) (Trigonomtery 1) Solutions
 L.K. Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 677 (+) PAPER B IIT JEE (0) (Trigoomtery ) Solutios TOWARDS IIT JEE IS NOT A JOURNEY, IT S A BATTLE, ONLY THE TOUGHEST WILL SURVIVE
L.K. Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 677 (+) PAPER B IIT JEE (0) (Trigoomtery ) Solutios TOWARDS IIT JEE IS NOT A JOURNEY, IT S A BATTLE, ONLY THE TOUGHEST WILL SURVIVE
*H31123A0228* 1. (a) Find the value of at the point where x = 2 on the curve with equation. y = x 2 (5x 1). (6)
 C3 past papers 009 to 01 physicsandmathstutor.comthis paper: January 009 If you don't find enough space in this booklet for your working for a question, then pleasecuse some loose-leaf paper and glue it
C3 past papers 009 to 01 physicsandmathstutor.comthis paper: January 009 If you don't find enough space in this booklet for your working for a question, then pleasecuse some loose-leaf paper and glue it
Parametrized Surfaces
 Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Parametrized Surfaces Recall from our unit on vector-valued functions at the beginning of the semester that an R 3 -valued function c(t) in one parameter is a mapping of the form c : I R 3 where I is some
Γ ΓΥΜΝΑΣΙΟΥ & Α ΛΥΚΕΙΟΥ
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΘ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2018 22 ΑΠΡΙΛΙΟΥ 2018 Γ ΓΥΜΝΑΣΙΟΥ & Α ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΘ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2018 22 ΑΠΡΙΛΙΟΥ 2018 Γ ΓΥΜΝΑΣΙΟΥ & Α ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ
HOMEWORK 4 = G. In order to plot the stress versus the stretch we define a normalized stretch:
 HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
HOMEWORK 4 Problem a For the fast loading case, we want to derive the relationship between P zz and λ z. We know that the nominal stress is expressed as: P zz = ψ λ z where λ z = λ λ z. Therefore, applying
New bounds for spherical two-distance sets and equiangular lines
 New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
New bounds for spherical two-distance sets and equiangular lines Michigan State University Oct 8-31, 016 Anhui University Definition If X = {x 1, x,, x N } S n 1 (unit sphere in R n ) and x i, x j = a
the total number of electrons passing through the lamp.
 1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
1. A 12 V 36 W lamp is lit to normal brightness using a 12 V car battery of negligible internal resistance. The lamp is switched on for one hour (3600 s). For the time of 1 hour, calculate (i) the energy
Γ ΓΥΜΝΑΣΙΟΥ & Α ΛΥΚΕΙΟΥ
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΕ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2014 6 ΑΠΡΙΛΙΟΥ 2014 Γ ΓΥΜΝΑΣΙΟΥ & Α ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΕ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2014 6 ΑΠΡΙΛΙΟΥ 2014 Γ ΓΥΜΝΑΣΙΟΥ & Α ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΗ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ ΑΠΡΙΛΙΟΥ 2017 Β & Γ ΛΥΚΕΙΟΥ.
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΗ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2017 30 ΑΠΡΙΛΙΟΥ 2017 Β & Γ ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΗ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2017 30 ΑΠΡΙΛΙΟΥ 2017 Β & Γ ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level
 UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level * 6 3 1 7 7 7 6 4 0 6 * MATHEMATICS (SYLLABUS D) 4024/21 Paper 2 October/November 2013 Candidates answer
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS General Certificate of Education Ordinary Level * 6 3 1 7 7 7 6 4 0 6 * MATHEMATICS (SYLLABUS D) 4024/21 Paper 2 October/November 2013 Candidates answer
Solution to Review Problems for Midterm III
 Solution to Review Problems for Mierm III Mierm III: Friday, November 19 in class Topics:.8-.11, 4.1,4. 1. Find the derivative of the following functions and simplify your answers. (a) x(ln(4x)) +ln(5
Solution to Review Problems for Mierm III Mierm III: Friday, November 19 in class Topics:.8-.11, 4.1,4. 1. Find the derivative of the following functions and simplify your answers. (a) x(ln(4x)) +ln(5
2 2 2 The correct formula for the cosine of the sum of two angles is given by the following theorem.
 5 TRIGONOMETRIC FORMULAS FOR SUMS AND DIFFERENCES The fundamental trignmetric identities cnsidered earlier express relatinships amng trignmetric functins f a single variable In this sectin we develp trignmetric
5 TRIGONOMETRIC FORMULAS FOR SUMS AND DIFFERENCES The fundamental trignmetric identities cnsidered earlier express relatinships amng trignmetric functins f a single variable In this sectin we develp trignmetric
Second Order RLC Filters
 ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
ECEN 60 Circuits/Electronics Spring 007-0-07 P. Mathys Second Order RLC Filters RLC Lowpass Filter A passive RLC lowpass filter (LPF) circuit is shown in the following schematic. R L C v O (t) Using phasor
43603H. (NOV1243603H01) WMP/Nov12/43603H. General Certificate of Secondary Education Higher Tier November 2012. Unit 3 10 11 H
 Centre Number Surname Candidate Number For Examiner s Use Other Names Candidate Signature Examiner s Initials General Certificate of Secondary Education Higher Tier November 2012 Pages 3 4 5 Mark Mathematics
Centre Number Surname Candidate Number For Examiner s Use Other Names Candidate Signature Examiner s Initials General Certificate of Secondary Education Higher Tier November 2012 Pages 3 4 5 Mark Mathematics
( ) 2 and compare to M.
 Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Problems and Solutions for Section 4.2 4.9 through 4.33) 4.9 Calculate the square root of the matrix 3!0 M!0 8 Hint: Let M / 2 a!b ; calculate M / 2!b c ) 2 and compare to M. Solution: Given: 3!0 M!0 8
Review of Essential Skills- Part 1. Practice 1.4, page 38. Practise, Apply, Solve 1.7, page 57. Practise, Apply, Solve 1.
 Review of Essential Skills- Part Operations with Rational Numbers, page. (e) 8 Exponent Laws, page 6. (a) 0 + 5 0, (d) (), (e) +, 8 + (h) 5, 9. (h) x 5. (d) v 5 Expanding, Simplifying, and Factoring Algebraic
Review of Essential Skills- Part Operations with Rational Numbers, page. (e) 8 Exponent Laws, page 6. (a) 0 + 5 0, (d) (), (e) +, 8 + (h) 5, 9. (h) x 5. (d) v 5 Expanding, Simplifying, and Factoring Algebraic
Phys460.nb Solution for the t-dependent Schrodinger s equation How did we find the solution? (not required)
 Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Phys460.nb 81 ψ n (t) is still the (same) eigenstate of H But for tdependent H. The answer is NO. 5.5.5. Solution for the tdependent Schrodinger s equation If we assume that at time t 0, the electron starts
Numerical Analysis FMN011
 Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Numerical Analysis FMN011 Carmen Arévalo Lund University carmen@maths.lth.se Lecture 12 Periodic data A function g has period P if g(x + P ) = g(x) Model: Trigonometric polynomial of order M T M (x) =
Reminders: linear functions
 Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Reminders: linear functions Let U and V be vector spaces over the same field F. Definition A function f : U V is linear if for every u 1, u 2 U, f (u 1 + u 2 ) = f (u 1 ) + f (u 2 ), and for every u U
Γ ΓΥΜΝΑΣΙΟΥ & Α ΛΥΚΕΙΟΥ
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΗ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2017 30 ΑΠΡΙΛΙΟΥ 2017 Γ ΓΥΜΝΑΣΙΟΥ & Α ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΗ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2017 30 ΑΠΡΙΛΙΟΥ 2017 Γ ΓΥΜΝΑΣΙΟΥ & Α ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ
Chapter 1 Complex numbers
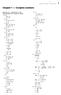 Complex numbers MC Qld- Chapter Complex numbers Exercise A Operations on and representations of complex numbers a u ( i) 8i b u + v ( i) + ( + i) + i c u + v ( i) + ( + i) i + + i + 8i d u v ( i) ( + i)
Complex numbers MC Qld- Chapter Complex numbers Exercise A Operations on and representations of complex numbers a u ( i) 8i b u + v ( i) + ( + i) + i c u + v ( i) + ( + i) i + + i + 8i d u v ( i) ( + i)
8. f = {(-1, 2), (-3, 1), (-5, 6), (-4, 3)} - i.) ii)..
 இர மத ப பண கள வ ன க கள 1.கணங கள ம ச ப கள ம 1. A ={4,6.7.8.9}, B = {2,4,6} C= {1,2,3,4,5,6 } i. A U (B C) ii. A \ (C \ B). 2.. i. (A B)' ii. A (BUC) iii. A U (B C) iv. A' B' v. A\ (B C) 3. A = { 1,4,9,16
இர மத ப பண கள வ ன க கள 1.கணங கள ம ச ப கள ம 1. A ={4,6.7.8.9}, B = {2,4,6} C= {1,2,3,4,5,6 } i. A U (B C) ii. A \ (C \ B). 2.. i. (A B)' ii. A (BUC) iii. A U (B C) iv. A' B' v. A\ (B C) 3. A = { 1,4,9,16
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΕ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ ΑΠΡΙΛΙΟΥ 2014 Β & Γ ΛΥΚΕΙΟΥ.
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΕ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 014 6 ΑΠΡΙΛΙΟΥ 014 Β & Γ ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΕ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 014 6 ΑΠΡΙΛΙΟΥ 014 Β & Γ ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ
2 2 2 The correct formula for the cosine of the sum of two angles is given by the following theorem.
 5 TRIGONOMETRIC FORMULAS FOR SUMS AND DIFFERENCES The fundamental trignmetric identities cnsidered earlier express relatinships amng trignmetric functins f a single variable In this sectin we develp trignmetric
5 TRIGONOMETRIC FORMULAS FOR SUMS AND DIFFERENCES The fundamental trignmetric identities cnsidered earlier express relatinships amng trignmetric functins f a single variable In this sectin we develp trignmetric
2 Composition. Invertible Mappings
 Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
Arkansas Tech University MATH 4033: Elementary Modern Algebra Dr. Marcel B. Finan Composition. Invertible Mappings In this section we discuss two procedures for creating new mappings from old ones, namely,
b. Use the parametrization from (a) to compute the area of S a as S a ds. Be sure to substitute for ds!
 MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
MTH U341 urface Integrals, tokes theorem, the divergence theorem To be turned in Wed., Dec. 1. 1. Let be the sphere of radius a, x 2 + y 2 + z 2 a 2. a. Use spherical coordinates (with ρ a) to parametrize.
 L.K.Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 4677 + {JEE Mai 04} Sept 0 Name: Batch (Day) Phoe No. IT IS NOT ENOUGH TO HAVE A GOOD MIND, THE MAIN THING IS TO USE IT WELL Marks:
L.K.Gupta (Mathematic Classes) www.pioeermathematics.com MOBILE: 985577, 4677 + {JEE Mai 04} Sept 0 Name: Batch (Day) Phoe No. IT IS NOT ENOUGH TO HAVE A GOOD MIND, THE MAIN THING IS TO USE IT WELL Marks:
Section 7.7 Product-to-Sum and Sum-to-Product Formulas
 Section 7.7 Product-to-Sum and Sum-to-Product Fmulas Objective 1: Express Products as Sums To derive the Product-to-Sum Fmulas will begin by writing down the difference and sum fmulas of the cosine function:
Section 7.7 Product-to-Sum and Sum-to-Product Fmulas Objective 1: Express Products as Sums To derive the Product-to-Sum Fmulas will begin by writing down the difference and sum fmulas of the cosine function:
Partial Differential Equations in Biology The boundary element method. March 26, 2013
 The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
The boundary element method March 26, 203 Introduction and notation The problem: u = f in D R d u = ϕ in Γ D u n = g on Γ N, where D = Γ D Γ N, Γ D Γ N = (possibly, Γ D = [Neumann problem] or Γ N = [Dirichlet
Probability and Random Processes (Part II)
 Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Probability and Random Processes (Part II) 1. If the variance σ x of d(n) = x(n) x(n 1) is one-tenth the variance σ x of a stationary zero-mean discrete-time signal x(n), then the normalized autocorrelation
Fractional Colorings and Zykov Products of graphs
 Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
Fractional Colorings and Zykov Products of graphs Who? Nichole Schimanski When? July 27, 2011 Graphs A graph, G, consists of a vertex set, V (G), and an edge set, E(G). V (G) is any finite set E(G) is
14 ح ر وجع ومطابق لألصل اليدوى وي طبع على مسئولية اللجنة الفنية. a b x a x b c. a b c
 ر وجع ومطابق لألصل اليدوى وي طبع على مسئولية اللجنة الفنية ا االسم التوقيع التاريخ االسم التوقيع التاريخ 4 ح ث.ع.ج / أول ARAB REPUBLIC OF EGYPT Ministry of Education General Secondary Education Certificate
ر وجع ومطابق لألصل اليدوى وي طبع على مسئولية اللجنة الفنية ا االسم التوقيع التاريخ االسم التوقيع التاريخ 4 ح ث.ع.ج / أول ARAB REPUBLIC OF EGYPT Ministry of Education General Secondary Education Certificate
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS
 CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
CHAPTER 48 APPLICATIONS OF MATRICES AND DETERMINANTS EXERCISE 01 Page 545 1. Use matrices to solve: 3x + 4y x + 5y + 7 3x + 4y x + 5y 7 Hence, 3 4 x 0 5 y 7 The inverse of 3 4 5 is: 1 5 4 1 5 4 15 8 3
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΘ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ ΑΠΡΙΛΙΟΥ 2018 Β & Γ ΛΥΚΕΙΟΥ.
 ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΘ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2018 22 ΑΠΡΙΛΙΟΥ 2018 Β & Γ ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ
ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ IΘ ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ 2018 22 ΑΠΡΙΛΙΟΥ 2018 Β & Γ ΛΥΚΕΙΟΥ www.cms.org.cy ΘΕΜΑΤΑ ΣΤΑ ΕΛΛΗΝΙΚΑ ΚΑΙ ΑΓΓΛΙΚΑ PAPERS IN BOTH GREEK AND ENGLISH ΚΥΠΡΙΑΚΗ ΜΑΘΗΜΑΤΙΚΗ ΟΛΥΜΠΙΑΔΑ
Exercises 10. Find a fundamental matrix of the given system of equations. Also find the fundamental matrix Φ(t) satisfying Φ(0) = I. 1.
 Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Exercises 0 More exercises are available in Elementary Differential Equations. If you have a problem to solve any of them, feel free to come to office hour. Problem Find a fundamental matrix of the given
Paper Reference. Paper Reference(s) 6665/01 Edexcel GCE Core Mathematics C3 Advanced. Thursday 11 June 2009 Morning Time: 1 hour 30 minutes
 Centre No. Candidate No. Paper Reference(s) 6665/01 Edexcel GCE Core Mathematics C3 Advanced Thursday 11 June 2009 Morning Time: 1 hour 30 minutes Materials required for examination Mathematical Formulae
Centre No. Candidate No. Paper Reference(s) 6665/01 Edexcel GCE Core Mathematics C3 Advanced Thursday 11 June 2009 Morning Time: 1 hour 30 minutes Materials required for examination Mathematical Formulae
ΚΥΠΡΙΑΚΗ ΕΤΑΙΡΕΙΑ ΠΛΗΡΟΦΟΡΙΚΗΣ CYPRUS COMPUTER SOCIETY ΠΑΓΚΥΠΡΙΟΣ ΜΑΘΗΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΠΛΗΡΟΦΟΡΙΚΗΣ 24/3/2007
 Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Οδηγίες: Να απαντηθούν όλες οι ερωτήσεις. Όλοι οι αριθμοί που αναφέρονται σε όλα τα ερωτήματα μικρότεροι του 10000 εκτός αν ορίζεται διαφορετικά στη διατύπωση του προβλήματος. Αν κάπου κάνετε κάποιες υποθέσεις
Approximation of distance between locations on earth given by latitude and longitude
 Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Approximation of distance between locations on earth given by latitude and longitude Jan Behrens 2012-12-31 In this paper we shall provide a method to approximate distances between two points on earth
Finite Field Problems: Solutions
 Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
Finite Field Problems: Solutions 1. Let f = x 2 +1 Z 11 [x] and let F = Z 11 [x]/(f), a field. Let Solution: F =11 2 = 121, so F = 121 1 = 120. The possible orders are the divisors of 120. Solution: The
D Alembert s Solution to the Wave Equation
 D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
D Alembert s Solution to the Wave Equation MATH 467 Partial Differential Equations J. Robert Buchanan Department of Mathematics Fall 2018 Objectives In this lesson we will learn: a change of variable technique
DESIGN OF MACHINERY SOLUTION MANUAL h in h 4 0.
 DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
DESIGN OF MACHINERY SOLUTION MANUAL -7-1! PROBLEM -7 Statement: Design a double-dwell cam to move a follower from to 25 6, dwell for 12, fall 25 and dwell for the remader The total cycle must take 4 sec
Section 8.2 Graphs of Polar Equations
 Section 8. Graphs of Polar Equations Graphing Polar Equations The graph of a polar equation r = f(θ), or more generally F(r,θ) = 0, consists of all points P that have at least one polar representation
Section 8. Graphs of Polar Equations Graphing Polar Equations The graph of a polar equation r = f(θ), or more generally F(r,θ) = 0, consists of all points P that have at least one polar representation
Fourier Series. MATH 211, Calculus II. J. Robert Buchanan. Spring Department of Mathematics
 Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Fourier Series MATH 211, Calculus II J. Robert Buchanan Department of Mathematics Spring 2018 Introduction Not all functions can be represented by Taylor series. f (k) (c) A Taylor series f (x) = (x c)
Integrals in cylindrical, spherical coordinates (Sect. 15.7)
 Integrals in clindrical, spherical coordinates (Sect. 5.7 Integration in spherical coordinates. Review: Clindrical coordinates. Spherical coordinates in space. Triple integral in spherical coordinates.
Integrals in clindrical, spherical coordinates (Sect. 5.7 Integration in spherical coordinates. Review: Clindrical coordinates. Spherical coordinates in space. Triple integral in spherical coordinates.
