2.1 Διαιρετότητα, ισοϋπόλοιποι αριθμοί. q Z, a = b q + r.
|
|
|
- Ἀριστομάχη Μαγγίνας
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Κεφάλαιο 2 Θεωρία Αριθμών Κύριες βιβλιογραφικές αναφορές για αυτό το Κεφάλαιο είναι οι Hardy and Wright 1979 και Graham, Knuth, and Patashnik Διαιρετότητα, ισοϋπόλοιποι αριθμοί Θεώρημα 2.1 Αν a, b Z, b > 0, τότε υπάρχουν μοναδικοί q Z, (το πηλίκο), και (το υπόλοιπο), τέτοιοι ώστε r {0, 1,..., b 1}, a = b q + r. Ορισμός 2.1 (Διαιρετότητα, ισοϋπόλοιποι αριθμοί) Αν το υπόλοιπο είναι 0 τότε a = bq και λέμε τότε ότι ο b διαιρεί τον a. Γράφουμε b a. Το ίδιο λέμε ακόμη και όταν ο b είναι αρνητικός (χωρίς να μιλάμε τότε για το υπόλοιπο της διαίρεσης). Αν δύο αριθμοί a 1, a 2 δίνουν το ίδιο υπόλοιπο r διαιρούμενοι διά b τότε λέμε ότι είναι ισοϋπόλοιποι διά b ή ισοϋπολοιποι modb. Γράφουμε επίσης σε αυτή την περίπτωση a 1 a 2 (b) ή a 1 = a 2 mod b. Είναι φανερό ότι δύο ακέραιοι είναι ισοϋπόλοιποι modb αν και μόνο αν το b διαιρεί τη διαφορά τους Υπολογίστε τα πηλίκα και υπόλοιπα των διαιρέσεων 5/3 και -5/3. Στη γλώσσα python η πράξη / υπολογίζει το πηλίκο της διαίρεσης των δύο ακεραίων ορισμάτων της ενώ η πράξη % υπολογίζει το υπόλοιπο. Εκτελέστε και τις δύο παραπάνω διαιρέσεις στην python. [Του Θεωρήματος 2.1:] Η ακέραια ευθεία Z διαμερίζεται στα σύνολα (διαστήματα) της μορφής {kb, kb + 1, kb + 2,..., kb + (b 1)}, 51
2 52 ΚΕΦΑΛΑΙΟ 2. ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ στα διαστήματα δηλ. από το ένα πολλαπλάσιο του b στο επόμενο. Ο αριθμός a ανήκει σε ένα μοναδικό τέτοιο διάστημα, έστω στο διάστημα [qb, (q + 1)b) Z. Αυτό σημαίνει ότι υπάρχει ένα r {0, 1,..., b 1} τέτοιο ώστε a = qb + r. Ας υποθέσουμε τώρα ότι το a μπορεί να γραφεί και με τη μορφή a = q b + r, όπου q Z, r {0, 1,..., b 1}. Αφαιρώντας κατά μέλη τις δύο παραπάνω σχέσεις παίρνουμε r r = (q q)b, δηλ. ότι ο αριθμός r r είναι κάποιο ακέραιο πολλαπλάσιο του b. Επειδή όμως έχουμε ότι 0 r < b, 0 r < b, b < r r < b, και το μόνο πολλαπλάσιο του b σε αυτό το εύρος είναι το 0. Άρα r = r και επίσης q = q, οπότε έχουμε αποδείξει και τη μοναδικότητα του ζεύγους πηλίκου, υπολοίπου πέρα από την ύπαρξη Αποδείξτε τις παρακάτω βασικές ιδιότητες της διαιρετότητας: 1. a ±a 2. a b, b a = a = ±b 3. a b, b c = a c 4. a b, a c = a kb + lc, k, l Z 5. a = b mod c, a = b mod c = a ± a = b ± b mod c 6. a = b mod c, a = b mod c = a a = b b mod c Αν a b και k 1 δείξτε a k b k. Ορισμός 2.2 (Ακέραιο μέρος, κλασματικό μέρος) Με x συμβολίζουμε το ακέραιο μέρος του πραγματικού αριθμού x, δηλ. το μεγαλύτερο ακέραιο k που ικανοποιεί k x. Επίσης με {x} συμβολίζουμε το κλασματικό μέρος του πραγματικού αριθμού x, δηλ. {x} = x x Δείξτε ότι n άρτιος αν και μόνο αν n = 2 n/ Πόσοι ακέραιοι 1000 δε διαιρούνται ούτε από το 3 ούτε από το Δείξτε 3 n 3 n. Παραγοντοποιήστε το n 3 n πρώτα. Εναλλακτικά χρησιμοποιήστε την Άσκηση 2.2: αν r είναι το υπόλοιπο του n διά 3 τότε n 3 n = r 3 r mod 3 και άρα αρκεί να εξετάσετε όλα τα διαφορετικά r.
3 2.2. ΜΕΓΙΣΤΟΣ ΚΟΙΝΟΣ ΔΙΑΙΡΕΤΗΣ, ΕΛΑΧΙΣΤΟ ΚΟΙΝΟ ΠΟΛΛΑΠΛΑΣΙΟ, ΑΛΓΟΡΙΘΜΟΣ ΤΟΥ ΕΥΚΛΕΙΔΗ Δείξτε ότι το τετράγωνο κάθε περιττού είναι της μορφής 8n Το γινόμενο δύο ακεραίων της μορφής 6n + 5 είναι της μορφής 6n Δείξτε ότι 5 n 5 n. Χρησιμοποιήστε την Άσκηση 2.2 και εξετάστε όλα τα δυνατά υπόλοιπα του n διά Δείξτε ότι 9 n 3 + (n + 1) 3 + (n + 2) 3. Μπορείτε να το λύσετε χρησιμοποιώντας και πάλι την Άσκηση 2.2. Αν βαριέστε να εξετάσετε και τις 9 περιπτώσεις τότε μπορείτε να χρησιμοποιήσετε το παρακάτω απλό πρόγραμμα σε python. for r in range(9): k = r**3+(r+1)**3+(r+2)**3 print k%9 Εναλλακτικά μπορείτε να κάνετε πράξεις στο δεξί μέλος και να χρησιμοποιήσετε την Άσκηση Η ακολουθία Fibonacci ορίζεται ως εξής: Δείξτε με επαγωγή ότι: (α) 2 f n 3 n. (β) 3 f n 4 n. (γ) 4 f n 6 n Δείξτε ότι (2 + 3) n είναι περιττός. f 1 = f 2 = 1, f n = f n 1 + f n 2 για n 3. Δείξτε πρώτα χρησιμοποιώντας το διωνυμικό θεώρημα (a + b) N = N j=0 ( N j ) a j b N j ότι (2 + 3) n + (2 3) n είναι ακέραιος και μάλιστα άρτιος. Έπειτα παρατηρήστε ότι 1 < (2 3) n < Μέγιστος κοινός διαιρέτης, ελάχιστο κοινό πολλαπλάσιο, αλγόριθμος του Ευκλείδη Ορισμός 2.3 (Μέγιστος κοινός διαιρέτης) Αν είναι a, b θετικοί ακέραιοι τότε ονομάζουμε μέγιστο κοινό διαιρέτη των a, b το μέγιστο d που διαιρεί και το a και το b. Το συμβολίζουμε με (a, b). Ορισμός 2.4 (Ελάχιστο κοινό πολλαπλάσιο) Αν είναι a, b θετικοί ακέραιοι τότε ονομάζουμε ελάχιστο κοινό πολλαπλάσιο των a, b το ελάχιστο n τέτοιο ώστε και το a και το b διαιρούν το n. Το συμβολίζουμε με [a, b]. Οι παραπάνω ορισμοί γενικεύονται κατά προφανή τρόπο σε περισσότερους από δύο αριθμούς.
4 54 ΚΕΦΑΛΑΙΟ 2. ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Παράδειγμα 2.1 Έχουμε Επίσης (10, 15) = 5, [10, 15] = 30. (7, 11) = 1, [7, 11] = 77. Για κάθε θετικό ακέραιο a έχουμε (1, a) = 1, [1, a] = a, (a, a) = a, [a, a] = a. Θεώρημα 2.2 Αν a, b είναι δύο θετικοί ακέραιοι τότε υπάρχουν δύο ακέραιοι k, l τέτοιοι ώστε (a, b) = ka + lb. Έστω το σύνολο S = {xa + yb : x, y Z} όλων των ακέραιων γραμμικών συνδυασμών των a, b. Κάθε στοιχείο του S διαιρείται από το (a, b). Ας είναι d ο μικρότερος θετικός ακέραιος του S. Αν d = ka + lb τότε κάθε πολλαπλάσιο του d είναι επίσης στο S. Θα δείξουμε ότι ισχύει και το αντίστροφο, ότι κάθε στοιχείο του S δηλ. είναι πολλαπλάσιο του d. Έστω u = xa + yb, με x, y Z και ας γράψουμε την ακέραια διαίρεση u/d: u = qd + r, 0 r < d. Είναι φανερό ότι r = u qd S (αφού το S είναι κλειστό ως προς ακέραιους γραμμικούς συνδυασμούς). Αν r > 0 αυτό αντιφάσκει με το γεγονός ότι το d είναι το μικρότερο θετικό στοιχείο του S. Άρα r = 0 και u = qd όπως θέλαμε να δείξουμε. Αφού a, b S έχουμε ότι το d διαιρεί τα a, b αλλά, από την άλλη, (a, b) d, το οποίο σημαίνει ότι ο d είναι ένας κοινός διαιρέτης των a, b, άρα d (a, b). Όμως, όπως παρατηρήσαμε στην αρχή, (a, b) d, άρα d = (a, b) και άρα (a, b) S και γράφεται ως ακέραιος γραμμικός συνδυασμός των a, b Δείξτε ότι ο μέγιστος κοινός διαιρέτης k ακεραίων επίσης γράφεται ως ακέραιος γραμμικός συνδυασμός των ακεραίων αυτών. Επαγωγή ως προς k και χρήση του Θεωρήματος 2.2. Πόρισμα 2.1 Αν a, b είναι θετικοί ακέραιοι και d a, d b τότε d (a, b). O d διαιρεί κάθε ακέραιο γραμμικό συνδυασμό των a, b άρα και το (a, b) λόγω του Θεωρήματος 2.2. Ορισμός 2.5 (Πολλαπλασιαστικό αντίστροφο mod ένα ακέραιο) Λέμε ότι δύο ακέραιοι x, y είναι πολλαπλασιαστικά αντίστροφα modb αν xy = 1 mod b. Συνήθως γράφουμε y = x ή y = x 1 αν το b υποννοείται. Θεώρημα 2.3 Ας είναι a, b 1 δύο ακέραιοι. Τότε υπάρχει ακέραιος x τέτοιος ώστε ax = 1 mod b αν και μόνο αν (a, b) = 1. (Υπάρχει δηλ. πολλαπλασιαστικό αντίστροφο του a mod b.)
5 2.2. ΜΚΔ, ΕΚΠ, ΑΛΓΟΡΙΘΜΟΣ ΤΟΥ ΕΥΚΛΕΙΔΗ 55 Αν d = (a, b) > 1 τότε για κάθε x Z έχουμε ότι d ax 1, και άρα είναι αδύνατο ο b να διαιρεί το ax 1. Αντίστροφα, αν (a, b) = 1 τότε από το Θεώρημα 2.2 έχουμε ότι υπάρχουν ακέραιοι x, y τέτοιοι ώστε 1 = ax + by απ όπου προκύπτει ότι ax = 1 mod b Αν x, y είναι δύο πολλαπλασιαστικά αντίστροφα modb του a τότε x = y mod b. Πώς μπορείς κανείς να υπολογίσει το μέγιστο κοινό διαιρέτη δύο θετικών ακεραίων; Λήμμα 2.1 Αν a b είναι δύο θετικοί ακέραιοι τότε 1. Αν b a τότε (a, b) = b. 2. Αν b a τότε (a, b) = (b, r) όπου r > 0 είναι το υπόλοιπο της διαίρεσης a/b. Η πρώτη πρόταση είναι προφανής. Αν a = qb + r είναι η ακέραια διαίρεση a/b τότε r = a qb άρα (a, b) r και, αφού (a, b) b έπεται ότι (a, b) (b, r). Όμως (b, r) a και άρα (b, r) (a, b), άρα (a, b) = (b, r), όπως έπρεπε να δείξουμε. Η προηγούμενη πρόταση είναι ουσιαστικά ο αλγόριθμος του Ευκλείδη για τον υπολογισμό του μέγιστου κοινού διαιρέτη δύο θετικών ακεραίων a, b. Δηλ. αντικαθιστούμε τον μεγαλύτερο από τους δύο, έστω a, από το υπόλοιπο της διαίρεσής του διά του μικροτέρου. Αν το υπόλοιπο αυτό είναι 0 (δηλ. αν b a) τότε η απάντηση είναι b. Αλλιώς συνεχίζουμε με τον υπολογισμό του (b, a mod b) μέχρι το a mod b να βγει 0. Ιδού μια υλοποίηση του αλγορίθμου αυτού στη γλώσσα python: def gcd(a, b): # find the gcd of a, b, where a >= b print a, b r = a % b # if a < b then this will reverse them at the next call if r == 0: return b else: return gcd(b, r) Η εντολή print που έχουμε βάλει ως πρώτη εντολή της συνάρτησης αυτής είναι απλά για να μας πληροφορεί ποιων αριθμών το μέγιστο κοινό διαιρέτη υπολογίζει πράγμα που μας βοηθάει να δούμε από ποιο ενδιάμεσα στάδια περνάει ο αλγόριθμος. Αν π.χ. καλέσουμε τη συνάρτηση με τους αριθμούς δίνοντας print gcd(7735, 3003) τότε παίρνουμε , 3003 που είναι οι ενδιάμεσες κλήσεις στη συνάρτηση μαζί με το τελικό αποτέλεσμα (91).
6 56 ΚΕΦΑΛΑΙΟ 2. ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ 2.3 Πρώτοι αριθμοί Ορισμός 2.6 (Πρώτος αριθμός) Ένας ακέραιος n > 1 λέγεται πρώτος αριθμός αν δεν έχει μη τετριμμένους διαιρέτες, αν δηλ. a n, a > 1 = a = n. Ένας ακέραιος n > 1 που δεν είναι πρώτος λέγεται σύνθετος αριθμός. Η ακολουθία των πρώτων αριθμών έχει το αρχικό κομμάτι 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79,.... Η ακολουθία των σύνθετων αριθμών έχει το αρχικό κομμάτι 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, Ελέγξτε αν οι αριθμοί 101, 103, 107, 111, 113, 121 είναι πρώτοι Αν ο n > 1 δεν είναι πρώτος τότε έχει κάποιο γνήσιο διαιρέτη (όχι το 1 ή το n δηλ.) d <= n. Αφού δεν είναι πρώτος θα έχει κάποιο γνήσιο διαιρέτη k. Υποθέστε ότι k > n και εξετάστε το μέγεθος του n/k Με βάση το αποτέλεσμα της Άσκησης 2.16 για να ελέγξουμε αν ένα θετικός ακέραιος n είναι πρώτος αρκεί να ελέγξουμε αν τον διαιρεί κάποιος από τους ακεραίους από το 2 έως τον ακέραιο n. Αυτή τη μέθοδο υλοποιεί η παρακάτω συνάρτηση python. def isprime(n): if n<=1: return False d = 2 while d*d <= n: # Check only up to the square root of n if n%d == 0: return False d = d+1 return True Δοκιμάστε την παραπάνω συνάρτηση σε κάποιους αριθμούς και καταλάβετε πώς δουλεύει. Μπορείτε επίσης να υπολογίσετε όλους τους πρώτους έως το 49 με την εντολή print [x for x in range(2,50) if isprime(x)] οπότε παίρνετε [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47] Την ίδια δουλειά κάνει και η παρακάτω συνάρτηση αλλά είναι κάπως πιο γρήγορη γιατί αποφεύγει να κάνει τον πολλπλασιασμό d*d αντικαθιστώντας τον με μερικές προσθέσεις (που είναι συνήθως πιο γρήγορες στην υλοποίηση, ειδικά για πολύ μεγάλους αριθμούς). def isprime(n): if n<=1: return False d = 2
7 2.3. ΠΡΩΤΟΙ ΑΡΙΘΜΟΙ 57 d2 = 4 while d2 <= n: # Check only up to the square root of n if n%d == 0: return False d2 = d2 + d + d +1 d = d+1 return True Γιατί δουλεύει; Έστω n σύνθετος και υποθέστε ότι ο μικρότερος πρώτος παράγοντας p του n είναι > n 1/3. Δείξτε τότε ότι ο n είναι γινόμενο δύο πρώτων (όχι αναγκαστικά διαφορετικών μεταξύ τους). Θεώρημα 2.4 Υπάρχουν άπειροι πρώτοι αριθμοί. Ας υποθέσουμε ότι υπάρχουν πεπερασμένοι μόνο πρώτοι αριθμοί, οι p 1, p 2,..., p n, και έστω k = p 1 p 2 p n + 1. Με βάση την υπόθεσή μας ο k δεν είναι πρώτος, άρα έχει κάποιο μη τετριμμένο διαιρέτη s, και ας υποθέσουμε ότι ο s είναι ο μικρότερος μη τετριμμένος διαιρέτης του k. Τότε ο s πρέπει να είναι πρώτος, αλλιώς θα είχε κι αυτός ένα μη τετριμμένο διαιρέτη, που θα ήταν και διαιρέτης του k και μικρότερος από τον s, πράγμα που αντιφάσκει με το ότι ο s είναι ο μικρότερος μη τετριμμένος διαιρέτης του k. Αφού ο s είναι πρώτος τότε είναι κάποιος από τους p 1, p 2,..., p n, έστω s = p t. Όμως k = 1 mod p t, άτοπο Δείξτε ότι υπάρχουν οσοδήποτε μεγάλα διαστήματα [a, b] N που δεν περιέχουν πρώτους αριθμούς. Υπάρχει πρώτος αριθμός ανάμεσα στους αριθμούς 10! + 2, 10! + 3, 10! + 4,..., 10! + 10; Βρείτε τους μικρότερους 5 διαδοχικούς σύνθετους ακεραίους. Βρείτε 10 6 διαδοχικούς ακεραίους που να είναι σύνθετοι. Ο αριθμός και οι επόμενοι 8 αριθμοί είναι όλοι σύνθετοι Ας είναι p 1 = 2, p 2 = 3, p 3 = 5, p 4,... οι πρώτοι αριθμοί σε αύξουσα σειρά. Χρησιμοποιώντας τη μέθοδο του Ευκλείδη (για το το ότι υπάρχουν άπειροι πρώτοι, Θεώρημα 2.4) δείξτε ότι χρησιμοποιώντας επαγωγή. Θεώρημα 2.5 Αν p πρώτος αριθμός και p ab τότε p a ή p b. p n 2 2n 1,
8 58 ΚΕΦΑΛΑΙΟ 2. ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Έστω ab = kp, k Z, και p a. Αφού p πρώτος αυτό σημαίνει ότι (p, a) = 1, και άρα, από το Θεώρημα 2.2, 1 = xa + yp για κάποιους x, y Z. Πολλαπλασιάζοντας επί b παίρνουμε άρα p b όπως έπρεπε να δείξουμε. b = xab + ypb = xkp + ybp = p(ak + yb) Παρατήρηση 2.1 Ομοίως αν p a 1 a 2 a k τότε το p διαιρεί κάποιο από τα a j (επαγωγή ως προς k). Θεώρημα 2.6 (Θεμελιώδες Θεώρημα της Αριθμητικής) Κάθε ακέραιος n > 1 μπορεί να γραφεί με μοναδικό τρόπο ως γινόμενο πρώτων αριθμών στη μορφή n = p e 1 1 pe 2 2 per r όπου p 1 < p 2 < < p r είναι διαφορετικοί πρώτοι αριθμοί και r, e 1, e 2,..., e r είναι θετικοί ακέραιοι. Παρατήρηση 2.2 Ένας άλλος τρόπος να εκφράσει κανείς αυτό το αποτέλεσμα είναι να πει ότι για κάθε ακέραιο είναι μοναδικά καθορισμένο το ποιοι πρώτοι αριθμοί (και πόσες φορές ο καθένας) εμφανίζονται αν τον διασπάσουμε πολλαπλασιαστικά όσο περισσότερο μπορούμε. Όποτε δηλ. υπάρχει κάποιος μη τετριμμένος διαιρέτης a του αριθμού n τότε γράφουμε n = a n a και συνεχίζουμε διασπώντας τους δύο ακεραίους a και n a όσο αυτό είναι δυνατό (μέχρι αυτοί να γίνουν πρώτοι δηλαδή). [ του Θεωρήματος 2.6] Είναι φανερό (ακολουθώντας την προηγούμενη παρατήρηση) ότι κάθε ακέραιος n > 1 μπορεί να γραφεί ως γινόμενο πρώτων. Απλά διασπάμε συνεχώς σε γινόμενο μικρότερων αριθμών, όσο μπορούμε να το κάνουμε αυτό. Όταν δε μπορούμε πλέον έχουμε φτάσει σε γινόμενο πρώτων. Αν θέλουμε μπορούμε να δώσουμε και μια πιο τυπική (αλλά όχι περισσότερο διαφωτιστική) απόδειξη με επαγωγή ως προς n. Συνεχίζουμε με επαγωγή για τη μοναδικότητα του αναπτύγματος σε γινόμενο πρώτων. Για n = 2 προφανώς ισχύει (η μικρότερη περίπτωση του n). Ας υποθέσουμε τώρα ότι ισχύει το θεώρημα για όλους τους ακεραίους μικροτερους από n και πάμε να το αποδείξουμε για το n. Ας υποθέσουμε ότι n = p 1 p 2 p r = q 1 q 2 q s, όπου p 1, p 2,..., q 1, q 2,... πρώτοι αριθμοί, όχι κατ ανάγκη πρώτοι μεταξύ τους. Τότε, με βάση το Θεώρημα 2.5 και την παρατήρηση που το ακολουθεί, έπεται ότι το q 1 είναι ένα από τα q 1, q 2,.... Διαγράφοντας το p 1 και από τις δύο μεριές προκύπτει ένας μικρότερος ακέραιος n = n/p 1 που γράφεται με δύο τρόπους ως γινόμενο πρώτων. Από επαγωγή αυτοί οι τρόποι πρέπει να είναι οι ίδιοι. Λήμμα 2.2 Αν a, b 1 τότε a b αν και μόνο αν όλοι οι πρώτοι αριθμοί που εμφανίζονται στην ανάλυση του a εμφανίζονται και στην ανάλυση του b και μάλιστα σε εκθέτη μεγαλύτερο ή ίσο από τον εκθέτη τους στον a. Ας υποθέσουμε ότι ο πρώτος p εμφανίζεται στην ανάλυση του a με εκθέτη e 1: a = p e
9 2.3. ΠΡΩΤΟΙ ΑΡΙΘΜΟΙ 59 (ακολουθούν διαφορετικοί πρώτοι). Αν a b τότε b = ka, για κάποιο k Z, οπότε b = ka = kp e και άρα ο p εμφανίζεται στον b με εκθέτη τουλάχιστον e. Η αντίστροφη κατεύθυνση είναι εξίσου φανερή αφού αν και a = p e 1 1 pe 2 2 pe k k b = p e 1 1 pe 2 2 pe k k p e k+1 k+1 pe r r με e j e j, j = 1, 2,..., k, τότε είναι προφανές ότι ο b είναι πολλαπλάσιο του a Ας είναι a, b 1 δύο ακέραιοι. Δείξτε ότι στον (a, b) εμφανίζονται ακριβώς εκείνοι οι πρώτοι αριθμοί που εμφανίζονται και στον a και στον b και μάλιστα με εκθέτη ίσο με τον ελάχιστο εκθέτη που έχουν στους a, b. Ομοίως δείξτε ότι στο [a, b] εμφανίζονται ακριβώς εκείνοι οι πρώτοι αριθμοί που εμφανίζονται στον a ή στον b και μάλιστα με εκθέτη ίσο με το μέγιστο εκθέτη που έχουν στους a, b. Γενικεύστε για περισσότερους από δύο ακεραίους. Χρησιμοποιήστε το Λήμμα Αν a, b 1 είναι ακέραιοι δείξτε ότι (a, b)[a, b] = a b Αν a, b > 0 είναι μεταξύ τους πρώτοι βρείτε τον (a 2 + b 2, a + b) Αν a άρτιος και b περιττός δείξτε (a, b) = (a/2, b). Αν και οι δύο είναι άρτιοι δείξτε (a, b) = 2(a/2, b/2) Αν (a, b) = 1 και c a + b δείξτε (c, a) = (c, b) = Αν α είναι ρίζα του πολυωνύμου x n + c n 1 x n 1 + c n 2 x n c 1 x + c 0, όπου c 0, c 1,..., c n 1 Z, δείξτε ότι αν το α δεν είναι ακέραιος τότε είναι άρρητος. Δείξτε ότι οι αριθμοί 2, 3 5, είναι άρρητοι. Υποθέστε όχι και γράψτε α = k l Βρείτε την ανάλυση του σε γινόμενο πρώτων. με (k, l) = 1 και l > 1. Ας είναι p κάποιος πρώτος διαιρέτης του l Βρείτε όλους τους πρώτους που διαιρούν το 10!. Ομοίως για τον αριθμό ( 30 10) Περιγράψτε όλους τους θετικούς ακεραίους που έχουν ακριβώς 3 διαιρέτες (συμπεριλαμβανομένου του 1 και τους εαυτού τους). Ομοίως για ακριβώς 4 διαιρέτες. Ομοίως για ακριβώς 5 διαιρέτες.
10 60 ΚΕΦΑΛΑΙΟ 2. ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Δείξτε ότι κάθε θετικός ακέραιος γράφεται σα γινόμενο ενός τέλειου τετραγώνου και ενός αριθμού ελεύθερου τετραγώνων (αυτοί είναι οι ακέραιοι πο υ δε διαιρούνται από το p 2 για κανένα πρώτο p) Δείξτε ότι η δύναμη με την οποία ο πρώτος p εμφανίζεται στο n! είναι το άθροισμα n/p + n/p 2 + n/p 3 +. Παρατηρήστε ότι το άθροισμα αυτό έχει πεπερασμένους σε πλήθος μη μηδενικούς όρους αφού για αρκετά μεγάλο j θα έχουμε n/p j < 1. Βρείτε την ανάλυση του 20! σε γινόμενο πρώτων. Πόσα μηδενικά υπάρχουν στο τέλος του αριθμού 1000!; Πόσα αν τον ίδιο αριθμό τον γράψουμε στο 8-αδικό σύστημα; Ποια ζεύγη ακεραίων a, b έχουν μέγιστο κοινό διαιρέτη (a, b) = 18 και ελάχιστο κοινό πολλαπλάσιο [a, b] = 240; Δείξτε c ab = c (a, c)(b, c) Δείξτε / Q Δείξτε log 2 3 / Q Δείξτε ότι ο αριθμός δεν είναι ποτέ ακέραιος αν n Δείξτε (a, b) = (a + b, [a, b]) n Πόσα ζεύγη θετικών ακεραίων a, b υπάρχουν με [a, b] = n. Η απάντηση εξαρτάται από την ανάλυση του n σε πρώτους παράγοντες Δείξτε ότι υπάρχουν άπειροι πρώτοι της μορφής 6k + 5. Δείξτε πρώτα ότι όλοι οι πρώτοι είναι της μορφής 6k+1 ή 6k+5. Υποθέστε ότι υπάρχουν πεπερασμένοι σε πλήθος πρώτοι της μορφής 6k + 5, οι p 1, p 2,..., p r, και εξετάστε τον αριθμό n = 6p 1 p 2 p r Αν πάρουμε ένα σύνολο από n + 1 διαφορετικούς ακεραίους από 1 έως 2n δείξτε ότι υπάρχει κάποιος στο σύνολο που διαιρεί κάποιον άλλο αριθμό του συνόλου.
11 Βιβλιογραφία Κεφαλαίου [1] Ronald L Graham, Donald E Knuth, and Oren Patashnik. Concrete Mathematics [2] Godfrey Harold Hardy and Edward Maitland Wright. An introduction to the theory of numbers. Oxford University Press,
12 62 ΒΙΒΛΙΟΓΡΑΦΙΑ ΚΕΦΑΛΑΙΟΥ
Θεωρια Αριθµων Προβληµατα
 Θεωρια Αριθµων Προβληµατα Μιχάλης Κολουντζάκης Τµήµα Μαθηµατικών και Εφαρµοσµένων Μαθηµατικών Πανεπιστήµιο Κρήτης Βούτες 700 3 Ηράκλειο 6 Απριλίου 205 Πολλές από τις παρακάτω ασκήσεις είναι από το ϐιβλίο
Θεωρια Αριθµων Προβληµατα Μιχάλης Κολουντζάκης Τµήµα Μαθηµατικών και Εφαρµοσµένων Μαθηµατικών Πανεπιστήµιο Κρήτης Βούτες 700 3 Ηράκλειο 6 Απριλίου 205 Πολλές από τις παρακάτω ασκήσεις είναι από το ϐιβλίο
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 10: Αριθμητική υπολοίπων - Κυκλικές ομάδες: Διαιρετότητα - Ευκλείδειος αλγόριθμος - Κατάλοιπα Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 10: Αριθμητική υπολοίπων - Κυκλικές ομάδες: Διαιρετότητα - Ευκλείδειος αλγόριθμος - Κατάλοιπα Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Πανεπιστήμιο Πειραιά Τμήμα Ψηφιακών Συστημάτων. Κρυπτογραφία. Θεωρία αριθμών Αλγεβρικές δομές. Χρήστος Ξενάκης
 Πανεπιστήμιο Πειραιά Τμήμα Ψηφιακών Συστημάτων Κρυπτογραφία Θεωρία αριθμών Αλγεβρικές δομές Χρήστος Ξενάκης Το σύνολο των ακεραίων Ζ = {..., -2, -1, 0, 1, 2,...} Το σύνολο των φυσικών Ν = {0, 1, 2,...}
Πανεπιστήμιο Πειραιά Τμήμα Ψηφιακών Συστημάτων Κρυπτογραφία Θεωρία αριθμών Αλγεβρικές δομές Χρήστος Ξενάκης Το σύνολο των ακεραίων Ζ = {..., -2, -1, 0, 1, 2,...} Το σύνολο των φυσικών Ν = {0, 1, 2,...}
Στοιχεία Θεωρίας Αριθμών & Εφαρμογές στην Κρυπτογραφία
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Σημειώσεις Διαλέξεων Στοιχεία Θεωρίας Αριθμών & Εφαρμογές στην Κρυπτογραφία Επιμέλεια σημειώσεων: Καλογερόπουλος Παναγιώτης
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Σημειώσεις Διαλέξεων Στοιχεία Θεωρίας Αριθμών & Εφαρμογές στην Κρυπτογραφία Επιμέλεια σημειώσεων: Καλογερόπουλος Παναγιώτης
4.2 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ
 14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
14 4 ΕΥΚΛΕΙΔΕΙΑ ΔΙΑΙΡΕΣΗ Ας υποθέσουμε ότι θέλουμε να βρούμε το πηλίκο και το υπόλοιπο της διαίρεσης του με τον Σύμφωνα με το γνωστό αλγόριθμο της διαίρεσης, το πηλίκο θα είναι ένας ακέραιος κ, τέτοιος,
Βασική Άλγεβρα. Ασκήσεις (εκδοχή )
 Βασική Άλγεβρα Ασκήσεις 05-6 (εκδοχή 8--05) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόμενα σελίδα Ασκήσεις Διαιρετότητα στους ακέραιους, ισοτιμίες Ασκήσεις Ακέραιοι odulo, Θεώρημα του Euler
Βασική Άλγεβρα Ασκήσεις 05-6 (εκδοχή 8--05) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόμενα σελίδα Ασκήσεις Διαιρετότητα στους ακέραιους, ισοτιμίες Ασκήσεις Ακέραιοι odulo, Θεώρημα του Euler
Ο μαθητής που έχει μελετήσει το κεφάλαιο της θεωρίας αριθμών θα πρέπει να είναι σε θέση:
 Ο μαθητής που έχει μελετήσει το κεφάλαιο της θεωρίας αριθμών θα πρέπει να είναι σε θέση: Να γνωρίζει: την αποδεικτική μέθοδο της μαθηματικής επαγωγής για την οποία πρέπει να γίνει κατανοητό ότι η αλήθεια
Ο μαθητής που έχει μελετήσει το κεφάλαιο της θεωρίας αριθμών θα πρέπει να είναι σε θέση: Να γνωρίζει: την αποδεικτική μέθοδο της μαθηματικής επαγωγής για την οποία πρέπει να γίνει κατανοητό ότι η αλήθεια
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ
 Διαιρετότητα Μαθαίνω Πολλαπλάσια ενός φυσικού αριθμού α είναι όλοι οι αριθμοί που προκύπτουν από τον πολλαπλασιασμό του με όλους τους φυσικούς αριθμούς, δηλαδή οι αριθμοί: 0, α, 2 α, 3 α, 4 α,... Το μηδέν
Διαιρετότητα Μαθαίνω Πολλαπλάσια ενός φυσικού αριθμού α είναι όλοι οι αριθμοί που προκύπτουν από τον πολλαπλασιασμό του με όλους τους φυσικούς αριθμούς, δηλαδή οι αριθμοί: 0, α, 2 α, 3 α, 4 α,... Το μηδέν
Βασική Άλγεβρα. Ασκήσεις (εκδοχή )
 Βασική Άλγεβρα Ασκήσεις 0-4 (εκδοχή 5--04) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόµενα σελίδα Ασκήσεις ιαιρετότητα στους ακέραιους, ισοτιµίες Ασκήσεις Ακέραιοι odulo, Θεώρηµα του Euler 7
Βασική Άλγεβρα Ασκήσεις 0-4 (εκδοχή 5--04) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόµενα σελίδα Ασκήσεις ιαιρετότητα στους ακέραιους, ισοτιµίες Ασκήσεις Ακέραιοι odulo, Θεώρηµα του Euler 7
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ ΑΝΔΡΕΣΑΚΗΣ ΔΗΜΗΤΡΗΣ ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.1.2. ΠΡΑΞΕΙΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ
 ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.1.2. ΠΡΑΞΕΙΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / ΠΡΟΣΘΕΣΗ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ 12+ 7 = 19 Οι αριθμοί 12 και 7 ονομάζονται ενώ το 19 ονομάζεται.. 3+5 =, 5+3 =...
ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ ΕΝΟΤΗΤΑ Α.1.2. ΠΡΑΞΕΙΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΚΑΙ ΙΔΙΟΤΗΤΕΣ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΗΜΕΡΟΜΗΝΙΑ / / ΠΡΟΣΘΕΣΗ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ 12+ 7 = 19 Οι αριθμοί 12 και 7 ονομάζονται ενώ το 19 ονομάζεται.. 3+5 =, 5+3 =...
2ογελ ΣΥΚΕΩΝ 2ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
f(t) = (1 t)a + tb. f(n) =
 Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Παράρτημα Αʹ Αριθμήσιμα και υπεραριθμήσιμα σύνολα Αʹ1 Ισοπληθικά σύνολα Ορισμός Αʹ11 (ισοπληθικότητα) Εστω A, B δύο μη κενά σύνολα Τα A, B λέγονται ισοπληθικά αν υπάρχει μια συνάρτηση f : A B, η οποία
Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης. Οταν το πρόβλημα έχει πεπερασμ
 Μαθηματικά Πληροφορικής 2ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μαθηματικά Πληροφορικής 2ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μορφές αποδείξεων. Μαθηματικά Πληροφορικής 2ο Μάθημα. Μορφές αποδείξεων (συνέχεια) Εξαντλητική μέθοδος
 Μορφές αποδείξεων Μαθηματικά Πληροφορικής ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μορφές αποδείξεων Μαθηματικά Πληροφορικής ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο 1
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 7 Φεβρουαρίου 03 Ασκηση. είξτε ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Λυσεις Ασκησεων - Φυλλαδιο ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 7 Φεβρουαρίου 03 Ασκηση. είξτε ότι
4.2 4.3 ΕΥΚΛΕΙ ΕΙΑ ΙΑΙΡΕΣΗ ΙΑΙΡΕΤΟΤΗΤΑ
 1 4.2 4.3 ΕΥΚΛΕΙ ΕΙΑ ΙΑΙΡΕΣΗ ΙΑΙΡΕΤΟΤΗΤΑ ΘΕΩΡΙΑ 1. Θεώρηµα Αν α, β ακέραιοι µε β 0, τότε υπάρχουν µοναδικοί ακέραιοι κ και υ, έτσι ώστε α = κβ + υ µε 0 υ < β. 2. Τέλεια διαίρεση Αν το υπόλοιπο υ της Ευκλείδειας
1 4.2 4.3 ΕΥΚΛΕΙ ΕΙΑ ΙΑΙΡΕΣΗ ΙΑΙΡΕΤΟΤΗΤΑ ΘΕΩΡΙΑ 1. Θεώρηµα Αν α, β ακέραιοι µε β 0, τότε υπάρχουν µοναδικοί ακέραιοι κ και υ, έτσι ώστε α = κβ + υ µε 0 υ < β. 2. Τέλεια διαίρεση Αν το υπόλοιπο υ της Ευκλείδειας
Οι φυσικοί αριθμοί. Παράδειγμα
 Οι φυσικοί αριθμοί Φυσικοί Αριθμοί Είναι οι αριθμοί με τους οποίους δηλώνουμε πλήθος ή σειρά. Για παράδειγμα, φυσικοί αριθμοί είναι οι: 0, 1,, 3,..., 99, 100,...,999, 1000, 0... Χωρίζουμε τους Φυσικούς
Οι φυσικοί αριθμοί Φυσικοί Αριθμοί Είναι οι αριθμοί με τους οποίους δηλώνουμε πλήθος ή σειρά. Για παράδειγμα, φυσικοί αριθμοί είναι οι: 0, 1,, 3,..., 99, 100,...,999, 1000, 0... Χωρίζουμε τους Φυσικούς
Περιεχόμενα. Κεφάλαιο 3 Οι ιδιότητες των αριθμών... 37 3.1 Αριθμητικά σύνολα... 37 3.2 Ιδιότητες... 37 3.3 Περισσότερες ιδιότητες...
 Περιεχόμενα Πρόλογος... 5 Κεφάλαιο Βασικές αριθμητικές πράξεις... 5. Τέσσερις πράξεις... 5. Σύστημα πραγματικών αριθμών... 5. Γραφική αναπαράσταση πραγματικών αριθμών... 6.4 Οι ιδιότητες της πρόσθεσης
Περιεχόμενα Πρόλογος... 5 Κεφάλαιο Βασικές αριθμητικές πράξεις... 5. Τέσσερις πράξεις... 5. Σύστημα πραγματικών αριθμών... 5. Γραφική αναπαράσταση πραγματικών αριθμών... 6.4 Οι ιδιότητες της πρόσθεσης
Οι Φυσικοί Αριθμοί. Παρατήρηση: Δεν στρογγυλοποιούνται αριθμοί τηλεφώνων, Α.Φ.Μ., κωδικοί αριθμοί κλπ. Πρόσθεση Φυσικών αριθμών
 Οι Φυσικοί Αριθμοί Γνωρίζουμε ότι οι αριθμοί είναι ποσοτικές έννοιες και για να τους γράψουμε χρησιμοποιούμε τα αριθμητικά σύμβολα. Οι αριθμοί μετρούν συγκεκριμένα πράγματα και φανερώνουν το πλήθος της
Οι Φυσικοί Αριθμοί Γνωρίζουμε ότι οι αριθμοί είναι ποσοτικές έννοιες και για να τους γράψουμε χρησιμοποιούμε τα αριθμητικά σύμβολα. Οι αριθμοί μετρούν συγκεκριμένα πράγματα και φανερώνουν το πλήθος της
11. Ποιες είναι οι άμεσες συνέπειες της διαίρεσης;
 10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
Σημειωματάριο μαθήματος 1ης Νοε. 2017
 Σημειωματάριο μαθήματος 1ης Νοε. 2017 Παραδείγματα συναρτήσεων. Αναδρομικές συναρτήσεις. Ξεκινήσαμε πακετάροντας παλαιότερό μας κώδικα για τον υπολογισμό των διαιρετών ενός φυσικού αριθμού σε συνάρτηση.
Σημειωματάριο μαθήματος 1ης Νοε. 2017 Παραδείγματα συναρτήσεων. Αναδρομικές συναρτήσεις. Ξεκινήσαμε πακετάροντας παλαιότερό μας κώδικα για τον υπολογισμό των διαιρετών ενός φυσικού αριθμού σε συνάρτηση.
* * * ( ) mod p = (a p 1. 2 ) mod p.
 Θεωρια Αριθμων Εαρινο Εξαμηνο 2016 17 Μέρος Α: Πρώτοι Αριθμοί Διάλεξη 1 Ενότητα 1. Διαιρετότητα: Διαιρετότητα, διαιρέτες, πολλαπλάσια, στοιχειώδεις ιδιότητες. Γραμμικοί Συνδυασμοί (ΓΣ). Ενότητα 2. Πρώτοι
Θεωρια Αριθμων Εαρινο Εξαμηνο 2016 17 Μέρος Α: Πρώτοι Αριθμοί Διάλεξη 1 Ενότητα 1. Διαιρετότητα: Διαιρετότητα, διαιρέτες, πολλαπλάσια, στοιχειώδεις ιδιότητες. Γραμμικοί Συνδυασμοί (ΓΣ). Ενότητα 2. Πρώτοι
ΚΕΦΑΛΑΙΟ 2: Ημιαπλοί Δακτύλιοι
 ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
> ln 1 + ln ln n = ln(1 2 3 n) = ln(n!).
 η Διάλεξη: Άρρητοι αριθμοί Το σύνολο Q των ρητών αριθμών είναι το Q = { m n : m Z, n N}. αριθμός που δεν είναι ρητός λέγεται άρρητος. Ενας πραγματικός Ασκηση: Αποδείξτε ότι το άθροισμα και το γινόμενο
η Διάλεξη: Άρρητοι αριθμοί Το σύνολο Q των ρητών αριθμών είναι το Q = { m n : m Z, n N}. αριθμός που δεν είναι ρητός λέγεται άρρητος. Ενας πραγματικός Ασκηση: Αποδείξτε ότι το άθροισμα και το γινόμενο
F 5 = (F n, F n+1 ) = 1.
 Λύσεις Θεμάτων Θεωρίας Αριθμών 1. (α) Να δειχθεί ότι ο πέμπτος αριθμός της μορφής Fermat, δηλαδή ο F 5 2 25 + 1 διαιρείται από το 641. (β) Εστω F n η ακολουθία των αριθμών Fermat, δηλαδή F n 2 2n + 1,
Λύσεις Θεμάτων Θεωρίας Αριθμών 1. (α) Να δειχθεί ότι ο πέμπτος αριθμός της μορφής Fermat, δηλαδή ο F 5 2 25 + 1 διαιρείται από το 641. (β) Εστω F n η ακολουθία των αριθμών Fermat, δηλαδή F n 2 2n + 1,
ΚΕΦΑΛΑΙΟ 2 Ο ΠΟΛΥΩΝΥΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ
 ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ 10 ΕΠΑΝΑΛΗΨΕΙΣ ΑΠΟ ΠΡΟΗΓΟΥΜΕΝΕΣ ΤΑΞΕΙΣ α ) Ταυτότητες 1. (a-β)(a+β)=a - b. (a ± b ) = a ± ab + b 3 3 3 3. (a ± b ) = a ± 3a b + 3ab
ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ - ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ Ο ΠΟΛΥΩΝΥΜΑ 10 ΕΠΑΝΑΛΗΨΕΙΣ ΑΠΟ ΠΡΟΗΓΟΥΜΕΝΕΣ ΤΑΞΕΙΣ α ) Ταυτότητες 1. (a-β)(a+β)=a - b. (a ± b ) = a ± ab + b 3 3 3 3. (a ± b ) = a ± 3a b + 3ab
Αριθμοθεωρητικοί Αλγόριθμοι
 Αλγόριθμοι που επεξεργάζονται μεγάλους ακέραιους αριθμούς Μέγεθος εισόδου: Αριθμός bits που απαιτούνται για την αναπαράσταση των ακεραίων. Έστω ότι ένας αλγόριθμος λαμβάνει ως είσοδο έναν ακέραιο Ο αλγόριθμος
Αλγόριθμοι που επεξεργάζονται μεγάλους ακέραιους αριθμούς Μέγεθος εισόδου: Αριθμός bits που απαιτούνται για την αναπαράσταση των ακεραίων. Έστω ότι ένας αλγόριθμος λαμβάνει ως είσοδο έναν ακέραιο Ο αλγόριθμος
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 1: Εισαγωγή- Χαρακτηριστικά Παραδείγματα Αλγορίθμων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 1: Εισαγωγή- Χαρακτηριστικά Παραδείγματα Αλγορίθμων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
KΕΦΑΛΑΙΟ 1 ΧΡΗΣΙΜΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΕΝΝΟΙΕΣ. { 1,2,3,..., n,...
 KΕΦΑΛΑΙΟ ΧΡΗΣΙΜΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΕΝΝΟΙΕΣ Βασικές έννοιες διαιρετότητας Θα συµβολίζουµε µε, τα σύνολα των φυσικών αριθµών και των ακεραίων αντιστοίχως: {,,3,,, } { 0,,,,, } = = ± ± ± Ορισµός Ένας φυσικός αριθµός
KΕΦΑΛΑΙΟ ΧΡΗΣΙΜΕΣ ΜΑΘΗΜΑΤΙΚΕΣ ΕΝΝΟΙΕΣ Βασικές έννοιες διαιρετότητας Θα συµβολίζουµε µε, τα σύνολα των φυσικών αριθµών και των ακεραίων αντιστοίχως: {,,3,,, } { 0,,,,, } = = ± ± ± Ορισµός Ένας φυσικός αριθµός
Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης. Οταν το πρόβλημα έχει πεπερασμ
 Μαθηματικά Πληροφορικής 4ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
Μαθηματικά Πληροφορικής 4ο Μάθημα Τμήμα Πληροφορικής και Τηλεπικοινωνιών Πανεπιστήμιο Αθηνών Μορφές αποδείξεων Υπάρχουν πολλά είδη αποδείξεων. Εδώ θα δούμε τα πιο κοινά: Εξαντλητική μέθοδος ή μέθοδος επισκόπησης.
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Κεφάλαιο 2. Παραγοντοποίηση σε Ακέραιες Περιοχές
 Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 2
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt016/nt016.html Πέµπτη 7 Οκτωβρίου 016 Ασκηση 1. Βρείτε όλους
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt016/nt016.html Πέµπτη 7 Οκτωβρίου 016 Ασκηση 1. Βρείτε όλους
Αλγεβρικές Δομές και Αριθμοθεωρία
 Κεφάλαιο 9 Αλγεβρικές Δομές και Αριθμοθεωρία 9.1 Εισαγωγή Θα παρουσιάσουμε κάποια στοιχεία από Θεωρία Αριθμών και ελάχιστα από Θεωρία Ομάδων. Οι γνώσεις αυτές είναι οι ελάχιστες απαραίτητες για την κατανόηση
Κεφάλαιο 9 Αλγεβρικές Δομές και Αριθμοθεωρία 9.1 Εισαγωγή Θα παρουσιάσουμε κάποια στοιχεία από Θεωρία Αριθμών και ελάχιστα από Θεωρία Ομάδων. Οι γνώσεις αυτές είναι οι ελάχιστες απαραίτητες για την κατανόηση
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Στοιχεία Θεωρίας Αριθμών & Εφαρμογές στην Κρυπτογραφία
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Σημειώσεις Διαλέξεων Στοιχεία Θεωρίας Αριθμών & Εφαρμογές στην Κρυπτογραφία Επιμέλεια σημειώσεων: Χρήστος Κούτρας Γιώργος
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών Σημειώσεις Διαλέξεων Στοιχεία Θεωρίας Αριθμών & Εφαρμογές στην Κρυπτογραφία Επιμέλεια σημειώσεων: Χρήστος Κούτρας Γιώργος
Χαρακτήρες διαιρετότητας ΜΚΔ ΕΚΠ Ανάλυση αριθμού σε γινόμενο πρώτων παραγόντων
 Χαρακτήρες διαιρετότητας ΜΚΔ ΕΚΠ Ανάλυση αριθμού σε γινόμενο πρώτων παραγόντων TINΑ ΒΡΕΝΤΖΟΥ www.ma8eno.gr www.ma8eno.gr Σελίδα 1 Ορισμός Ευκλείδεια διαίρεση ονομάζεται η πράξη κατά την οποία ένας αριθμός
Χαρακτήρες διαιρετότητας ΜΚΔ ΕΚΠ Ανάλυση αριθμού σε γινόμενο πρώτων παραγόντων TINΑ ΒΡΕΝΤΖΟΥ www.ma8eno.gr www.ma8eno.gr Σελίδα 1 Ορισμός Ευκλείδεια διαίρεση ονομάζεται η πράξη κατά την οποία ένας αριθμός
Ασκήσεις1 Πολυώνυμα. x x c. με το. b. Να βρεθούν όλες οι τιμές των a, Να βρεθεί ο μκδ και το εκπ τους
 Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
Κεφάλαιο 1 Πρότυπα. Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο.
 Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
 Επιμέλεια: xr.tsif Σελίδα 1 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΜΑΘΗΤΙΚΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ ΤΕΥΧΟΣ 6ο ΑΣΚΗΣΕΙΣ 501-600 Αφιερωμένο σε κάθε μαθητή που ασχολείται ή πρόκειται να ασχοληθεί με Μαθηματικούς διαγωνισμούς
Επιμέλεια: xr.tsif Σελίδα 1 ΠΡΟΤΕΙΝΟΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ΓΙΑ ΜΑΘΗΤΙΚΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ ΤΕΥΧΟΣ 6ο ΑΣΚΗΣΕΙΣ 501-600 Αφιερωμένο σε κάθε μαθητή που ασχολείται ή πρόκειται να ασχοληθεί με Μαθηματικούς διαγωνισμούς
ΠΑΡΑΓΡΑΦΟΣ 1. 2 ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ
 ΠΑΡΑΓΡΑΦΟΣ 1. 2 ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΑΣΚΗΣΕΙΣ ΜΕ ΑΘΡΟΙΣΜΑΤΑ ΚΑΙ ΑΦΑΙΡΕΣΕΙΣ ( 1 ) Να υπολογίσετε τις παραστάσεις Α = 3 + 23 + 19 Β = 8 +13 +45-7 Γ = 3 + 0 Α = 3+23 +19 =
ΠΑΡΑΓΡΑΦΟΣ 1. 2 ΠΡΟΣΘΕΣΗ ΑΦΑΙΡΕΣΗ ΚΑΙ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΦΥΣΙΚΩΝ ΑΡΙΘΜΩΝ ΑΣΚΗΣΕΙΣ ΜΕ ΑΘΡΟΙΣΜΑΤΑ ΚΑΙ ΑΦΑΙΡΕΣΕΙΣ ( 1 ) Να υπολογίσετε τις παραστάσεις Α = 3 + 23 + 19 Β = 8 +13 +45-7 Γ = 3 + 0 Α = 3+23 +19 =
β) 3 n < n!, n > 6 i i! = (n + 1)! 1, n 1 i=1
 Κεφάλαιο 2: Στοιχεία Λογικής - Μέθοδοι Απόδειξης 1. Να αποδειχθεί ότι οι λογικοί τύποι: (p ( (( p) q))) (p q) και p είναι λογικά ισοδύναμοι. Θέλουμε να αποδείξουμε ότι: (p ( (( p) q))) (p q) p, ή με άλλα
Κεφάλαιο 2: Στοιχεία Λογικής - Μέθοδοι Απόδειξης 1. Να αποδειχθεί ότι οι λογικοί τύποι: (p ( (( p) q))) (p q) και p είναι λογικά ισοδύναμοι. Θέλουμε να αποδείξουμε ότι: (p ( (( p) q))) (p q) p, ή με άλλα
Περιεχόμενα. Κεφάλαιο 3 Οι ιδιότητες των αριθμών Αριθμητικά σύνολα Ιδιότητες Περισσότερες ιδιότητες...
 Περιεχόμενα Πρόλογος 5 Κεφάλαιο Βασικές αριθμητικές πράξεις 5 Τέσσερις πράξεις 5 Σύστημα πραγματικών αριθμών 5 Γραφική αναπαράσταση πραγματικών αριθμών 6 Οι ιδιότητες της πρόσθεσης και του πολλαπλασιασμού
Περιεχόμενα Πρόλογος 5 Κεφάλαιο Βασικές αριθμητικές πράξεις 5 Τέσσερις πράξεις 5 Σύστημα πραγματικών αριθμών 5 Γραφική αναπαράσταση πραγματικών αριθμών 6 Οι ιδιότητες της πρόσθεσης και του πολλαπλασιασμού
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
4.4 ΜΕΓΙΣΤΟΣ ΚΟΙΝΟΣ ΔΙΑΙΡΕΤΗΣ - ΕΛΑΧΙΣΤΟ ΚΟΙΝΟ ΠΟΛΛΑΠΛΑΣΙΟ
 158 44 ΜΕΓΙΣΤΟΣ ΚΟΙΝΟΣ ΔΙΑΙΡΕΤΗΣ - ΕΛΑΧΙΣΤΟ ΚΟΙΝΟ ΠΟΛΛΑΠΛΑΣΙΟ Μέγιστος Κοινός Διαιρέτης Έστω α, β δύο ακέραιοι Ένας ακέραιος δ λέγεται κοινός διαιρέτης των α και β, όταν είναι διαιρέτης και του α και του
158 44 ΜΕΓΙΣΤΟΣ ΚΟΙΝΟΣ ΔΙΑΙΡΕΤΗΣ - ΕΛΑΧΙΣΤΟ ΚΟΙΝΟ ΠΟΛΛΑΠΛΑΣΙΟ Μέγιστος Κοινός Διαιρέτης Έστω α, β δύο ακέραιοι Ένας ακέραιος δ λέγεται κοινός διαιρέτης των α και β, όταν είναι διαιρέτης και του α και του
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας.
 Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
9 Πολυώνυμα Διαίρεση πολυωνύμων
 4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 2
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt014/nt014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt014/nt014.html https://sites.google.com/site/maths4edu/home/14
b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.
![b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0. b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.](/thumbs/63/49387122.jpg) Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Συνεχή Κλάσματα. Εμμανουήλ Καπνόπουλος Α.Μ 282
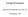 Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις Επαναληψης
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις Επαναληψης ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 22 Μαΐου 2013 Ασκηση 1. (1) Να λυθεί η γραµµική
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις Επαναληψης ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 22 Μαΐου 2013 Ασκηση 1. (1) Να λυθεί η γραµµική
Άλγεβρα Α Λυκείου Κεφάλαιο 2ο. οι πράξεις και οι ιδιότητές τους
 οι πράξεις και οι ιδιότητές τους Μερικές ακόμη ταυτότητες (επιπλέον από τις αξιοσημείωτες που βρίσκονται στο σχολικό βιβλίο) ) Διαφορά δυνάμεων με ίδιο εκθέτη: ειδικά αν ο εκθέτης ν είναι άρτιος υπάρχει
οι πράξεις και οι ιδιότητές τους Μερικές ακόμη ταυτότητες (επιπλέον από τις αξιοσημείωτες που βρίσκονται στο σχολικό βιβλίο) ) Διαφορά δυνάμεων με ίδιο εκθέτη: ειδικά αν ο εκθέτης ν είναι άρτιος υπάρχει
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 13 Μαρτίου 2013 Ασκηση 1. Αφού ϐρείτε την
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Α. Μπεληγιάννης - Σ. Παπαδάκης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt.html Τετάρτη 13 Μαρτίου 2013 Ασκηση 1. Αφού ϐρείτε την
Ερωτήσεις πολλαπλής επιλογής
 Ερωτήσεις πολλαπλής επιλογής 1. * Η µέθοδος της µαθηµατικής επαγωγής χρησιµοποιείται για την απόδειξη προτάσεων Ρ (ν), όταν Α. ν R Β. ν Q Γ. ν R*. ν N Ε. κανένα από τα προηγούµενα 2. * Για τους ακεραίους
Ερωτήσεις πολλαπλής επιλογής 1. * Η µέθοδος της µαθηµατικής επαγωγής χρησιµοποιείται για την απόδειξη προτάσεων Ρ (ν), όταν Α. ν R Β. ν Q Γ. ν R*. ν N Ε. κανένα από τα προηγούµενα 2. * Για τους ακεραίους
( ) ( ) Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή x. αντικ σταση στο που = α. [ ο αριθµ ός πουτο µηδεν ίζει
 μέρος πρώτο v v 1 v 1 Γενική μορφή πολυωνύμου: ( ) 1 1 Όροι του ( ) v v v P = a v + av 1 + av +... + a + a 1 + a, ν Ν, α ν R Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή. P : a, a, a,...,
μέρος πρώτο v v 1 v 1 Γενική μορφή πολυωνύμου: ( ) 1 1 Όροι του ( ) v v v P = a v + av 1 + av +... + a + a 1 + a, ν Ν, α ν R Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή. P : a, a, a,...,
2. Να γράψετε έναν αριθμό που είναι μεγαλύτερος από το 3,456 και μικρότερος από το 3,457.
 1. Ένα κεφάλαιο ενός βιβλίου ξεκινάει από τη σελίδα 32 και τελειώνει στη σελίδα 75. Από πόσες σελίδες αποτελείται το κεφάλαιο; Αν το κεφάλαιο ξεκινάει από τη σελίδα κ και τελειώνει στη σελίδα λ, από πόσες
1. Ένα κεφάλαιο ενός βιβλίου ξεκινάει από τη σελίδα 32 και τελειώνει στη σελίδα 75. Από πόσες σελίδες αποτελείται το κεφάλαιο; Αν το κεφάλαιο ξεκινάει από τη σελίδα κ και τελειώνει στη σελίδα λ, από πόσες
Αναδρομικές ακολουθίες και Θεωρία Αριθμών
 Αναδρομικές ακολουθίες και Θεωρία Αριθμών Εμμανουήλ Καπνόπουλος Επιβλέπων καθηγητής Ιωάννης Αντωνιάδης Μεταπτυχιακή Εργασία Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπιστήμιο Κρήτης Ηράκλειο Οκτώβριος
Αναδρομικές ακολουθίες και Θεωρία Αριθμών Εμμανουήλ Καπνόπουλος Επιβλέπων καθηγητής Ιωάννης Αντωνιάδης Μεταπτυχιακή Εργασία Τμήμα Μαθηματικών και Εφαρμοσμένων Μαθηματικών Πανεπιστήμιο Κρήτης Ηράκλειο Οκτώβριος
2 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΛΓΕΒΡΙΚΕΣ ΔΟΜΕΣ
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΛΓΕΒΡΙΚΕΣ ΔΟΜΕΣ Η θεωρία αριθμών και οι αλγεβρικές δομές τα τελευταία χρόνια χρησιμοποιούνται όλο και περισσότερο στην κρυπτολογία. Αριθμο-θεωρητικοί αλγόριθμοι χρησιμοποιούνται σήμερα
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ ΑΛΓΕΒΡΙΚΕΣ ΔΟΜΕΣ Η θεωρία αριθμών και οι αλγεβρικές δομές τα τελευταία χρόνια χρησιμοποιούνται όλο και περισσότερο στην κρυπτολογία. Αριθμο-θεωρητικοί αλγόριθμοι χρησιμοποιούνται σήμερα
τη µέθοδο της µαθηµατικής επαγωγής για να αποδείξουµε τη Ϲητούµενη ισότητα.
 Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Τµηµα Μαθηµατικων Εισαγωγή στην Αλγεβρα Τελική Εξέταση 15 Φεβρουαρίου 2017 1. (Οµάδα Α) Εστω η ακολουθία Fibonacci F 1 = 1, F 2 = 1 και F n = F n 1 + F n 2, για n
Αριστοτελειο Πανεπιστηµιο Θεσσαλονικης Τµηµα Μαθηµατικων Εισαγωγή στην Αλγεβρα Τελική Εξέταση 15 Φεβρουαρίου 2017 1. (Οµάδα Α) Εστω η ακολουθία Fibonacci F 1 = 1, F 2 = 1 και F n = F n 1 + F n 2, για n
A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις
![A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις](/thumbs/93/111356738.jpg) ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ ΑΣΚΗΣΗ η Αν α +β +γ = αβγ και α + β + γ, να δείξετε ότι το πολυώνυμο P()=(α β) +(β γ) + γ α είναι το μηδενικό πολυώνυμο. Από την ταυτότητα του Euler α +β +γ -αβγ = (α + β + γ)[(α-β)
ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ ΑΣΚΗΣΗ η Αν α +β +γ = αβγ και α + β + γ, να δείξετε ότι το πολυώνυμο P()=(α β) +(β γ) + γ α είναι το μηδενικό πολυώνυμο. Από την ταυτότητα του Euler α +β +γ -αβγ = (α + β + γ)[(α-β)
Η Ευκλείδεια διαίρεση
 1 Η Ευκλείδεια διαίρεση Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρηµα Αποδεικνύεται ότι για οποιουσδήποτε ακέραιους α και β, β 0, ισχύει το παρακάτω θεώρηµα και διατυπώνεται ως εξής : Αν α και β ακέραιοι µε β
1 Η Ευκλείδεια διαίρεση Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρηµα Αποδεικνύεται ότι για οποιουσδήποτε ακέραιους α και β, β 0, ισχύει το παρακάτω θεώρηµα και διατυπώνεται ως εξής : Αν α και β ακέραιοι µε β
ΛΥΣΕΙΣ ΤΩΝ ΑΣΚΗΣΕΩΝ ΕΠΑΝΑΛΗΨΗΣ ΓΙΑ ΤΙΣ ΓΙΟΡΤΕΣ (ΑΡΙΘΜΗΤΙΚΗ)
 ΛΥΣΕΙΣ ΤΩΝ ΑΣΚΗΣΕΩΝ ΕΠΑΝΑΛΗΨΗΣ ΓΙΑ ΤΙΣ ΓΙΟΡΤΕΣ (ΑΡΙΘΜΗΤΙΚΗ) 1. Ένα κεφάλαιο ενός βιβλίου ξεκινάει από τη σελίδα 32 και τελειώνει στη σελίδα 75. Από πόσες σελίδες αποτελείται το κεφάλαιο; Αν το κεφάλαιο
ΛΥΣΕΙΣ ΤΩΝ ΑΣΚΗΣΕΩΝ ΕΠΑΝΑΛΗΨΗΣ ΓΙΑ ΤΙΣ ΓΙΟΡΤΕΣ (ΑΡΙΘΜΗΤΙΚΗ) 1. Ένα κεφάλαιο ενός βιβλίου ξεκινάει από τη σελίδα 32 και τελειώνει στη σελίδα 75. Από πόσες σελίδες αποτελείται το κεφάλαιο; Αν το κεφάλαιο
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
bca = e. H 1j = G 2 H 5j = {f G j : f(0) = 1}
 Αλγεβρα Ι, Χειμερινο Εξαμηνο 2017 18 Ασκησεις που συζητηθηκαν στο φροντιστηριο Το [Α] συμβολίζει το φυλλάδιο ασκήσεων που θα βρείτε στην ιστοσελίδα του μαθήματος επιλέγοντας «Άλλες Ασκήσεις». 1. Πόσες
Αλγεβρα Ι, Χειμερινο Εξαμηνο 2017 18 Ασκησεις που συζητηθηκαν στο φροντιστηριο Το [Α] συμβολίζει το φυλλάδιο ασκήσεων που θα βρείτε στην ιστοσελίδα του μαθήματος επιλέγοντας «Άλλες Ασκήσεις». 1. Πόσες
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 11: Αριθμητική υπολοίπων-δυνάμεις Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 11: Αριθμητική υπολοίπων-δυνάμεις Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Σημειώσεις Ανάλυσης Ι. Θεωρούμε γνωστούς τους φυσικούς αριθμούς
 Σημειώσεις Ανάλυσης Ι 1. Οι ρητοί αριθμοί Θεωρούμε γνωστούς τους φυσικούς αριθμούς 1, 2, 3, και τις πράξεις (πρόσθεση - πολλαπλασιασμό)μεταξύ αυτών. Οι φυσικοί αριθμοί είναι επίσης διατεταγμένοι με κάποια
Σημειώσεις Ανάλυσης Ι 1. Οι ρητοί αριθμοί Θεωρούμε γνωστούς τους φυσικούς αριθμούς 1, 2, 3, και τις πράξεις (πρόσθεση - πολλαπλασιασμό)μεταξύ αυτών. Οι φυσικοί αριθμοί είναι επίσης διατεταγμένοι με κάποια
ΠΟΛΥΩΝΥΜΑ. Κεφάλαιο 2ο: Ερωτήσεις του τύπου Σωστό-Λάθος
 Κεφάλαιο 2ο: ΠΟΛΥΩΝΥΜΑ Ερωτήσεις του τύπου Σωστό-Λάθος 1. * Οι πραγματικοί αριθμοί είναι σταθερά πολυώνυμα. Σ Λ 2. * Το σταθερό πολυώνυμο 0 λέγεται μηδενικό πολυώνυμο. Σ Λ 3. * Κάθε σταθερό και μη μηδενικό
Κεφάλαιο 2ο: ΠΟΛΥΩΝΥΜΑ Ερωτήσεις του τύπου Σωστό-Λάθος 1. * Οι πραγματικοί αριθμοί είναι σταθερά πολυώνυμα. Σ Λ 2. * Το σταθερό πολυώνυμο 0 λέγεται μηδενικό πολυώνυμο. Σ Λ 3. * Κάθε σταθερό και μη μηδενικό
Πολυώνυµα - Πολυωνυµικές εξισώσεις
 4 ΚΕΦΑΛΑΙΟ Πολυώνυµα - Πολυωνυµικές εξισώσεις Ορισµός πολυωνύµου Ονοµάζoυµε ΠΟΛΥΩΝΥΜΟ του κάθε παράσταση της µορφής α ν ν +α ν- ν- + +α +α 0, ν ΙΝ και α 0, α,, α ν-, α ν ΙR. Παρατηρήσεις α. Τα α ν ν, α
4 ΚΕΦΑΛΑΙΟ Πολυώνυµα - Πολυωνυµικές εξισώσεις Ορισµός πολυωνύµου Ονοµάζoυµε ΠΟΛΥΩΝΥΜΟ του κάθε παράσταση της µορφής α ν ν +α ν- ν- + +α +α 0, ν ΙΝ και α 0, α,, α ν-, α ν ΙR. Παρατηρήσεις α. Τα α ν ν, α
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥΣΤΗΝ ΑΛΓΕΒΡΑ. Άρτιοι αριθμοί ονομάζονται οι αριθμοί που διαιρούνται με το 2 και περιττοί εκείνοι
 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥΣΤΗΝ ΑΛΓΕΒΡΑ 1)Ποιοι αριθμοί ονομάζονται άρτιοι και ποιοι περιττοί ; Άρτιοι αριθμοί ονομάζονται οι αριθμοί που διαιρούνται με το 2 και περιττοί εκείνοι που δεν διαιρούνται
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥΣΤΗΝ ΑΛΓΕΒΡΑ 1)Ποιοι αριθμοί ονομάζονται άρτιοι και ποιοι περιττοί ; Άρτιοι αριθμοί ονομάζονται οι αριθμοί που διαιρούνται με το 2 και περιττοί εκείνοι που δεν διαιρούνται
7.Αριθμητική παράσταση καλείται σειρά αριθμών που συνδέονται με πράξεις μεταξύ τους. Το αποτέλεσμα της αριθμητικής παράστασης ονομάζεται τιμή της.
 ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ Α.1.2 1. Οι ιδιότητες της πρόσθεσης των φυσικών αριθμών είναι οι εξής : Αντιμεταθετική ιδιότητα π.χ. α+β=β+α Προσετεριστική ιδιότητα π.χ. α+β+γ=(α+β)+γ=α+(β+γ) 2.Η πραξη της αφαίρεσης
ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ Α.1.2 1. Οι ιδιότητες της πρόσθεσης των φυσικών αριθμών είναι οι εξής : Αντιμεταθετική ιδιότητα π.χ. α+β=β+α Προσετεριστική ιδιότητα π.χ. α+β+γ=(α+β)+γ=α+(β+γ) 2.Η πραξη της αφαίρεσης
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Aπάντηση Απόλυτη τιμή αριθμού είναι η απόσταση του αριθμού από το 0. Συμβολίζεται με 3 = 3-3 = 3 + και και είναι πάντα θετικός αριθμός. Π.
 ΜΕΡΟΣ Α : Α Λ Γ Ε Β ΡΑ ΚΕΦΑΛΑΙΟ 1ο ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1.1 Πράξεις με πραγματικούς αριθμούς Α. Οι πραγματικοί αριθμοί και πράξεις τους 1. Γράψε τα βασικότερα σύνολα τιμών: Aπάντηση Ν{0,1,,,4,5,6,..+
ΜΕΡΟΣ Α : Α Λ Γ Ε Β ΡΑ ΚΕΦΑΛΑΙΟ 1ο ΟΙ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ 1.1 Πράξεις με πραγματικούς αριθμούς Α. Οι πραγματικοί αριθμοί και πράξεις τους 1. Γράψε τα βασικότερα σύνολα τιμών: Aπάντηση Ν{0,1,,,4,5,6,..+
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ
 ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
ιαιρετότητα Στοιχεία Θεωρίας Αριθµών «Ο Αλγόριθµος της ιαίρεσης» Αριθµητική Υπολοίπων 0 r < d και a = d q +r
 ιαιρετότητα Στοιχεία Θεωρίας Αριθµών ο a διαιρεί τον b: συµβολισµός: a b Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς a b και a c a (b + c) a b a bc, για κάθε c Z +
ιαιρετότητα Στοιχεία Θεωρίας Αριθµών ο a διαιρεί τον b: συµβολισµός: a b Ορέστης Τελέλης telelis@unipi.gr Τµήµα Ψηφιακών Συστηµάτων, Πανεπιστήµιο Πειραιώς a b και a c a (b + c) a b a bc, για κάθε c Z +
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Λυσεις Ασκησεων - Φυλλαδιο 1
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 1 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt01b/nt01b.html Πέµπτη 1 Οκτωβρίου 01 Ασκηση 1. είξτε ότι
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Λυσεις Ασκησεων - Φυλλαδιο 1 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt01b/nt01b.html Πέµπτη 1 Οκτωβρίου 01 Ασκηση 1. είξτε ότι
1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης
 1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης Στη συγκεκριμένη ενότητα εξετάζουμε θέματα σχετικά με την αριθμητική πεπερασμένης ακρίβειας που χρησιμοποιούν οι σημερινοί υπολογιστές και τα
1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης Στη συγκεκριμένη ενότητα εξετάζουμε θέματα σχετικά με την αριθμητική πεπερασμένης ακρίβειας που χρησιμοποιούν οι σημερινοί υπολογιστές και τα
3.1 ΕΞΙΣΩΣΕΙΣ 1 ΟΥ ΒΑΘΜΟΥ
 ΚΕΦΑΛΑΙΟ : ΕΞΙΣΩΣΕΙΣ. ΕΞΙΣΩΣΕΙΣ ΟΥ ΒΑΘΜΟΥ ΜΕΘΟΔΟΛΟΓΙΑ : ΑΠΛΗ ΜΟΡΦΗ Κάθε εξίσωση που έχει ή μπορεί να πάρει τη μορφή : α+β=0 ή α=-β () λέγεται εξίσωση ου βαθμού (ή πρωτοβάθμια εξίσωση), με άγνωστο το, ενώ
ΚΕΦΑΛΑΙΟ : ΕΞΙΣΩΣΕΙΣ. ΕΞΙΣΩΣΕΙΣ ΟΥ ΒΑΘΜΟΥ ΜΕΘΟΔΟΛΟΓΙΑ : ΑΠΛΗ ΜΟΡΦΗ Κάθε εξίσωση που έχει ή μπορεί να πάρει τη μορφή : α+β=0 ή α=-β () λέγεται εξίσωση ου βαθμού (ή πρωτοβάθμια εξίσωση), με άγνωστο το, ενώ
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Ασκησεις Επαναληψης. ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος :
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις Επαναληψης ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt015/nt015.html Τρίτη Ιουνίου 015 Ασκηση 1. (1) Να λυθεί η γραµµική
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις Επαναληψης ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt015/nt015.html Τρίτη Ιουνίου 015 Ασκηση 1. (1) Να λυθεί η γραµµική
Ε Μέχρι 18 Μαΐου 2015.
 Ε Μέχρι 18 Μαΐου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες άρα
Ε Μέχρι 18 Μαΐου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες άρα
ΠΟΛΥΩΝΥΜΑ. Κεφάλαιο 2ο: Ερωτήσεις του τύπου Σωστό-Λάθος
 Κεφάλαιο ο: ΠΟΛΥΩΝΥΜΑ Ερωτήσεις του τύπου Σωστό-Λάθος 1. * Οι πραγματικοί αριθμοί είναι σταθερά πολυώνυμα. Σ Λ. * Το σταθερό πολυώνυμο 0 λέγεται μηδενικό πολυώνυμο. Σ Λ 3. * Κάθε σταθερό και μη μηδενικό
Κεφάλαιο ο: ΠΟΛΥΩΝΥΜΑ Ερωτήσεις του τύπου Σωστό-Λάθος 1. * Οι πραγματικοί αριθμοί είναι σταθερά πολυώνυμα. Σ Λ. * Το σταθερό πολυώνυμο 0 λέγεται μηδενικό πολυώνυμο. Σ Λ 3. * Κάθε σταθερό και μη μηδενικό
ΕΥΡΕΣΗ ΜΕΓΙΣΤΟΥ ΚΟΙΝΟΥ ΔΙΑΙΡΕΤΗ
 ΕΥΡΕΣΗ ΜΕΓΙΣΤΟΥ ΚΟΙΝΟΥ ΔΙΑΙΡΕΤΗ Το πρόβλημα: Δεδομένα: δύο ακέραιοι a και b Ζητούμενο: ο μέγιστος ακέραιος που διαιρεί και τους δύο δοσμένους αριθμούς, γνωστός ως Μέγιστος Κοινός Διαιρέτης τους (Greatest
ΕΥΡΕΣΗ ΜΕΓΙΣΤΟΥ ΚΟΙΝΟΥ ΔΙΑΙΡΕΤΗ Το πρόβλημα: Δεδομένα: δύο ακέραιοι a και b Ζητούμενο: ο μέγιστος ακέραιος που διαιρεί και τους δύο δοσμένους αριθμούς, γνωστός ως Μέγιστος Κοινός Διαιρέτης τους (Greatest
Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5
 Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5 Α Σύνολα αριθμών Για τα σύνολα των αριθμών γνωρίζουμε ότι N Z Q R. ) Το N= { 0,,,,... } είναι το σύνολο των φυσικών αριθμών. ) Το Z = { 0, ±, ±, ±,... } είναι το σύνολο
Ιγνάτιος Ιωαννίδης Χρήσιμες Γνώσεις 5 Α Σύνολα αριθμών Για τα σύνολα των αριθμών γνωρίζουμε ότι N Z Q R. ) Το N= { 0,,,,... } είναι το σύνολο των φυσικών αριθμών. ) Το Z = { 0, ±, ±, ±,... } είναι το σύνολο
Αλγόριθμοι για αυτόματα
 Κεφάλαιο 8 Αλγόριθμοι για αυτόματα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 8.1 Πότε ένα DFA αναγνωρίζει κενή ή άπειρη γλώσσα Δοθέντος ενός DFA M καλούμαστε
Κεφάλαιο 8 Αλγόριθμοι για αυτόματα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 8.1 Πότε ένα DFA αναγνωρίζει κενή ή άπειρη γλώσσα Δοθέντος ενός DFA M καλούμαστε
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Ασκησεις - Φυλλαδιο 3 ιδασκοντες: Ν. Μαρµαρίδης - Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt2014/nt2014.html https://sites.google.com/site/maths4edu/home/14
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ. Ασκησεις - Επανάληψης. ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος :
 ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις - Επανάληψης ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt015b/nt015b.html Πέµπτη 1 Ιανουαρίου 016 Ασκηση 1. (1) Να λυθεί
ΘΕΩΡΙΑ ΑΡΙΘΜΩΝ Τµηµα Β Ασκησεις - Επανάληψης ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/numbertheory/nt015b/nt015b.html Πέµπτη 1 Ιανουαρίου 016 Ασκηση 1. (1) Να λυθεί
Υπολογισμός της δύναμης z=x b modn
 Υπολογισμός της δύναμης z=x b modn 1.Γράφουμε τον εκθέτη b στο δυαδικό σύστημα αρίθμησης i b = b i όπου i= 0 bi {0,1} I==0,1,,l-1.Εφαρμόζουμε έπειτα τον εξής αλγόριθμο: z=1 for I=l-1 downto 0 do z=z modn
Υπολογισμός της δύναμης z=x b modn 1.Γράφουμε τον εκθέτη b στο δυαδικό σύστημα αρίθμησης i b = b i όπου i= 0 bi {0,1} I==0,1,,l-1.Εφαρμόζουμε έπειτα τον εξής αλγόριθμο: z=1 for I=l-1 downto 0 do z=z modn
x 2 + y 2 = z 2 x = 3, y = 4, z = 5 x 2 + y 2 = z 2 (2.1)
 Πυθαγόρειες Τριάδες Χριστίνα Ιατράκη Ημερομηνία παράδοσης -10-014 1 Εισαγωγικά Ορισμός 1.1 Πυθαγόρεια τριάδα καλείται κάθε τριάδα ακέραιων (x, y, z) που είναι μη τετριμμένη λύση της εξίσωσης Μια τέτοια
Πυθαγόρειες Τριάδες Χριστίνα Ιατράκη Ημερομηνία παράδοσης -10-014 1 Εισαγωγικά Ορισμός 1.1 Πυθαγόρεια τριάδα καλείται κάθε τριάδα ακέραιων (x, y, z) που είναι μη τετριμμένη λύση της εξίσωσης Μια τέτοια
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ Πίνακας περιεχομένων Κεφάλαιο 1 - ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ... 2 Κεφάλαιο 2 ο - ΤΑ ΚΛΑΣΜΑΤΑ... 6 Κεφάλαιο 3 ο - ΔΕΚΑΔΙΚΟΙ ΑΡΙΘΜΟΙ... 10 ΣΩΤΗΡΟΠΟΥΛΟΣ ΝΙΚΟΣ 1 Κεφάλαιο 1 - ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ
ΜΑΘΗΜΑΤΙΚΑ Α ΓΥΜΝΑΣΙΟΥ Πίνακας περιεχομένων Κεφάλαιο 1 - ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ... 2 Κεφάλαιο 2 ο - ΤΑ ΚΛΑΣΜΑΤΑ... 6 Κεφάλαιο 3 ο - ΔΕΚΑΔΙΚΟΙ ΑΡΙΘΜΟΙ... 10 ΣΩΤΗΡΟΠΟΥΛΟΣ ΝΙΚΟΣ 1 Κεφάλαιο 1 - ΟΙ ΦΥΣΙΚΟΙ ΑΡΙΘΜΟΙ
ΠΕΡΙΕΧΟΜΕΝΑ 1 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΑΚΟΛΟΥΘΙΕΣ ΑΡΙΘΜΩΝ EΞΙΣΩΣΕΙΣ...47 ΠΡΟΛΟΓΟΣ... 9
 ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ... 9 1 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ...11 1.1 Βασικές θεωρητικές γνώσεις... 11 1.. Λυμένα προβλήματα... 19 1. Προβλήματα προς λύση... 4 1.4 Απαντήσεις προβλημάτων Πραγματικοί αριθμοί... 0 ΑΚΟΛΟΥΘΙΕΣ
ΠΕΡΙΕΧΟΜΕΝΑ ΠΡΟΛΟΓΟΣ... 9 1 ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ...11 1.1 Βασικές θεωρητικές γνώσεις... 11 1.. Λυμένα προβλήματα... 19 1. Προβλήματα προς λύση... 4 1.4 Απαντήσεις προβλημάτων Πραγματικοί αριθμοί... 0 ΑΚΟΛΟΥΘΙΕΣ
Ασκήσεις4 48. P AP τριγωνικό. Αφού δείξτε ότι ο A δεν είναι διαγωνίσιμος, βρείτε αντιστρέψιμο A 1 3 1
 Ασκήσεις4 48 Ασκήσεις4 Τριγωνισιμότητα Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Θεώρημα: είναι τριγωνίσιμος αν και μόνο αν ( x ) γινόμενο πρωτοβάθμιων παραγόντων
Ασκήσεις4 48 Ασκήσεις4 Τριγωνισιμότητα Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Θεώρημα: είναι τριγωνίσιμος αν και μόνο αν ( x ) γινόμενο πρωτοβάθμιων παραγόντων
4.2 ΔΙΑΙΡΕΣΗ ΠΟΛΥΩΝΥΜΩΝ
 4 ΔΙΑΙΡΕΣΗ ΠΟΛΥΩΝΥΜΩΝ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΘΕΩΡΗΜΑ (ΤΑΥΤΟΤΗΤΑ ΤΗΣ ΔΙΑΙΡΕΣΗΣ) Για κάθε ζεύγος πολυωνύμων ( και ( με ( 0 υπάρχουν δυο μοναδικά πολυώνυμα ( και (, τέτοια ώστε : ( ( όπου το ( ή είναι το μηδενικό
4 ΔΙΑΙΡΕΣΗ ΠΟΛΥΩΝΥΜΩΝ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΘΕΩΡΗΜΑ (ΤΑΥΤΟΤΗΤΑ ΤΗΣ ΔΙΑΙΡΕΣΗΣ) Για κάθε ζεύγος πολυωνύμων ( και ( με ( 0 υπάρχουν δυο μοναδικά πολυώνυμα ( και (, τέτοια ώστε : ( ( όπου το ( ή είναι το μηδενικό
Ορισμένες σελίδες του βιβλίου
 Ορισμένες σελίδες του βιβλίου 7. Θεωρούμε το σύνολο αναφοράς 0,,. Να οριστούν τα σύνολα: Α. των τριψηφίων αριθμών που σχηματίζουν τα στοιχεία του Ω. Β. των τριψηφίων αριθμών με διαφορετικά ψηφία Γ. των
Ορισμένες σελίδες του βιβλίου 7. Θεωρούμε το σύνολο αναφοράς 0,,. Να οριστούν τα σύνολα: Α. των τριψηφίων αριθμών που σχηματίζουν τα στοιχεία του Ω. Β. των τριψηφίων αριθμών με διαφορετικά ψηφία Γ. των
Επαναληπτικές Ασκήσεις
 Επαναληπτικές Ασκήσεις Έστω ότι το υπόλοιπο της διαίρεσης ενός πολυωνύμου ( x ) α Να γράψετε την ταυτότητα της διαίρεσης β Να βρείτε τα 0 και Ρ γ Αν το πολυώνυμο ( x) είναι x να βρείτε: x + x είναι 3x
Επαναληπτικές Ασκήσεις Έστω ότι το υπόλοιπο της διαίρεσης ενός πολυωνύμου ( x ) α Να γράψετε την ταυτότητα της διαίρεσης β Να βρείτε τα 0 και Ρ γ Αν το πολυώνυμο ( x) είναι x να βρείτε: x + x είναι 3x
Θεώρημα Βolzano. Κατηγορία 1 η. 11.1 Δίνεται η συνάρτηση:
 Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
3 o Καλοκαιρινό Μαθηµατικό σχολείο Ε.Μ.Ε. Λεπτοκαρυά Πιερίας 2009
 3 o Καλοκαιρινό Μαθηµατικό σχολείο Ε.Μ.Ε. Λεπτοκαρυά Πιερίας 2009 ιαιρετότητα και Ισοτιµίες Β και Γ Λυκείου Αλέξανδρος Γ. Συγκελάκης ags@math.uoc.gr Ιούλιος 2009 1 ιαιρετοτητα και Ισοτιµιες ΠΡΟΛΟΓΟΣ Το
3 o Καλοκαιρινό Μαθηµατικό σχολείο Ε.Μ.Ε. Λεπτοκαρυά Πιερίας 2009 ιαιρετότητα και Ισοτιµίες Β και Γ Λυκείου Αλέξανδρος Γ. Συγκελάκης ags@math.uoc.gr Ιούλιος 2009 1 ιαιρετοτητα και Ισοτιµιες ΠΡΟΛΟΓΟΣ Το
Μ Α Θ Η Μ Α Τ Ι Κ Α Γ ΓΥΜΝΑΣΙΟΥ ΖΕΡΒΟΣ ΜΑΝΟΛΗΣ
 Μ Α Θ Η Μ Α Τ Ι Κ Α Γ ΓΥΜΝΑΣΙΟΥ ΖΕΡΒΟΣ ΜΑΝΟΛΗΣ 1 ΜΕΡΟΣ Α ΚEΦΑΛΑΙΟ 1 Ο ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ 1.1 ΠΡΑΞΕΙΣ ΜΕ ΠΡΑΓΜΑΤΙΚΟΥΣ ΑΡΙΘΜΟΥΣ Α. Οι πραγματικοί αριθμοί και οι πράξεις τους 1. ΕΡΩΤΗΣΗ Τι ονομάζουμε
Μ Α Θ Η Μ Α Τ Ι Κ Α Γ ΓΥΜΝΑΣΙΟΥ ΖΕΡΒΟΣ ΜΑΝΟΛΗΣ 1 ΜΕΡΟΣ Α ΚEΦΑΛΑΙΟ 1 Ο ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ 1.1 ΠΡΑΞΕΙΣ ΜΕ ΠΡΑΓΜΑΤΙΚΟΥΣ ΑΡΙΘΜΟΥΣ Α. Οι πραγματικοί αριθμοί και οι πράξεις τους 1. ΕΡΩΤΗΣΗ Τι ονομάζουμε
K. Μυλωνάκης Αλγεβρα B Λυκείου
 ΠΟΛΥΩΝΥΜΑ Ονομάζουμε μονώνυμο του x κάθε πραγματικό αριθμό ή κάθε παράσταση της μορφής αx ν, όπου α είναι πραγμ. αριθμός και ν ένας θετικός ακέραιος. Π.χ. οι παραστάσεις 2χ 4, -3χ 2, 7 είναι μονώνυμα του
ΠΟΛΥΩΝΥΜΑ Ονομάζουμε μονώνυμο του x κάθε πραγματικό αριθμό ή κάθε παράσταση της μορφής αx ν, όπου α είναι πραγμ. αριθμός και ν ένας θετικός ακέραιος. Π.χ. οι παραστάσεις 2χ 4, -3χ 2, 7 είναι μονώνυμα του
