σχήμα 4γ Ωστόσο μόλις προσθέσουμε άλλους τέσσερις κύκλους (σαν ρόμβο) το τετράγωνο εξαφανίζεται από μία οκταγωνική ή και κυκλική διάταξη (σχήμα 6)
|
|
|
- Ἀριστομάχη Αλεβίζος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Οι παρακάτω σημειώσεις βασίζονται στο βιβλίο Τέχνη και Οπτική Αντίληψη, κεφάλαιο Σχήμα, σελ , του Rudolf Arnheim, Εκδόσεις Θεμέλιο, Πρόκειται για μια σύντομη επισκόπηση των βασικών εννοιών στις οποίες αναφέρεται ο Αrnheim με χρήση των παραδειγμάτων του για να διαφωτιστεί η έννοια του σχήματος και η έννοια της απλότητας. Η σύνοψη αυτή βασίζεται στις προφορικές παραδόσεις του μαθήματος Εικαστική Σύνθεση 2 το Δ' εξάμηνο και απευθύνεται στους φοιτητές του μαθήματος. Οι εικόνες και τα σχετικά σχόλια συνοδεύουν το κείμενο επεξηγηματικά ώστε να γίνουν πιο εύγλωττα κατανοητές κάποιες από τις θεωρητικές έννοιες στην εφαρμοφή τους. Σχήμα 'Ενα σχήμα ορίζεται από τα όρια του. Δεν προσδιορίζεται από άλλες ιδιότητες, όπως είναι η χωρική διάταξη, το αν είναι ορθό ή ανάστροφο, η γειτονία του με άλλα σχήματα, το χρώμα και η υφή. Ωστόσο η αντίληψη που έχουμε για ένα σχήμα επηρρεάζεται από κάποιες από αυτές τις ιδιότητες. Η αντιληπτική εμπειρία ενός αισθητού σχήματος επηρρεάζεται από την προηγούμενη εμπειρία μας. Σαν συνέπεια η κοινωνική γνώση συμπληρώνει την φυσιολογική και στο δυτικό πολιτισμό πχ. το σχήμα υπόκειται στους προοπτικούς νόμους και στην αδιαφάνεια των επιφανειών. Ενώ σε έναν πρωτόγονο ένα τετράγωνο σχεδιασμένο με προοπτική ενός σημείου, απλά παύει να είναι πια τετράγωνο, εμείς αναγνωρίζουμε σχήματα ακόμα και όταν καλύπτονται εν μέρη από άλλα σαν ολόκληρα. Ακόμη και όταν τους λείπει ένα τμήμα μπορούμε να συμπληρώσουμε αυτόματα το υπόλοιπο, πχ μια φέτα πεπόνι παραπέμπει στο ολόκληρο φρούτο. Eπίσης το περιεχόμενο ενός σχήματος επηρρεάζει την αντίληψη που έχουμε γι αυτό και ένα αυτοκίνητο που λειτουργεί γίνεται διαφορετικά αντιληπτό από ένα που δεν έχει μηχανή. Κατ' αντίθεση στον αρχαίο αιγυπτιακό πολιτισμό ή σε καποιους ιθαγενείς της Πολυνησίας αυτά τα χαρακτηριστικά δεν ισχύουν και τα σχήματα αψηφούν την προοπτική ή παρουσιάζονται σαν διάφανα με το περιεχόμενο τους. Άρα το σχήμα επηρρεάζεται από το εννοιολογικό του περιεχόμενο το οποίο και του προσδίδει ορισμένα αναπόσπαστα με την αναγνωρισή του χαρακτηριστικά. Αναγνωρίζουμε ένα αντικείμενο από τα μέρη του χωρίς να χρειαζόμαστε τα όρια του. Πχ ένα ανθρώπινο πρόσωπο γίνεται κατανοητό και μόνο από τα μέρη που το απαρτίζουν. σχήμα 1 Επίδραση στην αντίληψη του σχήματος έχει και η χωρική - χρονική σχέση ενός σχήματος με το περιβάλον του, δηλαδή το τι άλλο βρίσκεται κοντά του ή το τι έχει προηγηθεί ή το τι ακολουθεί.
2 Ένα παράδειγμα βλέπουμε στο σχήμα 2. Στο 2α αντιλαμβανόμαστε ένα τρίγωνο που είναι προσκολλημένο σε μία κάθετη. Αν όμως δούμε την σχηματική αλληλουχία του σχήματος 2β εύκολα αντιλαμβανόμαστε το ίδιο σχήμα σαν ένα τετράγωνο που είναι κρυμμένο πίσω από ένα επίπεδο. σχήμα 2α σχήμα 2β Άλλος παράγοντας επίδρασης στην αντίληψη μας για το σχήμα είναι η προηγούμενη εμπειρία μας αφού με βάση αυτό που ξέρουμε προχωρούμε σε υποθέσεις για να αναγνωρίσουμε και να κατατάξουμε ό,τι βλέπουμε. σχήμα 3 Έτσι η προηγούμενη γνώση και η προσδοκία επηρρεάζουν την αντίληψη που έχουμε για ένα σχήμα. Αν περιμένουμε να δούμε κάποιον όλοι οι άνθρωποι που μας πλησιάζουν μοιάζουν μ αυτόν. Στο σχήμα 3 η διαγώνιος λουρίδα που περιέχεται μέσα στο ορθογώνιο δεν μας λέει κάτι. Παρόλα αυτά αν μας πουν ότι είναι ο λαιμός μιας καμηλοπάρδαλης που περνά έξω από ένα παράθυρο αυτό γίνεται εύκολα πιστευτό λόγω της ομοιότητας με σχετικές εικόνες. Τότε το συγκεκριμένο σχήμα παίρνει ένα άλλο νόημα. Χωρίς να έχει αλλάξει τίποτα σ αυτό το αντιλαμβανόμαστε σαν τμήμα ενός όλου που συνεχίζει έξω από το συγκεκριμένο πλαίσιο. Όμως, στην ίδια την εικόνα δεν υπάρχει η ένδειξη για το πως θα την διαβάσουμε. Η αναγνώριση που αναφέρουμε δεν συμβαίνει ανεξάρτητα από το περιβάλον που υπάρχει η εικόνα, ή χωρίς κάποια "βοήθεια". Χρειαζόμαστε μία ένδειξη που να μας δείξει το δρόμο: μια πρόσφατη επίσκεψη σε ζωολογικό κήπο, ένα σχετικό ντοκυμαντερ, τοποθέτηση της εικόνας μέσα σε περιβάλον ζούγκλας. Όταν δοθούν τα κατάλληλα ερεθίσματα ένα σχήμα μπορεί να αποκτήσει ένα άλλο νόημα, χωρίς να μεταβληθεί καθόλου από μόνο του. Αυτό σημαίνει ότι ένα σχήμα είναι ένα δοχείο έτοιμο να το γεμίσουμε με ιδέες και επίσης πως κάποιες φορές αυτές οι ιδέες εισχωρούν από μόνες τους στο σχήμα μας αν δεν προσέξουμε τα γειτονικά σ αυτό μηνύματα. Σχετικά ο Gombrich λέει "'Οσο μεγαλύτερη βιολογική σχέση έχει ένα σχήμα με μας τόσο περισσότερες πιθανότητες έχει να είμαστε σε ετοιμότητα να το το αναγνωρίσουμε και συνεπώς
3 να είναι πιο ανεκτικά τα κριτήρια της μορφολογικής μας συμφωνίας". σχήμα4α σχήμα 4β σχήμα 4γ Ένα σχήμα μπορεί να μην γίνει αντιληπτό αν παρουσιαστεί μέσα σε ένα νέο περίγυρο. Για παράδειγμα το σχήμα 4α δεν αναγνωρίζεται το ίδιο εύκολα στο παράδειγμα 4β (επιμένουμε να βλέπουμε πρώτα ένα τετράγωνο) ή και μόνο αν το επιδιώξουμε στο παράδειγμα 4γ. Ωστόσο το μόνο στοιχείο που έχει παραλλαχτεί είναι ο περίγυρός του. Υπάρχουν διαφορετικές προτεραιότητες στην αναγνωρισιμότητα των σχημάτων; Γιατί κάποια σχήματα προτιμούνται έναντι άλλων; Για παράδειγμα, ας πάρουμε 4 μαύρους κύκλους. Το πιο άμεσο συμπέρασμα που καταλήγουμε είναι ότι ανήκουν σε ένα τετράγωνο και ορίζουν τις γωνίες του (σχήμα5α). Όμως τι μας κάνει να είμαστε τόσο σίγουροι; Σύμφωνα με τα σχήματα 5β και 5γ οι ίδιοι κύκλοι θα μπορούσαν να ορίζουν τα σχήματα αυτά και άπειρα άλλα. Ωστόσο αυτο δεν φαίνεται να μας απασχόλησε ούτε για ένα λεπτό προηγουμένως σαν ιδέα και ακόμη και τώρα δεν φαίνεται ιδιαίτερα πειστικό. σχήμα 5 Ωστόσο μόλις προσθέσουμε άλλους τέσσερις κύκλους (σαν ρόμβο) το τετράγωνο εξαφανίζεται από μία οκταγωνική ή και κυκλική διάταξη (σχήμα 6) σχήμα 6
4 Λευκοί κύκλοι ή τετράγωνα εμφανίζονται για τους περισσότερους ανθρώπους στα κέντρα των τεσσάρων γραμμών στο σχήμα 7. Γιατί όμως βλέπουμε κύκλο ή τετράγωνα και όχι άλλο σχήμα; σχήμα 7 Τελικά τι μας κάνει να αναγνωρίζουμε κάποια σχήματα ευκολότερα ή καθαρότερα ή συχνότερα από άλλα; Αν ανατρέξουμε στη θεωρία της Gestalt η απάντηση φαίνεται απλή: αναγνωρίζουμε τα πρώτα τα πιο απλά, πιο αρμονικά, πιο συμμετρικά σχήματα για αυτό και ο κύκλος και το τετράγωνο πάντα προηγούνται. Η βασική αρχή που καθορίζει την προτεραιότητα αναγνώρισης κάποιων σχημάτων έναντι άλλων όπως εκφράζεται μέσα από την θεωρία της Gestalt ορίζει πως: "Κάθε διάταξη ερεθισμάτων τείνει να γίνει αντιληπτή με τέτοιο τρόπο ώστε η προκύπτουσα δομή να είναι η απλούστερη που επιτρέπεται απο τις δεδομένες συνθήκες." Απλότητα Τι εννοούμε με τον όρο απλότητα; Είναι μια έννοια σχετική, υποκειμενική, ή καθορίζει κάποιους νόμους αντικειμενικά που μας επιτρέπουν να κατανοούμε σταθερά κάποιες δομές σαν απλές και άλλες όχι; Η απλότητα αναφέρεται πάντα σε μία διάταξη που είναι δοσμένη με τέτοιο τρόπο ώστε όταν μας παρουσιάζεται να μπορούμε να την "παρακολουθήσουμε": να μπορούμε να φανταστούμε τις σχέσεις μεταξύ που έχουν τα πράγματα που είναι διατεταγμένα κατ' αυτήν και επομένως να μπορούμε να τα θυμηθούμε. Όμως αναφερόμαστε σε οπτικά ερεθίσματα. Η οπτική γλώσσα είναι πιο άμεση από την λογική και λειτουργεί με τους δικούς της νόμους. Επίσης αυτό που μπορούμε να καταλάβουμε σχετίζεται άμεσα μ' αυτό που ξέρουμε ήδη, την εμπειρία και την τριβή με το αντικείμενο. Ένα έργο τέχνης μπορει να μας φανεί πολύπλοκο αν δεν είμαστε εξοικιωμένοι με το συγκεκριμένο εικαστικό ιδίωμα αλλά να αρχίσουμε να το καταλαβαίνουμε καλύτερα αν αποκτήσουμε την ανάλογη τριβή με το αντικείμενο. Αντίθετα ένα άλλο έργο μπορεί να μας φανεί απλό αν αγνοούμε κάποιες από τις παραμέτρους της κατασκευής του και να γίνει αντιληπτή η πολυπλοκότητα του όταν μας αναφερθούν και αυτοί. Η κατανόηση συγκεκριμένων οπτικών ερεθισμάτων σαν απλά είναι σίγουρα μια υποκειμενική διαδικασία, που εξαρτάται από τις γνώσεις και την δυνατότητά μας να επεξεργαστούμε τα συγκεκριμένα δεδομένα, έχει όμως και ένα αντικειμενικό παράλληλο. Το υποκειμενικό και αντικειμενικό αποτέλεσμα δεν είναι υποχρεωτικό να συμπίπτουν και αυτό εξαρτάται από την οπτική καλλιέργεια του θεατή ή την προσδοκία. Το πιο εύκολο παράδειγμα είναι να θεωρούμε ένα αποτέλεσμα πολύπλοκο κια υτό αντικειμανικά να είναι απλό. Αυτό γίνεται γιατί ο άπειρος θεατής δεν ξέρει τι να δει και πως να προσεγγίζει την έννοια που ο Arnheim ορίζει σαν "απλότητα". Για αρχή ας αναρωτηθούμε: Είναι αρκετή
5 η καταμέτρηση των συστατικών ενός όλου και η αρίθμηση των μερών του για να αποφασίσουμε αν είναι πολύπλοκο ή απλό; Σχετικά πειράματα με μία σειρα μαύρων και άσπρων κύβων έδειξαν πως όχι. Όταν ζητήθηκε να τοποθετηθούν 7 κύβοι - 3 μαύροι και 4 άσπροι - στην πιο απλή σειρά, από τα παραδείγματα α και β που αποτελούνται από δύο άνισα τμήματα άσπρου και μαύρου τόνου επιλέχθηκε το παράδειγμα γ που περιέχει τα περισσότερα διακριτά στοιχεία (σχήμα 8). Αυτό σημαίνει ότι η απλότητα είναι ανεξάρτητη από τον αριθμό των στοιχείων και σχετική με τις έννοιες της ισορροπίας και της κανονικότητας. Η διαδοχή άσπρων και μαύρων κύβων δημιουργεί μία σειρά από ίσα διαστήματα χωρίς κλιμάκωση. Το τετράγωνο είναι ένα σχήμα μη ιεραρχημένο άρα χωρίς εντάσεις που επιτρέπει την εύκολη λογική και οπτική κατανόηση της διαδοχής άσπρων και μαύρων τετραγώνων. Η εναλλαγή τετραγώνων γίνεται ρυθμική, έχει ροή. Τα άλλα παραδείγματα δεν μας βοηθούν να κατανοήσουμε ένα σκεπτικό. Παρουσιάζουν μια αδικαιολόγητη οπτική ανισότητα και γι αυτό μας μπερδεύουν. Άρα είναι η ομαλή οπτική κατανομή ερεθισμάτων που ευνοεί την ευκολότερη κατανόηση ενός σχήματος. σχήμα 8 Κατά το ίδιο σκεπτικό από το τετράγωνο και το σκαληνό τρίγωνο του σχημ. 9 προτιμάται σαν απλούστερο το τετράγωνο και ας έχει δύο παραπάνω στοιχεία (μία πλευρά συν μία γωνία). Ωστόσο σαν σχήμα είναι ισορροπημένο και συμμετρικό. Όλα τα μέρη του είναι ισότιμα, οι πλευρές και οι γωνίες του ίσες και δεν είναι ιεραρχημένο. Το σκαληνό τρίγωνο απεναντίας παρουσιάζει ιδιαίτερα ανισομερή κατανομή τόσο στις πλευρές όσο και στις γωνίες του. σχήμα 9 Συχνά η συντομότερη λύση δεν είναι και η απλούστερη. Για παράδειγμα αν θέλουμε να ενώσουμε τα σημεία Α και Β στην περιφέρεια ενός κύκλου ο συντομότερος δρόμος, το ευθύγραμμο τμήμα ΑΒ δεν είναι και η καλύτερη λύση από την πλευρά της απλότητας. Το ευθύγραμμο τμήμα τέμνει τον κύκλο και δημιουργεί την αίσθηση έλλειψης, του αυθαίρετου κοψίματος και της ασυμμετρίας (σχήμα 10). Αντίθετα το τόξο ΑΒ το οποίο συμπληρώνει τον κύκλο είναι μία λύση ευχάριστη και αρμονική.
6 σχήμα 10 Από τα παραπάνω παραδείγματα έχει γίνει φανερό ότι η απλότητα δεν σχετίζεται με την απλοΐκότητα και δεν επηρρεάζεται από τον αριθμό των στοιχείων ή από συντομεύσεις. "Ο Julian Hockberg έχει αποπειραθεί να την ορίσει ως εξής (χρησιμοιώντας τον όρο "καλύτερη μορφή"). "'Οσο μικρότερο το ποσό της πληροφορίας που απαιτείται για να οριστεί μια δεδομένη οργάνωση συγκριτικά με άλλες εναλλακτικές λύσεις, τόσο πιο πιθανό είναι ότι η εικόνα θα γίνει αντιληπτή κατ αυτόν τον τρόπο" [εννοεί ως απλή]. Στο σχ. 10 το γκρι τόξο ΑΒ συμπληρώνει το σχήμα και η πληροφορία που δίνουμε είναι: ένας κύκλος. Σκεφτείτε την περιγραφή που χρειαζόμαστε για να καλύψουμε την περίπτωση του τμήματος ΑΒ. Ιδιαίτερη σημασία αποκτά το γεγονός ότι τα στοιχεία στα οποία αναφερόμαστε παραπάνω δεν χρειάζεται να είναι σχεδιασμένα στο χαρτί αλλά μπορεί να γίνονται αντιληπτά έτσι στην πραγματικότητα. Για παράδειγμα "ένας κύβος από σύρμα και σχεδιασμένος με κεντρική προοπτική περιέχει γωνίες και ακμές ενός μόνου μεγέθους όταν γίνεται αντιληπτός ως τρισδιάστατος κύβος στο χώρο, αλλά γωνίες τουλάχιστον εννέα διαφορετικών μεγεθών και ακμές δέκα διαφορετικών μεγεθών στο δισδιάστατο σχέδιο. Γι αυτόν το λόγο, ο τρισδιάστατος κύβος θεωρείται απλούστερος από την δισδιάστατη προβολή του" (Arnheim, σ.74). Ας δούμε ξανά μερικά ερωτήματα που προκύπτουν στην προσπάθεια να διευκρινήσουμε την έννοια της απλότητας. Τα παιδικά σχέδια είναι χαρακτηριστική περίπτωση απλότητας. Είναι όμως έργα τέχνης; Ένα έργο τέχνης μπορεί να αποτελείται από ένα μόνο σχήμα. Είναι όμως απλοΐκό; Ένα ποίημα είναι πιο περίπλοκο από ένα λαικό τραγούδι;
7 Εικόνα 1(αριστερά): Jean Dubbufet, Will to Power (Volonté de puissance), January Λάδι με βότσαλα, άμμο Εικόνα 2: Anish Kapoor, Turning the World Upside Down, 2010 Εικόνα 2(δεξιά): Anish Kapoor, Turning the World Upside Down, 2010 γυαλί και σχοινί σε καμβά x 88.9 εκ. Για τον Dubbufet (Εικόνα 1) "η τέχνη των παρανοικών και η τέχνη των παιδιών έγιναν μοντέλα" (Αρνασον: 414) για να αναπτύξει τα έργα του.. Ο λόγος που ο Dubbufet κινήθηκε προς αυτές τις κατευθύνσεις ήταν η σχεδιαστική αμεσότητα και η "βίαιη εκφραστική δύναμη" αυτών των σχεδίων. Στην Εικόνα 1 το έργο του φαίνεται απλοικό και πρωτόγονο. Ας προσθέσουμε όμως μερικά ακόμη στοιχεία: "Η χαρακτηριστική τεχνική του Dubbufet.. βασίζονταν πάνω σε ένα παχύ υπόβαθρο, κατασκευασμένο από άμμο, χώμα, σταθεροποιητικά και άλλα μυστηριώδη υλικά με τα οποία ο καλλιτέχνης έκανε τη μίξη των χρωμάτων. Οι μορφές ήταν χαραγμένες πάνω στο υπόβαθρο αυτό, και το σύνολο παρουσίαζε διάφορες χαρακιές, ουλές και κάθε είδους κακοποιήσεις που θα μπορούσαν να του δώσουν τον χαρακτήρα του απτού και του πραγματικου." Άν είχαμε την ευκαιρία να δούμε από κοντά το συγκεκριμένο έργο του θα αντιλαμβανόμασταν ακόμα καλύτερα αυτό που πληροφορούμαστε όταν μαθαίνουμε τα υλικά του. Πρόκειται για μιά μελέτη στην υφή και στις σχέσεις διαφορετικών υλικών οργανομένων σύμφωνα με μια πρωτόγoνη αισθητική. Το έργο αυτό είναι προιόν επεξεργασίας πολλών πληροφοριών και εικαστικής γνώσης. Το ότι χρησιμοποιεί ένα απλοϊκό φορμά παρουσίασης επειδή αυτό εκφράζει καλύτερα το σκοπό του δεν το κάνει και το ίδιο απλοϊκό. Απεναντίας του δίνει άλλη μία εκφραστική διάσταση. Ωστόσο όλα τα στοιχεία που σαν υλικά είναι ετερόκλητα σε υφή και σε ένταση αλλά και σε κατηγορία καταφέρνει να τα παρουσιάζει ενοποιημένα και ξεκάθαρα στο καινούργιο σύνολο που είναι το έργο του. Ο Anish Kapoor (Εικ.2) έχει παρουσιάσει μία συμμετρική μορφή που αντανακλά στο μεταλλικό περίβλημα της τον περιβάλοντα χώρο. Με πρώτη ματιά το έργο είναι ένα απλοΐκό σχήμα. Ο τίτλος 'γυρνώντας ανάποδα τον κόσμο' μας δίνει μία ιδέα πως έχει διπλή εφαρμογή. Το έργο μπορεί ανά πάσα στιγμή να γυρίσει ανάποδα χωρίς να αλλάξει ενώ λόγω της κυρτότητας της επιφάνεια του ο γύρω κόσμος του περιγράφεται ανάποδα. Το υλικό που έχει χρησιμοποιηθεί, η ένταξη στο έργο του περιβάλοντα χώρου και η διττή του σημασία σαν αυτούσια μορφή και σαν αντανάκλαση του περιγύρου της δίνουν μια πολλαπλή λειτουργία στο συγκεκριμένο έργο. Αυτό που κάνει το έργο απλό δεν είναι το απλοΐκό σχήμα που τελικά ανακαλύπτουμε πως είναι προιόν πολύπλοκης σκέψης. Είναιαπλό γιατί η μορφή του και η λειτουργία του παρουσιάζονται με τρόπο σύμφωνο: κανένα χαρακτηριστικό ή ιδιότητα του έργου δεν αναιρεί την δυνατότητα αναστροφής του.
8 Όπως διευκρινίζει ο Arnheim "Όταν κάποιος επιθυμεί να πει ή να κάνει κάτι, οφείλει να ασχοληθεί με δύο ερωτήματα: ποιά είναι η απλούστερη δομή η οποία θα εξυπηρετήσει τον αντικειμενικό σκοπό (φειδωλία) και ποιός είναι ο απλούστερος τρόπος για να οργανώσει αυτήν την δομή (απλούστερη τάξη);"(arnheim, σ.74) Μιά παράμετρος που επηρρεάζει την αρχή της φειδωλίας είναι η χρήση. Απλά αντικείμενα μας ευχαριστούν εφόσον πληρούν βασικές αλλά περιορισμένες λειτουργίες (πχ τα μαχαίρια να κόβουν) όμως όλα τα έργα τέχνης θεωρούνται περίπλοκα. Και η αλήθεια είναι ότι σε κανένα είδος τέχνης τα σχήματα δεν είναι στοιχείωδη, ακόμα και σε προιστορικά σχέδια ή στα αφαιρετικά έργα του Mondrian. Εικόνα 3: Χερούλια από πόρτες στην είσοδο του κολυμβητηρίου Kildeshovshallen έξω από την Κοπεγχάγη. Το κτίριο κτίστηκε μεταξύ του Το γνωστό πρόβλημα, 'ποιό χερούλι πρέπει να σπρώξω;' στην πρώτη περίπτωση αντιμετωπίστηκε πολύ έξυπνα. Κόκκινο όχι, πρασινο ναι. Στην δεύτερη περίπτωση συνοδεύτηκε και από την διευκρίνησε "TRAEK" [τράβα] στα δανέζικα. Μετά απλοποιήθηκε και έμεινε μόνο η λέξη "TRAEK". Στην τέταρτη περίπτωση το κόκκινο - απαγορευτικο- σήμα συνοδεύεται απο τη λέξη "TRAEK". Δηλαδή δεν πρέπει να μπω από δω, αλλά αν ναι να τραβήξω;;; Ότι ξεκίνησε σαν μια απλή και κατατοπιστική ιδέα κατέληξε μπερδεμένη και ασαφής. Αυτό το παράδειγμα εξηγεί τι δεν είναι απλό. Σαν συμπέρασμα, ο απλούστερος σχεδιασμός γίνεται πολύπλοκος (δυσνόητος, ασαφής στο σκοπό του) όταν δεν εξυπηρετεί με καθαρότητα την λειτουργία για την οποία έχει γίνει. Κατά τον ίδιο τρόπο δεν μπορεί να εννοηθεί απλότητα όταν υπάρχουν αντιφάσεις και αλληλοακυρώσεις στην οργάνωση ενός οπτικού συστήματος, όποιο και να είναι αυτό. Εικόνα 4: George Seurat, Κυριακή στην μεγάλη Βόλτα, Λάδι σε καμβά, 207Χ308 εκ., Χαρακτηριστικό παράδειγμα υποταγής στους ίδιους σχεδιαστικούς νόμους. Ρούχα, κεφάλια. άνθρωποι, δέντρα, ζώα ακολουθούν την ίδια σχεδιαστική λογική χωρίς όμως να χάνουν την αυτοτέλεια ή την επιθυμητή ευκρίνεια. Κοιτάξτε την γυναικεία φιγούρα δεξιά και την κεντρική μετωπική φιγούρα. Αποτελούνται από παρόμοια απαλά καμπυλόγραμμα σχήματα. Κοιτάξτε όλες τις φιγούρες στο έργο και μετά παρατηρείστε τις απαλές καμπυλότητες των δέντρων πάνω δεξιά και της ακρης του γρασιδιού με το ποτάμι στην αριστερή μεριά. Γραμμές και σχήματα ακολουθούν τον ίδιο απαλά καμπύλο χαρακτήρα. Την ίδια απαλότητα συναντούμε και στα χρώματα του έργου: δεν υπάρχουν βίαια περάσματα στα πλασίματα των όγκων μέσα στη
9 φωτεινή ή την σκιερή περιοχή του έργου. Παρότι αυτές οι δύο έχουν τονική αντίθεση και τα χρώματα της φωτεινής περιοχής είναι λαμπερά δεν υπάρχει ένταση, επίθεση οπτικά από το χρώμα. Όλο το έργο διατηρεί την απόφαση της ηρεμίας σε χρώματα, σχήματα, γραμμές, τόνους, που υποστηρίζουν το ευχάριστο θέμα του. Έτσι καταφέρνει να μεταδώσει το επιθυμητό κλίμα της κυριακάτικης βόλτας με κάθε στοιχείο του. Εξαιτίας αυτής της συμφωνίας το έργο είναι ευανάγνωστο, καθαρό, βρίσκουμε αυτονόητο ότι κάθε σημείο του πρέπει να είναι έτσι. Αυτή είναι η απλότητά του. Τα ποιήματα, τα έργα τέχνης, τα φιλοσοφικά δοκίμια είναι τόσο πολύπλοκα όσο αυτό είναι αναγκαίο. Αν περνούν το όριο του αναγκαίου γίνονται φλύαρα, αδύναμα, περιττά. 'Ένα ακόμη βασικό τους χαρακτηριστικό είναι ότι η δομή που διαθέτουν καθορίζει την λειτουργία κάθε λεπτομέρειας τους στο σύνολο προς ώφελος του συνόλου. Στα έργα τέχνης κάθε μέρος υποτάσσεται στην οργάνωση του όλου: τα επιμέρους στοιχεία υποστηρίζουν την κεντρική μορφή και στο σύνολο διακρίνουμε μία ομοιογένεια. Σ ένα τοπίο ο ουρανός, η θάλασσα και οι άνθρωποι φαίνονται όμοια γιατί υπακούουν στους ίδιους σχεδιαστικούς νόμους. Αυτό δε σημαίνει παραποίηση της φύσης των πραγμάτων αλλά υποταγή τους σε ένα σύστημα οπτικό που εξυπηρετεί τον ίδιο σκοπό, χωρίς να αυτοαναιρείται. Εικόνα 5: Takashi Murakami, "Tan Tan Bo, 2001, ακρυλικό σε καμβά και σε σανίδα, 141 ¾ by 212 5/8 by 2 5/8 inch, Το έργο του Takashi Murakami διατηρεί μια κατάσταση οπτικής πολυφωνίας υπό έλεγχο με την χρωματική και σχηματική οικονομία. Η επανάληψη του κυκλικού σχήματος και η χρήση καμπύλων γραμμών, συνδυάζεται με μία χρωματική παλέτα χωρίς επιθετικές εξάρσεις. Η αντιπαράθεση στις έννοιες του απλού και του πολύπλοκου σαν ανοικτός διάλογος είναι κυρίαρχη στην δημιουργία του έργου καθώς η σύνθεση ξεκινάει από την αναφορά της σε μια μια απλοϊκή θεματική και ένα εξίσου απλοϊκό σχήμα. Η γενικευμένη και σχηματική αναφορά σε καρτούν με μια μορφή που θυμίζει αρκετά τον Μίκυ Μαους γίνεται η βάση για την παρουσίαση ενός πλήθους κυκλικών στοιχείων που έχουν εκρηκτικό χαρακτήρα στην κατανομή τους στην επιφάνεια του έργου. Τα σχήματα που απλώνονται στην επιφάνεια του έργου δεν είναι ωστόσο ασύνδετα μεταξύ τους. Η σχηματική πολυφωνία διατηρείται σε αρμονία από την επαναληπτικότητα σχημάτων και χρωμάτων. Όλα τα διαφορετικά στοιχεία υποτάσσονται σε μια κοινή λογική και έχουν
10 ιεραρχηθεί χρωματικά και σχηματικά, και κατά μεγέθη έτσι ώστε να μην διαταράσσουν την ανάγνωση του κεντρικού σχήματος. Για παράδειγμα το μαύρο σχήμα στο κάτω μέρος του δημιουργεί ένα σκοτεινό 'άνοιγμα προς τα μέσα ή ένα άλλο επίπεδο βάθους πάνω στο οποίο οι κάπως συγκλίνουσες γραμμώσεις τακτοποιούν τα καμπυλόγραμμα σχήματα που τοποθετούνται μπροστά του. Η ακαταστασία της ποικιομορφίας συντάσσεται τακτικά και δεν ενοχλεί στην αντίληψη του μαύρου σχήματος καθαυτό (σαν μέγεθος και σχήμα, ή τόνο αυτό δεν αλλοιώνεται). Τα σχήματα γεμίζουν την επιφάνεια και την κάνουν δυνατή, οπτικά ευχάριστη. Σκεφτείτε το έργο χωρίς αυτά στο συγκεκριμένο σημείο. Θα ήταν το ίδιο έργο σαν εντύπωση αν το μεγάλο μαύρο σχήμα παρέμενε απλώς μαύρο; Η φύση ευννοεί την απλότητα, τίποτε δεν γίνεται αν δεν είναι απαραίτητο. "Η φύση δεν κάνει τίποτε άσκοπα και το περισσότερο είναι άσκοπο όταν μπορεί να γίνει με το λιγότερο" υποστήριζε ο Ισαάκ Νεύτωνας. Βασική προυπόθεση πρακτικής εφαρμογής μιας τέτοιας ιδέας είναι η κατανόηση των ορίων δηλαδή μια καθαρή τοποθέτηση γαι το τι είναι αυτό στο οποίο στοχεύουμε ώστε να ξεκαθαριστεί η ασάφεια στο "λιγότερο" και το "περισσότερο". Είναι σημαντικό να κατανοούμε στα οπτικά συστήματα τις συμβάσεις τους. Αυτές οι "συμβάσεις" είναι το σύστημα που ομαδικοποιεί και κωδικοποιεί σε απλά ευκολονόητα και απτά οπτικά δεδομένα το τι "επιτρέπεται, τι επιβάλεται" και τι "αποβάλεται" οπτικά από το σύστημα. Τι δηλαδή το χαρακτηρίζει, τι το οργανώνει, τι συγκρατεί τα μέρη του, πως αυτά λειτουργούν. Είναι βασικό να διαχωριστεί η απλότητα από την απλοϊκότητα, την υπεραπλούστευση ή τον μινιμαλισμό. Άρα το ερώτημα που επιμένει είναι: ποιά είναι η απλούστερη λύση όταν ασχολούμαστε με πολύπλοκα οπτικά συστήματα; Ένας νόμος της oπτικής αντίληψης από την θεωρία της Gestalt απαντά πως: Κάθε διάταξη ερεθισμάτων τείνει να γίνει αντιληπτή με τέτοιο τρόπο ώστε η προκύπτουσα δομή να είναι η απλούστερη που επιτρέπεται από τις δεδομένες συνθήκες. Ισοπέδοση και Όξυνση. σχήμα 11 Τα πρώτα ζεύγη σχημάτων στο σχ11 παρουσιάζουν μία ελαφριά απόκλιση από την συμμετρία. Οταν ζητήθηκε σε τυχαίο δείγμα παρατηρητών να αποδώσουν τα σχήματα χωρίς πια να τα βλέπουν κάποιοι τα "επανέφεραν" σε μια κατάσταση συμμετρίας και κάποιοι άλλοι ώθησαν τις ανομοιότητες στα άκρα. Η τάση αυτή να μεταφέρουμε ένα σχήμα σε μια κατάσταση έντονης αρμονίας ή δυασαρμονίας όταν αυτή υπάρχει σε αμφιβολία ορίζεται από την θεωρία της Gestalt με την αρχή της "συνοπτικότητας" Ο νόμος της συνοπτικότητας [Pragnatz] ορίζει ότι κάθε δομή τείνει να γίνει όσο το δυνατόν πιο ξεκάθαρη. Αυτό σημαίνει ότι κάθε δομή περικλείει μέσα της μια τάση είτε για να εξισορροπηθούν τα επιμέρους στοιχεία της, είτε για να οξυνθούν οι αντιθέσεις τους με σκοπό να γίνεται το σύνολο πιο εύκολα και ξεκάθαρα αντιληπτό.
11 Αυτό δε σημαίνει ότι η "ισοπέδοση" αποκλείει και την ταυτόχρονη όξυνση" στο ίδιο ακριβώς σχήμα. Η διαδικασία αυτή συμβαίνει κατά τον ίδιο τρόπο που η μνήμη μας αμβλύνει και οξύνει την ανάμνηση κάποιων περιστατικών. Την ίδια στιγμή που κάτι παίρνει τεράστιες διαστάσεις κάτι άλλο έχει υποβαθμιστεί, έτσι ώστε η προτεραιότητα να δωθεί σε μια τάξη πραγμάτων που δημιουργεί και την υποκειμενική ανάμνηση. Στην προκειμένη περίπτωση όμως δεν αναφερόμαστε στον υποκειμενισμό μιας ανάμνησης αλλά στην εγγενή τάση ενός οπτικού συστήματος. Ενδιαφέρον στην κατανόηση της "συνοπτικότητας" έχει το γεγονός ότι στην τέχνη η επικράτηση της μιας επιλογής πάνω στην άλλη καταλήγει σε διαφορετικά οπτικά ιδιώματα. Η ισοπέδωση οδηγεί στον κλασικισμό, η όξυνση στον εξπρεσσιονισμό. Εικόνα 6: Jean-Auguste-Dominique Ingres, La Grande Odalisque, 1814, Λάδι σε καμβά 91 x 162 εκ. Εικόνα 7: Ernst Ludwig Kirchner, Κοπέλα με γιαπωνέζικη ομπρέλλα, 1909, 77Χ69 εκ.
12 Οι εικόνες 6 και 7 είναι δύο εκδοχές στο θέμα του γυναικείου γυμνού υπό την επίδραση του νεοκλασικισμού και του εξπρεσσιονισμού αντίστοιχα. Κάθε επιλογή που έχει γίνει ενισχύει την τάση του συνόλου για ηρεμία ή ένταση. Το ζητούμενο και των δύο καλλιτεχνών είναι κοινό: ο αισθησιασμός που συνδέεται με τον εξωτισμό. Το ενδιαφέρον είναι ότι καμία από τις δύο εικόνες δεν δίνει προτεραιότητα στις φυσικές αναλογίες και τον ρεαλισμό με την έννοια της ακριβής αντιστοίχησης της πραγματικότητας με το σχέδιο. Αυτό αφήνει να φανεί ξεκάθαρα το γεγονός πως οι επιλογές για την οργάνωση των έργων έγιναν με κριτήρια οπτικά. Στην περίπτωση του Ingres ο επιμηκυσμένος κορμός της 'οδαλίσκης' του έχει επιτρέψει να εντάξει στη σύνθεση μία οριζόντια οβάλ γραμμή η οποία υποστηρίζεται οπτικά από άλλους δύο τέτοιους άξονες. Τα χρώματα είναι αρμονικά, με υποβαθμισμένες αντιθέσεις. Αντίθετα ο Kirchner έχει στηρίξει την σύνθεση του σε διαγώνιο διάταξη ενώ το έργο του έχει πολλούς, σχεδόν κερματισμένους άξονες, σαν μικρά ευθύγραμμα τμήματα που τέμνονται σε αντίθεση. Τα χρώματά του είναι σε αντίθεση, ταυτόχρονη ή συμπληρωματικών και έτσι η οπτική κόντρα των νοητών αξόνων αλλά και των γραμμών που βλέπουμε στο σχέδιο συνεχίζεται και χρωματικά. σχήμα 12α σχήμα 12β σχήμα 12γ Αν αφαιρεθεί η εικόνα και παρατηρήσουμε τους άξονες των δύο συνθέσεων καταλήγουμε στα θέματα
13 του σχήματος 12γ. Είναι πια φανερή στο ένα σχήμα η τάση για σχέσεις που ορίζουν οπτικά έναν ήρεμο αισθησιασμό και επιτείνουν την 'κυκλικότητα'. Στην άλλη περίπτωση οι διασταυρωμένες κοφτές γραμμές ορίζουν ένα πεδίο έντασης. Μέσα σ αυτά τα συνθετικά πλαίσια, υποστηριγμένα κατάλληλα από τα χρώματα όλα τα στοιχεία του έργου υποτάσσονται στην ήρεμη αρμονία ή στην έντονη διάσπαση. Τι σημαίνει μέρος ενός όλου; Κάποια πράγματα τα αντιλαμβανόμαστε συγκριτικά. Το χρώμα είναι ένα απο αυτά κι ένα άλλο το μέγεθος. Ένα πρόσωπο είναι χλωμό κοντά σε κάτι κόκκινο και ροζωπό κοντά σε κάτι κίτρινοπράσινο. Μια γραμμή φαίνεται πιο έντονα κυκλική όταν περιστοιχίζεται από γωνίες. Αυτή η αλληλεπίδραση μεταξύ διαφορετικών στοιχείων δημιουργεί σύνολα διαφορετικά σε δυναμισμό και δυνατότητες από τα μεμονωμένα μέρη τους. Πόσο όμως είναι δυνατόν το όλο να επηρρεάσει τα μέρη ή να αντισταθεί στον τεμαχισμό του; Το επόμενο ζήτημα που πρέπει να ξεκαθαρίσουμε είναι ο τρόπος που ξεχωρίζουν τα στοιχεία ενός συνόλου. Πως υποδιαιρούμε; Τι σημαίνει χωρίζω ένα σύνολο στα μέρη του; σχήμα 13 Ένα περίπλοκο σχήμα γίνεται πολύ ευκολότερα αντιληπτό όταν διασπάται σε απλά σχήματα. Μόλις αντιληφτούμε το σχήμα 13 σαν σύνθεση ενός παραλληλογράμμου και ενός τριγώνου αποκαθίσταται "η ένταση παύει, η εικόνα κατασταλάζει, και φαίνεται φυσική και οριστική". σχήμα 14 Στο σχημα 14 έχουν διαιρεθεί στη μέση ένα τετράγωνο, ένα ορθογώνιο με αναλογία 1:2 και ένα 'χρυσό' ορθογώνιο. Στην πρώτη περίπτωση προκύπτουν δυο αρκετά μακρόστενα ορθογώνια και εύκολα παραδεχόμαστε ότι είναι ένας διαχωρισμός ενός τετραγώνου στη μέση. Στη δεύτερη περίπτωση από τον διαχωρισμό του ορθογωνίου προκύπτουν δύο τετράγωνα. Επίσης εύκολα το ορθογώνιο εξαφανίζεται και γίνεται πια αντιληπτό σαν το άθροισμα δύο τετραγώνων. Στην τρίτη περίπτωση από την υποδιαίρεση στο μισό ενός 'χρυσού' ορθογωνίου τα άλλα δύο ορθογώνια που
14 προκύπτουν διατηρούν μια αυτάρκει μέσα στο αρμονικό σύνολο. Στα δύο πρώτα παραδέιγματα ολοφάνερα κυριαρχεί η εικόνα του τετραγώνου γιατί είναι ένα απλό, μη ιεραρχημένο, ξεκάθαρο σχήμα. Σε σχέση με τα επιμέρους μακρόστενα τμήματα ή το επιμήκες παραλληλόγραμμο το τετράγωνο υπερτερεί σαν σχήμα. Είναι λοιπόν αυτό που αντιλαμβανόμαστε και η προτεραιότητα αυτή επηρρεάζει την αντίληψη που έχουμε σε ότι άλλο συμβαίνει. Το τετράγωνο, "χωρίζεται" ή "ενώνεται" στο μυαλό μας βάσι αυτής της κατανόησης. Η επιλογή της σχέσης όλου και μερών καθορίζεται από την απλότητα του όλου έναντι των μερών στα οποία χωρίζεται. σχήμα 15 Στο σχ 15 βλέπουμε ότι η διαίρεση επηρρεάζεται και από την εγγύτητα. Τα δύο σχήματα στα άκρα παρουσιάζουν δύο διαφορετικές αλλά ευδιάκριτες σχέσεις. Τα δύο μεσαία σχήματα είναι πιο ασαφή για την σχέση των μερών τους και γι' αυτό μας 'υποχρεώνουν' να προσθέσουμε εμείς κάποια δεδομένα. Αντιλαμβανόμαστε κάποιο ορθογώνιο πιο μπροστά από το άλλο στην ανάγκη να αξιολογήσουμε με κάποιο τρόπο την πληροφορία που μας δίνουν. Ο διαχωρισμός σε αυθαίρετα τμήματα είναι απλός τεμαχισμός που μπορεί να συμβεί τυχαία, μηχανικά και απρογραμμάτιστα. Για να διαχωριστεί ένα μέρος του συνόλου ωστόσο πρέπει πρώτα να γίνει αντιληπτή η δομή. Στο διαχωρισμό των μερών η δομή του όλου διατηρείται. Αν δεν υπάρχει δομή δεν έχει νόημα η συζήτηση για μέρη. Το μέρος, σε αντίθεση από το τμήμα είναι λειτουργικό στοιχείο του συνόλου, επομένως συνεργάζεται για να συμβεί το όλο. Ο ρόλος του κάθε μέρους καθορίζεται από την δομή του όλου έτσι ώστε το κάθε μέρος έχει μια συγκεκριμένη λειτουργία στο σύνολο. Τα μέρη που αποτελούν ένα σύνολο δεν είναι απλά προσθέσιμα ώστε με μια υπεράνθρωπη δύναμη να αποκτούν σαν όλο παραπάνω αξία. Τα μέρη και το όλον αλληλοεξαρτούνται. Το μέρος είναι απαραίτητο στο σύνολο και καθορίζει/διαμορφώνει την τελική εικόνα του συνόλου που ανήκει. Ο Arnheim τονίζει ότι "είναι σημαντικό να διακρίνουμε μεταξύ γνησίων μερών - δηλαδή τμημάτων που αντιπροσωπεύουν ένα διαχωριζόμενο υποσύνολο εντός της συνολικής διάρθρωσης- και απλών αποτμήσεων ή κομματιών δηλαδή τμημάτων διαχωριζόμεων μόνο εν σχέσει προς μια περιορισμένη τοπική διάρθρωση ή προς ρήγματα μη εγγενή με την εικόνα" (Arnheim: 94). Ομοιότητα Η σύγκριση που μας επιτρέπει να συνδέουμε και να αξιολογούμε στοιχεία συμβαίνει μόνο όταν υπάρχει μεταξύ τους κάποια κοινή βάση. Έτσι ενώ η ομοιότητα και ο διαχωρισμός είναι δύο πόλοι αντίθετοι που ανάμεσα τους παίρνουν νόημα οι συγκρίσεις. Ούτως ή άλλως στην περίπτωση που έχει επιτευχθεί μία απόλυτη ομοιογένεια σ ένα σύνολο το αποτέλεσμα ήταν η κατάρευση κάθε συστήματος δόμησης και συχνά η μονοτονία. Η ομοιότητα λοιπόν είναι απαραίτητη προϋπόθεση για την ομαδοποίηση στοιχείων και την διάκριση μεταξύ τους, δηλαδή την επισήμανση των διαφορών.
15 σχήμα 16 σχήμα 17 σχήμα 18 σχήμα 19 σχήμα 20 Στα σχήματα παρουσιάζονται τρόποι ομαδοποίησης: λόγω ομοιότητας μεγέθους, λόγω διαφοράς σχήματος, λόγω διαφοράς στη φωτεινότητα, λόγω χωρικής θέσης και λόγω κατεύθυνσης. Στα παραδείγματα αυτά επειδή τα εικονιζόμενα στοιχεία είναι πολύ απλά οι ομοιότητες είναι χαλαρές. Όπως αναφέρει ο Arnheim "οι παράγοντες ομοιότητας είναι πιο αποτελεσματικοί όταν στηρίζουν διατάξεις"( Arnheim:99). Αυτό σημαίνει ότι σε πιο πολύπλοκα συστήματα οι ομοιότητες δημιουργούν πιο έντονες τάσεις συνάφειας γιατί παρουσιάζονται περισσότερο αναγκαίες για να τα κατανοήσουμε και να τα απλοποιήσουμε. Σαν συνέπεια γίνονται πιο εύκολα και ευχάριστα κατανοητές.
16 Eικόνα 8: Henry Matisse, Blue Nude IV, γκουάς σε χαρτί [κολάζ]1952. Το έργο αυτό του Matisse η ανθρώπινη φιγούρα έχει κατακερματιστεί. Όμως πρόκειται για ένα έργο όπου βλέπουμε ένα συνεχές αναδιπλωμένο ανθρώπινο σώμα. Αυτό γίνεται γιατί εφαρμόζοντας την ομοιότητα στο σχήμα, την συνέχεια λόγω κατεύθυνσης (βλ. σημ. Gestalt) και το χρώμα, ομαδοποιούμε και συνδέουμε τα αποκομμένα στοιχεία. Έτσι, τα κενά που δημιουργούνται και επιτρέπουν στο σχέδιο να 'ανασάνει' λειτουργούν σχεδιαστικά αλλά δεν παρεμβαίνουν νοηματικά. Υπάρχει μία άμεση εμπλοκή του θεατή στο να συμπληρώσει τις πληροφορίες που ο καλλιτέχνης παραλείπει ή να κωδικοποιήσει ανάλογα αυτές που παραποιεί. Ο Matisse δημιουργεί ένα οπτικό σύστημα που έχει συνοχή και συνέπεια και σου επιβάλλεται με την δύναμη της οπτικής του αυτονομίας. Μπορεί να μην είναι "αρεστό" σ 'ολους τους θεατές για προσωπικούς λόγους, αλλά η συστηματική του οργάνωση και η εικαστική αυτονομία του (έξω από την αναπαράσταση της πραγματικότητας διεκδικεί μόνο ζωγραφικές+οπτικές αξίες) κάνουν το έργο αυτό σημαντικό και αξιοπρόσεκτο. Παρατηρείστε τις παραλληλότητες: στις γραμμές του ανασηκωμένου χεριού και του ξαπλωμένου ποδιού, όσο και στο μπροστά χέρι και στο ανασηκωμένο πόδι. Παρότι η σύνθεση περικλείεται σε ένα παραλληλόγραμμο έχει σχεδιαστεί με καμπυλόγραμμα ως επι το πλείστον σχήματα, ενώ οι κατευθύνσεις του άνω χεριου, δεξιού χεριού, ξαπλωμένου ποδιού και ανασηκωμένου ποδιού δίνουν μία περιστροφική, χαλαρή κινητικότητα στο σύνολο.
17 Εικόνα 9: Pablo Picasso, Νεαρή γυναίκα με μαντολίνο, Λάδι σε σανίδα, Στο έργο αυτό αρχικά ξεχωρίζουμε το κυρίως θέμα από το απαλό πράσινο φόντο. Τα οπτικά στοιχεία χωρίζονται σε δύο υποκατηγορίες: ανάλογα με το χρώμα και το σχήμα. Σύμφωνα με χρώμα διακρίνουμε τις ομάδες των κίτρινων, ανοιχτών βιολέ, ανοικτών μπλεπράσινων και κόκκινων στοιχείων. Συμφωνα με το σχήμα διακρίνουμε τα απαλά οβάλ, τα τριγωνικά φωτεινά μπλεπράσινα και τα κόκκινα και τα ροζωπά παραλληλόγραμμα. Σ αυτό το έργο η δομή και η αφήγηση επικαλύπτονται. Το πρόσωπο απορροφάται στο οβάλ υπογάλαζο χρώμα και το σχήμα του εντάσσεται στο χρωματικό σχήμα σαν χρωματική κηλίδα. Τα χέρια συμμορφώνονται στην καμπύλη που σχηματίζεται από ένα γενικευμένο τριγωνοειδές σχήμα το οποίο εξυπηρετεί περισσότερο την συνολική οπτική δομή παρά αναφέρεται στην ρεαλιστική αναπαράσταση ενός χεριού. Το μαντολίνο είναι άθροισμα κυκλικών σχημάτων στο οποίο διαμοιράζονται δύο από τα βασικά χρώματα της σύνθεσης. Μικρά τριγωνικά σχήματα 'σφηνώνουν την φιγούρα στη θέση της: παρατηρείστε τον εξισορροπιστικό ρόλο που έχει το κίτρινο τρίγωνο στην δεξιά πλευρά της σύνθεσης και το κόκκινο στην κάτω αριστερή πλευρά. Οι κλίσεις που δημιουργούνται από το μαντολίνο και το κίτρινο τρίγωνο όσο και από το κόκκινο και κίτρινο τρίγωνο υπογραμμίζουν την κλίση του κεφαλιού δίνοντας μια κίνηση προς τα πίσω και πάνω. Η γυναίκα φαίνεται να γέρνει απαλά το κεφάλι της, ενώ οι ευθείες γραμμές της πολυθρόνας τοποθετούν την φιγούρα με σταθερότητα στη θέση της.
18 Εικόνα 10: "Fernand Léger, "Study for the 'Skating Rink' Curtain", ακουαρέλα σε χαρτόνι, 38X45 εκ., 1921 Στο έργο αυτό του Léger τα οπτικά στοιχεία λογω της ομαδοποίησης του χρώματος και του σχήματος δημιουργούν υποομάδες που λόγω συνέχειας ή κατεύθυνσης ενοποιούνται με νοητούς άξονες. Αυτή η συνθετική οργάνωση δίνει κίνηση και ρυθμό στη σύνθεση. Παρατηρείστε τις ομάδες των ωχροκίτρινων και των μαύρων παραλληλογράμμων καθώς επίσης και την επαναληπτική, σχεδόν συμμετρική σχέση των πορτοκαλί και μπλέ κυκλικών σχημάτων. Η επανάληψη στο σχήμα του ρόμβου ενοποιεί την κάτω περιοχή της σύνθεσης και δημιουργεί τακτικό ρυθμό με την εναλλαγή χρώματος και τόνου. Στο πάνω μέρος είναι κάποια κάθετα τοποθετημένα παραλληλόγραμμα σχήματα που εναλλάσονται με τα λευκά κενά. Οι δύο αυτές περιοχές, πάνω και κάτω είναι πιο ήρεμες, αν και ρυθμικές και αντιδιαστέλλονται στην περιστροφική αναστάτωση του κέντρου. Εικόνα 11: Wassily Kandinsky, Reciprocal Accord, Η σύνθεση αυτή ονομάζεται "αμοιβαία συμφωνία" και βλέποντάς την καταλαβαίνουμε πολύ εύκολα το σκεπτικό της. Τα δύο βασικά μαύρα σχήματα που την συγκροτούν οργανώνονται με
19 μια χαλαρή αίσθηση συμμετρίας. Το στοιχείο που ενοποιεί την σύνθεση είναι η σχηματική ομοιότητα που λειτουργεί σαν συγγένεια, ομαδοποιώντας τα σχήματα που λειτουργούν σε αντίστοιξη μεταξύ τους. Κυκλικά, τριγωνικά και ακανόνιστα στοιχεία ομαδοποιούνται αυτόματα και αναπτύσουν σχέσεις τόσο σαν υποομάδες που έχουν κοινά μέλη όσο και με 'εσωτερικούς διαλόγους και σχέσεις αντίθεσης μεταξύ τους. Κάτω από αυτό το πρίσμα θα μπορούσαμε να δούμε μια ταυτόσημη οργάνωση στο έργο αυτό και στη συγγένεια των σχημάτων με το έργο του Murakami. Εικόνα 12: Josef Albers, από τη σειρά Graphic Tectonic, Ascention και To Mont Alban, λιθογραφία, 44Χ21 εκ., 60X48 εκ αντίστοιχα, Ο Αlbers ήταν καθηγητής στη σχολή του Bauhaus και μετέπειτα ένας από πιο καταξιωμένους δασκάλους τέχνης στην Αμερική. Όποιο και να ήταν το μέσο που χρησιμοποιούσε, η δουλειά του στόχευε να αναδείξει την "ομορφιά της απλής γεωμετρίας και την τεχνική επιδεξιότητα" όσο και την ασυμφωνία μεταξύ του φυσικού γεγονότος και του ψυχικού αποτελέσματος". Τα αποστασιωποιημένα αλλά απλά σχέδια του, οργανώνουν με ομαδοποιήσεις [λογω κατεύθυνσης, γειτονίας και φωτεινής διαφοροποίησης] σχέσεις όπου το προοπτικό βάθος εμφανίζεται και καταρρίπτεται. Τα έργα της Εικόνας 17 διαθέτουν καθαρότητα, ευκρίνεια και είναι τόσο πολύπλοκα όσα και απλά. Από αυτήν την έννοια ο Albers αγγίζει μία ποιητική συντομία και δεν είναι τυχαίο ότι το έργο του είναι από τα πρώτα έργα αφηρημένης τέχνης που αναγνωρίστηκε η ποιητικότητα στην αναπαραστατική αφαίρεση. Οι γεωμετρικές συνθέσεις του Albers έχουν μια οπτική πυκνότητα που βρίσκεται στην υπέρβαση της απλής, περιγραφικής οπτικής πληροφορίας. Κατασκευάζουν μέσα γνώριμα οπτικά στοιχεία όπως η τρισδιάστατη απεικόνιση της προοπτικής στη γεωμετρία έναν κόσμο καινούργιων οπτικών σχέσεων, όπου η γνώριμη οπτική σαφήνεια καταρρίπτεται για να προτείνει μέσα από την ευθεία γραμμή και την καθαρότητα νέες οπτικές σχέσεις.
20 Βιβλιογραφία Arnason H. H., ιστορία της Σύγχρονης Τέχνης, Παρατηρητής, 1995, Θεσσαλονίκη Arnheim, Τέχνη και Οπτική Αντίληψη, Θεμέλιο, Germain Bazin, Baroque and Rococo, Thames and Hudson, 1964 Wollheim, R. Art and its objects, Pelican,1970. Βακαλό Γεώργιος, Οπτική Σύνταξη, Νεφέλη, 1988 Γκόμπριχ, Ερνστ, Το χρονικό της Τέχνης, Μορφωτικό Ίδρυμα Εθνικής Τραπέζης, 1998 Ρήντ, Χέρμπερτ, Λεξικό Εικαστικών Τεχνών, Υποδομή Όπως αναρτήθηκαν από το διαδίκτυο τον Νοέμβριο του Anish Kapoor challenges perceptions in a mind-bending show at the ICA %20Dubuffet&page=1&f=People&cr= %C3%A8re
Άλλος παράγοντας επίδρασης στην αντίληψη μας για το σχήμα που επηρρεάζεται και α πό την προηγούμενη εμπειρία μας είναι τι ανάλογη προσδοκία υπάρχει,.
 Οι παρακάτω σημειώσεις βασίζονται στο βιβλίο Τέχνη και Οπτική Αντίληψη, κεφάλαιο Σχήμα, σελ 57-112, του Rudolf Arnheim, Εκδόσεις Θεμέλιο, 2005. Πρόκειται για μια σύντομη επισκόπηση των βασικών εννοιών
Οι παρακάτω σημειώσεις βασίζονται στο βιβλίο Τέχνη και Οπτική Αντίληψη, κεφάλαιο Σχήμα, σελ 57-112, του Rudolf Arnheim, Εκδόσεις Θεμέλιο, 2005. Πρόκειται για μια σύντομη επισκόπηση των βασικών εννοιών
ΘΕΜΑΤΑ ΤΕΧΝΗΣ Β και Γ ΛΥΚΕΙΟΥ. Ηρεμία, στατικότατα, σταθερότητα
 ΘΕΜΑΤΑ ΤΕΧΝΗΣ Β και Γ ΛΥΚΕΙΟΥ (μάθημα κατεύθυνσης) Τι είναι η δομή και η σύνθεση ενός εικαστικού έργου. Είναι η οργάνωση όλων των στοιχείων ενός έργου σε ένα ενιαίο σύνολο με στόχο να εκφράσουν κάποια
ΘΕΜΑΤΑ ΤΕΧΝΗΣ Β και Γ ΛΥΚΕΙΟΥ (μάθημα κατεύθυνσης) Τι είναι η δομή και η σύνθεση ενός εικαστικού έργου. Είναι η οργάνωση όλων των στοιχείων ενός έργου σε ένα ενιαίο σύνολο με στόχο να εκφράσουν κάποια
Μιχάλης Μακρή EFIAP. www.michalismakri.com
 Μιχάλης Μακρή EFIAP www.michalismakri.com Γιατί κάποιες φωτογραφίες είναι πιο ελκυστικές από τις άλλες; Γιατί κάποιες φωτογραφίες παραμένουν κρεμασμένες σε γκαλερί για μήνες ή και για χρόνια για να τις
Μιχάλης Μακρή EFIAP www.michalismakri.com Γιατί κάποιες φωτογραφίες είναι πιο ελκυστικές από τις άλλες; Γιατί κάποιες φωτογραφίες παραμένουν κρεμασμένες σε γκαλερί για μήνες ή και για χρόνια για να τις
«Το χρώμα είναι το πλήκτρο. Το μάτι είναι το σφυρί. Η ψυχή είναι το πιάνο με τις πολλές χορδές»
 ΑΝΑΛΥΣΗ ΤΟΥ ΧΡΩΜΑΤΟΣ «Το χρώμα είναι το πλήκτρο. Το μάτι είναι το σφυρί. Η ψυχή είναι το πιάνο με τις πολλές χορδές» W. kandinsky Το χρώμα είναι αναπόσπαστα δεμένο με ότι βλέπουμε γύρω μας. Από τον γύρω
ΑΝΑΛΥΣΗ ΤΟΥ ΧΡΩΜΑΤΟΣ «Το χρώμα είναι το πλήκτρο. Το μάτι είναι το σφυρί. Η ψυχή είναι το πιάνο με τις πολλές χορδές» W. kandinsky Το χρώμα είναι αναπόσπαστα δεμένο με ότι βλέπουμε γύρω μας. Από τον γύρω
Υλικά, Γραμμές και Τεχνικές στο Ελεύθερο Σχέδιο
 Κ Ε Φ Α Λ Α Ι Ο Α Υλικά, Γραμμές και Τεχνικές στο Ελεύθερο Σχέδιο Σκοπός Σκοπός του κεφαλαίου αυτού είναι να γνωρίσουν οι μαθητές τα υλικά που χρειάζονται για το ελεύθερο σχέδιο και τον τρόπο που θα τα
Κ Ε Φ Α Λ Α Ι Ο Α Υλικά, Γραμμές και Τεχνικές στο Ελεύθερο Σχέδιο Σκοπός Σκοπός του κεφαλαίου αυτού είναι να γνωρίσουν οι μαθητές τα υλικά που χρειάζονται για το ελεύθερο σχέδιο και τον τρόπο που θα τα
Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 2. ΣΥΝΘΕΤΙΚΗ ΙΣΟΡΡΟΠΙΑ
 Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 2. ΣΥΝΘΕΤΙΚΗ ΙΣΟΡΡΟΠΙΑ Η συμμετρική και η ασύμμετρη οργάνωση Κάθε καλλιτεχνικό έργο μπορεί να έχει συνθετική ενότητα και να είναι ολοκληρωμένο ως σύνολο, αλλά χρειάζεται
Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 2. ΣΥΝΘΕΤΙΚΗ ΙΣΟΡΡΟΠΙΑ Η συμμετρική και η ασύμμετρη οργάνωση Κάθε καλλιτεχνικό έργο μπορεί να έχει συνθετική ενότητα και να είναι ολοκληρωμένο ως σύνολο, αλλά χρειάζεται
ΣΥΝΘΕΤΙΚΕΣ ΑΡΧΕΣ ΕΙΚΟΝΩΝ
 ΣΥΝΘΕΤΙΚΕΣ ΑΡΧΕΣ ΕΙΚΟΝΩΝ ΣΥΝΘΕΣΗ: Οργάνωση ενός συνόλου από επιμέρους στοιχεία σε μια ενιαία διάταξη Αρχική ιδέα σύνθεσης Μορφή της σύνθεσης Δομή της σύνθεσης ΟΠΤΙΚΗ ΔΟΜΗ ΤΗΣ ΣΥΝΘΕΣΗΣ Βασικό λεξιλόγιο
ΣΥΝΘΕΤΙΚΕΣ ΑΡΧΕΣ ΕΙΚΟΝΩΝ ΣΥΝΘΕΣΗ: Οργάνωση ενός συνόλου από επιμέρους στοιχεία σε μια ενιαία διάταξη Αρχική ιδέα σύνθεσης Μορφή της σύνθεσης Δομή της σύνθεσης ΟΠΤΙΚΗ ΔΟΜΗ ΤΗΣ ΣΥΝΘΕΣΗΣ Βασικό λεξιλόγιο
Βασικοί κανόνες σύνθεσης στη φωτογραφία
 Βασικοί κανόνες σύνθεσης στη φωτογραφία Πάτρα, Δεκέμβρης 2012 Ποια είναι η σχέση ανάμεσα στην τέχνη και την πληροφόρηση; Πώς μπορεί η φωτογραφία να είναι τέχνη, εάν είναι στενά συνδεδεμένη με την αυτόματη
Βασικοί κανόνες σύνθεσης στη φωτογραφία Πάτρα, Δεκέμβρης 2012 Ποια είναι η σχέση ανάμεσα στην τέχνη και την πληροφόρηση; Πώς μπορεί η φωτογραφία να είναι τέχνη, εάν είναι στενά συνδεδεμένη με την αυτόματη
Γράμματα και αριθμοί
 5 Γράμματα και αριθμοί 5.1 Γενικά Στα τεχνικά σχέδια χρησιμοποιούμε γράμματα και αριθμούς, όταν θέλουμε να δώσουμε περισσότερες πληροφορίες, όπως να χαρακτηρίσουμε χώρους ή υλικά, να δείξουμε την πορεία
5 Γράμματα και αριθμοί 5.1 Γενικά Στα τεχνικά σχέδια χρησιμοποιούμε γράμματα και αριθμούς, όταν θέλουμε να δώσουμε περισσότερες πληροφορίες, όπως να χαρακτηρίσουμε χώρους ή υλικά, να δείξουμε την πορεία
1. Εισαγωγή. 2. Τεχνικές και «κρατούμενα»
 1. Εισαγωγή Η προσέγγιση των Μαθηματικών της Β Δημοτικού από το παιδί προϋποθέτει την κατανόηση των μαθηματικών εννοιών που παρουσιάστηκαν στην Α Δημοτικού και την εξοικείωση του παιδιού με τις πράξεις
1. Εισαγωγή Η προσέγγιση των Μαθηματικών της Β Δημοτικού από το παιδί προϋποθέτει την κατανόηση των μαθηματικών εννοιών που παρουσιάστηκαν στην Α Δημοτικού και την εξοικείωση του παιδιού με τις πράξεις
ΣΥΝΘΕΤΙΚΕΣ ΑΡΧΕΣ ΕΙΚΟΝΩΝ
 ΣΥΝΘΕΤΙΚΕΣ ΑΡΧΕΣ ΕΙΚΟΝΩΝ ΤΙ ΡΩΤΑΜΕ ΜΙΑ ΕΙΚΟΝΑ ; ΤΙ ΜΑΣ ΑΦΗΓΕΙΤΑΙ ΜΙΑ ΕΙΚΟΝΑ ; ΠΩΣ ΜΑΣ ΤΟ ΑΦΗΓΕΙΤΑΙ ΜΙΑ ΕΙΚΟΝΑ ; ΣΥΝΘΕΣΗ: Οργάνωση ενός συνόλου από επιμέρους στοιχεία σε μια ενιαία διάταξη Αρχική ιδέα σύνθεσης
ΣΥΝΘΕΤΙΚΕΣ ΑΡΧΕΣ ΕΙΚΟΝΩΝ ΤΙ ΡΩΤΑΜΕ ΜΙΑ ΕΙΚΟΝΑ ; ΤΙ ΜΑΣ ΑΦΗΓΕΙΤΑΙ ΜΙΑ ΕΙΚΟΝΑ ; ΠΩΣ ΜΑΣ ΤΟ ΑΦΗΓΕΙΤΑΙ ΜΙΑ ΕΙΚΟΝΑ ; ΣΥΝΘΕΣΗ: Οργάνωση ενός συνόλου από επιμέρους στοιχεία σε μια ενιαία διάταξη Αρχική ιδέα σύνθεσης
ΣΤΕΡΕΟΣΚΟΠΙΚΕΣ ΕΙΚΟΝΕΣ
 ΣΤΕΡΕΟΣΚΟΠΙΚΕΣ ΕΙΚΟΝΕΣ Η προοπτική εικόνα, είναι, όπως είναι γνωστό, η προβολή ενός χωρικού αντικειμένου, σε ένα επίπεδο, με κέντρο προβολής, το μάτι του παρατηρητή. Η εικόνα αυτή, θεωρούμε ότι αντιστοιχεί
ΣΤΕΡΕΟΣΚΟΠΙΚΕΣ ΕΙΚΟΝΕΣ Η προοπτική εικόνα, είναι, όπως είναι γνωστό, η προβολή ενός χωρικού αντικειμένου, σε ένα επίπεδο, με κέντρο προβολής, το μάτι του παρατηρητή. Η εικόνα αυτή, θεωρούμε ότι αντιστοιχεί
Μιχάλης Μακρή EFIAP. Copyright: 2013 Michalis Makri
 Μιχάλης Μακρή EFIAP Copyright: 2013 Michalis Makri Copyright: 2013 Michalis Makri Less is more Less but better Copyright: 2013 Michalis Makri Ο μινιμαλισμός ορίζεται ως η εξάλειψη όλων των στοιχείων που
Μιχάλης Μακρή EFIAP Copyright: 2013 Michalis Makri Copyright: 2013 Michalis Makri Less is more Less but better Copyright: 2013 Michalis Makri Ο μινιμαλισμός ορίζεται ως η εξάλειψη όλων των στοιχείων που
Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 1. ΣΥΝΘΕΤΙΚΗ ΕΝΟΤΗΤΑ ΚΑΙ ΑΡΜΟΝΙΑ
 Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 1. ΣΥΝΘΕΤΙΚΗ ΕΝΟΤΗΤΑ ΚΑΙ ΑΡΜΟΝΙΑ Ανέκαθεν η οπτική επικοινωνία συγκρίνεται με τη μουσική. Η έννοια της σύνθεσης αρμόζει τόσο στη μουσική όσο και στον εικαστικό σχεδιασμό
Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 1. ΣΥΝΘΕΤΙΚΗ ΕΝΟΤΗΤΑ ΚΑΙ ΑΡΜΟΝΙΑ Ανέκαθεν η οπτική επικοινωνία συγκρίνεται με τη μουσική. Η έννοια της σύνθεσης αρμόζει τόσο στη μουσική όσο και στον εικαστικό σχεδιασμό
Γεωµετρικές έννοιες και µετρήσεις µεγεθών. (ή, διαφορετικά, αντίληψη του χώρου)
 Γεωµετρικές έννοιες και µετρήσεις µεγεθών (ή, διαφορετικά, αντίληψη του χώρου) αντιλήψεις παιδιών (κι όχι µόνο) τι είναι γεωµετρία; Όταν αντιμετωπίζω προβλήματα γεωμετρίας νιώθω σαν να κάνω ένα είδος μεταγνωστικής
Γεωµετρικές έννοιες και µετρήσεις µεγεθών (ή, διαφορετικά, αντίληψη του χώρου) αντιλήψεις παιδιών (κι όχι µόνο) τι είναι γεωµετρία; Όταν αντιμετωπίζω προβλήματα γεωμετρίας νιώθω σαν να κάνω ένα είδος μεταγνωστικής
Μαθηματικά: Αριθμητική και Άλγεβρα. Μάθημα 10 ο, Τμήμα Α
 Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 10 ο, Τμήμα Α Ορθογώνιο παραλληλόγραμμο 3 cm 5 cm Ο τύπος όπως είναι γραμμένος δείχνει ότι μπορούμε να πολλαπλασιάσουμε δύο μήκη. Ε=3cm x 5cm=15cm 2. Πώς καταλαβαίνετε
Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 10 ο, Τμήμα Α Ορθογώνιο παραλληλόγραμμο 3 cm 5 cm Ο τύπος όπως είναι γραμμένος δείχνει ότι μπορούμε να πολλαπλασιάσουμε δύο μήκη. Ε=3cm x 5cm=15cm 2. Πώς καταλαβαίνετε
ραστηριότητες στο Επίπεδο 1.
 ραστηριότητες στο Επίπεδο 1. Στο επίπεδο 0, στις πρώτες τάξεις του δηµοτικού σχολείου, όπου στόχος είναι η οµαδοποίηση των γεωµετρικών σχηµάτων σε οµάδες µε κοινά χαρακτηριστικά στη µορφή τους, είδαµε
ραστηριότητες στο Επίπεδο 1. Στο επίπεδο 0, στις πρώτες τάξεις του δηµοτικού σχολείου, όπου στόχος είναι η οµαδοποίηση των γεωµετρικών σχηµάτων σε οµάδες µε κοινά χαρακτηριστικά στη µορφή τους, είδαµε
Σταυρούλα Πατσιομίτου
 Αριστοτέλους Μεταφυσικά 1078 α 30 Σταυρούλα Πατσιομίτου spatsiomitou@sch.gr Σ υνδέονται τα Μαθηματικά με την Αισθητική, με την Τέχνη, με την Τεχνολογία. Πόσο σημαντικό είναι να γνωρίζουμε την Ιστορία τους;
Αριστοτέλους Μεταφυσικά 1078 α 30 Σταυρούλα Πατσιομίτου spatsiomitou@sch.gr Σ υνδέονται τα Μαθηματικά με την Αισθητική, με την Τέχνη, με την Τεχνολογία. Πόσο σημαντικό είναι να γνωρίζουμε την Ιστορία τους;
6 Γεωμετρικές κατασκευές
 6 Γεωμετρικές κατασκευές 6.1 Γενικά Στα σχέδια εφαρμόζουμε γεωμετρικές κατασκευές, προκειμένου να επιλύσουμε προβλήματα που απαιτούν μεγάλη σχεδιαστική και κατασκευαστική ακρίβεια. Τα γεωμετρικά - σχεδιαστικά
6 Γεωμετρικές κατασκευές 6.1 Γενικά Στα σχέδια εφαρμόζουμε γεωμετρικές κατασκευές, προκειμένου να επιλύσουμε προβλήματα που απαιτούν μεγάλη σχεδιαστική και κατασκευαστική ακρίβεια. Τα γεωμετρικά - σχεδιαστικά
Χωρικές σχέσεις και Γεωμετρικές Έννοιες στην Προσχολική Εκπαίδευση
 Χωρικές σχέσεις και Γεωμετρικές Έννοιες στην Προσχολική Εκπαίδευση Ενότητα 6: Γεωμετρικά σχήματα και μεγέθη δύο και τριών διαστάσεων Δημήτρης Χασάπης Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία
Χωρικές σχέσεις και Γεωμετρικές Έννοιες στην Προσχολική Εκπαίδευση Ενότητα 6: Γεωμετρικά σχήματα και μεγέθη δύο και τριών διαστάσεων Δημήτρης Χασάπης Τμήμα Εκπαίδευσης και Αγωγής στην Προσχολική Ηλικία
1.1. ΓΕΙΝΙΚΑ ΟΡΙΣΜΟΙ Με ποιο τρόπο μπορούμε να σχεδιάσουμε έναν τρισδιάστατο χώρο ή αντικείμενο, πάνω σ ένα χαρτί δύο διαστάσεων?
 ΣΧΕΔΙΑΣΤΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ - Εξεταστέα ύλη Β εξαμήνου 2011 1.1. ΓΕΙΝΙΚΑ ΟΡΙΣΜΟΙ Με ποιο τρόπο μπορούμε να σχεδιάσουμε έναν τρισδιάστατο χώρο ή αντικείμενο, πάνω σ ένα χαρτί δύο διαστάσεων? Τρεις μέθοδοι προβολών
ΣΧΕΔΙΑΣΤΙΚΗ ΜΕΘΟΔΟΛΟΓΙΑ - Εξεταστέα ύλη Β εξαμήνου 2011 1.1. ΓΕΙΝΙΚΑ ΟΡΙΣΜΟΙ Με ποιο τρόπο μπορούμε να σχεδιάσουμε έναν τρισδιάστατο χώρο ή αντικείμενο, πάνω σ ένα χαρτί δύο διαστάσεων? Τρεις μέθοδοι προβολών
 Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
Β Γραφικές παραστάσεις - Πρώτο γράφημα Σχεδιάζοντας το μήκος της σανίδας συναρτήσει των φάσεων της σελήνης μπορείτε να δείτε αν υπάρχει κάποιος συσχετισμός μεταξύ των μεγεθών. Ο συνήθης τρόπος γραφικής
ΠΑΙΖΩ ΚΑΙ ΚΑΤΑΛΑΒΑΙΝΩ ΜΑΘΗΜΑΤΙΚΑ
 1oς ΚΥΚΛΟΣ - ΠΑΙΖΟΥΜΕ ΚΑΙ ΜΑΘΑΙΝΟΥΜΕ ΤΟΥΣ ΑΡΙΘΜΟΥΣ Α Ενότητα Ανακαλύπτουμε τις ιδιότητες των υλικών μας, τα τοποθετούμε σε ομάδες και διατυπώνουμε κριτήρια ομαδοποίησης Οι μαθητές μαθαίνουν να αναπτύσσουν
1oς ΚΥΚΛΟΣ - ΠΑΙΖΟΥΜΕ ΚΑΙ ΜΑΘΑΙΝΟΥΜΕ ΤΟΥΣ ΑΡΙΘΜΟΥΣ Α Ενότητα Ανακαλύπτουμε τις ιδιότητες των υλικών μας, τα τοποθετούμε σε ομάδες και διατυπώνουμε κριτήρια ομαδοποίησης Οι μαθητές μαθαίνουν να αναπτύσσουν
Σύμβολα και σχεδιαστικά στοιχεία. Μάθημα 3
 Σύμβολα και σχεδιαστικά στοιχεία Μάθημα 3 Τα αρχιτεκτονικά σύμβολα αποτελούν μια διεθνή, συγκεκριμένη και απλή γλώσσα. Είναι προορισμένα να γίνονται κατανοητά από τον καθένα, ακόμα και από μη ειδικούς.
Σύμβολα και σχεδιαστικά στοιχεία Μάθημα 3 Τα αρχιτεκτονικά σύμβολα αποτελούν μια διεθνή, συγκεκριμένη και απλή γλώσσα. Είναι προορισμένα να γίνονται κατανοητά από τον καθένα, ακόμα και από μη ειδικούς.
ΕΛΕΥΘΕΡΟ - ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ Β Ενιαίου Λυκείου (Μάθημα : Κατεύθυνσης)
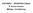 ΕΛΕΥΘΕΡΟ - ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ Β Ενιαίου Λυκείου (Μάθημα : Κατεύθυνσης) ΓΕΝΙΚΟΙ ΣΚΟΠΟΙ ΚΑΙ ΣΤΟΧΟΙ Το μάθημα απευθύνεται σε μαθητές με ειδικό ενδιαφέρον για το ΣΧΕΔΙΟ (Ελεύθερο και Προοπτικό) και που ενδέχεται
ΕΛΕΥΘΕΡΟ - ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ Β Ενιαίου Λυκείου (Μάθημα : Κατεύθυνσης) ΓΕΝΙΚΟΙ ΣΚΟΠΟΙ ΚΑΙ ΣΤΟΧΟΙ Το μάθημα απευθύνεται σε μαθητές με ειδικό ενδιαφέρον για το ΣΧΕΔΙΟ (Ελεύθερο και Προοπτικό) και που ενδέχεται
Επεξεργασία Χαρτογραφικής Εικόνας
 Επεξεργασία Χαρτογραφικής Εικόνας Διδάσκων: Αναγνωστόπουλος Χρήστος Κώδικες μετρήσεων αντικειμένων σε εικόνα Χρωματικά μοντέλα: Munsell, HSB/HSV, CIE-LAB Κώδικες μετρήσεων αντικειμένων σε εικόνες Η βασική
Επεξεργασία Χαρτογραφικής Εικόνας Διδάσκων: Αναγνωστόπουλος Χρήστος Κώδικες μετρήσεων αντικειμένων σε εικόνα Χρωματικά μοντέλα: Munsell, HSB/HSV, CIE-LAB Κώδικες μετρήσεων αντικειμένων σε εικόνες Η βασική
1ο χειμ. Εξαμηνο, 2013-2014
 1ο χειμ. Εξαμηνο, 2013-2014 Συνθεση πινακίδας παρουσίασης συνθετικά και γεωμετρικά στοιχεία Εισαγωγη στην Αρχιτεκτονικη Συνθεση Θεμα 1ο ΜΑΡΓΑΡΙΤΑ ΓΡΑΦΑΚΟΥ Καθηγήτρια της Σχολης Αρχιτεκτονων Ε.Μ.Π. Εικονογραφηση
1ο χειμ. Εξαμηνο, 2013-2014 Συνθεση πινακίδας παρουσίασης συνθετικά και γεωμετρικά στοιχεία Εισαγωγη στην Αρχιτεκτονικη Συνθεση Θεμα 1ο ΜΑΡΓΑΡΙΤΑ ΓΡΑΦΑΚΟΥ Καθηγήτρια της Σχολης Αρχιτεκτονων Ε.Μ.Π. Εικονογραφηση
Γεωμετρία. 63. Σε περίπτωση που η αρχή, το σημείο Ο, βρίσκεται πάνω σε μια ευθεία χχ τότε η
 Γεωμετρία Κεφάλαιο 1: Βασικές γεωμετρικές έννοιες Β.1.1 61.Η ευθεία είναι βασική έννοια της γεωμετρίας που την αντιλαμβανόμαστε ως την γραμμή που αφήνει ο κανόνας (χάρακας).συμβολίζεται με μικρά γράμματα
Γεωμετρία Κεφάλαιο 1: Βασικές γεωμετρικές έννοιες Β.1.1 61.Η ευθεία είναι βασική έννοια της γεωμετρίας που την αντιλαμβανόμαστε ως την γραμμή που αφήνει ο κανόνας (χάρακας).συμβολίζεται με μικρά γράμματα
Το σκηνικό μας είναι πλέον έτοιμο για εισάγουμε τα υπόλοιπα αντικείμενα του έργου μας.
 Εισαγωγή έτοιμου σκηνικού Όπως είδαμε και στο προηγούμενο κεφάλαιο, το Scratch παρέχει επίσης μία πληθώρα από έτοιμα σκηνικά. Για να εισάγουμε ένα έτοιμο σκηνικό, πηγαίνουμε στην καρτέλα Υπόβαθρα του σκηνικού
Εισαγωγή έτοιμου σκηνικού Όπως είδαμε και στο προηγούμενο κεφάλαιο, το Scratch παρέχει επίσης μία πληθώρα από έτοιμα σκηνικά. Για να εισάγουμε ένα έτοιμο σκηνικό, πηγαίνουμε στην καρτέλα Υπόβαθρα του σκηνικού
Επίλυση Προβλημάτων με Χρωματισμό. Αλέξανδρος Γ. Συγκελάκης asygelakis@gmail.com
 Επίλυση Προβλημάτων με Χρωματισμό Αλέξανδρος Γ. Συγκελάκης asygelakis@gmail.com 1 Η αφορμή συγγραφής της εργασίας Το παρακάτω πρόβλημα που τέθηκε στο Μεταπτυχιακό μάθημα «Θεωρία Αριθμών» το ακαδημαϊκό
Επίλυση Προβλημάτων με Χρωματισμό Αλέξανδρος Γ. Συγκελάκης asygelakis@gmail.com 1 Η αφορμή συγγραφής της εργασίας Το παρακάτω πρόβλημα που τέθηκε στο Μεταπτυχιακό μάθημα «Θεωρία Αριθμών» το ακαδημαϊκό
ΔΙΑΦΗΜΙΣΤΙΚΗ ΕΚΣΤΡΑΤΕΙΑ
 ΔΙΑΦΗΜΙΣΤΙΚΗ ΕΚΣΤΡΑΤΕΙΑ Advertising Layout: Το «περίγραμμα» στην έντυπη διαφήμιση Παρουσίαση: Μάνος Περακάκης Βιβλιογραφία: Διαφήμιση, Γιώργος Χ. Ζώτος Το «περίγραµµα» (Layout) Αποτελεί έκφραση της έντυπης
ΔΙΑΦΗΜΙΣΤΙΚΗ ΕΚΣΤΡΑΤΕΙΑ Advertising Layout: Το «περίγραμμα» στην έντυπη διαφήμιση Παρουσίαση: Μάνος Περακάκης Βιβλιογραφία: Διαφήμιση, Γιώργος Χ. Ζώτος Το «περίγραµµα» (Layout) Αποτελεί έκφραση της έντυπης
AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙ ΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ
 AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙ ΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ ΕΞΕΤΑΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕ ΙΟ 17 Σεπτεμβρίου 2014 ΘΕΜΑ: Σύνθεση με τρία
AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙ ΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙ ΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ ΕΞΕΤΑΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕ ΙΟ 17 Σεπτεμβρίου 2014 ΘΕΜΑ: Σύνθεση με τρία
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με τρία αντικείμενα ΓΕΝΙΚΕΣ ΟΔΗΓΙΕΣ: Η σύνθεση περιλαμβάνει
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με τρία αντικείμενα ΓΕΝΙΚΕΣ ΟΔΗΓΙΕΣ: Η σύνθεση περιλαμβάνει
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΔΥΟ (2)
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΔΥΟ (2) ΖΗΤΟΥΝΤΑΙ: 1. Απεικόνιση του θέματος στον καθορισμένο
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΠΕΜΠΤΗ 18 ΙΟΥΝΙΟΥ 2015 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ ΔΥΟ (2) ΖΗΤΟΥΝΤΑΙ: 1. Απεικόνιση του θέματος στον καθορισμένο
ΕΡΩΤΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ
 ΚΕΦΑΛΑΙΟ 1 ΕΡΩΤΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ Τι είναι ένα ευθύγραμμο τμήμα ΑΒ; Πώς ονομάζονται τα σημεία Α και Β; 1 ος ορισμός : Είναι η «ίσια» γραμμή που ενώνει τα δύο σημεία Α και Β. 2 ος ορισμός : Είναι
ΚΕΦΑΛΑΙΟ 1 ΕΡΩΤΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ Τι είναι ένα ευθύγραμμο τμήμα ΑΒ; Πώς ονομάζονται τα σημεία Α και Β; 1 ος ορισμός : Είναι η «ίσια» γραμμή που ενώνει τα δύο σημεία Α και Β. 2 ος ορισμός : Είναι
Gestalt. Το σύνολο είναι διαφορετικό σε δυναμική από στο άθροισμα των μερών του.
 Οι παρακάτω σημειώσεις περιέχουν κάποιες διευκρινήσεις και εικόνες που παρουσιάστηκαν και σχολιάστηκαν στα πλαίσια του μαθήματος Εικαστική Σύνθση 2, στο τμήμα ΕΑΔΣΑ, του ΤΕΙ Σερρών από την Νίνα Κοταμανίδου
Οι παρακάτω σημειώσεις περιέχουν κάποιες διευκρινήσεις και εικόνες που παρουσιάστηκαν και σχολιάστηκαν στα πλαίσια του μαθήματος Εικαστική Σύνθση 2, στο τμήμα ΕΑΔΣΑ, του ΤΕΙ Σερρών από την Νίνα Κοταμανίδου
710 -Μάθηση - Απόδοση
 710 -Μάθηση - Απόδοση Διάλεξη 6η Ποιοτική αξιολόγηση της Κινητικής Συμπεριφοράς Παρατήρηση III Η διάλεξη αυτή περιλαμβάνει: Διαδικασία της παρατήρησης & της αξιολόγησης Στόχοι και περιεχόμενο παρατήρησης
710 -Μάθηση - Απόδοση Διάλεξη 6η Ποιοτική αξιολόγηση της Κινητικής Συμπεριφοράς Παρατήρηση III Η διάλεξη αυτή περιλαμβάνει: Διαδικασία της παρατήρησης & της αξιολόγησης Στόχοι και περιεχόμενο παρατήρησης
710 -Μάθηση - Απόδοση
 710 -Μάθηση - Απόδοση Διάλεξη 6η Ποιοτική αξιολόγηση της Κινητικής Παρατήρηση Αξιολόγηση & Διάγνωση Η διάλεξη αυτή περιλαμβάνει: Διαδικασία της παρατήρησης & της αξιολόγησης Στόχοι και περιεχόμενο παρατήρησης
710 -Μάθηση - Απόδοση Διάλεξη 6η Ποιοτική αξιολόγηση της Κινητικής Παρατήρηση Αξιολόγηση & Διάγνωση Η διάλεξη αυτή περιλαμβάνει: Διαδικασία της παρατήρησης & της αξιολόγησης Στόχοι και περιεχόμενο παρατήρησης
Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας. Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης:
 Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης: παρόμοιο με του Cabri με αρκετές όμως διαφορές στην αρχιτεκτονική
Οδηγίες για το SKETCHPAD Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Με την εκτέλεση του Sketchpad παίρνουμε το παρακάτω παράθυρο σχεδίασης: παρόμοιο με του Cabri με αρκετές όμως διαφορές στην αρχιτεκτονική
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας. Παρουσίαση 12 η. Θεωρία Χρώματος και Επεξεργασία Έγχρωμων Εικόνων
 Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Παρουσίαση 12 η Θεωρία Χρώματος και Επεξεργασία Έγχρωμων Εικόνων Εισαγωγή (1) Το χρώμα είναι ένας πολύ σημαντικός παράγοντας περιγραφής, που συχνά απλουστεύει κατά
Ψηφιακή Επεξεργασία και Ανάλυση Εικόνας Παρουσίαση 12 η Θεωρία Χρώματος και Επεξεργασία Έγχρωμων Εικόνων Εισαγωγή (1) Το χρώμα είναι ένας πολύ σημαντικός παράγοντας περιγραφής, που συχνά απλουστεύει κατά
ΓΕΩΜΕΤΡΙΑ Α ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΙΔΑΚΤΕΑ ΕΞΕΤΑΣΤΕΑ ΥΛΗ
 ΥΛΗ ΚΑΙ ΟΔΗΓΙΕΣ ΔΙΔΑΣΚΑΛΙΑΣ ΣΧΟΛ. ΕΤΟΣ 2014-15 ΓΕΩΜΕΤΡΙΑ Α ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΙΔΑΚΤΕΑ ΕΞΕΤΑΣΤΕΑ ΥΛΗ Από το βιβλίο «Ευκλείδεια Γεωμετρία Α και Β Ενιαίου Λυκείου» των Αργυρόπουλου Η., Βλάμου
ΥΛΗ ΚΑΙ ΟΔΗΓΙΕΣ ΔΙΔΑΣΚΑΛΙΑΣ ΣΧΟΛ. ΕΤΟΣ 2014-15 ΓΕΩΜΕΤΡΙΑ Α ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΔΙΔΑΚΤΕΑ ΕΞΕΤΑΣΤΕΑ ΥΛΗ Από το βιβλίο «Ευκλείδεια Γεωμετρία Α και Β Ενιαίου Λυκείου» των Αργυρόπουλου Η., Βλάμου
Χώρος και Οπτικοακουστικά Μέσα
 Χώρος και Οπτικοακουστικά Μέσα ΘΕΩΡΙΑ [ΧΡΩΜΑ] (Τετάρτη 19/10/2016) Διδάσκων Δρ. Βασίλης Ψαρράς 3 η Διάλεξη [AVA340] 3 ο εξάμηνο (2016) Όλες οι διαλέξεις αποθηκεύονται στην πλατφόρµα opencourses.ionio.gr
Χώρος και Οπτικοακουστικά Μέσα ΘΕΩΡΙΑ [ΧΡΩΜΑ] (Τετάρτη 19/10/2016) Διδάσκων Δρ. Βασίλης Ψαρράς 3 η Διάλεξη [AVA340] 3 ο εξάμηνο (2016) Όλες οι διαλέξεις αποθηκεύονται στην πλατφόρµα opencourses.ionio.gr
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ
 9 ο ΜΑΘΗΜΑ ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ Πότε κάνουμε ομαδοποίηση των παρατηρήσεων; Όταν το πλήθος των τιμών μιας μεταβλητής είναι αρκετά μεγάλο κάνουμε ομαδοποίηση των παρατηρήσεων. Αυτό συμβαίνει είτε
9 ο ΜΑΘΗΜΑ ΟΜΑΔΟΠΟΙΗΣΗ ΤΩΝ ΠΑΡΑΤΗΡΗΣΕΩΝ Πότε κάνουμε ομαδοποίηση των παρατηρήσεων; Όταν το πλήθος των τιμών μιας μεταβλητής είναι αρκετά μεγάλο κάνουμε ομαδοποίηση των παρατηρήσεων. Αυτό συμβαίνει είτε
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΣΗΣ ΚΑΙ ΑΓΩΓΗΣ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΗΛΙΚΙΑ. Μάθημα: «Παιδικό σχέδιο: σύγχρονες προσεγγίσεις»
 ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΣΗΣ ΚΑΙ ΑΓΩΓΗΣ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΗΛΙΚΙΑ Μάθημα: «Παιδικό σχέδιο: σύγχρονες προσεγγίσεις» Διδάσκουσα: Κούβου Ουρανία Φοιτήτρια: Παπαϊωάννου Αργυρώ
ΕΘΝΙΚΟ ΚΑΙ ΚΑΠΟΔΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΤΜΗΜΑ ΕΚΠΑΙΔΕΥΣΗΣ ΚΑΙ ΑΓΩΓΗΣ ΣΤΗΝ ΠΡΟΣΧΟΛΙΚΗ ΗΛΙΚΙΑ Μάθημα: «Παιδικό σχέδιο: σύγχρονες προσεγγίσεις» Διδάσκουσα: Κούβου Ουρανία Φοιτήτρια: Παπαϊωάννου Αργυρώ
Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα
 Ασκήσεις της Ενότητας 2 : Ζωγραφίζοντας με το ΒΥΟΒ -1- α. Η χρήση της πένας Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα Υπάρχουν εντολές που μας επιτρέπουν να επιλέξουμε το χρώμα της πένας, καθώς και το
Ασκήσεις της Ενότητας 2 : Ζωγραφίζοντας με το ΒΥΟΒ -1- α. Η χρήση της πένας Κεφάλαιο 1: Κίνηση και γεωμετρικά σχήματα Υπάρχουν εντολές που μας επιτρέπουν να επιλέξουμε το χρώμα της πένας, καθώς και το
ισδιάστατοι μετασχηματισμοί ΚΕΦΑΛΑΙΟ 4: ισδιάστατοι γεωμετρικοί μετασχηματισμοί
 ΚΕΦΑΛΑΙΟ 4: ισδιάστατοι γεωμετρικοί μετασχηματισμοί Πολλά προβλήματα λύνονται μέσω δισδιάστατων απεικονίσεων ενός μοντέλου. Μεταξύ αυτών και τα προβλήματα κίνησης, όπως η κίνηση ενός συρόμενου μηχανισμού.
ΚΕΦΑΛΑΙΟ 4: ισδιάστατοι γεωμετρικοί μετασχηματισμοί Πολλά προβλήματα λύνονται μέσω δισδιάστατων απεικονίσεων ενός μοντέλου. Μεταξύ αυτών και τα προβλήματα κίνησης, όπως η κίνηση ενός συρόμενου μηχανισμού.
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2008 ΛΥΣΕΙΣ
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2008 ΛΥΣΕΙΣ Μάθημα: ΓΡΑΦΙΚΕΣ ΤΕΧΝΕΣ Ημερομηνία και ώρα εξέτασης: Τρίτη, 3 Ιουνίου 2008
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2008 ΛΥΣΕΙΣ Μάθημα: ΓΡΑΦΙΚΕΣ ΤΕΧΝΕΣ Ημερομηνία και ώρα εξέτασης: Τρίτη, 3 Ιουνίου 2008
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΕΞΕΤΑΣΗ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ KAI ΥΠΟΨΗΦΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΓΕΛ-ΕΠΑΛ ΕΞΕΤΑΣΗ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
ΑΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ KAI ΥΠΟΨΗΦΙΩΝ ΕΠΑΝΑΛΗΠΤΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΓΕΛ-ΕΠΑΛ ΕΞΕΤΑΣΗ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
ΕΛΕΥΘΕΡΟ - ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ
 ΕΛΕΥΘΕΡΟ - ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ Γ' Ενιαίου Λυκείου (Μάθημα : Κατεύθυνσης) ΓΕΝΙΚΟΙ ΣΚΟΠΟΙ ΚΑΙ ΣΤΟΧΟΙ Το μάθημα απευθύνεται σε μαθητές με ειδικό ενδιαφέρον για το ΕΛΕΥΘΕΡΟ-ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ ( Εικαστική και Αρχιτεκτονική
ΕΛΕΥΘΕΡΟ - ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ Γ' Ενιαίου Λυκείου (Μάθημα : Κατεύθυνσης) ΓΕΝΙΚΟΙ ΣΚΟΠΟΙ ΚΑΙ ΣΤΟΧΟΙ Το μάθημα απευθύνεται σε μαθητές με ειδικό ενδιαφέρον για το ΕΛΕΥΘΕΡΟ-ΠΡΟΟΠΤΙΚΟ ΣΧΕΔΙΟ ( Εικαστική και Αρχιτεκτονική
Η ζωή και ο Θάνατος στο Υλικό Σύμπαν
 Η ζωή και ο Θάνατος στο Υλικό Σύμπαν Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Τμήμα Φυσικής- Πανεπιστήμιο Αθηνών Η Γεωμετρία Του Σύμπαντος Όταν αναφερόμαστε σε μια γεωμετρία, θεωρούμε ως αυτονόητη
Η ζωή και ο Θάνατος στο Υλικό Σύμπαν Δρ Μάνος Δανέζης Επίκουρος Καθηγητής Αστροφυσικής Τμήμα Φυσικής- Πανεπιστήμιο Αθηνών Η Γεωμετρία Του Σύμπαντος Όταν αναφερόμαστε σε μια γεωμετρία, θεωρούμε ως αυτονόητη
ΠΑΡΟΥΣΙΑΣΗ ΣΤΑΤΙΣΤΙΚΩΝ ΔΕΔΟΜΕΝΩΝ
 ο Κεφάλαιο: Στατιστική ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΟΡΙΣΜΟΙ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός: Λέγεται ένα σύνολο στοιχείων που θέλουμε να εξετάσουμε με ένα ή περισσότερα χαρακτηριστικά. Μεταβλητές X: Ονομάζονται
ο Κεφάλαιο: Στατιστική ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΚΑΙ ΟΡΙΣΜΟΙ ΣΤΗ ΣΤΑΤΙΣΤΙΚΗ ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ Πληθυσμός: Λέγεται ένα σύνολο στοιχείων που θέλουμε να εξετάσουμε με ένα ή περισσότερα χαρακτηριστικά. Μεταβλητές X: Ονομάζονται
Διαγράμματα. Νίκος Σκουλίδης, Σημειώσεις Φυσικής Α` Γυμνασίου, , Διαγράμματα_1_0.docx
 Διαγράμματα Στα περισσότερα από τα Φύλλα Εργασίας που εργαστήκατε και συμπληρώσατε, είχατε να σχεδιάσετε και ένα διάγραμμα. Ίσως ήταν η πρώτη φορά που ασχοληθήκατε με αυτό το αντικείμενο και να σας φάνηκε
Διαγράμματα Στα περισσότερα από τα Φύλλα Εργασίας που εργαστήκατε και συμπληρώσατε, είχατε να σχεδιάσετε και ένα διάγραμμα. Ίσως ήταν η πρώτη φορά που ασχοληθήκατε με αυτό το αντικείμενο και να σας φάνηκε
ΑΡΧΗ 1ΗΣ ΑΠΟ 3 ΣΕΛΙ ΕΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ
 ΑΡΧΗ 1ΗΣ ΑΠΟ 3 ΣΕΛΙ ΕΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ ΕΞΕΤΑΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ 18 Σεπτεμβρίου 2013 ΘΕΜΑ: «Σύνθεση
ΑΡΧΗ 1ΗΣ ΑΠΟ 3 ΣΕΛΙ ΕΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΞΕΤΑΣΕΩΝ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΛΛΗΝΩΝ ΕΞΩΤΕΡΙΚΟΥ ΕΞΕΤΑΣΗ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ 18 Σεπτεμβρίου 2013 ΘΕΜΑ: «Σύνθεση
Δύο κύριοι τρόποι παρουσίασης δεδομένων. Παράδειγμα
 Δύο κύριοι τρόποι παρουσίασης δεδομένων Παράδειγμα Με πίνακες Με διαγράμματα Ονομαστικά δεδομένα Εδώ τα περιγραφικά μέτρα (μέσος, διάμεσος κλπ ) δεν έχουν νόημα Πήραμε ένα δείγμα από 25 άτομα και τα ρωτήσαμε
Δύο κύριοι τρόποι παρουσίασης δεδομένων Παράδειγμα Με πίνακες Με διαγράμματα Ονομαστικά δεδομένα Εδώ τα περιγραφικά μέτρα (μέσος, διάμεσος κλπ ) δεν έχουν νόημα Πήραμε ένα δείγμα από 25 άτομα και τα ρωτήσαμε
Α ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ ΓΕΛ I.
 Γεωμετρία Α ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ ΓΕΛ I. Εισαγωγή Η διδασκαλία της Γεωμετρίας στην Α Λυκείου εστιάζει στο πέρασμα από τον εμπειρικό στο θεωρητικό τρόπο σκέψης, με ιδιαίτερη έμφαση στη μαθηματική απόδειξη. Οι
Γεωμετρία Α ΤΑΞΗ ΗΜΕΡΗΣΙΟΥ ΓΕΛ I. Εισαγωγή Η διδασκαλία της Γεωμετρίας στην Α Λυκείου εστιάζει στο πέρασμα από τον εμπειρικό στο θεωρητικό τρόπο σκέψης, με ιδιαίτερη έμφαση στη μαθηματική απόδειξη. Οι
Δημιουργία μοντέλου αισθητικών κριτηρίων για αποτελεσματικό οπτικό σχεδιασμό εκπαιδευτικών ιστότοπων
 8 ο Πανελλήνιο Συνέδριο των Εκπαιδευτικών για τις ΤΠΕ «Αξιοποίηση των Τεχνολογιών της Πληροφορίας και της Επικοινωνίας στη Διδακτική Πράξη» Σύρος, 26-28 Ιουνίου 2015 ΥΠΟ ΤΗΝ ΑΙΓΙΔΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΟΛΙΤΙΣΜΟΥ,
8 ο Πανελλήνιο Συνέδριο των Εκπαιδευτικών για τις ΤΠΕ «Αξιοποίηση των Τεχνολογιών της Πληροφορίας και της Επικοινωνίας στη Διδακτική Πράξη» Σύρος, 26-28 Ιουνίου 2015 ΥΠΟ ΤΗΝ ΑΙΓΙΔΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΟΛΙΤΙΣΜΟΥ,
Γραμμή. Σημείο. κεφαλαίο γράμμα. Κάθε γραμμή. αποτελείται. Ευθεία κι αν αρχή και χωρίς. τέλος! x x
 1. Οι Πρωταρχικές Γεωμετρικές Έννοιες Σημείο Γραμμή Δεν έχει διαστάσεις!! Υπάρχει μόνο στο μυαλό μας. Συμβολίζεται με κεφαλαίο γράμμα. Κάθε γραμμή αποτελείται από άπειρα σημεία. Ευθεία Δεν είναι εύκολο
1. Οι Πρωταρχικές Γεωμετρικές Έννοιες Σημείο Γραμμή Δεν έχει διαστάσεις!! Υπάρχει μόνο στο μυαλό μας. Συμβολίζεται με κεφαλαίο γράμμα. Κάθε γραμμή αποτελείται από άπειρα σημεία. Ευθεία Δεν είναι εύκολο
Γνωστική Ψυχολογία Ι (ΨΧ32)
 Γνωστική Ψυχολογία Ι (ΨΧ32) Διάλεξη 6 Μηχανισμοί επεξεργασίας οπτικού σήματος Οι άλλες αισθήσεις Πέτρος Ρούσσος Η αντιληπτική πλάνη του πλέγματος Hermann 1 Πλάγια αναστολή Η πλάγια αναστολή (lateral inhibition)
Γνωστική Ψυχολογία Ι (ΨΧ32) Διάλεξη 6 Μηχανισμοί επεξεργασίας οπτικού σήματος Οι άλλες αισθήσεις Πέτρος Ρούσσος Η αντιληπτική πλάνη του πλέγματος Hermann 1 Πλάγια αναστολή Η πλάγια αναστολή (lateral inhibition)
Στα 1849 ο Sir David Brewster περιγράφει τη μακροσκοπική μηχανή λήψης και παράγονται οι πρώτες στερεοσκοπικές φωτογραφίες (εικ. 5,6).
 ΣΤΕΡΕΟΣΚΟΠΙΑ Η στερεοσκοπία είναι μια τεχνική που δημιουργεί την ψευδαίσθηση του βάθους σε μια εικόνα. Στηρίζεται στο ότι η τρισδιάστατη φυσική όραση πραγματοποιείται διότι κάθε μάτι βλέπει το ίδιο αντικείμενο
ΣΤΕΡΕΟΣΚΟΠΙΑ Η στερεοσκοπία είναι μια τεχνική που δημιουργεί την ψευδαίσθηση του βάθους σε μια εικόνα. Στηρίζεται στο ότι η τρισδιάστατη φυσική όραση πραγματοποιείται διότι κάθε μάτι βλέπει το ίδιο αντικείμενο
Ανάπτυξη Χωρικής Αντίληψης και Σκέψης
 Ανάπτυξη Χωρικής Αντίληψης και Σκέψης Clements & Sarama, 2009; Sarama & Clements, 2009 Χωρική αντίληψη και σκέψη Προσανατολισμός στο χώρο Οπτικοποίηση (visualization) Νοερή εικονική αναπαράσταση Νοερή
Ανάπτυξη Χωρικής Αντίληψης και Σκέψης Clements & Sarama, 2009; Sarama & Clements, 2009 Χωρική αντίληψη και σκέψη Προσανατολισμός στο χώρο Οπτικοποίηση (visualization) Νοερή εικονική αναπαράσταση Νοερή
ΚΑΤΑΣΚΕΥΗ ΠΙΝΑΚΩΝ ΚΑΙ ΣΧΗΜΑΤΩΝ ΣΤΟ ΔΟΚΙΜΙΟ ΕΡΕΥΝΗΤΙΚΗΣ ΕΡΓΑΣΙΑΣ: Μερικές χρήσιμες(;) υποδείξεις. Βασίλης Παυλόπουλος
 ΚΑΤΑΣΚΕΥΗ ΠΙΝΑΚΩΝ ΚΑΙ ΣΧΗΜΑΤΩΝ ΣΤΟ ΔΟΚΙΜΙΟ ΕΡΕΥΝΗΤΙΚΗΣ ΕΡΓΑΣΙΑΣ: Μερικές χρήσιμες(;) υποδείξεις Βασίλης Παυλόπουλος Διάγραμμα της παρουσίασης Πότε (δεν) χρειάζονται πίνακες και σχήματα σε μια ερευνητική
ΚΑΤΑΣΚΕΥΗ ΠΙΝΑΚΩΝ ΚΑΙ ΣΧΗΜΑΤΩΝ ΣΤΟ ΔΟΚΙΜΙΟ ΕΡΕΥΝΗΤΙΚΗΣ ΕΡΓΑΣΙΑΣ: Μερικές χρήσιμες(;) υποδείξεις Βασίλης Παυλόπουλος Διάγραμμα της παρουσίασης Πότε (δεν) χρειάζονται πίνακες και σχήματα σε μια ερευνητική
ΠΟΥ ΔΙΑΔΙΔΕΤΑΙ ΤΟ ΦΩΣ
 1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
1 ΦΩΣ Στο μικρόκοσμο θεωρούμε ότι το φως έχει δυο μορφές. Άλλοτε το αντιμετωπίζουμε με τη μορφή σωματιδίων που ονομάζουμε φωτόνια. Τα φωτόνια δεν έχουν μάζα αλλά μόνον ενέργεια. Άλλοτε πάλι αντιμετωπίζουμε
ΕΝΟΤΗΤΑ 4 ΕΙΔΗ ΓΡΑΜΜΩΝ, ΕΙΔΗ ΤΡΙΓΩΝΩΝ, ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΑ, ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ
 ΕΝΟΤΗΤΑ 4 ΕΙΔΗ ΓΡΑΜΜΩΝ, ΕΙΔΗ ΤΡΙΓΩΝΩΝ, ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΑ, ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Εκτίμηση και μέτρηση Μ3.6 Εκτιμούν, μετρούν, ταξινομούν και κατασκευάζουν γωνίες (με ή χωρίς τη χρήση της
ΕΝΟΤΗΤΑ 4 ΕΙΔΗ ΓΡΑΜΜΩΝ, ΕΙΔΗ ΤΡΙΓΩΝΩΝ, ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΑ, ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΙ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΑΡΙΘΜΟΙ Εκτίμηση και μέτρηση Μ3.6 Εκτιμούν, μετρούν, ταξινομούν και κατασκευάζουν γωνίες (με ή χωρίς τη χρήση της
ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO
 1 ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΜΑΘΗΤΗ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 1. Τοποθέτησε μια χελώνα στην επιφάνεια εργασίας. 2. Με ποια εντολή γράφει η χελώνα μας;.. 3. Γράψε την εντολή για να πάει
1 ΚΑΤΑΣΚΕΥΗ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΩΝ ΜΕ ΧΡΗΣΗ LOGO ΦΥΛΛΑ ΕΡΓΑΣΙΑΣ ΜΑΘΗΤΗ ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 1 1. Τοποθέτησε μια χελώνα στην επιφάνεια εργασίας. 2. Με ποια εντολή γράφει η χελώνα μας;.. 3. Γράψε την εντολή για να πάει
Μαθηματικά: Αριθμητική και Άλγεβρα. Μάθημα 3 ο, Τμήμα Α. Τρόποι απόδειξης
 Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 3 ο, Τμήμα Α Ο πυρήνας των μαθηματικών είναι οι τρόποι με τους οποίους μπορούμε να συλλογιζόμαστε στα μαθηματικά. Τρόποι απόδειξης Επαγωγικός συλλογισμός (inductive)
Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 3 ο, Τμήμα Α Ο πυρήνας των μαθηματικών είναι οι τρόποι με τους οποίους μπορούμε να συλλογιζόμαστε στα μαθηματικά. Τρόποι απόδειξης Επαγωγικός συλλογισμός (inductive)
VAN HIELE GEOMETRY TEST * (USISKIN) ΟΔΗΓΙΕΣ
 VAN HIELE GEOMETRY TEST * (USISKIN) ΟΔΗΓΙΕΣ Μην γυρίσετε την επόμενη σελίδα πριν σας το πουν. Για το test αυτό πρέπει να γνωρίζετε ότι: Δεν επηρεάζει τη βαθμολογία σου στο σχολείο. Χρησιμοποιείται αποκλειστικά
VAN HIELE GEOMETRY TEST * (USISKIN) ΟΔΗΓΙΕΣ Μην γυρίσετε την επόμενη σελίδα πριν σας το πουν. Για το test αυτό πρέπει να γνωρίζετε ότι: Δεν επηρεάζει τη βαθμολογία σου στο σχολείο. Χρησιμοποιείται αποκλειστικά
Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 5. ΣΥΝΘΕΤΙΚΟΣ ΡΥΘΜΟΣ
 Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 5. ΣΥΝΘΕΤΙΚΟΣ ΡΥΘΜΟΣ Ο ρυθμός είναι μια έννοια που ξεκινάει από την επαναλαμβανόμενη αλλαγή κατά τακτά χρονικά διαστήματα κάποιας χαρακτηριστικής κατάστασης. Στη μουσική
Β. ΚΑΝΟΝΕΣ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 5. ΣΥΝΘΕΤΙΚΟΣ ΡΥΘΜΟΣ Ο ρυθμός είναι μια έννοια που ξεκινάει από την επαναλαμβανόμενη αλλαγή κατά τακτά χρονικά διαστήματα κάποιας χαρακτηριστικής κατάστασης. Στη μουσική
ΕΝΤΟΛΕΣ. 7.1 Εισαγωγικό μέρος με επεξήγηση των Εντολών : Επεξήγηση των εντολών που θα
 7.1 Εισαγωγικό μέρος με επεξήγηση των Εντολών : Επεξήγηση των εντολών που θα ΕΝΤΟΛΕΣ χρησιμοποιηθούν παρακάτω στα παραδείγματα Βάζοντας την εντολή αυτή σε οποιοδήποτε αντικείμενο μπορούμε να αλλάζουμε
7.1 Εισαγωγικό μέρος με επεξήγηση των Εντολών : Επεξήγηση των εντολών που θα ΕΝΤΟΛΕΣ χρησιμοποιηθούν παρακάτω στα παραδείγματα Βάζοντας την εντολή αυτή σε οποιοδήποτε αντικείμενο μπορούμε να αλλάζουμε
ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ. Η διαίρεση καλείται Ευκλείδεια και είναι τέλεια όταν το υπόλοιπο είναι μηδέν.
 ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
ΕΝΟΤΗΤΑ 8 ΔΙΣΔΙΑΣΤΑΤΗ ΓΕΩΜΕΤΡΙΑ
 ΕΝΟΤΗΤΑ 8 ΔΙΣΔΙΑΣΤΑΤΗ ΓΕΩΜΕΤΡΙΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΓΕΩΜΕΤΡΙΑ Διερεύνηση σχημάτων και χώρου Γ1.1 Περιγράφουν και κατασκευάζουν διάφορα είδη γραμμών (ανοιχτές, κλειστές, ευθείες, καμπύλες) και δισδιάστατα
ΕΝΟΤΗΤΑ 8 ΔΙΣΔΙΑΣΤΑΤΗ ΓΕΩΜΕΤΡΙΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ ΓΕΩΜΕΤΡΙΑ Διερεύνηση σχημάτων και χώρου Γ1.1 Περιγράφουν και κατασκευάζουν διάφορα είδη γραμμών (ανοιχτές, κλειστές, ευθείες, καμπύλες) και δισδιάστατα
Φυσικά μεγέθη. Φυσική α λυκείου ΕΙΣΑΓΩΓΗ. Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα. Β.
 ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
ΕΙΣΑΓΩΓΗ Φυσικά μεγέθη Όλα τα φυσικά μεγέθη τα χωρίζουμε σε δύο κατηγορίες : Α. τα μονόμετρα Β. τα διανυσματικά Μονόμετρα ονομάζουμε τα μεγέθη εκείνα τα οποία για να τα γνωρίζουμε χρειάζεται να ξέρουμε
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2007
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2007 Μάθημα: ΓΡΑΦΙΚΕΣ ΤΕΧΝΕΣ Ημερομηνία και ώρα εξέτασης: Τετάρτη, 6 Ιουνίου 2007 7:30
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ ΚΑΙ ΠΟΛΙΤΙΣΜΟΥ ΔΙΕΥΘΥΝΣΗ ΑΝΩΤΕΡΗΣ ΚΑΙ ΑΝΩΤΑΤΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΥΠΗΡΕΣΙΑ ΕΞΕΤΑΣΕΩΝ ΠΑΓΚΥΠΡΙΕΣ ΕΞΕΤΑΣΕΙΣ 2007 Μάθημα: ΓΡΑΦΙΚΕΣ ΤΕΧΝΕΣ Ημερομηνία και ώρα εξέτασης: Τετάρτη, 6 Ιουνίου 2007 7:30
AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙ ΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΥΤΕΡΑ 17 ΙΟΥΝΙΟΥ 2013 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕ ΙΟ
 AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙ ΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΥΤΕΡΑ 17 ΙΟΥΝΙΟΥ 2013 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕ ΙΟ ΘΕΜΑ: Σύνθεση με τέσσερα αντικείμενα. ΓΕΝΙΚΕΣ Ο ΗΓΙΕΣ: Το προς σχεδίαση
AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙ ΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΥΤΕΡΑ 17 ΙΟΥΝΙΟΥ 2013 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕ ΙΟ ΘΕΜΑ: Σύνθεση με τέσσερα αντικείμενα. ΓΕΝΙΚΕΣ Ο ΗΓΙΕΣ: Το προς σχεδίαση
AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ Ο ΗΓΙΕΣ
 AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙ ΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΥΤΕΡΑ 17 ΙΟΥΝΙΟΥ 2013 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕ ΙΟ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ ΥΟ (2) ΖΗΤΟΥΝΤΑΙ: 1. Απεικόνιση του θέματος στον καθορισμένο
AΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙ ΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΕΥΤΕΡΑ 17 ΙΟΥΝΙΟΥ 2013 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕ ΙΟ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ ΥΟ (2) ΖΗΤΟΥΝΤΑΙ: 1. Απεικόνιση του θέματος στον καθορισμένο
ΔΗΜΙΟΥΡΓΙΑ. ΠΛΑΤΦΟΡΜΑΣ αω. και ΔΙΑΣΠΑΣΗ ΤΗΣ ΔΗΜΙΟΥΡΓΙΑΣ ΤΩΝ αλφα ωμεγα ΑΡΤΕΜΗΣ ΣΩΡΡΑΣ ΜΕΡΟΣ 13 Ο
 ΔΗΜΙΟΥΡΓΙΑ ΠΛΑΤΦΟΡΜΑΣ αω και ΔΙΑΣΠΑΣΗ ΤΗΣ ΔΗΜΙΟΥΡΓΙΑΣ ΤΩΝ αλφα ωμεγα αω ΑΡΤΕΜΗΣ ΣΩΡΡΑΣ ΜΕΡΟΣ 13 Ο δημιουργια ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΤΗΣ ΠΛΑΤΦΟΡΜΑΣ ΑΝΑΠΤΥΞΗΣ ΔΟΜΗΣ ΚΑΙ ΔΟΜΗΣΗΣ ΤΗΣ ΔΗΜΙΟΥΡΓΙΑΣ ΤΩΝ αλφα ΚΑΙ ΤΟΥ ωμεγα
ΔΗΜΙΟΥΡΓΙΑ ΠΛΑΤΦΟΡΜΑΣ αω και ΔΙΑΣΠΑΣΗ ΤΗΣ ΔΗΜΙΟΥΡΓΙΑΣ ΤΩΝ αλφα ωμεγα αω ΑΡΤΕΜΗΣ ΣΩΡΡΑΣ ΜΕΡΟΣ 13 Ο δημιουργια ΚΑΙ ΚΑΤΑΣΚΕΥΗ ΤΗΣ ΠΛΑΤΦΟΡΜΑΣ ΑΝΑΠΤΥΞΗΣ ΔΟΜΗΣ ΚΑΙ ΔΟΜΗΣΗΣ ΤΗΣ ΔΗΜΙΟΥΡΓΙΑΣ ΤΩΝ αλφα ΚΑΙ ΤΟΥ ωμεγα
Οφθαλμαπάτες (Optical illusions)
 Οφθαλμαπάτες (Optical illusions) Το φαινόμενο της οφθαλμαπάτης συνίσταται στο ότι εσφαλμένα αντιλαμβανόμαστε κάτι διαφορετικό, απ αυτό που βλέπουν τα μάτια μας, ή δυσκολευόμαστε να έχουμε μια σαφή σντίληψη
Οφθαλμαπάτες (Optical illusions) Το φαινόμενο της οφθαλμαπάτης συνίσταται στο ότι εσφαλμένα αντιλαμβανόμαστε κάτι διαφορετικό, απ αυτό που βλέπουν τα μάτια μας, ή δυσκολευόμαστε να έχουμε μια σαφή σντίληψη
Για μια αποτελεσματική Παρουσίαση
 Για μια αποτελεσματική Παρουσίαση Παναγιώτης Αντωνίου 6 ΣΗΜΕΙΑ ΣΤΙΣ ΠΑΡΟΥΣΙΑΣΕΙΣ Σχεδίαση σωστής δομής Προετοιμασία ξεκάθαρων διαφανειών Ακριβής διαχείριση της παρουσίασης Προφορά & Προβολή : Προετοιμασία
Για μια αποτελεσματική Παρουσίαση Παναγιώτης Αντωνίου 6 ΣΗΜΕΙΑ ΣΤΙΣ ΠΑΡΟΥΣΙΑΣΕΙΣ Σχεδίαση σωστής δομής Προετοιμασία ξεκάθαρων διαφανειών Ακριβής διαχείριση της παρουσίασης Προφορά & Προβολή : Προετοιμασία
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ Δευτέρα, 24 Ιουνίου 2019 ΖΗΤΟΥΝΤΑΙ: 1. Απεικόνιση
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ Δευτέρα, 24 Ιουνίου 2019 ΖΗΤΟΥΝΤΑΙ: 1. Απεικόνιση
Εισαγωγή στο Χρώμα. Εισαγωγή στο χρώμα και την ανάπτυξη της συνθετικής λειτουργίας των
 Στέλιος Μιχαήλ Ε.Ε.Κ.Κ. 8 Δεκεμβρίου 2010 Εισαγωγή στο Χρώμα Εισαγωγή στο χρώμα και την ανάπτυξη της συνθετικής λειτουργίας των χρωμάτων. Το φως ως στοιχείο που ειδικεύει και τροποποιεί το χρώμα. Θα μιλήσουμε
Στέλιος Μιχαήλ Ε.Ε.Κ.Κ. 8 Δεκεμβρίου 2010 Εισαγωγή στο Χρώμα Εισαγωγή στο χρώμα και την ανάπτυξη της συνθετικής λειτουργίας των χρωμάτων. Το φως ως στοιχείο που ειδικεύει και τροποποιεί το χρώμα. Θα μιλήσουμε
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Α. ΣΤΟΙΧΕΙΑ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 6. ΧΩΡΟΣ
 Α. ΣΤΟΙΧΕΙΑ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 6. ΧΩΡΟΣ Ο καλλιτέχνης μπορεί να συμπεριλάβει ή να αγνοήσει τη διάσταση του χώρου στην απεικόνιση που εκτελεί. Όταν περιγράφει το βάθος του οπτικού πεδίου με διάφορους
Α. ΣΤΟΙΧΕΙΑ ΤΗΣ ΓΡΑΦΙΣΤΙΚΗΣ ΕΚΦΡΑΣΗΣ 6. ΧΩΡΟΣ Ο καλλιτέχνης μπορεί να συμπεριλάβει ή να αγνοήσει τη διάσταση του χώρου στην απεικόνιση που εκτελεί. Όταν περιγράφει το βάθος του οπτικού πεδίου με διάφορους
Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ
 Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ ΕΙΣΑΓΩΓΗ Η Γενικευμένη Γεωμετρία, που θα αναπτύξουμε στα παρακάτω κεφάλαια, είναι μία «Νέα Γεωμετρία», η οποία προέκυψε από την ανάγκη να γενικεύσει ορισμένα σημεία της Ευκλείδειας
Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ ΕΙΣΑΓΩΓΗ Η Γενικευμένη Γεωμετρία, που θα αναπτύξουμε στα παρακάτω κεφάλαια, είναι μία «Νέα Γεωμετρία», η οποία προέκυψε από την ανάγκη να γενικεύσει ορισμένα σημεία της Ευκλείδειας
Χρωματίζουμε τα σημεία του επιπέδου με τρία χρώματα. Αποδείξτε ότι υπάρχουν δύο
 1.1 ΠΡΟΒΛΗ ΜΑ Χρωματίζουμε τα σημεία του επιπέδου με δύο χρώματα. Αποδείξτε ότι υπάρχουν δύο τουλάχιστον σημεία με το ίδιο χρώμα που απέχουν απόσταση 1. Έστω ότι χρωματίζουμε τα σημεία του επιπέδου κόκινα
1.1 ΠΡΟΒΛΗ ΜΑ Χρωματίζουμε τα σημεία του επιπέδου με δύο χρώματα. Αποδείξτε ότι υπάρχουν δύο τουλάχιστον σημεία με το ίδιο χρώμα που απέχουν απόσταση 1. Έστω ότι χρωματίζουμε τα σημεία του επιπέδου κόκινα
Και τώρα τι κάνω; Σημαντικότερο απ όλα είναι να διαβάσεις και να ευχαριστηθείς την ιστορία και τις πληροφορίες για τον κόσμο των χρωμάτων
 Και τώρα τι κάνω; Σημαντικότερο απ όλα είναι να διαβάσεις και να ευχαριστηθείς την ιστορία και τις πληροφορίες για τον κόσμο των χρωμάτων Να ποια είναι τα υλικά που θα χρειαστείς: γκρι χαρτόνι (100 γραμμαρίων)
Και τώρα τι κάνω; Σημαντικότερο απ όλα είναι να διαβάσεις και να ευχαριστηθείς την ιστορία και τις πληροφορίες για τον κόσμο των χρωμάτων Να ποια είναι τα υλικά που θα χρειαστείς: γκρι χαρτόνι (100 γραμμαρίων)
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ
 ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΑΣΚΗΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΜΑΖΑΣ ΘΕΣΗΣ ΚΕΝΤΡΟΥ ΜΑΖΑΣ ΡΟΠΗΣ ΑΔΡΑΝΕΙΑΣ ΣΩΜΑΤΩΝ ΓΕΝΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ Α. Υπολογισμός της θέσης του κέντρου μάζας συστημάτων που αποτελούνται από απλά διακριτά μέρη. Τα απλά διακριτά
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΨΥΧΟΛΟΓΙΑ (ΨΧ 00)
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΨΥΧΟΛΟΓΙΑ (ΨΧ 00) Πέτρος Ρούσσος ΔΙΑΛΕΞΗ 5 Έννοιες και Κλασική Θεωρία Εννοιών Έννοιες : Θεμελιώδη στοιχεία από τα οποία αποτελείται το γνωστικό σύστημα Κλασική θεωρία [ή θεωρία καθοριστικών
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΨΥΧΟΛΟΓΙΑ (ΨΧ 00) Πέτρος Ρούσσος ΔΙΑΛΕΞΗ 5 Έννοιες και Κλασική Θεωρία Εννοιών Έννοιες : Θεμελιώδη στοιχεία από τα οποία αποτελείται το γνωστικό σύστημα Κλασική θεωρία [ή θεωρία καθοριστικών
ΣΚΙΑΓΡΑΦΙΑ. Γενικές αρχές και έννοιες
 ΣΚΙΑΓΡΑΦΙΑ Γενικές αρχές και έννοιες Στο σύστημα προβολής κατά Monge δεν μας δίνεται η δυνατότητα ν αντιληφθούμε άμεσα τα αντικείμενα του χώρου, παρά μόνο αφού συνδυάσουμε τις δύο προβολές του αντικειμένου
ΣΚΙΑΓΡΑΦΙΑ Γενικές αρχές και έννοιες Στο σύστημα προβολής κατά Monge δεν μας δίνεται η δυνατότητα ν αντιληφθούμε άμεσα τα αντικείμενα του χώρου, παρά μόνο αφού συνδυάσουμε τις δύο προβολές του αντικειμένου
Βασικές Γεωμετρικές έννοιες
 Βασικές Γεωμετρικές έννοιες Σημείο Με την άκρη του μολυβιού μου ακουμπώντας την σε ένα κομμάτι χαρτί αφήνω ένα σημάδι το οποίο το λέω σημείο. Το σημείο το δίνω όνομα γράφοντας πάνω απ αυτό ένα κεφαλαίο
Βασικές Γεωμετρικές έννοιες Σημείο Με την άκρη του μολυβιού μου ακουμπώντας την σε ένα κομμάτι χαρτί αφήνω ένα σημάδι το οποίο το λέω σημείο. Το σημείο το δίνω όνομα γράφοντας πάνω απ αυτό ένα κεφαλαίο
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 1ο «ΑΛΓΕΒΡΑ»
 ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΥ ΜΕΡΣ ο «ΑΛΓΕΒΡΑ». Να υπολογίσετε την τιμή της παράστασης: Α = ( + ) 4( ) 8, όταν = 0,45. Απλοποιούμε πρώτα την παράσταση : Α = ( + ) 4( ) 8 = = + 6 4 + 4 8
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΥ ΜΕΡΣ ο «ΑΛΓΕΒΡΑ». Να υπολογίσετε την τιμή της παράστασης: Α = ( + ) 4( ) 8, όταν = 0,45. Απλοποιούμε πρώτα την παράσταση : Α = ( + ) 4( ) 8 = = + 6 4 + 4 8
Μαθηματική Εισαγωγή Συναρτήσεις
 Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Φυσικός Ραδιοηλεκτρολόγος (MSc) ο Γενικό Λύκειο Καστοριάς Καστοριά, Ιούλιος 14 A. Μαθηματική Εισαγωγή Πράξεις με αριθμούς σε εκθετική μορφή Επίλυση βασικών μορφών εξισώσεων Συναρτήσεις Στοιχεία τριγωνομετρίας
Συστήματα συντεταγμένων
 Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
ΚΥΚΛΟ. κάθετη στη χορδή ΑΒ. τη χορδή. του κέντρου Κ από. (βλέπε σχήμα).
 ΑΣΚΗΣΕΙΣ ΣΤΟΝ ΚΥΚΛΟ 1. Να κατασκευάσετε έναν κύκλο και να πάρετε μια χορδή του ΑΒ. Από το κέντρο Κ του κύκλου να φέρετε κάθετη στη χορδή ΑΒ η οποία τέμνει τη χορδή στο σημείο Μ. Να διαπιστώσετε με μέτρηση
ΑΣΚΗΣΕΙΣ ΣΤΟΝ ΚΥΚΛΟ 1. Να κατασκευάσετε έναν κύκλο και να πάρετε μια χορδή του ΑΒ. Από το κέντρο Κ του κύκλου να φέρετε κάθετη στη χορδή ΑΒ η οποία τέμνει τη χορδή στο σημείο Μ. Να διαπιστώσετε με μέτρηση
Το ταξίδι στην 11η διάσταση
 Το ταξίδι στην 11η διάσταση Το κείμενο αυτό δεν αντιπροσωπεύει το πώς παρουσιάζονται οι 11 διστάσεις βάση της θεωρίας των υπερχορδών! Είναι περισσότερο «τροφή για σκέψη» παρά επιστημονική άποψη. Οι σκέψεις
Το ταξίδι στην 11η διάσταση Το κείμενο αυτό δεν αντιπροσωπεύει το πώς παρουσιάζονται οι 11 διστάσεις βάση της θεωρίας των υπερχορδών! Είναι περισσότερο «τροφή για σκέψη» παρά επιστημονική άποψη. Οι σκέψεις
Κεφάλαιο 6: Ζωγραφική
 Κεφάλαιο 6: Ζωγραφική... Σε αυτό το κεφάλαιο: 6.1 Ζωγραφική 6.2 Απλά ζωγράφισε 6.3 Χρώμα, σκιά και μέγεθος 6.4 Παράδειγμα... «Ζωγραφίζω πράγματα που σκέφτομαι, όχι πράγματα που βλέπω!» (Πικάσο) 6.1 Ζωγραφική
Κεφάλαιο 6: Ζωγραφική... Σε αυτό το κεφάλαιο: 6.1 Ζωγραφική 6.2 Απλά ζωγράφισε 6.3 Χρώμα, σκιά και μέγεθος 6.4 Παράδειγμα... «Ζωγραφίζω πράγματα που σκέφτομαι, όχι πράγματα που βλέπω!» (Πικάσο) 6.1 Ζωγραφική
Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά. Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων
 Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων Εισαγωγή Η χώρα μας απέκτησε Νέα Προγράμματα Σπουδών και Νέα
Γράφοντας ένα σχολικό βιβλίο για τα Μαθηματικά Μαριάννα Τζεκάκη Αν. Καθηγήτρια Α.Π.Θ. Μ. Καλδρυμίδου Αν. Καθηγήτρια Πανεπιστημίου Ιωαννίνων Εισαγωγή Η χώρα μας απέκτησε Νέα Προγράμματα Σπουδών και Νέα
Οδηγίες για το CABRI - GEOMETRY II Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας
 Οδηγίες για το CABRI - GEOMETRY II Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Εκτελώντας το πρόγραμμα παίρνουμε ένα παράθυρο εργασίας Γεωμετρικών εφαρμογών. Τα βασικά κουμπιά και τα μενού έχουν την παρακάτω
Οδηγίες για το CABRI - GEOMETRY II Μωυσιάδης Πολυχρόνης - Δόρτσιος Κώστας Εκτελώντας το πρόγραμμα παίρνουμε ένα παράθυρο εργασίας Γεωμετρικών εφαρμογών. Τα βασικά κουμπιά και τα μενού έχουν την παρακάτω
WEB DESIGN Ο σχεδιασμός στο Web Design
 WEB DESIGN Ο σχεδιασμός στο Web Design ΠΑΤΣΙΑΛΟΥ ΚΩΝΣΤΑΝΤΙΝΑ Web Design Είναι ο σχεδιασμός και η δημιουργία δικτυακών τόπων. Περιλαμβάνει : την αρχιτεκτονική πληροφοριών, τη διεπαφή χρήστη και την πλοήγηση.
WEB DESIGN Ο σχεδιασμός στο Web Design ΠΑΤΣΙΑΛΟΥ ΚΩΝΣΤΑΝΤΙΝΑ Web Design Είναι ο σχεδιασμός και η δημιουργία δικτυακών τόπων. Περιλαμβάνει : την αρχιτεκτονική πληροφοριών, τη διεπαφή χρήστη και την πλοήγηση.
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ. ΘΕΜΑ: Σύνθεση με τέσσερα (4) αντικείμενα
 AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΔΕΥΤΕΡΑ 26 ΙΟΥΝΙΟΥ 2017 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με τέσσερα (4)
AΡΧΗ 1ΗΣ ΣΕΛΙΔΑΣ ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΕΙΔΙΚΩΝ ΜΑΘΗΜΑΤΩΝ ΔΕΥΤΕΡΑ 26 ΙΟΥΝΙΟΥ 2017 ΚΟΙΝΗ ΕΞΕΤΑΣΗ ΟΛΩΝ ΤΩΝ ΥΠΟΨΗΦΙΩΝ ΣΤΟ ΕΛΕΥΘΕΡΟ ΣΧΕΔΙΟ ΘΕΜΑ: Σύνθεση με τέσσερα (4)
