Εφαρμοσμένα Μαθηματικά ΙΙ
|
|
|
- Τυρώ Ηλιόπουλος
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD
2 Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται από ένα μη κενό σύνολο διανυσμάτων V, ένα σώμα F (π.χ. ή ) και δύο πράξεις: Πρέπει να οριστούν Σύνολο Συντελεστών κατάλληλα O V είναι κλειστός Την πρόσθεση διανυσμάτων: ως προς τις δύο + + : V V V ( xy, ) x+ y, xy, V πράξεις, δηλ ον βαθμωτό πολλαπλασιασμό: x+ y, ax V : F V V ( a, x) ax, α Fκαι x V Η πρόσθεση διανυσμάτων ορίζεται με τέτοιο τρόπο ώστε να ικανοποιεί τις: 1) x+ y= y+ x, xy, V ( ) ( ) 2) x+ y + z= x+ y+ z, xyz,, V 3) O V : x+ O= O+ x= x, x V 4) x V, ( x) V : x+ ( x) = O Ο βαθμωτός πολλαπλασιασμός ορίζεται με τέτοιο τρόπο ώστε να ικανοποιεί τις: ( ) ( ) 5) ab x = a b x, a, b F και x V ( ) 6) a x+ y = ax+ ay, a Fκαι x, y V ( ) 7) a+ b x= ax+ bx, a, b Fκαι x V 8) 1 x= x, x V Αντιμεταθετική Ιδιότητα (o 1 είναι η μονάδα του F) Προσεταιριστική Ιδιότητα Ουδέτερο στοιχείο (Μηδενικό διάνυσμα) Αντίθετο διάνυσμα Περιέχει τουλάχιστον το μηδενικό διάνυσμα Προσοχή: Στο βαθμωτό πολ/σμο η αντιμεταθετική ιδιότητα δεν απαιτείται Επιμεριστική Ιδιότητα ως προς την + στο V Επιμεριστική Ιδιότητα ως προς την + στο F
3 Ιδιότητες Διανυσματικών Χώρων Για κάθε F-διανυσματικό χώροv ισχύουν: o μηδενικό διάνυσμα είναι μοναδικό o αντίθετο διάνυσμα ενός διανύσματος είναι μοναδικό ( k l) v = kv lv, k, l F, v V 0 v= O, v V ko = O, k F 1 v= v, v V ( ) Παρατήρηση: Αν ο V περιέχει ένα διάνυσμα διάφορο του μηδενικού τότε περιέχει άπειρα διανύσματα
4 Βασικοί Διανυσματικοί Χώροι Το σύνολο των γεωμετρικών διανυσμάτων είναι -διανυσματικός χώρος. (Στη γραμμική άλγεβρα θεωρούμε διανύσματα θέσης: Όλα τα βέλη έχουν αρχή την αρχή των αξόνων) Το σύνολο χώρος. όλων των διατεταγμένων -άδων είναι -διανυσματικός Τα σύνολα Q,, C αποτελούν διανυσματικούς χώρους επί του εαυτού τους. Το σύνολο C είναι επίσης Q και -διανυσματικός χώρος. Το σύνολο των πολυωνύμων P [ x ] με πραγματικούς συντελεστές, βαθμού είναι -διανυσματικός χώρος. Το σύνολο των πραγματικών συναρτήσεων είναι -διανυσματικός χώρος. f : A με A A, Το σύνολο όλων των πινάκων M ( ) m F είναι F-διανυσματικός χώρος.
5 Συμβολισμός διανυσμάτων του v Ένα διάνυσμα ισοδύναμους τρόπους: 1. Ως διατεταγμένη -άδα αριθμών: 2. Ως πίνακας στήλη: μπορεί να γραφεί με τους ακόλουθους v= v1, v2,, v ( ) v v v v 1 2 = Στον απειροστικό λογισμό αντίστοιχα χρησιμοποιούσαμε το συμβολισμό: v = v1, v2,, v Πολλές φορές, για εξοικονόμηση χώρου, το τελευταίο βολεύει να το γράφουμε ως ανάστροφο πίνακα γραμμή: [ ] v= v1 v2 v Εναλλακτικοί τρόποι γραφής του συμβόλου του διανύσματος: v, v, v, v
6 Διανυσματικοί Υποχώροι Ορισμός Έστω ένας F-διανυσματικός χώροςv, τότε ένα μη κενό υποσύνολο του V καλείται F-διανυσματικός υποχώρος του V, αν αυτό είναι F διανυσματικός χώρος ως προς τις πράξεις της πρόσθεσης και του πολλαπλασιασμού του V. Ένα μη κενό υποσύνολο W ενός F διανυσματικού χώρουv, τότε V θα είναι F διανυσματικός υποχώρος του V, αν και μόνο αν αυτό είναι κλειστό ως προς τις πράξεις της πρόσθεσης και του πολλαπλασιασμού, δηλ αν-ν ισχύουν οι εξής 2 ιδιότητες: u+ v W, u, v W kw W, k F, w W ή ισοδύναμα αν-ν ισχύει ότι ku+ lv W, k, l F, u, v W Ένας διανυσματικός υποχώρος του V περιέχει πάντοτε το μηδενικό στοιχείο του V (είναι μη κενός) Ο ίδιος ο V και το μονοσύνολο { O} είναι F-διανυσματικοί υποχώροι του V. Ονομάζονται τετριμμένοι. Κάθε άλλος υποχώρος του V ονομάζεται γνήσιος.
7 Παραδείγματα Διανυσματικών Υποχώρων Το σύνολο όλων των διαγώνιων πινάκων υποχώρο του. M ( ) F D ( ) F αποτελεί F-διανυσματικό K ( ) F Τo σύνολο όλων των κάτω τριγωνικών πινάκων αποτελεί F-διανυσματικό υποχώρο του M ( F ). Το ίδιο ισχύει και για το σύνολο των άνω τριγωνικών πινάκων. A ( ) F Τo σύνολο όλων των συμμετρικών πινάκων υποχώρο του. M ( ) F S ( ) F αποτελεί F-διανυσματικό Οι -υποχώροι του είναι μόνον α) ο και b) το {0} Οι -υποχώροι του 2 είναι μόνον α) ο, b) το {(0,0)} και c) κάθε ευθεία που διέρχεται από την αρχή των αξόνων. 3 Οι -υποχώροι του είναι μόνον α) ο, b) το {(0,0,0)}, c) κάθε ευθεία που διέρχεται από την αρχή των αξόνων και d) κάθε επίπεδο που διέρχεται από την αρχή των αξόνων. Παρατήρηση: k l Το σύνολο δεν αποτελεί διανυσματικό υποχώρο του, 2 3 µε k < l
8 Χώρος παραγόμενος από διανύσματα Το σύνολο όλων των γραμμικών συνδυασμών s διανυσμάτων ενός διανυσματικού χώρου V αποτελεί διανυσματικό υποχώρο του V. { :,,,..., } W = w w= kv + kv + + kv k k k F s s 1 2 s Ο χώρος αυτός καλείται: χώρος παραγόμενος από τα διανύσματα και είναι ο μικρότερος υποχώρος του V που περιέχει τα v 1, v 2,..., vs Τα διανύσματα v v v καλούνται γεννήτορες του χώρου V.,,..., s 1 2 Συμβολισμός: spa{ v, v,..., v } ή S( { v, v,..., v }) 1 2 s 1 2 Ένας χώρος μπορεί να παράγεται από περισσότερα του ενός σύνολα (διάφορα μεταξύ τους) διανυσμάτων ν V spa{ v, v,..., v } και vs+ 1 v1, v2,..., vs Α = 1 2 s = V spa{ v, v,..., v, v } s 1 2 s s+ 1 v1, v2,..., vs Αν στους γεννήτορες ενός χώρου υπάρχει το μηδενικό διάνυσμα, τότε αυτό μπορούμε να το διαγράψουμε από τους γεννήτορες καθώς ισχύει ότι: spa( S) = spa( S { O}) Το ίδιο μπορεί να γίνει και για οποιοδήποτε διάνυσμα v μπορεί να γραφεί ως γραμμικός συνδυασμός των υπολοίπων spa( S) = spa( S { v})
9 4 Θεμελιώδεις Υποχώροι 1. Μηδενοχώρος (ή πυρήνας) ενός πίνακα Το σύνολο λύσεων του ομογενούς συστήματος Am x 1 = Om 1 { } N( A) = x F : Ax = O ονομάζεται μηδενοχώρος του A και είναι F-διανυσματικός υποχώρος του F 2. Χώρος Στηλών (ή πεδίο) ενός πίνακα Το σύνολο m { m 1 m 1 για κ ποιο } A ( ) = b F : A x = b, ά x F ονομάζεται είναι χώρος στηλών του Α και είναι F-διανυσματικός m υποχώρος του F Αν A= [ C1 C2 C ] όπου C j ή j στήλη του Α τότε ( A) = spa{ C1, C2,..., C} δηλ. είναι το σύνολο όλων των Γραμμικών Συνδυασμών των στηλών του Α Το σύστημα Ax = b έχει λύση αν-ν b A ( )
10 4 Θεμελιώδεις Υποχώροι 3. Αριστερός Μηδενοχώρος ενός πίνακα Το σύνολο λύσεων του ομογενούς συστήματος A mxm 1 = O 1 { 1} { 1} N( A ) = x F : A x= O = x F : x A= O m m ονομάζεται αριστερός μηδενοχώρος του A και είναι F-διανυσματικός m υποχώρος του F. (Ισούται με τον μηδενοχώρο του αναστρόφου του Α) 4. Χώρος Γραμμών ενός πίνακα Το σύνολο { m m 1 1 για κ ποιο } A ( ) = b F : A x = b, ά x F m ονομάζεται είναι χώρος γραμμών του Α και είναι F-διανυσματικός υποχώρος του F. (Ισούται με τον χώρο στηλών του αναστρόφου του Α) Αν A= [ 1 2 m ] όπου ή i γραμμή του Α τότε i ( A ) = spa{ 1, 2,..., } δηλ. είναι το σύνολο όλων των Γραμμικών Συνδυασμών των γραμμών του Α
11 Πίνακες με ίδιο Χώρο Γραμμών Δύο πίνακες Α και Β έχουν τον ίδιο Χώρο Γραμμών αν οι ανηγμένες κλιμακωτές μορφές τους έχουν ακριβώς τις ίδιες μη μηδενικές γραμμές. Πίνακες με ίδιο Χώρο Στηλών Δύο πίνακες Α και Β έχουν τον ίδιο Χώρο Στηλών αν οι ανηγμένες κλιμακωτές μορφές των αναστρόφων τους έχουν ακριβώς τις ίδιες μη μηδενικές γραμμές. Χώρος Γραμμών/Στηλών γινομένου πινάκων Αν το γινόμενο AB ορίζεται τότε ισχύουν τα ακόλουθα: ( AB) ( B) (χώρος στηλών του ΑΒ) ( ) ( AB) ( A) (χώρος γραμμών του ΑΒ)
12 Γραμμική Ανεξαρτησία Έστω ένας διανυσματικός χώρος V α διανύσματα v1, v2,..., vs V καλούνται Γραμμικά Ανεξάρτητα αν από κάθε γραμμικό συνδυασμό cv 1 1+ cv cv s s= O προκύπτει ότι: c1 = c2 = = c s = 0 Στην περίπτωση που για κάποιο, c καλούνται Γραμμικά Eξαρτημένα i 0 i Ένα πεπερασμένο σύνολο K V, K χαρακτηρίζεται Γραμμικά Ανεξάρτητο (αντίστοιχα Εξαρτημένο) αν τα στοιχεία του Κ είναι Γραμμικά Ανεξάρτητα (αντίστοιχα Εξαρτημένα). Το κενό σύνολο θεωρείται Γραμμικά Ανεξάρτητο
13 Γραμμική Ανεξαρτησία Το μηδενικό διάνυσμα ενός χώρου V είναι γραμμικά εξαρτημένο Κάθε μη μηδενικό διάνυσμα ενός χώρου V είναι γραμμικά ανεξάρτητο Δύο μη συγγραμμικά διανύσματα του Τρία μη συνεπίπεδα διανύσματα του, 2 Δύο διανύσματα του είναι γραμμικά εξαρτημένα αν-ν το ένα είναι πολλαπλάσιο του άλλου, δηλ. αν είναι συγγραμμικά., 2, 3 είναι γραμμικά ανεξάρτητα είναι γραμμικά ανεξάρτητα Τρία συνεπίπεδα διανύσματα του, 2 είναι γραμμικά εξαρτημένα k k > Ένα σύνολο διανυσμάτων του με είναι γραμμικά εξαρτημένο Ένα σύνολο διανυσμάτων είναι γραμμικά εξαρτημένο αν-ν κάποιο διάνυσμα του συνόλου μπορεί να γραφεί ως γραμμικός συνδυασμός των υπολοίπων Κάθε υποσύνολο γραμμικά ανεξαρτήτων διανυσμάτων είναι επίσης γραμμικά ανεξάρτητο σύνολο διανυσμάτων Κάθε υπερσύνολο γραμμικά εξαρτημένων διανυσμάτων είναι επίσης γραμμικά εξαρτημένο σύνολο διανυσμάτων. Κάθε σύνολο που περιέχει το μηδενικό διάνυσμα είναι γραμμικά εξαρτημένο.
14 Βρονσκιανή (Wroskia) f = f ( x),f = f ( x),...,f = f ( x) είναι συναρτήσεις διαφορίσιμες Αν φορές συνεχώς στο τότε η Βρονσκιανή τους είναι η ακόλουθη ορίζουσα: W( x) = f ( x) f ( x) f ( x) 1 2 f '( x) f '( x) f '( x) 1 2 f ( x) f ( x) f ( x) ( 1) ( 1) ( 1) 1 2 Αν η W( x) δεν είναι εκ ταυτότητος μηδέν τότε οι 1 2 ( είναι γραμμικά ανεξάρτητες στο C 1) (, + ) f,f,...,f W( x) = 0, x Προσοχή: Αν τότε αυτό δεν σημαίνει αναγκαστικά ότι οι είναι γραμμικά εξαρτημένες. (Απαιτούνται και άλλες συνθήκες) f 1,f 2,...,f
15 Άθροισμα και Ευθύ Άθροισμα Υποχώρων Άθροισμα Αν U,W διανυσματικοί υποχώροι του V τότε το άθροισμα των χώρων U και W ορίζεται ως U + W = { v: v= x+ y, για κάποια x U και y W} o άθροισμα των υποχώρων U,W είναι υποχώρος του V και μάλιστα ο μικρότερος υποχώρος του V που περιέχει και τους δύο υποχώρους. U W U Προσοχή: H ένωση των U,W δεν αποτελεί εν γένει υποχώρο του V, ενώ αντίθετα η τομή τους αποτελεί πάντοτε υποχώρο του V. W Ευθύ άθροισμα V = U W O V γράφεται ως ευθύ άθροισμα των υποχώρων του U και W: αν κάθε στοιχείο του V γράφεται με μοναδικό τρόπο ως άθροισμα ενός στοιχείου του U και ενός στοιχείου του W ή ισοδύναμα αν ισχύουν τα ακόλουθα: V = U + W U W = { 0}
16 Βάση ενός διανυσματικού χώρου Τα διανύσματα v1, v2,..., vs V αποτελούν βάση του V αν-ν 1) Είναι γραμμικά ανεξάρτητα 2) Παράγουν τον χώρο: V = spa{ v1, v2,..., v s } Μία βάση αποτελεί ταυτόχρονα το μέγιστο ανεξάρτητο σύνολο του V και το ελάχιστο παράγον σύνολο του V Ένας χώρος μπορεί να έχει πολλές βάσεις. 3 2 π.χ. Οι χώροι και έχουν άπειρες βάσεις Κάθε διάνυσμα του V γράφεται κατά μοναδικό τρόπο ως γραμμικός συνδυασμός των διανυσμάτων της βάσης (οι σταθερές που πολλαπλασιάζουν κάθε διάνυσμα της βάσης ονομάζονται συντεταγμένες ως προς τη συγκεκριμένη βάση. Προσοχή: Έχει σημασία η σειρά γραφής!) Διάσταση ενός διανυσματικού χώρου Όλες οι βάσεις ενός χώρου διαθέτουν το ίδιο πλήθος στοιχείων. Ο αριθμός αυτός καλείται διάσταση του χώρου. Συμβολισμός: dimv Ο μηδενικός υποχώρος {0} δεν έχει βάση. Δεχόμαστε όμως ότι dim{0}=0 Στα πλαίσια του μαθήματος θα ασχοληθούμε μόνο με χώρους πεπερασμένης διάστασης. dim =, dim Mm ( F) = m, dim P ( ) = + 1 Ένας χώρος πεπερασμένης διάστασης έχει μία τουλάχιστον βάση
17 Βάση-Διάσταση Απαιτούνται τόσα διανύσματα όσα έχει η βάση για να παραχθεί ο χώρος. Όλα τα υπόλοιπα είναι γραμμικός συνδυασμός αυτών. Αν τα 1 2 είναι γραμμικά ανεξάρτητα και = {,,..., } τότε θα είναι s V spa w1 w2 w s Αν dimv είναι. Τα εξαρτημένα. dimv v, v,..., v V = k, k = τότε το μέγιστο πλήθος γραμμικά ανεξαρτήτων διανυσμάτων > διανύσματα του χώρου V είναι πάντοτε γραμμικά v, v,..., v V Αν τότε για να αποτελούν 1 2 βάση του V αρκεί να ισχύει ένα από τα ακόλουθα: α) είναι γραμμικά ανεξάρτητα β) παράγουν τον V Το πλήθος των ελεύθερων μεταβλητών ενός ομογενούς συστήματος ισούται με dim N( A) ενώ το πλήθος των μεταβλητών με οδηγό ισούται με dim A ( ) UW, Αν δύο υποχώροι πεπερασμένης διάστασης του V τότε ισχύουν: dim U + W = dimu + dimw dim V W ( ) ( ) ( U W) = U + W dim dim dim UW, Αν δύο υποχώροι πεπερασμένης διάστασης του V με τότε ισχύουν: dimu dimw Α ν dimu = dimw U = W U W
18 Βάση-Διάσταση S = { v, v,..., v m } V = spa( S) Αν 1 2 και τότε υπάρχει ένα υποσύνολο του S, το οποίο αποτελεί βάση του V. Επομένως κάθε σύνολο που παράγει τον V ανάγεται σε μια βάση, αγνοώντας εν ανάγκη ορισμένα διανύσματα Κάθε γραμμικά ανεξάρτητο σύνολο του V μπορεί να επεκταθεί σε μία βάση, επισυνάπτοντας εν ανάγκη περισσότερα διανύσματα Κανονικές Βάσεις συνήθων διανυσματικών χώρων: Το σύνολο των διανυσμάτων e = (0,0,...,0,1,0,...,0), i = 1,..., όπου στη θέση i έχουν μονάδα και παντού αλλού μηδέν M ( ) i 2 Το σύνολο των x πινάκων eij όπου στη θέση i,j έχουν μονάδα και παντού αλλού μηδέν j P [ ] x Το σύνολο των +1 e ij μονωνύμων: 0 0 = i 2 {1, xx,,..., x }
19 Βαθμίδα (ή βαθμός ή τάξη) πίνακα Βαθμίδα ενός πίνακα A ονομάζεται η διάσταση του χώρου στηλών του Α raka= dim A ( ) Εκφράζει το μέγιστο πλήθος ανεξάρτητων στηλών/γραμμών του Α. Ισούται με το πλήθος των οδηγών στοιχείων κατά την απαλοιφή Gauss. Ισούται και με την τάξη της μεγαλύτερης μη μηδενικής ελάσσονας ορίζουσας του Α. Ισχύει: rak( A) = rak( A ) δηλ. το μέγιστο πλήθος των ανεξάρτητων στηλών ενός πίνακα ισούται με το μέγιστο πλήθος των ανεξάρτητων γραμμών του Ισχύει: 0 rak( A ) mi( m, ) m rak( A ) = 0 A = O m m m rak( A ) = det( A) 0, δηλ ο Α είναι αντιστρέψιμος Ισχύει: dim N( A ) + rak( A ) = Πλήθος ελεύθερων μεταβλητών στο Ax=0 m m Πλήθος μεταβλητών με οδηγό στο Ax=0 Επίσης: dim N( A ) + rak( A ) = m m m Πλήθος στηλών Πλήθος γραμμών
20 Θεμελιώδεις Υποχώροι (Σύνοψη) Για τους 4 θεμελιώδεις υποχώρους ισχύουν τα ακόλουθα: m A ( ), A ( ) N( A), N( A ) dim A ( ) = dim A ( ) = rak( A) dim N( A) = rak( A) m Η διάσταση του μηδενοχώρου καλείται μηδενικότητα (ullity) dim N( A ) = m rak( A) = A ( ) NA ( ) m = A ( ) NA ( ) Το εσωτερικό τους γινόμενο είναι ίσο με μηδέν: vu= 0 Κάθε διάνυσμα του Κάθε διάνυσμα του A ( ) είναι ορθογώνιο με κάθε διάνυσμα του N( A ) A ( ) είναι ορθογώνιο με κάθε διάνυσμα του N( A)
21 Απαλοιφή Gauss, Γραμμική Ανεξαρτησία και Χώροι Γραμμών / Στηλών πίνακα Αν στον πίνακα Α εφαρμόσουμε απαλοιφή Gauss και πάρουμε τον κλιμακωτό U, τότε οι μη μηδενικές γραμμές του U είναι γραμμικά ανεξάρτητες, ενώ γραμμικά ανεξάρτητες είναι επίσης και οι στήλες με οδηγό. Το πλήθος των γραμμικά ανεξάρτητων γραμμών και στηλών είναι το ίδιο και ίσο με τη βαθμίδα του πίνακα Α (ή του U). A ( ) Χώρος Γραμμών Οι στοιχειώδεις πράξεις κατά την μετατροπή του Α σε κλιμακωτή μορφή U δεν επηρεάζουν τον παραγόμενο χώρο γραμμών. Δηλ. ( A ) = U ( ) A ( ) Χώρος Στηλών Οι στοιχειώδεις πράξεις κατά την μετατροπή του Α σε κλιμακωτή μορφή U επηρεάζουν τον παραγόμενο χώρο στηλών, δηλ. ( A) U ( ) αλλά αφήνουν ανεπηρέαστες τις θέσεις των γραμμικά ανεξάρτητων στηλών.
22 Βάσεις των θεμελιωδών υποχώρων Ο πίνακας Α μετατρέπεται σε κλιμακωτή μορφή U με απαλοιφή Gauss. Τότε: A ( ) Χώρος Γραμμών Oι γραμμικά ανεξάρτητες (μη μηδενικές) γραμμές του U αποτελούν βάση του U ( ) και συνεπώς και του A ( ) A ( ) Mία βάση του A ( ) αποτελείται από τα διανύσματα στήλες του Α που αντιστοιχούν στις στήλες των οδηγών στοιχείων του U N( A) Μηδενοχώρος Υπολογίζουμε το πλήθος των ελεύθερων μεταβλητών (στήλες χωρίς οδηγό). Αν το πλήθος είναι μηδέν τότε ο N(A) έχει ως βάση το κενό σύνολο. Διαφορετικά μία βάση του Ν(Α) αποτελείται από τα διανύσματα που παίρνουμε επιλύοντας το σύστημα Αx=0 θέτοντας με τη σειρά κάθε ελεύθερη μεταβλητή ίση με τη μονάδα, μηδενίζοντας τις υπόλοιπες ελεύθερες μεταβλητές. N( A ) Χώρος Στηλών Αριστερός Μηδενοχώρος Εργαζόμαστε όπως και στον Ν(Α), αλλά με τον A. Εναλλακτικά αν EA = U τότε οι τελευταίες m rak( A) γραμμές του E αποτελούν βάση του υποχώρου Ο πίνακας E αποτελείται από το γινόμενο όλων των στοιχειωδών πινάκων που περιγράφουν τα βήματα της απαλοιφής Gauss. Μπορεί να υπολογιστεί απ ευθείας και ως ( Am Im) Gauss ( U E)
23 Επίλυση συστήματος Για το ομογενές σύστημα rak( A) rak( A) = Am x= O Έχει μοναδική λύση (τη μηδενική) Έχει άπειρες λύσεις ισχύουν τα επόμενα: Για το σύστημα b A ( ) b A ( ) N( A) N( A) { O} { O} = Am x= b ισχύουν τα επόμενα: o σύστημα έχει λύση (μία ή άπειρες) o σύστημα είναι αδύνατο o σύστημα είναι αδύνατο ή έχει μοναδική λύση o σύστημα είναι αδύνατο ή έχει άπειρες λύσεις
24 Βαθμίδα πίνακα και Επίλυση συστήματος Am x= b rak( A) = m = Μία λύση rak( A) = < m rak( A) = m < Καμία ή μία λύσεις Άπειρες λύσεις rak( A) < m, rak( A) < Καμία ή άπειρες λύσεις Θεώρημα ouché Capelli rak( A) = rak( A b) = rak( A) = rak( A b) < rak( A) < rak( A b) o σύστημα έχει μοναδική λύση o σύστημα άπειρες λύσεις o σύστημα είναι αδύνατο
25 Μοναδική λύση συστήματος Όλες οι επόμενες προτάσεις είναι ισοδύναμες: Το σύστημα Υπάρχει ο αντίστροφος Το ομογενές σύστημα Το σύστημα det( A) 0 N( A) = { O} dim N( A ) = 0 Ax = b A ( ) = A ( ) = F rak( A) = Ax = b έχει μοναδική λύση A 1 Ax = O έχει λύση A x= b έχει μοναδική λύση (τη μηδενική). b F Τετράγωνος πίνακας Η ανηγμένη κλιμακωτή μορφή του Α είναι ο ταυτοτικός πίνακας Οι γραμμές του Α είναι γραμμικά ανεξάρτητες παράγουν τον χώρο και αποτελούν βάση του. Το ίδιο ισχύει και για τις στήλες του Α. F I
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
ΜΑΣ121: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο , Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: 2 ώρες 18 Νοεμβρίου, 2017
 ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
Παραδείγματα (2 ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος
 Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Έστω ο υποχώρος W του R 5 που παράγεται από τα διανύσματα v=(,,-,,), v=(,,-,6,8), v=(,,,,6), v=(,,5,,8), v5=(,7,,,9). a)
Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Έστω ο υποχώρος W του R 5 που παράγεται από τα διανύσματα v=(,,-,,), v=(,,-,6,8), v=(,,,,6), v=(,,5,,8), v5=(,7,,,9). a)
Παραδείγματα Διανυσματικοί Χώροι (3)
 Παραδείγματα Διανυσματικοί Χώροι () Παράδειγμα Δίνεται ο πίνακας A = 6. Να υπολογισθούν οι θεμελιώδεις υποχώροι που σχετίζονται με τον πίνακα Α. Να βρεθεί η διάστασή του κάθε ενός και από μία βάση τους.
Παραδείγματα Διανυσματικοί Χώροι () Παράδειγμα Δίνεται ο πίνακας A = 6. Να υπολογισθούν οι θεμελιώδεις υποχώροι που σχετίζονται με τον πίνακα Α. Να βρεθεί η διάστασή του κάθε ενός και από μία βάση τους.
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος
 6/6/06 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 0 Δίνεται ο πίνακας A =. Nα υπολογίσετε την βαθμίδα του και να βρείτε τη διάσταση και από μία βάση α) του μηδενοχώρου
6/6/06 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 0 Δίνεται ο πίνακας A =. Nα υπολογίσετε την βαθμίδα του και να βρείτε τη διάσταση και από μία βάση α) του μηδενοχώρου
Κεφάλαιο 4 ιανυσµατικοί Χώροι
 Κεφάλαιο 4 ιανυσµατικοί Χώροι 4 ιανυσµατικοί χώροι - Βασικοί ορισµοί και ιδιότητες ιανυσµατικοί Χώροι Ένας ιανυσµατικός Χώρος V (δχ) είναι ένα σύνολο από µαθηµατικά αντικείµενα (αριθµούς, διανύσµατα, πίνακες,
Κεφάλαιο 4 ιανυσµατικοί Χώροι 4 ιανυσµατικοί χώροι - Βασικοί ορισµοί και ιδιότητες ιανυσµατικοί Χώροι Ένας ιανυσµατικός Χώρος V (δχ) είναι ένα σύνολο από µαθηµατικά αντικείµενα (αριθµούς, διανύσµατα, πίνακες,
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος
 Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Πίνακες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Πίνακες Μητρώα Πίνακας: Ορθογώνια διάταξη αριθμών σε γραμμές και στήλες
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Πίνακες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Πίνακες Μητρώα Πίνακας: Ορθογώνια διάταξη αριθμών σε γραμμές και στήλες
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Πίνακες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Πίνακες Μητρώα Πίνακας: Ορθογώνια διάταξη αριθμών σε γραμμές και στήλες
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Πίνακες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Πίνακες Μητρώα Πίνακας: Ορθογώνια διάταξη αριθμών σε γραμμές και στήλες
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 19/6/2018 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα
 Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Διανυσματικοί Χώροι και Υπόχωροι: Βάσεις και Διάσταση Ανδριανός Ε Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Διανυσματικοί Χώροι και Υπόχωροι: Βάσεις και Διάσταση Ανδριανός Ε Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Παραδείγματα (2) Διανυσματικοί Χώροι
 Παραδείγματα () Διανυσματικοί Χώροι Παράδειγμα 7 Ελέγξτε αν τα ακόλουθα σύνολα διανυσμάτων είναι γραμμικά ανεξάρτητα ή όχι: α) v=(,4,6), v=(,,), v=(7,,) b) v=(,4), v=(,), v=(4,) ) v=(,,), v=(5,,), v=(5,,)
Παραδείγματα () Διανυσματικοί Χώροι Παράδειγμα 7 Ελέγξτε αν τα ακόλουθα σύνολα διανυσμάτων είναι γραμμικά ανεξάρτητα ή όχι: α) v=(,4,6), v=(,,), v=(7,,) b) v=(,4), v=(,), v=(4,) ) v=(,,), v=(5,,), v=(5,,)
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικά Συστήματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικό Σύστημα a11x1 + a12x2 + + a1 nxn = b1 a x + a x + +
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικά Συστήματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικό Σύστημα a11x1 + a12x2 + + a1 nxn = b1 a x + a x + +
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 2004 Θέμα 1 ο. 4
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 00 Θέμα 1 ο Έστω U ο υπόχωρος του που παράγεται από τα στοιχεία (1-11α) (10β) (5-γ) και (-δ) (I) Να προσδιορίσετε τις αναγκαίες
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 00 Θέμα 1 ο Έστω U ο υπόχωρος του που παράγεται από τα στοιχεία (1-11α) (10β) (5-γ) και (-δ) (I) Να προσδιορίσετε τις αναγκαίες
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών «Γραµµική Άλγεβρα Ι» (ΕΜ111) Χειµερινό Εξάµηνο 2006-2007, ιδάσκων: Ι. Τσαγράκης 5 Ο ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Έστω V ένας διανυσµατικός χώρος επί
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών «Γραµµική Άλγεβρα Ι» (ΕΜ111) Χειµερινό Εξάµηνο 2006-2007, ιδάσκων: Ι. Τσαγράκης 5 Ο ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Έστω V ένας διανυσµατικός χώρος επί
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
2.0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ
 .0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Έστω διανύσματα που ανήκουν στο χώρο δ i = ( a i, ai,, ai) i =,,, και έστω γραμμικός συνδυασμός των i : xδ + x δ + + x δ = b που ισούται με το διάνυσμα b,
.0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Έστω διανύσματα που ανήκουν στο χώρο δ i = ( a i, ai,, ai) i =,,, και έστω γραμμικός συνδυασμός των i : xδ + x δ + + x δ = b που ισούται με το διάνυσμα b,
1. Για καθένα από τους ακόλουθους διανυσματικούς χώρους βρείτε μια βάση και τη διάσταση. 3. U x y z x y z x y. {(,, ) } a b. c d
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί
 Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ηµεροµηνία Αποστολής στον Φοιτητή: 12 Οκτωβρίου 2007
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 1) ΕΡΓΑΣΙΑ 1 η Ηµεροµηνία Αποστολής στον Φοιτητή: 1 Οκτωβρίου 007 Ηµεροµηνία παράδοσης της Εργασίας: 9 Νοεµβρίου 007. Πριν από την λύση κάθε άσκησης
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 1) ΕΡΓΑΣΙΑ 1 η Ηµεροµηνία Αποστολής στον Φοιτητή: 1 Οκτωβρίου 007 Ηµεροµηνία παράδοσης της Εργασίας: 9 Νοεµβρίου 007. Πριν από την λύση κάθε άσκησης
Παραδείγματα (1 ο σετ) Διανυσματικοί Χώροι
 Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού:
Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού:
a 11 a 1n b 1 a m1 a mn b n
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 13 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 28/4/2014 ΧΚουρουνιώτης (ΠανΚρήτης) Διάλεξη 13 28/4/2014 1 / 14 Πίνακες πάνω από σώμα K Πίνακες πάνω από σώμα K Το σύνολο των m n
Γραμμική Άλγεβρα ΙΙ Διάλεξη 13 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 28/4/2014 ΧΚουρουνιώτης (ΠανΚρήτης) Διάλεξη 13 28/4/2014 1 / 14 Πίνακες πάνω από σώμα K Πίνακες πάνω από σώμα K Το σύνολο των m n
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
= 7. Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις
 1. Εισαγωγή Δίνεται η συνάρτηση μεταφοράς = = 1 + 6 + 11 + 6 = + 6 + 11 + 6 =. 2 Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις L = 0 # και L $ % &'
1. Εισαγωγή Δίνεται η συνάρτηση μεταφοράς = = 1 + 6 + 11 + 6 = + 6 + 11 + 6 =. 2 Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις L = 0 # και L $ % &'
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
n = dim N (A) + dim R(A). dim V = dim ker L + dim im L.
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 9 Γραμμικοί Ισομορφισμοί Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 9 19/3/2014 1 / 12 Γραμμικές απεικονίσεις και υπόχωροι Εικόνα
Γραμμική Άλγεβρα ΙΙ Διάλεξη 9 Γραμμικοί Ισομορφισμοί Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 9 19/3/2014 1 / 12 Γραμμικές απεικονίσεις και υπόχωροι Εικόνα
Γραμμική Άλγεβρα Ι,
 Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Κεφάλαιο 7 Βάσεις και ιάσταση
 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].
![D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ]. D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].](/thumbs/60/44272313.jpg) 4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
Γραµµικη Αλγεβρα Ι. Ακαδηµαϊκο Ετος Βοηθος Ασκησεων: Χ. Ψαρουδάκης
 Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Γραμμική Αλγεβρα ΙΙ Διάλεξη 7 Βάσεις Διάσταση Χρήστος Κουρουνιώτης Πανεπισ τήμιο Κρήτης 7/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 7 7/3/ / 1
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 7 Διάσταση Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 7/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 7 7/3/2014 1 / 1 Εάν ένα υποσύνολο S του διανυσματικού χώρου V παράγει το V,
Γραμμική Άλγεβρα ΙΙ Διάλεξη 7 Διάσταση Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 7/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 7 7/3/2014 1 / 1 Εάν ένα υποσύνολο S του διανυσματικού χώρου V παράγει το V,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών «Γραμμική Άλγεβρα» (ΗΥ119) Χειμερινό Εξάμηνο 009-010 Διδάσκων: Ι. Τσαγράκης 6 Ο ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Δείξτε ότι η απεικόνιση τον ker f. Είναι η
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών «Γραμμική Άλγεβρα» (ΗΥ119) Χειμερινό Εξάμηνο 009-010 Διδάσκων: Ι. Τσαγράκης 6 Ο ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Δείξτε ότι η απεικόνιση τον ker f. Είναι η
n. Έστω αποτελείται από όλους τους πίνακες που αντιμετατίθενται με ένα συγκεκριμένο μη μηδενικό nxn πίνακα Τ:
 Η ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ καθώς είναι από τα σημαντικότερα κομμάτια της Άλγεβρας με τις περισσότερες εφαρμογές ΔΕΝ πρέπει να αποστηθίζεται και κυρίως ΔΕΝ πρέπει να γίνεται αντιπαθητική. Για τη σωστή εκμάθηση
Η ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ καθώς είναι από τα σημαντικότερα κομμάτια της Άλγεβρας με τις περισσότερες εφαρμογές ΔΕΝ πρέπει να αποστηθίζεται και κυρίως ΔΕΝ πρέπει να γίνεται αντιπαθητική. Για τη σωστή εκμάθηση
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος
 9/6/5 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 5 Δίνεται ο πίνακας A 5. Αν διαγωνοποιείται να τον διαγωνοποιήσετε και στη συνέχεια να k υπολογίσετε το A όπου k θετικός
9/6/5 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 5 Δίνεται ο πίνακας A 5. Αν διαγωνοποιείται να τον διαγωνοποιήσετε και στη συνέχεια να k υπολογίσετε το A όπου k θετικός
Ασκήσεις2 8. ; Αληθεύει ότι το (1, 0, 1, 2) είναι ιδιοδιάνυσμα της f ; b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα της γραμμικής απεικόνισης 3 3
 Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Εφαρμοσμένα Μαθηματικά ΙΙ 10ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί Επιμέλεια: Ι. Λυχναρόπουλος. Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f b) f : R R f y, ( +, y
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί Επιμέλεια: Ι. Λυχναρόπουλος. Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f b) f : R R f y, ( +, y
Διανύσµατα στο επίπεδο
 Διανύσµατα στο επίπεδο Ένα διάνυσµα v έχει αρχικό και τελικό σηµείο. Χαρακτηρίζεται από: διεύθυνση (ευθεία επί της οποίας κείται φορά (προς ποια κατεύθυνση της ευθείας δείχνει µέτρο (το µήκος του, v ή
Διανύσµατα στο επίπεδο Ένα διάνυσµα v έχει αρχικό και τελικό σηµείο. Χαρακτηρίζεται από: διεύθυνση (ευθεία επί της οποίας κείται φορά (προς ποια κατεύθυνση της ευθείας δείχνει µέτρο (το µήκος του, v ή
1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]
![1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x] 1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]](/thumbs/77/75945202.jpg) σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ
 ΤΜΗΜΑ ΔΙΕΘΝΟΥΣ ΕΜΠΟΡΙΟΥ ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΑ: ) ΠΙΝΑΚΕΣ ) ΟΡΙΖΟΥΣΕΣ ) ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4) ΠΑΡΑΓΩΓΟΙ ΜΑΡΙΑ ΡΟΥΣΟΥΛΗ ΚΕΦΑΛΑΙΟ ΠΙΝΑΚEΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΟΡΙΣΜΟΣ Πίνακας
ΤΜΗΜΑ ΔΙΕΘΝΟΥΣ ΕΜΠΟΡΙΟΥ ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΑ: ) ΠΙΝΑΚΕΣ ) ΟΡΙΖΟΥΣΕΣ ) ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4) ΠΑΡΑΓΩΓΟΙ ΜΑΡΙΑ ΡΟΥΣΟΥΛΗ ΚΕΦΑΛΑΙΟ ΠΙΝΑΚEΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΟΡΙΣΜΟΣ Πίνακας
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 25/9/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 5/9/07 Διδάσκων: Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Να δειχθεί ότι το πεδίο F( x, y) = y cos x + y,sin x
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Εξέταση Σεπτεμβρίου 5/9/07 Διδάσκων: Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) Να δειχθεί ότι το πεδίο F( x, y) = y cos x + y,sin x
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Σεπτεμβρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Σεπτεμβρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, Αυγούστου 00 Θέμα. (μονάδες.5) α) [μονάδες: 0.5] Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Σεπτεμβρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, Αυγούστου 00 Θέμα. (μονάδες.5) α) [μονάδες: 0.5] Υπολογίστε
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4
 Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ. Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες,
 ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες, παριστάνεται με την εξής ορθογώνια διάταξη: α11 α12 α1n α21 α22 α2n A = αm1 αm2 αmn Ορισμός 2: Δύο πίνακες Α και Β είναι ίσοι, και γράφουμε
ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες, παριστάνεται με την εξής ορθογώνια διάταξη: α11 α12 α1n α21 α22 α2n A = αm1 αm2 αmn Ορισμός 2: Δύο πίνακες Α και Β είναι ίσοι, και γράφουμε
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 2 η Ημερομηνία Αποστολής στον Φοιτητή: 28 Νοεμβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΚΕΦΑΛΑΙΟ 1: Πρότυπα. x y x z για κάθε x, y, R με την ιδιότητα 1R. x για κάθε x R, iii) υπάρχει στοιχείο 1 R. ii) ( x y) z x ( y z)
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΠΑΝΑΛΗΠΤΙΚΗ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ 5 Ιουλίου 2009
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΠΑΝΑΛΗΠΤΙΚΗ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ 5 Ιουλίου 009 Θέμα (0 μονάδες) Έστω U = (, y, z, w) = z, y = w υποσύνολο του και V ο υπόχωρος
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΠΑΝΑΛΗΠΤΙΚΗ ΤΕΛΙΚΗ ΕΞΕΤΑΣΗ 5 Ιουλίου 009 Θέμα (0 μονάδες) Έστω U = (, y, z, w) = z, y = w υποσύνολο του και V ο υπόχωρος
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - 02/07/08) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
 Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ. ρ Χρήστου Νικολαϊδη
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ ρ Χρήστου Νικολαϊδη Δεκέμβριος Περιεχόμενα Κεφάλαιο : σελ. Τι είναι ένας πίνακας. Απλές πράξεις πινάκων. Πολλαπλασιασμός πινάκων.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ ρ Χρήστου Νικολαϊδη Δεκέμβριος Περιεχόμενα Κεφάλαιο : σελ. Τι είναι ένας πίνακας. Απλές πράξεις πινάκων. Πολλαπλασιασμός πινάκων.
Συστήματα συντεταγμένων
 Συστήματα συντεταγμένων Χρησιμοποιούνται για την περιγραφή της θέσης ενός σημείου στον χώρο. Κοινά συστήματα συντεταγμένων: Καρτεσιανό (x, y, z) Πολικό (r, θ) Καρτεσιανό σύστημα συντεταγμένων Οι άξονες
Συστήματα συντεταγμένων Χρησιμοποιούνται για την περιγραφή της θέσης ενός σημείου στον χώρο. Κοινά συστήματα συντεταγμένων: Καρτεσιανό (x, y, z) Πολικό (r, θ) Καρτεσιανό σύστημα συντεταγμένων Οι άξονες
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ορίζουσες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Ορίζουσα H Ορίζουσα είναι ένας αριθμός και ορίζεται μόνον για τετραγωνικούς
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ορίζουσες Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Ορίζουσα H Ορίζουσα είναι ένας αριθμός και ορίζεται μόνον για τετραγωνικούς
Βάση και Διάσταση Διανυσματικού Χώρου
 Βάση και Διάσταση Διανυσματικού Χώρου Έστω V ένας διανυσματικός χώρος επί του σώματος F. Ορισμός : Ένα υποσύνολο S του διανυσματικού χώρου V θα λέμε ότι είναι βάση του V αν ισχύει Α) Η θήκη του S παράγει
Βάση και Διάσταση Διανυσματικού Χώρου Έστω V ένας διανυσματικός χώρος επί του σώματος F. Ορισμός : Ένα υποσύνολο S του διανυσματικού χώρου V θα λέμε ότι είναι βάση του V αν ισχύει Α) Η θήκη του S παράγει
Συστήματα Αυτομάτου Ελέγχου & Ρυθμίσεως Μηχανών : Στοιχεία Γραμμικής Άλγεβρας
 Συστήματα Αυτομάτου Ελέγχου & Ρυθμίσεως Μηχανών : Στοιχεία Γραμμικής Άλγεβρας Κων/νος Ι. Κυριακόπουλος Καθηγητής ΕΜΠ (http://users.tua.gr/kkyria/) Kostas J. Kyriakopoulos - Σ.Α.Ε. ΙΙ 1 Βασικές Έννοιες
Συστήματα Αυτομάτου Ελέγχου & Ρυθμίσεως Μηχανών : Στοιχεία Γραμμικής Άλγεβρας Κων/νος Ι. Κυριακόπουλος Καθηγητής ΕΜΠ (http://users.tua.gr/kkyria/) Kostas J. Kyriakopoulos - Σ.Α.Ε. ΙΙ 1 Βασικές Έννοιες
0 + a = a + 0 = a, a k, a + ( a) = ( a) + a = 0, 1 a = a 1 = a, a k, a a 1 = a 1 a = 1,
 I ΠΙΝΑΚΕΣ 11 Σώμα 111 Ορισμός: Ενα σύνολο k εφοδιασμένο με δύο πράξεις + και ονομάζεται σώμα αν ικανοποιούνται οι παρακάτω ιδιότητες: (Α (α (Προσεταιριστική ιδιότητα της πρόσθεσης (a + b + c = a + (b +
I ΠΙΝΑΚΕΣ 11 Σώμα 111 Ορισμός: Ενα σύνολο k εφοδιασμένο με δύο πράξεις + και ονομάζεται σώμα αν ικανοποιούνται οι παρακάτω ιδιότητες: (Α (α (Προσεταιριστική ιδιότητα της πρόσθεσης (a + b + c = a + (b +
, ορίζουμε deta = ad bc. Πρόταση Ένας πίνακας Α είναι αντιστρέψιμος τότε και μόνο αν deta 0.
 Για κάθε πίνακα Α ορίζουμε μία τιμή που λέγεται ορίζουσα και συμβολίζεται deta ή Α Ο ορισμός γίνεται επαγωγικά για = 2, 3, 4, και ισχύουν τα εξής: a b Για 22 πίνακα Α = c d, ορίζουμε deta = ad bc a 1 b
Για κάθε πίνακα Α ορίζουμε μία τιμή που λέγεται ορίζουσα και συμβολίζεται deta ή Α Ο ορισμός γίνεται επαγωγικά για = 2, 3, 4, και ισχύουν τα εξής: a b Για 22 πίνακα Α = c d, ορίζουμε deta = ad bc a 1 b
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai217/lai217html Παρασκευή 17 Νοεµβρίου 217 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai217/lai217html Παρασκευή 17 Νοεµβρίου 217 Ασκηση
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1. Τελεστές και πίνακες. 1. Τελεστές και πίνακες Γενικά. Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο.
 ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.
![b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0. b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.](/thumbs/63/49387122.jpg) Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: Οκτωβρίου 005) Η Άσκηση στην εργασία αυτή είναι
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: Οκτωβρίου 005) Η Άσκηση στην εργασία αυτή είναι
Γραμμική Αλγεβρα ΙΙ Διάλεξη 1 Εισαγωγή Χρήστος Κουρουνιώτης Πανεπισ τήμιο Κρήτης 19/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 1 19/2/ / 13
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 1 Εισαγωγή Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 1 19/2/2014 1 / 13 Εισαγωγή Τι έχουμε μάθει; Στο πρώτο μάθημα Γραμμικής Άλγεβρας
Γραμμική Άλγεβρα ΙΙ Διάλεξη 1 Εισαγωγή Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 1 19/2/2014 1 / 13 Εισαγωγή Τι έχουμε μάθει; Στο πρώτο μάθημα Γραμμικής Άλγεβρας
x 2 = b 1 2x 1 + 4x 2 + x 3 = b 2. x 1 + 2x 2 + x 3 = b 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
Κεφάλαιο 1 Πρότυπα. Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο.
 Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai218/lai218html Παρασκευή 23 Νοεµβρίου 218 Ασκηση 1
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai218/lai218html Παρασκευή 23 Νοεµβρίου 218 Ασκηση 1
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Γραμμικά Συστήματα- Απαλοιφή Gauss Επιμέλεια: I. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Γραμμικά Συστήματα- Απαλοιφή Gauss Επιμέλεια: I. Λυχναρόπουλος. Χρησιμοποιείστε απαλοιφή Gauss για να επιλύσετε τα ακόλουθα συστήματα: 5x 8y = 5x= + y
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Γραμμικά Συστήματα- Απαλοιφή Gauss Επιμέλεια: I. Λυχναρόπουλος. Χρησιμοποιείστε απαλοιφή Gauss για να επιλύσετε τα ακόλουθα συστήματα: 5x 8y = 5x= + y
[A I 3 ] [I 3 A 1 ].
![[A I 3 ] [I 3 A 1 ]. [A I 3 ] [I 3 A 1 ].](/thumbs/65/54189091.jpg) ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΤΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΣΕΠΤΕΜΒΡΙΟΥ 9 (α) Να ϐρεθεί ο αντίστροφος του πίνακα A = 6 4 (ϐ) Εστω b, b, b στο R Να λύθεί το σύστηµα x = b 6x + x + x = b x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΤΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΣΕΠΤΕΜΒΡΙΟΥ 9 (α) Να ϐρεθεί ο αντίστροφος του πίνακα A = 6 4 (ϐ) Εστω b, b, b στο R Να λύθεί το σύστηµα x = b 6x + x + x = b x
X = {(x 1, x 2 ) x 1 + 2x 2 = 0}.
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 4 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 26/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 4 26/2/2014 1 / 12 Υποσύνολα ενός διανυσματικού χώρου. Πότε είναι ένα υποσύνολο X ενός
Γραμμική Άλγεβρα ΙΙ Διάλεξη 4 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 26/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 4 26/2/2014 1 / 12 Υποσύνολα ενός διανυσματικού χώρου. Πότε είναι ένα υποσύνολο X ενός
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Ορίζουσες Επιμέλεια: Ι. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Ορίζουσες Επιμέλεια: Ι. Λυχναρόπουλος. Υπολογίστε τις ακόλουθες ορίζουσες a) 4 b) c) a b + a) 4 4 Παρατήρηση: Προσέξτε ότι ο συμβολισμός της ορίζουσας
Εφαρμοσμένα Μαθηματικά ΙΙ 7ο Σετ Ασκήσεων (Λύσεις) Ορίζουσες Επιμέλεια: Ι. Λυχναρόπουλος. Υπολογίστε τις ακόλουθες ορίζουσες a) 4 b) c) a b + a) 4 4 Παρατήρηση: Προσέξτε ότι ο συμβολισμός της ορίζουσας
Kεφάλαιο 4. Συστήματα διαφορικών εξισώσεων. F : : F = F r, όπου r xy
 4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
n! k! (n k)!, = k k 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n ) τον n n ταυτοτικό πίνακα,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n ) τον n n ταυτοτικό πίνακα,
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Παραδείγματα Γραμμικοί Μετασχηματισμοί
 Παραδείγματα Γραμμικοί Μετασχηματισμοί Παράδειγμα Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f + 4 4+ b) f : R R με f + a+ b ac c) f : P M με f ( a + b + c + d ) d b d f :
Παραδείγματα Γραμμικοί Μετασχηματισμοί Παράδειγμα Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f + 4 4+ b) f : R R με f + a+ b ac c) f : P M με f ( a + b + c + d ) d b d f :
Κεφάλαιο 1 Συστήματα γραμμικών εξισώσεων
 Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Γραμμική Άλγεβρα Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών
Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Γραμμική Άλγεβρα Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών
Γραμμική Άλγεβρα II Εαρινό εξάμηνο
 Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων
 Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12)
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 5 Οκτωβρίου 006 Ηµεροµηνία παράδοσης της Εργασίας: 0 Νοεµβρίου 006.
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 5 Οκτωβρίου 006 Ηµεροµηνία παράδοσης της Εργασίας: 0 Νοεµβρίου 006.
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 6
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 6 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2018/lai2018html Παρασκευή 7 εκεµβρίου 2018 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 6 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2018/lai2018html Παρασκευή 7 εκεµβρίου 2018 Ασκηση
Δακτύλιοι και Πρότυπα Ασκήσεις 6. Η ύλη των ασκήσεων αυτών είναι η Ενότητα6, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα.
 Δακτύλιοι και Πρότυπα 0-7 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα Βρείτε τη ρητή κανονική μορφή και μια κανονική μορφή Jorda του M( ) 0 0 Έστω
Δακτύλιοι και Πρότυπα 0-7 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα Βρείτε τη ρητή κανονική μορφή και μια κανονική μορφή Jorda του M( ) 0 0 Έστω
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 6
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 6 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2017/lai2017html Παρασκευή 15 εκεµβρίου 2017
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Λυσεις Ασκησεων - Φυλλαδιο 6 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2017/lai2017html Παρασκευή 15 εκεµβρίου 2017
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα
 Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
, b, έχει λύση αν και μόνο αν rank( A) rank( A b) είναι οι συνήθεις διατεταγμένες βάσεις των,
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις8: Γραμμικές Απεικονίσεις και Πίνακες Βασικά σημεία Ορισμός πίνακα γραμμικής απεικόνισης, παραδείγματα Ανάκτηση γραμμικής απεικόνισης από πίνακά της Ιδιότητες (πίνακας
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις8: Γραμμικές Απεικονίσεις και Πίνακες Βασικά σημεία Ορισμός πίνακα γραμμικής απεικόνισης, παραδείγματα Ανάκτηση γραμμικής απεικόνισης από πίνακά της Ιδιότητες (πίνακας
1 1 A = x 1 x 2 x 3. x 4. R 2 3 : a + b + c = x + y + z = 0. R 2 3 : a + x = b + y = c + z = 0
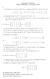 Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
1 x x x x 1 x x x x 1 x x x x 1 (10) B 2, B 1. (10)
 Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ. ΕΝΟΤΗΤΑ: Διανυσματικοί Χώροι (1) ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Διανυσματικοί Χώροι (1) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Διανυσματικοί Χώροι (1) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα
 ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2009-2010 Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Ένα σύνολο m εξισώσεων n αγνώστων που έχει την ακόλουθη
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2009-2010 Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Ένα σύνολο m εξισώσεων n αγνώστων που έχει την ακόλουθη
