n! k! (n k)!, = k k 1
|
|
|
- Λουκᾶς Κοντόσταυλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n ) τον n n ταυτοτικό πίνακα, με det(a) την ορίζουσα ενός τετραγωνικού πίνακα A, με F ένα τυχαίο σώμα και με F[x] το δακτύλιο των πολυωνύμων στη μεταβλητή x με συντελεστές από το F Πράξεις Πινάκων 1 Υπολογίστε τον πίνακα n για n N 2 Δίνονται οι πίνακες A = ( ), B = , C = (α) Δείξτε ότι AB = 7I και BA = C (β) Χρησιμοποιώντας το (α), υπολογίστε τον πίνακα C n για n N 3 Ενας πίνακας A R n n λέγεται στοχαστικός αν τα στοιχεία του είναι μη αρνητικοί αριθμοί και το άθροισμα των στοιχείων οποιασδήποτε γραμμής του A είναι ίσο με 1 (α) Δείξτε ότι ένας πίνακας A R n n με στοιχεία μη αρνητικούς αριθμούς είναι στοχαστικός αν και μόνο αν ισχύει AX = X, όπου X R n 1 είναι ο πίνακας - στήλη όλα τα στοιχεία του οποίου είναι ίσα με 1 (β) Συνάγετε ότι το γινόμενο δύο οποιωνδήποτε n n στοχαστικών πινάκων είναι επίσης n n στοχαστικός πίνακας 1
2 4 Για ακεραίους 0 k n γράφουμε ( ) n = k n! k! (n k)!, όπου m! = 1 2 m για θετικούς ακεραίους m και 0! = 1 κατά σύμβαση (α) Δείξτε ότι ( ) n = k ( ) n 1 + k ( ) n 1 για 1 k n 1 k 1 (β) Αν A, B είναι τετραγωνικοί πίνακες επί του F της ίδιας διάστασης και AB = BA, δείξτε ότι A m B n = B n A m για όλα τα m, n N (γ) Αν A, B είναι τετραγωνικοί πίνακες επί του F της ίδιας διάστασης και AB = BA, δείξτε ότι n ( ) n (A + B) n = A k B n k k για κάθε n N k=0 5 Δίνονται πίνακες A F m n, B F n p και C F p q (α) Εκφράστε το στοιχείο (i, j) του γινομένου ABC ως συνάρτηση των στοιχείων των A, B και C (β) Γενικότερα, έστω A 1, A 2,, A p πίνακες για τους οποίους ορίζεται το γινόμενο A 1 A 2 A p Εκφράστε το στοιχείο (i, j) του πίνακα A 1 A 2 A p ως συνάρτηση των στοιχείων των A 1, A 2,, A p 6 Εστω A, B F n n δύο άνω τριγωνικοί πίνακες (α) Δείξτε ότι ο πίνακας AB είναι επίσης άνω τριγωνικός (β) Αν κάθε στοιχείο στην κύρια διαγώνιο του B είναι ίσο με μηδέν, δείξτε ότι το ίδιο ισχύει για τον AB (γ) Αν κάθε στοιχείο στην κύρια διαγώνιο του A είναι ίσο με μηδέν, δείξτε ότι το ίδιο ισχύει για τον AB (δ) Αν A 1, A 2,, A n F n n είναι άνω τριγωνικοί πίνακες κάθε στοιχείο στην κύρια διαγώνιο των οποίων είναι ίσο με μηδέν, δείξτε ότι A 1 A 2 A n = O 2
3 ( a b 7 Δίνεται πίνακας A = c d ) F 2 2 (α) Δείξτε ότι A 2 (a + d)a + (ad bc) I = O (β) Βρείτε όλους τους πίνακες A F 2 2 για τους οποίους ισχύει A 2 = O (γ) Βρείτε όλους τους πίνακες A F 2 2 για τους οποίους ισχύει A 2 = I (δ) Βρείτε όλους τους πίνακες A R 2 2 για τους οποίους ισχύει A 2 = I 8 Εστω πίνακες A, B, P F n n (α) Αν ο P είναι αντιστρέψιμος και AP = O, δείξτε ότι A = O (β) Αν ο P είναι αντιστρέψιμος και P B = O, δείξτε ότι B = O (γ) Αν AB = BA, A 2 = B 2 και ο A + B είναι αντιστρέψιμος, δείξτε ότι A = B 9 Δίνονται οι πίνακες A = και B = A I (α) Υπολογίστε τον πίνακα B και δείξτε ότι B 2 = O (β) Συνάγετε ότι ο A είναι αντιστρέψιμος και υπολογίστε τον αντίστροφό του (γ) Υπολογίστε τον πίνακα A n για n N 10 Υπολογίστε τους πίνακες λ 1 n 0 (α) 0 λ 1, (β) 0 0 λ n για n N και λ F 11 Δίνεται ο n n πίνακας A = (α) Υπολογίστε τους πίνακες A 2 και A (β) Υπολογίστε τον πίνακα A m για τυχαίο m N 3
4 12 Για τυχαίο πίνακα A F n n συμβολίζουμε με tr(a) το άθροισμα των στοιχείων της κύριας διαγωνίου (ίχνος) του A (α) Για A, B F n n και λ F, δείξτε ότι: tr(λa) = λtr(a), tr(a + B) = tr(a) + tr(b), tr(ab) = tr(ba) (β) Αν για τη συνάρτηση ϕ : F n n F ισχύουν ϕ(λa) = λϕ(a), ϕ(a + B) = ϕ(a) + ϕ(b), ϕ(ab) = ϕ(ba) για όλους τους πίνακες A, B F n n και κάθε λ F, δείξτε ότι υπάρχει c F τέτοιο ώστε ϕ(a) = c tr(a) για κάθε A F n n 13 Δίνεται πίνακας A F n n (α) Υπολογίστε το ίχνος tr(a 2 ) ως συνάρτηση των στοιχείων του A (β) Συνάγετε ότι αν F = R και ο πίνακας A είναι συμμετρικός, τότε tr(a 2 ) 0 και η ισότητα ισχύει μόνο για το μηδενικό πίνακα 14 Υπάρχει θετικός ακέραιος n και πίνακες A, B, C C n n τέτοιοι ώστε (α) AB BA = I; (β) AB BA = A και AC = I; 15 Δίνεται πίνακας A F n n (α) Αν ο A είναι συμμετρικός, δείξτε ότι ο πίνακας P t AP είναι συμμετρικός για κάθε P F n n (β) Αν ο P t AP είναι συμμετρικός για κάποιον αντιστρέψιμο πίνακα P F n n, δείξτε ότι ο A είναι συμμετρικός πίνακας 4
5 16 Για ποιους θετικούς ακεραίους n ισχύει καθένα από τα εξής; (α) Αν ο πίνακας A F n n είναι συμμετρικός, τότε και ο A 2 είναι συμμετρικός (β) Αν A R n n και ο πίνακας A 2 είναι συμμετρικός, τότε και ο A είναι συμμετρικός (γ) Αν ο πίνακας A R n n είναι αντιστρέψιμος και ο A 2 είναι συμμετρικός, τότε ο A είναι συμμετρικός (δ) Αν A R n n και ο πίνακας (A + B) 2 είναι συμμετρικός για κάθε συμμετρικό πίνακα B R n n, τότε ο A είναι συμμετρικός 17 Εστω πίνακας A F n n Βρείτε όλους τους πίνακες B F n n για τους οποίους ισχύει AB = BA στις εξής περιπτώσεις: (α) A = , (β) A = , (γ) ο A είναι διαγώνιος και τα στοιχεία του στην κύρια διαγώνιο είναι διαφορετικά ανά δύο, (δ) A = 0 0 0, (ε) A = Εστω πίνακας A F n n (α) Αν ισχύει AB = BA για κάθε διαγώνιο πίνακα B F n n, δείξτε ότι ο A είναι διαγώνιος πίνακας (β) Αν ισχύει AB = BA για κάθε B F n n, δείξτε ότι A = λi για κάποιο λ F (γ) Αν ισχύει AB = BA για κάθε πίνακα B F n n τα στοιχεία στην κύρια διαγώνιο του οποίου είναι ίσα με μηδέν, δείξτε ότι A = λi για κάποιο λ F (δ) Αν ισχύει AP = P A για κάθε αντιστρέψιμο πίνακα P F n n, δείξτε ότι A = λi για κάποιο λ F (ε) Για ποιους πίνακες A ισχύει AB = BA για κάθε άνω τριγωνικό πίνακα B F n n, τα στοιχεία στην κύρια διαγώνιο του οποίου είναι ίσα με μηδέν; 19 Ενας πίνακας A C n n θα λέγεται καλός αν κάθε πίνακας X C n n γράφεται με μοναδικό τρόπο στη μορφή X = Y + Z, όπου Y, Z C n n είναι πίνακες με AY = Y A και AZ = ZA Δείξτε ότι ο A είναι καλός αν και μόνο αν A 2 = λi n για κάποιο μη μηδενικό λ C 5
6 20 Ενας τετραγωνικός πίνακας A λέγεται μηδενοδύναμος αν ισχύει A m = O για κάποιο θετικό ακέραιο m (α) Δείξτε ότι δεν υπάρχουν αντιστρέψιμοι μηδενοδύναμοι πίνακες (β) Δείξτε ότι αν ο πίνακας A είναι άνω τριγωνικός και όλα τα στοιχεία πάνω στην κύρια διαγώνιο του A είναι ίσα με μηδέν, τότε ο A είναι μηδενοδύναμος (γ) Δείξτε ότι αν οι A, B είναι μηδενοδύναμοι πίνακες και BA = λab για κάποιο λ F, τότε ο A + B είναι επίσης μηδενοδύναμος πίνακας (δ) Δώστε παράδειγμα 2 2 μηδενοδύναμων πινάκων A, B τέτοιων ώστε ο A + B να είναι αντιστρέψιμος πίνακας (ε) Βρείτε όλους τους 2 2 μηδενοδύναμους πίνακες Συνάγετε ότι αν οι A, B και A + B είναι 2 2 μηδενοδύναμοι πίνακες, τότε AB = BA = O (στ) Αληθεύει ότι αν οι A, B και A+B είναι 3 3 μηδενοδύναμοι πίνακες, τότε AB = O ή BA = λab για κάποιο λ F; 21 Βρείτε όλους τους αντιστρέψιμους πίνακες A R n n με στοιχεία μη αρνητικούς αριθμούς για τους οποίους τα στοιχεία του αντίστροφου πίνακα A 1 είναι επίσης μη αρνητικοί αριθμοί: (α) για n = 2, (β) για τυχαίο θετικό ακέραιο n 22 Εστω A F m n και B F n m Δείξτε ότι ο πίνακας I m AB είναι αντιστρέψιμος αν και μόνο αν ο πίνακας I n BA είναι αντιστρέψιμος 23 Συμβολίζουμε με K n (F) το σύνολο όλων των πινάκων της μορφής BC CB, όπου B, C F n n (α) Δείξτε ότι tr(a) = 0 για κάθε πίνακα A F n n που μπορεί να γραφεί ως άθροισμα πεπερασμένου πλήθους στοιχείων του K n (F) ( ) ( ) ( ) (β) Δείξτε ότι οι πίνακες, και ανήκουν στο K (F) (γ) Δείξτε ότι κάθε πίνακας A F n n ίχνους μηδέν μπορεί να γραφεί ως άθροισμα πεπερασμένου πλήθους στοιχείων του K n (F) 6
7 Στοιχειώδεις Μετασχηματισμοί και Γραμμικά Συστήματα 24 Υπολογίστε την ανηγμένη κλιμακωτή μορφή του πίνακα 1 2 n n + 1 n + 2 2n n 2 n + 1 n 2 n + 2 n 2 για n 2 25 Να λύσετε τα συστήματα των γραμμικών εξισώσεων: x 1 + x 2 + x 3 = 1 x 2 + x 3 + x 4 = 1 (α) x 3 + x 4 + x 5 = 1 (β) x 98 + x 99 + x 100 = 1 x 1 + x 3 + x 5 = 1 x 2 + x 4 + x 6 = 1 x 3 + x 5 + x 7 = 1 x 96 + x 98 + x 100 = 1 πάνω σε τυχαίο σώμα F 26 Για τις διάφορες τιμές του λ R, να λύσετε το σύστημα των γραμμικών εξισώσεων: (α) (γ) { λx1 + x 2 = 1 x 1 + λx 2 = λ για τυχαίο ακέραιο n 3 (β) λx 1 + x 2 + x 3 = 1 x 1 + λx 2 + x 3 = λ x 1 + x 2 + λx 3 = λ 2 λx 1 + x x n 1 + x n = 1 x 1 + λx x n 1 + x n = λ x 1 + x λx n 1 + x n = λ n 2 x 1 + x x n 1 + λx n = λ n 1 27 Δίνονται θετικοί ακέραιοι m, p και μη αντιστρέψιμος πίνακας A F n n (α) Δείξτε ότι υπάρχει μη μηδενικός πίνακας B F n p, τέτοιος ώστε AB = O (β) Δείξτε ότι υπάρχει μη μηδενικός πίνακας C F m n, τέτοιος ώστε CA = O 7
8 28 Δίνεται πίνακας A F m n με m < n (α) Δείξτε ότι το ομογενές γραμμικό σύστημα Ax = 0 έχει μη τετριμμένη λύση (β) Αν το σώμα F είναι άπειρο, δείξτε ότι το σύστημα Ax = 0 έχει άπειρες λύσεις 29 Εστω πίνακες A F n m και B F m n με AB = I n (α) Δείξτε ότι το ομογενές γραμμικό σύστημα Bx = 0 δεν έχει μη τετριμμένη λύση (β) Συνάγετε ότι ισχύει n m (γ) Αν n = m, δείξτε ότι ισχύει επίσης BA = I n 30 Δίνεται πίνακας A F m n Δείξτε ότι οι ακόλουθες προτάσεις είναι ισοδύναμες: (i) Το γραμμικό σύστημα Ax = b έχει το πολύ μία λύση για κάθε b F m (ii) Το ομογενές γραμμικό σύστημα Ax = 0 έχει μόνο την τετριμμένη λύση 31 Δίνεται πίνακας A F n n Δείξτε ότι οι ακόλουθες προτάσεις είναι ισοδύναμες: (i) Ο πίνακας A είναι αντιστρέψιμος (ii) Το γραμμικό σύστημα Ax = b έχει μοναδική λύση για κάθε b F n (iii) Το γραμμικό σύστημα Ax = b έχει μοναδική λύση για κάποιο b F n (iv) Το γραμμικό σύστημα Ax = b έχει λύση για κάθε b F n 32 Δίνεται πίνακας A Q m n και b Q m Δείξτε ότι αν το γραμμικό σύστημα Ax = b έχει μιγαδική λύση x C n, τότε το σύστημα αυτό έχει και ρητή λύση x Q n 33 Δίνονται σύνολο S με n στοιχεία και μη κενά υποσύνολα A 1, A 2,, A n+1 του S Χρησιμοποιώντας την Άσκηση 28, δείξτε ότι υπάρχουν μη κενά, ξένα μεταξύ τους σύνολα δεικτών I, J {1, 2,, n + 1} τέτοια ώστε i I A i = j J A j 8
9 34 Υπολογίστε τον αντίστροφο των n n πινάκων: (α) A n = 1 λ λ 2 λ n λ λ n λ n , (β) B n = για λ F και n 2, αντίστοιχα 35 Δίνεται ο πίνακας A n = n n n n n n n R n n (α) Υπολογίστε τον αντίστροφο του A n για n = 2, 3, 4, 5 (β) Υπολογίστε τον αντίστροφο του A n για τυχαίο θετικό ακέραιο n 36 Δίνεται ο πίνακας A n = (α) Για ποιες τιμές του n είναι ο πίνακας A n αντιστρέψιμος; R n n (β) Υπολογίστε τον αντίστροφο του A n, όταν αυτός υπάρχει 37 Εστω πίνακας A C n n (α) Αν κάθε στοιχείο της κύριας διαγωνίου του A είναι ίσο με n και καθένα από τα υπόλοιπα στοιχεία του A έχει μέτρο μικρότερο ή ίσο του 1, δείξτε ότι ο πίνακας A είναι αντιστρέψιμος (β) Ισχύει το ίδιο αν υποθέσουμε ότι κάθε στοιχείο της διαγωνίου του A είναι ίσο με n 1; 9
10 38 Εστω πίνακες A, B F n n Αν υπάρχουν ακέραιοι m 1 και p 0 τέτοιοι ώστε AB m = (I B) p, δείξτε ότι ο πίνακας B είναι αντιστρέψιμος 39 Εστω πίνακες A, B C n n με AB = BA και έστω P = A + B + I (α) Αν P x = 0 για κάποιο x C n, δείξτε ότι (A + I) k x = ( B) k x για κάθε k N (β) Αν A m = B m+1 = I για κάποιο θετικό ακέραιο m, δείξτε ότι ο πίνακας P είναι αντιστρέψιμος (γ) Αληθεύει το (β) χωρίς την υπόθεση ότι AB = BA; 40 Εστω πίνακες A, B F n n (α) Αν AB = A + B, δείξτε ότι AB = BA (β) Αν P F n n είναι αντιστρέψιμος πίνακας και ισχύει A = P B(A + P ), δείξτε ότι ABP = P BA (γ) Αληθεύει το (β) χωρίς την υπόθεση ότι ο P είναι αντιστρέψιμος; Ορίζουσες 41 Ποιο είναι το πρόσημο του όρου a 13 a 25 a 31 a 46 a 52 a 64 στο ανάπτυγμα της 6 6 ορίζουσας det(a ij ); 42 Δείξτε ότι (α) det (β) det 1 a a 2 + bc 1 b b 2 + ac 1 c c 2 + ab 1 a a 2 a 3 + bcd 1 b b 2 b 3 + acd 1 c c 2 c 3 + abd 1 d d 2 d 3 + abc = 2 det = 0 1 a a 2 1 b b 2 1 c c 2, για a, b, c, d F 10
11 43 Υπολογίστε τις n n ορίζουσες: (α) det (β) det n 1 1 n Θεωρούμε την n n ορίζουσα α + β α c n β α + β α β α + β = det α β α + β α β α + β για α, β F (α) Δείξτε ότι c n = (α + β)c n 1 αβ c n 2 για n 2, όπου c 0 = 1 κατά σύμβαση (β) Συνάγετε έναν τύπο για το c n της μορφής c n = p n (α, β), όπου p n (x, y) Z[x, y] είναι πολυώνυμο με ακέραιους συντελεστές 45 Εστω ο n n πίνακας A n της Άσκησης 35 (α) Υπολογίστε την ορίζουσα του A n για n = 1, 2, 3, 4, 5 (β) Υπολογίστε την ορίζουσα του A n για τυχαίο θετικό ακέραιο n (γ) Υπολογίστε τον προσαρτημένο πίνακα του A n για τυχαίο θετικό ακέραιο n (δ) Να λύσετε το σύστημα γραμμικών εξισώσεων A n x = b, όπου b είναι η στήλη μήκους n όλα τα στοιχεία της οποίας είναι ίσα με 1 46 Δείξτε ότι η ορίζουσα του προσαρτημένου πίνακα ενός πίνακα A F n n είναι ίση με (det(a)) n 1 47 Εστω αντιστρέψιμος πίνακας A F n n Δείξτε ότι το άθροισμα των στοιχείων του αντίστροφου πίνακα A 1 είναι ίσο με 1/ det(a) επί το άθροισμα των οριζουσών των n πινάκων που προκύπτουν αντικαθιστώντας μια από τις n γραμμές του A με τη γραμμή (1 1 1) 11
12 48 Δίνεται θετικός ακέραιος m (α) Αν για δύο n n πίνακες A = (a ij ) και B = (b ij ) με στοιχεία ακέραιους αριθμούς ισχύει a ij b ij (mod m) για 1 i, j n, δείξτε ότι det(a) det(b) (mod m) (β) Δείξτε ότι ο πίνακας A = είναι αντιστρέψιμος R Εστω ο n n πίνακας A = a 1 a 2 a n a 2 1 a 2 2 a 2 n a1 n 1 a2 n 1 an n 1, όπου a 1, a 2,, a n είναι στοιχεία ενός σώματος F (α) Δείξτε ότι det(a) = 1 i<j n (a j a i ) (β) Αν τα a 1, a 2,, a n είναι διαφορετικά ανά δύο, συνάγετε ότι ο πίνακας A είναι αντιστρέψιμος και δείξτε ότι το άθροισμα των στοιχείων του A 1 είναι ίσο με 1 (γ) Δείξτε ότι a 1 a 2 a n a 2 1 a 2 2 a 2 n det a n 2 1 a n 2 2 a n 2 n a n 1 a n 2 a n n = (a 1 + a a n ) 1 i<j n (a j a i ) 12
13 50 Υπολογίστε την n n ορίζουσα x 1 + y 1 x 2 + y 1 x n + y 1 det (x 1 + y 1 )(x 1 + y 2 ) (x 2 + y 1 )(x 2 + y 2 ) (x n + y 1 )(x n + y 2 ) (x 1 + y 1 ) (x 1 + y n 1 ) (x n + y 1 ) (x n + y n 1 ) για πραγματικούς αριθμούς x 1,, x n, y 1,, y n 1 51 Εστω f(t) η ορίζουσα του n n πίνακα c 1 t a t a t a t b t c 2 t a t a t b t b t c 3 t a t b t b t b t c n t, όπου a, b, c 1, c 2,, c n C και έστω το πολυώνυμο ϕ(t) = (c 1 t)(c 2 t) (c n t) (α) Δείξτε ότι f(a) = ϕ(a) και ότι f(b) = ϕ(b) (β) Αν a b, δείξτε ότι f(0) = bϕ(a) aϕ(b) b a 52 Να υπολογίσετε την ορίζουσα του (k + 1) (k + 1) πίνακα ( n ) ( n ( 0 1) n k) ( n+1 ) ( n+1 ) ( A(n, k) = n+1 ) 0 1 k, ( n+k ) ( n+k ) ) 0 1 όπου ( ) m r = m! Υπόδειξη: ( m r!(m r)! r ) ( = m 1 ) ( r + m 1 ) r 1 ( n+k k 13
14 53 Εστω A, B F n n και a 1, a 2,, a n, b 1, b 2,, b n, x 1, x 2,, x n F (α) Δείξτε ότι η ορίζουσα του πίνακα A + B είναι ίση με το άθροισμα των οριζουσών των 2 n πινάκων που προκύπτουν από τον A αντικαθιστώντας κάποιες από τις στήλες του A (πιθανώς καμιά ή και όλες) με τις αντίστοιχες στήλες του B (β) Υπολογίστε την n n ορίζουσα a 1 b 1 + x 1 a 1 b 2 a 1 b n det a 2 b 1 a 2 b 2 + x 2 a 2 b n a n b 1 a n b 2 a n b n + x n (γ) Υπολογίστε το όριο lim n ( 1) n/2 n! det ( 1) n 1 n 54 Εστω η n n ορίζουσα d n = det 1 1! 1 2! 1 n! 1 1 2! n! 1 1 3! (n+1)! 1 1 (n+1)! (2n 1)! (α) Υπολογίστε τη d n για n = 2 και n = 3 (β) Δείξτε ότι d n = 1!2! (n 1)! n!(n + 1)! (2n 1)! det ( n ) ( n 1 2) ( n+1 2 ( 2n 1 n ) ( n+1 3 ) ( 2n 1 n+1 ) ) ( n n) ( n+1 ) n+1 ) ( 2n 1 2n 1 (γ) Υπολογίστε τη d n για τυχαίο θετικό ακέραιο n 14
15 55 Εστω ακέραιος n 2 και a 0, a 1,, a n 1 R (α) Δείξτε ότι det = a a 1 +2a a n 2 a n a 0 a 1 a 2 a n 2 a n 1 (β) Υπάρχει πίνακας A τα στοιχεία του οποίου ανήκουν στο σύνολο { 1, 0, 1}, τέτοιος ώστε det(a) = 2010; 56 Εστω θετικοί ακέραιοι n, m και x 0, x 1,, x m 1 F (α) Αν A F n n και B = (b ij ) F m m, δείξτε ότι b 11 A b 12 A b 1m A b 21 A b 22 A b 2m A det = (det(a))m (det(b)) n b m1 A b m2 A b mm A (β) Εστω ο m 2 m 2 πίνακας C m = (c ij ), όπου 0 i, j m 2 1, με στοιχεία c ij = x s 0 r 0 x s 1 r 1, όπου i = r 0 +mr 1, j = s 0 +ms 1 και r 0, r 1, s 0, s 1 {0, 1,, m 1} Δείξτε ότι ( 2m det(c m ) = (x i x j )) 57 Εστω πίνακες A F n n, B F n m και D F m m (α) Δείξτε ότι ( A B det O D ) i>j = det(a) det(d) (β) Εστω ότι A, B R n n (δηλαδή F = C και n = m) Δείξτε ότι ( ) A B det = det(a ib) det(a + ib) B A και συνάγετε ότι ( A B det B A 15 ) 0
16 58 Εστω πίνακες A, B, C, D F n n (α) Δείξτε ότι αν ο A είναι αντιστρέψιμος και AC = CA, τότε ( ) A B det = det(ad CB) C D (β) Ισχύει το συμπέρασμα του (α) χωρίς την υπόθεση AC = CA; 59 Εστω πίνακες A F m n και B F n m (α) Αν m > n, δείξτε ότι det(ab) = 0 (β) Αν m n, δείξτε ότι det(ab) = S det(a S ) det(b S ), όπου στο άθροισμα του δεξιού μέλους το S = {j 1 < j 2 < < j m } διατρέχει όλα τα υποσύνολα του {1, 2,, n} με m στοιχεία, A S είναι ο m m πίνακας με στήλες τις j 1, j 2,, j m στήλες του A και B S είναι ο m m πίνακας με γραμμές τις j 1, j 2,, j m γραμμές του B (γ) Για τυχαίο πίνακα Q R n m, δείξτε ότι det(q t Q) 0 60 Δείξτε ότι det a 1 a 2 a 3 a n a n a 1 a 2 a n 1 a n 1 a n a 1 a n 2 ( n 1 n = ( 1) n 1 j=0 k=1 ζ jk a k ), a 2 a 3 a 4 a 1 όπου ζ = e 2πi/n Συνάγετε ότι n n 1 2 n 1 det n 1 n 1 n n 1 (n + 1) nn 1 = ( 1) 2 16
17 61 Εστω n n πίνακας A, καθένα από τα στοιχεία του οποίου είναι ίσο με 1 ή 1 (α) Δείξτε ότι η ορίζουσα του A είναι ακέραιο πολλαπλάσιο του 2 n 1 (β) Για δοσμένο n, υπολογίστε την ελάχιστη θετική τιμή που μπορεί να λάβει η ορίζουσα του A 62 Βρείτε όλους τους θετικούς ακεραίους n που έχουν την εξής ιδιότητα: η ορίζουσα κάθε συμμετρικού n n πίνακα με στοιχεία ακεραίους αριθμούς και μηδενικά πάνω στην κύρια διαγώνιο είναι άρτιος αριθμός 63 Υπάρχει πίνακας A R n n τέτοιος ώστε A 2 = I; (α) Απαντήστε το ερώτημα αυτό για n = 2, για n = 3, για τυχαίο θετικό ακέραιο n (β) Βρείτε όλους τους θετικούς ακεραίους n για τους οποίους υπάρχουν αντιστρέψιμοι πίνακες A, B R n n τέτοιοι ώστε A 2 + B 2 = O 64 Εστω ότι A, B R 2 2 είναι συμμετρικοί αντιστρέψιμοι πίνακες Δείξτε ότι ο A 2 + B 2 είναι επίσης αντιστρέψιμος πίνακας Ισχύει το ίδιο για n n πίνακες; 65 Δίνεται σώμα F (α) Αν το F έχει τουλάχιστον τρία στοιχεία, δείξτε ότι κάθε πίνακας A F n n μπορεί να γραφεί ως άθροισμα δύο αντιστρέψιμων πινάκων, ένας από τους οποίους είναι άνω τριγωνικός και ο άλλος κάτω τριγωνικός (β) Αν n 2, δείξτε ότι κάθε πίνακας A F n n μπορεί να γραφεί ως άθροισμα δύο αντιστρέψιμων πινάκων 66 Δίνεται θετικός ακέραιος n και τυχαίοι πραγματικοί αριθμοί a ij για 1 i, j n με i j Δείξτε ότι υπάρχουν πραγματικοί αριθμοί a ii {0, 1} για 1 i n, τέτοιοι ώστε ο πίνακας A = (a ij ) R n n να είναι αντιστρέψιμος 17
18 67 Δείξτε ότι: (α) Αν A 1, A 2,, A n+1 F n n είναι τυχαίοι πίνακες, τότε υπάρχουν λ 1, λ 2,, λ n+1 F, όχι όλα μηδέν, τέτοια ώστε det(λ 1 A 1 + λ 2 A λ n+1 A n+1 ) = 0 (β) Υπάρχουν πίνακες A 1, A 2 R 2 2 με την εξής ιδιότητα: αν λ 1, λ 2 είναι τυχαίοι πραγματικοί αριθμοί, όχι και οι δύο μηδέν, τότε det(λ 1 A 1 + λ 2 A 2 ) 0 (γ) Υπάρχουν πίνακες A 1, A 2, A 3, A 4 R 4 4 με την εξής ιδιότητα: αν λ 1, λ 2, λ 3, λ 4 είναι τυχαίοι πραγματικοί αριθμοί, όχι όλοι μηδέν, τότε det(λ 1 A 1 + λ 2 A 2 + λ 3 A 3 + λ 4 A 4 ) 0 Τάξη Πίνακα Συμβολίζουμε με rank(a) την τάξη ενός πίνακα A F m n, δηλαδή το μεγαλύτερο φυσικό αριθμό k για τον οποίο υπάρχει μη μηδενική k k υποορίζουσα του A και υπενθυμίζουμε ότι η τάξη ενός πίνακα δε μεταβάλλεται όταν εκτελούμε στοιχειώδεις μετασχηματισμούς στις γραμμές (ή στις στήλες) του πίνακα αυτού 68 Υπολογίστε την τάξη του πίνακα της Άσκησης 24 για κάθε θετικό ακέραιο n 69 Δίνεται θετικός ακέραιος n Ποια είναι η μέγιστη δυνατή τάξη ενός μηδενοδύναμου πίνακα A F n n (δηλαδή n n πίνακα με A m = O για κάποιο θετικό ακέραιο m); 70 Για τυχαίους πίνακες A F m n και B F n p δείξτε ότι: (α) rank(ab) rank(a) (β) rank(ab) rank(b) 71 Δίνεται πίνακας A F m n Δείξτε ότι οι ακόλουθες προτάσεις είναι ισοδύναμες: (α) rank(a) = m (β) Υπάρχει μία m m υποορίζουσα του A η οποία είναι διάφορη του μηδενός (γ) Το γραμμικό σύστημα Ax = b είναι συμβιβαστό για κάθε b F m 1 (δ) Υπάρχει πίνακας B F n m τέτοιος ώστε AB = I m 18
19 72 Δίνεται πίνακας A F m n Δείξτε ότι οι ακόλουθες προτάσεις είναι ισοδύναμες: (α) rank(a) = n (β) Υπάρχει μία n n υποορίζουσα του A η οποία είναι διάφορη του μηδενός (γ) Το γραμμικό σύστημα Ax = b έχει το πολύ μία λύση για κάθε b F m 1 (δ) Το ομογενές γραμμικό σύστημα Ax = 0 έχει μόνο την τετριμμένη λύση x = 0 (ε) Υπάρχει πίνακας C F n m τέτοιος ώστε CA = I n 73 Για τυχαίο πίνακα A F m n δείξτε ότι: (α) rank(p AQ) rank(a) για P F m m και Q F n n (β) rank(p A) = rank(a) για κάθε αντιστρέψιμο πίνακα P F m m (γ) rank(aq) = rank(a) για κάθε αντιστρέψιμο πίνακα Q F n n (δ) rank(p AQ) = rank(a) για όλους τους αντιστρέψιμους P F m m και Q F n n 74 Δείξτε ότι rank(a+b) rank(a)+rank(b) για τυχαίους πίνακες A, B F m n 75 Δείξτε ότι rank(i A 1 A 2 A m ) για τυχαίους πίνακες A 1, A 2,, A m F n n m rank(i A i ) i=1 76 Δίνεται ακέραιος n 2 Ποια είναι η ελάχιστη και ποια η μέγιστη τιμή της τάξης ενός n n πίνακα, τα στοιχεία του οποίου είναι ακριβώς οι ακέραιοι 1, 2,, n 2 ; 77 Εστω θετικός ακέραιος n και πίνακας A = (a ij ) R n n με a ij = { 0, αν i = j, 1, διαφορετικά (α) Αν ο n είναι άρτιος, δείξτε ότι ο πίνακας A είναι αντιστρέψιμος (β) Εστω ότι ο n είναι περιττός Ποιες είναι οι δυνατές τιμές της τάξης του A; 78 Εστω A ένας n n πίνακας με τις εξής ιδιότητες: Κάθε στοιχείο της κύριας διαγωνίου του A είναι ίσο με μηδέν και καθένα από τα υπόλοιπα στοιχεία του A είναι ίσο με 1 ή με 2010 Δείξτε ότι rank(a) n 1 19
20 79 Δίνεται πίνακας A R n n για τον οποίο ισχύει A t + A = J n I n, όπου J n είναι ο n n πίνακας κάθε στοιχείο του οποίου είναι ίσο με 1 (α) Δείξτε ότι rank(a) n 1 (β) Δώστε παράδειγμα τέτοιου πίνακα με rank(a) = n 1 (γ) Για n 2, δώστε παράδειγμα τέτοιου πίνακα με rank(a) = n Ο Διανυσματικός Χώρος F n 1 Ορίζουμε τον πυρήνα ενός πίνακα A F m n ως ker(a) := {x F n 1 : Ax = 0} και την απεικόνιση L A : F n 1 F m 1 θέτοντας L A (x) = Ax για x F n 1 80 Δίνεται πίνακας A F m n Δείξτε ότι οι ακόλουθες συνθήκες είναι ισοδύναμες: (α) Οι στήλες του A παράγουν το χώρο F m 1 (β) Το γραμμικό σύστημα Ax = b είναι συμβιβαστό για κάθε b F m 1 (γ) Η απεικόνιση L A : F n 1 F m 1 είναι επί (δ) rank(a) = m 81 Δίνεται πίνακας A F m n Δείξτε ότι οι ακόλουθες συνθήκες είναι ισοδύναμες: (α) Οι στήλες του A είναι γραμμικώς ανεξάρτητα στοιχεία του F m 1 (β) Το ομογενές γραμμικό σύστημα Ax = 0 έχει μόνο την τετριμμένη λύση x = 0 (γ) Η απεικόνιση L A : F n 1 F m 1 είναι 1 1 (δ) rank(a) = n 82 Εστω διακεκριμένοι πραγματικοί αριθμοί λ 1, λ 2,, λ n που δεν ανήκουν στο σύνολο { 1, 2,, n} Δείξτε ότι οι στήλες του πίνακα 1 λ λ λ n+1 1 λ λ 1 +n 1 1 λ 2 +2 λ 2 +n 1 1 λ n+2 λ n+n είναι γραμμικώς ανεξάρτητα διανύσματα του R n 1 20
21 83 Εστω W το σύνολο των στοιχείων (x 1 x 2 x n ) t του διανυσματικού χώρου F n 1 που ικανοποιούν τη σχέση x 1 + x x n = 0 (α) Δείξτε ότι το W είναι υπόχωρος του F n 1 (β) Υπολογίστε τη διάσταση του W και βρείτε μια βάση αυτού 84 Δίνεται πίνακας A F m n (α) Δείξτε ότι η διάσταση του υπόχωρου του F m 1 που παράγεται από τις στήλες του A είναι ίση με την τάξη του A (β) Συνάγετε ότι η διάσταση του υπόχωρου του F m 1 που παράγεται από τις στήλες του A είναι ίση με τη διάσταση του υπόχωρου του F n 1 που παράγεται από τις στήλες του A t 85 Δείξτε ότι dim ker(a) = n rank(a) για κάθε πίνακα A F m n 86 Βρείτε όλους τους υπόχωρους W του R n 1 με την ιδιότητα: αν (x 1 x 2 x n ) t W και σ είναι μετάθεση του συνόλου {1, 2,, n}, τότε (x σ(1) x σ(2) x σ(n) ) t W Ποιες είναι οι δυνατές τιμές της διάστασης ενός τέτοιου υπόχωρου; 87 Δείξτε ότι για κάθε υπόχωρο W του χώρου F n 1 υπάρχουν θετικός ακέραιος r και πίνακας A F r n τέτοιοι ώστε W = ker(a) 88 Δείξτε ότι για τον προσαρτημένο πίνακα adj(a) ενός πίνακα A F n n ισχύουν: (α) Αν rank(a) = n, τότε rank(adj(a)) = n (β) Αν rank(a) = n 1, τότε rank(adj(a)) = 1 (γ) Αν rank(a) n 2, τότε rank(adj(a)) = 0 89 Βρείτε όλους τους θετικούς ακεραίους n που έχουν την εξής ιδιότητα: αν A = (a ij ) είναι n n πίνακας με στοιχεία μη μηδενικούς πραγματικούς αριθμούς, τότε είναι δυνατόν να πολλαπλασιάσουμε κάθε στοιχείο a ij του A με κάποιον θετικό πραγματικό αριθμό b ij έτσι ώστε ο πίνακας που θα προκύψει να έχει ορίζουσα μηδέν 21
22 Αφηρημένοι Διανυσματικοί Χώροι Συμβολίζουμε με dim(v ) τη διάσταση ενός διανυσματικού χώρου V και με F n [x] τον F-διανυσματικό χώρο όλων των πολυωνύμων p(x) F[x] βαθμού μικρότερου ή ίσου του n 90 Για τα διανύσματα v 1, v 2,, v n ενός διανυσματικού χώρου V επί του F ισχύουν οι ισότητες n a ij v j = 0 V, i = 1, 2,, m j=1 για κάποιους συντελεστές a ij F, όπου 0 V είναι το μηδενικό στοιχείο του V Αν η τάξη του πίνακα A = (a ij ) F m n είναι ίση με n, δείξτε ότι v 1 = v 2 = = v n = 0 V 91 Δίνονται γραμμικώς ανεξάρτητα διανύσματα u 1, u 2,, u n ενός διανυσματικού χώρου V και διανύσματα v 1, v 2,, v m που παράγουν το V Χρησιμοποιήστε την Άσκηση 28 για να δείξετε ότι n m 92 Υπολογίστε τη διάσταση των παρακάτω υπόχωρων του F n n : (α) του υπόχωρου των άνω τριγωνικών n n πινάκων, (β) του υπόχωρου των άνω τριγωνικών n n πινάκων, κάθε στοιχείο στην κύρια διαγώνιο των οποίων είναι ίσο με μηδέν, (γ) του υπόχωρου των συμμετρικών n n πινάκων, (δ) του υπόχωρου των αντισυμμετρικών n n πινάκων 93 Δίνεται το σύνολο W n = {A F n n : tr(a) = 0} όλων των n n πινάκων με στοιχεία από το F, το ίχνος των οποίων είναι ίσο με μηδέν (α) Δείξτε ότι το W n είναι γνήσιος υπόχωρος του F n n Ποια είναι η διάστασή του; (β) Συνάγετε ότι οποιοιδήποτε πίνακες A 1, A 2,, A n 2 F n n με tr(a i ) = 0 για 1 i n 2 είναι γραμμικώς εξαρτημένα στοιχεία του F n n (γ) Βρείτε γραμμικώς ανεξάρτητα στοιχεία A 1, A 2,, A n 2 του F n n, τέτοια ώστε tr(a i ) = 1 για 1 i n 2 (δ) Εστω πίνακας B F n n ο οποίος δεν είναι πολλαπλάσιο του I n και έστω πίνακες A 1, A 2,, A n 2 F n n Αν ισχύει A i B = BA i για 1 i n 2, δείξτε ότι οι A 1, A 2,, A n 2 είναι γραμμικώς εξαρτημένα στοιχεία του F n n 22
23 94 Εστω V το σύνολο των πινάκων στο F m n των οποίων τα στοιχεία κάθε γραμμής και κάθε στήλης έχουν άθροισμα μηδέν (α) Δείξτε ότι ο V είναι γραμμικός υπόχωρος του F m n (β) Βρείτε μια βάση του V για m = 2 και τυχαίο n (γ) Βρείτε μια βάση του V για τυχαία m και n (δ) Συνάγετε ότι dim(v ) = (m 1)(n 1) 95 Δίνονται πολυώνυμα φ 0 (x), φ 1 (x),, φ n (x) F n [x] (α) Αν το φ i (x) έχει βαθμό ίσο με i για 0 i n (οπότε το φ 0 (x) είναι μη μηδενικό σταθερό πολυώνυμο), δείξτε ότι η (φ 0 (x), φ 1 (x),, φ n (x)) είναι βάση του F n [x] (β) Εστω a F Συνάγετε από το (α) ότι τα πολυώνυμα φ i (x) = (x a) i για 0 i n αποτελούν τα στοιχεία μιας βάσης του F n [x] (γ) Αν F = C, εκφράστε ένα τυχαίο πολυώνυμο p(x) F n [x] ως γραμμικό συνδυασμό των στοιχείων της βάσης του ερωτήματος (β) 96 Εστω a F (α) Δείξτε ότι το σύνολο W = {p(x) F n [x] : p(a) = 0} είναι γνήσιος υπόχωρος του διανυσματικού χώρου F n [x] (β) Αν p 0 (x), p 1 (x),, p n (x) F n [x] και p i (a) = 0 για 0 i n, δείξτε ότι τα p 0 (x), p 1 (x),, p n (x) είναι γραμμικώς εξαρτημένα στοιχεία του F n [x] (γ) Εστω μη μηδενικό στοιχείο b F Δείξτε ότι υπάρχουν γραμμικώς ανεξάρτητα p 0 (x), p 1 (x),, p n (x) F n [x], τέτοια ώστε p i (a) = b για 0 i n 97 Δίνονται ανά δύο διακεκριμένα στοιχεία a 1, a 2,, a n ενός σώματος F και τα πολυώνυμα φ(x) = (x a 1 )(x a 2 ) (x a n ) και φ i (x) = φ(x)/(x a i ) για 1 i n του F[x] (α) Δείξτε ότι τα φ 1 (x), φ 2 (x),, φ n (x) είναι γραμμικώς ανεξάρτητα στοιχεία του F-διανυσματικού χώρου F[x] (β) Δείξτε ότι κάθε πολυώνυμο p(x) F[x] με βαθμό μικρότερο του n γράφεται στη μορφή p(x) = c 1 φ 1 (x) + c 2 φ 2 (x) + + c n φ n (x) με c i = p(a i) φ (a i ) για 1 i n 23
24 98 Δίνονται τα στοιχεία φ i (x) = x i (1 + x) n i του F n [x] για 0 i n (α) Δείξτε ότι η B n = (φ 0 (x), φ 1 (x),, φ n (x)) είναι βάση του F n [x] (β) Για 0 k n, εκφράστε το μονώνυμο x k ως γραμμικό συνδυασμό των στοιχείων της βάσης B n (γ) Αν n = 4, πράξτε ομοίως για το πολυώνυμο p(x) = 1 + x + x 2 + x 3 + x 4 99 Δίνεται διανυσματικός χώρος V διάστασης n και υπόχωροί του U και W Δείξτε ότι οι ακόλουθες προτάσεις είναι ισοδύναμες: (i) V = U W (ii) V = U + W και dim(u) + dim(w ) = n (iii) Υπάρχουν βάσεις B και C των U και W, αντίστοιχα, με B C =, η ένωση των οποίων είναι βάση του V (iv) Για οποιεσδήποτε βάσεις B και C των U και W, αντίστοιχα, ισχύει B C = και η ένωση B C είναι βάση του V 100 Εστω V n = R n [x] Συμβολίζουμε με U n το σύνολο των πολυωνύμων p(x) V n για τα οποία ισχύει p( x) = p(x) και με W n το σύνολο των πολυωνύμων q(x) V n για τα οποία ισχύει q( x) = q(x) (α) Δείξτε ότι τα σύνολα U n και W n είναι υπόχωροι του διανυσματικού χώρου V n (β) Υπολογίστε τις διαστάσεις των U n και W n (γ) Δείξτε ότι V n = U n W n 101 Δίνεται ένας F-διανυσματικός χώρος V διάστασης n και ένας γνήσιος υπόχωρος U του V Δείξτε ότι ο U είναι ίσος με την τομή όλων των υπόχωρων διάστασης n 1 του V που περιέχουν τον U 102 Δίνεται διανυσματικός χώρος V διάστασης n (α) Εστω U και W υπόχωροι του V διάστασης k και n 1, αντίστοιχα Δείξτε ότι η διάστασης της τομής U W είναι ίση με k 1 ή k και ότι ισχύει dim(u W ) = k U W (β) Αν W 1, W 2 είναι δύο διαφορετικοί υπόχωροι του V διάστασης n 1, ποιες είναι οι δυνατές τιμές της διάστασης του W 1 W 2 ; (γ) Εστω ακέραιος 1 r n Αν W 1, W 2,, W r είναι υπόχωροι του V διάστασης n 1, ποιες είναι οι δυνατές τιμές της διάστασης του W 1 W 2 W r ; 24
25 103 Δίνονται υπόχωροι U, V, W ενός διανυσματικού χώρου (α) Δείξτε ότι U W + V W (U + V ) W (β) Ισχύει πάντοτε η ισότητα στο (α); (γ) Αν οι U, V, W έχουν πεπερασμένη διάσταση, δείξτε ότι dim(u + V + W ) dim(u) + dim(v ) + dim(w ) dim(u V ) dim(u W ) dim(v W ) + dim(u V W ) (δ) Αν οι U, V, W έχουν πεπερασμένη διάσταση, συνάγετε από το (γ) ότι dim(u) + dim(v ) + dim(w ) dim(u + V + W ) m, όπου m είναι ο μέγιστος των ακεραίων dim(u V ) + dim(u W ), dim(u V ) + dim(v W ) και dim(u W ) + dim(v W ) 104 Ενα πολυώνυμο a 0 +a 1 x+ +a n x n F n [x] λέγεται συμμετρικό (ή παλινδρομικό) αν ισχύει a i = a n i για 0 i n Συμβολίζουμε W n με το σύνολο των συμμετρικών πολυωνύμων του F n [x] (α) Δείξτε ότι το W n είναι υπόχωρος του διανυσματικού χώρου F n [x] (β) Δείξτε ότι τα πολυώνυμα p i (x) = x i + x n i για 0 i n/2 αποτελούν τα στοιχεία μιας βάσης του W n και συνάγετε ότι dim(w n ) = n/2 + 1 (γ) Δείξτε ότι τα πολυώνυμα φ i (x) = x i + x i x n i για 0 i n/2 αποτελούν επίσης τα στοιχεία μιας βάσης του W n Θέτουμε τώρα F = R Ενα συμμετρικό πολυώνυμο a 0 + a 1 x + + a n x n R n [x] λέγεται μονότροπο αν 0 a 0 a 1 a n/2 (δ) Δείξτε ότι ένα συμμετρικό πολυώνυμο p(x) R n [x] είναι μονότροπο αν και μόνο αν οι συντεταγμένες του p(x) ως προς τη βάση του του W n στο ερώτημα (γ) είναι μη αρνητικοί αριθμοί (ε) Συνάγετε ότι αν τα πολυώνυμα p(x) R n [x] και q(x) R m [x] είναι συμμετρικά και μονότροπα, τότε το γινόμενό τους p(x)q(x) R n+m [x] είναι επίσης συμμετρικό και μονότροπο 25
26 105 Εστω S ένα σύνολο m διανυσμάτων το οποίο παράγει ένα διανυσματικό χώρο V διάστασης n 2 Υποθέτουμε ότι το άθροισμα οποιωνδήποτε m 1 στοιχείων του S είναι συγγραμμικό με το στοιχείο του S που περισσεύει (δύο διανύσματα λέγονται συγγραμμικά αν είναι γραμμικώς εξαρτημένα) (α) Δείξτε ότι n m 1 (β) Δείξτε ότι το άθροισμα των στοιχείων του S είναι ίσο με το μηδενικό διάνυσμα 106 Εστω διανυσματικός χώρος V πάνω σε ένα άπειρο σώμα Δείξτε ότι ο V δεν είναι ίσος με την ένωση πεπερασμένου πλήθους γνήσιων υποχώρων του 107 Εστω δύο βάσεις B και C ενός διανυσματικού χώρου V πεπερασμένης διάστασης (α) Δείξτε ότι για κάθε v C υπάρχει u B τέτοιο ώστε το σύνολο (B {u}) {v} να είναι βάση του χώρου V (β) Δείξτε ότι για κάθε v C υπάρχει u B τέτοιο ώστε τα σύνολα (B {u}) {v} και (C {v}) {u} να είναι και τα δύο βάσεις του χώρου V 108 Εστω διανυσματικός χώρος V διάστασης n και έστω A ένας n n πίνακας με στοιχεία διανύσματα του V Δώστε απόδειξη ή αντιπαράδειγμα για την ακόλουθη πρόταση: Αν κάθε γραμμή του A είναι βάση του V, τότε είναι δυνατόν να αναδιαταχθεί κάθε γραμμή του A έτσι ώστε κάθε στήλη του πίνακα που θα προκύψει να είναι επίσης βάση του V 26
27 Γραμμικές Απεικονίσεις Για F-διανυσματικούς χώρους V και W, συμβολίζουμε με L(V, W ) τον F-διανυσματικό χώρο όλων των γραμμικών απεικονίσεων T : V W Ο δυϊκός χώρος V του V είναι ο F-διανυσματικός χώρος L(V, F) όλων των γραμμικών μορφών T : V F 109 Δίνονται ακέραιοι 1 k n και η απεικόνιση T : F n F n η οποία ορίζεται θέτοντας T (x) = (x 1,, x k, 0,, 0) για x = (x 1, x 2,, x n ) F n (α) Δείξτε ότι η T είναι γραμμική απεικόνιση και ότι T (T (x) = T (x) για κάθε x F n (β) Βρείτε τον πυρήνα και την εικόνα της T και υπολογίστε τις διαστάσεις τους (γ) Για ποιες τιμές των k και n είναι η T ισομορφισμός διανυσματικών χώρων; (δ) Υπολογίστε τον πίνακα της T ως προς τη συνήθη βάση του F n 110 Δίνεται ο γραμμικός μετασχηματισμός T : F n F n που ορίζεται θέτοντας T (x) = (x 1 x 2, x 2 x 3,, x n x 1 ) για x = (x 1, x 2,, x n ) F n (όπου για n = 1 έχουμε T (x) = 0 για κάθε x F, κατά σύμβαση) (α) Δείξτε ότι η T είναι γραμμική απεικόνιση (β) Βρείτε τον πυρήνα και την εικόνα της T και υπολογίστε τις διαστάσεις τους (γ) Εστω n = 2 και F = R Δείξτε ότι για x R 2, το T (x) είναι η ορθογώνια προβολή του 2x στην ευθεία x 1 + x 2 = Δίνεται η γραμμική απεικόνιση F-διανυσματικών χώρων T : V U και υπόχωρος W του V (α) Δείξτε ότι η εικόνα T (W ) = {T (w) : w W } του W ως προς την απεικόνιση T είναι υπόχωρος του U (β) Αν ο V έχει πεπερασμένη διάσταση, δείξτε ότι το ίδιο ισχύει για την εικόνα T (W ) και ότι dim T (W ) dim(w ) 112 Δίνεται διανυσματικός χώρος V Βρείτε όλες τις γραμμικές απεικονίσεις T : V V με την εξής ιδιότητα: τα διανύσματα v και T (v) είναι γραμμικώς εξαρτημένα για κάθε v V 113 Δίνεται γραμμικός μετασχηματισμός T : V V ενός διανυσματικού χώρου V και διάνυσμα x V Αν ισχύουν T m (x) = 0 και T m 1 (x) 0 για κάποιο θετικό ακέραιο m, δείξτε ότι τα διανύσματα x, T (x), T 2 (x),, T m 1 (x) είναι γραμμικώς ανεξάρτητα 27
28 114 Δίνεται γραμμικός μετασχηματισμός T : V V ενός διανυσματικού χώρου V (α) Αν x 1, x 2,, x 2 k είναι στοιχεία του V και ισχύουν T m (x m ) 0 και T 2m (x m ) = 0 για 1 m 2 k, δείξτε ότι τα διανύσματα x 1, x 2, x 4,, x 2 k είναι γραμμικώς ανεξάρτητα (β) Αν ο V έχει πεπερασμένη διάσταση, δείξτε ότι υπάρχει θετικός ακέραιος m τέτοιος ώστε ker(t m ) Im(T m ) = {0} 115 Δίνεται διανυσματικός χώρος V, στοιχεία v 1, v 2,, v n V και γραμμικός μετασχηματισμός T : V V Αν T (v 1 ) = v 1, T (v i ) = v i 1 + v i για 2 i n και το v 1 είναι μη μηδενικό διάνυσμα, δείξτε ότι το {v 1, v 2,, v n } είναι γραμμικώς ανεξάρτητο υποσύνολο του V 116 Δίνεται διανυσματικός χώρος V διάστασης n Αν {u 1,, u n+1 } και {v 1,, v n+1 } είναι υποσύνολα του V με n+1 στοιχεία, κάθε γνήσιο υποσύνολο καθενός από τα οποία είναι γραμμικώς ανεξάρτητο, δείξτε ότι υπάρχει γραμμικός ισομορφισμός T : V V τέτοιος ώστε τα διανύσματα T (u i ) και v i να είναι γραμμικώς εξαρτημένα για κάθε i με 1 i n Εστω V ο υπόχωρος του F m n που αποτελείται από τους πίνακες τα στοιχεία κάθε γραμμής και κάθε στήλης των οποίων έχουν άθροισμα μηδέν (βλέπε Άσκηση 94) Για X V, έστω T (X) F (m 1) (n 1) ο πίνακας που προκύπτει από τον X διαγράφοντας την τελευταία γραμμή και στήλη (α) Δείξτε ότι η T : V F (m 1) (n 1) είναι γραμμική απεικόνιση (β) Δείξτε ότι η T είναι ισομορφισμός διανυσματικών χώρων (γ) Συνάγετε ότι dim(v ) = (m 1)(n 1) 118 Για A F p m και θετικό ακέραιο n θεωρούμε την απεικόνιση T : F m n F p n η οποία ορίζεται θέτοντας T (X) = AX για X F m n (α) Δείξτε ότι η απεικόνιση T είναι γραμμική (β) Αν p = m και ο πίνακας A είναι αντιστρέψιμος, δείξτε ότι η T είναι ισομορφισμός διανυσματικών χώρων (γ) Αν η T είναι ισομορφισμός διανυσματικών χώρων, δείξτε ότι p = m και ότι ο πίνακας A είναι αντιστρέψιμος 119 Δίνεται γραμμική απεικόνιση F-διανυσματικών T : V W Αν ο V έχει πεπερασμένη διάσταση, δείξτε ότι dim(v ) = dim ker(t ) + dim Im(T ) 28
29 120 Εστω γραμμικοί μετασχηματισμοί S, T : V V ενός F-διανυσματικού χώρου V (α) Δείξτε ότι ο περιορισμός της T στον υπόχωρο ker(st ) του V ορίζει μια γραμμική απεικόνιση R : ker(st ) ker(s) (β) Δείξτε ότι ker(r) = ker(t ) και ότι Im(R) = ker(s) Im(T ) (γ) Αν ο V έχει πεπερασμένη διάσταση, συνάγετε ότι dim ker(st ) dim ker(s) + dim ker(t ) και ότι η ισότητα ισχύει αν και μόνο αν ker(s) Im(T ) 121 Δίνεται η γραμμική απεικόνιση F-διανυσματικών χώρων T : V U και υπόχωρος W του U (α) Δείξτε ότι η αντίστροφη εικόνα T 1 (W ) = {v V : T (v) W } του W ως προς την T είναι υπόχωρος του V (β) Εστω π : U U/W ο φυσικός επιμορφισμός του U επί του χώρου πηλίκο U/W Δείξτε ότι T 1 (W ) = ker(s), όπου S είναι η σύνθεση π T : V U/W (γ) Αν οι V και U έχουν πεπερασμένη διάσταση, δείξτε ότι dim T 1 (W ) dim(v ) dim(u) + dim(w ) 122 Εστω F-διανυσματικοί χώροι V 0, V 1,, V m, V m+1 με V 0 = V m+1 = {0} Αν υπάρχουν γραμμικές απεικονίσεις T i : V i V i+1 για 0 i m, τέτοιες ώστε ker(t i ) = Im(T i 1 ) για κάθε 1 i m, δείξτε ότι m ( 1) i dim(v i ) = 0 i=1 123 Εστω F-διανυσματικός χώρος V διάστασης n και γραμμικές απεικονίσεις S, T : V V Δείξτε ότι: (α) Αν Im(T ) = ker(t ), τότε ο n είναι άρτιος ακέραιος (β) Αν Im(S) = ker(s), Im(T ) = ker(t ), Im(S) Im(T ) = Im(ST ) και ST = T S, τότε ο n είναι ακέραιο πολλαπλάσιο του Για A F m n θεωρούμε την απεικόνιση T A : F n m F η οποία ορίζεται θέτοντας T A (X) = tr(ax) για X F n m (α) Δείξτε ότι η T A είναι γραμμική απεικόνιση για κάθε A F m n (β) Αν T A : F n m F είναι η μηδενική απεικόνιση, δείξτε ότι A = O (γ) Εστω T : F m n (F n m ) η απεικόνιση που ορίζεται θέτοντας T (A) = T A για A F m n Δείξτε ότι η T είναι γραμμική απεικόνιση (δ) Δείξτε ότι για κάθε γραμμική απεικόνιση L : F n m F υπάρχει μοναδικός πίνακας A F m n τέτοιος ώστε L = T A 29
30 125 Εστω πίνακες A, B F m n (α) Αν υπάρχει αντιστρέψιμος πίνακας P F m m τέτοιος ώστε B = P A, δείξτε ότι για x F n 1 ισχύει η ισοδυναμία Ax = 0 Bx = 0 (β) Αν για x F n 1 ισχύει η ισοδυναμία Ax = 0 Bx = 0, δείξτε ότι υπάρχει αντιστρέψιμος πίνακας P F m m τέτοιος ώστε B = P A Τάξη Γραμμικής Απεικόνισης Υπενθυμίζουμε ότι η τάξη μιας γραμμικής απεικόνισης T : V W ορίζεται ως rank(t ) = dim Im(T ) Ειδικότερα, για κάθε πίνακα A F m n η τάξη της γραμμικής απεικόνισης L A : F n 1 F m 1 που ορίζεται θέτοντας L A (x) = Ax για x F n 1 είναι ίση με τη διάσταση του υπόχωρου του F m 1 που παράγεται από τις στήλες του A και συνεπώς (Άσκηση 84) ίση με rank(a) 126 Δίνονται διανυσματικοί χώροι V και W πεπερασμένης διάστασης και γραμμική απεικόνιση T : V W (α) Δείξτε ότι η T είναι μονομορφισμός αν και μόνο αν rank(t ) = dim(v ) (β) Δείξτε ότι η T είναι επιμορφισμός αν και μόνο αν rank(t ) = dim(w ) (γ) Συνάγετε ότι η T είναι ισομορφισμός αν και μόνο αν rank(t ) = dim(v ) = dim(w ) 127 Δίνονται F-διανυσματικοί χώροι U, V, W πεπερασμένης διάστασης και γραμμικές απεικονίσεις T : U V και S : V W (α) Δείξτε ότι rank(st ) min{rank(s), rank(t )} (β) Συνάγετε ότι rank(ab) min{rank(a), rank(b)} για πίνακες A F m n και B F n p 128 Δίνεται F-διανυσματικός χώρος V διάστασης n και γραμμικές απεικονίσεις S, T, R : V V (α) Δείξτε ότι rank(s + T ) rank(s) + rank(t ) (β) Δείξτε ότι rank(s) + rank(t ) n + rank(st ) (γ) Δείξτε ότι rank(sr) + rank(rt ) rank(r) + rank(srt ) 30
31 129 Εστω πίνακας A F n n Ποια είναι η μέγιστη δυνατή τιμή της τάξης του A (α) αν A 2 = O; (β) αν A 3 = O; 130 Δίνεται F-διανυσματικός χώρος V διάστασης n και γραμμικός μετασχηματισμός S : V V Ορίζουμε το γραμμικό μετασχηματισμό T : V V θέτοντας T (x) = x S(x) για x V (α) Δείξτε ότι S(T (x)) = T (S(x) για κάθε x V (β) Δείξτε ότι rank(s) + rank(t ) n (γ) Δείξτε ότι οι ακόλουθες συνθήκες είναι ισοδύναμες: (i) V = Im(S) Im(T ) (ii) Im(S) Im(T ) = {0} (iii) rank(s) + rank(t ) = n (iv) Im(S) = ker(t ) (v) ker(s) = Im(T ) (vi) S(T (x)) = T (S(x)) = 0 για κάθε x V Για τυχαίο πίνακα A F n n συνάγετε τα εξής: (δ) rank(a) + rank(i A) n (ε) Ισχύει rank(a) + rank(i A) = n αν και μόνο αν A 2 = A 131 Δείξτε ότι: (α) Για τυχαίους πίνακες A, B F n n ισχύει rank(ab) rank(ba) n/2 (β) Υπάρχουν πίνακες A, B F n n ώστε rank(ab) rank(ba) = n/2 (γ) Αν για τους A, B F n n ισχύει AB = O και οι πίνακες A + A t και B + B t είναι αντιστρέψιμοι, δείξτε ότι rank(a) = rank(b) = n/2 132 Εστω διανύσματα u, v C n με u 0 Δείξτε ότι υπάρχει συμμετρικός πίνακας P C n n τέτοιος ώστε P u = v 31
32 Πίνακας μιας Γραμμικής Απεικόνισης 133 Δίνονται διανυσματικοί χώροι V και W διάστασης n και m, αντίστοιχα, και γραμμική απεικόνιση T : V W Εστω A F m n ο πίνακας της T ως προς τυχαίες βάσεις των V και W (α) Δείξτε ότι rank(t ) = rank(a) Συνάγετε ότι η T είναι: (β) μονομορφισμός αν και μόνο αν rank(a) = n, (γ) επιμορφισμός αν και μόνο αν rank(a) = m, (δ) ισομορφισμός αν και μόνο αν ο πίνακας A είναι αντιστρέψιμος 134 Θεωρούμε την απεικόνιση T : R n [x] R n [x] που ορίζεται θέτοντας T (p(x)) = p(x) p (x) για p(x) R n [x] (α) Δείξτε ότι η απεικόνιση T είναι γραμμική (β) Βρείτε τον πίνακα της T ως προς τη βάση (1, x,, x n ) του R n [x] (γ) Συνάγετε ότι η T είναι γραμμικός ισομορφισμός και υπολογίστε το ίχνος της (δ) Βρείτε όλα τα πολυώνυμα p(x) R n [x] για τα οποία ισχύει T (p(x)) = x n (ε) Υπολογίστε το σταθερό όρο του p(x) R n [x], αν T (p(x)) = 1 + x + + x n 135 Εστω A F p m, θετικός ακέραιος n και η γραμμική απεικόνιση T : F m n F p n η οποία ορίζεται θέτοντας T (X) = AX για X F m n (βλέπε Άσκηση 118) (α) Υπολογίστε τον πίνακα της T ως προς τις συνήθεις βάσεις (κατάλληλα διατεταγμένες) των F m n και F p n (β) Δείξτε ότι rank(t ) = n rank(a) (γ) Συνάγετε ότι η T είναι ισομορφισμός διανυσματικών χώρων αν και μόνο αν p = m και ο πίνακας A είναι αντιστρέψιμος (δ) Αν p = m, δείξτε ότι tr(t ) = n tr(a), όπου με tr(t ) συμβολίζουμε το ίχνος του πίνακα της T ως προς οποιαδήποτε βάση του F m n (βλέπε Άσκηση 146) 32
33 136 Δίνονται πίνακες A F p m και B F n q και η γραμμική απεικόνιση T : F m n F p q η οποία ορίζεται θέτοντας T (X) = AXB για X F m n (α) Δείξτε ότι η απεικόνιση T είναι γραμμική (β) Δείξτε ότι η T είναι ισομορφισμός διανυσματικών χώρων αν και μόνο αν p = m, q = n και οι πίνακες A και B είναι αντιστρέψιμοι (γ) Υπολογίστε τον πίνακα της T ως προς τις συνήθεις βάσεις (κατάλληλα διατεταγμένες) των F m n και F p q (δ) Εστω ότι ισχύουν p = m και q = n Δείξτε ότι tr(t ) = tr(a) tr(b) και ότι det(t ) = (det(a)) n (det(b)) m, όπου με tr(t ) και det(t ) συμβολίζουμε το ίχνος και την ορίζουσα του πίνακα της T ως προς οποιαδήποτε βάση του F m n (βλέπε Άσκηση 146) 137 Συμβολίζουμε με V n τον πραγματικό διανυσματικό χώρο διάστασης 2 n μια βάση του οποίου είναι το σύνολο όλων των υποσυνόλων του συνόλου [n] := {1, 2,, n} Θεωρούμε τη γραμμική απεικόνιση ϕ n : V n V n που ορίζεται θέτοντας ϕ n (S) = T [n] ( 1) S T T για κάθε S [n] Για παράδειγμα, για n = 2 έχουμε ϕ n ({1, 2}) = {1} {2}+{1, 2} Υπολογίστε το ίχνος και την ορίζουσα της ϕ n Συνάγετε ότι η ϕ n είναι αντιστρέψιμη για κάθε θετικό ακέραιο n ( ) Ir O 138 Δίνεται ο πίνακας J r = F O O n n, όπου 0 r n (α) Αν n 2, δείξτε ότι ο πίνακας J r μπορεί να γραφεί ως άθροισμα δύο αντιστρέψιμων πινάκων τα στοιχεία των οποίων ανήκουν στο σύνολο { 1, 0, 1} (β) Συνάγετε από το (α) ότι αν n 2, τότε κάθε πίνακας A F n n μπορεί να γραφεί ως άθροισμα δύο αντιστρέψιμων πινάκων 33
34 139 Εστω επί απεικόνιση f : R n n {0, 1,, n} για την οποία ισχύει f(ab) min {f(a), f(b)} για όλους τους πίνακες A, B R n n Δείξτε ότι f(a) = rank(a) για κάθε A R n n ως εξής: (α) Δείξτε ότι f(p A) = f(ap ) = f(a) για κάθε A R n n και κάθε αντιστρέψιμο πίνακα P R n n (β) Για A R n n δείξτε ότι f(a) = f(j k ), όπου k = rank(a) και J k είναι ο διαγώνιος πίνακας τάξης k με στοιχεία 1,, 1, 0,, 0 στην κύρια διαγώνιο (γ) Δείξτε ότι f(j k ) f(j k+1 ) για k = 0, 1,, n 1 (δ) Συνάγετε ότι f(a) = rank(a) για κάθε A R n n 140 Θεωρούμε γραμμικό μετασχηματισμό T : V V ενός F-διανυσματικού χώρου V και θέτουμε Fix(T ) = {x V : T (x) = x} (α) Δείξτε ότι το Fix(T ) είναι υπόχωρος του V (β) Δείξτε γενικότερα ότι για κάθε λ F, το σύνολο V λ (T ) = {x V : T (x) = λx} είναι υπόχωρος του V (γ) Εστω ότι ο V έχει πεπερασμένη διάσταση Δείξτε ότι Fix(T ) {0} αν και μόνο αν υπάρχει y V τέτοιο ώστε y x T (x) για κάθε x V (δ) Εστω ότι ο V έχει πεπερασμένη διάσταση και έστω k N Δείξτε ότι dim Fix(T ) k αν και μόνο αν υπάρχει διατεταγμένη βάση του V ως προς την οποία ο πίνακας της T έχει τη μορφή ( ) Ik B O C (ε) Ισχύει το (γ) χωρίς την υπόθεση ότι ο V έχει πεπερασμένη διάσταση; 34
35 141 Δίνεται γραμμικός μετασχηματισμός T : V V ενός F-διανυσματικού χώρου V για τον οποίο ισχύει T (T (x)) = T (x) για κάθε x V (α) Δείξτε ότι Im(T ) = Fix(T ) (όπου το Fix(T ) ορίστηκε στην Άσκηση 140) (β) Δείξτε ότι V = ker(t ) Fix(T ) (γ) Εστω ότι ο V έχει πεπερασμένη διάσταση Δείξτε ότι υπάρχει διατεταγμένη βάση του V ως προς την οποία ο πίνακας της T έχει τη μορφή ( ) Ir O O O 142 Δίνεται γραμμικός μετασχηματισμός T : V V ενός F-διανυσματικού χώρου V για τον οποίο ισχύει T (T (x)) = x για κάθε x V (α) Δείξτε ότι ο T είναι γραμμικός ισομορφισμός (β) Θεωρούμε τους υπόχωρους Fix(T ) και U = {x V : T (x) = x} του V που ορίστηκαν στην Άσκηση 140 Δείξτε ότι x + T (x) Fix(T ) και x T (x) U για κάθε x V Υποθέτουμε τώρα ότι ισχύει 1 1 στο F (δηλαδή ότι η χαρακτηριστική του F είναι διάφορη του 2) (γ) Δείξτε ότι V = Fix(T ) U (δ) Εστω ότι ο V έχει πεπερασμένη διάσταση n Δείξτε ότι υπάρχει διατεταγμένη βάση του V ως προς την οποία ο πίνακας της T έχει τη μορφή ( ) Ik O O I n k 35
36 143 Δίνεται γραμμικός μετασχηματισμός T : V V ενός R-διανυσματικού χώρου V για τον οποίο ισχύει T (T (x)) = x για κάθε x V (α) Δείξτε ότι ο T είναι γραμμικός ισομορφισμός (β) Δείξτε ότι για κάθε μη μηδενικό διάνυσμα x V, τα διανύσματα x και T (x) είναι γραμμικώς ανεξάρτητα Υποθέτουμε τώρα ότι ο V έχει πεπερασμένη διάσταση n (γ) Δείξτε ότι υπάρχει βάση του V της μορφής {u 1,, u m } {T (u 1 ),, T (u m )} και συνάγετε ότι ο n είναι άρτιος ακέραιος (δ) Δείξτε ότι υπάρχει διατεταγμένη βάση του V ως προς την οποία ο πίνακας της T έχει τη μορφή ( ) O Im O I m 144 Εστω F-διανυσματικός χώρος V διάστασης n και γραμμική απεικόνιση T : V V Εστω επίσης W m = Im(T m ) για θετικούς ακεραίους m (α) Δείξτε ότι αν ισχύουν T m = O για κάποιο θετικό ακέραιο m και W i {0}, τότε dim(w i+1 ) < dim(w i ) (β) Δείξτε ότι υπάρχει θετικός ακέραιος m, τέτοιος ώστε T m = O αν και μόνο αν υπάρχει βάση του V ως προς την οποία ο πίνακας της T είναι άνω τριγωνικός και κάθε στοιχείο στην κύρια διαγώνιό του είναι ίσο με μηδέν (γ) Δείξτε ότι αν T n = O και T n 1 O, τότε υπάρχει βάση του V ως προς την οποία ο πίνακας της T είναι ίσος με (δ) Δείξτε ότι αν T m = O για κάποιο θετικό ακέραιο m, τότε T n = O 36
37 Ομοιότητα Πινάκων Υπενθυμίζουμε ότι δύο πίνακες A, B F n n λέγονται όμοιοι αν υπάρχει αντιστρέψιμος πίνακας P F n n, τέτοιος ώστε B = P 1 AP 145 Δίνεται πίνακας A F n n (α) Εστω ότι A = λi για κάποιο λ F Δείξτε ότι αν B F n n είναι πίνακας όμοιος με τον A, τότε B = A (β) Εστω ότι A λi για κάθε λ F Δείξτε ότι υπάρχει πίνακας B F n n διάφορος του A, ο οποίος είναι όμοιος με τον A 146 Δίνονται όμοιοι πίνακες A, B F n n (α) Δείξτε ότι tr(a) = tr(b), ότι det(a) = det(b) και ότι rank(a) = rank(b) (β) Δείξτε ότι οι πίνακες A m και B m είναι όμοιοι για κάθε m N (γ) Δείξτε ότι οι πίνακες φ(a) και φ(b) είναι όμοιοι για κάθε πολυώνυμο φ(x) F[x] (δ) Εστω n 2 και C, D R n n Αν για κάθε ακέραιο m 2 οι πίνακες C m και D m είναι όμοιοι, είναι υποχρεωτικά οι C και D όμοιοι; 147 Δίνεται ο πίνακας C = Fn n, όπου n 2 (α) Δείξτε ότι αν ο πίνακας A F n n είναι όμοιος με τον C, τότε A 2 = O και A O (β) Για n = 2, δείξτε ότι κάθε μη μηδενικός πίνακας A F 2 2 με A 2 = O είναι όμοιος με τον C (γ) Για n = 3, δείξτε ότι κάθε μη μηδενικός πίνακας A F 3 3 με A 2 = O είναι όμοιος με τον C (δ) Ισχύει το ίδιο για n = 4; 148 Να εξετάσετε αν είναι όμοιοι οι ακόλουθοι πίνακες: (α) F4 4 και F
38 (β) F4 4 και F4 4 ( Ir O 149 Δίνονται ακέραιοι 0 r n και ο πίνακας J r = O O ) F n n (α) Δείξτε ότι για κάθε πίνακα A F n n που είναι όμοιος με τον J r ισχύει A 2 = A (β) Δείξτε ότι αν για τον πίνακα A F n n ισχύει A 2 = A, τότε ο A είναι όμοιος με τον J r όπου r = rank(a) ( Ik O 150 Δίνονται ακέραιοι 0 k n και ο πίνακας J k = O I n k ) F n n (α) Δείξτε ότι για κάθε πίνακα A F n n που είναι όμοιος με τον J k ισχύει A 2 = I (β) Δείξτε ότι αν για τον πίνακα A F n n έχουμε A 2 = I και ισχύει 1 1 στο F, τότε ο A είναι όμοιος με τον J k για κάποια τιμή του k (γ) Αληθεύει το (β) χωρίς την υπόθεση ότι ισχύει 1 1 στο F; ( O Im 151 Δίνεται ο πίνακας J m = O I m ) F 2m 2m (α) Δείξτε ότι για κάθε πίνακα A F 2m 2m που είναι όμοιος με τον J m ισχύει A 2 = I (β) Δείξτε ότι αν για τον πίνακα A F n n ισχύει A 2 = I, τότε ο n είναι άρτιος και ο A είναι όμοιος με τον πίνακα J m για m = n/2 152 Εστω 1 λ λ 0 A n (λ) = F n n λ για λ F Δείξτε ότι οι πίνακες A n (λ) και A n (µ) είναι όμοιοι για τυχαία μη μηδενικά στοιχεία λ, µ F 38
39 Χαρακτηριστικό Πολυώνυμο Γράφουμε χ A (x) = det(a xi) για το χαρακτηριστικό πολυώνυμο ενός τετραγωνικού πίνακα A 153 Εστω ο n n πίνακας A n = , όπου n 2 (α) Υπολογίστε το χαρακτηριστικό πολυώνυμο του A n (β) Για ποιες τιμές του n είναι ο A n αντιστρέψιμος; 154 Εστω θετικοί ακέραιοι p, q Συμβολίζουμε με J τον πίνακα καταλλήλων διαστάσεων, κάθε στοιχείο του οποίου είναι ίσο με 1 Υπολογίστε το χαρακτηριστικό πολυώνυμο: (α) του p p πίνακα J + qi p, ( qip J (β) του (p + q) (p + q) πίνακα J pi q ) 155 Εστω αντιστρέψιμος πίνακας A F n n με χ A (x) = (λ 1 x)(λ 2 x) (λ n x), για κάποια λ i F (α) Δείξτε ότι λ i 0 για κάθε δείκτη i και ότι χ A 1(x) = ( 1 λ 1 x)( 1 λ 2 x) ( 1 λ n x) (β) Αν ο A είναι όμοιος με τον A 1 και ο n είναι περιττός, δείξτε ότι λ i { 1, 1} για έναν τουλάχιστον δείκτη 1 i n 156 Για πίνακες A F m n και B F n m δείξτε ότι x n det(xi m AB) = x m det(xi n BA) 39
40 157 Εστω πίνακας A F n n τα στοιχεία κάθε γραμμής και κάθε στήλης του οποίου έχουν άθροισμα μηδέν Αν A ij είναι ο πίνακας που προκύπτει από τον A διαγράφοντας την i γραμμή και τη j στήλη και χ A (x) = n i=0 c i x i, δείξτε ότι c 1 = ( 1) i+j 1 n det(a ij ) Συνάγετε ότι η απόλυτη τιμή της det(a ij ) είναι ανεξάρτητη των i και j 158 Εστω F-διανυσματικοί χώροι V 0, V 1,, V m, V m+1 με V 0 = V m+1 = {0} και γραμμικές απεικονίσεις f i : V i V i+1 για 0 i m, τέτοιες ώστε ker f i = Im f i 1 για κάθε 1 i m Εστω γραμμικοί ενδομορφισμοί T i : V i V i για 1 i m, τέτοιοι ώστε T i+1 f i = f i T i για 1 i m 1 Αν p i (x) είναι το χαρακτηριστικό πολυώνυμο του T i : V i V i για 1 i m, δείξτε ότι p 1 (x) p 3 (x) = p 2 (x) p 4 (x) για m = 2, για m = 3, για τυχαίο θετικό ακέραιο m Συνάγετε από τα παραπάνω το ζητούμενο της Άσκησης Εστω ένα άπειρο σώμα F και A F n n Αν ο πίνακας (A+B) 2 είναι συμμετρικός για κάθε συμμετρικό πίνακα B F n n για τον οποίο ο A+B είναι αντιστρέψιμος, δείξτε ότι ο A είναι συμμετρικός πίνακας 160 Δείξτε ότι: (α) Κάθε 2 2 πίνακας με στοιχεία πραγματικούς αριθμούς μπορεί να γραφεί στη μορφή B 2 + ci, με B R 2 2 και c R (β) Κάθε 2 2 πίνακας με στοιχεία πραγματικούς αριθμούς μπορεί να γραφεί στη μορφή B 2 + C 2, με B, C R 2 2 (γ) Για κάθε θετικό ακέραιο n υπάρχει n n πίνακας με στοιχεία πραγματικούς αριθμούς ο οποίος δεν μπορεί να γραφεί στη μορφή B 2 + C 2, όπου B, C R n n είναι πίνακες με BC = CB 40
= k. n! k! (n k)!, k=0
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n τον n n ταυτοτικό πίνακα,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n τον n n ταυτοτικό πίνακα,
( A = A = 3 5 A 2 + B 2.
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
1 1 A = x 1 x 2 x 3. x 4. R 2 3 : a + b + c = x + y + z = 0. R 2 3 : a + x = b + y = c + z = 0
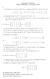 Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
ΜΑΣ121: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο , Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: 2 ώρες 18 Νοεμβρίου, 2017
 ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.
![b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0. b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.](/thumbs/63/49387122.jpg) Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2018/lai2018html Παρασκευή 12 Οκτωβρίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai2018/lai2018html Παρασκευή 12 Οκτωβρίου
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]
![1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x] 1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]](/thumbs/77/75945202.jpg) σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
Ασκήσεις2 8. ; Αληθεύει ότι το (1, 0, 1, 2) είναι ιδιοδιάνυσμα της f ; b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα της γραμμικής απεικόνισης 3 3
 Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Γραμμική Άλγεβρα II Εαρινό εξάμηνο
 Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
Γραµµικη Αλγεβρα Ι. Ακαδηµαϊκο Ετος Βοηθος Ασκησεων: Χ. Ψαρουδάκης
 Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων
 Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
Λύσεις και Υποδείξεις Επιλεγµένων Ασκήσεων 11 1 i) ii) 1 1 1 0 1 1 0 0 0 x = 0 x +x 4 +x 5 = x = 1 Λύνοντας ως προς x και στη συνέχεια ως προς x 4, ϐρίσκουµε ότι η γενική λύση του συστήµατος είναι η 5άδα
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 19/6/2018 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Αλγεβρικές Δομές Ι. 1 Ομάδα I
 Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
Αλγεβρικές Δομές Ι 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω G μια προσθετική ομάδα S ένα μη κενό σύνολο και M(S G το σύνολο όλων των συναρτήσεων f : S G. Δείξτε ότι το σύνολο M(S G είναι ομάδα με πράξη την πρόσθεση
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
1. Για καθένα από τους ακόλουθους διανυσματικούς χώρους βρείτε μια βάση και τη διάσταση. 3. U x y z x y z x y. {(,, ) } a b. c d
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
βαθμού 1 με A 2. Υπολογίστε τα χαρακτηριστικά και ελάχιστα πολυώνυμα των
 Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Ορισμός ελαχίστου πολυωνύμου γραμμικής απεικόνισης και ιδιότητές του Κριτήριο διαγωνισιμότητας
Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Ορισμός ελαχίστου πολυωνύμου γραμμικής απεικόνισης και ιδιότητές του Κριτήριο διαγωνισιμότητας
2 3x 5x x
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ ΚΑΤΕΥΘΥΝΣΗ ΣΤΑΤΙΣΤΙΚΗ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΑΣΚΗΣΕΙΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Ι ΙΩΑΝΝΗΣ Σ ΣΤΑΜΑΤΙΟΥ ΣΑΜΟΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕ ΚΑΤΕΥΘΥΝΣΗ ΣΤΑΤΙΣΤΙΚΗ ΚΑΙ ΧΡΗΜΑΤΟΟΙΚΟΝΟΜΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΑΣΚΗΣΕΙΣ ΕΦΑΡΜΟΣΜΕΝΗΣ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Ι ΙΩΑΝΝΗΣ Σ ΣΤΑΜΑΤΙΟΥ ΣΑΜΟΣ ΧΕΙΜΕΡΙΝΟ ΕΞΑΜΗΝΟ
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί
 Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Γραμμική Άλγεβρα Ι,
 Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Διανύσµατα στο επίπεδο
 Διανύσµατα στο επίπεδο Ένα διάνυσµα v έχει αρχικό και τελικό σηµείο. Χαρακτηρίζεται από: διεύθυνση (ευθεία επί της οποίας κείται φορά (προς ποια κατεύθυνση της ευθείας δείχνει µέτρο (το µήκος του, v ή
Διανύσµατα στο επίπεδο Ένα διάνυσµα v έχει αρχικό και τελικό σηµείο. Χαρακτηρίζεται από: διεύθυνση (ευθεία επί της οποίας κείται φορά (προς ποια κατεύθυνση της ευθείας δείχνει µέτρο (το µήκος του, v ή
Αλγεβρικές Δομές ΙΙ. 1 Ομάδα I. Ά σ κ η σ η 1.1 Έστω R ένας δακτύλιος. Δείξτε ότι το σύνολο
 Αλγεβρικές Δομές ΙΙ 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω R ένας δακτύλιος. Δείξτε ότι το σύνολο C(R) = {a R/ax = xa, για κάθε x R} είναι υποδακτύλιος του R, και λέγεται κέντρο του δακτυλίου R. Ά σ κ η σ η 1.2
Αλγεβρικές Δομές ΙΙ 1 Ομάδα I Ά σ κ η σ η 1.1 Έστω R ένας δακτύλιος. Δείξτε ότι το σύνολο C(R) = {a R/ax = xa, για κάθε x R} είναι υποδακτύλιος του R, και λέγεται κέντρο του δακτυλίου R. Ά σ κ η σ η 1.2
Γραμμική Άλγεβρα II. Ασκήσεις με Υποδείξεις - Απαντήσεις. Περιεχόμενα
 Γραμμική Άλγεβρα II Ασκήσεις με Υποδείξεις - Απαντήσεις ΜΜ Περιεχόμενα Ασκήσεις0: Όμοιοι Πίνακες Ασκήσεις: Πολυώνυμα 6 Ασκήσεις: Ιδιοτιμές και Ιδιοδιανύσματα Ασκήσεις: Διαγωνισιμότητα Ασκήσεις4: Τριγωνισιμότητα
Γραμμική Άλγεβρα II Ασκήσεις με Υποδείξεις - Απαντήσεις ΜΜ Περιεχόμενα Ασκήσεις0: Όμοιοι Πίνακες Ασκήσεις: Πολυώνυμα 6 Ασκήσεις: Ιδιοτιμές και Ιδιοδιανύσματα Ασκήσεις: Διαγωνισιμότητα Ασκήσεις4: Τριγωνισιμότητα
Κεφάλαιο 2 Πίνακες - Ορίζουσες
 Κεφάλαιο Πίνακες - Ορίζουσες Βασικοί ορισμοί και πίνακες Πίνακες Παραδείγματα: Ο πίνακας πωλήσεων ανά τρίμηνο μίας εταιρείας για τρία είδη που εμπορεύεται: ο Τρίμηνο ο Τρίμηνο 3 ο Τρίμηνο ο Τρίμηνο Είδος
Κεφάλαιο Πίνακες - Ορίζουσες Βασικοί ορισμοί και πίνακες Πίνακες Παραδείγματα: Ο πίνακας πωλήσεων ανά τρίμηνο μίας εταιρείας για τρία είδη που εμπορεύεται: ο Τρίμηνο ο Τρίμηνο 3 ο Τρίμηνο ο Τρίμηνο Είδος
ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ. Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες,
 ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες, παριστάνεται με την εξής ορθογώνια διάταξη: α11 α12 α1n α21 α22 α2n A = αm1 αm2 αmn Ορισμός 2: Δύο πίνακες Α και Β είναι ίσοι, και γράφουμε
ΘΕΩΡΙΑ ΠΙΝΑΚΩΝ Ορισμός 1: Ένας πίνακας Α με m γραμμές και n στήλες, παριστάνεται με την εξής ορθογώνια διάταξη: α11 α12 α1n α21 α22 α2n A = αm1 αm2 αmn Ορισμός 2: Δύο πίνακες Α και Β είναι ίσοι, και γράφουμε
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
Κεφάλαιο 6 Ιδιοτιμές και Ιδιοδιανύσματα
 Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
A, και εξετάστε αν είναι διαγωνίσιμη.
 Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Θεώρημα (Κριτήριο διαγωνισιμότητας) Ένας είναι διαγωνίσιμος αν και μόνο αν ( x) γινόμενο διακεκριμένων
Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Θεώρημα (Κριτήριο διαγωνισιμότητας) Ένας είναι διαγωνίσιμος αν και μόνο αν ( x) γινόμενο διακεκριμένων
1 Ορίζουσες. Άσκηση 1.1 Θεωρούμε τον πίνακα. 1 x x x x 1 x x x x 1 x x x x 1 A =
 1 Ορίζουσες Άσκηση 1.1 Θεωρούμε τον πίνακα 1 x x x x 1 x x x x 1 x x x x 1, όπου x είναι τυχόν στοιχείο του σώματος R. Να βρεθούν όλες οι τιμές του x για τις οποίες ο πίνακας A δεν είναι αντιστρέψιμος.
1 Ορίζουσες Άσκηση 1.1 Θεωρούμε τον πίνακα 1 x x x x 1 x x x x 1 x x x x 1, όπου x είναι τυχόν στοιχείο του σώματος R. Να βρεθούν όλες οι τιμές του x για τις οποίες ο πίνακας A δεν είναι αντιστρέψιμος.
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii2018/laii2018.html Παρασκευή 23 Μαρτίου 2018
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii2018/laii2018.html Παρασκευή 23 Μαρτίου 2018
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
Κεφάλαιο 7 Βάσεις και ιάσταση
 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1. Τελεστές και πίνακες. 1. Τελεστές και πίνακες Γενικά. Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο.
 ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
ΤΕΤΥ Εφαρμοσμένα Μαθηματικά 1 Τελεστές και πίνακες 1. Τελεστές και πίνακες Γενικά Τι είναι συνάρτηση? Απεικόνιση ενός αριθμού σε έναν άλλο. Ανάλογα, τελεστής είναι η απεικόνιση ενός διανύσματος σε ένα
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - 02/07/08) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
 Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών «Γραµµική Άλγεβρα Ι» (ΕΜ111) Χειµερινό Εξάµηνο 2006-2007, ιδάσκων: Ι. Τσαγράκης 5 Ο ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Έστω V ένας διανυσµατικός χώρος επί
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών «Γραµµική Άλγεβρα Ι» (ΕΜ111) Χειµερινό Εξάµηνο 2006-2007, ιδάσκων: Ι. Τσαγράκης 5 Ο ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Έστω V ένας διανυσµατικός χώρος επί
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 2 η Ημερομηνία Αποστολής στον Φοιτητή: 28 Νοεμβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Ασκήσεις4 48. P AP τριγωνικό. Αφού δείξτε ότι ο A δεν είναι διαγωνίσιμος, βρείτε αντιστρέψιμο A 1 3 1
 Ασκήσεις4 48 Ασκήσεις4 Τριγωνισιμότητα Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Θεώρημα: είναι τριγωνίσιμος αν και μόνο αν ( x ) γινόμενο πρωτοβάθμιων παραγόντων
Ασκήσεις4 48 Ασκήσεις4 Τριγωνισιμότητα Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Θεώρημα: είναι τριγωνίσιμος αν και μόνο αν ( x ) γινόμενο πρωτοβάθμιων παραγόντων
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 3 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2018/laii2018html Παρασκευή 23 Μαρτίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 3 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2018/laii2018html Παρασκευή 23 Μαρτίου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
ΚΕΦΑΛΑΙΟ 1: Πρότυπα. x y x z για κάθε x, y, R με την ιδιότητα 1R. x για κάθε x R, iii) υπάρχει στοιχείο 1 R. ii) ( x y) z x ( y z)
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai208/lai208html Παρασκευή 2 Οκτωβρίου 208 Ασκηση Να γράψετε
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai208/lai208html Παρασκευή 2 Οκτωβρίου 208 Ασκηση Να γράψετε
t t Αν κάποιος από αυτούς είναι αντιστρέψιμος, υπολογίστε τον αντίστροφό του. 2. Υπολογίστε την ορίζουσα του Δείξτε τα εξής.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις4: Ορίζουσες Βασικά σημεία Ορισμός και ιδιότητες οριζουσών (ιδιότητες γραμμών και στηλών, αναπτύγματα οριζουσών, det( B) det( )det( B)) Ένας τετραγωνικός πίνακας είναι
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις4: Ορίζουσες Βασικά σημεία Ορισμός και ιδιότητες οριζουσών (ιδιότητες γραμμών και στηλών, αναπτύγματα οριζουσών, det( B) det( )det( B)) Ένας τετραγωνικός πίνακας είναι
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2019/laii2019html Παρασκευή 1 Μαρτίου 2019 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2019/laii2019html Παρασκευή 1 Μαρτίου 2019 Ασκηση
Κεφάλαιο 1 Πρότυπα. Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο.
 Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii8/laii8html Παρασκευή 4 Ιουνίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii8/laii8html Παρασκευή 4 Ιουνίου
Εάν A = τότε ορίζουμε την ορίζουσα του πίνακα ως τον αριθμό. det( A) = = ( 2)4 3 1 = 8 3 = 11. τότε η ορίζουσά του πίνακα ισούται με
 Κεφάλαιο Ορίζουσες Βασικοί ορισμοί a b Εάν A τότε ορίζουμε την ορίζουσα του πίνακα ως τον αριθμό a b ad bc Συμβολίζουμε την ορίζουσα του πίνακα και ως A Εάν A τότε ( ) 8 Εάν a a a A a a a a a a τότε η
Κεφάλαιο Ορίζουσες Βασικοί ορισμοί a b Εάν A τότε ορίζουμε την ορίζουσα του πίνακα ως τον αριθμό a b ad bc Συμβολίζουμε την ορίζουσα του πίνακα και ως A Εάν A τότε ( ) 8 Εάν a a a A a a a a a a τότε η
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 2004 Θέμα 1 ο. 4
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 00 Θέμα 1 ο Έστω U ο υπόχωρος του που παράγεται από τα στοιχεία (1-11α) (10β) (5-γ) και (-δ) (I) Να προσδιορίσετε τις αναγκαίες
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 00 Θέμα 1 ο Έστω U ο υπόχωρος του που παράγεται από τα στοιχεία (1-11α) (10β) (5-γ) και (-δ) (I) Να προσδιορίσετε τις αναγκαίες
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος
 6/6/06 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 0 Δίνεται ο πίνακας A =. Nα υπολογίσετε την βαθμίδα του και να βρείτε τη διάσταση και από μία βάση α) του μηδενοχώρου
6/6/06 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 0 Δίνεται ο πίνακας A =. Nα υπολογίσετε την βαθμίδα του και να βρείτε τη διάσταση και από μία βάση α) του μηδενοχώρου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2019/laii2019html Παρασκευή 1 Μαρτίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2019/laii2019html Παρασκευή 1 Μαρτίου
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας.
 Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai218/lai218html Παρασκευή 23 Νοεµβρίου 218 Ασκηση 1
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai218/lai218html Παρασκευή 23 Νοεµβρίου 218 Ασκηση 1
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 7
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 7 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebrai/lai2018/lai2018.html Παρασκευή 14 εκεµβρίου 2018 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 7 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebrai/lai2018/lai2018.html Παρασκευή 14 εκεµβρίου 2018 Ασκηση
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Copyright: Ψωμόπουλος Ευάγγελος, Eκδόσεις Zήτη, Γ έκδοση: Μάρτιος 2012, Θεσσαλονίκη
 Kάθε γνήσιο αντίτυπο φέρει την υπογραφή του συγγραφέα ISBN 978-960-456-314-2 Copyright: Ψωμόπουλος Ευάγγελος, Eκδόσεις Zήτη, Γ έκδοση: Μάρτιος 2012, Θεσσαλονίκη Tο παρόν έργο πνευματικής ιδιοκτησίας προστατεύεται
Kάθε γνήσιο αντίτυπο φέρει την υπογραφή του συγγραφέα ISBN 978-960-456-314-2 Copyright: Ψωμόπουλος Ευάγγελος, Eκδόσεις Zήτη, Γ έκδοση: Μάρτιος 2012, Θεσσαλονίκη Tο παρόν έργο πνευματικής ιδιοκτησίας προστατεύεται
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
(a + b) n = a k b n k, k. (a + b) p = a p + b p. k=0. n! k! (n k)! k =
 ΒΑΣΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2016 Χρήστος Α. Αθανασιάδης Συμβολίζουμε με Z m το δακτύλιο των ακεραίων modulo m, με ā Z m την κλάση (mod m) του a Z και με M n (R) το δακτύλιο
ΒΑΣΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2016 Χρήστος Α. Αθανασιάδης Συμβολίζουμε με Z m το δακτύλιο των ακεραίων modulo m, με ā Z m την κλάση (mod m) του a Z και με M n (R) το δακτύλιο
[A I 3 ] [I 3 A 1 ].
![[A I 3 ] [I 3 A 1 ]. [A I 3 ] [I 3 A 1 ].](/thumbs/65/54189091.jpg) ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΤΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΣΕΠΤΕΜΒΡΙΟΥ 9 (α) Να ϐρεθεί ο αντίστροφος του πίνακα A = 6 4 (ϐ) Εστω b, b, b στο R Να λύθεί το σύστηµα x = b 6x + x + x = b x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΤΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΣΕΠΤΕΜΒΡΙΟΥ 9 (α) Να ϐρεθεί ο αντίστροφος του πίνακα A = 6 4 (ϐ) Εστω b, b, b στο R Να λύθεί το σύστηµα x = b 6x + x + x = b x
7 ΑΛΓΕΒΡΑ ΜΗΤΡΩΝ. 7.2 ΜΗΤΡΕΣ ΕΙΔΙΚΗΣ ΜΟΡΦΗΣ (Ι)
 77 78 7 ΑΛΓΕΒΡΑ ΜΗΤΡΩΝ. 7. ΕΙΣΑΓΩΓΗ Η Άλγεβρα των μητρών οι πινάκων είναι ιδιαίτερα χρήσιμη για την επίλυση συστημάτων καθώς επίσης στις επιστήμες της οικονομετρίας και της στατιστικής. ΟΡΙΣΜΟΣ: Μήτρα
77 78 7 ΑΛΓΕΒΡΑ ΜΗΤΡΩΝ. 7. ΕΙΣΑΓΩΓΗ Η Άλγεβρα των μητρών οι πινάκων είναι ιδιαίτερα χρήσιμη για την επίλυση συστημάτων καθώς επίσης στις επιστήμες της οικονομετρίας και της στατιστικής. ΟΡΙΣΜΟΣ: Μήτρα
Ασκήσεις1 Πολυώνυμα. x x c. με το. b. Να βρεθούν όλες οι τιμές των a, Να βρεθεί ο μκδ και το εκπ τους
 Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑ ΠΙΝΑΚΩΝ. (ii) Αν ο Β m+1, με m N, αντιστρέφεται, τότε και ο Β αντιστρέφεται
 ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑ ΠΙΝΑΚΩΝ 1) Έστω A, Β Μ n (R) τέτοιοι, ώστε A + Β = Ι n. Να δείξετε ότι : A = A 2 κκκ Β = Β 2 ΑΑ = Ο 2) Έστω A, Β Μ n (R), με A = A 2 και ΑΑ + ΒΒ = Ο. Να δειχθεί ότι ΑΑ = ΒΒ
ΕΝΔΕΙΚΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑ ΠΙΝΑΚΩΝ 1) Έστω A, Β Μ n (R) τέτοιοι, ώστε A + Β = Ι n. Να δείξετε ότι : A = A 2 κκκ Β = Β 2 ΑΑ = Ο 2) Έστω A, Β Μ n (R), με A = A 2 και ΑΑ + ΒΒ = Ο. Να δειχθεί ότι ΑΑ = ΒΒ
Εφαρμοσμένα Μαθηματικά ΙΙ 10ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί Επιμέλεια: Ι. Λυχναρόπουλος. Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f b) f : R R f y, ( +, y
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί Επιμέλεια: Ι. Λυχναρόπουλος. Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f b) f : R R f y, ( +, y
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii18/laii18html Παρασκευή 9 Μαρτίου 18 Ασκηση 1 Θεωρούµε
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii18/laii18html Παρασκευή 9 Μαρτίου 18 Ασκηση 1 Θεωρούµε
Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων
 7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai217/lai217html Παρασκευή 17 Νοεµβρίου 217 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai217/lai217html Παρασκευή 17 Νοεµβρίου 217 Ασκηση
ΚΕΦΑΛΑΙΟ 2. Γραμμικοί Κώδικες. 2.1 Η έννοια του Γραμμικού κώδικα
 ΚΕΦΑΛΑΙΟ 2 Γραμμικοί Κώδικες 2.1 Η έννοια του Γραμμικού κώδικα Μέχρι τώρα θεωρούσαμε έναν κώδικα C με παραμέτρους (n, M, d) απλώς ως ένα υποσύνολο του συνόλου A n, όπου A είναι ένα αλφάβητο. Είχαμε, όμως,
ΚΕΦΑΛΑΙΟ 2 Γραμμικοί Κώδικες 2.1 Η έννοια του Γραμμικού κώδικα Μέχρι τώρα θεωρούσαμε έναν κώδικα C με παραμέτρους (n, M, d) απλώς ως ένα υποσύνολο του συνόλου A n, όπου A είναι ένα αλφάβητο. Είχαμε, όμως,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2018/laii2018html Παρασκευή 9 Μαρτίου 2018 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 1 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2018/laii2018html Παρασκευή 9 Μαρτίου 2018 Ασκηση
Gauss. x + y + z = 2 3x + 3y z = 6 x y + z = 1. x + y + z = r x y = 0 3x + y + sz = s 0
 Γραμμική Άλγεβρα Κεφάλαιο Πίνακες και απαλοιφή Gauss. Ποια συνθήκη πρέπει να ικανοποιούν τα y, y 2, y 3 ώστε τα διανύσματα (0, y ), (, y 2 ), (2, y 3 ) να είναι στην ίδια ευθεία; Η ευθεία που περνάει από
Γραμμική Άλγεβρα Κεφάλαιο Πίνακες και απαλοιφή Gauss. Ποια συνθήκη πρέπει να ικανοποιούν τα y, y 2, y 3 ώστε τα διανύσματα (0, y ), (, y 2 ), (2, y 3 ) να είναι στην ίδια ευθεία; Η ευθεία που περνάει από
1 x x x x 1 x x x x 1 x x x x 1 (10) B 2, B 1. (10)
 Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
Δακτύλιοι και Πρότυπα Ασκήσεις 3. Στις παρακάτω ασκήσεις κάθε δακτύλιος είναι μη τετριμμένος μεταθετικός δακτύλιος. N ( a)
 11 Δακτύλιοι και Πρότυπα 2016-17 Ασκήσεις 3 Η ύλη των ασκήσεων αυτών είναι η Ενότητα3, Ελεύθερα πρότυπα Στις παρακάτω ασκήσεις κάθε δακτύλιος είναι μη τετριμμένος μεταθετικός δακτύλιος 1 Δείξτε ότι το
11 Δακτύλιοι και Πρότυπα 2016-17 Ασκήσεις 3 Η ύλη των ασκήσεων αυτών είναι η Ενότητα3, Ελεύθερα πρότυπα Στις παρακάτω ασκήσεις κάθε δακτύλιος είναι μη τετριμμένος μεταθετικός δακτύλιος 1 Δείξτε ότι το
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικοί Μετασχηματισμοί Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικοί Μετασχηματισμοί Γραμμικός Μετασχηματισμός ή
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: Οκτωβρίου 005) Η Άσκηση στην εργασία αυτή είναι
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: Οκτωβρίου 005) Η Άσκηση στην εργασία αυτή είναι
x 2 = b 1 2x 1 + 4x 2 + x 3 = b 2. x 1 + 2x 2 + x 3 = b 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].
![D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ]. D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].](/thumbs/60/44272313.jpg) 4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 4 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebrai/lai2018/lai2018.html Παρασκευή 23 Νοεµβρίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 4 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebrai/lai2018/lai2018.html Παρασκευή 23 Νοεµβρίου
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Εφαρμοσμένη Θεωρία Πινάκων. Quiz 3. Σύντομες Λύσεις
 Τμήμα Μηχανικών Οικονομίας και Διοίκησης Εφαρμοσμένη Θεωρία Πινάκων Γ. Καραγιώργος ykarag@aegean.gr Quiz Σύντομες Λύσεις Άσκηση. Δείξτε ότι η απεικόνιση u, v = u v + 5u v, όπου u = (u, u ), v = (v, v ),
Τμήμα Μηχανικών Οικονομίας και Διοίκησης Εφαρμοσμένη Θεωρία Πινάκων Γ. Καραγιώργος ykarag@aegean.gr Quiz Σύντομες Λύσεις Άσκηση. Δείξτε ότι η απεικόνιση u, v = u v + 5u v, όπου u = (u, u ), v = (v, v ),
 Μαρινα Μπομπολακη Κανονικη Μορϕη Jordan Πτυχιακη Εργασια Πανεπιστήμιο Αιγαίου, Τμήμα Μαθηματικών Σάμος Μαρτίου 27 Εισηγητης: Ευστράτιος Πρασίδης Επιτροπη Βασίλειος Μεταϕτσής Νικόλαος Παπαλεξίου Θα ήθελα
Μαρινα Μπομπολακη Κανονικη Μορϕη Jordan Πτυχιακη Εργασια Πανεπιστήμιο Αιγαίου, Τμήμα Μαθηματικών Σάμος Μαρτίου 27 Εισηγητης: Ευστράτιος Πρασίδης Επιτροπη Βασίλειος Μεταϕτσής Νικόλαος Παπαλεξίου Θα ήθελα
Έντυπο Yποβολής Αξιολόγησης ΓΕ
 Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
, 1 0 9 1, 2. A a και το στοιχείο της i γραμμής και j
 Κεφάλαιο Πίνακες Βασικοί ορισμοί και πίνακες Πίνακες Παραδείγματα: Ο πίνακας πωλήσεων ανά τρίμηνο μίας εταιρείας για τρία είδη που εμπορεύεται: ο Τρίμηνο ο Τρίμηνο ο Τρίμηνο ο Τρίμηνο Είδος Α 56 Είδος
Κεφάλαιο Πίνακες Βασικοί ορισμοί και πίνακες Πίνακες Παραδείγματα: Ο πίνακας πωλήσεων ανά τρίμηνο μίας εταιρείας για τρία είδη που εμπορεύεται: ο Τρίμηνο ο Τρίμηνο ο Τρίμηνο ο Τρίμηνο Είδος Α 56 Είδος
Κεφάλαιο 9 1 Ιδιοτιμές και Ιδιοδιανύσματα
 Σελίδα από 58 Κεφάλαιο 9 Ιδιοτιμές και Ιδιοδιανύσματα 9. Ορισμοί... 9. Ιδιότητες... 9. Θεώρημα Cayley-Hamlto...9 9.. Εφαρμογές του Θεωρήματος Cayley-Hamlto... 9.4 Ελάχιστο Πολυώνυμο...40 Ασκήσεις του Κεφαλαίου
Σελίδα από 58 Κεφάλαιο 9 Ιδιοτιμές και Ιδιοδιανύσματα 9. Ορισμοί... 9. Ιδιότητες... 9. Θεώρημα Cayley-Hamlto...9 9.. Εφαρμογές του Θεωρήματος Cayley-Hamlto... 9.4 Ελάχιστο Πολυώνυμο...40 Ασκήσεις του Κεφαλαίου
Κεφάλαιο 3 ΣΤΟΙΧΕΙΑ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ
 Κεφάλαιο 3 ΣΤΟΙΧΕΙΑ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Στο πρώτο μέρος αυτού του κεφαλαίου συνοψίζουμε όσα είναι απαραίτητα για την εύρεση ιδιοτιμών και ιδιοδιανυσμάτων ενός τετραγωνικού πίνακα Στο δεύτερο μέρος αναπτύσσονται
Κεφάλαιο 3 ΣΤΟΙΧΕΙΑ ΓΡΑΜΜΙΚΗΣ ΑΛΓΕΒΡΑΣ Στο πρώτο μέρος αυτού του κεφαλαίου συνοψίζουμε όσα είναι απαραίτητα για την εύρεση ιδιοτιμών και ιδιοδιανυσμάτων ενός τετραγωνικού πίνακα Στο δεύτερο μέρος αναπτύσσονται
ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ
 ΤΜΗΜΑ ΔΙΕΘΝΟΥΣ ΕΜΠΟΡΙΟΥ ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΑ: ) ΠΙΝΑΚΕΣ ) ΟΡΙΖΟΥΣΕΣ ) ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4) ΠΑΡΑΓΩΓΟΙ ΜΑΡΙΑ ΡΟΥΣΟΥΛΗ ΚΕΦΑΛΑΙΟ ΠΙΝΑΚEΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΟΡΙΣΜΟΣ Πίνακας
ΤΜΗΜΑ ΔΙΕΘΝΟΥΣ ΕΜΠΟΡΙΟΥ ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΣΤΑ ΓΕΝΙΚΑ ΜΑΘΗΜΑΤΙΚΑ ΚΕΦΑΛΑΙΑ: ) ΠΙΝΑΚΕΣ ) ΟΡΙΖΟΥΣΕΣ ) ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ 4) ΠΑΡΑΓΩΓΟΙ ΜΑΡΙΑ ΡΟΥΣΟΥΛΗ ΚΕΦΑΛΑΙΟ ΠΙΝΑΚEΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΟΡΙΣΜΟΣ Πίνακας
Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος 3. Αν A 5 4, B 4, C να υπολογίσετε τις ακόλουθες πράξεις 4 3 8 3 7 3 (αν έχουν νόημα): α) AB, b) BA, c) CB, d) C B,
Εφαρμοσμένα Μαθηματικά ΙΙ 5ο Σετ Ασκήσεων (Λύσεις) Πίνακες Επιμέλεια: I. Λυχναρόπουλος 3. Αν A 5 4, B 4, C να υπολογίσετε τις ακόλουθες πράξεις 4 3 8 3 7 3 (αν έχουν νόημα): α) AB, b) BA, c) CB, d) C B,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ. ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Άλγεβρα των Πινάκων (2) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών «Γραμμική Άλγεβρα» (ΗΥ119) Χειμερινό Εξάμηνο 009-010 Διδάσκων: Ι. Τσαγράκης 6 Ο ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Δείξτε ότι η απεικόνιση τον ker f. Είναι η
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών «Γραμμική Άλγεβρα» (ΗΥ119) Χειμερινό Εξάμηνο 009-010 Διδάσκων: Ι. Τσαγράκης 6 Ο ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Δείξτε ότι η απεικόνιση τον ker f. Είναι η
ΚΕΦΑΛΑΙΟ 5: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 5: 5. ΟΡΙΣΜΟΙ Έστω U και V δύο διανυσματικοί χώροι. Μια συνάρτηση F : U V θα λέγεται γραμμική απεικόνιση (ή ομομορφισμός, ή απλά μορφισμός εάν ικανοποιεί τις συνθήκες (i F ( u + = u + για κάθε
ΚΕΦΑΛΑΙΟ 5: 5. ΟΡΙΣΜΟΙ Έστω U και V δύο διανυσματικοί χώροι. Μια συνάρτηση F : U V θα λέγεται γραμμική απεικόνιση (ή ομομορφισμός, ή απλά μορφισμός εάν ικανοποιεί τις συνθήκες (i F ( u + = u + για κάθε
