ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
|
|
|
- ÊΠρομηθεύς Βιτάλης
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 5: ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΥΠΟΧΩΡΟΙ ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ Δ.Χ. ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ 009
2
3
4
5
6
7
8 ΓΡΑΜΜΙΚΩΣ ΕΞΑΡΤΗΜΕΝΑ & ΓΡΑΜΜΙΚΩΣ ΑΝΕΞΑΡΤΗΤΑ ΔΙΑΝΥΣΜΑΤΑ ΓΡΑΜΜΙΚΩΣ ΕΞΑΡΤΗΜΕΝΑ ΔΙΑΝΥΣΜΑΤΑ: Τα διανύσματα 1,,, k ενός m διανυσματικού χώρου είναι γραμμικώς εξαρτημένα ανν υπάρχουν συντελεστές λ1, λ,, λk με τουλάχιστον έναν από αυτούς 0, τέτοιοι ώστε: λ + λ + + λ = 1 1 k k 0 Παρατήρηση (άλλος ορισμός): Τα διανύσματα 1,,, k ενός διανυσματικού χώρου m είναι γραμμικώς εξαρτημένα ανν τουλάχιστον ένα από αυτά μπορεί να γραφτεί ως γραμμικός συνδυασμός των υπολοίπων. Απόδειξη {γραμμικώς εξαρτημένα} ανν { τουλάχιστον ένα λi 0 τ.ω. λ11+ λ+ + λii + λkk= 0 λ1 λ λk } i = 1 k λi λi λi (δηλ. το i γράφεται ως γραμμικός συνδυασμός των υπολοίπων). ΓΡΑΜΜΙΚΩΣ ΑΝΕΞΑΡΤΗΤΑ ΔΙΑΝΥΣΜΑΤΑ: Τα διανύσματα 1,,, k ενός m διανυσματικού χώρου είναι γραμμικώς ανεξάρτητα ανν δεν είναι γραμμικώς εξαρτημένα. Δηλαδή, ανν η σχέση: λ11+ λ+ + λkk = 0 ισχύει μόνο για λ1 = λ = = λ k = 0. Δηλ. δεν υπάρχει ούτε ένα λi 0 τ.ω. λ11+ λ+ + λkk = 0 Παρατήρηση: Η σχέση λ11+ λ+ + λ = 0 γράφεται ισοδύναμα ως: k k λ1 λ = 0 λ k [ ] 1 k πίνακας με στήλες τις συνιστώσες των διανυσμάτων το οποίο είναι ένα ομογενές σύστημα της μορφής Ax = 0. Άρα, για να εξετάσουμε αν τα διανύσματα 1,,, k είναι γραμμικώς εξαρτημένα ή γραμμικώς ανεξάρτητα, σχηματίζουμε τον πίνακα A = [ 1 k ] και εξετάζουμε αν το σύστημα Ax = 0 έχει μοναδική λύση τη x = 0 ή έχει άπειρες λύσεις. Συγκεκριμένα: α) Αν ra ( ) = k τότε τα διανύσματα είναι γραμμικώς ανεξάρτητα (το σύστημα Ax = 0 έχει μοναδική λύση τη x = 0 ) β) Αν ra ( ) < k τότε τα διανύσματα είναι γραμμικώς εξαρτημένα (το σύστημα Ax = 0 έχει άπειρες λύσεις)
9 4 Παράδειγμα: Εξετάστε αν τα παρακάτω διανύσματα του είναι γραμμικώς ανεξάρτητα ή όχι. 1 = (1,,0,1), = (,0,, 1), = ( 1,,,0) Λύση λ1 λ λ λ1 λ λ λ+ λ= 0 λ 1 + λ 0 + λ = = 0 λ + λ λ1 λ λ1 0 λ 0 = λ 0 A x A = ( 1) (+) (+) /4 1/4 (+) (+) = U ra ( ) = {πλήθος μη-μηδενικών γραμμών του U}=, δηλ. ra ( ) < k= και επομένως, το σύστημα Ax = 0 έχει άπειρες λύσεις, δηλ. υπάρχει ( λ1, λ, λ) (0,0,0) τ.ω. λ11+ λ+ λ= 0. Επομένως, τα 1,, είναι γραμμικώς εξαρτημένα. Σημείωση: Στο τελευταίο παράδειγμα, ξεκινήσαμε τη διαδικασία από τη σχέση λ11+ λ+ λ= 0, για λόγους κατανόησης. Μπορούσαμε να ξεκινήσουμε φτιάχνοντας κατευθείαν τον πίνακα Α με στήλες τις συνιστώσες των διανυσμάτων 1,,. Άσκηση: Εξετάστε αν τα παρακάτω διανύσματα του όχι. 1 = (1,7,6,), = (, 1,5,4), = (,,0, 1) Λύση 4 είναι γραμμικώς ανεξάρτητα ή, 4 = (0,4,,1) Ο πίνακας με στήλες τις συνιστώσες των διανυσμάτων 1,,, γράφεται ως: A =
10 Μπορούμε, να βρούμε την ra ( ) υπολογίζοντας πρώτα τον U, όπως κάναμε στο προηγούμενο παράδειγμα. Εναλλακτικά, επειδή ο Α είναι τετραγωνικός μπορούμε να υπολογίσουμε την ορίζουσα του. Έχουμε (κάνετε αν θέλετε μόνοι σας τον υπολογισμό): det A = 56, δηλαδή det A 0 και άρα το ομογενές σύστημα Ax = 0 έχει μοναδική λύση τη x = 0. Άρα, τα 1,,, είναι γραμμικώς ανεξάρτητα. 4 ΣΗΜΑΝΤΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ 1) Κάθε διάνυσμα 1 0 μόνο του, είναι γραμμικώς ανεξάρτητο, γιατί η σχέση λ 11 = 0 ισχύει μόνο εάν λ 1 = π.χ. η σχέση λ 0 1 = ισχύει μόνο για λ 1 = 0. ) Αντίθετα, το μηδενικό διάνυσμα 0 μόνο του, είναι γραμμικώς εξαρτημένο, γιατί η σχέση λ 1 0 = 0 ισχύει και για λ1 0. ) Επίσης, αν ένα από τα 1,,, k είναι το 0 τότε είναι γραμμικώς εξαρτημένα. π.χ. έστω 1,0,, k, τότε σίγουρα ισχύει: k = 0, δηλαδή λ = 1 0 4) Αν 1,,, k είναι γραμμικώς εξαρτημένα τότε και τα 1,,, k, k + 1,, ρ είναι γραμμικώς εξαρτημένα. (Δηλαδή, αν σε ένα πλήθος γραμμικώς εξαρτημένων διανυσμάτων βάλουμε και άλλα διανύσματα, τότε όλα μαζί είναι και πάλι γραμμικώς εξαρτημένα). 5) Αν από ένα πλήθος γραμμικώς ανεξάρτητων διανυσμάτων βγάλουμε κάποια αυτά τότε όσα μένουν είναι και πάλι γραμμικώς ανεξάρτητα. π.χ. αν θεωρήσουμε τα διανύσματα: 1 = (1,7,6,), = (, 1,5,4), = (,,0, 1), 4 = (0,4,,1) που όπως είδαμε στην παραπάνω άσκηση είναι γραμμικώς ανεξάρτητα, τότε: τα 1,, είναι γραμμικώς ανεξάρτητα. τα 1,, 4 είναι γραμμικώς ανεξάρτητα. τα 1,, 4 είναι γραμμικώς ανεξάρτητα. τα,, είναι γραμμικώς ανεξάρτητα. 4 τα 1, είναι γραμμικώς ανεξάρτητα., είναι γραμμικώς ανεξάρτητα, κ.λ.π. τα 1
11 m 6) Αν k > m τότε τα διανύσματα 1,,, k είναι σίγουρα γραμμικώς εξαρτημένα. Αυτό μπορεί να εξηγηθεί ως εξής: ο πίνακας A = [ 1 k ] είναι m k, άρα ra ( ) mi( mk, ) = m< k, και άρα το ομογενές σύστημα Ax = 0 έχει άπειρες λύσεις. Έτσι: ή περισσότερα διανύσματα του είναι πάντα γραμμικώς εξαρτημένα 4 ή περισσότερα διανύσματα του είναι πάντα γραμμικώς εξαρτημένα 4 5 ή περισσότερα διανύσματα του είναι πάντα γραμμικώς εξαρτημένα κ.λ.π. m 7) Δυο διανύσματα 1, είναι γραμμικώς εξαρτημένα, ανν λ τ.ω. = λ. 1 π.χ. τα 1 = (,1,0, ), = ( 4,,0, 6), είναι γραμμικώς εξαρτημένα, γιατί = 1 αντίθετα, τα 1 = (,1,0, ), = ( 4,,0, 6) είναι γραμμικώς ανεξάρτητα, γιατί λ τ.ω. = λ. 1 ΓΡΑΜΜΙΚΗ ΕΞΑΡΤΗΣΗ & ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΣΤΟΝ Αν φανταστούμε τα διανύσματα του ως «βελάκια» με αρχή το (0,0) και τέλος τη θέση (x,y) των συνιστωσών του, τότε από την παραπάνω παρατήρηση 7, προκύπτει ότι δύο διανύσματα στον είναι γραμμικώς εξαρτημένα ανν είναι συνευθειακά π.χ. 1 = (,1) και = (4, ), όπου = Επομένως, μη-συνευθειακά διανύσματα του είναι γραμμικώς ανεξάρτητα. π.χ. αν 1 = (,1) και = (4,1), τότε λ τ.ω. = λ. 1
12 Επίσης, στην παρατήρηση 6, είδαμε ότι ή περισσότερα διανύσματα του είναι πάντα γραμμικώς εξαρτημένα. Για παράδειγμα, για οποιαδήποτε διανύσματα 1,,, τουλάχιστον ένα από αυτά γράφεται ως γραμμικός συνδυασμός των άλλων δυο (π.χ. = λ1 1+ λ ) και άρα,, είναι γραμμικώς εξαρτημένα. τα 1 Άσκηση: Έστω 1 = (,1), = (4,1), =,. Βρείτε λ1, λ τέτοια ώστε = λ11+ λ. Κατόπιν, δείξτε το σχηματικά χρησιμοποιώντας τον κανόνα του παραλληλογράμμου. Λύση 4 4 λ 1 = λ1 1+ λ 1 / = λ λ 1 + = 1 / 1 1 λ δηλ. θέλουμε να λύσουμε το σύστημα: 4 λ1 1 1 = λ /. Έχουμε: 4 1/ Ab = 1 1 / (+) 4 0 5/ Ανάδρομη αντικατάσταση: η 5 5 εξίσωση: λ = λ = 6 1 η εξίσωση: λ λ = λ1+ 4 = λ1 = 6 Επομένως: 5 =
13 ΓΡΑΜΜΙΚΗ ΕΞΑΡΤΗΣΗ & ΓΡΑΜΜΙΚΗ ΑΝΕΞΑΡΤΗΣΙΑ ΣΤΟΝ Αν φανταστούμε τα διανύσματα του ως «βελάκια» με αρχή το (0,0,0) και τέλος τη θέση (x,y,z) των συνιστωσών του, τότε από την παραπάνω παρατήρηση 7, προκύπτει ότι δύο διανύσματα στον είναι γραμμικώς εξαρτημένα ανν είναι συνευθειακά π.χ. 1 = ( 1,, 5) και = (, 9,15), όπου = 1 δηλαδή και τα δύο βρίσκονται στην ίδια ευθεία που περνά από το 0 = (0,0,0) Επομένως, δύο μη-συνευθειακά διανύσματα του είναι γραμμικώς ανεξάρτητα. π.χ. αν 1 = ( 1,, 5) και = (,6,15), τότε λ τ.ω. = λ. 1 Σημείωση: Τρία διανύσματα στον είναι γραμμικώς εξαρτημένα ανν είναι συνεπίπεδα. Δηλαδή, ανήκουν στο ίδιο επίπεδο που περνά από το 0 = (0,0,0). Επίσης, στην παρατήρηση 6, είδαμε ότι 4 ή περισσότερα διανύσματα του είναι πάντα γραμμικώς εξαρτημένα. Για παράδειγμα, για 4 οποιαδήποτε διανύσματα 1,,, 4, τουλάχιστον ένα από αυτά γράφεται ως γραμμικός συνδυασμός των άλλων τριών (π.χ. 4 = λ1 1+ λ + λ ) και άρα τα 1,,, είναι γραμμικώς εξαρτημένα. 4 m Θεώρημα: Έστω τα διανύσματα 1,,, k ενός διανυσματικού χώρου. Το σύνολο των γραμμικών συνδυασμών τους, δηλαδή το σύνολο: m V = { τ.ω. = λ1 1+ λ + + λκ με 1,,, k λ λ λκ } m είναι διανυσματικός υπόχωρος του.
14 m ΟΡΙΣΜΟΣ: Έστω V ένας διανυσματικός υπόχωρος του. Λέμε ότι τα διανύσματα m 1,,, k του παράγουν τον V αν: 1) 1,,, k V και ) V, λ 1, λ,, λκ, τ.ω. = λ11+ λ+ + λ κ k (δηλ. κάθε διάνυσμα του V μπορεί να γραφτεί ως γραμμικός συνδυασμός των 1,,, k ) Συμβολισμός: V = 1,,, k σημαίνει ότι τα 1,,, k παράγουν το V ΒΑΣΕΙΣ & ΔΙΑΣΤΑΣΗ ΔΙΑΝΥΣΜΑΤΙΚΟΥ ΧΩΡΟΥ ΟΡΙΣΜΟΣ: Βάση ενός διανυσματικού χώρου V είναι ένα σύνολο γραμμικώς ανεξάρτητων διανυσμάτων που παράγουν το V. Με άλλα λόγια, το σύνολο { } B = 1,,, k είναι βάση του V αν: 1) 1,,, k V και ) 1,,, k είναι γραμμικώς ανεξάρτητα και ) V, λ 1, λ,, λk, τ.ω. = λ1 1+ λ + + λk k (δηλ. κάθε διάνυσμα του V μπορεί να γραφτεί ως γραμμικός συνδυασμός των 1,,, k ) Σημ.: Σ αυτή την περίπτωση, η k-άδα ( λ1, λ,, λk ) είναι μοναδική για κάθε διάνυσμα V, και τα λ1, λ,, λk ονομάζονται συνιστώσες του ως προς τη βάση B. Παράδειγμα: Δείξτε ότι το σύνολο = { e 1, e, e B } όπου e 1 = (1,0,0), e = (0,1,0), e = (0,0,1) είναι βάση του. Ποιες είναι οι συνιστώσες του διανύσματος = (1,,5) ως προς τη βάση B. Λύση 1) Καθένα από τα e 1, e, e είναι άδα πραγματικών αριθμών. Άρα: e1, e, e ) Ο πίνακας με τις συνιστώσες των e 1, e, e είναι: A = = I που έχει det A = 1, δηλαδή det A 0 και άρα το ομογενές σύστημα Ax = 0 έχει μοναδική λύση τη x = 0. Άρα, τα e 1, e, e είναι γραμμικώς ανεξάρτητα. ) Κάθε = ( x, y, z) γράφεται ως:
15 x x y= 0+ y+ 0= x0+ y1+ z0 z 0 0 z δηλαδή: = xe 1+ ye + ze Έτσι, το διάνυσμα = (1,,5) γράφεται ως = 1e 1 e + 5e και άρα, οι συνιστώσες B = e, e, e είναι οι 1,,5 του ως προς τη βάση { } 1 Σημείωση: Όταν μας ενδιαφέρει η σειρά των διανυσμάτων σε μια βάση τότε αυτή ονομάζεται διατεταγμένη βάση. Έτσι στο τελευταίο παράδειγμα, οι συνιστώσες του ως προς τη διατεταγμένη βάση B = { e 1, e, e } είναι οι 1,,5, ενώ οι συνιστώσες του B = e, e, e είναι οι,1,5 ως προς τη διατεταγμένη βάση { } 1 Άσκηση: Το σύνολο = { 1,, B } με 1 = (0,1,), = (,,6), = ( 1,, 8) είναι μια διατεταγμένη βάση του. Βρείτε τις συνιστώσες του διανύσματος = (1,,5) ως προς τη B. Λύση Ψάχνουμε τη μοναδική άδα ( λ1, λ, λ ) τ.ω. = λ1 1+ λ + λ. Έχουμε: λ1 = λ11 + λ+ λ = λ11+ λ+ λ = 1 λ λ δηλαδή, έχουμε να λύσουμε το σύστημα Απαλοιφή Gauss: εναλλαγή Ab = ( 1) (+) 0 1 λ1 1 1 λλ = (+). ( ) = U d Ανάδρομη αντικατάσταση: η 8 εξίσωση: λ = 8 λ = η εξίσωση: λ λ 8 5 = 1 λ + = 1 λ = 6 1 η εξίσωση: 5 8 λ λ λ = λ1+ = λ1 = 6 Άρα, = , και συνεπώς οι συνιστώσες του = (1,,5) 6 διατεταγμένη βάση = { 1,, B } είναι,, 6 ως προς τη
16 Παρατήρηση: Κάθε διανυσματικός χώρος έχει άπειρες βάσεις. Δηλαδή, υπάρχουν άπειρα σύνολα γραμμικώς ανεξάρτητων διανυσμάτων που παράγουν το V. (Εξαίρεση αποτελεί ο τετριμμένος υπόχωρος { 0 } που το πλήθος των βάσεων του είναι 0) Πρόταση: Καθεμιά από τις άπειρες βάσεις ενός διανυσματικού χώρου V έχει το ίδιο πλήθος διανυσμάτων. ΟΡΙΣΜΟΣ: Διάσταση ενός διανυσματικού χώρου V είναι το πλήθος διανυσμάτων κάθε βάσης του V και συμβολίζεται με dim( V ). Σημείωση: dim( V ) = [μέγιστο πλήθος γραμμικώς ανεξάρτητων διανυσμάτων του V ] π.χ. σε ένα διανυσματικό χώρο με dim( V ) =, μπορούμε να βρούμε: 1 γραμμικώς ανεξάρτητο διάνυσμα (που είναι κάθε μη-μηδενικό του διάνυσμα μόνο του) άδες με γραμμικώς ανεξάρτητα διανύσματα άδες με γραμμικώς ανεξάρτητα διανύσματα ενώ δεν υπάρχει: 4άδα ή 5άδα ή 6άδα κ.λ.π. με γραμμικώς ανεξάρτητα διανύσματα Παρατήρηση: dim( ) = m Δηλαδή: dim( ) =, m dim( ) =, 4 dim( ) = 4, κ.λ.π. Παρατήρηση: Αν ο διανυσματικός χώρος V παριστάνει μια ευθεία του που περνά από το (0,0) ή μια ευθεία του που περνά από το (0,0,0), τότε: dim( V ) = 1 π.χ. ο χώρος L= {( x, y) \ x y = 0} έχει dim( L ) = 1 ενώ ο W = {( x, y, z) \ x y+ z = 0 & x+ y z = 0} έχει dim( W ) = 1 Παρατήρηση: Αν ο διανυσματικός χώρος V παριστάνει ένα επίπεδο του από το (0,0,0), τότε: dim( V ) = π.χ. ο χώρος E = {( x, y, z) \ x y+ z = 0} έχει dim( E ) = που περνά Παρατήρηση: Γενικά, ο χώρος V = {( x1, x,, x) \ α1x1+ αx + + αx = 0} (όπου τουλάχιστον ένα από τα α1, α,, α είναι 0) έχει dim( V) = 1 W = ( x, x, x, x ) 4 \ x + x 5x + x = 0 έχει dim( W ) = π.χ. ο χώρος { } Παρατήρηση: Ο τετριμμένος υπόχωρος W = { 0 } το γραμμικώς εξαρτημένο διάνυσμα 0. Άρα, dimw = 0 οποιουδήποτε αποτελείται μόνο από
17 Παρατήρηση: Αν dim( V) = k, τότε οποιοδήποτε σύνολο k γραμμικώς ανεξάρτητων διανυσμάτων του V είναι βάση του. π.χ. -- οποιοδήποτε σύνολο γραμμικώς ανεξάρτητων διανυσμάτων του (δηλ. μησυνευθειακών διανυσμάτων του ) είναι βάση του. -- οποιοδήποτε σύνολο γραμμικώς ανεξάρτητων διανυσμάτων του (δηλ. μησυνεπίπεδων διανυσμάτων του ) είναι βάση του οποιοδήποτε σύνολο 4 γραμμικώς ανεξάρτητων διανυσμάτων του είναι βάση του οποιοδήποτε σύνολο 5 γραμμικώς ανεξάρτητων διανυσμάτων του είναι βάση του. κ.λ.π. Επίσης, -- οποιοδήποτε μη-μηδενικό διάνυσμα μιας ευθείας του που περνά από το (0,0) ή μιας ευθείας του που περνά από το (0,0,0), είναι βάση της. -- οποιοδήποτε σύνολο γραμμικώς ανεξάρτητων διανυσμάτων ενός επιπέδου του που περνά από το (0,0,0) είναι βάση του. Συμπέρασμα: Αν για ένα διανυσματικό χώρο V ξέρουμε ότι dim( V) = k, τότε για να δείξουμε ότι ένα σύνολο B = { 1,,, k } (που έχει k διανύσματα) είναι βάση του V, αρκεί να δείξουμε ότι: 1) 1,,, k V και ) 1,,, k είναι γραμμικώς ανεξάρτητα Σημείωση: Έστω W είναι υπόχωρος του V, τότε: α) dimw dimv β) αν dimw = dimv, τότε W = V π.χ. Έστω W είναι υπόχωρος του V = και τότε: 1) W = dimw = ) αν W επίπεδο που περνά από το 0 = (0,0,0) τότε dimw = < dimv ) αν W ευθεία που περνά από το 0 = (0,0,0) τότε dimw = 1< dimv W = τότε dimw = 0 < dimv 4) αν { 0} Θεώρημα: Οι στήλες κάθε αντιστρέψιμου πίνακα A, αποτελούν βάση του Εξήγηση: { A αντιστρέψιμος πίνακας} ανν {det A 0} ανν {το σύστημα Ax = 0 έχει μοναδική λύση τη x = 0 } ανν {οι στήλες του A είναι γραμμικώς ανεξάρτητα διανύσματα}. Όμως, οποιαδήποτε ανεξάρτητα διανύσματα αποτελούν βάση του. Άρα, οι στήλες του A αποτελούν βάση του. Παράδειγμα: Δείξτε ότι το σύνολο {,, } = ( 1, 4, 8) είναι βάση του. B = με 1 = (0,1,) 1, = (,,6),
18 Λύση 0 1 Έχουμε: A = 1 4 και άρα: det A = + = ( ) + ( 8 + ) = δηλ. det 0 B =,, είναι βάση του A και άρα το { } 1 Παρατήρηση: det I = 1 0. Άρα, οι στήλες του I αποτελούν βάση του ΟΡΙΣΜΟΣ: Κανονική βάση ενός διανυσματικού χώρου διανύσματα τις στήλες του I. { } π.χ. η κανονική βάση του είναι η 1, η κανονική βάση του είναι η 0, 1, η κανονική βάση του είναι η 0, 1, 0, κ.λ.π. είναι η βάση που έχει ως του. α) Τι παριστάνει γεωμετρικά; β) Βρείτε μια βάση και τη διάσταση του. γ) Ελέγξτε αν το διάνυσμα b = ( 1,1,) ανήκει στον V. Αν ναι, τότε βρείτε τις συνιστώσες του ως προς τη βάση που βρήκατε στο προηγούμενο ερώτημα. Λύση α) ο V παριστάνει ένα επίπεδο που περνά από το 0 = (0,0,0). β) για κάθε διάνυσμα = ( x, y, z) V τα x, yz, ικανοποιούν την εξίσωση: x y+ z = 0 x= y z y z δηλ. τα διανύσματα V είναι της μορφής: = y, με yz,. z 1 δηλ. y 1 z = + 0, με yz, (*) 0 1 Άσκηση: Έστω ο διανυσματικός υπόχωρος V = {( x, y, z) \ x y+ z = 0}
19 δηλ. κάθε διάνυσμα του V μπορεί να γραφτεί ως γραμμικός συνδυασμός των 1 διανυσμάτων 1 = 1 και = 0, τα οποία επιπλέον ανήκουν στον V αφού 0 1 ικανοποιούν την εξίσωση x y+ z = 0 Άρα, V = 1, (δηλ. ο V παράγεται από τα 1, ) Ελέγχουμε αν τα 1, είναι και γραμμικώς ανεξάρτητα. Έχουμε: 1 A = ( 1/) 1 0 1/ 0 1 (+) (+) 1 0 1/ = U 0 0 Άρα, ra= ( ) δηλαδή ra ( ) = και άρα τα 1, είναι γραμμικώς ανεξάρτητα. Επομένως, έχουμε δείξει ότι: 1) 1, V, και ) τα 1, είναι γραμμικώς ανεξάρτητα, και ) κάθε διάνυσμα του V μπορεί να γραφτεί ως γραμμικός συνδυασμός των 1, Επομένως, το σύνολο { 1, } είναι μια βάση του V. Άρα, κάθε βάση του V έχει διανύσματα. Άρα, dim( V ) = Σημείωση: Η εξίσωση x y+ z = 0 μπορεί να θεωρηθεί ως ομογενές σύστημα 1 με πίνακα A = [ 1 1] = U και άρα βασική μεταβλητή τη x και ελεύθερες τις yz., Η γενική λύση του Ax = 0 είναι η (*). Γενικά, σε μια τέτοια λύση τα μη-μηδενικά διανύσματα που πολλαπλασιάζονται με τις ελεύθερες μεταβλητές είναι πάντα βάση του V (δεν χρειάζεται να το δείχνουμε όπως κάναμε πιο πάνω για λόγους κατανόησης). γ) Το b = ( 1,1,) ανήκει στον V γιατί 1 1+ = 0, δηλαδή οι συνιστώσες του ικανοποιούν την εξίσωση x y+ z = 0. Επειδή λοιπόν b V και { 1, } μια βάση του V, αυτό συνεπάγεται ότι υπάρχει μοναδική άδα ( λ1, λ ) τ.ω. b = λ11+ λ. Έχουμε: λ b = λ λ 1 = λ11 + λ 0 1 = λ 1 λ 1 δηλαδή, έχουμε να λύσουμε το σύστημα = λ. Επειδή, έχουμε ήδη κάνει τη διαδικασία A U, δεν χρειάζεται να κάνουμε όλη απαλοιφές τη διαδικασία απαλοιφής Gauss A b U d απαλοιφές. Αρκεί να εφαρμόσουμε στο b τα ίδια στάδια απαλοιφής που εφαρμόσαμε στη διαδικασία A U. Έχουμε: απαλοιφές
20 1 b = 1 ( 1/) (+) 1 / (+) 1 / = d 0 1 λ Άρα: λ = 1 0 1/ 1 / 0 1 λ = 0 0 λ 0 Ανάδρομη αντικατάσταση: η εξίσωση: 0λ1+ 0λ = 0, που ισχύει ( λ1, λ) η εξίσωση: 1 λ = λ = 1 η εξίσωση: λ1 λ = 1 λ1 = 1 λ1 = 1 Άρα, b = 1+, και συνεπώς οι συνιστώσες του b = ( 1,1,) ως προς τη διατεταγμένη βάση { 1, } είναι 1,. Παρατήρηση: επειδή dim( ) =, το b = ( 1,1,) ως διάνυσμα του που είναι, θα έχει συνιστώσες ως προς μια βάση του. Για παράδειγμα, οι συνιστώσες του ως προς την κανονική βάση του είναι 1,1,. Όμως, το b ανήκει και στο επίπεδο { (,, ) \ 0 } V = x y z x y+ z = του συνιστώσες ως προς μια βάση του V. και επειδή dim( V ) =, το b θα έχει 1,,..., k μια μ. Τότε και το Θεώρημα: Έστω V είναι ένας πραγματικός διανυσματικός χώρος και { } βάση του V. Έστω u V με u = μ μ μ,...,, u,,..., είναι βάση του V. σύνολο { } 1 i 1 i+ 1 k i i k k όπου 0 i Παράδειγμα: Στην παραπάνω άσκηση βρήκαμε ότι μια βάση του διανυσματικού χώρου { (,, ) \ 0 1 V = x y z x y+ z = } είναι η { 1, }, με 1 = 1 και = Μια άλλη βάση του V μπορούμε να βρούμε αν αντικαταστήσουμε το 1 με ένα διάνυσμα u της μορφής: u = μ1 1+ μ, όπου μ 1 0, 1 7 π.χ. u = 1 = 1 0 = 0 1 και άρα, μια άλλη βάση του V είναι η { u, } Επίσης, μια άλλη βάση παίρνουμε αν αντικαταστήσουμε το μορφής: u = μ1 1+ μ, όπου μ 0. με ένα διάνυσμα w της
21 1 1 π.χ. w= 1+ = = και άρα, μια άλλη βάση του V είναι η { w } 1, Μ αυτόν τον τρόπο, εφόσον γνωρίζουμε ήδη μια βάση του V, μπορούμε να βρούμε άπειρες άλλες βάσεις του. Άσκηση: Έστω ο διανυσματικοί υπόχωροι V = {( x, y, z) \ x y+ z = 0} { (,, ) \ 0 W = x y z x y = } του. α) Γράψτε το σύνολο V W. Είναι διανυσματικός υπόχωρος του β) Βρείτε μια βάση και τη διάσταση του V W γ) Τι παριστάνει γεωμετρικά το V W ; Λύση α) V W = {( x, y, z) \ x y+ z = 0 & x y = 0}. και και γιατί; Η τομή δύο υπόχωρων ενός διανυσματικού χώρου είναι επίσης διανυσματικός υπόχωρος του ίδιου χώρου. Οι V και W είναι υπόχωροι του, άρα και η τομή V W είναι υπόχωρος του. β) για κάθε διάνυσμα = ( x, y, z) V W } 1 1 x x y+ z = 0 y = 0 x y = z 0 0 Έχουμε: A x 1 1 ( 1) (+) A = τα x, yz, ικανοποιούν το σύστημα: = U x Όμως, Ax = 0 Ux = 0 y 0 = z 0 βασικές μεταβλητές: x, y ελεύθερη μεταβλητή: z Ανάδρομη αντικατάσταση: η εξίσωση: y z = 0 y = z 1 η εξίσωση: x y+ z = 0 x z+ z = 0 x = z δηλ. τα διανύσματα V W είναι της μορφής: z = z, με z. z
22 1 δηλ. = z 1, με z 1 1 Επομένως, μια βάση του V W είναι το μονοσύνολο 1. 1 Άρα, κάθε βάση του V W έχει 1 διάνυσμα. Άρα, dim( V W) = 1 1 γ) Όλα τα διανύσματα του V W γράφονται ως = z 1 με z. Άρα, το V 1 παριστάνει την ευθεία του διανύσματος (1,1,1) του [δηλ. την ευθεία που διέρχεται από το σημείο (0,0,0) και το σημείο (1,1,1)] W ΠΡΟΤΑΣΗ 1: Σε κάθε κλιμακωτό πίνακα U, οι μη-μηδενικές γραμμές είναι γραμμικώς ανεξάρτητα διανύσματα π.χ. αν U =, τότε τα διανύσματα r 1 1, r = 0 =, r = είναι γραμμικώς ανεξάρτητα Εξήγηση: ο πίνακας με στήλες τα r 1, r, r 0 0 είναι ο 1 0 A =. Για να βρούμε την τάξη του δεν χρειάζεται να τον κάνουμε κλιμακωτό. Αρκεί να παρατηρήσουμε ότι A = που είναι κλιμακωτός με μη-μηδενικές γραμμές. Άρα, r( A ) =. Όμως, για κάθε πίνακα A, ισχύει r( A ) r( A) =. Επομένως, ra= ( ) (όσες δηλαδή και οι στήλες του) και συνεπώς τα r 1, r, r είναι γραμμικώς ανεξάρτητα. ΠΡΟΤΑΣΗ : Σε κάθε κλιμακωτό πίνακα U, οι στήλες που περιέχουν οδηγούς είναι γραμμικώς ανεξάρτητα διανύσματα
23 π.χ. αν U =, τότε τα διανύσματα 0 1, = =, 4 = είναι γραμμικώς ανεξάρτητα Εξήγηση: ο πίνακας με στήλες τα 1,, είναι ο A =, που είναι ήδη σε κλιμακωτή μορφή και έχει οδηγούς σε κάθε στήλη. Άρα, ra= ( ) (όσες δηλαδή και οι στήλες του) και συνεπώς τα 1,, είναι γραμμικώς ανεξάρτητα. ΧΩΡΟΣ ΣΤΗΛΩΝ ενός ΠΙΝΑΚΑ m Έστω ένας πίνακας A. Οι στήλες του A είναι διανύσματα του. Αυτά m παράγουν έναν διανυσματικό υπόχωρο του που ονομάζεται χώρος στηλών του A, και συμβολίζεται ως R ( A). Δηλ. αν 1,,, οι στήλες του A, τότε R ( A) = 1,,, Δηλ. ο R ( A) περιέχει όλα τα διανύσματα b m που γράφονται ως γραμμικοί συνδυασμοί των 1,,,. m π.χ. αν 1 A = τότε R ( A) =, 6, 9, Παρατήρηση: Για να ανήκει ένα διάνυσμα b στον R ( A), πρέπει να υπάρχουν λ1, λ,, λ τ.ω. b = λ11 + λ+ + λ το οποίο είναι ισοδύναμο με: λ1 λ1 [ ] 1 λ λ b = b = A Ax = b πίνακας με στήλες λ λ τις συνιστώσες των διανυσμάτων x Δηλαδή, b R ( A) ανν {το σύστημα Ax = b έχει λύση (μοναδική ή άπειρες)} Άσκηση: Εξετάστε αν το διάνυσμα b = ( 1,0,4) 1 A = ανήκει στο χώρο στηλών του πίνακα
24 Λύση Για να ανήκει το διάνυσμα b = ( 1,0,4) στον R ( A), πρέπει να υπάρχουν λ1, λ, λ, λ λ1 λ τ.ω. 0 λ 1 λ 6 λ 9 λ = = λ λ 4 b A x Δηλαδή, πρέπει το σύστημα Ax = b να έχει λύση (μοναδική ή άπειρες). Έχουμε: 1 1 ( ) 1 Ab 1 1 = (+) ( ) (+) (+) = U d όπου Ax = b Ux = d. Η η εξίσωση δίνει 0= 1 και άρα το σύστημα Ax = b δεν έχει καμία λύση. Επομένως, το b δεν ανήκει στον R ( A). Παρατήρηση: Αν ra ( ) = m(δηλ. ο U δεν έχει καμία μηδενική γραμμή) τότε έχουμε δει ότι το σύστημα Ax = b έχει λύση (μοναδική αν m= ή άπειρες αν m< ) για κάθε m b. Δηλαδή, σ αυτήν την περίπτωση: ( ) m R A ΠΑΡΑΤΗΡΗΣΕΙΣ Για ένα κλιμακωτό πίνακα U οι στήλες που περιέχουν οδηγούς αποτελούν μια βάση του R ( U ). Άρα: dim R ( U) = r( U) Αν A U τότε: απαλοιφές {ένα υποσύνολο των στηλών του A είναι γραμμικώς ανεξάρτητα διανύσματα} ανν {οι αντίστοιχες στήλες του U είναι γραμμικώς ανεξάρτητα διανύσματα} Συμπέρασμα: Αν A U τότε οι στήλες του A που αντιστοιχούν στις στήλες του απαλοιφές U που έχουν τους οδηγούς αποτελούν μια βάση του R ( A). Άρα: dim R ( A) = ra ( ) Γενικά, R( A) R ( U ) Παράδειγμα: Δείξτε ότι R( A) R ( U ), για τον πίνακα Λύση 1 Είδαμε παραπάνω ότι U = Άρα: {μια βάση του R ( U )} = {1 η & η στήλη του U } = Επομένως, ο R ( U ) περιέχει διανύσματα της μορφής: 1 A = , 0 0
25 1 λ1+ λ = λ10+ λ δηλ. της μορφής: = λ Όμως, π.χ. η η στήλη του A, δηλαδή η 9 δεν μπορεί να γραφτεί σ αυτή τη μορφή. Άρα, 9 R ( U ) και επομένως R( A) R ( U ). Άσκηση: Βρείτε τη διάσταση και μια βάση του διανυσματικού χώρου V που παράγεται από τα διανύσματα 1 = (1,, 4), = (,0, 1), = (0,6, 1), 4 = (1, 4, 9). Τι παριστάνει ο V γεωμετρικά; Λύση Σημείωση: V = 1,,, 4 και V υπόχωρος του Σχηματίζουμε τον πίνακα A με στήλες τα 1,,, Δηλαδή: 4 A = Άρα: V R ( A) Έπειτα, βρίσκουμε τον αντίστοιχο κλιμακωτό πίνακα: A = (+) (1/ 6) = U (+) (+) Επομένως, έχουμε ra= ( ) (= πλήθος μη-μηδενικών γραμμών του U ) Άρα, dim R ( A) = dimv = {μια βάση του V } = {μια βάση του R ( A) } = { 1, } (δηλ. οι στήλες του A που αντιστοιχούν στις στήλες του U που έχουν τους οδηγούς) Γεωμετρικά, ο V παριστάνει το επίπεδο του που ορίζεται από τα σημεία 0,1 και, δηλαδή από τα σημεία: (0,0,0), (1,,4) και (,0, 1). Αν θέλουμε να βρούμε μια εξίσωση αυτού του επιπέδου, εργαζόμαστε ως εξής: Κάθε επίπεδο του που περνά από το (0,0,0) έχει εξίσωση της μορφής: α x + βy+ γz = 0 με τουλάχιστον ένα από τα α, βγ, να είναι 0. Επειδή, περνά και από τα (1,, 4) και (,0, 1) θα πρέπει: α α 1 + β ( ) + γ 4= 0 α β 4γ ( 1) 0} + = { 0 } β = α + β + γ = α γ = 0 1 γ 0 Όμως, 1 4 ( ) (+) Βασικές μεταβλητές: α, β Ελεύθερη μεταβλητή: γ
26 Ανάδρομη αντικατάσταση: η 1 εξίσωση: 6β 1γ = 0 β = γ 6 1 η 1 1 εξίσωση: α β + 4γ = 0 α γ + 4γ = 0 α = γ 6 Άρα, το ζητούμενο επίπεδο έχει εξίσωση: γ x+ y+ z = 0 x+ y+ z = 0 x+ 1y+ 6z = δηλαδή, V = {( x, y, z) \ x+ 1y+ 6z = 0} ΧΩΡΟΣ ΓΡΑΜΜΩΝ ενός ΠΙΝΑΚΑ m Έστω ένας πίνακας A. Οι m γραμμές του A είναι διανύσματα του. Αυτά παράγουν έναν διανυσματικό υπόχωρο του που ονομάζεται χώρος γραμμών του A. Συμβολίζεται ως ( A R ), γιατί συμπίπτει με το χώρο στηλών του A π.χ. αν A = τότε R ( A ) =, 6, δηλ. ο ( A 4 R ) περιέχει όλα τα διανύσματα b που μπορούν να γραφτούν ως γραμμικοί συνδυασμοί των, 6,, δηλ. ως b = λ λ 6 + λ Παρατήρηση: Είδαμε παραπάνω ότι b R ( A) ανν {το σύστημα Ax = b έχει λύση (μοναδική ή άπειρες)}. Συμπέρασμα: b ( A R ) ανν {το σύστημα A x = b έχει λύση (μοναδική ή άπειρες)} ΠΑΡΑΤΗΡΗΣΕΙΣ Για ένα κλιμακωτό πίνακα U, οι μη-μηδενικές γραμμές αποτελούν μια βάση του ( U R ). Άρα: dim R ( U ) = r( U) Αν A U τότε: ( R A ) R ( U ) απαλοιφές (δηλαδή σε αντίθεση με τους χώρους στηλών των A και U που γενικά διαφέρουν, οι χώροι γραμμών τους ταυτίζονται) Συμπέρασμα: Αν A U τότε οι μη-μηδενικές γραμμές του U αποτελούν μια απαλοιφές βάση του ( A R ). Άρα: dim R ( A ) = ra ( )
27 π.χ. Έστω 1 1 A = Είδαμε παραπάνω ότι U = Άρα: dim R ( A ) = (=πλήθος μη-μηδενικών γραμμών του U ) 1 0 και {μια βάση του R ( A )} = {οι μη-μηδενικές γραμμές του U } =, 0 1 ΜΗΔΕΝΟΧΩΡΟΣ ενός ΠΙΝΑΚΑ Έστω ένας πίνακας A m. Το σύνολο λύσεων του ομογενούς συστήματος Ax = 0 είναι διανυσματικός υπόχωρος του που συμβολίζεται ως N ( A) και ονομάζεται μηδενόχωρος του A. Απόδειξη: προφανώς N ( A), αφού μια λύση του Ax = 0 είναι η x = 0. Επίσης, N ( A) αφού τα διανύσματα x που ικανοποιούν το σύστημα Ax = 0 ανήκουν στον. Επιπλέον, έστω x 1 και x δύο οποιεσδήποτε λύσεις του Ax = 0. Δηλαδή, x1, x N ( A). Τότε: Ax ( 1+ x) = Ax1+ Ax = 0+ 0= 0. Άρα, και ( x1+ x) N ( A). Δηλαδή το N ( A) είναι κλειστό ως προς την πρόσθεση. Επίσης, A( λx1) = λ( Ax1) = λ0= 0. Άρα, και ( λx1) N ( A), x1 N ( A) & λ. Δη λαδή το N ( A) είναι και κλειστό ως προς τον πολλαπλασιασμό με πραγματικό αριθμό. Συνεπώς, το N ( A) είναι διανυσματικός υπόχωρος του ΠΑΡΑΤΗΡΗΣΕΙΣ Αν A U τότε ξέρουμε ότι Ax = 0 Ux = 0. Επομένως: N( A) N ( U ) απαλοιφές dim N ( A) = r( A) = (πλήθος των ελεύθερων μεταβλητών) Αν ra ( ) = (δηλ. οδηγοί σε κάθε στήλη του U, δηλ. καμία ελεύθερη μεταβλητή) τότε το σύστημα Ax = 0 έχει μοναδική λύση τη x = 0. Άρα: ( A ) = { 0 N } (δηλ, ο τετριμμένος υπόχωρος του ) και dim N ( A ) = 0 Σ αυτήν την περίπτωση ο N ( A) δεν έχει καμία βάση Άσκηση: Βρείτε τη διάσταση και μια βάση του μηδενόχωρου του πίνακα 1 A =
28 Λύση 1 Είδαμε παραπάνω ότι U = Άρα: dim N( A) = r( A) dim N( A) = 4 dim N ( A) = Για να βρούμε μια βάση του N ( A) πρέπει να λύσουμε το σύστημα Ax = 0, το οποίο έχει 1 x 0 τις ίδιες λύσεις με το Ux y = z =. 0 w Βασικές μεταβλητές: x, z Ελεύθερες μεταβλητές: yw, Ανάδρομη αντικατάσταση: η 4 εξίσωση: ικανοποιείται ( xyzw,,, ) η 1 εξίσωση: z+ w= 0 z = w 1 η 1 εξίσωση: x y z w 0 x y = + + w + w= 0 x = y w y w y Άρα, ο N ( A) έχει διανύσματα της μορφής: x = 1, δηλαδή της μορφής: w w y w 1 y 1 0 x = 1 = y w w 0 + 1/, με yw, 0 1 w Επομένως, μια βάση του N ( A) είναι η 1 1 0, 0 1/. 0 1 Παρατήρηση: Το σύνολο λύσεων ενός μη-ομογενούς συστήματος Ax = b δεν είναι διανυσματικός χώρος, αφού αν x 1 και x δύο οποιεσδήποτε λύσεις του, τότε: A( x1+ x) = Ax1+ Ax = b + b = b b, δηλ. το ( x1+ x) δεν είναι λύση του Ax = b. Άρα, το σύνολο λύσεων της Ax = b δεν είναι κλειστό ως προς την πρόσθεση. Άρα, δεν είναι διανυσματικός χώρος.
29 m ΟΡΙΣΜΟΣ: Έστω ένας πίνακας A. Ο μηδενόχωρος του A, δηλαδή ο N ( A ) ονομάζεται αριστερός μηδενόχωρος του A. Παρατήρηση: από τη σχέση dim N ( A) = r( A) προκύπτει ότι dim N ( A ) = m r( A) [μιας και ο A έχει m στήλες και επιπλέον ra ( ) = ra ( )] Άσκηση: Βρείτε τη διάσταση και μια βάση του αριστερού μηδενόχωρου του πίνακα 1 A = Τι παριστάνει γεωμετρικά αυτός ο χώρος; 1 0 Λύση Από την προηγούμενη άσκηση, ξέρουμε ότι ra= ( ). Άρα, για τη διάσταση του N ( A ) έχουμε: dim N( A ) = m r( A) dim N( A ) = dim N ( A ) = 1 Για να βρούμε μια βάση του ( A N ) πρέπει να λύσουμε το σύστημα A x = 0. Έχουμε: 1 1 ( ) ( ) ( ) A = 6 (+) ( ) 9 (+) 0 6 εναλλαγή 0 6 (+) 5 0 (+) = U όπου χρησιμοποιήσαμε το συμβολισμό U για να ξεχωρίζουμε τον κλιμακωτό που μας δίνει ο A, από τον κλιμακωτό U που μας δίνει ο A. 1 1 x 0 A x 0 U x = = y = z Βασικές μεταβλητές: x, y Ελεύθερη μεταβλητή: z Ανάδρομη αντικατάσταση: 4 η & η εξίσωση: ικανοποιούνται ( xyz,, ) η εξίσωση: y+ z = 0 y = z 1 η εξίσωση: x + y z = 0 x+ ( z) z = 0 x = 5z 5z Άρα, ο N ( A ) έχει διανύσματα της μορφής: x = z, δηλαδή της μορφής: z 5 5 x = z, με z. Επομένως, μια βάση του ( A N ) είναι η. 1 1
30 Ο N ( A ) παριστάνει την ευθεία του (5,,1). που ορίζεται από τα σημεία (0,0,0) και ΣΥΝΟΠΤΙΚΕΣ ΠΑΡΑΤΗΡΗΣΕΙΣ: Έστω ένας πίνακας A m. Για να βρούμε τις διαστάσεις και βάσεις των R( A), R( A ), N ( A) και N ( A ) εργαζόμαστε ως εξής: 1) A U απαλοιφές ) ra= ( ) (πλήθος μη-μηδενικών γραμμών του U ) ) Υπολογίζουμε τις διαστάσεις των R( A), R( A ), N ( A) και N ( A ) από τις σχέσεις: dim R ( A) = ra ( ), dim R ( A ) = ra ( ), dim N ( A) = r( A), dim N ( A ) = m r( A) 4) {μια βάση του R ( A) } = {οι στήλες του A που αντιστοιχούν στις στήλες του U που έχουν τους οδηγούς} 5) {μια βάση του R ( A )} = {οι μη-μηδενικές γραμμές του U } 6) Αν dim N ( A ) = 0, τότε N ( A ) = { 0 } και άρα ο N ( A) δεν έχει βάση. Αν dim N ( A ) > 0, τότε λύνουμε το σύστημα Ux = 0 ως προς τις βασικές μεταβλητές (εκείνες δηλαδή τις μεταβλητές που αντιστοιχούν στις στήλες του U που έχουν τους οδηγούς) σε συνάρτηση με τις ελεύθερες μεταβλητές. Η γενική λύση γράφεται ως γραμμικός συνδυασμός «κάποιων» διανυσμάτων του έχοντας ως συντελεστές τις ελεύθερες μεταβλητές. Αυτά τα «κάποια» διανύσματα αποτελούν όλα μαζί μια βάση του N ( A). 7) Αν dim N ( A ) = 0, τότε N ( A ) = { 0 } και άρα ο N ( A ) δεν έχει βάση. Αν dim N ( A ) > 0, τότε A U και κατόπιν, λύνουμε το σύστημα U x = 0 ως απαλοιφές προς τις βασικές μεταβλητές (εκείνες δηλαδή τις μεταβλητές που αντιστοιχούν στις στήλες του U που έχουν τους οδηγούς) σε συνάρτηση με τις ελεύθερες μεταβλητές. m Η γενική λύση γράφεται ως γραμμικός συνδυασμός «κάποιων» διανυσμάτων του έχοντας ως συντελεστές τις ελεύθερες μεταβλητές. Αυτά τα «κάποια» διανύσματα αποτελούν όλα μαζί μια βάση του N ( A ). Παρατήρηση: Οποιοδήποτε διανυσματικό χώρο μπορούμε να τον γράψουμε ως το χώρο στηλών R ( A) ή ως μηδενόχωρο N ( A) κάποιου πίνακα A. Συγκεκριμένα: Αν ξέρουμε ότι ένας χώρος V έχει ως βάση ή τουλάχιστον παράγεται από τα διανύσματα 1,,, k τότε θέτουμε A=[πίνακας με στήλες τα 1,,, k ] και άρα, V R ( A). Αν ξέρουμε ότι τα διανύσματα ( x1, x,, x ) του V ικανοποιούν μια ή περισσότερες εξισώσεις της μορφής α1x1+ αx+ + αx = 0, τότε θέτουμε A=[πίνακας με στήλες τους συντελεστές κάθε μεταβλητής σ αυτές τις εξισώσεις] και άρα, V N ( A).
31 π.χ. αν V = 1,,, 4 με 1 = (1,, 4), = (,0, 1), = (0,6, 1), 4 = (1, 4, 9), τότε V R ( A), όπου A = ο πίνακας με στήλες τα 1,,, π.χ. αν V = {( x, y, z) \ x y+ 6z = 0} τότε ο V αποτελείται από τις λύσεις ( x, yz, ) της εξίσωσης x y+ 6z = 0 η οποία ισοδύναμα γράφεται ως [ 1 x 6 ] y= [0]. Δηλαδή, V N ( A) όπου A = [ z 1 6] π.χ. αν V = {( x, y, z) \ x = y = z} τότε ο V αποτελείται από τις λύσεις του x = = y x z x z = 0. Δηλαδή, = + = z 1 0 A = { x y } { x y } συστήματος V N ( A) όπου ΠΡΟΤΑΣΗ 1: Έστω ένας πίνακας A. Οι χώροι R ( A) και N ( A ) είναι m συμπληρωματικοί ο ένας στον άλλο στον. Δηλαδή, ικανοποιούν και τις επόμενες ιδιότητες: m R ( A) & ( m N A ) dim R( A) + dim N ( A ) = dim m R( A) N ( A ) = 0 { } ΠΡΟΤΑΣΗ : Έστω ένας πίνακας A. Οι χώροι R ( A ) και N ( A) είναι συμπληρωματικοί ο ένας στον άλλο στον. Δηλαδή, ικανοποιούν και τις επόμενες ιδιότητες: ( R A ) & N ( A) dim ( R A ) + dim N ( A) = dim R( A ) N ( A) = 0 { } m m m Πόρισμα: R ( A) ανν dim N ( A ) = 0 [δηλ. ra ( ) = m] Άσκηση (παλαιότερο θέμα): Έστω οι πραγματικοί διανυσματικοί υπόχωροι V = { ( x, y, z ) \ x+ y = 0 } και { W = ( x, y, z) \ x y+ z = 0} του. α) Τι παριστάνουν γεωμετρικά οι χώροι V και W και ποια η διάσταση του καθενός; β) Βρείτε μια βάση και τη διάσταση του υποχώρου V W. Τι παριστάνει αυτός ο χώρος γεωμετρικά; γ) Βρείτε μια βάση του υποχώρου του που είναι συμπληρωματικός του V W.
32 Λύση α) Και οι δυο χώροι περιέχουν άδες ( x, yz, ) πραγματικών αριθμών που ικανοποιούν μια εξίσωση της μορφής α x + βy+ γz = 0. Άρα, καθένας από τους χώρους V και W παριστάνει ένα επίπεδο που περνά από το 0 = (0,0,0). Επομένως, dimv = και dimw = β) V W = {( x, y, z) \ x+ y = 0 & x y+ z = 0} δηλαδή ο V W αποτελείται από τις λύσεις του συστήματος: x x+ y= 0 0} y= x y+ z = 0 z A 0 δηλαδή, ο V W N ( A), όπου A = Έχουμε: 1 0 ( 1) A = = U (+) 0 1 Όμως, Ax = 0 Ux = 0 Βασικές μεταβλητές: x, y Ελεύθερη μεταβλητή: z Ανάδρομη αντικατάσταση: η 1 εξίσωση: y+ z = 0 y= z 1 η 1 εξίσωση: x + y= 0 x+ z = 0 x= z z 1 Άρα, ο V W έχει διανύσματα της μορφής: x = z, δηλαδή της μορφής: z / x = z 1/, με z 1 / Επομένως, μια βάση του V W είναι το μονοσύνολο 1/. 1 Επειδή η βάση έχει 1 διάνυσμα, συμπεραίνουμε ότι dim( V W ) = 1 Ο V W παριστάνει την ευθεία του που ορίζεται από τα σημεία (0,0,0) και ( /,1/,1). Δηλαδή, τα επίπεδα V και W τέμνονται σε αυτήν την ευθεία. x
33 γ) Επειδή V W N ( A), συμπεραίνουμε ότι ο συμπληρωματικός στον V W είναι ο χώρος γραμμών του A, δηλαδή ο R ( A ). Μια βάση του R ( A ) είναι οι μημηδενικές γραμμές του U, δηλαδή {μια βάση του R ( A )}= 1 0, 0 1
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Σεπτεμβρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Σεπτεμβρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, Αυγούστου 00 Θέμα. (μονάδες.5) α) [μονάδες: 0.5] Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Σεπτεμβρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, Αυγούστου 00 Θέμα. (μονάδες.5) α) [μονάδες: 0.5] Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών «Γραμμική Άλγεβρα» (ΗΥ119) Χειμερινό Εξάμηνο 009-010 Διδάσκων: Ι. Τσαγράκης 6 Ο ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Δείξτε ότι η απεικόνιση τον ker f. Είναι η
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τμήμα Επιστήμης Υπολογιστών «Γραμμική Άλγεβρα» (ΗΥ119) Χειμερινό Εξάμηνο 009-010 Διδάσκων: Ι. Τσαγράκης 6 Ο ΦΥΛΛΑΔΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Δείξτε ότι η απεικόνιση τον ker f. Είναι η
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων εξέτασης προόδου στο μάθημα «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων εξέτασης προόδου στο μάθημα «Γραμμική Άλγεβρα» (ΗΥ9) Θέμα. (μονάδες.0) Οι ορίζουσες των πινάκων ABC,, βρεθούν οι ορίζουσες των πινάκων:
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων εξέτασης προόδου στο μάθημα «Γραμμική Άλγεβρα» (ΗΥ9) Θέμα. (μονάδες.0) Οι ορίζουσες των πινάκων ABC,, βρεθούν οι ορίζουσες των πινάκων:
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119) ΜΕΡΟΣ 6: ΓΡΑΜΜΙΚΕΣ ΑΠΕΙΚΟΝΙΣΕΙΣ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ ΤΟΥ ΜΑΘΗΜΑΤΟΣ ΗΡΑΚΛΕΙΟ
Παραδείγματα (2) Διανυσματικοί Χώροι
 Παραδείγματα () Διανυσματικοί Χώροι Παράδειγμα 7 Ελέγξτε αν τα ακόλουθα σύνολα διανυσμάτων είναι γραμμικά ανεξάρτητα ή όχι: α) v=(,4,6), v=(,,), v=(7,,) b) v=(,4), v=(,), v=(4,) ) v=(,,), v=(5,,), v=(5,,)
Παραδείγματα () Διανυσματικοί Χώροι Παράδειγμα 7 Ελέγξτε αν τα ακόλουθα σύνολα διανυσμάτων είναι γραμμικά ανεξάρτητα ή όχι: α) v=(,4,6), v=(,,), v=(7,,) b) v=(,4), v=(,), v=(4,) ) v=(,,), v=(5,,), v=(5,,)
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
2.0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ
 .0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Έστω διανύσματα που ανήκουν στο χώρο δ i = ( a i, ai,, ai) i =,,, και έστω γραμμικός συνδυασμός των i : xδ + x δ + + x δ = b που ισούται με το διάνυσμα b,
.0 ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ ΚΑΙ ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Έστω διανύσματα που ανήκουν στο χώρο δ i = ( a i, ai,, ai) i =,,, και έστω γραμμικός συνδυασμός των i : xδ + x δ + + x δ = b που ισούται με το διάνυσμα b,
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Διανυσματικοί Χώροι Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Διανυσματικός Χώρος επί του F Αλγεβρική δομή που αποτελείται
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Παραδείγματα (1 ο σετ) Διανυσματικοί Χώροι
 Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού:
Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού:
D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].
![D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ]. D = / Επιλέξτε, π.χ, το ακόλουθο απλό παράδειγμα: =[IA 1 ].](/thumbs/60/44272313.jpg) 4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
4. Φυλλάδιο Ασκήσεων IV σύντομες λύσεις, ενδεικτικές απαντήσεις πολλαπλής επιλογής 4.. Άσκηση. Χρησιμοποιήστε τη διαδικασία Gauss-Jordan γιά να βρείτε τους αντιστρόφους των παρακάτω πινάκων, αν υπάρχουν.
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-9) ΜΕΡΟΣ 7: ΙΔΙΟΤΙΜΕΣ & ΙΔΙΟΔΙΑΝΥΣΜΑΤΑ ΔΙΑΓΩΝΙΟΠΟΙΗΣΗ ΠΙΝΑΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ ΙΩΑΝΝΗΣ Α. ΤΣΑΓΡΑΚΗΣ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (ΗΥ-9) ΜΕΡΟΣ 7: ΙΔΙΟΤΙΜΕΣ & ΙΔΙΟΔΙΑΝΥΣΜΑΤΑ ΔΙΑΓΩΝΙΟΠΟΙΗΣΗ ΠΙΝΑΚΩΝ ΣΗΜΕΙΩΣΕΙΣ ΑΠΟ ΤΙΣ ΠΑΡΑΔΟΣΕΙΣ
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος
 Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών «Γραµµική Άλγεβρα Ι» (ΕΜ111) Χειµερινό Εξάµηνο 2006-2007, ιδάσκων: Ι. Τσαγράκης 5 Ο ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Έστω V ένας διανυσµατικός χώρος επί
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ - Τµήµα Εφαρµοσµένων Μαθηµατικών «Γραµµική Άλγεβρα Ι» (ΕΜ111) Χειµερινό Εξάµηνο 2006-2007, ιδάσκων: Ι. Τσαγράκης 5 Ο ΦΥΛΛΑ ΙΟ ΑΣΚΗΣΕΩΝ Άσκηση 1: Έστω V ένας διανυσµατικός χώρος επί
Βάση και Διάσταση Διανυσματικού Χώρου
 Βάση και Διάσταση Διανυσματικού Χώρου Έστω V ένας διανυσματικός χώρος επί του σώματος F. Ορισμός : Ένα υποσύνολο S του διανυσματικού χώρου V θα λέμε ότι είναι βάση του V αν ισχύει Α) Η θήκη του S παράγει
Βάση και Διάσταση Διανυσματικού Χώρου Έστω V ένας διανυσματικός χώρος επί του σώματος F. Ορισμός : Ένα υποσύνολο S του διανυσματικού χώρου V θα λέμε ότι είναι βάση του V αν ισχύει Α) Η θήκη του S παράγει
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα
 Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Διανυσματικοί Χώροι και Υπόχωροι: Βάσεις και Διάσταση Ανδριανός Ε Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής
Γραμμική Άλγεβρα και Μαθηματικός Λογισμός για Οικονομικά και Επιχειρησιακά Προβλήματα Ενότητα: Διανυσματικοί Χώροι και Υπόχωροι: Βάσεις και Διάσταση Ανδριανός Ε Τσεκρέκος Τμήμα Λογιστικής & Χρηματοοικονομικής
1 1 A = x 1 x 2 x 3. x 4. R 2 3 : a + b + c = x + y + z = 0. R 2 3 : a + x = b + y = c + z = 0
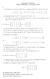 Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 19/6/2018 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 9/6/08 Διδάσκων: Ι. Λυχναρόπουλος Έστω A= k και w = 3 0. Να βρεθεί η τιμή του k για την οποία
Παραδείγματα (2 ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος
 Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Έστω ο υποχώρος W του R 5 που παράγεται από τα διανύσματα v=(,,-,,), v=(,,-,6,8), v=(,,,,6), v=(,,5,,8), v5=(,7,,,9). a)
Παραδείγματα ( ο σετ) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα Έστω ο υποχώρος W του R 5 που παράγεται από τα διανύσματα v=(,,-,,), v=(,,-,6,8), v=(,,,,6), v=(,,5,,8), v5=(,7,,,9). a)
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
Κεφάλαιο 7 Βάσεις και ιάσταση
 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
Εφαρμοσμένα Μαθηματικά ΙΙ 10ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί Επιμέλεια: Ι. Λυχναρόπουλος. Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f b) f : R R f y, ( +, y
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Γραμμικοί Μετασχηματισμοί Επιμέλεια: Ι. Λυχναρόπουλος. Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f b) f : R R f y, ( +, y
Γραμμική Άλγεβρα Ι Εξέταση Φεβρουαρίου. Επώνυμο. Όνομα. ΑΜ (13 ψηφία) Σύνολο
 1 Γραμμική Άλγεβρα Ι 009-10 Εξέταση Φεβρουαρίου Επώνυμο Όνομα ΑΜ (1 ψηφία) Ημ/ία Αίθουσα 1 5 Σύνολο Α Η εξέταση αποτελείται από 5 Θέματα. Το άθροισμα των μονάδων είναι 1, το άριστα 10 και η βάση 5. Απαντήστε
1 Γραμμική Άλγεβρα Ι 009-10 Εξέταση Φεβρουαρίου Επώνυμο Όνομα ΑΜ (1 ψηφία) Ημ/ία Αίθουσα 1 5 Σύνολο Α Η εξέταση αποτελείται από 5 Θέματα. Το άθροισμα των μονάδων είναι 1, το άριστα 10 και η βάση 5. Απαντήστε
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
1. Για καθένα από τους ακόλουθους διανυσματικούς χώρους βρείτε μια βάση και τη διάσταση. 3. U x y z x y z x y. {(,, ) } a b. c d
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.
![b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0. b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.](/thumbs/63/49387122.jpg) Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Παραδείγματα Διανυσματικοί Χώροι
 Παραδείγματα Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού: με V και
Παραδείγματα Διανυσματικοί Χώροι Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με y, V και του πολλαπλασιασμού: με V και
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί
 Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Παραδείγματα Διανυσματικοί Χώροι (3)
 Παραδείγματα Διανυσματικοί Χώροι () Παράδειγμα Δίνεται ο πίνακας A = 6. Να υπολογισθούν οι θεμελιώδεις υποχώροι που σχετίζονται με τον πίνακα Α. Να βρεθεί η διάστασή του κάθε ενός και από μία βάση τους.
Παραδείγματα Διανυσματικοί Χώροι () Παράδειγμα Δίνεται ο πίνακας A = 6. Να υπολογισθούν οι θεμελιώδεις υποχώροι που σχετίζονται με τον πίνακα Α. Να βρεθεί η διάστασή του κάθε ενός και από μία βάση τους.
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 2 η Ημερομηνία Αποστολής στον Φοιτητή: 28 Νοεμβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
, ορίζουμε deta = ad bc. Πρόταση Ένας πίνακας Α είναι αντιστρέψιμος τότε και μόνο αν deta 0.
 Για κάθε πίνακα Α ορίζουμε μία τιμή που λέγεται ορίζουσα και συμβολίζεται deta ή Α Ο ορισμός γίνεται επαγωγικά για = 2, 3, 4, και ισχύουν τα εξής: a b Για 22 πίνακα Α = c d, ορίζουμε deta = ad bc a 1 b
Για κάθε πίνακα Α ορίζουμε μία τιμή που λέγεται ορίζουσα και συμβολίζεται deta ή Α Ο ορισμός γίνεται επαγωγικά για = 2, 3, 4, και ισχύουν τα εξής: a b Για 22 πίνακα Α = c d, ορίζουμε deta = ad bc a 1 b
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ. Διανυσματικός χώρος
 Διανυσματικός χώρος ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ Ορισμός Διανυσματικός χώρος V πάνω στο σύνολο πραγματικός διανυσματικός χώρος V λέγεται κάθε σύνολο εφοδιασμένο με τις πράξεις της πρόσθεσης μεταξύ των στοιχείων
Διανυσματικός χώρος ΔΙΑΝΥΣΜΑΤΙΚΟΙ ΧΩΡΟΙ Ορισμός Διανυσματικός χώρος V πάνω στο σύνολο πραγματικός διανυσματικός χώρος V λέγεται κάθε σύνολο εφοδιασμένο με τις πράξεις της πρόσθεσης μεταξύ των στοιχείων
Διανύσµατα στο επίπεδο
 Διανύσµατα στο επίπεδο Ένα διάνυσµα v έχει αρχικό και τελικό σηµείο. Χαρακτηρίζεται από: διεύθυνση (ευθεία επί της οποίας κείται φορά (προς ποια κατεύθυνση της ευθείας δείχνει µέτρο (το µήκος του, v ή
Διανύσµατα στο επίπεδο Ένα διάνυσµα v έχει αρχικό και τελικό σηµείο. Χαρακτηρίζεται από: διεύθυνση (ευθεία επί της οποίας κείται φορά (προς ποια κατεύθυνση της ευθείας δείχνει µέτρο (το µήκος του, v ή
X = {(x 1, x 2 ) x 1 + 2x 2 = 0}.
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 4 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 26/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 4 26/2/2014 1 / 12 Υποσύνολα ενός διανυσματικού χώρου. Πότε είναι ένα υποσύνολο X ενός
Γραμμική Άλγεβρα ΙΙ Διάλεξη 4 Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 26/2/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 4 26/2/2014 1 / 12 Υποσύνολα ενός διανυσματικού χώρου. Πότε είναι ένα υποσύνολο X ενός
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος
 6/6/06 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 0 Δίνεται ο πίνακας A =. Nα υπολογίσετε την βαθμίδα του και να βρείτε τη διάσταση και από μία βάση α) του μηδενοχώρου
6/6/06 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 0 Δίνεται ο πίνακας A =. Nα υπολογίσετε την βαθμίδα του και να βρείτε τη διάσταση και από μία βάση α) του μηδενοχώρου
Γραµµική Αλγεβρα. Ενότητα 3 : ιανυσµατικοί Χώροι και Υπόχωροι. Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής
 Γραµµική Αλγεβρα Ενότητα 3 : ιανυσµατικοί Χώροι και Υπόχωροι Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Γραµµική Αλγεβρα Ενότητα 3 : ιανυσµατικοί Χώροι και Υπόχωροι Ευστράτιος Γαλλόπουλος Τµήµα Μηχανικών Η/Υ & Πληροφορικής Αδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Ασκήσεις2 8. ; Αληθεύει ότι το (1, 0, 1, 2) είναι ιδιοδιάνυσμα της f ; b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα της γραμμικής απεικόνισης 3 3
 Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Γραμμική Αλγεβρα ΙΙ Διάλεξη 7 Βάσεις Διάσταση Χρήστος Κουρουνιώτης Πανεπισ τήμιο Κρήτης 7/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 7 7/3/ / 1
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 7 Διάσταση Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 7/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 7 7/3/2014 1 / 1 Εάν ένα υποσύνολο S του διανυσματικού χώρου V παράγει το V,
Γραμμική Άλγεβρα ΙΙ Διάλεξη 7 Διάσταση Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 7/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 7 7/3/2014 1 / 1 Εάν ένα υποσύνολο S του διανυσματικού χώρου V παράγει το V,
Έστω ε μια ευθεία του καρτεσιανού επιπέδου, με εξίσωση ) ένα σημείο εκτός αυτής. Θέλουμε y (1)
 7 ΕΜΒΑΔΟΝ ΤΡΙΓΩΝΟΥ Απόσταση Σημείου από Ευθεία Έστω ε μια ευθεία του καρτεσιανού επιπέδου, με εξίσωση M ( x, y ) ένα σημείο εκτός αυτής Θέλουμε y να υπολογίσουμε την απόσταση d( M, ε) του ε σημείου M από
7 ΕΜΒΑΔΟΝ ΤΡΙΓΩΝΟΥ Απόσταση Σημείου από Ευθεία Έστω ε μια ευθεία του καρτεσιανού επιπέδου, με εξίσωση M ( x, y ) ένα σημείο εκτός αυτής Θέλουμε y να υπολογίσουμε την απόσταση d( M, ε) του ε σημείου M από
1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]
![1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x] 1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]](/thumbs/77/75945202.jpg) σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
Γραµµικη Αλγεβρα Ι. Ακαδηµαϊκο Ετος Βοηθος Ασκησεων: Χ. Ψαρουδάκης
 Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
Γραµµικη Αλγεβρα Ι Ακαδηµαϊκο Ετος 2011-2012 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml 21-2 - 2012
1 x x x x 1 x x x x 1 x x x x 1 (10) B 2, B 1. (10)
 Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 2004 Θέμα 1 ο. 4
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 00 Θέμα 1 ο Έστω U ο υπόχωρος του που παράγεται από τα στοιχεία (1-11α) (10β) (5-γ) και (-δ) (I) Να προσδιορίσετε τις αναγκαίες
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ-ΦΕΒΡΟΥΑΡΙΟΣ 00 Θέμα 1 ο Έστω U ο υπόχωρος του που παράγεται από τα στοιχεία (1-11α) (10β) (5-γ) και (-δ) (I) Να προσδιορίσετε τις αναγκαίες
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - 02/07/08) ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ
 Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Ονοματεπώνυμο:......... Α.Μ....... Ετος... ΑΙΘΟΥΣΑ:....... I. (περί τις 55μ. = ++5++. Σωστό ή Λάθος: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ (Εξ. Ιουνίου - //8 ΕΠΙΛΕΓΜΕΝΕΣ ΑΠΑΝΤΗΣΕΙΣ (αʹ Αν AB = BA όπου A, B τετραγωνικά και
Περιεχόμενα. Πρόλογος 3
 Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Πρόλογος Η χρησιμότητα της Γραμμικής Άλγεβρας είναι σχεδόν αυταπόδεικτη. Αρκεί μια ματιά στο πρόγραμμα σπουδών, σχεδόν κάθε πανεπιστημιακού τμήματος θετικών επιστημών, για να διαπιστώσει κανείς την παρουσία
Κεφάλαιο 4 ιανυσµατικοί Χώροι
 Κεφάλαιο 4 ιανυσµατικοί Χώροι 4 ιανυσµατικοί χώροι - Βασικοί ορισµοί και ιδιότητες ιανυσµατικοί Χώροι Ένας ιανυσµατικός Χώρος V (δχ) είναι ένα σύνολο από µαθηµατικά αντικείµενα (αριθµούς, διανύσµατα, πίνακες,
Κεφάλαιο 4 ιανυσµατικοί Χώροι 4 ιανυσµατικοί χώροι - Βασικοί ορισµοί και ιδιότητες ιανυσµατικοί Χώροι Ένας ιανυσµατικός Χώρος V (δχ) είναι ένα σύνολο από µαθηµατικά αντικείµενα (αριθµούς, διανύσµατα, πίνακες,
= 7. Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις
 1. Εισαγωγή Δίνεται η συνάρτηση μεταφοράς = = 1 + 6 + 11 + 6 = + 6 + 11 + 6 =. 2 Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις L = 0 # και L $ % &'
1. Εισαγωγή Δίνεται η συνάρτηση μεταφοράς = = 1 + 6 + 11 + 6 = + 6 + 11 + 6 =. 2 Στο σημείο αυτό θα υπενθυμίσουμε κάποιες βασικές ιδιότητες του μετασχηματισμού Laplace, δηλαδή τις L = 0 # και L $ % &'
ΣΥΣΤΗΜΑΤΑ. 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις)
 6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
6 ΣΥΣΤΗΜΑΤΑ 6.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ (Επαναλήψεις-Συμπληρώσεις) Η εξίσωση αx βy γ Στο Γυμνάσιο διαπιστώσαμε με την βοήθεια παραδειγμάτων ότι η εξίσωση αx βy γ, με α 0 ή β 0, που λέγεται γραμμική εξίσωση,
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
ΜΑΘΗΜΑΤΑ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΝΥΣΜΑΤΑ 1 ΜΑΘΗΜΑ 1 ο +2 ο ΕΝΝΟΙΑ ΔΙΑΝΥΣΜΑΤΟΣ Διάνυσμα ορίζεται ένα προσανατολισμένο ευθύγραμμο τμήμα, δηλαδή ένα ευθύγραμμο τμήμα
Παραδείγματα Γραμμικοί Μετασχηματισμοί
 Παραδείγματα Γραμμικοί Μετασχηματισμοί Παράδειγμα Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f + 4 4+ b) f : R R με f + a+ b ac c) f : P M με f ( a + b + c + d ) d b d f :
Παραδείγματα Γραμμικοί Μετασχηματισμοί Παράδειγμα Να εξετασθεί αν είναι γραμμικές οι ακόλουθες συναρτήσεις: a) f : R R με f + 4 4+ b) f : R R με f + a+ b ac c) f : P M με f ( a + b + c + d ) d b d f :
Γραμμική Άλγεβρα Ι,
 Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα
 Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
Ασκήσεις1 Πολυώνυμα. x x c. με το. b. Να βρεθούν όλες οι τιμές των a, Να βρεθεί ο μκδ και το εκπ τους
 Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
AX=B (S) A A X=A B I X=A B X=A B I X=A B X=A B X=A B X X
 . Επίλυση γραμμικού συστήματος με χρήση αντιστρόφου Πρόταση Θεωρούμε ένα τετραγωνικό γραμμικό σύστημα (δηλαδή ο αριθμός των εξισώσεων είναι ίσος με τον αριθμό των αγνώστων) AX=B (S). Αν ο πίνακας Α είναι
. Επίλυση γραμμικού συστήματος με χρήση αντιστρόφου Πρόταση Θεωρούμε ένα τετραγωνικό γραμμικό σύστημα (δηλαδή ο αριθμός των εξισώσεων είναι ίσος με τον αριθμό των αγνώστων) AX=B (S). Αν ο πίνακας Α είναι
ΜΑΣ121: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο , Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: 2 ώρες 18 Νοεμβρίου, 2017
 ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
ΜΑΣ: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ I Εαρινό εξάμηνο 07-08, Διδάσκων: Γιώργος Γεωργίου ΕΝΔΙΑΜΕΣΗ ΕΞΕΤΑΣΗ, Διάρκεια: ώρες 8 Νοεμβρίου, 07 Δίνονται 4 προβλήματα που αντιστοιχούν σε 0 μονάδες με άριστα το 00! ΟΝΟΜΑ: Αρ.
Γραμμική Άλγεβρα II Εαρινό εξάμηνο
 Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
Κεφάλαιο 1 Συστήματα γραμμικών εξισώσεων
 Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Γραμμική Άλγεβρα Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών
Κεφάλαιο Συστήματα γραμμικών εξισώσεων Παραδείγματα από εφαρμογές Γραμμική Άλγεβρα Παράδειγμα : Σε ένα δίκτυο (αγωγών ή σωλήνων ή δρόμων) ισχύει ο κανόνας των κόμβων όπου το άθροισμα των εισερχόμενων ροών
ΚΕΦΑΛΑΙΟ 1: Πρότυπα. x y x z για κάθε x, y, R με την ιδιότητα 1R. x για κάθε x R, iii) υπάρχει στοιχείο 1 R. ii) ( x y) z x ( y z)
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai217/lai217html Παρασκευή 17 Νοεµβρίου 217 Ασκηση
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai217/lai217html Παρασκευή 17 Νοεµβρίου 217 Ασκηση
2x y = 1 x + y = 5. 2x y = 1. x + y = 5. 2x y = 1 4x + 2y = 0. 2x y = 1 4x + 2y = 2
 Σημειώσεις μαθήματος Μ22 Γραμμική Άλγεβρα Ι Βασισμένες στο βιβλίο του GStrang Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2 Εισαγωγή Αυτές οι σημειώσεις καλύπτουν την ύλη του μαθήματος
Σημειώσεις μαθήματος Μ22 Γραμμική Άλγεβρα Ι Βασισμένες στο βιβλίο του GStrang Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2 Εισαγωγή Αυτές οι σημειώσεις καλύπτουν την ύλη του μαθήματος
Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων
 7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
[A I 3 ] [I 3 A 1 ].
![[A I 3 ] [I 3 A 1 ]. [A I 3 ] [I 3 A 1 ].](/thumbs/65/54189091.jpg) ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΤΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΣΕΠΤΕΜΒΡΙΟΥ 9 (α) Να ϐρεθεί ο αντίστροφος του πίνακα A = 6 4 (ϐ) Εστω b, b, b στο R Να λύθεί το σύστηµα x = b 6x + x + x = b x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΕΞΕΤΑΣΕΩΝ ΤΗΣ ΕΞΕΤΑΣΤΙΚΗΣ ΠΕΡΙΟ ΟΥ ΣΕΠΤΕΜΒΡΙΟΥ 9 (α) Να ϐρεθεί ο αντίστροφος του πίνακα A = 6 4 (ϐ) Εστω b, b, b στο R Να λύθεί το σύστηµα x = b 6x + x + x = b x
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος )
 ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
ΕΠΑΝΑΛΗΨΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΟΥ ( α μέρος ) Ερωτήσεις Θεωρίας Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε
Ευκλείδειοι Χώροι. Ορίζουµε ως R n, όπου n N, το σύνολο όλων διατεταµένων n -άδων πραγµατικών αριθµών ( x
 Ευκλείδειοι Χώροι Ορίζουµε ως R, όπου N, το σύνολο όλων διατεταµένων -άδων πραγµατικών αριθµών x, x,, x ) Tο R λέγεται ευκλείδειος -χώρος και τα στοιχεία του λέγονται διανύσµατα ή σηµεία Το x i λέγεται
Ευκλείδειοι Χώροι Ορίζουµε ως R, όπου N, το σύνολο όλων διατεταµένων -άδων πραγµατικών αριθµών x, x,, x ) Tο R λέγεται ευκλείδειος -χώρος και τα στοιχεία του λέγονται διανύσµατα ή σηµεία Το x i λέγεται
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai218/lai218html Παρασκευή 23 Νοεµβρίου 218 Ασκηση 1
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Τµηµα Β (ΑΡΤΙΟΙ) Ασκησεις - Φυλλαδιο 4 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebrai/lai218/lai218html Παρασκευή 23 Νοεµβρίου 218 Ασκηση 1
2.2 ΓΕΝΙΚΗ ΜΟΡΦΗ ΕΞΙΣΩΣΗΣ ΕΥΘΕΙΑΣ
 63 ΓΕΝΙΚΗ ΜΟΡΦΗ ΕΞΙΣΩΣΗΣ ΕΥΘΕΙΑΣ Η Εξίσωση Αx + Βy + Γ = 0, με Α 0 ή Β 0 Έστω ε μια ευθεία στο καρτεσιανό επίπεδο Αν η ευθεία ε τέμνει τον άξονα yy στο σημείο Σ (, 0 β ) και έχει συντελεστή διεύθυνσης
63 ΓΕΝΙΚΗ ΜΟΡΦΗ ΕΞΙΣΩΣΗΣ ΕΥΘΕΙΑΣ Η Εξίσωση Αx + Βy + Γ = 0, με Α 0 ή Β 0 Έστω ε μια ευθεία στο καρτεσιανό επίπεδο Αν η ευθεία ε τέμνει τον άξονα yy στο σημείο Σ (, 0 β ) και έχει συντελεστή διεύθυνσης
x 2 = x 2 1 + x 2 2. x 2 = u 2 + x 2 3 Χρησιµοποιώντας το συµβολισµό του ανάστροφου, αυτό γράφεται x 2 = x T x. = x T x.
 Κεφάλαιο 4 Μήκη και ορθές γωνίες Μήκος διανύσµατος Στο επίπεδο, R 2, ϐρίσκουµε το µήκος ενός διανύσµατος x = (x 1, x 2 ) χρησιµοποιώντας το Πυθαγόρειο ϑεώρηµα : x 2 = x 2 1 + x 2 2. Στο χώρο R 3, εφαρµόζουµε
Κεφάλαιο 4 Μήκη και ορθές γωνίες Μήκος διανύσµατος Στο επίπεδο, R 2, ϐρίσκουµε το µήκος ενός διανύσµατος x = (x 1, x 2 ) χρησιµοποιώντας το Πυθαγόρειο ϑεώρηµα : x 2 = x 2 1 + x 2 2. Στο χώρο R 3, εφαρµόζουµε
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss Jordan
 Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss Jodan Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y 6 με απαλοιφή Gauss. Ο επαυξημένος πίνακας του συστήματος
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss Jodan Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y 6 με απαλοιφή Gauss. Ο επαυξημένος πίνακας του συστήματος
Κεφάλαιο 6 Ιδιοτιμές και Ιδιοδιανύσματα
 Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
n = dim N (A) + dim R(A). dim V = dim ker L + dim im L.
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 9 Γραμμικοί Ισομορφισμοί Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 9 19/3/2014 1 / 12 Γραμμικές απεικονίσεις και υπόχωροι Εικόνα
Γραμμική Άλγεβρα ΙΙ Διάλεξη 9 Γραμμικοί Ισομορφισμοί Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 19/3/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 9 19/3/2014 1 / 12 Γραμμικές απεικονίσεις και υπόχωροι Εικόνα
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ. ΕΝΟΤΗΤΑ: Διανυσματικοί Χώροι (2) ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Διανυσματικοί Χώροι (2) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΝΟΤΗΤΑ: Διανυσματικοί Χώροι (2) ΙΟΝΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΔΙΔΑΣΚΩΝ: Βλάμος Παναγιώτης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα
 ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2009-2010 Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Ένα σύνολο m εξισώσεων n αγνώστων που έχει την ακόλουθη
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2009-2010 Μαθηματικά για Οικονομολόγους ΙI-Μάθημα 4 Γραμμικά Συστήματα ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Ι Ένα σύνολο m εξισώσεων n αγνώστων που έχει την ακόλουθη
Πίνακες >>A = [ 1,6; 7, 11]; Ή τον πίνακα >> B = [2,0,1; 1,7,4; 3,0,1]; Πράξεις πινάκων
![Πίνακες >>A = [ 1,6; 7, 11]; Ή τον πίνακα >> B = [2,0,1; 1,7,4; 3,0,1]; Πράξεις πινάκων Πίνακες >>A = [ 1,6; 7, 11]; Ή τον πίνακα >> B = [2,0,1; 1,7,4; 3,0,1]; Πράξεις πινάκων](/thumbs/25/6063576.jpg) Πίνακες Ένας πίνακας είναι μια δισδιάστατη λίστα από αριθμούς. Για να δημιουργήσουμε ένα πίνακα στο Matlab εισάγουμε κάθε γραμμή σαν μια ακολουθία αριθμών που ξεχωρίζουν με κόμμα (,) ή κενό (space) και
Πίνακες Ένας πίνακας είναι μια δισδιάστατη λίστα από αριθμούς. Για να δημιουργήσουμε ένα πίνακα στο Matlab εισάγουμε κάθε γραμμή σαν μια ακολουθία αριθμών που ξεχωρίζουν με κόμμα (,) ή κενό (space) και
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικά Συστήματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικό Σύστημα a11x1 + a12x2 + + a1 nxn = b1 a x + a x + +
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Γραμμικά Συστήματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Γραμμικό Σύστημα a11x1 + a12x2 + + a1 nxn = b1 a x + a x + +
Σημειώσεις για το μάθημα: «Βασικές Αρχές Θεωρίας Συστημάτων» (Μέρος Α )
 Χρήστος Ι Σχοινάς Αν Καθηγητής ΔΠΘ Σημειώσεις για το μάθημα «Βασικές Αρχές Θεωρίας Συστημάτων» (Μέρος Α ) ΞΑΝΘΗ, 008 - - - - ΚΕΦΑΛΑΙΟ ΔΙΑΝΥΣΜATA Ορισμοί και ιδιότητες Συχνά, σε διάφορα προβλήματα στα Μαθηματικά,
Χρήστος Ι Σχοινάς Αν Καθηγητής ΔΠΘ Σημειώσεις για το μάθημα «Βασικές Αρχές Θεωρίας Συστημάτων» (Μέρος Α ) ΞΑΝΘΗ, 008 - - - - ΚΕΦΑΛΑΙΟ ΔΙΑΝΥΣΜATA Ορισμοί και ιδιότητες Συχνά, σε διάφορα προβλήματα στα Μαθηματικά,
Gauss. x + y + z = 2 3x + 3y z = 6 x y + z = 1. x + y + z = r x y = 0 3x + y + sz = s 0
 Γραμμική Άλγεβρα Κεφάλαιο Πίνακες και απαλοιφή Gauss. Ποια συνθήκη πρέπει να ικανοποιούν τα y, y 2, y 3 ώστε τα διανύσματα (0, y ), (, y 2 ), (2, y 3 ) να είναι στην ίδια ευθεία; Η ευθεία που περνάει από
Γραμμική Άλγεβρα Κεφάλαιο Πίνακες και απαλοιφή Gauss. Ποια συνθήκη πρέπει να ικανοποιούν τα y, y 2, y 3 ώστε τα διανύσματα (0, y ), (, y 2 ), (2, y 3 ) να είναι στην ίδια ευθεία; Η ευθεία που περνάει από
ΚΕΦΑΛΑΙΟ 1 Ο ΔΙΑΝΥΣΜΑΤΑ
 ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΤΗΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΟΥ Β ΛΥΚΕΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 ΚΕΦΑΛΑΙΟ 1 Ο ΔΙΑΝΥΣΜΑΤΑ 1. ΘΕΜΑ ΚΩΔΙΚΟΣ_18556 Δίνονται τα διανύσματα α και β με ^, και,. α Να
ΘΕΜΑΤΑ ΚΑΙ ΑΠΑΝΤΗΣΕΙΣ ΤΗΣ ΤΡΑΠΕΖΑΣ ΘΕΜΑΤΩΝ ΓΙΑ ΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΟΥ Β ΛΥΚΕΙΟΥ ΣΧΟΛΙΚΟ ΕΤΟΣ 014-015 ΚΕΦΑΛΑΙΟ 1 Ο ΔΙΑΝΥΣΜΑΤΑ 1. ΘΕΜΑ ΚΩΔΙΚΟΣ_18556 Δίνονται τα διανύσματα α και β με ^, και,. α Να
1.3 ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ
 ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Ορισμός : αν λ πραγματικός αριθμός με 0 και μη μηδενικό διάνυσμα τότε σαν γινόμενο του λ με το ορίζουμε ένα διάνυσμα
ΚΕΦΑΛΑΙΟ Ο : ΔΙΑΝΥΣΜΑΤΑ - ΕΝΟΤΗΤΑ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ ΑΡΙΘΜΟΥ ΜΕ ΔΙΑΝΥΣΜΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ Ορισμός : αν λ πραγματικός αριθμός με 0 και μη μηδενικό διάνυσμα τότε σαν γινόμενο του λ με το ορίζουμε ένα διάνυσμα
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4
 Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
Γραµµικη Αλγεβρα Ι Επιλυση Επιλεγµενων Ασκησεων Φυλλαδιου 4 ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθος Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://wwwmathuoigr/ abeligia/linearalgebrai/laihtml
Kεφάλαιο 4. Συστήματα διαφορικών εξισώσεων. F : : F = F r, όπου r xy
 4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
4 Εισαγωγή Kεφάλαιο 4 Συστήματα διαφορικών εξισώσεων Εστω διανυσματικό πεδίο F : : F = Fr, όπου r x, και είναι η ταχύτητα στο σημείο πχ ενός ρευστού στο επίπεδο Εστω ότι ψάχνουμε τις τροχιές κίνησης των
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος
 9/6/5 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 5 Δίνεται ο πίνακας A 5. Αν διαγωνοποιείται να τον διαγωνοποιήσετε και στη συνέχεια να k υπολογίσετε το A όπου k θετικός
9/6/5 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 5 Δίνεται ο πίνακας A 5. Αν διαγωνοποιείται να τον διαγωνοποιήσετε και στη συνέχεια να k υπολογίσετε το A όπου k θετικός
Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο
 Ασκήσεις6 7 Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο και Βασικά σημεία Το σύνηθες εσωτερικό γινόμενο στο και (ορισμοί και ιδιότητες) Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορθογώνιο συμπλήρωμα
Ασκήσεις6 7 Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο και Βασικά σημεία Το σύνηθες εσωτερικό γινόμενο στο και (ορισμοί και ιδιότητες) Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορθογώνιο συμπλήρωμα
ΚΕΦ.6:ΤΕΤΡΑΓΩΝΙΚΕΣ ΜΟΡΦΕΣ. ΣΥΜΜΕΤΡΙΚΟΙ ΠΙΝΑΚΕΣ
 ΚΕΦ:ΤΕΤΡΑΓΩΝΙΚΕΣ ΜΟΡΦΕΣ ΣΥΜΜΕΤΡΙΚΟΙ ΠΙΝΑΚΕΣ Τετραγωνικές μορφές: Συναρτήσεις με τύπο Q ν α ι j j, j [ ] ν α α ν αν α νν ν Τ Χ ΑΧ Για παράδειγμα εάν v Q α + α + α + α α + α + α + α δηλ a a a a α + α + α
ΚΕΦ:ΤΕΤΡΑΓΩΝΙΚΕΣ ΜΟΡΦΕΣ ΣΥΜΜΕΤΡΙΚΟΙ ΠΙΝΑΚΕΣ Τετραγωνικές μορφές: Συναρτήσεις με τύπο Q ν α ι j j, j [ ] ν α α ν αν α νν ν Τ Χ ΑΧ Για παράδειγμα εάν v Q α + α + α + α α + α + α + α δηλ a a a a α + α + α
Γραμμική Άλγεβρα Ενότητα 2: Διανυσματικοί χώροι
 Γραμμική Άλγεβρα Ενότητα 2: Διανυσματικοί χώροι Ευάγγελος Ράπτης Τμήμα Πληροφορικής 5 Μάθημα 5 Τετάρτη 10 Οκτωβρίου 2012 Με το σημερινό 9 μάθημα αρχίζουμε τη μελέτη των Διανυσματικών χώρων, μία πολύ βασική
Γραμμική Άλγεβρα Ενότητα 2: Διανυσματικοί χώροι Ευάγγελος Ράπτης Τμήμα Πληροφορικής 5 Μάθημα 5 Τετάρτη 10 Οκτωβρίου 2012 Με το σημερινό 9 μάθημα αρχίζουμε τη μελέτη των Διανυσματικών χώρων, μία πολύ βασική
x 2 = b 1 2x 1 + 4x 2 + x 3 = b 2. x 1 + 2x 2 + x 3 = b 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΕΞΕΤΑΣΕΙΣ ΣΕΠΤΕΜΒΡΙΟΥ 008-9 ΛΥΣΕΙΣ = 1 (Ι) Να ϐρεθεί ο αντίστροφος του πίνακα 6 40 1 0 A 4 1 1 1 (ΙΙ) Εστω b 1, b, b 3 στο R Να λύθεί το σύστηµα x = b 1 x 1 + 4x + x 3 = b x 1 + x + x
Κεφάλαιο 9 1 Ιδιοτιμές και Ιδιοδιανύσματα
 Σελίδα από 58 Κεφάλαιο 9 Ιδιοτιμές και Ιδιοδιανύσματα 9. Ορισμοί... 9. Ιδιότητες... 9. Θεώρημα Cayley-Hamlto...9 9.. Εφαρμογές του Θεωρήματος Cayley-Hamlto... 9.4 Ελάχιστο Πολυώνυμο...40 Ασκήσεις του Κεφαλαίου
Σελίδα από 58 Κεφάλαιο 9 Ιδιοτιμές και Ιδιοδιανύσματα 9. Ορισμοί... 9. Ιδιότητες... 9. Θεώρημα Cayley-Hamlto...9 9.. Εφαρμογές του Θεωρήματος Cayley-Hamlto... 9.4 Ελάχιστο Πολυώνυμο...40 Ασκήσεις του Κεφαλαίου
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss-Jordan Παραγοντοποίηση LU, LDU
 Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss-Jordan Παραγοντοποίηση LU, LDU Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x+ y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y
Παραδείγματα Απαλοιφή Gauss Απαλοιφή Gauss-Jordan Παραγοντοποίηση LU, LDU Επιμέλεια: Ι. Λυχναρόπουλος Παράδειγμα x y Να επιλυθεί το ακόλουθο σύστημα: x+ y 6 Σε μορφή πινάκων το σύστημα γράφεται ως: x y
Θα ξέρεις τι λέγεται γραμμική εξίσωση με δύο αγνώστους. Λέγεται κάθε εξίσωση της μορφής αχ +βψ =γ. Θα ξέρεις τι είναι το σύστημα εξισώσεων
 1. Θα ξέρεις τι λέγεται γραμμική εξίσωση με δύο αγνώστους. Λέγεται κάθε εξίσωση της μορφής αχ +βψ =γ. Θα ξέρεις τι είναι το σύστημα εξισώσεων Είναι ομάδα από δύο ή περισσότερες εξισώσεις των οποίων ζητάμε
1. Θα ξέρεις τι λέγεται γραμμική εξίσωση με δύο αγνώστους. Λέγεται κάθε εξίσωση της μορφής αχ +βψ =γ. Θα ξέρεις τι είναι το σύστημα εξισώσεων Είναι ομάδα από δύο ή περισσότερες εξισώσεις των οποίων ζητάμε
7 Μάθημα Πορεία μελέτης Άσκηση Πορεία μελέτης
 Περιεχόμενα I Εναρξη μαθήματος 5 II Αρχικά μαθήματα 7 1 Μάθημα 1 7 1.1 Εισαγωγή............................... 7 1.2 Πορεία μελέτης............................ 7 1.3 Γραμμικά συστήματα.........................
Περιεχόμενα I Εναρξη μαθήματος 5 II Αρχικά μαθήματα 7 1 Μάθημα 1 7 1.1 Εισαγωγή............................... 7 1.2 Πορεία μελέτης............................ 7 1.3 Γραμμικά συστήματα.........................
( A = A = 3 5 A 2 + B 2.
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης , (1)
 1 ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης (1) όπου οι συντελεστές είναι δοσµένες συνεχείς συναρτήσεις ορισµένες σ ένα ανοικτό διάστηµα. Ορισµός 1. Ορίζουµε τον διαφορικό τελεστή µέσω της
1 ΘΕΩΡΙΑ: Έστω η οµογενής γραµµική διαφορική εξίσωση τάξης (1) όπου οι συντελεστές είναι δοσµένες συνεχείς συναρτήσεις ορισµένες σ ένα ανοικτό διάστηµα. Ορισµός 1. Ορίζουµε τον διαφορικό τελεστή µέσω της
