Ispitna pitanja iz Osnova hemije
|
|
|
- Πύρρος Κουρμούλης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 I grupa pitanja Ispitna pitanja iz Osnova hemije 1. Hijerarhija materijala, smeše, metode razdvajanja smeša Materija: supstance i energija (polje). Supstance se dele na homogene i heterogene supstance. Heterogene smeše (supstance) se mogu razdvojiti fizičkim metodama. Sastavljene su od homogenih komponenti. Osobine smeše zavise od osobina komponenti i njihovog odnosa u smeši (svaka zadržava karakteristična svojstva). Uniforman sastav (homogena supstanca) čista supstanca ili rastvor (homogena smeša). Homogena smeša uniformna materija promenljivog sastava. Takodje se mogu fizički razdvojiti na komponente. Čiste supstance se dele na jedinjenja i elemente.
2 Jedinjenja su supstance određenog i stalnog hemijskog sastava koje se sastoje od dva ili više elemenata. Hemijski se mogu razdvojiti na komponente. Elementi su osnovne supstance od kojih je sacinjena materija i ne mogu se dalje deliti. 118 (90 u prirodi). Metode razdvajanja : filitriranje taloženje rastvaranje (odvajenje rastvorljivog i nerastvorljivog) odlivanje (dekantovanje) centrifugiranje flotacija dijaliza destilacija frakciona destilacija topljenje sublimacija kristalizacija hromatografija. 2. Fizičke i hemijske osobine supstanci Fizičke osobine: Boja Gustina Tvrdoća Tačka topljenja Tačka ključanja Rastvorljivost (mora se naglasiti u kom rastvaraču) Kristalni oblik Provodljivost toplote i električne energije Hemijske osobine ukazuju na supstance tokom hemijskih promena. Inertnost, reaktivnost, korozivnost, zapaljivost. Osobine se dele na intenzivne i ekstenzivne. Ekstenzivne zavise od količine (masa, koncentracija, pritisak,...), intenzivne ne (gustina, boja, T.T., T.K.,...). 3. Nomenklatura neorganskih jedinjenja Jonska jedinjenja.
3 Katjoni: Monoatomski: -Ako ima jedno oksidaciono stanje onda IME+jon, ako ima vise, treba naglasiti (rimski broj u zagradi). Višeatomski katjoni imaju karakteristična imena (amonijum jon, hidronijum jon) Anjoni: Monoatomski: -IME+ID (hlorid, bromid). Složeni: -Najčešći nastavak -AT, onaj koji ima jedan atom kiseonika manje od -AT jona ali isto naelektrisanje ima nastavak -IT (sulfat, sulfit). Kada u seriji postoji više od četiri različita oksianjona (halogeni elementi) tada se koriste i prefiksi. Prefiks per- ukazuje da jon ima jedan kiseonik više nego jon koji se završava na -at (najviše oksidaciono stanje) a prefiks hipo- ukazuje na jedan kiseonik manje nego jon koji se završava na it Primer: ClO 4 - perhloratat ClO 3 - hlorat ClO 2 - hlorit ClO- hipohlorit Cl- hlorid Soli se imenuju tako što se na ime katjona (oduzimajući dodatak jon ) dodaje ime anjona. U slučaju kiselih soli između imena katjona i anjona dodaje se hidrogen NaHCO 3 Natrijum hidrogen karbonat. Analogno za bazne soli sa dodatkom hidroksid. Baza: IME+HIDROKSID. Kiselina IME+KISELINA Imena kovalentnih jedinjenja se izvode tako što se prvo u imenu navede ime atoma manje elektronegativnosti sa rimskim oksidacionim brojem u zagradi pa onda ime atoma veće elektronegativnosti kao da je anjon. Primer: CO 2 ugljenik(iv)-oksid (ugljen-dioksid)
4 4. Zakon o održanju masa, otkiće, primeri, posledice Ukupna masa supstance koja učestvuje u hemijskoj promeni (hemijsoj reakciji) ne menja se. Zakon o održanju mase Otkrio ga je francuski hemičar Lavoazije krajem 18. veka. Tačnost zakona potvrđena je početkom 20. veka. Nemački hemičar Landolt je sa tačnošću od 10-6 g. Ali po Ajnštajnovoj teoriji realtivnosti jedan deo mase mora preći u energiju. Doduše, ove promene su reda veličine te ne nose naročitu težinu u hemijskim proračunima. Primer zakona: Pri sagorevanju papira, primećuje se prividno smanjenje mase, ali ako bismo uhvatili sve produkte sagorevanja (ugljen-dioksid, vodu, pepeo) i izmerili ih, ustanovili bismo da je masa jednaka početnoj masi papira. Ovo se može uzeti kao dokaz nevaženja Flogistonske teorije. Posledica ovog zakona jeste zakon neuništivosti materije, a i zakon održanja energije može se izvesti kao zaključak relativističkih razmatranja. 5. Zakon stalnih masenih odnosa, daltonidi, bertolidi 6. Daltonova atomska teorija Elementi se međusobno jedine u stalnim masenim odnosima zbog čega je sastav emijskih jedinjenja stalan bez obzira na način na koji su ona dobijena Zakon stalnih masenih odnosa, Prust, Bertole se protivio. Primer za stalni maseni odnos sinteza vode (daltonid, po Daltonu koji je zagovarao Prustov stav). Zapaženo da kod legura metala može doći do različitog odnosa usled defekta (kristalne) rešetke. Ukupno naelektrisanje mora biti nula, nastaju bertolidi zbog toga. FeO žarenjem u Fe 0.95 O. Još neki primeri bertolida su gvožđe-sulfid, a čak i sadržaj cinka u cink-oksidu varira unutar tesnih granica. 4 postulata Daltonove torije: 1. Svaki element je sastavljen od izuzetno malih čestica koje se zovu atomi. 2. Svi atomi istog elementa su identični; atomi različitih elemenata su različiti i imaju različite osobine (uključujući i masu)
5 3. Atomi jednog elementa ne mogu se promeniti u atome drugog elementa hemijskim reakcijama; atomi se ne stvaraju niti uništavaju 4. Jedinjenja se stvaraju kada se atomi više elementa kombinuju; dato jedinjenje uvek ima isti broj i vrstu atoma. 7. Zakon umnoženih masenih odnosa Ako dva elementa meñusobno grade dva ili više jedinjenja onda se stalna masa jednog elementa jedini sa različitim masama drugog elementa, a te različite mase drugog elementa stoje u odnosu malih celih brojeva. Primer Azotovi oksidi. Primeri: NO, N 2 O, NO Thompson-ov i Milikan-ov eksperiment 9. Radioaktivnost Thompson posmatrao katodne zrake, primetio da su nezavisni od materijala katode, da skreću u električnom polju, negativno naelektrisani. Odredio je brzinu katodnih zraka i specifično naelektrisanje elektrona. Milikan je merio naelektrisanja elektrona balansirajući naelektrisane kapljice ulja u električnom polju. Na osnovu mnogobrojnih ponavljanja eksperimenta dolazi do zaključka da je svako naelektrisanje celobrojni umnožak e= C. Na osnovu Tompsonovog eksperimenta onda je određena i masa elektrona ( kg). Otkrio je Bekerel u rudi, Pjer i Marija izolovali radioaktivni element, polonijum a zatim radijum (po kojem radioaktivnost dobija ime). Raderford (radeci kod Tompsona) ispitivao prirodu radioaktivnosti. Otkrio tri tipa zračenja iz radioaktivne supstance: α zraci, β zraci i γ zraci α: jezgra He β: elektroni γ: fotoni velike energije, elektromagnetni talasi talasne dužine između nm i 0.1 nm. 10. Rutherford-ov model atoma Tompson predlaže model pudinga od šljiva, gde bi naelektrisanje unutar atoma bilo difuzno raspodeljeno. Raderford je vršio eksperiment difrakcije α čestica na tankoj zlatnoj foliji. Našli rasejane čestice, zbun. Pretpostavio da postoji pozitivno jezgro i elektron na velikom rastojanju od njega. Kasnije otkriveno da se jezgro
6 sastoji od protona i neutrona. Otkriće neutrona uslovljeno ispitivanjem izotopa. 11. Moderno shvatanje strukture atoma Sastoji se od jezgra i el. omotača. Elementarne čestice. Za hemiju bitni elektron proton i neutron. e je jedinica naelektrisanja u hemiji. Atomi su elektroneutralni. Jezgro je vrlo malo u odnosu na el. omotač, ostatak prazan prostor. Elektrostatičke sile drže elektrone koji se kreću oko jezgra. Mase atoma su izuzetno male g red veličine i izražavaju se u AMU (jedinica atomske mase) kg = m(p) ~ m(n) ~ 1AMU. Dimenzija reda veličine angstrema, m. 12. Relativna atomska i molekulska masa, izotopi, masena spektrometrija Relativna zato što se izražava u odnosu na masu drugog elementa. U početku su se koristili vodonik i kiseonik, ali se o g. koristi ugljenik. Izražava se u AMU. AMU je 1/12 mase ugljenikovog izotopa 12 C. Određuju se pomoću masene spektroskopije (izotopski sastav). Atomi istog elementa koji se razlikuju po broju neutrona u jezgru a samim tim i po masi nazivaju se izotopi. Atomski ili redni broj broj protona u jezgru. Piše se u subskriptu (dole) sa leve strane hemijskog simbola i nije ga obavezno navoditi jer je broj protona već odreñen samim hemijskom simbolom elementa Maseni broj ukupni broj protona + neutrona. Piše se u superskriptu (gore) sa leve strane hemijskog simbola. Izotopi imaju ista hemijska svojstva osim brzine reakcije (zbog mase, izotopski efekat). Fizičke osobine su drugačije. Dva nuklida su izobari ukoliko imaju isti maseni broj a različiti redni broj. Dva nuklida su izotoni ukoliko imaju isti broj neutrona a različiti broj protona u jezgru. Prosečna atomska masa. Defekt mase-energija u nuklearnim reakcijama. Masena spektroskopija-jonizovani uzorak se ubrzava el. poljem, razdvaja po masama magnetnim poljem. 13. Periodni sistem elemenata, Mendeljejev, Mozli Pomocu atomskih masa elementi se mogu urediti. Mendeljev uredjuje po rastućoj atomskoj masi, veruje da relativna atomska masa određuje osobine elementa. Oni koji nedostaju još uvek nisu otkriveni, osobine elementa moraju odgovarati njegovom položaju u sistemu. Periodni zakon
7 osobine se periodično smenjuju po atomskoj masi. Predviđa osobine neotkrivenih elemenata. Postoje problemi u periodnom sistemu, neslaganja od predviđenog (Argon teži od Kalijuma). Mozli eksperimentalno (bombardovanjem katodnim zracima elementa koji se ispituje i analizom frekvencije izlaznog zračenja) dokazuje da atome treba ređati po atomskom broju (broj protona u jezgru). Periodni zakon: Osobine elemenata su periodična funkcija njihovih atomskih brojeva Danas znamo da osobine zavise od broja i rasporeda elektrona u omotaču, ali kako je broj elektrona jednak broju protona, Mozlijevo uređenje je validno. 14. Molekuli, molekulske, empirijske i strukturne formule 15. Jonska jedinjenja i joni Atom je najmanji reprezent jednog elementa. Def. molekula: Molekul je skup od dva ili više atoma koji su čvrsto vezani hemijskom vezom. Molekul se ponaša različito od atoma koji ga grade. Elementi se nalaze u molekulskom obliku nekad (H 2, O 2, F 2, N 2, I 2, Cl 2, Br 2 ). Jedinjenja se sastoje od atoma barem dva elementa. Jedinjenja koja se sastoje od molekula se zovu molekulska jedinjenja (za razliku od jonskih jedinjenja). Molekulske formule daju stvaran broj i tip atoma koji grade molekul (H 2 O, H 2 O 2 ) Empirijske daju samo informaciju o njihovom odnosu (HO za H 2 O 2 ). Eksperimenti daju empirijske formule, za jonska kristalna jedinjenja je moguće samo empirijsku formulu dati. Strukturne formule crteži koji pored broja i tipa molekula prikazuju i strukturu molekula, orijentaciju hemijskih veza u prostoru. Razlikuju alotropske modifikacije C i dijamant i grafit. Joni- naelektrisane čestice, mogu biti mono i poliatomski. Katjon pozitivan, anjon negativan. Naelektrisanje se piše u superskriptu (Ag +, Fe 3+ ). Elektroni se primaju i otpuštaju da bi se postigla struktura najbližeg plemenitog gasa, u prirodi naelektrisanja do +3 najčešća. (Lantanoidi idu i do tetravalentnog stanja).
8 Jonska jedinjenja, katjoni i anjoni se međusobno privlače, gradeći kristalnu rešetku. Metali sa nemetalima ih grade. Molekulska samo nemetali medjusobom. Samo empirijska formula, beskonačni nizovi ponavljajućih strukturakristalna rešetka. 16. Mol, molarna masa, elementalna analiza 1mol = broj atoma u 12g ugljenikovog izotopa 12 C. Avogadrov broj N = Molarna masa, masa jednog mola čestica, dobija se sabiranjem relativnih atomskih masa elemenata koji grade molekul. Formulska masa je dobijena sabiranjem relativnih atomskih masa svih elemenata u empirijskoj formuli. Relativna atomska masa je brojno jednaka molarnoj, ali u različitim jedinicama. g/mol i AMU. Na osnovu analize nekog uzorka znamo u kom (masenom ili brojnom) odnosu različiti elementi ulaze u njegov sastav. Pomoću ovoga možemo napisati empirijsku formulu, često prvi korak pri analizi nepoznatog uzorka. 17. Steheometrija, izračunavanje preko jednačina hemijskih reakcija Kako se atomi jednog elementa ne mogu prevesti u atome drugog elementa, ukupan broj atoma nekog elementa mora biti isti u reaktantima i proizvodima reakcije. Zakon održanja mase, zakon stalnih masenih odnosa. Stehiometrijski koeficijenti broj molekula nekog jedinjenja koji ulazi/izlazi u neku reakciju. 18. Energija i unutrašnja energija, funkcije stanja, vrste sistema, I zakon termodinamike Energija je sposobnost tela da vrši rad ili predaje toplotu kinetička i potencijalna. U hemiji bitna elektrostatička energija. Hemijska energija je potencijalna energija zarobljena u nekom jedinjenju. Kinetička energija na mikroskali - temperatura. E se izražava u džulima, J. Kalorija 1cal = 4.184J. Nutricionistička cal je 1kcal. I takon TD: Energija je stalna, ne može se uništiti niti stvoriti, samo se njen oblik može menjati.
9 Unitračnja energija je zbir svih kinetičkih i potencijalnih E. Ne može se izračinati/izmeriti tačno, već do na aditivnu konsatntu. Promena E dobro definisana. Promena energije jednaka je razmenjenoj toploti + izvršeni rad. Kad sistem prima toplotu proces je endotermni, kada vezuje proces je egzotermni. Nešto je funkcija stanja kada zavisi samo od početnog i krajnjeg položaja, a ne od puta između ta dva. Razlika potencijalne energije npr. 19. Entalpija Eksperimenti se izvode pri P=const. A = -P V (minus jer sistem vrši rad) H = E+PV H = (E+PV) = Q+A-A = Q Promena entalpije jednaka je razmenjenoj toploti pri konstantnom pritisku. Za hemiju značajna jer se promena entalpije može lako eksperimentalno meriti, za razliku od unutrašnje energije. H<0 egzoterman (aluminotermija), H>0 endoterman. Promena entalpije je funkcija stanja. 20. Entalpija hemijske reakcije H = H krajnje - H pocetno = H proizvoda - H reaktanata. Sinteza vode je egzotermna, termohemijska reakcija. Entalpija je ekstenzivna, zavisi od količine uzorka koji reaguje. Promena entalpije povratne reakcije jednaka je negativnoj promeni entalpije direktne reakcije. Bitno je stanje u kome se nalaze reaktanti, jer entalpija bitno zavisi od toga, obavezno navesti. 21. Eksperimentalno određivanje entalpije hemijske reakcije, kalorimetrija Može se odrediti merenjem razmenjene toplote sistema i okoline. Toplotni kapacitet je jednak potrebnoj količini energije da bi se sistem zagrejao za jedan stepen K. Molarni, specifični... U kalorimetru se zapali uzorak, meri se promena temperature sredine (vode). Kada je P const H = Q, kada je V=const onda je H~Q. 22. Hesov zakon, standardne entalpije nastajanja
10 Entalpija je funkcija stanja, da bi znali entalpiju reakcije dovoljno je znati entalpiju reaktanata i proizvoda. Entalpija reakcije je jednaka zbiru entalpija međukoraka. Hesov zakon: Ako se reakcija odigrava u nizu koraka, H reakcije će biti jednaka zbiru promena entalpija svih koraka. Standardne entalpije nastajanja, jednake entalpiji (izmišljene) reakcije sinteze počevši od elemenata. Sve pri normalnim uslovima. Entalpije nastajanja za sve elemente su po definiciji nula. Entalpija reakcije jednaka je razlici formacionih entalpija proizvoda i reaktanata. 23. Spontanost hemijskih reakcija Entropija, II zakon termodinamike Entropija verovatnoća. Sistem teži da pređe u najverovatnije stanje (najveća S). Promena entropije jednaka je promeni entropije sistema + okoline. Jedini istinski izolovan sistem univerzum. Da bi nepovratni proces bio spontan promena entropije mora biti veća od 0. S(T=0) = 0 treći zakon TD. 25. Promena entropije sistema i okoline u hemijskim reakcijama 26. Slobodna energija Definisane su standardne molarne entropije za jedinjenja (pri standardnim uslovima). Nisu nula za elemente, povećavaju se sa molarnom masom, veće kod gasova nego kod tečnosti nego kod solida. Povećavaju se sa brojem atoma koji grade molekul. Promena entropije sistema pri reakciji jednaka je razlici standardnih molarnih entropija proizvoda i reaktantata (puta odgovarajući stehiometrijski koeficijent). Sistem nije izolovan, razmenjuje toplotu sa okolinom. Promena entropije okoline data je kao količnik negativne razmenjene toplote sa okolinom i temperature okoline. Ako je P const onda količnik negativne promene entalpije i temperature okoline. Spontanost S>0. S = Ssistema + Sokoline = Ssistema - Hsistema/T -T S = Hsistema T Ssistema = G G = 0 ravnoteža G<0 spontano
11 27. Kvantna teorija G>0 nije spontano Zove se slobodna energija zato što je brojno jednaka maksimalnom mogućem radu koji sistem može da izvrši. G funkcija stanja. Može se izračunati preko standardnih G za reaktante i proizvode (kao i entropija), za slobodne elemente u svom osnovnom stanju je nula. Tri problema klasične fizike: 1. Emisija svetlosti sa usijanih objekata (crno telo) 2. Fotoelektrični efekat izbijanje elektrona sa površine metala pomoću svetlosti 3. Emisija svetlosti sa pobuñenih atoma gasa emisioni spektri (neonska lampa) Zračenje crnog tela rešio Plank, pretpostavio da je zračenje u vidu paketića, kvantova. Atomi mogu primati i otpuštati energiju samo u diskretnim nivoima. Rešilo problem crnog tela. Emituje se energija jednaka celobrojnom umnošku energije kvanta. Pomoću kvantne teorije objašnjen fotoelektrični efekat. Brzina elektrona ne zavisi od intenziteta snopa, nego samo od talasne dužine. Manifestacija dvojne prirodne svetlosti. Razređeni gasovi otpuštaju i apsorbuju zračenje na tačno određenim talasnim dužinama (energijama). Balmerova serija Elektromagnetno zračenje, dvojna priroda svetlosti 29. Borov atomski model EM zračenje manifestuje osobine i talasnog i čestičnog. Talasno - interferencija, difrakcija, prelamanje. Čestično impuls (fotoefekat). Svemu se može pridružiti (De Broljeva) talasna dužina, dualizam materije. Bor pretpostavio da se elektroni kreću po kružnim orbitama oko jezgra (planetarni model). Po klasičnoj fizici bi onda gubili energiju zračenjem i kolabirali na jezgro što se ne dešava. Rešenje stabilne orbite. Borove postulati:
12 1. Samo orbite određenog radijusa, koje odgovaraju određenim energijama elektrona su dozvoljene da ih zauzimaju elektroni u atomu 2. Elektron koji se nalazi u dozvoljenoj orbiti ima odgovarajuću energiju i nalazi se u dozvoljenom energetskom stanju. Elektron koji se nalazi u dozvoljenom energetskom stanju neće otpuštati energiju i neće pasti na jezgro 3. Elektron apsorbuje i emituje energiju samo kada prelazi iz jednog dozvoljenog stanja u drugo. Ova energija se emituje ili apsorbje u vidu elektromagnetnog zračenja tj. fotona energije E = hν. Prvo, najniže stanje osnovno. Svako sledeće je pobuđeno. Beskonačno daleki energetski nivo, atom je jonizovan. 30. Limiti Borovog atomskog modela Odlično radi samo prilikom objašnjavanja spektra atomskog vodonika, za sve ostale atome postoje značajne greške. "Klasičan" je, opisuje elektron samo kao česticu ne uzima u obzir njegovu talasnu prirodu. 1. Elektroni postoje samo na odreñenim diskretnim (diskretno -ima jednu vrednost) energetskim nivoima, koji su opisni kvantnim brojevima 2. Pri prelasku elektrona sa jednog nivoa na drugi emituje se ili se apsorbuje energija. 31. Talasna priroda materije, Hajzenbergov princip neodređenosti Zračenje se ponaša i kao čestica i kao talas. Elektroni takođe. Pridruživanje svemu talasne dužine λ = h/p. p - impuls. Za elektrone talasna dužina bliska X zracima. Difrakcija elektrona, interferencija. Elektronski mirkoskop. Talas nije lokalizovan. Ako čestica ima talasnu prirodu, da li je ona lokalizovana? Hajzenbergov princip neodređenosti kaže da je principijelno nemoguće odrediti položaj i impuls neke čestice istovremeno (posledica nekomutativnosti operatora merenja). 32. Kvantna mehanika i atomske orbitale (atoma vodonika) Šredingerova jednačina, talasne funkcije. Talasne funkcije se pridružuju elektronu u elektrostatičkom polju protona. Sama talasna funkcija nema fizički smisao, njen kvadrat jednak je gustini verovatnoće pronalaska čestice na nekom mestu.
13 Kvadrat talasne fukncije ~ gustini elektronskog oblaka. Orbitala je deo prostora u kome je verovatnoća da pronalaženje elektrona 90%. Orbitale su okarakterisane sa 4 broja. Glavni kvantni broj n određuje energiju elektrona, rastojanje od jezgra. Od 0 do INF. Sporedni kvantni broj određuje igled orbitale. l između 0 i n-1. Magnetni kvantni broj određuje orijentaciju orbitale, ima vrednosti od l do +l (sa nulom). Spinski - spin elektrona ±1/2. Glavni odredjuje nivo/ljusku, sporedni podnivo. U vodoniku sve orbitale istog glavnog broja imaju istu E. 33. Izgled atomskih orbitala (atoma vodonika) 34. Višeelektronski atomi s sferne, n-1 sfernih čvorova. p orbitale kikiriki, 3 komada, javljaju se na n = 2. d se javljaju na n = 3, ima ih 5. Četiri izgledaju kao 2 p orbitale pod pravim uglom, dok peta izgleda kao p orbitala sa gumom za plivanje. f na n = 4, ima ih 7... Orbitala nema energiju sama po sebi, već elektron koji se u njoj nalazi, ali je E orbitale ustaljen izraz. Orbitala bez elektrona- prazna/virtuelna, pogodna pri teoretskim razmatranjima. U višeelektronskim atomima postoji i međusobno elektronsko odbijanje. Potrebno je znati položaje da bi se izračunalo, kvantna ne dozvoljava. Koriste se druge metode... Međuelektronsko odbijanje utiče na razdvajanje orbitala unutar jednog nivoa po energijama (cepanje). Pritom ono ne utiče na izgled orbitale, nego samo na energiju. Energija raste sa porastom sporednog kvantnog broja. 35. Spin elektrona, posledice spina Spin je svojstvo materije. Otkrili ga Štern i Gerlah u svom eksperimentu. Atomi srebra različito skreću pri prolasku kroz nehomogeno magnetno polje. Razlika koja dovodi do ovoga je magnetne prirode i uslovljena je spinom. Spin je jednak broju rotacija koje čestica treba da napravi da bi se
14 preslikala u samu sebe. Za elektron moguća su dva stanja spina +1/2 i - 1/ Elektronaska konfiguracija, Paulijev princip, Hundovo pravilo Princip opisuje svojstvo prirode, nikada se ne može narušiti. Paulijev princip: dva elektrona u istom atomu ne mogu imati ista sva četiri kvantna broja. Posledica je da se u jednu orbitalu mogu smestiti samo dva elektrona i to različitih spinova. Elektronska konfiguracija je raspored elektrona unutar elektronskog omotača. Definisana je sa po 4 kvantna broja za svaki elektron omotača. Da bi poznavali elektronsku konfiguraciju atoma potrebno je da znamo energije njegovih orbitala + Paulijev princp. Orbitale se popunjavaju po porastu energije (prvo najmanje). U tome nam pomaže Hundovo pravilo: Za degenerisane obitale najniže energetsko stanje je ono u kome je broj elektrona sa istim spinom maksimalan. Šematski prikaz, kućice, plemenit gas+nastavak...h He Li Be B C N Ne Na Valentni nivo najviši nivo (sve posle poslednjeg plemenitog gasa). Potpuno popunjeni (unutrašnji) nivoi ne učestvuju u hemijskim reakcijama, samo valentni nivo. 37. Atomski radijusi, efektivno naelektrisanje jezgra Efektivno naelektrisanje jednako je naelektrisanju jezgra umanjenom za broj elektrona na nižim energetskim nivoima- Gausov zakon. Raste niz periodu. Atomski radijusi opadaju niz periodu, efektivno naelektrisanje je veće pa je veća i sila privlačenja. Atomski radijusi rastu niz grupu, veći je glavni kvantni broj, veće su energije elektrona, veće rastojanje od jezgra. 38. Jonski radijusi, jonizaciona energija, afinitet prema elektronu Jonski prečnici su prečnici jona. Određeni eksperimentalno na osnovu rastojanja između jona u kristalnim rešetkama. Katjoni su uvek manji od neutralnog atoma (elektron manje, manji je omotač, manje odbijanje među elektronima), dok su anjoni veći (dodatak elektrona povećava međuelektronsko odbijanje, šire se na veći prostor).
15 Što je katjon naelektrisaniji prečnik mu je manji, a anjonu veći. Jonizaciona energija je minimalna energija koju je protebno dovesti atomu nekog elementa u gasovitom stanju da bi se on jonizovao. Druga energija jonizacije jednaka je energiji koju je potrebno dovesti već jonizovanom atomu da bi prešao u dvostruko jonizovano stanje. Treća... Dva energetski suprotna procesa: -Udaljavanje elektrona od jezgra, energija raste. -Smanjenje međuelektronskog odbijanja, energija opada. Jonizaciona energija je uvek pozitivna... Druga je veća od prve. Nagli skok kada se uklanjaju elektroni iz unutrašnih energetskih nivoa. E_jon raste po periodi, a opada po grupi, objašnjenje isto kao za atomske radijuse. Afinitet prema elektronu: energija koja se oslobodi ili veže pri dodavanju jednog elektrona neutralnom elementu u gasovitom stanju. Opet dva suprotna procesa: Elektron je bliže jezgru, energija se oslobađa. Elektron je bliže drugim elektronim, energija raste (vezuje se). Elektronegativnost može biti i pozitivna i negativna. U prirodi se češće sreće negativna. Afinitet prema elektronu raste (negativniji je) u periodi (sa leva na desno) a opada u grupi (odozgo nadole). Plemeniti gasovi imaju afinitet veći od 0 zbog svoje stabilne konfiguracije. 39. Periodni sistem elemenata, periode, grupe, podela Periodni sistem elemenata- elementi poređani po njihovom rednom broju i osobinama. U periodama su sadržani elementi sa istim maksimalnim kvantnim brojem. Periode - horizontale. U nekim grupama su sadržani elementi sličnih hemijskih osobina. Predstavljeni su kolonama u periodnoj tablici. Podela se još može uvesti na: -Metale, nalaze se u levom delu periodnog sistema i čine gotovo ¾ ukupnog broja elemenata. Imaju specifičan sjaj, elastičnost, mogu da se kuju, dobri su provodnici toplote i elektriciteta. Svi su u čvrstom stanju sem žive koja je tečna sve do -39. Imaju male jonizacione energije i lako grade katjone. Metali iz glavnih grupa otpuštaju elektrone gradeći konfiguraciju stabilong gasa, dok prelazni se mogu naći u više različitih stanja, nevezanih za plemenite gasove.
16 Sa metalima grade jonska jedinjenja, dok među sobom grade legure. Oksidi metala su većinom bazni. -Metaloidi, nalaze se na prelazu između metala i nemetala. Imaju osobine i metala i nemetala. Vizuelno liče na metale (metalni sjaj), ali ne provode ni toplotu ni struju. Krti su. Neki su poluprovodnici i koriste se u izradi čipova. -Nemetali se nalaza ne desnom kraju periodnog sistema. Za razliku od metala vrlo su raznoliki. Sedam njih su dvoatomni molekuli: (O 2, N 2, H 2, F 2, Cl 2 ), tečni Br 2, i čvrsti I 2. Ostali su u čvrstom stanju i mogu biti i izrazito meki (S), kao i tvrdi (dijamant). Tačke topljenja su im niže nego metalima, ali ima i izuzetaka (dijamant na 3570 C). Loše provode struju i toplotu, imaju izuzezno velike jonizacione energije i negativne afinitete prema elektronu. Lako grade anjone radi postizanja konfiguracije idealnog gasa. Sa metalima grade jonska jedinjenja, dok među sobom grade kovelentna. Oksidi su im kiseli. Takođe postoji podela na S, P, D i F elemente.
17 II grupa pitanja 1. Vrste hemijske veze, pravilo okteta 2. Jonska veza Jonska, kovalentna i metalna. Elektronska konfiguracija plemenitih gasova je vrlo stabilna. Imaju velike jonizacione energije, mali afinitet prema elektronu. Inertni su. Atomi teže da budu u najstabilnijem stanju, odnosno istoj konfiguraciji kao najbliži plemeniti gas. Pravilo okteta glasi: Atomi će gubiti ili dobijati ili deliti elektrone da bi postigli elektronsku konfiguraciju plemenitog gasa. Postoje izuzetci od ovog pravila, prelazni metali npr. Pri jonizaciji prelaznih metala je bilo koji elektronski gas predaleko. Veoma važno pravilo kod određivanja elektronske konfiguracije jona prelaznh metala: Kada se stvara katjon uvek se elektron uzima iz onog podnivoa koji ima veći glavni kvantni broj n. Jonska veza je suštinski elektrostatičko privlačenje između raznoimeno naelektrisanih jona. Uglavnom između katjona metala i anjona nemetala. Elektron sa katjona je prešao na anjon, te su se joni uredili u kristalnu rešetku privučeni samo elektrostatičkim silama. Standardne entalpije nastajanja svih jonskih jedinjenja su veoma negativne nastajanje jonskih jedinjenja je egzoterman proces Prilikom nastajanja jonkih jedinjenja sa dešavaju tri stvari:
18 - Uklanja se elektron iz atoma metala da bi nastao katjon. Za ovo je potrebno utošiti energiju jonizacije to je uvek endotermno - Dodaje se elektron atomu nemetala da bi se dobio anjon afinitet prema elektronu - uglavnom egzoterman proces (elementi koji imaju mali ili pozitivan afinitet prema elektronu ne grade anjone) - Nastali katjon i anjon se spajaju u čvrsto jonsko jedinjenje, uvek egotermno Energija poslednjeg dela procesa tumači se kao energija kristalne rešetke, tj ona energija koju je potrebno uložiti da bise kristalna rešetka razgradila. Ona zavisi od pakovanja jona u rešetku, kao i od odnosa njihovih veličina (sličnija veličina znači veću energiju). 3. Kovalentna veza, Luisovi simboli Češća od jonske veze. Za razliku od jonske veze, kovalentna jedinjenja su i gasovita (fosgen) i tečna (benzen) i čvrsta. Luisovi simboli valentni elektroni su predstavljeni tačkicama. Pogodni za s i p elemente, za d ne. Dve tačke predstavljaju popunjenu orbitalu, a jedna polupopunjenu. Luis je zaključio da atomi ne moraju da otpuštaju ili primaju elektrone, mogu da ih dele kako bi postigli konfiguraciju plemenitog gasa. Tako se dva vodonika jednine u H 2 u kome oba imaju konfiguraciju plemenitog gasa He. Nastajanje kovalentne veze sve sile koje učestvuju: - Privlačenje između jezgra jednog atoma i elektrona drugog atoma - Odbijanje između elektrona dva atoma - Odbijanje između jezgara dva atoma Kvantna mehanika pokazuje da se elektronski par lokalizuje između jezgara. H 2 postoji zato što su jezgra privučena negativnim naelektrisanjem nagomilanim između njih. Elektronski par radi kao lepak koji drži atome povezanim. Višestruke veze kada atomi dele više od jednog elektronskog para veza je višestruka. 2 para dvostruka, 3 para trostruka. Dvostruka je kraća i jača od nednostruke, dok je trostruka kraća i jača od dvostruke. 4. Polarnost kovalentne veze, elektronegativnost Kovalentna veza može biti polarna i nepolarna. Nepolarna nastaje između dva atoma istog elementa (H 2 F 2 ).
19 U kovalentnoj vezi dva atoma različitih elemenata uvek jedan atom jače privlači elektronski oblak. Usled toga elektronski oblak se deformiše i približi atomu koji ga više privlači. Tada dolazi do prostornog izdvajanja naelektrisanih oblasti, koje obrazuju dipol. Jonska veza se može sagledati kao eksteman primer kovalentne gde je elektron u potpunosti prešao sa jednog na drugi atom. Veličina koja opisuje polarnost je elektronegativnost. Elektronegativnost je mera sposobnosti atoma da privuče zajednički elektronski par unutar molekula. Veća elektronegativnost odgovara većem privlačenju. Elektronegativnost je eksperimentalno određena preko energija disociacija hemijskih veza različitih molekula (istorijski je bila definisana kao polovina zbira jonizacione energije i afiniteta prema elektronu). Fluor je najelektronegativniji (4), dok je cezijum najmanje elektronegativan (0.7). Elektronegativnost raste po periodi, dok po grupi opada. Dipolni momenat molekula povezan je sa razlikom elektronegativnosti atoma koji ga čine. Dipolni momenat molekula koji nisu sačinjeni isključivo od atoma jednog elementa takođe može biti nula. Dipolni momenat je vektorska veličina pa ukupno može biti nula, čak i ako delovi molekula imaju dipolni momenat različit od nule. CH 4 CCl Rezonancija, rezonantne strukture, izuzeci od pravila okteta Za neke molekule možemo napisati više različitih Luisovih formula, koje su medju sobom jednake. Primer je O 3. Eksperimentalno je pokazano da su sve veze u O 3 jednake, ne postoji jedna dvostruka i jedna jednostruka. To znači da se ozon nalazi između ove dve strukture u mešanom stanju. NO 3 - anjon ima tri rezonantne strukture. Pravilo okteta, pored prelaznih metala, ne važi ni u ovim slučajevima: a) Molekuli sa neparnim brojem valentnih elektrona b) Molekuli u kojima jedan atom ima manje od osam elektrona c) Molekuli u kojima jedan atom ima više od osam elektrona a) ClO 2, NO, NO 2. Molekul NO ima 11 valentnih elektrona i za njega su moguće dve Luisove strukture:
20 b) Ovakvo odstupanje se najčešće javlja kod bora i berilijuma. Primer BF 3. Formalno je moguće zadovoljiti pravilo okteta, ali se onda pozitivno naelektrisanje nalazi na fluoru koji je najelektronegativniji element, te je takvo stanje malo verovatno. Levo, rezonante strukture. Desno, verovatnija struktura. Ovi molekuli su Luisove kiseline jer na centralnom atomu postoji jedna prazna valentna orbitala. Oni će reagovati sa Luisovim bazama koje imaju na centralnom atomu jedan nevezivni elektronski par dajući soli. U solima svi atomi imaju pun oktet. c) Najčešći tip odstupanja od pravila okteta. Primer PCl 5 : Ovde oko atoma fosfora imamo 10 elektrona. Toliko elektrona ne može da stane u 3s i 3p orbitale fosfora. Moramo proširiti valentnu ljusku fosfora sa (praznim) 3d orbitalama koje su sledeće po energiji. Centralni atom mora biti iz treće ili kasnije periode. Ostali primer ovog narušavanja pravila okteta su SF 4, AsF 6 -, ICl 4 -
21 6. Geometrija molekula AB n tipa 7. VSEPR model Linearni, trigonalno planarni, tetraedarski, trigonalno bipiramidalni, oktaedarski. AB 2 : Linearni i savijeni AB 3 ; trigonalno planarni, trigonalno piramidalni, T oblik. Vezivni elektronski par je elektronski par koji učestvuje u građenju veze. U Luisovim formulama se obeležavaju crticama. Nevezivni elektronski par ne učestvuje u vezi. Drugi naziv je slobodan. U Luisovim formulama predstavljen je sa dve tačke. Elektronski domen se sastoji od vezivnog para, nevezivnog para ili višestruke veze. VSEPR model se koristi kod predviđanja strukture molekula tipa AB n gde je A p-element. Po VSEPR modelu, molekul će biti strukture u kojoj su elektronski domeni centralnog atoma najudeljeniji međusobno. Ako ima 3 domena, onda trigonalno planarni (120 ), 4 tetraedarski (109.5 )... Takođe nevezivni par je veći od vezivnog, kao što i višestruka veza jače odbija susedne elektronske domene. Time je objašnjen defekt ugla u molekulu vode (104.5 umesto ). Kada centralni atom ima 5 elektronskih domena tada se javljaju položaji koji nisu međusobno ekvivalentni. Aksijalni položaj ima 3 atoma pod 90 i jedan pod 180. Ekvatorijalni dva pod 120 i dva pod 90. Ispostavlja se da je ekvatorijalni položaj malo stabilniji od aksijalnog. Tako da kod AB 4 molekula, u kome A ima 5 domena, nevezivni par se nalazi u ekvatorijalnom položaju. Kod AB 3 se oba nevezivna para nalaze u ekvatorijalnom položaju. AB 6 -svi ekvivalentni. Oblici složenih molekula se mogu odrediti primenom VSEPR na deo po deo. 8. Teorija valentne veze Da bi došlo do kovalentne veze, mora doći do preklapanja orbitala.
22 9. Hibridizacija 10. Višestruke veze 11. MO teorija Čeono preklapanje gradi sigma vezu, dok bočno gradi pi vezu. s orbitale ne mogu da grade pi vezu. Orbitale koje grade vezu su po pravilu polu popunjene (jedan elektron). Uvek prvo nastaje sigma veza i znatno je jača od pi veze. Bitno: Teorija valentne veze podrazumeva da dolazi do promene samo u valentnim ljuskama oba atoma pri građenju molekula. Iako teorija valentne veze lepo radi za dvoatomske molekule, za poliatomske ne baš. Ugao između p orbitala je 90. U skladu sa time bi ugao u vodi trebalo da bude 90, a on je CH 4, dve p orbitale mogu da vežu dva vodonika pod 90, a u metanu ima 4 vodonika pod Da bi ove probleme rešili uvodi se pojam hibridizacije. Ona je samo model, ne oslikava stvarno stanje i ne zadovoljava Šredingerovu jednačinu. Hibridizacija podrazumeva da se orbitale različitih podnivoa izmešaju, izjednače po energiji i obliku. Takve orbitale se zovu hibridne orbitale. Po energiji one su između orbitala od kojih su nastale. Moguće je i mešanje i d orbitala (sp3d npr). Preostale d orbitale ostaju nepromenjene po energiji i obliku. Sp linearna, sp2 trigonalno planarna, sp3, tetraedarska, sp3d trigonalno bipiramidalna, sp3d2 oktaedarska. Dva atoma koja se vezuju kovalentno uvek se prvo vezuju preko sigma veze, čeono. Nakon toga, ako su atomi dovoljno blizu i ako imaju slobodne elektrone, mogu graditi bočne pi veze. Pi veze grade samo atomi iz druge periode meñusobno i sa atomima iz treće i viših perioda. Atomi iz treće periode zbog svoje veličine ne grade p veze ni međusobno ni sa atomima viših perioda. Postoji O=O, S=O, ali S=S ne postoji! Pi vezu grade nehibridizovane p orbitale (nekad i d, ali ređe). Tako nastaju dvostruke i trostruke veze. C 2 H 4 dvostruka, C 2 H 2 trostruka. Molekulsko orbitalna teorija takođe model, zasniva se na kvantnomehaničkom pristupu i rešavanju Šredingerove jednačine.
23 Elektroni u molekulu su opisani specifičnim talasnim funkcijama koje se zovu MOLEKULSKE ORBITALE (MO). Molekulske orbitale su dosta slične atomskim obitalama; svaka može da primi samo po dva elektrona različitog spina, imaju enegiju koja se može izračunati, molekulska orbitala se može prikazati kao kontura koja obuhvata prostor u kome je verovatnoća nalaženja elektrona 90% MO teorija molekul vodonika Rekli smo da veza u molekulu H 2 nastaje preklapanjem dve 1s atomske orbitale dva atoma vodonika. MO teorija proširuje ovu ideju i tvrdi da: Preklapajem atomskih orbitala nastaju molekulske orbitale Kad god se dve atomske orbitale preklapaju nastaju dve molekulske orbitale. (kad se preklapaju četiri atomske orbitale nastaju četiri molekulske orbitale) Od dve molekulske orbitale nastale preklapanjem 1s atomskih orbitala atoma vodonika jedna MO je niže energije a druga MO je više energije. MO niže energije je znatno povoljnija od druge MO, a i od orbitala pre kombinovanja. Ona ima najmanju energiju. Zbog toga ona učestvuje u građenju veze i naziva se vezivnom MO. Druga MO se naziva antivezivnom (ima smisla, veća energija, manje stabilna veza ). Vezivna se označava kao σ 1s a nevezivna kao σ*1s. * ukazuje da je orbitala antivezivna a 1s u indeksu ukazuje da je ta molekulska orbitala nastala preklapanjem 1s atomskih orbitala. Vezivne orbitale nastaju kada se preklope istoznačne atomske orbitale e atoma (znak određen talasnom funkcijom), dok antivezivne nastaju preklapanjem raznoznačnih orbitala. (npr. svaka p orbitala ima pozitivan i negativan krak itd.) 13. Konstrukcija MO dijagrama, red veze MO dijagrami način grafičkog prikazivanja MO. Po y osi energija, levo i desno se nalaze AO atoma koji učestvuju u vezi. Svaka MO može da primi po 2 elektrona suprotnog spina, za njih važi Paulijev princip. Za H 2 molekul je vezano stanje energetski povoljnije te on postoji, dok je za He 2 to znatno nepovoljnije nego za dva nevezana atoma He.
24 Red veze je definisan kao polovina razlike broja vezivnih i broja antivezivnih elektrona. 14. MO dijagrami dvoatomnih molekula elemenata druge periode Pravila za crtanje MO dijagrama: 1. Broj nastalih MO mora biti jednak broju kombinovanih atomskih orbitala 2. Da bi se atomske orbitale mogle kombinovati moraju biti bliskih energija i moraju imati odgovarajuću simetriju 3. Efikasnost kombinovanja atomskih orbitala je proporcionalna njihovom prekapanju što se bolje preklapaju vezivna MO će imati nižu energiju a antivezivna MO višu 4. Svaka MO može da primi maksimalno dva elektrona suprotnih spinova 5. Ako su dve ili više MO degenerisane (imaju iste energije) popunjavaće se u skladu sa Hundovim pravilom. Kod B 2, C 2, N 2 su π 2p i σ 2p zamenile mesto. 15. Elektronska konfiguracija i osobine molekula Paramegnetičnost i dijamegnetičnost se objasnjavaju elektronskom konfiguracijom.
25 Molekuli koji imaju nesparene elektrone bivaju privučeni magnetnim poljem i pojačavaju njegov intenzitet. Oni se nazivaju paramegneticima. Nasuprot njima, molekuli kojima su spareni svi elektroni, su odbijeni magnetnim poljem i nazivaju se dijamagnetičnim. Na osnovu elektronske konfiguracije se takođe može odrediti red veze. 16. Međumolekulske interakcije, jon-dipol i dipol-dipol interakcije Jon dipol interakcije se javljaju između, zamislite, jona i dipola. Što je veće naelektrisanje jona, to je interakcija jača. Što je veći dipolni momenat, interakcija je jača. Na osnovu jon dipol interakcija dolazi do rastvaranja jonskih jedinjenja u polarnim rastvaračima. Dipol-dipol interakcije se javljaju između dipolnih molekula. Veoma zavise od međusobne orijentacije molekula i opadaju sa kubom rastojanja. Zbog kompikovane zavisnosti teško je izračunati njihov uticaj. Utiču na temperaturu ključanja (povećavaju je). 17. Međumolekulske interakcije, Londonove sile Čak i nepolarni molekuli mogu dobiti dipolni momenat. Ovaj pojava zove se polarizacija. Polarizabilnost je veličina koja određuje koliki će biti dipolni momenat polarizovanog molekula. Ona definiše kolika je sposobnost elektronskog oblaka nekog molekula da se deformiše. Veća polarizabilnost znači jače Londonove sile. Veličina molekula utiče na polarizabilnost (veće veće). Kompaktni molekuli su manje polarizabilni od nekompaktnih. Londonove sile postoje uvek i između svih molekula, bitne su za fizičke osobine supstanci. Pomoću nijh se objašnjava zašto plemeniti gasovi i drugi nepolarni molekuli na niskim temperaturama prelaze u tečno stanje. 18. Međumolekulske interakcije, vodonične veze Vodonična veza je specifičan tip međumolekulske interakcije koja se javlja H vezan za neki izrazito elektronegativan atom (F, O, N). To uzrokuje postojanje dipolnog momenta koji onda utiče na osobine supstance. U ovoj interakciji učestvuju TRI atoma: H atom, atom za koji je H vezan i trećeg elektronegativnog atoma koji ima slobodan elektronski par. H atom (parcijalno pozitivan) biva privučen u blizinu slobodnog elektrongkog para i tako nastaje interakcija u vidu vodonične veze. Jačina ovih veza zavisi od polarnosti molekula koji sadrži vodonik i elektronegativnosti trećeg atoma koji u vezi učestvuje. Ova interakcija je slabija od jon-dipol, ali je jača od dipol-dipol i Londonove.
26 Zbog vodonične veze je tačka ključanja vode znatno veća nego što bi bila da ove interakcije nema. 18. Viskoznost, površinski napon tečnosti, fazne promene 19. Napon pare 20. Fazni dijagrami Viskoznost je pojava slepljivanja delova fluida i međusobno i uz zidove suda kao posledica interakcije između molekula fluida. Logično, što je ta interakcija jača, to je fluid viskozniji. Površinski napon je na isti način zavisi od međumolekulskih interakcija: što su one jače to molekuli fluida teže da budu bliže jedni drugima što se primećuje kao površinski napon tečnosti (težnja da slobodna površina bude minimizirana). Fazni prelazi su promena agregatnog stanja neke supstance. Prelaskom iz čvrstog u tečno i iz tečnog u gasovito, smanjuje se uređenost strukture i povećavaju međumolekulska rastojanja. Za takve promene je potrebna neka energija. Ta energija je nazvana specifična toplota topljenja/isparavanja i jednaka je količini energije koju je potrebno dovesti po jedinici mase supstance da bi ona promenila fazu u kojoj se nalazi. Što su međumolekulske interakcije jače to su ove energije veće. Fazni prelazi nisu mogući pod bilo kojim uslovima. Na faznom dijagramu su to tačke koje se nalaze na granici između dve faze. Iznad neke temperature nije moguće kondenzovati gas u tečnost. Granična temperatura se naziva kritičnom, a pritisak i zapremina koji vladaju u tom trenutku se takođe nazivaju kritičnim. Kada se iznad neke tečnosti u sudu sav gas evakuiše, jedan deo tečnosti će iz suda ispariti, preći u gasnu fazu. Pritisak te pare naziva se naponom pare. Kada se uspostavi to ravnotežno stanje broj molekula koji uđu u tečnost (kondenzuju se) jednak je onom koji iz nje izađu (ispare). Ovakva ravnoteža se naziva dinamičkom. Što je temperatura veća, veće su energije molekula, pa je kondenzovanje manje verovatno, dok isparavanje postaje verovatnije. Stoga se napon pare tečnosti povećava. Kada se napon pare izjednači sa okolnim pritiskom, dolazi do spontanog formiranja velikih količina para. Ta pojava naziva se ključanje tečnosti. Tačka ključanja je temperatura na kojoj dolazi do istog. Ona, očigledno, zavisi od temperature. Normalna tačka ključanja je pri pritisku od 1atm. Grafička reprezentacija faze u kojoj se supstanca nalazi na nekom pritisku i temperaturi.
27 21. Rastvori, komponente rastvora, proces rastvaranja Rastvor je homogena smeša dve ili više supstanci. Rastvarač je supstanca koja je u višku ili supstanca čija je faza zadržana! Rastvorena supstanca ona druga Postojanje međumolekulskih interakcija između dve supstance omogućava rastvaranje jedne u drugoj. Do rastvaranja supstance dolazi kada je interakcija rastvarač-rastvorena supstanca slična (veća) od interakcije rastvarač-rastvarač i interakcije među rastvorenom supstancom. 22. Energetske promene prilikom rastvaranja Treba razgraditi kristalnu strukturu supstance koja se rastvara (endotermno). Treba razmaći molekule rastvarača, kako bi se napravio prostor za rastvorenu supstancu (takođe endotermno). Mešanje ove dve supstance je egzotermno zbog interakcija između rastvarča i rastvorene supstance. Ukupna promena energije ova tri odvojena procesa utiče na to da li će rastvaranje biti endo ili egzotermno. Egzotermno magnezijum sulfat, endotermno amonijum nitrat. Polarno u polarnom, nepolarno u nepolarnom... Polarno-nepolarno ne, jer medjusobna interakcija nije dovoljna da nadonkadi kidanje međusobne interakcije u polarnoj supstanci. 23. Spontanost rastvaranja Gibsova slobodna energija. Promena entropije je pozitivna iz uređenijeg u manje uređeno stanje. Jedino što može da spreči spontanost rastvaranja
28 je velika entalpija rastvaranja. Gasovi se uvek rastvaraju jer su im međumolekulske interakcije skoro Zasićenost rastvora, rastvorljivost i temperatura, rastvorljivost i pritisak Konačna količina neke supstance se može rastvoriti u nekoj količini rastvarača (na datoj temperaturi). Kada je rastvorena baš ta maksimalna količina supstance rastvor je zasićen. Rastvorljivost neke supstance u nekom rastvaraču na nekoj temperaturi definisana je kao količnik maksimalne mase rastvorene supstance i mase rastvarača. Nezasićen rastvor sadrži manju količinu rastvorene supstance od maksimalne. Prezasićen rastvor sadrži veću količinu do maksimalne (ovakvo metastabilno stanje postiže se pravljenjem rastvora na većoj (manjoj) temperaturi i naglim hlađenjem (grejanjem), tako da supstanca ne iskristališe). Rastvorljivost u vodi generalno raste sa temperaturom (veća temperatura znači da je T S član u Gibsovoj sl. E. veći pa je G<0). Rastvorljivost gasova se smanjuje sa temperaturom (isti razlog kao i napon pare, veca kineticka energija omogucava molekulima gasa da pobegnu iz tečnosti). Prilikom rastvaranja tečnosti i čvrstih tela u tečnostima pritisak ne igra ulogu (kako V=const). Dok za rastvaranje gasova važi da što je veći pritisak to je veća rastvorljivost. Henrijev zakon Način predstavljanja koncentracije rastvora Procentna koncentracija Molski (molarni) udeo Molaritet (koncentracija) Molalitet 26. Koligativne osobine rastvora, smanjenje napona pare Napon pare rastvora je niži od napona pare čistog rastvarača. Parcijalni napon pare neke komponente rastvora zavisi jedino od temperature. Ukupan pritisak jednak je zbiru parcijalnih pritisaka pomnoženih sa molskim udelom te komponente u rastvoru. To je tvrdnja Raulovog zakona.:
29 Kada je supstanca B neisparljiva (so npr) p b =0. Pa je onda p=p a x a. Dokle god je B neisparljiva, ovaj rezultat ne zavisi od toga koja je to supstanca, pa je ova osobija koligativna. Kako je x a <0 vidimo da se napon pare smanjuje. 27. Koligativne osobine rastvora, povišenje temperature ključanja Dodavanjem neke supstance u rastvarač, napon pare se smanjuje. Kako je tačka ključanja ona u kojoj je pritisak pare jednak okolnom pritisku, tačka ključanja se povećava. T = K b b b molalitet rastvora K b Ebulioskopska konstanta T promena temperature ključanja 28. Koligativne osobine rastvora, sniženje temperature mržnjenja Pri mržnjenju rastvora čestice rastvora se vezuju jedna za drugu gradeći kristal. To čini da rastvorene čestice budu koncentrovanije, odnosno sistem je prešao u uređenije stanje. S<0. Razmatrajući ovo pomoću Gibsove slobodne energije dolazimo do toga da se T mora smanjiti da bi proces ponovo bio spontan. T = K f b b molalitet rastvora K f Krioskopska konstanta T promena temperature mržnjenja 29. Koligativne osobine rastvora, osmotski pritisak Kada se sa različitih strana polupropustne membrane nalaze rastvori različitih koncentracija doći će do difuzije molekula rastvarača iz oblasti manje koncentracije u oblast veće koncentracije (povećanje entropije). Ovaj proces se zaustavlja kada sistem dođe u dinamičku ravnotežu. Čestice koje se sudaraju sa membranom i kroz nju prolaze na nju vrše neki pritisak. Π = crt c je ovde koncentracija rastvora. 30. Koloidne čestice, koloidini rastvori
30 Koloidni su rastvori koji sadrže čestice dimenzija od 10 do 2000 angstrema. To mogu biti biološki molekuli (proteini), neorganske čestice (AgCl). Mogu se nalaziti i u tečnosti i u gasu. Zbog svoje karakteristične veličine dolazi do rasejanja svetlosti (Tindalov efekat), što se može upotrebiti za određivanje veličina koloidnih čestica. Same koloidne čestice poseduju veliku površinsku energiju koja potiče od visokog stepena disperzije. Zato bi se očekivalo da će spontano da se istalože, ali to nije slučaj. Mogi biti hidrofilni i hidrofobni. Hidrofilni na svojoj površini imaju grupe koje interaguju sa vodom i zbog toga su izuzetno dobro rastvorljivi. Hidrofobni se lako talože. Njih je moguće stabilizovati dodavanjem naelektrisanih čestica na njihovu površinu ili hemijskih stabilizatora (Natrijum stearat, koji je sastojak sapuna omogućava stabilizaciju lipidnih čestica na površini kože, te omogućava njihovo rastvaranje). Ne mogu se procediti, isuviše mali. Jedini način koagulacija (zgrušavanje). Koloidi se talože neutralizacijom jona na njihovoj površini, promenom ph, dodavanjem određenih polimera koji se lepe za njihovu površinu i time međusobno povezuju koloidne čestice, zagrevanjem,...
31 III grupa pitanja 1. Hemijska ravnoteža Ravnoteža nastupa onda kada se brzine polazne i povratne reakcije izjednače. aa + bb cc + dd v k pol = v pov a b pol [ A] [ B] = k pov [ C] c [ D] d Ovo važi i za reakcije koje se odigravaju u više stupnjeva, jer onda polazne i povratne brzine za svaki stupanj moraju biti jednake, tj. sve brzine moraju biti jednake. 2. Konstanta hemijske ravnoteže, zakon o dejstvu masa Iz prethodnih izraza se dobija: k k pol pov c [ C] [ D] = a [ A] [ B] c [ C] [ D] K = a [ A] [ B] d b d b Prethodni izraz poznat je kao zakon o dejstvu masa, a K je konstanta hemijske ravnoteže. Iz jednačine stanja idealnog gasa, moguće je za gasove izraziti koncentraciju preko pritiska i konstante, te se odatle izvodi konstanta hemijske reakcije izražena preko parcijalnih pritisaka gasova koji učestvuju u reakciji. Onda je konstanta izražena u koncentracijama K c, a konstanta izražena u pritiscima K p. Što je vrednost konstante ravnoteže veća, to je ravnoteža više pomerena ka stvaranju produkata reakcije. 3. Ravnoteže u heterogenim i homogenim sistemima Homogeni: Ravnoteže u gasovitim sistemima p c C a A p p p d D b B = K p
32 Ova konstanta vredi za određenu temperaturu. Takođe podleže Le Šateljeovom principu i sa povećanjem pritiska se pomera u smeru nastanka manjeg broja molekula. Ovo ne važi za reakcije u kojima je konstanta bezdimenziona, tj. gde se polazi od, i dobija isti broj molekula. Ravnoteže u rastvorima c d [ C] [ D] K c = a b [ A] [ B] Podleže pomeranju ravnoteže sa promenom koncentracije. Heterogeni: Sistem čvrsto-gasovito Primer: CaCO 3 ( s) CaO( s) + CO2 ( g) Ovde u izraz za ravnotežu ulazi samo koncentracija, ili parcijalni pritisak ugnjen-dioksida. (Primer 2: odvodnjena so kao sredstvo za sušenje, npr. kalcijum-hlorid) Sistem čvrsto-tečno Ovakav sistem čini čvrsta supstanca u ravnoteži sa svojim zasićenim rastvorom. B m + A ( s) mb ( aq) + na ( aq) n Konstanta za tu ravnotežu je: + m n K c = [ B ] [ A ] Ona se naziva proizvodom rastvorljivosti i obeležava se jos i sa K s. Kako koncentracija jona zavisi od rastvorljivosti soli, tako je ova konstanta povezana sa rastvorljivošću soli. Sistem tečno-tečno Ako se supstanca A rastvara u dve tečnosti koje se međusobno ne mešaju, one će se razdeliti i uspostaviće se ravnoteža: A A ( faza1) ( faza2) Konstanta ravnoteže je ovde:
33 K = A A ( faza2) ( faza1) Ovaj odnos naziva se Nernstovim zakonom deljenja, a konstanta se nativa koeficijentom deljenja. Činjenica da se rastvori ponašaju ovako koristi se u organskoj hemiji za rastavljanje smeša. 4. Faktori koji utiču na ravnotežu, katalizatori Uticaj pritiska i koncentracije (videti pitanje 2.) Uticaj temperature: Jedna reakcija od dve (polazne i povratne) je egzotermna a druga endotermna. Spoljna temperatura utiče na ravnotežu tako što se pri visokim temperaturama favorizuje endotermna a pri niskim temperaturama egzotermna reakcija. Ovo ne znači da je najadekvatniji temperaturni uslov onaj najekstremniji. 5. Elektrolitička disocijacija, elektroliti Elektrolitička disocija je proces razlaganja supstanci na jone. Elektroliti su one supstance čiji vodeni rastvor provodi električnu struju, dok su neelektroliti ostale supstance. Elektroliti se dele na jake i na slabe na osnovu konstante disocijacije. Konstanta disocijacije jeste konstanta ravnoteže reakcije razlaganja datog elektrolita na jone. Ako je dovoljno visoka, može se smatrati da elektrolit potpuno disosuje, tj. da je jak, dok elektroliti koji disosuju manje od 1% se mogu smatrati slabim. 6. Teorije kiselina i baza Arenijusova teorija Kiseline su supstance koje u vodenom rastvoru disosuju dajući jone vodonika H + (bolje rečeno, hidronijum jone H 3 O + ). Baze su one susptance koje u vodenom rastvoru disosuju dajući hidroksidne jone OH -. Luisova teorija Baza su donori slobodno elektronskog para, dok su kiseline akceptori slobodnog elektronskog para. Protolitička teorija
34 Kiseline su donori protona, baze su akceptori protona. Nastaju konjugovano kiselo bazni parovi. Baze primajući elektron postaju konjugovane kiseline koje sada teže da ga otpuste, i obrnuto za kiseline. 7. Jačina kiselina i baza po protolitičkoj teoriji Jačina kiselina i baza zavisi od njihove konstante disocijacije. Kod kiselina ona se naziva kiselinskom konstantom K a, a kod baza baznom konstantom K b. Jačina kiselina je mera koliko protona one mogu da otpuste. Jakih neorganskih kiselina ima 7, po jačini su: hlorovodonična, jodovodonična, bromovodonična, azotna, sumporna, hlorna, perhlorna. Kiseline se po broju protona koje mogu da otpuste dele na monobazne, dvobazne i trobazne. Polibazne kiseline imaju sve manje i manje konstante kiselosti za svaku sledeću disocijaciju. Jake baze su sve baze alkalnih i neke baze zemno-alkalnih metala. Sve baze se dele na monokisele, dvokisele i trokisele, zavisno od toga koliko imaju hidroksidnih grupa. 8. Jonski proizvod vode i ph Čista voda je vrlo slabo jonizovana na hidronijum i hidroksid jone. Konstanta ravnoteže te reakcije naziva se jonskim proizvodom vode: [ H ][ OH ] = K w = 10 mol / dm Brojna vrednost vredi na 25 C, dok je pri nižim temperaturama manja, a na višim veća. Ako uzememo u datom izrazu u obzir koncentraciju vodenih molekula od 55.4 mol/dm 3 dobijamo konstantu jonizacije vode na sobnoj temperaturi, mol 2 /dm 6. Kako čista voda sadrži jednaku koncentraciju vodonkovih i hidroksidnih jona ( mol/dm 3 ) ona je neutralna. Ako bi vodeni rastvor sadržao više vodoničnih jona ponašao bi se kiselo, a obrnuto bazno. Može se uvesti veličina ph: ph = log[ H + ] Pa je onda rastvor sa ph sedam neutralan, dok je onaj sa ph manjim od sedam kiseo, a sa višim bazan. Analogno se uvodi i veličina poh. 9. Neutralizacija i soli Neutralizacija je reakcija između baze i kiseline u kojoj obavezno nastaju so i voda.
35 10. Hidroliza 11. Puferi Soli se dele na neutralne, nastale potpunom neutralizacijom, bazne, nastale nepotpunom neutralizacijom polikisele baze, i kisele, nastale nepotpunom neutralizacijom polibazne kiseline. Hidroliza je reakcija između jakih konjugovanih kiselina ili baza i vode, u kojoj dolazi do cepanja molekula vode. Hidrolizom jakih konjigovanih baza nastaju hidroksidni joni, a konjigovanih kiselina vodonični joni. Odavde sledi da će soli nastale neutralizacijom jake baze slabom kiselinom reagovati bazno, i obrnuto. Soli nastale neutralizacijom jake baze jakom kiselinom gradiće neutralne rastvore, a ph soli nastalih iz slabih baza i slabih kiselina zavise od jačine baza i kiselina koje su učestvovale. Puferi su sistemi koji se opiru promeni ph vrednosti. Sastoje se od slabe kiseline i njene soli sa jakom bazom ili od slabe baze i njene soli sa jakom kiselinom. Puferi se opiru promeni ph vrednosti tako što joni nastali disocijacijama soli i kiseline/baze se međusobno nadoknađuju prateći Le Šateljeov princip, čime se minimizuje promena ph pri dodavanju stranih vodoničnih ili hidroksidnih jona. Konstanta kiselosti/baznosti mora ostati ista, te dolazi do preraspodele koncentracija soli i kiseline/baze do uspostavljanja nove ravnoteže. 12. Proizvod rastvorljivosti Pitanje 2. Ravnoteže u rastvorima. 13. Oksidaciona i redukciona sredstva, određivanje oksidacionih brojeva, sređivanje oksido-redukcionih reakcija. Oksido-redukcione reakcije su procesi u kojima dolazi do prenosa elektrona sa jednog na drugi molekul (atom, jon). Oksidaciono sredstvo jeste ona supstanca koja se redukuje u reakciji, redukciono sredstvo se oksiduje (oksidacija je otpuštanje elektrona, redukcija primanje elektrona). Oksidacioni brojevi određuju se u odnosu na sledeća pravila: Kiseonik je u svim jedinjenjima -2 sem u peroksidima i superoksidima gde je -1 i -½. Vodonik je +1 sem u hidridima metala, gde je -1.. Fluor je uvek -1, a ostali halogeni elementi su -1 u binarnim jedinjenjima osim sa kiseonikom ili elektronegativnijim elementima, gde su pozitivni. 14. Galvanska ćelija, način rada, primeri
36 Galvanska ćelija je spreg u kojem se prenos elektrona u redoks reakcijama dešava preko provodnika a ne preko direktnog kontakta. Sastoji se iz dve elektrode uronjene u rastvore elektrolita između kojih je omogućena razmena jona (pomoću polupropusne membrane ili sonog mosta) U spregu sa slike će teći elektroni i u polu-ćelijama će se odigravati polureakcije: Zn( s) Zn Cu e 2+ ( aq) + 2e Cu( s) Cink je ovde anoda, dok je bakar katoda. 15. EMS galvanske ćelije Voltmetar prikalen na galvanski spreg prikazaće EMS tog sprega. Standardna EMS definisana je pri uslovima sobne temperature i koncentracije rastvora od 1 mol/dm 3. Svakoj od reakcija pridružuje se redukcioni potencijal te se EMS izračunava kao: E = E( katode) E( anode) 16. Standardni elektrodni potencijal polureakcija, naponski niz metala Eksperimentalno se standardni redoks potencijali za razne polureakcije određuju mereći EMS galvanskog elementa sastavljenog od polu-ćelije koja se ispituje i od standardne vodonične elektrode (staklen cilindar u kojem se nalazi platinska folija povezana sa provodnikom preko platinske
37 žice uronjenim u rastvor ph vrednosti 1) Za SVE se uzima standardni redoks potencijal 0.0 V. Naponski niz metala je tako sastavljen da svi metali koji se nalaze pre vodonika se rastvaraju u kiselinama uz izdvajanje vodonika dok se plemeniti metali posle vodonika ne rastvaraju u kiselinama. Naponski niz: Li > K > Sr > Ca > Na > Mg > Al > Zn > Cr > Fe > Cd > Co > Ni > Sn > Pb > H > Cu > Ag > Hg > Pt > Au 17. Nernstova jednačina Nernstova jednačina opisuje zavisnost EMS od koncentracije i glasi: E = E Tj : 0 RT lnq nf RT E = E logq nf Gde je F Faradejeva konstanta, a n broj razmenjenih elektrona. Q predstavlja konstantu ravnoteže u datoj reakciji. 18. Koncentracioni spreg Na osnovu Nernstove jednačine moguće je zaključiti da će se čak i između elektroda napravljenih od istog materijala javiti EMS ako su koncentracije rastvora različite u polu-ćelijama. Ovakvi spregovi se koriste u konstrukciji ph-metra. 19. Olovni akumulator Olovni akumulator sastoji se od 6 redno vezanih galvanskih elemenata od po 2V. Katoda se sastoji od olovo(iv)-oksida a anoda od čistog Pb. Obe su uronjene u sumpornu kiselinu. Reakcije koje se dešavaju su: EMS za ovaj spreg je 2.041V. Kako su reaktanti čvrsti uklanja se potreba za bilo kakvim dodatnim razdvajanjem elektroda, a EMS onda zavisi samo od koncentracije sumporne kiseline. Tokom pražnjenja ćelije nastaje olovo-sulfat, koji se taloži na elektrodama. Punjenje kondenzatora odvija se sledećom reakcijom:
38 20. Korozija i zaštita od korozije Kako skoro svi metali oksiduju kada se nađu na vazduhu, potrebno je sprečiti štetu koja time nastaje. Ovo se dešava jer je standardni redukcioni potencijal većine metala niži od redoks potencijala kiseonika, te će se metal ponašati kao anoda. Rešava se zaštitnim bojama, galvanizacijom ili katodnom zaštitom. Galvanizacija se bazira na tome da neki drugi metal, npr. cink, ima niži potencijal od gvožđa koje treba da se zaštiti, te će se ponašati kao anoda umesto gvožđa. Sličan postupak katodne zaštite jeste postavljanje žrtvenih anoda duž metalnih konstrukcije koje će se trošiti umesto metala koji štitimo.
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
MEĐUMOLEKULSKE SILE JON-DIPOL DIPOL VODONIČNE NE VEZE DIPOL DIPOL-DIPOL DIPOL-INDUKOVANI INDUKOVANI JON-INDUKOVANI DISPERZNE SILE
 MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
MEĐUMLEKULSKE SILE JN-DIPL VDNIČNE NE VEZE DIPL-DIPL JN-INDUKVANI DIPL DIPL-INDUKVANI INDUKVANI DIPL DISPERZNE SILE MEĐUMLEKULSKE SILE jake JNSKA VEZA (metal-nemetal) KVALENTNA VEZA (nemetal-nemetal) METALNA
Osnovne veličine, jedinice i izračunavanja u hemiji
 Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže:
 HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
U unutrašnja energija H entalpija S entropija G 298. G Gibsova energija TERMOHEMIJA I TERMODINAMIKA HEMIJSKA TERMODINAMIKA
 HEMIJSKA TERMODINAMIKA Bavi se energetskim promenama pri odigravanju hemijskih reakcija. TERMODINAMIČKE FUNKCIJE STANJA U unutrašnja energija H entalpija S entropija Ako su određene na standardnom pritisku
HEMIJSKA TERMODINAMIKA Bavi se energetskim promenama pri odigravanju hemijskih reakcija. TERMODINAMIČKE FUNKCIJE STANJA U unutrašnja energija H entalpija S entropija Ako su određene na standardnom pritisku
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
 Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO?
 HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
1. razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MOLEKULA HEMIJSKA VEZA
 EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI
 dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
Rastvori i osobine rastvora
 Rastvori i osobine rastvora U srpskom jeziku reč rasvor predstavlja homogenu tečnu smešu. U engleskom reč solution predstavlja više od toga smešu dva gasa, legure (homogene smeše dva metala)... Na ovom
Rastvori i osobine rastvora U srpskom jeziku reč rasvor predstavlja homogenu tečnu smešu. U engleskom reč solution predstavlja više od toga smešu dva gasa, legure (homogene smeše dva metala)... Na ovom
Termohemija. C(s) + O 2 (g) CO 2 (g) H= -393,5 kj
 Termohemija Termodinamika proučava energiju i njene promene Termohemija grana termodinamike odnosi izmeñu hemijske reakcije i energetskih promena koje se pri tom dešavaju C(s) + O 2 (g) CO 2 (g) H= -393,5
Termohemija Termodinamika proučava energiju i njene promene Termohemija grana termodinamike odnosi izmeñu hemijske reakcije i energetskih promena koje se pri tom dešavaju C(s) + O 2 (g) CO 2 (g) H= -393,5
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne
 Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
Geometrija molekula Lusiove formule su dvodimezione i ne daju nam nikakve informacije o geometriji molekula Srećom postoje razvijene eksperimentalne metode (rentgenska kristalografija, NMR spektroskopija...)
U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni
 HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Osnovne teoreme diferencijalnog računa
 Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Osnovne teoreme diferencijalnog računa Teorema Rolova) Neka je funkcija f definisana na [a, b], pri čemu važi f je neprekidna na [a, b], f je diferencijabilna na a, b) i fa) fb). Tada postoji ξ a, b) tako
Fizika Biologija i druge prirodne nauke. Dva glavna vida materije su masa i energija. E = m c 2
 HEMIJA je nauka o materiji i njenim promenama Fizika Biologija i druge prirodne nauke Dva glavna vida materije su masa i energija. Ajnštajnova veza između energije i materije E = m c 2 Materija ima dualna
HEMIJA je nauka o materiji i njenim promenama Fizika Biologija i druge prirodne nauke Dva glavna vida materije su masa i energija. Ajnštajnova veza između energije i materije E = m c 2 Materija ima dualna
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA
 SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA Atomi su veoma sitne čestice Još niko nije uspeo da vidi atom Još nije konstruisan takav mikroskop koji će omogućiti da se vidi atom Najbolji
SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA Atomi su veoma sitne čestice Još niko nije uspeo da vidi atom Još nije konstruisan takav mikroskop koji će omogućiti da se vidi atom Najbolji
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Drugi zakon termodinamike
 Drugi zakon termodinamike Uvod Drugi zakon termodinamike nije univerzalni prirodni zakon, ne važi za sve sisteme, naročito ne za neobične sisteme (mikrouslovi, svemirski uslovi). Zasnovan je na zajedničkom
Drugi zakon termodinamike Uvod Drugi zakon termodinamike nije univerzalni prirodni zakon, ne važi za sve sisteme, naročito ne za neobične sisteme (mikrouslovi, svemirski uslovi). Zasnovan je na zajedničkom
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
n (glavni ) 1, 2, 3,.. veličina orbitale i njena energija E= -R(1/n 2 )
 Kvantni brojevi Jedna atomska orbitala je definisana sa tri kvantna broja n l m l Elektroni su rasporedjeni u nivoima i podnivoima n l definiše nivo definiše podnivo ukupni broj orbitala u podnivou: 2
Kvantni brojevi Jedna atomska orbitala je definisana sa tri kvantna broja n l m l Elektroni su rasporedjeni u nivoima i podnivoima n l definiše nivo definiše podnivo ukupni broj orbitala u podnivou: 2
2log. se zove numerus (logaritmand), je osnova (baza) log. log. log =
 ( > 0, 0)!" # > 0 je najčešći uslov koji postavljamo a još je,, > 0 se zove numerus (aritmand), je osnova (baza). 0.. ( ) +... 7.. 8. Za prelazak na neku novu bazu c: 9. Ako je baza (osnova) 0 takvi se
( > 0, 0)!" # > 0 je najčešći uslov koji postavljamo a još je,, > 0 se zove numerus (aritmand), je osnova (baza). 0.. ( ) +... 7.. 8. Za prelazak na neku novu bazu c: 9. Ako je baza (osnova) 0 takvi se
RASTVORI. više e komponenata. Šećer u vodi, O 2 u vodi, zubne plombe, vazduh, morska voda
 RASTVORI Rastvori su homogene smeše e 2 ili više e komponenata Šećer u vodi, O 2 u vodi, zubne plombe, vazduh, morska voda Fizička stanja rastvora Rastvori mogu da postoje u bilo kom od 3 agregatna stanja:
RASTVORI Rastvori su homogene smeše e 2 ili više e komponenata Šećer u vodi, O 2 u vodi, zubne plombe, vazduh, morska voda Fizička stanja rastvora Rastvori mogu da postoje u bilo kom od 3 agregatna stanja:
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Idealno gasno stanje-čisti gasovi
 Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Kiselo bazni indikatori
 Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Rastvori rastvaračem rastvorenom supstancom
 Rastvori Rastvor je homogen sistem sastavljen od najmanje dvije supstance-jedne koja je po pravilu u velikom višku i naziva se rastvaračem i one druge, koja se naziva rastvorenom supstancom. Rastvorene
Rastvori Rastvor je homogen sistem sastavljen od najmanje dvije supstance-jedne koja je po pravilu u velikom višku i naziva se rastvaračem i one druge, koja se naziva rastvorenom supstancom. Rastvorene
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
 Kvantna optika Toplotno zračenje Apsorpciona sposobnost tela je sposobnost apsorbovanja energije zračenja iz intervala l, l+ l na površini tela ds za vreme dt. Apsorpciona moć tela je sposobnost apsorbovanja
Kvantna optika Toplotno zračenje Apsorpciona sposobnost tela je sposobnost apsorbovanja energije zračenja iz intervala l, l+ l na površini tela ds za vreme dt. Apsorpciona moć tela je sposobnost apsorbovanja
= T 2. AgBr (s) + ½ Cl 2(g) + ½ Br 2(g) = AgCl (s) O (l) O (g) +1/2O 2(g) H 2(g) =H 2. značaj navođenja agregatnog stanja
 TERMOEMIJA Termohemija proučava toplotne promene koje prate hemijske reakcije, fazne prelaze (topljenje, isparavanje, sublimacija, polimorfne promene), rastvaranje supstance, razblaživanje rastvora itd.
TERMOEMIJA Termohemija proučava toplotne promene koje prate hemijske reakcije, fazne prelaze (topljenje, isparavanje, sublimacija, polimorfne promene), rastvaranje supstance, razblaživanje rastvora itd.
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
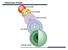 Dalton (803) Tomson (904) Raderford (9) Bor (93) Šredinger (96) OTKRIĆA OSNOVNIH SASTOJAKA ATOMA Do početka XX veka važila je Daltonova atomska teorija o nedeljivosti atoma. Karjem XIX i početkom XX veka
Dalton (803) Tomson (904) Raderford (9) Bor (93) Šredinger (96) OTKRIĆA OSNOVNIH SASTOJAKA ATOMA Do početka XX veka važila je Daltonova atomska teorija o nedeljivosti atoma. Karjem XIX i početkom XX veka
4.7. Zadaci Formalizam diferenciranja (teorija na stranama ) 343. Znajući izvod funkcije x arctg x, odrediti izvod funkcije x arcctg x.
 4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
4.7. ZADACI 87 4.7. Zadaci 4.7.. Formalizam diferenciranja teorija na stranama 4-46) 340. Znajući izvod funkcije arcsin, odrediti izvod funkcije arccos. Rešenje. Polazeći od jednakosti arcsin + arccos
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
BIOFIZIKA TERMO-FIZIKA
 BIOFIZIKA TERMO-FIZIKA Akademik, prof. dr Jovan P. Šetrajčić jovan.setrajcic@df.uns.ac.rs Univerzitet u Novom Sadu Departman za fiziku PMF Powered byl A T E X 2ε! p. / p. 2/ Termika FENOMENOLOŠKA TEORIJA
BIOFIZIKA TERMO-FIZIKA Akademik, prof. dr Jovan P. Šetrajčić jovan.setrajcic@df.uns.ac.rs Univerzitet u Novom Sadu Departman za fiziku PMF Powered byl A T E X 2ε! p. / p. 2/ Termika FENOMENOLOŠKA TEORIJA
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
SPEKTROSKOPIJA SPEKTROSKOPIJA
 Spektroskopija je proučavanje interakcija elektromagnetnog zraka (EMZ) sa materijom. Elektromagnetno zračenje Proces koji se odigrava Talasna dužina (m) Energija (J) Frekvencija (Hz) γ-zračenje Nuklearni
Spektroskopija je proučavanje interakcija elektromagnetnog zraka (EMZ) sa materijom. Elektromagnetno zračenje Proces koji se odigrava Talasna dužina (m) Energija (J) Frekvencija (Hz) γ-zračenje Nuklearni
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
OSNOVI HEMIJSKE TERMODINAMIKE I TERMOHEMIJA
 OSNOVI HEMIJSKE TERMODINAMIKE I TERMOHEMIJA OSNOVI HEMIJSKE TERMODINAMIKE Hemjska termodnamka proučava promene energje (toplotn efekat) pr odgravanju hemjskh reakcja. MATERIJA ENERGIJA? Energja je dskontnualna
OSNOVI HEMIJSKE TERMODINAMIKE I TERMOHEMIJA OSNOVI HEMIJSKE TERMODINAMIKE Hemjska termodnamka proučava promene energje (toplotn efekat) pr odgravanju hemjskh reakcja. MATERIJA ENERGIJA? Energja je dskontnualna
MEHANIKA FLUIDA. Isticanje kroz otvore sa promenljivim nivoom tečnosti
 MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
MEHANIKA FLUIDA Isticanje kroz otvore sa promenljivim nivoom tečnosti zadatak Prizmatična sud podeljen je vertikalnom pregradom, u kojoj je otvor prečnika d, na dve komore Leva komora je napunjena vodom
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
5 Ispitivanje funkcija
 5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
TALASNO-MEHANI MEHANIČKI MODEL ATOMA
 TALASNO-MEHANI MEHANIČKI MODEL ATOMA TALASNO-MEHANI MEHANIČKI MODEL ATOMA Kompton (19): svetlost ima i talasnu i korpuskularnu prirodu. Luj De Brolj (193): elektron ima i korpuskularnu i talasnu prirodu.
TALASNO-MEHANI MEHANIČKI MODEL ATOMA TALASNO-MEHANI MEHANIČKI MODEL ATOMA Kompton (19): svetlost ima i talasnu i korpuskularnu prirodu. Luj De Brolj (193): elektron ima i korpuskularnu i talasnu prirodu.
Kovalentna veza , CO 2. U molekulima H 2
 Kovalentna veza U molekulima H 2, N 2, O 2, CO 2, NH 3, H 2 O,... ili molekulima organskih jedinjenja ne postoje joni. To je veza između atoma i ona se bitno razlikuje od jonske veze a naziva se kovalentnom
Kovalentna veza U molekulima H 2, N 2, O 2, CO 2, NH 3, H 2 O,... ili molekulima organskih jedinjenja ne postoje joni. To je veza između atoma i ona se bitno razlikuje od jonske veze a naziva se kovalentnom
JONSKA VEZA (metal-nemetal) KOVALENTNA VEZA (nemetal-nemetal) METALNA VEZA (metal-metal) jake H N. prelazne VODONIČNA VEZA H F
 HEMIJSKE VEZE HEMIJSKE VEZE I GRAĐA JEDINJENJA,, I deo Postoje tri osnovna tipa veza (primarne veze) i one imaju najveći uticaj na svojstva jedinjenja. Pored njih postoje i dopunske (sekundarne) veze između
HEMIJSKE VEZE HEMIJSKE VEZE I GRAĐA JEDINJENJA,, I deo Postoje tri osnovna tipa veza (primarne veze) i one imaju najveći uticaj na svojstva jedinjenja. Pored njih postoje i dopunske (sekundarne) veze između
Verovatnoća i Statistika I deo Teorija verovatnoće (zadaci) Beleške dr Bobana Marinkovića
 Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
Verovatnoća i Statistika I deo Teorija verovatnoće zadaci Beleške dr Bobana Marinkovića Iz skupa, 2,, 00} bira se na slučajan način 5 brojeva Odrediti skup elementarnih dogadjaja ako se brojevi biraju
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
PERIODNI SISTEM ELEMENATA
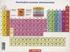 PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
C 273,15, T 273,15, 1 1 C 1 50 C 273,15 K 50K 323,15K 50K 373,15K C 40 C 40 K
 1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
Rastvori Osnovni pojmovi i izračunavanja
 Rastvori Osnovni pojmovi i izračunavanja Disperzni sistem je smeša u kojoj su jedna ili više supstanci raspršene u nekoj drugoj supstanci u obliku sitnih čestica. Disperzni sredstvo je supstanca u kojoj
Rastvori Osnovni pojmovi i izračunavanja Disperzni sistem je smeša u kojoj su jedna ili više supstanci raspršene u nekoj drugoj supstanci u obliku sitnih čestica. Disperzni sredstvo je supstanca u kojoj
GASNO STANJE.
 GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
TERMALNOG ZRAČENJA. Plankov zakon Stefan Bolcmanov i Vinov zakon Zračenje realnih tela Razmena snage između dve površine. Ž. Barbarić, MS1-TS 1
 OSNOVNI ZAKONI TERMALNOG ZRAČENJA Plankov zakon Stefan Bolcmanov i Vinov zakon Zračenje realnih tela Razmena snage između dve površine Ž. Barbarić, MS1-TS 1 Plankon zakon zračenja Svako telo čija je temperatura
OSNOVNI ZAKONI TERMALNOG ZRAČENJA Plankov zakon Stefan Bolcmanov i Vinov zakon Zračenje realnih tela Razmena snage između dve površine Ž. Barbarić, MS1-TS 1 Plankon zakon zračenja Svako telo čija je temperatura
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
IZVODI ZADACI (I deo Najpre da se podsetimo tablice i osnovnih pravila:. C0.. (. ( n n n-. (a a lna 6. (e e 7. (log a 8. (ln ln a (>0 9. ( 0 0. (>0 (ovde je >0 i a >0. (cos. (cos - π. (tg kπ cos. (ctg
KVADRATNA FUNKCIJA. Kvadratna funkcija je oblika: Kriva u ravni koja predstavlja grafik funkcije y = ax + bx + c. je parabola.
 KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
KVADRATNA FUNKCIJA Kvadratna funkcija je oblika: = a + b + c Gde je R, a 0 i a, b i c su realni brojevi. Kriva u ravni koja predstavlja grafik funkcije = a + b + c je parabola. Najpre ćemo naučiti kako
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA!
 DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA! Polazna znanja zakoni o: Održanju mase Stalnom (utvrdjenom) sastavu Umnoženim odnosima Zakon o održanju mase masa supstance ne menja
DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA! Polazna znanja zakoni o: Održanju mase Stalnom (utvrdjenom) sastavu Umnoženim odnosima Zakon o održanju mase masa supstance ne menja
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
Elektrotehnički fakultet univerziteta u Beogradu 17.maj Odsek za Softversko inžinjerstvo
 Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Elektrotehnički fakultet univerziteta u Beogradu 7.maj 009. Odsek za Softversko inžinjerstvo Performanse računarskih sistema Drugi kolokvijum Predmetni nastavnik: dr Jelica Protić (35) a) (0) Posmatra
Doc. dr Milena Đukanović
 Doc. dr Milena Đukanović milenadj@ac.me ATOMSKA STRUKTURA MATERIJE: 500 g.p.n.e. Empedokle svijet se sastoji od četiri osnovna elementa: zemlja, vazduh, vatra i voda. 400 g.p.n.e. Demokrit svijet je sagrađen
Doc. dr Milena Đukanović milenadj@ac.me ATOMSKA STRUKTURA MATERIJE: 500 g.p.n.e. Empedokle svijet se sastoji od četiri osnovna elementa: zemlja, vazduh, vatra i voda. 400 g.p.n.e. Demokrit svijet je sagrađen
