Στα ισοζύγια χρησιµοποιείται συχνά ο όρος σύστηµα, που αναφέρεται σε οτιδήποτε µπορεί να περιορισθεί µε την χρήση ορίων (γραµµών).
|
|
|
- Ἀριστόβουλος Δασκαλόπουλος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 1. ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ 1.1. Ισοζύγια µάζας Η εφαρµογή του νόµου διατήρησης της µάζας στην επίλυση προβληµάτων της βιοµηχανίας τροφίµων είναι γνωστή σαν προσδιορισµός των ισοζυγίων µάζας. Ένα αναλυτικό ισοζύγιο µάζας είναι απόλυτα απαραίτητο για τον σωστό σχεδιασµό και την αποτελεσµατική λειτουργία ενός εργοστασίου επεξεργασίας τροφίµων, γιατί δίνει πληροφορίες: α) για τις απαιτήσεις σε υλικά, πρώτες ύλες, και για τον όγκο παραγωγής, στοιχεία που είναι απαραίτητα για τον προσδιορισµό του κόστους παραγωγής, β) για την ανακύκλωση παραπροϊόντων και το µέγεθος των εγκαταστάσεων επεξεργασίας αποβλήτων, γ) για τον προσδιορισµό ή έλεγχο της απόδοσης µιας γραµµής παραγωγής ή ολόκληρου του εργοστασίου, δ) για τον προσδιορισµό των προδιαγραφών αγοράς µηχανολογικού εξοπλισµού και κατασκευής αποθηκευτικών χώρων, ε) πληροφορίες που είναι απαραίτητες για τον προσδιορισµό των ισοζυγίων ενέργειας. Τα ισοζύγια µάζας στηρίζονται στην αρχή ότι η ύλη δεν µπορεί να δηµιουργηθεί από το µηδέν, ούτε και να καταστραφεί ολοσχερώς. Με βάση την αρχή αυτή η ροή πρώτων υλών, προϊόντων και παραπροϊόντων που συµµετέχουν σε µια επεξεργασία περιγράφεται από την εξίσωση : εισερχόµενα υλικά = εξερχόµενα υλικά + συσσωρευµένα υλικά ή ΣΥΝΟΛΟ ΠΡΩΤΩΝ ΥΛΩΝ = ΣΥΝΟΛΟ ΠΡΟΪΟΝΤΩΝ, ΠΑΡΑΠΡΟΪΟΝΤΩΝ, ΑΠΟΒΛΗΤΩΝ + ΣΥΝΟΛΟ ΣΥΣΣΩΡΕΥΜΕΝΩΝ ΥΛΩΝ Αν η συσσώρευση είναι µηδέν, τότε έχουµε σταθερή κατάσταση οπότε : ΕΙΣΕΡΧΟΜΕΝΑ ΥΛΙΚΑ = ΕΞΕΡΧΟΜΕΝΑ ΥΛΙΚΑ Αν η συσσώρευση δεν είναι µηδέν, τότε η συγκέντρωση υλικών στο σύστηµα αλλάζει µε τον χρόνο, οπότε έχουµε επεξεργασία υπό ασταθή κατάσταση. Φάση ασταθούς κατάστασης έχουµε συνήθως κατά την έναρξη λειτουργίας µιας συνεχούς επεξεργασίας, που αντιστοιχεί στη περίοδο ρύθµισης, αλλά καταλήγει τελικά στη σταθερή κατάσταση µετά την σταθεροποίηση των συνθηκών επεξεργασίας. Στα ισοζύγια χρησιµοποιείται συχνά ο όρος σύστηµα, που αναφέρεται σε οτιδήποτε µπορεί να περιορισθεί µε την χρήση ορίων (γραµµών). Για την δηµιουργία ενός ισοζυγίου µάζας απαιτούνται : α) η επιλογή του συστήµατος, στο οποίο αναφέρεται το ισοζύγιο. Αυτό απαιτεί τον καθορισµό συµβατικών ορίων, τα οποία επιλέγονται µε τρόπον ώστε να συναντούν µόνο τις διαδροµές εκείνων των υλικών που παρουσιάζουν ενδιαφέρον στο ισοζύγιο µάζας. Οτιδήποτε βρίσκεται έξω από τα όρια θεωρείται ότι βρίσκεται έξω από το σύστηµα και αντίθετα. Για την σωστή επιλογή και οριοθέτηση του συστήµατος πρέπει να είναι γνωστό οτιδήποτε επηρεάζει αποφασιστικά την κατανοµή των διαφόρων υλικών (πρώτων υλών, προϊόντων, κλπ.) κατά την πορεία της επεξεργασίας. Ακόµη για την επίλυση του ισοζυγίου είναι απαραίτητη η κατασκευή ενός διαγράµµατος ροής που περιγράφει την επεξεργασία που περιλαµβάνει το σύστηµα. 1
2 β) η επιλογή µιας βάσης υπολογισµού. Συχνά σαν βάση χρησιµοποιείται ορισµένο βάρος ενός υλικού που µπαίνει ή βγαίνει από το σύστηµα, ενώ άλλες φορές κάποια χρονική περίοδος λειτουργίας της επεξεργασίας (π.χ. 1 ώρα). Κατά την επιλογή της βάσης καταβάλλεται προσπάθεια να βρει ένα συστατικό (υλικό), που µπαίνει στο σύστηµα µόνο από µια διαδροµή (ρεύµα) και βγαίνει από το σύστηµα πάλι µόνο από µια διαδροµή. Αν υπάρχει τέτοιο συστατικό, αυτό επιλέγεται σαν βάση και όλα τα αποτελέσµατα υπολογίζονται αναφορικά µε την βάση αυτή. Σε περίπτωση απουσίας ενός τέτοιου συστατικού, σαν βάση επιλέγεται το συστατικό που εµφανίζεται στις λιγότερες διαδροµές (ρεύµατα) που περιέχονται στο σύστηµα. Για την επίλυση ενός ισοζυγίου µάζας, απαιτείται συνήθως η δηµιουργία συστήµατος εξισώσεων. Για κάθε άγνωστη ποσότητα που πρέπει να προσδιορισθεί, είναι απαραίτητη η δηµιουργία µιας ανεξάρτητης εξίσωσης που περιέχει τον άγνωστο αυτό. Κατά κανόνα το σύστηµα εξισώσεων που πρέπει να λυθεί περιλαµβάνει την εξίσωση ισοζυγίου µάζας για το σύνολο των υλικών που µπαίνουν ή βγαίνουν από το σύστηµα (ολικό ισοζύγιο) και µια εξίσωση για κάθε ένα (χωριστά) συστατικό, που µπαίνει ή βγαίνει από το σύστηµα. Με άλλα λόγια οι εξισώσεις του ισοζυγίου µάζας αποτελούν µαθηµατικές διατυπώσεις των παρακάτω εκφράσεων της αρχής διατήρησης της µάζας : ολική µάζα που µπαίνει = ολική µάζα που βγαίνει στο σύστηµα από το σύστηµα και µάζα συστατικού που = µάζα συστατικού που µπαίνει στο σύστηµα βγαίνει από το σύστηµα Ο βαθµός ευκολίας της επίλυσης ενός προβλήµατος ισοζυγίου µάζας καθορίζεται από την επιδεξιότητα µε την οποία έγινε η επιλογή του συστήµατος και της βάσης υπολογισµών. Παραδείγµατα επίλυσης ισοζυγίων µάζας : ΠΑΡΑ ΕΙΓΜΑ 1. Σε ένα συµπυκνωτήρα τροφοδοτείται χυµός µε 8% στερεά που συµπυκνώνεται προς χυµό µε 22% στερεά συστατικά. Πόσο νερό πρέπει να εξατµισθεί (από το εισερχόµενο) για να πραγµατοποιηθεί η συµπύκνωση αυτή. Χ Kg νερού 1 Kg αραιού χυµού Ψ Kg χυµού µε ΣΥΜΠΥΚΝΩΤΗΡΑΣ µε 8% στερεά 22% στερεά Σχ. 1.1 ιάγραµµα ροής παραδείγµατος 1 2
3 ΛΥΣΗ : Το Σχ. 2.7., περιγράφει το ισοζύγιο µάζας γύρω από τον συµπυκνωτήρα χυµού. Στην περίπτωση αυτή δεν µπαίνει πρόβληµα επιλογής και οριοθέτησης του συστήµατος, αφού πρόκειται για µια φάση επεξεργασίας. Αντίθετα, πρέπει να γίνει επιλογή της βάσης για τους υπολογισµούς. Υπάρχουν τέσσερις δυνατότητες επιλογής : α) το καθαρό νερό, β) τα στερεά του χυµού, γ) ο ακατέργαστος χυµός (µε 8% στερεά) και δ) ο συµπυκνωµένος χυµός (µε 22% στερεά). Η πρώτη επιλογή αποκλείεται, γιατί το καθαρό νερό περιέχεται σε δύο ρεύµατα που βγαίνουν από το σύστηµα. Από την άλλη µεριά τα στερεά του χυµού δεν προσφέρουν ευκολόχρηστη βάση, αφού τ αποτελέσµατα θα πρέπει να εκφρασθούν σαν Kg εξατµιζόµενου νερού ανά Kg στερεών που εισέρχονται στο σύστηµα και θα απαιτηθεί ένας πρόσθετος υπολογισµός για τον προσδιορισµό του εξατµιζόµενου νερού σαν συνάρτηση της µάζας του εισερχόµενου (ασυµπύκνωτου) ή του εξερχόµενου (συµπυκνωµένου) χυµού. Τόσο ο ακατέργαστος χυµός, όσο και ο συµπυκνωµένος προσφέρουν µια εξίσου κατάλληλη βάση. Λαµβάνουµε λοιπόν σαν βάση το 1 Κg χυµού µε 8% στερεά και ονοµάζουµε Χ τα Kg νερού, που πρέπει να εξατµισθεί και Ψ τα Kg του παραγόµενου συµπυκνωµένου χυµού. ηµιουργούµε τις εξισώσεις που αναφέρονται στο ισοζύγιο µάζας : Ολικό ισοζύγιο µάζας : Χ + Ψ = 1 (1) Ισοζύγιο µάζας για τα στερεά συστατικά : 1 x 0,08 = Ψ x 0,22 (2) Ισοζύγιο µάζας για το νερό : 1 x 0,92 = Ψ x 0,78 + X (3) Η λύση του συστήµατος των εξισώσεων (1) και (2) δίνει : Χ = 0,636 Kg εξατµιζόµενου νερού / Kg εισερχόµενου χυµού, και Ψ = 0,364 Kg νέου χυµού µε 22% στερεά / Kg εισερχόµενου χυµού ΠΑΡΑ ΕΙΓΜΑ 2. Για την αποφυγή απώλειας αρωµατικών συστατικών κατά την συµπύκνωση πορτοκαλοχυµού µε εξάτµιση γίνεται συµπύκνωση του αραιού χυµού µέχρι περιεκτικότητας 58% σε στερεά σε εξατµιστήρες κενού και ακολουθεί ανάµιξη αυτού µε φρέσκο (ασυµπύκνωτο) χυµό για παραγωγή µίγµατος µε 42 % στερεά. Αναλυτικότερα, όπως φαίνεται στο Σχ. 2.8., ο φρέσκος χυµός µε 12,5 % στερεά περνά από ειδικά φίλτρα (finishers), όπου χωρίζεται σε στραγγισµένο καθαρό χυµό, σε χυµό µε αιωρούµενα στερεά (πούλπα-pulp) και άλλα κλάσµατα που θεωρούνται αµελητέας ποσότητας. Από τον φρέσκο χ χυµό, που τροφοδοτεί τα α φίλτρα, το 80 % κατά βάρος περνά στους εξατµιστήρες κενού, ενώ το υπόλοιπο 20%, που δεν περνά στους εξατµιστήρες (χυµός µε πούλπα), χρησιµοποιείται για αραίωση του συµπυκνωµένου χυµού (53% στερεά) µέχρι επίτευξης της τελικής επιθυµητής περιεκτικότητας του χυµού σε στερεά (42%). Ζητείται να υπολογισθούν : α) Το βάρος του εξατµιζόµενου νερού ανά 100 Kg φρέσκου χυµού που τροφοδοτείται στο σύστηµα. 3
4 β) Η περιεκτικότητα σε στερεά των ρευµάτων που βγαίνουν από τα φίλτρα. γ) Η αναλογία βάρους συµπυκνωµένου προς ασυµπύκνωτο χυµό στο τελικό προϊόν. αµελητέο κλάσµα στερεών 20Kg χυµός µε πούλπα (αιωρούµενα στερεά) 100Kg φρέσκου χυµού 80Kg χυµός ΦΙΛΤΡΑ ΕΞΑΤΜΙΣΤΗΡΑΣ ΑΝΑΜΙΚΤΗΡΑΣ µε 12,5% στραγγισµένος µε 58% στερεά καθαρός χυµός στερεά X Kg νερού Ψ Kg χυµού µε 42% στερεά Σχ ιάγραµµα ροής για παραγωγή συµπυκνωµένου πορτοκαλοχυµού α) Προσδιορισµός της ποσότητας του εξατµιζόµενου νερού. Επιλέγεται ένα σύστηµα τέτοιο, ώστε τα όρια του να κόβουν µόνον ρεύµατα που περιέχουν νερό και που µπαίνουν και βγαίνουν από το σύστηµα. Τα όρια του συστήµατος αυτού παριστάνονται στο Σχ 2.8. από την διακεκοµµένη γραµµή. Σαν βάση υπολογισµού λαµβάνονται τα 100 Kg φρέσκου χυµού. Έστω Χ = Kg εξατµιζόµενου νερού, και Ψ = Κg του προϊόντος (τελικός χυµός), Τότε µε εφαρµογή του ισοζυγίου µάζας προκύπτουν οι εξισώσεις : Ολικό ισοζύγιο µάζας του συστήµατος, δηλ. Σύνολον εισερχόµενων υλικών = σύνολον εξερχόµενων υλικών 100 = Χ + Ψ Ισοζύγιο µάζας πάνω στα στερεά, δηλ. Εισερχόµενα στερεά = εξερχόµενα στερεά 100 x 0,125 = Ψ x 0,42 Με επίλυση του συστήµατος των παραπάνω δύο εξισώσεων προκύπτει : Ψ = 29,8 Κg τελικού προϊόντος (χυµού µε 42% στερεά) και Χ = 70,2 Κg εξατµιζόµενου νερού / 100 Κg φρέσκου χυµού β) Προσδιορισµός της περιεκτικότητας σε στερεά κάθε ρεύµατος (κλάσµατος), που φεύγει από τα φίλτρα. 80 Κg µε Ζ Κg µε Ε Ξ Α Τ Μ Ι Σ Τ Η Ρ Α Σ Μ% στερεά 8% στερεά 4
5 70,2 Κg νερό Σχ Ισοζύγιο µάζας µόνο γύρω από τον εξατµιστήρα κενού. Θεωρώντας τον εξατµιστήρα σαν ένα σύστηµα, ονοµάζω Μ % την ζητούµενη περιεκτικότητα σε στερεά του εξερχόµενου ρεύµατος από τα φίλτρα, που τροφοδοτεί τον εξατµιστήρα. Αν Ζ Kg συµπυκνωµένου χυµού µε 58 % στερεά παράγονται από τον εξατµιστήρα, από το ισοζύγιο µάζας προκύπτουν οι εξισώσεις: Ολικό ισοζύγιο µάζας : 80 = Ζ + 70,2 Ισοζύγιο µάζας πάνω στα στερεά : 80 x M / 100 = Z x 0,58 Με επίλυση του συστήµατος των δύο παραπάνω εξισώσεων έχω ότι : και Ζ = 9,8 Kg χυµού µε 58 % στερεά Μ = 7,08 % στερεά Για τον προσδιορισµό της περιεκτικότητας στερεών (έστω Ρ %) στο κλάσµα των 20 Κg πούλπας, που φεύγει από τα φίλτρα, εξετάζεται το ισοζύγιο µάζας, που παριστάνεται στο Σχ Κg µε Ρ % στερεά 100 Kg φρέσκου χυµού 80 Kg µε Φ Ι Λ Τ Ρ Α µε 12,5 % στερεά 7,08 % στερεά Σχ Ισοζύγιο µάζας γύρω από τα φίλτρα Εφαρµόζεται το ισοζύγιο µάζας πάνω στα στερεά οπότε έχω : 100 x 0,125 = 80 x 0, x P/100, που δίνει Ρ = 34,2 % στερεά στο κλάσµα των 20 Κg γ) Αναλογία βάρους συµπυκνωµένου προς ασυµπύκνωτο χυµό : Από τα ευρεθέντα παραπάνω η ζητούµενη αναλογία θα είναι : α = 9,8 / 20 = 1 / 2 περίπου 1.2. Ισοζύγια Ενέργειας Η εφαρµογή του νόµου διατήρησης της ενέργειας στην επίλυση προβληµάτων, που αφορούν προσδιορισµό των διαφόρων ροών ενέργειας γύρω από µια γραµµή επεξεργασίας, είναι γνωστή σαν προσδιορισµός ισοζυγίων ενέργειας. Τα ισοζύγια ενέργειας είναι απαραίτητα : α) για τον καθορισµό των αναγκών µιας επεξεργασίας σε λειτουργικά µέσα, δηλ. ατµό, ζεστό - κρύο νερό, ηλεκτρική ε ενέργεια, κλπ. ίνουν κατά συνέπεια πληροφορίες απαραίτητες για τον υπολογισµό του κόστους επεξεργασίας. 5
6 β) για τον σχεδιασµό και εγκατάσταση µιας γραµµής επεξεργασίας, αφού δίνουν πληροφορίες απαραίτητες για την σύνταξη προδιαγραφών, που αφορούν µηχανήµατα εναλλαγής θερµότητας και εξοπλισµό παραγωγής των λειτουργικών µέσων (ατµολέβητες, αεροσυµπιεστές, κλπ.) Τα ισοζύγια ενέργειας χρησιµοποιούνται κατά τον ίδιο τρόπο όπως και τα ισοζύγια µάζας. Η εξίσωση πάνω στην οποία στηρίζεται το ισοζύγιο ενέργειας είναι µία έκφραση του νόµου διατήρησης της ενέργειας : Συνολική ενέργεια = Συνολική ενέργεια εισερχόµενη στο σύστηµα εξερχόµενη στο σύστηµα Σε περίπτωση που παρατηρείται συσσώρευση ενέργειας, το σύστηµα βρίσκεται υπό ασταθή κατάσταση. Όπως στη περίπτωση των ισοζυγίων µάζας έτσι και στα ισοζύγια ενέργειας, το σύστηµα περνά από µια φάση ρύθµισης, που χαρακτηρίζεται από ασταθή κατάσταση, για να καταλήξει σε παρατεταµένη λειτουργία µε µηδενική συσσώρευση ενέργειας ή όπως λέγεται, υπό σταθερή κατάσταση Η ενέργεια µπορεί να εµφανισθεί µε πολλές µορφές. Μερικές κοινές µορφές ενέργειας είναι η θερµότητα, η ενθαλπία, η µ µηχανική ενέργεια και η ηλεκτρική ενέργεια. Κατά την εφαρµογή του ισοζυγίου ενέργειας πρέπει να ληφθεί υπόψη το γεγονός, ότι κατά την διάρκεια της επεξεργασίας το σύστηµα µπορεί να µετατρέψει µια µορφή ενέργειας σε µια άλλη. Έτσι ένα συνολικό ισοζύγιο ενέργειας µπορεί να περιγραφεί από την εξίσωση : Εισερχόµενη ενέργεια = Εξερχόµενη ενέργεια ή Η1 + (ΜΕ)1 + C1 + G1 = H2 + (ME)2 + C2 + G2 + Q + W όπου Η = Ενθαλπία (στην πραγµατικότητα εννοείται η αλλαγή ενθαλπίας από κάποιο επίπεδο αναφοράς ή συµβατική βάση). ΜΕ = Μηχανική Ενέργεια C = Χηµική Ενέργεια G = Ηλεκτρική Ενέργεια Q = Θερµότητα W = Παραχθέν Έργο Η συχνότερη και χρησιµότερη εφαρµογή των ισοζυγίων ενέργειας αφορά τον προσδιορισµό των ροών θερµικής ενέργειας γύρω από ένα σύστηµα ή µια γραµµή επεξεργασίας. Γι αυτό η έµφαση στο σηµείο αυτό δίνεται στην επίδειξη χειρισµού προβληµάτων ισοζυγίων θερµικής ενέργειας : ΠΑΡΑ ΕΙΓΜΑ 3. Σε µια γραµµή απόσµησης ακατέργαστων λαδιών, το ακατέργαστο λάδι προθερµαίνεται σ ένα σωληνοειδή εναλλάκτη, που λειτουργεί µε αντιροή (αντίθετη ροή προϊόντος και θερµαντικού µέσου). Το θερµαντικό µέσο είναι συµπυκνωµένος ατµός (νερό), που περνά µέσα από τα τοιχώµατα του εναλλάκτη µε παροχή Κg / hr. Το ακατέργαστο λάδι µπαίνει στον εναλλάκτη σε θερµοκρασία 21,2 C και βγαίνει µε παροχή Κg / hr. Αν η θερµοκρασία εξόδου του ζεστού νερού είναι 43,3 C, ζητείται η θερµοκρασία εξόδου του λαδιού από τον εναλλάκτη. ίνονται : ειδική θερµότητα λαδιού, CpΛ = 0,5 Kcal / Kg C ειδική θερµότητα νερού, CpΝ = 1,0 Kcal / Kg C λάδι µε ΤΛ1 = 21,1 C 4450 Kg / hr ζεστό λάδι ΤΛ2 = ; 6
7 νερό µε ΤΝ2 = 43,3 C ζεστό νερό ΤΝ1 = 100 C 2270 Kg / hr ΛΥΣΗ : Ο ίδιος ο εναλλάκτης θερµότητας αποτελεί στη προκειµένη περίπτωση το σύστηµα και έτσι δεν χρειάζεται να γίνει καµία επιλογή συστήµατος. Σαν βάση υπολογισµού λαµβάνεται η λειτουργία του εναλλάκτη για 1 ώρα. Σύµφωνα µε τον νόµο διατήρησης της ενέργειας έχουµε : Εισερχόµενη ενθαλπία = Εξερχόµενη ενθαλπία ή ενθαλπία ενθαλπία ενθαλπία ενθαλπία εισερχόµενου + εισερχόµενου = εξερχόµενου + εξερχόµενου λαδιού (Q1) νερού (Q2) λαδιού (Q3) νερού (Q4) Συµβατικά, σαν θερµοκρασία αναφοράς (ΤΑ) λαµβάνεται η θερµοκρασία των 21,1 C, που είναι η χαµηλότερη θερµοκρασία του συστήµατος. ΣΗΜ. : αυτό δεν πρέπει να γίνεται στις περιπτώσεις που η εξίσωση του ισοζυγίου ενέργειας περιέχει ενθαλπίες, που πάρθηκαν από τους πίνακες ατµού (σελ.33). Αυτό, επειδή οι ενθαλπίες των πινάκων αυτών υπολογίστηκαν µε θερµοκρασία αναφοράς τους 0 C (ή τους 32 F). Είναι φανερό ότι στις περιπτώσεις αυτές επιβάλλεται η χρησιµοποίηση των 0 C (ή 32 F) σαν θερµοκρασία αναφοράς. Με τον τρόπο αυτό, το ρεύµα του εισερχόµενου λαδιού ( µε θερµοκρασία 21,2 C) θεωρείται, ότι έχει ενθαλπία (δηλ. περιέχει εσωτερική ενέργεια) ίση µε το µηδέν. Εισερχόµενη ενθαλπία : Q1 = mλ. CpΛ. (TΛ1 - TA) = ,5. (21,1-21,1) = 0 Kcal Q1 = mn. CpN. (TN1 - TA) = (100-21,2 0 = Kcal Εξερχόµενη ενθαλπία : Q3 = mλ. CpΛ. (TΛ2 - TA) = ,5. (TΛ2-21,1) Kcal Q4 = mν. CpΝ. (TΝ2 - TA) = (43,3-21,1) = 50,394 Kcal Από το ισοζύγιο ενέργειας προκύπτει ότι : Q3 = Q1 + Q2 - Q4 και µε αντικατάσταση αυτών έχω : ΤΛ ,5 = ,394, η οποία δίνει : ΤΛ2 = 78,95 C ή περίπου 79 C άρα Η θερµοκρασία του λαδιού στην έξοδο του εναλλάκτη θα είναι 79 C περίπου. 7
8 ΠΡΩΤΕΣ ΥΛΕΣ: ma, mb, mγ ΕΝΕΡΓΕΙΑ ΠΡΩΤΩΝ ΥΛΩΝ ΠΡΟΪΟΝΤΑ: mx, mψ. mz ΕΝΕΡΓΕΙΑ ΠΡΟΪΟΝΤΩΝ Εισερχόµενα ΜΟΝΑ Α ΕΠΕΞΕΡΓΑΣΙΑΣ παρακρατούµενη µάζα παρακρατούµενη ενέργεια Εξερχόµενα ΠΡΟΣΤΙΘΕΜΕΝΗ ΕΝΕΡΓΕΙΑ ( θερµική, µηχανική, ηλεκτρική,χηµική,κ.α ) ΑΠΟΒΛΗΤΑ: mλ, mν, mο ΑΠΩΛΕΙΕΣ ΕΝΕΡΓΕΙΑΣ ΕΝΕΡΓΕΙΑ ΑΠΟΒΛΗΤΩΝ Σχ. 1. Σχηµατική παράσταση ροής µάζας και ενέργειας γύρω από µια µονάδα επεξεργασίας 8
9 9
10 1.3. Μικτά ισοζύγια (Ισοζύγια Μάζας - Ενέργειας) Στην πράξη πολύ συχνά η επίλυση ενός ισοζυγίου ενέργειας προαπαιτεί την γνώση κάποιων στοιχείων, που προέρχονται από την επίλυση ισοζυγιών µάζας γύρο από κάποια φάση επεξεργασίας ή γύρω από την γραµµή επεξεργασίας συνολικά. Με άλλα λόγια, στις περιπτώσεις αυτές απαιτείται ταυτόχρονη επίλυση ισοζυγίων µάζας και ενέργειας. Τα ισοζύγια αυτού του τύπου είναι γνωστά σαν µικτά ισοζύγια. Στο Σχ 2.12 δίνεται η σχηµατική παράσταση της ροής µάζας και ενέργειας γύρω από µια µονάδα επεξεργασίας. ΠΑΡΑ ΕΙΓΜΑ 4. Χυµός πορτοκαλιού µε 10% στερεά, θερµοκρασία 20 C, και παροχή 15 τόνους / ώρα τροφοδοτείται προς συµπύκνωση σε µονοβάθµιο εξατµιστή, που λειτουργεί υπό κενό και επιτρέπει σηµείο βρασµού του χυµού στους 70 C. Ο παρεχόµενος υδρατµός στον εξατµιστήρα έχει απόλυτη πίεση 2,0245Κρ/cm². Αν η επιθυµητή τελική συγκέντρωση στερεών στον συµπυκνωµένο χυµό είναι 50% να υπολογιστεί η απαιτούµενη παροχή ατµού για την επεξεργασία αυτή. ίνεται: Ειδική θερµότητα αραιού χυµού : Cp1 = 0,914 Kcal / gr. C. Eιδική θερµότητα συµπ/νου χυµού: Cp2 = 0,800 kcal / gr. C. T1=20 C X1=10%στερεά m1= Kgr/hr mn ( ατµός εξατµισµένος ) ΤΝ = 70 C ma =? TA =120 C, P = 2,0245 Kp / cm² m2 =? X2 = 50 % ( υγρό συµπύκνωµα ) Τ2 = 70 C mσ = ma Σχ ιάγραµµα ροής εξατµιστή Από τον πίνακα υδρατµών (σελ. 33) βρίσκω ότι για πίεση (Ρ) 2,0245 αντιστοιχεί θερµοκρασία βρασµού = θερµοκρασία ατµού = 120 C και ότι οι ενθαλπίες των ρευµάτων είναι : ρεύµα ατµού 120 C : ΗΑ = 646,0 Kcal / Kg ρεύµα ατµού 70 C : HΝ = 627,3 Kcal / Kg ρεύµα συµπυκν. ατµού 70 C : ΗΣ = 69,93 Kcal / Kg ( νερού ) Το ισοζύγιο ενέργειας γύρω από τον εξατµιστήρα (Σχ ) δίνεται από την εξίσωση : Θερµότητα + θερµότητα = θερµότητα + θερµότητα + θερµότητα αρ. χυµού ατµού τελ. χυµού υδρατµών συµπ.ατµού 10
11 H µαθηµατική διατύπωση αυτής δίνει : m1.cp1.(t1-0) +ma. HA = m2.cp2.(t2-0) + mn. HN + mσ. ΗΣ ( 1 ) Στην εξίσωση αυτή, εκτός από το ζητούµενο ma, έχω άγνωστες τις ροές m2 και mν. Για τον υπολογισµό τους, προσδιορίζω το ισοζύγιο µάζας γύρω από τον εξατµιστήρα : m1 x1 mν ολικό ισοζύγιο : m1 = mn + m2 ή µάζας = mn + m2 ( 2 ) ισοζύγιο πάνω : m1. x1= m2. X2 ή m2 στα στερεά ,1= m2. X2 ( 3 ) x2 Από την επίλυση του συστήµατος των εξισώσεων ( 2 ) και ( 3 ) έχω : m1 = Kgr / hr πυκνού χυµού και mν = Kgr /hr παραγόµενο νερό ( υδρατµοί ). Με αντικατάσταση, των ευρεθέντων, στην εξίσωση ( 1 ) θα έχω : ,914. ( 20-0 ) + ma. 646 = ,8. ( 70-0 ) + ma. 69, ,3 όπου υπάρχει άγνωστος µόνο το ma, διότι ma = mσ, αφού είναι προφανές ότι η παροχή του συµπυκνώµατος ( υγρού ) ατµού mσ θα ισούται µε την παροχή τροφοδοσίας ατµού ma (ο ατµός προσφέρει την λανθάνουσα θερµότητα εξάτµισης που περιέχει και υγροποιείται). Από την επίλυση της παραπάνω εξίσωσης προκύπτει ότι : ma = ,8 Kgr / hr η απαιτούµενη παροχή ατµού. ΠΑΡΑ ΕΙΓΜΑ 5. Οινοποιείο διαθέτει τρεις ποιότητες κρασιών, που οι περιεκτικότητές τους δίνονται στον παρακάτω πίνακα, και θέλει να παράγει ένα τσέρυ µε 16 % αλκοόλη και 3 % σάκχαρα. Ζητείται η αναλογία τροφοδοσίας των 3 κρασιών προς τον αναµικτήρα για την παραγωγή του προϊόντος. Τύπος % αλκοόλη % σάκχαρα Κρασί Α 14,6 0,2 Κρασί Β 16,7 1,0 Κρασί Γ 17,0 12,0 ( 14,6 / 0,2 ) Κρασί Α x Kgr ( 16,7 / 1,0 ) Κρασί Β ψ Κgr ΤΣΕΡΥ 100 Kgr ΑΝΑΜΙΚΤΗΡΑΣ (16% / 3%) ( 17,0 / 12 ) Κρασί Γ Z Kgr 11
12 Σχ ιάγραµµα ροής αναµικτήρα οινοποιείου ΛΥΣΗ : Παίρνουµε σαν βάση υπολογισµού τα 100 Kgr τελικού προϊόντος. Έστω ότι για την παραγωγή αυτού απαιτούνται Χ, Υ και Ζ Kgr από τα κρασιά Α, Β, και Γ αντίστοιχα. Για την επίλυση του προβλήµατος, δηµιουργούµε σύστηµα 3 εξισώσεων : ( α ) το ολικό ισοζύγιο µάζας δίνει : Χ + Υ + Ζ = 100 ( β ) το ισοζύγιο µάζας ως προς την αλκοόλη µας δίνει : 0,146. Χ + 0,167. Υ + 0,17. Ζ = 0, ( γ ) το ισοζύγιο µάζας ως προς τα σάκχαρα είναι : 0,002. Χ + 0,01. Υ + 0,12. Ζ = 0, Επιλύνοντας το παραπάνω σύστηµα των εξισώσεων α, β, γ, έχω ότι απαιτούνται : Χ = 36,4 Kgr κρασιού Α Υ = 42,8 Kgr κρασιού Β Ζ = 20,8 Kgr κρασιού Γ Σύνολο = 100,0 Kgr µίγµα (τσέρυ ) Στα δοθέντα παραπάνω παραδείγµατα εφαρµογής των ισοζυγίων, είχαµε µόνο µια µονάδα επεξεργασίας ή µια γραµµή παραγωγής που περιείχε 2 3 µονάδες επεξεργασίας. Στις βιοµηχανίες τροφίµων όµως έχουµε συνήθως µια ολοκληρωµένη γραµµή παραγωγής ή ολόκληρο το εργοστάσιο που περιλαµβάνει πολλές επιµέρους µονάδες επεξεργασίας (βλ. Σχ και 2.16). Εδώ απαιτείται ένα ολοκληρωµένο διάγραµµα ροής, που να παριστάνει όλες τις εναλλακτικές ή παράλληλες διαδροµές της πρώτης ύλης και των ενδιάµεσων προϊόντων. Ένα τέτοιο ολοκληρωµένο διάγραµµα ροής, που παριστάνει την επεξεργασία τυρογάλακτος, δίνει το Σχ Στις περιπτώσεις αυτές, για να επιλύσουµε τα ισοζύγια, ακολουθούµε συνήθως την διαδικασία της σταδιακής εφαρµογής των ισοζυγίων γύρω από κάθε µονάδα χωριστά, µέχρι να ολοκληρωθεί η γραµµή επεξεργασίας ή το εργοστάσιο. Χαρακτηριστικό παράδειγµα αποτελεί η γραµµή επεξεργασίας σόγιας για την παραγωγή σογιέλαιου και ζωοτροφής ( Σχ. 2 ) 12
13 ΣΟΓΙΑ (σύστασης ) : 18% Λάδι 35% Πρωτεΐνη 27,1% Υδατάνθρακες 9,4% Κυτταρίνες 10,5% Υγρασία ΑΛΕΣΗ ΚΑΙ ΣΥΝΘΛΙΨΗ Ψ1 ΣΟΓΙΟΠΙΤΑ (ΜΕ 6% ΛΑ Ι) Χ1 ΛΑ Ι ΣΟΓΙΑΣ ΕΚΧΥΛΙΣΗ Χ 2 Ψ 2 ΕΞΑΝΙΟ (σ.β:65 C) ΕΚΧΥΛΙΣΜΑ (ΛΑ Ι + ΕΞΑΝΙΟ) ΥΠΟΛΕΙΜΜΑ (ΠΙΤΑ ΜΕ 0,5%ΛΑ Ι) (όλο το νερό + εξάνιο) (θέρµανση σε 3στάδια) ΞΗΡΑΝΣΗ ΞΗΡΑΝΣΗ (θέρµανση σε εναλ. θερµότ. ~90 C) Ψ3 Χ3 ΛΑ Ι ΣΟΓΙΑΣ ΝΕΡΟ ΖΩΟΤΡΟΦΗ (ΠΙΤΑ ΜΕ ΥΓΡΑΣΙΑ8%) ΕΞΑΝΙΟ 13
14 Σχ. 2. ιάγραµµα ροής ( απλοποιηµένο ) παραγωγής σογιέλαιου ΟΡΡΟΣ ( ΤΥΡΟΓΑΛΑ ) ΙΑΧΩΡΙΣΜΟΣ ΤΡΙΜΜΑΤΩΝ ΤΥΡΙ ΙΑΧΩΡΙΣΜΟΣ ΛΙΠΟΥΣ ΣΥΜΠΥΚΝΩΣΗ ΑΠΟΜΟΝΩΣΗ ΚΛΑΣΜΑΤΩΝ ΕΞΑΤΜΙΣΗ ΑΝΤΙΣΤΡΟΦΗ ΟΣΜΩΣΗ ΑΠΟΜΟΝΩΣΗ ΠΡΩΤΕΪΝΩΝ ΑΦΑΛΑΤΩΣΗ ΣΥΜΠΥΚΝΩΜΑ ΟΡΡΟΥ ΥΠΕΡ ΙΗΘΗΣΗ ΘΕΡΜΑΝΣΗ ΟΞΥΝΙΣΗ ΦΥΓΟΚΕΝΤΡΙΣΗ ΕΝΑΛΛΑΓΗ ΙΟΝΤΩΝ ΗΛΕΚΤΡΟ ΙΑ- ΛΥΣΗ ΣΥΜΠΥΚΝΩΜΑ ΥΠΕΡ ΙΗΘΗΣΗΣ ΙΗΘΗΜΑ ΥΠΕΡ ΙΗΘΗΣΗΣ ΟΡΡΟΣ ΧΩΡΙΣ ΠΡΩΤΕΪΝΕΣ ΟΥΣΙΩΣΗ ΠΡΩΤΕΪΝΙΚΟΥ ΟΡΡΟΥ ΞΗΡΑΝΣΗ ΣΥΜΠΥΚΝΩΣΗ ΣΚΟΝΗ ΟΡΡΟΥ ΤΥΡΙ ΤΥΡΙ ΠΡΩΤΕΪΝΗ (ΣΚΟΝΗ) ΑΦΑΛΑΤΩΣΗ ΠΡΩΤΕΪΝΗ ΟΡΡΟΥ ΠΑΓΩΤΑ ΠΑΙ ΙΚΕΣ ΤΡΟΦΕΣ ΖΩΟΤΡΟΦΗ ΛΑΚΤΟΖΗ-ΒΙΟΜΑΖΑ ΑΦΑΛΑΤΩΜΕΝΗ 14
15 ΟΡΡΟΥ ΚΡΕΜΑ ΟΡΡΟΥ ΙΑΤΡΙΚΑ ΠΡΟΪΟΝΤΑ ΣΚΟΝΗ ΖΩΟΤΡΟΦΗ ΤΥΡΙ Σχ. 3. ιάγραµµα ροής επεξεργασίας ορρού ( τυρογάλακτος ) ΠΑΡΑ ΕΙΓΜΑ 6. Με βάση το διάγραµµα ροής του Σχ Nα υπολογιστεί η παραγωγή τελικών προϊόντων (σογιέλαιου και σογιόπιττας για ζωοτροφή) στη γραµµή επεξεργασίας σόγιας. ΛΥΣΗ : Σαν βάση υπολογισµού λαµβάνονται τα 1000 Kgr πρώτης ύλης, δηλαδή καρπού σόγιας, του οποίου η σύσταση δίνεται στον πίνακα που συνοδεύει το διάγραµµα ροής. Εξετάζω την πρώτη µονάδα επεξεργασίας, δηλαδή την µονάδα άλεσης και σύνθλιψης : 1000 Kgr σόγιας µε 18 % λάδι ΑΛΕΣΗ ΣΥΝΘΛΙΨΗ και Χ1 Kgr λάδι Ψ1 Kgr σογιόπιττα µε 6 % λάδι Αν Χ1 Kgr το παραγόµενο σογιέλαιο, και Ψ1 Kgr η σογιόπιττα έχω : Ολικό ισοζύγιο µάζας : 1000 = Χ1 + Ψ1 Ισοζύγιο µάζας ως προς το λάδι : ,18 = Χ1. 1,0 + Ψ1. 0,06 Η επίλυση του συστήµατος µας δίνει : Χ1 = 127,7 Kgr σογιέλαιο και Ψ1 = 872,3 Kgr σογιόπιττας Ακολουθεί η εξέταση της µονάδας εκχύλισης της σογιόπιττας για την παραλαβή του υπόλοιπου λαδιού : εξάνιο ( διαλύτης ) Εκχύλισµα : Χ2 Kgr λάδι στo εξάνιο 872,3 Kgr σογιόπιττα. ΕΚΧΥΛΙΣΗ µε 6 % λάδι Υπόλειµµα: Ψ2 Kgr σογιόπιττα µε 0,5 % λάδι Ο διαλύτης εξάνιο, για απλούστευση των υπολογισµών, δεν λαµβάνεται υπόψη στο ισοζύγιο µάζας, δεδοµένου ότι ανακυκλώνεται και δεν περιλαµβάνεται στα τελικά προϊόντα της γραµµής επεξεργασίας, όπως φαίνεται και στο ολοκληρωµένο διάγραµµα ροής. Έτσι λαµβάνουµε σαν Χ2 τα Kgr του σογιέλαιου που παραλήφθηκαν από την πίττα και είναι διαλυµένα στο εξάνιο (εκχύλισµα) και Ψ2 τα Kgr του υπολείµµατος (µε περιεκτικότητα 0,5% σε λάδι) της εκχυλισθείσας πίττας, χωρίς την ποσότητα του εξανίου που έχει συγκρατήσει κατά την εκχύλιση. 15
16 Εφαρµόζω τα ισοζύγια µάζας στη µονάδα της εκχύλισης : Χ2 = 48,3 Kgr του σογιέλαιου διαλυµένα στο εξάνιο Ψ2 = 824 Kgr σογιόπιττα µε 0,5 % λάδι χωρίς το εξάνιο Κατόπιν εξετάζουµε την µονάδα ξήρανσης της σογιόπιττας : Εξάνιο Σογιόπιττα 824 Kgr ( υπόλειµµα εκχύλισης ΞΗΡΑΝΣΗ Υγρασία ( Η2Ο ) Ψ3 Kgr χωρίς το εξάνιο ) Πίττα µε 8% νερό Χ3 Kgr Στη εφαρµογή του ισοζυγίου µάζας δεν περιλαµβάνεται και πάλι το εξάνιο, όπως και προηγουµένως. Εξ άλλου υποθέτουµε, ότι όλο το νερό που περιείχε αρχικά η σόγια (πρώτη ύλη), περιέχεται τώρα σαν υγρασία στη σογιόπιττα (υπόλειµµα εκχύλισης). Έτσι θα έχουµε : Ολικό ισοζύγιο µάζας (χωρίς το εξάνιο ) : 842 = Χ3 + Ψ3 Ισοζύγιο µάζας ως προς το νερό : ,105 = Χ3.0,08 + Ψ3. 1,0 Η επίλυση του συστήµατος δίνει : Χ3 = 42,5 Kgr νερού και Ψ3 = 781,5 Kgr πίττας ( ζωοτροφή ) Άρα 1000 Kgr καρπού σόγιας δίνουν σαν τελικά προϊόντα : Σογιέλαιο = 127,7 + 48,3 = 176 Kgr Ζωοτροφή ( πίττα µε 8% υγρασία ) = 781,5 Kgr 16
17 17
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ. Προσδιορισµός ισοζυγίων µάζας
 ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ Προσδιορισµός ισοζυγίων µάζας Κατά τον προσδιορισµό των ισοζυγίων µάζας γίνεται εφαρµογή του νόµου διατήρησης της µάζας στην επίλυση προβληµάτων που αναφέρονται:
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ Προσδιορισµός ισοζυγίων µάζας Κατά τον προσδιορισµό των ισοζυγίων µάζας γίνεται εφαρµογή του νόµου διατήρησης της µάζας στην επίλυση προβληµάτων που αναφέρονται:
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ. Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για:
 ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για: Πληροφορίες για τις απαιτήσεις σε υλικά και πρώτες ύλες Πληροφορίες για τον όγκο παραγωγής Πληροφορίες
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΚΑΙ ΕΝΕΡΓΕΙΑΣ Στην βιομηχανία τροφίμων προκύπτουν ερωτήματα για: Πληροφορίες για τις απαιτήσεις σε υλικά και πρώτες ύλες Πληροφορίες για τον όγκο παραγωγής Πληροφορίες
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα : Εξάτμιση (2/2), 2ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Ισοζύγια μάζας
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα : Εξάτμιση (2/2), 2ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Ισοζύγια μάζας
Ειδική Ενθαλπία, Ειδική Θερµότητα και Ειδικός Όγκος Υγρού Αέρα
 θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
θερµοκρασία που αντιπροσωπεύει την θερµοκρασία υγρού βολβού. Το ποσοστό κορεσµού υπολογίζεται από την καµπύλη του σταθερού ποσοστού κορεσµού που διέρχεται από το συγκεκριµένο σηµείο. Η απόλυτη υγρασία
Πολυβάθµιοι Συµπυκνωτές
 Ο ατµός συµπυκνώνεται από το νερό το οποίο θερµαίνεται, ενώ ο αέρας διαφεύγει από την κορυφή του ψυκτήρα και απάγεται από την αντλία κενού µε την οποία επικοινωνεί ο ψυκτήρας. Το θερµό νερό που προκύπτει
Ο ατµός συµπυκνώνεται από το νερό το οποίο θερµαίνεται, ενώ ο αέρας διαφεύγει από την κορυφή του ψυκτήρα και απάγεται από την αντλία κενού µε την οποία επικοινωνεί ο ψυκτήρας. Το θερµό νερό που προκύπτει
Ισοζύγια Μάζας. 1. Eισαγωγή
 Ισοζύγια Μάζας 1. Eισαγωγή Οποιαδήποτε χηµική διεργασία όπου υπάρχουν αλληλεπιδράσεις µεταξύ δύο ή περισσότερων υλικών µπορεί να αναλυθεί µε βάση τα ισοζύγια υλικών. Γενικά, υπάρχουν δύο διαφορετικές περιπτώσεις
Ισοζύγια Μάζας 1. Eισαγωγή Οποιαδήποτε χηµική διεργασία όπου υπάρχουν αλληλεπιδράσεις µεταξύ δύο ή περισσότερων υλικών µπορεί να αναλυθεί µε βάση τα ισοζύγια υλικών. Γενικά, υπάρχουν δύο διαφορετικές περιπτώσεις
10 Ισοζύγια Μάζας & Ενέργειας
 10 Ισοζύγια Μάζας & Ενέργειας Ένα ισοζύγιο μάζας (ή υλικού) στηρίζεται στην αρχή διατήρηση της μάζας, που λέει ότι η μάζα δε δημιουργείται ούτε καταστρέφεται, αλλά μόνο αλλάζει μορφή ή φάση, Η ανάλυση
10 Ισοζύγια Μάζας & Ενέργειας Ένα ισοζύγιο μάζας (ή υλικού) στηρίζεται στην αρχή διατήρηση της μάζας, που λέει ότι η μάζα δε δημιουργείται ούτε καταστρέφεται, αλλά μόνο αλλάζει μορφή ή φάση, Η ανάλυση
Ε. Παυλάτου, 2017 ΔΙΕΡΓΑΣΙΕΣ
 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ 2 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία) και εξερχόμενα ρεύματα (προϊόντα) Διάγραμμα
ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ 2 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία) και εξερχόμενα ρεύματα (προϊόντα) Διάγραμμα
M V n. nm V. M v. M v T P P S V P = = + = σταθερή σε παραγώγιση, τον ορισµό του συντελεστή διαστολής α = 1, κυκλική εναλλαγή 3
 Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος εκεµβρίου 04- (//04. ίνονται οι ακόλουθες πληροφορίες για τον διθειάνθρακα (CS. Γραµµοµοριακή µάζα 76.4 g/mol, κανονικό σηµείο ζέσεως 46 C, κανονικό
Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος εκεµβρίου 04- (//04. ίνονται οι ακόλουθες πληροφορίες για τον διθειάνθρακα (CS. Γραµµοµοριακή µάζα 76.4 g/mol, κανονικό σηµείο ζέσεως 46 C, κανονικό
ΕΞΑΤΜΙΣΗ Θοδωρής Καραπάντσιος
 ΕΞ ΕΞΑΤΜΙΣΗ Θοδωρής Καραπάντσιος ΕΞ.1 Εισαγωγή Αντικείµενο της συµπύκνωσης είναι κατά κύριο λόγο η αποµάκρυνση νερού, µε εξάτµιση, από ένα υδατικό διάλυµα που περιέχει µια ή περισσότερες διαλυµένες ουσίες,
ΕΞ ΕΞΑΤΜΙΣΗ Θοδωρής Καραπάντσιος ΕΞ.1 Εισαγωγή Αντικείµενο της συµπύκνωσης είναι κατά κύριο λόγο η αποµάκρυνση νερού, µε εξάτµιση, από ένα υδατικό διάλυµα που περιέχει µια ή περισσότερες διαλυµένες ουσίες,
ΤΡΟΠΟΙ ΕΚΦΡΑΣΗΣ ΤΗΣ ΠΕΡΙΕΚΤΙΚΟΤΗΤΑΣ
 ΜΕΘΟ ΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΣΤΑ ΙΑΛΥΜΑΤΑ ιάλυµα ονοµάζουµε το οµογενές µίγµα δύο ή περισσοτέρων ουσιών. Στο Γυµνάσιο εξετάζουµε µόνο τα διαλύµατα εκείνα που αποτελούνται από δύο ουσίες. Η µία
ΜΕΘΟ ΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΣΤΑ ΙΑΛΥΜΑΤΑ ιάλυµα ονοµάζουµε το οµογενές µίγµα δύο ή περισσοτέρων ουσιών. Στο Γυµνάσιο εξετάζουµε µόνο τα διαλύµατα εκείνα που αποτελούνται από δύο ουσίες. Η µία
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης
 ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
ΠΡΟΒΛΗΜΑΤΑ Υ/Υ ΕΚΧΥΛΙΣΗΣ Κ. Μάτης Πρόβληµα 36. Μια υγρή τροφοδοσία 3,5 kg/s, που περιέχει µια διαλυτή ουσία Β διαλυµένη σε συστατικό Α, πρόκειται να διεργαστεί µε ένα διαλύτη S σε µια µονάδα επαφής καθ
ΕΦΑΡΜΟΓΗ ΕΠΕΞΕΡΓΑΣΙΑ ΤΥΡΟΓΑΛΟΥ ΜΕ ΕΞΑΤΜΙΣΗ ΥΠΟ ΚΕΝΟ
 ΕΦΑΡΜΟΓΗ ΕΠΕΞΕΡΓΑΣΙΑ ΤΥΡΟΓΑΛΟΥ ΜΕ ΕΞΑΤΜΙΣΗ ΥΠΟ ΚΕΝΟ Πηγή: Mr.Εmilio Turchi - VEOLIA WS & T Italia Επιµέλεια: Κων/νος I. Νάκος SHIELCO LTD SHIELCO Τεχνολογίες Περιβάλλοντος ΕΠΕ Σελίδα 1/5 1. Εισαγωγή Ανάλογα
ΕΦΑΡΜΟΓΗ ΕΠΕΞΕΡΓΑΣΙΑ ΤΥΡΟΓΑΛΟΥ ΜΕ ΕΞΑΤΜΙΣΗ ΥΠΟ ΚΕΝΟ Πηγή: Mr.Εmilio Turchi - VEOLIA WS & T Italia Επιµέλεια: Κων/νος I. Νάκος SHIELCO LTD SHIELCO Τεχνολογίες Περιβάλλοντος ΕΠΕ Σελίδα 1/5 1. Εισαγωγή Ανάλογα
ΠΑΡΑ ΕΙΓΜΑ ΚΥΚΛΟΥ RANKINE
 ΠΑΡΑ ΕΙΓΜΑ ΚΥΚΛΟΥ RANKINE Σε ένα κύκλο RANKINE, το σύστηµα ( kg) εισέρχεται στο στρόβιλο σε κατάσταση υπέρθερµου ατµού σε πίεση 0 bar και θερµοκρασία 00 0 C, η δε πίεση στο συµπυκνωτή είναι 0,0 bar Να
ΠΑΡΑ ΕΙΓΜΑ ΚΥΚΛΟΥ RANKINE Σε ένα κύκλο RANKINE, το σύστηµα ( kg) εισέρχεται στο στρόβιλο σε κατάσταση υπέρθερµου ατµού σε πίεση 0 bar και θερµοκρασία 00 0 C, η δε πίεση στο συµπυκνωτή είναι 0,0 bar Να
Η χρήση ατμού είναι ευρέως διαδεδομένη σχεδόν σε όλη την βιομηχανία. Ο ατμός
 Η χρήση ατμού είναι ευρέως διαδεδομένη σχεδόν σε όλη την βιομηχανία. Ο ατμός μεταφέρει μεγάλη ποσότητα ενέργειας με την μορφή θερμότητας και χρησιμοποιείται στην παραγωγική διαδικασία για την επιτάχυνση
Η χρήση ατμού είναι ευρέως διαδεδομένη σχεδόν σε όλη την βιομηχανία. Ο ατμός μεταφέρει μεγάλη ποσότητα ενέργειας με την μορφή θερμότητας και χρησιμοποιείται στην παραγωγική διαδικασία για την επιτάχυνση
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ & ΕΝΕΡΓΕΙΑΣ
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ & ΕΝΕΡΓΕΙΑΣ Ένα ισοζύγιο μάζας (ή υλικού) στηρίζεται στην αρχή διατήρηση της μάζας, που λέει ότι η μάζα δε δημιουργείται ούτε καταστρέφεται, αλλά μόνο αλλάζει μορφή ή
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ & ΕΝΕΡΓΕΙΑΣ Ένα ισοζύγιο μάζας (ή υλικού) στηρίζεται στην αρχή διατήρηση της μάζας, που λέει ότι η μάζα δε δημιουργείται ούτε καταστρέφεται, αλλά μόνο αλλάζει μορφή ή
ΠΡΟΒΛΗΜΑΤΑ ΕΚΠΛΥΣΗΣ. Πρόβληµα 30. Η καυστική σόδα παράγεται µε την επεξεργασία ενός διαλύµατος ανθρακικού νατρίου σε νερό (25 kg/s Na 2
 ΠΡΟΒΛΗΜΑΤΑ ΕΚΠΛΥΣΗΣ Πρόβληµα 30. Η καυστική σόδα παράγεται µε την επεξεργασία ενός διαλύµατος ανθρακικού νατρίου σε νερό (25 kg/s Na 2 CO 3 ) µε τη θεωρητική απαίτηση σε υδροξείδιο του ασβεστίου. Αφού
ΠΡΟΒΛΗΜΑΤΑ ΕΚΠΛΥΣΗΣ Πρόβληµα 30. Η καυστική σόδα παράγεται µε την επεξεργασία ενός διαλύµατος ανθρακικού νατρίου σε νερό (25 kg/s Na 2 CO 3 ) µε τη θεωρητική απαίτηση σε υδροξείδιο του ασβεστίου. Αφού
Μηχανική Τροφίµων. Θερµικές Ιδιότητες Τροφίµων. Η έννοια του «τροφίµου»
 Μηχανική Τροφίµων Θερµικές Ιδιότητες Τροφίµων Η έννοια του «τροφίµου» Στην µηχανική τροφίµων πολλές φορές χρησιµοποιούµε τον όρο τρόφιµο. Σε αντίθεση όµως µε άλλα επιστηµονικά πεδία της επιστήµης των τροφίµων,
Μηχανική Τροφίµων Θερµικές Ιδιότητες Τροφίµων Η έννοια του «τροφίµου» Στην µηχανική τροφίµων πολλές φορές χρησιµοποιούµε τον όρο τρόφιµο. Σε αντίθεση όµως µε άλλα επιστηµονικά πεδία της επιστήµης των τροφίµων,
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ
 ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
ΙΣΟΡΡΟΠΙΑ ΦΑΣΕΩΝ ΚΑΙ ΤΑΣΗ ΑΤΜΩΝ 2 Διεργασίες Πολυφασικών συστημάτων Πολλές διεργασίες στη Χημική Μηχανική στηρίζονται στη μεταφορά μάζας μεταξύ διαφορετικών φάσεων (αέρια, υγρή, στερεή) Εξάτμιση-Εξάχνωση
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής. Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά)
 ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΒΙΟΜΗΧΑΝΙΚΗ ΑΠΟΣΤΑΚΤΙΚΗ ΣΤΗΛΗ : Ερωτήσεις πολλαπλής επιλογής (Σηµείωση: Σκεφθείτε και δικαιολογήσετε τη σωστή απάντηση κάθε φορά) Η απόσταξη στηρίζεται στη διαφορά που υπάρχει στη σύσταση ισορροπίας των
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ. Περιεχόµενο & Χρησιµότητα. Στα πολλά ΜΑΘΗΜΑΤΙΚΑ! Καλώς ήλθατε. της ΜΗΧΑΝΙΚΗΣ ΤΡΟΦΙΜΩΝ! Έχετε κάποια ερώτηση?
 ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ Περιεχόµενο & Χρησιµότητα Καλώς ήλθατε στο µάθηµα της ΜΗΧΑΝΙΚΗΣ ΤΡΟΦΙΜΩΝ! Έχετε κάποια ερώτηση? ΝΑΙ..ΝΑΙ...ΝΑΙ.!! Σε τι διαφέρει από τα άλλα µαθήµατα της κατεύθυνσης??? Στα πολλά ΜΑΘΗΜΑΤΙΚΑ!
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ Περιεχόµενο & Χρησιµότητα Καλώς ήλθατε στο µάθηµα της ΜΗΧΑΝΙΚΗΣ ΤΡΟΦΙΜΩΝ! Έχετε κάποια ερώτηση? ΝΑΙ..ΝΑΙ...ΝΑΙ.!! Σε τι διαφέρει από τα άλλα µαθήµατα της κατεύθυνσης??? Στα πολλά ΜΑΘΗΜΑΤΙΚΑ!
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Liquid Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Περιοχές
Παραδείγµατα ροής ρευστών (Moody κλπ.)
 Παραδείγµατα ροής ρευστών (Mooy κλπ.) 005-006 Παράδειγµα 1. Να υπολογισθεί η πτώση πίεσης σε ένα σωλήνα από χάλυβα του εµπορίου µήκους 30.8 m, µε εσωτερική διάµετρο 0.056 m και τραχύτητα του σωλήνα ε 0.00005
Παραδείγµατα ροής ρευστών (Mooy κλπ.) 005-006 Παράδειγµα 1. Να υπολογισθεί η πτώση πίεσης σε ένα σωλήνα από χάλυβα του εµπορίου µήκους 30.8 m, µε εσωτερική διάµετρο 0.056 m και τραχύτητα του σωλήνα ε 0.00005
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού
 5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
5.3 Υπολογισμοί ισορροπίας φάσεων υγρού-υγρού Η αρχική εξίσωση που χρησιμοποιείται για τους υπολογισμούς της ΙΦΥΥ είναι η ικανοποίηση της βασικής θερμοδυναμικής απαίτησης της ισότητας των τάσεων διαφυγής
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2015-2016 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ ΜΟΝΑΔΕΣ ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 3 ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 4 ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 5 Επιφάνεια
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2015-2016 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ ΜΟΝΑΔΕΣ ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 3 ΒΑΣΙΚΕΣ ΚΑΙ ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 4 ΠΑΡΑΓΟΜΕΝΕΣ ΔΙΑΣΤΑΣΕΙΣ 5 Επιφάνεια
ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΙΑΧΕΙΡΙΣΗΣ ΕΝΕΡΓΕΙΑΚΩΝ ΠΟΡΩΝ ΘΕΡΜΟ ΥΝΑΜΙΚΗ Ι 1
 ΘΕΡΜΟ ΥΝΑΜΙΚΗ Ι ιδάσκων: Καθ. Α.Γ.Τοµπουλίδης ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΙΑΧΕΙΡΙΣΗΣ ΕΝΕΡΓΕΙΑΚΩΝ ΠΟΡΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ, ΚΟΖΑΝΗ Εαρινό εξάµηνο 2003-2004 Άσκηση 1: Κυλινδρικό έµβολο περιέχει αέριο το
ΘΕΡΜΟ ΥΝΑΜΙΚΗ Ι ιδάσκων: Καθ. Α.Γ.Τοµπουλίδης ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΙΑΧΕΙΡΙΣΗΣ ΕΝΕΡΓΕΙΑΚΩΝ ΠΟΡΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΥΤΙΚΗΣ ΜΑΚΕ ΟΝΙΑΣ, ΚΟΖΑΝΗ Εαρινό εξάµηνο 2003-2004 Άσκηση 1: Κυλινδρικό έµβολο περιέχει αέριο το
Enrico Fermi, Thermodynamics, 1937
 I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
I. Θερµοδυναµικά συστήµατα Enrico Feri, herodynaics, 97. Ένα σώµα διαστέλλεται από αρχικό όγκο. L σε τελικό όγκο 4. L υπό πίεση.4 at. Να υπολογισθεί το έργο που παράγεται. W - -.4 at 5 a at - (4..) - -
1 Aπώλειες θερμότητας - Μονωτικά
 1 Aπώλειες θερμότητας - Μονωτικά 1.1 Εισαγωγή Όταν ένα ρευστό ρέει μέσα σ' έναν αγωγό και η θερμοκρασία του διαφέρει από τη θερμοκρασία του περιβάλλοντος, τότε μεταδίδεται θερμότητα: από το ρευστό προς
1 Aπώλειες θερμότητας - Μονωτικά 1.1 Εισαγωγή Όταν ένα ρευστό ρέει μέσα σ' έναν αγωγό και η θερμοκρασία του διαφέρει από τη θερμοκρασία του περιβάλλοντος, τότε μεταδίδεται θερμότητα: από το ρευστό προς
(α) (β) (γ) ή (δ) gallons/h? ΙΣΟΖΥΓΙΟ ΑΙΜΟΚΑΘΑΡΣΗΣ ΝΕΦΡΟΠΑΘΩΝ
 Πρόβλημα Α. O δευτερογενής καθαρισμός των αστικών υγρών αποβλήτων αποτελείται από δυο συνεχόμενα τμήματα, του αερισμού και της διαύγασης (κατακάθισης). Τη χώνευση / αφομοίωση επιβλαβών ουσιών από το ρεύμα
Πρόβλημα Α. O δευτερογενής καθαρισμός των αστικών υγρών αποβλήτων αποτελείται από δυο συνεχόμενα τμήματα, του αερισμού και της διαύγασης (κατακάθισης). Τη χώνευση / αφομοίωση επιβλαβών ουσιών από το ρεύμα
ΕΦΑΡΜΟΓΗ ΜΟΝΑ Α ΑΝΑΚΥΚΛΩΣΗΣ ΝΕΡΟΥ ΚΑΙ ΜΗ ΕΝΙΚΗΣ ΑΠΟΡΡΙΨΗΣ ΥΓΡΩΝ ΑΠΟΒΛΗΤΩΝ
 ΕΦΑΡΜΟΓΗ ΜΟΝΑ Α ΑΝΑΚΥΚΛΩΣΗΣ ΝΕΡΟΥ ΚΑΙ ΜΗ ΕΝΙΚΗΣ ΑΠΟΡΡΙΨΗΣ ΥΓΡΩΝ ΑΠΟΒΛΗΤΩΝ Πηγή: Mr.Matteo Villa HAR srl. Επιµέλεια: Κων/νος I. Νάκος SHIELCO Ltd Σελίδα 1/5 O οίκος HAR srl, Ιταλίας εξειδικεύεται στον σχεδιασµό
ΕΦΑΡΜΟΓΗ ΜΟΝΑ Α ΑΝΑΚΥΚΛΩΣΗΣ ΝΕΡΟΥ ΚΑΙ ΜΗ ΕΝΙΚΗΣ ΑΠΟΡΡΙΨΗΣ ΥΓΡΩΝ ΑΠΟΒΛΗΤΩΝ Πηγή: Mr.Matteo Villa HAR srl. Επιµέλεια: Κων/νος I. Νάκος SHIELCO Ltd Σελίδα 1/5 O οίκος HAR srl, Ιταλίας εξειδικεύεται στον σχεδιασµό
ΕΠΕΞΕΡΓΑΣΙΑ ΤΡΟΦΙΜΩΝ
 ΕΠΕΞΕΡΓΑΣΙΑ ΤΡΟΦΙΜΩΝ Συμπύκνωση Τι είναι η συμπύκνωση Είναι η διαδικασία με την οποία απομακρύνουμε μέρος της υγρασίας του τροφίμου, αφήνοντας όμως αρκετή ώστε αυτό να παραμένει ρευστό (> 20-30%). Εφαρμόζεται
ΕΠΕΞΕΡΓΑΣΙΑ ΤΡΟΦΙΜΩΝ Συμπύκνωση Τι είναι η συμπύκνωση Είναι η διαδικασία με την οποία απομακρύνουμε μέρος της υγρασίας του τροφίμου, αφήνοντας όμως αρκετή ώστε αυτό να παραμένει ρευστό (> 20-30%). Εφαρμόζεται
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ
 ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ Στη χημική μηχανική έχουμε να κάνουμε με διεργασίες. Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική). Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα
ΔΙΕΡΓΑΣΙΕΣ ΔΙΑΓΡΑΜΜΑ ΡΟΗΣ Στη χημική μηχανική έχουμε να κάνουμε με διεργασίες. Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική). Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα
Αναερόβιες Μονάδες για την παραγωγή βιο-αερίου από βιοµάζα
 Αναερόβιες Μονάδες για την παραγωγή βιο-αερίου από βιοµάζα Βιο-αέριο? Το αέριο που παράγεται από την ζύµωση των οργανικών, ζωικών και φυτικών υπολειµµάτων και το οποίο µπορεί να χρησιµοποιηθεί για την
Αναερόβιες Μονάδες για την παραγωγή βιο-αερίου από βιοµάζα Βιο-αέριο? Το αέριο που παράγεται από την ζύµωση των οργανικών, ζωικών και φυτικών υπολειµµάτων και το οποίο µπορεί να χρησιµοποιηθεί για την
Περιεκτικότητα διαλύματος ονομάζουμε την ποσότητα της διαλυμένης ουσίας που περιέχεται σε ορισμένη μάζα ή όγκο διαλύματος.
 Διαλύματα Περιεκτικότητες 11 Αν ο καθηγητής Χημείας έδινε στους μαθητές του τη δυνατότητα να παρασκευάσουν στο Εργαστήριο Χημείας, ο καθένας χωριστά, ένα υδατικό διάλυμα ζάχαρης, είναι προφανές ότι το
Διαλύματα Περιεκτικότητες 11 Αν ο καθηγητής Χημείας έδινε στους μαθητές του τη δυνατότητα να παρασκευάσουν στο Εργαστήριο Χημείας, ο καθένας χωριστά, ένα υδατικό διάλυμα ζάχαρης, είναι προφανές ότι το
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 2: Ψυχομετρία, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Υπολογισμός των
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 2: Ψυχομετρία, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Υπολογισμός των
ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ
 ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ 1. Πώς ορίζεται η περίσσεια αέρα και η ισχύς μίγματος σε μία καύση; 2. Σε ποιές περιπτώσεις παρατηρείται μή μόνιμη μετάδοση της θερμότητας; 3. Τί είναι η αντλία
ΥΠΟΔΕΙΓΜΑ ΘΕΩΡΗΤΙΚΩΝ ΕΡΩΤΗΣΕΩΝ ΕΞΕΤΑΣΕΩΝ 1. Πώς ορίζεται η περίσσεια αέρα και η ισχύς μίγματος σε μία καύση; 2. Σε ποιές περιπτώσεις παρατηρείται μή μόνιμη μετάδοση της θερμότητας; 3. Τί είναι η αντλία
ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ
 . ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
. ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΧΗΜΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΠΟΛΥΦΑΣΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΩΤΗΡΗΣ ΤΣΙΒΙΛΗΣ, Καθ. ΕΜΠ 135 ΔΙΑΓΡΑΜΜΑΤΑ ΦΑΣΕΩΝ 1 2 3 4 1 στερεό (solid) 2 υγρό (liquid) 3 ατμός (vapor) 4 αέριο (gas) A 1+2+3
Υπολογισµοί του Χρόνου Ξήρανσης
 Η πραγµατική επιφάνεια ξήρανσης είναι διασπαρµένη και ασυνεχής και ο µηχανισµός από τον οποίο ελέγχεται ο ρυθµός ξήρανσης συνίσταται στην διάχυση της θερµότητας και της µάζας µέσα από το πορώδες στερεό.
Η πραγµατική επιφάνεια ξήρανσης είναι διασπαρµένη και ασυνεχής και ο µηχανισµός από τον οποίο ελέγχεται ο ρυθµός ξήρανσης συνίσταται στην διάχυση της θερµότητας και της µάζας µέσα από το πορώδες στερεό.
2 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ
 ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 2 ΣΗΜΑΝΤΙΚΟΙ ΟΡΟΙ Αδιαβατικό σύστημα Ισοβαρές σύστημα Ισόχωρο σύστημα Ισοθερμοκρασιακό σύστημα Μεταβλητή διαδρομής (συνάρτηση μετάβασης) Καταστατική μεταβολή (σημειακή
ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ 2 ΣΗΜΑΝΤΙΚΟΙ ΟΡΟΙ Αδιαβατικό σύστημα Ισοβαρές σύστημα Ισόχωρο σύστημα Ισοθερμοκρασιακό σύστημα Μεταβλητή διαδρομής (συνάρτηση μετάβασης) Καταστατική μεταβολή (σημειακή
1bar. bar; = = y2. mol. mol. mol. P (bar)
 Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος Σεπτεµβρίου -3 (7//4). Σηµειώστε µέσα στην παρένθεση δίπλα σε κάθε µέγεθος αν είναι εντατικό (Ν) ή εκτατικό (Κ): όγκος (Κ), θερµοκρασία (Ν), πυκνότητα
Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξέταση: Περίοδος Σεπτεµβρίου -3 (7//4). Σηµειώστε µέσα στην παρένθεση δίπλα σε κάθε µέγεθος αν είναι εντατικό (Ν) ή εκτατικό (Κ): όγκος (Κ), θερµοκρασία (Ν), πυκνότητα
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ. Μεταφορά θερµότητας Εναλλάκτες θερµότητας
 ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ Μεταφορά θερµότητας Εναλλάκτες θερµότητας Μεταφορά θερµότητας Για την θέρµανση ενός σώµατος (γενικότερα) ή ενός τροφίµου (ειδικότερα) απαιτείται µεταφορά θερµότητας από ένα θερµαντικό
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ Μεταφορά θερµότητας Εναλλάκτες θερµότητας Μεταφορά θερµότητας Για την θέρµανση ενός σώµατος (γενικότερα) ή ενός τροφίµου (ειδικότερα) απαιτείται µεταφορά θερµότητας από ένα θερµαντικό
ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ
 ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ 1. Να υπολογιστεί η μαζική παροχή του ατμού σε (kg/h) που χρησιμοποιείται σε ένα θερμαντήρα χυμού με τα παρακάτω στοιχεία: αρχική θερμοκρασία χυμού 20 C, τελική θερμοκρασία
ΥΠΟΔΕΙΓΜΑ ΑΣΚΗΣΕΩΝ ΓΡΑΠΤΩΝ ΕΞΕΤΑΣΕΩΝ 1. Να υπολογιστεί η μαζική παροχή του ατμού σε (kg/h) που χρησιμοποιείται σε ένα θερμαντήρα χυμού με τα παρακάτω στοιχεία: αρχική θερμοκρασία χυμού 20 C, τελική θερμοκρασία
Εξάτµιση. Ο Εξατµιστήρας
 Εξάτµιση Ορισµός Στη βιοµηχανία τροφίµων, η εξάτµιση αναφέρεται στη φυσική διεργασία η οποία συνίσταται στην αποµάκρυνση του νερού ενός υγρού τροφίµου έτσι ώστε να ληφθεί ένα υγρό τρόφιµο µε υψηλότερη
Εξάτµιση Ορισµός Στη βιοµηχανία τροφίµων, η εξάτµιση αναφέρεται στη φυσική διεργασία η οποία συνίσταται στην αποµάκρυνση του νερού ενός υγρού τροφίµου έτσι ώστε να ληφθεί ένα υγρό τρόφιµο µε υψηλότερη
Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί:
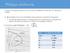 Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Ψύξη με εκτόνωση Η ψύξη ενός αερίου ρεύματος είναι δυνατή με αδιαβατική εκτόνωση του. Μπορεί να συμβεί: A. Mε ελεύθερη εκτόνωση σε βαλβίδα στραγγαλισμού: ισενθαλπική διεργασία σε χαμηλές θερμοκρασίες,
Χημεία Α Λυκείου. Διαλύματα
 Διαλύματα Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων ουσιών, οι οποίες αποούν τα συστατικά του διαλύματος. Από τα συστατικά αυτά, εκείνο που έχει την ίδια φυσική κατάσταση με αυτή του διαλύματος
Διαλύματα Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων ουσιών, οι οποίες αποούν τα συστατικά του διαλύματος. Από τα συστατικά αυτά, εκείνο που έχει την ίδια φυσική κατάσταση με αυτή του διαλύματος
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 8: Εκχύλιση, 1ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Τύποι εκχύλισης
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου (21/6/2017)
 Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Τμήμα Χημείας Μάθημα: Φυσικοχημεία Ι Εξέταση: Περίοδος Ιουνίου -7 (//7). Δίνεται η θεμελιώδης εξίσωση για την εσωτερική ενέργεια ενός συστήματος ενός συστατικού όπου κατάλληλη σταθερά. Να προσδιορίσετε
Για την επίλυση αυτής της άσκησης, αλλά και όλων των παρόμοιων χρησιμοποιούμε ιδιότητες των αναλογιών (χιαστί)
 ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΔΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυμάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούμε ή
ΜΕΘΟΔΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΔΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυμάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούμε ή
Προβλήματα εκχύλισης
 Προβλήματα εκχύλισης Πηγή: Μαρίνου-Κουρή, Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, εκδ. Παπασωτηρίου, Αθήνα, 1994 1. Εκχύλιση ακετόνης από νερό με χλωροβενζόλιο σε μονοβάθμιο εκχυλιστήρα. 100 kg διαλύματος
Προβλήματα εκχύλισης Πηγή: Μαρίνου-Κουρή, Παρλιάρου-Τσάμη, Ασκήσεις Φυσικών Διεργασιών, εκδ. Παπασωτηρίου, Αθήνα, 1994 1. Εκχύλιση ακετόνης από νερό με χλωροβενζόλιο σε μονοβάθμιο εκχυλιστήρα. 100 kg διαλύματος
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης
 ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
ΕΦΑΡΜΟΓΕΣ ΑΠΟΡΡΟΦΗΣΗΣ ΑΕΡΙΩΝ Κ. Μάτης Πρόβληµα 1. Ένα µίγµα αερίων που περιέχει 65% του Α, 5% Β, 8% C και % D βρίσκεται σε ισορροπία µ' ένα υγρό στους 350 Κ και 300 kn/m. Αν η τάση ατµών των καθαρών συστατικών
ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ. (χωρίς αντίδραση)
 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ (χωρίς αντίδραση) 2 Ε. Παυλάτου, 2017 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία)
ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ (χωρίς αντίδραση) 2 Ε. Παυλάτου, 2017 ΔΙΕΡΓΑΣΙΕΣ Διεργασία: περιγράφει μετατροπή της ύλης (φυσική ή χημική ή βιολογική) Στις διεργασίες περιγράφονται τα εισερχόμενα ρεύματα (τροφοδοσία)
2 ln P. AS H = n H S P P0 V T. nt A nt P nt P P P. nt P. AS ln P 7 R.
 Τµήµα Φαρµακευτικής Μάθηµα: Φυσικοχηµεία Εξετάσεις: Περίοδος Ιουνίου - (.6.). Αν η εξίσωση A, όπου Α και σταθερές, είναι θεµειώδης εξίσωση ενός συστήµατος, V να υποογισθούν οι καταστατικές εξισώσεις του
Τµήµα Φαρµακευτικής Μάθηµα: Φυσικοχηµεία Εξετάσεις: Περίοδος Ιουνίου - (.6.). Αν η εξίσωση A, όπου Α και σταθερές, είναι θεµειώδης εξίσωση ενός συστήµατος, V να υποογισθούν οι καταστατικές εξισώσεις του
ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΨΥΞΗΣ ΜΕ ΑΠΟΡΡΟΦΗΣΗ
 ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΨΥΞΗΣ ΜΕ ΑΠΟΡΡΟΦΗΣΗ Ψύξη µε Απορρόφηση (Absorption). Η µέθοδος αυτή σε αντίθεση µε τις κλασσικές ψυκτικές διατάξεις µηχανικής συµπίεσης χρησιµοποιεί δυο εργαζόµενα σώµατα. Αυτά είναι το
ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ ΨΥΞΗΣ ΜΕ ΑΠΟΡΡΟΦΗΣΗ Ψύξη µε Απορρόφηση (Absorption). Η µέθοδος αυτή σε αντίθεση µε τις κλασσικές ψυκτικές διατάξεις µηχανικής συµπίεσης χρησιµοποιεί δυο εργαζόµενα σώµατα. Αυτά είναι το
ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ
 Άσκηση 16 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Σε μια βιομηχανικ εγκατάσταση ένα ρεύμα υγρού πρέπει να θερμανθεί από τους 25 C στους 75 C ( περ = 25 C). Να εξεταστούν οι εξς εναλλακτικές λύσεις: (α) Η θέρμανση
Άσκηση 16 ΠΑΝΕΠΙΣΤΗΜΙΟ ΔΥΤΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ Σε μια βιομηχανικ εγκατάσταση ένα ρεύμα υγρού πρέπει να θερμανθεί από τους 25 C στους 75 C ( περ = 25 C). Να εξεταστούν οι εξς εναλλακτικές λύσεις: (α) Η θέρμανση
Βασικές Διεργασίες Μηχανικής Τροφίμων
 Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 1: Εξάτμιση (1/2), 2ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Σκοπός συμπύκνωσης
Βασικές Διεργασίες Μηχανικής Τροφίμων Ενότητα 1: Εξάτμιση (1/2), 2ΔΩ Τμήμα: Επιστήμης Τροφίμων και Διατροφής Του Ανθρώπου Σταύρος Π. Γιαννιώτης, Καθηγητής Μηχανικής Τροφίμων Μαθησιακοί Στόχοι Σκοπός συμπύκνωσης
6 η Οκτωβρίου 2013. Παρουσίαση της. Σουντουρλής Μιχάλης, Διπλωματούχος Χημικός Μηχανικός
 6 η Οκτωβρίου 2013 Παρουσίαση της Σουντουρλής Μιχάλης, Διπλωματούχος Χημικός Μηχανικός Εικόνα 1: Εγκατάσταση μονάδας «ΦΥΤΟΕΝΕΡΓΕΙΑ Α.Ε.» στο Παραλίμνιο Σερρών (2011) Α. Η Εταιρεία Η «ΦΥΤΟΕΝΕΡΓΕΙΑ Α.Ε.»
6 η Οκτωβρίου 2013 Παρουσίαση της Σουντουρλής Μιχάλης, Διπλωματούχος Χημικός Μηχανικός Εικόνα 1: Εγκατάσταση μονάδας «ΦΥΤΟΕΝΕΡΓΕΙΑ Α.Ε.» στο Παραλίμνιο Σερρών (2011) Α. Η Εταιρεία Η «ΦΥΤΟΕΝΕΡΓΕΙΑ Α.Ε.»
ΜΕΘΟ ΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΙΑΛΥΜΑΤΑ
 ΜΕΘΟ ΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυµάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούµε ή να
ΜΕΘΟ ΟΛΟΓΙΑ ΓΙΑ ΤΗΝ ΕΠΙΛΥΣΗ ΑΣΚΗΣΕΩΝ ΠΟΥ ΑΦΟΡΟΥΝ ΙΑΛΥΜΑΤΑ Οι ασκήσεις διαλυµάτων που αφορούν τις περιεκτικότητες % w/w, % w/v και % v/v χωρίζονται σε 3 κατηγορίες: α) Ασκήσεις όπου πρέπει να βρούµε ή να
1 Η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ ΚΑΡΔΙΤΣΑ ΔΙΑΛΥΜΑΤΑ
 1 Η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ ΚΑΡΔΙΤΣΑ ΔΙΑΛΥΜΑΤΑ ΗΛΙΑΣ ΝΟΛΗΣ-ΚΩΝΣΤΑΝΤΙΝΙΔΗΣ ΘΕΟΔΩΡΟΣ 2012 Διαλύματα Διάλυμα ονομάζεται κάθε ομογενές μείγμα δύο ή περισσοτέρων συστατικών. Κάθε
1 Η ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ ΤΜΗΜΑ ΔΙΑΤΡΟΦΗΣ ΚΑΙ ΔΙΑΙΤΟΛΟΓΙΑΣ ΚΑΡΔΙΤΣΑ ΔΙΑΛΥΜΑΤΑ ΗΛΙΑΣ ΝΟΛΗΣ-ΚΩΝΣΤΑΝΤΙΝΙΔΗΣ ΘΕΟΔΩΡΟΣ 2012 Διαλύματα Διάλυμα ονομάζεται κάθε ομογενές μείγμα δύο ή περισσοτέρων συστατικών. Κάθε
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ
 ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2016-2017 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ 2 ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Ε. Παυλάτου, 2017 ΓΝΩΣΤΙΚΟ ΕΠΙΠΕΔΟ Η διδασκαλία και εμπέδωση θεμελιακών εννοιών που σχετίζονται
ΑΝΑΛΥΣΗ ΣΥΣΤΗΜΑΤΩΝ ΧΗΜΙΚΗΣ ΜΗΧΑΝΙΚΗΣ 2016-2017 2 Ο ΕΞΑΜΗΝΟ Ε. ΠΑΥΛΑΤΟΥ ΑΝΑΠΛ. ΚΑΘΗΓΗΤΡΙΑ ΕΜΠ 2 ΣΚΟΠΟΣ ΜΑΘΗΜΑΤΟΣ Ε. Παυλάτου, 2017 ΓΝΩΣΤΙΚΟ ΕΠΙΠΕΔΟ Η διδασκαλία και εμπέδωση θεμελιακών εννοιών που σχετίζονται
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens. ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction
 Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
Associate. Prof. M. Krokida School of Chemical Engineering National Technical University of Athens ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ- ΥΓΡΟΥ Liquid- Liquid Extraction ΕΚΧΥΛΙΣΗ ΙΣΟΡΡΟΠΙΑΣ ΓΙΑ ΜΕΡΙΚΩΣ ΑΝΑΜΙΞΙΜΑ ΣΥΣΤΗΜΑΤΑ Τριγωνικές
6.2. ΤΗΞΗ ΚΑΙ ΠΗΞΗ, ΛΑΝΘΑΝΟΥΣΕΣ ΘΕΡΜΟΤΗΤΕΣ
 45 6.1. ΓΕΝΙΚΑ ΠΕΡΙ ΦΑΣΕΩΝ ΜΕΤΑΤΡΟΠΕΣ ΦΑΣΕΩΝ Όλα τα σώµατα,στερεά -ά-αέρια, που υπάρχουν στη φύση βρίσκονται σε µια από τις τρεις φάσεις ή σε δύο ή και τις τρεις. Όλα τα σώµατα µπορεί να αλλάξουν φάση
45 6.1. ΓΕΝΙΚΑ ΠΕΡΙ ΦΑΣΕΩΝ ΜΕΤΑΤΡΟΠΕΣ ΦΑΣΕΩΝ Όλα τα σώµατα,στερεά -ά-αέρια, που υπάρχουν στη φύση βρίσκονται σε µια από τις τρεις φάσεις ή σε δύο ή και τις τρεις. Όλα τα σώµατα µπορεί να αλλάξουν φάση
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ
 ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 2 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ Κυριακή, 16 Απριλίου 2006 Ώρα: 10:30 13.00 Προτεινόµενες Λύσεις ΜΕΡΟΣ Α 1. α) Η πυκνότητα του υλικού υπολογίζεται από τη m m m σχέση d
ΕΝΩΣΗ ΚΥΠΡΙΩΝ ΦΥΣΙΚΩΝ 2 Η ΠΑΓΚΥΠΡΙΑ ΟΛΥΜΠΙΑ Α ΦΥΣΙΚΗΣ Β ΓΥΜΝΑΣΙΟΥ Κυριακή, 16 Απριλίου 2006 Ώρα: 10:30 13.00 Προτεινόµενες Λύσεις ΜΕΡΟΣ Α 1. α) Η πυκνότητα του υλικού υπολογίζεται από τη m m m σχέση d
R T ενώ σε ολοκληρωµένη, αν θεωρήσουµε ότι οι ενθαλπίες αλλαγής φάσεως είναι σταθερές στο διάστηµα θερµοκρασιών που εξετάζουµε, είναι
 Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξετάσεις: Περίοδος Σεπτεµβρίου 007-0 (.9.00) Θέµα. Η τάση ατµών του στερεού µονοξειδίου του άνθρακα σε 60 K είναι.6 kpa και σε 65 K είναι. kpa. Η τάση ατµών του υγρού
Τµήµα Χηµείας Μάθηµα: Φυσικοχηµεία Ι Εξετάσεις: Περίοδος Σεπτεµβρίου 007-0 (.9.00) Θέµα. Η τάση ατµών του στερεού µονοξειδίου του άνθρακα σε 60 K είναι.6 kpa και σε 65 K είναι. kpa. Η τάση ατµών του υγρού
Απορρόφηση Αερίων (2)
 Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Απορρόφηση Αερίων (2) Λεπτομερής Ανάλυση Θεωρούμε έναν πύργο απορρόφησης που μπορεί να περιέχει δίσκους ή να είναι τύπου πληρωτικού υλικού ή άλλου τύπου. Τελικός σκοπός είναι να βρούμε το μέγεθος του πύργου.
Μηχανική Τροφίμων. Θεμελιώδεις Έννοιες Μηχανικής. Μέρος 1 ο. Συστήματα μονάδων
 Μηχανική Τροφίμων Θεμελιώδεις Έννοιες Μηχανικής Μέρος 1 ο Συστήματα μονάδων Διεθνές σύστημα (S.I). Έχει υιοθετηθεί αποκλειστικά στην μηχανική και τις επιστήμες. Οι τρεις βασικές μονάδες είναι το μέτρο
Μηχανική Τροφίμων Θεμελιώδεις Έννοιες Μηχανικής Μέρος 1 ο Συστήματα μονάδων Διεθνές σύστημα (S.I). Έχει υιοθετηθεί αποκλειστικά στην μηχανική και τις επιστήμες. Οι τρεις βασικές μονάδες είναι το μέτρο
2 Μετάδοση θερμότητας με εξαναγκασμένη μεταφορά
 2 Μετάδοση θερμότητας με εξαναγκασμένη μεταφορά 2.1 Εισαγωγή Η θερμοκρασιακή διαφορά μεταξύ δυο σημείων μέσα σ' ένα σύστημα προκαλεί τη ροή θερμότητας και, όταν στο σύστημα αυτό περιλαμβάνεται ένα ή περισσότερα
2 Μετάδοση θερμότητας με εξαναγκασμένη μεταφορά 2.1 Εισαγωγή Η θερμοκρασιακή διαφορά μεταξύ δυο σημείων μέσα σ' ένα σύστημα προκαλεί τη ροή θερμότητας και, όταν στο σύστημα αυτό περιλαμβάνεται ένα ή περισσότερα
4.1 Η ΕΝΝΟΙΑ ΤΗΣ ΕΞΙΣΩΣΗΣ
 1 4.1 Η ΕΝΝΟΙΑ ΤΗΣ ΕΞΙΣΩΣΗΣ ΘΕΩΡΙΑ 1. Εξίσωση µε έναν άγνωστο: Ονοµάζουµε µία ισότητα η οποία περιέχει αριθµούς και ένα γράµµα που είναι ο άγνωστος της εξίσωσης.. Λύση ή ρίζα της εξίσωσης : Είναι ο αριθµός
1 4.1 Η ΕΝΝΟΙΑ ΤΗΣ ΕΞΙΣΩΣΗΣ ΘΕΩΡΙΑ 1. Εξίσωση µε έναν άγνωστο: Ονοµάζουµε µία ισότητα η οποία περιέχει αριθµούς και ένα γράµµα που είναι ο άγνωστος της εξίσωσης.. Λύση ή ρίζα της εξίσωσης : Είναι ο αριθµός
ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΡΜΟ ΥΝΑΜΙΚΗΣ
 ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΡΜΟ ΥΝΑΜΙΚΗΣ. Μια νοικοκυρά µαγειρεύει σε χύτρα, η οποία είναι: (α) ακάλυπτη, (β) καλυµµένη µε ελαφρύ καπάκι και (γ) καλυµµένη µε βαρύ καπάκι. Σε ποια περίπτωση ο χρόνος µαγειρέµατος θα
ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΡΜΟ ΥΝΑΜΙΚΗΣ. Μια νοικοκυρά µαγειρεύει σε χύτρα, η οποία είναι: (α) ακάλυπτη, (β) καλυµµένη µε ελαφρύ καπάκι και (γ) καλυµµένη µε βαρύ καπάκι. Σε ποια περίπτωση ο χρόνος µαγειρέµατος θα
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ. Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας
 ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve Coons. Για εκπαιδευτικό
ΦΑΙΝΟΜΕΝΑ ΜΕΤΑΦΟΡΑΣ ΙΙ Διδάσκων: Παπασιώπη Νυμφοδώρα Αναπληρώτρια Καθηγήτρια Ε.Μ.Π. Ενότητα 9 η : Μεταφορά Μάζας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creatve Coons. Για εκπαιδευτικό
ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ.Ε. ΜΕ ΚΡΟΥΣΤΙΚΕΣ ΙΕΓΕΡΣΕΙΣ
 ΣΧΟΛΗ. Ν. ΟΚΙΜΩΝ ΜΑΘΗΜΑ: ΘΕΩΡΙΑ ΚΥΚΛΩΜΑΤΩΝ ΙΙ ΕΙΣΑΓΩΓΗ ΣΤΑ Σ.Α.Ε. ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ.Ε. ΜΕ ΚΡΟΥΣΤΙΚΕΣ ΙΕΓΕΡΣΕΙΣ ρ. Α. Μαγουλάς Οκτώβριος 4 Η συνάρτηση δ ( και η παράγωγός της Ορίζεται ως εξής: δ ( ανωµαλο
ΣΧΟΛΗ. Ν. ΟΚΙΜΩΝ ΜΑΘΗΜΑ: ΘΕΩΡΙΑ ΚΥΚΛΩΜΑΤΩΝ ΙΙ ΕΙΣΑΓΩΓΗ ΣΤΑ Σ.Α.Ε. ΕΠΙΛΥΣΗ ΓΡΑΜΜΙΚΩΝ.Ε. ΜΕ ΚΡΟΥΣΤΙΚΕΣ ΙΕΓΕΡΣΕΙΣ ρ. Α. Μαγουλάς Οκτώβριος 4 Η συνάρτηση δ ( και η παράγωγός της Ορίζεται ως εξής: δ ( ανωµαλο
Διαλύματα - Περιεκτικότητες διαλυμάτων Γενικά για διαλύματα
 Διαλύματα - Περιεκτικότητες διαλυμάτων Γενικά για διαλύματα Μάθημα 6 6.1. SOS: Τι ονομάζεται διάλυμα, Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων καθαρών ουσιών. Παράδειγμα: Ο ατμοσφαιρικός αέρας
Διαλύματα - Περιεκτικότητες διαλυμάτων Γενικά για διαλύματα Μάθημα 6 6.1. SOS: Τι ονομάζεται διάλυμα, Διάλυμα είναι ένα ομογενές μίγμα δύο ή περισσοτέρων καθαρών ουσιών. Παράδειγμα: Ο ατμοσφαιρικός αέρας
ΑΣΚΗΣΕΙΣ ΣΥΣΚΕΥΩΝ ΘΕΡΜΙΚΩΝ ΔΙΕΡΓΑΣΙΩΝ. 1η ενότητα
 1η ενότητα 1. Εναλλάκτης σχεδιάζεται ώστε να θερμαίνει 2kg/s νερού από τους 20 στους 60 C. Το θερμό ρευστό είναι επίσης νερό με θερμοκρασία εισόδου 95 C. Οι συντελεστές συναγωγής στους αυλούς και το κέλυφος
1η ενότητα 1. Εναλλάκτης σχεδιάζεται ώστε να θερμαίνει 2kg/s νερού από τους 20 στους 60 C. Το θερμό ρευστό είναι επίσης νερό με θερμοκρασία εισόδου 95 C. Οι συντελεστές συναγωγής στους αυλούς και το κέλυφος
ΤΕΛΟΣ 1ΗΣ ΑΠΟ 4 ΣΕΛΙ ΕΣ
 ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 26 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ ΚΑΙ ΚΛΙΜΑΤΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ
ΑΡΧΗ 1ΗΣ ΣΕΛΙ ΑΣ ΝΕΟ ΣΥΣΤΗΜΑ Γ ΗΜΕΡΗΣΙΩΝ ΠΑΝΕΛΛΑ ΙΚΕΣ ΕΞΕΤΑΣΕΙΣ HMEΡΗΣΙΩΝ ΕΠΑΓΓΕΛΜΑΤΙΚΩΝ ΛΥΚΕΙΩΝ ΠΕΜΠΤΗ 26 ΜΑΪΟΥ 2016 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΣΤΟΙΧΕΙΑ ΨΥΞΗΣ ΚΑΙ ΚΛΙΜΑΤΙΣΜΟΥ ΣΥΝΟΛΟ ΣΕΛΙ ΩΝ: ΤΕΣΣΕΡΙΣ (4) ΘΕΜΑ
1. Εναλλάκτες θερµότητας (Heat Exchangers)
 1. Εναλλάκτες θερµότητας (Heat Exangers) Οι εναλλάκτες θερµότητας είναι συσκευές µε τις οποίες επιτυγχάνεται η µεταφορά ενέργειας από ένα ρευστό υψηλής θερµοκρασίας σε ένα άλλο ρευστό χαµηλότερης θερµοκρασίας.
1. Εναλλάκτες θερµότητας (Heat Exangers) Οι εναλλάκτες θερµότητας είναι συσκευές µε τις οποίες επιτυγχάνεται η µεταφορά ενέργειας από ένα ρευστό υψηλής θερµοκρασίας σε ένα άλλο ρευστό χαµηλότερης θερµοκρασίας.
Energy resources: Technologies & Management
 Energy resources: Technologies & Management Θεωρία της καύσης Δρ Γεώργιος Σκόδρας Αναπληρωτής Καθηγητής Σκοπός της καύσης είναι η μετατροπή της χημικής ενέργειας που περιέχεται στο καύσιμο σε θερμική ενέργεια
Energy resources: Technologies & Management Θεωρία της καύσης Δρ Γεώργιος Σκόδρας Αναπληρωτής Καθηγητής Σκοπός της καύσης είναι η μετατροπή της χημικής ενέργειας που περιέχεται στο καύσιμο σε θερμική ενέργεια
ΘΕΡΜΟΔΥΝΑΜΙΚΗ II Χειμερινό Εξάμηνο Η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΕΡΓ. ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ II Χειμερινό Εξάμηνο 006-007 3 Η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Άσκηση Ένας κύλινδρος με όγκο 0,4 3 περιέχει μίγμα CH 4 και αέρα (Ο, % - Ν, 79%
ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΙΑΣ ΕΡΓ. ΡΕΥΣΤΟΜΗΧΑΝΙΚΗΣΣΤΡΟΒΙΛΟΜΗΧΑΝΩΝ ΘΕΡΜΟΔΥΝΑΜΙΚΗ II Χειμερινό Εξάμηνο 006-007 3 Η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Άσκηση Ένας κύλινδρος με όγκο 0,4 3 περιέχει μίγμα CH 4 και αέρα (Ο, % - Ν, 79%
ΕΝ ΕΙΚΤΙΚΑ ΠΑΡΑ ΕΙΓΜΑΤΑ ΚΡΙΤΗΡΙΩΝ ΑΞΙΟΛΟΓΗΣΗΣ. Παράδειγµα κριτηρίου αξιολόγησης σύντοµης διάρκειας στην Ενότητα 2.3 (Σχέση Βιοµηχανίας και Ενέργειας)
 ΕΝ ΕΙΚΤΙΚΑ ΠΑΡΑ ΕΙΓΜΑΤΑ ΚΡΙΤΗΡΙΩΝ ΑΞΙΟΛΟΓΗΣΗΣ Παράδειγµα κριτηρίου αξιολόγησης σύντοµης διάρκειας στην Ενότητα 2.3 (Σχέση Βιοµηχανίας και Ενέργειας) ΣΤΟΙΧΕΙΑ ΜΑΘΗΤΗ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΑΞΗ:... ΤΜΗΜΑ:...
ΕΝ ΕΙΚΤΙΚΑ ΠΑΡΑ ΕΙΓΜΑΤΑ ΚΡΙΤΗΡΙΩΝ ΑΞΙΟΛΟΓΗΣΗΣ Παράδειγµα κριτηρίου αξιολόγησης σύντοµης διάρκειας στην Ενότητα 2.3 (Σχέση Βιοµηχανίας και Ενέργειας) ΣΤΟΙΧΕΙΑ ΜΑΘΗΤΗ ΟΝΟΜΑΤΕΠΩΝΥΜΟ:... ΤΑΞΗ:... ΤΜΗΜΑ:...
6. Παράδειγµα Εφαρµογής του EMAS στον Τοµέα Τροφίµων & Ποτών
 6. Παράδειγµα Εφαρµογής του EMAS στον Τοµέα Τροφίµων & Ποτών Όνοµα Εταιρίας: Τοµέας: Αριθµός Εργαζοµένων: 80 Χώρα: Τυνησία Siozitex Παραγωγή Ελαιολάδου και Σαπωνιού 6.1. Εισαγωγή Η Siozitex είναι µια επιχείρηση
6. Παράδειγµα Εφαρµογής του EMAS στον Τοµέα Τροφίµων & Ποτών Όνοµα Εταιρίας: Τοµέας: Αριθµός Εργαζοµένων: 80 Χώρα: Τυνησία Siozitex Παραγωγή Ελαιολάδου και Σαπωνιού 6.1. Εισαγωγή Η Siozitex είναι µια επιχείρηση
Μηχανική και Ανάπτυξη Διεργασιών
 Μηχανική και Ανάπτυξη Διεργασιών Κωστής Μαγουλάς, Καθηγητής Επαμεινώνδας Βουτσάς, Επ. Καθηγητής 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ . ΟΡΙΣΜΟΣ Οι διαχωρισμοί είναι οι πιο συχνά παρατηρούμενες διεργασίες
Μηχανική και Ανάπτυξη Διεργασιών Κωστής Μαγουλάς, Καθηγητής Επαμεινώνδας Βουτσάς, Επ. Καθηγητής 7ο Εξάμηνο, Σχολή Χημικών Μηχανικών ΕΜΠ . ΟΡΙΣΜΟΣ Οι διαχωρισμοί είναι οι πιο συχνά παρατηρούμενες διεργασίες
Χηµεία Θετικής Κατεύθυνσης Β Λυκείου 2001
 Χηµεία Θετικής Κατεύθυνσης Β Λυκείου 001 Ζήτηµα 1 ο Στις ερωτήσεις 1.1-1.4, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1.1 Η εξαέρωση ενός
Χηµεία Θετικής Κατεύθυνσης Β Λυκείου 001 Ζήτηµα 1 ο Στις ερωτήσεις 1.1-1.4, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1.1 Η εξαέρωση ενός
ΞΗΡΑΝΤΗΡΙΟ ΠΥΡΗΝΑΣ ΜΗΧΑΝΟΛΟΓΙΚΗ ΜΕΛΕΤΗ
 ΕΡΓΟΔΟΤΗΣ: ΕΡΓΟ: ΞΗΡΑΝΤΗΡΙΟ ΠΥΡΗΝΑΣ ΤΟΠΟΘΕΣΙΑ: ΜΗΧΑΝΟΛΟΓΙΚΗ ΜΕΛΕΤΗ ΚΑΡΥΩΤΑΚΗ 5 Α 166 73 ΒΟΥΛΑ ΤΗΛ. 210 8995934, ΦΑΞ 210 8951760 e-mail info@inik.gr 1 1. ΤΕΧΝΙΚΟ ΥΠΟΜΝΗΜΑ α. Ονοματεπώνυμο του ιδιοκτήτη
ΕΡΓΟΔΟΤΗΣ: ΕΡΓΟ: ΞΗΡΑΝΤΗΡΙΟ ΠΥΡΗΝΑΣ ΤΟΠΟΘΕΣΙΑ: ΜΗΧΑΝΟΛΟΓΙΚΗ ΜΕΛΕΤΗ ΚΑΡΥΩΤΑΚΗ 5 Α 166 73 ΒΟΥΛΑ ΤΗΛ. 210 8995934, ΦΑΞ 210 8951760 e-mail info@inik.gr 1 1. ΤΕΧΝΙΚΟ ΥΠΟΜΝΗΜΑ α. Ονοματεπώνυμο του ιδιοκτήτη
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο
 Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
Συστήματα Βιομηχανικών Διεργασιών 6ο εξάμηνο Μέρος ο : Εισαγωγικά (διαστ., πυκν., θερμ., πίεση, κτλ.) Μέρος 2 ο : Ισοζύγια μάζας Μέρος 3 ο : 9 ο μάθημα Εκτός ύλης ΔΠΘ-ΜΠΔ Συστήματα Βιομηχανικών Διεργασιών
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ. Εξάτμιση - Αφυδάτωση
 ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ Εξάτμιση - Αφυδάτωση Εξάτμιση Η διεργασία απομάκρυνσης νερού από διαλύματα με βρασμό (συμπύκνωση διαλυμάτων ζάχαρης, χυμών κλπ) Παράμετροι επεξεργασίας: Η συγκέντρωση του ρευστού Διαλυτότητα
ΜΗΧΑΝΙΚΗ ΤΡΟΦΙΜΩΝ Εξάτμιση - Αφυδάτωση Εξάτμιση Η διεργασία απομάκρυνσης νερού από διαλύματα με βρασμό (συμπύκνωση διαλυμάτων ζάχαρης, χυμών κλπ) Παράμετροι επεξεργασίας: Η συγκέντρωση του ρευστού Διαλυτότητα
ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ
 ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ 2 ΕΝΘΑΛΠΙΑ ΣΧΗΜΑΤΙΣΜΟΥ ΕΝΩΣΗΣ Ο θερμοτονισμός ή η θερμότητα της αντίδρασης εκφράζει τη μεταβολή ενέργειας λόγω της χημικής αντίδρασης Η απαιτούμενη ενέργεια για το σχηματισμό
ΙΣΟΖΥΓΙΑ ΕΝΕΡΓΕΙΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ 2 ΕΝΘΑΛΠΙΑ ΣΧΗΜΑΤΙΣΜΟΥ ΕΝΩΣΗΣ Ο θερμοτονισμός ή η θερμότητα της αντίδρασης εκφράζει τη μεταβολή ενέργειας λόγω της χημικής αντίδρασης Η απαιτούμενη ενέργεια για το σχηματισμό
2.3 Περιεκτικότητα διαλύματος Εκφράσεις περιεκτικότητας
 1 Η θεωρία του μαθήματος με ερωτήσεις. 2.3 Περιεκτικότητα διαλύματος Εκφράσεις περιεκτικότητας Ερωτήσεις θεωρίας με απάντηση 3-1. Τι ονομάζεται περιεκτικότητα ενός διαλύματος; Είναι μία έκφραση που δείχνει
1 Η θεωρία του μαθήματος με ερωτήσεις. 2.3 Περιεκτικότητα διαλύματος Εκφράσεις περιεκτικότητας Ερωτήσεις θεωρίας με απάντηση 3-1. Τι ονομάζεται περιεκτικότητα ενός διαλύματος; Είναι μία έκφραση που δείχνει
Μετασχηµατισµοί Laplace, Αναλογικά Συστήµατα, ιαφορικές Εξισώσεις
 ΚΕΦΑΛΑΙΟ 2 Μετασχηµατισµοί Laplace, Αναλογικά Συστήµατα, ιαφορικές Εξισώσεις 2.1 ΕΙΣΑΓΩΓΗ Όπως έχουµε δει, για να προσδιορίσουµε τις αποκρίσεις ενός κυκλώµατος, πρέπει να λύσουµε ένα σύνολο διαφορικών
ΚΕΦΑΛΑΙΟ 2 Μετασχηµατισµοί Laplace, Αναλογικά Συστήµατα, ιαφορικές Εξισώσεις 2.1 ΕΙΣΑΓΩΓΗ Όπως έχουµε δει, για να προσδιορίσουµε τις αποκρίσεις ενός κυκλώµατος, πρέπει να λύσουµε ένα σύνολο διαφορικών
ηµήτρη Γεωργακάκη, Καθηγητή Γ.Π.Α.
 ΠΑΡΑΓΩΓΗ ΚΑΙ ΕΚΜΕΤΑΛΛΕΥΣΗ ΒΙΟΑΕΡΙΟΥ ΑΠΟ ΠΤΗΝΟ-ΚΤΗΝΟΤΡΟΦΙΚΑ ΑΠΟΒΛΗΤΑ ηµήτρη Γεωργακάκη, Καθηγητή Γ.Π.Α. ΣΤΟΧΟΣ ΤΗΣ ΠΑΡΑΓΩΓΗΣ ΒΙΟΑΕΡΙΟΥ : ΣΤΑΘΕΡΗ ΚΑΙ ΣΥΝΕΧΗΣ ΠΑΡΑΓΩΓΗ ΤΟΥ ΣΕ ΒΑΘΟΣ ΧΡΟΝΟΥ ΣΤΟΧΟΣ ΤΗΣ ΕΚΜΕΤΑΛΛΕΥΣΗΣ
ΠΑΡΑΓΩΓΗ ΚΑΙ ΕΚΜΕΤΑΛΛΕΥΣΗ ΒΙΟΑΕΡΙΟΥ ΑΠΟ ΠΤΗΝΟ-ΚΤΗΝΟΤΡΟΦΙΚΑ ΑΠΟΒΛΗΤΑ ηµήτρη Γεωργακάκη, Καθηγητή Γ.Π.Α. ΣΤΟΧΟΣ ΤΗΣ ΠΑΡΑΓΩΓΗΣ ΒΙΟΑΕΡΙΟΥ : ΣΤΑΘΕΡΗ ΚΑΙ ΣΥΝΕΧΗΣ ΠΑΡΑΓΩΓΗ ΤΟΥ ΣΕ ΒΑΘΟΣ ΧΡΟΝΟΥ ΣΤΟΧΟΣ ΤΗΣ ΕΚΜΕΤΑΛΛΕΥΣΗΣ
ΕΝΑΛΛΑΚΤΕΣ ΘΕΡΜΟΤΗΤΑΣ
 ΚΕΦΑΛΑΙΟ 4 ΕΝΑΛΛΑΚΤΕΣ ΘΕΡΜΟΤΗΤΑΣ 4.1 Εισαγωγή - τύποι εναλλακτών Εναλλάκτες θερμότητας είναι οι συσκευές στις οποίες έχουμε μεταφορά ε- νέργειας, με τη μορφή θερμότητας, μεταξύ δύο ρευστών που βρίσκονται
ΚΕΦΑΛΑΙΟ 4 ΕΝΑΛΛΑΚΤΕΣ ΘΕΡΜΟΤΗΤΑΣ 4.1 Εισαγωγή - τύποι εναλλακτών Εναλλάκτες θερμότητας είναι οι συσκευές στις οποίες έχουμε μεταφορά ε- νέργειας, με τη μορφή θερμότητας, μεταξύ δύο ρευστών που βρίσκονται
ηµήτρης Τσίνογλου ρ. Μηχανολόγος Μηχανικός
 Μετάδοση Θερµότητας ηµήτρης Τσίνογλου ρ. Μηχανολόγος Μηχανικός ΤΕΙ Σερρών Μετάδοση Θερµότητας 1 Εισαγωγή στη Μετάδοση Θερµότητας Κεφάλαιο 1 ΤΕΙ Σερρών Μετάδοση Θερµότητας Ορισµός Μετάδοση θερµότητας: «Μεταφορά
Μετάδοση Θερµότητας ηµήτρης Τσίνογλου ρ. Μηχανολόγος Μηχανικός ΤΕΙ Σερρών Μετάδοση Θερµότητας 1 Εισαγωγή στη Μετάδοση Θερµότητας Κεφάλαιο 1 ΤΕΙ Σερρών Μετάδοση Θερµότητας Ορισµός Μετάδοση θερµότητας: «Μεταφορά
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ
 ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
ΠΑΡΑΔΕΙΓΜΑΤΑ ΕΚΧΥΛΙΣΗ ΥΓΡΟΥ ΥΓΡΟΥ Παράδειγμα 1 Σε μονάδα εκχύλισης μιας μόνο βαθμίδας πραγματοποιείται εκχύλιση οξικού οξέος από νερό με χρήση βουτανόλης. Η τροφοδοσία παροχής F= 100 kg/h περιέχει οξικό
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2014 ÊÏÑÕÖÁÉÏ ÅÕÏÓÌÏÓ
 ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΧΗΜΕΙΑ Ηµεροµηνία: Τετάρτη 3 Απριλίου 014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ Για τις ερωτήσεις Α1 έως και Α4 να γράψετε στο τετράδιό σας τον αριθµό
ΤΑΞΗ: ΚΑΤΕΥΘΥΝΣΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΧΗΜΕΙΑ Ηµεροµηνία: Τετάρτη 3 Απριλίου 014 ιάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ Για τις ερωτήσεις Α1 έως και Α4 να γράψετε στο τετράδιό σας τον αριθµό
Ε. Παυλάτου, 2017 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ
 1 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ 2 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ Βασικές έννοιες Στοιχειομετρία-Στοιχειομετρικοί συντελεστές-στοιχειομετρική αναλογία Περιοριστικό αντιδρών Αντιδρών σε περίσσεια Μετατροπή (κλάσμα,
1 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ 2 ΙΣΟΖΥΓΙΑ ΜΑΖΑΣ ΜΕ ΑΝΤΙΔΡΑΣΗ Βασικές έννοιες Στοιχειομετρία-Στοιχειομετρικοί συντελεστές-στοιχειομετρική αναλογία Περιοριστικό αντιδρών Αντιδρών σε περίσσεια Μετατροπή (κλάσμα,
ΧΗΜΕΙΑ Β ΤΑΞΗΣ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2003
 ΧΗΜΕΙΑ Β ΤΑΞΗΣ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ 1ο Στις ερωτήσεις 1.1-1.4, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1.1 Από
ΧΗΜΕΙΑ Β ΤΑΞΗΣ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 00 ΘΕΜΑ 1ο Στις ερωτήσεις 1.1-1.4, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση. 1.1 Από
ΚΑΝΟΝΕΣ ΚΛΑΣΜΑΤΩΝ ΙΟΝΙΣΜΟΥ ΓΙΑ ΔΙΠΡΩΤΙΚΑ ΟΞΕΑ Στην περίπτωση διπρωτικού οξέως µε σταθερές pk A και pk B ελέγχουµε την τιµή του ph 1η περίπτωση.
 ΚΑΝΟΝΕΣ ΚΛΑΣΜΑΤΩΝ ΙΟΝΙΣΜΟΥ ΓΙΑ ΔΙΠΡΩΤΙΚΑ ΟΞΕΑ Στην περίπτωση διπρωτικού οξέως µε σταθερές pk A και pk B ελέγχουµε την τιµή του ph 1η περίπτωση ph pk A pk B Τότε α 0 (διπρωτικού) = α 0 (µονοπρωτικού) α
ΚΑΝΟΝΕΣ ΚΛΑΣΜΑΤΩΝ ΙΟΝΙΣΜΟΥ ΓΙΑ ΔΙΠΡΩΤΙΚΑ ΟΞΕΑ Στην περίπτωση διπρωτικού οξέως µε σταθερές pk A και pk B ελέγχουµε την τιµή του ph 1η περίπτωση ph pk A pk B Τότε α 0 (διπρωτικού) = α 0 (µονοπρωτικού) α
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ. Ερωτήσεις Επανάληψης
 Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Δ' Εξάμηνο ΦΥΣΙΚΕΣ ΔΙΕΡΓΑΣΙΕΣ Ερωτήσεις Επανάληψης 1 0.8 0.6 x D = 0.95 y 0.4 x F = 0.45 0.2 0 0 0.2 0.4 0.6 0.8 1 x B = 0.05 Σχήμα 1. Δεδομένα ισορροπίας y-x για δυαδικό μίγμα συστατικών Α και Β και οι
Θερμοδυναμική Ενότητα 4:
 Θερμοδυναμική Ενότητα 4: Ισοζύγια Ενέργειας και Μάζας σε ανοικτά συστήματα Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Θερμοδυναμική Ενότητα 4: Ισοζύγια Ενέργειας και Μάζας σε ανοικτά συστήματα Κυρατζής Νικόλαος Τμήμα Μηχανικών Περιβάλλοντος και Μηχανικών Αντιρρύπανσης ΤΕ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
εύτερος Θερμοδυναμικός Νόμος Εντροπία ιαθέσιμη ενέργεια Εξέργεια
 εύτερος Θερμοδυναμικός Νόμος Εντροπία ιαθέσιμη ενέργεια Εξέργεια Χαρακτηριστικά Θερμοδυναμικών Νόμων 0 ος Νόμος Εισάγει την έννοια της θερμοκρασίας Αν Α Γ και Β Γ τότε Α Β, όπου : θερμική ισορροπία ος
εύτερος Θερμοδυναμικός Νόμος Εντροπία ιαθέσιμη ενέργεια Εξέργεια Χαρακτηριστικά Θερμοδυναμικών Νόμων 0 ος Νόμος Εισάγει την έννοια της θερμοκρασίας Αν Α Γ και Β Γ τότε Α Β, όπου : θερμική ισορροπία ος
1. Παράρτηµα. Θερµοδυναµικής της ατµόσφαιρας
 1. Παράρτηµα. Θερµοδυναµικής της ατµόσφαιρας Αδιαβατικές µεταβολές στην ατµόσφαιρα Ο ατµοσφαιρικός αέρας µπορεί να θεωρηθεί ως µίγµα δύο αερίων, του ξηρού αέρα ο οποίος αποτελεί ιδανικό αέριο, µε την γνωστή
1. Παράρτηµα. Θερµοδυναµικής της ατµόσφαιρας Αδιαβατικές µεταβολές στην ατµόσφαιρα Ο ατµοσφαιρικός αέρας µπορεί να θεωρηθεί ως µίγµα δύο αερίων, του ξηρού αέρα ο οποίος αποτελεί ιδανικό αέριο, µε την γνωστή
ΧΗΜΕΙΑ Β ΤΑΞΗΣ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 2003
 ΧΗΜΕΙΑ Β ΤΑΞΗΣ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1.1-1.4, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
ΧΗΜΕΙΑ Β ΤΑΞΗΣ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ 003 ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ 1ο Στις ερωτήσεις 1.1-1.4, να γράψετε στο τετράδιό σας τον αριθµό της ερώτησης και δίπλα το γράµµα που αντιστοιχεί στη σωστή απάντηση.
Εφαρμοσμένη Θερμοδυναμική
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφαρμοσμένη Θερμοδυναμική Ενότητα 2: Ιδιότητες Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Εφαρμοσμένη Θερμοδυναμική Ενότητα 2: Ιδιότητες Χατζηαθανασίου Βασίλειος Καδή Στυλιανή Τμήμα Ηλεκτρολόγων Μηχανικών και Μηχανικών Η/Υ Άδειες
