Institutional Repository - Library & Information Centre - University of Thessaly 10/11/ :03:54 EET
|
|
|
- Ἀλεξανδρεύς Αντωνόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΒΓΖΑΝΤΙΑΚΟΙ ΝΑΟΙ ΤΗΣ ΒΟΡΕΙΟΥ ΗΠΕΙΡΟΥ Η ΚΟΙΜΗΣΙΣ ΤΗΣ ΘΕΟΤΟΚΟΥ Ό Ναός τον Βραχογ ο ραντξη. Πρός νότον τοΰ Αργυρόκαστρου έκτείνεται είς μήκος ικανών σταδίων έπίμηκες λεκανοπέδιον περικλειόμενον ένθεν καί ένθεν 6πό υψηλής διπλής βουνοσειράς βορειοανατολικές διη- κούσης, διασχίζεται δέ κατά μήκος 6πό τοΰ Δρύνου, παραποτάμου τοΰ Άωου, καί δυσμικως τούτου ύπδ τής έξ Ίωαννίνων αμαξιτού. Άφθονα είναι τά έκατέρωθεν τής πεδιάδος χωρία, κείμενα άλλα έπΐ των υπωρειών, άλλα έπ αύτών των αύχένων των πέριξ δρέων' κατά δε τό 7(Υν στάδιον τής άπό Ίωαννίνων άμαξιτοΰ εύρίσκονται έν δεξιά, πλήν άλλων, τά χωρία Επισκοπή καί δλίγον τι βορειότερον τό χωρίον Βραχογοραντζής, άπέναντι δέ τούτων, έπΐ τοΰ έτέρου χείλους τοΰ λεκανοπεδίου, τό χωρίον Ζερβάτι. Έν τοϊς χωρίοις τούτοις υπάρχει άνά εις βυζαντιακός ναός τιμώμενος, ώς καί ό τοΰ Λαμπόβου, έπ όνόματι τής Θεοτόκου (Κοιμήσεως). Περί τοΰ έν τψ πρώτω χωρίφ ναοΰ, τής άλλοτε Επισκοπής τής Μητροπόλεως Δρυνοπόλεως, έγράψαμεν έν έτέριρ άρθρφ δημοσιευομένφ έν τώ ύπό τοΰ Υπουργείου των Εκκλησιαστικών έκδιόομένφ Άρχαιολογικψ Δελτίφ, θά άναφέρωμεν δέ ένταΰθα περί των δύο άλλων. * * * 'Ο ναός τοΰ Βραχογοραντζή δύναται νάχαρακτηρισθή'μικρο- σκοπικός έν σχέσει πρός τούς ναούς τοΰ Ααμπόβου καί τής Έπι-
2 244 Πρακτικά τοΰ 1914 σκοπής, άλλ ούχ'ι άνευ ένδιαφέροντος (είκ. 1, 2, 3, 4). Στερούμενος νάρθηκος σχηματίζει έπίμηκες τετράπλευρον μήκους 7.60, πλάτους 6.86, καί χωρίζεται διά τοξωτών άνοιγμάτων εις τρία διαμερίσματα ή κλίτη, ών τό μέσον είναι'διπλάσιον των δύο πλαγίων (είκ. 2)' τδ πρώτον καλύπτεται ύπδ ήμικυκλικής καμάρας, τα δέ άλλα υπό καμάρας ίσης πρός τό τέταρτον τοΰ κύκλου (είκ. 3). Είκ. 1. Ναός Βραχογοραντζη. Τό ν μέρος των άκρων τοξωτών ανοιγμάτων στηρίζεται συγχωνευόμενον έπΐ τών στενών πλευρών τοΰ ναοΰ, τό δέ άλλο μέρος ώς καί τά λοιπά άνοίγματα επί τών τριών δκτωγωνίων στηριγμάτων (είκ. 4). Μικροτέρα είς ύψος καί όλίγον είς πλάτος τής μέσης καμάρας έξέχει πρός τά όπισθεν μόνον ή μέση ήμικυκλική κόγχη,
3 ΒνξαντιακοΙ ναοί τής Βορείου Ήπειρον. 245 πρός δέ τα πλάγια διαμερίσματα άντιστοιχοϋσι μικραί ήμικυκλικαί την τομήν κόγχαι βάθους έλάσσονος τοΰ πάχους τοΰ τοίχου (είκ. 2). ΈπΙ τοΰ δευτέρου έκ των όπισθεν τοξωτοΰ ανοίγματος έδρά- Είκ. 2. Ναόν Βραχογοραντζή κάτοψις. ζεται ό τροΰλλος, μετά ύψηλοΰ σχετικως κυλινδρικού τυμπάνου, άπολήγων άνω κωνοειδως ώς καί πάντες οί λοιποί ναοί τής περιοχής (πβλ. Βερσάκης, Άρχ. Δελτίον Τομ. Α' 1915 σ. 31, είκ. 1, 3, 4-8). Ή έσωτερική διάμετρος τούτου είναι μικρότερα τοΰ πλάτους τοΰ μέσου διαμερίσματος και ίση προς τδ τοξωτόν άνοι-
4 246 Πρακπκά τοϋ 1914 γμα- έκ τούτου ό τροΰλλος δεν στηρίζεται επί τετραγώνου, άλλα έπΐ έπιμήκους τετράπλευρου βάσεως (είκ. 2). Προς έξουδετέρωσιν της άνωμαλίας ταύτης κατεσκεύασαν τά κατά μήκος τοΰ ναοΰ πλάγια τοιχώματα τοΰ τετράπλευρου συγκλίνοντα βαθμηδόν πρός τά άνω κατά καμπύλην γραμμήν άρχομένην άπό τής εφαπτομένης τοΰ τόξου μέχρι τής βάσεως τοΰ τυμπάνου. Άπό τής εφαπτομένης ταύτης κατεσκεύασαν δεύτερον τοξωτόν κοίλωμα ύπεράνω τοΰ τοξωτού άνοίγματος, υπό δέ τά κράσπεδα τής ένθάδε διανοιγομένης μέσης καμάρας δύο τοξωτά χείλη άντιστοιχοΰντα πρός τό τοξωτόν κοίλωμα (είκ 3, 4). Διά κακοτέχνου λύσεως έπετεύχθη στερεά πως τετράγωνος βάσις καί συνεβιβάσθησαν τά άπό τής έκπονησεως τοΰ σχεδίου κακώς έξευρεθέντα καί διϊστάμενα άρχιτεκτονικά σχήματα.
5 Βυζαντιακοϊ ναοί της Βορείου Ηπείρου. 247 Ή τετράγωνος βάσις συγχωνεύεται προς τό τόμπανον διά σφαιρικών τριγωνικών τμημάτων. ΈπΙ της τετράπλευρου η τετραγώνου βάσεως στηριζόμενα έρείοονται έξω τοΰ ναοΰ δύο σαγματοειδη πλάγια κατασκευάσματα προς την βάσιν τοΰ τυμπάνου, τέσσαρα δέ τοξωτά παράθυρα εναλλάσσονται προς τοξωτάς κόγχας (εικ. 1, 3). Έξ δλου τοΰ οικοδομήματος μόνον μέρη τινά τοΰ τρούλλου διετήρησάν πως την πρώτην μορφήν, πάντα δέ τά λοιπά μετεσκευάσθησαν η άνιρκοδομήθησαν. Προς τό μέτωπον τοΰ ναοΰ προσετέθη καί έτερον διαμέρισμα, δυνάμενον νά άναπληρώση τόν έλλείποντα νάρθηκα (είκ. 1). Έάν δ ναός έχωρίζετο διά τοίχου κατά τό πρώτον μετά τό μέτωπον πολυγωνικόν στήριγμα καί ή μέση καμάρα διεσταυ-
6 248 Πρακτικά τον 1914 ροΰτο πρός δμοίαν έγκαρσίαν διακόπτουσαν τά συνεχή πλάγια διαμερίσματα, θά είχομεν οπωσδήποτε ναόν μετά νάρθηκος καί μετά κεντρικού σταυροθολίου. Νΰν δμως όμοιάζει δ ναός πρός βεβιασμένην μορφήν βασιλικής. 'Ολόκληρος δ εσωτερικός χώρος καλύπτεται, ως συνήθως, ύπό τοιχογραφιών, αί'τινες δμως έβλάβησαν, άν δεν κατεστρά- φησαν, υπό τοΰ καπνού τών κηρίων καί τών άλλων φώτων. "Αν δέ ληφθή 6π δψιν δτι ούδέν παράθυρον όπάρχει νΰν έν τφ ναώ, έκ δέ τού τρούλλου άμυδρόν μόνον διέρχεται φώς, δύναταί τις νά φαντασθή όποιον σκότος καλύπτει τό έσωτερικόν, έξ ου αί υπό τοΰ καπνού μελανθεΐσαι τοιχογραφία! φαίνονται ετι σκοτει- νότεραγ μόνον δι ίσχυροΰ τεχνητού φωτός καί μετά προηγού- μενον καθαρισμόν τών εικόνων ήδύνατό τις νά μελετήση ταΰτα ώς καί τήν μετά λαξευμάτων καί εικόνων ξυλίνην είκονόστασιν. Επειδή δέ έστερούμην τών μέσων τούτων, πρός δέ καί τών μέσων λήψεως καταλλήλων άπεικασμάτων, παρητήθην τής τε μελέτης καί τής δημοσιεύσεως τών άνω καί τών τοιχογραφιών τών λοιπών ναών τής Ηπείρου. Ένεκα τής καταστάσεως τού ναού δύσκολος καθίσταται ή προσπάθεια χρονολογήσεως αυτού. Έκ τής βεβιασμένης λύσεως αρχιτεκτονικών τινων μορφών θά παρεδεχόμην μεταβατικήν τινα περίοδον, καί δή τήν άπό τής δευτέρας βυζαντιακής προ τήν τρίτην. * * * 'Ο ναός τοϋ Ζερβατίου Καί ούτος στερούμενος νάρθηκος έχει σχήμα τετραπλεύρου μήκους 10, 90, πλάτους 7,58, καί χωρίζεται διά τοξωτών ανοιγμάτων εις τρία καμαρωτά διαμερίσματα ή κλίτη, ών τό μέσον, δλίγον μόνον πλατύτερον τών πλαγίων διασταυροΰται πρός δμοιον εγκάρσιον σκέλος (είκ. 5-6). Τό μέσον κλιτός είναι ύψηλότερον τών άλλων, άλλά άπό τοΰ σημείου τής διασταυρώσεως μέχρι τοΰ όπισθίου τοίχου τού ναού ή διαφορά είναι έλάσσων
7 ΒυξαντιακοΙ ναοί τής Βορείου Ηπείρου. 249 Ενεκα παχυτέρας κατασκευής της καμάρας. Τό^έξέχον μέρος ταύτης άπολήγει κατά τό πρόσθιον κράσπεδον τοΰ ανοίγματος εις τοξωτόν χείλος (είκ. 7), ένισχύθη δ ούτως ή καμάρα, ϊνα μείζονα παράσχη αντοχήν τή πιέσει τοΰ τρούλλου. Οδτος άπολήγει άνω ώς τοΰ προηγουμένου ναοΰ, Εχει κυλινδρικόν τύμπανον μετά τοξωτών παραθύρων καί διά (σφαιρικών Είκ. δ. Ζερβατίου ναός. τριγωνικών τμημάτων συγχωνεύεται προς τό δπ αυτό τετράγωνον άνοιγμα (είκ. 7). Τά βαστάζοντα τάς καμάρας τοξωτά ανοίγματα εχουσι διάφορον μέγεθος, τοΰ μέσου υπερβαίνοντος τό πρώτον καί τούτου τό τελευταΐον. Τά κάτωθι τοΰ τρούλλου μέρη τούτου καί τοΰ μέσου τόξου στηρίζονται τό μέν μέσον επί κίονος, τά δε τοΰ άλλου επί τετραγώνου στηρίγματος (είκ. 6, 7, 8).
8 250 Πρακτικά τον 1914 "Εκαστον κλιτός απολήγει εις τρεις έξεχούσας δπισθεν έλάσ- Είκ. 6. Ζερβατίον ναόν κάτοψις. σονας κόγχας, ών αί πλάγιαι είναι έξωτερικώς πολυγωνικαί,' ήμι- κυκλική δέ ή μέση. ΑίάκμαΙ των γωνιών των πρώτων έξέχοοσαι
9 ΒυξαντιακοΙ ναοί της Βορείου Ηπείρου. 251 καί σχηματίζουσαι τριμερές δοοντωτόν κράσπεοον χωρίζουσι την πρισματικήν επιφάνειαν τής κόγχης εις τοξωτάς παραθυροειοεΐς κοιλότητας. X >ε- 3. -R* 3- Ν Προκύπτει λοιπόν σχήμα πως βασιλικής άνευ νάρθηκος' οι εγκαρσίου δμως τοίχου μετά τό μέσον τόξον θά μεταβάλλετο το σχήμα εις ισοσκελές περίπου σταυροθόλιον μετά νάρθηκος.
10 262 Πρακτικά τοϋ 1914 Καί τούτου τοΰ ναοϋ οε τοίχοι πάντες έκαλύφθησαν διά τοιχογραφιών, δύο δέ άπεικάσματα, & μόνον κατώρθωσα νά εχω, παρέχουσι δείγμα τοΰ είδους καί της διατηρήσεως αυτών (εεκ. 9, 10). Έλήφθησαν αδται κατά τδ παρά τήν πλαγίαν είσοδον πρώτον τόξον και τό πλάγιον δεξιόν κλιτός, δπου ύπηρχεν έκ της εισόδου ολίγον φώς. Ή ήλικία τών τοιχογραφιών τούτων ΕΙκ. 8. Ζερβατίον ναόν τομή εγκάρσιά. καθορίζεται, έξ δσων άναφέρεται ύπεράνω της κυρίας εισόδου οΰτω ΊΙγέρθη έκ βάθρων και Ιστορήθη 6 πάνσεπτος και θείος ναός της ϋπεραγίας ενδόξου Δεσποίνης ημών Θεοτόκου κα'ι αειπάρθενου Μαρίας: Καί η συνδρομή δε όλων γέγονεν. Ίστορήθη δε καί χειρός (η)εμού τοϋ αμαρτωλού Μιχαήλ Νικολάου. "Ετος ΖΡΙδ.= (1605). Φαίνεται δμως 8τι πρόκειται περί άνοικοδομήσεως ναοϋ άρ-
11 ΒυξαντιακοΙ ναοί της Βορείου Ηπείρου. 263 χαιοτέρου, οβτινος ή πρώτη κατασκευή δέν θά απείχε χρονολογικές τής κατασκευής των προηγουμένων. Άν καί τα πάντα άνενεώθησαν έν τφ ναω, διατηρούνται ένιαχοΰ, λ. χ. παρά τήν Εικ. 9. Ζερβατίον ναού τοιχογραφία. πλαγίαν θύραν, ί'χνη τοίχου έμοίου προς τόν έν τφ ναω τού Λαμ- πόβου. Σφζεται δ έτι έν τοΐς άνω χωρίοις ή παράδωσις καθ ήν συγχρόνως φκοδομήθησαν οί τέσσαρες ναοί Λαμπόβου, Έπισκο-
12 254 Πρακτικά τοϋ 1914 πής, Βραχογοραντζή καί Ζερβατίου. Ίσως νά υπήρχον έν τού- τοις ναοί από της πρώτης ήδη περιόδου, άντικατασταθέντες έν ταϊς έπομέναις περιόδοις δί άλλων. Είκ. 10. Ζερβατίου ναόν άριοτεροΰ κλιτούς τοιχογραφία. Καί μετά τούς χρόνους, καθ ούς ίστορήθη ύπό τού Νικολάου ό ναός, έπεσκευάσθη οδτος καί μετεβλήθη διά προσθηκών προστφων καί διαμερισμάτων έν τφ μετώπφ, δι άνυψώσεως έξω-
13 Βυζαντιακοι ναοί τής Βορείου Ήπειρον. 255 τερικώς τής στέγης (είκ. 5) καί άλλων. Ένεκα των έπισκευών τούτων, ούδεμία εξωτερική επιφάνεια διετήρησε την πρώτην κατασκευήν. * ψ * Ο ναός τής Κοκαμιάς *Αν άμέσως μετά τά 70ον στάδιον τής άπδ Ίωαννίνων άμα- Είκ. 11. Κοκαμιάς μονή και ναός. ξιτοο στραφώμεν άριστερά, άκολουθοΰντες τήν πρδς τό Δέλβινον καί 'Αγίους Σαράντα άγουσαν μέχρι τοΰ 101ου περίπου σταδίου μετά τδ Δέλβινον, καί εντεύθεν πάλιν άκολουθήσωμεν ήμιονικήν όδόν μέχρι βουνώδους παρά τήν θάλασσαν τοποθεσίας νοτίως τής Νιβίτσης, θά εΰρωμεν μεταξύ βραχωδών υπωρειών τά έρείπια τής μονής τής Κοκαμιάς μετά μικροσκοπικοΰ έν αύτή ναού τής Θεοτόκου (είκ ).
14 256 Πρακτικά τοΰ 1914 Ούτος είναι τρίκογχος (είκ. 13) καί εχει μέγεθος κατά τον μείζονα άξονα τοϋ τετραπλεύρου, έφ ου έρείδονται αί κόγχαι , κατά δέ τον έτερον Διασχίζεται κατά μήκος ύπό ένδς μόνου κλίτους καμαρωτού πλάτους ίσου προς την μέσην κόγχην, μικροτέραν οδσαν των πλαγίων. Αύται συμπίπτουσι προς τό κέντρον τοΰ ναοΰ καί εκβάλλουσι πρός Ιν εκατέρωθεν τοξωτόν Είκ. 12. Κοκαμιας ναόν όπιοΰία οψις. όρθογώνιον την τομήν κοίλωμα. Ή μεταξύ των δυο τούτων τοξωτών κοιλωμάτων άπόστασις είναι μείζων τοΰ πλάτους τοΰ μέσου κλίτους, σχηματίζουσι δέ τά μέτωπα των έξεχόντων έκατέρωθεν τοξωτών χειλέων, έξ ών έμετρήθη ή άπόστασις, τάς δύο πλευράς τετραγώνου άνοίγματος. Διακοπτομένου τοΰ μέσου'κλίτους κατ ϊσην άπόστασιν έν τψ κέντρφ, σχηματίζονται αί ετεραι δύο
15 ΒυξαντιακοΙ ναοί της Βορείου Ηπειρον. 257 Είκ. 13. Κοκομιάς ναόν κάτοψίζ. 17
Βασικές Γεωμετρικές έννοιες
 Βασικές Γεωμετρικές έννοιες Σημείο Με την άκρη του μολυβιού μου ακουμπώντας την σε ένα κομμάτι χαρτί αφήνω ένα σημάδι το οποίο το λέω σημείο. Το σημείο το δίνω όνομα γράφοντας πάνω απ αυτό ένα κεφαλαίο
Βασικές Γεωμετρικές έννοιες Σημείο Με την άκρη του μολυβιού μου ακουμπώντας την σε ένα κομμάτι χαρτί αφήνω ένα σημάδι το οποίο το λέω σημείο. Το σημείο το δίνω όνομα γράφοντας πάνω απ αυτό ένα κεφαλαίο
Ή από τής 30 Ιουνίου μέχρι τής 10 Ιουλίου διαρκέσασα κατά τό
 264 Πρακτικά τής Αρχαιολογικής 'Εταιρείας 1950 12- ΑΝΑΣΚΑΦΗ ΕΝ ΤΗΝΩι Ή από τής 30 Ιουνίου μέχρι τής 10 Ιουλίου διαρκέσασα κατά τό παρόν έτος άνασκαφική μου εργασία έν Τήνφ δεν κατέστη δυνατόν λόγφ τοΰ
264 Πρακτικά τής Αρχαιολογικής 'Εταιρείας 1950 12- ΑΝΑΣΚΑΦΗ ΕΝ ΤΗΝΩι Ή από τής 30 Ιουνίου μέχρι τής 10 Ιουλίου διαρκέσασα κατά τό παρόν έτος άνασκαφική μου εργασία έν Τήνφ δεν κατέστη δυνατόν λόγφ τοΰ
01 Ιερός ναός Αγίου Γεωργίου ΓουμένισσΗΣ
 Ιερός ναός Αγίου Γεωργίου ΓουμένισσΗΣ Ιερός ναός Αγίου Γεωργίου ΓουμένισσΗΣ Το περίτεχνο τέμπλο του Αγίου Γεωργίου με τα πλευρικά τμήματά του Α Ν Α Δ Ε Ι Ξ Η Τ Ω Ν Μ Ε Τ Α Β Υ Ζ Α Ν Τ Ι Ν Ω Ν Μ Ν Η Μ Ε
Ιερός ναός Αγίου Γεωργίου ΓουμένισσΗΣ Ιερός ναός Αγίου Γεωργίου ΓουμένισσΗΣ Το περίτεχνο τέμπλο του Αγίου Γεωργίου με τα πλευρικά τμήματά του Α Ν Α Δ Ε Ι Ξ Η Τ Ω Ν Μ Ε Τ Α Β Υ Ζ Α Ν Τ Ι Ν Ω Ν Μ Ν Η Μ Ε
Δελτίον XAE 4 ( ), Περίοδος Δ'. Στη μνήμη του Γεωργίου Α. Σωτηρίου ( ) Σελ Ανδρέας ΣΤΥΛΙΑΝΟΥ ΑΘΗΝΑ 1966
 Μία τοιχογραφία της Κοιμήσεως της Θεοτόκου του ΙΑ αιώνος, εις τον ναόν του Αγίου Νικολάου της Στέγης (Κακοπετριά, Κύπρος).(Σημείωμα εις μνήμην του αειμνήστου Καθηγητού Γεωργίου Α. Σωτηρίου) (πίν. 75-76)
Μία τοιχογραφία της Κοιμήσεως της Θεοτόκου του ΙΑ αιώνος, εις τον ναόν του Αγίου Νικολάου της Στέγης (Κακοπετριά, Κύπρος).(Σημείωμα εις μνήμην του αειμνήστου Καθηγητού Γεωργίου Α. Σωτηρίου) (πίν. 75-76)
Ιερός Ναός Αγίων Ιάσωνος και Σωσιπάτρου ΚΕΡΚΥΡΑ
 Ιερός Ναός Αγίων Ιάσωνος και Σωσιπάτρου ΚΕΡΚΥΡΑ Μάριος Χειμαριός Μάριος Χειμαριός, Κέρκυρα, Ιερός Ναός Αγίων Ιάσωνος και Σωσιπάτρου (Αρχιτεκτονική/ Ιστορία ) www.24grammata.com1 1.ΕΙΣΑΓΩΓΗ Στην περιοχή
Ιερός Ναός Αγίων Ιάσωνος και Σωσιπάτρου ΚΕΡΚΥΡΑ Μάριος Χειμαριός Μάριος Χειμαριός, Κέρκυρα, Ιερός Ναός Αγίων Ιάσωνος και Σωσιπάτρου (Αρχιτεκτονική/ Ιστορία ) www.24grammata.com1 1.ΕΙΣΑΓΩΓΗ Στην περιοχή
Ιερός Ναός Αγίου Νικολάου, Πλατάνι Αχαΐας
 ΕΘΝΙΚΌ ΑΣΤΕΡΟΣΚΟΠΕΊΟ ΑΘΗΝΏΝ ΓΕΩΔΥΝΑΜΙΚΌ ΙΝΣΤΙΤΟΎΤΟ Π3.2.2 Μνημείο Αιγίου Ιερός Ναός Αγίου Νικολάου, Πλατάνι Αχαΐας Μονόχωρος τρίκογχος μετά τρούλου και τριμερή νάρθηκα ναός, του οποίου η κατασκευή τοποθετείται
ΕΘΝΙΚΌ ΑΣΤΕΡΟΣΚΟΠΕΊΟ ΑΘΗΝΏΝ ΓΕΩΔΥΝΑΜΙΚΌ ΙΝΣΤΙΤΟΎΤΟ Π3.2.2 Μνημείο Αιγίου Ιερός Ναός Αγίου Νικολάου, Πλατάνι Αχαΐας Μονόχωρος τρίκογχος μετά τρούλου και τριμερή νάρθηκα ναός, του οποίου η κατασκευή τοποθετείται
2 Β Βάσεις παραλληλογράµµου Βαρύκεντρο Γ Γεωµετρική κατασκευή Γεωµετρικός τόπος (ς) Γωνία Οι απέναντι πλευρές του. Κέντρο βάρους τριγώνου, δηλ. το σηµ
 1 ΛΕΞΙΚΟ ΓΕΩΜΕΤΡΙΚΩΝ ΟΡΩΝ Α Ακτίνιο Ακτίνα κύκλου Ακτίνα σφαίρας Άκρα ευθύγραµµου τµήµατος Αµβλεία γωνία Αµβλυγώνιο Ανάλογα ευθύγραµµα τµήµατα Αντιδιαµετρικό σηµείο Αντικείµενες ηµιευθείες Άξονας συµµετρίας
1 ΛΕΞΙΚΟ ΓΕΩΜΕΤΡΙΚΩΝ ΟΡΩΝ Α Ακτίνιο Ακτίνα κύκλου Ακτίνα σφαίρας Άκρα ευθύγραµµου τµήµατος Αµβλεία γωνία Αµβλυγώνιο Ανάλογα ευθύγραµµα τµήµατα Αντιδιαµετρικό σηµείο Αντικείµενες ηµιευθείες Άξονας συµµετρίας
Ε Ρ Ω Τ Η Σ Ε Ι Σ Θ Ε Ω Ρ Ι Α Σ.
 Μ Ν Σ Υ Κ Σ Ε Ρ Ω Τ Η Σ Ε Ι Σ Θ Ε Ω Ρ Ι Σ. 1. Να γράψετε τους τύπους του εμβαδού των : (α) τετραγώνου (β) ορθογωνίου παραλληλογράμμου (γ) παραλληλογράμμου (δ) τριγώνου (ε) ορθογωνίου τριγώνου (στ) τραπεζίου.
Μ Ν Σ Υ Κ Σ Ε Ρ Ω Τ Η Σ Ε Ι Σ Θ Ε Ω Ρ Ι Σ. 1. Να γράψετε τους τύπους του εμβαδού των : (α) τετραγώνου (β) ορθογωνίου παραλληλογράμμου (γ) παραλληλογράμμου (δ) τριγώνου (ε) ορθογωνίου τριγώνου (στ) τραπεζίου.
Επίμετρον. Εργασίαι στερεώσεως βυζαντινών μνημείων κατά το έτος 1923
 Επίμετρον. Εργασίαι στερεώσεως βυζαντινών μνημείων κατά το έτος 1923 Δελτίον XAE 11 (1924), Τεύχη α'-β', Περίοδος Β' Σελ. 90-94 ΑΘΗΝΑ 1924 ΕΠΙΜΕΤΡΟΝ ΕΡΓΑΣΙΑ! ΣΤΕΡΕΠΣΕΠΣ ΒΥΖΑΝΤΙΝΠΝ ΜΝΗΜΕΙΠΝ ΚΑΤΑ ΤΟ ΕΤΟΣ
Επίμετρον. Εργασίαι στερεώσεως βυζαντινών μνημείων κατά το έτος 1923 Δελτίον XAE 11 (1924), Τεύχη α'-β', Περίοδος Β' Σελ. 90-94 ΑΘΗΝΑ 1924 ΕΠΙΜΕΤΡΟΝ ΕΡΓΑΣΙΑ! ΣΤΕΡΕΠΣΕΠΣ ΒΥΖΑΝΤΙΝΠΝ ΜΝΗΜΕΙΠΝ ΚΑΤΑ ΤΟ ΕΤΟΣ
Μύες του πυελικού τοιχώματος
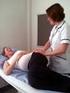 Μύες Πυέλου Μύες του πυελικού τοιχώματος Συμβάλλουν στο σχηματισμό των εσωτερικών πλάγιων τοιχωμάτων της πυελικής κοιλότητας. Εκφύονται μέσα από τη πυελική κοιλότητα αλλά καταφύονται έξω από αυτήν (μηριαίο).
Μύες Πυέλου Μύες του πυελικού τοιχώματος Συμβάλλουν στο σχηματισμό των εσωτερικών πλάγιων τοιχωμάτων της πυελικής κοιλότητας. Εκφύονται μέσα από τη πυελική κοιλότητα αλλά καταφύονται έξω από αυτήν (μηριαίο).
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ ( α μέρος )
 Πυθαγόρειο ενικό Λύκειο Σάμου ΕΠΝΛΗΨΗ ΕΩΜΕΤΡΙΣ ΛΥΚΕΙΟΥ ( α μέρος ) Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
Πυθαγόρειο ενικό Λύκειο Σάμου ΕΠΝΛΗΨΗ ΕΩΜΕΤΡΙΣ ΛΥΚΕΙΟΥ ( α μέρος ) Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό
Β.1.8. Παραπληρωματικές και Συμπληρωματικές γωνίες Κατά κορυφήν γωνίες
 Β.1.6. Είδη γωνιών Κάθετες ευθείες 1. Ορθή γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 90 ο. 2. Οξεία γωνία λέγεται κάθε γωνία με μέτρο μικρότερο των 90 ο. 3. Αμβλεία γωνία λέγεται κάθε γωνία
Β.1.6. Είδη γωνιών Κάθετες ευθείες 1. Ορθή γωνία λέγεται η γωνία της οποίας το μέτρο είναι ίσο με 90 ο. 2. Οξεία γωνία λέγεται κάθε γωνία με μέτρο μικρότερο των 90 ο. 3. Αμβλεία γωνία λέγεται κάθε γωνία
Κείμενο Εκκλησίας του Τιμίου Σταυρού στο Πελέντρι. Ελληνικά
 1 Κείμενο Εκκλησίας του Τιμίου Σταυρού στο Πελέντρι Ελληνικά 2 ΕΚΚΛΗΣΙΑ ΤΟΥ ΤΙΜΙΟΥ ΣΤΑΥΡΟΥ ΣΤΟ ΠΕΛΕΝΤΡΙ Η εκκλησία του Τιμίου Σταυρού στο Πελέντρι φαίνεται να χτίστηκε λίγο μετά τα μέσα του 12 ου αιώνα
1 Κείμενο Εκκλησίας του Τιμίου Σταυρού στο Πελέντρι Ελληνικά 2 ΕΚΚΛΗΣΙΑ ΤΟΥ ΤΙΜΙΟΥ ΣΤΑΥΡΟΥ ΣΤΟ ΠΕΛΕΝΤΡΙ Η εκκλησία του Τιμίου Σταυρού στο Πελέντρι φαίνεται να χτίστηκε λίγο μετά τα μέσα του 12 ου αιώνα
Ένα υγρό σε δοχείο και το υδροστατικό παράδοξο.
 Ένα υγρό σε δοχείο και το υδροστατικό παράδοξο. Ας μελετήσουμε τι συμβαίνει, όταν ένα υγρό περιέχεται σε ένα ακίνητο δοχείο. Τι δυνάμεις ασκεί στο δοχείο; Τι σχέση έχουν αυτές με το βάρος του υγρού; Εφαρμογή
Ένα υγρό σε δοχείο και το υδροστατικό παράδοξο. Ας μελετήσουμε τι συμβαίνει, όταν ένα υγρό περιέχεται σε ένα ακίνητο δοχείο. Τι δυνάμεις ασκεί στο δοχείο; Τι σχέση έχουν αυτές με το βάρος του υγρού; Εφαρμογή
'Αριθμός 811 Ο ΠΕΡΙ ΠΡΟΣΤΑΣΙΑΣ ΘΗΡΑΜΑΤΟΣ ΚΑΙ ΑΓΡΙΩΝ ΠΤΗΝΩΝ ΝΟΜΟΣ (ΚΕΦ. 65 ΚΑΙ ΝΟΜΟΙ 9 ΤΟΥ 1964 ΚΑΙ 76 ΤΟΥ 1965)
 740 μεθ' όδου άγούσης έκ του χωρίου «Σπαθαρικόν» προς την πάλαιαν κυρίαν όδόν 'Αποστόλου 'Ανδρέα 'Αμμοχώστου παρά την βορειοδυτικήν γωνίαν του τεμαχίου αρ. 27 του Κυβερνητικού Χώρο μετρικού Σχεδίου άρ.
740 μεθ' όδου άγούσης έκ του χωρίου «Σπαθαρικόν» προς την πάλαιαν κυρίαν όδόν 'Αποστόλου 'Ανδρέα 'Αμμοχώστου παρά την βορειοδυτικήν γωνίαν του τεμαχίου αρ. 27 του Κυβερνητικού Χώρο μετρικού Σχεδίου άρ.
Επαναληπτικές Ασκήσεις
 Β' Γυμν. - Επαναληπτικές Ασκήσεις 1 Άσκηση 1 Απλοποίησε τις αλγεβρικές παραστάσεις (α) 2y 2z 8ω 8ω 2y 2z (β) 1x 2y 3z 3 3 z 2z z 2 x y Επαναληπτικές Ασκήσεις Άλγεβρα - Γεωμετρία Άσκηση 2 Υπολόγισε την
Β' Γυμν. - Επαναληπτικές Ασκήσεις 1 Άσκηση 1 Απλοποίησε τις αλγεβρικές παραστάσεις (α) 2y 2z 8ω 8ω 2y 2z (β) 1x 2y 3z 3 3 z 2z z 2 x y Επαναληπτικές Ασκήσεις Άλγεβρα - Γεωμετρία Άσκηση 2 Υπολόγισε την
Μύες Θώρακα - Κορμού
 Μύες Θώρακα - Κορμού Μύες μαστικής περιοχής Μύες πρόσθιου θωρακικού τοιχώματος Μύες κοιλιακού τοιχώματος Μύες ράχης Μύες οπίσθιου κοιλιακού τοιχώματος 1 2 3 1 Μείζων θωρακικός 1 Ελάσσων θωρακικός 2 3Υποκλείδιος
Μύες Θώρακα - Κορμού Μύες μαστικής περιοχής Μύες πρόσθιου θωρακικού τοιχώματος Μύες κοιλιακού τοιχώματος Μύες ράχης Μύες οπίσθιου κοιλιακού τοιχώματος 1 2 3 1 Μείζων θωρακικός 1 Ελάσσων θωρακικός 2 3Υποκλείδιος
Γ Ε Ω Μ Ε Τ Ρ Ι Α - Κ Ε Φ Α Λ Α Ι Ο 1
 Ε Ω Μ Ε Τ Ρ Ι Α - Κ Ε Φ Α Λ Α Ι Ο 1 Εμβαδά Επίπεδων Σχημάτων & Πυθαγόρειο Θεώρημα Η συλλογή των ασκήσεων προέρχεται από μια ποικιλία πηγών, σημαντικότερες από τις οποίες είναι το Mathematica.gr, παλιότερα
Ε Ω Μ Ε Τ Ρ Ι Α - Κ Ε Φ Α Λ Α Ι Ο 1 Εμβαδά Επίπεδων Σχημάτων & Πυθαγόρειο Θεώρημα Η συλλογή των ασκήσεων προέρχεται από μια ποικιλία πηγών, σημαντικότερες από τις οποίες είναι το Mathematica.gr, παλιότερα
ΓΕΩΜΕΤΡΙΑ ΤΗΣ Α ΛΥΚΕΙΟΥ. ΚΕΦΑΚΑΙΟ 3 ο -ΤΡΙΓΩΝΑ
 ΓΕΩΜΕΤΡΙΑ ΤΗΣ Α ΛΥΚΕΙΟΥ ΟΙ ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΑΠΟΤΕΛΟΥΝ ΜΕΡΟΣ ΤΟΥ ΘΕΜΑΤΟΣ Α ΤΩΝ ΕΞΕΤΑΣΕΩΝ (ΘΕΜΑ ΘΕΩΡΙΑΣ) Α. ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ - ΛΑΘΟΥΣ ΚΕΦΑΚΑΙΟ 3 ο -ΤΡΙΓΩΝΑ 1. Ένα τρίγωνο είναι οξυγώνιο όταν έχει
ΓΕΩΜΕΤΡΙΑ ΤΗΣ Α ΛΥΚΕΙΟΥ ΟΙ ΕΡΩΤΗΣΕΙΣ ΚΛΕΙΣΤΟΥ ΤΥΠΟΥ ΑΠΟΤΕΛΟΥΝ ΜΕΡΟΣ ΤΟΥ ΘΕΜΑΤΟΣ Α ΤΩΝ ΕΞΕΤΑΣΕΩΝ (ΘΕΜΑ ΘΕΩΡΙΑΣ) Α. ΕΡΩΤΗΣΕΙΣ ΣΩΣΤΟΥ - ΛΑΘΟΥΣ ΚΕΦΑΚΑΙΟ 3 ο -ΤΡΙΓΩΝΑ 1. Ένα τρίγωνο είναι οξυγώνιο όταν έχει
5o Φύλλο Ασκήσεων. Γενικής Παιδείας. ΑΣΚΗΣΗ 1η. ΑΣΚΗΣΗ 2η. Να βρείτε τα διαστήματα μονοτονίας και τα ακρότατα των συναρτήσεων :
 ΛΥΚΕΙΟ Μ Α Θ Η Μ Α Τ Ι Κ Α Γ Λ Υ Κ Ε Ι Ο Υ Κ E Φ Α Λ Α Ι Ο Δ Ι Α Φ Ο Ρ Ι Κ Ο Σ 1ο Λ Ο Γ Ι Σ Μ Ο Σ ΤΡΙΜΗΣ ΠΑΝΤΕΛΗΣ ΜΑΘΗΜΑΤΙΚΟΣ Γενικής Παιδείας 5o Φύλλο Ασκήσεων ΑΣΚΗΣΗ 1η Να βρείτε τα διαστήματα μονοτονίας
ΛΥΚΕΙΟ Μ Α Θ Η Μ Α Τ Ι Κ Α Γ Λ Υ Κ Ε Ι Ο Υ Κ E Φ Α Λ Α Ι Ο Δ Ι Α Φ Ο Ρ Ι Κ Ο Σ 1ο Λ Ο Γ Ι Σ Μ Ο Σ ΤΡΙΜΗΣ ΠΑΝΤΕΛΗΣ ΜΑΘΗΜΑΤΙΚΟΣ Γενικής Παιδείας 5o Φύλλο Ασκήσεων ΑΣΚΗΣΗ 1η Να βρείτε τα διαστήματα μονοτονίας
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ
 ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ 1)Τι ονομάζεται διχοτόμος μιας γωνίας ; Διχοτόμος γωνίας ονομάζεται η ημιευθεία που έχει αρχή την κορυφή της γωνίας και τη χωρίζει σε δύο ίσες γωνίες. 2)Να
ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ 1)Τι ονομάζεται διχοτόμος μιας γωνίας ; Διχοτόμος γωνίας ονομάζεται η ημιευθεία που έχει αρχή την κορυφή της γωνίας και τη χωρίζει σε δύο ίσες γωνίες. 2)Να
ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ
 ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό σας. ΚΕΦΑΛΑΙΟ 1 1. Να συμπληρώσετε
ΕΠΑΝΑΛΗΨΗ Β ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Να βρείτε στην αντίστοιχη σελίδα του σχολικού σας βιβλίου το ζητούμενο της κάθε ερώτησης που δίνεται παρακάτω και να το γράψετε στο τετράδιό σας. ΚΕΦΑΛΑΙΟ 1 1. Να συμπληρώσετε
Γεωμετρία. 63. Σε περίπτωση που η αρχή, το σημείο Ο, βρίσκεται πάνω σε μια ευθεία χχ τότε η
 Γεωμετρία Κεφάλαιο 1: Βασικές γεωμετρικές έννοιες Β.1.1 61.Η ευθεία είναι βασική έννοια της γεωμετρίας που την αντιλαμβανόμαστε ως την γραμμή που αφήνει ο κανόνας (χάρακας).συμβολίζεται με μικρά γράμματα
Γεωμετρία Κεφάλαιο 1: Βασικές γεωμετρικές έννοιες Β.1.1 61.Η ευθεία είναι βασική έννοια της γεωμετρίας που την αντιλαμβανόμαστε ως την γραμμή που αφήνει ο κανόνας (χάρακας).συμβολίζεται με μικρά γράμματα
ΕΡΩΤΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ
 ΚΕΦΑΛΑΙΟ 1 ΕΡΩΤΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ Τι είναι ένα ευθύγραμμο τμήμα ΑΒ; Πώς ονομάζονται τα σημεία Α και Β; 1 ος ορισμός : Είναι η «ίσια» γραμμή που ενώνει τα δύο σημεία Α και Β. 2 ος ορισμός : Είναι
ΚΕΦΑΛΑΙΟ 1 ΕΡΩΤΗΣΕΙΣ ΓΕΩΜΕΤΡΙΑΣ Α ΓΥΜΝΑΣΙΟΥ Τι είναι ένα ευθύγραμμο τμήμα ΑΒ; Πώς ονομάζονται τα σημεία Α και Β; 1 ος ορισμός : Είναι η «ίσια» γραμμή που ενώνει τα δύο σημεία Α και Β. 2 ος ορισμός : Είναι
Γ Ε Ω Μ Ε Τ Ρ Ι Α - Κ Ε Φ Α Λ Α Ι Ο 2
 Ε Ω Μ Ε Τ Ρ Ι - Κ Ε Φ Λ Ι Ο 2 Τριγωνομετρία ΛΟΟΣ ΕΥΘΥΡΜΜΩΝ ΤΜΗΜΤΩΝ α α β α β α β 1. ν 2, να υπολογίσετε τους λόγους :,, β β β α β 2. Σε ένα ισόπλευρο τρίγωνο με πλευρά 6 cm και ύψος, να υπολογίσετε τους
Ε Ω Μ Ε Τ Ρ Ι - Κ Ε Φ Λ Ι Ο 2 Τριγωνομετρία ΛΟΟΣ ΕΥΘΥΡΜΜΩΝ ΤΜΗΜΤΩΝ α α β α β α β 1. ν 2, να υπολογίσετε τους λόγους :,, β β β α β 2. Σε ένα ισόπλευρο τρίγωνο με πλευρά 6 cm και ύψος, να υπολογίσετε τους
4 η εκάδα θεµάτων επανάληψης
 4 η εκάδα θεµάτων επανάληψης 3. ίνεται τετράγωνο µε κέντρο Ο και το µέσο του. Η τέµνει την στο. είξτε ότι = Το τρίγωνο είναι ορθογώνιο και ισοσκελές i Ο = 4 Τα ορθογώνια τρίγωνα και έχουν = και = άρα είναι
4 η εκάδα θεµάτων επανάληψης 3. ίνεται τετράγωνο µε κέντρο Ο και το µέσο του. Η τέµνει την στο. είξτε ότι = Το τρίγωνο είναι ορθογώνιο και ισοσκελές i Ο = 4 Τα ορθογώνια τρίγωνα και έχουν = και = άρα είναι
Ορισµοί. Ένα τετράπλευρο λέγεται εγγεγραµµένο σε κύκλο, αν οι κορυφές του είναι σηµεία του κύκλου.
 6.5 6.6 ΘΩΡΙ. Ορισµοί Ένα τετράπλευρο λέγεται εγγεγραµµένο σε κύκλο, αν οι κορυφές του είναι σηµεία του κύκλου. Ένα τετράπλευρο λέγεται εγγράψιµο σε κύκλο, όταν µπορεί να γραφεί κύκλος που να διέρχεται
6.5 6.6 ΘΩΡΙ. Ορισµοί Ένα τετράπλευρο λέγεται εγγεγραµµένο σε κύκλο, αν οι κορυφές του είναι σηµεία του κύκλου. Ένα τετράπλευρο λέγεται εγγράψιµο σε κύκλο, όταν µπορεί να γραφεί κύκλος που να διέρχεται
 ΚΕΦΑΛΑΙΟ 1 ο ΠΡΩΤΑΡΧΙΚΕΣ ΓΕΩΜΕΤΡΙΚΕΣ ΕΝΝΟΙΕΣ Τα αξιώματα είναι προτάσεις που δεχόμαστε ως αληθείς, χωρίς απόδειξη: Από δύο σημεία διέρχεται μοναδική ευθεία. Για κάθε ευθεία υπάρχει τουλάχιστον ένα σημείο
ΚΕΦΑΛΑΙΟ 1 ο ΠΡΩΤΑΡΧΙΚΕΣ ΓΕΩΜΕΤΡΙΚΕΣ ΕΝΝΟΙΕΣ Τα αξιώματα είναι προτάσεις που δεχόμαστε ως αληθείς, χωρίς απόδειξη: Από δύο σημεία διέρχεται μοναδική ευθεία. Για κάθε ευθεία υπάρχει τουλάχιστον ένα σημείο
Σωστό -λάθος. 3) Δύο ευθείες κάθετες προς μία τρίτη ευθεία είναι μεταξύ τους παράλληλες.
 Σωστό -λάθος Α. Για καθεμιά από τις παρακάτω προτάσεις να γράψετε στο τετράδιό σας τον αριθμό της και, ακριβώς δίπλα, την ένδειξη (Σ), αν η πρόταση είναι σωστή, ή (Λ), αν αυτή είναι λανθασμένη. 1) Οι οξείες
Σωστό -λάθος Α. Για καθεμιά από τις παρακάτω προτάσεις να γράψετε στο τετράδιό σας τον αριθμό της και, ακριβώς δίπλα, την ένδειξη (Σ), αν η πρόταση είναι σωστή, ή (Λ), αν αυτή είναι λανθασμένη. 1) Οι οξείες
Στο προοπτικό ανάγλυφο για τη ευθεία του ορίζοντα χρησιμοποιούμε ένα δεύτερο κατακόρυφο επίπεδο Π 1
 ΠΡΟΟΠΤΙΚΟ ΑΝΑΓΛΥΦΟ Το προοπτικό ανάγλυφο, όπως το επίπεδο προοπτικό, η στερεοσκοπική εικόνα κ.λπ. είναι τρόποι παρουσίασης και απεικόνισης των αρχιτεκτονικών συνθέσεων. Το προοπτικό ανάγλυφο είναι ένα
ΠΡΟΟΠΤΙΚΟ ΑΝΑΓΛΥΦΟ Το προοπτικό ανάγλυφο, όπως το επίπεδο προοπτικό, η στερεοσκοπική εικόνα κ.λπ. είναι τρόποι παρουσίασης και απεικόνισης των αρχιτεκτονικών συνθέσεων. Το προοπτικό ανάγλυφο είναι ένα
ΚΥΚΛΟ. κάθετη στη χορδή ΑΒ. τη χορδή. του κέντρου Κ από. (βλέπε σχήμα).
 ΑΣΚΗΣΕΙΣ ΣΤΟΝ ΚΥΚΛΟ 1. Να κατασκευάσετε έναν κύκλο και να πάρετε μια χορδή του ΑΒ. Από το κέντρο Κ του κύκλου να φέρετε κάθετη στη χορδή ΑΒ η οποία τέμνει τη χορδή στο σημείο Μ. Να διαπιστώσετε με μέτρηση
ΑΣΚΗΣΕΙΣ ΣΤΟΝ ΚΥΚΛΟ 1. Να κατασκευάσετε έναν κύκλο και να πάρετε μια χορδή του ΑΒ. Από το κέντρο Κ του κύκλου να φέρετε κάθετη στη χορδή ΑΒ η οποία τέμνει τη χορδή στο σημείο Μ. Να διαπιστώσετε με μέτρηση
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7
 ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
ΑΡΧΗ 1ης ΣΕΛΙΔΑΣ ΘΕΜΑ 1 Ο : ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ : ΦΥΣΙΚΗ ΚΑΤΕΥΘΥΝΣΗΣ ΤΑΞΗ : Γ ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ ΠΕΡΙΟΔΟΥ : ΝΟΕΜΒΡΙΟΣ 2015 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ : 7 Στις παρακάτω ερωτήσεις 1 έως 4 να γράψετε στο τετράδιό σας
Κείμενο Αγίου Νικολάου της Στέγης. Ελληνικά
 1 Κείμενο Αγίου Νικολάου της Στέγης Ελληνικά 2 Ο Άγιος Νικόλαος της Στέγης Πήρε το όνομα του μετά την προσθήκη της δεύτερης Στέγης του ναού τον 13ον αιώνα, για την προστασία του από τα χιόνα και τη βροχή.
1 Κείμενο Αγίου Νικολάου της Στέγης Ελληνικά 2 Ο Άγιος Νικόλαος της Στέγης Πήρε το όνομα του μετά την προσθήκη της δεύτερης Στέγης του ναού τον 13ον αιώνα, για την προστασία του από τα χιόνα και τη βροχή.
ΕΠΑΝΑΛΗΨΗ ΓΕΩΜΕΤΡΙΑΣ Β ΛΥΚΕΙΟΥ
 ΕΠΝΛΗΨΗ ΕΩΜΕΤΡΙΣ ΛΥΚΕΙΟΥ 1 Σε τρίγωνο με > και ορθόκεντρο Η να δείξετε ότι: Δίνεται τρίγωνο στο οποίο ισχύει: α β γ βγ Να δείξετε ότι: A 10 Δίνεται τρίγωνο με πλευρές α, β, γ και διάμεσο μα ν ισχύει η
ΕΠΝΛΗΨΗ ΕΩΜΕΤΡΙΣ ΛΥΚΕΙΟΥ 1 Σε τρίγωνο με > και ορθόκεντρο Η να δείξετε ότι: Δίνεται τρίγωνο στο οποίο ισχύει: α β γ βγ Να δείξετε ότι: A 10 Δίνεται τρίγωνο με πλευρές α, β, γ και διάμεσο μα ν ισχύει η
ΘΕΩΡΙΑ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΓΙΑ ΤΗΝ Α ΓΥΜΝΑΣΙΟΥ Α. ΓΩΝΙΕΣ - ΚΥΚΛΟΣ
 ΘΕΩΡΙΑ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΓΙΑ ΤΗΝ Α ΓΥΜΝΑΣΙΟΥ Α. ΓΩΝΙΕΣ - ΚΥΚΛΟΣ 1. Απόσταση δύο σηµείων Α και Β είναι το µήκος του ευθύγραµµου τµήµατος που τα ενώνει. 2. Γωνία είναι το µέρος του επιπέδου που βρίσκεται µεταξύ
ΘΕΩΡΙΑ ΣΤΗ ΓΕΩΜΕΤΡΙΑ ΓΙΑ ΤΗΝ Α ΓΥΜΝΑΣΙΟΥ Α. ΓΩΝΙΕΣ - ΚΥΚΛΟΣ 1. Απόσταση δύο σηµείων Α και Β είναι το µήκος του ευθύγραµµου τµήµατος που τα ενώνει. 2. Γωνία είναι το µέρος του επιπέδου που βρίσκεται µεταξύ
ΜΑΘΗΜΑ 7ο ΜΕΡΟΣ Α Η ΔΟΜΗ ΤΩΝ ΗΜΙΣΦΑΙΡΙΩΝ
 ΜΑΘΗΜΑ 7ο ΜΕΡΟΣ Α Η ΔΟΜΗ ΤΩΝ ΗΜΙΣΦΑΙΡΙΩΝ Η ΛΕΥΚΗ ΟΥΣΙΑ ΤΩΝ ΗΜΙΣΦΑΙΡΙΩΝ ΤΟΥ ΕΓΚΕΦΑΛΟΥ Η λευκή ουσία συντίθεται από εμύελες νευρικές ίνες διαφόρων διαμέτρων και νευρογλοία Οι νευρικές ίνες κατατάσσονται
ΜΑΘΗΜΑ 7ο ΜΕΡΟΣ Α Η ΔΟΜΗ ΤΩΝ ΗΜΙΣΦΑΙΡΙΩΝ Η ΛΕΥΚΗ ΟΥΣΙΑ ΤΩΝ ΗΜΙΣΦΑΙΡΙΩΝ ΤΟΥ ΕΓΚΕΦΑΛΟΥ Η λευκή ουσία συντίθεται από εμύελες νευρικές ίνες διαφόρων διαμέτρων και νευρογλοία Οι νευρικές ίνες κατατάσσονται
ΕΙΔΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΑΠΟ ΟΠΛΙΣΜΕΝΟ ΚΑΙ ΠΡΟΕΝΤΕΤΑΜΕΝΟ ΣΚΥΡΟΔΕΜΑ. Γ. Παναγόπουλος Καθηγητής Εφαρμογών, ΤΕΙ Σερρών
 ΕΙΔΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΑΠΟ ΟΠΛΙΣΜΕΝΟ ΚΑΙ ΠΡΟΕΝΤΕΤΑΜΕΝΟ ΣΚΥΡΟΔΕΜΑ Γ. Παναγόπουλος Καθηγητής Εφαρμογών, ΤΕΙ Σερρών Κελύφη οπλισμένου σκυροδέματος Κελύφη Ο/Σ Καμπύλοι επιφανειακοί φορείς μικρού πάχους Εντατική
ΕΙΔΙΚΕΣ ΚΑΤΑΣΚΕΥΕΣ ΑΠΟ ΟΠΛΙΣΜΕΝΟ ΚΑΙ ΠΡΟΕΝΤΕΤΑΜΕΝΟ ΣΚΥΡΟΔΕΜΑ Γ. Παναγόπουλος Καθηγητής Εφαρμογών, ΤΕΙ Σερρών Κελύφη οπλισμένου σκυροδέματος Κελύφη Ο/Σ Καμπύλοι επιφανειακοί φορείς μικρού πάχους Εντατική
Οσφυϊκό Πλέγµα και Νεύρα
 Οσφυϊκό Πλέγµα και Νεύρα Εισαγωγή Σχηµατισµός Κλάδοι του Οσφυϊκού Πλέγµατος Μηριαίο Νεύρο (Ο2-Ο4) Εισαγωγή Η κινητικότητα και η γενική αισθητικότητα του κάτω άκρου εξυπηρετούνται από τους τελικούς κλάδους
Οσφυϊκό Πλέγµα και Νεύρα Εισαγωγή Σχηµατισµός Κλάδοι του Οσφυϊκού Πλέγµατος Μηριαίο Νεύρο (Ο2-Ο4) Εισαγωγή Η κινητικότητα και η γενική αισθητικότητα του κάτω άκρου εξυπηρετούνται από τους τελικούς κλάδους
Κτηνιατρικόν Συμβούλιον Κύπρου. Έγένετο τη 9η 'Οκτωβρίου 1969.
 761 'Αριθμός 813 Ο ΠΕΡΙ ΕΓΓΡΑΦΗΣ ΚΤΗΝΙΑΤΡΩΝ ΝΟΜΟΣ, ΚΕΦ. 103 Κτηνιατρικόν Συμβούλιον Κύπρου Διορισμός δυνάμει τοΰ άρθρου 3 (1), (β) και (γ) Ενασκούν τάς εξουσίας δι' ών περιβέβληται δυνάμει τοΰ εδαφίου
761 'Αριθμός 813 Ο ΠΕΡΙ ΕΓΓΡΑΦΗΣ ΚΤΗΝΙΑΤΡΩΝ ΝΟΜΟΣ, ΚΕΦ. 103 Κτηνιατρικόν Συμβούλιον Κύπρου Διορισμός δυνάμει τοΰ άρθρου 3 (1), (β) και (γ) Ενασκούν τάς εξουσίας δι' ών περιβέβληται δυνάμει τοΰ εδαφίου
ΘΕΜΑΤΑ ΣΤΗΝ ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ
 Επιμέλεια: ιώργος Ράπτης ΘΕΤ ΣΤΗΝ ΕΩΕΤΡΙ ΛΥΚΕΙΟΥ ΘΕ 1 ο. Να αποδείξετε ότι το εμβαδό τραπεζίου με βάσεις 1, και ύψος υ δίνεται από τον τύπο: ( 1+ ) υ Ε= ονάδες 1 B. ν φν, λν και αν είναι: η γωνία, η πλευρά
Επιμέλεια: ιώργος Ράπτης ΘΕΤ ΣΤΗΝ ΕΩΕΤΡΙ ΛΥΚΕΙΟΥ ΘΕ 1 ο. Να αποδείξετε ότι το εμβαδό τραπεζίου με βάσεις 1, και ύψος υ δίνεται από τον τύπο: ( 1+ ) υ Ε= ονάδες 1 B. ν φν, λν και αν είναι: η γωνία, η πλευρά
9. ΑΝΑΣΚΑΦΗ ΒΟΡΕΙΩΣ ΤΗΣ ΒΑΣΙΛΙΚΗΣ ΤΟΥ ΑΓΙΟΥ ΔΗΜΗΤΡΙΟΥ ΘΕΣΣΑΛΟΝΙΚΗΣ
 9. ΑΝΑΣΚΑΦΗ ΒΟΡΕΙΩΣ ΤΗΣ ΒΑΣΙΛΙΚΗΣ ΤΟΥ ΑΓΙΟΥ ΔΗΜΗΤΡΙΟΥ ΘΕΣΣΑΛΟΝΙΚΗΣ Έν συνεχεία των προ ετών ύπο της Αρχαιολογικής Εταιρείας διά τοϋ Γ. Σωτηρίου γενομένων σκαφικών ερευνών, βορείως τής βασιλικής τοϋ 'Αγίου
9. ΑΝΑΣΚΑΦΗ ΒΟΡΕΙΩΣ ΤΗΣ ΒΑΣΙΛΙΚΗΣ ΤΟΥ ΑΓΙΟΥ ΔΗΜΗΤΡΙΟΥ ΘΕΣΣΑΛΟΝΙΚΗΣ Έν συνεχεία των προ ετών ύπο της Αρχαιολογικής Εταιρείας διά τοϋ Γ. Σωτηρίου γενομένων σκαφικών ερευνών, βορείως τής βασιλικής τοϋ 'Αγίου
Ο Ιερός Ναός του Αγ. Παντελεήμονος στη Μεσαιωνική Πόλη της Ρόδου
 28/07/2019 Ο Ιερός Ναός του Αγ. Παντελεήμονος στη Μεσαιωνική Πόλη της Ρόδου / Ορθόδοξες Προβολές Στη βορειοανατολική ακμή των τειχών της μεσαιωνικής πόλης της Ρόδου και σε απόσταση μόλις Παντελεήμονος.
28/07/2019 Ο Ιερός Ναός του Αγ. Παντελεήμονος στη Μεσαιωνική Πόλη της Ρόδου / Ορθόδοξες Προβολές Στη βορειοανατολική ακμή των τειχών της μεσαιωνικής πόλης της Ρόδου και σε απόσταση μόλις Παντελεήμονος.
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Ιστορία Κατασκευών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ιστορία Κατασκευών Ενότητα 3.3: Θολοδομικά Συστήματα Θολοδομικά συστήματα στο Βυζάντιο Δρ Σταματίνα Γ. Μαλικούτη Τμήμα Πολιτικών
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Ιστορία Κατασκευών Ενότητα 3.3: Θολοδομικά Συστήματα Θολοδομικά συστήματα στο Βυζάντιο Δρ Σταματίνα Γ. Μαλικούτη Τμήμα Πολιτικών
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΗΤΙΚΗ ΓΕΩΜΕΤΡΙΑ
 ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΗΤΙΚΗ ΓΕΩΜΕΤΡΙΑ ΟΡΙΣΜΟΙ Ευθύγραμμο τμήμα είναι το κομμάτι της ευθείας που έχει αρχή και τέλος. Ημιευθεια Είναι το κομμάτι της ευθείας που έχει αρχή αλλά όχι
ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΘΕΩΡΗΤΙΚΗ ΓΕΩΜΕΤΡΙΑ ΟΡΙΣΜΟΙ Ευθύγραμμο τμήμα είναι το κομμάτι της ευθείας που έχει αρχή και τέλος. Ημιευθεια Είναι το κομμάτι της ευθείας που έχει αρχή αλλά όχι
Σημείο Επίπεδο ο χώρος η ευθεία η έννοια του σημείου μεταξύ δύο άλλων σημείων και η έννοια της ισότητας δύο σχημάτων.
 ΜΑΘΗΜΑ 1 αόριστες έννοιες Έννοιες που είναι τόσο απλές και οικείες από την εμπειρία μας, ώστε δεν μπορούμε να βρούμε πιο απλές με τη βοήθεια των οποίων να τις περιγράψουμε Σημείο Επίπεδο ο χώρος η ευθεία
ΜΑΘΗΜΑ 1 αόριστες έννοιες Έννοιες που είναι τόσο απλές και οικείες από την εμπειρία μας, ώστε δεν μπορούμε να βρούμε πιο απλές με τη βοήθεια των οποίων να τις περιγράψουμε Σημείο Επίπεδο ο χώρος η ευθεία
ΑΣΚHΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΟΥ
 ΣΚHΣΙΣ ΠΝΛΗΨΗΣ ΜΘΗΜΤΙΚΩΝ ΥΜΝΣΙΟΥ ΦΥΛΧΤΟΣ Π. ΣΜΪΛΗ. ΜYΡΙΙΝΝΗΣ. 1. Να λύσετε τις εξισώσεις : α) χ (χ 1) 3 = (1+5χ) β) x (3 3 x) 1 3(1 x) γ ) χ 3(χ ) +7 =( 3)( 5) 3χ δ) 5χ 19 3-(4χ-5) =χ (6χ 5) ε) 4 x 5 x
ΣΚHΣΙΣ ΠΝΛΗΨΗΣ ΜΘΗΜΤΙΚΩΝ ΥΜΝΣΙΟΥ ΦΥΛΧΤΟΣ Π. ΣΜΪΛΗ. ΜYΡΙΙΝΝΗΣ. 1. Να λύσετε τις εξισώσεις : α) χ (χ 1) 3 = (1+5χ) β) x (3 3 x) 1 3(1 x) γ ) χ 3(χ ) +7 =( 3)( 5) 3χ δ) 5χ 19 3-(4χ-5) =χ (6χ 5) ε) 4 x 5 x
4 η εκάδα θεµάτων επανάληψης
 4 η εκάδα θεµάτων επανάληψης 3. ίνεται τετράγωνο µε κέντρο Ο και Μ το µέσο του. Η Μ τέµνει την στο. είξτε ότι = Το τρίγωνο είναι ορθογώνιο και ισοσκελές i ΟΜ = 4 Τα ορθογώνια τρίγωνα Μ και Μ έχουν Μ =
4 η εκάδα θεµάτων επανάληψης 3. ίνεται τετράγωνο µε κέντρο Ο και Μ το µέσο του. Η Μ τέµνει την στο. είξτε ότι = Το τρίγωνο είναι ορθογώνιο και ισοσκελές i ΟΜ = 4 Τα ορθογώνια τρίγωνα Μ και Μ έχουν Μ =
'Αριθμός 808 Ο ΠΕΡΙ ΠΡΟΣΤΑΣΙΑΣ ΘΗΡΑΜΑΤΟΣ ΚΑΙ ΑΓΡΙΩΝ ΠΤΗΝΩΝ ΝΟΜΟΣ (ΚΕΦ. 65 ΚΑΙ ΝΟΜΟΙ 9 ΤΟΥ 1964 ΚΑΙ 76 ΤΟΥ 1965)
 722 'Αριθμός 808 Ο ΠΕΡΙ ΠΡΟΣΤΑΣΙΑΣ ΘΗΡΑΜΑΤΟΣ ΚΑΙ ΑΓΡΙΩΝ ΠΤΗΝΩΝ ΝΟΜΟΣ (ΚΕΦ. 65 ΚΑΙ ΝΟΜΟΙ 9 ΤΟΥ 1964 ΚΑΙ 76 ΤΟΥ 1965) Διάταγμα δυνάμει του άρθρου 20 Ό Υπουργός 'Εσωτερικών, ένασκών τάς διά του άρθρου 20
722 'Αριθμός 808 Ο ΠΕΡΙ ΠΡΟΣΤΑΣΙΑΣ ΘΗΡΑΜΑΤΟΣ ΚΑΙ ΑΓΡΙΩΝ ΠΤΗΝΩΝ ΝΟΜΟΣ (ΚΕΦ. 65 ΚΑΙ ΝΟΜΟΙ 9 ΤΟΥ 1964 ΚΑΙ 76 ΤΟΥ 1965) Διάταγμα δυνάμει του άρθρου 20 Ό Υπουργός 'Εσωτερικών, ένασκών τάς διά του άρθρου 20
ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ. Η διαίρεση καλείται Ευκλείδεια και είναι τέλεια όταν το υπόλοιπο είναι μηδέν.
 ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
Ο Σκελετός της Πυέλου
 Ο Σκελετός της Πυέλου E Johnson Αν. Καθηγήτρια Εργαστήριο Ανατοµίας Η Πύελος το κατώτερο σηµείο του κορµού προς τα κάτω συνέχεια της κοιλιάς η πυελική κοιλότητα = κατώτερο τµήµα της κοιλιακής χώρας εντοπίζεται
Ο Σκελετός της Πυέλου E Johnson Αν. Καθηγήτρια Εργαστήριο Ανατοµίας Η Πύελος το κατώτερο σηµείο του κορµού προς τα κάτω συνέχεια της κοιλιάς η πυελική κοιλότητα = κατώτερο τµήµα της κοιλιακής χώρας εντοπίζεται
Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ
 Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ ΕΙΣΑΓΩΓΗ Η Γενικευμένη Γεωμετρία, που θα αναπτύξουμε στα παρακάτω κεφάλαια, είναι μία «Νέα Γεωμετρία», η οποία προέκυψε από την ανάγκη να γενικεύσει ορισμένα σημεία της Ευκλείδειας
Η ΓΕΝΙΚΕΥΜΕΝΗ ΓΕΩΜΕΤΡΙΑ ΕΙΣΑΓΩΓΗ Η Γενικευμένη Γεωμετρία, που θα αναπτύξουμε στα παρακάτω κεφάλαια, είναι μία «Νέα Γεωμετρία», η οποία προέκυψε από την ανάγκη να γενικεύσει ορισμένα σημεία της Ευκλείδειας
ΚΩΝΙΚΕΣ ΤΟΜΕΣ. Κεφάλαιο 4ο: Ερωτήσεις του τύπου «Σωστό - Λάθος» k R
 Κεφάλαιο 4ο: ΚΩΝΙΚΕΣ ΤΟΜΕΣ Α. ΚΥΚΛΟΣ Ερωτήσεις του τύπου «Σωστό - Λάθος» 1. * Η εξίσωση ( x x ) + ( y y ) = k, k R είναι πάντοτε εξίσωση κύκλου. o o. * Η εξίσωση x + y + Ax + By + Γ = 0 παριστάνει κύκλο
Κεφάλαιο 4ο: ΚΩΝΙΚΕΣ ΤΟΜΕΣ Α. ΚΥΚΛΟΣ Ερωτήσεις του τύπου «Σωστό - Λάθος» 1. * Η εξίσωση ( x x ) + ( y y ) = k, k R είναι πάντοτε εξίσωση κύκλου. o o. * Η εξίσωση x + y + Ax + By + Γ = 0 παριστάνει κύκλο
ΛΥΚΕΙΟ ΑΓΙΑΣ ΦΥΛΑΞΕΩΣ ΣΧΟΛ. ΧΡΟΝΙΑ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ Α ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ
 ΛΥΚΕΙΟ ΑΙΑΣ ΦΥΛΑΞΕΩΣ ΣΧΟΛ. ΧΡΟΝΙΑ - ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ Α ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΑΛΕΡΑ. Να λύσετε τα πιο κάτω συστήματα: α) χ+ψ=7 β)3κ+λ=4 γ) +y= δ)χ+ψ= χ-ψ=- 5κ=+3λ -y-y =7 4χψ=3.Να γίνουν οι πράξεις: α)
ΛΥΚΕΙΟ ΑΙΑΣ ΦΥΛΑΞΕΩΣ ΣΧΟΛ. ΧΡΟΝΙΑ - ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ Α ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΑΛΕΡΑ. Να λύσετε τα πιο κάτω συστήματα: α) χ+ψ=7 β)3κ+λ=4 γ) +y= δ)χ+ψ= χ-ψ=- 5κ=+3λ -y-y =7 4χψ=3.Να γίνουν οι πράξεις: α)
2 η εκάδα θεµάτων επανάληψης
 η εκάδα θεµάτων επανάληψης. Έστω τρίγωνο µε + Ένα πρόχειρο σχήµα είναι το διπλανό
η εκάδα θεµάτων επανάληψης. Έστω τρίγωνο µε + Ένα πρόχειρο σχήµα είναι το διπλανό
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΩΝ Β ΓΥΜΝΑΣΙΟΥ ΜΕΡΟΣ 2ο «ΓΕΩΜΕΤΡΙΑ»
 ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΜΘΗΜΤΙΚΩΝ ΥΜΝΣΙΟΥ ΜΕΡΟΣ ο «ΕΩΜΕΤΡΙ». 1. Να υπολογίσετε τα εμβαδά των σχημάτων,, χρησιμοποιώντας ως μονάδα μέτρησης εμβαδών το. Τι παρατηρείτε; ρίσκουμε ότι τα εμβαδά των,, είναι : 5,
ΕΠΝΛΗΠΤΙΚΕΣ ΣΚΗΣΕΙΣ ΜΘΗΜΤΙΚΩΝ ΥΜΝΣΙΟΥ ΜΕΡΟΣ ο «ΕΩΜΕΤΡΙ». 1. Να υπολογίσετε τα εμβαδά των σχημάτων,, χρησιμοποιώντας ως μονάδα μέτρησης εμβαδών το. Τι παρατηρείτε; ρίσκουμε ότι τα εμβαδά των,, είναι : 5,
ΓΕΩΜΕΤΡΙΑ Α ΓΥΜΝΑΣΙΟΥ
 ΚΕΦΑΛΑΙΟ 1 Ο Βασικές Γεωμετρικές Έννοιες ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Μια τεντωμένη κλωστή με άκρα δύο σημεία Α και Β μας δίνει μια εικόνα της έννοιας του.. Τα σημεία Α και Β λέγονται.. 2. Τι ονομάζεται ευθεία;..
ΚΕΦΑΛΑΙΟ 1 Ο Βασικές Γεωμετρικές Έννοιες ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ 1. Μια τεντωμένη κλωστή με άκρα δύο σημεία Α και Β μας δίνει μια εικόνα της έννοιας του.. Τα σημεία Α και Β λέγονται.. 2. Τι ονομάζεται ευθεία;..
ΣΚΙΑΓΡΑΦΙΑ. Γενικές αρχές και έννοιες
 ΣΚΙΑΓΡΑΦΙΑ Γενικές αρχές και έννοιες Στο σύστημα προβολής κατά Monge δεν μας δίνεται η δυνατότητα ν αντιληφθούμε άμεσα τα αντικείμενα του χώρου, παρά μόνο αφού συνδυάσουμε τις δύο προβολές του αντικειμένου
ΣΚΙΑΓΡΑΦΙΑ Γενικές αρχές και έννοιες Στο σύστημα προβολής κατά Monge δεν μας δίνεται η δυνατότητα ν αντιληφθούμε άμεσα τα αντικείμενα του χώρου, παρά μόνο αφού συνδυάσουμε τις δύο προβολές του αντικειμένου
Οι γωνίες και που ονομάζονται «εντός εναλλάξ γωνίες» και είναι ίσες. «εντός-εκτός και επί τα αυτά μέρη γωνίες» και είναι ίσες.
 ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΔΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» ΤΑΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΓΕΩΜΕΤΡΙΑ ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ 1. Μεσοκάθετος ενός ευθύγραμμου τμήματος ΑΒ ονομάζεται η ευθεία που είναι κάθετη
ΠΡΟΤΥΠΟ ΠΕΙΡΑΜΑΤΙΚΟ ΛΥΚΕΙΟ ΑΝΑΒΡΥΤΩΝ ΜΑΘΗΜΑΤΑ ΓΙΑ ΤΟΝ ΔΙΑΓΩΝΙΣΜΟ «ΘΑΛΗΣ» ΤΑΞΗ Α ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ: ΓΕΩΜΕΤΡΙΑ ΒΑΣΙΚΕΣ ΓΝΩΣΕΙΣ 1. Μεσοκάθετος ενός ευθύγραμμου τμήματος ΑΒ ονομάζεται η ευθεία που είναι κάθετη
Institutional Repository - Library & Information Centre - University of Thessaly 12/01/2016 21:56:54 EET - 148.251.235.206
 3. ΜΥΚΗΝΑΪΚΟΙ ΤΑΦΟΙ ΑΛΥΚΗΣ ΓΛΥΦΑΔΟΣ Την νέαν ταύτην άνασκαφήν παρά την 'Αλυκήν Γλυφάδος, οπού κατά τά έ'τη 1954 και 1955 ειχον άνασκαφή πολλοί μυκηναϊκών χρόνων θαλαμοειδείς τάφοι, κατέστησεν άναγκαίαν
3. ΜΥΚΗΝΑΪΚΟΙ ΤΑΦΟΙ ΑΛΥΚΗΣ ΓΛΥΦΑΔΟΣ Την νέαν ταύτην άνασκαφήν παρά την 'Αλυκήν Γλυφάδος, οπού κατά τά έ'τη 1954 και 1955 ειχον άνασκαφή πολλοί μυκηναϊκών χρόνων θαλαμοειδείς τάφοι, κατέστησεν άναγκαίαν
Φύλλο 3. Δράσεις με το λογισμικό The geometer s Sketchpad. Το περιβάλλον του λογισμικού αυτού είναι παρόμοιο μ εκείνο του Cabri II
 Φύλλο 3 1 ράσεις με το λογισμικό The geometer s Sketchpad Το περιβάλλον του λογισμικού αυτού είναι παρόμοιο μ εκείνο του Cabri II όμως έχει τη δικιά του φιλοσοφία και το δικό του τρόπο συνεργασίας με το
Φύλλο 3 1 ράσεις με το λογισμικό The geometer s Sketchpad Το περιβάλλον του λογισμικού αυτού είναι παρόμοιο μ εκείνο του Cabri II όμως έχει τη δικιά του φιλοσοφία και το δικό του τρόπο συνεργασίας με το
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΜΕΤΡΙΚΕΣ ΣΧΕΣΕΙΣ. ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ Κεφάλαιο 9ο: Ερωτήσεις του τύπου «Σωστό-Λάθος»
 ΕΩΜΕΤΡΙΑ Β ΥΚΕΙΟΥ Κεφάλαιο 9ο: ΜΕΤΡΙΚΕ ΧΕΕΙ Ερωτήσεις του τύπου «ωστό-άθος» Να χαρακτηρίσετε με (σωστό) ή (λάθος) τις παρακάτω προτάσεις. 1. * Αν σε τρίγωνο ΑΒ ισχύει ΑΒ = Α + Β, τότε το τρίγωνο είναι:
ΕΩΜΕΤΡΙΑ Β ΥΚΕΙΟΥ Κεφάλαιο 9ο: ΜΕΤΡΙΚΕ ΧΕΕΙ Ερωτήσεις του τύπου «ωστό-άθος» Να χαρακτηρίσετε με (σωστό) ή (λάθος) τις παρακάτω προτάσεις. 1. * Αν σε τρίγωνο ΑΒ ισχύει ΑΒ = Α + Β, τότε το τρίγωνο είναι:
ΑΡΧΑΙΟ ΕΛΛΗΝΙΚΟ ΘΕΑΤΡΟ. υπαίθρια αμφιθεατρική κατασκευή ημικυκλικής κάτοψης γύρω από μια κυκλική πλατεία
 ΑΡΧΑΙΟ ΕΛΛΗΝΙΚΟ ΘΕΑΤΡΟ υπαίθρια αμφιθεατρική κατασκευή ημικυκλικής κάτοψης γύρω από μια κυκλική πλατεία Μέρη αρχαίου θεάτρου σκηνή: ορθογώνιο, μακρόστενο κτίριο προσκήνιο: στοά με κίονες μπροστά από τη
ΑΡΧΑΙΟ ΕΛΛΗΝΙΚΟ ΘΕΑΤΡΟ υπαίθρια αμφιθεατρική κατασκευή ημικυκλικής κάτοψης γύρω από μια κυκλική πλατεία Μέρη αρχαίου θεάτρου σκηνή: ορθογώνιο, μακρόστενο κτίριο προσκήνιο: στοά με κίονες μπροστά από τη
Περί χριστιανικών μνημείων Λοκρίδος
 Περί χριστιανικών μνημείων Λοκρίδος Γ. ΚΟΛΛΙΑΣ Δελτίον XAE 4 (1934-1936), Περίοδος Γ' Σελ. νζ -ξδ ΑΘΗΝΑ 1938 ΥΠΟΜΝΗΜΑ Ύπο Γ. ΚΟΛΙΑ. ΠΕΡΙ ΧΡΙΣΤΙΑΝΙΚΩΝ ΜΝΗΜΕΙΩΝ ΛΟΚΡΙΔΟΣ Α' ΚΡΥΠΤΗ ΑΤΑΛΑΝΤΗΣ 'Εντός της 'Αταλάντης
Περί χριστιανικών μνημείων Λοκρίδος Γ. ΚΟΛΛΙΑΣ Δελτίον XAE 4 (1934-1936), Περίοδος Γ' Σελ. νζ -ξδ ΑΘΗΝΑ 1938 ΥΠΟΜΝΗΜΑ Ύπο Γ. ΚΟΛΙΑ. ΠΕΡΙ ΧΡΙΣΤΙΑΝΙΚΩΝ ΜΝΗΜΕΙΩΝ ΛΟΚΡΙΔΟΣ Α' ΚΡΥΠΤΗ ΑΤΑΛΑΝΤΗΣ 'Εντός της 'Αταλάντης
ΟΠΙΣΘΙΟ ΚΟΙΛΙΑΚΟ ΤΟΙΧΩΜΑ ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΙΑΤΡΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ
 ΟΠΙΣΘΙΟ ΚΟΙΛΙΑΚΟ ΤΟΙΧΩΜΑ ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΙΑΤΡΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ ΟΣΤΑ (ΟΣΦΥΙΚΟΙ ΣΠΟΝΔΥΛΟΙ ΙΕΡΟ) ΟΣΦΥΙΚΟΙ ΣΠΟΝΔΥΛΟΙ Μεγαλύτεροι σε μέγεθος και όγκο, με κοντούς και παχείς αυχένες, ευρύτερες
ΟΠΙΣΘΙΟ ΚΟΙΛΙΑΚΟ ΤΟΙΧΩΜΑ ΠΑΥΛΟΣ Γ. ΚΑΤΩΝΗΣ ΙΑΤΡΙΚΗ ΣΧΟΛΗ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΚΡΗΤΗΣ ΟΣΤΑ (ΟΣΦΥΙΚΟΙ ΣΠΟΝΔΥΛΟΙ ΙΕΡΟ) ΟΣΦΥΙΚΟΙ ΣΠΟΝΔΥΛΟΙ Μεγαλύτεροι σε μέγεθος και όγκο, με κοντούς και παχείς αυχένες, ευρύτερες
Μαθηματικά: Αριθμητική και Άλγεβρα. Μάθημα 10 ο, Τμήμα Α
 Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 10 ο, Τμήμα Α Ορθογώνιο παραλληλόγραμμο 3 cm 5 cm Ο τύπος όπως είναι γραμμένος δείχνει ότι μπορούμε να πολλαπλασιάσουμε δύο μήκη. Ε=3cm x 5cm=15cm 2. Πώς καταλαβαίνετε
Μαθηματικά: Αριθμητική και Άλγεβρα Μάθημα 10 ο, Τμήμα Α Ορθογώνιο παραλληλόγραμμο 3 cm 5 cm Ο τύπος όπως είναι γραμμένος δείχνει ότι μπορούμε να πολλαπλασιάσουμε δύο μήκη. Ε=3cm x 5cm=15cm 2. Πώς καταλαβαίνετε
24 ΔΙΑΓΩΝΙΣΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ Α ΛΥΚΕΙΟΥ ΔΙΑΓΩΝΙΣΜΑ 1 Ο. ΘΕΜΑ 2 Ο : Δίνεται ΑΒΓ ισοσκελές (ΑΒ=ΑΓ) τρίγωνο.αν ΒΔ και ΓΕ οι διχοτόμοι των γωνιών Β και
 ΔΙΩΝΙΣΜ 1 Ο ΘΕΜ 1 Ο : ) Να αποδείξετε ότι : Το ευθύγραμμο τμήμα που ενώνει τα μέσα τα των δύο πλευρών τριγώνου είναι παράλληλο προς την τρίτη πλευρά και ίση με το μισό της.(13 μονάδες) ) Να χαρακτηρίσετε
ΔΙΩΝΙΣΜ 1 Ο ΘΕΜ 1 Ο : ) Να αποδείξετε ότι : Το ευθύγραμμο τμήμα που ενώνει τα μέσα τα των δύο πλευρών τριγώνου είναι παράλληλο προς την τρίτη πλευρά και ίση με το μισό της.(13 μονάδες) ) Να χαρακτηρίσετε
ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΜΠΥΛΕΣ
 ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΜΠΥΛΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει: 1. Να σχεδιάζει γεωμετρικές καμπύλες (ελλειψοειδή, ωοειδή, παραβολή, υπερβολή, έλικα, σπείρα) εφαρμόζοντας τους
ΓΕΩΜΕΤΡΙΚΕΣ ΚΑΜΠΥΛΕΣ ΣΤΟΧΟΙ: Με τη συμπλήρωση της ενότητας αυτής ο/η μαθητής/τρια πρέπει: 1. Να σχεδιάζει γεωμετρικές καμπύλες (ελλειψοειδή, ωοειδή, παραβολή, υπερβολή, έλικα, σπείρα) εφαρμόζοντας τους
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ
 ΠΝΠΤΙΣ ΣΣΙΣ > 90. 1. ίνεται ισοσκελές τρίγωνο µε = και 0 πό την κορυφή φέρνουµε τις ηµιευθείες x κάθετη στην πλευρά και y κάθετη στην πλευρά που τέµνουν την στα σηµεία και αντίστοιχα. Να αποδείξετε α)
ΠΝΠΤΙΣ ΣΣΙΣ > 90. 1. ίνεται ισοσκελές τρίγωνο µε = και 0 πό την κορυφή φέρνουµε τις ηµιευθείες x κάθετη στην πλευρά και y κάθετη στην πλευρά που τέµνουν την στα σηµεία και αντίστοιχα. Να αποδείξετε α)
ΗΜΕΡΟΛΟΓΙΟ 2016 Εκκλησίες της Σωτήρας. Πρόγραμμα Μαθητικών Θρησκευτικών Περιηγήσεων «Συνοδοιπόροι στα ιερά προσκυνήματα του τόπου μας»
 ΗΜΕΡΟΛΟΓΙΟ 2016 Εκκλησίες της Σωτήρας Πρόγραμμα Μαθητικών Θρησκευτικών Περιηγήσεων «Συνοδοιπόροι στα ιερά προσκυνήματα του τόπου μας» ΙΑΝΟΥΑΡΙΟΣ Αγία Θέκλα Βρίσκεται 7χλμ νότια από το κέντρο της Σωτήρας.
ΗΜΕΡΟΛΟΓΙΟ 2016 Εκκλησίες της Σωτήρας Πρόγραμμα Μαθητικών Θρησκευτικών Περιηγήσεων «Συνοδοιπόροι στα ιερά προσκυνήματα του τόπου μας» ΙΑΝΟΥΑΡΙΟΣ Αγία Θέκλα Βρίσκεται 7χλμ νότια από το κέντρο της Σωτήρας.
2.3 ΜΕΣΟΚΑΘΕΤΟΣ ΕΥΘΥΓΡΑΜΜΟΥ ΤΜΗΜΑΤΟΣ
 1 3 ΜΕΣΚΘΕΤΣ ΕΥΘΥΡΜΜΥ ΤΜΗΜΤΣ ΘΕΩΡΙ Μεσοκάθετος ευθυγράµµου τµήµατος Λέγεται η ευθεία που διέρχεται από το µέσο του ευθυγράµµου τµήµατος και είναι κάθετη σ αυτό. Ιδιότητα : Κάθε σηµείο της µεσοκαθέτου ενός
1 3 ΜΕΣΚΘΕΤΣ ΕΥΘΥΡΜΜΥ ΤΜΗΜΤΣ ΘΕΩΡΙ Μεσοκάθετος ευθυγράµµου τµήµατος Λέγεται η ευθεία που διέρχεται από το µέσο του ευθυγράµµου τµήµατος και είναι κάθετη σ αυτό. Ιδιότητα : Κάθε σηµείο της µεσοκαθέτου ενός
Αριθμός 301 Ο ΠΕΡΙ ΠΡΟΣΤΑΣΙΑΣ ΤΩΝ ΛΟΥΟΜΕΝΩΝ ΕΝ ΤΗ ΘΑΛΑΣΣΗ ΝΟΜΟΣ 1968 (ΝΟΜΟΣ 72 ΤΟΥ 1968)
 294 Αριθμός 301 Ο ΠΕΡΙ ΠΡΟΣΤΑΣΙΑΣ ΤΩΝ ΛΟΥΟΜΕΝΩΝ ΕΝ ΤΗ ΘΑΛΑΣΣΗ ΝΟΜΟΣ 1968 (ΝΟΜΟΣ 72 ΤΟΥ 1968) Διάταγμα δυνάμει τοΰ άρθρου 3 Ό 'Υπουργός Συγκοινωνιών και "Εργων, ένασκών τάς δυνάμει τοΰ άρθρου 3 του περί
294 Αριθμός 301 Ο ΠΕΡΙ ΠΡΟΣΤΑΣΙΑΣ ΤΩΝ ΛΟΥΟΜΕΝΩΝ ΕΝ ΤΗ ΘΑΛΑΣΣΗ ΝΟΜΟΣ 1968 (ΝΟΜΟΣ 72 ΤΟΥ 1968) Διάταγμα δυνάμει τοΰ άρθρου 3 Ό 'Υπουργός Συγκοινωνιών και "Εργων, ένασκών τάς δυνάμει τοΰ άρθρου 3 του περί
ΜΕΣΑΙΩΝΙΚΑ ΕΥΒΟΙΑΣ. Institutional Repository - Library & Information Centre - University of Thessaly 13/08/ :30:33 EEST
 214 ΑΡΧΑΙΟΛΟΓΙΚΟΝ ΔΕΛΤΙΟΝ 19 (1964) : ΧΡΟΝΙΚΑ ΜΕΣΑΙΩΝΙΚΑ ΕΥΒΟΙΑΣ a. Άγια Παρασκευή 1. Χαλκϊς Αί στέγαι τής μεγάλης ταύτης βασιλικής είχον ύποστή ζημίας είς τάς κεράμους καί τάς ύπ αύτάς ξυλίνας κατασκευάς.
214 ΑΡΧΑΙΟΛΟΓΙΚΟΝ ΔΕΛΤΙΟΝ 19 (1964) : ΧΡΟΝΙΚΑ ΜΕΣΑΙΩΝΙΚΑ ΕΥΒΟΙΑΣ a. Άγια Παρασκευή 1. Χαλκϊς Αί στέγαι τής μεγάλης ταύτης βασιλικής είχον ύποστή ζημίας είς τάς κεράμους καί τάς ύπ αύτάς ξυλίνας κατασκευάς.
Συνοπτική Θεωρία Μαθηματικών Α Γυμνασίου
 Web page: www.ma8eno.gr e-mail: vrentzou@ma8eno.gr Η αποτελεσματική μάθηση δεν θέλει κόπο αλλά τρόπο, δηλαδή ma8eno.gr Συνοπτική Θεωρία Μαθηματικών Α Γυμνασίου Αριθμητική - Άλγεβρα Γεωμετρία Άρτιος λέγεται
Web page: www.ma8eno.gr e-mail: vrentzou@ma8eno.gr Η αποτελεσματική μάθηση δεν θέλει κόπο αλλά τρόπο, δηλαδή ma8eno.gr Συνοπτική Θεωρία Μαθηματικών Α Γυμνασίου Αριθμητική - Άλγεβρα Γεωμετρία Άρτιος λέγεται
ΘΕΜΑΤΑ & ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΜΑΘΗΜΑΤΙΚΩΝ Α ΓΥΜΝΑΣΙΟΥ
 ΘΕΜΤ & ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΣ ΜΘΗΜΤΙΚΩΝ ΥΜΝΣΙΟΥ ΘΕΜ 1. α) Να συµπληρώσετε τις παρακάτω ισότητες. α+0=.. α 1=. α-α=.. α:α=. 0 α=. 0:α=. Το α είναι ένας αριθµός διαφορετικός του 0. β) Στις παρακάτω προτάσεις να
ΘΕΜΤ & ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΣ ΜΘΗΜΤΙΚΩΝ ΥΜΝΣΙΟΥ ΘΕΜ 1. α) Να συµπληρώσετε τις παρακάτω ισότητες. α+0=.. α 1=. α-α=.. α:α=. 0 α=. 0:α=. Το α είναι ένας αριθµός διαφορετικός του 0. β) Στις παρακάτω προτάσεις να
ΓΕΩΜΕΤΡΙΑ Β ΛΥΚΕΙΟΥ (ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ)
 ΩΜΤΡΙ ΛΥΚΙΟΥ (ΤΡΠΖ ΘΜΤΩΝ) GI_V_GEO_2_18975 ίνεται τρίγωνο AB με AB=9, A=15. πό το βαρύκεντρο φέρνουμε ευθεία παράλληλη στην πλευρά B που τέμνει τις AB,A στα,e αντίστοιχα. α) Να αποδείξετε ότι A = 2 AB
ΩΜΤΡΙ ΛΥΚΙΟΥ (ΤΡΠΖ ΘΜΤΩΝ) GI_V_GEO_2_18975 ίνεται τρίγωνο AB με AB=9, A=15. πό το βαρύκεντρο φέρνουμε ευθεία παράλληλη στην πλευρά B που τέμνει τις AB,A στα,e αντίστοιχα. α) Να αποδείξετε ότι A = 2 AB
ΚΕΦΑΛΑΙΟ 1 Ο ΓΕΩΜΕΤΡΙΑ
 ΜΕΡΟΣ ΚΕΦΛΙΟ 1 Ο ΕΩΜΕΤΡΙ 1.1 ΙΣΟΤΗΤ ΤΡΙΩΝΩΝ 1. Ποια ονομάζονται κύρια και ποια δευτερεύοντα στοιχεία τριγώνων; Κύρια στοιχεία ενός τριγώνου ονομάζουμε τις πλευρές και τις γωνίες του. Δευτερεύοντα στοιχεία
ΜΕΡΟΣ ΚΕΦΛΙΟ 1 Ο ΕΩΜΕΤΡΙ 1.1 ΙΣΟΤΗΤ ΤΡΙΩΝΩΝ 1. Ποια ονομάζονται κύρια και ποια δευτερεύοντα στοιχεία τριγώνων; Κύρια στοιχεία ενός τριγώνου ονομάζουμε τις πλευρές και τις γωνίες του. Δευτερεύοντα στοιχεία
1 ΘΕΩΡΙΑΣ...με απάντηση
 1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
Ειδικά θέματα στη ροπή αδράνειας του στερεού.
 Ειδικά θέματα στη ροπή αδράνειας του στερεού Η συνική ροπή αδράνειας ως άθροισμα επί μέρους ροπών αδράνειας Έστω το τυχαίο στερεό του σχήματος που αποτελείται από επιμέρους τμήματα Α,Β,Γ,Δ Η ροπή αδράνειας
Ειδικά θέματα στη ροπή αδράνειας του στερεού Η συνική ροπή αδράνειας ως άθροισμα επί μέρους ροπών αδράνειας Έστω το τυχαίο στερεό του σχήματος που αποτελείται από επιμέρους τμήματα Α,Β,Γ,Δ Η ροπή αδράνειας
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ. 3 2 x. β)
 ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x. Να λυθούν οι εξισώσεις: α) 3x x 3 3 5x x β) 4 3 x x x 0
ΜΑΘΗΜΑΤΙΚΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ. Να λυθούν οι εξισώσεις και οι ανισώσεις : α) γ) x x 3x 7x 9 4 5 0 x x x 3 6 3 4 β) δ) 3x x 3 x 4 3 5 x x. 4 4 3 5 x. Να λυθούν οι εξισώσεις: α) 3x x 3 3 5x x β) 4 3 x x x 0
γ) Να σχεδιάσετε τις γραφικές παραστάσεις απομάκρυνσης - χρόνου, για τα σημεία Α, Β και Γ, τα οποία απέχουν από το ελεύθερο άκρο αντίστοιχα,,
 1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
1. Κατά μήκος μιας ελαστικής χορδής μεγάλου μήκους που το ένα άκρο της είναι ακλόνητα στερεωμένο, διαδίδονται δύο κύματα, των οποίων οι εξισώσεις είναι αντίστοιχα: και, όπου και είναι μετρημένα σε και
ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών Προγραμμάτων Σπουδών. Αναπληρωτής Καθηγητής ΤΕΧΝΙΚΟ ΚΑΤΑΣΚΕΥΑΣΤΙΚΟ ΣΧΕΔΙΟ Ι ΑΛΥΤΕΣ ΑΣΚΗΣΕΙΣ
 ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΥΠΟΥΡΓΕΙΟ ΕΘΝΙΚΗΣ ΠΑΙΔΕΙΑΣ & ΘΡΗΣΚΕΥΜΑΤΩΝ ΕΙΔΙΚΗ ΥΠΗΡΕΣΙΑ ΔΙΑΧΕΙΡΙΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΟΥ ΠΡΟΓΡΑΜΜΑΤΟΣ ΕΚΠΑΙΔΕΥΣΗ & ΑΡΧΙΚΗ ΕΠΑΓΓΕΛΜΑΤΙΚΗ ΚΑΤΑΡΤΙΣΗ (Ε.Π.Ε.Α.Ε.Κ. ΙΙ) ΚΑΤΗΓΟΡΙΑ ΠΡΑΞΕΩΝ: 2.2.2.α. Αναμόρφωση Προπτυχιακών
ΑΞΟΝΟΜΕΤΡΙΑ. Εισαγωγή
 ΑΞΟΝΟΜΕΤΡΙΑ Εισαγωγή Η προβολή τρισδιάστατου αντικειμένου πάνω σε δισδιάστατη επιφάνεια αποτέλεσε μια από τις βασικές αναζητήσεις μεθόδων απεικόνισης και απασχόλησε από πολύ παλιά τους ανθρώπους. Με την
ΑΞΟΝΟΜΕΤΡΙΑ Εισαγωγή Η προβολή τρισδιάστατου αντικειμένου πάνω σε δισδιάστατη επιφάνεια αποτέλεσε μια από τις βασικές αναζητήσεις μεθόδων απεικόνισης και απασχόλησε από πολύ παλιά τους ανθρώπους. Με την
3.4 Ι ΙΟΤΗΤΕΣ ΠΑΡΑΛΛΗΛΟΓΡΑΜΜΟΥ
 1 3.4 ΙΙΤΗΤΕΣ ΠΡΛΛΗΛΡΜΜΥ ΡΘΩΝΙΥ ΡΜΥ ΤΕΤΡΩΝΥ ΤΡΠΕΖΙΥ ΙΣΣΚΕΛΥΣ ΤΡΠΕΖΙΥ ΘΕΩΡΙ 1. Ιδιότητες παραλληλογράµµου Το σηµείο τοµής των διαγωνίων του είναι κέντρο συµµετρίας (Το κέντρο συµµετρίας) ι διαγώνιες διχοτοµούνται,
1 3.4 ΙΙΤΗΤΕΣ ΠΡΛΛΗΛΡΜΜΥ ΡΘΩΝΙΥ ΡΜΥ ΤΕΤΡΩΝΥ ΤΡΠΕΖΙΥ ΙΣΣΚΕΛΥΣ ΤΡΠΕΖΙΥ ΘΕΩΡΙ 1. Ιδιότητες παραλληλογράµµου Το σηµείο τοµής των διαγωνίων του είναι κέντρο συµµετρίας (Το κέντρο συµµετρίας) ι διαγώνιες διχοτοµούνται,
ΜΥΚΗΝΑΪΚΗ ΑΡΧΙΤΕΚΤΟΝΙΚΗ
 ΜΥΚΗΝΑΪΚΗ ΑΡΧΙΤΕΚΤΟΝΙΚΗ Εισαγωγικά: ΟΡΙΣΜΟΣ: Με τον όρο μυκηναϊκός πολιτισμός χαρακτηρίζεται ο προϊστορικός πολιτισμός της ΎστερηςΕποχήςτουΧαλκούαπότο1600-1100 π. Χ. που αναπτύχθηκε κυρίως στην κεντρική
ΜΥΚΗΝΑΪΚΗ ΑΡΧΙΤΕΚΤΟΝΙΚΗ Εισαγωγικά: ΟΡΙΣΜΟΣ: Με τον όρο μυκηναϊκός πολιτισμός χαρακτηρίζεται ο προϊστορικός πολιτισμός της ΎστερηςΕποχήςτουΧαλκούαπότο1600-1100 π. Χ. που αναπτύχθηκε κυρίως στην κεντρική
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 1 ΙΟΥΝΙΟΥ 019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΘΕΜΑ Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 1 ΙΟΥΝΙΟΥ 019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΘΕΜΑ Α Στις ερωτήσεις Α1-Α4 να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης
ΧΑΡΤΟΓΡΑΦΙΚΕΣ ΠΡΟΒΟΛΕΣ
 ΣΧΟΛΗ ΝΑΥΤΙΚΩΝ ΔΟΚΙΜΩΝ ΜΑΘΗΜΑ: ΘΕΩΡΗΤΙΚΗ ΝΑΥΤΙΛΙΑ Καθηγητής Δρ. Α. Παλληκάρης ΧΑΡΤΟΓΡΑΦΙΚΕΣ ΠΡΟΒΟΛΕΣ Νοέμβριος 2016 ΕΝΔΕΙΚΤΙΚΗ ΔΙΑΔΙΚΑΣΙΑ ΑΠΕΙΚΟΝΙΣΗΣ ΤΗΣ ΕΠΙΦΑΝΕΙΑΣ ΤΗΣ ΓΗΣ ΣΕ ΕΠΙΠΕΔΟ (ΚΑΤΑΣΚΕΥΗ ΧΑΡΤΩΝ)
ΣΧΟΛΗ ΝΑΥΤΙΚΩΝ ΔΟΚΙΜΩΝ ΜΑΘΗΜΑ: ΘΕΩΡΗΤΙΚΗ ΝΑΥΤΙΛΙΑ Καθηγητής Δρ. Α. Παλληκάρης ΧΑΡΤΟΓΡΑΦΙΚΕΣ ΠΡΟΒΟΛΕΣ Νοέμβριος 2016 ΕΝΔΕΙΚΤΙΚΗ ΔΙΑΔΙΚΑΣΙΑ ΑΠΕΙΚΟΝΙΣΗΣ ΤΗΣ ΕΠΙΦΑΝΕΙΑΣ ΤΗΣ ΓΗΣ ΣΕ ΕΠΙΠΕΔΟ (ΚΑΤΑΣΚΕΥΗ ΧΑΡΤΩΝ)
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ.
 ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΤΟ ΥΛΙΚΟ ΕΧΕΙ ΑΝΤΛΗΘΕΙ ΑΠΟ ΤΑ ΨΗΦΙΑΚΑ ΕΚΠΑΙΔΕΥΤΙΚΑ ΒΟΗΘΗΜΑΤΑ ΤΟΥ ΥΠΟΥΡΓΕΙΟΥ ΠΑΙΔΕΙΑΣ http://www.study4exams.gr/ ΕΧΕΙ ΤΑΞΙΝΟΜΗΘΕΙ ΑΝΑ ΕΝΟΤΗΤΑ ΚΑΙ ΑΝΑ ΤΥΠΟ ΓΙΑ ΔΙΕΥΚΟΛΥΝΣΗ ΤΗΣ ΜΕΛΕΤΗΣ ΣΑΣ ΚΑΛΗ ΕΠΙΤΥΧΙΑ ΣΤΗ
ΨΗΦΙΑΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΒΟΗΘΗΜΑ «ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ» 5 o ΔΙΑΓΩΝΙΣΜΑ ΜΑΡΤΙΟΣ 2017: ΘΕΜΑΤΑ
 ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
ΦΥΣΙΚΗ ΟΜΑΔΑΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ 5 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑΤΑ ΘΕΜΑ Α Στις προτάσεις 1-4 να γράψετε στο τετράδιό σας τον αριθμό της πρότασης και δίπλα το γράμμα που αντιστοιχεί στη φράση, η οποία
Ερωτήσεις τύπου «Σωστό - Λάθος» Σωστό Λάθος
 Εγγράψιμα και περιγράψιμα τετράπλευρα Ερωτήσεις τύπου «Σωστό - Λάθος» Σωστό Λάθος 1. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι παραλληλόγραμμο.. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι
Εγγράψιμα και περιγράψιμα τετράπλευρα Ερωτήσεις τύπου «Σωστό - Λάθος» Σωστό Λάθος 1. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι παραλληλόγραμμο.. Ένα τετράπλευρο είναι εγγράψιμο σε κύκλο αν είναι
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
Φύλλο 2. Δράσεις με το λογισμικό Cabri-geometry 3D
 1 Φύλλο 2 Δράσεις με το λογισμικό Cabri-geometry 3D Το περιβάλλον του λογισμικού αυτού είναι παρόμοιο με το αντίστοιχο λογισμικό του Cabri II. Περιέχει γενικές εντολές και εικονίδια που συμπεριλαμβάνουν
1 Φύλλο 2 Δράσεις με το λογισμικό Cabri-geometry 3D Το περιβάλλον του λογισμικού αυτού είναι παρόμοιο με το αντίστοιχο λογισμικό του Cabri II. Περιέχει γενικές εντολές και εικονίδια που συμπεριλαμβάνουν
Απέναντι πλευρές παράλληλες
 5. 5.5 ΘΩΡΙ. Παραλληλόγραµµο πέναντι πλευρές παράλληλες. Ιδιότητες παραλληλογράµµου πέναντι πλευρές ίσες πέναντι γωνίες ίσες Οι διαγώνιοι διχοτοµούνται Το σηµείο τοµής των διαγωνίων είναι κέντρο συµµετρίας
5. 5.5 ΘΩΡΙ. Παραλληλόγραµµο πέναντι πλευρές παράλληλες. Ιδιότητες παραλληλογράµµου πέναντι πλευρές ίσες πέναντι γωνίες ίσες Οι διαγώνιοι διχοτοµούνται Το σηµείο τοµής των διαγωνίων είναι κέντρο συµµετρίας
ΔΙΑΣΤΑΣΕΙΣ. Διαστάσεις σε κύκλους, τόξα, γωνίες κώνους Μέθοδοι τοποθέτησης διαστάσεων
 ΔΙΑΣΤΑΣΕΙΣ Διαστάσεις σε κύκλους, τόξα, γωνίες κώνους Μέθοδοι τοποθέτησης διαστάσεων Η Σωστή τοποθετηση Διαστασεων στο Μηχανολογικο Σχεδιο ειναι απαραιτητη για τη Σωστή Κατασκευή Εχετε κατι να παρατηρησετε;
ΔΙΑΣΤΑΣΕΙΣ Διαστάσεις σε κύκλους, τόξα, γωνίες κώνους Μέθοδοι τοποθέτησης διαστάσεων Η Σωστή τοποθετηση Διαστασεων στο Μηχανολογικο Σχεδιο ειναι απαραιτητη για τη Σωστή Κατασκευή Εχετε κατι να παρατηρησετε;
ΠΩΣ ΕΙΧΝΩ ΟΤΙ ΥΟ ΕΥΘΕΙΕΣ ΕΙΝΑΙ ΠΑΡΑΛΛΗΛΕΣ 1. είχνω ότι τέµνονται από τρίτη ευθεία και σχηµατίζονται γωνίες
 ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΧΟΛΙΑ στη γεωµετρία της Α τάξης ΠΩΣ ΕΙΧΝΩ ΟΤΙ ΥΟ ΕΥΘΕΙΕΣ ΕΙΝΑΙ ΚΑΘΕΤΕΣ 1. είχνω ότι η γωνία τους είναι 90 ο 2. είχνω ότι είναι διχοτόµοι δύο εφεξής και παραπληρωµατικών γωνιών. 3. είχνω ότι
ΠΑΡΑΤΗΡΗΣΕΙΣ ΣΧΟΛΙΑ στη γεωµετρία της Α τάξης ΠΩΣ ΕΙΧΝΩ ΟΤΙ ΥΟ ΕΥΘΕΙΕΣ ΕΙΝΑΙ ΚΑΘΕΤΕΣ 1. είχνω ότι η γωνία τους είναι 90 ο 2. είχνω ότι είναι διχοτόµοι δύο εφεξής και παραπληρωµατικών γωνιών. 3. είχνω ότι
ΝΑΟΣ ΑΓΙΑ ΑΙΚΑΤΕΡΙΝΗΣ
 ΝΑΟΣ ΑΓΙΑ ΑΙΚΑΤΕΡΙΝΗΣ Στον 11 ο αιώνα χρονολογείται η αγία Αικατερίνη στην Πλάκα, κοντά στο μνημείο του Λυσικράτους. Έχει χτιστεί πάνω σε ερείπια αρχαίου ναού της Αρτέμιδος. Η στέγαση του κεντρικού τμήματος,
ΝΑΟΣ ΑΓΙΑ ΑΙΚΑΤΕΡΙΝΗΣ Στον 11 ο αιώνα χρονολογείται η αγία Αικατερίνη στην Πλάκα, κοντά στο μνημείο του Λυσικράτους. Έχει χτιστεί πάνω σε ερείπια αρχαίου ναού της Αρτέμιδος. Η στέγαση του κεντρικού τμήματος,
ΔΟΜΗ ΞΥΛΟΥ ΔΟΜΗ ΞΥΛΟΥ 6. ΠΕΡΙΓΡΑΦΗ ΚΥΤΤΑΡΩΝ ΠΛΑΤΥΦΥΛΛΩΝ. Δομή Ξύλου - Θεωρία. Στέργιος Αδαμόπουλος
 ΔΟΜΗ ΞΥΛΟΥ 6. ΠΕΡΙΓΡΑΦΗ ΚΥΤΤΑΡΩΝ ΠΛΑΤΥΦΥΛΛΩΝ Τύποι και ρόλος κυττάρων πλατυφύλλων Μέλη αγγείων: αγωγά στοιχεία Ίνες: στερεωτικά στοιχεία (σπάνια και αγωγά) Τραχεϊδες: αγωγά και στερεωτικά στοιχεία Παρεγχυματικά
ΔΟΜΗ ΞΥΛΟΥ 6. ΠΕΡΙΓΡΑΦΗ ΚΥΤΤΑΡΩΝ ΠΛΑΤΥΦΥΛΛΩΝ Τύποι και ρόλος κυττάρων πλατυφύλλων Μέλη αγγείων: αγωγά στοιχεία Ίνες: στερεωτικά στοιχεία (σπάνια και αγωγά) Τραχεϊδες: αγωγά και στερεωτικά στοιχεία Παρεγχυματικά
ΤΟ ΑΡΧΑΙΟ ΘΕΑΤΡΟ ΤΗΣ ΛΙΝΔΟΥ ΣΟΦΙΑ ΒΑΣΑΛΟΥ ΒΠΠΓ
 ΤΟ ΑΡΧΑΙΟ ΘΕΑΤΡΟ ΤΗΣ ΛΙΝΔΟΥ ΣΟΦΙΑ ΒΑΣΑΛΟΥ ΒΠΠΓ Περιγραφή μνημείου Το αρχαίο θέατρο της Λίνδου διαμορφώνεται στους πρόποδες της δυτικής πλαγιάς του βράχου της λινδιακής ακρόπολης. Το κοίλο χωρίζεται σε
ΤΟ ΑΡΧΑΙΟ ΘΕΑΤΡΟ ΤΗΣ ΛΙΝΔΟΥ ΣΟΦΙΑ ΒΑΣΑΛΟΥ ΒΠΠΓ Περιγραφή μνημείου Το αρχαίο θέατρο της Λίνδου διαμορφώνεται στους πρόποδες της δυτικής πλαγιάς του βράχου της λινδιακής ακρόπολης. Το κοίλο χωρίζεται σε
ΛΥΣΕΙΣ ΙΑΓΩΝΙΣΜΑ ΓΕΩΜΕΤΡΙΑ Α ΛΥΚΕΙΟΥ 08/04/10
 ΥΣΙΣ ΙΑΩΝΙΣΜΑ ΩΜΤΡΙΑ Α ΥΚΙΟΥ ΘΜΑ ο 08/04/0 Α. Να αποδείξετε ότι η διάµεσος ορθογωνίου τριγώνου που φέρουµε από την κορυφή της ορθής γωνίας είναι ίση µε το µισό της υποτείνουσας. Θεωρία σχολικό βιβλίο σελ.09
ΥΣΙΣ ΙΑΩΝΙΣΜΑ ΩΜΤΡΙΑ Α ΥΚΙΟΥ ΘΜΑ ο 08/04/0 Α. Να αποδείξετε ότι η διάµεσος ορθογωνίου τριγώνου που φέρουµε από την κορυφή της ορθής γωνίας είναι ίση µε το µισό της υποτείνουσας. Θεωρία σχολικό βιβλίο σελ.09
