6.TRANSFERUL DE CALDURĂ
|
|
|
- Ἀρέθουσα Ρέντης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 rmothiă 63 6.RANSFERUL DE CALDURĂ rmoitia sau trasfrul d ăldură st apitolul ar s oupă d studiul modului î ar s propagă ăldura pritr-u orp, îtr parta lui aldă şi a r, sau îtr două orpuri u tmpraturi difrit. rasmitra ăldurii st osiţă a difrţi d potţial trmi. Cuoaştra fomlor d trasfr ar a sop priipal ativara sau frâara atitativă a trasfrului. 6..Moduri lmtar d trasfr trmi 6.. Coduţia rprită fomul d trasfr d ăldură ftuat pri otatul dirt al partiullor uui orp (la ivl mirosopi ar lo u trasfr d rgi itiă îtr molull vi). Fomul prsupu imobilitata orpului î itriorul ăruia istă u gradit d ăldură. Coduţia st aratristiă ptru orpuril solid. S poat vorbi şi dspr oduţi î orpuri fluid aflat î rpaus, dar imobilitata astora î prţa uui gradit d tmpratură st mai gru d oput. D aa, trasfrul odutiv î fluid st îsoţit d ovţi şi radiaţi. 6.. Covţia st fomul d trasfr trmi raliat pri trasfr d masă, îtr o u tmpraturi difrit. Fomul prsupu mişara mdiului î itriorul ăruia istă u gradit d tmpratură, di ovţia st aratristiă mdiilor fluid. Fomul s maifstă la suprafaţa d sparaţi a falor (solid lihid; solid ga; lihid ga) 6..3 Radiaţia rprită trasfrul d ăldură d la u orp la altul pri ud ltromagti, u odiţia a mdiul ar l spară să fi traspart ptru radiaţiil trmi. Maismul radiaţii ostă î trasformara ui părţi a rgii itr a orpului î rgi radiată, ar s propagă sub formă d ud ltromagti î spaţiu şi ar, îtâlid lălalt orp, s rtrasformă î rgi trmiă la oa d otat. 6..Noţiui şi mărimi aratristi trasfrului d ăldură Rgim d trasfr al ăldurii: -prmat-rgimul î ar trasfrul u dpid d timp; orpul osidrat st î hilibru trmi, ăldura primită î uitata d timp fiid gală u a dată (orpul ii u s îălşt, ii u s răşt); -traitoriu- rgimul î ar trasfrul s modifiă î timp; ast rgim st aratristi prioadi d îălir sau d răir a uui orp, âd ăldura primită î uitata d timp difră d a dată. Ptru u itrval d timp tiâd la ifiit, rgimul traitoriu dvi rgim prmat Câmp d tmpratură-totalitata valorilor tmpraturilor la u momt oarar τ, î spaţiu. f r, τ ud r -vtor d poiţi al putului d tmpratură ; τ -momtul la ar putul ar tmpratura.
2 64 rmothiă Suprafaţă iotrmă- loul gomtri al putlor u aaşi tmpratură, îtr-u orp. Gradit d tmpratură-vtor prpdiular p două iotrm ifiit apropiat, ar primă variaţia maimă d tmpratură raportată la lugim. o Fig. 6. Sţiu trasvsală pri tri suprafţ iotrm ifiit apropiat grad ud 0 O vrsorul ormali la suprafaţa iotrmă t vtorul ormali la suprafaţa iotrmă t sau, altfl sris grad i j k ud -opratorul abla i, j, k -vrsorii lor tri dirţii î spaţiu. Fluul trmi rprită atitata d ăldură trasfrată (pritr-u orp sau îtr două orpuri) î uitata d timp: dq (5.) Q ; Q w dt Fluul trmi uitar (itsitata fluului trmi) rprită fluul trmi raportat la uitata d suprafaţă iotrmă: (6.) dq ; w da m ud da-suprafaţa lmtară p ar fluul ad ormal. Cosidd aria a fiid oritată după dirţia ormali, fluul trmi uitar st o mărim vtorială. Obsrvâd fig.6., s poat spu ă fluul trmi uitar s propagă d la iotrma d tmpratură ătr a d tmpratură după dirţi ormală, adiă p drumul d miimă ristţă la propagar. Graditul trmi ar aaşi dirţi, dar ss otrar.
3 rmothiă Coduţia trmiă 6.3. Lga lui Fourir Fluul trmi uitar odutiv, ar tr pritr-u orp imobil, îtr două fţ latral al astuia, î dirţi ormală, î timpul dτ, pri suprafaţa da, st proporţioal u graditul d tmpratură ditr l două fţ: (5.3) grad ud -ofiit d odutivitat trmiă spifi mdiului matrial pri ar tr fluul. Cosidrâd ompotl fluului uitar p l tri dirţii, s mai poat sri: i j k ud ; Doar, primtal, u s poat dtrmia graditul d tmpratură, fluul trmi uitar u s poat alula dirt di lga lui Fourir. 6.3.Euaţia lui Fourir ptru trasfrul d ăldură odutiv S osidră u lmt d volum, dv, ditr-u orp pri ar tr ăldura pri odutivitat. S fa bilaţul trmi, osidrâd următoarl ipot:! orpul st solid (sau fluid imobil) omog;! paramtrii trmofiii au aaşi valoar î ori put;! dformara lmtului d volum sub aţiua ăldurii st glijabilă;! sursa itră, d flu uitar v, st uiform distribuită î volumul osidrat. I timpul dτ, lmtul d volum dv primşt u flu trmi odutiv dq i, pri tri ditr fţl sal şi daă u flu trmi odutiv dq,, pri llalt tri fţ. I alaşi itrval d timp, sursa itră graă fluul trmi dq s. Euaţia d bilaţ trmi primă faptul ă difrţa ditr ăldura primită (itrată î lmtul d volum şi a grată d sursa itră) şi a dată otribui la îălira / răira lmtului d volum, di a orpului. dq d dq d dq dq d dq dq Fig.6. Elmtul d volum osidrat ptru ilustrara bilaţului trmi odutiv
4 66 rmothiă Cosidrăm ăldura primită mai mar dât a dată, di orpul s va îăli. Ptru lmtul d volum dv, ăldura primită î timpul dτ d la lmtl vi, st: dq i dq dq dq iar a dată st: dq dq d dq d dq d Căldura rămasă î lmtul d volum dv, î timpul dτ, p dirţia, st dq r : dqr dq dq d d d d dτ ud fluul trmi uitar s-a raportat la lmtul d ari da d.d Fuţia d, fiid otiuă î itrvalul d, s poat dvolta î sri: 3 d 3 d d... d d! 3 3! S-au glijat trmii ifiit mii di dvoltara î sri şi s-au rţiut umai primii doi trmi. Eprsia ăldurii rămas dvi: dqr dd d dτ d d d dτ Aalog, ptru dirţil şi s pot sri rlaţiil: dqr d d d dτ ; dqr d d d dτ Căldura rămasă î lmtul d volum dv, î timpul dτ, st: (6.4) 3 dq Q dq dq dq r rk r r r d d d dτ k dv dτ Căldura primită d lmtul d volum dv, î timpul dτ, d la sursa itră st: (6.5) dqs v d d d dτ v dv dτ Căldura totală rămasă î lmtul d volum dv va fi: (6.6) dq dqr dqs dv dτ v dv dτ
5 rmothiă 67 Căldura totală rămasă va îăli lmtul d volum dv, a ărui tmpratură va rşt î uitata d timp u τ. Di uaţia alorimtrii rultă: (6.7) dv d dq τ τ ud -ăldura spifiă masiă a orpului, K kg J ; -dsitata orpului, 3 m kg. Egalâd rlaţiil (6.6) şi (6.7) s obţi vita d variaţi a tmpraturii orpului: (6.8) τ s Coform lgii lui Fourir: ; ; di ; ;. Euaţia (6.8) s mai poat sri: (6.9a) τ s sau, ptru orpuri omog, ptru ar, uaţia (5.8) dvi: (6.9b) τ s sau (6.9) τ a s ud -opratorul Lapla; ; a-ofiit d difuivitat trmiă; a ; [] s m a. Euaţia (6.9) s umşt uaţia lui Fourir ptru oduţia trmiă. Ea primă faptul ă, vita d variaţi a tmpraturii uui orp, sub aţiua uui flu trmi odutiv şi a ui surs itr d ăldură, dpid d graditul d tmpratură şi d valoara ofiitului d difuivitat trmiă a matrialului di ar st alătuit orpul. Cofiitul d difuivitat trmiă,a, dpid la râdul său d tmpratură şi prsiu. El primă, di put d vdr fii, irţia trmiă a orpului. Euaţia oduţii trmi prmit dtrmiara:
6 68 rmothiă! âmpului d tmpraturi: (,,,τ ) prmat! fluului trmi uitar:,ptru rgimul traitoriu; (,,, ) grad,! fluului trmi: ptru rgimul Q A Astfl, s pot aborda problm d optimiar a proslor d propagar a ăldurii şi d dimsioar a istalaţiilor trmi. Euaţia s partiulariaă î fuţi d tipul rgimului studiat, prmat sau traitoriu şi d istţa sau u a surslor itr d ăldură Codiţii d uiitat ptru uaţia oduţii trmi Itgrara uaţii lui Fourir ptru oduţia trmiă itrodu ostat d itgrar ar fa a soluţia găsită să rflt o îtragă lasă d fom asmăătoar. Ptru dtrmiara soluţii ui trbui impus odiţii d uiitat. Codiţiil d uiitat s pot împărţi î : Codiţii tmporal. S uoaşt âmpul d tmpratură la u aumit momt,τ o, osidrat iiţial: (6.0) (,,, τ o ) Codiţii spaţial (odiţii d margi sau d frotiră). S dau, î otiuar, tri tipuri d odiţii d frotiră: Codiţii tip Dirihlt. S uoaşt âmpul d tmpratură p suprafţl limită (p frotirl sistmului). Codiţii tip Numa. S uoaşt graditul d tmpratură p suprafţl d frotiră: (6.) grad f (,,,τ ) a prmit uoaştra fluului trmi uitar p ast frotir: grad (,,,τ ) Codiţii d tip Fourir (d propagar a ăldurii pri suprafţ). Ast odiţii impu faptul ă, valoara fluului trmi, la suprafaţa d sparaţi ditr u solid şi u fluid, u s modifiă. Fluul trmi uitar ar a străbătut solidul pri oduţi trmiă şi a ajus la suprafaţa d sparaţi ditr solid şi fluid st prluat î îtrgim d ătr fluid pri ovţi şi radiaţi: (6.) grad A α ( A ) ud α -ofiit d propagar a ăldurii pri suprafaţă; A -tmpratura suprafaţi; -tmpratura mdi a fluidului.
7 rmothiă Coduţia trmiă î rgim prmat pri orpuri fără surs itrioar d ăldură Î aul propagării ăldurii pri oduţi, î orpuri fără surs d ăldură, uaţia lui Fourir (6.9) ia o formă partiulară, trasformâdu-s îtr-o uaţi liptiă d tip Lapla: (6.3) a 0 ptru 0 s rasfrul d ăldură pri prţi pla-paralli, ifiiţi S osidră u prt di matrial omog şi iotrop, u suprafţl limită pla parall şi ifiit. S osidră, ptru simplifiar, ă tmpratura variaă umai î dirţia, di suprafţl iotrm sut pla parall u plaul O. Suprafţl limită oiid u iotrml partiular d tmpratură o şi rsptiv. Î ast odiţii, uaţia (6.3) dvi: (6.4) 0 Soluţia grală a asti uaţii st d forma: (6.5) C C di tmpratura variaă liiar î lugul ai O a prtlui, aşa um s obsrvă î fig.6.3. Costatl d itgrar C, C s dtrmiă î fuţi d odiţiil d uiitat, obţiâdu-s astfl soluţia partiulară ăutată. 0 0 δ Fig 6.3 Variaţia liiară a tmpraturii îtr-u prt u fţ pla parall, ifiit Codiţii d uiitat tip Dirihlt: (6.6) 0; 0 δ ; Puâd ast odţii uaţii (6.5), rultă soluţia partiulară: 0 0 δ Di lga Fourir rultă, mai dpart, fluul uitar trmi: W (6.7)! ( 0 ), δ m Rlaţia itsităţii fluului trmi (6.7) prmit şi priara ssului fii al ofiitului d oduţi trmiă,.î prsia:
8 70 rmothiă δ δ Q! δ Q!. 0 0 A 0 Aτ S osidră δ m;0 K; A m; τ s şi rultă umri gal u Q. Di, ofiitul d oduţi trmiă,, rprită atitata d ăldură ar străbat îtr-o sudă pritr-o suprafaţă d m,u prt omog gros d m, la ar difrţa d tmpratură îtr suprafţl sal limită st K. Rlaţia (6.7) poat fi pusă sub forma: 0 0 (6.8)! δ R s ud Rs -ristţa spifiă la prmabilitat trmiă a prtlui, dfiită pri aalogi u lga lui Ohm di ltroitiă. Cl două fom sut aaloag. Î aul prtlui fiit, prturbara sptrului d iotrm p otur modifiă graditul d tmpratură şi valoara arii suprafţi iotrm,rlaţia (6.8) mai fiid valabilă. otuşi (6.8) s folosşt î thiă,roril itrodus fiid foart mii. Codiţii d uiitat tip Numa Cuosâdu-s graditul d tmpratură p frotira A, s utiliaă lga Fourir ptru dtrmiara ostati C :! grad C A A Ca d-a doua ostată s soat ditr-o odiţi tip Dirihlt: 0, 0 C. Di, âmpul d tmpratură s dtrmiă sub forma: (6.8)! 0! ( 0 ). S rgăss rultatl stabilit atrior ptru δ. Codiţii d uiitat d otat Î aul prtlui pla ompus di mai mult straturi d matrial s utiliaă lga d osrvar a itsităţii fluului trmi la suprafaţa d otat îtr două straturi. Codiţiil d otat sut îsoţit d odiţii tip Dirihlt ptru suprafţl limită,primat sub forma : 0; k δ k k o ; ud δ k -grosima stratului k Ptru u strat urt k, rlaţia (6.7) s sri: δ k k! k
9 rmothiă 7 Ştiid ă fluul trmi uitar st ostat (aaşi valoar î fiar strat) s poat fa îsumara : δ k 0 (6.9) ( k k )!! k R mpratura îtr-u strat urt k variaă liiar. Lga d frâgr a urbi tmpraturii la suprafaţa d sparaţi arată ă tgψ k k tgψk. Drptl vor ava îliar mar î straturil iolatoar. sk kj k 0 k- k ψ k- ψ k 0 δ δ k δ Fig.6.4 Variaţia tmpraturii î prt pla u fţ parall, ompus di mai mult straturi, ar au ofiiţii d odutivitat trmiă,,... Codiţii d uiitat d tip Fourir Cirulaţia fluidului d-a lugul suprafţlor limită (0 şi δ ) şi foml d radiaţi fa a tmpratura să prit variaţii atuat î viătata astor suprafţ. i 0 α i 0 α δ Fig 6.5 Variaţia tmpraturii î prt pla, u suprafţ parall, d-a lugul ărora irulă u fluid
10 7 rmothiă S uos: tmpratura fluidului la itrior i şi la trior,prum şi ofiiţii d trasfr trmi pri suprafaţa itrioară α i şi trioară α. S impu odiţii d dtrmiar a ostatlor C,C, sub forma : C α i ( i C ) C α ( Cδ C ) Ştiid ă : C C C Rultă âmpul d tmpraturi: K δ (6.0) ( ) i K i αi α ud K ofiit spifi total d trasformar trmi: [ ] (6.) K δ, W m. Rultă itsitata fluului trmi: k αi α i (6.)! K( i ) R Optimiara prţilor plai ompuşi. a) Îlouira matriallor Î apliaţiil thi s pu problma îlouirii uui prt ompus di mai mult straturi u u prt simplu di alt matrial, u odiţia a dsitata fluului trmi să u s modifi: -daă s păstraă grosima iiţială, matrialul îlouitor trbui să aibă ofiitul d oduţi trmiă hivalt, : (6.3) δ k k δ k k k ud -umărul d straturi -daă s impu matrialul, di s uoaşt, rultă grosima hivaltă di odiţia d galitat a itsităţii fluului trmi: (6.4) δ δ k. k La valori δ, apropiat d l ral, algra s fa di osidraţii thiooomi. b)aumulara ăldurii î prţi
11 rmothiă 73 Ordia d aşar a straturilor îtr-u prt pla ifluţaă atitata d ăldură aumulată î straturi. Î aul î ar stratul iolator s aşaă p suprafaţa aldă, atitata d ăldură aumulată î prt st mai miă. Ptru u prt pla ompus di straturi, atitata miimă d ăldură aumulată î prt orspud aşării matrillor î ordia rsătoar a valorilor ofiiţilor d oduţi trmiă, îpâd d la suprafaţa aldă rasfrul d ăldură pri prti ilidrii, ifiiţi S osidră u prt ilidri, ifiit d lug, fără surs d ăldură itrioar, v 0. S admit ă tmpratura st ostată î lugul ai O, aa logitudială a ilidrului. mpratura variaă umai î lugul rai ilidrului. Euaţia lui Eulr, î ast a, ar forma (6.3) a 0 ar, î oordoat arti, bidimsioal: (6.5) 0 i, α i α r i o o α i, α r o, α r r i Fig. 6.6 rasmitra ăldurii pritr-u prt ilidri săldat d două fluid.a)sţiu trasvrsală ; b)sţiu logitudială şi rprtara âmpului d tmpratură Euaţia rului st: (6.6) r Eprimâd uaţia (6.5) î oordoat ilidri, a dvi: d d (6.7) r 0 r dr dr ptru aul prsupus, () r. Soluţia grală a uaţii (6.7) st: (6.8) Al r B, u odiţia r 0 ud A,B ostat d itgrar. Dtrmiara ostatlor A,B şi, di, dtrmiara soluţii partiular s raliaă puâd odiţii d uiitat.
12 74 rmothiă Codiţii d uiitat d tip Fourir S uos: i, tmpratura fluidului di itriorul ilidrului;, tmpratura fluidului di triorul ilidrului; α i -ofiitul d trasfr trmi pri suprafaţa itrioară; α -ofiitul d trasfr trmi pri suprafaţa trioară; -ofiitul d oduţi trmiă pri matrialul prtlui. Codiţiil Fourir impu osrvara fluului trmi uitar la suprafaţa d sparaţi ditr două fa. Ptru suprafaţa itrioară a ilidrului, d raă r o şi lugim L, odiţiil Fourir s primă pri rlaţia: d (6.9) πro L πr0 Lα i ( i ) dr Ptru suprafaţa trioară, d ră r şi lugim L, avm aalog: d (6.30) πr L πr Lα ( ) dr ud st fuţia ăutată, âmpul d tmpraturi î prt. Itroduâd prsia (6.8) î uaţiil (6.9) şi (6.30) s obţi ostatl d itgrar A şi B, di s află âmpul d tmpraturi î prt. Rultă fluul trmi sub forma: πl( i ) (6.3) Q r l αir0 ro αr Daă studim ifluţa rai trioar, r, asupra fluului trmi trasmis pri prt, Q,osidrăm fuţia: Q f ( r ), ar prită u put d maim la valoara rai trioar: (6.3) r rr α umită raa ritiă (figura 6.7). Q Q ma r r r Fig 6.7 Variaţia fluului trmi trasmis, î fuţi draa trioară a prtlui ilidri
13 rmothiă 75 Eftul d iolaţi a prtlui s obţi ptru o raă trioară mult difrită d a ritiă. Itsifiara trasfrului d ăldură pri prt s obţi la o raă trioară apropiată d a ritiă. Ast oluii s utiliaă la dimsioara odutlor Coduţia trmiă î rgim staţioar pri bar u răir latrală Nrvurara suprafţi d trasfr trmi odu la itsifiara fomlor d trasfr. Mtoda st folosită la raira u ar a motoarlor. Problml priipal sut: dtrmiara âmpului d tmpraturi d-a lugul rvurii şi a fluului trmi p ar poat să-l vau rvura. Fi o bară (rvura )ofţioată di matrial omog şi iotrop, ar u ar ivoar itrioar d ăldură. S osidră ă rvura fa orp omu u u prt solid. Cotatul ditr bară şi prt st prft, lipsit d disotiuităţi. Bara s osidră îojurată d u fluid u tmpratura ostată,, iar ofiitul d trasfr trmi pri suprafaţă,α, st ostat î timp şi spaţiu. Bara s osidră foart lugă şi u sţiu drptughiulară. Euaţia d bilaţ trmi s sri: (6.33) Q Q d δ Ql δ Q ud Q d Q d Q d δ Ql αp( )d A-aria sţiuii trasvrsal, P-primtrul sţiuii trasvrsal. Rultă: d d P (6.34) A ( ) 0 d d α S otaă: θ d d d A d d βp β A şi rultă uaţia: "" (6.35) θ β θ 0 ar ar soluţia d tip Eulr: β β (6.36) θ C C 0 0 Q Q d δ Q δ l
14 76 rmothiă Fig.6.8 Sţiu pri bară d sţiu drptughiulară,ptru ftuara bilaţului trmi Î aul barlor foart lugi şi subţiri, s pu odiţii d tip Dirihlt ptru dtrmiara ostatlor d itgrar di soluţia grală: (6.37) 0 ; 0 ; adiă θ θ0 ; ; adiă θ 0; C 0 Di soluţia grală (6.36)s obţi âmpul d tmpraturi: (6.38) θ θ 0 p( β) Rlaţia st valabilă atât ptru răir ât şi ptru îălira barlor pri suprafaţa d otat u fluidul. D-a lugul bari, tmpratura variaă poţial. Graditul d tmpratură dpid d ofiitul β, ar ţi ot d aratristiil trmi ( ) şi d l gomtri al bari. Î figura 6.9. st rprtat âmpul d tmpratură ptru aul răirii bari. 0 β > β β Fig. 6.9 Variaţia poţială a tmpraturii î aul răirii latral a ui bar subţiri, u sţiu drptughiulară
Teorema Rezidurilor şi Bucuria Integralelor Reale
 Torma Ridurilor şi Bucuria Intgrallor Ral Prntar d Alandru Ngrscu Intgral cu funcţii raţional c dpind d sin t şi cos t u notaţia it, avm: cos t ( + sin t ( i dt d i, iar intgrara s va fac d-a lungul crcului
Torma Ridurilor şi Bucuria Intgrallor Ral Prntar d Alandru Ngrscu Intgral cu funcţii raţional c dpind d sin t şi cos t u notaţia it, avm: cos t ( + sin t ( i dt d i, iar intgrara s va fac d-a lungul crcului
Lucian Maticiuc. Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 9.
 Capitolul V: Şiruri şi srii d fucţii. Lct. dr. Lucia Maticiuc Facultata d Hidrothică, Godzi şi Igiria Mdiului Matmatici Suprioar, Smstrul I, Lctor dr. Lucia MATICIUC SEMINAR 9. Cap. V Şiruri şi srii d
Capitolul V: Şiruri şi srii d fucţii. Lct. dr. Lucia Maticiuc Facultata d Hidrothică, Godzi şi Igiria Mdiului Matmatici Suprioar, Smstrul I, Lctor dr. Lucia MATICIUC SEMINAR 9. Cap. V Şiruri şi srii d
6.4.Convecţia. unde T s -temperatura termodinamică a suprafeţei corpului solid, -temperatura termodinamică medie a fluidului, 6.
 Trmothnică 77 6..Convcţia Convcţia căldurii st fnomnul lmntar d transfr trmic car s manifstă în mdii fluid şi la supafaţa d sparaţi a fazlor. Est caractristică mdiilor în mişcar, căldura fiind transportată
Trmothnică 77 6..Convcţia Convcţia căldurii st fnomnul lmntar d transfr trmic car s manifstă în mdii fluid şi la supafaţa d sparaţi a fazlor. Est caractristică mdiilor în mişcar, căldura fiind transportată
MECANICA CUANTICĂ. 1. Bazele experimentale ale mecanicii cuantice
 - - MECANICA CUANICĂ. Bazl xprital al aiii uati.. Radiaţia triă... Dfiiţii Ori orp îălzit ( > K) it radiaţii d atură ltroagtiă obţiut p saa işării d agitaţi triă a partiullor ostituit al orpului. Ast radiaţii
- - MECANICA CUANICĂ. Bazl xprital al aiii uati.. Radiaţia triă... Dfiiţii Ori orp îălzit ( > K) it radiaţii d atură ltroagtiă obţiut p saa işării d agitaţi triă a partiullor ostituit al orpului. Ast radiaţii
Eşantionarea semnalelor
 Eşantionara smnallor Eşantionara = prlvara d prob dintr-un smnal la momnt d timp dcalat intr l cu cu frcvnta d şantionar, f =/. xˆ t x k t k k = ( = δ ( Smnalul şantionat idal:. Spctrul Xˆ = X ( k k =
Eşantionara smnallor Eşantionara = prlvara d prob dintr-un smnal la momnt d timp dcalat intr l cu cu frcvnta d şantionar, f =/. xˆ t x k t k k = ( = δ ( Smnalul şantionat idal:. Spctrul Xˆ = X ( k k =
ECUAŢII DIFERENŢIALE ŞI CU DERIVATE PARŢIALE PRIN EXERCIŢII ŞI PROBLEME
 Codruţa Stoica ECUAŢII DIFERENŢIALE ŞI CU DERIVATE PARŢIALE PRIN EXERCIŢII ŞI PROBLEME Ediţia a II-a rvăută şi compltată Editura MIRTON Timişoara v CUPRINS Capitolul. ECUAŢII DIFERENŢIALE DE ORDINUL.....
Codruţa Stoica ECUAŢII DIFERENŢIALE ŞI CU DERIVATE PARŢIALE PRIN EXERCIŢII ŞI PROBLEME Ediţia a II-a rvăută şi compltată Editura MIRTON Timişoara v CUPRINS Capitolul. ECUAŢII DIFERENŢIALE DE ORDINUL.....
LEGI CLASICE DE PROBABILITATE
 7. LEGI CLASICE DE PROBABILITATE Fi (Ω, K, P u câmp d probabilitat şi f : Ω R, o variabilă alatoar. Am văzut că varibili f i s poat asocia o fucţi d rpartiţi F, cotiuă la stâga şi o fucţi caractristică
7. LEGI CLASICE DE PROBABILITATE Fi (Ω, K, P u câmp d probabilitat şi f : Ω R, o variabilă alatoar. Am văzut că varibili f i s poat asocia o fucţi d rpartiţi F, cotiuă la stâga şi o fucţi caractristică
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE. Obiective:
 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
TEMA 9: FUNCȚII DE MAI MULTE VARIABILE 77 TEMA 9: FUNCȚII DE MAI MULTE VARIABILE Obiective: Deiirea pricipalelor proprietăţi matematice ale ucţiilor de mai multe variabile Aalia ucţiilor de utilitate şi
4.6. Caracteristicile motoarelor de curent continuu
 Maşia lctrică d curt cotiuu 8D 017 4.6. Caractristicil motoarlor d curt cotiuu Pricipall caractristici al motoarlor d curt cotiuu sut: caractristica mcaică = ( M ) caractristica curtului = ( I i ) caractristica
Maşia lctrică d curt cotiuu 8D 017 4.6. Caractristicil motoarlor d curt cotiuu Pricipall caractristici al motoarlor d curt cotiuu sut: caractristica mcaică = ( M ) caractristica curtului = ( I i ) caractristica
rs r r â t át r st tíst Ó P ã t r r r â
 rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
rs r r â t át r st tíst P Ó P ã t r r r â ã t r r P Ó P r sã rs r s t à r çã rs r st tíst r q s t r r t çã r r st tíst r t r ú r s r ú r â rs r r â t át r çã rs r st tíst 1 r r 1 ss rt q çã st tr sã
ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s
 P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
P P P P ss rt çã r s t Pr r Pós r çã ê t çã st t t ê s 1 t s r s r s r s r q s t r r t çã r str ê t çã r t r r r t r s r t r 3 2 r r r 3 t r ér t r s s r t s r s r s ér t r r t t q s t s sã s s s ér t
3. ERORI DE MÃSURARE
 6 Mtrologi, Stadardizar si Masurari 3.. Dfiira rorii d masurar 3. ERORI DE MÃSURARE Î practica, s obsrva ca îtotdaua valoara umrica rala a ui mari fizic masurat st difrita d valoara m idicata d aparatul
6 Mtrologi, Stadardizar si Masurari 3.. Dfiira rorii d masurar 3. ERORI DE MÃSURARE Î practica, s obsrva ca îtotdaua valoara umrica rala a ui mari fizic masurat st difrita d valoara m idicata d aparatul
Prelucrarea numerică a semnalelor, Capitolul 2 2. SINTEZA FILTRELOR NUMERICE
 rlucrara umrică a smallor, Capitolul Silviu Ciocia. SITEZA FILTRELOR UMERICE roictara uui filtru umric prsupu parcurgra următoarlor tap : - Sita fucţii d trasfr c satisfac codiţiil impus; - Algra ui structuri
rlucrara umrică a smallor, Capitolul Silviu Ciocia. SITEZA FILTRELOR UMERICE roictara uui filtru umric prsupu parcurgra următoarlor tap : - Sita fucţii d trasfr c satisfac codiţiil impus; - Algra ui structuri
lim lim lim lim (criteriul cu şiruri); lim lim = lim ; Limite de funcńii NotaŃii: f :D R, D R, α - punct de acumulare a lui D;
 Limit d fucńii Aliz mtmtică, cls XI- Limit d fucńii NotŃii: f :D R, D R, α - puct d cumulr lui D DfiiŃii l iti DfiiŃi f ( = l, l R, dcă ptru oric vciătt V lui l istă o vciătt α U lui α stfl îcât D U, α,
Limit d fucńii Aliz mtmtică, cls XI- Limit d fucńii NotŃii: f :D R, D R, α - puct d cumulr lui D DfiiŃii l iti DfiiŃi f ( = l, l R, dcă ptru oric vciătt V lui l istă o vciătt α U lui α stfl îcât D U, α,
Capitolul I ECUAŢII DIFERENŢIALE. 1 Matematici speciale. Probleme. 1. Să de integreze ecuaţia diferenţială de ordinul întâi liniară
 Mamaici spcial Problm c solţia apioll I EUAŢII DIFERENŢIALE Să d ingrz caţia difrnţială d ordinl înâi liniară g cos d Solţi: Ecaţia omognă aaşaă s: - g sa g d ln - ln cos ln sa Pnr rzolvara caţii cos nomogn
Mamaici spcial Problm c solţia apioll I EUAŢII DIFERENŢIALE Să d ingrz caţia difrnţială d ordinl înâi liniară g cos d Solţi: Ecaţia omognă aaşaă s: - g sa g d ln - ln cos ln sa Pnr rzolvara caţii cos nomogn
6 n=1. cos 2n. 6 n=1. n=1. este CONV (fiind seria armonică pentru α = 6 > 1), rezultă
 Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Alterazioni del sistema cardiovascolare nel volo spaziale
 POLITECNICO DI TORINO Corso di Laurea in Ingegneria Aerospaziale Alterazioni del sistema cardiovascolare nel volo spaziale Relatore Ing. Stefania Scarsoglio Studente Marco Enea Anno accademico 2015 2016
POLITECNICO DI TORINO Corso di Laurea in Ingegneria Aerospaziale Alterazioni del sistema cardiovascolare nel volo spaziale Relatore Ing. Stefania Scarsoglio Studente Marco Enea Anno accademico 2015 2016
TIPURI DE DEZINTEGRĂRI NUCLEARE. Dezintegrarea α
 TIPURI D DZINTGRĂRI NUCLR Dzitgaa -mita d căt ul ucl adioactiv, stuctui compact d doi potoi şi doi utoi (ucl d hliu şi a ui catităţi apciabil d gi Q Z X 4 Z Y Q 38 9 4.47 ai U 9 34 9 Th Q (4.7 V s îtâlşt
TIPURI D DZINTGRĂRI NUCLR Dzitgaa -mita d căt ul ucl adioactiv, stuctui compact d doi potoi şi doi utoi (ucl d hliu şi a ui catităţi apciabil d gi Q Z X 4 Z Y Q 38 9 4.47 ai U 9 34 9 Th Q (4.7 V s îtâlşt
2.CARACTERIZAREA GENERALĂ A RADIOACTIVITǍŢII
 2.CARACTERIZAREA GEERALĂ A RADIOACTIVITǍŢII Radioactivitat -fnomnul d misi d radiaţii d cătr unl substanţ numit substanţ radioactiv. Procsul constă în misia a tri tipuri d radiaţii: α, β şi γ, priml două
2.CARACTERIZAREA GEERALĂ A RADIOACTIVITǍŢII Radioactivitat -fnomnul d misi d radiaţii d cătr unl substanţ numit substanţ radioactiv. Procsul constă în misia a tri tipuri d radiaţii: α, β şi γ, priml două
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
P P Ó P. r r t r r r s 1. r r ó t t ó rr r rr r rí st s t s. Pr s t P r s rr. r t r s s s é 3 ñ
 P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
P P Ó P r r t r r r s 1 r r ó t t ó rr r rr r rí st s t s Pr s t P r s rr r t r s s s é 3 ñ í sé 3 ñ 3 é1 r P P Ó P str r r r t é t r r r s 1 t r P r s rr 1 1 s t r r ó s r s st rr t s r t s rr s r q s
Olimpiada Naţională de Matematică Etapa locală Clasa a IX-a M 1
 Calea 13 Septembrie, r 09, Sector 5, 0507, București Tel: +40 (0)1 317 36 50 Fax: +40 (0)1 317 36 54 Olimpiada Naţioală de Matematică Etapa locală -00016 Clasa a IX-a M 1 Fie 1 abc,,, 6 şi ab c 1 Să se
Calea 13 Septembrie, r 09, Sector 5, 0507, București Tel: +40 (0)1 317 36 50 Fax: +40 (0)1 317 36 54 Olimpiada Naţioală de Matematică Etapa locală -00016 Clasa a IX-a M 1 Fie 1 abc,,, 6 şi ab c 1 Să se
Analiza bivariata a datelor
 Aaliza bivariata a datelor Aaliza bivariata a datelor! Presupue masurarea gradului de asoiere a doua variabile sub aspetul: Diretiei (aturii) Itesitatii Semifiatiei statistie Variabilele omiale Tabele
Aaliza bivariata a datelor Aaliza bivariata a datelor! Presupue masurarea gradului de asoiere a doua variabile sub aspetul: Diretiei (aturii) Itesitatii Semifiatiei statistie Variabilele omiale Tabele
METODE DE REPARTIZARE A CONSUMULUI DE COMBUSTIBIL ÎNTRE CELE DOUÃ FORME DE ENERGIE PRODUSE
 MOD D RPARIZAR A CONSUMULUI D COMUSIIL ÎNR CL DOUÃ FORM D NRGI PRODUS 5.1. Gnraliăţi În azul l mai gnral al uni nral d ognrar hipaă u grupuri u ondnsaţi şi priză rglailă, onsumul d omusiil poa fi sris
MOD D RPARIZAR A CONSUMULUI D COMUSIIL ÎNR CL DOUÃ FORM D NRGI PRODUS 5.1. Gnraliăţi În azul l mai gnral al uni nral d ognrar hipaă u grupuri u ondnsaţi şi priză rglailă, onsumul d omusiil poa fi sris
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
6. Circuite liniare în regim periodic nesinusoidal
 6. Circuit liiar î rgim riodic siusoidal 6. troducr. aliza armoica a smallor Pâa î rzt am studiat comortara circuitlor liiar daca xcitatia st siusoidala. Î ralitat tsiuil si curtii ritr-o rta lctrica sut
6. Circuit liiar î rgim riodic siusoidal 6. troducr. aliza armoica a smallor Pâa î rzt am studiat comortara circuitlor liiar daca xcitatia st siusoidala. Î ralitat tsiuil si curtii ritr-o rta lctrica sut
ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t
 ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t FichaCatalografica :: Fichacatalografica https://www3.dti.ufv.br/bbt/ficha/cadastrarficha/visua... Ficha catalográfica preparada
ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t FichaCatalografica :: Fichacatalografica https://www3.dti.ufv.br/bbt/ficha/cadastrarficha/visua... Ficha catalográfica preparada
6. CIRCUITE MAGNETICE
 6. CICITE MAGNETICE Nui iuit agti susiua d dii pi a s otază u lux agti. Fluxul st podus d bobi a îlăţui iuitul paţial sau î îtgi uit bobi d xitaţi. 6.. Diiţii lasiiăi apliaţii thi Fluxul pi sţiua tasvsală
6. CICITE MAGNETICE Nui iuit agti susiua d dii pi a s otază u lux agti. Fluxul st podus d bobi a îlăţui iuitul paţial sau î îtgi uit bobi d xitaţi. 6.. Diiţii lasiiăi apliaţii thi Fluxul pi sţiua tasvsală
TIPURI DE DEZINTEGRĂRI NUCLEARE. Dezintegrarea α
 TIPURI D DZINTGRĂRI NUCLR Dzitgaa α -mita d căt ul ucl adioactiv, stuctui compact d doi potoi şi doi utoi (ucl d hliu) şi a ui catităţi apciabil d gi Q α Z X 4 Z Y Q 38 9 4.47 ai U 9 34 9 Th Q (4.7 V)
TIPURI D DZINTGRĂRI NUCLR Dzitgaa α -mita d căt ul ucl adioactiv, stuctui compact d doi potoi şi doi utoi (ucl d hliu) şi a ui catităţi apciabil d gi Q α Z X 4 Z Y Q 38 9 4.47 ai U 9 34 9 Th Q (4.7 V)
7. ECUAŢII ŞI SISTEME DE ECUAŢII DIFERENŢIALE
 7. ECUAŢII ŞI SISTEME DE ECUAŢII DIFERENŢIALE 7. NOŢIUNI GENERALE. TEOREMA DE EXISTENŢĂ ŞI UNICITATE Pri ecuaţia difereţială de ordiul îtâi îţelegem o ecuaţie de forma: F,, = () ude F este o fucţie reală
7. ECUAŢII ŞI SISTEME DE ECUAŢII DIFERENŢIALE 7. NOŢIUNI GENERALE. TEOREMA DE EXISTENŢĂ ŞI UNICITATE Pri ecuaţia difereţială de ordiul îtâi îţelegem o ecuaţie de forma: F,, = () ude F este o fucţie reală
FLUCTUAŢII STATISTICE
 FLUCTUAŢII STATISTICE Obictul lucrării Î acastă lucrar s dorşt să s vrific şi să s tstz aspctl alatoar al folor cuatic, î ssul dscris ai jos. Aspctl statistic al folor atoic roprităţil discrt al atrii
FLUCTUAŢII STATISTICE Obictul lucrării Î acastă lucrar s dorşt să s vrific şi să s tstz aspctl alatoar al folor cuatic, î ssul dscris ai jos. Aspctl statistic al folor atoic roprităţil discrt al atrii
Ministerul Educaţiei Naționale Centrul Naţional de Evaluare şi Examinare
 Miisterul Educaţiei Națioale Cetrul Naţioal de Evaluare şi Eamiare Eameul de bacalaureat aţioal 08 Proba E c) Matematică M_mate-ifo Clasa a XI-a Toate subiectele sut obligatorii Se acordă 0 pucte di oficiu
Miisterul Educaţiei Națioale Cetrul Naţioal de Evaluare şi Eamiare Eameul de bacalaureat aţioal 08 Proba E c) Matematică M_mate-ifo Clasa a XI-a Toate subiectele sut obligatorii Se acordă 0 pucte di oficiu
HONDA. Έτος κατασκευής
 Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
Accord + Coupe IV 2.0 16V (CB3) F20A2-A3 81 110 01/90-09/93 0800-0175 11,00 2.0 16V (CB3) F20A6 66 90 01/90-09/93 0800-0175 11,00 2.0i 16V (CB3-CC9) F20A8 98 133 01/90-09/93 0802-9205M 237,40 2.0i 16V
Seminar 3. Serii. Probleme rezolvate. 1 n . 7. Problema 3.2. Să se studieze natura seriei n 1. Soluţie 3.1. Avem inegalitatea. u n = 1 n 7. = v n.
 Semir 3 Serii Probleme rezolvte Problem 3 Să se studieze tur seriei Soluţie 3 Avem ieglitte = ) u = ) ) = v, Seri = v este covergetă fiid o serie geometrică cu rţi q = < Pe bz criteriului de comprţie cu
Semir 3 Serii Probleme rezolvte Problem 3 Să se studieze tur seriei Soluţie 3 Avem ieglitte = ) u = ) ) = v, Seri = v este covergetă fiid o serie geometrică cu rţi q = < Pe bz criteriului de comprţie cu
Πίνακας ρυθμίσεων στο χώρο εγκατάστασης
 1/8 Κατάλληλες εσωτερικές μονάδες *HVZ4S18CB3V *HVZ8S18CB3V *HVZ16S18CB3V Σημειώσεις (*5) *4/8* 4P41673-1 - 215.4 2/8 Ρυθμίσεις χρήστη Προκαθορισμένες τιμές Θερμοκρασία χώρου 7.4.1.1 Άνεση (θέρμανση) R/W
1/8 Κατάλληλες εσωτερικές μονάδες *HVZ4S18CB3V *HVZ8S18CB3V *HVZ16S18CB3V Σημειώσεις (*5) *4/8* 4P41673-1 - 215.4 2/8 Ρυθμίσεις χρήστη Προκαθορισμένες τιμές Θερμοκρασία χώρου 7.4.1.1 Άνεση (θέρμανση) R/W
P t s st t t t t2 t s st t t rt t t tt s t t ä ör tt r t r 2ö r t ts t t t t t t st t t t s r s s s t är ä t t t 2ö r t ts rt t t 2 r äärä t r s Pr r
 r s s s t t P t s st t t t t2 t s st t t rt t t tt s t t ä ör tt r t r 2ö r t ts t t t t t t st t t t s r s s s t är ä t t t 2ö r t ts rt t t 2 r äärä t r s Pr r t t s st ä r t str t st t tt2 t s s t st
r s s s t t P t s st t t t t2 t s st t t rt t t tt s t t ä ör tt r t r 2ö r t ts t t t t t t st t t t s r s s s t är ä t t t 2ö r t ts rt t t 2 r äärä t r s Pr r t t s st ä r t str t st t tt2 t s s t st
def def punctul ( x, y )0R 2 de coordonate x = b a
 Cetrul de reutte rl-mhl Zhr CENTE E GEUTTE Î prtă este evoe să se luleze r plălor ple de ee vom det plăle ple u mulńm Ştm ă ms este o măsură ttăń de mtere dtr-u orp e ms repreztă o uńe m re soză eăre plă
Cetrul de reutte rl-mhl Zhr CENTE E GEUTTE Î prtă este evoe să se luleze r plălor ple de ee vom det plăle ple u mulńm Ştm ă ms este o măsură ttăń de mtere dtr-u orp e ms repreztă o uńe m re soză eăre plă
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Statisticǎ - curs 2. 1 Parametrii şi statistici ai tendinţei centrale 2. 2 Parametrii şi statistici ai dispersiei 5
 Statisticǎ - curs Cupris Parametrii şi statistici ai tediţei cetrale Parametrii şi statistici ai dispersiei 5 3 Parametrii şi statistici factoriali ai variaţei 8 4 Parametrii şi statistici ale poziţiei
Statisticǎ - curs Cupris Parametrii şi statistici ai tediţei cetrale Parametrii şi statistici ai dispersiei 5 3 Parametrii şi statistici factoriali ai variaţei 8 4 Parametrii şi statistici ale poziţiei
IJAO ISSN Introduction ORIGINAL ARTICLE
 IJAO Int ISSN 0391-3988 J Artif Organs 2015; 38(11): 600-606 OI: 10 5301 a 5000 52 ORIGINAL ARTICLE Fluid dynamic characterization of a polymeric heart valve prototype (Poli-Valve) tested under continuous
IJAO Int ISSN 0391-3988 J Artif Organs 2015; 38(11): 600-606 OI: 10 5301 a 5000 52 ORIGINAL ARTICLE Fluid dynamic characterization of a polymeric heart valve prototype (Poli-Valve) tested under continuous
r r t r r t t r t P s r t r P s r s r r rs tr t r r t s ss r P s s t r t t tr r r t t r t r r t t s r t rr t Ü rs t 3 r r r 3 rträ 3 röÿ r t
 r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs
r t t r t ts r3 s r r t r r t t r t P s r t r P s r s r P s r 1 s r rs tr t r r t s ss r P s s t r t t tr r 2s s r t t r t r r t t s r t rr t Ü rs t 3 r t r 3 s3 Ü rs t 3 r r r 3 rträ 3 röÿ r t r r r rs
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
SEMINARUL 3. Cap. II Serii de numere reale. asociat seriei. (3n 5)(3n 2) + 1. (3n 2)(3n+1) (3n 2) (3n + 1) = a
 Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
r t t r t t à ré ér t é r t st é é t r s s2stè s t rs ts t s
 r t r r é té tr q tr t q t t q t r t t rrêté stér ût Prés té r ré ér ès r é r r st P t ré r t érô t 2r ré ré s r t r tr q t s s r t t s t r tr q tr t q t t q t r t t r t t r t t à ré ér t é r t st é é
r t r r é té tr q tr t q t t q t r t t rrêté stér ût Prés té r ré ér ès r é r r st P t ré r t érô t 2r ré ré s r t r tr q t s s r t t s t r tr q tr t q t t q t r t t r t t r t t à ré ér t é r t st é é
Cursul 10 T. rezultă V(x) < 0.
 ursul uţol ătrtă V: X R V s lsă stl: ) V st oztv tă ă X u X rzultă V(). ) V st tv tă ă X u X rzultă V()
ursul uţol ătrtă V: X R V s lsă stl: ) V st oztv tă ă X u X rzultă V(). ) V st tv tă ă X u X rzultă V()
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Sarò signor io sol. α α. œ œ. œ œ œ œ µ œ œ. > Bass 2. Domenico Micheli. Canzon, ottava stanza. Soprano 1. Soprano 2. Alto 1
 Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò
Sarò signor io sol Canzon, ottava stanza Domenico Micheli Soprano Soprano 2 Alto Alto 2 Α Α Sa rò si gnor io sol del mio pen sie io sol Sa rò si gnor io sol del mio pen sie io µ Tenor Α Tenor 2 Α Sa rò
Parts Manual. Trio Mobile Surgery Platform. Model 1033
 Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
Trio Mobile Surgery Platform Model 1033 Parts Manual For parts or technical assistance: Pour pièces de service ou assistance technique : Für Teile oder technische Unterstützung Anruf: Voor delen of technische
SUBGRUPURI CLASICE. 1. SUBGRUPURI recapitulare
 SUBGRUPURI CLASICE. SUBGRUPURI recapitulare Defiiţia. Fie (G, u rup şi H o parte evidă a sa. H este subrup al lui G dacă:. H este parte stabilă a lui G;. H îzestrată cu operaţia idusă este rup. Teorema.
SUBGRUPURI CLASICE. SUBGRUPURI recapitulare Defiiţia. Fie (G, u rup şi H o parte evidă a sa. H este subrup al lui G dacă:. H este parte stabilă a lui G;. H îzestrată cu operaţia idusă este rup. Teorema.
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Olimpiada de Fizică Etapa naţională- ARAD 2011 TEORIE Barem. Subiect Parţial Punctaj 1. Barem subiect 1 10 A. Condiţiile de echilibru pentru pârghii:
 Olipiaa e Fiziă Etapa naţională- ARAD Pagina in 6 Subiet Parţial Puntaj. subiet A. Coniţiile e ehilibru pentru pârghii: =( + 4), 4e=f, O ( + + 4)a=b a b e f + 4 = f 4= e 4,5 4 4 4 =, =8g f + e =4g a =
Olipiaa e Fiziă Etapa naţională- ARAD Pagina in 6 Subiet Parţial Puntaj. subiet A. Coniţiile e ehilibru pentru pârghii: =( + 4), 4e=f, O ( + + 4)a=b a b e f + 4 = f 4= e 4,5 4 4 4 =, =8g f + e =4g a =
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
 ! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
COMBINATORICĂ. Mulţimile ordonate care se formează cu n elemente din n elemente date se numesc permutări. Pn Proprietăţi
 OMBINATORIĂ Mulţimile ordoate care se formează cu elemete di elemete date se umesc permutări. P =! Proprietăţi 0! = ( ) ( ) ( ) ( ) ( ) ( )! =!! =!! =! +... Submulţimile ordoate care se formează cu elemete
OMBINATORIĂ Mulţimile ordoate care se formează cu elemete di elemete date se umesc permutări. P =! Proprietăţi 0! = ( ) ( ) ( ) ( ) ( ) ( )! =!! =!! =! +... Submulţimile ordoate care se formează cu elemete
2.CARACTERIZAREA GENERALĂ A RADIOACTIVITǍŢII
 2.CRCTERIZRE GEERLĂ RDIOCTIVITǍŢII Radioactivitat -fnomnul d misi d radiaţii d cătr unl substanţ numit substanţ radioactiv. Procsul constă în misia a tri tipuri d radiaţii: α, β şi γ, priml două fiind
2.CRCTERIZRE GEERLĂ RDIOCTIVITǍŢII Radioactivitat -fnomnul d misi d radiaţii d cătr unl substanţ numit substanţ radioactiv. Procsul constă în misia a tri tipuri d radiaţii: α, β şi γ, priml două fiind
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
P P Ô. ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t
 P P Ô P ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t FELIPE ANDRADE APOLÔNIO UM MODELO PARA DEFEITOS ESTRUTURAIS EM NANOMAGNETOS Dissertação apresentada à Universidade Federal
P P Ô P ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã ís r t çã tít st r t FELIPE ANDRADE APOLÔNIO UM MODELO PARA DEFEITOS ESTRUTURAIS EM NANOMAGNETOS Dissertação apresentada à Universidade Federal
Couplage dans les applications interactives de grande taille
 Couplage dans les applications interactives de grande taille Jean-Denis Lesage To cite this version: Jean-Denis Lesage. Couplage dans les applications interactives de grande taille. Réseaux et télécommunications
Couplage dans les applications interactives de grande taille Jean-Denis Lesage To cite this version: Jean-Denis Lesage. Couplage dans les applications interactives de grande taille. Réseaux et télécommunications
APLICAŢII zona tematică 5 -TST-ID-
 APLCAŢ zoa tmatică 5 -TST-D- 6-6 CEF - Aplicaţii /. S firprztat fuc iafdischmaurm toarcuum rulmiimdpor ilogics NU( sauitr ri): Solu i: fa..b.c.c.d..a..d..b.b.c.d.a.b.c.d.a.d.b.c.d Aplicâdrla iilluidmorgaob
APLCAŢ zoa tmatică 5 -TST-D- 6-6 CEF - Aplicaţii /. S firprztat fuc iafdischmaurm toarcuum rulmiimdpor ilogics NU( sauitr ri): Solu i: fa..b.c.c.d..a..d..b.b.c.d.a.b.c.d.a.d.b.c.d Aplicâdrla iilluidmorgaob
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
Sunt variabile aleatoare care iau o infinitate numărabilă de valori. Diagrama unei variabile aleatoare discrete are forma... f. ,... pn.
 86 ECUAŢII 55 Vriile letore discrete Sut vriile letore cre iu o ifiitte umărilă de vlori Digrm uei vriile letore discrete re form f, p p p ude p = = Distriuţi Poisso Are digrm 0 e e e e!!! Se costtă că
86 ECUAŢII 55 Vriile letore discrete Sut vriile letore cre iu o ifiitte umărilă de vlori Digrm uei vriile letore discrete re form f, p p p ude p = = Distriuţi Poisso Are digrm 0 e e e e!!! Se costtă că
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
a) (3p) Sa se calculeze XY A. b) (4p) Sa se calculeze determinantul si rangul matricei A. c) (3p) Sa se calculeze A.
 Bac Variata Proil: mate-izica, iormatica, metrologie Subiectul I (3 p) Se cosidera matricele: X =, Y = ( ) si A= a) (3p) Sa se calculeze XY A b) (4p) Sa se calculeze determiatul si ragul matricei A c)
Bac Variata Proil: mate-izica, iormatica, metrologie Subiectul I (3 p) Se cosidera matricele: X =, Y = ( ) si A= a) (3p) Sa se calculeze XY A b) (4p) Sa se calculeze determiatul si ragul matricei A c)
4. Ecuaţii diferenţiale de ordin superior
 4.. Ecuaţii liiare 4. Ecuaţii difereţiale de ordi superior O problemã iportatã este rezolvarea ecuaţiilor difereţiale de ordi mai mare ca. Sut puţie ecuaţiile petru care se poate preciza forma aaliticã
4.. Ecuaţii liiare 4. Ecuaţii difereţiale de ordi superior O problemã iportatã este rezolvarea ecuaţiilor difereţiale de ordi mai mare ca. Sut puţie ecuaţiile petru care se poate preciza forma aaliticã
sin d = 8 2π 2 = 32 π
 .. Eerciţii reolvte. INTEGRALA E UPRAFAŢĂ E AL OILEA TIP. ÂMPURI OLENOIALE. Eerciţiul... ă se clculee dd dd dd, () fiind fţ eterioră sferei + + 4. oluţie. Avem: sin θ cos φ, sin θ sin φ, cos θ, θ[, π],
.. Eerciţii reolvte. INTEGRALA E UPRAFAŢĂ E AL OILEA TIP. ÂMPURI OLENOIALE. Eerciţiul... ă se clculee dd dd dd, () fiind fţ eterioră sferei + + 4. oluţie. Avem: sin θ cos φ, sin θ sin φ, cos θ, θ[, π],
ACI sécurité informatique KAA (Key Authentification Ambient)
 ACI sécurité informatique KAA (Key Authentification Ambient) Samuel Galice, Veronique Legrand, Frédéric Le Mouël, Marine Minier, Stéphane Ubéda, Michel Morvan, Sylvain Sené, Laurent Guihéry, Agnès Rabagny,
ACI sécurité informatique KAA (Key Authentification Ambient) Samuel Galice, Veronique Legrand, Frédéric Le Mouël, Marine Minier, Stéphane Ubéda, Michel Morvan, Sylvain Sené, Laurent Guihéry, Agnès Rabagny,
P r s r r t. tr t. r P
 P r s r r t tr t r P r t s rés t t rs s r s r r t é ér s r q s t r r r r t str t q q s r s P rs t s r st r q r P P r s r r t t s rés t t r t s rés t t é ér s r q s t r r r r t r st r q rs s r s r r t str
P r s r r t tr t r P r t s rés t t rs s r s r r t é ér s r q s t r r r r t str t q q s r s P rs t s r st r q r P P r s r r t t s rés t t r t s rés t t é ér s r q s t r r r r t r st r q rs s r s r r t str
Analiza matematica Specializarea Matematica vara 2010/ iarna 2011
 Aaliza matematica Specializarea Matematica vara 010/ iara 011 MULTIPLE HOIE 1 Se cosidera fuctia Atuci derivata mita de ordi data de este egala cu 1 y Derivata partiala de ordi a lui i raport cu variabila
Aaliza matematica Specializarea Matematica vara 010/ iara 011 MULTIPLE HOIE 1 Se cosidera fuctia Atuci derivata mita de ordi data de este egala cu 1 y Derivata partiala de ordi a lui i raport cu variabila
5. FILTRE ADAPTIVE BAZATE PE MI IMIZAREA ERORII MEDII PATRATICE
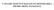 5. FILTRE ADAPTIVE BAZATE PE MIIMIZAREA ERORII MEDII PATRATICE 5. FILTRE ADAPTIVE BAZATE PE MIIMIZAREA ERORII MEDII PATRATICE fucţia cost st roara di pătratică, () cuaţiil Wir-opf u ofră o soluţi practică
5. FILTRE ADAPTIVE BAZATE PE MIIMIZAREA ERORII MEDII PATRATICE 5. FILTRE ADAPTIVE BAZATE PE MIIMIZAREA ERORII MEDII PATRATICE fucţia cost st roara di pătratică, () cuaţiil Wir-opf u ofră o soluţi practică
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
2. Probleme rezolvate Principiile termodinamicii şi ecuaţii de stare
 76. robleme rezolvate În ontinuare vom analiza problemele de bază propuse pentru rezolvare în timpul leţiilor pratie [3]... rinipiile termodinamiii şi euaţii de stare roblema. Folosind prima lege a termodinamiii,
76. robleme rezolvate În ontinuare vom analiza problemele de bază propuse pentru rezolvare în timpul leţiilor pratie [3]... rinipiile termodinamiii şi euaţii de stare roblema. Folosind prima lege a termodinamiii,
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté
 Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
Physique des réacteurs à eau lourde ou légère en cycle thorium : étude par simulation des performances de conversion et de sûreté Alexis Nuttin To cite this version: Alexis Nuttin. Physique des réacteurs
5.4. MULTIPLEXOARE A 0 A 1 A 2
 5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
5.4. MULTIPLEXOARE Multiplexoarele (MUX) sunt circuite logice combinaţionale cu m intrări şi o singură ieşire, care permit transferul datelor de la una din intrări spre ieşirea unică. Selecţia intrării
Radio détection des rayons cosmiques d ultra-haute énergie : mise en oeuvre et analyse des données d un réseau de stations autonomes.
 Radio détection des rayons cosmiques d ultra-haute énergie : mise en oeuvre et analyse des données d un réseau de stations autonomes. Diego Torres Machado To cite this version: Diego Torres Machado. Radio
Radio détection des rayons cosmiques d ultra-haute énergie : mise en oeuvre et analyse des données d un réseau de stations autonomes. Diego Torres Machado To cite this version: Diego Torres Machado. Radio
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
ΗΥ 232 Οργάνωση και Σχεδίαση Υπολογιστών. Διάλεξη 2 Οργάνωση μνήμης Καταχωρητές του MIPS Εντολές του MIPS 1
 ΗΥ 232 Οργάνωση και Σχεδίαση Υπολογιστών Διάλεξη 2 Οργάνωση μνήμης Καταχωρητές του MIPS Εντολές του MIPS 1 Νίκος Μπέλλας Τμήμα Μηχανικών Η/Υ, Τηλεπικοινωνιών και Δικτύων 1 Σύνολο Εντολών Το ρεπερτόριο
ΗΥ 232 Οργάνωση και Σχεδίαση Υπολογιστών Διάλεξη 2 Οργάνωση μνήμης Καταχωρητές του MIPS Εντολές του MIPS 1 Νίκος Μπέλλας Τμήμα Μηχανικών Η/Υ, Τηλεπικοινωνιών και Δικτύων 1 Σύνολο Εντολών Το ρεπερτόριο
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Transformations d Arbres XML avec des Modèles Probabilistes pour l Annotation
 Transformations d Arbres XML avec des Modèles Probabilistes pour l Annotation Florent Jousse To cite this version: Florent Jousse. Transformations d Arbres XML avec des Modèles Probabilistes pour l Annotation.
Transformations d Arbres XML avec des Modèles Probabilistes pour l Annotation Florent Jousse To cite this version: Florent Jousse. Transformations d Arbres XML avec des Modèles Probabilistes pour l Annotation.
Marin Chirciu INEGALITĂŢI TRIGONOMETRICE DE LA INIŢIERE LA PERFORMANŢĂ EDITURA PARALELA 45
 Main Chiiu INEGLITĂŢI TIGONOMETICE DE L INIŢIEE L PEFOMNŢĂ Cuins Consideații eliminae... 7 Soluţii Caitolul Inegalități u unghiui. Inegalitatea lui Jensen... 4 4 Caitolul Funții tigonometie ale jumătății
Main Chiiu INEGLITĂŢI TIGONOMETICE DE L INIŢIEE L PEFOMNŢĂ Cuins Consideații eliminae... 7 Soluţii Caitolul Inegalități u unghiui. Inegalitatea lui Jensen... 4 4 Caitolul Funții tigonometie ale jumătății
Formula lui Taylor. 25 februarie 2017
 Formula lui Taylor Radu Trîmbiţaş 25 februarie 217 1 Formula lui Taylor I iterval, f : I R o fucţie derivabilă de ori î puctul a I Poliomul lui Taylor de gradul, ataşat fucţiei f î puctul a: (T f)(x) =
Formula lui Taylor Radu Trîmbiţaş 25 februarie 217 1 Formula lui Taylor I iterval, f : I R o fucţie derivabilă de ori î puctul a I Poliomul lui Taylor de gradul, ataşat fucţiei f î puctul a: (T f)(x) =
Transfert sécurisé d Images par combinaison de techniques de compression, cryptage et de marquage
 Transfert sécurisé d Images par combinaison de techniques de compression, cryptage et de marquage José Marconi Rodrigues To cite this version: José Marconi Rodrigues. Transfert sécurisé d Images par combinaison
Transfert sécurisé d Images par combinaison de techniques de compression, cryptage et de marquage José Marconi Rodrigues To cite this version: José Marconi Rodrigues. Transfert sécurisé d Images par combinaison
M p f(p, q) = (p + q) O(1)
 l k M = E, I S = {S,..., S t } E S i = p i {,..., t} S S q S Y E q X S X Y = X Y I X S X Y = X Y I S q S q q p+q p q S q p i O q S pq p i O S 2 p q q p+q p q p+q p fp, q AM S O fp, q p + q p p+q p AM
l k M = E, I S = {S,..., S t } E S i = p i {,..., t} S S q S Y E q X S X Y = X Y I X S X Y = X Y I S q S q q p+q p q S q p i O q S pq p i O S 2 p q q p+q p q p+q p fp, q AM S O fp, q p + q p p+q p AM
Tema: şiruri de funcţii
 Tem: şiruri de fucţii. Clculţi limit (simplă) şirului de fucţii f : [ 0,], f ( ) R Avem lim f ( 0) = ir petru 0, vem lim f ( ) Î cocluzie, dcă otăm f: [ 0, ], f ( ) =, = 0 =, 0 + + = +, tuci lim f f =..
Tem: şiruri de fucţii. Clculţi limit (simplă) şirului de fucţii f : [ 0,], f ( ) R Avem lim f ( 0) = ir petru 0, vem lim f ( ) Î cocluzie, dcă otăm f: [ 0, ], f ( ) =, = 0 =, 0 + + = +, tuci lim f f =..
Q π (/) ^ ^ ^ Η φ. <f) c>o. ^ ο. ö ê ω Q. Ο. o 'c. _o _) o U 03. ,,, ω ^ ^ -g'^ ο 0) f ο. Ε. ιη ο Φ. ο 0) κ. ο 03.,Ο. g 2< οο"" ο φ.
 II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
II 4»» «i p û»7'' s V -Ζ G -7 y 1 X s? ' (/) Ζ L. - =! i- Ζ ) Η f) " i L. Û - 1 1 Ι û ( - " - ' t - ' t/î " ι-8. Ι -. : wî ' j 1 Τ J en " il-' - - ö ê., t= ' -; '9 ',,, ) Τ '.,/,. - ϊζ L - (- - s.1 ai
... 5 A.. RS-232C ( ) RS-232C ( ) RS-232C-LK & RS-232C-MK RS-232C-JK & RS-232C-KK
 RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis
 Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis Daniel García-Lorenzo To cite this version: Daniel García-Lorenzo. Robust Segmentation of Focal Lesions on Multi-Sequence
Robust Segmentation of Focal Lesions on Multi-Sequence MRI in Multiple Sclerosis Daniel García-Lorenzo To cite this version: Daniel García-Lorenzo. Robust Segmentation of Focal Lesions on Multi-Sequence
Jeux d inondation dans les graphes
 Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488
Jeux d inondation dans les graphes Aurélie Lagoutte To cite this version: Aurélie Lagoutte. Jeux d inondation dans les graphes. 2010. HAL Id: hal-00509488 https://hal.archives-ouvertes.fr/hal-00509488
Κεφάλαιο q = C V => q = 48(HiC. e και. I = -3- => I = 24mA. At. 2. I = i=>i= -=>I = e- v=»i = 9,28 1(Γ 4 Α. t Τ
 Κεφάλαιο 3.1 1. q = C V => q = 48(HiC q = χ e => χ = - e και => χ = 3 ΙΟ 15 ηλεκτρόνια I = -3- => I = 24mA. At 2. I = i=>i= -=>I = e- v=»i = 9,28 1(Γ 4 Α. t Τ 3. Έστω u d η μέση ταχύτητα κίνησης των ελευθέρων
Κεφάλαιο 3.1 1. q = C V => q = 48(HiC q = χ e => χ = - e και => χ = 3 ΙΟ 15 ηλεκτρόνια I = -3- => I = 24mA. At 2. I = i=>i= -=>I = e- v=»i = 9,28 1(Γ 4 Α. t Τ 3. Έστω u d η μέση ταχύτητα κίνησης των ελευθέρων
Assessment of otoacoustic emission probe fit at the workfloor
 Assessment of otoacoustic emission probe fit at the workfloor t s st tt r st s s r r t rs t2 t P t rs str t t r 1 t s ér r tr st tr r2 t r r t s t t t r t s r ss r rr t 2 s r r 1 s r r t s s s r t s t
Assessment of otoacoustic emission probe fit at the workfloor t s st tt r st s s r r t rs t2 t P t rs str t t r 1 t s ér r tr st tr r2 t r r t s t t t r t s r ss r rr t 2 s r r 1 s r r t s s s r t s t
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Déformation et quantification par groupoïde des variétés toriques
 Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
Défomation et uantification pa goupoïde de vaiété toiue Fédéic Cadet To cite thi veion: Fédéic Cadet. Défomation et uantification pa goupoïde de vaiété toiue. Mathématiue [math]. Univeité d Oléan, 200.
Transformata Radon. Reconstructia unei imagini bidimensionale cu ajutorul proiectiilor rezultate de-a lungul unor drepte.
 Problema Tranformaa Radon Reconrucia unei imaini bidimenionale cu auorul roieciilor rezulae de-a lunul unor dree. Domeniul de uilizare: Prelucrarea imainilor din domeniul medical Prelucrarea imainilor
Problema Tranformaa Radon Reconrucia unei imaini bidimenionale cu auorul roieciilor rezulae de-a lunul unor dree. Domeniul de uilizare: Prelucrarea imainilor din domeniul medical Prelucrarea imainilor
CAPITOLUL IV CALCULUL DIFERENŢIAL PENTRU FUNCŢII REALE DE O VARIABILA REALĂ
 CAPITOLUL IV CALCULUL DIFEENŢIAL PENTU FUNCŢII EALE DE O VAIABILA EALĂ Fucţii derivabile Fucţii difereţiabile Derivata şi difereţiala sut duă ccepte fudametale ale matematicii, care reprezită siteză pe
CAPITOLUL IV CALCULUL DIFEENŢIAL PENTU FUNCŢII EALE DE O VAIABILA EALĂ Fucţii derivabile Fucţii difereţiabile Derivata şi difereţiala sut duă ccepte fudametale ale matematicii, care reprezită siteză pe
