U unutrašnja energija H entalpija S entropija G 298. G Gibsova energija TERMOHEMIJA I TERMODINAMIKA HEMIJSKA TERMODINAMIKA
|
|
|
- Θήρων Καλλιγάς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 HEMIJSKA TERMODINAMIKA Bavi se energetskim promenama pri odigravanju hemijskih reakcija. TERMODINAMIČKE FUNKCIJE STANJA U unutrašnja energija H entalpija S entropija Ako su određene na standardnom pritisku imaju oznaku G Gibsova energija G 298 Temperatura na kojoj je određena veličina
2 SISTEM objekat ili skup objekata koji se pručavaju OKOLINA sve van sistema
3 SISTEM SISTEM kada toplota prelazi iz okoline u sistem Endoterman proces kada toplota prelazi iz sistema u okolinu q > 0 q < 0 Egzoterman proces REAKCIONI SISTEM REAKCIONI SISTEM CaCO 3 (s) CaO(s) + CO 2 (g) CH 4 (g) + 2 O 2 (g) CO 2 (g) + 2 H 2 O(g)
4 U unutrašnja energija obuhvata sve moguće oblike energije sistema PROMENA UNUTRAŠNJE ENERGIJE SISTEMA ΔU = q + w Toplota koju sistem prima/odaje Rad koji se vrši na sistemu (ili vrši sistem) w = p ΔV
5 I ZAKON TERMODINAMIKE (ZAKON O ODRŽANJU ENERGIJE) energija se ne može uništiti, niti stvoriti, već se razmenjuje sa okolinom q = ΔU w Toplota koju sistem odaje/prima = Promena unutrašnje energije sistema + Rad koji se vrši na sistemu (ili vrši sistem)
6 IZOHORNI PROCES Proces koji se odigrava pri stalnoj zapremini. V = const. V = const. ΔV =0 w = 0 q = ΔU w q Sistem q q v = ΔU
7 IZOBARNI PROCES Proces koji se odigrava pri stalnom pritisku. p = const. Rad Rad q p = ΔU w q p = ΔU + pδv q Sistem q q p = (U 2 U 1 ) + p(v 2 V 1 ) q p = (U 2 + pv 2 ) (U 1 + pv 1 ) H = U + pv q p = ΔH entalpija
8 TOPLOTA HEMIJSKE REAKCIJE Toplota koju sistem razmeni sa okolinom prilikom potpunog prelaska reaktanata koji se nalaze na temperaturi T u proizvode reakcije na istoj temperaturi T, prema stehiometrijskoj jednačini. Pri konstantnom pritisku jednaka je promeni entalpije. Δ r H Za p = p Endoterman proces Egzoterman proces Entalpija, H PROIZVODI Entalpija, H REAKTANTI REAKTANTI PROIZVODI H proizvoda > H reaktanata H proizvoda < H reaktanata
9 SISTEM SISTEM kada toplota prelazi iz okoline u sistem kada toplota prelazi iz sistema u okolinu q > 0 q < 0 Endoterman proces Egzoterman proces REAKCIONI SISTEM REAKCIONI SISTEM CaCO 3 (s) CaO(s) + CO 2 (g) CH 4 (g) + 2 O 2 (g) CO 2 (g) + 2 H 2 O(g) Δ r H > 0 Δ r H < 0
10 STANDARDNA PROMENA ENTALPIJE STVARANJA JEDINJENJA Toplota koja se oslobodi ili utroši pri nastajanju jednog mola jedinjenja od hemijskih elemenata u najstabilnijem obliku, pri standardnom pritisku. Δ f H Ag(s) + 1/2 Cl 2 (g) AgCl (s) p = Pa t = 25 o C ΔH = 127,1 kj mol 1 Δ f H (AgCl, s) = 127,1 kj mol 1 Standardnim entalpijama stvaranja (formiranja) elemenata u najstabilnijem obliku pripisana je vrednost nula. Δ f H (Br 2, l) = 0 Δ f H (Br 2, g) = 111,9 kj mol 1
11 STANDARDNE PROMENE ENTALPIJE STVARANJA JEDINJENJA Δ f H
12 IZRAČUNAVANJE STANDARDNE PROMENE ENTALPIJE REAKCIJE Δ r H = i ν A A + ν B B ν C C + ν D D ν Δ i f H proizvodi) ν iδ i( f i H i (reaktanti) 1 C 3 H 8 (g) + 5 O 2 (g) 3 CO 2 (g) + 4 H 2 O(l) p r o i z v o d i r e a k t a n t i Δ r H = 3 Δ f H [CO 2 (g)] + 4 Δ f H [H 2 O(l)] { 1 Δ f H [C 3 H 8 (g) ]+ 5 Δ f H [O 2 (g)]} Δ r H = 3x ( 393,5) + 4 x ( 285,8) ( 103,8) = 2219,9 kj mol 1 TERMOHEMIJSKA JEDNAČINA C 3 H 8 (g) + 5 O 2 (g) 3 CO 2 (g) + 4 H 2 O(l) Δ r H = 2219,9 kj mol 1
13 Entalpija je srazmerna količini supstanci 2H 2 (g) + O 2 (g) 2H 2 O(l) /2 ΔH = 571,6 kj/mol /2 EGZO H 2 (g) + 1/2O 2 (g) H 2 O(l) ΔH = 285,8 kj/mol Promena entalpije suprotne reakcije 2H 2 O(l) 2H 2 (g) + O 2 (g) ΔH = 571,6 kj/mol ENDO
14 HESOV ZAKON Promena entalpije hemijske reakcije ne zavisi od puta kojim se reakcija odvija, već samo od početnog i krajnjeg stanja. JEDNAČINA = JEDNAČINA 1 + JEDNAČINA ΔH = ΔH 1 + ΔH C ΔH 2 B ΔH = ΔH 1 + ΔH 2 ΔH 1 A
15 HESOV ZAKON primer C(s) + 1/2 O 2 (g) CO (g) ΔH =? 1 2 C(s) + O 2 (g) CO 2 (g) ΔH 1 = 393,5 kj mol 1 2 CO(g) + O 2 (g) 2 CO 2 (g) ΔH 2 = 566,0 kj mol 1 1/2)x 1 2 1/2 C(s) + O 2 (g) CO 2 (g) ΔH 1 = 393,5 kj mol 1 CO 2 (g) CO(g) + 1/2 O 2 (g) ( 1/2)x ΔH 2 = ( 1/2)x( 566,0) kj mol 1 C(s) + 1/2 O 2 (g) CO (g) ΔH = 393, = 110,5 kj mol 1
16 IZRAČUNAVANJE STANDARDNE PROMENE ENTALPIJE REAKCIJE REAKTANTI PROIZVODI Δ r H ΔH = H (proizvodi) H (reaktanti) REAKTANTI ELEMENTI ΔH 1 = Σ Δ f H (reaktanti) ELEMENTI PROIZVODI ΔH 2 = Σ Δ f H (proizvodi) REAKTANTI PROIZVODI Δ r H = ΔH 1 + ΔH 2 Δ r H = Σ Δ f H (proizvodi) ΣΔ f H (reaktanti)
17 ENTALPIJA HEMIJSKE VEZE Promena entalpije pri raskidanju jednog mola hemijskih veza u gasovitoj supstanci. H 2 (g) 2 H(g) ΔH = +436 kj mol 1 Endoterman proces Cl 2 (g) 2 Cl(g) ΔH = +243 kj mol 1 Obrazovanje veza egzoterman proces H(g) + Cl(g) HCl(g) ΔH = 431 kj mol 1 H(g) + F(g) HF(g) ΔH = 565 kj mol 1
18 SPONTANOST ODIGRAVANJA HEMIJSKE REAKCIJE Promena entalpije nije merilo spontanosti procesa. Mnogi spontani procesi su egzotermni, tj. odvijaju se uz sniženje energije. Rđanje gvožđa na vazduhu u prisustvu vlage: 2Fe(s) + ³/ ² O 2(g) + 3H 2 O(l) 2Fe(OH) 3 (s) Δ r H = 788,6 kj mol 1 Eksplozivna reakcija vodonika i kiseonika inicirana varnicom: 2H 2 (g) + O 2 (g) 2H 2 O(l) Δ r H = 571,6 kj mol 1 ALI Topljenje leda na sobnoj temperaturi: H 2 O(s) H 2 O(l) Δ r H = 6 kj mol 1
19 Pored promene energije sistema za spontanost nekog procesa bitna je i Promena uređenosti sistema H 2 O(s) H 2 O(l) ΔH = + 6 kj mol 1 Promena uređenosti sistema se iskazuje kao promena entropije.
20 S Entropija; mera neuređenosti sistema S = k lnw Bolcmanova konstanta Broj (mikro)stanja određenog sistema III ZAKON TERMODINAMIKE Na apsolutnoj nuli (0 K) i pri standardnom pritisku entropija čiste supstance je nula. STANDARDNE MOLARNA ENTROPIJA Entropija jednog mola supstance pri standardnom pritisku.
21 STANDARDNA MOLARNA ENTROPIJA S
22 PROMENA ENTROPIJE PROCESA Do porasta entropije dolazi: ΔS = S krajnje S početno 1. Kada supstanca prelazi iz čvrstog u tečno; iz tečnog u gasovito stanje čvrsto tečno gas
23 PROMENA ENTROPIJE PROCESA Do porasta entropije dolazi: ΔS = S krajnje S početno gas 2. Sa porastom temperature Entropija tečno čvrsto ključanje topljenje Temperatura 3. Rastvaranjem čvrste supstance rastvorena supstanca + rastvarač rastvor
24 STANDARDNA PROMENE ENTROPIJE REAKCIJE Δ r S = i ν A A + ν B B ν C C + ν D D νi Si ( proizvodi) νisi ( reaktanti) i CaCO 3 (s) CaO(s) + CO 2 (g) p r o i z v o d i r e a k t a n t i ΔS = 1 x S [CO 2 (g)] + 1 x S [CaO(s)] 1 x S [CaCO 3 (s) ] ΔS = 1x 39,8 + 1x 213,6 1 x 92,2 = 160,5 J mol 1 K 1 Δ r S > 0kod reakcija koje se odvijaju uz povećanje količine gasovitih supstanci
25 G SLOBODNA ENERGIJA SPONTANOST HEMIJSKIH REAKCIJA ENERGETSKI FAKTOR FAKTOR VEROVATNOĆE GIBSOVA SLOBODNA ENERGIJA G = H TS Slobodna energija je funkcija stanja ΔG = G krajnje G početno Δ r G = G proizvodi G reaktanti
26 G SLOBODNA ENERGIJA Δ r G = i ν Δ i f G proizvodi) ν iδ i( f i G i (reaktanti) Predznak promene slobodne energije predstavlja kriterijum spontanosti odigravanja reakcije pri konstantnoj temperaturi i pritisku 1. ΔG negativno reakcija je spontana 2. ΔG pozitivno reakcija nije spontana 3. ΔG jednako nuli sistem je u ravnoteži Na konstantnom pritisku i temperaturi reakcije se odvijaju u onom smeru u kome dolazi do smanjenja slobodne energije sistema.
27 G SLOBODNA ENERGIJA Nespontani proces Slobodna energija, G REAKTANTI PROIZVODI G proizvoda > G reaktanata ΔG >0 Spontani proces Slobodna energija, G REAKTANTI PROIZVODI G proizvoda < G reaktanata ΔG <0
28 VEZA IZMEĐU ΔG, ΔH i ΔS G = H TS Gibs Helmholcova jednačina ΔG = ΔH TΔS ENERGETSKI FAKTOR Egzotermne reakcije (ΔH) imaju veću šansu da budu spontane FAKTOR VEROVATNOĆE Ako su proizvodi u stanju veće neuređenosti (ΔS) veća je šansa da je reakcija spontana
29 STANDARDNA PROMENA SLOBODNE ENERGIJE ΔG Gibs Helmholcova jednačina za standardne uslove 1. ΔG negativno reakcija je spontana pri standardnim uslovima CaO(s) + CO 2 (g, Pa) CaCO 3 (s) Δ G na 25 o C= 130,4 kj mol 1 2. ΔG pozitivno reakcija nije spontana AgCl(s) Ag + (aq, c = 1 mol dm 3 ) + Cl (aq, c = 1 mol dm 3 ) Δ G na 25 o C= + 55,7 kj mol 1 3. ΔG jednako nuli sistem je u ravnoteži na 100 o C ΔG = ΔH TΔS H 2 O(l) H 2 O(g, Pa) Δ G = 0 kj mol 1
30 UTICAJ TEMPERATURE NA SPONTANOST REAKCIJE ΔG = ΔH TΔS ΔH ө ΔS ө ΔG ө Komentar I < 0 > 0 II > 0 < 0 III > 0 > 0 IV < 0 < 0
31 UTICAJ TEMPERATURE NA SPONTANOST REAKCIJE ΔG = ΔH TΔS ΔH ө ΔS ө ΔG ө Komentar I < 0 > 0 uvek < 0 Reakcija spontana na svim temperaturama; suprotna reakcija uvek nespontana II > 0 < 0 uvek > 0 Reakcija nespontana na svim temperaturama; suprotna reakcija uvek spontana III > 0 > 0 IV < 0 < 0
32 UTICAJ TEMPERATURE NA SPONTANOST REAKCIJE ΔG = ΔH TΔS ΔH ө ΔS ө ΔG ө Komentar I < 0 > 0 uvek < 0 Reakcija spontana na svim temperaturama; suprotna reakcija uvek nespontana II > 0 < 0 uvek > 0 Reakcija nespontana na svim temperaturama; suprotna reakcija uvek spontana Cu(s) + H 2 O(g) CuO(s) + H 2 (g) ΔH = + 84,5 kj mol 1 Δ S = 0,0487 kj mol 1 K 1 ΔG = ΔH TΔS = 84,5 + Tx0,0487 kj mol 1
33 UTICAJ TEMPERATURE NA SPONTANOST REAKCIJE ΔG = ΔH TΔS ΔH ө ΔS ө ΔG ө Komentar I < 0 > 0 uvek < 0 Reakcija spontana na svim temperaturama; suprotna reakcija uvek nespontana II > 0 < 0 uvek > 0 Reakcija nespontana na svim temperaturama; suprotna reakcija uvek spontana III > 0 > 0 > 0 na niskim temperaturama < 0 na visokim temperaturama IV < 0 < 0 < 0 na niskim temperaturama > 0 na visokim temperaturama Reakcija nespontana na niskim temperaturama; postaje spontana na višim temperaturama Reakcija spontana na niskim temperaturama; na višim temperaturama suprotna reakcija postaje spontana
34 UTICAJ TEMPERATURE NA SPONTANOST REAKCIJE ΔG = ΔH TΔS ΔH ө ΔS ө ΔG ө Komentar III > 0 > 0 > 0 na niskim temperaturama < 0 na visokim temperaturama CaCO 3 (s) CaO(s) + CO 2 (g) Reakcija nespontana na niskim temperaturama; postaje spontana na višim temperaturama Δ H = + 178,3 kj mol 1 Δ S = + 0,1605 kj mol 1 K 1 ΔG = ΔH TΔS = 178,3 Tx0,1605 kj mol 1
35 UTICAJ TEMPERATURE NA SPONTANOST REAKCIJE ΔG = ΔH TΔS ΔH ө ΔS ө ΔG ө Komentar III > 0 > 0 > 0 na niskim temperaturama < 0 na visokim temperaturama CaCO 3 (s) CaO(s) + CO 2 (g) Reakcija nespontana na niskim temperaturama; postaje spontana na višim temperaturama ΔG = ΔH TΔS = 178,3 Tx0,1605 kj mol 1 Na visokim temperaturama: 2000 K ΔG =178,3 321,0 = 142,7 kj mol 1
36 UTICAJ TEMPERATURE NA SPONTANOST REAKCIJE ΔG = ΔH TΔS ΔH ө ΔS ө ΔG ө Komentar III > 0 > 0 > 0 na niskim temperaturama < 0 na visokim temperaturama CaCO 3 (s) CaO(s) + CO 2 (g) Reakcija nespontana na niskim temperaturama; postaje spontana na višim temperaturama ΔG = ΔH TΔS = 178,3 Tx0,1605 kj mol 1 U slučaju niske temperature: 298 K ΔG =178,3 47,8 = + 130,5 kj mol 1
37 UTICAJ TEMPERATURE NA SPONTANOST REAKCIJE CaCO 3 (s) CaO(s) + CO 2 (g) ΔG = ΔH TΔS = 178,3 Tx0,1605 kj mol 1 Na kojoj temperaturi ΔG menja predznak? ΔG = 0 ΔG = ΔH TΔS = 0 T = ΔH /ΔS T = Δ H = 178,3 kj mol 1 Δ S 0,1605 kj mol 1 K 1= 1110 K
38 UTICAJ TEMPERATURE NA SPONTANOST REAKCIJE Reakcija K sa vodom spontana na svim temperaturama Dehidratacija CuSO 4 5H 2 O spontana samo na povišenim T ΔG > 0 ΔG > 0 ΔG > 0 ΔH < 0 ΔS < 0 ΔH > 0 ΔS < 0 ΔG < 0 ΔH < 0 ΔS > 0 ΔH > 0 ΔS > 0 ΔG < 0 ΔG < 0 Temperatura Temperatura Temperatura
OSNOVI HEMIJSKE TERMODINAMIKE I TERMOHEMIJA
 OSNOVI HEMIJSKE TERMODINAMIKE I TERMOHEMIJA OSNOVI HEMIJSKE TERMODINAMIKE Hemjska termodnamka proučava promene energje (toplotn efekat) pr odgravanju hemjskh reakcja. MATERIJA ENERGIJA? Energja je dskontnualna
OSNOVI HEMIJSKE TERMODINAMIKE I TERMOHEMIJA OSNOVI HEMIJSKE TERMODINAMIKE Hemjska termodnamka proučava promene energje (toplotn efekat) pr odgravanju hemjskh reakcja. MATERIJA ENERGIJA? Energja je dskontnualna
Termohemija. C(s) + O 2 (g) CO 2 (g) H= -393,5 kj
 Termohemija Termodinamika proučava energiju i njene promene Termohemija grana termodinamike odnosi izmeñu hemijske reakcije i energetskih promena koje se pri tom dešavaju C(s) + O 2 (g) CO 2 (g) H= -393,5
Termohemija Termodinamika proučava energiju i njene promene Termohemija grana termodinamike odnosi izmeñu hemijske reakcije i energetskih promena koje se pri tom dešavaju C(s) + O 2 (g) CO 2 (g) H= -393,5
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Drugi zakon termodinamike
 Drugi zakon termodinamike Uvod Drugi zakon termodinamike nije univerzalni prirodni zakon, ne važi za sve sisteme, naročito ne za neobične sisteme (mikrouslovi, svemirski uslovi). Zasnovan je na zajedničkom
Drugi zakon termodinamike Uvod Drugi zakon termodinamike nije univerzalni prirodni zakon, ne važi za sve sisteme, naročito ne za neobične sisteme (mikrouslovi, svemirski uslovi). Zasnovan je na zajedničkom
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
= T 2. AgBr (s) + ½ Cl 2(g) + ½ Br 2(g) = AgCl (s) O (l) O (g) +1/2O 2(g) H 2(g) =H 2. značaj navođenja agregatnog stanja
 TERMOEMIJA Termohemija proučava toplotne promene koje prate hemijske reakcije, fazne prelaze (topljenje, isparavanje, sublimacija, polimorfne promene), rastvaranje supstance, razblaživanje rastvora itd.
TERMOEMIJA Termohemija proučava toplotne promene koje prate hemijske reakcije, fazne prelaze (topljenje, isparavanje, sublimacija, polimorfne promene), rastvaranje supstance, razblaživanje rastvora itd.
TERMODINAMIKA.
 TERMODINAMIKA http://www.ffh.bg.ac.rs/geografi_fh_procesi.html 1 Termodinamika naučna disciplina koja proučava energetske promene koje prate univerzalne procese u prirodi kao i vezu tih promena sa osobinama
TERMODINAMIKA http://www.ffh.bg.ac.rs/geografi_fh_procesi.html 1 Termodinamika naučna disciplina koja proučava energetske promene koje prate univerzalne procese u prirodi kao i vezu tih promena sa osobinama
TERMODINAMIKA. Sistem i okruženje
 TERMODINAMIKA Sistem i okruženje SISTEM je deo sveta koji nas zanima; to je bilo koji objekat, bilo koja količina materije, bilo koji deo prostora, izabran za ispitivanje i izdvojen (misaono) od svega
TERMODINAMIKA Sistem i okruženje SISTEM je deo sveta koji nas zanima; to je bilo koji objekat, bilo koja količina materije, bilo koji deo prostora, izabran za ispitivanje i izdvojen (misaono) od svega
Gibbs-ova slobodna energija
 ibbs-ova slobodna energija Reakcija će se odvijati spontano ili ne, zavisno od toga de li je praćena porastom entropije univerzuma ili ne: ri = const: S S S univerzuma sistema okruzenja S univerzuma H
ibbs-ova slobodna energija Reakcija će se odvijati spontano ili ne, zavisno od toga de li je praćena porastom entropije univerzuma ili ne: ri = const: S S S univerzuma sistema okruzenja S univerzuma H
Rastvori Osnovni pojmovi i izračunavanja
 Rastvori Osnovni pojmovi i izračunavanja Disperzni sistem je smeša u kojoj su jedna ili više supstanci raspršene u nekoj drugoj supstanci u obliku sitnih čestica. Disperzni sredstvo je supstanca u kojoj
Rastvori Osnovni pojmovi i izračunavanja Disperzni sistem je smeša u kojoj su jedna ili više supstanci raspršene u nekoj drugoj supstanci u obliku sitnih čestica. Disperzni sredstvo je supstanca u kojoj
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Termohemija. Energetske promene pri fizičkim i hemijskim procesima
 Termohemija Energetske promene pri fizičkim i hemijskim procesima Poglavlje 2.2 Termohemija Termohemija je deo termodinamike i bavi se proučavanjem toplotom razmenjenom pri hemijskim i fizičkim promenama,
Termohemija Energetske promene pri fizičkim i hemijskim procesima Poglavlje 2.2 Termohemija Termohemija je deo termodinamike i bavi se proučavanjem toplotom razmenjenom pri hemijskim i fizičkim promenama,
BIOFIZIKA TERMO-FIZIKA
 BIOFIZIKA TERMO-FIZIKA Akademik, prof. dr Jovan P. Šetrajčić jovan.setrajcic@df.uns.ac.rs Univerzitet u Novom Sadu Departman za fiziku PMF Powered byl A T E X 2ε! p. / p. 2/ Termika FENOMENOLOŠKA TEORIJA
BIOFIZIKA TERMO-FIZIKA Akademik, prof. dr Jovan P. Šetrajčić jovan.setrajcic@df.uns.ac.rs Univerzitet u Novom Sadu Departman za fiziku PMF Powered byl A T E X 2ε! p. / p. 2/ Termika FENOMENOLOŠKA TEORIJA
Osnovne veličine, jedinice i izračunavanja u hemiji
 Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
za reverzibilan kružni proces količina toplote koju je sistem na svojoj nižoj temperaturi T 1 predao okolini i ponovo prešao u početno stanje
 ENROPIJA Spontani procesi u prirodi se uvek odvijaju u određenom smeru (npr. prelazak toplote sa toplijeg na hladnije telo) što nije moguće opisati termodinamičkim funkcijama do sad obrađenim. Nulti zakon
ENROPIJA Spontani procesi u prirodi se uvek odvijaju u određenom smeru (npr. prelazak toplote sa toplijeg na hladnije telo) što nije moguće opisati termodinamičkim funkcijama do sad obrađenim. Nulti zakon
Promene termodinamičkih funkcija na putu do ravnoteže i u ravnoteži
 romene termodinamičkih funkcija na putu do ravnoteže i u ravnoteži Helmholcova slobodna energija-2.5.1.,2.5.2. Gibsova slobodna energija-2.5.3. Gibs-Helmholcova jednačina-2.5.4. Reverzibilni i ireverzibilni
romene termodinamičkih funkcija na putu do ravnoteže i u ravnoteži Helmholcova slobodna energija-2.5.1.,2.5.2. Gibsova slobodna energija-2.5.3. Gibs-Helmholcova jednačina-2.5.4. Reverzibilni i ireverzibilni
Prvi zakon termodinamike
 Prvi zakon termodinamike Uvod Prvi princip termodinamike je apsolutni prirodni zakon koji važi za sve pojave koje se odigravaju na svim prostornim nivoima (mikro, makro i mega svetu). Zasnovan je na brojnim
Prvi zakon termodinamike Uvod Prvi princip termodinamike je apsolutni prirodni zakon koji važi za sve pojave koje se odigravaju na svim prostornim nivoima (mikro, makro i mega svetu). Zasnovan je na brojnim
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Termohemija. Energetske promene pri fizičkim i hemijskim procesima
 Termohemija Energetske promene pri fizičkim i hemijskim procesima Poglavlje 2.2 Termohemija Termohemija je deo termodinamike i bavi se proučavanjem toplotom razmenjenom pri hemijskim i fizičkim promenama,
Termohemija Energetske promene pri fizičkim i hemijskim procesima Poglavlje 2.2 Termohemija Termohemija je deo termodinamike i bavi se proučavanjem toplotom razmenjenom pri hemijskim i fizičkim promenama,
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
TOPLOTA I RAD, PRVI ZAKON TERMODINAMIKE
 TOPLOTA I RAD, PRI ZAKON TERMODINAMIKE Mehanički rad u termodinamici uvek predstavlja razmenu energije izmedju sistema i okoline. Mehanički rad se javlja kao rezultat delovanja sile duž puta: W Fdl W Fdl
TOPLOTA I RAD, PRI ZAKON TERMODINAMIKE Mehanički rad u termodinamici uvek predstavlja razmenu energije izmedju sistema i okoline. Mehanički rad se javlja kao rezultat delovanja sile duž puta: W Fdl W Fdl
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Termodinamika se bavi materijom u svim agregatnim stanjima.
 Termodinamika - Termo toplota - Dinamika promena, snaga Termodinamika je oblast fizike koja se bavi odnosima između toplote i drugih oblika energije. Konkretno objašnjava kako se toplotna energija pretvara
Termodinamika - Termo toplota - Dinamika promena, snaga Termodinamika je oblast fizike koja se bavi odnosima između toplote i drugih oblika energije. Konkretno objašnjava kako se toplotna energija pretvara
Reverzibilni procesi
 Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
Reverzbln proces Reverzbln proces: proces pr koja sste nkada nje vše od beskonačno ale vrednost udaljen od ravnoteže, beskonačno ala proena spoljašnjh uslova ože vratt sste u blo koju tačku, proena ože
TERMODINAMIKA osnovni pojmovi energija, rad, toplota
 TERMODINAMIKA osnovni pojmovi energija, rad, toplota TERMODINAMIKA TERMO TOPLO nauka o kretanju toplote DINAMO SILA Termodinamika-nauka odnosno naučna disciplina koja ispituje odnose između promena u sistemima
TERMODINAMIKA osnovni pojmovi energija, rad, toplota TERMODINAMIKA TERMO TOPLO nauka o kretanju toplote DINAMO SILA Termodinamika-nauka odnosno naučna disciplina koja ispituje odnose između promena u sistemima
Energetska priroda toplote Mejer i Džul (R. Mayer, , i J. Joul, ) W. Thomson S. Carnot J. W. Gibbs
 ERMODINAMIKA ermodinamika naučna disciplina koja proučava energetske promene koje prate univerzalne procese u prirodi kao i vezu tih promena sa osobinama materije koja učestvuje u njima. ermodinamika je
ERMODINAMIKA ermodinamika naučna disciplina koja proučava energetske promene koje prate univerzalne procese u prirodi kao i vezu tih promena sa osobinama materije koja učestvuje u njima. ermodinamika je
entropije Entropija raste ako se krećemo od čvrstog preko tečnog do gasovitog stanja: S čvrsto < S tečno << S gas
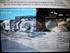 ,4,4, Odreñivanje promene entropije,4,4,, romena entropije pri promeni faza Molekular ularna interpretacija entropije Entropija raste ako se krećemo od čvrstog preko tečnog do gasovitog stanja: čvrsto
,4,4, Odreñivanje promene entropije,4,4,, romena entropije pri promeni faza Molekular ularna interpretacija entropije Entropija raste ako se krećemo od čvrstog preko tečnog do gasovitog stanja: čvrsto
C P,m C V,m = R C P C V = nr
 I zakon termodinamike du dq + dw + dw e dh du + pd du U U d + d d + u d,m,m R nr dh Izotermski procesi: p d + H H d w nr ln R ln Izotermski reverzibilni zapreminski rad gasa u I.G.S. w pδ Izotermski revetzibilni
I zakon termodinamike du dq + dw + dw e dh du + pd du U U d + d d + u d,m,m R nr dh Izotermski procesi: p d + H H d w nr ln R ln Izotermski reverzibilni zapreminski rad gasa u I.G.S. w pδ Izotermski revetzibilni
GASNO STANJE.
 GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
GASNO STANJE http://www.ffh.bg.ac.rs/geografi_fh_procesi.html AGREGATNA STANJA MATERIJE Četiri agregatna stanja materije na osnovu stepena uređenosti, tj. odnosa termalne energije čestica i energije međumolekulskih
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
NULTI I PRVI ZAKON TERMODINAMIKE
 NULTI I PRVI ZAKON TERMODINAMIKE NULTI ZAKON (princip)termodinamike ako su dva sistema A i B u međusobnom termičkom kontaktu, i u ravnoteži sa trećim sistemom C onda su u ravnoteži i jedan sa drugim Ako
NULTI I PRVI ZAKON TERMODINAMIKE NULTI ZAKON (princip)termodinamike ako su dva sistema A i B u međusobnom termičkom kontaktu, i u ravnoteži sa trećim sistemom C onda su u ravnoteži i jedan sa drugim Ako
H T. C P,m C V,m = R C P C V = nr U T U V T H P. Izotermski procesi: I zakon termodinamike. Izotermski reverzibilni zapreminski rad gasa u I.G.S.
 I zakon termodinamike du dq dw dh du pd C U dw e C,m C,m = R C C = nr C H du C d U d C d d u dh C p d H d Izotermski procesi: w nr ln R ln w p Izotermski reverzibilni zapreminski rad gasa u I.G.S. Izotermski
I zakon termodinamike du dq dw dh du pd C U dw e C,m C,m = R C C = nr C H du C d U d C d d u dh C p d H d Izotermski procesi: w nr ln R ln w p Izotermski reverzibilni zapreminski rad gasa u I.G.S. Izotermski
Kiselo bazni indikatori
 Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
C P,m C V,m = R C P C V = nr
 I zakon termodinamike du dq + dw + dw e dh du + pd du C U U C d + d C d + u d C,m C,m R C C nr dh Izotermski procesi: C p C d + H H d w nr ln R ln Izotermski reverzibilni zapreminski rad gasa u I.G.S.
I zakon termodinamike du dq + dw + dw e dh du + pd du C U U C d + d C d + u d C,m C,m R C C nr dh Izotermski procesi: C p C d + H H d w nr ln R ln Izotermski reverzibilni zapreminski rad gasa u I.G.S.
TOPLOTA. Primjeri. * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem.
 1.OSNOVNI POJMOVI TOPLOTA Primjeri * KALORIKA Nauka o toploti * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem. * TD SISTEM To je bilo koje makroskopsko tijelo ili grupa tijela,
1.OSNOVNI POJMOVI TOPLOTA Primjeri * KALORIKA Nauka o toploti * TERMODINAMIKA Razmatra prenos energije i efekte tog prenosa na sistem. * TD SISTEM To je bilo koje makroskopsko tijelo ili grupa tijela,
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
21/5/2008. Θερµοχηµεία
 Θερµοχηµεία Θερµοχηµεία Είναι η µελέτη των θερµικών φαινοµένων που συνοδεύουν µια χηµική αντίδραση. Θερµότητα αντίδρασης υπό σταθερή πίεση Θερµότητα αντίδρασης υπό σταθερή πίεση Η θερµοδυναµική συνάρτηση
Θερµοχηµεία Θερµοχηµεία Είναι η µελέτη των θερµικών φαινοµένων που συνοδεύουν µια χηµική αντίδραση. Θερµότητα αντίδρασης υπό σταθερή πίεση Θερµότητα αντίδρασης υπό σταθερή πίεση Η θερµοδυναµική συνάρτηση
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Termodinamički zakoni
 Termodinamički zakoni Stanje sistema Opisano je preko varijabli stanja tlak volumen temperatura unutrašnja energija Makroskopsko stanje izoliranog sistema može se specificirati jedino ako je sistem u unutrašnjoj
Termodinamički zakoni Stanje sistema Opisano je preko varijabli stanja tlak volumen temperatura unutrašnja energija Makroskopsko stanje izoliranog sistema može se specificirati jedino ako je sistem u unutrašnjoj
HEMIJSKA RAVNOTEŽA HEMIJSKA RAVNOTEŽA. N 2 O 4 (g) 2NO 2 (g) DINAMIČKA RAVNOTEŽA
 DINAMIČKA RAVNOTEŽA U toku hemijske reakije konentraije reaktanata opaaju, konentraije proizvoa reakije rastu. Posle nekog vremena o početka reakije nema merljive promene konentraije reaktanata ili proizvoa
DINAMIČKA RAVNOTEŽA U toku hemijske reakije konentraije reaktanata opaaju, konentraije proizvoa reakije rastu. Posle nekog vremena o početka reakije nema merljive promene konentraije reaktanata ili proizvoa
Postupak rješavanja bilanci energije
 Postupak rješavanja bilanci energije 1. Postaviti procesnu shemu 2. Riješiti bilancu tvari 3. Napisati potreban oblik jednadžbe za bilancu energije (zatvoreni otvoreni sustav) 4. Odabrati referentno stanje
Postupak rješavanja bilanci energije 1. Postaviti procesnu shemu 2. Riješiti bilancu tvari 3. Napisati potreban oblik jednadžbe za bilancu energije (zatvoreni otvoreni sustav) 4. Odabrati referentno stanje
2. TERMODINAMIKA 2.1. Prvi zakon termodinamike
 . ERMODINAMIKA.. rvi zakon termodinamike ermodinamika je naučna disciplina koja proučava energetske promene koje prate univerzalne procese u prirodi kao i vezu tih promena sa osobinama materije koja učestvuje
. ERMODINAMIKA.. rvi zakon termodinamike ermodinamika je naučna disciplina koja proučava energetske promene koje prate univerzalne procese u prirodi kao i vezu tih promena sa osobinama materije koja učestvuje
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Molekularna fizika i termodinamika. Molekularna fizika i termodinamika. Molekularna fizika i termodinamika. Molekularna fizika i termodinamika
 Molekularna fizika proučava strukturu i svojstva supstanci polazeći od molekularno -kinetičke teorije: supstance su sastavljene od vrlo malih čestica (molekula, atoma i jona) koji se nalaze u stalnom haotičnom
Molekularna fizika proučava strukturu i svojstva supstanci polazeći od molekularno -kinetičke teorije: supstance su sastavljene od vrlo malih čestica (molekula, atoma i jona) koji se nalaze u stalnom haotičnom
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
C P,m C V,m = R C P C V = nr
 I zakon termodinamike du dq+ dw+ dw e dh du+ pd du U U d+ d d+ u d,m,m R nr dh Izotermski procesi: p d + H H d wnr ln R ln Izotermski reverzibilni zapreminski rad gasa u I.G.. w p Izotermski revetzibilni
I zakon termodinamike du dq+ dw+ dw e dh du+ pd du U U d+ d d+ u d,m,m R nr dh Izotermski procesi: p d + H H d wnr ln R ln Izotermski reverzibilni zapreminski rad gasa u I.G.. w p Izotermski revetzibilni
Idealno gasno stanje-čisti gasovi
 Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
Idealno gasno stanje-čisti gasovi Parametri P, V, T i n nisu nezavisni. Odnos između njih eksperimentalno je utvrđeni izražava se kroz gasne zakone. Gasni zakoni: 1. ojl-maritov: PVconst. pri konstantnim
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
TERMODINAMIČKI PARAMETRI su veličine kojima opisujemo stanje sistema.
 TERMODINAMIKA U svakodnevnom govoru, često dolazi greškom do koriščenja termina temperatura i toplota u istom značenju. U fizici, ova dva termina imaju potpuno različito značenje. Razmatračemo kako se
TERMODINAMIKA U svakodnevnom govoru, često dolazi greškom do koriščenja termina temperatura i toplota u istom značenju. U fizici, ova dva termina imaju potpuno različito značenje. Razmatračemo kako se
HEMIJSKE RAVNOTEŽE. a = f = f c.
 II RAČUNSKE VEŽBE HEMIJSKE RAVNOTEŽE TEORIJSKI DEO I POJAM AKTIVNOSTI JONA Razblaženi rastvori (do 0,1 mol/dm ) u kojima je interakcija između čestica rastvorene supstance zanemarljiva ponašaju se kao
II RAČUNSKE VEŽBE HEMIJSKE RAVNOTEŽE TEORIJSKI DEO I POJAM AKTIVNOSTI JONA Razblaženi rastvori (do 0,1 mol/dm ) u kojima je interakcija između čestica rastvorene supstance zanemarljiva ponašaju se kao
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
SPONTANI PROCESI II ZAKON TERMODINAMIKE
 SPONANI PROCESI II ZAKON ERMODINAMIKE I zakon termodinamike se bavi termodinamičkim procesom kao procesom koji je praćen ekvivalentnošću različitih oblika energije bez ikakvih ograničenja odnosno ne govori
SPONANI PROCESI II ZAKON ERMODINAMIKE I zakon termodinamike se bavi termodinamičkim procesom kao procesom koji je praćen ekvivalentnošću različitih oblika energije bez ikakvih ograničenja odnosno ne govori
Heterogene ravnoteže taloženje i otapanje. u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima
 Heterogene ravnoteže taloženje i otapanje u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima Ako je BA teško topljiva sol (npr. AgCl) dodatkom
Heterogene ravnoteže taloženje i otapanje u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima Ako je BA teško topljiva sol (npr. AgCl) dodatkom
Obrada signala
 Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zavrxni ispit iz Matematiqke analize 1
 Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
Pismeni dio ispita iz Matematike Riješiti sistem jednačina i diskutovati rješenja u zavisnosti od parametra a:
 Zenica, 70006 + y+ z+ 4= 0 y+ z : i ( q) : = = y + z 4 = 0 a) Napisati pavu p u kanonskom, a pavu q u paametaskom obliku b) Naći jednačinu avni koja polazi koz pavu p i okomita je na pavu q ate su pave
Zenica, 70006 + y+ z+ 4= 0 y+ z : i ( q) : = = y + z 4 = 0 a) Napisati pavu p u kanonskom, a pavu q u paametaskom obliku b) Naći jednačinu avni koja polazi koz pavu p i okomita je na pavu q ate su pave
Kemijska termodinamika
 Kemijska termodinamika 1. Entalpija reakcije NH 3 (aq) + HCl(aq) NH 4 Cl(aq) odreñena je u reakcijskom kalorimetru. U kalorimetrijskoj posudi nalazilo se 20 cm 3 otopine NH 3 koncentracije 0,1 mol dm 3.
Kemijska termodinamika 1. Entalpija reakcije NH 3 (aq) + HCl(aq) NH 4 Cl(aq) odreñena je u reakcijskom kalorimetru. U kalorimetrijskoj posudi nalazilo se 20 cm 3 otopine NH 3 koncentracije 0,1 mol dm 3.
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
TERMOENERGETIKA. Boričić Aleksandra
 TERMOENERGETIKA Boričić Aleksandra Šta proučava termodinamika? Termodinamika je nauka koja proučava pojave vezane za međusobno pretvaranje jednog oblika energije u drugi. Termodinamika analizira i definiše
TERMOENERGETIKA Boričić Aleksandra Šta proučava termodinamika? Termodinamika je nauka koja proučava pojave vezane za međusobno pretvaranje jednog oblika energije u drugi. Termodinamika analizira i definiše
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
1.Θερμοχημεία. Η έννοια της ενθαλπίας
 1 ΧΗΜΕΙΑ Γ ΛΥΚΕΙΟΥ-Χ.Κ.ΦΙΡΦΙΡΗΣ 1.Θερμοχημεία Η έννοια της ενθαλπίας 1.Δίνεται το παρακάτω σχεδιάγραμμα 2.Να υπολογίσετε το ποσό θερμότητας που εκλύεται ή απορροφάται κατά την πραγματοποίηση της αντίδρασης
1 ΧΗΜΕΙΑ Γ ΛΥΚΕΙΟΥ-Χ.Κ.ΦΙΡΦΙΡΗΣ 1.Θερμοχημεία Η έννοια της ενθαλπίας 1.Δίνεται το παρακάτω σχεδιάγραμμα 2.Να υπολογίσετε το ποσό θερμότητας που εκλύεται ή απορροφάται κατά την πραγματοποίηση της αντίδρασης
Klasifikacija blizu Kelerovih mnogostrukosti. konstantne holomorfne sekcione krivine. Kelerove. mnogostrukosti. blizu Kelerove.
 Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
13.1. Termodinamički procesi O K O L I N A. - termodinamički sustav: količina tvari unutar nekog zatvorenog volumena
 13. TERMODINAMIKA - dio fizike koji proučava vezu izmeñu topline i drugih oblika energije (mehanički rad) - toplinski strojevi: parni stroj, hladnjak, motori s unutrašnjim izgaranjem - makroskopske veličine:
13. TERMODINAMIKA - dio fizike koji proučava vezu izmeñu topline i drugih oblika energije (mehanički rad) - toplinski strojevi: parni stroj, hladnjak, motori s unutrašnjim izgaranjem - makroskopske veličine:
Fizika Biologija i druge prirodne nauke. Dva glavna vida materije su masa i energija. E = m c 2
 HEMIJA je nauka o materiji i njenim promenama Fizika Biologija i druge prirodne nauke Dva glavna vida materije su masa i energija. Ajnštajnova veza između energije i materije E = m c 2 Materija ima dualna
HEMIJA je nauka o materiji i njenim promenama Fizika Biologija i druge prirodne nauke Dva glavna vida materije su masa i energija. Ajnštajnova veza između energije i materije E = m c 2 Materija ima dualna
Statistička interpretacija entropije Funkcije stanja
 Statistička interpretacija entropije Funkcije stanja Entalpija - pogledajmo izobarni proces iz stanja 1 u stanje 2 - rad koji je obavio sustav dan je W = P dv = P dv = P V 2 V 1 - iz prvog zakona termodinamike
Statistička interpretacija entropije Funkcije stanja Entalpija - pogledajmo izobarni proces iz stanja 1 u stanje 2 - rad koji je obavio sustav dan je W = P dv = P dv = P V 2 V 1 - iz prvog zakona termodinamike
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
5 Ispitivanje funkcija
 5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
MATEMATIKA I 1.kolokvij zadaci za vježbu I dio
 MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
C 273,15, T 273,15, 1 1 C 1 50 C 273,15 K 50K 323,15K 50K 373,15K C 40 C 40 K
 1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
1 Zadatak temperatura K- C Telo A se nalazi na temperaturi 50 C i zagreje se za 50 K. Telo B se nalazi na temperaturi 313 K.i zagreje se za 40 C. Koje je telo toplije posle zagravanja i kolika je razlika
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
2ο Σύνολο Ασκήσεων. Λύσεις 6C + 7H 2 C 6 H H διαφορά στο θερμικό περιεχόμενο των προϊόντων και των αντιδρώντων καλείται
 1 2ο Σύνολο Ασκήσεων Λύσεις Άσκηση 1: 6C + 7H 2 C 6 H 14 H1 6C + 7H 2 ΔΗ αντίδρασης H2 C 6 + H 14 C + H 2 H αντίδραση είναι εξώθερμη Άσκηση 2 - H διαφορά στο θερμικό περιεχόμενο των προϊόντων και των αντιδρώντων
1 2ο Σύνολο Ασκήσεων Λύσεις Άσκηση 1: 6C + 7H 2 C 6 H 14 H1 6C + 7H 2 ΔΗ αντίδρασης H2 C 6 + H 14 C + H 2 H αντίδραση είναι εξώθερμη Άσκηση 2 - H διαφορά στο θερμικό περιεχόμενο των προϊόντων και των αντιδρώντων
Hemijska termodinamika
 Poglavlje 2.1 Osnovni pojmovi Hemijska termodinamika Termodinamički sistem Termodinamičke osobine Stanje sistema Parametri stanja Termodinamička ravnoteža Termodinamički proces Energija Rad Toplota Prvi
Poglavlje 2.1 Osnovni pojmovi Hemijska termodinamika Termodinamički sistem Termodinamičke osobine Stanje sistema Parametri stanja Termodinamička ravnoteža Termodinamički proces Energija Rad Toplota Prvi
Moguća i virtuelna pomjeranja
 Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Dnamka sstema sa vezama Moguća vrtuelna pomjeranja f k ( r 1,..., r N, t) = 0 (k = 1, 2,..., K ) df k dt = r + t = 0 d r = r dt moguća pomjeranja zadovoljavaju uvjet: df k = d r + dt = 0. t δ r = δx +
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
