-Tehnike karakterizacije proteina

HTML
DOWNLOAD

Μέγεθος: px

Εμφάνιση ξεκινά από τη σελίδα:

Download "-Tehnike karakterizacije proteina"

Κύρος Βαρουξής
7 χρόνια πριν
Προβολές:

1 Univerzitet u Tuzli Farmaceutski fakultet Doktorski studij Školska: 2014/2015 -Biotehnološke metode u proizvodnji rekombinantnih proteina -Tehnike karakterizacije proteina Dr.sc. Aida Smajlović, docent

mutageni primer (5 -CAACAAGAAATTCGGGGTTTTCAAAGCTG-3 ) i sintetisani gen (C3S) za stefin B -primer SB3

2 MUTAGENEZA I krug PCR produkt 100 bp H75W -primer SB3 for, mutageni primer (5 - CCAGTCTCTGCCGTGGGAGAACAAACCGCTG-3 ) P36G P79S i sintetisani gen (C3S) za stefin B -primer SB3 for, mutageni primer (5 -CAACAAGAAATTCGGGGTTTTCAAAGCTG-3 ) i sintetisani gen (C3S) za stefin B -primer SB3 for, mutageni primer (5 - CACGAGAACAAATCGCTGACTCTG-3 ) i sintetisani gen (C3S) za stefin B 100 bp II krug PCR produkt 300 bp 300 bp

3 II krug PCR produkt 300 bp restrikcija (BamHI i NdeI); 5-10 U enzima ligacija pgem -Teasy transformacija detekcija plazmida colony PCR bijelih kolonija Provjera tačnosti nukleotidne sekvence metodom kapilarne elektroforezom kompetentne ćelije E.coli DH5α Plavo-bijeli test 300 bp

coli BL21(DE3)plysS segment 300 bp ekspresija 300 bp vektor pet11a

4 pgem - Teasy 300 bp restrikcija enzimima BamHI i NdeI ligacija transformacija Kompetentne ćelije E.coli BL21(DE3)plysS segment 300 bp ekspresija 300 bp vektor pet11a Kompetentne ćelije E.coli BL21(DE3)plysS 2 OD600 1,8 1,6 1,4 1,2 1 0,8 0,6 0,4 0, vrijeme [h] 8 10 H75W

Ekspresija proteina 1 2 3 M OD600 2 1,8 1,6 1,4 1,2 1 0,8 0,6 0,4 0,2 0 0 0,2 ml 1 M IPTG 2 4 6 vrijeme [h] 8 10 H75W Slika 14: Vremenska zavisnost rasta kompetentnih ćelija BL21(DE3)plysS sa

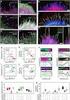
5 Ekspresija proteina M OD ,8 1,6 1,4 1,2 1 0,8 0,6 0,4 0, ,2 ml 1 M IPTG vrijeme [h] 8 10 H75W Slika 14: Vremenska zavisnost rasta kompetentnih ćelija BL21(DE3)plysS sa proteinom H75W. Strelicom je označeno vrijeme dodatka IPTG. 11 kda 66 kda 45 kda 30 kda 20,1 kda 14,4 kda Slika 15: Vremenska zavisnost ekspresije H75W rekombinantnog proteina praćena NaDS-PAGE. Traka M-LMW proteinski standard; Traka 1-proteinska frakcija odmah po dodatku IPTG; Traka 2-proteinska frakcija tri sata po dodatku IPTG; Traka 3-proteinska frakcija prije dodatka induktora ekspresije (IPTG).

6 Primjena fluorescentne spektroskopije: -Strukturna karakterizacija humanog serum albumina -Svijanje i odvijanje humanog serum albumina -Karakterizacija interakcije humanog serum albumina i antibiotika

7 Humani serum albumin Humani serum albumin je protein sa jednim polipeptidnim lancem, molekulske mase približno 67 kda. Sintetizira se u jetri i njegov poluživot iznosi 19 dana. Glavni je nosač masnih kiselina i lijekova, inhibira slobodne radikale kiseonika i inaktiviše toksične lipofilne metabolite bilirubina Zreli protein sadrži 585 aminokiselina, 17 disulfidnih veza i jednu slobodnu sulfhidrilnu grupu (Cys 34)

8 Aminokiselinska sekvenca MKWVTFISLL FLFSSAYSRG VFRRDAHKSE VAHRFKDLGE ENFKALVLIA FAQYLQQCPF EDHVKLVNEV TEFAKTCVAD ESAENCDKSL HTLFGDKLCT VATLRETYGE MADCCAKQEP ERNECFLQHK DDNPNLPRLV RPEVDVMCTA FHDNEETFLK KYLYEIARRH PYFYAPELLF FAKRYKAAFT ECCQAADKAA CLLPKLDELR DEGKASSAKQ RLKCASLQKF GERAFKAWAV ARLSQRFPKA EFAEVSKLVT DLTKVHTECC HGDLLECADD RADLAKYICE NQDSISSKLK ECCEKPLLEK SHCIAEVEND EMPADLPSLA ADFVESKDVC KNYAEAKDVF LGMFLYEYAR RHPDYSVVLL LRLAKTYETT LEKCCAAADP HECYAKVFDE FKPLVEEPQN LIKQNCELFE QLGEYKFQNA LLVRYTKKVP QVSTPTLVEV SRNLGKVGSK CCKHPEAKRM PCAEDYLSVV LNQLCVLHEK TPVSDRVTKC CTESLVNRRP CFSALEVDET YVPKEFNAET FTFHADICTL SEKERQIKKQ TALVELVKHK PKATKEQLKA VMDDFAAFVE KCCKADDKET CFAEEGKKLV AASQAALGL DAHKSE VAHRFKDLGE ENFKALVLIA FAQYLQQCPF EDHVKLVNEV TEFAKTCVAD ESAENCDKSL HTLFGDKLCT VATLRETYGE MADCCAKQEP ERNECFLQHK DDNPNLPRLV RPEVDVMCTA FHDNEETFLK KYLYEIARRH PYFYAPELLF FAKRYKAAFT ECCQAADKAA CLLPKLDELR DEGKASSAKQ RLKCASLQKF GERAFKAWAV ARLSQRFPKA EFAEVSKLVT DLTKVHTECC HGDLLECADD RADLAKYICE NQDSISSKLK ECCEKPLLEK SHCIAEVEND EMPADLPSLA ADFVESKDVC KNYAEAKDVF LGMFLYEYAR RHPDYSVVLL LRLAKTYETT LEKCCAAADP HECYAKVFDE FKPLVEEPQN LIKQNCELFE QLGEYKFQNA LLVRYTKKVP QVSTPTLVEV SRNLGKVGSK CCKHPEAKRM PCAEDYLSVV LNQLCVLHEK TPVSDRVTKC CTESLVNRRP CFSALEVDET YVPKEFNAET FTFHADICTL SEKERQIKKQ TALVELVKHK PKATKEQLKA VMDDFAAFVE KCCKADDKET CFAEEGKKLV AASQAALGL

9 Fluorescentna spektroskopija Strukturna karakterizacija humanog serum albumina Svijanje i odvijanje humanog serum albumina Karakterizacija interakcije humanog serum albumina i lijekova

10 Struktura humanog serum albumina 3 domene povezane disulfidnim vezama (domena I, II i III ) svaka domena sastoji se od 2 poddomene: IA i IB IIA i IIB IIIA i IIIB

11 Fluorescentna spektroskopija Strukturna karakterizacija humanog serum albumina Svijanje i odvijanje humanog serum albumina Karakterizacija interakcije humanog serum albumina i lijekova

(Na 2 HPO 4 ) 0,02 M Fosfatni pufer (ph = 7) A 280 = 0,692 Ex: 292 nm

12 Goveđi serum albumin (BSA) (A 280 =0,692, A 280 =1,241) Urea CH 4 N 2 O (1M 6M) Kalij dihidrogen fosfat (KH 2 PO 4 ) Dinatrij hidrogen fosfat (Na 2 HPO 4 ) 0,02 M Fosfatni pufer (ph = 7) A 280 = 0,692 Ex: 292 nm Ex: 295 nm Em: ( ) nm A 280 = 1,241 Ex: 292 nm Ex: 295 nm Em: ( ) nm

13 Fluorescentna spektroskopija Strukturna karakterizacija humanog serum albumina Svijanje i odvijanje humanog serum albumina Karakterizacija interakcije humanog serum albumina i lijekova

potpuno denaturisanog u 6M urei, snimljeni u području

14 Emisijski fluorescentni spektri nativnog goveđeg serum albumina u 0M urei, djelimično denturisanog u 1 5 M urei i potpuno denaturisanog u 6M urei, snimljeni u području nm pri ekscitaciji od 292 nm nakon ravnotežne denaturacije od 3,5h.

15 Fluorescentna spektroskopija Strukturna karakterizacija humanog serum albumina Svijanje i odvijanje humanog serum albumina Karakterizacija interakcije humanog serum albumina i lijekova analgetici antikancerogeni lijekovi

Spektrofotometar UV-mini 1240 (Shimadzu) Odvagati 0,5 g HSA, staviti u odmjernu tikvicu od

16 Priprema fosfatnog pufera WTW ph-metar (Mettler Tolerado USA) 0,2 M KH 2 PO 4 (41,3 ml ) 0,2 M Na 2 HPO 4 (58,7 ml ) 1,17 g NaCl ph= 7,38 i ph= 6,5 Priprema rastvora HSA Spektrofotometar UV-mini 1240 (Shimadzu) Odvagati 0,5 g HSA, staviti u odmjernu tikvicu od 25mL i dopuniti destilovanom vodom. Odpipetirati 15mL i dopuniti sa 40mL destilovane vode. A 280 =2,521

17 Priprema uzoraka HSA BSA 9M urea 6M GdnHCl Uzorci Rekombinantni humani serum albumin, HSA, ph 7,4 Rekombinantni humani serum albumin, HSA u 2M urei, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G1, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G1 u 2M urei, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G2, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G2 u 2M urei, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G3, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G3 u 2M urei, ph 7,4

Priprema uzoraka Antibiotici (različiti proizvođači, lijekovi, koji se koriste kao alternativa) G1 G2 G3 Uzorci Rekombinantni humani serum albumin, HSA, ph 7,4 Rekombinantni humani serum albumin, HSA

18 Priprema uzoraka Antibiotici (različiti proizvođači, lijekovi, koji se koriste kao alternativa) G1 G2 G3 Uzorci Rekombinantni humani serum albumin, HSA, ph 7,4 Rekombinantni humani serum albumin, HSA u 2M urei, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G1, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G1 u 2M urei, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G2, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G2 u 2M urei, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G3, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G3 u 2M urei, ph 7,4

19 intenzitet fluorescence (a.u.) HSA HSA, 2M urea 60 G G talasna dužina [nm] Uzorci Rekombinantni humani serum albumin, HSA, ph 7,4 Rekombinantni humani serum albumin, HSA u 2M urei, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G1, ph 7,4 Rekombinantni humani serum albumin, sistem HSA-G1 u 2M urei, ph 7,4

20 Snimanje spektara Spektrofluorometar RF-5301 (Shimadzu) - Spektri su snimani u području nm - Ekscitaciji 292nm - Otvor na ekscitacijskom i emisionom monohromatoru 1,5 nm.

21 Fluorescentni spektri sistema HSA- Fluorouracil pri ph 7,38 i ekscitaciji 292 nm

22 U uzorcima je korišten volumen proteina od 700 µl (A 280 = 2,521). Fluorescentni emisijski spektri su snimljeni u području od 300 do 500 nm, pri ekscitaciji na 292 nm, pri seriji različitih koncentracija fluorouracila. Ovi spektri su pokazali da je intenzitet fluorescence u uzorku sa maksimalnom koncentracijom lijeka 1,47x manji u odnosu na slijepu probu (HSA bez fluorouracila), što znači da se lijek postepeno veže za HSA.

23 Fluorescentni spektri sistema HSA- Fluorouracil pri ph 6,5 i ekscitaciji 292 nm

24 U uzorcima je korišten volumen proteina od 700 µl (A 280 = 2,521). Fluorescentni emisijski spektri su snimljeni u području od 300 do 650 nm, pri ekscitaciji na 292 nm, pri seriji različitih koncentracija fluorouracila. Ovi spektri su pokazali da je intenzitet fluorescence u uzorku sa maksimalnom koncentracijom lijeka 1,18x manji u odnosu na slijepu probu (HSA bez Fluorouracila), što znači da se lijek postepeno veže za HSA.

25 Fluorescentni spektri sistema HSA- Doxorubicin pri ph 7,38 i ekscitaciji 292 nm

26 U uzorcima je korišten volumen proteina od 700 µl (A 280 = 2,521). Fluorescentni emisijski spektri su snimljeni u području od 300 do 650 nm, pri ekscitaciji na 292 nm, pri seriji različitih koncentracija doxorubicina. Ovi spektri su pokazali da je intenzitet fluorescence u uzorku sa maksimalnom koncentracijom lijeka 2,72x manji u odnosu na slijepu probu (HSA bez Doxorubicina), što znači da se lijek postepeno veže za HSA.

27 Fluorescentni spektri sistema HSA- Doxorubicin pri ph 6,5 i ekscitaciji 292 nm

28 U uzorcima je korišten volumen proteina od 700 µl (A 280 = 2,521). Fluorescentni emisijski spektri su snimljeni u području od 300 do 650 nm, pri ekscitaciji na 292 nm, pri seriji različitih koncentracija doxorubicina. Ovi spektri su pokazali da je intenzitet fluorescence u uzorku sa maksimalnom koncentracijom lijeka 6,59x manji u odnosu na slijepu probu (HSA bez Doxorubicina), što znači da se lijek postepeno veže za HSA.

Σχετικά έγγραφα

Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom

Kolegij: Obrada industrijskih otpadnih voda Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom Zadatak: Ispitati učinkovitost procesa koagulacije/flokulacije na obezbojavanje