16. skupine. dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
|
|
|
- Σταματία Βαρβάρα Σκλαβούνος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Elementi 16. skupine Elementi 16. skupine nazivaju se halkogenim elementima (grč. chalkós + génesis tvore rude ), jer su sastavni dio ruda (Cu-, Zn-, Fe-, Pb-, Hg-; kao sulfidi, oksidi, selenidi, teluridi itd.). U 16. skupini elemenata periodnog sustava nalaze se sljedeći elementi: kisik (O), sumpor (S), selenij (Se), telurij (Te) i polonij (Po). Kisik i sumpor su nemetali, selenij i telurij polumetali (metaloidi), a polonij je radioaktivan metal. U prirodi dolaze u spojevima i kao elementarni uviše alotropskih modifikacija i svi imaju šest valentnih elektrona: [X] ns 2 np 4. 1
2 Fizička svojstva halkogenih elemenata Kisik Sumpor Selenij Telurij Formula O 2 S 8 Se 8, Se n Te n Agregacijsko stanje plinovito čvrsto čvrsto čvrsto Talište / o C -218,4 118, Vrelište / o C -182,9 444, Boja bezbojan žut crven, siv srebrnobijeli Atomski polumjer / pm Ionski polumjer / pm Elektronegativnost 3,5 2,5 2,4 2,1 E Θ / V: X H 2 X 1,23 0,14-0,40-0,72 Kemijska svojstva halkogenih elemenata Halkogeni elementi tvore ionske spojeve s metalima male E i i male elektronegativnosti (primanjem 2e od metala tvore X ione), a kovalentne s nemetalima velike E i i velike elektronegativnosti. Sumpor, selenij, telurij i polonij tvore spojeve s negativnim oksidacijskim brojem -2 i -1 s vodikom i metalima, a s pozitivnim oksidacijskim brojem +2, +4 i +6 s elektronegativnijim elementima (kisikom i halogenim elementima). 2
3 Kisik u spojevima ima uvijek negativan oksidacijski broj (-2 u oksidima, -1 u peroksidima, -1/2 u superoksidima, -1/3 u ozonidima) osim u spojevima s fluorom (npr. OF 2, oksidacijski broj +2). Rasprostranjenost halkogenih elemenata Kisik w = 49,2 %; spojevi kisika, w(o 2 )=23%u zraku Sumpor w = 0,06 %; rude sulfida, sulfata; S 8 u SAD (vulkanskog podrijetla ili nastaje bakterijskim razlaganjem CaSO 4 ) Selenij i w = %; kao elementarni uz S 8 ; Tl Telurij minerali koji sadrže dž sulfide kao selenidi i teluridi. 3
4 Kisik Kisik je najrasprostraniji element na Zemlji. Volumni udio elementarnog kisika u zraku iznosi 20,9 %, a maseni udio 23 %. Kisik, ik O 2 (g), je pri sobnoj temperaturit plin bez boje, okusa i mirisa. Kisik ne gori ali podržava gorenje i život na zemlji bez kisika je nemoguć. Tekući kisik,o 2 (l) je tamnoplave boje, paramagnetičan je i dobiva se ukapljivanjem zraka i frakcijskom destilacijom. Postoje dvije alotropske modifikacije kisika:.. O 2 (g), kisik O Ȯ..... O O O 3 (g), ozon : O O: :.... O O : Ozon je modrikasti plin karakterističnog mirisa i stvara se u Zemljinoj atmosferi na visini km prilikom električnog pražnjenja uz djelovanje UV zračenja. Freoni uništavaju ozonski sloj (ozonske rupe). Molekula ozona, O 3 je dijamagnetična polarna molekula i zbog polarnosti je topljivost O 3 (g) u vodi 50 puta veća od topljivosti O 2 (g). 4
5 Laboratorijsko dobivanje kisika Zagrijavanjem (termičkim raspadom) klorata ili permanganata: Δ 2KClO 3 3( (c) 2KCl(s) +3O 2 2(g) 2KMnO 4 (c) Δ K 2 MnO 4 (s) + MnO 2 (s) + O 2 (g) Zagrijavanjem (termičkim raspadom) nekih oksida metala (HgO, Ag 2 O) 2Ag 2 O(s) 4Ag(s) + O 2 (g) Elektrolizom vode: K( ): 4H 2 O(l) + 4e 2H 2 (g)+ 4OH (aq) A(+): 4OH (aq) O 2 (g) + 2H 2 O(l) + 4e. Hofmannov aparat 5
6 Ukoliko katodni i anodni prostor nisu odijeljeni tada nastaje praskavac, eksplozivna smjesa vodika i kisika uomjeru 2:1. Dobivanje (a) i svojstva (b) praskavca Industrijsko dobivanje kisika Elektrolizom vodenih otopina (na anodi): A(+): 4OH (aq) O 2 (g) + 2H 2 O(l) + 4e. Ukapljivanjem - likvefakcijom zraka te naknadnom frakcijskom destilacijom tekućeg zraka [t v (O 2 ): -183 o C, t v (N 2 ): -195,8 o C, t v (Ar): -185,7 o C]. 6
7 Upotreba kisika Kisik (zrak) se upotrebljava pri proizvodnji željeza u visokoj peći, kao i dobivanju čelika. U proizvodnji metala (prevođenje sulfida u okside). U proizvodnji spojeva koji sadrže kisik: organskih i anorganskih. Zajedno s etinom upotrebljava se za autogeno zavarivanje. U biološkoj obradi otpadnih voda. U medicini (respiratori). Kisik i zagađivanje atmosfere Izgaranjem fosilnih goriva (ugljena, nafte, zemnog plina) i u metalurškim procesima nastaju sumporovi oksidi: S+O 2 (g) SO 2 (g), 2SO 2 (g) + O 2 (g) 2SO 3 (g). Reakcijom dušika sa kisikom nastaju otrovni plinovi dušikov(ii) oksid i dušikov(iv) oksid N 2 (g) + O 2 (g) 2NO(g); 2NO(g) + O 2 (g) 2NO 2 (g). Nastali plinovi (SO 2, SO 3 i NO 2 ) reagiraju u zraku sa vodom i tako nastaju kisele kiše (H 2 SO 3,H 2 SO 4 i HNO 3 ). SO 2 (g) + H 2 O(l) H 2 SO 3 (aq); SO 3 (g) + H 2 O(l) H 2 SO 4 (aq); 3NO 2 (g) + H 2 O(l) 2HNO 3 (aq) + NO(g). 7
8 Posljedice kiselih kiša Skulptura na jednom dvorcu u Westphaliji u Njemačkoj fotografirana 1908.g. i 1968.g. Nepotpunim izgaranjem fosilnih goriva nastaju i ugljikov(ii) oksid (CO) koji je otrovan te ugljikov(iv) oksid (CO 2 ) koji nije otrovan, ali onemogućava pristup zraku (kisiku). 2C(s) + O 2 (g) 2CO(g), 2CO(g) + O 2 (g) 2CO 2 (g). Dio ugljikovog(iv) oksida biljke koriste za fotosintezu, no suvišak ugljikovog(iv) oksida, metan (CH 4 ) i vodena para (H 2 O) u atmosferi apsorbiraju infracrveno zračenje zbog čega dolazi do zagrijavanja Zemlje i globalnih klimatskih promjena globalno zatopljenje. 8
9 Spojevi kisika Oksidi Oksidi su spojevi elemenata i kisika oksidacijskog broja -2 koji sadrže oksidni ion, O. Okside tvore svi elementi osim He, Ne, Ar, Kr, a mogu se podijeliti na bazične, kisele, neutralne i amfoterne. Moraju ispunjavati jedan od tri uvjeta: a) da se otapaju u vodi (topljivi) b) da reagiraju s kiselinama ili lužinama (topljivi i netopljivi) c) da reagiraju s bazičnim ili kiselim oksidima (topljivi i netopljivi u vodi). Bazični oksidi su oksidi metala topljivi u vodi jer s vodom daju baze. U vodi su topljivi ionski oksidi 1. skupine i oksidi Ca, Sr, Ba: CaO(s) + H 2 O(l) Ca(OH) 2 (aq) Na 2 O(s) + H 2 O(l) 2NaOH(aq). Oksidi metala koji su topljivi u vodi, kao i netopljivi, mogu reagirati s kiselinama ili mogu reagirati s kiselim oksidima i dati soli: MgO(s) + 2HCl(aq) MgCl 2 (aq) + H 2 O Δ CaO(s) + SiO 2 (s) CaSiO 3 (s). 9
10 Kiseli oksidi su oksidi nemetala jer otopljeni u vodi tvore kiselinu: SO 2 (g) + H 2 O(l) H 2 SO 3 (aq) CO 2 (g) + H 2 O(l) H 2 CO 3 (aq) P 4 O 10 (s) + 6H 2 O(l) 4H 3 PO 4 (aq). Topljivi i netopljivi u vodi oksidi nemetala reagiraju s bazama, a isto tako i s bazičnim oksidima i daju soli: SO 2 (g) + 2 NaOH(aq) Na 2 SO 3 (aq)+ H 2 O(l) SiO 2 (l) + 2 NaOH(l) Na 2 SiO 3 (l) + H 2 O(g) Δ SiO 2 (s) + CaO(s) CaSiO 3 (s) Svojstvo da kiseli i bazični oksidi međusobno reagiraju koristi se u industriji stakla i metalurgiji. Staklo je kruta otopina kiselih i bazičnih oksida. Neutralni oksidi ne reagiraju s vodom, ne otapaju se niti u kiselinama niti u bazama i ne mogu neutralizirati ni kiseline ni baze. Neutralni oksidi su: N 2 O, CO i NO. 10
11 Amfoterni oksidi imaju bazična i kisela svojstva. Čine ih elementi duž linije između metala i nemetala i elementi u sredini periodnog sustava. Oni reagiraju s jakim kiselinama kao bazni oksidi, a s jakim bazama kao kiseli oksidi. ZnO(s) + 2H + (aq) Zn 2+ (aq) + H 2 O(l) ZnO(s) + 2OH (aq) + H 2 O(l) [Zn(OH) 4 ] (aq) Al 2O 3 3( (s)+ 6H + (aq) 2Al 3+ (aq) +3H 2 O(l) () Al 2 O 3 (s)+ 2OH (aq) + 3H 2 O(l) 2[Al(OH) 4 ] (aq). Voda najvažniji od svih oksida i najvažniji kemijski spoj na Zemlji neophodna je za sve žive organizme bez vode nema života (zbog toga se i traži u Svemiru). molekula vode je trokutaste strukture s kutem od 104,5 o između dvije O H veze. 11
12 Zbog velike razlike u koeficijentu elektronegativnosti između vodika i kisika, molekula vode je izrazito dipolnog karaktera. Kisikovi atomi molekula vode koji su djelomično negativno nabijeni i i vodikovi i atomi koji su djelomično pozitivno nabijeni međusobno se privlače, što posredstvom vodikove veze dovodi do asocijacije molekula i u tekućem i u čvrstom agregatnom stanju. Zahvaljujući svojoj velikoj moći otapanja (dipolni karakter!) prirodna voda nije nikada potpuno čista. Obično voda sadrži nešto otopljenih soli raznih minerala kroz čije slojeve je prošla. Osobito je značajno prirodno o onečišćenje vode s ionima Ca 2+, Mg 2+ i Fe 2+, jer se prilikom uparavanja (kuhanja) takve vode ili dodatkom sapuna stvaraju netopljivi produkti. Zbog toga se voda koja sadrži te ione naziva tvrda voda. Takva voda sadrži veliki broj najrazličitijih iona. O kojim je ionima riječ i u kojoj koncentraciji se nalaze u vodi može se vidjeti na etiketi bilo koje vode kupljene u trgovini. 12
13 Tvrdoću vode mjerimo tzv. stupnjevima tvrdoće ( o dh): 1 o njemačke tvrdoće = 10 mg dm 3 CaO 1 o francuske tvrdoće = 10 mg dm 3 CaCO 3. Klasifikacija vode po tvrdoći prema Hartegradenu: 0 dh - 4 dh jako meka voda 4 dh - 8 dh meka voda 8 dh - 18 dh srednje tvrda voda 18 dh - 30 dh tvrda voda > 30 dh jako tvrda voda 13
14 Iako je tvrdoća vode uvjetovana i Mg 2+ ife 2+ ionima, prisustvo Ca 2+ iona je najvažnije. Postoje 2 tipa tvrdoće: a) prolazna, koju čine hidrogenkarbonatni ioni (HCO 3 ) i odgovarajuća količina metalnih iona. b) stalna, kod koje je u u vodi prisutan neki drugi anion (ne hidrogenkarbonatni) uz odgovarajuću količinu metalnih iona. Naziv prolazna tvrdoća osniva se na činjenici da se takva tvrdoća može ukloniti kuhanjem vode: Ca HCO 3 CaCO 3 (s) + CO 2 (g) + H 2 O(l) Reakcija je povratna i hidrogenkarbonatni ion može ponovo nastati kada voda koja djeluje na kalcijev karbonat sadrži ugljikov(iv) oksid. Stalagmiti Stalaktiti 14
15 Kuhanje vode je ujedno i najjednostavniji način da se smanji tvrdoća vode, tj. da se voda omekša. Drugi postupci mekšanja temelje se na: a) dodavanju karbonatnih iona u otopinu tvrde vode (najčešće otopina Na 2 CO 3 ) čime se istaloži CaCO 3 : Ca 2+ (aq) + CO 3 (aq) CaCO 3 (s) b) dodavanju lužine (najčešće otopina Ca(OH) 2 ) kojom se HCO 3 ioni prevode u CO 3 i istalože kao CaCO 3 : HCO 3 (aq) + OH (aq) CO 3 (aq) + H 2 O Ca 2+ (aq) + 2HCO 2+ 3 (aq) + Ca (aq) + 2OH (aq) 2CaCO 3 (s) + 2H 2 O(l) Pri tome se dio OH iona istaloži i u obliku hidroksida zbog prisutnih Mg 2+ ife 2+ iona: Mg 2+ (aq)+ 2OH (aq) Mg(OH) 2 (s); Fe 2+ (aq)+ 2OH (aq) Fe(OH) 2 (s). 15
16 Danas se ioni iz vode uklanjaju ionskim izmjenjivačima. Kao ionski izmjenjivači najprije su se upotrebljavali prirodni silikatni minerali permutit i zeolit, dok se danas koriste izmjenjivači na bazi smola koje imaju mrežastu strukturu. U kationskom izmjenjivaču izmjenjuju se kationi sa H + ionima te se onda takva voda propušta kroz anionski izmjenjivač u kojem se izmjenjuju anioni sa OH ionima čime se dobiva deionizirana voda. To se može prikazati sljedećim jednostavnim jednadžbama kemijske reakcije: 2H smola + Ca 2+ (aq) Ca smola + 2H + (aq) 2OH smola + SO 4 (aq) + 2H + (aq) SO 4 smola + 2H 2 O(l). Peroksidi Peroksidi su spojevi kisika oksidacijskog broja -1 koji sadrže peroksidni ion, O 2-2. Skupini peroksida pripada vodikov peroksid (H 2 O 2 ) i metalni peroksidi. Struktura H 2 O 2 16
17 U laboratorijskim uvjetima H 2 O 2 se može dobiti djelovanjem kiseline na čvrsti barijev peroksid (a), dok se industrijski danas dobiva iz 2-alkilantrakinona (b). a) BaO 2 (s) + 2 H 3 O + (aq) Ba 2+ (aq) + H 2 O 2 (aq) + 2H 2 O(l) b) Vodikov peroksid ovisno o uvjetima može djelovati kao oksidans i kao reducens te kao vrlo slaba dvoprotonska kiselina. Oksidans (u kiselom mediju): H 2 O 2 (aq) + 2H + (aq) + 2e 2H 2 O(l) Reducens (u kiselom mediju): H 2 O 2 (aq) 2H + (aq) + O 2 (g) + 2e Oksidans (u alkalnom mediju): HO + +2e (aq) H 2 O(l) 3OH (aq) Reducens (u alkalnom mediju): HO (aq) + OH (aq) O 2 (g) + H 2 O(l) + 2e 17
18 Vodikov peroksid koji u trgovinu dolazi kao vodena otopina masenog udjela 3-33 % raspada se na vodu i kisik (reakcija disproporcioniranja): 2H 2O 2 2( (aq) 2H 2 O(l) () +O 2 2(g) (g). Zbog njegovog oksidacijskog ili redukcijskog djelovanja upotrebljava se u kemiji, medicini, za bojanje kose, kao raketno gorivo s hidrazinom (NH 2 NH 2 )itd. U tekstilnoj industriji koristi se za bijeljenje (većinom celuloznih materijala). H 2 O 2 (aq) H 2 O(l) + O(g). 35 Sumpor, selenij i telurij Svi se mogu naći u više alotropskih modifikacija. Sumpor se može naći u više od dvije alotropske modifikacije, a najvažnije j dvije kristalne forme (gdje dolazi u obliku S 8 molekula) su rompska koja pri 95,5 o C prelazi u monoklinsku (t t =118,9 o C). Na višim temperaturama (t 200 o C) nastaju S n -lanci, a između 444, o C S n,s 4,S 2,S. Sumpor (rompski) 18
19 I selenij i telurij dolaze u više alotropskih modifikacija, a sva tri elementa, sumpor, selenij i telurij dolaze i kao amorfni. Selenij i telurij Polonij se može naći u uranovim rudama, a nastaje i radioaktivnim raspadom drugih elemenata. Zbog veličine atoma je preklapanje p-orbitala nemoguće zbog njihove veće udaljenosti (S, Se, Te). Zato se atomi povezuju samo jednostrukom σ-vezom i nastaju zatvorene ili lančaste strukture. Sumpor dolazi u dva kristalna oblika, kao rompski i monoklinski žute boje (enantiotropija), a rompska modifikacija je stabilnija. S 8 -stabilna molekula do t o C kada prelazi u lančasti μ-s n (smeđi), dok su Se 8 ite 8 nestabilne molekule. S n, Se n, Te n sve stabilniji lančast radikali, jer imaju nesparen elektron na kraju lanca. 19
20 Sumpor se upotrebljava za proizvodnju sumporne kiseline, za vulkanizaciju gume, za dobivanje sumpornih spojeva i za proizvodnju baruta. Minerali koji se koriste kao izvori za sumporne spojeve PbS HgS FeS 2 ZnS galenit cinabarit (cinober) pirit sfalerit Spojevi sumpora Sumporovodik (H 2 S) - spoj sumpora sa oksidacijskim brojem -2. Sumporovodik se dobiva iz metalnih sulfida: FeS(s) + 2HCl(aq) H 2 S(g) + FeCl 2 (aq). H 2 S (g) je otrovan plin mirisa na trula jaja, otapanjem u vodi daje slabu diprotonsku sumporovodičnu kiselinu, H 2 S(aq): H 2 S(aq) 2 H + (aq) + S 2- (aq). Ona u reakciji s baznim oksidima i bazama daje dvije vrste soli: hidrogensulfide (HS ) i sulfide (S ), od čega hidrogensulfide samo s alkalijskim elementima. 20
21 U spojeve sumpora sa oksidacijskim brojem +4 pripadaju sumporov(iv) oksid (SO 2 )isumporasta kiselina (H 2 SO 3 ).. Industrijsko dobivanje SO 2 (g) iz sumpora i sulfida: a) S(s) + O 2 (g) SO 2 (g) b) 2ZnS(s) + 3O 2 (g) 2ZnO(s) + 2SO 2 (g). Laboratorijsko dobivanje: Na 2 SO 3 (s) + H 2 SO 4 (aq) Na 2 SO 4 (aq) + SO 2 (g) + H 2 O(l). Na 2 SO 3 (s) + H 2 SO 4 (aq) Na 2 SO 4 (aq) + SO 2 (g) + H 2 O(l) SO 2 (g) + H 2 O(l) H 2 SO 3 (aq) HSO 3 (aq) + H 2 O(l) + I 2 (aq) HSO 4 (aq) + 2I (aq) + 2H + (aq) 5HSO 3 (aq) + 2MnO 4 (aq) + H + 5SO 4 (aq) + 2Mn 2+ +3H 2 O(l) 21
22 SO 2 (g) je otrovan plin bockavog mirisa. Otapanjem u vodi daje slabu diprotonsku sumporastu kiselinu, H 2 SO 3 (aq). H 2 O(l) () +SO 2 2(g) H 2SO 3 3( (aq). Sumporasta kiselina daje dvije vrste soli, hidrogensulfite (HSO 3 ) i sulfite (SO 3 ). Sumporov dioksid, sumporasta kiselina i sulfiti su reducensi: 2MnO 4 (aq)+ 6H + (aq)+ 5SO 3 (aq) 5SO 4 (aq) + 2Mn 2+ (aq) + 3H 2 O(l). U spojeve sumpora sa oksidacijskim brojem +6 pripadaju sumporov(vi) oksid (SO 3 ) i sumporna kiselina (H 2 SO 4 ). Sumporov(VI) oksid je pri normalnim okolnostima lako hlapljivalji tekućina (pri 16,8 o C krutina, polimer), a u plinovitom stanju molekula SO 3 je rezonantni sp 2 -hibrid. SO 3 je anhidrid sumporne kiseline. SO 3 (g) SO 3 (s) 22
23 Ishodna tvar za dobivanje sumporovog(vi) oksida je SO 2 (g) koji se dobiva izgaranjem S(s) ili prženjem sulfidne rude. Dobivanje SO 3 ( o C uz katalizator Pt ili V 2 O 5 ): 2SO 2 (g) + O 2 (g) 2SO 3 (g). S obzirom da je reakcija egzotermna SO 3 se mora odvoditi iz reakcijske smjese. Dobivanje H 2 SO 4 kontaktni postupak Dobiveni SO 3 (g) se slabo otapa u vodi, zato se otapa u koncentriranoj sumpornoj kiselini (98 %) uz dodatak vode (hlađenje), nastaje koncentrirana kiselina masenog udjela 98 %. oleum je otopina SO 3 u konc. H 2 SO 4 SO 3 (g) + H 2 O(l) H 2 SO 4 (aq) H 2 SO 4 (aq) + SO 3 (g) H 2 S 2 O 7 (aq) sumporna kiselina pirosumporna kiselina H 2 S 2 O 7 (aq) + H 2 O(l) 2H 2 SO 4 (aq) 23
24 Struktura sumporne kiseline je tetraedarska: Sumporna kiselina (w = 96 %) je bezbojna uljasta tekućina (ρ =1,84gcm 3 ). Njena velika uporaba temelji se na njezinom trima svojstvima: a) kiselinskom (jaka kiselina) - čista H 2 SO 4 otapa mnoge tvari, čak i kristalinične ionske spojeve - u vodenim otopinama praktički potpuno disocira (prvi stupanj disocijacije): H 2 SO 4 H + + HSO 4 ; K a =oko10 3 mol dm 3 HSO 4 H + + SO 4 ; K a =1, mol dm 3 - daje dvije vrste soli: sulfate i hidrogensulfate b) oksidacijskom - H 2 SO 4 je srednje jako oksidacijsko sredstvo, ali samo kada je vruća i koncentrirana: Cu(s) + HSO 4 (aq)+ 3H + (aq) Cu 2+ (aq) + SO 2 (g) + 2H 2 O(l). 24
25 c) dehidratacijskom - čista H 2 SO 4 pokazuje sklonost da na sebe veže vodu pri čemu nastaju hidrati H 2 SO 4 ; prilikom te reakcije oslobađaju se znatne količine topline - zbog toga se često upotrebljava za sušenje Pokus: šećer + H 2 SO 4 konc.; C 12 H 22 O C + 11 H 2 O Tiosulfati derivati sumporne kiseline. Tiosumporna kiselina (H 2 S 2 O 3 ) nije poznata jer je nestabilna i raspada se, ali su poznate soli te kiseline, tiosulfati (S 2 O 3 ): Prikaz tetraedarske strukture tiosulfatnog iona, S 2 O 3 Natrijev tiosulfat (Na 2 S 2 O 3 ) otapa netopljive srebrne halogenide i upotrebljava se kao fiksir u fotografskoj industriji: AgBr(s) + 2S 2 O 3 (aq) [(Ag(S 2 O 3 ) 2 ] 3 (aq) + Br (aq). 25
26 Upotrebljava se i kao reducens u jodometriji (analitičkoj kemiji): nekom oksidansu (KMnO 4, H 2 O 2, Fe 3+ itd.) dodaje se višak KI(s), a izlučeni I 2 je ekvivalentan količini oksidansa. Količina I 2 se odredi titracijom s Na 2 S 2 O 3 (aq) uz škrob kao indikator (adicijski spoj škroba i I 2 daje ljubičastu boju): S 2 O 3 (aq) + I 2 (aq) 2I (aq) + S 4 O 6 (aq). 26
Vodik. dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Vodik Najzastupljeniji element u svemiru (maseni udio iznosi 90 %) i sastavni dio Zvijezda. Na Zemlji je po masenom udjelu deseti element po zastupljenosti. Zemljina gravitacija premalena je da zadrži
Vodik Najzastupljeniji element u svemiru (maseni udio iznosi 90 %) i sastavni dio Zvijezda. Na Zemlji je po masenom udjelu deseti element po zastupljenosti. Zemljina gravitacija premalena je da zadrži
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
17. skupine. dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Elementi 17. skupine Elementi 17. skupine nazivaju se halogenim elementima (grč.-háls + génesis tvorac soli ). U prirodi se nalaze kao soli. Halogeni elementi su nemetali: fluor (F), klor (Cl), brom (Br),
Elementi 17. skupine Elementi 17. skupine nazivaju se halogenim elementima (grč.-háls + génesis tvorac soli ). U prirodi se nalaze kao soli. Halogeni elementi su nemetali: fluor (F), klor (Cl), brom (Br),
Heterogene ravnoteže taloženje i otapanje. u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima
 Heterogene ravnoteže taloženje i otapanje u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima Ako je BA teško topljiva sol (npr. AgCl) dodatkom
Heterogene ravnoteže taloženje i otapanje u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima Ako je BA teško topljiva sol (npr. AgCl) dodatkom
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
Otopine elektrolita. elektroliti tvari koje kada su rastaljene ili otopljene u vodi provode struju pomoću jona
 Otopine elektrolita elektroliti tvari koje kada su rastaljene ili otopljene u vodi provode struju pomoću jona ioni (gr. oni koji putuju ) električki pozitivno i negativno nabijene čestice, nastaju raspadanjem
Otopine elektrolita elektroliti tvari koje kada su rastaljene ili otopljene u vodi provode struju pomoću jona ioni (gr. oni koji putuju ) električki pozitivno i negativno nabijene čestice, nastaju raspadanjem
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Alkalijski i zemnoalkalijski metali
 Elementi 1. i 2. skupine Sljedeći faktori utječu na svojstva alkalijskih i zemnoalkalijskih elemenata : Alkalijski i zemnoalkalijski metali elektronska konfiguracija veličina atoma i iona energija ionizacije
Elementi 1. i 2. skupine Sljedeći faktori utječu na svojstva alkalijskih i zemnoalkalijskih elemenata : Alkalijski i zemnoalkalijski metali elektronska konfiguracija veličina atoma i iona energija ionizacije
ŠTO JE ANORGANSKA KEMIJA? Organska kemija je definirana kao kemija ugljikovodikovih spojeva i njihovih derivata Ali što je s CO, CO 2 ili HCN..
 ŠTO JE ANORGANSKA KEMIJA? Organska kemija je definirana kao kemija ugljikovodikovih spojeva i njihovih derivata Ali što je s CO, CO 2 ili HCN.. Anorganska kemija se može najkraće definirati kao sve ostalo
ŠTO JE ANORGANSKA KEMIJA? Organska kemija je definirana kao kemija ugljikovodikovih spojeva i njihovih derivata Ali što je s CO, CO 2 ili HCN.. Anorganska kemija se može najkraće definirati kao sve ostalo
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ. Γενικής Παιδείας Χημεία Α Λυκείου ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ. Επιμέλεια: ΒΑΣΙΛΗΣ ΛΟΓΟΘΕΤΗΣ
 ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ Γενικής Παιδείας Χημεία Α Λυκείου Επιμέλεια: ΒΑΣΙΛΗΣ ΛΟΓΟΘΕΤΗΣ e-mail: info@iliaskos.gr www.iliaskos.gr 1 57 1.. 1 kg = 1000 g 1 g = 0,001 kg 1
ΗΛΙΑΣΚΟΣ ΦΡΟΝΤΙΣΤΗΡΙΑ ΥΠΗΡΕΣΙΕΣ ΠΑΙΔΕΙΑΣ ΥΨΗΛΟΥ ΕΠΙΠΕΔΟΥ Γενικής Παιδείας Χημεία Α Λυκείου Επιμέλεια: ΒΑΣΙΛΗΣ ΛΟΓΟΘΕΤΗΣ e-mail: info@iliaskos.gr www.iliaskos.gr 1 57 1.. 1 kg = 1000 g 1 g = 0,001 kg 1
KERAMIKA, BETON I DRVO
 VJEŽBE: četvrtak, 12:15-14:00 KERAMIKA, BETON I DRVO Vježba 1. Ionske i kovalentne strukture Prof.dr.sc. Lidija Ćurković STRUKTURA ČVRSTIH (krutih) TVARI ovisi o: 1. VRSTI VEZA IZMEĐU STRUKTURNIH JEDINICA
VJEŽBE: četvrtak, 12:15-14:00 KERAMIKA, BETON I DRVO Vježba 1. Ionske i kovalentne strukture Prof.dr.sc. Lidija Ćurković STRUKTURA ČVRSTIH (krutih) TVARI ovisi o: 1. VRSTI VEZA IZMEĐU STRUKTURNIH JEDINICA
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
panagiotisathanasopoulos.gr
 . Παναγιώτης Αθανασόπουλος Χηµικός ιδάκτωρ Παν. Πατρών. Οξειδοαναγωγή Παναγιώτης Αθανασόπουλος Χημικός, Διδάκτωρ Πανεπιστημίου Πατρών 95 Χηµικός ιδάκτωρ Παν. Πατρών 96 Χηµικός ιδάκτωρ Παν. Πατρών. Τι ονοµάζεται
. Παναγιώτης Αθανασόπουλος Χηµικός ιδάκτωρ Παν. Πατρών. Οξειδοαναγωγή Παναγιώτης Αθανασόπουλος Χημικός, Διδάκτωρ Πανεπιστημίου Πατρών 95 Χηµικός ιδάκτωρ Παν. Πατρών 96 Χηµικός ιδάκτωρ Παν. Πατρών. Τι ονοµάζεται
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
1 η Σειρά προβλημάτων στο μάθημα Εισαγωγική Χημεία
 1 η Σειρά προβλημάτων στο μάθημα Εισαγωγική Χημεία Ημ. Παράδοσης: Δευτέρα 25/11/2013 11 πμ 1. Οι αντιδράσεις οξειδοαναγωγής σώζουν ζωές!!! Οι αερόσακοι στα αυτοκίνητα, όταν ανοίγουν γεμίζουν με άζωτο το
1 η Σειρά προβλημάτων στο μάθημα Εισαγωγική Χημεία Ημ. Παράδοσης: Δευτέρα 25/11/2013 11 πμ 1. Οι αντιδράσεις οξειδοαναγωγής σώζουν ζωές!!! Οι αερόσακοι στα αυτοκίνητα, όταν ανοίγουν γεμίζουν με άζωτο το
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
13. skupine. dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Elementi 13. skupine U 13. skupini periodnog sustava nalaze se sljedeći elementi: bor (B), aluminij (Al), galij (Ga), indij (In) i talij (Tl). B je polumetal, dok su ostali elementi metali. U elementarnom
Elementi 13. skupine U 13. skupini periodnog sustava nalaze se sljedeći elementi: bor (B), aluminij (Al), galij (Ga), indij (In) i talij (Tl). B je polumetal, dok su ostali elementi metali. U elementarnom
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
ΦΡΟΝΤΙΣΤΗΡΙΟ Μ.Ε. ΣΥΜΒΟΛΟ ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Α ΛΥΚΕΙΟΥ ΑΝΤΙ ΡΑΣΕΙΣ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Α ΛΥΚΕΙΟΥ ΑΝΤΙ ΡΑΣΕΙΣ Όλες οι αντιδράσεις που ζητούνται στη τράπεζα θεµάτων πραγµατοποιούνται. Στην πλειοψηφία των περιπτώσεων απαιτείται αιτιολόγηση της πραγµατοποίησης των αντιδράσεων.
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ Α ΛΥΚΕΙΟΥ ΑΝΤΙ ΡΑΣΕΙΣ Όλες οι αντιδράσεις που ζητούνται στη τράπεζα θεµάτων πραγµατοποιούνται. Στην πλειοψηφία των περιπτώσεων απαιτείται αιτιολόγηση της πραγµατοποίησης των αντιδράσεων.
Kiselo bazni indikatori
 Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Kiselo bazni indikatori Slabe kiseline ili baze koje imaju različite boje nejonizovanog i jonizovanog oblika u rastvoru Primer: slaba kiselina HIn(aq) H + (aq) + In (aq) nejonizovani oblik jonizovani oblik
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
14. skupine. dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Elementi 14. skupine U 14. skupini periodnog sustava nalaze se sljedeći elementi: ugljik (C), silicij (Si), germanij (Ge), kositar (Sn), olovo (Pb). Cjenemetal, SiiGesupolumetali, asn i Pb metali. U elementarnom
Elementi 14. skupine U 14. skupini periodnog sustava nalaze se sljedeći elementi: ugljik (C), silicij (Si), germanij (Ge), kositar (Sn), olovo (Pb). Cjenemetal, SiiGesupolumetali, asn i Pb metali. U elementarnom
γ) Βa(ΟΗ) 2 (aq) + ΗBr(aq)
 Θέμα 2 ο 2.1. Να συμπληρώσετε τις χημικές εξισώσεις (προϊόντα και συντελεστές) των παρακάτω αντιδράσεων που γίνονται όλες. α) CaI 2 (aq) + AgNO 3 (aq) β) Cl 2 (g) + H 2 S(aq) γ) Βa(ΟΗ) 2 (aq) + ΗBr(aq)
Θέμα 2 ο 2.1. Να συμπληρώσετε τις χημικές εξισώσεις (προϊόντα και συντελεστές) των παρακάτω αντιδράσεων που γίνονται όλες. α) CaI 2 (aq) + AgNO 3 (aq) β) Cl 2 (g) + H 2 S(aq) γ) Βa(ΟΗ) 2 (aq) + ΗBr(aq)
3. ΧΗΜΙΚΕΣ ΑΝΤΙΔΡΑΣΕΙΣ
 23 3. ΧΗΜΙΚΕΣ ΑΝΤΙΔΡΑΣΕΙΣ 1. Βλέπε θεωρία σελ. 83. 2. α) (χημική εξίσωση) β) (δύο μέλη) (ένα βέλος >) γ) (αντιδρώντα) δ) (τμήμα ύλης ομογενές που χωρίζεται από το γύρω του χώρο με σαφή όρια). ε) (που οδηγούν
23 3. ΧΗΜΙΚΕΣ ΑΝΤΙΔΡΑΣΕΙΣ 1. Βλέπε θεωρία σελ. 83. 2. α) (χημική εξίσωση) β) (δύο μέλη) (ένα βέλος >) γ) (αντιδρώντα) δ) (τμήμα ύλης ομογενές που χωρίζεται από το γύρω του χώρο με σαφή όρια). ε) (που οδηγούν
Χηµεία Α Γενικού Λυκείου
 Χηµεία Α Γενικού Λυκείου Απαντήσεις στα θέματα της Τράπεζας Θεμάτων Συγγραφή απαντήσεων: 'Αρης Ασλανίδης Χρησιμοποιήστε τους σελιδοδείκτες (bookmarks) στο αριστερό μέρος της οθόνης για την πλοήγηση μέσα
Χηµεία Α Γενικού Λυκείου Απαντήσεις στα θέματα της Τράπεζας Θεμάτων Συγγραφή απαντήσεων: 'Αρης Ασλανίδης Χρησιμοποιήστε τους σελιδοδείκτες (bookmarks) στο αριστερό μέρος της οθόνης για την πλοήγηση μέσα
Ερωτήσεις πολλαπλης επιλογής στην οξειδοαναγωγή (1ο κεφάλαιο Γ Θετική 2015)
 Ερωτήσεις πολλαπλης επιλογής στην οξειδοαναγωγή (1ο κεφάλαιο Γ Θετική 2015) 1. Σε ποια απο τις παρακάτω ενώσεις το Ν έχει αριθμό οξέιδωσης +5 A. ΗΝΟ 2 C ΚΝΟ 3 B. ΝΗ 3 D Ν 2 Ο 3 2. Σε ποια απο τις παρακάτω
Ερωτήσεις πολλαπλης επιλογής στην οξειδοαναγωγή (1ο κεφάλαιο Γ Θετική 2015) 1. Σε ποια απο τις παρακάτω ενώσεις το Ν έχει αριθμό οξέιδωσης +5 A. ΗΝΟ 2 C ΚΝΟ 3 B. ΝΗ 3 D Ν 2 Ο 3 2. Σε ποια απο τις παρακάτω
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
elementi dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Prijelazni elementi Prijelazni elementi se nalaze od 3. do 12. skupine periodičnog sustava elemenata (d-orbitale), s elektronskom konfiguracijom: [X] ns 2 (n-1)d x, x = 1-10. Svi prijelazni metali imaju
Prijelazni elementi Prijelazni elementi se nalaze od 3. do 12. skupine periodičnog sustava elemenata (d-orbitale), s elektronskom konfiguracijom: [X] ns 2 (n-1)d x, x = 1-10. Svi prijelazni metali imaju
EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZVOR EMISIJE
 Prof. dr. sc. Z. Prelec INŽENJERSTO ZAŠTITE OKOLIŠA Poglavlje: (Emisija u atmosferu) List: 1 EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZOR EMISIJE Izgaranje - najveći uzrok
Prof. dr. sc. Z. Prelec INŽENJERSTO ZAŠTITE OKOLIŠA Poglavlje: (Emisija u atmosferu) List: 1 EMISIJA ŠTETNIH SASTOJAKA U ATMOSFERU IZ PROCESA IZGARANJA IZGARANJE - IZOR EMISIJE Izgaranje - najveći uzrok
ΕΞΕΤΑΣΕΙΣ ΣΤΗ ΓΕΝΙΚΗ ΧΗΜΕΙΑ
 ΕΞΕΤΑΣΕΙΣ ΣΤΗ ΓΕΝΙΚΗ ΧΗΜΕΙΑ (Επιλέγετε δέκα από τα δεκατρία θέματα) ΘΕΜΑΤΑ 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος; Γιατί; (α) Από τα στοιχεία Mg, Al, Cl, Xe, C και Ρ, τον μεγαλύτερο
ΕΞΕΤΑΣΕΙΣ ΣΤΗ ΓΕΝΙΚΗ ΧΗΜΕΙΑ (Επιλέγετε δέκα από τα δεκατρία θέματα) ΘΕΜΑΤΑ 1. Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος; Γιατί; (α) Από τα στοιχεία Mg, Al, Cl, Xe, C και Ρ, τον μεγαλύτερο
ΟΝΟΜΑΣΙΑ F - HF Υδροφθόριο S 2- H 2 S Υδρόθειο Cl - HCl Υδροχλώριο OH - H 2 O Οξείδιο του Υδρογόνου (Νερό) NO 3 HNO 3. Νιτρικό οξύ SO 3 H 2 SO 3
 1 Να συμπληρωθεί ο παρακάτω πίνακα οξέων: ΟΝΟΜΑΣΙΑ F HF Υδροφθόριο S 2 H 2 S Υδρόθειο Cl HCl Υδροχλώριο OH H 2 O Υδρογόνου (Νερό) NO 3 HNO 3 οξύ SO 3 H 2 SO 3 Θειώδε οξύ Br HBr Υδροβρώμιο 2 SO 4 H 2 SO
1 Να συμπληρωθεί ο παρακάτω πίνακα οξέων: ΟΝΟΜΑΣΙΑ F HF Υδροφθόριο S 2 H 2 S Υδρόθειο Cl HCl Υδροχλώριο OH H 2 O Υδρογόνου (Νερό) NO 3 HNO 3 οξύ SO 3 H 2 SO 3 Θειώδε οξύ Br HBr Υδροβρώμιο 2 SO 4 H 2 SO
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
C kao nukleofil (Organometalni spojevi)
 C kao nukleofil (Organometalni spojevi) 1 Nastajanje nukleofilnih C atoma i njihova adicija na karbonilnu grupu Ukupan proces je jedan od najkorisnijih sintetskih postupaka za stvaranje C-C veze 2 Priroda
C kao nukleofil (Organometalni spojevi) 1 Nastajanje nukleofilnih C atoma i njihova adicija na karbonilnu grupu Ukupan proces je jedan od najkorisnijih sintetskih postupaka za stvaranje C-C veze 2 Priroda
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
15. (V B) skupina. N, P, As, Sb, Bi ns 2 np 3
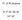 15. (V B) skupina N, P, As, Sb, Bi ns 2 np 3 melti ng point/ o C boiling point/ o C ionization energy/ ev I II III IV V coval ent radius / nm ionic radius X 3+ / nm bond energy kj mol -1 koeficijent elektronegativnosti
15. (V B) skupina N, P, As, Sb, Bi ns 2 np 3 melti ng point/ o C boiling point/ o C ionization energy/ ev I II III IV V coval ent radius / nm ionic radius X 3+ / nm bond energy kj mol -1 koeficijent elektronegativnosti
A B C D. v v k k. k k
 Brzina kemijske reakcije proporcionalna je aktivnim masama reagirajućih tvari!!! 1 A B C D v2 1 1 2 2 o C D m A B v m n o p v v k k m A B o C D p C a D n A a B A B C D 1 2 1 2 o m p n 1 2 n v v k k K a
Brzina kemijske reakcije proporcionalna je aktivnim masama reagirajućih tvari!!! 1 A B C D v2 1 1 2 2 o C D m A B v m n o p v v k k m A B o C D p C a D n A a B A B C D 1 2 1 2 o m p n 1 2 n v v k k K a
ΙΑΓΩΝΙΣΜΑ 1 Ο ( 1 Ο ΚΕΦΑΛΑΙΟ)
 ΙΑΓΩΝΙΣΜΑ 1 Ο ( 1 Ο ΚΕΦΑΛΑΙΟ) ΘΕΜΑ 1 Ο Να εξηγήσετε ποιες από τις παρακάτω προτάσεις είναι σωστές και να διορθώσετε τις λανθασµένες: 1. Τα άτοµα όλων των στοιχείων είναι διατοµικά.. Το 16 S έχει ατοµικότητα
ΙΑΓΩΝΙΣΜΑ 1 Ο ( 1 Ο ΚΕΦΑΛΑΙΟ) ΘΕΜΑ 1 Ο Να εξηγήσετε ποιες από τις παρακάτω προτάσεις είναι σωστές και να διορθώσετε τις λανθασµένες: 1. Τα άτοµα όλων των στοιχείων είναι διατοµικά.. Το 16 S έχει ατοµικότητα
Κανόνες διαλυτότητας για ιοντικές ενώσεις
 Κανόνες διαλυτότητας για ιοντικές ενώσεις 1. Ενώσεις των στοιχείων της Ομάδας 1A και του ιόντος αμμωνίου (Ιόντα: Li +, Na +, K +, Rb +, Cs +, NH 4+ ) είναι ευδιάλυτες, χωρίς εξαίρεση: πχ. NaCl, K 2 S,
Κανόνες διαλυτότητας για ιοντικές ενώσεις 1. Ενώσεις των στοιχείων της Ομάδας 1A και του ιόντος αμμωνίου (Ιόντα: Li +, Na +, K +, Rb +, Cs +, NH 4+ ) είναι ευδιάλυτες, χωρίς εξαίρεση: πχ. NaCl, K 2 S,
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
ΑΡΙΘΜΟΣ ΟΞΕΙΔΩΣΗΣ - ΓΡΑΦΗ ΧΗΜΙΚΩΝ ΤΥΠΩΝ- ΟΝΟΜΑΤΟΛΟΓΙΑ
 ΑΡΙΘΜΟΣ ΟΞΕΙΔΩΣΗΣ - ΓΡΑΦΗ ΧΗΜΙΚΩΝ ΤΥΠΩΝ- ΟΝΟΜΑΤΟΛΟΓΙΑ Τι είναι ο αριθμός οξείδωσης Αριθμό οξείδωσης ενός ιόντος σε μια ετεροπολική ένωση ονομάζουμε το πραγματικό φορτίο του ιόντος. Αριθμό οξείδωσης ενός
ΑΡΙΘΜΟΣ ΟΞΕΙΔΩΣΗΣ - ΓΡΑΦΗ ΧΗΜΙΚΩΝ ΤΥΠΩΝ- ΟΝΟΜΑΤΟΛΟΓΙΑ Τι είναι ο αριθμός οξείδωσης Αριθμό οξείδωσης ενός ιόντος σε μια ετεροπολική ένωση ονομάζουμε το πραγματικό φορτίο του ιόντος. Αριθμό οξείδωσης ενός
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA
 Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA Relativna skala masa elemenata: atomska jedinica mase 1/12 mase atoma ugljika C-12. Unificirana jedinica atomske mase (u)
Pripremila i uredila: Doc. dr. sc. Blaženka Foretić OSNOVE KEMIJSKOG RAČUNANJA Relativna skala masa elemenata: atomska jedinica mase 1/12 mase atoma ugljika C-12. Unificirana jedinica atomske mase (u)
ΚΕΦΑΛΑΙΟ 3: ΟΞΕΑ ΒΑΣΕΙΣ ΑΛΑΤΑ ΟΞΕΙ ΙΑ - ΑΝΤΙ Ρ Α ΣΕΙΣ
 Χηµεία Α Λυκείου Φωτεινή Ζαχαριάδου 1 από 10 ( α πό τράπεζα θεµάτων) ΚΕΦΑΛΑΙΟ 3: ΟΞΕΑ ΒΑΣΕΙΣ ΑΛΑΤΑ ΟΞΕΙ ΙΑ - ΑΝΤΙ Ρ Α ΣΕΙΣ 1. Να συµπληρώσετε τα προϊόντα και τους συντελεστές στις επόµενες χηµικές εξισώσεις
Χηµεία Α Λυκείου Φωτεινή Ζαχαριάδου 1 από 10 ( α πό τράπεζα θεµάτων) ΚΕΦΑΛΑΙΟ 3: ΟΞΕΑ ΒΑΣΕΙΣ ΑΛΑΤΑ ΟΞΕΙ ΙΑ - ΑΝΤΙ Ρ Α ΣΕΙΣ 1. Να συµπληρώσετε τα προϊόντα και τους συντελεστές στις επόµενες χηµικές εξισώσεις
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
stehiometrijska valencija
 Oksidacijski broj i stehiometrijska valencija Stehiometrijska valencija predstavlja broj valentnih veza koje atom stvara s drugim atomima u molekuli. Valencija je dakle, sposobnost atoma da se veže s određenim
Oksidacijski broj i stehiometrijska valencija Stehiometrijska valencija predstavlja broj valentnih veza koje atom stvara s drugim atomima u molekuli. Valencija je dakle, sposobnost atoma da se veže s određenim
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
UKUPAN BROJ OSVOJENIH BODOVA
 ŠIFRA DRŽAVNO TAKMIČENJE II razred UKUPAN BROJ OSVOJENIH BODOVA Test regledala/regledao...... Podgorica,... 008. godine 1. Izračunati steen disocijacije slabe kiseline, HA, ako je oznata analitička koncentracija
ŠIFRA DRŽAVNO TAKMIČENJE II razred UKUPAN BROJ OSVOJENIH BODOVA Test regledala/regledao...... Podgorica,... 008. godine 1. Izračunati steen disocijacije slabe kiseline, HA, ako je oznata analitička koncentracija
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2014. ÄÉÁÍüÇÓÇ
 ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΧΗΜΕΙΑ Ηµεροµηνία: Τετάρτη 23 Απριλίου 2014 ιάρκεια Εξέτασης: 2 ώρες ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιο σας τον αριθµό κάθε µίας από τις ερωτήσεις A1 έως A4 και δίπλα
ΤΑΞΗ: ΜΑΘΗΜΑ: ΘΕΜΑ Α Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΧΗΜΕΙΑ Ηµεροµηνία: Τετάρτη 23 Απριλίου 2014 ιάρκεια Εξέτασης: 2 ώρες ΕΚΦΩΝΗΣΕΙΣ Να γράψετε στο τετράδιο σας τον αριθµό κάθε µίας από τις ερωτήσεις A1 έως A4 και δίπλα
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Παραδοχές στις οποίες στις οποίες στηρίζεται ο αριθμός οξείδωσης
 Αριθμός Οξείδωσης ή τυπικό σθένος Είναι ένας αριθμός που εκφράζει την ενωτική ικανότητα των στοιχείων με βάση ορισμένες παραδοχές. Η χρησιμοποίηση του επιβλήθηκε για τους πιο κάτω λόγους : Χρησιμεύει στη
Αριθμός Οξείδωσης ή τυπικό σθένος Είναι ένας αριθμός που εκφράζει την ενωτική ικανότητα των στοιχείων με βάση ορισμένες παραδοχές. Η χρησιμοποίηση του επιβλήθηκε για τους πιο κάτω λόγους : Χρησιμεύει στη
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Prirodne znanosti kemija
 Prirodne znanosti kemija 1. Kemija proučava: sastav građu svojstva i promjene tvari 2. Ostale su prirodne znanosti: fizika biologija astronomija geologija molekularna biologija 3. Vrste kemijske industrije:
Prirodne znanosti kemija 1. Kemija proučava: sastav građu svojstva i promjene tvari 2. Ostale su prirodne znanosti: fizika biologija astronomija geologija molekularna biologija 3. Vrste kemijske industrije:
Napomena: Zadaci za DZ su označeni plavom bojom!
 DODATNI ZADACI ZA DOMAĆU ZADAĆU I VJEŽBU (uz Seminar 05 i 06) Napomena: Zadaci za DZ su označeni plavom bojom! 1. Koliko je grama fosforne kiseline i kalcijeva hidroksida potrebno za dobivanje 100 g kalcijeva
DODATNI ZADACI ZA DOMAĆU ZADAĆU I VJEŽBU (uz Seminar 05 i 06) Napomena: Zadaci za DZ su označeni plavom bojom! 1. Koliko je grama fosforne kiseline i kalcijeva hidroksida potrebno za dobivanje 100 g kalcijeva
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
2.1. Να χαρακτηρίσετε τις επόμενες προτάσεις ως σωστές (Σ) ή λανθασμένες (Λ);
 Θέμα 2ο 2.1. Να χαρακτηρίσετε τις επόμενες προτάσεις ως σωστές (Σ) ή λανθασμένες (Λ); α) Η διαφορά του ατομικού αριθμού από το μαζικό αριθμό ισούται με τον αριθμό νετρονίων του ατόμου. β) Το 19 Κ + έχει
Θέμα 2ο 2.1. Να χαρακτηρίσετε τις επόμενες προτάσεις ως σωστές (Σ) ή λανθασμένες (Λ); α) Η διαφορά του ατομικού αριθμού από το μαζικό αριθμό ισούται με τον αριθμό νετρονίων του ατόμου. β) Το 19 Κ + έχει
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
ΑΠΑΝΤΗΣΕΙΣ ΤΩΝ ΑΣΚΗΣΕΩΝ
 ΑΠΑΝΤΗΣΕΙΣ ΤΩΝ ΑΣΚΗΣΕΩΝ Ε.1. Γ. Ε.. Β. Ε.. Α. Ε.4. Α. Ε.5. Γ. Ε.6. Β. Ε.7. Δ. Ε.8. Δ. Ε.9. Γ. Ε.1. Γ. Ε.11. Δ. Ε.1. Β. Ε.1. α: Σ, β:σ, γ:σ, δ:σ, ε:λ (είναι σωστό μόνο για ιοντικές ενώσεις, στις ομοιοπολικές
ΑΠΑΝΤΗΣΕΙΣ ΤΩΝ ΑΣΚΗΣΕΩΝ Ε.1. Γ. Ε.. Β. Ε.. Α. Ε.4. Α. Ε.5. Γ. Ε.6. Β. Ε.7. Δ. Ε.8. Δ. Ε.9. Γ. Ε.1. Γ. Ε.11. Δ. Ε.1. Β. Ε.1. α: Σ, β:σ, γ:σ, δ:σ, ε:λ (είναι σωστό μόνο για ιοντικές ενώσεις, στις ομοιοπολικές
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Χημικές Αντιδράσεις. Εισαγωγική Χημεία
 Χημικές Αντιδράσεις Εισαγωγική Χημεία Κατηγορίες Χημικών Αντιδράσεων Πέντε κυρίως κατηγορίες: Σύνθεσης Διάσπασης Απλής αντικατάστασης Διπλής αντικατάστασης Καύσης Αντιδράσεις σύνθεσης Ένωση δύο ή περισσότερων
Χημικές Αντιδράσεις Εισαγωγική Χημεία Κατηγορίες Χημικών Αντιδράσεων Πέντε κυρίως κατηγορίες: Σύνθεσης Διάσπασης Απλής αντικατάστασης Διπλής αντικατάστασης Καύσης Αντιδράσεις σύνθεσης Ένωση δύο ή περισσότερων
3. Υπολογίστε το μήκος κύματος de Broglie (σε μέτρα) ενός αντικειμένου μάζας 1,00kg που κινείται με ταχύτητα1 km/h.
 1 Ο ΚΕΦΑΛΑΙΟ ΑΣΚΗΣΕΙΣ 1. Ποια είναι η συχνότητα και το μήκος κύματος του φωτός που εκπέμπεται όταν ένα e του ατόμου του υδρογόνου μεταπίπτει από το επίπεδο ενέργειας με: α) n=4 σε n=2 b) n=3 σε n=1 c)
1 Ο ΚΕΦΑΛΑΙΟ ΑΣΚΗΣΕΙΣ 1. Ποια είναι η συχνότητα και το μήκος κύματος του φωτός που εκπέμπεται όταν ένα e του ατόμου του υδρογόνου μεταπίπτει από το επίπεδο ενέργειας με: α) n=4 σε n=2 b) n=3 σε n=1 c)
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
PROSTORNI STATIČKI ODREĐENI SUSTAVI
 PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
Kiselo-bazne ravnoteže
 Uvod u biohemiju (školska 2016/17.) Kiselo-bazne ravnoteže NB: Prerađena/adaptirana prezentacija američkih profesora! Primeri kiselina i baza iz svakodnevnog života Arrhenius-ova definicija kiselina i
Uvod u biohemiju (školska 2016/17.) Kiselo-bazne ravnoteže NB: Prerađena/adaptirana prezentacija američkih profesora! Primeri kiselina i baza iz svakodnevnog života Arrhenius-ova definicija kiselina i
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
HALKOGENI ELEMENTI HALKOGENI ELEMENTI
 HALKGENI ELEMENTI HALKGENI ELEMENTI 16. grupa Periodnog sistema elemenata. Kiseonik najrasprostranjeniji element na Zemlji: 45,5 mas.% litosfere 23 mas.% (21 vol.%) atmosfere 86 mas.% hidrosfere umpor
HALKGENI ELEMENTI HALKGENI ELEMENTI 16. grupa Periodnog sistema elemenata. Kiseonik najrasprostranjeniji element na Zemlji: 45,5 mas.% litosfere 23 mas.% (21 vol.%) atmosfere 86 mas.% hidrosfere umpor
C M. V n: n =, (D): V 0,M : V M P = ρ ρ V V. = ρ
 »»...» -300-0 () -300-03 () -3300 3.. 008 4 54. 4. 5 :.. ;.. «....... :. : 008. 37.. :....... 008.. :. :.... 54. 4. 5 5 6 ... : : 3 V mnu V mn AU 3 m () ; N (); N A 6030 3 ; ( ); V 3. : () 0 () 0 3 ()
»»...» -300-0 () -300-03 () -3300 3.. 008 4 54. 4. 5 :.. ;.. «....... :. : 008. 37.. :....... 008.. :. :.... 54. 4. 5 5 6 ... : : 3 V mnu V mn AU 3 m () ; N (); N A 6030 3 ; ( ); V 3. : () 0 () 0 3 ()
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
ΟΜΟΣΠΟΝΔΙΑ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑΔΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2019 Β ΦΑΣΗ
 ΤΑΞΗ: ΜΑΘΗΜΑ: A ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΧΗΜΕΙΑ Ημερομηνία: Σάββατο 20 Απριλίου 2019 Διάρκεια Εξέτασης: 2 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α1. Δίνεται στοιχείο Χ το οποίο έχει οκτώ ηλεκτρόνια στην εξωτερική του στιβάδα.
ΤΑΞΗ: ΜΑΘΗΜΑ: A ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΧΗΜΕΙΑ Ημερομηνία: Σάββατο 20 Απριλίου 2019 Διάρκεια Εξέτασης: 2 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α1. Δίνεται στοιχείο Χ το οποίο έχει οκτώ ηλεκτρόνια στην εξωτερική του στιβάδα.
Α ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΑ 2-3) ( ) ΘΕΜΑ Α Α1.
 Α ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΑ 2-3) (5 2 2017) ΘΕΜΑ Α Α1. Επιλέξτε τη σωστή απάντηση σε καθεμία από τις επόμενες ερωτήσεις : 1. Σε ποια από τις επόμενες ενώσεις το χλώριο έχει μεγαλύτερο αριθμό
Α ΛΥΚΕΙΟΥ ΕΠΑΝΑΛΗΠΤΙΚΟ ΔΙΑΓΩΝΙΣΜΑ (ΚΕΦΑΛΑΙΑ 2-3) (5 2 2017) ΘΕΜΑ Α Α1. Επιλέξτε τη σωστή απάντηση σε καθεμία από τις επόμενες ερωτήσεις : 1. Σε ποια από τις επόμενες ενώσεις το χλώριο έχει μεγαλύτερο αριθμό
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Χηµεία Α Γενικού Λυκείου
 Χηµεία Α Γενικού Λυκείου Απαντήσεις στα θέματα της Τράπεζας Θεμάτων Συγγραφή απαντήσεων: 'Αρης Ασλανίδης Χρησιμοποιήστε τους σελιδοδείκτες (bookmarks) στο αριστερό μέρος της οθόνης για την πλοήγηση μέσα
Χηµεία Α Γενικού Λυκείου Απαντήσεις στα θέματα της Τράπεζας Θεμάτων Συγγραφή απαντήσεων: 'Αρης Ασλανίδης Χρησιμοποιήστε τους σελιδοδείκτες (bookmarks) στο αριστερό μέρος της οθόνης για την πλοήγηση μέσα
ΝΟΜΟΣ ΤΗΣ ΠΕΡΙΟ ΙΚΟΤΗΤΑΣ : Οι ιδιότητες των χηµικών στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
 1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα
1. Ο ΠΕΡΙΟ ΙΚΟΣ ΠΙΝΑΚΑΣ Οι άνθρωποι από την φύση τους θέλουν να πετυχαίνουν σπουδαία αποτελέσµατα καταναλώνοντας το λιγότερο δυνατό κόπο και χρόνο. Για το σκοπό αυτό προσπαθούν να οµαδοποιούν τα πράγµατα
13) DRŽAVNA MATURA LJETO 2014.
 288 13) DRŽAVNA MATURA LJETO 2014. C Kamenac su karbonati kao što je CaCO 3, otapaju se u kiselinama prema jednadžbi CaCO 3(s) + 2H + (aq) Ca 2+ (aq) + CO 2(g) + H 2O(l). Otopina amonijaka je lužnata (NH
288 13) DRŽAVNA MATURA LJETO 2014. C Kamenac su karbonati kao što je CaCO 3, otapaju se u kiselinama prema jednadžbi CaCO 3(s) + 2H + (aq) Ca 2+ (aq) + CO 2(g) + H 2O(l). Otopina amonijaka je lužnata (NH
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
ΜΑΞΙΜΟΣ ΚΟΤΕΛΙΔΑΣ. β) Να βρεθεί σε ποια οµάδα και σε ποια περίοδο του Περιοδικού Πίνακα ανήκουν.
 ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΘΕΜΑΤΑ: 03490 ΗΜΕΡΟΜΗΝΙΑ: 27/5/2014 ΟΙ ΚΑΘΗΓΗΤΕΣ: ΜΑΞΙΜΟΣ ΚΟΤΕΛΙΔΑΣ ΕΚΦΩΝΗΣΕΙΣ Θέμα 2ο Α) Για τα στοιχεία: 12 Μg και 8 Ο α) Να κατανεµηθούν τα ηλεκτρόνιά τους σε στιβάδες. (µονάδες 2) β)
ΜΑΘΗΜΑ: ΧΗΜΕΙΑ ΘΕΜΑΤΑ: 03490 ΗΜΕΡΟΜΗΝΙΑ: 27/5/2014 ΟΙ ΚΑΘΗΓΗΤΕΣ: ΜΑΞΙΜΟΣ ΚΟΤΕΛΙΔΑΣ ΕΚΦΩΝΗΣΕΙΣ Θέμα 2ο Α) Για τα στοιχεία: 12 Μg και 8 Ο α) Να κατανεµηθούν τα ηλεκτρόνιά τους σε στιβάδες. (µονάδες 2) β)
KEMIJSKA RAVNOTEŽA II
 Fakultet kemijskog inženjerstva i tehnologije Sveučilišta u Zagrebu Seminar 09 EMIJSA RAVNOTEŽA II Ravnoteže u otopinama elektrolita 2 dr. s. Biserka Tkalče dr. s. Lidija Furač EMIJSA RAVNOTEŽA II ONJUGIRANE
Fakultet kemijskog inženjerstva i tehnologije Sveučilišta u Zagrebu Seminar 09 EMIJSA RAVNOTEŽA II Ravnoteže u otopinama elektrolita 2 dr. s. Biserka Tkalče dr. s. Lidija Furač EMIJSA RAVNOTEŽA II ONJUGIRANE
Χ ΗΜΙΚΕΣ Α Ν Τ ΙΔΡΑΣΕΙΣ
 53 Χ ΗΜΙΚΕΣ Α Ν Τ ΙΔΡΑΣΕΙΣ Χημική αντίδραση ονομάζουμε κάθε χημικό φαινόμενο. Δηλαδή, κάθε φαινόμενο στο οποίο έχουμε αναδιάταξη των ηλεκτρονίων ( e ) της εξωτερικής στιβάδας των ατόμων που παίρνουν μέρος
53 Χ ΗΜΙΚΕΣ Α Ν Τ ΙΔΡΑΣΕΙΣ Χημική αντίδραση ονομάζουμε κάθε χημικό φαινόμενο. Δηλαδή, κάθε φαινόμενο στο οποίο έχουμε αναδιάταξη των ηλεκτρονίων ( e ) της εξωτερικής στιβάδας των ατόμων που παίρνουν μέρος
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Χηµεία Α Γενικού Λυκείου
 Χηµεία Α Γενικού Λυκείου Απαντήσεις στα θέματα της Τράπεζας Θεμάτων Συγγραφή απαντήσεων: 'Αρης Ασλανίδης Χρησιμοποιήστε τους σελιδοδείκτες (bookmarks) στο αριστερό μέρος της οθόνης για την πλοήγηση μέσα
Χηµεία Α Γενικού Λυκείου Απαντήσεις στα θέματα της Τράπεζας Θεμάτων Συγγραφή απαντήσεων: 'Αρης Ασλανίδης Χρησιμοποιήστε τους σελιδοδείκτες (bookmarks) στο αριστερό μέρος της οθόνης για την πλοήγηση μέσα
3. Να συμπληρωθούν οι παρακάτω αντιδράσεις:
 1. Να συμπληρωθούν οι παρακάτω αντιδράσεις: 2N 2 + 3H 2 2NH 3 4Na + O 2 2Να 2 Ο Fe + Cl 2 FeCl 2 Zn + Br 2 ZnBr 2 2K + S K 2 S 2Ca + O 2 2CaO Na + Ca -------- C + O 2 CO 2 H 2 + Br 2 2HBr CaO + H 2 O Ca(OH)
1. Να συμπληρωθούν οι παρακάτω αντιδράσεις: 2N 2 + 3H 2 2NH 3 4Na + O 2 2Να 2 Ο Fe + Cl 2 FeCl 2 Zn + Br 2 ZnBr 2 2K + S K 2 S 2Ca + O 2 2CaO Na + Ca -------- C + O 2 CO 2 H 2 + Br 2 2HBr CaO + H 2 O Ca(OH)
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ (ΚΕΦ 2-3 ) ΚΥΡΙΑΚΗ 4 ΔΕΚΕΜΒΡΙΟΥ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 4
 ΑΡΧΗ 1 ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ (ΚΕΦ 2-3 ) ΚΥΡΙΑΚΗ 4 ΔΕΚΕΜΒΡΙΟΥ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 4 ΘΕΜΑ Α Α1. Στον σύγχρονο Περιοδικό Πίνακα τα χημικά στοιχεία έχουν ταξινομηθεί: α. κατ αύξοντα ατομικό
ΑΡΧΗ 1 ΗΣ ΣΕΛΙΔΑΣ ΔΙΑΓΩΝΙΣΜΑ ΧΗΜΕΙΑΣ Α ΛΥΚΕΙΟΥ (ΚΕΦ 2-3 ) ΚΥΡΙΑΚΗ 4 ΔΕΚΕΜΒΡΙΟΥ 2016 ΣΥΝΟΛΟ ΣΕΛΙΔΩΝ 4 ΘΕΜΑ Α Α1. Στον σύγχρονο Περιοδικό Πίνακα τα χημικά στοιχεία έχουν ταξινομηθεί: α. κατ αύξοντα ατομικό
