KERAMIKA, BETON I DRVO
|
|
|
- Ζοροβάβελ Φραγκούδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 VJEŽBE: četvrtak, 12:15-14:00 KERAMIKA, BETON I DRVO Vježba 1. Ionske i kovalentne strukture Prof.dr.sc. Lidija Ćurković
2 STRUKTURA ČVRSTIH (krutih) TVARI ovisi o: 1. VRSTI VEZA IZMEĐU STRUKTURNIH JEDINICA 2. SLAGANJU STRUKTURNIH JEDINICA VEZE U KERAMICI Ionske i/ili kovalentne. Veza u keramici nije čista ionska ni čista kovalentna veza, već smjesa ionske i kovalentne.
3 STRUKTURA KERAMIKE Kod keramičkih materijala susrećemo dvije grupe kristala na osnovi primarnih (međuatomskih, kemijskih) veza: 1. IONSKE KRISTALE 2. KOVALENTNE KRISTALE JAKOST VEZE: JAKE SLABE KOVALENTNA IONSKA METALNA FIZIKALNE VEZE UDIO IONSKOG KARAKTERA VEZE: % (ionskog karaktera) = {1-exp[-0,25(X A -X B ) 2 ]} 100 X A = elektronegativnost elementa A X B = elektronegativnost elementa B
4 CaF 2 : veliki udio ionskog karaktera veze (89 %) SiC: mali udio ionskog karaktera veze (12 %)
5 IONSKO / KOVALENTNI KARAKTER VEZE Nema 100 % ionskog karaktera veze O % ionskog karaktera H 2, N 2, Cl 2
6 Materijal Postotak ionskog karaktera veze CaF 2 89 MgO 73 NaCl 67 Al 2 O 3 63 SiO 2 51 Si 3 N 4 30 ZnS 18 SiC 12
7 IONSKE STRUKTURE IONSKI KRISTALI nastaju tako da manji kationi popunjavaju praznine između većih aniona.
8 IONSKA VEZA - nastaje spajanjem ATOMA METALA s ATOMIMA NEMETALA. Kako nastaju ioni? METALI imaju malu energiju ionizacije i lako tvore POZITIVNE IONE koje nazivamo KATIONI neutralni atom NEMETALI imaju veliki afinitet prema elektronu pa lako tvore NEGATIVNE IONE koje nazivamo ANIONI kation (+) anion (-)
9 IONSKA VEZA valentni elektron IONSKA VEZA je veza koju uzrokuje elektrostatsko privlačenje suprotno nabijenih iona.
10 IONSKE STRUKTURE IONSKI KRISTALI nastaju tako da manji kationi popunjavaju praznine između većih aniona. Koordinacijski broj i vrsta praznine (koordinacijski poliedar) koji kationi popunjavaju ovisi o omjeru r kationa /r aniona. ANION KATION r K /r A r K /r A r K /r A stabilno stabilno nestabilno ZA STABILNU KORDINACIJU KATIONI I ANIONI MORAJU BITI U KONTAKTU!
11 IONSKE STRUKTURE ANION KATION MAKSIMALNI RADIJUS KATIONA? MINIMALNI RADIJUS KATIONA?
12 IONSKI KRISTALI nastaju tako da manji kationi popunjavaju praznine između većih aniona. Koordinacijski broj i vrsta praznine (koordinacijski poliedar) koji kationi popunjavaju ovisi o omjeru r kationa /r aniona. r K /r A < 0,155 KB = 2 (linearni raspored) 0,155 < r K /r A < 0,225 KB = 3 (trigonalne praznine) 0,225 < r K /r A < 0,414 KB = 4 (tetraedarske praznine) 0,414 < r K /r A < 0,732 KB = 6 (oktaedarske praznine)
13 0,732 < r K /r A < 1,000 KB = 8 (kubična praznina) r K /r A >1,000 KB = 12 (kuboktaedarska praznina)
14 Položaj intersticijskih mjesta (praznina) u FCC, BCC i HCP jediničnoj ćeliji: Oktaedarska FCC Tetraedarska FCC Oktaedarska HCP Oktaedarska BCC Tetraedarska BCC Tetraedarska HCP
15 Veličina i broj tetraedarskih i oktaedarskih mjesta u BCC, FCC i HCP jediničnu ćeliju. Veličina intersticijskih mjesta je dana ovisno o omjeru r kationa /r aniona. Broj intersticijskih mjesta je broj mjesta koji pripada jednoj jediničnoj ćeliji. Jedinična ćelija Veličina tetraedarskog mjesta, r kationa /r aniona Veličina oktaedarskog mjesta, r kationa /r aniona Broj tetraedarskih mjesta koji pripadaju jednoj jediničnoj ćeliji Broj oktaedarskih mjesta koji pripadaju jednoj jediničnoj ćeliji BCC 0,291 0, FCC 0,225 0, HCP 0,225 0, Tetraedarska praznina Tetraedarska praznina Oktaedarska praznina Oktaedarska praznina Tetraedarska praznina > oktaedarske Oktaedarska praznina > tetraedarske
16 Računanje minimalnog omjera radijusa kationa i aniona (r K /r A ) za koordinacijski broj 3 r K Kation r A Anion cos 30 = 3 / 2 r r A 1-3 / 2 K = = 3 / 2 0,155 Minimalni omjer polumjera kationa i aniona za koordinacijski broj 3 je 0,155.
17 Računanje minimalnog omjera radijusa kationa i aniona (r K /r A ) za koordinacijski broj 6 ili maksimalnog omjera radijusa kationa i aniona (r K /r A ) za koordinacijski broj 4 Primjer struktura HALITA (NaCl) ANION KATION
18 Računanje minimalnog omjera radijusa kationa i aniona (r K /r A ) za koordinacijski broj 8 ili maksimalnog omjera radijusa kationa i aniona (r K /r A ) za koordinacijski broj 6. Primjer struktura CsCl ANION KATION
19 Računanje teorijske gustoće NaCl na temelju njegove kristalne strukture Cl- Na+ a Za NaCl strukturu, parametar jedinične ćelije a = 2 ( r Na + + r Cl - ), gdje je r radijus iona. a Stvarna gustoća = 2,16 g/cm 3
20 IONSKE STRUKTURE - neke uobičajne strukture Struktura halita (NaCl) (radi se o dvije isprepletene plošno centrirane kubične rešetke (FCC). r kationa = r Na+ = 0,102 nm Cl - r aniona = r Cl- = 0,181 nm Cl - Cl - Cl - Na + Cl - r kationa /r aniona = 0,56 KB = 6 prvih susjeda (iona druge vrste) Cl - Cl - : FCC jedinična ćelija Na + : u oktaedarskim prazninama Istu kristalnu strukturu imaju: LiCl, MgO, CaO, MnO, FeO, CoO, NiO, itd.
21 IONSKI STRUKTURE Struktura CsCl. r kationa = r Cs+ = 0,170 nm r aniona = r Cl- = 0,181 nm r kationa /r aniona = 0,94 KB = 8 prvih susjeda (iona druge vrste) Ci - : SC jedinična ćelija Cs + : u kubičnoj praznini
22 Struktura α-al 2 O 3 keramike (korund). Najstabilniji kristalni oblik Al 2 O 3 je mineral korund. Istu strukturu imaju: Fe 2 O 3, Cr 2 O 3, Ti 2 O 3, V 2 O 3. To je najvažniji čisti oksid u području keramike. Struktura korunda se zasniva na heksagonskom najgušćem slaganju kisikovih iona (ABABABAB...) sa ionima aluminija smještenim u 2/3 oktaedarskih intersticijskih mjesta.
23 IONSKE STRUKTURE primjer kompleksne strukture (tri kemijska elementa) PEROVSKITNA STRUKTURA Struktura perovskita: CaTiO 3. FCC jedinična ćelija sa ionima Ca 2+ i O 2-, a ion Ti 4+ u oktaedarskom intersticijskom mjestu.
24 KOVALENTE STRUKTURE Struktura SFALERITA (ZnS) -kovalentna veza dominira. r kationa = r (Zn 2+ ) = 0,06 nm S 2- S 2- r aniona = r (S 2- ) = 0,184 nm S 2- Zn 2+ S 2- r kationa /r aniona = 0,33 KB = 4 S 2- : FCC jedinična ćelija Zn 2+ u tetraedarskim prazninama elektronegativnost (Zn) = 1,6 elektronegativnost (S) = 2,5 % (ionskog karaktera ZnS) = {1-exp[-0,25(X A -X B ) 2 ]} 100 = 18 % X A = elektronegativnost elementa A; X B = elektronegativnost elementa B
25 Neke uobičajne strukture keramike Struktura Cezijev klorid (CsCl) Natrijev klorid (NaCl) Jedinična ćelija SC FCC Kemijska formula MX MX Fluorit (CaF 2 ) FCC MX 2 Silikati (SiO 2 ) FCC MX 2 Korund (Al 2 O 3 ) heksagonska M 2 O 3 Perovskit (CaTiO 3 ) Spinel (MgAlO 4 ) SC M`M``X 3 FCC M`M``X 4
26 KOVALENTNI KRISTALI: Struktura kristala u kojoj su atomi povezani kovalentnom vezom određena je brojem kovalentnih veza svakog pojedinog atoma i usmjerenošću tih veza. Koordinacijski broj određuje se relacijom: 8-N, gdje je N broj valentnih elektrona. Istu kristalnu strukturu ima npr. SiC, dijamant, Si, Ge,...
27 KOVALENTNI KRISTALI Najveći dio svjetske proizvodnje stakla čine silikatna stakla. Osnovna komponenta silikatnog stakla je SiO 2, a strukturna jedinica je tetraedar. SILIKATNA STRUKTURA osnova tetraedar. O 4- Si O O
28 KOVALENTNI KRISTALI KRISTALNA STRUKTURA KRISTOBALITA SiO 2 može imati KRISTALNU STRUKTURU (npr. kvarc, kristobalit) ili AMORFNU STRUKTURU (npr. staklo)
29 AMORFNA STRUKTURA struktura silikatnog stakla
KERAMIKA BETON I DRVO Podloge za vježbe
 FAKULTET STROJARSTVA I BRODOGRADNJE SVEUČILIŠTE U ZAGREBU Zavod za materijale KERAMIKA BETON I DRVO Podloge za vježbe prof. dr. sc. Lidija Ćurković izv. prof. dr. sc. Vera Rede Marijana Majić Renjo, mag.
FAKULTET STROJARSTVA I BRODOGRADNJE SVEUČILIŠTE U ZAGREBU Zavod za materijale KERAMIKA BETON I DRVO Podloge za vježbe prof. dr. sc. Lidija Ćurković izv. prof. dr. sc. Vera Rede Marijana Majić Renjo, mag.
MATERIJALI I. web stranici e-kolegija: Prof. dr. sc. Lidija Ćurković
 MATERIJALI I Prof. dr. sc. Lidija Ćurković 16/10/2017 Copyright: Prof. dr. sc. Lidija Ćurković MATERIJALI I (SATNICA: 2+1) PREDAVANJA (2 školska sata): ponedjeljak, 16:15-18:00 (A dvorana); utorak, 8-10
MATERIJALI I Prof. dr. sc. Lidija Ćurković 16/10/2017 Copyright: Prof. dr. sc. Lidija Ćurković MATERIJALI I (SATNICA: 2+1) PREDAVANJA (2 školska sata): ponedjeljak, 16:15-18:00 (A dvorana); utorak, 8-10
MATERIJALI I.
 MATERIJALI I Predmetni nastavnici: Prof. dr. sc. Lidija Ćurković Prof. dr. sc. Zdravko Schauperl Doc. dr. sc. Alar Željko 2. PREDAVANJE IZ MATERIJALA I ODRŽAT ĆE SE U SUBOTU 3.10.2015. OD 12:15 DO 14:00
MATERIJALI I Predmetni nastavnici: Prof. dr. sc. Lidija Ćurković Prof. dr. sc. Zdravko Schauperl Doc. dr. sc. Alar Željko 2. PREDAVANJE IZ MATERIJALA I ODRŽAT ĆE SE U SUBOTU 3.10.2015. OD 12:15 DO 14:00
Doc. dr Milena Đukanović
 Doc. dr Milena Đukanović milenadj@ac.me ČVRSTO AGREGATNO STANJE: Materijale u čvrstom agregatnom stanju možemo podijeliti na: Monokristalne Polikristalne Polimerne Amorfne. Riječ kristal se do kraja srednjeg
Doc. dr Milena Đukanović milenadj@ac.me ČVRSTO AGREGATNO STANJE: Materijale u čvrstom agregatnom stanju možemo podijeliti na: Monokristalne Polikristalne Polimerne Amorfne. Riječ kristal se do kraja srednjeg
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
1. razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MOLEKULA HEMIJSKA VEZA
 EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
EMIJSKE VEZE 1 razred gimnazije- opšti i prirodno-matematički smer STRUKTURA MLEKULA Molekul je najsitnija čestica koja se sastoji od dva ili više istih atoma, a to su molekuli elemenata: Cl 2, 2, N 2,
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Mašinski fakultet Sarajevo Univerzitet u Sarajevu MATERIJALI 1. prezentacija predavanja za šk.god. 2009/2010
 Mašinski fakultet Sarajevo Univerzitet u Sarajevu MATERIJALI 1 prezentacija predavanja za šk.god. 2009/2010 predavanja pripremio viši asistent Ismar HAJRO mr. dipl.ing.maš. KRATAK PREGLED KURSA MATERIJALI
Mašinski fakultet Sarajevo Univerzitet u Sarajevu MATERIJALI 1 prezentacija predavanja za šk.god. 2009/2010 predavanja pripremio viši asistent Ismar HAJRO mr. dipl.ing.maš. KRATAK PREGLED KURSA MATERIJALI
Otopine elektrolita. elektroliti tvari koje kada su rastaljene ili otopljene u vodi provode struju pomoću jona
 Otopine elektrolita elektroliti tvari koje kada su rastaljene ili otopljene u vodi provode struju pomoću jona ioni (gr. oni koji putuju ) električki pozitivno i negativno nabijene čestice, nastaju raspadanjem
Otopine elektrolita elektroliti tvari koje kada su rastaljene ili otopljene u vodi provode struju pomoću jona ioni (gr. oni koji putuju ) električki pozitivno i negativno nabijene čestice, nastaju raspadanjem
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
KEMIJA SKRIPTA ZA DRŽAVNU MATURU. Kristina Kučanda. ožujak 2015.
 KEMIJA SKRIPTA ZA DRŽAVNU MATURU Kristina Kučanda ožujak 2015. Autor: Kristina Kučanda streberica.gimnazijalka@yahoo.com prema: Ispitni katalog za državnu maturu u šk. god. 2013/2014., Kemija, NCVVO www.ncvvo.hr
KEMIJA SKRIPTA ZA DRŽAVNU MATURU Kristina Kučanda ožujak 2015. Autor: Kristina Kučanda streberica.gimnazijalka@yahoo.com prema: Ispitni katalog za državnu maturu u šk. god. 2013/2014., Kemija, NCVVO www.ncvvo.hr
Τμήμα Γεωτεχνολογίας & Περιβάλλοντος
 Τμήμα Γεωτεχνολογίας & Περιβάλλοντος Ολιβινικά βιομηχανικά πετρώματα στο Βούρινο της υτικής Μακεδονίας Σπουδάστρια : Κουζέλη Ευλαμπία Επιβλέπων : Επίκ. Καθ. Ανδρέας Ιορδανίδης Γενικά χαρακτηριστικά του
Τμήμα Γεωτεχνολογίας & Περιβάλλοντος Ολιβινικά βιομηχανικά πετρώματα στο Βούρινο της υτικής Μακεδονίας Σπουδάστρια : Κουζέλη Ευλαμπία Επιβλέπων : Επίκ. Καθ. Ανδρέας Ιορδανίδης Γενικά χαρακτηριστικά του
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο. Φυσική Συμπυκνωμένης Ύλης. Ενότητα 2. Βασίλειος Γιαννόπαπας
 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Φυσική Συμπυκνωμένης Ύλης Ενότητα 2 Βασίλειος Γιαννόπαπας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μετσόβιο Πολυτεχνείο Φυσική Συμπυκνωμένης Ύλης Ενότητα 2 Βασίλειος Γιαννόπαπας Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Kovalentna veza Za razliku od ionske veze gdje se veza ostvaruje prijenosom elektrona, kod kovalentne veze ona se ostvaruje tako da u toj vezi atomi dijele jedan ili više zajedničkih elektronskih parova.
Kovalentna veza Za razliku od ionske veze gdje se veza ostvaruje prijenosom elektrona, kod kovalentne veze ona se ostvaruje tako da u toj vezi atomi dijele jedan ili više zajedničkih elektronskih parova.
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
elektronskog para samo jednog od atoma u vezi
 KOMPLEKSNI SPOJEVI Spojevi u kojima se nalaze skupine atoma koji su povezani u više ili manje stabilne jedinice u krutom, tekućem, otopljenom i plinovitom stanju. Koordinacijski spojevi jer imaju koordinacijsku
KOMPLEKSNI SPOJEVI Spojevi u kojima se nalaze skupine atoma koji su povezani u više ili manje stabilne jedinice u krutom, tekućem, otopljenom i plinovitom stanju. Koordinacijski spojevi jer imaju koordinacijsku
ZNANOST O METALIMA Zbirka riješenih zadataka
 SVEUČILIŠTE U ZAGREBU METALURŠKI FAKULTET T. Matković, P.Matković, Lj.Slokar ZNANOST O METALIMA Zbirka riješenih zadataka Sisak, 010. SADRŽAJ: 1. KRISTALNE STRUKTURE METALA... 1.1. Praznine (šupljine)
SVEUČILIŠTE U ZAGREBU METALURŠKI FAKULTET T. Matković, P.Matković, Lj.Slokar ZNANOST O METALIMA Zbirka riješenih zadataka Sisak, 010. SADRŽAJ: 1. KRISTALNE STRUKTURE METALA... 1.1. Praznine (šupljine)
PROSTORNI STATIČKI ODREĐENI SUSTAVI
 PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
Vodik. dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Vodik Najzastupljeniji element u svemiru (maseni udio iznosi 90 %) i sastavni dio Zvijezda. Na Zemlji je po masenom udjelu deseti element po zastupljenosti. Zemljina gravitacija premalena je da zadrži
Vodik Najzastupljeniji element u svemiru (maseni udio iznosi 90 %) i sastavni dio Zvijezda. Na Zemlji je po masenom udjelu deseti element po zastupljenosti. Zemljina gravitacija premalena je da zadrži
Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design
 Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Supplemental Material for Estimation of grain boundary segregation enthalpy and its role in stable nanocrystalline alloy design By H. A. Murdoch and C.A. Schuh Miedema model RKM model ΔH mix ΔH seg ΔH
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
ΓΗ ΚΑΙ ΣΥΜΠΑΝ. Εικόνα 1. Φωτογραφία του γαλαξία μας (από αρχείο της NASA)
 ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
ΓΗ ΚΑΙ ΣΥΜΠΑΝ Φύση του σύμπαντος Η γη είναι μία μονάδα μέσα στο ηλιακό μας σύστημα, το οποίο αποτελείται από τον ήλιο, τους πλανήτες μαζί με τους δορυφόρους τους, τους κομήτες, τα αστεροειδή και τους μετεωρίτες.
U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni
 HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
HEMIJSKA VEZA ELEKTRONSKA TEORIJA VALENCE U stvaranju hemijske veze među atomima učestvuju samo elektroni u najvišem energetskom nivou valentni elektroni Atomi teže da postignu oktet elektrona na poslednjem
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Uvod u anorgansku kemiju Poglavlje
 Poglavlje Ključni pojmovi esencijalni elementi homeostaza polumjer atoma energija ionizacije afinitet prema elektronu relativni koeficijent elektronegativnosti 1 Ciljevi Uvod u anorgansku kemiju Definirati
Poglavlje Ključni pojmovi esencijalni elementi homeostaza polumjer atoma energija ionizacije afinitet prema elektronu relativni koeficijent elektronegativnosti 1 Ciljevi Uvod u anorgansku kemiju Definirati
Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže:
 HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
HEMIJSKE VEZE Pri međusobnom spajanju atoma nastaje energetski stabilniji sistem. To se postiže: - prelaskom atoma u pozitivno i negativno naelektrisane jone koji se međusobno privlače, jonska veza - sparivanjem
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Čvrsto stanje osobine
 Fizička hemija II Doc. dr Gordana Ćirić-Marjanović Čvrsto stanje može biti kristalno ili amorfno. Čvrsto stanje osobine Kristalne čvrste supstancije generalno pokazuju oštru tačku topljenja; ispitivanja
Fizička hemija II Doc. dr Gordana Ćirić-Marjanović Čvrsto stanje može biti kristalno ili amorfno. Čvrsto stanje osobine Kristalne čvrste supstancije generalno pokazuju oštru tačku topljenja; ispitivanja
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PRIMJER 3. MATLAB filtdemo
 PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
1. ΧΗΜΙΚΟΙ ΕΣΜΟΙ ΣΤΑ ΣΤΕΡΕΑ
 1. ΧΗΜΙΚΟΙ ΕΣΜΟΙ ΣΤΑ ΣΤΕΡΕΑ ΓΕΝΙΚΑ Η στερεά, η υγρή και η αέρια κατάσταση αποτελούν τις τρεις, συνήθεις στο γήινο περιβάλλον, καταστάσεις της ύλης. ιαφέρουν η µία από την άλλη σε κάποια απλά γνωρίσµατα:
1. ΧΗΜΙΚΟΙ ΕΣΜΟΙ ΣΤΑ ΣΤΕΡΕΑ ΓΕΝΙΚΑ Η στερεά, η υγρή και η αέρια κατάσταση αποτελούν τις τρεις, συνήθεις στο γήινο περιβάλλον, καταστάσεις της ύλης. ιαφέρουν η µία από την άλλη σε κάποια απλά γνωρίσµατα:
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Dijagonalizacija operatora
 Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
II. RAZRED SULFIDI (SELENIDI, TELURIDI, ARZENIDI, ANTIMONIDI) IN SULFOSOLI (KOMPLEKSNI SULFIDI)
 II. RAZRED SULFIDI (SELENIDI, TELURIDI, ARZENIDI, ANTIMONIDI) IN SULFOSOLI (KOMPLEKSNI SULFIDI) Žveplo v litosferi: 470 µg/g kot - S 2- - sulfidi, s kovinskimi kationi. Nastopanje v magmatskih, metamorfnih
II. RAZRED SULFIDI (SELENIDI, TELURIDI, ARZENIDI, ANTIMONIDI) IN SULFOSOLI (KOMPLEKSNI SULFIDI) Žveplo v litosferi: 470 µg/g kot - S 2- - sulfidi, s kovinskimi kationi. Nastopanje v magmatskih, metamorfnih
Heterogene ravnoteže taloženje i otapanje. u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima
 Heterogene ravnoteže taloženje i otapanje u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima Ako je BA teško topljiva sol (npr. AgCl) dodatkom
Heterogene ravnoteže taloženje i otapanje u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima Ako je BA teško topljiva sol (npr. AgCl) dodatkom
Αλληλεπίδραση ακτίνων-χ με την ύλη
 Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων
Άσκηση 8 Αλληλεπίδραση ακτίνων-χ με την ύλη Δ. Φ. Αναγνωστόπουλος Τμήμα Μηχανικών Επιστήμης Υλικών Πανεπιστήμιο Ιωαννίνων Ιωάννινα 2013 Άσκηση 8 ii Αλληλεπίδραση ακτίνων-χ με την ύλη Πίνακας περιεχομένων
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Κεφάλαιο 1. Έννοιες και παράγοντες αντιδράσεων
 Κεφάλαιο 1 Έννοιες και παράγοντες αντιδράσεων Σύνοψη Το κεφάλαιο αυτό είναι εισαγωγικό του επιστημονικού κλάδου της Οργανικής Χημείας και περιλαμβάνει αναφορές στους πυλώνες της. Ειδικότερα, εδώ παρουσιάζεται
Κεφάλαιο 1 Έννοιες και παράγοντες αντιδράσεων Σύνοψη Το κεφάλαιο αυτό είναι εισαγωγικό του επιστημονικού κλάδου της Οργανικής Χημείας και περιλαμβάνει αναφορές στους πυλώνες της. Ειδικότερα, εδώ παρουσιάζεται
GLAZBENA UMJETNOST. Rezultati državne mature 2010.
 GLAZBENA UJETNOST Rezultati državne mature 2010. Deskriptivna statistika ukupnog rezultata PARAETAR VRIJEDNOST N 112 k 61 72,5 St. pogreška mjerenja 5,06 edijan 76,0 od 86 St. devijacija 15,99 Raspon 66
GLAZBENA UJETNOST Rezultati državne mature 2010. Deskriptivna statistika ukupnog rezultata PARAETAR VRIJEDNOST N 112 k 61 72,5 St. pogreška mjerenja 5,06 edijan 76,0 od 86 St. devijacija 15,99 Raspon 66
IMOBILIZACIJA AKTIVNIH TVARI ZA BIOLOŠKO PREPOZNAVANJE
 IMBILIZACIJA AKTIVI TVARI ZA BILŠK PREPZAVAJE EZIMI ATITIJELA RECEPTRI MIKRRGAIZMI ŽIVTIJSKE ILI BILJE STAICE ŽIVTIJSKA I BILJA VLAKA KLJUČI PRCES PRI IZRADI BISEZRA IMBILIZACIJA BILŠKE TVARI - AJČEŠĆE
IMBILIZACIJA AKTIVI TVARI ZA BILŠK PREPZAVAJE EZIMI ATITIJELA RECEPTRI MIKRRGAIZMI ŽIVTIJSKE ILI BILJE STAICE ŽIVTIJSKA I BILJA VLAKA KLJUČI PRCES PRI IZRADI BISEZRA IMBILIZACIJA BILŠKE TVARI - AJČEŠĆE
7.14 Προβλήματα για εξάσκηση
 7.14 Προβλήματα για εξάσκηση 7.1 Το ορυκτό οξείδιο του αλουμινίου (Corundum, Al 2 O 3 ) έχει κρυσταλλική δομή η οποία μπορεί να περιγραφεί ως HCP πλέγμα ιόντων οξυγόνου με τα ιόντα αλουμινίου να καταλαμβάνουν
7.14 Προβλήματα για εξάσκηση 7.1 Το ορυκτό οξείδιο του αλουμινίου (Corundum, Al 2 O 3 ) έχει κρυσταλλική δομή η οποία μπορεί να περιγραφεί ως HCP πλέγμα ιόντων οξυγόνου με τα ιόντα αλουμινίου να καταλαμβάνουν
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
Na/K (mole) A/CNK
 Li, W.-C., Chen, R.-X., Zheng, Y.-F., Tang, H., and Hu, Z., 206, Two episodes of partial melting in ultrahigh-pressure migmatites from deeply subducted continental crust in the Sulu orogen, China: GSA
Li, W.-C., Chen, R.-X., Zheng, Y.-F., Tang, H., and Hu, Z., 206, Two episodes of partial melting in ultrahigh-pressure migmatites from deeply subducted continental crust in the Sulu orogen, China: GSA
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO?
 HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
HEMIJSKA VEZA ŠTA DRŽI STVARI (ATOME) ZAJEDNO? U OKVIRU OVOG POGLAVLJA ĆEMO RADITI Jonska i kovalentna veza. Metalna veza. Elektronska teorija hemijske veze. Struktura molekula. Međumolekulske interakcije.
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΗΛΕΚΤΡΟΛΟΓΙΚΑ ΥΛΙΚΑ. Ενότητα 7: ΚΕΡΑΜΙΚΑ ΛΙΤΣΑΡΔΑΚΗΣ ΓΕΩΡΓΙΟΣ ΤΗΜΜΥ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΛΟΓΙΚΑ ΥΛΙΚΑ Ενότητα 7: ΚΕΡΑΜΙΚΑ ΛΙΤΣΑΡΔΑΚΗΣ ΓΕΩΡΓΙΟΣ ΤΗΜΜΥ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΛΟΓΙΚΑ ΥΛΙΚΑ Ενότητα 7: ΚΕΡΑΜΙΚΑ ΛΙΤΣΑΡΔΑΚΗΣ ΓΕΩΡΓΙΟΣ ΤΗΜΜΥ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Dvoatomna linearna rešetka
 Dvoatomna linearna rešetka Promatramo linearnu rešetku s dva različita atom u elementarnoj ćeliji. Konstanta rešetke je a. Udaljenost između susjednih različih atoma je a/2 Mase atoma su M 1 i M 2. (Neka
Dvoatomna linearna rešetka Promatramo linearnu rešetku s dva različita atom u elementarnoj ćeliji. Konstanta rešetke je a. Udaljenost između susjednih različih atoma je a/2 Mase atoma su M 1 i M 2. (Neka
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Kristalna struktura. Kruta (čvrsta) tijela:
 Kruta (čvrsta) tijela: Kristalna struktura Kristalna tijela metali (bakar, željezo,... ) šečer (kristalni), kuhinjska sol dijamanti i drago kamenje razni kristali i minerali kristalno staklo, pahulje snijega,
Kruta (čvrsta) tijela: Kristalna struktura Kristalna tijela metali (bakar, željezo,... ) šečer (kristalni), kuhinjska sol dijamanti i drago kamenje razni kristali i minerali kristalno staklo, pahulje snijega,
APROKSIMACIJA FUNKCIJA
 APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
APROKSIMACIJA FUNKCIJA Osnovni koncepti Gradimir V. Milovanović MF, Beograd, 14. mart 2011. APROKSIMACIJA FUNKCIJA p.1/46 Osnovni problem u TA Kako za datu funkciju f iz velikog prostora X naći jednostavnu
ELEKTRIČNA STRUJA KROZ TEKUĆINE. Elektrolitička disocijacija. čista destilirana voda izolator, uz npr. NaCl bolja vodljivost
 ELEKTRIČNA STRUJA KROZ TEKUĆINE Elektrolitička disocijacija čista destilirana voda izolator, uz npr. NaCl bolja vodljivost otopine kiselina, lužina ili soli = elektroliti pozitivni i negativni ioni povećavaju
ELEKTRIČNA STRUJA KROZ TEKUĆINE Elektrolitička disocijacija čista destilirana voda izolator, uz npr. NaCl bolja vodljivost otopine kiselina, lužina ili soli = elektroliti pozitivni i negativni ioni povećavaju
STVARANJE VEZE C-C POMO]U ORGANOBORANA
![STVARANJE VEZE C-C POMO]U ORGANOBORANA STVARANJE VEZE C-C POMO]U ORGANOBORANA](/thumbs/55/37829094.jpg) STVAAJE VEZE C-C PM]U GAAA 2 6 rojne i raznovrsne reakcije * idroborovanje alkena i reakcije alkil-borana 3, Et 2 (ili TF ili diglim) Ar δ δ 2 2 3 * cis-adicija "suprotno" Markovnikov-ljevom pravilu *
STVAAJE VEZE C-C PM]U GAAA 2 6 rojne i raznovrsne reakcije * idroborovanje alkena i reakcije alkil-borana 3, Et 2 (ili TF ili diglim) Ar δ δ 2 2 3 * cis-adicija "suprotno" Markovnikov-ljevom pravilu *
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
ΙΑΦΑ Φ ΝΕΙ Ε ΕΣ Ε ΧΗΜΕ Μ Ι Ε ΑΣ ΓΥΜΝ Μ ΑΣΙΟΥ H
 Hταξινόµηση των στοιχείων τάξη Γ γυµνασίου Αναγκαιότητα ταξινόµησης των στοιχείων Μέχρι το 1700 µ.χ. ο άνθρωπος είχε ανακαλύψει µόνο 15 στοιχείακαι το 1860 µ.χ. περίπου 60στοιχεία. Σηµαντικοί Χηµικοί της
Hταξινόµηση των στοιχείων τάξη Γ γυµνασίου Αναγκαιότητα ταξινόµησης των στοιχείων Μέχρι το 1700 µ.χ. ο άνθρωπος είχε ανακαλύψει µόνο 15 στοιχείακαι το 1860 µ.χ. περίπου 60στοιχεία. Σηµαντικοί Χηµικοί της
ΘΕΜΑΤΑ ΑΠΟ ΠΜΔΧ ΣΧΕΤΙΚΑ ΜΕ ΤΟ 1 ΚΕΦΑΛΑΙΟ ΤΗΣ Γ ΛΥΚΕΙΟΥ
 ΘΕΜΑΤΑ ΑΠΟ ΠΜΔΧ ΣΧΕΤΙΚΑ ΜΕ ΤΟ ΚΕΦΑΛΑΙΟ ΤΗΣ Γ ΛΥΚΕΙΟΥ 27 ος ΠΜΔΧ Γ ΛΥΚΕΙΟΥ 30 03 203. Στοιχείο Μ το οποίο ανήκει στην πρώτη σειρά στοιχείων μετάπτωσης, σχηματίζει ιόν Μ 3+, που έχει 3 ηλεκτρόνια στην υποστιβάδα
ΘΕΜΑΤΑ ΑΠΟ ΠΜΔΧ ΣΧΕΤΙΚΑ ΜΕ ΤΟ ΚΕΦΑΛΑΙΟ ΤΗΣ Γ ΛΥΚΕΙΟΥ 27 ος ΠΜΔΧ Γ ΛΥΚΕΙΟΥ 30 03 203. Στοιχείο Μ το οποίο ανήκει στην πρώτη σειρά στοιχείων μετάπτωσης, σχηματίζει ιόν Μ 3+, που έχει 3 ηλεκτρόνια στην υποστιβάδα
Program za tablično računanje Microsoft Excel
 Program za tablično računanje Microsoft Excel Teme Formule i funkcije Zbrajanje Oduzimanje Množenje Dijeljenje Izračun najveće vrijednosti Izračun najmanje vrijednosti 2 Formule i funkcije Naravno da je
Program za tablično računanje Microsoft Excel Teme Formule i funkcije Zbrajanje Oduzimanje Množenje Dijeljenje Izračun najveće vrijednosti Izračun najmanje vrijednosti 2 Formule i funkcije Naravno da je
OSNOVE TEHNOLOGIJE PROMETA
 OSNOVE TEHNOLOGIJE PROMETA MODUL: Tehnologija teleomuniacijsog rometa FAKULTET PROMETNIH ZNANOSTI Predavači: Doc.dr.sc. Štefica Mrvelj Maro Matulin, dil.ing. Zagreb, ožuja 2009. Oće informacije Konzultacije:
OSNOVE TEHNOLOGIJE PROMETA MODUL: Tehnologija teleomuniacijsog rometa FAKULTET PROMETNIH ZNANOSTI Predavači: Doc.dr.sc. Štefica Mrvelj Maro Matulin, dil.ing. Zagreb, ožuja 2009. Oće informacije Konzultacije:
INŽENJERSTVO NAFTE I GASA. 2. vežbe. 2. vežbe Tehnologija bušenja II Slide 1 of 50
 INŽENJERSTVO NAFTE I GASA Tehnologija bušenja II 2. vežbe 2. vežbe Tehnologija bušenja II Slide 1 of 50 Proračuni trajektorija koso-usmerenih bušotina 2. vežbe Tehnologija bušenja II Slide 2 of 50 Proračun
INŽENJERSTVO NAFTE I GASA Tehnologija bušenja II 2. vežbe 2. vežbe Tehnologija bušenja II Slide 1 of 50 Proračuni trajektorija koso-usmerenih bušotina 2. vežbe Tehnologija bušenja II Slide 2 of 50 Proračun
13. skupine. dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Elementi 13. skupine U 13. skupini periodnog sustava nalaze se sljedeći elementi: bor (B), aluminij (Al), galij (Ga), indij (In) i talij (Tl). B je polumetal, dok su ostali elementi metali. U elementarnom
Elementi 13. skupine U 13. skupini periodnog sustava nalaze se sljedeći elementi: bor (B), aluminij (Al), galij (Ga), indij (In) i talij (Tl). B je polumetal, dok su ostali elementi metali. U elementarnom
ΣΥΣΤΑΣΗ ΤΟΥ ΦΛΟΙΟΥ ΤΗΣ ΓΗΣ.
 ΣΥΣΤΑΣΗ ΤΟΥ ΦΛΟΙΟΥ ΤΗΣ ΓΗΣ. Η σύσταση του φλοιού ουσιαστικά καθορίζεται από τα πυριγενή πετρώματα μια που τα ιζήματα και τα μεταμορφωμένα είναι σε ασήμαντες ποσότητες συγκριτικά. Η δημιουργία των βασαλτικών-γαββρικών
ΣΥΣΤΑΣΗ ΤΟΥ ΦΛΟΙΟΥ ΤΗΣ ΓΗΣ. Η σύσταση του φλοιού ουσιαστικά καθορίζεται από τα πυριγενή πετρώματα μια που τα ιζήματα και τα μεταμορφωμένα είναι σε ασήμαντες ποσότητες συγκριτικά. Η δημιουργία των βασαλτικών-γαββρικών
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
ΥΛΙΚΑ ΠΑΡΟΝ ΚΑΙ ΜΕΛΛΟΝ
 ΥΛΙΚΑ ΠΑΡΟΝ ΚΑΙ ΜΕΛΛΟΝ Ι 5 Δομή ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ Κρυσταλλικά υλικά Άμορφα υλικά Κρύσταλλος είναι ένα υλικό που παρουσιάζει τρισδιάστατη περιοδική τάξη ατόμων,
ΥΛΙΚΑ ΠΑΡΟΝ ΚΑΙ ΜΕΛΛΟΝ Ι 5 Δομή ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΑΣ ΥΛΙΚΩΝ Κρυσταλλικά υλικά Άμορφα υλικά Κρύσταλλος είναι ένα υλικό που παρουσιάζει τρισδιάστατη περιοδική τάξη ατόμων,
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Μοναδική πηγή Cr είναι τα χρωμιούχα μέλη της ομάδας των σπινελλίων: R 2+ R
 ΧΡΩΜΙΟ Μοναδική πηγή Cr είναι τα χρωμιούχα μέλη της ομάδας των σπινελλίων: R 2+ R 3+ 2 O 4 όπου: R 2+ = Mg, Fe 2+, Mn, Zn, Ni R 3+ = Cr, Al, Fe 3+, Ti, V 3+ Γενικός τύπος χρωμίτη: (Fe 2+, Mg)O.(Cr, Al,
ΧΡΩΜΙΟ Μοναδική πηγή Cr είναι τα χρωμιούχα μέλη της ομάδας των σπινελλίων: R 2+ R 3+ 2 O 4 όπου: R 2+ = Mg, Fe 2+, Mn, Zn, Ni R 3+ = Cr, Al, Fe 3+, Ti, V 3+ Γενικός τύπος χρωμίτη: (Fe 2+, Mg)O.(Cr, Al,
1. PODELA MATERIJALA
 1. PODELA MATERIJALA metali keramika polimeri VRSTE MATERIJALA kompoziti Metalni materijali Keramički materijali Polimeri Kompozitni materijali metal + keramika polimeri + keramika metal + polimeri Slika
1. PODELA MATERIJALA metali keramika polimeri VRSTE MATERIJALA kompoziti Metalni materijali Keramički materijali Polimeri Kompozitni materijali metal + keramika polimeri + keramika metal + polimeri Slika
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Sample BKC-10 Mn. Sample BKC-23 Mn. BKC-10 grt Path A Path B Path C. garnet resorption. garnet resorption. BKC-23 grt Path A Path B Path C
 0.5 0.45 0.4 0.35 0.3 Sample BKC-10 Mn BKC-10 grt Path A Path B Path C 0.12 0.1 0.08 Mg 0.25 0.06 0.2 0.15 0.04 0.1 0.05 0.02 0 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 Core Rim 0.9 0.8 Fe 0 0 0.01 0.02
0.5 0.45 0.4 0.35 0.3 Sample BKC-10 Mn BKC-10 grt Path A Path B Path C 0.12 0.1 0.08 Mg 0.25 0.06 0.2 0.15 0.04 0.1 0.05 0.02 0 0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 Core Rim 0.9 0.8 Fe 0 0 0.01 0.02
Θεµατικό Περιεχόµενο Μαθήµατος
 Θεµατικό Περιεχόµενο Μαθήµατος 1. Κρυσταλικές δοµές Ιονική ακτίνα Ενέργεια πλέγµατος Πυκνές διατάξεις 4εδρικές 8εδρικές οπές Μέταλλα ιοντικά στερεά Πώς περιγράφεται η δοµή τους Πως προσδιορίζεται η δοµή
Θεµατικό Περιεχόµενο Μαθήµατος 1. Κρυσταλικές δοµές Ιονική ακτίνα Ενέργεια πλέγµατος Πυκνές διατάξεις 4εδρικές 8εδρικές οπές Μέταλλα ιοντικά στερεά Πώς περιγράφεται η δοµή τους Πως προσδιορίζεται η δοµή
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Kovalentna veza , CO 2. U molekulima H 2
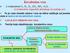 Kovalentna veza U molekulima H 2, N 2, O 2, CO 2, NH 3, H 2 O,... ili molekulima organskih jedinjenja ne postoje joni. To je veza između atoma i ona se bitno razlikuje od jonske veze a naziva se kovalentnom
Kovalentna veza U molekulima H 2, N 2, O 2, CO 2, NH 3, H 2 O,... ili molekulima organskih jedinjenja ne postoje joni. To je veza između atoma i ona se bitno razlikuje od jonske veze a naziva se kovalentnom
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
ΓΕΩΧΗΜΕΙΑ Δ ΕΞΑΜΗΝΟ ΕΙΣΑΓΩΓΗ- ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑΤΟΣ. Χριστίνα Στουραϊτη
 1 ΓΕΩΧΗΜΕΙΑ Δ ΕΞΑΜΗΝΟ ΕΙΣΑΓΩΓΗ- ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑΤΟΣ Χριστίνα Στουραϊτη ΠΡΟΓΡΑΜΜΑ ΜΑΘΗΜΑΤΩΝ ΓΕΩΧΗΜΕΙΑΣ Δ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2018-2019 ΕΒΔΟΜΑΔΑ ΠΕΡΙΕΧΟΜΕΝΟ ΔΙΔΑΣΚΟΥΣΑ 1 η 2 η Εισαγωγή- Επεξηγήσεις,
1 ΓΕΩΧΗΜΕΙΑ Δ ΕΞΑΜΗΝΟ ΕΙΣΑΓΩΓΗ- ΠΕΡΙΕΧΟΜΕΝΑ ΜΑΘΗΜΑΤΟΣ Χριστίνα Στουραϊτη ΠΡΟΓΡΑΜΜΑ ΜΑΘΗΜΑΤΩΝ ΓΕΩΧΗΜΕΙΑΣ Δ ΕΞΑΜΗΝΟ ΑΚΑΔΗΜΑΪΚΟ ΕΤΟΣ 2018-2019 ΕΒΔΟΜΑΔΑ ΠΕΡΙΕΧΟΜΕΝΟ ΔΙΔΑΣΚΟΥΣΑ 1 η 2 η Εισαγωγή- Επεξηγήσεις,
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze:
 Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
Hemijska veza Kada su atomi povezani jedan sa drugim tada kažemo da izmeñu njih postoji hemijska veza Generalno postoji tri vrste hemijske veze: Jonska, Kovalentna i Metalna Luisovi simboli veoma zgodan
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
