logo.pdf Oddelek za fiziko Avtor: Marjeta Tušek Ljubljana,
|
|
|
- Ἀρτεμᾶς Κοτζιάς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 logo.pdf Oddelek za fiziko Avtor: Marjeta Tušek Ljubljana, 1
2 Kazalo 1 UVOD 3 2 OSNOVE JEDRSKE MAGNETNE RESONANCE Magnetne lastnosti jeder in resonanca Radiofrekvenčni pulz Jedrska relaksacija Signal proste precesije in spinski odmev SLIKANJE Z MAGNETNO RESONANCO Gradienti magnetnega polja Fourierjeva transformacija in k -prostor Izbira rezine Oprema laboratorija za MR slikanje POPAČITVE IN ARTEFAKTI Artefakti zaradi gibanja vzorca Artefakti zaradi merilne naprave Artefakti zaradi zajemanja signala HITRE METODE SLIKANJA Metoda spinskega odmeva RARE Gibbsovo zvonjenje Odprava popačitev Gibbsovega zvonjenja PRIPRAVA EKSPERIMENTA 27 2
3 1 UVOD 2 OSNOVE JEDRSKE MAGNETNE RESONANCE 2.1 Magnetne lastnosti jeder in resonanca Slikanje z magnetno resonanco uspeva, ker lahko opazujemo, kako se jedro atoma v nekem vzorcu odziva na zunanje magnetno polje. Poglejmo najprej klasično sliko. Magnetni moment, ki nastane zaradi gibanja protona okoli težišča atoma, lahko izračunamo po enačbi 1 p m = e 0 Γ, (1) 2m p kjer je Γ = m r v vrtilna količina, s katero je magnetni moment vzporeden, e 0 je osnovni naboj, m p pa je masa protona. Proton se vede kot majhen magnetni dipol in homogeno magnetno polje deluje nanj z navorom (enačba 2) M = p m B = e 0 Γ B. (2) 2m p Če sedaj preidemo v kvantno mehaniko, lahko vektor vrtilne količine zapišimo z operatorjem ˆ I ˆ Γ = ˆ I. (3) Zaradi vrtilne količine oziroma spina lahko jedru pripišemo magnetni dipolni moment ˆ µ = γˆ Γ, (4) kjer je γ giromagnetno razmerje, γ = gµ N /, in je značilno za vsako posamezno jedro. Giromagnetno razmerje za proton je približno γ = 42, 6MHz/T. Količina µ N predstavlja jedrski magneton, µ N = e /2m p Am 2. Magnetni dipol ima tudi jedro vodika ( 1 H), kar je pomembno za slikanje z magnetno resonanco, saj približno 70% človeškega telesa sestavlja voda. Le pri jedrih, ki imajo neničelni skupni magnetni dipolni moment, kar pomeni, da imajo liho število protonov, lahko opazujemo pojav jedrske magnetne resonance. Ostala jedra, ki jih tudi lahko izkoriščamo za slikanje z jedrsko magnetno resonanco, so predvsem izotop ogljika ( 13 C), natrij ( 23 Na) in fosfor ( 31 P ). Dokler so jedra s spinom izven magnetnega polja, so magnetni dipolni momenti naključno usmerjeni. V magnetnem polju pa temu ni več tako, kar lepo prikazuje slika 1 [sersa]. Interakcijo magnetnega dipolnega momenta z zunanjim magnetnim poljem opiše Hamiltonov operator (enačba 5) Ĥ = B ˆ µ = B ˆ I. (5) Če delujemo s statičnim magnetnim poljem B 0 v smeri osi z, se enačba 5 zapiše kot Ĥ = B 0 µ z = γ B 0 Î z. (6) 3
4 Slika 1: Slika a) prikazuje jedra s spinom v odsotnosti magnetnega polja. Slika b) pa prikazuje orientacijo jeder v prisotnosti zunanjega magnetnega polja. Lastne vrednosti tega operatorja so za jedra s spinom I enaka E m = γ B 0 m, (7) kjer je m magnetno kvantno število in lahko zasede vrednosti m = I, I + 1,..., I 1, I. Osnovno stanje jedra s spinom I, ki je izven magnetnega polja 2I + 1 krat degenerirano, se v prisotnosti zunanjega magnetnega polja razcepi na 2I + 1 energijskih stanj. Temu pojavu pravimo Zeemanov razcep (slika 2). Za proton so možne vrednosti magnetnega dipolnega momenta µ z = ±γ /2, saj velja, da je I = 1/2. Torej se proton v statičnem zunanjem magnetnem polju lahko razcepi na dve energijski stanji (m = ±1/2), na paralelno oziroma antiparalelno stanje glede na projekcijo magnetnega dipolnega momenta na smer statičnega zunanjega magnetnega polja. Slika 2: Zeemanov razcep za jedra s spinom 1/2. Paralelno stanje je energijsko ugodnejše od antiparalelnega. Porazdelitev števila delcev po energijskih nivojih, ko je sistem v ravnotežju, se pokorava Boltzmanovi enačbi, ki velja za vse podobne pojave v naravi (enačba 8) N a = e Ea Ep kt N p = e E kt 1 E kt, (8) kjer so N a in N p števila spinov v antiparalelni in paralelni smeri, E a in E p so ustrezne energije, k je Boltzmanova konstanta in T je absolutna temperatura. Pri sobni temperaturi je razlika v zasednosti dveh nivojev približno milijoninka vseh jeder, vendar prav ta višek jeder v nižjem energijskem nivoju povzroči 4
5 nastanek malenkostne magnetizacije vzorca M 0. Ta razlika nam omogoča opazovanje absorbcije elektromagnetnega valovanja v snovi, na čemer temelji tudi magnetna resonanca. Če ta presežek protonov s spinom paralelnim na smer zunanjega magnetnega polja pomnožimo z dipolnim magnentim momentom za posamezen spin γ /2 in vpeljemo gostoto protonov na enoto volumna ρ 0, lahko določimo ravnovesno stanje magnetizacije M 0 M 0 = ρ 0γ 2 2 4kT B 0. (9) Prehod jeder iz enega v drugi energijski nivo se zgodi pri absorbciji ali osvoboditvi energije. Prehod lahko simuliramo z oscilirajočim magnetnim poljem, vendar le pod pogojem, da energija tega polja ustreza razliki energij dveh stanj, kar imenujemo resonančni pogoj. Razlika v energijah dveh sosednjih nivojev je sorazmerna z jakostjo magnetnega polja E = γ B 0. (10) Od tod lahko dobimo frekvenco valovanja, ki izzove prehod med dvema nivojema: oziroma krožno frekvenco ν 0 = E h = γ 2π B 0 (11) ω 0 = 2πγ 0 = γb 0. (12) Pri MR resonančno frekvenco pri kateri se zgodi prehod med Zeemanovimi nivoji imenujemo Larmorjeva frekvenca. Kot lahko vidimo iz enačb 11 in 12 je ta odvisna od vrste jeder oziroma njihovega giromagnetnega razmerja ter od jakosti zunanjega magnetnega polja. Magnetna polja, ki jih uporabljamo pri MR poskusih, so zelo močna, od 0.5T do 3T, magnenti momenti jeder pa so, kot smo že omenili, velikostnega reda jedrskega magnetona (µ N Am 2 ), zato so resonančne frekvence večinoma v radiofrekvenčnem območju (RF) 1 600MHz. MR signal je sorazmeren z magentizacijo vzorca M 0 (enačba 9) in je tem večji, čim večja je protonska gostota in čim močenjše je magnetno polje B 0. Večjo magnetizacijo in s tem večji signal, bi lahko dobili tudi z močno ohladitvijo vzorcev, vendar smo pri MR slikanju živih bioloških vzorce vedno omejeni na sobno temperaturo. 2.2 Radiofrekvenčni pulz Jedra s spinom si lahko klasično predstavljamo kot majhne vrteče se magnetke, ki se v odsotnosti magnetnega polja usmerijo kaotično, tako da je njihova skupna magnetizacija M 0 enaka nič. Če pa jih izpostavimo magnetnemu polju B 0, pa začnejo precesirati okrog smeri polja in vektor skupne magnetizacije M 0, ki je vsota vseh magnetnih momentov jeder, je različne od nič. V zunanjem magnetnem polju B občuti jedro z magnentim momentom µ navor µ B. Sprememba vrtilne količine je enaka sunku navora d < Γ > dt =< µ > B. (13) 5
6 Za spreminjanje pričakovane vrednosti magnetnega momenta lahko sedaj s pomočjo enačbe 4 zapišemo: d < µ > dt = γ < µ > B. (14) Jedrska magnetizacija M je definirana kot vsota posameznih jedrskih magnetnih momentov µ i znotraj ustrezno majhnega dela vzorca prostornine V M = i V µ i V = n < µ >, (15) kjer je n število opazovanih jeder. Če sedaj enačbo 14 pomnožimo z n dobimo dm = γm dt B, (16) ki opisuje časovno spreminjanje magnetizacije v odvisnoti od zunanjega magnetnega polja. Najprej si poglejmo, kaj se dogaja v vrtečem se koordiantnem sistemu. Iz klasične mehanike vemo, da je časovni odvod magnetizacije M(t) v mirujočem koordinatnem sistemu, ki kroži s frekvenco ω r = (0, 0, ω r ) enak dm = δ M dt δt + ω r M. (17) Iz enačbe 16 in enačbe 17 lahko dobimo enačbo gibanja magnetizacije v vrtečem se koordinatnem sistemu δ M δt kjer je B ef efektivno magnetno polje = γ M B ef, (18) B ef = B + ω r γ. (19) Predpostavimo, da imamo vzorec v statičnem magnetnem polju B = (0, 0, B 0 ) in da vrtimo koordinatni sistem s frekvenco ω r = (0, 0, ω r ). Tedaj je efektivno magnento polje enako B ef = (0, 0, B 0 ) + 1 γ (0, 0, ω r). Če sedaj za ω r izberemo frekvenco ω r = γb 0, kar je Larmorjeva frekvenca, vidimo, da je B ef = 0. To pomeni, da magnetizacija v vrtečem se koordiantnem sistemu miruje oziroma da v laboratorijskem koordinatnem sistemu precesira okoli statičnega magnetnega polja B 0 z Larmorjevo frekvenco ω 0 = γb 0. Sedaj pa dodajmo statičnemu magnetnemu polju B 0 še vrteče se magnetno polje B 1. Polje v vrtečem se koordinatnem sistemu, ki se vrti z Larmorjevo frekvenco, usmerimo v smeri x,, torej pravokotno na smer statičnega magnetnega polja (kot je prikazano na sliki 3). Tedaj je B ef = (B 1, 0, 0). Enačba 18 opisuje sedaj precesijo s frekvenco γb 1, okrog polja B 1 v vrtečem se sistemu. Če je magnentno polje B 1 vklopljeno čas t p, potem se v tem času magentizacija zasuče okrog osi x, za kot θ = γb 1 t p. (20) 6
7 Slika 3: Jedrska precesija (levo) in sukanje magnetizacije pri RF pulzu (desno). Magnetno polje B 1 pripada RF valovanju s katerim obsevamo jedra. Takšno RF valovanje najlažje dosežemo z RF tuljavami, ki so del nihajnega kroga uglašenega na Larmorjevo frekvenco opazovanih jeder. S primerno izbiro jakosti RF valovanja (B 1 ) in trajanja RF sunka (t p ), lahko dosežemo, da se magnetizacija odkloni od ravnovesne lege za poljuben kot θ. Najpogosteje uporabljamo t. i. sunek 90 in sunek 180, kjer smo s prvim odklonili magnetizacijo za kot 90 in s drugim za kot 180. Enačba 18 dobro opisuje spreminjanje jedrske magnetizacije v sistemu izoliranih jeder. Taka jedra ne interagirajo med sabo, ravno tako pa ne z mrežo. Do opisa realnejše slike dogajanja moramo to enačbo še dopolniti z opisom procesa relaksacije. 2.3 Jedrska relaksacija Enačba 16 je osnova Blochovim enačbam. Leta 1946 je Felix Bloch formuliral set enačb, ki opisujejo gibanje jedrskega spina v magnetnem polju pod vplivom RF sunkov. Enačbo 16 je popravil, in sicer tako, da je upošteval, da se jedra po izklopu RF pulzov relaksirajo nazaj v ravnovesno lego, kjer se vzpostavi ravnovesna magnetizacija M 0. Predvideval je, da se v z - smeri in xy - ravnini relaksirajo na različna načina. Ko sistem spinov z dodatnim, vrtečim se magnetnim poljem B 1, zmotimo iz ravnovesnega stanja, se bo po končanem RF pulzu le to zopet začelo vzpostavljati. Ta proces imenujemo spinsko - mrežna relaksacija oziroma longitudinalna relaksacija, saj poteka spreminjanje magnetizacije vzdolž smeri magnetnega polja (slika 4). Za njen nastanek je odgovoren prenos energije (sklopitve) med jedri in mrežnimi nihanji. Hitrost longitudinalne relaksacije, ki nam jo opiše karakteristični čas T 1, je zaradi zelo različne stopnje sklopitve med jedri in mrežnimi nihanji zelo različna med različnimi snovmi. Predvsem so velike razlike med tekočimi in trdnimi snovmi. V trdnih vzorcih je longitudinalna relaksacija mnogo počasnejša kot v tekočinah. Tako imamo v tekočinah relaksacijske čase T 1 v razponu od nekaj 100ms pa do več sekund (za vodo je približno 3s), v trdnih vzorcih pa je lahko T 1 dolg tudi več ur. Opis spinsko mrežne relaksacije opisuje enačba 21 dm z dt = M 0 M z T 1. (21) Rešitev te enačbe nam opiše longitudinalno relaksacijo 7
8 Slika 4: Prikaz longitudinalne relaksacije (rumena puščica) takoj po RF pulzu ter njeno vračanje v ravnovesno lego. Mz (t) = Mz (0)e t/t1 + M0 (1 e t/t1 ), (22) kar nam prikazuje tudi slika 5. Slika 5: Longitudinalna relaksacija. Ko sistem zmotimo iz ravnovesne lege pa se poleg izginjanje longitudinalne magnetizacije zgodi še nekaj drugega. Protoni začnejo pridobivati na fazni koherenci, kar okrepi magnetizacijo v xy - ravnini oziroma t. i. transverzalno magnetizacijo. Ko ugasnemo RF sunek, protoni izgubljajo fazno koherenco in magnetizacija Mxy se začne vračati v svojo ravnovesno lego Mxy = 0 (slika 6). Zmanjševanje transverzalne relaksacije je posledica interkacije med posameznimi jedri, saj ima vsako posamezno jedro različne lokalne interakcije s svojimi sosedi, kar pomeni, da posamezna jedra čutijo različno B0 in se njihove Larmorjeve frekvence razlikujejo. Pri tej relaksaciji ni prišlo do izmenjave energij med jedri in mrežo in je zato v splošnem tudi njena hitrost precej drugačna kot hitrost longitudinalne magnetizacije. Slika 6: Prikaz zmanjševanja transverzalne relaksacije (rumena puščica). 8
9 Čas upadanja transverzalne magnetizacije opiše karakteristični čas T 2, ki ga imenujemo tudi spinsko - spinski relaksacijski čas. Relaksacijski časi T 2 so v tekočinah velikostnega reda od nekaj 10ms pa do nekaj sekund (za vodo je T 2 približno 2s), v trdninah pa so mnogo krajši in znašajo lahko tudi samo nekaj µs. Opis transverzalne relaksacije opisuje enačba 23 dm xy dt = M xy T 2. (23) Rešitev, ki nam opiše transverzalno relaksacijo pa se glasi in je prikazana na sliki 7. M xy (t) = M xy (0)e t/t2 (24) Slika 7: Transverzalna relaksacija. Enačbi relaksacije 21 in 23 pravilno opisujeta spreminjanje magnetizacije samo v primeru statičnega magnetnega polja B 0. Spreminjanje magentizacije pod vplivom poljubnega magnetnega polja B(t) pa opišemo s kombinacijo enačbe gibanja 16 z enačbami relaksacije 21 in 23. Tako dobimo Blochove enačbe, ki nam opisujejo spreminjanje magnetizacije pod vplivom magnetnega polja dm x dt dm y dt = γ( M B) x M x T 2, (25) = γ( M B) y M y T 2, (26) dm z dt = γ( M B) z + M 0 M z T 1. (27) 2.4 Signal proste precesije in spinski odmev Po sunku 90 se torej magnetizacija začne vrteti okoli osi statičnega magnetnega polja z Larmorjevo frekvenco. Zaradi tega vrtenja se skozi RF tuljavo spreminja magnetni pretok in v RF tuljavi se inducira električna napetost. Ta je največja takoj po sunku 90, saj ima takrat magnetizacija tudi največjo možno projekcijo na ravnino pravokotno na smer statičnega magnetnega polja. V tuljavi inducirana napetost je namreč sorazmerna s komponento magnetizacije, ki spreminja magnetni pretok skozi tuljavo, torej s tranverzalno komponento 9
10 magnetizacije M xy in s frekvenco njenega vrtenja. Čez čas se transverzalna magnetizacija zaradi relaksacije začne zmanjševati in induciran signal postane vse manjši. Ta proces je prikazan na sliki 8. Z merjenjem inducirane napetosti lahko tako spremljamo razpadanje transverzalne komponente magnetizacije; pravimo, da na ta način posnamemo signal proste precesije. Ker je signal proste precesije sorazmeren z velikostjo magnetizacije in frekvenco njene precesije, obe količini pa sta sorazmerni z jakostjo magnetnega polja, velja, da je induciran signal oziroma MR signal sorazmeren s kvadratom magnetnega polja. Slika 8: Pulzni eksperiment. Tukaj moramo še omeniti, da v realnih razmerah nimamo nikoli popolnoma homogenega zunanjega magnetnega polja, ampak imamo vedno krajevne odmike od srednje vrednosti magnetnega polja v vzorcu. Zaradi njih se magnetizacija v različnih delih vzorca suče z različnimi precesijskimi hitrostmi in signal proste precesije ne upada več samo zaradi transverzalne relaksacije, ampak tudi zaradi razorientacije magnetizacije v vorcu. Posledica tega je, da signal proste precesije ne upada več s karakterističnim časom T 2, ampak s krajšim časom T2 1 = 1 + γ < B0 2 >. (28) T 2 T 2 Torej v idelano homogenem polju in neviskoznem vzorcu (vodi) velja, da je T 1 = T 2 = T2, v nehomogenem (realnem) polju in neviskoznem vzorcu je T 1 = T 2 > T2 in v nehomogenem polju in realnem vzorcu (biološko tkvivo) je T 1 > T 2 > T2. Z namenom, da bi v MR slikah dosegli čim boljše razmerje med signalom in šumom, težijo načrtovalci MR tomografskih sistemov k izgradnji vse močnejših magnetov. Do neke mere lahko povečamo razmerje med signalom in šumom tudi s povprečevanjem (seštevanjem) signalov, vendar utegne biti to zelo zamudno, saj se pri tem povečuje razmerje med signalom in šumom s kvadratnim korenom od števila povprečitev. Na primer, izboljšanje razmerja signal - šum, ki ga dosežemo s podvojitvijo gostote magnetnega polja, bi lahko dosegli pri nespremenjem magnetnem polju šele s šestnajstimi ponovitvami. Signal proste precesije torej izvira iz transverzalne magnetizacije vseh jeder, ki so vzbujena s pulzom in običajno vsebuje komponente, ki imajo različne frekvence in se zmanjšujejo z različno hitrostjo. Te komponente lahko analiziramo, če naredimo Fourierjevo transformacijo (FT) signala proste precesije, ki omogoča povezavo med informacijo vsebovano v časovni domeni in frekvenčnem 10
11 spektru. FT sinusnega časovnega poteka je ozka črta v frekvenčni skali, če pa je časovni signal sestavljen iz dveh zelo različnih frekvenc, dobimo v frekvenčni skali dve črti. O FT in izmerjenem signalu proste precesije bomo več povedali v naslednjih poglavjih. Kot je že bilo poudarjeno, se zaradi nehomogenosti magnetnega polja fazna koherenca jedrskih spinov hitro izgubi, kar preprečuje določanje pravega T 2 v vzorcu. Toda v procesu izgubljanja faze lahko efektivno zamenjamo smer precesije, kar pripelje do pojava odmeva. Takoj po sunku 90 imajo tako hitra kot tudi počasna jedra enako fazo precesije in signal proste precesije je takrat največji. Po prenehanju delovanja pulza pa začenjo jedra izgubljati fazo s časovno konstanto T2. Če v času τ po začetnem pulzu dovedemo 180 pulz, se magnetizacija v xy - ravnini obrne za kot 180 okrog osi x. Rezultat je, da so v času τ po 180 pulzu vsa jedra ponovno zbrana, kar da signal, ki ga imenujemo spinski odmev. Signal proste precesije, ki po sunku 90 začne padati kot funkcija e t/τ, se po času 2τ zaradi sunka 180 spet močno dvigne kot nekakšen odmev začetnega signala. Višina odmeva je za e 2τ/T2 nižja od signala, ki sledi takoj po sunku 90. Ta postopek je prikazan na spodnji sliki (slika 9). Slika 9: Spinski odmev. 3 SLIKANJE Z MAGNETNO RESONANCO Osnovna naloga slikanja z MR je rekonstrukcija slike preseka telesa. Da bi to dosegli, je treba v prostoru izmeriti MR - signal in iz njega dekodirati prostorski položaj jeder. V prejšnjem poglavju je opisano, kako dobimo MR - signal, ki izvira, ne glede na obliko vzorca, iz vseh jeder v vzorcu. Tako ne moremo ločiti od kje prihaja signal. Prostorsko kodiranje pa lahko dosežemo z gradienti magnetnega polja. 3.1 Gradienti magnetnega polja Osnovna enačba, na kateri temelji slikanje z magnetno resonanco, je enačba 12, ki pravi da je resonančna frekvenca spina sorazmerna z magnetnim poljem, ki ga občuti. Z gradienti magnetnega polja dosežemo, da čutijo spini v različnih delih vzorca različno magnetno polje. To pomeni, da se v različnih deloh vzorca 11
12 vrtijo z različnimi frekvencami. Ponavadi se uporabljajo enodimenizionalni linerani gradientni magentnega polja G x, G y in G z. S poljubno kombinacijo vseh treh gradientnih magnetnih polj lahko dosežemo linearno naraščajoče polje v poljubni smeri. Poglejmo si primer (slika 10), kjer poleg polja B 0 deluje tudi linearni gradient magnetnega polja G x vzdolž osi x in imamo B(x) = B 0 + G x x (29) ω = ω 0 + γg x x. (30) Vidimo, da je frekvenca s katero precesirajo jedra v izbrani točki neposredno odvisna od njene koordinate x. Amplituda spektra pri določeni frekvenci je sorazmerna številu jeder, ki precesirajo s to frekvenco, to pa so le jedra, ki imajo enako koordinato x. FT signala proste precesije v prisotnosti linearnega gradienta polja G x predstavlja zato enodimenzionalno projekcijo objekta na os x. Slika 10: Homogeno (levo), gradientno (sredina) in sešteto (desno) magnetno polje. 3.2 Fourierjeva transformacija in k -prostor Poglejmo si sedaj postopek rekonstrukcije MR slike s FT bolj natančno. V MRI aparatu najprej izberemo koordinatni sistem, ki je izbran tako, da z-os teče vzdolž osi aparata. V aparatu imamo konstantno magnetno polje velikosti B 0, ki je usmerjeno vzdolž z-osi. Poleg tega lahko, kot smo že omenili, s pomočjo pomožnih tuljav proizvedemo tudi poljubne časovno odvisne gradiente magnetnega polja v vseh treh smereh koordinatnih osi (slika 11). Gradienti so izbrani tako, da spreminajo le z-komponento bazičnega polja. Pri izbranih gradientih magnetnega polja, se velikost magnetnega polja v aparatu izraža z enačbo B(x, y, z, t) = B 0 + xg x (t) + yg y (t) + zg z (t). (31) Od tod takoj dobimo zvezo, ki opisuje vpliv gradientov magnetnega polja na Larmorjevo krožno hitrost precesije jeder. Dobimo ω(x, y, z, t) = ω 0 + xγg x (t) + yγg y (t) + zγg z (t), (32) kjer smo z ω 0 = γb 0 označili krožno hitrost proste precesije. 12
13 Slika 11: Gradienti magnetnega polja v vseh treh smereh. Z 90 RF pulzom odklonimo jedra. Ta začnejo hkrati precesirati, oziroma na začetku imajo vsa isto fazo, nato pa s časom zaradi različnih krožnih hitrosti (32) izgubljajo fazo. Celotna faza, ki jo pridobi jedro v položaju (x, y, z) v časovnem intervalu [0, t] je enaka ω 0 t + xγ t 0 G x (u)du + yγ t 0 G y (u)du + zγ t 0 G z (u)du. (33) Signal, ki ga izmerimo na tuljavi takoj po pulzu 90 je vsota signalov vseh delov vzorca in ga lahko sedaj s pomočjo enačbe 33 zapišemo kot ( t t t ) s(t) = ρ(x, y, z) cos ω 0 t + xγ G x (u)du + yγ G y (u)du + zγ G z (u)du dx dy dz, R (34) kjer je ρ(x, y, z) gostota jeder v točki (x, y, z). Enakovredno bi lahko namesto integrala po celotnem R 3, integrirali le po telesu. V našem zapisu samo privzamemo, da je gostota jeder zunaj telesa enaka 0. Poleg tega je tak zapis nekoliko bolj simetričen glede na Fourierovo transformacijo, ki jo bomo kasneje uporabili. Signal v (34) je za nadaljno analizo potrebno še nekoliko obdelati. Potrebno je izvesti demodulacijo. Najprej nekoliko prilagodimo oznake; naj bo x = (x, y, z), fazo v (33) pa na kratko zapišimo z ω 0 t + φ(t). Izmerjeni signal (34) je sedaj s(t) = ρ( x) cos (ω 0 t + φ(t))d x. R 3 V postopku demodulacije signal s(t) najprej pomnožimo s signalom cos ω 0 t. Dobimo s(t) cos ω 0 t = ρ( x) cos ω 0 t cos (ω 0 t + φ(t))d x = R 3 = ρ( x) cos φ(t) + cos (2ω 0t + φ(t)) d x. R 2 3 V integralu na desni imamo signal cos (2ω 0 t + φ(t)), ki ima zelo veliko frekvenco. Z uporabo visokofrekvenčnega filtra H odfiltriramo te visoke frekvence. Dobimo cos φ(t) H(s(t) cos ω 0 t) = ρ( x) d x. (35) R 2 3 Če začetni signal s(t) (enačba 34) pomnožimo še s signalom sin ω 0 t, po filtraciji visokih frekvenc dobimo sin φ(t) H(s(t) sin ω 0 t) = ρ( x) d x. (36) R
14 Od tu naprej lahko privzamemo, da bo obdelava podatkov potekala v računalniku, zato lahko enačbe prepišemo v kompleksni obliki. Enačbo (36) pomnožimo z imaginarno enoto i in prištejemo enačbi (35). Dobimo 2H(s(t) cos ω 0 t) + i2h(s(t) sin ω 0 t) = ρ( x)e iφ(t) d x. (37) R 3 in Uvedimo še oznake ( K(t) = γ t 0 G x (u)du, γ t 0 G y (u)du, γ t 0 ) G z (u)du (38) ( ) S K(t) = 2H(s(t) cos ω 0 t) + i2h(s(t) sin ω 0 t). (39) S čimer smo definiriali t. i. k prostor, kjer je k x = γ t 0 G x(u)du, k y = γ t 0 G y(u)du in k z = γ t 0 G z(u)du. Nazadnje pridemo do iskane zveze ( ) S K = R 3 ρ( x)e i x K d x. (40) ( ) V enačbi (40) je funkcija S K, ki jo pridobimo iz meritev, iščemo pa porazdelitev jeder v telesu ρ( x) in iz oblike enačbe je razvidno, da je S K ( ) ravno Fourierova transformiranka funkcije ρ( x). Funkcijo ρ( x) tako dobimo z obratno Fourierovo transformacijo. Iz matematične analize vemo, da je Fourierjeva transformacija funkcije f (f : R 3 C) definirana kot F ( ω) = f( t)e i ω t d t (41) R 3 ter da je njen inverz enak f( t) = 1 (2π) 3 R 3 F ( ω)e i ω t d ω. (42) Sedaj lahko na enačbi 40 uporabimo inverzno FT in dobimo ρ( x) = 1 ( ) K (2π) 3 e i x K d x. (43) R 3 S Za( določitev ) funkcije gostote jeder v telesu ρ( x) torej moramo poznati funkcijo S K za vse K R 3. Vse skupaj sedaj lahko povzamemo v sledeč postopek meritve; za izbrani K 0 R 3 izberemo gradiente G x (t), G y (t), G z (t) in čas t 0 tako, glej (38), da je K(t 0 ) = K 0. Po enačbi (39) ( je (filtrirana ) in kompleksna) vrednost izmerjenega signala ob času t 0 ravno S K0. To ponovimo za vse mogoče K R 3 in nato s pomočjo (43) izračunamo iskano gostoto ρ( x). 14
15 Opisani postopek načeloma deluje, vendar s praktičnega stališča ni uporaben. Najprej vidimo, da celoten postopek merjenja traja dolgo časa, ker naenkrat zajamemo le eno vrednost funkcije S, poleg tega pa nehomogenost magnetnega polja v MR aparatu povzroči, da se signal (34) oz. (37) s časom zelo hitro zaduši in s tem onemogoča zanesljivo meritev. Obema težavama se lahko izognemo tako, da predhodno izberemo rezino slikanja ter da pri slikanju uporabimo spinski odmev. 3.3 Izbira rezine Ker MR - signal izvira iz cele prostornine vzorca, lahko pred zajetjem signala izoliramo presek, za katerega želimo rekonstruirati sliko. To dosežemo s kombinirano uporabo gradienta G z in RF - oblikovanega pulza (slika 12). Ker običajno želimo vzbuditi jedra v rezini s škatlastim profilom bomo to najlažje dosegli, če bomo na sistem delovali z RF pulzom oblike sinc(x) = sin(x) x, saj nam da FT sinc funkcije škatlast profil. Tako obliko pulza imenujemo oblikovan oziroma mehek pulz. Resonančni pogoj bo izpolnjen samo za jedra, ki so v ravnini, pravokotni na ta gradient, tako, da bo signal izviral iz ozkega področja z debelino, ki je odvisna od obsega frekvenc, vsebovanih v RF - pulzu, in od velikosti gradienta magnetnega polja. 90 pulz je torej selektiven, z omejenim frekvenčnim območjem. Z večjim gradientom in istim pulzom bi bila debelina rezine tanjša. Slika 12: Izbira rezine. Nezaželjena posledica tega gradienta sta različna precesijska frekvenca posamezne plasti rezine in izguba fazne povezave jeder, ki bi bila brez gradienta po 90 pulzu prisotna. Posledica tega je majhen signal proste precesije, zato dodamo nasprotno predznačen gradient G z, ki povzroči ponovno zbiranje, tako da je izmerjeni signal ponovno fazno koherenten in zato veliko večji, kot bi bil brez tega dodatka. S tem, ko smo predhodno izbrali rezino slikanja, lahko sedaj za določitev gostote jeder v telesu ρ( x), uporabimo inverzno 2D FT (enačba 42) v xy ravnini in dobimo ρ(x, y) = 1 S (k x k y ) e i(kxx+kyy) dk x dk y. (44) 2π S 15
16 Metoda je sestavljena iz dveh delov: opazujemo fazo in frekvenco signala, ki ju uporabimo za prostorsko dekodiranje signala. Prvi del je uporaba t. i. faznega gradienta (G y ), ki mu postopoma spreminjamo amplitudo. Večja amplituda tega gradienta povzroči hitrejšo precesijo v izbrani točki in to ima za posledico serijo signalov, ki se v izbranem času zavrte za različne kote in se zato med sabo ločijo po fazah. V drugem delu pa uporabimo t. i. bralni gradient (G x ), ki povzroči frekvenčno kodiranje signala v vzorcu. Na sliki 13a je prikazan princip faznega kodiranja; trem namišljenim jedrom dovedemo RF pulz. Zaradi gradienta so le - ta v različnih poljih in začnejo precesirati z različnimi frekvencami (t = 0). Po času t = t lahko izmerimo razliko v fazah signalov (precesijski koti) kot posledico različnih precesijskih hitrosti. Na sliki 13b pa so na poenostavljeni sliki, ki predpostavlja, da so jedrski spini v enem samem delčku prostora, ilustrirani štirje od običajno 128 ali 256 fazno kodiranih korakov. V tem primeru je povečanje faznega gradienta G y v vsakem koraku dovolj močno, da zavrti fazni kot za določeno vrednost, v našem primeru 90. Tako vsak korak da signal, ki je fazno premaknjen za 90 za isto točko vzorca. V praksi ta proces ponavljamo v majhnih korakih z enakomernimi faznimi zamiki, ki pokrijejo polni kot. Število korakov določa dimenzijo matrike, ki mora biti zaradi hitrega računanja FT enaka 2 n (64, 128, 256, 512.) Slika 13: Slika a) prikazuje princip faznega kodiranja, slika b) pa princip 2D - FT. G y je pravokoten na G x in ena kobinacija teh dveh gradientov da eno črto podatkov. Ostale črte dobimo s spremembo amplitude G y. S spreminjanjem velikosti in trajanja gradienta lahko torej zajamemo različne točke v k prostoru. 3.4 Oprema laboratorija za MR slikanje Najpomembnejši del laboratorija za MR slikanje je seveda magnet od katerega zahtevamo, da ustvarja zelo močno ter čimbolj homogeno statično magnetno polje. Čim večja je jakost magneta, tem boljšo ločljivost slike lahko dobimo oziroma boljše razmerje med signalom in šumom pri izbrani ločljivosti. Tipično so jakosti polja velikostnega reda nekaj tesla (T), kar ustreza precesijskim frekvencam vodikovih jeder velikostnega red 100M Hz. Najpogosteje se uporabljajo 16
17 superprevodni magneti, ki se poleg stalnega močnega magnetnega polja odlikujejo tudi z zelo dobro stabilnostjo polja. Slabost superprevodnih magnetov je vzdrževanje tempreature pri 4K, za kar potrebujemo drag tekoči helij. Samo magnetno polje magneta ni nikoli dovolj homogeno, pa tudi vsak nov vzorec zaradi različne susceptibilnosti na svoj način poruši homogenost magnetnega polja. Zato je potrebno homogenost magneta izboljševati z dodatnimi t. i. shim tuljavami. Z ustrezno linearno kombinacijo teh polj lahko izboljšamo homogenost magnetnega polja v vzorcu. Poleg teh tuljav potrebujemo seveda tudi gradientne tuljave, ki so osnova za slikanje z MR, za ustvarjanje gradientnega polja v željeni smeri x, y ali z. Jakost teh gradientov je velikostnega reda 10mT/m. Naslednji nepogrešljivi element je RF sonda oziroma tuljavica v katero vstavimo vzorec. RF sonda je v bistvu nihajni krog uglašen na precesijske frekvence jeder. Od sonde zahtevamo, da ustvarja kar se da homogeno, vrteče se magnetno polje B 1. Zaradi potrebe po zelo visokih lastnih frekvencah nihajnega kroga, običajna solenoidna tuljava ni primerna, ker ima previsoko induktivnost. Zato se pogosteje uporabljajo sedlaste tuljave. Drugi del potrebne opreme za slikanje z MR pa predstavljajo elektronske komponente, ki povezujejo magnet z računalnikom in tako omogočajo izvajanje pulznih zporedij, zajem signala in njegovo obdelavo. Najpomembnejši del elektronske opreme je seveda računalnik, ki skrbi za izvajanje zaporedij za slikanje z MR, ima nadzor nad vso spremljajočo elektronsko opremo in računa slike iz zajetega MR - signala. Računalnik je namenjen tudi nadaljnji obdelavi slik in njihovem arhiviranju. Zelo pomemben del elektronske opreme pri MR slikanju je tudi MR spektrometer, ki je sestavljen iz več elektronskih komponent, kot so RF oscilator, generator oblik signalov, modulator, frekvenčni filtri,... Naloga spektrometra je, da pretvori sprejeti visokofrekvenčni RF signal v nižje frekvenčno področje in ga digitalizira. Ravno tako oblikuje RF in gradientne sunke, poskrbi, da je njihovo trajanje ustrezno ter, da je faza RF sunkov pravilna. Pod elektronsko opremo spada še RF oddajnik, ki skrbi za ojačitev šibkih RF sunkov iz spektrometra v močne RF sunke, ki jih vodimo na RF sondo. Sunkovna moč teh oddajnikov je več kw. Naj omenim še gradientne ojačevalnike, ki delujejo v področju slišnih frekvenc in ojačajo obliko gradientnih sunkov, ki jih dobijo iz spektrometra. Vsaka gradientna tuljava ima svoj gradientni ojačevalnik. Skica najpomembnejših delov opreme za slikanje z MR je prikazana na spodnji sliki (slika 14). Slika 14: Skica pomembnejših delov sistema za slikanje z MR. 17
18 4 POPAČITVE IN ARTEFAKTI Pri slikanju z magnetno resonanco lahko nastanejo razne popačitve oziroma t. i. artefakti, ki se pojavijo na sliki, vendar niso del slikanega vzroca. Artefakti lahko nastanejo zaradi premikanja pacienta oziroma vzorca, lahko so posledica nehomogenosti magnetnega polja oziroma so posledica interakcije med magnetom in različnimi tuljavami. Večina artefaktov pa je povezanih z samimi sekvencami slikanja, izbranimi parametri ter algoritmi za rekonstrukcijo slike. Zaradi pojava artefaktov lahko dobimo napačno sliko vzorca, kar lahko v primeru klinične uporabe vodi tudi do napačne diagnoze, zato je nujno da se artefaktov zavedamo in jih poskušamo odpraviti. V tem poglavju jih bomo omenili le nekaj. Glede na to, kaj je posledica izvora artefaktov, jih lahko v splošnem razdelimo na artefakte, ki so posledica našega vzorca, na artefakte, ki so posledica samega merilnega sistema ter na artefakti, ki se pojavijo zaradi eksperimentalne metodologije oziroma obdelave slike. 4.1 Artefakti zaradi gibanja vzorca V raziskovalne namene večinoma uporabljamo statične vzorce, kjer artefaktov zaradi premikanja ni. Vendar pa je slikanje z MR zelo razširjeno v klinični uporabi, kjer v večini primerov slikamo paciente, kjer zelo težko dosežemo popolno mirovanje, zato je nujno da poznamo artefakte, ki jih povzroča premikanje pacientov ter jih poskušamo odpraviti. Gibanje delov bolnika med zajemanjem signala vodi do neskladja v fazni koherenci in amplitudi transverzalne magnetizacije, kar lahko na sliki opazimo kot t. i. ghosting in bleščanje (slika 15). Ti artefakti se pojavijo v smeri faznega gradienta, ne glede na to v kateri smeri se je dejansko zgodil premik. Taka gibanja, ki povzročajo artefakte, so predvsem dihanje, bitje srca, žilno utripanje, mežikanje, požiranje... Do popačenja lahko pride tudi zaradi izkrivljenega glavnega magnetnega polja v prisotnosti feromagnetnih materialov, ki jih lahko ima pacient. Opazimo prostorsko izkrivljenost, področje manjšega signala, obkroženo s področjem visoke intenzitete ali področja obročev z visoko intenziteto. Slika 15: Popačenje MR slike zaradi dihanja pacienta med slikanjem. 18
19 4.2 Artefakti zaradi merilne naprave Artefakti lahko nastanejo tudi zaradi nehomogenosti v zunanjem magnetnem polju, ki nam lahko povzroči izkrivljanja tako v intenziteti kot v prostoru. Artefakti so lahko tudi posledica padca moči gradientov, kar je vidno kot stisnjenost slike vzdolž osi preobremenjenga gradienta. Nastanejo zaradi padca moči v gradientnem ojačevalcu, zaradi česar je gradient manjši od tistega, ki ga pričakuje računalnik. Artefakti, ki nastanejo zaradi nehomogenosti RF - odklonskega kota se kažejo kot zaplate s povečano ali zmanjšano intenziteto signala. Nastanejo zaradi sprememb jakosti RF pulza, ki so potrebne za odklon protonov za 90 ali 180 v izbrani rezini. 4.3 Artefakti zaradi zajemanja signala Ti artefakti so posledica načina zbiranja podatkov, njihove obdelave ter rekonstrukcije slike. Pri slikanju lahko premer slikanega vzorca preseže vidno polje, kar imenujemo popačenje zaradi potujevanja. Artefakt se pojavi zaradi majhne hitrosti vzorčenja v frekvenčno kodirani smeri. Napaka izgleda kot serija sledi slik vzdolž frekvenčno kodirane osi slikanega objekta (slika 16). Slika 16: Artefakti zaradi potujevanja. Artefakti nastanejo tudi zaradi kemijskega premika, ki v tkivu nastane zaradi razlike v Larmorjevi frekvenci vodikovih molekul v vodi in v maščobi. Popačenje zaradi kemijskega premika nastane samo vzdolž frekvenčno kodirane osi kot pas visoke ali nizke intenzitete na robu strukture z visoko vsebnostjo maščobe. V tej osi sta tako za nekaj točkovnih elementov zamaknjeni sliki; ena pripada vodi, druga maščobi. Poznamo pa tudi popačenje zaradi t.i. skrajšanja, kar poznamo kot Gibbsovo zvonjenje (slika 17). Skrajšana Fourierjeva vrsta ali končno število sinusnih valov ne more popolnoma opisati hitrih sprememb. Popačenje ima zaradi tega obliko pasov visoke in nizke intenzitete, ki so vzporedni področjem hitrih sprememb. To popačenje lahko povzroči težavo pri opisu majhnih struktur kot na primer meniskus pri kolenu. O Gibbsovem pojavu oziroma Gibbsovemu zvonjenju ter kako se ga vsaj deloma znebiti, bomo več povedali v naslednjih poglavjih. 19
20 Slika 17: Gibbsovo zvonjenje. 5 HITRE METODE SLIKANJA Običajna metoda slikanja z magnetno resonanco, ki temelji na uporabi spinskega omeva, je zelo stabilna in da kontrastno bogate slike. Vendar pa je pogosto prepočasna, da bi bila primerna za klinično uporabo, ki narekuje le nekaj minuten čas zajemnja slikovnega signala. Težava metode spinskega slikanja s spinskim odmevom je v tem, da zajemamo pri njej vsakič le signal ene same vrstice slike v k - prostoru. Čas zajemnja signala lahko zapišemo kot t = pnt R, (45) kjer je p število povprečevanj, n število vrstic slike in TR (repetition time) čas med dvema sosednjima korakoma. Torej celoten zajem signala traja toliko časa, kot ima slika vrstic, pomnoženo s časom ponavljanja zaporedja TR, s katerim merimo čas zajemanja signala med dvema zaporednima vrsticama. Pri nekaterih metodah slikanja je čas TR lahko precej dolg, saj le tako lahko dosežemo primeren slikovni kontrast. To še posebej velja za slikanje s T2 in s protonsko obtežitvijo. Tako lahko slikanje traja tudi več minut. To težavo lahko odpravimo tako, da uporabimo zaporedje z več zaporednimi spinskimi odmevi in v vsakem odmevu zajamemo signal iz nove vrstice k - prostora, čas TR pa ostane enako dolg ter se s tem ohrani tudi željeni kontrast slike. To zaporedje slikanja se imenuje Rapid Acquisition with Relaxation Enhancement (RARE). RARE metoda slikanja je od običajne metode slikanja s spinskim odmevom hitrejša tolikokrat kolikor je zaporednih spinskih odmevov v zaporedju RARE, to število tudi imenujemo turbo faktor (N). 5.1 Metoda spinskega odmeva Da bi bolje razumeli princip delovanja matode RARE, si najprej poglejmo običajno tehniko slikanja s spinskim odmevom, na kateri temelji hitra metoda RARE. Z 90 pulzom vzbudimo jedra vzorca v precesijo ter hkrati vklopimo tudi gradient Gz s katerim izberemo rezino slikanja. Z gradientoma Gy in Gx definiramo vrstico, ki jo želimo prebrati v k - prostoru. Recimo, da imamo konstantno velikost bralnega gradienta in da zajemamo signal v N različnih točkah s časovnim intervalom vzorčenja T 20
21 k x = γg 0 T j; j = 0, 1,..., N 1. (46) S tem v korakih zajamemo vse točke pozitivnega poltraka k x. Da zajamemo tudi točke negativnega poltraka, pred začetkom zajemanja vklopimo za polovični čas nameravanega zajemnaja signala, še negativni bralni gradient G x : G x T 2 = G xnt. S tem smo dobili signal za vse željene točke k x ravnine, vendar le pri vrednosti k y = 0. Da bomo lahko naredili 2D rekonstrukcijo, moramo zajem opraviti še za vse ostale vrednosti k y, tako da bom res zajeli signal iz celotnega k prostora. To naredimo z faznim gradientom. Pred začetkom zajemanja signala za nek fiksen čas t y vklopimo fazni gradient G y v y smeri. Njegova vrednost se ob vsaki ponovitvi zajema signala po času TR enakomerno poveča. Tako smo dosegli zajem signala pri različnih vrednostih k y. Po vklopu gradientov za izbiro vrstice pa sledi sunek 180, ki ustvari spinski odmev, ki ga s pomočjo bralnega gradienta zabeležimo. Celotno zaporedje ponovimo tolikokrat kot je potrebno, da preberemo vse vrstice k - ravnine (kot je opisano zgoraj), pri čemer lahko z različno izbiro parametrov TE (echo time) in TR določamo željen kontrast. Pri metodi spinskega odmeva moramo torej zaporedje velikokrat ponavljati, kar je lahko časovno zelo zamudno. Zaporedje za slikanje s spinskim odmevom je prikazano na spodnji sliki (slika 18) Slika 18: Zaporedje za slikanje s spinskim odmevom. 5.2 RARE Metoda RARE lahko bistveno skrajša čas zajemanja signala, saj nam omogoča beleženje signala več vrstic hkrati pri eni vzbuditvi. Ideja tehnike večkratnega spinskega odmeva je, da po eni vzbuditvi s pulzom 90 z več zaporednimi pulzi 180 ustvarimo več spinskih odmevov, s katerimi posnamemo različne dele k - ravnine. Spinske odmeve lahko ponavljamo, dokler nam T 2 relaksacija ne uniči signala. Osnovna sekvenca je prikazana na spodnji shemi (slika 19) Začetni del je enak kot pri običajnem slikanju s spinskim odmevom. Najprej z 90 pulzom vzbudimo jedra vzorca v precesijo, čemur sledi signal proste precesije ter hkrati z ustreznim gradientom G z izberemo rezino, ki jo želimo posneti. Nato generiramo več pulzov 180 ter posledično zabeležimo več spinskih odmevov. Pomembna razlika med tehniko slikanja s spinskim odmevom in RARE pa je ravno v uporabi faznih gradientov, ki jih tu vklopimo po vsakem pulzu
22 Slika 19: Zaporedje za slikanje z metodo RARE. posebej. Na ta način k - prostor razdelimo na bloke, ki jih posnamemo znotraj ene ponovitve zaporedja. Teh je toliko, kolikor je zaporednih odmevov (N) zaporedja RARE. V vsakem odmevu zajamemo signal ene vrstice k - prostora iz naslednjega bloka. Na primer, če ima slika M vrstic in M stolpcev in je turbo faktor, kar predstavlja število odmevov, enak N, potem bomo imeli k - prostor razdeljen na N blokov po M/N vrstic. V prvi ponovitvi zaporedja bomo zajeli signal prve vrstice prvega bloka, prve vrstice drugega bloka,...,prve vrstice N - tega bloka. Temu bo sledila druga ponovitev, v kateri bomo zajeli drugo vrstico prvega bloka, drugo vrstico drugega bloka,..., drugo vrstico N - tega bloka. V zadnji (M/N) ponovitvi zaporedja bomo zajeli signal M/N - te vrtsice prvega bloka, M/N - te vrstice drugega bloka,... in M/N - te vrstice N - tega bloka. Različni bloki si lahko v k - prostoru sledijo zaporedno (sekvenčno vzorčenje k - prostora), lahko so razvrščeni od sredine navzven (centrično vzorčenje k - prostora) ali pa od roba proti sredini (obratno centrično vzorčenje k - prostora). Vsi trije različni pristopi so prikazani na sliki 20, kjer je v prvem odmevu zaporedja RARE vzorčena vrstica rdečega bloka, v drugem odmevu vrstica modrega bloka, v tretjem odmevu vrstica zelenega bloka in v četrtem odmevu vrstica modrega bloka. V zaporednih izvedbah zaporedja RARE za primer b) in c), kjer so bloki razdeljeni na spodnjo in zgornjo polovico, vzorčimo najprej vrstice zgornjih polovic blokov in nato vrstice spodnjih polovic blokov. Slika 20: Različni načini razvrstitve blokov vzorčenja signala v k - prostoru za N = 4: a) sekvenčna, b) centrična in c) obratno centrična. Torej, če imamo zaporednih odmevov N oziroma imamo k - prostor razdeljen na N blokov, smo hitrost beleženja signala povečali za N - krat v primerjavi z običajno tehniko slikanja s spinskim odmevom. Na primer, če je čas slikanja 22
23 z metodo spinskega odmeva slike velikosti približno 256T R, kar je velikostnega red 256s, se čas slikanja z metodo RARE, ki ima turbo faktor 16, skrajša na 256T R/16 16s. Na sliki 21 pa si poglejmo, kako se z pulznim zaporedjem RARE gibljemo po k ravnini. Slika 21: Pot po k ravnini pri metodi RARE. Po vzbuditvi jeder v precesijo smo v izhodišči k = 0. Z vklopom gradienta G x se pomaknemo v točko A, od koder nas pulz 180 prezrcali v točko B. Pulz 180 namreč spremeni predznak fazi, kar pomeni spremembo predznaka pri k x in k y, torej zrcaljenje čez izhodišče k - ravnine. S kratkim vklopom faznega gradienta G y se premaknemo v točko C, nato pa vklopimo bralni gradient, ki premika vektor proti točki D. Med tem časom vzorčimo signal spinskega odmeva. Ko dosežemo maksimalni k x, se z vklopom G y, ki ima nasproten predznak kot prej, ponovno premaknemo v točko A, od tam pa z novim pulzom 180 v točko B. Nato se z drugo vrednostjo faznega gradienta G y pomaknemo v točko E, kjer enako kot prej posnamemo spinski odmev vrstice v novem bloku z naslednjo vrednostjo k y. In, kot smo že omenili, to branje vrstic v blokih k - ravnine lahko s pulzi 180 ponavljamo tako dolgo, dokler T 2 relaksacija ne pokvari signala. Hitra metoda slikanja RARE ima mnoge prednosti. Njena uporabnost je predvsem v tem, da zelo hitro lahko dobimo gostotno ali T 2 uteženo sliko. Signal MR slike se spreminja v odvisnosti od parametrov meritve TE in TR, kar nam opisuje tudi spodnja enačba ( ) signal ρe T E T 2 1 e T R T 1. (47) Pri metodi slikanja RARE imamo dolge čase ponavljanja zaporedja, torej T R oziroma T R T 1, in kratke TE, s čimer dobimo gostotno uteženo sliko, oziroma imamo TE primerljiv s časom spinsko - spinske relaksacije (T 2 ), kar nam da T 2 utežene slike. Zaradi hitrosti zajemanja signala metode večkratnega spinskega odmeva se lahko znebimo artefaktov, ki bi jih lahko povzročalo pacientovo gibanje med samim slikanjem. Kljub temu da je metoda hitrega slikanja RARE zelo uporabna in v klinični uporabi danes praktično nepogrešljiva, ima kar nekaj pomanjkljivosti, saj je zelo občutljiva in lahko kljub vsemu še vedno pride do pojava več različnih artefak- 23
24 tov, predvsem tistih, ki so posledica zajemanja signala, obdelave podatkov ter rekonstrukcije slike. 5.3 Gibbsovo zvonjenje Pri metodi RARE imamo torej k - prostor razdeljen na bloke, ki si lahko sledijo zaporedno, centrično ali obratno centrično (slika 20). Poglejmo si primer, kjer si bloki sledijo centrično. Po vsaki vzbuditvi najprej posnamemo signale, ki pripadajo najmanjšim vrednostim k y. Različne vrednosti k y lahko označimo z indeksi, ki povedo, v kateri vrstici gor ali dol iz središča k ravnine so. Primer zaporedja izbranih k y po eni vzbuditvi je lahko 0, 16, 17, 32, 33, 48, 49, 64, 65, 80, 81, 96, 97, 112, 113, 128. To je 16 vrednsoti k y, ki jih posnamemo s 16 zaporednimi spinskimi odmevi. Ostale dobimo tako, da navedeno zaporedje namesto v 0 začnemo v 8, 7, 6,..., +7 (razen 0). Tako zajamemo vseh 256 točk k ravnine. Tak način zajemanja ima prednost, da so nižji bloki posneti čim prej po vzbujanju jeder, kjer imamo še dovolj signala, saj nam nižji bloki določajo kontrast slike. Pomanjkljivost zajemanja signala po blokih pa je, da potek signalov vrstic različnih blokov ne poteka zvezno, ampak v korakih. Posledica tega nezveznega poteka signalov je popačitev slik v obliki Gibbsovega zvonjenja. Gibbsove zvonjenje je na sliki vidno v obliki več pasov (obročev) z visoko in nizko intenziteto. Ti pasovi so vzporedni s hitrimi spremembami v intenziteti signala. Posledica Gibbsovega zvonjenja je lahko tudi navidezno razširjanje robov. Slika 22: Primer Gibbsovega zvonjenje. Gibbsovo zvonjenje se pojavi kot posledica uporabe Fourierjeve transformacije pri rekonstrukcije MR slike, ker uporabimo podatke za rekonstrukcijo le iz končno velikega območja k ravnine in imamo tako skrajšano Fourierjevo vrsto. Na sliki 23a je prikazan signal, ki nam kaže primer nezvezenga poteka intenzitete signala vrstic. Če na tem signalu uporabimo Fourierjevo transformacijo, vidimo (slika 23b), da na obeh straneh nezveznosti dobimo več valov, kar nam opisuje Gibbsovo zvonjenje. Če bi lahko uporabili podatke iz neskončnega k prostora teh valov ne bi dobili, ampak bi dobili zopet stopničasto funkcijo, kot je prikazno na sliki 23b pod valovi. 24
25 Slika 23: a) Grafičen prikaz razlike v intenziteti signala. b) Grafičen prikaz Fourierjeve transformacije signala, ki ima nezvezen prehod intenzitete. Slika 24: Gibbsovo zvonjenje, ki ga dobimo zaradi skrajšane FT pri nezveznih prehodih intenzitete. 5.4 Odprava popačitev Gibbsovega zvonjenja Za odpravo popačitev v obliki Gibbsovega zvonjenja je v uporabi več različnih načinov in metod. V diplomski nalogi pa smo preizkusili in predstavili dve različni, nekoliko novejši, metodi. Ker so signali vrstic zaporednih blokov zajeti v zaporedno zakasnjenih spinskih odmevih (med njimi je časovna zakasnitev TE), so zaradi procesa spinsko - spinske jedrske relaksacije različno močno T 2 obteženi. Tako signal vrstice j - tega bloka, ki je zajet v j - tem odmevu ob čau jte, zapišemo z enačbo ( ) S j = ρe jt E T 2 1 e T R T 1. (48) Kot smo že omenili, je posledica različne obtežitve signalov vrstic različnih blokov popačitev v obliki Gibbsovega zvonjenja. Tem popačitvam bi se lahko izognili, če bi odpravili odvisnost signalov od zaporedja blokov zajema signala, kar pomeni neodvisnost enačbe 48 od j. Do neke mere lahko to dosežemo tako, da signale vrstic pred rekonstrukcijo slike množimo s faktorjem upada signala zaradi spinsko - spinske relaksacije S j = S j ρe jt E T 2. (49) Ta pristop zahteva poznavanje relaksacijskega časa T 2 vzorca, kar v osnovi ni težavno, če je vzorec homogen in ima en sam relaksacijski čas T 2. Vendar pa je 25
26 pri slikanju z magnetno resonanco večina vzorcev zelo heterogenih in ima precej različne relaksacijske čase v različnih delih vzorca. V teh primerih se tak pristop precej slabše obnese, saj moramo uporabiti nekakšen pričakovan povprečen T 2 relaksacijski čas vzorca. Zato smo poizkusili zmanjšati vpliv Gibbsovega zvonjenja še z drugo metodo. Poglejmo si primer za sekvenčno vzorčenje k - prostora (slika 20a)). Denimo, da indeks i označuje pri sekvenčnem zaporedju zaporedno vrstico posameznega bloka in zaseda vrednosti od 0 (prva vrstica) pa do M/N 1 (zadnja vrstica). Indeks blokov j pa naj se giblje od 1 (prvi blok) do N (zadnji blok). Zvezni prehod signalov vrstic med bloki lahko dosežemo tako, da se signali različnih vrstic znotraj istega bloka tako spreminjajo, da eksponentno padajo proti signalu prve vrstice naslednjega bloka (slika 25). Slika 25: Potek relativnih signalov vrstic pri sekvenčni razporeditvi blokov zajemanja signalov v zaporedju RARE, kjer je z rdečo označen nezvezen potek signalov vrstic, ki ga dobimo z običajnim zaporedjem RARE, medtem ko je z modro označen zvezen potek signalov vrstic, ki ga dobimo z spreminjajočim časom ponavljanja zaporedja. To padanje bi zopet lahko dosegli z ustreznim množenjem vrstic pred rekonstrukcijo slike, lahko pa za to padanje poskrbimo tudi s premišljenim zajemanjem signalov vrstic z različnim indekosm i, saj vse vrstice istega indeksa i zajamemo v isti i - ti ponovitvi zaporedja RARE. Poleg tega pa lahko na signal i - te ponovitve vplivamo tudi tako, da ustrezno spremenimo čas ponavljanja zaporedja TR. Tega bomo odslej imenovali kar T R i. Z združevanjem obeh zahteve po zveznem in eksponentnem padanju signalov zaporednih vrstic ter zahteve po ustreznem spreminjanju časa ponavljanja zaporedja T R i dobimo naslednjo enačbo ( ) ( ) ρe (j+i/(m/n))t E T 2 1 e T R T 1 = ρe jt E T 2 1 e T R i T 1. (50) Rešitev zgornje enačbe je neodvisna od indeksa blokov j, saj se ta okrajša in je tako rešitev odvisna le od indeksa i in parametrov slikanja ( )) T R i = T 1 ln (1 e (i/(m/n))t E T 2 1 e T R T 1. (51) 26
27 V običajnih pogojih slikanja je čas spinskega odmeva TE mnogo krajši od relaksacijskega časa T 2 vzorca. Poleg tega lahko na intenziteto signala vplivamo preko spreminjanja časa ponavljanja zaporedja le, kadar ta ni predlog v primerjavi s T 1. Če je ta velikostnega reda T 1 ali celo krajši od T 1, se zgornja enačba poenostavi v obliko ( T R i = T R 1 (i/(m/n))t E ). (52) T 2 Za izračun T R i moramo še vedno poznati relaksacijski čas T 2, a je od točnega poznavanja tega končni rezultat slike manj odvisen kot pri prvi predstavljeni metodi množenja signalov vrstic pred rekonstrukcijo slike. 6 PRIPRAVA EKSPERIMENTA Literatura 27
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
11 Slikanje z jedrsko magnetno resonanco
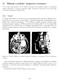 11 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
11 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
12 Slikanje z jedrsko magnetno resonanco
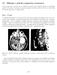 12 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
12 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Matematika 2. Diferencialne enačbe drugega reda
 Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
diferencialne enačbe - nadaljevanje
 12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Petek, 12. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
Analiza 2 Rešitve 14. sklopa nalog
 Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU
 NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU Equatio n Section 6Vsebina poglavja: Navor kot vektorski produkt ročice in sile, magnetni moment, navor na magnetni moment, d'arsonvalov ampermeter/galvanometer.
NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU Equatio n Section 6Vsebina poglavja: Navor kot vektorski produkt ročice in sile, magnetni moment, navor na magnetni moment, d'arsonvalov ampermeter/galvanometer.
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
Reševanje sistema linearnih
 Poglavje III Reševanje sistema linearnih enačb V tem kratkem poglavju bomo obravnavali zelo uporabno in zato pomembno temo linearne algebre eševanje sistemov linearnih enačb. Spoznali bomo Gaussovo (natančneje
Poglavje III Reševanje sistema linearnih enačb V tem kratkem poglavju bomo obravnavali zelo uporabno in zato pomembno temo linearne algebre eševanje sistemov linearnih enačb. Spoznali bomo Gaussovo (natančneje
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
VEKTORJI. Operacije z vektorji
 VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba.
 1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
vezani ekstremi funkcij
 11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant.
 Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Vaja: Odbojnostni senzor z optičnimi vlakni. Namen vaje
 Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
1 Fibonaccijeva stevila
 1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
Osnove matematične analize 2016/17
 Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
DISKRETNA FOURIERJEVA TRANSFORMACIJA
 29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
Navadne diferencialne enačbe
 Navadne diferencialne enačbe Navadne diferencialne enačbe prvega reda V celotnem poglavju bo y = dy dx. Diferencialne enačbe z ločljivima spremeljivkama Diferencialna enačba z ločljivima spremeljivkama
Navadne diferencialne enačbe Navadne diferencialne enačbe prvega reda V celotnem poglavju bo y = dy dx. Diferencialne enačbe z ločljivima spremeljivkama Diferencialna enačba z ločljivima spremeljivkama
FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22. junij Navodila
 FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22 junij 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Veljale bodo samo rešitve na papirju, kjer
FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22 junij 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Veljale bodo samo rešitve na papirju, kjer
17. Električni dipol
 17 Električni dipol Vsebina poglavja: polarizacija prevodnika (snovi) v električnem polju, električni dipolni moment, polarne in nepolarne snovi, dipol v homogenem in nehomogenem polju, potencial in polje
17 Električni dipol Vsebina poglavja: polarizacija prevodnika (snovi) v električnem polju, električni dipolni moment, polarne in nepolarne snovi, dipol v homogenem in nehomogenem polju, potencial in polje
Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja D R priredi neko število f (x) R.
 II. FUNKCIJE 1. Osnovni pojmi 2. Sestavljanje funkcij 3. Pregled elementarnih funkcij 4. Zveznost Kaj je funkcija? Definicija Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja D R priredi
II. FUNKCIJE 1. Osnovni pojmi 2. Sestavljanje funkcij 3. Pregled elementarnih funkcij 4. Zveznost Kaj je funkcija? Definicija Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja D R priredi
Najprej zapišemo 2. Newtonov zakon za cel sistem v vektorski obliki:
 NALOGA: Po cesi vozi ovornjak z hirosjo 8 km/h. Tovornjak je dolg 8 m, širok 2 m in visok 4 m in ima maso 4 on. S srani začne pihai veer z hirosjo 5 km/h. Ob nekem času voznik zaspi in ne upravlja več
NALOGA: Po cesi vozi ovornjak z hirosjo 8 km/h. Tovornjak je dolg 8 m, širok 2 m in visok 4 m in ima maso 4 on. S srani začne pihai veer z hirosjo 5 km/h. Ob nekem času voznik zaspi in ne upravlja več
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
UPOR NA PADANJE SONDE V ZRAKU
 UPOR NA PADANJE SONDE V ZRAKU 1. Hitrost in opravljena pot sonde pri padanju v zraku Za padanje v zraku je odgovorna sila teže. Poleg sile teže na padajoče telo deluje tudi sila vzgona, ki je enaka teži
UPOR NA PADANJE SONDE V ZRAKU 1. Hitrost in opravljena pot sonde pri padanju v zraku Za padanje v zraku je odgovorna sila teže. Poleg sile teže na padajoče telo deluje tudi sila vzgona, ki je enaka teži
Tema 1 Osnove navadnih diferencialnih enačb (NDE)
 Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
Matematika. Funkcije in enačbe
 Matematika Funkcije in enačbe (1) Nariši grafe naslednjih funkcij: (a) f() = 1, (b) f() = 3, (c) f() = 3. Rešitev: (a) Linearna funkcija f() = 1 ima začetno vrednost f(0) = 1 in ničlo = 1/. Definirana
Matematika Funkcije in enačbe (1) Nariši grafe naslednjih funkcij: (a) f() = 1, (b) f() = 3, (c) f() = 3. Rešitev: (a) Linearna funkcija f() = 1 ima začetno vrednost f(0) = 1 in ničlo = 1/. Definirana
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
 I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
SEMINARSKA NALOGA Funkciji sin(x) in cos(x)
 FAKULTETA ZA MATEMATIKO IN FIZIKO Praktična Matematika-VSŠ(BO) Komuniciranje v matematiki SEMINARSKA NALOGA Funkciji sin(x) in cos(x) Avtorica: Špela Marinčič Ljubljana, maj 2011 KAZALO: 1.Uvod...1 2.
FAKULTETA ZA MATEMATIKO IN FIZIKO Praktična Matematika-VSŠ(BO) Komuniciranje v matematiki SEMINARSKA NALOGA Funkciji sin(x) in cos(x) Avtorica: Špela Marinčič Ljubljana, maj 2011 KAZALO: 1.Uvod...1 2.
Če je električni tok konstanten (se ne spreminja s časom), poenostavimo enačbo (1) in dobimo enačbo (2):
 ELEKTRIČNI TOK TEOR IJA 1. Definicija enote električnega toka Električni tok je gibanje električno nabitih delcev v trdnih snoveh (kovine, polprevodniki), tekočinah ali plinih. V kovinah se gibljejo prosti
ELEKTRIČNI TOK TEOR IJA 1. Definicija enote električnega toka Električni tok je gibanje električno nabitih delcev v trdnih snoveh (kovine, polprevodniki), tekočinah ali plinih. V kovinah se gibljejo prosti
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Definicija. definiramo skalarni produkt. x i y i. in razdaljo. d(x, y) = x y = < x y, x y > = n (x i y i ) 2. i=1. i=1
 Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
INDUCIRANA NAPETOST (11)
 INDUCIRANA NAPETOST_1(11d).doc 1/17 29.3.2007 INDUCIRANA NAPETOST (11) V tem poglavju bomo nadgradili spoznanja o magnetnih pojavih v stacionarnih razmerah (pri konstantnem toku) z analizo razmer pri časovno
INDUCIRANA NAPETOST_1(11d).doc 1/17 29.3.2007 INDUCIRANA NAPETOST (11) V tem poglavju bomo nadgradili spoznanja o magnetnih pojavih v stacionarnih razmerah (pri konstantnem toku) z analizo razmer pri časovno
Matrike. Poglavje II. Matrika je pravokotna tabela realnih števil. Na primer: , , , 0 1
 Poglavje II Matrike Matrika je pravokotna tabela realnih števil Na primer: [ ] 1 1 1, 2 3 1 1 0 1 3 2 1, 0 1 4 [ ] 2 7, Matrika je sestavljena iz vrstic in stolpcev Vrstici matrike [ ] 1 1 1 2 3 1 [ ]
Poglavje II Matrike Matrika je pravokotna tabela realnih števil Na primer: [ ] 1 1 1, 2 3 1 1 0 1 3 2 1, 0 1 4 [ ] 2 7, Matrika je sestavljena iz vrstic in stolpcev Vrstici matrike [ ] 1 1 1 2 3 1 [ ]
MERITVE LABORATORIJSKE VAJE. Študij. leto: 2011/2012 UNIVERZA V MARIBORU. Skupina: 9
 .cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
.cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
cot x ni def. 3 1 KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA (A) Merske enote stopinja [ ] radian [rad] 1. Izrazi kot v radianih.
![cot x ni def. 3 1 KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA (A) Merske enote stopinja [ ] radian [rad] 1. Izrazi kot v radianih. cot x ni def. 3 1 KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA (A) Merske enote stopinja [ ] radian [rad] 1. Izrazi kot v radianih.](/thumbs/72/66438140.jpg) TRIGONOMETRIJA (A) Merske enote KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA stopinja [ ] radian [rad] 80 80 0. Izrazi kot v radianih. 0 90 5 0 0 70. Izrazi kot v stopinjah. 5 8 5 (B) Definicija kotnih funkcij
TRIGONOMETRIJA (A) Merske enote KOTNE FUNKCIJE POLJUBNO VELIKEGA KOTA stopinja [ ] radian [rad] 80 80 0. Izrazi kot v radianih. 0 90 5 0 0 70. Izrazi kot v stopinjah. 5 8 5 (B) Definicija kotnih funkcij
Gradniki TK sistemov
 Gradniki TK sistemov renos signalov v višji rekvenčni legi Vsebina Modulacija in demodulacija Vrste analognih modulacij AM M FM rimerjava spektrov analognih moduliranih signalov Mešalniki Kdaj uporabimo
Gradniki TK sistemov renos signalov v višji rekvenčni legi Vsebina Modulacija in demodulacija Vrste analognih modulacij AM M FM rimerjava spektrov analognih moduliranih signalov Mešalniki Kdaj uporabimo
MAGNETNI MATERIALI. 1. Mehkomagnetni materiali 2. Trdomagnetni materiali
 MAGNETNI MATERIALI 1. Mehkomagnetni materiali 2. Trdomagnetni materiali Magnetni materiali in njihove lastnosti Slika 5.1 Magnetenje različnih vrst snovi Magnetne lastnosti snovi v B = µ v H Permeabilnost
MAGNETNI MATERIALI 1. Mehkomagnetni materiali 2. Trdomagnetni materiali Magnetni materiali in njihove lastnosti Slika 5.1 Magnetenje različnih vrst snovi Magnetne lastnosti snovi v B = µ v H Permeabilnost
3. VAJA IZ TRDNOSTI. Rešitev: Pomik v referenčnem opisu: u = e y 2 e Pomik v prostorskem opisu: u = ey e. e y,e z = e z.
 3. VAJA IZ TRDNOSTI (tenzor deformacij) (pomiki togega telesa, Lagrangev in Eulerjev opis, tenzor velikih deformacij, tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Gumijasti
3. VAJA IZ TRDNOSTI (tenzor deformacij) (pomiki togega telesa, Lagrangev in Eulerjev opis, tenzor velikih deformacij, tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Gumijasti
3. AMPEROV ZAKON. SLIKA: Zanka v magnetnem polju. Integral komponente magnetnega polja v smeri zanke je sorazmeren toku, ki ga zanka oklepa.
 3. AMPEROV ZAKON Equation Section 3 Vsebina poglavja: Integral polja po zaključeni zanki je sorazmeren toku, ki ga zanka objame. Izračuni polja s pomočjo Amperovega zakona za: tokovno premico, solenoid,
3. AMPEROV ZAKON Equation Section 3 Vsebina poglavja: Integral polja po zaključeni zanki je sorazmeren toku, ki ga zanka objame. Izračuni polja s pomočjo Amperovega zakona za: tokovno premico, solenoid,
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA
 Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
Domače naloge za 2. kolokvij iz ANALIZE 2b VEKTORSKA ANALIZA. Naj bo vektorsko polje R : R 3 R 3 dano s predpisom R(x, y, z) = (2x 2 + z 2, xy + 2yz, z). Izračunaj pretok polja R skozi površino torusa
Kvadratne forme. Poglavje XI. 1 Definicija in osnovne lastnosti
 Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
11.5 Metoda karakteristik za hiperbolične PDE
 11.5 Metoda karakteristik za hiperbolične PDE Hiperbolična kvazi linearna PDE ima obliko au xx + bu xy + cu yy = f, (1) kjer so a, b, c, f funkcije x, y, u, u x in u y, ter velja b 2 4ac > 0. Če predpostavimo,
11.5 Metoda karakteristik za hiperbolične PDE Hiperbolična kvazi linearna PDE ima obliko au xx + bu xy + cu yy = f, (1) kjer so a, b, c, f funkcije x, y, u, u x in u y, ter velja b 2 4ac > 0. Če predpostavimo,
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
3.1 Reševanje nelinearnih sistemov
 3.1 Reševanje nelinearnih sistemov Rešujemo sistem nelinearnih enačb f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n ) = 0. f n (x 1, x 2,..., x n ) = 0. Pišemo F (x) = 0, kjer je x R n in F : R n
3.1 Reševanje nelinearnih sistemov Rešujemo sistem nelinearnih enačb f 1 (x 1, x 2,..., x n ) = 0 f 2 (x 1, x 2,..., x n ) = 0. f n (x 1, x 2,..., x n ) = 0. Pišemo F (x) = 0, kjer je x R n in F : R n
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
S53WW. Meritve anten. RIS 2005 Novo Mesto
 S53WW Meritve anten RIS 2005 Novo Mesto 15.01.2005 Parametri, s katerimi opišemo anteno: Smernost (D, directivity) Dobitek (G, gain) izkoristek (η=g/d, efficiency) Smerni (sevalni) diagram (radiation pattern)
S53WW Meritve anten RIS 2005 Novo Mesto 15.01.2005 Parametri, s katerimi opišemo anteno: Smernost (D, directivity) Dobitek (G, gain) izkoristek (η=g/d, efficiency) Smerni (sevalni) diagram (radiation pattern)
Spoznajmo sedaj definicijo in nekaj osnovnih primerov zaporedij števil.
 Zaporedja števil V matematiki in fiziki pogosto operiramo s približnimi vrednostmi neke količine. Pri numeričnemu računanju lahko npr. število π aproksimiramo s števili, ki imajo samo končno mnogo neničelnih
Zaporedja števil V matematiki in fiziki pogosto operiramo s približnimi vrednostmi neke količine. Pri numeričnemu računanju lahko npr. število π aproksimiramo s števili, ki imajo samo končno mnogo neničelnih
Dragi polinom, kje so tvoje ničle?
 1 Dragi polinom, kje so tvoje ničle? Vito Vitrih FAMNIT - Izlet v matematično vesolje 17. december 2010 Polinomi: 2 Polinom stopnje n je funkcija p(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, a i R.
1 Dragi polinom, kje so tvoje ničle? Vito Vitrih FAMNIT - Izlet v matematično vesolje 17. december 2010 Polinomi: 2 Polinom stopnje n je funkcija p(x) = a n x n + a n 1 x n 1 +... + a 1 x + a 0, a i R.
vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov
 28. 3. 11 UV- spektrofotometrija Biuretska metoda Absorbanca pri λ=28 nm (A28) UV- spektrofotometrija Biuretska metoda vstopni žarek intenziteta I Lowrijeva metoda Bradfordova metoda Bradfordova metoda
28. 3. 11 UV- spektrofotometrija Biuretska metoda Absorbanca pri λ=28 nm (A28) UV- spektrofotometrija Biuretska metoda vstopni žarek intenziteta I Lowrijeva metoda Bradfordova metoda Bradfordova metoda
VAJE IZ NIHANJA. 3. Pospešek nihala na vijačno vzmet je: a. stalen, b. največji v skrajni legi, c. največji v ravnovesni legi, d. nič.
 VAJE IZ NIHANJA Izberi pravilen odgovor in fizikalno smiselno utemelji svojo odločitev. I. OPIS NIHANJA 1. Slika kaže nitno nihalo v ravnovesni legi in skrajnih legah. Amplituda je razdalja: a. Od 1 do
VAJE IZ NIHANJA Izberi pravilen odgovor in fizikalno smiselno utemelji svojo odločitev. I. OPIS NIHANJA 1. Slika kaže nitno nihalo v ravnovesni legi in skrajnih legah. Amplituda je razdalja: a. Od 1 do
POROČILO. št.: P 1100/ Preskus jeklenih profilov za spuščen strop po točki 5.2 standarda SIST EN 13964:2004
 Oddelek za konstrkcije Laboratorij za konstrkcije Ljbljana, 12.11.2012 POROČILO št.: P 1100/12 680 01 Presks jeklenih profilov za spščen strop po točki 5.2 standarda SIST EN 13964:2004 Naročnik: STEEL
Oddelek za konstrkcije Laboratorij za konstrkcije Ljbljana, 12.11.2012 POROČILO št.: P 1100/12 680 01 Presks jeklenih profilov za spščen strop po točki 5.2 standarda SIST EN 13964:2004 Naročnik: STEEL
11. Vaja: BODEJEV DIAGRAM
 . Vaja: BODEJEV DIAGRAM. Bodejev diagram sestavljata dva grafa: a) amplitudno frekvenčni diagram in b) fazno frekvenčni diagram Decibel je enota za razmerje dveh veličin. Definicija: B B 0log0 A A db Bodejeve
. Vaja: BODEJEV DIAGRAM. Bodejev diagram sestavljata dva grafa: a) amplitudno frekvenčni diagram in b) fazno frekvenčni diagram Decibel je enota za razmerje dveh veličin. Definicija: B B 0log0 A A db Bodejeve
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
7. VAJA IZ MEHANIKE TRDNIH TELES. (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji)
 7. VAJA IZ MEHANIKE TRDNIH TELES (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Pomik deformabilnega telesa je glede na kartezijski koordinatni sistem
7. VAJA IZ MEHANIKE TRDNIH TELES (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Pomik deformabilnega telesa je glede na kartezijski koordinatni sistem
primer reševanja volumskega mehanskega problema z MKE
 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE p p RAK: P-XII//74 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE L
Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE p p RAK: P-XII//74 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE L
Afina in projektivna geometrija
 fina in projektivna geometrija tožnice () kiciraj stožnico v evklidski ravnini R, ki je določena z enačbo 6 3 8 + 6 =. Rešitev: tožnica v evklidski ravnini je krivulja, ki jo določa enačba a + b + c +
fina in projektivna geometrija tožnice () kiciraj stožnico v evklidski ravnini R, ki je določena z enačbo 6 3 8 + 6 =. Rešitev: tožnica v evklidski ravnini je krivulja, ki jo določa enačba a + b + c +
8. Posplošeni problem lastnih vrednosti
 8. Posplošeni problem lastnih vrednosti Bor Plestenjak NLA 13. april 2010 Bor Plestenjak (NLA) 8. Posplošeni problem lastnih vrednosti 13. april 2010 1 / 15 Matrični šop Dani sta kvadratni n n matriki
8. Posplošeni problem lastnih vrednosti Bor Plestenjak NLA 13. april 2010 Bor Plestenjak (NLA) 8. Posplošeni problem lastnih vrednosti 13. april 2010 1 / 15 Matrični šop Dani sta kvadratni n n matriki
II. LIMITA IN ZVEZNOST FUNKCIJ
 II. LIMITA IN ZVEZNOST FUNKCIJ. Preslikave med množicami Funkcija ali preslikava med dvema množicama A in B je predpis f, ki vsakemu elementu x množice A priredi natanko določen element y množice B. Važno
II. LIMITA IN ZVEZNOST FUNKCIJ. Preslikave med množicami Funkcija ali preslikava med dvema množicama A in B je predpis f, ki vsakemu elementu x množice A priredi natanko določen element y množice B. Važno
Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni izrek.
 DN#3 (januar 2018) 3A Teme, ki jih preverja domača naloga: Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni
DN#3 (januar 2018) 3A Teme, ki jih preverja domača naloga: Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni
MATEMATIKA 1 UNIVERZITETNI ŠTUDIJSKI PROGRAM BIOKEMIJA 1. LETNIK
 abc MATEMATIKA 1 UNIVERZITETNI ŠTUDIJSKI PROGRAM BIOKEMIJA 1. LETNIK ŠTEVILA PRIBLIŽNO RAČUNANJE PRIBLIŽNO RAČUNANJE Ta fosil dinozavra je star 7 milijonov in šest let, pravi paznik v muzeju.??? Ko sem
abc MATEMATIKA 1 UNIVERZITETNI ŠTUDIJSKI PROGRAM BIOKEMIJA 1. LETNIK ŠTEVILA PRIBLIŽNO RAČUNANJE PRIBLIŽNO RAČUNANJE Ta fosil dinozavra je star 7 milijonov in šest let, pravi paznik v muzeju.??? Ko sem
