PRILOGA I 1. DEFINICIJE IZRAZOV IN NJIHOVI SIMBOLI
|
|
|
- Γιώργος Μέλιοι
- 6 χρόνια πριν
- Προβολές:
Transcript
1 PRILOGA I 1. DEFINICIJE IZRAZOV IN NJIHOVI SIMBOLI 1$3(72677(ý(1-$ 9 RNYLUX WHJD SUDYLOQLND MH WUHED NRW QDSHWRVW WHþHQMD Y L]UDþXQLK ]D GHOH REUHPHQMHQH QD WODN upoštevati vrednosti, kakor sledi: þh MHNOR QH L]ND]XMH VSRGQMH LQ ]JRUQMH QDSHWRVWL WHþHQMD MH SRWUHEQR XSRãWHYDWL QDMQLåMR YUHGQRVWGRJRYRUQHQDSHWRVWLWHþHQMD5 p 0,2 ; þhmhnorl]nd]xmhvsrgqmrlq]jruqmrqdshwrvwwhþhqmdmhwuhedxsrãwhydwlyuhgqrvw - R el ali - R eh 0,92 ali - R p 0, TLAK PORUŠITVE V RNYLUXWHJDSUDYLOQLNDWODNSRUXãLWYHSRPHQLWODNSULNDWHUHPVHSRMDYLSODVWLþQDQHVWDELOQRVW WMQDMYLãMLWODNGRVHåHQPHGSUHVNXVRPSRUXãLWYH]QRWUDQMLPYRGQLPWODNRP 1.3. SIMBOLI Simboli, uporabljeni v tej prilogi, pomenijo: P h KLGUDYOLþQL preskusni tlak, v barih, P r = tlak porušitve jeklenke, izmerjen med preizkusom s porušitvijo z notranjim vodnim tlakom, v barih, P rt L]UDþXQDQLQDMQLåMLWHRUHWLþQLWODNSRUXãLWYHYEDULK R e YUHGQRVW QDSHWRVWL WHþHQMD XSRãWHYDQD Y VNODGX ] SUL GRORþDQMX YUHGQRVWL 5 NL VH XSRUDEOMD]DL]UDþXQGHORYREUHPHQMHQLKVWODNRPY1PP 2, R el QDMPDQMãDYUHGQRVWVSRGQMHQDSHWRVWLWHþHQMDNLMRMDPþLSURL]YDMDOHFMHNOHQNHY1PP 2, R eh QDMPDQMãDYUHGQRVW]JRUQMHQDSHWRVWLWHþHQMDNLMRMDPþLproizvajalec jeklenke, v N/mm 2, R p 0,2 GRJRYRUQDQDSHWRVWWHþHQMD NLMRMDPþLSURL]YDMDOHFY1PP 2, R m QDMPDQMãDYUHGQRVWQDWH]QHWUGQRVWLNLMRMDPþLSURL]YDMDOHFMHNOHQNHY1PP 2, D QDMPDQMãDUDþXQVNDGHEHOLQDVWHQHYDOMDVWHJDSODãþD jeklenke, v mm, D = imenski zunanji premer jeklenke, v mm, d = premer trna pri upogibnem preskusu, v mm, R mt = dejanska natezna trdnost, v N/mm 2
2 1.4. NORMALIZACIJA Izraz 'normalizacija' je v tem pravilniku uporabljen v skladu z njegovo definicijo v 68.WRþNL6,67 EN 10052: RUPDOL]DFLMLODKNRVOHGLSRSXãþDQMHSULHQDNRPHUQLWHPSHUDWXULQLåMLRGVSRGQMHWUDQVIRUPDFLMVNH WRþNH$ c1 ) jekla POBOLJŠANJE,]UD]SREROMãDQMHR]QDþXMHWRSORWQRREGHODYRL]GHODQHMHNOHQNHSULNDWHULMHNOHQNRVHJUejemo na HQDNRPHUQR WHPSHUDWXUR YLãMR RG JRUQMH WUDQVIRUPDFLMVNH WRþNH MHNOD $ c3 ). Jeklenko nato ohlajamo s hitrostjo, ki ne presega 80 % hitrosti ohlajanja, ki bi jo dosegli s hlajenjem v vodi temperature 20 o & QDWR SD MR SRSXãþDPR SUL HQDNRPHUQL WHPSHUDWXUL QLåML RG VSRGQMH WUDQVIRUPDFLMVNHWRþNHMHNOD$F Toplotna obdelava mora biti takšna, da v jeklenki ne pride do razpok. Jeklenk ni dovoljeno kaliti v vodi brez dodatkov. 7(+1,ý1(=$+7(9( 2.1. UPORABLJENA JEKLA Jeklo opredeljujejo poswrshn QMHJRYHJD SULGRELYDQMD QMHJRYD NHPLþQD VHVWDYD LQ WRSORWQD obdelava izdelane jeklenke ter njegove mehanske lastnosti. Proizvajalec mora navesti ustrezne podatke, ob upoštevanju zahtev, naštetih spodaj. Vsako spremembo teh podatkov je treba, s stališþd ES pregleda tipa, obravnavati kot spremembo tipa jekla. a) Postopek pridobivanja Postopek pridobivanja mora biti opredeljen z navedbo uporabljenega procesa (na primer: PDUWLQRYNDNLVLNRYNRQYHUWRUHOHNWURSHþLQXSRUDEOMHQHJDSRVWRSNDSRPLUMHQMD b).hplþqdvhvwdyd.hplþqdvhvwdydprudqdydmdwlyvdm QDMYHþMRYVHEQRVWåYHSODLQIRVIRUMDYYVHKSULPHULK vsebnost ogljika, mangana in silicija v vseh primerih, YVHEQRVWQLNOMDNURPDPROLEGHQDLQYDQDGLMDþHVRQDPHUQRGRGDQLNRWOHJLUQLHOHPHQWL Vsebnosti ogljika, mangana, silicija in, kjer je primerno, niklja, kroma, molibdena in vanadija PRUDMRELWLGDQHVWDNLPLWROHUDQFDPLGDUD]OLNHPHGQDMQLåMRLQQDMYLãMRYUHGQRVWMR]DYVDNRãDUåR ne presegajo:
3 za ogljik: - 0,06 %, kadar je najvišja vsebnost manjša od 0,30 %, - 0,07 %, kadar je najvišja vsebnost enaka ali višja od 0,30 %; za mangan in silicij: - 0,30 %; za krom: - 0,30 %, kadar je najvišja vsebnost manjša od 1,5 %, - 0,50 %, kadar je najvišja vsebnost enaka ali višja od 1,5 %; za nikelj: - 0,40 %; za molibden: - 0,15 %; za vanadij: - 0,10 %. c) Toplotna obdelava Toplotna obdelava mora biti definirana s temperaturo, VþDVRPY]GUåHYDQMDWHWHPSHUDWXUHLQ]YUVWR hladilnega medija, ki se uporablja v posamezni fazi obdelave (normalizacija, ki ji sledi ali ne sledi SRSXãþDQMHDOLSREROMãDQMH 7HPSHUDWXUD DYVWHQLWL]DFLMH SUHG NDOMHQMHP DOL QRUPDOL]DFLMR PRUD ELWL Y]GUåHYDna v mejah odstopanja 35 o &QDY]JRUDOLQDY]GRO,VWRYHOMD]DWHPSHUDWXURSRSXãþDQMD Zahteve, ki morajo biti izpolnjene Uporabljeno mora biti pomirjeno jeklo, odporno proti staranju. Celotna jeklenka mora biti toplotno obdelana, bodisi z normalizdflmrnlmlvohgldolqhvohglsrsxãþdqmherglvlvndomhqmhpnlpxvohgl SRSXãþDQMH9VHEQRVWåYHSODLQYVHEQRVWIRVIRUMDYY]RUFXOLWLQHQHVPHELWL]DYVDNHJDYHþMDRG 0,035 YVRWDYVHEQRVWLREHKSDQHVPHELWLYHþMDRG 9VHEQRVWåYHSODLQYVebnost fosforja YNRQþQHPL]GHONXQHVPHELWL]DYVDNHJDYHþMDRG %, vsota vsebnosti obeh pa ne sme biti YHþMDRG % Proizvajalec sme uporabljati jekla, RSUHGHOMHQD Y OH þh VR RGREUHQD NRW MHNOD ]D izdelavo jeklenk iz celega. 'UåDYD þodqlfd PRUD QD ]DKWHYR SRVODWL GUXJLP GUåDYDP þodqlfdp VH]QDP PDWHULDORY NL MLK QD njenem ozemlju uporabljajo za izdelavo jeklenk, na katere se nanaša ta pravilnik.
4 =DJRWRYOMHQH PRUDMR ELWL PRåQRVWL L]YDMDQMD QHRGYLVQLK DQDOL] SRVHEHM ãh ]D Sreverjanje YVHEQRVWL åyhsod LQ IRVIRUMD ] ]DKWHYDPL L] 7H DQDOL]H PRUDMR ELWL RSUDYOMHQH ERGLVL QD vzorcih, vzetih iz polizdelkov, kakršne proizvajalec jekla dobavlja proizvajalcu jeklenk, bodisi na GRNRQþDQLKMHNOHQNDK 2ERGORþLWYL]DMHPDQMHY]Rrcev iz jeklenke se lahko vzame vzorec iz ene od jeklenk, ki so bile L]EUDQH ]D PHKDQVNH SUHVNXVH GRORþHQH Y DOL ]D SUHVNXV V SRUXãLWYLMR ] QRWUDQMLP YRGQLP WODNRPGRORþHQY,=5$ý81'(/292%5(0(1-(1,+67/$ Najmanjša debelina stene mora biti vsaj enaka najvišji od naslednjih treh vrednosti: 3K ' - D =, K kjer je vrednost R manjša od naslednjih dveh vrednosti: 1) R e ; 2) 0,75 R m ]DQRUPDOL]LUDQHDOLQRUPDOL]LUDQHLQSRSXãþDQHMHNOHQNH 0,85 R m za poboljšane jeklenke ' - D = + PP - a = 1,5 mm. ýh MH NRQYHNVQR GQR L]GHODQR V NRYDQMHP L] FHYL PRUD ELWL GHEHOLQD VWHQH PHUMHQD QD sredini izoblikovanega dna, najmanj 1,5 a Debelina konkavnega dna jekleqnh QH VPH ELWL PDQMãD RG D ]QRWUDM REPRþMD SUHPHUD podstavka jeklenke. =D ]DJRWRYLWHY XVWUH]QH SRUD]GHOLWYH QDSHWRVWL VH PRUDGHEHOLQDVWHQMHNOHQNHQDREPRþMX SUHKRGDPHGYDOMDVWRVWHQRLQGQRPSRYHþHYDWLSRVWRSRPD 2.3. KONSTRUKCIJA IN PROIZVODNJA Proizvajalec mora preveriti debelino sten vsake jeklenke ter stanje notranjih in zunanjih površin, zato da zagotovi, da: GHEHOLQDVWHQHQDQREHQHPPHVWXQLPDQMãDRGGHEHOLQHSUHGSLVDQHYQDþUWX na notranjih in zunanjih površinah jeklenke ni napak, ki bi lahko škodljivo vplivale na varnost jeklenke pri uporabi.
5 Ovalnost valjastega dela jeklenke mora biti omejena na tako vrednost, da razlika med QDMYHþMLP LQ QDMPDQMãLP ]XQDQMLP SUHPHURP QD LVWHP SUHVHNX QL YHþMD RG SRYSUHþQH vrednosti teh dveh premerov. 0DNVLPDOQRRGVWRSDQMHRVLYDOMDVWHJDGHODMHNOHQNHRGUDYQHþUWHQHVPHSUHVHJDWLPPQDPHWHU GROåLQH ýhvrqdmhnohqnrsulwumhqlsrgvwdynlprudmrelwlgryromprþqllql]ghodqll]pdwhuldodnlmh JOHGH NRUR]LMH ]GUXåOjiv z vrsto jekla, iz katerega je narejena jeklenka. Oblika podstavka mora MHNOHQNL ]DJRWDYOMDWL XVWUH]QR VWDELOQRVW 3RGVWDYNL QH VPHMR RPRJRþDWL ]DGUåHYDQMD YRGH DOL dovoljevati vdora vode v prostor med podstavkom in jeklenko. 3. PRESKUSI 3.1. MEHANSKI PRESKUSI Splošne zahteve 5D]HQþHWDSUDYLOQLNGRORþDGUXJDþHPRUDMRELWLPHKDQVNLSUHVNXVLL]YHGHQLYVNODGX] naslednjimi standardi: SIST EN : natezni preskus jekel, SIST EN ISO : preskus trdote po Brinellu, EURONORM 6-55: upogibni preskus jekel, EURONORM 12-XSRJLEQLSUHVNXVMHNOHQLKSORþHYLQLQWUDNRYWDQMãLKRGPP SIST EN :2000 -XGDUQLSUHVNXVSUHL]NXãDQFD]]DUH]R9OHåHþHJDQDGYHKSRGSRUDK Vsi mehanski preskusi za preverjanje kakovosti jekel, uporabljenih za jeklenke, morajo biti L]YHGHQLQDSUHVNXãDQFLKY]HWLK]GRNRQþDQLKMHNOHQN Vrste preskusov in merila preskušanja 1D YVDNL SUHVNXVQL MHNOHQNL PRUDMR ELWL RSUDYOMHQL HQ QDWH]QL SUHVNXV Y Y]GROåQL VPHUL ãwlumh upogibnl SUHVNXVL Y RERGQL VPHUL LQ þh GHEHOLQD VWHQH GRSXãþD MHPDQMH SUHVNXãDQFHY ãlulqh QDMPDQMPPWULMHSUHVNXVLXGDUQHåLODYRVWL3UHVNXãDQFL]DSUHVNXVXGDUQHåLODYRVWLPRUDMRELWL RGY]HWL Y SUHþQL VPHUL þh SD GHEHOLQD LQDOL SUHPHU MHNOHQNH RQHPRJRþDWD odvzem preskušanca ãlulqhqdmpdqmppysuhþqlvphulqdmergrsuhvnxãdqfl]dxgduqhsuhvnxvhrgy]hwlyy]groåql smeri.
6 Natezni preskus 3UHVNXãDQHFPRUDXVWUH]DWLGRORþLORP SIST EN :2002, dodatek D, kadar je njegova debelina PPDOLYHþ SIST EN :2002, dodatek B, kadar je njegova debelina manjša od 3 mm. Tedaj morata ELWLãLULQDLQGROåLQDSUHVNXãDQFDR]LURPDPPQHJOHGHQDQMHJRYRGHEHOLQR Površini preskušanca, ki ustrezata notranji in zunanji površini jeklenke, ne smeta biti strojno obdelani. 5D]WH]HNL]UDåHQYRGVWRWNLKQHVPHELWLPDQMãLRG 5 PW Poleg tega raztezek ne sme biti manjši od: 14 %, kadar je preskus izveden v skladu s SIST EN :2002, dodatek D 11 %, kadar je preskus izveden v skladu s SIST EN :2002, dodatek B Vrednost, ugotovljena kot natezna trdnost, ne sme biti manjša od R m. 9UHGQRVWQDSHWRVWLWHþHQMDNLQDMMRGRORþLQDWH]QLSUHVNXVPRUDELWLWDNDNDNUãQRXSRUDEOMDPRY sklagx]sull]udþxqxmhnohqnh*ruqmdqdshwrvwwhþhqmdprudelwlgrorþhqdl]gldjudpdqdshwrvw -UD]WH]HNDOLSRNDNãQLGUXJLHQDNRQDWDQþQLPHWRGL 9UHGQRVWXJRWRYOMHQDNRWQDSHWRVWWHþHQMDQHVPHELWLPDQMãDRG5 eh, R el ali R p0,2, odvisno od posameznega primera Upogibni preskus Upogibni preskus mora biti opravljen na preskušancih, ki jih pridobimo tako, da UD]UHåHPRSUVWDQãLULQHPPQDGYDHQDNRGROJDGHODRGNDWHULKVPHELWLYVDNVWURMQRREGHODQOH na robovih. Ploskve preskušancev, ki ustrezajo notranji oziroma zunanji površini stene valja, ne smejo biti obdelane z odrezavanjem Upogibni preskus mora biti opravljen s trnom premera d in dvema podpornima YDOMþNRPDNLVWDQDPHGVHERMQLRGGDOMHQRVWLGD 9HVþDs preskusa mora biti notranja površina prstana v stiku s trnom Preskušanec med upogibanjem navznoter okoli trna ne sme razpokati, dokler se razdalja med njegovima notranjima površinama ne zmanjša na vrednost, enako premeru trna (glej skico v Prilogi III).
7 Razmerje (n) med premerom trna in debelino preskušanca ne sme presegati vrednosti iz naslednje tabele: Dejanska natezna trdnost R mt v N/mm 2 Vrednost n GRYNOMXþQR 2 QDGGRYNOMXþQR 3 QDGGRYNOMXþQR 4 QDGGRYNOMXþQR 5 QDGGRYNOMXþQR 6 QDGGRYNOMXþQR 7 nad UHVNXVLXGDUQHåLODYRVWL 3UHVNXVL XGDUQH ålodyrvwl PRUDMR ELWL RSUDYljeni na preskušancih tipa SIST EN : VLSUHVNXVLXGDUQHåLODYRVWLPRUDMRELWLRSUDYOMHQLSULWHPSHUDWXULPLQXV o C. Zareza mora biti pravokotna na obe površini stene jeklenke. 3UHVNXãDQHFXSRUDEOMHQ]DSUHVNXVXGDUQHåLODYRVWLQHVPHELWL zravnan in mora biti obdelan na vseh svojih šestih ploskvah, vendar le toliko, da dobimo ravne površine ploskve. 1LWL SRYSUHþQD YUHGQRVW XGDUQH ålodyrvwl GREOMHQD Y WUHK SUHVNXVLK XGDUQH ålodyrvwl Y Y]GROåQLDOLSUHþQLVPHULLQYVDNDQLWLQREena posamezna, s preskusi dobljena vrednost, ne sme biti PDQMãDRGXVWUH]QHYUHGQRVWLL]UDåHQHY-FP 2, navedene v naslednji tabeli: povprhþmhwuhk preskušancev vsaka posamezna vrednost jekla, katerih R m QLYHþML od 650 N/mm 2 jekla, katerih R m MHYHþML od 650 N/mm 2 Y]GROåQR SUHþQR Y]GROåQR SUHþQR
8 3.2 PRESKUS PORUŠITVE Z NOTRANJIM VODNIM TLAKOM Preskusne zahteve -HNOHQNHQDNDWHULKL]YDMDPRWDSUHVNXVPRUDMRLPHWLR]QDNHQDYHGHQHYWRþNL Preskus porušitve z notranjim vodnim tlakom mora biti opravljen v dveh zaporednih VWRSQMDK ] XSRUDER SUHVNXVQH SURJH NL RPRJRþD SRYHþHYDQMH WODND Y MHNOHQNL ] HQDNRPHUQR hitrostjo, dokler se jeklenka ne poruši in hkrati zapisovanje krivulje spreminjanja tlaka v odvisnosti RGþDVD3UHVNXVPRUDELWLRSUDYOMHQSULVREQLWHPSHUDWXUL 0HGSUYRVWRSQMRPRUDELWLKLWURVWSRYHþHYDQMDWODNDYHVþDVHQDNDGRYUHGQRVWLWODNDSUL NDWHULVH]DþQHSODVWLþQDGHIRUPDFLMD7DKLWURVWQHVPHSUHVHJDWLEDUV Od ]DþHWNDSODVWLþQHGHIRUPDFLMHQDSUHMGUXJDVWRSQMDGRWRNPHGLMDL]þUSDONHQHVPHELWLYHþMLRG dvakratne vrednosti dotoka v prvi stopnji in mora biti konstanten, dokler ne pride do porušitve jeklenke Interpretacija rezultatov Interpretacija rezultatov preskusa porušitve z notranjim vodnim tlakom mora obsegati: SUHXþLWHYNULYXOMHWODN-þDV]DGRORþLWHYWODNDSRUXãLWYH pregled mesta porušitve in oblike njegovih robov, v primeru jeklenk s konkavnim dnom preveritev, ali se pri preskusu nll]erþlorgqrmhnohqnh Izmerjeni tlak porušitve (P r PRUDELWLYLãMLRGYUHGQRVWLGDQH]HQDþER 3 UW = D 5 ' D P 3UHVNXVSRUXãLWYH]QRWUDQMLPYRGQLPWODNRPMHNOHQNHQHVPHSRY]URþLWLUD]SDGDMHNOHQNH na kose Glavni lom ne sme biti krhkega tipa, t. j. robovi loma ne smejo biti radialni, ampak nagnjeni glede na ravnino premera, in morajo izkazovati kontrakcijo. /RPMHVSUHMHPOMLYOHþHL]SROQMXMHQDVOHGQMH]DKWHYH 1. Pri jeklenkah, pri katerih debelina 'a' ne presega 7,5 mm: (a) YHþMLGHOORPDPRUDELWLQHGYRPQRY]GROåHQ (b) lom mora biti nerazvejan, FORPQHVPHLPHWLQDVWDYNRYYRERGQLVPHUL]DYHþNRW o na nobenem koncu svojega glavnega dela,
9 (d) lom ne sme segati v tiste dele jeklenke, NLVRYHþNRW-NUDWGHEHOHMãLRGQDMYHþMH debeline, izmerjene na polovici višine jeklenke, (e) pri jeklenkah s konveksnim dnom lom ne sme segati do sredine dna jeklenke. V naslednjih primerih je dovoljeno, da zahteva (d) ni izpolnjena: (a) pulvwråþdvwhpyudwxmhnohqnhdolnrqyhnvqhpvsrgqmhpgqxndgduorpqhvhjdyghohmhnohqnh katerih premer je za faktor 0,75 manjši od imenskega zunanjega premera jeklenke, (b) pri konkavnem dnu: kadar razdalja med skrajnim prednjim koncem loma in ravnino dna jeklenke presega petkratnik debeline 'a', 3UL MHNOHQNDK SUL NDWHULK GHEHOLQD D SUHVHJD PP PRUD ELWL YHþML GHO ORPD QHGYRPQR Y]GROåHQ /RPQRPHVWRQHVPHSRND]DWLQREHQHRþLWQHQDSDNHYNRYLQL 35(6.86=1,+$-2ý,07/$ HNOHQNHNLVRSUHGPHWWHJDSUHVNXVDPRUDMRLPHWLR]QDNHQDYHGHQHYWRþNL 3UHVNXV ] QLKDMRþLP WODNRP PRUD ELWL RSUDYOMHQ QD GYHK MHNOHQNDK ]D NDWHUL SURL]YDMDOHF MDPþLGDYUD]XPQLKPHMDKSUHGVWDYOMDWDQDMQLåMHQDþUWRYDQHYUHGQRVWLREuporabi nekorozivnega fluida. 3UHVNXVPRUDSRWHNDWL]QLKDQMHPWODþQHREUHPHQLWYH1DMYLãMLWODNSULQLKDMXPRUDELWLHQDN tlaku P h ali dvema tretjinama tega tlaka. 1DMQLåMLWODNSULQLKDMXQHVPHSUHVHJDWL % najvišjega tlaka pri nihaju. Najmanjše število nihajev in najvišja frekvenca preskušanja sta navedena v naslednji tabeli: Najvišji uporabljeni tlak P h 2/3 P h Najmanjše število nihajev Najvišja frekvenca, v nihajih na minuto 5 12 Temperatura, merjena na zunanji steni jeklennhphgsuhvnxvrpqhvphsuhvhþl o C. 3UHVNXVYHOMD]DXVSHãQHJDþHMHNOHQNDSUHVWDQH]DKWHYDQRãWHYLORQLKDMHYQHGDEL]DþHODSXãþDWL
10 +,'5$9/,ý1,35(6.86 7ODNYRGHYMHNOHQNLPRUDQDUDãþDWLHQDNRPHUQRGRNOHUQHGRVHåHYUHGQRVWL3 h Jeklenka mora ostati pod tlakom P h GRYROMGROJRGDMHPRJRþHXJRWRYLWLGDWODNQHNDåH ]QDPHQMSDGDQMDLQGDQLQREHQHJDSXãþDQMD Po preskusu jeklenka ne sme kazati nobenih trajnih deformacij Vsaka preskušena jeklenka, ki ne izpolnjuje zahtev preskusa, mora biti zavrnjena PREVERJANJE HOMOGENOSTI JEKLENKE Ta preskus obsega preverjanje, da se nobeni dve mesti na zunanji steni jeklenke ne razlikujeta po WUGRWL]DYHþNRW+%3UHYHUMDQMHPRUDELWLRSUDYOMHQRQDGYHKSUHþQLKpresekih jeklenke blizu YUDWXMHNOHQNHLQGQDQDãWLULKPHGVHERMHQDNRRGGDOMHQLKWRþNDK 3.6. PREVERJANJE HOMOGENOSTI SERIJE Ta preskus, ki ga opravi proizvajalec, obsega preverjanje morebitne napake pri izbiri osnovnega PDWHULDOD SORþHYLQH SDOLF FHvi) ali pri postopku toplotne obdelave. Preskus se opravi s SUHVNXãDQMHP WUGRWH DOL NDNãQR GUXJR XVWUH]QR PHWRGR 3UL QRUPDOL]LUDQLK D QH SRSXãþDQLK jeklenkah, tega preskusa ni treba opraviti na vsaki jeklenki PREVERJANJE DNA (DNOV) NA JEKLENKAH Dno jeklenke je treba prerezati v meridianski ravnini, eno od tako nastalih površin prereza spolirati in pregledati pod 5 do 10-NUDWQRSRYHþDYR -HNOHQNDMHQHXVWUH]QDþHSUHJOHGRGNULMHUD]SRNHDOLþHVRGLPHQ]LMHNDWHUHNROLSRUHDOLYNOMXþND tako velike,gdrjurådmryduqrvw 4. ES PREGLED TIPA (6SUHJOHGWLSDQDYHGHQYþOHQXSUDYLOQLNDVHODKNRRSUDYLWXGL]DGUXåLQHMHNOHQN 'UXåLQDMHNOHQNSRPHQLMHNOHQNHL]GHODQHYLVWLWRYDUQLNLVHUD]OLNXMHMR]JROMSRGROåLQLYHQGDU v okviru naslednjih omejitev: QDMPDQMãDGROåLQDPRUDELWLYVDMWULNUDWYHþMDRGSUHPHUDMHNOHQNH QDMYHþMDGROåLQDQHVPHELWLYHþNRW-NUDWYHþMDRGGROåLQHSUHVNXãHQHMHNOHQNH
11 3URVLOHF]D(6SUHJOHGWLSDPRUD]DYVDNRGUXåLQRMHNOHQNSUHGORåLWLGRNXPHQWDFLMRSRWUHEno za izvedbo v nadaljevanju opisanih preskusov, in dati priglašenemu organu na razpolago serijo 50 jeklenk, izmed katerih le-ta izbere potrebno število jeklenk za izvedbo preskusov, navedenih v nadaljevanju, ter na zahtevo priglašenega organa podati morebitne dodatne informacije. Prosilec PRUD QDYHVWL YUVWR LQ WUDMDQMH WRSORWQH REGHODYH LQ WHPSHUDWXUH 3ULGRELWL LQ SUHGORåLWL PRUD FHUWLILNDWHãDUåQLKDQDOL]]DMHNORL]NDWHUHJDVRMHNOHQNHSURL]YHGHQH 4.2. V postopku ES pregleda tipa mora priglašeni organ: Preveriti, ali: VRL]UDþXQLSUHGSLVDQLYSUDYLOQL GHEHOLQH VWHQ GYHK MHNOHQN L]SROQMXMHMR ]DKWHYH L] SUL þhphu PRUDMR ELWL PHULWYH RSUDYOMHQH QD WUHK SUHþQLK SUHUH]LK LQ SR FHORWQHP RERGX Y]GROåQLK SUHVHNRY GQD LQ YUDWX jeklenke, so izpolnjene zahteve, predpisane v 2.1 in 2.3.3, vse jeklenke, ki jih izbere priglašeni organ, izpolnjujejo zahteve, predpisane v 2.3.2, VR]XQDQMHLQQRWUDQMHSRYUãLQHMHNOHQNEUH]NDNUãQLKNROLQDSDNNLELODKNRSRY]URþLOHGD MHNOHQNHQHELELOHYHþYDUQe Opraviti naslednje preskuse na izbranih jeklenkah: SUHVNXVHGRORþHQHYQDGYHKMHNOHQNDKýHMHGROåLQDMHNOHQNHPPDOLYHþPRUDWD ELWL QDWH]QL SUHVNXV Y Y]GROåQL VPHUL LQ XSRJLEQL SUHVNXV RSUDYOMHQD QD SUHVNXãDQFLK odvzetih s spodnmhjdlq]jruqmhjdghodsodãþd SUHVNXVGRORþHQYQDGYHKMHNOHQNDK SUHVNXVGRORþHQYQDGYHKMHNOHQNDK SUHVNXVGRORþHQYQDHQLMHNOHQNL SUHVNXVGRORþHQYQDYVHKY]RUþQLKMHNOHQNDK ýhvruh]xowdwlsuhvnxvry]dgryromlylpora priglašeni organ izdati potrdilo o ES pregledu tipa, v skladu z vzorcem iz Priloge IV. 5. ES UGOTAVLJANJE SKLADNOSTI 5.1. Za potrebe ES ugotavljanja skladnosti mora proizvajalec jeklenk: 3UHGORåLWLSULJODãHQHPXRUJDQXSRWUGLORR(6SUHJOHGXtipa,
12 3UHGORåLWL SULJODãHQHPX RUJDQX FHUWLILNDWH R ãduåqlk DQDOL]DK MHNHO GREDYOMHQLK ]D proizvodnjo jeklenk,,phwlgrnd]lodrvohgomlyrvwlãduåhmhnodl]ndwhuhmhelodsurl]yhghqdsrvdph]qdmhnohqnd 3UHGORåLWLSULJODãHQHPXRUJDQXGRNXPHQWHNLVHQDQDãDMRQDWRSORWQRREGHODYRLQVOXåLMRNRW dokazilo, da so od njega dobavljene jeklenke bodisi v normaliziranem bodisi poboljšanem stanju, in dokumente, ki navajajo uporabljeno toplotno obdelavo, 3UHGORåLWLSULJODãHQHPXRUJDQXVH]QDPMHNOHQN]QDYHGERãWHYLONLQR]QDNGRORþHQLK YWRþNL 5.2. POSTOPEK ES UGOTAVLJANJA SKLADNOSTI Med izvajanjem postopka ES ugotavljanja skladnosti mora priglašeni organ: preveriti, ali je bilo pridobljeno potrdilo o ES pregledu tipa in ali so jeklenke skladne z njim, preveriti dokumente, ki navajajo podatke o materialih, SUHYHULWL DOL VR L]SROQMHQH WHKQLþQH ]DKWHYH GRORþHQH Y WRþNL LQ ãh SRVHEHM SUHYHULWL ] YL]XDOQLPSUHJOHGRP]XQDQMRVWLSRPRåQRVWLSDWXGLQRWUDQMRVWLMHNOHQNDOLVRSURL]YDMDOþHYD proizvodnja in preskusi, opravljeni v skladu z 2.3.1, zadovoljivi; vizualni pregled mora biti opravljen na najmanj 10 SUHGORåHQLKMHNOHQN L]YHVWLSUHVNXVHGRORþHQHYLQ SUHYHULWLDOLVRSRGDWNLNLMLKMHSUHGORåLOSURL]YDMDOHFYVH]QDPXQDYHGHQHPYWRþQL WRVHRSUDYL]QDNOMXþQLPSUHYHUMDQMHP oceniti rezultate preskusov homogenosti serije, ki jih je opravil proizvajalec v skladu s 3.6. ýhvruh]xowdwlsuhvnxvry]dgryromlylprudsuljodãhqlrujdql]gdwlsrwuglorres skladnosti v skladu z vzorcem iz Priloge V. =DGYHYUVWLSUHVNXVRYGRORþHQLKYLQMHWUHEDQDNOMXþQRY]HWLSRGYHMHNOHQNLL] YVDNHRGVHULMMHNOHQNDOLGHORYWHKVHULMNLVRELOLL]GHODQLL]LVWHãDUåHLQQDNDWHULKMHELOD opravljena predpisana toplotna obdelava pod enakimi pogoji. Na eni od jeklenk morajo biti opravljeni preskusi, predpisani v 3.1 (mehanski preskusi), na drugi pa SUHVNXVSUHGSLVDQYSUHVNXVVSRUXãLWYLMR]QRWUDQMLPYRGQLPWODNRPýHVHL]NDåHGDMHELO SUHVNXVRSUDYOMHQQDSDþQRDOLGDMHELODQDUHMHQDQDSDNDSULPHUMHQMXJDMHSRWUHEQRSRQRYLWL ýhvhhghqdolyhþsuhvnxvryl]ndåhmrnrwohghoqrqh]dgryromlylprudsuljodãhqlrujdqxjrwrylwl vzrok.
13 ýhqhxvwuh]qrvwqlsrvohglfdwrsorwqhreghodye, se serija zavrne. ýh MH QHXVWUH]QRVW SRVOHGLFD WRSORWQH REGHODYH PRUD SURL]YDMDOHF SRQRYLWL WRSORWQR obdelavo celotne serije jeklenk. Po ponovljeni toplotni obdelavi: PRUDSURL]YDMDOHFRSUDYLWLSUHVNXVGRORþHQY mora priglašeni organ osudylwlyvhsuhvnxvhgrorþhqhysuyhplqguxjhprgvwdynx ýhmhnohqnhqlvrsrqryqrwrsorwqrreghodqhdolþhuh]xowdwlsuhyhumdqmdlqsuhvnxvrysrsrqryomhql WRSORWQLREGHODYLQHL]SROQMXMHMR]DKWHYGRORþHQLKYWHPSUDYLOQLNXVHVHULMD]DYUQH 5.2,]ELUD SUHVNXãDQFHY LQ L]YHGED YVHK SUHVNXVRY PRUDWD SRWHNDWL Y QDY]RþQRVWL LQ SRG nadzorom predstavnika priglašenega organa. 3R L]YHGEL YVHK SUHGSLVDQLK SUHVNXVRY PRUD ELWL Y QDY]RþQRVWL LQ SRG QDG]RURP predstavnika priglašenega organa, na vvhkmhnohqndkl]vhulmhrsudyomhqklgudyolþqlsuhvnxvgrorþhq v IZVZETJE IZ ES UGOTAVLJANJA SKLADNOSTI 3ULMHNOHQNDKL]Y]HWLKL](6XJRWDYOMDQMDVNODGQRVWLQDSRGODJLþOHQDWHJDSUDYLOQLNDPRUDYVH preskuse in preglede, predpisane v 5.2, opraviti proizvajalec na svojo odgovornost. 3URL]YDMDOHF PRUD SUHGORåLWL SULJODãHQHPX RUJDQX YVR GRNXPHQWDFLMR WHU SRURþLOD R SUHVNXVLK LQ pregledih. 6. OZNAKE IN NAPISI 2]QDNHLQQDSLVLGRORþHQLYWHMWRþNLPRUDMRELWLYWLVQMHQLYLGQRþLWOMLYRLQQH]Erisljivo na vratu jeklenke. Pri jeklenkah, katerih prostornina ne presega 15 litrov, so lahko oznake in napisi vtisnjeni bodisi na vratu jeklenke bodisi na kakem drugem dovolj debelem delu jeklenke. Slika, ki prikazuje oznake in napise, je v Prilogi II.
14 6.1. VTISKOVANJE OZNAK.RWRGVWRSDQMHRG]DKWHYWRþNH3ULORJH,SUDYLOQLNDNLXUHMDWODþQHSRVRGHWLSDMHNOHQNHPRUD proizvajalec vtisniti oznako ES pregleda tipa v naslednjem zaporedju: SUL MHNOHQNDK NL VR SR GRORþLOLK þohqd WHJD SUDYLOQLND SUHGPHW (6 SUHJOHGD WLSD Ln ES ugotavljanja skladnosti: -VWLOL]LUDQDþUNDε, - serijska številka 1 po tem pravilniku, - YHOLNDH þundh NL R]QDþXMHMR GUåDYR NL MH L]GDOD SRWUGLOR R (6 SUHJOHGX WLSD WHU zadnji dve številki leta, v katerem je bilo izdano potrdilo o ES pregledu tipa, - številka potrdila o ES pregledu tipa (npr. ε 1 D 79 45); -SULMHNOHQNDKNLVRSRGRORþLOLKþOHQDWHJDSUDYLOQLNDL]Y]HWHL](6XJRWDYOMDQMDVNODGQRVWL - VWLOL]LUDQDþUNDεRENURåHQDVãHVWHURNRWQLNRP - serijska številka 1 po tem pravilniku, dodeljena v kronološkem vrstnem redu sprejemanja, - YHOLNDHþUNDHNLR]QDþXMHMRGUåDYRNLMHL]GDODSRWUGLORR(6SUHJOHGXWLSDWHU]DGQMLGYH številki leta, v katerem je bilo izdano potrdilo o ES pregledu tipa, - številka potrdila o ES pregledu tipa (npr. ε 1 D 79 54)..RWRGVWRSDQMHRG]DKWHYWRþNH3ULORJH,,SUDYLOQLNDNLXUHMDWODþQHSRVRGHWLSDMHNOHQNHPRUD priglašeni organ pritrditi oznako za ES skladnost v naslednjem zaporedju: PDODþUNDH YHOLNDH þundh NL R]QDþXMHMR GUåDYR Y NDWHUL MH ELOR RSUDYOMHQR (6 XJRWDYOMDQMH VNODGQRVWL SR SRWUHEL GRSROQMHQRH ] HQR R]LURPD GYHPD þundpd NL R]QDþXMHWD RåMH WHULWRULDOQRREPRþMHYWHMGUåDYL oznaka priglašenega organa ki jo pritrdi predstavnik tega organa skupaj s predstavnikovo oznako, kolikor je to primerno, šesterokotnik, datum ES ugotavljanja skladnosti: leto/ mesec, (npr. e D 80/01) NAPISI, KI SE NANAŠAJO NA PROIZVODNJO Proizvajalec mora vtisniti naslednje napise, ki se nanašajo na proizvodnjo: Glede jekla: ãwhyloþqryuhgqrvw5y1pp 2 QDNDWHULWHPHOMLL]UDþXQ VLPERO 1 MHNOHQND Y QRUPDOL]LUDQHP VWDQMX DOL QRUPDOL]LUDQHP LQ SRSXãþDQHP VWDQMX DOL simbol T (jeklenka v poboljšanem stanju),
15 *OHGHKLGUDYOLþQHJDSUHVNXVD vrednost preskusnega tlaka v barih, ki ji sledi simbol 'bar', Glede tipa jeklenke: 0DVD MHNOHQNH Y NLORJUDPLK YNOMXþQR ] YVHPL QRWUDQMLPL GHOL WRGD EUH] YHQWLOD LQ QDMPDQMãD SURVWRUQLQD Y OLWULK NL MR MDPþL SURL]YDMDOHF MHNOHQNH âwhyloþql YUHGQRVWL PDVH LQ SURVWRUQLQH morataelwl]drnuråhqlqdhqrghflpdonr3ulsurvwruqlqlprudelwlyuhgqrvw]drnuråhqdqdy]grosul masi pa navzgor, Glede izvora: YHOLNDH þundh NL R]QDþXMHMR GUåDYR L]YRUD NDWHULP VOHGLWD R]QDND SURL]YDMDOFD LQ VHULMVND številka.
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
ANALIZNE METODE ZA PREVERJANJE SESTAVE DOL2ý(1,+ 6/$'.25-(9 NAMENJENIH ZA PREHRANO LJUDI UVOD
 PRILOGA 3 ANALIZNE METODE ZA PREVERJANJE SESTAVE DOL2ý(1,+ 6/$'.25-(9 NAMENJENIH ZA PREHRANO LJUDI 1. Priprava vzorca za analizo UVOD Vzorec, ki je bil dostavljen v laboratorij, temeljito premešamo. 2GY]DPHPR
PRILOGA 3 ANALIZNE METODE ZA PREVERJANJE SESTAVE DOL2ý(1,+ 6/$'.25-(9 NAMENJENIH ZA PREHRANO LJUDI 1. Priprava vzorca za analizo UVOD Vzorec, ki je bil dostavljen v laboratorij, temeljito premešamo. 2GY]DPHPR
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Logatherm WPL 14 AR T A ++ A + A B C D E F G A B C D E F G. kw kw /2013
 WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
MET2'( '2/2ý$1-$.$ ,+.$5$.7(5,67,. SLADKORJA PRI INTERVENCIJSKEM ODKUPU. , (. =$ '2'(/-(9$1-( 72ý.
 PRILOGA 4 MET2'( '2/2ý$1-$.$.292671,+.$5$.7(5,67,. SLADKORJA PRI INTERVENCIJSKEM ODKUPU, 326723(. =$ '2'(/-(9$1-( 72ý. METODA 1 '2/2ý$1-( 96(%1267, 3(3(/$,QãWUXPHQW ]D PHUMHQMH SUHYRGQRVWL NRQGXNWRPHWHU
PRILOGA 4 MET2'( '2/2ý$1-$.$.292671,+.$5$.7(5,67,. SLADKORJA PRI INTERVENCIJSKEM ODKUPU, 326723(. =$ '2'(/-(9$1-( 72ý. METODA 1 '2/2ý$1-( 96(%1267, 3(3(/$,QãWUXPHQW ]D PHUMHQMH SUHYRGQRVWL NRQGXNWRPHWHU
Bočna zvrnitev upogibno obremenjenih elementov s konstantnim prečnim prerezom
 D. Beg, študijsko gradivo za JK, april 006 KK FGG UL Bočna zvrnitev upogibno obremenjenih elementov s konstantnim prečnim prerezom Nosilnost na bočno zvrnitev () Elemente, ki niso bočno podprti in so upogibno
D. Beg, študijsko gradivo za JK, april 006 KK FGG UL Bočna zvrnitev upogibno obremenjenih elementov s konstantnim prečnim prerezom Nosilnost na bočno zvrnitev () Elemente, ki niso bočno podprti in so upogibno
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
PRILOGA VI POTRDILO O SKLADNOSTI. (Vzorci vsebine) POTRDILO O SKLADNOSTI ZA VOZILO HOMOLOGIRANEGA TIPA
 PRILOGA VI POTRDILA O SKLADNOSTI (Vzorci vsebine) A POTRDILO O SKLADNOSTI ZA VOZILO HOMOLOGIRANEGA TIPA Stran 1 POTRDILO O SKLADNOSTI ZA VOZILO HOMOLOGIRANEGA TIPA (1) (številka potrdila o skladnosti:)
PRILOGA VI POTRDILA O SKLADNOSTI (Vzorci vsebine) A POTRDILO O SKLADNOSTI ZA VOZILO HOMOLOGIRANEGA TIPA Stran 1 POTRDILO O SKLADNOSTI ZA VOZILO HOMOLOGIRANEGA TIPA (1) (številka potrdila o skladnosti:)
POROČILO. št.: P 1100/ Preskus jeklenih profilov za spuščen strop po točki 5.2 standarda SIST EN 13964:2004
 Oddelek za konstrkcije Laboratorij za konstrkcije Ljbljana, 12.11.2012 POROČILO št.: P 1100/12 680 01 Presks jeklenih profilov za spščen strop po točki 5.2 standarda SIST EN 13964:2004 Naročnik: STEEL
Oddelek za konstrkcije Laboratorij za konstrkcije Ljbljana, 12.11.2012 POROČILO št.: P 1100/12 680 01 Presks jeklenih profilov za spščen strop po točki 5.2 standarda SIST EN 13964:2004 Naročnik: STEEL
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
CM707. GR Οδηγός χρήσης... 2-7. SLO Uporabniški priročnik... 8-13. CR Korisnički priručnik... 14-19. TR Kullanım Kılavuzu... 20-25
 1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
+105 C (plošče in trakovi +85 C) -50 C ( C)* * Za temperature pod C se posvetujte z našo tehnično službo. ϑ m *20 *40 +70
 KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
l 5 Levo: Površinski profil referenčne dolžine in dolžina vrednotenja; Desno: srednja linija profila
 referenčna linija profila l=l=l=l=l 1 2 3 4 5... referenčna dolžina l 1 l 2 l 3 l 4 l 5 l n dolžina vrednotenja Levo: Površinski profil referenčne dolžine in dolžina vrednotenja; Desno: srednja linija
referenčna linija profila l=l=l=l=l 1 2 3 4 5... referenčna dolžina l 1 l 2 l 3 l 4 l 5 l n dolžina vrednotenja Levo: Površinski profil referenčne dolžine in dolžina vrednotenja; Desno: srednja linija
ARHITEKTURA DETAJL 1, 1:10
 0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
0.15 0.25 3.56 0.02 0.10 0.12 0.10 SESTV S2 polimer-bitumenska,dvoslojna(po),... 1.0 cm po zahtevah SIST DIN 52133 in nadstandardno, (glej opis v tehn.poročilu), npr.: PHOENIX STR/Super 5 M * GEMINI P
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL
 POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Statistična analiza. doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo Univerza v Ljubljani- Fakulteta za farmacijo
 Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Osnove matematične analize 2016/17
 Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
Osnove matematične analize 216/17 Neža Mramor Kosta Fakulteta za računalništvo in informatiko Univerza v Ljubljani Kaj je funkcija? Funkcija je predpis, ki vsakemu elementu x iz definicijskega območja
POPIS DEL IN PREDIZMERE
 POPIS DEL IN PREDIZMERE ZEMELJSKI USAD v P 31 - P 32 ( l=18 m ) I. PREDDELA 1.1 Zakoličba, postavitev in zavarovanje prečnih profilov m 18,0 Preddela skupaj EUR II. ZEMELJSKA DELA 2.1 Izkop zemlje II.
POPIS DEL IN PREDIZMERE ZEMELJSKI USAD v P 31 - P 32 ( l=18 m ) I. PREDDELA 1.1 Zakoličba, postavitev in zavarovanje prečnih profilov m 18,0 Preddela skupaj EUR II. ZEMELJSKA DELA 2.1 Izkop zemlje II.
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Definicija. definiramo skalarni produkt. x i y i. in razdaljo. d(x, y) = x y = < x y, x y > = n (x i y i ) 2. i=1. i=1
 Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Osnove sklepne statistike
 Univerza v Ljubljani Fakulteta za farmacijo Osnove sklepne statistike doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo e-pošta: mitja.kos@ffa.uni-lj.si Intervalna ocena oz. interval zaupanja
Univerza v Ljubljani Fakulteta za farmacijo Osnove sklepne statistike doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo e-pošta: mitja.kos@ffa.uni-lj.si Intervalna ocena oz. interval zaupanja
Primeri: naftalen kinolin spojeni kinolin
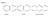 Primeri: naftalen kinolin spojeni kinolin 3 skupne strani 7 skupnih strani 5 skupnih strani 6 skupnih atomov 8 skupnih atomov 6 skupnih atomov orto spojen sistem orto in peri spojena sistema mostni kinolin
Primeri: naftalen kinolin spojeni kinolin 3 skupne strani 7 skupnih strani 5 skupnih strani 6 skupnih atomov 8 skupnih atomov 6 skupnih atomov orto spojen sistem orto in peri spojena sistema mostni kinolin
IZZIVI DRUŽINSKE MEDICINE. U no gradivo zbornik seminarjev
 IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
Varnost opreme pod tlakom (2. del)
 Univerza v Ljubljani - Fakulteta za kemijo in kemijsko tehnologijo KATEDRA ZA TEHNIŠKO VARNOST Delovne priprave in naprave II Varnost opreme pod tlakom (2. del) Boris Jerman Priloge PrPPOPT Priloga I -
Univerza v Ljubljani - Fakulteta za kemijo in kemijsko tehnologijo KATEDRA ZA TEHNIŠKO VARNOST Delovne priprave in naprave II Varnost opreme pod tlakom (2. del) Boris Jerman Priloge PrPPOPT Priloga I -
ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ
 GR ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ H OLJLAJNYOMÁSÚ SZEGECSELŐ M4/M12 SZEGECSEKHEZ HASZNÁLATI UTASÍTÁS - ALKATRÉSZEK SLO OLJNO-PNEVMATSKI KOVIČAR ZA ZAKOVICE
GR ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ H OLJLAJNYOMÁSÚ SZEGECSELŐ M4/M12 SZEGECSEKHEZ HASZNÁLATI UTASÍTÁS - ALKATRÉSZEK SLO OLJNO-PNEVMATSKI KOVIČAR ZA ZAKOVICE
The Thermal Comfort Properties of Reusable and Disposable Surgical Gown Fabrics Original Scientific Paper
 24 The Thermal Comfort Properties of Surgical Gown Fabrics 1 1 2 1 2 Termofiziološke lastnosti udobnosti kirurških oblačil za enkratno in večkratno uporabo december 2008 marec 2009 Izvleček Kirurška oblačila
24 The Thermal Comfort Properties of Surgical Gown Fabrics 1 1 2 1 2 Termofiziološke lastnosti udobnosti kirurških oblačil za enkratno in večkratno uporabo december 2008 marec 2009 Izvleček Kirurška oblačila
SPECIFIKACIJA MALT ZA ZIDOVE 1.del Malta za grobi in fini omet (malta za zunanji in notranji omet prevod avtorja izvlečka)
 SIST EN 998-1 (januar 2004, angl) (izvleček) SPECIFIKACIJA MALT ZA ZIDOVE 1.del Malta za grobi in fini omet (malta za zunanji in notranji omet prevod avtorja izvlečka) 1. Obseg in področje uporabe EN 998-1
SIST EN 998-1 (januar 2004, angl) (izvleček) SPECIFIKACIJA MALT ZA ZIDOVE 1.del Malta za grobi in fini omet (malta za zunanji in notranji omet prevod avtorja izvlečka) 1. Obseg in področje uporabe EN 998-1
4. DEL. Določbe za pakiranje in cisterne
 4. DEL Določbe za pakiranje in cisterne POGLAVJE 4.1 UPORABA EMBALAŽE, TUDI VSEBNIKOV IBC IN VELIKE EMBALAŽE Uvodni opombi OPOMBA 1: Embalažne skupine Zaradi pakiranja so nevarne snovi vseh razredov,
4. DEL Določbe za pakiranje in cisterne POGLAVJE 4.1 UPORABA EMBALAŽE, TUDI VSEBNIKOV IBC IN VELIKE EMBALAŽE Uvodni opombi OPOMBA 1: Embalažne skupine Zaradi pakiranja so nevarne snovi vseh razredov,
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant.
 Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Vaje: Električni tokovi
 Barbara Rovšek, Bojan Golli, Ana Gostinčar Blagotinšek Vaje: Električni tokovi 1 Merjenje toka in napetosti Naloga: Izmerite tok, ki teče skozi žarnico, ter napetost na žarnici Za izvedbo vaje potrebujete
Barbara Rovšek, Bojan Golli, Ana Gostinčar Blagotinšek Vaje: Električni tokovi 1 Merjenje toka in napetosti Naloga: Izmerite tok, ki teče skozi žarnico, ter napetost na žarnici Za izvedbo vaje potrebujete
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
1 Fibonaccijeva stevila
 1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
GEOMETRIJA V RAVNINI DRUGI LETNIK
 GEOMETRIJA V RAVNINI DRUGI LETNIK 2 1 Geometrija v ravnini 1.1 Osnove geometrije Točka je tisto, kar nima delov. Črta je dolžina brez širine. Ploskev je tisto, kar ima samo dolžino in širino. Osnovni zakoni,
GEOMETRIJA V RAVNINI DRUGI LETNIK 2 1 Geometrija v ravnini 1.1 Osnove geometrije Točka je tisto, kar nima delov. Črta je dolžina brez širine. Ploskev je tisto, kar ima samo dolžino in širino. Osnovni zakoni,
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
Snov v električnem polju. Električno polje dipola (prvi način) Prvi način: r + d 2
 Snov v lktričnm polju lktrično polj ipola (prvi način) P P - Prvi način: z r = r Δr r = r Δr Δr Δ r - r r r r r r Δr rδr =, = 4πε r r 4πε r r r r = r cos, r r r = r cos. r Vlja: = cos, r r r r r = cos,
Snov v lktričnm polju lktrično polj ipola (prvi način) P P - Prvi način: z r = r Δr r = r Δr Δr Δ r - r r r r r r Δr rδr =, = 4πε r r 4πε r r r r = r cos, r r r = r cos. r Vlja: = cos, r r r r r = cos,
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Petek, 12. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Matematika 1. Gabrijel Tomšič Bojan Orel Neža Mramor Kosta
 Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
PRILOGA 1. "Porušitveni tlak" pomeni najmanjši tlak, ki povzroči, da aerosolni razpršilnik eksplodira ali se razpoči.
 PRILOGA 1 1. DEFINICIJE 1.1. Tlak "Tlak" pomeni notranji tlak, ki je izražen v barih (relativni tlak). 1.2. Preskusni tlak "Preskusni tlak" pomeni tlak, s katerim je lahko ne napolnjen aerosolni razpršilnik
PRILOGA 1 1. DEFINICIJE 1.1. Tlak "Tlak" pomeni notranji tlak, ki je izražen v barih (relativni tlak). 1.2. Preskusni tlak "Preskusni tlak" pomeni tlak, s katerim je lahko ne napolnjen aerosolni razpršilnik
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Zaporedna in vzporedna feroresonanca
 Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
1. TVORBA ŠIBKEGA (SIGMATNEGA) AORISTA: Največ grških glagolov ima tako imenovani šibki (sigmatni) aorist. Osnova se tvori s. γραψ
 TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
TVORBA AORISTA: Grški aorist (dovršnik) izraža dovršno dejanje; v indikativu izraža poleg dovršnosti tudi preteklost. Za razliko od prezenta ima aorist posebne aktivne, medialne in pasivne oblike. Pri
Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni izrek.
 DN#3 (januar 2018) 3A Teme, ki jih preverja domača naloga: Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni
DN#3 (januar 2018) 3A Teme, ki jih preverja domača naloga: Kotne funkcije poljubnega kota. Osnovne zveze med funkcijamo istega kota. Uporaba kotnih funkcij v poljubnem trikotniku. Kosinusni in sinusni
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Naziv: Prijemalo FTV panelov za vertikalne fasade Oznaka: PVF (60, 80, 100, 120, 133, 150, 172, 200 in 240 mm) NAVODILA ZA UPORABO
 Naziv: Prijemalo FTV panelov za vertikalne fasade Oznaka: PVF (60, 80, 100, 120, 133, 150, 172, 200 in 240 mm) NAVODILA ZA UPORABO VSEBINA UVOD - SPLOŠNE INFORMACIJE 3 Namen navodil 3 Proizvajalec 3 Identifikacija
Naziv: Prijemalo FTV panelov za vertikalne fasade Oznaka: PVF (60, 80, 100, 120, 133, 150, 172, 200 in 240 mm) NAVODILA ZA UPORABO VSEBINA UVOD - SPLOŠNE INFORMACIJE 3 Namen navodil 3 Proizvajalec 3 Identifikacija
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Prenos znanja in izkušenj za razvoj trga solarnih ogrevalnih sistemov. Kakovost solarnih ogrevalnih sistemov. Ljubljana, 4. in 5. 6.
 Prenos znanja in izkušenj za razvoj trga solarnih ogrevalnih sistemov Ljubljana, 4. in 5. 6. 2009 Kakovost solarnih ogrevalnih sistemov dr. Ciril Arkar, Univerza v Ljubljani, Fakulteta za strojništvo Kakovost
Prenos znanja in izkušenj za razvoj trga solarnih ogrevalnih sistemov Ljubljana, 4. in 5. 6. 2009 Kakovost solarnih ogrevalnih sistemov dr. Ciril Arkar, Univerza v Ljubljani, Fakulteta za strojništvo Kakovost
Matematka 1 Zadaci za drugi kolokvijum
 Matematka Zadaci za drugi kolokvijum 8 Limesi funkcija i neprekidnost 8.. Dokazati po definiciji + + = + = ( ) = + ln( ) = + 8.. Odrediti levi i desni es funkcije u datoj tački f() = sgn, = g() =, = h()
Matematka Zadaci za drugi kolokvijum 8 Limesi funkcija i neprekidnost 8.. Dokazati po definiciji + + = + = ( ) = + ln( ) = + 8.. Odrediti levi i desni es funkcije u datoj tački f() = sgn, = g() =, = h()
Slika 5: Sile na svetilko, ki je obešena na žici.
 4. poglavje: Sile 5. Cestna svetilka visi na sredi 10 m dolge žice, ki je napeta čez cesto. Zaradi teže svetilke (30 N) se žica za toliko povesi, da pride sredina za 30 cm niže kot oba konca. Kako močno
4. poglavje: Sile 5. Cestna svetilka visi na sredi 10 m dolge žice, ki je napeta čez cesto. Zaradi teže svetilke (30 N) se žica za toliko povesi, da pride sredina za 30 cm niže kot oba konca. Kako močno
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
KAKO IZGUBLJAMO TOPLOTO V STANOVANJSKI HIŠI
 KAKO IZGUBLJAMO TOPLOTO V STANOVANJSKI HIŠI Toplotne izgube v stanovanjski hiši neposredno vplivajo na višino finančnih sredstev, ki jih porabimo za vzdrževanje ugodne klime v hladnih zimskih mesecih.
KAKO IZGUBLJAMO TOPLOTO V STANOVANJSKI HIŠI Toplotne izgube v stanovanjski hiši neposredno vplivajo na višino finančnih sredstev, ki jih porabimo za vzdrževanje ugodne klime v hladnih zimskih mesecih.
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Matematika vaja. Matematika FE, Ljubljana, Slovenija Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija
 Matematika 1 3. vaja B. Jurčič Zlobec 1 1 Univerza v Ljubljani, Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija Matematika FE, Ljubljana, Slovenija 2011 Določi stekališča zaporedja a
Matematika 1 3. vaja B. Jurčič Zlobec 1 1 Univerza v Ljubljani, Fakulteta za Elektrotehniko 1000 Ljubljana, Tržaška 25, Slovenija Matematika FE, Ljubljana, Slovenija 2011 Določi stekališča zaporedja a
TRDNOST (VSŠ) - 1. KOLOKVIJ ( )
 TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
DIMENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE
 TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
TEORIJA ETONSKIH KONSTRUKCIJA T- DIENZIONISANJE PRAVOUGAONIH POPREČNIH PRESEKA NAPREGNUTIH NA PRAVO SLOŽENO SAVIJANJE 3.5 f "2" η y 2 D G N z d y A "" 0 Z a a G - tačka presek koja određje položaj sistemne
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
KONSTRUKTORSKA GRADBENA FIZIKA. Analiza ios aplikacije Condensation in primerjava z analitično dobljenimi rezultati
 KONSTRUKTORSKA GRADBENA FIZIKA Analiza ios aplikacije Condensation in primerjava z analitično dobljenimi rezultati Timotej Čižek štud. leto 2013/2014 Condensation je preprosta aplikacija, ki deluje na
KONSTRUKTORSKA GRADBENA FIZIKA Analiza ios aplikacije Condensation in primerjava z analitično dobljenimi rezultati Timotej Čižek štud. leto 2013/2014 Condensation je preprosta aplikacija, ki deluje na
primer reševanja volumskega mehanskega problema z MKE
 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE p p RAK: P-XII//74 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE L
Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE p p RAK: P-XII//74 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE L
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
vezani ekstremi funkcij
 11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
IZRAČUN MEHANSKIH PARAMETROV NADZEMNEGA VODA
 Univerza v Ljubljani Fakulteta za elektrotehniko IZRAČUN MEHANSKIH PARAMETROV NADZEMNEGA VODA Seminar pri predmetu Razdelilna in industrijska omrežja Maja Mikec Profesor: dr. Grega Bizjak Študijsko leto
Univerza v Ljubljani Fakulteta za elektrotehniko IZRAČUN MEHANSKIH PARAMETROV NADZEMNEGA VODA Seminar pri predmetu Razdelilna in industrijska omrežja Maja Mikec Profesor: dr. Grega Bizjak Študijsko leto
