2 ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ ( ΔΙΑΙΡΕΙ ΚΑΙ ΒΑΣΙΛΕΥΕ )
|
|
|
- Νανα Ταρσούλη
- 8 χρόνια πριν
- Προβολές:
Transcript
1 ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ ( ΔΙΑΙΡΕΙ ΚΑΙ ΒΑΣΙΛΕΥΕ )
2 74 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα. Εισαγωγή Στο κεφάλαιο αυτό θα εξετάσουμε μεθόδους σχεδιασμού και ανάλυσης αλγορίθμων που βασίζονται στην αναγωγή του αρχικού προβλήματος σε ένα ή περισσότερα, αλλά μικρότερου μεγέθους. Ακριβέστερα, θα πρόκειται για στιγμιότυπα του ίδιου προβλήματος, όπου κάποια καλώς ορισμένη παράμετρος που εκφράζει το μέγεθος του στιγμιοτύπου θα είναι μικρότερη. Εάν η αναγωγή μπορεί να γίνει για το αρχικό πρόβλημα, τότε μπορεί να επιτευχθεί και για τα υποπροβλήματα. Έχουμε τότε την επαναλαμβανόμενη αναγωγή σε όλο και μικρότερα υποπροβλήματα, δηλαδή την αναδρομική εφαρμογή της. Όταν τα υποπροβλήματα γίνουν αρκετά μικρά, μπορούν να λυθούν εύκολα, παρέχοντας την λύση και στο αρχικό (μεγάλο) πρόβλημα. Συνήθως, οι μέθοδοι αυτές είναι γνωστές με την επωνυμία "Διαίρει και Βασίλευε" (Δ & Β). Ας θεωρήσουμε προς στιγμήν το πρόβλημα της αναζήτησης λίστας στοιχείων, που αναλύθηκε στο Κεφάλαιο. Κατά την διαδοχική αναζήτηση, η σύγκριση με το πρώτο στοιχείο ανάγει την επίλυση σε μικρότερο στιγμιότυπο που ορίζεται από την υπολίστα των - στοιχείων. Το μέγεθος ελαττώθηκε μεν από σε -, όχι όμως σημαντικά αφού η επίλυση του στιγμιότυπου με - στοιχεία στοιχίζει σχεδόν όσο και για. Αντίθετα, με τη δυαδική αναζήτηση, η διάσπαση παράγει στιγμιότυπα με / περίπου στοιχεία και αυτό οδήγησε σε έναν σαφώς βελτιωμένο αλγόριθμο. Πρέπει δηλαδή η διάσπαση να γίνεται σε στιγμιότυπα με αρκετά μικρότερο μέγεθος. Ακριβέστερα, είναι γενική αρχή για κάθε μέθοδο, ότι πρέπει να διατηρείται μια ισοτιμία μεταξύ των διαφόρων παραγόντων, εφόσον δεν υπάρχουν στοιχεία που να επιβάλλουν την προτίμηση ενός από άλλους. Για την μέθοδο Δ & Β αυτό μεταφράζεται στην προσπάθεια της ισοδιάσπασης, όπου δηλαδή το αρχικό στιγμιότυπο μεγέθους ανάγεται σε k στιγμιότυπα (συνήθως k=), που πρέπει να έχουν μέγεθος περίπου /k. Άλλωστε, ένα έργο πολύ μικρού μεγέθους θα τελειώσει μεν πολύ γρήγορα, όμως αυτό δεν φαίνεται να ωφελεί όταν συνεπάγεται ότι υπάρχει και ένα έργο πολύ μεγάλου μεγέθους που χρειάζεται πολύ μεγαλύτερο χρόνο. Αυτό πρέπει να είναι διαισθητικά τουλάχιστον σωστό, σε ορισμένες όμως περιπτώσεις επιδέχεται και μαθηματική απόδειξη: Ας θεωρήσουμε την περίπτωση διάσπασης σε δύο υποπροβλήματα, μεγεθών και αντίστοιχα, όπου =, το μέγεθος του αρχικού προβλήματος. Υποθέτουμε ότι ο χρόνος επίλυσης κάθε υποπροβλήματος μεγέθους m, με κάποια μέθοδο, είναι Τ(m). Τότε και για τα δύο υποπροβλήματα απαιτείται συνολικά χρόνος Τ( ) T( ) = T( ) T(- ) = : f( ) Για την λύση του αρχικού προβλήματος συνήθως θα απαιτείται και ο επιπλέον χρόνος που χρειάζεται για την διάσπαση ή, ισοδύναμα, για τον συνδυασμό των δυο επιμέρους λύσεων. Ας εξετάσουμε όμως μόνο τον χρόνο f( ), στην περίπτωση όπου η συνάρτηση Τ και η παράγωγος της Τ είναι ως προς m αυστηρά αύξουσες. Για παράδειγμα αυτό συμβαίνει σε περιπτώσεις που απαντώνται σε πολλά προβλήματα, όπου Τ(m) = cm με >, T(m) = ml(m), κ.α.
3 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 75 Για ελάχιστο της f χρειαζόμαστε δηλαδή 0 = f ( ) = T ( ) -T (- ), T ( ) = T (- ). Επειδή όμως η T είναι αυστηρά αύξουσα, αυτό μπορεί να ισχύει μόνο όταν: Επίσης, και επειδή T αύξουσα, ισχύει: άρα πρόκειται πράγματι για ελάχιστο. = - δηλαδή = / =. f ( ) = T ( ) T ( ) > 0. Η αναδρομική φύση της μεθόδου παρέχει και μια αναδρομική διατύπωση για την πολυπλοκότητα, οπότε συνήθως διευκολύνεται και η ανάλυση του αλγορίθμου. Έτσι στο κεφάλαιο αυτό θα ασχοληθούμε αρκετά με αναδρομικές σχέσεις. Τέλος, παρατηρούμε ότι η επαναλαμβανόμενη αναγωγή του σε /, /4,... (στο παράδειγμα της ισοδιάσπασης σε δυο υποπροβλήματα) οδηγεί σε λογαριθμικό αριθμό βημάτων και αυτό συνήθως οδηγεί σε αλγορίθμους που είναι βέλτιστοι. Ιδιαίτερη θέση ανάμεσα στις μεθόδους αναδρομικής αναγωγής σε μικρότερα προβλήματα κατέχει ο "ταχύς μετασχηματισμός Fouie" που θα αναλυθεί ξεχωριστά στο επόμενο κεφάλαιο.. Γενική ανάλυση της μεθόδου Δ & Β Θα αναλύσουμε την μέθοδο Δ & Β για την περίπτωση της αναδρομικής ισοδιάσπασης σε δυο υποπροβλήματα. Δεν βλάπτεται η γενικότητα αν υποθέσουμε ότι το μέγεθος, του αρχικού στιγμιότυπου, είναι δύναμη του δύο, δηλαδή = p, p = log. Θα διακρίνουμε δυο περιπτώσεις εφαρμογής της μεθόδου. Στην πρώτη περίπτωση απαιτείται η λύση ενός μόνο από τα δύο υποπροβλήματα που προκύπτουν από μια διάσπαση, ενώ στη δεύτερη απαιτούνται οι λύσεις και των δυο, προκειμένου να ευρεθεί η λύση του αμέσως μεγαλύτερου προβλήματος. Συναντήσαμε την πρώτη περίπτωση στη μέθοδο της δυαδικής αναζήτησης, όπου με μια σύγκριση η αναζήτηση
4 76 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα περιορίζεται σε μια μόνο από τις δυο υπολίστες του μισού μήκους. Με την πρώτη διάσπαση θα έχουμε υποστιγμιότυπα, μεγέθους / το καθένα, που πάλι είναι δύναμη του (όπου p το p-). Με τη δεύτερη διάσπαση θα έχουμε 4 υποστιγμιότυπα, μεγέθους /4= p- το καθένα. Γενικά, στην διάσπαση αριθμ. j, θα έχουμε j υποστιγμιότυπα, μεγέθους p-j =/ j το καθένα. Είναι φανερό, ότι θα προχωρήσουμε το πολύ μέχρι την διάσπαση p, όπου το κάθε στιγμιότυπο θα έχει μέγεθος. Μπορεί, για κάποιο λόγο, να συμφέρει να σταματήσουμε νωρίτερα. Υποθέτουμε επομένως ότι έχουμε k διασπάσεις, όπου k p, ότι οι διασπάσεις αριθμούνται από την τελευταία προς την πρώτη. Επειδή όλα τα στιγμιότυπα στην ίδια διάσπαση i είναι ισομεγέθη, μπορούμε να υποθέσουμε ότι όλα απαιτούν το ίδιο χρόνο, έστω Τ(i). Η Εικόνα.- δείχνει τις αντιστοιχίες, που έχουμε μέχρι στιγμής, όταν =6, p=4 και σύνολο διασπάσεων k=3. Πλή θος στιγμιοτύπων j = p-i Μέ γ ε θ ος κά θε στιγμιότυπου p-j = i Στιγμιότυπα και χρόνος που απαιτεί το καθένα 6 j=0, i=4 Τ(4) 8 j=, i=3 Τ(3) Τ(3) j=, i= Τ() 4 Τ() 5 Τ() 6 Τ() 7 8 j=3, i= Τ() 8 Τ() 9 Τ() 0 Τ() Τ() Τ() 3 Τ() 4 Τ() 5 Εικόνα.- Δέντρο Διάσπασης Στην πρώτη περίπτωση, όπου απαιτείται η λύση μόνο ενός εκ των δυο στιγμιότυπων μιας διάσπασης, ο χρόνος Τ(i), είναι ίσος με το χρόνο που απαιτείται για ένα στιγμιότυπο στην αμέσως από κάτω διάσπαση, δηλαδή Τ(i-), συν τον επιπλέον χρόνο που θα χρειασθεί να βρεθεί η λύση του στιγμιότυπου από τη λύση του προηγούμενου. Ας είναι Ε(i) αυτός ο επιπλέον χρόνος. Για παράδειγμα, στην περίπτωση της δυαδικής αναζήτησης, η μια σύγκριση που ανάγει το πρόβλημα στην αναζήτηση με τη μισή κάθε φορά λίστα είναι ο επιπλέον "χρόνος" και είναι ο ίδιος για όλες τις διασπάσεις i, Ε(i)=. Γενικότερα,
5 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 77 Τ(i) = Τ(i-) Ε(i), (.-) όπου i = i o,...,p (στην Εικόνα.- ο αρχικός δείκτης είναι i o = ). Πάντα όμως θα ξέρουμε τον χρόνο που απαιτείται στην κατώτατη διάσπαση, δηλαδή θα έχουμε και την αρχική συνθήκη όπου b είναι γνωστός αριθμός. Τ(i o ) = b, (.-) Η λύση της αναδρομικότητας (.-), με την αρχική συνθήκη (.-), γίνεται εύκολα με την αλλεπάλληλη εφαρμογή της: Τ(i) = Τ(i-)Ε(i) = [Τ(i-)Ε(i-)]E(i) = T(i-)E(i-)E(i) = [T(i-3)E(i-)]E(i-)E(i) =, οπότε τελικά προκύπτει η λύση T( i ) = b E( j ) i j= io i = i o,...,p, (.-3) όπου όταν i=i o το άθροισμα είναι κενό και συμφωνούμε τότε να το παίρνουμε ίσο με μηδέν. Ο χρόνος, που απαιτείται για το αρχικό στιγμιότυπο, δίνεται από την (.-3) με i=p, δηλαδή p T( p ) = b E( j ). (.-4) j= io Στην δεύτερη περίπτωση, όπου απαιτείται η λύση και των δυο υποπροβλημάτων, ο χρόνος Τ(i) θα είναι ίσος με τον χρόνο Τ(i-) Τ(i-) = Τ(i-) που χρειάζεται για κάθε ένα από τα δυο μικρότερα στιγμιότυπα της διάσπασης i, συν τον επιπλέον χρόνο Ε(i), που απαιτείται για να επιτευχθεί η λύση του στιγμιότυπου από την λύση των άλλων δύο. Έτσι, έχουμε αρχικά: Τ(i) = Τ(i-) Ε(i). (.-5) Αυτό όμως πρέπει να γίνει για όλα τα στιγμιότυπα της διάσπασης i, που είναι σε πλήθος p-i. Αν λοιπόν καλέσουμε τ(i) τον χρόνο που απαιτείται συνολικά, για όλα τα στιγμιότυπα της διάσπασης i, έχουμε τ( i ) p i T( i ) p i { T( i ) E( i )} p i = = = T( i ) p i E( i ). Επειδή τ(i-) = p-(i-) Τ(i-),
6 78 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα βρίσκουμε τον αναδρομικό τύπο τ(i) = τ(i-) p-i Ε(i), i=i o,...,p. (.-6) Η αρχική συνθήκη είναι pio pio τ( i ) = T( i ) = b (.-7) o o Επομένως, όπως και με την προηγούμενη περίπτωση, i τ( i ) p i o b p = j E( j ), (.-8) j= io με την ίδια συμφωνία για το κενό άθροισμα, όταν i=i o. Και πάλι, ο χρόνος που απαιτείται για το αρχικό στιγμιότυπο δίνεται από την (.-8) με i = p και είναι: τ(p)= p-p p io p j T( p ) = ( p ) = Τ(p) = Τ(p) τ b E( j ). p j= io Τα παραπάνω έδειξαν τον τρόπο παραγωγής αναδρομικών σχέσεων και υπολογισμού της πολυπλοκότητας γενικά, για την μέθοδο του Δ & Β. Η υπόθεση = p δεν είναι ουσιαστική. Άλλες φορές μπορεί να συμφέρει μια άλλη υπόθεση, όπως = p - και συνήθως, ό,τι κι αν είναι ο, η γενική αυτή μεθοδολογία μπορεί να ακολουθηθεί, ίσως με λίγη παραπάνω άλγεβρα..3 Παραδείγματα Ήδη στο Κεφάλαιο συναντήσαμε παράδειγμα όπου εφαρμόσθηκε η μέθοδος Δ & Β, συγκεκριμένα την δυαδική αναζήτηση (Π.0-0). Εξετάζουμε τώρα τρία ακόμα παραδείγματα που αφορούν αναδρομικές σχέσεις. Από την προηγούμενη παράγραφο γνωρίζουμε ήδη για μέθοδο επίλυσης αναδρομικότητας, την αλλεπάλληλη εφαρμογή της. Το πρώτο παράδειγμα δείχνει μια ακόμα (γενική) μέθοδο επίλυσης αναδρομικότητας, αυτή της χαρακτηριστικής εξίσωσης, εφαρμοσμένη στην κλασσική περίπτωση των αριθμών Fiboacci. Ενώ δε η αναδρομικότητα εμφανίζεται στη μέθοδο Δ & Β για την ανάλυση της, το δεύτερο παράδειγμα αφορά και μια μέθοδο όπου η ίδια η Δ & Β εφαρμόζεται για τον υπολογισμό όρου αναδρομικής ακολουθίας. Μια ακόμα γενική μέθοδος επίλυσης αναδρομικότητας, αυτή των γεννητριών συναρτήσεων, περιγράφεται με το τρίτο παράδειγμα. ΠΑΡΑΔΕΙΓΜΑ Π.3-. Λύση αναδρομικής σχέσης μέσω της χαρακτηριστικής εξίσωσης. Ακολουθία Fiboacci.
7 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 79 Οι αριθμοί Fibboacci εμφανίζονται σε διάφορες εφαρμογές και ορίζονται από την αναδρομική σχέση f = f - f -,, (.3-) που συνοδεύεται με δύο αρχικές συνθήκες, όπως π.χ. f 0 = 0, f =. (.3-) Η παρακάτω μέθοδος επίλυσης της αναδρομικότητας εφαρμόζεται και σε άλλες περιπτώσεις γενικότερα και αποδίδεται στον DeMoive. Η μέθοδος συνίσταται στην αναζήτηση λύσεων συγκεκριμένης μορφής, στην περίπτωση μας της μορφής f =. Αντικατάσταση στην αναδρομική σχέση δίνει ή, μετά από διαίρεση με -, = = 0. (.3-3) Η εξίσωση αυτή προκύπτει και αμέσως με απλή εξέταση της αρχικής αναδρομικής σχέσης και καλείται "χαρακτηριστική εξίσωση". Παρατηρούμε επιπλέον ότι η αναδρομική σχέση είναι γραμμική και ομογενής, δηλαδή η συλλογή των αγνώστων αριστερά δίνει ένα γραμμικό συνδυασμό f -f - -f - =0 (από τον οποίο προκύπτει αμέσως η χαρακτηριστική εξίσωση) και δεν υπάρχουν άλλοι όροι (το δεξιό μέλος είναι μηδέν). Επομένως, όπως εύκολα μπορούμε να επαληθεύσουμε, εάν φ, φ είναι δυο λύσεις τότε η c φ c φ είναι επίσης λύση, η γενική λύση της αναδρομικότητας. Οι δε σταθερές c, c ορίζονται από τις συμπληρωματικές συνθήκες, στην περίπτωση μας f 0 = 0, f =. Η γενική αυτή μέθοδος βρίσκεται σε πλήρη αντιστοιχία με την γνωστή μέθοδο επίλυσης στοιχειωδών γραμμικών διαφορικών εξισώσεων. Στην περίπτωση της ακολουθίας Fiboacci, η λύση της χαρακτηριστικής εξίσωσης δίνει τις γνωστές από την στοιχειώδη άλγεβρα τιμές της χρυσής τομής άρα τις λύσεις,, και τη γενική λύση = ( - 5 )/, = ( 5 )/, (.3-4) f = c c. Η εφαρμογή των συνθηκών (.3-) δίνει τις σχέσεις c c = 0, c c =, από όπου c = / 5, c = -/ 5, οπότε τελικά
8 80 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα ( ) =. (.3-5) 5 f Ο υπολογισμός όμως των τιμών f από τον τύπο αυτό για μεγάλα εισάγει σοβαρές ανακρίβειες. Έτσι είναι προτιμότερος ο υπολογισμός από κάποιον άλλον αλγόριθμο. Μπορούν για παράδειγμα να βρεθούν οι αριθμοί f k για όλα τα k μέχρι κάποιο μεγάλο απ' ευθείας από την αναδρομική σχέση. Ο αναδρομικός αλγόριθμος που προκύπτει αμέσως fuctio F() if < the etu (* δεν εκτελείται *) else etu F(-) F(-), δεν είναι καλός. Εκτός από τα λογιστικά της αναδρομικής υλοποίησης υπολογίζει τιμές της F() =: f πολλές φορές παραπάνω απ' ότι χρειάζεται, π.χ. την F() πέντε φορές την F(3) φορές, κ.α. Η χρήση μιας μεταβλητής t για την προσωρινή διάσωση της τιμής f k- δίνει τον παρακάτω αλγόριθμο που απαιτεί μόνο τους αναγκαίους υπολογισμούς : (* F(k) = f k, g = f k- *) (* αρχικές τιμές *) g = 0 (* g = f 0 *) f = (* f = f *) Αλγόριθμος Fiboacci- (*υπολογισμός τιμών για k *) fo k = to do t = f (* προσωρινή διάσωση της πιο πρόσφατης τιμής, t=f k- *) f = f g (* υπολογισμός νέας τιμής, f k = f k- f k- *) g = t (* προαγωγή της τιμής f k- στην f k- για τον επόμενο υπολογισμό *) F(k) = f (* αποθήκευση της τιμής f k *) ed k-loop Π.3- ΠΑΡΑΔΕΙΓΜΑ Π.3-. Υπολογισμός όρου αναδρομικής ακολουθίας με υποδιαίρεση του μεγέθους του προβλήματος. Το παράδειγμα Fiboacci. Περιγράφουμε την εφαρμογή της μεθόδου Δ&Β ή παραλλαγής της σε αναδρομικό υπολογισμό, όταν ζητείται ένας μόνο όρος για κάποιο μεγάλο. Αντί τότε να υπολογίσουμε όλους τους προηγούμενους όρους f k, υπολογίζουμε μόνο μερικούς από
9 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 8 αυτούς που θα μας οδηγήσουν στο ζητούμενο. Για να γίνει αυτό χρησιμοποιούμε δυνάμεις του και επαναδιατυπώνουμε την αναδρομική σχέση στη μορφή. v k = Av k, όπου v k, v k διανύσματα και Α πίνακας. Αντί τότε να εφαρμόσουμε διαδοχικά την αναδρομική σχέση φορές για να βρούμε τον -στό όρο, άρα και όλους τους ενδιάμεσους, σχηματίζουμε επαγωγικά τις δυνάμεις Β 0 = Α, Β = Α = Β 0 Β 0, Β = Α 4 = Β A m Β,..., Β m = = B m- B m-, οπότε υπολογίζουμε διαδοχικά τους όρους Β 0 V 0 = AV 0, B (B 0 V 0 ) = A (AV 0 ) =A 3 V 0, B (B (B 0 V 0 )) = A 7 V 0, κ.ο.κ., μέχρι να σχηματίσουμε τον επιθυμητό όρο V = A V 0. Για παράδειγμα, αν = 33 = 5 0, υπολογίζουμε τους Β 0,Β,...,Β 5 και τους όρους V =B 0 V 0, V 3 = B 5 V. Προφανώς η δυαδική αναπαράσταση του, ή ισοδύναμα οι διαδοχικές διαιρέσεις δια του, παράγουν τις απαραίτητες δυνάμεις που χρειάζονται. Η μέθοδος μπορεί να θεωρηθεί ως αναγωγή σε πεπερασμένη σειρά μικρότερων προβλημάτων αν για αρχικό μέγεθος προβλήματος θεωρηθεί ο, επόμενο μικρότερο μέγεθος ο / κ.ο.κ. Η γενική αυτή ιδέα πρέπει να προσαρμόζεται ως προς τους ακριβείς δείκτες κατά περίπτωση. Το παράδειγμα Π.0-5 εξηγεί πλήρως τον υπολογισμό δυνάμεων που χρησιμοποιείται και εδώ. Υπολογισμός του αριθμού Fiboacci f για μεγάλα. Επειδή υπάρχουν δυο στοιχεία εισόδου v k- = [f k-, f k- ] T για τον υπολογισμό του f k στην αναδρομική σχέση, χρειαζόμαστε πίνακα και διανύσματα, άρα γράφουμε v k f A f k k = Av k A f = k f = = 0 k,. Ας υποθέσουμε για παράδειγμα ότι θέλουμε να υπολογίσουμε τον f 39. Χρειαζόμαστε τον υπολογισμό του v 39 = [f 38, f 39 ] T, με δεδομένο το v = [f 0, f ] T. Εδώ συμφέρει η δυαδική ανάλυση του - = 38 = 5, δηλαδή να υπολογισθούν οι Β = Α, Β = Α 4 = Β Β και Β 5 = Α 3 (μέσω του Β 3 = Β Β = Α 8, Β 4 = Β 3 Β 3 = Α 6, Β 5 = Β 4 Β 4 ). Τότε v 39 = B 5 (B (B v )) = A 34 v = A 38 v, απ' όπου και διαβάζουμε τη ζητούμενη τιμή f 39. Για να διατυπώσουμε τον αλγόριθμο παρατηρούμε πρώτα επαγωγικά ότι όλες οι δυνάμεις του Α έχουν την μορφή A a = β β a β =,,... Εύκολα αυτό διαπιστώνεται για = με α = 0, β = και μετά αποδεικνύεται επαγωγικά μέσω της Α = ΑΑ, οπότε προκύπτει και ότι α =β, β = α β. Ειδικότερα μας ενδιαφέρει ο υπολογισμός του Α μέσω του A, δηλαδή οι τιμές α, β μέσω των α, β. Ο πολλαπλασιασμός Α = A A δίνει
10 8 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα α = α β, α = α β β Άρα, αν οι μεταβλητές α, β χρησιμοποιούνται για τις εκάστοτε τιμές α, β (και ανανεώνονται στις α, β ) ισχύει ο υπολογισμός t = β α = α t β = αβ t. Παρόμοια, η ανανέωση των τιμών του διανύσματος [g, g ] T από την σχέση g g g A g, δηλαδή ο υπολογισμός του νέου ζεύγους g = f k-, g = f k από το ζεύγος g = f k-, g = f k, γίνεται από τον αλγόριθμο t = βg g = αg t g = βg αg t, όπου α = α, β = β. Έτσι για τον υπολογισμό του f υπολογίζουμε το διάνυσμα [g, g ] T = [f -, f ] T μετά από συνεχείς ανανεώσεις μέσω του αλγορίθμου: Αλγόριθμος Fiboacci - m = log g = 0 (* g = f 0 *) g = (* g = f *) = - B = A (Αναλυτικότερα η εντολή Β=Α υλοποιείται με τις α=0 (που αντιστοιχεί στην α=α ), β= (που αντιστοιχεί β=β ). Στο σημείο αυτό και αφού πάντα οι τιμές α,β ορίζουν τον πίνακα Β, έχει τεθεί Β = 0 ) fo k = to m do if οdd(μονός) the g B g g g (αναλυτικότερα: t=βf, g =αg t, g =βg αg t) if > the B B (αναλυτικότερα: t=β, α=αt, β=αβt) = / (* συνήθως αρκεί = / *)
11 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 83 ed-fo Π.3- ΠΑΡΑΔΕΙΓΜΑ Π.3-3. Μέθοδος των γεννητριών συναρτήσεων (των δυναμοσειρών) για την επίλυση γραμμικών αναδρομικών σχέσεων. Έστω ότι η δοθείσα αναδρομική σχέση συνδέει τους όρους α, a -, a -m, m και ότι είναι γραμμική, δηλαδή μπορεί να τεθεί στη μορφή F(a, a -, a -m ) := c a c - a - c -m a -m = 0, m, (.3-4) όπου c i είναι γνωστοί αριθμοί. Με τις αρχικές συνθήκες δίνονται οι πρώτοι m όροι α 0,, α m-. Θεωρούμε τότε μια δυναμοσειρά g(): = =0 a = a 0 a a, (.3-5) της οποίας οι συντελεστές είναι οι όροι της ζητούμενης ακολουθίας και πρέπει να προσδιοριστούν. Σχηματίζουμε την ποσότητα F(g()), g(),, m g()) = c g()c - g() c -m m g() = c [a 0 a a m- m- a m m a ] c - [a 0 a a m- m- a m- m a - ] c -m [a 0 m a m a -m ] =(c a 0 ) (c a c - a 0 ) (c a m- c - a m- c -m a 0 ) m- (c a m c - a m- c -m a 0 ) m (c a c - a - c -m a -m ), οπότε από την (.3-4) (c c - c -m m )g()=(c a 0 )(c a c - a 0 ) (c a m- c - a m- c - ma 0 ) m-. (.3-5) Όλοι οι συντελεστές στη (.3-5) είναι γνωστοί λόγω των αρχικών συνθηκών, επομένως από τη σχέση αυτή βρίσκουμε ένα συγκεκριμένο τύπο για την g, ως πηλίκο δυο πολυωνύμων. Ας σημειωθεί ότι ο συντελεστής της g() στο α μέλος είναι το ίδιο πολυώνυμο p(), βαθμού m, που ορίζει την χαρακτηριστική εξίσωση p()=0 του
12 84 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα Π.3-. Γνωρίζοντας τώρα την g, μπορούμε να την αναπτύξουμε σε δυναμοσειρά (με επίσης αρκετό κόπο) και να προσδιορίσουμε έτσι τους συντελεστές στην (.3-4). Ας δούμε πώς εφαρμόζεται η μέθοδος στην περίπτωση της ακολουθίας Fiboacci. Η αναδρομική σχέση γίνεται F(a, a -, a - ) = a -a - -a - =0 (.3-6) και δίνονται οι όροι a 0, a, έστω a 0 =0, a =. Βρίσκουμε τότε F(g()), g(), g() = g() - g() - g() = (-- )g(c) = (a 0 a a )-(a 0 a a - )-(a 0 a 3 a - ) -a 0 (a -a 0 ) (a -a - -a - ) = 0(-0) o Άρα (-- )g() = ή g =. (.3-7) ( ) Απομένει τώρα να αναπτύξουμε την g σε δυναμοσειρά. Ένας τρόπος για να επιτευχθεί αυτό είναι να παραγοντοποιηθεί το πολυώνυμο στον παρανομαστή και στη συνέχεια να διασπαστεί το κλάσμα σε άθροισμα κλασμάτων της μορφής Α, Β Γ οι οποίοι και αναπτύσσονται εύκολα σε δυναμοσειρά. Στη συγκεκριμένη περίπτωση, οι ρίζες της εξίσωσης -- =0 (που είναι η χαρακτηριστική εξίσωση του παραδείγματος 3.-) είναι = ( 5) /, = ( 5) / (.3-8) οπότε ο παρανομαστής παραγοποιείται στη μορφή -- = -(- )(- ) και το κλάσμα (.3-7) έχει διάσπαση g ( ) = = ( )( ) = α β. (.3-9) Μόνοι άγνωστοι είναι οι α, β οι που προσδιορίζονται με εξίσωση συντελεστών όταν στο β μέλος γίνει η πρόσθεση:
13 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 85 Άρα ( )( ) = ( α β ) ( α β ) ( )( ) αβ = - και a β = 0,.
14 86 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα οπότε a =, = β, και με, γνωστά από την (.3-8). Τότε από την (.3-9): ( ) g =. (.3-0) Για την ανάπτυξη των επιμέρους κλασμάτων σε δυναμοσειρά, χρησιμοποιούμε τη γνωστή ταυτότητα =, απ όπου βρίσκουμε ότι για κάθε γ 0, = = γ γ γ γ γ γ γ άρα από την (.3-0) g()= = = 0, απ όπου προσδιορίζονται οι συντελεστές του αναπτύγματος της g, δηλαδή οι όροι της ακολουθίας Fiboacci. a 0 =0, ( ) = = = = α (επιβεβαιώνοντας έτσι τις αρχικές συνθήκες) και ( ) 5 = = α που συμφωνεί με την (.3-5).
15 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 87 Π Αλγόριθμος του Stasse για πολλαπλασιασμό πινάκων Ας θεωρήσουμε πίνακες. Η παρακάτω μέθοδος βρίσκει το γινόμενο Α Β=C για πίνακες με 7 πολλαπλασιασμούς, αντί για 8 που συνήθως απαιτούνται: Πρώτα βρίσκουμε τις ποσότητες = ( a a )( b b ) 5 = ( a a ) b = ( a a ) b 6 = ( a a)( b b ) 3 = a( b b ) 7 = ( a a )( b b ) = a ( b b ) 4 και μετά υπολογίζουμε τα στοιχεία c ij του C από τις σχέσεις: c = c = 3 5, c = c = Έτσι, ο C υπολογίζεται με μ=7 πολλαπλασιασμούς και α=8 προσθέσεις. Είναι ουσιώδες να μη χρησιμοποιηθεί η αντιμεταθετικότητα του πολλαπλασιασμού στα παραπάνω, γιατί δεν ισχύει όταν τα διάφορα στοιχεία είναι πίνακες, για τους οποίους θέλουμε να εφαρμόσουμε την μέθοδο. Όταν = k (δύναμη του ) τότε μια ισοδιάσπαση των πινάκων σε υποπίνακες, A A B A B = A A B B C B = C C C C =, δίνει τη δυνατότητα εφαρμογής των παραπάνω, μόνο που τώρα αντί τα α ij, b ij, i, c ij να είναι αριθμοί, είναι πίνακες k- k-. Έτσι, χρειαζόμαστε 7 πολλαπλασιασμούς τέτοιων πινάκων (που ο καθένας θα γίνει με την ίδια μέθοδο) και 8 προσθέσεις. Επομένως, θα ισχύει µ ( k ) = 7 µ ( κ - ), µ > 0 µ ( 0 ) =, για τους πολλαπλασιασμούς, ενώ για τις προσθαφαιρέσεις ισχύει k a( k ) = 8( ) 7a( k ), k > 0 a( 0 ) = 0. Η λύση των αναδρομικών σχέσεων δίνει:
16 88 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα log log. µ( k ) k = 7 = 7 = < (αριθμός πολλαπλασιασμών του απλοϊκού αλγορίθμου) και k k k a( k ) = 8( ) 7a( k ) = 8( ) 7 8( ) 7 a( k ) k k k3 3 = 8( ) 7 8( ) 7 8( ) 7 a( k 3 ) =... = 7 = = k k- i i ki k 7 8( ) 8( ) i i=0 i=0 ( ) k- 7 4 k k i k = ( q / )( ) ( 7 / 4 ) ( q / )( ) ( / ) = = i=0 ( 7 / 4 ) ή k = a( k ) 6 6 < 8 3 k (αριθμός προσθαφαιρέσεων του απλοϊκού αλγορίθμου)..5 Δ & Β για διάταξη λίστας. Αλγόριθμος Quicksot Ας είναι L το αρχικό διάνυσμα-λίστα. Επιλέγουμε κάποιον αντιπρόσωπο και διασπάμε την αρχική λίστα σε δυο υπολίστες έτσι ώστε όλοι οι αντιπρόσωποι της μιας να είναι μικρότεροι του και όλοι της άλλης να είναι μεγαλύτεροι. Επαναλαμβάνουμε το ίδιο με κάθε μία από τις δύο υπολίστες, οπότε έχουμε τώρα 4 υπολίστες με τα στοιχεία της ης μικρότερα από αυτά της ης, που είναι μικρότερα από αυτά της 3ης, που είναι μικρότερα από αυτά της 4ης. Επαναλαμβάνουμε με κάθε μια από τις 4 υπολίστες κ.ο.κ. μέχρις ότου ολόκληρη η λίστα να είναι διαταγμένη. Χρειαζόμαστε επομένως έναν αλγόριθμο διάσπασης της τυχαίας υπολίστας της L, για την οποία δεχόμαστε ότι περιλαμβάνει τα στοιχεία L(k),...,L(m). Είσοδος στον αλγόριθμο θα είναι οι δείκτες των ορίων της υπολίστας, δηλαδή οι k, m καθώς και τα στοιχεία της L. Ο αλγόριθμος θα επιστρέφει έναν δείκτη i που ορίζει την θέση του μετά την διάσπαση, δηλαδή L(i) =, και βέβαια την νέα υπολίστα με L(j) για k j i, L(j) για i j m. Χρειαζόμαστε και έναν απλό τρόπο επιλογής του για την διάσπαση. Η επιλογή αυτή θα μπορούσε να γίνεται "έξυπνα" πριν από κάθε χρήση και ο δείκτης, τέτοιος ώστε = L() πριν τη διάσπαση, να δίνεται σαν είσοδος. Εδώ για λόγους απλούστευσης και αυτοματισμού, αφήνουμε αυθαίρετα τον αλγόριθμο διάσπασης να επιλέγει το πρώτο στοιχείο της υπολίστας, δηλαδή = L(k). Η Εικόνα.5- περιγράφει την εφαρμογή του αλγορίθμου διάσπασης.
17 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 89 k L(k) k Αλγόριθμος Διάσπασης i m m Εικόνα.5- Ένας καλός αλγόριθμος διάσπασης χρησιμοποιεί δύο δείκτες με αρχικές τιμές i k και j m και περισώζει κάπου το έτσι ώστε η θέση L(i) να είναι διαθέσιμη για την αποθήκευση ενός άλλου στοιχείου. Ο j ελαττώνεται συνεχώς κατά μέχρι να συμβεί L(j)<. Τότε το L(j) ανήκει στην πάνω υπολίστα και αποθηκεύεται στην θέση i, ενώ η θέση j καθίσταται διαθέσιμη για την αποθήκευση άλλου στοιχείου. Τώρα αρχίζει η αύξηση του i συνεχώς κατά μέχρι να συμβεί L(i)> (ή και ). Τότε το L(i) ανήκει στην κάτω υπολίστα και αποθηκεύεται στην διαθέσιμη θέση j. Επανερχόμαστε στην ελάττωση του j και επαναλαμβάνουμε την διαδικασία. Κάποτε θα συμβεί i=j και αυτή είναι η θέση για να τοποθετηθεί το. Ο αλγόριθμος έχει και το πλεονέκτημα ότι κάθε στοιχείο που μετακινείται, μετακινείται μόνο μια φορά εκτός από το που μετακινείται δύο φορές. Παρατηρείστε ότι, εκτός του L(k), όλοι οι αντιπρόσωποι συγκρίνονται με το, μια φορά άρα ο αλγόριθμος απαιτεί m-k συγκρίσεις. Μπορούμε τώρα να διατυπώσουμε έναν απλό αναδρομικό αλγόριθμο που απλώς «οδηγεί» την αναδρομική χρήση του αλγορίθμου διάσπασης. Αλγόριθμος quicksot (L, k, m) if k<m the do Αλγόριθμος διάσπασης για L,k,m,i quicksot(l,k,i-) quicksot(l,i,m) ed Εάν η αναδρομική διατύπωση μεταφερθεί και σε αναδρομική υλοποίηση, οι τιμές των k,m χρειάζεται να φυλάγονται σε «στοίβα» (stack).
18 90 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα ΠΧΠ. Ας εξετάσουμε την περίπτωση που το αποτέλεσμα κάθε εφαρμογής του αλγορίθμου διάσπασης περιγράφεται από την Εικόνα.5-, δηλαδή το καταλήγει να είναι ακραίο στοιχείο της λίστας άρα μια από τις δυο υπολίστες είναι κενή. Έχουμε έτσι ένα παράδειγμα όπου η διάσπαση σε υποπροβλήματα δεν είναι ισότιμη και παραβιάζεται η αρχή της εξισορρόπησης (.). k Αλγόριθμος Διάσπασης ή m πάνω λίστα κενή κάτω λίστα κενή δηλ. i=k ή i=m Εικόνα.5- Μπορεί πράγματι να βρεθεί ένα αρχικό διάνυσμα L με στοιχεία για το οποίο θα συμβεί η παραπάνω περίπτωση. Τότε οι m-k συγκρίσεις του αλγορίθμου διάσπασης γίνονται - την πρώτη φορά (m=, k=), - συγκρίσεις την η κ.λ.π. Τελικά θα έχουμε... ( ) = ( ) / = θ / συγκρίσεις ( ) Μπορεί να δειχθεί ότι η παραπάνω περίπτωση είναι και χειρότερη. Άρα, ΠΧΠ ( ) = ( ) / = θ ( / ) ΠΜΟ. Πρόκειται για άλλο ένα παράδειγμα σχετικά πολύπλοκης ανάλυσης. Δεχόμαστε ότι ΠΜΟ(i) = 0, για i. Την πρώτη φορά που θα εφαρμοσθεί ο αλγόριθμος διάσπασης (k =, m = ) θα γίνουν m-k = - συγκρίσεις και θα προκύψουν δυο υπολίστες, μια με i- και μια με -i στοιχεία, που πρέπει να διαταχθούν πάλι με quicksot. Οι δυνατές τιμές του i είναι,...,. Άρα η μέση τιμή για όλες τις (ισοπίθανες) περιπτώσεις ως προς i είναι [ ΠΜΟ( i ) ΠΜΟ( i) ] i=
19 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 9 Προσθέτοντας και τις αρχικές - συγκρίσεις βρίσκουμε την αναδρομική ανισότητα i= 0 ΠΜΟ(0) = 0, ΠΜΟ() = 0. ΠΜΟ() - ΠΜΟ( i),, (.5-) Θα αποδείξουμε με επαγωγή ότι ΠΜΟ() 3/ log, για. Αν =, βρίσκουμε αμέσως ΠΜΟ()=-(/) 0 = < 3=(3/) (log) και η αποδεικτέα σχέση επαληθεύεται. Δεχόμαστε τότε ότι η σχέση αυτή ισχύει για i =,...,(-) και θα την αποδείξουμε για i = 3 (η τιμή = δεν μας ενδιαφέρει πλέον). Η παραδοχή αυτή δίνει για 3 ΠΜΟ() 3 i log i i= = 3 3 i log i = l - 3 l i= ( ) ( ) l d ( ) Η τελευταία ανισότητα προκύπτει από απλή επιθεώρηση εμβαδών στις γραφικές παραστάσεις της f():= l() και του αθροίσματος (αυστηρότερα: μπορεί κάποιος να χρησιμοποιήσει το γεγονός ότι η f είναι "κυρτή" συνάρτηση). Επειδή l( ) d = l( ) = l( ) 4 4 ισχύει 3 l( ) l( ) 3 3 ΠΜΟ() - = l 4 l l l 4l l 3 log ( ) ( ) ( ) i= i l ( ) i ( ) ( ) ( ) Καταλήγουμε ότι ΠΜΟ() = Ο(log) και όπως γνωρίζουμε (.) αυτό χαρακτηρίζει έναν βέλτιστο αλγόριθμο. Η ιδιότητα αυτή δικαιολογεί και το όνομα quicksot (quick: γρήγορος). Ο αλγόριθμος οφείλεται στον C. A. R. Hoae και βασίζεται στην παρατήρηση ότι η συστηματική σύγκριση διαδοχικών στοιχείων παράγει αργούς αλγορίθμους, όπως με τον αλγόριθμο bubblesot, άρα είναι προτιμότερη η σύγκριση μεταξύ στοιχείων που βρίσκονται σε κάποια απόσταση. Παρενθετικά, η ανάλυση της ΠΜΟ() για την μέθοδο quicksot μπορεί να ακολουθήσει μια τεχνική που απαντάται στην ανάλυση μεθόδων πεπερασμένων
20 9 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα στοιχείων και μερικές φορές αναφέρεται και ως "Λήμμα του Gowall". Επειδή η τεχνική αυτή έχει ευρύτερη εφαρμογή την περιγράφουμε εδώ. Ας θεωρήσουμε μια συνάρτηση για την οποία F () α() β ()F(), για 0 (.5-) Εννοείται ότι οι F, α, β είναι αρκετά λείες συναρτήσεις του, δηλαδή υπάρχουν οι παράγωγοι που χρειαζόμαστε και είναι συνεχείς όταν αυτό είναι απαραίτητο. Τότε ισχύει το φράγμα F() F( 0 )e β()-β( 0 ) e β() a(t)e -β(t) dt (.5-3) 0 Για να αποδειχθεί αυτό από την δοθείσα σχέση (.5-) μεταφέρουμε τον όρο β ()F() στο αριστερό μέλος και πολλαπλασιάζουμε επί e -β(). Παρατηρούμε τότε ότι [F ()-β ()F()]e -β() = (F()e- β() ) a()e -β(), 0 Ολοκληρώνοντας τότε βρίσκουμε F()e -β() - F( 0 )e -β( 0 ) 0 που είναι η σχέση (.5-3). a(t)e -β(t) dt, Όταν όμως κάποιος επιτύχει το φράγμα (.5-3) για την F, μπορεί να το αντικαταστήσει στην (.5-), ενισχύοντας την ανισότητα και επιτυγχάνοντας έτσι και ένα φράγμα για την F. Για να εφαρμόσουμε την τεχνική αυτή στην περίπτωσή μας, θέτουμε i= 0 ( i) F( ) = ΠΜΟ. Στην θέση της παραγώγου F () έχουμε το διακριτό αντίστοιχο [F() - F(-)]/ = F()-F(-) = ΠΜΟ(). Έτσι η αρχική ανισότητα (.5-) γράφεται και F () (-) F(-). Το συνεχές αντίστοιχο θα ήταν F () F(),
21 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 93 όπου για μια ποιοτική αρχική ανάλυση, θέτουμε για και για -. Η σχέση αυτή αντιστοιχεί στην (.5-) με α()= και β ()=/, άρα β()=l(). Τότε ( ) l( ) β e = e =, κ.ο.κ. οπότε με 0 =, F( 0 )=F()=0, καταλήγουμε στην αντίστοιχη της (.5-3) ανισότητα και τότε F( ) t t dt = l( ) F () = ΠΜΟ() F() = l() = l(), Άρα ΠΜΟ() = Ο(l()), όπως και πριν. Ακριβέστερη ανάλυση μπορεί να επιδιωχθεί χωρίς προσφυγή στο συνεχές αντίστοιχο, αλλά μεταφέροντας τα βήματα της απόδειξης της (.5-3), ένα-προς-ένα στο διακριτό τους αντίστοιχο. Ένα τέχνασμα για να πάρει κανείς μια ιδέα για την ΠΜΟ χωρίς να εμπλακεί σε δύσκολη ανάλυση είναι το εξής: Αντί να θεωρήσει όλες τις περιπτώσεις για να επιτύχει τον μέσο όρο των συγκρίσεων, μετράει τις συγκρίσεις για συγκεκριμένες περιπτώσεις που φαίνονται να εκφράζουν μια μέση, ή μια καλύτερη, ή άλλη περίπτωση. Ας θεωρήσουμε για παράδειγμα ότι = p - κι ας δεχθούμε ότι θα συμβαίνει ο αλγόριθμος διάσπασης να κόβει την κάθε υπολίστα ακριβώς στα δύο, περνώντας το ακριβώς στη μέση. Αν Q(p) είναι ο αριθμός των συγκρίσεων για στοιχεία, τότε Q(p-) είναι ο αριθμός για p- - στοιχεία κλπ., ενώ Q() είναι ο αριθμός για -= στοιχείο, άρα Q()=0. Εύκολα μπορούμε να δούμε ότι ισχύει η αναδρομική σχέση p Q( p ) = Q( p ), που μπορεί να λυθεί αν εφαρμοσθεί η αρχική συνθήκη Q()=0. Βρίσκουμε ότι ( ) ( ) ( ) Q( p ) = p ( ) = log = O log. Ο αλγόριθμος quicksot δεν είναι «i place» αφού χρειάζεται επιπλέον χώρο ανάλογο του για την διαχείριση της στοίβας των k,m. Βελτιώσεις που μπορούν να γίνουν:. Είδαμε πως αν επιλέγεται τέτοιο που να καταλήγει στο «κέντρο» της υπολίστας μετά την εφαρμογή του αλγορίθμου διάσπασης, τότε έχουμε αρκετά καλό αριθμό συγκρίσεων Ο(log). Παρατηρούμε επίσης ότι η αυτόματη επιλογή =L(k) δεν δίνει καλή απόδοση, ακόμα και σε περιπτώσεις όπου τα πράγματα θα έπρεπε να ήταν πολύ εύκολα. Η επιλογή του έχει επομένως σημασία. Στρατηγικές για την επιλογή του υπάρχουν, απαιτούν κάποιες επιπλέον πράξεις αλλά συμφέρουν γιατί τελικώς μειώνουν την ΠΜΟ. Μια τέτοια στρατηγική είναι να διαλέξει
22 94 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα κανείς ένα δείκτη q στην τύχη μεταξύ k και m και να χρησιμοποιήσει =L(q). Μια άλλη είναι να διαλέξει τον να είναι ο μεσαίος από τους L(k), L( (km)/) ) και L(m).. Ο χρόνος διαχείρισης της στοίβας αξίζει να καταναλώνεται όταν ο είναι μεγάλος. Για μικρά όμως πληρώνει κανείς πιο πολύ γι αυτό τον χρόνο παρά για τις συγκρίσεις. Έτσι εφαρμόζει κανείς quicksot για μεγάλα και όταν οι υπολίστες φτάσουν να έχουν αρκετά μικρό μέγεθος (εμπειρικά, γύρω στο 0) τότε χρησιμοποιεί κάποιον άλλον αλγόριθμο για την διάταξή τους. 3. Αντί να αφήσει κάποιος την διαχείριση της στοίβας (στον αναδρομικό αλγόριθμο) στην διάθεση του compile (κάποιας γλώσσας) είναι καλύτερα να γράψει μια μη αναδρομική παραλλαγή του αλγορίθμου, όπου θα γίνονται μόνο τα αναγκαία PUSH και ΡΟΡ στην στοίβα. Χρησιμοποιούνται κι άλλες ιδέες - βελτιώσεις που δεν θα μας απασχολήσουν εδώ..6 Shellsot Ο Αλγόριθμος Shellsot έχει αρκετό ενδιαφέρον, προγραμματίζεται εύκολα και είναι γρήγορος. Η ανάλυσή του όμως είναι πολύ δύσκολη και όπως θα δούμε υπάρχουν ανοιχτά θέματα. Η μέθοδος: Επιλέγεται μια ακολουθία από «βήματα» h t, h t-,...,h, h = (όπως θα διαπιστώσουμε εύκολα, η τιμή h = εξασφαλίζει ότι το αποτέλεσμα θα είναι σωστό). Για κάθε h k η λίστα των στοιχείων χωρίζεται σε h k υπολίστες. Η πρώτη υπολίστα περιέχει τα στοιχεία, h k, h k κ.λ.π., το δεύτερο τα, h k, h k, κ.λ.π. Η κάθε υπολίστα διατάσσεται με την εφαρμογή ενός (κάποιου) αλγορίθμου. ΠΑΡΑΔΕΙΓΜΑ Π.6-. Να εφαρμοσθεί η Shellsot για L T = [ ] και με ακολουθία βημάτων 7, 5, 4, 3,,. Τα στοιχεία που ανήκουν κάθε φορά στην ίδια υπολίστα δηλώνονται με συνδετικές γραμμές:
23 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 95 h= h= h= h= h= h= Π.6- Στο τέλος (h=) έχουμε μια υπολίστα (την αρχική) που η διάταξή της εξασφαλίζει και την διάταξη της αρχικής λίστας. Υπάρχουν βέβαια αρκετές φυσιολογικές ερωτήσεις, όπως: Τι αλγόριθμος είναι καλό να χρησιμοποιείται για την διάταξη κάθε υπολίστας; Αφού για h= ολόκληρη η αρχική λίστα διατάσσεται με τον αλγόριθμο που χρησιμοποιείται για τις υπολίστες, είναι πράγματι καλύτερος ο Shellsot από τον αλγόριθμο αυτό; Ποιά είναι η καλύτερη επιλογή βημάτων; Παρατηρούμε ότι κάθε φορά οι υπολίστες είναι «αρκετά διαταγμένες» από τα προηγούμενα βήματα και ότι όσο προχωρούμε προς τα τελευταία βήματα τόσο πιο πολύ περιμένουμε ότι θα χρειαστούν ελάχιστες αλλαγές για τη διάταξή τους. Έτσι, για την διάταξη κάθε υπολίστας, καλό είναι να χρησιμοποιήσουμε έναν αλγόριθμο
24 96 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα που δεν απαιτεί πολλές συγκρίσεις όταν η λίστα είναι σχεδόν έτοιμη. Ένας τέτοιος αλγόριθμος είναι αυτός της Παρεμβολής, βλ. Π.3-3 Είναι ο Shellsot καλύτερος από τον αλγόριθμο της Παρεμβολής; Όταν h= τότε οι δύο αλγόριθμοι συμπίπτουν, αλλά η λίστα έχει προετοιμασθεί αρκετά από τα προηγούμενα βήματα. Αν χρησιμοποιήσουμε μόνο h= τότε έχουμε την ΠΧΠ της παρεμβολής, δηλαδή. Αν χρησιμοποιήσουμε δύο βήματα, h και h = τότε μπορεί να δειχθεί ότι η ΠΧΠ του Shellsot βελτιώνεται σημαντικά σε.7 5/3 με καλύτερη τιμή για h την h Πιο πολλά βήματα δίνουν ακόμα πιο καλή βελτίωση. Το ερώτημα της καλύτερης επιλογής βημάτων είναι μάλλον ανοιχτό, αφού έχουμε μόνο μερικές απαντήσεις: αν h k = k -, για k log τότε ΠΧΠ() 3/. Σημειώστε εδώ ότι ο υπολογισμός ενός h από το προηγούμενο (ή επόμενο) γίνεται πολύ εύκολα σε γλώσσα assembly με μετατόπιση κατά bit. πειραματικές μελέτες με το να φτάνει μέχρι και έχουν δείξει ότι η ακολουθία βημάτων h k k : = ( 3 ) / με k t, όπου t := μικρότερος ακέραιος με την ιδιότητα ht, δίνει πολύ καλούς χρόνους. Σημειώστε ότι κάθε h υπολογίζεται με αναγωγικό τύπο από το προηγούμενο ή επόμενο: h k = 3h k, h k = (h k - ) / 3 έχει αποδειχθεί ότι αν για h χρησιμοποιηθούν όλες οι δυνατές τιμές της μορφής i 3 j (που είναι < ) τότε ΠΧΠ() (log) Επειδή όμως υπάρχουν πολλά τέτοια h, απαιτούνται πολλά περάσματα που επιβάλλουν σημαντική λογιστική επιβάρυνση. Επομένως, αυτή η επιλογή δεν είναι ιδιαίτερα χρήσιμη εκτός αν το είναι πολύ μεγάλο. Τέλος, η αποδοτικότητα της μεθόδου οφείλεται στο ότι η χρήση κάποιου h δεν καταστρέφει την πρόοδο που έχει ήδη επιτευχθεί από τα προηγούμενα h.
25 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 97.7 BUCKET και RADIX SORT Μέχρι στιγμής, οι αλγόριθμοι που εξετάσαμε χρησιμοποιούν μόνο την υπόθεση ότι οι αντιπρόσωποι (keys) είναι στοιχεία ενός γραμμικά διαταγμένου συνόλου. Υπάρχουν όμως περιπτώσεις που γνωρίζουμε πιο πολλά για τους αντιπροσώπους, όπως π.χ. ότι είναι 5-ψήφιοι αριθμοί. Σε τέτοιες περιπτώσεις χρησιμοποιούνται αλγόριθμοι «BUCKET» (κάδος) ή «αλγόριθμοι που κάνουν διάταξη με κατανομή». Αυτοί οι αλγόριθμοι χωρίζουν πρώτα τους αντιπροσώπους σε σωρούς. Στον ίδιο σωρό πάνε όσα ονόματα αρχίζουν από Α, σε άλλο σωρό όσα αρχίζουν από Β, κ.λπ., ή: σε άλλον σωρό όσοι αριθμοί αρχίζουν από, στον ίδιο όσοι αρχίζουν από κ.λπ. Μετά γίνεται διάταξη - εσωτερικά - του κάθε σωρού χωριστά και τέλος, συνδυάζονται οι σωροί για να κατασκευαστεί η διαταγμένη λίστα. Ο κάθε σωρός μπορεί να διαταχθεί με τον ίδιο τρόπο οπότε έχουμε αναδρομικό αλγόριθμο. Για να εξετάσουμε την πολυπλοκότητα ενός αλγορίθμου BUCKETSORT πρέπει να παρατηρήσουμε ότι ο αλγόριθμος έχει τρεις φάσεις και ότι η κάθε φάση απαιτεί το δικό της είδος πράξεων. Φάση Κατανομής (σε σωρούς). Ας δεχθούμε ότι χρησιμοποιούνται k σωροί. Εδώ ο αλγόριθμος εξετάζει κάθε αντιπρόσωπο μια φορά, π.χ. συγκρίνοντάς τον με k τιμές που αντιστοιχούν σε ( είναι ενδεικτικές για) κάθε έναν από τους k σωρούς, για να αποφασίσει σε ποιο σωρό ανήκει ο αντιπρόσωπος. Μετά τοποθετεί τον αντιπρόσωπο στον σωρό του, που σημαίνει κάποια παραπάνω προσπάθεια π.χ. να υπολογίσει μερικούς δείκτες. Αν δεν ξέρουμε άλλες ειδικές λεπτομέρειες το μόνο που μπορούμε να πούμε γι αυτή τη φάση είναι ότι η προσπάθεια είναι ανάλογη του. Φάση διάταξης (του κάθε σωρού). Ας δεχθούμε ότι για την διάταξη του κάθε σωρού χρησιμοποιείται ένας αλγόριθμος που απαιτεί S(m) συγκρίσεις, όταν ο σωρός έχει m στοιχεία. Αν λοιπόν, από την Φάση Κατανομής, προέκυψαν i στοιχεία στο σωρό i=,...,k, τότε για όλους τους k σωρούς θα χρειαστούν k i= S( i ) συγκρίσεις Φάση συνδυασμού (των διαταγμένων πλέον σωρών για να κατασκευαστεί η τελική, διαταγμένη, λίστα). Στην χειρότερη περίπτωση, μπορεί να χρειαστεί να αντιγράψει (να μεταφέρει) ο αλγόριθμος όλους τους αντιπροσώπους, ένα προς ένα, από τους σωρούς στην λίστα. Άρα, η προσπάθεια είναι ανάλογη του. Ας δεχθούμε ότι S(m)=cmlogm (γιατί;) κι ας υποθέσουμε ότι όλοι οι σωροί έχουν τον ίδιο αριθμό στοιχείων μετά την κατανομή, δηλαδή i =/k. Τότε από την Φάση Διάταξης θα έχουμε αριθμό συγκρίσεων
26 98 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα k c( / k )log( / k ) = c log( / k ), = i όπου η σταθερά c εξαρτάται από τον συγκεκριμένο αλγόριθμο που χρησιμοποιήθηκε σ αυτή την φάση και είναι ανεξάρτητη των, k. Παρατηρούμε τότε ότι όσο μεγαλύτερος είναι ο αριθμός των σωρών k τόσο λιγότερες συγκρίσεις χρειάζονται. Όμως δεν είναι πάντα εφικτός ο καθορισμός του k (και η επιτυχία να είναι i =/k), εκτός αν γνωρίζουμε κι άλλες λεπτομέρειες για το συγκεκριμένο πρόβλημα. Μια άλλη λύση θα ήταν η αναδρομική εφαρμογή BUCKETSORT για τη δημιουργία όλο και μικρότερων σωρών. Αυτό όμως επιβαρύνει σημαντικά «τα λογιστικά» του αλγορίθμου και, γενικά, δεν συμφέρει εκτός από την παρακάτω περίπτωση. RADIX SORT. Τυπική περίπτωση εφαρμογής της μεθόδου Radi είναι όταν οι αντιπρόσωποι είναι ακέραιοι, π.χ. 5-ψήφιοι. Ένας αναδρομικός αλγόριθμος θα μπορούσε αρχικά να χωρίσει τους αριθμούς σε 0 σωρούς, ανάλογα με το πρώτο ψηφίο (αν δηλαδή το πρώτο ψηφίο είναι 0,,...,9), μετά να χωρίσει κάθε σωρό σε 0 σωρούς ανάλογα με το δεύτερο ψηφίο κ.λπ. Το πρόβλημα βέβαια εξακολουθεί να υπάρχει αφού δημιουργούνται όλο και πιο πολλοί «υπό-σωροί» άλλων υπο-σωρών και πρέπει να τηρείται αυστηρή λογιστική μέχρι να γίνει πλήρης διάταξη. Το ενδιαφέρον όμως είναι πως αν ο χωρισμός γίνεται από το τελευταίο ψηφίο (ή bit, ή γράμμα, ή πεδίο) τότε οι σωροί μπορούν «να συγκολληθούν» σ ένα μεγάλο σωρό προτού προχωρήσει κανείς σε άλλο διαχωρισμό σύμφωνα με το επόμενο (από δεξιά προς τα αριστερά) στοιχείο! Έτσι απαλείφεται το πρόβλημα της λογιστικής και, με την αναδρομικότητα, δεν χρησιμοποιείται άλλος αλγόριθμος για εσωτερική διάταξη σωρών. ΠΑΡΑΔΕΙΓΜΑ Π.7-. RADIX SORT για την λίστα 4808, 9734, 9087, 90583, 530, 655, 78397, 4800, 0097, 6535, 4983, 9083, 8664, 3807 (=4). Θα γίνουν 5 διαχωρισμοί ανάλογα με το ο,ο,...,5ο (από δεξιά προς τα αριστερά) ψηφίο σε σωρούς 0,,...,9. Μετά από κάθε διαχωρισμό θα γίνεται και «συναρμολόγηση». ος Διαχωρισμός Στο σωρό μπαίνουν οι 4808, 4800 Στο σωρό μπαίνουν οι 9734, 530, 0097 Στο σωρό 3 μπαίνουν οι , 498 3, Στο σωρό 4 μπαίνουν οι Στο σωρό 5 μπαίνουν οι 65 5, Στο σωρό 7 μπαίνουν οι 908 7, , Στους υπόλοιπους σωρούς δεν τοποθετούνται αριθμοί και οι σωροί συναρμολογούνται σε νέα λίστα με τη σειρά: Σωρός 0,Σωρός,...,Σωρός 9:
27 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ , 4800, 9734, 530, 0097,..., 9087, 78397, 3807, 7 ος Διαχωρισμός και συναρμολόγηση: 480 0, 53 0, , 65 5, 653 5,..., Σωρός 0 Σωρός Σωρός 9 Συνεχίζοντας με τον ίδιο τρόπο βεβαιωθείτε ότι μετά τον 3ο Διαχωρισμό ο Σωρός 9 θα περιέχει μετά τον 4ο ο Σωρός 0 θα περιέχει και ότι μετά τον 5ο επιτυγχάνεται η διαταγμένη λίστα. Παρακολουθείστε τους αντιπροσώπους που αρχίζουν και διαφέρουν μόνο στον 3ο (από δεξιά) δείκτη. Στους δύο πρώτους διαχωρισμούς και οι δύο πέφτουν στον ίδιο σωρό, στον τρίτο διαχωρισμό φυσικά πέφτουν σε διαφορετικούς σωρούς και στους υπόλοιπους δύο πέφτουν πάλι στον ίδιο σωρό. Τι εξασφαλίζει ότι στο τέλος θα εμφανισθούν στην σωστή τους θέση; Π.7- Ανάλυση: Η βασική πράξη στον RADIX SORT δεν είναι πλέον η σύγκριση αντιπροσώπων μεταξύ τους αλλά η τοποθέτησή τους σε σωρούς (που απαιτεί π.χ. καθορισμό του σωρού και ορισμό δεικτών-poites). Μπορεί να αποδειχθεί ότι η ΠΧΠ είναι ανάλογη του. Αυτή είναι μικρότερη του κάτω φράγματος της.. Γιατί;.8 Συμβολή και Megesot Δίνονται δύο διαταγμένες λίστες (αντιπροσώπων) Α και Β. Συμβολή είναι η κατασκευή μιας νέας διαταγμένης λίστας C, που περιέχει τα στοιχεία των Α και Β. Απλή λύση: Συγκρίνονται το πρώτο από τα εναπομένοντα στοιχεία της Α με το πρώτο από τα εναπομένοντα στοιχεία της Β. Το μικρότερο τοποθετείται στην C. ΠΑΡΑΔΕΙΓΜΑ Π.8-. Α={3, 0,, 6} Β={8, 4, 5} Σύγκριση 3 με 8 A B C
28 00 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα Σύγκριση 0 με 8 A B C Σύγκριση 0 με 4 A B C κ.λ.π. Π.8- Φυσικά, όταν εξαντληθούν τα στοιχεία μιας από τις Α ή Β, τα εναπομείναντα στοιχεία της άλλης προσαρτώνται στο τέλος της C χωρίς παραπέρα συγκρίσεις. Αλγόριθμος MERGE {όπου η Α έχει και η Β έχει m στοιχεία}. i j k l while i ad j m do if a i < b j the do c k a i ; i i ed else do c k b i ; j j ed ed if i> the move b j,...,b m to c k,...,c m else move a i,...,a to c k,...,c m Ανάλυση: Ας είναι ΠΧΠ(,m) ο αριθμός των συγκρίσεων στην χειρότερη περίπτωση. Μετά από κάθε σύγκριση ελαττώνεται κατά ο αριθμός των στοιχείων της Α ή της Β, ενώ της άλλης παραμένει ο ίδιος. Γεωμετρικά, το αρχικό ορθογώνιο (όλα τα στοιχεία της Α και όλα τα m στοιχεία της Β στην Εικόνα.8-α) θα μετατραπεί στο μικρότερο ορθογώνιο της.8-β (αν α <b ) ή της.8-γ (αν b <a ), μετά την η σύγκριση. Μετά από κάθε σύγκριση το υπάρχον ορθογώνιο θα περιορίζεται σε κάποιο μικρότερο από το οποίο θα λείπει η αριστερή κάθετη ή η κάτω οριζόντια γραμμή. Η χειρότερη περίπτωση θα είναι όταν φτάσουμε στο ορθογώνιο-σημείο της πάνω δεξιά γωνίας, όπου δηλαδή θα έχουν απομείνει τα στοιχεία α και b m και όπου με μια ακόμα σύγκριση τελειώνουμε. Κάθε σύγκριση που γίνεται σημαίνει μετάβαση από ένα σημείο σε διπλανό (πάνω ή δεξιά), με αρχή από το κάτω αριστερά σημείο (,) και τέλος στο πάνω δεξιά (,m).
29 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 0 B m. B m. B m.... A... A... A (α) (β) (γ) Εικόνα.8- Η πορεία από το αρχικό στο τελικό σημείο μπορεί να γίνει με ( ) ( m ) = m μεταβάσεις (συγκρίσεις), στις οποίες προστίθεται και η μια τελική σύγκριση α με b m, δίνοντας συνολικά ΠXΠ(, m) = m συγκρίσεις. Η περίπτωση m=, όπου δηλαδή οι δύο λίστες Α και Β είναι ισάριθμες, έχει ενδιαφέρον αφού μπορούμε να δείξουμε ότι τότε ο MERGE είναι βέλτιστος: αν θέσουμε m=, στην παραπάνω ανάλυση βρίσκουμε ενώ ισχύει και το ΠXΠ( ): = ΠXΠ(, ) =, ΘΕΩΡΗΜΑ Θ.8-. Για οποιοδήποτε σωστό αλγόριθμο για συμβολή, όταν οι Α και Β έχουν από στοιχεία η κάθε μία, χρειάζονται στην χειρότερη περίπτωση τουλάχιστον - συγκρίσεις. Απόδειξη: Αφού εξετάζουμε την χειρότερη περίπτωση μπορούμε να δώσουμε ό,τι iput θέλουμε. Ας θεωρήσουμε οποιονδήποτε σωστό αλγόριθμο και ας εξετάσουμε τις εισόδους για τρεις περιπτώσεις: I : b <a <...<b j <a j <...<b <a I j : ίδιο με το Ι μόνο που τα α j και b j έχουν εναλλαγεί, δηλαδή α j <b j. I j : ίδιο με το Ι μόνο που τα α j, b j έχουν εναλλαγεί, δηλαδή b j < b j < a j... Ισχυριζόμαστε ότι ο αλγόριθμος (όποιος κι αν είναι) είναι υποχρεωμένος, για το Ι:
30 0 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα (i) να συγκρίνει α i με b i, για όλα τα i=,...,, Αφού b i <a i θα τοποθετηθεί στην C το b i. Αμέσως μετά (ii) για όλα τα i=,...,(-) να συγκρίνει α i με b i. Αφού α i < b i θα τοποθετηθεί στην C το α i. Αν δεν εφάρμοζε το (i) τότε για κάποιο j, <j<, ο αλγόριθμος δεν θα έκανε την σύγκριση α j με b j. Άρα, θα έδινε το ίδιο αποτέλεσμα για το Ι και για το Ι j. Αυτό είναι άτοπο αφού ο αλγόριθμος είναι σωστός. Το ίδιο ισχύει για το (ii) και τα Ι και Ι j. Τώρα από (i) & (ii) έχουμε αντίστοιχα ένα ελάχιστο από και - συγκρίσεις, δηλαδή - συγκρίσεις. Θ.8- Όταν m=, παρατηρούμε ότι ο MERGE αντιστοιχεί σε ακολουθιακή αναζήτηση της λίστας Α, που όπως γνωρίζουμε υστερεί σε σύγκριση με άλλους αλγορίθμους π.χ. δυαδική αναζήτηση. Υπάρχουν επομένως καλύτεροι αλγόριθμοι για συμβολή, τουλάχιστον αυτοί που κατά κάποιο τρόπο αντιστοιχούν σε δυαδική αναζήτηση. Το σημαντικό όμως στοιχείο για τον MERGE οφείλεται στο γεγονός ότι δεν κάνει παλινδρομήσεις μέσα στις λίστες Α και Β κι αυτό έχει σημασία π.χ στην εξωτερική διάταξη (.9). Megesot: Ένας αλγόριθμος για διάταξη, που είναι μάλιστα βέλτιστος ως προς την ΠΧΠ, προκύπτει με αναδρομική συμβολή, όπου λίστες συνενώνονται σε μεγαλύτερες διαταγμένες λίστες μέχρις ότου επιτευχθεί η μεγάλη λίστα. Ας είναι = p. Πρώτα έχουμε λίστες του ενός στοιχείου και τις συμβάλλουμε κατά ζεύγη πληρώνοντας έτσι ( σύγκριση/ζεύγος) (/ ζεύγη) = / συγκρίσεις Τώρα έχουμε / λίστες των δύο στοιχείων και τις συμβάλλουμε κατά ζεύγη. Από το Θ.8- κάθε ζεύγος απαιτεί *-=4- συγκρίσεις, έτσι συνολικά απαιτούνται (4-)*/4=(-/4) συγκρίσεις. Γενικά, θα υπάρχουν / j λίστες των j στοιχείων και θα απαιτούνται από το Θ.8- j j j ( ( ) ) / = ( / ) συγκρίσεις, για j=0,...,(p-). Αθροίζοντας ως προς j βρίσκουμε ότι συνολικά ο Megesot απαιτεί
31 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 03 ΠΧΠ( ) = log συγκρίσεις Η τιμή αυτή βέβαια δεν παραβιάζει το κάτω φράγμα της. και είναι κοντά σ αυτό, συμπίπτει στον κυρίαρχο όρο log και, επομένως, μπορούμε να πούμε ότι ο megesot είναι (σχεδόν) βέλτιστος..9 Εξωτερική Διάταξη Εδώ θεωρούμε (όπως συχνά συμβαίνει) ότι ο αριθμός των στοιχείων ή αρχείων μιας λίστας είναι τόσο μεγάλος που δεν είναι δυνατόν να έχουμε όλα τα στοιχεία στην άμεση (ταχεία) μνήμη του υπολογιστή, που έστω ότι έχει χωρητικότητα για m το πολύ στοιχεία, όπου m<. Σε τέτοιες περιπτώσεις έχει βαρύτητα ο χρόνος μεταφοράς δεδομένων μεταξύ της άμεσης μνήμης και της εξωτερικής συσκευής στην οποία είναι αποθηκευμένα τα στοιχεία της λίστας. Ο χρόνος αυτός είναι αρκετά μεγαλύτερος από τον χρόνο των συγκρίσεων στην άμεση μνήμη. Επίσης, σημαντικό είναι να χρησιμοποιούνται ακολουθιακές διαδικασίες αντί για π.χ. δυαδικές, αφού οι μη ακολουθιακές διαδικασίες απαιτούν (με τις παλινδρομήσεις τους) χρόνο για επανατυλίξεις ταινιών, για εντοπισμό περιοχών σε δίσκο κ.λπ. Έτσι, αξίζει να χρησιμοποιηθεί ο MERGE. Ας δούμε πώς μπορεί να γίνει εξωτερική διάταξη στην αρκετά απλή αλλά όχι τόσο συχνή περίπτωση που διαθέτουμε 4 ταινίες Τ ο, Τ, Τ, Τ 3 για αποθήκευση. Όλα τα στοιχεία αρχικά είναι αποθηκευμένα στην Τ ο, έχουν πλήθος (μεγάλο), ενώ η άμεση μνήμη μπορεί να συγκρατήσει και διατάξει μόνο m<< απ αυτά. Έτσι, διαβάζουμε (μεταφέρουμε από την Τ ο στην άμεση μνήμη) τα στοιχεία αυτά ανά m κάθε φορά (ίσως λιγότερα την τελευταία φορά, αν ο δεν είναι ακέραιο πολλαπλάσιο του m), τα οποία και διατάσσονται με κάποιο αλγόριθμο. Οι διαταγμένες ομάδες m στοιχείων αποθηκεύονται εναλλακτικά στις Τ και Τ 3, αρχίζοντας με την τοποθέτηση της πρώτης m-άδας στην T. Εδώ τελειώνει η πρώτη φάση, δηλαδή η κατασκευή και κατανομή των διαταγμένων m-άδων. Αμέσως μετά γίνεται επανατύλιξη των ταινιών κι ένας διαχωρισμός τους σε ταινίες εισόδου (οι Τ και Τ 3, που κρατούν τις διαταγμένες m-άδες) και σε ταινίες εξόδου (οι Τ ο και Τ, που θα παραλάβουν εξαγόμενα). Τώρα αρχίζει η δεύτερη φάση, που κάνει συμβολή πολλές φορές (POLYPHASE MERGE): Κάνουμε συμβολή της πρώτης m-άδας από Τ με την πρώτη m-άδα από Τ 3 και το αποτέλεσμα - μια διαταγμένη ομάδα από m στοιχείατοποθετείται στην Τ ο. Αυτό γίνεται με χρήση του MERGE, άρα στην άμεση μνήμη υπάρχουν πάντα τα δύο στοιχεία (ένα από κάθε m-άδα) που συγκρίνονται, κι όταν φύγει το ένα για την Τ ο διαβάζεται το επόμενο και θα συγκριθεί με αυτό που απόμεινε. Επαναλαμβάνουμε με τις δεύτερες m-άδες από Τ και Τ 3 και τοποθετούμε το αποτέλεσμα στην Τ. Συνεχίζουμε μέχρι να εξαντληθούν με όλα τα ζεύγη από Τ και Τ 3, τοποθετώντας τα εξαγόμενα εναλλακτικά σε Τ ο και Τ. Αν μείνει μονή m-άδα την τοποθετούμε όπως
32 04 ΑΛΓΟΡΙΘΜΟΙ: εισαγωγικά θέματα και παραδείγματα είναι στην ταινία που έχει σειρά. Αλλάζουμε τις ταινίες εισόδου σε ταινίες εξόδου και αντίστροφα και επαναλαμβάνουμε με τις m-άδες. Συνεχίζουμε με τον ίδιο τρόπο μέχρι να διαταχθεί ολόκληρη η λίστα. Ενδιάμεσα φυσικά χρειάζονται και οι σχετικές επανατυλίξεις. ΠΑΡΑΔΕΙΓΜΑ Π.9-. Να ακολουθηθεί ο προηγούμενος αλγόριθμος για την λίστα που εμφανίζεται στην ταινία Τ ο της Εικόνας.9-, με m=4. Τα αποτελέσματα δείχνονται στην Εικόνα.9-. Το σύμβολο σημειώνει το τέλος μιας διαταγμένης ομάδας ενώ το δείχνει το τέλος της ταινίας (δεν υπάρχουν άλλα στοιχεία στην ταινία). Τ Μετά από την η Φάση: Τ Τ η Φάση, ο πέρασμα: Τ Τ η Φάση, ο πέρασμα: Τ Τ η Φάση, 3ο πέρασμα: Τ Εικόνα.9- Παράδειγμα εξωτερικής διάταξης Π.9- Ανάλυση: Οι βασικές πράξεις είναι συγκρίσεις, επανατυλίξεις (τεσσάρων ταινιών ταυτόχρονα), καθώς και πλήρη περάσματα από τα δεδομένα (μεταφορές από ταινίες σε μνήμη και αντίστροφα).
33 . ΑΝΑΔΡΟΜΙΚΗ ΑΝΑΓΩΓΗ ΣΕ ΜΙΚΡΟΤΕΡΑ ΠΡΟΒΛΗΜΑΤΑ 05 Ας είναι k ο αριθμός των στοιχείων (αντιπροσώπων, αρχείων) που έχει η κάθε αρχική διαταγμένη ομάδα (στον προηγούμενο αλγόριθμο k=m) κι ας υποθέσουμε ότι και η τελευταία ομάδα έχει k στοιχεία ώστε :=/k να είναι ακέραιος. Έτσι, προτού μπει ο αλγόριθμος στην η φάση, δηλαδή με το συμπλήρωμα της ης Φάσης, έχουν γίνει τα παρακάτω: Ένα πλήρες πέρασμα από τα δεδομένα: κάθε στοιχείο από την ταινία εισόδου T μεταφέρεται στην άμεση μνήμη, όπου γίνονται μερικές συγκρίσεις και κάποτε το στοιχείο αυτό μεταφέρεται σε μια ταινία εξόδου. Μία επανατύλιξη. σ συγκρίσεις. Αν ο αλγόριθμος που χρησιμοποιείται για εσωτερική διάταξη (π.χ. Heapsot) χρειάζεται S(k) συγκρίσεις για να διατάξει τα k στοιχεία (π.χ. για την Heapsot S(k) klogk, βλ.., στη χειρότερη περίπτωση) έχουμε σ=s(k), επειδή έχουν διαταχθεί ομάδες των k στοιχείων. Στη η φάση παρατηρούμε ότι έχουμε τόσα πλήρη περάσματα από τα δεδομένα και τόσες επανατυλίξεις όσα και τα περάσματα από την loop «while» αυτής της φάσης. Αρχίζουμε την η φάση με ομάδες των k στοιχείων. Μετά το πρώτο πέρασμα έχουμε / ομάδες στις ταινίες των k στοιχείων, εκτός ίσως από την τελευταία. Μετά το δεύτερο πέρασμα έχουμε /4 ομάδες κ.λπ. Έτσι, συμπεραίνουμε ότι ο αριθμόςτων πλήρων περασμάτων από τα δεδομένα και ο αριθμόςτων επανατυλίξεων (κι από τις δύο φάσεις) είναι log. Επειδή =/k, όσο μεγαλύτερο είναι το k (δηλαδή όσο μεγαλύτερες σε μέγεθος και μικρότερες σε αριθμό είναι οι αρχικές ομάδες) τόσο πιο λίγο είναι το κόστος επανατυλίξεων και μεταφορών δεδομένων. Φυσικά, στον προηγούμενο αλγόριθμο k=m και το m είναι σταθερό με τον υπολογιστή που έχουμε, έτσι δεν μπορούμε να το αυξήσουμε. Αυτή όμως η (αναμενόμενη) παρατήρηση έχει εφαρμογές σε άλλες περιπτώσεις εξωτερικής διάταξης, που δεν θα εξετάσουμε εδώ. Ας πάρουμε τώρα k=m, οπότε έχουμε log( / m ) επανατυλίξεις και πλήρη περάσματα από τα δεδομένα. Μας απομένει ο υπολογισμός του αριθμού των συγκρίσεων που μέχρι στιγμής, από την η φάση, είναι σ = (/m)s(m), π.χ. για τον Heapsot είναι σ = ( / m)mlogm = logm. Στη η φάση μετράμε τις συγκρίσεις του MERGE: Κατά το ο πέρασμα ο MERGE έχει διατάξει /=(/m) ζεύγη των m στοιχείων και χρειάζεται m- συγκρίσεις για το κάθε ζεύγος (στη χειρότερη περίπτωση) δηλαδή (/m)(m-) συγκρίσεις. Παρόμοια, κατά το πέρασμα αριθμός i χρειάζονται i i ( m ) = i m συγκρίσεις. Άρα, από όλα τα log περάσματα προκύπτουν συνολικά
Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 9: ΒΑΣΙΚΕΣ ΤΕΧΝΙΚΕΣ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΑΝΑΛΥΣΗΣ ΑΛΓΟΡΙΘΜΩΝ ΕΞΙΣΟΡΡΟΠΗΣΗ, ΔΙΑΙΡΕΙ ΚΑΙ ΒΑΣΙΛΕΥΕ
 Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 9: ΒΑΣΙΚΕΣ ΤΕΧΝΙΚΕΣ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΑΝΑΛΥΣΗΣ ΑΛΓΟΡΙΘΜΩΝ ΕΞΙΣΟΡΡΟΠΗΣΗ, ΔΙΑΙΡΕΙ ΚΑΙ ΒΑΣΙΛΕΥΕ Δημήτριος Κουκόπουλος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα
Σχεδίαση και Ανάλυση Αλγορίθμων Ενότητα 9: ΒΑΣΙΚΕΣ ΤΕΧΝΙΚΕΣ ΣΧΕΔΙΑΣΜΟΥ ΚΑΙ ΑΝΑΛΥΣΗΣ ΑΛΓΟΡΙΘΜΩΝ ΕΞΙΣΟΡΡΟΠΗΣΗ, ΔΙΑΙΡΕΙ ΚΑΙ ΒΑΣΙΛΕΥΕ Δημήτριος Κουκόπουλος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Πεπερασμένες και Διαιρεμένες Διαφορές Εισαγωγή Θα εισάγουμε την έννοια των διαφορών με ένα
Αλγόριθμοι και Πολυπλοκότητα
 Αλγόριθμοι και Πολυπλοκότητα Διαίρει και Βασίλευε Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Διαίρει και Βασίλευε Divide and Conquer Η τεχνική διαίρει και βασίλευε αναφέρεται
Αλγόριθμοι και Πολυπλοκότητα Διαίρει και Βασίλευε Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Διαίρει και Βασίλευε Divide and Conquer Η τεχνική διαίρει και βασίλευε αναφέρεται
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων
 Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
ΕΠΛ231 Δομές Δεδομένων και Αλγόριθμοι 4. Παραδείγματα Ανάλυσης Πολυπλοκότητας Ανάλυση Αναδρομικών Αλγόριθμων
 ΕΠΛ31 Δομές Δεδομένων και Αλγόριθμοι 4. Παραδείγματα Ανάλυσης Πολυπλοκότητας Ανάλυση Αναδρομικών Αλγόριθμων Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα
ΕΠΛ31 Δομές Δεδομένων και Αλγόριθμοι 4. Παραδείγματα Ανάλυσης Πολυπλοκότητας Ανάλυση Αναδρομικών Αλγόριθμων Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( ))
![ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( )) ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( ))](/thumbs/17/113546.jpg) ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 6: ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (Θ.Μ.Τ.) [Θεώρημα Μέσης Τιμής Διαφορικού Λογισμού του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 6: ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (Θ.Μ.Τ.) [Θεώρημα Μέσης Τιμής Διαφορικού Λογισμού του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
Διάλεξη 04: Παραδείγματα Ανάλυσης
 Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα
Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα
Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων
 Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα
Διάλεξη 04: Παραδείγματα Ανάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: - Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα
ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου
 ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου Κεφάλαιο ο Αλγεβρικές Παραστάσεις ΛΕΜΟΝΙΑ ΜΠΟΥΤΣΚΟΥ Γυμνάσιο Αμυνταίου ΜΑΘΗΜΑ Α. Πράξεις με πραγματικούς αριθμούς ΑΣΚΗΣΕΙΣ ) ) Να συμπληρώσετε τα κενά ώστε στην κατακόρυφη στήλη
ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου Κεφάλαιο ο Αλγεβρικές Παραστάσεις ΛΕΜΟΝΙΑ ΜΠΟΥΤΣΚΟΥ Γυμνάσιο Αμυνταίου ΜΑΘΗΜΑ Α. Πράξεις με πραγματικούς αριθμούς ΑΣΚΗΣΕΙΣ ) ) Να συμπληρώσετε τα κενά ώστε στην κατακόρυφη στήλη
Κατακερματισμός (Hashing)
 Κατακερματισμός (Hashing) O κατακερματισμός είναι μια τεχνική οργάνωσης ενός αρχείου. Είναι αρκετά δημοφιλής μέθοδος για την οργάνωση αρχείων Βάσεων Δεδομένων, καθώς βοηθάει σημαντικά στην γρήγορη αναζήτηση
Κατακερματισμός (Hashing) O κατακερματισμός είναι μια τεχνική οργάνωσης ενός αρχείου. Είναι αρκετά δημοφιλής μέθοδος για την οργάνωση αρχείων Βάσεων Δεδομένων, καθώς βοηθάει σημαντικά στην γρήγορη αναζήτηση
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
Μαθηματικά Γ Γυμνασίου
 Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 13: Αλγόριθμοι-Μεγάλων ακεραίων- Εκθετοποίηση- Πολλαπλασιασμός πινάκων -Strassen Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 13: Αλγόριθμοι-Μεγάλων ακεραίων- Εκθετοποίηση- Πολλαπλασιασμός πινάκων -Strassen Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Περιεχόμενα μεθόδευση του μαθήματος
 Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ
 ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΚΕΦΑΛΑΙΟ 5 ΑΚΟΛΟΥΘΙΕΣ ΑΡΙΘΜΗΤΙΚΗ ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟΔΟΣ
 ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 5 ΑΚΟΛΟΥΘΙΕΣ ΑΡΙΘΜΗΤΙΚΗ ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟΔΟΣ ΓΙΑΝΝΗΣ ΠΑΤΕΡΑΣ ΜΑΘΗΜΑΤΙΚΟΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΑΚΟΛΟΥΘΙΕΣ ΚΕΦΑΛΑΙΟ 5 ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ακολουθία ονομάζουμε
ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΚΕΦΑΛΑΙΟ 5 ΑΚΟΛΟΥΘΙΕΣ ΑΡΙΘΜΗΤΙΚΗ ΓΕΩΜΕΤΡΙΚΗ ΠΡΟΟΔΟΣ ΓΙΑΝΝΗΣ ΠΑΤΕΡΑΣ ΜΑΘΗΜΑΤΙΚΟΣ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ ΑΚΟΛΟΥΘΙΕΣ ΚΕΦΑΛΑΙΟ 5 ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ακολουθία ονομάζουμε
0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2
![0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2 0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2](/thumbs/59/43483993.jpg) ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
7. Αν υψώσουμε και τα δύο μέλη μιας εξίσωσης στον κύβο (και γενικά σε οποιαδήποτε περιττή δύναμη), τότε προκύπτει
 8 7y = 4 y + y ( 8 7y) = ( 4 y + y) ( y) + 4 y y 4 y = 4 y y 8 7y = 4 y + ( 4 y) = ( 4 y y) ( 4 y) = 4( 4 y)( y) ( 4 y) 4( 4 y)( y) = 0 ( 4 y) [ 4 y 4( y) ] = 4 ( 4 y)( y + 4) = 0 y = ή y = 4) 0 4 H y
8 7y = 4 y + y ( 8 7y) = ( 4 y + y) ( y) + 4 y y 4 y = 4 y y 8 7y = 4 y + ( 4 y) = ( 4 y y) ( 4 y) = 4( 4 y)( y) ( 4 y) 4( 4 y)( y) = 0 ( 4 y) [ 4 y 4( y) ] = 4 ( 4 y)( y + 4) = 0 y = ή y = 4) 0 4 H y
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ
 ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ ΕΠΙΜΕΛΕΙΑ : ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΕΥΡΙΠΙΔΟΥ 80 ΝΙΚΑΙΑ ΝΕΑΠΟΛΗ ΤΗΛΕΦΩΝΟ 0965897 ΔΙΕΥΘΥΝΣΗ ΣΠΟΥΔΩΝ ΒΡΟΥΤΣΗ ΕΥΑΓΓΕΛΙΑ ΜΠΟΥΡΝΟΥΤΣΟΥ ΚΩΝ/ΝΑ ΑΥΓΕΡΙΝΟΣ ΒΑΣΙΛΗΣ ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ Η έννοια του μιγαδικού
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 07-08 Αριθμητική Ολοκλήρωση Εισαγωγή Έστω ότι η f είναι μία φραγμένη συνάρτηση στο πεπερασμένο
Διδάσκων: Παναγιώτης Ανδρέου
 Διάλεξη 04: ΠαραδείγματαΑνάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: -Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα -Γραμμική
Διάλεξη 04: ΠαραδείγματαΑνάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: -Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα -Γραμμική
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
Αναζήτηση. 1. Σειριακή αναζήτηση 2. Δυαδική Αναζήτηση. Εισαγωγή στην Ανάλυση Αλγορίθμων Μάγια Σατρατζέμη
 Αναζήτηση. Σειριακή αναζήτηση. Δυαδική Αναζήτηση Εισαγωγή στην Ανάλυση Αλγορίθμων Μάγια Σατρατζέμη Παραδοχή Στη συνέχεια των διαφανειών (διαλέξεων) η ασυμπτωτική έκφραση (συμβολισμός Ο, Ω, Θ) του χρόνου
Αναζήτηση. Σειριακή αναζήτηση. Δυαδική Αναζήτηση Εισαγωγή στην Ανάλυση Αλγορίθμων Μάγια Σατρατζέμη Παραδοχή Στη συνέχεια των διαφανειών (διαλέξεων) η ασυμπτωτική έκφραση (συμβολισμός Ο, Ω, Θ) του χρόνου
Εισαγωγή στην Ανάλυση Αλγορίθμων
 Εισαγωγή στην Ανάλυση Αλγορίθμων (4) Μεθοδολογία αναδρομικών σχέσεων (Ι) Με επανάληψη της αναδρομής Έστω όπου r και a είναι σταθερές. Βρίσκουμε τη σχέση που εκφράζει την T(n) συναρτήσει της T(n-) την T(n)
Εισαγωγή στην Ανάλυση Αλγορίθμων (4) Μεθοδολογία αναδρομικών σχέσεων (Ι) Με επανάληψη της αναδρομής Έστω όπου r και a είναι σταθερές. Βρίσκουμε τη σχέση που εκφράζει την T(n) συναρτήσει της T(n-) την T(n)
Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές
 0 Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Για να λύσουμε μια πολυωνυμική εξίσωση P(x) 0 (ή μια πολυωνυμική ανίσωση P(x)
0 Πολυωνυμικές εξισώσεις και ανισώσεις Εξισώσεις και ανισώσεις που ανάγονται σε πολυωνυμικές Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Για να λύσουμε μια πολυωνυμική εξίσωση P(x) 0 (ή μια πολυωνυμική ανίσωση P(x)
Υπολογιστικά & Διακριτά Μαθηματικά
 Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 5: Αναδρομικές σχέσεις - Υπολογισμός Αθροισμάτων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
Υπολογιστικά & Διακριτά Μαθηματικά Ενότητα 5: Αναδρομικές σχέσεις - Υπολογισμός Αθροισμάτων Στεφανίδης Γεώργιος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για
11. Ποιες είναι οι άμεσες συνέπειες της διαίρεσης;
 10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
10. Τι ονομάζουμε Ευκλείδεια διαίρεση και τέλεια διαίρεση; Όταν δοθούν δύο φυσικοί αριθμοί Δ και δ, τότε υπάρχουν δύο άλλοι φυσικοί αριθμοί π και υ, έτσι ώστε να ισχύει: Δ = δ π + υ. Ο αριθμός Δ λέγεται
(18 ο ) ΚΛΑΣΜΑΤΙΚΗ ΑΝΑΓΩΓΗ - ΙI: «διάμεσος &θεσιακή επιλογή στοιχείου»
 (8 ο ) ΚΛΑΣΜΑΤΙΚΗ ΑΑΓΩΓΗ - ΙI: «διάμεσος &θεσιακή επιλογή στοιχείου» Το πρόβλημα του διαμέσου στοιχείου: ένα θεμελιακό πρόβλημα Συναντήσαμε ήδη αρκετές φορές το πρόβλημα του να «κόψουμε» ένα σύνολο στοιχείων
(8 ο ) ΚΛΑΣΜΑΤΙΚΗ ΑΑΓΩΓΗ - ΙI: «διάμεσος &θεσιακή επιλογή στοιχείου» Το πρόβλημα του διαμέσου στοιχείου: ένα θεμελιακό πρόβλημα Συναντήσαμε ήδη αρκετές φορές το πρόβλημα του να «κόψουμε» ένα σύνολο στοιχείων
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ
 Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Συναρτήσεις Όταν αναφερόμαστε σε μια συνάρτηση, ουσιαστικά αναφερόμαστε σε μια σχέση ή εξάρτηση. Στα μαθηματικά που θα μας απασχολήσουν, με απλά λόγια, η σχέση
Ε π ι μ έ λ ε ι α Κ Ο Λ Λ Α Σ Α Ν Τ Ω Ν Η Σ 1 Συναρτήσεις Όταν αναφερόμαστε σε μια συνάρτηση, ουσιαστικά αναφερόμαστε σε μια σχέση ή εξάρτηση. Στα μαθηματικά που θα μας απασχολήσουν, με απλά λόγια, η σχέση
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Αλγόριθμοι Ταξινόμησης Μέρος 2
 Αλγόριθμοι Ταξινόμησης Μέρος 2 Μανόλης Κουμπαράκης 1 Προχωρημένοι Αλγόριθμοι Ταξινόμησης Στη συνέχεια θα παρουσιάσουμε τρείς προχωρημένους αλγόριθμους ταξινόμησης: treesort, quicksort και mergesort. 2
Αλγόριθμοι Ταξινόμησης Μέρος 2 Μανόλης Κουμπαράκης 1 Προχωρημένοι Αλγόριθμοι Ταξινόμησης Στη συνέχεια θα παρουσιάσουμε τρείς προχωρημένους αλγόριθμους ταξινόμησης: treesort, quicksort και mergesort. 2
Ανάλυση αλγορίθμων. Χρόνος εκτέλεσης: Αναμενόμενη περίπτωση. - απαιτεί γνώση της κατανομής εισόδου
 Ανάλυση αλγορίθμων Παράμετροι απόδοσης ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι πόροι, π.χ. μνήμη, επικοινωνία (π.χ. σε κατανεμημένα συστήματα) Προσπάθεια υλοποίησης Ανάλυση της απόδοσης Θεωρητική
Ανάλυση αλγορίθμων Παράμετροι απόδοσης ενός αλγόριθμου: Χρόνος εκτέλεσης Απαιτούμενοι πόροι, π.χ. μνήμη, επικοινωνία (π.χ. σε κατανεμημένα συστήματα) Προσπάθεια υλοποίησης Ανάλυση της απόδοσης Θεωρητική
ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΩΝ 36 η Εθνική Μαθηματική Ολυμπιάδα «Ο ΑΡΧΙΜΗΔΗΣ» 23 Φεβρουαρίου 2019 Θέματα και ενδεικτικές λύσεις μεγάλων τάξεων
 ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Πανεπιστημίου (Ελευθερίου Βενιζέλου) 34 06 79 ΑΘΗΝΑ Τηλ 036653 367784 Fax: 036405 e mail : info@hmsgr wwwhmsgr GREEK MATHEMATICAL SOCIETY 34, Paneistimiou (Εleftheriou Venizelou)
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ Πανεπιστημίου (Ελευθερίου Βενιζέλου) 34 06 79 ΑΘΗΝΑ Τηλ 036653 367784 Fax: 036405 e mail : info@hmsgr wwwhmsgr GREEK MATHEMATICAL SOCIETY 34, Paneistimiou (Εleftheriou Venizelou)
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 6α: Αναζήτηση Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos. Για εκπαιδευτικό
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 6α: Αναζήτηση Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commos. Για εκπαιδευτικό
A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις
![A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις A N A B P Y T A ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ. 1 (α + β + γ) [(α-β) 2 +(α-γ) 2 +(β-γ) 2 ] και τις υποθέσεις](/thumbs/93/111356738.jpg) ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ ΑΣΚΗΣΗ η Αν α +β +γ = αβγ και α + β + γ, να δείξετε ότι το πολυώνυμο P()=(α β) +(β γ) + γ α είναι το μηδενικό πολυώνυμο. Από την ταυτότητα του Euler α +β +γ -αβγ = (α + β + γ)[(α-β)
ΑΣΚΗΣΕΙΣ ΠΟΛΥΩΝΥΜΩΝ ΑΣΚΗΣΗ η Αν α +β +γ = αβγ και α + β + γ, να δείξετε ότι το πολυώνυμο P()=(α β) +(β γ) + γ α είναι το μηδενικό πολυώνυμο. Από την ταυτότητα του Euler α +β +γ -αβγ = (α + β + γ)[(α-β)
Διδάσκων: Παναγιώτης Ανδρέου
 Διάλεξη 6: ΠαραδείγματαΑνάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: -Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα -Γραμμική
Διάλεξη 6: ΠαραδείγματαΑνάλυσης Πολυπλοκότητας/Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: -Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, παραδείγματα -Γραμμική
2. Να γράψετε έναν αριθμό που είναι μεγαλύτερος από το 3,456 και μικρότερος από το 3,457.
 1. Ένα κεφάλαιο ενός βιβλίου ξεκινάει από τη σελίδα 32 και τελειώνει στη σελίδα 75. Από πόσες σελίδες αποτελείται το κεφάλαιο; Αν το κεφάλαιο ξεκινάει από τη σελίδα κ και τελειώνει στη σελίδα λ, από πόσες
1. Ένα κεφάλαιο ενός βιβλίου ξεκινάει από τη σελίδα 32 και τελειώνει στη σελίδα 75. Από πόσες σελίδες αποτελείται το κεφάλαιο; Αν το κεφάλαιο ξεκινάει από τη σελίδα κ και τελειώνει στη σελίδα λ, από πόσες
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 3: Ασυμπτωτικός συμβολισμός Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 3: Ασυμπτωτικός συμβολισμός Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
V. Διαφορικός Λογισμός. math-gr
 V Διαφορικός Λογισμός Παντελής Μπουμπούλης, MSc, PhD σελ blospotcom, bouboulismyschr ΜΕΡΟΣ Η έννοια της Παραγώγου Α Ορισμός Εφαπτομένη καμπύλης συνάρτησης: Έστω μια συνάρτηση και A, ένα σημείο της C Αν
V Διαφορικός Λογισμός Παντελής Μπουμπούλης, MSc, PhD σελ blospotcom, bouboulismyschr ΜΕΡΟΣ Η έννοια της Παραγώγου Α Ορισμός Εφαπτομένη καμπύλης συνάρτησης: Έστω μια συνάρτηση και A, ένα σημείο της C Αν
9 Πολυώνυμα Διαίρεση πολυωνύμων
 4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
d k 10 k + d k 1 10 k d d = k i=0 d i 10 i.
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Μεταθέσεις και πίνακες μεταθέσεων
 Παράρτημα Α Μεταθέσεις και πίνακες μεταθέσεων Το παρόν παράρτημα βασίζεται στις σελίδες 671 8 του βιβλίου: Γ. Χ. Ψαλτάκης, Κβαντικά Συστήματα Πολλών Σωματιδίων (Πανεπιστημιακές Εκδόσεις Κρήτης, Ηράκλειο,
Παράρτημα Α Μεταθέσεις και πίνακες μεταθέσεων Το παρόν παράρτημα βασίζεται στις σελίδες 671 8 του βιβλίου: Γ. Χ. Ψαλτάκης, Κβαντικά Συστήματα Πολλών Σωματιδίων (Πανεπιστημιακές Εκδόσεις Κρήτης, Ηράκλειο,
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
ΚΕΦΑΛΑΙΟ 5 ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΚΕΦΑΛΑΙΟ 5 ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Εισαγωγή Οι γεννήτριες συναρτήσεις είναι ένα από τα ισχυρά εργαλεία για μια ενοποιημένη αντιμετώπιση πολλών κατηγοριών προβλημάτων απαρίθμησης Ο Lplce έθεσε πρώτος τις
ΚΕΦΑΛΑΙΟ 5 ΓΕΝΝΗΤΡΙΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Εισαγωγή Οι γεννήτριες συναρτήσεις είναι ένα από τα ισχυρά εργαλεία για μια ενοποιημένη αντιμετώπιση πολλών κατηγοριών προβλημάτων απαρίθμησης Ο Lplce έθεσε πρώτος τις
Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων
 Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων Με τον όρο μη γραμμικές εξισώσεις εννοούμε εξισώσεις της μορφής: f( ) 0 που προέρχονται από συναρτήσεις f () που είναι μη γραμμικές ως προς. Περιέχουν δηλαδή
Αριθμητική εύρεση ριζών μη γραμμικών εξισώσεων Με τον όρο μη γραμμικές εξισώσεις εννοούμε εξισώσεις της μορφής: f( ) 0 που προέρχονται από συναρτήσεις f () που είναι μη γραμμικές ως προς. Περιέχουν δηλαδή
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα
 Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
ΚΕΦΑΛΑΙΟ 2: Ημιαπλοί Δακτύλιοι
 ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
n ίδια n διαφορετικά n n 0 n n n 1 n n n n 0 4
 Διακριτά Μαθηματικά Ι Επαναληπτικό Μάθημα 1 Συνδυαστική 2 Μεταξύ 2n αντικειμένων, τα n είναι ίδια. Βρείτε τον αριθμό των επιλογών n αντικειμένων από αυτά τα 2n αντικείμενα. Μεταξύ 3n + 1 αντικειμένων τα
Διακριτά Μαθηματικά Ι Επαναληπτικό Μάθημα 1 Συνδυαστική 2 Μεταξύ 2n αντικειμένων, τα n είναι ίδια. Βρείτε τον αριθμό των επιλογών n αντικειμένων από αυτά τα 2n αντικείμενα. Μεταξύ 3n + 1 αντικειμένων τα
(CLR, κεφάλαιο 32) Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Παραστάσεις πολυωνύµων Πολυωνυµική Παρεµβολή ιακριτός Μετασχηµατισµός Fourier
 Ταχύς Μετασχηµατισµός Fourier CLR, κεφάλαιο 3 Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Παραστάσεις πολυωνύµων Πολυωνυµική Παρεµβολή ιακριτός Μετασχηµατισµός Fourier Ταχύς Μετασχηµατισµός Fourier
Ταχύς Μετασχηµατισµός Fourier CLR, κεφάλαιο 3 Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Παραστάσεις πολυωνύµων Πολυωνυµική Παρεµβολή ιακριτός Μετασχηµατισµός Fourier Ταχύς Μετασχηµατισµός Fourier
ΚΕΦΑΛΑΙΟ 2 Ο ΕΞΙΣΩΣΕΙΣ-ΑΝΙΣΩΣΕΙΣ
 ΚΕΦΑΛΑΙΟ Ο ΕΞΙΣΩΣΕΙΣ-ΑΝΙΣΩΣΕΙΣ. ΕΞΙΣΩΣΕΙΣ ΟΥ ΒΑΘΜΟΥ.3 ΠΡΟΒΛΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ ΟΥ ΒΑΘΜΟΥ Α. Επίλυση εξισώσεων δευτέρου βαθμού με ανάλυση σε γινόμενο παραγόντων 1. ΕΡΩΤΗΣΗ Ποια εξίσωση λέγεται εξίσωση ου βαθμού
ΚΕΦΑΛΑΙΟ Ο ΕΞΙΣΩΣΕΙΣ-ΑΝΙΣΩΣΕΙΣ. ΕΞΙΣΩΣΕΙΣ ΟΥ ΒΑΘΜΟΥ.3 ΠΡΟΒΛΗΜΑΤΑ ΕΞΙΣΩΣΕΩΝ ΟΥ ΒΑΘΜΟΥ Α. Επίλυση εξισώσεων δευτέρου βαθμού με ανάλυση σε γινόμενο παραγόντων 1. ΕΡΩΤΗΣΗ Ποια εξίσωση λέγεται εξίσωση ου βαθμού
Προβλήματα, αλγόριθμοι, ψευδοκώδικας
 Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
ΑΛΓΕΒΡΑ Τ Ν Ο Π Σ Ι Κ Η Τ Λ Η
 Τ Ν Ο Π Σ Ι Κ Η Τ Λ Η ΑΛΓΕΒΡΑ Τα ςημαντικότερα ςημεία τησ θεωρίασ Ερωτήςεισ εμπζδωςησ- απαντήςεισ Μεθοδολογία αςκήςεων Προτεινόμενεσ αςκήςεισ του βιβλίου - διεξοδική ανάλυςη των λφςεων (ςκζψη-βήματα-επεξήγηςη
Τ Ν Ο Π Σ Ι Κ Η Τ Λ Η ΑΛΓΕΒΡΑ Τα ςημαντικότερα ςημεία τησ θεωρίασ Ερωτήςεισ εμπζδωςησ- απαντήςεισ Μεθοδολογία αςκήςεων Προτεινόμενεσ αςκήςεισ του βιβλίου - διεξοδική ανάλυςη των λφςεων (ςκζψη-βήματα-επεξήγηςη
Παντελής Μπουμπούλης, M.Sc., Ph.D. σελ. 2 math-gr.blogspot.com, bouboulis.mysch.gr
 VI Ολοκληρώματα Παντελής Μπουμπούλης, MSc, PhD σελ mth-grlogspotcom, ououlismyschgr ΜΕΡΟΣ Αρχική Συνάρτηση Ορισμός Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ Αρχική συνάρτηση ή παράγουσα της στο Δ
VI Ολοκληρώματα Παντελής Μπουμπούλης, MSc, PhD σελ mth-grlogspotcom, ououlismyschgr ΜΕΡΟΣ Αρχική Συνάρτηση Ορισμός Έστω f μια συνάρτηση ορισμένη σε ένα διάστημα Δ Αρχική συνάρτηση ή παράγουσα της στο Δ
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER
 4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
4. ΚΕΦΑΛΑΙΟ ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΥ FOURIER Σκοπός του κεφαλαίου είναι να παρουσιάσει μερικές εφαρμογές του Μετασχηματισμού Fourier (ΜF). Ειδικότερα στο κεφάλαιο αυτό θα περιγραφούν έμμεσοι τρόποι
(Γραμμικές) Αναδρομικές Σχέσεις
 (Γραμμικές) Αναδρομικές Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις
(Γραμμικές) Αναδρομικές Σχέσεις Διδάσκοντες: Φ. Αφράτη, Δ. Φωτάκης Επιμέλεια διαφανειών: Δ. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις
Συνεχή Κλάσματα. Εμμανουήλ Καπνόπουλος Α.Μ 282
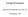 Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014
 ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
Θεωρία Πληροφορίας. Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Θεωρία Πληροφορίας Διάλεξη 4: Διακριτή πηγή πληροφορίας χωρίς μνήμη Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Ατζέντα Διακριτή πηγή πληροφορίας χωρίς μνήμη Ποσότητα πληροφορίας της πηγής Κωδικοποίηση
Α ΜΕΡΟΣ - ΑΛΓΕΒΡΑ. Α. Οι πραγματικοί αριθμοί και οι πράξεις τους
 Α ΜΕΡΟΣ - ΑΛΓΕΒΡΑ Κεφάλαιο 1 ο ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ 1.1 Πράξεις με πραγματικούς αριθμούς Α. Οι πραγματικοί αριθμοί και οι πράξεις τους 1. Ποιοι αριθμοί ονομάζονται: α) ρητοί β) άρρητοι γ) πραγματικοί;
Α ΜΕΡΟΣ - ΑΛΓΕΒΡΑ Κεφάλαιο 1 ο ΑΛΓΕΒΡΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ 1.1 Πράξεις με πραγματικούς αριθμούς Α. Οι πραγματικοί αριθμοί και οι πράξεις τους 1. Ποιοι αριθμοί ονομάζονται: α) ρητοί β) άρρητοι γ) πραγματικοί;
Μη γράφετε στο πίσω μέρος της σελίδας
 Εισαγωγή στο Σχεδιασμό & την Ανάλυση Αλγορίθμων Εξέταση Ιουνίου 2015 Σελ. 1 από 7 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες
Εισαγωγή στο Σχεδιασμό & την Ανάλυση Αλγορίθμων Εξέταση Ιουνίου 2015 Σελ. 1 από 7 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος
 Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Διαίρει-και-Βασίλευε. Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Διαίρει-και-Βασίλευε 2
 Διαίρει-και-Βασίλευε Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Διαίρει-και-Βασίλευε 2 Διαίρει-και-Βασίλευε Γενική µέθοδος σχεδιασµού αλγορίθµων: Διαίρεση σε ( 2) υποπροβλήµατα (σηµαντικά) µικρότερου µεγέθους.
Διαίρει-και-Βασίλευε Αλγόριθµοι & Πολυπλοκότητα (Χειµώνας 2011) Διαίρει-και-Βασίλευε 2 Διαίρει-και-Βασίλευε Γενική µέθοδος σχεδιασµού αλγορίθµων: Διαίρεση σε ( 2) υποπροβλήµατα (σηµαντικά) µικρότερου µεγέθους.
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ
 ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
Συνέχεια συνάρτησης σε διάστημα. Η θεωρία και τι προσέχουμε. x, ισχύει: lim f (x) f ( ).
 Κεφάλαιο 4 Συνέχεια συνάρτησης σε διάστημα 411 Ερώτηση θεωρίας 1 Η θεωρία και τι προσέχουμε Πότε μια συνάρτηση f θα λέμε ότι είναι συνεχής σε ένα ανοικτό διάστημα (, ) αβ; Απάντηση Μια συνάρτηση f θα λέμε
Κεφάλαιο 4 Συνέχεια συνάρτησης σε διάστημα 411 Ερώτηση θεωρίας 1 Η θεωρία και τι προσέχουμε Πότε μια συνάρτηση f θα λέμε ότι είναι συνεχής σε ένα ανοικτό διάστημα (, ) αβ; Απάντηση Μια συνάρτηση f θα λέμε
Διδάσκων: Κωνσταντίνος Κώστα Διαφάνειες: Δημήτρης Ζεϊναλιπούρ ΕΠΛ 035 Δομές Δεδομένων και Αλγόριθμοι για Ηλ. Μηχ. και Μηχ. Υπολ.
 Διάλεξη : Παραδείγματα Ανάλυσης Πολυπλοκότητας / Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, 6 παραδείγματα
Διάλεξη : Παραδείγματα Ανάλυσης Πολυπλοκότητας / Ανάλυση Αναδρομικών Αλγόριθμων Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: Παραδείγματα Ανάλυσης Πολυπλοκότητας : Μέθοδοι, 6 παραδείγματα
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο
 Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
Κεφάλαιο 5. Το Συμπτωτικό Πολυώνυμο Σύνοψη Στο κεφάλαιο αυτό παρουσιάζεται η ιδέα του συμπτωτικού πολυωνύμου, του πολυωνύμου, δηλαδή, που είναι του μικρότερου δυνατού βαθμού και που, για συγκεκριμένες,
1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης
 1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης Στη συγκεκριμένη ενότητα εξετάζουμε θέματα σχετικά με την αριθμητική πεπερασμένης ακρίβειας που χρησιμοποιούν οι σημερινοί υπολογιστές και τα
1 Αριθμητική κινητής υποδιαστολής και σφάλματα στρογγύλευσης Στη συγκεκριμένη ενότητα εξετάζουμε θέματα σχετικά με την αριθμητική πεπερασμένης ακρίβειας που χρησιμοποιούν οι σημερινοί υπολογιστές και τα
Θεώρημα Βolzano. Κατηγορία 1 η. 11.1 Δίνεται η συνάρτηση:
 Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
2ογελ ΣΥΚΕΩΝ 2ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β Λυκει(ου ο ΓΕΛ ΣΥΚΕΩΝ ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Β ΛΥΚΕΙΟΥ ογελ ΣΥΚΕΩΝ ογελ ΣΥΚΕΩΝ ΣΧΟΛΙΚΟ ΕΤΟΣ -4 ΠΟΛΥΩΝΥΜΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ Επιμέλεια: ΧΑΛΑΤΖΙΑΝ ΠΑΥΛΟΣ
Στ Τάξη. Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1
 Ενδεικτική Οργάνωση Ενοτήτων Στ Τάξη Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1 15 Αρ3.1 Απαγγέλουν, διαβάζουν, γράφουν και αναγνωρίζουν ποσότητες αριθμών Επανάληψη μέχρι το 1 000
Ενδεικτική Οργάνωση Ενοτήτων Στ Τάξη Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1 15 Αρ3.1 Απαγγέλουν, διαβάζουν, γράφουν και αναγνωρίζουν ποσότητες αριθμών Επανάληψη μέχρι το 1 000
A. ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών
 Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών Συμβολισμοί Σε αναλογία με τους ορισμούς συμβολίζουμε μια ακολουθία: 1 είτε μέσω του διανυσματικού ορισμού, παραθέτοντας αναγκαστικά
Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών Συμβολισμοί Σε αναλογία με τους ορισμούς συμβολίζουμε μια ακολουθία: 1 είτε μέσω του διανυσματικού ορισμού, παραθέτοντας αναγκαστικά
(a 1, b 1 ) (a 2, b 2 ) = (a 1 a 2, b 1 b 2 ).
 ΕΜ0 - Διακριτά Μαθηματικά Ιανουαρίου 006 Άσκηση - Λύσεις Πρόβλημα [0 μονάδες] Εστω L και L δύο κυκλώματα σε ένα γράφημα G. Εστω a μία ακμή που ανήκει και στο L και στο L και έστω b μία ακμή που ανήκει
ΕΜ0 - Διακριτά Μαθηματικά Ιανουαρίου 006 Άσκηση - Λύσεις Πρόβλημα [0 μονάδες] Εστω L και L δύο κυκλώματα σε ένα γράφημα G. Εστω a μία ακμή που ανήκει και στο L και στο L και έστω b μία ακμή που ανήκει
1ο Κεφάλαιο: Συστήματα
 ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
ο Κεφάλαιο: Συστήματα Γραμμικά συστήματα i. Ποια εξίσωση λέγεται γραμμική; ii. Πως μεταβάλλεται η ευθεία y, 0 ή 0 για τις διάφορες τιμές των α,β,γ; iii. Τι ονομάζεται λύση μιας γραμμικής εξίσωσης; iv.
3. Προσομοίωση ενός Συστήματος Αναμονής.
 3. Προσομοίωση ενός Συστήματος Αναμονής. 3.1. Διατύπωση του Προβλήματος. Τα συστήματα αναμονής (queueing systems), βρίσκονται πίσω από τα περισσότερα μοντέλα μελέτης της απόδοσης υπολογιστικών συστημάτων,
3. Προσομοίωση ενός Συστήματος Αναμονής. 3.1. Διατύπωση του Προβλήματος. Τα συστήματα αναμονής (queueing systems), βρίσκονται πίσω από τα περισσότερα μοντέλα μελέτης της απόδοσης υπολογιστικών συστημάτων,
A. ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
ΚΕΦΑΛΑΙΟ 4 ο : ΑΝΙΣΩΣΕΙΣ ΤΟ 2 Ο ΘΕΜΑ
 ΚΕΦΑΛΑΙΟ 4 ο : ΑΝΙΣΩΣΕΙΣ ΤΟ 2 Ο ΘΕΜΑ Άσκηση 1 Δίνονται οι ανισώσεις: 3x και 2 x α) Να βρείτε τις λύσεις τους (Μονάδες 10) β) Να βρείτε το σύνολο των κοινών τους λύσεων (Μονάδες 15) α) Έχουμε 3x 2x x 2
ΚΕΦΑΛΑΙΟ 4 ο : ΑΝΙΣΩΣΕΙΣ ΤΟ 2 Ο ΘΕΜΑ Άσκηση 1 Δίνονται οι ανισώσεις: 3x και 2 x α) Να βρείτε τις λύσεις τους (Μονάδες 10) β) Να βρείτε το σύνολο των κοινών τους λύσεων (Μονάδες 15) α) Έχουμε 3x 2x x 2
2.1 2.2 ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ
 ΚΕΦΑΛΑΙΟ Ο : ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ - ΕΝΟΤΗΤΕΣ :.... ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΜΕΘΟΔΟΛΟΓΙΑ : ΠΡΑΓΜΑΤΙΚΟ & ΦΑΝΤΑΣΤΙΚΟ ΜΕΡΟΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Έστω ένας μιγαδικός αριθμός,
ΚΕΦΑΛΑΙΟ Ο : ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ - ΕΝΟΤΗΤΕΣ :.... ΕΝΝΟΙΑ ΤΟΥ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ ΠΡΑΞΕΙΣ ΣΤΟ ΣΥΝΟΛΟ ΤΩΝ ΜΙΓΑΔΙΚΩΝ ΜΕΘΟΔΟΛΟΓΙΑ : ΠΡΑΓΜΑΤΙΚΟ & ΦΑΝΤΑΣΤΙΚΟ ΜΕΡΟΣ ΜΙΓΑΔΙΚΟΥ ΑΡΙΘΜΟΥ Έστω ένας μιγαδικός αριθμός,
Μεθοδολογία Επίλυσης Προβλημάτων ============================================================================ Π. Κυράνας - Κ.
 Μεθοδολογία Επίλυσης Προβλημάτων ============================================================================ Π. Κυράνας - Κ. Σάλαρης Πολλές φορές μας δίνεται να λύσουμε ένα πρόβλημα που από την πρώτη
Μεθοδολογία Επίλυσης Προβλημάτων ============================================================================ Π. Κυράνας - Κ. Σάλαρης Πολλές φορές μας δίνεται να λύσουμε ένα πρόβλημα που από την πρώτη
1.1 ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ
 . ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ : ΓΡΑΜΜΙΚΗ ΕΞΙΣΩΣΗ Η εξίσωση με και 0 ή 0 λέγεται γραμμική εξίσωση. Οι μεταβλητές είναι οι άγνωστοι της εξίσωσης αυτής. Οι αριθμοί λέγονται συντελεστές των αγνώστων
. ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ ΣΤΟΙΧΕΙΑ ΘΕΩΡΙΑΣ : ΓΡΑΜΜΙΚΗ ΕΞΙΣΩΣΗ Η εξίσωση με και 0 ή 0 λέγεται γραμμική εξίσωση. Οι μεταβλητές είναι οι άγνωστοι της εξίσωσης αυτής. Οι αριθμοί λέγονται συντελεστές των αγνώστων
Αλγόριθμοι για αυτόματα
 Κεφάλαιο 8 Αλγόριθμοι για αυτόματα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 8.1 Πότε ένα DFA αναγνωρίζει κενή ή άπειρη γλώσσα Δοθέντος ενός DFA M καλούμαστε
Κεφάλαιο 8 Αλγόριθμοι για αυτόματα Κύρια βιβλιογραφική αναφορά για αυτό το Κεφάλαιο είναι η Hopcroft, Motwani, and Ullman 2007. 8.1 Πότε ένα DFA αναγνωρίζει κενή ή άπειρη γλώσσα Δοθέντος ενός DFA M καλούμαστε
ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ. Σύμφωνα με τα παραπάνω, για μια αριθμητική πρόοδο που έχει πρώτο όρο τον ...
 ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ Ορισμός : Μία ακολουθία ονομάζεται αριθμητική πρόοδος, όταν ο κάθε όρος της, δημιουργείται από τον προηγούμενο με πρόσθεση του ίδιου πάντοτε αριθμού. Ο σταθερός αριθμός που προστίθεται
ΑΡΙΘΜΗΤΙΚΗ ΠΡΟΟΔΟΣ Ορισμός : Μία ακολουθία ονομάζεται αριθμητική πρόοδος, όταν ο κάθε όρος της, δημιουργείται από τον προηγούμενο με πρόσθεση του ίδιου πάντοτε αριθμού. Ο σταθερός αριθμός που προστίθεται
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ
 ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΣΥΝΟΠΤΙΚΗ ΘΕΩΡΕΙΑ ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.Καρτάλη 8 Βόλος Τηλ. 43598 ΠΊΝΑΚΑΣ ΠΕΡΙΕΧΟΜΈΝΩΝ 3. Η ΕΝΝΟΙΑ ΤΗΣ ΠΑΡΑΓΩΓΟΥ... 5 ΜΕΘΟΔΟΛΟΓΙΑ ΛΥΜΕΝΑ ΠΑΡΑΔΕΙΓΜΑΤΑ...
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 4: Αναδρομικές σχέσεις και ανάλυση αλγορίθμων Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 4: Αναδρομικές σχέσεις και ανάλυση αλγορίθμων Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Συνοπτική Μεθοδολογία Ασκήσεων IP Fragmentation. Ασκήσεις στο IP Fragmentation
 Συνοπτική Μεθοδολογία Ασκήσεων IP Fragmentation Οι σημειώσεις που ακολουθούν περιγράφουν τις ασκήσεις IP Fragmentation που θα συναντήσετε στο κεφάλαιο 3. Η πιο συνηθισμένη και βασική άσκηση αναφέρεται
Συνοπτική Μεθοδολογία Ασκήσεων IP Fragmentation Οι σημειώσεις που ακολουθούν περιγράφουν τις ασκήσεις IP Fragmentation που θα συναντήσετε στο κεφάλαιο 3. Η πιο συνηθισμένη και βασική άσκηση αναφέρεται
APEIROSTIKOS LOGISMOS I
 APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 4. Άσκηση : Υπολογίστε, αν υπάρχουν, τα παρακάτω όρια. Αν χρειάζεται, υπολογίστε τα αντίστοιχα πλευρικά όρια. + 4 3 + +,
APEIROSTIKOS LOGISMOS I ΟΛΟΗΜΕΡΟ ΕΡΓΑΣΤΗΡΙΟ ΠΡΟΒΛΗΜΑΤΩΝ Λύσεις ασκήσεων φυλλαδίου 4. Άσκηση : Υπολογίστε, αν υπάρχουν, τα παρακάτω όρια. Αν χρειάζεται, υπολογίστε τα αντίστοιχα πλευρικά όρια. + 4 3 + +,
Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύ
 Θεωρία Υπολογισμού Ενότητα 24: Μη Ντεντερμινιστικές Μηχανές Turing Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Θεωρία Υπολογισμού Ενότητα 24: Μη Ντεντερμινιστικές Μηχανές Turing Τμήμα Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
Εισαγωγή στους Αλγορίθμους
 Εισαγωγή στους Αλγορίθμους Ενότητα 5η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Η Μέθοδος «Διαίρει & Βασίλευε» Η Μέθοδος
Εισαγωγή στους Αλγορίθμους Ενότητα 5η Διδάσκων Χρήστος Ζαρολιάγκης Καθηγητής Τμήμα Μηχανικών Η/Υ & Πληροφορικής Πανεπιστήμιο Πατρών Email: zaro@ceid.upatras.gr Η Μέθοδος «Διαίρει & Βασίλευε» Η Μέθοδος
(Γραμμικές) Αναδρομικές Σχέσεις
 (Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες:. Φωτάκης. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
(Γραμμικές) Αναδρομικές Σχέσεις ιδάσκοντες:. Φωτάκης. Σούλιου Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Αναδρομικές Σχέσεις Αναπαράσταση
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος
 Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
Παραδείγματα Διανυσματικοί Χώροι Ι. Λυχναρόπουλος Παράδειγμα Έστω το σύνολο V το σύνολο όλων των θετικών πραγματικών αριθμών εφοδιασμένο με την ακόλουθη πράξη της πρόσθεσης: y y με, y V και του πολλαπλασιασμού
ΓΥΜΝΑΣΙΟ ΚΑΣΤΕΛΛΑΝΩΝ ΜΕΣΗΣ ΑΛΓΕΒΡΑ
 ΑΛΓΕΒΡΑ ΠΡΟΑΠΑΙΤΟΥΜΕΝΑ ΑΠΟ Α ΓΥΜΝΑΣΙΟΥ Ομόσημοι Ετερόσημοι αριθμοί Αντίθετοι Αντίστροφοι αριθμοί Πρόσθεση ομόσημων και ετερόσημων ρητών αριθμών Απαλοιφή παρενθέσεων Πολλαπλασιασμός και Διαίρεση ρητών αριθμών
ΑΛΓΕΒΡΑ ΠΡΟΑΠΑΙΤΟΥΜΕΝΑ ΑΠΟ Α ΓΥΜΝΑΣΙΟΥ Ομόσημοι Ετερόσημοι αριθμοί Αντίθετοι Αντίστροφοι αριθμοί Πρόσθεση ομόσημων και ετερόσημων ρητών αριθμών Απαλοιφή παρενθέσεων Πολλαπλασιασμός και Διαίρεση ρητών αριθμών
με Τέλος πάντων, έστω ότι ξεκινάει ένα άλλο υποθετικό σενάριο που απλά δεν διευκρινίζεται. Για το i) θα έχουμε , 2
 Άσκηση 75 Σε έναν οργανισμό, αρχικά υπάρχουν 04800 βακτήρια. Μετά από 1 ώρα υπάρχουν 10400 βακτήρια, μετά από ώρες 5100 βακτήρια, και γενικά ο αριθμός των βακτηρίων υποδιπλασιάζεται κάθε μια ώρα. α) Πόσα
Άσκηση 75 Σε έναν οργανισμό, αρχικά υπάρχουν 04800 βακτήρια. Μετά από 1 ώρα υπάρχουν 10400 βακτήρια, μετά από ώρες 5100 βακτήρια, και γενικά ο αριθμός των βακτηρίων υποδιπλασιάζεται κάθε μια ώρα. α) Πόσα
Δυναμικός Κατακερματισμός. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Δυναμικός Κατακερματισμός 1 Κατακερματισμός Τι αποθηκεύουμε στους κάδους; Στα παραδείγματα δείχνουμε μόνο την τιμή του πεδίου κατακερματισμού Την ίδια την εγγραφή (ως τρόπος οργάνωσης αρχείου) μέγεθος
Δυναμικός Κατακερματισμός 1 Κατακερματισμός Τι αποθηκεύουμε στους κάδους; Στα παραδείγματα δείχνουμε μόνο την τιμή του πεδίου κατακερματισμού Την ίδια την εγγραφή (ως τρόπος οργάνωσης αρχείου) μέγεθος
( ) ( ) Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή x. αντικ σταση στο που = α. [ ο αριθµ ός πουτο µηδεν ίζει
 μέρος πρώτο v v 1 v 1 Γενική μορφή πολυωνύμου: ( ) 1 1 Όροι του ( ) v v v P = a v + av 1 + av +... + a + a 1 + a, ν Ν, α ν R Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή. P : a, a, a,...,
μέρος πρώτο v v 1 v 1 Γενική μορφή πολυωνύμου: ( ) 1 1 Όροι του ( ) v v v P = a v + av 1 + av +... + a + a 1 + a, ν Ν, α ν R Τοα R σημαίνει ότι οι συντελεστές δεν περιέχουν την μεταβλητή. P : a, a, a,...,
