ΜΕΤΑΠΤΥΧΙΑΚΗ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
|
|
|
- Ῥεβέκκα Μπότσαρης
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΡΑΜΜΑ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΥΧΡΟΝΕΣ ΕΦΑΡΜΟΕΣ -άμμα και -Βήτα συναρτήσεις ΜΕΤΑΠΤΥΧΙΑΚΗ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΑΣΙΑ Σούρλα Δ. Βασιλική Επιλέπουσα : Κοκολοιαννάκη. Χρυσή Αν. Καθηήτρια Πανεπιστημίου Πατρών Πάτρα Ιούνιος
2
3 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΠΡΟΡΑΜΜΑ ΣΠΟΥΔΩΝ ΜΑΘΗΜΑΤΙΚΑ ΚΑΙ ΣΥΧΡΟΝΕΣ ΕΦΑΡΜΟΕΣ -άμμα και -Βήτα συναρτήσεις ΜΕΤΑΠΤΥΧΙΑΚΗ ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΑΣΙΑ Σούρλα Δ. Βασιλική Επιλέπουσα : Χρυσή Κοκολοιαννάκη Αν. Καθηήτρια Πανεπιστημίου Πατρών Εκρίθηκε από την τριμελή επιτροπή την η Ιουνίου Χρ. Κοκολοιαννάκη Β. Παπαεωρίου Ευ. Πετροπούλου Αν. Καθηήτρια Καθηητής Επίκουρος Καθηήτρια Πανεπιστημίου Πατρών Πανεπιστημίου Πατρών Πανεπιστημίου Πατρών Πάτρα Ιούνιος
4 Σούρλα Δ. Βασιλική Πτυχιούχος Μαθηματικός Πανεπιστημίου Πατρών Cogh Σούρλα Δ. Βασιλική. Με επιφύλαξη παντός δικαιώματος. All gh v. Απαορεύεται η αντιραφή αποθήκευση και διανομή της παρούσας ερασίας εξ ολοκλήρου ή τμήματος αυτής ια εμπορικό σκοπό. Επιτρέπεται η ανατύπωση αποθήκευση και διανομή ια σκοπό μη κερδοσκοπικό εκπαιδευτικής ή ερευνητικής φύσης υπό την προϋπόθεση να αναφέρεται η πηή προέλευσης και να διατηρείται το παρόν μήνυμα. Ερωτήματα που αφορούν τη χρήση της ερασίας ια κερδοσκοπικό σκοπό πρέπει να απευθύνονται προς τον συραφέα. Οι απόεις και τα συμπεράσματα που περιέχονται σε αυτό το έραφο εκφράουν τον συραφέα και δεν πρέπει να ερμηνευτεί ότι εκφράουν τις επίσημες θέσεις του Πανεπιστημίου Πατρών. 4
5 ΠΕΡΙΛΗΨΗ Η νωστή συνάρτηση Eul : R > είναι μια από τις σπουδαιότερες ειδικές συναρτήσεις στην Ανάλυση και όχι μόνο και συνδέεται με το και το σύμολο Pochh : C ℵ Άμεσα συνδεδεμένη με τη άμμα συνάρτηση είναι η συνάρτηση Βήτα : R > R >. Το 8 οι Rl D και E Pgu εισήααν το -Pochh σύμολo: ια C R και και με τη οήθεια αυτού όρισαν την -άμμα συνάρτηση : ℵ l > C \ Z και την -Βήτα συνάρτηση : R > R > Οι συναρτήσεις αυτές είναι -ενικεύσεις των και συναρτήσεων με την έννοια ότι ια και ια. Έκτοτε αρκετοί έχουν ασχοληθεί με τις ιδιότητες αυτών καθώς και με την εύρεση φραμάτων ανισοτήτων και ασυμπτωτικών σχέσεων των και καθώς και συναρτήσεων που τις περιέχουν. Στην παρούσα διπλωματική ερασία ίνεται μία όσο το δυνατόν καλύτερη καταραφή των νωστών αποτελεσμάτων καθώς επίσης και αποτελεσμάτων που αφορούν τις -ήτα συναρτήσεις και -υπερεωμετρικές. Επιπλέον δίνουμε και νέες ανισότητες ια τις και συναρτήσεις. ΛΕΞΕΙΣ ΚΛΕΙΔΙΑ -άμμα -Βήτα συναρτήσεις -Pochh σύμολο 5
6 6
7 ASTRACT Th wll-ow Eul uco : R > o o h o uul uco Al coc wh Pochh ol C ℵ Dcl coc wh h G uco h uco : R > R >. : I 8 Rl D E Pgu ouc h -Pochh ol : C R h h -G uco : ℵ l > C \ Z h - uco : R > R > W o h h uco -glo o uco o. Th cocg o o h ov uco ul oc lo w uco volvg h. w ow ul o -G - -Z - goc uco. I o w gv o o ul o uco. KEY WORDS -G uco - uco -Pochh ol. 7
8 8
9 ΠΙΝΑΚΑΣ ΠΕΡΙΕΧΟΜΕΝΩΝ Περίληη 5 Ac..7 Περιεχόμενα...9 Εισαωή.. Κεφάλαιο Σελίδα Ι. Βασικές συναρτήσεις..... άμμα Συνάρτηση..... Βήτα συνάρτηση Ζήτα συνάρτηση Υπερεωμετρικές συναρτήσεις Mg-Ll συναρτήσεις 8 II. -Συναρτήσεις Pochh σύμολο άμμα συνάρτηση.... -δίαμμα συνάρτηση 4.4 Βήτα συνάρτηση 6.5 Ζήτα συνάρτηση 9.6 Υπερεωμετρική συνάρτηση..7 Mg-Ll συναρτήσεις...6 III. Προτάσεις και θεωρήματα ια τις -Συναρτήσεις 4 ραφήματα...6 Βιλιοραφία 6 9
10
11 ΕΙΣΑΩΗ Οι συναρτήσεις -άμμα > είναι -ενίκευση των νωστών συναρτήσεων άμμα και όταν το τείνει στη μονάδα τότε οι συναρτήσεις τείνουν στις συναρτήσεις. Οι συναρτήσεις προέκυαν από τη σύνδεση της συνδυαστικής και της θεωρίας μέτρου όπως αναφέρεται στην ερασία [] και στη ιλιοραφία της. Πράματι έστω λέεται συνδυαστικό μέτρο αν ακέραιος. Δηλαδή αν μ ένα μέτρο σ ένα διάστημα I [ R. Το μέτρο μ M ℵ η οστή ροπή του μ είναι μη αρνητικός μ μ που είναι ο μετασχηματισμός Mll του I μ τότε το μ είναι συνδυαστικό μέτρο αν και μόνο αν M μ ℵ ℵ. Το πιο νωστό παράδειμα σχέσης συνδυαστικής και θεωρίας μέτρου είναι το που μετρά το σύνολο των μεταθέσεων ενός συνόλου με στοιχεία. Ο μετασχηματισμός Mll του μέτρου R > : είναι η κλασική άμμα συνάρτηση ια Οι ροπές του μέτρου είναι το. Πράματι : R > Χρησιμοποιώντας το σύμολο Pochh : το ράφεται : Οι C ℵ. αυξανόμενοι παραοντικοί αριθμοί : ια R και ℵ που προκύπτουν από τη ενική μορφή του Pochh συμόλου : ια C R και ℵ έχουν σχέση με το σύνολο των μεταθέσεων T των ισομορφισμών κλάσεων- επίπεδων δένδρων με ρία l oo με συκεκριμένες ιδιότητες. Αποδεικνύεται [] και ιλιοραφία της ότι T.
12 Ο μετασχηματισμός Mll του μέτρου > ια R > δηλαδή : είναι η -άμμα συνάρτηση ια R > C η οποία συνδέεται με την μέσω της ισότητας : Οι > C \ Z αυξανόμενοι παραοντικοί αριθμοί εμφανίονται ως οι ροπές της συνάρτησης : ενικότερα ισχύει η ισότητα : T. Λόω της σχέσης των συναρτήσεων και είναι λοικό να αποδειχθούν ια την ιδιότητες και σχέσεις οι οποίες είναι αντίστοιχες των ιδιοτήτων και σχέσεων που αφορούν στη συνάρτηση και λέονται ενικεύσεις αυτών. Αυτές τις ιδιότητες και σχέσεις καταράαμε και αποδείξαμε αναλυτικά καθώς επίσης και τις αντίστοιχες ια τις συναρτήσεις Mg-Ll υπερεωμετρικές και ήτα συναρτήσεις οι οποίες συνδέονται με τις άμμα συναρτήσεις. Στο ο κεφάλαιο αναφέρουμε ορισμούς και σημαντικές ιδιότητες χωρίς αποδείξεις των νωστών μας συναρτήσεων άμμα Βήτα υπερεωμετρικών F c και των Mg-Ll συναρτήσεων. Στο ο κεφάλαιο ράφονται οι ορισμοί ια τις ενικεύσεις των ανωτέρω συναρτήσεων και αποδεικνύονται αναλυτικά οι αντίστοιχες ιδιότητες που ικανοποιούν. Στο ο κεφάλαιο αποδεικνύονται προτάσεις και θεωρήματα ια τις ανωτέρω συναρτήσεις.
13 Ι. Βασικές συναρτήσεις. άμμα Συνάρτηση Ορισμός.. [ 4] : Η συνάρτηση άμμα ορίεται ισοδυνάμως με τους κάτωθι τρόπους : μέσω του ολοκληρώματος : R >. που δόθηκε από τον Eul και μέσω του άπειρου ορίου : l που δόθηκε από τους Eul-Gu. Χρησιμοποιώντας το σύμολο του Pochh... ℵ. που ορίεται ως : C ℵ. ο ορισμός. μπορεί να πάρει τη μορφή : l μέσω του απειροινομένου : / C \ Z ℵ που δόθηκε από τους W όπου.4.5 l... l η σταθερά Eul-Mco. Ιδιότητες της άμμα συνάρτησης [ 4] : Z {}
14 4 π ± ±... π 5 6 π 7 π 8 π διπλασιασμού του Lg π Lg Dulco Foul τύπος 9 π π R > R > τύπος του Gu Ορισμός.. : Η λοαριθμική παράωος της άμμα συνάρτησης λέεται δίαμμα συνάρτηση ή διαφορετικά και ορίεται ως εξής : ' l....6 Ιδιότητες της δίαμμα συνάρτησης : C ℵ ια : Η τάξης παράωος της δίνεται : C ℵ 4
15 . Βήτα συνάρτηση Ορισμός.. [ 4] : συνάρτηση Βήτα ορίεται ια R > R > ισοδυνάμως από τα ολοκληρώματα : π co Ιδιότητες της Βήτα συνάρτησης [ 4] : 4. Ζήτα συνάρτηση Ορισμός.. [] : Ορίουμε ως ήτα συνάρτηση την έκφραση : R > R >. Παρατήρηση : ια η. μας δίνει τη συνάρτηση :. νωστή ως συνάρτηση του R. 5
16 Ιδιότητες της Ζήτα συνάρτησης [9] : π π π R R > R > Ιδιότητες της συνάρτησης R [9] : π π π π co R >.4 Υπερεωμετρικές συναρτήσεις Ορισμός.4. [ 5] : Η υπερεωμετρική συνάρτηση Gu F c δίνεται υπό μορφήν σειράς : F c C c C \ Z. c και είναι λύση της διαφορικής εξίσωσης : '' ' [ c ] 6
17 Ορισμός.4. [ 5] : Η υπερεωμετρική συνάρτηση F c δίνεται υπό μορφήν ολοκληρώματος : F c c c c R > Rc > g π. Ιδιότητες υπερεωμετρικής συνάρτησης [] : F c F c F F 4 F c c c c c R c > c 5 F c F c c c 6 F c F c c 7 [ ] F c F c ℵ ℵ Ορισμός.4. [5] : Η ενικευμένη υπερεωμετρική συνάρτηση F δίνεται υπό μορφήν σειράς : F C.4 είναι λύση της διαφορικής εξίσωσης : [ θ θ θ ] w όπου θ και w F και συκλίνει ια πεπερασμένα αν συκλίνει ια αν και αποκλίνει ια όλα τα αν >. 7
18 .5 Mg-Ll συναρτήσεις Ορισμός.5. [5] : Η Mg-Ll συνάρτηση με μια παράμετρο ορίεται ως εξής : E R >.5 Ορισμός.5. [5] : Η Mg-Ll συνάρτηση δυο παραμέτρων ορίεται ως εξής : E R R >.6 Ορισμός.5. [5] : Η ενικευμένη Mg-Ll συνάρτηση ορίεται ως εξής : E α C R R >.7 Παρατήρηση : Η συνάρτηση.7 ια δίνει την.6 και η.6 ια δίνει την.5. 8
19 II. -Συναρτήσεις. -Pochh σύμολο Η έκφραση :. παρουσιάεται σε πολλά προλήματα της Συνδυαστικής Ανάλυσης []. Σημειώνουμε ότι ια προκύπτει το νωστό Pochh σύμολο. Η επαναλαμανόμενη εμφάνιση της έκφρασης. οδήησε στην εισαωή της - άμμα συνάρτησης. Ορισμός.. [] : Η έκφραση : ια C R και ονομάεται -Pochh σύμολo. ℵ. Ιδιότητες ια το -Pochh σύμολο [] : C \ Z > ℵ. C \ Z > ℵ.4 9
20 Συνεπώς προκύπτει Όπως είναι νωστό ακόμα Άρα.. -άμμα συνάρτηση Ορισμός.. [] : Η -άμμα συνάρτηση ορίεται από την ισότητα : l > C \ Z.5 Σημείωση : Παρατηρούμε ότι όταν τότε. Θεώρημα.. [] : Η -άμμα συνάρτηση ράφεται ως εξής : > C \ Z R >.6
21 Στον ορισμό.4 της άμμα συνάρτησης l αντικαθιστούμε το με οπότε :. l l l Πολλαπλασιάουμε και τα δυο μέλη της τελευταίας ισότητας με οπότε προκύπτει : l l.5 Πρόταση.. [] : Η -άμμα συνάρτηση ικανοποιεί τη σχέση : ια R > C.7 Θεωρούμε το ολοκλήρωμα και θέτουμε συνεπώς..6.
22 Σημείωση : ια προκύπτει το νωστό ολοκλήρωμα Gu. Ιδιότητες της -άμμα συνάρτησης > [ 6] : R 4 ℵ 5 6 Z C \ > ℵ 7 π ℵ 8 R 9 όπου l... l π π
23 ρτησης συν αμμα της τητα ιδι ά ό..6 Αντικαθιστούμε στην.6 όπου το R οπότε : 4 Η ιδιότητα ια ℵ δίνει : 5 Προκύπτει από την ιδιότητα 4 ια. 6 Από την σχέση.5 έχουμε : συμολου τητα ιδι Pochh ό l l l l l.5 7 Αντικαθιστoύμε στην.6 όπου το οπότε : συναρτησης αμμα της τητα ιδι ό π 8 Στην ιδιότητα 5 της άμμα συνάρτησης αντικαθιστούμε όπου το και ρίσκουμε : Θέτουμε όπου με και οπότε :
24 4 Πολλαπλασιάουμε και τα δύο μέλη της ανωτέρω σχέσης με οπότε προκύπτει :.6 9 Από την σχέση.6 παίρνουμε :.5 / / όπου η σταθερά Eul-Mcho.6 ά ά ό π π ρτησης συν μμα της τητα ιδι 4 π π. -δίαμμα συνάρτηση Ορισμός.. [] : Η λοαριθμική παράωος της -άμμα συνάρτησης ονομάεται -δίαμμα συνάρτηση και ορίεται ως εξής : ' l >.8 Ιδιότητες της -δίαμμα συνάρτησης > [ 6] : l ℵ.9 l.
25 5 Η οστή παράωος της δίνεται : ℵ. Παίρνoυμε τον λοάριθμο και στα δύο μέλη της σχέσης.6 οπότε έχουμε : l l ] l[ Παραωίουμε ως προς οπότε :.8 ' l ] l[.6 l l l Επειδή η ισότητα.9 ια ίνεται : l l l l Η σχέση αυτή θα δειχθεί με τη μέθοδο της επαωής. Παραωίοντας την.9 ως προς : ' ' ' η οποία είναι η. ια. Έστω ότι ισχύει ια δηλαδή : Θα δείξουμε ότι ισχύει ια δηλαδή : Πράματι :
26 ' [ ] που είναι η προς απόδειξη σχέση..4 Βήτα συνάρτηση Ορισμός.4. [] : Ορίουμε ως Βήτα συνάρτηση την έκφραση : > R > R >. Ιδιότητες της -Βήτα συνάρτησης > [ 6] :
27 7 9 > ] [ ℵ Χρησιμοποιώντας τις παρακάτω σχέσεις: η σχέση. μετασχηματίεται : ρτησης συν ητα της τητα ιδι ά ό Στον ορισμό της Βήτα συνάρτησης αντικαθιστoύμε το με και το με συναρτησης τα της τητα ιδι - ή ό Β Θεωρούμε το ολοκλήρωμα : και θέτουμε άρα οπότε :.8 ά ή ό ρτησης συν τα της τητα ιδι Β 4 Εφαρμόοντας την ιδιότητα 9 της άμμα συνάρτησης στον ορισμό της Βήτα συνάρτησης προκύπτει το εξής :
28 8 5 Αντικαθιστούμε στον ορισμό της Βήτα συνάρτησης το με : 6 Αντικαθιστούμε στον ορισμό της Βήτα συνάρτησης το με : 7 Αντικαθιστούμε στον ορισμό της Βήτα συνάρτησης το με : 8 Αντικαθιστούμε στον ορισμό της Βήτα συνάρτησης το με : 9 Εφαρμόοντας την ιδιότητα στον ορισμό της Βήτα συνάρτησης και θέτοντας όπου το και όπου το προκύπτει : Αντικαθιστούμε στον ορισμό της Βήτα συνάρτησης το με και το με : συναρτησης της τητα αμμα ιδι ό 4 ] [
29 .5 Ζήτα συνάρτηση Ορισμός.5. [] : Ορίουμε ως ήτα συνάρτηση με μορφή σειράς : > R > R >. Ορισμός.5. [6] : Ορίουμε ως R ήτα συνάρτηση με μορφή ολοκληρώματος : >.4 Ιδιότητες της ήτα συνάρτησης > και > [ 6] : l l ια όλες τις αποδείξεις των ανωτέρω ιδιοτήτων θα χρησιμοποιήσουμε τον ορισμό.. Η σχέση αυτή θα δειχθεί με τη μέθοδο της επαωής. η οποία είναι η προς απόδειξη σχέση ια. Έστω ότι ισχύει ια δηλαδή : 9
30 . Θα δείξουμε ότι ισχύει ια δηλαδή : Πράματι : Από τον ορισμό έχουμε : Εφαρμόουμε ια : ' Όμως ξέρουμε από τη σχέση. ια : l Άρα l. Ξαναράφουμε το ως l οπότε από την σχέση. προκύπτει : l l l l οπότε ια l επιπλέον έχουμε Συνεπώς l 4 Η σχέση αυτή θα δειχθεί με τη μέθοδο της επαωής. ια ισχύει διότι : Έστω ότι ισχύει ια δηλαδή : Θα δείξουμε ότι ισχύει ια δηλαδή : Πράματι
31 [ ] [ ] 5 Προκύπτει άμεσα από τις σχέσεις. και.. 6 Από τον ορισμό.5. έχουμε ότι : ν ν ν ν.6 Υπερεωμετρική συνάρτηση Ορισμός.6. : Η υπερεωμετρική συνάρτηση Gu δίνεται F υπό μορφήν σειράς : F C C \ Z >.5 Ορισμός.6. : Η υπερεωμετρική συνάρτηση δίνεται υπό F μορφήν σειράς : F C C \ Z >.6 Ορισμός.6. : Η υπερεωμετρική συνάρτηση F c δίνεται υπό μορφήν σειράς :
32 F C >.7 Σημείωση : Οι ορισμοί.6. και.6. προκύπτουν από την ερασία [] ια κατάλληλες τιμές των παραμέτρων. Ιδιότητες της υπερεωμετρικής συνάρτησης F > : F F F F ℵ F Προκύπτει άμεσα από τον ορισμό. Η σχέση αυτή θα δειχθεί με τη μέθοδο της επαωής. ια η προς απόδειξη σχέση ίνεται : F F η οποία ισχύει διότι : F F Έστω ότι ισχύει ια δηλαδή : F F
33 Θα δείξουμε ότι ισχύει ια δηλαδή : F F Πράματι : F F F Θεωρούμε την συνάρτηση και υπολοίουμε τις παραώους της: ' '' '''
34 4 Επαωικά προκύπτει : Στη συνέχεια υπολοίουμε τις αντίστοιχες τιμές ια : ' ' ' '' ' Αναπτύσσουμε την ύρω από το : F. Θεώρημα.6. : Αν R R > > > Z τότε ια όλα τα πεπερασμένα ισχύει : F.8 Έχουμε συναρτησης αμμα της ιδιοτητα και Από τις ανωτέρω σχέσεις προκύπτει : συναρτησης ητα της ιδιοτητα Β
35 5 Από την ανωτέρω σχέση και τον ορισμό.6 έχουμε : F Επειδή από την τελευταία ισότητα προκύπτει η προς απόδειξη σχέση : F Σημείωση : Στην ερασία [] έχει δειχθεί η πιο ενική σχέση : F Θεώρημα.6. : Αν R R > > τότε ια όλα τα πεπερασμένα ισχύει : F.9 Στην απόδειξη του θεωρήματος.6. δείξαμε ότι ισχύει : Από τον ορισμό.5 και χρησιμοποιώντας την ανωτέρω σχέση έχουμε :
36 6 F α 4 ό συναρτησης υπερεωμετρικης της τητα ιδι Σημείωση : Στην ερασία [] έχει δειχθεί η πιο ενική σχέση : F.7 Mg-Ll συναρτήσεις Ορισμός.7. [4] : Έστω R C R R R > η Mg- Ll συνάρτηση ορίεται από την ακόλουθη σειρά : E. Ιδιότητες της συνάρτησης Mg-Ll [4] : E E / E / E R.
37 7 Από τον ορισμό. προκύπτει :. E.6.7 E Η ισοδυναμία προκύπτει αν θέσουμε στην αποδειχθείσα σχέση όπου το. E E E. Ξεκινώντας από το δεύτερο μέλος :. E E ό συναρτησης της τητα αμμα ιδι. E Έστω C R R > τότε : E E E. Ξεκινώντας από το πρώτο μέλος και χρησιμοποιώντας τη σχέση. έχουμε :
38 8 E E E E / /.7.7 E /. E 4 Αν C R R > και ℵ τότε : E E.4 Η σχέση αυτή θα δειχθεί με τη μέθοδο της επαωής. E η οποία είναι η προς απόδειξη σχέση ια. Έστω ότι ισχύει ια δηλαδή : E E. Θα δείξουμε ότι ισχύει ια δηλαδή :
39 9 E E Πράματι E E E 5 Έστω C R R > και R τότε : E E.5 Κατ αρχήν ισχύει : συναρτησης αμμα τη ς ιδιοτητα. Ξεκινώντας από το πρώτο μέλος της σχέσης.5 και λαμάνοντας υπόιν την προηούμενη σχέση : E που είναι το ητούμενο αποτέλεσμα.
40 4 III. Προτάσεις και θεωρήματα ια τις -Συναρτήσεις Θεώρημα.. [6] : Έστω > > και. Τότε η συνάρτηση ικανοποιεί την παρακάτω ανίσωση :. ια και. ια την απόδειξη των ανισοτήτων. θα χρειαστούμε το κάτωθι λήμμα : Λήμμα.. : Έστω > και. Τότε η συνάρτηση ικανοποιεί την παρακάτω ανίσωση :. ια και. / / ια / τότε : / / / / /
41 4 / / Άρα η ανίσωση ίνεται : / ια / τότε : / / / / / / / Άρα η ανίσωση ίνεται : / Με πρόσθεση κατά μέλη των παραπάνω σχέσεων : / / Συνεπώς / / Τελικά Ομοίως προκύπτει η αντίστροφη ανισότητα ια.
42 4 Απόδειξη Θεωρήματος.. : Αντικαθιστούμε όπου το και όπου το στη σχέση. : Ομοίως προκύπτει η αντίστροφη ανισότητα ια. Πόρισμα.. [6] : Έστω >. Τότε η συνάρτηση ικανοποιεί την παρακάτω ανίσωση :. ή.4 Αντικαθιστούμε όπου το στη σχέση. : Aπό την ιδιότητα 5 της -Βήτα συνάρτησης : Αν θέσουμε όπου το στη σχέση. : Aπό την ιδιότητα 6 της -Βήτα συνάρτησης :
43 4 Θεώρημα.. [6] : ια το ινόμενο των συναρτήσεων με και ισχύουν οι παρακάτω ανισώσεις :.5 Θέτουμε όπου το στις ανισότητες. οπότε προκύπτει : Δηλαδή Πρόταση.. [] : Η παράωος ως προς της συνάρτησης δίνεται από την ισότητα : log R >.6 Παραωίοντας την έκφραση προκύπτει :
44 44 log log log που είναι το ητούμενο. Θεώρημα..4 [] : Έστω θετικά ορισμένη συνάρτηση στο. Θεωρούμε ότι > και λοαριθμικά κυρτή τότε. ια να δείξουμε ότι αρκεί να δείξουμε χρησιμοποιώντας την.5 : l log l log Εφόσον όμως είναι λοαριθμικά κυρτή ισχύει : log log log Εφόσον επιπλέον ισχύει η σχέση : έχουμε : log log log log log log log log log log log log log log log log log log
45 45 log log l log l log log l log l log log log l Επομένως. Θεώρημα..5 [ 6] : Η συνάρτηση l ια > είναι λύση της ραμμικής μερικής διαφορικής εξίσωσης :.7 Λοαριθμίουμε τη σχέση.6 οπότε : l l l l l l l ' '
46 46 l l l l ' l ' l Με αντικατάσταση των ανωτέρω σχέσεων στην δοθείσα σχέση παίρνουμε το ητούμενο. Θεώρημα..6 [6] : Έστω η συνάρτηση l ια >. Τότε η συνάρτηση είναι πλήρως μονότονη. Λοαριθμίουμε τη σχέση.6 οπότε : l l l l l l l '.8 " Επαωικά ρίσκουμε : Αφού τότε η οποία είναι πλήρως μονότονη ια > αφού είναι πλήρως μονότονη ια >.
47 47 Θεώρημα..7 [ 6]: Η -άμμα συνάρτηση είναι λοαριθμικά κυρτή στο. Από τη σχέση.8 συμπεραίνουμε άμεσα ότι η -άμμα συνάρτηση είναι λοαριθμικά κυρτή στο. Θεώρημα..8 ενίκευση του τύπου διπλασιασμού Lg ια την [6] : Η -άμμα συνάρτηση ικανοποιεί την παρακάτω ισότητα : π ια R > C.9 Αν στη σχέση θέσουμε προκύπτει : Αν τώρα θέσουμε u προκύπτει : u u u u u u Από την ιδιότητα της -άμμα συνάρτησης ια ξέρουμε π και επειδή επίσης η ανωτέρω σχέση ίνεται :
48 48 π π π Θεώρημα.. [8] : Ισχύει η παρακάτω ισότητα : c l π > c. Λαμάνοντας υπόη τη σχέση : π [] και τη.6 η -Βήτα συνάρτηση παίρνει την παρακάτω μορφή : c c c c c c c c c c c π π π c c c c π π Άρα c l π c c l
49 49 c c c c l c c l Επειδή l > και l l l θα ισχύει : c l π l Θεώρημα.. [8] : Ισχύει η παρακάτω ισότητα : l >. Λαμάνοντας υπόη τη σχέση : π [] και τη.6 προκύπτει : π π Ομοίως π Με διαίρεση κατά μέλη των δυο παραπάνω σχέσεων προκύπτει : π π
50 5 Άρα l αφού l Θεώρημα.. : Η συνάρτηση > και ℵ ικανοποιεί τις παρακάτω ανισότητες : l l. όπου... και η σταθερά του Eul. Η ισότητα ισχύει ια. Από τη σχέση. ια έχουμε : ' > ' ια δεδομένη αυστηρώς φθίνουσα θετική συνάρτηση με l g ισχύει η σχέση: g g g g Συνεπώς αν θεωρήσουμε ότι g και g τότε ια την ' ισχύει :
51 5 ' Ολοκληρώνοντας την ανωτέρω σχέση από έως δεδομένου ότι η σειρά συκλίνει προκύπτει : ' ] l[ ] l[ ] l[ ] l[ ] l[ ] l[ ] l[ ] l[ l l l l Ολοκληρώνοντας ξανά την παραπάνω ανίσωση από έως δεδομένου του ότι η σειρά συκλίνει προκύπτει : l l Υπολοίουμε το ολοκλήρωμα l θέτοντας w και w w w w οπότε :
52 5 l l l l l l l w w w w w w w w Τελικά η παραπάνω ανίσωση ίνεται : l l l l l l l l l l l l l l l Από τη σχέση. προκύπτει : l l l l l l επιπλέον λόω του ότι : l... l l l τελικά έχουμε : l l η οποία είναι η..
53 5 Τέλος ια παίρνουμε : l l η οποία ισχύει διότι. Πόρισμα..5 : Η συνάρτηση > ικανοποιεί τις παρακάτω ανισότητες : l l. όπου η σταθερά του Eul. Οι ανισότητες προκύπτουν από την. ια. l l l l Πόρισμα..6 : Ισχύουν οι παρακάτω ανισότητες ια το π : π όπου η σταθερά του Eul.
54 54 Αν στην. αντικαταστήσουμε όπου το και δεδομένου του ότι π προκύπτει : l l l l π π Πόρισμα..7 : Η συνάρτηση > και ℵ ικανοποιεί τις παρακάτω ανισότητες : l l.5 όπου... και η σταθερά του Eul. Η ισότητα ισχύει ια. Αν στη σχέση. αντικαταστήσουμε το από την ιδιότητα της προκύπτει :
55 55 l l l l l l l l Θέτοντας το προκύπτει : l l l l l l ο.ε.δ.
56 56 Σημείωση : Το θεώρημα.. και τα πορίσματα..5 και..6 αποτελούν - ενίκευση του θεωρήματος και πορίσματος της ερασίας []. Ανάλοο θεώρημα με το θεώρημα.. έχει δειχθεί με την ίδια μέθοδο και στην ερασία [] όπου σημειώνονται λάθη και δεν αποτελεί -ενίκευση του θεωρήματος της ερασίας [] όπως θα έπρεπε. Πόρισμα..8 : Η συνάρτηση > ικανοποιεί τις παρακάτω ανισότητες : l l.6 όπου... και η σταθερά του Eul. Από την.5 έχουμε : l l l l Πολλαπλασιάοντας τις ανωτέρω σχέσεις κατά μέλη προκύπτει :
57 57 l l Πολλαπλασιάοντας την ανωτέρω σχέση κατά μέλη με την παρακάτω : l l προκύπτει τελικά : l l l l l l l l l l l l
58 58 Υπολοίουμε τα εκθετικά : l l l l l l l l l l l l l l Τελικά προκύπτει : l l l l. Θεώρημα..9 [7] : Έστω > και >. Τότε η θετική συνάρτηση φθίνει ως προς και ως προς. Έστω > και >. Τότε η θετική συνάρτηση φθίνει ως προς ια > και > ν και αυξάνεται ως προς ια > ν ν ν.
59 Όπως είδαμε και παραπάνω ια > και > : Επίσης ια > και > : ν ν ν ν ν ν ν ν Από τις δυο τελευταίες σχέσεις καταλήουμε στο ητούμενο. Παραωίοντας την σχέση. ως προς : log ν ν ν.7 Αν > τότε ια ν > > ν ν > log ν >. Έτσι από την σχέση.7 συμπεραίνουμε ότι η φθίνει με >. Αν και ν log ν. Έτσι η αυξάνει με >. ν Θεώρημα.. [7] : Έστω η R ήτα συνάρτηση. Τότε ισχύει η ανίσωση : >.8 Έστω g δυο μη αρνητικές συναρτήσεις με πραματικούς αριθμούς τέτοιους ώστε να ισχύει η ανισότητα Schw : g g g Έτσι εφαρμόοντας στην ανίσωση αυτή : καταλήουμε : και μέσω του ορισμού.5. έχουμε : g 59
60 6 Όμως από την ιδιότητα της συνάρτησης προκύπτει τελικά : που είναι το ητούμενο. Θεώρημα.. [7] : Έστω u η R ήτα συνάρτηση. Τότε ισχύει η ανίσωση : v u v u v u v u / / / /.9 όπου > > v u και v u >. Θεωρούμε την ανισότητα ol ια > : g g Εφαρμόοντας την ανίσωση αυτή ια : u και v g καταλήουμε : v u v u v u v u
61 6 v u v u v u v u Όμως από τον ορισμό.5. έχουμε : / / / / v u v u v u v u που είναι η.9.
62 ΡΑΦΗΜΑΤΑ 5 ράφημα της άμμα συνάρτησης. Σχήμα ράφημα της άμμα συνάρτησης ια 5. Σχήμα ράφημα της άμμα συνάρτησης ια. Σχήμα 4 6
63 ράφημα της Βήτα συνάρτησης. Σχήμα 4 ράφημα της Βήτα συνάρτησης ια 5. Σχήμα 5 Σημείωση : Παρατηρούμε ότι τα σχήματα και είναι ανάλοα με το σχήμα καθώς και το σχήμα 5 με το σχήμα 4. 6
64 ΒΙΒΛΙΟΡΑΦΙΑ [] M. Aow I. A. Sgu 97. oo o hcl Fuco wh Foul Mhcl Tl Dov Nw Yo. [] R. D E. Pgu 7. O hgoc uco -Pochh ol Dvulgco Mc [] R. D C. O E. Pgu. O h -g -uo Cl Euo Joul o Mhc [4] G. A. Dogo R. A. Cu. Th -Mg-Ll Fuco I. J. Co. Mh. Scc [5] A. Kl. Svv J. Tullo 6. Tho Alco o Fcol Dl Euo Elv. [6] C.G. Koolog. Po Iul o Gl - G Z Fuco I. J. Co. Mh. Scc [7] C.G. Koolog- V. K. So o o h -G uco L Mhch LXVIII I.- o:.448/.68.. [8] V. K. A l o h -G - Fuco I. Mh. Fou [9] W. Mgu F. Ohg R. P. So 966. Foul Tho o h Scl Fuco o Mhcl Phc Sg-Vlg Nw Yo Ic. [] SF. Movc. Pow ouc Iul o h uco I. Joul o Mh. Al [] S. Mu G. M. ullh. A Igl Ro o So - goc Fuco I. Mh. Fou [] E. D. Rvll 96. Scl Fuco Chl Pulhg Co Nw Yo. [] Z. Sc. Pow ouc ul o h uco Kguvc J. Mh [4] Παναιώτης Σιαφαρίκας 7. Ειδικές Συναρτήσεις Εκδόσεις Πανεπιστημίου Πατρών. 64
Θεώρημα Βolzano. Κατηγορία 1 η. 11.1 Δίνεται η συνάρτηση:
 Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
- ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 6: ΜΗ ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΣΤΟ R - ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΤΟ ΑΠΕΙΡΟ - ΠΕΠΕΡΑΣΜΕΝΟ ΟΡΙΟ ΑΚΟΛΟΥΘΙΑΣ [Κεφ..6: Μη Πεπερασμένο Όριο στο R - Κεφ..7: Όρια Συνάρτησης
Εισαγωγή στις Συναρτήσεις Πλοήγησης (Navigation Functions - NF)
 Εισαωή στις Συναρτήσεις Πλοήησης (Navigation Functions - NF) Οι συναρτήσεις πλοήησης είναι μια μεθοδολοία που εισήααν οι Rimon και Koditschek ια τον προραμματισμό κίνησης (motion planning) ενός ρομπότ,
Εισαωή στις Συναρτήσεις Πλοήησης (Navigation Functions - NF) Οι συναρτήσεις πλοήησης είναι μια μεθοδολοία που εισήααν οι Rimon και Koditschek ια τον προραμματισμό κίνησης (motion planning) ενός ρομπότ,
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014
 ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
ΜΕΓΙΣΤΙΚΟΣ ΤΕΛΕΣΤΗΣ 18 Σεπτεμβρίου 2014 Περιεχόμενα 1 Εισαγωγή 2 2 Μεγιστικός τελέστης στην μπάλα 2 2.1 Βασικό θεώρημα........................ 2 2.2 Γενική περίπτωση μπάλας.................. 6 2.2.1 Στο
κυρτές συναρτήσεις. Αν η g είναι γνησίως αύξουσα τότε η gof : είναι κυρτή. . Θα δείξουμε ότι η h είναι γνησίως αύξουσα.
 Άσκηση Έστω f, g: κυρτές συναρτήσεις Αν η g είναι γνησίως αύξουσα τότε η gof : είναι κυρτή Λύση Θα δείξουμε ότι η h ( ) Θέτουμε h( ) gof ( ) g f ( ) είναι γνησίως αύξουσα h( ) g f ( ) f ( ) Έχουμε ότι
Άσκηση Έστω f, g: κυρτές συναρτήσεις Αν η g είναι γνησίως αύξουσα τότε η gof : είναι κυρτή Λύση Θα δείξουμε ότι η h ( ) Θέτουμε h( ) gof ( ) g f ( ) είναι γνησίως αύξουσα h( ) g f ( ) f ( ) Έχουμε ότι
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου].
![ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου]. ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ.2.6 Μέρος Β του σχολικού βιβλίου].](/thumbs/52/29746903.jpg) ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ..6 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1. ΘΕΜΑ Β Να μελετηθούν ως προς την μονοτονία
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 8: ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ [Ενότητα Μονοτονία Συνάρτησης του κεφ..6 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1. ΘΕΜΑ Β Να μελετηθούν ως προς την μονοτονία
Συνθήκες Θ.Μ.Τ. Τρόπος αντιμετώπισης: 1. Για να ισχύει το Θ.Μ.Τ. για μια συνάρτηση f σε ένα διάστημα [, ] (δηλαδή για να υπάρχει ένα τουλάχιστον (, )
![Συνθήκες Θ.Μ.Τ. Τρόπος αντιμετώπισης: 1. Για να ισχύει το Θ.Μ.Τ. για μια συνάρτηση f σε ένα διάστημα [, ] (δηλαδή για να υπάρχει ένα τουλάχιστον (, ) Συνθήκες Θ.Μ.Τ. Τρόπος αντιμετώπισης: 1. Για να ισχύει το Θ.Μ.Τ. για μια συνάρτηση f σε ένα διάστημα [, ] (δηλαδή για να υπάρχει ένα τουλάχιστον (, )](/thumbs/65/53019709.jpg) Κατηγορία η Συνθήκες ΘΜΤ Τρόπος αντιμετώπισης: Για να ισχύει το ΘΜΤ για μια συνάρτηση σε ένα διάστημα [, ] (δηλαδή για να υπάρχει ένα τουλάχιστον (, ) τέτοιο ώστε ( ) ( a) '( ) ) πρέπει: a Η συνάρτηση
Κατηγορία η Συνθήκες ΘΜΤ Τρόπος αντιμετώπισης: Για να ισχύει το ΘΜΤ για μια συνάρτηση σε ένα διάστημα [, ] (δηλαδή για να υπάρχει ένα τουλάχιστον (, ) τέτοιο ώστε ( ) ( a) '( ) ) πρέπει: a Η συνάρτηση
2. Αν έχουμε μια συνάρτηση f η οποία είναι συνεχής σε ένα διάστημα Δ.
 Κατηγορία η Εύρεση μονοτονίας Τρόπος αντιμετώπισης:. Αν έχουμε μια συνάρτηση f η οποία είναι συνεχής σε ένα διάστημα Δ. Αν f( ) σε κάθε εσωτερικό σημείο του Δ, τότε η f είναι γνησίως αύξουσα σε όλο το
Κατηγορία η Εύρεση μονοτονίας Τρόπος αντιμετώπισης:. Αν έχουμε μια συνάρτηση f η οποία είναι συνεχής σε ένα διάστημα Δ. Αν f( ) σε κάθε εσωτερικό σημείο του Δ, τότε η f είναι γνησίως αύξουσα σε όλο το
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ
 ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ - ΠΑΠΑΔΟΠΟΥΛΟΣ ΜΑΡΙΝΟΣ ΠΕΡΙΕΧΟΜΕΝΑ. Τίτλος Θεματικές Ενότητες Σελίδες. Δυο λόγια προς τους μαθητές.
 ΠΕΡΙΕΧΟΜΕΝΑ Τίτλος Θεματικές Ενότητες Σελίδες Προλογικό Σημείωμα Δυο λόγια προς τους μαθητές. ΚΕΦΑΛΑΙΟ 1 ο Όρια Συνέχεια Συνάρτησης 1-177 Μέρος 1 ο ΣΥΝΑΡΤΗΣΕΙΣ 1-85 Μάθημα 1 Έννοια συνάρτησης Πεδίο ορισμού
ΠΕΡΙΕΧΟΜΕΝΑ Τίτλος Θεματικές Ενότητες Σελίδες Προλογικό Σημείωμα Δυο λόγια προς τους μαθητές. ΚΕΦΑΛΑΙΟ 1 ο Όρια Συνέχεια Συνάρτησης 1-177 Μέρος 1 ο ΣΥΝΑΡΤΗΣΕΙΣ 1-85 Μάθημα 1 Έννοια συνάρτησης Πεδίο ορισμού
Κεφάλαιο 4: Διαφορικός Λογισμός
 ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
ΣΥΓΧΡΟΝΗ ΠΑΙΔΕΙΑ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ Κεφάλαιο 4: Διαφορικός Λογισμός Μονοτονία Συνάρτησης Tζουβάλης Αθανάσιος Κεφάλαιο 4: Διαφορικός Λογισμός Περιεχόμενα Μονοτονία συνάρτησης... Λυμένα παραδείγματα...
x R, να δείξετε ότι: i)
 ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ Γ ΛΥΚΕΙΟΥ Έστω μια συνάρτηση f παραγωγίσιμη στο R για την οποία ισχύουν: f ( ), f ( ) για κάθε R και f ( ) f ( ) α) Να βρείτε τον τύπο της f για κάθε R g( ) β) Αν g είναι
ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΨΗΣ Γ ΛΥΚΕΙΟΥ Έστω μια συνάρτηση f παραγωγίσιμη στο R για την οποία ισχύουν: f ( ), f ( ) για κάθε R και f ( ) f ( ) α) Να βρείτε τον τύπο της f για κάθε R g( ) β) Αν g είναι
ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ
 Νίκος Ζανταρίδης (Φροντιστήριο Πυραμίδα) ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ Ένα γενικό θέμα Ανάλυσης Χρήσιμες Προτάσεις Ασκήσεις για λύση Μικρό βοήθημα για τον υποψήφιο μαθητή της Γ Λυκείου λίγο πριν τις εξετάσεις Απρίλιος
Νίκος Ζανταρίδης (Φροντιστήριο Πυραμίδα) ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ Ένα γενικό θέμα Ανάλυσης Χρήσιμες Προτάσεις Ασκήσεις για λύση Μικρό βοήθημα για τον υποψήφιο μαθητή της Γ Λυκείου λίγο πριν τις εξετάσεις Απρίλιος
x είναι f 1 f 0 f κ λ
 3 Ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ [Κεφάλαια, Μέρος Β' του σχολικού βιβλίου] ΘΕΜΑ Α.Βλέπε σχολικό βιβλίο, σελίδα 4.. Βλέπε σχολικό βιβλίο, σελίδα 88, 89. 3. α) ΣΩΣΤΟ, διότι αν η f παραγωγίσιμη στο χ
3 Ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ [Κεφάλαια, Μέρος Β' του σχολικού βιβλίου] ΘΕΜΑ Α.Βλέπε σχολικό βιβλίο, σελίδα 4.. Βλέπε σχολικό βιβλίο, σελίδα 88, 89. 3. α) ΣΩΣΤΟ, διότι αν η f παραγωγίσιμη στο χ
1.8 ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ 73 8 ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ρισμός της συνέχειας Έστω οι συναρτήσεις g h παρακάτω σχήματα των οποίων οι γραφικές παραστάσεις δίνονται στα C h 6 l ( C l g( C g l l (a Παρατηρούμε ότι:
ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ 73 8 ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ρισμός της συνέχειας Έστω οι συναρτήσεις g h παρακάτω σχήματα των οποίων οι γραφικές παραστάσεις δίνονται στα C h 6 l ( C l g( C g l l (a Παρατηρούμε ότι:
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ
 ΝΙΚΟΣ ΑΛΕΞΑΝΔΡΗΣ ΜΑΘΗΜΑΤΙΚΟΣ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΣΥΝΔΥΑΣΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΝΙΚΟΣ ΑΛΕΞΑΝΔΡΗΣ ΠΤΥΧΙΟΥΧΟΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΑΘΗΝΩΝ (ΕΚΠΑ) ΔΙΑΔΙΚΤΥΑΚΟ
ΝΙΚΟΣ ΑΛΕΞΑΝΔΡΗΣ ΜΑΘΗΜΑΤΙΚΟΣ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΠΡΟΤΕΙΝΟΜΕΝΑ ΘΕΜΑΤΑ ΣΥΝΔΥΑΣΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΝΙΚΟΣ ΑΛΕΞΑΝΔΡΗΣ ΠΤΥΧΙΟΥΧΟΣ ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΑΘΗΝΩΝ (ΕΚΠΑ) ΔΙΑΔΙΚΤΥΑΚΟ
Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους
 ΜΑΘΗΜΑΤΙΚΑ, 6-7 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΠΙΚ. ΚΑΘ. ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους 6-7. Περιοδικές Συναρτήσεις) Έστω συνεχής συνάρτηση f : R R περιοδική
ΜΑΘΗΜΑΤΙΚΑ, 6-7 ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΟΙΚΟΝΟΜΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ ΕΠΙΚ. ΚΑΘ. ΣΤΑΥΡΟΣ ΤΟΥΜΠΗΣ Λύσεις Εξετάσεων Φεβρουαρίου Ακ. Έτους 6-7. Περιοδικές Συναρτήσεις) Έστω συνεχής συνάρτηση f : R R περιοδική
********* Β ομάδα Κυρτότητα Σημεία καμπής*********
 ********* Β ομάδα Κυρτότητα Σημεία καμπής********* 5 Για την δύο φορές παραγωγίσιμη στο R συνάρτηση ισχύει: e για κάθε R. Να αποδείξετε ότι η γραφική παράσταση της δεν παρουσιάζει σημείο καμπής. Υποθέτουμε
********* Β ομάδα Κυρτότητα Σημεία καμπής********* 5 Για την δύο φορές παραγωγίσιμη στο R συνάρτηση ισχύει: e για κάθε R. Να αποδείξετε ότι η γραφική παράσταση της δεν παρουσιάζει σημείο καμπής. Υποθέτουμε
Φίλη μαθήτρια, φίλε μαθητή,
 Φίλη μαθήτρια, φίλε μαθητή, Το βιβλίο αυτό, όπως και το πρώτο τεύχος, είναι εναρμονισμένο με την πρόσφατα καθορισμένη ύλη και απευθύνεται στους μαθητές της Γ Λυκείου που έχουν επιλέξει τον προσανατολισμό
Φίλη μαθήτρια, φίλε μαθητή, Το βιβλίο αυτό, όπως και το πρώτο τεύχος, είναι εναρμονισμένο με την πρόσφατα καθορισμένη ύλη και απευθύνεται στους μαθητές της Γ Λυκείου που έχουν επιλέξει τον προσανατολισμό
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 10: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ
 ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ Άσκηση.
Η ΒΟΗΘΗΤΙΚΗ ΣΥΝΑΡΤΗΣΗ ΚΑΙ ΟΙ ΑΝΙΣΟΤΙΚΕΣ ΣΧΕΣΕΙΣ ΣΥΝΕΔΡΙΟ Ε.Μ.Ε. ΤΕΤΑΡΤΗ
 Η ΒΟΗΘΗΤΙΚΗ ΣΥΝΑΡΤΗΣΗ ΚΑΙ ΟΙ ΑΝΙΣΟΤΙΚΕΣ ΣΧΕΣΕΙΣ ΣΥΝΕΔΡΙΟ Ε.Μ.Ε. ΤΕΤΑΡΤΗ 7 007 ΑΤΜΑΤΖΙΔΗΣ ΑΘΑΝΑΣΙΟΣ ΚΑΘΗΓΗΤΗΣ Μ.Ε. Όλα ξεκίνησαν όταν μαθητές της Γ Λυκείου Κατεύθυνσης με ρώτησαν με πόσους τρόπους μπορούν
Η ΒΟΗΘΗΤΙΚΗ ΣΥΝΑΡΤΗΣΗ ΚΑΙ ΟΙ ΑΝΙΣΟΤΙΚΕΣ ΣΧΕΣΕΙΣ ΣΥΝΕΔΡΙΟ Ε.Μ.Ε. ΤΕΤΑΡΤΗ 7 007 ΑΤΜΑΤΖΙΔΗΣ ΑΘΑΝΑΣΙΟΣ ΚΑΘΗΓΗΤΗΣ Μ.Ε. Όλα ξεκίνησαν όταν μαθητές της Γ Λυκείου Κατεύθυνσης με ρώτησαν με πόσους τρόπους μπορούν
ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 7: ΣΥΝΕΠΕΙΕΣ ΘΕΩΡΗΜΑΤΟΣ ΜΕΣΗΣ ΤΙΜΗΣ
 ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 7: ΣΥΝΕΠΕΙΕΣ ΘΕΩΡΗΜΑΤΟΣ ΜΕΣΗΣ ΤΙΜΗΣ [Κεφ..6: Συνέπειες του Θεωρήματος της Μέσης Τιμής πλην της Ενότητας Μονοτονία Συνάρτησης του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 7: ΣΥΝΕΠΕΙΕΣ ΘΕΩΡΗΜΑΤΟΣ ΜΕΣΗΣ ΤΙΜΗΣ [Κεφ..6: Συνέπειες του Θεωρήματος της Μέσης Τιμής πλην της Ενότητας Μονοτονία Συνάρτησης του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
ΗΡΑΚΛΕΙΤΟΣ ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΗΡΑΚΛΕΙΤΟΣ ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β') ΔΕΥΤΕΡΑ 28 ΜΑΪΟΥ 2012
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β') ΔΕΥΤΕΡΑ 28 ΜΑΪΟΥ 2012 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΜΑ
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β') ΔΕΥΤΕΡΑ 28 ΜΑΪΟΥ 2012 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ ΘΕΜΑ
ΦΡΟΝΤΙΣΤΗΡΙΟ ΜΕΣΗΣ ΕΚΠΑΙΔΕΥΣΗΣ ΗΡΑΚΛΕΙΤΟΣ ΚΩΛΕΤΤΗ
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β') ΔΕΥΤΕΡΑ 5 ΜΑΪΟΥ 5 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ & ΤΕΧΝΟΛΟΓΙΚΉΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) Ε Ν Δ Ε
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΚΑΙ ΕΠΑΛ (ΟΜΑΔΑ Β') ΔΕΥΤΕΡΑ 5 ΜΑΪΟΥ 5 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ & ΤΕΧΝΟΛΟΓΙΚΉΣ ΚΑΤΕΥΘΥΝΣΗΣ (ΚΑΙ ΤΩΝ ΔΥΟ ΚΥΚΛΩΝ) Ε Ν Δ Ε
35 Χρήσιμες Προτάσεις με αποδείξεις Γ Λυκείου Μαθηματικά Κατεύθυνσης
 4 5 35 Χρήσιμες Προτάσεις με αποδείξεις Γ Λυκείου Μαθηματικά Κατεύθυνσης Περίληψη: Στο ένθετο αυτό περιλαμβάνονται 35 βασικές προτάσεις, μικρά λήμματα χρήσιμα για τις εξετάσεις. Μας βοηθούν να «ξεκλειδώνουμε»
4 5 35 Χρήσιμες Προτάσεις με αποδείξεις Γ Λυκείου Μαθηματικά Κατεύθυνσης Περίληψη: Στο ένθετο αυτό περιλαμβάνονται 35 βασικές προτάσεις, μικρά λήμματα χρήσιμα για τις εξετάσεις. Μας βοηθούν να «ξεκλειδώνουμε»
Πανελλήνιες Εξετάσεις Ημερήσιων Γενικών Λυκείων. Εξεταζόμενο Μάθημα: Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης, Ημ/νία: 27 Μαΐου 2013
 Πανελλήνιες Εξετάσεις Ημερήσιων Γενικών Λυκείων Εξεταζόμενο Μάθημα: Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης, Ημ/νία: 27 Μαΐου 2013 Απαντήσεις Θεμάτων Θεμα Α Α1. Θεωρία σχολικού βιβλίου σελ. 334-335
Πανελλήνιες Εξετάσεις Ημερήσιων Γενικών Λυκείων Εξεταζόμενο Μάθημα: Μαθηματικά Θετικής και Τεχνολογικής Κατεύθυνσης, Ημ/νία: 27 Μαΐου 2013 Απαντήσεις Θεμάτων Θεμα Α Α1. Θεωρία σχολικού βιβλίου σελ. 334-335
ΟΙ πιο πάνω έννοιες εκφράζουν όπως λέμε τη μονοτονία της συνάρτησης.
 3 Μονοτονία συναρτήσεων 3 Μονοτονία συναρτήσεων 3Α Μονοτονία συνάρτησης Έστω f μία συνάρτηση με πεδίο ορισμού Γνησίως αύξουσα συνάρτηση Η συνάρτηση f λέγεται γνησίως αύξουσα στο Δ αν για κάθε, Δ, με
3 Μονοτονία συναρτήσεων 3 Μονοτονία συναρτήσεων 3Α Μονοτονία συνάρτησης Έστω f μία συνάρτηση με πεδίο ορισμού Γνησίως αύξουσα συνάρτηση Η συνάρτηση f λέγεται γνησίως αύξουσα στο Δ αν για κάθε, Δ, με
Για να εκφράσουμε τη διαδικασία αυτή, γράφουμε: :
 Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
Η θεωρία στα μαθηματικά προσανατολισμού Γ υκείου Τι λέμε συνάρτηση με πεδίο ορισμού το σύνολο ; Έστω ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το μία διαδικασία (κανόνα), με την
y = 2 x και y = 2 y 3 } ή
 ΘΕΜΑ Έστω οι μιγαδικοί αριθμοί z, w για τους οποίους ισχύουν οι σχέσεις z = και w i =. i). Να βρείτε το γεωμετρικό τόπο των εικόνων των z και w. ii). Να αποδείξετε ότι δεν υπάρχουν μιγαδικοί αριθμοί z,
ΘΕΜΑ Έστω οι μιγαδικοί αριθμοί z, w για τους οποίους ισχύουν οι σχέσεις z = και w i =. i). Να βρείτε το γεωμετρικό τόπο των εικόνων των z και w. ii). Να αποδείξετε ότι δεν υπάρχουν μιγαδικοί αριθμοί z,
ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ
 ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ Ορισμοί Μία συνάρτηση f λέγεται: 1 γνησίως αύξουσα σ' ένα υποσύνολο Β του πεδίου ορισμού της όταν για κάθε 1, Β με 1 < ισχύει ότι f( 1 ) < f( ) γνησίως φθίνουσα σ' ένα υποσύνολο Β
ΜΟΝΟΤΟΝΙΑ ΣΥΝΑΡΤΗΣΗΣ Ορισμοί Μία συνάρτηση f λέγεται: 1 γνησίως αύξουσα σ' ένα υποσύνολο Β του πεδίου ορισμού της όταν για κάθε 1, Β με 1 < ισχύει ότι f( 1 ) < f( ) γνησίως φθίνουσα σ' ένα υποσύνολο Β
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α. , έχει κατακόρυφη ασύμπτωτη την x 0.
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α Άσκηση Θεωρούμε τον παρακάτω ισχυρισμό: «Αν η συνάρτηση την» ορίζεται στο τότε δεν μπορεί να έχει κατακόρυφη ασύμπτωτη ) Να χαρακτηρίσετε τον παραπάνω ισχυρισμό γράφοντας
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΓΕΝΙΚΑ ΘΕΜΑ Α Άσκηση Θεωρούμε τον παρακάτω ισχυρισμό: «Αν η συνάρτηση την» ορίζεται στο τότε δεν μπορεί να έχει κατακόρυφη ασύμπτωτη ) Να χαρακτηρίσετε τον παραπάνω ισχυρισμό γράφοντας
Θεώρημα Bolzano. ΑΠΑΝΤΗΣΗ. Έστω μια συνάρτηση f, ορισμένη σε ένα κλειστό διάστημα [, ]. Αν: η f είναι συνεχής στο [, ] και, επιπλέον, ισχύει
![Θεώρημα Bolzano. ΑΠΑΝΤΗΣΗ. Έστω μια συνάρτηση f, ορισμένη σε ένα κλειστό διάστημα [, ]. Αν: η f είναι συνεχής στο [, ] και, επιπλέον, ισχύει Θεώρημα Bolzano. ΑΠΑΝΤΗΣΗ. Έστω μια συνάρτηση f, ορισμένη σε ένα κλειστό διάστημα [, ]. Αν: η f είναι συνεχής στο [, ] και, επιπλέον, ισχύει](/thumbs/62/47577709.jpg) Θεώρημα Bolzno. ΑΠΑΝΤΗΣΗ Έστω μια συνάρτηση f, ορισμένη σε ένα κλειστό διάστημα [, ]. Αν: η f είναι συνεχής στο [, ] και, επιπλέον, ισχύει f f 0, τότε υπάρχει ένα, τουλάχιστον, 0 (, ) τέτοιο, ώστε f( 0
Θεώρημα Bolzno. ΑΠΑΝΤΗΣΗ Έστω μια συνάρτηση f, ορισμένη σε ένα κλειστό διάστημα [, ]. Αν: η f είναι συνεχής στο [, ] και, επιπλέον, ισχύει f f 0, τότε υπάρχει ένα, τουλάχιστον, 0 (, ) τέτοιο, ώστε f( 0
40 Ασκήσεις στον ΟΛΟΚΛΗΡΩΤΙΚΟ ΛΟΓΙΣΜΟ ( Επεξεργασία του ΜΑΝΩΛΗ ΨΑΡΡΑ)
 Άσκηση η 4 Ασκήσεις στον ΟΛΟΚΛΗΡΩΤΙΚΟ ΛΟΓΙΣΜΟ ( Επεξεργασία του ΜΑΝΩΛΗ ΨΑΡΡΑ) Έστω f, g είναι συνεχείς συναρτήσεις στο διάστημα, να δείξετε: Α. (Ανισότητα των Cauchy-Schwarz) Β.( Ανισότητα του Minkowski)
Άσκηση η 4 Ασκήσεις στον ΟΛΟΚΛΗΡΩΤΙΚΟ ΛΟΓΙΣΜΟ ( Επεξεργασία του ΜΑΝΩΛΗ ΨΑΡΡΑ) Έστω f, g είναι συνεχείς συναρτήσεις στο διάστημα, να δείξετε: Α. (Ανισότητα των Cauchy-Schwarz) Β.( Ανισότητα του Minkowski)
Προσομοίωση προαγωγικών εξετασεων Άλγεβρας Β Λυκείου Σχ. έτος
 Προσομοίωση προαγωγικών εξετασεων Άλγεβρας Β Λυκείου Σχ. έτος 04-05 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 05-06 ΤΑΞΗ: Β ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΛΓΕΒΡΑ ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ ΘΕΜΑΤΑ (4) ΘΕΜΑ ο Α.Να χαρακτηρίσετε
Προσομοίωση προαγωγικών εξετασεων Άλγεβρας Β Λυκείου Σχ. έτος 04-05 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΣΧΟΛΙΚΟΥ ΕΤΟΥΣ 05-06 ΤΑΞΗ: Β ΛΥΚΕΙΟΥ ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΑΛΓΕΒΡΑ ΠΡΟΣΟΜΟΙΩΣΗ ΘΕΜΑΤΩΝ ΘΕΜΑΤΑ (4) ΘΕΜΑ ο Α.Να χαρακτηρίσετε
και γνησίως αύξουσα στο 0,
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Α1. Σχολικό βιβλίο σελ 6 (i) A. Σχολικό βιβλίο σελ 141 Α. Σχολικό βιβλίο σελ 46-47 Α4. α. Λ β. Σ γ. Λ δ. Σ ε. Σ ΘΕΜΑ Β Β1. Ισχύει D f επειδή 1 1 1 Για κάθε η f είναι παραγωγίσιμη
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΘΕΜΑ Α Α1. Σχολικό βιβλίο σελ 6 (i) A. Σχολικό βιβλίο σελ 141 Α. Σχολικό βιβλίο σελ 46-47 Α4. α. Λ β. Σ γ. Λ δ. Σ ε. Σ ΘΕΜΑ Β Β1. Ισχύει D f επειδή 1 1 1 Για κάθε η f είναι παραγωγίσιμη
ΑΝΑΛΥΣΗ 1 ΔΕΚΑΤΟ ΕΝΑΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ ΔΕΚΑΤΟ ΕΝΑΤΟ ΜΑΘΗΜΑ, 9--3 Μ. Παπαδημητράκης. Σήμερα θα δούμε κάποια πράγματα για μια σημαντική ειδική κατηγορία σειρών, εκείνες που έχουν όλους τους προσθετέους τους μη-αρνητικούς. Και θα αρχίσουμε
ΑΝΑΛΥΣΗ ΔΕΚΑΤΟ ΕΝΑΤΟ ΜΑΘΗΜΑ, 9--3 Μ. Παπαδημητράκης. Σήμερα θα δούμε κάποια πράγματα για μια σημαντική ειδική κατηγορία σειρών, εκείνες που έχουν όλους τους προσθετέους τους μη-αρνητικούς. Και θα αρχίσουμε
A. ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
ΜΑΘΗΜΑΤΙΚΑ. 1 ο ΔΙΑΓΩΝΙΣΜΑ ΘΕΜΑ 1 ο. ΘΕΜΑ 2 ο. 0, αν x
 Γ' ΛΥΚΕΙΟΥ-ΤΕΧΝΟΛΟΓΙΚΩΝ/ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΩΡΙΑ. Πότε δύο συναρτήσεις και g είναι ίσες;. Πότε μία συνάρτηση με πεδίο ορισμού Α λέγεται " " ; 3. Πότε μία συνάρτηση λέγεται συνεχής στο σημείο o του πεδίου
Γ' ΛΥΚΕΙΟΥ-ΤΕΧΝΟΛΟΓΙΚΩΝ/ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΘΕΩΡΙΑ. Πότε δύο συναρτήσεις και g είναι ίσες;. Πότε μία συνάρτηση με πεδίο ορισμού Α λέγεται " " ; 3. Πότε μία συνάρτηση λέγεται συνεχής στο σημείο o του πεδίου
A. ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
8Α ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ A ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ Πότε μια συνάρτηση λέγεται συνεχής σε ένα σημείο του πεδίου ορισμού o της ; Απάντηση : ( ΟΜΟΓ, 6 ΟΜΟΓ, 9 Β, ΟΜΟΓ, 5 Έστω μια συνάρτηση και ένα σημείο του πεδίου
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΔΕΥΤΕΡΑ 11 ΙΟΥΝΙΟΥ 2018 ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΔΕΥΤΕΡΑ ΙΟΥΝΙΟΥ 8 ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Σελίδα από Φάνης Μαργαρώνης Φροντιστήρια Ρούλα Μακρή Τομέας μαθηματικών ΘΕΜΑ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΔΕΥΤΕΡΑ ΙΟΥΝΙΟΥ 8 ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ ΣΤΑ ΘΕΜΑΤΑ ΤΩΝ ΜΑΘΗΜΑΤΙΚΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Σελίδα από Φάνης Μαργαρώνης Φροντιστήρια Ρούλα Μακρή Τομέας μαθηματικών ΘΕΜΑ
ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ. Το Θεώρημα και το Πόρισμα ισχύουν σε διαστήματα και όχι σε ένωση διαστημάτων.
 ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ Θεώρημα Αν μια συνάρτηση f είναι συνεχής σε ένα διάστημα Δ και ισχύει f () = 0 για κάθε εσωτερικό σημείο του Δ, τότε η f είναι σταθερή σ' όλο το διάστημα Δ. Πόρισμα Αν δύο συναρτήσεις
ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ Θεώρημα Αν μια συνάρτηση f είναι συνεχής σε ένα διάστημα Δ και ισχύει f () = 0 για κάθε εσωτερικό σημείο του Δ, τότε η f είναι σταθερή σ' όλο το διάστημα Δ. Πόρισμα Αν δύο συναρτήσεις
5o Επαναληπτικό Διαγώνισμα 2016
 5o Επαναληπτικό Διαγώνισμα 6 Διάρκεια: 3 ώρες ΘΕΜΑ A Α Έστω μια συνάρτηση f ορισμένη σε ένα διάστημα Δ Να αποδείξετε ότι αν η f είναι συνεχής στο Δ και f για κάθε εσωτερικό σημείο του Δ, να αποδείξετε
5o Επαναληπτικό Διαγώνισμα 6 Διάρκεια: 3 ώρες ΘΕΜΑ A Α Έστω μια συνάρτηση f ορισμένη σε ένα διάστημα Δ Να αποδείξετε ότι αν η f είναι συνεχής στο Δ και f για κάθε εσωτερικό σημείο του Δ, να αποδείξετε
Προτεινόμενες λύσεις. f (x) f (x ) f (x) f (x ) f (x) f (x ) (x x ). f (x) f (x ) lim[f (x) f (x )] lim (x x ) lim[f (x) f (x )] 0 lim f (x) f (x ),
![Προτεινόμενες λύσεις. f (x) f (x ) f (x) f (x ) f (x) f (x ) (x x ). f (x) f (x ) lim[f (x) f (x )] lim (x x ) lim[f (x) f (x )] 0 lim f (x) f (x ), Προτεινόμενες λύσεις. f (x) f (x ) f (x) f (x ) f (x) f (x ) (x x ). f (x) f (x ) lim[f (x) f (x )] lim (x x ) lim[f (x) f (x )] 0 lim f (x) f (x ),](/thumbs/88/117311736.jpg) Πανελλαδικές Εξετάσεις 8 Μαθηματικά Προσανατολισμού /6/8 ΘΕΜΑ Α Προτεινόμενες λύσεις Α Αφού η f είναι παραγωγίσιμη στο σημείο του πεδίου ορισμού της, ισχύει ότι: Για κάθε έχουμε: Επομένως ισχύει ότι: Δηλαδή:
Πανελλαδικές Εξετάσεις 8 Μαθηματικά Προσανατολισμού /6/8 ΘΕΜΑ Α Προτεινόμενες λύσεις Α Αφού η f είναι παραγωγίσιμη στο σημείο του πεδίου ορισμού της, ισχύει ότι: Για κάθε έχουμε: Επομένως ισχύει ότι: Δηλαδή:
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ. Να εξετάσετε αν είναι ίσες οι συναρτήσεις f, g όταν: x x 2 x x. x x g x. ln x ln x 1 και
 Α ΟΜΑΔΑ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Να εξετάσετε αν είναι ίσες οι συναρτήσεις, όταν: () με R και (). Σ Υ Ν Α Ρ Τ Η Σ Ε Ι Σ Το πεδίο ορισμού της είναι A R. Επομένως A A R Α Θα εξετάσουμε αν για κάθε R ισχύει.
Α ΟΜΑΔΑ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Να εξετάσετε αν είναι ίσες οι συναρτήσεις, όταν: () με R και (). Σ Υ Ν Α Ρ Τ Η Σ Ε Ι Σ Το πεδίο ορισμού της είναι A R. Επομένως A A R Α Θα εξετάσουμε αν για κάθε R ισχύει.
[ α π ο δ ε ί ξ ε ι ς ]
![[ α π ο δ ε ί ξ ε ι ς ] [ α π ο δ ε ί ξ ε ι ς ]](/thumbs/78/78384597.jpg) Γ' Λυκείου Κατεύθυνση [ α π ο δ ε ί ξ ε ι ς ] ε ξ ε τ α σ τ έ α ς ύ λ η ς 7-8 Επιμέλεια Κόλλας Αντώνης Όριο πολυωνυμικής στο Αν P( = αν ν + αν ν +... + α + α είναι πολυώνυμο του και, τότε: P( P( P( =...
Γ' Λυκείου Κατεύθυνση [ α π ο δ ε ί ξ ε ι ς ] ε ξ ε τ α σ τ έ α ς ύ λ η ς 7-8 Επιμέλεια Κόλλας Αντώνης Όριο πολυωνυμικής στο Αν P( = αν ν + αν ν +... + α + α είναι πολυώνυμο του και, τότε: P( P( P( =...
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου
 Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
ΕΚΤΙΜΗΣΗ ΠΟΣΟΣΤΙΑΙΩΝ ΣΗΜΕΙΩΝ ΓΙΑ ΕΠΙΛΕΓΜΕΝΟ ΕΚΘΕΤΙΚΟ ΠΛΗΘΥΣΜΟ ΑΠΟ k ΠΛΗΘΥΣΜΟΥΣ
 ΚΩΝΣΤΑΝΤΙΝΟΣ Γ. ΑΓΓΕΛΟΥ ΕΚΤΙΜΗΣΗ ΠΟΣΟΣΤΙΑΙΩΝ ΣΗΜΕΙΩΝ ΓΙΑ ΕΠΙΛΕΓΜΕΝΟ ΕΚΘΕΤΙΚΟ ΠΛΗΘΥΣΜΟ ΑΠΟ k ΠΛΗΘΥΣΜΟΥΣ ΜΕΤΑΠΤΥΧΙΑΚΗ ΔΙΑΤΡΙΒΗ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΔΙΑΤΜΗΜΑΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΜΑΘΗΜΑΤΙΚΑ
ΚΩΝΣΤΑΝΤΙΝΟΣ Γ. ΑΓΓΕΛΟΥ ΕΚΤΙΜΗΣΗ ΠΟΣΟΣΤΙΑΙΩΝ ΣΗΜΕΙΩΝ ΓΙΑ ΕΠΙΛΕΓΜΕΝΟ ΕΚΘΕΤΙΚΟ ΠΛΗΘΥΣΜΟ ΑΠΟ k ΠΛΗΘΥΣΜΟΥΣ ΜΕΤΑΠΤΥΧΙΑΚΗ ΔΙΑΤΡΙΒΗ ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΔΙΑΤΜΗΜΑΤΙΚΟ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥΔΩΝ «ΜΑΘΗΜΑΤΙΚΑ
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( ))
![ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( )) ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να εξετάσετε αν ισχύουν οι υποθέσεις του Θ.Μ.Τ. για την συνάρτηση στο διάστημα [ 1,1] τέτοιο, ώστε: C στο σημείο (,f( ))](/thumbs/17/113546.jpg) ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 6: ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (Θ.Μ.Τ.) [Θεώρημα Μέσης Τιμής Διαφορικού Λογισμού του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 6: ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ (Θ.Μ.Τ.) [Θεώρημα Μέσης Τιμής Διαφορικού Λογισμού του κεφ..5 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
5ο Επαναληπτικό διαγώνισμα στα Μαθηματικά κατεύθυνσης της Γ Λυκείου Θέμα A
 5ο Επαναληπτικό διαγώνισμα στα Μαθηματικά κατεύθυνσης της Γ Λυκείου 7-8 Θέμα A A Έστω μια συνάρτηση f παραγωγίσιμη σ ένα διάστημα στο οποίο όμως η f είναι συνεχής Αν η f διατηρεί πρόσημο στο α,,β ότι το
5ο Επαναληπτικό διαγώνισμα στα Μαθηματικά κατεύθυνσης της Γ Λυκείου 7-8 Θέμα A A Έστω μια συνάρτηση f παραγωγίσιμη σ ένα διάστημα στο οποίο όμως η f είναι συνεχής Αν η f διατηρεί πρόσημο στο α,,β ότι το
Να χαρακτηρίσετε ως σωστές (Σ) ή λάθος (Λ) τις παρακάτω προτάσεις :
 Δ Ι Α Γ Ω Ν Ι Σ Μ Α Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Θ Ε Τ Ι Κ Η Σ Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Η Σ Κ Α Τ Ε Υ Θ Υ Ν Σ Η Σ Γ Λ Υ Κ Ε Ι Ο Υ Θ Ε Μ Α 1 Ο Έστω μια συνάρτηση, η οποία είναι ορισμένη σε ένα κλειστό διάστημα. Αν
Δ Ι Α Γ Ω Ν Ι Σ Μ Α Μ Α Θ Η Μ Α Τ Ι Κ Ω Ν Θ Ε Τ Ι Κ Η Σ Τ Ε Χ Ν Ο Λ Ο Γ Ι Κ Η Σ Κ Α Τ Ε Υ Θ Υ Ν Σ Η Σ Γ Λ Υ Κ Ε Ι Ο Υ Θ Ε Μ Α 1 Ο Έστω μια συνάρτηση, η οποία είναι ορισμένη σε ένα κλειστό διάστημα. Αν
Συνέχεια συνάρτησης σε κλειστό διάστημα
 8 Συνέχεια συνάρτησης σε κλειστό διάστημα Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ 1 Μια συνάρτηση f θα λέμε ότι είναι: i Συνεχής σε ένα ανοιχτό διάστημα (α,β) όταν είναι συνεχής σε κάθε σημείο του διαστήματος (α,β)
8 Συνέχεια συνάρτησης σε κλειστό διάστημα Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ 1 Μια συνάρτηση f θα λέμε ότι είναι: i Συνεχής σε ένα ανοιχτό διάστημα (α,β) όταν είναι συνεχής σε κάθε σημείο του διαστήματος (α,β)
Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. Ημερομηνία: Πέμπτη 20 Απριλίου 2017 Διάρκεια Εξέτασης: 3 ώρες ΕΚΦΩΝΗΣΕΙΣ
 ΑΠΟ /4/7 έως τις /4/7 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Πέμπτη Απριλίου 7 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α Έστω μία συνάρτηση f ορισμένη σε ένα διάστημα
ΑΠΟ /4/7 έως τις /4/7 ΤΑΞΗ: ΜΑΘΗΜΑ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Ημερομηνία: Πέμπτη Απριλίου 7 Διάρκεια Εξέτασης: 3 ώρες ΘΕΜΑ Α ΕΚΦΩΝΗΣΕΙΣ Α Έστω μία συνάρτηση f ορισμένη σε ένα διάστημα
Εξεταστέα ύλη μαθηματικών Α Λυκείου 2017
 Εξεταστέα ύλη μαθηματικών Α Λυκείου 2017 Α Λυκείου Γεωμετρία Κεφάλαιο 3 3.1 Είδη και στοιχεία τριγώνων 3.2 1 ο Κριτήριο ισότητας τριγώνων (εκτός της απόδειξης του θεωρήματος) 3.3 2 ο Κριτήριο ισότητας
Εξεταστέα ύλη μαθηματικών Α Λυκείου 2017 Α Λυκείου Γεωμετρία Κεφάλαιο 3 3.1 Είδη και στοιχεία τριγώνων 3.2 1 ο Κριτήριο ισότητας τριγώνων (εκτός της απόδειξης του θεωρήματος) 3.3 2 ο Κριτήριο ισότητας
Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει να είναι σε θέση:
 Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει να είναι σε θέση:. Να μπορεί να βρίσκει απο τη γραφική παράσταση μιας συνάρτησης το πεδίο ορισμού της το σύνολο τιμών της την τιμή της σε ένα σημείο..
Ο μαθητής που έχει μελετήσει τo κεφάλαιο αυτό θα πρέπει να είναι σε θέση:. Να μπορεί να βρίσκει απο τη γραφική παράσταση μιας συνάρτησης το πεδίο ορισμού της το σύνολο τιμών της την τιμή της σε ένα σημείο..
Απαντήσεις στα Μαθηματικά Κατεύθυνσης 2016
 ΘΕΜΑ Α Απαντήσεις στα Μαθηματικά Κατεύθυνσης 6 Α.. Σχολ. Βιβλίο, Θεωρία, σελ.6-(i) Α.. Σχολ. Βιβλίο, Θεωρία, σελ. 4 Α. Σχολ. Βιβλίο, Θεωρία, σελ. 46,47 Α.4. α. Λ β. Σ γ. Λ δ. Σ ε. Σ ΘΕΜΑ Β B. Η συνάρτηση
ΘΕΜΑ Α Απαντήσεις στα Μαθηματικά Κατεύθυνσης 6 Α.. Σχολ. Βιβλίο, Θεωρία, σελ.6-(i) Α.. Σχολ. Βιβλίο, Θεωρία, σελ. 4 Α. Σχολ. Βιβλίο, Θεωρία, σελ. 46,47 Α.4. α. Λ β. Σ γ. Λ δ. Σ ε. Σ ΘΕΜΑ Β B. Η συνάρτηση
g x είναι συνάρτηση 1 1 στο Ag = R αλλά δεν είναι γνησίως
 ΘΕΜΑ Α Α. Απόδειξη θεωρήματος σελ. 99 σχολικού βιβλίου. Α. α. Ψευδής β. Θεωρούμε τη συνάρτηση, 0 g, 0 η οποία έχει γραφική παράσταση (σχήμα σχολικού βιβλίου σελ.5): y O y=g() Η g είναι συνάρτηση στο Ag
ΘΕΜΑ Α Α. Απόδειξη θεωρήματος σελ. 99 σχολικού βιβλίου. Α. α. Ψευδής β. Θεωρούμε τη συνάρτηση, 0 g, 0 η οποία έχει γραφική παράσταση (σχήμα σχολικού βιβλίου σελ.5): y O y=g() Η g είναι συνάρτηση στο Ag
Λύσεις των θεμάτων των Πανελλαδικών Εξετάσεων στα Μαθηματικά Προσανατολισμού 2016
 Λύσεις των θεμάτων των Πανελλαδικών Εξετάσεων στα Μαθηματικά Προσανατολισμού 16 ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΗΜΕΡΗΣΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ
Λύσεις των θεμάτων των Πανελλαδικών Εξετάσεων στα Μαθηματικά Προσανατολισμού 16 ΛΥΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΤΩΝ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΗΜΕΡΗΣΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 17-10-13 Μ. Παπαδημητράκης. 1 Την προηγούμενη φορά αναφέραμε (και αποδείξαμε στην περίπτωση n = 2) το θεώρημα που λέει ότι, αν n N, n 2, τότε για κάθε y 0 υπάρχει μοναδική μηαρνητική
ΑΝΑΛΥΣΗ 1 ΠΕΜΠΤΟ ΜΑΘΗΜΑ, 17-10-13 Μ. Παπαδημητράκης. 1 Την προηγούμενη φορά αναφέραμε (και αποδείξαμε στην περίπτωση n = 2) το θεώρημα που λέει ότι, αν n N, n 2, τότε για κάθε y 0 υπάρχει μοναδική μηαρνητική
5.1.1 Η θεωρία και τι προσέχουμε
 Κεφάλαιο 5 Συνέχεια συνάρτησης σε διάστημα Συνέπειες του Θεωρήματος Bolzano 5.. Η θεωρία και τι προσέχουμε Τα κύρια χαρακτηριστικά μιας συνεχούς συνάρτησης f ορισμένης σε ένα διάστημα Δ, είναι: i. Η γραφική
Κεφάλαιο 5 Συνέχεια συνάρτησης σε διάστημα Συνέπειες του Θεωρήματος Bolzano 5.. Η θεωρία και τι προσέχουμε Τα κύρια χαρακτηριστικά μιας συνεχούς συνάρτησης f ορισμένης σε ένα διάστημα Δ, είναι: i. Η γραφική
0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2
![0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2 0x2 = 2. = = δηλαδή η f δεν. = 2. Άρα η συνάρτηση f δεν είναι συνεχής στο [0,3]. Συνεπώς δεν. x 2. lim f (x) = lim (2x 1) = 3 και x 2 x 2](/thumbs/59/43483993.jpg) ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 8: ΘΕΩΡΗΜΑ BOLZANO - ΠΡΟΣΗΜΟ ΣΥΝΑΡΤΗΣΗΣ - ΘΕΩΡΗΜΑ ΕΝΔΙΑΜΕΣΩΝ ΤΙΜΩΝ - ΘΕΩΡΗΜΑ ΜΕΓΙΣΤΗΣ ΚΑΙ ΕΛΑΧΙΣΤΗΣ ΤΙΜΗΣ - ΣΥΝΟΛΟ ΤΙΜΩΝ ΣΥΝΕΧΟΥΣ ΣΥΝΑΡΤΗΣΗΣ
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ. και σε κάθε γειτονιά του z
 7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Ένα σημείο λέγεται ανώμαλο σημείο της συνάρτησης f( ) αν η f( ) δεν είναι αναλυτική στο και σε κάθε γειτονιά του υπάρχει ένα τουλάχιστον
7. ΑΝΩΜΑΛΑ ΣΗΜΕΙΑ, ΠΟΛΟΙ ΚΑΙ ΤΟ ΘΕΩΡΗΜΑ ΤΩΝ ΟΛΟΚΛΗΡΩΤΙΚΩΝ ΥΠΟΛΟΙΠΩΝ Ένα σημείο λέγεται ανώμαλο σημείο της συνάρτησης f( ) αν η f( ) δεν είναι αναλυτική στο και σε κάθε γειτονιά του υπάρχει ένα τουλάχιστον
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΤΕΛΕΥΤΑΙΑ ΕΠΑΝΑΛΗΨΗ ΑΝΑΛΥΣΗ ΟΛΟΚΛΗΡΩΜΑΤΑ ΜΙΧΑΛΗΣ ΜΑΓΚΟΣ
 ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΤΕΛΕΥΤΑΙΑ ΕΠΑΝΑΛΗΨΗ ΑΝΑΛΥΣΗ ΟΛΟΚΛΗΡΩΜΑΤΑ ΜΙΧΑΛΗΣ ΜΑΓΚΟΣ . ΔΙΑΒΑΖΩ ΤΗ ΘΕΩΡΙΑ ΑΠΟ ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ Σελ.303: Ορισμός (Αρχική συνάρτηση ή παράγουσα) Σελ.304: Απόδειξη του
ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Γ ΛΥΚΕΙΟΥ ΤΕΛΕΥΤΑΙΑ ΕΠΑΝΑΛΗΨΗ ΑΝΑΛΥΣΗ ΟΛΟΚΛΗΡΩΜΑΤΑ ΜΙΧΑΛΗΣ ΜΑΓΚΟΣ . ΔΙΑΒΑΖΩ ΤΗ ΘΕΩΡΙΑ ΑΠΟ ΤΟ ΣΧΟΛΙΚΟ ΒΙΒΛΙΟ Σελ.303: Ορισμός (Αρχική συνάρτηση ή παράγουσα) Σελ.304: Απόδειξη του
M. J. Lighthill. g(y) = f(x) e 2πixy dx, (1) d N. g (p) (y) =
 Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
Μεθοδική Επανα λήψή. Επιμέλεια Κων/νος Παπασταματίου. Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες. Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ.
 Μεθοδική Επανα λήψή Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 Βόλος Τηλ. 4 598 Επιμέλεια Κων/νος Παπασταματίου Περιεχόμενα Συνοπτική Θεωρία με Ερωτήσεις Απαντήσεις...
Μεθοδική Επανα λήψή Θεωρία - Λεξιλόγιο Βασικές Μεθοδολογίες Φροντιστήριο Μ.Ε. «ΑΙΧΜΗ» Κ. Καρτάλη 8 Βόλος Τηλ. 4 598 Επιμέλεια Κων/νος Παπασταματίου Περιεχόμενα Συνοπτική Θεωρία με Ερωτήσεις Απαντήσεις...
2 ο Διαγώνισμα Ύλη: Συναρτήσεις
 ο Διαγώνισμα 08-9 Ύλη: Συναρτήσεις Θέμα Α Α. Θεωρήστε τον παρακάτω ισχυρισμό: «Αν μια συνάρτηση : είναι - τότε είναι και γνησίως μονότονη.» α) Να χαρακτηρίσετε τον ισχυρισμό γράφοντας στο τετράδιό σας
ο Διαγώνισμα 08-9 Ύλη: Συναρτήσεις Θέμα Α Α. Θεωρήστε τον παρακάτω ισχυρισμό: «Αν μια συνάρτηση : είναι - τότε είναι και γνησίως μονότονη.» α) Να χαρακτηρίσετε τον ισχυρισμό γράφοντας στο τετράδιό σας
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ. f ( x) 0 0 2x 0 x 0
 ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΑΠΑΝΤΗΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΚΑΙ ΟΙΚΟΝΟΜΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 8 ΜΑΪΟΥ 6 ΘΕΜΑ Α Α. Θεωρία, βλ. σχολικό βιβλίο
ΠΑΝΕΛΛΗΝΙΕΣ ΕΞΕΤΑΣΕΙΣ ΗΜΕΡΗΣΙΩΝ ΓΕΝΙΚΩΝ ΛΥΚΕΙΩΝ ΑΠΑΝΤΗΣΕΙΣ ΤΩΝ ΘΕΜΑΤΩΝ ΣΤΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΚΑΙ ΟΙΚΟΝΟΜΙΚΩΝ ΣΠΟΥΔΩΝ Γ ΛΥΚΕΙΟΥ (ΝΕΟ ΣΥΣΤΗΜΑ) 8 ΜΑΪΟΥ 6 ΘΕΜΑ Α Α. Θεωρία, βλ. σχολικό βιβλίο
X = συνεχης. Είναι εμφανές ότι αναγκαία προϋπόθεση για την ύπαρξη της ροπογεννήτριας
 Ροπογεννήτριες (mome geerig fucios), πιθανογεννήτριες (robbiliy geerig fucios) και χαρακτηριστικές συναρτήσεις (chrcerisic fucios) Η ροπογεννήτρια συνάρτηση της τμ είναι η πραγματική συνάρτηση πραγματικής
Ροπογεννήτριες (mome geerig fucios), πιθανογεννήτριες (robbiliy geerig fucios) και χαρακτηριστικές συναρτήσεις (chrcerisic fucios) Η ροπογεννήτρια συνάρτηση της τμ είναι η πραγματική συνάρτηση πραγματικής
ΟΡΙΑ ΣΥΝΕΧΕΙΑ: Τύποι - Βασικές έννοιες
 Τύποι - Βασικές έννοιες Όρια - Συνέχεια 37. ΟΡΙΑ ΣΥΝΕΧΕΙΑ: Τύποι - Βασικές έννοιες Με τη βοήθεια του παρακάτω θεωρήματος διευκολύνεται ο υπολογισμός ορίων (άλγεβρα ορίων): Αν τα όρια lim f () και lim g()
Τύποι - Βασικές έννοιες Όρια - Συνέχεια 37. ΟΡΙΑ ΣΥΝΕΧΕΙΑ: Τύποι - Βασικές έννοιες Με τη βοήθεια του παρακάτω θεωρήματος διευκολύνεται ο υπολογισμός ορίων (άλγεβρα ορίων): Αν τα όρια lim f () και lim g()
Α3. Σχολικό βιβλίο σελ. 142 Γεωμετρική ερμηνεία του θ. Fermat: Στο σημείο (x o, f(x o )) η εφαπτομένη της C f είναι οριζόντια.
 ΑΠΑΝΤΗΣΕΙΣ ΠΡΟΣΟΜΟΙΗΣΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 8 ΜΑΡΤΙΟΥ 08 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α Α. Σχολικό βιβλίο σελ. 76 Α. α. Ψ β. Σχολικό
ΑΠΑΝΤΗΣΕΙΣ ΠΡΟΣΟΜΟΙΗΣΗΣ ΠΑΝΕΛΛΑΔΙΚΩΝ ΕΞΕΤΑΣΕΩΝ Γ ΤΑΞΗΣ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΤΕΤΑΡΤΗ 8 ΜΑΡΤΙΟΥ 08 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΜΑ Α Α. Σχολικό βιβλίο σελ. 76 Α. α. Ψ β. Σχολικό
Κατηγορία 1 η. Σταθερή συνάρτηση Δίνεται παραγωγίσιμη συνάρτηση f : 0, f '( x) 0 για κάθε εσωτερικό σημείο x του Δ
 Κατηγορία η Σταθερή συνάρτηση Τρόπος αντιμετώπισης: Για να αποδείξουμε ότι μια συνάρτηση είναι σταθερή σε ένα διάστημα Δ πρέπει: η συνάρτηση να είναι συνεχής στο Δ '( ) 0 για κάθε εσωτερικό σημείο του
Κατηγορία η Σταθερή συνάρτηση Τρόπος αντιμετώπισης: Για να αποδείξουμε ότι μια συνάρτηση είναι σταθερή σε ένα διάστημα Δ πρέπει: η συνάρτηση να είναι συνεχής στο Δ '( ) 0 για κάθε εσωτερικό σημείο του
Τελευταία Επανάληψη. την ευθεία x=1 και τoν x x. 2 1 x. Λύση. x 2 1 x 0, άρα. x 1 x. x x 1. γ) x 1 e x x 1 x e ln x 1 x f x.
 Δίνεται η συνάρτηση ln Τελευταία Επανάληψη α) Να βρείτε το πεδίο ορισμού της β) Να μελετήσετε την ως προς την μονοτονία της γ) Να βρείτε το πλήθος των ριζών της εξίσωσης e, δ) Να υπολογίσετε το εμβαδόν
Δίνεται η συνάρτηση ln Τελευταία Επανάληψη α) Να βρείτε το πεδίο ορισμού της β) Να μελετήσετε την ως προς την μονοτονία της γ) Να βρείτε το πλήθος των ριζών της εξίσωσης e, δ) Να υπολογίσετε το εμβαδόν
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να μελετήσετε ως προς τη μονοτονία και τα ακρότατα τις παρακάτω συναρτήσεις: f (x) = 0 x(2ln x + 1) = 0 ln x = x = e x =
 ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 0: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
ΚΕΦΑΛΑΙΟ ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 0: ΕΥΡΕΣΗ ΤΟΠΙΚΩΝ ΑΚΡΟΤΑΤΩΝ [Ενότητα Προσδιορισμός των Τοπικών Ακροτάτων - Θεώρημα Εύρεση Τοπικών Ακροτάτων του κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
ΜΑΘΗΜΑΤΙΚΑ Γ ΛΥΚΕΙΟΥ ΟΜΑΔΕΣ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ : ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΠΡΟΛΟΓΟΣ Σε κάθε ενότητα αυτού του βιβλίου θα βρείτε : Βασική θεωρία με τη μορφή ερωτήσεων Μεθοδολογίες και σχόλια
(a 1, b 1 ) (a 2, b 2 ) = (a 1 a 2, b 1 b 2 ).
 ΕΜ0 - Διακριτά Μαθηματικά Ιανουαρίου 006 Άσκηση - Λύσεις Πρόβλημα [0 μονάδες] Εστω L και L δύο κυκλώματα σε ένα γράφημα G. Εστω a μία ακμή που ανήκει και στο L και στο L και έστω b μία ακμή που ανήκει
ΕΜ0 - Διακριτά Μαθηματικά Ιανουαρίου 006 Άσκηση - Λύσεις Πρόβλημα [0 μονάδες] Εστω L και L δύο κυκλώματα σε ένα γράφημα G. Εστω a μία ακμή που ανήκει και στο L και στο L και έστω b μία ακμή που ανήκει
f x x, ν Ν-{0,1} είναι παραγωγίσιμη στο R
 ΟΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Θέμα Α Α Να αποδείξετε ότι η συνάρτηση ν ν και ισχύει f ν f, νν-{,} είναι παραγωγίσιμη στο R
ΟΕΦΕ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 4 ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΘΕΤΙΚΗ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗ ΚΑΤΕΥΘΥΝΣΗ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Θέμα Α Α Να αποδείξετε ότι η συνάρτηση ν ν και ισχύει f ν f, νν-{,} είναι παραγωγίσιμη στο R
ΘΕΩΡΗΜΑ ΜΕΣΗΣ ΤΙΜΗΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ
 Διατύπωση: Αν μια συνάρτηση είναι: συνεχής στο κλειστό διάστημα [ α β] και παραγωγίσιμη στο ανοικτό διάστημα ( α β) τότε υπάρχει ένα τουλάχιστον ξ ( α β) τέτοιο ώστε: ( ( β) ( α) β α Γεωμετρικά αυτό σημαίνει
Διατύπωση: Αν μια συνάρτηση είναι: συνεχής στο κλειστό διάστημα [ α β] και παραγωγίσιμη στο ανοικτό διάστημα ( α β) τότε υπάρχει ένα τουλάχιστον ξ ( α β) τέτοιο ώστε: ( ( β) ( α) β α Γεωμετρικά αυτό σημαίνει
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Β ΦΑΣΗ Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ / ΣΠΟΥ ΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7 Ε_3.Μλ3ΘΟ(ε) ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ / ΣΠΟΥ ΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ηµεροµηνία: Τετάρτη 9 Απριλίου 7 ιάρκεια Εξέτασης: 3 ώρες
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7 Ε_3.Μλ3ΘΟ(ε) ΤΑΞΗ: Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ / ΣΠΟΥ ΩΝ ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ Ηµεροµηνία: Τετάρτη 9 Απριλίου 7 ιάρκεια Εξέτασης: 3 ώρες
ΓΙΩΡΓΟΣ ΚΟΡΩΝΑΚΗΣ. ΑΛΛΑΓΗ ΜΕΤΑΒΛΗΤΗΣ ΣΤΟ ΟΡΙΣΜΕΝΟ ΟΛΟΚΛΗΡΩΜΑ Διδακτική προσέγγιση
 ΓΙΩΡΓΟΣ ΚΟΡΩΝΑΚΗΣ ΑΛΛΑΓΗ ΜΕΤΑΒΛΗΤΗΣ ΣΤΟ ΟΡΙΣΜΕΝΟ ΟΛΟΚΛΗΡΩΜΑ Διδακτική προσέγγιση Αφορμή γι αυτή τη σύντομη εργασία έδωσε μια ημερίδα διδασκαλίας των Μαθηματικών, η οποία οργανώθηκε από το Σχολικό Σύμβουλο
ΓΙΩΡΓΟΣ ΚΟΡΩΝΑΚΗΣ ΑΛΛΑΓΗ ΜΕΤΑΒΛΗΤΗΣ ΣΤΟ ΟΡΙΣΜΕΝΟ ΟΛΟΚΛΗΡΩΜΑ Διδακτική προσέγγιση Αφορμή γι αυτή τη σύντομη εργασία έδωσε μια ημερίδα διδασκαλίας των Μαθηματικών, η οποία οργανώθηκε από το Σχολικό Σύμβουλο
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΑΡΑΓΩΓΟΥ - ΠΑΡΑΓΩΓΟΣ ΚΑΙ ΣΥΝΕΧΕΙΑ [Κεφ. 2.1: Έννοια της Παραγώγου του σχολικού βιβλίου].
![ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΑΡΑΓΩΓΟΥ - ΠΑΡΑΓΩΓΟΣ ΚΑΙ ΣΥΝΕΧΕΙΑ [Κεφ. 2.1: Έννοια της Παραγώγου του σχολικού βιβλίου]. ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΑΡΑΓΩΓΟΥ - ΠΑΡΑΓΩΓΟΣ ΚΑΙ ΣΥΝΕΧΕΙΑ [Κεφ. 2.1: Έννοια της Παραγώγου του σχολικού βιβλίου].](/thumbs/61/45920216.jpg) ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΑΡΑΓΩΓΟΥ - ΠΑΡΑΓΩΓΟΣ ΚΑΙ ΣΥΝΕΧΕΙΑ [Κεφ 1: Έννοια της Παραγώγου του σχολικού βιβλίου] ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1 ΘΕΜΑ Β Να βρείτε την παράγωγο της συνάρτησης
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΑΡΑΓΩΓΟΥ - ΠΑΡΑΓΩΓΟΣ ΚΑΙ ΣΥΝΕΧΕΙΑ [Κεφ 1: Έννοια της Παραγώγου του σχολικού βιβλίου] ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα 1 ΘΕΜΑ Β Να βρείτε την παράγωγο της συνάρτησης
Συνεχή Κλάσματα. Εμμανουήλ Καπνόπουλος Α.Μ 282
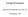 Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
Συνεχή Κλάσματα Εμμανουήλ Καπνόπουλος Α.Μ 282 5 Νοεμβρίου 204 Ορισμός και ιδιότητες: Ορισμός: Έστω a 0, a, a 2,...a n ανεξάρτητες μεταβλητές, n N σχηματίζουν την ακολουθία {[a 0, a,..., a n ] : n N} όπου
Λύσεις του διαγωνίσματος στις παραγώγους
 Λύσεις του διαγωνίσματος στις παραγώγους Θέμα ο Α Έστω ότι f ), για κάθε α, ), β) Επειδή η f είναι συνεχής στο θα είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα α, ] και [, β) Επομένως, για ισχύει
Λύσεις του διαγωνίσματος στις παραγώγους Θέμα ο Α Έστω ότι f ), για κάθε α, ), β) Επειδή η f είναι συνεχής στο θα είναι γνησίως αύξουσα σε κάθε ένα από τα διαστήματα α, ] και [, β) Επομένως, για ισχύει
13 Μονοτονία Ακρότατα συνάρτησης
 3 Μονοτονία Ακρότατα συνάρτησης Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρημα Αν μια συνάρτηση f είναι συνεχής σ ένα διάστημα Δ, τότε: Αν f ( ) > 0για κάθε εσωτερικό του Δ, η f είναι γνησίως αύξουσα στο Δ. Αν
3 Μονοτονία Ακρότατα συνάρτησης Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Θεώρημα Αν μια συνάρτηση f είναι συνεχής σ ένα διάστημα Δ, τότε: Αν f ( ) > 0για κάθε εσωτερικό του Δ, η f είναι γνησίως αύξουσα στο Δ. Αν
ΕΠΙΛΥΣΗ ΕΞΙΣΩΣΕΩΝ ΚΑΙ ΑΝΙΣΩΣΕΩΝ ΣΥΝΑΡΤΗΣΙΑΚΩΝ ΜΟΡΦΩΝ MIAΣ ΜΕΤΑΒΛΗΤΗΣ
 ΕΠΙΛΥΣΗ ΕΞΙΣΩΣΕΩΝ ΚΑΙ ΑΝΙΣΩΣΕΩΝ ΣΥΝΑΡΤΗΣΙΑΚΩΝ ΜΟΡΦΩΝ MIAΣ ΜΕΤΑΒΛΗΤΗΣ Στα παρακάτω γίνεται μία προσπάθεια, ομαδοποίησης των ασκήσεων επίλυσης εξισώσεων και ανισώσεων, συναρτησιακών μορφών, συνεχών συναρτήσεων,
ΕΠΙΛΥΣΗ ΕΞΙΣΩΣΕΩΝ ΚΑΙ ΑΝΙΣΩΣΕΩΝ ΣΥΝΑΡΤΗΣΙΑΚΩΝ ΜΟΡΦΩΝ MIAΣ ΜΕΤΑΒΛΗΤΗΣ Στα παρακάτω γίνεται μία προσπάθεια, ομαδοποίησης των ασκήσεων επίλυσης εξισώσεων και ανισώσεων, συναρτησιακών μορφών, συνεχών συναρτήσεων,
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρα 10 Ιουνίου 2019 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ. (Ενδεικτικές Απαντήσεις)
 ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρα Ιουνίου 9 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (Ενδεικτικές Απαντήσεις) ΘΕΜΑ Α Αα) Ορισμός σχολικού βιβλίου σελ 5 Έστω Α ένα υποσύνολο
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Γ ΗΜΕΡΗΣΙΟΥ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Δευτέρα Ιουνίου 9 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ (Ενδεικτικές Απαντήσεις) ΘΕΜΑ Α Αα) Ορισμός σχολικού βιβλίου σελ 5 Έστω Α ένα υποσύνολο
ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 4: ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΟΥ ΧΩΡΙΟΥ [Κεφ.3.7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ
![ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 4: ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΟΥ ΧΩΡΙΟΥ [Κεφ.3.7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟ 4ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 4: ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΟΥ ΧΩΡΙΟΥ [Κεφ.3.7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ](/thumbs/54/33927053.jpg) ΚΕΦΑΛΑΙΟ ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΟΥ ΧΩΡΙΟΥ [Κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ ΘΕΜΑ Β Άσκηση. Να υπολογίσετε το εμβαδόν του χωρίου που περικλείεται από τη γραφική
ΚΕΦΑΛΑΙΟ ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΕΜΒΑΔΟΝ ΕΠΙΠΕΔΟΥ ΧΩΡΙΟΥ [Κεφ..7 Μέρος Β του σχολικού βιβλίου]. ΑΣΚΗΣΕΙΣ ΘΕΜΑ Β Άσκηση. Να υπολογίσετε το εμβαδόν του χωρίου που περικλείεται από τη γραφική
Παράδειγμα 14.2 Να βρεθεί ο μετασχηματισμός Laplace των συναρτήσεων
 Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
Κεφάλαιο 4 Μετασχηματισμός aplace 4. Μετασχηματισμός aplace της εκθετικής συνάρτησης e Είναι Άρα a a a u( a ( a ( a ( aj F( e e d e d [ e ] [ e ] ( a e (c ji, με a (4.9 a a a [ e u( ] a, με a (4.3 Η σχέση
ΑΣΚΗΣΕΙΣ ΠΙΘΑΝΟΤΗΤΩΝ του Παν. Λ. Θεοδωρόπουλου 0
 ΑΣΚΗΣΕΙΣ ΠΙΘΑΝΟΤΗΤΩΝ του Παν. Λ. Θεοδωρόπουλου 0 Η Θεωρία Πιθανοτήτων είναι ένας σχετικά νέος κλάδος των Μαθηματικών, ο οποίος παρουσιάζει πολλά ιδιαίτερα χαρακτηριστικά στοιχεία. Επειδή η ιδιαιτερότητα
ΑΣΚΗΣΕΙΣ ΠΙΘΑΝΟΤΗΤΩΝ του Παν. Λ. Θεοδωρόπουλου 0 Η Θεωρία Πιθανοτήτων είναι ένας σχετικά νέος κλάδος των Μαθηματικών, ο οποίος παρουσιάζει πολλά ιδιαίτερα χαρακτηριστικά στοιχεία. Επειδή η ιδιαιτερότητα
9 Πολυώνυμα Διαίρεση πολυωνύμων
 4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
ΜΑΘΗΜΑΤΙΚΑ II ΕΚΦΩΝΗΣΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ II ΕΠΑΛ (ΟΜΑ Α Β ) ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α A Έστω f µια συνάρτηση ορισµένη σε ένα διάστηµα Αν F είναι µια παράγουσα της f στο, τότε να αποδείξετε ότι: όλες οι συναρτήσεις της µορφής G() F() + c, c
ΜΑΘΗΜΑΤΙΚΑ II ΕΠΑΛ (ΟΜΑ Α Β ) ΕΚΦΩΝΗΣΕΙΣ ΘΕΜΑ Α A Έστω f µια συνάρτηση ορισµένη σε ένα διάστηµα Αν F είναι µια παράγουσα της f στο, τότε να αποδείξετε ότι: όλες οι συναρτήσεις της µορφής G() F() + c, c
1.1. Διαφορική Εξίσωση και λύση αυτής
 Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
Εισαγωγή στις συνήθεις διαφορικές εξισώσεις 9 Διαφορική Εξίσωση και λύση αυτής Σε ότι ακολουθεί με τον όρο συνάρτηση θα εννοούμε μια πραγματική συνάρτηση μιας πραγματικής μεταβλητής, ορισμένη σε ένα διάστημα
ΑΝΑΛΥΣΗ 2. Μ. Παπαδημητράκης.
 ΑΝΑΛΥΣΗ Μ. Παπαδημητράκης. 1 ΔΕΚΑΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ Χρησιμοποιούμε τα σύμβολα f και f() d για να συμβολίσουμε όλα μαζί τα αόριστα ολοκληρώματα της f σε ένα διάστημα I. Δηλαδή, γράφουμε f = f + c ή f() d =
ΑΝΑΛΥΣΗ Μ. Παπαδημητράκης. 1 ΔΕΚΑΤΟ ΤΡΙΤΟ ΜΑΘΗΜΑ Χρησιμοποιούμε τα σύμβολα f και f() d για να συμβολίσουμε όλα μαζί τα αόριστα ολοκληρώματα της f σε ένα διάστημα I. Δηλαδή, γράφουμε f = f + c ή f() d =
1. Υπολογίστε, όπου αυτές υπάρχουν, τις παραγώγους των συναρτήσεων:
 Υπολογίστε, όπου αυτές υπάρχουν, τις παραγώγους των συναρτήσεων:, g, h Απάντηση: Η με έχει παράγωγο 4 Μπορούμε όμως να εργαστούμε ως εξής: Είναι άρα 4 Η g με g έχει παράγωγο : g Η συνάρτηση h με h έχει
Υπολογίστε, όπου αυτές υπάρχουν, τις παραγώγους των συναρτήσεων:, g, h Απάντηση: Η με έχει παράγωγο 4 Μπορούμε όμως να εργαστούμε ως εξής: Είναι άρα 4 Η g με g έχει παράγωγο : g Η συνάρτηση h με h έχει
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ
 Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
Μ Α Θ Η Μ Α Τ Α Γ Λ Υ Κ Ε Ι Ο Υ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ ΚΑΙ ΣΠΟΥΔΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ (Α ΜΕΡΟΣ: ΣΥΝΑΡΤΗΣΕΙΣ) Επιμέλεια: Καραγιάννης Ιωάννης, Σχολικός Σύμβουλος Μαθηματικών
Ασκήσεις Επανάληψης Γ Λυκείου
 Ασκήσεις Επανάληψης Γ Λυκείου Ασκήσεις Επανάληψης σε όλο το εύρος της διδακτέας ύλης Κων/νος Παπασταματίου Κ. Καρτάλη 8 (με Δημητριάδος) Τηλ. 4 598 Θε ματα Δεσμω ν 98- Επιμέλεια Κων/νος Παπασταματίου Σελίδα
Ασκήσεις Επανάληψης Γ Λυκείου Ασκήσεις Επανάληψης σε όλο το εύρος της διδακτέας ύλης Κων/νος Παπασταματίου Κ. Καρτάλη 8 (με Δημητριάδος) Τηλ. 4 598 Θε ματα Δεσμω ν 98- Επιμέλεια Κων/νος Παπασταματίου Σελίδα
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ. Μαθηματικά. Β μέρος
 ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ 2 5 +32 17 2= 1156 Μαθηματικά Β μέρος 8 9 15 Δ=2 δ Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών και Σπουδών Οικονομίας
ΥΠΟΥΡΓΕΙΟ ΠΑΙΔΕΙΑΣ, ΕΡΕΥΝΑΣ ΚΑΙ ΘΡΗΣΚΕΥΜΑΤΩΝ ΙΝΣΤΙΤΟΥΤΟ ΕΚΠΑΙΔΕΥΤΙΚΗΣ ΠΟΛΙΤΙΚΗΣ 2 5 +32 17 2= 1156 Μαθηματικά Β μέρος 8 9 15 Δ=2 δ Γ ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Ομάδας Προσανατολισμού Θετικών Σπουδών και Σπουδών Οικονομίας
d k 10 k + d k 1 10 k d d = k i=0 d i 10 i.
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
ΜΕΘΟΔΟΙ ΠΟΥ ΧΡΕΙΑΖΟΝΤΑΙ ΜΙΑ ΔΕΥΤΕΡΗ ΜΑΤΙΑ
 ΜΕΘΟΔΟΙ ΠΟΥ ΧΡΕΙΑΖΟΝΤΑΙ ΜΙΑ ΔΕΥΤΕΡΗ ΜΑΤΙΑ? Εύρεση πεδίου ορισμού σε συνθέσεις.. Δίνεται η γν. αύξουσα συνάρτηση :[ -, ] R. Α. Να βρεθεί το πεδίο ορισμού της g () = ( + ) + ( + ). Β. Να βρεθεί η μονοτονία
ΜΕΘΟΔΟΙ ΠΟΥ ΧΡΕΙΑΖΟΝΤΑΙ ΜΙΑ ΔΕΥΤΕΡΗ ΜΑΤΙΑ? Εύρεση πεδίου ορισμού σε συνθέσεις.. Δίνεται η γν. αύξουσα συνάρτηση :[ -, ] R. Α. Να βρεθεί το πεδίο ορισμού της g () = ( + ) + ( + ). Β. Να βρεθεί η μονοτονία
Ελληνική Μαθηματική Εταιρεία Παράρτημα Νομού Εύβοιας ΕΞΕΤΑΣΕΙΣ 2008 ΜΑΘΗΜΑ : ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ
 Ελληνική Μαθηματική Εταιρεία Παράρτημα Νομού Εύβοιας ΕΞΕΤΑΣΕΙΣ 8 ΜΑΘΗΜΑ : ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ: ΘΕΜΑ ο : Α. Θεωρία, σχολικό βιβλίο σελίδα 5 Α. Θεωρία, σχολικό βιβλίο σελίδα 9 Β. α) Σ, β) Σ,
Ελληνική Μαθηματική Εταιρεία Παράρτημα Νομού Εύβοιας ΕΞΕΤΑΣΕΙΣ 8 ΜΑΘΗΜΑ : ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ ΑΠΑΝΤΗΣΕΙΣ: ΘΕΜΑ ο : Α. Θεωρία, σχολικό βιβλίο σελίδα 5 Α. Θεωρία, σχολικό βιβλίο σελίδα 9 Β. α) Σ, β) Σ,
