ΟΠΤΙΚΗ Ι ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ. ηµήτρης Παπάζογλου. ιατµηµατικό Μεταπτυχιακό Πρόγραµµα Σπουδών «Οπτική και Όραση»
|
|
|
- ŌÁĒ Κωνσταντόπουλος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΟΠΤΙΚΗ Ι ΛΥΜΕΝΕΣ ΑΣΚΗΣΕΙΣ ηµήτρης Παπάζογλου ιατµηµατικό Μεταπτυχιακό Πρόγραµµα Σπουδών «Οπτική και Όραση» Πανεπιστήµιο Κρήτης 2005
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41 Διατμηματικό Μεταπτυχιακό πρόγραμμα "Οπτική και Όραση"
42 Διατμηματικό Μεταπτυχιακό πρόγραμμα "Οπτική και Όραση"
43
44
45
46 ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Οπτική Ι, ιδάσκων: ηµήτρης Παπάζογλου 1. Να υπολογιστούν οι θέσεις των χαρακτηριστικών σηµείων καθώς και η θέση και η διάµετρος της κόρης εισόδου και κόρης εξόδου στο παρακάτω σύστηµα. H ισχύς των φακών είναι αντίστοιχα +10D, -5D, +10D. (ο αποκλίνων φακός είναι αµφίκοιλος και συµµετρικός, οι συγκλίνοντες είναι επιπεδόκυρτοι, η διάµετρος όλων των οπτικών είναι 30 mm, ενώ όλες οι αποστάσεις δίνονται σε mm) n= Λύση Για τον 1 ο συγκλίνοντα επιπεδόκυρτο φακό µπορούµε να γράψουµε: Γνωρίζοντας ότι: M D DP1 D = = P1 1 P1 1 d 3mm D= = = 2 mm, P1 = 10 n 1.5 ο πίνακας που περιγράφει τον 1 ο συγκλίνοντα φακό γίνεται: M m = m Από το παραπάνω πίνακα υπολογίζουµε τις θέσεις των κυρίων επιπέδων καθώς και την ενεργό εστιακή απόσταση. 1 m HH 1 M 1 M Z = = 0, Z = = 2 mm, 1 1(2,2) 1 1(1,1) H H M1(2,1) M1(2,1) f e 1 1 = = 100 mm M 1(2,1) 2 3 1
47 ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Οπτική Ι, ιδάσκων: ηµήτρης Παπάζογλου Κατ αναλογία αφού ο 3 ος φακός είναι ίδιος µε τον 1 ο αλλά απλώς αντεστραµµένος θα περιγράφεται από τον ακόλουθο πίνακα: M m = , 3 1 m ενώ οι θέσεις των κυρίων επιπέδων αντίστοιχα δίνονται από τις σχέσεις: H H 1 M 1 M Z = = 2 mm, Z = = 0, 3 3(2,2) 3 3(1,1) H H M3(2,1) M3(2,1) f e 3 1 = = 100 mm M 1(2,1) 2 3 Από την άλλη πλευρά ο αποκλίνων αµφίκοιλος φακός µπορεί να περιγραφεί µε τον παρακάτω πίνακα: M 2 ' D DP 2 2 D = = P P 1 P [2 PD ] 1 D P όπως γνωρίζουµε η ολική ισχύς του φακού δίνεται από το στοιχείο (2,1) του πίνακα οπότε µπορούµε να υπολογίσουµε την ισχύ P του 2 κάθε ενός από τα διόπτρα που αποτελούν τον αµφίκοιλο αποκλίνοντα φακό 1 : D d 1.5mm 1mm n DP P = 5m P = = 2.49m 2 2 = = = D2 2 = 2[2 2 2] P P PD Έτσι συνολικά ο αποκλίνων φακός περιγράφεται από τον πίνακα: M m = 5m , 2 1 ενώ οι θέσεις των κυρίων επιπέδων αντίστοιχα δίνονται από τις σχέσεις: 1 απορρίπτουµε την λύση την θετική λύση αφού τα δίοπτρα είναι κοίλα 2
48 ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Οπτική Ι, ιδάσκων: ηµήτρης Παπάζογλου M 1 M Z = = 0.5 mm, Z = = 0.5 mm, 2 2(2,2) 3 2(1,1) H H M2(2,1) M2(2,1) f e 3 1 = = 200mm M 2(2,1) Γνωρίζοντας τις θέσεις των κυρίων επιπέδων καθενός από τους φακούς που αποτελούν το σύστηµα µπορούµε να περιγράψουµε το συνολικό σύστηµα ως εξής: M = M T M T M, tot όπου Τ 1, πίνακας µετατόπισης που περιγράφει την διάδοση από το πίσω κύριο επίπεδο του 1 ου φακού έως το εµπρός κύριο επίπεδο του 2 ου και Τ 2, πίνακας µετατόπισης που περιγράφει την διάδοση από το πίσω κύριο επίπεδο του 2 ου φακού έως το εµπρός κύριο επίπεδο του 3 ου φακού Σχήµα 1. Περιγραφή του κάθε στοιχείου του συστήµατος µε τα κύρια επίπεδα του (όλες οι αποστάσεις αναφέρονται σε mm) 3
49 Έτσι συνολικά έχουµε: ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Οπτική Ι, ιδάσκων: ηµήτρης Παπάζογλου M tot m m 1 0 = 1 1 = 1 10m m m m m = = 10 m m 1 10 m m m = 1 1 = 10 m m m = 1 1 = 10m m m = m Με βάση τον παραπάνω πίνακα που περιγράφει το συνολικό σύστηµα µπορούµε να υπολογίσουµε τις θέσεις των κυρίων επιπέδων και των δεσµικών σηµείων καθώς και ενεργό εστιακή απόσταση: 1 M 1 M tot Z H = = 29 mm, Z = = 29 mm, M tot(2,2) tot tot(1,1) H tot (2,1) Mtot(2,1) f e tot 1 = = 80 mm M tot(2,1) (Οι θέσεις των κύριων επιπέδων του συστήµατος µετρώνται αντίστοιχα από το εµπρός κύριο επίπεδο του 1 ου φακού και το πίσω κύριο επίπεδο του 3 ου φακού.) Το σύστηµα βρίσκεται στον αέρα εποµένως τα δεσµικά σηµεία βρίσκονται πάνω στα κύρια επίπεδα. 80 H 10.5 H 80 F F Σχήµα 2. Χαρακτηριστικά σηµεία του συστήµατος (όλες οι αποστάσεις αναφέρονται σε mm) 4
50 ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Οπτική Ι, ιδάσκων: ηµήτρης Παπάζογλου Για να υπολογίσουµε την θέση της κόρης εισόδου και της κόρης εξόδου στο παραπάνω σύστηµα θα πρέπει να εντοπίσουµε το διάφραγµα ανοίγµατος του συστήµατος απεικονίζοντας το άνοιγµα κάθε φακού στον χώρο του αντικειµένου. Ξεκινώντας από τον τρίτο φακό αντικαθιστούµε τον φακό µε άνοιγµα της ίδιας διαµέτρου (30 mm) προσεγγιστικά θεωρούµε ότι το διάφραγµα βρίσκεται στο µέσο του φακού. Για να απεικονίσουµε το παραπάνω διάφραγµα µε την βοήθεια του 1 ου και του 2 ου φακού αρκεί να υπολογίσουµε τον πίνακα Μ 1,2 που περιγράφει τους δύο φακούς 2 : M m 1 0 = = 5m m m = 1 1 = 5m 1 10m m = m ,2 1 1 Με βάση τον παραπάνω πίνακα που περιγράφει το υποσύστηµα των δύο πρώτων φακών µπορούµε να υπολογίσουµε τις θέσεις των κυρίων επιπέδων και των δεσµικών σηµείων καθώς και ενεργό εστιακή απόσταση: Z = 18.4 mm, Z = 36.7 mm, f = 163.3mm 1,2 1,2 H H Θεωρώντας ότι το φως διαδίδεται από αριστερά προς τα δεξιά, το διάφραγµα µε το οποίο αντικαταστήσαµε τον τρίτο φακό βρίσκεται σε απόσταση s = 36.7 mm+ 20 mm+ 1.5 mm= 58.2 mm από το «εµπρός 3» κύριο επίπεδο του υποσυστήµατος των δύο πρώτων φακών οπότε µπορούµε να υπολογίσουµε την θέση s του ειδώλου του χρησιµοποιώντας την σχέση: e 1, sf s s f s f 1,2 + = s = = 1,2 1,2 90.4mm 18.4 ~58.2 Οι διαστάσεις του ειδώλου δίνονται µέσω της εγκάρσιας µεγέθυνσης: s 90.4 D = MT D = D = 30 mm = 46.6 mm H 1,2 H 1,2 s Σε αυτή την περίπτωση χρησιµοποιούµε µέρος των υπολογισµών που έχουµε ήδη κάνει για το Μ tot 3 σύµφωνα µε την αντίστροφη διάδοση που θεωρούµε 5
51 ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Οπτική Ι, ιδάσκων: ηµήτρης Παπάζογλου Με αντίστοιχο τρόπο αντικαθιστούµε τον 2 ο φακό µε άνοιγµα της ίδιας διαµέτρου (30 mm) ενώ θεωρούµε και πάλι προσεγγιστικά ότι το διάφραγµα βρίσκεται στο µέσο του φακού. Απεικονίζουµε το παραπάνω διάφραγµα µε την βοήθεια του 1 ου φακού χρησιµοποιώντας τα χαρακτηριστικά σηµεία του που ήδη γνωρίζουµε. Θεωρώντας ότι το φως διαδίδεται από αριστερά προς τα δεξιά, το διάφραγµα µε το οποίο αντικαταστήσαµε τον 2 ο φακό βρίσκεται σε απόσταση s = 2 mm mm= 22.7 mm από το «εµπρός» κύριο επίπεδο του πρώτου φακού οπότε µπορούµε να υπολογίσουµε και πάλι την θέση s και την µεγέθυνση του: sf s s s f s f 1 + = = = mm ~20.7 Οι διαστάσεις του ειδώλου δίνονται µέσω της εγκάρσιας µεγέθυνσης: s 29.4 D = MT D = D = 30 mm = 38.8 mm s Το τελευταίο άνοιγµα που πρέπει να απεικονίσουµε είναι αυτό που ορίζεται από τον πρώτο φακό του συστήµατος σε αυτή όµως την περίπτωση διάφραγµα µε το οποίο αντικαθιστούµε τον πρώτο φακό έχει ως είδωλο τον εαυτό του για υποθετική διάδοση από αριστερά προς τα δεξιά. Έτσι το άνοιγµα που παρουσιάζει το µικρότερο γωνιακό άνοιγµα για αξονικό αντικείµενο 1.5 είναι αυτό που ορίζεται από τον πρώτο 77.7 φακό και εποµένως ο πρώτος φακός αποτελεί και το διάφραγµα ανοίγµατος του συστήµατος. Η κόρη εισόδου ταυτίζεται σε αυτή την περίπτωση µε το διάφραγµα ανοίγµατος ενώ η κόρη εξόδου αποτελεί το είδωλο της κόρης εισόδου µέσω του συνολικού συστήµατος στον 6
52 ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Οπτική Ι, ιδάσκων: ηµήτρης Παπάζογλου χώρο του ειδώλου. Για να υπολογίσουµε την θέση και τις διαστάσεις της κόρης εξόδου απεικονίζουµε την κόρη εισόδου χρησιµοποιώντας τα χαρακτηριστικά σηµεία του συνολικού συστήµατος. Έτσι αφού η κόρη εισόδου απέχει κατά s = 29 mm mm = 27.5 mm υπολογίζουµε για την κόρη εξόδου: sftot + = s = = 41.9mm s s f s f tot Οι διαστάσεις της κόρης εξόδου δίνονται µέσω της εγκάρσιας µεγέθυνσης: s 41.9 D = MT D = D = 30 mm = 45.7 mm s 27.5 tot κόρη εισόδου 23.4 H H F F κόρη εξόδου Σχήµα 2. Χαρακτηριστικά σηµεία και κόρη εισόδου, εξόδου του συστήµατος (όλες οι αποστάσεις αναφέρονται σε mm) 7
ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr
 ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr 1. Να σχεδιάσετε την διάδοση των ακτίνων στα παρακάτω οπτικά συστήµατα F F
ιατµηµατικό µεταπτυχιακό πρόγραµµα «Οπτική και Όραση» Ασκήσεις Οπτική Ι ιδάσκων: ηµήτρης Παπάζογλου Email: dpapa@iesl.forth.gr 1. Να σχεδιάσετε την διάδοση των ακτίνων στα παρακάτω οπτικά συστήµατα F F
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ
 ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
ΕΡΑΣΤΗΡΙ ΕΦΑΡΜΣΜΕΝΗΣ ΠΤΙΚΗΣ Άσκηση 1: Λεπτοί φακοί Εξεταζόμενες γνώσεις. Εξίσωση κατασκευαστών των φακών. Συστήματα φακών. Διαγράμματα κύριων ακτινών. Είδωλα και μεγέθυνση σε λεπτούς φακούς. Α. Λεπτοί
Οπτική και κύματα. Δημήτρης Παπάζογλου Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης
 Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@materal.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Θεωρία πινάκων Διάνυσμα ακτίνας Παραξονική προσέγγιση ta διάνυσμα ακτίνας y αριθμητικό
Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@materal.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Θεωρία πινάκων Διάνυσμα ακτίνας Παραξονική προσέγγιση ta διάνυσμα ακτίνας y αριθμητικό
1. Ιδιότητες φακών. 1 Λεπτοί φακοί. 2 Απριλίου Βασικές έννοιες
 . Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
. Ιδιότητες φακών 2 Απριλίου 203 Λεπτοί φακοί. Βασικές έννοιες Φακός είναι ένα οπτικό σύστημα με δύο διαθλαστικές επιφάνειες. Ο απλούστερος φακός έχει δύο σφαιρικές επιφάνειες αρκετά κοντά η μία με την
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. G. Mitsou
 ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ Διάθλαση σε σφαιρική επιφάνεια Φακοί Ορισμοί Λεπτοί φακοί Συγκλίνοντες φακοί Δημιουργία ειδώλων Αποκλίνοντες φακοί Γενικοί τύποι φακών Σύστημα λεπτών φακών σε επαφή Ασκήσεις Διάθλαση
Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@materials.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική
 Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@maerals.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική Η ιδέα την απεικόνισης Σημειακή πηγή Στιγματική απεικόνιση Η ανακατεύθυνση
Οπτική και κύματα Δημήτρης Παπάζογλου dpapa@maerals.uoc.gr Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γεωμετρική Οπτική Η ιδέα την απεικόνισης Σημειακή πηγή Στιγματική απεικόνιση Η ανακατεύθυνση
ΕΚΦΕ ΕΥΒΟΙΑΣ. ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ
 ΕΚΦΕ ΕΥΒΟΙΑΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 Διάρκεια: 60 min ΣΑΒΒΑΤΟ 06/12/2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Μαθητές: Σχολική Μονάδα 1.
ΕΚΦΕ ΕΥΒΟΙΑΣ ΠΡΟΚΡΙΜΑΤΙΚΟΣ ΔΙΑΓΩΝΙΣΜΟΣ ΓΙΑ ΤΗΝ ΕΠΙΛΟΓΗ ΟΜΑΔΑΣ ΜΑΘΗΤΩΝ ΓΙΑ ΤΗΝ 13 η ΕΥΡΩΠΑΪΚΗ ΟΛΥΜΠΙΑΔΑ ΕΠΙΣΤΗΜΩΝ EUSO 2015 Διάρκεια: 60 min ΣΑΒΒΑΤΟ 06/12/2014 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ Μαθητές: Σχολική Μονάδα 1.
Μελέτη συστήματος φακών με τη Μέθοδο του Newton
 Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
Μελέτη συστήματος φακών με τη Μέθοδο του Newton.Σκοπός Σκοπός της άσκησης είναι η μελέτη της εστιακής απόστασης συστήματος φακών, η εύρεση της ισοδύναμης εστιακής απόστασης του συστήματος αυτού καθώς και
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ OΠΤΙΚΑ ΣΤΟΙΧΕΙΑ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 www.pmoira.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ
 ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
ΕΡΓΑΣΤΗΡΙΟ ΤΕΧΝΟΛΟΓΙΑΣ ΟΠΤΙΚΩΝ ΟΡΓΑΝΩΝ Άσκηση 4. Διαφράγματα. Θεωρία Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα. Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ
 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Αντώνης Πουλιάσης Φυσικός M.Sc. 12 ο ΓΥΜΝΑΣΙΟ ΠΕΡΙΣΤΕΡΙΟΥ Πουλιάσης Αντώνης Φυσικός M.Sc. 2 Ανάκλαση Είδωλα σε κοίλα και κυρτά σφαιρικά κάτοπτρα Γεωμετρική
Φυσική Εικόνας & Ήχου Ι (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 3: Γενικά περί φακών Αθανάσιος Αρααντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών Τεχνών Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 3: Γενικά περί φακών Αθανάσιος Αρααντινός Τμήμα Φωτογραφίας & Οπτικοακουστικών Τεχνών Το περιεχόμενο
Ο15. Κοίλα κάτοπτρα. 2. Θεωρία. 2.1 Γεωμετρική Οπτική
 Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
Ο15 Κοίλα κάτοπτρα 1. Σκοπός Σκοπός της άσκησης είναι η εύρεση της εστιακής απόστασης κοίλου κατόπτρου σχετικά μεγάλου ανοίγματος και την μέτρηση του σφάλματος της σφαιρικής εκτροπής... Θεωρία.1 Γεωμετρική
Εστιομετρία φακών και κατόπτρων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ, ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Εστιομετρία
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Εθνικό και Καποδιστριακό Πανεπιστήμιο Αθηνών ΣΧΟΛΗ ΘΕΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΤΟΜΕΑΣ ΑΣΤΡΟΦΥΣΙΚΗΣ, ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΜΗΧΑΝΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΑΣΤΡΟΝΟΜΙΑΣ ΚΑΙ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Εστιομετρία
ΑΣΚΗΣΗ 8 Μελέτη φακών
 Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
Απαραίτητα όργανα και υλικά ΑΣΚΗΣΗ 8 Μελέτη φακών 8. Απαραίτητα όργανα και υλικά. Οπτική τράπεζα.. Πέτασμα. 3. Συγκεντρωτικός φακός. 4. Φωτεινή πηγή. 5. Διάφραγμα με δακτύλιο και οπή. 6. Φίλτρο κόκκινο
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34
 Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
Γεωμετρική Οπτική ΚΕΦΑΛΑΙΟ 34 Γεωμετρική Οπτική Γνωρίζουμε τα βασικά Δηλαδή, πως το φως διαδίδεται και αλληλεπιδρά με σώματα διαστάσεων πολύ μεγαλύτερων από το μήκος κύματος. Ανάκλαση: Προσπίπτουσα ακτίνα
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
ΚΥΜΑΤΙΚΗ - ΟΠΤΙΚΗ 181 ΕΠΙΠΕ Ο ΙΟΠΤΡΟ. ΕΠΙΠΕ ΕΣ ΙΑΘΛΩΣΕΣ ΕΠΙΦΑΝΕΙΕΣ: Ο τύπος των επιπέδων διόπτρων
 ΚΥΜΑΤΙΚΗ - ΟΠΤΙΚΗ 8 ΕΠΙΠΕ Ο ΙΟΠΤΡΟ ΕΠΙΠΕ ΕΣ ΙΑΘΛΩΣΕΣ ΕΠΙΦΑΝΕΙΕΣ: Ο τύπος των επιπέδων διόπτρων προκύπτει από τον τύπο των σφαιρικών διόπτρων όταν R=. = Από τ σχέσ αυτή φαίνεται ότι το πρόσµο του είναι
ΚΥΜΑΤΙΚΗ - ΟΠΤΙΚΗ 8 ΕΠΙΠΕ Ο ΙΟΠΤΡΟ ΕΠΙΠΕ ΕΣ ΙΑΘΛΩΣΕΣ ΕΠΙΦΑΝΕΙΕΣ: Ο τύπος των επιπέδων διόπτρων προκύπτει από τον τύπο των σφαιρικών διόπτρων όταν R=. = Από τ σχέσ αυτή φαίνεται ότι το πρόσµο του είναι
ΟΠΤΙΚΕΣ ΔΙΑΦΟΡΕΣ ΜΕΤΑΞΥ ΟΦΘΑΛΜΙΚΩΝ ΦΑΚΩΝ ΚAI ΦΑΚΩΝ ΕΠΑΦΗΣ
 ΟΠΤΙΚΕΣ ΔΙΑΦΟΡΕΣ ΜΕΤΑΞΥ ΟΦΘΑΛΜΙΚΩΝ ΦΑΚΩΝ ΚAI ΦΑΚΩΝ ΕΠΑΦΗΣ Σ. Πλαΐνης, MSc, PhD Ινστιτούτο Οπτικής και Όρασης, Σχολή Επιστηµών Υγείας, Πανεπιστήµιο Κρήτης O. Λουκαΐδης, MSc Optical House, Ρόδος 1. Εισαγωγή
ΟΠΤΙΚΕΣ ΔΙΑΦΟΡΕΣ ΜΕΤΑΞΥ ΟΦΘΑΛΜΙΚΩΝ ΦΑΚΩΝ ΚAI ΦΑΚΩΝ ΕΠΑΦΗΣ Σ. Πλαΐνης, MSc, PhD Ινστιτούτο Οπτικής και Όρασης, Σχολή Επιστηµών Υγείας, Πανεπιστήµιο Κρήτης O. Λουκαΐδης, MSc Optical House, Ρόδος 1. Εισαγωγή
Generated by Foxit PDF Creator Foxit Software http://www.foxitsoftware.com For evaluation only. ΑΣΚΗΣΗ 10 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ
 ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΑΣΚΗΣΗ 0 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΟΥ . Γεωμετρική οπτική ΜΕΡΟΣ ΠΡΩΤΟ ΒΑΣΙΚΕΣ ΘΕΩΡΗΤΙΚΕΣ ΓΝΩΣΕΙΣ Η Γεωμετρική οπτική είναι ένας τρόπος μελέτης των κυμάτων και χρησιμοποιείται για την εξέταση μερικών
ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΟΠΤΙΚΑ ΣΤΟΙΧΕΙΑ : ΚΑΤΟΠΤΡΑ ΔΙΟΠΤΡΑ ΦΑΚΟΙ Συγγραφή Επιμέλεια: Παναγιώτης Φ. Μοίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ.
Μεγεθυντικός φακός. 1. Σκοπός. 2. Θεωρία. θ 1
 Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
Μεγεθυντικός φακός 1. Σκοπός Οι μεγεθυντικοί φακοί ή απλά μικροσκόπια (magnifiers) χρησιμοποιούνται για την παρατήρηση μικροσκοπικών αντικειμένων ώστε να γίνουν καθαρά παρατηρήσιμες οι λεπτομέρειες τους.
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1,β ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΜΟΝΟΧΡΩΜΑΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ
 ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1,β ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΜΟΝΟΧΡΩΜΑΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ ΣΚΟΠΟΙ η εξάσκηση στην παρατήρηση και περιγραφή φαινοµένων, όπως το φαινόµενο της συµβολής των κυµάτων η παρατήρηση των αποτελεσµάτων
ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 1,β ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΜΟΝΟΧΡΩΜΑΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ ΣΚΟΠΟΙ η εξάσκηση στην παρατήρηση και περιγραφή φαινοµένων, όπως το φαινόµενο της συµβολής των κυµάτων η παρατήρηση των αποτελεσµάτων
ΑΚΤΥΛΙΟΙ ΤΟΥ ΝΕΥΤΩΝΑ
 ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΑΣΚΗΣΗ ΝΟ4 ΑΚΤΥΛΙΟΙ ΤΟΥ ΝΕΥΤΩΝΑ Γ. Μήτσου εκέµβριος 007 Α. ΘΕΩΡΙΑ Εισαγωγή Στο πείραµα αυτό θα προσδιορίσουµε το µήκος
ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΑΣΚΗΣΗ ΝΟ4 ΑΚΤΥΛΙΟΙ ΤΟΥ ΝΕΥΤΩΝΑ Γ. Μήτσου εκέµβριος 007 Α. ΘΕΩΡΙΑ Εισαγωγή Στο πείραµα αυτό θα προσδιορίσουµε το µήκος
Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός
 Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός Μάθημα: Φυσική Τμήματα:,.. Τάξη: Α Ομάδα Προσανατολισμού 1,3,4 Καθηγητές: Περ. Εβδομ: 2 ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΥΛΗ ΠΕΡΙΟΔΟΙ ΗΜΕΡΟΜΗΝΙΕΣ Φυσικά Μεγέθη Μονάδες
Προγραμματισμός Ύλης Έτους Τάξη Α Κοινός Κορμός Μάθημα: Φυσική Τμήματα:,.. Τάξη: Α Ομάδα Προσανατολισμού 1,3,4 Καθηγητές: Περ. Εβδομ: 2 ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΥΛΗ ΠΕΡΙΟΔΟΙ ΗΜΕΡΟΜΗΝΙΕΣ Φυσικά Μεγέθη Μονάδες
ΤΕΙ ΑΘΗΝΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER
 ΤΕΙ ΑΘΗΝΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER ΑΣΚΗΣΗ ΝΟ2 ΜΕΤΡΗΣΗ ΤΗΣ ΤΑΧΥΤΗΤΑΣ ΤΟΥ ΦΩΤΟΣ Γ. Μήτσου Οκτώβριος 2007 Α. Θεωρία Εισαγωγή Η ταχύτητα του φωτός
ΤΕΙ ΑΘΗΝΑΣ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΧΗΜΕΙΑΣ & Τ/Υ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LASER ΑΣΚΗΣΗ ΝΟ2 ΜΕΤΡΗΣΗ ΤΗΣ ΤΑΧΥΤΗΤΑΣ ΤΟΥ ΦΩΤΟΣ Γ. Μήτσου Οκτώβριος 2007 Α. Θεωρία Εισαγωγή Η ταχύτητα του φωτός
Σχηματισμός ειδώλων. Εισαγωγή
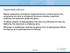 Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
Σχηματισμός ειδώλων Είδωλα πραγματικών αντικειμένων σχηματίζονται όταν οι ακτίνες φωτός (που εκπέμπονται από αυτά τα αντικέιμενα) συναντούν επίπεδες ή καμπύλες επιφάνειες που βρίσκονται μεταξύ δύο μέσων.
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
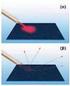 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ. β' νόμος της ανάκλασης: Η γωνία πρόσπτωσης και η γωνία ανάκλασης είναι ίσες.
 ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΝΑΚΛΑΣΗ Η ακτίνα (ή η δέσμη) πριν ανακλασθεί ονομάζεται προσπίπτουσα ή αρχική, ενώ μετά την ανάκλαση ονομάζεται ανακλώμενη. Η γωνία που σχηματίζει η προσπίπτουσα με την κάθετη στην επιφάνεια στο σημείο
ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ
 http://www.economics.edu.gr 1 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΚΕΦΑΛΑΙΟ 1 ο : ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΑΣΚΗΣΕΙΣ ΥΠΟ ΕΙΓΜΑΤΑ ( τρόποι επίλυσης παρατηρήσεις σχόλια ) ΑΣΚΗΣΗ 1 Έστω ο πίνακας παραγωγικών δυνατοτήτων µιας
http://www.economics.edu.gr 1 ΑΡΧΕΣ ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΚΕΦΑΛΑΙΟ 1 ο : ΒΑΣΙΚΕΣ ΕΝΝΟΙΕΣ ΑΣΚΗΣΕΙΣ ΥΠΟ ΕΙΓΜΑΤΑ ( τρόποι επίλυσης παρατηρήσεις σχόλια ) ΑΣΚΗΣΗ 1 Έστω ο πίνακας παραγωγικών δυνατοτήτων µιας
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
Κεφάλαιο 32 Φως: Ανάκλασηκαι ιάθλαση Γεωµετρική θεώρηση του Φωτός Ανάκλαση ηµιουργίαειδώλουαπόκάτοπτρα. είκτης ιάθλασης Νόµος του Snell Ορατό Φάσµα και ιασπορά Εσωτερική ανάκλαση Οπτικές ίνες ιάθλαση σε
ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ
 ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Όταν προσπίπτει φως σε μια διεπιφάνεια που σχηματίζεται μεταξύ δύο οπτικά διαφορετικών μέσων, ένα μέρος του υφίσταται ανάκλαση ενώ το υπόλοιπο διέρχεται από το πρώτο στο δεύτερο
ΕΥΘΥΓΡΑΜΜΗ ΔΙΑΔΟΣΗ ΤΟΥ ΦΩΤΟΣ Όταν προσπίπτει φως σε μια διεπιφάνεια που σχηματίζεται μεταξύ δύο οπτικά διαφορετικών μέσων, ένα μέρος του υφίσταται ανάκλαση ενώ το υπόλοιπο διέρχεται από το πρώτο στο δεύτερο
Φυσική Εικόνας & Ήχου Ι (Ε)
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 4: Υπολογισμός της εστιακής απόστασης f από τη γραμμική μεγέθυνση Μ Αθανάσιος Αραβαντινός Τμήμα Φωτογραφίας
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Φυσική Εικόνας & Ήχου Ι (Ε) Ενότητα 4: Υπολογισμός της εστιακής απόστασης f από τη γραμμική μεγέθυνση Μ Αθανάσιος Αραβαντινός Τμήμα Φωτογραφίας
Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ34. Ιούλιος 2008 KYMATIKH. ιάρκεια: 210 λεπτά
 Κυµατική ΦΥΕ4 5/7/8 Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ4 Ιούλιος 8 KYMATIKH ιάρκεια: λεπτά Θέµα ο (Μονάδες:.5) A) Θεωρούµε τις αποστάσεις
Κυµατική ΦΥΕ4 5/7/8 Ελληνικό Ανοικτό Πανεπιστήµιο Ενδεικτικές Λύσεις Θεµάτων Τελικών εξετάσεων στη Θεµατική Ενότητα ΦΥΕ4 Ιούλιος 8 KYMATIKH ιάρκεια: λεπτά Θέµα ο (Μονάδες:.5) A) Θεωρούµε τις αποστάσεις
7.1 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ
 7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
7.1 ΑΣΚΗΣΗ 7 ΜΕΤΡΗΣΗ ΤΗΣ ΕΣΤΙΑΚΗΣ ΑΠΟΣΤΑΣΗΣ ΦΑΚΩΝ ΘΕΩΡΙΑ Όταν φωτεινή παράλληλη δέσμη διαδιδόμενη από οπτικό μέσο α με δείκτη διάθλασης n 1 προσπίπτει σε άλλο οπτικό μέσο β με δείκτη διάθλασης n 2 και
ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ. Ερωτήσεις κλειστού τύπου. Ερωτήσεις ανοικτού τύπου
 ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
ΟΠΤΙΚΗ Περιεχόμενα ΓΕΩΜΕΤΡΙΚΗ ΟΠΤΙΚΗ... 2 Ερωτήσεις κλειστού τύπου... 2 Ερωτήσεις ανοικτού τύπου... 2 Ασκήσεις... 3 ΚΥΜΑΤΙΚΗ ΟΠΤΙΚΗ... 4 Ερωτήσεις κλειστού τύπου... 4 Ερωτήσεις ανοικτού τύπου... 4 Ασκήσεις...
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0
 Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
Οι δύο θεμελιώδεις παράμετροι προσδιορισμού της ταχύτητας του φωτός στο κενό: Διηλεκτρική σταθερά ε0 Μαγνητική διαπερατότητα μ0 1 c 0 0 Όταν το φως αλληλεπιδρά με την ύλη, το ηλεκτρομαγνητικό πεδίο του
4. Όρια ανάλυσης οπτικών οργάνων
 4. Όρια ανάυσης οπτικών οργάνων 29 Μαΐου 2013 1 Περίθαση Οι αρχές ειτουργίας των οπτικών οργάνων που περιγράψαμε μέχρι στιγμής βασίζονται στη γεωμετρική οπτική, δηαδή την περιγραφή του φωτός ως ακτίνες
4. Όρια ανάυσης οπτικών οργάνων 29 Μαΐου 2013 1 Περίθαση Οι αρχές ειτουργίας των οπτικών οργάνων που περιγράψαμε μέχρι στιγμής βασίζονται στη γεωμετρική οπτική, δηαδή την περιγραφή του φωτός ως ακτίνες
LASER 3 ΣΥΜΒΟΛΗ ΚΑΙ ΠΕΡΙΘΛΑΣΗ ΦΩΤΟΣ LASER ΜΕΤΡΗΣΗ ΣΤΑΘΕΡΑΣ ΛΕΠΤΟΥ ΠΛΕΓΜΑΤΟΣ ΚΑΙ ΤΗΣ ΑΚΤΙΝΑΣ ΜΙΚΡΩΝ ΚΟΚΚΩΝ
 LASER 3 ΣΥΜΒΟΛΗ ΚΑΙ ΠΕΡΙΘΛΑΣΗ ΦΩΤΟΣ LASER ΜΕΣΩ ΙΑΦΑΝΩΝ ΥΛΙΚΩΝ ΜΕΤΡΗΣΗ ΣΤΑΘΕΡΑΣ ΛΕΠΤΟΥ ΠΛΕΓΜΑΤΟΣ ΚΑΙ ΤΗΣ ΑΚΤΙΝΑΣ ΜΙΚΡΩΝ ΚΟΚΚΩΝ A. ΘΕΩΡΙΑ 1. Περίθλαση 1.1 Εισαγωγή Μια βασική ιδιότητα των κυµάτων είναι ότι
LASER 3 ΣΥΜΒΟΛΗ ΚΑΙ ΠΕΡΙΘΛΑΣΗ ΦΩΤΟΣ LASER ΜΕΣΩ ΙΑΦΑΝΩΝ ΥΛΙΚΩΝ ΜΕΤΡΗΣΗ ΣΤΑΘΕΡΑΣ ΛΕΠΤΟΥ ΠΛΕΓΜΑΤΟΣ ΚΑΙ ΤΗΣ ΑΚΤΙΝΑΣ ΜΙΚΡΩΝ ΚΟΚΚΩΝ A. ΘΕΩΡΙΑ 1. Περίθλαση 1.1 Εισαγωγή Μια βασική ιδιότητα των κυµάτων είναι ότι
Φυσικά Μεγέθη Μονάδες Μέτρησης
 ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΚΟΙΝΟΥ ΚΟΡΜΟΥ ΤΑΞΗ: Α Λυκείου Προσανατολισμού 1,3,4. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ
ΓΓ/Μ ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ. Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα
 ΓΓ/Μ6 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ' Τάξη
ΓΓ/Μ6 05-06 ΣΥΣΤΗΜΑ ΠΑΙΔΕΙΑΣ ΟΡΟΣΗΜΟ Τεύχος 6ο: Διάθλαση του φωτός Φακοί & οπτικά όργανα ΕΚΔΟΤΙΚΕΣ ΤΟΜΕΣ ΟΡΟΣΗΜΟ ΠΕΡΙΟΔΙΚΗ ΕΚΔΟΣΗ ΓΙΑ ΤΟ ΓΥΜΝΑΣΙΟ ΚΑΙ ΤΟ ΛΥΚΕΙΟ Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α Φυσική για την Γ' Τάξη
Σχήμα 9-1: (α) Το σύνθετο μικροσκόπιο του Janssen (1595) στο Middleburg Museum (β) Το μικροσκόπιο του van Leeuwenhoek (1670).
 Equation Chapter (Next) Section 1 Είδαμε στο κεφ. 6 ότι μπορούμε να χρησιμοποιήσουμε ένα συγκλίνοντα φακό για να παρατηρήσουμε ένα αντικείμενο σε μεγέθυνση. Όσο εύκολος κι αν είναι στη χρήση ο μεγεθυντικός
Equation Chapter (Next) Section 1 Είδαμε στο κεφ. 6 ότι μπορούμε να χρησιμοποιήσουμε ένα συγκλίνοντα φακό για να παρατηρήσουμε ένα αντικείμενο σε μεγέθυνση. Όσο εύκολος κι αν είναι στη χρήση ο μεγεθυντικός
Μελέτη φάσµατος εκποµπής Hg µε φράγµα περίθλασης
 Ο7 Μελέτη φάσµατος εκποµπής Hg µε φράγµα περίλασης 1 Σκοπός Στην άσκηση αυτή α µελετήσουµε το φάσµα εκποµπής του υδραργύρου και α προσδιορίσουµε τα µήκη κύµατος των φασµατικών του γραµµών µε τη βοήεια
Ο7 Μελέτη φάσµατος εκποµπής Hg µε φράγµα περίλασης 1 Σκοπός Στην άσκηση αυτή α µελετήσουµε το φάσµα εκποµπής του υδραργύρου και α προσδιορίσουµε τα µήκη κύµατος των φασµατικών του γραµµών µε τη βοήεια
Υπολογισμός της ισχύος συστήματος λεπτών φακών σε επαφή
 Υπολογισμός της ισχύος συστήματος λεπτών φακών σε επαφή 1. Σκοπός Στην άσκηση αυτή θα προσδιορίσουμε την εστιακή απόσταση που διαμορφώνει ένα σύστημα λεπτών φακών που βρίσκονται σε επαφή μεταξύ τους και
Υπολογισμός της ισχύος συστήματος λεπτών φακών σε επαφή 1. Σκοπός Στην άσκηση αυτή θα προσδιορίσουμε την εστιακή απόσταση που διαμορφώνει ένα σύστημα λεπτών φακών που βρίσκονται σε επαφή μεταξύ τους και
Υπολογισµός της ισχύος συστήµατος λεπτών φακών σε επαφή
 Ο6 Υπογισµός της ισχύος συστήµατος λεπτών φακών σε επαφή. Σκοπός Στην άσκηση αυτή θα προσδιορίσουµε την εστιακή απόσταση που διαµορφώνει ένα σύστηµα λεπτών φακών που βρίσκονται σε επαφή µεταξύ τους και
Ο6 Υπογισµός της ισχύος συστήµατος λεπτών φακών σε επαφή. Σκοπός Στην άσκηση αυτή θα προσδιορίσουµε την εστιακή απόσταση που διαµορφώνει ένα σύστηµα λεπτών φακών που βρίσκονται σε επαφή µεταξύ τους και
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
s s f 25 s ' 10 10 s ' 10 α) s ' 16.7 β) S=10 cm, άρα το αντικείμενο βρίσκεται πάνω στην εστία.
 ΑΣΚΗΣΗ 1 Δύο κάτοπτρα σχηματίζουν ορθή γωνία, όπως φαίνεται στο σχήμα. Στο σημείο Ο υπάρχει ένα αντικείμενο. Να προσδιορίσετε τη θέση των ειδώλων που σχηματίζονται ΑΣΚΗΣΗ 2 Κοίλο σφαιρικό κάτοπτρο έχει
ΑΣΚΗΣΗ 1 Δύο κάτοπτρα σχηματίζουν ορθή γωνία, όπως φαίνεται στο σχήμα. Στο σημείο Ο υπάρχει ένα αντικείμενο. Να προσδιορίσετε τη θέση των ειδώλων που σχηματίζονται ΑΣΚΗΣΗ 2 Κοίλο σφαιρικό κάτοπτρο έχει
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
Μηχανική ΙI. Μετασχηµατισµοί Legendre. της : (η γραφική της παράσταση δίνεται στο ακόλουθο σχήµα). Εάν
 Τµήµα Π. Ιωάννου & Θ. Αποστολάτου 7/5/2000 Μηχανική ΙI Μετασχηµατισµοί Legendre Έστω µια πραγµατική συνάρτηση. Ορίζουµε την παράγωγο συνάρτηση της : (η γραφική της παράσταση δίνεται στο ακόλουθο σχήµα).
Τµήµα Π. Ιωάννου & Θ. Αποστολάτου 7/5/2000 Μηχανική ΙI Μετασχηµατισµοί Legendre Έστω µια πραγµατική συνάρτηση. Ορίζουµε την παράγωγο συνάρτηση της : (η γραφική της παράσταση δίνεται στο ακόλουθο σχήµα).
Φυσική IΙ. Ενότητα 13: Γεωμετρική οπτική. Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών
 Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
Φυσική IΙ Ενότητα 13: Γεωμετρική οπτική Κουζούδης Δημήτρης Πολυτεχνική Σχολή Τμήμα Χημικών Μηχανικών Σκοποί ενότητας Η κυματική φύση του φωτός: διάθλαση, ανάκλαση, απορρόφηση Γωνίες πρόσπτωσης, ανάκλασης
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ
 ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Άσκηση 4: Σφάλματα φακών: Ι Σφαιρική εκτροπή Εξεταζόμενες γνώσεις: σφάλματα σφαιρικής εκτροπής. Α. Γενικά περί σφαλμάτων φακών Η βασική σχέση του Gauss 1/s +1/s = 1/f που
ΕΡΓΑΣΤΗΡΙΟ ΕΦΑΡΜΟΣΜΕΝΗΣ ΟΠΤΙΚΗΣ Άσκηση 4: Σφάλματα φακών: Ι Σφαιρική εκτροπή Εξεταζόμενες γνώσεις: σφάλματα σφαιρικής εκτροπής. Α. Γενικά περί σφαλμάτων φακών Η βασική σχέση του Gauss 1/s +1/s = 1/f που
Παρατηρήσεις στη δηµιουργία του στάσιµου*
 Παρατηρήσεις στη δηµιουργία του στάσιµου* Κατά µήκος γραµµικού ελαστικού µέσου το οποίο ταυτίζεται µε τον άξονα χ χ, διαδίδονται κατά αντίθετη φορά, δύο εγκάρσια αρµονικά κύµατα, ίδιου πλάτους και ίδιας
Παρατηρήσεις στη δηµιουργία του στάσιµου* Κατά µήκος γραµµικού ελαστικού µέσου το οποίο ταυτίζεται µε τον άξονα χ χ, διαδίδονται κατά αντίθετη φορά, δύο εγκάρσια αρµονικά κύµατα, ίδιου πλάτους και ίδιας
Με k1 = 1.220, k2 = 2.232, k3 = 3.238, and n = 1,2,3,
 ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ Ι ΠΟΜ 114(Ε) ΟΠΤΙΚΗ ιάθλαση φωτός µέσω σχισµής, γύρω από µικρό δοκάρι και µέσω µικρής οπής
ΤΕΧΝΟΛΟΓΙΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΓΕΩΠΛΗΡΟΦΟΡΙΚΗΣ ΕΡΓΑΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ Ι ΠΟΜ 114(Ε) ΟΠΤΙΚΗ ιάθλαση φωτός µέσω σχισµής, γύρω από µικρό δοκάρι και µέσω µικρής οπής
LASER 4. ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΜΕΓΕΘΩΝ ΤΟΥ ΙΟ ΙΚΟΥ LASER ΑΙΣΘΗΤΙΚΗΣ ΚΑΙ ΦΥΣΙΚΟΘΕΡΑΠΕΙΑΣ GaAs (ΤΥΠΟΥ FE-LA 10)
 LASER 4 ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΜΕΓΕΘΩΝ ΤΟΥ ΙΟ ΙΚΟΥ LASER ΑΙΣΘΗΤΙΚΗΣ ΚΑΙ ΦΥΣΙΚΟΘΕΡΑΠΕΙΑΣ GaAs (ΤΥΠΟΥ FE-LA 10) Α. ΘΕΩΡΙΑ Για την κατανόηση και καλύτερη εκτέλεση αυτής της άσκησης, είναι απαραίτητη η γνώση
LASER 4 ΜΕΛΕΤΗ ΧΑΡΑΚΤΗΡΙΣΤΙΚΩΝ ΜΕΓΕΘΩΝ ΤΟΥ ΙΟ ΙΚΟΥ LASER ΑΙΣΘΗΤΙΚΗΣ ΚΑΙ ΦΥΣΙΚΟΘΕΡΑΠΕΙΑΣ GaAs (ΤΥΠΟΥ FE-LA 10) Α. ΘΕΩΡΙΑ Για την κατανόηση και καλύτερη εκτέλεση αυτής της άσκησης, είναι απαραίτητη η γνώση
4ο ιαγώνισµα - Κύµατα. Θέµα 1ο
 4ο ιαγώνισµα - Κύµατα Ηµεροµηνία : εκέµβρης 2012 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα 1ο Στις ερωτήσεις 1.1 1.4 επιλέξτε την σωστη απάντηση (4 5 = 20 µονάδες ) 1.1. Οταν ένα κύµα συχνότητας
4ο ιαγώνισµα - Κύµατα Ηµεροµηνία : εκέµβρης 2012 ιάρκεια : 3 ώρες Ονοµατεπώνυµο: Βαθµολογία % Θέµα 1ο Στις ερωτήσεις 1.1 1.4 επιλέξτε την σωστη απάντηση (4 5 = 20 µονάδες ) 1.1. Οταν ένα κύµα συχνότητας
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ
 ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
ΒΑΣΙΚΕΣ ΑΡΧΕΣ ΤΗΣ ΟΠΤΙΚΗΣ Μάθημα προς τους ειδικευόμενους γιατρούς στην Οφθαλμολογία, Στο Κ.Οφ.Κ.Α. την 18/11/2003. Υπό: Δρος Κων. Ρούγγα, Οφθαλμιάτρου. 1. ΑΝΑΚΛΑΣΗ ΤΟΥ ΦΩΤΟΣ Όταν μια φωτεινή ακτίνα ή
Γεωμετρική Οπτική. Πρόκειται δηλαδή για μια ισοφασική επιφάνεια που ονομάζεται μέτωπο κύματος.
 Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
Γεωμετρική Οπτική Στη Γεωμετρική Οπτική επεξεργαζόμαστε τα φαινόμενα ωσάν το φως να αποτελείται μόνο από σωματίδια, ώστε να εξασφαλίζεται την εύκολη ερμηνεία των φαινομένων της ευθύγραμμης διάδοσης του
3. Απλά οπτικά όργανα
 3. Απλά οπτικά όργανα 20 Απριλίου 2013 1 Διαφράγματα Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός αντικειμένου. Μας
3. Απλά οπτικά όργανα 20 Απριλίου 2013 1 Διαφράγματα Στο σχεδιασμό οπτικών οργάνων πρέπει να λάβει κανείς υπόψη και άλλες παραμέτρους πέρα από το πού και πώς σχηματίζεται το είδωλο ενός αντικειμένου. Μας
Σφάλματα φακών (Σφαιρικό - Χρωματικό).
 O12 Σφάλματα φακών (Σφαιρικό - Χρωματικό). 1. Σκοπός Στην άσκηση αυτή υπολογίζονται πειραματικά δυο από τα πιο σημαντικά οπτικά σφάλματα (η αποκλίσεις) που παρουσιάζονται όταν φωτεινές ακτίνες διέλθουν
O12 Σφάλματα φακών (Σφαιρικό - Χρωματικό). 1. Σκοπός Στην άσκηση αυτή υπολογίζονται πειραματικά δυο από τα πιο σημαντικά οπτικά σφάλματα (η αποκλίσεις) που παρουσιάζονται όταν φωτεινές ακτίνες διέλθουν
Προσδιορισµός των χαρακτηριστικών (ιδιο-)συχνοτήτων και κανονικών τρόπων ταλάντωσης µε χρήση συµµετριών
 Μηχανική ΙΙ Τµήµα Ιωάννου-Αποστολάτου 6 Μαϊου 2001 Προσδιορισµός των χαρακτηριστικών (ιδιο-)συχνοτήτων και κανονικών τρόπων ταλάντωσης µε χρήση συµµετριών Θεωρούµε ότι 6 ίσες µάζες συνδέονται µε ταυτόσηµα
Μηχανική ΙΙ Τµήµα Ιωάννου-Αποστολάτου 6 Μαϊου 2001 Προσδιορισµός των χαρακτηριστικών (ιδιο-)συχνοτήτων και κανονικών τρόπων ταλάντωσης µε χρήση συµµετριών Θεωρούµε ότι 6 ίσες µάζες συνδέονται µε ταυτόσηµα
Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ
 ΟΜΑΔΑ ΟΝΟΜΑΤΕΠΩΝΥΜΑ ΜΑΘΗΤΩΝ 1)... 2)... 3)... ΗΜΕΡΟΜΗΝΙΑ : Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ Με το πείραµα αυτό θα προσδιορίσουµε: Σκοπός
ΟΜΑΔΑ ΟΝΟΜΑΤΕΠΩΝΥΜΑ ΜΑΘΗΤΩΝ 1)... 2)... 3)... ΗΜΕΡΟΜΗΝΙΑ : Υπολογισμός της εστιακής απόστασης f λεπτού συμμετρικού συγκλίνοντος φακού απο τη γραμμική μεγέθυνση Μ Με το πείραµα αυτό θα προσδιορίσουµε: Σκοπός
Β ΚΥΚΛΟΣ ΠΡΟΣΟΜΟΙΩΤΙΚΩΝ ΙΑΓΩΝΙΣΜΑΤΩΝ ΣΥΓΧΡΟΝΟ Ενδεικτικές Απαντήσεις A Λυκείου Νοέµβριος 2013 ΘΕΜΑ Α ΘΕΜΑ Β
 Ενδεικτικές Απαντήσεις Λυκείου Νοέµβριος 0. β Φυσική ΘΕΜΑ Α γενιικής παιιδείίας. γ. β. γ 5. α 6. α Λάθος β Σωστό γ Λάθος δ Λάθος ε Σωστό. α β γ δ ε ΘΕΜΑ Β. Α. ευθύγραµµη οµαλή κίνηση Β. ακινησία Γ. ευθύγραµµη
Ενδεικτικές Απαντήσεις Λυκείου Νοέµβριος 0. β Φυσική ΘΕΜΑ Α γενιικής παιιδείίας. γ. β. γ 5. α 6. α Λάθος β Σωστό γ Λάθος δ Λάθος ε Σωστό. α β γ δ ε ΘΕΜΑ Β. Α. ευθύγραµµη οµαλή κίνηση Β. ακινησία Γ. ευθύγραµµη
P = 0 1/2 1/ /2 1/
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-37: Εφαρµοσµένες Στοχαστικές ιαδικασίες - Εαρινό Εξάµηνο 206 ιδάσκων : Π. Τσακαλίδης 7ο Φροντιστήριο Επιµέλεια : Κωνσταντίνα Φωτιάδου Ασκηση. Μια Μαρκοβιανή
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-37: Εφαρµοσµένες Στοχαστικές ιαδικασίες - Εαρινό Εξάµηνο 206 ιδάσκων : Π. Τσακαλίδης 7ο Φροντιστήριο Επιµέλεια : Κωνσταντίνα Φωτιάδου Ασκηση. Μια Μαρκοβιανή
1. Σκοπός της άσκησης... 1. 2. Στοιχεία θεωρίας... 1. 2.1 Γεωμετρική οπτική... 1. 2.2 Ο νόμος της ανάκλασης... 1. 2.3 Ο νόμος της διάθλασης...
 1. Λεπτοί Φακοί Σελίδα 1. Σκοπός της άσκησης.... 1 2. Στοιχεία θεωρίας... 1 2.1 Γεωμετρική οπτική... 1 2.2 Ο νόμος της ανάκλασης... 1 2.3 Ο νόμος της διάθλασης... 2 2.4 Είδωλα & παραξονική προσέγγιση...
1. Λεπτοί Φακοί Σελίδα 1. Σκοπός της άσκησης.... 1 2. Στοιχεία θεωρίας... 1 2.1 Γεωμετρική οπτική... 1 2.2 Ο νόμος της ανάκλασης... 1 2.3 Ο νόμος της διάθλασης... 2 2.4 Είδωλα & παραξονική προσέγγιση...
Άσκηση 1 (α) ============================================================== Έχουµε L = π, εποµένως η σειρά Fourier είναι: 1 2 a. cos. a n. b n.
 http://elear.maths.gr/, maths@maths.gr, Τηλ: 69795 Ενδεικτικές απαντήσεις 6ης Γραπτής Εργασίας ΠΛΗ 7-8: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
http://elear.maths.gr/, maths@maths.gr, Τηλ: 69795 Ενδεικτικές απαντήσεις 6ης Γραπτής Εργασίας ΠΛΗ 7-8: Οι φοιτητές θα κάνουν την δική τους εργασία σκεπτόµενοι πάνω στις ενδεικτικές απαντήσεις. Σε περίπτωση
( ) { } ( ) ( ( ) 2. ( )! r! e j ( ) Κίνηση στερεών σωμάτων. ω 2 2 ra. ω j. ω i. ω = ! ω! r a. 1 2 m a T = T = 1 2 i, j. I ij. r j. d 3! rρ. r! e!
 Κίνηση στερεών σωμάτων ΦΥΣ 11 - Διαλ.30 1 q Κίνηση στερεού σώµατος: Ø Υπολογισµός της κινητικής ενέργειας Ø Θεωρήσαµε ότι ένα σώµα διακριτής ή συνεχούς κατανοµής µάζας q Η κινητική ενέργεια δίνεται από
Κίνηση στερεών σωμάτων ΦΥΣ 11 - Διαλ.30 1 q Κίνηση στερεού σώµατος: Ø Υπολογισµός της κινητικής ενέργειας Ø Θεωρήσαµε ότι ένα σώµα διακριτής ή συνεχούς κατανοµής µάζας q Η κινητική ενέργεια δίνεται από
Φωτογραφική μηχανή - Αρχή λειτουργίας.
 Ο25 Φωτογραφική μηχανή - Αρχή λειτουργίας. 1 Σκοπός Στην άσκηση αυτή γίνεται μία παρουσίαση των βασικών στοιχείων της φωτογραφικής μηχανής (φακός φωτοφράκτης - διάφραγμα αισθητήρας) καθώς και μία σύντομη
Ο25 Φωτογραφική μηχανή - Αρχή λειτουργίας. 1 Σκοπός Στην άσκηση αυτή γίνεται μία παρουσίαση των βασικών στοιχείων της φωτογραφικής μηχανής (φακός φωτοφράκτης - διάφραγμα αισθητήρας) καθώς και μία σύντομη
P (A B) = P (A) + P (B) P (A B).
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-217: Πιθανότητες - Εαρινό Εξάµηνο 2007 ιδάσκων : Π. Τσακαλίδης Λύσεις Πρώτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης : 08/10/2007 Ηµεροµηνία Παράδοσης : 18/10/2007
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-217: Πιθανότητες - Εαρινό Εξάµηνο 2007 ιδάσκων : Π. Τσακαλίδης Λύσεις Πρώτης Σειράς Ασκήσεων Ηµεροµηνία Ανάθεσης : 08/10/2007 Ηµεροµηνία Παράδοσης : 18/10/2007
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ
 ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΑΣΚΗΣΕΙΣ ΚΥΜΑΤΙΚΗΣ ΟΠΤΙΚΗΣ ΑΣΚΗΣΗ 1: Ένα οπτικό φράγμα με δυο σχισμές που απέχουν μεταξύ τους απόσταση =0.0 mm είναι τοποθετημένο σε απόσταση =1,0 m από μια οθόνη. Το οπτικό φράγμα με τις δυο σχισμές φωτίζεται
ΑΣΚΗΣΗ 17. Περίθλαση µε Laser
 ΑΣΚΗΣΗ 17 Περίθλαση µε Laser ΣΥΣΚΕΥΕΣ: Οπτική τράπεζα µε οθόνη, πηγή Laser, φράγµα, σχισµή, διάφραγµα µε τρύπα στην οποία στερεώνεται λεπτό σύρµα, µικρόµετρο, µέτρο. ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ: Συµβολή φωτός:
ΑΣΚΗΣΗ 17 Περίθλαση µε Laser ΣΥΣΚΕΥΕΣ: Οπτική τράπεζα µε οθόνη, πηγή Laser, φράγµα, σχισµή, διάφραγµα µε τρύπα στην οποία στερεώνεται λεπτό σύρµα, µικρόµετρο, µέτρο. ΘΕΩΡΗΤΙΚΗ ΕΙΣΑΓΩΓΗ: Συµβολή φωτός:
Φύση του φωτός. Θεωρούμε ότι το φως έχει διττή φύση: διαταραχή που διαδίδεται στο χώρο. μήκος κύματος φωτός. συχνότητα φωτός
 Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Γεωμετρική Οπτική Φύση του φωτός Θεωρούμε ότι το φως έχει διττή φύση: ΚΥΜΑΤΙΚΗ Βασική ιδέα Το φως είναι μια Η/Μ διαταραχή που διαδίδεται στο χώρο Βασική Εξίσωση Φαινόμενα που εξηγεί καλύτερα (κύμα) μήκος
Α. Ροπή δύναµης ως προς άξονα περιστροφής
 Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
Μηχανική στερεού σώµατος, Ροπή ΡΟΠΗ ΔΥΝΑΜΗΣ Α. Ροπή δύναµης ως προς άξονα περιστροφής Έστω ένα στερεό που δέχεται στο άκρο F Α δύναµη F όπως στο σχήµα. Στο Ο διέρχεται άξονας περιστροφής κάθετος στο στερεό
Περίθλαση από µία σχισµή.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 71 7. Άσκηση 7 Περίθλαση από µία σχισµή. 7.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την συµπεριφορά των µικροκυµάτων
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 71 7. Άσκηση 7 Περίθλαση από µία σχισµή. 7.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης είναι η γνωριµία των σπουδαστών µε την συµπεριφορά των µικροκυµάτων
Γραµµικά πολωµένο φως - Ο νόµος του Malus
 Ο10 Γραµµικά πολωµένο φως - Ο νόµος του Malus 1. Σκοπός Στην άσκηση αυτή θα επιβεβαιώσουµε πειραµατικά την προβλεπόµενη σχέση ανάµεσα στη διεύθυνση πόλωσης του φωτός και της έντασής του, καθώς αυτό διέρχεται
Ο10 Γραµµικά πολωµένο φως - Ο νόµος του Malus 1. Σκοπός Στην άσκηση αυτή θα επιβεβαιώσουµε πειραµατικά την προβλεπόµενη σχέση ανάµεσα στη διεύθυνση πόλωσης του φωτός και της έντασής του, καθώς αυτό διέρχεται
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική. Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΟΠΤΙΚΗ (Ηλεκτροµαγνητισµός-Οπτική) Γεωµετρική Οπτική (Μάθηµα
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΟΠΤΙΚΗ (Ηλεκτροµαγνητισµός-Οπτική) Γεωµετρική Οπτική (Μάθηµα
Φυσικές Επιστήμες Σχολή Θετικών Επιστημών και Τεχνολογίας
 ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΙΚΡΟΣΚΟΠΗΣΗ Εργαστηριακές Ασκήσεις Βιολογίας I Φυσικές Επιστήμες Σχολή Θετικών Επιστημών και Τεχνολογίας Παξινού Ευγενία Για την επιστήμη της Βιολογίας, το μικροσκόπιο αποτέλεσε τη μεγαλύτερη
ΕΙΣΑΓΩΓΗ ΣΤΗ ΜΙΚΡΟΣΚΟΠΗΣΗ Εργαστηριακές Ασκήσεις Βιολογίας I Φυσικές Επιστήμες Σχολή Θετικών Επιστημών και Τεχνολογίας Παξινού Ευγενία Για την επιστήμη της Βιολογίας, το μικροσκόπιο αποτέλεσε τη μεγαλύτερη
0, x < 0 1+x 8, 0 x < 1 1 2, 1 x < x 8, 2 x < 4
 Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-7: Πιθανότητες-Χειµερινό Εξάµηνο 5 ιδάσκων : Π. Τσακαλίδης Φροντιστήριο 7 Συνεχείς Τυχαίες Μεταβλητές Επιµέλεια : Κωνσταντίνα Φωτιάδου Ασκηση. Εστω
Πανεπιστήµιο Κρήτης - Τµήµα Επιστήµης Υπολογιστών ΗΥ-7: Πιθανότητες-Χειµερινό Εξάµηνο 5 ιδάσκων : Π. Τσακαλίδης Φροντιστήριο 7 Συνεχείς Τυχαίες Μεταβλητές Επιµέλεια : Κωνσταντίνα Φωτιάδου Ασκηση. Εστω
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ
 ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΗΛΕΚΤΡΟΝΙΚΗ ΜΙΚΡΟΣΚΟΠΙΑ ΔΡ. ΒΑΣΙΛΕΙΟΣ ΜΠΙΝΑΣ Τμήμα Φυσικής, Πανεπιστήμιο Κρήτης Email: binasbill@iesl.forth.gr Thl. 1269 Crete Center for Quantum Complexity and Nanotechnology Department of Physics, University
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ
 ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2017 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2017 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
Διαγώνισμα Φυσικής Γ Λυκείου. Αρμονικό κύμα Συμβολή Στάσιμα
 Διαγώνισμα Φυσικής Γ Λυκείου Αρμονικό κύμα Συμβολή Στάσιμα ~~ Διάρκεια 3 ώρες ~~ Θέμα Α 1) Δύο σημεία ενός γραμμικού ομογενούς ελαστικού μέσου, στο οποίο έχει δημιουργηθεί στάσιμο εγκάρσιο κύμα, βρίσκονται
Διαγώνισμα Φυσικής Γ Λυκείου Αρμονικό κύμα Συμβολή Στάσιμα ~~ Διάρκεια 3 ώρες ~~ Θέμα Α 1) Δύο σημεία ενός γραμμικού ομογενούς ελαστικού μέσου, στο οποίο έχει δημιουργηθεί στάσιμο εγκάρσιο κύμα, βρίσκονται
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική. Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΟΠΤΙΚΗ (Ηλεκτροµαγνητισµός-Οπτική) Γεωµετρική Οπτική (Μάηµα
Ηλεκτρομαγνητισμός - Οπτική - Σύγχρονη Φυσική Ενότητα: Οπτική Βαρουτάς Δημήτρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών ΟΠΤΙΚΗ (Ηλεκτροµαγνητισµός-Οπτική) Γεωµετρική Οπτική (Μάηµα
HMY 333 Φωτονική. Διάλεξη 04 Απεικόνιση. Οι λόγοι για τους οποίους χρησιμοποιούμε τους φακούς:
 1 2 HMY 333 Φωτονική Διάλεξη 04 Απεικόνιση Το ηλεκτρομαγνητικό φάσμα μπορεί να χρησιμοποιηθεί για τις επικοινωνίες (π.χ. ραδιοκύματα ή οπτικές ίνες). Ένας άλλος τομέας χρήσης της ηλεκτρομαγνητικής ακτινοβολίας
1 2 HMY 333 Φωτονική Διάλεξη 04 Απεικόνιση Το ηλεκτρομαγνητικό φάσμα μπορεί να χρησιμοποιηθεί για τις επικοινωνίες (π.χ. ραδιοκύματα ή οπτικές ίνες). Ένας άλλος τομέας χρήσης της ηλεκτρομαγνητικής ακτινοβολίας
Κεφάλαιο 33 ΦακοίκαιΟπτικάΣτοιχεία. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 33 ΦακοίκαιΟπτικάΣτοιχεία ΠεριεχόµεναΚεφαλαίου 33 Λεπτοί Φακοί- ιάδοση Ακτίνας Εξίσωση Λεπτού Φακού-Μεγέθυνση Συνδυασµός Φακών ΟιεξίσωσητουΟπτικού Φωτογραφικές Μηχανές : Ψηφιακές και Φιλµ ΤοΑνθρώπινοΜάτι;
Κεφάλαιο 33 ΦακοίκαιΟπτικάΣτοιχεία ΠεριεχόµεναΚεφαλαίου 33 Λεπτοί Φακοί- ιάδοση Ακτίνας Εξίσωση Λεπτού Φακού-Μεγέθυνση Συνδυασµός Φακών ΟιεξίσωσητουΟπτικού Φωτογραφικές Μηχανές : Ψηφιακές και Φιλµ ΤοΑνθρώπινοΜάτι;
Fundamentals of Lasers
 Fundamentals of Lasers Συνθήκη κατωφλίου: Ας υποθέσουμε ένα μέσο με καταστάσεις i> και k>, με ενέργειες Ε i, Ε k. Ένα Η/Μ κύμα που διαδίδεται σε αυτό το μέσο θα μεταβάλλει την έντασή του σύμφωνα με τη
Fundamentals of Lasers Συνθήκη κατωφλίου: Ας υποθέσουμε ένα μέσο με καταστάσεις i> και k>, με ενέργειες Ε i, Ε k. Ένα Η/Μ κύμα που διαδίδεται σε αυτό το μέσο θα μεταβάλλει την έντασή του σύμφωνα με τη
Φυσικά Μεγέθη Μονάδες Μέτρησης
 ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΤΑΞΗ: Α Προσανατολισμού 2. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ ΔΙΔΑΚΤΕΑ ΔΕΙΚΤΕΣ
ΓΝΩΣΤΙΚΟ ΑΝΤΙΚΕΙΜΕΝΟ: ΦΥΣΙΚΗ A ΛΥΚΕΙΟΥ ΤΑΞΗ: Α Προσανατολισμού 2. ΚΕΦΑΛΑΙΑ ΕΝΟΤΗΤΕΣ ΜΑΘΗΣΙΑΚΑ ΑΠΟΤΕΛΕΣΜΑΤΑ ΔΕΙΚΤΕΣ ΕΠΙΤΥΧΙΑΣ Οι μαθητές και οι μαθήτριες να είναι σε θέση να: ΑΝΤΙΣΤΟΙΧΑ ΔΙΔΑΚΤΕΑ ΔΕΙΚΤΕΣ
ΚΕΦΑΛΑΙΟ 11Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση
 ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
ΚΕΦΑΛΑΙΟ Α «Γεωμετρική οπτική - οπτικά όργανα» Εισαγωγή - Ανάκλαση Μαρία Κατσικίνη katsiki@auth.gr users.auth.gr/~katsiki Ηφύσητουφωτός 643-77 Netwon Huygens 69-695 Το φως είναι δέσμη σωματιδίων Το φως
Εφαρμοσμένη Οπτική. Γεωμετρική Οπτική
 Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
Εφαρμοσμένη Οπτική Γεωμετρική Οπτική Κύρια σημεία του μαθήματος Η προσέγγιση της γεωμετρικής οπτικής Νόμοι της ανάκλασης και της διάθλασης Αρχή του Huygens Αρχή του Fermat Αρχή της αντιστρεψιμότητας (principle
Ευθυγραµµίζοντας ένα τηλεσκόπιο
 Ευθυγραµµίζοντας ένα τηλεσκόπιο Τι είναι ευθυγράµµιση Πρόκειται για τη διαδικασία ευθυγράµµισης των οπτικών και µηχανικών αξόνων όλων των οπτικών στοιχείων του τηλεσκοπίου. Όταν τα στοιχεία αυτά ευθυγραµµιστούν
Ευθυγραµµίζοντας ένα τηλεσκόπιο Τι είναι ευθυγράµµιση Πρόκειται για τη διαδικασία ευθυγράµµισης των οπτικών και µηχανικών αξόνων όλων των οπτικών στοιχείων του τηλεσκοπίου. Όταν τα στοιχεία αυτά ευθυγραµµιστούν
ΟΠΤΙΚΗ ΟΦΘΑΛΜΙΚΩΝ ΦΑΚΩΝ Κ ΦΑΚΩΝ ΕΠΑΦΗΣ. A. ιαφορές µεταξύ γυαλιών και φακών επαφής / διαθλαστικής χειρουργικής
 ΟΠΤΙΚΗ ΟΦΘΑΛΜΙΚΩΝ ΦΑΚΩΝ Κ ΦΑΚΩΝ ΕΠΑΦΗΣ A. ιαφορές µεταξύ γυαλιών και φακών επαφής / διαθλαστικής χειρουργικής Για την διόρθωση του διαθλαστικού σφάλµατος του οφθαλµού (µυωπία, υπερµετρωπία, αστιγµατισµός)
ΟΠΤΙΚΗ ΟΦΘΑΛΜΙΚΩΝ ΦΑΚΩΝ Κ ΦΑΚΩΝ ΕΠΑΦΗΣ A. ιαφορές µεταξύ γυαλιών και φακών επαφής / διαθλαστικής χειρουργικής Για την διόρθωση του διαθλαστικού σφάλµατος του οφθαλµού (µυωπία, υπερµετρωπία, αστιγµατισµός)
ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ LASER
 ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΜΟΝΟΧΡΩΜΑΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ ΣΚΟΠΟΙ H εξάσκηση στην παρατήρηση και περιγραφή φαινοµένων, όπως το φαινόµενο της συµβολής των κυµάτων H παρατήρηση των αποτελεσµάτων της διάδοσης της
ΜΕΤΡΗΣΗ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ ΜΟΝΟΧΡΩΜΑΤΙΚΗΣ ΑΚΤΙΝΟΒΟΛΙΑΣ ΣΚΟΠΟΙ H εξάσκηση στην παρατήρηση και περιγραφή φαινοµένων, όπως το φαινόµενο της συµβολής των κυµάτων H παρατήρηση των αποτελεσµάτων της διάδοσης της
Οµάδα Ασκήσεων #3-Λύσεις
 Οµάδα Ασκήσεων #3-Λύσεις Πρόβληµα # (α) Ο βραχίονας είναι επίπεδος. Μπορούµε να βρούµε τον προσπελάσιµο χώρο εργασίας µε µια βήµα-προς-βήµα προσέγγιση. Πρώτα βρίσκουµε το χώρο που καλύπτεται όταν η άρθρωση-3
Οµάδα Ασκήσεων #3-Λύσεις Πρόβληµα # (α) Ο βραχίονας είναι επίπεδος. Μπορούµε να βρούµε τον προσπελάσιµο χώρο εργασίας µε µια βήµα-προς-βήµα προσέγγιση. Πρώτα βρίσκουµε το χώρο που καλύπτεται όταν η άρθρωση-3
Περίθλαση από ακµή και από εµπόδιο.
 ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
ρ. Χ. Βοζίκης Εργαστήριο Φυσικής ΙΙ 63 6. Άσκηση 6 Περίθλαση από ακµή και από εµπόδιο. 6.1 Σκοπός της εργαστηριακής άσκησης Σκοπός της άσκησης αυτής, καθώς και των δύο εποµένων, είναι η γνωριµία των σπουδαστών
α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση
 Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
Λύση ΑΣΚΗΣΗ 1 α) Η γενική εξίσωση του αρµονικού κύµατος είναι. Συγκρίνοντάς την µε µία από τις δύο εξισώσεις των τρεχόντων κυµάτων, έστω την εξίσωση, προκύπτει: και Με αντικατάσταση στη θεµελιώδη εξίσωση
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ
 ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2016 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
ΑΣΚΗΣΗ 3 ΣΥΓΚΛΙΝΟΝΤΕΣ ΚΑΙ ΑΠΟΚΛΙΝΟΝΤΕΣ ΦΑΚΟΙ ΑΣΚΗΣΗ 3-2016 1 Σκοπός Σε αυτή την άσκηση ο φοιτητής χειρίζεται βασικά οπτικά όργανα όπως είναι οι λεπτοί φακοί. Στο πρώτο μέρος υπολογίζεται η εστιακή απόσταση
Γραµµικά πολωµένο φως - Ο νόµος του Malus
 Ο10 Γραµµικά πολωµένο φως - Ο νόµος του Malus 1. Σκοπός Στην άσκηση αυτή θα επιβεβαιώσουµε πειραµατικά την προβλεπόµενη σχέση ανάµεσα στη διεύθυνση πόλωσης του φωτός και της έντασής του, καθώς αυτό διέρχεται
Ο10 Γραµµικά πολωµένο φως - Ο νόµος του Malus 1. Σκοπός Στην άσκηση αυτή θα επιβεβαιώσουµε πειραµατικά την προβλεπόµενη σχέση ανάµεσα στη διεύθυνση πόλωσης του φωτός και της έντασής του, καθώς αυτό διέρχεται
Φύση και διάδοση φωτός
 Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Κυματική Φύση και διάδοση φωτός Ακτινικό μοντέλο διάδοσης. Στο κεφάλαιο των κυμάτων αναπαραστήσαμε τη διάδοση των κυμάτων με τα κυματομέτωπα. Μια απλούστευση
Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Κυματική Φύση και διάδοση φωτός Ακτινικό μοντέλο διάδοσης. Στο κεφάλαιο των κυμάτων αναπαραστήσαμε τη διάδοση των κυμάτων με τα κυματομέτωπα. Μια απλούστευση
Σχήµα 1. ιατάξεις πρισµάτων που προσοµοιώνουν τη λειτουργία των φακών. (α) Συγκλίνων. (β) Αποκλίνων
 Ο3 Γενικά περί φκών. Γενικά Φκός ονοµάζετι κάθε οµογενές, ισότροπο κι διφνές οπτικό µέσο που διµορφώνετι πό δυο σφιρικές επιφάνειες (ή πό µι σφιρική κι µι επίπεδη). Βσική () () Σχήµ. ιτάξεις πρισµάτων
Ο3 Γενικά περί φκών. Γενικά Φκός ονοµάζετι κάθε οµογενές, ισότροπο κι διφνές οπτικό µέσο που διµορφώνετι πό δυο σφιρικές επιφάνειες (ή πό µι σφιρική κι µι επίπεδη). Βσική () () Σχήµ. ιτάξεις πρισµάτων
ΣΥΜΒΟΛΟΜΕΤΡΟ MICHELSON ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΜΗΚΟΥΣ ΚΥΜΑΤΟΣ LASER He-Ne
 ΤΕΙ ΘΗΝΣ ΤΜΗΜ ΦΥΣΙΚΗΣ ΧΗΜΕΙΣ & Τ/Υ ΕΡΓΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LAE ΣΚΗΣΗ ΝΟ ΣΥΜΒΟΛΟΜΕΤΡΟ MICHELON ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΜΗΚΟΥΣ ΚΥΜΤΟΣ LAE He-Ne Γιώργος Μήτσου πρίλιος 007 . ΘΕΩΡΙ Εισαγωγή Τα
ΤΕΙ ΘΗΝΣ ΤΜΗΜ ΦΥΣΙΚΗΣ ΧΗΜΕΙΣ & Τ/Υ ΕΡΓΣΤΗΡΙΟ ΦΥΣΙΚΗΣ ΟΠΤΙΚΗΣ - ΟΠΤΟΗΛΕΚΤΡΟΝΙΚΗΣ & LAE ΣΚΗΣΗ ΝΟ ΣΥΜΒΟΛΟΜΕΤΡΟ MICHELON ΠΡΟΣ ΙΟΡΙΣΜΟΣ ΜΗΚΟΥΣ ΚΥΜΤΟΣ LAE He-Ne Γιώργος Μήτσου πρίλιος 007 . ΘΕΩΡΙ Εισαγωγή Τα
( ) ( ) ( )! r a. Στροφορμή στερεού. ω i. ω j. ω l. ε ijk. ω! e i. ω j ek = I il. ! ω. l = m a. = m a. r i a r j. ra 2 δ ij. I ij. ! l. l i.
 Στροφορμή στερεού q Η στροφορµή του στερεού γράφεται σαν: q Αλλά ο τανυστής αδράνειας έχει οριστεί σαν: q H γωνιακή ταχύτητα δίνεται από: ω = 2 l = m a ra ω ω ra ω e a ΦΥΣ 211 - Διαλ.31 1 r a I j = m a
Στροφορμή στερεού q Η στροφορµή του στερεού γράφεται σαν: q Αλλά ο τανυστής αδράνειας έχει οριστεί σαν: q H γωνιακή ταχύτητα δίνεται από: ω = 2 l = m a ra ω ω ra ω e a ΦΥΣ 211 - Διαλ.31 1 r a I j = m a
