ΚΕΦΑΛΑΙΟ 2 Ο 2. ΙΞΩ ΕΣ ΡΕΥΣΤΟ (VISCOUS FLUID)

Transcript

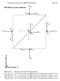
1 ΚΕΦΑΛΑΙΟ Ο. ΙΞΩ ΕΣ ΡΕΥΣΤΟ (VISCOUS FUID) Ο Ισαάκ Νεύτωνας έγραψε το 687 στο περίφηµο βιβλίο του Principia Mathematica "The resistance which arises from the lack of slipperiness originating in a fluid, other things being equal, is proportional to the velocity by which the parts of the fluid are being separated from each other". Αντίσταση (resistance) σηµαίνει διατµητική τάση (shear stress), και ταχύτητα µε την οποία µέρη του ρευστού αποχωρίζονται ("velocity by which the parts of the fluid are being separated") σηµαίνει κλίση ταχύτητας (velocity gradient). Η σταθερά αναλογίας (proportionality constant) µεταξύ αυτών των ποσοτήτων είναι το ιξώδες ή έλειψη ολισθηρότητας (lack of slipperiness). Σε µία διάσταση αυτός ο νόµος µπορεί να γραφεί ως: τ yx d u η d y x Ο Stokes το 845 τελικά έγραψε αυτόν τον νόµο σε τρισδιάστατη µαθηµατική µορφή και το 856 τα πειράµατα του Poiseuille σε ένα τριχοειδές ρεόµετρο (capillary rheometer) απέδειξαν τον νόµο του Νεύτωνα πειραµατικά. Εάν η σταθερό και ανεξάρτητο από τον ρυθµό διάτµησης τότε το ρευστό λέγεται Νευτώνειο και το σύµβολο µ χρησιµοποιείται για να δηλώσει ιξώδες. Οµως σε πολλά ρευστά το ιξώδες εξαρτάται από τον ρυθµό διάτµησης. - Εάν η µειώνεται µε τον ρυθµό διάτµησης, το ρευστό λέγεται ρευστό διατµητικής λέπτυνσης (shear-thinning fluid), και - Εάν η αυξάνει µε τον ρυθµό διάτµησης, το ρευστό λέγεται ρευστό διατµητικής πάχυνσης (shear-thickening fluid). Παρακάτω η απλούστερη ροή που µπορεί να παραχθεί σε ένα ρεολογικό εργαστήριο παρουσιάζεται πρώτα (απλή διάτµηση - simple shear) και εν συνεχεία παρουσιάζονται διάφορα παραδείγµατα για ρευστά διατµητικής λέπτυνσης και πάχυνσης. Απλή διάτµηση (simple shear) Αυτή η ροή µπορεί να δηµιουργηθεί στον χώρο µεταξύ δύο παράλληλων πλακών όταν αποχωρίζονται προς αντίθετες κατευθύνσεις µε µία σχετική ταχύτητα V (βλέπε Σχήµα -). Η

2 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - διατµητική τάση (shear stress) είναι: τ yx Ο ρυθµός διάτµησης ή η κλίση ταχύτητας είναι: γ& d u d y F A x V h Σχήµα -: Απεικόνιση της απλής διατµητικής ροής. Σχήµα -: Παραδείγµατα όπου το ιξώδες εξαρτάται από τον ρυθµό διάτµησης (Macosco, 994)

3 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 3 Εκτατικό ιξώδες ή ιξώδες εφαλκυσµού (extensional viscosity): Ο Trouton το 96 µελετησε την ροή σκληρών υλικών (stiff materials) όπως το λειωµένο γυαλί (molten glass). Επειδή τέτοια υλικά έχουν πολύ µεγάλο ιξώδες, µπόρεσε να τα εξετάσει σε εφελκυσµό µε πολύ λίγη χαλάρωση λόγω βάρους (sagging due to gravity). Βρήκε ότι η αναλογία µεταξύ τάσης και κλίσης ταχύτητας είναι τρεις φορές µεγαλύτερη απ την αντίστοιχη τιµή σε διάτµηση. Αυτή η καινούρια ποσότητα λέγεται εκτατικό ιξώδες και είναι σύµφωνη µε τον νόµο του Νεύτωνα όταν γραφεί σε τρεις διαστάσεις. Σχήµα -3:Το εκτατικό ιξώδες τήγµατος πολυστυρενίου στους 6 o C (Munstedt).. ΚΛΙΣΗ ΤΑΧΥΤΗΤΑΣ (VEOCITY GRADIENT) Για να γενικεύσουµε τον νόµο του Νεύτωνα σε τρεις διαστάσεις, µπορούµε να χρησιµοποιήσουµε τον τανυστή τάσης αλλά χρειαζόµαστε έναν τρόπο να καθορίσουµε την κλίση ταχύτητας σε ένα σηµείο στο ρευστό. Σ αυτή την περίπτωση ενδιαφερόµαστε να υπολογίσουµε την ταχύτητα µε την οποία τα διάφορα µέρη του ρευστού αποµακρύνονται µεταξύ τους, όπως ανέφερε ο Νεύτωνας. Θεωρούµε το Σχήµα -4 παρακάτω. Γενικά, η ταχύτητα στο ρευστό είναι συνάρτηση της θέσης και του χρόνου.

4 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 4 v v ( x, t ) Η ταχύτητα στο σηµείο P είναι v και στο Q είναι v+dv. Η σχετική αλλαγή dv µπορεί να υπολογισθεί ως: v d v.dx or d v.dx x όπου είναι ο τανυστής της κλίσης ταχύτητας. Αυτός ο νέος τανυστής όπως και όλοι οι άλλοι έχει δύο κατευθύνσεις: µία είναι η κατεύθυνση της ταχύτητας και η άλλη της κλίσης και ορίζεται ως: ( vi x T v ) or v T j Στον πίνακα - οι συνιστώσες του ή σφαιρικές συντεταγµένες. v x j i T ( v) δίνοται σε καρτεσιανές, κυλινδρικές και Σχήµα -4: Σχετική ταχύτητα, dv, µεταξύ σηµείων P και Q που µετακινούνται σε ένα ρευστό.

5 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 5 ΠΙΝΑΚΑΣ -: Συνιστώσες του ή ( v) T Καρτεσιανές Συντεταγµένες - Rectangular Coordinates (x, y, z) xx v x / x xy v x / y xz v x / z yx v y / x yy v y / y yz v y / z zx v z / x zy v z / y zz v z / z Κυλινδρικές Συντεταγµένες - Cylindrical Coordinates (r, θ, z) rr v r / r rθ v r /r θ - v θ /r rz v r / z θ r v θ / r zr v z / r θθ θ /r θ +v r /r θ z v θ / z zθ v z /r θ zz v z / z Σφαιρικές Συντεεγµένες - Spherical Coordinates (r,θ,φ ) rr v r / r θ r v θ / r φ r v φ / r rθ v r /r θ - v θ /r θθ v θ /r θ +v r /r φθ φθ v φ /r θ rφ v r /rsinθ φ - v φ /r θφ v θ /rsinθ φ - vφ cotθ /r φφ v φ /rsinθ φ +v r /r+ v θ cotθ /r

6 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 6 ΠΑΡΑ ΕΙΓΜΑ.: Υπολόγισε για µονοαξονικό µόνιµο εφελκυσµό (steady uniaxial extension), απλή µόνιµη διάτµηση (simple steady shear) και µόνιµη περιστροφή στερεού σώµατος (solid body rotation). i. Εφελκυσµός (extension): Από την κινηµατική της ροής (kinematics of the flow) για µονοαξονικό εφελκυσµό (uniaxial extension), µπορούµε να γράψουµε: ij & ε - & ε / όπου ε& είναι ο ρυθµός εφελκυσµού που ορίζεται ως: ii. ε& d dt Απλή µόνιµη διάτµηση (steady simple shear): ij γ& - & ε / όπου γ& είναι ο ρυθµός διάτµησης. Επισηµαίνεται ότι, επειδή v T, έχουµε ( v ) ij γ& iii. Περιστροφή στερεού σώµατος (solid body rotation): Εάν Ω είναι η γωνιακή ταχύτητα (angular velocity) τότε - Ω Ω Ετσι µπορούµε να δούµε ότι ο τανυστής κλίσης ταχύτητας δεν είναι µηδέν για περιστροφή στερεού σώµατος. Περιστροφή δεν µπορεί να προκαλέσεις διατµητική τάση. Ετσι πρέπει να

7 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 7 βρούµε τρόπο να απαλείψουµε την επίδραση της επιροής από το, έτσι ώστε να µπορέσουµε να συσχετίσουµε τον τανυστή τάσης µε τον νέο τανυστή για την κλίση ταχύτητας. Αυτός θα είναι ο γενικευµένος νόµος του Νεύτωνα σε τρεις διαστάσεις... ΤΑΝΥΣΤΗΣ ΡΥΘΜΟΥ ΠΑΡΑΜΟΡΦΩΣΗΣ Μπορούµε να απαλείψουµε την περιστροφή (rotation) από τον τανυστή κλίσης της ταχύτητας για να ικανοποιήσουµε την αρχή της αδιαφορίας του υλικού (material indifference requirement). Ο σκοπός µας είναι να βρούµε έναν τανυστή για να περιγράψουµε παραµόρφωση ο οποίος θα µας βοηθήσει αργότερα για να αναπτύξουµε καταστατικές εξισώσεις ρεολογίας. Το τελικό αποτέλεσµα είναι ο τανυστής ρυθµού παραµόρφωσης (rate of deformation tensor), D, ο οποίος ορίζεται ως: D ( v ) T + v Επισηµαίνεται ότι ο τανυστής είναι τώρα συµµετρικός και µπορεί να συσχετισθεί µε τον τανυστή τάσης. Απο την άλλη πλευρά, ( v) T ή v δεν είναι συµµετρικοί επειδή περιλαµβάνουν την επίδραση της περιστροφής. Ο τανυστής προκύπτει από το άθροισµα του D και W, όπου ο D περιγράφει τον ρυθµό παραµόρφωσης και ο W περιγράφει τον ρυθµό περιστροφής.

8 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 8 ΠΑΡΑ ΕΙΓΜΑ.: Υπολόγισε D και W για µόνιµο µονοαξονικό εφελκυσµό, απλή διάτµηση και περιστροφή στερεού σώµατος όπως επίσης και τις αναλοίωτες τους: i. Μόνιµος Μονοαξονικός Εφελκυσµός (Steady Uniaxial Extension): Τα αποτελέσµατα είναι: ij ij ji D ( + & ε ) - & ε - & ε W ij Αυτή η ροή λέγεται αστρόβιλη (irrotational) επειδή W. Οι αναλοίωτες είναι: ii. II D [ ( tr I D tr D D ) - tr ( D III D ) ] tr ε& 3 D Μόνιµη Απλή ιάτµηση (Steady simple shear): D ij & γ & γ - 3ε& W ij - & γ & γ I D, II D γ& I W, II W γ&,, III III D W iii. Περιστροφή Στερεού Σώµατος (Solid Body Rotation):

9 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ Ω D ij W ij Ω ij I, W II W Ω, III W Από αυτό το παράδειγµα βλέπουµε ότι: - W δίνει την γωνιακή περιστροφή στο υλικό σε οποιοδήποτε σηµείο. - Για περιστροφή στερεού σώµατος έχουµε µόνο W - D χαρακτηρίζει τον ρυθµό εφελκυσµού σε κάποιο σηµείο - Για µονοαξονικό εφελκυσµό, W (αστρόβιλη ροή - flow irrotational) Για όλες τις ροές βλέπουµε ότι I D. Αυτό ισχύει για ασυµπίεστα υλικά επειδή tr ( D ) i vi. v I D D αντιπροσωπεύει τον τοπικό ρυθµό αλλαγής µήκους (local rate of change in length). Μπορούµε να αποδείξουµε την ακόλουθη σχέση. d d x d x. D.d x d t Τελικά είναι χρήσιµο να επισηµάνουµε ότι D είναι η χρονική παράγωγος του B στο όριο µικρών παραµορφώσεων. Για να το αποδείξουµε αρχίζουµε από τον τανυστή παραµόρφωσης F, Παίρνουµε την χρονική παράγωγο: d x F. d x ( d x) F ( d x ).d x + F. t t t Επειδή dx' είναι σταθερό στο χρόνο t', τότε ο τελευταίος όρος είναι µηδέν. Ετσι µπορούµε να γράψουµε ότι:

10 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - F &. d x.d x Ή χρησιµοποιώντας την εξίσωση για dx, F &. F Επειδή ενδιαφερόµαστε για το στιγµιαίο ρυθµό διαχωρισµού, παίρνουµε το όριο όπως το x' πλησιάζει το x, τότε: lim x x F I and lim x x F& Το Σχήµα -5 απεικονίζει την δεύτερη αναλοίωτη σαν συνάρτηση της τρίτης για απλή διάτµηση και εφελκυσµό. 6 Simple shear or planar extension IID 8 4 Uniaxial and biaxial extension 5 III D Σχήµα -5: Η απεικόνιση των αναλοίωτων του τανυστή του ρυθµού παραµόρφωσης έγκειται στον χώρο µεταξύ των δύο καµπυλών που αντιστοιχούν σε απλή διάατµηση και µονοαξονικό εφελκυσµό ασυµπίεστου υγρού I D.

11 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ -.3. ΝΕΥΤΩΝΕΙΟ ΥΓΡΟ (NEWTONIAN FUID) Το Νευτώνειο ρευστό σε τρεις διαστάσεις ορίζεται ως: τ η D ή αναφορικά µε το ολικό τανυστή τάσης, T - p I + η D Για απλή διάτµηση αυτή η εξίσωση γίνεται, & γ T ij - p + η & γ Ετσι, τ η & γ, N τ -τ, N τ T τ 33 Για Νευτώνεια ρευστά, το ιξώδες είναι ανεξάρτητο του ρυθµού διάτµησης και εξαρτάται µόνο από την θερµοκρασία και λίγο από την πίεση. Στις επόµενες σελίδες, το ιξώδες δίνεται για διάφορα υλικά σε θερµοκρασία περιβάλλοντος. Σε άλλο πίνακα δίνονται οι ρυθµοί διάτµησης για γνωστές διεργασίες. Μπορούµε να διαπιστώσουµε ότι οι ρυθµοί διάτµησης ποικίλουν από -6 σε διεργασίες καθίζησης λεπτής σκόνης (sedimentation of fine powders) µέχρι 7 σε διεργασίες λίπανης (lubrication). Πίνακας -: Το ιξώδες µερικών γνωστών ρευστών σε θερµοκρασία περιβάλλοντος. -

12 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - Πίνακας -3: Το ιξώδες µερικών γνωστών ρευστών σε διάφορους ρυθµούς διάτµησης που εξαρτώνται από τις διεργασίες.4. ΤΟ ΓΕΝΙΚΕΥΜΕΝΟ ΙΞΩ ΕΣ ΡΕΥΣΤΟ (GENERA VISCOUS FUID) Γενικά για την µοντελοποίηση του ιξώδους µερικών ρευστών που εξαρτάται από τον ρυθµό διάτµησης, η γενική θεωρία του ιξώδες ρευστού χρησιµοποιείται που έχει σαν βάση τον γενικευµένο νόµο του Νεύτωνα σε τρεις διαστάσεις. Γενικά µπορούµε να γράψουµε ότι η τάση εξαρτάται από τον ρυθµό παραµόρφωσης, T f ( D ) Ανα πτύσσοντας µπορούµε να γράψουµε, T 3 D D D 3 D f + f Επειδή D I για ασυµπίεστα ρευστά, f -p. Χρησιµοποιώντας το θεώρηµα των Cayley- Hamilton για να εκφράσουµε µεγαλύτερες δυνάµεις του D σαν συναρτήσεις µικρότερων, µπορούµε να γράψουµε + f + f +... T - p I + η D + η ( D)

13 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 3 Όπου η, and η είναι αριθµητικές συναρτήσεις (scalar functions) των αναλοίωτων του D. T - p I + η ( IID, IIID ) D + η ( IID, IIID )( D) Αυτή η καταστατική εξίσωση είναι γνωστή σαν το ρευστό Reiner-Rivlin (Reiner-Rivlin fluid). Το Νευτώνειο ρευστό είναι απλά µία ειδική περίπτωση. Ο όρος µε το η προβλέπει κάθετες τάσεις σε µόνιµη διατµητική ροή (steady shear flow), αλλά οι προβλέψεις δεν συµφωνούν µε τις πειραµατικές µετρήσεις. Οι προβλέψεις είναι: T T T 33 T - p η & γ - p + η & γ Σε απλή διάτµηση όλα τα ρευστά που επιδεικνύουν κάθετες τάσεις, δείχνουν θετική πρώτη διαφορά κάθετων τάσεων (positive N ) και αρνητική δεύτερη διαφορά κάθετων τάσεων (negative N ) µε N <<Ν (για τήγµατα πολυµερών ο λόγος είναι -/7). Σωστή πρόβλεψη µπορεί να επιτευχθεί µε την χρήση του τανυστή B για να περιγράψουµε παραµόρφωση. Επειδή ο όρος µε το η δίνει ποιοτικά λανθασµένα αποτελέσµατα, συνήθως απαλείφεται. Ετσι το µοντέλο για το γενικευµένο ιξώδες ρευστό µπορεί να γραφεί: T I + η ( II - p D, D III ) D Επιπρόσθετα για απλή διάτµηση III D η σωστή µορφή είναι: T - p I + η ( IID ) D or τ η ( II Το µοντέλο αυτό είναι γνωστό σαν γενικευµένο ιξώδες ρευστό (general viscous fluid). Υπάρχουν πολλές µορφές. D ) D.5. ΕΚΘΕΤΙΚΟ ΡΕΥΣΤΌ (POWER AW FUID) Η πιό γνωστή µορφή του γενικευµένου ιξώδες ρευστού είναι το εκθετικό µοντέλο (power law model) που σε τρείς διαστάσεις γράφεται: τ ij (n-)/ m II D ( Dij ) Αυτή η εξίσωση συχνά εφαρµόζεται σε µόνιµη απλή διάτµηση για την οποία,

14 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 4 II D γ& Ετσι, για µόνιµη διάτµηση, το µοντέλο power law γράφεται: τ τ n m & γ or η Γενικά αυτή η εξίσωση ισχύει για να αντιπροσωπεύσει το ιξώδες για διατµητικές τάσεις µεγαλύτερες από µία ορισµένη τιµή (yield stress). Πειραµατικά το ιξώδες πολλών ρευστών προσεγγίζει µία τιµή (Νευτώνειο ιξώδες) σε πολύ µικρές διατµητικές τάσεις. Οµως το εκθετικό µοντέλο δίνει άπειρο ιξώδες όπως η διατµητική τάση προσεγγίζει σταδιακά το µηδέν (βλέπε Σχήµα -6). m & γ n-.6. ΤΟ ΜΟΝΤΕΛΟ CROSS (CROSS MODE) Ο Cross πρότεινε ένα µοντέλο που δίνει µία σταθερή τιµή στους πολύ µικρούς ρυθµούς διάτµησης (Νευτώνειο ιξώδες) και µία άλλη σταθερή τιµή στους µεγάλους ρυθµούς διάτµησης. Το µοντέλο αυτό είναι γνωστό σαν µοντέλο Cross και γράφεται: η -η η - +( o η K II D Τυπικά για πολύ µικρούς ρυθµούς διάτµησης ή ) ( -n ) / µοντέλο Cross παίρνει τη µορφή εκθετικού µοντέλου, ή για η >> η II D, η προσεγγίζει η. Σε µεσαίες τιµές το ( n- ) ( η -η ) ( η -η ) m & γ where m -n K o η η m & γ Βλέπε Σχήµα παρακάτω για σύγκριση πειραµατικών δεδοµένων µε το µοντέλο Cross. o n-

15 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 5 Σχήµα -6: Το ιξώδες τήγµατος του πολυµερούς ABS σε τρείς θερµοκρασίες; οι συνεχείς γραµµές παριστούν το µοντέλο του Cross και οι διακεκοµένες το εκθετικό µοντέλο (Macosco, 994)..7. ΑΛΛΑ ΙΞΩ Η ΜΟΝΤΕΛΑ (OTHER VISCOUS MODES) Για να ταιριάξει (εφαρµόσει) πειραµατικές µετρήσεις καλύτερα, οι Yasuda et al (98) πρότειναν το εξής µοντέλο: η -η η - ( -n ) / o η α [ + α λ II D ] Αυτό το µοντέλο είναι ισοδύναµο µε αυτό του Cross µε µία πέµπτη µεταβλητή, α. Με α, η εξίσωση αυτή είναι γνωστή σαν µοντέλο Carreau (βλέπε Σχήµα -7). Συχνά η δεν παρατηρείται και ως εκ τούτου τίθεται ίσον µε το. Αυτό είναι το µοντέλο του Ellis και από το Σχήµα -7 µπορεί να παρατητρηθεί οτι ταιρίαζει (fits) µε τα πειράµατα αρκετά καλά. Το µοντέλο Ellis συνήθως γράφεται σαν συνάρτηση της δεύτερης αναλοίωτης του τανυστή τάσης σαν: η η + II k τ α -

16 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 6 Υπάρχουν πολλά άλλα µοντέλα ιξώδους. Οµως πρέπει να κατανοηθεί ότι όσο πιό πολύπλοκα µοντέλα χρησιµοποιούνται, τόσο πιο λίγα είναι τα προβλήµατα που µπορούν να λυθούν αναλυτικά. Σε τέτοιες περιπτώσεις αριθµητικές µεθόδους µπορούν να χρησιµοποιηθούν. Σχήµα -7: Το ιξώδες τήγµατος ενός πολυπροπυλενίου (PP) και ενός γραµµικού πολυεθυλενίου χαµηλής πυκνότητας (DPE); Οι συνεχείς γραµµές είναι οι εφαρµογές (fits) των µοντέλων Cross και Carreau αντίστοιχα (from Mitsoulis and Hatzikiriakos, 3).

17 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 7 ΠΑΡΑ ΕΙΓΜΑ -: Ροή εκθετικού ρευστού δια µέσου κυλινδρικού αγωγού Καθόρισε την σχέση µεταξύ διαφοράς πίεσης p -p και ογκοµετρικής παροχής ενός εκθετικού ρευστού δια µέσου ενός κυλινδρικού αγωγού (Σχήµα -8) υποθέτοντας ότι (a) η ροή είναι µόνιµη, γραµµική και ασυµπίεστη (b) η βαρύτητα παίζει αµελητέο ρόλο; και (c) ισόθερµες συνθήκες ισχύουν. Figure -8: Ροή δια µέσου κυλινδρικού αγωγού Από τις παραδοχές τοθ προβλήµατος και χρησιµοποιώντας κυλινδρικές συντεταγµένες, περιµένουµε vx (r ), v, and vr vx θ Ετσι, η εξίσωση συνεχείας ικανοποιείται και η εξίσωση ορµής παίρνει την µορφή: Επειδή το p - + (r τ rx ) x r x p / x είναι µόνο συνάρτηση του x και ο δεύτερος όρος συνάρτηση µόνο του r, µπορούµε να γράψουµε: d p d (r τ rx ) d x r d x Η εξίσωση µπορεί να ολοκληρωθεί και χρησιµοποιώντας τ r x m - d vx d r n µπορούµε να ολοκληρώσουµε δεύτερη φορά,

18 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 8 R ) p - p ( o w R r rx τ τ και R r - /n + R m /n+ w /n x τ v Οι κατανοµές ταχύτητας εµφανίζονται παρακάτω για διάφορες τιµές του n (Σχήµα -9), Ολοκληρώνοντας την κατανοµή ταχύτητας κατά πλάτος της διατοµής (cross sectional area), η ογκοµετρική παροχή παράγεται ως, m R ) p - p ( /n + 3 R d r d r Q /n R π θ π vx Τελικά µπορούµε να γράψουµε µία εξίσωση για το ρυθµό διάτµησης στο τοίχωµα, 4 n R 4 Q dr d 3 x R w π γ v & Αυτά τα αποτελέσµατα θα χρησιµοποιηθούν αργότερα για να αναλύσουµε µετρήσεις από ροή σε κυλινδρικούς αγωγούς. Σχήµα -9: Κατανοµές ταχύτητας σε κυλινδρικό αγωγό για εκθετικό ρευστό.

19 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ ΠΛΑΣΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ (PASTIC BEHAVIOUR) Τα πλαστικά υλικά δείχνουν λίγη ή καθόλου παραµόρφωση όταν ασκηθεί τάση µέχρι µίας ορισµένης τιµής. Πάνω από αυτή την τιµή (yield stress) το υλικό ρέει. Παραδείγµατα περιλαµβάνουν πυκνά αιωρήµατα (concentrated suspensions), µπογιές και χρώµατα (house paints), υλικά τροφίµων όπως η µαγιονέζα και το ketchup. Ενα απλό µοντέλο για πλαστική συµπεριφορά είναι το µοντέλο του Χούκ (Hookean) σε τάσεις κάτω από την τάση yield και Νευτώνεια συµπεριφορά (Newtonian behaviour) για τάσεις πάνω απο την τάση yield (Bingham model) τ G γ τ η γ& + τ y for for τ < τ τ τ y y Το µοντέλο µπορεί και να γραφεί ως: τ γ& η γ& + τ y for for τ < τ τ τ y y Για ενα πιο γενικό µοντέλο, το ιξώδες µπορεί να επιδείξει διατµητική λέπτυνση ή πάχυνση. Για την περίπτωση προβληµάτων σε τρείς διαστάσεις, πρέπει να χρησιµοποιήσουµε ένα κατάλληλο κριτήριο για ροή για την τάση yield. Σ αυτή την περίπτωση η τάση αντικαθίσταται από κάποια αναλοίωτη του τανυστή τάσης. Ενα τέτοιο κατάλληλο κριτήριο είναι αυτό του Von Mises, τ G B τ y τ η + II D / for for IIτ < τ y II τ τ y Στα σχήµατα παρακάτω διάφορα παραδείγµατα πλαστικής συµπεριφοράς απεικονίζονται (Σχήµατα -a, b and c και Σχήµα -).

20 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - Σχήµα -: Πλαστική συµπεριφορά Bingham (a) διατµητική τάση σαν συνάρτηση της διατµητικής παραµόρφωσης (shear stress versus strain) σε σταθερό ρυθµό διάτµησης (b) διατµητική τάση σαν συνάρτηση του ρυθµού διάτµησης (c) πειραµατικές µετρήσεις ροής διαφόρων υλικών τροφίµων που επιδεικνύουν yield stress και ψευδοπλαστική συµπεριφορά.

21 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - Σχήµα -: Εφαρµογές του µοντέλου Bingham σε πειραµατικές µετρήσεις σε αιώρηµα 6 vol% iron oxide in mineral oil (a)περιοχή υψηλών διατµητικών τάσεων ( high shear rate range), (b)περιοχή χαµηλών διατµητικών τάσεων και (c) όλες οι µετρήσεις µαζί σε λογαριθµική κλίµακα.

22 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ -.9. ΑΛΛΑ ΙΞΩ ΟΠΛΑΣΤΙΚΑ ΜΟΝΤΕΛΑ (OTHER VISCOPASTIC MODE) Ο Casson πρότεινε το εξής µοντέλο για τα ιξωδοπλαστικά υλικά. Σε µία διάσταση µπορεί να γραφεί ως, γ& τ < τ y / / / τ ( η γ& ) + τ y for τ τ y Το µοντέλο Casson model µπορεί σε πολλές περιπτώσεις να ταιριάξει µε τα πειραµατικά δεδοµένα καλύτερα από το µοντέλο Bingham (Σχήµατα -, και -3). ιάφορες µελέτες έχουν δείξει ότι στις µικρές διατµητικές τάσεις υπάρχει µια Νευτώνεια περιοχή, αντί για Χούκεια (βλέπε παράδειγµα στο Σχήµα παρακάτω). Σ αυτές τις περιπτώσεις το µοντέλο µε τα δύο ιξώδη µπορεί να χρησιµοποιηθεί που µπορεί να γραφεί ως: τ η D τ y τ II D / + m II (n-)/ D Πολλές άλλες παραλλαγές υπάρχουν που παρέχουν ευκολίες στην αριθµητική ανάλυση για την αποφυγή ασυνέχειας στην καµπύλη ροής κ.λ.π. D for for for II / D II / D & γ C > & γ C

23 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 3 (a) (b) Σχήµα -: Τα δεδοµένα του σχήµατος - απεικονισµένα ως (a) ιξώδες σαν συνάρτηση του ρυθµού διάτµησης και (b) ιξώδες σαν συνάρτηση της διατµητικής τάσης (Macosco 994). Figure -3: Σύγκριση των εφαρµογών των µοντέλων Bingham και Casson σε πειραµατικές µετρήσεις αιωρήµατος οξειδίου του σιδήρου. γ&

24 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ ΕΞΙΣΩΣΕΙΣ ΙΣΟΖΥΓΙΩΝ (BAANCE EQUATIONS) Για να εφαρµόσουµε τα ιξώδη µοντέλα σε πολύπλοκα προβλήµατα ροής, χρειαζόµαστε τις εξισώσεις συνεχείας, ορµής ή κίνησης και κατάλληλες οριακές συνθήκες. Για ανισόθερµα προβλήµατα η εξίσωση ενέργειας πρέπει να χρησιµοποιηθεί. Για ασυµπίεστα ρευστά αυτές οι εξισώσεις είναι:. Εξίσωση συνεχείας ή µικροσκοπικό ισοζύγιο µάζας. Εξίσωση ορµής D v ρ D t Κατάλληλες οριακές συνθήκες είναι:. v. T + ρ g - Σε στερεές επιφάνειες (solid boundaries), η ταχύτητα µη-ολίσθησης (no-slip), και µη διαπερατότητας (no-penetration) ισχύουν vt vs u r f a c e vn -Σε διεπιφάνειες ρευστού-ρευστού, οι ταχύτητες και οι τάσεις των δύο ρευστών (a και b) εφαπτόµενα στην διεπιφάνεια πρέπει να είναι ίσες. vt a vt b ( nˆ. T. tˆ ) ( nˆ. T. tˆ ) a -Οι ταχύτητες κάθετα σε διεπιφάνειες ρευστού-ρευστού είναι πάλι µηδέν, και το ισοζύγιο κάθετων τάσεων πρέπει να περιλαµβάνει την διεπιφανειακή τάση Γ και την καµπυλότητα της επιφάνειας. nˆ. T. nˆ 3. Εξίσωση ενέργειας (energy equation) ( ) a v na ( v nb nˆ. T. nˆ b ) b + H Γ Λόγω της µετάπτωσης της µηχανικής ενέργειας σε θερµική, ρευστά σε ροή προκαλούν έκλυση θερµότητας (dissipation of mechanical energy) και αυτή πρέπει να λαµβάνεται υπ όψιν:

25 ΙΞΩ ΕΣ ΡΕΥΣΤΟ - Κ - 5 ρ U t -. ρ U v -.q + T : D όπου U είναι η εσςτερική ενέγεια και q ο θερµικός ρυθµός ροής θερµότητας ανά µονάδα επιφάνειας (conductive heat flux). Αυτή η εξίσωση µπορεί να εκφρασθεί µε κύρια µεταβλητή την θερµοκρασία (υποθέτοντας σταθερή θερµική αγωγιµότητα και µη-έκλυση ενέργειας από χηµικές αντιδράσεις κ.λ.π.) ρ cˆ p D T D t k T T + T : D Ο τελευταίος όρος είναι ο σκεδασµός (µετάπτωση) ενέργειας (energy dissipation) που µερικές φορές µπορεί να είναι πολύ σηµαντικός (π.χ. ροή τηγµάτων πολυµερών σε µεγάλους ρυθµούς ροής). Η λύση ανισόθερµων προβληµάτων µπορεί να είναι σηµαντικά δύσκολη και επίπονη λόγω της εξάρτησης του ιξώδους από την θερµοκρασία. Ετσι οι εξισώσεις ροής και ενέργειας πρέπει να λυθούν ταυτόχρονα.. ΒΙΒΛΙΟΓΡΑΦΙΑ Barnes H.A, Hutton J.F., and Walters K., An Introduction to Rheology, Elsevier, Amsterdam 989 Dealy J.M., Rheometers for Molten Plastics, Van Nostrand Reinhold, New York 983. Dealy J.M. and K.F. Wissbrun, Melt Rheology and Its Role in Plastics Processing, Van Nostrand Reinhold, New York 99. Mitsoulis E, Hatzikiriakos SG, Polymer Eng Sci., Rheol. Acta, 4, 39-3 (3). Macosco C.W., Rheology: Principles, Measurements and Applications, VCH, ondon 994. Munstedt, H., J. Rheol. 4, 847 (98) Yasuda K, Armstrong RC, Cohen RE, Rheol Acta,, (98)