Electromagnetic Engineering MAPTele
|
|
|
- Σίλας Καραβίας
- 7 χρόνια πριν
- Προβολές:
Transcript
1 lcomagc gg MAPTl 8-9 Faculdad d ghaa Pogam lcomagc wavs Popagao Icdc Wavguds Tasmsso ls Radao Iês Cavalho Asssa Pofsso Faculdad d ghaa, Uvsdad do Poo ms@f.up.p
2 Popagao Faculdad d ghaa Sudg maal a good book o lcomagsm: Mcowav gg, Davd Poa, Addso-Wsl Fld ad Wav lcomagcs, Davd K. Chg, Addso-Wsl aspacs of lcus poblms o cdc, wavguds ad asmsso ls hp://pagas.f.up.p/~ms// 89 Icdc
3 fohcomg lcus Faculdad d ghaa lcomagc Wavs Pla wav cdc oda Wavguds wk Tasmsso Ls 6/ ad / Radao 89 Icdc
4 Pla wav cdc Faculdad d ghaa Cos omal cdc flco ad asmsso coffcs saoa wav fac wh pfc coduco mulpl facs oblqu cdc ppdcula ad paalll polaaos flco ad asmsso coffcs fac wh pfc coduco oal al flco 89 Icdc 4
5 Mall s quaos losslss mda Faculdad d ghaa H µ H ε H H ε µ lcc fld magc fld dlcc pmv magc pmabl ( ε ε ε ) ( µ ) µ µ 8 µ ε c m/s ε µ H ε µ H wav quaos losslss mda 89 Icdc 5
6 Pla lcomagc wavs mpoal pssos Faculdad d ghaa Pla wav losslss mda lal polad alog popagag alog No: h a soluos of wav quaos losslss mda cos( ω k)ˆ v f s h amplud ( ω πf ) ω s h agula fquc k ω µε s h wavumb k s h phas vloc µ ε π λ cosω ( ) f cos( k) λ cosω ( k) T / dco of popagao 89 Icdc 6
7 Hlmhol s quaos Faculdad d ghaa wav quaos ε µ H H ε µ phaso oao: ( ) X cos( ω φ) phaso s X X jφ Hlmhol s quaos k H k ( k ω µε ) H No: { } j ( ) ( ω φ R X ) R { X } jω phaso of d( ) d s jωx mpoa θ j ( θ ) ( θ ) cos j s 89 Icdc 7
8 Pla lcomagc wavs phaso oao Faculdad d ghaa Pla wavs losslss mda jkaˆ jkaˆ H pˆ H pˆ h wav popagag alog h â k ω µε s h wavumb dco pˆ ad pˆ h dca h polaao dco No: h polaao dco of h lcomagc wav s dfd b h polaao dco of h lcc fld 89 Icdc 8
9 Pla lcomagc wavs phasos Faculdad d ghaa No: H ˆ aˆ ( a ) ( H ) ε µ Ω s h sc mpdac of h mdum lcc ad magc flds a ppdcula o ach oh ad o h dco of popagao asvs lcomagc (TM) wav 89 Icdc 9
10 Pla lcomagc wavs phasos Faculdad d ghaa ampl jkaˆ pˆ jkaˆ H ph H ˆ H ˆ ˆ ( a ) ( a H ) W h lcc ad magc fld phasos of a GH TM wav popagag alog h dco f spac. Th wav s lal polad alog h dco ad h lcc fld amplud s V/m V/m ˆ ˆ p aˆ ˆ ˆ ˆ ˆ π f k ω µ ε π ad/m c jπ ˆ V/m µ π ε H Ω j π ( aˆ ) ˆ A/m π 89 Icdc
11 Pla lcomagc wavs phasos Faculdad d ghaa ampl jkaˆ pˆ jkaˆ H ph H ˆ H ˆ ˆ ( a ) ( a H ) Th lcc fld phaso of a TM wav popagag a omagc mdum wh dlcc j 4π ( 4 ) cosa 4 s gv b ˆ V/m Fd h fqucof h wav ad oba h magc fld phaso. kaˆ 4π ( 4) ˆ ˆ ˆ kaˆ 4π ( ˆ 4ˆ) ˆ a k 4π 4 π m 4π (ˆ 4ˆ) aˆ.6 ˆ.8ˆ π 5.º 89 Icdc
12 Pla lcomagc wavs phasos Faculdad d ghaa ampl jkaˆ pˆ jkaˆ H ph H ˆ H ˆ ˆ ( a ) ( a H ) Th lcc fld phaso of a TM wav popagag a omagc mdum wh dlcc j 4π ( 4 ) cosa 4 s gv b ˆ V/m Fd h fqucof h wav ad oba h magc fld phaso. k ω µ ε ω µ ε k π m µ ε π f c f.5 GH ε 4, µ ˆ.6ˆ.8ˆ a µ µ µ 6π ε ε ε Ω H π j4π ( 4) (.8ˆ.6ˆ) A/m 89 Icdc
13 Icdc of a TM wav a a pla bouda Faculdad d ghaa flcd â agl of cdc θ asmd pla of cdc pla â θ θ θ pla coag h omal o h bouda sufac ad h vco dcag h dco of popagao of h cd wav â cd mdum ( ε, µ σ ), mdum ( ε, µ σ ), dcos of popagao: aˆ aˆ aˆ s θ ˆ s θ s θ ˆ ˆ ˆ ˆ ˆ 89 Icdc
14 Sll s laws law of flco Faculdad d ghaa wavfo go wh cosa phas â / O pla wavs wavfos a ppdcula o â / A pos O ad A hav h sam phas A B â / / pos O ad A hav h sam phas θ θ O θ phas k ds. / / AO koa k â mdum ε, µ σ ( ), mdum ε, µ σ ( ), / / OO sθ OO sθ θ θ ω kω µε v f 89 Icdc 4
15 Sll s laws law of faco Faculdad d ghaa pla wavs wavfos a ppdcula o â â / A / O pos O ad A hav h sam phas / pos O ad B hav h sam phas A B â phas k ds. θ θ / k AO k OB θ O / OO k sθ k OO sθ / â mdum ( ε, µ σ ), mdum ( ε, µ σ ), sθ sθ k k v v f f ω kω µε v f 89 Icdc 5
16 Id of faco Faculdad d ghaa Id of faco ao of h spd of lgh f spac o ha h mdum lag low spd c v f : losslss mda µ ε vf µ ε µ ε µ ε sθ s θ v v f f sθ sθ Sll s law of faco 89 Icdc 6
17 Bouda codos Faculdad d ghaa ( ) ( H H ) J S ( D D ) ρs ( B B ) aˆ aˆ aˆ aˆ,a,a B,om B,om â l b h omal o h fac pog fom mdum o mdum â mdum ( ε, µ σ ), mdum ( ε, µ σ ), a B om couos Ha couos f J S Dom couos f ρ S couos No: J S ad ρ ol dal coducos S 89 Icdc 7
18 Bouda codos dal coducos Faculdad d ghaa Idal coducos σ û mdum ( ε, µ σ ), sk dph δ π f µσ mdum ( ε, µ σ ), D cod cod H B cod cod J S ρ S ampl σ J ρ S S aˆ ˆ a ( H H ) ( D D ) aˆ H H ˆ D D,aaˆ a,omaˆ 89 Icdc 8
19 Nomal cdc Faculdad d ghaa omal cdc θ θ θ s s θ θ θ θ mdum mdum â H H â cd flcd H H jk ˆ jk jk ˆ ˆ jk ˆ mdum ( jk jk )ˆ H H H jk jk ˆ H â asmd H jk ˆ jk ˆ mdum 89 Icdc 9
20 89 Icdc Faculdad d ghaa Nomal cdc flco ad asmsso coffcs bouda codos mdum mdum â H H â â H couous a couous a H ( ) f J S ( ) jk jk ˆ H jk jk ˆ mdum mdum jk ˆ H jk ˆ a H H
21 Nomal cdc flco ad asmsso coffcs Faculdad d ghaa Γ τ flco coffc asmsso coffc â H H â H â No mdum mdum. Γ τ. Γ. τ 4. jk jk ( Γ )ˆ τ jk ˆ mdum ( jk jk )ˆ H jk jk ˆ mdum H jk ˆ jk ˆ 89 Icdc
22 Nomal cdc saoa wav Faculdad d ghaa jk jk ( Γ )ˆ Γ τ τ jk jk [( Γ) Γ ]ˆ â H H â τ jk Γ jk ( jk )ˆ ˆ H â s ( ) j j mdum Γ mdum τ τ jk ˆ j s ( k )ˆ Γ popagag wav saoa wav 89 Icdc
23 Nomal cdc mama ad mma Faculdad d ghaa jk jk ( Γ )ˆ jk j k ( Γ )ˆ Γ Γ jθγ â H H â [ Γ cos( θ k ) ] ( Γ s ( k ) ) Γ θ Γ ( θ k ) Γ Γ cos Γ H â mdum mdum Γ τ jk ˆ j s ( k )ˆ τ Γ mama: mma: cos θγ k m θγ ( ) π k Γ ( θ Γ k ) ( ) ( θ π ) [ ] cos MAX Γ k ( Γ ) ( ) m MAX 89 Icdc
24 Nomal cdc cdc o dal coduco Faculdad d ghaa f mdum s losslss ( σ ) jk jk ( Γ )ˆ f mdum s dal coduco ( σ ) Γ τ â H H â o popagag wav, ol saoa wav jk jk ( )ˆ j s ( k )ˆ H â mdum Γ τ mdum µ ε σ j ωε mama: MAX ( )π k ad MAX mma: m π k ad m 89 Icdc 4
25 Avag pow cad b lcomagc wav Faculdad d ghaa avag pow cad b h wav acoss sufac A: P av S da A av S av R { H } * avag Pog s vco da daˆ ppdcula o sufac A ad wh fsmal absolu valu da A 89 Icdc 5
26 Avag Pog s vco fo TM wavs Faculdad d ghaa TM wavs H aˆ H ˆ a A ( B C) ( A C) B C( A B) ( aˆ ) * H * * {( ) aˆ ( ˆ )} * a * aˆ * S av R * aˆ S av R { H } * avag Pog s vco pos alog h popagao dco 89 Icdc 6
27 Avag pow fo TM wavs losslss mda Faculdad d ghaa TM wavs losslss mda H aˆ ˆ H a jkaˆ pˆ s al S md R * aˆ S av aˆ ( W/m ) P av S da A av L A b h sufac ppdcula o h popagag dco da da aˆ P av S av A ( W) P av o A ( W) S av s cosa 89 Icdc 7
28 Avag cd, flcd ad asmd pow Faculdad d ghaa P P av, av, o o A A P P av, av, Γ â H H â P av, o A P P P av, av, av, P P P P av, av, av, av, τ Γ mpoa H P av mdum S da A av â Γ mdum τ S av A Γ τ o A 89 Icdc 8
29 Nomal cdc mulpl facs Faculdad d ghaa mdum mdum mdum o M M M. mda ad f. jk ˆ all wavs a lal polad alog d flco ad asmsso coffcs: fac : fac : fac : Γ Γ Γ Γ ad ad ad τ τ τ 89 Icdc 9
30 Nomal cdc mulpl facs Faculdad d ghaa mdum mdum d mdum jk ( ) ( τ ) jk d τ ( jk τ ) τ τ jk d jk ( d ) Γ jk ( ) Γ τ Γ τ jk d jk jkd ( Γτ ) jkd jk ( d ) Γ τ Γ Γ τ jk d jk jkd jk( d ) τ Γ Γ τ τ ΓΓτ j4k d jk jkd jk( d ) Γ Γ τ Γ Γ τ j4k d jk j5kd jk( d ) τ Γ Γ τ j5kd jk( d ) Γ Γ τ M M M 89 Icdc
31 Nomal cdc mulpl facs Faculdad d ghaa mdum mdum mdum mdum mdum mdum jk jk jk M M M jk jk d d jkd j4k d j6k d τ Γ τ Γ τ τ Γ Γ τ τ Γ Γ L Γ jk d jkd j k d ( Γ Γ Γ Γ L) τ τ Γ 4 Γ τ τ Γ jk d jkd ( Γ Γ ) jk d τ τγ Γ jkd ΓΓ Γ Γ Γ Γ jk d jk d 89 Icdc
32 Nomal cdc mulpl facs Faculdad d ghaa mdum mdum mdum mdum mdum mdum jk jk jk M M M jk jk d d jkd jk d jk d jk d j5k d jk d j7k d jk d τ τ τ τ Γ Γ τ τ Γ Γ τ τ Γ Γ L τ j τ ( k k) d jkd j4kd j6k d ( Γ Γ Γ Γ Γ Γ L) τ τ ( kk) d jkd ( Γ Γ ) j τ ( k k ) j d τ jkd Γ Γ 89 Icdc
33 89 Icdc Faculdad d ghaa Nomal cdc a mulpl facs alav appoach mdum mdum mdum d M M M mdum mdum mdum d ( ) H jk jk jk jk ˆ ˆ mdum jk jk jk jk jk ( ) H jk jk jk jk ˆ ˆ mdum H jk jk ˆ ˆ mdum
34 Mulpl facs bouda codos Faculdad d ghaa dlcc mda J S a H a couous couous mdum mdum mdum d d jk d jk d jk d jk d jk d jk d 4 quaos 4 ukows (,, ), assumg 89 Icdc 4
35 89 Icdc 5 Faculdad d ghaa Mulpl facs bouda codos mdum mdum mdum d d jk d jk d jk d jk d jk d jk d k j d k j Γ Γ Γ Γ ( ) d k j d k k j Γ Γ τ τ pvous pssos, as pcd
36 Mulpl facs ampls Faculdad d ghaa mdum mdum mdum lmao of flcos a fac b sg mdum mdum s a machg dvc d ampls lmaos of fls lss Auao of ada chos (vsbl aplas) 89 Icdc 6
37 Mulpl facs l/4 asfom Faculdad d ghaa lma flcos jkd Γ Γ mdum mdum mdum jkd jkd jkd ( ) ( )( ) ( ) d l/4 asfom : jk d k d mπ, m odd g Γ Γ Γ Γ τ Γ jk d jk d ( k k ) j d τ jkd Γ wavlgh mdum d m λ, odd 4 m g 89 Icdc 7
38 l/4 asfom dff wavlgh Faculdad d ghaa Γ Γ Γ Γ Γ mdum mdum mdum f p dsg fquc λ, p v f p vloc mdum d v d 4 jkd ( ) fquc f Γ Γ jk d f p Γ Γ Γ Γ τ Γ jk d jk d ( k k ) j d τ jkd Γ * P P f c Γ Γ 4 ( cos( kd )) Γ cos( k d) F cos F cos δ δ wh Γ F Γ π δ k d f f p 89 Icdc 8
39 l/4 asfom dff wavlgh Faculdad d ghaa P P f c F cos δ F cos δ wh F Γ Γ ad π δ f f p mdum mdum mdum Γ F f δ Γ F f δ d P P f c F F F F π π 5π δ 89 Icdc 9
40 Poblm Faculdad d ghaa fomula No: coduco 89 Icdc 4
41 Poblm Faculdad d ghaa A pla lcomagc wav wh h followg lcc fld phaso popagas a ad s cd omall o a fac a wh a omagc mdum wh facv d ha occups h go >. Fd j4π ˆ ( V/m) a) h flco ad asmsso coffcs; b) h lcc fld phasos of h flcd ad asmd wavs; c) h avag Pogvcos of h cd, flcd ad asmd wavs; d) h faco of cd pow ha s asmd o mdum. fomula 89 Icdc 4
42 Poblm Faculdad d ghaa fomula P P f c F cos δ F cos δ F Γ Γ π δ f f p 89 Icdc 4
43 Oblqu cdc of a TM wav a a pla bouda Faculdad d ghaa TM wav H aˆ. omal o pla of cdc ad H a pla â flcd θ â asmd â θ jk aˆ ˆ ppdcula polaao θ â. paalllo pla of cdc jk aˆ ( ˆ s ˆ ) θ paalll polaao cd mdum ε, µ σ ( ), mdum ε, µ σ ( ), Gal cas: jk aˆ a ( ) jk ˆ ˆ s ˆ ˆ θ,, paalll polaao ppdcula polaao 89 Icdc 4
44 Ppdcula ad paalll polaaos covo ppdcula polaao paalll polaao Faculdad d ghaa â H â â H â θ θ θ H θ θ θ H â â H H mdum mdum mdum mdum Compos of, paalll o h fac kp h dco 89 Icdc 44
45 Ppdcula polaao lcc ad magc flds Faculdad d ghaa cd aˆ s θ ˆ ˆ jkaˆ ˆ H aˆ flcd aˆ s θ ˆ jkaˆ ˆ H aˆ jkaˆ θ ( s θ ˆ cos ) ˆ ˆ s θ ˆ ˆ jkaˆ θ ( s θ ˆ cos ) ˆ â â H θ θ H θ H â asmd mdum mdum aˆ s θ ˆ ˆ jkaˆ ˆ H aˆ jkaˆ θ ( s θ ˆ cos ) ˆ laoshps bw ad obad fom bouda codos, 89 Icdc 45
46 Ppdcula polaao lcc ad magc flds Faculdad d ghaa bouda codos a couous H a couous ( f J S ) â H â a θ θ θ H H H H â jksθ jk sθ jk sθ jk sθ jk sθ cos θ jk sθ H mdum mdum k sθ k sθ ( ) 89 Icdc 46
47 Ppdcula polaao flco ad asmsso coffcs ( ) â H Faculdad d ghaa â θ θ θ H â H mdum mdum Γ τ flco coffc asmsso coffc 89 Icdc 47
48 Ppdcula polaao flco ad asmsso coffcs Γ τ flco coffc asmsso coffc â H Faculdad d ghaa â o θ θ θ H. Γ τ (as omal cdc) â. s possbl ha Γ (Bws s agl) θ θ B H s θ s θ mdum mdum s θ B µ ε ( µ µ ) µ ε ol wh µ µ. f mdum s dal coduco, Γ τ 89 Icdc 48
49 lcc fld mdum ppdcula polaao Faculdad d ghaa jk aˆ ˆ jk aˆ ˆ â H â Γ τ aˆ s θ aˆ s θ θ θ θ H jk jk jk sθ [( τ Γ ) Γ ] ˆ â τ jk jk jks ( ) ˆ jk aˆ θ ˆ Γ H τ jk aˆ θ ˆ jγ s jks ( k ) ˆ mdum mdum wav popagag alog â wav popagag alog, wh dpd amplud 89 Icdc 49
50 Mama ad mma mdum ppdcula polaao jk aˆ ˆ aˆ aˆ jk aˆ s θ s θ ˆ â H Faculdad d ghaa â j ( ksθ k ) ( jk Γ ) ˆ Γ Γ jθ Γ θ θ θ H [ Γ cos( θ k ) ] Γ s( θ k θ ) [ ] Γ Γ cos Γ Γ cos Γ ( θ k ) â H mdum mdum mama: k ( θ π ) MAX Γ mma: Γ k [ θ ( ) π ] m ( ) ( Γ ) MAX Γ m 89 Icdc 5
51 Icdc o dal coduco ppdcula polaao Faculdad d ghaa If mdum s dal coduco Γ τ â H jk jk cos ( )ˆ jk sθ θ θ θ jk sθ j s( k )ˆ â wav popagag alog, wh dpd amplud H mdum dal coduco mama: ( ) π MAX k MAX mma: π m k m 89 Icdc 5
52 Paalll polaao lcc ad magc flds Faculdad d ghaa cd aˆ s θ ˆ ˆ jk aˆ ˆ s jkaˆ H ˆ flcd aˆ H s θ ( ˆ ) θ ˆ jk aˆ ˆ jk aˆ ˆ s θ ˆ ˆ ( ˆ s ˆ ) θ â H H θ θ â θ H â asmd mdum mdum aˆ s θ ˆ ˆ jkaˆ ( ˆ s θ ˆ ) laoshps bw, ad jkaˆ H ˆ obad fom bouda codos 89 Icdc 5
53 Paalll polaao lcc ad magc flds Faculdad d ghaa bouda codos a couous H a couous ( f J S ) â â H H â â a H H H θ θ θ θ θ θ H H â â jk sθ jk sθ cos θ jk sθ H jk sθ jk sθ jk sθ H mo mdum mo mdum k s θ k sθ ( ) ( ) 89 Icdc 5
54 Paalll polaao flco ad asmsso coffcs Faculdad d ghaa ( ) ( ) â H â θ θ H θ H â mdum mdum Γ τ flco coffc asmsso coffc 89 Icdc 54
55 Paalll polaao flco ad asmsso coffcs Faculdad d ghaa Γ τ flco coffc asmsso coffc â H θ θ H â o θ. Γ τ â. s possbl ha Γ H (Bws s agl) θ θ B s θ s θ mdum mdum s θ B µ ε ( ε ε ) µ ε wh µ µ s θ B ( ε ε ). If mdum s dal coduco, Γ τ 89 Icdc 55
56 lcc fld mdum paalll polaao Faculdad d ghaa jk τ Γ aˆ jkaˆ ( ˆ s θ ˆ ) ( cos ˆ s ˆ θ ) jk aˆ ( ˆ s θ ˆ ) θ jk aˆ a ( ˆ ) jk ˆ s θ ˆ Γ ( ˆ s θ ˆ ) â H θ θ θ H â Γ τ â τ Γ Γ jk sθ jk sθ jk aˆ ( ˆ s θ ˆ ) jk jk ( ) ˆ jk jk ( ) s θ ˆ H mdum mdum τ jγ jk aˆ jk sθ s ( ˆ s θ ˆ ) ( k ) ˆ Γ jk sθ cos ( k ) s θ ˆ 89 Icdc 56
57 lcc fld mdum paalll polaao Faculdad d ghaa wav popagag alog â â H â jk aˆ τ ( ˆ s ) θ ˆ θ θ θ H jk sθ jγ s ( k ) cos ˆ θ â jk sθ Γ cos ( k ) s ˆ θ H mdum mdum wavs popagag alog, wh dpd ampluds 89 Icdc 57
58 Mama ad mma mdum paalll polaao Faculdad d ghaa jk aˆ jkaˆ ( cos ˆ s ˆ ) ( cos ˆ s ˆ ) θ θ θ θ a ( ) ( ) jk jk j a a a jk βˆ ˆ ˆ ˆ ˆ s θ ˆ â H â jk aˆ jk aˆ jk ( aˆ aˆ ) ( Γ ) jk ( ) Γ θ θ θ H Γ Γ jθ Γ â [ Γ cos( θγ k ) ] Γ s ( θ k θ ) [ ] Γ cos H ( θ k ) Γ Γ cos Γ mdum mdum mama: k mma: ( θγ π ) [ θγ ( ) π ] MAX m k ( Γ ) ( Γ ) MAX m 89 Icdc 58
59 Icdc o dal coduco paalll polaao Faculdad d ghaa f mdum s dal coduco Γ τ â H j a [( ) ( ) ] jk jk a a jk a jk ˆ ˆ ˆ ˆ ˆ s θ ˆ jk sθ jk sθ cos ( k ) ( k ) s θ ˆ s ˆ â θ θ H wavs popagag alog, wh dpd ampluds mdum dal coduco mama of : MAX ( ) k π mma of : m π k MAX m 89 Icdc 59
60 Mallc wavguds jksθ : j s ( k )ˆ : j jk sθ jksθ s cos ( k ) ( k ) s θ ˆ ˆ Faculdad d ghaa ppdcula polaao: paalll polaao: a a π k π k θ θ mdum dal coduco fo boh polaaos, a coducg pla paalll π o h pla could b sd a k whou modfg lcc fld mdum π k 89 Icdc 6
61 Mallc wavguds Faculdad d ghaa lcomagc wav s gudd b h wo coducg sufacs mallc wavgud could b possbl o gud a lcomagc wav wh ol dlcc mda? θ θ mdum dal coduco β π 89 Icdc 6
62 Dlcc wavguds Faculdad d ghaa gal cas: ach cdc pa of h wav s asmd o dlcc dlcc dlcc dlcc af som dsac, h lcomagc wav mdum s cosdabl auad gall, dlcc mda do gud lcomagc wavs ffcl θ θ h soluo would b o hav o g asmd o mdum s hs possbl? 89 Icdc 6
63 Toal al flco Faculdad d ghaa Sll s law of faco: s θ sθ â flcd â asmd > θ > θ θ θ Ccal agl: θ c θ such ha θ 9º θ c acs θ â cd θ θ c o asmd wav o mdum mdum mdum Toal al flco s θ s θc s θ ± s θ ± j s θ s θ 89 Icdc 6
64 Toal al flco Faculdad d ghaa Toal al flco: s θ ± j s θ â flcd â asmd θ Losslss ad omagc mda: µ ε θ θ µ ε ε â Rflco coffcs: cd mdum mdum Γ Γ Γ Γ Γ cos cos θ m j ( ) s θ ± j ( ) s θ Γ θ ± j ( ) s θ ± j ( ) s θ Γ Γ 89 Icdc 64
65 Toal al flco vasc wavs Faculdad d ghaa spaal vaao of flds mdum : jk aˆ â flcd â asmd aˆ s θ ˆ ˆ θ θ jk ( sθ ) θ ± j s θ â cd mdum mdum k s jk θ sθ wav popagag alog amplud dcasg poall wh vasc flds 89 Icdc 65
66 Poblm Faculdad d ghaa Th lcc fld of a ufom pla wav popagag a s gv b jπ (4 ) ˆ. Ths wav s cd o a fac wh a dlcc mdum wh facv d ha occups h go >. Fd (a) (b) (c) (d) () h dco of popagao of h cd wav ad h agl of cdc; h magc fld phaso of h cd wav; h popagao dcos of h flcd ad asmd wavs. h lcc fld phasos of h flcd ad asmd wavs h faco of h cd pow ha s asmd o h dlcc fomula 89 Icdc 66
67 Poblm Faculdad d ghaa fomula 89 Icdc 67
68 Poblm Faculdad d ghaa fomula Losslss mda: 89 Icdc 68
Reflection & Transmission
Rflc & Tasmss 4 D. Ray Kw Rflc & Tasmss - D. Ray Kw Gmc Opcs (M wavs flc fac - asmss cdc.. Sll s Law: s s 3. Ccal agl: s c / 4. Tal flc wh > c ly f > Rflc & Tasmss - D. Ray Kw Pla Wav λ wavfs λ λ. < ;
ECE 222b Applied Electromagnetics Notes Set 3b
C b Appl lcomancs Nos S 3b Insuco: Pof. Val Loman Dpamn of lccal an Compu nnn Unvs of Calfona San Do Rflcon an Tansmsson. Nomal ncnc T R T R Fs fn h manc fls: 3 Rflcon an Tansmsson T R T R T R T R R T
LAPLACE TRANSFORM TABLE
LAPLACE TRANSFORM TABLE Th Laplac afom of am mpl fuco a gv h Tabl. Fuco U mpul U Sp U Ramp Expoal Rpad Roo S Co Polyomal Dampd Dampd co f δ u -a -a co,,... -a -a co F / / /a /a / /!/ /a a/a Thom : Shf
George S. A. Shaker ECE477 Understanding Reflections in Media. Reflection in Media
Geoge S. A. Shake C477 Udesadg Reflecos Meda Refleco Meda Ths hadou ages a smplfed appoach o udesad eflecos meda. As a sude C477, you ae o equed o kow hese seps by hea. I s jus o make you udesad how some
ECE 222b Applied Electromagnetics Notes Set 3a
C b lid lcomagnics Nos S 3a Insuco: Pof. Viali Lomakin Damn of lcical and Comu ngining Univsi of Califonia San Digo Unifom Plan Wavs Consid Mawll s quaions: In a losslss mdium ε and µ a al and σ : Sinc
Linear electro-optic effect:
EE6.4686.568 Elcto-optcs Elcto-optc optc ffct: D ρ, B E, t B, D H j, t D ε E P εe K ffct 3 P ε χ E χ E χ E 3..., La lcto-optc ffct: ε ε χ χ E ε E jk, j j jk k k Pockls ffct Wh o E appld, ε ε ε ε x ε 33
i i (3) Derive the fixed-point iteration algorithm and apply it to the data of Example 1.
Howor#3 urvval Aalyss Na: Huag Xw 黃昕蔚 Quso: uppos ha daa ( follow h odl ( ( > ad <
UNIVERSITÀ DEGLI STUDI DI BOLOGNA. DIPARTIMENTO DI INGEGNERIA ELETTRICA Viale Risorgimento n BOLOGNA (ITALIA) FOR THE CURRENT DISTRIBUTION
UVERSÀ DEG SUD D BOOGA DPAREO D GEGERA EERCA Vl Rogo - 36 BOOGA (AA AAYCA SOUOS FOR HE CURRE DSRBUO A RUHERFORD CABE WH SRADS. F. Bch Ac h gocl o of h ol co coffc og h of Rhfo cl vg. h olo fo h gl l c
Chapter 1 Fundamentals in Elasticity
D. of o. NU Fs s ν ss L. Pof. H L ://s.s.. D. of o. NU. Po Dfo ν Ps s - Do o - M os - o oos : o o w Uows o: - ss - - Ds W ows s o qos o so s os. w ows o fo s o oos s os of o os. W w o s s ss: - ss - -
Chapter 4 : Linear Wire Antenna
Chapt 4 : Lina Wi Antnna nfinitsima Dipo Sma Dipo Finit Lngth Dipo Haf-Wavngth Dipo Lina mnts na o on nfinit Pfct Conductos nfinitsima Dipo Lngth
Reflection Models. Reflection Models
Reflecon Models Today Types of eflecon models The BRDF and eflecance The eflecon equaon Ideal eflecon and efacon Fesnel effec Ideal dffuse Thusday Glossy and specula eflecon models Rough sufaces and mcofaces
ELE 3310 Tutorial 11. Reflection of plane waves Wave impedance of the total field
L 0 Tuto Rfcton of pn wvs Wv mpdnc of th tot fd Rfcton of M wvs Rfcton tks pc whn n M wv hts on bound. Pt of th wv gts fctd, nd pt of t gts tnsmttd. Popgton dctons nd mptuds of th fctd nd tnsmttd wvs dpnd
.. ntsets ofa.. d ffeom.. orp ism.. na s.. m ooth.. man iod period I n open square. n t s e t s ofa \quad d ffeom \quad orp ism \quad na s \quad m o
G G - - -- - W - - - R S - q k RS ˆ W q q k M G W R S L [ RS - q k M S 4 R q k S [ RS [ M L ˆ L [M O S 4] L ˆ ˆ L ˆ [ M ˆ S 4 ] ˆ - O - ˆ q k ˆ RS q k q k M - j [ RS ] [ M - j - L ˆ ˆ ˆ O ˆ [ RS ] [ M
Physics 401 Final Exam Cheat Sheet, 17 April t = 0 = 1 c 2 ε 0. = 4π 10 7 c = SI (mks) units. = SI (mks) units H + M
Maxwell' s Equations in vauum E ρ ε Physis 4 Final Exam Cheat Sheet, 7 Apil E B t B Loent Foe Law: F q E + v B B µ J + µ ε E t Consevation of hage: J + ρ t µ ε ε 8.85 µ 4π 7 3. 8 SI ms) units q eleton.6
W τ R W j N H = 2 F obj b q N F aug F obj b q Ψ F aug Ψ ( ) ϱ t + + p = 0 = 0 Ω f = Γ Γ b ϱ = (, t) = (, t) Ω f Γ b ( ) ϱ t + + p = V max 4 3 2 1 0-1 -2-3 -4-4 -3-2 -1 0 1 2 3 4 x 4 x 1 V mn V max
!"!# ""$ %%"" %$" &" %" "!'! " #$!
" "" %%"" %" &" %" " " " % ((((( ((( ((((( " %%%% & ) * ((( "* ( + ) (((( (, (() (((((* ( - )((((( )((((((& + )(((((((((( +. ) ) /(((( +( ),(, ((((((( +, 0 )/ (((((+ ++, ((((() & "( %%%%%%%%%%%%%%%%%%%(
!!" #7 $39 %" (07) ..,..,.. $ 39. ) :. :, «(», «%», «%», «%» «%». & ,. ). & :..,. '.. ( () #*. );..,..'. + (# ).
1 00 3 !!" 344#7 $39 %" 6181001 63(07) & : ' ( () #* ); ' + (# ) $ 39 ) : : 00 %" 6181001 63(07)!!" 344#7 «(» «%» «%» «%» «%» & ) 4 )&-%/0 +- «)» * «1» «1» «)» ) «(» «%» «%» + ) 30 «%» «%» )1+ / + : +3
Errata Sheet. 2 k. r 2. ts t. t t ... cos n W. cos nx W. W n x. Page Location Error Correction 2 Eq. (1.3) q dt. W/m K. 100 Last but 6 2.
Eaa S Pag can E Ccn Eq. (. q q k W/ K k W/ K A A 6 n as bu 6 s q lns s q T k T k Q.. Wall s aus n gvn Wall s aus a an C. 7 n, lf kc cs ( s sn kc cs ( s sn s f cs k sn cs k sn quan C ( s C ( s an ln 6 sn
webpage :
Amn Halloc Mah Ecss / 7 E-mal : amn@shhs bpag : shhs/amn MATH EXERCISES GRADIENT DIVERGENCE CURL DEL NABLA OERATOR LALACIAN OERATOR CONTINUITY AND NAVIER-STOKES EQUATIONS VECTOR RODUCTS I and hn scala
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
ITU-R P (2012/02) &' (
ITU-R P.530-4 (0/0) $ % " "#! &' ( P ITU-R P. 530-4 ii.. (IPR) (ITU-T/ITU-R/ISO/IEC).ITU-R http://www.itu.int/itu-r/go/patents/en. ITU-T/ITU-R/ISO/IEC (http://www.itu.int/publ/r-rec/en ) () ( ) BO BR BS
General theorems of Optical Imaging systems
Gnral thorms of Optcal Imagng sstms Tratonal Optcal Imagng Topcs Imagng qualt harp: mags a pont sourc to a pont Dstorton fr: mags a shap to a smlar shap tgmatc Imagng Imags a pont sourc to a nfntl sharp
C 1 D 1. AB = a, AD = b, AA1 = c. a, b, c : (1) AC 1 ; : (1) AB + BC + CC1, AC 1 = BC = AD, CC1 = AA 1, AC 1 = a + b + c. (2) BD 1 = BD + DD 1,
1 1., BD 1 B 1 1 D 1, E F B 1 D 1. B = a, D = b, 1 = c. a, b, c : (1) 1 ; () BD 1 ; () F; D 1 F 1 (4) EF. : (1) B = D, D c b 1 E a B 1 1 = 1, B1 1 = B + B + 1, 1 = a + b + c. () BD 1 = BD + DD 1, BD =
= 0.927rad, t = 1.16ms
P 9. [a] ω = 2πf = 800rad/s, f = ω 2π = 27.32Hz [b] T = /f = 7.85ms [c] I m = 25mA [d] i(0) = 25cos(36.87 ) = 00mA [e] φ = 36.87 ; φ = 36.87 (2π) = 0.6435 rad 360 [f] i = 0 when 800t + 36.87 = 90. Now
2?nom. Bacc. 2 nom. acc. S <u. >nom. 7acc. acc >nom < <
K+P K+P PK+ K+P - _+ l Š N K - - a\ Q4 Q + hz - I 4 - _+.P k - G H... /.4 h i j j - 4 _Q &\\ \\ ` J K aa\ `- c -+ _Q K J K -. P.. F H H - H - _+ 4 K4 \\ F &&. P H.4 Q+ 4 G H J + I K/4 &&& && F : ( -+..
2013/2012. m' Z (C) : V= (E): (C) :3,24 m/s. (A) : T= (1-z).g. (D) :4,54 m/s
( ) 03/0 - o l P z o M l =.P S. ( ) m' Z l=m m=kg m =,5Kg g=0/kg : : : : Q. (A) : V= (B) : V= () : V= (D) : V= (): : V :Q. (A) :4m/s (B) :0,4 m/s () :5m/s (D) :0,5m/s (): : M T : Q.3 (A) : T=(-z).g (B)
! " #! $ %&! '( #)!' * +#, " -! %&! "!! ! " #$ % # " &' &'... ()* ( +, # ' -. + &', - + &' / # ' -. + &' (, % # , 2**.
! " #! $ %&! '( #)!' * +#, " -! %&! "!!! " #$ % # " &' &'... ()* ( +, # ' -. + &', - + &' / 0123 4 # ' -. + &' (, % #. -5 0126, 2**., 2, + &' %., 0, $!, 3,. 7 8 ', $$, 9, # / 3:*,*2;
! "# $ % $&'& () *+ (,-. / 0 1(,21(,*) (3 4 5 "$ 6, ::: ;"<$& = = 7 + > + 5 $?"# 46(A *( / A 6 ( 1,*1 B"',CD77E *+ *),*,*) F? $G'& 0/ (,.
! " #$%&'()' *('+$,&'-. /0 1$23(/%/4. 1$)('%%'($( )/,)$5)/6%6 7$85,-9$(- /0 :/986-$, ;2'$(2$ 1'$-/-$)('')5( /&5&-/ 5(< =(4'($$,'(4 1$%$2/996('25-'/(& ;/0->5,$ 1'$-/%'')$(($/3?$%9'&-/?$( 5(< @6%-'9$
ΠΑΡΑΡΤΗΜΑ Ι AΠΑΝΤΗΣΕΙΣ ΚΕΦΑΛΑΙΟ 6. I z. nia 2 2 3/2. ni a 3/2 3/2. I,min. I,max. = 511 A/m, ( HII,max HII,min)/ HII,max. II,min.
ΠΑΡΑΡΤΗΜΑ Ι ΠΑΡΑΡΤΗΜΑ Ι AΠΑΝΤΗΣΕΙΣ ΚΕΦΑΛΑΙΟ 6 I 6/ ( + π) 4πa 6/ I nia + + / / ( a + ) a ( d ) ni a II a + ( d/ ) ai I a + ( d/) / / I,ma 75 A/m, I,min 676 A/m, ( I,ma I,min )/ I,ma,545 II,ma 75 A/m, II,min
webpage :
Amin Haliloic Mah Eciss E-mail : amin@shkhs wbpa : wwwshkhs/amin MATH EXERISES GRADIENT DIVERGENE URL DEL NABLA OERATOR LALAIAN OERATOR ONTINUITY AND NAVIER-STOKES EQUATIONS VETOR RODUTS I and hn scala
*❸341❸ ❸➈❽❻ ❸&❽❼➅❽❼❼➅➀*❶❹❻❸ ➅❽❹*➃❹➆❷❶*➈❹1➈. Pa X b P a µ b b a ➁❽❽❷➂➂%&'%➁❽➈❽)'%➁❽❽'*➂%➁❽➄,-➂%%%,❹❽➀➂'❹➄%,❹❽❹'&,➅❸%&❹-❽❻ ,❹❽➀➂'❹➄%,❹❽❹'&,➅❸%&❹-❽❻
*❸34❸ ➁❽❽❷➂➂%&'%➁❽➈❽)'%➁❽❽'*➂%➁❽➄,-➂%%%,❹❽➀➂'❹➄%,❹❽❹'&,➅❸%&❹-❽❻,❹❽➀➂'❹➄%,❹❽❹'&,➅❸%&❹-❽❻ -3*98❻➀*➁❽4❹❹** ~ N( µσ, )**σ **-❹➄❹8❹* µ*➆4❹➂➂*➁➆*❽➀➂❹➄*➂➂* *➁3 Pa ( < b) * ➀8*-9❼4➂❸*-❹❶➀➈-❸❸*-❽4&➄❹➈*➀8*-❹3➀9❼*8❽*-❽❼➄➂➀3*❸❽4&➄❹➈*❹➄❽3*➀&❼➄❽3❸❹*❻3➂
ΖΕΡΔΑΛΗΣ ΣΩΤΗΡΙΟΣ ΤΟ ΟΥΤΙ ΣΤΗ ΒΕΡΟΙΑ (1922-ΣΗΜΕΡΑ) ΘΕΣΣΑΛΟΝΙΚΗ 2005 1
(1922- ) 2005 1 2 .1.2 1.1.2-3 1.2.3-4 1.3.4-5 1.4.5-6 1.5.6-10.11 2.1 2.2 2.3 2.4.11-12.12-13.13.14 2.5 (CD).15-20.21.22 3 4 20.,,.,,.,.,,.,.. 1922., (= )., (25/10/2004), (16/5/2005), (26/1/2005) (7/2/2005),,,,.,..
The Multi-Soliton Solutions to The KdV Equation by Hirota Method
Progrss Appld Mhcs Vol. 8, o., 4, pp. -5 OI:.968/69 ISS 95-5X [Pr] ISS 95-58 [Ol].cscd..cscd.org Th Mul-Solo Soluos o Th KdV Equo y Hro Mhod MA L [],* [] pr of Mhcs Sccs, zhou Uvrsy, zhou, Ch. *Corrspodg
ITU-R P ITU-R P (ITU-R 204/3 ( )
1 ITU-R P.530-1 ITU-R P.530-1 (ITU-R 04/3 ) (007-005-001-1999-1997-1995-1994-199-1990-1986-198-1978)... ( ( ( 1 1. 1 : - - ) - ( 1 ITU-R P.530-1..... 6.3. :. ITU-R P.45 -. ITU-R P.619 -. ) (ITU-R P.55
V r,k j F k m N k+1 N k N k+1 H j n = 7 n = 16 Ṽ r ñ,ñ j Ṽ Ṽ j x / Ṽ W 2r V r D N T T 2r 2r N k F k N 2r Ω R 2 n Ω I n = { N: n} n N R 2 x R 2, I n Ω R 2 u R 2, I n x k+1 = x k + u k, u, x R 2,
Κεφάλαιο 2 Διαχείριση Σηµάτων σε Ψηφιακά Συστήµατα Ελέγχου
Κεφάλαιο 2 Διαχείριση Σηµάτων σε Ψηφιακά Συστήµατα Ελέγχου u Μετατροπή Αναλογικού Σήµατος σε Ψηφιακό (A/D Conversion) Ο µετασχηµατισµός Ζ u Μαθηµατική Ανάλυση της Διαδικασίας A/D Μετατροπή Ψηφιακού Σήµατος
Chapter 15 Identifying Failure & Repair Distributions
Chape 5 Idefyg Falue & Repa Dsbuos Paamee Esmao maxmum lkelhood esmao C. Ebelg, Io o Relably & Maaably Chape 5 Egeeg, d ed. Wavelad Pess, Ic. Copygh 00 Maxmum Lkelhood Esmao (MLE) Fd esmaes fo he dsbuo
Lifting Entry (continued)
ifting Entry (continued) Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion Planar state equations MARYAN 1 01 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu
!#$%!& '($) *#+,),# - '($) # -.!, '$%!%#$($) # - '& %#$/0#!#%! % '$%!%#$/0#!#%! % '#%3$-0 4 '$%3#-!#, '5&)!,#$-, '65!.#%
" #$%& '($) *#+,),# - '($) # -, '$% %#$($) # - '& %#$0##% % '$% %#$0##% % '1*2)$ '#%3$-0 4 '$%3#-#, '1*2)$ '#%3$-0 4 @ @ @
ΗΜ & Διάδοση ΗΜ Κυμάτων
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΗΜ & Διάδοση ΗΜ Κυμάτων Ενότητα : Κυματική Εξίσωση & Επίπεδο ΗΜ Κύμα Σαββαΐδης Στυλιανός Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ Υψίσυχνη θεωρητική υποδειγµατοποίηση ηλεκτρικών καλωδίων
) * +, -. + / - 0 1 2 3 4 5 6 7 8 9 6 : ; < 8 = 8 9 >? @ A 4 5 6 7 8 9 6 ; = B? @ : C B B D 9 E : F 9 C 6 < G 8 B A F A > < C 6 < B H 8 9 I 8 9 E ) * +, -. + / J - 0 1 2 3 J K 3 L M N L O / 1 L 3 O 2,
Κεφάλαιο 2 Διαχείριση Σηµάτων σε Ψηφιακά Συστήµατα Ελέγχου
Κεφάλαιο 2 Διαχείριση Σηµάτων σε Ψηφιακά Συστήµατα Ελέγχου u Μετατροπή Αναλογικού Σήµατος σε Ψηφιακό (A/D Conversion) Ο µετασχηµατισµός Ζ u Μαθηµατική Ανάλυση της Διαδικασίας A/D Μετατροπή Ψηφιακού Σήµατος
➆t r r 3 r st 40 Ω r t st 20 V t s. 3 t st U = U = U t s s t I = I + I
tr 3 P s tr r t t 0,5A s r t r r t s r r r r t st 220 V 3r 3 t r 3r r t r r t r r s e = I t = 0,5A 86400 s e = 43200As t r r r A = U e A = 220V 43200 As A = 9504000J r 1 kwh = 3,6MJ s 3,6MJ t 3r A = (9504000
... 5 A.. RS-232C ( ) RS-232C ( ) RS-232C-LK & RS-232C-MK RS-232C-JK & RS-232C-KK
RS-3C WIWM050 014.1.9 P1 :8... 1... 014.0.1 1 A... 014.0. 1... RS-3C()...01.08.03 A.. RS-3C()...01.08.03 3... RS-3C()... 003.11.5 4... RS-3C ()... 00.10.01 5... RS-3C().008.07.16 5 A.. RS-3C().0 1.08.
Fourier Series. Fourier Series
ECE 37 Z. Aliyazicioglu Elecrical & Compuer Egieerig Dep. Cal Poly Pomoa Periodic sigal is a fucio ha repeas iself every secods. x() x( ± ) : period of a fucio, : ieger,,3, x() 3 x() x() Periodic sigal
Teen Physique. 131 Luke Smith Lance Manibog Donail Nikooei 4 137
T hysq Fst Lst 20 Avo Vs 1 20 21 Rdy z 16 21 56 Ms Sz 8 56 67 Dy Gdy 15 67 82 Adw L 11 82 94 Do Csos 12 94 98 Jss Vs 6 98 103 Jss Mo 13 103 105 Dvd K 10 105 107 Jo By 9 107 112 Js Gtt 3 112 114 Ty MKy
( ) ΘΕ ΑΝ4 / 2 0. α) β) f(x) f ( x) cos x
Η ΑΝΕΠ Η Η Ν Ω Ν Ω ΑΘΗ Α ΑΝIV Ε ε ά ει Ν επ ε β ί 5 (3-9-5) Επώ : Ό α: ΑΝ Ν: ΘΕ ΑΝ Τα π α Chebyshev T ( ) α π ω μ ( ) y y y (,,, ) π [,] Η ω α α α π α μ / d d T ( ) Tm ( ) [ T ( )] Α απ f ( ) 3, [,], α
η η η η GAR = 1 F RR η F RR F AR F AR F RR η F RR F AR µ µ µ µ µ µ Γ R N=mxn W T X x mean X W T x g W P x = W T (x g x mean ) X = X x mean P x = W T X d P x P i, i = 1, 2..., G M s t t
Calculus and Differential Equations page 1 of 17 CALCULUS and DIFFERENTIAL EQUATIONS
alculus and Diffrnial Equaions pag of 7 ALULUS and DIFFERENTIAL EQUATIONS Th following 55 qusions concrn calculus and diffrnial quaions. In his vrsion of h am, h firs choic is always h corrc on. In h acual
Κεφάλαιο 3 Κίνηση σε 2 και 3 Διαστάσεις
Κεφάλαιο 3 Κίνηση σε και 3 Διαστάσεις Κίνηση υλικού σημείου στο επίπεδο ( -D) και στο χώρο (3 -D). Ορισμός διανυσμάτων για την μελέτη της -D 3-D κίνησης: Θέση, Μετατόπιση Μέση και στιγμιαία ταχύτητα Μέση
Original Lambda Lube-Free Roller Chain
ambda (ub-fr) llr Ca Orgal ambda ub-fr llr Ca ambda a rass prduvy ad savs my. du maa m. Elma prdu ama. du dwm. g lf ad lw maa ambda as us spal l-mprgad busgs prvd lubra ad prlg war lf. mb Tmpraur: 10 C
( ) ( ) ( ) ( ) ( ) λ = 1 + t t. θ = t ε t. Continuum Mechanics. Chapter 1. Description of Motion dt t. Chapter 2. Deformation and Strain
Continm Mechanics. Official Fom Chapte. Desciption of Motion χ (,) t χ (,) t (,) t χ (,) t t Chapte. Defomation an Stain s S X E X e i ij j i ij j F X X U F J T T T U U i j Uk U k E ( F F ) ( J J J J)
Microscopie photothermique et endommagement laser
Microscopie photothermique et endommagement laser Annelise During To cite this version: Annelise During. Microscopie photothermique et endommagement laser. Physique Atomique [physics.atom-ph]. Université
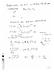Prblma dl smipian Cas i cs ω µ Cas sin cs i cs Cas fas [ ] [ ] ] [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ttal S S J L J J L A d I I A d I d I V d d V V d d V n J n J ˆ 0 ˆ ˆ ˆ 0 ˆ 0 ˆ ˆ ˆ 0 S S S S i i
Α Ρ Ι Θ Μ Ο Σ : 6.913
Α Ρ Ι Θ Μ Ο Σ : 6.913 ΠΡΑΞΗ ΚΑΤΑΘΕΣΗΣ ΟΡΩΝ ΔΙΑΓΩΝΙΣΜΟΥ Σ τ η ν Π ά τ ρ α σ ή μ ε ρ α σ τ ι ς δ ε κ α τ έ σ σ ε ρ ι ς ( 1 4 ) τ ο υ μ ή ν α Ο κ τ ω β ρ ί ο υ, η μ έ ρ α Τ ε τ ά ρ τ η, τ ο υ έ τ ο υ ς δ
ΚΕΦΑΛΑΙΟ 11 ΕΠΙΠΕ Ο ΚΥΜΑ
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ ΕΠΙΠΕ Ο ΚΥΜΑ. Η λύση της µονοδιάστατης εξίσωσης κύµατος Ιδιαίτερο θεωρητικό αλλά πρακτικό ενδιαφέρον εµφανίζει η περίπτωση ενός ο- µοιόµορφου επίπεδου ηλεκτροµαγνητικού κύµατος που διαδίδεται
! " # $ % & $ % & $ & # " ' $ ( $ ) * ) * +, -. / # $ $ ( $ " $ $ $ % $ $ ' ƒ " " ' %. " 0 1 2 3 4 5 6 7 8 9 : ; ; < = : ; > : 0? @ 8? 4 A 1 4 B 3 C 8? D C B? E F 4 5 8 3 G @ H I@ A 1 4 D G 8 5 1 @ J C
Ó³ Ÿ , º 7(156).. 62Ä69. Š Œ œ ƒˆˆ ˆ ˆŠ. .. ŠÊ²Ö μ 1,. ƒ. ²ÓÖ μ 2. μ ± Ê É É Ê Ò μ μ, Œμ ±
Ó³ Ÿ. 009.. 6, º 7(156.. 6Ä69 Š Œ œ ƒˆˆ ˆ ˆŠ ˆŒ ˆ - ˆ ƒ ˆ ˆ ˆŸ Š -Œ ˆ Šˆ ˆ.. ŠÊ²Ö μ 1,. ƒ. ²ÓÖ μ μ ± Ê É É Ê Ò μ μ, Œμ ± É ÉÓ μ Ò ÕÉ Ö ²μ Í Ò - μ Ò ² É Ö ³ ÖÉÓ Ì ÒÎ ² ÖÌ, μ²ó ÊÕÐ Ì ±μ ± 4- μ Ò. This paper
Lifting Entry 2. Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion MARYLAND U N I V E R S I T Y O F
ifting Entry Basic planar dynamics of motion, again Yet another equilibrium glide Hypersonic phugoid motion MARYAN 1 010 avid. Akin - All rights reserved http://spacecraft.ssl.umd.edu ifting Atmospheric
Faculdade de Engenharia. Transmission Lines ELECTROMAGNETIC ENGINEERING MAP TELE 2008/2009
Facudad d Ennharia Transmission ins EECTROMAGNETC ENGNEERNG MAP TEE 8/9 Transmission ins Facudad d Ennharia transmission ins wavuids supportin TEM wavs most common typs para-pat wavuids coaxia wavuids
Ó³ Ÿ , º 1(199).. 66Ä79 .. Ê 1. Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ±
Ó³ Ÿ. 216.. 13, º 1(199).. 66Ä79 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ Œ Ÿ ƒˆÿ ˆ Œ ƒ ˆ ˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± μé ³± Ì ²ÖÉ É ±μ É μ É Í ³μÉ Î μ ²μ± ²Ó μ³ μ- Éμ± Ö ² ±É ± ³ ÏÉ Ì ±μ²ó± Ì ³ ±, Ò
ƒˆˆ-ˆœ œ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ
Ó³ Ÿ. 2018.. 15, º 6218).. 467Ä475 ˆ ˆŠ Œ ˆ ˆ Œ ƒ Ÿ. ˆŸ ƒˆˆ-ˆœ œ Ÿ ˆ ˆ Š ˆˆ ƒ ˆ ˆˆ.. Ê 1 Œμ ±μ ± μ Ê É Ò Ê É É ³. Œ.. μ³μ μ μ, Œμ ± μ± μ, ÎÉμ ³μ Ë ± Í Ö ³³ É Î ±μ, μ ² μ μ ƒ ²Ó ÉÊ μ² μ ²μÉ μ É É μ Ô -
Ó³ Ÿ º 3[120] Particles and Nuclei, Letters No. 3[120]
![Ó³ Ÿ º 3[120] Particles and Nuclei, Letters No. 3[120]](/thumbs/62/47071815.jpg "Ó³ Ÿ º 3[120] Particles and Nuclei, Letters No. 3[120]")
Ó³ Ÿ. 2004. º 3[120] Particles and Nuclei, Letters. 2004. No. 3[120] Š 621.384.633.5/6 Š ˆ ˆ Šˆ Šˆ Š ˆ Ÿ Ÿ ˆ ˆ.. Œ ϱµ 1,.. µ 1,.. ³ µ 1,. Œ. Ò 1, ƒ.. Ê ±µ 1 Ñ Ò É ÉÊÉ Ö ÒÌ ² µ, Ê Œµ ±µ ± µ Ê É Ò É ÉÊÉ
Ó³ Ÿ , º 2(131).. 105Ä ƒ. ± Ï,.. ÊÉ ±μ,.. Šμ ² ±μ,.. Œ Ì ²μ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê
Ó³ Ÿ. 2006.. 3, º 2(131).. 105Ä110 Š 537.311.5; 538.945 Œ ƒ ˆ ƒ Ÿ ˆŠ ˆ ƒ Ÿ ƒ ˆ œ ƒ Œ ƒ ˆ ˆ Š ˆ 4 ². ƒ. ± Ï,.. ÊÉ ±μ,.. Šμ ² ±μ,.. Œ Ì ²μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê ³ É É Ö μ ² ³ μ É ³ Í ² Ö Ê³ μ μ ³ É μ μ μ²ö
ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ
7/4/017 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εισαγωγή στις Κεραίες Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Μηχανισμός Ακτινοβολίας
Κεραίες & Ασύρματες Ζεύξεις
Κεραίες & Ασύρματες Ζεύξεις ΓΡΑΜΜΙΚΕΣ ΚΕΡΑΙΕΣ Το μάθημα αυτό πραγματεύεται το αντικείμενο των κεραιών και των Ασύρματων Ζεύξεων. Περιέχει τη θεμελίωση και τις βασικές έννοιες /αρχές που διέπουν τόσο τα
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού.
Νόµοςπεριοδικότητας του Moseley:Η χηµική συµπεριφορά (οι ιδιότητες) των στοιχείων είναι περιοδική συνάρτηση του ατοµικού τους αριθµού. Περιοδικός πίνακας: α. Είναι µια ταξινόµηση των στοιχείων κατά αύξοντα
ibemo Kazakhstan Republic of Kazakhstan, West Kazakhstan Oblast, Aksai, Pramzone, BKKS office complex Phone: ; Fax:
Εφαρμογές της κβαντομηχανικής. Εφαρμογές της κβαντομηχανικής
Εφαρμογές της κβαντομηχανικής ΠΙΑΣ Ελεύθερο σωματίδιο σε μια διάσταση Σωματίδιο κινούμενο ελεύθερα στον άξονα σε σταθερό δυναμικό ανεξάρτητο του : V ˆ( () V ξίσωση Schrödinger: d d H ˆ H ˆ ˆ() () () d
ο ο 3 α. 3"* > ω > d καΐ 'Ενορία όλις ή Χώρί ^ 3 < KN < ^ < 13 > ο_ Μ ^~~ > > > > > Ο to X Η > ο_ ο Ο,2 Σχέδι Γλεγμα Ο Σ Ο Ζ < o w *< Χ χ Χ Χ < < < Ο
18 ρ * -sf. NO 1 D... 1: - ( ΰ ΐ - ι- *- 2 - UN _ ί=. r t ' \0 y «. _,2. "* co Ι». =; F S " 5 D 0 g H ', ( co* 5. «ΰ ' δ". o θ * * "ΰ 2 Ι o * "- 1 W co o -o1= to»g ι. *ΰ * Ε fc ΰ Ι.. L j to. Ι Q_ " 'T
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ
3/5/016 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Παραδείγματα Κεραιών Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Δίπολο Hetz L d
Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / / + 3 / / / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " #
Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / 0 1 2 / + 3 / / 1 2 3 / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " # $ % $ ' $ % ) * % @ + * 1 A B C D E D F 9 O O D H
X t m X t Y t Z t Y t l Z t k X t h x Z t h z Z t Y t h y z X t Y t Z t E. G γ. F θ. z Θ Γ. γ F θ
R X t m X t Y t Z t Y t l Z t k X t hxz t hzz t Y t hy z X t Y t Z t E F { f( y z; θ); θ Θ R p } θ G { g( y z; γ); γ Γ R q } γ ΘΓ z ΘΓ F θ θ γ F θ G γ G γ E [] = () h( y, z) dydz h( z) () h( y z) dydz
/&25*+* 24.&6,2(2**02)' 24
!! "#$ % (33 &' ())**,"-.&/(,01.2(*(33*( ( &,.*(33*( ( 2&/((,*(33*( 24 /&25** 24.&6,2(2**02)' 24 " 0 " ( 78,' 4 (33 72"08 " 2/((,02..2(& (902)' 4 #% 7' 2"8(7 39$:80(& 2/((,* (33; (* 3: &
Masters Bikini 45+ A up to 5'4"
Mss Bk 45+ A p 5'4" Fs Ls 178 C Cvs 24 5 178 182 D M 1 2 182 186 S L 7 1 186 194 D Chs 21 4 194 273 C Bshp 12 3 273 Mss Bk 45+ B v 5'4" Fs Ls 179 Khy D 8 1 179 18 A Rd 12 3 18 183 F Ivy 26 5 183 27 Jdy
Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ. Παππάς Χρήστος Επίκουρος Καθηγητής
ΗΛΕΚΤΡΟΝΙΚΗ ΟΜΗ ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΑΤΟΜΩΝ Παππάς Χρήστος Επίκουρος Καθηγητής ΤΟ ΜΕΓΕΘΟΣ ΤΩΝ ΑΤΟΜΩΝ Ατομική ακτίνα (r) : ½ της απόστασης μεταξύ δύο ομοιοπυρηνικών ατόμων, ενωμένων με απλό ομοιοπολικό δεσμό.
ϕ be a scalar field. The gradient is the vector field defined by
Amn Halloc Math Ecss E-mal : amn@sthths bpa : sthths/amn MATH EXERCISES GRADIENT DIVERGENCE CURL DEL NABLA OERATOR LALACIAN OERATOR CONTINUITY AND NAVIER-STOKES EQUATIONS VECTOR RODUCTS I and thn scala
Κεφάλαιο 2 Διαχείριση Σηµάτων σε Ψηφιακά Συστήµατα Ελέγχου
Κεφάλαιο 2 Διαχείριση Σηµάτων σε Ψηφιακά Συστήµατα Ελέγχου Μετατροπή Αναλογικού Σήµατος σε Ψηφιακό (A/D Conversion) Ο µετασχηµατισµός Ζ Μαθηµατική Ανάλυση της ιαδικασίας A/D Μετατροπή Ψηφιακού Σήµατος
Ó³ Ÿ , º 1(130).. 7Ä ±μ. Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê
Ó³ Ÿ. 006.. 3, º 1(130).. 7Ä16 Š 530.145 ˆ ƒ ˆ ˆŒ ˆŸ Š ƒ.. ±μ Ñ Ò É ÉÊÉ Ö ÒÌ ² μ, Ê É μ ² Ö Ó μ μ Ö μ μ²õ μ É μ ÌÉ ±ÊÎ É ² ³ É μ - Î ±μ μ ÊÌ ±μ Ëμ ³ μ- ±² μ ÒÌ ³μ ²ÖÌ Ê ±. ³ É ÔÉμ μ μ μ Ö, Ö ²ÖÖ Ó ±μ³
Molekulare Ebene (biochemische Messungen) Zelluläre Ebene (Elektrophysiologie, Imaging-Verfahren) Netzwerk Ebene (Multielektrodensysteme) Areale (MRT, EEG...) Gene Neuronen Synaptische Kopplung kleine
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 21-7722479 - e-mail:
ALFA ROMEO. Έτος κατασκευής
145 1.4 i.e. AR33501 66 90 10/94-01/01 0802-1626M 237,40 1.4 i.e. 16V AR33503 76 103 12/96-01/01 0802-1627M 237,40 1.6 i.e. AR33201 76 103 10/94-01/01 0802-1628M 237,40 1.6 i.e. 16V AR67601 88 120 12/96-01/01
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΣΧΟΛΗ ΕΠΙΣΤΗΜΩΝ ΤΗΣ ΙΟΙΚΗΣΗΣ ΠΡΟΓΡΑΜΜΑ ΜΕΤΑΠΤΥΧΙΑΚΩΝ ΣΠΟΥ ΩΝ ΜΕΤΑΠΤΥΧΙΑΚΟ ΙΠΛΩΜΑ ΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΜΕ. Ι..Ε.
ΑΣΚΗΣΗ 1 ΟΜΑ Α 2 Στην ακόλουθη άσκηση σας δίνονται τα έξοδα ανά µαθητή και οι ετήσιοι µισθοί (κατά µέσο όρο) των δασκάλων για 51 πολιτείες της Αµερικής. Τα δεδοµένα είναι για τη χρονιά 1985. Οι µεταβλητές
2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς. 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η. 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν. 5. Π ρ ό τ α σ η. 6.
Π Ε Ρ Ι Ε Χ Ο Μ Ε Ν Α 1. Ε ι σ α γ ω γ ή 2. Α ν ά λ υ σ η Π ε ρ ι ο χ ή ς 3. Α π α ι τ ή σ ε ι ς Ε ρ γ ο δ ό τ η 4. Τ υ π ο λ ο γ ί α κ τ ι ρ ί ω ν 5. Π ρ ό τ α σ η 6. Τ ο γ ρ α φ ε ί ο 1. Ε ι σ α γ ω
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ
ΠΕΡΙΟΔΙΚΟΣ ΠΙΝΑΚΑΣ ΣΤΟΙΧΕΙΩΝ Περίοδοι περιοδικού πίνακα Ο περιοδικός πίνακας αποτελείται από 7 περιόδους. Ο αριθμός των στοιχείων που περιλαμβάνει κάθε περίοδος δεν είναι σταθερός, δηλ. η περιοδικότητα
1 B0 C00. nly Difo. r II. on III t o. ly II II. Di XR. Di un 5.8. Di Dinly. Di F/ / Dint. mou. on.3 3 D. 3.5 ird Thi. oun F/2. s m F/3 /3.
. F/ /3 3. I F/ 7 7 0 0 Mo ode del 0 00 0 00 A 6 A C00 00 0 S 0 C 0 008 06 007 07 09 A 0 00 0 00 0 009 09 A 7 I 7 7 0 0 F/.. 6 6 8 8 0 00 0 F/3 /3. fo I t o nt un D ou s ds 3. ird F/ /3 Thi ur T ou 0 Fo
ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ
8/3/018 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΑΣΥΡΜΑΤΕΣ ΕΠΙΚΟΙΝΩΝΙΕΣ Εισαγωγή στις Κεραίες Αθανάσιος Κανάτας Καθηγητής Παν/μίου Πειραιώς Μηχανισμός Ακτινοβολίας
Problem 7.19 Ignoring reflection at the air soil boundary, if the amplitude of a 3-GHz incident wave is 10 V/m at the surface of a wet soil medium, at what depth will it be down to 1 mv/m? Wet soil is
#%" )*& ##+," $ -,!./" %#/%0! %,!
-!"#$% -&!'"$ & #("$$, #%" )*& ##+," $ -,!./" %#/%0! %,! %!$"#" %!#0&!/" /+#0& 0.00.04. - 3 3,43 5 -, 4 $ $.. 04 ... 3. 6... 6.. #3 7 8... 6.. %9: 3 3 7....3. % 44 8... 6.4. 37; 3,, 443 8... 8.5. $; 3
[ ] [ ] ( ) 1 1 ( 1. ( x) Q2bi
![[ ] [ ] ( ) 1 1 ( 1. ( x) Q2bi](/thumbs/40/22110731.jpg "[ ] [ ] ( ) 1 1 ( 1. ( x) Q2bi")
NSW BOS Mhics Esio Soluios 8 F dowlod d pi fo wwwiuco Do o phoocopy opyigh 8 iuco Q L u 5 d ( ) c u u 5 Q Qc ( ) ( ) d 5 u d c d d l c d [ ] [ ] ( ) d l ( ) l l Qd L u fo > ( ) u d Wh u ; wh u d d ( u
ϕ n n n n = 1,..., N n n {X I, Y I } {X r, Y r } (x c, y c ) q r = x a y a θ X r = [x r, y r, θ r ] X I = [x I, y I, θ I ] X I = R(θ)X r R(θ) R(θ) = cosθ sinθ 0 sinθ cosθ 0 0 0 1 Ẋ I = R(θ)Ẋr y r ẏa r
HMY 799 1: Αναγνώριση Συστημάτων
HMY 799 : Αναγνώριση Συστημάτων Διαλέξεις 3 4 Στοχαστικά/τυχαία / χ διανύσματα Ντετερμινιστικά και στοχαστικά σήματα στο πεδίο της συχνότητας Στοχαστικά σήματα και γραμμικά συστήματα Deterministic and
Άσκηση. υπολογιστούν τα Ω, F, T, φ, So, και P. Λύση: Το σήμα πρέπει να τροποποιηθεί ώστε να έλθει στη μορφή S(t)=So sin(ωt+φ)
Ένα σήμα περιγράφεται από τις σχέσεις: S(t)= sin(ωt+φ) (πλάτος) με Ω κυκλική συχνότητα Ω = πf = /R (ισχύς) με R αντίσταση φόρτου. Επίσης ισχύει Ι(t) = Io sin (Ωt +φ) και = Io R. και Άσκηση Δίνεται σήμα
Da se podsetimo Algoritam optimizacije. Odrediti vrednosti parametara kola koje će garantovati da odziv F(x, p) ima željenu vrednost F * (x).
Aotam otmzac Da s odstmo Aotam otmzac Aotam otmzac Aotam otmzac : Oddt vdost aamtaa oa [,... ] o ć aatovat da odzv (x, ma žu vdost * (x. Mtod: až mmuma fuc š E(x,; (oma za vattatvu ocu odstuaa dobo od
(... )..!, ".. (! ) # - $ % % $ & % 2007
(! ), "! ( ) # $ % & % $ % 007 500 ' 67905:5394!33 : (! ) $, -, * +,'; ), -, *! ' - " #!, $ & % $ ( % %): /!, " ; - : - +', 007 5 ISBN 978-5-7596-0766-3 % % - $, $ &- % $ % %, * $ % - % % # $ $,, % % #-
ECE Spring Prof. David R. Jackson ECE Dept. Notes 2
ECE 634 Spring 6 Prof. David R. Jackson ECE Dept. Notes Fields in a Source-Free Region Example: Radiation from an aperture y PEC E t x Aperture Assume the following choice of vector potentials: A F = =
The ε-pseudospectrum of a Matrix
The ε-pseudospectrum of a Matrix Feb 16, 2015 () The ε-pseudospectrum of a Matrix Feb 16, 2015 1 / 18 1 Preliminaries 2 Definitions 3 Basic Properties 4 Computation of Pseudospectrum of 2 2 5 Problems
ITU-R SA (2010/01)! " # $% & '( ) * +,
(010/01)! " # $% & '( ) * +, SA ii.. (IPR) (ITU-T/ITU-R/ISO/IEC).ITU-R 1 1 http://www.itu.int/itu-r/go/patents/en. (http://www.itu.int/publ/r-rec/en ) () ( ) BO BR BS BT F M P RA S RS SA SF SM SNG TF V
Example 1: THE ELECTRIC DIPOLE
Example 1: THE ELECTRIC DIPOLE 1 The Electic Dipole: z + P + θ d _ Φ = Q 4πε + Q = Q 4πε 4πε 1 + 1 2 The Electic Dipole: d + _ z + Law of Cosines: θ A B α C A 2 = B 2 + C 2 2ABcosα P ± = 2 ( + d ) 2 2