Могућности и планови ЕПС на пољу напонско реактивне подршке. Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије
|
|
|
- Σωστράτη Καζαντζής
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Могућности и планови ЕПС на пољу напонско реактивне подршке Излагач: Милан Ђорђевић, мастер.ел.тех.и рачунар. ЈП ЕПС Производња енергије 1
2 Обавезе ЈП ЕПС као КПС... ЗАКОН О ЕНЕРГЕТИЦИ ЧЛАН 94. Енергетски субјект који обавља делатност производње електричне енергије (у даљем тексту: Произвођач електричне енергије), у складу са овим законом, има право да:... 4)понуди оператору преносног, односно дистрибутивног система помоћне услуге, у складу са техничким карактеристикама и правилима о раду преносног и дистрибутивног система и правилима о раду тржишта електричне енергије... ЧЛАН 95. Електране из члана 94. став 1. овог закона које су прикључене на преносни, односно дистрибутивни систем морају да буду технички оспособљене и погонски спремне за пружање помоћних услуга у складу са правилима о раду преносног, односно дистрибутивног система и у складу са њиховим специфичним технологијама, Помоћне услуге се набављају на тржишним принципима, уз поштовање принципа јавности и недискриминације, на начин утврђен правилима о раду тржишта електричне енергије. 2
3 Обавезе ЈП ЕПС као КПС ПРАВИЛА О РАДУ ПРЕНОСНОГ СИСТЕМА 6.2. ВРСТЕ И ОБИМ ПОМОЋНИХ И СИСТЕМСКИХ УСЛУГА Корисник преносног система који са ЈП ЕМС има закључен уговор о пружању помоћних услуга дужан је да одржава у исправном стању сву опрему неопходну за пружање помоћних услуга која су његово средство, и да тренутно обавести ЈП ЕМС о промени на својим капацитетима по питању могућности и квалитета пружања ових услуга Помоћну услугу регулације напона морају пружити све генераторске јединице прикључене на преносни систем у складу са својим техничким карактеристикама УПРАВЉАЊЕ ПРЕНОСНИМ СИСТЕМОМ Напон се превасходно регулише издавањем одговарајућих налога за генерисање или апсорпцију реактивне енергије у свим генераторским јединицама које су у погону, те синхроним компензаторима и статичким компензационим постројењима који имају уговорну обавезу за пружање системске услуге регулације напона. 3
4 Могућности генераторских јединица ЈП ЕПС у погледу генерисања/апсорбовања реактивне снаге Qind Qcap ТЕ и ТЕТО Mvar -289 Mvar ХЕ Mvar -526 Mvar Укупно Mvar -815 Mvar 4
5 Могућности генераторских јединица ЈП ЕПС у погледу генерисања реактивне снаге Qmax (Mvar) ТЕНТ А 964 ТЕНТ Б 327 ТЕ Колубара А 170 TE Морава 90 ТЕ Костолац А 213 ТЕ Костолац Б 432 ТЕТО Нови Сад 200 ТЕТО Зрењанин 114 ХЕ Ђердап ХЕ Ђердап 2 55 ХЕ Пирот 36 ХЕ Врла 1 33 ХЕ Врла 2 15 ХЕ Врла 3 18 ХЕ Врла 4 15 ХЕ Бајина Башта 118 РХЕ Бајина Башта 110 ХЕ Зворник 72 ХЕ Бистрица 30 ХЕ Потпећ 26 ХЕ Увац 16 ХЕ Кокин Брод 11 5
6 Могућности генераторских јединица ЈП ЕПС у погледу апсорбовања реактивне снаге Qmin (Mvar) ТЕНТ А -161 ТЕНТ Б 0 ТЕ Колубара А -28 TE Морава 0 ТЕ Костолац А -20 ТЕ Костолац Б -39 ТЕТО Нови Сад -17 ТЕТО Зрењанин -24 ХЕ Ђердап ХЕ Ђердап 2-5 ХЕ Пирот -20 ХЕ Врла 1 0 ХЕ Врла 2 0 ХЕ Врла 3 0 ХЕ Врла 4 0 ХЕ Бајина Башта 12 РХЕ Бајина Башта -110 ХЕ Зворник -24 ХЕ Бистрица 0 ХЕ Потпећ -3 ХЕ Увац -16 ХЕ Кокин Брод 0 6
7 Могућности генераторских јединица ЈП ЕПС у погледу генерисања/апсорбовања реактивне снаге ГЈ повезане на 110kV преносну мрежу ГЈ повезане на 220kV преносну мрежу ГЈ повезане на 400kV преносну мрежу Qmax = 1.083Mvar Qmin = -157Mvar Qmax = 911Mvar Qmin = -157Mvar Qmax = 1.595Mvar Qmin = -501Mvar 7
8 Могућности генераторских јединица ЈП ЕПС у погледу генерисања/апсорбовања реактивне снаге из мреже Утицајни фактори: Губици реактивне снаге на блок трансформатору (ΔQBT) Вредност реактивне снаге сопствене потрошње (Qsp) {ΔQBT} {Qmax,Qmin} BT {Qsp} {Qmax,Qmin} TSP G 8
9 Могућности генераторских јединица ЈП ЕПС у погледу генерисања/апсорбовања реактивне снаге из мреже Qind Qcap ТЕ и ТЕТО Mvar -841 Mvar ХЕ 734 Mvar -841 Mvar Укупно Mvar Mvar 9
10 Могућности генераторских јединица ЈП ЕПС у погледу предаје реактивне снаге у мрежу Qmax (Mvar) ТЕНТ А 616 ТЕНТ Б 211 ТЕ Колубара А 136 TE Морава 71 ТЕ Костолац А 171 ТЕ Костолац Б 329 ТЕТО Нови Сад 173 ТЕТО Зрењанин 100 ХЕ Ђердап ХЕ Ђердап 2 34 ХЕ Пирот 26 ХЕ Врла 1 27 ХЕ Врла 2 12 ХЕ Врла 3 14 ХЕ Врла 4 13 ХЕ Бајина Башта 64 РХЕ Бајина Башта 37 ХЕ Зворник 60 ХЕ Бистрица 18 ХЕ Потпећ 20 ХЕ Увац 13 ХЕ Кокин Брод 9 10
11 Могућности генераторских јединица ЈП ЕПС у погледу преузимања реактивне снаге из мреже Qmin (Mvar) ТЕНТ А -456 ТЕНТ Б -96 ТЕ Колубара А -52 TE Морава -12 ТЕ Костолац А -48 ТЕ Костолац Б -114 ТЕТО Нови Сад -33 ТЕТО Зрењанин -29 ХЕ Ђердап ХЕ Ђердап 2-25 ХЕ Пирот -28 ХЕ Врла 1-4 ХЕ Врла 2-2 ХЕ Врла 3-2 ХЕ Врла 4-2 ХЕ Бајина Башта -38 РХЕ Бајина Башта -183 ХЕ Зворник -32 ХЕ Бистрица -11 ХЕ Потпећ -8 ХЕ Увац -19 ХЕ Кокин Брод -2 11
12 Могућности генераторских јединица ЈП ЕПС у погледу ГЈ повезане на 110kV преносну мрежу предаје/прeузимања реактивне снаге из мреже ГЈ повезане на 220kV преносну мрежу ГЈ повезане на 400kV преносну мрежу Qmax = 878Mvar Qmin = -299Mvar Qmax = 562Mvar Qmin = -464Mvar Qmax = 1.101Mvar Qmin = -919Mvar 12
13 Q [Mvar] Могућности генераторских јединица ЈП ЕПС у погледу предаје/прeузимања реактивне снаге из мреже Предаја реактивне снаге у мрежу kV 220kV 400kV Преузимање реактивне снаге из мреже 13
14 Могућности ГЈ у зависности од вредности напона у тачки прикључења 14
15 Могућности ГЈ у зависности од вредности напона у тачки прикључења UG=UG,max Област рада са максималним доступним капацитетом реактивне снаге UG=UG,min 15
16 Могућности ГЈ у зависности од вредности напона у тачки прикључења Um [kv] Qm [Mvar] 16
17 Будућа побољшања 69Mvar 60Mvar 17
18 Будућа побољшања 2Mvar 14Mvar 18
19 ХВАЛА НА ПАЖЊИ 19
1.2. Сличност троуглова
 математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
З А Х Т Е В ЗА ИЗДАВАЊЕ МИШЉЕЊА О УСЛОВИМА И МОГУЋНОСТИМА ПРИКЉУЧЕЊА ОБЈЕКТА ЗА ПРОИЗВОДЊУ ЕЛЕКТРИЧНЕ ЕНЕРГИЈЕ. Мишљење се прибавља у сврху:
 ПР-ЕНГ-01.87/01 З А Х Т Е В ЗА ИЗДАВАЊЕ МИШЉЕЊА О УСЛОВИМА И МОГУЋНОСТИМА ПРИКЉУЧЕЊА ОБЈЕКТА ЗА ПРОИЗВОДЊУ ЕЛЕКТРИЧНЕ ЕНЕРГИЈЕ Мишљење се прибавља у сврху: Подаци о странци: Пословно име: (Пословно име
ПР-ЕНГ-01.87/01 З А Х Т Е В ЗА ИЗДАВАЊЕ МИШЉЕЊА О УСЛОВИМА И МОГУЋНОСТИМА ПРИКЉУЧЕЊА ОБЈЕКТА ЗА ПРОИЗВОДЊУ ЕЛЕКТРИЧНЕ ЕНЕРГИЈЕ Мишљење се прибавља у сврху: Подаци о странци: Пословно име: (Пословно име
УРЕДБУ О УСЛОВИМА И ПОСТУПКУ СТИЦАЊА СТАТУСА ПОВЛАШЋЕНОГ ПРОИЗВОЂАЧА ЕЛЕКТРИЧНЕ ЕНЕРГИЈЕ I. ПРЕДМЕТ
 На основу члана 56. став 9. Закона о енергетици ( Службени гласник РС, бр. 57/11, 80/11 исправка, 93/12 и 124/12) и члана 42. став 1. Закона о Влади ( Службени гласник РС, бр. 55/05, 71/05-исправка, 101/07,
На основу члана 56. став 9. Закона о енергетици ( Службени гласник РС, бр. 57/11, 80/11 исправка, 93/12 и 124/12) и члана 42. став 1. Закона о Влади ( Службени гласник РС, бр. 55/05, 71/05-исправка, 101/07,
налазе се у диелектрику, релативне диелектричне константе ε r = 2, на међусобном растојању 2 a ( a =1cm
 1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
Appendix 1. Prilozi Plana Razvoja prenosnog sistema R.Srbije za period (2031.) -word dokumeti-
 Appendix 1 Prilozi Plana Razvoja prenosnog sistema R.Srbije za period 2017.- 2026.(2031.) -word dokumeti- Sadržaj Prilog 5.1 - Planovi izgradnje, povlacenja i revitalizacije kapaciteta u JP EPS do 2026.godine...
Appendix 1 Prilozi Plana Razvoja prenosnog sistema R.Srbije za period 2017.- 2026.(2031.) -word dokumeti- Sadržaj Prilog 5.1 - Planovi izgradnje, povlacenja i revitalizacije kapaciteta u JP EPS do 2026.godine...
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 2004
 РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 004 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор 100 VA има напон и реактансу кратког споја u 4% и x % респективно При номиналном оптерећењу
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 004 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор 100 VA има напон и реактансу кратког споја u 4% и x % респективно При номиналном оптерећењу
ПРАВИЛА О РАДУ ПРЕНОСНОГ СИСТЕМА. октобар, године
 ПРАВИЛА О РАДУ ПРЕНОСНОГ СИСТЕМА октобар, 2015. године На основу члана 116. Закона о енергетици (Службени гласник РС бр. 145/2014) и члана 44. Статута Јавног предузећа Електромрежа Србије, Београд (Службени
ПРАВИЛА О РАДУ ПРЕНОСНОГ СИСТЕМА октобар, 2015. године На основу члана 116. Закона о енергетици (Службени гласник РС бр. 145/2014) и члана 44. Статута Јавног предузећа Електромрежа Србије, Београд (Службени
ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ -
 ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ - ЦЕНЕ ПРОИЗВОДЊЕ И ДИСТРИБУЦИЈЕ ВОДЕ И ЦЕНЕ САКУПЉАЊА, ОДВОђЕЊА И ПРЕЧИШЋАВАЊА ОТПАДНИХ ВОДА НА НИВОУ ГРУПАЦИЈЕ ВОДОВОДА
ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ - ЦЕНЕ ПРОИЗВОДЊЕ И ДИСТРИБУЦИЈЕ ВОДЕ И ЦЕНЕ САКУПЉАЊА, ОДВОђЕЊА И ПРЕЧИШЋАВАЊА ОТПАДНИХ ВОДА НА НИВОУ ГРУПАЦИЈЕ ВОДОВОДА
Теорија електричних кола
 др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
г) страница aa и пречник 2RR описаног круга правилног шестоугла јесте рац. бр. јесу самерљиве
 в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
Положај сваке тачке кружне плоче је одређен са поларним координатама r и ϕ.
 VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
Предмет: Задатак 4: Слика 1.0
 Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Утицај дистрибуираних извора електричне енергије на мрежу
 INFOTEH-JAHORINA Vol. 13, March 2014. Утицај дистрибуираних извора електричне енергије на мрежу Младен Бањанин, Јована Тушевљак Електротехнички факултет Источно Сарајево, Босна и Херцеговина banjanin@ymail.com,
INFOTEH-JAHORINA Vol. 13, March 2014. Утицај дистрибуираних извора електричне енергије на мрежу Младен Бањанин, Јована Тушевљак Електротехнички факултет Источно Сарајево, Босна и Херцеговина banjanin@ymail.com,
2. Наставни колоквијум Задаци за вежбање ОЈЛЕРОВА МЕТОДА
 . колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
. колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
L кплп (Калем у кплу прпстпперипдичне струје)
 L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
Теорија електричних кола
 Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
Теорија електричних кола
 Др Милка Потребић, ванредни професор, Теорија електричних кола, предавања, Универзитет у Београду Електротехнички факултет, 07. Вишефазне електричне системе је патентирао српски истраживач Никола Тесла
Др Милка Потребић, ванредни професор, Теорија електричних кола, предавања, Универзитет у Београду Електротехнички факултет, 07. Вишефазне електричне системе је патентирао српски истраживач Никола Тесла
ТРАПЕЗ РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ. Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце
 РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
Анализа Петријевих мрежа
 Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
ПЛАН РАЗВОЈА ПРЕНОСНОГ СИСТЕМА - за период до године -
 ПЛАН РАЗВОЈА ПРЕНОСНОГ СИСТЕМА - за период до 2015. године - САДРЖАЈ ПРИЛОЗИ ИНДЕКС СЛИКА ИНДЕКС ТАБЕЛА iii iv v 1. УВОД 1 2. ПРОГНОЗА ПОТРОШЊЕ 5 2.1 УВОДНЕ ПОСТАВКЕ 5 2.2 МЕТОДОЛОГИЈА 5 2.2.1 Прогноза
ПЛАН РАЗВОЈА ПРЕНОСНОГ СИСТЕМА - за период до 2015. године - САДРЖАЈ ПРИЛОЗИ ИНДЕКС СЛИКА ИНДЕКС ТАБЕЛА iii iv v 1. УВОД 1 2. ПРОГНОЗА ПОТРОШЊЕ 5 2.1 УВОДНЕ ПОСТАВКЕ 5 2.2 МЕТОДОЛОГИЈА 5 2.2.1 Прогноза
ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (13Е013ЕНТ) - септембар 2018
 Универзитет у Београду Електротехнички факултет Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (3Е03ЕНТ) - септембар 08 Трофазни уљни дистрибутивни индустријски трансформатор има номиналне
Универзитет у Београду Електротехнички факултет Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (3Е03ЕНТ) - септембар 08 Трофазни уљни дистрибутивни индустријски трансформатор има номиналне
2.3. Решавање линеарних једначина с једном непознатом
 . Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
. Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 2 (13Е013ЕП2) октобар 2016.
 ЕНЕРГЕТСКИ ПРЕТВАРАЧИ (3Е03ЕП) октобар 06.. Батерија напона B = 00 пуни се преко трофазног полууправљивог мосног исправљача, који је повезан на мрежу 3x380, 50 Hz преко трансформатора у спрези y, са преносним
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ (3Е03ЕП) октобар 06.. Батерија напона B = 00 пуни се преко трофазног полууправљивог мосног исправљача, који је повезан на мрежу 3x380, 50 Hz преко трансформатора у спрези y, са преносним
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
ЛИНЕАРНА ФУНКЦИЈА. k, k 0), осна и централна симетрија и сл. 2, x 0. У претходном примеру неке функције су линеарне а неке то нису.
 ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
Први корак у дефинисању случајне променљиве је. дефинисање и исписивање свих могућих eлементарних догађаја.
 СЛУЧАЈНА ПРОМЕНЉИВА Једнодимензионална случајна променљива X је пресликавање у коме се сваки елементарни догађај из простора елементарних догађаја S пресликава у вредност са бројне праве Први корак у дефинисању
СЛУЧАЈНА ПРОМЕНЉИВА Једнодимензионална случајна променљива X је пресликавање у коме се сваки елементарни догађај из простора елементарних догађаја S пресликава у вредност са бројне праве Први корак у дефинисању
ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА
 ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА 1. Допуни шта недостаје: а) 5m = dm = cm = mm; б) 6dm = m = cm = mm; в) 7cm = m = dm = mm. ПОЈАМ ПОВРШИНЕ. Допуни шта недостаје: а) 10m = dm = cm = mm ; б) 500dm = a
ПОВРШИНа ЧЕТВОРОУГЛОВА И ТРОУГЛОВА 1. Допуни шта недостаје: а) 5m = dm = cm = mm; б) 6dm = m = cm = mm; в) 7cm = m = dm = mm. ПОЈАМ ПОВРШИНЕ. Допуни шта недостаје: а) 10m = dm = cm = mm ; б) 500dm = a
ПИТАЊА ЗА КОЛОКВИЈУМ ИЗ ОБНОВЉИВИХ ИЗВОРА ЕНЕРГИЈЕ
 ПИТАЊА ЗА КОЛОКВИЈУМ ИЗ ОБНОВЉИВИХ ИЗВОРА ЕНЕРГИЈЕ 1. Удео снаге и енергије ветра у производњи електричне енергије - стање и предвиђања у свету и Европи. 2. Навести називе најмање две међународне организације
ПИТАЊА ЗА КОЛОКВИЈУМ ИЗ ОБНОВЉИВИХ ИЗВОРА ЕНЕРГИЈЕ 1. Удео снаге и енергије ветра у производњи електричне енергије - стање и предвиђања у свету и Европи. 2. Навести називе најмање две међународне организације
Закони термодинамике
 Закони термодинамике Први закон термодинамике Први закон термодинамике каже да додавање енергије систему може бити утрошено на: Вршење рада Повећање унутрашње енергије Први закон термодинамике је заправо
Закони термодинамике Први закон термодинамике Први закон термодинамике каже да додавање енергије систему може бити утрошено на: Вршење рада Повећање унутрашње енергије Први закон термодинамике је заправо
Управљање системима за дистрибуцију природног гаса применом вишекритеријумске анализе
 Универзитет у Београду Машински факултет Бранка М. Тубин-Митровић Управљање системима за дистрибуцију природног гаса применом вишекритеријумске анализе докторска дисертација Београд, 2016 UNIVERSITY OF
Универзитет у Београду Машински факултет Бранка М. Тубин-Митровић Управљање системима за дистрибуцију природног гаса применом вишекритеријумске анализе докторска дисертација Београд, 2016 UNIVERSITY OF
Вектори vs. скалари. Векторске величине се описују интензитетом и правцем. Примери: Померај, брзина, убрзање, сила.
 Вектори 1 Вектори vs. скалари Векторске величине се описују интензитетом и правцем Примери: Померај, брзина, убрзање, сила. Скаларне величине су комплетно описане само интензитетом Примери: Температура,
Вектори 1 Вектори vs. скалари Векторске величине се описују интензитетом и правцем Примери: Померај, брзина, убрзање, сила. Скаларне величине су комплетно описане само интензитетом Примери: Температура,
МОБИЛНЕ МАШИНЕ I. ttl. хидростатички системи, хидростатичке компоненте: вентили, главни разводници, командни разводници.
 МОБИЛНЕ МАШИНЕ I предавање 8.2 \ хидростатички системи, хидростатичке компоненте: вентили, главни разводници, командни разводници Хидростатички погонски системи N e M e e N h p Q F M m m v m m F o M v
МОБИЛНЕ МАШИНЕ I предавање 8.2 \ хидростатички системи, хидростатичке компоненте: вентили, главни разводници, командни разводници Хидростатички погонски системи N e M e e N h p Q F M m m v m m F o M v
3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни
 ТАЧКА. ПРАВА. РАВАН Талес из Милета (624 548. пре н. е.) Еуклид (330 275. пре н. е.) Хилберт Давид (1862 1943) 3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни Настанак геометрије повезује
ТАЧКА. ПРАВА. РАВАН Талес из Милета (624 548. пре н. е.) Еуклид (330 275. пре н. е.) Хилберт Давид (1862 1943) 3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни Настанак геометрије повезује
Универзитет у Крагујевцу Факултет за машинство и грађевинарство у Краљеву Катедра за основне машинске конструкције и технологије материјала
 Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
ПРАВИЛА О РАДУ ДИСТРИБУТИВНОГ СИСТЕМА
 ПРАВИЛА О РАДУ ДИСТРИБУТИВНОГ СИСТЕМА Верзија 1.0 децембар, 2009. године На основу члана 107. Закона о енергетици (''Службени гласник Републике Србије'' број 84/04) и чл. 32. ст. 1. т. 9. Одлуке о измени
ПРАВИЛА О РАДУ ДИСТРИБУТИВНОГ СИСТЕМА Верзија 1.0 децембар, 2009. године На основу члана 107. Закона о енергетици (''Службени гласник Републике Србије'' број 84/04) и чл. 32. ст. 1. т. 9. Одлуке о измени
Управни одбор Републичке агенције за електронске комуникације на седници од 27. маја године, донео је ПРАВИЛНИК
 На основу чл. 8. став 1. тачка 1), 23. став 1, 37. став 3. и 38. став 3. Закона о електронским комуникацијама ( Службени гласник РС, број 44/10 ), члана 12. став 1. тачка 1) и члана 16. тачка 4. Статута
На основу чл. 8. став 1. тачка 1), 23. став 1, 37. став 3. и 38. став 3. Закона о електронским комуникацијама ( Службени гласник РС, број 44/10 ), члана 12. став 1. тачка 1) и члана 16. тачка 4. Статута
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ
 СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
b) Израз за угиб дате плоче, ако се користи само први члан реда усвојеног решења, је:
 Пример 1. III Савијање правоугаоних плоча За правоугаону плочу, приказану на слици, одредити: a) израз за угиб, b) вредност угиба и пресечних сила у тачки 1 ако се користи само први члан реда усвојеног
Пример 1. III Савијање правоугаоних плоча За правоугаону плочу, приказану на слици, одредити: a) израз за угиб, b) вредност угиба и пресечних сила у тачки 1 ако се користи само први члан реда усвојеног
ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ
 ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ предмет: ОСНОВИ МЕХАНИКЕ студијски програм: ЗАШТИТА ЖИВОТНЕ СРЕДИНЕ И ПРОСТОРНО ПЛАНИРАЊЕ ПРЕДАВАЊЕ БРОЈ 2. Садржај предавања: Систем сучељних сила у равни
ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ предмет: ОСНОВИ МЕХАНИКЕ студијски програм: ЗАШТИТА ЖИВОТНЕ СРЕДИНЕ И ПРОСТОРНО ПЛАНИРАЊЕ ПРЕДАВАЊЕ БРОЈ 2. Садржај предавања: Систем сучељних сила у равни
6.2. Симетрала дужи. Примена
 6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
Школска 2010/2011 ДОКТОРСКЕ АКАДЕМСКЕ СТУДИЈЕ
 Школска 2010/2011 ДОКТОРСКЕ АКАДЕМСКЕ СТУДИЈЕ Прва година ИНФОРМАТИЧКЕ МЕТОДЕ У БИОМЕДИЦИНСКИМ ИСТРАЖИВАЊИМА Г1: ИНФОРМАТИЧКЕ МЕТОДЕ У БИОМЕДИЦИНСКИМ ИСТРАЖИВАЊИМА 10 ЕСПБ бодова. Недељно има 20 часова
Школска 2010/2011 ДОКТОРСКЕ АКАДЕМСКЕ СТУДИЈЕ Прва година ИНФОРМАТИЧКЕ МЕТОДЕ У БИОМЕДИЦИНСКИМ ИСТРАЖИВАЊИМА Г1: ИНФОРМАТИЧКЕ МЕТОДЕ У БИОМЕДИЦИНСКИМ ИСТРАЖИВАЊИМА 10 ЕСПБ бодова. Недељно има 20 часова
Писмени испит из Метода коначних елемената
 Београд,.0.07.. За приказани билинеарни коначни елемент (Q8) одредити вектор чворног оптерећења услед задатог линијског оптерећења p. Користити природни координатни систем (ξ,η).. На слици је приказан
Београд,.0.07.. За приказани билинеарни коначни елемент (Q8) одредити вектор чворног оптерећења услед задатог линијског оптерећења p. Користити природни координатни систем (ξ,η).. На слици је приказан
СТРАТЕШКИ И РАЗВОЈНИ ПРОЈЕКТИ
 СТРАТЕШКИ И РАЗВОЈНИ ПРОЈЕКТИ ЕЛЕКТРОПРИВРЕДЕ СРБИЈЕ ЈП Електропривреда Србије МИСИЈА Електропривреде Србије је сигурно снабдевање свих купаца електричном енергијом, под тржишно најповољнијим условима,
СТРАТЕШКИ И РАЗВОЈНИ ПРОЈЕКТИ ЕЛЕКТРОПРИВРЕДЕ СРБИЈЕ ЈП Електропривреда Србије МИСИЈА Електропривреде Србије је сигурно снабдевање свих купаца електричном енергијом, под тржишно најповољнијим условима,
КАТЕДРА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ И ПОГОНЕ ЛАБОРАТОРИЈА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 1
 КАТЕДРА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ И ПОГОНЕ ЛАБОРАТОРИЈА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 1 Лабораторијска вежба број 1 МОНОФАЗНИ ФАЗНИ РЕГУЛАТОР СА ОТПОРНИМ И ОТПОРНО-ИНДУКТИВНИМ ОПТЕРЕЋЕЊЕМ
КАТЕДРА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ И ПОГОНЕ ЛАБОРАТОРИЈА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 1 Лабораторијска вежба број 1 МОНОФАЗНИ ФАЗНИ РЕГУЛАТОР СА ОТПОРНИМ И ОТПОРНО-ИНДУКТИВНИМ ОПТЕРЕЋЕЊЕМ
ПРАВИЛА О РАДУ ДИСТРИБУТИВНОГ СИСТЕМА
 На основу члана 107. Закона о енергетици (''Службени гласник Републике Србије'' број 84/04) и члана 32. став 1. тачка 9. Одлуке о измени Одлуке о оснивању јавних предузећа за дистрибуцију електричне енергије
На основу члана 107. Закона о енергетици (''Службени гласник Републике Србије'' број 84/04) и члана 32. став 1. тачка 9. Одлуке о измени Одлуке о оснивању јавних предузећа за дистрибуцију електричне енергије
Tестирање хипотеза. 5.час. 30. март Боjана Тодић Статистички софтвер март / 10
 Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
5.2. Имплицитни облик линеарне функције
 математикa за VIII разред основне школе 0 Слика 6 8. Нацртај график функције: ) =- ; ) =,5; 3) = 0. 9. Нацртај график функције и испитај њен знак: ) = - ; ) = 0,5 + ; 3) =-- ; ) = + 0,75; 5) = 0,5 +. 0.
математикa за VIII разред основне школе 0 Слика 6 8. Нацртај график функције: ) =- ; ) =,5; 3) = 0. 9. Нацртај график функције и испитај њен знак: ) = - ; ) = 0,5 + ; 3) =-- ; ) = + 0,75; 5) = 0,5 +. 0.
АНАЛОГНА ЕЛЕКТРОНИКА ЛАБОРАТОРИЈСКЕ ВЕЖБЕ
 ЕЛЕКТРОТЕХНИЧКИ ФАКУЛТЕТ У БЕОГРАДУ КАТЕДРА ЗА ЕЛЕКТРОНИКУ АНАЛОГНА ЕЛЕКТРОНИКА ЛАБОРАТОРИЈСКЕ ВЕЖБЕ ВЕЖБА БРОЈ 2 ПОЈАЧАВАЧ СНАГЕ У КЛАСИ Б 1. 2. ИМЕ И ПРЕЗИМЕ БР. ИНДЕКСА ГРУПА ОЦЕНА ДАТУМ ВРЕМЕ ДЕЖУРНИ
ЕЛЕКТРОТЕХНИЧКИ ФАКУЛТЕТ У БЕОГРАДУ КАТЕДРА ЗА ЕЛЕКТРОНИКУ АНАЛОГНА ЕЛЕКТРОНИКА ЛАБОРАТОРИЈСКЕ ВЕЖБЕ ВЕЖБА БРОЈ 2 ПОЈАЧАВАЧ СНАГЕ У КЛАСИ Б 1. 2. ИМЕ И ПРЕЗИМЕ БР. ИНДЕКСА ГРУПА ОЦЕНА ДАТУМ ВРЕМЕ ДЕЖУРНИ
предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА
 Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
Анализа техно-економских услова изградње соларне електране на крову пословне зграде Електротехничког института Никола Тесла
 Стручни рад UDK:621.311.243 BIBLID:0350-8528(2014),24.p.41-56 doi:10.5937/zeint24-4934 Анализа техно-економских услова изградње соларне електране на крову пословне зграде Електротехничког института Никола
Стручни рад UDK:621.311.243 BIBLID:0350-8528(2014),24.p.41-56 doi:10.5937/zeint24-4934 Анализа техно-економских услова изградње соларне електране на крову пословне зграде Електротехничког института Никола
ТЕХНИЧКА ПРЕПОРУКА БР. 16 ОСНОВНИ ТЕХНИЧКИ ЗАХТЕВИ ЗА ПРИКЉУЧЕЊЕ МАЛИХ ЕЛЕКТРАНА НА ДИСТРИБУТИВНИ СИСТЕМ
 ТЕХНИЧКА ПРЕПОРУКА БР. 16 ОСНОВНИ ТЕХНИЧКИ ЗАХТЕВИ ЗА ПРИКЉУЧЕЊЕ МАЛИХ ЕЛЕКТРАНА НА ДИСТРИБУТИВНИ СИСТЕМ ИЗДАВАЧ: Техничко уређење: Коректура: Рачунарска обрада цртежа: ЈП ЕПС ДИРЕКЦИЈА ЗА ДИСТРИБУЦИЈУ
ТЕХНИЧКА ПРЕПОРУКА БР. 16 ОСНОВНИ ТЕХНИЧКИ ЗАХТЕВИ ЗА ПРИКЉУЧЕЊЕ МАЛИХ ЕЛЕКТРАНА НА ДИСТРИБУТИВНИ СИСТЕМ ИЗДАВАЧ: Техничко уређење: Коректура: Рачунарска обрада цртежа: ЈП ЕПС ДИРЕКЦИЈА ЗА ДИСТРИБУЦИЈУ
Управни одбор Републичке агенције за електронске комуникације, на седници од 25. октобра године, донео је ПРАВИЛНИК
 На основу чл. 8. став 1. тачка 1), 23. став 1, 37. став 3. и 38. став 3. Закона о електронским комуникацијама ( Службени гласник РС, бр. 44/10 и 60/13-УС), члана 12. став 1. тачка 1) и члана 16. тачка
На основу чл. 8. став 1. тачка 1), 23. став 1, 37. став 3. и 38. став 3. Закона о електронским комуникацијама ( Службени гласник РС, бр. 44/10 и 60/13-УС), члана 12. став 1. тачка 1) и члана 16. тачка
Динамика. Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе:
 Њутнови закони 1 Динамика Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе: када су објекти довољно велики (>димензија атома) када се крећу брзином много мањом
Њутнови закони 1 Динамика Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе: када су објекти довољно велики (>димензија атома) када се крећу брзином много мањом
Примена првог извода функције
 Примена првог извода функције 1. Одреди дужине страница два квадрата тако да њихов збир буде 14 а збир површина тих квадрата минималан. Ре: x + y = 14, P(x, y) = x + y, P(x) = x + 14 x, P (x) = 4x 8 Први
Примена првог извода функције 1. Одреди дужине страница два квадрата тако да њихов збир буде 14 а збир површина тих квадрата минималан. Ре: x + y = 14, P(x, y) = x + y, P(x) = x + 14 x, P (x) = 4x 8 Први
ПРАВИЛНИК О БЕЗБЕДНОСТИ МАШИНА ( Службени гласник РС, број 36/09)
 Република Србија МИНИСТАРСТВО EКОНОМИЈЕ И РЕГИОНАЛНОГ РАЗВОЈА Сектор за инфраструктуру квалитета ВОДИЧ ЗА ПРИМЕНУ ПРАВИЛНИКА О БЕЗБЕДНОСТИ МАШИНА И ТАБЕЛА УСКЛАЂЕНОСТИ СА ДИРЕКТИВОМ 2006/42/ЕЗ ЕВРОПСКОГ
Република Србија МИНИСТАРСТВО EКОНОМИЈЕ И РЕГИОНАЛНОГ РАЗВОЈА Сектор за инфраструктуру квалитета ВОДИЧ ЗА ПРИМЕНУ ПРАВИЛНИКА О БЕЗБЕДНОСТИ МАШИНА И ТАБЕЛА УСКЛАЂЕНОСТИ СА ДИРЕКТИВОМ 2006/42/ЕЗ ЕВРОПСКОГ
ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције. Diffie-Hellman размена кључева
 ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2/13 Diffie-Hellman размена кључева први алгоритам са јавним
ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2/13 Diffie-Hellman размена кључева први алгоритам са јавним
LICENCA ZA OBAVLJANJE DJELATNOSTI MEĐUNARODNE TRGOVINE ELEKTRIČNOM ENERGIJOM
 Bosna i Hercegovina Бocна и Χерцеговина DRŽAVNA REGULATORNA KOMISIJA ДРЖАВНА РЕГУЛАТОРНА КОМИСИЈА ZA ELEKTRIČNU ENERGIJU ЗА ЕЛЕКТРИЧНУ ЕНЕРГИЈУ LICENCA ZA OBAVLJANJE DJELATNOSTI MEĐUNARODNE TRGOVINE ELEKTRIČNOM
Bosna i Hercegovina Бocна и Χерцеговина DRŽAVNA REGULATORNA KOMISIJA ДРЖАВНА РЕГУЛАТОРНА КОМИСИЈА ZA ELEKTRIČNU ENERGIJU ЗА ЕЛЕКТРИЧНУ ЕНЕРГИЈУ LICENCA ZA OBAVLJANJE DJELATNOSTI MEĐUNARODNE TRGOVINE ELEKTRIČNOM
Прокупље 04. Aприл 2013.
 СЛУЖБЕНИ ЛИСТ ОПШТИНЕ ПРОКУПЉЕ ГОДИНА XIV Број 2 Прокупље 04. Aприл 2013. Лист излази према потреби Годишња претплата: 1.000 дин. Цена овог броја износи: 40 дин. Рок за рекламацију: 10 дана 1 На основу
СЛУЖБЕНИ ЛИСТ ОПШТИНЕ ПРОКУПЉЕ ГОДИНА XIV Број 2 Прокупље 04. Aприл 2013. Лист излази према потреби Годишња претплата: 1.000 дин. Цена овог броја износи: 40 дин. Рок за рекламацију: 10 дана 1 На основу
Количина топлоте и топлотна равнотежа
 Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
I Наставни план - ЗЛАТАР
 I Наставни план - ЗЛААР I РАЗРЕД II РАЗРЕД III РАЗРЕД УКУО недељно годишње недељно годишње недељно годишње годишње Σ А1: ОАЕЗНИ ОПШЕОРАЗОНИ ПРЕДМЕИ 2 5 25 5 2 1. Српски језик и књижевност 2 2 4 2 2 1.1
I Наставни план - ЗЛААР I РАЗРЕД II РАЗРЕД III РАЗРЕД УКУО недељно годишње недељно годишње недељно годишње годишње Σ А1: ОАЕЗНИ ОПШЕОРАЗОНИ ПРЕДМЕИ 2 5 25 5 2 1. Српски језик и књижевност 2 2 4 2 2 1.1
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
ОБРАЗАЦ ЗА ПРИЈАВУ ТЕХНИЧКОГ РЕШЕЊА
 ЕЛЕКТРОНСКИ ФАКУЛТЕТ У НИШУ ОБРАЗАЦ ЗА ПРИЈАВУ ТЕХНИЧКОГ РЕШЕЊА У складу са одредбама Правилника о поступку и начину вредновања, и квантативном исказивању научноистраживачких резултата истраживача, који
ЕЛЕКТРОНСКИ ФАКУЛТЕТ У НИШУ ОБРАЗАЦ ЗА ПРИЈАВУ ТЕХНИЧКОГ РЕШЕЊА У складу са одредбама Правилника о поступку и начину вредновања, и квантативном исказивању научноистраживачких резултата истраживача, који
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x,
 РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
Р Е Ш Е Њ Е О ОДОБРЕЊУ ТИПА МЕРИЛА године
 САВЕЗНА РЕПУБЛИКА ЈУГОСЛАВИЈА САВЕЗНО МИНИСТАРСТВО ПРИВРЕДЕ И УНУТРАШЊЕ ТРГОВИНЕ САВЕЗНИ ЗАВОД ЗА МЕРЕ И ДРАГОЦЕНЕ МЕТАЛЕ 11 000 Београд, Мике Аласа 14, поштански фах 384 телефон: (011) 328-2736, телефакс:
САВЕЗНА РЕПУБЛИКА ЈУГОСЛАВИЈА САВЕЗНО МИНИСТАРСТВО ПРИВРЕДЕ И УНУТРАШЊЕ ТРГОВИНЕ САВЕЗНИ ЗАВОД ЗА МЕРЕ И ДРАГОЦЕНЕ МЕТАЛЕ 11 000 Београд, Мике Аласа 14, поштански фах 384 телефон: (011) 328-2736, телефакс:
МЕТОДОЛОГИЈА ЗА ИЗРАДУ ИЗВЕШТАЈА ПРОПИСАНИХ ОДЛУКОМ О ИЗВЕШТАВАЊУ О АДЕКВАТНОСТИ КАПИТАЛА БАНКЕ ПРИЛОГ 1. Извештај о капиталу банке Образац КАП
 СЕКТОР ЗА КОНТРОЛУ ПОСЛОВАЊА БАНАКА Датум последњег ажурирања: 12.1.2017. МЕТОДОЛОГИЈА ЗА ИЗРАДУ ИЗВЕШТАЈА ПРОПИСАНИХ ОДЛУКОМ О ИЗВЕШТАВАЊУ О АДЕКВАТНОСТИ КАПИТАЛА БАНКЕ Овом методологијом се детаљно објашњавају
СЕКТОР ЗА КОНТРОЛУ ПОСЛОВАЊА БАНАКА Датум последњег ажурирања: 12.1.2017. МЕТОДОЛОГИЈА ЗА ИЗРАДУ ИЗВЕШТАЈА ПРОПИСАНИХ ОДЛУКОМ О ИЗВЕШТАВАЊУ О АДЕКВАТНОСТИ КАПИТАЛА БАНКЕ Овом методологијом се детаљно објашњавају
Р Е Ш Е Њ Е О ОДОБРЕЊУ ТИПА МЕРИЛА
 САВЕЗНА РЕПУБЛИКА ЈУГОСЛАВИЈА САВЕЗНО МИНИСТАРСТВО ПРИВРЕДЕ И УНУТРАШЊЕ ТРГОВИНЕ САВЕЗНИ ЗАВОД ЗА МЕРЕ И ДРАГОЦЕНЕ МЕТАЛЕ 11 000 Београд, Мике Аласа 14, поштански фах 384 телефон: (011) 3282-736, телефакс:
САВЕЗНА РЕПУБЛИКА ЈУГОСЛАВИЈА САВЕЗНО МИНИСТАРСТВО ПРИВРЕДЕ И УНУТРАШЊЕ ТРГОВИНЕ САВЕЗНИ ЗАВОД ЗА МЕРЕ И ДРАГОЦЕНЕ МЕТАЛЕ 11 000 Београд, Мике Аласа 14, поштански фах 384 телефон: (011) 3282-736, телефакс:
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
ОГРАНИЧЕЊА И ЗАБРАНЕ ЗА ДУГОТРАЈНЕ ОРГАНСКЕ ЗАГАЂУЈУЋЕ СУПСТАНЦЕ (РОРѕ)
 ПРИЛОГ 2. ОГРАНИЧЕЊА И ЗАБРАНЕ ЗА ДУГОТРАЈНЕ ОРГАНСКЕ ЗАГАЂУЈУЋЕ СУПСТАНЦЕ (РОРѕ) ДИО А Листа забрањених РОРѕ супстанци из Стокхолмске конвенције о дуготраjним органским загађивачима Назив супстанце CAS
ПРИЛОГ 2. ОГРАНИЧЕЊА И ЗАБРАНЕ ЗА ДУГОТРАЈНЕ ОРГАНСКЕ ЗАГАЂУЈУЋЕ СУПСТАНЦЕ (РОРѕ) ДИО А Листа забрањених РОРѕ супстанци из Стокхолмске конвенције о дуготраjним органским загађивачима Назив супстанце CAS
УСЛОВИ ЗА КОРИШЋЕЊЕ ПРИВРЕМЕНЕ ЛИЦЕНЦЕ ЗА ОБАВЉАЊЕ ДЈЕЛАТНОСТИ МЕЂУНАРОДНЕ ТРГОВИНЕ ЕЛЕКТРИЧНОМ ЕНЕРГИЈОМ
 Bosna i Hercegovina Бocна и Χерцеговина DRŽAVNA REGULATORNA KOMISIJA ДРЖАВНА РЕГУЛАТОРНА КОМИСИЈА ZA ELEKTRIČNU ENERGIJU ЗА ЕЛЕКТРИЧНУ ЕНЕРГИЈУ УСЛОВИ ЗА КОРИШЋЕЊЕ ПРИВРЕМЕНЕ ЛИЦЕНЦЕ ЗА ОБАВЉАЊЕ ДЈЕЛАТНОСТИ
Bosna i Hercegovina Бocна и Χерцеговина DRŽAVNA REGULATORNA KOMISIJA ДРЖАВНА РЕГУЛАТОРНА КОМИСИЈА ZA ELEKTRIČNU ENERGIJU ЗА ЕЛЕКТРИЧНУ ЕНЕРГИЈУ УСЛОВИ ЗА КОРИШЋЕЊЕ ПРИВРЕМЕНЕ ЛИЦЕНЦЕ ЗА ОБАВЉАЊЕ ДЈЕЛАТНОСТИ
6.5 Површина круга и његових делова
 7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
Слика 1. Слика 1.2 Слика 1.1
 За случај трожичног вода приказаног на слици одредити: а Вектор магнетне индукције у тачкама А ( и ( б Вектор подужне силе на проводник са струјом Систем се налази у вакууму Познато је: Слика Слика Слика
За случај трожичног вода приказаног на слици одредити: а Вектор магнетне индукције у тачкама А ( и ( б Вектор подужне силе на проводник са струјом Систем се налази у вакууму Познато је: Слика Слика Слика
10.3. Запремина праве купе
 0. Развијени омотач купе је исечак чији је централни угао 60, а тетива која одговара том углу је t. Изрази површину омотача те купе у функцији од t. 0.. Запремина праве купе. Израчунај запремину ваљка
0. Развијени омотач купе је исечак чији је централни угао 60, а тетива која одговара том углу је t. Изрази површину омотача те купе у функцији од t. 0.. Запремина праве купе. Израчунај запремину ваљка
Ваљак. cm, а површина осног пресека 180 cm. 252π, 540π,... ТРЕБА ЗНАТИ: ВАЉАК P=2B + M V= B H B= r 2 p M=2rp H Pосн.пресека = 2r H ЗАДАЦИ:
 Ваљак ВАЉАК P=B + M V= B H B= r p M=rp H Pосн.пресека = r H. Површина омотача ваљка је π m, а висина ваљка је два пута већа од полупрчника. Израчунати запремину ваљка. π. Осни пресек ваљка је квадрат површине
Ваљак ВАЉАК P=B + M V= B H B= r p M=rp H Pосн.пресека = r H. Површина омотача ваљка је π m, а висина ваљка је два пута већа од полупрчника. Израчунати запремину ваљка. π. Осни пресек ваљка је квадрат површине
Писмени испит из Теорије плоча и љуски. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама.
 Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. = 0.2 dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2.
Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. = 0.2 dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2.
Колоквијум траје 150 минута. Дозвољено је поседовање само једне свеске за рад и концепт. Прецртати оно што није за преглед.
 Универзитет у Београду, Електротехнички факултет, Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (3Е3ЕНТ) Колоквијум децембар 8. Трофазни уљни енергетски трансформатор има следеће
Универзитет у Београду, Електротехнички факултет, Катедра за енергетске претвараче и погоне ЕНЕРГЕТСКИ ТРАНСФОРМАТОРИ (3Е3ЕНТ) Колоквијум децембар 8. Трофазни уљни енергетски трансформатор има следеће
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ
 7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
Смер: Друмски саобраћај. Висока техничка школа струковних студија у Нишу ЕЛЕКТРОТЕХНИКА СА ЕЛЕКТРОНИКОМ
 Испит из предмета Електротехника са електроником 1. Шест тачкастих наелектрисања Q 1, Q, Q, Q, Q 5 и Q налазе се у теменима правилног шестоугла, као на слици. Познато је: Q1 = Q = Q = Q = Q5 = Q ; Q 1,
Испит из предмета Електротехника са електроником 1. Шест тачкастих наелектрисања Q 1, Q, Q, Q, Q 5 и Q налазе се у теменима правилног шестоугла, као на слици. Познато је: Q1 = Q = Q = Q = Q5 = Q ; Q 1,
КОНКУРСНА ДОКУМЕНТАЦИЈА
 ЈГСП "НОВИ САД" Футошки пут 46, Нови Сад Позив за подношење понуда је објављен на Порталу јавних набавки и интернет стани наручиоца: 08.10.2015. године. Рок за подношење понуда: 16.10.2015. године до 11.00
ЈГСП "НОВИ САД" Футошки пут 46, Нови Сад Позив за подношење понуда је објављен на Порталу јавних набавки и интернет стани наручиоца: 08.10.2015. године. Рок за подношење понуда: 16.10.2015. године до 11.00
ПРАВИЛА ЗА РАСПОДЕЛУ ПРЕКОГРАНИЧНИХ ПРЕНОСНИХ КАПАЦИТЕТА НА ГРАНИЦАМА РЕГУЛАЦИОНЕ ОБЛАСТИ ЈП ЕМС ЗА ПЕРИОД ГОД ГОД.
 На основу члана 72. и 126. Закона о енергетици (''Службени гласник РС'', бр.57/2011, 80/2011-исправка, 93/2012 и 124/2012), члана 18. Закона о јавним предузећима (''Службени гласник РС'', бр.119/2012,
На основу члана 72. и 126. Закона о енергетици (''Службени гласник РС'', бр.57/2011, 80/2011-исправка, 93/2012 и 124/2012), члана 18. Закона о јавним предузећима (''Службени гласник РС'', бр.119/2012,
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА
 РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 005 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор има сљедеће податке: 50kVA 0 / 0kV / kv Yy6 релативна реактанса кратког споја је x %
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 005 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор има сљедеће податке: 50kVA 0 / 0kV / kv Yy6 релативна реактанса кратког споја је x %
Флукс, електрична енергија, електрични потенцијал
 Флукс, електрична енергија, електрични потенцијал 1 Електрични флукс Ако линије поља пролазе кроз површину A која је нормална на њих Производ EA је флукс, Φ Генерално: Φ E = E A cos θ 2 Електрични флукс,
Флукс, електрична енергија, електрични потенцијал 1 Електрични флукс Ако линије поља пролазе кроз површину A која је нормална на њих Производ EA је флукс, Φ Генерално: Φ E = E A cos θ 2 Електрични флукс,
МАТРИЧНА АНАЛИЗА КОНСТРУКЦИЈА
 Београд, 21.06.2014. За штап приказан на слици одредити најмању вредност критичног оптерећења P cr користећи приближан поступак линеаризоване теорије другог реда и: а) и један елемент, слика 1, б) два
Београд, 21.06.2014. За штап приказан на слици одредити најмању вредност критичног оптерећења P cr користећи приближан поступак линеаризоване теорије другог реда и: а) и један елемент, слика 1, б) два
РЕШЕНИ ЗАДАЦИ СА РАНИЈЕ ОДРЖАНИХ КЛАСИФИКАЦИОНИХ ИСПИТА
 РЕШЕНИ ЗАДАЦИ СА РАНИЈЕ ОДРЖАНИХ КЛАСИФИКАЦИОНИХ ИСПИТА 006. Задатак. Одредити вредност израза: а) : за, и 69 0, ; б) 9 а) Како је за 0 и 0 дати израз идентички једнак изразу,, : : то је за дате вредности,
РЕШЕНИ ЗАДАЦИ СА РАНИЈЕ ОДРЖАНИХ КЛАСИФИКАЦИОНИХ ИСПИТА 006. Задатак. Одредити вредност израза: а) : за, и 69 0, ; б) 9 а) Како је за 0 и 0 дати израз идентички једнак изразу,, : : то је за дате вредности,
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
Упутство за избор домаћих задатака
 Упутство за избор домаћих задатака Студент од изабраних задатака области Математике 2: Комбинаторика, Вероватноћа и статистика бира по 20 задатака. Студент може бирати задатке помоћу програмског пакета
Упутство за избор домаћих задатака Студент од изабраних задатака области Математике 2: Комбинаторика, Вероватноћа и статистика бира по 20 задатака. Студент може бирати задатке помоћу програмског пакета
ОБЛАСТИ: 1) Тачка 2) Права 3) Криве другог реда
 ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
Мониторинг квалитета ваздуха Града Новог Сада у години
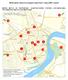 Мониторинг квалитета ваздуха Града Новог Сада у 2009. години МЕРНА МЕСТА ЗА УЗОРКОВАЊЕ ЈЕДНОЧАСОВНИХ УЗОРАКА АЗОТДИОКСИДA, УГЉЕНМОНОКСИДА И УГЉЕНДИОКСИДА А1. Поликлиника, Хајдук Вељкова 2, Нови Сад ГВИ
Мониторинг квалитета ваздуха Града Новог Сада у 2009. години МЕРНА МЕСТА ЗА УЗОРКОВАЊЕ ЈЕДНОЧАСОВНИХ УЗОРАКА АЗОТДИОКСИДA, УГЉЕНМОНОКСИДА И УГЉЕНДИОКСИДА А1. Поликлиника, Хајдук Вељкова 2, Нови Сад ГВИ
ЗБИРКА РИЈЕШЕНИХ ЗАДАТАКА ИЗ МАТЕМАТИКЕ ЗА ПРИЈЕМНИ ИСПИТ
 Универзитет у Источном Сарајеву Електротехнички факултет НАТАША ПАВЛОВИЋ ЗБИРКА РИЈЕШЕНИХ ЗАДАТАКА ИЗ МАТЕМАТИКЕ ЗА ПРИЈЕМНИ ИСПИТ Источно Сарајево,. године ПРЕДГОВОР Збирка задатака је првенствено намијењена
Универзитет у Источном Сарајеву Електротехнички факултет НАТАША ПАВЛОВИЋ ЗБИРКА РИЈЕШЕНИХ ЗАДАТАКА ИЗ МАТЕМАТИКЕ ЗА ПРИЈЕМНИ ИСПИТ Источно Сарајево,. године ПРЕДГОВОР Збирка задатака је првенствено намијењена
Арбитража Регулаторне комисије за електричну енергију у Федерацији Босне и Херцеговине ФЕРК у саставу: у поступку арбитраже по тужби.
 Број:05-04-925-13/19/06 Мостар, 31.05.2007. године Арбитража Регулаторне комисије за електричну енергију у Федерацији Босне и Херцеговине ФЕРК у саставу: Зденко Шимуновић, предсједник ФЕРК-а Ђулизара Хаџимустафић,
Број:05-04-925-13/19/06 Мостар, 31.05.2007. године Арбитража Регулаторне комисије за електричну енергију у Федерацији Босне и Херцеговине ФЕРК у саставу: Зденко Шимуновић, предсједник ФЕРК-а Ђулизара Хаџимустафић,
ЕЛЕКТРОНИКЕ ЗА УЧЕНИКЕ ТРЕЋЕГ РАЗРЕДА
 МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА РЕПУБЛИКЕ СРБИЈЕ ЗАЈЕДНИЦА ЕЛЕКТРОТЕХНИЧКИХ ШКОЛА РЕПУБЛИКЕ СРБИЈЕ ДВАДЕСЕТ ДРУГО РЕГИОНАЛНО ТАКМИЧЕЊЕ ОДГОВОРИ И РЕШЕЊА ИЗ ЕЛЕКТРОНИКЕ ЗА УЧЕНИКЕ ТРЕЋЕГ
МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА РЕПУБЛИКЕ СРБИЈЕ ЗАЈЕДНИЦА ЕЛЕКТРОТЕХНИЧКИХ ШКОЛА РЕПУБЛИКЕ СРБИЈЕ ДВАДЕСЕТ ДРУГО РЕГИОНАЛНО ТАКМИЧЕЊЕ ОДГОВОРИ И РЕШЕЊА ИЗ ЕЛЕКТРОНИКЕ ЗА УЧЕНИКЕ ТРЕЋЕГ
КРУГ. У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице.
 КРУГ У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице. Архимед (287-212 г.п.н.е.) 6.1. Централни и периферијски угао круга Круг
КРУГ У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице. Архимед (287-212 г.п.н.е.) 6.1. Централни и периферијски угао круга Круг
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
Прорачун токова снага рачунским путем и софтверским програмима Мatlab и Аtp
 Прорачун токова снага рачунским путем и софтверским програмима Мatlab и Аtp Стефан Чурлић Факултет техничких наука, Чачак Електротехничко и рачунарско инжењерство, индустријска електроенергетика, 2017/2018
Прорачун токова снага рачунским путем и софтверским програмима Мatlab и Аtp Стефан Чурлић Факултет техничких наука, Чачак Електротехничко и рачунарско инжењерство, индустријска електроенергетика, 2017/2018
Погодност за одржавање, Расположивост, Марковљеви ланци
 Погност за ржавање, Расположивост, Марковљеви ланци Погност за ржавање Одржавање обухвата све радње (осим рутинског сервисирања у току рада као што је замена горива или сличне мање активности) чији је
Погност за ржавање, Расположивост, Марковљеви ланци Погност за ржавање Одржавање обухвата све радње (осим рутинског сервисирања у току рада као што је замена горива или сличне мање активности) чији је
Релејне заштите које се координирају са погонским дијаграмом, функцијама система регулације побуде и заштитама електроенергетског система
 Stručni rad UDK:621.316.925:621.313.322 BIBLID:0350-8528(2016),26.p.85-99 doi:10.5937/zeint26-12300 Релејне заштите које се координирају са погонским дијаграмом, функцијама система регулације побуде и
Stručni rad UDK:621.316.925:621.313.322 BIBLID:0350-8528(2016),26.p.85-99 doi:10.5937/zeint26-12300 Релејне заштите које се координирају са погонским дијаграмом, функцијама система регулације побуде и
8.5 ЛАБОРАТОРИЈСКА ВЕЖБА 5 Задатак вежбе: PI регулација брзине напонски управљаним микромотором једносмерне струје
 Регулација електромоторних погона 8.5 ЛАБОРАТОРИЈСКА ВЕЖБА 5 Задатак вежбе: регулација брзине напонски управљаним микромотором једносмерне струје Увод Simulik модел На основу упрошћеног блок дијаграма
Регулација електромоторних погона 8.5 ЛАБОРАТОРИЈСКА ВЕЖБА 5 Задатак вежбе: регулација брзине напонски управљаним микромотором једносмерне струје Увод Simulik модел На основу упрошћеног блок дијаграма
Семинарски рад из линеарне алгебре
 Универзитет у Београду Машински факултет Докторске студије Милош Живановић дипл. инж. Семинарски рад из линеарне алгебре Београд, 6 Линеарна алгебра семинарски рад Дата је матрица: Задатак: a) Одредити
Универзитет у Београду Машински факултет Докторске студије Милош Живановић дипл. инж. Семинарски рад из линеарне алгебре Београд, 6 Линеарна алгебра семинарски рад Дата је матрица: Задатак: a) Одредити
Писмени испит из Теорије површинских носача. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама.
 Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2. За плочу
Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2. За плочу
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
