Επιχειρησιακή Έρευνα I
|
|
|
- Θωθ Βάμβας
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Επιχειρησιακή Έρευνα I Operations/Operational Research (OR) Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis
2 Περιεχόμενα EE 1&2 Εισαγωγή Μαθηματικός Προγραμματισμός - Γραμμικός Προγραμματισμός Βελτιστοποίηση δικτύων Μαθηματικός Προγραμματισμός - Ακέραιος Προγραμματισμός Μαθηματικός Προγραμματισμός - Δυναμικός προγραμματισμός Μαθηματικός Προγραμματισμός - Μη γραμμικός προγραμματισμός 2
3 Περιεχόμενα EE 1 Εισαγωγή Γραμμικός Προγραμματισμός Μοντελοποίηση Προβλημάτων Επίλυση Προβλημάτων Γραφική μέθοδος Μέθοδος Simplex Μέθοδος μεγάλου Μ Δυϊκότητα Βελτιστοποίηση δικτύων Πρόβλημα της συντομότερης διαδρομής Πρόβλημα του ελάχιστου ζευγνύοντος δέντρου Πρόβλημα μέγιστης ροής Πρόβλημα ροής ελαχίστου κόστους 3
4 Παραδείγματα Μοντελοποίησης
5 Παράδειγμα 1 Η επιχείρηση Whitt Window είναι µια επιχείρηση µε 3 µόνο υπαλλήλους οι οποίοι κατασκευάζουν δύο διαφορετικών ειδών παράθυρα: παράθυρα µε ξύλινο πλαίσιο και παράθυρα µε µεταλλικό πλαίσιο. Η επιχείρηση βγάζει ένα κέρδος 60 για κάθε παράθυρο µε ξύλινο πλαίσιο και 30 για κάθε παράθυρο µε µεταλλικό πλαίσιο. Ο υπάλληλος A κατασκευάζει παράθυρα µε ξύλινο πλαίσιο και µπορεί να παράγει 6 την ηµέρα. Ο υπάλληλος Β κατασκευάζει παράθυρα µε µεταλλικό πλαίσιο και µπορεί να παράγει 4 την ηµέρα. Ο υπάλληλος Γ κατασκευάζει τα τζάµια και µπορεί να παράγει 48 τετραγωνικά µέτρα την ηµέρα. Για κάθε παράθυρο µε ξύλινο πλαίσιο χρησιµοποιούνται 6 τ.µ γυαλί και για κάθε παράθυρο µε µεταλλικό πλαίσιο 8 τ.µ. Η επιχείρηση θέλει να προσδιορίσει πόσα παράθυρα από το κάθε είδος πρέπει να παράγει κάθε µέρα έτσι ώστε να µεγιστοποιήσει το συνολικό κέρδος της. 5
6 Παράδειγμα 1 Μεταβλητές απόφασης x1, x2. Max Z = 6x1 + 3x2 Περιορισμοί σε ανθρώπινο δυναμικό Χ 1 <=6 Χ 2 <=4 6Χ 1 + 8Χ 2 <=48 6
7 Παράδειγμα 2 Έστω τρείς αγροτικές κοινότητες Κ1, Κ2, Κ3 στις οποίες η κυβέρνηση έχει παραχωρήσει δυνατότητα χρήσης 400, 600 και 300 εκτάριων γης αντίστοιχα. Επίσης, έχει παραχωρήσει δυνατότητα χρήσης 600, 800 και 375 κυβικών νερού ανά κοινότητα. Τα αγροτικά προϊόντα που είναι κατάλληλα για παραγωγή είναι το ζαχαρότευτλο, το βαμβάκι και το σιτάρι. Συνολικά, η κυβέρνηση δε θέλει να καλλιεργηθούν περισσότερα από 600 εκτάρια σε ζαχαρότευτλο, 500 σε βαμβάκι και 325 σε σιτάρι Η κατανάλωση νερού ανά εκτάριο είναι 3 κυβικά για το ζαχαρότευτλο, 2 κυβικά για το βαμβάκι και 1 κυβικό για το σιτάρι. Κάθε κοινότητα θα καλλιεργεί το ίδιο ποσοστό του εδάφους με μια άλλη κοινότητα. Δηλαδή δεν μπορεί μια κοινότητα να καλλιεργήσει το 100% του εδάφους της και μια άλλη το 20% του εδάφους που της παραχωρείται Η παραγόμενη αξία είναι 4Κ ευρώ ανά εκτάριο με ζαχαρότευτλα, 3Κ ευρώ ανά εκτάριο βαμβακιού και 1Κ ευρώ ανά εκτάριο σιταριού Πόσο να καλλιεργήσει και από τι προϊόν κάθε κοινότητα για να μεγιστοποιηθεί το κέρδος; 7
8 Παράδειγμα 2 Πόσο να καλλιεργήσει και από τι προϊόν κάθε κοινότητα για να μεγιστοποιηθεί το κέρδος; Μεταβλητές απόφασης: Χ Κ1ΠΙ, Χ Κ1Π2, Χ Κ1Π3, Χ Κ2Π1, Χ Κ2Π2, Χ Κ2Π3, Χ Κ3ΠΙ, Χ Κ3Π2, Χ Κ3Π3 Περιορισμοί: Στα εκτάρια Χ Κ1ΠΙ + Χ Κ1Π2 + Χ Κ1Π3 <=400 Χ Κ2ΠΙ + Χ Κ2Π2 + Χ Κ2Π3 <=600 Χ Κ3ΠΙ + Χ Κ3Π2 + Χ Κ3Π3 <=300 Στα Προϊόντα Χ Κ1ΠΙ + Χ Κ2Π1 + Χ Κ3Π1 <=600 Χ Κ1Π2 + Χ Κ2Π2 + Χ Κ3Π2 <=500 Χ Κ1Π3 + Χ Κ2Π3 + Χ Κ3Π3 <=325 Στο νερό 3Χ Κ1ΠΙ + 2Χ Κ1Π2 + Χ Κ1Π3 <=600 3Χ Κ2ΠΙ + 2Χ Κ2Π2 + Χ Κ2Π3 <=800 3Χ Κ3ΠΙ + 2Χ Κ3Π2 + Χ Κ3Π3 <=375 Στις κοινωνικές συμφωνίες Χ Κ1ΠΙ + ΧΚ 1Π2 + ΧΚ 1Π3 400 = Χ Κ2ΠΙ + ΧΚ 2Π2 + ΧΚ 2Π3 600 = Χ Κ3ΠΙ + ΧΚ 3Π2 + ΧΚ 3Π
9 Παράδειγμα 2 Πόσο να καλλιεργήσει και από τι προϊόν κάθε κοινότητα για να μεγιστοποιηθεί το κέρδος; Η παραγόμενη αξία είναι 4Κ ευρώ ανά εκτάριο με ζαχαρότευτλα, 3Κ ευρώ ανά εκτάριο βαμβακιού και 1Κ ευρώ ανά εκτάριο σιταριού Max Z=4Χ Κ1ΠΙ + 4Χ Κ2Π1 + 4Χ Κ3Π1 + 3Χ Κ1Π2 + 3Χ Κ2Π2 + 3Χ Κ3Π2 + Χ Κ1Π3 + Χ Κ2Π3 + Χ Κ3Π3 Χ Κ1ΠΙ + Χ Κ1Π2 + Χ Κ1Π3 <=400 Χ Κ2ΠΙ + Χ Κ2Π2 + Χ Κ2Π3 <=600 Χ Κ3ΠΙ + Χ Κ3Π2 + Χ Κ3Π3 <=300 Χ Κ1ΠΙ + Χ Κ2Π1 + Χ Κ3Π1 <=600 Χ Κ1Π2 + Χ Κ2Π2 + Χ Κ3Π2 <=500 Χ Κ1Π3 + Χ Κ2Π3 + Χ Κ3Π3 <=325 3Χ Κ1ΠΙ + 2Χ Κ1Π2 + Χ Κ1Π3 <=600 3Χ Κ2ΠΙ +2Χ Κ2Π2 + Χ Κ2Π3 <=800 3Χ Κ3ΠΙ +2Χ Κ3Π2 + Χ Κ3Π3 <=375 Χ Κ1ΠΙ + ΧΚ 1Π2 + ΧΚ 1Π3 400 Χ Κ2ΠΙ + ΧΚ 2Π2 + ΧΚ 2Π3 600 = Χ Κ2ΠΙ + ΧΚ 2Π2 + ΧΚ 2Π3 600 = Χ Κ3ΠΙ + ΧΚ 3Π2 + ΧΚ 3Π3 300 Χ Κ1ΠΙ + ΧΚ 1Π2 + ΧΚ 1Π3 400 = Χ Κ3ΠΙ + ΧΚ 3Π2 + ΧΚ 3Π
10 Παράδειγμα 3 Μια χαλυβουργική μονάδα θέλει να μειώσει τους παραγόμενους ρύπους κατά 60 εκατομμύρια μονάδες σε στερεά σωματίδια, 150 εκατομμύρια μονάδες σε οξείδια του θείου και 125 εκατομμύρια μονάδες σε υδρογονάνθρακες Για να το πετύχει αυτό, η μονάδα μπορεί να χρησιμοποιήσει μεθόδους μείωσης ρύπων όπως (α) να αυξήσει το ύψος των καπνοδόχων, (β) να τοποθετήσει φίλτρα ή/και (γ) να χρησιμοποιεί καλύτερο καύσιμο Η πηγές ρύπανσης είναι δύο. Οι κάμινοι εμφύσησης και οι ανοικτές κάμινοι. Για κάθε μια μέθοδο μείωσης ρύπων έχουμε αντίστοιχη μείωση ανά πηγή ρύπανσης βάσει του πίνακα: Ρυπαντής Ψηλότερες Καπνοδόχοι Φίλτρα Καλύτερα Καύσιμα Κάμινοι Εμφύσησης Ανοικτές Κάμινοι Κάμινοι Εμφύσησης Ανοικτές Κάμινοι Κάμινοι Εμφύσησης Στερεά Σωμ Οξείδια θείου Υδρογονάθ Ανοικτές Κάμινοι 10
11 Παράδειγμα 3 Η ετήσια δαπάνη (χρημ. μον.) ανά μέθοδο μείωσης των ρύπων ανά πηγή ρύπανσης δίνεται βάσει του πίνακα: Κάμινοι Εμφύσησης Ανοικτές Κάμινοι Ψηλότερες Καπνοδόχοι 8 10 Φίλτρα 7 6 Καλύτερα Καύσιμα 11 9 Το πρόβλημα είναι να βρεθεί η σωστή αναλογία χρήσης κάθε μεθόδου μείωσης ρύπων ανά πηγή ρύπανσης για να ελαχιστοποιηθεί το κόστος. Οι μεταβλητές απόφασης είναι: Κάμινοι Εμφύσησης Ανοικτές Κάμινοι Ψηλότερες Καπνοδόχοι x 1 x 2 Φίλτρα x 3 x 4 Καλύτερα Καύσιμα x 5 x 6 11
12 Παράδειγμα 3 Ποια είναι η σωστή αναλογία χρήσης κάθε μεθόδου μείωσης ρύπων ανά πηγή ρύπανσης για να ελαχιστοποιηθεί το κόστος; Min (Z) = 8Χ Χ 2 + 7Χ 3 +6Χ Χ 5 + 9Χ 6 Μεταβλητές απόφασης: Χ 1, Χ 2, Χ 3, Χ 4, Χ 5, Χ 6. Περιορισμοί: Ρύπανσης 12Χ 1 + 9Χ Χ 3 +20Χ Χ Χ 6 >=60 35Χ Χ Χ 3 +31Χ Χ Χ 6 >=150 37Χ Χ Χ 3 +24Χ Χ Χ 6 >=125 Αναλογίας Χ j <=1 για κάθε j=1,2,3..6 Μη αρνητικότητας Χ j >=0 για κάθε j=1,2,
13 Παράδειγμα 4 Ένα εργοστάσιο παράγει μέχρι 5 τύπους προϊόντων (Π1, Π2,..., Π5) χρησιμοποιώντας δύο διαδικασίες Δ1 και Δ2.Μετά την αφαίρεση του κόστους των πρώτων υλών, κάθε μονάδα προϊόντος επιφέρει το ακόλουθο κέρδος Π1 Π2 Π3 Π4 Π Κάθε μονάδα προϊόντος απαιτεί ορισμένο χρόνο στην κάθε διαδικασία: Π1 Π2 Π3 Π4 Π5 Δ Δ Η τελική συναρμολόγηση κάθε μονάδας του κάθε προϊόντος απαιτεί 20 εργατοώρες. Το εργοστάσιο έχει 3 μηχανές για την διαδικασία Δ1 και 2 μηχανές για την Δ2 και επίσης λειτουργεί 6 ημέρες την εβδομάδα, με 2 βάρδιες των 8 ωρών την ημέρα. 8 εργάτες εργάζονται στην συναρμολόγηση και ο καθένας κάνει μία βάρδια την ημέρα. Το πρόβλημα είναι η εύρεση του βέλτιστου ποσού παραγωγής του κάθε προϊόντος έτσι ώστε να μεγιστοποιηθεί το κέρδος. 13
14 Παράδειγμα 4 Max(z) = 550x x x x x 5 Περιορισμοί Μηχανών: 3 μηχανές για Δ1 * 96 ώρες / εβδομάδα = 288 ώρες / εβδομάδα, οπότε: 12x x x x 5 <=288 2 μηχανές για Δ2 * 96 ώρες / εβδομάδα = 192 ώρες / εβδομάδα, οπότε: 10x 1 + 8x x 3 <= 192 Περιορισμοί Εργατών: 8 εργάτες x 48 ώρες / εβδομάδα = 384 ώρες / εβδομάδα. Επειδή κάθε μονάδα προϊόντος απαιτεί 20 ώρες έχουμε: 20x x x x x 5 <=384 14
15 Παράδειγμα 4 Max(z) = 550x1+ 600x2+ 350x3+ 400x4+ 200x5 S.t. 12x1 + 20x2+ 25x4+ 15x5<=288 10x1 + 8x2+ 16x3 <= x1+ 20x2+ 20x3+ 20x4+ 20x5<=384 x1,x2,x3,x4,x5>=0 15
16 Παράδειγμα 5 Η ανάπτυξη των ζώων επηρεάζεται πολύ από τρία βασικά στοιχεία διατροφής: "πρωτεΐνη", "άλατα" και "βιταμίνες". Τα ελάχιστα ημερήσια ποσά είναι: 70gr πρωτεΐνη, 3gr άλατα και 10mg βιταμίνη. Υπάρχουν πέντε τύποι διατροφής (Α,Β,Γ,Δ,Ε) διαθέσιμα για την ικανοποίηση των απαιτήσεων. Το περιεχόμενο ανά κιλό κάθε είδους διατροφής είναι: Τύπος Διατροφής Πρωτεΐνη (gr) Άλατα (gr) Βιταμίνη (mgr) Α Β Γ Δ Ε Το κόστος ενός κιλού τους κάθε είδους διατροφής σε χρηματικές μονάδες είναι: Τύπος Διατροφής Α Β Γ Δ Ε Κόστος (χρ. μον) Το πρόβλημα είναι η εύρεση συνδυασμού τύπων διατροφής που ικανοποιεί τις διατροφικές απαιτήσεις με το ελάχιστο κόστος. 16
17 Παράδειγμα 5 Μεταβλητές απόφασης x j, j=1, 2,... 5 min z = 2x 1 + 7x 2 + 4x 3 + 3x 4 + 5x 5 με τους περιορισμούς: 0.30x x x x x 5 => x x x x x 5 =>3 0.05x x x x x 5 =>10 X j >=0, j= 1, 2,..., 5 17
18 Παράδειγμα 6 Ένα εργοστάσιο επιπλοποιίας κατασκευάζει τραπέζια, καρέκλες, γραφεία και βιβλιοθήκες. Οι βασικές πρώτες ύλες είναι το ξύλο καρυδιάς και το MDF. Επίσης κάθε έπιπλο χρειάζεται ανθρωποώρες εργασίας. Ο ακόλουθος πίνακας παρουσιάζει τις απαιτήσεις κάθε μονάδας παραγωγής: Είδος MDF(ft 3 ) Καρυδιά(ft 3 ) Εργατοώρες Τραπέζι Καρέκλα Γραφείο Βιβλιοθήκη Η παραγωγή σχεδιάζεται για μια περίοδο 10 ημερών. Για την περίοδο αυτή υπάρχουν διαθέσιμα 1500ft 3 MDF και 1000ft 3 καρυδιά. Το ξύλο MDF κοστίζει 100χ.μ./ft 3 και το ξύλο καρυδιάς 250χ.μ./ft 3. Το κόστος της ανθρωποώρας είναι 500χ.μ. και υπάρχουν 10 εργάτες που εργάζονται μια βάρδια (8ωρο) ανά ημέρα. Κάθε τραπέζι πωλείται 3100χ.μ., κάθε καρέκλα πωλείται 2100χ.μ. κάθε γραφείο 5100χ.μ. και τέλος, κάθε βιβλιοθήκη πωλείται 6900χ.μ. Το πρόβλημα είναι η εύρεση του αριθμού των ειδών για το μέγιστο κέρδος του εργοστασίου. (κέρδος μονάδας= τιμή πώλησης μονάδας μείον το κόστος μονάδας) Π.χ. κέρδος ανά τραπέζι = 3100 (5* * *500) = 600χ.μ 18
19 Παράδειγμα 6 max z = 600x T + 250x K + 750x Γ + 450x Β με τους ακόλουθους περιορισμούς που οφείλονται στα περιορισμένα υλικά (MDF και καρυδιά) και στις ανθρωποώρες που είναι διαθέσιμα: 5x Τ + x Κ + 9x Γ + 12x Β <=1500 2x Τ + 3x Κ + 4x Γ + x Β <=1000 3x Τ + 2x Κ + 5x Γ + 10x Β <=800 x Τ, x Κ, x Γ, x Β >=0. 19
20 Παράδειγμα 7 Έστω το παρακάτω µοντέλο γραµµικού προγραµµατισµού: max z = 4x 1 + 5x 2 Κάτω από τις συνθήκες: 3x 1 + 1x x 1 + 5x 2 = 6 6x 1 + 4x 2 6 x 1 0, x 2 0 Να εκφράσετε το παρακάτω µοντέλο στην τυποποιηµένη του µορφή, εισάγοντας, αν είναι απαραίτητο, επιπρόσθετες µεταβλητές. Λύστε το πρόβληµα με τον solver. z - 4x1-5x2 - Mx4 - Mx6 = 0 3x1 + 1x2 + x3 = 27 5x1 + 5x2 + x4 = 6 6x1 + 4x2 - x5 + x6 = 6 20
21 Παράδειγμα 8 Έστω το παρακάτω µοντέλο γραµµικού προγραµµατισµού: min z = 5x 1-6x 2 Κάτω από τις συνθήκες: x 1 + 3x 2 6 x 1 + x 2-1 3x 1 + 2x 2 3 x 2 0 Να εκφράσετε το παρακάτω µοντέλο στην τυποποιηµένη του µορφή, εισάγοντας, αν είναι απαραίτητο, επιπρόσθετες µεταβλητές Λύστε το πρόβληµα. Ερµηνεύστε την βέλτιστη λύση και τις τιµές των επιπρόσθετων µεταβλητών. Ποια είναι η ερµηνεία της κάθε µιας από τις µεταβλητές αυτές; max - z = -5x1 + 6x2 -z + 5x1-6x2 + Mx6= 0 x1 + 3x2 + x3 = 6 -x1 - x2 + x4 = 1 3x1 + 2x2 -x5 + x6 = 3 21
Επιχειρησιακή Έρευνα I
 Επιχειρησιακή Έρευνα I Operations/Operational Research (OR) Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα EE 1&2 Εισαγωγή Μαθηματικός Προγραμματισμός - Γραμμικός
Επιχειρησιακή Έρευνα I Operations/Operational Research (OR) Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα EE 1&2 Εισαγωγή Μαθηματικός Προγραμματισμός - Γραμμικός
Επιχειρησιακή Έρευνα I
 Επιχειρησιακή Έρευνα I Operations/Operational Research (OR) Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα EE 1&2 Εισαγωγή Μαθηματικός Προγραμματισμός - Γραμμικός
Επιχειρησιακή Έρευνα I Operations/Operational Research (OR) Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα EE 1&2 Εισαγωγή Μαθηματικός Προγραμματισμός - Γραμμικός
Επιχειρησιακή Έρευνα I
 Επιχειρησιακή Έρευνα I Operations/Operational Research (OR) Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Παραδείγματα Μοντελοποίησης Παράδειγμα 1 Οι φοιτητές του ΤΜΟΔ ως γνωστό-
Επιχειρησιακή Έρευνα I Operations/Operational Research (OR) Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Παραδείγματα Μοντελοποίησης Παράδειγμα 1 Οι φοιτητές του ΤΜΟΔ ως γνωστό-
Επιχειρησιακή Έρευνα I
 Επιχειρησιακή Έρευνα I Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα 1. Εισαγωγή 2. Γραμμικός Προγραμματισμός 1. Μοντελοποίηση 2. Μέθοδος Simplex (C) Copyright Α.
Επιχειρησιακή Έρευνα I Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα 1. Εισαγωγή 2. Γραμμικός Προγραμματισμός 1. Μοντελοποίηση 2. Μέθοδος Simplex (C) Copyright Α.
Επιχειρησιακή Έρευνα I
 Επιχειρησιακή Έρευνα I Operations/Operational Research (OR) Κωστής Μαμάσης Παρασκευή 9: : Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα EE & Εισαγωγή Μαθηματικός Προγραμματισμός - Γραμμικός Προγραμματισμός
Επιχειρησιακή Έρευνα I Operations/Operational Research (OR) Κωστής Μαμάσης Παρασκευή 9: : Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα EE & Εισαγωγή Μαθηματικός Προγραμματισμός - Γραμμικός Προγραμματισμός
Ανάλυση ευαισθησίας. Άσκηση 3 Δίνεται ο παρακάτω τελικός πίνακας Simplex. Επιχειρησιακή Έρευνα Γκόγκος Χρήστος
 Τμήμα Μηχανικών Πληροφορικής ΤΕ Ακαδημαϊκό έτος 2016-2017 Άρτα Επιχειρησιακή Έρευνα Γκόγκος Χρήστος Μεταπτυχιακό Μηχανικών Η/Υ και Δικτύων Μεταπτυχιακό Μηχανικών Η/Υ και Δικτύων ΣΕΤ ΑΣΚΗΣΕΩΝ 3 Ανάλυση
Τμήμα Μηχανικών Πληροφορικής ΤΕ Ακαδημαϊκό έτος 2016-2017 Άρτα Επιχειρησιακή Έρευνα Γκόγκος Χρήστος Μεταπτυχιακό Μηχανικών Η/Υ και Δικτύων Μεταπτυχιακό Μηχανικών Η/Υ και Δικτύων ΣΕΤ ΑΣΚΗΣΕΩΝ 3 Ανάλυση
Επιχειρησιακή Έρευνα I
 Επιχειρησιακή Έρευνα I Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα 1. Εισαγωγή 2. Γραμμικός Προγραμματισμός 1. Μοντελοποίηση 2. Μέθοδος Simplex 1. Αλγόριθμός Simplex
Επιχειρησιακή Έρευνα I Κωστής Μαμάσης Παρασκευή 09:00 12:00 Σημειώσεις των Α. Platis, K. Mamasis Περιεχόμενα 1. Εισαγωγή 2. Γραμμικός Προγραμματισμός 1. Μοντελοποίηση 2. Μέθοδος Simplex 1. Αλγόριθμός Simplex
Α) δηλώνουν τις ποσότητες που, ανάλογα με το πρόβλημα, θα παραχθούν, επενδυθούν, αγοραστούν, κατασκευαστούν κ.λπ.
 1. 0 γραμμικός προγραμματισμός μπορεί να εφαρμοστεί στη διαχείριση αγροτικής παραγωγής για τη βέλτιστη κατανομή πόρων όπως., με τρόπο που να οδηγεί στη μεγιστοποίηση των κερδών. Α) διαθέσιμης προς καλλιέργειας
1. 0 γραμμικός προγραμματισμός μπορεί να εφαρμοστεί στη διαχείριση αγροτικής παραγωγής για τη βέλτιστη κατανομή πόρων όπως., με τρόπο που να οδηγεί στη μεγιστοποίηση των κερδών. Α) διαθέσιμης προς καλλιέργειας
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΣΗΜΕΙΩΣΕΙΣ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΣΗΜΕΙΩΣΕΙΣ Δ.Α.Π. Ν.Δ.Φ.Κ. ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΕΙΡΑΙΩΣ www.dap-papei.gr ΠΑΡΑΔΕΙΓΜΑ 1 ΑΣΚΗΣΗ 1 Η FASHION Α.Ε είναι μια από
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΤΜΗΜΑ ΟΡΓΑΝΩΣΗΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΕΩΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΣΗΜΕΙΩΣΕΙΣ Δ.Α.Π. Ν.Δ.Φ.Κ. ΠΑΝΕΠΙΣΤΗΜΙΟΥ ΠΕΙΡΑΙΩΣ www.dap-papei.gr ΠΑΡΑΔΕΙΓΜΑ 1 ΑΣΚΗΣΗ 1 Η FASHION Α.Ε είναι μια από
Τμήμα Διοίκησης Επιχειρήσεων
 Τμήμα Διοίκησης Επιχειρήσεων ΠΟΣΟΤΙΚΕΣ ΜΕΘΟΔΟΙ ΣΤΗ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ Ενότητα 1: Γραµµικός προγραµµατισµός(γ.π.) ιδάσκων: Βασίλειος Ισµυρλής Τηλ:6979948174, e-mail: vasismir@gmail.com http://vasilis-ismyrlis.webnode.gr/
Τμήμα Διοίκησης Επιχειρήσεων ΠΟΣΟΤΙΚΕΣ ΜΕΘΟΔΟΙ ΣΤΗ ΔΙΟΙΚΗΣΗ ΕΠΙΧΕΙΡΗΣΕΩΝ Ενότητα 1: Γραµµικός προγραµµατισµός(γ.π.) ιδάσκων: Βασίλειος Ισµυρλής Τηλ:6979948174, e-mail: vasismir@gmail.com http://vasilis-ismyrlis.webnode.gr/
Τμήμα Διεθνούς Εμπορίου Επιχειρησιακή έρευνα. Επιχειρησιακή Έρευνα
 ΤΕΙ Δυτικής Μακεδονίας Τμήμα Διεθνούς Εμπορίου Επιχειρησιακή Έρευνα Προβλήματα Διαμόρφωση μαθηματικού μοντέλου Γραφική λύση Επίλυση με τη μέθοδο Simplex Δρ. Ζαχαρούλα Καλογηράτου 1 Πρόβλημα 1. Εργαστήριο
ΤΕΙ Δυτικής Μακεδονίας Τμήμα Διεθνούς Εμπορίου Επιχειρησιακή Έρευνα Προβλήματα Διαμόρφωση μαθηματικού μοντέλου Γραφική λύση Επίλυση με τη μέθοδο Simplex Δρ. Ζαχαρούλα Καλογηράτου 1 Πρόβλημα 1. Εργαστήριο
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 2: Τεχνικές Μοντελοποίησης, Εφαρμογές Μοντελοποίησης Γραμμικών Προβλημάτων Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 2: Τεχνικές Μοντελοποίησης, Εφαρμογές Μοντελοποίησης Γραμμικών Προβλημάτων Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Επιχειρησιακή Έρευνα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #1: Ασκήσεις Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #1: Ασκήσεις Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το παρόν εκπαιδευτικό
Ανάλυση Ευαισθησίας µε τη χρήση του Solver
 Ανάλυση Ευαισθησίας µε τη χρήση του Solver Πρόβληµα 1 Μια εταιρία κατασκευής τηλεοράσεων κατασκευάζει τέσσερα µοντέλα τηλεοράσεων Μ1, Μ2, Μ3 και Μ4. Κάθε µοντέλο για να παραχθεί απαιτεί χρόνο συναρµολόγησης
Ανάλυση Ευαισθησίας µε τη χρήση του Solver Πρόβληµα 1 Μια εταιρία κατασκευής τηλεοράσεων κατασκευάζει τέσσερα µοντέλα τηλεοράσεων Μ1, Μ2, Μ3 και Μ4. Κάθε µοντέλο για να παραχθεί απαιτεί χρόνο συναρµολόγησης
 Άσκηση 1 Ένα κεντρικό βιβλιοπωλείο ειδικεύεται στα λογοτεχνικά βιβλία και τα βιβλία τέχνης. Προκειμένου να προωθήσει μια νέα συλλογή λογοτεχνικών βιβλίων και βιβλίων τέχνης, η διεύθυνση του βιβλιοπωλείου
Άσκηση 1 Ένα κεντρικό βιβλιοπωλείο ειδικεύεται στα λογοτεχνικά βιβλία και τα βιβλία τέχνης. Προκειμένου να προωθήσει μια νέα συλλογή λογοτεχνικών βιβλίων και βιβλίων τέχνης, η διεύθυνση του βιβλιοπωλείου
3.7 Παραδείγματα Μεθόδου Simplex
 3.7 Παραδείγματα Μεθόδου Simplex Παράδειγμα 1ο (Παράδειγμα 1ο - Κεφάλαιο 2ο - σελ. 10): Το πρόβλημα εκφράζεται από το μαθηματικό μοντέλο: max z = 600x T + 250x K + 750x Γ + 450x B 5x T + x K + 9x Γ + 12x
3.7 Παραδείγματα Μεθόδου Simplex Παράδειγμα 1ο (Παράδειγμα 1ο - Κεφάλαιο 2ο - σελ. 10): Το πρόβλημα εκφράζεται από το μαθηματικό μοντέλο: max z = 600x T + 250x K + 750x Γ + 450x B 5x T + x K + 9x Γ + 12x
ΠΡΩΤΟ ΣΕΤ ΑΣΚΗΣΕΩΝ-ΓΡΑΦΙΚΗ ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΟΣ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 ΠΡΩΤΟ ΣΕΤ ΑΣΚΗΣΕΩΝ-ΓΡΑΦΙΚΗ ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΟΣ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΑΣΚΗΣΗ 1 Ένας κτηµατίας πρέπει να καθορίσει πόσα στρέµµατα καλαµποκιού και σιταριού να φυτέψει αυτή τη χρονιά. Ένα στρέµµα σιταριού
ΠΡΩΤΟ ΣΕΤ ΑΣΚΗΣΕΩΝ-ΓΡΑΦΙΚΗ ΕΠΙΛΥΣΗ ΠΡΟΒΛΗΜΑΤΟΣ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΑΣΚΗΣΗ 1 Ένας κτηµατίας πρέπει να καθορίσει πόσα στρέµµατα καλαµποκιού και σιταριού να φυτέψει αυτή τη χρονιά. Ένα στρέµµα σιταριού
Διδάσκων: Νίκος Λαγαρός
 ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ 4 η Σειρά Ασκήσεων του Μαθήματος «ΕΙΣΑΓΩΓΗ ΣΤΗN ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ» Διδάσκων: Νίκος Λαγαρός Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες Χρήσης Creative
ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΕΜΠ 4 η Σειρά Ασκήσεων του Μαθήματος «ΕΙΣΑΓΩΓΗ ΣΤΗN ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΣΥΣΤΗΜΑΤΩΝ» Διδάσκων: Νίκος Λαγαρός Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες Χρήσης Creative
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1
 ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1 1 Βελτιστοποίηση Στην προσπάθεια αντιμετώπισης και επίλυσης των προβλημάτων που προκύπτουν στην πράξη, αναπτύσσουμε μαθηματικά μοντέλα,
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ ΚΕΦΑΛΑΙΟ 1 1 Βελτιστοποίηση Στην προσπάθεια αντιμετώπισης και επίλυσης των προβλημάτων που προκύπτουν στην πράξη, αναπτύσσουμε μαθηματικά μοντέλα,
Β. Τυπική μορφή (κανόνες μετατροπής, προβλήματα μετατροπής) - Λυμένο πρόβλημα 2, Ασκήσεις 2,3,4,5.
 Άλυτες Ασκήσεις ΓΠ Α. Μέρη ενός προβλήματος ΓΠ - Λυμένο πρόβλημα 1, Άσκηση 1. Β. Τυπική μορφή (κανόνες μετατροπής, προβλήματα μετατροπής) - Λυμένο πρόβλημα 2, Ασκήσεις 2,3,4,5. Γ. Διατύπωση μαθηματικού
Άλυτες Ασκήσεις ΓΠ Α. Μέρη ενός προβλήματος ΓΠ - Λυμένο πρόβλημα 1, Άσκηση 1. Β. Τυπική μορφή (κανόνες μετατροπής, προβλήματα μετατροπής) - Λυμένο πρόβλημα 2, Ασκήσεις 2,3,4,5. Γ. Διατύπωση μαθηματικού
Γραμμικός Προγραμματισμός
 Μια εταιρεία παράγει κέικ δύο κατηγοριών, απλά και πολυτελείας: Ένα απλό κέικ αποδίδει κέρδος 1 ευρώ. Ένα κέικ πολυτελείας αποδίδει κέρδος 6 ευρώ. Η καθημερινή ζήτηση του απλού κέικ είναι 200. Η καθημερινή
Μια εταιρεία παράγει κέικ δύο κατηγοριών, απλά και πολυτελείας: Ένα απλό κέικ αποδίδει κέρδος 1 ευρώ. Ένα κέικ πολυτελείας αποδίδει κέρδος 6 ευρώ. Η καθημερινή ζήτηση του απλού κέικ είναι 200. Η καθημερινή
maximize z = 50x x 2 κάτω από τους περιορισμούς (εβδομαδιαίο κέρδος, χρηματικές μονάδες)
 Ένας κοσμηματοπώλης, κατασκευάζει μπρασελέ και κολιέ αναμειγνύοντας ασήμι με κάποιο άλλο μέταλλο. Το μοντέλο π.γ.π. που ανέπτυξε για την εύρεση της εβδομαδιαίας παραγωγής (x 1 μπρασελέ και x 2 κολιέ) η
Ένας κοσμηματοπώλης, κατασκευάζει μπρασελέ και κολιέ αναμειγνύοντας ασήμι με κάποιο άλλο μέταλλο. Το μοντέλο π.γ.π. που ανέπτυξε για την εύρεση της εβδομαδιαίας παραγωγής (x 1 μπρασελέ και x 2 κολιέ) η
Εισαγωγή στο Γραμμικό Προγραμματισμό. Χειμερινό Εξάμηνο
 Εισαγωγή στο Γραμμικό Προγραμματισμό Χειμερινό Εξάμηνο 2016-2017 Εισαγωγή Ασχολείται με το πρόβλημα της άριστης κατανομής των περιορισμένων πόρων μεταξύ ανταγωνιζόμενων δραστηριοτήτων μιας επιχείρησης
Εισαγωγή στο Γραμμικό Προγραμματισμό Χειμερινό Εξάμηνο 2016-2017 Εισαγωγή Ασχολείται με το πρόβλημα της άριστης κατανομής των περιορισμένων πόρων μεταξύ ανταγωνιζόμενων δραστηριοτήτων μιας επιχείρησης
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ. Κεφάλαιο 2 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού
 ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Κεφάλαιο 2 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού 1 Μεταξύ δύο περιορισμών, ο ένας πρέπει να ισχύει Έστω ότι για την κατασκευή ενός προϊόντος
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Κεφάλαιο 2 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού 1 Μεταξύ δύο περιορισμών, ο ένας πρέπει να ισχύει Έστω ότι για την κατασκευή ενός προϊόντος
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D.
 Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Γραμμικός προγραμματισμός: Εισαγωγή Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών ΤμήμαΠληροφορικής Διάλεξη 3 η /2017 Γραμμικός προγραμματισμός Είναι μια μεθοδολογία
Βασίλειος Μαχαιράς Πολιτικός Μηχανικός Ph.D. Γραμμικός προγραμματισμός: Εισαγωγή Πανεπιστήμιο Θεσσαλίας Σχολή Θετικών Επιστημών ΤμήμαΠληροφορικής Διάλεξη 3 η /2017 Γραμμικός προγραμματισμός Είναι μια μεθοδολογία
2. ΣΥΓΚΕΝΤΡΩΤΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΠΑΡΑΓΩΓΗΣ
 2. ΣΥΓΚΕΝΤΡΩΤΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΠΑΡΑΓΩΓΗΣ Ο Συγκεντρωτικός Προγραμματισμός Παραγωγής (Aggregae Produion Planning) επικεντρώνεται: α) στον προσδιορισμό των ποσοτήτων ανά κατηγορία προϊόντων και ανά χρονική
2. ΣΥΓΚΕΝΤΡΩΤΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΠΑΡΑΓΩΓΗΣ Ο Συγκεντρωτικός Προγραμματισμός Παραγωγής (Aggregae Produion Planning) επικεντρώνεται: α) στον προσδιορισμό των ποσοτήτων ανά κατηγορία προϊόντων και ανά χρονική
2.1. ΑΠΛΑ ΠΑΡΑΔΕΙΓΜΑΤΑ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 . ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ. ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ( Linear Programming ) Ο Γραμμικός Προγραμματισμός είναι μια τεχνική που επιτρέπει την κατανομή των περιορισμένων πόρων μιας επιχείρησης με τον πιο
. ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ. ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ( Linear Programming ) Ο Γραμμικός Προγραμματισμός είναι μια τεχνική που επιτρέπει την κατανομή των περιορισμένων πόρων μιας επιχείρησης με τον πιο
Επιχειρησιακή Έρευνα
 Επιχειρησιακή Έρευνα Ενότητα 1: Εισαγωγή στο Γραμμικό Προγραμματισμό (1 ο μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
Επιχειρησιακή Έρευνα Ενότητα 1: Εισαγωγή στο Γραμμικό Προγραμματισμό (1 ο μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
Μοντελοποίηση προβληµάτων
 Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Θεωρία γράφων
Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Σχεδιασµός Αλγορίθµων Ακέραιος προγραµµατισµός Αποδοτικοί Αλγόριθµοι Μη Αποδοτικοί Αλγόριθµοι Θεωρία γράφων
Τ.Ε.Ι. Πειραιά Π.Μ.Σ. ΕΠΙΣΤΗΜΗ ΤΩΝ ΑΠΟΦΑΣΕΩΝ ΜΕ ΠΛΗΡΟΦΟΡΙΑΚΑ ΣΥΣΤΗΜΑΤΑ
 Τ.Ε.Ι. Πειραιά Π.Μ.Σ. ΕΠΙΣΤΗΜΗ ΤΩΝ ΑΠΟΦΑΣΕΩΝ ΜΕ ΠΛΗΡΟΦΟΡΙΑΚΑ ΣΥΣΤΗΜΑΤΑ Ακαδημαϊκό Έτος: 2013-2014 (Χειμερινό Εξάμηνο) Μάθημα: Σχεδιασμός Αλγορίθμων και Επιχειρησιακή Έρευνα Καθηγητής: Νίκος Τσότσολας Εργασία
Τ.Ε.Ι. Πειραιά Π.Μ.Σ. ΕΠΙΣΤΗΜΗ ΤΩΝ ΑΠΟΦΑΣΕΩΝ ΜΕ ΠΛΗΡΟΦΟΡΙΑΚΑ ΣΥΣΤΗΜΑΤΑ Ακαδημαϊκό Έτος: 2013-2014 (Χειμερινό Εξάμηνο) Μάθημα: Σχεδιασμός Αλγορίθμων και Επιχειρησιακή Έρευνα Καθηγητής: Νίκος Τσότσολας Εργασία
Μίγμα προϊόντων (product mix)
 ΠΡΟΒΛΗΜΑΤΑ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ 2 Μίγμα προϊόντων (product mix) Σε τέτοιου είδους προβλήματα, ο στόχος της βελτιστοποίησης είναι να βρεθεί η πιο κερδοφόρα λύση με βάση περιορισμένους πόρους εν συγκρίσει επιθυμητών
ΠΡΟΒΛΗΜΑΤΑ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ 2 Μίγμα προϊόντων (product mix) Σε τέτοιου είδους προβλήματα, ο στόχος της βελτιστοποίησης είναι να βρεθεί η πιο κερδοφόρα λύση με βάση περιορισμένους πόρους εν συγκρίσει επιθυμητών
ΜΑΘΗΜΑΤΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΘΕΜΑ 1 ΜΑΘΗΜΑΤΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ένα παραγωγικό σύστημα χρησιμοποιεί δύο διαδικασίες, τις D1 και D2, κάθε μία από τις οποίες συμπαράγει δύο προϊόντα Α και Β σε διαφορετικές αναλογίες, χρησιμοποιώντας
ΘΕΜΑ 1 ΜΑΘΗΜΑΤΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ένα παραγωγικό σύστημα χρησιμοποιεί δύο διαδικασίες, τις D1 και D2, κάθε μία από τις οποίες συμπαράγει δύο προϊόντα Α και Β σε διαφορετικές αναλογίες, χρησιμοποιώντας
Περιεχόμενα Πρόλογος 5ης αναθεωρημένης έκδοσης ΚΕΦΆΛΆΙΟ 1 Ο ρόλος της επιχειρησιακής έρευνας στη λήψη αποφάσεων ΚΕΦΆΛΆΙΟ 2.
 Περιεχόμενα Πρόλογος 5ης αναθεωρημένης έκδοσης... 11 Λίγα λόγια για βιβλίο... 11 Σε ποιους απευθύνεται... 12 Τι αλλάζει στην 5η αναθεωρημένη έκδοση... 12 Το βιβλίο ως διδακτικό εγχειρίδιο... 14 Ευχαριστίες...
Περιεχόμενα Πρόλογος 5ης αναθεωρημένης έκδοσης... 11 Λίγα λόγια για βιβλίο... 11 Σε ποιους απευθύνεται... 12 Τι αλλάζει στην 5η αναθεωρημένη έκδοση... 12 Το βιβλίο ως διδακτικό εγχειρίδιο... 14 Ευχαριστίες...
Επιχειρησιακή Έρευνα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #6: Στοχαστικός Γραμμικός Προγραμματισμός Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #6: Στοχαστικός Γραμμικός Προγραμματισμός Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων
Μέθοδοι Βελτιστοποίησης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μέθοδοι Βελτιστοποίησης Ενότητα # 5: Πολυστοχαστικός Προγραμματισμός Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μέθοδοι Βελτιστοποίησης Ενότητα # 5: Πολυστοχαστικός Προγραμματισμός Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων
Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ Π Ρ Ο Γ Ρ Α Μ Μ Α Τ Ι Σ Μ Ο Σ
 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΦΕΒΡΟΥΑΡΙΟΣ 013 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ Π Ρ Ο Γ Ρ Α Μ Μ Α Τ Ι Σ Μ Ο Σ ΘΕΜΑ 1 ο : Για το μοντέλο του π.γ.π. που ακολουθεί maximize
ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΦΕΒΡΟΥΑΡΙΟΣ 013 ΤΟΜΕΑΣ ΣΤΑΤΙΣΤΙΚΗΣ, ΠΙΘΑΝΟΤΗΤΩΝ & ΕΠΙΧΕΙΡΗΣΙΑΚΗΣ ΕΡΕΥΝΑΣ Μ Α Θ Η Μ Α Τ Ι Κ Ο Σ Π Ρ Ο Γ Ρ Α Μ Μ Α Τ Ι Σ Μ Ο Σ ΘΕΜΑ 1 ο : Για το μοντέλο του π.γ.π. που ακολουθεί maximize
1. ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 Η επιχειρησιακή έρευνα επικεντρώνεται στη λήψη αποφάσεων από επιχειρήσεις οργανισμούς, κράτη κτλ. Στα πλαίσια της επιχειρησιακής έρευνας εξετάζονται οι ακόλουθες περιπτώσεις : Γραμμικός προγραμματισμός
Η επιχειρησιακή έρευνα επικεντρώνεται στη λήψη αποφάσεων από επιχειρήσεις οργανισμούς, κράτη κτλ. Στα πλαίσια της επιχειρησιακής έρευνας εξετάζονται οι ακόλουθες περιπτώσεις : Γραμμικός προγραμματισμός
Επιχειρησιακή Έρευνα
 Επιχειρησιακή Έρευνα Ενότητα 6: Εφαρμογές Γραμμικού Προγραμματισμού (2 ο μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
Επιχειρησιακή Έρευνα Ενότητα 6: Εφαρμογές Γραμμικού Προγραμματισμού (2 ο μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
ιαµόρφωση Προβλήµατος
 Γραµµικός Προγραµµατισµός ιαµόρφωση Προβλήµατος Η παρουσίαση προετοιµάστηκε από τον Ν.Α. Παναγιώτου ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Περιεχόµενα Παρουσίασης 1. Γενικά Στοιχεία Γραµµικού
Γραµµικός Προγραµµατισµός ιαµόρφωση Προβλήµατος Η παρουσίαση προετοιµάστηκε από τον Ν.Α. Παναγιώτου ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ Επιχειρησιακή Έρευνα Περιεχόµενα Παρουσίασης 1. Γενικά Στοιχεία Γραµµικού
Επιχειρησιακή έρευνα (ασκήσεις)
 Επιχειρησιακή έρευνα (ασκήσεις) ΤΕΙ Ηπείρου (Τμήμα Λογιστικής και Χρηματοοικονομικής) Γκόγκος Χρήστος (06-01-2015) 1. Γραφική επίλυση προβλημάτων Γραμμικού Προγραμματισμού A) Με τη βοήθεια της γραφικής
Επιχειρησιακή έρευνα (ασκήσεις) ΤΕΙ Ηπείρου (Τμήμα Λογιστικής και Χρηματοοικονομικής) Γκόγκος Χρήστος (06-01-2015) 1. Γραφική επίλυση προβλημάτων Γραμμικού Προγραμματισμού A) Με τη βοήθεια της γραφικής
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 1: Δυϊκή Θεωρία, Οικονομική Ερμηνεία Δυϊκού Προβλήματος Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΓΡΑΜΜΙΚΟΣ & ΔΙΚΤΥΑΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Ενότητα 1: Δυϊκή Θεωρία, Οικονομική Ερμηνεία Δυϊκού Προβλήματος Σαμαράς Νικόλαος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Επιχειρησιακή Έρευνα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #3: Ακέραιος Προγραμματισμός Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #3: Ακέραιος Προγραμματισμός Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης
Άσκηση 5. Εργοστάσια. Συστήματα Αποφάσεων Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης
 Άσκηση Μια μεγάλη εταιρεία σκοπεύει να μπει δυναμικά στην αγορά αναψυκτικών της χώρας διαθέτοντας συνολικά 7 μονάδες κεφαλαίου. Το πρόβλημα που αντιμετωπίζει είναι αν πρέπει να κατασκευάσει ένα κεντρικό
Άσκηση Μια μεγάλη εταιρεία σκοπεύει να μπει δυναμικά στην αγορά αναψυκτικών της χώρας διαθέτοντας συνολικά 7 μονάδες κεφαλαίου. Το πρόβλημα που αντιμετωπίζει είναι αν πρέπει να κατασκευάσει ένα κεντρικό
Διαδικασία μετατροπής σε τυπική μορφή
 ΤΕΙ Δυτικής Μακεδονίας -Τμήμα Διοίκησης επιχειρήσεων- Μάθημα: Ποσοτικές μέθοδοι στη διοίκηση επιχειρήσεων- ΣΤ Εξάμηνο Ημερομηνία: Τρίτη 25 ΑΠΡ 2017, 1 η γραπτή Πρόοδος Εκπαιδευτής: Βασίλειος Ισμυρλής,
ΤΕΙ Δυτικής Μακεδονίας -Τμήμα Διοίκησης επιχειρήσεων- Μάθημα: Ποσοτικές μέθοδοι στη διοίκηση επιχειρήσεων- ΣΤ Εξάμηνο Ημερομηνία: Τρίτη 25 ΑΠΡ 2017, 1 η γραπτή Πρόοδος Εκπαιδευτής: Βασίλειος Ισμυρλής,
ΤΕΙ Χαλκίδας Σχολή Διοίκησης και Οικονομίας Τμήμα Διοίκησης Επιχειρήσεων
 ΤΕΙ Χαλκίδας Σχολή Διοίκησης και Οικονομίας Τμήμα Διοίκησης Επιχειρήσεων Επιχειρησιακή Έρευνα Τυπικό Εξάμηνο: Δ Αλέξιος Πρελορέντζος Εισαγωγή Ορισμός 1 Η συστηματική εφαρμογή ποσοτικών μεθόδων, τεχνικών
ΤΕΙ Χαλκίδας Σχολή Διοίκησης και Οικονομίας Τμήμα Διοίκησης Επιχειρήσεων Επιχειρησιακή Έρευνα Τυπικό Εξάμηνο: Δ Αλέξιος Πρελορέντζος Εισαγωγή Ορισμός 1 Η συστηματική εφαρμογή ποσοτικών μεθόδων, τεχνικών
ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ IΙ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ IΙ Ακαδ. Έτος 2018-2019 Διδάσκων: Β. ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegean.gr Τηλ: 2271035468
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΙΓΑΙΟΥ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΟΙΚΟΝΟΜΙΑΣ ΚΑΙ ΔΙΟΙΚΗΣΗΣ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ IΙ Ακαδ. Έτος 2018-2019 Διδάσκων: Β. ΚΟΥΤΡΑΣ Επικ. Καθηγητής v.koutras@fme.aegean.gr Τηλ: 2271035468
σει κανένα modem των 128Κ. Θα κατασκευάσει συνολικά = 320,000 τεμάχια των 64Κ και το κέρδος της θα γίνει το μέγιστο δυνατό, ύψους 6,400,000.
 Σ ένα εργοστάσιο ειδών υγιεινής η κατασκευή των πορσελάνινων μπανιέρων έχει διαμορφωθεί σε τρία διαδοχικά στάδια : καλούπωμα, λείανση και βάψιμο. Στον πίνακα που ακολουθεί καταγράφονται τα ωριαία δεδομένα
Σ ένα εργοστάσιο ειδών υγιεινής η κατασκευή των πορσελάνινων μπανιέρων έχει διαμορφωθεί σε τρία διαδοχικά στάδια : καλούπωμα, λείανση και βάψιμο. Στον πίνακα που ακολουθεί καταγράφονται τα ωριαία δεδομένα
Λύσεις θεμάτων Επιχειρησιακής Έρευνας (17/09/2014)
 Λύσεις θεμάτων Επιχειρησιακής Έρευνας (17/09/2014) Θέμα 1 Μια επιχείρηση χρησιμοποιεί 3 πρώτες ύλες Α, Β, Γ για να παράγει 2 προϊόντα Π1 και Π2. Για την παραγωγή μιας μονάδας προϊόντος Α απαιτούνται 1
Λύσεις θεμάτων Επιχειρησιακής Έρευνας (17/09/2014) Θέμα 1 Μια επιχείρηση χρησιμοποιεί 3 πρώτες ύλες Α, Β, Γ για να παράγει 2 προϊόντα Π1 και Π2. Για την παραγωγή μιας μονάδας προϊόντος Α απαιτούνται 1
Κεφάλαιο 2ο: Συστημική Προσέγγιση Προβλημάτων
 2.1 Εισαγωγή Κεφάλαιο 2ο: Συστημική Προσέγγιση Προβλημάτων Από τα συστήματα radar, νηοπομπών, οπλικά και επιχειρησιακά συστήματα, γεννάται η επιχειρησιακή έρευνα που εξελίσσεται στη συνέχεια, κατά την
2.1 Εισαγωγή Κεφάλαιο 2ο: Συστημική Προσέγγιση Προβλημάτων Από τα συστήματα radar, νηοπομπών, οπλικά και επιχειρησιακά συστήματα, γεννάται η επιχειρησιακή έρευνα που εξελίσσεται στη συνέχεια, κατά την
Αλγοριθµική Επιχειρησιακή Ερευνα. Χειµερινό Εξάµηνο 2013-2014. Ασκήσεις. 1. Ενα διυλιστήριο µπορεί να επεξεργαστεί τρία είδη ακατέργαστου πετρελαίου :
 Αλγοριθµική Επιχειρησιακή Ερευνα Χειµερινό Εξάµηνο 2013-2014 Ασκήσεις 1. Ενα διυλιστήριο µπορεί να επεξεργαστεί τρία είδη ακατέργαστου πετρελαίου : - το πρώτο προερχόµενο από την Αφρική, το οποίο ονοµάζεται
Αλγοριθµική Επιχειρησιακή Ερευνα Χειµερινό Εξάµηνο 2013-2014 Ασκήσεις 1. Ενα διυλιστήριο µπορεί να επεξεργαστεί τρία είδη ακατέργαστου πετρελαίου : - το πρώτο προερχόµενο από την Αφρική, το οποίο ονοµάζεται
ΜΑΘΗΜΑ: ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ-ΘΕΜΑΤΑ ΕΞΕΤΑΣΤΙΚΗΣ ΙΟΥΛΙΟΥ 2014
 ΠΑΝΕΠΙΣΤΗΜΙΟΥΠΟΛΗ - ΡΙΟ 00 ΠΑΤΡΑ UNIVERSITY CAMPUS-RIO 00 PATRAS, GR ΜΑΘΗΜΑ: ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ-ΘΕΜΑΤΑ ΕΞΕΤΑΣΤΙΚΗΣ ΙΟΥΛΙΟΥ 0 ΘΕΜΑ ( Μονάδες ) Στο παρακάτω πρόβληµα γ.π c max = + s. t + - + + + 0 +,,
ΠΑΝΕΠΙΣΤΗΜΙΟΥΠΟΛΗ - ΡΙΟ 00 ΠΑΤΡΑ UNIVERSITY CAMPUS-RIO 00 PATRAS, GR ΜΑΘΗΜΑ: ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ-ΘΕΜΑΤΑ ΕΞΕΤΑΣΤΙΚΗΣ ΙΟΥΛΙΟΥ 0 ΘΕΜΑ ( Μονάδες ) Στο παρακάτω πρόβληµα γ.π c max = + s. t + - + + + 0 +,,
ΔΕΟ13(ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΛΙΟΥ )
 ΔΕΟ13(ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΛΙΟΥ ) ΑΣΚΗΣΗ 1 Μια εταιρεία ταχυμεταφορών διατηρεί μια αποθήκη εισερχομένων. Τα δέματα φθάνουν με βάση τη διαδικασία Poion με μέσο ρυθμό 40 δέματα ανά ώρα. Ένας υπάλληλος
ΔΕΟ13(ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΙΟΥΛΙΟΥ ) ΑΣΚΗΣΗ 1 Μια εταιρεία ταχυμεταφορών διατηρεί μια αποθήκη εισερχομένων. Τα δέματα φθάνουν με βάση τη διαδικασία Poion με μέσο ρυθμό 40 δέματα ανά ώρα. Ένας υπάλληλος
Παραλλαγές του Προβλήματος Μεταφοράς Το Πρόβλημα Μεταφόρτωσης και το Πρόβλημα Αναθέσεων Γεωργία Φουτσιτζή ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα
 Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Παραλλαγές του Προβλήματος Μεταφοράς Το Πρόβλημα Μεταφόρτωσης και το Πρόβλημα Αναθέσεων Γεωργία Φουτσιτζή ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα To Πρόβλημα Μεταφοράς
Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 Παραλλαγές του Προβλήματος Μεταφοράς Το Πρόβλημα Μεταφόρτωσης και το Πρόβλημα Αναθέσεων Γεωργία Φουτσιτζή ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα To Πρόβλημα Μεταφοράς
Ασκήσεις γραφικής επίλυσης
 Ασκήσεις γραφικής επίλυσης Άσκηση 1- (Παράδειγµα 3.4 βιβλίου) Σε ένα πτηνοτροφείο χρησιµοποιείται για την καθηµερινή διατροφή ενός συνόλου πτηνών ένα µείγµα αποτελούµενο από δύο είδη δηµητριακών: το είδος
Ασκήσεις γραφικής επίλυσης Άσκηση 1- (Παράδειγµα 3.4 βιβλίου) Σε ένα πτηνοτροφείο χρησιµοποιείται για την καθηµερινή διατροφή ενός συνόλου πτηνών ένα µείγµα αποτελούµενο από δύο είδη δηµητριακών: το είδος
Δυναμικότητα (GWh) A B C Ζήτηση (GWh) W X Y Z
 Άσκηση Η εταιρία ηλεκτρισμού ELECTRON έχει τρείς μονάδες ηλεκτροπαραγωγής Α, Β, C και θέλει να καλύψει τη ζήτηση σε τέσσερις πόλεις W, Χ, Υ, Ζ. Η μέγιστη παραγωγή, η απαιτούμενη ζήτηση και το κόστος μεταφοράς
Άσκηση Η εταιρία ηλεκτρισμού ELECTRON έχει τρείς μονάδες ηλεκτροπαραγωγής Α, Β, C και θέλει να καλύψει τη ζήτηση σε τέσσερις πόλεις W, Χ, Υ, Ζ. Η μέγιστη παραγωγή, η απαιτούμενη ζήτηση και το κόστος μεταφοράς
Γραμμικός Προγραμματισμός και Βελτιστοποίηση (Εργαστήριο 3)
 Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός και Βελτιστοποίηση (Εργαστήριο 3) Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Μάρτιος 2015 Δρ. Δημήτρης Βαρσάμης Γραμμικός Προγραμματισμός (E 3) Μάρτιος
Τμήμα Μηχανικών Πληροφορικής Γραμμικός Προγραμματισμός και Βελτιστοποίηση (Εργαστήριο 3) Δρ. Δημήτρης Βαρσάμης Επίκουρος Καθηγητής Μάρτιος 2015 Δρ. Δημήτρης Βαρσάμης Γραμμικός Προγραμματισμός (E 3) Μάρτιος
Τμήμα Εφαρμοσμένης Πληροφορικής
 Τμήμα Εφαρμοσμένης Πληροφορικής ΑΛΓΟΡΙΘΜΟΙ ΓΡΑΜΜΙΚΗΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ 8 Ο ΕΞΑΜΗΝΟ ΣΑΜΑΡΑΣ ΝΙΚΟΛΑΟΣ, ΕΠ. ΚΑΘΗΓΗΤΗΣ Δυϊκή Θεωρία (1) Θεώρημα : Το δυϊκό πρόβλημα του γραμμικού προβλήματος 0 0 1 1 2 2 0 0 T
Τμήμα Εφαρμοσμένης Πληροφορικής ΑΛΓΟΡΙΘΜΟΙ ΓΡΑΜΜΙΚΗΣ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗΣ 8 Ο ΕΞΑΜΗΝΟ ΣΑΜΑΡΑΣ ΝΙΚΟΛΑΟΣ, ΕΠ. ΚΑΘΗΓΗΤΗΣ Δυϊκή Θεωρία (1) Θεώρημα : Το δυϊκό πρόβλημα του γραμμικού προβλήματος 0 0 1 1 2 2 0 0 T
Διαχείριση Εφοδιαστικής Αλυσίδας
 Διαχείριση Εφοδιαστικής Αλυσίδας 4 η Διάλεξη: Βελτιστοποίηση πολλαπλών στόχων (Μulti-objective optimization) 2019 Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Ατζέντα Εισαγωγή στην βελτιστοποίηση
Διαχείριση Εφοδιαστικής Αλυσίδας 4 η Διάλεξη: Βελτιστοποίηση πολλαπλών στόχων (Μulti-objective optimization) 2019 Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Ατζέντα Εισαγωγή στην βελτιστοποίηση
Οργάνωση και Διοίκηση Εργοστασίων. Σαχαρίδης Γιώργος
 Οργάνωση και Διοίκηση Εργοστασίων Σαχαρίδης Γιώργος Πρόβλημα 1 Μία εταιρεία έχει μία παραγγελία για την παραγωγή κάποιου προϊόντος. Με τις 2 υπάρχουσες βάρδιες (40 ώρες την εβδομάδα η καθεμία) μπορούν
Οργάνωση και Διοίκηση Εργοστασίων Σαχαρίδης Γιώργος Πρόβλημα 1 Μία εταιρεία έχει μία παραγγελία για την παραγωγή κάποιου προϊόντος. Με τις 2 υπάρχουσες βάρδιες (40 ώρες την εβδομάδα η καθεμία) μπορούν
Επιχειρησιακή Έρευνα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #1: Γραμμικός Προγραμματισμός Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #1: Γραμμικός Προγραμματισμός Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες
Γραμμικός Προγραμματισμός
 Γραμμικός Προγραμματισμός Παράδειγμα ΕΠΙΠΛΟΞΥΛ Η βιοτεχνία ΕΠΙΠΛΟΞΥΛ παράγει δύο βασικά προϊόντα: τραπέζια και καρέκλες υψηλής ποιότητας. Η διαδικασία παραγωγής και για τα δύο προϊόντα περιλαμβάνει την
Γραμμικός Προγραμματισμός Παράδειγμα ΕΠΙΠΛΟΞΥΛ Η βιοτεχνία ΕΠΙΠΛΟΞΥΛ παράγει δύο βασικά προϊόντα: τραπέζια και καρέκλες υψηλής ποιότητας. Η διαδικασία παραγωγής και για τα δύο προϊόντα περιλαμβάνει την
Επιχειρησιακή Έρευνα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #: Εφαρμογές του Γραμμικού Προγραμματισμού Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Επιχειρησιακή Έρευνα Ενότητα #: Εφαρμογές του Γραμμικού Προγραμματισμού Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων
Επιχειρησιακή Έρευνα Εφαρμογές και Λογισμικό Γραμμικού Προγραμματισμού
 Επιχειρησιακή Έρευνα Εφαρμογές και Λογισμικό Γραμμικού Προγραμματισμού Νίκος Τσάντας ιατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών Τμήμ. Μαθηματικών Μαθηματικά των Υπολογιστών και των Αποφάσεων Ακαδημαϊκό
Επιχειρησιακή Έρευνα Εφαρμογές και Λογισμικό Γραμμικού Προγραμματισμού Νίκος Τσάντας ιατμηματικό Πρόγραμμα Μεταπτυχιακών Σπουδών Τμήμ. Μαθηματικών Μαθηματικά των Υπολογιστών και των Αποφάσεων Ακαδημαϊκό
ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Μια μαθηματική τεχνική Ευρύτατο φάσμα εφαρμογών Προβλήματα με γραμμικότητα ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΙΣΑΓΩΓΗ Ο Γραμμικός Προγραμματισμός επιλύει, κάτω από ορισμένες προϋποθέσεις,
ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Μια μαθηματική τεχνική Ευρύτατο φάσμα εφαρμογών Προβλήματα με γραμμικότητα ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΙΣΑΓΩΓΗ Ο Γραμμικός Προγραμματισμός επιλύει, κάτω από ορισμένες προϋποθέσεις,
3.12 Το Πρόβλημα της Μεταφοράς
 312 Το Πρόβλημα της Μεταφοράς Σ αυτή την παράγραφο και στις επόμενες μέχρι το τέλος του κεφαλαίου θα ασχοληθούμε με μερικά σπουδαία είδη προβλημάτων γραμμικού προγραμματισμού Οι ειδικές αυτές περιπτώσεις
312 Το Πρόβλημα της Μεταφοράς Σ αυτή την παράγραφο και στις επόμενες μέχρι το τέλος του κεφαλαίου θα ασχοληθούμε με μερικά σπουδαία είδη προβλημάτων γραμμικού προγραμματισμού Οι ειδικές αυτές περιπτώσεις
Fermat, 1638, Newton Euler, Lagrange, 1807
 Εισαγωγή Μαθ Προγρ Κλασικά Προβλ Επεκτάσεις Υπολογιστικές Μέθοδοι στη Θεωρία Αποφάσεων Ενότητα 1 Εισαγωγή Αντώνης Οικονόμου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Προπτυχιακό πρόγραμμα σπουδών 3 Μαρτίου
Εισαγωγή Μαθ Προγρ Κλασικά Προβλ Επεκτάσεις Υπολογιστικές Μέθοδοι στη Θεωρία Αποφάσεων Ενότητα 1 Εισαγωγή Αντώνης Οικονόμου Τμήμα Μαθηματικών Πανεπιστήμιο Αθηνών Προπτυχιακό πρόγραμμα σπουδών 3 Μαρτίου
Πληροφοριακά Συστήματα Διοίκησης. Επισκόπηση μοντέλων λήψης αποφάσεων Τεχνικές Μαθηματικού Προγραμματισμού
 Πληροφοριακά Συστήματα Διοίκησης Επισκόπηση μοντέλων λήψης αποφάσεων Τεχνικές Μαθηματικού Προγραμματισμού Σημασία μοντέλου Το μοντέλο δημιουργεί μια λογική δομή μέσω της οποίας αποκτούμε μια χρήσιμη άποψη
Πληροφοριακά Συστήματα Διοίκησης Επισκόπηση μοντέλων λήψης αποφάσεων Τεχνικές Μαθηματικού Προγραμματισμού Σημασία μοντέλου Το μοντέλο δημιουργεί μια λογική δομή μέσω της οποίας αποκτούμε μια χρήσιμη άποψη
Άσκηση 21. Συστήματα Αποφάσεων Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης
 Εταιρία παράγει σκυρόδεμα με το οποίο προμηθεύει σε καθημερινή βάση διάφορες οικοδομικές επιχειρήσεις. Το σκυρόδεμα παράγεται σε δύο εργοτάξια της εταιρίας, το Α και το Β. Με τα σημερινά δεδομένα, υπάρχει
Εταιρία παράγει σκυρόδεμα με το οποίο προμηθεύει σε καθημερινή βάση διάφορες οικοδομικές επιχειρήσεις. Το σκυρόδεμα παράγεται σε δύο εργοτάξια της εταιρίας, το Α και το Β. Με τα σημερινά δεδομένα, υπάρχει
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού
 Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γεωργία Φουτσιτζή-Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 τελευταία ενημέρωση: 21/10/2016
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γεωργία Φουτσιτζή-Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 τελευταία ενημέρωση: 21/10/2016
ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ (Linear Programming) Από το βιβλίο: Κώστογλου, Β. (2015). Επιχειρησιακή Έρευνα. Θεσσαλονίκη: Εκδόσεις Τζιόλα. 1 Το Πρόβλημα των Περιορισμένων Πόρων Κάθε επιχειρηματική δραστηριότητα
ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ (Linear Programming) Από το βιβλίο: Κώστογλου, Β. (2015). Επιχειρησιακή Έρευνα. Θεσσαλονίκη: Εκδόσεις Τζιόλα. 1 Το Πρόβλημα των Περιορισμένων Πόρων Κάθε επιχειρηματική δραστηριότητα
Επιχειρησιακή Έρευνα
 Επιχειρησιακή Έρευνα Ενότητα 9: Ειδικές περιπτώσεις επίλυσης με τη μέθοδο simplex (1o μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
Επιχειρησιακή Έρευνα Ενότητα 9: Ειδικές περιπτώσεις επίλυσης με τη μέθοδο simplex (1o μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ. ΕΞΕΤΑΣΗ ΣΤΗΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ Έβδομο Εξάμηνο
 ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΞΕΤΑΣΗ ΣΤΗΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ Έβδομο Εξάμηνο Διδάσκων: Ι. Κολέτσος Κανονική Εξέταση 2007 ΘΕΜΑ 1 Διαιτολόγος προετοιμάζει ένα μενού
ΣΧΟΛΗ ΕΦΑΡΜΟΣΜΕΝΩΝ ΜΑΘΗΜΑΤΙΚΩΝ & ΦΥΣΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΕΞΕΤΑΣΗ ΣΤΗΝ ΕΠΙΧΕΙΡΗΣΙΑΚΗ ΕΡΕΥΝΑ ΛΥΣΕΙΣ ΘΕΜΑΤΩΝ Έβδομο Εξάμηνο Διδάσκων: Ι. Κολέτσος Κανονική Εξέταση 2007 ΘΕΜΑ 1 Διαιτολόγος προετοιμάζει ένα μενού
Επιχειρησιακή Έρευνα
 Επιχειρησιακή Έρευνα Ενότητα 5: Εφαρμογές Γραμμικού Προγραμματισμού (1 ο μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
Επιχειρησιακή Έρευνα Ενότητα 5: Εφαρμογές Γραμμικού Προγραμματισμού (1 ο μέρος) Μπεληγιάννης Γρηγόριος Σχολή Οργάνωσης και Διοίκησης Επιχειρήσεων Τμήμα Διοίκησης Επιχειρήσεων Αγροτικών Προϊόντων & Τροφίμων
ΕΝΔΕΙΚΤΙΚΑ ΠΡΟΒΛΗΜΑΤΑ
 Πρόβλημα 1 ΕΝΔΕΙΚΤΙΚΑ ΠΡΟΒΛΗΜΑΤΑ Η εταιρεία GALAXY INDUSTRIES διαθέτει στην αγορά 2 είδη πλάκες πεζοδρομίου: τη Space Ray και τη Galaxy Ray. Τα 2 είδη κατασκευάζονται σε δωδεκάδες από την ίδια βασική πρώτη
Πρόβλημα 1 ΕΝΔΕΙΚΤΙΚΑ ΠΡΟΒΛΗΜΑΤΑ Η εταιρεία GALAXY INDUSTRIES διαθέτει στην αγορά 2 είδη πλάκες πεζοδρομίου: τη Space Ray και τη Galaxy Ray. Τα 2 είδη κατασκευάζονται σε δωδεκάδες από την ίδια βασική πρώτη
ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ (Γ.Π.).) (LINEAR PROGRAMMING)
 ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ (Γ.Π.).) (LINEAR PROGRAMMING) Δρ. Βασιλική Καζάνα Αναπλ. Καθηγήτρια ΤΕΙ Καβάλας, Τμήμα Δασοπονίας & Διαχείρισης Φυσικού Περιβάλλοντος Δράμας Εργαστήριο Δασικής Διαχειριστικής
ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ (Γ.Π.).) (LINEAR PROGRAMMING) Δρ. Βασιλική Καζάνα Αναπλ. Καθηγήτρια ΤΕΙ Καβάλας, Τμήμα Δασοπονίας & Διαχείρισης Φυσικού Περιβάλλοντος Δράμας Εργαστήριο Δασικής Διαχειριστικής
Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΕΙΣΗΓΗΤΗΣ: Δρ. Ιωάννης Σ. Τουρτούρας Μηχανικός Παραγωγής & Διοίκησης
Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΜΑΘΗΜΑΤΙΚΗ ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΠΡΟΒΛΗΜΑΤΩΝ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΕΙΣΗΓΗΤΗΣ: Δρ. Ιωάννης Σ. Τουρτούρας Μηχανικός Παραγωγής & Διοίκησης
ΜΑΘΗΜΑ 3 Ο ΠΟΣΟΤΙΚΕΣ ΜΕΘΟ ΟΙ ΣΤΗΝ ΛΗΨΗ ΑΠΟΦΑΣΕΩΝ (εργαστήριο) ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2012-2013-ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ
 ΜΑΘΗΜΑ 3 Ο ΠΟΣΟΤΙΚΕΣ ΜΕΘΟ ΟΙ ΣΤΗΝ ΛΗΨΗ ΑΠΟΦΑΣΕΩΝ (εργαστήριο) ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2012-2013-ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ Προβλήµατα Ακέραιου Προγραµµατισµού Ι Τα προβλήµατα Ακέραιου Προγραµµατισµού, ανήκουν γενικά σε 3
ΜΑΘΗΜΑ 3 Ο ΠΟΣΟΤΙΚΕΣ ΜΕΘΟ ΟΙ ΣΤΗΝ ΛΗΨΗ ΑΠΟΦΑΣΕΩΝ (εργαστήριο) ΑΚΑ ΗΜΑΙΚΟ ΕΤΟΣ 2012-2013-ΕΑΡΙΝΟ ΕΞΑΜΗΝΟ Προβλήµατα Ακέραιου Προγραµµατισµού Ι Τα προβλήµατα Ακέραιου Προγραµµατισµού, ανήκουν γενικά σε 3
 1. Στις 30 Απριλίου τα κοστολογικά στοιχεία της βιομηχανίας PLASTIC ΑΒΕΕ είχαν ως εξής : Αγορά πρώτων υλών 72.000 Τελικό απόθεμα πρώτων υλών 12.000 Αρχικό απόθεμα πρώτων υλών 3.000 Άμεση εργασία 9.500
1. Στις 30 Απριλίου τα κοστολογικά στοιχεία της βιομηχανίας PLASTIC ΑΒΕΕ είχαν ως εξής : Αγορά πρώτων υλών 72.000 Τελικό απόθεμα πρώτων υλών 12.000 Αρχικό απόθεμα πρώτων υλών 3.000 Άμεση εργασία 9.500
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ ΔΙΑΛΕΞΗ 6 η -Η ΔΥΙΚΗ ΜΕΘΟΔΟΣ SIMPLEX
 ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2013-2014 ΔΙΑΛΕΞΗ 6 η -Η ΔΥΙΚΗ ΜΕΘΟΔΟΣ SIMPLEX ΔΥΙΚΟΤΗΤΑ Κάθε πρόβλημα γραμμικού προγραμματισμού συνδέεται με εάν άλλο πρόβλημα γραμμικού προγραμματισμού
ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΑΚ. ΕΤΟΣ 2013-2014 ΔΙΑΛΕΞΗ 6 η -Η ΔΥΙΚΗ ΜΕΘΟΔΟΣ SIMPLEX ΔΥΙΚΟΤΗΤΑ Κάθε πρόβλημα γραμμικού προγραμματισμού συνδέεται με εάν άλλο πρόβλημα γραμμικού προγραμματισμού
Μοντελοποίηση και Τεχνικοοικονομική Ανάλυση Εφοδιαστικής Αλυσίδας Βιοκαυσίμων
 Μοντελοποίηση και Τεχνικοοικονομική Ανάλυση Εφοδιαστικής Αλυσίδας Βιοκαυσίμων Αιμ. Κονδύλη, Ι. Κ. Καλδέλλης, Χρ. Παπαποστόλου ΤΕΙ Πειραιά, Τμήμα Μηχανολογίας Απρίλιος 2007 Στόχοι της εργασίας Η τεχνική
Μοντελοποίηση και Τεχνικοοικονομική Ανάλυση Εφοδιαστικής Αλυσίδας Βιοκαυσίμων Αιμ. Κονδύλη, Ι. Κ. Καλδέλλης, Χρ. Παπαποστόλου ΤΕΙ Πειραιά, Τμήμα Μηχανολογίας Απρίλιος 2007 Στόχοι της εργασίας Η τεχνική
Συστήματα Παραγωγής ΠΑΡΑΔΕΙΓΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ
 Συστήματα Παραγωγής ΠΑΡΑΔΕΙΓΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Περιεχόμενα 1 Γενικά στοιχεία γραμμικού προγραμματισμού 2 Παράδειγμα γραμμικού προγραμματισμού και γραφικής επίλυσης του 3 Γραμμικός προγραμματισμός
Συστήματα Παραγωγής ΠΑΡΑΔΕΙΓΜΑ ΓΡΑΜΜΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ Περιεχόμενα 1 Γενικά στοιχεία γραμμικού προγραμματισμού 2 Παράδειγμα γραμμικού προγραμματισμού και γραφικής επίλυσης του 3 Γραμμικός προγραμματισμός
Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ
 Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ 1 η Διάλεξη: Αναδρομή στον Μαθηματικό Προγραμματισμό 2019, Πολυτεχνική Σχολή Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Περιεχόμενα 1. Γραμμικός Προγραμματισμός
Διαχείριση Εφοδιαστικής Αλυσίδας ΙΙ 1 η Διάλεξη: Αναδρομή στον Μαθηματικό Προγραμματισμό 2019, Πολυτεχνική Σχολή Εργαστήριο Συστημάτων Σχεδιασμού, Παραγωγής και Λειτουργιών Περιεχόμενα 1. Γραμμικός Προγραμματισμός
Εισαγωγή στο Γραμμικό Προγραμματισμό
 Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 Εισαγωγή στο Γραμμικό Προγραμματισμό Φουτσιτζή Γεωργία-Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 15/10/2016 1 Περιεχόμενα Γραμμικός
Τμήμα Μηχανικών Πληροφορικής ΤΕ 2017-2018 Εισαγωγή στο Γραμμικό Προγραμματισμό Φουτσιτζή Γεωργία-Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 15/10/2016 1 Περιεχόμενα Γραμμικός
ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ. Γραφική λύση προβλημάτων Γραμμικού Προγραμματισμού
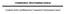 ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Γραφική λύση προβλημάτων Γραμμικού Προγραμματισμού Πρόγραμμα Γενικό γραμμικό πρόβλημα με πολύγωνη περιοχή εφικτών λύσεων Να λυθεί το παρακάτω γραμμικό πρόγραμμα: ma z μ. π. 4
ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Γραφική λύση προβλημάτων Γραμμικού Προγραμματισμού Πρόγραμμα Γενικό γραμμικό πρόβλημα με πολύγωνη περιοχή εφικτών λύσεων Να λυθεί το παρακάτω γραμμικό πρόγραμμα: ma z μ. π. 4
Περιεχόμενα. Πρόλογος Η ιοικητική Επιστήμη στην Κοινωνία της Πληροφορίας... 17
 Πρόλογος... 13 1. Η ιοικητική Επιστήμη στην Κοινωνία της Πληροφορίας... 17 1.1. Εισαγωγή... 19 1.2. Ένα μοντέλο ανάλυσης οργανισμού... 21 1.3. Νέες τάσεις στην οργανωτική δομή των επιχειρήσεων... 23 1.4.
Πρόλογος... 13 1. Η ιοικητική Επιστήμη στην Κοινωνία της Πληροφορίας... 17 1.1. Εισαγωγή... 19 1.2. Ένα μοντέλο ανάλυσης οργανισμού... 21 1.3. Νέες τάσεις στην οργανωτική δομή των επιχειρήσεων... 23 1.4.
ΠΔΕ253 2 η εργασία Προσοχή! Είναι ένα αρχικό version. Κατά την παρουσίαση των βίντεο θα διορθωθούν τυχόν λάθη σε πράξεις στην άσκηση 1.
 ΠΔΕ253 2 η εργασία 2014 15 Προσοχή! Είναι ένα αρχικό version. Κατά την παρουσίαση των βίντεο θα διορθωθούν τυχόν λάθη σε πράξεις στην άσκηση 1. Λύση άσκησης 3 Έστω με Eπείγοντα περιστατικά x "" = o αριθμός
ΠΔΕ253 2 η εργασία 2014 15 Προσοχή! Είναι ένα αρχικό version. Κατά την παρουσίαση των βίντεο θα διορθωθούν τυχόν λάθη σε πράξεις στην άσκηση 1. Λύση άσκησης 3 Έστω με Eπείγοντα περιστατικά x "" = o αριθμός
Χρήστος Ι. Σχοινάς Αν. Καθηγητής ΔΠΘ. Συμπληρωματικές σημειώσεις για το μάθημα: «Επιχειρησιακή Έρευνα ΙΙ»
 Χρήστος Ι. Σχοινάς Αν. Καθηγητής ΔΠΘ Συμπληρωματικές σημειώσεις για το μάθημα: «Επιχειρησιακή Έρευνα ΙΙ» 2 ΔΥΝΑΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Προβλήματα ελάχιστης συνεκτικότητας δικτύου Το πρόβλημα της ελάχιστης
Χρήστος Ι. Σχοινάς Αν. Καθηγητής ΔΠΘ Συμπληρωματικές σημειώσεις για το μάθημα: «Επιχειρησιακή Έρευνα ΙΙ» 2 ΔΥΝΑΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ Προβλήματα ελάχιστης συνεκτικότητας δικτύου Το πρόβλημα της ελάχιστης
The Product Mix Problem
 Προσδιοριστικές Μέθοδοι Επιχειρησιακής Έρευνας 1 The Product Mix Problem Τα προβλήματα αυτά αναφέρονται σε συστήματα τα οποία εκμεταλλευόμενα τους περιορισμένους πόρους που έχουν στη διάθεσή του, παράγουν
Προσδιοριστικές Μέθοδοι Επιχειρησιακής Έρευνας 1 The Product Mix Problem Τα προβλήματα αυτά αναφέρονται σε συστήματα τα οποία εκμεταλλευόμενα τους περιορισμένους πόρους που έχουν στη διάθεσή του, παράγουν
Ακέραιος Γραμμικός Προγραμματισμός
 Τμήμα Πληροφορικής & Τηλεπικοινωνιών Πανεπιστήμιο Ιωαννίνων 2018-2019 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος- Γεωργία Φουτσιτζή Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος
Τμήμα Πληροφορικής & Τηλεπικοινωνιών Πανεπιστήμιο Ιωαννίνων 2018-2019 Ακέραιος Γραμμικός Προγραμματισμός Γκόγκος Χρήστος- Γεωργία Φουτσιτζή Επιχειρησιακή Έρευνα τελευταία ενημέρωση: 12/01/2017 1 Ακέραιος
Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ
 Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΙΣΗΓΗΤΗΣ: Δρ. Ιωάννης Σ. Τουρτούρας Μηχανικός Παραγωγής & Διοίκησης Δ.Π.Θ. Χρηματοδότηση Το παρόν εκπαιδευτικό
Τ.Ε.Ι. ΑΝΑΤΟΛΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΚΑΙ ΘΡΑΚΗΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΓΡΑΜΜΙΚΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ ΕΙΣΗΓΗΤΗΣ: Δρ. Ιωάννης Σ. Τουρτούρας Μηχανικός Παραγωγής & Διοίκησης Δ.Π.Θ. Χρηματοδότηση Το παρόν εκπαιδευτικό
Μέθοδοι Βελτιστοποίησης
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μέθοδοι Βελτιστοποίησης Ενότητα # 5: Ασκήσεις Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το παρόν
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Μέθοδοι Βελτιστοποίησης Ενότητα # 5: Ασκήσεις Αθανάσιος Σπυριδάκος Καθηγητής Τμήμα Διοίκησης Επιχειρήσεων Άδειες Χρήσης Το παρόν
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ. Κεφάλαιο 3 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού
 ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Κεφάλαιο 3 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού 1 Σχέση γραμμικού και ακέραιου προγραμματισμού Ενα πρόβλημα ακέραιου προγραμματισμού είναι
ΑΚΕΡΑΙΟΣ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΣ & ΣΥΝΔΥΑΣΤΙΚΗ ΒΕΛΤΙΣΤΟΠΟΙΗΣΗ Κεφάλαιο 3 Μορφοποίηση Προβλημάτων Ακέραιου Προγραμματισμού 1 Σχέση γραμμικού και ακέραιου προγραμματισμού Ενα πρόβλημα ακέραιου προγραμματισμού είναι
Επιχειρησιακή Έρευνα - Επαναληπτική Εξέταση Οκτώβριος 2007
 Επιχειρησιακή Έρευνα - Επαναληπτική Εξέταση Οκτώβριος 2007 Επιτρέπεται µια σελίδα Α4 σηµειώσεων. Γράψτε ΜΟΝΟ τέσσερα θέµατα (αν υπάρχει 5 ο ΕΝ λαµβάνεται υπόψη) άριστα 3,5 θέµατα. Κάθε θέµα έχει ίδια αξία,
Επιχειρησιακή Έρευνα - Επαναληπτική Εξέταση Οκτώβριος 2007 Επιτρέπεται µια σελίδα Α4 σηµειώσεων. Γράψτε ΜΟΝΟ τέσσερα θέµατα (αν υπάρχει 5 ο ΕΝ λαµβάνεται υπόψη) άριστα 3,5 θέµατα. Κάθε θέµα έχει ίδια αξία,
Μοντέλα Διανομής και Δικτύων
 Μοντέλα Διανομής και Δικτύων 10-03-2017 2 Πρόβλημα μεταφοράς (1) Τα προβλήματα μεταφοράς ανακύπτουν συχνά σε περιπτώσεις σχεδιασμού διανομής αγαθών και υπηρεσιών από τα σημεία προσφοράς προς τα σημεία
Μοντέλα Διανομής και Δικτύων 10-03-2017 2 Πρόβλημα μεταφοράς (1) Τα προβλήματα μεταφοράς ανακύπτουν συχνά σε περιπτώσεις σχεδιασμού διανομής αγαθών και υπηρεσιών από τα σημεία προσφοράς προς τα σημεία
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού
 Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 τελευταία ενημέρωση: 21/10/2016 1 Γραφική μέθοδος
Η γραφική μέθοδος επίλυσης προβλημάτων Γραμμικού Προγραμματισμού Γκόγκος Χρήστος ΤΕΙ Ηπείρου Επιχειρησιακή Έρευνα Τμήμα Μηχανικών Πληροφορικής ΤΕ 2016-2017 τελευταία ενημέρωση: 21/10/2016 1 Γραφική μέθοδος
ΠΡΟΒΛΗΜΑΤΑ ΕΛΑΧΙΣΤΟΠΟΙΗΣΗΣ
 ΠΡΟΒΛΗΜΑΤΑ ΕΛΑΧΙΣΤΟΠΟΙΗΣΗΣ Ελαχιστοποίηση κόστους διατροφής Ηεπιχείρηση ζωοτροφών ΒΙΟΤΡΟΦΕΣ εξασφάλισε µια ειδική παραγγελίααπό έναν πελάτη της για την παρασκευή 1.000 κιλών ζωοτροφής, η οποία θα πρέπει
ΠΡΟΒΛΗΜΑΤΑ ΕΛΑΧΙΣΤΟΠΟΙΗΣΗΣ Ελαχιστοποίηση κόστους διατροφής Ηεπιχείρηση ζωοτροφών ΒΙΟΤΡΟΦΕΣ εξασφάλισε µια ειδική παραγγελίααπό έναν πελάτη της για την παρασκευή 1.000 κιλών ζωοτροφής, η οποία θα πρέπει
ΤΟ ΔΥΑΔΙΚΟ ΠΡΟΒΛΗΜΑ. Θεωρίες δυϊσμού Θεώρημα Thevenin-Norton. Συστήματα Αποφάσεων Εργαστήριο Συστημάτων Αποφάσεων και Διοίκησης
 ΤΟ ΔΥΑΔΙΚΟ ΠΡΟΒΛΗΜΑ Θεωρίες δυϊσμού Θεώρημα Thevenin-Norton minu = b 1 Π 1 + b Π + + b m Π m ΔΥΑΔΙΚΟ X 1 X X n Π 1 α 11 a 1... a 1n b 1 Π α 1 a... a n b............ Π m a m1 a m a mn b m c 1 c... c n maxz
ΤΟ ΔΥΑΔΙΚΟ ΠΡΟΒΛΗΜΑ Θεωρίες δυϊσμού Θεώρημα Thevenin-Norton minu = b 1 Π 1 + b Π + + b m Π m ΔΥΑΔΙΚΟ X 1 X X n Π 1 α 11 a 1... a 1n b 1 Π α 1 a... a n b............ Π m a m1 a m a mn b m c 1 c... c n maxz
Μοντελοποίησης και Βελτιστοποίηση Εφοδιαστικών Αλυσίδων 7 Ο εξάμηνο
 Πανεπιστήμιο Δυτικής Μακεδονίας Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μοντελοποίησης και Βελτιστοποίηση Εφοδιαστικών Αλυσίδων 7 Ο εξάμηνο 2 η ΕΡΓΑΣΙΑ ΜΑΘΗΜΑΤΟΣ ΔΕΚΕΜΒΡΙΟΣ 2012 Μιχαήλ Γεωργιάδης
Πανεπιστήμιο Δυτικής Μακεδονίας Τμήμα Μηχανικών Πληροφορικής & Τηλεπικοινωνιών Μοντελοποίησης και Βελτιστοποίηση Εφοδιαστικών Αλυσίδων 7 Ο εξάμηνο 2 η ΕΡΓΑΣΙΑ ΜΑΘΗΜΑΤΟΣ ΔΕΚΕΜΒΡΙΟΣ 2012 Μιχαήλ Γεωργιάδης
Δυναμικότητα (GWh) A B C Ζήτηση (GWh) W X Y Z
 Άσκηση 0 Η εταιρία ηλεκτρισμού ELECTRON έχει τρείς μονάδες ηλεκτροπαραγωγής Α, Β, C και θέλει να καλύψει τη ζήτηση σε τέσσερις πόλεις W, Χ, Υ, Ζ. Η μέγιστη παραγωγή, η απαιτούμενη ζήτηση και το κόστος
Άσκηση 0 Η εταιρία ηλεκτρισμού ELECTRON έχει τρείς μονάδες ηλεκτροπαραγωγής Α, Β, C και θέλει να καλύψει τη ζήτηση σε τέσσερις πόλεις W, Χ, Υ, Ζ. Η μέγιστη παραγωγή, η απαιτούμενη ζήτηση και το κόστος
Συνδυαστική Βελτιστοποίηση
 Διδάσκων: Ξενίδης Δημήτριος (xenides@uop.gr) Τόπος Διδασκαλίας: Αίθουσα Υ5 Ημέρα και Ώρα Διδασκαλίας: Παρασκευή 10:00-14:00 Βιβλίο Μαθήματος: Elementary Linear Programming with Applications Σελίδα στο
Διδάσκων: Ξενίδης Δημήτριος (xenides@uop.gr) Τόπος Διδασκαλίας: Αίθουσα Υ5 Ημέρα και Ώρα Διδασκαλίας: Παρασκευή 10:00-14:00 Βιβλίο Μαθήματος: Elementary Linear Programming with Applications Σελίδα στο
