ΜΟΝΤΕΛΟΠΟΙΗΣΗ ΧΡΟΝΙΚΗΣ ΑΠΟΚΡΙΣΗΣ ΚΑΙ ΚΑΤΑΝΑΛΩΣΗΣ ΕΝΕΡΓΕΙΑΣ ΚΥΚΛΩΜΑΤΩΝ CMOS

Transcript

1 Λάμπρος Σ. Μπισδούνης Δp. Ηλεκτρολόγος Μηχνικός ΧΑΝΙΑ - 200

2 Οργάνωση της προυσίσης Εισγωγή στις τεχνικές εξομοίωσης κι μοντελοποίησης κυκλωμάτων CMOS LSI. Αντικείμενο της προυσίσης. Χρονική πόκριση κι κτνάλωση ενέργεις ντιστροφέ CMOS. Τεχνικές νγωγής λογικών πυλών CMOS σε ισοδύνμους ντιστροφείς. Συμπεράσμτ. 2

3 Εισγωγή Στο πρελθόν, η επλήθευση (verification) ενός ηλεκτρονικού κυκλώμτος γινότν με τη διδικσί του bread-boarding. Η ολοκλήρωση μεγάλου ριθμού τρνζίστορ σε έν κύκλωμ πυριτίου (chip), κθιστά πρίτητη τη χρήση εργλείων εξομοίωσης (CAD tools). Η εξομοίωση πρέπει ν πρέχει κρίβει κι τχύτητ. Γι την ποδοτική εξομοίωση των κυκλωμάτων LSI στ διάφορ επίπεδ της διδικσίς σχεδισμού, πιτούντι ρκετοί τύποι εξομοίωσης: Εξομοίωση σε επίπεδο συμπεριφοράς (behavioral level) Εξομοίωση σε επίπεδο κτχωρητή (RTL level) Λογική εξομοίωση σε επίπεδο πύλης ή δικόπτη (gate or switch level) Χρονική εξομοίωση (timing simulation) Κυκλωμτική εξομοίωση (circuit simulation) 3

4 Εισγωγή Όσο μετκινούμστε προς τ κάτω στην ιερρχί, η κρίβει της εξομοίωσης υξάνετι με συνέπει όμως τη μείωση της τχύτητάς της. 4

5 Εισγωγή Οι βσικοί τρόποι μοντελοποίησης χρονικής πόκρισης κι κτνάλωσης ενέργεις κυκλωμάτων που χρησιμοποιούντι σε επίπεδο πύλης κι δικόπτη είνι: Μοντελοποίηση με χρήση πινάκων νφοράς Μοντελοποίηση με εμπειρικές εξισώσεις Μοντελοποίηση με ισοδύνμ κυκλώμτ RC Μοντελοποίηση με βάση νάλυση της πόκρισης του ντιστροφέ CMOS Aντικείμενο της προυσίσης ποτελεί η μοντελοποίηση κυκλωμάτων CMOS με βάση την νάλυση της πόκρισης του ντιστροφέ CMOS, σε συνδυσμό με τεχνικές νγωγής πυλών σε ισοδύνμους ντιστροφείς. Οι τεχνικές μοντελοποίησης που βσίζοντι στην νάλυση του ντιστροφέ πρέχουν υψηλή κρίβει με μικρούς χρόνους υπολογισμού (περίπου 2 τάξεις μεγέθους μικρότερους πό τους κυκλωμτικούς εξομοιωτές). 5

6 Αντικείμενo της προυσίσης Ανάπτυξη νλυτικών μοντέλων χρονικής πόκρισης κι κτνάλωσης ενέργεις του ντιστροφέ CMOS. Από τη μοντελοποίηση της χρονικής πόκρισης προκύπτουν νλυτικές εκφράσεις γι την κθυστέρηση κι το χρόνο μετάβσης της τάσης εξόδου του ντιστροφέ. Η δυνμική κτνάλωση ενέργεις εξρτάτι μονάχ πό το χωρητικό φορτίο κι την τάση τροφοδοσίς κι είνι εύκολο ν νλυθεί. Έτσι, δίνετι έμφση στον υπολογισμό της κτνάλωσης ενέργεις βρχυκυκλώμτος, που εξρτάτι πό το χρόνο μετάβσης εισόδου, την τάση τροφοδοσίς, το φορτίο εξόδου κι τ εσωτερικά χρκτηριστικά του ντιστροφέ. Κτά την νάπτυξη των μοντέλων, ποφεύγετι η χρήση ριθμητικών μεθόδων κι δεδομένων που προέρχοντι πό προγενέστερες κυκλωμτικές εξομοιώσεις, έτσι ώστε οι εκφράσεις που προκύπτουν ν είνι πλές κι ν οδηγούν σε μικρό χρόνο υπολογισμού. 6

7 Αντικείμενo της προυσίσης Τ προτεινόμεν νλυτικά μοντέλ προυσιάζουν υξημένη κρίβει επειδή ε- κτός πό τις κύριες επιδράσεις: της κλίσης κυμτομορφής εισόδου του χωρητικού φορτίου κι του ρεύμτος του τρνζίστορ φόρτισης ή εκφόρτισης, συμπεριλμβάνουν κι τις επιδράσεις: in PMOS CM DD Ip IC M IC L out του ρεύμτος βρχυκυκλώμτος κι της χωρητικότητς σύζευξης εισόδου εξόδου NMOS In CL Η κρίβει λλά κι η τχύτητ υπολογισμού του μοντέλου εξρτάτι πό τις εξισώσεις που χρησιμοποιούντι γι το ρεύμ υποδοχής των τρνζίστορ, οι οποίες πρέπει ν είνι έγκυρες γι τρνζίστορ μικρού μήκους κνλιού (submicron transistors). 7

8 Αντικείμενo της προυσίσης Ανάπτυξη μεθοδολογίς νγωγής λογικών πυλών σε ισοδύνμους ντιστροφείς. Η νγωγή βσίζετι στην νάλυση της δυνμικής συμπεριφοράς των σειρικά κι πράλληλ συνδεδεμένων τρνζίστορ, ότν λειτουργούν ως κλάδος φόρτισης ή εκφόρτισης του κόμβου εξόδου κι ως κλάδος βρχυκυκλώμτος. Κτά την νγωγή λμβάνοντι υπόψη οι επιδράσεις: του χωρητικού φορτίου εξόδου, του χρόνου μετάβσης των εισόδων, του ριθμού των εισόδων που βρίσκοντι υπό μετάβση, της θέσης των εισόδων που βρίσκοντι υπό μετάβση, του φινομένου σώμτος (body effect), κι των χωρητικοτήτων των εσωτερικών κόμβων. 8

9 Ανάλυση του ντιστροφέ CMOS Φινόμενο κορεσμού τχύτητς φορέων (velocity saturation effect) σε τρνζίστορ υπομικρομέτρου (submicron transistors): Μη γρμμική σχέση μετξύ της τχύτητς φορέων κι του ηλεκτρικού πεδίου κνλιού Το ρεύμ υποδοχής στην περιοχή κορεσμού δεν περιγράφετι με κρίβει χρησιμοποιώντς κλσσικές τετργωνικές εξισώσεις όπου I D ~ ( GS - TH ) 2 9

10 Ανάλυση του ντιστροφέ CMOS Μοντελοποίηση του φινομένου κορεσμού τχύτητς φορέων με την εισγωγή του δείκτη κορεσμού τχύτητς φορέων (-power law MOS model): I D I DO GS DD T T, > Περιοχή κορεσμού DS DO I D IDO GS DO DD T T 2 DS, Γρμμική περιοχή DS DO I DO : I D γι GS DS DD DO : DS γι GS DD DO DO GS DD T T 2 0

11 Ανάλυση του ντιστροφέ CMOS in DD 0, ( t/ τ), DD, 0 t < t t > 0 τ τ PMOS DD C d d L + C M dt dt d out in out dt + I I p n 0 in CM IC M Ip IC L out d dt out I C c p L m I + C τ DD n M +, I C p L I n + C M, t 0 0 < t η t τ > τ NMOS In CL c m C CM + C L M

12 Ανάλυση του ντιστροφέ CMOS n p TN DD TP DD ÊáíïíéêüðïéçìÝíç ÔÜóç Ðåñéï Þ Ðåñéï Þ 2 Ðåñéï Þ 4 Ðåñéï Þ 5A Õðïêáôçãïñßá Á -udop ÃñáììÞ êïñåóìïý PMOS Åßóïäïò Õðïêáôçãïñßá Â Ðåñéï Þ 3 Êáôçãïñßá Â Ðåñéï Þ 5B Êáôçãïñßá Á Ðåñéï Þ udon 0 n -p ÊáíïíéêïðïéçìÝíïò ñüíïò x t / τ ÃñáììÞ êïñåóìïý NMOS 2

13 Ανάλυση του ντιστροφέ CMOS ΚΑΤΗΓΟΡΙΑ Α: ΓΡΗΓΟΡΕΣ ΕΙΣΟΔΟΙ Περιοχή, 0 x n: NMOS ποκοπή, PMOS γρμμική GSP TN / 2 p u c y ( e n ) out + m n, y A p n 2 n lp 2 k A lp lp, u ( p) Περιοχή 2, n x x satp : NMOS περιοχή κόρου, PMOS γρμμική περιοχή Γρμμική προσέγγιση του ρεύμτος του PMOS: I I + S x n p pmin dop ( ) I k lp ( + ) C C DD L M D0p τ p /2 3

14 Ανάλυση του ντιστροφέ CMOS ( ) ( ) ( ) ( ) 2 + out m pmin sn n u + c x n + R + I d x n + [ Sd x n / 2] [ A x n n ]/( + ) A sn k sn τ ( + ) C C DD L M k sn I D0n d n DD( CL + CM ) ( ) n τ R y e ( ny n ) Συνθήκη κόρου PMOS: u u. Το σημείο x satp υπολογίζετι με τη βοήθει n νπτυγμάτων Taylor δευτέρου βθμού των u out κι u dop στο σημείο x n p. Περιοχή 3, x satp x p, NMOS, PMOS περιοχή κόρου A u u c x x n A sn n sp out 23 + m + + x p n ( ) ( ) + p + Περιοχή 4, p x, NMOS περιοχή κόρου, PMOS περιοχή ποκοπής u u + c x out 23 m A n sn p ( ) x + n n + Περιοχή 5Α, x x satn, NMOS περιοχή κόρου, PMOS περιοχή ποκοπής u u + c out 23 m out A sn n Asn n x + n dop ( ) n + ( ) n ( ) 4

15 Ανάλυση του ντιστροφέ CMOS Περιοχή 6, x x satn, NMOS γρμμική περιοχή, PMOS περιοχή ποκοπής A ( n) n u u ( x xsatn ) out ln / 2 k ln τ don e A ln C + C, ( ) DD L M Το x satn υπολογίζετι πό την έκφρση της u out στην Περιοχή 5Α γι u out u don ΚΑΤΗΓΟΡΙΑ B: ΑΡΓΕΣ ΕΙΣΟΔΟΙ Περιοχή 5Β, x satn x, NMOS γρμμική περιοχή, PMOS κόρος, ποκοπή Αμελητέ επίδρση του I p στο διάστημ x satn x p u out u satn e 2A ln ( x n) ( n + )/ ( ( xsatn n) n + )/ n Περιοχή 6, x, NMOS γρμμική περιοχή, PMOS περιοχή ποκοπής u out u [] e ( ) n ( ) A n x ln Το x satn υπολογίζετι πό την έκφρση της u out στην Περιοχή 4 ή 3 γι u out u don με τη βοήθει νπτυγμάτων Taylor δευτέρου βθμού / 2, u satn. u don xsatn n n n 2 5

16 Ανάλυση του ντιστροφέ CMOS Κθυστέρηση του ντιστροφέ: t DHL t ( τ/ 2) x τ ( τ/ 2) Yποκτηγορί Α : Περιοχή 5A x 0.5 c m A + sn u n ( n) n n n + + Κτηγορί A: Περιοχή 5A ν u [] 0.5 κι Περιοχή 4 ν u [] 0.5 x 0.5 y y 2 2y 2y 2 2 ( 2y ) Κτηγορί Β: Περιοχή 4 ν u [-p] 0.5 κι Περιοχή 3 ν u [-p] x 0.5 w w 2 2w 2w 2 2 ( 2w ) 0 Υποκτηγορί Β : Περιοχή 3 y i κι w i : συντελεστές νπτύγμτος Taylor της u out στις περιοχές 4 κι 3 ντίστοιχ. 6

17 Ανάλυση του ντιστροφέ CMOS Ενεργός χρόνος μετάβσης εξόδου ντιστροφέ: τ tr DD 0.7 d out t t dt 0.5 Περιοχή 5A: du out s dx x x 0.5 τ 0.7 s s A sn ( n) n Περιοχή 4: s c m A sn ( x n) n 0.5 Περιοχή 3: s c + m A sp A sn ( x n) 0.5 ( x p) p 0.5 n 7

18 Ανάλυση του ντιστροφέ CMOS Κτνάλωση ενέργεις ντιστροφέ CMOS: Σττική (ρεύμ διρροής διάχυσης-υποστρώμτος, υποκτωφλίου, πύλης) Δυνμική (φόρτιση κι εκφόρτιση χωρητικού φορτίου) Βρχυκυκλώμτος (γώγιμο μονοπάτι DD γείωση κτά τη μετγωγή) Δυνμική κτνάλωση ενέργεις: Υπολογίζετι εύκολ. Δεν εξρτάτι πό τ εσωτερικά χρκτηριστικά της πύλης, κι την κλίση κυμτομορφής εισόδου. τ I C d DD L dt tr DD 0 E 2 D DD I DD dt DD CL dout CLDD 0 0 out E D 0 0 8

19 Ανάλυση του ντιστροφέ CMOS Kτνάλωση ενέργεις βρχυκυκλώμτος: Συμπεριλμβάνοντι οι επιδράσεις της C M κι του ρεύμτος διμέσου της C gs του τρνζίστορ βρχυκυκλώμτος: x3 0 ESC DD I SCτ dx din ISC Ip IC gsp IC Cgsp Cgsp gsp dt τ x 2 DD E 0 sc DD 2 ( x satp x 2 ) (x satp + x 2 2x ) S 2C gsp τ DD + DD ( p k sp + ) τ ( p x satp ) p + ( p x 3 ) p + C gsp 2 DD ( x 3 x satp ) 9

20 Ανάλυση του ντιστροφέ CMOS ΠΑΡΑΜΕΤΡΟΙ NMOS PMOS L (μm) W (μm) I DO (ma) T () DO () DD 5 C L 0.2 pf 20

21 Ανάλυση του ντιστροφέ CMOS 2

22 Ανάλυση του ντιστροφέ CMOS 22

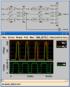
23 Ανάλυση του ντιστροφέ CMOS 9 8 ÌÞêïò êáíáëéïý 0.8 ìm C L 0.2 pf C L 0 [emu-94] ÅíÝñãåéá âñá õêõêëþìáôïò (pjoule) [Auve-98] [Saku-90] [Hede-87-93] SPICE [een-84] ÌïíôÝëï ñüíïò ìåôüâáóçò åéóüäïõ (nsec) 23

24 Ανγωγή σττικών πυλών σε ισοδύνμους ντιστροφείς Η νγωγή περιλμβάνει τη μοντελοποίηση: των σειρικά συνδεδεμένων τρνζίστορ ότν λειτουργούν ως κλάδος φόρτισης ή εκφόρτισης της εξόδου των πυλών των σειρικά συνδεδεμένων τρνζίστορ ότν λειτουργούν ως κλάδος βρχυκυκλώμτος των πυλών των πράλληλ συνδεδεμένων τρνζίστορ κι της περίπτωσης χρονικά επικλυπτόμενων εισόδων Κτά την νγωγή λμβάνοντι υπόψη οι επιδράσεις: του χωρητικού φορτίου εξόδου του χρόνου μετάβσης των εισόδων του ριθμού των εισόδων που βρίσκοντι υπό μετάβση της θέσης των εισόδων που βρίσκοντι υπό μετάβση του φινομένου σώμτος (body effect) κι των χωρητικοτήτων των εσωτερικών κόμβων ΚΑΤΑΝΑΛΩΣΗΣ ΕΝΕΡΓΕΙΑΣ ΚΥΚΛΩΜΑΤΑ CMOS 24

25 Σειρικά τρνζίστορ ως κλάδος φόρτισης ή εκφόρτισης Ενλλκτικές εξισώσεις μοντέλου δύνμης που περιέχουν το πλάτος κνλιού: Περιοχή κόρου: ( ) I P ( W/ L) D C GS T ( ), DS > DO Γρμμική περιοχή: I P ( W / L) 2, D L GS T DS DO ( GS T) 2 P Φινόμενο σώμτος (body effect): ( b b ) T TO + γ 2φ + SB 2 φ T TO + γ SB Ανλύετι μι NAND πύλη N εισόδων. Οι NOR πύλες νλύοντι συμμετρικά. Αρχικά εξετάζετι η χειρότερη (πό άποψη DS DO κθυστέρησης) περίπτωση: τυτόχρονες μετβάσεις σε όλες τις εισόδους. C p C p2 C pn in in2 inn DD in in2 inn out A M M 2 M N C n C n2 C nn C L 25

26 Σειρικά τρνζίστορ ως κλάδος φόρτισης ή εκφόρτισης t ON : χρόνος ένρξης γωγής λυσίδς ON : τάση κόμβου Α γι t t ON M : περιοχή κόρου έως t t satn κι στη συνέχει γρμμική περιοχή M 2 M N : μόνιμ στη γρμμική περιοχή Περιοχή οροπεδίου [τ, t satn ] ότν t satn τ (μετάβση εισόδων τχύτερη πό μετάβση εξόδου) Η A θεωρείτι γρμμική στο διάστημ [t ON, τ]: A + ON P τ t ON ON ( t t ) ON Γι ν υπολογιστεί το W eq πρέπει πρώτ ν υπολογιστούν η τάση οροπεδίου P κι οι τιμές t ON κι ON. 26

27 Σειρικά τρνζίστορ ως κλάδος φόρτισης ή εκφόρτισης Υπολογισμός τάσης οροπεδίου: W W W W K 2 3, ID IDK [ n ( γ ) ] P W L + C DD TO P N TK TOn + Si N γ i N / ( ), Si ( ) P W L k L K ( )( ) N i DD TOn 2 DD TK P ( ) DD N 2 N, θ 2 N. A out M M K C n + C L I D I CK C K I DK Υπολογισμός t ON κι ON : I Cmi C DD t + τ. mi ICni i ( C C ) GS [ t ] T [ t ] 0 t i ON i i i i ( γ ) mi [ t TOn + + i+ [ i+ ] C m2 DD DD ( C + C ) m2 n2 t2 τ. τ ni, in in in C m2 C m3 M M 2 M 3 C n + C L 2 3 C n2 C n3 ON in t 3 t 2 t t ON

28 Σειρικά τρνζίστορ ως κλάδος φόρτισης ή εκφόρτισης Υπολογισμός W eq : Δύο περιπτώσεις t satn τ κι t satn τ. Περίπτωση : ( ) [ ] in n D C TO A I P W L +γ I ( + γ ) P L W C in D A TOn ( ) in ( ) Περιοχή Β I D PL( W / L) DD TOn ( + γ ) A ( out A) TOn W eq / 2 Περιοχή Α: t (τ + t ON ) / 2 Περιοχή Οροπεδίου: A P, in DD A N N W ( N )( + γ ) out Wt () out N N ( ) DD TOn ( ) W 06. W[ t t ] + W[ t t 0] eq satn out / 2 Υπολογισμός του t satn πό την Περιοχή 5Α του ντιστροφέ: ( γ ) [ ] n P + out P DD TO P / 2 28

29 Σειρικά τρνζίστορ ως κλάδος φόρτισης ή εκφόρτισης Περίπτωση 2: Περιοχή Α: t (t ON + t satn ) / 2, t satn γι μηδενικό ρεύμ βρχυκυκλώμτος. [ in n ( γ ) ], out n ( + γ ) C d out P W dt L + Περιοχή Β: L C TO A W( t) W N ( N )( + γ ) ( in TO n ) N out / 2 [ ] P A in TO A / 2 ( ) W 06. W[ t t ] + W[ t t 0] eq satn out t satn πό την Περιοχή 3 ή 4 του ντιστροφέ 29

30 Σειρικά τρνζίστορ ως κλάδος φόρτισης ή εκφόρτισης Επίδρση ριθμού κι θέσης εισόδων υπό μετάβση: Τ τρνζίστορ με μετάβση στην είσοδο προυσιάζουν μικρότερη γωγιμότητ πό εκείν που είνι σε κτάστση μόνιμης γωγής (λόγω μικρότερης G ). Ότν η μετάβση εισόδων είνι ρκετά τχύτερη πό τη μετάβση εξόδου, η περίπτωση μετάβσης στις εισόδους που βρίσκοντι πλησιέστερ στην έξοδο προυσιάζει γρηγορότερη εκφόρτιση (λόγω των εσωτερικών χωρητικοτήτων). Όσο η μετάβση εισόδων γίνετι βρδύτερη πό εκείνη της εξόδου, η περίπτωση μετάβσης σε εισόδους κοντά στη γείωση οδηγεί σε γρηγορότερη εκφόρτιση, λόγω της μικρότερης T κι της μεγλύτερης GS των ντίστοιχων τρνζίστορ. Οι κυμτομορφές εξόδου γι διάφορους συνδυσμούς μετβάσεων εισόδων προυσιάζουν πράλληλη μεττόπιση νάλογ με τις εισόδους υπό μετάβση. Συνεπώς W eq m W eq -worst (m >). O συντελεστής m εξρτάτι πό: Θέση κι ριθμό εισόδων υπό μετάβση W: W W + + W N Σχέση κυμτομορφών εισόδου κι εξόδου G (I DON τ) / (C L DD ). 30

31 Σειρικά τρνζίστορ ως κλάδος φόρτισης ή εκφόρτισης Κυκλωμτικές εξομοιώσεις έχουν δείξει ότι ο m εξρτάτι εκθετικά πό το G: G m m + ( m m )[ e 02. ] vf vs vf d ( ) Είσοδοι m vf m vs υπό Αριθμός εισόδων (N) μετάβση , , , , 2, 3 3

32 Σειρικά τρνζίστορ ως κλάδος φόρτισης ή εκφόρτισης Υπολογισμός ισοδύνμης εισόδου γι χρονικά επικλυπτόμενες εισόδους: Η ισοδύνμη είσοδος κθορίζετι πό τον κλάδο που μετφέρει το ρεύμ φόρτισης ή εκφόρτισης κι το ρεύμ βρχυκυκλώμτος. Η τχύτητ φόρτισης ή εκφόρτισης κθορίζετι κυρίως πό τις εισόδους με την πιο ργή μετάβση. Ισοδύνμος χρόνος εκκίνησης: t 0 max (t, t 2,... t N ). Οι είσοδοι (k) που έχουν ξεπεράσει τ 2/3 DD ότν η μετάβση που τελειώνει τελευτί φτάνει στο λογικό κτώφλι DD /2, θεωρούντι στθερές στη τιμή DD. Ισοδύνμος χρόνος μετάβσης: τ m i i [ t t 0 ] DD m m N k ( t t ) endi 0 32

33 Σειρικά τρνζίστορ ως κλάδος βρχυκυκλώμτος Με εξίρεση των εσωτερικών χωρητικοτήτων, η τάση εξόδου δεν εξρτάτι πό τη θέση των υπό μετάβση εισόδων, λλά μόνο πό το πλήθος τους W eq q WL, W W W W. 2 Αριθμός εισόδων Αριθμός εισόδων υπό μετάβση L Λόγω των εσωτερικών χωρητικοτήτων η φόρτιση είνι ργότερη γι μετάβση εισόδων που βρίσκοντι κοντά στη γείωση. ( C C + C ) k CO ri Ci rk C i C C + C + C gdk i gdi gsi ni, q r L L O i N+ i N N in in in2 inn in2 C gd C gs C gd2 C gs2 C gdn C gsn DD 2 3 N M M 2 out M N inn C n C n2 C n3 C nn k: υποδοχή του ου τρνζίστορ M k με μετάβση στην είσοδο C L 33

34 Σειρικά τρνζίστορ ως κλάδος βρχυκυκλώμτος Ισοδύνμη χωρητικότητ σύζευξης εισόδου εξόδου: C M3 in M M 2 out C CMN C M C M2 in2 C MN in out M eq m i MN i m: ριθμός εισόδων υπό μετάβση CMNk rk Cgdk + rk+ Cgsk r k N+ k N in3 M 3 k: κροδέκτης υποδοχής του τρνζίστορ (M k ) με μετάβση στην είσοδο Η ισοδύνμη χωρητικότητ εισόδου-γείωσης (ή τροφοδοσίς γείωσης ότν πρόκειτι γι PMOS) που πιτείτι γι τον υπολογισμό της ενέργεις βρχυκυκλώμτος υπολογίζετι με πρόμοιο τρόπο. 34

35 Πράλληλ συνδεδεμέν τρνζίστορ, m N: ριθμός των τρνζίστορ με μετάβση στην είσοδο. W eq m i W Γι χρονικά επικλυπτόμενες μετβάσεις εισόδων: S i 0: γι τρνζίστορ των οποίων η είσοδος ρχίζει ν μετβίνει μετά το χρονικό σημείο όπου η είσοδος με την τχύτερη μετάβση φτάνει στην τελική της τιμή. Η φόρτιση ή εκφόρτιση ρχίζει με την ένρξη μετάβσης σε μι είσοδο. Ισοδύνμος χρόνος εκκίνησης: t 0 min ( t, t 2,, t m ) Το τρνζίστορ με την τχύτερη μετάβση στην είσοδο έχει τη μεγλύτερη συμμετοχή στη φόρτιση ή εκφόρτιση. τ min ( tend t0, tend2 t0,, tendm t0 ) Το W eq είνι μι μη γρμμική συνάρτηση των χρόνων μετάβσης των m εισόδων που προσεγγίζετι πό μι εκθετική συνάρτηση: t t S i e endi Γι το τρνζίστορ με την τχύτερη μετάβση S i ενώ γι τ υπόλοιπ S i <. Κλάδος βρχυκυκλώμτος: W eq χωρίς S i λλά με ισοδύνμη είσοδο πό σειρικά τρνζίστορ. i W 5. [( 0 ) τ ] m S W eq i i i 35

36 Χρονική πόκριση πυλών 36

37 Χρονική πόκριση πυλών 37

38 Κθυστέρηση πυλών 38

39 Κθυστέρηση πυλών 39

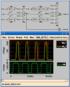
40 Ενέργει βρχυκυκλώμτος πυλών 4 ÌïíôÝëï SPICE NAND 3 åéóüäùí 3 ÌïíôÝëï SPICE NAND 4 åéóüäùí ÅíÝñãåéá Âñá õêõêëþìáôïò (pjoule) ÌåôÜâáóç óå üëåò ôéò åéóüäïõò ÌåôÜâáóç ìüíï óôçí in ÌåôÜâáóç ìüíï óôçí in3 ÅíÝñãåéá âñá õêõêëþìáôïò (pjoule) ÌåôÜâáóç óå üëåò ôéò åéóüäïõò ÌåôÜâáóç ìüíï óôçí in ÌåôÜâáóç ìüíï óôçí in ñüíïò ìåôüâáóçò åéóüäïõ (nsec) ñüíïò ìåôüâáóçò åéóüäïõ (nsec) 40

41 Συμπεράσμτ Ανπτύχθηκν νλυτικά μοντέλ χρονικής πόκρισης κι κτνάλωσης ενέργεις του ντιστροφέ CMOS, γι τεχνολογίες υπομικρομέτρου. Με βάση την μοντελοποίηση της χρονικής πόκρισης, πράχθηκν νλυτικές εκφράσεις γι την κθυστέρηση κι το χρόνο μετάβσης εξόδου του ντιστροφέ. Δόθηκε έμφση στη μοντελοποίηση της κτνάλωσης ενέργεις βρχυκυκλώμτος, που εξρτάτι πό το χρόνο μετάβσης εισόδου, την τάση τροφοδοσίς, το χωρητικό φορτίο κι τ εσωτερικά χρκτηριστικά του ντιστροφέ. Με σκοπό την υξημένη κρίβει, συμπεριλήφθησν οι επιδράσεις του ρεύμτος βρχυκυκλώμτος κι της χωρητικότητς σύζευξης εισόδου-εξόδου. Με σκοπό το μειωμένο χρόνο υπολογισμού, ποφεύχθηκε η χρήση ριθμητικών μεθόδων κι δεδομένων πό προγενέστερες κυκλωμτικές εξομοιώσεις. Ανπτύχθηκε μεθοδολογί νγωγής σττικών πυλών CMOS σε ισοδύνμους ντιστροφείς, η οποί βσίστηκε στην νάλυση της δυνμικής συμπεριφοράς των σειρικά κι πράλληλ συνδεδεμένων τρνζίστορ. Κτά την νγωγή συμπεριλήφθησν οι επιδράσεις όλων των σημντικών πργόντων που επηρεάζουν τη λειτουργί των σττικών πυλών. 4

42 Επεκτάσεις Μοντελοποίηση σύνθετων σττικών πυλών CMOS που περιλμβάνουν συνδυσμό πό σειρικά κι πράλληλ συνδεδεμέν τρνζίστορ, στους κλάδους φόρτισης ή εκφόρτισης κι βρχυκυκλώμτος. Μοντελοποίηση πυλών δυνμικής λογικής (π.χ. Domino logic). Μοντελοποίηση σττικών πυλών που ποτελούντι πό τρνζίστορ περάσμτος (pass transistors). Μοντελοποίηση επίδρσης των γρμμών σύνδεσης στη χρονική πόκριση των πυλών, γι τεχνολογίες πολύ μικρού μήκους κνλιού (deep-submicron technologies). 42