Ugljikohidrati i glikoliza
|
|
|
- Σουσάννα Βουγιουκλάκης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Ugljikohidrati i glikoliza Seminar 11b 1 1. Suspenzija stanica kvasca uzgajana je u anaerobnim uvjetima te se glukoza fermentirala u etanol i O 2. Ako se želi promatrati količina 14 O 2, na kojem mjestu je potrebno ugraditi 14 u glukozu? a) Na ugljicima 1 i 6; b) Na ugljicima 3 i 4; c) Na ugljicima 3 i Ako se u gore navedenu suspenziju doda inhibitor alkohol dehidrogenaze, stanice će umirati zbog toga što: a) Piruvat se neće sintetizirati pa neće biti preteče za sintezu glukoze te će stanice ostati bez energije; b) Mora se dodati još ATP kako bi započela razgradnja glukoze u ovim uvjetima. c) NAD + koji je potreban za odvijanje glikolize se ne obnavlja te je cijeli proces zaustavljen i ne dolazi do sinteze ATP. 2 1
2 3. Mutant kvasca ima defektnu triozafosfat izomerazu koja je katalitički inaktivna. Što od navedenog očekujete u anaerobnim uvjetima? a) Omjer sintetiziranog ATP/razgrađena glukoza biti će identičan kao i u normalnim stanicama; b) Omjer sintetiziranog ATP/razgrađena glukoza biti će ½ onoga što se inače dobiva u normalnim stanicama. c) Omjer sitetiziranog ATP/razgrađena glukoza biti će nula. 4. Mehanizam glceraldehid-3-fosfat dehidrogenaze ne uključuje: a) Fosforilaciju supstrata s ATP; b) Oksidaciju i fosforilaciju supstrata; c) Kovalentni međuprodukt Iako je glukoza glavni šećer koji se razgrađuje glikolizm, drugi šećeri kao što su galaktoza i fruktoza često su prisutni u krvi. Ovi šećeri: a) Ne mogu se metabolizirati glikolitičkim putem; b) Moraju se prvo pretvoriti u glukozu kako bi se metabolizirali; c) Metaboliziraju se glikolitičkim putom zbog toga što se pretvaraju u međuprodukte ovog puta. 6. Tri glavna regulacijska enzima u glikolitičkom putu su: a) heksokinaza, fosfofrukto-kinaza i piruvat kinaza; b) fosfofrukto-kinaza, gliceraldehid-3-fosfat dehidrogenaza i piruvat kinaza; c) heksokinaza, fosfofrukto-kinaza i gliceraldehid-3-fosfat dehidrogenaza. 4 2
3 7. Koji enzim glikolitičkog puta cijepa šećer sa šest - atoma na dva produkta od 3- atoma? a) fosfogluko-izomeraza; b) enolaza; c) aldolaza. 8. Koji od navedenih nisu produkti glikolize ako se glukoza razgrađuje do piruvata? a) 2 ATP b) 2 NAD + c) 2 2 O 5 9. Galaktozemia nastaje kao nedostatak kojeg enzima? a) Galaktokinaze b) Glukoza-1-fosfat-uridil transferaze c) Laktaze. 10. Koja je od navedenih molekula uključena u proces kojeg nazivamo stimulacijom prema naprijed? a) fruktoza-2,6-bisfosfat b) IF-1 c) inzulin 6 3
4 Monosaharidi Monosaharidi najjednostavniji ugljikohidrati. To su aldehidi ili ketoni s 2 ili više hidroksilnih skupina Najmanji n = 3 (TRIOZE) i to su gliceraldehid i dihidroksiaceton Aldoze sadrže aldehidnu skupinu Ketoze sadrže keto-skupinu 7 Stereoizomeri Općenito, molekula s n asimetričnih centara ima 2 n stereoizomernih oblika. Za npr. aldotrioze n = 1 i postoje 2 stereoizomera D- i L-gliceraldehid. Oni su enantiomeri (zrcalne slike) O O 2 O D-gliceraldehid 8 4
5 Niz D-aldoza 9 Niz D-ketoza 10 5
6 ANOMERI su oblici istog šećera koji se razlikuju po konformaciji na anomernom atomu ugljika. Anomerni ugljik je onaj ugljik koji je u necikličkom (linearnom) obliku šećera u sastavu aldehidne ili keto-skupine. U aldozama to je 1, a u ketozama 2. Na anomernom ugljiku zbiva se nukleofilna adicija prilikom ciklizacije šećera. Kod glukoze: O O O O O 2 O D-glukoza 2 O O O O O O 2 O O α-d-glukopiranoza O O O O O α-anomer je onaj kod kojeg se Oskupina anomernog ugljika i najveći supstituent na ostatku prstena (ovdje 2 O na 5) nalaze na suprotnim stranama prstena. Kod β-anomera ove dvije skupine su na istoj strani prstena. 2 O O O β-d-glukopiranoza O 11 O 12 6
7 EPIMERI: dva šećera su epimeri ako se razlikuju po konfiguraciji na samo jednom asimetričnom ugljiku koji nije anomerni. O O O O O 2 O D -glukoza O O O O O 2 O D -m anoza 2 -epimer D -glukoze O O O O O 2 O D -galaktoza 4 -epimer D -glukoze L-ŠEĆERI su zrcalna slika odgovarajućih D-šećera. U usporedbi s D-šećerima istog naziva imaju suprotnu konfiguraciju na svim kiralnim centrima. O O O O O 2 O D -glukoza O O O O O 2 O L-glukoza 13 Disaharidi Dva šećera povezana O-glikozidnom vezom 14 7
8 Polisaharidi (glikani) Monosaharidi povezani glikozidnim vezama, linearni ili razgranati jer se glikozidna veza može ostvariti s bilo kojom hidroksilnom skupinom monosaharida -eluloza - β(1-4) polimer glukoze -Škrob - α(1-4) i α(1-6) -Glikogen - α(1-4) i α(1-6) 15 Zadatak 1. Izračunajte ukupni oksidacijski broj ugljika u: a) glukozi b) piruvatu c) laktatu d) glicerolu 16 8
9 Rješenje Oksidacijski broj svakog pojedinog atoma ugljika računa se kao u anorganskim spojevima, osim što se - veze ne računaju: a) Glukoza: ukupni oksidacijski broj je 0. O O +1 0 O 0 0 O 0 O -1 2 O 17 Rješenje O O O 3 piruvat NAD + + NAD + laktat-dehidrogenaza O O O 3 laktat b) Piruvat: ukupni oksidacijski broj je +2. Iz ovoga rezultata vidimo da se pri pretvorbi glukoze (0) u dva piruvata (+4) ugljikov skelet ukupno mora oksidirati tj. izgubiti 4 elektrona. To se zbiva u jedinoj redoks-reakciji glikolize koju katalizira gliceraldehid-3-fosfatdehidrogenaza. Svaka molekula NAD + pri tome prima po jedan par elektrona. O O 3 O 18 9
10 Rješenje O O O 3 piruvat NAD + + NAD + laktat-dehidrogenaza O O O 3 laktat c) Laktat: ukupni oksidacijski broj je 0. Mliječno kiselo vrenje u sumarnoj reakciji ne dovodi do neto oksidacije niti redukcije bilo kojeg metabolita. Svrha njegove posljednje reakcije, koju katalizira laktat-dehidrogenaza, je regeneracija NAD + utrošenog u reakciji gliceraldehid-3-fosfatdehidrogenaze. Ovom regeneracijom održava se konstantan omjer NAD+/NAD, neophodan za odvijanje glikolize. O O O 3 d) Glicerol: ukupni oksidacijski broj je O O 2 O 19 Glikoliza 20 10
11
12 23 Zadatak 1. Dodamo li glukozu obilježenu s 14 na -1 u sustav u kojem se odvija glikoliza, koji će atomi biti obilježeni u: a) piruvatu b) laktatu (u mišiću) c) etanolu (u kvascu) 24 12
13 Rješenje O O * * * 2 O * 2 O P O O O ATP ADP ATP ADP O O O O O O O O O O O O O 2 O 2 O P 2 O P 2 O P glukoza glukoza-6-fosfat fruktoza-6-fosfat fruktoza-1,6-bisfosfat * 2 O P O 2 O dihidroksiaceton-fosfat + P O i + NAD O O~ P O O O O NAD ADP ATP 2 O O O O O P 2 O P * 2 O P * 2 O P * 2 O * gliceraldehid-3-fosfat 1,3-bisfosfoglicerat 3-fosfoglicerat 2-fosfoglicerat O O O O ADP ATP O P O 2 * * 3 piruvat fosfoenolpiruv 25 Rješenje b) laktat nastaje iz piruvata na sljedeći način O O NAD + NAD O O + + O O 3 * * piruvat 3 laktat c) etanol nastaje iz piruvata na sljedeći način O O O NAD + + NAD + 2 O O 2 O 3 3 * * * 3 piruvat acetaldehid etanol 26 13
14 Zadatak 2. Anorganski fosfat označen s 32 P dodan je s glukozom u stanični ekstrakt jetre te je inkubiran bez prisutstva kisika. Nakon kratkog vremena 1,3-BPG izolirate iz smjese. Na kojim ugljicima očekujete pronalazak radioaktivnog fosfata? Ukoliko inkubirate kroz duže vrijeme, hoće li se mjesto obilježavanja promijeniti? Zašto? 27 Rješenje: Nakon kratke inkubacije, označeni fosfat se pojavljuje na -1 1,3BPG-a. Anorganski fosfat ulazi u glikolizu u koraku kataliziranom s gliceraldehid 3-fosfat dehidrogenazom: Nakon duže inkubacije, radioaktivna oznaka će biti na -1 i -3 1,3-BPG-a jer korak poslije nastajanja 1,3-BPG-a uključuje fosforilaciju ADP-a u ATP, koji će biti radioaktivno obilježen na γ - položaju: 28 14
15 U drugim glikolitičkim reakcijama, radioaktivni ATP može fosforilirati -1 fruktoza 6-fosfata i -6 glukoze, oba su ekvivalenta -3 u 1,3-BPG-u. 29 Zadatak 3. Kod anaerobne degradacije glukoze preko glikolize, ukupno ne dolazi do oksidacije ili redukcije supstrata. No, slobodna energija potrebna za sintezu ATP-a dolazi iz povoljnih reakcija transfera elekrona. Koji metabolički intermedijer je elektron donor, a koji je elektron akceptor kad je glukoza razgrađena glikolitičkom fermentacijom: a) u mišiću b) u kvascu 30 15
16 31 Rješenje a) Elektron donor je GAP čija se aldehidna skupina oksidira u karboksilnu (1,3-BPG). Elektron akceptor je piruvat čija ketonska skupina se reducira u hidroksilnu skupinu laktata. b) Elektron donor je ponovno GAP. Elektron akceptor je acetaldehid koji se reducira u etanol
17 Zadatak 4. U staničnim uvjetima, koje su reakcije glikolize gotovo ireverzibilne? 33 Rješenje zadatka 4. - Prevorba glukoze u glukoza-6-fosfat pomoću heksokinaze; - Pretvorba fruktoza-6-fosfata u fruktoza-1,6-bisfosfat pomoću fosforukto kinaze; - Pretvorba fosfoenolpiruvata u piruvat pomoću piruvat kinaze
18 Zadatak 5. Zbog čega je za mišić povoljno da izlučuje mliječnu kiselinu u krv tijekom intezivnog vježbanja? 35 Rješenje zadatka 5. Mliječna kiselina je jaka kiselina. Ukoliko bi ostala u stanici, p stanice bi se smanjio te bi moglo doći do denaturacije proteina a time i do oštećenja mišića
19 Zadatak 6. Koja je fiziološka prednost za pankreas da ima transporter glukoze, GLUT2 s velikom K M? 37 Rješenje zadatka 6. GLUT2 transportira glukozu kada je koncentracija glukoze u krvi visoka, a to je upravo koncentracija kod koje β-stanice pankreasa izlučuju inzulin
20 Zadatak 7. Predvidite utjecaje sljedećih mutacija na odvijanje glikolize u stanicama jetre: a) Gubitak alosteričkog mjesta vezanja za ATP na fosfofruktokinazi; b) Gubitak veznog mjesta za citrat na fosfofruktokinazi; c) Gubitak fosfatazne domene na bifunkcionalnom enzimu koji kontrolira razinu fruktoza-2,6-bisfosfata; d) Gubitak veznog mjesta za fruktoza-1,6-bisfosfat na piruvat kinazi. 39 Rješenje zadatka 7. a) Povećanje b) Povećanje c) Povećanje d) Smanjenje 40 20
Glukoneogeneza i regulacija glukoneogeneze
Glukoneogeneza i regulacija glukoneogeneze Boris Mildner Glukoneogeneza Sinteza ugljikohidrata iz jednostavnih preteča Put od fosfoenolpiruvata do glukoza 6-fosfata zajednički je za mnoge preteče ugljikohidrata.
Put pentoza fosfata. B. Mildner. Put pentoza fosfata
Put pentoza fosfata B. Mildner Put pentoza fosfata Svrha ovog puta je: A) da se stanici omogući dovoljno NADPH, koji služi kao reducens u biosintetskim reakcijama kao i u zaštiti stanica od kisikovih radikala.
Glukoneogeneza. Glukoneogeneza. Glukoneogeneza. poteka v jetrih in ledvični skorji, v citoplazmi in delno v mitohondrijih.
poteka v jetrih in ledvični skorji, v citoplazmi in delno v mitohondrijih. Izhodne spojine:, laktat, in drugi intermediati cikla TKK glukogene aminokisline, glicerol Kaj pa maščobne kisline? Ireverzibilne
METABOLIZEM OGLJIKOVIH HIDRATOV
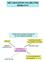METABOLIZEM OGLJIKOVIH HIDRATOV KAKO CELICA DOBI GLUKOZO IN OSTALE MONOSAHARIDE? HRANA ZNOTRAJCELIČNI GLIKOGEN ali ŠKROB razgradnja s prebavnimi encimi GLUKOZA in ostali monosaharidi fosforilitična cepitev
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
3.1 Granična vrednost funkcije u tački
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Ugljeni hidrati. Uvod. masti, belančevine CO 2. O + hν + hlorofil fotosinteza + H 2. glukoza. skrob. ishrana. ishrana glikogen. celuloza.
Ugljeni hidrati Uvod C 2 + 2 + hν + hlorofil fotosinteza glukoza skrob ishrana celuloza ishrana glikogen masti, belančevine glukoza C 2 + 2 + energija 1 Definicija Ugljeni hidrati su polihidroksi aldehidi,
Seminar 13.b. Glikogen GLIKOGEN. B. Mildner
Seminar 13.b Glikogen B. Mildner GLIKOGEN 1 Glikogen Nereducirani kraj Glikogen je jako dostupni skladišni oblik glukoze; kao i jako velik, razgranat polimer; Glukozne jedinice su povezane α-1,4-glikozidnim
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
Riješeni zadaci: Nizovi realnih brojeva
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
METABOLIZEM OGLJIKOVIH HIDRATOV
METABLIZEM GLJIKVIH HIDRATV KAK CELICA DBI GLUKZ IN STALE MNSAHARIDE? HRANA ZNTRAJCELIČNI GLIKGEN ali ŠKRB razgradnja s prebavnimi encimi GLUKZA in ostali monosaharidi fosforilitična cepitev prenos do
Elementi spektralne teorije matrica
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
4. razred gimnazije - opšti i prirodno-matematički smer UGLJENI HIDRATI
. razred gimnazije - opšti i prirodno-matematički smer 07 UGLJENI IDRATI Ugljeni hidrati su najrasprostranjenija jedinjenja u živom svetu. rganska jedinjenja ugljenika, vodonika i kiseonika u kojima je
41. Jednačine koje se svode na kvadratne
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Glikoliza. Metabolične poti. Organizacija metaboličnih poti Ciklična pot (intermediati se reciklirajo) Kako poteka oksidacija goriv v našem organizmu?
Glikoliza Sežig v bombnem kalorimetru organizacija in osnove uravnavanja metaboličnih poti aerobna glikoliza anaerobna glikoliza vstop drugih sladkorjev v glikolizo glicerolfosfatni in malat-aspartatni
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
7 Algebarske jednadžbe
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
CIKLUS LIMUNSKE KISELINE (CLK)
SVEUČILIŠTE U ZAGREBU FAKULTET KEMIJSKOG INŽENJERSTVA I TEHNOLOGIJE CIKLUS LIMUNSKE KISELINE (CLK) Doc. dr. sc. Dragana Vuk Metabolička sudbina piruvata 1. Oksidacijska dekarboksilacija piruvata 2. Ciklus
Računarska grafika. Rasterizacija linije
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Eliminacijski zadatak iz Matematike 1 za kemičare
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Matematika 1 - vježbe. 11. prosinca 2015.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Operacije s matricama
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Zavrxni ispit iz Matematiqke analize 1
Građevinski fakultet Univerziteta u Beogradu 3.2.2016. Zavrxni ispit iz Matematiqke analize 1 Prezime i ime: Broj indeksa: 1. Definisati Koxijev niz. Dati primer niza koji nije Koxijev. 2. Dat je red n=1
Sortiranje prebrajanjem (Counting sort) i Radix Sort
Sortiranje prebrajanjem (Counting sort) i Radix Sort 15. siječnja 2016. Ante Mijoč Uvod Teorem Ako je f(n) broj usporedbi u algoritmu za sortiranje temeljenom na usporedbama (eng. comparison-based sorting
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
fotosinteza CO 2 + H 2 soli vinske kiseline). sunceva svetlost
UGLJENI IDRATI (U) ( n n n ) + katalizator fotosinteza sunceva svetlost zelene biljke (hlorofil) molekuli (+)-glukoze povezuju se u velike molekule skroba i celuloze celuloza (potporni skelet biljke) masti,
ELEKTROTEHNIČKI ODJEL
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Ispitivanje toka i skiciranje grafika funkcija
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Kaskadna kompenzacija SAU
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Linearna algebra 2 prvi kolokvij,
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Ciklus limunske kiseline-2
Ciklus limunske kiseline-2 Boris Mildner Katabolizam proteina, masti i ugljikohidrata u tri faze staničnog disanja. Faza 1.: oksidacija masnih kiselina, masti i ugljikohidrata kako bi nastao acetil-coa.
1 Promjena baze vektora
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
TRIGONOMETRIJA TROKUTA
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
[ C][ D] [ A][ B] Integracija metabolizma. Metabolički putevi koji omogućuju život izuzetno su složeni i međusobno isprepleteni
![[ C][ D] [ A][ B] Integracija metabolizma. Metabolički putevi koji omogućuju život izuzetno su složeni i međusobno isprepleteni](/thumbs/66/55930464.jpg "[ C][ D] [ A][ B] Integracija metabolizma. Metabolički putevi koji omogućuju život izuzetno su složeni i međusobno isprepleteni")
Metabolički putevi koji omogućuju život izuzetno su složeni i međusobno isprepleteni Integracija metabolizma Mitohondriji u štapićima Svi metabolički putevi moraju udovoljiti dvama uvjetima 1. individualne
SEKUNDARNE VEZE međumolekulske veze
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
4. Koji od navedenih enzima pripada vrsti hidroksilaza? a) heksokinaza; b) kimotripsin; c) glikogen fosforilaza; d) trioza fosfat izomeraza.
Osnove biokemije zadaća 7. 1. Što je točno o zimogenima? a) protoproteini su jedna vrsta zimogena; b) zimogene inhibiraju inhibitori proteina; c) zimogeni su enzimski neaktivni; d) zimogeni cijepaju proteaze.
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
( , 2. kolokvij)
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Dvanaesti praktikum iz Analize 1
Dvaaesti praktikum iz Aalize Zlatko Lazovi 20. decembar 206.. Dokazati da fukcija f = 5 l tg + 5 ima bar jedu realu ulu. Ree e. Oblast defiisaosti fukcije je D f = k Z da postoji ula fukcije a 0, π 2.
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
5. Karakteristične funkcije
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
SISTEMI NELINEARNIH JEDNAČINA
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
Teorijske osnove informatike 1
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
numeričkih deskriptivnih mera.
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Uvod u metabolizam - procesi izgradnje i razgradnje u živoj stanici
Metabolizam Uvod u metabolizam - procesi izgradnje i razgradnje u živoj stanici Izv. prof. dr. sc. Lidija Šver jelokupnost svih kemijskih pretvorbi u stanici ili organizmu Pretvorba (transformacija) tvari
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
Numerička matematika 2. kolokvij (1. srpnja 2009.)
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
OKSIDACIJSKA FOSFORILACIJA
OKSIDACIJSKA FOSFORILACIJA Sinteza ATP B. Mildner & M. Kekez 2012. 1. Što od navedenog nije dio Mittchelove kemiosmotske hipoteze? a) Dio energije koji se dobiva transportom elektrona koristi se za dobivanje
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
18. listopada listopada / 13
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
1.4 Tangenta i normala
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
Linearna algebra 2 prvi kolokvij,
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
Svetlosna energija absorbuje se hlorofilima u biljnim ćelijama. Hloroplast
Svetlosna energija absorbuje se hlorofilima u biljnim ćelijama Hloroplast Procesom ćelijskog disanja deponovana energija u šećerima erima prevodi se u ATP i druge energetske metabolite. Istovremeno se
Tipovi reakcija u kemiji organskih spojeva
Tipovi reakcija u kemiji organskih spojeva J. Lovrić U stanicama se događaju mnogobrojne enzimski specifične reakcije: npr. razgradnja složenih molekula (ugljikohidrata ili proteina) do jednostavnih kao
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
IZVODI ZADACI (I deo)
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Glikogen (razgradnja, sinteza i njihova regulacija) Boris Mildner
Glikogen (razgradnja, sinteza i njihova regulacija) Boris Mildner Čestice glikogena u hepatocitima. Glikogen, čestice za pohranjivanje glukoze, u hepatocitima se nalazi u citoplazmi blizu tubula endoplazmatske
2. KOLOKVIJ IZ MATEMATIKE 1
2 cos(3 π 4 ) sin( + π 6 ). 2. Pomoću linearnih transformacija funkcije f nacrtajte graf funkcije g ako je, g() = 2f( + 3) +. 3. Odredite domenu funkcije te odredite f i njenu domenu. log 3 2 + 3 7, 4.
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
DOLOČANJE)ENCIMSKE)AKTIVNOSTI)V)KLINIČNE)NAMENE)
DLČANJEENCIMSKEAKTIVNSTIVKLINIČNENAMENE 20encimovseru=nskopregledujevkliniki 1954sougotovilipovezanostsrčnegainfarktainpovišanekonc. aspartataminotransferazevserumu danesnarapolagovelikoabzapreciznodoločanjekoncproteinov
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med =
100g maslaca: 751kcal = 20g : E maslac E maslac = (751 x 20)/100 E maslac = 150,2kcal 100g med: 320kcal = 30g : E med E med = (320 x 30)/100 E med = 96kcal 100g mleko: 49kcal = 250g : E mleko E mleko =
radni nerecenzirani materijal za predavanja
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
, Zagreb. Prvi kolokvij iz Analognih sklopova i Elektroničkih sklopova
Grupa A 29..206. agreb Prvi kolokvij Analognih sklopova i lektroničkih sklopova Kolokvij se vrednuje s ukupno 42 boda. rijednost pojedinog zadatka navedena je na kraju svakog zadatka.. a pojačalo na slici
Računarska grafika. Rasterizacija linije
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Riješeni zadaci: Limes funkcije. Neprekidnost
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Periodičke izmjenične veličine
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
Ugljikohidrati. Boris Mildner
Ugljikohidrati Boris Mildner Ugljikohidrati Ugljikohidrati su najzastupljenije biomolekule na Zemlji. Svake godine fotosintezom se pretvara 100x10 9 tona CO 2 i H 2 O u celulozu i druge biljne proizvode.
Matematička analiza 1 dodatni zadaci
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
Aminokiseline. Anabolizam azotnihjedinjenja: Biosinteza aminokiselina, glutationa i biološki aktivnih amina 22.12.2014
Anabolizam azotnihjedinjenja: Biosinteza aminokiselina, glutationa i biološki aktivnih amina Predavanja iz opšte biohemije Školska 2014/2015. godina Aminokiseline 1 Metabolizam aminokiselina Proteini iz
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
RIJEŠENI ZADACI I TEORIJA IZ
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Sume kvadrata. mn = (ax + by) 2 + (ay bx) 2.
Sume kvadrata Koji se prirodni brojevi mogu prikazati kao zbroj kvadrata dva cijela broja? Propozicija 1. Ako su brojevi m i n sume dva kvadrata, onda je i njihov produkt m n takoder suma dva kvadrata.
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
PRIMJER 3. MATLAB filtdemo
PRIMJER 3. MATLAB filtdemo Prijenosna funkcija (IIR) Hz () =, 6 +, 3 z +, 78 z +, 3 z +, 53 z +, 3 z +, 78 z +, 3 z +, 6 z, 95 z +, 74 z +, z +, 9 z +, 4 z +, 5 z +, 3 z +, 4 z 3 4 5 6 7 8 3 4 5 6 7 8
TRIGONOMETRIJSKE FUNKCIJE I I.1.
TRIGONOMETRIJSKE FUNKCIJE I I Odredi na brojevnoj trigonometrijskoj kružnici točku Et, za koju je sin t =,cost < 0 Za koje realne brojeve a postoji realan broj takav da je sin = a? Izračunaj: sin π tg
3. OSNOVNI POKAZATELJI TLA
MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
Funkcije dviju varjabli (zadaci za vježbu)
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva