Potenciálna energia Niekoľko prípadových štúdií
|
|
|
- Χλόη Αγγελόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Potenciálna energia Niekoľko prípadových štúdií Odvodiť správny vzorec pre potenciálnu energiu môže myť niekedy dosť ťažké, najmä ak ešte nemáme poznatky z abstraktnejšej teoretickej mechaniky (naučí vás to kolega Fecko). Preto sa tu nepokúsim sformulovať nejaké rigorózne postupy ako vyrábať Feynmanovu zbierku vzorcov pre energiu Namiesto toho rozoberiem niekoľko špeciálnych prípadov, možno to prinesie nejaké poučenie. 1
2 Potenciálna energia na pružine Poloha z = 0 je poloha nedeformovanej pružiny. To nie je rovnovážna poloha guličky, lebo pružina sa predĺžia pod vplyvom tiaže guličky. Gulička môže ostať v kľude v bode, keď sila pružiny vyrovná silu tiaže, teda keď hodnoty na obr. sú z-zložky síl Rovnovážna poloha guličky má teda súradnicu Voľme bod z 0 za referenčný bod a vypočítajme prácu, ktorú vykoná trpaslík, keď guličku potiahne za lano tak, aby sa prakticky nulovou rýchlosťou presunula do ľubovoľného bodu z > z 0. V bode z teda musí pôsobiť silou, ktorej z-zložka bude lebo práve vtedy celková sila na guličku bude nulová a gulička nebude zrýchľovať. 2
3 Potenciálna energia na pružine Všimnime si, že na skúmaný fyzikálny systém, guličku, pôsobia dva externé objekty. Zem tiažovou silou a pružina silou z deformácie. Trpaslík, ktorého sme použili, je vlastne náš známy trpaslíkbrzdár, tentokrát nepoužívajúci kopiju ale lano. Vypočítame jeho prácu a dostaneme súhrnnú potenciálnu energiu, v našom prípade hodnoty na obr. sú z-zložky síl Výraz mgz poznáme. Výraz 1 2 Kz2 je nový vzrec do Feynmanovej zbierky, potenciálna energia pružnosti. 3
4 Potenciálna energia na pružine Analýzou práce jedného trpaslíka sme vyčarali prácu dvoch externých objektov za dve zložky potenciálnej energie častice. Celková energia guličky teda bude Pohybová rovnica guličky je Overme, že celková energia guličky sa zachováva hodnoty na obr. sú z-zložky síl Po dosadení za ma z z pohybovej rovnice dostaneme Energia je konštantná, zachováva sa. 4
5 Potenciálna energia pružiny Pozrime sa teraz na situáciu z iného uhla pohľadu. Za fyzikálny systém, ktorý študujeme budeme považovať pružinu, ktorá nech má zanedbateľnú hmotnosť. Teda nemá ani kinetickú energiu, i keď sa prípadne bude hýbať (deformovať). Súradnica z = 0 znamená nedeformovanú pružinu. Trpaslík, keď chce pružinu deformovať, musí pôsobiť silou F z = Kz a vykoná pritom prácu (štartujúc z referenčného bodu z = 0) Potenciálna energia deformovanej pružiny teda je Všimnime si, že tu sme nečarali prácu nejakého externého objektu za potenciálnu energiu pružiny. Táto energia pružnosti je naozaj obsiahnutá vnútri pružiny. 5
6 Potenciálna energia pružiny verzus potenciálna energia guličky na pružine Všimnime si, že keď sme ako systém uvažovali guličku a pružina bol len externý objekt, tiež sme odvodili výraz Aj ten výraz sme odvodzovali pomocou trpaslíka, ale bol tu výrazný rozdiel oproti čistej pružine. Pri guličke sme potenciálnou energiou nahradili (vyčarali) prácu externého objektu, pružiny. A potom sme povedali, že do energetickej bilancie už nebudeme rátať prácu pružiny, hoci zelená sila stále pri pohybe guličky pracuje. Energia pružnosti čistej pružiny je v akomsi zmysle poctivejšia energia než potenciálna energia guličky od pružnosti, ktorá je len vyčaraná práca. Celé to zdĺhavo popisujeme najmä preto, že Feynmanovu zbierku energetických vzorcov nemôžme používať bez rozmýšľania, musíme vedieť, ktorý z tých vzorcov je len vyčaraná práca, a potom prácu vyčaraných objektov už nezarátavať do energetickej bilancie. 6
7 Vyčaraná energia verzus nevyčaraná energia Vo Feynmanovej zbierke energetických vzorcov teda môžeme mať vzorce dvoch typov: vyčarané vzorce a nevyčarané vzorce. Medzi nimi je rozdiel. hociktorý vyčaraný vzorec môžem zo zbierky vynechať, ale potom musím do energetickej bilancie zarátať (na pravú stranu) prácu príslušného externého objektu. Zákon zachovania energie bude fungovať v zovšeobecnej forme s prácou na pravej strane. nevyčaraný vzorec nemôžem zo zbierky vynechať, prestal by fungovať zákon zachovania energie. Nevyčaraný vzorec sa nedá rozumne nahradiť prácou čohosi na pravej strane. Lebo príslušnú prácu nekonajú externé objekty ale vnútorné komponenty, napríklad molekuly, v pružine. Nevyčaraná energia pružnosti pružiny sa prejaví aj tak, že v istom zmysle sa dá identifikovať, kde sa tá energia nachádza (miestne), teda že v tej pružine. Dalo by sa to overiť aj takým pokusom. Stlačím pružinu a fixujem jej deformáciu nejakým špagátom. Potom ju stlačenú hodím do kyseliny, špagát sa rozpustí. Aký bude rozdiel oproti pokusu, keď do kyseliny hodím nestlačenú pružinu? Teplota kyseliny, v ktorej sa rozpustila stlačená pružina sa zvýši oproti pokusu s nestlačenou pružinou. 7
8 Potenciálna energia pružiny Pre nehmotnú pružinu neviem rozumne napísať pohybovú rovnicu, takže neviem skontrolovať či sa zachováva v čase jej energia. Ale odvodený výraz je zjavne energiou, lebo ak zavesím na deformovanú pružinu teleso a uvoľním ho, vie ho pružina vytiahnuť vyššie a vykonať prácu a keď tú prácu spočítam, zjavne to bude sedieť s nájdeným vzorcom pre jej energiu. Priateľskejší objekt na skúmanie zachovania energie, ktorej časťou je energia pružnosti je kmitajúca tyč, s ktorou sme sa už zoznámili, takže v ďalšom budeme skúmať energetickú bilanciu kmitajúcej tyče ako iného fyzikálneho zvieraťa. 8
9 Opakovanie: pozdĺžna deformácia pružnej tyče Deformácia tyče v nejakom okamihu je zadaná funkciou u(x), ktorá udáva posunutie prierezu tyče, ktorý sa pôvodne nachádzal v mieste x. Malý objemový element tyče dĺžky dx pri deformácii zmení svoju dĺzku, jeho nová dĺžka bude Takže relatívne predĺženie voči pôvodnej dĺžke dx bude Funkcia ε(x) udáva relatívne predĺženie tyče v mieste x. Ak Na prierez tyče v mieste x pôsobí napätie σ(x) (napätie je sila/plocha), potom platí Hookov zákon Predstavme si teraz, že máme zadanú deformáciu tyče ako funkciu u(x) a chceme vypočítať potenciálnu energiu tyče v dôsledku tej deformácie. Ľahšie sa to odvodí v diskrétnom modeli pružiniek, lebo deformačnú energiu jednej pružinky poznáme. 9
10 Pripomienka Limita kontinua bola vyšlo: Chápme to ako kvazimikroskopický model kontinua. Aké budú jeho parametre ρ, E? Ak prierez guličky je S, potom jedna gulička s hmotnosťou m pripadá na objem SΔ a bude ρ = m/(sδ). Ak sa pružina predĺži o u, treba na to silu F = ku. Dĺžka nedeformovanej pružiny je Δ, relatívne predĺženie u/δ, napätie F/S a dostaneme V modeli s guličkami vyšlo a takto to vyšlo v efektívnej teórii bez odvolávania sa na guličky. Hurá! 10
11 Posunutia koncov i-tej pružiny sú u(x i 1 ) a u(x i ), pôvodná dĺžka tej pružinky bola Δ, deformovaná dĺžka je Δ + u x i u x i 1, predĺženie pružinky teda je u x i u x i 1 Potenciálna energia i-tej pružinky teda je Vzťah konštánt E spojitého modelu a k diskrétneho modelu je a teda energia pružnosti celej tyče je 11
12 Vzorec prejde v spojitom modeli na integrál Potenciálnej energie pružnosti v pozdĺžne deformovanej tyči je teda kde E je Youngov modul pružnosti a uviedli sme explicitne aj časový okamih t. Kinetickú energiu tyče nájdeme ľahko. Hmotnosť objemového elementy tyče je ρdv, jeho okamžitá rýchlosť je u(t, x)/ t a teda Celková energia tyče teda je 12
13 Energia deformácie tyče bez aproximácie diskrétnymi pružinami Chceme zistiť deformačnú energiu tyče. Tyč rozdelíme na elementy dĺžky dx, jeden taký element je nakreslený červeno. Zavoláme na pomoc trpaslíkov brzdárov, každý dostane na starosť jeden element tyče. Zapichne si do toho elementu svoju brzdiacu kopiju a dáva pozor, aby zrýchlenie elementu počas nasledujúcich manipulácií bolo stále nulové. Preto sleduje sily, ktorými okolité elementy pôsobia na jemu zverený element a neustále ich vyrovnáva, aby celková sila pôsobiaca na element a teda aj jeho zrýchlenie bolo nulové. 13
14 Energia deformácie tyče bez aproximácie diskrétnymi pružinami Element susediaci s červeným elementom zľava naň pôsobí silou element susediaci sprava silou Trpaslík brzdár teda musí vyvíjať silu 14
15 Energia deformácie tyče bez aproximácie diskrétnymi pružinami Mám rozostavených trpaslíkov. Nech aktuálny stav deformácie tyče je daný funkciou u(x). Konečná deformácia, ktorú chcem dosiahnuť je u(x). Dosiahnem to tak, že ako veľký šéf postupne posúvam trpaslíkov o malé kúsky δ u x. Tieto malé pridávané deformácie sú pri rôznych x navzájom nezávislé, rôznej veľkosti a vykonávané v ľubovoľnom poradí. Všetko kvôli tomu, aby som sa presvedčil, že výsledná deformačná energia nezávisí na ceste, teda na detailnom postupe ako som z referenčného stavu u x = 0, prišiel k stavu u(x). Keďže trpaslíci vyrovnávajú všetky sily na nulu, ja ako veľký šéf nekonám pri manipuláciách žiadnu prácu, ale zato trpaslíci pri malom posunutí δ u x vykonajú prácu 15
16 Energia deformácie tyče bez aproximácie diskrétnymi pružinami Celková práca, ktorú vykonajú pri mojich manipuláciách trpaslíci pri zmene bude Použijem per partes, uvedomím si, že okraje neprispejú, lebo tam sú všetky deformácie stále nulové a dostanem 16
17 Energia deformácie tyče bez aproximácie diskrétnymi pružinami Teraz sčítam cez všetky malé prídavky deformácií δ u(x) a dostanem pre celkovú prácu trpaslíkov A toto je presne deformačná energia pružnej tyče. 17
18 Vlnenie tyče zachovanie energie Pohybová rovnica tyče je vlnová rovnica Dokážeme, že ak deformácia u(t, x) spĺňa pohybovú rovnica, energia sa zachováva. Počítajme časovú deriváciu energie keď sme dosadili za druhú časovú deriváciu pravú stranu pohybovej rovnice 18
19 Máme zatiaľ Na prvý člen použijeme per partes (podľa premennej integrovania, teda x) a dostaneme Člen v hranatých zátvorkách je nulový, lebo na hraniciach je deformácia nulová. Sčítance v integráli sú rovnaké ale s opačným znamienkom, takže celkovo dostávame nulu. Časová derivácia energie je teda nulová, energia je konštantná, zachováva sa. Pre naše nové fyzikálne zviera, pružnú tyč, sme našli výraz pre energiu (do Feynmanovej zbierky vzorcov) a ukázali sme, že aj pre toto zviera platí zákon zachovania energie. 19
20 Keď sme vyšetrovali guličku na pružine z energetického hľadiska, za fyzikálny systém sme považovali guličku a pružina bola vonkajší objekt. Prácu sily od pružiny sme vyčarali za potenciálnu energiu guličky Potom sme vyšetrovali samostatne pružinu ako fyzikálny objekt a našli sme, že jej potenciálna energia (nič vyčaraného!) je To, čo by sme radi videli je vyšetrovať spojený fyzikálny systém pružina plus gulička z hľadiska zákona zachovania energie. Neurobili sme to, lebo sme nemali pohybovú rovnicu pre pružinu (nemali sme ani vzorec pre kinetickú energiu pružiny). Nahradíme teraz pružinu pružnou tyčou, o ktorej vieme všetko a vyšetríme pohyb a zákon zachovania energie pre systém gulička nalepená na tyči 20
21 Gulička na pružnej tyči x u(x) x+u(x) kľudový stav deformovaný stav ξ súradnica guličky, meraná od konca nedeformovanej tyče. Tyč (nedeformovaná) má dĺžku L. x identifikuje prierezy tyče (je to vzdialenosť prierezu od začiatku tyče v nedeformovanom stave). x je vlastne meno prierezu tyče. ξ-súradnica prierezu tyče s menom x v deformovanom stave je ξ x = L + x + u(x). Koniec tyče má súradnicu ξ L = ξ, lebo to je súčasne súradnica guličky, teda u L = ξ. Napätie na konci tyče je Sila, ktorou gulička pôsobí na tyč je F = σ L S, tyč na guličku silou σ L S. 21
22 Gulička na pružnej tyči x u(x) x+u(x) kľudový stav deformovaný stav Pohybové rovnice teda budú 22
23 Energetická bilancia samotnej pružnej tyče Napravo je výkon sily, ktorou externý objekt, gulička, pôsobí na tyč, takže energetická bilancia tyče je v poriadku. Energia samotnej tyče sa nezachováva, ale jej zmena je krytá prácou externého objektu guličky. Super! 23
24 Energetická bilancia samotnej guličky F je sila, ktorou tyč pôsobí na guličku, dξ/dt je rýchlosť konca tyče a aj guličky), takže napravo máme výkon sily, ktorou tyč pôsobí na guličku. Takže zmena energie guličky je krytá prácou externého objektu, tyče. Super! Všimnime si, že za energiu guličky sme považovali len jej kinetickú energiu. Nemali sme žiadnu potenciálnu energiu pružnosti ako pri guličke na pružine. Práca tyče sa totiž nedá vyčarať za akúsi efektívnu potenciálnu energiu guličky. Práca tyče totiž nie je daná len začiatočným a koncovým stavom guličky, lebo medzitým vnútorné vlnenie tyče mohlo vyzerať od prípadu k prípadu všelijako, takže práca vykonaná vonkajším objektom 24 závisí na ceste.
25 Energetická bilancia sústavy tyč plus gulička Dajúc dokopy výsledky získané pre samotnú tyč a pre samotnú guličku dostaneme Celková energia sústavy tyč plus gulička sa teda zachováva! 25
26 Môže vzniknúť otázka, prečo sa to pri pružine dá vyčarať a pri tyči nie. V čom sú tyč a pružina odlišné? Nuž, musí to byť tak, že pri pružine sme švindľovali. Vedeckejšie povedané, dačo sme zanedbávali. Zanedbávali sme dynamiku pružiny. Pre pružinu sme nepísali žiadnu pohybovú rovnicu! Pritom aj po pružine sa zjavne môže šíriť akési vlnenie, čo sme neuvažovali. Pružina instantne reagovala na pohyb guličky rovnomerným roztiahnutím. Rigoróznejšou analýzou, čo a ako sme pri pružine zanedbávali, sa pre istotu zaoberať nebudeme. Výsledkom zanedbaní bolo, že práca pružiny nad guličkou nezávisela na ceste a mohli sme prácu vyčarať za efektívnu potenciálnu energiu guličky. 26
27 Energia a interakcia na diaľku Uvažujme dve častice pôsobiace na seba gravitačne. Pohybové rovnice sú Pre časticu majme zatiaľ len jeden vzorec v zbierke: kinetickú energiu Separátne pre každú časticu je to ok, lebo zmena energie prvej častice je krytá výkonom sily, ktorou druhá častica pôsobí na prvú a podobne zmena energie druhej častice je krytá výkonom sily, ktorou na ňu pôsobí prvá častica. Problém nastane, pre systém oboch častíc: sumárna energia sa nezachováva, ako sme to bolo pri kontaktnej interakci. Podľa zákona akcie a reakcie majú síce sily opačné znamienko, ibaže častice nemusia mať rovnakú rýchlosť, ako mali objekty v prípade kontaktnej interakcie (ktoré sa dotýkali), takže suma pravých strán sa nevynuluje. Pritom žiadny ďalší vonkajší objekt nepôsobí! Záver: buď sa energia nezachováva, alebo sme na niečo zabudli. 27
28 Energia a interakcia na diaľku Vyšetrime podrobnejšie, ako je to z energiou sústavy dvoch častíc Všimnime si ale, že výraz na pravej strane sa dá písať ako časová derivácia akejsi funkcie polôh dvoch častíc. (Geniálne sa pozriem na ten vzťah a vidím!) Takže platí Našli sme nový vzorec do Feynmanovej zbierky! Ale pozor. Náš systém sa skladá z dvoch častíc, ale nepribudol vzorec aplikovateľný na každú časticu zvlášť! Pribudol vzorec pre dvojčastičie. Až dve častice chápané ako jeden systém majú nový vzorec. 28
29 Energia a interakcia na diaľku Zákon zachovania energie pre dve gravitujúce častice teda zachránil nový vzorec Hovoríme tomu interakčná energia dvoch gravitujúcich častíc, nachádzajúcich sa v polohách Ԧr 1, Ԧr 2. Máme ale problém s interpretáciou práce ako spôsobu transferu energie. Pre energiu prvej častice platí čo hovorí, že energia častice narastá (uvažujeme teraz približujúce sa častice) pritekaním energie, ako hovorí výkon na pravej strane. Ibaže energia druhej častice neklesá, ale tiež narastá. Kto to platí? Formálna odpoveď je jednoduchá, kinetické energie oboch častíc narastajú na úkor ich interakčnej energie, ktorá klesá (stáva sa viac zápornou). Ibaže akosi necítime, že by interakčná energia bol fyzikálny objekt, z ktorého odteká energia tak, že by konal prácu nad časticami. Viac by sa nám páčilo, keby sme energetické náklady mohli zosobniť, ako keď firma hodí na krk stratu konkrétnemu zamestnancovi. Čo keby tak existoval tretí objekt, ktorý by tú prácu naozaj konal? 29
Matematika Funkcia viac premenných, Parciálne derivácie
 Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Matematika 2-01 Funkcia viac premenných, Parciálne derivácie Euklidovská metrika na množine R n všetkých usporiadaných n-íc reálnych čísel je reálna funkcia ρ: R n R n R definovaná nasledovne: Ak X = x
Matematika prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad
 Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
Matematika 3-13. prednáška 4 Postupnosti a rady 4.5 Funkcionálne rady - mocninové rady - Taylorov rad, MacLaurinov rad Erika Škrabul áková F BERG, TU Košice 15. 12. 2015 Erika Škrabul áková (TUKE) Taylorov
Cvičenie č. 4,5 Limita funkcie
 Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
Cvičenie č. 4,5 Limita funkcie Definícia ity Limita funkcie (vlastná vo vlastnom bode) Nech funkcia f je definovaná na nejakom okolí U( ) bodu. Hovoríme, že funkcia f má v bode itu rovnú A, ak ( ε > )(
1. Limita, spojitost a diferenciálny počet funkcie jednej premennej
 . Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
. Limita, spojitost a diferenciálny počet funkcie jednej premennej Definícia.: Hromadný bod a R množiny A R: v každom jeho okolí leží aspoň jeden bod z množiny A, ktorý je rôzny od bodu a Zadanie množiny
M6: Model Hydraulický systém dvoch zásobníkov kvapaliny s interakciou
 M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
M6: Model Hydraulický ytém dvoch záobníkov kvapaliny interakciou Úlohy:. Zotavte matematický popi modelu Hydraulický ytém. Vytvorte imulačný model v jazyku: a. Matlab b. imulink 3. Linearizujte nelineárny
Obvod a obsah štvoruholníka
 Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Obvod a štvoruholníka D. Štyri body roviny z ktorých žiadne tri nie sú kolineárne (neležia na jednej priamke) tvoria jeden štvoruholník. Tie body (A, B, C, D) sú vrcholy štvoruholníka. strany štvoruholníka
Relatívna deformácia je úmerná napätiu.
 Relatívna deformácia je úmerná napätiu. Konštanta úmernosti v tomto vzťahu je dôležitá materiálová konštanta, nazýva sa Youngov modul pružnosti E (modul pružnosti v tlaku) a vo vzťahu pre súvislosť relatívnej
Relatívna deformácia je úmerná napätiu. Konštanta úmernosti v tomto vzťahu je dôležitá materiálová konštanta, nazýva sa Youngov modul pružnosti E (modul pružnosti v tlaku) a vo vzťahu pre súvislosť relatívnej
Prechod z 2D do 3D. Martin Florek 3. marca 2009
 Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
Počítačová grafika 2 Prechod z 2D do 3D Martin Florek florek@sccg.sk FMFI UK 3. marca 2009 Prechod z 2D do 3D Čo to znamená? Ako zobraziť? Súradnicové systémy Čo to znamená? Ako zobraziť? tretia súradnica
6 Limita funkcie. 6.1 Myšlienka limity, interval bez bodu
 6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
6 Limita funkcie 6 Myšlienka ity, interval bez bodu Intuitívna myšlienka ity je prirodzená, ale definovať presne pojem ity je značne obtiažne Nech f je funkcia a nech a je reálne číslo Čo znamená zápis
Motivácia Denícia determinantu Výpo et determinantov Determinant sú inu matíc Vyuºitie determinantov. Determinanty. 14. decembra 2010.
 14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
14. decembra 2010 Rie²enie sústav Plocha rovnobeºníka Objem rovnobeºnostena Rie²enie sústav Príklad a 11 x 1 + a 12 x 2 = c 1 a 21 x 1 + a 22 x 2 = c 2 Dostaneme: x 1 = c 1a 22 c 2 a 12 a 11 a 22 a 12
Ekvačná a kvantifikačná logika
 a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
a kvantifikačná 3. prednáška (6. 10. 004) Prehľad 1 1 (dokončenie) ekvačných tabliel Formula A je ekvačne dokázateľná z množiny axióm T (T i A) práve vtedy, keď existuje uzavreté tablo pre cieľ A ekvačných
ZADANIE 1_ ÚLOHA 3_Všeobecná rovinná silová sústava ZADANIE 1 _ ÚLOHA 3
 ZDNIE _ ÚLOH 3_Všeobecná rovinná silová sústv ZDNIE _ ÚLOH 3 ÚLOH 3.: Vypočítjte veľkosti rekcií vo väzbách nosník zťženého podľ obrázku 3.. Veľkosti známych síl, momentov dĺžkové rozmery sú uvedené v
ZDNIE _ ÚLOH 3_Všeobecná rovinná silová sústv ZDNIE _ ÚLOH 3 ÚLOH 3.: Vypočítjte veľkosti rekcií vo väzbách nosník zťženého podľ obrázku 3.. Veľkosti známych síl, momentov dĺžkové rozmery sú uvedené v
7 Derivácia funkcie. 7.1 Motivácia k derivácii
 Híc, P Pokorný, M: Matematika pre informatikov a prírodné vedy 7 Derivácia funkcie 7 Motivácia k derivácii S využitím derivácií sa stretávame veľmi často v matematike, geometrii, fyzike, či v rôznych technických
Híc, P Pokorný, M: Matematika pre informatikov a prírodné vedy 7 Derivácia funkcie 7 Motivácia k derivácii S využitím derivácií sa stretávame veľmi často v matematike, geometrii, fyzike, či v rôznych technických
Látka ako kontinuum 1
 Látka ako kontinuum 1 Objekty okolo nás sú spravidla látkovej povahy. Čo presne nazývame látka nie je dobre definované. V slovenskej terminológii pretrvávajú zvyklosti zavedené niekedy v rámci ideologického
Látka ako kontinuum 1 Objekty okolo nás sú spravidla látkovej povahy. Čo presne nazývame látka nie je dobre definované. V slovenskej terminológii pretrvávajú zvyklosti zavedené niekedy v rámci ideologického
MIDTERM (A) riešenia a bodovanie
 MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
MIDTERM (A) riešenia a bodovanie 1. (7b) Nech vzhl adom na štandardnú karteziánsku sústavu súradníc S 1 := O, e 1, e 2 majú bod P a vektory u, v súradnice P = [0, 1], u = e 1, v = 2 e 2. Aký predpis bude
7. FUNKCIE POJEM FUNKCIE
 7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
7. FUNKCIE POJEM FUNKCIE Funkcia f reálnej premennej je : - každé zobrazenie f v množine všetkých reálnych čísel; - množina f všetkých usporiadaných dvojíc[,y] R R pre ktorú platí: ku každému R eistuje
PRIEMER DROTU d = 0,4-6,3 mm
 PRUŽINY PRUŽINY SKRUTNÉ PRUŽINY VIAC AKO 200 RUHOV SKRUTNÝCH PRUŽÍN PRIEMER ROTU d = 0,4-6,3 mm èíslo 3.0 22.8.2008 8:28:57 22.8.2008 8:28:58 PRUŽINY SKRUTNÉ PRUŽINY TECHNICKÉ PARAMETRE h d L S Legenda
PRUŽINY PRUŽINY SKRUTNÉ PRUŽINY VIAC AKO 200 RUHOV SKRUTNÝCH PRUŽÍN PRIEMER ROTU d = 0,4-6,3 mm èíslo 3.0 22.8.2008 8:28:57 22.8.2008 8:28:58 PRUŽINY SKRUTNÉ PRUŽINY TECHNICKÉ PARAMETRE h d L S Legenda
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2012/2013 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/18
Motivácia pojmu derivácia
 Derivácia funkcie Motivácia pojmu derivácia Zaujíma nás priemerná intenzita zmeny nejakej veličiny (dráhy, rastu populácie, veľkosti elektrického náboja, hmotnosti), vzhľadom na inú veličinu (čas, dĺžka)
Derivácia funkcie Motivácia pojmu derivácia Zaujíma nás priemerná intenzita zmeny nejakej veličiny (dráhy, rastu populácie, veľkosti elektrického náboja, hmotnosti), vzhľadom na inú veličinu (čas, dĺžka)
Moderné vzdelávanie pre vedomostnú spoločnosť Projekt je spolufinancovaný zo zdrojov EÚ M A T E M A T I K A
 M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
M A T E M A T I K A PRACOVNÝ ZOŠIT II. ROČNÍK Mgr. Agnesa Balážová Obchodná akadémia, Akademika Hronca 8, Rožňava PRACOVNÝ LIST 1 Urč typ kvadratickej rovnice : 1. x 2 3x = 0... 2. 3x 2 = - 2... 3. -4x
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2014/2015 ARMA modely časť 2: moving average modely(ma) p.1/24 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA)
 ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
ARMA modely čast 2: moving average modely (MA) Beáta Stehlíková Časové rady, FMFI UK, 2011/2012 ARMA modely časť 2: moving average modely(ma) p.1/25 V. Moving average proces prvého rádu - MA(1) ARMA modely
1. písomná práca z matematiky Skupina A
 1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
1. písomná práca z matematiky Skupina A 1. Vypočítajte : a) 84º 56 + 32º 38 = b) 140º 53º 24 = c) 55º 12 : 2 = 2. Vypočítajte zvyšné uhly na obrázku : β γ α = 35 12 δ a b 3. Znázornite na číselnej osi
3. Striedavé prúdy. Sínusoida
 . Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
. Striedavé prúdy VZNIK: Striedavý elektrický prúd prechádza obvodom, ktorý je pripojený na zdroj striedavého napätia. Striedavé napätie vyrába synchrónny generátor, kde na koncoch rotorového vinutia sa
4 Dynamika hmotného bodu
 61 4 Dynamika hmotného bodu V predchádzajúcej kapitole - kinematike hmotného bodu sme sa zaoberali pohybom a pokojom telies, čiže formou pohybu. Neriešili sme príčiny vzniku pohybu hmotného bodu. A práve
61 4 Dynamika hmotného bodu V predchádzajúcej kapitole - kinematike hmotného bodu sme sa zaoberali pohybom a pokojom telies, čiže formou pohybu. Neriešili sme príčiny vzniku pohybu hmotného bodu. A práve
Start. Vstup r. O = 2*π*r S = π*r*r. Vystup O, S. Stop. Start. Vstup P, C V = P*C*1,19. Vystup V. Stop
 1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
1) Vytvorte algoritmus (vývojový diagram) na výpočet obvodu kruhu. O=2xπxr ; S=πxrxr Vstup r O = 2*π*r S = π*r*r Vystup O, S 2) Vytvorte algoritmus (vývojový diagram) na výpočet celkovej ceny výrobku s
Základné poznatky molekulovej fyziky a termodynamiky
 Základné poznatky molekulovej fyziky a termodynamiky Opakovanie učiva II. ročníka, Téma 1. A. Príprava na maturity z fyziky, 2008 Outline Molekulová fyzika 1 Molekulová fyzika Predmet Molekulovej fyziky
Základné poznatky molekulovej fyziky a termodynamiky Opakovanie učiva II. ročníka, Téma 1. A. Príprava na maturity z fyziky, 2008 Outline Molekulová fyzika 1 Molekulová fyzika Predmet Molekulovej fyziky
,Zohrievanie vody indukčným varičom bez pokrievky,
 Farba skupiny: zelená Označenie úlohy:,zohrievanie vody indukčným varičom bez pokrievky, Úloha: Zistiť, ako závisí účinnosť zohrievania vody na indukčnom variči od priemeru použitého hrnca. Hypotéza: Účinnosť
Farba skupiny: zelená Označenie úlohy:,zohrievanie vody indukčným varičom bez pokrievky, Úloha: Zistiť, ako závisí účinnosť zohrievania vody na indukčnom variči od priemeru použitého hrnca. Hypotéza: Účinnosť
Zložené funkcie a substitúcia
 3. kapitola Zložené funkcie a substitúcia Doteraz sme sa pri funkciách stretli len so závislosťami medzi dvoma premennými. Napríklad vzťah y=x 2 nám hovoril, ako závisí premenná y od premennej x. V praxi
3. kapitola Zložené funkcie a substitúcia Doteraz sme sa pri funkciách stretli len so závislosťami medzi dvoma premennými. Napríklad vzťah y=x 2 nám hovoril, ako závisí premenná y od premennej x. V praxi
Termodynamika. Doplnkové materiály k prednáškam z Fyziky I pre SjF Dušan PUDIŠ (2008)
 ermodynamika nútorná energia lynov,. veta termodynamická, Izochorický dej, Izotermický dej, Izobarický dej, diabatický dej, Práca lynu ri termodynamických rocesoch, arnotov cyklus, Entroia Dolnkové materiály
ermodynamika nútorná energia lynov,. veta termodynamická, Izochorický dej, Izotermický dej, Izobarický dej, diabatický dej, Práca lynu ri termodynamických rocesoch, arnotov cyklus, Entroia Dolnkové materiály
Goniometrické rovnice a nerovnice. Základné goniometrické rovnice
 Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Goniometrické rovnice a nerovnice Definícia: Rovnice (nerovnice) obsahujúce neznámu x alebo výrazy s neznámou x ako argumenty jednej alebo niekoľkých goniometrických funkcií nazývame goniometrickými rovnicami
Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín. Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť.
 Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť. Ktoré fyzikálne jednotky zodpovedajú sústave SI: a) Dĺžka, čas,
Kontrolné otázky na kvíz z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej a nesprávnych odpovedí sa môže v teste meniť. Ktoré fyzikálne jednotky zodpovedajú sústave SI: a) Dĺžka, čas,
6 APLIKÁCIE FUNKCIE DVOCH PREMENNÝCH
 6 APLIKÁCIE FUNKCIE DVOCH PREMENNÝCH 6. Otázky Definujte pojem produkčná funkcia. Definujte pojem marginálny produkt. 6. Produkčná funkcia a marginálny produkt Definícia 6. Ak v ekonomickom procese počet
6 APLIKÁCIE FUNKCIE DVOCH PREMENNÝCH 6. Otázky Definujte pojem produkčná funkcia. Definujte pojem marginálny produkt. 6. Produkčná funkcia a marginálny produkt Definícia 6. Ak v ekonomickom procese počet
24. Základné spôsoby zobrazovania priestoru do roviny
 24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
24. Základné spôsoby zobrazovania priestoru do roviny Voľné rovnobežné premietanie Presné metódy zobrazenia trojrozmerného priestoru do dvojrozmernej roviny skúma samostatná matematická disciplína, ktorá
Komplexné čísla, Diskrétna Fourierova transformácia 1
 Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
Komplexné čísla, Diskrétna Fourierova transformácia Komplexné čísla C - množina všetkých komplexných čísel komplexné číslo: z = a + bi, kde a, b R, i - imaginárna jednotka i =, t.j. i =. komplexne združené
AerobTec Altis Micro
 AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
AerobTec Altis Micro Záznamový / súťažný výškomer s telemetriou Výrobca: AerobTec, s.r.o. Pionierska 15 831 02 Bratislava www.aerobtec.com info@aerobtec.com Obsah 1.Vlastnosti... 3 2.Úvod... 3 3.Princíp
x x x2 n
 Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
Reálne symetrické matice Skalárny súčin v R n. Pripomeniem, že pre vektory u = u, u, u, v = v, v, v R platí. dĺžka vektora u je u = u + u + u,. ak sú oba vektory nenulové a zvierajú neorientovaný uhol
ELEKTRICKÉ POLE. Elektrický náboj je základná vlastnosť častíc, je viazaný na častice látky a vyjadruje stav elektricky nabitých telies.
 ELEKTRICKÉ POLE 1. ELEKTRICKÝ NÁBOJ, COULOMBOV ZÁKON Skúmajme napr. trenie celuloidového pravítka látkou, hrebeň suché vlasy, mikrotén slabý prúd vody... Príčinou spomenutých javov je elektrický náboj,
ELEKTRICKÉ POLE 1. ELEKTRICKÝ NÁBOJ, COULOMBOV ZÁKON Skúmajme napr. trenie celuloidového pravítka látkou, hrebeň suché vlasy, mikrotén slabý prúd vody... Príčinou spomenutých javov je elektrický náboj,
Analýza údajov. W bozóny.
 Analýza údajov W bozóny http://www.physicsmasterclasses.org/index.php 1 Identifikácia častíc https://kjende.web.cern.ch/kjende/sl/wpath_teilchenid1.htm 2 Identifikácia častíc Cvičenie 1 Na web stránke
Analýza údajov W bozóny http://www.physicsmasterclasses.org/index.php 1 Identifikácia častíc https://kjende.web.cern.ch/kjende/sl/wpath_teilchenid1.htm 2 Identifikácia častíc Cvičenie 1 Na web stránke
Matematika 2. časť: Funkcia viac premenných Letný semester 2013/2014
 Matematika 2 časť: Funkcia viac premenných Letný semester 2013/2014 RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk
Matematika 2 časť: Funkcia viac premenných Letný semester 2013/2014 RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk
Matematický model robota s diferenciálnym kolesovým podvozkom
 Matematický model robota s diferenciálnym kolesovým podvozkom Demonštračný modul Úlohy. Zostavte matematický model robota s diferenciálnym kolesovým podvozkom 2. Vytvorte simulačný model robota v simulačnom
Matematický model robota s diferenciálnym kolesovým podvozkom Demonštračný modul Úlohy. Zostavte matematický model robota s diferenciálnym kolesovým podvozkom 2. Vytvorte simulačný model robota v simulačnom
Zrýchľovanie vesmíru. Zrýchľovanie vesmíru. o výprave na kraj vesmíru a čo tam astronómovia objavili
 Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru
Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru a čo tam astronómovia objavili Zrýchľovanie vesmíru o výprave na kraj vesmíru
Logaritmus operácie s logaritmami, dekadický a prirodzený logaritmus
 KrAv11-T List 1 Logaritmus operácie s logaritmami, dekadický a prirodzený logaritmus RNDr. Jana Krajčiová, PhD. U: Najprv si zopakujme, ako znie definícia logaritmu. Ž: Ja si pamätám, že logaritmus súvisí
KrAv11-T List 1 Logaritmus operácie s logaritmami, dekadický a prirodzený logaritmus RNDr. Jana Krajčiová, PhD. U: Najprv si zopakujme, ako znie definícia logaritmu. Ž: Ja si pamätám, že logaritmus súvisí
Gramatická indukcia a jej využitie
 a jej využitie KAI FMFI UK 29. Marec 2010 a jej využitie Prehľad Teória formálnych jazykov 1 Teória formálnych jazykov 2 3 a jej využitie Na počiatku bolo slovo. A slovo... a jej využitie Definícia (Slovo)
a jej využitie KAI FMFI UK 29. Marec 2010 a jej využitie Prehľad Teória formálnych jazykov 1 Teória formálnych jazykov 2 3 a jej využitie Na počiatku bolo slovo. A slovo... a jej využitie Definícia (Slovo)
Úvod do lineárnej algebry. Monika Molnárová Prednášky
 Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
Úvod do lineárnej algebry Monika Molnárová Prednášky 2006 Prednášky: 3 17 marca 2006 4 24 marca 2006 c RNDr Monika Molnárová, PhD Obsah 2 Sústavy lineárnych rovníc 25 21 Riešenie sústavy lineárnych rovníc
Goniometrické funkcie
 Goniometrické funkcie Oblúková miera Goniometrické funkcie sú funkcie, ktoré sa používajú pri meraní uhlov (Goniometria Meranie Uhla). Pri týchto funkciách sa uvažuje o veľkostiach uhlov udaných v oblúkovej
Goniometrické funkcie Oblúková miera Goniometrické funkcie sú funkcie, ktoré sa používajú pri meraní uhlov (Goniometria Meranie Uhla). Pri týchto funkciách sa uvažuje o veľkostiach uhlov udaných v oblúkovej
Tomáš Madaras Prvočísla
 Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
Prvočísla Tomáš Madaras 2011 Definícia Nech a Z. Čísla 1, 1, a, a sa nazývajú triviálne delitele čísla a. Cele číslo a / {0, 1, 1} sa nazýva prvočíslo, ak má iba triviálne delitele; ak má aj iné delitele,
18. kapitola. Ako navariť z vody
 18. kapitola Ako navariť z vody Slovným spojením navariť z vody sa zvyknú myslieť dve rôzne veci. Buď to, že niekto niečo tvrdí, ale nevie to poriadne vyargumentovať, alebo to, že niekto začal s málom
18. kapitola Ako navariť z vody Slovným spojením navariť z vody sa zvyknú myslieť dve rôzne veci. Buď to, že niekto niečo tvrdí, ale nevie to poriadne vyargumentovať, alebo to, že niekto začal s málom
Matematika 2. časť: Analytická geometria
 Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Matematika 2 časť: Analytická geometria RNDr. Jana Pócsová, PhD. Ústav riadenia a informatizácie výrobných procesov Fakulta BERG Technická univerzita v Košiciach e-mail: jana.pocsova@tuke.sk Súradnicové
Chí kvadrát test dobrej zhody. Metódy riešenia úloh z pravdepodobnosti a štatistiky
 Chí kvadrát test dobrej zhody Metódy riešenia úloh z pravdepodobnosti a štatistiky www.iam.fmph.uniba.sk/institute/stehlikova Test dobrej zhody I. Chceme overiť, či naše dáta pochádzajú z konkrétneho pravdep.
Chí kvadrát test dobrej zhody Metódy riešenia úloh z pravdepodobnosti a štatistiky www.iam.fmph.uniba.sk/institute/stehlikova Test dobrej zhody I. Chceme overiť, či naše dáta pochádzajú z konkrétneho pravdep.
FUNKCIE N REÁLNYCH PREMENNÝCH
 FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE FUNKCIE N REÁLNYCH PREMENNÝCH RNDr. Kristína Rostás, PhD. PREDMET: Matematická analýza ) 2010/2011 1. DEFINÍCIA REÁLNEJ FUNKCIE
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY UNIVERZITY KOMENSKÉHO V BRATISLAVE FUNKCIE N REÁLNYCH PREMENNÝCH RNDr. Kristína Rostás, PhD. PREDMET: Matematická analýza ) 2010/2011 1. DEFINÍCIA REÁLNEJ FUNKCIE
Súčtové vzorce. cos (α + β) = cos α.cos β sin α.sin β cos (α β) = cos α.cos β + sin α.sin β. tg (α β) = cotg (α β) =.
 Súčtové vzorce Súčtové vzorce sú goniometrické hodnoty súčtov a rozdielov dvoch uhlov Sem patria aj goniometrické hodnoty dvojnásobného a polovičného uhla a pridám aj súčet a rozdiel goniometrických funkcií
Súčtové vzorce Súčtové vzorce sú goniometrické hodnoty súčtov a rozdielov dvoch uhlov Sem patria aj goniometrické hodnoty dvojnásobného a polovičného uhla a pridám aj súčet a rozdiel goniometrických funkcií
Fyzika. Úvodný kurz pre poslucháčov prvého ročníka bakalárskych programov v rámci odboru geológie. 3. prednáška energia, práca, výkon
 Fyzika Úvodný kurz pre poslucháčov prvého ročníka bakalárskych programov v rámci odboru geológie 3. prednáška energia, práca, výkon V súvislosti s gravitačným poľom (minulá prednáška) môžeme uvažovať napr.
Fyzika Úvodný kurz pre poslucháčov prvého ročníka bakalárskych programov v rámci odboru geológie 3. prednáška energia, práca, výkon V súvislosti s gravitačným poľom (minulá prednáška) môžeme uvažovať napr.
Numerické metódy matematiky I
 Prednáška č. 7 Numerické metódy matematiky I Riešenie sústav lineárnych rovníc ( pokračovanie ) Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc
Prednáška č. 7 Numerické metódy matematiky I Riešenie sústav lineárnych rovníc ( pokračovanie ) Prednáška č. 7 OBSAH 1. Metóda singulárneho rozkladu (SVD) Úvod SVD štvorcovej matice SVD pre menej rovníc
Einsteinove rovnice. obrázkový úvod do Všeobecnej teórie relativity. Pavol Ševera. Katedra teoretickej fyziky a didaktiky fyziky
 Einsteinove rovnice obrázkový úvod do Všeobecnej teórie relativity Pavol Ševera Katedra teoretickej fyziky a didaktiky fyziky (Pseudo)historický úvod Gravitácia / Elektromagnetizmus (Pseudo)historický
Einsteinove rovnice obrázkový úvod do Všeobecnej teórie relativity Pavol Ševera Katedra teoretickej fyziky a didaktiky fyziky (Pseudo)historický úvod Gravitácia / Elektromagnetizmus (Pseudo)historický
4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti
 4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti Výroková funkcia (forma) ϕ ( x) je formálny výraz (formula), ktorý obsahuje znak x, pričom x berieme z nejakej množiny M. Ak za x zvolíme
4. Výrokové funkcie (formy), ich definičný obor a obor pravdivosti Výroková funkcia (forma) ϕ ( x) je formálny výraz (formula), ktorý obsahuje znak x, pričom x berieme z nejakej množiny M. Ak za x zvolíme
STRIEDAVÝ PRÚD - PRÍKLADY
 STRIEDAVÝ PRÚD - PRÍKLADY Príklad0: V sieti je frekvencia 50 Hz. Vypočítajte periódu. T = = = 0,02 s = 20 ms f 50 Hz Príklad02: Elektromotor sa otočí 50x za sekundu. Koľko otáčok má za minútu? 50 Hz =
STRIEDAVÝ PRÚD - PRÍKLADY Príklad0: V sieti je frekvencia 50 Hz. Vypočítajte periódu. T = = = 0,02 s = 20 ms f 50 Hz Príklad02: Elektromotor sa otočí 50x za sekundu. Koľko otáčok má za minútu? 50 Hz =
LR(0) syntaktické analyzátory. doc. RNDr. Ľubomír Dedera
 LR0) syntaktické analyzátory doc. RNDr. Ľubomír Dedera Učebné otázky LR0) automat a jeho konštrukcia Konštrukcia tabuliek ACION a GOO LR0) syntaktického analyzátora LR0) syntaktický analyzátor Sám osebe
LR0) syntaktické analyzátory doc. RNDr. Ľubomír Dedera Učebné otázky LR0) automat a jeho konštrukcia Konštrukcia tabuliek ACION a GOO LR0) syntaktického analyzátora LR0) syntaktický analyzátor Sám osebe
Ako sa hravo naučiť počtu derivačnému
 Škola pre Mimoriadne Nadané Deti a Gymnázium, Teplická 7, 8 0 Bratislava Anino BELAN Ako sa hravo naučiť počtu derivačnému učebný text pre septimu osemročného gymnázia BRATISLAVA 06 Obsah Ako zachytiť
Škola pre Mimoriadne Nadané Deti a Gymnázium, Teplická 7, 8 0 Bratislava Anino BELAN Ako sa hravo naučiť počtu derivačnému učebný text pre septimu osemročného gymnázia BRATISLAVA 06 Obsah Ako zachytiť
RIEŠENIE WHEATSONOVHO MOSTÍKA
 SNÁ PMYSLNÁ ŠKOL LKONKÁ V PŠŤNO KOMPLXNÁ PÁ Č. / ŠN WSONOVO MOSÍK Piešťany, október 00 utor : Marek eteš. Komplexná práca č. / Strana č. / Obsah:. eoretický rozbor Wheatsonovho mostíka. eoretický rozbor
SNÁ PMYSLNÁ ŠKOL LKONKÁ V PŠŤNO KOMPLXNÁ PÁ Č. / ŠN WSONOVO MOSÍK Piešťany, október 00 utor : Marek eteš. Komplexná práca č. / Strana č. / Obsah:. eoretický rozbor Wheatsonovho mostíka. eoretický rozbor
URČENIE MOMENTU ZOTRVAČNOSTI FYZIKÁLNEHO KYVADLA
 54 URČENE MOMENTU ZOTRVAČNOST FYZKÁLNEHO KYVADLA Teoretický úvod: Fyzikálnym kyvadlom rozumieme teleso (napr. dosku, tyč), ktoré vykonáva periodický kmitavý pohyb okolo osi, ktorá neprechádza ťažiskom.
54 URČENE MOMENTU ZOTRVAČNOST FYZKÁLNEHO KYVADLA Teoretický úvod: Fyzikálnym kyvadlom rozumieme teleso (napr. dosku, tyč), ktoré vykonáva periodický kmitavý pohyb okolo osi, ktorá neprechádza ťažiskom.
Modul pružnosti betónu
 f cm tan α = E cm 0,4f cm ε cl E = σ ε ε cul Modul pružnosti betónu α Autori: Stanislav Unčík Patrik Ševčík Modul pružnosti betónu Autori: Stanislav Unčík Patrik Ševčík Trnava 2008 Obsah 1 Úvod...7 2 Deformácie
f cm tan α = E cm 0,4f cm ε cl E = σ ε ε cul Modul pružnosti betónu α Autori: Stanislav Unčík Patrik Ševčík Modul pružnosti betónu Autori: Stanislav Unčík Patrik Ševčík Trnava 2008 Obsah 1 Úvod...7 2 Deformácie
Smernicový tvar rovnice priamky
 VoAg1-T List 1 Smernicový tvar rovnice priamk RNDr.Viera Vodičková U: Medzi prevratné objav analtickej geometrie patrí to, že s priamkou nenarábame ako s geometrickým objektom, ale popisujeme ju rovnicou.
VoAg1-T List 1 Smernicový tvar rovnice priamk RNDr.Viera Vodičková U: Medzi prevratné objav analtickej geometrie patrí to, že s priamkou nenarábame ako s geometrickým objektom, ale popisujeme ju rovnicou.
Kontrolné otázky z jednotiek fyzikálnych veličín
 Verzia zo dňa 6. 9. 008. Kontrolné otázky z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej odpovede sa môže v kontrolnom teste meniť. Takisto aj znenie nesprávnych odpovedí. Uvedomte si
Verzia zo dňa 6. 9. 008. Kontrolné otázky z jednotiek fyzikálnych veličín Upozornenie: Umiestnenie správnej odpovede sa môže v kontrolnom teste meniť. Takisto aj znenie nesprávnych odpovedí. Uvedomte si
Život vedca krajší od vysnívaného... s prírodou na hladine α R-P-R
 Život vedca krajší od vysnívaného... s prírodou na hladine α R-P-R Ako nadprirodzené stretnutie s murárikom červenokrídlym naformátovalo môj profesijný i súkromný život... Osudové stretnutie s murárikom
Život vedca krajší od vysnívaného... s prírodou na hladine α R-P-R Ako nadprirodzené stretnutie s murárikom červenokrídlym naformátovalo môj profesijný i súkromný život... Osudové stretnutie s murárikom
Definícia parciálna derivácia funkcie podľa premennej x. Definícia parciálna derivácia funkcie podľa premennej y. Ak existuje limita.
 Teória prednáška č. 9 Deinícia parciálna deriácia nkcie podľa premennej Nech nkcia Ak eistje limita je deinoaná okolí bod [ ] lim. tak túto limit nazýame parciálno deriácio nkcie podľa premennej bode [
Teória prednáška č. 9 Deinícia parciálna deriácia nkcie podľa premennej Nech nkcia Ak eistje limita je deinoaná okolí bod [ ] lim. tak túto limit nazýame parciálno deriácio nkcie podľa premennej bode [
Pevné ložiská. Voľné ložiská
 SUPPORTS D EXTREMITES DE PRECISION - SUPPORT UNIT FOR BALLSCREWS LOŽISKA PRE GULIČKOVÉ SKRUTKY A TRAPÉZOVÉ SKRUTKY Výber správnej podpory konca uličkovej skrutky či trapézovej skrutky je dôležité pre správnu
SUPPORTS D EXTREMITES DE PRECISION - SUPPORT UNIT FOR BALLSCREWS LOŽISKA PRE GULIČKOVÉ SKRUTKY A TRAPÉZOVÉ SKRUTKY Výber správnej podpory konca uličkovej skrutky či trapézovej skrutky je dôležité pre správnu
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy
 Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/27
Jednotkový koreň (unit root), diferencovanie časového radu, unit root testy Beáta Stehlíková Časové rady, FMFI UK, 2013/2014 Jednotkový koreň(unit root),diferencovanie časového radu, unit root testy p.1/27
Základné vzťahy medzi hodnotami goniometrických funkcií
 Ma-Go-2-T List Základné vzťahy medzi hodnotami goniometrických funkcií RNDr. Marián Macko U: Predstav si, že ti zadám hodnotu jednej z goniometrických funkcií. Napríklad sin x = 0,6. Vedel by si určiť
Ma-Go-2-T List Základné vzťahy medzi hodnotami goniometrických funkcií RNDr. Marián Macko U: Predstav si, že ti zadám hodnotu jednej z goniometrických funkcií. Napríklad sin x = 0,6. Vedel by si určiť
Funkcie - základné pojmy
 Funkcie - základné pojmy DEFINÍCIA FUNKCIE Nech A, B sú dve neprázdne číselné množiny. Ak každému prvku x A je priradený najviac jeden prvok y B, tak hovoríme, že je daná funkcia z množiny A do množiny
Funkcie - základné pojmy DEFINÍCIA FUNKCIE Nech A, B sú dve neprázdne číselné množiny. Ak každému prvku x A je priradený najviac jeden prvok y B, tak hovoríme, že je daná funkcia z množiny A do množiny
, kde pre prípad obruč M + I/R 2 = 2 M.
 55 ročník Fyzikálnej olympiády v školskom roku 3/4 iešenie úloh domáceho kola kategórie A (ďalšie inormácie na http://ounizask a wwwolympiadysk) Kyvadlo vo valci iešenie: a) Ide o sústavu dvoch spojených
55 ročník Fyzikálnej olympiády v školskom roku 3/4 iešenie úloh domáceho kola kategórie A (ďalšie inormácie na http://ounizask a wwwolympiadysk) Kyvadlo vo valci iešenie: a) Ide o sústavu dvoch spojených
Diferenciálne rovnice
 Diferenciálne rovnice Juraj Tekel Katedra teoretickej fyziky a didaktiky fyziky FMFI UK Mlynska Dolina 842 48 Bratislava juraj(a)tekel(b)gmail(c)com http://fks.sk/~juro/phys_teaching.html Aktualizované
Diferenciálne rovnice Juraj Tekel Katedra teoretickej fyziky a didaktiky fyziky FMFI UK Mlynska Dolina 842 48 Bratislava juraj(a)tekel(b)gmail(c)com http://fks.sk/~juro/phys_teaching.html Aktualizované
HASLIM112V, HASLIM123V, HASLIM136V HASLIM112Z, HASLIM123Z, HASLIM136Z HASLIM112S, HASLIM123S, HASLIM136S
 PROUKTOVÝ LIST HKL SLIM č. sklad. karty / obj. číslo: HSLIM112V, HSLIM123V, HSLIM136V HSLIM112Z, HSLIM123Z, HSLIM136Z HSLIM112S, HSLIM123S, HSLIM136S fakturačný názov výrobku: HKL SLIMv 1,2kW HKL SLIMv
PROUKTOVÝ LIST HKL SLIM č. sklad. karty / obj. číslo: HSLIM112V, HSLIM123V, HSLIM136V HSLIM112Z, HSLIM123Z, HSLIM136Z HSLIM112S, HSLIM123S, HSLIM136S fakturačný názov výrobku: HKL SLIMv 1,2kW HKL SLIMv
M8 Model "Valcová a kužeľová nádrž v sérií bez interakcie"
 M8 Model "Valcová a kužeľová nádrž v sérií bez interakcie" Úlohy: 1. Zostavte matematický popis modelu M8 2. Vytvorte simulačný model v prostredí: a) Simulink zostavte blokovú schému, pomocou rozkladu
M8 Model "Valcová a kužeľová nádrž v sérií bez interakcie" Úlohy: 1. Zostavte matematický popis modelu M8 2. Vytvorte simulačný model v prostredí: a) Simulink zostavte blokovú schému, pomocou rozkladu
Ján Buša Štefan Schrötter
 Ján Buša Štefan Schrötter 1 KOMPLEXNÉ ČÍSLA 1 1.1 Pojem komplexného čísla Väčšine z nás je známe, že druhá mocnina ľubovoľného reálneho čísla nemôže byť záporná (ináč povedané: pre každé x R je x 0). Ako
Ján Buša Štefan Schrötter 1 KOMPLEXNÉ ČÍSLA 1 1.1 Pojem komplexného čísla Väčšine z nás je známe, že druhá mocnina ľubovoľného reálneho čísla nemôže byť záporná (ináč povedané: pre každé x R je x 0). Ako
Goniometrické substitúcie
 Goniometrické substitúcie Marta Kossaczká S goniometrickými funkciami ste sa už určite stretli, pravdepodobne predovšetkým v geometrii. Ich použitie tam ale zďaleka nekončí. Nazačiatoksizhrňme,čoonichvieme.Funkciesínusakosínussadajúdefinovať
Goniometrické substitúcie Marta Kossaczká S goniometrickými funkciami ste sa už určite stretli, pravdepodobne predovšetkým v geometrii. Ich použitie tam ale zďaleka nekončí. Nazačiatoksizhrňme,čoonichvieme.Funkciesínusakosínussadajúdefinovať
Úvod. Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...
 Úvod Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...) Postup pri riešení problémov: 1. formulácia problému 2. formulácia
Úvod Na čo nám je numerická matematika? Poskytuje nástroje na matematické riešenie problémov reálneho sveta (fyzika, biológia, ekonómia,...) Postup pri riešení problémov: 1. formulácia problému 2. formulácia
Spriahnute oscilatory
 Spriahnute oscilatory Juraj Tekel 1 Tema spriahnutych oscilatorov je na strednej skole vacsinou vynechana. Je vsak velmi zaujimava a velmi dolezita. Ide o situaciu, ked sa sustava sklada z viacerych telies,
Spriahnute oscilatory Juraj Tekel 1 Tema spriahnutych oscilatorov je na strednej skole vacsinou vynechana. Je vsak velmi zaujimava a velmi dolezita. Ide o situaciu, ked sa sustava sklada z viacerych telies,
Zadania. 4 Do prázdneho pohára v tvare valca s polomerom R vložíme kocku ľadu so stranou a a s hustotou ρ i
 0. Fyzikálny Náboj, 017 Zadania Zadania 1 Dvaja malí uvrešťaní fyzici sa na pieskovisku chvastajú, čí veľký brat vie behať rýchlejšie. Po urputnej výmene názorov, podporenej údermi lopatkou a nervydrásajúcim
0. Fyzikálny Náboj, 017 Zadania Zadania 1 Dvaja malí uvrešťaní fyzici sa na pieskovisku chvastajú, čí veľký brat vie behať rýchlejšie. Po urputnej výmene názorov, podporenej údermi lopatkou a nervydrásajúcim
Poznámky k prednáškam z Termodynamiky z Fyziky 1.
 Poznámky k prednáškam z Termodynamiky z Fyziky 1. Peter Bokes, leto 2010 1 Termodynamika Doposial sme si budovali predstavu popisu látky pomocou mechanických stupňov vol nosti, ako boli súradnice hmotného
Poznámky k prednáškam z Termodynamiky z Fyziky 1. Peter Bokes, leto 2010 1 Termodynamika Doposial sme si budovali predstavu popisu látky pomocou mechanických stupňov vol nosti, ako boli súradnice hmotného
u R Pasívne prvky R, L, C v obvode striedavého prúdu Činný odpor R Napätie zdroja sa rovná úbytku napätia na činnom odpore.
 Pasívne prvky, L, C v obvode stredavého prúdu Čnný odpor u u prebeh prúdu a napäta fázorový dagram prúdu a napäta u u /2 /2 t Napäte zdroja sa rovná úbytku napäta na čnnom odpore. Prúd je vo fáze s napätím.
Pasívne prvky, L, C v obvode stredavého prúdu Čnný odpor u u prebeh prúdu a napäta fázorový dagram prúdu a napäta u u /2 /2 t Napäte zdroja sa rovná úbytku napäta na čnnom odpore. Prúd je vo fáze s napätím.
Matematická analýza pre fyzikov IV.
 119 Dodatok - klasické riešenia PDR 8.1. Parciálne diferenciálne rovnice Príklady parciálnych diferenciálnych rovníc: Lalpaceova rovnica u = 0 Helmholtzova rovnica u = λu n Lineárna transportná rovnica
119 Dodatok - klasické riešenia PDR 8.1. Parciálne diferenciálne rovnice Príklady parciálnych diferenciálnych rovníc: Lalpaceova rovnica u = 0 Helmholtzova rovnica u = λu n Lineárna transportná rovnica
DOMÁCE ZADANIE 1 - PRÍKLAD č. 2
 Mechanizmy s konštantným prevodom DOMÁCE ZADANIE - PRÍKLAD č. Príklad.: Na obrázku. je zobrazená schéma prevodového mechanizmu tvoreného čelnými a kužeľovými ozubenými kolesami. Určte prevod p a uhlovú
Mechanizmy s konštantným prevodom DOMÁCE ZADANIE - PRÍKLAD č. Príklad.: Na obrázku. je zobrazená schéma prevodového mechanizmu tvoreného čelnými a kužeľovými ozubenými kolesami. Určte prevod p a uhlovú
Úloha 3.7 Teleso hmotnosti 2 kg sa pohybuje pozdĺž osi x tak, že jeho dráha je vyjadrená rovnicou
 3 Dynamika Newtonove pohybové zákony Úloha 3.1 Teleso tvaru kvádra leží na horizontálnej doske stola. Na jeho prednej stene sú pripevnené dve lanká v strede steny. Lanká napneme tak, že prvé zviera s čelnou
3 Dynamika Newtonove pohybové zákony Úloha 3.1 Teleso tvaru kvádra leží na horizontálnej doske stola. Na jeho prednej stene sú pripevnené dve lanká v strede steny. Lanká napneme tak, že prvé zviera s čelnou
Metodicko pedagogické centrum. Národný projekt VZDELÁVANÍM PEDAGOGICKÝCH ZAMESTNANCOV K INKLÚZII MARGINALIZOVANÝCH RÓMSKYCH KOMUNÍT
 Moderné vzdelávanie pre vedomostnú spoločnosť / Projekt je spolufinancovaný zo zdrojov EÚ Kód ITMS: 26130130051 číslo zmluvy: OPV/24/2011 Metodicko pedagogické centrum Národný projekt VZDELÁVANÍM PEDAGOGICKÝCH
Moderné vzdelávanie pre vedomostnú spoločnosť / Projekt je spolufinancovaný zo zdrojov EÚ Kód ITMS: 26130130051 číslo zmluvy: OPV/24/2011 Metodicko pedagogické centrum Národný projekt VZDELÁVANÍM PEDAGOGICKÝCH
Elektrónová štruktúra atómov
 Verzia z 29. októbra 2015 Elektrónová štruktúra atómov Atóm vodíka a jednoelektrónové atómy Najjednoduchším atómom je atóm vodíka. Skladá sa z jadra (čo je len jediný protón) a jedného elektrónu. Atóm
Verzia z 29. októbra 2015 Elektrónová štruktúra atómov Atóm vodíka a jednoelektrónové atómy Najjednoduchším atómom je atóm vodíka. Skladá sa z jadra (čo je len jediný protón) a jedného elektrónu. Atóm
RIEŠENIA 3 ČASŤ
 RIEŠENIA 3 ČASŤ - 2009-10 1. PRÁCA RAKETY Raketa s hmotnosťou 1000 kg vystúpila do výšky 2000 m nad povrch Zeme. Vypočítajte prácu, ktorú vykonali raketové motory, keď predpokladáme pohyb rakety v homogénnom
RIEŠENIA 3 ČASŤ - 2009-10 1. PRÁCA RAKETY Raketa s hmotnosťou 1000 kg vystúpila do výšky 2000 m nad povrch Zeme. Vypočítajte prácu, ktorú vykonali raketové motory, keď predpokladáme pohyb rakety v homogénnom
Návrh vzduchotesnosti pre detaily napojení
 Výpočet lineárneho stratového súčiniteľa tepelného mosta vzťahujúceho sa k vonkajším rozmerom: Ψ e podľa STN EN ISO 10211 Návrh vzduchotesnosti pre detaily napojení Objednávateľ: Ing. Natália Voltmannová
Výpočet lineárneho stratového súčiniteľa tepelného mosta vzťahujúceho sa k vonkajším rozmerom: Ψ e podľa STN EN ISO 10211 Návrh vzduchotesnosti pre detaily napojení Objednávateľ: Ing. Natália Voltmannová
Budený oscilátor s tlmením
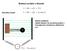 Budený oscilátor s tlmením Špeciálny prípad Možná realizácia: Nabité teliesko na nevodivej pružine v homogénnom striedavom elektrickom poli Budený oscilátor s tlmením Použijeme trik s komplexnými fázormi
Budený oscilátor s tlmením Špeciálny prípad Možná realizácia: Nabité teliesko na nevodivej pružine v homogénnom striedavom elektrickom poli Budený oscilátor s tlmením Použijeme trik s komplexnými fázormi
Hydromechanika II. Viskózna kvapalina Povrchové napätie Kapilárne javy. Doplnkové materiály k prednáškam z Fyziky I pre EF Dušan PUDIŠ (2013)
 Hyomechanika II Viskózna kvaaina Povchové naäie Kaiáne javy Donkové maeiáy k enáškam z yziky I e E Dušan PUDIŠ (013 Lamináne vs. Tubuenné úenie Pi úení eánej kvaainy ôsobia mezi voma susenými vsvami i
Hyomechanika II Viskózna kvaaina Povchové naäie Kaiáne javy Donkové maeiáy k enáškam z yziky I e E Dušan PUDIŠ (013 Lamináne vs. Tubuenné úenie Pi úení eánej kvaainy ôsobia mezi voma susenými vsvami i
Kmitavý pohyb telesa zaveseného na pružine (Aktivity súvisiace s kmitaním uskutočnené pomocou programu Coach 6) Michal Kriško FMFI UK
 Názov projektu: CIV Centrum Internetového vzdelávania FMFI Číslo projektu: SOP ĽZ 2005/1-046 ITMS: 11230100112 Kmitavý pohyb telesa zaveseného na pružine (Aktivity súvisiace s kmitaním uskutočnené pomocou
Názov projektu: CIV Centrum Internetového vzdelávania FMFI Číslo projektu: SOP ĽZ 2005/1-046 ITMS: 11230100112 Kmitavý pohyb telesa zaveseného na pružine (Aktivity súvisiace s kmitaním uskutočnené pomocou
4. JEDNODUCHÉ KVANTOVO-MECHANICKÉ SYSTÉMY - FYZIKÁLNY PRÍSTUP
 4. JEDNODUCHÉ KVANTOVO-MECHANICKÉ SYSTÉMY - FYZIKÁLNY PRÍSTUP Samozdružený operátor  sa dá napísať pomocou jeho vlastných čísiel a j a jeho vlastných stavov a j ako  = a j a j a j, (4.1) j kde súčet
4. JEDNODUCHÉ KVANTOVO-MECHANICKÉ SYSTÉMY - FYZIKÁLNY PRÍSTUP Samozdružený operátor  sa dá napísať pomocou jeho vlastných čísiel a j a jeho vlastných stavov a j ako  = a j a j a j, (4.1) j kde súčet
Bubliny, kvapky a krivosti
 Bubliny, kvapky a krivosti Marián Fecko KTF&DF, FMFI UK, Bratislava Text prednesený na Akadémii Trojstenu dňa 9.12.2011 1 Rozhranie medzi kvapalinou a vzduchom sa správa tak, akoby to bola pružná blanka.
Bubliny, kvapky a krivosti Marián Fecko KTF&DF, FMFI UK, Bratislava Text prednesený na Akadémii Trojstenu dňa 9.12.2011 1 Rozhranie medzi kvapalinou a vzduchom sa správa tak, akoby to bola pružná blanka.
Deliteľnosť a znaky deliteľnosti
 Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
Deliteľnosť a znaky deliteľnosti Medzi základné pojmy v aritmetike celých čísel patrí aj pojem deliteľnosť. Najprv si povieme, čo znamená, že celé číslo a delí celé číslo b a ako to zapisujeme. Nech a
Obsah. 1.1 Reálne čísla a ich základné vlastnosti... 7 1.1.1 Komplexné čísla... 8
 Obsah 1 Číselné obory 7 1.1 Reálne čísla a ich základné vlastnosti............................ 7 1.1.1 Komplexné čísla................................... 8 1.2 Číselné množiny.......................................
Obsah 1 Číselné obory 7 1.1 Reálne čísla a ich základné vlastnosti............................ 7 1.1.1 Komplexné čísla................................... 8 1.2 Číselné množiny.......................................
DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c)
 Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach Božena Mihalíková, Ivan Mojsej Strana 1 z 43 DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c) 1 Obyčajné diferenciálne rovnice 3 1.1 Úlohy
Prírodovedecká fakulta Univerzity P. J. Šafárika v Košiciach Božena Mihalíková, Ivan Mojsej Strana 1 z 43 DIFERENCÁLNE ROVNICE Matematická analýza (MAN 2c) 1 Obyčajné diferenciálne rovnice 3 1.1 Úlohy
9 Mechanika kvapalín. 9.1 Tlak v kvapalinách a plynoch
 137 9 Mechanika kvapalín V predchádzajúcich kapitolách sme sa zaoberali mechanikou pevných telies, telies pevného skupenstva. V nasledujúcich kapitolách sa budeme zaoberať mechanikou kvapalín a plynov.
137 9 Mechanika kvapalín V predchádzajúcich kapitolách sme sa zaoberali mechanikou pevných telies, telies pevného skupenstva. V nasledujúcich kapitolách sa budeme zaoberať mechanikou kvapalín a plynov.
FYZIKA DUSˇAN OLCˇA K - ZUZANA GIBOVA - OL GA FRICˇOVA Aprı l 2006
 FYZIKA DUŠAN OLČÁK - ZUZANA GIBOVÁ - OL GA FRIČOVÁ Apríl 2006 2 Obsah 1 o-g-f:mechanický pohyb tuhého telesa 5 1.1 Kinematika hmotného bodu......................... 6 1.1.1 Rýchlost a zrýchlenie pohybu....................
FYZIKA DUŠAN OLČÁK - ZUZANA GIBOVÁ - OL GA FRIČOVÁ Apríl 2006 2 Obsah 1 o-g-f:mechanický pohyb tuhého telesa 5 1.1 Kinematika hmotného bodu......................... 6 1.1.1 Rýchlost a zrýchlenie pohybu....................
Rozsah hodnotenia a spôsob výpočtu energetickej účinnosti rozvodu tepla
 Rozsah hodnotenia a spôsob výpočtu energetickej účinnosti príloha č. 7 k vyhláške č. 428/2010 Názov prevádzkovateľa verejného : Spravbytkomfort a.s. Prešov Adresa: IČO: Volgogradská 88, 080 01 Prešov 31718523
Rozsah hodnotenia a spôsob výpočtu energetickej účinnosti príloha č. 7 k vyhláške č. 428/2010 Názov prevádzkovateľa verejného : Spravbytkomfort a.s. Prešov Adresa: IČO: Volgogradská 88, 080 01 Prešov 31718523
Integrovanie racionálnych funkcií
 Integrovanie racionálnych funkcií Tomáš Madaras 2009-20 Z teórie funkcií už vieme, že každá racionálna funkcia (t.j. podiel dvoch polynomických funkcií) sa dá zapísať ako súčet polynomickej funkcie a funkcie
Integrovanie racionálnych funkcií Tomáš Madaras 2009-20 Z teórie funkcií už vieme, že každá racionálna funkcia (t.j. podiel dvoch polynomických funkcií) sa dá zapísať ako súčet polynomickej funkcie a funkcie
