MAGNETNI KOMPAS PTIC. Kazalo 1. Uvod Kaj so eksperimentalna dejstva in kakšna je teorija
|
|
|
- Πολυξένη Κωνσταντόπουλος
- 7 χρόνια πριν
- Προβολές:
Transcript
1 MAGNETNI KOMPAS PTIC BENJAMIN BATISTIĆ 23 NOVEMBER 2009 Kazalo 1. Uvod 1 2. Kaj so eksperimentalna dejstva in kakšna je teorija Zemeljsko magnetno polje Funkcionalne lastnosti magnetnega kompasa ptic Različne teorije delovanja magnetnega kompasa 3 3. Mehanizem para radikalov (RPM) Numerični eksperiment Magnetni kompas ptic je vezan na vid 7 4. RPM, od hipoteze do realnosti 8 5. Zaključek Osebno videnje problema 9 Literatura Uvod Osnovno vprašanje je, kako ptice selivke vedo kam leteti v času preseljevanja? Na hitro bi pomislili, da se morda naučijo prepoznavati okoljske znake, na primer, topografske značilnosti, zvezdna slika, dinamika sonca, skratka, takšno ali drugačno vrednotenje vidnega v skladu z neko izkušnjo. Človek si je sestavil kompas, ultimativno orientacijsko napravo, ki izkorišča prisotnost statičnega zemljinega magnetnega polja. Magnetni materiali čutijo v prisotosti zunanjega magnetnega polja navor, ki skuša zavrteti magnete tako, da so silnice obeh polj, zunanjega in tistega znotraj magneta, poravnane. Ptice vsekakor ne premorejo dobesedno iste mehanične naprave, lahko pa bi izkoriščale osnovno idejo in se orientirale na osnovi magnetnega polja. Slika magnetnega polja je zelo surova in izčiščena informacija, dovolj interpretacijsko enolična, da bi jo lahko evolucija preferirala in razvila učinkovit bio-detektor. Uporaba magnetnega kompasa pri pticah je dejansko dokazana, najprej za Erithacus rubeculo (Taščica) [1] in kasneje še za 17 ptic [2]. Naravno sledi naslednje vprašanje. Kaj je biofizikalni mehanizem za zaznavo magnetnih polj? Odgovora v resnici ne poznamo. 2. Kaj so eksperimentalna dejstva in kakšna je teorija 2.1. Zemeljsko magnetno polje. Geomagnetno polje je dipolno polje, katerega poli ležijo zelo blizu zemljinih geografskih polov, definiranih z osjo vrtenja. Silnice polja kažejo iz tal na antarktičnem polu in poniknejo v tla na arktičnem polu, 1
2 2 BENJAMIN BATISTIĆ 23 NOVEMBER 2009 Slika 1. Shematični prikaz zemljinega magnetnega polja. Vir: [2] vektor magnetnega polja je vzporeden zemljini površini skoraj natanko na polovici med poloma, na ekvatorju. Nagib (inklinacija) magnetnega polja je definiran s kotom, ki ga vektor magnetnega polja oklepa s horizontom, in je vzdolž vzporednika približno konstanten. Gostota magnetnega polja postopoma upada v smeri od pola (0.6 G) proti magnetnemu ekvatorju (0.3 G), približno simetrično na obeh hemisferah. Treba se je zavedati, da je zemeljsko magnetno polje precej šibko; tipična energija molekularnih dipolov v polju takšne gostote je za več kot 6 velikostnih redov manjša od tipične termodinamske fluktuacije k B T. Magnetno polje, v kolikor ga uspemo zaznavati, je precej zanesljiv vir informacij; tako nagib, kot tudi absolutna velikost polja, so dovolj, da lahko povemo kje, oziroma kako daleč ali kako blizu magnetnega pola ali ekvatorja smo Funkcionalne lastnosti magnetnega kompasa ptic. V pionirskih eksperimentih [2], sta par Wiltschko eksperimentalno demonstrirala principe in režime delovanja magnetnega kompasa pri pticah: Ptice za orientacijo uporabljajo informacijo o nagibu magnetnega polja, a ne zaznajo njegove smeri [2]. Tako doživljajo magnetno polje na južni oziroma severni hemisferi enako. Dodaten mehanizem, ali znanje, je potrebno pri pticah, ki prečkajo ekvator, da se na to prečkanje pravilno odzovejo. Izkaže se, da je magnetni kompas ptic ozko kalibriran na ambientalno magnetno polje in deluje le v ozkem magnetnem oknu. Na primer; taščice, ki so bivale v ambientalnem polju velikosti 0.46 G so bile popolnoma disorientirane za polja manjša od 0.34 G in podobno za polja večja od 0.6 G. Takšno vedenje bi bilo precej neznačilno, če bi ptice uporabljale mehanični kompas, kot si ga je omislil človek. Orientacijske sposobnosti ptic so močno odvisne od valovne dolžine ambientalne svetlobe ([6] in reference znotraj [5]). Izkaže se, da mora biti energija svetlobe dovolj velika, če želimo, da kompas deluje. Zanimiva so opažanja
3 MAGNETNI KOMPAS PTIC 3 Slika 2. Magnetni kompas ptic je inklinacijski (orientacija je vezana na nagib magnetnega polja). Ptice iz južne in severne poloble se selijo na osnovi istega mehanizma; ne razločijo polaritete magnetnega polja. Vir [2] [3], da taščice ne zmorejo orientacije v rumeno-oranžni svetlobi (z maksimumom pri 590 nm), čeprav se spekter krepko prekriva z zeleno svetlobo (širina nm), kjer je bila orientacija odlična, in rumeno svetlobo (širina nm), kjer orientacije ni bilo. Pri eksperimentih z golobi [7] so opazili, da se določeni predeli možganov, ki pripadajo optičnemu sistemu (nbor in tectum opticum) odzivajo na spremembe ambientalnega magnetnega polja, kar se izkaže pogojeno s prisotnostjo vidne svetlobe in zdravo (nepoškodovano) mrežnico (reference znotraj [5]). Zanimiv eksperiment, ki pravtako potrjuje domnevo, da je magnetni kompas ptic vezan na vidni sistem, pokaže, da je magnetna orientacija ptic lateralizirana [9] (bolj razvita v eni od možganskih polovic). Eksperiment so izvedli tako, da so pticam pokrili eno od očes in merili sposobnost orientacije. S pokritim levim očeom so se testne ptice orinetirale odlično, s pokritim desnim očesom pa sploh ne Različne teorije delovanja magnetnega kompasa. Med različnimi teoretičnimi modeli zaznavanja magnetnega polja, ki so bili predlagani, sta zaživela le dva. V prvem naj bi receptorji izrabljali mehanične lastnosti magnetnih delcev (mineral magnetit), v drugem pa naj bi fotoreceptorski mehanizem, odvisen od magnetnega polja, neposredno vplival na očesno transdukcijo (proces pri katerem senzorni receptor pretvori stimulus iz okolja v akcijski potencial, ki se prenese v možgane). Magnetoreceptor na magnetitni bazi v različnih modelih vsebuje ali prosto vrteče eno-domenske magnetitne delce ali fiksirane super-paramagnetne magnetitne delce ali pa tekoči kristal, ki vsebuje magnetitne delce (vse relevantne reference v [5]). V magnetnih poljih, podobno šibkih kot je zemeljsko, lahko superparamagnetni kristali generirajo dovolj velika magnetna polja, ki zaznavno vplivajo na dinamiko bližnjih kristalov. Interakcija med kristali lahko deformira celotno tkivo v katerega so ti kristali vpeti. Pravtako lahko medsebojno interagirajo celotne gruče kristalov, kar lahko privede do merljivih makroskopskih deformacij (pomembne reference znotraj [8]). V mehanizmih, ki delujejo na osnovi mehanike magnetitnih delcev, je zaenkrat težko prepoznati procese, ki bi pojasnili vse funkcionalne
4 4 BENJAMIN BATISTIĆ 23 NOVEMBER 2009 Slika 3. Magnetno odvisna reakcijska shema para radikalov. Tri faze: nastanek para, oscilacije S T in rekombinacija. Vir [5] lastnosti magnetnega kompasa ptic, kot so navedene v prejšnjem podpoglavju. Kakorkoli, narejenih je mnogo eksperimentov, ki kažejo, da ta mehanizem pojasni navigacijsko sposobnost živali kot so raki, ribe, želve,... Iz množice mehanizmov, ki delujejo na osnovi foto-stimulirane magnetorecepcije izpostavimo le najbolj popularnega, to je mehanizem radikalnih parov. Razlog za njegovo preferenco je v prvi vrsti vgrajena foto-občutljivost, ki je konsistentna z eksperimentalnimi opažanji in drugo, kar ga izpostavlja iz množice sorodnih kandidatov je, da lahko v specifičnih pogojih deluje v režimu dovolj majhnega magnetnega polja. 3. Mehanizem para radikalov (RPM) Osnovna ideja [4] mehanizma para radikalov (Radical Pair Mechanism, RPM), pojasni zaznavo šibkih magnetnih polj, na osnovi zaznave magnetno odvisne makroskopske populacije produktov, ki nastanejo v reakcijah pri katerih sodelujejo pari radikalov. Mehanizem sam ne razlaga kako se neko makro-kemično stanje substrata prevede v uporabni signal (transdukcija), ki ga lahko obdelujejo možgani, pač pa se osredotoča zgolj na dejstvo, da je lahko stanje substrata zelo občutljivo na prisotnost magnetnega polja. Najpreprostejša reakcija, v kateri sodelujejo pari radikalov bi bila preprosta rekombinacija elektronov, toda to samo po sebi ni bistveno, bistveno je, da se produkti diferencirajo glede na to, v kakšnem stanju, tripletnem ali singletnem, je bil radikalni par v trenutku reakcije. Reakcijska shema poteka preko treh korakov. 1) Natanek para. V prvem koraku vzbujena donorska molekula D prenese elektron na akceptorsko molekulo A, kar povzroči nastanek para radikalov D + +A. Da bi lahko opazovali efekte magnetnega polja, je pomembno, da par radikalov nastane v spinsko-koreliranem singletnem ali tripletnem stanju. Spinsko koreliran par radikalov lahko nastane, na primer, z fotoinduciranim prenosom elektrona. V takšnem primeru, se prenos sproži zaradi eksitacije donorja pri absorbciji fotona. Pred absorbcijo fotona bosta donor in akceptor skoraj zagotovo v singletnem stanju, torej bo singletno tudi vzbujeno stanje. Ker prenos elektona ne spremeni korelacije med spini, bo radikalni par pravtako v singletnem stanju. 2) Oscilacije singlet-triplet. Singletno stanje para radikalov ni lastno stanje skupnega Hamiltoniana, ki v tej sliki vključuje še hiperfino sklopitev s spinom jedra, zato sistem oscilira med singletnim in tripletnim stanjem. Moramo si predstavljati, da zaradi majhne razlike v hiperfini sklopitvi obeh radikalov, elektrona precedirata z
5 MAGNETNI KOMPAS PTIC 5 Slika 4. Delež tripletnih stanj p T (t) v odsotnosti zunanjega magnetnega polja, brez rekombinacije (zeleno) in z rekombinacijo (rdeče): A) brez zunanjega magnetnega polja B) v prisotnosti majhnega zunanjega magnetnega polja, kjer se pojavi majna modulacija s frekvenco Zeeemanove sklopitve, ki spremeni tripletni donos (modro). Vir [12] različnima frekvencama, kar privede do oscilacij skupnega spina. V tej sliki zanemarimo druge sklopitve in privzamemo, da so relaksacijski časi (časi potrebni za rekombinacijo), daljši od periode oscilacij med tripletnim in singletnim stanjem. 3) Reakcija. Končno, singletni in tripletni pari reagirajo in rezultirajo v različnih produktih, kar zmanjšuje populacijo radikalnih parov z ustreznimi hitrostmi k S in k T. Za izračun donosa produktov iz reakcije radikalnih parov v tripletnem stanju, privzamemo, da je radikalni par geometrično fiksiran v substratu in da je njegovo začetno stanje singletno. Tripletni donos Φ T je definiran kot količina produktov, ki prehaja preko tripletnega reakcijskega kanala, (1) Φ T = 0 k T T (t)dt, kjer je T (t) delež parov radikalov v tripletnem stanju v poljubnem času t in k T reakcijska konstanta, ki določa hitrost reakcij. T (t) lahko dobimo, če poznamo dinamiko statističnega operatorja ρ(t), (2) T (t) = Tr[Q T ρ(t)],
6 6 BENJAMIN BATISTIĆ 23 NOVEMBER 2009 kjer Tr A = i A ii, in Q T je projektor na tripletna stanja. operatorja zadošča stohastični Liouvillovi enačbi, Časovni razvoj statističnega (3) ρ = i [H, ρ] k S 2 [QS, ρ] + k S 2 [QT, ρ] +. Tukaj [A, B] = AB ± BA, Q S je projektor na singletna stanja, in H je spinski Hamiltonski operator. Začetni pogoj za statistični operator je ρ(0) = Q S /Tr Q S, ker je, po predpostavki, par radikalov ob nastanku v singletnem stanju. Zadnja dva člena v enačbi 3 opisujeta disipacijo radikalnih parov preko singletnega in tripletnega reakcijskega kanala, medtem ko prvi člen opisuje oscilacije med tripletnimi in singletnimi stanji. V modelu brez izgube splošnosti predpostavimo, da sta reakcijski hitrosti k S in k T od spina neodvisni, k S = k T = k, kar dopušča, da pišemo, (4) ρ(t) = 1 N e iht/ Q S e iht/ e kt. Tukaj je N število jedrskih spinskih stanj. Če vstavimo enačbo 4 v enačbo 2 dobimo, (5) T (t) = e kt N 4N 4N m=1 m=1 Q T mnq S mn cos [(ω m ω n )t], kjer ω i predstavlja energijo i-tega lastnega stanja Hamiltonjana H. Ko izračunamo še integral v enačbi 1 dobimo celoten tripletni donos, (6) φ T = 1 N 4N m=1 m=1 4N Q T mnq S mn k 2 k 2 + (ω m ω n ) 2. Pri dovolj šibkih magnetnih poljih Zeemanov effekt povzroči razcep sicer degeneriranih spinskih stanj in posledično oscilacije med tripletnim in singletnim stanjem. Oscilacije lahko povečajo tripletni donos Φ T, slika 4. Drugače je, če je magnetno polje preveliko, primerljivo z velikostjo hiperfine sklopitve. V tem primeru se singletna in tripletna stanja razcepijo preveč, kar privede do upada tripletnega donosa. Zanimiva fizika je torej v režimu šibkih polj (majhnih v primerjavi s hiperfino sklopitvijo), kjer je tripletni donos Φ T odvisen ne samo od jakosti magnetnega polja pač pa tudi od hitrosti reakcij k Numerični eksperiment. V članku [5], predstavi raziskovalna skupina zelo preprosto realizacijo modela parov radikalov. Za par radikalov j, j = 1, 2, kjer vsakemu pripada spin elektona S j in spin jedra I j z veliostjo 1/2, sestavijo Hamiltonian, (7) H(B) = H 1 (B) + H 2 (B), kjer, (8) H j (B) = γs (B + A j I j ). Tukaj je standardno γ = gµ B, kjer g=2 in µ B je Bohrov magneton. A j predstavlja tenzor hiperfine sklopitve, in je anizotropen. Anizotropnost tenzorja A omogoča odvisnost tripletnega donosa od rotacije magnetnega polja glede na glavne osi tenzorja. S tem postane takšen model operativen v smislu orientacije glede na
7 MAGNETNI KOMPAS PTIC 7 Slika 5. Odvisnost tripletnega donosa Φ T od hitrosti rekombinacije parov radikalov k in gostote zunanjega magnetnega polja B, ki tvori z z-osjo para radikalov kot 68 (prva slika), in odvisnost tripletnega donosa od gostote magnetnega polja ter kota magnetnega polja glede na z-os (druga slika). Vir [5] magnetno polje, kot ga opažamo pri pticah selivkah. V konkretnem eksperimentu konstruirajo anizotropnost z naslednjo izbiro tenzorjev, 10G 0 0 (9) A 1 = 0 10G in (10) A 2 = 5G G G Anizotropen je le tenzor A 1 in glavne osi obeh tenzorjev sovpadajo. Kljub preprostosti modela so dobljeni rezultati dovolj bogati. Kot lahko vidimo na sliki 5, lahko zelo majhno magnetno polje, manjše od 0.5G, povzroči znaten porast tripletnega donosa, ki je tem bolj izrazit čim manjša je hitrost rekombinacije k. Za večja magnetna polja opazimo upad tripletnega donosa. Morda bolj pomembno je, da se model odziva na variacije naklona magnetnega polja glede na os para radikalov, o čemer se lahko prepričamo na isti sliki 5. Kotna odvisnost tripletnega donosa je prikazana zgolj na intervalu [0, 90 ], zaradi simetrije na inverzijo smeri magnetnega polja in zrcaljena preko z-osi Magnetni kompas ptic je vezan na vid. Spoznali smo, da bi lahko ptice zaznavale obliko lokalne magnetne slike izkoriščajoč mehanizem para radikalov, vendar je nujno, da je molekularni sistem v katerem se mehanizem izvaja, orientacijsko fiksiran. Tega ne moremo pričakovati, če je reagent v tekoči fazi, kjer nenehno prerivanje med molekulami hitro izpovpreči vse anizotropne efekte. Radikali morajo biti vsaj delno imobilizirani in orientirani. V članku [5] predlagajo, da so celice, ki so odgovorne za zaznavo magnetnega polja porazdeljene po očesni mrežnici in poravnane s čepki in paličicami (fotoreceptorske celice). Prav tako, naj bi bile molekule, ki tvorijo ustrezne pare radikalov, orintacijsko fiksirane znotraj celice. Torej bodo celice na različnih mestih na mrežnici videle magneto polje pod različnimi koti in se posledično različno odzivale, pač v skladu z anizotropno naravo interakcije parov radikalov z magnetnim poljem..
8 8 BENJAMIN BATISTIĆ 23 NOVEMBER RPM, od hipoteze do realnosti Ali lahko uporabimo neko kemično reakcijo za ugotavljanje smeri magnetnega polja zemlje? Na prvi pogled bi bila večina poznavalcev skeptičnih. Interakcijska energija tipične molekule z zemeljskim magnetnim poljem velikosti 0.5 G je za več kot šest velikostnih redov manjša od termične energije tipične molekule, ki pa je dodatno še krat manjša od tipičnih vezavnih energij. Težko bi verjeli, da je kakšno kemično ravnovesno stanje sistema zaznavno odvisno od tako minorne perturbacije, kot je zemeljsko magnetno polje. Toda, kljub pomislekom smo se prepričali, kako smiseln je mehanizem parov radikalov z ozirom na vsa eksperimentalna dejstva. Raziskovalci s tega področja se zadnje čase precej trudijo definirati okvirje znotraj katerih naj bi se gibali specifični parametri molekule, ki bi ustrezale sistemu v katerem poteka RPM. Popularen potencialni kandidat v procesu RPM je molekula (protein) Cryptochroma, za katero je znano, da tvori stabilne radikalne pare, ki nastajajo pri absorbciji zeleno-modre svetlobe, v skladu z opažanji pri pticah in je hkrati dokazano prisotna v mrežnici (taščice) [10, 11]. Toda, ni še jasno pokazano, da se Cryptohroma ustrezno odziva v pogojih v katerih se orinetirajo ptiči (dovolj šibka magnetna polja). Poleg eksperimentalnih ocen imamo na voljo tudi teoretične ocene tipičnih parametrov na osnovi preprostih modelov (kot je omenjen v prejšnjem poglavju): Ustrezna molekula v RPM naj bi bila preprosta, sestavljena le iz nekaj molekul vodika in dušika, sicer bi kompleksne notranje sklopitve zasenčile prisotnost zemeljskega magnetnega polja. Eksperimenti kažejo, da se velikost hiper-fine sklopitve z jedri 1 H in 14 N, giblje na intervalu 1 G 0.1 G, kar da za oceno periode oscilacij med singletnim in tripletnim stanjem približno 10 ns. Dodatna občutljivost na magnetno polje je posledica Zeemanove interakcije magnetnih momentov dveh elektronov, ki prispeva še dodatno oscilacijo med singletnimi in tripletnimi stanji, ki ustreza periodi 700 ns v magnetnem polju velikosti 5 G [12]. Zahtevati moramo, da je življenjski čas (čas potreben za rekombinacijo) dosti daljši od periode oscilacij med tripletnim in singletnim stanjem. Temu pogoju zadostimo, če par radikalov vztraja v spinsko koreliranem stanju več kot 1 µs. V tem primeru mora biti k velikostnega reda 10 6 s 1. k T in k S naj bosta istega velikostnega reda, zato da bosta singletni in tripletni reakcijski kanal enakovredna. Račun pokaže [12, 13], da je relativna sprememba tripletnega donosa zaradi dodatnega magnetnega polja sigmoidno odvisna od življenjskega časa 1/k in postane neodvisna (saturira) od življenjskih časov daljših od 1 µs za magnetna polja velikosti 5 G. Zaradi tega si lahko mislimo, da bi daljši življenjski časi para radikalov morda predstavljali neučinkovitost, oziroma slabšo odzivnost. Aproksimativna teorija [12] nam da oceno razmika robov (tukaj si zamislimo rob orbitale), r e, dveh radikalov. Za življenjske čase, ki smo jih ocenili na 1 µs, mora biti ta razdalja manjša od 1.5 nm. Po drugi strani, pa iz zahteve, da je interakcija med radikali vsaj enakega velikostnega reda kot interakcija z zunanjim magnetnim poljem, če ne manjša, da za spodnjo mejo razmika med centri radikalov r c > 3.5 nm. Kar je preveč in nekonsistentno z oceno za r e. Teorija predpostavlja, da se lahko na določeni razdalji 0.2 nm < r c izničita izmenjalna in dipolna interakcija, kar bi pomenilo, da je premer radikala približno 0.5 nm.
9 MAGNETNI KOMPAS PTIC 9 Ker je magnetno polje šibko, so posledice polja verjetno zaznavne šele, ko se seštejejo prispevki na večjem volumnu. Izračuni dajo oceno, da je potrebno 10 8 parov radikalov na volumnu 0.4 mm 3, da bi lahko zanesljivo zaznavali anomalije velikostnega reda 2% zemeljskega magnetnega polja [8]. Precej živahno je preučevanje magnetorecepcije v povezavi z orientacijo ptic v prisotnosti oscilirajočega magnetnega polja in kvantne kontrole [14, 15, 16]. V eksperimentu [14], so bile ptice izpostavljene različnim frekvencam magnetnega polja (0.05 G in 26 glede na zemeljsko magnetno polje velikosti 0.47 G) na intervalu od 0.01 Mhz do 7 Mhz. Do frekvence 0.1 Mhz so se ptice orientirale normalno, na intervalu 0.1 Mhz 0.5 Mhz pa so kazale aksialno motnjo orientacije. To pomeni, da so se orientirale ali v pravo, ali v nasprotno smer z dobro definirano osjo. Aksialna motnja naj bi bila značilna za mejni režim delovanja magnetnega kompasa ptic. Nizko-frekvenčna polja, katerih perioda je dosti daljša od življenjskega časa para radikalov, lahko obravnavamo kot statična. Smiselno bi bilo pričakovati, da se prisotnost oscilirajočega polja izrazi pri frekvencah, ki sovpadajo z življenjskim časom para radikalov, kar da za oceno spodnje meje življenjskega časa > 0.2 µs. Da bi nadalje razumeli lastnosti para radikalov so poskusili, če se ptice na katero frekvenco, ki bi bila povezana z Zeemanovo interakcijo, odzivajo še posebej izrazito. Magnetni moment v prisotnosti zunanjega magnetnega polja B 0 prične precedirati okoli smeri polja z Larmorjevo frekvenco, ki je za elektronski spin enaka ν L = γ e B 0 /2π. Ptice so adaptirali na ambientalna polja, ki ustrezajo Larmorjevi frekvenci Mhz 0.42 G in 2.63 Mhz 0.42 G, ter spremljali kako so vrednosti velikosti magnentega polja pri katerih magnetni kompas odpove odvisne od frekvence. Izkaže se, zelo signifikantno, da relativnno šibko magnetno polje prave (Larmorjeve) frekvence zadošča za disorientacijo ptic, Slika 6. To resonančno vedenje pri frekvencah, ki ustrezajo Zeemanovi sklopitvi, pojasnjujejo z radikalnim parom, kjer eden od elektronov ne čuti hiperfine sklopitve z jedrom [12]. Kar moramo pričakovati na osnovi eksperimentov z oscilirajočim poljem, je presenetljiva stabilnost kvantne prepletenosti dveh ločenih radikalov. Na osnovi modeliranja ustrezne Lindbladove verzije časovnega razvoja statističnega operatorja (Master equation) se skuša kvantificirati robustnost na različne motnje zaradi sklopitve para radikalov z okolico [15] in posledice kvantne kontrole [16] na delovanje mehanizma para radikalov in s tem povezana možnost uporabe različnih tehnik kvantne kontrole za nadaljne raziskave na tem področju. 5. Zaključek Seznanili smo se s problematiko orientacije ptic na osnovi magnetnega polja. Vemo, da je magnetni kompas ptic inklinacijski, kar pomeni, da ptice zaznavajo nagib magnetnega polja ne pa tudi polaritete. Videli smo kako je delovanje kompasa pogojeno s prisotnostjo ustrezne svetlobe in kako bi lahko ta kompas našel svoj prostor v očesu. Podrobneje smo si ogledali model para radikalov, ki razlaga delovanje kompasa na osnovi foto-senzibilnih kemičnih procesov, nismo pa pozabili omeniti alternativ, ki delovanje kompasa razlagajo analogno s človeškim izdelkom - mehanično, s prisotnostjo magnetnih delcev. Na koncu smo kritično ovrednotili RPM in postavili okvirje katerim mora zadoščati realizacija takšnega mehanizma Osebno videnje problema. Kljub temu, da smo se osredotočili na mehanizem para radikalov na osnovi mnogih funkcionalnih lastnosti kompasa ptic, ki bi
10 10 BENJAMIN BATISTIĆ 23 NOVEMBER 2009 Slika 6. Orientacijske sposobnosti taščic v prisotnosti oscilirajočega magnetnega polja (puščice na robu kažejo porazdelitev po smeri, puščica na sredini ustreza povprečni smeri, dolžina le-te pa statistični signifikanci). (Levo) Odziv v lokalnem geomagnetnem polju. (Desno) Odziv v dvakrat večjem polju po treh urah adaptacije na spremenjene pogoje. (Zgornja diagrama) Orientacija brez prisotnosti oscilirajočega polja. (Spodnji diagrami) Ustrezajo odzivom v prisotnosti oscilirajočega polja različne jakosti. Vidimo, da so v prvem primeru (Levo) ptice pri Larmorjevi frekvenci Mhz disorientirane že pri zelo šibkem polju G, medtem ko se pri polovični in dvakratni Larmorjevi frekvenci orientirajo odlično še pri 10-krat močnejšem polju. Podobno opazimo tudi na diagramih, ki ustrezajo statičnemu magnetnemu polju velikosti 0.92 G. Vir [14] jih sicer težko pojasnili, ne bi izključeval alternativne teorije. Očitno RPM deluje dobro in pojasnjuje vse, v principu. Težava je v realizaciji, ki nikakor ne zadosti pogoju operativnosti v tako šibkih poljih kot je zemeljsko (razen v kakšnih pogojih, nezdružljivih z življenjem). Se pravi; bilo bi marsikaj boljše, če bi lahko magnetno polje, ki vpliva na kemične procese pri RPM nekako ojačali. To bi lahko dosegli, če bi družno z molekulami, ki so funkcionalne v RPM, sobivala kakšna skladno urejena super-paramagnetna struktura, ki bi ojačala lokalno magnetno polje, ampak katere mehanska odzivnost bi bila za magnetorecepcijo nebistvena. To bi predstavljalo nekakšno sintezo obeh principov.
11 MAGNETNI KOMPAS PTIC 11 Literatura 1. Wiltschko W, Merkel F, Verh. dt. zool. Ges., 59, (1966) 2. Wiltschko W, Wiltscho R, J. Exp. Biol., 199, (1969) 3. Wiltschko W, Wiltschko R, Erithacus rubecula. J. Comp. Physiol. A., 184, (1999) 4. Schulten K, Festkörperprobleme 22, (1982) 5. Ritz T, Adem S, Schulten K, Biophys J, 78, (2000) 6. Wiltschko W, Wiltschko R,. J. Exp. Biol, 204, (2001) 7. Semm P, Beason R C, Brain Res. Bull., 25, (1990) 8. Johnsen S, Lohmann K J,Nature Rev. Neuro., 6, (2005) 9. Wiltschko W, Traudt T, Gunturkun O, Prior H, Wiltschko R, Nature, 419, (2002) 10. Möller A, Segasser S, Wiltschko W, Schierwater B, Naturwissenschaften, 91, (2004) 11. Mouritsen H, Jenssen-B U, Liedvogel M, Feenders G, Stalleicken J, Dirks P, Weiler R, PNAS, 101, no.39, (2004) 12. Rodgers C T, Hore P J, PNAS, 106, no.2, (2009) 13. Timmel C R, Till U, Brocklehurst B, McLauchlan K A, Hore P J, Mol Phys, 95, (1998) 14. Thorsten R, Wiltschko R, Hore P J, Rodgers C T, Stapput K, Thalau P, Timmel C R, Wiltschko W, Biophys. J., 96, (2009) 15. Gauger E, Rieper E, Morton J J L, Benjamin S C, Vedral V, arxiv: v3 (2009) 16. Cai J, Guerreschi G G, Briegel H J, arxiv: v2 (2009)
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * FIZIKA NAVODILA ZA OCENJEVANJE. Petek, 10. junij 2016 SPLOŠNA MATURA
 Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Državni izpitni center *M16141113* SPOMLADANSKI IZPITNI ROK FIZIKA NAVODILA ZA OCENJEVANJE Petek, 1. junij 16 SPLOŠNA MATURA RIC 16 M161-411-3 M161-411-3 3 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Frekvenčna analiza neperiodičnih signalov. Analiza signalov prof. France Mihelič
 Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Frekvenčna analiza neperiodičnih signalov Analiza signalov prof. France Mihelič Vpliv postopka daljšanja periode na spekter periodičnega signala Opazujmo družino sodih periodičnih pravokotnih impulzov
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Petek, 12. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M543* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Petek,. junij 05 SPLOŠNA MATURA RIC 05 M543 M543 3 IZPITNA POLA Naloga Odgovor Naloga Odgovor Naloga Odgovor Naloga Odgovor
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU
 NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU Equatio n Section 6Vsebina poglavja: Navor kot vektorski produkt ročice in sile, magnetni moment, navor na magnetni moment, d'arsonvalov ampermeter/galvanometer.
NAVOR NA (TOKO)VODNIK V MAGNETNEM POLJU Equatio n Section 6Vsebina poglavja: Navor kot vektorski produkt ročice in sile, magnetni moment, navor na magnetni moment, d'arsonvalov ampermeter/galvanometer.
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
 I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
3. VAJA IZ TRDNOSTI. Rešitev: Pomik v referenčnem opisu: u = e y 2 e Pomik v prostorskem opisu: u = ey e. e y,e z = e z.
 3. VAJA IZ TRDNOSTI (tenzor deformacij) (pomiki togega telesa, Lagrangev in Eulerjev opis, tenzor velikih deformacij, tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Gumijasti
3. VAJA IZ TRDNOSTI (tenzor deformacij) (pomiki togega telesa, Lagrangev in Eulerjev opis, tenzor velikih deformacij, tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Gumijasti
17. Električni dipol
 17 Električni dipol Vsebina poglavja: polarizacija prevodnika (snovi) v električnem polju, električni dipolni moment, polarne in nepolarne snovi, dipol v homogenem in nehomogenem polju, potencial in polje
17 Električni dipol Vsebina poglavja: polarizacija prevodnika (snovi) v električnem polju, električni dipolni moment, polarne in nepolarne snovi, dipol v homogenem in nehomogenem polju, potencial in polje
Funkcije več spremenljivk
 DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
DODATEK C Funkcije več spremenljivk C.1. Osnovni pojmi Funkcija n spremenljivk je predpis: f : D f R, (x 1, x 2,..., x n ) u = f (x 1, x 2,..., x n ) kjer D f R n imenujemo definicijsko območje funkcije
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Poliedri Ines Pogačar 27. oktober 2009
 Poliedri Ines Pogačar 27. oktober 2009 Pri linearnem programiranju imamo opravka s končnim sistemom neenakosti in končno spremenljivkami, torej je množica dopustnih rešitev presek končno mnogo polprostorov.
Poliedri Ines Pogačar 27. oktober 2009 Pri linearnem programiranju imamo opravka s končnim sistemom neenakosti in končno spremenljivkami, torej je množica dopustnih rešitev presek končno mnogo polprostorov.
SLIKA 1: KRIVULJA BARVNE OBČUTLJIVOSTI OČESA (Rudolf Kladnik: Osnove fizike-2.del,..stran 126, slika 18.4)
 Naše oko zaznava svetlobo na intervalu valovnih dolžin približno od 400 do 800 nm. Odvisnost očesne občutljivosti od valovne dolžine je različna od človeka do človeka ter se spreminja s starostjo. Največja
Naše oko zaznava svetlobo na intervalu valovnih dolžin približno od 400 do 800 nm. Odvisnost očesne občutljivosti od valovne dolžine je različna od človeka do človeka ter se spreminja s starostjo. Največja
Energije in okolje 1. vaja. Entalpija pri kemijskih reakcijah
 Entalpija pri kemijskih reakcijah Pri obravnavi energijskih pretvorb pri kemijskih reakcijah uvedemo pojem entalpije, ki popisuje spreminjanje energije sistema pri konstantnem tlaku. Sistemu lahko povečamo
Entalpija pri kemijskih reakcijah Pri obravnavi energijskih pretvorb pri kemijskih reakcijah uvedemo pojem entalpije, ki popisuje spreminjanje energije sistema pri konstantnem tlaku. Sistemu lahko povečamo
MAGNETNI MATERIALI. 1. Mehkomagnetni materiali 2. Trdomagnetni materiali
 MAGNETNI MATERIALI 1. Mehkomagnetni materiali 2. Trdomagnetni materiali Magnetni materiali in njihove lastnosti Slika 5.1 Magnetenje različnih vrst snovi Magnetne lastnosti snovi v B = µ v H Permeabilnost
MAGNETNI MATERIALI 1. Mehkomagnetni materiali 2. Trdomagnetni materiali Magnetni materiali in njihove lastnosti Slika 5.1 Magnetenje različnih vrst snovi Magnetne lastnosti snovi v B = µ v H Permeabilnost
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Poglavje 10. Molekule Kovalentna vez
 Poglavje 10 Molekule Atomi se vežejo v molekule. Vezavo med atomi v molkuli posredujejo zunanji - valenčni elektroni. Pri vseh molekularnih vezeh negativni naboj elektronov posreduje med pozitinvimi ioni
Poglavje 10 Molekule Atomi se vežejo v molekule. Vezavo med atomi v molkuli posredujejo zunanji - valenčni elektroni. Pri vseh molekularnih vezeh negativni naboj elektronov posreduje med pozitinvimi ioni
Analiza 2 Rešitve 14. sklopa nalog
 Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
Analiza Rešitve 1 sklopa nalog Navadne diferencialne enačbe višjih redov in sistemi diferencialnih enačb (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) 6 + 8 0, (b)
12 Slikanje z jedrsko magnetno resonanco
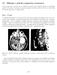 12 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
12 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
11 Slikanje z jedrsko magnetno resonanco
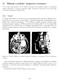 11 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
11 Slikanje z jedrsko magnetno resonanco Pri tej vaji bomo spoznali, da so nekatera atomska jedra magnetni dipoli, in predstavili njihovo obnašanje v zunanjem magnetnem polju. Seznanili se bomo tudi s
UNIVERZA V LJUBLJANI FMF, oddelek za fiziko seminar Laser na proste elektrone
 UNIVERZA V LJUBLJANI FMF, oddelek za fiziko seminar Laser na proste elektrone Bojan Žunkovič mentor: doc. dr. Matjaž Žitnik 7. maj 2007 Povzetek V preteklosti je bilo sinhrotronsko sevanje pri pospeševanju
UNIVERZA V LJUBLJANI FMF, oddelek za fiziko seminar Laser na proste elektrone Bojan Žunkovič mentor: doc. dr. Matjaž Žitnik 7. maj 2007 Povzetek V preteklosti je bilo sinhrotronsko sevanje pri pospeševanju
diferencialne enačbe - nadaljevanje
 12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
12. vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 diferencialne enačbe - nadaljevanje Ortogonalne trajektorije Dana je 1-parametrična družina krivulj F(x, y, C) = 0. Ortogonalne
e 2 4πε 0 r i r j Ze 2 4πε 0 r i j<i
 Poglavje 9 Atomi z več elektroni Za atom z enim elektronom smo lahko dobili analitične rešitve za lastne vrednosti in lastne funkcije energije. Pri atomih z več elektroni to ni mogoče in se moramo zadovoljiti
Poglavje 9 Atomi z več elektroni Za atom z enim elektronom smo lahko dobili analitične rešitve za lastne vrednosti in lastne funkcije energije. Pri atomih z več elektroni to ni mogoče in se moramo zadovoljiti
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba.
 1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
1. Osnovni pojmi Enačba, v kateri poleg neznane funkcije neodvisnih spremenljivk ter konstant nastopajo tudi njeni odvodi, se imenuje diferencialna enačba. Primer 1.1: Diferencialne enačbe so izrazi: y
5.6 Ostale lastnosti feromagnetnih materialov
 5.6 Ostale lastnosti feromagnetnih materialov Pri izdelavi magnetnih materialov imajo pomembno vlogo tudi nepravilnosti v njihovi strukturi. Če je material izdelan brez nepravilnosti, premikanje Blochovih
5.6 Ostale lastnosti feromagnetnih materialov Pri izdelavi magnetnih materialov imajo pomembno vlogo tudi nepravilnosti v njihovi strukturi. Če je material izdelan brez nepravilnosti, premikanje Blochovih
Tema 1 Osnove navadnih diferencialnih enačb (NDE)
 Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
Izpeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega
 Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
1 Fibonaccijeva stevila
 1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
REˇSITVE. Naloga a. b. c. d Skupaj. FAKULTETA ZA MATEMATIKO IN FIZIKO Oddelek za matematiko Verjetnost 2. kolokvij 23.
 Ime in priimek: Vpisna št: FAKULTETA ZA MATEMATIKO IN FIZIKO Oddelek za matematiko Verjetnost. kolokvij 3. januar 08 Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja. Nalog je 6,
Ime in priimek: Vpisna št: FAKULTETA ZA MATEMATIKO IN FIZIKO Oddelek za matematiko Verjetnost. kolokvij 3. januar 08 Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja. Nalog je 6,
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Matematika 1. Gabrijel Tomšič Bojan Orel Neža Mramor Kosta
 Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
Slika 5.1 Magnetenje različnih vrst snovi
 5. Magnetni materiali in njihove lastnosti Če opazujemo različne snovi v magnetnem polju, lahko pri vsaki ugotovimo magnetne lastnosti. Glede na izraženost magnetnih lastnosti oz. glede na obnašanje snovi
5. Magnetni materiali in njihove lastnosti Če opazujemo različne snovi v magnetnem polju, lahko pri vsaki ugotovimo magnetne lastnosti. Glede na izraženost magnetnih lastnosti oz. glede na obnašanje snovi
logo.pdf Oddelek za fiziko Avtor: Marjeta Tušek Ljubljana,
 logo.pdf Oddelek za fiziko Avtor: Marjeta Tušek Ljubljana, 1 Kazalo 1 UVOD 3 2 OSNOVE JEDRSKE MAGNETNE RESONANCE 3 2.1 Magnetne lastnosti jeder in resonanca............... 3 2.2 Radiofrekvenčni pulz.........................
logo.pdf Oddelek za fiziko Avtor: Marjeta Tušek Ljubljana, 1 Kazalo 1 UVOD 3 2 OSNOVE JEDRSKE MAGNETNE RESONANCE 3 2.1 Magnetne lastnosti jeder in resonanca............... 3 2.2 Radiofrekvenčni pulz.........................
Če je električni tok konstanten (se ne spreminja s časom), poenostavimo enačbo (1) in dobimo enačbo (2):
 ELEKTRIČNI TOK TEOR IJA 1. Definicija enote električnega toka Električni tok je gibanje električno nabitih delcev v trdnih snoveh (kovine, polprevodniki), tekočinah ali plinih. V kovinah se gibljejo prosti
ELEKTRIČNI TOK TEOR IJA 1. Definicija enote električnega toka Električni tok je gibanje električno nabitih delcev v trdnih snoveh (kovine, polprevodniki), tekočinah ali plinih. V kovinah se gibljejo prosti
7. VAJA IZ MEHANIKE TRDNIH TELES. (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji)
 7. VAJA IZ MEHANIKE TRDNIH TELES (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Pomik deformabilnega telesa je glede na kartezijski koordinatni sistem
7. VAJA IZ MEHANIKE TRDNIH TELES (tenzor deformacij II) (tenzor majhnih deformacij in rotacij, kompatibilitetni pogoji) NALOGA 1: Pomik deformabilnega telesa je glede na kartezijski koordinatni sistem
1. Newtonovi zakoni in aksiomi o silah:
 1. Newtonovi zakoni in aksiomi o silah: A) Telo miruje ali se giblje enakomerno, če je vsota vseh zunanjih sil, ki delujejo na telo enaka nič. B) Če rezultanta vseh zunanjih sil, ki delujejo na telo ni
1. Newtonovi zakoni in aksiomi o silah: A) Telo miruje ali se giblje enakomerno, če je vsota vseh zunanjih sil, ki delujejo na telo enaka nič. B) Če rezultanta vseh zunanjih sil, ki delujejo na telo ni
Kvadratne forme. Poglavje XI. 1 Definicija in osnovne lastnosti
 Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
Poglavje XI Kvadratne forme V zadnjem poglavju si bomo ogledali še eno vrsto preslikav, ki jih tudi lahko podamo z matrikami. To so tako imenovane kvadratne forme, ki niso več linearne preslikave. Kvadratne
Elektron u magnetskom polju
 Quantum mechanics 1 - Lecture 13 UJJS, Dept. of Physics, Osijek 4. lipnja 2013. Sadržaj 1 Bohrov magneton Stern-Gerlachov pokus Vrtnja elektrona u magnetskom polju 2 Nuklearna magnetska rezonancija (NMR)
Quantum mechanics 1 - Lecture 13 UJJS, Dept. of Physics, Osijek 4. lipnja 2013. Sadržaj 1 Bohrov magneton Stern-Gerlachov pokus Vrtnja elektrona u magnetskom polju 2 Nuklearna magnetska rezonancija (NMR)
+105 C (plošče in trakovi +85 C) -50 C ( C)* * Za temperature pod C se posvetujte z našo tehnično službo. ϑ m *20 *40 +70
 KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
Atomi, molekule, jedra
 Atomi, molekule, jedra B. Golli, PeF 25. maj 2015 Kazalo 1 Vodikov atom 5 1.1 Modeli vodikovega atoma........................... 5 1.2 Schrödingerjeva enačba za vodikov atom.................. 5 Nastavek
Atomi, molekule, jedra B. Golli, PeF 25. maj 2015 Kazalo 1 Vodikov atom 5 1.1 Modeli vodikovega atoma........................... 5 1.2 Schrödingerjeva enačba za vodikov atom.................. 5 Nastavek
Univerza v Novi Gorici Fakulteta za znanosti o okolju Okolje (I. stopnja) Meteorologija 2013/2014. Energijska bilanca pregled
 Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
Univerza v Novi Gorici Fakulteta za znanosti o okolu Okole (I. stopna) Meteorologia 013/014 Energiska bilanca pregled 1 Osnovni pomi energiski tok: P [W = J/s] gostota energiskega toka: [W/m ] toplota:q
8. Posplošeni problem lastnih vrednosti
 8. Posplošeni problem lastnih vrednosti Bor Plestenjak NLA 13. april 2010 Bor Plestenjak (NLA) 8. Posplošeni problem lastnih vrednosti 13. april 2010 1 / 15 Matrični šop Dani sta kvadratni n n matriki
8. Posplošeni problem lastnih vrednosti Bor Plestenjak NLA 13. april 2010 Bor Plestenjak (NLA) 8. Posplošeni problem lastnih vrednosti 13. april 2010 1 / 15 Matrični šop Dani sta kvadratni n n matriki
TRDNOST (VSŠ) - 1. KOLOKVIJ ( )
 TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
TRDNOST (VSŠ) - 1. KOLOKVIJ (17. 12. 03) Pazljivo preberite besedilo vsake naloge! Naloge so točkovane enakovredno (vsaka 25%)! Pišite čitljivo! Uspešno reševanje! 1. Deformiranje telesa je podano s poljem
Mehanizem feromagnetnih domen in magnetne aplikacije
 Seminar- 4. letnik Mehanizem feromagnetnih domen in magnetne aplikacije Avtor: Jože BUH Mentor: Dr. Denis ARČON 7. januar 2011 Povzetek Za permanentne (trde) magnete je značilno, da ostanejo namagneteni,
Seminar- 4. letnik Mehanizem feromagnetnih domen in magnetne aplikacije Avtor: Jože BUH Mentor: Dr. Denis ARČON 7. januar 2011 Povzetek Za permanentne (trde) magnete je značilno, da ostanejo namagneteni,
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
DISKRETNA FOURIERJEVA TRANSFORMACIJA
 29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
Matematika 2. Diferencialne enačbe drugega reda
 Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
Matematika 2 Diferencialne enačbe drugega reda (1) Reši homogene diferencialne enačbe drugega reda s konstantnimi koeficienti: (a) y 6y + 8y = 0, (b) y 2y + y = 0, (c) y + y = 0, (d) y + 2y + 2y = 0. Rešitev:
SATCITANANDA. F = e E sila na naboj. = ΔW e. Rudolf Kladnik: Fizika za srednješolce 3. Svet elektronov in atomov
 Ruolf Klnik: Fizik z srenješolce Set elektrono in too Električno olje (11), gibnje elce električne olju Strn 55, nlog 1 Kolikšno netost or releteti elektron, se njego kinetičn energij oeč z 1 kev? Δ W
Ruolf Klnik: Fizik z srenješolce Set elektrono in too Električno olje (11), gibnje elce električne olju Strn 55, nlog 1 Kolikšno netost or releteti elektron, se njego kinetičn energij oeč z 1 kev? Δ W
Snov v električnem polju. Električno polje dipola (prvi način) Prvi način: r + d 2
 Snov v lktričnm polju lktrično polj ipola (prvi način) P P - Prvi način: z r = r Δr r = r Δr Δr Δ r - r r r r r r Δr rδr =, = 4πε r r 4πε r r r r = r cos, r r r = r cos. r Vlja: = cos, r r r r r = cos,
Snov v lktričnm polju lktrično polj ipola (prvi način) P P - Prvi način: z r = r Δr r = r Δr Δr Δ r - r r r r r r Δr rδr =, = 4πε r r 4πε r r r r = r cos, r r r = r cos. r Vlja: = cos, r r r r r = cos,
Linearne preslikave. Poglavje VII. 1 Definicija linearne preslikave in osnovne lastnosti
 Poglavje VII Linearne preslikave V tem poglavju bomo vektorske prostore označevali z U,V,W,... Vsi vektorski prostori bodo končnorazsežni. Zaradi enostavnosti bomo privzeli, da je pripadajoči obseg realnih
Poglavje VII Linearne preslikave V tem poglavju bomo vektorske prostore označevali z U,V,W,... Vsi vektorski prostori bodo končnorazsežni. Zaradi enostavnosti bomo privzeli, da je pripadajoči obseg realnih
Katedra za farmacevtsko kemijo. Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks. 25/11/2010 Vaje iz Farmacevtske kemije 3 1
 Katedra za farmacevtsko kemijo Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks 25/11/2010 Vaje iz Farmacevtske kemije 3 1 Sinteza kompleksa [Mn 3+ (salen)oac] Zakaj uporabljamo brezvodni
Katedra za farmacevtsko kemijo Sinteza mimetika encima SOD 2. stopnja: Mn 3+ ali Cu 2+ salen kompleks 25/11/2010 Vaje iz Farmacevtske kemije 3 1 Sinteza kompleksa [Mn 3+ (salen)oac] Zakaj uporabljamo brezvodni
Definicija. definiramo skalarni produkt. x i y i. in razdaljo. d(x, y) = x y = < x y, x y > = n (x i y i ) 2. i=1. i=1
 Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
Funkcije več realnih spremenljivk Osnovne definicije Limita in zveznost funkcije več spremenljivk Parcialni odvodi funkcije več spremenljivk Gradient in odvod funkcije več spremenljivk v dani smeri Parcialni
V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant.
 Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Seminar I. Zemljin magnetizem. Fakulteta za matematiko in fiziko Univerza v Ljubljani. Avtor: Jure Zmrzlikar
 Seminar I Zemljin magnetizem Fakulteta za matematiko in fiziko Univerza v Ljubljani Avtor: Jure Zmrzlikar zmrzlikar.jure@gmail.com Mentor: prof. dr. Peter Prelovšek Junij 2012 Povzetek Magnetno polje Zemlje
Seminar I Zemljin magnetizem Fakulteta za matematiko in fiziko Univerza v Ljubljani Avtor: Jure Zmrzlikar zmrzlikar.jure@gmail.com Mentor: prof. dr. Peter Prelovšek Junij 2012 Povzetek Magnetno polje Zemlje
primer reševanja volumskega mehanskega problema z MKE
 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE p p RAK: P-XII//74 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE L
Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE p p RAK: P-XII//74 Reševanje mehanskih problemov z MKE primer reševanja volumskega mehanskega problema z MKE L
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
vezani ekstremi funkcij
 11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
11. vaja iz Matematike 2 (UNI) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 ekstremi funkcij več spremenljivk nadaljevanje vezani ekstremi funkcij Dana je funkcija f(x, y). Zanimajo nas ekstremi nad
Vaja: Odbojnostni senzor z optičnimi vlakni. Namen vaje
 Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
Namen vaje Spoznavanje osnovnih fiber-optičnih in optomehanskih komponent Spoznavanje načela delovanja in praktične uporabe odbojnostnega senzorja z optičnimi vlakni, Delo z merilnimi instrumenti (signal-generator,
