Organska bioelektronika. Karen Butina
|
|
|
- Ê Ταρσούλη
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Organska bioelektronika Karen Butina 16
2 Danes je nadvse popularno vse, kar je bio, eko in organsko, pa naj bo to sadje, zelenjava, mleko, žito, celo obleke in turistične aktivnosti. Da ne bi zaostajala za sodobnimi trendi, je organska in bio zdaj postala tudi elektronika! Najverjetneje si vsi predstavljamo, kaj pomeni organsko kmetijstvo in kakšen je biojogurt; kakšni pa sta organska in bioelektronika? Razlaga je pravzaprav izjemno preprosta: organska zgolj pomeni, da je sestavljena iz organskih snovi (torej takih, ki vsebujejo ogljik), bio pa pomeni, da gre za biokompatibilno, torej živim bitjem prijazno elektroniko. Organska bioelektronika je področje znanosti, ki prav zdaj kalí in je brez dvoma eno izmed najmlajših, vendar tudi najobetavnejših. Obljublja namreč nove ter inovativne terapije, in sicer predvsem na področju zdravljenja nevrodegenerativnih bolezni, kot sta npr. Parkinsonova in Alzheimerjeva bolezen veliki bremeni razvitega, starajočega se zahodnega sveta. Naši možgani so izjemnega pomena za delovanje celotnega telesa, saj obdelujejo podatke, pridobljene tako iz okolice kot iz notranjosti telesa, na osnovi katerih se potem odločajo o izvrševanju najrazličnejših dejanj. Fizično gledano so možgani pravzaprav velik skupek živčnih celic, razdeljen na posamezne dele, ki opravljajo različne naloge. Živčne celice se v možgane stekajo iz hrbtenjače, od koder živčna vlakna segajo v prav vse dele telesa. Glavna naloga živčevja je torej prenos informacij: čutilni živci prinašajo informacije v možgane, ki jih obdelajo ter pošljejo ukaze motoričnim živcem in drugim, ki ukaze izvršijo. Informacije se po živčnih celicah prenašajo v obliki električnih signalov, kjer ioni predstavljajo nosilce naboja. Opisane lastnosti možganov so vodile do vzpostavitve analogije med njimi in računalniki. Tudi slednji so namreč namenjeni obdelovanju podatkov in prenašajo informacije v obliki električnih signalov, le da kot nosilce naboja uporabljajo elektrone. Prav dejstvo, da gre za zelo podoben način prenosa informacij, je privedlo do ideje o možnosti interakcije med možgani in računalniki oz. drugimi elektronskimi napravami in elementi, kar je povzročilo nastanek organske bioelektronike. Pri nevrodegenerativnih boleznih se pogosto znajdemo v situaciji, ko določene živčne celice zaradi poškodbe ali bolezni ne opravljajo več svoje funkcije. Zato potrebujemo terapijo, ki bo omogočala kar se da pristno nadomestilo nedelujočih živčnih celic. 17
3 Organska bioelektronika KAKO DELUJEJO ŽIVČNE CELICE Za lažje razumevanje principov delovanja organske bioelektronike, s katerimi slednja posnema delovanje naših lastnih živčnih celic, bomo na začetku obnovili znanje o delovanju le-teh. Živčne celice oz. nevroni so ključne enote živčevja, ki vključuje možgane, hrbtenjačo in periferne ganglije, ki so zadolženi za prenos informacij iz možganov in hrbtenjače v vse dele telesa. Živčne celice so sestavljene iz some oz. telesa celice (kjer so tudi jedro in drugi pomembni organeli), aksona in dendritov. Prek dendritov živčna celica sprejema informacije od drugih živčnih celic, prek aksona pa posreduje informacije naprej. Živčna celica ima lahko več dendritov, a vedno samo en akson, ki se lahko pozneje razveji. Dendriti so običajno zelo kratki (merijo le nekaj sto mikrometrov), aksoni pa so lahko tudi daljši od enega metra. Informacije se med živčnimi celicami prenašajo po sinapsah, ki so lahko električne ali kemične. Ker so slednje mnogo pogostejše, se bomo v nadaljevanju osredotočili nanje. Sinapsa je pravzaprav stik med aksonom ene in dendritom ali somo drugega živčne celice. Kadar po aksonu potuje električni impulz, se na njegovem koncu odprejo posebni kanalčki, ki vanj spustijo pozitivno nabite kalcijeve ione. Ti povzročijo, da se iz konca aksona izločijo t. i. živčni prenašalci ali nevrotransmiterji skupina molekul, ki na dendrit druge živčne celice prenese določeno sporočilo. Na dendritu druge živčne celice, ki je fizično zelo blizu aksonu prve, so posebni receptorji, ki zaznajo izločene živčne prenašalce. Receptorji so zasidrani v membrano, ki je sama po sebi polarizirana, tako da je navznoter negativno nabita. Živčni prenašalci so lahko vzbujevalni (npr. acetilholin) ali zaviralni (npr. možgani periferno živčevje Živčna celica (Vir: morphonix. com) celično jedro dendriti hrbtenjača telo živčne celice akson periferno živčevje 18 sinapsa Živčni sistem v človeškem telesu (Vir: anatomisty.com)
4 GABA), njihovo izločanje pa povzroči bodisi depolarizacijo (izenačenje nabojev na obeh straneh membrane) bodisi hiperpolarizacijo (povečanje razlike v naboju med notranjo in zunanjo stranjo membrane) polarizirane postsinaptične membrane (dendrit ali soma). Depolarizacija se zgodi zaradi vdora pozitivno nabitih natrijevih ionov in se na ta način pozneje prenaša naprej tudi po aksonu živčne celice, ki je prejela vzbujevalni signal. Kadar govorimo o prenosu električnih impulzov po aksonu, se torej za tem skriva povsem preprosto odpiranje natrijevih kanalčkov, ki povzročijo depolarizacijo določenega dela membrane, kar povzroči, da se v naslednjem koraku depolarizira naslednji del itd., dokler signal ne doseže konca aksona, kjer se spet izločijo določeni živčni prenašalci. Kadar imamo opravka z zaviralnimi živčnimi prenašalci, prek postsinaptične membrane v dendrit oz. somo vdrejo negativno nabiti klorovi ioni, ki še dodatno polarizirajo membrano ter tako onemogočijo nastanek potenciala in prenos električnega impulza. ZAKAJ POTREBUJEMO UMETNE ŽIVČNE CELICE Zdaj vemo, kako delujejo živčne celice. Zagata, pred katero so se znašli znanstveniki, je bila, kakšen material bi bil primeren za uporabo v človeškem telesu in hkrati sposoben posnemati ključne lastnosti živčnih celic, tj. prevajanje električnega signala in v odgovor nanj sproščanje živčnih prenašalcev. Kot smo ugotovili že v uvodu, imamo v vsakdanjem življenju opravka s kopico elektronike, ki nadvse akson uspešno prevaja električne signale prek prenosa elektronov. Ena izmed danes dostopnih terapij za bolnike z določenimi nevrološkimi boleznimi, npr. Parkinsonovo boleznijo, pri katerih drugi načini zdravljenja odpovedo, je uporaba kovinskih elektrod za neposredno spodbujanje živčnih celic v delu možganov, ki je zaradi bolezni prizadet. V tem primeru je potreben kirurški poseg, s katerim elektrodo vstavijo v bolnikove možgane. Ko je elektroda na ustreznem mestu, neselektivno aktivira vse živčne celice, s katerimi je v stiku, zato ta terapija ni najbolj primerna zaradi vsaj dveh pomanjkljivosti: njeno delovanje je netipično, poleg tega pa težavo predstavljajo tudi kirurški posegi, saj je poleg elektrod v možgane treba v prsi vstaviti tudi generator za napajanje elektrod. Naslednja izmed možnih in občasno uporabljanih terapij temelji na dostavi živčnih prenašalcev in drugih molekul v tekočini, vendar tudi ta način ni popoln. Ne samo zato, ker je treba imeti celotno napeljavo majhnih cevi in črpalk speljano zunaj, ampak tudi zato, ker vnos tekočine ni zaželen, saj zmoti vezikli z živčnimi prenašalci sinapsa dendrit/soma receptorji za živčne prenašalce Sinapsa (Vir: www. nextplica.com) 19
5 Organska bioelektronika Obarvana živčna celica (gre za t. i. piramidalno živčno celico, kakršno najdemo v možganih); na desni strani je jasno vidno jedro celice, iz katerega izvirajo zelo kratki dendriti, na levo stran pa se razteza dolg akson, ki se na koncu razveji. 20 naravno ravnotežje koncentracij določenih snovi, ki so na mestu vnosa. Popolna terapija bi torej omogočala elektronsko uravnavano dostavo živčnih prenašalcev na želeno mesto brez odvečne tekočine. V praksi to pomeni, da bi moral biti material, iz katerega bi sestavili 'umetno' živčno celico, prevoden tako za elektrone kot za nabite organske delce oz. ione ter obenem še bniozdružljiv, da bi ga lahko vstavili v tkivo bolnika. PREVODNI POLIMERI Leta 2000 so Alan J. Heeger, Alan G. MacDiarmid in Hideki Shirakawa prejeli Nobelovo nagrado za odkritje t. i. prevodnih polimerov. Sintetični polimeri so danes najpogosteje uporabljeni materiali na svetu in najbolj značilni med njimi so premnoge vrste plastike. Vsi vemo, da plastika nikakor ne prevaja električnega toka; celo obratno pogosto jo uporabljajo kot izolator. Kakšni so torej prevodni polimeri ter kako lahko prevajajo elektrone in ione? Za prevodnost materiala morata biti izpolnjena dva ključna pogoja: med atomi morajo biti prisotne t. i. konjugirane vezi in material mora biti podvržen t. i. dopiranju, s katerim vanj vnesemo ali mu odvzamemo nosilce naboja. Konjugirane vezi so dvojne vezi, v katerih sta prisotna dva različna tipa vezi: vez σ (sigma) in vez π (pi). Prva od njiju je zelo močna in do nje pride zaradi prekrivanja atomskih orbital. Kadar so med posameznimi atomi prisotne izključno vezi te vrste, je material izvrsten izolator. Prav nasprotno je vez π šibka in orbitali se ne prekrivata, zato so elektroni znotraj teh vezi razmeroma mobilni. In prav ta mobilnost elektronov je ključna za prevodnost materiala. Prevodni polimeri sami po sebi pravzaprav niso posebno dobro prevodni, zato pa to njihovo lastnost lahko temeljito izboljšamo s t. i. dopiranjem, pri katerem v material vnesemo mobilne nosilce naboja, ki so bodisi pozitivni ali negativni. Dopiranje lahko poteka prek oksidacije oz. redukcije materiala, pri čemer pri oksidaciji nastanejo t. i. pozitivne luknje (odvzeli smo elektrone), pri redukciji pa dobimo presežek negativnega naboja. Kadar imamo pozitivne luknje, je material dobro prevoden za elektrone, kadar pa imamo več negativnega naboja, se po materialu dobro prevajajo pozitivno nabiti ioni. UMETNA ŽIVČNA CELICA Po nekoliko daljšem uvodu smo naposled prišli do bistva: ali je znanstvenikom res uspelo razviti umetno živčno celico? Skoraj! Za lažje razumevanje in predstavo bomo na hitro preleteli ves razvoj do končnega izdelka, ki je danes najbližje umetni živčni celici. Najprej so razvili t. i. organsko elektronsko ionsko črpalko (v nadaljevanju:
6 V organski bioelektroniki se zelo pogosto uporablja kombiniran prevodni polimer PEDOT:PSS, ki je sestavljen iz dveh komponent: poli(3,4-etilendioksitiopen)-a in poli(stirensulfonat)-a. PEDOT je oksidiran in ima zatorej presežek pozitivnega naboja, PSS pa ima, nasprotno, presežek negativnega naboja. Skupaj torej predstavljata idealen material, saj je PEDOT prevoden za elektrone, PSS pa za katione. (Vir: nanoudla.blogspot.se/) OEIČ). Gre za ploščato napravo, narejeno iz PEDOT:PSS-a, ki omogoča prostorsko in časovno nadzorovan prenos živčnih prenašalcev brez tekočine. Princip delovanja OEIČ je skrajno preprost: pravokotnik PEDOT:PSS-a je razdeljen na dva dela, 'anodo' in 'katodo', med katerima je za elektrone neprevoden kanalček. Ta kanalček se vzpostavi tako, da PEDOT čezmerno oksidiramo in tako izničimo njegove prevodne lastnosti. PEDOT je tisti, ki prevaja elektrone, kar torej pomeni, da se prek kanalčka lahko prevajajo samo kationi. Živčni prenašalci, kot so acetilholin, glutamat, aspartat in GABA, so pri določenih vrednostih ph pozitivno nabiti in se kot kationi lahko prenašajo po kanalčku. Na anodo torej nanesemo naš živčni prenašalec v tekočini. Da se ta ne bi razlila po vsej OEIČ, je slednja z izjemo anode in katode prekrita s hidrofobno plastjo (na katodo so sprva dajali le elektrolit, npr. raztopino soli). Zdaj imamo OEIČ razdeljeno na dve strani: na anodo, na kateri je pozitivno nabit živčni prenašalec, in na katodo, na kateri je elektrolit. Med anodo in katodo je kanalček, prek katerega lahko potujejo le kationi. In kako prepričati naše pozitivno nabite molekule živčnega prenašalca, da bi potovale prek kanalčka? Vzpostavimo električno napetost ali električni tok. Ob tem se anoda oksidira in katoda reducira, kot posledica presežka pozitivnih nabojev na strani anode in negativnih na strani katode pa naš živčni prenašalec potuje z anodne strani prek kanalčka na katodno stran. Z vzpostavitvijo električne napetosti oz. toka torej dosežemo, da se PEDOT:PSS bodisi oksidira ali reducira, kar lahko prikažemo s preprostima kemičnima reakcijama: Anoda (oksidacija): PEDOT 0 + kation + :PSS PEDOT + :PSS + kation + + e Katoda (redukcija): PEDOT + :PSS + kation + + e PEDOT 0 + kation + :PSS Koliko časa bo OEIČ delovala, je odvisno od količine PEDOT-a, ki se lahko oksidira, vendar t. i. pulzirajoča dostava, pri kateri se smer električnega toka menja, obljublja rešitev tudi za ta problem. M + M + M + smer transporta kationov Organska elektronska ionska črpalka OEIČ (Vir: com) elektrolit e e P + PSS + M + M + PSS + P 0 + V C + C + M + M + C+ C + PEDOT:PSS 21
7 Organska bioelektronika Živčne celice (shy5y) v laboratorijski kulturi (Vir: people.qc. cuny.edu/) 22 Kot smo že omenili, je bil na katodi sprva le elektrolit, v katerega so se prenašali živčni prenašalci, ki so prišli prek kanalčka. S pomočjo t. i. visokotlačne tekočinske kromatografije (angl. HPLC high performance liquid chromatography) smo potem ugotavljali, koliko živčnih prenašalcev je prek kanalčka pripotovalo do katode. Izkaže se, da je razmerje med številom elektronov (tega lahko izračunamo glede na podatke o napetosti oz. toku) in številom uspešno transportiranih živčnih prenašalcev linearno. To je bila seveda odlična novica za znanstvenike, saj je pomenila, da s spreminjanjem toka oz. napetosti lahko zelo dobro uravnavamo tudi količino dostavljenega živčnega prenašalca. Naslednji korak je bil, da so namesto elektrolita na katodo namestili kar živčne celice; kot večino drugih celic namreč lahko tudi živčne celice umetno vzgajamo v laboratorijskih kulturah. Že pri opisovanju delovanja živčnih celic smo omenili, da se kot posledica električnega impulza na presinaptični membrani odprejo kalcijevi kanalčki, kar sproži sproščanje živčnega prenašalca. S pomočjo posebnih barvil lahko pod mikroskopom vidimo kalcij in tako vemo, ali so se naše živčne celice odzvale na vzbujevalni živčni prenašalec (npr. acetilholin). Odziv živčnih celic po prehodu živčnega prenašalca skozi kanalček je dokazal, da je preneseni živčni prenašalec tudi biološko aktiven. Organska elektronska ionska črpalka je imela torej mnogo lastnosti, ki so bile zelo zaželene, vendar je bila njena oblika povsem neprimerna za nekaj, kar naj bi bilo umetna živčna celica. Zato so znanstveniki brez odvečnega zapletanja prvotno ploščato napravo preoblikovali tako, da so jo 'preganili'. Ob tem je prišlo tudi do spremembe v tem smislu, da je del, ki je v ploščati obliki bil kanalček, tu postal pravzaprav končni cilj pozitivno nabitega živčnega prenašalca. Princip delovanja je ostal enak kot pri OEIČ, le da imamo namesto raztopine z živčnim prenašalcem na anodi in elektrolita na katodi med njima še dodatno raztopino znotraj kanalčka, kjer živčni prenašalec pride v stik z okoljem. Nova napravica je podobna tanki injekcijski igli, ki ob dovajanju električnega toka v okolje sprošča živčne prenašalce. Prvi poskusi in vivo z umetno živčno celico so bili že narejeni na morskih prašičkih. Da bi se izognili kirurškim posegom in zapletom z napajanjem, je bila umetna živčna celica testirana na slušnem sistemu živali. Znotraj ušesa je čutilo za sluh v obliki zavite cevke, imenovane polž. Na spodnji steni polža so slušne čutnice, ki imajo na vrhu migetalke, nad njimi pa se razpenja tanka mrenica. Slušne čutnice so električno aktivne; sicer ne delujejo kot pravi živci, a so z njimi povezane. Razlikujemo dva tipa slušnih čutnic, notranje in zunanje,
8 pri čemer so notranje tiste, ki imajo ključne vlogo pri prevajanju dražljajev. Slednji so pravzaprav valovanje zraka, ki ga čutnice zaznajo prek migetalk. Ob depolarizaciji, ki se zgodi ob vdoru pozitivnih ionov kot posledica dražljaja, notranje čutnice izločijo živčni prenašalec glutamat. Presežne količine glutamata so za notranje čutnice in čutilne živčne celice, povezane z njimi, značilno strupene, medtem ko za zunanje čutnice in živčne celice, povezane z njimi, to ne velja. Ob prisotnosti prevelikih količin glutamata in poškodb živčnih celic lahko pride do izgube sluha. Zaradi razlike v odzivu na glutamat je bilo možno v ušesnem polžu preveriti delovanje umetne živčne celice. Izkazalo se je, da slednja deluje po pričakovanjih in je torej z njeno pomočjo mogoče dostaviti želene koncentracije živčnih prenašalcev (v našem primeru glutamata) na želeno mesto, v želenem časovnem obdobju in brez dodatne tekočine. Čudovita tehnologija, mar ne! S hidrofobna enkapsulacija PEDOT:PSS hiperoksidiran PEDOT:PSS substrat PET S anoda S rezervoar anoda T katoda T Čeprav je znanstvenikom za zdaj uspelo le odvzeti sluh nekaj morskim prašičkom, je izjemnega pomena to, da razpolagamo z dokazom, da umetna živčna celica deluje po pričakovanjih in tako odpira nove možnosti za uporabo v medicini. KAKO NAPREJ? Tako organsko elektronsko ionsko črpalko kot tudi 'umetno živčno celico' danes proizvaja švedsko podjetje Acreo. Sama oblikovna zasnova umetne živčne celice je že zelo dovršena, precej več dela pa bo potrebnega na področju njene karakterizacije, da bi definirali več snovi, ki jih lahko z njeno pomočjo dostavimo na želeno mesto, glede na namen pa bi bilo morda smotrno optimizirati tudi dostavne čase. Prostorsko uravnavanje je mogoče razmeroma preprosto doseči s širino kanalčka, po katerem potujejo pozitivno nabite molekule (govorili smo predvsem o živčnih prenašalcih). Najbolj pereče vprašanje pri vseh zadevi pa je, kako napajati umetno živčno celico, saj danes uporabljani način s priključnimi kabli več kot očitno ni najbolj optimalen. Glede na namen bi morda želeli električni tok tudi poljubno vključevati in izključevati, kar stvari še dodatno zaplete. V sklopu organske bioelektronike seveda poteka delo še na drugih Razvoj organske elektronske ionske črpalke do enkapsulirane oblike; S (angl. source) je tarčna raztopina torej tista, v kateri imamo živčni prenašalec, T (angl. target) pa je ciljna raztopina oz. elektrolit. (Vir: Simon et al., 2009.) Enkapsulirana oblika organske elektronske ionske črpalke (Vir: anoda, S katoda T 23
9 REVIJA ZA AVTOMATIZACIJO, ROBOTIKO, STROJNIŠTVO IN INFORMATIKO d. o. o., Novo mesto Stran januar 2013 / I številka 1 izhaja 4 x letno Stran 21 Stran 28 Stran 40 Organska bioelektronika področjih, ne zgolj na razvoju umetne živčne celice. Med obetavnejšimi projekti tako najdemo take, ki stremijo k uporabi prevodnih polimerov pri koronarni perkutani angioplastiki. Slednja je namenjena odpiranju zamašenih žil, kjer na zoženo mesto vstavijo mrežasto cevko, ki pripomore k ohranjanju širine žile (ŽIT 2013/5, str. 30). Premik mrežaste cevke, nastanek krvnega strdka okoli nje ali vnovična zamašitev žile kljub cevki so najpogostejši vzroki za srčni infarkt pri bolnikih, pri katerih je bila izvedena koronarna perkutana angioplastika. Prevodni polimeri so zaradi svoje izjemne biozdružljivosti in fleksibilnosti primerni za uporabo namesto mrežastih cevk, saj jih naše telo hitreje privzame za 'svoje'. Poleg tega se je izkazalo, da uporaba prevodnih polimerov omogoča hitrejšo regeneracijo, njihove prevodne lastnosti pa lahko izkoristimo za nove strategije sproščanja zdravil. viri in literatura V. Karagkiozaki, P. G. Karagiannidis, M. Gioti, P. Kavatzikidou, D. Georgiou, E. Georgaraki, S. Logothetidis: Bioelectronics meets nanomedicine for cardiovascular implants: PEDOT-based nanocoatings for tissue regeneration;. Biochimica et Biophysica Acta, K. C. Larsson, P. Kjäll, A. Richter- Dahlfors: Organic bioelectronics for electronic-to-chemical translation in modulation of neuronal signaling and machine-to-brain interfacing; Biochimica et Biophysica Acta, K. Svennersten, K. C. Larsson, M. Berggren, A. Richter-Dahlfors: Organic bioelectronics in nanomedicine; Biochimica et Biophysica Acta, D. T. Simon et al.: Organic electronics for precise delivery of neurotransmitters to modulate mammalian sensory function; Nature, K. Larsson: Organic bioelectronic devices to control cell signalling; Doktorska naloga, D. Simon, K. C. Larsson, M. Berggren, A. Richter-Dahlfors: Precise Neurotransmitter-Mediated Communication with Neurons In Vitro and In Vivo Using Organic Electronics; Journal of Biomechanical Science and Engineering, spletni naslovi about/organic_electronics. html?hl=sl&id=jbcraaaaqbaj prizes/chemistry/laureates/2000/ bioelectronics bioelectronics?l=en v8/n9/abs/nmat2494.html TISKOVINA - POŠTNINA PLAČANA PRI POŠTI 1102 Nadzor energetskih transformatorjev Sistemske rešitve za robotiko na ključ SIEMENS SIMATIC S7-1500! Bluetooth za brezžične meritve v industriji 24 Tovarna prihodnosti: raziskovalni projekt
10 oglas 25
Diferencialna enačba, v kateri nastopata neznana funkcija in njen odvod v prvi potenci
 Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Linearna diferencialna enačba reda Diferencialna enačba v kateri nastopata neznana funkcija in njen odvod v prvi potenci d f + p= se imenuje linearna diferencialna enačba V primeru ko je f 0 se zgornja
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 22. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 22. oktober 2013 Kdaj je zaporedje {a n } konvergentno, smo definirali s pomočjo limite zaporedja. Večkrat pa je dobro vedeti,
Tretja vaja iz matematike 1
 Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Tretja vaja iz matematike Andrej Perne Ljubljana, 00/07 kompleksna števila Polarni zapis kompleksnega števila z = x + iy): z = rcos ϕ + i sin ϕ) = re iϕ Opomba: Velja Eulerjeva formula: e iϕ = cos ϕ +
Funkcijske vrste. Matematika 2. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 2. april Gregor Dolinar Matematika 2
 Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Matematika 2 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 2. april 2014 Funkcijske vrste Spomnimo se, kaj je to številska vrsta. Dano imamo neko zaporedje realnih števil a 1, a 2, a
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 5. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 5. december 2013 Primer Odvajajmo funkcijo f(x) = x x. Diferencial funkcije Spomnimo se, da je funkcija f odvedljiva v točki
PONOVITEV SNOVI ZA 4. TEST
 PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
PONOVITEV SNOVI ZA 4. TEST 1. * 2. *Galvanski člen z napetostjo 1,5 V požene naboj 40 As. Koliko električnega dela opravi? 3. ** Na uporniku je padec napetosti 25 V. Upornik prejme 750 J dela v 5 minutah.
Odvod. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 10. december Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 10. december 2013 Izrek (Rolleov izrek) Naj bo f : [a,b] R odvedljiva funkcija in naj bo f(a) = f(b). Potem obstaja vsaj ena
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 21. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 21. november 2013 Hiperbolične funkcije Hiperbolični sinus sinhx = ex e x 2 20 10 3 2 1 1 2 3 10 20 hiperbolični kosinus coshx
KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK
 1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
1 / 24 KODE ZA ODKRIVANJE IN ODPRAVLJANJE NAPAK Štefko Miklavič Univerza na Primorskem MARS, Avgust 2008 Phoenix 2 / 24 Phoenix 3 / 24 Phoenix 4 / 24 Črtna koda 5 / 24 Črtna koda - kontrolni bit 6 / 24
Osnove elektrotehnike uvod
 Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Osnove elektrotehnike uvod Uvod V nadaljevanju navedena vprašanja so prevod testnih vprašanj, ki sem jih našel na omenjeni spletni strani. Vprašanja zajemajo temeljna znanja opredeljenega strokovnega področja.
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 14. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 14. november 2013 Kvadratni koren polinoma Funkcijo oblike f(x) = p(x), kjer je p polinom, imenujemo kvadratni koren polinoma
13. Jacobijeva metoda za računanje singularnega razcepa
 13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
13. Jacobijeva metoda za računanje singularnega razcepa Bor Plestenjak NLA 25. maj 2010 Bor Plestenjak (NLA) 13. Jacobijeva metoda za računanje singularnega razcepa 25. maj 2010 1 / 12 Enostranska Jacobijeva
8. Diskretni LTI sistemi
 8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
8. Diskreti LI sistemi. Naloga Določite odziv diskretega LI sistema s podaim odzivom a eoti impulz, a podai vhodi sigal. h[] x[] - - 5 6 7 - - 5 6 7 LI sistem se a vsak eoti impulz δ[] a vhodu odzove z
Kotne in krožne funkcije
 Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Kotne in krožne funkcije Kotne funkcije v pravokotnem trikotniku Avtor: Rok Kralj, 4.a Gimnazija Vič, 009/10 β a c γ b α sin = a c cos= b c tan = a b cot = b a Sinus kota je razmerje kotu nasprotne katete
Booleova algebra. Izjave in Booleove spremenljivke
 Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Izjave in Booleove spremenljivke vsako izjavo obravnavamo kot spremenljivko če je izjava resnična (pravilna), ima ta spremenljivka vrednost 1, če je neresnična (nepravilna), pa vrednost 0 pravimo, da gre
Transformator. Delovanje transformatorja I. Delovanje transformatorja II
 Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
Transformator Transformator je naprava, ki v osnovi pretvarja napetost iz enega nivoja v drugega. Poznamo vrsto različnih izvedb transformatorjev, glede na njihovo specifičnost uporabe:. Energetski transformator.
1. Trikotniki hitrosti
 . Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
. Trikotniki hitrosti. Z radialno črpalko želimo črpati vodo pri pogojih okolice z nazivnim pretokom 0 m 3 /h. Notranji premer rotorja je 4 cm, zunanji premer 8 cm, širina rotorja pa je,5 cm. Frekvenca
matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):
![matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij): matrike A = [a ij ] m,n αa 11 αa 12 αa 1n αa 21 αa 22 αa 2n αa m1 αa m2 αa mn se števanje po komponentah (matriki morata biti enakih dimenzij):](/thumbs/87/96579490.jpg) 4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
4 vaja iz Matematike 2 (VSŠ) avtorica: Melita Hajdinjak datum: Ljubljana, 2009 matrike Matrika dimenzije m n je pravokotna tabela m n števil, ki ima m vrstic in n stolpcev: a 11 a 12 a 1n a 21 a 22 a 2n
Delovna točka in napajalna vezja bipolarnih tranzistorjev
 KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
KOM L: - Komnikacijska elektronika Delovna točka in napajalna vezja bipolarnih tranzistorjev. Določite izraz za kolektorski tok in napetost napajalnega vezja z enim virom in napetostnim delilnikom na vhod.
SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK
 SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
SKUPNE PORAZDELITVE SKUPNE PORAZDELITVE VEČ SLUČAJNIH SPREMENLJIVK Kovaec vržemo trikrat. Z ozačimo število grbov ri rvem metu ( ali ), z Y a skuo število grbov (,, ali 3). Kako sta sremelivki i Y odvisi
NEPARAMETRIČNI TESTI. pregledovanje tabel hi-kvadrat test. as. dr. Nino RODE
 NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
NEPARAMETRIČNI TESTI pregledovanje tabel hi-kvadrat test as. dr. Nino RODE Parametrični in neparametrični testi S pomočjo z-testa in t-testa preizkušamo domneve o parametrih na vzorcih izračunamo statistike,
IZPIT IZ ANALIZE II Maribor,
 Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
Maribor, 05. 02. 200. (a) Naj bo f : [0, 2] R odvedljiva funkcija z lastnostjo f() = f(2). Dokaži, da obstaja tak c (0, ), da je f (c) = 2f (2c). (b) Naj bo f(x) = 3x 3 4x 2 + 2x +. Poišči tak c (0, ),
UVOD GORIVNE CELICE...
 GORIVNE CELICE 1 Kazalo UVOD... 3 1 GORIVNE CELICE... 4 1.1 VRSTE IN LASTNOSTI GORIVNIH CELIC... 4 1.2 DELOVANJE GORIVNIH CELIC... 5 2 TEMELJI ELEKTROKEMIJE... 7 2.1 ELEKTROKEMIJSKE REAKCIJE... 7 2.2 ELEKTROKEMIJSKI
GORIVNE CELICE 1 Kazalo UVOD... 3 1 GORIVNE CELICE... 4 1.1 VRSTE IN LASTNOSTI GORIVNIH CELIC... 4 1.2 DELOVANJE GORIVNIH CELIC... 5 2 TEMELJI ELEKTROKEMIJE... 7 2.1 ELEKTROKEMIJSKE REAKCIJE... 7 2.2 ELEKTROKEMIJSKI
1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου...
 ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
ΑΠΟΖΗΜΙΩΣΗ ΘΥΜΑΤΩΝ ΕΓΚΛΗΜΑΤΙΚΩΝ ΠΡΑΞΕΩΝ ΣΛΟΒΕΝΙΑ 1. Έντυπα αιτήσεων αποζημίωσης... 2 1.1. Αξίωση αποζημίωσης... 2 1.1.1. Έντυπο... 2 1.1.2. Πίνακας μεταφράσεων των όρων του εντύπου... 3 1 1. Έντυπα αιτήσεων
p 1 ENTROPIJSKI ZAKON
 ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
ENROPIJSKI ZAKON REERZIBILNA srememba: moža je obrjea srememba reko eakih vmesih staj kot rvota srememba. Po obeh sremembah e sme biti obeih trajih srememb v bližji i dalji okolici. IREERZIBILNA srememba:
Kontrolne karte uporabljamo za sprotno spremljanje kakovosti izdelka, ki ga izdelujemo v proizvodnem procesu.
 Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
Kontrolne karte KONTROLNE KARTE Kontrolne karte uporablamo za sprotno spremlane kakovosti izdelka, ki ga izdeluemo v proizvodnem procesu. Izvaamo stalno vzorčene izdelkov, npr. vsako uro, vsake 4 ure.
CM707. GR Οδηγός χρήσης... 2-7. SLO Uporabniški priročnik... 8-13. CR Korisnički priručnik... 14-19. TR Kullanım Kılavuzu... 20-25
 1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
1 2 3 4 5 6 7 OFFMANAUTO CM707 GR Οδηγός χρήσης... 2-7 SLO Uporabniški priročnik... 8-13 CR Korisnički priručnik... 14-19 TR Kullanım Kılavuzu... 20-25 ENG User Guide... 26-31 GR CM707 ΟΔΗΓΟΣ ΧΡΗΣΗΣ Περιγραφή
Integralni račun. Nedoločeni integral in integracijske metrode. 1. Izračunaj naslednje nedoločene integrale: (a) dx. (b) x 3 +3+x 2 dx, (c) (d)
 Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Integralni račun Nedoločeni integral in integracijske metrode. Izračunaj naslednje nedoločene integrale: d 3 +3+ 2 d, (f) (g) (h) (i) (j) (k) (l) + 3 4d, 3 +e +3d, 2 +4+4 d, 3 2 2 + 4 d, d, 6 2 +4 d, 2
Numerično reševanje. diferencialnih enačb II
 Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Numerčno reševanje dferencaln enačb I Dferencalne enačbe al ssteme dferencaln enačb rešujemo numerčno z več razlogov:. Ne znamo j rešt analtčno.. Posamezn del dferencalne enačbe podan tabelarčno. 3. Podatke
Tabele termodinamskih lastnosti vode in vodne pare
 Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
Univerza v Ljubljani Fakulteta za strojništvo Laboratorij za termoenergetiko Tabele termodinamskih lastnosti vode in vodne pare po modelu IAPWS IF-97 izračunano z XSteam Excel v2.6 Magnus Holmgren, xsteam.sourceforge.net
MATEMATIČNI IZRAZI V MAFIRA WIKIJU
 I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
I FAKULTETA ZA MATEMATIKO IN FIZIKO Jadranska cesta 19 1000 Ljubljan Ljubljana, 25. marec 2011 MATEMATIČNI IZRAZI V MAFIRA WIKIJU KOMUNICIRANJE V MATEMATIKI Darja Celcer II KAZALO: 1 VSTAVLJANJE MATEMATIČNIH
Podobnost matrik. Matematika II (FKKT Kemijsko inženirstvo) Diagonalizacija matrik
 Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
Podobnost matrik Matematika II (FKKT Kemijsko inženirstvo) Matjaž Željko FKKT Kemijsko inženirstvo 14 teden (Zadnja sprememba: 23 maj 213) Matrika A R n n je podobna matriki B R n n, če obstaja obrnljiva
17. Električni dipol
 17 Električni dipol Vsebina poglavja: polarizacija prevodnika (snovi) v električnem polju, električni dipolni moment, polarne in nepolarne snovi, dipol v homogenem in nehomogenem polju, potencial in polje
17 Električni dipol Vsebina poglavja: polarizacija prevodnika (snovi) v električnem polju, električni dipolni moment, polarne in nepolarne snovi, dipol v homogenem in nehomogenem polju, potencial in polje
Poglavje 7. Poglavje 7. Poglavje 7. Regulacijski sistemi. Regulacijski sistemi. Slika 7. 1: Normirana blokovna shema regulacije EM
 Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
Slika 7. 1: Normirana blokovna shema regulacije EM Fakulteta za elektrotehniko 1 Slika 7. 2: Principielna shema regulacije AM v KSP Fakulteta za elektrotehniko 2 Slika 7. 3: Merjenje komponent fluksa s
*M * Osnovna in višja raven MATEMATIKA NAVODILA ZA OCENJEVANJE. Sobota, 4. junij 2011 SPOMLADANSKI IZPITNI ROK. Državni izpitni center
 Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Državni izpitni center *M40* Osnovna in višja raven MATEMATIKA SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sobota, 4. junij 0 SPLOŠNA MATURA RIC 0 M-40-- IZPITNA POLA OSNOVNA IN VIŠJA RAVEN 0. Skupaj:
Lastnosti in delovanje polimerne gorivne celice
 FAKULTETA ZA STROJNIŠTVO Laboratorij za termoenergetiko LABORATORIJSKA VAJA Lastnosti in delovanje polimerne gorivne celice Mitja Mori, Mihael Sekavčnik CILJ VAJE - Spoznati sestavo in vrste gorivnih celic.
FAKULTETA ZA STROJNIŠTVO Laboratorij za termoenergetiko LABORATORIJSKA VAJA Lastnosti in delovanje polimerne gorivne celice Mitja Mori, Mihael Sekavčnik CILJ VAJE - Spoznati sestavo in vrste gorivnih celic.
Zaporedja. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 15. oktober Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 15. oktober 2013 Oglejmo si, kako množimo dve kompleksni števili, dani v polarni obliki. Naj bo z 1 = r 1 (cosϕ 1 +isinϕ 1 )
Če je električni tok konstanten (se ne spreminja s časom), poenostavimo enačbo (1) in dobimo enačbo (2):
 ELEKTRIČNI TOK TEOR IJA 1. Definicija enote električnega toka Električni tok je gibanje električno nabitih delcev v trdnih snoveh (kovine, polprevodniki), tekočinah ali plinih. V kovinah se gibljejo prosti
ELEKTRIČNI TOK TEOR IJA 1. Definicija enote električnega toka Električni tok je gibanje električno nabitih delcev v trdnih snoveh (kovine, polprevodniki), tekočinah ali plinih. V kovinah se gibljejo prosti
Zaporedna in vzporedna feroresonanca
 Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
Visokonapetostna tehnika Zaporedna in vzporedna feroresonanca delovanje regulacijskega stikala T3 174 kv Vaja 9 1 Osnovni pogoji za nastanek feroresonance L C U U L () U C () U L = U L () U C = ωc V vezju
+105 C (plošče in trakovi +85 C) -50 C ( C)* * Za temperature pod C se posvetujte z našo tehnično službo. ϑ m *20 *40 +70
 KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
KAIFLEX ST Tehnični podatki Material Izjemno fleksibilna zaprtocelična izolacija, fleksibilna elastomerna pena (FEF) Opis Uporaba Temperaturno območje Toplotna prevodnost W/(m K ) pri različnih srednjih
vaja Izolacija kromosomske DNA iz vranice in hiperkromni efekt. DNA RNA Protein. ime deoksirbonukleinska kislina ribonukleinska kislina
 transkripcija translacija Protein 12. vaja Izolacija kromosomske iz vranice in hiperkromni efekt sladkorji deoksiriboza riboza glavna funkcija dolgoročno shranjevanje genetskih informacij prenos informacij
transkripcija translacija Protein 12. vaja Izolacija kromosomske iz vranice in hiperkromni efekt sladkorji deoksiriboza riboza glavna funkcija dolgoročno shranjevanje genetskih informacij prenos informacij
1. Definicijsko območje, zaloga vrednosti. 2. Naraščanje in padanje, ekstremi. 3. Ukrivljenost. 4. Trend na robu definicijskega območja
 ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
ZNAČILNOSTI FUNKCIJ ZNAČILNOSTI FUNKCIJE, KI SO RAZVIDNE IZ GRAFA. Deinicijsko območje, zaloga vrednosti. Naraščanje in padanje, ekstremi 3. Ukrivljenost 4. Trend na robu deinicijskega območja 5. Periodičnost
1 Fibonaccijeva stevila
 1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
1 Fibonaccijeva stevila Fibonaccijevo število F n, kjer je n N, lahko definiramo kot število načinov zapisa števila n kot vsoto sumandov, enakih 1 ali Na primer, število 4 lahko zapišemo v obliki naslednjih
PROCESIRANJE SIGNALOV
 Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Rešive pisega izpia PROCESIRANJE SIGNALOV Daum: 7... aloga Kolikša je ampliuda reje harmoske kompoee arisaega periodičega sigala? f() - -3 - - 3 Rešiev: Časova fukcija a iervalu ( /,/) je lieara fukcija:
Kvantni delec na potencialnem skoku
 Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
Kvantni delec na potencialnem skoku Delec, ki se giblje premo enakomerno, pride na mejo, kjer potencial naraste s potenciala 0 na potencial. Takšno potencialno funkcijo zapišemo kot 0, 0 0,0. Slika 1:
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
DISKRETNA FOURIERJEVA TRANSFORMACIJA
 29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
29.03.2004 Definicija DFT Outline DFT je linearna transformacija nekega vektorskega prostora dimenzije n nad obsegom K, ki ga označujemo z V K, pri čemer ima slednji lastnost, da vsebuje nek poseben element,
TRANSPORT RAZTOPIN. Agronomija - UNI
 TRANSPORT RAZTOPIN Agronomija - UNI Transport na celičnem nivoju oz. transport preko membrane je osnova za transport na višjih nivojih (tkiva). Pomen biološki membran (plazmalema, tonoplast,...) homeostaza
TRANSPORT RAZTOPIN Agronomija - UNI Transport na celičnem nivoju oz. transport preko membrane je osnova za transport na višjih nivojih (tkiva). Pomen biološki membran (plazmalema, tonoplast,...) homeostaza
The Thermal Comfort Properties of Reusable and Disposable Surgical Gown Fabrics Original Scientific Paper
 24 The Thermal Comfort Properties of Surgical Gown Fabrics 1 1 2 1 2 Termofiziološke lastnosti udobnosti kirurških oblačil za enkratno in večkratno uporabo december 2008 marec 2009 Izvleček Kirurška oblačila
24 The Thermal Comfort Properties of Surgical Gown Fabrics 1 1 2 1 2 Termofiziološke lastnosti udobnosti kirurških oblačil za enkratno in večkratno uporabo december 2008 marec 2009 Izvleček Kirurška oblačila
Reševanje sistema linearnih
 Poglavje III Reševanje sistema linearnih enačb V tem kratkem poglavju bomo obravnavali zelo uporabno in zato pomembno temo linearne algebre eševanje sistemov linearnih enačb. Spoznali bomo Gaussovo (natančneje
Poglavje III Reševanje sistema linearnih enačb V tem kratkem poglavju bomo obravnavali zelo uporabno in zato pomembno temo linearne algebre eševanje sistemov linearnih enačb. Spoznali bomo Gaussovo (natančneje
Galvanski členi. Mentor: Gregor Skačej. 24. september 2009
 Galvanski členi Blaž Šterbenc Mentor: Gregor Skačej 24. september 2009 Povzetek V seminarju bom na kratko opisal zgodovinski razvoj galvanskih členov, obravnaval nernstovo enačbo uporaba za izračun električnih
Galvanski členi Blaž Šterbenc Mentor: Gregor Skačej 24. september 2009 Povzetek V seminarju bom na kratko opisal zgodovinski razvoj galvanskih členov, obravnaval nernstovo enačbo uporaba za izračun električnih
Izpeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega
 Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
Izeljava Jensenove in Hölderjeve neenakosti ter neenakosti Minkowskega 1. Najosnovnejše o konveksnih funkcijah Definicija. Naj bo X vektorski rostor in D X konveksna množica. Funkcija ϕ: D R je konveksna,
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant.
 Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Poglavje IV Determinanta matrike V tem poglavju bomo vpeljali pojem determinante matrike, spoznali bomo njene lastnosti in nekaj metod za računanje determinant 1 Definicija Preden definiramo determinanto,
Matematika 1. Gabrijel Tomšič Bojan Orel Neža Mramor Kosta
 Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
Matematika Gabrijel Tomšič Bojan Orel Neža Mramor Kosta 6. november 200 Poglavje 2 Zaporedja in številske vrste 2. Zaporedja 2.. Uvod Definicija 2... Zaporedje (a n ) = a, a 2,..., a n,... je predpis,
STANDARD1 EN EN EN
 PRILOGA RADIJSKE 9,000-20,05 khz naprave kratkega dosega: induktivne aplikacije 315 600 khz naprave kratkega dosega: aktivni medicinski vsadki ultra nizkih moči 4516 khz naprave kratkega dosega: železniške
PRILOGA RADIJSKE 9,000-20,05 khz naprave kratkega dosega: induktivne aplikacije 315 600 khz naprave kratkega dosega: aktivni medicinski vsadki ultra nizkih moči 4516 khz naprave kratkega dosega: železniške
Funkcije. Matematika 1. Gregor Dolinar. Fakulteta za elektrotehniko Univerza v Ljubljani. 12. november Gregor Dolinar Matematika 1
 Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1 Gregor Dolinar Fakulteta za elektrotehniko Univerza v Ljubljani 12. november 2013 Graf funkcije f : D R, D R, je množica Γ(f) = {(x,f(x)) : x D} R R, torej podmnožica ravnine R 2. Grafi funkcij,
Matematika 1. Gregor Dolinar. 2. januar Fakulteta za elektrotehniko Univerza v Ljubljani. Gregor Dolinar Matematika 1
 Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Mtemtik 1 Gregor Dolinr Fkultet z elektrotehniko Univerz v Ljubljni 2. jnur 2014 Gregor Dolinr Mtemtik 1 Izrek (Izrek o povprečni vrednosti) Nj bo m ntnčn spodnj mej in M ntnčn zgornj mej integrbilne funkcije
Na pregledni skici napišite/označite ustrezne točke in paraboli. A) 12 B) 8 C) 4 D) 4 E) 8 F) 12
 Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Predizpit, Proseminar A, 15.10.2015 1. Točki A(1, 2) in B(2, b) ležita na paraboli y = ax 2. Točka H leži na y osi in BH je pravokotna na y os. Točka C H leži na nosilki BH tako, da je HB = BC. Parabola
Kotni funkciji sinus in kosinus
 Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Kotni funkciji sinus in kosinus Oznake: sinus kota x označujemo z oznako sin x, kosinus kota x označujemo z oznako cos x, DEFINICIJA V PRAVOKOTNEM TRIKOTNIKU: Kotna funkcija sinus je definirana kot razmerje
Iterativno reševanje sistemov linearnih enačb. Numerične metode, sistemi linearnih enačb. Numerične metode FE, 2. december 2013
 Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
Numerične metode, sistemi linearnih enačb B. Jurčič Zlobec Numerične metode FE, 2. december 2013 1 Vsebina 1 z n neznankami. a i1 x 1 + a i2 x 2 + + a in = b i i = 1,..., n V matrični obliki zapišemo:
IONOTROPNI in METABOTROPNI receptorji. Klara Kropivšek
 IONOTROPNI in METABOTROPNI receptorji Klara Kropivšek Membranski receptorji Specializirani integralni membranski proteini. Vezava ekstracelularnih mediatorjev - ligandov (hormoni, nevrotransmiterji, citokini
IONOTROPNI in METABOTROPNI receptorji Klara Kropivšek Membranski receptorji Specializirani integralni membranski proteini. Vezava ekstracelularnih mediatorjev - ligandov (hormoni, nevrotransmiterji, citokini
13. Vaja: Reakcije oksidacije in redukcije
 1. Vaja: Reakcije oksidacije in redukcije a) Osnove: Oksidacija je reakcija pri kateri posamezen element (reducent) oddaja elektrone in se pri tem oksidira (oksidacijsko število se zviša). Redukcija pa
1. Vaja: Reakcije oksidacije in redukcije a) Osnove: Oksidacija je reakcija pri kateri posamezen element (reducent) oddaja elektrone in se pri tem oksidira (oksidacijsko število se zviša). Redukcija pa
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
Statistična analiza. doc. dr. Mitja Kos, mag. farm. Katedra za socialno farmacijo Univerza v Ljubljani- Fakulteta za farmacijo
 Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Statistična analiza opisnih spremenljivk doc. dr. Mitja Kos, mag. arm. Katedra za socialno armacijo Univerza v Ljubljani- Fakulteta za armacijo Statistični znaki Proučevane spremenljivke: statistični znaki
Tema 1 Osnove navadnih diferencialnih enačb (NDE)
 Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
Matematične metode v fiziki II 2013/14 Tema 1 Osnove navadnih diferencialnih enačb (NDE Diferencialne enačbe v fiziki Večina osnovnih enačb v fiziki je zapisana v obliki diferencialne enačbe. Za primer
KONSTRUKTORSKA GRADBENA FIZIKA. Analiza ios aplikacije Condensation in primerjava z analitično dobljenimi rezultati
 KONSTRUKTORSKA GRADBENA FIZIKA Analiza ios aplikacije Condensation in primerjava z analitično dobljenimi rezultati Timotej Čižek štud. leto 2013/2014 Condensation je preprosta aplikacija, ki deluje na
KONSTRUKTORSKA GRADBENA FIZIKA Analiza ios aplikacije Condensation in primerjava z analitično dobljenimi rezultati Timotej Čižek štud. leto 2013/2014 Condensation je preprosta aplikacija, ki deluje na
Najprej zapišemo 2. Newtonov zakon za cel sistem v vektorski obliki:
 NALOGA: Po cesi vozi ovornjak z hirosjo 8 km/h. Tovornjak je dolg 8 m, širok 2 m in visok 4 m in ima maso 4 on. S srani začne pihai veer z hirosjo 5 km/h. Ob nekem času voznik zaspi in ne upravlja več
NALOGA: Po cesi vozi ovornjak z hirosjo 8 km/h. Tovornjak je dolg 8 m, širok 2 m in visok 4 m in ima maso 4 on. S srani začne pihai veer z hirosjo 5 km/h. Ob nekem času voznik zaspi in ne upravlja več
Spoznajmo sedaj definicijo in nekaj osnovnih primerov zaporedij števil.
 Zaporedja števil V matematiki in fiziki pogosto operiramo s približnimi vrednostmi neke količine. Pri numeričnemu računanju lahko npr. število π aproksimiramo s števili, ki imajo samo končno mnogo neničelnih
Zaporedja števil V matematiki in fiziki pogosto operiramo s približnimi vrednostmi neke količine. Pri numeričnemu računanju lahko npr. število π aproksimiramo s števili, ki imajo samo končno mnogo neničelnih
21. Viri napetosti. Viri napetosti 21.
 21. Viri napetosti Vsebina polavja: elektromotorna sila, eneratorska napetost, električni tokokro, baterije, sončna celica. Generatorska sila. Do sedaj smo se ukvarjali le z učinki električnea polja, ne
21. Viri napetosti Vsebina polavja: elektromotorna sila, eneratorska napetost, električni tokokro, baterije, sončna celica. Generatorska sila. Do sedaj smo se ukvarjali le z učinki električnea polja, ne
vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov. 6. vaja Kvan*ta*vno določanje proteinov
 28. 3. 11 UV- spektrofotometrija Biuretska metoda Absorbanca pri λ=28 nm (A28) UV- spektrofotometrija Biuretska metoda vstopni žarek intenziteta I Lowrijeva metoda Bradfordova metoda Bradfordova metoda
28. 3. 11 UV- spektrofotometrija Biuretska metoda Absorbanca pri λ=28 nm (A28) UV- spektrofotometrija Biuretska metoda vstopni žarek intenziteta I Lowrijeva metoda Bradfordova metoda Bradfordova metoda
Primeri: naftalen kinolin spojeni kinolin
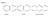 Primeri: naftalen kinolin spojeni kinolin 3 skupne strani 7 skupnih strani 5 skupnih strani 6 skupnih atomov 8 skupnih atomov 6 skupnih atomov orto spojen sistem orto in peri spojena sistema mostni kinolin
Primeri: naftalen kinolin spojeni kinolin 3 skupne strani 7 skupnih strani 5 skupnih strani 6 skupnih atomov 8 skupnih atomov 6 skupnih atomov orto spojen sistem orto in peri spojena sistema mostni kinolin
Električni naboj, ki mu pravimo tudi elektrina, označimo s črko Q, enota zanj pa je C (Coulomb-izgovorimo "kulon") ali As (1 C = 1 As).
 1 UI.DOC Elektrina - električni naboj (Q) Elementarni delci snovi imajo lastnost, da so nabiti - nosijo električni naboj-elektrino. Protoni imajo pozitiven naboj, zato je jedro pozitivno nabito, elektroni
1 UI.DOC Elektrina - električni naboj (Q) Elementarni delci snovi imajo lastnost, da so nabiti - nosijo električni naboj-elektrino. Protoni imajo pozitiven naboj, zato je jedro pozitivno nabito, elektroni
IZZIVI DRUŽINSKE MEDICINE. U no gradivo zbornik seminarjev
 IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
IZZIVI DRUŽINSKE MEDICINE Uno gradivo zbornik seminarjev študentov Medicinske fakultete Univerze v Mariboru 4. letnik 2008/2009 Uredniki: Alenka Bizjak, Viktorija Janar, Maša Krajnc, Jasmina Rehar, Mateja
PITAGORA, ki je večino svojega življenja posvetil številom, je bil mnenja, da ves svet temelji na številih in razmerjih med njimi.
 ZGODBA O ATOMU ATOMI V ANTIKI Od nekdaj so se ljudje spraševali iz česa je zgrajen svet. TALES iz Mileta je trdil, da je osnovna snov, ki gradi svet VODA, kar pa sploh ni presenetljivo. PITAGORA, ki je
ZGODBA O ATOMU ATOMI V ANTIKI Od nekdaj so se ljudje spraševali iz česa je zgrajen svet. TALES iz Mileta je trdil, da je osnovna snov, ki gradi svet VODA, kar pa sploh ni presenetljivo. PITAGORA, ki je
25. Viri napetosti. Vir napetosti(25).doc
 25. Viri napetosti Vsebina polavja: elektromotorna sila, eneratorska napetost, električni tokokro, baterije, sončna celica. Generatorska sila. Do sedaj smo se ukvarjali le z učinki električnea polja, ne
25. Viri napetosti Vsebina polavja: elektromotorna sila, eneratorska napetost, električni tokokro, baterije, sončna celica. Generatorska sila. Do sedaj smo se ukvarjali le z učinki električnea polja, ne
Avto na vodik in gorivne celice
 OSNOVNA ŠOLA ŽELEZNIKI Avto na vodik in gorivne celice Raziskovalna naloga Področje: naravoslovno - tehniško Avtorji: Matija Rihtaršič, Vid Šolar, Gašper Potočnik, Jakob Bernik, Luka Galjot, 9. razred
OSNOVNA ŠOLA ŽELEZNIKI Avto na vodik in gorivne celice Raziskovalna naloga Področje: naravoslovno - tehniško Avtorji: Matija Rihtaršič, Vid Šolar, Gašper Potočnik, Jakob Bernik, Luka Galjot, 9. razred
Energije in okolje 1. vaja. Entalpija pri kemijskih reakcijah
 Entalpija pri kemijskih reakcijah Pri obravnavi energijskih pretvorb pri kemijskih reakcijah uvedemo pojem entalpije, ki popisuje spreminjanje energije sistema pri konstantnem tlaku. Sistemu lahko povečamo
Entalpija pri kemijskih reakcijah Pri obravnavi energijskih pretvorb pri kemijskih reakcijah uvedemo pojem entalpije, ki popisuje spreminjanje energije sistema pri konstantnem tlaku. Sistemu lahko povečamo
TRANSPORT RAZTOPIN. Agronomija - UNI 2005/06
 TRANSPORT RAZTOPIN Transport na celičnem nivoju oz. transport preko membrane je osnova za transport na višjih nivojih (tkiva). Pomen biološki membran (plazmalema, tonoplast,...) homeostaza rastlinske celice
TRANSPORT RAZTOPIN Transport na celičnem nivoju oz. transport preko membrane je osnova za transport na višjih nivojih (tkiva). Pomen biološki membran (plazmalema, tonoplast,...) homeostaza rastlinske celice
Splošno o interpolaciji
 Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Splošno o interpolaciji J.Kozak Numerične metode II (FM) 2011-2012 1 / 18 O funkciji f poznamo ali hočemo uporabiti le posamezne podatke, na primer vrednosti r i = f (x i ) v danih točkah x i Izberemo
Fazni diagram binarne tekočine
 Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Fazni diagram binarne tekočine Žiga Kos 5. junij 203 Binarno tekočino predstavljajo delci A in B. Ti se med seboj lahko mešajo v različnih razmerjih. V nalogi želimo izračunati fazni diagram take tekočine,
Gimnazija Krˇsko. vektorji - naloge
 Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
Vektorji Naloge 1. V koordinatnem sistemu so podane točke A(3, 4), B(0, 2), C( 3, 2). a) Izračunaj dolžino krajevnega vektorja točke A. (2) b) Izračunaj kot med vektorjema r A in r C. (4) c) Izrazi vektor
ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI. Membranski separacijski procesi: diafiltracija, elektrodializa, reverzna osmoza, pervaporacija
 ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI Membranski separacijski procesi: diafiltracija, elektrodializa, reverzna osmoza, pervaporacija Membranski separacijski procesi v biotehnologiji proces mikrofiltracija
ZAKLJUČNI PROCESI V BIOTEHNOLOGIJI Membranski separacijski procesi: diafiltracija, elektrodializa, reverzna osmoza, pervaporacija Membranski separacijski procesi v biotehnologiji proces mikrofiltracija
Logatherm WPL 14 AR T A ++ A + A B C D E F G A B C D E F G. kw kw /2013
 WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
WP 14 R T d 9 10 11 53 d 2015 811/2013 WP 14 R T 2015 811/2013 WP 14 R T Naslednji podatki o izdelku izpolnjujejo zahteve uredb U 811/2013, 812/2013, 813/2013 in 814/2013 o dopolnitvi smernice 2010/30/U.
Vaje: Električni tokovi
 Barbara Rovšek, Bojan Golli, Ana Gostinčar Blagotinšek Vaje: Električni tokovi 1 Merjenje toka in napetosti Naloga: Izmerite tok, ki teče skozi žarnico, ter napetost na žarnici Za izvedbo vaje potrebujete
Barbara Rovšek, Bojan Golli, Ana Gostinčar Blagotinšek Vaje: Električni tokovi 1 Merjenje toka in napetosti Naloga: Izmerite tok, ki teče skozi žarnico, ter napetost na žarnici Za izvedbo vaje potrebujete
ZGRADBA ATOMA IN PERIODNI SISTEM
 ZGRADBA ATOMA IN PERIODNI SISTEM Kemijske lastnosti elementov se periodično spreminjajo z naraščajočo relativno atomsko maso oziroma kot vemo danes z naraščajočim vrstnim številom. Dmitrij I. Mendeljejev,
ZGRADBA ATOMA IN PERIODNI SISTEM Kemijske lastnosti elementov se periodično spreminjajo z naraščajočo relativno atomsko maso oziroma kot vemo danes z naraščajočim vrstnim številom. Dmitrij I. Mendeljejev,
VEKTORJI. Operacije z vektorji
 VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
VEKTORJI Vektorji so matematični objekti, s katerimi opisujemo določene fizikalne količine. V tisku jih označujemo s krepko natisnjenimi črkami (npr. a), pri pisanju pa s puščico ( a). Fizikalne količine,
Gradniki TK sistemov
 Gradniki TK sistemov renos signalov v višji rekvenčni legi Vsebina Modulacija in demodulacija Vrste analognih modulacij AM M FM rimerjava spektrov analognih moduliranih signalov Mešalniki Kdaj uporabimo
Gradniki TK sistemov renos signalov v višji rekvenčni legi Vsebina Modulacija in demodulacija Vrste analognih modulacij AM M FM rimerjava spektrov analognih moduliranih signalov Mešalniki Kdaj uporabimo
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ
 GR ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ H OLJLAJNYOMÁSÚ SZEGECSELŐ M4/M12 SZEGECSEKHEZ HASZNÁLATI UTASÍTÁS - ALKATRÉSZEK SLO OLJNO-PNEVMATSKI KOVIČAR ZA ZAKOVICE
GR ΠΡΙΤΣΙΝΑΔΟΡΟΣ ΛΑΔΙΟΥ ΑΕΡΟΣ ΓΙΑ ΠΡΙΤΣΙΝΙΑ M4/M12 ΟΔΗΓΙΕΣ ΧΡΗΣΗΣ - ΑΝΤΑΛΛΑΚΤΙΚΑ H OLJLAJNYOMÁSÚ SZEGECSELŐ M4/M12 SZEGECSEKHEZ HASZNÁLATI UTASÍTÁS - ALKATRÉSZEK SLO OLJNO-PNEVMATSKI KOVIČAR ZA ZAKOVICE
FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22. junij Navodila
 FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22 junij 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Veljale bodo samo rešitve na papirju, kjer
FAKULTETA ZA STROJNIŠTVO Matematika 4 Pisni izpit 22 junij 212 Ime in priimek: Vpisna št: Navodila Pazljivo preberite besedilo naloge, preden se lotite reševanja Veljale bodo samo rešitve na papirju, kjer
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL
 POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
POROČILO 3.VAJA DOLOČANJE REZULTANTE SIL Izdba aje: Ljubjana, 11. 1. 007, 10.00 Jan OMAHNE, 1.M Namen: 1.Preeri paraeogramsko praio za doočanje rezutante nezporedni si s skupnim prijemaiščem (grafično)..dooči
Inverzni problem lastnih vrednosti evklidsko razdaljnih matrik
 Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Peter Škvorc Inverzni problem lastnih vrednosti evklidsko razdaljnih matrik DIPLOMSKO DELO UNIVERZITETNI
Univerza v Ljubljani Fakulteta za računalništvo in informatiko Fakulteta za matematiko in fiziko Peter Škvorc Inverzni problem lastnih vrednosti evklidsko razdaljnih matrik DIPLOMSKO DELO UNIVERZITETNI
Državni izpitni center SPOMLADANSKI IZPITNI ROK *M * NAVODILA ZA OCENJEVANJE. Sreda, 3. junij 2015 SPLOŠNA MATURA
 Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
Državni izpitni center *M15143113* SPOMLADANSKI IZPITNI ROK NAVODILA ZA OCENJEVANJE Sreda, 3. junij 2015 SPLOŠNA MATURA RIC 2015 M151-431-1-3 2 IZPITNA POLA 1 Naloga Odgovor Naloga Odgovor Naloga Odgovor
MERITVE LABORATORIJSKE VAJE. Študij. leto: 2011/2012 UNIVERZA V MARIBORU. Skupina: 9
 .cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
.cwww.grgor nik ol i c NVERZA V MARBOR FAKTETA ZA EEKTROTEHNKO, RAČNANŠTVO N NFORMATKO 2000 Maribor, Smtanova ul. 17 Študij. lto: 2011/2012 Skupina: 9 MERTVE ABORATORJSKE VAJE Vaja št.: 4.1 Določanj induktivnosti
Laboratorij za termoenergetiko. Vodikove tehnologije in PEM gorivne celice
 Laboratorij za termoenergetiko Vodikove tehnologije in PEM gorivne celice Pokrivanje svetovnih potreb po energiji premog 27% plin 22% biomasa 10% voda 2% sonce 0,4% veter 0,3% nafta 32% jedrska 6% geoterm.
Laboratorij za termoenergetiko Vodikove tehnologije in PEM gorivne celice Pokrivanje svetovnih potreb po energiji premog 27% plin 22% biomasa 10% voda 2% sonce 0,4% veter 0,3% nafta 32% jedrska 6% geoterm.
Elektroni in ioni. Piezoelektrični pojav. Termoelektrični pojav
 39 Elektroni in ioni Piezo- in termoelektrika Termični elektroni Curki elektronov Odklon curka v poljih Relativistični odklon Masni spektrometer ionov Naboji na kapljicah Elektroni v snovi Dielektričnost
39 Elektroni in ioni Piezo- in termoelektrika Termični elektroni Curki elektronov Odklon curka v poljih Relativistični odklon Masni spektrometer ionov Naboji na kapljicah Elektroni v snovi Dielektričnost
Glukoneogeneza. Glukoneogeneza. Glukoneogeneza. poteka v jetrih in ledvični skorji, v citoplazmi in delno v mitohondrijih.
 poteka v jetrih in ledvični skorji, v citoplazmi in delno v mitohondrijih. Izhodne spojine:, laktat, in drugi intermediati cikla TKK glukogene aminokisline, glicerol Kaj pa maščobne kisline? Ireverzibilne
poteka v jetrih in ledvični skorji, v citoplazmi in delno v mitohondrijih. Izhodne spojine:, laktat, in drugi intermediati cikla TKK glukogene aminokisline, glicerol Kaj pa maščobne kisline? Ireverzibilne
IZVODI ZADACI ( IV deo) Rešenje: Najpre ćemo logaritmovati ovu jednakost sa ln ( to beše prirodni logaritam za osnovu e) a zatim ćemo
 IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
IZVODI ZADACI ( IV deo) LOGARITAMSKI IZVOD Logariamskim izvodom funkcije f(), gde je >0 i, nazivamo izvod logarima e funkcije, o jes: (ln ) f ( ) f ( ) Primer. Nadji izvod funkcije Najpre ćemo logarimovai
