REAALAINETE KESKUS JAAK SÄRAK
|
|
|
- Μέλισσα Τοκατλίδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 REAALAINETE KESKUS JAAK SÄRAK TALLINN
2 DESCRIPTIVE GEOMETRY Study aid for daily and distance learning courses Compiler Jaak Särak Edited by Tallinn College of Engineering This publication is meant for the students of the faculties of constructions, architecture, transport and mechanical engineering. This publication contains projections of points, lines, planes and solid figures on plane surfaces (on technical drawings) by the method of Monge s orthogonal projections, also it contains projections of solid figures in there dimensional room (aonometric projections). There is graphical solving of measurement eercises included; intersection of solid figures with planes and mutual intersection of them. Drawings of spread surfaces of solid figures are also handled. At the end of publication there are principles of making projections of the shadows of solid figures and quoted orthogonal projections SAATEKS Käesolevas õppematerjalis on esitatud kujutava geomeetria kursus, mis vastab selle aine programmidele Tallinna Tehnikakõrgkoolis. Varjude osa ja perspektiiviõpetust (käesolevas loengukonspektis ei ole) käsitletakse arhitektuurieriala üliõpilastele eraldi õppeprogrammides (käesolevas loengukonspektis on varjude osa toodud täiendusena aine programmile ning jääb arhitektuurieriala üliõpilastele ka napiks). Antud väljaanne on võrreldes eelmise loengukonspektiga, mis on välja antud a, parandatud ja täiendatud, ümber töötatud on kõik joonised ning lisatud ka uusi näiteid. Tallinnas 30. juulil a. Koostaja 2
3 SISUKORD 1. SISSEJUHATUS , SELLE SISU JA EESMÄRK JOONISTE VORMISTAMINE TÕSIASJU ELEMENTAARGEOMEETRIAST PROJEKTSIOONIDE LIIGID JA ELEMENDID TSENTRAALPROJEKTSIOON Projektsioonide üldomadused: PARALLEELPROJEKTSIOON Paralleelprojektsioonide omadused: RISTPROJEKTSIOON Sirglõigu ristprojektsioon Nurga ristprojektsioon Ristprojektsiooni omadused AKSONOMEETRIA RISTAKSONOMEETRIA Ristisomeetria Standardne ristdimeetria KALDAKSONOMEETRIA Frontaalne kalddimeetria e. kabinetprojektsioon Frontaalne kaldisomeetria Horisontaalne kaldisomeetria PUNKTI JA SIRGE PROJEKTSIOONID MONGE I MEETOD. PUNKTI KAKSVAADE Punkti kaksvaade Punkti asukoht ruumiveerandite järgi PUNKTI KOLMVAADE (E.ÜLDASENDILINE PUNKT) SIRGJOONE KAKSVAADE JA KOLMVAADE SIRGLÕIGU JAOTAMINE ANTUD VAHEKORRAS ERIASENDILISED SIRGED HORISONTAAL H FRONTAAL F PROFIILSIRGE S SIRGE JÄLGPUNKTID SIRGETE VASTASTIKUSED ASENDID PARALLEELSED SIRGED LÕIKUVAD SIRGED KIIVSIRGED SIRGLÕIGU PIKKUS. KALDENURGAD TÄISNURKSE KOLMNURGA VÕTE SIRKLIVÕTE TASAPINNA PROJEKTSIOON. JÄLJED TASAPINNA MÄÄRAMINE TASAPINNA JÄLJED ERIASENDILISED TASAPINNAD NIVOOPINNAD PROJEKTEERIVAD TASAPINNAD PUNKT JA SIRGE TASAPINNAL
4 11.1. PUNKT JA SIRGE ERIASENDILISEL TASAPINNAL PUNKT JA SIRGE ÜLDASENDILISEL TASAPINNAL TASAPINNA NIVOOJOONED TASAPINNA HORISONTAAL TASAPINNA FRONTAAL TASAPINNA LANGUSJOONED. KALDENURGAD TASAPINNA LANGUSJOONED TASAPINNA KALDENURGAD SIRGE JA TASAPINNA LÕIKUMINE SIRGE JA TASAPINNA LÕIKUMINE SIRGE JA TASAPINNA PARALLEELSUS TASAPINDADE VASTASTIKUSED ASENDID TASAPINNA LÕIKUMINE EKRAANI RISTTASAPINNAGA TASAPINDADE LÕIKUMISE ÜLDJUHTUM TASAPINDADE PARALLEELSUS TASAPINNA NORMAAL NURGAD SIRGETE JA TASAPINDADE VAHEL NURK KAHE SIRGE VAHEL NURK KAHE TASAPINNA VAHEL NURK SIRGJOONE JA TASAPINNA VAHEL LISAPROJEKTEERIMINE LISAEKRAANI VÕTE Punkti projekteerimine lisaekraanile Tasapinna muutmine ekraani risttasapinnaks Sirgjoone muutmine ekraani normaaliks OBJEKTI PÖÖRAMISVÕTE Pööramine ümber ekraani normaali Pööramine ümber nivoosirge TASAPINNALISE KUJUNDI ORIGINAALVORMI TULETAMINE PÖÖRAMISE TEEL KEHA JA SIRGE LÕIKUMINE TAHUKA LÕIKUMINE SIRGEGA KERA LÕIKUMINE SIRGEGA SILINDRI LÕIKUMINE SIRGEGA KOONUSE LÕIKUMINE SIRGEGA TAHUKA LÕIKUMINE TASAPINNAGA TAHUKA LÕIKUMINE ERIASENDILISE TASAPINNAGA TAHUKA LÕIKUMINE ÜLDASENDILISE TASAPINNAGA PÖÖRDPINDADE LÕIKAMINE TASAPINNAGA SFÄÄRI JA PÖÖRDSILINDRI LÕIKED PÖÖRDKOONUSE LÕIKED TAHUKATE LÕIKUMINE. PINNALAOTUSED HULKTAHUKAD TAHUKATE PINNALAOTUSED TAHUKATE LÕIKUMINE PÖÖRDKEHADE LÕIKUMINE KÕVERPINNA JA TASAPINNA LÕIKUMINE KÕVERPINNA JA SIRGJOONE LÕIKUMINE ABITASAPINDADE VÕTE LÕIKEJOONTE TULETAMISEL ABISFÄÄRIDE VÕTE LÕIKEJOONE TULETAMISEL Kontsentrilised abisfäärid
5 Ekstsentrilised abisfäärid NIVOOSIRGETE (ABISIRGETE) VÕTE Silindrite lõikumine VARJUD PÕHIMÕISTED VARJUDE KONSTRUEERIMINE KAKSVAATEL VARJUD AKSONOMEETRILISTEL KUJUTISTEL KVOODITUD RISTPROJEKTSIOON PUNKTI JA SIRGJOONE KVOODITUD RISTPROJEKTSIOON PINDADE RISTPROJEKTSIOONID JA NENDE LÕIKUMISED Pindade ristprojektsioonid Tasapindade lõikumine Pöördpinna lõikumine tasapinnaga KATUSED ANTUD KALDENURGAGA PIND LÄBI ANTUD JUHTJOONE Tasapind läbi antud sirge. Muldkeha kalded Etteantud kaldega pind läbi antud kõverjoone TOPOGRAAFILISE PINNA LÕIKUMINE TEISTE PINDADEGA Ühesuguse kaldega tasapinna lõikumine topograafilise pinnaga Mullatööde piirete määramine topograafilistel pindadel KORDAMISEKS SOOVITATAV KIRJANDUS
6 1. SISSEJUHATUS 1.1. Kujutav geomeetria, selle sisu ja eesmärk Kujutav geomeetria on geomeetria eriharu, milles käsitletakse: 1) objektidest tasapinnaliste kujutiste (jooniste) tuletamist; 2) ruumigeomeetriliste ülesannete lahendamist kujutiste abil. Kui geomeetria muudes harudes (stereomeetria, analüütiline geomeetria) lahendatakse ülesanded arvutuslike meetoditega, siis kujutavas geomeetrias lahendatakse kõik graafiliselt. Seega on siin joonisel eriline koht. Siin on joonis põhivahend, mujal illustreeriva tähendusega. Seega peab joonis üheselt määrama kujutatud objekti kõik geomeetrilised omadused. Kui see tingimus on täidetud, siis nimetatakse teda objekti määravaks jooniseks. Kõige tähtsamad on tehnilised joonised, mille järgi toimub nn jooniste lugemine, s.o objekti kuju, suuruse ja tema osade vastastikuse asendi kindlakstegemine joonise järgi. Kujutava geomeetria eesmärgid: 1) teoreetilise aluse andmine jooniste lugemiseks ja valmistamiseks ning sellega aluse rajamine tehnilisele joonestamisele ja muudele joonestamise harudele; 2) inimese ruumikujutluse arendamine. Hästi väljaarenenud ruumikujutlus on eriti tähtis konstruktoritel, arhitektidel, ehitusinseneridel jne. Kujutav geomeetria on õppeaine, kus kõik järgnev õppematerjal tugineb eelneval, seepärast tuleb kõik eelnev alati üle korrata ja selgeks teha. Mõne osa vahelejätmine põhjustab edasise mittemõistmist. Kujutav geomeetria on õppeaine, mis nõuab kujutlemisoskust. Kujutlemisraskuste ületamiseks kasutage abivahendeid, tehke mudeleid jne. Harjutusülesanded, kordamisküsimused Jooniste vormistamine 1. Vahendid Pliiatsid kõvadusega 3H, 2H, H, F, HB,B,2B (vene tähistusega 3T, 2T,T,TM, M, 2M) Sirklid: mõõtsirkel, joonsirkel Kumm, žilett, nuga, kustutusplaat, kleeplint, kolmnurgad Mõõtjoonlaud, mõõtkavajoonlaud, lekaalid, mall, trafaretid, pehme harjake, tušiga töötamise vahendid, joonsuled, rapidograafid (0,25; 0,35; 0,5; 0,7; 1,0) Personaalarvuti CAD projekteerimisega, kasutades erinevaid joonestusprogramme 2. Normkiri Kiri on joonise lahutamatu osa. Joonise kvaliteet oleneb kirja korrektsusest. Kiri kirjutatakse, ei joonestata. Ladina tähestik: A B C D E F G H I J K L M N O P Q R S Š T U V W Õ Ä Ö Ü X Y Z 6
7 a b c d e f g h i j k l m n o p q r s š t u v w õ ä ö ü y z Kreeka tähestik: Αα - alfa Ββ - beeta Γγ - gamma δ - delta Εε - epsilon Ζζ - dzeeta Ηη - eeta Θθ - teeta Ιι - joota Κκ - kappa Λλ - lambda Μµ - müü Νν - nüü Ξξ - ksii Οο- omikron Ππ - pii Ρρ - roo Σσ - sigma Ττ - tau Υυ - üpsilon ϑϕ - fii Χχ - hii Ψψ - psii Ωω - oomega Numbrid: Kirja suuruseks loetakse suurtähe kõrgust h = (2,5; 3,5; 5; 7; 10; 14; 20) millimeetrites. Vastavalt kirja kõrgusele on kirjal number. ISO 3098/1 järgi on kahte tüüpi kirja A- ja B-tüüpi; nii püst- kui kaldkirja. Joonisel 1 on toodud B- tüüpi kaldkirja nr 5 näide koos mõõtudega. Meie kasutame töödes B-tüüpi kaldkirja. Väiketähe kõrgus c = (7/10) h a. Harjutusülesanded: 5 ISO h 1,5 f 1,5 15 ο 1 ISO 81 taip 0,5 Formaat A4 a d 3,5 c 7 b 297 Tähtede vahe a = (2/10) h b. 25 Ridade alusjoonte vahe b = (14/10)h Sõnade vahe min Graafilised tööd ja kontrolltööd: 420 Ain Kaasik MI e = (6/10) h Kirja joone jämedus Formaat A3 d = (1/10) h Tsentreerimisjoon Väiketähtede üla- ja alapikendus f = (3/10)h Tähe laius (taval.) g = ( 6/10) h 3. Formaadid Formaadid (paberi mõõdud): (siin Raamjoon Formaadi äärejoon Joonis 1. a kirja näidis (B tüüpi kaldkiri nr 5); b jooniste lehtede formaadid A4 ja A3. toome ainult põhiformaadid.) A A A A A
8 Kirjanurk (vt joonis 2) kujutavas geomeetrias on väiksem kui insenerigraafikas TTK Ain Kuusik 3437 MI-11 Hulktahu lõige Nr 3 10 Töö nimetus Üliõpilaspileti või õppemärkmiku number Töö number Joonis 2. Graafilistel töödel kasutatav kirjanurk Mõõtkavad. 1:2; 1:5; 1:10; 1:20; 1:50 jne vähendav suurus; 1:1 loomulik suurus; 2:1; 5:1; 10:1; 20:1; 40:1; 100:1; 200:1 jne suurendav. Joonte liigid. Joonise hõlpsamaks lugemiseks ja joonisest arusaamiseks on kehtestatud kindlad joonte liigid, määratud nende jämedused, kasutusalad. Pidev jämejoon: Kriipsjoon: Kriips-kakspunktpeenjoon: Kriips-punktpeenjoon s nähtavad kontuur- ja üleminekujooned, pidev jämejoon ehk põhijoon, lõigete kontuurid. Joone jämedus s = 0,5...1,4 mm, meie võtame s = 0,7...0,9 mm. Arvutijoonistel võtame s = 0,7 mm s/2 või s nähtamatud kontuurjooned, nähtamatud üleminekujooned s/2 liikuvate osade äärmised asendid s/2 mitmesugused telg ja tsentrijooned Pidev peen- s/2 igasugused abijooned, viirutusjooned, joon: viitejooned, projektsioonteljed, tasapindade jäljed, painutusjooned pinnalaotusel jne Pidev vabakäejoon: Murretega peenjoon: Jämendatud s/2 katkestusjooned, kohtlõike ja -vaate üleminekujoon s/2 pikad katkestusjooned s.1,5s lõikepinna asukohta ehk kulgemist 8
9 kriipsud: näitavad jooned (ISO128-24:1999(E) järgi kriips-punktpeenjoont jämendatud joonte vahel ei ole vaja kasutada) Joonte jämedused ja nende kasutusala vastab standardile ISO128-24:1999(E) ja nende kasutusala insenerigraafikas on tunduvalt laiem Tõsiasju elementaargeomeetriast 1. Kaks sirgjoont, mis on paralleelsed kolmandaga, on paralleelsed omavahel. 2. Kui paralleelsed sirged lõikavad nurga haarasid, siis lõigud, milleks paralleelid jaotavad nurga ühe haara, on võrdelised lõikudega, milleks nad jaotavad nurga teise haara. 3. Sirgjoon ja tasapind on paralleelsed, kui tasapinnal leidub antud sirgega paralleelne lõik. 4. Kaks tasapinda on paralleelsed, kui ühe tasapinna kahel lõikuval sirgel on kummalgi oma paralleel teisel tasapinnal. 5. Sirgjoon ja tasapind on teineteisega risti, kui tasapinnal leidub kaks lõikuvat sirget, mis on risti antud sirgega. 6. Kaks tasapinda, mis on paralleelsed kolmandaga, on paralleelsed ka omavahel. 7. Paralleelsete tasapindade lõikamisel tasapinnaga tekivad paralleelsed lõikesirged. 8. Kolme tasapinna lõikesirged on kas paralleelsed või lõikuvad kõik ühes punktis. 9. Tasapinna normaal (ristsirge) on risti iga sirgega, mis asetseb sellel tasapinnal. 10. Igast punktist saab läbi panna üheainsa sirge, mis on risti antud tasapinnaga. 11. Igast punktist saab läbi panna üheainsa tasapinna, mis on risti antud sirgega. 12. Iga tasapind, mis läbib antud tasapinna normaali, on selle antud tasapinnaga risti. 13. Kui sirge ei ole risti antud tasapinnaga, siis saab temast läbi panna ühe tasapinna, mis on antud tasapinnaga risti. Selle tasapinna määrab antud sirge koos tasapinna iga normaaliga, mis lõikab antud sirget. 14. Kahe kiivsirge vahelist nurka mõõdetakse tavalise nurgaga, mille haarad on paralleelsed nende kiivsirgetega. 15. Kahetahulist nurka mõõdetakse nurgaga, mille haarad asetsevad teine teisel tahul ja on risti tahkude lõikejoonega. Kahetahulist nurka võib mõõta ka nurgaga nende tasapindade normaalide vahel. 2. PROJEKTSIOONIDE LIIGID JA ELEMENDID Kujutise saamist objektist nimetatakse projekteerimiseks Tsentraalprojektsioon Kirjeldataval projekteerimisel lähtuvad kõik kiired ühest punktist (tsentrist S) s.o tsentraalprojekteerimine ja saadavat kujutist nimetatakse tsentraalprojektsiooniks e perspektiiviks. Seega A B C on ABC tsentraalprojektsioon. Igale S D A M N C B C' ε Joonis 3. Tsentraalprojektsioon M'=N' 9
10 ruumipunktile saab leida selle meetodiga projektsiooni, välja arvatud ekraaniga paralleelsete kiirtega projekteerimisel. See tähendab, et punkti D projektsiooni me ei saa. Kiir SD ε ja punkti D kujutist lõplikul kaugusel ei ole. Elemendid: tasapind ε ekraan e projektsioonipind sellel saadakse kujutis; punkt S projekteerimistsenter e silmapunkt; kiired SA, SB, SC kujutamiskiired e projekteerivad kiired Projektsioonide üldomadused 1. Punkti projektsioon ekraanil on seda punkti läbiva kujutamiskiire ja ekraani lõikepunkt. See kirjutatakse nii: A SA ε (A prim on kiire SA ja ekraani ε lõikepunkt). 2. Mistahes objekti projektsioon koosneb selle objekti punktide projektsioonidest. Punktid sirgel B C projekteeruvad B C -le. Kõverjoonte projektsiooni on just punktide kaudu lihtne teha. 3. Sirgjoone projektsioon on üldjuhul sirge, sest ta on sirgjoont projekteeriva tasapinna ja ekraani lõikesirge. Erijuhul punkt M K. 4. Kui punkt on mingil joonel, siis selle punkti projektsioon on selle joone projektsioonil. S 5. Kui tasapinnalist kujundit projekteerivad kiired asetsevad kõik kujundi tasapinnas (vt A B joonis 4), siis see kujund projekteerub sirglõiguks s.o tasapinna sirgkujutis, ning sirgjoone punktikujuline projektsioon C sirgjoone punktkujutis. 6. Objekti üksainus projektsioon ilma C' lisaandmeteta ei määra seda objekti ruumis. Nagu punkti A projektsioon silmapunktist S võib olla tegelikult ükskõik kus sellel kiirel SA Paralleelprojektsioon ε Joonis 4. Projektsioonide üldomadused tasapinnalist kujundit projekteerivad kiired asuvad kõik kujundi tasapinnas Kui kujutamiskiired on omavahel paralleelsed, siis on see paralleelprojekteerimine; vastav kujutis aga paralleelprojektsioon. Paralleelprojekteerimist võib võtta ka kui tsentraalprojekteerimise erijuhtu, kus silmapunkt on viidud lõpmata kaugele (S ). Siin antakse S asemel kujutamiskiirte siht K (vt joonis 5). C A B K ε Paralleelprojektsioonid jagunevad kald- ja ristprojektsioonideks. Ristprojektsiooni nimetatakse ka ortogonaalprojektsiooniks. C' Joonis 5. Paralleelprojektsioon 10
11 Paralleelprojektsioonide omadused Kehtivad p 2.1. omadused 1...6, lisaks veel aga järgmised. 7. Kui sirglõik on paralleelne ekraaniga, siis tema paralleelprojektsioon sellel ekraanil on pikkuselt võrdne ja paralleelne lõigu enesega. Tõestus: AB ε ja asetseb tasapinnal µ, µ ε (vt joonis 6). µ ja ε lõikamisel tasapinnaga ABB A tekivad paralleelsed lõikesirged, siis A B AB; ABB A rööpkülik ja A B =AB. B C A D µ C'=D' ε Joonis 6. Paralleelprojektsioonide omadused: sirglõik on paralleelne ekraaniga 8. Sirgjoone lõigud on võrdelised oma paralleelprojektsioonidega. Tõestus: kui sirgjoon AC ja tema paralleelprojektsioon A C asuvad samal projekteerival tasapinnal, siis sirged kas lõikuvad või on paralleelsed. Lõikepunkt L; AA BB CC ; siis lõikavad nad nurga haaradest võrdelised lõigud (vt 1.3. p2), seega AB : BC = A B : B C (vt joonis 7). Siit järeldub: 1) lõigu keskpunkt projekteerub sama lõigu kujutise keskpunktiks; 2) kolmnurga raskuskese (mediaanide lõikepunkt) projekteerub kujutiskolmnurga raskuskeskmeks. Sirglõigu paralleelprojektsioon võib olla lõigust kas lühem või pikem või võrdne. Projektsiooni pikkuse ja lõigu enda suhet nimetatakse moondeteguriks (m). Näiteks lõigu AB moondetegur m = A B AB; valemist AB BC = A B B C ; A B /AB = B C / BC = m; A B = m AB ja B C = m BC ning sõltuvalt kujundi, kiirte ja ekraani asendist võib paralleelprojektsiooni pikkus muutuda 0, seega ka moondeteguri m vahemik on 0 m. ε L=L' A B C' C Joonis 7. Paralleelprojektsioonide omadused: sirgjoone lõigud on võrdelised oma paralleelprojektsioonidega 9. Paralleelsete sirgete paralleelprojektsioonid on üldjuhul jälle paralleelsed sirged. Tõestus: AB CD siis ka π τ, sest ka AA CC ja tekivad lõikesirged A B C D. Erandid: 1. Kui paralleelid on kujutamiskiirtega paralleelsed, siis projekteeruvad nad punktideks. ε A π G τ B C M C' =G' Joonis 8. Paralleelprojektsioonide omadused: paralleelsete sirgete paralleelprojektsioonid D N D' 11
12 Märkus: punkt 9 aga ei ole pööratav, st ei saa öelda, et kui A B C D, siis ka AB CD, sest ka AG, mis on kiivne sirge, ei ole paralleelne CD-ga A B A G = C D, aga AG CD. 2. Kui sirged, sõltumata nende arvust, asuvad ühel ja samal tasapinnal, mis on kiirtega paralleelne, siis nad projekteeruvad üheks ainsaks sirgeks. 10. Paralleelsed sirged on võrdelised oma paralleelprojektsioonidega. Tõestus: tasapindadel π ja τ lõigud A M AB ja C N CD, saame A B M ja C D N, kus A M = AB ja C N = CD; siit AB CD = A B C D või A B AB = C D CD = m, st paralleelsetel lõikudel on sama moondetegur. 11. Kui tasapinnaline kujund on paralleelne ekraaniga, siis tema paralleelprojektsioon on kongruentne kujundi endaga. Kujund γ mistahes lõik temal on paralleelne lõiguga ekraanil ε kui kujundi tasapind on paralleelne ekraaniga ε k A ' γ' A γ Joonis 9. Paralleelprojektsioonide omadused: tasapinnaline kujund on paralleelne ekraaniga B ε, s.o lause 7 põhjal ja seda moondevabalt; järelikult A B = AB γ ja γ on kongruentsed. Kui aga kujundi tasapind on paralleelne kujutamiskiirtega (vt 2.1 p 5), siis tema paralleelprojektsiooniks on sirglõik. Võrreldes paralleelprojekteerimist tsentraalprojekteerimisega, võib välja tuua järgmist. 1. Paralleelprojekteerimisel säilib sirgjoonte paralleelsus ja lõikude lihtsuhe. Objektide mõõtmed on vähem moonutatud kui tsentraalprojektsioonil. 2. Paralleelprojektsiooni tuletamine on tunduvalt lihtsam tsentraalprojektsiooni tuletamisest. Tehnikas eelistatakse paralleelprojektsiooni, eriti aga ristprojektsioone Ristprojektsioon Kui kujutamiskiired on risti ekraaniga, siis saadud kujutis on ristprojektsioon. Ta kuulub paralleelprojektsioonide hulka ja tema kohta kehtivad kõik paralleelprojektsioonide omaduste M M' ε L=L' ε N ϕ A L N'=L' Joonis 10. Paralleelprojektsioonide omadused: tasapinnaline kujund on paralleelne kujutamiskiirtega ϕ K K' B M Joonis 11. Ristprojektsiooni omadused: sirglõigu ristprojektsioon k 12
13 laused (vt 2.1 ja 2.2). Sirgjoone kaldenurk ϕ, teravnurk ( ), selle sirgjoone ja tema ristprojektsiooni vahel sellele tasapinnale. Nurga tipp L on sirgjoone ja ekraani lõikepunkt. Nurk ϕ on sirgjoone kaldenurk Sirglõigu ristprojektsioon Tõmbame abijoone A M AB (vt jn 11). Tekib A B M, sealt A B = A M cosϕ, aga A M = AB, siis AB = AB cosϕ. Siit järeldub, et sirglõigu ristprojektsioon ei saa olla lõigust enesest pikem. Ta on aga piires 0...AB-ni. Et A B AB = cosϕ = m, siit cos ϕ = m (moondetegur), seega 0 m Nurga ristprojektsioon Nurga ristprojektsioon võib olla nurgast enesest kas väiksem, suurem või võrdne. Sõltub nurga tasapinna asendist ekraani ja kiirte suhtes: a S b π a) kui nurga tasapind on risti ekraaniga, siis nurga ristprojektsioon on kas 0 või 180; b) kui nurga tasapind on paralleelne ekraaniga, siis projektsioon on võrdne nurga enesega (vt 2. 2 p11). b' a' ε Nurga ristprojektsioon Kui a//a' ja b ε, siis 90 =90 ' Ristprojektsiooni omadused Lisaks eelpooltoodud omadustele on ristprojektsioonil veel järgmised omadused. 12. Sirglõigu ristprojektsiooni pikkus võrdub sirglõigu enda pikkuse ja kaldenurga koosinuse korrutisega (vt jn 11) (vt Sirglõigu ristprojektsiooni pikkus). 13. Täisnurk projekteerub ristprojekteerimisel täisnurgaks, kui tema üks haar asetseb ekraanil või on sellega paralleelne, teine haar aga pole selle ekraaniga risti. Tõestus: kui a ja b on täisnurga haarad ja a ja b nende haarade ristprojektsioonid ekraanil. Haar a aga on paralleelne ekraaniga (a ε), siis a s, sest s ε ja a ε. a b, seega a π ja b asub projektsioonpinnal π ning paralleelprojektsioonide omaduse (7.) põhjal a a (sest a ε), järelikult ka a π ja a b. 13a. Nurk, mille üks haar asetseb ekraanil või on ekraaniga paralleelne ning mille ristprojektsioon on täisnurk, on ka ise täisnurk. Meil on kolmnurgad ACB ja AC B, seal nurk ϕ(a, A= c ε Joonis 12. Ristprojektsiooni omadused: nurga ristprojektsioon β B= ϕ b b' a ϕ' a' α C k C' Joonis 13. Ristprojektsiooni omadused: nurga ristprojektsioon 13
14 b) ja tema projektsioon ϕ (a b ). Koosinuslause põhjal nendest kolmnurkadest c 2 = a 2 + b 2-2ab cos ϕ c 2 = (a ) 2 + (b ) 2-2a b cos ϕ, siit nende valemite vasakust poolest saame, et c 2 - c 2 = 0. Lahutades ka paremad pooled saame- a 2 - (a ) 2 + b 2 -(b ) 2-2abcos ϕ + 2a b cosϕ =0 Kolmnurkadest BCC ja ACC leiame, et a 2 - (a ) 2 = k 2 = b 2 -(b ) 2. Pannes selle eelmisesse valemisse asemele, saame 2k 2-2abcos ϕ + 2a b cos ϕ = 0 aga k/a = sinα ja k/b = sinβ; a /a = cosα ja b /b= cosβ siis teisendades eelmist valemit saame: sinα sinβ - cosϕ + cosα cosβ cosϕ = 0. cosϕ cosα sin β Siit cosϕ =, cosα cos β kus 0 < ϕ < 180; 0 α; β AKSONOMEETRIA Objekti kujutis peab olema lihtne, mõõdetav ja piltlik. Lihtne mida vähem jooni, seda lihtsam. Mõõdetav seda parem, mida rohkem tasapinnalisi kujundeid on projekteerunud moondevabalt. Piltlik seda parem mida hõlpsamini me tema järgi objekti ära tunneme; selleks tuleb objekt seada kiirte ja ekraani suhtes üldasendisse, s.o asendisse, mille puhul võimalikult palju objekti servi ja tahke on kiirte suhtes kaldu. Kõige piltlikuma kujutise saame tsentraalprojekteerimisega. Seda tehakse arhitektuuris. Hõlpsasti saab aga piltlikke (ruumilisi) kujutisi aksonomeetriliste kujutiste abil. Aksonomeetriliste projektsioonide esmaseks ülesandeks on ilmekate (ruumiliste) kujutiste saamine. Seda kujutamismeetodit nimetatakse aksonomeetriaks (kreeka keeles akson telg, metreo mõõdan). Ilmekuse saavutamiseks tuleb ese asetada võimalikult üldisesse asendisse ekraanide suhtes ning siduda mingi kindla teljestiku ja koordinaatidega. Andmetena kasutame aksonomeetriliste projektsioonide saamiseks kaksvaadet. Tegevuse järjekord selleks on järgmine. 1. Objekt seotakse ruumilise ristteljestikuga objekti iga punkt saab oma koordinaadid selles teljestikus. 2. Joonestatakse teljestiku kujutis. 3. Konstrueeritakse objekti enda kujutis teljestiku kujutise baasil, kasutades selleks saadud objekti punktide koordinaate selles teljestikus. Tulemuseks saame objekti aksonomeetrilise kujutise. Suur tähtsus on telgede asendil ja moondeteguritel telgede suhtes. Siin on moondetegur telgedel oleva ühiklõigu aksonomeetrilise kujutise ja tema loomuliku suuruse suhe erinevate telgede suundades. Moondetegurid: m = O 0 A 0 OA; m y = O 0 B 0 OB; 14
15 m z = O 0 C 0 OC, O A C γ siit näiteks: z α C B O 0 A 0 = m OA, kus Z β z OA = O O 0 A 0 m jne X A B Lähtuvalt teljestiku Y asendist ja telgede ε y moondetegurite vahekorrast liigitatakse aksonomeetrilisi y kujutisi järgmiselt. Joonis 14. Aksonomeetria teljestik 1. Kui moondetegur on kõikide telgede suundades ühesugune (m = m y = m z ), siis aksonomeetrilised kujutised on isomeetrilised e. võrdmõõdulised (ristisomeetria, frontaalne kaldisomeetria, horisontaalne kaldisomeetria). 2. Kui kahe telje suunas on moondetegur ühesugune, kolmanda suunas aga erinev (m = m z ; m y m z ), siis kujutised on dimeetrilised e. kahemõõdulised (ristdimeetria, frontaalne kalddimeetria, horisontaalne kalddimeetria). 3. Kui moondetegur on kõikide telgede suunas erinev (m m y m z ), siis aksonomeetrilised kujutised on trimeetrilised e. kolmemõõdulised (risttrimeetria, frontaalne kaldtrimeetria, horisontaalne kaldtrimeetria). Praktikas harilikult trimeetriat ei kasutata. Aksonomeetria põhiteoreem ütleb: tasapinnale joonestatud kolme lõiku, mis algavad kõik ühest punktist, kuid ei asetse ühel sirgel, võib alati vaadelda ristteljestiku ühikkolmiku paralleelprojektsioonina. Selle teoreemi alusel võib teljestiku ühikkolmiku paralleelprojektsiooni joonestada vabalt, ainsa kitsendusega, et kogu teljestiku kujutis ei tohi asetseda ühel sirgel Ristaksonomeetria Ristaksonomeetria jaguneb: a) ristisomeetria; b) ristdimeetria. 1. Ristteljestiku telgede ristprojektsioonid on jälgkolmnurga kõrgussirgeteks. Kolmnurka XYZ, mille tippudeks on telgede jälgpunktid ja külgedeks on koordinaatpindade XOY, YOZ ja ZOX jälgsirged, nimetatakse telgede jälgkolmnurgaks (vt joonis 14). 2. Moondeteguritevaheline seos: m = O 0 /O = cosα ; m y = O 0 y/oy = cosβ; m z = O 0 z/oz = cosγ Ristprojektsiooni puhul on telgede moondetegurite ruutude summa võrdne 2, s.o Tõestus vt [1] lk m 2 + m y 2 + m z 2 = 2. 15
16 3. Kahe koordinaattelje tasapinnal (või selle paralleeltasapinnal) asetseva ringjoone ristaksonomeetrilise kujutise (ellipsi) pikem telg on risti kolmanda koordinaattelje kujutisega. Telgede suurused on: pikem telg a = r; Tõestus vt[1] lk Ristisomeetria 2 y m z 2 z m y 2 yz m lühem telg b = r 1 ; b = r 1 ; b = r 1. Kasutades ekraanide suhtes ristuvaid kiiri ja teljestikku, kus kõik teljed on ekraanide suhtes võrdse nurga all, saame ristisomeetria teljestiku (vt jn 15). Teljestik: Siin on moondetegurid kõikide telgede suunas võrdsed: m = m y = m z, siis m 2 + m 2 y +m 2 z = 2, siit 3m 2 = 2 (selle väite tõestuse võib leida [1], lk ). 2 Järelikult moondeteguri väärtus on: m = m y = mz = = 0, 82 ; 3 2 s.o cos α = m =, st telgede kalle ekraanide suhtes on α = β = γ = Seetõttu 3 on ka nurgad telgede kujutiste vahel kõik võrdsed, st suurusega 120. Teljestiku kujutist koos moondeteguritega ja praktikas nende asemel kasutatavate taandatud moondeteguritega vt joonisel 15. Tegelikult moondetegurit m = 0,82 ei kasutata, vaid seda suurendatakse km = 1,0, kus tegur k = 1,0 = 1,22 ; st joonestamisel muudetakse mõõtkava ja seda uut moondetegurit 0,82 nimetatakse taandatatud moondeteguriks. Ringjooned need muutuvad ellipsiteks, mille pikem pooltelg a = kr = 1, 22r, 2 lühem pooltelg b = kr 1 m = kr 1 2 0, 71r. 3 Edukalt saab ellipseid konstrueerida kasutades kõõlude meetodit. Kera ristisomeetriline kujund on ring, millel raadius R = 1,22 r. Joonisel 18a on kujutatud risttahuka ristisomeetriline kujutis Standardne ristdimeetria Kui kasutada ekraanide suhtes ristuvaid kiiri, on kaks koordinaattelge ( ja y) võrdsete ja kolmas (z) telg erineva kalde all ekraanide suhtes ja saame täisnurkse ristdimeetria. Kõige levinum on standardne ristdimeetria, kus y- ja z-teljed on ja -telg ekraani suhtes kaldu. Teljestik (vt joonis 16). Moondetegurid telgede suunas m y = m z = 2m (või m = m z = 2m y ) [(2m ) 2 + (2m ) m = 9m 2 2 ], aga 9m = 2, siit m = 1 2 0,47 3 = ja m = = 2 2 0, 94 3 = y m z. 16
17 m=0,82 km=1 120 z mz=0,82 kmz=1 120 R z 120 my=0,82 kmy=1 m=my=mz= 2/3=0,82 k=1/m=1/0,82=1,22 y R z y r C B b O A a D R=2b b a a b a b y Ellipsi teljed: BD=2b CA=2a Ellipsi poolteljed: a=1,22r b=0,71r Joonis 15. Ristisomeetria teljestik, selle joonestamine ja kuubi ristisomeetriline kujutis Praktikas ei kasutata moondetegureid m = 0.47; m y = 0,94 ja m z = 0,94. Kõik moondetegurid korrutatakse teguriga k = 1 = 3 2 1, 06. Võetakse km 4 = 1/2 ja km y = km z = 1, need on m y taandatud moondetegurid ning kujutis tekib 1,06 korda originaalist suurem. Telgede joonestamiseks nurgad 0 - ja y 0 -telje ning z 0 -telje ristsihi vahel on ja ' Kuna tan /8 ja tan võib need nurgad tangensite kaudu välja joonestada. 8 Ringjooned (vt joonis16) Ringjooned muutuvad ellipsiteks, mille poolteljed on a = 1,06r; 17
18 ja 2 b kr m y r 1 1 = 1 = 1,06 0, 35r ; (kusjuures suhe 9 2 ning b kr m r 7 2 = 1 = 1,06 0, 95r. 9 Kera joonestatakse raadiusega R = 1,06r ringina. b1 = a Kui moondetegurid telgede suunas on m :m y :m z = 1:1/2:1, siis nurgad on peegelpildis. 1 3 ) z0 z0 C v25' 00 7v10' 7 A0 00 B0 y0 0 km=0,5 kmy=1,0 m=0,47 my=0,94 y0 0 z b1 a m/my/mz=0,5/1/1 a=1,06r b1=a/3 b2=0,9a a 0 b2 a b1 y Joonis 16. Standardse ristdimeetria teljestik, selle joonestamine ja kuubi standardne ristdimeetriline kujutis Kumba, kas ristisomeetriat või ristdimeetriat kasutada, sõltub objektist, tähtis on, et ei oleks kahjustatud piltlikkust. Viilkatusega hoone kujutis isomeetrias jääb igal juhul ilmetuks Kaldaksonomeetria Kaldaksonomeetria jaguneb: - frontaalne kaldisomeetria, - frontaalne kalddimeetria, - horisontaalne kaldisomeetria, - horisontaalne kalddimeetria (ei kasutata). Ristaksonomeetrias on tihti vähemalt üks detaili pind ekraaniga risti (projekteerub sirgjooneks). Sellega kaotab objekti kujutis aga oma piltlikkuse. Ristaksonomeetrias on ka objekti teljestik tavaliselt ekraani suhtes risti, et aga piltlikkust säilitada, siis välditakse teljestiku sellist asendit. 18
19 Kaldprojektsiooni puhul aga ei ole vaja vältida selliseid teljestiku lihtsaid eriasendeid, seepärast kasutataksegi praktilises kaldaksonomeetrias teljestiku ja ekraani vastastikust asendit, kus kaks telge asetsevad vahetult ekraanil (st ekraaniks on üks koordinaatpind). Kolmas telg on siis ekraaniga risti Frontaalne kalddimeetria e. kabinetprojektsioon Ekraaniks võetakse vertikaalne koordinaatpind Oz, mis on paralleelne objekti fassaadpinnaga. Teljed ja z ühtivad oma kaldprojektsioonidega ja moondetegurid z0 nendel telgedel m = m z = 1. Kaldkiirte sihi valime nii, et moondetegur m y = 0,5. Kuna y-telje moondetegur võrdub kiirte kaldenurga kootangensiga m y = OB 0 / OB = cotϕ = 0.5, siis kiirte kaldenurk ekraani suhtes ϕ 63. y-telje kaldenurk on ekraanil 45 (võib olla ka 30 või 60 ). Ringid frontaaltasapinnal (või sellega paralleelsel pinnal) on loomulikus suuruses. Teistel tasapindadel projekteeruvad ringjooned ellipsiteks, mille suur pooltelg a = 1,07R asub -telje 7 14' 0 OD m= 1,0 O0 mz= 1,0 7 14' my=0,5 b=0,33r a=1,07r o 45 o (30 või 60 ) b=0,33r a=1,07r y0 Joonis 17. Kabinetprojektsiooni teljestik, selle Joonis 17. joonestamine Kabinetprojektsiooni ja ringjoone teljestik, kujutised selle ekraanidel. joonestamine ja ringjoone kujutised ekraanidel. suhtes nurga all 7 14 (horisontaaltasapinnal) ja z-telje suhtes ka 7 14 (vertikaalsel profiilpinnal). Väike pooltelg b = 0,33R. Frontaalset kalddimeetriat nimetatakse ka kabinetprojektsiooniks. Joonisel 18b on kujutatud risttahuka kabinetprojektsioon. z a. b. z y y Joonis18. Ühesuguste mõõtudega risttahuka aksonomeetriliste kujutiste näited: a ristisomeetriline kujutis; b kujutis frontaalses kalddimeetrias e kabinetprojektsioonis Frontaalne kaldisomeetria Ekraaniks võetakse siin samuti vertikaalne z-koordinaatpind. Objekti fassaadpind on paralleelne ekraaniga. Teljed ja z ühtivad oma kaldprojektsioonidega, siis m = m z = 1. 19
20 Kui aga kaldkiirte siht on selline, et m y = 1 (sel juhul kiirte kaldenurk ekraani suhtes ϕ = 45 ) ja moondetegurid telgede suunas m = m y = m z = 1:1:1. y-telje kaldenurk ekraanil on 45 (võib ka 30 või 60 kui vaja) (vt jn 19). zo Horisontaalne kaldisomeetria Ekraaniks ε 0 võetakse horisontaalne y-pind. Siin - ja y-telg ühtivad oma kaldprojektsioonidega horisontaalsel põhipinnal ja moondetegurid m = m y = 1. z-telje moondetegur aga võrdub kiirte kaldenurga kootangensiga m z = OC 0 /OC = cotϕ. Kui kiirte kaldenurk ekraani suhtes ϕ = 45, siis m z = 1 (see on horisontaalse kaldisomeetria puhul kõige rohkem kasutatav kaldenurk) (vt jn 20). o m=1,0 mz=1,0 my=1,0 45 yo Joonis 19.Frontaalse kaldisomeetria teljestik o o o (30 või 60 ) y-telje kaldenurk soovitatakse võtta ω = 30, kuid võib kasutada ka 45 ja 60. Objekti kõik horisontaalpinnad ja -lõiked projekteeruvad moondevabalt (seal saame ka põhiplaani). Horisontaalset kaldisomeetriat on otstarbekas kasutada arhitektuursetel joonistel. mz=1,0 z0 30 o o (45 või 60 ) Joonis 20. Horisontaalse kaldisomeetria teljestik 0 m=1,0 my=1,0 y0 4. PUNKTI JA SIRGE PROJEKTSIOONID 4.1. Monge i meetod. Punkti kaksvaade Monge i meetod seisneb järgmises. Objektist tuletatakse kaks ristprojektsiooni ekraanidel, mis on teineteisega risti. Seejärel pööratakse ekraanid koos kujutistega joonise tasapinnale. Saame objekti kaksvaate. Sageli on vaja veel täiendavaid vaateid (ristprojektsioone) või lõikeid ja projekteerida neid teistele tasapindadele ja pöörata joonise tasapinnale. Niiviisi saadud joonist, mis koosneb mitmest omavahel seotud ristprojektsioonist, nimetatakse mituvaateks. Meetod sai nime kuulsa prantsuse matemaatiku ja suure geomeetria spetsialisti, inseneri, ühiskonna- ja riigitegelase Gaspard Monge järgi, kes elas aastatel Gaspard Monge andis oma raamatus Géométrie déscriptive (1799) kokkukuuluvate ristprojektsioonide meetodi ja rajas sellele kogu kujutava geomeetria teooria. 20
21 Punkti kaksvaade Meil on kaks teineteisega ristuvat ekraani ε 1 ja ε 2 ; kusjuures ε 1 ε 2 (vt jn 21). Siin joonisel: ε 1 horisontaalne põhiekraan; ε 2 vertikaalne esiekraan; ekraanide lõikesirge - telg; projekteerivad kiired: K 1 põhikiir (K 1 ε 1 ), K 2 esikiir (K 2 ε 2 ); punkti A ristprojektsioon põhiekraanil A (s.o p A põhiprojektsioon, tema pealtvaade e horisontaalprojektsioon); punkti A ristprojektsioon esiekraanil A (s.o p A a. b. ε2 A" B=B" A K2 C" ε1 K1 A Vaade ε2 suunas Vaade ε1 suunas C=C' ε2 B=B" ε1 A A" C" Vaade suunas C=C' Vaade ε2 suunas Joonis 21. Punkti kaksvaade: a punktid ruuminurgas ja nende projektsioonid teineteisega ristuvatele ekraanidele; b samade punktide joonis (kaksvaade) esiprojektsioon, tema eestvaade e frontaalprojektsioon); sirge A A p A projektsioone ühendav sidejoon, mis on alati risti -teljega (A A - telg); -telg kaksvaate telg. Pöörates põhiekraani (ε 1 ) esiekraani (ε 2 ) tasapinnale, s.o joonise tasapinnale, saame p A joonise (2 vaadet), mis koosneb p A kahest teineteisega seotud vaatest A ja A ja mida nimetatakse punkti A kaksvaateks. Kaksvaate omadused A2 1. Sidejoon A A. ε2 2. Punkti A kaugus põhiekraanist seda mõõdetakse A" A1 eestvaatel punkti A projektsiooni (A ) kaugusega -teljest A A = AA. Punkti A kaugus esiekraanist seda mõõdetakse pealtvaatel punkti A projektsiooni (A ) kaugusega -teljest A A A = AA. 3. Kui punkt on esiekraanil (nagu p B), siis tema ε1 esiprojektsioon B B [p B eestvaade (B ) langeb kokku p B Joonis 22. Punkti asukoht enesega ruumis], punkti B pealtvaade (B ), aga on -teljel. ruumis tema Põhiekraanil oleva punkti puhul aga (nagu p C) p C kaksvaate järgi. pealtvaade C C, eestvaade (C ) aga on -teljel. 4. Joonise pinda võib aga soovi kohaselt tõlgendada kas põhi- või esiekraanina (vt jn 22). 14. Punkti kaksvaade määrab punkti asukoha ristuvate ekraanide suhtes üheselt, joonise pinna suhtes aga kaheselt (vt jn 22). 21
22 Kui joonise pinnaks võtta põhiekraan, näeksime punkti A asukohaga A 1, kui aga joonise pinnaks võtta esiekraan, näeksime sama punkti asukohaga A 2. Punkt asub seega jooniste erivariantide järgi kahel kohal A 1 ja A 2. Tegelikult, kui murrame joonise pinna kokku ruumi nurgaks, saame esialgse tulemuse mõlemad punktid, nii A 1 kui A 2, langevad kokku punktis A, st, ruumis A 1 A 2 A Punkti asukoht ruumiveerandite järgi Ristuvad tasapinnad ε 1 ja ε 2 jagavad ruumi neljaks ruumiveerandiks (vt jn 23 ): I ekraani ees ja põhiekraanist üleval pool; II esiekraani taga ja põhiekraanist üleval pool; III esiekraani taga ja põhiekraanist allpool; IV esiekraani ees ja põhiekraanist allpool B C' C ε2 A" B" B D C A C'' ε1 D" A D' Kui joonise pinnaks võtame esiekraani ε 2, siis pöörates ekraani ε 1 joonise pinnale, saame punktide kaksvaated, nii nagu on näidatud joonisel 24. Joonis 23. Ristuvad tasapinnad jagavad ruumi neljaks ruumiveerandiks D Kui punkti kaksvaated langevad kokku, siis punkt asub tasapinnal ξ, mis poolitab II ja IV veerandit (vt jn 25). ε1 2. B -y C' ε2 +z ' ' 0 A D' 1. +y ε ' C' ' D'' D 3. C C'' 4. -z ε2 C'' D'' D' Joonis 24. Punkti asukoht ruumiveerandite järgi joonisel (kaksvaatel) ja joonise saamine 22
23 ε1 ξ 2. -y F' 3. F ε2 +z F'' 0 G'' -z 1. G' G +y 4. ξ ε F''=F' G'=G" ε2 Joonis 25. Punkti asukoht ruumiveerandites, kui punkti kaksvaated langevad kokku Tabelis 1 on toodud punktide koordinaatide märgid, kui punktid asuvad erinevates ruumiveerandites. Punktide asukohad ruumiveerandites vastavad joonistele 23 ja 24. Punktide koordinaatide märgid vastavates ruumiveerandites Punkt Punkti asukoht ruumiveerandis y z A I B II + + C III + D IV + + Tabel 1. Siin on punkti A kõik koordinaadid positiivsed, kuna punkti koordinaatlõigud vastavatel telgedel langevad kokku telgede positiivse suunaga (vastasel juhul oleks koordinaadid negatiivsed). Koordinaat määrab punkti A kauguse külgekraanist e 3 (punkti A laiuse koordinaat), seda mõõdetakse mööda -telge või paralleelselt -teljega. Koordinaat y määrab punkti A kauguse esiekraanist e 2 (punkti A sügavuse koordinaat), seda mõõdetakse mööda y-telge või paralleelselt y-teljega. Koordinaat z määrab punkti A kauguse põhiekraanist e 1 (punkti A kõrguse koordinaat), seda mõõdetakse mööda z-telge või paralleelselt z-teljega. Näide punkti koordinaatide märkimise kohta: A(20; 15; 35), st punkti A koordinaatide väärtused on järgmised = 20 mm, y = 15 mm ja z = 35 mm. Joonisel 26 on toodud näide punktide K(40; 35; 10); E(15; -20; -15) ja F(30; 10; -30) kaksvaate joonestamiseks, kus punktid on vastavalt I, III ja IV ruumiveerandis. 23
24 4.2. Punkti kolmvaade (e üldasendiline punkt) Punkti kaksvaade määrab punkti asukoha ekraanide suhtes üheselt. Keerukama objekti puhul peaks neid punkte olema väga palju ja punktide tähiseid samuti väga palju. Joonis läheb liiga kirjuks ja isegi segaseks. Seetõttu on tehnilises joonestamises üldse loobutud punktide tähistamisest. Kuid kui punktid on tähistamata, siis ei määra kaksvaade tihti enam objekti üheselt. Näiteks vaatame kaksvaadet, mis on näidatud joonisel 27 a. Sellise kaksvaate võivad anda erinevad objektid. Joonisel 27 annavad samasuguse kaksvaate nii detailid 27 b, c kui ka d. Kui kaksvaade ei määra objekti üheselt, siis võetakse kasutusele lisaristprojektsioonid lisaekraanidele. Esimene täiendav ekraan võetakse risti -teljega. Ta on risti nii põhikui esiekraaniga ja tähistatakse ε 3 ning nimetatakse külgekraaniks. Külgekraan lõikab nii põhi- kui esiekraani vastavalt mööda telgesid y ja z. Objekti ristprojektsioon külgekraanil s.o objekti vasakvaade e. külgvaade. Punktist A saame siis projektsioonid ekraanidel ε 1, ε 2 ja ε 3 : pealtvaate A, eestvaate A ja külgvaate A (vt jn 28). Punkti A kaugus külgekraanist on AA. Ekraanide lõikesirged võetakse ristkoordinaadistiku teljestikuks Oyz. Kehad c ja d ei ole kaksvaatega lõplikult määratud. a. K" 40 K' E' F' F" E" z y1 Joonis 26. Näide punktide kaksvaadete konstrueerimiseks nende koordinaatide järgi Ekraanid on koordinaatpinnad (vt jn 28): põhiekraan ε 1 y (ykoordinaatpind); esiekraan ε 2 z (z-koordinaatpind); b. c. d. külgekraan ε 3 yz (yz-koordinaatpind). Joonis 27. Kaksvaatega määramata detailide variante Punkti A kaugused ekraanidest on: 0 = OA = A A s.o p A kaugus külgekraanist e p A külgkvoot; y 0 = OA y = AA s.o p A kaugus esiekraanist e p A esikvoot; z 0 = OA z = A A s.o p A kaugus põhiekraanist e p A põhikvoot. Need on punkti A koordinaadid. Kirjutatakse näiteks nii A(2; 5; 3), kui = 2; y = 5 ja z = 3. Saadud joonist, mis koosneb punkti A kolmest omavahel seotud ristprojektsioonist, nimetatakse punkti A kolmvaateks. 24
25 z z ε2 ε2 ε3 A" 0 y0 z0 A 0 y0 z0 ε1 Az y0 A z0 0 O ε3 A"' z0 y0 Ay 0 y ε1 a. b. A" A 0 y0 0 Az y0 z0 z0 z0 O y0 Ay 0 y1 y0 Ay 45 Abisirge A"' y3 Joonis 28. Punkti A kolmvaade: a punkt A ruuminurgas ja tema projektsioonid teineteisega ristuvatele ekraanidele; b sama punkti A joonis (kolmvaade), kus põhi- ja külgekraan on pööratud esiekraani tasandile Pöörates ekraanid joonise tasapinda, saame punkti kolmvaate (vt jn 28 b). Siin joonisel: A A on püstsidejoon; A A z rõhtsidejoon. Kaugused A z A = A A = y 0 s.o kolmvaate peaomadus s.o ühtlasi ka p A y-koordinaat. Koordinaatlõigud 0 ja z 0 on: OA = A z A = 0 s.o p A -koordinaat; OA z = A A = z 0 s.o p A z-koordinaat. Punkti kaks projektsiooni kolmvaatel määravad ära üheselt ka kolmanda projektsiooni. Siin on nagu 2 kaksvaadet: 1) eestvaade pealtvaatega; 2) eestvaade külgvaatega. Punkti projektsioonid võib anda ka koordinaatide järgi ja need projektsioonid võivad asetseda ükskõik millises veerandis I, II, III või IV. Näitena vaatame joonisel 26 toodud punktide K(40; 35; 10) ja F(30; 10; -30) kolmvaateid (vt jn 29). K" z 10 K"' F' 10 0 y3 K' F" y1 F"' Joonis 29. Näide punktide kaksvaadete konstrueerimiseks nende koordinaatide järgi, kus punkt K on I ja punkt F on IV ruumiveerandis 25
26 4.3. Sirgjoone kaksvaade ja kolmvaade Sirgjoon on määratud oma kahe punktiga, iga punkt aga kaksvaatega või kolmvaatega. Seega sirgjoon on määratud oma 2 punkti kaksvaatega või kolmvaatega. Järelikult sirgjoone projekteerimiseks piisab, kui on teada tema otspunktide koordinaadid. Sirgjoone projekteerimisel: 1) leida otspunktide ristprojektsioonid; 2) ühendada samanimelised punktide projektsioonid pideva jämejoonega. Kui võtta sirgel mingi punkt M, siis selle punkti projektsioonid asuvad sirge AB pealt- ja eestvaatel nii, et sidejoon M M on risti -teljega (vt jn 30). Üldjuhul, ε2 kui sirget AB nimetada sirgeks s, siis s" sirge s on määratud oma s" kaksvaatega, ja kui ühegi punkti π s projektsiooni ei ole sirgel määratud (nagu joonisel 31a), siis võime sirgel τ võtta vabalt mõned punktid. Nende punktide projektsioonid asuvad s' sidejoontel sirge s vastavatel ε1 s' projektsioonidel. Sirge s pealtvaate määrab projekteeritav tasapind τ. Eestvaate projekteeritav tasapind π; kusjuures τ ε 1 ja π ε 2 ; ning τ ja π lõikejoon on sirge s (vt jn 31b). Joon. 30. Sirge kaksvaade ja punkt sirgel Joonis 31. Sirge projektsioonide saamine Kui meil on vaja saada kolmandat vaadet, külgvaadet sirgest s, millel on kaksvaade olemas, valime sirgel s vabalt kaks punkti M ja N ning tuletame nende punktide külgvaated kaksvaate kaudu. Siin on kaks varianti (vt jn 32): I variant: M M = M z M ja N N = N z N kanname rõhtsatele sidejoontele M ja N st risti z-teljega. Saadud punktid N ja M ühendame ja saame s ; II variant: punktide M ja N kaugused esiekraanist kanname pealtvaatelt üle 45 joontega või kaartega, selleks tõmbame rõhtsad sidejooned punktide põhiprojektsioonidest M ja N (risti y-teljega) kuni y-teljeni. A" a. b. M" B" M' 4.4. Sirglõigu jaotamine antud vahekorras Antud teemat selgitame näite abil (vt jn 33). Jaotame sirglõigu AB vahekorras 3:2, nii et AM = 3. Sirglõigu jaotamiseks tõmbame ükskõik kas eestvaatel või pealtvaatel ühest MB 2 sirglõigu otspunktist vabalt mingi nurga all sirge, nagu joonisel 33 on see tõmmatud pealtvaatel punktist A, ja kanname sellele 5 jaotust ühtlaste vahedega, kuna meil on vaja sirge jagada suhtes 26
27 3:2. Seejärel ühendame sirgega viimase jaotuse punktiga B, saame sirge 5. Lõpuks tõmbame kolmanda jaotuse kohalt paralleelse sirge kuni sirgeni AB, saame punkti M (3M'+5). Sealt saame sidejoonega punkti M teise projektsiooni. M" M' z s" s'" N" O N"' N' s' y1 M"' y3. A" Joonis 32. Sirge kolmvaate konstrueerimine sirge kaksvaatest M' M" B" 3 5 Joonis 33. Sirge jaotamine etteantud vahekorras 5. ERIASENDILISED SIRGED Üldasendiline sirge s.o sirge, mis ei ole ühegi ekraaniga paralleelne ega asetse ühelgi ekraanil. Eriasendiline sirge on mõne ekraaniga paralleelne või asetseb mõnel neist. Ekraaniga paralleelseid sirgeid nimetatakse nivoosirgeteks. Need on: horisontaal, s.o põhiekraaniga paralleelne sirge (tähistatakse h ); frontaal, s.o esiekraaniga paralleelne sirge (tähistatakse f ); profiilsirge, s.o külgekraaniga paralleelne sirge (tähistatakse s ) Horisontaal h Horisontaali eestvaade h -teljega, siis A B = AB sirglõik projekteerub põhiekraanile õiges pikkuses. Originaalsuuruses on ka esikaldenurk ϕ 2 (kaldenurk esiekraani suhtes, sest selle tasapind on põhiekraaniga paralleelne). Punkt E h, s.o horisontaali esijälg, sirge h lõikepunkt esitahuga E h Ε h. Põhijälg horisontaalil puudub, sest h ε 1. Kui h ε 2 ja h ε 1, siis E h E h h (horisontaal projekteerub esiekraanile punktiks). X ε1 Eh=Eh" A A" Eh' ϕ2 h h' ε2 h" B" ϕ2 B Eh=Eh" Eh' A" ϕ2 h" B" Joonis 34. Horisontaalsirge, tema projektsioonid, pikkus ja kaldenurk h' 27
28 5.2. Frontaal f Frontaali pealtvaade f -teljega (vt jn 35). Esiekraanile projekteeruvad originaalsuuruses frontaali pikkus (siin lõik AB, milline on frontaalil A B = AB) ja frontaali põhikaldenurk ϕ 1 ; põhiekraanil aga A B -telg. Frontaalil puudub esijälg, sest f ε 2, frontaali põhijäljeks on punkt P(P,P ), frontaali lõikepunkt põhiekraaniga. Kui sirge f on paralleelne esi- ja külgekraaniga (f p) (vt jn 35c); siis f -teljega ja f ε 1, frontaalsirge f põhiprojektsioon on punkt. Kui sirge s on paralleelne põhi- ja esiekraaniga s h f; siis f -teljega ja s ε 3, sirge s külgprojektsioon on punkt. ε2 B" Pf" A" f" ϕ1 A Pf=Pf' f" B f Pf" A" ϕ1 f' ε1 B" ϕ1 f' Pf=Pf' a. b. c. f" f'=p=p' f ε1//ε2//ε3 Joonis 35. Frontaalsirge: a frontaalsirge piltkujutis, tema projektsioonid ekraanidel, pikkus ja kaldenurk; b sama frontaalsirge joonis; c frontaalsirge joonis, kui f ε Profiilsirge s Profiilsirge pealt- ja eestvaade on üldjuhul sirged ühel ja samal sidejoonel (vt jn 36). Erandjuhul võib üks projektsioonidest olla punkt. Kui sirgel ei ole punkte fikseeritud, siis kaksvaade ei määra üheselt profiilsirget, sest projekteeruvad pinnad esi- ja põhitasapinnale τ ja π langevad ε2 s'' s π=τ m ε1 s'' s' a. s' b. Joonis 36. Profiilsirge: a piltkujutis, b selle joonis A" B" s'' s' z y1 a. b. s'' y3 ühte ja külgekraanile ei teki lõikesirget (vt jn 37). Joonis 37. Profiilsirge joonis: a sirge on määratud kahe punktiga; b sirge ei ole määratud punktidega 28
29 NÄIDE Meil on sirge kaksvaade ja sellel punkti M eestvaade M. Leida punkti asukoht sirgel, tema pealtvaade. Lahendusel on siin kaks varianti. 1. variant: tuleb leida sirge külgvaade ja punkt M kanda sidejoontega üle sellele sirgele (vt jn var.). 2. variant: tõmbame vabas suunas mingi nurga all A B suhtes sirge A 0 B = A B nii, et ta läbiks sirget A B, sinna kanname A 0 M 0 = A M. Sirglõigud jagunevad nagu A M M B. Tõmbame M 0 M B 0 B A 0 A, saame M (vt jn var). ' M'' z '' M''' ' M'' ' M' 1. variant y1 '' y3 ' M' M0 A0 Vabas suunas 2. variant--a0='' M0='M'' Joonis 38. Punkti asukoha leidmine sirgel 6. SIRGE JÄLGPUNKTID Sirgjoone ja ekraani lõikepunkti nimetatakse selle sirge jälgpunktiks (e. jäljeks). Kui sirge s ei ole ühegi ekraaniga paralleelne, siis on tal 3 jälgpunkti: põhijälg P s ε 1 ; esijälg E s ε 2 ; külgjälg K s ε 3. Põhijälg P (vt jn 39a) asetseb põhiekraanil ε 1 ja sirgel s, seega selle punkti eestvaade P asetseb -teljel ja samaaegselt sirge eestvaatel (sirge eestvaade tuleb pikendada -teljeni) seega P = -telg s. Sidejoonega leiame ka pealtvaates punkti P pealtvaate P. Analoogselt saame leida esijälje E projektsioonid (E s -telg ja tõmbame sidejoone punktist E kuni sidejoon lõikub s saame eestvaatel E ). Joonisel 39 on näidatud sirge põhijälje ja esijälje leidmine sirge kahe erineva asendi korral. 29
30 ε2 E''=E E''=E P'' s'' s E' s' P =P ε1 s'' P'' a. P =P s' E' t'' P'' P =P t' b. E' E''=E Joonis 39. Sirge jälgpunktide leidmine: a sirge ühe otsa pikendamisel saame põhijälje ja teise otsa pikendamisel esijälje; b sirge pikendamisel läbib sirge põhiekraani ja sama sirge otsa pikendamisel lõikub ta esiekraaniga (aksonomeetrilist kujutist ei ole näidatud) 7. SIRGETE VASTASTIKUSED ASENDID Kaks sirgjoont võivad olla paralleelsed, lõikuvad või kiivsed. Kuidas otsustada, milline on kaksvaate järgi sirgete vastastikune asend ruumis? Seda vaatame järgnevalt Paralleelsed sirged Paralleelsed sirged projekteeruvad üldjuhul igale ekraanile paralleelsete sirgetena (vt jn 40a). Kui a b, siis ka a b ja a b. Õige on üldjuhul ka vastupidine väide: kui a b ja a b, siis ka a b. Erandiks on aga profiilsirged et otsustada, kas sirged on paralleelsed, peab siin olema ka külgvaade. Kui külgvaatel sirgete projektsioonid lõikuvad, on nad kiivsed (vt jn 40c). a'' a' a. Üldjuhus b'' b' z a'' a''' b'' b'' a'' b''' y3 a' a' b' b' b. y1 Erandid, kui a ja b//ε3 c. z y1 b''' a''' y3 Sirgjoonte paralleelsuse tunnus: kui sirgete samanimelised projektsioonid on omavahel paralleelsed, kuid pole risti kaksvaate teljega, siis need sirged on paralleelsed. Joonis 40. Paralleelsete sirgete joonised: a üldjuhus; b ja c erandid, kui sirged on paralleelsed külgekraaniga 30
31 7.2. Lõikuvad sirged Lõikuvad sirged a ja b läbivad nende lõikepunkti L. Järelikult eestvaates a ja b lõikuvad, saame punkti L, ja pealtvaates a ja b lõikuvad saame L. Nende sirgete lõikepunkt pealtvaates L ja eestvaates L asuvad ühel ja samal sidejoonel (vt jn 41a). Kahe sirge lõikumise tunnus kaksvaate järgi: kui kahe sirge samanimeliste projektsioonide lõikepunktid asetsevad ühel ja samal sidejoonel ning kummagi sirge mõlemad projektsioonid pole risti -teljega, siis need sirged ruumis lõikuvad. a. a'' a' L'' L' b'' Kui ühe sirge mõlemad projektsioonid on risti -teljega (need on profiilsirged), siis võib olla tegemist kas ristuvate või kiivsete sirgetega seda näitab sirgete külgvaade (vt jn 41b), kas külgvaates sirgete projektsioonid Joonis 41. Lõikuvad sirged: a üldjuhus; b erand, kui üks sirgetest samal sidejoonel on profiilsirge, siis tuleb teha ka külgvaade lõikuvad või mitte. Siin joonisel 41b külgvaates A B ja C D lõikepunkti sidejoonel ei esine, järelikult sirged AB ja CD on kiivsed Kiivsirged b' z C'' ' '' C''' M''=N'' M''' ' '' N''' D''' D'' D' y3 M' N' C' b. Kiivsirged ei ole paralleelsed ega lõiku, järelikult kiivsirgete kaksvaade ei rahulda lõikumise ega paralleelsuse tunnust see on kiivsuse tunnus. Praktikas tuleb sageli lahendada ülesanne, et leida, kumb sirge läheb teisest üle (kui vaadata ülevalt) või kumb sirge teise eest läbi (eestvaates). y1 b'' M''=N'' U'' a'' V'' M' U'=V' b' N' a. a' C'' ' C' b. ' D'' D' z y1 '' '' C''' D''' y3 Joonis 42. Kiivsirged: a üldjuhus; b sirged võivad projekteeruda kas ühel või ka kahel ekraanil paralleelsetena Sirgetel a ja b punktid U ja V 31
Ruumilise jõusüsteemi taandamine lihtsaimale kujule
 Kodutöö nr.1 uumilise jõusüsteemi taandamine lihtsaimale kujule Ülesanne Taandada antud jõusüsteem lihtsaimale kujule. isttahuka (joonis 1.) mõõdud ning jõudude moodulid ja suunad on antud tabelis 1. D
Kodutöö nr.1 uumilise jõusüsteemi taandamine lihtsaimale kujule Ülesanne Taandada antud jõusüsteem lihtsaimale kujule. isttahuka (joonis 1.) mõõdud ning jõudude moodulid ja suunad on antud tabelis 1. D
MATEMAATIKA TÄIENDUSÕPE MÕISTED, VALEMID, NÄITED, ÜLESANDED LEA PALLAS VII OSA
 MATEMAATIKA TÄIENDUSÕPE MÕISTED, VALEMID, NÄITED, ÜLESANDED LEA PALLAS VII OSA SISUKORD 57 Joone uutuja Näited 8 58 Ülesanded uutuja võrrandi koostamisest 57 Joone uutuja Näited Funktsiooni tuletisel on
MATEMAATIKA TÄIENDUSÕPE MÕISTED, VALEMID, NÄITED, ÜLESANDED LEA PALLAS VII OSA SISUKORD 57 Joone uutuja Näited 8 58 Ülesanded uutuja võrrandi koostamisest 57 Joone uutuja Näited Funktsiooni tuletisel on
Geomeetrilised vektorid
 Vektorid Geomeetrilised vektorid Skalaarideks nimetatakse suurusi, mida saab esitada ühe arvuga suuruse arvulise väärtusega. Skalaari iseloomuga suurusi nimetatakse skalaarseteks suurusteks. Skalaarse
Vektorid Geomeetrilised vektorid Skalaarideks nimetatakse suurusi, mida saab esitada ühe arvuga suuruse arvulise väärtusega. Skalaari iseloomuga suurusi nimetatakse skalaarseteks suurusteks. Skalaarse
KORDAMINE RIIGIEKSAMIKS VII teema Vektor. Joone võrrandid.
 KORDMINE RIIGIEKSMIKS VII teema Vektor Joone võrrandid Vektoriaalseid suuruseid iseloomustavad a) siht b) suund c) pikkus Vektoriks nimetatakse suunatud sirglõiku Vektori alguspunktiks on ja lõpp-punktiks
KORDMINE RIIGIEKSMIKS VII teema Vektor Joone võrrandid Vektoriaalseid suuruseid iseloomustavad a) siht b) suund c) pikkus Vektoriks nimetatakse suunatud sirglõiku Vektori alguspunktiks on ja lõpp-punktiks
KORDAMINE RIIGIEKSAMIKS V teema Vektor. Joone võrrandid.
 KORDMINE RIIGIEKSMIKS V teema Vektor Joone võrrandid Vektoriaalseid suuruseid iseloomustavad a) siht b) suund c) pikkus Vektoriks nimetatakse suunatud sirglõiku Vektori alguspunktiks on ja lõpp-punktiks
KORDMINE RIIGIEKSMIKS V teema Vektor Joone võrrandid Vektoriaalseid suuruseid iseloomustavad a) siht b) suund c) pikkus Vektoriks nimetatakse suunatud sirglõiku Vektori alguspunktiks on ja lõpp-punktiks
Planeedi Maa kaardistamine G O R. Planeedi Maa kõige lihtsamaks mudeliks on kera. Joon 1
 laneedi Maa kaadistamine laneedi Maa kõige lihtsamaks mudeliks on kea. G Joon 1 Maapinna kaadistamine põhineb kea ümbeingjoontel, millest pikimat nimetatakse suuingjooneks. Need suuingjooned, mis läbivad
laneedi Maa kaadistamine laneedi Maa kõige lihtsamaks mudeliks on kea. G Joon 1 Maapinna kaadistamine põhineb kea ümbeingjoontel, millest pikimat nimetatakse suuingjooneks. Need suuingjooned, mis läbivad
Analüütilise geomeetria praktikum II. L. Tuulmets
 Analüütilise geomeetria praktikum II L. Tuulmets Tartu 1985 2 Peatükk 4 Sirge tasandil 1. Sirge tasandil Kui tasandil on antud afiinne reeper, siis iga sirge tasandil on selle reeperi suhtes määratud lineaarvõrrandiga
Analüütilise geomeetria praktikum II L. Tuulmets Tartu 1985 2 Peatükk 4 Sirge tasandil 1. Sirge tasandil Kui tasandil on antud afiinne reeper, siis iga sirge tasandil on selle reeperi suhtes määratud lineaarvõrrandiga
Vektorid II. Analüütiline geomeetria 3D Modelleerimise ja visualiseerimise erialale
 Vektorid II Analüütiline geomeetria 3D Modelleerimise ja visualiseerimise erialale Vektorid Vektorid on arvude järjestatud hulgad (s.t. iga komponendi väärtus ja positsioon hulgas on tähenduslikud) Vektori
Vektorid II Analüütiline geomeetria 3D Modelleerimise ja visualiseerimise erialale Vektorid Vektorid on arvude järjestatud hulgad (s.t. iga komponendi väärtus ja positsioon hulgas on tähenduslikud) Vektori
Ehitusmehaanika harjutus
 Ehitusmehaanika harjutus Sõrestik 2. Mõjujooned /25 2 6 8 0 2 6 C 000 3 5 7 9 3 5 "" 00 x C 2 C 3 z Andres Lahe Mehaanikainstituut Tallinna Tehnikaülikool Tallinn 2007 See töö on litsentsi all Creative
Ehitusmehaanika harjutus Sõrestik 2. Mõjujooned /25 2 6 8 0 2 6 C 000 3 5 7 9 3 5 "" 00 x C 2 C 3 z Andres Lahe Mehaanikainstituut Tallinna Tehnikaülikool Tallinn 2007 See töö on litsentsi all Creative
DEF. Kolmnurgaks nim hulknurka, millel on 3 tippu. / Kolmnurgaks nim tasandi osa, mida piiravad kolme erinevat punkti ühendavad lõigud.
 Kolmnurk 1 KOLMNURK DEF. Kolmnurgaks nim hulknurka, millel on 3 tippu. / Kolmnurgaks nim tasandi osa, mida piiravad kolme erinevat punkti ühendavad lõigud. Kolmnurga tippe tähistatakse nagu punkte ikka
Kolmnurk 1 KOLMNURK DEF. Kolmnurgaks nim hulknurka, millel on 3 tippu. / Kolmnurgaks nim tasandi osa, mida piiravad kolme erinevat punkti ühendavad lõigud. Kolmnurga tippe tähistatakse nagu punkte ikka
Lokaalsed ekstreemumid
 Lokaalsed ekstreemumid Öeldakse, et funktsioonil f (x) on punktis x lokaalne maksimum, kui leidub selline positiivne arv δ, et 0 < Δx < δ Δy 0. Öeldakse, et funktsioonil f (x) on punktis x lokaalne miinimum,
Lokaalsed ekstreemumid Öeldakse, et funktsioonil f (x) on punktis x lokaalne maksimum, kui leidub selline positiivne arv δ, et 0 < Δx < δ Δy 0. Öeldakse, et funktsioonil f (x) on punktis x lokaalne miinimum,
MATEMAATIKA TÄIENDUSÕPE MÕISTED, VALEMID, NÄITED LEA PALLAS XII OSA
 MATEMAATIKA TÄIENDUSÕPE MÕISTED, VALEMID, NÄITED LEA PALLAS XII OSA SISUKORD 8 MÄÄRAMATA INTEGRAAL 56 8 Algfunktsioon ja määramata integraal 56 8 Integraalide tabel 57 8 Määramata integraali omadusi 58
MATEMAATIKA TÄIENDUSÕPE MÕISTED, VALEMID, NÄITED LEA PALLAS XII OSA SISUKORD 8 MÄÄRAMATA INTEGRAAL 56 8 Algfunktsioon ja määramata integraal 56 8 Integraalide tabel 57 8 Määramata integraali omadusi 58
Kompleksarvu algebraline kuju
 Kompleksarvud p. 1/15 Kompleksarvud Kompleksarvu algebraline kuju Mati Väljas mati.valjas@ttu.ee Tallinna Tehnikaülikool Kompleksarvud p. 2/15 Hulk Hulk on kaasaegse matemaatika algmõiste, mida ei saa
Kompleksarvud p. 1/15 Kompleksarvud Kompleksarvu algebraline kuju Mati Väljas mati.valjas@ttu.ee Tallinna Tehnikaülikool Kompleksarvud p. 2/15 Hulk Hulk on kaasaegse matemaatika algmõiste, mida ei saa
20. SIRGE VÕRRANDID. Joonis 20.1
 κ ËÁÊ Â Ì Ë Æ Á 20. SIRGE VÕRRANDID Sirget me võime vaadelda kas tasandil E 2 või ruumis E 3. Sirget vaadelda sirgel E 1 ei oma mõtet, sest tegemist on ühe ja sama sirgega. Esialgu on meie käsitlus nii
κ ËÁÊ Â Ì Ë Æ Á 20. SIRGE VÕRRANDID Sirget me võime vaadelda kas tasandil E 2 või ruumis E 3. Sirget vaadelda sirgel E 1 ei oma mõtet, sest tegemist on ühe ja sama sirgega. Esialgu on meie käsitlus nii
2.2.1 Geomeetriline interpretatsioon
 2.2. MAATRIKSI P X OMADUSED 19 2.2.1 Geomeetriline interpretatsioon Maatriksi X (dimensioonidega n k) veergude poolt moodustatav vektorruum (inglise k. column space) C(X) on defineeritud järgmiselt: Defineerides
2.2. MAATRIKSI P X OMADUSED 19 2.2.1 Geomeetriline interpretatsioon Maatriksi X (dimensioonidega n k) veergude poolt moodustatav vektorruum (inglise k. column space) C(X) on defineeritud järgmiselt: Defineerides
Mitmest lülist koosneva mehhanismi punktide kiiruste ja kiirenduste leidmine
 TALLINNA TEHNIKAÜLIKOOL MEHAANIKAINSTITUUT Dünaamika kodutöö nr. 1 Mitmest lülist koosnea mehhanismi punktide kiiruste ja kiirenduste leidmine ariant ZZ Lahendusnäide Üliõpilane: Xxx Yyy Üliõpilase kood:
TALLINNA TEHNIKAÜLIKOOL MEHAANIKAINSTITUUT Dünaamika kodutöö nr. 1 Mitmest lülist koosnea mehhanismi punktide kiiruste ja kiirenduste leidmine ariant ZZ Lahendusnäide Üliõpilane: Xxx Yyy Üliõpilase kood:
Funktsiooni diferentsiaal
 Diferentsiaal Funktsiooni diferentsiaal Argumendi muut Δx ja sellele vastav funktsiooni y = f (x) muut kohal x Eeldusel, et f D(x), saame Δy = f (x + Δx) f (x). f (x) = ehk piisavalt väikese Δx korral
Diferentsiaal Funktsiooni diferentsiaal Argumendi muut Δx ja sellele vastav funktsiooni y = f (x) muut kohal x Eeldusel, et f D(x), saame Δy = f (x + Δx) f (x). f (x) = ehk piisavalt väikese Δx korral
HAPE-ALUS TASAKAAL. Teema nr 2
 PE-LUS TSL Teema nr Tugevad happed Tugevad happed on lahuses täielikult dissotiseerunud + sisaldus lahuses on võrdne happe analüütilise kontsentratsiooniga Nt NO Cl SO 4 (esimeses astmes) p a väärtused
PE-LUS TSL Teema nr Tugevad happed Tugevad happed on lahuses täielikult dissotiseerunud + sisaldus lahuses on võrdne happe analüütilise kontsentratsiooniga Nt NO Cl SO 4 (esimeses astmes) p a väärtused
Graafiteooria üldmõisteid. Graaf G ( X, A ) Tippude hulk: X={ x 1, x 2,.., x n } Servade (kaarte) hulk: A={ a 1, a 2,.., a m } Orienteeritud graafid
 Graafiteooria üldmõisteid Graaf G ( X, A ) Tippude hulk: X={ x 1, x 2,.., x n } Servade (kaarte) hulk: A={ a 1, a 2,.., a m } Orienteeritud graafid Orienteerimata graafid G(x i )={ x k < x i, x k > A}
Graafiteooria üldmõisteid Graaf G ( X, A ) Tippude hulk: X={ x 1, x 2,.., x n } Servade (kaarte) hulk: A={ a 1, a 2,.., a m } Orienteeritud graafid Orienteerimata graafid G(x i )={ x k < x i, x k > A}
; y ) vektori lõpppunkt, siis
 III kusus VEKTOR TASANDIL. JOONE VÕRRAND *laia matemaatika teemad. Vektoi mõiste, -koodinaadid ja pikkus: http://www.allaveelmaa.com/ematejalid/vekto-koodinaadid-pikkus.pdf Vektoite lahutamine: http://allaveelmaa.com/ematejalid/lahutaminenull.pdf
III kusus VEKTOR TASANDIL. JOONE VÕRRAND *laia matemaatika teemad. Vektoi mõiste, -koodinaadid ja pikkus: http://www.allaveelmaa.com/ematejalid/vekto-koodinaadid-pikkus.pdf Vektoite lahutamine: http://allaveelmaa.com/ematejalid/lahutaminenull.pdf
,millest avaldub 21) 23)
 II kursus TRIGONOMEETRIA * laia matemaatika teemad TRIGONOMEETRILISTE FUNKTSIOONIDE PÕHISEOSED: sin α s α sin α + s α,millest avaldu s α sin α sα tan α, * t α,millest järeldu * tα s α tα tan α + s α Ülesanne.
II kursus TRIGONOMEETRIA * laia matemaatika teemad TRIGONOMEETRILISTE FUNKTSIOONIDE PÕHISEOSED: sin α s α sin α + s α,millest avaldu s α sin α sα tan α, * t α,millest järeldu * tα s α tα tan α + s α Ülesanne.
Sissejuhatus mehhatroonikasse MHK0120
 Sissejuhatus mehhatroonikasse MHK0120 2. nädala loeng Raavo Josepson raavo.josepson@ttu.ee Loenguslaidid Materjalid D. Halliday,R. Resnick, J. Walker. Füüsika põhikursus : õpik kõrgkoolile I köide. Eesti
Sissejuhatus mehhatroonikasse MHK0120 2. nädala loeng Raavo Josepson raavo.josepson@ttu.ee Loenguslaidid Materjalid D. Halliday,R. Resnick, J. Walker. Füüsika põhikursus : õpik kõrgkoolile I köide. Eesti
Matemaatiline analüüs I iseseisvad ülesanded
 Matemaatiline analüüs I iseseisvad ülesanded Leidke funktsiooni y = log( ) + + 5 määramispiirkond Leidke funktsiooni y = + arcsin 5 määramispiirkond Leidke funktsiooni y = sin + 6 määramispiirkond 4 Leidke
Matemaatiline analüüs I iseseisvad ülesanded Leidke funktsiooni y = log( ) + + 5 määramispiirkond Leidke funktsiooni y = + arcsin 5 määramispiirkond Leidke funktsiooni y = sin + 6 määramispiirkond 4 Leidke
Vektori u skalaarkorrutist iseendaga nimetatakse selle vektori skalaarruuduks ja tähistatakse (u ) 2 või u 2 u. u v cos α = u 2 + v 2 PQ 2
 Vektorite sklrkorrutis Vtleme füüsikkursusest tuntud olukord, kus kehle mõjub jõud F r j keh teeb selle jõu mõjul nihke s Konkreetsuse huvides olgu kehks rööbsteel liikuv vgun Jõud F r mõjugu vgunile rööbstee
Vektorite sklrkorrutis Vtleme füüsikkursusest tuntud olukord, kus kehle mõjub jõud F r j keh teeb selle jõu mõjul nihke s Konkreetsuse huvides olgu kehks rööbsteel liikuv vgun Jõud F r mõjugu vgunile rööbstee
9. AM ja FM detektorid
 1 9. AM ja FM detektorid IRO0070 Kõrgsageduslik signaalitöötlus Demodulaator Eraldab moduleeritud signaalist informatiivse osa. Konkreetne lahendus sõltub modulatsiooniviisist. Eristatakse Amplituuddetektoreid
1 9. AM ja FM detektorid IRO0070 Kõrgsageduslik signaalitöötlus Demodulaator Eraldab moduleeritud signaalist informatiivse osa. Konkreetne lahendus sõltub modulatsiooniviisist. Eristatakse Amplituuddetektoreid
Geomeetria põhivara. Jan Willemson. 19. mai 2000.a.
 Geomeetria põhivara Jan Willemson 19. mai 2000.a. 1 Kolmnurk Kolmnurgas tasub mõelda järgmistest lõikudest ja sirgetest: kõrgused, nurgapoolitajad, välisnurkade poolitajad, külgede keskristsirged, mediaanid,
Geomeetria põhivara Jan Willemson 19. mai 2000.a. 1 Kolmnurk Kolmnurgas tasub mõelda järgmistest lõikudest ja sirgetest: kõrgused, nurgapoolitajad, välisnurkade poolitajad, külgede keskristsirged, mediaanid,
PLASTSED DEFORMATSIOONID
 PLAED DEFORMAIOONID Misese vlavustingimus (pinegte ruumis) () Dimensineerimisega saab kõrvaldada ainsa materjali parameetri. Purunemise (tugevuse) kriteeriumid:. Maksimaalse pinge kirteerium Laminaat puruneb
PLAED DEFORMAIOONID Misese vlavustingimus (pinegte ruumis) () Dimensineerimisega saab kõrvaldada ainsa materjali parameetri. Purunemise (tugevuse) kriteeriumid:. Maksimaalse pinge kirteerium Laminaat puruneb
Eesti koolinoorte XLVIII täppisteaduste olümpiaadi
 Eesti koolinoorte XLVIII täppisteaduste olümpiaadi lõppvoor MATEMAATIKAS Tartus, 9. märtsil 001. a. Lahendused ja vastused IX klass 1. Vastus: x = 171. Teisendame võrrandi kujule 111(4 + x) = 14 45 ning
Eesti koolinoorte XLVIII täppisteaduste olümpiaadi lõppvoor MATEMAATIKAS Tartus, 9. märtsil 001. a. Lahendused ja vastused IX klass 1. Vastus: x = 171. Teisendame võrrandi kujule 111(4 + x) = 14 45 ning
ITI 0041 Loogika arvutiteaduses Sügis 2005 / Tarmo Uustalu Loeng 4 PREDIKAATLOOGIKA
 PREDIKAATLOOGIKA Predikaatloogika on lauseloogika tugev laiendus. Predikaatloogikas saab nimetada asju ning rääkida nende omadustest. Väljendusvõimsuselt on predikaatloogika seega oluliselt peenekoelisem
PREDIKAATLOOGIKA Predikaatloogika on lauseloogika tugev laiendus. Predikaatloogikas saab nimetada asju ning rääkida nende omadustest. Väljendusvõimsuselt on predikaatloogika seega oluliselt peenekoelisem
4.2.5 Täiustatud meetod tuletõkestusvõime määramiseks
 4.2.5 Täiustatud meetod tuletõkestusvõime määramiseks 4.2.5.1 Ülevaade See täiustatud arvutusmeetod põhineb mahukate katsete tulemustel ja lõplike elementide meetodiga tehtud arvutustel [4.16], [4.17].
4.2.5 Täiustatud meetod tuletõkestusvõime määramiseks 4.2.5.1 Ülevaade See täiustatud arvutusmeetod põhineb mahukate katsete tulemustel ja lõplike elementide meetodiga tehtud arvutustel [4.16], [4.17].
Vektoralgebra seisukohalt võib ka selle võrduse kirja panna skalaarkorrutise
 Jõu töö Konstanse jõu tööks lõigul (nihkel) A A nimetatakse jõu mooduli korrutist teepikkusega s = A A ning jõu siirde vahelise nurga koosinusega Fscos ektoralgebra seisukohalt võib ka selle võrduse kirja
Jõu töö Konstanse jõu tööks lõigul (nihkel) A A nimetatakse jõu mooduli korrutist teepikkusega s = A A ning jõu siirde vahelise nurga koosinusega Fscos ektoralgebra seisukohalt võib ka selle võrduse kirja
Funktsioonide õpetamisest põhikooli matemaatikakursuses
 Funktsioonide õpetamisest põhikooli matemaatikakursuses Allar Veelmaa, Loo Keskkool Funktsioon on üldtähenduses eesmärgipärane omadus, ülesanne, otstarve. Mõiste funktsioon ei ole kasutusel ainult matemaatikas,
Funktsioonide õpetamisest põhikooli matemaatikakursuses Allar Veelmaa, Loo Keskkool Funktsioon on üldtähenduses eesmärgipärane omadus, ülesanne, otstarve. Mõiste funktsioon ei ole kasutusel ainult matemaatikas,
KOMBINATSIOONID, PERMUTATSIOOND JA BINOOMKORDAJAD
 KOMBINATSIOONID, PERMUTATSIOOND JA BINOOMKORDAJAD Teema 3.1 (Õpiku peatükid 1 ja 3) Jaan Penjam, email: jaan@cs.ioc.ee Diskreetne Matemaatika II: Kombinatoorika 1 / 31 Loengu kava 1 Tähistusi 2 Kombinatoorsed
KOMBINATSIOONID, PERMUTATSIOOND JA BINOOMKORDAJAD Teema 3.1 (Õpiku peatükid 1 ja 3) Jaan Penjam, email: jaan@cs.ioc.ee Diskreetne Matemaatika II: Kombinatoorika 1 / 31 Loengu kava 1 Tähistusi 2 Kombinatoorsed
Kontekstivabad keeled
 Kontekstivabad keeled Teema 2.1 Jaan Penjam, email: jaan@cs.ioc.ee Rekursiooni- ja keerukusteooria: KV keeled 1 / 27 Loengu kava 1 Kontekstivabad grammatikad 2 Süntaksipuud 3 Chomsky normaalkuju Jaan Penjam,
Kontekstivabad keeled Teema 2.1 Jaan Penjam, email: jaan@cs.ioc.ee Rekursiooni- ja keerukusteooria: KV keeled 1 / 27 Loengu kava 1 Kontekstivabad grammatikad 2 Süntaksipuud 3 Chomsky normaalkuju Jaan Penjam,
4.1 Funktsiooni lähendamine. Taylori polünoom.
 Peatükk 4 Tuletise rakendusi 4.1 Funktsiooni lähendamine. Talori polünoom. Mitmetes matemaatika rakendustes on vaja leida keerulistele funktsioonidele lihtsaid lähendeid. Enamasti konstrueeritakse taolised
Peatükk 4 Tuletise rakendusi 4.1 Funktsiooni lähendamine. Talori polünoom. Mitmetes matemaatika rakendustes on vaja leida keerulistele funktsioonidele lihtsaid lähendeid. Enamasti konstrueeritakse taolised
Vektorid. A=( A x, A y, A z ) Vektor analüütilises geomeetrias
 ektorid Matemaatikas tähistab vektor vektorruumi elementi. ektorruum ja vektor on defineeritud väga laialt, kuid praktikas võime vektorit ette kujutada kui kindla arvu liikmetega järjestatud arvuhulka.
ektorid Matemaatikas tähistab vektor vektorruumi elementi. ektorruum ja vektor on defineeritud väga laialt, kuid praktikas võime vektorit ette kujutada kui kindla arvu liikmetega järjestatud arvuhulka.
Kirjeldab kuidas toimub programmide täitmine Tähendus spetsifitseeritakse olekuteisendussüsteemi abil Loomulik semantika
 Operatsioonsemantika Kirjeldab kuidas toimub programmide täitmine Tähendus spetsifitseeritakse olekuteisendussüsteemi abil Loomulik semantika kirjeldab kuidas j~outakse l~oppolekusse Struktuurne semantika
Operatsioonsemantika Kirjeldab kuidas toimub programmide täitmine Tähendus spetsifitseeritakse olekuteisendussüsteemi abil Loomulik semantika kirjeldab kuidas j~outakse l~oppolekusse Struktuurne semantika
Koduseid ülesandeid IMO 2017 Eesti võistkonna kandidaatidele vol 4 lahendused
 Koduseid ülesandeid IMO 017 Eesti võistkonna kandidaatidele vol 4 lahendused 17. juuni 017 1. Olgu a,, c positiivsed reaalarvud, nii et ac = 1. Tõesta, et a 1 + 1 ) 1 + 1 ) c 1 + 1 ) 1. c a Lahendus. Kuna
Koduseid ülesandeid IMO 017 Eesti võistkonna kandidaatidele vol 4 lahendused 17. juuni 017 1. Olgu a,, c positiivsed reaalarvud, nii et ac = 1. Tõesta, et a 1 + 1 ) 1 + 1 ) c 1 + 1 ) 1. c a Lahendus. Kuna
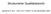 α α α α α α α α α α α α α α α α α α α α α α α α α α α α β χ δ ε φ γ η ι ϕ κ λ µ ν ο π θ ρ σ τ υ ϖ ω ξ ψ ζ αα ββ χχ δδ εε φφ γγ ηη ιι ϕϕ κκ λλ µµ νν οο
α α α α α α α α α α α α α α α α α α α α α α α α α α α α β χ δ ε φ γ η ι ϕ κ λ µ ν ο π θ ρ σ τ υ ϖ ω ξ ψ ζ αα ββ χχ δδ εε φφ γγ ηη ιι ϕϕ κκ λλ µµ νν οο
TARTU ÜLIKOOL Teaduskool. STAATIKA TASAKAALUSTAMISTINGIMUSED Koostanud J. Lellep, L. Roots
 TARTU ÜLIKOOL Teaduskool STAATIKA TASAKAALUSTAMISTINGIMUSED Koostanud J. Lellep, L. Roots Tartu 2008 Eessõna Käesoleva õppevahendi kasutajana on mõeldud eelkõige täppisteaduste vastu huvi tundvaid gümnaasiumi
TARTU ÜLIKOOL Teaduskool STAATIKA TASAKAALUSTAMISTINGIMUSED Koostanud J. Lellep, L. Roots Tartu 2008 Eessõna Käesoleva õppevahendi kasutajana on mõeldud eelkõige täppisteaduste vastu huvi tundvaid gümnaasiumi
LOOGIKA ELEMENTE MATEMAATIKAS. GEOMEETRIA AKSIOMAATILISEST ÜLESEHITUSEST. Koostanud Hilja Afanasjeva
 LOOGIKA ELEMENTE MATEMAATIKAS. GEOMEETRIA AKSIOMAATILISEST ÜLESEHITUSEST EESSÕNA Koostanud Hilja Afanasjeva Enne selle teema käsitlemist avame mõned materjalist arusaamiseks vajalikud mõisted hulgateooriast.
LOOGIKA ELEMENTE MATEMAATIKAS. GEOMEETRIA AKSIOMAATILISEST ÜLESEHITUSEST EESSÕNA Koostanud Hilja Afanasjeva Enne selle teema käsitlemist avame mõned materjalist arusaamiseks vajalikud mõisted hulgateooriast.
Smith i diagramm. Peegeldustegur
 Smith i diagramm Smith i diagrammiks nimetatakse graafilist abivahendit/meetodit põhiliselt sobitusküsimuste lahendamiseks. Selle võttis 1939. aastal kasutusele Philip H. Smith, kes töötas tol ajal ettevõttes
Smith i diagramm Smith i diagrammiks nimetatakse graafilist abivahendit/meetodit põhiliselt sobitusküsimuste lahendamiseks. Selle võttis 1939. aastal kasutusele Philip H. Smith, kes töötas tol ajal ettevõttes
Matemaatiline analüüs I iseseisvad ülesanded
 Matemaatiline analüüs I iseseisvad ülesanded. Leidke funktsiooni y = log( ) + + 5 määramispiirkond.. Leidke funktsiooni y = + arcsin 5 määramispiirkond.. Leidke funktsiooni y = sin + 6 määramispiirkond.
Matemaatiline analüüs I iseseisvad ülesanded. Leidke funktsiooni y = log( ) + + 5 määramispiirkond.. Leidke funktsiooni y = + arcsin 5 määramispiirkond.. Leidke funktsiooni y = sin + 6 määramispiirkond.
Jätkusuutlikud isolatsioonilahendused. U-arvude koondtabel. VÄLISSEIN - COLUMBIA TÄISVALATUD ÕÕNESPLOKK 190 mm + SOOJUSTUS + KROHV
 U-arvude koondtabel lk 1 lk 2 lk 3 lk 4 lk 5 lk 6 lk 7 lk 8 lk 9 lk 10 lk 11 lk 12 lk 13 lk 14 lk 15 lk 16 VÄLISSEIN - FIBO 3 CLASSIC 200 mm + SOOJUSTUS + KROHV VÄLISSEIN - AEROC CLASSIC 200 mm + SOOJUSTUS
U-arvude koondtabel lk 1 lk 2 lk 3 lk 4 lk 5 lk 6 lk 7 lk 8 lk 9 lk 10 lk 11 lk 12 lk 13 lk 14 lk 15 lk 16 VÄLISSEIN - FIBO 3 CLASSIC 200 mm + SOOJUSTUS + KROHV VÄLISSEIN - AEROC CLASSIC 200 mm + SOOJUSTUS
Vektor. Joone võrrand. Analüütiline geomeetria.
 Vektor. Joone võrrand. Analüütiline geomeetria. Hele Kiisel, Hugo Treffneri Gümnaasium Analüütilise geomeetria teemad on gümnaasiumi matemaatikakursuses jaotatud kaheks osaks: analüütiline geomeetria tasandil,
Vektor. Joone võrrand. Analüütiline geomeetria. Hele Kiisel, Hugo Treffneri Gümnaasium Analüütilise geomeetria teemad on gümnaasiumi matemaatikakursuses jaotatud kaheks osaks: analüütiline geomeetria tasandil,
1 Funktsioon, piirväärtus, pidevus
 Funktsioon, piirväärtus, pidevus. Funktsioon.. Tähistused Arvuhulki tähistatakse üldlevinud viisil: N - naturaalarvude hulk, Z - täisarvude hulk, Q - ratsionaalarvude hulk, R - reaalarvude hulk. Piirkonnaks
Funktsioon, piirväärtus, pidevus. Funktsioon.. Tähistused Arvuhulki tähistatakse üldlevinud viisil: N - naturaalarvude hulk, Z - täisarvude hulk, Q - ratsionaalarvude hulk, R - reaalarvude hulk. Piirkonnaks
Arvuteooria. Diskreetse matemaatika elemendid. Sügis 2008
 Sügis 2008 Jaguvus Olgu a ja b täisarvud. Kui leidub selline täisarv m, et b = am, siis ütleme, et arv a jagab arvu b ehk arv b jagub arvuga a. Tähistused: a b b. a Näiteks arv a jagab arvu b arv b jagub
Sügis 2008 Jaguvus Olgu a ja b täisarvud. Kui leidub selline täisarv m, et b = am, siis ütleme, et arv a jagab arvu b ehk arv b jagub arvuga a. Tähistused: a b b. a Näiteks arv a jagab arvu b arv b jagub
HULGATEOORIA ELEMENTE
 HULGATEOORIA ELEMENTE Teema 2.2. Hulga elementide loendamine Jaan Penjam, email: jaan@cs.ioc.ee Diskreetne Matemaatika II: Hulgateooria 1 / 31 Loengu kava 2 Hulga elementide loendamine Hulga võimsus Loenduvad
HULGATEOORIA ELEMENTE Teema 2.2. Hulga elementide loendamine Jaan Penjam, email: jaan@cs.ioc.ee Diskreetne Matemaatika II: Hulgateooria 1 / 31 Loengu kava 2 Hulga elementide loendamine Hulga võimsus Loenduvad
Tallinna Tehnikaülikool Mehaanikainstituut Deformeeruva keha mehaanika õppetool. Andrus Salupere STAATIKA ÜLESANDED
 Tallinna Tehnikaülikool Mehaanikainstituut Deformeeruva keha mehaanika õppetool Andrus Salupere STAATIKA ÜLESANDED Tallinn 2004/2005 1 Eessõna Käesolev ülesannete kogu on mõeldud kasutamiseks eeskätt Tallinna
Tallinna Tehnikaülikool Mehaanikainstituut Deformeeruva keha mehaanika õppetool Andrus Salupere STAATIKA ÜLESANDED Tallinn 2004/2005 1 Eessõna Käesolev ülesannete kogu on mõeldud kasutamiseks eeskätt Tallinna
28. Sirgvoolu, solenoidi ja toroidi magnetinduktsiooni arvutamine koguvooluseaduse abil.
 8. Sigvoolu, solenoidi j tooidi mgnetinduktsiooni vutmine koguvooluseduse il. See on vem vdtud, kuid mitte juhtme sees. Koguvooluseduse il on sed lihtne teh. Olgu lõpmt pikk juhe ingikujulise istlõikeg,
8. Sigvoolu, solenoidi j tooidi mgnetinduktsiooni vutmine koguvooluseduse il. See on vem vdtud, kuid mitte juhtme sees. Koguvooluseduse il on sed lihtne teh. Olgu lõpmt pikk juhe ingikujulise istlõikeg,
Skalaar, vektor, tensor
 Peatükk 2 Skalaar, vektor, tensor 1 2.1. Sissejuhatus 2-2 2.1 Sissejuhatus Skalaar Üks arv, mille väärtus ei sõltu koordinaatsüsteemi (baasi) valikust Tüüpiline näide temperatuur Vektor Füüsikaline suurus,
Peatükk 2 Skalaar, vektor, tensor 1 2.1. Sissejuhatus 2-2 2.1 Sissejuhatus Skalaar Üks arv, mille väärtus ei sõltu koordinaatsüsteemi (baasi) valikust Tüüpiline näide temperatuur Vektor Füüsikaline suurus,
Eesti koolinoorte XLI täppisteaduste olümpiaad
 Eesti koolinoorte XLI täppisteaduste olümpiaad MATEMAATIKA III VOOR 6. märts 994. a. Lahendused ja vastused IX klass.. Vastus: a) neljapäev; b) teisipäev, kolmapäev, reede või laupäev. a) Et poiste luiskamise
Eesti koolinoorte XLI täppisteaduste olümpiaad MATEMAATIKA III VOOR 6. märts 994. a. Lahendused ja vastused IX klass.. Vastus: a) neljapäev; b) teisipäev, kolmapäev, reede või laupäev. a) Et poiste luiskamise
KATEGOORIATEOORIA. Kevad 2010
 KTEGOORITEOORI Kevad 2010 Loengukonspekt Lektor: Valdis Laan 1 1. Kategooriad 1.1. Hulgateoreetilistest alustest On hästi teada, et kõigi hulkade hulka ei ole olemas. Samas kategooriateoorias sooviks me
KTEGOORITEOORI Kevad 2010 Loengukonspekt Lektor: Valdis Laan 1 1. Kategooriad 1.1. Hulgateoreetilistest alustest On hästi teada, et kõigi hulkade hulka ei ole olemas. Samas kategooriateoorias sooviks me
KATEGOORIATEOORIA. Kevad 2016
 KTEGOORITEOORI Kevad 2016 Loengukonspekt Lektor: Valdis Laan 1 1. Kategooriad 1.1. Hulgateoreetilistest alustest On hästi teada, et kõigi hulkade hulka ei ole olemas. Samas kategooriateoorias sooviks me
KTEGOORITEOORI Kevad 2016 Loengukonspekt Lektor: Valdis Laan 1 1. Kategooriad 1.1. Hulgateoreetilistest alustest On hästi teada, et kõigi hulkade hulka ei ole olemas. Samas kategooriateoorias sooviks me
HSM TT 1578 EST 6720 611 954 EE (04.08) RBLV 4682-00.1/G
 HSM TT 1578 EST 682-00.1/G 6720 611 95 EE (0.08) RBLV Sisukord Sisukord Ohutustehnika alased nõuanded 3 Sümbolite selgitused 3 1. Seadme andmed 1. 1. Tarnekomplekt 1. 2. Tehnilised andmed 1. 3. Tarvikud
HSM TT 1578 EST 682-00.1/G 6720 611 95 EE (0.08) RBLV Sisukord Sisukord Ohutustehnika alased nõuanded 3 Sümbolite selgitused 3 1. Seadme andmed 1. 1. Tarnekomplekt 1. 2. Tehnilised andmed 1. 3. Tarvikud
Skalaar, vektor, tensor
 Peatükk 2 Skalaar, vektor, tensor 1 2.1. Sissejuhatus 2-2 2.1 Sissejuhatus Skalaar Üks arv, mille väärtus ei sõltu koordinaatsüsteemi (baasi) valikust Tüüpiline näide temperatuur Vektor Füüsikaline suurus,
Peatükk 2 Skalaar, vektor, tensor 1 2.1. Sissejuhatus 2-2 2.1 Sissejuhatus Skalaar Üks arv, mille väärtus ei sõltu koordinaatsüsteemi (baasi) valikust Tüüpiline näide temperatuur Vektor Füüsikaline suurus,
(Raud)betoonkonstruktsioonide üldkursus 33
 (Raud)betoonkonstruktsioonide üldkursus 33 Normaallõike tugevusarvutuse alused. Arvutuslikud pinge-deormatsioonidiagrammid Elemendi normaallõige (ristlõige) on elemendi pikiteljega risti olev lõige (s.o.
(Raud)betoonkonstruktsioonide üldkursus 33 Normaallõike tugevusarvutuse alused. Arvutuslikud pinge-deormatsioonidiagrammid Elemendi normaallõige (ristlõige) on elemendi pikiteljega risti olev lõige (s.o.
Tallinna Tehnikaülikool Mehaanikainstituut Rakendusmehaanika õppetool. Andrus Salupere. Loengukonspekt EMR5170, EMR0020, 4,0 AP
 Tallinna Tehnikaülikool Mehaanikainstituut Rakendusmehaanika õppetool Andrus Salupere DÜNAAMIKA Loengukonspekt EMR5170, EMR0020, 4,0 AP Tallinn 2003/2004/2005 Eessõna Käesolev loengukonspekt on mõeldud
Tallinna Tehnikaülikool Mehaanikainstituut Rakendusmehaanika õppetool Andrus Salupere DÜNAAMIKA Loengukonspekt EMR5170, EMR0020, 4,0 AP Tallinn 2003/2004/2005 Eessõna Käesolev loengukonspekt on mõeldud
Eesti LIV matemaatikaolümpiaad
 Eesti LIV matemaatikaolümpiaad 31. märts 007 Lõppvoor 9. klass Lahendused 1. Vastus: 43. Ilmselt ei saa see arv sisaldada numbrit 0. Iga vähemalt kahekohaline nõutud omadusega arv sisaldab paarisnumbrit
Eesti LIV matemaatikaolümpiaad 31. märts 007 Lõppvoor 9. klass Lahendused 1. Vastus: 43. Ilmselt ei saa see arv sisaldada numbrit 0. Iga vähemalt kahekohaline nõutud omadusega arv sisaldab paarisnumbrit
Eesti koolinoorte 43. keemiaolümpiaad
 Eesti koolinoorte 4. keeiaolüpiaad Koolivooru ülesannete lahendused 9. klass. Võrdsetes tingiustes on kõikide gaaside ühe ooli ruuala ühesugune. Loetletud gaaside ühe aarruuala ass on järgine: a 2 + 6
Eesti koolinoorte 4. keeiaolüpiaad Koolivooru ülesannete lahendused 9. klass. Võrdsetes tingiustes on kõikide gaaside ühe ooli ruuala ühesugune. Loetletud gaaside ühe aarruuala ass on järgine: a 2 + 6
sin 2 α + cos 2 sin cos cos 2α = cos² - sin² tan 2α =
 KORDAMINE RIIGIEKSAMIKS III TRIGONOMEETRIA ) põhiseosed sin α + cos sin cos α =, tanα =, cotα =, cos sin + tan =, tanα cotα = cos ) trigonomeetriliste funktsioonide täpsed väärtused α 5 6 9 sin α cos α
KORDAMINE RIIGIEKSAMIKS III TRIGONOMEETRIA ) põhiseosed sin α + cos sin cos α =, tanα =, cotα =, cos sin + tan =, tanα cotα = cos ) trigonomeetriliste funktsioonide täpsed väärtused α 5 6 9 sin α cos α
T~oestatavalt korrektne transleerimine
 T~oestatavalt korrektne transleerimine Transleerimisel koostatakse lähtekeelsele programmile vastav sihtkeelne programm. Transleerimine on korrektne, kui transleerimisel programmi tähendus säilib. Formaalsemalt:
T~oestatavalt korrektne transleerimine Transleerimisel koostatakse lähtekeelsele programmile vastav sihtkeelne programm. Transleerimine on korrektne, kui transleerimisel programmi tähendus säilib. Formaalsemalt:
KEEMIAÜLESANNETE LAHENDAMISE LAHTINE VÕISTLUS
 KEEMIAÜLESANNETE LAHENDAMISE LAHTINE VÕISTLUS Nooem aste (9. ja 10. klass) Tallinn, Tatu, Kuessaae, Nava, Pänu, Kohtla-Jäve 11. novembe 2006 Ülesannete lahendused 1. a) M (E) = 40,08 / 0,876 = 10,2 letades,
KEEMIAÜLESANNETE LAHENDAMISE LAHTINE VÕISTLUS Nooem aste (9. ja 10. klass) Tallinn, Tatu, Kuessaae, Nava, Pänu, Kohtla-Jäve 11. novembe 2006 Ülesannete lahendused 1. a) M (E) = 40,08 / 0,876 = 10,2 letades,
2.1. Jõud ja pinged 2-2
 1 Peatükk 2 Pinge 2.1. Jõud ja pinged 2-2 2.1 Jõud ja pinged Kehale mõjuvad välisjõud saab jagada kahte rühma. 1. Pindjõud ehk kontaktjõud on põhjustatud keha kontaktist teiste kehade või keskkondadega.
1 Peatükk 2 Pinge 2.1. Jõud ja pinged 2-2 2.1 Jõud ja pinged Kehale mõjuvad välisjõud saab jagada kahte rühma. 1. Pindjõud ehk kontaktjõud on põhjustatud keha kontaktist teiste kehade või keskkondadega.
Staatika ja kinemaatika
 Staatika ja kinemaatika MHD0071 I. Staatika Leo eder Mehhatroonikainstituut Mehaanikateaduskond allinna ehnikaülikool 2016 Sisukord I Staatika 1. Sissejuhatus. 2. Newtoni seadused. 3. Jõud. 4. ehted vektoritega.
Staatika ja kinemaatika MHD0071 I. Staatika Leo eder Mehhatroonikainstituut Mehaanikateaduskond allinna ehnikaülikool 2016 Sisukord I Staatika 1. Sissejuhatus. 2. Newtoni seadused. 3. Jõud. 4. ehted vektoritega.
Eesti koolinoorte XLIX täppisteaduste olümpiaad
 Eesti koolinoorte XLIX täppisteaduste olümpiaad MATEMAATIKA PIIRKONDLIK VOOR 26. jaanuaril 2002. a. Juhised lahenduste hindamiseks Lp. hindaja! 1. Juhime Teie tähelepanu sellele, et alljärgnevas on 7.
Eesti koolinoorte XLIX täppisteaduste olümpiaad MATEMAATIKA PIIRKONDLIK VOOR 26. jaanuaril 2002. a. Juhised lahenduste hindamiseks Lp. hindaja! 1. Juhime Teie tähelepanu sellele, et alljärgnevas on 7.
6 Mitme muutuja funktsioonid
 6 Mitme muutu funktsioonid Reaalarvude järjestatud paaride (x, ) hulga tasandi punktide hulga vahel on üksühene vastavus, st igale paarile vastab üks kindel punkt tasandil igale tasandi punktile vastavad
6 Mitme muutu funktsioonid Reaalarvude järjestatud paaride (x, ) hulga tasandi punktide hulga vahel on üksühene vastavus, st igale paarile vastab üks kindel punkt tasandil igale tasandi punktile vastavad
6.6 Ühtlaselt koormatud plaatide lihtsamad
 6.6. Ühtlaselt koormatud plaatide lihtsamad paindeülesanded 263 6.6 Ühtlaselt koormatud plaatide lihtsamad paindeülesanded 6.6.1 Silindriline paine Kui ristkülikuline plaat on pika ristküliku kujuline
6.6. Ühtlaselt koormatud plaatide lihtsamad paindeülesanded 263 6.6 Ühtlaselt koormatud plaatide lihtsamad paindeülesanded 6.6.1 Silindriline paine Kui ristkülikuline plaat on pika ristküliku kujuline
O15. Prisma aine dispersiooni määramine goniomeetri abil.
 O. Prisma aine dispersiooni määramine goniomeetri abil. 1.VALGUSE DISPERSIOON 1.1. Teoreetilised alused Prisma abil saame lahutada uuritava valguse spektriks ning määrata murdumisnäitaja n sõltuvuse lainepikkusest.
O. Prisma aine dispersiooni määramine goniomeetri abil. 1.VALGUSE DISPERSIOON 1.1. Teoreetilised alused Prisma abil saame lahutada uuritava valguse spektriks ning määrata murdumisnäitaja n sõltuvuse lainepikkusest.
Pinge. 2.1 Jõud ja pinged
 Peatükk 2 Pinge 1 2.1. Jõud ja pinged 2-2 2.1 Jõud ja pinged Kehale mõjuvad välisjõud saab jagada kahte rühma. 1. Pindjõud ehk kontaktjõud on põhjustatud keha kontaktist teiste kehade või keskkondadega.
Peatükk 2 Pinge 1 2.1. Jõud ja pinged 2-2 2.1 Jõud ja pinged Kehale mõjuvad välisjõud saab jagada kahte rühma. 1. Pindjõud ehk kontaktjõud on põhjustatud keha kontaktist teiste kehade või keskkondadega.
MATEMAATILISEST LOOGIKAST (Lausearvutus)
 TARTU ÜLIKOOL Teaduskool MATEMAATILISEST LOOGIKAST (Lausearvutus) Õppematerjal TÜ Teaduskooli õpilastele Koostanud E. Mitt TARTU 2003 1. LAUSE MÕISTE Matemaatilise loogika ühe osa - lausearvutuse - põhiliseks
TARTU ÜLIKOOL Teaduskool MATEMAATILISEST LOOGIKAST (Lausearvutus) Õppematerjal TÜ Teaduskooli õpilastele Koostanud E. Mitt TARTU 2003 1. LAUSE MÕISTE Matemaatilise loogika ühe osa - lausearvutuse - põhiliseks
ALGEBRA I. Kevad Lektor: Valdis Laan
 ALGEBRA I Kevad 2013 Lektor: Valdis Laan Sisukord 1 Maatriksid 5 1.1 Sissejuhatus....................................... 5 1.2 Maatriksi mõiste.................................... 6 1.3 Reaalarvudest ja
ALGEBRA I Kevad 2013 Lektor: Valdis Laan Sisukord 1 Maatriksid 5 1.1 Sissejuhatus....................................... 5 1.2 Maatriksi mõiste.................................... 6 1.3 Reaalarvudest ja
Deformatsioon ja olekuvõrrandid
 Peatükk 3 Deformatsioon ja olekuvõrrandid 3.. Siire ja deformatsioon 3-2 3. Siire ja deformatsioon 3.. Cauchy seosed Vaatleme deformeeruva keha meelevaldset punkti A. Algolekusontemakoor- dinaadid x, y,
Peatükk 3 Deformatsioon ja olekuvõrrandid 3.. Siire ja deformatsioon 3-2 3. Siire ja deformatsioon 3.. Cauchy seosed Vaatleme deformeeruva keha meelevaldset punkti A. Algolekusontemakoor- dinaadid x, y,
Joonis 1. Teist järku aperioodilise lüli ülekandefunktsiooni saab teisendada võnkelüli ülekandefunktsiooni kujul, kui
 Ülesnded j lhendused utomtjuhtimisest Ülesnne. Süsteem oosneb hest jdmisi ühendtud erioodilisest lülist, mille jonstndid on 0,08 j 0,5 ning õimendustegurid stlt 0 j 50. Leid süsteemi summrne ülendefuntsioon.
Ülesnded j lhendused utomtjuhtimisest Ülesnne. Süsteem oosneb hest jdmisi ühendtud erioodilisest lülist, mille jonstndid on 0,08 j 0,5 ning õimendustegurid stlt 0 j 50. Leid süsteemi summrne ülendefuntsioon.
Ülesanne 4.1. Õhukese raudbetoonist gravitatsioontugiseina arvutus
 Ülesanne 4.1. Õhukese raudbetoonist gravitatsioontugiseina arvutus Antud: Õhuke raudbetoonist gravitatsioontugisein maapinna kõrguste vahega h = 4,5 m ja taldmiku sügavusega d = 1,5 m. Maapinnal tugiseina
Ülesanne 4.1. Õhukese raudbetoonist gravitatsioontugiseina arvutus Antud: Õhuke raudbetoonist gravitatsioontugisein maapinna kõrguste vahega h = 4,5 m ja taldmiku sügavusega d = 1,5 m. Maapinnal tugiseina
NÄIDE KODUTÖÖ TALLINNA TEHNIKAÜLIKOOL. Elektriajamite ja jõuelektroonika instituut. AAR0030 Sissejuhatus robotitehnikasse
 TALLINNA TEHNIKAÜLIKOOL Elektriajamite ja jõuelektroonika instituut AAR000 Sissejuhatus robotitehnikasse KODUTÖÖ Teemal: Tööstusroboti Mitsubishi RV-6SD kinemaatika ja juhtimine Tudeng: Aleksei Tepljakov
TALLINNA TEHNIKAÜLIKOOL Elektriajamite ja jõuelektroonika instituut AAR000 Sissejuhatus robotitehnikasse KODUTÖÖ Teemal: Tööstusroboti Mitsubishi RV-6SD kinemaatika ja juhtimine Tudeng: Aleksei Tepljakov
MATEMAATILINE ANAL U US II Juhend TT U kaug oppe- uli opilastele
 MATEMAATILINE ANALÜÜS II Juhend TTÜ kaugõppe-üliõpilastele TALLINNA TEHNIKAÜLIKOOL Matemaatikainstituut MATEMAATILINE ANALÜÜS II Juhend TTÜ kaugõppe-üliõpilastele Tallinn 24 3 MATEMAATILINE ANALÜÜS II
MATEMAATILINE ANALÜÜS II Juhend TTÜ kaugõppe-üliõpilastele TALLINNA TEHNIKAÜLIKOOL Matemaatikainstituut MATEMAATILINE ANALÜÜS II Juhend TTÜ kaugõppe-üliõpilastele Tallinn 24 3 MATEMAATILINE ANALÜÜS II
Tuletis ja diferentsiaal
 Peatükk 3 Tuletis ja diferentsiaal 3.1 Tuletise ja diferentseeruva funktsiooni mõisted. Olgu antud funktsioon f ja kuulugu punkt a selle funktsiooni määramispiirkonda. Tuletis ja diferentseeruv funktsioon.
Peatükk 3 Tuletis ja diferentsiaal 3.1 Tuletise ja diferentseeruva funktsiooni mõisted. Olgu antud funktsioon f ja kuulugu punkt a selle funktsiooni määramispiirkonda. Tuletis ja diferentseeruv funktsioon.
Prisma. Lõik, mis ühendab kahte mitte kuuluvat tippu on prisma diagonaal d. Tasand, mis. prisma diagonaal d ja diagonaaltasand (roheline).
 Prism Prisms nimese ulu, mille s u on vsvl rlleelsee j võrdsee ülgedeg ulnurgd, ning ülejäänud ud on rööüliud, millel on ummgi ulnurgg üine ülg. Prlleelseid ulnuri nimese rism õjdes j nende ulnurde ülgi
Prism Prisms nimese ulu, mille s u on vsvl rlleelsee j võrdsee ülgedeg ulnurgd, ning ülejäänud ud on rööüliud, millel on ummgi ulnurgg üine ülg. Prlleelseid ulnuri nimese rism õjdes j nende ulnurde ülgi
Elastsusteooria tasandülesanne
 Peatükk 5 Eastsusteooria tasandüesanne 143 5.1. Tasandüesande mõiste 144 5.1 Tasandüesande mõiste Seeks, et iseoomustada pingust või deformatsiooni eastse keha punktis kasutatakse peapinge ja peadeformatsiooni
Peatükk 5 Eastsusteooria tasandüesanne 143 5.1. Tasandüesande mõiste 144 5.1 Tasandüesande mõiste Seeks, et iseoomustada pingust või deformatsiooni eastse keha punktis kasutatakse peapinge ja peadeformatsiooni
Eesti koolinoorte 58. füüsikaolümpiaad
 Eesti koolinoorte 58. füüsikaolümpiaad 29. jaanuar 2011. a. Piirkondlik voor. Gümnaasiumi ülesannete lahendused Eessõna Allpool on toodud iga ülesande üks õige lahenduskäik (mõnel juhul ka enam. Kõik alternatiivsed
Eesti koolinoorte 58. füüsikaolümpiaad 29. jaanuar 2011. a. Piirkondlik voor. Gümnaasiumi ülesannete lahendused Eessõna Allpool on toodud iga ülesande üks õige lahenduskäik (mõnel juhul ka enam. Kõik alternatiivsed
2. HULGATEOORIA ELEMENTE
 2. HULGATEOORIA ELEMENTE 2.1. Hulgad, nende esitusviisid. Alamhulgad Hulga mõiste on matemaatika algmõiste ja seda ei saa def ineerida. Me võime vaid selgitada, kuidas seda abstraktset mõistet endale kujundada.
2. HULGATEOORIA ELEMENTE 2.1. Hulgad, nende esitusviisid. Alamhulgad Hulga mõiste on matemaatika algmõiste ja seda ei saa def ineerida. Me võime vaid selgitada, kuidas seda abstraktset mõistet endale kujundada.
3. LOENDAMISE JA KOMBINATOORIKA ELEMENTE
 3. LOENDAMISE JA KOMBINATOORIKA ELEMENTE 3.1. Loendamise põhireeglid Kombinatoorika on diskreetse matemaatika osa, mis uurib probleeme, kus on tegemist kas diskreetse hulga mingis mõttes eristatavate osahulkadega
3. LOENDAMISE JA KOMBINATOORIKA ELEMENTE 3.1. Loendamise põhireeglid Kombinatoorika on diskreetse matemaatika osa, mis uurib probleeme, kus on tegemist kas diskreetse hulga mingis mõttes eristatavate osahulkadega
RF võimendite parameetrid
 RF võimendite parameetrid Raadiosageduslike võimendite võimendavaks elemendiks kasutatakse põhiliselt bipolaarvõi väljatransistori. Paraku on transistori võimendus sagedusest sõltuv, transistor on mittelineaarne
RF võimendite parameetrid Raadiosageduslike võimendite võimendavaks elemendiks kasutatakse põhiliselt bipolaarvõi väljatransistori. Paraku on transistori võimendus sagedusest sõltuv, transistor on mittelineaarne
Lexical-Functional Grammar
 Lexical-Functional Grammar Süntaksiteooriad ja -mudelid 2005/06 Kaili Müürisep 6. aprill 2006 1 Contents 1 Ülevaade formalismist 1 1.1 Informatsiooni esitus LFG-s..................... 1 1.2 a-struktuur..............................
Lexical-Functional Grammar Süntaksiteooriad ja -mudelid 2005/06 Kaili Müürisep 6. aprill 2006 1 Contents 1 Ülevaade formalismist 1 1.1 Informatsiooni esitus LFG-s..................... 1 1.2 a-struktuur..............................
2. Optilised instrumendid
 Sisukord 2. Optilised instrumendid... 2 2.0 Tutvumine mikroskoobiga... 2 2.0.1 Sissejuhatus ja teoreetiline ülevaade... 2 2.1 Pikksilma suurendus, vaateväli ja lahutusvõime... 7 2.1.1 Tööülesanne... 7
Sisukord 2. Optilised instrumendid... 2 2.0 Tutvumine mikroskoobiga... 2 2.0.1 Sissejuhatus ja teoreetiline ülevaade... 2 2.1 Pikksilma suurendus, vaateväli ja lahutusvõime... 7 2.1.1 Tööülesanne... 7
Fotomeetria. Laineoptika
 Fotomeetria 1. Päikese ja Maa vaheline kaugus on 1,5 10 8 km. Kui kaua tuleb valgus Päikeselt Maale? (Vastus: 500 s) 2. Fizeau ajaloolises katses valguse kiiruse määramiseks oli 720 hambaga hammasratta
Fotomeetria 1. Päikese ja Maa vaheline kaugus on 1,5 10 8 km. Kui kaua tuleb valgus Päikeselt Maale? (Vastus: 500 s) 2. Fizeau ajaloolises katses valguse kiiruse määramiseks oli 720 hambaga hammasratta
 ΕΛΛΗΝΙΚΑ Χ Ρ ΗΜ ΑΤ ΙΣ Τ ΗΡ ΙΑ CISCO EXPO 2009 G. V a s s i l i o u - E. K o n t a k i s g.vassiliou@helex.gr - e.k on t ak is@helex.gr 29 Α π ρ ι λ ί ο υ 20 0 9 Financial Services H E L E X N O C A g e
ΕΛΛΗΝΙΚΑ Χ Ρ ΗΜ ΑΤ ΙΣ Τ ΗΡ ΙΑ CISCO EXPO 2009 G. V a s s i l i o u - E. K o n t a k i s g.vassiliou@helex.gr - e.k on t ak is@helex.gr 29 Α π ρ ι λ ί ο υ 20 0 9 Financial Services H E L E X N O C A g e
Sissejuhatus. Kinemaatika
 Sissejuhatus Enamuse füüsika ülesannete lahendamine taandub tegelikult suhteliselt äikese hulga ideede rakendamisele (öeldu kehtib ka teiste aldkondade, näiteks matemaatika kohta). Seega on aja õppida
Sissejuhatus Enamuse füüsika ülesannete lahendamine taandub tegelikult suhteliselt äikese hulga ideede rakendamisele (öeldu kehtib ka teiste aldkondade, näiteks matemaatika kohta). Seega on aja õppida
Matemaatiline analüüs IV praktikumiülesannete kogu a. kevadsemester
 Matemaatiline analüüs IV praktikumiülesannete kogu 4. a. kevadsemester . Alamhulgad ruumis R m. Koonduvad jadad. Tõestage, et ruumis R a) iga kera s.o. ring) U r A) sisaldab ruutu keskpunktiga A = a,b),
Matemaatiline analüüs IV praktikumiülesannete kogu 4. a. kevadsemester . Alamhulgad ruumis R m. Koonduvad jadad. Tõestage, et ruumis R a) iga kera s.o. ring) U r A) sisaldab ruutu keskpunktiga A = a,b),
PEATÜKK 5 LUMEKOORMUS KATUSEL. 5.1 Koormuse iseloom. 5.2 Koormuse paiknemine
 PEATÜKK 5 LUMEKOORMUS KATUSEL 5.1 Koormuse iseloom (1) P Projekt peab arvestama asjaolu, et lumi võib katustele sadestuda paljude erinevate mudelite kohaselt. (2) Erinevate mudelite rakendumise põhjuseks
PEATÜKK 5 LUMEKOORMUS KATUSEL 5.1 Koormuse iseloom (1) P Projekt peab arvestama asjaolu, et lumi võib katustele sadestuda paljude erinevate mudelite kohaselt. (2) Erinevate mudelite rakendumise põhjuseks
5. TUGEVUSARVUTUSED PAINDELE
 TTÜ EHHTROONKNSTTUUT HE00 - SNTEHNK.5P/ETS 5 - -0-- E, S 5. TUGEVUSRVUTUSE PNELE Staatika üesandes (Toereaktsioonide eidmine) vaadatud näidete ause koostada taade sisejõuepüürid (põikjõud ja paindemoment)
TTÜ EHHTROONKNSTTUUT HE00 - SNTEHNK.5P/ETS 5 - -0-- E, S 5. TUGEVUSRVUTUSE PNELE Staatika üesandes (Toereaktsioonide eidmine) vaadatud näidete ause koostada taade sisejõuepüürid (põikjõud ja paindemoment)
Ülesannete numbrid on võetud ülesannete kogust L.Lepmann jt. Ülesandeid gümnaasiumi matemaatika lõpueksamiks valmistumisel Tln Ül.
 Ülesannete numbrid on võetud ülesannete kogust L.Lepmann jt. Ülesandeid gümnaasiumi matemaatika lõpueksamiks valmistumisel Tln.6 I kursus NÄIDISTÖÖ nr.: Astmed.. Arvutada avaldise täpne väärtus. 8 * (,8)
Ülesannete numbrid on võetud ülesannete kogust L.Lepmann jt. Ülesandeid gümnaasiumi matemaatika lõpueksamiks valmistumisel Tln.6 I kursus NÄIDISTÖÖ nr.: Astmed.. Arvutada avaldise täpne väärtus. 8 * (,8)
Ehitusmehaanika. EST meetod
 Ehitusmehaanika. EST meetod Staatikaga määramatu kahe avaga raam /44 4 m q = 8 kn/m 00000000000000000000000 2 EI 4 EI 6 r r F EI p EI = 0 kn p EI p 2 m 00 6 m 00 6 m Andres Lahe Mehaanikainstituut Tallinna
Ehitusmehaanika. EST meetod Staatikaga määramatu kahe avaga raam /44 4 m q = 8 kn/m 00000000000000000000000 2 EI 4 EI 6 r r F EI p EI = 0 kn p EI p 2 m 00 6 m 00 6 m Andres Lahe Mehaanikainstituut Tallinna
Ecophon Line LED. Süsteemi info. Mõõdud, mm 1200x x x600 T24 Paksus (t) M329, M330, M331. Paigaldusjoonis M397 M397
 Ecophon Line LED Ecophon Line on täisintegreeritud süvistatud valgusti. Kokkusobiv erinevate Focus-laesüsteemidega. Valgusti, mida sobib kasutada erinevates ruumides: avatud planeeringuga kontorites; vahekäigus
Ecophon Line LED Ecophon Line on täisintegreeritud süvistatud valgusti. Kokkusobiv erinevate Focus-laesüsteemidega. Valgusti, mida sobib kasutada erinevates ruumides: avatud planeeringuga kontorites; vahekäigus
Energiabilanss netoenergiavajadus
 Energiabilanss netoenergiajadus 1/26 Eelmisel loengul soojuskadude arvutus (võimsus) φ + + + tot = φ φ φ juht v inf φ sv Energia = tunnivõimsuste summa kwh Netoenergiajadus (ruumis), energiakasutus (tehnosüsteemis)
Energiabilanss netoenergiajadus 1/26 Eelmisel loengul soojuskadude arvutus (võimsus) φ + + + tot = φ φ φ juht v inf φ sv Energia = tunnivõimsuste summa kwh Netoenergiajadus (ruumis), energiakasutus (tehnosüsteemis)
VFR navigatsioon I (Mõisted ja elemendid I)
 VFR navigatsioon I (Mõisted ja elemendid I) 1. Suunad ja nende tähistamine. 2. Maakera ja sellega seonduv. 3. Maa magnetism. 4. Kursid (suunanurkade tüübid). 5. Navigatsiooniline kiiruste kolmnurk Min
VFR navigatsioon I (Mõisted ja elemendid I) 1. Suunad ja nende tähistamine. 2. Maakera ja sellega seonduv. 3. Maa magnetism. 4. Kursid (suunanurkade tüübid). 5. Navigatsiooniline kiiruste kolmnurk Min
Sirgete varraste vääne
 1 Peatükk 8 Sirgete varraste vääne 8.1. Sissejuhatus ja lahendusmeetod 8-8.1 Sissejuhatus ja lahendusmeetod Käesoleva loengukonspekti alajaotuses.10. käsitleti väändepingete leidmist ümarvarrastes ja alajaotuses.10.3
1 Peatükk 8 Sirgete varraste vääne 8.1. Sissejuhatus ja lahendusmeetod 8-8.1 Sissejuhatus ja lahendusmeetod Käesoleva loengukonspekti alajaotuses.10. käsitleti väändepingete leidmist ümarvarrastes ja alajaotuses.10.3
7.7 Hii-ruut test 7.7. HII-RUUT TEST 85
 7.7. HII-RUUT TEST 85 7.7 Hii-ruut test Üks universaalsemaid ja sagedamini kasutust leidev test on hii-ruut (χ 2 -test, inglise keeles ka chi-square test). Oletame, et sooritataval katsel on k erinevat
7.7. HII-RUUT TEST 85 7.7 Hii-ruut test Üks universaalsemaid ja sagedamini kasutust leidev test on hii-ruut (χ 2 -test, inglise keeles ka chi-square test). Oletame, et sooritataval katsel on k erinevat
Tehniline Mehaanika. I. Staatika II. Tugevusõpetus III. Kinemaatika IV. Dünaamika V. Masinaelemendid /aparaatide detailid/ I STAATIKA
 Tehniline Mehaanika I. Staatika II. Tugevusõpetus III. Kinemaatika IV. Dünaamika V. Masinaelemendid /aparaatide detailid/ I STTIK 1.1. Põhimõisted Staatika on jäikade kehade tasakaaluõpetus. Ta uurib tingimus,
Tehniline Mehaanika I. Staatika II. Tugevusõpetus III. Kinemaatika IV. Dünaamika V. Masinaelemendid /aparaatide detailid/ I STTIK 1.1. Põhimõisted Staatika on jäikade kehade tasakaaluõpetus. Ta uurib tingimus,
