Αλγόριθμοι Περικοπής και Απομάκρυνσης Κρυμμένων Επιφανειών
|
|
|
- Ἠώς Ζαχαρίου
- 9 χρόνια πριν
- Προβολές:
Transcript
1 Γραφικά & Οπτικοποίηση Κεφάλαιο 5 Αλγόριθμοι Περικοπής και Απομάκρυνσης Κρυμμένων Επιφανειών
2 Εισαγωγή Το οπτικό μας πεδίο είναι περιορισμένο ενώ παράλληλα υπάρχει παρεμπόδιση μεταξύ αντικειμένων βλέπουμε ένα πολύ μικρό κομμάτι των αντικειμένων που αποτελούν τον κόσμο Οι αλγόριθμοι περικοπής αφαιρούν αντικείμενα που δεν σχετίζονται με την δημιουργία της εικόνας συγκεκριμένου καρέ επειδή: Βρίσκονται εκτός του οπτικού πεδίου (περικοπή στο οπτικό πεδίο) Παρεμποδίζονται από άλλα αντικείμενα (περικοπή παρεμποδιζομένων) Παρεμποδίζονται από έμπροσθεν όψεις του ίδιου αντικειμένου (περικοπή πίσω όψεων) Περικοπή στο οπτικό πεδίο: Αφαιρεί τα στοιχειώδη αντικείμενα εκτός του πεδίου παρατήρησης Υλοποιείται με αλγόριθμους αποκοπής στις 3Δ 2
3 Εισαγωγή (2) Περικοπή πίσω όψεων: Αφαιρεί τα στοιχειώδη σχήματα που αποκρύπτονται από μπροστινά στοιχειώδη σχήματα του ίδιου αντικειμένου Χρησιμοποιεί γι αυτό τα κανονικά διανύσματα Tο πρόβλημα της παρεμπόδισης: Καθορισμός των ορατών αντικειμένων σε κάθε τμήμα της εικόνας Επιλύεται με τον υπολογισμό του πρώτου αντικειμένου που τέμνεται από κάθε ακτίνα προερχόμενη από το σημείο παρατήρησης Για σωστή δημιουργία εικόνας πρέπει να λυθεί το πρόβλημα της παρεμπόδισης 3
4 Εισαγωγή (3) Αλγόριθμοι Απομάκρυνσης Κρυμμένων Επιφανειών (ΑΚΕ) Σκοπός: Εξάλειψη των κρυμμένων επιφανειών των αντικειμένων διαχείριση του προβλήματος παρεμπόδισης Οι αλγόριθμοι ΑΚΕ περιλαμβάνουν ταξινόμηση των στοιχειωδών αντικειμένων: Η ταξινόμηση στην διάσταση Z (βάθος) είναι αναγκαία καθώς η ορατότητα εξαρτάται από τη διάταξη βάθους Η ταξινόμηση στις διαστάσεις X, Y επιταχύνει την ταξινόμηση της διάστασης Z, καθώς τα στοιχειώδη αντικείμενα που δεν επικαλύπτονται στις διαστάσεις X, Y δεν παρεμποδίζονται Οι αλγόριθμοι ΑΚΕ κατηγοριοποιούνται σύμφωνα με τον χώρο λειτουργίας τους: Χώρος αντικειμένων Χώρος εικόνας 4
5 Γενική μορφή ΑΚΕ χώρου αντικειμένων: for κάθε στοιχειώδες αντικείμενο { Βρες το ορατό μέρος //(σύγκριση με όλα τα στοιχειώδη αντικείμενα) Σχεδίασε το ορατό μέρος } Η πολυπλοκότητα είναι O(P 2 ), όπου P # στοιχειωδών αντικειμένων Γενική μορφή ΑΚΕ χώρου εικόνας: for κάθε εικονοστοιχείο { Εισαγωγή (4) Βρες το πλησιέστερο στοιχειώδες αντικείμενο Σχεδίασε το εικονοστοιχείο με το χρώμα του πλησιέστερου στοιχειώδους αντικειμένου } Η πολυπλοκότητα είναι O(pP), όπου p # εικονοστοιχείων εικόνας 5
6 Εισαγωγή (5) Το υπολογιστικό κόστος των αλγορίθμων ΑΚΕ είναι μεγάλο παρά την υλοποίηση σε υλικό και την παράλληλη επεξεργασία Πολλά στοιχειώδη αντικείμενα μπορούν να απαλειφθούν χωρίς την χρήση αλγορίθμων ΑΚΕ Η περικοπή πίσω όψεων εξαλείφει περίπου τα μισά στοιχειώδη αντικείμενα (πίσω όψεις) με έλεγχο κόστους O(P) Η περικοπή στο οπτικό πεδίο αφαιρεί τα στοιχειώδη αντικείμενα που βρίσκονται εκτός του οπτικού πεδίου με κόστος O(Pv), όπου v το μέσο πλήθος κορυφών ανά στοιχειώδες αντικείμενο Η περικοπή παρεμποδιζομένων κοστίζει επίσης O(P) ΣΥΜΠΕΡΑΣΜΑ: Πρόβλημα είναι η απόδοση των αλγορίθμων ΑΚΕ (O(P 2 ) ή O(pP) ανάλογα με τον χώρο λειτουργίας τους) 6
7 Περικοπή Πίσω Όψεων Τα ορατά πολύγωνα ενός αντικειμένου είναι αυτά που βρίσκονται στο έναντι του παρατηρητή ημισφαίριο των αντικειμένων Αν, από κατασκευή μοντέλων, οι πίσω όψεις τους δεν είναι ορατές περικοπή αυτών. Οι απαιτήσεις είναι: Να μην υπάρχει σύνορο Να είναι 2Δ πολλαπλότητες Να είναι αδιαφανή Η κυρτότητα δεν αποτελεί εμπόδιο Οι πίσω όψεις ανιχνεύονται με τον υπολογισμό της γωνίας που σχηματίζεται από το κανονικό διάνυσμα ˆn του πολυγώνου (κατευθυνόμενο από το αδιαφανές στερεό προς τα έξω) και το διάνυσμα παρατήρησης ˆv 7
8 Περικοπή Πίσω Όψεων (2) Αν η γωνία > 90 o τότε το πολύγωνο είναι πίσω όψη Ο έλεγχος αυτός γίνεται με το εσωτερικό γινόμενο διανυσμάτων: vn ˆ ˆ 0 Η περικοπή πίσω όψεων είναι πολύ αποτελεσματική καθώς εξαλείφει περίπου το 50% των πολυγώνων Καθώς ο έλεγχος πίσω όψης & ο υπολογισμός του κανονικού διανύσματος & του διανύσματος παρατήρησης κάθε πολυγώνου απαιτούν σταθερό χρόνο η πολυπλοκότητα είναι O(P), όπου P το πλήθος των πολυγώνων 8
9 Περικοπή στο Οπτικό Πεδίο Ο μετασχηματισμός παρατήρησης καθορίζει το οπτικό πεδίο του παρατηρητή Το πεδίο οριοθετείται από μέγιστη & ελάχιστη τιμή βάθους, και ορίζει ένα 3Δ στερεό που ονομάζεται στερεό παρατήρησης Η μορφή του στερεού παρατήρησης μπορεί να είναι: Κόλουρη πυραμίδα {προοπτική προβολή} Ορθογώνιο παραλληλεπίπεδο {ορθογραφική ή παράλληλη προβολή} Σκοπός: Εξάλειψη στοιχειωδών αντικειμένων εκτός του στερεού παρατήρησης Λαμβάνει χώρα μετά τον μετασχηματισμό από ΣΣΠ σε ΚΧΟ, και πριν την διαίρεση με w (για την προοπτική προβολή) Η περικοπή στο οπτικό πεδίο γίνεται στις 3Δ με χρήση 3Δ αποκοπής 9
10 Περικοπή στο Οπτικό Πεδίο (2) Αντικείμενα προς αποκοπή: Σημεία Ευθύγραμμα Τμήματα Πολύγωνα Η αποκοπή σημείου είναι τετριμμένη Η αποκοπή ευθύγραμμου τμήματος & πολυγώνου ανάγεται στον υπολογισμό των τομών ενός ευθυγράμμου τμήματος με τα επίπεδα του αντικειμένου αποκοπής Στις 3Δ, το εσωτερικό του αντικειμένου αποκοπής ορίζεται ως: x x x min y y y min z z z min max max max (1) 10
11 Περικοπή στο Οπτικό Πεδίο (3) Στην ορθογραφική ή παράλληλη προβολή χρησιμοποιείται ο ORTHO πίνακας M που απεικονίζει τα επίπεδα αποκοπής στο -1 & 1 έτσι ώστε: x y z min min min x y z max max max PERSP Στην προοπτική προβολή, ο πίνακας M (πριν τη διαίρεση με w) απεικονίζει τα επίπεδα αποκοπής στο w & w έτσι ώστε: Η τιμή του w δεν είναι σταθερή (είναι το z e του σημείου) Η αποκοπή με βάση το w ονομάζεται ομογενής αποκοπή 1 1 x y z w min min min x y z w max max max 11
12 Περικοπή στο Οπτικό Πεδίο (4) Για ευθύγραμμο τμήμα σε παραμετρική μορφή: l(t) = (1-t)p 1 + tp 2 από το p 1 = [x 1, y 1, z 1, w 1 ] T στο p 2 = [x 2, y 2, z 2, w 2 ] T, η τιμή του w μπορεί να βρεθεί με παρεμβολή ως εξής: (1-t)w 1 + tw 2 και οι ανισότητες (1) μπορούν να χρησιμοποιηθούν για να ορίσουν το κομμάτι του ευθυγράμμου τμήματος που βρίσκεται εντός του αντικειμένου αποκοπής: ((1 t) w tw ) (1 t) x tx (1 t) w tw ((1 t) w tw ) (1 t) y ty (1 t) w tw ((1 t) w tw ) (1 t) z tz (1 t) w tw (2) 12
13 Περικοπή στο Οπτικό Πεδίο (5) Επιλύοντας τις 6 ανισότητες ως προς t βρίσκουμε τα 6 σημεία τομής του ευθυγράμμου τμήματος με τα επίπεδα αποκοπής: : t x1 w1 ( x x ) ( w w ) : t x1 w1 ( x x ) ( w w ) ά : t y1 w1 ( y y ) ( w w ) ά : t y1 w1 ( y y ) ( w w ) (3) : t z1 w1 ( z z ) ( w w ) : t z1 w1 ( z z ) ( w w )
14 Αλγόριθμοι Αποκοπής στις 3Δ Οι περισσότεροι αλγόριθμοι αποκοπής 2Δ επεκτείνονται εύκολα στις 3Δ διευθετώντας κατάλληλα: Τον υπολογισμό των τομών Τον έλεγχο εντός / εκτός Αποκοπή Ευθυγράμμου Τμήματος Cohen Sutherland στις 3Δ Στις 3Δ, χρησιμοποιούνται 6 ψηφία για την κωδικοποίηση των 27 διαμερίσεων του 3Δ χώρου, που ορίζονται από τα επίπεδα του αντικειμένου αποκοπής: ο 1 ψηφίο: Θέσε 1 για z zmax, αλλιώς 0 ο 2 ψηφίο: Θέσε 1 για z zmin, αλλιώς 0 ο 3 ψηφίο: Θέσε 1 για y ymax, αλλιώς 0 ο 4 ψηφίο: Θέσε 1 για y ymin, αλλιώς 0 ο 5 ψηφίο: Θέσε 1 για x xmax, αλλιώς ο 6 ψηφίο: Θέσε 1 για x xmin, αλλιώς
15 Αλγόριθμοι Αποκοπής στις 3Δ (2) Ένας 6-ψήφιος κωδικός ανατίθεται σε ένα 3Δ σημείο ανάλογα με ποια από τις 27 διαμερίσεις του 3Δ χώρου βρίσκεται Έστω c 1, c 2 οι 6-ψήφιοι κωδικοί των κορυφών p 1, p 2 ενός ευθυγράμμου τμήματος: Αν c1 c αποδοχή ευθυγράμμου τμήματος Αν c1 c απόρριψη ευθυγράμμου τμήματος Ψευδοκώδικας του CS στις 3Δ: CS_Clip_3D ( vertex p1, p2 ) { } int c1, c2; vertex I; plane R; c1 = mkcode (p1); c2 = mkcode (p2); if ((c1 c2) == 0) /* p1p2 βρίσκεται εντός */ else if ((c1 & c2)!= 0) /* p1p2 βρίσκεται εκτός */ else { R = /* επίπεδο αντικ. αποκοπής με (ψηφίο c1!= ψηφίο c2) */ i = intersect_plane_line (R, (p1,p2)); if outside (R, p1) CS_Clip_3D(i, p2); else CS_Clip_3D(p1, i);} 15
16 Αλγόριθμοι Αποκοπής στις 3Δ (3) Διαφέρει από τον 2Δ αλγόριθμο ως προς: Τον υπολογισμό των τομών Τον έλεγχο εντός / εκτός Υπολογισμός τομών: Υπολογισμός τομής επιπέδου-ευθείας στις 3Δ αντί του υπολογισμού τομής ευθείας-ευθείας στις 2Δ Τα όρια αποκοπής δεν δίνονται στον ψευδοκώδικα: Για την ορθογραφική ή παράλληλη προβολή, είναι σταθερά επίπεδα & χρησιμοποιούνται αλγόριθμοι τομής επιπέδου-ευθείας Για την προοπτική προβολή (ομογενείς συντεταγμένες), χρησιμοποιούνται οι εξισώσεις (3) Έλεγχος εντός / εκτός αντικειμένου αποκοπής: Μπορεί να γίνει με έλεγχο προσήμου στην τιμή της εξίσωσης επιπέδου R για τις συντεταγμένες του p 1 16
17 Αλγόριθμοι Αποκοπής στις 3Δ (4) Αποκοπή Ευθυγράμμου Τμήματος Liang Barsky 3Δ Το ευθύγραμμο τμήμα προς αποκοπή δίνεται με τις κορυφές του p 1 και p 2 (όπως πριν) Στην ορθογραφική ή παράλληλη προβολή, το αντικείμενο αποκοπής είναι ένας κύβος και στις 3Δ προστίθεται η ανισότητα για την z συντεταγμένη: z z t z z min Στην προοπτική προβολή (ομογενείς συντεταγμένες), χρησιμοποιούνται οι ανισότητες (2) που ορίζουν το τμήμα του παραμετρικού ευθύγραμμου τμήματος εντός του αντικειμένου αποκοπής: ( w t w) x t x w t w max ( w t w) y t y w t w ( w t w) z t z w t w όπου x x x, y y y, z z z
18 Αλγόριθμοι Αποκοπής στις 3Δ (5) Αυτές οι ανισότητες έχουν την κοινή μορφή tp i q i για i= 1,2,,6 όπου: p1 x w q1 x1 w1 p x w q w x p y w q y w p4 y w q4 w1 y1 p5 z w q5 z1 w1 p z w q w z Οι λόγοι (q i / p i ) αντιστοιχούν στις παραμετρικές τιμές της τομής του ευθύγραμμου τμήματος με το επίπεδο αποκοπής i Ο υπόλοιπος αλγόριθμος παραμένει όπως στις 2Δ 18
19 Αλγόριθμοι Αποκοπής στις 3Δ (6) Αποκοπή Πολυγώνου Sutherland Hodgman 3Δ Στις 3Δ το αντικείμενο αποκοπής είναι το στερεό παρατήρησης, αντί ενός κυρτού πολυγώνου Ο αλγόριθμος αποτελείται από 6 αλυσιδωτά στάδια, ένα για κάθε όψη του στερεού παρατήρησης Διαφορές από τον 2Δ αλγόριθμο: Η υπορουτίνα inside_test τροποποιείται ώστε να ελέγχει αν ένα σημείο βρίσκεται εντός επιπέδου ισοδύναμο με έλεγχο προσήμου εξίσωσης του επιπέδου για τις συντεταγμένες του σημείου Η υπορουτίνα intersect_lines πρέπει να αντικατασταθεί από την intersect_plane_line για τον υπολογισμό τομής ακμής πολυγώνου με επίπεδο του όγκου αποκοπής οι εξισώσεις (3) χρησιμοποιούνται για την προοπτική προβολή 19
20 Περικοπή Παρεμποδιζομένων Απόρριψη στοιχειωδών αντικειμένων που κρύβονται από άλλα στοιχειώδη αντικείμενα πλησιέστερα στον παρατηρητή Σκοπός: Αποδοτική απόρριψη μεγάλου πλήθους στοιχειωδών αντικειμένων πριν την εφαρμογή ακριβών αλγορίθμων ΑΚΕ Σύνολο ορατών επιφανειών: Υποσύνολο στοιχειωδών αντικειμένων που αποτυπώνονται σε τουλάχιστον ένα εικονοστοιχείο της εικόνας Υπολογισμός σφιχτού υπερσυνόλου του συνόλου ορατών επιφανειών ώστε τα υπόλοιπα στοιχειώδη αντικείμενα να περικοπούν Αυτό το υπερσύνολο καλείται δυνητικά ορατό σύνολο (ΔΟΣ) Η περικοπή παρεμποδιζομένων δεν εξακριβώνει ποια τμήματα των στοιχειωδών αντικειμένων αποκρύπτονται αλγόριθμοι ΑΚΕ Αντίθετα εξακριβώνει ποια στοιχειώδη αντικείμενα ΔΕΝ είναι (εξ ολοκλήρου) ορατά και τα απορρίπτει, υπολογίζοντας το ΔΟΣ 20
21 Περικοπή Παρεμποδιζομένων (2) (a) σύνολο ορατών επιφανειών (b) όλα τα στοιχειώδη αντικείμενα (c) ΔΟΣ 21
22 Περικοπή Παρεμποδιζομένων (3) Το ΔΟΣ χρησιμοποιείται σαν είσοδος στους αλγόριθμους ΑΚΕ Η περικοπή παρεμποδιζομένων κοστίζει O(P), όπου P το # στοιχειωδών αντικειμένων 2 κατηγορίες περικοπής παρεμποδιζομένων: Περικοπή Παρεμποδιζομένων από-σημείο: Επιλύει το πρόβλημα παρεμπόδισης για ένα σημείο παρατήρησης Κατάλληλη για εξωτερικές σκηνές Περικοπή Παρεμποδιζομένων από-περιοχή: Επιλύει το πρόβλημα περικοπής για μια περιοχή του χώρου Κατάλληλη για πυκνές εσωτερικές σκηνές Κατάλληλη για στατικές σκηνές εξαιτίας των υπολογισμών προεπεξεργασίας 22
23 Περικοπή Παρεμποδιζομένων από-περιοχή Πολλές εφαρμογές αποτελείται από σύνολο κυρτών περιοχών (κελιά), συνδεδεμένα με πύλες Απλή μορφή: σκηνή αποτελείται από 2Δ σχέδιο δαπέδου, τα κελιά και οι πύλες είναι παράλληλα με τον x και τον y άξονα Τα στοιχειώδη αντικείμενα είναι ορατά μεταξύ κελιών μόνο μέσω των πυλών Το κελί c a μπορεί να είναι ορατό από το κελί c b μέσω του c m, αν υπάρχουν ευθείες ορατότητας που ενώνουν κατάλληλα τις πύλες τους Ο αλγόριθμος απαιτεί ένα βήμα προ-επεξεργασίας Εκτελείται μόνο μια φορά αν τα κελιά και οι πύλες είναι στατικά Κατασκευάζει τον πίνακα ΔΟΣ & ένα δέντρο BSP Πίνακας ΔΟΣ: Δίνει το ΔΟΣ για κάθε κελί που μπορεί να βρίσκεται ο παρατηρητής Η ορατότητα είναι συμμετρική ο πίνακας ΔΟΣ είναι συμμετρικός 23
24 Περικοπή Παρεμποδιζομένων από-περιοχή (2) Κατασκευάζεται, ξεκινώντας από κάθε κελί c & αναδρομικά επισκέπτεται όλα τα προσβάσιμα κελιά από τον γράφο γειτνίασης, όσο υπάρχουν ευθείες ορατότητας που επιτρέπουν την ορατότητα από το c Έτσι κατασκευάζεται το δέντρο ορατότητας (stab tree) του c, που ορίζει το ΔΟΣ Δέντρο BSP: Χρησιμοποιεί διαχωριστικά επίπεδα, που μπορεί να είναι όρια κελιών, για να διαμερίσει αναδρομικά την σκηνή Τα φύλλα αναπαριστούν τα κελίά Ένα ισορροπημένο δέντρο BSP χρησιμοποιείται για τον εντοπισμό του κελιού που περιέχει ένα σημείο, σε χρόνο O(log 2 n c ), όπου n c το # των κελιών Κατά την εκτέλεση, τα βήματα που οδηγούν στη δημιουργία εικόνας του ΔΟΣ για ένα σημείο παρατήρησης v είναι: 1. Προσδιορισμός κελιού c του v χρησιμοποιώντας το δέντρο BSP 2. Προσδιορισμός του ΔΟΣ του c χρησιμοποιώντας τον πίνακα ΔΟΣ 3. Αποτύπωση του ΔΟΣ στην οθόνη 24
25 Περικοπή Παρεμποδιζομένων από-περιοχή (3) (a) Σκηνή μοντελοποιημένη με κελιά και πύλες (b) Δέντρα τομής (stab trees) κελιών (c) Πίνακας ΔΟΣ (d) δέντρο ΒSP Το ΔΟΣ δεν αλλάζει όσο το v παραμένει στο ίδιο κελί Τα πρώτα 2 βήματα εκτελούνται μόνο όταν το v περνά το όριο ενός κελιού Κατά την εκτέλεση, χρησιμοποιούνται μόνο το δέντρο BSP και ο πίνακας ΔΟΣ 25
26 Η περικοπή παρεμποδιζομένων μπορεί να βελτιστοποιηθεί αν συνδυαστεί με περικοπή στο οπτικό πεδίο και πίσω όψεων Η δημιουργία εικόνας μπορεί να περιοριστεί σε στοιχειώδη αντικείμενα που βρίσκονται ταυτόχρονα εντός του οπτικού πεδίου και του ΔΟΣ Το στερεό παρατήρησης δημιουργείται αναδρομικά και μικραίνει από κελί σε κελί του δέντρου ορατότητας Ψευδοκώδικας: main() { } Περικοπή Παρεμποδιζομένων από-περιοχή (4) προσδιορισμός κελιού c του σημείου παρατήρησης με χρήση δέντρου BSP; προσδιορισμός του ΔΟΣ κελιού c με χρήση πίνακα ΔΟΣ; f = αρχικό οπτικό πεδίο; portal render(c, f, PVS); /* PVS = ΔΟΣ*/ 26
27 Περικοπή Παρεμποδιζομένων από-περιοχή (5) portal render(cell c, frustum f, list PVS); { } for κάθε πολύγωνο R στο c { } if ((R είναι πύλη) & (c ΔΟΣ)) { } /* η πύλη R οδηγεί στο κελί c */ /* υπολογισμός νέου οπτικού πεδίου f */ f = clip frustum(f, R); if (f <> empty) portal render(c, f, PVS); else if (R είναι πύλη) {} else { } /* R δεν είναι πύλη*/ /* εφαρμογή περικοπής πίσω όψεων*/ if (!back face(r)) { /* εφαρμογή περικοπής στο οπτικό πεδίο*/ } R = clip poly(f, R); if (R <> empty) render(r ); 27
28 Περικοπή Παρεμποδιζομένων από-περιοχή (6) Η εντολή f = clip frustum(f, R) υπολογίζει την τομή του τρέχοντος οπτικού πεδίου f & του όγκου που σχηματίζεται από το σημείο παρατήρησης & του πολυγώνου πύλης R Αν παράγονται περίεργα κυρτά σχήματα, μπορεί να μην υπάρξει υποστήριξη από το υλικό Λύση: Αντικατάσταση του f από το περιβάλλον κιβώτιό του 28
29 Περικοπή Παρεμποδιζομένων από-περιοχή (7) Παράδειγμα: Προσδιορίζεται το κελί (E), στο οποίο βρίσκεται ο παρατηρητής v, με BSP Τα αντικείμενα του κελιού περικόπτονται ως προς το αρχικό οπτικό πεδίο f 1 Η πρώτη πύλη, που οδηγεί στο κελί D του ΔΟΣ, περιορίζει το οπτικό πεδίο στο f 2 Τα αντικείμενα του κελιού D περικόπτονται ως προς το f 2 Η δεύτερη πύλη που οδηγεί στο κελί Α περιορίζει το οπτικό πεδίο στο f 3 Τα αντικείμενα του κελιού Α περικόπτονται ως προς το f 3 Η αναδρομή σταματά εδώ δεν υπάρχουν άλλα πολύγωνα πύλες στο f 3 29
30 Περικοπή Παρεμποδιζομένων από-σημείο Luebke: Εσωτερικές σκηνές με κελιά και πύλες Η εικόνα δημιουργείται ξεκινώντας από το τρέχον κελί Τα στοιχειώδη αντικείμενα πρέπει να είναι ορατά μέσω της προβολής των πυλών, αν αυτές βρίσκονται εντός των ορίων αποκοπής Αναδρομικές κλήσεις για κελιά στα οποία οδηγούν οι πύλες Σε κάθε βήμα, οι νέες πύλες τέμνονται με τις παλιές μέχρι να μην απομείνει τίποτα Υπολογίζεται μια υπερεκτίμηση (παράθυρο) της τομής των πυλών, ώστε να μειωθεί η πολυπλοκότητα 30
31 Περικοπή Παρεμποδιζομένων από-σημείο (2) Δεν μπορούμε να υποθέσουμε την ύπαρξη κελιών & πυλών για εξωτερικές σκηνές Οι διαμερισμένες περιοχές τέτοιων σκηνών δεν θα είχαν συνοχή σχετικά με τα χαρακτηριστικά παρεμπόδισης Η περικοπή παρεμποδιζομένων από-σημείο επιλύει το πρόβλημα για ένα σημείο παρατήρησης το ΔΟΣ δεν υπολογίζεται, άρα δεν απαιτείται πολλή προ-επεξεργασία εν αντιθέσει με την περικοπή παρεμποδιζομένων από-περιοχή Η ιδέα πίσω από αυτή την τεχνική είναι ο παρεμποδιστής: Ο παρεμποδιστής είναι ένα στοιχειώδες αντικείμενο, ή συνδυασμός στοιχειωδών αντικειμένων, που παρεμποδίζουν μεγάλο πλήθος άλλων στοιχειωδών αντικειμένων (παρεμποδιζόμενοι) ως προς συγκεκριμένο σημείο παρατήρησης Η περιοχή που ορίζεται από το σημείο παρατήρησης και τον παρεμποδιστή είναι ο χώρος παρεμπόδισης 31
32 Περικοπή Παρεμποδιζομένων από-σημείο (3) Τα στοιχειώδη αντικείμενα εντός του χώρου παρεμπόδισης περικόπτονται Τα μερικώς παρεμποδιζόμενα αντικείμενα προωθούνται στους αλγορίθμους ΑΚΕ Δύο βήματα απαιτούνται για την περικοπή παρεμποδιζομένων ως προς σημείο παρατήρησης v: Δημιουργία συνόλου καλών παρεμποδιστών για το v Περικοπή παρεμποδιζομένων χρησιμοποιώντας τους παρεμποδιστές 32
33 Περικοπή Παρεμποδιζομένων από-σημείο (4) Επίπεδοι παρεμποδιστές, ταξινομημένοι ανάλογα με την επιφάνεια προβολής τους, προτείνονται από τους Coorg & Teller: Η συνάρτηση ταξινόμησης: f ί A( nv ˆ ˆ) όπου το A η επιφάνεια του επίπεδου παρεμποδιστή, το μοναδιαίο κανονικό του διάνυσμα και ˆv το διάνυσμα από το σημείο παρατήρησης προς το κέντρο του επίπεδου παρεμποδιστή Ένα σύνηθες είδος επιπέδου παρεμποδιστή είναι ο αντιπρόσωπος ενός αντικειμένου Ο αντιπρόσωπος είναι ένα κυρτό πολύγωνο, κάθετο στην κατεύθυνση παρατήρησης, εγγεγραμμένο εντός του χώρου παρεμπόδισης του παρεμποδιστή v 2 ˆn 33
34 Περικοπή Παρεμποδιζομένων από-σημείο (5) Η περικοπή παρεμποδιζομένων επιταχύνεται αν υπάρχει μια ιεραρχική περιγραφή της σκηνής με περιβάλλοντες όγκους Ξεκινώντας από το υψηλότερο επίπεδο, ένας περιβάλλων όγκος που βρίσκεται εξ ολοκλήρου εντός/εκτός του χώρου παρεμπόδισης αγνοείται/αποτυπώνεται στην οθόνη Ένας περιβάλλων όγκος που τέμνει τον χώρο παρεμπόδισης, διασπάται στο επόμενο επίπεδο 34
35 Περικοπή Παρεμποδιζομένων από-σημείο (6) Η περικοπή παρεμποδιζομένων πάσχει από το πρόβλημα της μερικής παρεμπόδισης: Ένα αντικείμενο μπορεί να μην βρίσκεται στον χώρο παρεμπόδισης κανενός στοιχειώδους αντικειμένου δεν περικόπτεται, παρόλο που μπορεί να βρίσκεται στον χώρο παρεμπόδισης κάποιου συνδυασμού γειτονικών στοιχειωδών αντικειμένων Γι αυτό, έχουν αναπτυχθεί αλγόριθμοι που συγχωνεύουν χώρους παρεμπόδισης : Ο Παπαϊωάννου πρότεινε μια επέκταση του επίπεδου παρεμποδιστή, τον στερεό παρεμποδιστή, που διευθετεί το πρόβλημα της μερικής παρεμπόδισης δημιουργώντας έναν επίπεδο παρεμποδιστή για ολόκληρο τον όγκο ενός αντικειμένου 35
36 Απομάκρυνση Κρυμμένων Επιφανειών Οι αλγόριθμοι ΑΚΕ δίνουν την τελική λύση στο πρόβλημα της παρεμπόδισης (ορατότητας) Τα ορατά στοιχειώδη αντικείμενα (ή τμήματά τους) πρέπει να σχεδιάζονται απευθείας Οι αλγόριθμοι ΑΚΕ ταξινομούν τα αντικείμενα που τέμνονται από τις ακτίνες προβολής Αυτή η ταξινόμηση καταλήγει στη σύγκριση 2 σημείων: p 1 =[x 1, y 1, z 1 ] T and p 2 =[x 2, y 2, z 2 ] T Αν είναι πάνω στην ίδια ακτίνα τότε αποτελούν ένα ζεύγος παρεμπόδισης το πλησιέστερο παρεμποδίζει το άλλο 2 περιπτώσεις: Ορθογραφική προβολή: αν οι ακτίνες προβολής είναι παράλληλες στο z, τότε 2 σημεία είναι ζεύγος παρεμπόδισης αν: (x 1 = x 2 ) και (y 1 = y 2 ) 36
37 Απομάκρυνση Κρυμμένων Επιφανειών (2) Προοπτική προβολή: πρέπει να γίνει η προοπτική διαίρεση για να βρεθεί αν 2 σημεία είναι ζεύγος παρεμπόδισης. Η συνθήκη είναι: (x 1 / z 1 = x 2 / z 2 ) και (y 1 / z 1 = y 2 / z 2 ) Στην προοπτική προβολή, η ακριβή προοπτική διαίρεση γίνεται έτσι κι αλλιώς κατά την μετάβαση από ΣΣΠ σε ΚΧΟ, εντός του μετασχηματισμού παρατήρησης 37
38 Απομάκρυνση Κρυμμένων Επιφανειών (3) Μετασχηματίζει το προοπτικό στερεό παρατήρησης σε ορθογώνιο παραλληλεπίπεδο γίνονται συγκρίσεις των x και y συντεταγμένων για τον καθορισμό των ζευγών παρεμπόδισης Για αυτό το λόγο η ΑΚΕ γίνεται μετά το μετασχηματισμό παρατήρησης στον ΚΧΟ Διατήρηση της z συντεταγμένης για την ΑΚΕ, κατά τον μετασχηματισμό παρατήρησης Οι περισσότεροι αλγόριθμοι ΑΚΕ εκμεταλλεύονται τη συνάφεια υπολογισμοί τομής αντικαθίστανται με αυξητικούς υπολογισμούς: Συνάφεια επιφάνειας Συνάφεια αντικειμένων Συνάφεια γραμμών σάρωσης Συνάφεια ακμής Συνάφεια μεταξύ καρέ 38
39 Αλγόριθμος Z-buffer Αρχικά απορρίφθηκε λόγω της υψηλής απαίτησης σε μνήμη Σήμερα είναι υλοποιημένος σε κάθε κάρτα γραφικών Διατηρεί 2Δ μνήμη τιμών βάθους (Z-buffer) με την ίδια χωρική ανάλυση με τον καταχωρητή εικόνας 1:1 αντιστοιχία μεταξύ των στοιχείων των καταχωρητών εικόνας & βάθους Κάθε στοιχείο του καταχωρητή βάθους φυλάσσει το ελάχιστο βάθος μέχρι στιγμής για το αντίστοιχο εικονοστοιχείο του καταχωρητή εικόνας Ο καταχωρητής βάθους αρχικοποιείται στη μέγιστη τιμή βάθους, συνήθως στο όπισθεν επίπεδο αποκοπής Κατά τη σχεδίαση υπολογίζονται για κάθε στοιχειώδες αντικείμενο τα (z p, c p ) για κάθε εικονοστοιχείο p = (x p, y p ), όπου z p το βάθος του αντικειμένου στο p, και c p το χρώμα του στο p 39
40 Αλγόριθμος Z-buffer (2) Καταχωρητής Καταχωρητής 3Δ σκηνή Εικόνας Βάθους Αν οι τιμές βάθους μειώνονται καθώς απομακρυνόμαστε από το σημείο παρατήρησης, ο κύριος έλεγχος του Z-buffer είναι: if (z-buffer[xp, yp] < zp) { } f-buffer[xp, yp] = cp; /* ενημέρωση καταχωρητή εικόνας */ z-buffer[xp, yp] = zp; /* ενημέρωση καταχωρητή βάθους */ 40
41 Αλγόριθμος Z-buffer (3) Για τον υπολογισμό του βάθους z p σε κάθε εικονοστοιχείο που καλύπτει ένα αντικείμενο, τίθεται θέμα απόδοσης: Ο υπολογισμός τομής του αντικειμένου με την ακτίνα που ορίζεται από το σημείο παρατήρησης και το εικονοστοιχείο είναι ακριβός Εκμεταλλευόμαστε τη συνάφεια επιφάνειας. Έστω η εξίσωση επιπέδου του στοιχειώδους αντικειμένου: Για το βάθος παίρνουμε: F (x, y, z) = ax + by + cz + d =0 F (x, y) = z = - d/c - (a/c)x - (b/c)y F υπολογίζεται αυξητικά από το εικονοστοιχείο (x, y) στο (x+1, y) αφού: F (x+1, y) F (x, y) = - a/c Προσθέτοντας την σταθερή πρώτη διαφορά της F στο x ή y, υπολογίζεται το βάθος από εικονοστοιχείο σε εικονοστοιχείο με κόστος μιας πρόσθεσης 41
42 Αλγόριθμος Z-buffer (4) Στην πράξη, οι τιμές βάθους στις κορυφές ενός επίπεδου στοιχειώδους αντικειμένου παρεμβάλλονται κατά μήκος των ακμών και των γραμμών σάρωσης Το ίδιο συμβαίνει και για το χρωματικό διάνυσμα Η πολυπλοκότητα του αλγορίθμου Z-buffer είναι O(Ps), όπου P # των στοιχειωδών αντικειμένων και s ο μέσος # των εικονοστοιχείων που καλύπτει ένα αντικείμενο Στην πράξη, όσο αυξάνει το P, το s μειώνεται αναλογικά O(p), όπου p το # των εικονοστοιχείων Πλεονεκτήματα αλγορίθμου Z-buffer : Απλός Σταθερή απόδοση Μειονεκτήματα αλγορίθμου Z-buffer : Δυσκολία στην αντιμετώπιση κάποιων ειδικών εφέ (π.χ. διαφάνεια) 42
43 Αλγόριθμος Z-buffer (5) Το αποτέλεσμα έχει σταθερή ανάλυση, που οφείλεται στη φύση του χώρου εικόνας Z-fighting: προβλήματα αριθμητικής σύγκρισης βάθους, αν τα όρια αποκοπής ορίζουν μεγάλη διάσταση βάθους Ο καταχωρητής βάθους που υπολογίζεται κατά τη σχεδίαση, μπορεί να χρησιμοποιηθεί με πολλούς τρόπους: Επιτρέπει τη συγχώνευση βάθους 2 ή περισσότερων εικόνων. Έστω (f a, z a ) και (f b, z b ) οι καταχωρητές εικόνας και βάθους 2 τμημάτων μιας σκηνής. Μπορούν να συγχωνευθούν με την επιλογή του τμήματος με την μικρότερη τιμή βάθους σε κάθε εικονοστοιχείο: for(x=0; x<xres; x++){ } for(y=0; y<yres; y++) { Fc[x,y] = (Za[x,y]>Zb[x,y])? Fa[x,y]:Fb[x,y]; Zc[x,y] = (Za[x,y]>Zb[x,y])? Za[x,y]:Zb[x,y]; } 43
44 Αλγόριθμος Z-buffer (6) Πολλοί άλλοι υπολογισμοί μπορούν να γίνουν με τον Z-buffer: Προσδιορισμός σκιών Μετατροπή επιφανειών σε ογκοστοιχεία Υπολογισμοί Voronoi Ανακατασκευή 3Δ αντικειμένων Ανίχνευση συμμετρίας Ανάκτηση 3Δ αντικειμένων 44
45 Αλγόριθμος BSP Η δυαδική διαμέριση χώρου (BSP) είναι ένας αλγόριθμος χώρου αντικειμένων που χρησιμοποιεί ένα δυαδικό δέντρο για να υποδιαιρεί αναδρομικά τον χώρο Τα δεδομένα στους κόμβους αντιπροσωπεύουν τα πολύγωνα της σκηνής Οι εσωτερικοί κόμβοι διαμερίζουν το χώρο σε σχέση με το επίπεδο του πολυγώνου τους, ώστε οι απόγονοι που είναι στο αριστερό υποδέντρο να είναι στη μια μεριά του επιπέδου και εκείνοι που είναι στο δεξί να είναι στην άλλη 45
46 Αλγόριθμος για την κατασκευή δέντρου BSP: BuildBSP(BSPnode, polygondb); { Αλγόριθμος BSP (2) Επιλογή πολυγώνου (επιπέδου) Pi από polygondb; Ανάθεση Pi στο BSPnode; /* Διαμερισμός των πολυγώνων της σκηνής ανάλογα με τη μεριά που βρίσκονται σε σχέση με το επίπεδο Pi, διαίρεση των πολυγώνων που τέμνουν το Pi */ Partition(Pi, polygondb, polygondbl, polygondbr); if (polygondbl!= empty) BuildBSP(BSPnode->Left,polygonDBL); if (polygondbr!= empty) BuildBSP(BSPnode->Right,polygonDBR); } Σημαντική η επιλογή του επιπέδου διαμερισμού P i, ώστε να δημιουργηθεί ένα ισοσταθμισμένο δέντρο BSP Επιλέγεται ένα επίπεδο, που διαιρεί τη σκηνή σε 2 τμήματα που κατά προσέγγιση έχουν την ίδια πληθικότητα 46
47 Αλγόριθμος BSP (3) Κατά τη διαμέριση, πολύγωνα που τέμνουν το επίπεδο διαιρούνται επιτυγχάνεται με την επέκταση ενός αλγορίθμου αποκοπής ώστε να δίνει τόσο τα εσωτερικά όσο και τα εξωτερικά τμήματα του πολυγώνου Δέντρα BSP χρησιμοποιούνται για την εμφάνιση μιας σκηνής χωρίς τις κρυμμένες επιφάνειες Για ένα σημείο παρατήρησης v και έναν κόμβο του δέντρου BSP, όλα τα πολύγωνα που βρίσκονται στην ίδια διαμέριση με το v δεν μπορούν να κρύβονται από πολύγωνα της άλλης διαμέρισης τα πολύγωνα της άλλης διαμέρισης σχεδιάζονται πρώτα 47
48 Αλγόριθμος BSP (4) Ψευδοκώδικας: DisplayBSP(BSPnode, v); { if IsLeaf(BSPnode) Render(BSPnode->Polygon) else if (v στην άριστερή διαμέριση του BSPnode->Polygon) { DisplayBSP(BSPnode->Right, v); Render(BSPnode->Polygon); DisplayBSP(BSPnode->Left, v); } else /* v στην δεξιά διαμέριση του BSPnode->Polygon */ { DisplayBSP(BSPnode->Left, v); Render(BSPnode->Polygon); DisplayBSP(BSPnode->Right, v); } } 48
49 Αλγόριθμος BSP (5) Ο αλγόριθμος DisplayBSP κοστίζει O(P) Ο αλγόριθμος BuildBSP κοστίζει O(P 2 ) Η συνολική πολυπλοκότητα του αλγορίθμου BSP είναι O(P 2 ) Για στατικές σκηνές, η BuildBSP δε χρησιμοποιείται συχνά. Για κάθε νέα θέση του σημείου παρατήρησης, μόνο η DisplayBSP χρησιμοποιείται ο αλγόριθμος BSP είναι κατάλληλος για στατικές σκηνές, αλλά ΟΧΙ κατάλληλος για δυναμικές σκηνές 49
50 Ταξινομεί τα πολύγωνα ανάλογα με την απόστασή τους από τον παρατηρητή και τα σχεδιάζει με αντίστροφη σειρά (από πίσω προς τα εμπρός) Ονομάζεται επίσης αλγόριθμος ζωγράφου Για την ταξινόμηση χρησιμοποιούνται οι ελάχιστες τιμές βάθους: DepthSort(polygonDB); { Αλγόριθμος Ταξινόμησης Κατά Βάθος /* Ταξινόμησε την polygondb σύμφωνα με το ελάχιστο z */ for κάθε πολύγωνο στο polygondb βρες MINZ και MAXZ; ταξινόμησε το polygondb σύμφωνα με το MINZ; επίλυση επικαλύψεων στο z; σχεδίασε τα πολύγωνα με τη σειρά της ταξινομημένης λίστας; } Επικαλύψεις στο z έχουμε όταν επικαλύπτονται οι εκτάσεις z των πολυγώνων δύσκολη ταξινόμηση αφού άγνωστο ποιο είναι πλησιέστερο μερικές φορές αδύνατη η ταξινόμηση 50
51 Αλγόριθμος Ταξινόμησης Κατά Βάθος (2) Πολύγωνα που δεν μπορούν να ταξινομηθούν: Όταν επικαλύπτονται οι z εκτάσεις δυο πολύγωνων R και Q, γίνονται μια σειρά ελέγχων αυξανόμενης πολυπλοκότητας για να βρεθεί η σωστή σειρά στη λίστα σχεδίασης Αν ένας από τους παρακάτω ελέγχους είναι θετικός τότε το Q δεν αποκρύπτεται από το R: 1. Δεν επικαλύπτονται οι x-εκτάσεις των R και Q 2. Δεν επικαλύπτονται οι y-εκτάσεις των R και Q 51
52 Αλγόριθμος Ταξινόμησης Κατά Βάθος (3) 3. Το R βρίσκεται ολόκληρο στον ημιχώρο του επιπέδου του Q στον οποίο δεν βρίσκεται το σημείο παρατήρησης v. Αυτό διαπιστώνεται ελέγχοντας αν το πρόσημο της εξίσωσης επιπέδου του Q είναι ίδιο για όλες τις κορυφές του R και διαφορετικό από αυτό για το v: όπου sign(f Q (r i )) sign(f Q (v)), r i R f Q (x, y, z) = a Q x + b Q y + c Q z + d Q = 0 είναι η εξίσωση επιπέδου του πολύγωνου Q 4. Το Q βρίσκεται ολόκληρο στον ημιχώρο του επιπέδου του R στον οποίο βρίσκεται και το σημείο παρατήρησης v. Αυτό διαπιστώνεται ελέγχοντας αν το πρόσημο της εξίσωσης επιπέδου του R είναι ίδιο για όλες τις κορυφές του Q καθώς και για το v: όπου sign(f R (q i )) = sign(f R (v)), q i Q f R (x, y, z) = a R x + b R y + c R z + d R = 0 είναι η εξίσωση επιπέδου του πολύγωνου R 52
53 Αλγόριθμος Ταξινόμησης Κατά Βάθος (4) (a) R πίσω από Q (b) Q μπροστά από R 5. Δεν επικαλύπτονται οι προβολές των R και Q Αν κανένας από τους 5 ελέγχους δεν ισχύει, εναλλάσσουμε τα R και Q και επαναλαμβάνονται οι έλεγχοι 3, 4 Οι έλεγχοι 1, 2, 5 είναι συμμετρικοί δε χρειάζονται επανάληψη Αν και πάλι δε βρεθεί η σωστή σειρά, το R χωρίζεται σε 2 πολύγωνα από το επίπεδο του Q, τα νέα πολύγωνα αντικαθιστούν το R και η παραπάνω διαδικασία επαναλαμβάνεται 53
54 Αλγόριθμος Ταξινόμησης Κατά Βάθος (5) Η ταξινόμηση κατά βάθος είναι αλγόριθμος χώρου αντικειμένων εκτός από το τελευταίο βήμα (χώρος εικόνας) Μια βελτιστοποίηση είναι να σχεδιάζονται τα πολύγωνα από εμπρος προς τα πίσω: Διαδοχικά πολύγωνα σχεδιάζονται μόνο σε εικονοστοιχεία που δεν έχουν ήδη καλυφθεί από πλησιέστερα πολύγωνα Η σχεδίαση σταματά όταν όλα τα εικονοστοιχεία της εικόνας έχουν καλυφθεί τουλάχιστον μια φορά Κόστος βήματος ταξινόμησης O(Plog 2 P) Η επίλυση των z επικαλύψεων κοστίζει (χειρότερη) O(P 2 ) Ο αλγόριθμος είναι αργός για πολύπλοκες σκηνές Θετικό: Μπορεί να αντιμετωπίσει εύκολα τη διαφάνεια 54
55 Αλγόριθμος Εκπομπής Ακτίνων Για κάθε εικονοστοιχείο p παρακολουθείται μια ακτίνα Η ακτίνα καθορίζεται από το σημείο παρατήρησης v και το διάνυσμα p v Υπολογισμός τομών με όλα τα στοιχειώδη αντικείμενα της σκηνής και η πλησιέστερη στο v ορίζει το ορατό αντικείμενο Βασικός αλγόριθμος: RayCasting(primitiveDB, v); { } } for κάθε εικονοστοιχείο p { minp = MAXINT; for κάθε αντικείμενο R στην primitivedb { } /* υπολογισμός τομής της ακτίνας (v,p) με το R */ I = intersect_primitive_ray(r,v,p); /* MAXINT αν κανένα */ if ( i-v < minp) { } p -> nearest_primitive = R; minp = i-v 55
56 Αλγόριθμος Εκπομπής Ακτίνων (2) Η εκπομπή ακτίνων δεν εκμεταλλεύεται τη συνάφεια O(pP) Πολύ γενική μέθοδος Μπορεί να επιταχυνθεί με παράλληλη επεξεργασία Ο αλγόριθμος εκπομπής ακτίνων εφαρμόζεται πριν ή μετά την προοπτική προβολή: Στην 1 η περίπτωση, οι ακτίνες είναι οι ακτίνες προβολής Στη 2 η περίπτωση, οι ακτίνες είναι παράλληλες μεταξύ τους και κάθετες στο επίπεδο προβολής Η εκπομπή ακτίνων κατατάσσεται είτε ως αλγόριθμος χώρου αντικειμένων είτε χώρου εικόνας 56
57 Περίληψη Στον παρακάτω πίνακα εμφανίζονται οι πολυπλοκότητες και ο χώρος λειτουργίας των αλγορίθμων ΑΚΕ που παρουσιάστηκαν: 57
58 Θέματα Απόδοσης Αλγόριθμοι Περικοπής, ΑΚΕ, Παρακολούθησης Ακτίνας και άλλοι, χρειάζονται υπολογισμούς τομής Οι υπολογισμοί τομής είναι ακριβοί Τεχνικές που επιταχύνουν τους υπολογισμούς τομής: Περιβάλλοντες Όγκοι (Bounding volumes) Υποδιαίρεση Χώρου 58
59 Περιβάλλοντες Όγκοι Ένας τρόπος να μειωθεί το κόστος υπολογισμού τομών με ένα πολύπλοκο μοντέλο, είναι να ομαδοποιήσουμε τα στοιχειώδη αντικείμενα σε ένα περιβάλλοντα όγκο Μπορεί π.χ. να είναι ένα ορθογώνιο παραλληλεπίπεδο, ή σφαίρα Μπορεί να μην είναι κλειστός 59
60 Περιβάλλοντες Όγκοι (2) Τομή με τον περιβάλλοντα όγκο δεν συνεπάγεται απαραίτητα τομή με το μοντέλο, αφού υπάρχει κενός χώρος μεταξύ του όγκου και του μοντέλου Αντίθετα, μη τομή με τον περιβάλλοντα όγκο συνεπάγεται μη τομή με το μοντέλο που περιέχει 60
61 Περιβάλλοντες Όγκοι (3) Όταν δεν τέμνεται ο περιβάλλοντας όγκος, δεν γίνεται έλεγχος τομής με το μοντέλο εξοικονόμηση υπολογισμών Ένας καλός περιβάλλον όγκος πρέπει: Να είναι απλός Να ελαχιστοποιεί τον κενό χώρο Με το πρώτο οι έλεγχοι τομής γίνονται αποτελεσματικοί Με το δεύτερο θα υπάρχουν κατά το δυνατόν λιγότερες λάθος προειδοποιήσεις Αυτά τα 2 είναι συνήθως αντικρουόμενα: Πρέπει να επιτευχθεί συμβιβασμός 61
62 Περιβάλλοντες Όγκοι (4) Ο περιβάλλον όγκος ορθογώνιο παραλληλεπιπέδο σχηματίζεται παίρνοντας το μέγιστο και το ελάχιστο των συντεταγμένων των κορυφών του μοντέλου Ορίζονται από 6 επίπεδα κάθετα στους κύριους άξονες και γι αυτό ονομάζονται περιβάλλοντα κιβώτια ευθυγραμμισμένα με τους άξονες (AABBs) Περιέχουν πολύ κενό χώρο 62
63 Περιβάλλοντες Όγκοι (5) Προσανατολισμένα περιβάλλοντα κιβώτια (OBBs) είναι ορθογώνια παραλληλεπίπεδα προσανατολισμένα αυθαίρετα OBBs περιέχουν λιγότερο κενό χώρο από τα AABBs Ιεραρχικοί περιβάλλοντες όγκοι (hierarchical bounding volumes) συμβιβάζουν καλύτερα την απλότητα και τον κενό χώρο Περιλαμβάνους τις ιεραρχίες k-dops (πολύεδρα που έχουν πλευρές με προκαθορισμένους προσανατολισμούς) και ιεραρχίες OBBs Δημιουργούνται δέντρα με εγκυβωτισμένους όγκους Ρίζα: περιβάλλον όγκος που περιέχει όλο το μοντέλο Κόμβοι: μικρότεροι όγκοι που εσωκλείουν τμήματα του μοντέλου Φύλλα: στοιχειώδη αντικείμενα Η δομή δέντρου περιορίζει την περιοχή των πιθανών τομών 63
64 Περιβάλλοντες Όγκοι (6) Άλλη ιεραρχική μέθοδος είναι τα προοδευτικά περιβλήματα Ακολουθία από περιβλήματα που περικλείουν πιο στενά το μοντέλο Κάθε περίβλημα περικλείει όλα τα επόμενα περιβλήματα Όλα τα περιβλήματα περικλείουν ολόκληρο το μοντέλο Τα εξωτερικά περιβλήματα είναι πιο απλά αλλά με περισσότερο κενό χώρο Τα εσωτερικά περιβλήματα είναι πιο σύνθετα αλλά με λιγότερο κενό χώρο Έναρξη από τα εξωτερικά περιβλήματα (πιο απλά), όσο υπάρχουν τομές 64
65 Περιβάλλοντες Όγκοι (7) Ψευδοκώδικας για ιεραρχικό έλεγχο τομής ενός μοντέλου M IntersectionTest(M) { if BottomLevel(M) return(llintersectiontest(m)) else if LLIntersectionTest(BoundingVolume(M)) { v = false; for κάθε τμήμα M->C v = (v IntersectionTest(M->C)); return(v); } else return (false); } LLIntersectionTest: εκτελεί εξαντλητικό έλεγχο τομής για κάθε στοιχειώδες αντικείμενο της παραμέτρου του M->C: αντιπροσωπεύει ένα τμήμα στο αμέσως πιο κάτω επίπεδο της ιεραρχίας 65
66 Υποδιαίρεση Χώρου Υποδιαίρεση 3Δ χώρου σε ένα διατεταγμένο σύνολο κελιών Τα κελιά προσδιορίζουν έμμεσα τη χωρική σχέση των αντικειμένων που τα καταλαμβάνουν 2 αντικείμενα ενδέχεται να τέμνονται αν καταλαμβάνουν κοινά κελιά Η διάταξη των κελιών προσδιορίζει την ενδεχόμενη παρεμπόδιση ενός αντικειμένου από κάποιο άλλο αντικείμενο Οι τεχνικές υποδιαίρεσης χώρου απαιτούν ειδικές δομές δεδομένων και επεξεργασία για να καταχωρηθούν τα αντικείμενα στις δομές αυτές Οκταδικό δέντρο: ιεραρχική τεχνική υποδιαίρεσης 3Δ χώρου Υποδιαιρεί αναδρομικά ένα αρχικό κελί σε 8 υποκελιά Η υποδιαίρεση σταματά: Όταν φτάσει σε κελί με στοιχειώδης μέγεθος (ογκοστοιχείο) Όταν η πολυπλοκότητα του αντικειμένου μέσα στο κελί είναι μικρότερη από δεδομένο όριο 66
67 Υποδιαίρεση Χώρου (2) Στην περικοπή, αγνοούνται τα μοντέλα που δεν καλύπτουν τα κελιά που μας ενδιαφέρουν: Στην περικοπή στο οπτικό πεδίο, λαμβάνονται υπόψη μόνο τα κελιά που είναι κοινά με το οπτικό πεδίο Στην περικοπή παρεμποδιζομένων, ελέγχονται μόνο αντικείμενα που καταλαμβάνουν κελιά με τις ίδιες x,y συντατεγμένες Το οκταδικό δέντρο έχει περισσότερα επίπεδα για σκηνές με μεγαλύτερη πολυπλοκότητα 67
Γραφικά Ι. Ενότητα 5: Αλγόριθμοι Περικοπής και Απομάκρυνσης Κρυμμένων Επιφανειών
 Γραφικά Ι Ενότητα 5: Αλγόριθμοι Περικοπής και Απομάκρυνσης Κρυμμένων Επιφανειών Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 5 Αλγόριθμοι Περικοπής και Απομάκρυνσης
Γραφικά Ι Ενότητα 5: Αλγόριθμοι Περικοπής και Απομάκρυνσης Κρυμμένων Επιφανειών Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 5 Αλγόριθμοι Περικοπής και Απομάκρυνσης
Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ. 3ο Μάθημα Αποκοπή. Γραφικα. Ευάγγελος Σπύρου
 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε
Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε 3Δ Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Αποκοπή ευθείας σε 2Δ Αποκοπή πολυγώνου σε 2Δ Αποκοπή σε
Διδάσκων: Φοίβος Μυλωνάς
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #08 Αποκοπή (εισαγωγή) Σημειακή Αποκοπή Αποκοπή Ευθύγραμμων Τμημάτων (line
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #08 Αποκοπή (εισαγωγή) Σημειακή Αποκοπή Αποκοπή Ευθύγραμμων Τμημάτων (line
Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα. Παπαπαύλου Χρήστος ΑΜ: 6609
 Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα Παπαπαύλου Χρήστος ΑΜ: 6609 Αναπαράσταση μοντέλου Το 3D μοντέλο το αποθηκεύουμε στην μνήμη με τις εξής δομές δεδομένων: Λίστα κορυφών Λίστα τριγώνων
Απαλλακτική Εργασία Γραφικά & Εικονική Πραγματικότητα Παπαπαύλου Χρήστος ΑΜ: 6609 Αναπαράσταση μοντέλου Το 3D μοντέλο το αποθηκεύουμε στην μνήμη με τις εξής δομές δεδομένων: Λίστα κορυφών Λίστα τριγώνων
Κεφάλαιο 8. Οπτικοποίηση Απαλοιφή
 Κεφάλαιο 8. Οπτικοποίηση Απαλοιφή Oι οπτικές επιδράσεις, που μπορεί να προκαλέσει μια εικόνα στους χρήστες, αποτελούν ένα από τα σπουδαιότερα αποτελέσματα των λειτουργιών γραφικών με Η/Υ. Τον όρο της οπτικοποίησης
Κεφάλαιο 8. Οπτικοποίηση Απαλοιφή Oι οπτικές επιδράσεις, που μπορεί να προκαλέσει μια εικόνα στους χρήστες, αποτελούν ένα από τα σπουδαιότερα αποτελέσματα των λειτουργιών γραφικών με Η/Υ. Τον όρο της οπτικοποίησης
Γραφικά Ι. Ενότητα 4: Προβολές και Μετασχηματισμοί Παρατήρησης. Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Γραφικά Ι Ενότητα 4: Προβολές και Μετασχηματισμοί Παρατήρησης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 4 Προβολές και Μετασχηματισμοί Παρατήρησης Εισαγωγή
Γραφικά Ι Ενότητα 4: Προβολές και Μετασχηματισμοί Παρατήρησης Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 4 Προβολές και Μετασχηματισμοί Παρατήρησης Εισαγωγή
Στο Κεφάλαιο 5 µελετώντας την προβολή του τρισδιάστατου χώρου στο επίπεδο της κάµερας εξετάστηκε
 Κεφάλαιο 6 Αποκοπή (clipping) Στο Κεφάλαιο 5 µελετώντας την προβολή του τρισδιάστατου χώρου στο επίπεδο της κάµερας εξετάστηκε η διαδικασία προβολής µεµονωµένων σηµείων και µόνο προς το τέλος του κεφαλαίου
Κεφάλαιο 6 Αποκοπή (clipping) Στο Κεφάλαιο 5 µελετώντας την προβολή του τρισδιάστατου χώρου στο επίπεδο της κάµερας εξετάστηκε η διαδικασία προβολής µεµονωµένων σηµείων και µόνο προς το τέλος του κεφαλαίου
Γραφικά με Η/Υ Αποκοπή
 Γραφικά με Η/Υ Αποκοπή Βασικές λειτουργίες απεικόνισης μετατροπή των φυσικών συντεταγμένων, ενός αντικειμένου, σε συντεταγμένες της συσκευής απεικόνισης (δημιουργία μετασχηματισμού απεικόνισης) αφαίρεση
Γραφικά με Η/Υ Αποκοπή Βασικές λειτουργίες απεικόνισης μετατροπή των φυσικών συντεταγμένων, ενός αντικειμένου, σε συντεταγμένες της συσκευής απεικόνισης (δημιουργία μετασχηματισμού απεικόνισης) αφαίρεση
Γραφικά με Η/Υ Αποκοπή
 Γραφικά με Η/Υ Αποκοπή Αποκοπή Οι αλγόριθμοι αποκοπής έχουν σχεδιαστεί έτσι ώστε να είναι αποτελεσματικοί στο να εντοπίζουν τα τμήματα μίας σκηνής ή ενός αντικειμένου σε συντεταγμένες προβολής που βρίσκονται
Γραφικά με Η/Υ Αποκοπή Αποκοπή Οι αλγόριθμοι αποκοπής έχουν σχεδιαστεί έτσι ώστε να είναι αποτελεσματικοί στο να εντοπίζουν τα τμήματα μίας σκηνής ή ενός αντικειμένου σε συντεταγμένες προβολής που βρίσκονται
Εργαστήριο Τεχνολογίας Πολυμέσων & Γραφικών, Τ.Ε.Π Π.Μ, Μάθημα: Γραφικά με Η/Υ
 ΓΡΑΦΙΚΑ Γέμισμα ΑΛΓΟΡΙΘΜΟΙ ΓΕΜΙΣΜΑΤΟΣ Για τις πλεγματικές οθόνες υπάρχουν: Αλγόριθμοι γεμίσματος:, που στηρίζονται στη συνάφεια των pixels του εσωτερικού ενός πολυγώνου Αλγόριθμοι σάρωσης: που στηρίζονται
ΓΡΑΦΙΚΑ Γέμισμα ΑΛΓΟΡΙΘΜΟΙ ΓΕΜΙΣΜΑΤΟΣ Για τις πλεγματικές οθόνες υπάρχουν: Αλγόριθμοι γεμίσματος:, που στηρίζονται στη συνάφεια των pixels του εσωτερικού ενός πολυγώνου Αλγόριθμοι σάρωσης: που στηρίζονται
Γραφικά Υπολογιστών & Εικονική Πραγματικότητα. Μετασχηματισμός απεικόνισης & Αλγόριθμοι αποκοπής
 Γραφικά Υπολογιστών & Εικονική Πραγματικότητα Μετασχηματισμός απεικόνισης & Αλγόριθμοι αποκοπής Βασικές λειτουργίες απεικόνισης μετατροπή του παγκόσμιου συστήματος συντεταγμένων, ενός αντικειμένου, σε
Γραφικά Υπολογιστών & Εικονική Πραγματικότητα Μετασχηματισμός απεικόνισης & Αλγόριθμοι αποκοπής Βασικές λειτουργίες απεικόνισης μετατροπή του παγκόσμιου συστήματος συντεταγμένων, ενός αντικειμένου, σε
Τι είναι Αποκοπή (clip)?
 Αποκοπή Τι είναι Αποκοπή (clip)? Η διαδικασία απεικόνισης μόνο των τμημάτων των αντικειμένων που βρίσκονται μέσα σε μια περιοχή Από μεγαλύτερη 2Δ σκηνή στην οποία έχουμε ήδη τιμές για τα piels Κατά την
Αποκοπή Τι είναι Αποκοπή (clip)? Η διαδικασία απεικόνισης μόνο των τμημάτων των αντικειμένων που βρίσκονται μέσα σε μια περιοχή Από μεγαλύτερη 2Δ σκηνή στην οποία έχουμε ήδη τιμές για τα piels Κατά την
Γραφικά Υπολογιστών: Μέθοδοι Ανίχνευσης Επιφανειών (Surface Detection Methods)
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Μέθοδοι Ανίχνευσης Επιφανειών (Surface Detection Methods) Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Μέθοδοι Ανίχνευσης Επιφανειών (Surface Detection Methods) Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα
Γεωμετρικές Σκιές. Θ. Θεοχάρης Ι. Κακαδιάρης - Γ. Πασσαλής
 Γεωμετρικές Σκιές Θ. Θεοχάρης Ι. Κακαδιάρης - Γ. Πασσαλής Περιεχόμενα Σ1 Χαρακτηριστικά Σκιών στα Γραφικά Σ2 Απλές Σκιές Σ3 Σύγχρονοι Αλγόριθμοι Σκιών 2 Εισαγωγή (1) Οι σκιές είναι σημαντικές στην κατανόηση
Γεωμετρικές Σκιές Θ. Θεοχάρης Ι. Κακαδιάρης - Γ. Πασσαλής Περιεχόμενα Σ1 Χαρακτηριστικά Σκιών στα Γραφικά Σ2 Απλές Σκιές Σ3 Σύγχρονοι Αλγόριθμοι Σκιών 2 Εισαγωγή (1) Οι σκιές είναι σημαντικές στην κατανόηση
ΚΕΦΑΛΑΙΟ 5: ΑΠΕΙΚΟΝΙΣΗ ΚΑΙ ΑΠΟΚΟΠΗ
 ΚΕΦΑΛΑΙΟ 5: ΑΠΕΙΚΟΝΙΣΗ ΚΑΙ ΑΠΟΚΟΠΗ Ένα γεωμετρικό μοντέλο είναι μια αριθμητική περιγραφή ενός αντικειμένου, που περιλαμβάνει το μέγεθος, το σχήμα, καθώς και άλλες ιδιότητές του. Η περιγραφή του μοντέλου
ΚΕΦΑΛΑΙΟ 5: ΑΠΕΙΚΟΝΙΣΗ ΚΑΙ ΑΠΟΚΟΠΗ Ένα γεωμετρικό μοντέλο είναι μια αριθμητική περιγραφή ενός αντικειμένου, που περιλαμβάνει το μέγεθος, το σχήμα, καθώς και άλλες ιδιότητές του. Η περιγραφή του μοντέλου
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων
 Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
Ειδικά θέματα Αλγορίθμων και Δομών Δεδομένων (ΠΛΕ073) Απαντήσεις 1 ου Σετ Ασκήσεων Άσκηση 1 α) Η δομή σταθμισμένης ένωσης με συμπίεση διαδρομής μπορεί να τροποποιηθεί πολύ εύκολα ώστε να υποστηρίζει τις
Κλασσική παρατήρηση & παρατήρηση με υπολογιστή
 Κλασσική παρατήρηση & παρατήρηση με υπολογιστή Πολλέςαπότιςεργασίεςσχεδίασης (αρχιτεκτονικό, μηχανολογικό σχέδιο, κινούμενα σχέδια) γίνονται με υπολογιστή Ο χρήστης θα πρέπει να μπορεί να παράξει «κλασικές»
Κλασσική παρατήρηση & παρατήρηση με υπολογιστή Πολλέςαπότιςεργασίεςσχεδίασης (αρχιτεκτονικό, μηχανολογικό σχέδιο, κινούμενα σχέδια) γίνονται με υπολογιστή Ο χρήστης θα πρέπει να μπορεί να παράξει «κλασικές»
Η διαδικασία Παραγωγής Συνθετικής Εικόνας (Rendering)
 Υφή Η διαδικασία Παραγωγής Συνθετικής Εικόνας (Rendering) Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3D Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης Απομάκρυνση Πίσω Επιφανειών
Υφή Η διαδικασία Παραγωγής Συνθετικής Εικόνας (Rendering) Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3D Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης Απομάκρυνση Πίσω Επιφανειών
Σχεδίαση Αλγορίθμων -Τμήμα Πληροφορικής ΑΠΘ - Εξάμηνο 4ο
 Πολλαπλασιασμός μεγάλων ακεραίων (1) Για να πολλαπλασιάσουμε δύο ακεραίους με n 1 και n 2 ψηφία με το χέρι, θα εκτελέσουμε n 1 n 2 πράξεις πολλαπλασιασμού Πρόβλημα ρβημ όταν έχουμε πολλά ψηφία: A = 12345678901357986429
Πολλαπλασιασμός μεγάλων ακεραίων (1) Για να πολλαπλασιάσουμε δύο ακεραίους με n 1 και n 2 ψηφία με το χέρι, θα εκτελέσουμε n 1 n 2 πράξεις πολλαπλασιασμού Πρόβλημα ρβημ όταν έχουμε πολλά ψηφία: A = 12345678901357986429
Αποκοπή 4.1. Εργα: : & ΣΚΕΠΣΙΣ (ΕΠΕΑΚ - ΥΠΕΠΘ) Τµήµα Πληροφορικής 1 2 (SCS) Θέση παρατηρητή. Θέσεις αντικειµένων και φωτεινών πηγών
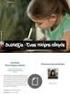 Αποκοπή Αποκοπή αντικειµένου (π.χ. πολυγώνου) ως προς αντικείµενο αποκοπής (π.χ. πολύγωνο, πυραµίδα, κύβος). Για αποφυγή αντεστραµµένης εµφάνισης αντικειµένων όπισθεν παρατηρητή. Για σηµαντική µείωση όγκου
Αποκοπή Αποκοπή αντικειµένου (π.χ. πολυγώνου) ως προς αντικείµενο αποκοπής (π.χ. πολύγωνο, πυραµίδα, κύβος). Για αποφυγή αντεστραµµένης εµφάνισης αντικειµένων όπισθεν παρατηρητή. Για σηµαντική µείωση όγκου
Κεφάλαιο 7. Τρισδιάστατα Μοντέλα
 Κεφάλαιο 7. 7.1 ομές εδομένων για Γραφικά Υπολογιστών. Οι δομές δεδομένων αποτελούν αντικείμενο της επιστήμης υπολογιστών. Κατά συνέπεια πρέπει να γνωρίζουμε πώς οργανώνονται τα γεωμετρικά δεδομένα, προκειμένου
Κεφάλαιο 7. 7.1 ομές εδομένων για Γραφικά Υπολογιστών. Οι δομές δεδομένων αποτελούν αντικείμενο της επιστήμης υπολογιστών. Κατά συνέπεια πρέπει να γνωρίζουμε πώς οργανώνονται τα γεωμετρικά δεδομένα, προκειμένου
Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch
 Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch Ματθές Δημήτριος 1, Μαγουλάς Αντώνιος 2 1 Εκπαιδευτικός Πληροφορικής ΠΕ86, dimmat@gmail.com 2 Εκπαιδευτικός Πληροφορικής ΠΕ03, amagul@yahoo.com
Ένας απλός και γρήγορος αλγόριθμος για την αποκοπή γραμμών στο Scratch Ματθές Δημήτριος 1, Μαγουλάς Αντώνιος 2 1 Εκπαιδευτικός Πληροφορικής ΠΕ86, dimmat@gmail.com 2 Εκπαιδευτικός Πληροφορικής ΠΕ03, amagul@yahoo.com
Πληροφορική 2. Αλγόριθμοι
 Πληροφορική 2 Αλγόριθμοι 1 2 Τι είναι αλγόριθμος; Αλγόριθμος είναι ένα διατεταγμένο σύνολο από σαφή βήματα το οποίο παράγει κάποιο αποτέλεσμα και τερματίζεται σε πεπερασμένο χρόνο. Ο αλγόριθμος δέχεται
Πληροφορική 2 Αλγόριθμοι 1 2 Τι είναι αλγόριθμος; Αλγόριθμος είναι ένα διατεταγμένο σύνολο από σαφή βήματα το οποίο παράγει κάποιο αποτέλεσμα και τερματίζεται σε πεπερασμένο χρόνο. Ο αλγόριθμος δέχεται
Μετασχηματισμοί Παρατήρησης και Προβολές
 Μετασχ. Γραφικά Παρατήρησης Υπολογιστών και Προβολές Μετασχηματισμοί Παρατήρησης και Προβολές Γ. Γ. Παπαϊωάννου, - 2008 Στάδια Προβολής στο Επίπεδο Περνάμε από WCS στοτοπικόσύστημα συντεταγμένων του παρατηρητή
Μετασχ. Γραφικά Παρατήρησης Υπολογιστών και Προβολές Μετασχηματισμοί Παρατήρησης και Προβολές Γ. Γ. Παπαϊωάννου, - 2008 Στάδια Προβολής στο Επίπεδο Περνάμε από WCS στοτοπικόσύστημα συντεταγμένων του παρατηρητή
Γραφικά με υπολογιστές. Διδάσκων: Φοίβος Μυλωνάς. Διάλεξη #07
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #07 Γραμμές και Πολύγωνα: Εισαγωγή Αναπαράσταση 2D και 3D Χρωματισμός πολυγώνων
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Χειμερινό εξάμηνο Γραφικά με υπολογιστές Διδάσκων: Φοίβος Μυλωνάς fmylonas@ionio.gr Διάλεξη #07 Γραμμές και Πολύγωνα: Εισαγωγή Αναπαράσταση 2D και 3D Χρωματισμός πολυγώνων
Μετασχηματισμός Παρατήρησης
 Μετασχηματισμός Παρατήρησης Παγκόσμιο Σύστημα Συντεταγμένων Σύστημα Συντεταγμένων Παρατηρητή. Σύνθεση βασικών μετασχηματισμών. Καθορίζει όρια αποκοπής & παραμέτρους προβολής Θα εξετάσουμε ΜΠ Ι και Θέσεις
Μετασχηματισμός Παρατήρησης Παγκόσμιο Σύστημα Συντεταγμένων Σύστημα Συντεταγμένων Παρατηρητή. Σύνθεση βασικών μετασχηματισμών. Καθορίζει όρια αποκοπής & παραμέτρους προβολής Θα εξετάσουμε ΜΠ Ι και Θέσεις
Γραφικά Υπολογιστών: Αποκοπή στις 3D Διαστάσεις
 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Αποκοπή στις 3D Διαστάσεις Πασχάλης Ράπτης ttp://aetos.it.teite.gr/~praptis praptis@it.teite.gr 2 Περιεχόμενα Θα δούμε μερικά demos προοπτικών προβολών
ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Αποκοπή στις 3D Διαστάσεις Πασχάλης Ράπτης ttp://aetos.it.teite.gr/~praptis praptis@it.teite.gr 2 Περιεχόμενα Θα δούμε μερικά demos προοπτικών προβολών
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων
 5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
5ο Μάθημα Αλγόριθμοι Σχεδίασης Βασικών Σχημάτων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Ευθεία Κύκλος Έλλειψη Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Ευθεία 3 Κύκλος
Παράλληλοι Αλγόριθμοι: Ανάλυση Εικόνας και Υπολογιστική Γεωμετρία. Πέτρος Ποτίκας CoReLab 4/5/2006
 Παράλληλοι Αλγόριθμοι: Ανάλυση Εικόνας και Υπολογιστική Γεωμετρία Πέτρος Ποτίκας CoReLab 4/5/2006 Επισκόπηση Ετικέτες σε συνιστώσες (Component labelling) Hough μετασχηματισμοί (transforms) Πλησιέστερος
Παράλληλοι Αλγόριθμοι: Ανάλυση Εικόνας και Υπολογιστική Γεωμετρία Πέτρος Ποτίκας CoReLab 4/5/2006 Επισκόπηση Ετικέτες σε συνιστώσες (Component labelling) Hough μετασχηματισμοί (transforms) Πλησιέστερος
Γραφικά και Εικονική Πραγματικότητα Απαλλακτική εργασία 2012. Παπαπαύλου Χρήστος ΑΜ: 6609
 Γραφικά και Εικονική Πραγματικότητα Απαλλακτική εργασία 2012 0B Παπαπαύλου Χρήστος ΑΜ: 6609 Περιεχόμενα Πίνακας Περιεχομένων...2 Περιεχόμενα...2 Προγραμματιστικές λεπτομέρειες υλοποίησης...3 geom.h...3
Γραφικά και Εικονική Πραγματικότητα Απαλλακτική εργασία 2012 0B Παπαπαύλου Χρήστος ΑΜ: 6609 Περιεχόμενα Πίνακας Περιεχομένων...2 Περιεχόμενα...2 Προγραμματιστικές λεπτομέρειες υλοποίησης...3 geom.h...3
επιστρέφει το αμέσως μεγαλύτερο από το x στοιχείο του S επιστρέφει το αμέσως μικρότερο από το x στοιχείο του S
 Μελετάμε την περίπτωση όπου αποθηκεύουμε ένα (δυναμικό) σύνολο στοιχειών,, τα οποίo είναι υποσύνολο του. Υποστηριζόμενες λειτουργίες αναζήτηση(s,x): εισαγωγή(s,x): διαγραφή(s,x): διάδοχος(s,x): προκάτοχος(s,x):
Μελετάμε την περίπτωση όπου αποθηκεύουμε ένα (δυναμικό) σύνολο στοιχειών,, τα οποίo είναι υποσύνολο του. Υποστηριζόμενες λειτουργίες αναζήτηση(s,x): εισαγωγή(s,x): διαγραφή(s,x): διάδοχος(s,x): προκάτοχος(s,x):
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
Αναπαράσταση & Απλοποίηση Μοντέλων
 Γραφικά & Οπτικοποίηση Κεφάλαιο 6 Αναπαράσταση & Απλοποίηση Μοντέλων Εισαγωγή Οι 3Δ εικόνες στα Γραφικά αποτελούνται από διάφορα σχήματα & δομές: Γεωμετρικά σχήματα (π.χ. σφαίρες) Μαθηματικές επιφάνειες
Γραφικά & Οπτικοποίηση Κεφάλαιο 6 Αναπαράσταση & Απλοποίηση Μοντέλων Εισαγωγή Οι 3Δ εικόνες στα Γραφικά αποτελούνται από διάφορα σχήματα & δομές: Γεωμετρικά σχήματα (π.χ. σφαίρες) Μαθηματικές επιφάνειες
Ενδεικτική πολυ-εργασία 1 - εφαρμογή στην υπολογιστική όραση
 Ενδεικτική πολυ-εργασία 1 - εφαρμογή στην υπολογιστική όραση Εντοπισμός ενός σήματος STOP σε μια εικόνα. Περιγράψτε τη διαδικασία με την οποία μπορώ να εντοπίσω απλά σε μια εικόνα την ύπαρξη του παρακάτω
Ενδεικτική πολυ-εργασία 1 - εφαρμογή στην υπολογιστική όραση Εντοπισμός ενός σήματος STOP σε μια εικόνα. Περιγράψτε τη διαδικασία με την οποία μπορώ να εντοπίσω απλά σε μια εικόνα την ύπαρξη του παρακάτω
Πρόβληµα Απόκρυψης. Ποιο είναι το εµφανές αντικείµενο (χρώµα) σε κάθε σηµείο του επιπέδου προβολής;
 Πρόβληµα Απόκρυψης Ποιο είναι το εµφανές αντικείµενο (χρώµα) σε κάθε σηµείο του επιπέδου προβολής; Σ Εµφανές αντικείµενο στο σηµείο Σ Επίπεδο προβολής Χωρίζονται σε αλγόριθµους απόκρυψης ακµών και επιφανειών.
Πρόβληµα Απόκρυψης Ποιο είναι το εµφανές αντικείµενο (χρώµα) σε κάθε σηµείο του επιπέδου προβολής; Σ Εµφανές αντικείµενο στο σηµείο Σ Επίπεδο προβολής Χωρίζονται σε αλγόριθµους απόκρυψης ακµών και επιφανειών.
Ταξινόμηση: Εισαγωγικά. Ταξινόμηση (Sor ng) Αλγόριθμοι Απλής Ταξινόμησης. Βασικά Βήματα των Αλγορίθμων
 Ταξινόμηση: Εισαγωγικά Ταξινόμηση (Sor ng) Ορέστης Τελέλης Βασικό πρόβλημα για την Επιστήμη των Υπολογιστών. π.χ. αλφαβητική σειρά, πωλήσεις ανά τιμή, πόλεις με βάση πληθυσμό, Μπορεί να είναι ένα πρώτο
Ταξινόμηση: Εισαγωγικά Ταξινόμηση (Sor ng) Ορέστης Τελέλης Βασικό πρόβλημα για την Επιστήμη των Υπολογιστών. π.χ. αλφαβητική σειρά, πωλήσεις ανά τιμή, πόλεις με βάση πληθυσμό, Μπορεί να είναι ένα πρώτο
ΣΧΕΔΙΑΣΗ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ ΜΕ Η/Υ (Computer Aided Design)
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΧΕΔΙΑΣΗ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ ΜΕ Η/Υ (Computer Aided Design) Ενότητα # 2: Στερεοί Μοντελοποιητές (Solid Modelers) Δρ Κ. Στεργίου
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΣΧΕΔΙΑΣΗ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ ΜΕ Η/Υ (Computer Aided Design) Ενότητα # 2: Στερεοί Μοντελοποιητές (Solid Modelers) Δρ Κ. Στεργίου
Αλγόριθμοι και πολυπλοκότητα Συγχωνευτική Ταξινόμηση
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Συγχωνευτική Ταξινόμηση Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Συγχωνευτική Ταξινόμηση (Merge Sort) 7 2 9 4 2 4 7 9 7 2 2 7 9 4
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Αλγόριθμοι και πολυπλοκότητα Συγχωνευτική Ταξινόμηση Ιωάννης Τόλλης Τμήμα Επιστήμης Υπολογιστών Συγχωνευτική Ταξινόμηση (Merge Sort) 7 2 9 4 2 4 7 9 7 2 2 7 9 4
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
1 ΘΕΩΡΙΑΣ...με απάντηση
 1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
1 ΘΕΩΡΙΑΣ.....με απάντηση ΑΛΓΕΒΡΑ Κεφάλαιο 1 0 Εξισώσεις Ανισώσεις 1. Τι ονομάζεται Αριθμητική και τι Αλγεβρική παράσταση; Ονομάζεται Αριθμητική παράσταση μια παράσταση που περιέχει πράξεις μεταξύ αριθμών.
Αλγόριθμοι Ταξινόμησης Μέρος 2
 Αλγόριθμοι Ταξινόμησης Μέρος 2 Μανόλης Κουμπαράκης 1 Προχωρημένοι Αλγόριθμοι Ταξινόμησης Στη συνέχεια θα παρουσιάσουμε τρείς προχωρημένους αλγόριθμους ταξινόμησης: treesort, quicksort και mergesort. 2
Αλγόριθμοι Ταξινόμησης Μέρος 2 Μανόλης Κουμπαράκης 1 Προχωρημένοι Αλγόριθμοι Ταξινόμησης Στη συνέχεια θα παρουσιάσουμε τρείς προχωρημένους αλγόριθμους ταξινόμησης: treesort, quicksort και mergesort. 2
Απεικόνιση Υφής. Μέρος Α Υφή σε Πολύγωνα
 Απεικόνιση Γραφικά ΥφήςΥπολογιστών Απεικόνιση Υφής Μέρος Α Υφή σε Πολύγωνα Γ. Γ. Παπαϊωάννου, - 2008 Τι Είναι η Υφή; Η υφή είναι η χωρική διαμόρφωση των ποιοτικών χαρακτηριστικών της επιφάνειας ενός αντικειμένου,
Απεικόνιση Γραφικά ΥφήςΥπολογιστών Απεικόνιση Υφής Μέρος Α Υφή σε Πολύγωνα Γ. Γ. Παπαϊωάννου, - 2008 Τι Είναι η Υφή; Η υφή είναι η χωρική διαμόρφωση των ποιοτικών χαρακτηριστικών της επιφάνειας ενός αντικειμένου,
Αποκοπή ευθυγράμμων τμημάτων
 Αλγόριθμος των Cohen-Sutherland Αποκοπή ευθυγράμμων τμημάτων Χαρακτηριστικά (Attrbutes LEFT : αριστερά της ευθείας LEFT RIGHT: δεξιά της ευθείας RIGHT ΤΟΡ : άνω της ευθείας TO BOTTO: κάτω της ευθείας BOTTO
Αλγόριθμος των Cohen-Sutherland Αποκοπή ευθυγράμμων τμημάτων Χαρακτηριστικά (Attrbutes LEFT : αριστερά της ευθείας LEFT RIGHT: δεξιά της ευθείας RIGHT ΤΟΡ : άνω της ευθείας TO BOTTO: κάτω της ευθείας BOTTO
Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας
 Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας Η πρώτη οθόνη μετά την εκτέλεση του προγράμματος διαφέρει κάπως από τα προηγούμενα λογισμικά, αν και έχει αρκετά κοινά στοιχεία. Αποτελείται
Οδηγίες για το Geogebra Μωυσιάδης Πολυχρόνης Δόρτσιος Κώστας Η πρώτη οθόνη μετά την εκτέλεση του προγράμματος διαφέρει κάπως από τα προηγούμενα λογισμικά, αν και έχει αρκετά κοινά στοιχεία. Αποτελείται
ΚΕΦΑΛΑΙΟ 3 Ο 3.2 Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η. (Σ) όπου α, β, α, β, είναι οι
 ΚΕΦΑΛΑΙΟ 3 Ο ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 3. Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η ΓΡΑΦΙΚΗ ΕΠΙΛΥΣΗ ΤΟΥ. Ποια είναι η μορφή ενός συστήματος δύο γραμμικών εξισώσεων, δύο αγνώστων; Να δοθεί παράδειγμα.
ΚΕΦΑΛΑΙΟ 3 Ο ΣΥΣΤΗΜΑΤΑ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ 3. Η ΕΝΝΟΙΑ ΤΟΥ ΓΡΑΜΜΙΚΟΥ ΣΥΣΤΗΜΑΤΟΣ ΚΑΙ Η ΓΡΑΦΙΚΗ ΕΠΙΛΥΣΗ ΤΟΥ. Ποια είναι η μορφή ενός συστήματος δύο γραμμικών εξισώσεων, δύο αγνώστων; Να δοθεί παράδειγμα.
Απαραίτητες αφού 3Δ αντικείμενα απεικονίζονται σε 2Δ συσκευές. Θέση παρατηρητή. 3Δ Μετασχ/σμός Παρατήρησης
 Προβολές Προβολές Απαραίτητες αφού 3Δ αντικείμενα απεικονίζονται σε Δ συσκευές. Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3Δ Μαθηματικά Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης
Προβολές Προβολές Απαραίτητες αφού 3Δ αντικείμενα απεικονίζονται σε Δ συσκευές. Θέσεις αντικειμένων και φωτεινών πηγών Θέση παρατηρητή 3Δ Μαθηματικά Μοντέλα 3Δ Μετασχ/σμοί Μοντέλου 3Δ Μετασχ/σμός Παρατήρησης
Εισαγωγή στην επιστήμη των υπολογιστών. Λογισμικό Υπολογιστών Κεφάλαιο 8ο Αλγόριθμοι
 Εισαγωγή στην επιστήμη των υπολογιστών Λογισμικό Υπολογιστών Κεφάλαιο 8ο Αλγόριθμοι 1 Έννοια Ανεπίσημα, ένας αλγόριθμος είναι μια βήμα προς βήμα μέθοδος για την επίλυση ενός προβλήματος ή την διεκπεραίωση
Εισαγωγή στην επιστήμη των υπολογιστών Λογισμικό Υπολογιστών Κεφάλαιο 8ο Αλγόριθμοι 1 Έννοια Ανεπίσημα, ένας αλγόριθμος είναι μια βήμα προς βήμα μέθοδος για την επίλυση ενός προβλήματος ή την διεκπεραίωση
Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Σχεδίαση γραμμών (Bresenham), Σχεδίασης Κύκλων, Γέμισμα Πολυγώνων Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιγραφή
ΕΠΑΝΑΛΗΨΗ Α ΓΥΜΝΑΣΙΟΥ
 ΕΠΑΝΑΛΗΨΗ Α ΓΥΜΝΑΣΙΟΥ ΘΕΩΡΙΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ Α.1. 1) Ποιοι φυσικοί αριθμοί λέγονται άρτιοι και ποιοι περιττοί; ( σ. 11 ) 2) Από τι καθορίζεται η αξία ενός ψηφίου σ έναν φυσικό αριθμό; ( σ. 11 ) 3) Τι
ΕΠΑΝΑΛΗΨΗ Α ΓΥΜΝΑΣΙΟΥ ΘΕΩΡΙΑ ΑΛΓΕΒΡΑ ΚΕΦΑΛΑΙΟ Α.1. 1) Ποιοι φυσικοί αριθμοί λέγονται άρτιοι και ποιοι περιττοί; ( σ. 11 ) 2) Από τι καθορίζεται η αξία ενός ψηφίου σ έναν φυσικό αριθμό; ( σ. 11 ) 3) Τι
Γραφικά Υπολογιστών: Εμφάνιση σε 2D
 1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Εμφάνιση σε 2D Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα Έννοιες παραθύρων (windowing) Αποκοπή (clipping)
1 ΤΕΙ Θεσσαλονίκης Τμήμα Πληροφορικής Γραφικά Υπολογιστών: Εμφάνιση σε 2D Πασχάλης Ράπτης http://aetos.it.teithe.gr/~praptis praptis@it.teithe.gr 2 Περιεχόμενα Έννοιες παραθύρων (windowing) Αποκοπή (clipping)
Γραφικά & Οπτικοποίηση. Κεφάλαιο 1. Εισαγωγή. Γραφικά & Οπτικοπίηση: Αρχές & Αλγόριθμοι Κεφάλαιο 1
 Γραφικά & Οπτικοποίηση Κεφάλαιο 1 Εισαγωγή Ιστορικά Ιστορική ανασκόπηση : 2 Ιστορικά (2) Ρυθμοί ανάπτυξης CPU και GPU 3 Εφαρμογές Ειδικά εφέ για ταινίες & διαφημίσεις Επιστημονική εξερεύνηση μέσω οπτικοποίησης
Γραφικά & Οπτικοποίηση Κεφάλαιο 1 Εισαγωγή Ιστορικά Ιστορική ανασκόπηση : 2 Ιστορικά (2) Ρυθμοί ανάπτυξης CPU και GPU 3 Εφαρμογές Ειδικά εφέ για ταινίες & διαφημίσεις Επιστημονική εξερεύνηση μέσω οπτικοποίησης
κυρτών και σύνθετων σωμάτων
 Τ.Ε.Ι. Αθηνών τμήμα Πληροφορικής Διπλωματική εργασία Ανίχνευση συγκρούσεων σε σκηνές 3Δ κυρτών και σύνθετων σωμάτων Κόνιαρης Χαράλαμπος Επιβλέπων καθηγητής : Δρ. Ιωάννης Πρατικάκης Περιληπτικά (1) Γενικά
Τ.Ε.Ι. Αθηνών τμήμα Πληροφορικής Διπλωματική εργασία Ανίχνευση συγκρούσεων σε σκηνές 3Δ κυρτών και σύνθετων σωμάτων Κόνιαρης Χαράλαμπος Επιβλέπων καθηγητής : Δρ. Ιωάννης Πρατικάκης Περιληπτικά (1) Γενικά
auth Αλγόριθμοι - Τμήμα Πληροφορικής ΑΠΘ - Εξάμηνο 4ο
 Σχεδίαση Αλγορίθμων Διαίρει και Βασίλευε http://delab.csd.auth.gr/courses/algorithms/ auth 1 Διαίρει και Βασίλευε Η γνωστότερη ρημέθοδος σχεδιασμού αλγορίθμων: 1. Διαιρούμε το στιγμιότυπο του προβλήματος
Σχεδίαση Αλγορίθμων Διαίρει και Βασίλευε http://delab.csd.auth.gr/courses/algorithms/ auth 1 Διαίρει και Βασίλευε Η γνωστότερη ρημέθοδος σχεδιασμού αλγορίθμων: 1. Διαιρούμε το στιγμιότυπο του προβλήματος
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος
 Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ποσοτικές Μέθοδοι στη Διοίκηση Επιχειρήσεων ΙΙ Σύνολο- Περιεχόμενο Μαθήματος Χιωτίδης Γεώργιος Τμήμα Λογιστικής και Χρηματοοικονομικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Ενδεικτική Οργάνωση Ενοτήτων. E Τάξη. Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1
 Ενδεικτική Οργάνωση Ενοτήτων E Τάξη Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1 Αρ3.1 Απαγγέλουν, διαβάζουν, γράφουν και αναγνωρίζουν ποσότητες αριθμών μέχρι το 1 000 000 000 8 Επανάληψη
Ενδεικτική Οργάνωση Ενοτήτων E Τάξη Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1 Αρ3.1 Απαγγέλουν, διαβάζουν, γράφουν και αναγνωρίζουν ποσότητες αριθμών μέχρι το 1 000 000 000 8 Επανάληψη
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
5. Απλή Ταξινόμηση. ομές εδομένων. Χρήστος ουλκερίδης. Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων
 Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 5. Απλή Ταξινόμηση 2 ομές εδομένων 4 5 Χρήστος ουλκερίδης Τμήμα Ψηφιακών Συστημάτων 11/11/2016 Εισαγωγή Η
Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 5. Απλή Ταξινόμηση 2 ομές εδομένων 4 5 Χρήστος ουλκερίδης Τμήμα Ψηφιακών Συστημάτων 11/11/2016 Εισαγωγή Η
Στ Τάξη. Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1
 Ενδεικτική Οργάνωση Ενοτήτων Στ Τάξη Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1 15 Αρ3.1 Απαγγέλουν, διαβάζουν, γράφουν και αναγνωρίζουν ποσότητες αριθμών Επανάληψη μέχρι το 1 000
Ενδεικτική Οργάνωση Ενοτήτων Στ Τάξη Α/Α Μαθηματικό περιεχόμενο Δείκτες Επιτυχίας Ώρες Διδ. 1 ENOTHTA 1 15 Αρ3.1 Απαγγέλουν, διαβάζουν, γράφουν και αναγνωρίζουν ποσότητες αριθμών Επανάληψη μέχρι το 1 000
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. Να βρείτε τις ασύμπτωτες της γραφικής παράστασης της συνάρτησης f με τύπο
 ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΑΣΥΜΠΤΩΤΕΣ - ΚΑΝΟΝΕΣ DE L HOSPITAL - ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΗΣ [Κεφ..9: Ασύμπτωτες Κανόνες de l Hospital Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
ΚΕΦΑΛΑΙΟ 3ο: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ : ΑΣΥΜΠΤΩΤΕΣ - ΚΑΝΟΝΕΣ DE L HOSPITAL - ΜΕΛΕΤΗ ΣΥΝΑΡΤΗΣΗΣ [Κεφ..9: Ασύμπτωτες Κανόνες de l Hospital Μέρος Β του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα. ΘΕΜΑ
Εισαγωγή στην Επεξεργασία Ερωτήσεων. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Εισαγωγή στην Επεξεργασία Ερωτήσεων Βάσεις Δεδομένων 2013-2014 Ευαγγελία Πιτουρά 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα Βάσεις
Εισαγωγή στην Επεξεργασία Ερωτήσεων Βάσεις Δεδομένων 2013-2014 Ευαγγελία Πιτουρά 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα Βάσεις
Μετασχηµατισµοί 2 &3
 Μετασχηµατισµοί &3 Περιγράφονται σαν σύνθεση βασικών: µετατόπιση, αλλαγή κλίµακας,περιστροφή, στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών
Μετασχηµατισµοί &3 Περιγράφονται σαν σύνθεση βασικών: µετατόπιση, αλλαγή κλίµακας,περιστροφή, στρέβλωση Χωρίζονται σε γεωµετρικούς (εδώ) και αξόνων (αντίστροφοι) Θέσεις αντικειµένων και φωτεινών πηγών
Προβλήματα, αλγόριθμοι, ψευδοκώδικας
 Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
Προβλήματα, αλγόριθμοι, ψευδοκώδικας October 11, 2011 Στο μάθημα Αλγοριθμική και Δομές Δεδομένων θα ασχοληθούμε με ένα μέρος της διαδικασίας επίλυσης υπολογιστικών προβλημάτων. Συγκεκριμένα θα δούμε τι
2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων
 2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Επανάληψη 3 Συσχετισμένοι 4 Γραμμικοί
2ο Μάθημα Μετασχηματισμοί 2Δ/3Δ και Συστήματα Συντεταγμένων Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Σύνοψη του σημερινού μαθήματος 1 Εισαγωγή 2 Επανάληψη 3 Συσχετισμένοι 4 Γραμμικοί
Εισαγωγή στην Επεξεργασία Ερωτήσεων. Βάσεις Δεδομένων Ευαγγελία Πιτουρά 1
 Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα 2 Βήματα Επεξεργασίας Τα βασικά βήματα στην επεξεργασία
Εισαγωγή στην Επεξεργασία Ερωτήσεων 1 Επεξεργασία Ερωτήσεων Θα δούμε την «πορεία» μιας SQL ερώτησης (πως εκτελείται) Ερώτηση SQL Ερώτηση ΣΒΔ Αποτέλεσμα 2 Βήματα Επεξεργασίας Τα βασικά βήματα στην επεξεργασία
21. ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 - ΔΗΜΙΟΥΡΓΩΝΤΑΣ ΜΕ ΤΟ BYOB BYOB. Αλγόριθμος Διαδικασία Παράμετροι
 21. ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 - ΔΗΜΙΟΥΡΓΩΝΤΑΣ ΜΕ ΤΟ BYOB BYOB Αλγόριθμος Διαδικασία Παράμετροι Τι είναι Αλγόριθμος; Οι οδηγίες που δίνουμε με λογική σειρά, ώστε να εκτελέσουμε μια διαδικασία ή να επιλύσουμε ένα
21. ΦΥΛΛΟ ΕΡΓΑΣΙΑΣ 4 - ΔΗΜΙΟΥΡΓΩΝΤΑΣ ΜΕ ΤΟ BYOB BYOB Αλγόριθμος Διαδικασία Παράμετροι Τι είναι Αλγόριθμος; Οι οδηγίες που δίνουμε με λογική σειρά, ώστε να εκτελέσουμε μια διαδικασία ή να επιλύσουμε ένα
Διάλεξη 14: Δέντρα IV B Δένδρα. Διδάσκων: Παναγιώτης Ανδρέου
 Διάλεξη 14: Δέντρα IV B Δένδρα Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: 2 3 Δένδρα, Εισαγωγή και άλλες πράξεις Άλλα Δέντρα: Β δένδρα, Β+ δέντρα, R δέντρα Διδάσκων: Παναγιώτης Ανδρέου ΕΠΛ231
Διάλεξη 14: Δέντρα IV B Δένδρα Στην ενότητα αυτή θα μελετηθούν τα εξής επιμέρους θέματα: 2 3 Δένδρα, Εισαγωγή και άλλες πράξεις Άλλα Δέντρα: Β δένδρα, Β+ δέντρα, R δέντρα Διδάσκων: Παναγιώτης Ανδρέου ΕΠΛ231
Γραφικά με Η/Υ. 3D Μοντέλα
 Γραφικά με Η/Υ 3D Μοντέλα Τρισδιάστατα μοντέλα Τρισδιάστατα μοντέλα Δομές και βάσεις δεδομένων Οργάνωση των γεωμετρικών δεδομένων σε βάσεις δεδομένων επεξεργάζονται μεγάλες ποσότητες γεωμετρικών δεδομένων
Γραφικά με Η/Υ 3D Μοντέλα Τρισδιάστατα μοντέλα Τρισδιάστατα μοντέλα Δομές και βάσεις δεδομένων Οργάνωση των γεωμετρικών δεδομένων σε βάσεις δεδομένων επεξεργάζονται μεγάλες ποσότητες γεωμετρικών δεδομένων
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΟΝΤΕΛΟΠΟΙΗΣΗ-ΨΗΦΙΑΚΗ ΣΥΝΘΕΣΗ ΕΙΚΟΝΩΝ Διδάσκων: Ν. ΝΙΚΟΛΑΙΔΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΟΝΤΕΛΟΠΟΙΗΣΗ-ΨΗΦΙΑΚΗ ΣΥΝΘΕΣΗ ΕΙΚΟΝΩΝ Διδάσκων: Ν. ΝΙΚΟΛΑΙΔΗΣ 3 η Σειρά Ασκήσεων 1. Ένα σωματίδιο με μάζα m=4 βρίσκεται αρχικά (t=0) στη θέση x=(2,2)
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΜΟΝΤΕΛΟΠΟΙΗΣΗ-ΨΗΦΙΑΚΗ ΣΥΝΘΕΣΗ ΕΙΚΟΝΩΝ Διδάσκων: Ν. ΝΙΚΟΛΑΙΔΗΣ 3 η Σειρά Ασκήσεων 1. Ένα σωματίδιο με μάζα m=4 βρίσκεται αρχικά (t=0) στη θέση x=(2,2)
Διαίρει και Βασίλευε. πρόβλημα μεγέθους Ν. διάσπαση. πρόβλημα μεγέθους k. πρόβλημα μεγέθους Ν-k
 Διαίρει και Βασίλευε πρόβλημα μεγέθους Ν διάσπαση πρόβλημα μεγέθους k πρόβλημα μεγέθους Ν-k Διαίρει και Βασίλευε πρόβλημα μεγέθους Ν διάσπαση επιλύουμε αναδρομικά τα υποπροβλήματα πρόβλημα μεγέθους k πρόβλημα
Διαίρει και Βασίλευε πρόβλημα μεγέθους Ν διάσπαση πρόβλημα μεγέθους k πρόβλημα μεγέθους Ν-k Διαίρει και Βασίλευε πρόβλημα μεγέθους Ν διάσπαση επιλύουμε αναδρομικά τα υποπροβλήματα πρόβλημα μεγέθους k πρόβλημα
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Εφαρμοσμένα Μαθηματικά ΙΙ 1ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες 2ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος
 Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
Εφαρμοσμένα Μαθηματικά ΙΙ ο Σετ Ασκήσεων (Λύσεις) Διανύσματα, Ευθείες Επίπεδα, Επιφάνειες ου βαθμού Επιμέλεια: Ι. Λυχναρόπουλος. Βρείτε το διάνυσμα με άκρα το Α(3,-,5) και Β(5,,-) ΑΒ=< 5 3, ( ), 5 >=
Π(n) : 1 + a + + a n = an+1 1 a 1. a 1. + a k+1 = ak+2 1
 Διακριτά Μαθηματικά [Rosen, κεφ. 5] Γιάννης Εμίρης Τμήμα Πληροφορικής & Τηλεπικοινωνιών, ΕΚΠΑ Νοέμβριος 2018 Επαγωγή και Αναδρομή [Rosen, κεφ. 5] Μαθηματική επαγωγή [Rosen 5.1] Μέθοδος απόδειξης μιας μαθηματικής
Διακριτά Μαθηματικά [Rosen, κεφ. 5] Γιάννης Εμίρης Τμήμα Πληροφορικής & Τηλεπικοινωνιών, ΕΚΠΑ Νοέμβριος 2018 Επαγωγή και Αναδρομή [Rosen, κεφ. 5] Μαθηματική επαγωγή [Rosen 5.1] Μέθοδος απόδειξης μιας μαθηματικής
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ
 ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 13: Αλγόριθμοι-Μεγάλων ακεραίων- Εκθετοποίηση- Πολλαπλασιασμός πινάκων -Strassen Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΙΣΑΓΩΓΗ ΣΤΗΝ ΑΝΑΛΥΣΗ ΑΛΓΟΡΙΘΜΩΝ Ενότητα 13: Αλγόριθμοι-Μεγάλων ακεραίων- Εκθετοποίηση- Πολλαπλασιασμός πινάκων -Strassen Μαρία Σατρατζέμη Τμήμα Εφαρμοσμένης Πληροφορικής Άδειες Χρήσης Το παρόν εκπαιδευτικό
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Φυσική για Μηχανικούς Ο νόμος του Gauss Εικόνα: Σε μια επιτραπέζια μπάλα πλάσματος, οι χρωματιστές γραμμές που βγαίνουν από τη σφαίρα αποδεικνύουν την ύπαρξη ισχυρού ηλεκτρικού πεδίου. Με το νόμο του Gauss,
Μορφές των χωρικών δεδομένων
 Μορφές των χωρικών δεδομένων Eάν θελήσουμε να αναπαραστήσουμε το περιβάλλον με ακρίβεια, τότε θα χρειαζόταν μιά απείρως μεγάλη και πρακτικά μη πραγματοποιήσιμη βάση δεδομένων. Αυτό οδηγεί στην επιλογή
Μορφές των χωρικών δεδομένων Eάν θελήσουμε να αναπαραστήσουμε το περιβάλλον με ακρίβεια, τότε θα χρειαζόταν μιά απείρως μεγάλη και πρακτικά μη πραγματοποιήσιμη βάση δεδομένων. Αυτό οδηγεί στην επιλογή
Ιωάννης Σ. Μιχέλης Μαθηματικός
 1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται αριθμητική και τι αλγεβρική παράσταση; Μία παράσταση, που περιέχει πράξεις με αριθμούς ονομάζεται αριθμητική παράσταση. Μία παράσταση, που περιέχει πράξεις
1 Άλγεβρα 1 ο Κεφάλαιο Ερώτηση 1 : Τι ονομάζεται αριθμητική και τι αλγεβρική παράσταση; Μία παράσταση, που περιέχει πράξεις με αριθμούς ονομάζεται αριθμητική παράσταση. Μία παράσταση, που περιέχει πράξεις
Γεωµετρικοί Αλγόριθµοι (CLR, κεφάλαιο 35)
 Γεωµετρικοί Αλγόριθµοι (CLR, κεφάλαιο 35) Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Γινόµενα σηµεία, τοµή ευθυγράµµων τµηµάτων Εύρεση κυρτών περιβληµάτων: Ο αλγόριθµος του Grm και ο αλγόριθµος του
Γεωµετρικοί Αλγόριθµοι (CLR, κεφάλαιο 35) Στην ενότητα αυτή θα µελετηθούν τα εξής θέµατα: Γινόµενα σηµεία, τοµή ευθυγράµµων τµηµάτων Εύρεση κυρτών περιβληµάτων: Ο αλγόριθµος του Grm και ο αλγόριθµος του
4ο Μάθημα Προβολές και Μετασχηματισμοί Παρατήρησης
 4ο Μάθημα Προβολές και Μετασχηματισμοί Παρατήρησης Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Προοπτική Προβολή Παράλληλη Προβολή Ορθογραφικές Προβολές Πλάγιες Παράλληλες
4ο Μάθημα Προβολές και Μετασχηματισμοί Παρατήρησης Γραφικα Τμήμα Πληροφορικής Πανεπιστήμιο Θεσσαλίας Ακ Έτος 2016-17 Εισαγωγή Προοπτική Προβολή Παράλληλη Προβολή Ορθογραφικές Προβολές Πλάγιες Παράλληλες
Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες)
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς
 Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
Κεφάλαιο 2: Διανυσματικός λογισμός συστήματα αναφοράς 2.1 Η έννοια του διανύσματος Ο τρόπος που παριστάνομε τα διανυσματικά μεγέθη είναι με τη μαθηματική έννοια του διανύσματος. Διάνυσμα δεν είναι τίποτε
Πρακτική Άσκηση σε σχολεία της δευτεροβάθμιας εκπαίδευσης
 Πρακτική Άσκηση σε σχολεία της δευτεροβάθμιας εκπαίδευσης Ενότητα 2: Απόδειξη Δέσποινα Πόταρη, Γιώργος Ψυχάρης Σχολή Θετικών επιστημών Τμήμα Μαθηματικό Η ΔΙΑΧΥΣΗ ΤΗΣ ΕΝΝΟΙΑΣ ΤΟΥ ΕΜΒΑΔΟΥ ΣΤΗΝ ΠΡΩΤΟΒΑΘΜΙΑ
Πρακτική Άσκηση σε σχολεία της δευτεροβάθμιας εκπαίδευσης Ενότητα 2: Απόδειξη Δέσποινα Πόταρη, Γιώργος Ψυχάρης Σχολή Θετικών επιστημών Τμήμα Μαθηματικό Η ΔΙΑΧΥΣΗ ΤΗΣ ΕΝΝΟΙΑΣ ΤΟΥ ΕΜΒΑΔΟΥ ΣΤΗΝ ΠΡΩΤΟΒΑΘΜΙΑ
Μετασχηματισμοί Μοντελοποίησης (modeling transformations)
 Μετασχηματισμοί Δ Μετασχηματισμοί Μοντελοποίησης (modeling trnformtion) Καθορισμός μετασχηματισμών των αντικειμένων Τα αντικείμενα περιγράφονται στο δικό τους σύστημα συντεταγμένων Επιτρέπει την χρήση
Μετασχηματισμοί Δ Μετασχηματισμοί Μοντελοποίησης (modeling trnformtion) Καθορισμός μετασχηματισμών των αντικειμένων Τα αντικείμενα περιγράφονται στο δικό τους σύστημα συντεταγμένων Επιτρέπει την χρήση
Εισ. Στην ΠΛΗΡΟΦΟΡΙΚΗ. Διάλεξη 7 η. Βασίλης Στεφανής
 Εισ. Στην ΠΛΗΡΟΦΟΡΙΚΗ Διάλεξη 7 η Βασίλης Στεφανής Αλγόριθμοι ταξινόμησης Στην προηγούμενη διάλεξη είδαμε: Binary search Λειτουργεί μόνο σε ταξινομημένους πίνακες Πώς τους ταξινομούμε? Πολλοί τρόποι. Ενδεικτικά:
Εισ. Στην ΠΛΗΡΟΦΟΡΙΚΗ Διάλεξη 7 η Βασίλης Στεφανής Αλγόριθμοι ταξινόμησης Στην προηγούμενη διάλεξη είδαμε: Binary search Λειτουργεί μόνο σε ταξινομημένους πίνακες Πώς τους ταξινομούμε? Πολλοί τρόποι. Ενδεικτικά:
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ. (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα.
 Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Μαθηματικά Α' Γυμ. - Ερωτήσεις Θεωρίας 1 ΕΡΩΤΗΣΕΙΣ (1) Ποιοι είναι οι φυσικοί αριθμοί; Γράψε τέσσερα παραδείγματα. (2) Ποιοι είναι οι άρτιοι και ποιοι οι περιττοί αριθμοί; Γράψε από τρία παραδείγματα.
Πόσες από αυτές τις σκακιέρες είναι αλήθεια διαφορετικές;
 Η ύλη συνοπτικά... Στοιχειώδης συνδυαστική Γεννήτριες συναρτήσεις Σχέσεις αναδρομής Θεωρία Μέτρησης Polyá Αρχή Εγκλεισμού - Αποκλεισμού Πόσες από αυτές τις σκακιέρες είναι αλήθεια διαφορετικές; Αυτές οι
Η ύλη συνοπτικά... Στοιχειώδης συνδυαστική Γεννήτριες συναρτήσεις Σχέσεις αναδρομής Θεωρία Μέτρησης Polyá Αρχή Εγκλεισμού - Αποκλεισμού Πόσες από αυτές τις σκακιέρες είναι αλήθεια διαφορετικές; Αυτές οι
Θέση και Προσανατολισμός
 Κεφάλαιο 2 Θέση και Προσανατολισμός 2-1 Εισαγωγή Προκειμένου να μπορεί ένα ρομπότ να εκτελέσει κάποιο έργο, πρέπει να διαθέτει τρόπο να περιγράφει τα εξής: Τη θέση και προσανατολισμό του τελικού στοιχείου
Κεφάλαιο 2 Θέση και Προσανατολισμός 2-1 Εισαγωγή Προκειμένου να μπορεί ένα ρομπότ να εκτελέσει κάποιο έργο, πρέπει να διαθέτει τρόπο να περιγράφει τα εξής: Τη θέση και προσανατολισμό του τελικού στοιχείου
ΠΑΡΑΔΕΙΓΜΑΤΑ ΘΕΜΑ Β. 2x 1. είναι Τότε έχουμε: » τον χρησιμοποιούμε κυρίως σε θεωρητικές ασκήσεις.
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ : ΣΥΝΑΡΤΗΣΗ - ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗ [Υποκεφάλαιο. Μονότονες συναρτήσεις Αντίστροφη συνάρτηση του σχολικού βιβλίου]. ΠΑΡΑΔΕΙΓΜΑΤΑ Παράδειγμα.
Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων ομές εδομένων
 Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 6. Δυαδικά Δέντρα 2 ομές εδομένων 4 5 Χρήστος ουλκερίδης Τμήμα Ψηφιακών Συστημάτων 18/11/2016 Εισαγωγή Τα
Πανεπιστήμιο Πειραιώς Σχολή Τεχνολογιών Πληροφορικής και Επικοινωνιών Τμήμα Ψηφιακών Συστημάτων 6. Δυαδικά Δέντρα 2 ομές εδομένων 4 5 Χρήστος ουλκερίδης Τμήμα Ψηφιακών Συστημάτων 18/11/2016 Εισαγωγή Τα
1 x m 2. degn = m 1 + m m n. a(m 1 m 2...m k )x m 1
 1 Πολυώνυμα και συσχετικός χώρος Ορισμός 3.1 Ενα μονώνυμο N στις μεταβλητές x 1, x 2,..., x n είναι ένα γινόμενο της μορφής x m 1 2...x m n n, όπου όλοι οι εκθέτες είναι φυσικοί αριθμοί. Ο βαθμός του μονωνύμου
1 Πολυώνυμα και συσχετικός χώρος Ορισμός 3.1 Ενα μονώνυμο N στις μεταβλητές x 1, x 2,..., x n είναι ένα γινόμενο της μορφής x m 1 2...x m n n, όπου όλοι οι εκθέτες είναι φυσικοί αριθμοί. Ο βαθμός του μονωνύμου
Τι είναι αλγόριθμος; Υποπρογράμματα (υποαλγόριθμοι) Βασικές αλγοριθμικές δομές
 Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
Ιόνιο Πανεπιστήμιο Τμήμα Πληροφορικής Εισαγωγή στην Επιστήμη των Υπολογιστών 2015-16 Αλγόριθμοι και Δομές Δεδομένων (Ι) (εισαγωγικές έννοιες) http://di.ionio.gr/~mistral/tp/csintro/ Μ.Στεφανιδάκης Τι είναι
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ 1 ο : Όριο Συνέχεια Συνάρτησης
 ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
ΜΑΘΗΜΑΤΙΚΑ Θετικής & Τεχνολογικής Κατεύθυνσης Β ΜΕΡΟΣ (ΑΝΑΛΥΣΗ) ΚΕΦ ο : Όριο Συνέχεια Συνάρτησης Φυλλάδιο Φυλλάδι555 4 ο ο.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ.α) ΕΝΝΟΙΑ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ
Αλγόριθμοι και Πολυπλοκότητα
 Αλγόριθμοι και Πολυπλοκότητα Διαίρει και Βασίλευε Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Διαίρει και Βασίλευε Divide and Conquer Η τεχνική διαίρει και βασίλευε αναφέρεται
Αλγόριθμοι και Πολυπλοκότητα Διαίρει και Βασίλευε Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Διαίρει και Βασίλευε Divide and Conquer Η τεχνική διαίρει και βασίλευε αναφέρεται
d k 10 k + d k 1 10 k d d = k i=0 d i 10 i.
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Φύλλο 2. Δράσεις με το λογισμικό Cabri-geometry 3D
 1 Φύλλο 2 Δράσεις με το λογισμικό Cabri-geometry 3D Το περιβάλλον του λογισμικού αυτού είναι παρόμοιο με το αντίστοιχο λογισμικό του Cabri II. Περιέχει γενικές εντολές και εικονίδια που συμπεριλαμβάνουν
1 Φύλλο 2 Δράσεις με το λογισμικό Cabri-geometry 3D Το περιβάλλον του λογισμικού αυτού είναι παρόμοιο με το αντίστοιχο λογισμικό του Cabri II. Περιέχει γενικές εντολές και εικονίδια που συμπεριλαμβάνουν
Γραφικά Ι. Ενότητα 1: Εισαγωγή. Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών
 Γραφικά Ι Ενότητα 1: Εισαγωγή Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 1 Εισαγωγή Ιστορικά Ιστορική ανασκόπηση : 3 Ιστορικά (2) Ρυθμοί ανάπτυξης CPU και
Γραφικά Ι Ενότητα 1: Εισαγωγή Θεοχάρης Θεοχάρης Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Ενότητα 1 Εισαγωγή Ιστορικά Ιστορική ανασκόπηση : 3 Ιστορικά (2) Ρυθμοί ανάπτυξης CPU και
ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ. Η διαίρεση καλείται Ευκλείδεια και είναι τέλεια όταν το υπόλοιπο είναι μηδέν.
 ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
ΑΛΓΕΒΡΑ 1 ο ΚΕΦΑΛΑΙΟ ΘΕΩΡΙΑ Α ΓΥΜΝΑΣΙΟΥ 1. Τι είναι αριθμητική παράσταση; Με ποια σειρά εκτελούμε τις πράξεις σε μια αριθμητική παράσταση ώστε να βρούμε την τιμή της; Αριθμητική παράσταση λέγεται κάθε
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Β ΛΥΚΕΙΟΥ
 ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΠΡΣΑΝΑΤΛΙΣΜΥ Β ΛΥΚΕΙΥ ΘΕΩΡΙΑ ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β ΛΥΚΕΙΥ Να δώσετε τους ορισμούς: διάνυσμα, μηδενικό διάνυσμα, μέτρο διανύσματος, μοναδιαίο διάνυσμα Διάνυσμα AB ονομάζεται ένα ευθύγραμμο
Συστήματα συντεταγμένων
 Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
Κεφάλαιο. Για να δημιουργήσουμε τρισδιάστατα αντικείμενα, που μπορούν να παρασταθούν στην οθόνη του υπολογιστή ως ένα σύνολο από γραμμές, επίπεδες πολυγωνικές επιφάνειες ή ακόμη και από ένα συνδυασμό από
