βαθμού 1 με A 2. Υπολογίστε τα χαρακτηριστικά και ελάχιστα πολυώνυμα των
|
|
|
- Δευκαλίων Μανωλάς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Ορισμός ελαχίστου πολυωνύμου γραμμικής απεικόνισης και ιδιότητές του Κριτήριο διαγωνισιμότητας με το ελάχιστο πολυώνυμο Συνιστώμενες ασκήσεις: -8, -,, 9,,, 6 Συμβολισμός: V είναι πεπερασμένης διάστασης -διανυσματικός χώρος, όπου ή Έστω a Βρείτε το ελάχιστο πολυώνυμο του b Εξετάστε αν ο είναι διαγωνίσιμος c Δείξτε ότι ο είναι αντιστρέψιμος και βρείτε ένα ( x) [ x] βαθμού με Υπολογίστε τα χαρακτηριστικά και ελάχιστα πολυώνυμα των , και εξετάστε αν οι, είναι όμοιοι 0 Έστω a Βρείτε το ελάχιστο πολυώνυμο του b Δείξτε ότι δεν υπάρχει τέτοιος ώστε Έστω ( v, v, v ) μια διατεταγμένη βάση του και : η γραμμική απεικόνιση που ορίζεται από ( v ) v v, ( v) v v v, ( v) v v Βρείτε το ελάχιστο πολυώνυμο της και εξετάστε αν υπάρχει διατεταγμένη βάση u του ώστε ( : u, u), όπου Α είναι ο πίνακας της άσκησης Θεωρούμε τη γραμμική απεικόνιση : [ x] [ x], ( ( x)) ( x) ( x) a Βρείτε το ελάχιστο πολυώνυμο της και εξετάστε αν η είναι διαγωνίσιμη b Βρείτε τη διάσταση κάθε ιδόχωρου της 6 Έστω τέτοιος ώστε ( I )( I )( 7 I ) 0 Εξετάστε αν ο είναι a διαγωνίσιμος, b αντιστρέψιμος 7 Να καθοριστούν όλοι οι τέτοιοι ώστε 0 και Tr 6 8 Να βρεθεί το χαρακτηριστικό πολυώνυμο και το ελάχιστο πολυώνυμο του Εξετάστε αν ο είναι διαγωνίσιμος ( ) τέτοια
2 Ασκήσεις 6 9 Έστω Βρείτε το ελάχιστο πολυώνυμο της γραμμικής απεικόνισης t :, ( ), και εξετάστε αν είναι διαγωνίσιμη 0 Αν : V V είναι μια γραμμική απεικόνιση τέτοια ώστε γράφεται κατά μοναδικό τρόπο ως 0 Δείξτε ότι ( x) ( x) για κάθε t Έστω και W ο υπόχωρος του άσκηση των Ασκήσεων είδαμε ότι di, τότε κάθε στοιχείο v V v v v v, όπου v ker( ),,0, που παράγεται από τα στοιχεία W Δείξτε ότι diw deg ( x ) Έστω,, C και D 0 C a Δείξτε ότι αν ο D είναι διαγωνίσιμος, τότε οι και C είναι διαγωνίσμοι b Ισχύει το αντίστροφο του a; Βρείτε το ελάχιστο πολυώνυμο του Γενικεύοντας την προηγούμενη, άσκηση βρείτε το ελάχιστο πολυώνυμο του a b b b b a b b b b a b b b b a και εξετάστε αν ο Α είναι διαγωνίσιμος, όπου 6 Δείξτε ότι ( x) x και ( x) ( x ), όπου , a Έστω a 0 0 b d 0 c e Αποδείξτε ότι ο Α είναι διαγωνίσιμος αν και μόνο αν a 0 b Να βρεθούν οι τιμές των abc,, ώστε ο πίνακας να είναι διαγωνίσιμος 8 Έστω a b 0 c 0 0 V I,,, Στην
3 Ασκήσεις 6 k 0 0 x 0 a Βρείτε τις τιμές του k ώστε deg ( ) b Για την τιμή του k που βρήκατε πριν, υπολογίστε τον με χρήση του ( x ) c Δείξτε ότι ο δεν είναι διαγωνίσιμος για κάθε θετικό ακέραιο 9 Να βρεθούν οι τιμές του c τέτοιες ώστε το πολυώνυμο ( x ) ( x x c ) να μηδενίζεται από τον πίνακα Έστω a a a Για καθεμιά από τις ακόλουθες περιπτώσεις βρείτε όλες τις τιμές του a (αν υπάρχουν) τέτοιες ώστε να αληθεύει η αναγραφόμενη ιδιότητα a Υπάρχει αντιστρέψιμος πίνακας P τέτοιος ώστε ο P P είναι άνω τριγωνικός b Υπάρχει αντιστρέψιμος πίνακας P τέτοιος ώστε ο P P είναι διαγώνιος c Ο πίνακας Α μηδενίζει το πολυώνυμο ( x )( x )( x 00) Έστω I Έστω, με τέτοιος ώστε I, I, I 0, I 0 a Να δειχθεί ότι οι Α, Β έχουν το ίδιο ελάχιστο πολυώνυμο b Αληθεύει ότι έχουν το ίδιο χαρακτηριστικό πολυώνυμο; c Εξετάστε αν οι, είναι τριγωνίσιμοι I για κάποιο θετικό ακέραιο και Tr Αποδείξτε ότι Έστω τέτοιος ώστε 9 0I 0 Δείξτε ότι ισχύει ακριβώς μία από τις παρακάτω περιπτώσεις I ή όμοιος με τον όμοιος με τον I ή Έστω, g : V V δυο γραμμικές απεικονίσεις τέτοιες ώστε για τα ελάχιστα πολυώνυμα ( x), ( x ) ισχύει ( ( x), ( x )) Έστω g g a Δείξτε ότι η γραμμική απεικόνιση g ( ) : V V είναι ένας ισομορφισμός b Δείξτε ότι αν ker {0 V }, τότε ker g {0 } ή V
4 Ασκήσεις a0 0 0 a 0 0 a 0 0 a Στην άσκηση, είδαμε ότι ( x ) ( ) ( x a x a 0) Δείξτε ότι ( x) ( ) ( x) 6 Έστω και ( x) [ x] Ο ( ) είναι αντιστρέψιμος αν και μόνο αν ( ( x), ( x)) 7 Έστω : V V μια γραμμική απεικόνιση και ( x) [ x] Δείξτε ότι ker ( ) ker d( ), όπου d( x) ( ( x), ( x)) 8 Έστω ένας αντιστρέψιμος, τριγωνίσιμος πίνακας τέτοιος ώστε ( x) ( x ) Δείξτε ότι 9 ( I ) 0 a Έστω b Έστω, τέτοιοι ώστε ( ) ( ) x x Δείξτε ότι οι, είναι όμοιοι C, D Δείξτε ότι ( x) ( x ) και ( x) ( x ), αλλά οι πίνακες CD, δεν είναι όμοιοι C D 0 Έστω Θεωρούμε τη γραμμική απεικόνιση R:, R( ) Αποδείξτε ότι a Αν ( x) [ x], τότε ( R )( ) ( ) για κάθε, και b ( x) ( x) R Αληθεύει ότι ( x) ( x) ; R C D Έστω, Ξέρουμε ότι ( x) ( x ) (βλ άσκηση 7) Αληθεύει ότι ( x) ( x ) ; Εξετάστε ποιες από τις ακόλουθες προτάσεις είναι σωστές Σε κάθε περίπτωση δώστε μια απόδειξη ή ένα αντιπαράδειγμα a Υπάρχει με ( x ) ( x )( x ) και ( x) ( x ) ( x ) b Έστω τέτοιος ώστε I 0 Τότε ο είναι διαγωνίσιμος Έστω 0 I με ( x) ( x )( x ) ( x 0) Να βρεθεί το ( x), όπου 0 Έστω με det 0 Δείξτε ότι υπάρχει μη μηδενικός με 0 Υπολογίστε 0 ένα τέτοιο όταν 0 0 Έστω τέτοιος ώστε Δείξτε ότι ο είναι διαγωνίσιμος και rank Tr( ) 6 Επαναληπτική άσκηση κατανόησης Εξετάστε ποιες από τις παρακάτω προτάσεις είναι σωστές Σε κάθε περίπτωση δώστε μια απόδειξη ή ένα αντιπαράδειγμα Έστω a 0 για κάποιο θετικό ακέραιο 0
5 Ασκήσεις 6 b αντιστρέψιμος (0) 0 c Αν, τότε ο είναι διαγωνίσιμος 0 d Έστω, Τότε ( x) ( x) 0 e Αν ο είναι αντιστρέψιμος, τότε ( x) ( x ) για κάθε
6 Ασκήσεις 66 Υποδείξεις/Απαντήσεις Ασκήσεις Το χαρακτηριστικό πολυώνυμο του είναι (μετά από λίγες πράξεις) x ( x) det x ( x ) ( x ) x Ξέρουμε ότι το ελάχιστο πολυώνυμο διαιρεί το χαρακτηριστικό πολυώνυμο και έχει τις ίδιες ρίζες με αυτό (βλ Πόρισμα και Θεώρημα 6) Άρα ( x) ( x )( x ) ή ( x) ( x ) ( x ) Ελέγχουμε αν ο ( I)( I) είναι ίσος με 0 Έχουμε ( )( ) Συνεπώς ( x) ( x )( x ), που είναι γινόμενο διακεκριμένων πρωτοβαθμίων μονικών παραγόντων Άρα ο πίνακας είναι διαγωνίσιμος σύμφωνα με το Πόρισμα Ο είναι αντιστρέψιμος αφού (0) 0 Από ( x) ( x )( x ) x 6x παίρνουμε 0 6 I I ( 6 ) ( 6 I) Ένα ζητούμενο ( x) είναι το ( x) ( x 6 I) Υπόδειξη: Εργαζόμενοι όπως στην προηγούμενη άσκηση βρίσκουμε ( x) ( x) ( x ), ( x) ( x ), ( x) ( x ) Οι, δεν είναι όμοιοι, γιατί όμοιοι πίνακες έχουν το ίδιο ελάχιστο πολυώνυμο (Πρόταση 8) a Απάντηση: ( ) x x b Υπόδειξη: Αν υπήρχε 0, άτοπο με, τότε κάθε ιδιοτιμή του θα ήταν ίση με 0 και άρα Απάντηση: Δεν υπάρχει καθώς x x x x ( ) ( ) ( ) ( ) Απάντηση: Θεωρώντας τη διατεταγμένη βάση {, xx, }, εύκολα βρίσκουμε ότι ο αντίστοιχος πίνακας της είναι ο Έχουμε ( x) ( x ), η δεν είναι διαγωνίσιμη και υπάρχει μοναδικός ιδιόχωρος οπότε η ζητούμενη διάσταση είναι di V ( ) 6 Έστω ( x) ( x )( x )( x 7) [ x] Έχουμε ( ) 0 και άρα ( x) ( x ) a Από την τελευταία σχέση και το γεγονός ότι το ( x ) είναι γινόμενο πρωτοβάθμιων διακεκριμένων μονικών παραγόντων στο [ x ], έπεται ότι το () x είναι γινόμενο
7 Ασκήσεις 67 πρωτοβάθμιων διακεκριμένων μονικών παραγόντων στο [ x ] Άρα ο είναι διαγωνίσιμος σύμφωνα με το Θεώρημα b ος τρόπος Από ( x) ( x ) και το Θεώρημα 6 έπεται ότι αν είναι μια ιδιοτιμή του, τότε,, 7 Άρα το 0 δεν είναι ιδιοτιμή του και επομένως ο είναι αντιστρέψιμος ος τρόπος Υπόδειξη Ο μηδενίζει ένα πολυώνυμο που έχει μη μηδενικό σταθερό όρο Άρα είναι αντιστρέψιμος, βλ άσκηση (Σημείωση Αυτός ο τρόπος δεν χρησιμοποιεί ιδιοτιμές ή ελάχιστο πολυώνυμο αλλά μόνο τον ορισμό αντιστρέψιμου πίνακα) 7 Επειδή, έχουμε ( x) x( x )( x ) Επειδή το 0 ( I)( I) x( x )( x ) είναι γινόμενο διακεκριμένων πρωτοβάθμιων μονικών παραγόντων στο [ x ], το ίδιο ισχύει και για το () x και επομένως ο Α είναι διαγωνίσιμος σύμφωνα με το Πόρισμα Επίσης, κάθε ιδιοτιμή του είναι ένας από τους αριθμούς 0,, Το άθροισμα των ιδιοτιμών του είναι 6 Επειδή ο είναι, συμπεραίνουμε ότι οι ιδιοτιμές είναι,, Συνεπώς ο είναι όμοιος με τον I Άρα I 8 Παρατηρούμε ότι 0 Ββ C, 0 D όπου, C, D (7) Έχουμε 0 ( x) ( x ) Άρα ( x) ( x )( x 7) C ( x) ( x 7) D C D ( ) ( ) συμπεραίνουμε ότι ( x) x ( x) ( x ) ( x) ( x) ( x) ( x) ( x ) ( x 7) σύμφωνα με την Πρόταση Από x x γιατί το ελάχιστο πολυώνυμο διαιρεί το χαρακτηριστικό πολυώνυμο Επειδή I 0, έχουμε ( ) ( ) x x Από ( x C ) ( x )( x 7) έπεται άμεσα ότι C ( x) ( x )( x 7) Έχουμε D ( x) x 7 Σύμφωνα με το Πόρισμα 0 ( x) ( ( x), ( x), ( x)) ( x ) ( x 7) C D Ο Α δεν είναι διαγωνίσιμος αφού το ελάχιστο πολυώνυμό του διαιρείται με το ) ( x ) (Πόρισμα 9 Απάντηση: x x Είναι διαγωνίσιμη σύμφωνα με το Θεώρημα ( ) 0 Υπόδειξη: Χρησιμοποιώντας το ελάχιστο πολυώνυμο, δείξτε ότι η είναι διαγωνίσιμη t t t Υπόδειξη: Αν ( x) [ x ], τότε ( ) ( ) και άρα ( ) 0 ( ) 0 k Υπόδειξη: Δείξτε ότι τα στοιχεία I,,,,, όπου k deg ( x), είναι μια βάση του W a Λύση: Αν ( x) ( ) * [ x ], τότε ( D) 0 ( C) Για ( x ) ( ) D x παίρνουμε D ( ) * 0 D( ) D( C) 0 0 D ( C) ( x) ( x), ( x) ( x) D C D
8 Ασκήσεις 68 Επειδή ο D είναι διαγωνίσιμος, το ( x ) είναι γινόμενο πρωτοβάθμιων διακεκριμένων μονικών D παραγόντων στο [ x ] και άρα το ίδιο ισχύει για καθένα από τα () x, C () x Άρα οι C, είναι διαγωνίσιμοι b Απάντηση: Δεν ισχύει Ένα παράδειγμα είναι C (), D Ο D δεν είναι 0 διαγωνίσιμος Υπόδειξη: Παρατηρήστε ότι και άρα ( x) x( x ) Υπόδειξη: Από την άσκηση ξέρουμε ότι ( x ) ( ) ( x a ( ) b )( x a b ) Δείξτε ότι αν b 0, τότε ( x a ( ) b)( x a b), b 0 ( x) x a, b aλύση: Το χαρακτηριστικό πολυώνυμο του Α είναι το ( x) ( x ) Από το Πόρισμα και το Θεώρημα 6 έπεται ότι το ελάχιστο πολυώνυμο του είναι ένα από τα ( x )( x ), ( x ) ( x ), ( x )( x ), ( x ) ( x ) Από το Πόρισμα, ο Α διαγωνοποιείται αν και μόνο αν το ελάχιστο πολυώνυμο είναι το ( x)( x ) Είναι σαφές ότι το ελάχιστο πολυώνυμο είναι το ( x)( x ) αν και μόνο αν ( I)( I) 0 Υπολογίζοντας βρίσκουμε a ( I)( I) ad ae b d 0 Επομένως ( I)( I) 0 a 0 (και b, c, d, e τυχαία) b Απάντηση: a 0 (και bc, τυχαία) 8 Απάντηση: a Έχουμε b Λύση: deg ( x) ( I) 0 k 0 ( ) ( ) 0 x x x x I Στην περίπτωση αυτή x x ( ) ( ) k I I c Λύση: Οι ιδιοτιμές του είναι,, Αν ο είναι διαγωνίσιμος για κάποιο, τότε θα είναι όμοιος με τον I και άρα ίσος με αυτόν, I Δηλαδή ο μηδενίζει το πολυώνυμο x Άρα ( ) x x Από το a έπεται ότι ( x ) ( x ) και επομένως ( x ) x Αυτό είναι άτοπο 9 Το καθώς εφαρμόζοντας την Πρόταση 0 προκύπτει ότι όλες οι ρίζες του x στο είναι απλές ( x ) ( x x c ) μηδενίζεται από τον πίνακα αν και μόνο αν ( ) ( ) ( ) x x x x c Όπως στην άσκηση, βρίσκουμε ότι ( x) ( x )( x ) Επειδή τα πολυώνυμα x, x είναι σχετικά πρώτα, έχουμε σύμφωνα με την Πρόταση ( x) ( x ) ( x x c) x x x c Από την Πρόταση έχουμε x 009 x x c 009 c 0 c
9 Ασκήσεις 69 0 Έχουμε ( x) det( xi) ( x a)( x )( x ) και οι ιδιοτιμές του Α είναι a,, a Επειδή για κάθε a το ( x ) είναι γινόμενο πρωτοβάθμιων παραγόντων στο [ x ], ο Α είναι τριγωνίσιμος για κάθε a (Θεώρημα ) b Αν a,, τότε ο Α έχει τρεις διακεκριμένες ιδιοτιμές και άρα είναι διαγωνίσιμος συμφωνα με το Πόρισμα 9 Αν a, τότε di V () rank( I ) 0 0 rank που είναι διάφορο της πολλαπλότητας () της ιδιοτιμής του Α Συνεπώς για a, ο Α δεν είναι διαγωνίσιμος σύμφωνα με το Θεώρημα 0 Όμοια αποδεικνύεται ότι για a, di V( ) ( ) και άρα ο Α δεν είναι διαγωνίσιμος Από τα παραπάνω έπεται ότι, δεδομένου του a, υπάρχει αντιστρέψιμος πίνακας διαγώνιος αν και μόνο αν a, P τέτοιος ώστε ο P P είναι c Αν ο Α μηδενίζει το ( x )( x )( x 00), τότε ισχύει ( x) ( x )( x )( x 00) Επειδή το είναι ιδιοτιμή του έχουμε x ( x ) σύμφωνα με το Θεώρημα 6, οπότε x ( x )( x )( x 00) που είναι άτοπο Άρα δεν υπάρχει a τέτοιο ώστε ο Α να μηδενίζει το ( x )( x )( x 00) Από την υπόθεση I συνάγουμε ότι Ο Α διαγωνοποιείται Πράγματι, το ελάχιστο πολυώνυμο () x του Α διαιρεί το x και επειδή το x έχει διακεκριμένες ρίζες στο (όπως προκύπτει εφαρμόζοντας την Πρόταση 0), το ίδιο συμβαίνει για το () x Άρα ο διαγωνοποιείται σύμφωνα με το Πόρισμα Κάθε ιδιοτιμή του Α ικανοποιεί τη σχέση Έστω,, (όχι αναγκαστικά διακεκριμένες) οι ιδιοτιμές του Α Ξέρουμε ότι Tr (Πόρισμα 7) Από την τριγωνική ανισότητα για μέτρα μιγαδικών παίρνουμε Tr Άρα η ανισότητα είναι ισότητα Συνεπώς οι μιγαδικοί αριθμοί,, έχουν το ίδιο πρωτεύον όρισμα Κάθε i έχει μέτρο αφού i Άρα Από τη σχέση Tr παίρνουμε Άρα η διαγώνια μορφή του Α είναι ο πίνακας I, οπότε PI P για κάποιον αντιστρέψιμο P Επομένως I a Ο Α μηδενίζει το x x x ( x )( x ) και άρα x x x Επειδή τα πολυώνυμα x και x είναι ανάγωγα στο [ ] ( ) ( )( ) x παίρνουμε ότι το () x είναι ένα από τα x, x, ( x )( x ) Από την υπόθεση I και το γεγονός ότι deg ( x) (ο πίνακας είναι ), παίρνουμε ( ) x x Με ανάλογο τρόπο προκύπτει ότι ( ) x x b Έχουμε ( x) ( x) (Πόρισμα ), deg ( x) deg ( x) (από το a), και τα ( x), ( x) έχουν τον ίδιο μεγιστοβάθμιο συντελεστή
10 Ασκήσεις 70 Άρα ( x) ( x) c Δεν είναι τριγωνίσιμοι σύμφωνα με το Θεώρημα γιατί το χαρακτηριστικό τους πολυώνυμο είναι το x που δεν είναι γινόμενο πρωτοβάθμιων πολυωνύμων στο [ x ] Από τη σχέση I έπεται ότι x x x x x Άρα έχουμε τρεις ( ) 9 0 ( )( ) περιπτώσεις ) ( ) x x I ) ( ) x x I ) ( x) ( x )( x ) διαγωνίσιμος (βλ Πόρισμα 9 ή Πόρισμα ) Στην περίπτωση αυτή, οι ιδιοτιμές του είναι οι,, ή οι,,σύμφωνα με το Θεώρημα 6 Άρα στην περίπτωση αυτή, ο είναι όμοιος με τον Οι τέσσερις πίνακες I, I, ή με τον, είναι ανά δύο μη όμοιοι (πχ έχουν διαφορετικά χαρακτηριστικά πολυώνυμα) και άρα ισχύει ακριβώς μια από τις ανωτέρω περιπτώσεις a Από το Θεώρημα 6 υπάρχουν a( x), b( x) [ x ] τέτοια ώστε ( x) a( x) ( x) b( x ) Άρα V ( g) a( g) g ( g) b( g) ( g) a( g ) Από ( g) a( g) έπεται ότι η γραμμική απεικόνιση ( g) : V V είναι επί Επειδή ο V V είναι πεπερασμένη διάστασης, η ( g) : V V είναι ισομορφισμός b Έστω ότι και ο ker και ο ker g είναι μη τετριμμένοι Τότε το 0 είναι ιδιοτιμή και της και της g Από το Θεώρημα 6 έπεται ότι το x διαιρεί και το ( x ) και το g ( x ), άτοπο αφού ( ( x), ( x )) g 6 Έστω ότι ( ( x), ( x)) Τότε από το Θεώρημα 6 έχουμε ( x) a( x) ( x) b( x) για κάποια a( x), b( x) [ x] Άρα ( ) a( ) I και ο ( ) είναι αντιστρέψιμος Αντίστροφα, έστω ότι ο ( ) είναι αντιστρέψιμος Έστω px ( ) ένας κοινός παράγοντας των ( x), ( x) με deg px ( ) Τότε ( x) p( x) c( x), ( x) p( x) d( x) για κάποια c( x), d( c) [ x] Από την πρώτη σχέση παίρνουμε ( ) p( ) c( ), οπότε det ( ) det p( )det c( ) και άρα det p ( ) 0, δηλαδή ο p ( ) είναι αντιστρέψιμος Από τη δεύτερη σχέση παίρνουμε 0 ( ) p( ) d( ) και επειδή ο p ( ) είναι αντιστρέψιμος έχουμε d( ) 0 Άρα ( x) d( x ) και deg ( x) deg d( x), άτοπο αφού ( x) p( x) d( x) και deg px ( ) 7 8 Υπόδειξη: Αν το είναι μια ιδιοτιμή του, τότε καθένα από τα n, n,,, είναι μια ιδιοτιμή του Επειδή, προκύπτει ότι,0, Συμπεράνετε ότι ( x ) ( ) ( x ) g
11 Ασκήσεις 7 9 Υπόδειξη: a Διακρίνετε περιπτώσεις αν το ελάχιστο πολυώνυμο έχει διακεκριμένες ρίζες ή πολλαπλή ρίζα Στην ειδική περίπτωση που ( x) ( x) ( x ), χρησιμοποιώντας a τριγωνοποίηση έπεται ότι αρκεί να δειχτεί ότι οι, 0 0 αυτοί είναι όμοιοι υπολογίζοντας έναν αντιστρέψιμο P τέτοιον ώστε b Όμοιοι πίνακες έχουν το ίδιο rank k k 0 Υπόδειξη: a Αποδείξτε ότι R ( ) για κάθε θετικό ακέραιο k b, είναι όμοιοι Δείξτε ότι οι πίνακες a b P P 0 0 b Αρκεί να δειχτεί ότι για κάθε ( x) [ x] ισχύει ( R ) 0 ( ) 0 Η ισοδυναμία αυτή έπεται από το a Γενικά δεν αληθεύει ότι ( x) ( x) καθώς έχουν βαθμούς αντίστοιχα v, v Απάντηση: Δεν αληθεύει Ένα αντιπαράδειγμα είναι, Έχουμε () x x 0 0 και ( ) x x a Λάθος γιατί το () x δεν διαιρεί το ( x ) (βλ Πόρισμα ) b Σωστό Έχουμε ότι ( ) x x x Αρκεί να δείξουμε ότι το x x δεν έχει διπλή ρίζα στο, γιατί τότε θα συμβαίνει το ίδιο για το () x και άρα ο θα είναι διαγωνίσιμος σύμφωνα με το Πόρισμα Έστω ότι το έχει κοινή ρίζα με την παράγωγό του a 0, τότε a a, οπότε ( ) x x x έχει διπλή ρίζα στο, οπότε θα ( x) x σύμφωνα με την Πρόταση 0 Αν ( a) 0 a a 0 a a 0 a Αλλά το a δεν είναι ρίζα του ( x) x, άτοπο Απάντηση: ( x) ( x ) ( x ) ( x 0) Απάντηση για το τελευταίο ερώτημα Ισχύει x x x οπότε ένας είναι ( 6 I) ( ) ( 6) Υπόδειξη: Ο είναι όμοιος με διαγώνιο πίνακα της μορφής diag(0,,0,,,,,, ) όπου a, b, c 0, a b c και rank b c Τότε ο 6 Απάντηση a Σ b Σ c Σ d Σ e Σ a b c είναι όμοιος με τον diag(0,,0,,,) a bc
A, και εξετάστε αν είναι διαγωνίσιμη.
 Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Θεώρημα (Κριτήριο διαγωνισιμότητας) Ένας είναι διαγωνίσιμος αν και μόνο αν ( x) γινόμενο διακεκριμένων
Ασκήσεις 6 Ασκήσεις Ελάχιστο Πολυώνυμο Βασικά σημεία Ορισμός ελαχίστου πολυωνύμου πίνακα και ιδιότητές του Θεώρημα (Κριτήριο διαγωνισιμότητας) Ένας είναι διαγωνίσιμος αν και μόνο αν ( x) γινόμενο διακεκριμένων
Ασκήσεις3 Διαγωνίσιμες Γραμμικές Απεικονίσεις
 Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις 5 Βασικά σημεία Ιδιότητες ιδιόχωρων: Έστω,, Ισχύουν τα εξής Ασκήσεις Διαγωνίσιμες Γραμμικές Απεικονίσεις κάποιες διακεκριμένες ιδιοτιμές της γραμμικής απεικόνισης : V V, όπου o Αν v v 0, όπου
Ασκήσεις3 Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα.
 Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
Ασκήσεις 0 Ασκήσεις Διαγωνισιμότητα Βασικά σημεία Διαγωνίσιμοι πίνακες: o Ορισμός και παραδείγματα o H -στήλη του P P είναι E αν και μόνο αν η -στήλη του P είναι ιδιοδιάνυσμα του που αντιστοιχεί στην ιδιοτιμή
b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.
![b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0. b. Για κάθε θετικό ακέραιο m και για κάθε A. , υπάρχουν άπειρα το πλήθος πολυώνυμα ( x) [ x] m και ( A) 0.](/thumbs/63/49387122.jpg) Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Ασκήσεις4 46 Ασκήσεις 4 Τριγωνίσιμες γραμμικές απεικονίσεις, Θεώρημα των Cayley-Hamilton Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Κριτήριο τριγωνισιμότητας
Ασκήσεις4 48. P AP τριγωνικό. Αφού δείξτε ότι ο A δεν είναι διαγωνίσιμος, βρείτε αντιστρέψιμο A 1 3 1
 Ασκήσεις4 48 Ασκήσεις4 Τριγωνισιμότητα Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Θεώρημα: είναι τριγωνίσιμος αν και μόνο αν ( x ) γινόμενο πρωτοβάθμιων παραγόντων
Ασκήσεις4 48 Ασκήσεις4 Τριγωνισιμότητα Βασικά σημεία Ορισμός τριγωνίσιμου πίνακα, ορισμός τριγωνίσιμης γραμμικής απεικόνισης Θεώρημα: είναι τριγωνίσιμος αν και μόνο αν ( x ) γινόμενο πρωτοβάθμιων παραγόντων
Γραμμική Άλγεβρα II Εαρινό εξάμηνο
 Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
Γραμμική Άλγεβρα II Εαρινό εξάμηνο 0-0 Υποδείξεις/Απαντήσεις των Ασκήσεων Περιεχόμενα Ασκήσεις Πολυώνυμα Ασκήσεις Ιδιοτιμές-Ιδιοδιανύσματα 6 Ασκήσεις Διαγωνίσιμες γραμμικές απεικονίσεις 9 Ασκήσεις4 Τριγωνίσιμες
Ασκήσεις2 8. ; Αληθεύει ότι το (1, 0, 1, 2) είναι ιδιοδιάνυσμα της f ; b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα της γραμμικής απεικόνισης 3 3
 Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
Ασκήσεις 8 Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμων και ιδιοδιανυσμάτων, υπολογισμός τους Σε διακεκριμένες ιδιοτιμές αντιστοιχούν γραμμικά ανεξάρτητα ιδιοδιανύσματα Αν ΑΧ=λΧ,
1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]
![1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x] 1. a. Έστω b. Να βρεθούν οι ιδιοτιμές και τα ιδιοδιανύσματα του A Έστω A και ( x) [ x]](/thumbs/77/75945202.jpg) σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
σκήσεις Ασκήσεις Ιδιοτιμές και ιδιοδιανύσματα Βασικά σημεία Ορισμός ιδιοτιμών και ιδιοδιανυσμάτων, υπολογισμός τους Ιδιόχωροι, διάσταση ιδιόχωρου, εύρεση βάσης ιδιόχωρου Σε διακεκριμένες ιδιοτιμές αντιστοιχούν
Ασκήσεις1 Πολυώνυμα. x x c. με το. b. Να βρεθούν όλες οι τιμές των a, Να βρεθεί ο μκδ και το εκπ τους
 Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
Aσκήσεις1 1 Βασικά σημεία Ευκλείδεια διαίρεση πολυωνύμων Ορισμός και ιδιότητες μκδ και εκπ Ιδιότητες σχετικών πρώτων πολυωνύμων Τα ανάγωγα πολυώνυμα στο [ ] και [ ] Ασκήσεις1 Πολυώνυμα Ανάλυση πολυωνύμου
Γραμμική Άλγεβρα II. Ασκήσεις με Υποδείξεις - Απαντήσεις. Περιεχόμενα
 Γραμμική Άλγεβρα II Ασκήσεις με Υποδείξεις - Απαντήσεις ΜΜ Περιεχόμενα Ασκήσεις0: Όμοιοι Πίνακες Ασκήσεις: Πολυώνυμα 6 Ασκήσεις: Ιδιοτιμές και Ιδιοδιανύσματα Ασκήσεις: Διαγωνισιμότητα Ασκήσεις4: Τριγωνισιμότητα
Γραμμική Άλγεβρα II Ασκήσεις με Υποδείξεις - Απαντήσεις ΜΜ Περιεχόμενα Ασκήσεις0: Όμοιοι Πίνακες Ασκήσεις: Πολυώνυμα 6 Ασκήσεις: Ιδιοτιμές και Ιδιοδιανύσματα Ασκήσεις: Διαγωνισιμότητα Ασκήσεις4: Τριγωνισιμότητα
Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου Όνομα συνοπτικές ενδεικτικές λύσεις
 Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 009 Όνομα συνοπτικές ενδεικτικές λύσεις ΑΜ Ημ/ία Αίθουσα 1 Σύνολο Η εξέταση αποτελείται από θέματα. Κάθε θέμα αξίζει 4 μονάδες. Το άριστα είναι μονάδες και η βάση
Γραμμική Άλγεβρα ΙΙ Εξέταση Σεπτεμβρίου 009 Όνομα συνοπτικές ενδεικτικές λύσεις ΑΜ Ημ/ία Αίθουσα 1 Σύνολο Η εξέταση αποτελείται από θέματα. Κάθε θέμα αξίζει 4 μονάδες. Το άριστα είναι μονάδες και η βάση
Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων
 7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
7 Βασικά σημεία Ασκήσεις6 Διαγωνοποίηση Ερμιτιανών Πινάκων Το σύνηθες εσωτερικό γινόμενο στο και Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορισμός, Ερμιτιανού πίνακα και μοναδιαίου πίνακα Ιδιότητες
,..., v n. W πεπερασμένα παραγόμενοι και dimv. Τα ακόλουθα είναι ισοδύναμα f είναι ισομορφιμός. f είναι 1-1. f είναι επί.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις7: Γραμμικές Απεικονίσεις Βασικά σημεία Ορισμός και παραδείγματα γραμμικών απεικονίσεων Σύνθεση γραμμικών απεικονίσεων, ισομορφισμοί Κάθε γραμμική απεικόνιση f : V W, όπου
1. Για καθένα από τους ακόλουθους διανυσματικούς χώρους βρείτε μια βάση και τη διάσταση. 3. U x y z x y z x y. {(,, ) } a b. c d
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις6: Βάση και Διάσταση Βασικά σημεία Βάση διανυσματικού χώρου (ορισμός, παραδείγματα, μοναδικότητα συντελεστών) Θεώρημα (ύπαρξη, πρώτη μορφή) Έστω V K μη μηδενικός με K πεπερασμένο
Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο
 Ασκήσεις6 7 Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο και Βασικά σημεία Το σύνηθες εσωτερικό γινόμενο στο και (ορισμοί και ιδιότητες) Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορθογώνιο συμπλήρωμα
Ασκήσεις6 7 Ασκήσεις6 Το σύνηθες εσωτερικό γινόμενο στο και Βασικά σημεία Το σύνηθες εσωτερικό γινόμενο στο και (ορισμοί και ιδιότητες) Ορθοκανονικές βάσεις και η μέθοδος Gram-Schmidt Ορθογώνιο συμπλήρωμα
Κεφάλαιο 6 Ιδιοτιμές και Ιδιοδιανύσματα
 Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
Κεφάλαιο 6 Ορισμοί Έστω Α ένας πίνακας με πραγματικά στοιχεία Ο πραγματικός ή μιγαδικός αριθμός λ καλείται ιδιοτιμή του πίνακα Α εάν υπάρχει μη μηδενικό διάνυσμα v με πραγματικά ή μιγαδικά στοιχεία τέτοιο
Δακτύλιοι και Πρότυπα Ασκήσεις 6. Η ύλη των ασκήσεων αυτών είναι η Ενότητα6, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα.
 Δακτύλιοι και Πρότυπα 0-7 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα Βρείτε τη ρητή κανονική μορφή και μια κανονική μορφή Jorda του M( ) 0 0 Έστω
Δακτύλιοι και Πρότυπα 0-7 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Εφαρμογές Θεωρημάτων Δομής στη Γραμμική Αλγεβρα Βρείτε τη ρητή κανονική μορφή και μια κανονική μορφή Jorda του M( ) 0 0 Έστω
Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 10
 Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 0 Επαναληπτικες Ασκησεις ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθοι Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laiihtml
Γραµµικη Αλγεβρα ΙΙ Ασκησεις - Φυλλαδιο 0 Επαναληπτικες Ασκησεις ιδασκοντες: Ν Μαρµαρίδης - Α Μπεληγιάννης Βοηθοι Ασκησεων: Χ Ψαρουδάκης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laiihtml
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii8/laii8html Παρασκευή 4 Ιουνίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β ΠΕΡΙΤΤΟΙ Ασκησεις - Φυλλαδιο 9 Επαναληπτικες Ασκησεις ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii8/laii8html Παρασκευή 4 Ιουνίου
Έντυπο Yποβολής Αξιολόγησης ΓΕ
 Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
, b, έχει λύση αν και μόνο αν rank( A) rank( A b) είναι οι συνήθεις διατεταγμένες βάσεις των,
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις8: Γραμμικές Απεικονίσεις και Πίνακες Βασικά σημεία Ορισμός πίνακα γραμμικής απεικόνισης, παραδείγματα Ανάκτηση γραμμικής απεικόνισης από πίνακά της Ιδιότητες (πίνακας
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις8: Γραμμικές Απεικονίσεις και Πίνακες Βασικά σημεία Ορισμός πίνακα γραμμικής απεικόνισης, παραδείγματα Ανάκτηση γραμμικής απεικόνισης από πίνακά της Ιδιότητες (πίνακας
Κεφάλαιο 1 Πρότυπα. Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο.
 Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Κεφάλαιο Πρότυπα Στο κεφάλαιο αυτό εισάγουμε την έννοια του προτύπου πάνω από δακτύλιο Ορισμοί και Παραδείγματα Παραδοχές Στo βιβλίο αυτό θα κάνουμε τις εξής παραδοχές Χρησιμοποιούμε προσθετικό συμβολισμό
Βασική Άλγεβρα. Ασκήσεις (εκδοχή )
 Βασική Άλγεβρα Ασκήσεις 0-4 (εκδοχή 5--04) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόµενα σελίδα Ασκήσεις ιαιρετότητα στους ακέραιους, ισοτιµίες Ασκήσεις Ακέραιοι odulo, Θεώρηµα του Euler 7
Βασική Άλγεβρα Ασκήσεις 0-4 (εκδοχή 5--04) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόµενα σελίδα Ασκήσεις ιαιρετότητα στους ακέραιους, ισοτιµίες Ασκήσεις Ακέραιοι odulo, Θεώρηµα του Euler 7
Βασική Άλγεβρα. Ασκήσεις (εκδοχή )
 Βασική Άλγεβρα Ασκήσεις 05-6 (εκδοχή 8--05) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόμενα σελίδα Ασκήσεις Διαιρετότητα στους ακέραιους, ισοτιμίες Ασκήσεις Ακέραιοι odulo, Θεώρημα του Euler
Βασική Άλγεβρα Ασκήσεις 05-6 (εκδοχή 8--05) Βασική Άλγεβρα Ασκήσεις Υποδείξεις/Απαντήσεις Περιεχόμενα σελίδα Ασκήσεις Διαιρετότητα στους ακέραιους, ισοτιμίες Ασκήσεις Ακέραιοι odulo, Θεώρημα του Euler
8.1 Διαγωνοποίηση πίνακα
 Κεφάλαιο 8 Κανονικές μορφές από 6 Κεφάλαιο 8 Κ Α Ν Ο Ν Ι Κ Ε Σ Μ Ο Ρ Φ Ε Σ 8. Διαγωνοποίηση πίνακα Ορισμός 8.α Ένας πίνακας M n ( ) oνομάζεται διαγωνοποιήσιμος στο αν υπάρχει αντιστρέψιμος πίνακας P M
Κεφάλαιο 8 Κανονικές μορφές από 6 Κεφάλαιο 8 Κ Α Ν Ο Ν Ι Κ Ε Σ Μ Ο Ρ Φ Ε Σ 8. Διαγωνοποίηση πίνακα Ορισμός 8.α Ένας πίνακας M n ( ) oνομάζεται διαγωνοποιήσιμος στο αν υπάρχει αντιστρέψιμος πίνακας P M
ΚΕΦΑΛΑΙΟ 2: Ημιαπλοί Δακτύλιοι
 ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ : Ημιαπλοί Δακτύλιοι Είδαμε στο κύριο θεώρημα του προηγούμενου κεφαλαίου ότι κάθε δακτύλιος διαίρεσης έχει την ιδιότητα κάθε πρότυπο είναι ευθύ άθροισμα απλών προτύπων Εδώ θα χαρακτηρίσουμε όλους
ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Burnside
 ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Bursde a b Θα αποδείξουμε εδώ ότι κάθε ομάδα τάξης pq ( p, q πρώτοι) είναι επιλύσιμη Το θεώρημα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιμοποίησε τη νέα
ΚΕΦΑΛΑΙΟ 8: Εφαρμογή: Το θεώρημα του Bursde a b Θα αποδείξουμε εδώ ότι κάθε ομάδα τάξης pq ( p, q πρώτοι) είναι επιλύσιμη Το θεώρημα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιμοποίησε τη νέα
B είναι ισοδύναμοι αν και μόνο αν υπάρχουν διατεταγμένες βάσεις ˆv του. , b, έχει λύση αν και μόνο αν rank( A) rank( A b)
 Ασκήσεις8: Γραμμικές Απεικονίσεις και Πίνακες Βασικά σημεία Ορισμός πίνακα γραμμικής απεικόνισης, παραδείγματα Ανάκτηση γραμμικής απεικόνισης από πίνακά της Ιδιότητες (πίνακας που αντιστοιχεί στο άθροισμα,
Ασκήσεις8: Γραμμικές Απεικονίσεις και Πίνακες Βασικά σημεία Ορισμός πίνακα γραμμικής απεικόνισης, παραδείγματα Ανάκτηση γραμμικής απεικόνισης από πίνακά της Ιδιότητες (πίνακας που αντιστοιχεί στο άθροισμα,
Δακτύλιοι και Πρότυπα Ασκήσεις 3. Στις παρακάτω ασκήσεις κάθε δακτύλιος είναι μη τετριμμένος μεταθετικός δακτύλιος. N ( a)
 11 Δακτύλιοι και Πρότυπα 2016-17 Ασκήσεις 3 Η ύλη των ασκήσεων αυτών είναι η Ενότητα3, Ελεύθερα πρότυπα Στις παρακάτω ασκήσεις κάθε δακτύλιος είναι μη τετριμμένος μεταθετικός δακτύλιος 1 Δείξτε ότι το
11 Δακτύλιοι και Πρότυπα 2016-17 Ασκήσεις 3 Η ύλη των ασκήσεων αυτών είναι η Ενότητα3, Ελεύθερα πρότυπα Στις παρακάτω ασκήσεις κάθε δακτύλιος είναι μη τετριμμένος μεταθετικός δακτύλιος 1 Δείξτε ότι το
Κεφάλαιο 9 1 Ιδιοτιμές και Ιδιοδιανύσματα
 Σελίδα από 58 Κεφάλαιο 9 Ιδιοτιμές και Ιδιοδιανύσματα 9. Ορισμοί... 9. Ιδιότητες... 9. Θεώρημα Cayley-Hamlto...9 9.. Εφαρμογές του Θεωρήματος Cayley-Hamlto... 9.4 Ελάχιστο Πολυώνυμο...40 Ασκήσεις του Κεφαλαίου
Σελίδα από 58 Κεφάλαιο 9 Ιδιοτιμές και Ιδιοδιανύσματα 9. Ορισμοί... 9. Ιδιότητες... 9. Θεώρημα Cayley-Hamlto...9 9.. Εφαρμογές του Θεωρήματος Cayley-Hamlto... 9.4 Ελάχιστο Πολυώνυμο...40 Ασκήσεις του Κεφαλαίου
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων
 ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
ΚΕΦΑΛΑΙΟ 3: Συνθήκες Αλυσίδων Μελετάμε εδώ τη συνθήκη της αύξουσας αλυσίδας υποπροτύπων και τη συνθήκη της φθίνουσας αλυσίδας υποπροτύπων Αυτές συνδέονται μεταξύ τους με την έννοια της συνθετικής σειράς
Δακτύλιοι και Πρότυπα Ασκήσεις 2. όπου a (4 i) (1 2 i), b i. Στη συνέχεια βρείτε κάθε τέτοιο d. b. Δείξτε ότι [ i] (4 i)
![Δακτύλιοι και Πρότυπα Ασκήσεις 2. όπου a (4 i) (1 2 i), b i. Στη συνέχεια βρείτε κάθε τέτοιο d. b. Δείξτε ότι [ i] (4 i) Δακτύλιοι και Πρότυπα Ασκήσεις 2. όπου a (4 i) (1 2 i), b i. Στη συνέχεια βρείτε κάθε τέτοιο d. b. Δείξτε ότι [ i] (4 i)](/thumbs/62/47831736.jpg) 6 Δακτύλιοι και Πρότυπα 016-17 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Περιοχές κυρίων ιδεωδών. 1. Θεωρούμε το δακτύλιο [ i]. a. Βρείτε ένα d [ i] με ( a, b) d, όπου a (4 i) (1 i), b 16 1 i.
6 Δακτύλιοι και Πρότυπα 016-17 Ασκήσεις Η ύλη των ασκήσεων αυτών είναι η Ενότητα, Περιοχές κυρίων ιδεωδών. 1. Θεωρούμε το δακτύλιο [ i]. a. Βρείτε ένα d [ i] με ( a, b) d, όπου a (4 i) (1 i), b 16 1 i.
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 2 η Ημερομηνία Αποστολής στον Φοιτητή: 28 Νοεμβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 8 Νοεμβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 6 Ιανουαρίου 0 Οι ασκήσεις
ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΠΟΛΥΩΝΥΜΟ ΠΙΝΑΚΑ: Έστω Α ένας n nπίνακας επί ενός σώματος F. Για χ στο F, ορίζεται το πολυώνυμο ( ως προς χ ) : h ( x) = det( A- xi ).
 1 ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΠΟΛΥΩΝΥΜΟ ΠΙΝΑΚΑ: Έστω Α ένας n nπίνακας επί ενός σώματος F. Για χ στο F, ορίζεται το πολυώνυμο ( ως προς χ ) : h ( x) = det( A- xi ). A n Πόρισμα 1: Ο βαθμός του χαρ/κου πολυωνύμου ενός
1 ΧΑΡΑΚΤΗΡΙΣΤΙΚΟ ΠΟΛΥΩΝΥΜΟ ΠΙΝΑΚΑ: Έστω Α ένας n nπίνακας επί ενός σώματος F. Για χ στο F, ορίζεται το πολυώνυμο ( ως προς χ ) : h ( x) = det( A- xi ). A n Πόρισμα 1: Ο βαθμός του χαρ/κου πολυωνύμου ενός
{ } ΠΛΗ 12: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι 2 η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ. Απαντήσεις. 1. (15 µονάδες)
 Σελίδα από 8 (5 µονάδες) ΠΛΗ : ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ Απαντήσεις i Εξηγείστε γιατί κάθε ένα από τα παρακάτω υποσύνολα του R δεν είναι υπόχωρος του R {[ xyz,, ] T z } {[ xyz,,
Σελίδα από 8 (5 µονάδες) ΠΛΗ : ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗ ΠΛΗΡΟΦΟΡΙΚΗ Ι η ΓΡΑΠΤΗ ΕΡΓΑΣΙΑ Απαντήσεις i Εξηγείστε γιατί κάθε ένα από τα παρακάτω υποσύνολα του R δεν είναι υπόχωρος του R {[ xyz,, ] T z } {[ xyz,,
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ: ΠΛΗΡΟΦΟΡΙΚΗ ΘΕ: ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΉ Ι (ΠΛΗ ) ΛΥΣΕΙΣ ΕΡΓΑΣΙΑΣ Οι πρώτες δύο ασκήσεις αναφέρονται στις έννοιες γραµµική ανεξαρτησία, γραµµικός
Θεωρία Galois. Πρόχειρες σημειώσεις (εκδοχή )
 Θεωρία Galos Πρόχειρες σημειώσεις 0- (εκδοχή -7-0) Περιεχόμενα 0 Υπενθυμίσεις και συμπληρώματα Ανάγωγα πολυώνυμα Ανάγωγα πολυώνυμα και σώματα Χαρακτηριστική σώματος Απλές ρίζες πολυωνύμων Ασκήσεις 0 Επεκτάσεις
Θεωρία Galos Πρόχειρες σημειώσεις 0- (εκδοχή -7-0) Περιεχόμενα 0 Υπενθυμίσεις και συμπληρώματα Ανάγωγα πολυώνυμα Ανάγωγα πολυώνυμα και σώματα Χαρακτηριστική σώματος Απλές ρίζες πολυωνύμων Ασκήσεις 0 Επεκτάσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΑΠΑΝΤΗΣΕΙΣ Α ΕΡΓΑΣΙΑΣ. ( 8 µον.) Η άσκηση αυτή αναφέρεται σε διαιρετότητα και ρίζες πολυωνύµων. a. Να λυθεί η εξίσωση
Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα
 Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα Ορισµοί Ιδιοτιµές και Ιδιοδιανύσµατα Έστω Α ένας πίνακας µε πραγµατικά στοιχεία Ο πραγµατικός ή µιγαδικός αριθµός λ καλείται ιδιοτιµή του πίνακα Α εάν υπάρχει µη
Κεφάλαιο 6 Ιδιοτιµές και Ιδιοδιανύσµατα Ορισµοί Ιδιοτιµές και Ιδιοδιανύσµατα Έστω Α ένας πίνακας µε πραγµατικά στοιχεία Ο πραγµατικός ή µιγαδικός αριθµός λ καλείται ιδιοτιµή του πίνακα Α εάν υπάρχει µη
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 3 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2018/laii2018html Παρασκευή 23 Μαρτίου
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Προτεινοµενες Ασκησεις - Φυλλαδιο 3 ιδασκων: Α Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://usersuoigr/abeligia/linearalgebraii/laii2018/laii2018html Παρασκευή 23 Μαρτίου
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 17 Οκτωβρίου 2011
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 7 Οκτωβρίου 0 Ημερομηνία παράδοσης της Εργασίας: 5 Νοεμβρίου 0 Οι ασκήσεις
Γραμμική Άλγεβρα Ι,
 Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
Γραμμική Άλγεβρα Ι, 207-8 Ασκήσεις2 και Ασκήσεις3: Γραμμοϊσοδύναμοι Πίνακες και Επίλυση Γραμμικών Συστημάτων Βασικά σημεία Γραμμοϊσοδυναμία πινάκων o Στοιχειώδεις πράξεις γραμμών o Ανηγμένη κλιμακωτή μορφή
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι
 ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 3
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii2018/laii2018.html Παρασκευή 23 Μαρτίου 2018
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 3 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii2018/laii2018.html Παρασκευή 23 Μαρτίου 2018
ΑΣΚΗΣΕΙΣ 7 ης ΕΒΔΟΜΑΔΑΣ
 ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Ακαδηµαϊκό έτος 5-6 ΜΑΘΗΜΑ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Καθηγητής: Σ Πνευµατικός ΑΣΚΗΣΕΙΣ 7 ης ΕΒΔΟΜΑΔΑΣ ΟΙ ΚΑΝΟΝΙΚΕΣ ΜΟΡΦΕΣ JORDAN Θεωρούµε ένα n-διάστατο διανυσµατικό χώρο E στο σώµα Κ = ή και
ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ Ακαδηµαϊκό έτος 5-6 ΜΑΘΗΜΑ ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Καθηγητής: Σ Πνευµατικός ΑΣΚΗΣΕΙΣ 7 ης ΕΒΔΟΜΑΔΑΣ ΟΙ ΚΑΝΟΝΙΚΕΣ ΜΟΡΦΕΣ JORDAN Θεωρούµε ένα n-διάστατο διανυσµατικό χώρο E στο σώµα Κ = ή και
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας.
 Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
Ποιες από τις παρακάτω προτάσεις είναι αληθείς; Δικαιολογήστε την απάντησή σας. 1. Κάθε πολυώνυμο ανάγωγο επί του Z είναι ανάγωγο επί του Q. Σωστό. 2. Κάθε πολυώνυμο ανάγωγο επί του Q είναι ανάγωγο επί
Μία απεικόνιση από ένα διανυσματικό χώρο V στον εαυτό του, L : V V την ονομάζουμε γραμμικό τελεστή στο V (ή ενδομορφισμό του V ). Ορισμός. L : V V γρα
 Γραμμική Άλγεβρα ΙΙ Διάλεξη 15 Αναλλοίωτοι Υπόχωροι, Ιδιόχωροι Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 2/5/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 15 2/5/2014 1 / 12 Μία απεικόνιση από ένα διανυσματικό
Γραμμική Άλγεβρα ΙΙ Διάλεξη 15 Αναλλοίωτοι Υπόχωροι, Ιδιόχωροι Χρήστος Κουρουνιώτης Πανεπιστήμιο Κρήτης 2/5/2014 Χ.Κουρουνιώτης (Παν.Κρήτης) Διάλεξη 15 2/5/2014 1 / 12 Μία απεικόνιση από ένα διανυσματικό
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobson
 ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Στο κεφάλαιο αυτό μελετάμε δακτυλίους του Art χρησιμοποιώντας το ριζικό του Jacobso. Ως εφαρμογή αποδεικνύουμε ότι κάθε δακτύλιος του Art είναι και της Noether. 4.1. Δακτύλιοι
ΚΕΦΑΛΑΙΟ 4: Ριζικό του Jacobso Στο κεφάλαιο αυτό μελετάμε δακτυλίους του Art χρησιμοποιώντας το ριζικό του Jacobso. Ως εφαρμογή αποδεικνύουμε ότι κάθε δακτύλιος του Art είναι και της Noether. 4.1. Δακτύλιοι
1 ιαδικασία διαγωνιοποίησης
 ιαδικασία διαγωνιοποίησης Εστω V ένας R-διανυσματικός χώρος (ή έναςc-διανυσματικός χώρος) διάστασης n. Είναι γνωστό ότι κάθε διάνυσμα (,,..., n ) του χώρου V μπορεί να παρασταθεί και σαν πίνακας στήλη
ιαδικασία διαγωνιοποίησης Εστω V ένας R-διανυσματικός χώρος (ή έναςc-διανυσματικός χώρος) διάστασης n. Είναι γνωστό ότι κάθε διάνυσμα (,,..., n ) του χώρου V μπορεί να παρασταθεί και σαν πίνακας στήλη
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
Διαγωνοποίηση μητρών. Στοιχεία Γραμμικής Άλγεβρας
 Διαγωνοποίηση μητρών Στοιχεία Γραμμικής Άλγεβρας Όμοιες μήτρες Ορισμός: Οι τετραγωνικές μήτρες Α=[α ij ] nxn & B=[b ij ] nxn όμοιες (Α~Β): αν υπάρχει ομαλή μήτρα Ρ τ.ώ. Β = Ρ -1 Α Ρ A~B Β~ Α Ρ ομαλή μήτρα
Διαγωνοποίηση μητρών Στοιχεία Γραμμικής Άλγεβρας Όμοιες μήτρες Ορισμός: Οι τετραγωνικές μήτρες Α=[α ij ] nxn & B=[b ij ] nxn όμοιες (Α~Β): αν υπάρχει ομαλή μήτρα Ρ τ.ώ. Β = Ρ -1 Α Ρ A~B Β~ Α Ρ ομαλή μήτρα
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
Κεφάλαιο Διανυσματικοί Χώροι Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: Διανυσματικοί Χώροι α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο
1 1 A = x 1 x 2 x 3. x 4. R 2 3 : a + b + c = x + y + z = 0. R 2 3 : a + x = b + y = c + z = 0
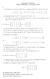 Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
Γραμμική Άλγεβρα Ι Θέματα Εξετάσεων Ιανουαρίου 6. (α Υπολογίστε τον πίνακα X R και την ορίζουσα det(x 5 αν AX = B + C και ( ( ( 3 3 A = B = C =. 4 3 (β Θεωρούμε πίνακα A R n n τέτοιον ώστε A = 4A 4I n.
t t Αν κάποιος από αυτούς είναι αντιστρέψιμος, υπολογίστε τον αντίστροφό του. 2. Υπολογίστε την ορίζουσα του Δείξτε τα εξής.
 Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις4: Ορίζουσες Βασικά σημεία Ορισμός και ιδιότητες οριζουσών (ιδιότητες γραμμών και στηλών, αναπτύγματα οριζουσών, det( B) det( )det( B)) Ένας τετραγωνικός πίνακας είναι
Γραμμική Άλγεβρα Ι, 07-8 Ασκήσεις4: Ορίζουσες Βασικά σημεία Ορισμός και ιδιότητες οριζουσών (ιδιότητες γραμμών και στηλών, αναπτύγματα οριζουσών, det( B) det( )det( B)) Ένας τετραγωνικός πίνακας είναι
Εφαρμοσμένα Μαθηματικά ΙΙ
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Εφαρμοσμένα Μαθηματικά ΙΙ Ιδιοτιμές - Ιδιοδιανύσματα Ιωάννης Λυχναρόπουλος Μαθηματικός, MSc, PhD Χαρακτηριστικά Ποσά Τετράγωνου Πίνακα (Ιδιοτιμές Ιδιοδιανύσματα)
Κεφάλαιο 7 Βάσεις και ιάσταση
 Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
Κεφάλαιο 7: Βάσεις και ιάσταση Σελίδα από 9 Κεφάλαιο 7 Βάσεις και ιάσταση n Στο Κεφάλαιο 5 είδαµε την έννοια της βάσης στο και στο Κεφάλαιο 6 µελετήσαµε διανυσµατικούς χώρους. Στο παρόν κεφάλαιο θα ασχοληθούµε
Θεώρημα Βolzano. Κατηγορία 1 η. 11.1 Δίνεται η συνάρτηση:
 Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
Κατηγορία η Θεώρημα Βolzano Τρόπος αντιμετώπισης:. Όταν μας ζητούν να εξετάσουμε αν ισχύει το θεώρημα Bolzano για μια συνάρτηση f σε ένα διάστημα [, ] τότε: Εξετάζουμε την συνέχεια της f στο [, ] (αν η
Κεφάλαιο 2. Παραγοντοποίηση σε Ακέραιες Περιοχές
 Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
Κεφάλαιο Παραγοντοποίηση σε Ακέραιες Περιοχές Γνωρίζουµε ότι στο Ÿ κάθε στοιχείο εκτός από το 0 και τα ± γράφεται ως γινόµενο πρώτων αριθµών κατά τρόπο ουσιαστικά µοναδικό Από τη Βασική Άλγεβρα ξέρουµε
Έντυπο Yποβολής Αξιολόγησης ΓΕ
 Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
Έντυπο Yποβολής Αξιολόγησης ΓΕ O φοιτητής συμπληρώνει την ενότητα «Υποβολή Εργασίας» και αποστέλλει το έντυπο σε δύο μη συρραμμένα αντίγραφα (ή ηλεκτρονικά) στον Καθηγητή-Σύμβουλο Ο Καθηγητής-Σύμβουλος
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ : ΠΛΗ12 «ΜΑΘΗΜΑΤΙΚΑ Ι» Επαναληπτική Τελική Εξέταση 16 Ιουλίου 2003
 http://edueapgr/pli/pli/studetshtm Page of 6 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ : ΠΛΗ «ΜΑΘΗΜΑΤΙΚΑ Ι» Επαναληπτική Τελική Εξέταση 6 Ιουλίου Απαντήστε όλα
http://edueapgr/pli/pli/studetshtm Page of 6 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ «ΠΛΗΡΟΦΟΡΙΚΗ» ΘΕΜΑΤΙΚΗ ΕΝΟΤΗΤΑ : ΠΛΗ «ΜΑΘΗΜΑΤΙΚΑ Ι» Επαναληπτική Τελική Εξέταση 6 Ιουλίου Απαντήστε όλα
ΠΛΗ ΛΥΣΕΙΣ ΕΡΓ_2 ΣΕΛ. 1/11
 ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: Νοεμβρίου 007 Ημερομηνία παράδοσης της Εργασίας: 4 Δεκεμβρίου 007 Πριν από την λύση κάθε άσκησης καλό
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: Νοεμβρίου 007 Ημερομηνία παράδοσης της Εργασίας: 4 Δεκεμβρίου 007 Πριν από την λύση κάθε άσκησης καλό
= k. n! k! (n k)!, k=0
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n τον n n ταυτοτικό πίνακα,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n τον n n ταυτοτικό πίνακα,
Κεφάλαιο 4 Διανυσματικοί Χώροι
 Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Κεφάλαιο Διανυσματικοί χώροι - Βασικοί ορισμοί και ιδιότητες Θεωρούμε τρία διαφορετικά σύνολα: α) Το σύνολο διανυσμάτων (πινάκων με μία στήλη) με στοιχεία το οποίο συμβολίζουμε με Σε αυτό το σύνολο γνωρίζουμε
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι
 Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
Εφαρμοσμένα Μαθηματικά ΙΙ 9ο Σετ Ασκήσεων (Λύσεις) Διανυσματικοί Χώροι Επιμέλεια: Ι. Λυχναρόπουλος. Δείξτε ότι ο V R εφοδιασμένος με τις ακόλουθες πράξεις (, a b) + (, d) ( a+, b+ d) και k ( ab, ) ( kakb,
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες
 ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιμοποιώντας τανυστικά γινόμενα και εφαρμόζοντας το θεώρημα των Wedderbur-Art ( 33) θα αποδείξουμε δύο θεμελιώδη θεωρήματα που αφορούν κεντρικές απλές άλγεβρες *
ΚΕΦΑΛΑΙΟ 6: Κεντρικές Απλές Άλγεβρες Χρησιμοποιώντας τανυστικά γινόμενα και εφαρμόζοντας το θεώρημα των Wedderbur-Art ( 33) θα αποδείξουμε δύο θεμελιώδη θεωρήματα που αφορούν κεντρικές απλές άλγεβρες *
A B. (f; B) = f(x 1 ) = a 11 x 1 + a k1 x k + 0.x k x n f(x 2 ) = a 12 x 1 + a k2 x k + 0.x k x n
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΑΣΚΗΣΕΙΣ III ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDAN 1 Εστω f : V V γραμμική απεικόνιση Εστω A = ker(f i ) και B = ker(f i+1 ) Δείξτε ότι (i) A B και (ii) f(b) A Αποδ: (i) Εστω x ker(f i ) Τότε f i (x)
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΑΣΚΗΣΕΙΣ III ΚΑΝΟΝΙΚΗ ΜΟΡΦΗ JORDAN 1 Εστω f : V V γραμμική απεικόνιση Εστω A = ker(f i ) και B = ker(f i+1 ) Δείξτε ότι (i) A B και (ii) f(b) A Αποδ: (i) Εστω x ker(f i ) Τότε f i (x)
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: Οκτωβρίου 005) Η Άσκηση στην εργασία αυτή είναι
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές Λύσεις ΕΡΓΑΣΙΑ η (Ηµεροµηνία Αποστολής στον Φοιτητή: Οκτωβρίου 005) Η Άσκηση στην εργασία αυτή είναι
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα
 Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
Παραδείγματα Ιδιοτιμές Ιδιοδιανύσματα Παράδειγμα Να βρείτε τις ιδιοτιμές και τα αντίστοιχα ιδιοδιανύσματα του πίνακα A 4. Επίσης να προσδιοριστούν οι ιδιοχώροι και οι γεωμετρικές πολλαπλότητες των ιδιοτιμών.
ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ 12) ΕΡΓΑΣΙΑ 1 η Ημερομηνία Αποστολής στον Φοιτητή: 20 Οκτωβρίου 2008
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) ΕΡΓΑΣΙΑ η Ημερομηνία Αποστολής στον Φοιτητή: 0 Οκτωβρίου 008 Ημερομηνία παράδοσης της Εργασίας: Νοεμβρίου 008 Πριν
ΚΕΦΑΛΑΙΟ 1: Πρότυπα. x y x z για κάθε x, y, R με την ιδιότητα 1R. x για κάθε x R, iii) υπάρχει στοιχείο 1 R. ii) ( x y) z x ( y z)
 ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΚΕΦΑΛΑΙΟ 1: Πρότυπα Στο κεφάλαιο αυτό θα υπενθυμίσουμε τις βασικές έννοιες που αφορούν πρότυπα πάνω από ένα δακτύλιο Θα περιοριστούμε στα πλέον απαραίτητα για αυτά που ακολουθούν στα άλλα κεφάλαια Η κατευθυντήρια
ΘΕΩΡΗΜΑ CAYLEY-HAMILTON. Έστω A πίνακας ν ν. Από το θεώρηµα Cayley-Hamilton συµπεραίνουµε ότι το σύνολο των πολυωνύµων p( λ ), ώστε p( A)
 Γραµµική Άλγεβρα ΙΙ Σελίδα από Μάθηµα 7 ο ΘΕΩΡΗΜΑ CYLEY-HMILTON Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 60 Ασκήσεις :,,, σελ 6 Ελάχιστο πολυώνυµο πίνακα Έστω πίνακας ν ν Από το θεώρηµα Cayley-Hamilton
Γραµµική Άλγεβρα ΙΙ Σελίδα από Μάθηµα 7 ο ΘΕΩΡΗΜΑ CYLEY-HMILTON Θεωρία : Γραµµική Άλγεβρα : εδάφιο 6, σελ 60 Ασκήσεις :,,, σελ 6 Ελάχιστο πολυώνυµο πίνακα Έστω πίνακας ν ν Από το θεώρηµα Cayley-Hamilton
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί
 Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Κεφάλαιο 5 Γραμμικοί Μετασχηματισμοί 5 Γενικά Γραμμικοί Μετασχηματισμοί Μία σχέση μεταξύ των στοιχείων δύο συνόλων Α,Β αντιστοιχίζει στοιχεία του Α με στοιχεία του Β άλλου μέσω ενός κανόνα που μπορεί να
Ε Μέχρι 31 Μαρτίου 2015.
 Ε Μέχρι 31 Μαρτίου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες
Ε Μέχρι 31 Μαρτίου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες
Δηλαδή η ρητή συνάρτηση είναι πηλίκο δύο ακέραιων πολυωνύμων. Επομένως, το ζητούμενο ολοκλήρωμα είναι της μορφής
 D ολοκλήρωση ρητών συναρτήσεων Το θέμα μας στην ενότητα αυτή είναι η ολοκλήρωση ρητών συναρτήσεων. Ας θυμηθούμε πρώτα ποιες συναρτήσεις ονομάζονται ρητές. Ορισμός: Μία συνάρτηση ονομάζεται ρητή όταν μπορεί
D ολοκλήρωση ρητών συναρτήσεων Το θέμα μας στην ενότητα αυτή είναι η ολοκλήρωση ρητών συναρτήσεων. Ας θυμηθούμε πρώτα ποιες συναρτήσεις ονομάζονται ρητές. Ορισμός: Μία συνάρτηση ονομάζεται ρητή όταν μπορεί
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/2017 Διδάσκων: Ι. Λυχναρόπουλος
 Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
Τμήμα Μηχανολόγων Μηχανικών Πανεπιστήμιο Θεσσαλίας Άσκηση (Μονάδες.5) Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση 8/6/07 Διδάσκων: Ι. Λυχναρόπουλος Προσδιορίστε το c R ώστε το διάνυσμα (,, 6 ) να ανήκει στο
1 x x x x 1 x x x x 1 x x x x 1 (10) B 2, B 1. (10)
 Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
Γραμμική Άλγεβρα, Τμήμα Β (Τζουβάρας/Χαραλάμπους) Φεβρουάριος 07 (I) Εστω n n πίνακας A τέτοιος ώστε A = 6A, έστω δ.χ. V με dim(v ) = n και f : V V η γραμμική απεικόνιση με πίνακα A ως πρός κάποια βάση
Ε Μέχρι 18 Μαΐου 2015.
 Ε Μέχρι 18 Μαΐου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες άρα
Ε Μέχρι 18 Μαΐου 2015. 1 Αντικείμενα: δακτύλιοι Fraleigh, 4.1. Ορισμός έννοιας «δακτυλίου». Χαρακτηρισμοί δακτυλίων και στοιχείων αυτών: Δακτύλιος R Στοιχεία δακτυλίου R / (= δεν έχει μηδενοδιαιρέτες άρα
ΑΠΑΝΤΗΣΕΙΣ , Β= 1 y, όπου y 0. , όπου y 0.
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Ι (ΘΕ ΠΛΗ ) ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΞΕΤΑΣΗ 9 Ιουνίου 8:-: ΑΠΑΝΤΗΣΕΙΣ Θέμα (Α) ( 5 μονάδες) Δίδονται οι πίνακες Α=,
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥΔΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ ΓΙΑ ΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ Ι (ΘΕ ΠΛΗ ) ΕΠΑΝΑΛΗΠΤΙΚΗ ΕΞΕΤΑΣΗ 9 Ιουνίου 8:-: ΑΠΑΝΤΗΣΕΙΣ Θέμα (Α) ( 5 μονάδες) Δίδονται οι πίνακες Α=,
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
x είναι f 1 f 0 f κ λ
 3 Ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ [Κεφάλαια, Μέρος Β' του σχολικού βιβλίου] ΘΕΜΑ Α.Βλέπε σχολικό βιβλίο, σελίδα 4.. Βλέπε σχολικό βιβλίο, σελίδα 88, 89. 3. α) ΣΩΣΤΟ, διότι αν η f παραγωγίσιμη στο χ
3 Ο ΔΙΑΓΩΝΙΣΜΑ ΕΝΔΕΙΚΤΙΚΕΣ ΑΠΑΝΤΗΣΕΙΣ [Κεφάλαια, Μέρος Β' του σχολικού βιβλίου] ΘΕΜΑ Α.Βλέπε σχολικό βιβλίο, σελίδα 4.. Βλέπε σχολικό βιβλίο, σελίδα 88, 89. 3. α) ΣΩΣΤΟ, διότι αν η f παραγωγίσιμη στο χ
ΚΕΦΑΛΑΙΟ 8: Εφαρµογή: Το θεώρηµα του Burnside
 ΚΕΦΑΛΑΙΟ 8: Εφαρµογή: Το θεώρηµα του Bursde Θα αποδείξουµε εδώ ότι κάθε οµάδα τάξης a q b (, q πρώτοι) είναι επιλύσιµη. Το θεώρηµα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιµοποίησε τη νέα τότε
ΚΕΦΑΛΑΙΟ 8: Εφαρµογή: Το θεώρηµα του Bursde Θα αποδείξουµε εδώ ότι κάθε οµάδα τάξης a q b (, q πρώτοι) είναι επιλύσιµη. Το θεώρηµα αυτό αποδείχτηκε από τον Bursde το 904 ο οποίος χρησιµοποίησε τη νέα τότε
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ
 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 6 Νοεµβρίου 005 Ηµεροµηνία Παράδοσης της Εργασίας
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΡΟΓΡΑΜΜΑ ΣΠΟΥ ΩΝ ΣΤΗΝ ΠΛΗΡΟΦΟΡΙΚΗ ΜΑΘΗΜΑΤΙΚΑ Ι (ΘΕ ΠΛΗ ) Ενδεικτικές λύσεις ΕΡΓΑΣΙΑ η Ηµεροµηνία Αποστολής στον Φοιτητή: 6 Νοεµβρίου 005 Ηµεροµηνία Παράδοσης της Εργασίας
Γραμμική Άλγεβρα Ι Εξέταση Φεβρουαρίου. Επώνυμο. Όνομα. ΑΜ (13 ψηφία) Σύνολο
 1 Γραμμική Άλγεβρα Ι 009-10 Εξέταση Φεβρουαρίου Επώνυμο Όνομα ΑΜ (1 ψηφία) Ημ/ία Αίθουσα 1 5 Σύνολο Α Η εξέταση αποτελείται από 5 Θέματα. Το άθροισμα των μονάδων είναι 1, το άριστα 10 και η βάση 5. Απαντήστε
1 Γραμμική Άλγεβρα Ι 009-10 Εξέταση Φεβρουαρίου Επώνυμο Όνομα ΑΜ (1 ψηφία) Ημ/ία Αίθουσα 1 5 Σύνολο Α Η εξέταση αποτελείται από 5 Θέματα. Το άθροισμα των μονάδων είναι 1, το άριστα 10 και η βάση 5. Απαντήστε
Κεφάλαιο 0. Μεταθετικοί ακτύλιοι, Ιδεώδη
 Κεφάλαιο 0 Μεταθετικοί ακτύλιοι, Ιδεώδη Το κεφάλαιο αυτό έχει προπαρασκευαστικό χαρακτήρα Θα καθιερώσουµε συµβολισµούς και θα υπενθυµίσουµε ορισµούς και στοιχειώδεις προτάσεις για δακτύλιους και ιδεώδη
Κεφάλαιο 0 Μεταθετικοί ακτύλιοι, Ιδεώδη Το κεφάλαιο αυτό έχει προπαρασκευαστικό χαρακτήρα Θα καθιερώσουµε συµβολισµούς και θα υπενθυµίσουµε ορισµούς και στοιχειώδεις προτάσεις για δακτύλιους και ιδεώδη
Κεφάλαιο 7 Ορθογώνιοι Πίνακες
 Κεφάλαιο 7 Ορθογώνιοι Πίνακες Εσωτερικό Γινόμενο και ορθογωνιότητα Έστω V ένας διανυσματικός χώρος, υπόχωρος του n. Κάθε συνάρτηση ορισμένη στο VV (την οποία θα συμβολίζουμε με ) ορίζει ένα εσωτερικό γινόμενο
Κεφάλαιο 7 Ορθογώνιοι Πίνακες Εσωτερικό Γινόμενο και ορθογωνιότητα Έστω V ένας διανυσματικός χώρος, υπόχωρος του n. Κάθε συνάρτηση ορισμένη στο VV (την οποία θα συμβολίζουμε με ) ορίζει ένα εσωτερικό γινόμενο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ. Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 2010 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ119)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ -ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ ΥΠΟΛΟΓΙΣΤΩΝ Λύσεις των Θεμάτων της Εξέτασης Ιανουαρίου 00 στο μάθημα: «Γραμμική Άλγεβρα» (ΗΥ9) Ηράκλειο, 7 Ιανουαρίου 00 Θέμα. (μονάδες.5) α) [μονάδες:.0]. Υπολογίστε
I. ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ. math-gr
 I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
I ΜΙΓΑΔΙΚΟΙ ΑΡΙΘΜΟΙ i e ΜΕΡΟΣ Ι ΟΡΙΣΜΟΣ - ΒΑΣΙΚΕΣ ΠΡΑΞΕΙΣ Α Ορισμός Ο ορισμός του συνόλου των Μιγαδικών αριθμών (C) βασίζεται στις εξής παραδοχές: Υπάρχει ένας αριθμός i για τον οποίο ισχύει i Το σύνολο
Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος
 6/6/06 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 0 Δίνεται ο πίνακας A =. Nα υπολογίσετε την βαθμίδα του και να βρείτε τη διάσταση και από μία βάση α) του μηδενοχώρου
6/6/06 Εφαρμοσμένα Μαθηματικά ΙΙ Τελική Εξέταση Ι. Λυχναρόπουλος Άσκηση (Μονάδες ) 0 Δίνεται ο πίνακας A =. Nα υπολογίσετε την βαθμίδα του και να βρείτε τη διάσταση και από μία βάση α) του μηδενοχώρου
( ) Άρα το 1 είναι ρίζα του P, οπότε το x 1 είναι παράγοντάς του. Το πηλίκο της διαίρεσης ( x 3x + 5x 3) : ( x 1) είναι:
 ( x) Άρα το είναι ρίζα του P, οπότε το x είναι παράγοντάς του 4 Το πηλίκο της διαίρεσης ( x 3x + 5x 3) : ( x ) είναι: 3 π ( x) = x + x x + 3 Η ταυτότητα της προηγούμενης διαίρεσης είναι: 4 3 x 3x + 5x
( x) Άρα το είναι ρίζα του P, οπότε το x είναι παράγοντάς του 4 Το πηλίκο της διαίρεσης ( x 3x + 5x 3) : ( x ) είναι: 3 π ( x) = x + x x + 3 Η ταυτότητα της προηγούμενης διαίρεσης είναι: 4 3 x 3x + 5x
7. Αν υψώσουμε και τα δύο μέλη μιας εξίσωσης στον κύβο (και γενικά σε οποιαδήποτε περιττή δύναμη), τότε προκύπτει
 8 7y = 4 y + y ( 8 7y) = ( 4 y + y) ( y) + 4 y y 4 y = 4 y y 8 7y = 4 y + ( 4 y) = ( 4 y y) ( 4 y) = 4( 4 y)( y) ( 4 y) 4( 4 y)( y) = 0 ( 4 y) [ 4 y 4( y) ] = 4 ( 4 y)( y + 4) = 0 y = ή y = 4) 0 4 H y
8 7y = 4 y + y ( 8 7y) = ( 4 y + y) ( y) + 4 y y 4 y = 4 y y 8 7y = 4 y + ( 4 y) = ( 4 y y) ( 4 y) = 4( 4 y)( y) ( 4 y) 4( 4 y)( y) = 0 ( 4 y) [ 4 y 4( y) ] = 4 ( 4 y)( y + 4) = 0 y = ή y = 4) 0 4 H y
Copyright: Ψωμόπουλος Ευάγγελος, Eκδόσεις Zήτη, Γ έκδοση: Μάρτιος 2012, Θεσσαλονίκη
 Kάθε γνήσιο αντίτυπο φέρει την υπογραφή του συγγραφέα ISBN 978-960-456-314-2 Copyright: Ψωμόπουλος Ευάγγελος, Eκδόσεις Zήτη, Γ έκδοση: Μάρτιος 2012, Θεσσαλονίκη Tο παρόν έργο πνευματικής ιδιοκτησίας προστατεύεται
Kάθε γνήσιο αντίτυπο φέρει την υπογραφή του συγγραφέα ISBN 978-960-456-314-2 Copyright: Ψωμόπουλος Ευάγγελος, Eκδόσεις Zήτη, Γ έκδοση: Μάρτιος 2012, Θεσσαλονίκη Tο παρόν έργο πνευματικής ιδιοκτησίας προστατεύεται
( A = A = 3 5 A 2 + B 2.
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι Χειμερινό Εξάμηνο 25 Ασκήσεις Για πίνακες A R m n και B R p q ορίζονται οι πίνακες AB και BA και ισχύει AB = BA Τι συμπεραίνετε για τα m, n, p, q; 2 Για A, B R n n : (α Δείξτε ότι (A
Θέµατα ( ικαιολογείστε πλήρως όλες τις απαντήσεις σας)
 Τµήµα Εφαρµοσµένων Μαθηµατικών Παν/µίου Κρήτης Εξεταστική περίοδος εαρινού εξαµήνου Πέµπτη, 2 Ιούνη 28 Γραµµική Αλγεβρα II ιδάσκων: Α. Τόγκας Θέµατα ( ικαιολογείστε πλήρως όλες τις απαντήσεις σας) Θέµα
Τµήµα Εφαρµοσµένων Μαθηµατικών Παν/µίου Κρήτης Εξεταστική περίοδος εαρινού εξαµήνου Πέµπτη, 2 Ιούνη 28 Γραµµική Αλγεβρα II ιδάσκων: Α. Τόγκας Θέµατα ( ικαιολογείστε πλήρως όλες τις απαντήσεις σας) Θέµα
ΛΥΣΕΙΣ ΦΥΛΛΑΔΙΟΥ 6 / ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ Γραμμικές απεικονίσεις, Αλλαγή βάσης, Ιδιοτιμές, Ιδιοδιανύσματα
 ΛΥΣΕΙΣ ΦΥΛΛΑΔΙΟΥ 6 / 009-0 ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ Γραμμικές απεικονίσεις, Αλλαγή βάσης, Ιδιοτιμές, Ιδιοδιανύσματα Έστω η γραμμική απεικόνιση T : με (α) Βρείτε τον πίνακα της T, I Ως προς την κανονική βάση
ΛΥΣΕΙΣ ΦΥΛΛΑΔΙΟΥ 6 / 009-0 ΠΟΛΙΤΙΚΟΙ ΜΗΧΑΝΙΚΟΙ Γραμμικές απεικονίσεις, Αλλαγή βάσης, Ιδιοτιμές, Ιδιοδιανύσματα Έστω η γραμμική απεικόνιση T : με (α) Βρείτε τον πίνακα της T, I Ως προς την κανονική βάση
Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης
 Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Ελάχιστο Πολυώνυµο Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 20 4. Ελάχιστο Πολυώνυµο Στην παρούσα παράγραφο
Τίτλος Μαθήματος: Γραμμική Άλγεβρα ΙΙ Ενότητα: Ελάχιστο Πολυώνυµο Διδάσκων: Καθηγητής Νικόλαος Μαρμαρίδης, Καθηγητής Ιωάννης Μπεληγιάννης Τμήμα: Μαθηματικών 20 4. Ελάχιστο Πολυώνυµο Στην παρούσα παράγραφο
9 Πολυώνυμα Διαίρεση πολυωνύμων
 4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
4ο Κεφάλαιο 9 Πολυώνυμα Διαίρεση πολυωνύμων Α ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Ορισμοί Μονώνυμο του x ονομάζουμε κάθε παράσταση της μορφής ν αx όπου α R, * ν N και x μια μεταβλητή που μπορεί να πάρει οποιαδήποτε
V (F ) = {(u 1, u 2, u 3 ) P 2 K F (u 1, u 2, u 3 ) = 0}
 1 Θεώρημα BEZOU T Ο δακτύλιος K[x 1,..., x n ] είναι περιοχή μονοσήμαντης ανάλυσης. Άρα κάθε πολυώνυμο f K[x 1,..., x n ] (που δεν είναι σταθερά, δηλαδή f / K) αναλύεται σε γινόμενο αναγώγων πολυωνύμων,
1 Θεώρημα BEZOU T Ο δακτύλιος K[x 1,..., x n ] είναι περιοχή μονοσήμαντης ανάλυσης. Άρα κάθε πολυώνυμο f K[x 1,..., x n ] (που δεν είναι σταθερά, δηλαδή f / K) αναλύεται σε γινόμενο αναγώγων πολυωνύμων,
n! k! (n k)!, = k k 1
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n ) τον n n ταυτοτικό πίνακα,
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Συμπληρωματικές Ασκήσεις Χειμερινό Εξάμηνο 2015 Χρήστος Α Αθανασιάδης Συμβολίζουμε με O το μηδενικό πίνακα καταλλήλων διαστάσεων, με I (ορισμένες φορές, με I n ) τον n n ταυτοτικό πίνακα,
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΣΤΑΤΙΣΤΙΚΗΣ ΜΑΣ 121: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟΥ 3
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΣΤΑΤΙΣΤΙΚΗΣ ΜΑΣ 11: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟΥ 3 1. Να βρείτε τις ιδιοτιμές και τα ιδιοδιανύσματα των πιο κάτω πινάκων: 1 0 3 1 1 1 1 1 3 1 1 4 a b.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΥΠΡΟΥ ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΚΑΙ ΣΤΑΤΙΣΤΙΚΗΣ ΜΑΣ 11: ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ Ι ΑΣΚΗΣΕΙΣ ΚΕΦΑΛΑΙΟΥ 3 1. Να βρείτε τις ιδιοτιμές και τα ιδιοδιανύσματα των πιο κάτω πινάκων: 1 0 3 1 1 1 1 1 3 1 1 4 a b.
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 2
 ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 2 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii2018/laii2018.html Παρασκευή 16 Μαρτίου 2018
ΓΡΑΜΜΙΚΗ ΑΛΓΕΒΡΑ ΙΙ Τµηµα Β (ΠΕΡΙΤΤΟΙ) Ασκησεις - Φυλλαδιο 2 ιδασκων: Α. Μπεληγιάννης Ιστοσελιδα Μαθηµατος : http://users.uoi.gr/abeligia/linearalgebraii/laii2018/laii2018.html Παρασκευή 16 Μαρτίου 2018
