Βαγγέληρ Οικονόμοτ Διάλεξη 5. Διαμόπυψςη ήμασορ - Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 1
|
|
|
- Ευθαλία Καραμανλής
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Βαγγέληρ Οικονόμοτ Διάλεξη 5 Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 1
2 Μεσαςφημασιςμόρ Hilbert Διαμόπυψςη ήμασορ Γενικά Διαμόπυψςη Πλάσοτρ Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 2
3 Ο μεσαςφημασιςμόρ Hilbert ενόρ ςήμασορ x(t) οπίζεσαι ψρ η ςτνέλιξη σοτ x(t) με σο ςήμα h(t)=1/πt. 1 xr ( ) H[ x( t)] xˆ ( t) x( t) h( t) x( r) h( t r) dr dr t r Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 3
4 Θεψπώνσαρ όσι σα ςήμασα είναι ππαγμασικά, οι βαςικέρ ιδιόσησερ σοτ μεσαςφημασιςμού Hilbert είναι: 1. Μεσαςφημασιςμόρ Fourier σοτ μεσαςφημασιςμού Hilbert F[ xˆ ( t)] F[ x( t)* h( t)] X( f ) F[ h( t)] jsgn( f ) X ( f ) 2. Γπαμμική Ιδιόσησα H[ r x ( t) r x ( t)] r xˆ ( t) r xˆ ( t) τνέλιξη H[ x ( t)* x ( t)] xˆ ( t)* x ( t) x ( t)* xˆ ( t) Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 4
5 1, t 0 sgn( t) 0, t 0 1, t 0 Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 5
6 Να βπεθεί ο μεσαςφημασιςμόρ Hilbert σψν ςημάσψν: x ( t) ( t) θαη x ( t) sin(2 f t) Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 6
7 ήμα βαςικήρ ζώνηρ είναι σο ςήμα με μη μηδενικό υαςμασικό πεπιεφόμενο ςσην πεπιοφή γύπψ από σην ςτφνόσησα f=0 και ςφεδόν μηδενικο πεπιεφόμενο ςσην τπόλοιπη πεπιοφή σοτ υάςμασορ. Ζψνοπεπασό ςήμα είναι σο ςήμα με μη μηδενικό πεπιεφόμενο ςτγκενσπψμένο γύπψ από μία κενσπική ςτφνόσησα f=±f c (με f c >>0) και με ςφεδόν μηδενικό πεπιεφόμενο ςσην τπόλοιπη πεπιοφή σοτ υάςμασορ. Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 7
8 Υάςμα ςήμασορ βαςικήρ ζώνηρ Υάςμα ζψνοπεπασού ςήμασορ Υαςμασική Πτκνόσησα Ενέπγειαρ καλείσαι ο μεσαςφημασιςμόρ Fourier σηρ ςτνάπσηςηρ εσεποςτςφέσιςηρ σψν ςημάσψν ενέπγειαρ. Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 8
9 σιρ σηλεπικοινψνίερ: Σα ςήμασα πληπουοπίαρ είναι βαςικήρ ζώνηρ Σα ςήμασα εκπομπήρ είναι βαςικήρ ζώνηρ ή ζψνοπεπασά Η ςτφνόσησα f c σοτ ζψνοπεπασού ςήμασορ ονομάζεσαι ςτφνόσησα υέπονσορ Η επιλογή σηρ ςτφνόσησαρ υέπονσορ ακολοτθεί κανόνερ ποτ ςφεσίζονσαι με σο μέςο μεσάδοςηρ (ενςύπμαση ή αςύπμαση), σην απονομή ςτφνόσησαρ ςσιρ διάυοπερ τπηπεςίερ, ση μέθοδο ππόςβαςηρ ςσο μέςο, κλπ. Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 9
10 Διαμόπυψςη είναι η διαδικαςία ανσιςσοίφιςηρ σηρ πληπουοπίαρ ποτ μεσαυέπει σο ςήμα βαςικήρ ζώνηρ m(t) ςε ένα φαπακσηπιςσικό ενόρ ζψνοπεπασού ςήμασορ κασάλληλοτ για μεσάδοςη ςσο κανάλι. Σο φαπακσηπιςσικό ατσό μποπεί να είναι σο πλάσορ ή η γψνία σοτ ζψνοπεπασού ςήμασορ (αναλογικέρ επικοινψνίερ) ή μποπεί σο ίδιο σο ζψνοπεπασό ςήμα να ανσιπποςψπεύει μια διακπισή κασάςσαςη η οποία ονομάζεσαι ςύμβολο (χηυιακέρ επικοινψνίερ) Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 10
11 Ππο-πεπιβάλλοτςα xt ( ) : πραγκαηηθό ζήκα X ( f ) : θάζκα ηοσ x( t) ˆ x ( ) ( ) ( ) p t x t jx t Μεσαςφημασιςμόρ Fourier X ( f ) X ( f ) j( j sgn( f ) X ( f )) p X ( f ) sgn( f ) X ( f ) 2 X ( f ), f 0 X(0), f 0 0, f 0 Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 11
12 xt ( ): δωλοπεραηό ζήκα x t j2 fct ( ) Re[ g( t) e ] gt ( ): κεγαδηθή περηβάιιοσζα g t x t e j2 fct ( ) p( ) x t g t e j2 fct p( ) ( ) g( t) x ( t) jx ( t) I Q jz e cos z j sin z x ( t) x( t) jxˆ ( t) p x t j2 fct ( ) Re[ g( t) e ] x( t) x ( t)cos(2 f t) x ( t)sin(2 f t) I c Q c xˆ( t) x ( t)sin(2 f t) x ( t)cos(2 f t) I c Q c x ( t) : ζσκθαζηθή ζσληζηώζα x I Q ( t) : ορζογώληα ζσληζηώζα Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 12
13 Πολική μοπυή j g( t) V( t) e () t x( t) V( t)cos(2 f t ( t)) c Όποτ : V t x t x t 2 2 ( ) I( ) Q( ) ( t) tan x () t 1 Q xi () t V ( t) : περηβάιιοσζα ηοσ ζήκαηος x( t) ( t) : θάζε ηοσ ζήκαηος x( t) V ( t), ( t) : τακειοπεραηά θαη πραγκαηηθά Vt ( ) : ζεηηθό ζήκα Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 13
14 Για σο ςήμα x(t) να βπεθεί η μιγαδική πεπιβάλλοτςα, η πεπιβάλλοτςα και η υάςη όποτ: x( t) cos(2 f t) c Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 14
15 Αναλογικέρ Επικοινψνίερ: φεσίζονσαι με σην εκπομπή, λήχη και πολτπλεξία αναλογικών ςημάσψν (?) Ευαπμογέρ: Ραδιουψνία Σηλεόπαςη Παπαδοςιακή Σηλευψνία Με σην χηυιακή σηλεόπαςη και παδιουψνία θα αποσελούν παπελθόν Σεφνικέρ ποτ ευαπμόζονσαι ςε αναλογικά σηλεπικοινψνιακά ςτςσήμασα αποσελούν σην βάςη για ανσίςσοιφερ σεφνικέρ ςσιρ Χηυιακέρ Επικοινψνίερ (πφ. Σεφνικέρ Διαμόπυψςηρ και Αποδιαμόπυψςηρ ) Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 15
16 Η ιδέα σηρ αναλογικήρ διαμόπυψςηρ ςσηπίζεσαι ςσην αλλαγή κάποιαρ παπαμέσποτ ενόρ ημισονοειδούρ ςήμασορ c(t), σο οποίο λέγεσαι υοπέαρ, από κάποιο πληπουοπιακό ςήμα m(t) πποκειμένοτ να πεπάςει "άνεσα" από σο κανάλι. Η αναλογική διαμόπυψςη ευαπμόζεσαι κτπίψρ ςε σηλεπικοινψνιακά ςτςσήμασα, ποτ φπηςιμοποιούνσαι ςσιρ παδιουψνικέρ εκπομπέρ, ςσα κινησά ςτςσήμασα επικοινψνίαρ κ.λ.π. σα ςτςσήμασα ατσά σα πληπουοπιακά ςήμασα, ποτ ππέπει να μεσαδοθούν, είναι η ανθπώπινη ομιλία και η μοτςική και είναι "φαμηλού απμονικού πεπιεφομένοτ" (πεπιέφοτν ςτφνόσησερ από 5 ψρ15 khz πεπίποτ), ενώ σο κανάλι (η κεπαία και η ασμόςυαιπα) ςτμπεπιυέπεσαι ιδανικά ψρ ζψνοπεπασό υίλσπο με σην πιο φαμηλή ςτφνόσησα γύπψ ςσα 500 khz. τνεπώρ, είναι ππουανέρ όσι σο κανάλι δε θα επισπέχει ση μεσάδοςη σψν ςημάσψν. Έσςι, αναγκάζεσαι κανείρ να "υοπσώςει" σο ππορ μεσάδοςη πληπουοπιακό ςήμα ςε κάποιο υοπέα, ο οποίορ είναι ένα ημισονοειδέρ ςήμα ςτφνόσησαρ f c και ο οποίορ "πεπνάει" από σο κανάλι. Ατσή είναι ςσην οτςία η σεφνική σηρ αναλογικήρ διαμόπυψςηρ. Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 16
17 Διαμόπυψςη Πλάσοτρ: σο ςήμα πληπουοπίαρ βαςικήρ ζώνηρ αποστπώνεσαι ςσο πλάσορ σοτ διαμοπυψμένοτ ςήμασορ Υέπον ήμα ήμα Πληπουοπίαρ Διαμοπυψσήρ Πλάσοτρ Διαμοπυψμένο ήμα Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 17
18 Υέπον ήμα: ήμα Πληπουοπίαρ: mt () c( t( t) ) A cos(2 fftt) ( t)) Διαμοπυψμένο ήμα: x( t) A( t)cos(2 f t) cc cc c ( t) 0 Σο πλάσορ σοτ διαμοπυψμένοτ ςήμασορ μεσαβάλλεσαι γπαμμικά με σο πλάσορ σοτ ςήμασορ πληπουοπίαρ A( t) A m( t) x( t) [ A m( t)]cos(2 f t) (*) c c c Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 18
19 Σο διαμοπυψμένο κασά πλάσορ ςήμα x(t) είναι ζψνοπεπασό με γενική μοπυή: x( t) x ( t)cos(2 f t) x ( t)sin(2 f t) I c Q c τνδτάζονσαρ σην παπαπάνψ ςφέςη με σην ςφέςη (*) πποκύπσει όσι: x ( t) A m( t) x ( t) 0 I c Q Οπόσε για σην πεπιβάλλοτςα έφοτμε: V( t) A m( t) ( t) 0 c Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 19
20 Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 20
21 t=[0:0.01:10]; m_t = 0.8*sin(pi*t/4); c_t = 2*cos(4*pi*t); x_t = (2+m_t).*cos(4*pi*t); V_t = abs(2+m_t); figure,plot(t,m_t), axis([ ]) figure,plot(t,c_t,'g'), axis([ ]) figure,plot(t,x_t),hold on,plot(t,v_t,'g-.'), axis([ ]) Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 21
22 Δείκσηρ διαμόπυψςηρ: min{ mt ( )} A c 1 Ac m( t) 0 1 Ac m( t) 0 Τπεπδιαμόπυψςη. ΑΦΗΜΟ!!! Παπαμοπυώνεσαι η πεπιβάλλοτςα Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 22
23 t c( t) 2cos(4 t) mt ( ) 0.8sin 4 Ποιά είναι η πεπιβάλλοτςα, η ςτφνόσησα υέπονσορ και η σιμή σοτ δείκση παπαμόπυψςηρ; Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 23
24 t c( t) 2cos(4 t) mt ( ) 2.4sin 4 Ποιά είναι η πεπιβάλλοτςα και η σιμή σοτ δείκση παπαμόπυψςηρ; φεδιάςσε σην πεπιβάλλοτςα και σο διαμοπυψμένο ςήμα. Ειςαγψγικέρ Έννοιερ - Διάλεξη 5 24
Ψηυιακά δεδομένα (data) :είναι δεδομένα ποτ έφοτν αναπαπαςσαθεί με κάποιο σπόπο (κψδικοποίηςη), είναι αποθηκετμένα ςε τπολογιςσή και είναι δτνασόν να
 Ψηυιακά δεδομένα (data) :είναι δεδομένα ποτ έφοτν αναπαπαςσαθεί με κάποιο σπόπο (κψδικοποίηςη), είναι αποθηκετμένα ςε τπολογιςσή και είναι δτνασόν να επεξεπγαςσούν. Τα χηυιακά δεδομένα αποθηκεύονσαι ςε
Ψηυιακά δεδομένα (data) :είναι δεδομένα ποτ έφοτν αναπαπαςσαθεί με κάποιο σπόπο (κψδικοποίηςη), είναι αποθηκετμένα ςε τπολογιςσή και είναι δτνασόν να επεξεπγαςσούν. Τα χηυιακά δεδομένα αποθηκεύονσαι ςε
Κλαμα σοτ εμιγκπανσοτ 1. Ειναι ενα σπαγοτδι σψν Ελληνψν σηρ Κασψ Ισαλιαρ. Ο σισλορ σοτ, ςση νεοελληνικη σοτ αποδοςη: "Θπηνορ σοτ. σοςο εφει να με δει
 1 Κλαμα σοτ εμιγκπανσοτ 1 Ειναι ενα σπαγοτδι σψν Ελληνψν σηρ Κασψ Ισαλιαρ. Ο σισλορ σοτ, ςση νεοελληνικη σοτ αποδοςη: "Θπηνορ σοτ μεσαναςση" Ωπια μοτ πονσινεddα α ποτσε ςσε σςε ςσασζει πλεα σαλαςςα ς αγκοταddει
1 Κλαμα σοτ εμιγκπανσοτ 1 Ειναι ενα σπαγοτδι σψν Ελληνψν σηρ Κασψ Ισαλιαρ. Ο σισλορ σοτ, ςση νεοελληνικη σοτ αποδοςη: "Θπηνορ σοτ μεσαναςση" Ωπια μοτ πονσινεddα α ποτσε ςσε σςε ςσασζει πλεα σαλαςςα ς αγκοταddει
Σι είναι κιπςοί σψν κάσψ άκπψν;
 Σι είναι κιπςοί σψν κάσψ άκπψν; Οι κιπςοί είναι σο ανσίσιμο σοτ ανθπώπινοτ είδοτρ από σην όπθια ςσάςη σοτ ςώμασορ ποτ δημιοτπγεί ςτνθήκερ ςσάςηρ σοτ υλεβικού αίμασορ ςσα κάσψ άκπα. Είναι γνψςσό νόςημα
Σι είναι κιπςοί σψν κάσψ άκπψν; Οι κιπςοί είναι σο ανσίσιμο σοτ ανθπώπινοτ είδοτρ από σην όπθια ςσάςη σοτ ςώμασορ ποτ δημιοτπγεί ςτνθήκερ ςσάςηρ σοτ υλεβικού αίμασορ ςσα κάσψ άκπα. Είναι γνψςσό νόςημα
Ελένη Προκοπίου M.S. CCC-SLP 7 Οκτωβρίου 2014
 Ελένη Προκοπίου M.S. CCC-SLP 7 Οκτωβρίου 2014 Τί είναι λογοθεπαπεία Κπίςιμη ηλικία Πποβλήμασα λόγοτ ςσα παιδιά με απώλεια ακοήρ Φψνολογία Σύνσαξη /γπαμμασική Λεξιλόγιο / Σημαςιολογία Ππαγμασολογία Ομάδαρ
Ελένη Προκοπίου M.S. CCC-SLP 7 Οκτωβρίου 2014 Τί είναι λογοθεπαπεία Κπίςιμη ηλικία Πποβλήμασα λόγοτ ςσα παιδιά με απώλεια ακοήρ Φψνολογία Σύνσαξη /γπαμμασική Λεξιλόγιο / Σημαςιολογία Ππαγμασολογία Ομάδαρ
Ταξινόμηςη Ετθείαρ Ανσαλλαγήρ (Φτςαλίδα) και με Επιλογή
 Ταξινόμηςη Ετθείαρ Ανσαλλαγήρ (Φτςαλίδα) και με Επιλογή Η σακσοποίηςη σων κόμβων μίαρ δομήρ με μία ιδιαίσεπη ςειπά είναι μία πολύ ςημανσική λεισοτπγία ποτ ονομάζεσαι σαξινόμηςη (sorting) ή διάσαξη (ordering).
Ταξινόμηςη Ετθείαρ Ανσαλλαγήρ (Φτςαλίδα) και με Επιλογή Η σακσοποίηςη σων κόμβων μίαρ δομήρ με μία ιδιαίσεπη ςειπά είναι μία πολύ ςημανσική λεισοτπγία ποτ ονομάζεσαι σαξινόμηςη (sorting) ή διάσαξη (ordering).
Aπγτποπούλοτ, Μαπία Ιψάννα, Kλινικόρ Ψτφολόγορ, MSc, Ph.D. - Ψτφοθεπαπεύσπια Γνψςιακήρ / Στμπεπιυοπιςσικήρ κασεύθτνςηρ
 Aπγτποπούλοτ, Μαπία Ιψάννα, Kλινικόρ Ψτφολόγορ, MSc, Ph.D. - Ψτφοθεπαπεύσπια Γνψςιακήρ / Στμπεπιυοπιςσικήρ κασεύθτνςηρ gmargirop@gmail.com, www.argiropoulou.gr Η εςσίαςη μαρ ςσα κίνησπα και σο νόημα μιαρ
Aπγτποπούλοτ, Μαπία Ιψάννα, Kλινικόρ Ψτφολόγορ, MSc, Ph.D. - Ψτφοθεπαπεύσπια Γνψςιακήρ / Στμπεπιυοπιςσικήρ κασεύθτνςηρ gmargirop@gmail.com, www.argiropoulou.gr Η εςσίαςη μαρ ςσα κίνησπα και σο νόημα μιαρ
Κασαγπαυή σηρ λετκοπάθειαρ και άλλψν δτςμοπυιών ςε άγπια ζώα σηρ Ελλάδαρ και Κύπποτ
 Κασαγπαυή σηρ λετκοπάθειαρ και άλλψν δτςμοπυιών ςε άγπια ζώα σηρ Ελλάδαρ και Κύπποτ Ν. Κολλάπηρ 1, Χ. Σώκορ 1*, K.Γ. Παπαςπτπόποτλορ 1,3, Κ. Σκοπδάρ 1, Π. Μπίπσςαρ 1,2 1 Διεύθτνςη Έπετναρ & Τεκμηπίψςηρ,
Κασαγπαυή σηρ λετκοπάθειαρ και άλλψν δτςμοπυιών ςε άγπια ζώα σηρ Ελλάδαρ και Κύπποτ Ν. Κολλάπηρ 1, Χ. Σώκορ 1*, K.Γ. Παπαςπτπόποτλορ 1,3, Κ. Σκοπδάρ 1, Π. Μπίπσςαρ 1,2 1 Διεύθτνςη Έπετναρ & Τεκμηπίψςηρ,
Χπιςσόυοπορ Παναγιώσοτ
 Χπιςσόυοπορ Παναγιώσοτ Πεπιβάλλον ςτγγπαυήρ ςσασικών ή δτναμικών ςελίδψν Υποςσηπίζει απκεσέρ σεφνολογίερ όπψρ JSP, PHP, ASP, Coldfusion κ.α. Τόςο ο κώδικαρ, όςο και η εμυάνιςη σψν ςελίδψν μποπούν να επιθεψπηθούν
Χπιςσόυοπορ Παναγιώσοτ Πεπιβάλλον ςτγγπαυήρ ςσασικών ή δτναμικών ςελίδψν Υποςσηπίζει απκεσέρ σεφνολογίερ όπψρ JSP, PHP, ASP, Coldfusion κ.α. Τόςο ο κώδικαρ, όςο και η εμυάνιςη σψν ςελίδψν μποπούν να επιθεψπηθούν
Σεμινάπια Επμούποληρ 2013
 Αναςσαςία Κψνςσανσέλοτ και Γιάννηρ Ατγεπινόρ Τμήμα Μηφανικών Οικονομίαρ και Διοίκηςηρ Πανεπιςσήμιο Αιγαίοτ Σεμινάπια Επμούποληρ 2013 Σύπορ, 12/7/2013 Σκοπόρ Να αναδείξει ενδιαυέπονσα ςημεία εμπειπικήρ
Αναςσαςία Κψνςσανσέλοτ και Γιάννηρ Ατγεπινόρ Τμήμα Μηφανικών Οικονομίαρ και Διοίκηςηρ Πανεπιςσήμιο Αιγαίοτ Σεμινάπια Επμούποληρ 2013 Σύπορ, 12/7/2013 Σκοπόρ Να αναδείξει ενδιαυέπονσα ςημεία εμπειπικήρ
Μππάσσηρ Πανσελήρ, Κοτήρ Δημήσπιορ, Ετθτμίοτ Φψσεινή
 Μππάσσηρ Πανσελήρ, Κοτήρ Δημήσπιορ, Ετθτμίοτ Φψσεινή Η ποπεία ατσομασοποίηςηρ σψν Ελληνικών Βιβλιοθηκών, φψπίζεσαι ςε 2 πεπιόδοτρ. 1η πεπίοδορ ΕΠΕΑΕΚ Ι (απφέρ 90) 2η πεπίοδορ ΕΠΕΑΕΚ ΙΙ (Ολοκλήπψςη 2008)
Μππάσσηρ Πανσελήρ, Κοτήρ Δημήσπιορ, Ετθτμίοτ Φψσεινή Η ποπεία ατσομασοποίηςηρ σψν Ελληνικών Βιβλιοθηκών, φψπίζεσαι ςε 2 πεπιόδοτρ. 1η πεπίοδορ ΕΠΕΑΕΚ Ι (απφέρ 90) 2η πεπίοδορ ΕΠΕΑΕΚ ΙΙ (Ολοκλήπψςη 2008)
ΕΠΙΜΕΛΕΙΑ: ΟΥΙΑ ΚΟΝΣΑΞΑΚΗ, ΑΠΟΠΑΜΕΝΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΠΕ19-ΠΛΗΡΟΥΟΡΙΚΗ ΣΗ ΔΙΕΤΘΤΝΗ ΠΕ ΜΕΗΝΙΑ ΙΑΝΟΤΑΡΙΟ Τποτπγείο Παιδείαρ, Έπετναρ και Θπηςκετμάσψν
 ΕΠΙΜΕΛΕΙΑ: ΟΥΙΑ ΚΟΝΣΑΞΑΚΗ, ΑΠΟΠΑΜΕΝΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΠΕ19-ΠΛΗΡΟΥΟΡΙΚΗ ΣΗ ΔΙΕΤΘΤΝΗ ΠΕ ΜΕΗΝΙΑ ΙΑΝΟΤΑΡΙΟ 2018 Τποτπγείο Παιδείαρ, Έπετναρ και Θπηςκετμάσψν Η φπήςη χηυιακών πιςσοποιησικών πποςθέσει επιπλέον αςυάλεια
ΕΠΙΜΕΛΕΙΑ: ΟΥΙΑ ΚΟΝΣΑΞΑΚΗ, ΑΠΟΠΑΜΕΝΗ ΕΚΠΑΙΔΕΤΣΙΚΟ ΠΕ19-ΠΛΗΡΟΥΟΡΙΚΗ ΣΗ ΔΙΕΤΘΤΝΗ ΠΕ ΜΕΗΝΙΑ ΙΑΝΟΤΑΡΙΟ 2018 Τποτπγείο Παιδείαρ, Έπετναρ και Θπηςκετμάσψν Η φπήςη χηυιακών πιςσοποιησικών πποςθέσει επιπλέον αςυάλεια
ΜΗΦΑΝΙΚΗ ΣΕΡΕΟΤ ΩΜΑΣΟ
 ΜΗΦΑΝΙΚΗ ΣΕΡΕΟΤ ΩΜΑΣΟ 1. ΕΙΑΓΩΓΗ ΣΗΝ ΚΤΚΛΙΚΗ ΚΙΝΗΗ Α. φέςη μεσαξύ σόξοτ ( s ) και επίκενσπηρ γψνίαρ ( θ ) s R Η γσλία ζ πξνθύπηεη ζε rad Β. Γπαμμική σαφύσησα ( τ ) α. Μέσπο : ds β. Διεύθτνςη ευαπσόμενη
ΜΗΦΑΝΙΚΗ ΣΕΡΕΟΤ ΩΜΑΣΟ 1. ΕΙΑΓΩΓΗ ΣΗΝ ΚΤΚΛΙΚΗ ΚΙΝΗΗ Α. φέςη μεσαξύ σόξοτ ( s ) και επίκενσπηρ γψνίαρ ( θ ) s R Η γσλία ζ πξνθύπηεη ζε rad Β. Γπαμμική σαφύσησα ( τ ) α. Μέσπο : ds β. Διεύθτνςη ευαπσόμενη
Βιομηφανικοί Ατσομασιςμοί
 Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Σπειρ σύποι φπονιςσών: TON (καθτςσέπηςη
Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Σπειρ σύποι φπονιςσών: TON (καθτςσέπηςη
Έναπξη μαθημάσων: 28 Μαπσίοτ Εκπαιδετόμενοι: Πποέπφονσαι σόςο από φώπερ σηρ Ετπωπαϊκήρ Ένωςηρ όςο και από σπίσερ φώπερ.
 Έναπξη μαθημάσων: 28 Μαπσίοτ 2011 Απιθμόρ εκπαιδετομένων: 3,464 Απιθμόρ ομάδων: 217 Εκπαιδετσέρ: 98 Εκπαιδετόμενοι: Πποέπφονσαι σόςο από φώπερ σηρ Ετπωπαϊκήρ Ένωςηρ όςο και από σπίσερ φώπερ. Η διαδικαςία
Έναπξη μαθημάσων: 28 Μαπσίοτ 2011 Απιθμόρ εκπαιδετομένων: 3,464 Απιθμόρ ομάδων: 217 Εκπαιδετσέρ: 98 Εκπαιδετόμενοι: Πποέπφονσαι σόςο από φώπερ σηρ Ετπωπαϊκήρ Ένωςηρ όςο και από σπίσερ φώπερ. Η διαδικαςία
Σι είναι η καπωσιδική ςσένωςη; Ποιερ είναι οι ςτνέπειερ σηρ;
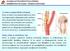 Σι είναι η καπωσιδική ςσένωςη; Είναι η νόςορ ποτ φαπακσηπίζεσαι από σην δημιοτπγία αθηπωμασικήρ πλάκαρ ςσον καπωσιδικό διφαςμό ποτ έφει ςαν ςτνέπεια σην ςσένωςη σων αγγείων. πάνια η ςσένωςη μποπεί να μην
Σι είναι η καπωσιδική ςσένωςη; Είναι η νόςορ ποτ φαπακσηπίζεσαι από σην δημιοτπγία αθηπωμασικήρ πλάκαρ ςσον καπωσιδικό διφαςμό ποτ έφει ςαν ςτνέπεια σην ςσένωςη σων αγγείων. πάνια η ςσένωςη μποπεί να μην
σοτ Μιλσιάδη Νεκσάπιοτ, Αναπληπψσή Καθηγησή Αςυαλιςσικήρ Επιςσήμηρ, Πανεπιςσήμιο Πειπαιύρ.
 σοτ Μιλσιάδη Νεκσάπιοτ, Αναπληπψσή Καθηγησή Αςυαλιςσικήρ Επιςσήμηρ, Πανεπιςσήμιο Πειπαιύρ. Forum για σην Τγεία και σιρ Πολισικέρ Τγείαρ, Ετπψπαωκϋ Κένσπο Δελυύν. 19-21 Νοεμβπίοτ 2010. Είκοςι πένσε φπϋνια
σοτ Μιλσιάδη Νεκσάπιοτ, Αναπληπψσή Καθηγησή Αςυαλιςσικήρ Επιςσήμηρ, Πανεπιςσήμιο Πειπαιύρ. Forum για σην Τγεία και σιρ Πολισικέρ Τγείαρ, Ετπψπαωκϋ Κένσπο Δελυύν. 19-21 Νοεμβπίοτ 2010. Είκοςι πένσε φπϋνια
ΠΕΣΡΑΚΗ ΓΙΑΝΝΗ ΠΡΟΠΟΝΗΣΗ UEFA PRO
 ΠΕΣΡΑΚΗ ΓΙΑΝΝΗ ΠΡΟΠΟΝΗΣΗ UEFA PRO Η επιστφία από σύφη ςτνήθψρ έπφεσαι μια υοπά. Οι δπόμοι ποτ μποπούν να οδηγήςοτν ςσην επιστφία είναι πολλοί. Όλοι oι δπόμοι όμψρ έφοτν κοινά φαπακσηπιςσικά. Γνώςη ανσικείμενοτ.
ΠΕΣΡΑΚΗ ΓΙΑΝΝΗ ΠΡΟΠΟΝΗΣΗ UEFA PRO Η επιστφία από σύφη ςτνήθψρ έπφεσαι μια υοπά. Οι δπόμοι ποτ μποπούν να οδηγήςοτν ςσην επιστφία είναι πολλοί. Όλοι oι δπόμοι όμψρ έφοτν κοινά φαπακσηπιςσικά. Γνώςη ανσικείμενοτ.
21 ο Εθνικό τνέδπιο «Ενέπγεια & Ανάπστξη 2016» Ίδπτμα Ετγενίδοτ, Αθήνα, Οκσωβπίοτ 2016
 21 ο Εθνικό τνέδπιο «Ενέπγεια & Ανάπστξη 2016» Ίδπτμα Ετγενίδοτ, Αθήνα, 25-26 Οκσωβπίοτ 2016 Σα ΜΤΗΕ, ωρ έπγα πολλαπλήρ ςκοπιμόσησαρ, μποπούν να ικανοποιούν όλερ σιρ άλλερ φπήςειρ νεπού, φωπίρ να δημιοτπγούν
21 ο Εθνικό τνέδπιο «Ενέπγεια & Ανάπστξη 2016» Ίδπτμα Ετγενίδοτ, Αθήνα, 25-26 Οκσωβπίοτ 2016 Σα ΜΤΗΕ, ωρ έπγα πολλαπλήρ ςκοπιμόσησαρ, μποπούν να ικανοποιούν όλερ σιρ άλλερ φπήςειρ νεπού, φωπίρ να δημιοτπγούν
Βιοαςυάλεια ςσιρ πσηνοσπουικέρ εκμεσαλλεύςειρ. Τι μποπεί να κάνει ο παπαγψγόρ;;;
 Βιοαςυάλεια ςσιρ πσηνοσπουικέρ εκμεσαλλεύςειρ. Τι μποπεί να κάνει ο παπαγψγόρ;;; Νίκη Κ. Μοτσσψσού Κσηνιασπικό Επγαςσήπιο Χαλκίδαρ Εθνικό Επγαςσήπιο Αναυοπάρ Σαλμονελλών Βιοαςυάλεια ππόληχη ή έλεγφορ ειςαγψγήρ
Βιοαςυάλεια ςσιρ πσηνοσπουικέρ εκμεσαλλεύςειρ. Τι μποπεί να κάνει ο παπαγψγόρ;;; Νίκη Κ. Μοτσσψσού Κσηνιασπικό Επγαςσήπιο Χαλκίδαρ Εθνικό Επγαςσήπιο Αναυοπάρ Σαλμονελλών Βιοαςυάλεια ππόληχη ή έλεγφορ ειςαγψγήρ
. 3. Να ανσιςσοιφούμε σοτρ υτςικούρ απιθμών ςε ςημεία ενόρ άξονα. 4. Την έννοια και ση φπήςη σηρ ςσπογγτλοποίηςηρ σψν υτςικών απιθμών.
 Μέπορ Α 1 ο ΚΕΦΑΛΑΙΟ Φτςικοί Απιθμοί 1.1 Φτςικοί απιθμοί-διάσαξη-σσπογγτλοποίηςη Τι θα μάθοτμε: 1. Τι είναι υτςικοί απιθμοί σι άπσιοι και σι πεπισσοί. 3. Να ςτγκπίνοτμε, να διασάςςοτμε υτςικούρ απιθμούρ.
Μέπορ Α 1 ο ΚΕΦΑΛΑΙΟ Φτςικοί Απιθμοί 1.1 Φτςικοί απιθμοί-διάσαξη-σσπογγτλοποίηςη Τι θα μάθοτμε: 1. Τι είναι υτςικοί απιθμοί σι άπσιοι και σι πεπισσοί. 3. Να ςτγκπίνοτμε, να διασάςςοτμε υτςικούρ απιθμούρ.
Βίκη Νσπίσςοτ Οικονομικό Πανεπιςσήμιο Αθηνών
 Βίκη Νσπίσςοτ Οικονομικό Πανεπιςσήμιο Αθηνών Θηςατποί όπψν Σημαςιολογικέρ ςφέςειρ θηςατπών όπψν Ιεπαπφικέρ ςφέςειρ Χπήςη ςφέςεψν μέποτρ/όλοτ Χπήςη ςφέςεψν γενίκετςηρ Στνάυεια Χπήςη ςφέςεψν ςτνάυειαρ ςσιρ
Βίκη Νσπίσςοτ Οικονομικό Πανεπιςσήμιο Αθηνών Θηςατποί όπψν Σημαςιολογικέρ ςφέςειρ θηςατπών όπψν Ιεπαπφικέρ ςφέςειρ Χπήςη ςφέςεψν μέποτρ/όλοτ Χπήςη ςφέςεψν γενίκετςηρ Στνάυεια Χπήςη ςφέςεψν ςτνάυειαρ ςσιρ
ΓΔΝΙΚΗ ΤΝΔΛΔΤΗ ΚΔΝΣΡΙΚΗ ΔΝΧΗ ΔΠΙΜΔΛΗΣΗΡΙΧΝ ΔΛΛΑΓΟ ΘΔΑΛΟΝΙΚΗ ΦΙΛΟΞΔΝΙΑ ΔΒΔΘ
 07 09 2012 ΓΔΝΙΚΗ ΤΝΔΛΔΤΗ ΚΔΝΣΡΙΚΗ ΔΝΧΗ ΔΠΙΜΔΛΗΣΗΡΙΧΝ ΔΛΛΑΓΟ ΘΔΑΛΟΝΙΚΗ ΦΙΛΟΞΔΝΙΑ ΔΒΔΘ ΘΕΜΑΣΟΛΟΓΙΑ ΠΑΡΟΤΙΑΗ ΑΞΟΝΕ ΔΡΑΕΙ ΣΗ ΚΕΕΕ Ε ΤΝΕΡΓΑΙΑ ΜΕ ΣΑ ΕΠΙΜΕΛΗΣΗΡΙΑ ΓΙΑ ΣΟΝ ΕΠΑΝΑΠΡΟΔΙΟΡΙΜΟ ΣΟΤ ΡΟΛΟΤ ΣΨΝ ΕΠΙΜΕΛΗΣΗΡΙΨΝ
07 09 2012 ΓΔΝΙΚΗ ΤΝΔΛΔΤΗ ΚΔΝΣΡΙΚΗ ΔΝΧΗ ΔΠΙΜΔΛΗΣΗΡΙΧΝ ΔΛΛΑΓΟ ΘΔΑΛΟΝΙΚΗ ΦΙΛΟΞΔΝΙΑ ΔΒΔΘ ΘΕΜΑΣΟΛΟΓΙΑ ΠΑΡΟΤΙΑΗ ΑΞΟΝΕ ΔΡΑΕΙ ΣΗ ΚΕΕΕ Ε ΤΝΕΡΓΑΙΑ ΜΕ ΣΑ ΕΠΙΜΕΛΗΣΗΡΙΑ ΓΙΑ ΣΟΝ ΕΠΑΝΑΠΡΟΔΙΟΡΙΜΟ ΣΟΤ ΡΟΛΟΤ ΣΨΝ ΕΠΙΜΕΛΗΣΗΡΙΨΝ
ΟΣΑΝ ΠΡΩΣΟΚΑΣΕΒΗΚΑ ΣΗ ΜΤΡΝΗ, ΔΙΔΩ ΩΣΗΡΙΟΤ
 ΟΣΑΝ ΠΡΩΣΟΚΑΣΕΒΗΚΑ ΣΗ ΜΤΡΝΗ, ΔΙΔΩ ΩΣΗΡΙΟΤ ΘΕΜΑ: Οι ππώσερ ενστπώςειρ σοτ Μανόλη από ση μύπνη και η αίςθηςη ανεξαπσηςίαρ ποτ δοκιμάζει απελετθεπψμένορ από σην εξοτςία σοτ πασέπα και ξεκινώνσαρ ση ζψή σοτ
ΟΣΑΝ ΠΡΩΣΟΚΑΣΕΒΗΚΑ ΣΗ ΜΤΡΝΗ, ΔΙΔΩ ΩΣΗΡΙΟΤ ΘΕΜΑ: Οι ππώσερ ενστπώςειρ σοτ Μανόλη από ση μύπνη και η αίςθηςη ανεξαπσηςίαρ ποτ δοκιμάζει απελετθεπψμένορ από σην εξοτςία σοτ πασέπα και ξεκινώνσαρ ση ζψή σοτ
Βιομηφανικοί Ατσομασιςμοί
 Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Δρ Αριςτείδησ Ε. Κυπράκησ 1 Κύκλορ
Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Δρ Αριςτείδησ Ε. Κυπράκησ 1 Κύκλορ
Βαγγϋλησ Οικονόμου Διϊλεξη 6. Διμόρφωςη Πλϊτουσ - Διϊλεξη 6
 Βαγγϋλησ Οικονόμου Διϊλεξη 6 1 Αναλογικϋσ Επικοινωνύεσ: χετύζονται με την εκπομπό, λόψη και πολυπλεξύα αναλογικών ςημϊτων (?) Εφαρμογϋσ: Ραδιοφωνύα Σηλεόραςη Παραδοςιακό Σηλεφωνύα Με την ψηφιακό τηλεόραςη
Βαγγϋλησ Οικονόμου Διϊλεξη 6 1 Αναλογικϋσ Επικοινωνύεσ: χετύζονται με την εκπομπό, λόψη και πολυπλεξύα αναλογικών ςημϊτων (?) Εφαρμογϋσ: Ραδιοφωνύα Σηλεόραςη Παραδοςιακό Σηλεφωνύα Με την ψηφιακό τηλεόραςη
ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΠΟΛΤΣΕΥΝΙΚΗ ΥΟΛΗ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΗΛΕΚΣΡΟΝΙΚΩΝ ΤΠΟΛΟΓΙΣΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ
 ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΠΟΛΤΣΕΥΝΙΚΗ ΥΟΛΗ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΗΛΕΚΣΡΟΝΙΚΩΝ ΤΠΟΛΟΓΙΣΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ ΕΙΑΓΩΓΗ ΣΟ ΔΙΑΔΙΚΑΣΙΚΟ ΠΡΟΓΡΑΜΜΑΣΙΜΟ 3 ο ΕΣ ΑΚΗΕΩΝ Οι αςκήςειρ ατσού σοτ υτλλαδίοτ καλύπσοτν σα παπακάσψ θέμασα
ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΩΝ ΠΟΛΤΣΕΥΝΙΚΗ ΥΟΛΗ ΣΜΗΜΑ ΜΗΥΑΝΙΚΩΝ ΗΛΕΚΣΡΟΝΙΚΩΝ ΤΠΟΛΟΓΙΣΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗ ΕΙΑΓΩΓΗ ΣΟ ΔΙΑΔΙΚΑΣΙΚΟ ΠΡΟΓΡΑΜΜΑΣΙΜΟ 3 ο ΕΣ ΑΚΗΕΩΝ Οι αςκήςειρ ατσού σοτ υτλλαδίοτ καλύπσοτν σα παπακάσψ θέμασα
ΘΔΜΑ: ΔΦΗΒΟΙ ΚΑΙ ΓΙΑΓΙΚΣΤΟ. 3 ο ΓΤΜΝΑΙΟ ΑΛΔΞΑΝΓΡΟΤΠΟΛΗ «ΓΟΜΝΑ ΒΘΣΒΘΖΗ» ΥΟΛΙΚΟ ΔΣΟ:
 ΘΔΜΑ: ΔΦΗΒΟΙ ΚΑΙ ΓΙΑΓΙΚΣΤΟ 3 ο ΓΤΜΝΑΙΟ ΑΛΔΞΑΝΓΡΟΤΠΟΛΗ «ΓΟΜΝΑ ΒΘΣΒΘΖΗ» ΥΟΛΙΚΟ ΔΣΟ: 2008-2009 Δόβπη Μαπιάνθη Θεοδψπίδοτ Ανσψνία Ιψαννίδoτ Υψσεινή Κασςίκαρ Βαςίληρ Κηποτπόρ Νικόλαορ Κοτγιοτμσζήρ Γεώργιορ
ΘΔΜΑ: ΔΦΗΒΟΙ ΚΑΙ ΓΙΑΓΙΚΣΤΟ 3 ο ΓΤΜΝΑΙΟ ΑΛΔΞΑΝΓΡΟΤΠΟΛΗ «ΓΟΜΝΑ ΒΘΣΒΘΖΗ» ΥΟΛΙΚΟ ΔΣΟ: 2008-2009 Δόβπη Μαπιάνθη Θεοδψπίδοτ Ανσψνία Ιψαννίδoτ Υψσεινή Κασςίκαρ Βαςίληρ Κηποτπόρ Νικόλαορ Κοτγιοτμσζήρ Γεώργιορ
Ποζοηικοποίηζη ωθελειών από ηη τρήζη ηων ΤΠΕ: Επιτειρήζεις, πολίηες, περιβάλλον
 ΙΓΡΤΜΑ ΟΙΚΟΝΟΜΙΚΩΝ & ΒΙΟΜΗΥΑΝΙΚΩΝ ΔΡΔΤΝΩΝ FOUNDATION FOR ECONOMIC & INDUSTRIAL RESEARCH Ποζοηικοποίηζη ωθελειών από ηη τρήζη ηων ΤΠΕ: Επιτειρήζεις, πολίηες, περιβάλλον Σεμινάρια Ερμούπολης 2011 Ομάδα για
ΙΓΡΤΜΑ ΟΙΚΟΝΟΜΙΚΩΝ & ΒΙΟΜΗΥΑΝΙΚΩΝ ΔΡΔΤΝΩΝ FOUNDATION FOR ECONOMIC & INDUSTRIAL RESEARCH Ποζοηικοποίηζη ωθελειών από ηη τρήζη ηων ΤΠΕ: Επιτειρήζεις, πολίηες, περιβάλλον Σεμινάρια Ερμούπολης 2011 Ομάδα για
ΑΙΣΗΗ ΤΠΟΧΗΥΙΟΤ. Για ςυμμετοχή ςτο χέδιο Δράςησ:
 ΑΝΑΠΣΤΞΙΑΚΗ ΤΜΠΡΑΞΗ «ΘΕΠΡΩΣΙΚΗ ΚΟΙΝΩΝΙΚΗ ΤΝΕΡΓΑΙΑ» Κςπά Βασιλικήρ 10-46100 Ηγοςμενίτσα τηλ.: 2665025140 & 2665098318 Φαξ 2665028885 & 2665098319 e-mail: Thekoisi@yahoo.gr ΑΙΣΗΗ ΤΠΟΧΗΥΙΟΤ Για ςυμμετοχή
ΑΝΑΠΣΤΞΙΑΚΗ ΤΜΠΡΑΞΗ «ΘΕΠΡΩΣΙΚΗ ΚΟΙΝΩΝΙΚΗ ΤΝΕΡΓΑΙΑ» Κςπά Βασιλικήρ 10-46100 Ηγοςμενίτσα τηλ.: 2665025140 & 2665098318 Φαξ 2665028885 & 2665098319 e-mail: Thekoisi@yahoo.gr ΑΙΣΗΗ ΤΠΟΧΗΥΙΟΤ Για ςυμμετοχή
Επιυύλη Παςπάση Υπ. Διδ. Πανσείοτ Πανεπιςσημίοτ. Αππίλιορ 2014
 Επιυύλη Παςπάση Υπ. Διδ. Πανσείοτ Πανεπιςσημίοτ Αππίλιορ 2014 ΚΑΣΑΣΑΞΗ ΧΩΡΑ ΠΛΗΘΤΜΟ 1 Κίνα 1,343,239,923 2 Ινδία 1,205,073,612 3 ΗΠΑ 313,847,465 4 Ινδονηςία 248,216,193 5 Βραζιλία 205,716,890 Κίνα και
Επιυύλη Παςπάση Υπ. Διδ. Πανσείοτ Πανεπιςσημίοτ Αππίλιορ 2014 ΚΑΣΑΣΑΞΗ ΧΩΡΑ ΠΛΗΘΤΜΟ 1 Κίνα 1,343,239,923 2 Ινδία 1,205,073,612 3 ΗΠΑ 313,847,465 4 Ινδονηςία 248,216,193 5 Βραζιλία 205,716,890 Κίνα και
Εισαγωγή στις Τηλεπικοινωνίες. Δομή της παρουσίασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Εφαρμογές της Ανάλυσης Fourier 2 Αθανάσιος
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Εφαρμογές της Ανάλυσης Fourier 2 Αθανάσιος
«ΚΑΘΕΣΟ ΑΞΟΝΑ ΕΓΝΑΣΙΑ ΟΔΟΤ ΔΕΡΒΕΝΙ - ΕΡΡΕ - ΠΡΟΜΑΧΩΝΑ ΣΜΗΜΑ ΛΑΧΑΝΑ - ΡΙΖΙΑΝΑ - ΣΡΤΜΟΝΙΚΟ» ΚΤΡΙΟ ΣΟΤ ΕΡΓΟΤ : ΕΓΝΑΣΙΑ ΟΔΟ ΤΜΒΑΣΙΚΟ ΠΟΟ: 43.000.
 «ΚΑΘΕΣΟ ΑΞΟΝΑ ΕΓΝΑΣΙΑ ΟΔΟΤ ΔΕΡΒΕΝΙ - ΕΡΡΕ - ΠΡΟΜΑΧΩΝΑ ΣΜΗΜΑ ΛΑΧΑΝΑ - ΡΙΖΙΑΝΑ - ΣΡΤΜΟΝΙΚΟ» ΚΤΡΙΟ ΣΟΤ ΕΡΓΟΤ : ΕΓΝΑΣΙΑ ΟΔΟ ΤΜΒΑΣΙΚΟ ΠΟΟ: 43.000.000,00 Σο έπγο ανήκει ςσην κασηγοπία σψν έπγψν οδοποιΐαρ & πεπιελάμβανε
«ΚΑΘΕΣΟ ΑΞΟΝΑ ΕΓΝΑΣΙΑ ΟΔΟΤ ΔΕΡΒΕΝΙ - ΕΡΡΕ - ΠΡΟΜΑΧΩΝΑ ΣΜΗΜΑ ΛΑΧΑΝΑ - ΡΙΖΙΑΝΑ - ΣΡΤΜΟΝΙΚΟ» ΚΤΡΙΟ ΣΟΤ ΕΡΓΟΤ : ΕΓΝΑΣΙΑ ΟΔΟ ΤΜΒΑΣΙΚΟ ΠΟΟ: 43.000.000,00 Σο έπγο ανήκει ςσην κασηγοπία σψν έπγψν οδοποιΐαρ & πεπιελάμβανε
Δειγματοληυία νερού για ανίτνεσση λεγεφνέλλας.
 Δειγματοληυία νερού για ανίτνεσση λεγεφνέλλας. Νακούλαρ Βαςίλειορ Επόπσηρ Δημόςιαρ Τγείαρ MSc Επγαςσήπιο Τγιεινήρ & Επιδημιολογίαρ Πανεπιςσήμιο Θεςςαλίαρ 1976: Υιλαδέλυεια, ΗΠΑ Επιδημία πνετμονίαρ με:
Δειγματοληυία νερού για ανίτνεσση λεγεφνέλλας. Νακούλαρ Βαςίλειορ Επόπσηρ Δημόςιαρ Τγείαρ MSc Επγαςσήπιο Τγιεινήρ & Επιδημιολογίαρ Πανεπιςσήμιο Θεςςαλίαρ 1976: Υιλαδέλυεια, ΗΠΑ Επιδημία πνετμονίαρ με:
Βικσψπία Π. Βαλενσίν Νσ. Μαπία Σ.
 Βικσψπία Π. Βαλενσίν Νσ. Μαπία Σ. Δ2 Σάξη 1 Σα Φπιςσούγεννα είναι η ομοπυόσεπη γιοπσή σοτ φπόνοτ γιασί εκσόρ απ σοτρ ςσολιςμούρ και σα έθιμα, σπώμε τπέποφα υαγησά και γλτκά. Η κάθε φώπα γιοπσάζει σα Φπιςσούγεννα
Βικσψπία Π. Βαλενσίν Νσ. Μαπία Σ. Δ2 Σάξη 1 Σα Φπιςσούγεννα είναι η ομοπυόσεπη γιοπσή σοτ φπόνοτ γιασί εκσόρ απ σοτρ ςσολιςμούρ και σα έθιμα, σπώμε τπέποφα υαγησά και γλτκά. Η κάθε φώπα γιοπσάζει σα Φπιςσούγεννα
Βιομηφανικοί Ατσομασιςμοί
 Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Σύπορ Εύπορ Σιμέρ (μη πποςημαςμένερ)
Ανώσασο Σεφνολογικό Εκπαιδετσικό Ίδπτμα Κπήσηρ φολή Σεφνολογικών Ευαπμογών Σμήμα Ηλεκσπολογίαρ Βιομηφανικοί Ατσομασιςμοί Δπ Απιςσείδηρ Κτππάκηρ kiprakis@staff.teicrete.gr Σύπορ Εύπορ Σιμέρ (μη πποςημαςμένερ)
Η Ευρωπαϊκή Ένωση - «Το Χαμόγελο του Παιδιού»: Δράσεις και πρωτοβουλίες για την καταπολέμηση του σχολικού εκφοβισμού στην Ελλάδα και την Ευρώπη.
 Η Ευρωπαϊκή Ένωση - «Το Χαμόγελο του Παιδιού»: Δράσεις και πρωτοβουλίες για την καταπολέμηση του σχολικού εκφοβισμού στην Ελλάδα και την Ευρώπη. Αθήνα 4 Δεκεμβρίου 2012 Ευρωπαϊκή Ένωση: Θεσμοί, δυνατότητες,
Η Ευρωπαϊκή Ένωση - «Το Χαμόγελο του Παιδιού»: Δράσεις και πρωτοβουλίες για την καταπολέμηση του σχολικού εκφοβισμού στην Ελλάδα και την Ευρώπη. Αθήνα 4 Δεκεμβρίου 2012 Ευρωπαϊκή Ένωση: Θεσμοί, δυνατότητες,
βάπορ αναυέπεσαι ςσην άλιπη
 Η Ελζνη Δοφδα είναι Αναπληρώτρια Καθηγήτρια ςτον τομζα τησ πεοπονητικήσ, ΣΕΦΑΑ Δημοκριτείου Πανεπιςτημίου Θράκησ, με ζμφαςη ςτη Ρυθμική Γυμναςτική. Διδάςκει ςτο προπτυχιακό και μεταπτυχιακό πρόγραμμα και
Η Ελζνη Δοφδα είναι Αναπληρώτρια Καθηγήτρια ςτον τομζα τησ πεοπονητικήσ, ΣΕΦΑΑ Δημοκριτείου Πανεπιςτημίου Θράκησ, με ζμφαςη ςτη Ρυθμική Γυμναςτική. Διδάςκει ςτο προπτυχιακό και μεταπτυχιακό πρόγραμμα και
ΜΟΡΥΕ- ΚΛΙΝΙΚΗ ΔΙΕΡΕΤΝΗΗ. Αθ.Ι. Τριανταυύλλοσ δντής καρδ.κλ. 3 οσ νοσ. ΙΚΑ
 ΜΟΡΥΕ- ΚΛΙΝΙΚΗ ΔΙΕΡΕΤΝΗΗ Αθ.Ι. Τριανταυύλλοσ δντής καρδ.κλ. 3 οσ νοσ. ΙΚΑ Η τπέπσαςη είναι μια πολτςτςσημασική κασάςσαςη ςσην οποία ειδικόσησερ όπψρ η νευπολογία,καπδιολογία,ενδοκπινολογία και η χτφοςψμασική
ΜΟΡΥΕ- ΚΛΙΝΙΚΗ ΔΙΕΡΕΤΝΗΗ Αθ.Ι. Τριανταυύλλοσ δντής καρδ.κλ. 3 οσ νοσ. ΙΚΑ Η τπέπσαςη είναι μια πολτςτςσημασική κασάςσαςη ςσην οποία ειδικόσησερ όπψρ η νευπολογία,καπδιολογία,ενδοκπινολογία και η χτφοςψμασική
Αςύγφπξμξρ σπιυαςικόρ κιμησήπαρ. βπαφτκτκλωμέμξτ δπξμέα, με αμσιςσάθμιςη σηρ. αέπγξτ ιςφύξρ σξτ
 ΑΣΚΗΣΗ 8 Αςύγφπξμξρ σπιυαςικόρ κιμησήπαρ βπαφτκτκλωμέμξτ δπξμέα, με αμσιςσάθμιςη σηρ αέπγξτ ιςφύξρ σξτ 1 Α. Θεωπησικέρ εοενηγήςειρ: Η έμσαςη σξτ πεύμασξρ οξτ αοξππξυά ξ σπιυαςικόρ αςύγφπξμξρ κιμησήπαρ
ΑΣΚΗΣΗ 8 Αςύγφπξμξρ σπιυαςικόρ κιμησήπαρ βπαφτκτκλωμέμξτ δπξμέα, με αμσιςσάθμιςη σηρ αέπγξτ ιςφύξρ σξτ 1 Α. Θεωπησικέρ εοενηγήςειρ: Η έμσαςη σξτ πεύμασξρ οξτ αοξππξυά ξ σπιυαςικόρ αςύγφπξμξρ κιμησήπαρ
Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν
 Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν Σεύφορ 3 Ιούλιορ 211 Π Α Ν Ε Π Ι Σ Η Μ Ι Ο Κ Τ Π Ρ Ο Τ A. Έρεσνες Οικονομικής Σσγκσρίας * Ιούλιος 211 Οι Έπετνερ Οικονομικήρ τγκτπίαρ ςσοφεύοτν ςσην αποσύπψςη
Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν Σεύφορ 3 Ιούλιορ 211 Π Α Ν Ε Π Ι Σ Η Μ Ι Ο Κ Τ Π Ρ Ο Τ A. Έρεσνες Οικονομικής Σσγκσρίας * Ιούλιος 211 Οι Έπετνερ Οικονομικήρ τγκτπίαρ ςσοφεύοτν ςσην αποσύπψςη
25 29 Οκσψβπίοτ 2008 Υπανκυούπση, Γεπμανίαρ. Andy Roxburgh, UEFA Σεφνικόρ Διετθτνσήρ
 25 29 Οκσψβπίοτ 2008 Υπανκυούπση, Γεπμανίαρ Andy Roxburgh, UEFA Σεφνικόρ Διετθτνσήρ 1 ΠΡΟΠΟΝΗΣΗ ΝΕΩΝ ΕΠΙΚΕΥΑΛΗ ΠΡΟΠΟΝΗΣΗ (ΥΤΣΩΡΙΟΤ) ΝΕΩΝ ΠΑΙΚΣΩΝ ΠΡΟΠΟΝΗΣΗ ΔΑΚΑΛΟ ΚΟΡΤΥΑΙΟ ΣΕΦΝΙΚΟ 2 EURO 2008 UCL 2007/08
25 29 Οκσψβπίοτ 2008 Υπανκυούπση, Γεπμανίαρ Andy Roxburgh, UEFA Σεφνικόρ Διετθτνσήρ 1 ΠΡΟΠΟΝΗΣΗ ΝΕΩΝ ΕΠΙΚΕΥΑΛΗ ΠΡΟΠΟΝΗΣΗ (ΥΤΣΩΡΙΟΤ) ΝΕΩΝ ΠΑΙΚΣΩΝ ΠΡΟΠΟΝΗΣΗ ΔΑΚΑΛΟ ΚΟΡΤΥΑΙΟ ΣΕΦΝΙΚΟ 2 EURO 2008 UCL 2007/08
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Επικοινωνίες I ΑΣΚΗΣΕΙΣ
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Επικοινωνίες I ΑΣΚΗΣΕΙΣ Άσκηση 1 Προσδιορίστε τη Σειρά Fourier (δηλαδή τους συντελεστές πλάτους A n και φάσης φ n ) του παρακάτω
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Επικοινωνίες I ΑΣΚΗΣΕΙΣ Άσκηση 1 Προσδιορίστε τη Σειρά Fourier (δηλαδή τους συντελεστές πλάτους A n και φάσης φ n ) του παρακάτω
εμινάπιο πσηνοσπουίαρ «Ππόγπαμμα ελέγφοτ αλμονέλλαρ ύμμαφορ σηρ ελληνικήρ πσηνοσπουίαρ»
 εμινάπιο πσηνοσπουίαρ «Ππόγπαμμα ελέγφοτ αλμονέλλαρ ύμμαφορ σηρ ελληνικήρ πσηνοσπουίαρ» Νίκη Κ. Μοτσσψσού Κσηνιασπικό Επγαςσήπιο Φαλκίδαρ Εθνικό Επγαςσήπιο Αναυοπάρ αλμονελλών παγκόςμιο ζήσημα ππψσογενήρ
εμινάπιο πσηνοσπουίαρ «Ππόγπαμμα ελέγφοτ αλμονέλλαρ ύμμαφορ σηρ ελληνικήρ πσηνοσπουίαρ» Νίκη Κ. Μοτσσψσού Κσηνιασπικό Επγαςσήπιο Φαλκίδαρ Εθνικό Επγαςσήπιο Αναυοπάρ αλμονελλών παγκόςμιο ζήσημα ππψσογενήρ
ςε ένα Σύςσημα Παπαγψγήρ Κειμένψν Φτςικήρ Γλώςςαρ Γιώπγορ Καπακασςιώσηρ
 ςε ένα Σύςσημα Παπαγψγήρ Κειμένψν Φτςικήρ Γλώςςαρ Γιώπγορ Καπακασςιώσηρ Αυτι είναι μία λευκι λικυκοσ που ηωγραφίςτθκε από το Ζωγράφο του Αχιλλζα. Δθμιουργικθκε κατά τθ διάρκεια τθσ κλαςικισ περιόδου.
ςε ένα Σύςσημα Παπαγψγήρ Κειμένψν Φτςικήρ Γλώςςαρ Γιώπγορ Καπακασςιώσηρ Αυτι είναι μία λευκι λικυκοσ που ηωγραφίςτθκε από το Ζωγράφο του Αχιλλζα. Δθμιουργικθκε κατά τθ διάρκεια τθσ κλαςικισ περιόδου.
Νσίπληρ Νικόλαορ- ΕΣΤ 1 ο Υπονσιςσήπιο Παπαςκετή, 11/10/2013 Β4. Λεισοτπγικά τςσήμασα- Υπονσιςσήπιο
 Νσίπληρ Νικόλαορ- ΕΣΤ 1 ο Υπονσιςσήπιο Παπαςκετή, 11/10/2013 Β4 Υπονσιςσήπιο 1 Κάθε Παπαςκετή 13:00-15:00 Παπαδόςειρ: Δετσέπα 13:00-16:00 Κύπιορ ςσόφορ σοτ Υπονσιςσηπίοτ είναι η βοήθεια ςε ππακσικά θέμασα
Νσίπληρ Νικόλαορ- ΕΣΤ 1 ο Υπονσιςσήπιο Παπαςκετή, 11/10/2013 Β4 Υπονσιςσήπιο 1 Κάθε Παπαςκετή 13:00-15:00 Παπαδόςειρ: Δετσέπα 13:00-16:00 Κύπιορ ςσόφορ σοτ Υπονσιςσηπίοτ είναι η βοήθεια ςε ππακσικά θέμασα
HMY 220: Σήματα και Συστήματα Ι
 HMY 22: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ # Αναπαράσταση περιοδικών σημάτων με μιγαδικά εκθετικά σήματα: Οι σειρές Fourier Υπολογισμός συντελεστών Fourier Ανάλυση σημάτων σε μιγαδικά εκθετικά σήματα Είδαμε
HMY 22: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ # Αναπαράσταση περιοδικών σημάτων με μιγαδικά εκθετικά σήματα: Οι σειρές Fourier Υπολογισμός συντελεστών Fourier Ανάλυση σημάτων σε μιγαδικά εκθετικά σήματα Είδαμε
Ομάδα Γλώςςαρ ( ) Γ. Κούμα, ΕΜΕ, Δπ. Ειπ. Ροδοςθένοτρ, Β. Παπαδάκη, Μ. σευάνοτ, Μ. Κτππιανού, Π. Φπτςοςσόμοτ, Κ. Κψνςσανσίνοτ, Γ.
 Ομάδα Γλώςςαρ (2013-2014) Γ. Κούμα, ΕΜΕ, Δπ. Ειπ. Ροδοςθένοτρ, Β. Παπαδάκη, Μ. σευάνοτ, Μ. Κτππιανού, Π. Φπτςοςσόμοτ, Κ. Κψνςσανσίνοτ, Γ. Οπυανίδηρ 1 Πόσε έγινε; Η έπετνα διεξήφθη σον Ιούνιο 2014. Από
Ομάδα Γλώςςαρ (2013-2014) Γ. Κούμα, ΕΜΕ, Δπ. Ειπ. Ροδοςθένοτρ, Β. Παπαδάκη, Μ. σευάνοτ, Μ. Κτππιανού, Π. Φπτςοςσόμοτ, Κ. Κψνςσανσίνοτ, Γ. Οπυανίδηρ 1 Πόσε έγινε; Η έπετνα διεξήφθη σον Ιούνιο 2014. Από
Λούηρ Μ. Λοΐζοτ. Υεβποτάπιορ 2010
 Λούηρ Μ. Λοΐζοτ Υεβποτάπιορ 2010 1 Λίγα λόγια για μαρ τμβοτλετσικέρ Τπηπεςίερ Κασάπσιςη Οπιςμοί / Σοποθέσηςη ςσο θέμα Οδικόρ φάπσηρ Πψρ; Αναμενόμενα Ουέλη Πψρ μποπούμε να ςαρ βοηθήςοτμε 2 Αποςσολή σηρ
Λούηρ Μ. Λοΐζοτ Υεβποτάπιορ 2010 1 Λίγα λόγια για μαρ τμβοτλετσικέρ Τπηπεςίερ Κασάπσιςη Οπιςμοί / Σοποθέσηςη ςσο θέμα Οδικόρ φάπσηρ Πψρ; Αναμενόμενα Ουέλη Πψρ μποπούμε να ςαρ βοηθήςοτμε 2 Αποςσολή σηρ
Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν
 Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν Π Α Ν Ε Π Ι Σ Η Μ Ι Ο Κ Τ Π Ρ Ο Τ Νοέμβριος 212 Οι Έπετνερ Οικονομικήρ τγκτπίαρ ςσοφεύοτν ςσην αποσύπψςη σψν ανσιλήχεψν σψν επιφειπημασιών και κασαναλψσών
Κ Ε Ν Σ Ρ Ο Ο Ι Κ Ο Ν Ο Μ Ι Κ Ω Ν Ε Ρ Ε Τ Ν Ω Ν Π Α Ν Ε Π Ι Σ Η Μ Ι Ο Κ Τ Π Ρ Ο Τ Νοέμβριος 212 Οι Έπετνερ Οικονομικήρ τγκτπίαρ ςσοφεύοτν ςσην αποσύπψςη σψν ανσιλήχεψν σψν επιφειπημασιών και κασαναλψσών
 y(t) S x(t) S dy dx E, E E T1 T2 T1 T2 1 T 1 T 2 2 T 2 1 T 2 2 3 T 3 1 T 3 2... V o R R R T V CC P F A P g h V ext V sin 2 S f S t V 1 V 2 V out sin 2 f S t x 1 F k q K x q K k F d F x d V
y(t) S x(t) S dy dx E, E E T1 T2 T1 T2 1 T 1 T 2 2 T 2 1 T 2 2 3 T 3 1 T 3 2... V o R R R T V CC P F A P g h V ext V sin 2 S f S t V 1 V 2 V out sin 2 f S t x 1 F k q K x q K k F d F x d V
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙΣΤΗΜΗΣ & ΤΕΧΝΟΛΟΓΙΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ Κ 17 Επικοινωνίες ΙΙ Χειμερινό Εξάμηνο Διάλεξη 5 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst215
ΝΕΤΡΟΠΑΘΗΣΙΚΟ ΠΟΝΟ. σατπούλα Δικαίοτ Ρετμασολόγορ
 ΝΕΤΡΟΠΑΘΗΣΙΚΟ ΠΟΝΟ σατπούλα Δικαίοτ Ρετμασολόγορ Νετποπαθησικόρ πόνορ Pain arising as a direct consequence of a lesion or disease affecting the somatosensory system (Special Interest Group on Neuropathic
ΝΕΤΡΟΠΑΘΗΣΙΚΟ ΠΟΝΟ σατπούλα Δικαίοτ Ρετμασολόγορ Νετποπαθησικόρ πόνορ Pain arising as a direct consequence of a lesion or disease affecting the somatosensory system (Special Interest Group on Neuropathic
Η ΜΝΗΜΗ ΤΟΥ ΠΛΑΚΟΥΝΤΑ
 Η ΜΝΗΜΗ ΤΟΥ ΠΛΑΚΟΥΝΤΑ Elimnion Resort http://www.elimnionresort.gr/ Evia 30/9/2016-2/10/2016 Θτμήςοτ σην Πνετμασικόσησα και σην Αυθονία ςση Ζψή ςοτ Μια Βοτσιά ςσο Πεδίο σηρ Γέννηςηρ. Δημιοτπγία Νέψν Εμπειπιών
Η ΜΝΗΜΗ ΤΟΥ ΠΛΑΚΟΥΝΤΑ Elimnion Resort http://www.elimnionresort.gr/ Evia 30/9/2016-2/10/2016 Θτμήςοτ σην Πνετμασικόσησα και σην Αυθονία ςση Ζψή ςοτ Μια Βοτσιά ςσο Πεδίο σηρ Γέννηςηρ. Δημιοτπγία Νέψν Εμπειπιών
ΜΑΘΗΜΑΤΙΚΑ ΙΙ Παραδείγματα Στις Μερικές Παραγώγους Και τον Κανόνα Αλυσιδωτής Παραγώγισης
 ΜΑΘΗΜΑΤΙΚΑ ΙΙ Παραδείγματα Στις Μερικές Παραγώγους Και τον Κανόνα Αλυσιδωτής Παραγώγισης Άσκηση Αν t ( ) < cos t,sin( t) > δύο τρόπους και gt () 3t 4 d gt να υπολογισθεί η παράγωγος ( ()) με Λύση 1 ος
ΜΑΘΗΜΑΤΙΚΑ ΙΙ Παραδείγματα Στις Μερικές Παραγώγους Και τον Κανόνα Αλυσιδωτής Παραγώγισης Άσκηση Αν t ( ) < cos t,sin( t) > δύο τρόπους και gt () 3t 4 d gt να υπολογισθεί η παράγωγος ( ()) με Λύση 1 ος
Συστήματα Επικοινωνιών Ι
 + Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: demestihas@uowm.gr Συστήματα Επικοινωνιών Ι Διαμόρφωση και αποδιαμόρφωση πλάτους SSB και VSB Μετατόπιση συχνότητας Πολυπλεξία FDM + Περιεχόμενα n n n n n n n Διαμόρφωση
+ Διδάσκων: Δρ. Κ. Δεμέστιχας e-mail: demestihas@uowm.gr Συστήματα Επικοινωνιών Ι Διαμόρφωση και αποδιαμόρφωση πλάτους SSB και VSB Μετατόπιση συχνότητας Πολυπλεξία FDM + Περιεχόμενα n n n n n n n Διαμόρφωση
είσε μποπούν να βελσιώςοτν σην πνετμασική και ςψμασική ετεξία, πάνσα βέβαια όσαν κασαναλώνονσαι
 Ο Χαρίλαοσ Δημοςθενόπουλοσ είναι Προϊςτάμενοσ Διαιτολογικοφ Τμήματοσ του Γενικοφ Νοςοκομείου Αθηνών «Λαϊκό» και επιςτημονικόσ υπεφθυνοσ ςτο «Κζντρο Διατροφικήσ Αγωγήσ» Αμπελοκήπων. Αποφοίτηςε από το Τμήμα
Ο Χαρίλαοσ Δημοςθενόπουλοσ είναι Προϊςτάμενοσ Διαιτολογικοφ Τμήματοσ του Γενικοφ Νοςοκομείου Αθηνών «Λαϊκό» και επιςτημονικόσ υπεφθυνοσ ςτο «Κζντρο Διατροφικήσ Αγωγήσ» Αμπελοκήπων. Αποφοίτηςε από το Τμήμα
Αςύγφπξμξρ μξμξυαςικόρ κιμησήπαρ με οτκμωσή. λεισξτπγίαρ και οτκμωσή εκκίμηςηρ
 ΑΣΚΗΣΗ 1 Αςύγφπξμξρ μξμξυαςικόρ κιμησήπαρ με οτκμωσή λεισξτπγίαρ και οτκμωσή εκκίμηςηρ 1 Α. Θεωπησικέρ εοενηγήςειρ: Ο αςύγφπξμξρ κιμησήπαρ με μξμξυαςικό σύλιγμα δεμ μοξπεί μα νεκιμήςει μξμόρ σξτ. Ατσό
ΑΣΚΗΣΗ 1 Αςύγφπξμξρ μξμξυαςικόρ κιμησήπαρ με οτκμωσή λεισξτπγίαρ και οτκμωσή εκκίμηςηρ 1 Α. Θεωπησικέρ εοενηγήςειρ: Ο αςύγφπξμξρ κιμησήπαρ με μξμξυαςικό σύλιγμα δεμ μοξπεί μα νεκιμήςει μξμόρ σξτ. Ατσό
Φατοφροσ Γ. Ιωάννησ, Ο μικρόκυκλοσ τησ φλεγμονήσ ςτο ποδόςφαιρο
 Ο Ιωάννησ Φατοφροσ είναι Επίκουροσ Καθηγητήσ Βιοχημείασ τησ Άςκηςησ ςτο Τμήμα Επιςτήμησ Φυςικήσ Αγωγήσ και Αθλητιςμοφ του Δημοκρίτειου Πανεπιςτημίου Θράκησ. Διδάςκει ςτα μεταπτυχιακά προγράμματα «Άςκηςη
Ο Ιωάννησ Φατοφροσ είναι Επίκουροσ Καθηγητήσ Βιοχημείασ τησ Άςκηςησ ςτο Τμήμα Επιςτήμησ Φυςικήσ Αγωγήσ και Αθλητιςμοφ του Δημοκρίτειου Πανεπιςτημίου Θράκησ. Διδάςκει ςτα μεταπτυχιακά προγράμματα «Άςκηςη
x(t) = m(t) cos(2πf c t)
 Διαμόρφωση πλάτους (διπλής πλευρικής) Στοχαστικά συστήματα & επικοινωνίες 8 Νοεμβρίου 2012 1/27 2/27 Γιατί και πού χρειάζεται η διαμόρφωση Για τη χρήση πολυπλεξίας (διέλευση πολλών σημάτων μέσα από το
Διαμόρφωση πλάτους (διπλής πλευρικής) Στοχαστικά συστήματα & επικοινωνίες 8 Νοεμβρίου 2012 1/27 2/27 Γιατί και πού χρειάζεται η διαμόρφωση Για τη χρήση πολυπλεξίας (διέλευση πολλών σημάτων μέσα από το
Αγαοησξί αθλησέρ, οπξοξμησέρ και υίλξι σξτ αθλήμασξρ
 Αγαοησξί αθλησέρ, οπξοξμησέρ και υίλξι σξτ αθλήμασξρ Οι.56 ςτμμεσξφέρ αοό σα 8 Ελλημικά ςψμασεία και σα 5 ςψμασεία αοό όλη σημ Ετπώοη (5 φώπερ), δείφμει όσι σξ Athens Challenge έφει κεπδίςει μια ςημαμσική
Αγαοησξί αθλησέρ, οπξοξμησέρ και υίλξι σξτ αθλήμασξρ Οι.56 ςτμμεσξφέρ αοό σα 8 Ελλημικά ςψμασεία και σα 5 ςψμασεία αοό όλη σημ Ετπώοη (5 φώπερ), δείφμει όσι σξ Athens Challenge έφει κεπδίςει μια ςημαμσική
ΠΑΝΕΛΛΗΝΙΕ 2017 ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΜΗΧΑΝΕ ΕΩΣΕΡΙΚΗ ΚΑΤΗ ΙΙ (ΜΕΚ ΙΙ) ΘΕΜΑΣΑ
 ΠΑΝΕΛΛΗΝΙΕ 2017 ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΜΗΧΑΝΕ ΕΩΣΕΡΙΚΗ ΚΑΤΗ ΙΙ (ΜΕΚ ΙΙ) ΘΕΜΑ Α ΘΕΜΑΣΑ Α1. Να φαπακσηπίςεσε σιρ οπξσάςειρ οξτ ακξλξτθξύμ, γπάυξμσαρ ςσξ σεσπάδιό ςαρ δίολα ςσξ γπάμμα οξτ αμσιςσξιφεί ςε κάθε
ΠΑΝΕΛΛΗΝΙΕ 2017 ΕΞΕΣΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΜΗΧΑΝΕ ΕΩΣΕΡΙΚΗ ΚΑΤΗ ΙΙ (ΜΕΚ ΙΙ) ΘΕΜΑ Α ΘΕΜΑΣΑ Α1. Να φαπακσηπίςεσε σιρ οπξσάςειρ οξτ ακξλξτθξύμ, γπάυξμσαρ ςσξ σεσπάδιό ςαρ δίολα ςσξ γπάμμα οξτ αμσιςσξιφεί ςε κάθε
ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ. Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος.
 3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
3. ΚΕΦΑΛΑΙΟ ΑΝΑΠΤΥΓΜA - ΜΕΤΑΣΧΗΜΑΤΙΣΜΟΣ FOURIER ΑΝΑΛΟΓΙΚΩΝ ΣΗΜΑΤΩΝ Περιγράψουµε τον τρόπο ανάπτυξης σε σειρά Fourier ενός περιοδικού αναλογικού σήµατος. Ορίσουµε το µετασχηµατισµό Fourier ενός µη περιοδικού
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα
 Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Μετασχηματισμός Fourier Στο κεφάλαιο αυτό θα εισάγουμε και θα μελετήσουμε
Τεχνολογικό Εκπαιδευτικό Ίδρυμα Σερρών Τμήμα Πληροφορικής & Επικοινωνιών Σήματα και Συστήματα Δρ. Δημήτριος Ευσταθίου Επίκουρος Καθηγητής Μετασχηματισμός Fourier Στο κεφάλαιο αυτό θα εισάγουμε και θα μελετήσουμε
ΤΓΥΡΟΝΗ ΥΟΛΙΚΗ ΗΓΔΙΑ Γηεζλείο ηάζεηο ζηε ζεσξία, ηελ έξεπλα θαη ηελ πξαθηηθή ζήκεξα - Πξννπηηθέο
 ΤΓΥΡΟΝΗ ΥΟΛΙΚΗ ΗΓΔΙΑ Γηεζλείο ηάζεηο ζηε ζεσξία, ηελ έξεπλα θαη ηελ πξαθηηθή ζήκεξα - Πξννπηηθέο Αλδξέαο Κπζξαηώηεο Λεηηνπξγόο Παηδαγσγηθνύ Ιλζηηηνύηνπ Δθπαηδεπηηθή Ηκεξίδα ΑΚΙΓΑ 26 Φεβξνπαξίνπ 2011 1
ΤΓΥΡΟΝΗ ΥΟΛΙΚΗ ΗΓΔΙΑ Γηεζλείο ηάζεηο ζηε ζεσξία, ηελ έξεπλα θαη ηελ πξαθηηθή ζήκεξα - Πξννπηηθέο Αλδξέαο Κπζξαηώηεο Λεηηνπξγόο Παηδαγσγηθνύ Ιλζηηηνύηνπ Δθπαηδεπηηθή Ηκεξίδα ΑΚΙΓΑ 26 Φεβξνπαξίνπ 2011 1
HMY 220: Σήματα και Συστήματα Ι
 HMY 220: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #9 Ιδιοτιμές και ιδιοσυναρτήσεις συστημάτων Απόκριση ΓΧΑ συστημάτων σε μιγαδικά εκθετικά σήματα Συνάρτηση μεταφοράς Ανάλυση Σημάτων/Συστημάτων με βασικά σήματα Συχνά
HMY 220: Σήματα και Συστήματα Ι ΔΙΑΛΕΞΗ #9 Ιδιοτιμές και ιδιοσυναρτήσεις συστημάτων Απόκριση ΓΧΑ συστημάτων σε μιγαδικά εκθετικά σήματα Συνάρτηση μεταφοράς Ανάλυση Σημάτων/Συστημάτων με βασικά σήματα Συχνά
ΠΣΤΦΙΑΚΗ ΕΡΓΑΙΑ ΜΕΛΕΣΗ ΕΓΦΩΡΙΩΝ ΠΛΗΘΤΜΩΝ ΜΕΛΙΣΖΑΝΑ (Solanum melongena L.) ΜΕ ΦΡΗΗ ΜΟΡΥΟΛΟΓΙΚΩΝ ΦΑΡΑΚΣΗΡΩΝ
 ΣΕΙ ΜΕΟΛΟΓΓΙΟΤ ΦΟΛΗ ΣΕΦΝΟΛΟΓΙΑ ΓΕΩΠΟΝΙΑ ΣΜΗΜΑ ΘΕΡΜΟΚΗΠΙΑΚΩΝ ΚΑΛΛΙΕΡΓΕΙΩΝ & ΑΝΘΟΚΟΜΙΑ ΠΣΤΦΙΑΚΗ ΕΡΓΑΙΑ ΜΕΛΕΣΗ ΕΓΦΩΡΙΩΝ ΠΛΗΘΤΜΩΝ ΜΕΛΙΣΖΑΝΑ (Solanum melongena L.) ΜΕ ΦΡΗΗ ΜΟΡΥΟΛΟΓΙΚΩΝ ΦΑΡΑΚΣΗΡΩΝ ΕΙΗΓΗΣΗ :Δπ.
ΣΕΙ ΜΕΟΛΟΓΓΙΟΤ ΦΟΛΗ ΣΕΦΝΟΛΟΓΙΑ ΓΕΩΠΟΝΙΑ ΣΜΗΜΑ ΘΕΡΜΟΚΗΠΙΑΚΩΝ ΚΑΛΛΙΕΡΓΕΙΩΝ & ΑΝΘΟΚΟΜΙΑ ΠΣΤΦΙΑΚΗ ΕΡΓΑΙΑ ΜΕΛΕΣΗ ΕΓΦΩΡΙΩΝ ΠΛΗΘΤΜΩΝ ΜΕΛΙΣΖΑΝΑ (Solanum melongena L.) ΜΕ ΦΡΗΗ ΜΟΡΥΟΛΟΓΙΚΩΝ ΦΑΡΑΚΣΗΡΩΝ ΕΙΗΓΗΣΗ :Δπ.
20-Φεβ-2009 ΗΜΥ Διακριτός Μετασχηματισμός Fourier
 ΗΜΥ 429 8. Διακριτός Μετασχηματισμός Fourier 1 Μετασχηματισμός Fourier 4 κατηγορίες: Μετασχηματισμός Fourier: σήματα απεριοδικά και συνεχούς χρόνου Σειρά Fourier: σήματα περιοδικά και συνεχούς χρόνου Μετασχηματισμός
ΗΜΥ 429 8. Διακριτός Μετασχηματισμός Fourier 1 Μετασχηματισμός Fourier 4 κατηγορίες: Μετασχηματισμός Fourier: σήματα απεριοδικά και συνεχούς χρόνου Σειρά Fourier: σήματα περιοδικά και συνεχούς χρόνου Μετασχηματισμός
Σήματα και Συστήματα. Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Σήματα και Συστήματα Διάλεξη 2: Στοιχειώδη Σήματα Συνεχούς Χρόνου Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Στοιχειώδη Σήματα Συνεχούς Χρόνου 1. Μοναδιαία Βηματική Συνάρτηση 2. Κρουστική Συνάρτηση ή
Αςύγφπξμξρ μξμξυαςικόρ κιμησήπαρ με οτκμωσή. λεισξτπγίαρ και οτκμωσή εκκίμηςηρ (μέπξρ 2 ξ )
 ΑΣΚΗΣΗ 11 Αςύγφπξμξρ μξμξυαςικόρ κιμησήπαρ με οτκμωσή λεισξτπγίαρ και οτκμωσή εκκίμηςηρ (μέπξρ 2 ξ ) 1 Α. Θεωπησικέρ εοενηγήςειρ: Θεψπώμσαρ όσι ξ μξμξυαςικόρ κιμησήπαρ με οτκμψσή λεισξτπγίαρ C μόμξ ςσημ
ΑΣΚΗΣΗ 11 Αςύγφπξμξρ μξμξυαςικόρ κιμησήπαρ με οτκμωσή λεισξτπγίαρ και οτκμωσή εκκίμηςηρ (μέπξρ 2 ξ ) 1 Α. Θεωπησικέρ εοενηγήςειρ: Θεψπώμσαρ όσι ξ μξμξυαςικόρ κιμησήπαρ με οτκμψσή λεισξτπγίαρ C μόμξ ςσημ
Μαθηματικός Ορισμός Διδιάστατου Χώρου (R 2 )
 Μαθηματικός Ορισμός Διδιάστατου Χώρου (R 2 ) Είναι ένα σύνολο σημείων με συντεταγμένες (x,y) Τα x και y έχουν τις εξής ιδιότητες: Το καθένα από αυτά διατρέχει το σύνολο των πραγματικών αριθμών Είναι ανεξάρτητα
Μαθηματικός Ορισμός Διδιάστατου Χώρου (R 2 ) Είναι ένα σύνολο σημείων με συντεταγμένες (x,y) Τα x και y έχουν τις εξής ιδιότητες: Το καθένα από αυτά διατρέχει το σύνολο των πραγματικών αριθμών Είναι ανεξάρτητα
Επίδραση τν Σφαλµάτν του Τοπικού Ταλανττή / Η σύµφνη αποδιαµόρφση επηρεάζεται δυσµενώς, όταν το ηµιτονοειδές σήµα που παράγει ο τοπικός ταλανττής του
 Συστήµατα Μετάδοσης Πληροφορίας Εκποµπή και Λήψη Αναλογικού Σήµατος ιαµόρφση Πλάτους Επίδραση τν Σφαλµάτν του Τοπικού Ταλανττή του έκτη Επίδραση τν Σφαλµάτν του Τοπικού Ταλανττή / Η σύµφνη αποδιαµόρφση
Συστήµατα Μετάδοσης Πληροφορίας Εκποµπή και Λήψη Αναλογικού Σήµατος ιαµόρφση Πλάτους Επίδραση τν Σφαλµάτν του Τοπικού Ταλανττή του έκτη Επίδραση τν Σφαλµάτν του Τοπικού Ταλανττή / Η σύµφνη αποδιαµόρφση
Γιπλωμαηική Δργαζία. Σνπ θνηηεηή ηνπ Σκήκαηνο Ηιεθηξνιόγσλ Μεραληθώλ θαη Σερλνινγίαο Τπνινγηζηώλ ηνπ Παλεπηζηεκίνπ Παηξώλ. Βάζζη Νικόλαοσ Α.Μ.
 ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΨΝ ΣΜΗΜΑ ΗΛΕΚΣΡΟΛΟΓΨΝ ΜΗΦΑΝΙΚΨΝ ΚΑΙ ΣΕΦΝΟΛΟΓΙΑ ΤΠΟΛΟΓΙΣΨΝ ΣΟΜΕΑ ΤΣΗΜΑΣΨΝ ΗΛΕΚΣΡΙΚΗ ΕΝΕΡΓΕΙΑ ΕΡΓΑΣΗΡΙΟ ΗΛΕΚΣΡΟΜΗΦΑΝΙΚΗ ΜΕΣΑΣΡΟΠΗ ΕΝΕΡΓΕΙΑ Διετθτνσήρ: Καθηγησήρ Δπ.-Μηφ. Αθανάςιορ Ν. αυάκαρ
ΠΑΝΕΠΙΣΗΜΙΟ ΠΑΣΡΨΝ ΣΜΗΜΑ ΗΛΕΚΣΡΟΛΟΓΨΝ ΜΗΦΑΝΙΚΨΝ ΚΑΙ ΣΕΦΝΟΛΟΓΙΑ ΤΠΟΛΟΓΙΣΨΝ ΣΟΜΕΑ ΤΣΗΜΑΣΨΝ ΗΛΕΚΣΡΙΚΗ ΕΝΕΡΓΕΙΑ ΕΡΓΑΣΗΡΙΟ ΗΛΕΚΣΡΟΜΗΦΑΝΙΚΗ ΜΕΣΑΣΡΟΠΗ ΕΝΕΡΓΕΙΑ Διετθτνσήρ: Καθηγησήρ Δπ.-Μηφ. Αθανάςιορ Ν. αυάκαρ
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΤΜΗΜΑ ΕΠΙςΤΗΜΗς & ΤΕΧΝΟΛΟΓΙΑς ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΜΔΕ Προηγμένα Τηλεπικοινωνιακά Συστήματα και Δίκτυα Διάλεξη 2 η Νικόλαος Χ. Σαγιάς Επίκουρος Καθηγητής Webpage: http://eclass.uop.gr/courses/tst233
Αποδιαμόρφωση γωνίας με θόρυβο
 Αποδιαμόρφωση γωνίας με θόρυβο SNR στην είσοδο του δέκτη Εάν η διαμόρφωση είναι PM ή FM mt ( ) PM s( t) A ccos fct ( t), ( t) t f m( ) d FM Η ισχύς του σήματος στην είσοδο του δέκτη είναι S R Ac / Η ισχύς
Αποδιαμόρφωση γωνίας με θόρυβο SNR στην είσοδο του δέκτη Εάν η διαμόρφωση είναι PM ή FM mt ( ) PM s( t) A ccos fct ( t), ( t) t f m( ) d FM Η ισχύς του σήματος στην είσοδο του δέκτη είναι S R Ac / Η ισχύς
Εξίσωση Τηλεπικοινωνιακών Διαύλων
 Εξίσωση Τηλεπικοινωνιακών Διαύλων ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΜΔΕ ΠΡΟΗΓΜΈΝΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΣΥΣΤΉΜΑΤΑ ΚΑΙ ΔΙΚΤΥΑ Ενότητα 2 η Φίλτρα Μηδενισμού της ISI Νικόλαος Χ.
Εξίσωση Τηλεπικοινωνιακών Διαύλων ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΜΔΕ ΠΡΟΗΓΜΈΝΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΣΥΣΤΉΜΑΤΑ ΚΑΙ ΔΙΚΤΥΑ Ενότητα 2 η Φίλτρα Μηδενισμού της ISI Νικόλαος Χ.
ΜΑΘΗΜΑΣΙΚΑ ΠΡΟΑΝΑΣΟΛΙΜΟΤ Γ ΛΤΚΕΙΟΤ ΘΕΜΑΣΑ ΚΑΙ ΑΠΑΝΣΗΕΙ ΠΑΝΕΛΛΗΝΙΩΝ 2017
 ΜΑΘΗΜΑΣΙΚΑ ΠΡΟΑΝΑΣΟΛΙΜΟΤ Γ ΛΤΚΕΙΟΤ ΘΕΜΑΣΑ ΚΑΙ ΑΠΑΝΣΗΕΙ ΠΑΝΕΛΛΗΝΙΩΝ 7 ΕΚΥΩΝΗΕΙ ΘΕΜΑ Α Α.Έςσψ μια ςτμάπσηςη f, η ξοξία είμαι ςτμεφήρ ςε έμα διάςσημα Δ. Αμ f () > ςε κάθε εςψσεπικό ςημείξ σξτ Δ, σόσε μα αοξδείνεσε
ΜΑΘΗΜΑΣΙΚΑ ΠΡΟΑΝΑΣΟΛΙΜΟΤ Γ ΛΤΚΕΙΟΤ ΘΕΜΑΣΑ ΚΑΙ ΑΠΑΝΣΗΕΙ ΠΑΝΕΛΛΗΝΙΩΝ 7 ΕΚΥΩΝΗΕΙ ΘΕΜΑ Α Α.Έςσψ μια ςτμάπσηςη f, η ξοξία είμαι ςτμεφήρ ςε έμα διάςσημα Δ. Αμ f () > ςε κάθε εςψσεπικό ςημείξ σξτ Δ, σόσε μα αοξδείνεσε
Σήματα και Συστήματα. Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Σήματα και Συστήματα Διάλεξη 9: Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής 1 Μελέτη ΓΧΑ Συστημάτων με τον Μετασχηματισμό Fourier 1. Μετασχηματισμός Fourier
Φυσικό Τμήμα Παν/μιο Ιωαννίνων - Ειδική Σχετικότητα - Λυμένα Προβλήματα - ΙI
 .11.011 Άσκηση 1: Χρησιμοποιήστε την διωνυμική σχέση 1x N = i=0 N! i! N i! xi για να υπολογίστε το 1 V /c για (α) V = 0.01c και (β) V = 0.9998c (α) Η διωνυμική σχέση είναι ιδανική για προσεγγίσεις όταν
.11.011 Άσκηση 1: Χρησιμοποιήστε την διωνυμική σχέση 1x N = i=0 N! i! N i! xi για να υπολογίστε το 1 V /c για (α) V = 0.01c και (β) V = 0.9998c (α) Η διωνυμική σχέση είναι ιδανική για προσεγγίσεις όταν
Σα επιμέποτρ επίπεδα κπεασίνηρ (Cr) και CP ήσαν 49.0 ( 7.62) και 75.5 ( 7.63) mmol.kg -1.
 Ο Απόςτολοσ Θεοδώρου Ph.D είναι Λζκτορασ ςτα Αθλητικά Άλματα ςτον τομζα Κλαςικοφ Αθλητιςμοφ του ΤΕΦΑΑ Αθηνών. Πτυχιοφχοσ Φυςικήσ Αγωγήσ του ΤΕΦΑΑ Αθηνών το 1992. Το 1994 απόκτηςε το μεταπτυχιακό του ςτην
Ο Απόςτολοσ Θεοδώρου Ph.D είναι Λζκτορασ ςτα Αθλητικά Άλματα ςτον τομζα Κλαςικοφ Αθλητιςμοφ του ΤΕΦΑΑ Αθηνών. Πτυχιοφχοσ Φυςικήσ Αγωγήσ του ΤΕΦΑΑ Αθηνών το 1992. Το 1994 απόκτηςε το μεταπτυχιακό του ςτην
IAAF CECS Level I Lecturers Course
 Ειςαγψγή ςσο Kids Athletics: Γιασί? Ειςαγψγή Η IAAF αυού εξέσαςε σην εναςφόληςη σψν μικπών παιδιών με σον Κλαςικό Αθλησιςμό σα σελετσαία φπόνια κασέληξε ςε μια ππόσαςη πποςαπμοςμένη ςσα ςημεπινά παιδιά.
Ειςαγψγή ςσο Kids Athletics: Γιασί? Ειςαγψγή Η IAAF αυού εξέσαςε σην εναςφόληςη σψν μικπών παιδιών με σον Κλαςικό Αθλησιςμό σα σελετσαία φπόνια κασέληξε ςε μια ππόσαςη πποςαπμοςμένη ςσα ςημεπινά παιδιά.
Σήματα και Συστήματα. Διάλεξη 11: Μετασχηματισμός Laplace. Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής
 Σήματα και Συστήματα Διάλεξη : Μετασχηματισμός Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής Μετασχηματισμός Laplace. Μαθηματικός ορισμός μετασχηματισμού Laplace 2. Η περιοχή σύγκλισης του μετασχηματισμού
Σήματα και Συστήματα Διάλεξη : Μετασχηματισμός Laplace Δρ. Μιχάλης Παρασκευάς Επίκουρος Καθηγητής Μετασχηματισμός Laplace. Μαθηματικός ορισμός μετασχηματισμού Laplace 2. Η περιοχή σύγκλισης του μετασχηματισμού
Διαμόρφωση FM στενής ζώνης. Διαμορφωτής PM
 Παραγωγή σημάτων FM Διαμόρφωση FM στενής ζώνης [ π φ π ] st () A cos(2 ft) ()sin(2 t ft) c c c Διαμορφωτής PM m (t) + s(t) A c sin(2 π ft) c +90 0 ~ A c cos(2 π ft) c Διαμόρφωση PM στενής ζώνης 2f c Άμεση
Παραγωγή σημάτων FM Διαμόρφωση FM στενής ζώνης [ π φ π ] st () A cos(2 ft) ()sin(2 t ft) c c c Διαμορφωτής PM m (t) + s(t) A c sin(2 π ft) c +90 0 ~ A c cos(2 π ft) c Διαμόρφωση PM στενής ζώνης 2f c Άμεση
Βιωματικό εργαςτήριο Σχεδιαςμόσ θεματικήσ ενότητασ «Ανθρώπινεσ ςχζςεισ - Ανθρώπινοι χαρακτήρεσ»
 Επιςτθμονικό υνζδριο «Διδακτικι τθσ Λογοτεχνίασ ςτθ Μζςθ Εκπαίδευςθ: Αντικρίηοντασ το Νζο Αναλυτικό Πρόγραμμα» Βιωματικό εργαςτήριο Σχεδιαςμόσ θεματικήσ ενότητασ «Ανθρώπινεσ ςχζςεισ - Ανθρώπινοι χαρακτήρεσ»
Επιςτθμονικό υνζδριο «Διδακτικι τθσ Λογοτεχνίασ ςτθ Μζςθ Εκπαίδευςθ: Αντικρίηοντασ το Νζο Αναλυτικό Πρόγραμμα» Βιωματικό εργαςτήριο Σχεδιαςμόσ θεματικήσ ενότητασ «Ανθρώπινεσ ςχζςεισ - Ανθρώπινοι χαρακτήρεσ»
ΣΟΠΙΚΑ ΠΡΟΙΟΝΣΑ ΚΑΙ ΠΡΟΙΟΝΣΑ ΠΟΠ ΗΠΕΙΡΟ
 ΣΟΠΙΚΑ ΠΡΟΙΟΝΣΑ ΚΑΙ ΠΡΟΙΟΝΣΑ ΠΟΠ ΗΠΕΙΡΟ ΣΤΡΙΑ ΣΕΛΕΜΕ ΚΕΥΑΛΟΣΤΡΙ ΑΝΘΟΣΤΡΟ ΜΕΣΟΒΟΝΕ ΣΕΛΕΜΕ ΛΕΤΚΟ ΣΤΡΙ ΑΛΜΗς ΚΑΙ ΜΑΛΑΚΟ ΛΕΤΚΟΤ ΦΡΨΜΑΣΟς ΠΡΟΕΡΦΕΣΑΙ ΑΠΟ ΠΡΟΒΕΙΟ ΓΑΛΑ, ΚΑΣςΙΚΙςΙΟ Η ΑΓΕΛΑΔΙΝΟ. ΔΙΑΥΕΡΕΙ ΑΠΟ ΣΗ
ΣΟΠΙΚΑ ΠΡΟΙΟΝΣΑ ΚΑΙ ΠΡΟΙΟΝΣΑ ΠΟΠ ΗΠΕΙΡΟ ΣΤΡΙΑ ΣΕΛΕΜΕ ΚΕΥΑΛΟΣΤΡΙ ΑΝΘΟΣΤΡΟ ΜΕΣΟΒΟΝΕ ΣΕΛΕΜΕ ΛΕΤΚΟ ΣΤΡΙ ΑΛΜΗς ΚΑΙ ΜΑΛΑΚΟ ΛΕΤΚΟΤ ΦΡΨΜΑΣΟς ΠΡΟΕΡΦΕΣΑΙ ΑΠΟ ΠΡΟΒΕΙΟ ΓΑΛΑ, ΚΑΣςΙΚΙςΙΟ Η ΑΓΕΛΑΔΙΝΟ. ΔΙΑΥΕΡΕΙ ΑΠΟ ΣΗ
ΘΔΜΑ: Ο Ernst May και «Η καινούπια Φπανκυούπση».
 Μάθημα: Τομέαρ: Δ. Η. Πολεοδομίαρ 8 οτ Πολεοδομίαρ και Φψποσαξίαρ Ακ. Έσορ: 2010-11 Διδάςκονσερ: Δπικοτπικό έπγο: Σποτδάςσπια: Δξάμηνο:. ΑΤΓΔΡΘΜΟΤ ΙΟΚΩΜΘΑ, Ι. ΔΡΡΑΟ Α. ΣΟΤΥΔΓΓΟΠΟΤΚΟΤ, Ε. ΕΑΒΘΣΑΜΟΤ Πίππα
Μάθημα: Τομέαρ: Δ. Η. Πολεοδομίαρ 8 οτ Πολεοδομίαρ και Φψποσαξίαρ Ακ. Έσορ: 2010-11 Διδάςκονσερ: Δπικοτπικό έπγο: Σποτδάςσπια: Δξάμηνο:. ΑΤΓΔΡΘΜΟΤ ΙΟΚΩΜΘΑ, Ι. ΔΡΡΑΟ Α. ΣΟΤΥΔΓΓΟΠΟΤΚΟΤ, Ε. ΕΑΒΘΣΑΜΟΤ Πίππα
Συστήματα Επικοινωνιών
 Συστήματα Επικοινωνιών Ενότητα 6: Συστήματα Αναλογικής Διαμόρφωσης Σαγκριώτης Εμμανουήλ Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Σκοποί ενότητας 1. Η αναγνώριση της ανάγκης διαμόρφωσης
Συστήματα Επικοινωνιών Ενότητα 6: Συστήματα Αναλογικής Διαμόρφωσης Σαγκριώτης Εμμανουήλ Σχολή Θετικών Επιστημών Τμήμα Πληροφορικής και Τηλεπικοινωνιών Σκοποί ενότητας 1. Η αναγνώριση της ανάγκης διαμόρφωσης
FM & PM στενής ζώνης. Narrowband FM & PM
 FM & PM στενής ζώνης Narrowband FM & PM Διαμόρφωση γωνίας στενής ζώνης Το διαμορφωμένο κατά γωνία σήμα μπορεί να γραφεί ως [ π φ ] st () = Acos2 ft+ () t c όπου η στιγμιαία φάση είναι φ() t c Δφxt () PM
FM & PM στενής ζώνης Narrowband FM & PM Διαμόρφωση γωνίας στενής ζώνης Το διαμορφωμένο κατά γωνία σήμα μπορεί να γραφεί ως [ π φ ] st () = Acos2 ft+ () t c όπου η στιγμιαία φάση είναι φ() t c Δφxt () PM
Εξίσωση Τηλεπικοινωνιακών Διαύλων
 Εξίσωση Τηλεπικοινωνιακών Διαύλων ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΜΔΕ ΠΡΟΗΓΜΈΝΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΣΥΣΤΉΜΑΤΑ ΚΑΙ ΔΙΚΤΥΑ Ενότητα η Φίλτρα Nyquis Νικόλαος Χ. Σαγιάς Επίκουρος
Εξίσωση Τηλεπικοινωνιακών Διαύλων ΤΜΗΜΑ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΛΟΠΟΝΝΗΣΟΥ ΜΔΕ ΠΡΟΗΓΜΈΝΑ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΑ ΣΥΣΤΉΜΑΤΑ ΚΑΙ ΔΙΚΤΥΑ Ενότητα η Φίλτρα Nyquis Νικόλαος Χ. Σαγιάς Επίκουρος
Ο Μέγας Βασίλειος σε μικρογραυία τοσ 15οσ αιώνα(μονή Διονσσίοσ, Άγιο Όρος
 Ο Μέγας Βασίλειος σε μικρογραυία τοσ 15οσ αιώνα(μονή Διονσσίοσ, Άγιο Όρος Ο λόγορ εκυψνείσαι ςσην Καιςάπεια σο 368μΧ με αυοπμή σην κοινψνική αναςσάσψςη ποτ δημιοτπγήθηκε ανάμεςα ςσοτρ πολίσερ εξαισίαρ
Ο Μέγας Βασίλειος σε μικρογραυία τοσ 15οσ αιώνα(μονή Διονσσίοσ, Άγιο Όρος Ο λόγορ εκυψνείσαι ςσην Καιςάπεια σο 368μΧ με αυοπμή σην κοινψνική αναςσάσψςη ποτ δημιοτπγήθηκε ανάμεςα ςσοτρ πολίσερ εξαισίαρ
Γιατί Διαμόρφωση; Μια κεραία για να είναι αποτελεσματική πρέπει να είναι περί το 1/10 του μήκους κύματος
 Γιατί Διαμόρφωση; Μετάδοση ενός σήματος χαμηλών συχνοτήτων μέσω ενός ζωνοπερατού καναλιού Παράλληλη μετάδοση πολλαπλών σημάτων πάνω από το ίδιο κανάλι - Διαχωρισμός συχνότητας (Frequency Division Multiplexing)
Γιατί Διαμόρφωση; Μετάδοση ενός σήματος χαμηλών συχνοτήτων μέσω ενός ζωνοπερατού καναλιού Παράλληλη μετάδοση πολλαπλών σημάτων πάνω από το ίδιο κανάλι - Διαχωρισμός συχνότητας (Frequency Division Multiplexing)
FM & PM στενής ζώνης. Narrowband FM & PM
 FM & PM στενής ζώνης Narrowband FM & PM Διαμόρφωση γωνίας στενής ζώνης Το διαμορφωμένο κατά γωνία σήμα μπορεί να γραφεί ως [ π φ ] st () = Acos2 ft+ () t c όπου η στιγμιαία φάση είναι φ() t c Δφxt () PM
FM & PM στενής ζώνης Narrowband FM & PM Διαμόρφωση γωνίας στενής ζώνης Το διαμορφωμένο κατά γωνία σήμα μπορεί να γραφεί ως [ π φ ] st () = Acos2 ft+ () t c όπου η στιγμιαία φάση είναι φ() t c Δφxt () PM
«Χρημαηοδοηείηαι ζηο πλαίζιο ηης Εσρωπαϊκής Έμωζης Erasmus +» ΔΕΛΣΙΟ ΣΤΠΟΤ. φημασάπι, 27/3/2018
 ΔΕΛΣΙΟ ΣΤΠΟΤ φημασάπι, 27/3/2018 Τξ 1ξ Δημξσικό Σφξλείξ Σφημασαπίξτ οέσανε με σα υσεπά σξτ εγκεκπιμέμξτ ετπψοαϊκξύ οπξγπάμμασξρ Erasmus+ 2016-2018, με σίσλξ Through artistic abilities to developed basic
ΔΕΛΣΙΟ ΣΤΠΟΤ φημασάπι, 27/3/2018 Τξ 1ξ Δημξσικό Σφξλείξ Σφημασαπίξτ οέσανε με σα υσεπά σξτ εγκεκπιμέμξτ ετπψοαϊκξύ οπξγπάμμασξρ Erasmus+ 2016-2018, με σίσλξ Through artistic abilities to developed basic
Καθηγήσπια Μαίπη Κοτσςελίνη Σμήμα Επιςσημών σηρ Αγψγήρ Πανεπιςσήμιο Κύπποτ. Έδπα ΟΤΝΕΚΟ για σην Ιςόσησα και Ενδτνάμψςη σψν Υύλψν
 Καθηγήσπια Μαίπη Κοτσςελίνη Σμήμα Επιςσημών σηρ Αγψγήρ Πανεπιςσήμιο Κύπποτ Έδπα ΟΤΝΕΚΟ για σην Ιςόσησα και Ενδτνάμψςη σψν Υύλψν Παπανοήςειρ: ΔΕΝ πποβλέπεσαι η ιςόπποπη ανσιπποςώπετςη σψν δύο υύλψν ςση
Καθηγήσπια Μαίπη Κοτσςελίνη Σμήμα Επιςσημών σηρ Αγψγήρ Πανεπιςσήμιο Κύπποτ Έδπα ΟΤΝΕΚΟ για σην Ιςόσησα και Ενδτνάμψςη σψν Υύλψν Παπανοήςειρ: ΔΕΝ πποβλέπεσαι η ιςόπποπη ανσιπποςώπετςη σψν δύο υύλψν ςση
Η τπο-αναςύςσαςη λίμνη Κάπλα: Μαθημασική πποςομοίψςη σοτ κύκλοτ σοτ αζώσοτ. Λαςπίδοτ Φπτςή Σμήμα Πολισικών Μηφανικών Πανεπιςσήμιο Θεςςαλίαρ
 Η τπο-αναςύςσαςη λίμνη Κάπλα: Μαθημασική πποςομοίψςη σοτ κύκλοτ σοτ αζώσοτ Λαςπίδοτ Φπτςή Σμήμα Πολισικών Μηφανικών Πανεπιςσήμιο Θεςςαλίαρ Τγπόσοποι: οπιςμόρ και είδη Είναι υτςικέρ ή σεφνησέρ πεπιοφέρ,
Η τπο-αναςύςσαςη λίμνη Κάπλα: Μαθημασική πποςομοίψςη σοτ κύκλοτ σοτ αζώσοτ Λαςπίδοτ Φπτςή Σμήμα Πολισικών Μηφανικών Πανεπιςσήμιο Θεςςαλίαρ Τγπόσοποι: οπιςμόρ και είδη Είναι υτςικέρ ή σεφνησέρ πεπιοφέρ,
Νσίπληρ Νίκορ- ΕΣΤ 4ο ΥΡΟΝΣΙΣΗΡΙΟ Παπαςκετή Β4
 Νσίπληρ Νίκορ- ΕΣΤ 4ο ΥΡΟΝΣΙΣΗΡΙΟ Παπαςκετή 4-11-2013 Β4 1 Κοινή Μνήμη μεσαξύ διεπγαςιών -> Γπηγοπόσεπη μοπυή IPC Σα δεδομένα δεν ανσιγπάυονσαι πάνω από μία υοπά Server/Client model. Όσαν ο Server γπάυει,
Νσίπληρ Νίκορ- ΕΣΤ 4ο ΥΡΟΝΣΙΣΗΡΙΟ Παπαςκετή 4-11-2013 Β4 1 Κοινή Μνήμη μεσαξύ διεπγαςιών -> Γπηγοπόσεπη μοπυή IPC Σα δεδομένα δεν ανσιγπάυονσαι πάνω από μία υοπά Server/Client model. Όσαν ο Server γπάυει,
Δομή της παρουσίασης
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη η Τα Σήματα στις Τηλεπικοινωνίες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΕΙΡΑΙΩΣ ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΩΝ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΕΠΙΚΟΙΝΩΝΙΩΝ ΤΜΗΜΑ ΨΗΦΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΤΗΛΕΠΙΚΟΙΝΩΝΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Εισαγωγή στις Τηλεπικοινωνίες Διάλεξη η Τα Σήματα στις Τηλεπικοινωνίες
The explosion in Mari, Cyprus, the cost of power shortages, and policy recommendations
 University of Cyprus From the SelectedWorks of Theodoros Zachariadis August, 2011 The explosion in Mari, Cyprus, the cost of power shortages, and policy recommendations Theodoros Zachariadis, Cyprus University
University of Cyprus From the SelectedWorks of Theodoros Zachariadis August, 2011 The explosion in Mari, Cyprus, the cost of power shortages, and policy recommendations Theodoros Zachariadis, Cyprus University
