ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
|
|
|
- Αττις Κυπραίος
- 9 χρόνια πριν
- Προβολές:
Transcript
1 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ Πεδίο ορισμού. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) f ( ) 5 6 ii) f ( ) 7 iii) iv) f( ) 4 f( ) 8 v) f ( ) 6 vi) f ( ) 0 5. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: 5 i) f( ) ii) f ( ) 4 9 iv) f( ) v) f( ) 8 4 iii) f( ) 5 5 vi) f( ). Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) f( ) ii) f( ) iii) f( ) iv) f( ) v) f( ) vi) f( ) Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) f( ) ii) f( ) iii) f( ) iv) f( ) v) f( ) vi) f( ) Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: 5 i) f( ) ii) f( ) iii) f( ) 5 5 v) f( ) 4 7 iv) f( ) 7 0 vi) f( ) Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) f ( ) 9 ii) f ( ) 4 0 iii) f ( ) 6 iv) f ( ) v) f ( ) vi) f ( )
2 7. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) f( ) 4 ii) f( ) iii) f( ) 5 iv) f( ) v) f( ) 5 vi) f( ) Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) iii) f ( ) 6 f( ) v) f( ) 4 7 ii) f( ) 9. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) iii) v) 4 0 iv) f( ) vi) f ( ) f ( ) ii) f ( ) 8 f( ) 4 5 iv) f( ) vi) 0. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) iii) f ( ) 4 4 ii) f( ) f( ). Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: f ( ) 6 9 f( ) 4 5 iv) f ( ) 4 5 i) f( ) ii) f ( ) 4 iii) f ( ) 6 iv) f( ) v) f( ) vi) f( ) 5. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) f( ) ii) f( ) ( )( 6) ( )( 5 )( ) 5 iii) f( ) ( )( )( 9). Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) 5 8 iv) f( ) ( 5 6)( ) f ( ) ( )( 6) ii) f ( ) ( 4)( ) 4
3 iii) f( ) ( )( ) 6 iv) f( ) 4 5 ( )( 6 9) 4. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) f ( ) ii) f( ) iii) f ( ) iv) f( ) v) f( ) vi) f ( ) 5. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) f ( ) ii) f ( ) iii) f ( ) 9 6. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) f ( ) ii) f ( ) iii) f ( ) 7. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: 5 i) ii) iii) Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) ii) iii) 9. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: i) ii) iii) iv) iv) iv) 5 0. Να βρείτε τα πεδία ορισμού των παρακάτω συναρτήσεων: 4 i) ii) iii) 4 5. Να βρείτε τα πεδία ορισμού των συναρτήσεων : i) f ( ) ii) g( ) iii) h( ) iv) k( ) v) s( ) ( ). Να βρείτε τα πεδία ορισμού των συναρτήσεων : i) a ( ) ii) ( ) iv) ( ) v) ( ) iii) ( ) 5
4 . Να βρείτε τα πεδία ορισμού των συναρτήσεων: i) f ( ) 5 ii)f() = iii) f ( ) iv) f ( ) v) f ( ) 4. Να βρείτε τα πεδία ορισμού των συναρτήσεων i) f( ) 5 iv) f( ) ii) f( ) 5 v) f( ) 5 iii) f( ) vi) f ( ) 5. Να βρείτε τα πεδία ορισμού των συναρτήσεων: i) f ( ) 5 5 iii) f( ) 49 ii) f( ) iv) f ( ) Να βρείτε τα πεδία ορισμού των συναρτήσεων : i) f ( ) ii) g( ) iii) h( ) 4 iv) k( ) v) 7. Να βρείτε τα πεδία ορισμού των συναρτήσεων: s ( ) vi) t ( ) i)f() = ii) f() = iii) f() = 8. Να βρείτε τα πεδία ορισμού των συναρτήσεων: i) f( ) ii) f( ) 5 4 iii) f( ) 9. Να βρεθούν τα πεδία ορισμού των συναρτήσεων: i) f( ) ii) f( ) iii) f ( ) 4 0. Να βρείτε τα πεδία ορισμού των συναρτήσεων : i) f( ) ii) g ( ) iv) k( ) v) s ( ) iii) h ( ) vi) t ( ). Να βρείτε το πεδίου ορισμού καθεμιάς από τις παρακάτω συναρτήσεις : i) f( ) ii) g ( ) iii) h( ) 6
5 iv) k( ) v) a ( ) vi) l( ). Nα βρείτε το πεδίο ορισμού των συναρτήσεων: i) f() = ii) f()= 4- iii)f()= - 4 iv) f() = 4 v) f()= vi) f()= 4 4 vii) f()=, αν 0 viii) f()=, αν 0. Να βρεθεί το πεδίο ορισμού των συναρτήσεων: i) f() = ii) f() = 5 iv) f () = 4 -, [0,6] vii) f()=, [6,7] iii) f() = v) f() = vi) f()=, [-,] viii) f() = -, [-,] i) f()= Τιμές συνάρτησης 4. Να εξετάσετε ποια από τα παρακάτω βελοδιαγράμματα παριστάνουν συνάρτηση:. Έστω η συνάρτηση f που παριστάνεται με το διπλανό βελοδιάγραμμα. Να βρείτε: i) το πεδίο ορισμού της f. ii) τα f(), f(0). iii)το σύνολο τιμών της f 5. Δίνεται η συνάρτηση f() = --4. ii) Να βρείτε τις τιμές α) f(0), β)f(-), γ) f(4), δ) f(5). iii) Να λύσετε την εξίσωση f() =-6 7
6 6. Δίνεται η συνάρτηση f ( ). ii) Να βρείτε τις τιμές 4 α) f(6), β)f(), γ) f 6, δ) f(). 5, 0 7. Δίνεται η συνάρτηση f( ). 7, 0 ii) Να βρείτε τις τιμές α) f(-), 5 β) f, γ) f(-), δ) f(0), ε) f, στ) f( ) iii) Να λύσετε την εξίσωση f() =., 8. Δίνεται η συνάρτηση f ( ), 0,. ii) Να διατάξετε από τη μικρότερη προς τη μεγαλύτερη τις τιμές α) f(-), β)f(5), γ) f, δ) f()., 9. Δίνεται η συνάρτηση f ( ) 4,,. ii) Να βρείτε τις τιμές α) f(-4), β)f(-), γ) f ( ), δ) f(), ε)f(), στ) f ( ) ζ) f(f(0)) η) f(f(-)) θ) f(f(6)), ό 40. Δίνεται η συνάρτηση f( )., ii) Να βρείτε τις τιμές α) f(0), β) f ( ), γ) δ) f, ε) 5 f 4 f,, στ) f( 5) 8
7 6, 4. Δίνεται η συνάρτηση f( ),. ii) Να βρείτε τις τιμές : α) f(0), β)f(-), γ) f(-), δ) f ( ), ε) 6 στ) f ζ) f η) f 4 θ) f ( 5 ) 4. Δίνεται η συνάρτηση f() = -. ii) Να βρείτε τις τιμές : α) f(-), β)f(-), γ) f(0), δ) f(), ε) f(f()), στ) f(f(5)) iii) Να υπολογίσετε τις παραστάσεις: α)f(α) β) f(α ) γ) a δ) f(α +β) +f(α-β) f, 4. Δίνεται η συνάρτηση f() = - +. ii) Να βρείτε τις τιμές : α) f(-), β)f(-), γ) f(0), δ) f, iii) Να υπολογίσετε την παράσταση: Α= f(α +β) +f(α-β) -(f(α)+ f(β)) iv) Να λύσετε την εξίσωση f ( ) f ( ) 44. Δίνεται η συνάρτηση f() = ii) Να βρείτε τις τιμές : α) f(-), β)f(5), γ) f(0), iii) Να υπολογίσετε τις παραστάσεις: α)f(-α) β) f(α ) γ) f(α-β) iv) Να λύσετε την εξίσωση: f() = v) Να λύσετε την ανίσωση: f ( ) f ( ) 45. Δίνεται η συνάρτηση f() = - -. ii) Να βρείτε την τιμή της παράστασης : Α= f()-f)-) iii) Να λύσετε την εξίσωση: f() = iv) Να γράψετε τον τύπο της f χωρίς το σύμβολο της απόλυτης τιμής v) Να λύσετε την ανίσωση: f ( f (4)) f( 6) f (0) Δίνεται η συνάρτηση f( ) 6. 8 ii) Να απλοποιήσετε τον τύπο της f iii) Να βρείτε τις τιμές : 9
8 α) f(), β)f(4), γ) f(-4) και δ) iv) Να λύσετε την εξίσωση: f() 0 f 47. Δίνεται η συνάρτηση f() = --. Να υπολογίσετε τα f(0), f(- ), f(α + l), f(), f(f(0)). 48. Δίνεται η συνάρτηση f ( )., 0 f( ).Να βρείτε τα f(0),f(),f(-),f() και, Δίνεται η συνάρτηση, Z f( ).Να βρείτε τα, Z f(0), f ( ), f (), f ( ) f ( ). 50. Δίνεται η συνάρτηση f() = 4. Να βρείτε τα R,τα οποία μέσω της f αντιστοιχούν στον αριθμό 5., 0 5. Δίνεται η συνάρτηση f( ). Να υπολογιστούν οι τιμές f(-), f(0), f()., 0 5. Δίνεται η συνάρτηση f με: f()= +4-. Να υπολογιστούν οι τιμές: i) f(α+β), ii) f(α ), iii) f(α), iv) f(α +) 5. Δίνεται η συνάρτηση f με f f 54. Δίνεται η συνάρτηση f()=, 0 f ( ) a,0. Να βρεθούν τα α,β αν είναι f(-)=f() και, -, (,] 55. Δίνεται η συνάρτηση f( ), (, ) i) Να βρείτε το πεδίο ορισμού της f ii) Να βρείτε τα f(0), f( ), f(l), f(π), αν 0. Υπολογίστε το f(-)-f(-) και f(α )+f(β )-f(-)., αν 0 a, Δίνεται η συνάρτηση f () = a i) Να βρείτε το πεδίο ορισμού της f. ii) Να βρείτε τα α, β ώστε f (-) = και f(l) =. a, 57. Δίνεται η συνάρτηση f () = a, i) Να βρείτε το α. 0
9 ii) Να βρείτε την f. iii) Να λύσετε την εξίσωση f () = Δίνεται η συνάρτηση f () =, R. Να λύσετε: i) την εξίσωση f () = - ii)την ανίσωση f() - f( +) < 59. Αν η συνάρτηση f: R R έχει τη μορφή: f (...) = (.. ) - (...) + να βρείτε τα f (-) και f (0) 60. Δίνεται η συνάρτηση f () = - -. Να υπολογίσετε τα: f(0), f(l), f(l- ), f(t-), f( ), f(-). 6. Δίνεται η συνάρτηση f () = -. i) Να υπολογίσετε τις παραστάσεις: f() f( ) α) 4 ii) Να λυθεί η εξίσωση: 6 -f(l)-f(0) = f() iii) Να βρείτε το α ώστε: f(α ) = 6. Δίνεται η συνάρτηση f () =. Να λύσετε: i) την εξίσωση f () = 0 ii) την εξίσωση f ( -) f () = iii) ανίσωση f () - 8f () <, στο (0, + ) 6. Δίνεται η συνάρτηση f (χ) = χ - να βρείτε το λ ώστε: i) f (λ ) = ii. f()=λ5, (,) 64. Δίνεται η συνάρτηση: f ( ), [,5)., [5,0) i) Να βρείτε το πεδίο ορισμού της f. β) f ( h) f () h ii) Να βρείτε αν υπάρχουν τα: f(-l), f(5 + ), f(), f() iii)να λύσετε την εξίσωση: f() + f (0) = 0 a, 65. Δίνεται η συνάρτηση f( ) 4 a, i) Να βρείτε το πεδίο ορισμού της f. ii) Να βρείτε τα α, β ώστε: f (0) + f () = 0 και f () = 64. iii)για α = 4 και β = 0 να λύσετε την εξίσωση: f(l) = f, 66. Έστω η συνάρτηση: f () =. Να βρείτε τους αριθμούς, f, f (-), f( ), f, f(l) 4
10 67. Αν είναι συνάρτηση η f () = iv) το α, v) τον τύπο της f, vi) τα f ( 5 ), f 5 vii) να λύσετε την εξίσωση f() = 4., a, να βρείτε: 68. Έστω η συνάρτηση: f () = a,. Αν f() =0, να βρείτε τα α και β., Προσδιορισμός παραμέτρου 69. Δίνεται η συνάρτηση f ( ) a για την οποία ισχύει f(4)=6 i) Να βρείτε τον αριθμό α ii) Να βρείτε τις τιμές f (-), f (-),f(0) και f() iii) Να λύσετε την εξίσωση f() = iv) Να λύσετε την ανίσωση f() <6 70. Δίνεται η συνάρτηση f ( ) a για την οποία ισχύει f(6)=9 i) Να βρείτε τον αριθμό α και το πεδίο ορισμού της f ii) Να βρείτε τις τιμές f (-) και f() 7. Δίνεται η συνάρτηση f ( ) a για την οποία ισχύει f(6)=9 i) Να βρείτε τον αριθμό α και το πεδίο ορισμού της f ii) Να βρείτε τις τιμές f (-) και f () a 7. Δίνεται η συνάρτηση f( ) για την οποία ισχύει f()=- i) Να βρείτε τον αριθμό α και το πεδίο ορισμού της f ii) Να βρείτε τις τιμές f (4) και f (-6) a 7. Δίνεται η συνάρτηση f( ) 4 i) Ποιο είναι το πεδίο ορισμού της f ii) Να βρείτε τον αριθμό α iii) Να λύσετε την εξίσωση f( ) iv) Να λύσετε την ανίσωση f() 0 για την οποία ισχύει f(-5)=- a 5, 74. Δίνεται η συνάρτηση f( ) για την οποία ισχύει f(-)= και f(5)=0., i) Να βρείτε τους αριθμούς α και β 5 ii) Να βρείτε τις τιμές f, f (),f() και f(4) iii)να λύσετε την εξίσωση f () f ( f ()) f ( 0) 0
11 75. Δίνεται η συνάρτηση f ( ) για την οποία ισχύει f()+ f(5)=7. i) Να βρείτε την τιμή του αριθμού λ ii) Να εξετάσετε αν οι αριθμοί 8 και - ανήκουν στο σύνολο τιμών της f iii) Να λύσετε την ανίσωση f() > Δίνεται η συνάρτηση f ( ) a για την οποία ισχύει f(-)=6. i) Να βρείτε τον αριθμό α ii) Θεωρούμε αριθμό β για τον οποίο ισχύει : f( ) f( ) 4 iii) Να λύσετε την ανίσωση f(+β) + f(-4) β. 77. Δίνεται η συνάρτηση f () για την οποία ισχύει f(0)=6 και f(-)=. i) Να βρείτε τους αριθμούς α και β f( ) f( ) ii) Να υπολογίσετε την τιμή της παράστασης: f( ) iii) Να λύσετε την ανίσωση f( f( 5)) 5. a, 78. Δίνεται η συνάρτηση f( ) a 8, Να βρείτε τον αριθμό α. για την οποία ισχύει f(-)= και f(5)=0. Προσδιορισμός τύπου συνάρτησης 79. Η εκτύπωση ευχετηρίων καρτών συμπεριλαμβάνει σταθερή χρέωση 0,90 καθώς και 0,0 για κάθε κάρτα που τυπώνεται. Σύμφωνα με τα παραπάνω,να βρείτε τη συνάρτηση που αποδίδει κάθε φορά το κόστος της εκτύπωσης σε σχέση με τον αριθμό των καρτών. 80. Από ένα τετράγωνο ΑΒΓΔ πλευράς 0cm κόβουμε ένα κομμάτι ΓΕΖΗ σχήματος ορθογωνίου,με διαστάσεις 4cm και cm, όπως φαίνεται στο διπλανό σχήμα. i) Να εκφράσετε το εμβαδόν του χρωματισμένου χωρίου σαν συνάρτηση του ii) να βρείτε το, ώστε το εμβαδόν του χρωματισμένου χωρίου να είναι 68 cm. Α 0 cm 4 cm Ζ cm Η Β Δ Ε Γ Ε 8. Στο επόμενο σχήμα είναι ΑΕ=4 cm και ΓΔ= cm,ενώ το τμήμα ΑΓ έχει μήκος 8 cm και το σημείο Β κινείται πάνω σ αυτό. Να εκφράσετε σαν συνάρτηση του : i) το εμβαδόν του χρωματισμένου χωρίου ii) Το μήκος ΕΒ+ΒΔ 4 cm Δ cm A cm B Γ
12 8. Σε μια κοινότητα όλοι οι καταναλωτές νερού πληρώνουν 6 πάγιο κάθε μήνα,ανεξαρτήτως αν καταναλώνουν ή όχι νερό.για τα πρώτα m νερού πληρώνουν 0,60 / m.για κάθε m επιπλέον από τα m πληρώνουν 0,80 / m.να βρεθεί συνάρτηση y=f() που να δίνει το κόστος (y) του νερού,αν σε έναν μήνα καταναλωθούν m νερό. Αποδεικτικές ασκήσεις 8. Δίνεται η συνάρτηση f ( ).Να γραφεί ο τύπος χωρίς τη χρήση απολύτων τιμών. 84. Δίνεται η συνάρτηση 5 f( ).Να γραφεί ο τύπος χωρίς τη χρήση απολύτων τιμών 85. Δίνεται η συνάρτηση f()=-5.να αποδείξετε ότι: i) f( ) f( ) f( ) 5 ii) f f f ( ) ( ) ( ) 86. Δίνεται η συνάρτηση f()=-+.να αποδείξετε ότι: f( ) f(4 ) f( ) 87. Δίνεται η συνάρτηση f()=.να αποδείξετε ότι: i) f( ) f( ) [f( ) f( )] ii) f ( ) 8 f ( ) f ( ) Δίνεται η συνάρτηση f()= +.Να αποδείξετε ότι: f( ) f( ) f( ). 89. Δίνεται η συνάρτηση f () =, α 0. Να δείξετε ότι: a f ( a) f ( ) f 90. Δίνεται η συνάρτηση f()= -.Να αποδείξετε ότι: f ( ) f ( ) f a. 9. Δίνεται η συνάρτηση f () = α + β, α 0, R. Να αποδείξετε ότι: για κάθε, y R y f ( ) f ( y) f, 9. Δίνεται η συνάρτηση f () = α, α < 0, R. Να αποδείξετε ότι: για κάθε, y R Συναρτησιακές σχέσεις f y f ( ) f ( y), 9. Δίνεται η συνάρτηση f: R R για την οποία ισχύει: f ( -) =5-8-f(+), για κάθε R. Να βρείτε την τιμή f(4). 94. Δίνεται η συνάρτηση f: R R για την οποία ισχύει f(-)=6 και η σχέση : f (+) =f()+, για κάθε R. Να βρείτε τις τιμές f(0) και f(). 95. Δίνεται η συνάρτηση f: R R για την οποία ισχύει f()=- και η σχέση : f (+5) =4+α, για κάθε R. Να βρείτε: 4
13 i) τον αριθμό α ii) τον τύπο f() της συνάρτησης 96. Δίνεται η συνάρτηση f: R R για την οποία ισχύει : f (+) =f()-(-), για κάθε R. Να βρείτε: i) την τιμή f() ii) τον τύπο f() της συνάρτησης 97. Δίνεται η συνάρτηση f: R R για την οποία ισχύει : f (-) =4-6-f(), για κάθε R. Να βρείτε: i) την τιμή f() ii) τον τύπο f() της συνάρτησης 98. Δίνεται η συνάρτηση f: R R για την οποία ισχύει: f ( -) = +, για κάθε R. Να βρείτε το f (). 99. Δίνεται η συνάρτηση f: R R για την οποία ισχύουν f(α) = και f(f(α)) = 7, να βρείτε το f(). 00. Δίνεται η συνάρτηση f : R R για την οποία ισχύει : f ( ) 6 f (997) για κάθε R. i) να βρείτε το f (997) ii) να βρείτε τον τύπο f() της συνάρτησης. 0. Δίνεται η συνάρτηση f : R R για την οποία ισχύει f ( ) 4 5 f () για κάθε R. i) να βρείτε το f () ii) να βρείτε τον τύπο f() της συνάρτησης. 0. Δίνεται η συνάρτηση f: R R για την οποία ισχύει: f ( y) = f () + f (y), για κάθε, y R. Να αποδείξετε ότι: i) f ()=0 ii) f f ( ), για κάθε Έστω η συνάρτηση f: R R για την οποία ισχύει: f ( ) f ( ), για κάθε χ R. Να βρείτε τα f(0) και f(l). 04. Έστω η συνάρτηση f για την οποία ισχύει η σχέση: f (α β) = f (α) + f (β), για κάθε α, β R i. Να εκφράσετε συναρτήσει του f(α) τους αριθμούς: f(α ), f(α ), f ( a ) ii. Να δείξετε ότι f() = 0 iii. Να εκφράσετε συναρτήσει του f(α) το f a iv. Αν f(0)=l, να υπολογίσετε τις τιμές f(00), f(0,l), f(000), f( 0 ) 05. Δίνεται συνάρτηση f για την οποία ισχύει αποδείξετε ότι η γραφική της παράσταση διέρχεται από το σημείο A,. f f για κάθε. Να 06. Δίνεται συνάρτηση f για την οποία ισχύει () f() f() για κάθε. Να αποδείξετε ότι η γραφική της παράσταση διέρχεται από την αρχή των αξόνων. 07. Δίνεται συνάρτηση f για την οποία ισχύει f y f f y για κάθε y, ότι η γραφική της παράσταση διέρχεται από την αρχή των αξόνων.. Να αποδείξετε 5
14 Συνδυαστικά θέματα a 08. Δίνεται η συνάρτηση f( ) για την οποία ισχύει f()=. i) Να βρείτε το πεδίο ορισμού της f ii) Nα βρείτε τον αριθμό α iii) Να γράψετε τον τύπο f() με πιο απλή μορφή iv) Nα λύσετε την ανίσωση f() < Δίνεται η συνάρτηση f( ) για την οποία ισχύει 9 i) Να βρείτε το πεδίο ορισμού της f ii) Nα βρείτε τον αριθμό α iii) Να γράψετε τον τύπο f() με πιο απλή μορφή iv) Nα λύσετε την εξίσωση f( ) v) Nα λύσετε την ανίσωση f( ) f (5). 4 a 0. Δίνεται η συνάρτηση f( ) για την οποία ισχύει f(-)=. i) Να βρείτε το πεδίο ορισμού της f ii) Nα βρείτε τον αριθμό α iii) Να γράψετε τον τύπο f() με πιο απλή μορφή iv) Nα λύσετε την ανίσωση f ( ) f ( ). Δίνεται η συνάρτηση f ( ) a για την οποία ισχύει f()-f(6)=4. ii) Να βρείτε το πεδίο ορισμού της f ii) Nα βρείτε τον αριθμό α 7 iii) Να μετατρέψετε το κλάσμα σε ισοδύναμο με ρητό παρονομαστή f () f(4). Δίνεται η συνάρτηση f ( ) ( ). i) Να βρείτε το πεδίο ορισμού της f ii) Να γράψετε τον τύπο f() με πιο απλή μορφή iii) να λύσετε την εξίσωση f() =.. Δίνεται η συνάρτηση f () = i) Να βρείτε το πεδίο ορισμού της f. ii) Να απλοποιηθεί ο τύπος της f. iii) Να λυθεί η ανίσωση f () < Δίνεται η συνάρτηση: f () = i) Να βρεθεί το πεδίο ορισμού Α της f. ii) Να απλοποιηθεί το τύπος της f. iii) Να λυθεί η ανίσωση f() >. 6
15 5. Δίνεται η συνάρτηση: f() = Να βρείτε το πεδίο ορισμού Α της f. i) Να απλοποιήσετε τον τύπο της f. ii) Να λυθεί η εξίσωση: f() =. iii) Να βρείτε το f ( ) με ρητό παρονομαστή. 6. Δίνεται η συνάρτηση: f ( ) (6 ) για την οποία ισχύει f(λ)=4. i) Να βρείτε τον αριθμό λ. ii) Να λύσετε την ανίσωση f( ) 7. iii) Για τους πραγματικούς αριθμούς α και β,να αποδείξετε ότι ισχύει f(α+β) = f(α)+f(β),αν και μόνο αν οι α και β είναι αντίστροφοι. 7. Δίνεται η συνάρτηση: f ( ) 8για την οποία ισχύει f(f(-))=55. i) Να βρείτε τον αριθμό λ. ii) Να βρείτε το πρόσημο των τιμών της f() για τις διάφορες τιμές του R. iii) Να βρείτε το πρόσημο της παράστασης f (0) f (0) f ( 0) f( ) iv) Να λύσετε την ανίσωση. f( ) 8. Δίνεται η συνάρτηση: f() = για την οποία ισχύει f(-4)=7. i) Να βρείτε το πεδίο ορισμού Α της f και τον αριθμό λ. ii) Να απλοποιήσετε τον τύπο της f. iii) Να βρείτε για ποιες τιμές του ορίζεται η παράσταση f(-4), iv) Να λύσετε την ανίσωση f( 4) Δίνεται η συνάρτηση: f () = i) Να βρείτε το πεδίο ορισμού Α της f. ii) Να δείξετε ότι για κάθε Α, f () = iii) Να λύσετε την εξίσωση: f () = iv) Να λύσετε την ανίσωση f() <, 0. Δίνεται η συνάρτηση f (),για την οποία ισχύει f()=- και f(f())=., i) Να βρείτε τους αριθμούς α και β. ii) Να βρείτε για ποιες τιμές του ισχύει f() = iii) Να λύσετε την ανίσωση: f (0) f (6) f ( f ( )) a,. Δίνεται η συνάρτηση f (), 7,για την οποία ισχύει f(-)=-7.
16 i) Να βρείτε τους αριθμούς α και β. ii) Να λύσετε την εξίσωση f() =-8 iii) Να μετατρέψετε το κλάσμα f( 6) f( 6) iv) Να λύσετε την ανίσωση (+) f(f(-6)). σε ισοδύναμο με ρητό παρονομαστή., [ 0,). Δίνεται η συνάρτηση f () 4, [,5) i) Να βρείτε το πεδίο ορισμού Α της f. ii) Να βρείτε τον αριθμό α iii) Να γράψετε την τιμή f ( 7) σαν κλάσμα με ρητό παρονομαστή.,. Δίνεται η συνάρτηση f () =, i) Να βρείτε το f ( ) και να το γράψετε με ρητό παρονομαστή. ii) Να βρείτε το f a a, α > 0. iii)αν f(f()) = λ 005, τότε να βρείτε το λ. 4. Δίνεται η συνάρτηση f () = f i) Να βρείτε το πεδίο ορισμού Α της f. ii) Να λύσετε τις εξισώσεις : α) f (5) f (0) f () β) γ) f f ( ) () 0 f (4) f f f [ ( 4) f()] (4) (), ( 5, ) 4, [4,8) ( ), [, 4).Οι αριθμοί f ( 0) και f(-4) είναι αντίστροφοι. 5. Δίνεται η συνάρτηση: f () = και η εξίσωση -+=0 ().Ισχύει : f ( ),όπου Δ η a 6 διακρίνουσα της εξίσωσης () i) Να βρείτε τον αριθμό α και το πεδίο ορισμού Α της f. ii) Αν και οι ρίζες της εξίσωσης (),να σχηματίσετε εξίσωση ου βαθμού,που να έχει ρίζες τους αριθμούς :f() και f() 6. Δίνεται η συνάρτηση: f ( ) 5. i) Να αποδείξετε ότι η εξίσωση f() = 0 έχει δύο λύσεις πραγματικές και άνισες για κάθε λ R. ii) Να βρείτε την τιμή του λ,ώστε για τις ρίζες και της εξίσωσης f() = 0 να ισχύει : iii) Για την τιμή του λ που βρήκατε στο ερώτημα (ii),να λύσετε τις ανισώσεις α) f ( ) f ( ) f ( ) β) f ( ) 8
17 , 7. Δίνεται η συνάρτηση f (), i) Να βρείτε τους αριθμούς α και β. ii) Να λύσετε την εξίσωση : f ( ) 4.,για την οποία ισχύουν f(-)= και f()=.. 4, 8. Δίνεται η συνάρτηση f () a,όπου α R.Γνωρίζουμε ότι η εξίσωση :, 8 f ( ) f (75) 0 () έχει μοναδική ρίζα. i) Να αποδείξετε ότι α=-. ii) Θεωρούμε τα ενδεχόμενα Α και Β ενός δειγματικού χώρου Ω για τα οποία ισχύουν: ( ) f (4),f(P(A))=0 και f ( ( )).Nα βρείτε την πιθανότητα Ρ(Β). 9
AΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ
 http://1lyk-ag-dimitr.att.sch.gr/ AΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ ΙΑΤΑΞΗ: 1. Έστω ότι α < β και γ < δ. Να αποδείξετε ότι: αγ αδ βγ + βδ > 0 2. Αν α -1, δείξτε ότι α 3 + 1 α 2 + α 3. Αν x>1 δείξτε ότι: 2x 3
http://1lyk-ag-dimitr.att.sch.gr/ AΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ ΙΑΤΑΞΗ: 1. Έστω ότι α < β και γ < δ. Να αποδείξετε ότι: αγ αδ βγ + βδ > 0 2. Αν α -1, δείξτε ότι α 3 + 1 α 2 + α 3. Αν x>1 δείξτε ότι: 2x 3
1. Nα λυθούν οι ανισώσεις. 2. Nα λυθούν οι ανισώσεις. 3. Nα βρεθούν οι κοινές λύσεις των ανισώσεων: 4. Nα βρεθούν οι κοινές λύσεις των ανισώσεων:
 ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΑΝΙΣΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 4 ο ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ. Nα λυθούν οι ανισώσεις α) 4 β) 4. Nα λυθούν οι ανισώσεις ( )( ) α) + > - (+) β). Nα βρεθούν οι κοινές λύσεις των ανισώσεων: ( ) ( ) 8 4 8 και
ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΑΝΙΣΩΣΕΙΣ ΚΕΦΑΛΑΙΟ 4 ο ΑΣΚΗΣΕΙΣ ΓΙΑ ΛΥΣΗ. Nα λυθούν οι ανισώσεις α) 4 β) 4. Nα λυθούν οι ανισώσεις ( )( ) α) + > - (+) β). Nα βρεθούν οι κοινές λύσεις των ανισώσεων: ( ) ( ) 8 4 8 και
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ ΚΑΤΑΚΟΡΥΦΗ-ΟΡΙΖΟΝΤΙΑ ΜΕΤΑΤΟΠΙΣΗ ΚΑΜΠΥΛΗΣ Να σχεδιάσετε στο ίδιο σύστημα αξόνων τις γραφικές παραστάσεις των συναρτήσεων: f ()=, g()= +3,h()= -3 Να σχεδιάσετε στο ίδιο σύστημα
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ ΚΑΤΑΚΟΡΥΦΗ-ΟΡΙΖΟΝΤΙΑ ΜΕΤΑΤΟΠΙΣΗ ΚΑΜΠΥΛΗΣ Να σχεδιάσετε στο ίδιο σύστημα αξόνων τις γραφικές παραστάσεις των συναρτήσεων: f ()=, g()= +3,h()= -3 Να σχεδιάσετε στο ίδιο σύστημα
ii) Να ποια τιμή του ώστε η εξίσωση (1) έχει μία διπλή πραγματική ρίζα; Έπειτα να βρεθεί η ρίζα αυτή. Ασκήσεις Άλγεβρας
 . Δίνεται η εξίσωση, (). i) Να βρεθεί ο αριθμός ώστε η εξίσωση () να έχει μία τουλάχιστον πραγματική ρίζα. ii) Να βρεθεί ο αριθμός ώστε η εξίσωση () να έχει δύο ίσες πραγματικές ρίζες. iii) Να βρεθεί ο
. Δίνεται η εξίσωση, (). i) Να βρεθεί ο αριθμός ώστε η εξίσωση () να έχει μία τουλάχιστον πραγματική ρίζα. ii) Να βρεθεί ο αριθμός ώστε η εξίσωση () να έχει δύο ίσες πραγματικές ρίζες. iii) Να βρεθεί ο
ΘΕΜΑΤΑ ΘΕΜΑ 1. α) Να λύσετε την εξίσωση : 2 2 2x. β) Αν α είναι η ϑετική εξίσωσης του ερωτήµατος (α), να λύσετε την ανίσωση : 1 x < α.
 ΘΕΜΑΤΑ ΘΕΜΑ 6 3 α) Να λύσετε την εξίσωση : 3 β) Αν α είναι η ϑετική εξίσωσης του ερωτήµατος (α), να λύσετε την ανίσωση : < α. ΘΕΜΑ α) Να λύσετε την ανίσωση : + < 7. β) Αν ο είναι λύση της ανίσωσης του
ΘΕΜΑΤΑ ΘΕΜΑ 6 3 α) Να λύσετε την εξίσωση : 3 β) Αν α είναι η ϑετική εξίσωσης του ερωτήµατος (α), να λύσετε την ανίσωση : < α. ΘΕΜΑ α) Να λύσετε την ανίσωση : + < 7. β) Αν ο είναι λύση της ανίσωσης του
1, 2, Β 3, 2,λ. 7, να 2 βρείτε την τιμή του k. x x y y Α)Να βρείτε τις τιμές των x,y για τις οποίες ορίζεται η παράσταση. Β)Να αποδείξετε ότι Α=-1
 ,, Β,,λ. Δίνονται τα σημεία Β.Αν τα Α,Β είναι συμμετρικά ως προς τον άξονα y y να βρείτε το λ. Β. Βρείτε τις τιμές του λ, ώστε το σημείο Β να βρίσκεται στο ο τεταρτημόριο του ορθοκανονικού συστήματος.
,, Β,,λ. Δίνονται τα σημεία Β.Αν τα Α,Β είναι συμμετρικά ως προς τον άξονα y y να βρείτε το λ. Β. Βρείτε τις τιμές του λ, ώστε το σημείο Β να βρίσκεται στο ο τεταρτημόριο του ορθοκανονικού συστήματος.
3. α) Να λύσετε την εξίσωση x 2 = 3. β) Να σχηματίσετε εξίσωση δευτέρου βαθμού με ρίζες, τις ρίζες της εξίσωσης του α) ερωτήματος.
 . Δίνεται η εξίσωση λ + 4(λ ) = 0, με παράμετρο λ R α) Να βρείτε τη διακρίνουσα της εξίσωσης. β) Να αποδείξετε ότι η παραπάνω εξίσωση έχει ρίζες πραγματικές για κάθε λ R. γ) Αν, είναι οι ρίζες της παραπάνω
. Δίνεται η εξίσωση λ + 4(λ ) = 0, με παράμετρο λ R α) Να βρείτε τη διακρίνουσα της εξίσωσης. β) Να αποδείξετε ότι η παραπάνω εξίσωση έχει ρίζες πραγματικές για κάθε λ R. γ) Αν, είναι οι ρίζες της παραπάνω
ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ. 1.Δίνεται η εξίσωση f x x 4x. Να βρείτε την τιμή του πραγματικού αριθμού λ για την οποία η
 ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ Δίνεται η εξίσωση fx x 4x Να βρείτε την τιμή του πραγματικού αριθμού λ για την οποία η εξίσωση f x 0 έχει: α) ρίζα το β) δύο ρίζες πραγματικές και άνισες γ) ρίζες ετερόσημες δ) Αν 3,
ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ Δίνεται η εξίσωση fx x 4x Να βρείτε την τιμή του πραγματικού αριθμού λ για την οποία η εξίσωση f x 0 έχει: α) ρίζα το β) δύο ρίζες πραγματικές και άνισες γ) ρίζες ετερόσημες δ) Αν 3,
6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ ΣΥΝΑΡΤΗΣΗΣ Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία (κανόνας), με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ακριβώς ένα στοιχείο
6.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ ΣΥΝΑΡΤΗΣΗΣ Συνάρτηση από ένα σύνολο Α σε ένα σύνολο Β λέγεται μια διαδικασία (κανόνας), με την οποία κάθε στοιχείο του συνόλου Α αντιστοιχίζεται σε ακριβώς ένα στοιχείο
ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ. α) Το σημείο (-1,1) ανήκει στη γραφική παράσταση της f; α) Να βρεθεί η τιμή του α, ώστε η τιμή της f στο χ 0 =2 να είναι 1.
 Γ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 1.Δίνεται η συνάρτηση f()= 4 1 α) Το σημείο (-1,1) ανήκει στη γραφική παράσταση της f; β) Αν χ=, ποια είναι η τιμή της f; γ) Αν f()=1, ποια είναι
Γ ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΓΕΝΙΚΗΣ ΠΑΙΔΕΙΑΣ ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ 1.Δίνεται η συνάρτηση f()= 4 1 α) Το σημείο (-1,1) ανήκει στη γραφική παράσταση της f; β) Αν χ=, ποια είναι η τιμή της f; γ) Αν f()=1, ποια είναι
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ - ΠΑΡΑΡΤΗΜΑ ΔΩΔΕΚΑΝΗΣΟΥ
 ΘΕΜΑ 1 Ένα Λύκειο έχει 400 μαθητές από τους οποίους οι 00 είναι μαθητές της Α τάξης. Αν επιλέξουμε τυχαία ένα μαθητή, η πιθανότητα να είναι μαθητής της Γ τάξης είναι 0%. Να βρείτε: i. Το πλήθος των μαθητών
ΘΕΜΑ 1 Ένα Λύκειο έχει 400 μαθητές από τους οποίους οι 00 είναι μαθητές της Α τάξης. Αν επιλέξουμε τυχαία ένα μαθητή, η πιθανότητα να είναι μαθητής της Γ τάξης είναι 0%. Να βρείτε: i. Το πλήθος των μαθητών
ΑΣΚΗΣΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ (1o Γ Λυκείου) να ανήκουν στη γραφική παράσταση της συνάρτησης f( x)
 ΑΣΚΗΣΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ (o Γ Λυκείου).Να βρεθούν οι τιμές των α, β R ώστε: Α) τα σημεία (, ),(, ) να ανήκουν στη γραφική παράσταση της συνάρτησης α +β. Β)τα σημεία ( 0, ),( e, ) να ανήκουν στην γραφική παράσταση
ΑΣΚΗΣΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ (o Γ Λυκείου).Να βρεθούν οι τιμές των α, β R ώστε: Α) τα σημεία (, ),(, ) να ανήκουν στη γραφική παράσταση της συνάρτησης α +β. Β)τα σημεία ( 0, ),( e, ) να ανήκουν στην γραφική παράσταση
ΘΕΜΑ 2 Αν Α, Β είναι ενδεχόμενα ενός δειγματικού χώρου Ω με Ρ(Α ) = 3Ρ(Α), Ρ(Β ) = 1/3 και () 3()
 ΘΕΜΑ 1 Ένα Λύκειο έχει 400 μαθητές από τους οποίους οι 00 είναι μαθητές της Α τάξης Αν επιλέξουμε τυχαία ένα μαθητή, η πιθανότητα να είναι μαθητής της Γ τάξης είναι 0% Να βρείτε: i Το πλήθος των μαθητών
ΘΕΜΑ 1 Ένα Λύκειο έχει 400 μαθητές από τους οποίους οι 00 είναι μαθητές της Α τάξης Αν επιλέξουμε τυχαία ένα μαθητή, η πιθανότητα να είναι μαθητής της Γ τάξης είναι 0% Να βρείτε: i Το πλήθος των μαθητών
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
 Άσκηση 1102 Δίνονται δύο ενδεχόμενα ενός δειγματικού χώρου Ω και οι πιθανότητες α) Να υπολογίσετε την (Μονάδες 9) β) i) Να υπολογίσετε με διάγραμμα Venn και να γράψετε στη γλώσσα των συνόλων το ενδεχόμενο:
Άσκηση 1102 Δίνονται δύο ενδεχόμενα ενός δειγματικού χώρου Ω και οι πιθανότητες α) Να υπολογίσετε την (Μονάδες 9) β) i) Να υπολογίσετε με διάγραμμα Venn και να γράψετε στη γλώσσα των συνόλων το ενδεχόμενο:
a = f( x ) =. (Μονάδες 8) 2 = =,από όπου προκύπτει ( υψώνοντας στο τετράγωνο ), x =, επομένως x = 0 x = ή Άσκηση 4679 Δίνεται η συνάρτηση:
 Άσκηση 4679 Δίνεται η συνάρτηση: a = + 4 f( x) x x α) Να βρείτε τις τιμές του πραγματικού αριθμού α, ώστε το πεδίο ορισμού της συνάρτησης f να είναι το σύνολο. (Μονάδες 0) β) Αν είναι γνωστό ότι η γραφική
Άσκηση 4679 Δίνεται η συνάρτηση: a = + 4 f( x) x x α) Να βρείτε τις τιμές του πραγματικού αριθμού α, ώστε το πεδίο ορισμού της συνάρτησης f να είναι το σύνολο. (Μονάδες 0) β) Αν είναι γνωστό ότι η γραφική
ΕΛΛΗΝΙΚΗ ΜΑΘΗΜΑΤΙΚΗ ΕΤΑΙΡΕΙΑ - ΠΑΡΑΡΤΗΜΑ ΔΩΔΕΚΑΝΗΣΟΥ
 ΘΕΜΑ 1 Ένα Λύκειο έχει 400 μαθητές από τους οποίους οι 00 είναι μαθητές της Α τάξης Αν επιλέξουμε τυχαία ένα μαθητή, η πιθανότητα να είναι μαθητής της Γ τάξης είναι 0% Να βρείτε: i Το πλήθος των μαθητών
ΘΕΜΑ 1 Ένα Λύκειο έχει 400 μαθητές από τους οποίους οι 00 είναι μαθητές της Α τάξης Αν επιλέξουμε τυχαία ένα μαθητή, η πιθανότητα να είναι μαθητής της Γ τάξης είναι 0% Να βρείτε: i Το πλήθος των μαθητών
Φεργαδιώτης Αθανάσιος ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΤΗΝ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ. Θέμα 2 ο (150)
 Φεργαδιώτης Αθανάσιος ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΤΗΝ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Θέμα ο (150) -- Τράπεζα θεμάτων Άλγεβρας Α Λυκείου Φεργαδιώτης Αθανάσιος -3- Τράπεζα θεμάτων Άλγεβρας Α Λυκείου Φεργαδιώτης Αθανάσιος ΚΕΦΑΛΑΙΟ
Φεργαδιώτης Αθανάσιος ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ ΣΤΗΝ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ Θέμα ο (150) -- Τράπεζα θεμάτων Άλγεβρας Α Λυκείου Φεργαδιώτης Αθανάσιος -3- Τράπεζα θεμάτων Άλγεβρας Α Λυκείου Φεργαδιώτης Αθανάσιος ΚΕΦΑΛΑΙΟ
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - 2 ο ΘΕΜΑ
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ ο : ΠΙΘΑΝΟΤΗΤΕΣ. Ένα τηλεοπτικό παιχνίδι παίζεται με ζεύγη αντιπάλων των δυο φύλων. Στο παιχνίδι συμμετέχουν άντρες: ο Δημήτρης (Δ), ο Κώστας (Κ), ο Μιχάλης (Μ) και γυναίκες:
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ - ο ΘΕΜΑ ΚΕΦΑΛΑΙΟ ο : ΠΙΘΑΝΟΤΗΤΕΣ. Ένα τηλεοπτικό παιχνίδι παίζεται με ζεύγη αντιπάλων των δυο φύλων. Στο παιχνίδι συμμετέχουν άντρες: ο Δημήτρης (Δ), ο Κώστας (Κ), ο Μιχάλης (Μ) και γυναίκες:
ΘΕΜΑ 2. βρείτε. (Μονάδες 15) με διαφορά ω.
 ΘΕΜΑ ΘΕΜΑ Έστω α, β πραγµατικοί αριθµοί για τους οποίους ισχύουν: α β = 4 και αβ + αβ = 0 α) Να αποδείξετε ότι: α + β = 5. (Μονάδες 0) β) Να κατασκευάσετε εξίσωση ου βαθµού µε ρίζες τους αριθµούς α, β
ΘΕΜΑ ΘΕΜΑ Έστω α, β πραγµατικοί αριθµοί για τους οποίους ισχύουν: α β = 4 και αβ + αβ = 0 α) Να αποδείξετε ότι: α + β = 5. (Μονάδες 0) β) Να κατασκευάσετε εξίσωση ου βαθµού µε ρίζες τους αριθµούς α, β
( 2) 1 0,. Αν ρ 1, ρ 2 οι ρίζες της (ε) και
 ΘΕΜΑ ο Δίνεται η συνάρτηση f με τύπο : f( ) α. Να βρείτε το πεδίο ορισμού της. β. Να βρείτε τα σημεία τομής της με τους άξονες αν υπάρχουν. γ. Αν α, β ρίζες της εξίσωσης: ΘΕΜΑ ο f ( ), να δείξετε ότι αβ+=0.
ΘΕΜΑ ο Δίνεται η συνάρτηση f με τύπο : f( ) α. Να βρείτε το πεδίο ορισμού της. β. Να βρείτε τα σημεία τομής της με τους άξονες αν υπάρχουν. γ. Αν α, β ρίζες της εξίσωσης: ΘΕΜΑ ο f ( ), να δείξετε ότι αβ+=0.
Άλγεβρα Α Λυκείου. Στέλιος Μιχαήλογλου
 Άλγεβρα Α Λυκείου Στέλιος Μιχαήλογλου wwwaskisopolisgr Άλγεβρα Α Λυκείου Οι πράξεις των πραγματικών αριθμών και οι ιδιότητες τους Αν οι αριθμοί α,β είναι αντίστροφοι, να αποδείξετε ότι: 7 4 : 8 0 7 Να
Άλγεβρα Α Λυκείου Στέλιος Μιχαήλογλου wwwaskisopolisgr Άλγεβρα Α Λυκείου Οι πράξεις των πραγματικών αριθμών και οι ιδιότητες τους Αν οι αριθμοί α,β είναι αντίστροφοι, να αποδείξετε ότι: 7 4 : 8 0 7 Να
Α Λυκείου Άλγεβρα Τράπεζα Θεμάτων Το Δεύτερο Θέμα
 Α Λυκείου Άλγεβρα Τράπεζα Θεμάτων Το Δεύτερο Θέμα Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον εκατοστό
Α Λυκείου Άλγεβρα Τράπεζα Θεμάτων Το Δεύτερο Θέμα Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον εκατοστό
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ ΤΟΥ ΚΕΦΑΛΑΙΟΥ 4
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ ΤΟΥ ΚΕΦΑΛΑΙΟΥ 4 ΛΥΣΗ ΤΗΣ ΕΞΙΣΩΣΗΣ α + β + γ = 0 α 0 Η ΕΝΝΟΙΑ ΤΗΣ ΙΑΚΡΙΝΟΥΣΑΣ 1. Να λυθούν οι παρακάτω εξισώσεις ως προς ή y: α) - 4 = 0 β) 3 = 4 γ) + - 15 = 0 δ) 5-18 -
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑ Ι ΑΚΤΙΚΗ ΕΝΟΤΗΤΑ ΤΟΥ ΚΕΦΑΛΑΙΟΥ 4 ΛΥΣΗ ΤΗΣ ΕΞΙΣΩΣΗΣ α + β + γ = 0 α 0 Η ΕΝΝΟΙΑ ΤΗΣ ΙΑΚΡΙΝΟΥΣΑΣ 1. Να λυθούν οι παρακάτω εξισώσεις ως προς ή y: α) - 4 = 0 β) 3 = 4 γ) + - 15 = 0 δ) 5-18 -
Άλγεβρα Α Λυκείου. Επαναληπτικά θέματα από διαγωνίσματα ΟΕΦΕ Πραγματικοί αριθμοί
 wwwaskisopolisgr Άλγεβρα Α Λυκείου Επαναληπτικά θέματα από διαγωνίσματα ΟΕΦΕ 006-08 Δίνεται ότι και y Πραγματικοί αριθμοί α) i Να βρεθούν τα όρια μεταξύ των οποίων περιέχεται το ii Να βρεθούν τα όρια μεταξύ
wwwaskisopolisgr Άλγεβρα Α Λυκείου Επαναληπτικά θέματα από διαγωνίσματα ΟΕΦΕ 006-08 Δίνεται ότι και y Πραγματικοί αριθμοί α) i Να βρεθούν τα όρια μεταξύ των οποίων περιέχεται το ii Να βρεθούν τα όρια μεταξύ
ΣΤ ΕΝΟΤΗΤΑ. Βασικές έννοιες των συναρτήσεων. ΣΤ.1 (6.1 παρ/φος σχολικού βιβλίου) ΣΤ.2 (6.2 παρ/φος σχολικού βιβλίου)
 ΣΤ ΕΝΟΤΗΤΑ Βασικές έννοιες των συναρτήσεων ΣΤ. (6. παρ/φος σχολικού βιβλίου) Η έννοια της συνάρτησης ΣΤ. (6. παρ/φος σχολικού βιβλίου) Γραφική παράσταση συνάρτησης ΣΤ.3 (6.3 παρ/φος σχολικού βιβλίου) Η
ΣΤ ΕΝΟΤΗΤΑ Βασικές έννοιες των συναρτήσεων ΣΤ. (6. παρ/φος σχολικού βιβλίου) Η έννοια της συνάρτησης ΣΤ. (6. παρ/φος σχολικού βιβλίου) Γραφική παράσταση συνάρτησης ΣΤ.3 (6.3 παρ/φος σχολικού βιβλίου) Η
ΘΕΜΑ 2. Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7,
 Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον εκατοστό όρο της. (Μονάδες 15) β) Να αποδείξετε ότι
Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον εκατοστό όρο της. (Μονάδες 15) β) Να αποδείξετε ότι
1. Να χαρακτηρίσετε τις παρακάτω προτάσεις με Σωστό (Σ) ή Λάθος (Λ). i)
 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΡΙΖΕΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΑΣΚΗΣΕΙΣ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ Να χαρακτηρίσετε τις παρακάτω προτάσεις με Σωστό (Σ) ή Λάθος (Λ), 0 i Αν αβ 0 τότε Αν β 0 τότε Αν α 0 τότε v Αν α 0 τότε v Αν α 0 τότε
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΡΙΖΕΣ ΠΡΑΓΜΑΤΙΚΩΝ ΑΡΙΘΜΩΝ ΑΣΚΗΣΕΙΣ ΑΝΤΙΚΕΙΜΕΝΙΚΟΥ ΤΥΠΟΥ Να χαρακτηρίσετε τις παρακάτω προτάσεις με Σωστό (Σ) ή Λάθος (Λ), 0 i Αν αβ 0 τότε Αν β 0 τότε Αν α 0 τότε v Αν α 0 τότε v Αν α 0 τότε
ΣΥΝΑΡΤΗΣΕΙΣ. 3. Μια μπάλα πέφτει από την κορυφή ενός πυργου. Το ύψος στο οποίο βρίσκετε μετά από t sec δίνεται από τη συνάρτηση f () x 75 3
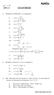 ΦΥΛ ΣΥΝΑΡΤΗΣΕΙΣ. Να βρεθούν τα Πεδία Ορισμων συναρτήσεων: i) f () 4 f () i f () 4 f () 6 5 v) f () 9 vi) f () v f () log() vi f () 4, i) f () 8, Να βρεθούν επίσης οι τιμές : n f ( 4),( f ),( f0),(),(0),(
ΦΥΛ ΣΥΝΑΡΤΗΣΕΙΣ. Να βρεθούν τα Πεδία Ορισμων συναρτήσεων: i) f () 4 f () i f () 4 f () 6 5 v) f () 9 vi) f () v f () log() vi f () 4, i) f () 8, Να βρεθούν επίσης οι τιμές : n f ( 4),( f ),( f0),(),(0),(
ΑΝΙΣΩΣΕΙΣ 2ου ΒΑΘΜΟΥ
 ΑΝΙΣΩΣΕΙΣ ου ΒΑΘΜΟΥ Αν έχω τριώνυμο της μορφής :,. Υπολογίζω την Διακρίνουσα 4 Αν Δ> τότε η εξίσωση έχει άνισες ρίζες έστω Ομόσημο του α Ετερόσημο του α, τότε: Ομόσημο του α Αν Δ= τότε η εξίσωση έχει διπλή
ΑΝΙΣΩΣΕΙΣ ου ΒΑΘΜΟΥ Αν έχω τριώνυμο της μορφής :,. Υπολογίζω την Διακρίνουσα 4 Αν Δ> τότε η εξίσωση έχει άνισες ρίζες έστω Ομόσημο του α Ετερόσημο του α, τότε: Ομόσημο του α Αν Δ= τότε η εξίσωση έχει διπλή
τότε για κάθε αριθμό ξ μεταξύ των f(α) και f(β) υπάρχει τουλάχιστον ένας x0 (α, β) τέτοιος ώστε να ισχύει f(x0)=ξ. Μονάδες 15
 ΔΙΑΓΩΝΙΣΜΑ ΣΤΑ ΟΡΙΑ ΚΑΙ ΣΤΗ ΣΥΝΕΧΕΙΑ ΘΕΜΑ o Α Να αποδείξετε ότι, αν μία συνάρτηση f είναι συνεχής στο κλειστό διάστημα [α, β] και f(α)f(β), τότε για κάθε αριθμό ξ μεταξύ των f(α) και f(β) υπάρχει τουλάχιστον
ΔΙΑΓΩΝΙΣΜΑ ΣΤΑ ΟΡΙΑ ΚΑΙ ΣΤΗ ΣΥΝΕΧΕΙΑ ΘΕΜΑ o Α Να αποδείξετε ότι, αν μία συνάρτηση f είναι συνεχής στο κλειστό διάστημα [α, β] και f(α)f(β), τότε για κάθε αριθμό ξ μεταξύ των f(α) και f(β) υπάρχει τουλάχιστον
ΘΕΜΑ 2. Δίνονται οι συναρτήσεις
 ΘΕΜΑ 2 Δίνονται οι συναρτήσεις (, x R 3 f ( x) = x και g x) = x α) Να δείξετε ότι οι γραφικές παραστάσεις των συναρτήσεων f, g τέμνονται σε τρία σημεία τα οποία και να βρείτε. (Μονάδες 13) β) Αν Α, Ο,
ΘΕΜΑ 2 Δίνονται οι συναρτήσεις (, x R 3 f ( x) = x και g x) = x α) Να δείξετε ότι οι γραφικές παραστάσεις των συναρτήσεων f, g τέμνονται σε τρία σημεία τα οποία και να βρείτε. (Μονάδες 13) β) Αν Α, Ο,
ΒΑΣΙΚΑ ΘΕΜΑΤΑ ΑΠΟ ΤΟ ΒΙΒΛΙΟ ΤΟΥ ΦΡΟΝΤΙΣΤΗΡΙΟΥ
 ΒΑΣΙΚΑ ΘΕΜΑΤΑ ΑΠΟ ΤΟ ΒΙΒΛΙΟ ΤΟΥ ΦΡΟΝΤΙΣΤΗΡΙΟΥ. Δύο ομάδες Ο, Ο παίζουν μεταξύ τους σε μια σχολική ποδοσφαιρική συνάντηση (οι αγώνες δεν τελειώνουν ποτέ με ισοπαλία). Νικήτρια θεωρείται η ομάδα που θα νικήσει
ΒΑΣΙΚΑ ΘΕΜΑΤΑ ΑΠΟ ΤΟ ΒΙΒΛΙΟ ΤΟΥ ΦΡΟΝΤΙΣΤΗΡΙΟΥ. Δύο ομάδες Ο, Ο παίζουν μεταξύ τους σε μια σχολική ποδοσφαιρική συνάντηση (οι αγώνες δεν τελειώνουν ποτέ με ισοπαλία). Νικήτρια θεωρείται η ομάδα που θα νικήσει
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ 1. Να λυθούν οι ανισώσεις: i) 2x 1 5
 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. Να λυθούν οι ανισώσεις: i) ii) iii) iv) 4 9 v) 7 4 vi). Να λυθούν οι ανισώσεις: i) ( ) 4 ii) ( ) ( ) iii) 4( ) ( ) ( ) iv) ( ) ( ) 7( ) v) 4 9 ( ). Να λυθούν οι παρακάτω
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. Να λυθούν οι ανισώσεις: i) ii) iii) iv) 4 9 v) 7 4 vi). Να λυθούν οι ανισώσεις: i) ( ) 4 ii) ( ) ( ) iii) 4( ) ( ) ( ) iv) ( ) ( ) 7( ) v) 4 9 ( ). Να λυθούν οι παρακάτω
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ
 ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
ΜΕΘΟΔΟΛΟΓΙΕΣ & ΑΣΚΗΣΕΙΣ ΓΙΑ ΤΗΝ ΑΛΓΕΒΡΑ ΤΗΣ Α ΛΥΚΕΙΟΥ Επιμέλεια : Παλαιολόγου Παύλος Μαθηματικός Αγαπητοί μαθητές. αυτό το βιβλίο αποτελεί ένα βοήθημα στην ύλη της Άλγεβρας Α Λυκείου, που είναι ένα από
ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ. και 25x i). Να κάνετε τις πράξεις στο πολυώνυμο.
 ΣΥΛΛΟΓΟΣ «Η ΕΛΛΗΝΙΚΗ ΠΑΙΔΕΙΑ» ΓΥΜΝΑΣΙΟ ΑΜΑΡΟΥΣΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΘΕΜΑ 1 Δίνονται τα πολυώνυμα (3x ) (5 x)(3x ) και 5x 9 i). Να κάνετε τις πράξεις στο πολυώνυμο. ii). Να βρείτε την τιμή του
ΣΥΛΛΟΓΟΣ «Η ΕΛΛΗΝΙΚΗ ΠΑΙΔΕΙΑ» ΓΥΜΝΑΣΙΟ ΑΜΑΡΟΥΣΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΘΕΜΑ 1 Δίνονται τα πολυώνυμα (3x ) (5 x)(3x ) και 5x 9 i). Να κάνετε τις πράξεις στο πολυώνυμο. ii). Να βρείτε την τιμή του
x y z xy yz zx, να αποδείξετε ότι x=y=z.
 ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦ. ο A. Ταυτότητες, ιδιότητες δυνάμεων, διάταξη.1 Να παραγοντοποιήσετε τις παρακάτω παραστάσεις: 1. 15a x 15a y 5a x 5a y. a x a x a x a x 3 3 4 3 3 3 3. x 4xy 16 4 y
ΑΣΚΗΣΕΙΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Α ΛΥΚΕΙΟΥ ΚΕΦ. ο A. Ταυτότητες, ιδιότητες δυνάμεων, διάταξη.1 Να παραγοντοποιήσετε τις παρακάτω παραστάσεις: 1. 15a x 15a y 5a x 5a y. a x a x a x a x 3 3 4 3 3 3 3. x 4xy 16 4 y
Στοιχεία Συναρτήσεων. 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: στ. x 1
 Στοιχεία Συναρτήσεων 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: 1 α. f() β. f() 3 6 8 3 1 γ. g() δ. g() ( 6)( 5) 4 ε. h() 4 στ. h() 4 ζ. ε. στ. 1 φ() η. 1 1 1 r() 5 6 1 r() 1 5 6 φ() 5. Στις
Στοιχεία Συναρτήσεων 1. Να βρεθεί το πεδίο ορισμού των παρακάτω συναρτήσεων: 1 α. f() β. f() 3 6 8 3 1 γ. g() δ. g() ( 6)( 5) 4 ε. h() 4 στ. h() 4 ζ. ε. στ. 1 φ() η. 1 1 1 r() 5 6 1 r() 1 5 6 φ() 5. Στις
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΑΛΓΕΒΡΑΣ Α ΛΥΚΕΙΟΥ
 ΘΕΜΑ ο Δίνεται η συνάρτηση f με τύπο : f( x) α. Να βρείτε το πεδίο ορισμού της. x x x x β. Να βρείτε τα σημεία τομής της με τους άξονες αν υπάρχουν. γ. Αν α, β ρίζες της εξίσωσης: ΘΕΜΑ ο Δίνεται η συνάρτηση
ΘΕΜΑ ο Δίνεται η συνάρτηση f με τύπο : f( x) α. Να βρείτε το πεδίο ορισμού της. x x x x β. Να βρείτε τα σημεία τομής της με τους άξονες αν υπάρχουν. γ. Αν α, β ρίζες της εξίσωσης: ΘΕΜΑ ο Δίνεται η συνάρτηση
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ. Β κύκλος
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Β κύκλος 6-7 ) Δίνεται η παραγωγίσιμη στο συνάρτηση f για την οποία ισχύει : α) Να δείξετε ότι f()=+e -, f ()+f()=, για κάθε και f()=e+ β) Να βρείτε το όριο ( y f(y)) γ) Να δείξετε
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Β κύκλος 6-7 ) Δίνεται η παραγωγίσιμη στο συνάρτηση f για την οποία ισχύει : α) Να δείξετε ότι f()=+e -, f ()+f()=, για κάθε και f()=e+ β) Να βρείτε το όριο ( y f(y)) γ) Να δείξετε
ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ. 3. Δίνονται τα σύνολα 2
 ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ ΣΥΝΟΛΑ-ΠΙΘΑΝΟΤΗΤΕΣ Έστω βασικό σύνολο Ω = {, 4, 5, 8, 0} και τα υποσύνολα του Ω, Α = {, 5, 0}, Β = {4, 8, 0} i) Να παραστήσετε με διάγραμμα Venn τα παραπάνω σύνολα ii) Να περιγράψετε
ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ ΣΥΝΟΛΑ-ΠΙΘΑΝΟΤΗΤΕΣ Έστω βασικό σύνολο Ω = {, 4, 5, 8, 0} και τα υποσύνολα του Ω, Α = {, 5, 0}, Β = {4, 8, 0} i) Να παραστήσετε με διάγραμμα Venn τα παραπάνω σύνολα ii) Να περιγράψετε
ΚΕΦΑΛΑΙΟ 4 ο : ΑΝΙΣΩΣΕΙΣ ΤΟ 2 Ο ΘΕΜΑ
 ΚΕΦΑΛΑΙΟ 4 ο : ΑΝΙΣΩΣΕΙΣ ΤΟ 2 Ο ΘΕΜΑ Άσκηση 1 Δίνονται οι ανισώσεις: 3x και 2 x α) Να βρείτε τις λύσεις τους (Μονάδες 10) β) Να βρείτε το σύνολο των κοινών τους λύσεων (Μονάδες 15) α) Έχουμε 3x 2x x 2
ΚΕΦΑΛΑΙΟ 4 ο : ΑΝΙΣΩΣΕΙΣ ΤΟ 2 Ο ΘΕΜΑ Άσκηση 1 Δίνονται οι ανισώσεις: 3x και 2 x α) Να βρείτε τις λύσεις τους (Μονάδες 10) β) Να βρείτε το σύνολο των κοινών τους λύσεων (Μονάδες 15) α) Έχουμε 3x 2x x 2
ΕΞΙΣΩΣΕΙΣ 2ου ΒΑΘΜΟΥ
 ΕΞΙΣΩΣΕΙΣ ου ΒΑΘΜΟΥ Τι ονομάζουμε εξίσωση ου βαθμού; o Εξίσωση ου βαθμού με ένα άγνωστο ονομάζουμε κάθε εξίσωση που γράφεται ή μπορεί να γραφεί στη μορφή με α π.χ 5 6 Τι ονομάζουμε εξίσωση ου βαθμού ελλιπούς
ΕΞΙΣΩΣΕΙΣ ου ΒΑΘΜΟΥ Τι ονομάζουμε εξίσωση ου βαθμού; o Εξίσωση ου βαθμού με ένα άγνωστο ονομάζουμε κάθε εξίσωση που γράφεται ή μπορεί να γραφεί στη μορφή με α π.χ 5 6 Τι ονομάζουμε εξίσωση ου βαθμού ελλιπούς
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Α ΜΕΡΟΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7-8 Α ΜΕΡΟΣ Δίνεται η παραγωγίσιμη στο συνάρτηση f για την οποία ισχύει : f ()+f()=, για κάθε και f()=e+ α) Να δείξετε ότι f()=+e -, β) Να βρείτε το όριο lim ( lim f(y)) y γ) Να δείξετε
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7-8 Α ΜΕΡΟΣ Δίνεται η παραγωγίσιμη στο συνάρτηση f για την οποία ισχύει : f ()+f()=, για κάθε και f()=e+ α) Να δείξετε ότι f()=+e -, β) Να βρείτε το όριο lim ( lim f(y)) y γ) Να δείξετε
ΚΕΦΑΛΑΙΟ 4 ο. Πίνακας διερεύνησης της εξίσωσης Εξίσωση: αx 2 +βx+γ=0 (α 0) (Ε) Έχει ΥΟ ρίζες άνισες που δίνονται από τους τύπους x 1,2 =
 ΕΞΙΩΕΙ-ΑΝΙΩΕΙ ου ΒΑΘΜΟΥ - 38 - ΚΕΦΑΑΙΟ 4 ΚΕΦΑΑΙΟ 4 ο Εξισώσεις - Ανισώσεις β βαθµού 5.1. Μορφή και διερεύνηση της εξίσωσης β βαθµού Άθροισµα και γινόµενο των ριζών της Κάθε εξίσωση β βαθµού πριν τη λύσουµε,
ΕΞΙΩΕΙ-ΑΝΙΩΕΙ ου ΒΑΘΜΟΥ - 38 - ΚΕΦΑΑΙΟ 4 ΚΕΦΑΑΙΟ 4 ο Εξισώσεις - Ανισώσεις β βαθµού 5.1. Μορφή και διερεύνηση της εξίσωσης β βαθµού Άθροισµα και γινόµενο των ριζών της Κάθε εξίσωση β βαθµού πριν τη λύσουµε,
ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ ΣΥΝΟΛΑ-ΠΙΘΑΝΟΤΗΤΕΣ
 ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ ΣΥΝΟΛΑ-ΠΙΘΑΝΟΤΗΤΕΣ Έστω βασικό σύνολο Ω = {, 4, 5, 8, 0} και τα υποσύνολα του Ω, Α = {, 5, 0}, Β = {4, 8, 0} i) Να παραστήσετε με διάγραμμα Venn τα παραπάνω σύνολα ii) Να περιγράψετε
ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ ΣΥΝΟΛΑ-ΠΙΘΑΝΟΤΗΤΕΣ Έστω βασικό σύνολο Ω = {, 4, 5, 8, 0} και τα υποσύνολα του Ω, Α = {, 5, 0}, Β = {4, 8, 0} i) Να παραστήσετε με διάγραμμα Venn τα παραπάνω σύνολα ii) Να περιγράψετε
Να αιτιολογήσετε την απάντησή σας µε τη βοήθεια και του ερωτήµατος α). ii) Να αποδείξετε ότι ισχύει η ανισότητα 1+α < 1+ α. α+α
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΑΝΙΣΩΣΕΙΣ 1. α) Να λύσετε τις ανισώσεις: x 5 3 και x x 1 0. β) Να βρείτε τις κοινές λύσεις των ανισώσεων του ερωτήµατος (α). x 1. ίνονται οι ανισώσεις: 3x 1
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΑΝΙΣΩΣΕΙΣ 1. α) Να λύσετε τις ανισώσεις: x 5 3 και x x 1 0. β) Να βρείτε τις κοινές λύσεις των ανισώσεων του ερωτήµατος (α). x 1. ίνονται οι ανισώσεις: 3x 1
Άλγεβρα Α Λυκείου Επαναληπτικές ασκήσεις
 Άλγεβρα Α Λυκείου Επαναληπτικές ασκήσεις Δημήτρης Πατσιμάς Στέλιος Μιχαήλογλου ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ ΣΥΝΟΛΑ-ΠΙΘΑΝΟΤΗΤΕΣ Έστω βασικό σύνολο Ω = {,,, 4, 5, 6,7,8,9, 0} και τα υποσύνολα του Ω, Α = {,,4,6},
Άλγεβρα Α Λυκείου Επαναληπτικές ασκήσεις Δημήτρης Πατσιμάς Στέλιος Μιχαήλογλου ΕΠΑΝΑΛΗΨΗ Α ΛΥΚΕΙΟΥ ΣΥΝΟΛΑ-ΠΙΘΑΝΟΤΗΤΕΣ Έστω βασικό σύνολο Ω = {,,, 4, 5, 6,7,8,9, 0} και τα υποσύνολα του Ω, Α = {,,4,6},
ρ πε α εμ των α ματ ών 2014 Ο Η ΡΗ Ο Ο Γ Ρ Θ μα 2ο
 ρ πε α εμ των α ματ ών 2014 Γ Ο Η ΡΗ Ο Ο Γ Ρ Θ μα 2ο Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον
ρ πε α εμ των α ματ ών 2014 Γ Ο Η ΡΗ Ο Ο Γ Ρ Θ μα 2ο Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον
( 2) 1 0,. Αν ρ 1, ρ 2 οι ρίζες της (ε) και
 ΘΕΜΑ ο Δίνεται η συνάρτηση f με τύπο : f( x) α Να βρείτε το πεδίο ορισμού της x x x x β Να βρείτε τα σημεία τομής της με τους άξονες αν υπάρχουν γ Αν α, β ρίζες της εξίσωσης: ΘΕΜΑ ο x x f ( x), να δείξετε
ΘΕΜΑ ο Δίνεται η συνάρτηση f με τύπο : f( x) α Να βρείτε το πεδίο ορισμού της x x x x β Να βρείτε τα σημεία τομής της με τους άξονες αν υπάρχουν γ Αν α, β ρίζες της εξίσωσης: ΘΕΜΑ ο x x f ( x), να δείξετε
β. Να βρείτε την πιθανότητα πραγματοποίησης καθενός από τα δύο ενδεχόμενα του ερωτήματος α).
 1.: Έννοια της Πιθανότητας Κεφάλαιο 1ο: Πιθανότητες ΑΣΚΗΣΗ 1 (_497) Ένα τηλεοπτικό παιχνίδι παίζεται με ζεύγη αντιπάλων των δυο φύλων. Στο παιχνίδι συμμετέχουν 3 άντρες: ο Δημήτρης (Δ), ο Κώστας (Κ), ο
1.: Έννοια της Πιθανότητας Κεφάλαιο 1ο: Πιθανότητες ΑΣΚΗΣΗ 1 (_497) Ένα τηλεοπτικό παιχνίδι παίζεται με ζεύγη αντιπάλων των δυο φύλων. Στο παιχνίδι συμμετέχουν 3 άντρες: ο Δημήτρης (Δ), ο Κώστας (Κ), ο
ΔΕΙΓΜΑΤΑ ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ B ΓΥΜΝΑΣΙΟΥ. 1 ο δείγμα
 ΔΕΙΓΜΑΤΑ ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ B ΓΥΜΝΑΣΙΟΥ 1 ο δείγμα Α. Θεωρία Α) Πότε ένα πολύγωνο λέγεται κανονικό; Β) Να δώσετε τον ορισμό της εγγεγραμμένης γωνίας σε κύκλο (Ο, ρ). (Να γίνει σχήμα) Γ) Ποια
ΔΕΙΓΜΑΤΑ ΘΕΜΑΤΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΘΗΜΑΤΙΚΩΝ B ΓΥΜΝΑΣΙΟΥ 1 ο δείγμα Α. Θεωρία Α) Πότε ένα πολύγωνο λέγεται κανονικό; Β) Να δώσετε τον ορισμό της εγγεγραμμένης γωνίας σε κύκλο (Ο, ρ). (Να γίνει σχήμα) Γ) Ποια
Ανισώσεις. Κώστας Γλυκός. Τράπεζα θεμάτων ΜΑΘΗΜΑΤΙΚΟΣ. εκδόσεις / 1 0 /
 Ανισώσεις Κώστας Γλυκός Τράπεζα θεμάτων ΙΙ Ι δδ ιι ι αα ίί ί ττ εε ρρ αα μμ αα θθ ήή μμ αα ττ αα 6 9 7. 3 0 0. 8 8. 8 8 Kgllykos..gr 5 / 1 0 / 0 1 6 εκδόσεις τηλ. Οικίας : 10-610.178 κινητό : 697-300.88.88
Ανισώσεις Κώστας Γλυκός Τράπεζα θεμάτων ΙΙ Ι δδ ιι ι αα ίί ί ττ εε ρρ αα μμ αα θθ ήή μμ αα ττ αα 6 9 7. 3 0 0. 8 8. 8 8 Kgllykos..gr 5 / 1 0 / 0 1 6 εκδόσεις τηλ. Οικίας : 10-610.178 κινητό : 697-300.88.88
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
Στέλιος Μιχαήλογλου - Δημήτρης Πατσιμάς
 Μεθοδική Επανάληψη www.askisopolis.gr Στέλιος Μιχαήλογλου - Δημήτρης Πατσιμάς Ε. Σύνολα i. Τι είναι το σύνολο; ii. Ποιοι είναι οι βασικοί τρόποι παράστασης συνόλων και τι γνωρίζετε γι αυτούς; iii. Πότε
Μεθοδική Επανάληψη www.askisopolis.gr Στέλιος Μιχαήλογλου - Δημήτρης Πατσιμάς Ε. Σύνολα i. Τι είναι το σύνολο; ii. Ποιοι είναι οι βασικοί τρόποι παράστασης συνόλων και τι γνωρίζετε γι αυτούς; iii. Πότε
Μαθηματικά Γ Γυμνασίου
 Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Α λ γ ε β ρ ι κ έ ς π α ρ α σ τ ά σ ε ι ς 1.1 Πράξεις με πραγματικούς αριθμούς (επαναλήψεις συμπληρώσεις) A. Οι πραγματικοί αριθμοί και οι πράξεις τους Διδακτικοί στόχοι Θυμάμαι ποιοι αριθμοί λέγονται
Ρητοί αριθμοί λέγονται οι αριθμοί που έχουν ή μπορούν να πάρουν τη μορφή
 ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ)-ΘΕΩΡΕΙΑ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμώv αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ)-ΘΕΩΡΕΙΑ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ Το σύνολο των πραγματικών αριθμών Υπενθυμίζουμε ότι το σύνολο των πραγματικών αριθμώv αποτελείται από τους ρητούς και τους άρρητους αριθμούς και παριστάνεται
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β, 8B, 9 Έστω Α ένα υποσύνολο του Ονομάζουμε
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β, 8B, 9 Έστω Α ένα υποσύνολο του Ονομάζουμε
B= πραγματοποιείται τουλάχιστον ένα από τα ενδεχόμενα Α και Β ii) B = πραγματοποιούνται ταυτόχρονα τα ενδεχόμενα Β και Γ iii)
 Πιθανότητες.3096. α) Αν Α,Β,Γ είναι τρία ενδεχόμενα ενός δειγματικού χώρου Ω ενός πειράματος τύχης που αποτελείται από απλά ισοπίθανα ενδεχόμενα, να διατυπώσετε λεκτικά τα παρακάτω ενδεχόμενα: i) A B ii)
Πιθανότητες.3096. α) Αν Α,Β,Γ είναι τρία ενδεχόμενα ενός δειγματικού χώρου Ω ενός πειράματος τύχης που αποτελείται από απλά ισοπίθανα ενδεχόμενα, να διατυπώσετε λεκτικά τα παρακάτω ενδεχόμενα: i) A B ii)
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΣΤΗ ΣΥΝΕΧΕΙΑ ΚΑΙ ΤΑ ΘΕΩΡΗΜΑΤΑ ΑΥΤΗΣ. x 0 για κάθε xεr και για την συνάρτηση g ισχύει i. Να βρείτε
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΤΑ ΣΤΗ ΣΥΝΕΧΕΙΑ ΚΑΙ ΤΑ ΘΕΩΡΗΜΑΤΑ ΑΥΤΗΣ Δίνεται η συνεχής συνάρτηση f : IR IR τέτοια ώστε f ( ) 1 για κάθε IR (1) και η γραφική της παράσταση διέρχεται από το σημείο i Να βρείτε τα κ και λ
ΕΠΑΝΑΛΗΠΤΙΚΑ ΤΑ ΣΤΗ ΣΥΝΕΧΕΙΑ ΚΑΙ ΤΑ ΘΕΩΡΗΜΑΤΑ ΑΥΤΗΣ Δίνεται η συνεχής συνάρτηση f : IR IR τέτοια ώστε f ( ) 1 για κάθε IR (1) και η γραφική της παράσταση διέρχεται από το σημείο i Να βρείτε τα κ και λ
1 ΔΙΑΓΩΝΙΣΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΛΥΚΕΙΩΝ ΤΗΣ ΡΟΔΟΥ ΤΗΣ Α ΤΑΞΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ ΔΙΑΓΩΝΙΣΜΑ 1 Ο
 1 ΔΙΑΓΩΝΙΣΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΛΥΚΕΙΩΝ ΤΗΣ ΡΟΔΟΥ ΤΗΣ Α ΤΑΞΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ ΔΙΑΓΩΝΙΣΜΑ 1 Ο ΘΕΜΑ 1 ο α) Αν χ 1, χ ρίζες της εξίσωσης αχ +βχ+γ=0, 0 να δείξετε ότι S 1 και P 1 Μον. 10 β) Έστω η συνάρτηση
1 ΔΙΑΓΩΝΙΣΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΛΥΚΕΙΩΝ ΤΗΣ ΡΟΔΟΥ ΤΗΣ Α ΤΑΞΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ ΔΙΑΓΩΝΙΣΜΑ 1 Ο ΘΕΜΑ 1 ο α) Αν χ 1, χ ρίζες της εξίσωσης αχ +βχ+γ=0, 0 να δείξετε ότι S 1 και P 1 Μον. 10 β) Έστω η συνάρτηση
- 11 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ
 - 11 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ) 1 Να βρεθεί η σχετική θέση των γραφικών παραστάσεων των συναρτήσεων f και g γα τις οποίες ισχύει: f()+1=g()+e (Η C f κάτω
- 11 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΣΥΝΑΡΤΗΣΕΙΣ (ΕΙΣΑΓΩΓΗ) 1 Να βρεθεί η σχετική θέση των γραφικών παραστάσεων των συναρτήσεων f και g γα τις οποίες ισχύει: f()+1=g()+e (Η C f κάτω
7. α) Να λύσετε την ανίσωση x 5 <4. β) Αν κάποιος αριθμός α επαληθεύει την παραπάνω ανίσωση, να αποδείξετε ότι
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΑΝΙΣΩΣΕΙΣ 1. α) Να λύσετε τις ανισώσεις: x 5 3 και x x 1 0. β) Να βρείτε τις κοινές λύσεις των ανισώσεων του ερωτήματος (α). x 1. Δίνονται οι ανισώσεις: 3x 1
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΑΝΙΣΩΣΕΙΣ 1. α) Να λύσετε τις ανισώσεις: x 5 3 και x x 1 0. β) Να βρείτε τις κοινές λύσεις των ανισώσεων του ερωτήματος (α). x 1. Δίνονται οι ανισώσεις: 3x 1
Τράπεζα Θεμάτων Άλγεβρα Α Λυκείου Κεφάλαιο 3 Θέμα 2. Επιμέλεια : Μιχάλης Γιάνναρος - Μαθηματικός
 Τράπεζα Θεμάτων Άλγεβρα Α Λυκείου Κεφάλαιο 3 Θέμα Επιμέλεια : Μιχάλης Γιάνναρος - Μαθηματικός Θεωρία ως και την 3. Ασκήσεις: -5 Θεωρία ως και την 3.3 Ασκήσεις: 6-8 Άσκηση Δίνεται η παράσταση: A= 3 5 +
Τράπεζα Θεμάτων Άλγεβρα Α Λυκείου Κεφάλαιο 3 Θέμα Επιμέλεια : Μιχάλης Γιάνναρος - Μαθηματικός Θεωρία ως και την 3. Ασκήσεις: -5 Θεωρία ως και την 3.3 Ασκήσεις: 6-8 Άσκηση Δίνεται η παράσταση: A= 3 5 +
β) Αν κάποιος αριθµός α επαληθεύει την παραπάνω ανίσωση, να αποδείξετε ότι 1 1 1 9 < α
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΑΝΙΣΩΣΕΙΣ 1. α) Να λύσετε τις ανισώσεις: x 5 3 και x x 1 0. β) Να βρείτε τις κοινές λύσεις των ανισώσεων του ερωτήµατος (α). x 1. ίνονται οι ανισώσεις: 3x 1
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΑΝΙΣΩΣΕΙΣ 1. α) Να λύσετε τις ανισώσεις: x 5 3 και x x 1 0. β) Να βρείτε τις κοινές λύσεις των ανισώσεων του ερωτήµατος (α). x 1. ίνονται οι ανισώσεις: 3x 1
ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου
 ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου Κεφάλαιο ο Αλγεβρικές Παραστάσεις ΛΕΜΟΝΙΑ ΜΠΟΥΤΣΚΟΥ Γυμνάσιο Αμυνταίου ΜΑΘΗΜΑ Α. Πράξεις με πραγματικούς αριθμούς ΑΣΚΗΣΕΙΣ ) ) Να συμπληρώσετε τα κενά ώστε στην κατακόρυφη στήλη
ΜΑΘΗΜΑΤΙΚΑ Γ Γυμνασίου Κεφάλαιο ο Αλγεβρικές Παραστάσεις ΛΕΜΟΝΙΑ ΜΠΟΥΤΣΚΟΥ Γυμνάσιο Αμυνταίου ΜΑΘΗΜΑ Α. Πράξεις με πραγματικούς αριθμούς ΑΣΚΗΣΕΙΣ ) ) Να συμπληρώσετε τα κενά ώστε στην κατακόρυφη στήλη
2 3x 4 0, να υπολογίσετε χωρίς να λύσετε την
 ΑΣΚΗΣΕΙΣ Α ΛΥΚΕΙΟΥ Κ.Κ. (θέματα προηγούμενων χρόνων) 1.Να υπολογίσετε τις τιμές των παραστάσεων : i. 16 81 6 3 ii. 64 64 64. Aν x1, xοι ρίζες της εξίσωσης x 3x 4 0, να υπολογίσετε χωρίς να λύσετε την εξίσωση,
ΑΣΚΗΣΕΙΣ Α ΛΥΚΕΙΟΥ Κ.Κ. (θέματα προηγούμενων χρόνων) 1.Να υπολογίσετε τις τιμές των παραστάσεων : i. 16 81 6 3 ii. 64 64 64. Aν x1, xοι ρίζες της εξίσωσης x 3x 4 0, να υπολογίσετε χωρίς να λύσετε την εξίσωση,
ΓΕΝΙΚΟ ΛΥΚΕΙΟ Λ. ΑΙΔΗΨΟΥ ΣΧΟΛ. ΕΤΟΣ ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ ΙΟΥΝΙΟΥ ΑΛΓΕΒΡΑ Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ
 ΓΕΝΙΚΟ ΛΥΚΕΙΟ Λ. ΑΙΔΗΨΟΥ ΣΧΟΛ. ΕΤΟΣ 01-013 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ ΙΟΥΝΙΟΥ ΑΛΓΕΒΡΑ Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Θέμα 1 ο Α. Έστω a ένας πραγματικός αριθμός. Να δώσετε τον ορισμό της απόλυτης
ΓΕΝΙΚΟ ΛΥΚΕΙΟ Λ. ΑΙΔΗΨΟΥ ΣΧΟΛ. ΕΤΟΣ 01-013 ΓΡΑΠΤΕΣ ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ ΠΕΡΙΟΔΟΥ ΜΑΪΟΥ ΙΟΥΝΙΟΥ ΑΛΓΕΒΡΑ Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ Θέμα 1 ο Α. Έστω a ένας πραγματικός αριθμός. Να δώσετε τον ορισμό της απόλυτης
Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ 1η κατηγορία: ΕΥΡΕΣΗ ΠΕΔΙΟΥ ΟΡΙΣΜΟΥ
 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ η κατηγορία: ΕΥΡΕΣΗ ΠΕΔΙΟΥ ΟΡΙΣΜΟΥ Για να βρούμε το πεδίο ορισμού μιας συνάρτησης, αρκεί να βρούμε τις τιμές του χ για τις οποίες ορίζονται οι πράξεις που αναγράφονται στο τύπο
Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ η κατηγορία: ΕΥΡΕΣΗ ΠΕΔΙΟΥ ΟΡΙΣΜΟΥ Για να βρούμε το πεδίο ορισμού μιας συνάρτησης, αρκεί να βρούμε τις τιμές του χ για τις οποίες ορίζονται οι πράξεις που αναγράφονται στο τύπο
Μαθηματικά Γενικής Παιδείας. iv) f(x)= v) f(x)= ln(x 2-4) vi) f(x) =, v) f(x) = 6 x 5. vi) vii) f(x) = ln(x 2-2) viii) f(x) = lnx 2.
 Ερωτήσεις ανάπτυξης Β. Να βρεθούν τα πεδία ορισμού των συναρτήσεων: 5 4 i) f() = ii) f()= iii) f()= iv) f()= ln( ) e v) f()= ln( -4) 4 4 vi) f() =, 5. Να βρείτε το πεδίο ορισμού των συναρτήσεων f με τύπο:
Ερωτήσεις ανάπτυξης Β. Να βρεθούν τα πεδία ορισμού των συναρτήσεων: 5 4 i) f() = ii) f()= iii) f()= iv) f()= ln( ) e v) f()= ln( -4) 4 4 vi) f() =, 5. Να βρείτε το πεδίο ορισμού των συναρτήσεων f με τύπο:
ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ
 ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: A ΑΛΓΕΒΡΑ ΘΕΜΑ A Α1. Να αποδείξετε ότι: αβ α β (Μονάδες 15) A. Χαρακτηρίστε ως Σωστό (Σ) ή Λάθος (Λ) τις ακόλουθες προτάσεις: 1. Η εξίσωση
ΘΕΜΑΤΑ ΠΡΟΑΓΩΓΙΚΩΝ ΑΠΟΛΥΤΗΡΙΩΝ ΕΞΕΤΑΣΕΩΝ ΜΑΪΟΣ ΙΟΥΝΙΟΣ ΤΑΞΗ: ΜΑΘΗΜΑ: A ΑΛΓΕΒΡΑ ΘΕΜΑ A Α1. Να αποδείξετε ότι: αβ α β (Μονάδες 15) A. Χαρακτηρίστε ως Σωστό (Σ) ή Λάθος (Λ) τις ακόλουθες προτάσεις: 1. Η εξίσωση
x 1 vii) f(x) 5 x 4 viii) 2 + γ) f (x) = στ) f (x) = e x -1 Β. Γραφική παράσταση Γ. Ίσες συναρτήσεις x 3 x 3 f(x), g(x) ιι)
 Α.Πεδίο ορισμού. Να προσδιορίσετε το πεδίο ορισμού των συναρτήσεων με τύπους ι) f() = v) f() 4 6 6 5 log 4 ii) f() = iii) f() = log ( ) iv) f() = log ( log 4(- )) vi) f() = 4 vii) f() 5 4 viii) f() ημ.
Α.Πεδίο ορισμού. Να προσδιορίσετε το πεδίο ορισμού των συναρτήσεων με τύπους ι) f() = v) f() 4 6 6 5 log 4 ii) f() = iii) f() = log ( ) iv) f() = log ( log 4(- )) vi) f() = 4 vii) f() 5 4 viii) f() ημ.
ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4. [ ] z, w. 3 f x, x 1,3 όπου 3 μιγαδικοί των οποίων οι εικόνες
![ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4. [ ] z, w. 3 f x, x 1,3 όπου 3 μιγαδικοί των οποίων οι εικόνες ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4. [ ] z, w. 3 f x, x 1,3 όπου 3 μιγαδικοί των οποίων οι εικόνες](/thumbs/55/37062184.jpg) ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4 1. i) Να δείξετε ότι υπάρχει μοναδικό 3 3 0 1, ώστε: 3 e, 1 ln 0 + 0 = 0 ii) Δίνεται ο μιγαδικός 3 z = ln + i, > 0 a) Να βρείτε την ελάχιστη απόσταση k της εικόνας του z από την αρχή
ΓΕΝΙΚΕΣ ΑΣΚΗΣΕΙΣ 4 1. i) Να δείξετε ότι υπάρχει μοναδικό 3 3 0 1, ώστε: 3 e, 1 ln 0 + 0 = 0 ii) Δίνεται ο μιγαδικός 3 z = ln + i, > 0 a) Να βρείτε την ελάχιστη απόσταση k της εικόνας του z από την αρχή
ΠΡΟΤΕΙΝΟΜΕΝΟΣ ΣΧΕΔΙΑΣΜΟΣ ΕΠΑΝΑΛΗΨΗΣ ΜΑΘΗΜΑΤΙΚΩΝ Γ ΓΥΜΝΑΣΙΟΥ
 ΕΚΠΑΙΔΕΥΤΗΡΙΑ ΓΥΜΝΑΣΙΟ ΑΜΑΡΟΥΣΙΟΥ ΠΡΟΤΕΙΝΟΜΕΝΟΣ ΣΧΕΔΙΑΣΜΟΣ ΕΠΑΝΑΛΗΨΗΣ ΜΑΘΗΜΑΤΙΚΩΝ Γ ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Επαναληπτικές Ασκήσεις (από σχολικό βιβλίο) (από βοήθημα Γ Γυμνασίου Πετσιά-Κάτσιου) Κεφάλαιο 1ο 17,
ΕΚΠΑΙΔΕΥΤΗΡΙΑ ΓΥΜΝΑΣΙΟ ΑΜΑΡΟΥΣΙΟΥ ΠΡΟΤΕΙΝΟΜΕΝΟΣ ΣΧΕΔΙΑΣΜΟΣ ΕΠΑΝΑΛΗΨΗΣ ΜΑΘΗΜΑΤΙΚΩΝ Γ ΓΥΜΝΑΣΙΟΥ ΑΛΓΕΒΡΑ Επαναληπτικές Ασκήσεις (από σχολικό βιβλίο) (από βοήθημα Γ Γυμνασίου Πετσιά-Κάτσιου) Κεφάλαιο 1ο 17,
Συνοπτική θεωρία - Τι να προσέχουμε Ασκήσεις Θέματα από Πανελλαδικές. γ) g( x) e 2. ln( x 1) 3. x x. ζ) ( x) ln(9 x2) ια) ( ) ln x 1
 Κεφ ο : Διαφορικός Λογισμός Συνοπτική θεωρία - Τι να προσέχουμε Θέματα από Πανελλαδικές Α Πεδίο ορισμού συνάρτησης (Περιορισμούς για το χ ) Όταν έχουμε κλάσμα πρέπει : παρονομαστής 0 Όταν έχουμε ρίζα πρέπει
Κεφ ο : Διαφορικός Λογισμός Συνοπτική θεωρία - Τι να προσέχουμε Θέματα από Πανελλαδικές Α Πεδίο ορισμού συνάρτησης (Περιορισμούς για το χ ) Όταν έχουμε κλάσμα πρέπει : παρονομαστής 0 Όταν έχουμε ρίζα πρέπει
1. Να προσδιορίσετε το πεδίο ορισμού των συναρτήσεων με τύπους. 2. Να βρεθεί ο λ R ώστε f(x) = ln ( x 2 +2λx+9) να έχει πεδίο ορισμού Α = R
 Α.Πεδίο ορισμού. Να προσδιορίσετε το πεδίο ορισμού των συναρτήσεων με τύπους ι) f() = 4 6 6 ii) f() = iii) f() = log ( ) iv) f() = log ( log 4(- )) v) 5 f() log vi) f() = 4 4 vii) f() 5 4 viii) f() ημ.
Α.Πεδίο ορισμού. Να προσδιορίσετε το πεδίο ορισμού των συναρτήσεων με τύπους ι) f() = 4 6 6 ii) f() = iii) f() = log ( ) iv) f() = log ( log 4(- )) v) 5 f() log vi) f() = 4 4 vii) f() 5 4 viii) f() ημ.
ΕΞΙΣΩΣΕΙΣ - 2 ου ΒΑΘΜΟΥ ΑΣΚΗΣΕΙΣ. 9). Να λυθούν οι εξισώσεις :
 ΕΞΙΣΩΣΕΙΣ - ου ΒΑΘΜΟΥ ΑΣΚΗΣΕΙΣ ). Να λυθούν οι εξισώσεις: α). + ( 3 ) 6 = 0 β). 4 ( 3 ) + 3 = 0 γ). + ( ) = 0 δ). 5 + 5 = 0 ε). 4( 3) + 5 + 6 6 = 0 στ).( + 3 ) ( 3 + ) ( 3 ) = 0 η). + (3 ) + (4 3 ) = 0
ΕΞΙΣΩΣΕΙΣ - ου ΒΑΘΜΟΥ ΑΣΚΗΣΕΙΣ ). Να λυθούν οι εξισώσεις: α). + ( 3 ) 6 = 0 β). 4 ( 3 ) + 3 = 0 γ). + ( ) = 0 δ). 5 + 5 = 0 ε). 4( 3) + 5 + 6 6 = 0 στ).( + 3 ) ( 3 + ) ( 3 ) = 0 η). + (3 ) + (4 3 ) = 0
Mαθηματικά Θετικής - Τεχνολογικής Κατεύθυνσης Γ. Λυκείου Ανάλυση Κεφ. 1 ο ΣΥΝΑΡΤΗΣΕΙΣ
 Γ. Λυκείου Ανάλυση Κεφ. ο Γ / ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΝΑΛΥΣΗ ΚΕΦΑΛΑΙΟ Ο ΣΥΝΑΡΤΗΣΕΙΣ ΙΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
Γ. Λυκείου Ανάλυση Κεφ. ο Γ / ΛΥΚΕΙΟΥ ΜΑΘΗΜΑΤΙΚΑ ΘΕΤΙΚΗΣ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ ΑΝΑΛΥΣΗ ΚΕΦΑΛΑΙΟ Ο ΣΥΝΑΡΤΗΣΕΙΣ ΙΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ ΑΝΤΙΣΤΡΟΦΗ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΟ ΣΥΝΑΡΤΗΣΗΣ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΑΝΙΣΩΣΕΙΣ Β ΒΑΘΜΟΥ. i) x 1
 ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΑΝΙΣΩΣΕΙΣ Β ΒΑΘΜΟΥ. Δίνεται το τριώνυμο : 3.Να βρείτε το πρόσημο των τιμών του τριωνύμου για : 3 4 i) 3 i 4 3. Να βρεθεί το πρόσημο των τριωνύμων : i) f ( ) 5 3 g( ) i h( ) 3. Να βρεθεί το
ΑΣΚΗΣΕΙΣ ΣΤΙΣ ΑΝΙΣΩΣΕΙΣ Β ΒΑΘΜΟΥ. Δίνεται το τριώνυμο : 3.Να βρείτε το πρόσημο των τιμών του τριωνύμου για : 3 4 i) 3 i 4 3. Να βρεθεί το πρόσημο των τριωνύμων : i) f ( ) 5 3 g( ) i h( ) 3. Να βρεθεί το
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ Β ΜΕΡΟΣ
 ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7-8 Β ΜΕΡΟΣ. Δίνεται η τέσσερις φορές παραγωγίσιμη στο συνάρτηση f τέτοια ώστε : f (4) () + f () () = ημ + συν, για κάθε και f() =, f () =, f () = - και f () () =. α) Να βρείτε τον
ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 7-8 Β ΜΕΡΟΣ. Δίνεται η τέσσερις φορές παραγωγίσιμη στο συνάρτηση f τέτοια ώστε : f (4) () + f () () = ημ + συν, για κάθε και f() =, f () =, f () = - και f () () =. α) Να βρείτε τον
Κ Ε Φ Α Λ Α Ι Ο 3 ο : Ε ξ ι σ ώ σ ε ι ς. 3.1 Εξισώσεις 1 ου Βαθμού. 3.2 Η εξίσωση x. 3.3 Εξισώσεις 2 ου Βαθμού. ρωτήσεις αντικειμενικού τύπουθέμα Α1-
 3. Εξισώσεις ου Βαθμού 3. Η εξίσωση 3.3 Εξισώσεις ου Βαθμού Διδακτικό υλικό Άλγεβρας Α Λυκείου (Κεφάλαιο 3 ο ) Κ Ε Φ Α Λ Α Ι Ο 3 ο : Ε ξ ι σ ώ σ ε ι ς ρωτήσεις αντικειμενικού τύπουθέμα Α- Εξεταστέα ύλη
3. Εξισώσεις ου Βαθμού 3. Η εξίσωση 3.3 Εξισώσεις ου Βαθμού Διδακτικό υλικό Άλγεβρας Α Λυκείου (Κεφάλαιο 3 ο ) Κ Ε Φ Α Λ Α Ι Ο 3 ο : Ε ξ ι σ ώ σ ε ι ς ρωτήσεις αντικειμενικού τύπουθέμα Α- Εξεταστέα ύλη
<Πεδία ορισμού ισότητα πράξεις σύνθεση>
 Συναρτήσεις 1 A Έστω μία συνάρτηση Να βρείτε το πεδίο ορισμού της συνάρτησης B Δίνεται η συνάρτηση Να βρείτε το πεδίο ορισμού των συναρτήσεων :, και Γ Να εξετάσετε
Συναρτήσεις 1 A Έστω μία συνάρτηση Να βρείτε το πεδίο ορισμού της συνάρτησης B Δίνεται η συνάρτηση Να βρείτε το πεδίο ορισμού των συναρτήσεων :, και Γ Να εξετάσετε
Μαθηματικά Προσανατολισμού Γ Λυκείου Κανιστράς Δημήτριος. Συναρτήσεις Όρια Συνέχεια Μια πρώτη επανάληψη Απαντήσεις των ασκήσεων.
 Άσκηση Μαθηματικά Προσανατολισμού Γ Λυκείου Κανιστράς Δημήτριος Συναρτήσεις Όρια Συνέχεια Μια πρώτη επανάληψη Απαντήσεις των ασκήσεων Μέρος ο i. Δίνεται η γνησίως μονότονη συνάρτηση f : A IR. Να αποδείξετε
Άσκηση Μαθηματικά Προσανατολισμού Γ Λυκείου Κανιστράς Δημήτριος Συναρτήσεις Όρια Συνέχεια Μια πρώτη επανάληψη Απαντήσεις των ασκήσεων Μέρος ο i. Δίνεται η γνησίως μονότονη συνάρτηση f : A IR. Να αποδείξετε
ΣΥΝΑΡΤΗΣΕΙΣ. 1.Να βρείτε το πεδίο ορισμού των συναρτήσεων: 1 1 x 4. x x x x x 5 iv) f ( x) v)f(x)=2x+ vi)f(x)= x 4x. x 2 2 1
 ) ( ) ΣΥΝΑΡΤΗΣΕΙΣ.Να βρείτε το πεδίο ορισμού των συναρτήσεων: 4 i) f ii)f iii)f()= 5 iv) f ( ) v)f()=+ vi)f()= 5 4 vii) f ( ) viii)f()=.να βρείτε το πεδίο ορισμού των συναρτήσεων: i) f ( ) 4 ii)f 9 iii)f()=
) ( ) ΣΥΝΑΡΤΗΣΕΙΣ.Να βρείτε το πεδίο ορισμού των συναρτήσεων: 4 i) f ii)f iii)f()= 5 iv) f ( ) v)f()=+ vi)f()= 5 4 vii) f ( ) viii)f()=.να βρείτε το πεδίο ορισμού των συναρτήσεων: i) f ( ) 4 ii)f 9 iii)f()=
2 είναι λύσεις της ανίσωσης 2x2 3x+1<0.
 ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΕΞΙΣΩΣΕΙΣ. α) Να βρείτε τις ρίζες της εξίσωσης x +0x=. x + 0x β) Να λύσετε την εξίσωση x. ίνεται η εξίσωση: x λx+(λ +λ )=0 (), λ R. α) Να προσδιορίσετε τον πραγµατικό αριθµό λ, ώστε η
ΤΡΑΠΕΖΑ ΘΕΜΑΤΩΝ, ΕΞΙΣΩΣΕΙΣ. α) Να βρείτε τις ρίζες της εξίσωσης x +0x=. x + 0x β) Να λύσετε την εξίσωση x. ίνεται η εξίσωση: x λx+(λ +λ )=0 (), λ R. α) Να προσδιορίσετε τον πραγµατικό αριθµό λ, ώστε η
1.1 ΠΡΑΞΕΙΣ ΜΕ ΠΡΑΓΜΑΤΙΚΟΥΣ ΑΡΙΘΜΟΥΣ. Α. Οι πραγματικοί αριθμοί και οι πράξεις τους ( ) ( ) ( ) ( ) ( ) ( ) είναι πραγματικός, γ) Το 3 είναι άρρητος,
 . ΠΡΑΞΕΙΣ ΜΕ ΠΡΑΓΜΑΤΙΚΟΥΣ ΑΡΙΘΜΟΥΣ Τηλ 0676-7 /0600 Α. Οι πραγματικοί αριθμοί και οι πράξεις τους. Να συμπληρωθούν τα κενά ώστε στην κατακόρυφη στήλη να προκύψει το έτος γέννησης σας : +....= 9.. = ( -
. ΠΡΑΞΕΙΣ ΜΕ ΠΡΑΓΜΑΤΙΚΟΥΣ ΑΡΙΘΜΟΥΣ Τηλ 0676-7 /0600 Α. Οι πραγματικοί αριθμοί και οι πράξεις τους. Να συμπληρωθούν τα κενά ώστε στην κατακόρυφη στήλη να προκύψει το έτος γέννησης σας : +....= 9.. = ( -
ςεδς ΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΘΕΜΑΤΑ ΓΙΑ ΕΞΕΤΑΣΕΙΣ ΕΠΙΜΕΛΕΙΑ Βαγγέλης Βαγγέλης Νικολακάκης Μαθηματικός
 01 ςεδς ΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΘΕΜΑΤΑ ΙΑ ΕΞΕΤΑΣΕΙΣ Βαγγέλης ΕΠΙΜΕΛΕΙΑ Βαγγέλης Νικολακάκης Μαθηματικός ΣΗΜΕΙΩΜΑ Το παραπάνω φυλλάδιο φτιάχτηκε για να προσφέρει λίγη βοήθεια κυρίως στους
01 ςεδς ΤΕΤΡΑΔΙΟ ΕΠΑΝΑΛΗΨΗΣ ΕΡΩΤΗΣΕΙΣ ΘΕΩΡΙΑΣ ΘΕΜΑΤΑ ΙΑ ΕΞΕΤΑΣΕΙΣ Βαγγέλης ΕΠΙΜΕΛΕΙΑ Βαγγέλης Νικολακάκης Μαθηματικός ΣΗΜΕΙΩΜΑ Το παραπάνω φυλλάδιο φτιάχτηκε για να προσφέρει λίγη βοήθεια κυρίως στους
3 η δεκάδα θεµάτων επανάληψης
 η δεκάδα θεµάτων επανάληψης. Έστω η συνάρτηση f() = 80 αν < < 0 αν 0 αν i ) Να υπολογιστεί η τιµή της παράστασης Α = f( ) + f(0) 5f() f + f( ) Αν Μ(, ) και Ν(, 0) να βρείτε την εξίσωση της ευθείας ΜΝ i
η δεκάδα θεµάτων επανάληψης. Έστω η συνάρτηση f() = 80 αν < < 0 αν 0 αν i ) Να υπολογιστεί η τιµή της παράστασης Α = f( ) + f(0) 5f() f + f( ) Αν Μ(, ) και Ν(, 0) να βρείτε την εξίσωση της ευθείας ΜΝ i
Α σ κήσεις για τ ι ς μέρες των Χριστ ουγεννι άτ ι κ ων διακ οπών
 Μαθηματικά Β Γυμνασίου Α σ κήσεις για τ ι ς μέρες των Χριστ ουγεννι άτ ι κ ων διακ οπών 1. Να χρησιμοποιήσετε μεταβλητές για να εκφράσετε με μια αλγεβρική παράσταση τις παρακάτω φράσεις: a. Η διαφορά δυο
Μαθηματικά Β Γυμνασίου Α σ κήσεις για τ ι ς μέρες των Χριστ ουγεννι άτ ι κ ων διακ οπών 1. Να χρησιμοποιήσετε μεταβλητές για να εκφράσετε με μια αλγεβρική παράσταση τις παρακάτω φράσεις: a. Η διαφορά δυο
Α ΛΥΚΕΙΟ ΓΕΡΑΚΑ. ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Σχολικό Έτος ΜΑΝΩΛΗ ΨΑΡΡΑ. Μανώλης Ψαρράς Σελίδα 1
 Α ΛΥΚΕΙΟ ΓΕΡΑΚΑ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Σχολικό Έτος 014-15 ΜΑΝΩΛΗ ΨΑΡΡΑ Μανώλης Ψαρράς Σελίδα 1 Α ΣΥΣΤΗΜΑΤΑ ΑΣΚΗΣΗ 1 η Να λυθούν γραφικά τα συστήματα: y y6 y 5 1 : 1 : 3 : y 6 0 y 5
Α ΛΥΚΕΙΟ ΓΕΡΑΚΑ ΑΣΚΗΣΕΙΣ ΕΠΑΝΑΛΗΨΗΣ ΣΤΗΝ ΑΛΓΕΒΡΑ Β ΛΥΚΕΙΟΥ Σχολικό Έτος 014-15 ΜΑΝΩΛΗ ΨΑΡΡΑ Μανώλης Ψαρράς Σελίδα 1 Α ΣΥΣΤΗΜΑΤΑ ΑΣΚΗΣΗ 1 η Να λυθούν γραφικά τα συστήματα: y y6 y 5 1 : 1 : 3 : y 6 0 y 5
Θέματα ενδοσχολικών εξετάσεων Άλγεβρας Α Λυκείου Σχ. έτος , Ν. Δωδεκανήσου ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ
 Θέματα ενδοσχολικών εξετάσεων Άλγεβρας Α Λυκείου Σχ. έτος 013-014, Ν. Δωδεκανήσου ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός
Θέματα ενδοσχολικών εξετάσεων Άλγεβρας Α Λυκείου Σχ. έτος 013-014, Ν. Δωδεκανήσου ΘΕΜΑΤΑ ΕΝΔΟΣΧΟΛΙΚΩΝ ΕΞΕΤΑΣΕΩΝ ΤΑΞΗ: Α ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΑΛΓΕΒΡΑ ΣΧΟΛΙΚΟ ΕΤΟΣ: 013-014 Επιμέλεια: Καραγιάννης Ιωάννης Σχολικός
ΑΣΚΗΣΕΙΣ ΣΤΑ ΠΟΛΥΩΝΥΜΑ (ΑΡΙΘΜΗΤΙΚΗ ΤΙΜΗ,ΠΡΑΞΕΙΣ,ΙΣΟΤΗΤΑ) P( x) ( 4) x ( 8) x ( 5 6) x 16 είναι το μηδενικό πολυώνυμο.
 ΑΣΚΗΣΕΙΣ ΣΤΑ ΠΟΛΥΩΝΥΜΑ (ΑΡΙΘΜΗΤΙΚΗ ΤΙΜΗ,ΠΡΑΞΕΙΣ,ΙΣΟΤΗΤΑ) 1. Δίνονται τα πολυώνυμα: P ( x) x x, Q( x) x x 1. Να βρεθούν: a) P( x) Q( x) ) P( x) Q( x) ) P( x) Q( x). Να βρεθεί η τιμή του λ R για την οποία
ΑΣΚΗΣΕΙΣ ΣΤΑ ΠΟΛΥΩΝΥΜΑ (ΑΡΙΘΜΗΤΙΚΗ ΤΙΜΗ,ΠΡΑΞΕΙΣ,ΙΣΟΤΗΤΑ) 1. Δίνονται τα πολυώνυμα: P ( x) x x, Q( x) x x 1. Να βρεθούν: a) P( x) Q( x) ) P( x) Q( x) ) P( x) Q( x). Να βρεθεί η τιμή του λ R για την οποία
ΑΣΚΗΣΕΙΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ
 www.apodeiis.gr ΑΣΚΗΣΕΙΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ 1 1. Να βρείτε το πεδίο ορισμού των συναρτήσεων: 1 i. ii. 1. Να βρείτε τα πεδία ορισμού των συναρτήσεων: i. 1 1 ii. ln. Δίνεται η συνάρτηση g, i. Να αποδείξετε
www.apodeiis.gr ΑΣΚΗΣΕΙΣ ΔΙΑΦΟΡΙΚΟΥ ΛΟΓΙΣΜΟΥ 1 1. Να βρείτε το πεδίο ορισμού των συναρτήσεων: 1 i. ii. 1. Να βρείτε τα πεδία ορισμού των συναρτήσεων: i. 1 1 ii. ln. Δίνεται η συνάρτηση g, i. Να αποδείξετε
Μονοτονία - Ακρότατα - 1 1 Αντίστροφη Συνάρτηση
 4 Μονοτονία - Ακρότατα - Αντίστροφη Συνάρτηση Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Μονοτονία συνάρτησης Μια συνάρτηση f λέγεται: Γνησίως αύξουσα σ' ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε,
4 Μονοτονία - Ακρότατα - Αντίστροφη Συνάρτηση Α. ΑΠΑΡΑΙΤΗΤΕΣ ΓΝΩΣΕΙΣ ΘΕΩΡΙΑΣ Μονοτονία συνάρτησης Μια συνάρτηση f λέγεται: Γνησίως αύξουσα σ' ένα διάστημα Δ του πεδίου ορισμού της, όταν για οποιαδήποτε,
ΘΕΜΑ 2. Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7,
 Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον εκατοστό όρο της. (Μονάδες 15) β) Να αποδείξετε ότι
Θεωρούμε την ακολουθία (α ν ) των θετικών περιττών αριθμών: 1, 3, 5, 7, α) Να αιτιολογήσετε γιατί η (α ν ) είναι αριθμητική πρόοδος και να βρείτε τον εκατοστό όρο της. (Μονάδες 15) β) Να αποδείξετε ότι
ΣΥΝΕΠΕΙΕΣ Θ.Μ.Τ. ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ ΕΥΡΕΣΗ ΣΥΝΑΡΤΗΣΗΣ
 Ενότητα 19 ΣΥΝΕΠΕΙΕΣ Θ.Μ.Τ. ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ ΕΥΡΕΣΗ ΣΥΝΑΡΤΗΣΗΣ 1). Να βρεθεί η συνάρτηση f όταν: i) A, f ()=3 5 f(0)=1, ii) A=, f ()=συν-ημ f(π)=, Ασκήσεις για λύση - iii) A=, f ()=4e 6 f '(0)=f(0)=1,
Ενότητα 19 ΣΥΝΕΠΕΙΕΣ Θ.Μ.Τ. ΣΤΑΘΕΡΗ ΣΥΝΑΡΤΗΣΗ ΕΥΡΕΣΗ ΣΥΝΑΡΤΗΣΗΣ 1). Να βρεθεί η συνάρτηση f όταν: i) A, f ()=3 5 f(0)=1, ii) A=, f ()=συν-ημ f(π)=, Ασκήσεις για λύση - iii) A=, f ()=4e 6 f '(0)=f(0)=1,
Επαναληπτικές ασκήσεις για το Πάσχα.
 Μαθηματικά B Γυμνασίου Επαναληπτικές ασκήσεις για το Πάσχα. Άλγεβρα. Κεφάλαιο 1 ο. 1. Να υπολογιστούν οι παρακάτω αριθμητικές παραστάσεις : 1 7 1 7 1 1 ) - 1 4 : ) -1 1 : 1 4 10 9 6. Να λυθούν οι εξισώσεις:
Μαθηματικά B Γυμνασίου Επαναληπτικές ασκήσεις για το Πάσχα. Άλγεβρα. Κεφάλαιο 1 ο. 1. Να υπολογιστούν οι παρακάτω αριθμητικές παραστάσεις : 1 7 1 7 1 1 ) - 1 4 : ) -1 1 : 1 4 10 9 6. Να λυθούν οι εξισώσεις:
Εκφωνήσεις και λύσεις των ασκήσεων της Τράπεζας Θεμάτων στην Άλγεβρα Α ΓΕΛ
 Κοίταξε τις µεθόδους, τις λυµένες ασκήσεις και τις ασκήσεις προς λύση των ενοτήτων 6, 7 του βοηθήµατος Μεθοδολογία Άλγεβρας και Στοιχείων Πιθανοτήτων Α Γενικού Λυκείου των Ευσταθίου Μ. και Πρωτοπαπά Ελ.
Κοίταξε τις µεθόδους, τις λυµένες ασκήσεις και τις ασκήσεις προς λύση των ενοτήτων 6, 7 του βοηθήµατος Μεθοδολογία Άλγεβρας και Στοιχείων Πιθανοτήτων Α Γενικού Λυκείου των Ευσταθίου Μ. και Πρωτοπαπά Ελ.
ΣΥΝΑΡΤΗΣΕΙΣ-ΟΡΙΟ-ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 ΣΥΝΑΡΤΗΣΕΙΣ-ΟΡΙΟ-ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΣΥΝΑΡΤΗΣΕΙΣ -ΟΡΙΟ ΣΥΝΕΧΕΙΑ Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο τουr Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα)
ΣΥΝΑΡΤΗΣΕΙΣ-ΟΡΙΟ-ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΣΥΝΑΡΤΗΣΕΙΣ -ΟΡΙΟ ΣΥΝΕΧΕΙΑ Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο τουr Ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α μια διαδικασία (κανόνα)
ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΘΕΜΑ Α
 ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
ΚΕΦΑΛΑΙΟ 1 ο : ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ ΕΝΟΤΗΤΑ 1: ΟΡΙΣΜΟΣ ΠΕΔΙΟ ΟΡΙΣΜΟΥ ΠΡΑΞΕΙΣ ΣΥΝΑΡΤΗΣΕΩΝ ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ ΒΑΣΙΚΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΛΥΜΕΝΑ ΘΕΜΑΤΑ Ερώτηση θεωρίας 1 ΘΕΜΑ Α Τι ονομάζουμε πραγματική συνάρτηση
Μαθηματικά Προσανατολισμού Γ Λυκείου Κανιστράς Δημήτριος. Συναρτήσεις Όρια Συνέχεια Μια πρώτη επανάληψη Απαντήσεις των ασκήσεων
 Μαθηματικά Προσανατολισμού Γ Λυκείου Κανιστράς Δημήτριος Συναρτήσεις Όρια Συνέχεια Μια πρώτη επανάληψη Απαντήσεις των ασκήσεων Άσκηση i. Δίνεται η γνησίως μονότονη συνάρτηση f : A IR. Να αποδείξετε ότι
Μαθηματικά Προσανατολισμού Γ Λυκείου Κανιστράς Δημήτριος Συναρτήσεις Όρια Συνέχεια Μια πρώτη επανάληψη Απαντήσεις των ασκήσεων Άσκηση i. Δίνεται η γνησίως μονότονη συνάρτηση f : A IR. Να αποδείξετε ότι
