Γενική Ισορροπία. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 19 Απριλίου 2013
|
|
|
- Οὐρανός Βιτάλης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50. Παρατήρηση. Στη γενική ισορροπία προσέξτε ότι οι καµπύλες αδιαφορίας των δύο καταναλωτών εφάπτονται µεταξύ τους. Αυτό γίνεται εύκολα αντιληπτό εάν παρατηρήστε ότι: 1 λόγω άριστης επιλογής πρέπει να εφάπτονται η κάθε µία µε τον εισοδηµατικό περιορισµό και 2 επειδή «καθαρίζουν» οι αγορές ϑα πρέπει η επαφή να λαµβάνει χώρα στο ίδιο σηµείο Θα πρέπει να εφάπτονται η µία στην άλλη. Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50. Εν γένει στην αρχική κατανοµή κάτι τέτοιο δεν ισχύει. Τι ϑα συνέβαινε αν ίσχυε κάτι τέτοιο; Προφανώς η αρχική κατανοµή ϑα ήταν και γενική ισορροπία µε λόγο τιµών την κοινή εφαπτοµένη. Ξεκινώντας από την αρχική κατανοµή, ας δούµε τα καλάθια που προτιµάει από την αρχική κατανοµή ο A. Αυτά λέγονται Uppr contour st του A στην κατανοµή. Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
2 U A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 U A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50. Ας κάνουµε το ίδιο και µε τον B. Παρατηρούµε ότι µεταξύ των δύο καµπυλών αδιαφορίας που διέρχονται από την αρχική κατανοµή, σχηµατίζεται ενός είδους «ϕακός».αυτά είναι τα σηµεία που προτιµού και οι δύο από την αρχική κατανοµή: Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 U A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
3 U A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 U A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 U A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 U A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
4 . Είναι αυτονόητο ότι οποιαδήποτε ανταλλαγή γίνει ϑα γίνει µέσα σε αυτόν τον ϕακό. ιότι µόνο εκεί µέσα και οι δύο είναι καλύτερα. Προσέξτε ότι αν πάµε µέσα σε ένα άλλο σηµείο του ϕακού, x στο οποίο οι καµπύλες αδιαφορίας των δύο τέµνονται (δεν εφάπτονται), πάλι ϑα σχηµατίζεται ένας ϕακός που και οι δύο ϑα προτιµούν από το x (και ασφαλώς και το ). Αυτό ϑα συνεχίζεται για όσο οι καµπύλες αδιαφορίας τέµνονται. Αν ϐρούµε σηµείο όπου εφάπτονται, τότε δε µπορεί να γίνει περαιτέρω ανταλλαγή διότι δεν υπάρχει σηµείο που και οι δύο να είναι καλύτερα: Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 U A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 x U A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 x Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
5 x Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 x Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Αποτελεσµατικότητα κατά Parto Η επαφή των καµπυλών αδιαφορίας σηµαίνει ότι δε µπορεί να γίνει άλλη ανταλλαγή. Τι σηµαίνει αυτή η επαφή; Οτι δε µπορεί η ϑέση κάποιου καταναλωτή να ϐελτιωθεί χωρίς να ϐλαφτεί η ϑέση άλλου. Οσο δεν υπήρχε επαφή, µπρούσαµε να ϐελτιώνουµε τη ϑέση του A (π.χ. µέσα στο ϕακό), χωρίς να χειροτερεύει η ϑέση του B. Για την ακρίβεια και ο B γινόταν καλύτερα. Με την επαφή όµως ο ϕακός εξαφανίζεται και για να ϐελτιωθεί κάποιος, πρέπει ο άλλος να γίνει χειρότερα (να πέσει σε χαµηλότερη καµπύλη αδιαφορίας). Αν ϐρούµε σηµείο όπου εφάπτονται, τότε δε µπορεί να γίνει περαιτέρω ανταλλαγή διότι δεν υπάρχει σηµείο που και οι δύο να είναι καλύτερα. Το uppr contour st του A ϐρίσκεται πάνω από την καµπύλη αδιαφορίας του B και τούµπαλιν: Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
6 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Αποτελεσµατικότητα κατά Parto Ορισµός Αυτό ακριβώς που περιγράψαµε είναι η αποτελεσµατικότητα κατά Parto. Τα σηµεία αυτά επαφής λέγονται άριστα κατά Parto. Μια κατανοµή λέγεται άριστη ή αποτελεσµατική κατά Parto εάν, ϕεύγοντας από αυτήν την κατανοµή, δε µπορεί να ϐελτιωθεί η ϑέση του ενός χωρίς να ϐλαφτεί η ϑέση κάποιου άλλου στην οικονοµία. Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
7 Αποτελεσµατικότητα κατά Parto Είναι µοναδικό αυτό το σηµείο επαφής µέσα στον ϕακό; Οχι, υπάρχουν άπειρα. είτε µερικά ενδεικτικά: Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
8 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
9 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Αποτελεσµατικότητα κατά Parto Παρατήρηση 1: συµπεριλαµβάνονται εκτός από τα σηµεία µέσα στο ϕακό, και σηµεία εκτός, σε όλο το κουτί. Ολα αυτά τα σηµεία ονοµάζονται «σύνολο Parto» ή γραµµή συµβάσεων. Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
10 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Σύνολο Parto ή γραμμή συμβάσεων Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Πρώτο Θεµελιώδες Θεώρηµα των Οικονοµικών της Ευηµερίας Ερώτηση: Η αγοραία ισορροπία τί ιδιότητες έχει όσον αφορά στην ευηµερία των καταναλωτών; Θεώρηµα Αν οι προτιµήσεις των καταναλωτών είναι τοπικά µη κορεσµένες (ή µονοτονικές) τότε κάθε Βαλρασιανή ισορροπία είναι αποτελεσµατική κατά Parto. Αυτό που µας λέει το 1ο Θ.Θ.Ο.Ε. είναι ότι η αγορά δεν κάνει «σπατάλες» ευηµερίας. Το µόνο που Ϲητάµε για να ισχύει είναι να µην έχουν οι καταναλωτές παχιές καµπύλες αδιαφορίας. Το ϑεώρηµα δεν κάνει κανενός είδους αξιολογική κρίση για τις αγοραίες ισορροπίες. Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
11 Πρώτο Θεµελιώδες Θεώρηµα των Οικονοµικών της Ευηµερίας Απόδειξη. Αν η ϐαλρασιανή ισορροπία x = (x A, 1 xa, 2 xb, 1 xb ) δεν είναι άριστη κατά Parto, 2 τότε ϑα υπάρχει µια άλλη εφικτή κατανοµή (y A, 1 ya, 2 yb, 1 yb ) που και οι δύο ϑα 2 προτιµούν. Τί σηµαίνει εφικτή; Οτι y A 1 + yb 1 = A 1 + B 1 (1) y A 2 + yb 2 = A 2 + B 2 (2) p 1 (y A 1 + yb 1 ) + p 2(y A 2 + yb 2 ) = p 1( A 1 + B 1 ) + p 2( A 2 + B 2 ) (3) Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Πρώτο Θεµελιώδες Θεώρηµα των Οικονοµικών της Ευηµερίας Απόδειξη. Αφού όµως η x είναι ϐαλρασιανή ισορροπία οι δύο καταναλωτές µεγιστοποιούν τη χρησιµότητά τους καταναλώνοντας x. Αυτό σηµαίνει ότι αν προτιµούν την y, δηλαδή αν y A A x A, y B B x B, το y ϑα είναι πιο ακριβό από το εισόδηµά τους µε τις τιµές της ισορροπίας x (αλλιώς ϑα το επέλεγαν αφού µεγιστοποιούν): p 1 y A 1 + p 2y A 2 > p 1 A 1 + p 2 A 2 p 1 y B 1 + p 2y B 2 > p 1 B 1 + p 2 B 2 (4) Προσθέτοντας λαµβάνουµε: p 1 (y A 1 + yb 1 ) + p 2(y A 2 + yb 2 ) > p 1( A 1 + B 1 ) + p 2( A 2 + B 2 ) (5) Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Πρώτο Θεµελιώδες Θεώρηµα των Οικονοµικών της Ευηµερίας Απόδειξη. Από την (3) όµως προκύπτει p 1 ( A 1 + B 1 ) + p 2( A 2 + B 2 ) > p 1( A 1 + B 1 ) + p 2( A 2 + B 2 ) (6) Ατοπο. Q.E.D. Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Πρώτο Θεµελιώδες Θεώρηµα των Οικονοµικών της Ευηµερίας 1 Γιατί ϑέλουµε οι προτιµήσεις να είναι µη κορεσµένες; 2 είτε σχήµα παρακάτω. Αν έχουµε παχιές καµπύλες αδιαφορίας το x είναι ϐαλρασιανή ισορροπία (µπορείτε να δείτε γιατί), αλλά δεν είναι κατά Parto άριστη αφού υπάρχει το y που ο B προτιµάει χωρίς να είναι χειρότερο για τον A. Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
12 x U A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 x y U A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Παράδειγµα Να ϐρεθεί το σύνολο Parto για την οικονοµία: U A (A 1, A 2 ) = 2 ln A 1 + ln A 2, A = (1, 0) U B (B 1, B 2 ) = ln B 1 + ln B 2, B = (0, 1) Να υπολογιστεί το σύνολο Parto. Το σύνολο Parto δίνεται από τις κατανοµές που ο ένας καταναλωτής (ας πούµε ο A) δε µπορεί να αυξήσει τη χρησιµότητά του χωρίς να ϐλαφτεί ο άλλος (ο B). Αυτό σηµαίνει ότι δεδοµένης της χρησιµότητας του B, η χρησιµότητα του A έχει µεγιστοποιηθεί (αλλιώς ϑα µπορούσε να την αυξήσει χωρίς να ϐλαφτεί ο B). Εποµένως το σύνολο Parto δίνεται από τις κατανοµές που µεγιστοποιούν τη χρησιµότητα του ενός δεδοµένης της χρησιµότητας του άλλου, ή µε άλλα λόγια που αποτελούν λύση του παρακάτω προβλήµατος µεγιστοποίησης: Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 Παράδειγµα max A1,A2,B1,B2 s.t. U A (A 1, A 2 ) = 2 ln A 1 + ln A 2 ln B 1 + ln B 2 = Û A 1 + B 1 = 1 A 2 + B 2 = 2 Σχηµατίζουµε τη Langrangian (Θυµηθείτε ότι A i = 1 B i ): L = 2 ln A 1 + ln A 2 + λ[û ln(1 A 1 ) ln(1 A 2 )] F.O.C. :L A1 = 0 2 = λ A 1 1 A 1 L A2 = 0 1 = λ A 2 1 A 2 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
13 Παράδειγµα ιαιρώντας παίρνουµε: 2A 2 A 1 = 1 A 2 1 A 1 2A 2 2A 2 A 1 = A 1 A 1 A 2 A 2 = A 1 2 A 1 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50 0 B A A 1 2 A 1 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου / 50
Γενική Ισορροπία-Ευηµερία. 2ο Θεµελιώδες Θεώρηµα των Οικονοµικών της ευηµερίας. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς.
 Γενική Ισορροπία-Ευηµερία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία-Ευηµερία 19 Απριλίου 2013 1 / 20 Το πρώτο Θ.Θ.Ο.Ε. µας λέει ότι κάθε Βαλρασιανή
Γενική Ισορροπία-Ευηµερία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία-Ευηµερία 19 Απριλίου 2013 1 / 20 Το πρώτο Θ.Θ.Ο.Ε. µας λέει ότι κάθε Βαλρασιανή
Notes. Notes. Notes. Notes. T A = ŵ A p 1 e A 1 p 2e A 2 T B = ŵ B p 1 e A 1 p 2e B 2. 1 x A. 2 x B
 Γενική Ισορροπία-Ευημερία Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Δεκεμβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Γενική Ισορροπία-Ευημερία 3 Δεκεμβρίου 2012 1 / 17 Το πρώτο Θ.Θ.Ο.Ε. μας λέει ότι κάθε
Γενική Ισορροπία-Ευημερία Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Δεκεμβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Γενική Ισορροπία-Ευημερία 3 Δεκεμβρίου 2012 1 / 17 Το πρώτο Θ.Θ.Ο.Ε. μας λέει ότι κάθε
Γενική Ισορροπία. Γενική ισορροπία και παραγωγή. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 19 Απριλίου 2013
 Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 013 1 / 60. Η παραγωγή στη γενική ισορροπία έχει πάλι µεγάλη αντιστοιχία
Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 013 1 / 60. Η παραγωγή στη γενική ισορροπία έχει πάλι µεγάλη αντιστοιχία
Μικροοικονοµική Θεωρία. Γενική ισορροπία και παραγωγή. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 24 Σεπτεµβρίου 2014
 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 4 Σεπτεµβρίου 014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 4 Σεπτεµβρίου 014 1 / 60. Η παραγωγή στη γενική ισορροπία έχει πάλι µεγάλη
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 4 Σεπτεµβρίου 014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 4 Σεπτεµβρίου 014 1 / 60. Η παραγωγή στη γενική ισορροπία έχει πάλι µεγάλη
Γενική Ισορροπία. Γενική ισορροπία - Ανταλλαγή. Γενική ισορροπία - Ανταλλαγή. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς.
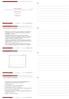 Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 2013 1 / 23. Η οικονοµία των δύο καταναλωτών µε δύο αγαθά που παρουσιάσαµε
Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 2013 1 / 23. Η οικονοµία των δύο καταναλωτών µε δύο αγαθά που παρουσιάσαµε
Μικροοικονοµική Θεωρία. Γενική ισορροπία - Ανταλλαγή. Γενική ισορροπία - Ανταλλαγή. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 23 Σεπτεµβρίου 2014
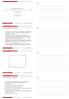 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 23 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 23 Σεπτεµβρίου 2014 1 / 23. Η οικονοµία των δύο καταναλωτών µε δύο αγαθά
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 23 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 23 Σεπτεµβρίου 2014 1 / 23. Η οικονοµία των δύο καταναλωτών µε δύο αγαθά
Γενική Ισορροπία- Υπαρξη και µοναδικότητα. Υπαρξη ϐαλρασιανής ισορροπίας. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς.
 Γενική Ισορροπία- Υπαρξη και µοναδικότητα Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία- Υπαρξη και µοναδικότητα 19 Απριλίου 2013 1 / 44 ύο Ϲητήµατα
Γενική Ισορροπία- Υπαρξη και µοναδικότητα Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία- Υπαρξη και µοναδικότητα 19 Απριλίου 2013 1 / 44 ύο Ϲητήµατα
Γενική Ισορροπία. Γενική ισορροπία vs Μερική ισορροπία. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 19 Απριλίου 2013
 Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 2013 1 / 30 Γενική ισορροπία - Εισαγωγή Γενική ισορροπία vs Μερική ισορροπία
Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 2013 1 / 30 Γενική ισορροπία - Εισαγωγή Γενική ισορροπία vs Μερική ισορροπία
Μικροοικονοµική Θεωρία. Τιµές και εισόδηµα. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 22 Σεπτεµβρίου 2014
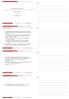 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 30 Τιµές και εισόδηµα Η συνάρτηση χρησιµότητας
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 30 Τιµές και εισόδηµα Η συνάρτηση χρησιµότητας
Κοινωνική επιλογή και Ευηµερία. Κοινωνική επιλογή. Κοινωνική επιλογή, το παράδοξο του Condorcet. Notes. Notes. Notes. Notes.
 Κοινωνική επιλογή και Ευηµερία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Κοινωνική επιλογή και Ευηµερία 19 Απριλίου 013 1 / 51 Κοινωνική επιλογή. Κοινωνική επιλογή.
Κοινωνική επιλογή και Ευηµερία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Κοινωνική επιλογή και Ευηµερία 19 Απριλίου 013 1 / 51 Κοινωνική επιλογή. Κοινωνική επιλογή.
Μικροοικονοµική Θεωρία. Ζήτηση ενός αγαθού ως συνάρτηση της τιµής. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 22 Σεπτεµβρίου 2014
 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 40 Ζήτηση ενός αγαθού ως συνάρτηση της τιµής
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 40 Ζήτηση ενός αγαθού ως συνάρτηση της τιµής
Καλάθι αγαθών. Σχέσεις προτίµησης. Ιδιότητες σχέσεων προτίµησης. Notes. Notes. Notes. Notes
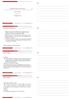 Θεωρία Καταναλωτή-Προτιµήσεις Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Θεωρία Καταναλωτή-Προτιµήσεις 22 Σεπτεµβρίου 2014 1 / 17 Προτιµήσεις καταναλωτών Θέλουµε
Θεωρία Καταναλωτή-Προτιµήσεις Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Θεωρία Καταναλωτή-Προτιµήσεις 22 Σεπτεµβρίου 2014 1 / 17 Προτιµήσεις καταναλωτών Θέλουµε
Γενική Ισορροπία. Παραδείγµατα γενικής ισορροπίας µε ανταλλαγή. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 19 Απριλίου 2013
 Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 2013 1 / 25 Παραδείγµατα γενικής ισορροπίας µε ανταλλαγή. ιαφορετικές προτιµήσεις
Γενική Ισορροπία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 19 Απριλίου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Γενική Ισορροπία 19 Απριλίου 2013 1 / 25 Παραδείγµατα γενικής ισορροπίας µε ανταλλαγή. ιαφορετικές προτιµήσεις
Διάλεξη 10. Γενική Ισορροπία VA 30
 Διάλεξη 10 Γενική Ισορροπία V 30 1 Μερική & Γενική Ισορροπία Μέχρι τώρα εξετάζαμε γενικά την αγορά ενός αγαθού μεμονωμένα. Το πώς δηλαδή η προσφορά και η ζήτηση επηρεάζονται από την τιμή του συγκεκριμένου
Διάλεξη 10 Γενική Ισορροπία V 30 1 Μερική & Γενική Ισορροπία Μέχρι τώρα εξετάζαμε γενικά την αγορά ενός αγαθού μεμονωμένα. Το πώς δηλαδή η προσφορά και η ζήτηση επηρεάζονται από την τιμή του συγκεκριμένου
Μικροοικονοµική Θεωρία. Συνάρτηση και καµπύλη κόστους. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 22 Σεπτεµβρίου 2014
 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 49 Συνάρτηση και καµπύλη κόστους Πολύ χρήσιµες
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 49 Συνάρτηση και καµπύλη κόστους Πολύ χρήσιµες
Notes. Notes. Notes. Notes. A B C x y z y z x z x y
 Κοινωνική επιλογή και Ευημερία Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Δεκεμβρίου 01 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Κοινωνική επιλογή και Ευημερία 3 Δεκεμβρίου 01 1 / 50 Κοινωνική επιλογή. Κοινωνική επιλογή.
Κοινωνική επιλογή και Ευημερία Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Δεκεμβρίου 01 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Κοινωνική επιλογή και Ευημερία 3 Δεκεμβρίου 01 1 / 50 Κοινωνική επιλογή. Κοινωνική επιλογή.
To 2 ο Θεμελιώδες Θεώρημα Ευημερίας
 o 2 ο Θεμελιώδες Θεώρημα Ευημερίας - Το 1 ο Θεώρημα Ευημερίας (FW) εξασφαλίζει ότι η ανταγωνιστική ισορροπία είναι άριστη κατά Pareto αλλά δεν εξασφαλίζει μια ίση διανομή των οικονομικών οφελών μεταξύ
o 2 ο Θεμελιώδες Θεώρημα Ευημερίας - Το 1 ο Θεώρημα Ευημερίας (FW) εξασφαλίζει ότι η ανταγωνιστική ισορροπία είναι άριστη κατά Pareto αλλά δεν εξασφαλίζει μια ίση διανομή των οικονομικών οφελών μεταξύ
Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία
 Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία Βασικές Υποθέσεις (i) Οι αγορές όλων των αγαθών είναι τέλεια ανταγωνιστικές. Οι καταναλωτές και οι επιχειρήσεις
Γενική Ανταγωνιστική Ισορροπία και Αποτελεσματικές κατά Pareto Κατανομές σε Ανταλλακτική Οικονομία Βασικές Υποθέσεις (i) Οι αγορές όλων των αγαθών είναι τέλεια ανταγωνιστικές. Οι καταναλωτές και οι επιχειρήσεις
1 = = = x x = x. 4 u = = = MRS MRS. x x. MRS = MRS = = x = x x [1] x12 x x W W
![1 = = = x x = x. 4 u = = = MRS MRS. x x. MRS = MRS = = x = x x [1] x12 x x W W 1 = = = x x = x. 4 u = = = MRS MRS. x x. MRS = MRS = = x = x x [1] x12 x x W W](/thumbs/82/86418028.jpg) Θέµα ο (α) Μια κατανοµή στο εσωτερικό του κουτιού Edgeworth είναι άριστη κατά areto αν MRS MRS Έχουµε τα ακόλουθα MRS 3 3 4 4 4 3 3 4 4 4, MRS 3 3 3 3 3 3 Στην αρχική κατανοµή βρίσκουµε 00 MRS(50, 00)
Θέµα ο (α) Μια κατανοµή στο εσωτερικό του κουτιού Edgeworth είναι άριστη κατά areto αν MRS MRS Έχουµε τα ακόλουθα MRS 3 3 4 4 4 3 3 4 4 4, MRS 3 3 3 3 3 3 Στην αρχική κατανοµή βρίσκουµε 00 MRS(50, 00)
Άριστες κατά Pareto Κατανομές
 Άριστες κατά Pareto Κατανομές - Ορισμός. Μια κατανομή x = (x, x ) = (( 1, )( 1, )) ονομάζεται άριστη κατά Pareto αν δεν υπάρχει άλλη κατανομή x = ( x, x ) τέτοια ώστε: U j( x j) U j( xj) για κάθε καταναλωτή
Άριστες κατά Pareto Κατανομές - Ορισμός. Μια κατανομή x = (x, x ) = (( 1, )( 1, )) ονομάζεται άριστη κατά Pareto αν δεν υπάρχει άλλη κατανομή x = ( x, x ) τέτοια ώστε: U j( x j) U j( xj) για κάθε καταναλωτή
Εξωτερικές Οικονοµίες
 Εξωτερικές Οικονοµίες Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 31 Μαΐου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Εξωτερικές Οικονοµίες 31 Μαΐου 2013 1 / 31 Εξωτερικότητες. Εξωτερικότητες. Ορισµός (Εξωτερικότητα)
Εξωτερικές Οικονοµίες Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 31 Μαΐου 2013 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Εξωτερικές Οικονοµίες 31 Μαΐου 2013 1 / 31 Εξωτερικότητες. Εξωτερικότητες. Ορισµός (Εξωτερικότητα)
31/05/2017. Κεφάλαιο 32 Ανταλλαγή. Μικροοικονομική. Ανταλλαγή. Ανταλλαγή. Πλάτος = A B. Μια σύγχρονη προσέγγιση
 31/05/017 HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 3 Ανταλλαγή Ανταλλαγή Δύο καταναλωτές, και. Τα αποθέματα των αγαθών τους 1 και είναι w = ( w1, w ) και w = ( w, w ). 1 π.χ.
31/05/017 HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 3 Ανταλλαγή Ανταλλαγή Δύο καταναλωτές, και. Τα αποθέματα των αγαθών τους 1 και είναι w = ( w1, w ) και w = ( w, w ). 1 π.χ.
HAL R. VARIAN. Μικροοικονομική. Μια σύγχρονη προσέγγιση. 3 η έκδοση
 HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 32 Ανταλλαγή Ανταλλαγή Δύο καταναλωτές, και. Τα αποθέματα των αγαθών τους 1 και 2 είναι π.χ. 1 2 w = ( w1, w2 ) και w w w w = ( 6,
HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Κεφάλαιο 32 Ανταλλαγή Ανταλλαγή Δύο καταναλωτές, και. Τα αποθέματα των αγαθών τους 1 και 2 είναι π.χ. 1 2 w = ( w1, w2 ) και w w w w = ( 6,
Μικροοικονοµική Θεωρία. Μονοπώλιο. Μονοπώλιο. Μονοπώλιο. Notes. Notes. Notes. Notes. Κώστας Ρουµανιάς. 23 Σεπτεµβρίου 2014
 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 23 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 23 Σεπτεµβρίου 2014 1 / 26 Ως τώρα, υποθέσαµε ότι οι αγορές είναι ανταγωνιστικές.
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 23 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 23 Σεπτεµβρίου 2014 1 / 26 Ως τώρα, υποθέσαµε ότι οι αγορές είναι ανταγωνιστικές.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος 2016-17 ΠΟΛΙΤΙΚΗ ΟΙΚΟΝΟΜΙΑ ΤΗΣ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass) 1 ιάλεξη2 Ανταγωνισμός, οικονομική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τµήµα Οικονοµικών Επιστηµών Ακαδηµαϊκό έτος 2016-17 ΠΟΛΙΤΙΚΗ ΟΙΚΟΝΟΜΙΑ ΤΗΣ ΚΟΙΝΩΝΙΚΗΣ ΠΟΛΙΤΙΚΗΣ (διαβάζουμε κεφ. 4 από Μ. Χλέτσο και σημειώσεις στο eclass) 1 ιάλεξη2 Ανταγωνισμός, οικονομική
Μικροοικονοµική Θεωρία. Οικονοµικές πολιτικές σε ανταγωνιστικό περιβάλλον. Deadweight loss: Νεκρή Ϲηµία. Notes. Notes. Notes. Notes.
 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 1 Οικονοµικές πολιτικές σε ανταγωνιστικό περιβάλλον.
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 22 Σεπτεµβρίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 22 Σεπτεµβρίου 2014 1 / 1 Οικονοµικές πολιτικές σε ανταγωνιστικό περιβάλλον.
Notes. Notes. Notes. Notes. C = p x x 1 + p y y 1. pxx + pyy = 160
 Ελαχιστοποίηση κόστους Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 9 Οκτωβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Ελαχιστοποίηση κόστους 9 Οκτωβρίου 2012 1 / 36 Κόστος Το πρόβλημα εύρεσης ενός άριστου καλαθιού
Ελαχιστοποίηση κόστους Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 9 Οκτωβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Ελαχιστοποίηση κόστους 9 Οκτωβρίου 2012 1 / 36 Κόστος Το πρόβλημα εύρεσης ενός άριστου καλαθιού
Notes. Notes. Notes. Notes. p x. x x
 Θεωρία ζήτησης Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 9 Οκτωβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία ζήτησης 9 Οκτωβρίου 2012 1 / 40 Ζήτηση ενός αγαθού ως συνάρτηση της τιμής Δεδομένου ότι ένας
Θεωρία ζήτησης Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 9 Οκτωβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία ζήτησης 9 Οκτωβρίου 2012 1 / 40 Ζήτηση ενός αγαθού ως συνάρτηση της τιμής Δεδομένου ότι ένας
Διάλεξη 3. Οικονομικά της ευημερίας. Οικονομικά της ευημερίας 3/9/2017. Περίγραμμα. Εργαλεία δεοντολογικής ανάλυσης
 Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης Συνθήκες για αποτελεσματικότητα κατά areto Συνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης Συνθήκες για αποτελεσματικότητα κατά areto Συνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Ανταγωνιστικές Οικονοµίες Ανταλλαγής
 Κεφάλαιο 1 Ανταγωνιστικές Οικονοµίες Ανταλλαγής 1.1 Οικονοµία Ανταλλαγής Οπως και στο προηγουµενο κεφάλαιο, υποθέτουµε ότι ο χώρος αγα- ϑών είναι διατεταγµένος χώρος µε norm E και το σύνολο κατανάλωσης
Κεφάλαιο 1 Ανταγωνιστικές Οικονοµίες Ανταλλαγής 1.1 Οικονοµία Ανταλλαγής Οπως και στο προηγουµενο κεφάλαιο, υποθέτουµε ότι ο χώρος αγα- ϑών είναι διατεταγµένος χώρος µε norm E και το σύνολο κατανάλωσης
Διάλεξη 3. Οικονομικά της ευημερίας 2/26/2016. Περίγραμμα. Εργαλεία δεοντολογικής ανάλυσης. Αποτελεσματικότητα κατά Pareto: ορισμός. ορισμός.
 Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης υνθήκες για αποτελεσματικότητα κατά areto υνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Περίγραμμα Διάλεξη Εργαλεία δεοντολογικής ανάλυσης υνθήκες για αποτελεσματικότητα κατά areto υνθήκες για ισορροπία σε ανταγωνιστικές αγορές Το πρώτο θεώρημα των οικονομικών της ευημερίας Το δεύτερο θεώρημα
Γενική Ανταγωνιστική Ισορροπία
 Γενική Ανταγωνιστική Ισορροπία - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών
Γενική Ανταγωνιστική Ισορροπία - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό Α. - Οι προτιμήσεις των καταναλωτών
Κεφάλαιο 32 Ανταλλαγή
 HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 32 Ανταλλαγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Ανάλυση μερικής ισορροπίας/ανάλυση γενικής ισορροπίας Τέλειος ανταγωνισμός/ατελής
HL R. VRIN Μικροοικονομική Μια σύγχρονη προσέγγιση 3 η έκδοση Εκδόσεις Κριτική Κεφάλαιο 32 Ανταλλαγή Ύλη για τη Μίκρο ΙΙ: όλο το κεφάλαιο Ανάλυση μερικής ισορροπίας/ανάλυση γενικής ισορροπίας Τέλειος ανταγωνισμός/ατελής
0 χ1 χ2 Ι2 χ3 Ι5 Ι3 χ
 ΠΝΕΠΙΣΤΗΜΙΟ ΜΚΕ ΟΝΙΣ - ΤΜΗΜ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΘΗΓΗΤΗΣ ΚΩΣΤΣ ΕΛΕΝΤΖΣ ΠΟΤΕΛΕΣΜΤ ΥΠΟΚΤΣΤΣΗΣ ΚΙ ΕΙΣΟ ΗΜΤΟΣ Ι1 χ/ Ρ=0 χ/ Ρ>0 χ/ Ρ
ΠΝΕΠΙΣΤΗΜΙΟ ΜΚΕ ΟΝΙΣ - ΤΜΗΜ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΘΗΓΗΤΗΣ ΚΩΣΤΣ ΕΛΕΝΤΖΣ ΠΟΤΕΛΕΣΜΤ ΥΠΟΚΤΣΤΣΗΣ ΚΙ ΕΙΣΟ ΗΜΤΟΣ Ι1 χ/ Ρ=0 χ/ Ρ>0 χ/ Ρ
Notes. Notes. Notes. Notes
 Θεωρία Καταναλωτή-Προτιμήσεις Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Οκτωβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία Καταναλωτή-Προτιμήσεις 3 Οκτωβρίου 2012 1 / 19 Προτιμήσεις καταναλωτών Θέλουμε
Θεωρία Καταναλωτή-Προτιμήσεις Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 3 Οκτωβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία Καταναλωτή-Προτιμήσεις 3 Οκτωβρίου 2012 1 / 19 Προτιμήσεις καταναλωτών Θέλουμε
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 2 5/9/2002 Απαντήστε σε μια από τις δυο ερωτήσεις. 3. Να υπολογιστεί η ανταγωνιστική ισορροπία και τα σημεία
 ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5/9/00 Απαντήστε σε μια από τις δυο ερωτήσεις. 1.Θεωρουμε οικονομία αποτελούμενη από ένα καταναλωτή, με προτιμήσεις U log+ logx,και περιουσία μόνο μια μονάδα του αγαθού
ΜΑΘΗΜΑΤΙΚΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ 5/9/00 Απαντήστε σε μια από τις δυο ερωτήσεις. 1.Θεωρουμε οικονομία αποτελούμενη από ένα καταναλωτή, με προτιμήσεις U log+ logx,και περιουσία μόνο μια μονάδα του αγαθού
ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ
 ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Κεφάλαιο 3 Οικονοµικά των Επιχειρήσεων Ε. Σαρτζετάκης 1 Καταναλωτική συµπεριφορά! Σκοπός αυτής της διάλεξης είναι να εξετάσουµε τον τρόπο µε τον οποίο οι καταναλωτές
ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Κεφάλαιο 3 Οικονοµικά των Επιχειρήσεων Ε. Σαρτζετάκης 1 Καταναλωτική συµπεριφορά! Σκοπός αυτής της διάλεξης είναι να εξετάσουµε τον τρόπο µε τον οποίο οι καταναλωτές
 ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ-ΜΑΘΗΜΑ ΠΕΜΠΤΟ-ΕΚΤΟ ΕΚΤΟ ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ-ΙΣΟΡΡΟΠΙΑ ΙΣΟΡΡΟΠΙΑ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ ΤΜΗΜΑ ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΥ ΣΧΕ ΙΑΣΜΟΥ & ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Ακαδηµαϊκό Έτος 2011-2012 ΕΠΙΧ Μικροοικονοµική
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ-ΜΑΘΗΜΑ ΠΕΜΠΤΟ-ΕΚΤΟ ΕΚΤΟ ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ-ΙΣΟΡΡΟΠΙΑ ΙΣΟΡΡΟΠΙΑ ΤΟΥ ΚΑΤΑΝΑΛΩΤΗ ΤΜΗΜΑ ΕΠΙΧΕΙΡΗΜΑΤΙΚΟΥ ΣΧΕ ΙΑΣΜΟΥ & ΠΛΗΡΟΦΟΡΙΑΚΩΝ ΣΥΣΤΗΜΑΤΩΝ Ακαδηµαϊκό Έτος 2011-2012 ΕΠΙΧ Μικροοικονοµική
Προσφορά Εργασίας Προτιμήσεις και Συνάρτηση Χρησιμότητας ( Χ,Α συνάρτηση χρησιμότητας U(X,A)
 Προσφορά Εργασίας - Έστω ότι υπάρχουν δύο αγαθά Α και Χ στην οικονομία. Το αγαθό Α παριστάνει τα διάφορα καταναλωτικά αγαθά. Το αγαθό Χ παριστάνει τον ελεύθερο χρόνο. Προτιμήσεις και Συνάρτηση Χρησιμότητας
Προσφορά Εργασίας - Έστω ότι υπάρχουν δύο αγαθά Α και Χ στην οικονομία. Το αγαθό Α παριστάνει τα διάφορα καταναλωτικά αγαθά. Το αγαθό Χ παριστάνει τον ελεύθερο χρόνο. Προτιμήσεις και Συνάρτηση Χρησιμότητας
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος Τμήμα Οικονομικών Επιστημών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 206-207 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου ο Πακέτο Ασκήσεων Ημερομηνία παράδοσης: Τρίτη Απριλίου
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 206-207 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου ο Πακέτο Ασκήσεων Ημερομηνία παράδοσης: Τρίτη Απριλίου
ΑΝΤΑΛΛΑΓΗ. Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα. και. και το αρχικό απόθεμα και.
 ΑΝΤΑΛΛΑΓΗ Άσκηση 5 Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα u ( x, x ) = x + x 1 2 1 2 και u ( x, x ) = x + x 1 2 1 2 Ω = (2,0) Ω = (0,1) και το αρχικό απόθεμα και. Να προσδιοριστεί
ΑΝΤΑΛΛΑΓΗ Άσκηση 5 Οι συναρτήσεις χρησιμότητας των ατόμων Α και Β είναι αντίστοιχα u ( x, x ) = x + x 1 2 1 2 και u ( x, x ) = x + x 1 2 1 2 Ω = (2,0) Ω = (0,1) και το αρχικό απόθεμα και. Να προσδιοριστεί
Διάλεξη 7. Εξίσωση Slutsky. Οι επιδράσεις µιας µεταβολής της
 Οι επιδράσεις µιας µεταβολής της τιµής Διάλεξη 7 Εξίσωση Slutsk Τι θα συµβεί όταν µειωθεί η τιµή ενός αγαθού; Αποτέλεσµα υποκατάστασης : το αγαθό γίνεται σχετικά πιο φτηνό και γι αυτό ο καταναλωτής υποκαθιστά
Οι επιδράσεις µιας µεταβολής της τιµής Διάλεξη 7 Εξίσωση Slutsk Τι θα συµβεί όταν µειωθεί η τιµή ενός αγαθού; Αποτέλεσµα υποκατάστασης : το αγαθό γίνεται σχετικά πιο φτηνό και γι αυτό ο καταναλωτής υποκαθιστά
Μικροοικονοµική Θεωρία. Προσφορά προϊόντος από επιχείρηση. Προσφορά προϊόντος από επιχείρηση. = 0 p = dc(q) Notes. Notes. Notes.
 Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 23 Σεπτεµβρίου 214 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 23 Σεπτεµβρίου 214 1 / 25 Προσφορά προϊόντος από επιχείρηση Ποια είναι
Μικροοικονοµική Θεωρία Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 23 Σεπτεµβρίου 214 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Μικροοικονοµική Θεωρία 23 Σεπτεµβρίου 214 1 / 25 Προσφορά προϊόντος από επιχείρηση Ποια είναι
Η θεωρία των επιλογών του καταναλωτή
 Η θεωρία των επιλογών του καταναλωτή Ο εισοδηµατικός περιορισµός του καταναλωτή Λίτρα Αριθµός από πίτσες απάνες για (σε ευρώ) απάνες για πίτσα (σε ευρώ) Συνολικές δαπάνες (σε ευρώ) 1 1. 1. 5 9 1 9 1. 1
Η θεωρία των επιλογών του καταναλωτή Ο εισοδηµατικός περιορισµός του καταναλωτή Λίτρα Αριθµός από πίτσες απάνες για (σε ευρώ) απάνες για πίτσα (σε ευρώ) Συνολικές δαπάνες (σε ευρώ) 1 1. 1. 5 9 1 9 1. 1
ΔΥΝΑΜΗ ΣΤΗΝ ΑΓΟΡΑ (Παράδειγμα: ΜΟΝΟΠΩΛΙΟ)
 Θεωρήματα Οικονομικών της Ευημερίας (1) Οι ανταγωνιστικές αγορές συντονίζουν τις αποφάσεις των καταναλωτών και των παραγωγών εξασφαλίζοντας Pareto αποτελεσματικές κατανομές των παραγωγικών πόρων και των
Θεωρήματα Οικονομικών της Ευημερίας (1) Οι ανταγωνιστικές αγορές συντονίζουν τις αποφάσεις των καταναλωτών και των παραγωγών εξασφαλίζοντας Pareto αποτελεσματικές κατανομές των παραγωγικών πόρων και των
Γενική Ανταγωνιστική Ισορροπία σε Οικονομία με Έναν Καταναλωτή και Έναν Παραγωγό
 Γενική Ανταγωνιστική Ισορροπία σε Οικονομία με Έναν Καταναλωτή και Έναν Παραγωγό - Ορισμός. Μια ανταγωνιστική οικονομία που διέπεται από το θεσμό της ατομικής ιδιοκτησίας είναι μια οικονομία όπου: (i)
Γενική Ανταγωνιστική Ισορροπία σε Οικονομία με Έναν Καταναλωτή και Έναν Παραγωγό - Ορισμός. Μια ανταγωνιστική οικονομία που διέπεται από το θεσμό της ατομικής ιδιοκτησίας είναι μια οικονομία όπου: (i)
Εισαγωγή. Αποτελεσματικότητα κατά Pareto. 1. ΑΝΤΑΓΩΝΙΣΜΟΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ (επεξεργασία σημειώσεων Β. Ράπανου)
 1. ΑΝΤΑΓΩΝΙΣΜΟΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ (επεξεργασία σημειώσεων Β. Ράπανου) Εισαγωγή Μια από τις πιο βασικές διακρίσεις στην οικονομική θεωρία είναι μεταξύ των εννοιών της οικονομικής αποτελεσματικότητας
1. ΑΝΤΑΓΩΝΙΣΜΟΣ ΚΑΙ ΟΙΚΟΝΟΜΙΚΗ ΑΠΟΤΕΛΕΣΜΑΤΙΚΟΤΗΤΑ (επεξεργασία σημειώσεων Β. Ράπανου) Εισαγωγή Μια από τις πιο βασικές διακρίσεις στην οικονομική θεωρία είναι μεταξύ των εννοιών της οικονομικής αποτελεσματικότητας
Κοινωνικοοικονομική Αξιολόγηση Επενδύσεων Διάλεξη 3 η. Αποτελεσματικότητα και Ευημερία
 Κοινωνικοοικονομική Αξιολόγηση Επενδύσεων Διάλεξη 3 η Αποτελεσματικότητα και Ευημερία Ζητήματα που θα εξεταστούν: Πότε και πως επιτυγχάνεται η οικονομική αποτελεσματικότητα Θεωρήματα των οικονομικών της
Κοινωνικοοικονομική Αξιολόγηση Επενδύσεων Διάλεξη 3 η Αποτελεσματικότητα και Ευημερία Ζητήματα που θα εξεταστούν: Πότε και πως επιτυγχάνεται η οικονομική αποτελεσματικότητα Θεωρήματα των οικονομικών της
Notes. Notes. Notes. Notes
 Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 26 Μαΐου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) 26 Μαΐου 2012 1 / 19 Εως τώρα τα αγαθά που θεωρήσαμε ότι καταναλώνει ο καταναλωτής ήταν ιδιωτικά αγαθά. Με απλά λόγια
Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 26 Μαΐου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) 26 Μαΐου 2012 1 / 19 Εως τώρα τα αγαθά που θεωρήσαμε ότι καταναλώνει ο καταναλωτής ήταν ιδιωτικά αγαθά. Με απλά λόγια
4.1 Ζήτηση για Ασφάλιση. Πλήρη κάλυψη.
 4. Ζήτηση για Ασφάλιση. Πλήρη κάλυψη. Η αγορά ασφαλιστικών συµφωνιών είναι µία ιδιαίτερη περίπτωση αγοράς δικαιωµάτων. Αντικείµενο της αγοράς αυτής είναι να δώσει την ευκαιρία µεταβίβασης εισοδήµατος από
4. Ζήτηση για Ασφάλιση. Πλήρη κάλυψη. Η αγορά ασφαλιστικών συµφωνιών είναι µία ιδιαίτερη περίπτωση αγοράς δικαιωµάτων. Αντικείµενο της αγοράς αυτής είναι να δώσει την ευκαιρία µεταβίβασης εισοδήµατος από
Οικονοµικό Πανεπιστήµιο Αθηνών. Ε. Ο. Σ. Μικροοικονοµική ΙΙ Εξετάσεις Ιανουαρίου ιδάσκων : Ρουµανιάς Κώστας
 Οικονοµικό Πανεπιστήµιο Αθηνών. Ε. Ο. Σ. Μικροοικονοµική ΙΙ Εξετάσεις Ιανουαρίου 2014 ιδάσκων : Ρουµανιάς Κώστας 24-2-2015 ΕΠΩΝΥΜΟ : ΟΝΟΜΑ : ΠΑΤΡΩΝΥΜΟ : ΑΡ. ΜΗΤΡΩΟΥ : Ο ΗΓΙΕΣ : Να απαντηθούν όλα τα ακόλουθα
Οικονοµικό Πανεπιστήµιο Αθηνών. Ε. Ο. Σ. Μικροοικονοµική ΙΙ Εξετάσεις Ιανουαρίου 2014 ιδάσκων : Ρουµανιάς Κώστας 24-2-2015 ΕΠΩΝΥΜΟ : ΟΝΟΜΑ : ΠΑΤΡΩΝΥΜΟ : ΑΡ. ΜΗΤΡΩΟΥ : Ο ΗΓΙΕΣ : Να απαντηθούν όλα τα ακόλουθα
ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι Ενότητα 3: Εργαλεία Κανονιστικής Ανάλυσης Κουτεντάκης Φραγκίσκος Γαληνού Αργυρώ Τμήμα Οικονομικών Επιστημών Άδειες Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ ΔΗΜΟΣΙΑ ΟΙΚΟΝΟΜΙΚΗ Ι Ενότητα 3: Εργαλεία Κανονιστικής Ανάλυσης Κουτεντάκης Φραγκίσκος Γαληνού Αργυρώ Τμήμα Οικονομικών Επιστημών Άδειες Χρήσης Το παρόν εκπαιδευτικό
Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας
 Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό
Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό
ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ
 Ένθετο Κεφάλαιο ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Μικροοικονομική Ε. Σαρτζετάκης 1 Καταναλωτική συμπεριφορά Σκοπός αυτής της διάλεξης είναι να εξετάσουμε τον τρόπο με τον οποίο οι καταναλωτές
Ένθετο Κεφάλαιο ΘΕΩΡΙΑ ΧΡΗΣΙΜΟΤΗΤΑΣ ΚΑΤΑΝΑΛΩΤΙΚΗ ΣΥΜΠΕΡΙΦΟΡΑ Μικροοικονομική Ε. Σαρτζετάκης 1 Καταναλωτική συμπεριφορά Σκοπός αυτής της διάλεξης είναι να εξετάσουμε τον τρόπο με τον οποίο οι καταναλωτές
Κεφάλαιο 1. Θεωρία Ζήτησης
 Κεφάλαιο 1 Θεωρία Ζήτησης Στο κεφάλαιο αυτό υποθέτουµε ότι καταναλωτής εισέρχεται στην αγορά µε πλούτο w > 0 και επιθυµεί να τον ανταλλάξει µε διάνυσµα αγαθών x που να µεγιστοποιεί τις προτιµήσεις του.
Κεφάλαιο 1 Θεωρία Ζήτησης Στο κεφάλαιο αυτό υποθέτουµε ότι καταναλωτής εισέρχεται στην αγορά µε πλούτο w > 0 και επιθυµεί να τον ανταλλάξει µε διάνυσµα αγαθών x που να µεγιστοποιεί τις προτιµήσεις του.
Notes. Notes. Notes. Notes
 Αγορές - Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 6 Δεκεμβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Αγορές - 6 Δεκεμβρίου 2012 1 / 26 Ως τώρα, υποθέσαμε ότι οι αγορές είναι ανταγωνιστικές. Μία συνέπεια των
Αγορές - Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 6 Δεκεμβρίου 2012 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Αγορές - 6 Δεκεμβρίου 2012 1 / 26 Ως τώρα, υποθέσαμε ότι οι αγορές είναι ανταγωνιστικές. Μία συνέπεια των
Μεγιστοποίηση της Χρησιμότητας
 Μεγιστοποίηση της Χρησιμότητας - Πρόβλημα Καταναλωτή: Επιλογή καταναλωτικού συνδυασμού x=(x, x ) υπό ένα σύνολο φυσικών, θεσμικών και οικονομικών περιορισμών κατά τρόπο ώστε να μεγιστοποιεί τη χρησιμότητά
Μεγιστοποίηση της Χρησιμότητας - Πρόβλημα Καταναλωτή: Επιλογή καταναλωτικού συνδυασμού x=(x, x ) υπό ένα σύνολο φυσικών, θεσμικών και οικονομικών περιορισμών κατά τρόπο ώστε να μεγιστοποιεί τη χρησιμότητά
Κεφάλαιο 5 R (2, 3) R (3, 0)
 Κεφάλαιο 5 Θα ξεκινήσουµε το κεφάλαιο αυτό βλέποντας ένα ακόµη παράδειγµα αναφορικά µε την ισορροπία που προκύπτει από την οπισθογενή επαγωγή (backwards induction) και την ισορροπία κατά Nash στην στρατηγική
Κεφάλαιο 5 Θα ξεκινήσουµε το κεφάλαιο αυτό βλέποντας ένα ακόµη παράδειγµα αναφορικά µε την ισορροπία που προκύπτει από την οπισθογενή επαγωγή (backwards induction) και την ισορροπία κατά Nash στην στρατηγική
Π 0,0 1,2 Κ 4,3 2,3 Π 2,0 5,3 9,10 Κ 4,4 7,2 6,0. (βʹ) 2 < 4q q > 1 2
 ΜΕΡΟΣ 1 Με κόκκινο σας δίνω τις σωστές απαντήσεις και τη συλλογιστική πίσω από την επιλογή της συγκεκριμένης απάντησης. Με μπλε χρώμα εξηγώ γιατί η συγκεκριμένη απάντηση είναι λάθος. 1. Από το θεώρημα
ΜΕΡΟΣ 1 Με κόκκινο σας δίνω τις σωστές απαντήσεις και τη συλλογιστική πίσω από την επιλογή της συγκεκριμένης απάντησης. Με μπλε χρώμα εξηγώ γιατί η συγκεκριμένη απάντηση είναι λάθος. 1. Από το θεώρημα
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ. Θεωρία Χρησιµότητας και Συµπεριφοράς του Καταναλωτή
 ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ Θεωρία Χρησιµότητας και Συµπεριφοράς του Καταναλωτή Εισαγωγή: Όπως γνωρίζουµε, το οικονοµικό πρόβληµα εστιάζεται στην αποτελεσµατική κατανοµή των ανεπαρκών οικονοµικών πόρων στις εναλλακτικές
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ Θεωρία Χρησιµότητας και Συµπεριφοράς του Καταναλωτή Εισαγωγή: Όπως γνωρίζουµε, το οικονοµικό πρόβληµα εστιάζεται στην αποτελεσµατική κατανοµή των ανεπαρκών οικονοµικών πόρων στις εναλλακτικές
Διάλεξη 3. Προτιµήσεις. Ορθολογισµός στην οικονοµική. Σχέσεις προτιµήσεων
 Ορθολογισµός στην οικονοµική Διάλεξη 3 Προτιµήσεις!1 Υπόθεση συµπεριφοράς: Ένας λήπτης αποφάσεων επιλέγει πάντοτε τον πλέον προτιµώµενο συνδυασµό από το σύνολο των εναλλακτικών συνδυασµών που έχει στη
Ορθολογισµός στην οικονοµική Διάλεξη 3 Προτιµήσεις!1 Υπόθεση συµπεριφοράς: Ένας λήπτης αποφάσεων επιλέγει πάντοτε τον πλέον προτιµώµενο συνδυασµό από το σύνολο των εναλλακτικών συνδυασµών που έχει στη
Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας
 Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό
Άριστες κατά Pareto Κατανομές και το Πρώτο Θεώρημα Ευημερίας - Υποθέτουμε μια οικονομία που αποτελείται από: Δύο καταναλωτές 1,. Μία επιχείρηση. Δύο αγαθά: τον ελεύθερο χρόνο Χ και το καταναλωτικό αγαθό
Θέµα: Μεγιστοποίηση χρησιµότητας και επιλογή
 ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ Ι Φροντιστήριο 3 Θέµα: Μεγιστοποίηση χρησιµότητας και επιλογή Γενική σηµείωση: Οι λύσεις των ασκήσεων του βιβλίου γίνονται µε τρόπο ώστε να κατανοηθεί καλύτερα η θεωρία. Οι περισσότερες
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΘΕΩΡΙΑ Ι Φροντιστήριο 3 Θέµα: Μεγιστοποίηση χρησιµότητας και επιλογή Γενική σηµείωση: Οι λύσεις των ασκήσεων του βιβλίου γίνονται µε τρόπο ώστε να κατανοηθεί καλύτερα η θεωρία. Οι περισσότερες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος Τμήμα Οικονομικών Επιστημών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 20-202 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Βασίλης Θ. Ράπανος Γεωργία Καπλάνογλου Ημερομηνία παράδοσης: Απριλίου 202 Οι
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 20-202 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Βασίλης Θ. Ράπανος Γεωργία Καπλάνογλου Ημερομηνία παράδοσης: Απριλίου 202 Οι
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2012-2013 Τμήμα Οικονομικών Επιστημών Εξέταση στο μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2012-2013 Τμήμα Οικονομικών Επιστημών Εξέταση στο μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου Εξεταστική περίοδος Φεβρουαρίου Η εξέταση αποτελείται από
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2012-2013 Τμήμα Οικονομικών Επιστημών Εξέταση στο μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου Εξεταστική περίοδος Φεβρουαρίου Η εξέταση αποτελείται από
2o Μάθηµα. Χαράλαµπος Χρήστου 1/7 Σηµειώσεις: ηµόσια Οικονοµική Ι/2 ο Μάθηµα
 2o Μάθηµα Αναφέραµε στο πρώτο µάθηµα τρόπους µε τους οποίους το κράτος επηρεάζει την οικονοµική συµπεριφορά µας. (νοµικό πλαίσιο, το κράτος αγοράζει και παράγει αγαθά και υπηρεσίες, ρυθµίζει τις πολιτικές
2o Μάθηµα Αναφέραµε στο πρώτο µάθηµα τρόπους µε τους οποίους το κράτος επηρεάζει την οικονοµική συµπεριφορά µας. (νοµικό πλαίσιο, το κράτος αγοράζει και παράγει αγαθά και υπηρεσίες, ρυθµίζει τις πολιτικές
Το Πρότυπο Υπόδειγμα του Διεθνούς Εμπορίου 5-1
 Το Πρότυπο Υπόδειγμα του Διεθνούς Εμπορίου 5-1 Επισκόπηση Μετρώντας την αξία της παραγωγής και της κατανάλωσης Ευημερία και όροι εμπορίου Επιδράσεις της οικονομικής ανάπτυξης Επιδράσεις διεθνών μεταβιβάσεων
Το Πρότυπο Υπόδειγμα του Διεθνούς Εμπορίου 5-1 Επισκόπηση Μετρώντας την αξία της παραγωγής και της κατανάλωσης Ευημερία και όροι εμπορίου Επιδράσεις της οικονομικής ανάπτυξης Επιδράσεις διεθνών μεταβιβάσεων
(1β) Μη Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος με Ενδογενές Πλήθος Επιχειρήσεων
 (β) Μη Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος με Ενδογενές Πλήθος Επιχειρήσεων Ελεύθερη Είσοδος και Ισορροπία Μηδενικών Κερδών - Η δυνατότητα νέων επιχειρήσεων να εισέρχονται ελεύθερα στην αγορά
(β) Μη Χωροθετικά Υποδείγματα Διαφοροποιημένου Προϊόντος με Ενδογενές Πλήθος Επιχειρήσεων Ελεύθερη Είσοδος και Ισορροπία Μηδενικών Κερδών - Η δυνατότητα νέων επιχειρήσεων να εισέρχονται ελεύθερα στην αγορά
Ορια Συναρτησεων - Ορισµοι
 Ορια Συναρτησεων - Ορισµοι Λυγάτσικας Ζήνων Βαρβάκειο Ενιαίο Πειραµατικό Λύκειο 3 Σεπτεµβρίου 205 Εισαγωγή Στην παράγραφο αυτή ϑα δούµε πως προκύπτει η ιδέα του ορίου στην προσπά- ϑεια να ορίσουµε την
Ορια Συναρτησεων - Ορισµοι Λυγάτσικας Ζήνων Βαρβάκειο Ενιαίο Πειραµατικό Λύκειο 3 Σεπτεµβρίου 205 Εισαγωγή Στην παράγραφο αυτή ϑα δούµε πως προκύπτει η ιδέα του ορίου στην προσπά- ϑεια να ορίσουµε την
Μικροοικονομική. Ενότητα 3: Ο καταναλωτής επιλέγει να μεγιστοποιήσει τη χρησιμότητά του. Σόρμας Αστέριος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη)
 Μικροοικονομική Ενότητα 3: Ο καταναλωτής επιλέγει να μεγιστοποιήσει τη χρησιμότητά του Σόρμας Αστέριος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Μικροοικονομική Ενότητα 3: Ο καταναλωτής επιλέγει να μεγιστοποιήσει τη χρησιμότητά του Σόρμας Αστέριος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2013 2014 Τμήμα Οικονομικών Επιστημών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2013 2014 Τμήμα Οικονομικών Επιστημών Χειμώνας Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Βασίλης Θ. Ράπανος Γεωργία Καπλάνογλου 1 ο Πακέτο Ασκήσεων. Απαντήσεις Ημερομηνία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2013 2014 Τμήμα Οικονομικών Επιστημών Χειμώνας Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Βασίλης Θ. Ράπανος Γεωργία Καπλάνογλου 1 ο Πακέτο Ασκήσεων. Απαντήσεις Ημερομηνία
Οικονοµικός ορθολογισµός
 Οικονοµικός ορθολογισµός Διάλεξη 5 Επιλογή!1 Η βασική παραδοχή για τη συµπεριφορά του λήπτη αποφάσεων είναι ότι αυτός/αυτή επιλέγει την πλέον προτιµώµενη εναλλακτική επιλογή που του/της είναι διαθέσιµη.
Οικονοµικός ορθολογισµός Διάλεξη 5 Επιλογή!1 Η βασική παραδοχή για τη συµπεριφορά του λήπτη αποφάσεων είναι ότι αυτός/αυτή επιλέγει την πλέον προτιµώµενη εναλλακτική επιλογή που του/της είναι διαθέσιµη.
Επιλογές του Καταναλωτή και Αποφάσεις Ζήτησης Εκδόσεις Κριτική
 5 Επιλογές του Καταναλωτή και Αποφάσεις Ζήτησης Τέσσερα βασικά στοιχεία του υποδείγματος επιλογής του καταναλωτή Το εισόδημα του καταναλωτή. Οι τιμές των αγαθών. Οι προτιμήσεις του καταναλωτή. Η υπόθεση
5 Επιλογές του Καταναλωτή και Αποφάσεις Ζήτησης Τέσσερα βασικά στοιχεία του υποδείγματος επιλογής του καταναλωτή Το εισόδημα του καταναλωτή. Οι τιμές των αγαθών. Οι προτιμήσεις του καταναλωτή. Η υπόθεση
ηµόσια Οικονοµική Βασίλης Ράπανος, Γεωργία Καπλάνογλου µόνο Τµήµα Ι.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδηµαϊκό έτος 2013-2014 Τµήµα Οικονοµικών Επιστηµών Εξεταστική περίοδος Απριλίου Εξέταση στο µάθηµα: ηµόσια Οικονοµική ιδασκαλία: Βασίλης Ράπανος, Γεωργία Καπλάνογλου Η εξέταση αποτελείται
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδηµαϊκό έτος 2013-2014 Τµήµα Οικονοµικών Επιστηµών Εξεταστική περίοδος Απριλίου Εξέταση στο µάθηµα: ηµόσια Οικονοµική ιδασκαλία: Βασίλης Ράπανος, Γεωργία Καπλάνογλου Η εξέταση αποτελείται
Ο λόγος των τιμών ισορροπίας είναι p ˆ. 2 pˆ 7 2 = Το εισόδημα των δύο ατόμων στις τιμές ισορροπίας είναι
 3 Ο λόγος των τιμών ισορροπίας είναι p ˆ pˆ pˆ. Στη συνέχεια αντικαθιστώντας στις εξισώσεις (V)-(X) βρίσκουμε τις ποσότητες ισορροπίας. Για να κάνουμε το παράδειγμα πιο συγκεκριμένο, ας υποθέσουμε ότι
3 Ο λόγος των τιμών ισορροπίας είναι p ˆ pˆ pˆ. Στη συνέχεια αντικαθιστώντας στις εξισώσεις (V)-(X) βρίσκουμε τις ποσότητες ισορροπίας. Για να κάνουμε το παράδειγμα πιο συγκεκριμένο, ας υποθέσουμε ότι
Επιλογή Ποιότητας και Κάθετη Διαφοροποίηση Προϊόντος
 Επιλογή Ποιότητας και Κάθετη Διαφοροποίηση Προϊόντος - Τα προϊόντα που παράγουν οι επιχειρήσεις μπορούν να διαφοροποιούνται ως προς ένα πλήθος χαρακτηριστικών. Παράδειγμα: Τα αυτοκίνητα διαφοροποιούνται
Επιλογή Ποιότητας και Κάθετη Διαφοροποίηση Προϊόντος - Τα προϊόντα που παράγουν οι επιχειρήσεις μπορούν να διαφοροποιούνται ως προς ένα πλήθος χαρακτηριστικών. Παράδειγμα: Τα αυτοκίνητα διαφοροποιούνται
Notes. Notes. Notes. Notes
 Θεωρία Καταναλωτή: Αβεβαιότητα Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 9 Οκτωβρίου 0 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία Καταναλωτή: Αβεβαιότητα 9 Οκτωβρίου 0 / 5 Ανάγκη θεωρίας επιλογής υπό αβεβαιότητα
Θεωρία Καταναλωτή: Αβεβαιότητα Κώστας Ρουμανιάς Ο.Π.Α. Τμήμα Δ. Ε. Ο. Σ. 9 Οκτωβρίου 0 Κώστας Ρουμανιάς (Δ.Ε.Ο.Σ.) Θεωρία Καταναλωτή: Αβεβαιότητα 9 Οκτωβρίου 0 / 5 Ανάγκη θεωρίας επιλογής υπό αβεβαιότητα
ΟΜΟΣΠΟΝ ΙΑ ΕΚΠΑΙ ΕΥΤΙΚΩΝ ΦΡΟΝΤΙΣΤΩΝ ΕΛΛΑ ΟΣ (Ο.Ε.Φ.Ε.) ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ ΕΠΑΝΑΛΗΠΤΙΚΑ ΘΕΜΑΤΑ 2017 Β ΦΑΣΗ ΜΑΘΗΜΑΤΙΚΑ ÅÐÉËÏÃÇ
 ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΘΕΜΑ Α Ηµεροµηνία: Σάββατο 8 Απριλίου 2017 ιάρκεια Εξέτασης: 3 ώρες Α1. Θεωρία. Σχολικό βιβλίο σελίδα 83 Α2. α) Σωστό β) Λάθος γ) Σωστό
ΤΑΞΗ: Β ΓΕΝΙΚΟΥ ΛΥΚΕΙΟΥ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ: ΘΕΤΙΚΩΝ ΣΠΟΥ ΩΝ ΜΑΘΗΜΑ: ΘΕΜΑ Α Ηµεροµηνία: Σάββατο 8 Απριλίου 2017 ιάρκεια Εξέτασης: 3 ώρες Α1. Θεωρία. Σχολικό βιβλίο σελίδα 83 Α2. α) Σωστό β) Λάθος γ) Σωστό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2012-2013 Τμήμα Οικονομικών Επιστημών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 202-20 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Βασίλης Θ. Ράπανος Γεωργία Καπλάνογλου ο Πακέτο Ασκήσεων Απαντήσεις Ημερομηνία
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 202-20 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Βασίλης Θ. Ράπανος Γεωργία Καπλάνογλου ο Πακέτο Ασκήσεων Απαντήσεις Ημερομηνία
Σηµειώσεις. Μικροοικονοµικής Θεωρίας ΙΙΙ (ΜΙΚΟ 201)
 Σηµειώσεις Μικροοικονοµικής Θεωρίας ΙΙΙ (ΜΙΚΟ 201) «Οικονοµική της Ευηµερίας» Βαγγέλης Τζουβελέκας Ρέθυµνο, 2003 ΚΕΦΑΛΑΙΟ 5 ΟΙΚΟΝΟΜΙΚΗ ΤΗΣ ΕΥΗΜΕΡΙΑΣ 5.1 Μη Ουδετερότητα των Φόρων Εάν υποθέσουµε ότι προς
Σηµειώσεις Μικροοικονοµικής Θεωρίας ΙΙΙ (ΜΙΚΟ 201) «Οικονοµική της Ευηµερίας» Βαγγέλης Τζουβελέκας Ρέθυµνο, 2003 ΚΕΦΑΛΑΙΟ 5 ΟΙΚΟΝΟΜΙΚΗ ΤΗΣ ΕΥΗΜΕΡΙΑΣ 5.1 Μη Ουδετερότητα των Φόρων Εάν υποθέσουµε ότι προς
Εξωτερικότητες και περιβαλλοντική πολιτική
 Εξωτερικότητες και περιβαλλοντική πολιτική Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 10 Απριλίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Εξωτερικότητες και περιβαλλοντική πολιτική 10 Απριλίου 2014 1 / 42 Κλιµατική
Εξωτερικότητες και περιβαλλοντική πολιτική Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 10 Απριλίου 2014 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Εξωτερικότητες και περιβαλλοντική πολιτική 10 Απριλίου 2014 1 / 42 Κλιµατική
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος Τμήμα Οικονομικών Επιστημών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 206-207 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου ο Πακέτο Ασκήσεων Απαντήσεις Σωστό-Λάθος (Δίπλα σε κάθε
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 206-207 Τμήμα Οικονομικών Επιστημών Χειμώνας-Άνοιξη Μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου ο Πακέτο Ασκήσεων Απαντήσεις Σωστό-Λάθος (Δίπλα σε κάθε
ΚΑΜΠΥΛΗ ENGEL ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΖΗΤΗΣΗΣ ΚΑΤΑ MARSHALL ΚΑΙ HICKS. 1. Η καµπύλη Engel
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ ΚΑΜΠΥΛΗ ENGEL ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΖΗΤΗΣΗΣ ΚΑΤΑ ARSALL ΚΑΙ ICKS. Η καµπύλη Egel Η καµπύλη Egel παράγεται από την
ΠΑΝΕΠΙΣΤΗΜΙΟ ΜΑΚΕ ΟΝΙΑΣ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΚΑΘΗΓΗΤΗΣ ΚΩΣΤΑΣ ΒΕΛΕΝΤΖΑΣ ΚΑΜΠΥΛΗ ENGEL ΚΑΙ Ι ΙΟΤΗΤΕΣ ΤΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΖΗΤΗΣΗΣ ΚΑΤΑ ARSALL ΚΑΙ ICKS. Η καµπύλη Egel Η καµπύλη Egel παράγεται από την
Λύσεις Πρώτου Πακέτου Ασκήσεων
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι 2016-17 Λύσεις Πρώτου Πακέτου Ασκήσεων Άσκηση 1 1. α) Αν βάλουµε την ποσότητα του αγαθού X στον οριζόντιο και την ποσότητα
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τμήμα Οικονομικών Επιστημών Μάθημα: Μικροοικονομική Θεωρία Ι 2016-17 Λύσεις Πρώτου Πακέτου Ασκήσεων Άσκηση 1 1. α) Αν βάλουµε την ποσότητα του αγαθού X στον οριζόντιο και την ποσότητα
Μικροοικονομική. Θεωρία Συμπεριφοράς Καταναλωτή
 Μικροοικονομική Θεωρία Συμπεριφοράς Καταναλωτή Συνολική και οριακή ρησιμότητα Η κατανάλωση αγαθών συνεπάγεται κάποια ικανοποίηση ή ρησιμότητα για τον καταναλωτή. Συνολική ρησιμότητα (U) είναι η συνολική
Μικροοικονομική Θεωρία Συμπεριφοράς Καταναλωτή Συνολική και οριακή ρησιμότητα Η κατανάλωση αγαθών συνεπάγεται κάποια ικανοποίηση ή ρησιμότητα για τον καταναλωτή. Συνολική ρησιμότητα (U) είναι η συνολική
Ιδιότητες καµπυλών ζήτησης
 Ιδιότητες καµπυλών ζήτησης Διάλεξη 6 ΖΗΤΗΣΗ Συγκριτική στατική ανάλυση των συναρτήσεων της κανονικής ζήτησης είναι η µελέτη του πώς οι συναρτήσεις κανονικής ζήτησης (, 2,) και (, 2,) αλλάζουν όταν οι τιµές,
Ιδιότητες καµπυλών ζήτησης Διάλεξη 6 ΖΗΤΗΣΗ Συγκριτική στατική ανάλυση των συναρτήσεων της κανονικής ζήτησης είναι η µελέτη του πώς οι συναρτήσεις κανονικής ζήτησης (, 2,) και (, 2,) αλλάζουν όταν οι τιµές,
Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrange
 64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
64 Ακρότατα υπό συνθήκη και οι πολλαπλασιαστές του Lagrage Ας υποθέσουµε ότι ένας δεδοµένος χώρος θερµαίνεται και η θερµοκρασία στο σηµείο,, Τ, y, z Ας υποθέσουµε ότι ( y z ) αυτού του χώρου δίδεται από
ιάλεξη 3 Προτιµήσεις ~ σηµαίνει ότι το x προτιµάται τουλάχιστο όσο και ~ f Ορθολογισµός στην οικονοµική Σχέσεις προτιµήσεων
 Ορθολογισµός στην οικονοµική ιάλεξη 3 Προτιµήσεις Υπόθεση συµπεριφοράς: Ένας λήπτης αποφάσεων επιλέγει πάντοτε τον πλέον προτιµώµενο συνδυασµό από το σύνολο των εναλλακτικών συνδυασµών που έχει στη διάθεση
Ορθολογισµός στην οικονοµική ιάλεξη 3 Προτιµήσεις Υπόθεση συµπεριφοράς: Ένας λήπτης αποφάσεων επιλέγει πάντοτε τον πλέον προτιµώµενο συνδυασµό από το σύνολο των εναλλακτικών συνδυασµών που έχει στη διάθεση
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ
 ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ 36 Κεφάλαιο 3ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ. Σ 4. Λ. Λ 3. Λ 4. Λ 3. Σ 4. Σ 43. Σ 4. Λ 5. Σ 44. Σ 5. Σ 6. Σ 45. Λ 6.
ΑΠΑΝΤΗΣΕΙΣ - ΥΠΟ ΕΙΞΕΙΣ ΣΤΙΣ ΕΡΩΤΗΣΕΙΣ 36 Κεφάλαιο 3ο: ΟΛΟΚΛΗΡΩΤΙΚΟΣ ΛΟΓΙΣΜΟΣ Απαντήσεις στις ερωτήσεις του τύπου Σωστό-Λάθος. Σ. Σ 4. Λ. Λ 3. Λ 4. Λ 3. Σ 4. Σ 43. Σ 4. Λ 5. Σ 44. Σ 5. Σ 6. Σ 45. Λ 6.
Α. Αυτάρκης Οικονομία
 σελ. από 9 Οικονομικό Πανεπιστήμιο Αθηνών Τμήμα Οικονομικής Επιστήμης Μάθημα: 473 Διεθνής Οικονομική Εαρινό Εξάμηνο 05 Καθηγητής: Γιώργος Αλογοσκούφης Φροντιστής: Αλέκος Παπαδόπουλος 8/5/05 Διαγραμματική
σελ. από 9 Οικονομικό Πανεπιστήμιο Αθηνών Τμήμα Οικονομικής Επιστήμης Μάθημα: 473 Διεθνής Οικονομική Εαρινό Εξάμηνο 05 Καθηγητής: Γιώργος Αλογοσκούφης Φροντιστής: Αλέκος Παπαδόπουλος 8/5/05 Διαγραμματική
ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 6 ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ-ΚΑΤΑΝΑΛΩΤΗ
 ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 6 ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ-ΚΑΤΑΝΑΛΩΤΗ ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ- ΚΑΤΑΝΑΛΩΤΗ ΔΙΑΡΘΡΩΣΗ ΘΕΜΑΤΙΚΩΝ ΕΝΟΤΗΤΩΝ ΚΕΦΑΛΑΙΟΥ Η θεωρία της οριακής
ΤΟΥΡΙΣΤΙΚΗ ΟΙΚΟΝΟΜΙΚΗ ΚΕΦΑΛΑΙΟ 6 ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ-ΚΑΤΑΝΑΛΩΤΗ ΘΕΩΡΙΑ ΠΡΟΤΙΜΗΣΕΩΝ ΚΑΙ ΕΠΙΛΟΓΩΝ ΤΟΥ ΤΟΥΡΙΣΤΑ- ΚΑΤΑΝΑΛΩΤΗ ΔΙΑΡΘΡΩΣΗ ΘΕΜΑΤΙΚΩΝ ΕΝΟΤΗΤΩΝ ΚΕΦΑΛΑΙΟΥ Η θεωρία της οριακής
6. Το Υπόδειγμα των Επικαλυπτόμενων Γενεών: Ανταλλαγή I
 6. Το Υπόδειγμα τν Επικαλυπτόμενν Γενεών: Ανταλλαγή I 6.. Ερτήσεις Σχολιάστε την εγκυρότητα τν παρακάτ προτάσεν. Αν πιστεύετε ότι μια πρόταση είναι σστή κάτ από ορισμένες προϋποθέσεις τότε να αναφέρετε
6. Το Υπόδειγμα τν Επικαλυπτόμενν Γενεών: Ανταλλαγή I 6.. Ερτήσεις Σχολιάστε την εγκυρότητα τν παρακάτ προτάσεν. Αν πιστεύετε ότι μια πρόταση είναι σστή κάτ από ορισμένες προϋποθέσεις τότε να αναφέρετε
Ηδονικές τιµές 10/31/10. Ρύπανση και πρόσοδοι (νοίκια) γης. Γεωργική γη. Δύο περιοχές. Δύο περιοχές Γεωργική γη
 Ρύπανση και πρόσοδοι (νοίκια) γης Ηδονικές τιµές Τι καθορίζει την τιµή της γης; η παρούσα αξία της ροής υπηρεσιών που προσδοκάται στο µέλλον Πρόσοδοι (νοίκι) και αξία ως ακίνητο Στην γεωργική καλλιέργεια
Ρύπανση και πρόσοδοι (νοίκια) γης Ηδονικές τιµές Τι καθορίζει την τιµή της γης; η παρούσα αξία της ροής υπηρεσιών που προσδοκάται στο µέλλον Πρόσοδοι (νοίκι) και αξία ως ακίνητο Στην γεωργική καλλιέργεια
3.1 Ανεξάρτητες αποφάσεις - Κατανομή χρόνου μεταξύ εργασίας και σχόλης
 3. ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΑΓΟΡΑΣ ΕΡΓΑΣΙΑΣ (ΝΕΟΚΛΑΣΙΚΟ ΥΠΟΔΕΙΓΜΑ). ΠΡΟΣΦΟΡΑ ΕΡΓΑΣΙΑΣ Ως προσφορά εργασίας ορίζεται το σύνολο των ωρών εργασίας που προσφέρονται προς εκμίσθωση μία δεδομένη χρονική στιγμή.
3. ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗ ΑΝΑΛΥΣΗ ΤΗΣ ΑΓΟΡΑΣ ΕΡΓΑΣΙΑΣ (ΝΕΟΚΛΑΣΙΚΟ ΥΠΟΔΕΙΓΜΑ). ΠΡΟΣΦΟΡΑ ΕΡΓΑΣΙΑΣ Ως προσφορά εργασίας ορίζεται το σύνολο των ωρών εργασίας που προσφέρονται προς εκμίσθωση μία δεδομένη χρονική στιγμή.
ΜΑΘΗΜΑ 4 Ο. 4.1 Ισορροπία Μονοψωνιακής Επιχείρησης που Χρησιµοποιεί Περισσότερες από µία Μεταβλητές Εισροές
 ΜΑΘΗΜΑ 4 Ο 4.1 Ισορροπία Μονοψωνιακής Επιχείρησης που Χρησιµοποιεί Περισσότερες από µία Μεταβλητές Εισροές Εάν οι αγορές των εισροών είναι µονοψωνιακές, οποιαδήποτε µεταβολή στις ποσότητες των παραγωγικών
ΜΑΘΗΜΑ 4 Ο 4.1 Ισορροπία Μονοψωνιακής Επιχείρησης που Χρησιµοποιεί Περισσότερες από µία Μεταβλητές Εισροές Εάν οι αγορές των εισροών είναι µονοψωνιακές, οποιαδήποτε µεταβολή στις ποσότητες των παραγωγικών
Βασικές έννοιες και ορισµοί. Ευθεία
 Βασικές έννοιες και ορισµοί Ευθεία a R n, a 0 = {x R n x = λa} Βασικές έννοιες και ορισµοί Ευθεία a R n, a 0 = {x R n x = λa} Υπερεπίπεδο α R, a R n P = {x R n ax = α} Βασικές έννοιες και ορισµοί Ευθεία
Βασικές έννοιες και ορισµοί Ευθεία a R n, a 0 = {x R n x = λa} Βασικές έννοιες και ορισµοί Ευθεία a R n, a 0 = {x R n x = λa} Υπερεπίπεδο α R, a R n P = {x R n ax = α} Βασικές έννοιες και ορισµοί Ευθεία
ΑΠΑΝΤΗΤΙΚΟ ΔΕΛΤΙΟ ΟΝΟΜΑΤΕΠΩΝΥΜΟ ΑΕΜ ΕΞΑΜΗΝΟ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΝΟΜΙΚΩΝ, ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΠΟΛΙΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ: ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΚΑΙ ΠΟΛΙΤΙΚΗΣ ΜΑΘΗΜΑ: Μικροοικονομική Ι ΔΙΔΑΣΚΩΝ: Νίκος
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΣΧΟΛΗ ΝΟΜΙΚΩΝ, ΟΙΚΟΝΟΜΙΚΩΝ ΚΑΙ ΠΟΛΙΤΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΜΗΜΑ ΟΙΚΟΝΟΜΙΚΩΝ ΕΠΙΣΤΗΜΩΝ ΤΟΜΕΑΣ: ΟΙΚΟΝΟΜΙΚΗΣ ΘΕΩΡΙΑΣ ΚΑΙ ΠΟΛΙΤΙΚΗΣ ΜΑΘΗΜΑ: Μικροοικονομική Ι ΔΙΔΑΣΚΩΝ: Νίκος
Άσκηση 3: Έστω η συνάρτηση χρησιμότητας για δύο αγαθά Χ και Υ έχει τη μορφή Cobb- Douglas U (X,Y) = X o,5 Y 0,5
 ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗΣ Σημείωση: Κάποιες από τις παρακάτω ασκήσεις θα λυθούν στην 3 η και 4 η διάλεξη του μαθήματος (στις ημερομηνίες που αναγράφονται στο πρόγραμμα) και οι υπόλοιπες θα αποτελέσουν προσωπική
ΜΙΚΡΟΟΙΚΟΝΟΜΙΚΗΣ Σημείωση: Κάποιες από τις παρακάτω ασκήσεις θα λυθούν στην 3 η και 4 η διάλεξη του μαθήματος (στις ημερομηνίες που αναγράφονται στο πρόγραμμα) και οι υπόλοιπες θα αποτελέσουν προσωπική
1. Με βάση τον κανόνα της ψηφοφορίας με απλή πλειοψηφία, η ποσότητα του δημόσιου αγαθού που θα παρασχεθεί είναι η κοινωνικά αποτελεσματική ποσότητα.
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2013-2014 Τμήμα Οικονομικών Επιστημών Εξεταστική περίοδος Ιουλίου Εξέταση στο μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου Η εξέταση αποτελείται από δύο
ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Ακαδημαϊκό έτος 2013-2014 Τμήμα Οικονομικών Επιστημών Εξεταστική περίοδος Ιουλίου Εξέταση στο μάθημα: Δημόσια Οικονομική Διδασκαλία: Γεωργία Καπλάνογλου Η εξέταση αποτελείται από δύο
Θεωρία Παιγνίων-Ολιγοπώλιο σε ποσότητες
 Θεωρία Παιγνίων-Ολιγοπώλιο σε ποσότητες Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 4 Μαρτίου 214 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Θεωρία Παιγνίων-Ολιγοπώλιο σε ποσότητες 4 Μαρτίου 214 1 / 14 Ενα απλούστατο παίγνιο
Θεωρία Παιγνίων-Ολιγοπώλιο σε ποσότητες Κώστας Ρουµανιάς Ο.Π.Α. Τµήµα. Ε. Ο. Σ. 4 Μαρτίου 214 Κώστας Ρουµανιάς (.Ε.Ο.Σ.) Θεωρία Παιγνίων-Ολιγοπώλιο σε ποσότητες 4 Μαρτίου 214 1 / 14 Ενα απλούστατο παίγνιο
