Učni pripomočki, učilo in model za spoznavanje (vrst) lesa

Transcript

1 Seminarska naloga pri predmetu Didaktika tehnike s seminarjem II, študijsko leto 2006/2007 Učni pripomočki, učilo in model za spoznavanje (vrst) lesa Katarina Golob Mentor: dr. Janez Jamšek Ljubljana, april 2007

2 Povzetek V seminarju so opisani učni pripomočki, učilo in model za spoznavanje (vrst) lesa v gozdu. To so didaktična plošča vrste lesa, posamezni večji vzorci lesa, knjižica z opisi najpogostejših domačih drevesnih vrst in model štora oziroma prečnega prereza debla. Ti pripomočki se uporabljajo v tehnični učilnici na prostem na temo spoznavanje vrst lesa in dreves v gozdu. Skozi seminar pisana je njihova namembnost, način uporabe in napotki za izdelavo. S pomočjo uporabe omenjenih pripomočkov bodo učenci prepoznali naše najpogostejše vrste lesa ter našteli njihove osnovne značilnosti in uporabo: bukev, hrast, smreko in lipo, ter znali ločiti les iglavca od listavca. 2

3 Kazalo vsebine 1 Uvod Navezava na učni načrt Pregled obstoječega gradiva Opis učnih pripomočkov, učila in modelov Didaktična tabla Vrste lesa... 4 Kako uporabljamo didaktično tablo?... 4 Izdelava didaktične table Vzorci lesa... 6 Katere vzorce lesa uporabljamo in zakaj?... 6 Dejavnosti ob uporabi vzorcev... 7 Priprava vzorcev Knjižica z opisi vrst lesa Model štora Sklep Literatura Viri Priloge Kazalo slik Slika 4.1: Didaktična tabla vrste lesa... 5 Slika 4.2: Vzorci lesa... 6 Slika 4.3: Tablice z poimenovanji vzorcev... 6 Slika 4.4: Prečni prerezi lesa s poimenovanimi vidnimi deli [2]... 7 Slika 4.5: Zelo dobro vidne traheje... 8 Slika 4.6: Lesni trakovi na vzorcu hrasta... 8 Slika 4.7: Lepo vidne pore pri hrastu... 8 Slika 4.8: Rez polena v prvi fazi priprave vzorca (svež les) Slika 4.9: Prikaz sušenja vzorcev Slika 4.10: Priporočen vzorec lesa Slika 4.11: Model štora Slika 4.12: Prikaz valovitih letnih na prečnem prerezu debla gabra Kazalo tabel in shem Tabela 4.1: Drevesna sestava gozdov v Sloveniji... 7 Tabela 4.2: V knjižici opisane drevesne vrste Tabela 4.3: Izsek iz knjižice z opisi drevesnih vrst Shema 4.1: Postopek ločevanja lesa iglavca in listavca

4 1 Uvod Pri pouku je zaželeno, da se čim več stvari demonstrira. Tako lahko prikažemo določene procese, predmete, dejavnosti. Cilj demonstriranja ni, da so učenci prepuščeni sami sebi, npr. da bi samo gledali, ampak, da aktivno opazujejo in pri tem zaznajo to, kar je na objektu ali procesu bistveno [1]. Zato je naloga učitelja, da z navodili, delovnimi listi in ostalimi pripomočki usmerja učenčevo opazovanje in dejavnosti ob tem. Ta seminar služi kot vodilo za izdelavo, pripravo in uporabo učnih pripomočkov, učil in modelov v tehnični učilnici na prostem z namenom spoznati les na splošno in prepoznati les naših najpogostejših drevesnih vrst. Predstavila bom didaktično tablo Vrste lesa, posamezne vzorce lesa, knjižico z opisi najpogostejših domačih in nekaj tujih drevesnih vrst ter model štora oziroma prereza debla. S pomočjo le teh bo učni proces bolj kvaliteten, bolj poln in maksimalno zapolnjen z aktivnostjo učencev, tako fizično kot miselno. Kajti, če novosti spoznavamo s čim več čutili, je učenje učinkovitejše [1]. Tako je tudi s pripomočki, ki sem jih pripravila: z njimi je možno zaposliti skoraj vse učenčeve čute (vid, otip, voh). 2 Navezava na učni načrt Les se obravnava v devetletni osnovni šoli v 6. razredu. Dejavnosti in obravnavana snov v tej učilnici na prostem s pomočjo učnih pripomočkov, učila in modela pokrivajo naslednje učne cilje, zapisane v učnem načrtu [2]: prepozna naše najpogostejše vrste lesa ter našteje njihove osnovne značilnosti in uporabo (uporaba didaktične table, vzorci lesa, knjižica z opisi domačih najpogostejših in nekaj tujih drevesnih vrst, model štora oziroma prereza debla) na podlagi prečnega prereza ugotovi zgradbo lesa (letnice, branike, stržen, skorja) (model štora oziroma prereza debla in vzorci lesa) 3 Pregled obstoječega gradiva Že ko sem pisala seminarsko nalogo na temo tehnične učilnice na prostem na temo spoznavanja lesa in dreves v gozdu, nisem zasledila nobene literature o izvedbi te učilnice, kaj še le o učnih pripomočkih. Zato mi je bil v največjo oporo pri tem seminarju prej omenjeni seminar, v katerem sem že dosti stvari o tem ž napisala. 4 Opis učnih pripomočkov, učila in modelov V tem poglavju bom podrobneje opisala način uporabe, dejavnosti, ki jih lahko s temi učnimi pripomočki, učilom in modelom izvajamo ter stvari, na katere je potrebno biti pozoren pri izdelavi le teh. Predvsem je pomembno primerno dimenzioniranje, da jih lahko brez težav prenašamo in nesemo tudi v naravo. Kot učni pripomoček so uporabljeni vzorci lesa in knjižica z opisi domačih najpogostejših in nekaj tujih drevesnih vrst; kot učilo didaktična tabla Vrste lesa in kot model štor oziroma prerez debla. 4.1 Didaktična tabla Vrste lesa Didaktična tabla Vrste lesa je zelo koristna pri spoznavanju vrst lesa. Njen namen je celovito predstaviti les naših najpogostejših drevesnih vrst. To pomeni, da je na tabli možno videti strukturo, barvo in specifične značilnosti posamezne vrste lesa, les je možno tudi potipati; učni proces je zaradi tega učinkovitejši. V nadaljevanju je opisano, kako to dosežemo. Kako uporabljamo didaktično tablo? Didaktično tablo postavimo na vidno mesto, tako da bo dostopna in vidna vsem učencem. Priporočljivo jo je uporabljati v kombinaciji s knjižico z opisi vrst lesa, katera je podrobneje opisana v razdelku 4.3. Najprej bom na kratko opisala njen izgled. Didaktična tabla meri 680 x 670 x 5 mm. Na njej je pritrjenih štirinajst vzorcev lesa najpogostejših domačih in dva vzorca tujih drevesnih vrst. Pod vsakim vzorcem lesa je jasno napisano njegovo ime. Na tabli so zastopani naslednji vzorci lesa: smreka, bukev, hrast, bor, jelka, jablana, lipa, jesen, gaber, češnja, oreh, breza, kostanj, macesen, balza in mahagoni. Čeprav balze in mahagonija ne 4

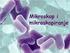
5 zasledimo v slovenskih gozdovih, sem ju na tablo vključila zaradi pogoste uporabe v modelarstvu (balza) in pojavnosti v pohištveni industriji (mahagoni). Vzorci lesa merijo 100 x 55 x 20 mm. Didaktična tabla je prikazana na sliki 4.1. Slika 4.1: Didaktična tabla vrste lesa. Izdelava didaktične table Za pomoč pri izdelavi je v prilogi sestavna tehnična risba z vsemi potrebnimi podatki. Podrobnejši opis z opombami in namigi glede izdelave pa je opisan v nadaljevanju tega razdelka. Priprava osnovne plošče Pri izdelavi didaktične table je potrebno nameniti največjo pozornost izbiri velikosti in materiala osnovne plošče, kamor pritrdimo vzorce; velikosti vzorcev in razporeditvi slednjih na ploščo. Zakaj? Izbira velikosti osnovne plošče igra veliko vlogo pri predstavitvi: plošča mora biti dovolj velika, da je primerna za uporabo v učilnici ali na prostem za učni proces na razdalji do 6m; prav tako ne sme biti prevelika, ker bi bila v tem primeru preveč okorna in nepraktična za prenašanje. Posledično je to tudi vzrok za primerno izbiro materiala tabla ne sme biti pretežka. Zato sem si za osnovno ploščo izbrala vezano ploščo dimenzij 670 x 680 x 5 mm. Takšna debelina plošče zadostuje, da je tabla dovolj trdna, da prenese težo šestnajstih vzorcev in da ni pretežka za prenašanje. Priprava vzorcev Ko se odločimo, kateri les posameznih drevesnih vrst bi radi predstavili, se ne bomo kar zapodili v gozd in podrli drevesa, katerih les bi potrebovali, ampak povprašamo na kakšni žagi, če imajo iskani les; pogledamo v drvarnico, stopimo do gozdarja, Prav nikoli pa samo zaradi enega kosa lesa ne podiramo celega drevesa. Pri izbiri vzorcev lesa pazimo, da se na njih res vidijo glavne in izstopajoče značilnosti posamezne vrste lesa (struktura, barva, specifične značilnosti,...). Seveda je za to potrebna tudi pravšnja velikost vzorca, primer vzorca je prikazan na sliki 4.2. Primer vzorca lesa breze: Vemo, da so samo za brezovino značilne parenhimske pege, zato izberemo tak kos lesa, kjer bodo te pege lepo vidne. Na tem mestu se moramo tudi odločiti, kako bomo zaščitili vzorce. Na svoji didaktični plošči vzorcev nisem lakirala predvsem iz enega razloga: če les polakiramo izgubi svojo značilno barvo. 5

6 Slika 4.2: Vzorci lesa. Vsako vrsto lesa je potrebno še poimenovati, zato pod vzorcem napišemo ime lesa, jaz sem posamezna imena s pirografom izžgala na majhne tablice (slika 4.3), katere sem nato pritrdila pod vzorec na tablo. Slika 4.3: Tablice z poimenovanji vzorcev. Preden vzorce pritrdimo na ploščo, jih je potrebno kar se le da dobro posušiti. Pri tem pazimo, da jih ne sušimo prehitro, saj nam bodo tako popokali. Pri nameščanju vzorcev na tablo pazimo tudi na dovolj velik razmak med njimi. 4.2 Vzorci lesa Tudi posamezni vzorci lesa veliko doprinesejo k izboljšanju učnega procesa. To so večji kosi lesa, ki jih damo učencem v roke. V bistvu z njimi najbolj aktiviramo učenčevo mišljenje in ga zaposlimo z dejavnosti. Katere vzorce lesa uporabljamo in zakaj? Za tehnično učilnico na prostem z naslovom spoznavanje dreves in lesa v gozdu ter dejavnosti, ki sem jih predvidevala izpeljati, potrebujemo vzorec lesa hrasta, bukve, bora, lipe, češnje ali oreha. In zakaj ravno te? Les hrasta je najprimernejši za opazovanje trahej (t. i. pore na prečnem prerezu) in lesnih trakov. Bukovina je zanimiva tudi zaradi možnosti opazovanja lesnih trakov. S pomočjo teh vzorcev lahko postopoma vpeljemo 6

7 naslednje pojme: venčasto porozen les (hrast), raztreseno porozen les (bukev, lipa) in polvenčasto porozen les (češnja, oreh). Za osvežitev spomina je na sliki 4.4 shematsko prikazana omenjena delitev. K tem vzorcem bi še dodala vzorec smreke, ki predstavlja največji delež posameznih drevesnih vrst v naših gozdovih glede na lesno zalogo (v povprečju zadnjih osmih let 32,4%) glej tabelo 4.1. Za pouk je toliko bolje, če uspemo pridobiti še kak dodaten vzorec lesa in ga učencem pokažemo kot zanimivost. Tabela 4.1: Drevesna sestava gozdov v Sloveniji, izračunana na podlagi lesne zaloge drevesnih vrst ter primerjava s preteklimi leti (povzeto po poročilu zavoda za gozdove Slovenije o gozdovih za leto 2005, [1]) (v % - od lesne zaloge) LETO smreka jelka bori macesen drugi iglavci bukev hrasti iglavci listavci ,7 9,1 5,9 1,3 0,2 31,7 6,7 49,2 50, ,5 9,0 6,1 1,3 0,1 31,6 6,8 49,0 51, ,5 8,5 6,0 1,2 0,2 31,6 6,9 48,4 51, ,3 8,3 6,0 1,2 0,2 31,6 6,9 48,0 52, ,3 8,2 6,0 1,2 0,2 31,6 7,0 47,9 52, ,3 7,9 5,8 1,2 0,3 31,5 7,0 47,5 52, ,4 7,8 5,7 1,2 0,3 31,7 6,9 47,4 52, ,2 7,7 5,8 1,2 0,3 31,7 7,0 47,1 52,9 Slika 4.4: Prečni prerezi lesa s poimenovanimi vidnimi deli [2]. Dejavnosti ob uporabi vzorcev preučevanje prerezov (prečni, radialni in tangencialni) Vsaki skupini damo po en vzorec lesa. Najboljše je, da imajo ob vpeljavi pojmov vsi enakega hrast. Omenjene prereze skupaj z učenci pokažemo na vzorcih. Kasneje damo več različnih lesov bukev, bor, češnjo ali oreh, ki si jih bodo čez čas zamenjali. o Prečni prerez Pri bukvi, hrastu, javorju, lahko opazujemo lesne trakove, ki so vidni kot svetleče, gladke lise bleščice. Pri hrastu so močno razvidne tudi traheje (cevke po katerih se prevaja hrana za drevo), zelo dobro vidne na sliki

8 Slika 4.5: Zelo dobro vidne traheje. o Tangencialni prerez Učenci opazujejo vzorec bukve in hrasta, kjer so trakovi prečno prerezani in vidni s prostim očesom kot črte, slika 4.6. Slika 4.6: Lesni trakovi na vzorcu hrasta. Lesni trakovi preučevanje posameznega kosa lesa Učence zaposlimo s preučevanjem posameznega kosa lesa. Prepričana sem, da bodo zagotovo uživali v tem. Tako bi pri zgoraj naštetih vzorcih z lupo opazovali pore (kje ležijo, kako velike so, koliko jih je ), glej sliko 4.7. Da bo preučevanje lažje, delajmo vsi na enaki vrsti lesa. Slika 4.7: Lepo vidne pore pri hrastu. 8

9 ocenjevanje starosti lesa, način rasti Učencem damo vzorec lesa, na katerem so lepo vidne letnice in branike, na primer vzorec bora. Povprašamo jih, kako bi lahko ocenili starost drevesa in kako je raslo. Primer navodila na učnem listu: 1. Na prečnem prerezu svojega vzorca preštej letnice in izmeri širino branik. Kaj lahko sklepaš iz svojih meritev? 2. Nariši les hrasta in označi posamezne strukture (letnice, traheje, trakove ) prepoznavanje lesa Tukaj bi se osredotočili le na najpogostejše drevesne vrste: bukev, hrast, smreko in lipo. Pripravimo jim vzorce lesa, za lipo priporočam, da je sveža, saj bo le tako imela svoj značilen vonj. Zelo dobra stvar, ki jo lahko izvedemo ob vzorcih lesa je, da učence naučimo ločiti les listavca od iglavca. Pri tem jih vodimo: ali so letnice in branike izrazito vidne? Če so, poglejmo naprej: ali so tudi izrazite traheje? Če je odgovor pritrdilen, potem je to zagotovo listavec. Iglavci imajo izrazite branike in letnice, vendar nimajo izrazitih trahej. Shematsko je proces prepoznavanja prikazan na shemi 1. Za te dejavnosti pripravimo tudi delovne liste, ki jim bodo kot vodilo pri»uporabi«vzorcev. Shema 4.1: Postopek ločevanja lesa iglavca in listavca Izrazito vidne letnice in branike DA NE Izrazite traheje? DA NE LISTAVEC LISTAVEC Priprava vzorcev Pri sami pripravi vzorcev se držimo istega načina pridobitve vzorca nikoli samo zaradi tega ne podiramo dreves. V začetni fazi dobimo poleno, priporočljivo je, da meri vsaj približno φ 200 x 250 mm. Pri vseh drevesnih vrstah tega ni mogoče dobiti; v tem primeru vzamemo manjšega. Vendar za vrste, katere priporočam za vzorce mislim, da glede velikosti ne bo problemov. Najpomembnejše pri vzorcu je, da zagotovimo prečni, radialni in tangencialni prerez. Priprava se razlikuje glede na to, ali delamo s svežim ali s suhim lesom. Če dobimo suh les, ga lahko kar odrežemo na izbrano velikost, kot sem že večkrat omenila, je najbolj priporočljiva 200 x 100 x 50 milimetrov, glej sliko Če se le da, je zelo dobro, da je na vzorcu še skorja, saj nam olajša prepoznavanje lesa. V nasprotnem primeru, če imamo svež les, pa je prva faza priprave, da naše poleno prerežemo vzdolžno tako, da rez poteka dober centimeter nad radialnim prerezom (glej sliko 4.8). 9

10 Slika 4.8: Rez polena v prvi fazi priprave vzorca (svež les). To naredimo zato, da ima les na razpolago večjo površino za sušenje. Pri tem poudarjam, da je potrebno les sušiti počasi, če ne še bolj izrazito poka. Žal se v večini primerov pokanju ne moremo popolnoma izogniti. Primer sušenja vzorcev je prikazan na sliki 4.9. Slika 4.9: Prikaz sušenja vzorcev. Ko se les posuši, ga naprej obdelujemo po prej omenjenem postopku. 10

11 Slika 4.10: Priporočen vzorec lesa. 4.3 Knjižica z opisi vrst lesa Knjižica vsebuje 21 strani; v njej so po abecednem vrstnem redu zbrani opisi naših in dveh tujih drevesnih vrst, glej tabelo 4.2: Naše drevesne vrste: Iglavci: - bor - jelka - macesen - smreka Tuje drevesne vrste: Listavca: - balza - mahagoni Listavci: - breza - bukev - češnja - hrast - hruška - jablana - javor - jesen - kostanj - lipa - oreh Tabela 4.2: V knjižici opisane drevesne vrste. Na začetku knjižice je kratko in pregledno podana razlaga osnovnih pojmov, ki so potrebni za razumevanje opisov. Primer razlage osnovnih pojmov iz knjižice: VENČASTO POROZEN LES les z dobro vidnimi porami na začetku ranega lesa POLVENČASTO POROZEN LES les, v katerem so v ranem lesu pore relativno večje ali pa so številčnejše (npr. češnja, oreh) 11

12 LETNICA vidna meja med branikami (lanskim kasnim lesom in letošnjim ranim lesom) Nato sledijo podrobnejši opisi posameznih drevesnih vrst, ki zajemajo opis, lastnosti, obdelavo in uporabo lesa. Kot sem že omenila v razdelku 4.1, je knjižico priporočljivo uporabiti v kombinaciji z didaktično tablo vrste lesa. Ko učenci gledajo določen vzorec lesa na tabli, si lahko obenem v knjižici preberejo lastnosti opazovanega vzorca. Knjižica jim je lahko tudi v veliko pomoč pri preučevanju»velikih«vzorcev lesa. Primer: Hrast Tabela 4.3: Izsek iz knjižice z opisi drevesnih vrst OPIS LESA Beljava ozka, sivo bela, jedrovina rumeno rjava do rjava, močno potemni. Les je venčasto porozen. Traheje so v ranem lesu velike, v kasnem lesu manjše, večkrat razporejene v radialnih nizih. Pore v ranem lesu in trakove razločno vidimo s prostim očesom. Trakovi so zelo široki. V tangencialnem prerezu so trakovi videti kot temne, do 5 cm dolge navpične črte, v radialnem prerezu pa kot različne bleščice. OBDELAVA Les se zmerno dobro suši, vendar počasi, ker je nagnjen k pokanju in veženju. Dobro se mehansko obdeluje, tudi struži in rezbari. Pri lepljenju v splošnem ne povzroča težav. Dobro se luži in lakira. LASTNOSTI LESA Gostota hrastovine je odvisna od širine branik in ima širok razpon, od nizke do visoke. Gostota absolutno suhega lesa: kg/m 3. Gostota zračno suhega lesa: kg/m 3. Les je trd, tlačna trdnost je visoka, upogibna trdnost je srednja do visoka. Modul elastičnosti je srednje velik do visok. Kovinski delci temno obarvajo les jedrovine. UPORABA rezan furnir pohištvo notranjo opremo obloge parket stavbno pohištvo: vrata, okna stopnice gradbeni les gradnje v vodi v ladjedelništvu za izdelavo vozil 12

13 4.4 Model štora Za predstavitev in razlago pojmov letnica, branika, skorja in stržen je primeren model štora oziroma prečni prerez debla, glej sliko Slika 4.11: Model štora. Pri tem so dobri primeri tudi štor pravega kostanja, bora, macesna ali hrasta, kjer lahko pokažemo tudi jedrovino in beljavo (te vrste imajo namreč obarvano jedrovino). Tak model uporabimo v razredu, lahko pa tudi zunaj, če v bližini ne najdemo kakšnega»pravega«štora. Vsekakor se pa splača dobiti prečni prerez debla gabra, prikazanega na sliki 4.12, ki ga lahko pokažemo kot zanimivost, saj ima le ta vrsta valovite letnice. Slika 4.12: Prikaz valovitih letnih na prečnem prerezu debla gabra. 13

14 5 Sklep Glavni namen seminarske naloge je bil predstaviti učne pripomočke, učila in modele v tehnični učilnici na prostem v okviru spoznavanja vrst lesa in dreves v gozdu. Naredila in opisala sem didaktično ploščo vrste lesa,»večje«vzorce lesa, knjižico z opisi štirinajstih najpogostejših domačih in dveh tujih drevesnih vrst, ter model štora oziroma prečnega prereza debla. Opisani pripomočki so enostavni za uporabo in izdelavo in popolnoma nenevarni za učence. Poglaviten način dela s pripomočki vključuje pridobitev čim več učenčevih neposrednih čutnih izkušenj. Posledično se prav zaradi stalne učenčeve aktivnosti močno izboljša kvaliteta učnega procesa. Ti pripomočki ne samo da zelo popestrijo tehnično učilnico na prostem, brez njih si izvedbe učilnice na prostem sploh ne morem predstavljati. Razmišljala sem tudi o izboljšavah didaktične table: na tablo bi lahko bili vzorci in ploščice z imeni pritrjeni z magneti. Kasneje bi bilo možno učencem zastaviti nalogo, kjer bi bile na tabli pritrjene ploščice z imeni lesa, učenec pa bi moral poiskati ustrezen vzorec k napisu ali obratno: na tabli bi bili pritrjeni vzorci, učenec mora poiskati pravilno ime zanj. Menim, da je zelo koristno učencem predstaviti čim več kvalitetnih didaktičnih pripomočkov, seveda skupaj s premišljenimi napotki in nalogami za opazovanje oziroma kakršne koli druge dejavnosti. 14

15 6 Literatura [1] A. Tomić, Izbrana poglavja iz didaktike: študijsko gradivo za pedagoško andragoško izobraževanje (Slovenija, Center FF za pedagoško izobraževanje, 1997). [2] Učni načrt : program osnovnošolskega izobraževanja. Tehnika in tehnologija (Slovenija, Ministrstvo za šolstvo, znanost in šport: Zavod RS za šolstvo, 2002) 7 Viri [1] Splošni podatki in dejstva o gozdovih v Sloveniji [ [2] J. Polanc, I. Leban, Les zgradba in lastnosti (Slovenija, Lesarska založba, 2004). 15

16 8 Priloge Tehnična risba Didaktična tabla vrste lesa 16

17 PRIMER DELOVNEGA LISTA: 1. Na sliki označi prereze lesa. 2. Označi posamezne strukture lesa: 3. Na prečnem prerezu svojega vzorca preštejte letnice in izmerite širino branik. Kaj lahko sklepate iz svojih meritev? 17

18 4. Nariši les hrasta in označi posamezne strukture (letnice, traheje, trakove ) 5. Naštete drevesne vrste razvrsti med iglavce ali listavce: iglavec listavec macesen bukev hrast smreka hruška tisa jelka oreh vrba bor lipa breza 18