Stanični kostur CITOSKELET. Uloge citoskeleta. Citoskelet. Mikrotubuli (mikrocjevčice) Citoskelet Međustanične veze Stanična stijenka
|
|
|
- Ἑκάβη Κομνηνός
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Citoskelet Međustanične veze Stanična CITOSKELET (grč. kytos + skeleton, osušeno tijelo, kostur) Stanični kostur Izv. prof. dr. sc. Lidija Šver Citoskelet Mreža vlakana, niti koja se proteže kroz citoplazmu Mikrotubuli Uloge citoskeleta 1. određuje oblik stanice (bitno za životinjsku stanicu!) 2. omogućava kretanje čitave stanice (bičevi, trepetljike, Note different pseudopodiji) thicknesses, i locations, organela and structures unutar stanice 3. regulira organizaciju unutarstaničnih struktura 4. pruža i omogućava mehaničku potporu stanici 0.25 µm Mikrofilamenti različita debljina, smještaj i građa vlakanaca Tri različita elementa citoskeleta Mikrotubuli (mikrocjevčice) INTERMEDIJARNI FILAMENTI MIKROTUBULI AKTINSKI FILAMENTI svako vlakno je sastavljeno od monomernih podjedinica različit smještaj mreže vlakanaca u stanici
2 Funkcija mikrotubula 1. Održavanje oblika stanice (otpornost na pritisak) 2. Pokretanje kromosoma tijekom diobe stanica (centrioli, diobeno vreteno) 3. Pokretanje organela zajedno s motoričkim proteinima (organizacija stanice kretanje vezikula i organela) 4. Pokretanje stanice (izgrađuju bičeve i trepetiljke) Prof. dr. sc. Lidija Šver Mikrotubuli nastaju udruživanjem tubulinskih dimera 24 nm 14 nm 5 nm heterodimer 8 nm mikrotubuli su sastavljeni od spiralno zavijenih α- i β- tubulinskih monomera (2 različite podjedinice = heterodimeri) jedan potpun uzvoj spirale sadržava 13 podjedinica (dakle, cijev čini 13 protofilamenata) šuplje cijevi promjera 24 nm, promjer lumena cijevi 14 nm duljina mikrotubula: od 200 nm do 25 µm polarnost mikrotubula + kraj (završava β- tubulinom); brzo rastući kraj - kraj (završava α- tubulinom); spontano gubi podjedinice Mikrotubuli nastaju udruživanjem (polimerizacijom) heterodimera uz energiju GTP-a Poluživot mikrotubula nekoliko minuta može se modificirati djelovanjem nekih spojeva Kolhicin alkaloid, inhibira polimerizaciju veže se za heterodimere i zaustavlja polimerizaciju zbog nedostatka raspoloživih heterodimera u citoplazmi koristi se u citogenetičkim analizama za zaustavljanje stanica u metafazi mitoze PRODUŽIVANJE MIKROTUBULA dodavanje dimera na + kraju SKRAĆIVANJE MIKROTUBULA dubitak dimera na - kraju Količina raspoloživog GTP-tubulina (ne ATP-a, razlika od aktinskih mikrofilamenata) kontrolira produživanje (polimerizaciju) i skraćivanje (depolimerizaciju) mikrotubula u procesu zvanom dinamička nestabilnost Polimerizaciju tubulina u mikrotubule kontroliraju raznolike tvorbe čiji je skupni naziv SREDIŠTA ORGANIZACIJE MIKROTUBULA (engl. microtubule organizing centers = MTOC) Tim tvorbama pripadaju: centrioli centromere kromosoma bazalna tjelešca (baza bičeva/trepetljika) Promjer: 0,15 µm Dužina: 0,3 0,5 µm 1 par u stanici koja se ne dijeli Podvostručenje (2 para) u S fazi interfaze Centrosom izgrađen od dva centriola
3 Udvostručavanje centrosoma prije diobe (G 1 - S faza) odvajaju se centrioli, a novi centrioli rastu iz kratke diskoidalne strukture pod pravim kutom na roditeljski centriol Mikrotubuli 9 tripleta (A, B i C mikrotubuli) Neksini (proteini koji povezuju susjedne triplete) MikrotubulA je potpun (13 podjedinica tvori jedan uzvoj spirale), mikrotubulib i C imaju zajedničku stijenku, tj. dijele podjedinice Zrakaste (radijalne) žbice Centriol A tubul Pericentriolarni materijal B tubul C tubul Mikrotubuli Pericentriolarni materijal i centrioli Polarni kraj (+) Minus krajevi mikrotubula u interfaznoj stanici su uloženi u matriks centrosoma (središte organizacije mikrotubula; MTOC) Plus krajevi su slobodni i rastu pericentriolarni materijal (matriks centrosoma) proteinska struktura u njima nastaju mikrotubuli diobenog vretena, dakle, centrosom je središte organizacije mikrotubula (MTOC) centrioli upravljaju polimerizacijom pojedinačnih mikrotubula koji se zrakasto šire od centriola stanice koje se više ne dijele (neuroni) otpuštaju mikrotubule iz centrosoma Kretanje mikrotubula tijekom diobe Sile povlačenja Sile guranja Mikrotubuli u diobi stanice centromere kao središta organizacije mikrotubula otpuštanje tubulinskih dimera na + kraju (skraćivanje kinetohornog mikrotubula) zbog proteina (MCAK) iz porodice kinezina koji se nalazi u kinetohorama Kinetohorne niti postaju kraće i povlače kromatide prema polovima Polarne niti vretena (one koje se nisu vezale za kromosome) postaju duže; na mjestima preklapanja dolazi do klizanja i odguravanja prema polovima skraćivanje kinetohornog mikrotubula centromera kinetohora kromosom otpušteni tubulinski dimeri
4 Mikrotubuli pomažu u organizaciji unutrašnjosti stanice Organele se pomiču duž mikrotubula uz pomoć motoričkih proteina (dineina i kinezina) uključeni su u pokretanje organela zajedno s motoričkim proteinima motorički proteini koji se pričvrste za receptore na organelama mogu hodati duž mikrotubula, ili, u nekim slučajevima, duž mikrofilamenata dinein laki lanac teški lanac kinezin dinein kinezin ATP Motorički protein (energija iz ATP-a) mjehurić Receptor na organelu za motorički protein Mikrotubul Prof. dr. sc. Lidija Šver minus kraj plus kraj Kretanje duž mikrotubula omogućavaju motorički proteini iz porodice dineina (prema minus kraju; tj. vrše transport organela od zrnatog ER prema Golgijevom aparatu ) i kinezina (prema plus kraju tj. od Golgijevog aparata prema ER) Laki lanci vežu teret koji se prenosi, a teški hidroliziraju ATP i vrše pokretanje. Uloga mikrotubula u unutarstaničnom pomicanju organela Pomicanje mjehurića između ER i GA, te GA i stanične membrane Transport mjehurića s neurotransmiterima u aksonima živčanih stanica Transport pigmenta melanina u pigmentnim stanicama Tijelo stanice (perikarion) ATP Mikrotubul mjehurić Akson Receptor na organelu za motorički protein Završetak aksona Transport u Motorički protein (energija iz ATP-a) Mikrotubul Transport iz stanicu stanice a) Motorički proteini koji se pričvrste za receptore na organelama mogu hodati duž mikrotubula, ili, u nekim slučajevima, duž mikrofilamenata. Mikrotubul Mjehurić 0.25 µm Mjehurić koji sadrži neurotransmitere može migrirati prema vršku aksona živčane stanice. Na slici se vide dva mjehurića koja se pomiču duž velikog aksona živčane stanice lignje (SEM). Trepetljike i bičevi dodatak stanicama koji im omogućuje pokretljivost trepetljike mnogo dužina: 2-10 µm bičevi jedan ili više dužina: µm promjer bičeva/trepetljika 0,3-0,5 µm epitelne stanice respiratornih puteva, jajovod, stanice kože, spermiji, rasplodne stanice nekih biljaka
5 Trepetljike i bičevi zajednička ultrastruktura bičeva i trepetljika je AKSONEMA sastavljena od snopa (9 dubleta +2) mikrotubula i njima pridruženih proteina aksonema 2 središnja tubula obavijena središnjom ovojnicom 9 parova (dubleta) tubula (tubul A potpun=13 podjedinica, tubul B ima 2-3 zajedničke podjedinice s tubulom A) minus krajevi trepetljika i bičeva usidreni su u bazalno tjelešce unutar stanice bazalno tjelešce je vrlo slično centriolu 9 tripleta tubula također ima ulogu MTOC-a na bazi svake trepetljike/biča na kraju bazalnog tjelešca, završava tubul C, a tubuli A i B nastavljaju se u bič/trepetljike cytosol Citoplazma Cilium Trepetljika/bič plasma Plazmatska membrane axoneme Aksonema basal Bazalno body (centriole) tjelešce (centriol) Uzorak µm Poprečni presjek kroz aksonemu Mikrotubuli Plazma Bazalno tjelešce 0.1 µm 0.1 µm Triplet Poprečni presjek kroz bazalno tjelešce Vanjski par mikrotubula Dineinske ručice Središnji mikrotubul Zrakaste žbice Vanjski susjedni parovi mikrotubula međusobno povezani proteinom neksinom Plazmatska S površine tubula A strše u parovima dineinske ručice Dineinske ručice povezuju susjedne tubule i omogućuju klizno pomicanje dubleta jedan duž drugoga Aktivacija s ATP jer dinein djeluje kao ATP-aza Poprečni presjek kroz trepetljike Klizanje i savijanje trepetljika postiže se dineinom Valovito gibanje trepetljika i bičeva širi se klizanjem susjednih dubleta u aksonemi jedni po drugima Dineinske ručice s mikrotubula A jednog dubleta vežu se za površinu mikrotubula B susjednog dubleta i hodaju po njemu prema minus kraju Klizanje susjednih parova nije slobodno; ograničava ga prisustvo neksina (povezuje međusobno susjedne dublete) i zrakastih žbica (povezuju središnje tubule s vanjskim) vanjska dineinska ručica unutarnja dineinska ručica vanjska dineinska ručica vanjski par mikrotubula (dublet) središnji tubuli plazmatska Kako se savijaju mikrocjevčice trepetljika/bičeva Bez povezivanja neksinom Izdvojeni parovi mikrotubula dinein uzrokuje klizanje susjednog para mikrotubula Susjedni mikrotubuli povezani neksinom Normalni bič dinein uzrokuje savijanje susjednog para mikrotubula
6 Mikrotubuli služe za gibanje bičeva i trepetljika Zbog povezujućih proteina (neksina i zrakastih žbica), sile klizanja uzrokuju savijanje trepetljika/bičeva KARTAGENEROV sindrom; nepokretne cilije zbog manjka dineinskih ručica; nepokretnost spermija i česte infekcije dišnih puteva Mikrotubuli Zaključci nađeni u središnjim dijelovima stanice sastavljeni su od α i β tubulina velike šuplje cijevi koje sastavlja energija iz GTP-a polarnost mikrotubula (+ i kraj) nastanak mikrotubula kontroliraju raznolike tvorbe = SREDIŠTA ORGANIZACIJE MIKROTUBULA Mreža mikrotubula u citoplazmi Služe za davanje oblika i čvrstoće stanici pokretanje trepetljika/bičeva, pokretanje organela i odvajanje kromosoma Mikrofilamenti (aktinski filamenti) mikroniti, mikrovlakna promjera 5-7 nm kuglaste podjedinice nanizane u dva međusobno isprepletena aktinska lanca ispod st. membrane u većini stanica u mišićnim stanicama čitava stanica; organizirane s miozinom Polimerizacija G-aktina u F-aktin = aktinski mikrofilamenti filamenti ili F-aktin nastaju polimerizacijom glubularnog aktina (G-aktina) isprepliću se dva lanca mikrofilamenti su u mrežu povezani su veznim proteinima Uloga mikrofilamenata 1. mišićna kontrakcija 2. promjene oblika stanice (ameboidno kretanje) 3. pokretanje (strujanje) citoplazme 4. dioba stanice (formiranje kontraktilnog prstena) 5. održavanje oblika stanice (otpornost na rastezanje) 6. povezivanje stanica (INTEGRINI, proteini membrane povezani s aktinskim mikrofilamentima s citoplazmatske strane i proteinom fibronektinom u izvanstaničnom matriksu) Mikrofilamenti koji imaju ulogu u staničnoj pokretljivosti sadrže, osim proteina aktina, i deblje niti proteina miozina klizanje miozinskih niti po aktinskim nitima skraćivanje stanice (kontrakcija) Aktinski filament Mišićna stanica Miozinski filament Miozinska ručica
7 Mehanizam mišićne kontrakcije Amoeboidno kretanje Kružno kretanje citoplazme Uključuje kontrakcije aktinskih i miozinskih niti sol-gel konverzija Kora (korteks) (ektoplazma): Gel-stanje s mrežom aktinskih niti Unutrašnjost (endoplazma): solstanje s aktinskim podjedinicama Izduživanje pseudopodija, lažne nožice Carra Elodea Stvaranje kontraktilnog prstena u citokinezi animalnih stanica Održavanje oblika stanice i njihovo povezivanje Stanica pričvršćena za izvanstanični matriks Citoplazma Aktin Stanična Pričvrsni proteini (integrini) Izvanstanični matriks (fibronektin)
8 Intermedijarna vlakna (filamenti) Udruživanje intermedijarnih filamenata vlaknati proteini izgrađeni od 8 podjedinica supernavijenih u deblje niti grade ih monomeri (50tak različitih proteina podijeljeni u VI skupina) udruženi u duga vlakna (2 nepolarna tetramera spojena po duljini) nisu polarne strukture poput mikrotubula i mikrofilamenata Prof. dr. sc. Lidija Šver Intermedijarna vlakna (filamenti) Jedinstvene monomerne podjedinice u različitim staničnim tipovima Keratini 20-tak polipeptida epitelne stanice; čvrsti nokti, kosa, Vimentin održavanje oblika stanice (fibroblasti, endotelne stanice i leukociti) čvrsto vezan na mikrotubule Dezmin mišićne stanice Neurofilamenti protežu se duž aksona zajedno s mikrotubulima čine citoskelet živčane stanice mikrotubuli uzdužno, intermedijarni filamenti poprečno određuju debljinu aksona i brzinu prijenosa impulsa Lamini 3 polipeptida (lamin A, B i C) gotovo sve stanice Prema smještaju - dva glavna tipa: jezgrini (lamini) citoplazmatski Uloga intermedijarnih filamenata 1. održavanje oblika stanice (otpornost na rastezanje) 2. učvršćivanje jezgre i određenih organela 3. formiranje jezgrine lamine 4. podržava produžetke živčanih stanica (aksone) 5. povezuje stanice međusobno Intermedijarni filamenti povezuju tkiva održavanje oblika stanice (otpornost na rastezanje) dezmosom tvore jezgrinu laminu na unutarnjoj strani jezgrine ovojnice lamini su važni tijekom mitoze fosforilacija lamina signal za razgradnju jezgrine ovojnice Lamini rastezanje sloja stanica u kojima postoje intermedijarni filamenti rastezanje sloja stanica u kojima ne postoje intermedijarni filamenti stanice ostaju netaknute i međusobno povezane stanice se rasprsnu Intermedijarni filamenti povezuju proteinske strukture međustaničnih veza (dezmosoma). Dezmosomi obično povezuju susjedne epitelne stanice, primjerice cilindrične stanice tankog crijeva. Fibrozna lamina (polipeptidi LAMINI)
9 Intermedijarni filamenti daju strukturni kontinuitet tkivima Žuti krugovi označavaju plazmatske membrane stanica Crvene crte ističu kontinuitet keratinskih vlakana između dviju stanica Zaključci: Intermedijarni filamenti sastavljeni su od monomernih podjedinica koje se razlikuju u različitim tipovima stanica imaju građevnu ulogu u stanici relativno postojane molekule nisu polarne strukture Citoskelet u prokariota ne postoji evolucijska srodnost proteina koji grade citoskelet prokariota i eukariota međutim, postoji sličnost u: trodimenzionalnoj stukturi funkciji (održavanju oblika stanice) polarnosti FtsZ (engl. Filamenting temperature-sensitive mutant Z) sličan proteinu tubulinu u eukariotskoj stanici stvara filamente u prisutnosti GTP-a, ali ti se filamenti ne grupiraju u cjevčice (tubuli) bitan tijekom diobe bakterijske stanice i nužan za dopremu drugih proteina koji formiraju novu staničnu stijenku između stanica koje se dijele Citoskelet u prokariota MreB i ParM MreB jedan od prokariotskih proteina koji je sličan aktinu sudjeluje u održavanju oblika stanice nalazi se ispod stanične membrane svih neokruglih bakterija ParM također sličan eukariotskom proteinu aktinu filamenti pokazuju dinamičku nestabilnost sudjeluju u odvajanju plazmidne DNA tijekom diobe bakterijske stanice mehanizmom koji je sličan mehanizmu kojim mikrotubuli eukariotske stanice dijele genski materijal Crescentin u bakteriji Caulobacter crescentus srodan intermedijarnim filamentima eukariotske stanice sudjeluje u održavanju oblika bakterijske stanice (spiralni oblik i oblik zareza), ali mehanizam nije poznat Međustanične veze animalnih stanica Međustanične veze udruživanje stanica, povezanost i komunikacija povezanost omogućuju glikoproteini (integralni proteini stanične membrane) i međustanični proteoglikani specijalna područja za povezivanje međustanične veze
10 Tipovi međustaničnih veza animalnih stanica Intermedijarni filamenti Epitelno tkivo Tijesni spojevi (konekson) 1. Čvrsti spoj (engl. tight junction) 2. Tijesni spoj (engl. gap junction) 3. Dezmosom i hemidezmosom DEZMOSOM Međustanični prostor Međustanični prostor Proteini čvrstog spoja Plazmatska Međustanični prostor Jezgra Bazalna Vezivno tkivo Međustanični prostor emidezmosomi ČVRSTI SPOJ Proteinski kanali TIJESNI SPOJ Uloga staničnih međustaničnih veza Čvrsti spojevi 1. povezivanje stanica (pričvrsni spojevi) 2. sprečavanje prolaska tvari kroz međustanični prostor (nepropusni spojevi) 3. komunikacija između stanica (kumunikacijski spojevi) ČVRSTI SPOJEVI engl. tight juntion nepropusni spoj između epitelnih stanica membrane susjednih stanica su se stopile i zabrtvile međustanični prostor (nema pukotine između njih) čvrsta barijera koja sprečava prolaz tvari (samo nekolicina otopljenih tvari može proći kroz ovaj čvrsti vez bez ulaska u samu epitelnu stanicu) mreža tankih lanaca u čvrstoj vezi sastavljena je od proteina koji dijele obje stanice TIJESNI SPOJEVI engl. gap junction komunikacijski spoj bočni dijelovi stanica 6 polipeptida (heksameri) u membrani stanice s hidrofilnom porom (promjer 1,5 nm) = KONEKSON 2 koneksona susjednih stanica i hidrofilne pore dviju susjednih stanica tvore hidrofilni kanal koji povezuje citoplazme Koneksoni = proteini koji tvore tijesne spojeve (hidrofilne kanale) i omogućuju prolaz malih čestica (Mr do 1500) između stanica (hormoni, camp i GMP, ioni) koje prenose poruke i usklađuju rad stanica u tkivu Tijesni spojevi (konekson) emidezmosomi
11 Dezmosom Međustanične veze u biljaka komunikacijski kanal (kao tijesni spoj u animalnih stanica) jažica (jažični kanal) jažice: mali okrugli ili ovalni dijelovi stijenke koji ostaju nezadebljali ako je jako zadebljala jažični kanal prolaz hranjivih tvari i komunikacija stanica plazmodezmije: citoplazmatske niti koje prolaze jažičnim kanalom sincicij Stanične stijenke Tijesni spojevi (konekson) emidezmosom DEZMOSOM i EMIDEZMOSOM pričvrsni spoj odmaknute st. membrane te povećan međustanični prostor (>30 nm, uobičajeno 20 nm) u međustaničnom prostoru nakupine guste tvari, također i s unutrašnje strane membrane susjednih stanica (pričvrsna ploča; >12 proteina + citokeratinski intermedijarni filamenti) Citoplazma prve stanice Citoplazma druge stanice 0.5 µm Plazmodezmiji Plazmatske membrane Plazmodezmije Plazmodezmij ma povezani kanali koji prolaze kroz staničnu stijenku biljnih stanica omogućuju izravnu vezu citoplazme jedne stanice sa citoplazmom susjedne stanice i prolaz raznih molekula (šećera, soli i aminokiselina) pa čak i nekih većih molekula Jažica Endoplazmatska mrežica Plazmodezmij Stanična Plazmatska cilindrični oblik, obložen plazmatskom membranom unutar plazmodezmija uska cjevasta struktura koja potječe od glatkog ER = dezmotubul dezmotubul u potpunosti ne ispunjava plazmodezmij ostatak ispunjen citosolom obiju stanica, proteinom aktinom, miozinom i nekim drugim proteinima plazmatska unakrsno povezujući glikan pektin celulozne mikrofibrile susjedne biljne stanice Plazmodezmij među veza u biljnom tkivu glatki endoplazmatski retikulum dezmotubul dezmotubul plazmodezmij središnja lamela miozin aktin primarna Simplast i apoplast plazmodezmij citoplazma vakuola apoplastni put (kroz staničnu stijenku) simplastni put (kroz citoplazmu) Simplast plazmodezmiji omogućavaju izravan protok malih molekula (šećeri, aminokiseline, ioni) i vode između stanica veće molekule mogu se transportirati pomoću aktinskih niti transport vode i drugih tvari niz koncentracijski gradijent koristi se u korijenu za unos hranjivih soli i vode iz tla od epidermalnih stanica (korijenovih dlačica) kroz primarnu koru korijena i endoderme (i pericikla) do ksilema kojim se prenose na veće udaljenosti Apoplast kretanje vode i hranjivih tvari koristeći kontinuitet staničnih stijenki i međustaničnih prostora kretanje vode po zakonima difuzije koristi se u korijenu za unos vode i mineralnih tvari iz tla
12 Stanična Stanična građena od celuloznih vlakana uronjenih u druge polisaharide i proteine debljine 0,2 µm sličnih funkcija kao izvanstanični matriks u animalnih stanica Središnja vakuola Središnja vakuola 1 µm Središnja vakuola Citosol Plazmatska Sekundarna Primarna Središnja lamela Plazmatska Biljna Plasmodezmiji Stanična značajna za biljne stanice, stanice gljiva i bakterija, neke jednostanične eukariote (alge) protoplast gola stanica, bez stanične stijenke staničnu stijenku nemaju animalne stanice, neke alge i protisti, te spolne rasplodne stanice biljaka izlučuje ju citoplazma, ali je mrtva struktura (osim plazmodezmija) Uloga stanične stijenke 1. zaštita stanice (od bakterija, virusa...) 2. održavanje oblika stanice (zbog znatnog unutarnjeg tlaka vakuola) 3. povezivanje biljnih stanica u tkivo 4. onemogućavanje prevelikog ulaska vode u stanicu 5. indirektno omogućava komunikaciju između stanica (plazmodezmije) 6. čvrste stanične stijenke specijaliziranih stanica (ksilemske stanice, sklerenhim, kolenhim) omogućuju uspravan položaj biljke, protivno gravitacijskoj sili Sastav stanične stijenke Sastav stanične stijenke Ugljikohidrati Celuloza Amilopektin i amiloza Pektini emiceluloza itin Pektin Križno povezujući glikan Celulozne mikrofibrile Središnja lamela Primarna Plazmatska Celuloza homopolimer β-glukoze; ostataka međusobno povezanih β-1,4-glikozidnom vezom nerazgranjena, nitasta molekula 4 C 2 O O O O O O α-glukoza O C C C C C C O O O O O 4 O C 2 O O O 1 O O β-glukoza β-glukoza β-1,4-glikozidna veza
13 Pektini Sastav stanične stijenke polimeri galakturonske kiseline protopektin (duže molekule) u blago kiselom mediju i uz djelovanje pektinaza prelazi u pektin lako oksidira i bubri maceracija (pektinaze i pektinesteraze) razgradnja do monosaharida najviše u primarnoj staničnoj stijenci i nezrelim plodovima Sastav stanične stijenke emiceluloza rezervna celuloza jako zadebljale stanične stijenke sjemenki (datulja, šparoga...) prilikom klijanja se razgrađuje do monosaharida i služi kao rezervna tvar biljna slonova kost Ekvadorska palma slonovača, Phytelephas aequatorialis itin Sastav stanične stijenke u staničnoj stijenci gljiva, a samo u nekim biljkama (primjerice, nekim algama) polimer derivata glukoze (N-acetil glukozamina) koji su međusobno spojeni β-1,4-glikozidnim vezama Sastav stanične stijenke Amilopektin mol. masa 5 x glukoznih ostataka povezanih α-1,6-glikozidnim vezama, razgranjena Razgranjenje na svakom glukoznom ostatku Amiloza mol. masa Linearna, nerazgranjena molekula glukoznih ostataka povezanih α-1,4-glikozidnim vezama Građa stanične stijenke 100-tinjak pravilno posloženih celuloznih niti miceli usporedno micelarnih snopova mikrofibrila međuprostori snopova ispunjeni vodom i dr. tvarima pravilan raspored mikrofibrila pruža staničnoj stijenki elastičnost i čvrstoću Orijentacija micela/mikrofibrila paralelan raspored mikrofibrila u istoj ravnini (plohi) Središnja lamela Primarna Plazmatska Pektin Topljiv protein Celulozni mikrofibrili emiceluloza mikrofibrile različitih ravnina pod kutom orijentacija micela/mikrofibrila vlaknasta plohe paralelne s uzdužnom osi stanice prstenasta plohe poprečne na uzdužnu os stanice spriralna - plohe kose na uzdužnu os stanice jezgra jezgra jezgra
14 Građa stanične stijenke središnja lamela tanki sloj koji povezuje dvije susjedne stanice izgrađuju ga ljepljivi polisaharidi pektin i hemiceluloza primarna naslanja se na središnju lamelu prema unutrašnjosti stanice tanji i fleksibilni sloj građen od celuloze, hemiceluloze, pektina i glikoproteina izlučuje ju mlada stanica sekundarna najdeblji sloj stanične stijenke nalazi se između primarne stanične stijenke i stanične membrane čini ga više laminarnih celuloznih slojeva, često s uklopljenim drugim tvarima (lignin) pruža glavnu čvrstoću i zaštitu biljnoj stanici sekundarna (S3) sekundarna (S2) sekundarna (S1) primarna središnja lamela Rast stanične stijenke tanka u embrionalnim stanicama (meristem) 80% hemiceluloza i pektin; elastična prati rast volumena stanice lamelarna struktura u ekvatorijalnoj ravnini mitotičkog aparata = ploča fuzija mjehurića; centrifugalni rast (od središta prema bočnim ma stanice majke = FRAGMOPLAST primarna sekundarna Citokineza biljne stanice Mjehurići GA koji stvaraju FRAGMOPLAST Stanična roditeljske stanice Nova Stanična ploča Primarna Sekundarna Plazmatska Jažica Plazmodezmij Središnja lamela Stanice kćeri Plalzmodezmij Protoplast Stanična algi Domena Bacteria i domena Archaea prokarioti (Procaryota) Domena Eukarya, eukarioti podijeljeni na nadcarstva/ carstva Protista, Plantae, Fungi i Animalia sadrži celulozu i različite glikoproteine umetanje dodatnih specifičnih polisaharida omogućuje taksonomiju algi (manozil, ksilani, agaroza, furceleran, ) osim toga, ugrađuje se sporopolenin, kalcijevi ioni, ortosilicijeva kiselina ( 4 SiO 4 ) progenote
15 Alge kremenjašice (dijatomeje, Diatomeae) Stanična gljiva izgrađena od hitina i drugih polisaharida u tri sloja (od stanične membrane prema van): sloj hitina sloj β-1,3-glukana i β-1,6-glukana (glukan je polimer D-glukoze koje međusobno povezane glikozidnom vezom) 3. su sloj glikoproteina koji sadrže šećer manozu manoproteini β-1,6-glukan β-1,3-glukan hitin fosfolipidni dvosloj stanične membrane Bojenje po Gram-u Stanična prokariota - bakterija bakterijske stanice imaju staničnu stijenku izgrađenu od peptidoglikana (mureina) polimer kojeg grade šećeri i aminokiseline polisaharidni lanci izgrađeni od šećera N-acetilglukozamina (NAG) i Nacetilmuraminske kiseline (NAM) povezani ß-1,4-glikozidnom vezom polisaharidni linearni lanci unakrsno povezani peptidima koji sadrže 4 do 5 Daminokiselina (gotovo svi ostali organizmi imaju proteine izgrađene samo od Laminokiselina).C.J. Gram god. upotrijebio je bazičnu boju crystal violet i otopinu joda koji povećava međudjelovanje boje i stanica. Nakon ispiranja u alkoholu i vodi, dio bakterija je bilo ljubičasto-plavo obojeno. Razlika u boji, posljedica je različite građe stanične stijenke između Gram+ (obojenih) i G (bezbojnih) bakterija. G+ bakterije imaju puno deblji sloj peptidoglikana u koji se upije plava boja i koja se ne ispere u alkoholu Lipopolisaharid Stanična Sloj peptidoglikana Stanična Vanjska Sloj peptidoglikana Plazmatska Plazmatska Protein Protein Gramnegativna bakterija Grampozitivna bakterija 20 µm Stanična prokariota - arheja Gram-pozitivne bakterije = mnogobrojni slojevi mureina (50-90% stanične stijenke) oko stanične membrane 1. polimerski lanci glikana (polimer šećera N-acetilglikozamina i Nacetiltalozaminuronske kiseline povezani β-1,3-glikozidnom vezom) unakrsno povezani peptidima kojeg grade L-aminokiseline metanogene arheje (vrste rodova Methanobacterium i Methanothermus) zadržavaju boju u debelom sloju peptidoglikana Gram-negativne bakterije = tanki sloj mureina (10% stanične stijenke) kojeg okružuje dodatni lipidni omotač (sloj lipopolisaharida i lipoproteina= vanjska ) ne zadržavaju boju nemaju peptidoglikan karakterističan za staničnu stijenku bakterija postoje 4 različita tipa stijenke: izgrađena od pseudopeptidoglikana (pseudomureina) Shema stanične stijenke Gram -negativne bakterije Shema stanične stijenke Gram -pozitivne bakterije žuto - sloj peptidoglikana (mureina) purpurno protein zeleno - teihoična kiselina smeđe fosfolipid narančasto - lipopolisaharid u potpunosti izgrađena od debelog sloja polisaharida vrste roda alococcus izgrađena od glikoproteina hipertermofili (vrste roda alobacterium) velika učestalost kiselih aminokiselina daje staničnoj stijenci ove skupine arheja negativni naboj što uzrokuje nestabilnost strukture koju neutralizira velika količina natrijevih iona posljedično tomu, ova skupina živi u uvjetima velike slanosti 4. u rodova Methanomicrobium i Desulfurococcus, je izgrađena samo od površinskog sloja proteina koji čine mrežu tzv. Ssloja
16 Dodatni kemijski spojevi stanične stijenke biljaka tijekom života biljke, ugradnja kemijskih tvari u staničnu stijenku kao posljedica diferencijacije: lignin tvari lipofilnog karaktera suberin kutin mineralizacija plazmatska sekundarna st. središnja lamela primarna st. celuloza hemiceluloza lignin protein osim strukturnih elemenata, unutar stanične stijenke postoje i nestrukturne sastavnice: brojni spojevi male molekulske mase [boje, alkoholi, terpeni, tanini, itd.] oligosaharidi (i polisaharidi) proteini (obično glikoproteini) neki od glikoproteina sudjeluju u procesima prepoznavanja čimbenik nepodudarnosti na površini tučka lektini - glikoproteini velike specifičnosti Zadebljanja stijenke služe za povećanje čvrstoće stijenke Primarna (debela) Primarna (tanka) Jažica Stanice parenhima Stanice kolenhima Zadebljanja stijenke jednoliko jako zadebljala = cjelovito zadebljala (sklereide) odebljanja su ograničena samo na pojedine dijelove stijenke = lokalna zadebljanja (uglovni kolenhim (bs)) Lokalna zadebljanja stanične stijenke dodatno povećanje čvrstoće stijenke kvrge, bodlje cistoliti (Urticaceae, Moraceae) inkrustacija (stvaranje kamene kore) držak (SiO2) e = epiderma ku = kutikula pp = palisadni parenhim hp = spužvasti parenhim cs = provodne žile st = puč (stoma) c = cistolit grozd (CaCO3)
CITO T SKE K L E ET E
 CITOSKELET ULOGE CITOSKELETNIH ELEMENATA ćelije gajene u kulturi aktinski filamenti mikrotubule intermedijarni filamenti enterocit specifičnost organizacija STRUKTURA -PRATEĆI PROTEINI FUNKCIJA debljina
CITOSKELET ULOGE CITOSKELETNIH ELEMENATA ćelije gajene u kulturi aktinski filamenti mikrotubule intermedijarni filamenti enterocit specifičnost organizacija STRUKTURA -PRATEĆI PROTEINI FUNKCIJA debljina
ORGANIZACIJA BILJNE STANICE
 NEŢIVI DIO STANICE ORGANIZACIJA BILJNE STANICE A. PROTOPLAST HIJALOPLAZMA (MATRIKS, CITOSOL) STANIČNI ORGANELI PLAZMALEMA LIZOSOMI ENDOPLAZMATSKI RETIKULUM GOLGIJEV APARAT RIBOSOMI SFEROSOMI CITOPLAZMA
NEŢIVI DIO STANICE ORGANIZACIJA BILJNE STANICE A. PROTOPLAST HIJALOPLAZMA (MATRIKS, CITOSOL) STANIČNI ORGANELI PLAZMALEMA LIZOSOMI ENDOPLAZMATSKI RETIKULUM GOLGIJEV APARAT RIBOSOMI SFEROSOMI CITOPLAZMA
Biologija ćelije CITOSKELET
 Biologija ćelije CITOSKELET Kompleksna mreža proteinskih filamenata 3 osnovna elementa: 1. Mikrofilamenti (prečnika oko 7 nm) od proteina aktina 2. Intermedijarni filamenti (oko 8-11 nm) - od 6 glavnih
Biologija ćelije CITOSKELET Kompleksna mreža proteinskih filamenata 3 osnovna elementa: 1. Mikrofilamenti (prečnika oko 7 nm) od proteina aktina 2. Intermedijarni filamenti (oko 8-11 nm) - od 6 glavnih
dinamična mreža proteinskih filamenata građeni od proteina koji mogu spontano da polimerišu u citoskeletne filamente FUNKCIJE: Oblik ćelije Funkciona
 CITOSKELET dinamična mreža proteinskih filamenata građeni od proteina koji mogu spontano da polimerišu u citoskeletne filamente FUNKCIJE: Oblik ćelije Funkciona polarnost Pozicioniranje organela Transport
CITOSKELET dinamična mreža proteinskih filamenata građeni od proteina koji mogu spontano da polimerišu u citoskeletne filamente FUNKCIJE: Oblik ćelije Funkciona polarnost Pozicioniranje organela Transport
BIOLOGIJA 1. Građa i kemijski sastav prokariotske i eukariotske stanice
 BIOLOGIJA 1 Živi i neživi sustavi sastoje se iz istih atoma. Između te dvije forme sustava uočavaju se jasne razlike: Anorganska supstanca slučajna raspodjela materije i energije Građa i kemijski sastav
BIOLOGIJA 1 Živi i neživi sustavi sastoje se iz istih atoma. Između te dvije forme sustava uočavaju se jasne razlike: Anorganska supstanca slučajna raspodjela materije i energije Građa i kemijski sastav
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
Membrane u stanici. Endomembranski sustav = endomembrane. Razlikuju se prema: Izv. prof. dr. sc. Lidija Šver. Razlika u odnosu proteina i lipida
 Membrane u stanici Endomembranski sustav, organeli stanice Izv. prof. dr. sc. Lidija Šver Razlikuju se prema: debljini molekulskom sastavu (i fosfolipida i proteina i ugljikohidrata) metaboličkom ponašanju
Membrane u stanici Endomembranski sustav, organeli stanice Izv. prof. dr. sc. Lidija Šver Razlikuju se prema: debljini molekulskom sastavu (i fosfolipida i proteina i ugljikohidrata) metaboličkom ponašanju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
PROSTORNI STATIČKI ODREĐENI SUSTAVI
 PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
PROSTORNI STATIČKI ODREĐENI SUSTAVI - svi elementi ne leže u istoj ravnini q 1 Z F 1 F Y F q 5 Z 8 5 8 1 7 Y y z x 7 X 1 X - svi elementi su u jednoj ravnini a opterećenje djeluje izvan te ravnine Z Y
Opća biologija. Predavač: Nina Popović, dipl. ing. biologije
 Opća biologija Predavač: Nina Popović, dipl. ing. biologije Okvirni sadržaj predmeta Osnove bioloških principa Principi znanstvenih metoda u biologiji Značajke života Osnove o stanici Osnove nasljeđivanja
Opća biologija Predavač: Nina Popović, dipl. ing. biologije Okvirni sadržaj predmeta Osnove bioloških principa Principi znanstvenih metoda u biologiji Značajke života Osnove o stanici Osnove nasljeđivanja
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
a M a A. Može se pokazati da je supremum (ako postoji) jedinstven pa uvodimo oznaku sup A.
 3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
3 Infimum i supremum Definicija. Neka je A R. Kažemo da je M R supremum skupa A ako je (i) M gornja meda skupa A, tj. a M a A. (ii) M najmanja gornja meda skupa A, tj. ( ε > 0)( a A) takav da je a > M
Funkcije dviju varjabli (zadaci za vježbu)
 Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
Funkcije dviju varjabli (zadaci za vježbu) Vidosava Šimić 22. prosinca 2009. Domena funkcije dvije varijable Ako je zadano pridruživanje (x, y) z = f(x, y), onda se skup D = {(x, y) ; f(x, y) R} R 2 naziva
zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju.
 zastori zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. (mm) (mm) za PROZOR im (mm) tv25 40360 360 400 330x330 tv25 50450 450 500 410x410
zastori zastori sunset curtain Kućište od željeza zaštićeno epoksidnim prahom, opruge od željeza. Lako i brzo se montiraju. (mm) (mm) za PROZOR im (mm) tv25 40360 360 400 330x330 tv25 50450 450 500 410x410
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Funkcije proteinov (pogojene s strukturo)
 Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje molekul (ligandov, npr. O2 v Hb, Mb) Uravnavanje - DNA-vezavni proteini
Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje molekul (ligandov, npr. O2 v Hb, Mb) Uravnavanje - DNA-vezavni proteini
Cenovnik spiro kanala i opreme - FON Inžinjering D.O.O.
 Cenovnik spiro kanala i opreme - *Cenovnik ažuriran 09.02.2018. Spiro kolena: Prečnik - Φ (mm) Spiro kanal ( /m) 90 45 30 Muf/nipli: Cevna obujmica: Brza diht spojnica: Elastična konekcija: /kom: Ø100
Cenovnik spiro kanala i opreme - *Cenovnik ažuriran 09.02.2018. Spiro kolena: Prečnik - Φ (mm) Spiro kanal ( /m) 90 45 30 Muf/nipli: Cevna obujmica: Brza diht spojnica: Elastična konekcija: /kom: Ø100
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
10. STABILNOST KOSINA
 MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
Cauchyjev teorem. Postoji više dokaza ovog teorema, a najjednostvniji je uz pomoć Greenove formule: dxdy. int C i Cauchy Riemannovih uvjeta.
 auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
auchyjev teorem Neka je f-ja f (z) analitička u jednostruko (prosto) povezanoj oblasti G, i neka je zatvorena kontura koja čitava leži u toj oblasti. Tada je f (z)dz = 0. Postoji više dokaza ovog teorema,
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
NOMENKLATURA ORGANSKIH SPOJEVA. Imenovanje aromatskih ugljikovodika
 NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
NOMENKLATURA ORGANSKIH SPOJEVA Imenovanje aromatskih ugljikovodika benzen metilbenzen (toluen) 1,2-dimetilbenzen (o-ksilen) 1,3-dimetilbenzen (m-ksilen) 1,4-dimetilbenzen (p-ksilen) fenilna grupa 2-fenilheptan
Funkcije proteinov (pogojene s strukturo)
 Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje določenih molekul (ligandov, npr. Hb, Mb) Uravnavanje procesov (DNA-vezavni
Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje določenih molekul (ligandov, npr. Hb, Mb) Uravnavanje procesov (DNA-vezavni
3. razred gimnazije- opšti i prirodno-matematički smer ALKENI. Aciklični nezasićeni ugljovodonici koji imaju jednu dvostruku vezu.
 ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
ALKENI Acikliči ezasićei ugljovodoici koji imaju jedu dvostruku vezu. 2 4 2 2 2 (etile) viil grupa 3 6 2 3 2 2 prope (propile) alil grupa 4 8 2 2 3 3 3 2 3 3 1-bute 2-bute 2-metilprope 5 10 2 2 2 2 3 2
Funkcije proteinov (pogojene s strukturo)
 Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje molekul (ligandov, npr. O2 v Hb, Mb) Uravnavanje - DNA-vezavni proteini
Funkcije proteinov (pogojene s strukturo) Oporna funkcija (strukturni proteini, npr keratini, kolagen...) Transport/skladiščenje molekul (ligandov, npr. O2 v Hb, Mb) Uravnavanje - DNA-vezavni proteini
Sekundarne struktura proteina Fibrilni proteini
 Sekundarne struktura proteina Fibrilni proteini Nivoi strukture proteina (strukturna hijerarhija) proteina Nivoi strukture proteina Primarna struktura Sekundarna struktura Super-sekundarna struktura Tercijarnastruktura
Sekundarne struktura proteina Fibrilni proteini Nivoi strukture proteina (strukturna hijerarhija) proteina Nivoi strukture proteina Primarna struktura Sekundarna struktura Super-sekundarna struktura Tercijarnastruktura
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1)
 Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
Inženjerska grafika geometrijskih oblika (5. predavanje, tema1) Prva godina studija Mašinskog fakulteta u Nišu Predavač: Dr Predrag Rajković Mart 19, 2013 5. predavanje, tema 1 Simetrija (Symmetry) Simetrija
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Akvizicija tereta. 5660t. Y= masa drva, X=masa cementa. Na brod će se ukrcati 1733 tona drva i 3927 tona cementa.
 Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
Akvizicija tereta. Korisna nosivost broda je 6 t, a na brodu ia 8 cu. ft. prostora raspoloživog za sještaj tereta pod palubu. Navedeni brod treba krcati drvo i ceent, a na palubu ože aksialno ukrcati 34
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
POVRŠINA TANGENCIJALNO-TETIVNOG ČETVEROKUTA
 POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
POVRŠIN TNGENIJLNO-TETIVNOG ČETVEROKUT MLEN HLP, JELOVR U mnoštvu mnogokuta zanimljiva je formula za površinu četverokuta kojemu se istoobno može upisati i opisati kružnica: gje su a, b, c, uljine stranica
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PT ISPITIVANJE PENETRANTIMA
 FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton,
 Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton, neutron Građa atoma Pozitron, neutrino, antineutrino Beta
Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton, neutron Građa atoma Pozitron, neutrino, antineutrino Beta
MATEMATIKA I 1.kolokvij zadaci za vježbu I dio
 MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
MATEMATIKA I kolokvij zadaci za vježbu I dio Odredie c 0 i kosinuse kueva koje s koordinanim osima čini vekor c = a b ako je a = i + j, b = i + k Odredie koliki je volumen paralelepipeda, čiji se bridovi
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Dijagonalizacija operatora
 Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE)
 (Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
(Enegane) List: PARNA POSTROJENJA ZA KOMBINIRANU PROIZVODNJU ELEKTRIČNE I TOPLINSKE ENERGIJE (ENERGANE) Na mjestima gdje se istovremeno troši električna i toplinska energija, ekonomičan način opskrbe energijom
Transmembranski transport iona i malih molekula
 Transmembranski transport iona i malih B. Mildner Transmembranski transport iona i malih Plazmatska membrana regulira promet. Osim plinova (O 2 i CO 2 ) i malih hidrofobnih, većina ne može čistom difuzijom
Transmembranski transport iona i malih B. Mildner Transmembranski transport iona i malih Plazmatska membrana regulira promet. Osim plinova (O 2 i CO 2 ) i malih hidrofobnih, većina ne može čistom difuzijom
INTEGRALNI RAČUN. Teorije, metodike i povijest infinitezimalnih računa. Lucija Mijić 17. veljače 2011.
 INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
INTEGRALNI RAČUN Teorije, metodike i povijest infinitezimalnih računa Lucija Mijić lucija@ktf-split.hr 17. veljače 2011. Pogledajmo Predstavimo gornju sumu sa Dodamo još jedan Dobivamo pravokutnik sa Odnosno
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Matematička analiza 1 dodatni zadaci
 Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Matematička analiza 1 dodatni zadaci 1. Ispitajte je li funkcija f() := 4 4 5 injekcija na intervalu I, te ako jest odredite joj sliku i inverz, ako je (a) I = [, 3), (b) I = [1, ], (c) I = ( 1, 0].. Neka
Riješeni zadaci: Nizovi realnih brojeva
 Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Riješei zadaci: Nizovi realih brojeva Nizovi, aritmetički iz, geometrijski iz Fukciju a : N R azivamo beskoači) iz realih brojeva i ozačavamo s a 1, a,..., a,... ili a ), pri čemu je a = a). Aritmetički
Prostorni spojeni sistemi
 Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
Prostorni spojeni sistemi K. F. (poopćeni) pomaci i stupnjevi slobode tijela u prostoru: 1. pomak po pravcu (translacija): dva kuta kojima je odreden orijentirani pravac (os) i orijentirana duljina pomaka
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
LANCI & ELEMENTI ZA KAČENJE
 LANCI & ELEMENTI ZA KAČENJE 0 4 0 1 Lanci za vešanje tereta prema standardu MSZ EN 818-2 Lanci su izuzetno pogodni za obavljanje zahtevnih operacija prenošenja tereta. Opseg radne temperature se kreće
LANCI & ELEMENTI ZA KAČENJE 0 4 0 1 Lanci za vešanje tereta prema standardu MSZ EN 818-2 Lanci su izuzetno pogodni za obavljanje zahtevnih operacija prenošenja tereta. Opseg radne temperature se kreće
Vesla, teleskopi, nosači za štapove za ribolov
 76 Vesla, teleskopi, nosači za štapove za ribolov vesla pala piatta rvena vesla obojana prozirnom poliuretanskom bojom, vrlo čvrsta, sa ravnom lopaticom. Imaju plastično ležište za rašlje Φ43mm. tr13 38180
76 Vesla, teleskopi, nosači za štapove za ribolov vesla pala piatta rvena vesla obojana prozirnom poliuretanskom bojom, vrlo čvrsta, sa ravnom lopaticom. Imaju plastično ležište za rašlje Φ43mm. tr13 38180
Mitohondriji i kloroplasti Stanično disanje Fotosinteza Evolucija metaboličkih reakcija
 Mitohondriji i kloroplasti Stanično disanje Fotosinteza Evolucija metaboličkih reakcija MITOHONDRIJI -u svim eukariotskim stanicama -njihov broj ovisi o metaboličkoj aktivnosti stanice (nekoliko stotina
Mitohondriji i kloroplasti Stanično disanje Fotosinteza Evolucija metaboličkih reakcija MITOHONDRIJI -u svim eukariotskim stanicama -njihov broj ovisi o metaboličkoj aktivnosti stanice (nekoliko stotina
Riješeni zadaci: Limes funkcije. Neprekidnost
 Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Riješeni zadaci: Limes funkcije. Neprekidnost Limes funkcije Neka je 0 [a, b] i f : D R, gdje je D = [a, b] ili D = [a, b] \ { 0 }. Kažemo da je es funkcije f u točki 0 jednak L i pišemo f ) = L, ako za
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
Linearna algebra 2 prvi kolokvij,
 Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Linearna algebra 2 prvi kolokvij, 27.. 20.. Za koji cijeli broj t je funkcija f : R 4 R 4 R definirana s f(x, y) = x y (t + )x 2 y 2 + x y (t 2 + t)x 4 y 4, x = (x, x 2, x, x 4 ), y = (y, y 2, y, y 4 )
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Zašto se baviti BOTANIKOM i
 BOTANIKA Zašto se baviti BOTANIKOM i biljkama? BOTANIKA Temelj za razumijevanje ostalih kolegija na studijima Šumarskoga fakulteta Kada završim fakultet cijeli radni vijek ću se baviti biljkama Ljubav
BOTANIKA Zašto se baviti BOTANIKOM i biljkama? BOTANIKA Temelj za razumijevanje ostalih kolegija na studijima Šumarskoga fakulteta Kada završim fakultet cijeli radni vijek ću se baviti biljkama Ljubav
4. Koji od navedenih enzima pripada vrsti hidroksilaza? a) heksokinaza; b) kimotripsin; c) glikogen fosforilaza; d) trioza fosfat izomeraza.
 Osnove biokemije zadaća 7. 1. Što je točno o zimogenima? a) protoproteini su jedna vrsta zimogena; b) zimogene inhibiraju inhibitori proteina; c) zimogeni su enzimski neaktivni; d) zimogeni cijepaju proteaze.
Osnove biokemije zadaća 7. 1. Što je točno o zimogenima? a) protoproteini su jedna vrsta zimogena; b) zimogene inhibiraju inhibitori proteina; c) zimogeni su enzimski neaktivni; d) zimogeni cijepaju proteaze.
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
 **** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
TRIGONOMETRIJA TROKUTA
 TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
TRIGONOMETRIJA TROKUTA Standardne oznake u trokutuu ABC: a, b, c stranice trokuta α, β, γ kutovi trokuta t,t,t v,v,v s α,s β,s γ R r s težišnice trokuta visine trokuta simetrale kutova polumjer opisane
VODA I BILJNE STANICE
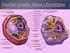 VODA I BILJNE STANICE Ž i v o t nastao u vodi ovisi o vodi BEZ VODE NEMA ŽIVOTA Voda - izvanredno velika uloga u životu biljaka - sastavni dio svih biljnih organizama potrebna za: - odvijanje svih fizioloških
VODA I BILJNE STANICE Ž i v o t nastao u vodi ovisi o vodi BEZ VODE NEMA ŽIVOTA Voda - izvanredno velika uloga u životu biljaka - sastavni dio svih biljnih organizama potrebna za: - odvijanje svih fizioloških
Pismeni ispit iz matematike Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: ( ) + 1.
 Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Pismeni ispit iz matematike 0 008 GRUPA A Riješiti sistem jednačina i diskutovati rješenja sistema u zavisnosti od parametra: λ + z = Ispitati funkciju i nacrtati njen grafik: + ( λ ) + z = e Izračunati
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
KONVEKSNI SKUPOVI. Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5. Back FullScr
 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 1. Neka su x, y R n,
KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 KONVEKSNI SKUPOVI Definicije: potprostor, afin skup, konveksan skup, konveksan konus. 1/5 1. Neka su x, y R n,
BIOLOGIJA SKRIPTA ZA DRŽAVNU MATURU. Marko Galić Kristina Kučanda
 BIOLOGIJA SKRIPTA ZA DRŽAVNU MATURU Marko Galić Kristina Kučanda 2 Autori: Marko Galić marko.gspn@gmail.com Kristina Kučanda streberica.gimnazijalka@yahoo.com prema: Ispitni katalog za državnu maturu u
BIOLOGIJA SKRIPTA ZA DRŽAVNU MATURU Marko Galić Kristina Kučanda 2 Autori: Marko Galić marko.gspn@gmail.com Kristina Kučanda streberica.gimnazijalka@yahoo.com prema: Ispitni katalog za državnu maturu u
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
3/25/2016. Hemijske komponente ćelije
 Hemijske komponente ćelije Molekuli u ćeliji Najbitniji molekuli u ćeliji su poznati. Putevi sinteze i razgradnje su poznati za većinu ćelijskih konstituenata. Hemijska energija pokreće biosintezu. Organizacija
Hemijske komponente ćelije Molekuli u ćeliji Najbitniji molekuli u ćeliji su poznati. Putevi sinteze i razgradnje su poznati za većinu ćelijskih konstituenata. Hemijska energija pokreće biosintezu. Organizacija
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
( ) p a. poklopac. Rješenje:
 5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
5 VJEŽB - RIJEŠENI ZDI IZ MENIKE LUID 1 1 Treb odrediti silu koj drži u rvnoteži poklopc B jedinične širine, zlobno vezn u točki, u položju prem slici Zdno je : =0,84 m; =0,65 m; =5,5 cm; =999 k/m B p
STOLICA FIRST MATE Model na preklop. Imitacija kože. KLUPA FIRST CLASS Model na preklop. Imitacija kože.
 STOLICE I STOLOVI STOLICA FIRST MATE Model na preklop. Imitacija kože. BOJA Širina (cm) Dubina (cm) Visina (cm) VE CHFSW VE CHFSB bijela sa plavim šavovima plava sa bijelim šavovima 40 48 45 40 48 45 KLUPA
STOLICE I STOLOVI STOLICA FIRST MATE Model na preklop. Imitacija kože. BOJA Širina (cm) Dubina (cm) Visina (cm) VE CHFSW VE CHFSB bijela sa plavim šavovima plava sa bijelim šavovima 40 48 45 40 48 45 KLUPA
PRAVAC. riješeni zadaci 1 od 8 1. Nađite parametarski i kanonski oblik jednadžbe pravca koji prolazi točkama. i kroz A :
 PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
PRAVAC iješeni adaci od 8 Nađie aameaski i kanonski oblik jednadžbe aca koji olai očkama a) A ( ) B ( ) b) A ( ) B ( ) c) A ( ) B ( ) a) n a AB { } i ko A : j b) n a AB { 00 } ili { 00 } i ko A : j 0 0
MEHANIKA FLUIDA. Prosti cevovodi
 MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
MEHANIKA FLUIDA Prosti ceooi zaatak Naći brzin oe kroz naglaak izlaznog prečnika =5 mm, postaljenog na kraj gmenog crea prečnika D=0 mm i žine L=5 m na čijem je prenjem el građen entil koeficijenta otpora
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Vodik. dr.sc. M. Cetina, doc. Tekstilno-tehnološki fakultet, Zavod za primijenjenu kemiju
 Vodik Najzastupljeniji element u svemiru (maseni udio iznosi 90 %) i sastavni dio Zvijezda. Na Zemlji je po masenom udjelu deseti element po zastupljenosti. Zemljina gravitacija premalena je da zadrži
Vodik Najzastupljeniji element u svemiru (maseni udio iznosi 90 %) i sastavni dio Zvijezda. Na Zemlji je po masenom udjelu deseti element po zastupljenosti. Zemljina gravitacija premalena je da zadrži
