3 SEDIMENTNE STRUKTURE
|
|
|
- ἐλπίς Αντωνιάδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 3 SEDIMENTNE STRUKTURE 3.1 UVOD fizičke osobine sedimenata koje su uglavnom odraz taložnih procesa, ali mogu biti i posttaložnog odnosno dijagenetskog podrijetla najčešće obuhvaćaju veličinu zrna morfologiju zrna građu sedimenta (značajke koje se u engleskoj literaturi označavaju s texture ) njihovim istraživanjem mogu se dobiti informacije o načinu, uvjetima i okolišima postanka sedimenata 3.2 VELIČINA ZRNA osnovni deskriptivni element siliciklastičnih sedimentnih stijena odraz je procesa trošenja i erozije, koji generiraju čestice različitih veličina i prirode transporta Ljestvice veličine čestica veličina čestica u sedimentima i sedimentnim stijenama kreće se u rasponu od nekoliko mikrometara (mikrona) do nekoliko metara tipovi geometrijske ljestvice logaritamske ljestvice 30
2 Udden-Wentworthova ljestvica najčešće korištena ljestvica za klasifikaciju i nomenklaturu sedimenata i sedimentnih stijena geometrijska ljestvica bazirana na broju 2 (1, 2, 4, 8, 16) Pojednostavljena ljestvica veličine čestica koja pokazuje Wentworthove kategorije i odgovarajuće kategorije u phi (Φ) jedinicama. Krumbeinova ljestvica modifikacija Udden-Wentworthove ljestvice s logaritamskim Φ jedinicama Φ=-log 2 d d-veličina zrna u mm Prim: veličina čestica pijeska kreće se između 0,0625mm i 2mm; tj. od 2-4 mm do 2 1 mm što u Φ jedinicama iznosi: Φ = -log = -(-4) = 4 Φ = -log = -(1) = 1 Ljestvica veličine čestica s odgovarajućim nazivljem. Preuzeto iz 3 Shema klasifikacije šljunkovito-pjeskovito-muljevitih sedimenata i sedimentnih stijena. 31
3 3.2.2 Metode određivanja veličine čestica (granulometrijskog sastava) odabir ovisi o rasponu veličine čestica stupnju konsolidacije sedimenta odnosno sedimentne stijene namjeni istraživanja podjela terenske laboratorijske terenske metode usporedba sa standardnim uzorcima usporedba istraživanog sedimenta sa standardnim uzorcima poznatih dimenzija zrna vrlo krupni pijesak krupni pijesak srednji pijesak Standardni uzorci koji služe za terensku odredbu veličine čestica. sitni pijesak vrlo sitni pijesak silt upotreba Mullerovog povećala povećalo s ljestvicama za mjerenje veličine čestica od 20 μm do 20 mm terensko sijanje po Azmonu za prahovito-pješčane, pješčane i pješčano-šljunkovite nevezane sedimente sijanje uzoraka kroz 3-5 sita mjerenje volumena svake pojedine frakcije u menzuri izračun volumnog udjela svake frakcije određivanje vrste sedimenta mjerenje brzine taloženja čestica za muljevite (glinovito-siltne) sedimente mjeri se vrijeme potrebno za taloženje sedimenta suspendiranog u vodi iz potrebnog vremena izračunava se (očitava iz tablica) promjer čestica u uzorku 32
4 laboratorijske metode izravno mjerenje kod analize šljunaka, breča i konglomerata pomično mjerilo, milimetarska traka, ravnalo mjeri se najveći promjer barem 300 zrna mjerenja mikroskopom kod analize pješčenjaka i siltita kad nije moguće dezintegrirati uzorak mjere se veličine slučajnih presjeka najmanje 300 zrna sijanje najvažnija metoda određivanja veličine zrna (prah - sitni šljunak) 5-7 sita frakcija dio uzorka koji sadrži zrna s dimenzijama ograničenim dimenzijama otvora gornjeg i donjeg sita priprema rasuti uzorak četvrtanje poluvezani ili vezani dezintegracija» moćenje u vodi (muljeviti sedimenti slabo vezani pješčenjaci)» vodikov peroksid (H 2 O 2 ) - slabo vezani glinovito-prašinasto-pješčani sedimenti 2H 2 O 2 2H 2 O + O 2 (pritisak dezinetegrira stijenu)» ultrazvuk - jače litificirani glinovito-prašinasto-pješčani sedimenti - djelovanje ultrazvuka na razmrvljeni i u vodi namočeni uzorak» kiseline (monokloroctena, octena, klorovodična) - otapanje kalcitnog cementa Prim: CaCO 3 + 2HCl CaCl 2 + CO 2 + H 2 O sijanje trešnja seta sita na vibracijskom aparatu mjerenje mase uzorka zaostalog na pojedinom situ (frakcija) izračunavanje masenog udjela svake pojedine frakcije Laboratorijska sita 33
5 sedimentacijska analiza određivanje veličine zrna na temelju brzine padanja čestica temelji sa na Stocksovu zakonu: veličina čestica (d) računa se mjerenjem vremena (t) potrebnog da bi čestice pale s visine h: uvjeti masa tekućine mora biti puno veća od mase uzorka uzorci sadrže čestice <0,05 mm (mala brzina padanja čestica) metode sedimentacija u Atterbergovom cilindru omogućava izdvajanje bilo koje željene frakcije uzorak se dispergira u vodi i stavi u cilindar izračuna se vrijeme potrebno za taloženje čestica većih od željene veličine (prim. 4µm) nakon tog vremena tekućina s česticama željene veličine i manjima ispusti se u posebnu posudu postupak se ponavlja više puta (dok tekućina u cilindru ne postane bistra) spora (oko 30 dana) Preuzeto iz 3 Prikaz postupka sedimentacijske analize metodom Atterbergovog cilindra. pipetna metoda koristi se za analize granulometrijskog sastava pipetiranjem u različitim vremenskim razmacima iz iste dubine suspendiranog uzorka određuje se promjena koncentracije uzorka koja ovisi o brzini taloženja, tj. o veličini čestica koje se talože svaka odpipetirana suspenzija se osuši i izvaže postotak svake pojedine frakcije izračuna se iz težine suhog ostatka početne koncentracije i razlike težina suhih ostataka svih ostalih koncentracija areometriranje temelji se na promjeni gustoće suspenzije u ovisnosti o brzini taloženja čestica mjerenjem promjena gustoće suspenzije u određenim vremenskim razmacima (t 1, t 2, t 3,..) potrebnim za taloženje čestica promjera d 1, d 2, d 3 izračunaju se udjeli sedimentiranih čestica Areometar Mjerenje gustoće tekućine areometrom. 34
6 mjerenje refrakcije ili disperzije svjetla koje prolazi kroz suspenziju sedigraf Preuzeto iz 2i SediGraph III 5210 tvrtke Micrometrics. VELIČINA ZRNA (u mm) > Izbor metoda određivanja veličine čestica u sedimentima VRSTA SEDIMENTA ILI STIJENE blokovi konglomerat/breča šljunak/drobina konglomerat/breča METODA izravno mjerenje izravno mjerenje i sijanje rupičastim sitima POTREBNA KOLIČINA UZORKA najmanje 300 pojedinačnih zrna > 300 zrna ili sijanje rupičastim sitima 2 0,063 pijesak pješčenjak 0,063 0,004 < 0,004 prah prahovnjak glina glinjak sijanje laboratorijskim sitima mjerenje mikroskopom sijanje mikrositima i sedimentacijska analiza sedimentacijska analiza mjerenje elektronskim mikroskopom g > 300 zrna g 1 5 g 0,1 0,5 g Grafički prikaz rezultata granulometrijskih analiza histogram krivulja učestalosti (frekvencijska krivulja) kumulativna granulometrijska krivulja histogram prikaz količine svake pojedine frakcije u obliku stupaca Rezultati analize granulometrijskog sastava prikazani u obliku histograma. 35
7 krivulja učestalosti (frekvencijska krivulja) na apscisu se nanesu veličine zrna, a na ordinatu njihova količina u % dobivenim točkama konstruira se krivulja daje brzu impresiju o distribuciji veličine čestica, o unimodalnom, bimodalnom ili polimodalnom sastavu Rezultati analize granulometrijskog sastava prikazani u obliku krivulja učestalosti. kumulativna granulometrijska krivulja najčešći način prikazivanja rezultata granulometrijskih analiza prikazuje cjelokupni sastav i raspored zrna iz nje se mogu direktno očitati udjeli pojedinih frakcija iz nje se mogu očitati ili izračunati važni granulometrijski parametri Rezultati analize granulometrijskog sastava prikazani u obliku kumulativne granulometrijske krivulje. Rezultati analize granulometrijskog sastava prikazani u obliku kumulativne granulometrijske krivulje. Veličina čestica na apscisi izražena je u mm i prikazana je na logaritamskoj skali. 36
8 3.2.4 Parametri veličine čestica (granulometrijski parametri) srednja veličina čestica (medijan) prosječna veličina zrna (mean) koeficijent sortiranosti koeficijent asimetrije srednja veličina čestica (medijan) - Md veličina čestica na 50% kumulativne granulometrijske krivulje A B Očitavanje medijana na kumulativnoj granulometrijskoj krivulji: A Φ jedinice; B mm prosječna veličina čestica (mean) - M aritmetički izračunata prosječna veličina čestica A B Izračunavanje prosječne veličine čestica na kumulativnoj granulometrijskoj krivulji: A Φ jedinice; B mm koeficijent sortiranosti - So pokazatelj distribucije veličine čestica faktori: izvor materijala granit će dati drugačiji materijal nego stariji pješčenjak veličina zrna sedimenta pijesak najčešće bolje sortirani od krupnozrnatih i sitnozrnatih jer se lako transportiraju, a time i sortiraju vjetrom i vodom taložni mehanizam naglo taloženi sedimenti (prim. olujni sedimenti) loša sortiranost sedimenti taloženi iz viskoznih tokova (prim. muljni tokovi) loša sortiranost sedimenti prerađeni vjetrom ili vodom (prim. pješčani sedimenti pustinja ili plaža) dobra sortiranost načini određivanja matematički izračun iz kumulativne granulometrijske krivulje usporedba s vizualnim komparatorima za procjenu sortiranosti čestica 37
9 matematički izračuni sortiranosti čestica iz kumulativne granulometrijske krivulje A B Utvrđivanje sortiranosti čestica u uzorku matematičkim izračunom: A standardne devijacije (Folk & Ward); B kvadratnog korijena P75/P25 (Trask & Krumbein). Folk & Ward Trask & Krumbein So sortiranost So sortiranost < 0,35 vrlo dobra 1-1,23 vrlo dobra 0,35-0,50 dobra 1,23-1,41 dobra 0,50-0,71 umjereno dobra 1,41-1,74 srednja 0,71-1,00 umjerena 1,74-2,00 loša 1,00-2,00 slaba >2,00 vrlo loša > 2,00 vrlo slaba Granične vrijednosti kategorija sortiranosti čestica. usporedba s vizualnim komparatorima za procjenu sortiranosti čestica Preuzeto iz 3 koeficijent asimetrije- Sk (skewness) pokazatelj simetričnosti distribucije čestica najbolje se vidi na krivulji učestalosti pozitivni Sk (prim. fluvijalni i eolski sedimenti) negativni Sk (prim. sedimenti plaža) Krivulja učestalosti sa simetričnom distribucijom čestica. Krivulja učestalosti s asimetričnom distribucijom čestica. 38
10 matematičko izračunavanje koeficijenta asimetrije Granulometrijske analize mogu se koristiti za razlikovanje sedimenata iz različitih okoliša i facijesa i daju podatke o taložnim procesima i uvjetima toka, međutim same za sebe nisu dovoljno pouzdane i najbolje ih je koristiti u kombinaciji s drugim karakteristikama sedimenta poput sedimentnih tekstura. 3.3 MORFOMETRIJSKE ZNAČAJKE ZRNA daju podatke o strukturno-teksturnim odlikama sedimenta služe pri rekonstrukciji i interpretaciji uvjeta transporta i okoliša taloženja oblik zrna sferičnost zaobljenost struktura površine zrna Oblik zrna približavanje nekog zrna manje-više pravilnim geometrijskim tijelima faktori primarni oblik minerala u matičnoj stijeni stupanj zaobljavanja i habanja tijekom transporta dijagenetske promjene Karakteristični oblici zrna Sferičnost zrna približavanje oblika zrna obliku kugle indeks sferičnosti (Is) Is = (Vz/Vk) 1/3 Vz-volumen zrna Vk-volumen kugle promjera kao i najmanji mogući opisani krug oko projekcije zrna Is 1; Is bliže jedinici zrno sličnije kugli viša sferičnost u praksi vizualno uspoređivanje zrna s grafičkom tablicom Preuzeto iz 3 Tablica za grafičko određivanje stupnja sferičnosti i zaobljenosti zrna. 39
11 3.3.3 Zaobljenost zrna odnos između uglova i bridova zrna prema polumjeru najvećeg mogućeg u zrno upisanog kruga proporcionalna je dužini i intenzitetu transporta, veličini zrna i njegovoj gustoći, a obrnuto proporcionalna s tvrdoćom zrna Prim: valutice šljunka dobro su zaobljene već nakon km transporta stupanj zaobljenosti kvarcnih zrna promjera 1,5-2 mm povećava se nakon transporta na udaljenost od 2000 km samo oko 5% Kategorije zaobljenosti za niskosferična i visokosferična zrna Struktura površine zrna može se istraživani na zrnima veličine pijeska i krupnijima istražuje se pomoću elektronskog mikroskopa strukture na površini zrna su značajke koje nastaju kao rezultat transportnog mehanizma i ponekad mogu imati dijagnostičko značenje Preuzeto iz 1 sedimenti visokoenergetskih plaža glacijalni sedimenti pustinjski sedimenti Elektronske mikrofotografije pješčanih kvarcnih zrna. orijentacija zrna način pakiranja zrna način podržavanja zrna (potpora) kontakti među zrnima 3.4 GRAĐA SEDIMENTA kontroliraju neke fizičke značajke sedimentnih stijena poput gustoće, poroznosti i permeabilnosti Orijentacija zrna produkt je interakcije transportno-taložnog medija (prim. vjetar, led, voda) sa sedimentom preferirana orijentacija česta kod pješčenjaka i konglomerata zrna i valutice su poredane svojom dužom osi u istome smjeru 40
12 transport klizanjem transport kotrljanjem u vodi imbricirane valutice Shematski prikaz orijentacije izduženih zrna (valutica) u odnosu na smjer struje. imbrikacija pojava karakteristična za plosnate valutice u šljuncima nošenim vodom valutice su naslonjene jedna na drugu i nagnute u smjeru suprotnom od smjera toka često se koristi za istraživanja paleotokova slučajno orijentirane valutice Imbricirane valutice s naznačenim smjerom prijenosa materijala Način pakiranja zrna utječe na poroznost i propusnost stijena kubično pakiranje visoka poroznost romboedarsko pakiranje niska poroznost ovisi o obliku, veličini zrna i sortiranosti lošija sortiranost manja poroznost Kubično i romboedarsko pakiranje zrna u sedimentu Način podržavanja zrna (potpora) klastpotporne stijene zrna su u međusobnom kontaktu Klastpotporni konglomerat; Manastir Krka. matrikspotporne stijene zrna plivaju u matriksu Preuzeto iz 1 Matrikspotporni konglomerat. 41
13 3.4.4 Kontakti među zrnima ukazuju na stupanj kompakcije sedimenta glavni tipovi točkasti zrna dodiruju jedan drugi u točkama dajući sedimentu zrnsku potporu tangencijalni zrna se dodiruju duž linija konkavno-konveksni zrna prodiru jedno u drugo suturirani zrna imaju zupčaste kontakte Vrste kontakata među zrnima. 3.5 MATRIKS I CEMENT zapunjavaju prostor među zrnima u strukturi klastičnih sedimenata (klastična struktura) matriks mehanički istaloženi sitni detritus (prim. glina ili prah) može biti taložen istovremeno s krupnijim česticama ili naknadno zapunjavajući porni prostor cement kemijski precipitirani autigeni mineral (prim. kalcit, silika, Fe-oksidi) cementacijom se smanjuje poroznost i permeabilnost sedimenta Primjeri klastične strukturemikroskopski izgled. strukturno nezreli sedimenti puno matriksa loša sortiranost uglata zrna strukturno zreli sedimenti malo matriksa sortiranost umjerena do dobra zrna poluzaobljena do zaobljena strukturno superzreli sedimenti nemaju matriksa vrlo dobra sortiranost zrna su dobro zaobljena primarna poroznost i permeabilnost rastu s porastom strukturne zrelosti jer zreliji sedimenti sadrže manje matriksa i više pornog prostora 3.6 STRUKTURNA ZRELOST Preuzeto iz 3 Preuzeto iz 3 42
AGREGAT. Asistent: Josip Crnojevac, mag.ing.aedif. SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU
 AGREGAT Asistent: Josip Crnojevac, mag.ing.aeif. jcrnojevac@gmail.com SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU JOSIP JURAJ STROSSMAYER UNIVERSITY OF OSIJEK 1 Pojela agregata PODJELA AGREGATA - PREMA
AGREGAT Asistent: Josip Crnojevac, mag.ing.aeif. jcrnojevac@gmail.com SVEUČILIŠTE JOSIPA JURJA STROSSMAYERA U OSIJEKU JOSIP JURAJ STROSSMAYER UNIVERSITY OF OSIJEK 1 Pojela agregata PODJELA AGREGATA - PREMA
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Grafičko prikazivanje atributivnih i geografskih nizova
 Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Grafičko prikazivanje atributivnih i geografskih nizova Biserka Draščić Ban Pomorski fakultet u Rijeci 17. veljače 2011. Grafičko prikazivanje atributivnih nizova Atributivni nizovi prikazuju se grafički
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom
 Kolegij: Obrada industrijskih otpadnih voda Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom Zadatak: Ispitati učinkovitost procesa koagulacije/flokulacije na obezbojavanje
Kolegij: Obrada industrijskih otpadnih voda Vježba: Uklanjanje organskih bojila iz otpadne vode koagulacijom/flokulacijom Zadatak: Ispitati učinkovitost procesa koagulacije/flokulacije na obezbojavanje
PT ISPITIVANJE PENETRANTIMA
 FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
FSB Sveučilišta u Zagrebu Zavod za kvalitetu Katedra za nerazorna ispitivanja PT ISPITIVANJE PENETRANTIMA Josip Stepanić SADRŽAJ kapilarni učinak metoda ispitivanja penetrantima uvjeti promatranja SADRŽAJ
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRERADA GROŽðA. Sveučilište u Splitu Kemijsko-tehnološki fakultet. Zavod za prehrambenu tehnologiju i biotehnologiju. Referati za vježbe iz kolegija
 Sveučilište u Splitu Kemijsko-tehnološki fakultet Zavod za prehrambenu tehnologiju i biotehnologiju Referati za vježbe iz kolegija PRERADA GROŽðA Stručni studij kemijske tehnologije Smjer: Prehrambena
Sveučilište u Splitu Kemijsko-tehnološki fakultet Zavod za prehrambenu tehnologiju i biotehnologiju Referati za vježbe iz kolegija PRERADA GROŽðA Stručni studij kemijske tehnologije Smjer: Prehrambena
Impuls i količina gibanja
 FAKULTET ELEKTROTEHNIKE, STROJARSTVA I BRODOGRADNJE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba 4 Impuls i količina gibanja Ime i prezime prosinac 2008. MEHANIKA
FAKULTET ELEKTROTEHNIKE, STROJARSTVA I BRODOGRADNJE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba 4 Impuls i količina gibanja Ime i prezime prosinac 2008. MEHANIKA
Trigonometrija 2. Adicijske formule. Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto
 Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
Trigonometrija Adicijske formule Formule dvostrukog kuta Formule polovičnog kuta Pretvaranje sume(razlike u produkt i obrnuto Razumijevanje postupka izrade složenijeg matematičkog problema iz osnova trigonometrije
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
Izravni posmik. Posmična čvrstoća tla. Laboratorijske metode određivanja kriterija čvratoće ( c i φ )
 Posmična čvrstoća tla Posmična se čvrstoća se često prikazuje Mohr-Coulombovim kriterijem čvrstoće u - σ dijagramu c + σ n tanφ Kriterij čvrstoće C-kohezija φ -kut trenja c + σ n tan φ φ c σ n Posmična
Posmična čvrstoća tla Posmična se čvrstoća se često prikazuje Mohr-Coulombovim kriterijem čvrstoće u - σ dijagramu c + σ n tanφ Kriterij čvrstoće C-kohezija φ -kut trenja c + σ n tan φ φ c σ n Posmična
Izbor statističkih testova Ana-Maria Šimundić
 Izbor statističkih testova Ana-Maria Šimundić Klinički zavod za kemiju Klinička jedinica za medicinsku biokemiju s analitičkom toksikologijom KBC Sestre milosrdnice Izbor statističkog testa Tajna dobrog
Izbor statističkih testova Ana-Maria Šimundić Klinički zavod za kemiju Klinička jedinica za medicinsku biokemiju s analitičkom toksikologijom KBC Sestre milosrdnice Izbor statističkog testa Tajna dobrog
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
( , 2. kolokvij)
 A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
A MATEMATIKA (0..20., 2. kolokvij). Zadana je funkcija y = cos 3 () 2e 2. (a) Odredite dy. (b) Koliki je nagib grafa te funkcije za = 0. (a) zadanu implicitno s 3 + 2 y = sin y, (b) zadanu parametarski
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
10. STABILNOST KOSINA
 MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
MEHANIKA TLA: Stabilnot koina 101 10. STABILNOST KOSINA 10.1 Metode proračuna koina Problem analize tabilnoti zemljanih maa vodi e na određivanje odnoa između rapoložive mičuće čvrtoće i proečnog mičućeg
6 SREDNJEZRNATI KLASTITI (PJEŠČENJACI)
 62 6 SREDNJEZRNATI KLASTITI (PJEŠČENJACI) veličina čestica: 2mm - 63μm 6.1 UVOD vrlo krupni pijesak krupni pijesak srednji pijesak sitni pijesak vrlo sitni pijesak litifikacija pijesak pješčenjak klastična
62 6 SREDNJEZRNATI KLASTITI (PJEŠČENJACI) veličina čestica: 2mm - 63μm 6.1 UVOD vrlo krupni pijesak krupni pijesak srednji pijesak sitni pijesak vrlo sitni pijesak litifikacija pijesak pješčenjak klastična
1.4 Tangenta i normala
 28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
28 1 DERIVACIJA 1.4 Tangenta i normala Ako funkcija f ima derivaciju u točki x 0, onda jednadžbe tangente i normale na graf funkcije f u točki (x 0 y 0 ) = (x 0 f(x 0 )) glase: t......... y y 0 = f (x
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI)
 IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
IZRAČUNAVANJE POKAZATELJA NAČINA RADA NAČINA RADA (ISKORIŠĆENOSTI KAPACITETA, STEPENA OTVORENOSTI RADNIH MESTA I NIVOA ORGANIZOVANOSTI) Izračunavanje pokazatelja načina rada OTVORENOG RM RASPOLOŽIVO RADNO
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Periodičke izmjenične veličine
 EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
EHNČK FAKULE SVEUČLŠA U RJEC Zavod za elekroenergeiku Sudij: Preddiploski sručni sudij elekroehnike Kolegij: Osnove elekroehnike Nosielj kolegija: Branka Dobraš Periodičke izjenične veličine Osnove elekroehnike
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Pošto pretvaramo iz veće u manju mjernu jedinicu broj 2.5 množimo s 1000,
 PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
PRERAČUNAVANJE MJERNIH JEDINICA PRIMJERI, OSNOVNE PRETVORBE, POTENCIJE I ZNANSTVENI ZAPIS, PREFIKSKI, ZADACI S RJEŠENJIMA Primjeri: 1. 2.5 m = mm Pretvaramo iz veće u manju mjernu jedinicu. 1 m ima dm,
Otpornost R u kolu naizmjenične struje
 Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
Otpornost R u kolu naizmjenične struje Pretpostavimo da je otpornik R priključen na prostoperiodični napon: Po Omovom zakonu pad napona na otporniku je: ( ) = ( ω ) u t sin m t R ( ) = ( ) u t R i t Struja
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
3 Klasifikacija tla i indeksni pokazatelji.
 3 Klasifikacija tla i indeksni pokazatelji. 3.1 Osnovne grupe tla Postoji niz različitih klasifikacija tla. Svakako, klasifikacija treba omogućiti da se pomoću jednostavnih pokusa svrstaju tla u grupe
3 Klasifikacija tla i indeksni pokazatelji. 3.1 Osnovne grupe tla Postoji niz različitih klasifikacija tla. Svakako, klasifikacija treba omogućiti da se pomoću jednostavnih pokusa svrstaju tla u grupe
Program testirati pomoću podataka iz sledeće tabele:
 Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
3. OSNOVNI POKAZATELJI TLA
 MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
MEHANIKA TLA: Onovni paraetri tla 4. OSNONI POKAZATELJI TLA Tlo e atoji od tri faze: od čvrtih zrna, vode i vazduha i njihovo relativno učešće e opiuje odgovarajući pokazateljia.. Specifična težina (G)
Mate Vijuga: Rijeseni zadaci iz matematike za srednju skolu
 16. UVOD U STATISTIKU Statistika je nauka o sakupljanju i analizi sakupljenih podatka u cilju donosenja zakljucaka o mogucem toku ili obliku neizvjesnosti koja se obradjuje. Frekventna distribucija - je
16. UVOD U STATISTIKU Statistika je nauka o sakupljanju i analizi sakupljenih podatka u cilju donosenja zakljucaka o mogucem toku ili obliku neizvjesnosti koja se obradjuje. Frekventna distribucija - je
ODREĐIVANJE MODULA STIŠLJIVOSTI U EDOMETRU
 SVEUČILIŠTE U ZAGREBU GEOTEHNIČKI FAKULTET ZORAN BAJSIĆ ODREĐIVANJE MODULA STIŠLJIVOSTI U EDOMETRU ZAVRŠNI RAD VARAŽDIN, 2012. SVEUČILIŠTE U ZAGREBU GEOTEHNIČKI FAKULTET ZAVRŠNI RAD ODREĐIVANJE MODULA
SVEUČILIŠTE U ZAGREBU GEOTEHNIČKI FAKULTET ZORAN BAJSIĆ ODREĐIVANJE MODULA STIŠLJIVOSTI U EDOMETRU ZAVRŠNI RAD VARAŽDIN, 2012. SVEUČILIŠTE U ZAGREBU GEOTEHNIČKI FAKULTET ZAVRŠNI RAD ODREĐIVANJE MODULA
Matematika 1 - vježbe. 11. prosinca 2015.
 Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Matematika - vježbe. prosinca 5. Stupnjevi i radijani Ako je kut φ jednak i rad, tada je veza između i 6 = Zadatak.. Izrazite u stupnjevima: a) 5 b) 7 9 c). d) 7. a) 5 9 b) 7 6 6 = = 5 c). 6 8.5 d) 7.
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
2.2 Srednje vrijednosti. aritmetička sredina, medijan, mod. Podaci (realizacije varijable X): x 1,x 2,...,x n (1)
 2.2 Srednje vrijednosti aritmetička sredina, medijan, mod Podaci (realizacije varijable X): x 1,x 2,...,x n (1) 1 2.2.1 Aritmetička sredina X je numerička varijabla. Aritmetička sredina od (1) je broj:
2.2 Srednje vrijednosti aritmetička sredina, medijan, mod Podaci (realizacije varijable X): x 1,x 2,...,x n (1) 1 2.2.1 Aritmetička sredina X je numerička varijabla. Aritmetička sredina od (1) je broj:
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
konst. Električni otpor
 Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
Sveučilište J. J. Strossmayera u sijeku Elektrotehnički fakultet sijek Stručni studij Električni otpor hmov zakon Pri protjecanju struje kroz vodič pojavljuje se otpor. Georg Simon hm je ustanovio ovisnost
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
- pravac n je zadan s točkom T(2,0) i koeficijentom smjera k=2. (30 bodova)
 MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
MEHANIKA 1 1. KOLOKVIJ 04/2008. grupa I 1. Zadane su dvije sile F i. Sila F = 4i + 6j [ N]. Sila je zadana s veličinom = i leži na pravcu koji s koordinatnom osi x zatvara kut od 30 (sve komponente sile
Novi Sad god Broj 1 / 06 Veljko Milković Bulevar cara Lazara 56 Novi Sad. Izveštaj o merenju
 Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Broj 1 / 06 Dana 2.06.2014. godine izmereno je vreme zaustavljanja elektromotora koji je radio u praznom hodu. Iz gradske mreže 230 V, 50 Hz napajan je monofazni asinhroni motor sa dva brusna kamena. Kada
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
GLAZBENA UMJETNOST. Rezultati državne mature 2010.
 GLAZBENA UJETNOST Rezultati državne mature 2010. Deskriptivna statistika ukupnog rezultata PARAETAR VRIJEDNOST N 112 k 61 72,5 St. pogreška mjerenja 5,06 edijan 76,0 od 86 St. devijacija 15,99 Raspon 66
GLAZBENA UJETNOST Rezultati državne mature 2010. Deskriptivna statistika ukupnog rezultata PARAETAR VRIJEDNOST N 112 k 61 72,5 St. pogreška mjerenja 5,06 edijan 76,0 od 86 St. devijacija 15,99 Raspon 66
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
STATISTIKA S M E I M N I AR R 7 : METODE UZORKA
 Fakultet za menadžment u turizmu i ugotiteljtvu, Opatija Sveučilišni preddiplomki tudij Polovna ekonomija u turizmu i ugotiteljtvu Noitelj kolegija: Prof. dr. c. Suzana Marković Aitentica: Jelena Komšić
Fakultet za menadžment u turizmu i ugotiteljtvu, Opatija Sveučilišni preddiplomki tudij Polovna ekonomija u turizmu i ugotiteljtvu Noitelj kolegija: Prof. dr. c. Suzana Marković Aitentica: Jelena Komšić
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
VOLUMEN ILI OBUJAM TIJELA
 VOLUMEN ILI OBUJAM TIJELA Veličina prostora kojeg tijelo zauzima Izvedena fizikalna veličina Oznaka: V Osnovna mjerna jedinica: kubni metar m 3 Obujam kocke s bridom duljine 1 m jest V = a a a = a 3, V
VOLUMEN ILI OBUJAM TIJELA Veličina prostora kojeg tijelo zauzima Izvedena fizikalna veličina Oznaka: V Osnovna mjerna jedinica: kubni metar m 3 Obujam kocke s bridom duljine 1 m jest V = a a a = a 3, V
Numerička matematika 2. kolokvij (1. srpnja 2009.)
 Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Numerička matematika 2. kolokvij (1. srpnja 29.) Zadatak 1 (1 bodova.) Teorijsko pitanje. (A) Neka je G R m n, uz m n, pravokutna matrica koja ima puni rang po stupcima, tj. rang(g) = n. (a) Napišite puni
Alarmni sustavi 07/08 predavanja 12. i 13. Detekcija metala, izvori napajanja u sustavima TZ
 Alarmni sustavi 07/08 predavanja 12. i 13. Detekcija metala, izvori napajanja u sustavima TZ pred.mr.sc Ivica Kuric Detekcija metala instrument koji detektira promjene u magnetskom polju generirane prisutnošću
Alarmni sustavi 07/08 predavanja 12. i 13. Detekcija metala, izvori napajanja u sustavima TZ pred.mr.sc Ivica Kuric Detekcija metala instrument koji detektira promjene u magnetskom polju generirane prisutnošću
2 PROCESI POSTANKA SEDIMENATA I SEDIMENTNIH STIJENA
 2 PROCESI POSTANKA SEDIMENATA I SEDIMENTNIH STIJENA sedimentne stijene nastaju djelovanjem fizičkih, kemijskih i bioloških procesa na površini ili plitko ispod površine Zemlje pri niskim temperaturama
2 PROCESI POSTANKA SEDIMENATA I SEDIMENTNIH STIJENA sedimentne stijene nastaju djelovanjem fizičkih, kemijskih i bioloških procesa na površini ili plitko ispod površine Zemlje pri niskim temperaturama
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II
 1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
1 UPUTSTVO ZA IZRADU GRAFIČKOG RADA IZ MEHANIKE II Zadatak: Klipni mehanizam se sastoji iz krivaje (ekscentarske poluge) OA dužine R, klipne poluge AB dužine =3R i klipa kompresora B (ukrsne glave). Krivaja
Konstruisanje. Dobro došli na... SREDNJA MAŠINSKA ŠKOLA NOVI SAD DEPARTMAN ZA PROJEKTOVANJE I KONSTRUISANJE
 Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
Dobro došli na... Konstruisanje GRANIČNI I KRITIČNI NAPON slajd 2 Kritični naponi Izazivaju kritične promene oblika Delovi ne mogu ispravno da vrše funkciju Izazivaju plastične deformacije Može doći i
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE GODINE 8. RAZRED TOČNI ODGOVORI
 21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
21. ŠKOLSKO/OPĆINSKO/GRADSKO NATJECANJE IZ GEOGRAFIJE 2014. GODINE 8. RAZRED TOČNI ODGOVORI Bodovanje za sve zadatke: - boduju se samo točni odgovori - dodatne upute navedene su za pojedine skupine zadataka
Metode i instrumenti za određivanje visinskih razlika. Zdravka Šimić
 Metode i instrumenti za određivanje visinskih razlika Zdravka Šimić Visinski prikaz terena - konfiguracija dio plana dio karte 2 Visinski prikaz terena Izohipse ili slojnice povezuju točke iste visine.
Metode i instrumenti za određivanje visinskih razlika Zdravka Šimić Visinski prikaz terena - konfiguracija dio plana dio karte 2 Visinski prikaz terena Izohipse ili slojnice povezuju točke iste visine.
VJEŽBE 3 BIPOLARNI TRANZISTORI. Slika 1. Postoje npn i pnp bipolarni tranziostori i njihovi simboli su dati na slici 2 i to npn lijevo i pnp desno.
 JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
JŽ 3 POLAN TANZSTO ipolarni tranzistor se sastoji od dva pn spoja kod kojih je jedna oblast zajednička za oba i naziva se baza, slika 1 Slika 1 ipolarni tranzistor ima 3 izvoda: emitor (), kolektor (K)
1 Promjena baze vektora
 Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Promjena baze vektora Neka su dane dvije različite uredene baze u R n, označimo ih s A = (a, a,, a n i B = (b, b,, b n Svaki vektor v R n ima medusobno različite koordinatne zapise u bazama A i B Zapis
Masa, Centar mase & Moment tromosti
 FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
FAKULTET ELEKTRTEHNIKE, STRARSTVA I BRDGRADNE - SPLIT Katedra za dinamiku i vibracije Mehanika 3 (Dinamika) Laboratorijska vježba Masa, Centar mase & Moment tromosti Ime i rezime rosinac 008. Zadatak:
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Opća bilanca tvari - = akumulacija u dif. vremenu u dif. volumenu promatranog sustava. masa unijeta u dif. vremenu u dif. volumen promatranog sustava
 Opća bilana tvari masa unijeta u dif. vremenu u dif. volumen promatranog sustava masa iznijeta u dif. vremenu iz dif. volumena promatranog sustava - akumulaija u dif. vremenu u dif. volumenu promatranog
Opća bilana tvari masa unijeta u dif. vremenu u dif. volumen promatranog sustava masa iznijeta u dif. vremenu iz dif. volumena promatranog sustava - akumulaija u dif. vremenu u dif. volumenu promatranog
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
DINAMIČKA MEHANIČKA ANALIZA (DMA)
 Karakterizacija materijala DINAMIČKA MEHANIČKA ANALIZA (DMA) Dr.sc.Emi Govorčin Bajsić,izv.prof. Zavod za polimerno inženjerstvo i organsku kemijsku tehnologiju Da li je DMA toplinska analiza ili reologija?
Karakterizacija materijala DINAMIČKA MEHANIČKA ANALIZA (DMA) Dr.sc.Emi Govorčin Bajsić,izv.prof. Zavod za polimerno inženjerstvo i organsku kemijsku tehnologiju Da li je DMA toplinska analiza ili reologija?
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
( , treći kolokvij) 3. Na dite lokalne ekstreme funkcije z = x 4 + y 4 2x 2 + 2y 2 3. (20 bodova)
 A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
A MATEMATIKA (.6.., treći kolokvij. Zadana je funkcija z = e + + sin(. Izračunajte a z (,, b z (,, c z.. Za funkciju z = 3 + na dite a diferencijal dz, b dz u točki T(, za priraste d =. i d =.. c Za koliko
Dijagonalizacija operatora
 Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Dijagonalizacija operatora Problem: Može li se odrediti baza u kojoj zadani operator ima dijagonalnu matricu? Ova problem je povezan sa sljedećim pojmovima: 1 Karakteristični polinom operatora f 2 Vlastite
Strukture podataka i algoritmi 1. kolokvij 16. studenog Zadatak 1
 Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
Strukture podataka i algoritmi 1. kolokvij Na kolokviju je dozvoljeno koristiti samo pribor za pisanje i službeni šalabahter. Predajete samo papire koje ste dobili. Rezultati i uvid u kolokvije: ponedjeljak,
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste
 PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
PREDNAPETI BETON Primjer nadvožnjaka preko autoceste 7. VJEŽBE PLAN ARMATURE PREDNAPETOG Dominik Skokandić, mag.ing.aedif. PLAN ARMATURE PREDNAPETOG 1. Rekapitulacija odabrane armature 2. Određivanje duljina
POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE
 **** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
**** MLADEN SRAGA **** 011. UNIVERZALNA ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE SKUP REALNIH BROJEVA α Autor: MLADEN SRAGA Grafički urednik: BESPLATNA - WEB-VARIJANTA Tisak: M.I.M.-SRAGA
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Heterogene ravnoteže taloženje i otapanje. u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima
 Heterogene ravnoteže taloženje i otapanje u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima Ako je BA teško topljiva sol (npr. AgCl) dodatkom
Heterogene ravnoteže taloženje i otapanje u vodi u prisustvu zajedničkog iona u prisustvu kompleksirajućegreagensa pri različitim ph vrijednostima Ako je BA teško topljiva sol (npr. AgCl) dodatkom
Zavod za tehnologiju, Katedra za alatne strojeve: GLODANJE
 Glodanje je postupak obrade odvajanjem čestica (rezanjem) obradnih površina proizvoljnih oblika. Izvodi se na alatnim strojevima, glodalicama, pri čemu je glavno (rezno) gibanje kružno kontinuirano i pridruženo
Glodanje je postupak obrade odvajanjem čestica (rezanjem) obradnih površina proizvoljnih oblika. Izvodi se na alatnim strojevima, glodalicama, pri čemu je glavno (rezno) gibanje kružno kontinuirano i pridruženo
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Uvod u neparametrijske testove. Usporedba. Neparametrijske inačice t-testa za dva nezavisna uzorka. dr. sc. Goran Kardum
 Uvod u neparametrijske testove dr. sc. Goran Kardum 1 Usporedba NACRT ISTRAŽIVANJA PARAMETRIJSKA PROCEDURA NEPARAMETRIJSKA PROCEDURA Dva nezavisna uzorka T-test Mann-Whitney U-test Dva zavisna uzorka T-test
Uvod u neparametrijske testove dr. sc. Goran Kardum 1 Usporedba NACRT ISTRAŽIVANJA PARAMETRIJSKA PROCEDURA NEPARAMETRIJSKA PROCEDURA Dva nezavisna uzorka T-test Mann-Whitney U-test Dva zavisna uzorka T-test
5. PARCIJALNE DERIVACIJE
 5. PARCIJALNE DERIVACIJE 5.1. Izračunajte parcijalne derivacije sljedećih funkcija: (a) f (x y) = x 2 + y (b) f (x y) = xy + xy 2 (c) f (x y) = x 2 y + y 3 x x + y 2 (d) f (x y) = x cos x cos y (e) f (x
5. PARCIJALNE DERIVACIJE 5.1. Izračunajte parcijalne derivacije sljedećih funkcija: (a) f (x y) = x 2 + y (b) f (x y) = xy + xy 2 (c) f (x y) = x 2 y + y 3 x x + y 2 (d) f (x y) = x cos x cos y (e) f (x
Značenje indeksa. Konvencija o predznaku napona
 * Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
* Opšte stanje napona Tenzor napona Značenje indeksa Normalni napon: indeksi pokazuju površinu na koju djeluje. Tangencijalni napon: prvi indeks pokazuje površinu na koju napon djeluje, a drugi pravac
Ĉetverokut - DOMAĆA ZADAĆA. Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke.
 Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
Ĉetverokut - DOMAĆA ZADAĆA Nakon odgledanih videa trebali biste biti u stanju samostalno riješiti sljedeće zadatke. 1. Duljine dijagonala paralelograma jednake su 6,4 cm i 11 cm, a duljina jedne njegove
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
1 Afina geometrija. 1.1 Afini prostor. Definicija 1.1. Pod afinim prostorom nad poljem K podrazumevamo. A - skup taqaka
 1 Afina geometrija 11 Afini prostor Definicija 11 Pod afinim prostorom nad poljem K podrazumevamo svaku uređenu trojku (A, V, +): A - skup taqaka V - vektorski prostor nad poljem K + : A V A - preslikavanje
1 Afina geometrija 11 Afini prostor Definicija 11 Pod afinim prostorom nad poljem K podrazumevamo svaku uređenu trojku (A, V, +): A - skup taqaka V - vektorski prostor nad poljem K + : A V A - preslikavanje
Dimenzioniranje nosaa. 1. Uvjeti vrstoe
 Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Dimenzioniranje nosaa 1. Uvjeti vrstoe 1 Otpornost materijala prouava probleme 1. vrstoe,. krutosti i 3. elastine stabilnosti konstrukcija i dijelova konstrukcija od vrstog deformabilnog materijala. Moraju
Uvod u neparametarske testove
 Str. 148 Uvod u neparametarske testove Predavač: Dr Mirko Savić savicmirko@ef.uns.ac.rs www.ef.uns.ac.rs Hi-kvadrat testovi c Str. 149 Koristi se za upoređivanje dve serije frekvencija. Vrste c testa:
Str. 148 Uvod u neparametarske testove Predavač: Dr Mirko Savić savicmirko@ef.uns.ac.rs www.ef.uns.ac.rs Hi-kvadrat testovi c Str. 149 Koristi se za upoređivanje dve serije frekvencija. Vrste c testa:
Osnovni elementi mehanike tla
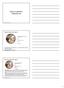 Osnovni elementi mehanike tla Tekstura sedimentnih stijena Cement naknadno izlučen u dijelu pornih prostora Pora Pora ispunjena vodom Matriks Zrno (klast) Shematski prikaz načina pakiranja zrna i načina
Osnovni elementi mehanike tla Tekstura sedimentnih stijena Cement naknadno izlučen u dijelu pornih prostora Pora Pora ispunjena vodom Matriks Zrno (klast) Shematski prikaz načina pakiranja zrna i načina
Gauss, Stokes, Maxwell. Vektorski identiteti ( ),
 Vektorski identiteti ( ), Gauss, Stokes, Maxwell Saša Ilijić 21. listopada 2009. Saša Ilijić, predavanja FER/F2: Vektorski identiteti, nabla, Gauss, Stokes, Maxwell... (21. listopada 2009.) Skalarni i
Vektorski identiteti ( ), Gauss, Stokes, Maxwell Saša Ilijić 21. listopada 2009. Saša Ilijić, predavanja FER/F2: Vektorski identiteti, nabla, Gauss, Stokes, Maxwell... (21. listopada 2009.) Skalarni i
ZBIRKA POTPUNO RIJEŠENIH ZADATAKA
 **** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
**** IVANA SRAGA **** 1992.-2011. ZBIRKA POTPUNO RIJEŠENIH ZADATAKA PRIRUČNIK ZA SAMOSTALNO UČENJE POTPUNO RIJEŠENI ZADACI PO ŽUTOJ ZBIRCI INTERNA SKRIPTA CENTRA ZA PODUKU α M.I.M.-Sraga - 1992.-2011.
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
PRORAČUN GLAVNOG KROVNOG NOSAČA
 PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
PRORAČUN GLAVNOG KROVNOG NOSAČA STATIČKI SUSTAV, GEOMETRIJSKE KARAKTERISTIKE I MATERIJAL Statički sustav glavnog krovnog nosača je slobodno oslonjena greda raspona l11,0 m. 45 0 65 ZAŠTITNI SLOJ BETONA
TABLICE I DIJAGRAMI iz predmeta BETONSKE KONSTRUKCIJE II
 TABLICE I DIJAGRAMI iz predmeta BETONSKE KONSTRUKCIJE II TABLICA 1: PARCIJALNI KOEFICIJENTI SIGURNOSTI ZA DJELOVANJA Parcijalni koeficijenti sigurnosti γf Vrsta djelovanja Djelovanje Stalno Promjenjivo
TABLICE I DIJAGRAMI iz predmeta BETONSKE KONSTRUKCIJE II TABLICA 1: PARCIJALNI KOEFICIJENTI SIGURNOSTI ZA DJELOVANJA Parcijalni koeficijenti sigurnosti γf Vrsta djelovanja Djelovanje Stalno Promjenjivo
SISTEMI NELINEARNIH JEDNAČINA
 SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
SISTEMI NELINEARNIH JEDNAČINA April, 2013 Razni zapisi sistema Skalarni oblik: Vektorski oblik: F = f 1 f n f 1 (x 1,, x n ) = 0 f n (x 1,, x n ) = 0, x = (1) F(x) = 0, (2) x 1 0, 0 = x n 0 Definicije
7 Algebarske jednadžbe
 7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
7 Algebarske jednadžbe 7.1 Nultočke polinoma Skup svih polinoma nad skupom kompleksnih brojeva označavamo sa C[x]. Definicija. Nultočka polinoma f C[x] je svaki kompleksni broj α takav da je f(α) = 0.
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
BETONSKE KONSTRUKCIJE 2
 BETONSE ONSTRUCIJE 2 vježbe, 31.10.2017. 31.10.2017. DATUM SATI TEMATSA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponljanje poznatih postupaka dimenzioniranja
BETONSE ONSTRUCIJE 2 vježbe, 31.10.2017. 31.10.2017. DATUM SATI TEMATSA CJELINA 10.- 11.10.2017. 2 17.-18.10.2017. 2 24.-25.10.2017. 2 31.10.- 1.11.2017. uvod ponljanje poznatih postupaka dimenzioniranja
Pismeni ispit iz matematike GRUPA A 1. Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj, zatim naći 4 z.
 Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
Pismeni ispit iz matematike 06 007 Napisati u trigonometrijskom i eksponencijalnom obliku kompleksni broj z = + i, zatim naći z Ispitati funkciju i nacrtati grafik : = ( ) y e + 6 Izračunati integral:
