STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
|
|
|
- Ευμελια Δαμασκηνός
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Dalton (803) Tomson (904) Raderford (9) Bor (93) Šredinger (96)
2 OTKRIĆA OSNOVNIH SASTOJAKA ATOMA Do početka XX veka važila je Daltonova atomska teorija o nedeljivosti atoma. Karjem XIX i početkom XX veka došlo se do otkrića subatomskih čestica. ELEKTRON Tomson odredio specifično naelektrisanje elektrona e =,76 0 C kg m Miliken odredio naelektrisanje elektrona e =, C PROTON m e = 9, kg Masa elektrona Bor (93) Dalton (803) Šredinger (96) Tomson je otkrio da je vodonikov jon najmanja čestica sa pozitivnim naelektrisanjem i da je verovatno prisutna u svim vrstama atoma. Ova čestica dobila je naziv proton (od grčke reči protos prvi). Tomson (904) Raderford (9)
3 OTKRIĆA OSNOVNIH SASTOJAKA ATOMA Nakon otkrića elektrona i protona: Tomsonov model atoma Pozitivno naelektrisanje je ravnomerno raspoređeneo po celoj zapremini atoma i neutralisano je elektronima utopljenim u moru pozitivnog elektriciteta. Dalton (803) Tomson (904) Raderford (9) Bor (93) Šredinger (96)
4 OTKRIĆA OSNOVNIH SASTOJAKA ATOMA Raderfordov ogled: bombardovanje listića metala α česticama ( 4 He + ) U slučaju ravnomerno raspoređenog pozitivnog i negativnog naelektrisanja, α čestice bi imale skoro pravolinijsku putanju uz malo skretanje pri prolazu korz listić metala Dalton (803) Eksperiment je pkazao da pored α čestica koje ne menjaju pravac ili malo skreću, postoji i mali broj onih koje skreću pod uglom > 90 o. Bor (93) Tomson (904) Raderford (9) Rutherford.exe Pozitivno naelektrisanje je skoncentrisano na malom prostoru atoma jezgro atoma. Elektroni kruže oko jezgra. Šredinger (96) Raderfordov model atoma Planetarni model atoma
5 OTKRIĆA OSNOVNIH SASTOJAKA ATOMA NEUTRON Čedvik je 93. otkrio čestice koje su nenaelektrisane i imaju masu približno jednaku masi protona. Dobile su naziv neutron. Elektroni Jezgro atoma (protoni i neutroni) ~0 4 m ~0 0 m Atom je složena čestica i sastoji se iz elektrona, protona i neutrona. Čestica Simbol Masa, kg Naelektrisanje, C Proton p, , nukleoni Neutron n, Elektron e 9,09 0 3,60 0 9
6 IZOTOPI Z N A Atomski broj (redni broj) broj protona u jezgru Broj neutrona u jezgru Maseni broj broj protona i neutrona u jezgru A = Z + N Nuklearni simbol elementa X A Z X Hemijski element se sastoji od atoma istog atomskog broja, Z. Z određuje položaj elementa u Periodnom sistemu elemenata i predstavlja broj protona, odnosno elektrona.
7 IZOTOPI Nuklearni simbol izotopa vodonika protijuma, deuterijuma i tricijuma Različiti maseni broj = IZOTOPI vodonika H H 3 H Jednaki atomski broj = vodonik = H
8 IZOTOPI IZOTOPI atomi koji sadrže isti broj protona, a različit broj neutrona. razlikuju se po masi, ali imaju ista hemijska svojstva. IZOTOPI HELIJUMA 3 4 He He Broj protona = Z = Broj neutrona = A Z = Broj protona = Z = Broj neutrona = A Z =
9 IZOTOPI Još neki primeri izotopa Element Izotopi vodonika Izotopi kiseonika Izotopi urana Simbol Atomski broj (Z) Maseni broj (A) Zastupljenost (%) H 99,985 D 0,05 T 3 nepostojan (radioaktivan) 6 O ,759 7 O 8 7 0,037 8 O 8 8 0,04 34 U , U , U ,745
10 IZOTOPI 9 C 0 6 C 6 C 6 C 3 6 C 4 6 C 5 6 C C Jedini stabilni izotopi Nestabilni izotopi se vremenom spontano raspadaju RADIOAKTIVNOST Dolazi do transmutacije elemenata (pretvaranja jedne atomske vrste u drugu) i gubitka mase koja se pretvara u energiju Praćeno oslobađanjem: α čestica (He + ), β čestica (elektroni), γ zraka (elektromagnetno zračenje malih λ ).
11 IZOTOPI Stabilnost jezgra zavisi od odnosa broja protona i neutrona. za lakša jezgra (do Z = 0) optimalno je Z = N za teža jezgra optimalno je Z < N (N =,5Z) Pojas stabilnosti jezgara atoma
12 SPEKTAR ELEKTROMAGNETNOG ZRAČENJA Elektromagnetno zračenje je talasne prirode c λ ν = c λ = ν Porast energije Vidljiva oblast Porast energije Porast talasne dužine
13 OSNOVNE POSTAVKE KVANTNE TEORIJE Spektar zračenja crnog tela Maks Plank kvantna priroda zračenja Intenzitet emitovanog zračenja Ultarljubičasta katastrofa Talasna dužina, nm h = 6, Js Energija koju zrači atom koji osciluje je diskontinualna. Emituje se u kvantima energije. Energija kvanta zavisi od frekvencije E = h ν Energija koja se emituje može biti samo celobrojni umnožak kvanta E = n h ν n =,, 3,... Plankova konstanta
14 OSNOVNE POSTAVKE KVANTNE TEORIJE Elektron Upadna svetlost Evakuisana posuda Pločica od fotoosetljiviog metala Albert Ajnštajn fotoelektrični efekat Za ν < ν o nema emisije elektrona Broj emitovanih elektrona intenzitetu svetlosti Kinetička energija elektrona ν Ajnštajnova pretpostavka: svetlost se emituje u česticama energije (fotoni) E = h ν Anoda Galvanometar 700 nm 550 nm v max =, m/s 440 nm v max = 6, 0 5 m/s Nema emitovanih elektrona Metal
15 OSNOVNE POSTAVKE KVANTNE TEORIJE Albert Ajnštajn Ajnšatajnova pretpostavka: fotoelektrični efekat svetlost se emituje u česticama energije (fotoni) E = h ν mv E h ν = E i + = E i + E i izlazni rad elektrona k E k kinetička energija elektrona Energija potrebna da se izbaci elektron (E k = 0) E = E i = h ν o E k = hν E i Sa porastom ν (opada λ) raste i kinetička energija e. ν < ν o 700 nm 550 nm v max =, m/s 440 nm v max = 6, 0 5 m/s Nema emitovanih elektrona Metal
16 ATOMSKI SPEKTRI KONTINUALNI SPEKTRI Porast energije Vidljiva oblast Intenzitet emitovanog zracenja Porast energije Porast talasne dužine Talasna dužina, nm Talasna dužina Supstance u gasovitom stanju daju LINIJSKE SPEKTRE Talasna dužina
17 ATOMSKI SPEKTRI Uski prorez Uzani snop svetlosti Cev sa pobuđenim H gasom Sočivo Prizma Ekran
18 SPEKTAR ATOMA VODONIKA u vidljivoj oblasti spektra Zavisnost talasnih dužina linija u atomskom spektru vodonika opisuje: Ridbergova jednačina = R λ n R Ridbergova konstanta n ceo nroj n > Poreklo spektralnih linija u atomskom spektru vodonika razrešio je Nils Bor postavljajući kvantno mehanički model atoma.
19 BOROV MODEL ATOMA VODONIKA PRVI BOROV POSTULAT Elektron se oko jezgra kreće po kružnoj putanji orbiti, pri čemu ne emituje i ne apsorbuje energiju. Orbita najbliža jezgru stacionarno energetsko stanje elektrona. Prvi kvantni uslov (mv)(rπ) = nh Impuls elektrona Dužina orbite Celobrojni umnožak Plankove konstante h ħ = Borova jedinica mvr = nħ π
20 BOROV MODEL ATOMA VODONIKA Izjednačavanjem centripetalne i Kulonove sile elektrostatičkog privlačenja uz korišćenje mvr = nħ Bor je dobio: Za n = ħ r n = n me k r ħ = 5, 9 pm me k = Poluprečnik bilo koje orbite proton r 4 = 6r r 3 = 9r r = 4r r r n = n r kvantni broj glavni kvantni broj
21 BOROV MODEL ATOMA VODONIKA Energija elektrona je jednaka zbiru kinetičke (kruženje elektrona oko jezgra) i potencijalne energije (položaj elektrona u odnosu na jezgro). Bor je dobio da je: E n = Rhc n Energija ektrona na bilo kojoj orbiti R konstanta proporcionalnosti R = R =, m Za n = E =, J Energija potrebna da se atom jonizuje (energija potrebna da se ukloni e sa prve orbite) ENERGIJA JONIZACIJE (E i ) Za mol H E i (H) = E =, J 6,0 0 3 mol = 3 kj mol
22 BOROV MODEL ATOMA VODONIKA Energija E 6 = E /36 E 5 = E /0 E 4 = E /6 E 3 = E /9 =,4 0 9 J E = E /4 = 5, J Kvantni broj E n = E n Za n E 0 E =,8 0 8 J Osnovno stanje e
23 BOROV MODEL ATOMA VODONIKA DRUGI BOROV POSTULAT Elektron može da apsorbuje ili emituje energiju samo ako je ispunjen drugi kvantni uslov: ΔE = hν E 3 E = ΔE = hν E 3 E = = 46 ( 38) = = 8 kj mol apsorpcija emisija E 3 E = ΔE = hν Emituje se zračenje karakteristično za dati prelaz
24 BOROV MODEL ATOMA VODONIKA DRUGI BOROV POSTULAT Elektron može da apsorbuje ili emituje energiju samo ako je ispunjen drugi kvantni uslov: Apsorbovna energija /mol Emitovana energija /mol Osnovno stanje Pobuđeno stanje Osnovno stanje
25 BOROV MODEL ATOMA VODONIKA Bor je izveo jednačinu: ΔE I = R n k n p ΔE = (hc)/λ λ = R n k n p Ukoliko se posmatraju nivoi n k = i n p > dobija se Ridbergova jednačina λ = R n n > R = R =, m
26 BOROV MODEL ATOMA VODONIKA λ = R n k n p Pašen Breket Pfund 8 kj mol 46 kj mol Lajmanova serija n k = i n p > Balmerova n k = i n p > λ λ R = n p R = n p Balmer 38 kj mol Pašenova serija n k = 3i n p >3 λ R 3 = n p Lajman 3 kj mol Breketova serija n k = 4i n p >4 λ = R 4 n p Pfundova serija n k = 5i n p >6 λ R 5 = n p
27 KVANTNI BROJEVI Prvi ili glavni kvantni broj, n Određuje glavni energetski nivo i udaljenost od jezgra. E Rhc = r n = n r n Vrednosti glavnog kvantnog broja n =,, 3,... Elektroni sa istom vrednošću n su u istoj elektronskoj ljusci. n Elektronska ljuska K L M N O P Q Maks. broj elektrona
28 Drugi ili orbitalni kvantni broj, l Nedostaci Borovog modela atoma: elektroni istog glavnog energetskog nivoa imaju isti sadržaj energije, elektronske orbite su kružnog oblika. Zomerfeld je uveo drugi kvantni broj kao objašnjenje cepanja spektralnih linija. Drugi ili azimutski kvantni broj, k,sa vrednostima od do n. Za n = 4, k =,, 3, 4 k = n kružna putanja k < n eliptična putanja Definiše oblik putanje elektrona i broj energetskih podnivoa.
29 Drugi ili orbitalni kvantni broj, l Definiše oblik putanje elektrona i broj energetskih podnivoa. Oznaka k je zamenjena oznakom l, a naziv je promenjen u orbitalni kvantni broj. Vrednosti orbitalnog kvantnog broja: l = 0,,,..., (n ) za n =, l = 0 za n =, l = 0 ili za n = 3, l = 0, ili za n = 4, l = 0,, ili 3 Svaki nivo, određen glavnim kvantnim brojem n, ima n podnivoa.
30 Drugi ili orbitalni kvantni broj, l Različiti oblici putanja elektrona (različiti orbitalni kvantni brojevi) dobili su posebne nazive. Vrednost, l Oznaka putanje 0 s p d 3 f s sharp (oštra) p principal (glavna) d diffuse (difuzna) f fundamental (osnovna) Oznaka podnivoa za prva 4 glavna kvantna broja n 3 4 l podnivo s s p 3s 3p 3d 4s 4p 4d 4f
31 Treći ili magnetni kvantni broj, m l Uveden radi objašnjenja Zemanovog efekta (razdvajanje spektralnih linija pod uticajem spoljašnjeg magnetnog polja). Degenerisani nivoi u njima se nalaze elektroni sa istim sadržajem energije (isti n i l). U magnetnom polju degenerisani nivoi se razdvajaju na pod podnivoe. Magnetni kvantni broj određuje pod podnivoe i pokazuje usmerenost orbite u prostoru. Vrednosti magnetnog kvantnog broja: m l = l, (l ),...,, 0,,..., (l ), l l = Svaki podnivo (određen kvantnim brojem l) ima l + pod podniva.
32 Četvrti ili spinski kvantni broj, m s Objašnjenje pojave dubleta spektralnih linija. Elektron Paralelan spoljašnjem magnetnom polju s =/ ħ Orbitni magnetni momenat Spinski magnetni momenat (spin elektrona) Antiparalelan spoljašnjem magnetnom polju s = / ħ Vrednosti spinskog kvantnog broja: m s = /, /
33 PAULIJEV PRINCIP ISKLJUČENJA Uatomu ne mogu postojati dva elektrona sa jednakim kvantnim brojevima. Prvi energetski nivo n = l = 0 Drugi energetski nivo n = l = m l = 0 m l = l = 0 m l = m l = 0 m l = 0 m s = / m s = + / m s = / m s = + / m s = / m s = + / m s = / m s = + / m s = / m s = + / e 8 e Maksimalan broj elektrona na podnivoima: s, p 6, d 0, f 4.
34 PAULIJEV PRINCIP ISKLJUČENJA Nivo n Broj e Maksimalan broj elektrona na podnivou s p d f Maksimalan broj elektrona na podnivoima: s, p 6, d 0, f 4. Maksimalan broj elektrona na energetskom nivou: n. Nivoi se popunjavaju elektronima po složenijim pravilima. n Ljuska K L M N O P Q Max. broj e
Doc. dr Milena Đukanović
 Doc. dr Milena Đukanović milenadj@ac.me ATOMSKA STRUKTURA MATERIJE: 500 g.p.n.e. Empedokle svijet se sastoji od četiri osnovna elementa: zemlja, vazduh, vatra i voda. 400 g.p.n.e. Demokrit svijet je sagrađen
Doc. dr Milena Đukanović milenadj@ac.me ATOMSKA STRUKTURA MATERIJE: 500 g.p.n.e. Empedokle svijet se sastoji od četiri osnovna elementa: zemlja, vazduh, vatra i voda. 400 g.p.n.e. Demokrit svijet je sagrađen
SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA
 SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA Atomi su veoma sitne čestice Još niko nije uspeo da vidi atom Još nije konstruisan takav mikroskop koji će omogućiti da se vidi atom Najbolji
SASTAV MATERIJE STRUKTURA ATOMA I PERODNI SISTEM ELEMENATA Atomi su veoma sitne čestice Još niko nije uspeo da vidi atom Još nije konstruisan takav mikroskop koji će omogućiti da se vidi atom Najbolji
STRUKTURA ATOMA. Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926)
 Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
Dalton (1803) Tomson (1904) Raderford (1911) Bor (1913) Šredinger (1926) TALASNO MEHANIČKI MODEL ATOMA Hipoteza de Brolja Elektroni i fotoni imaju dvojnu prirodu: talasnu i korpuskularnu. E = hν E = mc
Atomska fizika Sadržaj
 Kvantna svojstva elektromagnetnog zračenja. Ultravioletna katastrofa 79 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 81 Fotoelektrični efekat 83 Komptonovo rasejanje 86 Atomska fizika Sadržaj Atomski
Kvantna svojstva elektromagnetnog zračenja. Ultravioletna katastrofa 79 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 81 Fotoelektrični efekat 83 Komptonovo rasejanje 86 Atomska fizika Sadržaj Atomski
Atomska fizika Sadržaj
 Atomska fizika Sadržaj Kvantna svojstva elektromagnetnog zračenja. 86 Ultravioletna katastrofa 87 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 88 Fotoelektrični efekat 90 Komptonovo rasejanje 93 Atomski
Atomska fizika Sadržaj Kvantna svojstva elektromagnetnog zračenja. 86 Ultravioletna katastrofa 87 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 88 Fotoelektrični efekat 90 Komptonovo rasejanje 93 Atomski
Atomska fizika Sadržaj
 Kvantna svojstva elektromagnetnog zračenja. Ultravioletna katastrofa 363 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 365 Fotoelektrični efekat 367 Komptonovo rasejanje 370 Talasna priroda materije.
Kvantna svojstva elektromagnetnog zračenja. Ultravioletna katastrofa 363 Plankov zakon zračenja. Bolcmanov i Vinov zakon. 365 Fotoelektrični efekat 367 Komptonovo rasejanje 370 Talasna priroda materije.
 Kvantna optika Toplotno zračenje Apsorpciona sposobnost tela je sposobnost apsorbovanja energije zračenja iz intervala l, l+ l na površini tela ds za vreme dt. Apsorpciona moć tela je sposobnost apsorbovanja
Kvantna optika Toplotno zračenje Apsorpciona sposobnost tela je sposobnost apsorbovanja energije zračenja iz intervala l, l+ l na površini tela ds za vreme dt. Apsorpciona moć tela je sposobnost apsorbovanja
DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA!
 DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA! Polazna znanja zakoni o: Održanju mase Stalnom (utvrdjenom) sastavu Umnoženim odnosima Zakon o održanju mase masa supstance ne menja
DALTONOV ATOMSKI MODEL Nastao je čitavih 2300 godina posle DEMOKRITA! Polazna znanja zakoni o: Održanju mase Stalnom (utvrdjenom) sastavu Umnoženim odnosima Zakon o održanju mase masa supstance ne menja
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa u jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma
 Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Elektronska struktura atoma Raderfordov atomski model jezgro u sredini pozitivno naelektrisano skoro sva masa jezgru veoma malo Elektroni kruže oko jezgra elektrostatičke interakcije ih drže da ne napuste
Eliminacijski zadatak iz Matematike 1 za kemičare
 Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Za mnoge reakcije vrijedi Arrheniusova jednadžba, koja opisuje vezu koeficijenta brzine reakcije i temperature: K = Ae Ea/(RT ). - T termodinamička temperatura (u K), - R = 8, 3145 J K 1 mol 1 opća plinska
Linijski spektri. Užarena čvrsta tijela, tekućine i gasovi pri visokom pritisku i temperaturi emitiraju svjetlost s kontinuiranim valnim duljinama
 Bohrov model atoma Linijski spektri Daćemo malo detaljniji opis linijskih spektara jer ih je Borov model atoma uspio objasniti (za atom hidrogena) Užarena čvrsta tijela, tekućine i gasovi pri visokom pritisku
Bohrov model atoma Linijski spektri Daćemo malo detaljniji opis linijskih spektara jer ih je Borov model atoma uspio objasniti (za atom hidrogena) Užarena čvrsta tijela, tekućine i gasovi pri visokom pritisku
Fizika. Dualna priroda elektromagnetnog zračenja. Princip rada lasera. za studente Geodezije i geomatike. Doc.dr Ivana Stojković
 Fizika za studente Geodezije i geomatike Dualna priroda elektromagnetnog zračenja Princip rada lasera Docdr Ivana Stojković Istorijski razvoj shvatanja prirode svetlosti Korpuskularna teorija svetlosti
Fizika za studente Geodezije i geomatike Dualna priroda elektromagnetnog zračenja Princip rada lasera Docdr Ivana Stojković Istorijski razvoj shvatanja prirode svetlosti Korpuskularna teorija svetlosti
SAZNANJA O MATERIJI OD STAROG DO XIX VEKA
 SAZNANJA O MATERIJI OD STAROG DO XIX VEKA U najstarija vremena, čovek je svoja poimanja sveta iskazivao mitovima. MIT (mitos) reč, priča, kazivanje (grč.); MITOLOGIJA od, priča i (logos), reč, učenje.
SAZNANJA O MATERIJI OD STAROG DO XIX VEKA U najstarija vremena, čovek je svoja poimanja sveta iskazivao mitovima. MIT (mitos) reč, priča, kazivanje (grč.); MITOLOGIJA od, priča i (logos), reč, učenje.
UVOD U KVANTNU TEORIJU
 UVOD U KVANTNU TEORIJU UVOD U KVANTNU TEORIJU 1.) FOTOELEKTRIČKI EFEKT 2.) LINIJSKI SPEKTRI ATOMA 3.) BOHROV MODEL ATOMA 4.) CRNO TIJELO 5.) ČESTICE I VALOVI Elektromagnetsko zračenje UVOD U KVANTNU TEORIJU
UVOD U KVANTNU TEORIJU UVOD U KVANTNU TEORIJU 1.) FOTOELEKTRIČKI EFEKT 2.) LINIJSKI SPEKTRI ATOMA 3.) BOHROV MODEL ATOMA 4.) CRNO TIJELO 5.) ČESTICE I VALOVI Elektromagnetsko zračenje UVOD U KVANTNU TEORIJU
Periodni sistem elemenata
 Periodni sistem elemenata Periodni sistem elemenata je hemijska tablica u kojoj su po određenoj zakonitosti sistematizovani (poredani) hem.elem. Mendeljejev je je definisao Peridni zakon koji glasi: Hemujske
Periodni sistem elemenata Periodni sistem elemenata je hemijska tablica u kojoj su po određenoj zakonitosti sistematizovani (poredani) hem.elem. Mendeljejev je je definisao Peridni zakon koji glasi: Hemujske
I.13. Koliki je napon između neke tačke A čiji je potencijal 5 V i referentne tačke u odnosu na koju se taj potencijal računa?
 TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
TET I.1. Šta je Kulonova sila? elektrostatička sila magnetna sila c) gravitaciona sila I.. Šta je elektrostatička sila? sila kojom međusobno eluju naelektrisanja u mirovanju sila kojom eluju naelektrisanja
Osnovni primer. (Z, +,,, 0, 1) je komutativan prsten sa jedinicom: množenje je distributivno prema sabiranju
 RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
RAČUN OSTATAKA 1 1 Prsten celih brojeva Z := N + {} N + = {, 3, 2, 1,, 1, 2, 3,...} Osnovni primer. (Z, +,,,, 1) je komutativan prsten sa jedinicom: sabiranje (S1) asocijativnost x + (y + z) = (x + y)
3.1 Granična vrednost funkcije u tački
 3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
3 Granična vrednost i neprekidnost funkcija 2 3 Granična vrednost i neprekidnost funkcija 3. Granična vrednost funkcije u tački Neka je funkcija f(x) definisana u tačkama x za koje je 0 < x x 0 < r, ili
Atomi i jezgre 1.1. Atomi i kvanti 1.2. Atomska jezgra λ = h p E = hf, E niži
 tomi i jezgre.. tomi i kvanti.. tomska jezgra Kvant je najmanji mogući iznos neke veličine. Foton, čestica svjetlosti, je kvant energije: gdje je f frekvencija fotona, a h Planckova konstanta. E = hf,
tomi i jezgre.. tomi i kvanti.. tomska jezgra Kvant je najmanji mogući iznos neke veličine. Foton, čestica svjetlosti, je kvant energije: gdje je f frekvencija fotona, a h Planckova konstanta. E = hf,
HEMIJSKA VEZA TEORIJA VALENTNE VEZE
 TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
TEORIJA VALENTNE VEZE Kovalentna veza nastaje preklapanjem atomskih orbitala valentnih elektrona, pri čemu je region preklapanja između dva jezgra okupiran parom elektrona. - Nastalu kovalentnu vezu opisuje
kvantovanim elektronskim orbitama. set matematičkih i konceptualnih alata je stvoren do godine
 Dr Dejan Gvozdić Fizika : Elementi atomske i kvantne fizike 04 Dr Dejan Gvozdić.900. godina Rad Ma Planck-a na problemu zračenja crnog tela uvođenje kvanta energije.. 93. godina Niels Bohr predlog modela
Dr Dejan Gvozdić Fizika : Elementi atomske i kvantne fizike 04 Dr Dejan Gvozdić.900. godina Rad Ma Planck-a na problemu zračenja crnog tela uvođenje kvanta energije.. 93. godina Niels Bohr predlog modela
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu
 Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
Zadaci sa prethodnih prijemnih ispita iz matematike na Beogradskom univerzitetu Trigonometrijske jednačine i nejednačine. Zadaci koji se rade bez upotrebe trigonometrijskih formula. 00. FF cos x sin x
1. Određivanje odnosa q/m mikročestica
 FIZIČKA HEMIJA II Dr Gordana Ćirić-Marjanović, vanredni profesor 1. Određivanje odnosa q/m mikročestica Primena električnog i magnetnog polja predstavlja osnovni način za podešavanje kretanja naelektrisanih
FIZIČKA HEMIJA II Dr Gordana Ćirić-Marjanović, vanredni profesor 1. Određivanje odnosa q/m mikročestica Primena električnog i magnetnog polja predstavlja osnovni način za podešavanje kretanja naelektrisanih
I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI
 dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
dr Ljiljana Vojinović-Ješić I HEMIJSKI ZAKONI I STRUKTURA SUPSTANCI ZAKON STALNIH MASENIH ODNOSA (I stehiometrijski zakon, Prust, 1799) Maseni odnos elemenata u datom jedinjenju je stalan, bez obzira na
Rad, snaga, energija. Tehnička fizika 1 03/11/2017 Tehnološki fakultet
 Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Rad, snaga, energija Tehnička fizika 1 03/11/2017 Tehnološki fakultet Rad i energija Da bi rad bio izvršen neophodno je postojanje sile. Sila vrši rad: Pri pomjeranju tijela sa jednog mjesta na drugo Pri
Spektar X-zraka. Atomska fizika
 Spektar X-zraka Emitirana X- zraka Katoda Anoda Upadni elektron 1895. godine W. Röntgen opazio je nevidljivo (X-zrake) zračenje koje nastaje pri izboju u cijevi s razrijeđenim plinom. Rendgensko zračenje
Spektar X-zraka Emitirana X- zraka Katoda Anoda Upadni elektron 1895. godine W. Röntgen opazio je nevidljivo (X-zrake) zračenje koje nastaje pri izboju u cijevi s razrijeđenim plinom. Rendgensko zračenje
41. Jednačine koje se svode na kvadratne
 . Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
. Jednačine koje se svode na kvadrane Simerične recipročne) jednačine Jednačine oblika a n b n c n... c b a nazivamo simerične jednačine, zbog simeričnosi koeficijenaa koeficijeni uz jednaki). k i n k
TALASNO-MEHANI MEHANIČKI MODEL ATOMA
 TALASNO-MEHANI MEHANIČKI MODEL ATOMA TALASNO-MEHANI MEHANIČKI MODEL ATOMA Kompton (19): svetlost ima i talasnu i korpuskularnu prirodu. Luj De Brolj (193): elektron ima i korpuskularnu i talasnu prirodu.
TALASNO-MEHANI MEHANIČKI MODEL ATOMA TALASNO-MEHANI MEHANIČKI MODEL ATOMA Kompton (19): svetlost ima i talasnu i korpuskularnu prirodu. Luj De Brolj (193): elektron ima i korpuskularnu i talasnu prirodu.
Fizika atomskog jezgra Sadržaj
 Osnovne karakteristike atomskog jezgra 30 Defekt mase jezgra i energija veze 303 Stabilnost atomskog jezgra 305 Radioaktivni raspad 308 akon radioaktivnog raspada 309 Vrste radioaktivnog raspada 30 α-radioaktivni
Osnovne karakteristike atomskog jezgra 30 Defekt mase jezgra i energija veze 303 Stabilnost atomskog jezgra 305 Radioaktivni raspad 308 akon radioaktivnog raspada 309 Vrste radioaktivnog raspada 30 α-radioaktivni
Atomska jezgra. Atomska jezgra. Materija. Kristal. Atom. Elektron. Jezgra. Nukleon. Kvark. Stanica
 Atomska jezgra Materija Kristal Atom Elektron Jezgra Nukleon Stanica Kvark Razvoj nuklearne fizike 1896. rođenje nuklearne fizike Becquerel otkrio radioaktivnost 1899. Rutherford pokazao da postoje različite
Atomska jezgra Materija Kristal Atom Elektron Jezgra Nukleon Stanica Kvark Razvoj nuklearne fizike 1896. rođenje nuklearne fizike Becquerel otkrio radioaktivnost 1899. Rutherford pokazao da postoje različite
2.1 UVOD Tomsonov model Radefordov model atoma... 5
 1 S A D R Ž A J. MODELI ATOMA.1 UVOD.... Tomsonov model....3 Radefordov model atoma... 5.3.1 Eksperimenti rasijanja alfa čestica... 5.3. Radefordov planetarni model atoma... 8.4 BOROV MODEL ATOMA.4.1 Linijski
1 S A D R Ž A J. MODELI ATOMA.1 UVOD.... Tomsonov model....3 Radefordov model atoma... 5.3.1 Eksperimenti rasijanja alfa čestica... 5.3. Radefordov planetarni model atoma... 8.4 BOROV MODEL ATOMA.4.1 Linijski
Osnovne karakteristike atomskog jezgra
 Osnovne karakteristike atomskog jezgra Otkriće atomskog jezgra (Raderford, 1911., rasejanje α-čestica) - skoro celokupna masa atoma je skoncentrisana u prostoru dimenzija 10 15 m. Jezgro sadrži protone
Osnovne karakteristike atomskog jezgra Otkriće atomskog jezgra (Raderford, 1911., rasejanje α-čestica) - skoro celokupna masa atoma je skoncentrisana u prostoru dimenzija 10 15 m. Jezgro sadrži protone
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET SIGNALI I SISTEMI. Zbirka zadataka
 UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
UNIVERZITET U NIŠU ELEKTRONSKI FAKULTET Goran Stančić SIGNALI I SISTEMI Zbirka zadataka NIŠ, 014. Sadržaj 1 Konvolucija Literatura 11 Indeks pojmova 11 3 4 Sadržaj 1 Konvolucija Zadatak 1. Odrediti konvoluciju
SPEKTROSKOPIJA SPEKTROSKOPIJA
 Spektroskopija je proučavanje interakcija elektromagnetnog zraka (EMZ) sa materijom. Elektromagnetno zračenje Proces koji se odigrava Talasna dužina (m) Energija (J) Frekvencija (Hz) γ-zračenje Nuklearni
Spektroskopija je proučavanje interakcija elektromagnetnog zraka (EMZ) sa materijom. Elektromagnetno zračenje Proces koji se odigrava Talasna dužina (m) Energija (J) Frekvencija (Hz) γ-zračenje Nuklearni
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović
 DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
DISKRETNA MATEMATIKA - PREDAVANJE 7 - Jovanka Pantović Novi Sad April 17, 2018 1 / 22 Teorija grafova April 17, 2018 2 / 22 Definicija Graf je ure dena trojka G = (V, G, ψ), gde je (i) V konačan skup čvorova,
18. listopada listopada / 13
 18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
18. listopada 2016. 18. listopada 2016. 1 / 13 Neprekidne funkcije Važnu klasu funkcija tvore neprekidne funkcije. To su funkcije f kod kojih mala promjena u nezavisnoj varijabli x uzrokuje malu promjenu
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f
 IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f IspitivaƬe funkcija: 1. Oblast definisanosti funkcije (ili domen funkcije) D f 2. Nule i znak funkcije; presek sa y-osom IspitivaƬe
Elektron u magnetskom polju
 Quantum mechanics 1 - Lecture 13 UJJS, Dept. of Physics, Osijek 4. lipnja 2013. Sadržaj 1 Bohrov magneton Stern-Gerlachov pokus Vrtnja elektrona u magnetskom polju 2 Nuklearna magnetska rezonancija (NMR)
Quantum mechanics 1 - Lecture 13 UJJS, Dept. of Physics, Osijek 4. lipnja 2013. Sadržaj 1 Bohrov magneton Stern-Gerlachov pokus Vrtnja elektrona u magnetskom polju 2 Nuklearna magnetska rezonancija (NMR)
UNIVERZITET U NOVOM SADU FAKULTET TEHNIČKIH NAUKA. BOJE I OSVETLJENOST za studente animacije u inženjerstvu
 UNIVERZITET U NOVOM SADU FAKULTET TEHNIČKIH NAUKA Dušan Ilić BOJE I OSVETLJENOST za studente animacije u inženjerstvu NOVI SAD 2014 SADRŽAJ 1 Uvod 5 2 Svetlost kao elektromagnetni talas 7 2.1 Uvod................................
UNIVERZITET U NOVOM SADU FAKULTET TEHNIČKIH NAUKA Dušan Ilić BOJE I OSVETLJENOST za studente animacije u inženjerstvu NOVI SAD 2014 SADRŽAJ 1 Uvod 5 2 Svetlost kao elektromagnetni talas 7 2.1 Uvod................................
M086 LA 1 M106 GRP. Tema: Baza vektorskog prostora. Koordinatni sustav. Norma. CSB nejednakost
 M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
M086 LA 1 M106 GRP Tema: CSB nejednakost. 19. 10. 2017. predavač: Rudolf Scitovski, Darija Marković asistent: Darija Brajković, Katarina Vincetić P 1 www.fizika.unios.hr/grpua/ 1 Baza vektorskog prostora.
To je ujedno 1/12 mase atoma ugljika koja je određena eksperimentom i koja iznosi kg. Dakle mase nukleona:
 Nuklearna fizika_intro Osnovne sile u prirodi, građa atomske jezgre, nukleoni i izotopi, energija vezanja jezgre, radioaktivnost, osnovne vrste radioaktivnog zračenja i njihova svojstva, zakon radioaktivnog
Nuklearna fizika_intro Osnovne sile u prirodi, građa atomske jezgre, nukleoni i izotopi, energija vezanja jezgre, radioaktivnost, osnovne vrste radioaktivnog zračenja i njihova svojstva, zakon radioaktivnog
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15
 MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
MATRICE I DETERMINANTE - formule i zadaci - (Matrice i determinante) 1 / 15 Matrice - osnovni pojmovi (Matrice i determinante) 2 / 15 (Matrice i determinante) 2 / 15 Matrice - osnovni pojmovi Matrica reda
Elementi spektralne teorije matrica
 Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
Elementi spektralne teorije matrica Neka je X konačno dimenzionalan vektorski prostor nad poljem K i neka je A : X X linearni operator. Definicija. Skalar λ K i nenula vektor u X se nazivaju sopstvena
PRAVA. Prava je u prostoru određena jednom svojom tačkom i vektorom paralelnim sa tom pravom ( vektor paralelnosti).
 PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
PRAVA Prava je kao i ravan osnovni geometrijski ojam i ne definiše se. Prava je u rostoru određena jednom svojom tačkom i vektorom aralelnim sa tom ravom ( vektor aralelnosti). M ( x, y, z ) 3 Posmatrajmo
FTN Novi Sad Katedra za motore i vozila. Teorija kretanja drumskih vozila Vučno-dinamičke performanse vozila: MAKSIMALNA BRZINA
 : MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
: MAKSIMALNA BRZINA Maksimalna brzina kretanja F O (N) F OI i m =i I i m =i II F Oid Princip određivanja v MAX : Drugi Njutnov zakon Dokle god je: F O > ΣF otp vozilo ubrzava Kada postane: F O = ΣF otp
Operacije s matricama
 Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
Linearna algebra I Operacije s matricama Korolar 3.1.5. Množenje matrica u vektorskom prostoru M n (F) ima sljedeća svojstva: (1) A(B + C) = AB + AC, A, B, C M n (F); (2) (A + B)C = AC + BC, A, B, C M
III VEŽBA: FURIJEOVI REDOVI
 III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
III VEŽBA: URIJEOVI REDOVI 3.1. eorijska osnova Posmatrajmo neki vremenski kontinualan signal x(t) na intervalu definisati: t + t t. ada se može X [ k ] = 1 t + t x ( t ) e j 2 π kf t dt, gde je f = 1/.
radni nerecenzirani materijal za predavanja R(f) = {f(x) x D}
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Neka su D i K bilo koja dva neprazna skupa. Postupak f koji svakom elementu x D pridružuje točno jedan element y K zovemo funkcija
numeričkih deskriptivnih mera.
 DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
DESKRIPTIVNA STATISTIKA Numeričku seriju podataka opisujemo pomoću Numeričku seriju podataka opisujemo pomoću numeričkih deskriptivnih mera. Pokazatelji centralne tendencije Aritmetička sredina, Medijana,
Otkriće prirodne radioaktivnosti
 Otkriće prirodne radioaktivnosti Kruksove cevi Rentgen [Wilhem Konrad Rontgen, 1845-1923] Sir Wiliam Crookes 1832-1919 Iz Kruksovih cevi se emituje prodorno zračenje Otkriće Xzraka X-zraka - 1895 Prva
Otkriće prirodne radioaktivnosti Kruksove cevi Rentgen [Wilhem Konrad Rontgen, 1845-1923] Sir Wiliam Crookes 1832-1919 Iz Kruksovih cevi se emituje prodorno zračenje Otkriće Xzraka X-zraka - 1895 Prva
OM2 V3 Ime i prezime: Index br: I SAVIJANJE SILAMA TANKOZIDNIH ŠTAPOVA
 OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
OM V me i preime: nde br: 1.0.01. 0.0.01. SAVJANJE SLAMA TANKOZDNH ŠTAPOVA A. TANKOZDN ŠTAPOV PROZVOLJNOG OTVORENOG POPREČNOG PRESEKA Preposavka: Smičući napon je konsanan po debljini ida (duž pravca upravnog
Usavršavanje Borovog modela
 Usavršavanje Borovog modela Vilson-Sommerfeldova pravila kvantovanja Odakle dolaze: Bohr ovo pravilo kvantizacije momenta impulsa elektrona? mvr=nh/π Planck ovo pravilo kvantizacije energije elektromagnetnog
Usavršavanje Borovog modela Vilson-Sommerfeldova pravila kvantovanja Odakle dolaze: Bohr ovo pravilo kvantizacije momenta impulsa elektrona? mvr=nh/π Planck ovo pravilo kvantizacije energije elektromagnetnog
SEKUNDARNE VEZE međumolekulske veze
 PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
PRIMARNE VEZE hemijske veze među atomima SEKUNDARNE VEZE međumolekulske veze - Slabije od primarnih - Elektrostatičkog karaktera - Imaju veliki uticaj na svojstva supstanci: - agregatno stanje - temperatura
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri
 Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
Betonske konstrukcije 1 - vežbe 3 - Veliki ekscentricitet -Dodatni primeri 1 1 Zadatak 1b Čisto savijanje - vezano dimenzionisanje Odrediti potrebnu površinu armature za presek poznatih dimenzija, pravougaonog
OPŠTA TEORIJA ELEKTRONSKE PARAMAGNETNE REZONANCIJE
 OPŠTA TEORIJA ELEKTRONSKE PARAMAGNETNE REZONANCIJE Elektronska paramagnetna rezonancija (EPR), takođe poznata kao elektronska spinska rezonancija (ESR) ili elektronska magnetna rezonancija (EMR), je rezonantna
OPŠTA TEORIJA ELEKTRONSKE PARAMAGNETNE REZONANCIJE Elektronska paramagnetna rezonancija (EPR), takođe poznata kao elektronska spinska rezonancija (ESR) ili elektronska magnetna rezonancija (EMR), je rezonantna
IZVODI ZADACI (I deo)
 IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
IZVODI ZADACI (I deo) Najpre da se podsetimo tablice i osnovnih pravila:. C`=0. `=. ( )`= 4. ( n )`=n n-. (a )`=a lna 6. (e )`=e 7. (log a )`= 8. (ln)`= ` ln a (>0) 9. = ( 0) 0. `= (>0) (ovde je >0 i a
INTELIGENTNO UPRAVLJANJE
 INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
INTELIGENTNO UPRAVLJANJE Fuzzy sistemi zaključivanja Vanr.prof. Dr. Lejla Banjanović-Mehmedović Mehmedović 1 Osnovni elementi fuzzy sistema zaključivanja Fazifikacija Baza znanja Baze podataka Baze pravila
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama.
 Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
Apsolutno neprekidne raspodele Raspodele apsolutno neprekidnih sluqajnih promenljivih nazivaju se apsolutno neprekidnim raspodelama. a b Verovatno a da sluqajna promenljiva X uzima vrednost iz intervala
ELEKTROTEHNIČKI ODJEL
 MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
MATEMATIKA. Neka je S skup svih živućih državljana Republike Hrvatske..04., a f preslikavanje koje svakom elementu skupa S pridružuje njegov horoskopski znak (bez podznaka). a) Pokažite da je f funkcija,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika. Monotonost i ekstremi. Katica Jurasić. Rijeka, 2011.
 Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Veleučilište u Rijeci Stručni studij sigurnosti na radu Akad. god. 2011/2012. Matematika Monotonost i ekstremi Katica Jurasić Rijeka, 2011. Ishodi učenja - predavanja Na kraju ovog predavanja moći ćete:,
Uvod u atomsku fiziku
 Uvod u atomsku fiziku Do kraja 20. stoljeća Različiti modeli o grañi materije (atoma). J.J. Thomson Atom je pozitivno nabijena kuglica u kojoj su vrlo sitni elektroni ravnomjerno rasporeñeni. Atom kao
Uvod u atomsku fiziku Do kraja 20. stoljeća Različiti modeli o grañi materije (atoma). J.J. Thomson Atom je pozitivno nabijena kuglica u kojoj su vrlo sitni elektroni ravnomjerno rasporeñeni. Atom kao
XI dvoqas veжbi dr Vladimir Balti. 4. Stabla
 XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
XI dvoqas veжbi dr Vladimir Balti 4. Stabla Teorijski uvod Teorijski uvod Definicija 5.7.1. Stablo je povezan graf bez kontura. Definicija 5.7.1. Stablo je povezan graf bez kontura. Primer 5.7.1. Sva stabla
Obrada signala
 Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Obrada signala 1 18.1.17. Greška kvantizacije Pretpostavka je da greška kvantizacije ima uniformnu raspodelu 7 6 5 4 -X m p x 1,, za x druge vrednosti x 3 x X m 1 X m = 3 x Greška kvantizacije x x x p
Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton,
 Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton, neutron Građa atoma Pozitron, neutrino, antineutrino Beta
Elementarne čestice Elementarne ili osnovne ili fundamentalne čestice = Najmanji dijelovi od kojih je sastavljena tvar. Do 1950: Elektron, proton, neutron Građa atoma Pozitron, neutrino, antineutrino Beta
Ispitivanje toka i skiciranje grafika funkcija
 Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Ispitivanje toka i skiciranje grafika funkcija Za skiciranje grafika funkcije potrebno je ispitati svako od sledećih svojstava: Oblast definisanosti: D f = { R f R}. Parnost, neparnost, periodičnost. 3
Računarska grafika. Rasterizacija linije
 Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
Računarska grafika Osnovni inkrementalni algoritam Drugi naziv u literaturi digitalni diferencijalni analizator (DDA) Pretpostavke (privremena ograničenja koja se mogu otkloniti jednostavnim uopštavanjem
S t r a n a 1. 1.Povezati jonsku jačinu rastvora: a) MgCl 2 b) Al 2 (SO 4 ) 3 sa njihovim molalitetima, m. za so tipa: M p X q. pa je jonska jačina:
 S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
S t r a n a 1 1.Povezati jonsku jačinu rastvora: a MgCl b Al (SO 4 3 sa njihovim molalitetima, m za so tipa: M p X q pa je jonska jačina:. Izračunati mase; akno 3 bba(no 3 koje bi trebalo dodati, 0,110
RAD, SNAGA I ENERGIJA
 RAD, SNAGA I ENERGIJA SADRŢAJ 1. MEHANIĈKI RAD SILE 2. SNAGA 3. MEHANIĈKA ENERGIJA a) Kinetiĉka energija b) Potencijalna energija c) Ukupna energija d) Rad kao mera za promenu energije 4. ZAKON ODRŢANJA
RAD, SNAGA I ENERGIJA SADRŢAJ 1. MEHANIĈKI RAD SILE 2. SNAGA 3. MEHANIĈKA ENERGIJA a) Kinetiĉka energija b) Potencijalna energija c) Ukupna energija d) Rad kao mera za promenu energije 4. ZAKON ODRŢANJA
Skulptura mamuta, dužine samo 3.7cm koja je isklesana od mamutove kljove, delo je umetnika koji je živeo u severozapadnoj Nemačkoj pre godina.
 NUKLEARNA FIZIKA Skulptura mamuta, dužine samo 3.7cm koja je isklesana od mamutove kljove, delo je umetnika koji je živeo u severozapadnoj Nemačkoj pre 35000 godina. Koji fizički principi omogućavaju vremensko
NUKLEARNA FIZIKA Skulptura mamuta, dužine samo 3.7cm koja je isklesana od mamutove kljove, delo je umetnika koji je živeo u severozapadnoj Nemačkoj pre 35000 godina. Koji fizički principi omogućavaju vremensko
RIJEŠENI ZADACI I TEORIJA IZ
 RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
RIJEŠENI ZADACI I TEORIJA IZ LOGARITAMSKA FUNKCIJA SVOJSTVA LOGARITAMSKE FUNKCIJE OSNOVE TRIGONOMETRIJE PRAVOKUTNOG TROKUTA - DEFINICIJA TRIGONOMETRIJSKIH FUNKCIJA - VRIJEDNOSTI TRIGONOMETRIJSKIH FUNKCIJA
Fizika 2. Auditorne vježbe 12. Kvatna priroda svjetlosti. Ivica Sorić. Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstava
 Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstava Fizika Auditorne vježbe Kvatna priroda svjetlosti Ivica Sorić (Ivica.Soric@fesb.hr) Bohrovi postulati Elektron se kreće oko atomske
Fakultet elektrotehnike, strojarstva i brodogradnje Studij računarstava Fizika Auditorne vježbe Kvatna priroda svjetlosti Ivica Sorić (Ivica.Soric@fesb.hr) Bohrovi postulati Elektron se kreće oko atomske
Glava Energija Sunca
 Glava 2 Zračenje 2.1 Energija Sunca Sunce je zvezda koja se nalazi u centru Solarnog sistema. Sunce je skoro idealnog sfernog oblika i sastoji se od vrele plazme iprepletane magnetnim poljem. Njegov poluprečnik
Glava 2 Zračenje 2.1 Energija Sunca Sunce je zvezda koja se nalazi u centru Solarnog sistema. Sunce je skoro idealnog sfernog oblika i sastoji se od vrele plazme iprepletane magnetnim poljem. Njegov poluprečnik
Teorijske osnove informatike 1
 Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Teorijske osnove informatike 1 9. oktobar 2014. () Teorijske osnove informatike 1 9. oktobar 2014. 1 / 17 Funkcije Veze me du skupovima uspostavljamo skupovima koje nazivamo funkcijama. Neformalno, funkcija
Osnovne veličine, jedinice i izračunavanja u hemiji
 Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
Osnovne veličine, jedinice i izračunavanja u hemiji Pregled pojmova veličina i njihovih jedinica koje se koriste pri osnovnim izračunavanjima u hemiji dat je u Tabeli 1. Tabela 1. Veličine i njihove jedinice
PARCIJALNI IZVODI I DIFERENCIJALI. Sama definicija parcijalnog izvoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je,
 PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
PARCIJALNI IZVODI I DIFERENCIJALI Sama definicija parcijalnog ivoda i diferencijala je malo teža, mi se njome ovde nećemo baviti a vi ćete je, naravno, naučiti onako kako vaš profesor ahteva. Mi ćemo probati
SEMINAR IZ KOLEGIJA ANALITIČKA KEMIJA I. Studij Primijenjena kemija
 SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
SEMINAR IZ OLEGIJA ANALITIČA EMIJA I Studij Primijenjena kemija 1. 0,1 mola NaOH je dodano 1 litri čiste vode. Izračunajte ph tako nastale otopine. NaOH 0,1 M NaOH Na OH Jak elektrolit!!! Disoira potpuno!!!
ELEKTRONSKA STRUKTURA ATOMA
 ELEKTRONSKA STRUKTURA ATOMA EMISIJA I APSORPCIJA SVIJETLOSTI Zašto užarene tvari emitiraju svijetlost? električna žarulja neonka svijeća užareno željezo vatromet sunce... Vidljive zrake Ultraljubičaste
ELEKTRONSKA STRUKTURA ATOMA EMISIJA I APSORPCIJA SVIJETLOSTI Zašto užarene tvari emitiraju svijetlost? električna žarulja neonka svijeća užareno željezo vatromet sunce... Vidljive zrake Ultraljubičaste
5 Ispitivanje funkcija
 5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
5 Ispitivanje funkcija 3 5 Ispitivanje funkcija Ispitivanje funkcije pretodi crtanju grafika funkcije. Opšti postupak ispitivanja funkcija koje su definisane eksplicitno y = f() sadrži sledeće elemente:
( ) ( ) 2 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET. Zadaci za pripremu polaganja kvalifikacionog ispita iz Matematike. 1. Riješiti jednačine: 4
 UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
UNIVERZITET U ZENICI POLITEHNIČKI FAKULTET Riješiti jednačine: a) 5 = b) ( ) 3 = c) + 3+ = 7 log3 č) = 8 + 5 ć) sin cos = d) 5cos 6cos + 3 = dž) = đ) + = 3 e) 6 log + log + log = 7 f) ( ) ( ) g) ( ) log
HEMIJA. dr Dubravka Štajner dr Slavko Kervešan
 1954 EMIJA dr Dubravka Štajner dr Slavko Kervešan 1 Dr Dubravka Štajner, Dr Slavko Kevrešan EMIJA UNIVERZITET U NVM SADU PLJPRIVREDNI FAKULTET Novi Sad, 2014. EDIIJA SNVNI UDŽBENIK snivač i izdavač Edicije
1954 EMIJA dr Dubravka Štajner dr Slavko Kervešan 1 Dr Dubravka Štajner, Dr Slavko Kevrešan EMIJA UNIVERZITET U NVM SADU PLJPRIVREDNI FAKULTET Novi Sad, 2014. EDIIJA SNVNI UDŽBENIK snivač i izdavač Edicije
Klasifikacija blizu Kelerovih mnogostrukosti. konstantne holomorfne sekcione krivine. Kelerove. mnogostrukosti. blizu Kelerove.
 Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Klasifikacija blizu Teorema Neka je M Kelerova mnogostrukost. Operator krivine R ima sledeća svojstva: R(X, Y, Z, W ) = R(Y, X, Z, W ) = R(X, Y, W, Z) R(X, Y, Z, W ) + R(Y, Z, X, W ) + R(Z, X, Y, W ) =
Program testirati pomoću podataka iz sledeće tabele:
 Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
Deo 2: Rešeni zadaci 135 Vrednost integrala je I = 2.40407 42. Napisati program za izračunavanje koeficijenta proste linearne korelacije (Pearsonovog koeficijenta) slučajnih veličina X = (x 1,..., x n
2 tg x ctg x 1 = =, cos 2x Zbog četvrtog kvadranta rješenje je: 2 ctg x
 Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
Zadatak (Darjan, medicinska škola) Izračunaj vrijednosti trigonometrijskih funkcija broja ako je 6 sin =,,. 6 Rješenje Ponovimo trigonometrijske funkcije dvostrukog kuta! Za argument vrijede sljedeće formule:
antična Grčija - snov zgrajena iz atomov /rezultat razmišljanja/
 ZGRADBA ATOMA 1.1 - DALTON atom (atomos nedeljiv) antična Grčija - snov zgrajena iz atomov /rezultat razmišljanja/ dokaz izpred ~ 200 let Temelj so 3 zakoni: ZAKON O OHRANITVI MASE /Lavoisier, 1774/ ZAKON
ZGRADBA ATOMA 1.1 - DALTON atom (atomos nedeljiv) antična Grčija - snov zgrajena iz atomov /rezultat razmišljanja/ dokaz izpred ~ 200 let Temelj so 3 zakoni: ZAKON O OHRANITVI MASE /Lavoisier, 1774/ ZAKON
dt 2 I tretiramo kvantno-mehani ki, pokazati da vaºi
 Kvantna mehanika zadaci sa pro²lih rokova, emineter.wordpress.com Pismeni ispit, 31. avgust 015. 1. Kruti rotator u ravni momenta inercije I i elektri nog dipolnog momenta d se nalazi u elektri nom polju
Kvantna mehanika zadaci sa pro²lih rokova, emineter.wordpress.com Pismeni ispit, 31. avgust 015. 1. Kruti rotator u ravni momenta inercije I i elektri nog dipolnog momenta d se nalazi u elektri nom polju
(P.I.) PRETPOSTAVKA INDUKCIJE - pretpostavimo da tvrdnja vrijedi za n = k.
 1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
1 3 Skupovi brojeva 3.1 Skup prirodnih brojeva - N N = {1, 2, 3,...} Aksiom matematičke indukcije Neka je N skup prirodnih brojeva i M podskup od N. Ako za M vrijede svojstva: 1) 1 M 2) n M (n + 1) M,
PERIODNI SISTEM ELEMENATA
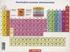 PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
PERIODNI SISTEM ELEMENATA 1/43 PERIODNI SISTEM ELEMENATA - Kratka istorija Otkriće elemenata do danas otktiveno još 11 elemenata 2011. IUPAC potvrdio otkriće 2 nova elementa: Flerovijum (Fl, Z = 114) i
radni nerecenzirani materijal za predavanja
 Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
Matematika 1 Funkcije radni nerecenzirani materijal za predavanja Definicija 1. Kažemo da je funkcija f : a, b R u točki x 0 a, b postiže lokalni minimum ako postoji okolina O(x 0 ) broja x 0 takva da je
OBRTNA TELA. Vladimir Marinkov OBRTNA TELA VALJAK
 OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
OBRTNA TELA VALJAK P = 2B + M B = r 2 π M = 2rπH V = BH 1. Zapremina pravog valjka je 240π, a njegova visina 15. Izračunati površinu valjka. Rešenje: P = 152π 2. Površina valjka je 112π, a odnos poluprečnika
1. Osnovi kvantne mehanike
 1. Osnovi kvantne mehanike Kao što je dobro poznato, foton, kao nosilac elektromagnetnog polja, osim što se ponaša kao talas (poseduje talasna svojstva - kao primer za to spomenućemo difrakciju svetlosti,
1. Osnovi kvantne mehanike Kao što je dobro poznato, foton, kao nosilac elektromagnetnog polja, osim što se ponaša kao talas (poseduje talasna svojstva - kao primer za to spomenućemo difrakciju svetlosti,
TERMALNOG ZRAČENJA. Plankov zakon Stefan Bolcmanov i Vinov zakon Zračenje realnih tela Razmena snage između dve površine. Ž. Barbarić, MS1-TS 1
 OSNOVNI ZAKONI TERMALNOG ZRAČENJA Plankov zakon Stefan Bolcmanov i Vinov zakon Zračenje realnih tela Razmena snage između dve površine Ž. Barbarić, MS1-TS 1 Plankon zakon zračenja Svako telo čija je temperatura
OSNOVNI ZAKONI TERMALNOG ZRAČENJA Plankov zakon Stefan Bolcmanov i Vinov zakon Zračenje realnih tela Razmena snage između dve površine Ž. Barbarić, MS1-TS 1 Plankon zakon zračenja Svako telo čija je temperatura
1 Afina geometrija. 1.1 Afini prostor. Definicija 1.1. Pod afinim prostorom nad poljem K podrazumevamo. A - skup taqaka
 1 Afina geometrija 11 Afini prostor Definicija 11 Pod afinim prostorom nad poljem K podrazumevamo svaku uređenu trojku (A, V, +): A - skup taqaka V - vektorski prostor nad poljem K + : A V A - preslikavanje
1 Afina geometrija 11 Afini prostor Definicija 11 Pod afinim prostorom nad poljem K podrazumevamo svaku uređenu trojku (A, V, +): A - skup taqaka V - vektorski prostor nad poljem K + : A V A - preslikavanje
Zadaci iz trigonometrije za seminar
 Zadaci iz trigonometrije za seminar FON: 1. Vrednost izraza sin 1 cos 6 jednaka je: ; B) 1 ; V) 1 1 + 1 ; G) ; D). 16. Broj rexea jednaqine sin x cos x + cos x = sin x + sin x na intervalu π ), π je: ;
Zadaci iz trigonometrije za seminar FON: 1. Vrednost izraza sin 1 cos 6 jednaka je: ; B) 1 ; V) 1 1 + 1 ; G) ; D). 16. Broj rexea jednaqine sin x cos x + cos x = sin x + sin x na intervalu π ), π je: ;
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A
 Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Kontrolni zadatak (Tačka, prava, ravan, diedar, poliedar, ortogonalna projekcija), grupa A Ime i prezime: 1. Prikazane su tačke A, B i C i prave a,b i c. Upiši simbole Î, Ï, Ì ili Ë tako da dobijeni iskazi
Iskazna logika 3. Matematička logika u računarstvu. novembar 2012
 Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
Iskazna logika 3 Matematička logika u računarstvu Department of Mathematics and Informatics, Faculty of Science,, Serbia novembar 2012 Deduktivni sistemi 1 Definicija Deduktivni sistem (ili formalna teorija)
5. Karakteristične funkcije
 5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
5. Karakteristične funkcije Profesor Milan Merkle emerkle@etf.rs milanmerkle.etf.rs Verovatnoća i Statistika-proleće 2018 Milan Merkle Karakteristične funkcije ETF Beograd 1 / 10 Definicija Karakteristična
Relativistička kvantna mehanika
 Relativistička kvantna mehanika zadaci sa prošlih rokova, emineter.wordpress.com Pismeni ispit, 8. jul 2016. 1. Pokazati da generatori Lorencove grupe S µν = i 4 [γµ, γ ν ] zadovoljavaju Lorencovu algebru:
Relativistička kvantna mehanika zadaci sa prošlih rokova, emineter.wordpress.com Pismeni ispit, 8. jul 2016. 1. Pokazati da generatori Lorencove grupe S µν = i 4 [γµ, γ ν ] zadovoljavaju Lorencovu algebru:
Kaskadna kompenzacija SAU
 Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Kaskadna kompenzacija SAU U inženjerskoj praksi, naročito u sistemima regulacije elektromotornih pogona i tehnoloških procesa, veoma često se primenjuje metoda kaskadne kompenzacije, u čijoj osnovi su
Linearna algebra 2 prvi kolokvij,
 1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
1 2 3 4 5 Σ jmbag smjer studija Linearna algebra 2 prvi kolokvij, 7. 11. 2012. 1. (10 bodova) Neka je dano preslikavanje s : R 2 R 2 R, s (x, y) = (Ax y), pri čemu je A: R 2 R 2 linearan operator oblika
