5. APLICATII ALE PRINCIPIILOR TERMODINAMICII
|
|
|
- Ἀριστομάχη Μανωλάς
- 7 χρόνια πριν
- Προβολές:
Transcript
1 5. APLIAII ALE PRINIPIILOR ERMODINAMIII 5..Ranamentul motoarelor termice Duă cum am văzut, al oilea rinciiu al termoinamicii a fost stabilit in analiza funcţionării maşinilor termice.ţinân seama că schimbul e calură intre corul e lucru şi termostate este reverşibil numai acă are loc în mo izoterm, şi că ciclul arnot este o transformare rerezentată rin ouă izoterme şi ouă aiabate, aşa cum am conşierat anterior, utem rerezenta ciclul astfel: Q 4 Q 3 ubliniem fatul că acă un sistem efectuează o transformare ciclică, schimbân călură cu ouă termostate e temeraturi ate, atunci unicul ciclu reverşibil este ciclul arnot. Maşina bitermă al cărui cor e lucru efectuează un ciclu reverşibil se numeşte maşină arnot, iar toate celelalte sunt maşini biterme ireverşibile. Presuunem că >, aică R( ) - sursa cală (încălzitor) şi R( ) - sursa rece (răcitor); Q > Q. Q este rimită e la R( ) şi Q este ceată sursei rece, lucrul mecanic efectuat e fiecare ciclu fiin: L Q - Q Pentru a caracteriza eficienţa funcţionării unei astfel e maşini se introuce noţiunea e ranament termic, care se efineşte ca: lucrulmecaniceciclu L η calurarimitaeciclu onform rinciiului al oilea δq 0 aică 3 Q δq δq δq δq 0 Integralele -3 şi 4- sunt zero entru că transformările sunt aiabatice şi rezultă: Q Q 0. Q Q a urmare, η Q 5. Din exreşia ranamentului se observă că acesta nu eine e substanţa e lucru ci este eterminat numai e temeraturile rezervoarelor termice (rima teoremă arnot). Ranamentul ciclului arnot mai mic ecât arată că în natură nu se oate realiza ecât converşia arţială a călurii în lucru mecanic şi că acest roces imlică în mo 4 3 4
2 obligatoriu cearea unei ărţi Q in călura rimită e substanţa e lucru, la o temeratura <. onverşia arţială a călurii în lucru mecanic arată la rânul său că acţiunea termică este mult eosebită e alte tiuri e acţiuni care se manifestă în natură. În urma roceselor ciclice, orice ti e acţiune se oate transforma integral în acţiune termică, ar acţiunea termică se transformă oar arţial în alte tiuri e acţiuni, conform rinciiului al II-lea. De aici, afirmaţia că rinciiul al oilea arată neechivalenţa calitativă intre călură şi lucru mecanic. Dacă maşina bitermă funcţionează uă un ciclu oarecare ireverşibil, atunci, Q ţinân seama e inegalitatea lui lausius relaţia < conuce la : Q η i < Deci, ranamentul maşinii termice ireverşibile care funcţionează, schimbân călură cu aceleaşi termostate ca maşina arnot, este întoteauna mai mic ecât ranamentul maşinii arnot. Exreşia 5. rerezintă conţinutul celei e-a oua teoreme arnot: ranamentul oricărei maşini biterme care funcţionează cu aceleaşi termostate e temeraturi şi, nu oate eăşi ranamentul maşinii ieale arnot. u alte cuvinte, ireverşibilitatea iminuează ranamentul e converşie a călurii în lucru mecanic, contribuin în lus la egraarea energiei interne. Pentru refacerea calităţii energiei interne este necesară toteauna o comensaţie. Ranamentul maşinilor termice în afară e fatul că nu oate avea valoarea, are o limită suerioară imusă e caacitatea energiei e a se transforma intr-o formă într-alta, e neechivalenţa calitativă intre călură şi lucru mecanic. Din relaţia (5.) rezultă că ranamentul maşinii arnot este subunitar şi cu atât mai mare cu cât / este mai mic. e oate calcula care in cele ouă surse influenţeaza mai mult ranamentul: η η şi întrucât > rezultă η η < Deci, variatia temeraturii sursei cale influenteaza mai uţin ranamentul ciclului arnot rin comaraţie cu variaţia temeraturii sursei reci. Altfel sus, ranamentul creşte acă scae temeratura sursei reci. ηciclului arnot este egal cu numai acă Q 0 şi 0, în contraicţie cu formularea e bază a rinciiului al II-lea al termoinamicii. În cazul în care Q 0 şi 0, izoterma se confună cu aiabata şi ciclul nu se oate închie. u alte cuvinte nu este oşibil un ciclu arnot cu rezervorul rece în stare e zero absolut. Dua estinaţia lor, maşinile termice se îmart în trei tiuri rinciale: -motoare termice -ome termice (ome e calură) -maşini frigorifice Motorele termice, esre care am vorbit, transformă Q în L; omele termice e seama unui L cheltuit şi a călurii luate e la meiu (cu temeratura mică), încălzesc coruri cu temeratura mai mare; maşini frigorifice care cu ajutorul lucrului mecanic, L cheltuit iau calura Q e la corul care se răceşte şi o transmite meiului înconjurător. Maşina arnot oate funcţiona şi ca maşină frigorifică. 5.
3 orul e lucru e seama lucrului mecanic efectuat e meiul exterior, rimeşte călura Q e la sursa rece şi transmite într-un ciclu călura Q Q L, sursei cale. Q 4 Q 3 Eficienţa unei maşini frigorifice este eterminată e coeficientul e răcire: Q Q ψ L Q Q şi oate fi o mărime subunitară, suraunitară sau zero. Eficienţa omei e călură: Q ϕ cu > 5.4 L Relaţia funamentală a termoinamicii. Alicaţii Princiiul zero introuce temeratura ca arametru e stare şi entru sistemele la echilibru arată că forţele generalizate sunt funcţii e cooronatele generalizate şi temeratură şi la fel energia internă: Ai Ai ( a, a,... an, ) şi ( a, a,... an, ) Princiiul I : exrimarea matematică infinitezimală: δq - δl şi finită: Q L cu convenţia că: entru Q>0 sistemul rimeşte călură;q<0, sistemul ceează călură;l>0, sistemul efectuează lucrul mecanic; L<0, asura sistemului se efectueaza lucrul mecanic. Princiiul al II-lea: exrimarea matematică infinitezimală δq ombinân exreşiile matematice ale rinciiului I şi al II-lea se obţine: δl, sau, δl 5.5 Aiai i Deci ecuaţia 5.6 rerezintă ecuatia funamentala a termoinamicii; egalitatea este valabila în cazul roceselor termoinamice reverşibile iar inegalitatea în cazul celor ireverşibile.omarân exreşiile, entru rocese cvaşistatice: δq cu δl 3
4 Aa i i i, rezultă că acă într-o iagramă (,), δl rerezinta aria e sub curba e transformare, în cooronate (,) aria e sub curba va rerezenta călura. Avantajele utilizarii iagramei (,) este comoă în sensul că ea rerezintă imeiat şi sugestiv atât calura schimbată în cursul ciclului cât şi lucrul mecanic rous e corul e lucru într-un ciclu: aria Q Q L ciclu ermite să se vaă în ce orţiuni ale ciclului calura este furnizata substanţei e lucru şi în ce orţiuni ea este rimită e la substanţa e lucru: unui aort reverşibil e călură îi coresune o creştere e entroie, iar unei ceări e călură, o micşorare a entroiei Relaţii iferenţiale e eenenţă între funcţiile e stare şi arametri e stare entru un sistem termoinamic şimlu tilizân relaţia funamentală a termoinamicii ot fi stabilite relaţii iferenţiale e eenenţă între funcţiile e stare entru un sistem termoinamic şimlu: 0 (,) : (,) (,) (,) ν
5 Deoarece (,) şi (,) sunt iferenţiale totale exacte, şi ; Foloşin aceste ientităţi se obţine: 5.8. v P care rerezintă o relaţie Maxwell (,) : (,) (,) (,) ν 5.0 Deoarece (,) şi (,) sunt iferenţiale totale exacte, şi ; Foloşin aceste ientităţi se obţine: 5. a oua relaţie Maxwell alculul energiei interne, entaliei şi entroiei Energia ( ) ν, 5
6 (,) ν 5.3 a să se rezolve ecuaţia integralo-iferenţială trebuie cunoscută eenenţa lui e temeratură şi ecuaţiile e stare ale sistemului termoinamic. νr Pentru gazul ieal: ct, rezultă 0 () ν Entalia (,) ν (, ) ν 5.5 νr Pentru gazul ieal: ct, rezultă 0 a urmare, (,) ν 0 Entroia (, ) ν eci ; rezultă ν 5.6 (, ) ν eci ; rezultă ν 5.7 (, ) eci - ;, 5.8 rezultă ( ) Pentru gazul ieal, exreşiile variaţiei e entroie se ot calcula, ţinân seama e ecuaţia e stare νr şi e fatul că const şi const. ν ν ln R ν ln νr ln
7 ν ν ln R ν ln νr ln (, ) νr νr ν R ln νr ln Procese termoinamice funamentale Procesele în care o marime termoinamica îşi astreaza valoarea constantă sunt conşierate rocese termoinamice funamentale atorită imortanţei lor teoretice şi alicative. Astfel e rocese sunt: rocese aiabatice, caracterizate rin Q0; rocese olitroice, caracterizate rin caacitatea calorica constanta; rocese izoterme, caracterizate rin temeratura constanta; rocese izocore, caracterizate rin volum constant; rocese izobare, caracterizate rin reşiune constantă. om stuia rincialele transformări termoinamice în veerea stabilirii legilor care le guvernează entru sisteme termoinamice şimle Procese aiabatice e numeşte transformare aiabatică transformarea termoinamică în cursul căreia sistemul nu rimeşte şi nici nu ceează călură: δq 0. În coniţii reale o transformare este aiabatica aca sistemul este înzestrat cu o bună izolaţie termică sau acă estinerea (sau comrimarea) gazului se face atât e rai încât, ractic nu are loc nici un fel e schimb e călură între sistem şi meiu. Deoarece entru o transformare reverşibilă rinciiul al oilea δq, în transformarea aiabatica 0. u alte cuvinte o transformare aiabatică reverşibilă este în acelaşi tim şi izentroică. ransformarea aiabatică oate fi şi ireverşibilă.de exemlu curgerea unui gaz real rintr-un tub rugos, înzestrat cu înveliş aiabatic care nu ermite schimbul e calură. urgerea gazului va fi, în consecinţă, aiabatică entru că nu rimeşte şi nici nu ceează călură. urgerea unui gaz real într-un tub rugos fiin însoţită întoteauna e frecare, care rouce o işiare e energie e către fluiul care curge, această transformare este ireverşibilă şi ca orice roces ireverşibil antrenează o creştere a entroiei: > δq. În cazul transformarii aiabatice ireverşibile examinată, δq 0, ar >0, eci transformarea aiabatică nu este şi izentroică. Prin urmare se oate sune că orice transformare izentroică a unui sistem izolat este aiabatică, însă reciroca nu este aevarată ecât în cazul transformarilor reverşibile. În acest aragraf ne referim la transformarile reverşibile ( 0) şi vom analiza relaţiile intre arametrii iverselor stări într-o transformare aiabatică reverşibilă. Pentru aceasta vom euce ecuaţia iferenţială a unei transformari izentroice. δq δq Daca transformarea este izentroică, 7
8 e une ; 5. u ajutorul acestor ecuaţii nu este greu să se obţină relaţia: 5.3 Aceasta relaţie nu este ecât ecuaţia iferenţialăa unei transformări izentroice. Ea exrimă variaţia mărimilor calorice şi ale sistemului în funcţie e mărimile sale termice şi într-o transformare izentroică. e noteaza cu k marimea : k 5.4 Marimea k se numeste exonentul transformarii izentroice, sau exonent izentroic. Ţinân cont e aceasta notaţie, relaţia ( 5.3) evine: ln k sau - k; ln - kln 5.5 ln Această ecuaţie iferenţială stabileşte o relaţie între şi într-o transformare izentroică. Integrân această relatie între ouă stări ale transformarii izentroice se obţine : ln k ln sau ln k ln 5.6 Dacă în intervalul conşierat exonentul izentroic ramâne constant, el oate fi scos e sub integrală şi astfel obţinem: k k k ln ln k 5.7 Aşaar, entru fiecare stare a sistemului care arcurge o transformare izentroica (cu k constant) avem: P k const 5.8 Aceasta ecuaţie este ecuaţia aiabatei, a lui Poisson. Dacă exonentul aiabatic variază cân sistemul îşi moifică starea şi acă se cunoaşte variaţia lui, atunci integrala se rezolvă numeric entru a găşi valoarea lui in valorile arametrilor in starea iniţială şi volumul in starea finală. e mai oate foloşi şi valoarea meie a lui k şi atunci ecuaţia Poisson este : k meiu const. une k meiu k ln 5.9 ln ubliniem ca ecuatiile transformarii izentroice sunt alicabile atât entru gaze cât şi entru lichie şi solie (n-am facut nici-o resuunere rivin şist termoinamic). 8
9 Exonentul izentroic caata o valoare senşibil iferita entru iversele faze e stare ale substantei. Astfel, entru lichie şi solie k este foarte mare şi sufera o variatie substantiala o ata cu temeratura. Pentru aa la 0 0 k în tim ce la t50 0, k iar la t00 0 k3000. Pentru gaze şi vaori k variaza (se micsoreaza) utin cu temeratura; entru majoritatea gazelor el este curins între,3 şi,7; k variaza uternic numai în vecinatatea curbei limita. În Fig... sunt rerezentate valorile exonentului izentroic k entru vaorii e aa. Pentru exonentul aiabatic al gazelor se euce exreşia ca fiin raortul intre călurile secifice sau molare la reşiune constantă şi volum constant: k Din k si in relatia ; ks v şi ca urmare γ k erfect γ k k ar alurile secifice şi molare ale gazului erfect variază foarte uţin în tim;e aceea, valoarea lui γ oate fi conşierată cu buna recizie, ractice ineenenta e temeratură. În ceea ce riveste relaţia intre temeratura a oua stări într-o transformare izentroică se oate scrie, ţinân seamai e ecuaţia Poisson, k k k k const., const sau const. Prin urmare, în cursul unei estineri izentroice (aiabatic reverşibilă) sistemul se răceşte,eci estinerea aiabatică reverşibilă este un roceeu eficient e răcire a gazelor (!) Lucrul mecanic în estinerea aiabatică δq ; entru transformarea izentroică - L ; L ( ) valabilă atât entru transformarea reverşibilă cât şi ireverşibilă. Ecuaţiile e mai jos nu ot fi foloşite ecât în cazul cân exonentul izentroic este constant sau se ia o valoare meie a acestuia. k k k k k L L k sau k 5.3 k k 9
10 Dat fiin că entru un gaz erfect energia internă nu eine ecât e temeratură şi calura secifica este constantă se obţine exreşia entru lucru mecanic: ( ) ( sau ν ν L L γ ) 5.3 ariaţia e entroie este nulă în rocesele aiabatice reverşibile, şi călura molară e asemenea ransformari olitroice e numesc transformari olitroice transformările entru care este constant şi aceste transformări satisfac ecuaţia: const. n 5.33 entru o valoare n arbitrară, constantă entru transformarea conşierată. n oartă numele e coeficient olitroic şi oate lua orice valori între - şi. Noţiunea e transformare olitroică a fost introusă rin analogie cu transformarea aiabatică ; iferenţa majoră intre aceste ouă transformări este că în tim ce k este o marime variabilă, n este o constantă. Într-o transformare olitroă sistemul oate rimi sau cea calură. Noţiunea e transformare olitroică este foloşită mai ales în stuiul roceselor e comrimare şi e estinere în motoarele cu gaz. Procesele reale e comrimare şi e estinere in motorele cu gaz şi in comresoare nu sunt e obicei nici aiabatice nici izotermice ci ocuă o oziţie intermeiară între aceste oua transformări. Din această cauză în ractică valorile lui n sunt curinse între şi k. Ecuaţia generală a transformării olitroice este eusă uă cum urmează: Q Q δ δ : la ct v v e notează echivalent sau n n şi rezultă: ( ) 0 ar n n Deci ecuaţia rocesului olitroic este: 0 n 5.34 Ecuaţia este alicabilă oricărui sistem termoinamic. Alicaţie entru gazul ieal. 0
11 o. Procesul aiabatic. 0 n γ γ νr γ νr 0 γ 0 si eci γ ct o. Procesul izoterm. 0 n 0 si eci ct νr νr 3 o. Procesul izocor. si eci n Pconst ct aiab ct. Lucrul mecanic e estinere efectuat e către sistem în cursul unei transformări olitroice se calculează in integrala: n L şi entru că rezultă: n n n L sau L 5.35 n n entru gazul erfect se obţin ecuaţiile: n R sau sau - L L L 5.36 n n n ălura furnizată sau rimită e sistem se etermina ornin e la rinciiul I al termoinamicii: Q ( ) L δq, 5.38 acă transformarea olitroă este efectuată e un gaz ieal (aroximaţia este valabilă în calculele inginereşti in transformările olitroe ale motoarelor cu gaz)
12 νr ( ); L 5.39 n ă analizăm eenenţa călurii molare olitroe entru gazul erfect e inicele olitroei; R ( γ ) n γ ; ; 5.40 n n n Fig. ariaţia călurii molare olitroe,, în funcţie e inicele olitroei γ n <n<γ izotermă Zona haşurată coresune roceselor olitroice caracteristice maşinilor termice. Raortul Q/L se oate interreta entru toate transformările în cazul gazului ieal. ( n) Q ( n γ ) ; L ( n -) Q ν Q γ n ( n) ; 5.4 L νr L γ γ Avem cazurile: Dacă n 0 sau 0 < n < atunci raortul Q/L > Dacă n atunci Q L Dacă < n < γ atunci raortul Q/L < şi eci gazul consumă călură entru a efectua lucru mecanic. Dacă n γ atunci Q 0. Dacă n > γ atunci Q/L < 0. ariaţia entroiei, aică iferenţa intre entroiile a ouă stări in cursul transformării olitroe este: 5.4 n ν eoarece este evient că: ecuaţia 5.4 caătă forma: n 5.43 ân entru transformarea olitroă este constantă atunci variaţia e entroie este:
13 ln 5.44 e vee că în transformarea olitroică entroia variază logaritmic în funcţie e temeratură. Pentru a utea etermina valoarea exonentului olitroic al unei transformări concrete a unui gaz trebuie să isunem e ate exerimentale legate e resectiva transformare. Proceeul cel mai como consta în foloşirea curbei transformării în iagrama (,). e logaritmează ecuaţia olitroei şi se obţine: n log log 5.45 log log În scara logaritmica curba olitroei evine reata iar n este anta acestei rete. Log Procese izoterme Log. Fig.5.5. Pentru gazul erfect transformarea izotermă este escrisă e legea Boyle-Mariotte: const., aică la temeratură constantă volumul variază în funcţie e reşiune uă o hierbolă. Izotermele gazelor reale şi ale corurilor lichie şi solie au forme mai comlicate. ezi Fig. 5.5 entru gazul real. Este imortant să amintim că erivata care este e fat coeficientul e comreşibilitate izotermă nu oate fi ozitivă entru nici-o substanţă şi eci creşterea reşiunii uă o izotermă etermină o scăere a volumului. Lucrul mecanic e estinere al unui sistem într-o transformare izotermă este eterminat cu relaţia generală: L 5.46 Pentru calculul integralei este necesar să se cunoască variaţia reşiunii în funcţie e volum e e izotermă fie in ecuatia e stare fie irect in ate exerimentale în acest ultim caz integrala calculânu-se rin metoe numerice. 3
14 Pentru gazul erfect, L se obţine cunoscân ecuaţia termică e stare: L R ln 5.47 alura, furnizată sistemului sau ceată e acesta într-o transformare izotermă se calculeaza cu ajutorul relaţiei: δq Q - ( ) 5.48 une şi sunt entroiile în cele oua stări. Dacă gazul este erfect, atunci in rinciiul I se ştie că în transformarea izotermă lucrul mecanic efectuat e gaz este egal cu cantitatea e călura rimită: L Q ariaţia e entroie într-o transformare izotermă se calculeaza astfel: (, ) (, ) 5.49 şi ţinân cont e ecuaţia lui Maxwell: 5.50 Dacă se cunosc volumele in starile şi atunci relaţia: (, ) (, ) 5.5 şi ţinân cont e ecuaţia lui Maxwell: 5.5 Pentru calcularea integralelor care intervin în ec (5.50, 5.5) este necesar să se cunoască valorile erivatelor arţiale ale substanţelor stuiate e izotermă. Aceste cantităţi ot fi calculate fie cu ajutorul ecuaţiilor e stare fie rin iferenţierea numerică sau grafică a atelor exerimentale asura relaţiilor existente între, şi. În cazul gazului erfect avem: νr νr ; 5.53 şi ca urmare: ν Rln ; νr ln 5.54 ălura molară într-o transformare izotermă este infinit e mare : aică sistemul este un termostat Procese izobarice Parametri e stare în transformarea izobară sunt legaţi rin ecuaţia care se euce ornin e la transformarea olitroă care are inicele n0: 4
15 5.55 De aici se vee că entru gaz cu cât temeratura sa este mai riicată cu atât este mai mare volumul său. Pentru gaze reale, lichie şi solie încălzirea este însoţită e o ilatare termică e-a lungul izobarei. Aceeaşi creştere a temeraturii rouce o ilatare mai accentuată unui gaz ecât unui lichi sau unui soli. Lucrul mecanic e estinere al unui sistem într-o transformare izobară este at e relaţia: L Pentru gaz erfect, avân ecuaţia e stare: νr L ν R( ) 5.57 ălura furnizată sistemului în timul încălzirii sale sau ceată e sistem în timul răcirii sale, într-o transformare izobară va fi eteminată, lecân e la rinciiul I: δq sau δq Q - (, ) (, ) 5.58 alorile entaliei entru cele oua stări ot fi aflate fie in tabelele cu rorietăţi termoinamice ale substanţelor fie cu ajutorul iagramelor e stare ale acestora. Diferenţa intre entaliile a ouă stări e e izobară oate fi exrimată la rânul sau uă cum urmează: (, ) (, ) 5.59 şi ţinân seama e exreşia călurii molare la reşiune constantă sau (, ) ( ), Q ν ν Dacă este ineenentă e temeratură, atunci relaţia evine: Q - ν ( ) 5.6 ariaţia e entroie într-o transformare izobară este ată e relaţia: (, ) (, ) 5.6 sau ν (, ) (, ) 5.63 În cazul în care călura secifică nu eine e temeratură în intervalul e temeratură conşierat, se obţine: (, ) (, ) ln 5.64 Deci se observă că în transformarea izobară entroia variază în funcţie e temeratură într-un mo logaritmic Procese izocore 5
16 Forma generală a izocorelor unui gaz real într-o, iagrama (,) şi (,) este rerezentata în fig. Parametri într-o stare ot fi eterminati cunoscân arametri într-o stare e referinţă şi foloşin iagramele e stare, ecuaţiile caracteristice şi tabelele cu rorietăţile termoinamice ale substanţei stuiate. Parametri e stare entru gazul ieal sunt legaţi rin ecuaţia care se oate etermina şi intr-o olitroă cu n tinzân la infinit. reşterea temeraturii gazului care se află într-un volum constant etermină toteauna creşterea reşiunii iar această creştere este cu atât mai raiă cu cât volumul este mai mic. Încălzirea gazelor reale şi a lichielor rovoacă tot o creştere a reşiunii; mai mult, această creştere este senşibil mai raiă în lichie ecât în gaze. Este interesant e remarcat o articularitate curioasă a izocorelor aei la temeraturi scăzute. e ştie că la temeratura e 3,98 o enşitatea aei este maximă la reşiune atmosferică normală. n stuiu etaliat arată că în acest omeniu al temeraturii izocorele aei sunt e forma rerezentata în Fig. 5.7; izocorele cu v< ml/g trec rin minim în vecinatatea unctului cu temeratura 3,98 0, iar izocora v ml/g este tangentă la curba e saturaţie. La stânga unctelor e minim izocorele au anta negativă, aică <0. Fig Izocorele aei entru v>, ml/g âna la valoarea v, ml/g, care coresune unctului trilu, au articularitatea că intersectează e oua ori curba e saturaţie: o ată cu anta ozitiva iar o ata cu anta negativa. Astfel, acă aa arcurge o transformare izocoră entru < A,încalzirea sistemului uce la micşorarea reşiunii. ân temeratura creşte sistemul care coresune izotermelor, ml/g<v<, ml/g trece e la starea cu o şingura faza la starea cu oua faze, iar aoi in nou la starea cu o şingură fază. Lucrul mecanic e estinere într-o transformare izocoră este zero. Aceasta se vee in relaţia : 6
17 L ar şi in L entru transformarea olitroică. alura furnizată sistemului într-o încălzire izocoră se calculează ornin e la rinciiul I: δq ; δq şi în consecinţă exreşia ei va fi: Q (, ) (, ) 5.66 Diferenţa intre energiile interne ale celor ouă stări entru transformarea izocoră se etermină in: (, ) ( ), ν Deci călura se etermină ca integrală in: Q ν Dacă se foloseşte călura molară sau secifică meie atunci: Q - ν me ( ) 5.68 iar acă călura molară este constantă ca în cazul gazului ieal exreşia evine: Q - ν ( ) 5.67 ariaţia entroiei într-o transformare izocoră se etermină astfel: (, ) (, ) 5.69 şi ţinân seama e relaţia Maxwell: ν (, ) (, ) 5.70 Dacă în intervalul secificat călura secifică este constantă atunci: (, ) (, ) ν ln 5.7 eci e-a lungul izocorei entroia variază logaritmic cu temeratura Laminarea. Efectul Joule -homson e stie in exerienta, ca aca un jet e gaz sau e lichi care curge e-a lungul unui tub sau al unei conucte, întâlneste un obstacol care rouce o micsorare brusca a sectiunii transversale a jetului, iar în continuare sectiunea jetului creste, atunci reşiunea gazului (lichiului) este toteauna mai mica ua obstacol ecât înainte e el. n asemenea obstacol se numeste rezistenta locala. Efectul micsorarii reşiunii jetului e flui motor care curge rintr-o gâtuire a unei conucte oarta numele e laminare. Laminarea este un roces frecvent în ractica: curgerea aei rintr-un robinet artial închis sau trecerea aerului rintr-un registru artial eschis. Efectul rous e isozitivele e gâtuire se manifesta rin micsorarea reşiunii ua rezistenta locala. Din unct e veere fizic, scaerea reşiunii ua o rezistenta locala se exlica rin işiarea fluxului e energie entru învingerea rezistentei locale. 7
18 tuiem curgerea unui gaz (lichi) e-a lungul unui tub care rezinta o rezistenta locala, e exemlu o iafragma. Înainte şi uă iafragmă secţiunea tubului este aceeaşi şi astfel vom neglija variaţia energiei cinetice a fluiului în curgere. În timul laminarii fluiul motor oate rimi calură, ar noi vom stuia cazul cân acest roces este aiabatic, aică curgerea fluiului rin iafragmă se face fără schimb e călură (ereţii tubului vor fi într-un înveliş aiabatic). ă conşierăm la un moment at o masă e gaz curinsă între cele ouă secţiuni, I înainte e rezistenţa locală şi II uă rezistenţa locală, e fat ouă istoane imonerabile (Fig.5.8.). Deoarece gazul curge este normal ca cele ouă istoane să se elaseze e-a lungul tubului. Notam cu aria secţiunii tubului aică aria istoanelor convenţionale şi cu,, şi,, resiunile, volumele şi resectiv temeraturile gazului înainte şi uă iafragmă. Într-un anumit interval e tim istonul I se va elasa e o istanta l iar istonul II e o istanta l >l eoarece resiunea şi ensitatea gazului sunt mai mici ua iafragma ecât înaintea ei. Lucrul mecanic efectuat entru elasarea istonului e istanta l va fi L I l cu volumul e gaz îmins e istonul I rin iafragma. Lucrul mecanic efectuat e istonul II care se elaseaza îmotriva resiunii va fi L II. Prin elasarea masei e gaz consierate se rouce într-un interval e tim at un lucru mecanic egal cu iferenta L II - L I -. Acest lucru mecanic este consumat entru învingerea rezistenţei locale; el se transformă în călură. Deoarece rocesul examinat este aiabatic lucrul mecanic este rezultatul variatiei energiei interne: L -( - ) Deci: - -( - ) şi Aică 5.7 Rezultatul obţinut este imortant aratân că: în urma laminării aiabatice valorile entaliei unui flui sunt aceleaşi înainte şi uă rezistenţa locală. Ne interesează cum variază alţi arametri sau funcţii în acest roces e laminare care este un roces ireversibil. Într-aevăr, acă imaginăm rocesul în sens invers (în tub se inverseaza sensul e curgere) toteauna se constată o micşorare a resiunii uă trecerea gazului rin rezistenţa locală. Acest fat este natural eoarece energia fluxului este consumată entru a învinge rezistenţa locală atât într-un sens cât şi în celălalt. 8
19 Întrucât transformarea este aiabatică şi ireversibilă, entroia gazului (lichiului), creşte. Înainte e a calcula entroia trebuie facută următoarea observaţie: ecuaţiile iferenţiale ale termoinamicii folosite entru calcularea variatiilor temeraturii, entroiei,etc sunt sunt alicabile transformarilor reversibile. Deci entru a le alica entru calculul variatiilor starii gazului în cazul laminarii aiabatice ireversibile in starea în starea, trebuie aleasa schema unei transformari reversibile care sa faca sa treaca fluiul consierat in aceeaşi stare (inainte e iafragma) în aceeaşi stare finala (e uă). a transformare reversibila se oate lua e exemlu o ilatare a gazului cu ceare (rimire ) e calură, astfel încât entalia gazului să ramână constantă: sre eosebire e laminarea aiabatică ireversibilă, ilatarea izentalică (<0) nu oate fi în acelaşi tim şi aiabatică; in δq - se vee că entru δq0 şi 0 entalia nu oate ramâne neschimbată, 0. Dacă se imaginează o transformare reversibilă aiabatică şi izentalică atunci gazul nu va suferi nici-o ilatare sau altfel sus starea gazului nu se va schimba şi eci nu va avea loc nici-o transformare. ariaţia entroiei gazului care rezultă in această transformare reversibilă (variatie care este egala cu cea a entroiei în laminarea gazului in starea în starea ) va fi: (, ) - (, ) 5.73 care se oate scrie, ţinân seama e relaţia funamentală: (, ) (, ) 5.74 sau (, ) (, ) 5.75 aceasta ultimă exresie este mai comoa entru ca <, şi in ecuaţie rezultă că întoteauna >, eci entroia creşte. ă examinăm acum variaţia temeraturii gazului sau lichiului în cursul laminării aiabatice. Întrucât această transformare este caracterizată rin coniţia const. entru rezolvarea acestei robleme este necesar sa calculăm valoarea erivatei P Din relaţia e ciclicitate: Pentru a evalua exresia termoinamicii: se orneşte e la relaţia funamentală a 9
20 ), ( ), (, şi ientificân termenii celor ouă ecuatii se obţine: ş i Marimea P se numeste coeficient e laminare aiabatică sau efect Joule- homson iferenţial şi se noteaza cu α. În cazul general α este iferit e zero. ariaţia temeraturii gazelor şi lichielor ca urmare a laminării aiabatice a rimit numele e efect Joule - homson. Marimea α se numeşte coeficient Joule - homson. Măsurân efectul Joule - homson iferenţial, aică o iferenţă finită e temeratură foarte mică, entru o iferenţă e resiune e acelaşi orin e marime e-o arte şi e alta a iafragmei, se oate etermina α şi aoi cunoscânu-l e α se oate construi iagrama (, ) a substanţei e stuiat, se ot etermina calura secifică, volumul secific şi alte funcţii calorice. ariaţia temeraturii gazului (sau lichiului) în rocesul e laminare aiabatică, în cazul unei schimbări însemnate a resiunii în zona e rezistenţă, a rimit numele e efect Joule-homson integral şi este escris e relaţia: 5.78 α în care şi sunt temeraturile fluiului înainte şi ua iafragmă. Efectul Joule homson integral oate atinge o valoare foarte mare. De exemlu, în laminarea aiabatică a vaorilor e aă e la kpa la 450 o âna la 98 kpa, temeratura vaorilor scae ână la 80 o, aică cu 70 o. e une urmatoarea întrebare: temeratura fluiului scae întoteauna într-o laminare aiabatică sau care este semnul efectului Joule- homson? Pentru că întoteauna > 0, semnul efectului Joule-homson iferenţial α este at e semnul exresiei:
21 este evient că acă < 5.80 atunci α < 0 iar laminarea aiabatică este însoţită e creşterea temeraturii fluiului. Dacă > 5.8 α > 0 iar laminarea aiabatică uce la micşorarea temeraturii fluiului. În sfârşit, acă 5.8 atunci α 0 aică temeratura fluiului ramâne neschimbată în laminarea aiabatică. Relaţia este aevarată entru gazul erfect, ceea ce înseamnă că în laminare gazul erfect nu îşi moifica temeratura. Deci efectul Joule-homson nu se manifestă ecât în gazele reale ( şi entru un gaz care se suune ec. an er Waals) şi în lichie. Fig.5.9. urba e inversie a azotului în iagrama (, ) Exerienţa arată că entru aceeaşi substanţă semnul lui α eine e omeniul stărilor acestei substanţe. tarea fluiului în care α este nul a căătat numele e unct e inversie al efectului Joule - homson. locul geometric al unctelor e inversie într-o iagramă e stare a unei substanţe se numeste curba e inversie a efectului Joule - homson. În Fig. 5.9 este rerezentata curba e inversie a azotului în iagrama (, ). În interiorul regiunii elimitate e curba e inversie α > 0, aică laminarea antrenează o răcire a gazului. În exteriorul curbei α <0 aică rocesul este însotit e o încalzire a gazului. urbele e inverşie a altor substante au o alura şimilara. Laminarea aiabatica oate fi foloşita ca un roceeu eficient entru racirea gazelor. Este clar ca un gaz nu se va raci ecât în cazul în care starea sa se va afla în regiunea în care α >0 aica în regiunea şituata sub curba e inverşie. Este interesant sa comaram acest roceeu e racire cu cel rin estinere aiabatica reversibilă esre care am vorbit într-un aragraf receent. om comara entru aceasta valorile erivatelor: si.
22 ltima erivată oate fi numită coeficient e ilatare aiabatică reversibilă (aica izentroică) şi rin analogie cu α o vom nota cu α şi oate fi rerezentat in ecuaţia e ciclicitate sub forma: şi tinân seama e ec Maxwell, se obţine : α otrivit ecuaţiei 5.8 coeficientul e laminare aiabatică (aică e ilatare aiabatică reversibilă) este 5.8 α şi se obţine: α α 5.83 Deoarece valorile lui şi sunt ozitive, α > α a urmare, se vee ca ilatarea aiabatică reversibilă (cu lucru mecanic exterior) asigură in unct e veere termoinamic, o răcire mai eficientă a unui gaz sau a unui lichi ecât laminarea aiabatică, aică o estinere aiabatică ireversibilă Destinerea aiabatică a unui gaz real în vi (etenta Joule) a examinăm încă o transformare ireversibilă tiică unui gaz real, ilatarea aiabatică în vi, fără lucru mecanic exterior. În cazul unui gaz erfect, stuiul exerimental al ilatării aiabatice fără lucru mecanic exterior a ermis lui Gay- Lussac şi aoi lui Joule să stabilească că temeratura gazului ieal nu variaza într-o astfel e transformare; acest fat a ermis să se enunţe o rorietate imortantă a gazelor erfecte: energia internă nu eine e volum. ă stuiem legile estinerii aiabatice a gazului real în vi, ornin e la exerimentul care resuune că şi la cel al gazului ieal un vas îmărţit în ouă ărţi rintr-un erete esărţitor mobil; o arte conţine gaz la temeratura în tim ce cealaltă este viată. asul este izolat aiabatic, eci nu există nici-un schimb e călură cu meiul exterior. La eblocarea eretelui gazul se estine în vi, eterminân o micşorare a resiunii, gazul ocuân întreg volumul. emeratura şi entroia variază în aceasta transformare şi variaţiile le vom calcula în cele ce urmează.
23 Primul rinciiu al termoinamicii se scrie: Q meiu δ P P P0 Dilatarea este aiabatică iar L 0 eoarece meiu 0, gazul estizânu-se fără efectuare e lucru mecanic. a urmare 0 şi eci const., aică în timul estinerii aiabatice a gazului în vi, energia internă a gazului rămâne neschimbată. ariaţia temeraturii gazului în funcţie e volum într-o transformare const. se etermină in relaţia: ), ( ), ( 5.84 Derivata arţială care intervine în această relaţie oate fi usă sub forma: şi v 5.85 şi înlocuin valoarea în ecuatia 5.84 se obţine: ), ( ), ( 5.86 Această relaţie arată că în cazul general temeratura gazului se micşorează în timul estinerii aiabatice în vi. Deoarece entru o substanţă reală avem întoteauna: > 0 şi >0 în transformarea examinată avem, <. Pentru un gaz erfect estinerea aiabatică în vi nu rouce nici-o variaţie a temeraturii: 0. erf şi ca urmare 0. erf
24 unoscân valorile şi nu este ificil cu ajutorul iagramelor e stare sau a tabelelor cu rorietăţile termoinamice să se afle valoarea resiunii gazului in vas uă ilatarea lui âna la resiunea.. În transformarea stuiată variaţia entroiei gazului este ată e relaţia evientă: (, ) (, ) 5.88 şi ţinân seama e relaţia: se obţine: (, ) (, ) 5.90 integrala in ec (5.90) se calculează cu ajutorul tabelelor rorietăţilor termoinamice ale gazelor (se construieste curba functiei /f() entru const, aoi se integrează aceasta curba între şi ). Întrucât integrala in membrul al oilea al acestei egalităţi este toteauna ozitivă, avem: >., aica în estinerea Joule, care este o transformare ireversibilă tiică, entroia creşte. Pentru un gaz ieal, înlocuin valoarea lui / in ecuaţia e stare R in relatia (5.90) se obţine: (, ) (, ) Rln 5.9 e constată aceeasi eenenţă e ti logaritmic a variaţiei entroiei entru gazul ieal PRINIPIL AL III-LEA AL ERMODINAMIII 6.. Formularea rinciiului al III-lea al termoinamicii La efinirea scării termoinamice a temeraturii s-a subliniat fatul ca ioteza existenţei unui sistem care ar avea temeratura termoinamica egala cu zero (zero absolut) este în contraicţie cu rinciiul al II-lea al termoinamicii. În schimb, existenţa unor stări cu temeraturi oricât e aroiate e zero absolut nu contravine nici unui rinciiu. Are eci sens să ne întrebăm ce evin anumite mărimi termoinamice atunci cân temeratura tine catre zero absolut. om stuia în secial entroia ca functie e şi sau şi. ν > 0 6. ν > 0 4
25 aică entroia este monotonă în raort cu : escreşte o ată cu escreşterea temeraturii. O teoremă matematică ne asigură atunci, că acă 0, entroia tine către o valoare finită sau - : lim lim 0 finit 6. 0 finit > 0 > 0 a urmare utem rerezenta grafic, (,) entru ouă valori ale volumului şi cu >. Fig.6.. Deenenta entroiei e cân 0 Fig. 6.a.contravine rinciiului al II-lea: acă efectuăm o comrimare izotermă (A B) şi aoi o estinere aiabatică(b ), constatăm că fluiul atinge starea entru 0 înainte ca volumul să fi atins volumul, eci contrazice afirmatia: fiecarei stari îi coresune o anumită entroie. erinţele rinciiului al II-lea nu sunt resectate ecât acă limita entroiei este aceeaşi fie finită sau infinită oricare ar fi volumul (in 6.b şi 6.c). În urma unor cercetări foarte amle asura comortării sistemelor la temeraturi foarte joase, W. Nernst (906) a ajuns la concluzia că în natură nu oate fi realizată ecât starea 6.c, amisă e rinciiul al II-lea al termoinamicii. Posibilitatea 6.b eşi conformă cu rinciiul al II-lea este interzisă e rinciiul Nernst. Deci în cazul 6.c, 0 const., 0 fiin o constantă care nu eine e arametri e stare. Această relaţie constituie exresia matematică a teoremei Nernst. eorema Nernst: La zero absolut entroia oricărui sistem termoinamic are o valoare constanta (un roces izoterm este şi izentroic sau izoterma e zero absolut coincie cu aiabata). 5
26 Analizân concluziile lui Nernst, Planck formuleaza cel e-al III-lea rinciiu al termoinamicii: în cazul sistemelor omogene conensate, entroia tine către o valoare limita nulă, cân temeratura tine catre zero absolut Formula nu se alica la sisteme olicomonente (solutii, aliaje ) şi soliele amorfe. Altă formulare a eoremei Nernst-Planck: la zero absolut entroia oricărui sistem termoinamic la echilibru este zero, sau izoterma e zero absolut coincie cu aiabata e zero. 6.. onsecintele rinciiului al III-lea 6... Princiiul al III-lea are rolul e a fixa valoarea constantei entroiei. Funcţiile termoinamice se etermină ânăla o constanta aitivă. alorile acestor constante nu ot fi cunoscute e baza rinciiilor I, II ; rinciiul al III-lea etermină funcţiile termoinamice ca valori absolute şi nu ca variaţii. δq 6.4 starea fiin aleasă arbitrar. sau δq Relaţia 6.5 este valabilă acă în omeniul e temeraturi 0 nu au loc transformări e stare e agregare sau transformări olimorfe. Dacă astfel e transformări au loc, integrarea se face e orţiuni şi se însumează entroiile care însoţesc transformările resective. Astfel, e exemlu, la încălzirea unui mol e substanţă soliă care în intervalul e temeratura 0 trece în stare lichiă şi aoi în stare e vaori, entroia molară la temeratura şi resiunea e atm va fi : t 0 λt, s v, l λv t t v v. g Imosibilitatea rinciială a atingerii temeraturii e zero absolut Fig. 6.. iclul arnot care conţine izoterma e zero absolut iclul arnot în (,) contine izoterma e zero absolut. Q/ Întrucât Q 0, şi 0 e întreg ciclul, se obţine un rezultat absur. Deci temeratura e 0 K nu este accesibilă. nii autori consieră inaccesibilitatea temeraturii e zero absolut ca un enunţ echivalent al rinciiului al III-lea. 6
27 Fig Pentru ca 0 cân 0, izocorele e şi trec rin origine. ariaţiile e temeratură entru fiecare treată e estinere aiabatică alcătuiesc un şir escrescător format in termeni care tin săse anuleze în aroiere e 0 K. Rezultă, că rintr-un numar finit e transformări izoterme temeratura e 0 K nu se oate atinge omortarea coeficientilor termici cân 0 K. α si β şi α 6.7 β 6.8 um lim (, ) 0, limα lim β 0 ) ) 0 În stările in vecinătatea stării e zero absolut, substanţele îşi ier rorietăţile e ilatare, e elasticitate termică, în acor cu exerienţa omortarea coeficientilor calorici cân 0 K şi ν 6.0 ν Prin integrare rezultă : ν ν (, ) şi (, ) Integralele trebuie să fie convergente. Entroiile in relaţiile 6.0 şi 6. sunt finite numai aca, 0 cân 0 K rezulta lim (, ) 0 lim (, )
28 6..5. Limitele rinciiului al III-lea a) Alicarea la un număr restrâns e sisteme imlică un gra e generalitate reus faţă e celelalte rinciii. e contesta că ar fi rinciiu entru că nu a introus nici-o funcţie e stare. b) Limitarea rinciiului al III-lea la sistemele conensate imlică criterii e valabilitate a moelelor fizice. Astfel, sistemul gaz ieal şi gaz real nu sunt în echilibru termoinamic la 0 K şi ecuaţiile lor e stare nu se alică entru 0 K (gazul se egenerează, aică gazul se găseşte în starea e egenerare, fenomen exlicat e statistica cuantică). Exemlu: ct ct. α β (,) ν (,) ν 0 0 (, ) ν( R ln ln s0 ) ν (, ) ν( ln Rln s ) 0 şi ca urmare 0 K imlica α, β 6.3.Limitele e alicabilitate ale rinciiilor a) Limita inferioară: nu se alica la microsisteme. nu are sens entru o articulă. Princiiul al II-lea stabileşte eosebirea intre forma microfizica e transmitere a energiei - calura şi forma macrofizică legată e variaţia arametrilor externi - lucrul mecanic. În cazul sistemelor ale caror imensiuni sunt comarabile cu imensiunile moleculare isare eosebirea intre notiunile e calura şi L şi e aceea entru aceste sisteme (macrosisteme) nu au sens arametrii termoinamici:, entroie, etc. b) Limita suerioară Postulatul termoinamic asura echilibrului termic, asura trecerii inevitabile a unui sistem izolat în stare e echilibru şi imosibilitatea e a ieşi e la sine in aceasta stare, recum şi legea creşterii entroiei în asemenea sisteme sunt rezultate ale generalizarii atelor exerimentale în sisteme e imensiuni finite. Extinerea necritică a acestor legi la sisteme e imensiuni infinite fără analizarea moificarilor rofune oate uce (a şi us) la concluzii neştiinţifice (moartea termică a universului). eoria morţii termice a fost formulata e lausius care scria: Energia lumii rămâne constantă, entroia lumii tine către valoarea maximă, eci mai evreme sau mai târziu niversul ajunge la echilibru termoinamic; atunci toate rocesele ar înceta şi lumea s-ar scufuna în stare e moarte termică. 8
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Emil Petrescu Viorel Păun
 Probleme de fizică Emil Petrescu iorel Păun October 6, 2004 Curins 4 ERMODINAMICĂ 72 72 Caitolul 4 ERMODINAMICĂ PROBLEMA 4.1 a Să se demonstreze că în cazul unui roces adiabatic alicat unui gaz ideal este
Probleme de fizică Emil Petrescu iorel Păun October 6, 2004 Curins 4 ERMODINAMICĂ 72 72 Caitolul 4 ERMODINAMICĂ PROBLEMA 4.1 a Să se demonstreze că în cazul unui roces adiabatic alicat unui gaz ideal este
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
1. NOŢIUNI TERMODINAMICE DE BAZĂ
 . NOŢIUNI TERMODINAMIE DE BAZĂ.. Noţiuni desre structura discretă a substanţei onceţia atomistă desre substanţă enunţată acum 5 ani de către Leuci şi Democrit, a fost confirmată în secolul al XIII-lea
. NOŢIUNI TERMODINAMIE DE BAZĂ.. Noţiuni desre structura discretă a substanţei onceţia atomistă desre substanţă enunţată acum 5 ani de către Leuci şi Democrit, a fost confirmată în secolul al XIII-lea
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
2.PRIMUL PRINCIPIU AL TERMODINAMICII
 0 Termotehnica.PRIMUL PRINCIPIU AL TERMODINAMICII Noţiunea de rinciiu defineşte o afirmaţie care nu se oate demonstra matematic. Princiiul rerezintă rezultatul studiilor exerimentale asura roceselor din
0 Termotehnica.PRIMUL PRINCIPIU AL TERMODINAMICII Noţiunea de rinciiu defineşte o afirmaţie care nu se oate demonstra matematic. Princiiul rerezintă rezultatul studiilor exerimentale asura roceselor din
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
5.1. Noţiuni introductive
 ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
ursul 13 aitolul 5. Soluţii 5.1. oţiuni introductive Soluţiile = aestecuri oogene de două sau ai ulte substanţe / coonente, ale căror articule nu se ot seara rin filtrare sau centrifugare. oonente: - Mediul
CALCULUL ENTALPIEI, ENTROPIEI ŞI A ENTALPIEI LIBERE LA DIFERITE TEMPERATURI
 CALCULUL ENALPIEI, ENROPIEI ŞI A ENALPIEI LIBERE LA DIFERIE EMPERAURI 1. Consideraţii teoretice Entalia H este o funcţie de două variabile de stare indeendente, şi, adică H = H(,), rezultă că: H H dh =
CALCULUL ENALPIEI, ENROPIEI ŞI A ENALPIEI LIBERE LA DIFERIE EMPERAURI 1. Consideraţii teoretice Entalia H este o funcţie de două variabile de stare indeendente, şi, adică H = H(,), rezultă că: H H dh =
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
FIZICĂ. Elemente de termodinamica. ş.l. dr. Marius COSTACHE
 FIZICĂ Elemente de termodinamica ş.l. dr. Marius COSTACHE 1 ELEMENTE DE TERMODINAMICĂ 1) Noţiuni introductive sistem fizic = orice porţiune de materie, de la o microparticulă la întreg Universul, porţiune
FIZICĂ Elemente de termodinamica ş.l. dr. Marius COSTACHE 1 ELEMENTE DE TERMODINAMICĂ 1) Noţiuni introductive sistem fizic = orice porţiune de materie, de la o microparticulă la întreg Universul, porţiune
Curs 2 Şiruri de numere reale
 Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
3 FUNCTII CONTINUE Noţiuni teoretice şi rezultate fundamentale Spaţiul euclidian R p. Pentru p N *, p 2 fixat, se defineşte R
 3 FUNCTII CONTINUE 3.. Noţiuni teoretice şi rezultate fundamentale. 3... Saţiul euclidian R Pentru N *, fixat, se defineşte R = R R R = {(x, x,, x : x, x,, x R} de ori De exemlu, R = {(x, y: x, yr} R 3
3 FUNCTII CONTINUE 3.. Noţiuni teoretice şi rezultate fundamentale. 3... Saţiul euclidian R Pentru N *, fixat, se defineşte R = R R R = {(x, x,, x : x, x,, x R} de ori De exemlu, R = {(x, y: x, yr} R 3
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Noțiuni termodinamice de bază
 Noțiuni termodinamice de bază Alexandra Balan Andra Nistor Prof. Costin-Ionuț Dobrotă COLEGIUL NAȚIONAL DIMITRIE CANTEMIR ONEȘTI Septembrie, 2015 http://fizicaliceu.wikispaces.com Noțiuni termodinamice
Noțiuni termodinamice de bază Alexandra Balan Andra Nistor Prof. Costin-Ionuț Dobrotă COLEGIUL NAȚIONAL DIMITRIE CANTEMIR ONEȘTI Septembrie, 2015 http://fizicaliceu.wikispaces.com Noțiuni termodinamice
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
1.10. Lucrul maxim. Ciclul Carnot. Randamentul motoarelor
 2a temperatura de inversie este T i =, astfel încât λT i şi Rb λ>0 pentru T
2a temperatura de inversie este T i =, astfel încât λT i şi Rb λ>0 pentru T
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Ovidiu Gabriel Avădănei, Florin Mihai Tufescu,
 vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
vidiu Gabriel Avădănei, Florin Mihai Tufescu, Capitolul 6 Amplificatoare operaţionale 58. Să se calculeze coeficientul de amplificare în tensiune pentru amplficatorul inversor din fig.58, pentru care se
riptografie şi Securitate
 riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
riptografie şi Securitate - Prelegerea 12 - Scheme de criptare CCA sigure Adela Georgescu, Ruxandra F. Olimid Facultatea de Matematică şi Informatică Universitatea din Bucureşti Cuprins 1. Schemă de criptare
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
Tipul F2. m coboară cu frecare ( 0,5 ) pe prisma de. masă M 9 kg şi unghi 45. Dacă prisma se deplasează pe orizontală fără frecare şi
 Tiul F. În sistemul din figură, corul de masă 4 kg m coboară cu frecare ( 0, ) e risma de 0 masă M 9 kg şi unghi 4. Dacă risma se delasează e orizontală fără frecare şi g 0 m/s, modulul acceleraţiei rismei
Tiul F. În sistemul din figură, corul de masă 4 kg m coboară cu frecare ( 0, ) e risma de 0 masă M 9 kg şi unghi 4. Dacă risma se delasează e orizontală fără frecare şi g 0 m/s, modulul acceleraţiei rismei
ENUNŢURI ŞI REZOLVĂRI 2013
 ENUNŢURI ŞI REZOLVĂRI 8. Un conductor de cupru ( ρ =,7 Ω m) are lungimea de m şi aria secţiunii transversale de mm. Rezistenţa conductorului este: a), Ω; b), Ω; c), 5Ω; d) 5, Ω; e) 7, 5 Ω; f) 4, 7 Ω. l
ENUNŢURI ŞI REZOLVĂRI 8. Un conductor de cupru ( ρ =,7 Ω m) are lungimea de m şi aria secţiunii transversale de mm. Rezistenţa conductorului este: a), Ω; b), Ω; c), 5Ω; d) 5, Ω; e) 7, 5 Ω; f) 4, 7 Ω. l
Ecuatii trigonometrice
 Ecuatii trigonometrice Ecuatiile ce contin necunoscute sub semnul functiilor trigonometrice se numesc ecuatii trigonometrice. Cele mai simple ecuatii trigonometrice sunt ecuatiile de tipul sin x = a, cos
Ecuatii trigonometrice Ecuatiile ce contin necunoscute sub semnul functiilor trigonometrice se numesc ecuatii trigonometrice. Cele mai simple ecuatii trigonometrice sunt ecuatiile de tipul sin x = a, cos
Ecuatii exponentiale. Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. a x = b, (1)
 Ecuatii exponentiale Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. Cea mai simpla ecuatie exponentiala este de forma a x = b, () unde a >, a. Afirmatia.
Ecuatii exponentiale Ecuatia ce contine variabila necunoscuta la exponentul puterii se numeste ecuatie exponentiala. Cea mai simpla ecuatie exponentiala este de forma a x = b, () unde a >, a. Afirmatia.
( ) Recapitulare formule de calcul puteri ale numărului 10 = Problema 1. Să se calculeze: Rezolvare: (
 Exemple e probleme rezolvate pentru curs 0 DEEA Recapitulare formule e calcul puteri ale numărului 0 n m n+ m 0 = 0 n n m =0 m 0 0 n m n m ( ) n = 0 =0 0 0 n Problema. Să se calculeze: a. 0 9 0 b. ( 0
Exemple e probleme rezolvate pentru curs 0 DEEA Recapitulare formule e calcul puteri ale numărului 0 n m n+ m 0 = 0 n n m =0 m 0 0 n m n m ( ) n = 0 =0 0 0 n Problema. Să se calculeze: a. 0 9 0 b. ( 0
Continue. Answer: a. Logout. e-desc» Concurs Phi» Quizzes» Setul 1 - Clasa a X-a» Attempt 1. 1 of 2 4/14/ :27 PM. Marks: 0/1.
 Concurs Phi: Setul 1 - Clasa a X-a 1 of 2 4/14/2008 12:27 PM Logout e-desc» Concurs Phi» Quizzes» Setul 1 - Clasa a X-a» Attempt 1 1 Un termometru cu lichid este gradat intr-o scara de temperatura liniara,
Concurs Phi: Setul 1 - Clasa a X-a 1 of 2 4/14/2008 12:27 PM Logout e-desc» Concurs Phi» Quizzes» Setul 1 - Clasa a X-a» Attempt 1 1 Un termometru cu lichid este gradat intr-o scara de temperatura liniara,
Tranzistoare bipolare şi cu efect de câmp
 apitolul 3 apitolul 3 26. Pentru circuitul de polarizare din fig. 26 se cunosc: = 5, = 5, = 2KΩ, = 5KΩ, iar pentru tranzistor se cunosc următorii parametrii: β = 200, 0 = 0, μa, = 0,6. a) ă se determine
apitolul 3 apitolul 3 26. Pentru circuitul de polarizare din fig. 26 se cunosc: = 5, = 5, = 2KΩ, = 5KΩ, iar pentru tranzistor se cunosc următorii parametrii: β = 200, 0 = 0, μa, = 0,6. a) ă se determine
4.PRINCIPIUL AL II -LEA AL TERMODINAMICII
 4.PRINCIPIUL AL II -LEA AL ERMODINAMICII Istoria acestui principiu este una dintre fascinantele aventuri ale ştiinţei, care a generat nenumărate paradoxuri, controverse şi predicţii tulburătoare (moartea
4.PRINCIPIUL AL II -LEA AL ERMODINAMICII Istoria acestui principiu este una dintre fascinantele aventuri ale ştiinţei, care a generat nenumărate paradoxuri, controverse şi predicţii tulburătoare (moartea
Functii Breviar teoretic 8 ianuarie ianuarie 2011
 Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
IV. CUADRIPOLI SI FILTRE ELECTRICE CAP. 13. CUADRIPOLI ELECTRICI
 V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
V. POL S FLTE ELETE P. 3. POL ELET reviar a) Forma fundamentala a ecuatiilor cuadripolilor si parametrii fundamentali: Prima forma fundamentala: doua forma fundamentala: b) Parametrii fundamentali au urmatoarele
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Cursul Măsuri reale. D.Rusu, Teoria măsurii şi integrala Lebesgue 15
 MĂSURI RELE Cursul 13 15 Măsuri reale Fie (,, µ) un spaţiu cu măsură completă şi f : R o funcţie -măsurabilă. Cum am văzut în Teorema 11.29, dacă f are integrală pe, atunci funcţia de mulţime ν : R, ν()
MĂSURI RELE Cursul 13 15 Măsuri reale Fie (,, µ) un spaţiu cu măsură completă şi f : R o funcţie -măsurabilă. Cum am văzut în Teorema 11.29, dacă f are integrală pe, atunci funcţia de mulţime ν : R, ν()
FC Termodinamica. November 24, 2013
 FC Termodinamica November 24, 2013 Cuprins 1 Noţiuni fundamentale (FC.01.) 2 1.1 Sistem termodinamic... 2 1.2 Stări termodinamice... 2 1.3 Procese termodinamice... 3 1.4 Parametri de stare... 3 1.5 Lucrul
FC Termodinamica November 24, 2013 Cuprins 1 Noţiuni fundamentale (FC.01.) 2 1.1 Sistem termodinamic... 2 1.2 Stări termodinamice... 2 1.3 Procese termodinamice... 3 1.4 Parametri de stare... 3 1.5 Lucrul
 10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
10. STABILIZATOAE DE TENSIUNE 10.1 STABILIZATOAE DE TENSIUNE CU TANZISTOAE BIPOLAE Stabilizatorul de tensiune cu tranzistor compară în permanenţă valoare tensiunii de ieşire (stabilizate) cu tensiunea
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
1.3 Baza a unui spaţiu vectorial. Dimensiune
 .3 Baza a unui spaţiu vectorial. Dimensiune Definiţia.3. Se numeşte bază a spaţiului vectorial V o familie de vectori B care îndeplineşte condiţiile de mai jos: a) B este liniar independentă; b) B este
.3 Baza a unui spaţiu vectorial. Dimensiune Definiţia.3. Se numeşte bază a spaţiului vectorial V o familie de vectori B care îndeplineşte condiţiile de mai jos: a) B este liniar independentă; b) B este
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R. 4.1 Proprietăţi topologice ale lui R Puncte de acumulare
 Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Capitolul 4 PROPRIETĂŢI TOPOLOGICE ŞI DE NUMĂRARE ALE LUI R În cele ce urmează, vom studia unele proprietăţi ale mulţimilor din R. Astfel, vom caracteriza locul" unui punct în cadrul unei mulţimi (în limba
Problema a II - a (10 puncte) Diferite circuite electrice
 Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
Olimpiada de Fizică - Etapa pe judeţ 15 ianuarie 211 XI Problema a II - a (1 puncte) Diferite circuite electrice A. Un elev utilizează o sursă de tensiune (1), o cutie cu rezistenţe (2), un întrerupător
CURS 5 TERMODINAMICĂ ŞI FIZICĂ STATISTICĂ
 CURS 5 ERMODINAMICĂ ŞI FIZICĂ SAISICĂ 5.. Noţiuni fundamentale. Corpurile macroscopice sunt formate din atomi şi molecule, constituenţi microscopici aflaţi într-o mişcare continuă, numită mişcare de agitaţie
CURS 5 ERMODINAMICĂ ŞI FIZICĂ SAISICĂ 5.. Noţiuni fundamentale. Corpurile macroscopice sunt formate din atomi şi molecule, constituenţi microscopici aflaţi într-o mişcare continuă, numită mişcare de agitaţie
2 Transformări liniare între spaţii finit dimensionale
 Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
Transformări 1 Noţiunea de transformare liniară Proprietăţi. Operaţii Nucleul şi imagine Rangul şi defectul unei transformări 2 Matricea unei transformări Relaţia dintre rang şi defect Schimbarea matricei
1. PROPRIETĂȚILE FLUIDELOR
 1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
1. PROPRIETĂȚILE FLUIDELOR a) Să se exprime densitatea apei ρ = 1000 kg/m 3 în g/cm 3. g/cm 3. b) tiind că densitatea glicerinei la 20 C este 1258 kg/m 3 să se exprime în c) Să se exprime în kg/m 3 densitatea
Aplicatii tehnice ale gazului perfect si ale transformarilor termodinamice
 Aplicatii tehnice ale gazului perfect si ale transformarilor termodinamice 4.. Gaze perfecte 4... Definirea gazului perfect Conform teoriei cinetico-moleculare gazul perfect este definit prin următoarele
Aplicatii tehnice ale gazului perfect si ale transformarilor termodinamice 4.. Gaze perfecte 4... Definirea gazului perfect Conform teoriei cinetico-moleculare gazul perfect este definit prin următoarele
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].
![Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36].](/thumbs/72/67648751.jpg) Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Componente şi circuite pasive Fig.3.85. Impedanţa condensatoarelor electrolitice SMD cu Al cu electrolit semiuscat în funcţie de frecvenţă [36]. Fig.3.86. Rezistenţa serie echivalentă pierderilor în funcţie
Valori limită privind SO2, NOx şi emisiile de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili
 Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Anexa 2.6.2-1 SO2, NOx şi de praf rezultate din operarea LPC în funcţie de diferite tipuri de combustibili de bioxid de sulf combustibil solid (mg/nm 3 ), conţinut de O 2 de 6% în gazele de ardere, pentru
Componente şi Circuite Electronice Pasive. Laborator 3. Divizorul de tensiune. Divizorul de curent
 Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
Laborator 3 Divizorul de tensiune. Divizorul de curent Obiective: o Conexiuni serie şi paralel, o Legea lui Ohm, o Divizorul de tensiune, o Divizorul de curent, o Implementarea experimentală a divizorului
II. 5. Probleme. 20 c 100 c = 10,52 % Câte grame sodă caustică se găsesc în 300 g soluţie de concentraţie 10%? Rezolvare m g.
 II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
II. 5. Problee. Care ete concentraţia procentuală a unei oluţii obţinute prin izolvarea a: a) 0 g zahăr în 70 g apă; b) 0 g oă cautică în 70 g apă; c) 50 g are e bucătărie în 50 g apă; ) 5 g aci citric
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
EDITURA PARALELA 45 MATEMATICĂ DE EXCELENŢĂ. Clasa a X-a Ediţia a II-a, revizuită. pentru concursuri, olimpiade şi centre de excelenţă
 Coordonatori DANA HEUBERGER NICOLAE MUŞUROIA Nicolae Muşuroia Gheorghe Boroica Vasile Pop Dana Heuberger Florin Bojor MATEMATICĂ DE EXCELENŢĂ pentru concursuri, olimpiade şi centre de excelenţă Clasa a
Coordonatori DANA HEUBERGER NICOLAE MUŞUROIA Nicolae Muşuroia Gheorghe Boroica Vasile Pop Dana Heuberger Florin Bojor MATEMATICĂ DE EXCELENŢĂ pentru concursuri, olimpiade şi centre de excelenţă Clasa a
Curs 2 DIODE. CIRCUITE DR
 Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Curs 2 OE. CRCUTE R E CUPRN tructură. imbol Relația curent-tensiune Regimuri de funcționare Punct static de funcționare Parametrii diodei Modelul cu cădere de tensiune constantă Analiza circuitelor cu
Forme de energie. Principiul I al termodinamicii
 Forme de energie. Principiul I al termodinamicii Există mai multe forme de energie, care se pot clasifica după natura modificărilor produse în sistemele termodinamice considerate şi după natura mişcărilor
Forme de energie. Principiul I al termodinamicii Există mai multe forme de energie, care se pot clasifica după natura modificărilor produse în sistemele termodinamice considerate şi după natura mişcărilor
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
z a + c 0 + c 1 (z a)
 1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
a. Caracteristicile mecanice a motorului de c.c. cu excitaţie independentă (sau derivaţie)
 Caracteristica mecanică defineşte dependenţa n=f(m) în condiţiile I e =ct., U=ct. Pentru determinarea ei vom defini, mai întâi caracteristicile: 1. de sarcină, numită şi caracteristica externă a motorului
Caracteristica mecanică defineşte dependenţa n=f(m) în condiţiile I e =ct., U=ct. Pentru determinarea ei vom defini, mai întâi caracteristicile: 1. de sarcină, numită şi caracteristica externă a motorului
CURS VII-IX. Capitolul IV: Funcţii derivabile. Derivate şi diferenţiale. 1 Derivata unei funcţii. Interpretarea geometrică.
 Lect dr Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr Lucian MATICIUC CURS VII-IX Capitolul IV: Funcţii derivabile Derivate şi diferenţiale 1
Lect dr Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr Lucian MATICIUC CURS VII-IX Capitolul IV: Funcţii derivabile Derivate şi diferenţiale 1
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
3 TRANSFORMĂRI SIMPLE DE STARE A GAZELOR
 34 ermotehica 3 RANSFORMĂRI SIMPLE DE SARE A GAZELOR Î termodiamică se cosideră că rocesele e care le suferă ageţii termici î iteriorul istalaţiilor termice sut comuse ditr-u asamblu de trasformări termodiamice
34 ermotehica 3 RANSFORMĂRI SIMPLE DE SARE A GAZELOR Î termodiamică se cosideră că rocesele e care le suferă ageţii termici î iteriorul istalaţiilor termice sut comuse ditr-u asamblu de trasformări termodiamice
VII.2. PROBLEME REZOLVATE
 Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
Teoria Circuitelor Electrice Aplicaţii V PROBEME REOVATE R7 În circuitul din fiura 7R se cunosc: R e t 0 sint [V] C C t 0 sint [A] Se cer: a rezolvarea circuitului cu metoda teoremelor Kirchhoff; rezolvarea
1.7. AMPLIFICATOARE DE PUTERE ÎN CLASA A ŞI AB
 1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
1.7. AMLFCATOARE DE UTERE ÎN CLASA A Ş AB 1.7.1 Amplificatoare în clasa A La amplificatoarele din clasa A, forma de undă a tensiunii de ieşire este aceeaşi ca a tensiunii de intrare, deci întreg semnalul
Principiul Inductiei Matematice.
 Principiul Inductiei Matematice. Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural. Metoda inductiei
Principiul Inductiei Matematice. Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural. Metoda inductiei
Progresii aritmetice si geometrice. Progresia aritmetica.
 Progresii aritmetice si geometrice Progresia aritmetica. Definitia 1. Sirul numeric (a n ) n N se numeste progresie aritmetica, daca exista un numar real d, numit ratia progresia, astfel incat a n+1 a
Progresii aritmetice si geometrice Progresia aritmetica. Definitia 1. Sirul numeric (a n ) n N se numeste progresie aritmetica, daca exista un numar real d, numit ratia progresia, astfel incat a n+1 a
Stabilizator cu diodă Zener
 LABAT 3 Stabilizator cu diodă Zener Se studiază stabilizatorul parametric cu diodă Zener si apoi cel cu diodă Zener şi tranzistor. Se determină întâi tensiunea Zener a diodei şi se calculează apoi un stabilizator
LABAT 3 Stabilizator cu diodă Zener Se studiază stabilizatorul parametric cu diodă Zener si apoi cel cu diodă Zener şi tranzistor. Se determină întâi tensiunea Zener a diodei şi se calculează apoi un stabilizator
Unitatea atomică de masă (u.a.m.) = a 12-a parte din masa izotopului de carbon
 ursul.3. Mării şi unităţi de ăsură Unitatea atoică de asă (u.a..) = a -a parte din asa izotopului de carbon u. a.., 0 7 kg Masa atoică () = o ărie adiensională (un nuăr) care ne arată de câte ori este
ursul.3. Mării şi unităţi de ăsură Unitatea atoică de asă (u.a..) = a -a parte din asa izotopului de carbon u. a.., 0 7 kg Masa atoică () = o ărie adiensională (un nuăr) care ne arată de câte ori este
6 n=1. cos 2n. 6 n=1. n=1. este CONV (fiind seria armonică pentru α = 6 > 1), rezultă
 Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Semiar 5 Serii cu termei oarecare Probleme rezolvate Problema 5 Să se determie atura seriei cos 5 cos Soluţie 5 Şirul a 5 este cu termei oarecare Studiem absolut covergeţa seriei Petru că cos a 5 5 5 şi
Esalonul Redus pe Linii (ERL). Subspatii.
 Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
Seminarul 1 Esalonul Redus pe Linii (ERL). Subspatii. 1.1 Breviar teoretic 1.1.1 Esalonul Redus pe Linii (ERL) Definitia 1. O matrice A L R mxn este in forma de Esalon Redus pe Linii (ERL), daca indeplineste
SEMINARUL 3. Cap. II Serii de numere reale. asociat seriei. (3n 5)(3n 2) + 1. (3n 2)(3n+1) (3n 2) (3n + 1) = a
 Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Capitolul II: Serii de umere reale. Lect. dr. Lucia Maticiuc Facultatea de Hidrotehică, Geodezie şi Igieria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucia MATICIUC SEMINARUL 3. Cap. II Serii
Modelare şi simulare Seminar 4 SEMINAR NR. 4. Figura 4.1 Reprezentarea evoluţiei sistemului prin graful de tranziţii 1 A A =
 SEMIR R. 4. Sistemul M/M// Caracteristici: = - intensitatea traficului - + unde Figura 4. Rerezentarea evoluţiei sistemului rin graful de tranziţii = rata medie de sosire a clienţilor în sistem (clienţi
SEMIR R. 4. Sistemul M/M// Caracteristici: = - intensitatea traficului - + unde Figura 4. Rerezentarea evoluţiei sistemului rin graful de tranziţii = rata medie de sosire a clienţilor în sistem (clienţi
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
V O. = v I v stabilizator
 Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
Stabilizatoare de tensiune continuă Un stabilizator de tensiune este un circuit electronic care păstrează (aproape) constantă tensiunea de ieșire la variaţia între anumite limite a tensiunii de intrare,
SEMINAR TRANSFORMAREA FOURIER. 1. Probleme
 SEMINAR TRANSFORMAREA FOURIER. Probleme. Să se precizeze dacă funcţiile de mai jos sunt absolut integrabile pe R şi, în caz afirmativ să se calculeze { transformata Fourier., t a. σ(t), t < ; b. f(t) σ(t)
SEMINAR TRANSFORMAREA FOURIER. Probleme. Să se precizeze dacă funcţiile de mai jos sunt absolut integrabile pe R şi, în caz afirmativ să se calculeze { transformata Fourier., t a. σ(t), t < ; b. f(t) σ(t)
8 Intervale de încredere
 8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
8 Intervale de încredere În cursul anterior am determinat diverse estimări ˆ ale parametrului necunoscut al densităţii unei populaţii, folosind o selecţie 1 a acestei populaţii. În practică, valoarea calculată
ALGEBRĂ ŞI ELEMENTE DE ANALIZĂ MATEMATICĂ FIZICĂ
 Sesiunea august 07 A ln x. Fie funcţia f : 0, R, f ( x). Aria suprafeţei plane delimitate de graficul funcţiei, x x axa Ox şi dreptele de ecuaţie x e şi x e este egală cu: a) e e b) e e c) d) e e e 5 e.
Sesiunea august 07 A ln x. Fie funcţia f : 0, R, f ( x). Aria suprafeţei plane delimitate de graficul funcţiei, x x axa Ox şi dreptele de ecuaţie x e şi x e este egală cu: a) e e b) e e c) d) e e e 5 e.
FIZICĂ. Bazele fizice ale mecanicii cuantice. ş.l. dr. Marius COSTACHE
 FIZICĂ Bazele fizice ale mecanicii cuantice ş.l. d. Maius COSTACHE 1 BAZELE FIZICII CUANTICE Mecanica cuantică (Fizica cuantică) studiază legile de mişcae ale micoaticulelo (e -, +,...) şi ale sistemelo
FIZICĂ Bazele fizice ale mecanicii cuantice ş.l. d. Maius COSTACHE 1 BAZELE FIZICII CUANTICE Mecanica cuantică (Fizica cuantică) studiază legile de mişcae ale micoaticulelo (e -, +,...) şi ale sistemelo
9. Statica solidului rigid...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
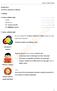 SEMINAR 9 STATICA SOLIDULUI RIGID CUPRINS 9. Statica solidului rigid...1 Curins...1 Introducere...1 9.1. Asecte teoretice...2 9.2. Alicaţii rezolvate...3 9. Statica solidului rigid În acest seminar se
SEMINAR 9 STATICA SOLIDULUI RIGID CUPRINS 9. Statica solidului rigid...1 Curins...1 Introducere...1 9.1. Asecte teoretice...2 9.2. Alicaţii rezolvate...3 9. Statica solidului rigid În acest seminar se
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Proiectarea filtrelor prin metoda pierderilor de inserţie
 FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
FITRE DE MIROUNDE Proiectarea filtrelor prin metoda pierderilor de inserţie P R Puterea disponibila de la sursa Puterea livrata sarcinii P inc P Γ ( ) Γ I lo P R ( ) ( ) M ( ) ( ) M N P R M N ( ) ( ) Tipuri
Exemple de probleme rezolvate pentru cursurile DEEA Tranzistoare bipolare cu joncţiuni
 Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
Problema 1. Se dă circuitul de mai jos pentru care se cunosc: VCC10[V], 470[kΩ], RC2,7[kΩ]. Tranzistorul bipolar cu joncţiuni (TBJ) este de tipul BC170 şi are parametrii β100 şi VBE0,6[V]. 1. să se determine
