Ε νικό και Καποδιστριακό Πανεπιστήμιο Α ηνών. Δι οτομίες Πο υπ οκότητας σε Προ ήματα Μέτρησης
|
|
|
- ÏἸάϊρος Παπανδρέου
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Ε νικό και Καποδιστριακό Πανεπιστήμιο Α ηνών Τμήμα Μα ηματικών Μεταπτυ ιακό Πρό ραμμα Λο ικής και Θε ρίας Α ορί μ ν και Υπο ο ισμού Δι οτομίες Πο υπ οκότητας σε Προ ήματα Μέτρησης Διπ ματική Ερ ασία του Στυ ιανού Δεσποτάκη Επι έπ ν: Άρης Πα ουρτζής Επίκουρος Κα η ητής Ιού ιος 2012
2
3 : 1. :.. ΙΙΙΙΙΙΙΙ 2. :. ΙΙΙΙΙΙΙΙ 3. :. ΙΙΙΙΙΙΙΙ
4 ii
5 iii Περί ηψη Στην παρούσα διπ ματική ερ ασία με ετάμε ε ρήματα δι οτομίας που αφορούν κυρί ς προ ήματα μέτρησης. Ένα εώρημα δι οτομίας ια μια κ άση προ ημάτ ν, στην υπο ο ιστική πο υπ οκότητα, είναι μια π ήρης ταξινόμηση τ ν προ- ημάτ ν της οικο ένειας σε υπο ο ιστικά εύκο α και σε υπο ο ιστικά δύσκο α προ ήματα, ρίς ενδιάμεσα προ ήματα. Εξαιτίας του ε ρήματος του Ladner δε μπορούμε να ρούμε δι οτομία ια ο όκ ηρες τις κ άσεις NP και #P, α ά παρ ό α αυτά υπάρ ουν με ά ες υποκ άσεις προ ημάτ ν που μοντε οποιούν πο ά φυσικά προ ήματα και ια τις οποίες υπάρ ουν ε ρήματα δι οτομίας. Ξεκινάμε με το μοντέ ο τ ν προ ημάτ ν ικανοποίησης περιορισμών ς πρό ημα απόφασης (CSP) και στη συνέ εια με ετάμε τις κ άσεις τ ν προ ημάτ ν μέτρησης ομομορφισμών ραφήματος, τ ν προ ημάτ ν μέτρησης ικανοποίησης περιορισμών (#CSP) και τ ν προ ημάτ ν Holant. Τέ ος, α κάνουμε μια σύντομη εισα ή στους ο ο ραφικούς α ορί μους, που είναι ειδικού τύπου πο υ νυμικοί α όρι μοι ια προ ήματα μέτρησης. Λέξεις κ ειδιά: Δι οτομία, Πρό ημα Ικανοποίησης Περιορισμών, Ομομορφισμοί Γραφήματος, Πρo ήματα Holant, Ο ο ραφικοί Α όρι μοι
6 iv
7 v Abstract In this thesis we study dichotomy theorems mainly of counting problems. A dichotomy theorem for a class of problems, in computational complexity, is a complete classification of the problems of this class in computationally easy and computationally hard problems, without intermediate problems. Due to Ladner s theorem we cannot find a dichotomy for the whole classes NP and #P, however there are large subclasses of NP (#P), that model many natural problems, for which dichotomy theorems exist. We begin with the framework of the decision version of constraint satifaction problems (CSP) and then we study the classes of graph homomorphisms problems, of counting constraint satisfaction problems (#CSP) and of Holant problems. Finally, we will make a brief introduction to holographic algorithms, a special type of polynomial-time algorithms for counting problems. Keywords: Dichotomy, Constraint Satisfaction Problem, Graph Homomorphisms, Holant Problems, Holographic Algorithms
8 vi
9 vii Ευ αριστίες Θα ή ε α με αφορμή αυτή τη διπ ματική να ευ αριστήσ ό ους μου τους κα η ητές ια τις νώσεις που μου πρόσφεραν και ια την ουσιαστική επιρροή που εί αν στη μέ ρι τώρα πορεία μου. Πιο συ κεκριμένα, α ή ε α να ευ αριστήσ τον κ. Πα ουρτζή ια την κα οδή ησή του ό ο αυτό το διάστημα, και τα ά α δύο μέ η τις τριμε ούς επιτροπής, κ. Ζά ο και κ. Φ τάκη. Επίσης α ή ε α να ευ αριστήσ τους κα η ητές μου κ. Κο ιόπου ο, κ. Θη υκό και κ. Κουτσουπιά ια τη στήριξή τους και τις συμ ου ές που μου πρόσφεραν. Επιπ έον, α ή ε α να ευ αριστήσ τον Ανδρέα ια την κα ή συνερ ασία που εί αμε κα ό η τη διάρκεια της συ ραφής αυτής της ερ ασίας. Να ευ αριστήσ επίσης, τους συμφοιτητές μου και φί ους μου στο μπ και την ερ αστηριακή ομάδα του Corelab ια τις ευ άριστες και δημιουρ ικές συζητήσεις που εί αμε. Τέ ος, α ή ε α να ευ αριστήσ την οικο ένειά μου ια την α άπη και τη στήριξη που μου έ ει προσφέρει ό α αυτά τα ρόνια.
10 viii
11 Περιε όμενα 1 Εισα ή Βασικοί Ορισμοί Το Θεώρημα του Ladner και οι Επιπτώσεις του Παραδεί ματα Δι οτομιών στην Πο υπ οκότητα Το CSP ς Πρό ημα Απόφασης Ορισμός του Προ ήματος Απόφασης Δυαδικό (Boolean) CSP Το Γενικό Μοντέ ο Προ ήματα Μέτρησης Ορισμοί και Παραδεί ματα Ομομορφισμοί Γραφήματος #CSP Προ ήματα Holant Ο ο ραφικοί Α όρι μοι Θε ρήματα Δι οτομίας ια το #CSP Κάποιες Ειδικές Περιπτώσεις Το #CSP με Βάρη Μι αδικούς Αρι μούς Γ σσάρι 47 Βι ιο ραφία 51 1
12 2 ΠΕΡΙΕΧΟΜΕΝΑ
13 Κεφά αιο 1 Εισα ή 1.1 Βασικοί Ορισμοί Σκοπός της Υπο ο ιστικής Πο υπ οκότητας είναι να ταξινομήσει τα διάφορα προ ήματα σε κ άσεις πο υπ οκότητας. Σε αυτή την παρά ραφο α ορίσουμε κάποιες ασικές κ άσεις πο υπ οκότητας και ανα ών, τα οποία α ρειαστούμε στη συνέ εια. Για μια πιο ανα υτική εισα ή, παραπέμπουμε στα [2, 34]. Όταν περιορίζουμε μια μη ανή Turing (TM) ς προς τον ρόνο που μπορεί να τρέξει, τότε προκύπτει ο παρακάτ ορισμός: Ορισμός Έστω f μια συνάρτηση από το N στο N. Θα λέμε ότι η TM M λειτουργεί σε χρόνο f(n), αν για κάθε συμβολοσειρά εισόδου x, ο χρόνος που χρειάζεται η M σε είσοδο x είναι το πολύ f( x ) 1. Ας υποθέσουμε ότι μια γλώσσα L (Σ { }) αποφασίζεται από μια TM η οποία λειτουργεί σε χρόνο f(n). Θα λέμε ότι L TIME(f(n)). Αν από την ά η περιορίσουμε τη μη ανή ς προς τον ώρο τον οποίο μπορεί να ρησιμοποιήσει, τότε έ ουμε τον παρακάτ ορισμό: Ορισμός Έστω f μια συνάρτηση από το N στο N. Θα λέμε ότι η TM M λειτουργεί σε χώρο f(n), αν για κάθε συμβολοσειρά εισόδου x, η M χρειάζεται χώρο το πολύ f( x ). Έστω L μια γλώσσα. Θα λέμε ότι L SPACE(f(n)) αν υπάρχει TM που αποφασίζει την L με τη χρήση το πολύ f(n) κελιών στην ταινία εργασίας της. Για μη-ντετερμινιστικές μη ανές Turing συμ ο ίζουμε τις κ άσεις πο υπ οκότητας με περιορισμό στο ρόνο και στο ώρο ς NTIME(f(n)) και NSPACE(f(n)) αντίστοι α. Ορίζουμε επίσης τις παρακάτ κ άσεις πο υπ οκότητας: 1 το x συμ ο ίζει το μήκος της συμ ο οσειράς x 3
14 4 ΚΕΦΑΛΑΙΟ 1. ΕΙΣΑΓΩΓΗ L = SPACE(log n) NL = NSPACE(log n) P = k>0 TIME(nk ) NP = k>0 NTIME(nk ) EXP = k>0 TIME(2nk ) PSPACE = k>0 SPACE(nk ) NPSPACE = k>0 NSPACE(nk ) Οι παραπάν κ άσεις συνδέονται μεταξύ τους ς εξής: L NL P NP PSPACE. Για τους περισσότερες από τους παραπάν ε κ εισμούς παραμένει ανοι τό το ερώτημα αν είναι νήσιοι ή ό ι. Το κεντρικό και πιο διάσημο ανοι τό ερώτημα της υπο ο ιστικής πο υπ οκότητας είναι η σ έση μεταξύ τ ν κ άσε ν P και NP, επειδή ια τα περισσότερα προ ήματα που συναντούμε στη ι ιο ραφία, αυτά που μπορούν να υ ούν αποτε εσματικά ανήκουν στο P και αυτά ια τα οποία δε ν ρίζουμε αποδοτικούς α ορί μους ανήκουν στο NP. Οι παραπάν ορισμοί αφορούν προ ήματα απόφασης ( ώσσες). Εμείς α ασ ο η ούμε κυρί ς με προ ήματα μέτρησης (συναρτήσεις), όπου ενδιαφερόμαστε ια το π ή ος τ ν ύσε ν ενός δοσμένου προ ήματος. Η κύρια κ άση ια τα προ ήματα μέτρησης είναι η εξής: Ορισμός (Valiant [36]). #P είναι η κλάση όλων των συναρτήσεων f : Σ N για τις οποίες, για κάθε x Σ, f(x) = acc M (x) για κάποια NP-TM M, όπου acc M (x) είναι το πλήθος των υπολογιστικών μονοπατιών της M που αποδέχονται με είσοδο x. Επίσης, η κ άση συναρτήσε ν που υπο ο ίζονται από μια ντετερμινιστική μη- ανή Turing πο υ νυμικού ρόνου είναι η FP. Το ανοι τό ερώτημα ια την πο υπ οκότητα τ ν προ ημάτ ν μέτρησης, αντίστοι ο αυτού του P vs. NP, είναι το εάν ισ ύει FP = #P ή FP #P, με το δεύτερο να ε ρείται πιο πι ανό. Για να δώσουμε αρ ότερα κάποια αποτε έσματα π ηρότητας, α ρησιμοποιήσουμε τις παρακάτ ανα ές: Ορισμός Θα λέμε ότι ένα πρόβλημα A ανάγεται σε ένα πρόβλημα B κατά Karp-αναγωγή (polynomial-time many one) και θα συμβολίζεται με A p m B, αν υπάρχει μια συνάρτηση f υπολογίσιμη σε πολυωνυμικό χρόνο, τέτοια ώστε για κάθε x, x A αν και μόνο αν f(x) B. Στην περίπτ ση συναρτήσε ν f A και f B, η παραπάν ανα ή ορίζεται ς εξής: f A (x) p m f B αν g FP, x f A (x) = g(f B (x)).
15 1.2. ΤΟ ΘΕΩΡΗΜΑ ΤΟΥ LADNER ΚΑΙ ΟΙ ΕΠΙΠΤΩΣΕΙΣ ΤΟΥ 5 Ορισμός Θα λέμε ότι ένα πρόβλημα A (ή συνάρτηση) ανάγεται σε ένα πρόβλημα B κατά Cook-αναγωγή (polynomial-time Turing) και θα συμβολίζεται με A p T B, αν η A μπορεί να υπολογιστεί από μια ντετερμινιστική TM M σε πολυωνυμικό χρόνο με τη χρήση ενός μαντείου (oracle) για τη B. Αν η M καλέσει μία μόνο φορά το μαντείο για τη B, τότε έχουμε την Cook [1] αναγωγή, που συμβολίζεται με A p [1] T B. Να σημειώσουμε ότι η Cook-ανα ή ισ ύει ό ι μόνο ια ώσσες (προ ήματα), α ά και ια συναρτήσεις. Για τα προ ήματα μέτρησης α ρησιμοποιήσουμε επίσης και την φειδ ή (parsimonious) ανα ή: Ορισμός Θα λέμε ότι ένα πρόβλημα μέτρησης #A ανάγεται σε ένα πρόβλημα μέτρησης #B με φειδωλή αναγωγή (parsimonious reduction) αν υπάρχει μια συνάρτηση f υπολογίσιμη σε πολυωνυμικό χρόνο τέτοια ώστε, για κάθε x, {y (x, y) A} = {z (f(x), z) B}. 1.2 Το Θεώρημα του Ladner και οι Επιπτώσεις του Όπ ς είπαμε ένα από κύρια ανοι τά προ ήματα είναι μια απόδειξη ια το αν ισ ύει ή ό ι ότι P NP. Από τη στι μή που το πρό ημα είναι ακόμη ανοι τό, το κα ύτερο που μπορούμε να ε πίζουμε είναι να κατατάξουμε κά ε πρό ημα στο NP να είναι είτε NP-complete είτε να ύνεται στο P. Η παραπάν πρόταση ισ ύει και ια τα προ ήματα μέτρησης, ό έ ειψης απόδειξης του FP #P, μπορούμε να κατατάξουμε κά ε πρό ημα στο #P έτσι ώστε να είναι είτε #P-complete είτε να ύνεται σε πο υ νυμικό ρόνο; Και στα δύο παραπάν ερ τήματα απάντησε αρνητικά ο Ladner με το παρακάτ εώρημά του [31]. Θεώρημα Αν P NP τότε υπάρχει μια γλώσσα L NP η οποία δεν ανήκει στο P αλλά ούτε είναι NP-complete. Η ακό ου η απόδειξη μπορεί να ρε εί στο [2] (με κάποιες επτομέρειες να παρα είπονται): Απόδειξη του θεωρήματος Έστ M i η μη ανή Turing που έ ει σαν περι- ραφή τη δυαδική αναπαράσταση του i. Ας ε ρήσουμε τη ώσσα SAT H = {ϕ01 nh(n) ϕ SAT n = ϕ }, όπου H : N N είναι η συνάρτηση που ορίζεται ς εξής: H(n) είναι ο μικρότερος αρι μός i < log log n τέτοιος ώστε ια κά ε x {0, 1} με x log n, η M i δίνει ς έξοδο το SAT H (x) μετά από το πο ύ i x i ήματα. Αν δεν υπάρ ει τέτοιος αρι μός i τότε H(n) = log log n.
16 6 ΚΕΦΑΛΑΙΟ 1. ΕΙΣΑΓΩΓΗ Μπορούμε να υπο ο ίσουμε την H(n) αναδρομικά υπο ο ίζοντας πρώτα τα H(k) ια k log n. Ο α όρι μος ρειάζεται να προσομοιώσει το πο ύ log log n μη ανές Turing ια κά ε είσοδο με μήκος το πο ύ log n και ια το πο ύ log log n (log n) log log n ήματα. Στο τέ ος κά ε τέτοιας προσομοί σης πρέπει να ε έ ουμε αν M i (x) = SAT H (x) και ια να το κάνουμε αυτό ρειαζόμαστε την τιμή του H(k) ια ένα k log n. Εύκο α μπορούμε να δούμε ότι ο συνο ικός υπο ο ισμός του H(n) ίνεται το πο ύ σε O(n 3 ) ήματα. Αυτό μας δεί νει και ότι η συνάρτηση H(n) είναι κα ώς ορισμένη. Τώρα ας υπο έσουμε ότι SAT H P, και άρα υπάρ ει μη ανή Turing M που ύνει το SAT H σε το πο ύ c n c ήματα ια κάποια στα ερά c. Θα υπάρ ει κάποιος αρι μός i > c τέτοιος ώστε M i = M. Εξ ορισμού, ια n > 2 2i, H(n) i, οπότε H(n) = O(1). Από την ά η μεριά, αν H(n) = O(1), τότε η H μπορεί να πάρει μόνο πεπερασμένου π ή ους τιμές, οπότε υπάρ ει ένα i τέτοιο ώστε H(n) = i, ια άπειρα σε π ή ος n. Από αυτό συμπεραίνουμε ότι η M i ύνει το SAT H σε ρόνο i n i, ιατί διαφορετικά αν υπήρ ε κάποιο x ια το οποίο η M i δε δίνει σ στό αποτέ εσμα μέσα σε αυτό το ρόνο, τότε ια σ εδόν ό α τα n > 2 x (εκτός ίσ ς από το 2 2i ) α ίσ υε H(n) i. Στις δύο τε ευταίες παρα ράφους δείξαμε ότι SAT H P αν και μόνο αν H(n) = O(1). Επιπ έον, η συνεπα ή της δεύτερης παρα ράφου ισ ύει ακόμη και αν υπο έσουμε μόνο ότι υπάρ ει στα ερά C τέτοια ώστε H(n) C ια άπειρα σε π ή ος n, που σημαίνει ότι αν SAT H P τότε το H(n) τείνει στο άπειρο όταν το n τείνει στο άπειρο. Έστ τώρα ότι SAT H P: από τα παραπάν συμπεραίνουμε ότι H(n) C ια κάποια στα ερά C, από το οποίο προκύπτει ότι το SAT H είναι απ ά το SAT αν κο ήσουμε σε κά ε στι μιότυπο το πο ύ πο υ νυμικά σε π ή ος 1. Αυτό όμ ς α σήμαινε ότι ένας πο υ νυμικός α όρι μος ια το SAT H α μπορούσε να ρησιμοποιη εί ια να υ εί το SAT σε πο υ νυμικό ρόνο, και άρα α ίσ υε P = NP. Ας υπο έσουμε τέ ος ότι το SAT H είναι NP-complete: οπότε υπάρ ει ανα- ώ ή r από το SAT στο SAT H που τρέ ει σε ρόνο O(n k ) ια κάποια στα ερά k. Έ ουμε ήδη δείξει ότι SAT H P, οπότε το H(n) τείνει στο άπειρο. Αφού η r τρέ ει σε ρόνο O(n k ), ια αρκετά με ά α n α πρέπει να στέ νει στι μιότυπα του SAT με έ ους n σε στι μιότυπα του SAT H με έ ους το πο ύ n H (n). Συνεπώς αρκετά με ά ους τύπους ψ, η ανα ή r τους στέ νει σε μια συμ ο οσειρά του τύπου ϕ01 ϕ H( ϕ ), όπου ϕ ένας τύπος μικρότερος κατά ένα στα ερό πο υ νυμικό παρά οντα. Πιο συ κεκριμένα α είναι ϕ ϕ H( ϕ ) = O( ψ i ), που σημαίνει ότι ϕ = o( ψ ). Εφαρμόζοντας αναδρομικά τη διαδικασία μέ ρι να φτάσουμε σε αρκετά μικρό τύπο, έ ουμε έναν α όρι μο πο υ νυμικού ρόνου ια το SAT, κάτι που έρ εται σε αντί εση με την υπό εση ότι P NP.
17 1.2. ΤΟ ΘΕΩΡΗΜΑ ΤΟΥ LADNER ΚΑΙ ΟΙ ΕΠΙΠΤΩΣΕΙΣ ΤΟΥ 7 Ας σημειώσουμε ότι η συ κεκριμένη τε νική που είδαμε στην απόδειξη, μπορεί να εφαρμοστεί και σε ά ες κ άσεις και έτσι να προκύψουν τα παρακάτ πορίσματα. Πόρισμα Αν υποθέσουμε ότι P NP, τότε υπάρχει μια άπειρη ιεραρχία από διαχωρισμένες κλάσεις πολυπλοκότητας μεταξύ του P και του NP. Απόδειξη. Θα εφαρμόσουμε τη τε νική της απόδειξης του ε ρήματος ια να δειξουμε ότι υπάρ ει ώσσα που δεν ανήκει στο P, ούτε η SAT H = def SAT H0 ανά εται σε αυτήν: Ας ε ρήσουμε τη ώσσα SAT H1 = {ϕ01 nh(n) ϕ SAT H0 n = ϕ }, όπου H είναι η συνάρτηση που ορίσαμε στην απόδειξη του Η SAT H1 είναι ό ι μόνο στο NP, α ά ανά εται και στην SAT H0 (αφού H είναι πο υ νυμικά υπο ο ίσιμη). Από την ά η μεριά, ρησιμοποιώντας τα ίδια επι ειρήματα όπ ς πριν, αν SAT H1 P α προέκυπτε ότι SAT H0 P. Επίσης μια ανα ή SAT H0 p SATH 1, α μας έδινε έναν πο υ νυμικό α όρι μο ια την SAT H0. Ας ε ρήσουμε τώρα την ακό ου η οικο ένεια σσών: SAT Hi = {ϕ01 nh(n) ϕ SAT Hi 1 n = ϕ }. Οι κ άσεις πο υπ οκότητας που ορίζονται από τις αντίστοι ες κ ειστότητες (closures) κατά Karp, αποτε ούν μια άπειρη ιεραρ ία κ άσε ν μεταξύ του P και του NP. Πόρισμα Αν FP #P τότε υπάρχει μια άπειρη ιεραρχία διαχωρισμένων κλάσεων πολυπλοκότητας μεταξύ του FP και του #P. Εκτός από τα τε νητά προ ήματα που περι ράψαμε στις παραπάν αποδειξεις (SAT H ), υπάρ ουν και κάποιοι φυσικοί υποψήφιοι που πιστεύουμε π ς δεν είναι ούτε NP-complete, και ούτε ν ρίζουμε αν ανήκουν στο P. Τέτοια προ ήματα είναι το πρό ημα ισομορφισμού ραφημάτ ν και το πρό ημα της παρα οντοποίησης ς πρό ημα απόφασης, δη αδή δοσμένου ενός ακεραίου n και ενός ακεραίου M με 1 M n, το ερώτημα είναι αν ο n έ ει διαιρέτη d με 1 < d < M. Για τα προ ήματα μέτρησης, μπορούμε να ε ρήσουμε αντίστοι α το πρό ημα του υπο ο ισμού του π ή ους τ ν διαιρετών ενός ακεραίου. Από την ά η μεριά, η π ειοψηφία τ ν προ ημάτ ν απόφασης (μέτρησης) που ν ρίζουμε και που προκύπτουν φυσικά, είναι είτε πο ύ εύκο α, δη αδή ανήκουν στο P(FP), είτε πο ύ δύσκο α, δη αδή είναι NP-complete(#P-complete). Από τη στι μή που δε μπορούμε να αποδείξουμε ότι αυτό ισ ύει ια ό α τα προ ήματα στο NP(#P), α έ αμε να ρούμε υποκ άσεις που περιέ ουν όσο το δυνατόν περισσότερα προ ήματα, τέτοιες ώστε τα προ ήματα που περιέ ονται σε αυτές να είναι είτε πο ύ εύκο α, είτε πο ύ δύσκο α. Μια τέτοιου είδους κ άση α πρέπει να είναι αρκετά περιορισμένη ώστε εώρημα αντίστοι ο με αυτό του Ladner να μην ισ ύει ια αυτή την κ άση, α ά παρά η α α έ αμε να είναι και όσο το δυνατόν πιο με ά η ίνεται. Έτσι α εί αμε πετύ ει να κα ορίσουμε π ήρ ς την πο υπ οκότητα τ ν προ ημάτ ν που περιέ ονται σε αυτή την κ άση. Τέτοιου είδους
18 8 ΚΕΦΑΛΑΙΟ 1. ΕΙΣΑΓΩΓΗ ε ρήματα στην υπο ο ιστική πο υπ οκότητα, όπου μια οικο ένεια προ ημάτ ν αποδεικνύεται ότι περιέ ει είτε πο ύ εύκο α, είτε πο ύ δύσκο α προ ήματα και τίποτα ενδιάμεσα, ονομάζονται ε ρήματα δι οτομίας (dichotomy theorems). 1.3 Παραδεί ματα Δι οτομιών στην Υπο ο- ιστική Πο υπ οκότητα Ένα από τα πρώτα ε ρήματα δι οτομίας στην υπο ο ιστική πο υπ οκότητα οφεί εται στους Jaeger, Vertigan και Welsh [26] και αφορά το πο υώνυμο Tutte ενός ραφήματος. Ορισμός Το πολυώνυμο Tutte ενός γραφήματος G είναι το: T (G; x, y) = A E (x 1) κ(v,a) κ(v,e) A ( V κ(v,a)) (y 1) όπου κ(v, A) = το πλήθος των συνεκτικών συνιστωσών του γραφήματος (V, A). Το πο υώνυμο Tutte ορίζεται ια κά ε μη κατευ υνόμενο ράφημα και δίνει π ηροφορίες ια το π ς ακρι ώς είναι συνεκτικό το ράφημα. Μερικά παραδεί ματα που μπρούν να ρε ούν στο ι ιο του Welsh [40] είναι τα εξής: το T (G; 1, 1) υπο ο ίζει το π ή ος τ ν δενδροπαρα όντ ν (spanning trees) του ραφήματος G. το T (G; 2, 1) υπο ο ίζει το π ή ος τ ν δασών (forests) στο G T (G; 1, 2) υπο ο ίζει το π ή ος τ ν υποσυνό ν από ακμές που είναι συνεκτικά και κα ύπτουν το G. το T (G; 2, 0) υπο ο ίζει το π ή ος τ ν ακυκ ικών προσανατο ισμών του G. Το ρ ματικό πο υώνυμο P (G; λ) ενός ραφήματος G με n κορυφές, m ακμές και k συνεκτικές συνιστώσες δίνεται από τον τύπο: P (G; λ) = ( 1) n k λ k T (G; 1 λ, 0). Αν ε ρήσουμε το λ έναν ετικό ακέραιο, τότε το P (G; λ) υπο ο ίζει το π ή ος τ ν λ- ρ ματισμών του G. Για στα ερά x, y το εώρημα δι οτομίας τ ν Jaeger, Vertigan και Welsh είναι πάν στο ακό ου ο πρό ημα: TUTTE(x, y):
19 1.3. ΠΑΡΑΔΕΙΓΜΑΤΑ ΔΙΧΟΤΟΜΙΩΝ ΣΤΗΝ ΠΟΛΥΠΛΟΚΟΤΗΤΑ 9 Είσοδος: Ένα ράφημα G. Ζητούμενο: T (G; x, y). Πιο συ κεκριμένα, απέδειξαν ότι το πρό ημα υπο ο ισμού του πο υ νύμου Tutte ενός ραφήματος στο σημείο (x, y) του επιπέδου, είναι #Phard εκτός εάν (x 1)(y 1) = 1 ή όταν το (x, y) ισούται με (1, 1), ( 1, 1), (0, 1), ( 1, 0), (i, i), ( i, i), (j, j 2 ) ή (j 2, j), όπου j = e 2πi/3. Επίσης οι Vertigan και Welsh [39] έδειξαν ότι αν περιοριστούμε στην περίπτ ση τ ν επίπεδ ν ραφημάτ ν, τότε και τα σημεία στην υπερ ο ή (x 1)(y 1) = 2 οδη ούν σε υπο ο ισμό του πο υ νύμου σε πο υ νυμικό ρόνο. Στο παραπάν σ ήμα, κά ε σημείο (x, y) του επιπέδου αντιστοι εί σε ένα πρό- ημα TUTTE(x, y). Σε κά ε κόκκινο σημείο, το πρό ημα ύνεται σε πο υ νυμικό ρόνο. Σε κά ε μπ ε σημείο το πρό ημα είναι #P-hard ενικά, α ά υπο ο ίζεται σε πο υ νυμικό ρόνο ια επίπεδα ραφήματα. Σε κά ε ά ο σημείο, το πρό ημα είναι #P-hard ακόμη και ια επίπεδα ραφήματα. Ένα ά ο εώρημα δι οτομίας που ήκε το 1990 ήταν ια το πρό ημα H- Χρ ματισμού. Ένας H-Χρ ματισμός ενός ραφήματος G είναι απ ά ένας ομομορφισμός από το G στο H. Για παράδει μα, αν H = K 3 τότε ο K 3 -Χρ ματισμός είναι απ ά το πρό ημα 3- ρ ματισμού ενός ραφήματος, και πιο ενικά αν H = K q τότε έ ουμε το πρό ημα του k- ρ ματισμού.
20 10 ΚΕΦΑΛΑΙΟ 1. ΕΙΣΑΓΩΓΗ Οι Hell και Nesetril [25] απέδειξαν ότι το πρό ημα του H-Χρ ματισμού είναι στο P αν το ράφημα H είναι διμερές, ενώ είναι NP-complete σε κά ε ά η περίπτ ση. Πο ά πρόσφατα ε ρήματα δι οτομίας αφορούν προ ήματα από τη στατιστική φυσική. Στην στατιστική φυσική μοντε οποιούν συστήματα spin σε ραφήματα, και έ ουν να υπο ο ίσουν τη συνάρτηση διαμέρισης (partition function) ενός συστήματος spin ένα ράφημα. Ένα από τα πιο με ετημένα μοντέ α στη στατιστική φυσική είναι το μοντέ ο Ising, που πρ τοεισή η τη δεκαετία του 1920 από τους Lenz και Ising ια να με ετήσουν τον φερρομα νητισμό (ferromagnetism). Ένα στι μιότυπο του μοντέ ου δίνεται από ένα σύνο ο από n τοπο εσίες, ένα σύνο ο από ενέρ ειες α η επίδρασης V ij ια κά ε ζεύ ος i, j από τοπο εσίες, μια ένταση μ νητικού πεδίου B, και μια αντίστροφη ερμοκρασία (inverse temperature) β. Κατάσταση του συστήματος που ορίζεται από αυτές τις παραμέτρους είναι είναι μία από τις 2 n πι ανές ανα έσεις σ από ±1 spins σε κά ε τοπο εσία. Η ενέρ εια μιας κατάστασης σ συμ ο ίζεται με H(σ) και ορίζεται ς: H(σ) = {i,j} V ij σ i σ j B k σ k. Το ενδιαφέρον κομμάτι σε αυτό το ά ροισμα είναι ο πρώτος όρος, που αποτε είται από τη συνεισφορά από τα ζεύ η τοπο εσιών. Η σημασία αυτής της έκφρασης έρ εται από την κατανομή Gibbs, σύμφ να με την οποία η πι ανότητα το σύστημα να ρίσκεται σε μια κατάσταση σ είναι ανά ο η της ποσότητας exp( βh(σ)). Από αυτό συμπεραίνουμε ότι η πι ανότητα μιας κατάστασης σ είναι 1/Z exp( βh(σ)), όπου ο παρά οντας κανονικοποίησης Z, που κα είται συνάρτηση διαμέρισης του συστήματος, είναι ο Z = exp( βh(σ)). σ { 1,1} n Να σημειώσουμε εδώ ότι ο υπο ο ισμός της συνάρτησης διαμέρισης του μοντέ ου Ising ισοδυναμεί με το πρό ημα TUTTE(x, y) με x, y τέτοια ώστε (x 1)(y 1) = 2. Α α σημαντικά μοντέ α της στατιστικής φυσικής είναι το μοντέ ο Hard-Core (που είναι ισοδύναμο με τον υπο ο ισμό τ ν ανεξάρτητ ν συνό ν σε ένα ράφημα), το μοντέ ο Potts και το μοντέ ο Antiferromagnetic Potts (που είναι ισοδύναμο με τον υπο ο ισμό του π ή ους τ ν ρ ματισμών ενός ραφήματος). Τα ε ρήματα δι οτομίας που έ ουμε αφορούν ειδικές περιπτώσεις αυτών τ ν μοντέ ν και ένε ότι η συνάρτηση διαμέρισης μπορεί να προσε ιστεί (FPRAS) κάτ από κάποιες τιμές μιας παραμέτρου του συστήματος. Για το μοντέ ο Ising η παράμετρος αυτή είναι η β. Αυτό που είναι πιο αξιοσημεί το με αυτές τις δι οτομίες είναι ότι συμπίπτουν με τις μετα άσεις φάσεις (phase transitions) που έ ουν αποδει εί από τους φυσικούς.
21 1.3. ΠΑΡΑΔΕΙΓΜΑΤΑ ΔΙΧΟΤΟΜΙΩΝ ΣΤΗΝ ΠΟΛΥΠΛΟΚΟΤΗΤΑ 11 Έτσι εάν η παράμετρος είναι κάτ από μια κρίσιμη τιμή, τότε το πρό ημα είναι εύκο ο, ενώ όταν η παράμετρος υπερ εί αυτή τη τιμή, τότε το πρό ημα ίνεται #P-hard, και επιπ έον το σύστημα α άζει φάση.
22 12 ΚΕΦΑΛΑΙΟ 1. ΕΙΣΑΓΩΓΗ
23 Κεφά αιο 2 Το Πρό ημα Ικανοποίησης Περιορισμών (CSP) ς Πρό ημα Απόφασης Σκοπός αυτού του κεφα αίου είναι να εισά ουμε το πρό ημα ικανοποίησης περιορισμών (constraint satisfaction problem ή απ ούστερα CSP) ς πρό ημα απόφασης και να παρουσιάσουμε ορισμένα από τα πιο σημαντικά αποτε έσματα ύρ από τη ε ρία του. Η προέ ευση του προ ήματος οφεί εται στον Ugo Montanari και συ κεκριμένα σε ένα άρ ρο του το 1974 [33] που ασ ο είται με το πρό ημα ια εφαρμο ές επεξερ ασίας εικόνας. Για μια πρώτη διαίσ ηση μπορούμε να σκεφτόμαστε το CSP σαν ένα ενικό ομο ενές π αίσιο που μοντε οποιεί πο ά ν στά συνδυαστικά προ ήματα. Παραδεί ματα τέτοι ν προ ημάτ ν είναι ραφο ε ρητικά ( ρ ματισμός ραφήματος, κά υψη κορυφών,...), το SAT, προ ήματα άσε ν δεδομέν ν, τε νητής νοημοσύνης, επι ειρησιακής έρευνας, ε τιστοποίησης και πο ά ά α. 2.1 Ορισμός του Προ ήματος Απόφασης Αρ ικά α εισά ουμε κάποιους ασικούς ορισμούς. Ορισμός Πεδίο (domain) ονομάζεται ένα πεπερασμένο σύνολο D από στοιχεία, που συνήθως θα συμβολίζεται ως D = {0, 1,, n 1}. Ορισμός O πληθικός αριθμός (cardinality) ενός πεδίου D θα συμβολίζεται ως D = n. Ορισμός Μια k-δική σχέση (relation) R στο πεδίο D θα είναι ένα υποσύνολο R D k. 13
24 14 ΚΕΦΑΛΑΙΟ 2. ΤΟ CSP ΩΣ ΠΡΟΒΛΗΜΑ ΑΠΟΦΑΣΗΣ Για παράδει μα αν έ ουμε ς πεδίο το σύνο ο D = {0, 1, 2}, μια διμε ής σ έση στο D είναι η L = {(0, 0), (0, 1), (0, 2), (1, 1), (1, 2), (2, 2)}. Ορισμός Ένας k-δικός περιορισμός είναι ένα κατηγόρημα εφαρμοζόμενο σε ένα διάνυσμα k μεταβλητών. Για παράδει μα τα C 1 (x, y) = (x = y), C 2 (x, y) = (x y) και C 3 (x, y, z) = (x y z x) είναι περιορισμοί. Από μια σ έση R μπορούμε να κατασκευάσουμε έναν περιορισμό R( x) τέτοιο ώστε το R να αντιστοι εί στο σύνο ο ύσε ν του R( x). Αν ια παράδει μα ε- ρήσουμε τη σ έση L που αναφέραμε προη ουμέν ς ια το πεδίο D = {0, 1, 2}, τότε ο περιορισμός L(x, y) αντιστοι εί στον περιορισμό x y ια το D. Επίσης να παρατηρήσουμε ότι μια σ έση R μπορεί να οδη ήσει σε περισσότερους του ενός περιορισμούς. Για παράδει μα οι R(x, y) και R(y, x) είναι διαφορετικοί περιορισμοί. Ήρ ε η ώρα να ορίσουμε το πρό ημα CSP. Ως είσοδος δίνεται ένας τύπος ϕ, ο οποίος είναι πεπερασμένη σύζευξη από περιορισμούς στο πεδίο D. Το ζητούμενο είναι αν ό οι οι περιορισμοί είναι ικανοποιήσιμοι, δη αδή αν υπάρ ει αποτίμηση στις μετα ητές έτσι ώστε να ικανοποιούνται ό οι οι περιορισμοί. Για παράδει μα αν έ ουμε τον τύπο (a = b) (b d) (d < c) (b < c) στο πεδίο D = {0, 1, 2, 3}, τότε η αποτίμηση a = 2, b = 2, c = 3, d = 2 δεν είναι ύση ιατί δεν ικανοποιείται ο δεύτερος περιορισμός. Η αποτίμηση όμ ς a = 1, b = 1, c = 3, d = 2 αποτε εί ύση, άρα ο τύπος είναι ικανοποιήσιμος. Ας δούμε τώρα μερικά παραδεί ματα προ ημάτ ν που μοντε οποιούνται από το π αίσιο του CSP. Το πιο απ ό ίσ ς παράδει μα είναι αυτό του 3- ρ ματισμού ενός ραφήματος. Σ αυτό το πρό ημα δίνεται ένα μη κατευ υνόμενο ράφημα και μας ρ τάνε αν μπορούμε να ρ ματίσουμε τις κορυφές του με τρία ρώματα έτσι ώστε οποιεσδήποτε δύο κορυφές ενώνονται με ακμή να έ ουν διαφορετικό ρώμα. Θα ε ρήσουμε ς πεδίο D το {0, 1, 2}, ένα στοι είο ια κά ε ρώμα και ς μετα ητές τις κορυφές του ραφήματος. Για παράδει μα στο ράφημα της εικόνας α έ ουμε μετα ητές το σύνο ο V = {a, b, c, d}. Τέ ος ό οι οι περιορισμοί α αντιστοι ούν στη σ έση και α υπάρ ει ένας ια κά ε ακμή. Στο παράδει μά οιπόν ο τύπος που α προκύψει ς είσοδος α είναι ο (a b) (a c) (b c) (a d) και μια ύση είναι η a = 0, b = 2, c = d = 1, άρα το ράφημα είναι 3- ρ ματίσιμο.
25 2.1. ΟΡΙΣΜΟΣ ΤΟΥ ΠΡΟΒΛΗΜΑΤΟΣ ΑΠΟΦΑΣΗΣ 15 Ένα ά ο παράδει μα προ ήματος που μοντε οποιείται ς CSP είναι η k- κά υψη κορυφών. Σ αυτό το πρό ημα δίνεται πά ι ς είσοδος ένα ράφημα και μας ρ τάνε αν υπάρ ουν το πο ύ k κορυφές που κα ύπτουν ό ες τις ακμές, δη αδή ια ακμή του ά ιστον το ένα άκρο της να ανήκει σ αυτές τις k το πο ύ κορυφές. Γι αυτό το πρό ημα α ε ρήσουμε ς πεδίο το D = {0, 1}, όπου τα στοι εία α αντιστοι ούν στην επι ο ή ή μη μιας κορυφής. Ως μετα ητές α ε ρήσουμε πά ι τις κορυφές του ραφήματος, δη αδή ια το παραπάν ράφημα α έ ουμε μετα ητές το σύνο ο V = {a, b, c, d}. Οι περιορισμοί α είναι δύο ειδών. Πρώτον, α υπάρ ει ένας περιορισμός C(x, y) ια κά ε ακμή {x, y} που α αντιστοι εί στη σ έση C = {(01), (10), (11)} και α εξασφα ίζει ότι ια κά ε ακμή α ά ουμε στο σύνο ο μας του ά ιστον ένα άκρο. Επίσης α υπάρ ει και ένας περιορισμός K που α περιέ ει ό ες τις μετα ητές και α εξασφα ίζει ότι το πο ύ k κορυφές έ ουν επι ε εί. Για το παραπάν ράφημα ο τύπος που α προκύψει είναι ο C(a, b) C(a, c) C(b, c) C(a, d) K(a, b, c, d). Έστ ότι ζητάμε μια 2-κά υψη κορυφών, οπότε μια ύση είναι η a = b = 1, c = d = 0. Πέρα από το ενικό CSP υπάρ ει και το παραμετρικό CSP. Η διαφορά του είναι ότι τώρα π έον το πρό ημα έ ει και μια παράμετρο S που είναι ένα σύνο ο σ έσε ν στο πεδίο D. Στο πρό ημα CSP(S) δίνεται πά ι ς είσοδος ένας τύπος ϕ α ά αυτή τη φορά ο τύπος είναι πεπερασμένη σύζευξη περιορισμών που αντιστοι ούν αποκ ειστικά σε σ έσεις από το S. Πά ι και σε αυτό το πρό ημα το ερώτημα είναι αν ο ϕ είναι ικανοποιήσιμος. Το ενικό CSP πρό ημα είναι ν στό ότι είναι NP-complete (αφού ια παράδει μα ο 3- ρ ματισμός είναι ειδική περίπτ σή του). Το ενδιαφέρον με το παραμετρικό CSP είναι δοσμένου ενός πεδίου D υπάρ ουν κάποιες παράμετροι S ια τις οποίες το πρό ημα CSP(S) ανήκει στο P. Ας ε ρήσουμε ια παράδει μα το δυαδικό πεδίο D = {0, 1}. Είδαμε ότι το CSP({C, K}) μοντε οποιεί το πρό- ημα k-κά υψης κορυφών, άρα είναι NP-complete. Το πρό ημα όμ ς CSP({ }) μοντε οποιεί το 2- ρ ματισμό ενός ραφήματος άρα ανήκει στο P.
26 16 ΚΕΦΑΛΑΙΟ 2. ΤΟ CSP ΩΣ ΠΡΟΒΛΗΜΑ ΑΠΟΦΑΣΗΣ 2.2 Δυαδικό (Boolean) CSP Σ αυτή την παρά ραφο α ασ ο η ούμε με το δυαδικό πεδίο D = {0, 1}. Αυτή είναι η πιο απ ή και ταυτό ρονα ενδιαφέρουσα περίπτ ση πεδίου. Μοντε οποιεί αρκετά φυσικά προ ήματα και υπάρ ουν και αρκετά ενδιαφέροντα αποτε έσματα ια το δυαδικό πεδίο, όπ ς το εώρημα του Schaefer ια το οποίο α μι ήσουμε παρακάτ. Το πιο κ ασικό παράδει μα προ ήματος που μοντε οποιείται ς CSP στο δυαδικό πεδίο είναι το 3SΑΤ. Ορισμός Λέμε ότι ένας τύπος είναι σε κανονική συζευκτική μορφή (conjunctive normal form ή απλούστερα CNF) όταν είναι σύζευξη από όρους, όπου κάθε όρος είναι διάζευξη από literals, όπου κάθε literal είτε μια μεταβλητή x, είτε η άρνησή της x. Στο πρό ημα 3SΑΤ δίνεται ς είσοδος ένας πεπερασμένος CNF τύπος ϕ στον οποίο κά ε όρος έ ει το πο ύ τρία literals και μας ρ τάνε αν είναι ικανοποιήσιμος. Είναι ν στό ότι το 3SΑΤ είναι NP-complete πρό ημα (Karp 1972) [30]. Για να μοντε οποιήσουμε το 3SΑΤ ς CSP ρειαζόμαστε τέσσερις σ έσεις, τις R 0 = {0, 1} 3 \ {000}, R 1 = {0, 1} 3 \ {001}, R 2 = {0, 1} 3 \ {011} και R 3 = {0, 1} 3 \ {111}. Έτσι ια παράδει μα μπορούμε να φτιάξουμε τους περιορισμούς (x y z) = R 0 (x, y, z), (x y z) = R 1 (x, y, z), (x ȳ z) = R 1 (x, z, y), ( x y z) = R 2 (y, x, z), κ..π. Είναι φανερό οιπόν ότι το 3SΑΤ αντιστοι εί στο CSP({R 0, R 1, R 2, R 3 }). Για να μπορέσουμε να διατυπώσουμε το εώρημα του Schaefer πρέπει πρώτα να αναφέρουμε κάποιους ορισμούς ια του περιορισμούς. Ορισμός Ένας όρος θα ονομάζεται: Horn αν περιέχει το πολύ ένα θετικό literal, δυϊκός Horn αν περιέχει το πολύ ένα αρνητικό literal, διζευκτικός αν περιέχει το πολύ δύο literals αφινικός αν μπορεί να περιγραφεί από μια αφινική εξίσωση modulo 2. Επίσης ένας τύπος ϕ = c 1 c p ονομάζεται Horn, δυϊκός Horn, διζευκτικός ή αφινικός αν κάθε όρος c i είναι Horn, δυϊκός Horn, διζευκτικός ή αφινικός αντίστοιχα. Για τον παραπάν ορισμό ε ρούμε πάντα ότι οι τύποι είναι σε CNF μορφή. Ας δούμε τώρα μερικά παραδεί ματα ια τους παραπάν ορισμούς: ο c 1 := ( x ȳ z) είναι Horn, ο c 2 := ( x y z) είναι δυϊκός Horn,
27 2.2. ΔΥΑΔΙΚΟ (BOOLEAN) CSP 17 ο c 3 := ( x y) είναι διζευκτικός, Horn και δυϊκός Horn, ο c 4 := (x y) είναι διζευκτικός και δυϊκός Horn, ο c 5 := (x + y + z = 1)mod2 είναι αφινικός, ο c 6 := (x = y) είναι αφινικός, διζευκτικός, Horn και δυϊκός Horn, ο c 7 := (x y) είναι αφινικός και διζευκτικός, Ενώ το ενικό SAT πρό ημα είναι NP-complete, υπάρ ουν κάποιες ειδικές περιπτώσεις του που ανήκουν στο P. Μία από αυτές είναι το HORNSAT, στο οποίο μας δίνεται ένας πεπερασμένος Horn τύπος ϕ και μας ρ τάνε αν είναι ικανοποιήσιμος. Όμοια μπορούμε να ορίσουμε και το πρό ημα DUALHORNSAT, στο οποίο ς είσοδος δίνεται ένας δυϊκός Horn τύπος. Ένας τύπος ϕ(x 1,, x k ) είναι Horn αν και μόνο αν ο τύπος ϕ( x 1,, x k ) είναι δυϊκός Horn. Συμπεραίνουμε οιπόν ότι και το DUALHORNSAT ύνεται σε πο υ νυμικό ρόνο. Αν τώρα περιορίσουμε τις εισόδους του προ ήματος να είναι μόνο διζευκτικοί τύποι, τότε προκύπτει το πρό ημα 2SAT, το οποίο είναι ν στό ότι ανήκει και αυτό στο P. Τέ ος, μπορούμε να ορίσουμε το πρό ημα AFFINESAT, στο οποίο δίνεται ς είσοδος ένας πεπερασμένος αφινικός τύπος ϕ και μας ρ τάνε αν είναι ικανοποιήσιμος. Ένας ά ος τρόπος να δούμε το ίδιο πρό ημα είναι ο εξής, μας δίνεται ς είσοδος ένα αφινικό σύστημα εξισώσε ν A x = b στον δακτύ ιο Z 2 και μας ρ τάνε αν έ ει ύση. Το AFFINESAT ύνεται κι αυτό σε πο υ νυμικό ρόνο αφού η ύπαρξει ύσης του συστήματος A x = b μπορεί να ε ε εί με τη μέ οδο απα οιφής Gauss. Ας δούμε ένα παράδει μα φυσικού προ ήματος που ύνεται ς AFFINESAT. Στο πρό ημα του 2- ρ ματισμού ραφήματος μας δίνεται ένα ράφημα G = (V, E) με V το σύνο ο κορυφών και το σύνο ο τ ν ακμών και μας ρ τάνε αν υπάρ ει συνάρτηση f : V {0, 1} τέτοια ώστε να ισ ύει f(x) f(y) ια κά ε ακμή (x, y) του ραφήματος. Θε ρούμε τη σ έση 2col = {01, 10}, η οποία αντιστοι εί στον αφινικό περιορισμό 2col(x, y) = (x + y = 1)mod2. Για κά ε ακμή οιπόν (x, y) E έ ουμε έναν περιορισμό (x + y = 1), και ό οι μαζί οι περιορισμοί φτιά νουν ένα αφινικό σύστημα εξισώσε ν A x = b στο Z 2, που μπορούμε στη συνέ εια να ύσουμε σε πο υ νυμικό ρόνο με τη μέ οδο απα οιφής Gauss και άρα να ύσουμε το πρό ημα 2- ρ ματισμού του G. Ανακεφα αιώνοντας, ν ρίζουμε ότι το πρό ημα 3SΑΤ είναι NP-complete, α ά τα προ ήματα HORNSAT, DUALHORNSAT, 2SAT και AFFINESAT ανήκουν ό α στο P. Ένα ά ο πρό ημα που α μας απασ ο ήσει στην πορεία είναι το πρό ημα NAE3SAT. Σ αυτό το πρό ημα ς είσοδο δε όμαστε πά ι έναν πεπερασμένο τύπο
28 18 ΚΕΦΑΛΑΙΟ 2. ΤΟ CSP ΩΣ ΠΡΟΒΛΗΜΑ ΑΠΟΦΑΣΗΣ ϕ = c 1 c p σε CNF μορφή με κά ε όρο να περιέ ει ακρι ώς 3 literals. Το ερώτημα όμ ς αυτή τη φορά είναι αν υπάρ ει αποτίμηση I τ ν μετα ητών έτσι ώστε ο ϕ να είναι α η ής και σε κά ε όρο c i να υάρ ει του ά ιστον ένα literal που αποτιμάται σε 1 και του ά ιστον ένα literal που αποτιμάται σε 0. Ο Schaefer το 1978 [35] έδειξε ότι το NAE3SAT είναι NP-complete. Ας δούμε τώρα π ς μπορούμε να μοντε οποιήσουμε το NAE3SAT σαν CSP. Έστ ότι έ ουμε μια παράμετρο S και ας υπο έσουμε ότι στο συνο ο S περιέ εται η σ έση nae = {001, 010, 011, 100, 101, 110}. Εύκο α μέσ της nae μπορούμε να φτιάξουμε τον περιορισμό neq(x, y) = nae(x, y, y), που δή ώνει ότι τα x, y είναι διαφορετικά μεταξύ τους. Με τη οή εια τ ν neq και nae μπορούμε τώρα να ορίσουμε τους παρακάτ περιορισμούς nae 1 (x, y, z) = nae(x, y, z) = v(neq(z, v) nae(x, y, v)) nae 2 (x, y, z) = nae(x, ȳ, z) = v(neq(y, v) nae 1 (x, v, z)) nae 3 (x, y, z) = nae( x, ȳ, z) = v(neq(x, v) nae 2 (v, y, z)) Παρατηρούμε ότι παρόμοια με το 3SΑΤ αυτοί οι περιορισμοί μας αρκούν ια να μοντε οποιήσουμε το NAE3SAT. Το NAE3SAT οιπόν είναι το CSP({nae}), άρα το CSP({nae}) είναι NP-complete. Θα ορίσουμε τώρα δύο τετριμμένες περιπτώσεις σ έσε ν. Ορισμός Έστω ένα d {0, 1}. Μια σχέση R ονομάζεται d-έγκυρη αν περιέχει το διάνυσμα (d, d,, d). Ένα σύνολο S από σχέσεις ονομάζεται d-έγκυρο αν κάθε σχέση R S είναι d-έγκυρη. Είναι φανερό ότι αν το S είναι 0-έ κυρο ή 1-έ κυρο τότε το CSP(S) ανήκει στο P, αφού αν δώσουμε σε κά ε μετα ητή την τιμή 0 ή 1 αντίστοι α τότε προκύπτει μια προφανής ύση. Τώρα π έον μπορούμε να διατυπώσουμε το εώρημα δι οτομίας του Schaefer [35]. Θεώρημα Έστω S ένα σύνολο από σχέσεις στο δυαδικό πεδίο {0, 1}. Αν το S είναι 0-έγκυρο, ή 1-έγκυρο ή Horn ή δυϊκό Horn, ή διζευκτικό,
29 2.2. ΔΥΑΔΙΚΟ (BOOLEAN) CSP 19 ή αφινικό, τότε το CSP(S) ανήκει στο P. Σε κάθε άλλη περίπτωση το CSP(S) είναι NPcomplete. Η πορεία της απόδειξης έ ει ς εξής, έ ουμε ήδη δει ό ες τις εύκο ες περιπτώσεις, δη αδή τις περιπτώσεις ια τις οποίες το CSP(S) ανήκει στο P. α δείξουμε ότι σε κά ε ά η περίπτ ση, δη αδή αν το S δεν ικανοποιεί μια από τις έξι συν ήκες του ε ρήματος, τότε το S α περιέ ει τη σ έση nae που αναφέραμε παραπάν. Σ αυτή την περίπτ ση και αφού το CSP({nae}) είδαμε ότι είναι NP-complete άρα και το CSP(S) α είναι NP-complete. Να σημειώσουμε εδώ ότι η απόδειξη που α αναφέρουμε δεν είναι η πρ τότυπη απόδειξη του Schaefer, η οποία είναι πιο πο ύπ οκη, α ά ασίζεται στο [1] και πριέ ει στοι εία κα ο ικής ά ε ρας. Πριν προ ρήσουμε στο κύριο μέρος της απόδειξης α πρέπει να αναφέρουμε μερικούς ακόμη ορισμούς. Ορισμός Καρτεσιανό γινόμενο (cartesian product) δύο σχέσεων R 1 D k και R 2 D m ονομάζεται η σχέση R 1 R 2 = {z D k+m x R 1, y R 2 : z i = x i για i = 1, 2,, k και z k+j = y j για j = 1, 2,, m}. Για παράδει μα αν έ ουμε R 1 = {(01), (23)} και R 2 = {(456), (789)}, τότε R 1 R 2 = {(01456), (01789), (23456), (23789)}. Ορισμός Προβολή (projection) μιας σχέσης R D k στην t-οστή συντεταγμένη είναι η σχέση pr t R = {z D x R : x t = z}. Παρόμοια μπορεί να οριστεί και η προ ο ή μιας σ έσης σε περισσότερες της μιας συντετα μένες. Για παράδει μα αν R = {(123), (456), (789)}, τότε η προ ο ή της R στην πρώτη και τρίτη συντετα μένη είναι η σ έση pr 1,3 R = {(13), (46), (79)} (= pr 1 R pr 3 R). Ορισμός Συνταύτιση (identification) μιας σχέσης R D k στις συντεταγμένες s και t ονομάζεται η σχέση R = {z D k 1 x R : x s = x t και z i = x i για i = 1, 2,, t 1, t + 1,, k}. Για παράδει μα αν R = {(122), (345), (777)}, τότε η συνταύτιση της R στις δύο τε ευταίες συντετα μένες είναι η σ έση R = {(12), (77)}. Με ά α ό ια η R είναι το συνο ο ύσε ν του περιορισμού R (x, y) που ορίζεται ς R (x, y) = R(x, y, y). Ορισμός Έστω ένα σύνολο S από σχέσεις. Θα λέμε ότι το S είναι κλειστό ως προς την πράξη op αν R S, op(r) S. Με άλλα λόγια, δε μπορούμε εφαρμόζοντας την πράξη op μέσα στο S να προκύψει μια σχέση έξω από αυτό.
30 20 ΚΕΦΑΛΑΙΟ 2. ΤΟ CSP ΩΣ ΠΡΟΒΛΗΜΑ ΑΠΟΦΑΣΗΣ Ορισμός Έστω ένα σύνολο σχέσεων S. Μπορούμε να κατασκευάσουμε ένα νέο σύνολο S το οποίο θα περιέχει όλες τις σχέσεις του S, όλες τις προβολές των σχέσεων του S, όλες τις προβολές των προβολών των σχέσεων του S, κ.λ.π. Αυτό το νέο σύνολο S το ονομάζουμε κλειστότητα προβολών (projection closure) του S. Για παράδει μα αν έ ουμε S = {R} με R = {(123), (456), (789)}, τότε φτιά- νουμε τις σ έσεις R 1 := pr 2,3 R = {(23), (56), (89)}, R 2 := pr 1,3 R = {(13), (46), (79)}, R 3 := pr 1,2 R = {(12), (45), (78)}, R 4 := pr 2 R 1 = {(3), (6), (9)}, R 5 := pr 1 R 1 = {(2), (5), (8)}, R 6 := pr 1 R 2 = {(1), (4), (7)}, Η κ ειστότητα προ ο ών του S είναι το σύνο ο S = S Έστ eq η σ έση ισότητας, δη αδή eq = {(d, d) d D}. 1 i 6 {R i }. Ορισμός Σύγκλωνο (co-clone) ενός συνόλου σχέσεων S, που συμβολίζεται ως S, ονομάζεται το μικρότερο (άπειρο) σύνολο σχέσεων τέτοιο ώστε: S S, eq S, το S είναι κλειστό ως προς το καρτεσιανό γινόμενο, το S είναι κλειστό ως προς τις προβολές, το S είναι κλειστό ως προς την συνταύτιση. Ο ό ος που ενδιαφερόμαστε ια τα σύ κ να είναι το παρακάτ εώρημα. Θεώρημα Για κάθε σύνολο σχέσεων S ισχύει ότι CSP(S) P CSP( S ) Με ά α ό ια τα σύ κ να είναι κάτι σαν κανονικές μορφές τ ν συνό ν σ έσε ν. Μπορεί να έ ουμε δύο διαφορετικά σύνο α S 1, S 2, α ά να ισ ύει S 1 = S 2, οπότε ό του παραπάν ε ρήματος δε ρειάζεται να τα αντιμετ πίσουμε ξε ριστά όσον αφορά την πο υπ οκότητα του CSPτους.
31 2.2. ΔΥΑΔΙΚΟ (BOOLEAN) CSP 21 Πόρισμα Έστω S 1 και S 2 δύο διαφορετικά μεταξύ τους σύνολα σχέσεων. Αν S 1 = S 2 τότε ισχύει ότι CSP(S 1 ) P CSP(S 2 ). Ορισμός Δικτυωτό (lattice) ονομάζουμε ένα μερικώς διατεταγμένο σύνολο στο οποίο οποιαδήποτε δύο στοιχεία έχουν ένα μοναδικό ελάχιστο άνω φράγμα (supremum) και ένα μοναδικό μέγιστο κάτω φράγμα (infimum). Αν S είναι το σύνο ο ό ν τ ν συ κ ών ν ό ν τ ν διαφορετικών σ έσε ν που ορίζονται στο πεδίο D = {0, 1}, τότε η δομή (S, ), δη αδή το S με τη σ έση διάταξης υποσυνό ου, αποτε εί ένα δικτυ τό. Το κα ό με αυτό το δικτυ τό στο δυαδικό πεδίο είναι ότι ν ρίζουμε π ήρ ς τη δομή του. Στο παραπάν δικτυ τό κά ε κυκ άκι αντιστοι εί σε ένα σύ κ νο στο δυαδικό πεδίο. Αν δυο σύ κ να ενώνονται με ραμμή τότε αυτό σημαίνει ότι το σύ κ νο που ρίσκεται πιο κάτ είναι υποσύνο ο αυτού που ρίσκεται από πάν.
32 22 ΚΕΦΑΛΑΙΟ 2. ΤΟ CSP ΩΣ ΠΡΟΒΛΗΜΑ ΑΠΟΦΑΣΗΣ Το επόμενο εώρημα [29, 28, 27] είναι εμέ ιος ί ος ια την απόδειξη του ε ρήματος του Schaefer. Θεώρημα Έστω δύο σύνολα σχέσεων S 1, S 2 με το S 1 πεπερασμένο. Αν ισχύει ότι S 1 S 2, τότε ισχύει και η αναγωγή CSP(S 1 ) P CSP(S 2 ). Από το παραπάν εώρημα μπορούμε να συμπεράνουμε τα εξής: 1. Αν ια ένα σύ κ νο S ισ ύει ότι CSP(S) P, τότε ια ό α τα σύ κ να S που ρίσκονται κάτ από το S, ισ ύει επίσης ότι CSP(S ) P. 2. Αν ια ένα σύ κ νο S ισ ύει ότι CSP(S) NP-complete, τότε ια ό α τα σύ κ να S που ρίσκονται πάν από το S, ισ ύει ότι CSP(S ) NPcomplete. Ας δούμε τώρα ξανά το εώρημα του Schaefer σε συνδυασμό με το δικτυ τό τ ν σύ κ ν ν. Τα σύ κ να που αντιστοι ούν στις έξι εύκο ες περιπτώσεις του ε ρήματος είναι τα εξής: 0-έ κυρο: ii 0, 1-έ κυρο: ii 1, Horn: ie 2 δυϊκό Horn: iv 2, διζευκτικό: id 2, αφινικό: il 2. Για αυτά οιπόν τα σύ κ να έ ουμε ήδη δει ότι τα αντίστοι α CSP ανήκουν στο P. Λό της παραπάν παρατήρησης και ια ό α τα σύ κ να που ρίσκονται από κάτ τους α ισ ύει το ίδιο. Αυτό αφήνει ανεξερεύνητα δύο μόνο σύ κ να, το BR, που αντιστοι εί σε ό ες τις δυνατές σ έσεις στο δυαδικό πεδίο D = {0, 1}, και το in 2, που είναι το σύ κ νο της σ έσης nae. Έ ουμε όμ ς δει ότι το CSP(nae) είναι NP-complete, άρα τα CSPπου αντιστοι ούν στα σύ κ να BR και in 2 είναι NP-complete, και αυτό ο οκ ηρώνει την απόδειξη του ε ρήματος δι οτομίας του Schaefer. Tο εώρημα του Schaefer μπορεί να εξειδικευτεί ακόμη πιο πο ύ. Πιο συ κεκριμένα στο [1] μπορούμε να δούμε αποτε έσματα π ηρότητας σε υποκ άσεις του P ( L, NL, L) ια τα CSP που ανήκουν στο P.
33 2.3. ΤΟ ΓΕΝΙΚΟ ΜΟΝΤΕΛΟ Το Γενικό Μοντέ ο Το 2002 ο Bulatov έδ σε ένα αποτέ εσμα δι οτομίας παρόμοιο με του Schaefer, α ά ια πεδίο με τρία στοι εία, δη αδή ια D = {0, 1, 2} [3]. Η ενική περίπτ ση ια οποιοδήποτε πεπερασμένο πεδίο παραμένει ανοι τή μέ ρι σήμερα [22].
34 24 ΚΕΦΑΛΑΙΟ 2. ΤΟ CSP ΩΣ ΠΡΟΒΛΗΜΑ ΑΠΟΦΑΣΗΣ
35 Κεφά αιο 3 Προ ήματα Μέτρησης Σ αυτό το κεφά αιο α παρουσιάσουμε τρεις σκε ετούς προ ημάτ ν που μοντε οποιούν πο ά προ ήματα μέτρησης. Πιο συ κεκριμένα α μι ήσουμε ια ομομορφισμούς ραφημάτ ν (graph homomorphisms), προ ήματα μέτρησης ικανοποίησης περιορισμών (#CSP ) και προ ήματα Holant και α δείξουμε ότι με τη σειρά που τα αναφέραμε κά ε ένα είναι ενίκευση του προη ούμενου. Γι αυτά τα προ ήματα έ ουν αποδει εί διάφορα ε ρήματα δι οτομίας τα οποία και α δούμε. Τέ ος α κάνουμε μια σύντομη εισα ή στους ο ο ραφικούς α όρι μους (holographic algorithms) που είναι πο υ νυμικοί α όρι μοι συ κεκριμένου τύπου ια προ ήματα μέτρησης. 3.1 Ορισμοί και Παραδεί ματα Το πρώτο και πιο απ ό μοντέ ο προ ήματος που α δούμε είναι το πρό ημα ομομορφισμών ραφήματος (graph homomorphisms problem). Έστ A = (A i,j ) C q q ένας πίνακας, ο οποίος εν ένει μπορεί να έ ει μι αδικά στοι εία. Αυτός ο πίνακας είναι και η παράμετρος του προ ήματος. Το πρό ημα ομομορφισμών ραφήματος, EVAL(A), είναι δοσμένου ενός ραφήματος G = (V, E), να υπο ο ίσουμε τη συνάρτηση διαμέρισης Z A (G) = σ:v [q] (u,v) E A σ(u),σ(v). Αν ο A είναι συμμετρικός πίνακας και το G είναι μη κατευ υνόμενο ράφημα, τότε έ ουμε το πρό ημα ομομορφισμών μη κατευ υνόμενου ραφήματος. Ανά ο α τώρα με το τι α επι έξουμε ς πίνακα A, μπορεί να προκύψει και ένα διαφορετικό πρό ημα και ενικά η συνάρτηση Z A (G) μπορεί να εκφράσει πο ές ενδιαφέρουσες ιδιότητες. Ας δούμε ορισμένα παραδεί ματα: 25
36 26 ΚΕΦΑΛΑΙΟ 3. ΠΡΟΒΛΗΜΑΤΑ ΜΕΤΡΗΣΗΣ Αν έσουμε A = κορυφών του G. Αν έσουμε A = ρ ματισμών του G. ( ), τότε η Z A (G) μετράει το π ή ος τ ν κα ύψε ν , τότε Z A (G) μετράει το π ή ος τ ν Πιο ενικά, αν A =....., τότε προκύπτει το πρό ημα του k- ρ ματισμού ραφήματος (ο πίνακας είναι k k). Επίσης ένα παράδει μα στο οποίο ο πίνακας δε παίρνει μόνο τιμές 0 και 1 είναι το πρό ημα του να μετρήσουμε το π ή ος τ ν ενα όμεν ν υπο ραφημάτ ν του G με άρτιο π ή ος ακμών. Αυτό το πρό ημα είναι ισοδύναμο με το να έσουμε A = ( ). Το δεύτερο μοντέ ο προ ημάτ ν που α εξετάσουμε είναι το #CSP. Έστ D = {1, 2,, d} ένα πεδίο. Μια ώσσα περιορισμών L είναι ένα πεπερασμένο σύνο ο συναρτήσε ν {f 1,, f h } ια τις οποίες η f i : D r i C είναι μια r i - με ής συνάρτηση ια κάποιο r i 1. Το πρό ημα #CSP(L) έ ει ς είσοδο ένα σύνο ο από n μετα ητές x = (x 1,, x n ) και μια συ ο ή I από m διανύσματα της μορφής (f, i 1,, i r ) στα οποία η f είναι μια r-με ής συνάρτηση στο L και i 1,, i r [n]. Το πρό ημα ζητάει και πά ι να υπο ο ίσουμε τη συνάρτηση διαμέρισης η οποία τώρα είναι η Z L (I) = x D n (f,i 1,,i r ) I f(x i1,, x ir ). Αν οι συναρτήσεις στην L έ ουν σαν πεδίο τιμών το {0, 1}, τότε μπορούμε να τις δούμε σαν σ έσεις και έ ουμε το πρό ημα #CSP(F) ρίς άρη. Όπ ς έπουμε, το #CSP είναι το αντίστοι ο πρό ημα μέτρησης του προ- ήματος απόφασης που είδαμε στο προη ούμενο κεφά αιο. Οπότε, όπ ς είναι αναμενόμενο, ένα παράδει μα προ ήματος που μοντε οποιείται σαν #CSP είναι το #3SAT. Πιο συ κεκριμένα μπορούμε να έσουμε D = {0, 1} και L =
37 3.1. ΟΡΙΣΜΟΙ ΚΑΙ ΠΑΡΑΔΕΙΓΜΑΤΑ 27 {f 0, f 1, f 2, f 3 }, όπου f 0 (x, y, z) = x y z, f 1 (x, y, z) = x y z, f 2 (x, y, z) = x ȳ z, f 3 (x, y, z) = x ȳ z, οπότε έπουμε ότι το #CSP(L) είναι ακρι ώς το πρό ημα #3SAT. Αναφέραμε στην εισα ή του κεφα αίου ότι το #CSP είναι ενίκευση του προ ήματος ομομορφισμών ραφήματος. Αυτό συμ αίνει ιατί αν στην L ε ρήσουμε μία μόνο συνάρτηση η οποία είναι διμε ής και εκφράζεται από τον πίνακα A και επίσης αντιστοι ήσουμε τις μετα ητές x 1,, x n στις κορυφές του ραφήματος G και τους περιορισμούς του I στις ακμές του G, τότε έ ουμε μοντε οποιήσει το πρό ημα ομομορφισμών ραφήματος σαν #CSP, άρα το πρώτο είναι ειδική περίπτ ση του δεύτερου. Το τρίτο και πιο ενικό μοντέ ο προ ήματος που α δούμε είναι πρό ημα Holant. Έστ [q] ένα πεδίο και F ένα πεπερασμένο σύνο ο συναρτήσε ν με μι αδικές τιμές και ορίσματα από το [q]. Το πρό ημα Holant(F ) είναι το εξής: είσοδος είναι μια τριάδα Ω = (G, F, π) (signature grid), όπου G = (V, E) είναι ένα ράφημα με ετικέτες στις κορυφές, και π είναι η συνάρτηση που σε κά ε κορυφή v V αντιστοι εί ς ετικέτα μια συνάρτηση f v F έτσι ώστε το π ή ος ορισμάτ ν που δέ εται η f v να είναι ίσο με το α μό της v. Ζητούμενο του προ ήματος είναι ο υπο ο ισμός της συνάρτησης Holant Ω = σ:e [q] v V f v (σ E(v) ). Ένα παράδει μα προ ήματος το οποίο μοντε οποιείται σαν Holant α ά έ ει αποδει εί ότι δεν μοντε οποιείται σαν πρό ημα ομομορφισμών ραφήματος [23] είναι το πρό ημα μέτρησης τέ ει ν ταιριασμάτ ν σε ένα ράφημα. Συ κεκριμένα ια να το μοντε οποιήσουμε σαν πρό ημα Holant έτουμε [q] = {0, 1} και F να περιέ ει ό ες τις EXACTONE συναρτήσεις, δη αδή τις συναρτήσεις που επιστρέφουν 1 αν ακρι ώς ένα όρισμά τους είναι 1 και 0 διαφορετικά. Σε κά ε κορυφή του G αντιστοι ούμε μια EXACTONE συνάρτηση με το κατά η ο π ή ος ορισμάτ ν. Το ινόμενο v V f v (σ E(v) ) ισούται με 1 αν το σ 1 (1) E είναι ένα τέ ειο ταίριασμα και ισούται με 0 διαφορετικά. Οπότε το Holant Ω μετράει το π ή ος τ ν τέ ει ν ταιριασμάτ ν του ραφήματος. Αν αντί ια τις EXACTONE συναρτήσεις ρησιμοποιήσουμε τις ATMOSTONE συναρτήσεις, τότε μετράμε το π ή ος ό ν τ ν (ό ι απαραίτητα τέ ει ν) ταιριασμάτ ν.
38 28 ΚΕΦΑΛΑΙΟ 3. ΠΡΟΒΛΗΜΑΤΑ ΜΕΤΡΗΣΗΣ Ορισμός Έστω A ένα σύνολο συναρτήσεων. Ορίζουμε το πρόβλημα Holant A ως υποπερίπτωση του Holant να είναι το πρόβλημα Holant A (F) = Holant(F A). Σ αυτή την υποπερίπτωση, καλούμε το A, ελεύθερα διαθέσιμες συναρτήσεις (freely available functions). Αν ε ρήσουμε ό ες τις συναρτήσεις ισότητας ς ε εύ ερα δια έσιμες, τότε η υποπερίπτ ση του Holant που δημιουρ είται είναι ακρι ώς το πρό ημα #CSP. Με ά α ό ια ισ ύει ότι #CSP(F) = Holant(F Equalities). Για να δούμε ότι το Holant είναι ενίκευση του #CSP κάνουμε τα εξής: αναπαριστούμε ένα στι μιότυπο του #CSP από ένα διμερές ράφημα, όπου το αριστερό μέρος (LHS) αντιστοι εί στις μετα ητές και το δεξί μέρος (RHS) αντιστοι εί στους περιορισμούς (στις συναρτήσεις). Η τριάδα εισόδου Ω του Holant είναι η εξής: Σε κά ε κορυφή-μετα ητή στο LHS αντιστοι ούμε μια συνάρτηση ισότητα (EQUALITY function) και σε κά ε κορυφή-περιορισμό στο RHS δίνουμε ς ετικέτα τον περιορισμό-συνάρτηση που αντιστοι εί σ αυτή τη κορυφή. Η EQUALITY συνάρτηση σε κά ε κορυφή-μετα ητή ανα κάζει τα προσκείμενες ακμές αν πάρουν την ίδια τιμή. Αυτό κάνει τις ανα έσεις τιμών στις ακμές ουσιαστικά να είναι ανα έσεις τιμών στις κορυφές που με της σειρά τους είναι ανα έσεις τιμών στις μετα ητές του LHS όπ ς στο #CSP. Β έπουμε οιπόν ότι το #CSP είναι ειδική περίπτ ση του προ ήματος Holant. Ας δούμε τώρα και κάποιες ά ες ειδικές περιπτώσεις του Holant. Ορισμός Έστω U το σύνολο όλων των μονομελών συναρτήσεων. Τότε ορίζουμε Holant (F) = Holant(F U). Ορισμός Έστω i η μονομελής συνάρτηση που δίνει τιμή 1 σε είσοδο i [q], και τιμή 0 σε κάθε άλλη είσοδο. Τότε ορίζουμε, Holant c (F) = Holant(F { 1,, q }). Είναι φανερό από τον ορισμό ότι το Holant c πειέ ει ς υποπερίπτ ση το Holant. Κάτι ά ο όμ ς που επίσης ισ ύει είναι ότι το Holant c περιέ ει ς υποπερίπτ ση και το #CSP [18]. Ό ό ος που ορίζουμε υποπεριπτώσεις του Holant είναι ιατί ενώ ιδανικά α έ αμε να ρούμε ε ρήματα δι οτομίας ια ό η την κ άση Holant, αν δε μπορούμε να το κάνουμε αυτό, τότε προσπα ούμε να ρούμε δι οτομίες σε όσο το δυνατόν
39 3.2. ΟΜΟΜΟΡΦΙΣΜΟΙ ΓΡΑΦΗΜΑΤΟΣ 29 με α ύτερες υποκ άσεις. Η εικόνα οιπόν τ ν κ ασε ν που έ ουμε ορίσει, είναι η παρακάτ. 3.2 Ομομορφισμοί Γραφήματος Θα δούμε τώρα συνοπτικά τα αποτε έσματα δι οτομίας που έ ουν αποδει εί ια τις κ άσεις προ ημάτ ν που ορίσαμε. Πρώτα α δούμε την περίπτ ση τ ν ομομορφισμών μη κατευ υνόμενου ραφήματος, δη αδή την περίπτ ση που ο πίνακας είναι συμμετρικός. Αν επιπ έον ο πίνακας περιέ ει τιμές μόνο στο {0, 1}, τότε οι Dyer και Greenhill [20] έδειξαν ότι αν το ράφημα H A που αντιστοι εί στον πίνακα A, δεν είναι π ήρες (complete) ή π ήρ ς διμερές (complete bipartite) τότε το πρό ημα είναι στο P. Σε κά ε ά η περίπτ ση το πρό ημα είναι #P-complete. Οι Bulatov και Grohe [8] στη συνέ εια επέκτειναν το αποτέ εσμα ια πίνακες με μη αρνητικά άρη και στο επόμενο κεφά αιο α δούμε περισσότερα ια το κριτήριό τους. Αρ ότερα οι Goldberg, Grohe, Jerrum και Thurley [24] απέδειξαν το αντίτοι ο εώρημα δι οτομίας ια ό ους τους συμμετρικούς πίνακες με στοι εία πρα ματικούς αρι μούς. Τέ ος, οι Cai, Chen και Lu [12] έδειξαν το παρακάτ ενικότερο εώρημα. Θεώρημα Έστω A ένας συμμετρικός πίνακας με στοιχεία μιγαδικούς αριθμούς. Τότε το να μετρήσουμε τους ομομορφισμούς στο H A γίνεται είτε σε πολυωνυμικό χρόνο, είτε το πρόβλημα είναι #P-hard.
40 30 ΚΕΦΑΛΑΙΟ 3. ΠΡΟΒΛΗΜΑΤΑ ΜΕΤΡΗΣΗΣ Για την περίπτ ση που έ ουμε και μη κατευ υνόμενα ραφήματα, δη αδή ια την περίπτ ση που ο πίνακας δεν είναι απαραίτητα συμμετρικός, οι Dyer, Goldberg και Paterson [19] έδειξαν ένα εώρημα δι οτομίας ια μια οικο ένεια ακυκ ικών κατευ υνόμεν ν ραφημάτ ν και ια πίνακες με στοι εία στο {0, 1}. To 2010 οι Cai και Chen [10] επέκτειναν το αποτέ εσμά τους ια ό α τα κατευ υνόμενα ραφήματα και ια πίνακες με μη-αρνητικά στοι εία. 3.3 #CSP Ας δούμε τώρα τα αποτε έσματα δι οτομίας ια το δυαδικό #CSP όπου το πεδίο είναι το D = {0, 1}. Για την περίπτ ση που δεν έ ουμε άρη, δη αδή οι συναρτήσεις είναι απ ά σ έσεις, οι Creignou και Hermann [17] έδειξαν ότι η μόνη εύκο η περίπτ ση είναι όταν έ ουμε αφινικές σ έσεις, ενώ σε κά ε ά η περίπτ ση το πρό ημα είναι #P-hard. Μπορούμε να ενικεύσουμε την έννοια τ ν αφινικών σ έσε ν και να ορίσουμε τις α νά αφινικές συναρτήσεις, οι οποίες είναι σαν τις αφινικές, απ ά αντί ια τιμές 0,1 παίρνουν τιμές 0, c, ια έναν παρά οντα c. Έστ επίσης P η κ άση ό ν τ ν συναρτήσε ν που μπορούν να εκφραστούν ς ινόμενο μονομε ών συναρτήσε ν, διμε ών συναρτήσε ν ισότητας και διμε ών συναρτήσε ν ανισότητας. Οι Dyer, Goldberg και Jerrum [18] έδειξαν το παρακάτ εώρημα. Θεώρημα Έστω F ένα σύνολο από μη-αρνητικές συναρτήσεις στο δυαδικό πεδίο. Το #CSP(F) είναι #P-hard εκτός εάν όλες οι συναρτήσεις στο F είναι αγνά αφινικές ή ανήκουν στην κλάση P, οπότε σε αυτή την περίπτωση το πρόβλημα ανήκει στο P. Το 2009 οι Bulatov, Dyer, Goldberg, Jalsenius και Richerby [7] απέδειξαν εώρημα δι οτομίας ια το δυαδικό #CSP όπου οι συναρτήσεις παίρνουν τιμές σε ό ους του πρα ματικούς αρι μούς, και ανεξάρτητα οι Cai, Lu και Xia [15] έκαναν το ίδιο ια τους μι αδικούς αρι μούς. Για τη ενική περίπτ ση στην οποία το πεδίο D μπορεί να είναι οποιοδήποτε πεπερασμένο σύνο ο, ο Boulatov [4] απέδειξε δι οτομία ια την περίπτ ση του #CSP ρίς άρη. Το κριτήριο όμ ς που έδ σε ια τη δι οτομία δεν ήταν ν στό αν είναι αποφασίσιμο. Οι Dyer και Richerby [21] στη συνέ εια απέδειξαν το ίδιο εώρημα δίνοντας ένα απ ούστερο κριτήριο και αποδεικνύοντας ότι είναι αποφασίσιμο. Φυσικά το νέο κριτήριο ήταν ισοδύναμο με αυτό του Bulatov. Θα μι ήσουμε πιο ανα υτικά ια αυτά τα δύο papers στο επόμενο κεφά αιο. Λί ο αρ ότερα οι Bulatov, Dyer, Goldberg, Jalsenius, Jerrum και Richerby [6] επέκτειναν το αποτέ εσμα τ ν Dyer και Richerby ια ετικά ρητά άρη. Στη συνέ εια οι Cai, Chen και Lu [13] έδειξαν δι οτομία ια ό α τα μη-αρνητικά άρη. Τέ ος, οι Cai και Chen [11] απέδειξαν τη ενική περίπτ ση ια άρη μι αδικούς αρι μούς, δίνοντας τρία
41 3.4. ΠΡΟΒΛΗΜΑΤΑ HOLANT 31 κριτήρια δι οτομίας που το αν είναι ή ό ι αποφασίσιμα παραμένει ανοι τό. Για το τε ευταίο αποτέ εσμα α δούμε πιο ανα υτικά την απόδειξη και τα κριτήρια στο επόμενο κεφά αιο. 3.4 Προ ήματα Holant Θα δούμε τώρα τι αποτε έσματα δι οτομίας υπάρ ουν ια τα ενικότερα μοντέ α τ ν Holant και Holant c. Οι Cai, Lu και Xia [15] απέδειξαν δι οτομία ια το συμμετρικό, δυαδικό μοντέ ο Holant με μι αδικά άρη. Αρ ότερα [16] επέκτειναν το αποτέ εσμά τους και ια τη μη συμμετρική περίπτ ση. Στο ίδιο paper [15] έδ σαν επίσης δι οτομία ια το συμμετρικό, δυαδικό μοντέ ο του Holant c με άρη πρα ματικούς αρι μούς. Τέ ος,οι Cai, Huang και Lu [14] επέκτειναν αυτό το αποτέ εσμα ια την περίπτ ση με μι αδικά άρη. Οι περισσότερες περιπτώσεις ια τη ενικότερη κ άση Holant παραμένουν ανοι- τές. 3.5 Ο ο ραφικοί Α όρι μοι Σ αυτή την παρά ραφο α κάνουμε μια εισα ή στους ο ο ραφικούς α όρι μους (holographic algorithms). Τους α όρι μους αυτούς τους εισή α ε ο Valiant [37] και είναι πο υ νυμικοί α όρι μοι ια διάφορα εξ τικά προ ήματα ια τα οποία πιο πριν δε ν ρίζαμε ότι ανήκαν στο P. Η ενική ιδέα είναι ότι ένα πρό ημα μέτρησης το ανά ουμε στο πρό ημα μέτρησης τέ ει ν ταιριασμάτ ν σε επίπεδα ραφήματα (ο ο ραφική ανα ή), ια το οποίο έ ουμε πο υ νυμικό α όρι μο, και έτσι προκύπτει πο υ νυμικός α όρι μος και ια το αρ ικό μας πρό ημα. Ορισμός Το πρόβλημα #PERFMATCH είναι το εξής: Είσοδος: Ένα μη κατευθυνόμενο γράφημα G = (V, E, W ) με βάρη. Ζητούμενο: PerfMatch(G) = w i,j, E (i,j) E όπου η άθροιση γίνεται για όλα τα τέλεια ταιριάσματα E του G. Αν τα άρη στις ακμές του ραφήματος είναι ό α ίσα με 1, τότε το PerfMatch(G) μετάει το π ή ος τ ν τέ ει ν ταιριασμάτ ν του ραφήματος G. Το αντίστοι ο πρό ημα απόφασης ν ρίζουμε ότι ανήκει στο P, α ά το παραπάν πρό ημα μέτρησης είναι #P-complete [36]. Για την περίπτ ση όμ ς τ ν επίπεδ ν ραφημάτ ν, το #PERFMATCH ανήκει στο FP (Fisher, Kasteleyn, Temberley, 1961). Πιο συ κεκριμένα ισ ύει το παρακάτ εώρημα.
Α όρι μοι και Πο υπ οκότητα 1η Σειρά Γραπτών Ασκήσε ν
 .. Α όρι μοι και Πο υπ οκότητα 1η Σειρά Γραπτών Ασκήσε ν CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Επιμέ εια διαφανειών: Χάρης Α ε ιδάκης 12 Δεκεμ ρίου, 2011 Outline. 1 Άσκηση 1. 2 Άσκηση 2. 3 Άσκηση 3. 4 Άσκηση 4. 5 Άσκηση
.. Α όρι μοι και Πο υπ οκότητα 1η Σειρά Γραπτών Ασκήσε ν CoReLab ΣΗΜΜΥ - Ε.Μ.Π. Επιμέ εια διαφανειών: Χάρης Α ε ιδάκης 12 Δεκεμ ρίου, 2011 Outline. 1 Άσκηση 1. 2 Άσκηση 2. 3 Άσκηση 3. 4 Άσκηση 4. 5 Άσκηση
Το Διανυσματικό Μοντέ ο
 4 Το Διανυσματικό Μοντέ ο Περιε όμενα Κεφα αίου 4.1 Εισα ή............................ 74 4.2 Βασικές Έννοιες........................ 74 4.2.1 Υπο ο ισμός Σημαντικότητας Όρ ν......... 76 4.2.2 Υπο ο ισμός
4 Το Διανυσματικό Μοντέ ο Περιε όμενα Κεφα αίου 4.1 Εισα ή............................ 74 4.2 Βασικές Έννοιες........................ 74 4.2.1 Υπο ο ισμός Σημαντικότητας Όρ ν......... 76 4.2.2 Υπο ο ισμός
Το Λο ικό Μοντέ ο. Περιε όμενα Κεφα αίου
 3 Το Λο ικό Μοντέ ο Περιε όμενα Κεφα αίου 3.1 Εισα ή............................ 52 3.2 Το Απ ό Λο ικό Μοντέ ο................... 52 3.2.1 Βασικές Έννοιες.................... 53 3.2.2 Τε εστές Γειτονικότητας
3 Το Λο ικό Μοντέ ο Περιε όμενα Κεφα αίου 3.1 Εισα ή............................ 52 3.2 Το Απ ό Λο ικό Μοντέ ο................... 52 3.2.1 Βασικές Έννοιες.................... 53 3.2.2 Τε εστές Γειτονικότητας
Ανάκτηση Π ηροφορίας στον Πα κόσμιο Ιστό
 9 Ανάκτηση Π ηροφορίας στον Πα κόσμιο Ιστό Περιε όμενα Κεφα αίου 9.1 Εισα ή............................ 204 9.2 Πα κόσμιος Ιστός και Μη ανές Αναζήτησης......... 204 9.2.1 Οι Προκ ήσεις του Πα κόσμιου Ιστού........
9 Ανάκτηση Π ηροφορίας στον Πα κόσμιο Ιστό Περιε όμενα Κεφα αίου 9.1 Εισα ή............................ 204 9.2 Πα κόσμιος Ιστός και Μη ανές Αναζήτησης......... 204 9.2.1 Οι Προκ ήσεις του Πα κόσμιου Ιστού........
Το Πι ανοκρατικό Μοντέ ο
 5 Το Πι ανοκρατικό Μοντέ ο Περιε όμενα Κεφα αίου 5.1 Εισα ή............................ 94 5.2 Βασικές Έννοιες Θε ρίας Πι ανοτήτ ν............ 95 5.3 Υπο ο ισμός Σ ετικότητας Ε ράφ ν............ 96 5.3.1
5 Το Πι ανοκρατικό Μοντέ ο Περιε όμενα Κεφα αίου 5.1 Εισα ή............................ 94 5.2 Βασικές Έννοιες Θε ρίας Πι ανοτήτ ν............ 95 5.3 Υπο ο ισμός Σ ετικότητας Ε ράφ ν............ 96 5.3.1
Κανονισμός Εκτε εστικής Επιτροπής
 Κανονισμός Εκτε εστικής Επιτροπής Περιφερειακής Ένωσης Δήμων (Π.Ε.Δ.) Ιονίων Νήσων Περιφερειακή Έν ση Δήμ ν (Π.Ε.Δ.) Ιονί ν Νήσ ν ΠΕΔ ΙΝ Ιανουάριος 2012 2 Περιε όμενα 1 Αντικείμενο 4 2 Σύν εση εκτε εστικής
Κανονισμός Εκτε εστικής Επιτροπής Περιφερειακής Ένωσης Δήμων (Π.Ε.Δ.) Ιονίων Νήσων Περιφερειακή Έν ση Δήμ ν (Π.Ε.Δ.) Ιονί ν Νήσ ν ΠΕΔ ΙΝ Ιανουάριος 2012 2 Περιε όμενα 1 Αντικείμενο 4 2 Σύν εση εκτε εστικής
Ο Κατά ο ος Υπο ραφών
 7 Ο Κατά ο ος Υπο ραφών Περιε όμενα Κεφα αίου 7.1 Εισα ή............................ 144 7.2 Μέ οδοι Εξα ής Υπο ραφών................ 144 7.2.1 Βασικές Μέ οδοι Εξα ής Υπο ραφών....... 145 7.2.2 Εξα ή Υπο
7 Ο Κατά ο ος Υπο ραφών Περιε όμενα Κεφα αίου 7.1 Εισα ή............................ 144 7.2 Μέ οδοι Εξα ής Υπο ραφών................ 144 7.2.1 Βασικές Μέ οδοι Εξα ής Υπο ραφών....... 145 7.2.2 Εξα ή Υπο
NP-complete problems. IS, 4-Degree IS,CLIQUE, NODE COVER, MAX CUT, MAX BISECTION, BISECTION WIDTH. NP-complete problems 1 / 30
 NP-complete problems IS, 4-Degree IS,CLIQUE, NODE COVER, MAX CUT, MAX BISECTION, BISECTION WIDTH Καλογερόπουλος Παναγιώτης (ΜΠΛΑ) NP-complete problems 1 / 30 Independent Set is NP-complete Ορισμός. Εστω
NP-complete problems IS, 4-Degree IS,CLIQUE, NODE COVER, MAX CUT, MAX BISECTION, BISECTION WIDTH Καλογερόπουλος Παναγιώτης (ΜΠΛΑ) NP-complete problems 1 / 30 Independent Set is NP-complete Ορισμός. Εστω
Παρά η η Δια είριση Δεδομέν ν
 17 Παρά η η Δια είριση Δεδομέν ν Ο όρος "με ά α δεδομένα" εμφανίστηκε στα μέσα της δεκαετίας του 2000 και έ ει έσει νέες προκ ήσεις στα ΣΔΒΔ. Συνοπτικά, οι προκ ήσεις αυτές απορρέουν κυρί ς από τον πο
17 Παρά η η Δια είριση Δεδομέν ν Ο όρος "με ά α δεδομένα" εμφανίστηκε στα μέσα της δεκαετίας του 2000 και έ ει έσει νέες προκ ήσεις στα ΣΔΒΔ. Συνοπτικά, οι προκ ήσεις αυτές απορρέουν κυρί ς από τον πο
Ο Αντεστραμμένος Κατά ο ος
 6 Ο Αντεστραμμένος Κατά ο ος Περιε όμενα Κεφα αίου 6.1 Εισα ή............................ 118 6.2 Η Δομή του Αντεστραμμένου Κατα ό ου........... 118 6.3 Χρήση του Κατα ό ου στην Επεξερ ασία Ερ τημάτ ν...
6 Ο Αντεστραμμένος Κατά ο ος Περιε όμενα Κεφα αίου 6.1 Εισα ή............................ 118 6.2 Η Δομή του Αντεστραμμένου Κατα ό ου........... 118 6.3 Χρήση του Κατα ό ου στην Επεξερ ασία Ερ τημάτ ν...
Κανονισμός Εποπτικού Συμ ου ίου
 Κανονισμός Εποπτικού Συμ ου ίου Περιφερειακής Ένωσης Δήμων (Π.Ε.Δ.) Ιονίων Νήσων Περιφερειακή Έν ση Δήμ ν (Π.Ε.Δ.) Ιονί ν Νήσ ν ΠΕΔ ΙΝ Ιανουάριος 2012 2 Περιε όμενα 1 Αντικείμενο του Κανονισμού 4 2 Σύν
Κανονισμός Εποπτικού Συμ ου ίου Περιφερειακής Ένωσης Δήμων (Π.Ε.Δ.) Ιονίων Νήσων Περιφερειακή Έν ση Δήμ ν (Π.Ε.Δ.) Ιονί ν Νήσ ν ΠΕΔ ΙΝ Ιανουάριος 2012 2 Περιε όμενα 1 Αντικείμενο του Κανονισμού 4 2 Σύν
Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Τε νο ο ίας Π ηροφορικής και Υπο ο ιστών. Διπ ματική Ερ ασία
 Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Τε νο ο ίας Π ηροφορικής και Υπο ο ιστών Υ οποίηση κατασκευής δέντρου επι εμάτ ν σε Hadoop Mapreduce Διπ ματική
Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Τε νο ο ίας Π ηροφορικής και Υπο ο ιστών Υ οποίηση κατασκευής δέντρου επι εμάτ ν σε Hadoop Mapreduce Διπ ματική
ΕΠΑΝΑΛΗΠΣΙΚΕ ΑΚΗΕΙ ΜΙΓΑΔΙΚΟΤ-ΟΡΙΑ-ΤΝΕΧΕΙΑ
 (ΠΕΡΙΕΧΕΙ ΑΚΗΕΙ ΚΑΙ ΑΠΟ ΣΗΝ ΣΡΑΠΕΖΑ ΘΕΜΑΣΩΝ ΣΗ Ε.Μ.Ε) ΑΚΗΗ 1 Έςτω ςυνεήσ ςυνάρτηςη :RR, με (0)=2 η οποία ικανοποιεί τη ςέςη ( ) 4 = 6 ια κά ε R α) Να βρείτε τισ τιμέσ (2) και (-2) β) Να απο είξετε τι υπάρει
(ΠΕΡΙΕΧΕΙ ΑΚΗΕΙ ΚΑΙ ΑΠΟ ΣΗΝ ΣΡΑΠΕΖΑ ΘΕΜΑΣΩΝ ΣΗ Ε.Μ.Ε) ΑΚΗΗ 1 Έςτω ςυνεήσ ςυνάρτηςη :RR, με (0)=2 η οποία ικανοποιεί τη ςέςη ( ) 4 = 6 ια κά ε R α) Να βρείτε τισ τιμέσ (2) και (-2) β) Να απο είξετε τι υπάρει
Κανονισμός Διοικητικού Συμ ου ίου
 Κανονισμός Διοικητικού Συμ ου ίου Περιφερειακής Ένωσης Δήμων (Π.Ε.Δ.) Ιονίων Νήσων Περιφερειακή Έν ση Δήμ ν (Π.Ε.Δ.) Ιονί ν Νήσ ν -3mm-3mm ΠΕΔ ΙΝ Ιανουάριος 2012 2 Περιε όμενα 1 Αντικείμενο του κανονισμού
Κανονισμός Διοικητικού Συμ ου ίου Περιφερειακής Ένωσης Δήμων (Π.Ε.Δ.) Ιονίων Νήσων Περιφερειακή Έν ση Δήμ ν (Π.Ε.Δ.) Ιονί ν Νήσ ν -3mm-3mm ΠΕΔ ΙΝ Ιανουάριος 2012 2 Περιε όμενα 1 Αντικείμενο του κανονισμού
Κανονισμός Οικονομικής Δια είρισης
 Κανονισμός Οικονομικής Δια είρισης Περιφερειακής Ένωσης Δήμων (Π.Ε.Δ.) Ιονίων Νήσων Περιφερειακή Έν ση Δήμ ν (Π.Ε.Δ.) Ιονί ν Νήσ ν ΠΕΔ ΙΝ Ιανουάριος 2012 2 Περιε όμενα Άρ ρο 1: Αντικείμενο Κανονισμού 4
Κανονισμός Οικονομικής Δια είρισης Περιφερειακής Ένωσης Δήμων (Π.Ε.Δ.) Ιονίων Νήσων Περιφερειακή Έν ση Δήμ ν (Π.Ε.Δ.) Ιονί ν Νήσ ν ΠΕΔ ΙΝ Ιανουάριος 2012 2 Περιε όμενα Άρ ρο 1: Αντικείμενο Κανονισμού 4
Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Τε νο ο ίας Π ηροφορικής και Υπο ο ιστών. Διπ ματική Ερ ασία
 Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Τε νο ο ίας Π ηροφορικής και Υπο ο ιστών Με έτη και Υ οποίηση Α ορί μ ν ια Βιο ο ικές Εφαρμο ές σε MapReduce Περι
Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Τε νο ο ίας Π ηροφορικής και Υπο ο ιστών Με έτη και Υ οποίηση Α ορί μ ν ια Βιο ο ικές Εφαρμο ές σε MapReduce Περι
Ανάπτυξη Βι ιο ήκης Γραφικών ια Ενσ ματ μένο Σύστημα
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ Ανάπτυξη Βι ιο ήκης Γραφικών ια Ενσ ματ μένο Σύστημα ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ Ανάπτυξη Βι ιο ήκης Γραφικών ια Ενσ ματ μένο Σύστημα ΔΙΠΛΩΜΑΤΙΚΗ ΕΡΓΑΣΙΑ
Απ ή υ οποίηση α ορί μου Fast Multipole Method ανεξάρτητου συνάρτησης πυρήνα
 Αριστοτέ ειο Πανεπιστήμιο Θεσσα ονίκης Πο υτε νική Σ ο ή Τμήμα Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Η εκτρονικής και Υπο ο ιστών Απ ή υ οποίηση α ορί μου Fast Multipole Method ανεξάρτητου
Αριστοτέ ειο Πανεπιστήμιο Θεσσα ονίκης Πο υτε νική Σ ο ή Τμήμα Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Η εκτρονικής και Υπο ο ιστών Απ ή υ οποίηση α ορί μου Fast Multipole Method ανεξάρτητου
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Αποτίμηση Αποτε εσματικότητας
 2 Αποτίμηση Αποτε εσματικότητας Περιε όμενα Κεφα αίου 2.1 Εισα ή............................ 26 2.2 Βασικά Μέτρα Αποτε εσματικότητας............. 26 2.2.1 Ανάκ ηση, Ακρί εια και Αστο ία........... 27 2.2.2
2 Αποτίμηση Αποτε εσματικότητας Περιε όμενα Κεφα αίου 2.1 Εισα ή............................ 26 2.2 Βασικά Μέτρα Αποτε εσματικότητας............. 26 2.2.1 Ανάκ ηση, Ακρί εια και Αστο ία........... 27 2.2.2
ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ
 1 ΚΕΦΑΛΑΙΟ 1 : ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 11 ΕΙΣΑΓΩΓΗ Σε ότι ακολουθεί συμβολίζουμε με το σύνολο των φυσικών αριθμών και με και R τα σύνολα των ακεραίων των ρητών και των πραγματικών αριθμών
1 ΚΕΦΑΛΑΙΟ 1 : ΠΡΑΓΜΑΤΙΚΕΣ ΣΥΝΑΡΤΗΣΕΙΣ ΠΟΛΛΩΝ ΜΕΤΑΒΛΗΤΩΝ 11 ΕΙΣΑΓΩΓΗ Σε ότι ακολουθεί συμβολίζουμε με το σύνολο των φυσικών αριθμών και με και R τα σύνολα των ακεραίων των ρητών και των πραγματικών αριθμών
ILP-Feasibility conp
 Διάλεξη 19: 23.12.2014 Θεωρία Γραμμικού Προγραμματισμού Γραφέας: Χαρίλαος Τζόβας Διδάσκων: Σταύρος Κολλιόπουλος 19.1 Θεωρία Πολυπλοκότητας και προβλήματα απόφασης Για να μιλήσουμε για προβλήματα και τον
Διάλεξη 19: 23.12.2014 Θεωρία Γραμμικού Προγραμματισμού Γραφέας: Χαρίλαος Τζόβας Διδάσκων: Σταύρος Κολλιόπουλος 19.1 Θεωρία Πολυπλοκότητας και προβλήματα απόφασης Για να μιλήσουμε για προβλήματα και τον
Υπολογιστική Πολυπλοκότητα
 Υπολογιστική Πολυπλοκότητα ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Γιατί κάποια (επιλύσιμα) προβλήματα είναι δύσκολο
Υπολογιστική Πολυπλοκότητα ημήτρης Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Υπολογιστική Πολυπλοκότητα Γιατί κάποια (επιλύσιμα) προβλήματα είναι δύσκολο
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ ΜΕΛΕΤΗ ΚΑΙ ΠΡΟΣΟΜΟΙΩΣΗ BLDC ΚΙΝΗΤΗΡΑ ΣΕ ΠΕΡΙΒΑΛΛΟΝ MATLAB/SIMULINK
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΙΚΩΝ ΒΙΟΜΗΧΑΝΙΚΩΝ ΔΙΑΤΑΞΕΩΝ ΚΑΙ ΣΥΣΤΗΜΑΤΩΝ ΑΠΟΦΑΣΕΩΝ ΜΕΛΕΤΗ ΚΑΙ ΠΡΟΣΟΜΟΙΩΣΗ BLDC ΚΙΝΗΤΗΡΑ ΣΕ ΠΕΡΙΒΑΛΛΟΝ MATLAB/SIMULINK
Θεωρία Υπολογισμού Άρτιοι ΑΜ. Διδάσκων: Σταύρος Κολλιόπουλος. eclass.di.uoa.gr. Περιγραφή μαθήματος
 Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Περιγραφή μαθήματος Θεωρία Υπολογισμού Άρτιοι ΑΜ Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας (Θεωρία Αλγορίθμων). Διδάσκων: Σταύρος Κολλιόπουλος
Θεωρία Υπολογισμού Αρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr
 Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
Θεωρία Υπολογισμού Άρτιοι ΑΜ Διδάσκων: Σταύρος Κολλιόπουλος eclass.di.uoa.gr Περιγραφή μαθήματος Σκοπός του μαθήματος είναι η εισαγωγή στη Θεωρία Υπολογισμού και στη Θεωρία Υπολογιστικής Πολυπλοκότητας
d(v) = 3 S. q(g \ S) S
 Διάλεξη 9: 9.11.2016 Θεωρία Γραφημάτων Διδάσκων: Σταύρος Κολλιόπουλος Γραφέας: Παναγιωτίδης Αλέξανδρος Θεώρημα 9.1 Εστω γράφημα G = (V, E), υπάρχει τέλειο ταίριασμα στο G αν και μόνο αν για κάθε S υποσύνολο
Διάλεξη 9: 9.11.2016 Θεωρία Γραφημάτων Διδάσκων: Σταύρος Κολλιόπουλος Γραφέας: Παναγιωτίδης Αλέξανδρος Θεώρημα 9.1 Εστω γράφημα G = (V, E), υπάρχει τέλειο ταίριασμα στο G αν και μόνο αν για κάθε S υποσύνολο
Θεωρία Γραφημάτων 6η Διάλεξη
 Θεωρία Γραφημάτων 6η Διάλεξη Α. Συμβώνης Εθνικο Μετσοβειο Πολυτεχνειο Σχολη Εφαρμοσμενων Μαθηματικων και Φυσικων Επιστημων Τομεασ Μαθηματικων Φεβρουάριος 2016 Α. Συμβώνης (ΕΜΠ) Θεωρία Γραφημάτων 6η Διάλεξη
Θεωρία Γραφημάτων 6η Διάλεξη Α. Συμβώνης Εθνικο Μετσοβειο Πολυτεχνειο Σχολη Εφαρμοσμενων Μαθηματικων και Φυσικων Επιστημων Τομεασ Μαθηματικων Φεβρουάριος 2016 Α. Συμβώνης (ΕΜΠ) Θεωρία Γραφημάτων 6η Διάλεξη
Υπολογιστική Πολυπλοκότητα
 Υπολογιστική Πολυπλοκότητα ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό
Υπολογιστική Πολυπλοκότητα ιδάσκοντες: Σ. Ζάχος,. Φωτάκης Επιμέλεια διαφανειών:. Φωτάκης Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Άδεια Χρήσης Το παρόν εκπαιδευτικό
q(g \ S ) = q(g \ S) S + d = S.
 Διάλεξη 9: 9.11.2016 Θεωρία Γραφημάτων Διδάσκων: Σταύρος Κολλιόπουλος Γραφέας: Παναγιωτίδης Αλέξανδρος & Σ. Κ. Θεώρημα 9.1 Εστω γράφημα G = (V, E), υπάρχει τέλειο ταίριασμα στο G αν και μόνο αν για κάθε
Διάλεξη 9: 9.11.2016 Θεωρία Γραφημάτων Διδάσκων: Σταύρος Κολλιόπουλος Γραφέας: Παναγιωτίδης Αλέξανδρος & Σ. Κ. Θεώρημα 9.1 Εστω γράφημα G = (V, E), υπάρχει τέλειο ταίριασμα στο G αν και μόνο αν για κάθε
Chapter 7, 8 : Time, Space Complexity
 CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 19 December 2008 1 1 Κλάση NP 2 Μη-Ντετερμινιστικές Μηχανές Turing: Eίναι δυνατόν σε μια συνολική κατάσταση να υπάρχουν πολλές δυνατές επόμενες
CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 19 December 2008 1 1 Κλάση NP 2 Μη-Ντετερμινιστικές Μηχανές Turing: Eίναι δυνατόν σε μια συνολική κατάσταση να υπάρχουν πολλές δυνατές επόμενες
12. ΑΝΙΣΩΣΕΙΣ Α ΒΑΘΜΟΥ. είναι δύο παραστάσεις μιας μεταβλητής x πού παίρνει τιμές στο
 ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
ΓΕΝΙΚΑ ΠΕΡΙ ΑΝΙΣΩΣΕΩΝ Έστω f σύνολο Α, g Α ΒΑΘΜΟΥ είναι δύο παραστάσεις μιας μεταβλητής πού παίρνει τιμές στο Ανίσωση με έναν άγνωστο λέγεται κάθε σχέση της μορφής f f g g ή, η οποία αληθεύει για ορισμένες
Επίπεδα Γραφήματα : Προβλήματα και Υπολογιστική Πολυπλοκότητα
 Αλγόριθμοι πολυωνυμικού χρόνου Ένας αλγόριθμος πολυωνυμικού χρόνου έχει χρόνο εκτέλεσης όπου είναι μία (θετική) σταθερά Κλάση πολυπλοκότητας : περιλαμβάνει τα προβλήματα που επιδέχονται λύση σε πολυωνυμικό
Αλγόριθμοι πολυωνυμικού χρόνου Ένας αλγόριθμος πολυωνυμικού χρόνου έχει χρόνο εκτέλεσης όπου είναι μία (θετική) σταθερά Κλάση πολυπλοκότητας : περιλαμβάνει τα προβλήματα που επιδέχονται λύση σε πολυωνυμικό
conp and Function Problems
 conp and Function Problems 1 Ένα πρόβλημα απόφασης λέμε ότι επιλύεται σε μηντετερμινιστικό πολυωνυμικό χρόνο αν υπάρχει ένας μηντετερμινιστικός αλγόριθμος που, εκμεταλλευόμενος μια τυχαία επιλογή, μπορεί
conp and Function Problems 1 Ένα πρόβλημα απόφασης λέμε ότι επιλύεται σε μηντετερμινιστικό πολυωνυμικό χρόνο αν υπάρχει ένας μηντετερμινιστικός αλγόριθμος που, εκμεταλλευόμενος μια τυχαία επιλογή, μπορεί
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 14. Χρονική Πολυπλοκότητα 17, 20, 24 Απριλίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να
Θεωρία Υπολογισμού και Πολυπλοκότητα Κεφάλαιο 14. Χρονική Πολυπλοκότητα 17, 20, 24 Απριλίου 2007 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να
ψ φ2 = k χ φ2 = 4k χ φ1 = χ φ1 + χ φ2 + 3 = 4(k 1 + k 2 + 1) + 1 ψ φ1 = ψ φ1 + χ φ2 = k k = (k 1 + k 2 + 1) + 1
 Ασκήσεις στο μάθημα της Λογικής 15 Οκτωβρίου 2015 Άσκηση 1. Να δειχτεί ότι δεν υπάρχουν τύποι μήκους 2,3,6 αλλά κάθε άλλο (θετικό ακέραιο) μήκος είναι δυνατό (άσκηση 2, σελίδα 39) Απόδειξη. Δείχνουμε πρώτα
Ασκήσεις στο μάθημα της Λογικής 15 Οκτωβρίου 2015 Άσκηση 1. Να δειχτεί ότι δεν υπάρχουν τύποι μήκους 2,3,6 αλλά κάθε άλλο (θετικό ακέραιο) μήκος είναι δυνατό (άσκηση 2, σελίδα 39) Απόδειξη. Δείχνουμε πρώτα
JEAN-CHARLES BLATZ 02XD34455 01RE52755
 ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ ΤΩΝ ΕΝ Ι ΑΜ ΕΣ ΩΝ ΟΙ Κ ΟΝΟΜ Ι Κ ΩΝ Κ ΑΤΑΣ ΤΑΣ ΕΩΝ ΤΗΣ ΕΤΑΙ ΡΙ ΑΣ Κ ΑΙ ΤΟΥ ΟΜ Ι ΛΟΥ Α Τρίµηνο 2005 ΑΝΩΝΥΜΟΣ Γ ΕΝΙ Κ Η ΕΤ ΑΙ Ρ Ι Α Τ ΣΙ ΜΕΝΤ ΩΝ Η Ρ ΑΚ Λ Η Σ ΑΡ. ΜΗ Τ Ρ. Α.Ε. : 13576/06/Β/86/096
ΟΡΘΗ ΕΠΑΝΑΛΗΨΗ ΤΩΝ ΕΝ Ι ΑΜ ΕΣ ΩΝ ΟΙ Κ ΟΝΟΜ Ι Κ ΩΝ Κ ΑΤΑΣ ΤΑΣ ΕΩΝ ΤΗΣ ΕΤΑΙ ΡΙ ΑΣ Κ ΑΙ ΤΟΥ ΟΜ Ι ΛΟΥ Α Τρίµηνο 2005 ΑΝΩΝΥΜΟΣ Γ ΕΝΙ Κ Η ΕΤ ΑΙ Ρ Ι Α Τ ΣΙ ΜΕΝΤ ΩΝ Η Ρ ΑΚ Λ Η Σ ΑΡ. ΜΗ Τ Ρ. Α.Ε. : 13576/06/Β/86/096
Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών
 Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών Συμβολισμοί Σε αναλογία με τους ορισμούς συμβολίζουμε μια ακολουθία: 1 είτε μέσω του διανυσματικού ορισμού, παραθέτοντας αναγκαστικά
Ισότητα, Αλγεβρικές και Αναλυτικές Ιδιότητες Πραγματικών Ακολουθιών Συμβολισμοί Σε αναλογία με τους ορισμούς συμβολίζουμε μια ακολουθία: 1 είτε μέσω του διανυσματικού ορισμού, παραθέτοντας αναγκαστικά
Ανάκτηση Π ηροφορίας. Συ ραφή Απόστο ος Ν. Παπαδόπου ος Ι άννης Μαν όπου ος Κ νσταντίνος Τσί ας. Κριτικός Ανα νώστης Δημήτριος Κατσαρός
 Ανάκτηση Π ηροφορίας Συ ραφή Απόστο ος Ν. Παπαδόπου ος Ι άννης Μαν όπου ος Κ νσταντίνος Τσί ας Κριτικός Ανα νώστης Δημήτριος Κατσαρός Συντε εστές Έκδοσης ΓΛΩΣΣΙΚΗ ΕΠΙΜΕΛΕΙΑ: Α. Ν. Παπαδόπου ος, Ι. Μαν
Ανάκτηση Π ηροφορίας Συ ραφή Απόστο ος Ν. Παπαδόπου ος Ι άννης Μαν όπου ος Κ νσταντίνος Τσί ας Κριτικός Ανα νώστης Δημήτριος Κατσαρός Συντε εστές Έκδοσης ΓΛΩΣΣΙΚΗ ΕΠΙΜΕΛΕΙΑ: Α. Ν. Παπαδόπου ος, Ι. Μαν
Επέκταση του συστήματος ανοι τού κώδικα Pig
 Επέκταση του συστήματος ανοι τού κώδικα Pig Εμμανουή Ζουμπου άκης AEM: 1462 Επι έπ ν κα η ητής: Αναστάσιος Γούναρης, Λέκτορας τμ. Π ηροφορικής Α.Π.Θ. Ιούνιος 2012 2 2 Abstract The tremendous Internet growth
Επέκταση του συστήματος ανοι τού κώδικα Pig Εμμανουή Ζουμπου άκης AEM: 1462 Επι έπ ν κα η ητής: Αναστάσιος Γούναρης, Λέκτορας τμ. Π ηροφορικής Α.Π.Θ. Ιούνιος 2012 2 2 Abstract The tremendous Internet growth
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι
 ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
ProapaitoÔmenec gn seic.
 ProapaitoÔmeec g seic. Α. Το σύνολο των πραγματικών αριθμών R και οι αλγεβρικές ιδιότητες των τεσσάρων πράξεων στο R. Το σύνολο των φυσικών αριθμών N = {1,, 3,... }. Προσέξτε: μερικά βιβλία (τα βιβλία
ProapaitoÔmeec g seic. Α. Το σύνολο των πραγματικών αριθμών R και οι αλγεβρικές ιδιότητες των τεσσάρων πράξεων στο R. Το σύνολο των φυσικών αριθμών N = {1,, 3,... }. Προσέξτε: μερικά βιβλία (τα βιβλία
u v 4 w G 2 G 1 u v w x y z 4
 Διάλεξη :.0.06 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος. Εισαγωγικοί ορισμοί Ορισμός. Γράφημα G καλείται ένα ζεύγος G = (V, E) όπου V είναι το σύνολο των κορυφών (ή κόμβων) και E
Διάλεξη :.0.06 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος. Εισαγωγικοί ορισμοί Ορισμός. Γράφημα G καλείται ένα ζεύγος G = (V, E) όπου V είναι το σύνολο των κορυφών (ή κόμβων) και E
Ε νικό Μετσό ιο Πο υτε νείο. Α όρι μοι Επανε ραφής Τροποποιημέν ν Ερ τημάτ ν ια Βατές Περι ραφικές Λο ικές
 dummy line Ε νικό Μετσό ιο Πο υτε νείο ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ Α όρι μοι Επανε ραφής Τροποποιημέν ν Ερ τημάτ ν ια Βατές Περι
dummy line Ε νικό Μετσό ιο Πο υτε νείο ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ & ΥΠΟΛΟΓΙΣΤΩΝ Α όρι μοι Επανε ραφής Τροποποιημέν ν Ερ τημάτ ν ια Βατές Περι
Θεωρία Υπολογισμού και Πολυπλοκότητα
 Θεωρία Υπολογισμού και Πολυπλοκότητα Κλάσεις P, NP NP-πληρότητα 15 Απριλίου 2008 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να περιγράψουμε με
Θεωρία Υπολογισμού και Πολυπλοκότητα Κλάσεις P, NP NP-πληρότητα 15 Απριλίου 2008 Δρ. Παπαδοπούλου Βίκη 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτε μπορούμε να περιγράψουμε με
Chapter 7, 8 : Time, Space Complexity
 CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 12 December 2008 1 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτεμπορούμεναπεριγράψουμεμεένααλγόριθμο μπορεί να
CSC 314: Switching Theory Chapter 7, 8 : Time, Space Complexity 12 December 2008 1 1 Υπολογίσιμα και Εφικτά Υπολογίσιμα Προβλήματα Είδαμε ότι 1. Οτιδήποτεμπορούμεναπεριγράψουμεμεένααλγόριθμο μπορεί να
M. J. Lighthill. g(y) = f(x) e 2πixy dx, (1) d N. g (p) (y) =
 Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
Εισαγωγή στην ανάλυση Fourier και τις γενικευμένες συναρτήσεις * M. J. Lighthill μετάφραση: Γ. Ευθυβουλίδης ΚΕΦΑΛΑΙΟ 2 Η ΘΕΩΡΙΑ ΤΩΝ ΓΕΝΙΚΕΥΜΕΝΩΝ ΣΥΝΑΡΤΗΣΕΩΝ ΚΑΙ ΤΩΝ ΜΕΤΑΣΧΗΜΑΤΙΣΜΩΝ ΤΟΥΣ FOURIER 2.1. Καλές
Πολλοί τρόποι περιγραφής αλγορίθμων. Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις
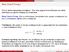 Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
Θέση Church-Turing Κανονική μορφή Kleene Θέση Church-Turing I Πολλοί τρόποι περιγραφής αλγορίθμων Όλοι είναι μηχανιστικά ισοδύναμοι και ειδικά ισοδύναμοι με μερικές αναδρομικές συναρτήσεις Θέση Church-Turing:
CSC 314: Switching Theory
 CSC 314: Switching Theory Course Summary 9 th January 2009 1 1 Θέματα Μαθήματος Ερωτήσεις Τι είναι αλγόριθμος? Τι μπορεί να υπολογιστεί? Απαντήσεις Μοντέλα Υπολογισμού Δυνατότητες και μη-δυνατότητες 2
CSC 314: Switching Theory Course Summary 9 th January 2009 1 1 Θέματα Μαθήματος Ερωτήσεις Τι είναι αλγόριθμος? Τι μπορεί να υπολογιστεί? Απαντήσεις Μοντέλα Υπολογισμού Δυνατότητες και μη-δυνατότητες 2
Ανάπτυξη Συστήματος Συστάσε ν Συνερ ατικής Διή ησης με ρήση Ιεραρ ικών Α ορί μ ν Κατάταξης
 ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Μεταπτυχιακή Διπλωματική Εργασία Ανάπτυξη Συστήματος Συστάσε ν Συνερ ατικής Διή ησης με ρήση Ιεραρ ικών Α ορί μ ν Κατάταξης της Μαριάννας Κουνέ
ΤΜΗΜΑ ΜΗΧΑΝΙΚΩΝ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΚΑΙ ΠΛΗΡΟΦΟΡΙΚΗΣ Μεταπτυχιακή Διπλωματική Εργασία Ανάπτυξη Συστήματος Συστάσε ν Συνερ ατικής Διή ησης με ρήση Ιεραρ ικών Α ορί μ ν Κατάταξης της Μαριάννας Κουνέ
a = a a Z n. a = a mod n.
 Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
Αλγεβρα Ι Χειμερινο Εξαμηνο 2017 18 Διάλεξη 1 Ενότητα 1. Πράξεις: Πράξεις στο σύνολο S, ο πίνακας της πράξης, αντιμεταθετικές πράξεις. Προσεταιριστικές πράξεις, το στοιχείο a 1 a 2 a n. Η πράξη «σύνθεση
0 + a = a + 0 = a, a k, a + ( a) = ( a) + a = 0, 1 a = a 1 = a, a k, a a 1 = a 1 a = 1,
 I ΠΙΝΑΚΕΣ 11 Σώμα 111 Ορισμός: Ενα σύνολο k εφοδιασμένο με δύο πράξεις + και ονομάζεται σώμα αν ικανοποιούνται οι παρακάτω ιδιότητες: (Α (α (Προσεταιριστική ιδιότητα της πρόσθεσης (a + b + c = a + (b +
I ΠΙΝΑΚΕΣ 11 Σώμα 111 Ορισμός: Ενα σύνολο k εφοδιασμένο με δύο πράξεις + και ονομάζεται σώμα αν ικανοποιούνται οι παρακάτω ιδιότητες: (Α (α (Προσεταιριστική ιδιότητα της πρόσθεσης (a + b + c = a + (b +
NP-πληρότητα. Λεωνίδας Παληός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων
 NP-πληρότητα Λεωνίδας Παληός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων Πολυωνυμικός μετασχηματισμός Ένας πολυωνυμικός μετασχηματισμός από την L 1 Σ 1 * στην L 2 Σ 2 * είναι μια συνάρτηση
NP-πληρότητα Λεωνίδας Παληός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων Πολυωνυμικός μετασχηματισμός Ένας πολυωνυμικός μετασχηματισμός από την L 1 Σ 1 * στην L 2 Σ 2 * είναι μια συνάρτηση
Λύσεις 4ης Σειράς Ασκήσεων
 Λύσεις 4ης Σειράς Ασκήσεων Άσκηση 1 Αναγάγουμε τν Κ 0 που γνωρίζουμε ότι είναι μη-αναδρομική (μη-επιλύσιμη) στην γλώσσα: L = {p() η μηχανή Turing Μ τερματίζει με είσοδο κενή ταινία;} Δοσμένης της περιγραφής
Λύσεις 4ης Σειράς Ασκήσεων Άσκηση 1 Αναγάγουμε τν Κ 0 που γνωρίζουμε ότι είναι μη-αναδρομική (μη-επιλύσιμη) στην γλώσσα: L = {p() η μηχανή Turing Μ τερματίζει με είσοδο κενή ταινία;} Δοσμένης της περιγραφής
(a + b) + c = a + (b + c), (ab)c = a(bc) a + b = b + a, ab = ba. a(b + c) = ab + ac
 Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
Σημειώσεις μαθήματος Μ1212 Γραμμική Άλγεβρα ΙΙ Χρήστος Κουρουνιώτης ΤΜΗΜΑ ΜΑΘΗΜΑΤΙΚΩΝ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ 2014 Κεφάλαιο 1 Διανυσματικοί Χώροι Στο εισαγωγικό μάθημα Γραμμικής Άλγεβρας ξεκινήσαμε μελετώντας
OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ
 Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Ο ΚΕΦΑΛΑΙΟ : ΟΡΙΟ ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ OΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΠΡΑΓΜΑΤΙΚΟΙ ΑΡΙΘΜΟΙ ΣΥΝΑΡΤΗΣΕΙΣ Έστω Α ένα υποσύνολο του Τι ονομάζουμε πραγματική συνάρτηση με πεδίο ορισμού το Α ; Απάντηση : ΕΣΠ Β Έστω
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου
 Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Η Θεωρία στα Μαθηματικά κατεύθυνσης της Γ Λυκείου wwwaskisopolisgr έκδοση 5-6 wwwaskisopolisgr ΣΥΝΑΡΤΗΣΕΙΣ 5 Τι ονομάζουμε πραγματική συνάρτηση; Έστω Α ένα υποσύνολο του Ονομάζουμε πραγματική συνάρτηση
Μαθηματικά. Ενότητα 2: Διαφορικός Λογισμός. Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη)
 Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
Μαθηματικά Ενότητα 2: Διαφορικός Λογισμός Σαριαννίδης Νικόλαος Τμήμα Διοίκησης Επιχειρήσεων (Κοζάνη) Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ
 ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΚΕΦΑΛΑΙΟ 3 ΤΟ ΔΙΩΝΥΜΙΚΟ ΘΕΩΡΗΜΑ Εισαγωγή Οι αριθμοί που εκφράζουν το πλήθος των στοιχείων ανά αποτελούν ίσως τους πιο σημαντικούς αριθμούς της Συνδυαστικής και καλούνται διωνυμικοί συντελεστές διότι εμφανίζονται
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ. Μια παράσταση που περιέχει πράξεις με μεταβλητές (γράμματα) και αριθμούς καλείται αλγεβρική, όπως για παράδειγμα η : 2x+3y-8
 ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
ΘΕΩΡΙΑ Β ΓΥΜΝΑΣΙΟΥ Άλγεβρα 1 ο Κεφάλαιο 1. Τι ονομάζουμε αριθμητική και τι αλγεβρική παράσταση; Να δώσετε από ένα παράδειγμα. Μια παράσταση που περιέχει πράξεις με αριθμούς, καλείται αριθμητική παράσταση,
Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Η εκτρικής Ισ ύος. Διπ ματική Ερ ασία
 Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Η εκτρικής Ισ ύος Εφαρμο ές της Θε ρίας Παι νί ν στα Μικροδίκτυα Διπ ματική Ερ ασία του ΠΕΤΡΟΥ Χ. ΑΡΙΣΤΕΙΔΟΥ Επι
Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Η εκτρικής Ισ ύος Εφαρμο ές της Θε ρίας Παι νί ν στα Μικροδίκτυα Διπ ματική Ερ ασία του ΠΕΤΡΟΥ Χ. ΑΡΙΣΤΕΙΔΟΥ Επι
Ε νικό Μετσό ιο Πο υτε νείο
 Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Τε νο ο ίας Π ηροφορικής και Υπο ο ιστών Ερ α είο Αυτοματοποιημένης Εξερεύνησης Απόδοσης - Επιφάνειας Υ ικού - Ισ
Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Τομέας Τε νο ο ίας Π ηροφορικής και Υπο ο ιστών Ερ α είο Αυτοματοποιημένης Εξερεύνησης Απόδοσης - Επιφάνειας Υ ικού - Ισ
Ε νικό Μετσό ιο Πο υτε νείο
 Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Μη ανο ό ν Μη ανικών Τομέας Ρευστών Ερ αστήριο Θερμικών Στρο ι ομη ανών Μονάδα Παρά η ης Υπο ο ιστικής Ρευστοδυναμικής& Βε τιστοποίησης Η συνε ής συζυ ής μέ οδος ια περιοδικές
Ε νικό Μετσό ιο Πο υτε νείο Σ ο ή Μη ανο ό ν Μη ανικών Τομέας Ρευστών Ερ αστήριο Θερμικών Στρο ι ομη ανών Μονάδα Παρά η ης Υπο ο ιστικής Ρευστοδυναμικής& Βε τιστοποίησης Η συνε ής συζυ ής μέ οδος ια περιοδικές
Αλγόριθµοι και Πολυπλοκότητα
 Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
Αλγόριθµοι και Πολυπλοκότητα Ν. Μ. Μισυρλής Τµήµα Πληροφορικής και Τηλεπικοινωνιών, Πανεπιστήµιο Αθηνών Καθηγητής: Ν. Μ. Μισυρλής () Αλγόριθµοι και Πολυπλοκότητα 15 Ιουνίου 2009 1 / 26 Εισαγωγή Η ϑεωρία
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ
 ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ ΘΕΤΙΚΩΝ ΣΠΟΥΔΩΝ - ΟΙΚΟΝΟΜΙΑΣ & ΠΛΗΡΟΦΟΡΙΚΗΣ Γ ΛΥΚΕΙΟΥ ΘΕΩΡΙΑ & ΑΠΟΔΕΙΞΕΙΣ Επιμέλεια: Βασίλης Κράνιας wwwe-mathsgr ΑΝΑΛΥΣΗ Τι ονομάζουμε πραγματική συνάρτηση Έστω Α ένα υποσύνολο
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά
 Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
Διακριτά Μαθηματικά ΙΙ Χρήστος Νομικός Τμήμα Μηχανικών Η/Υ και Πληροφορικής Πανεπιστήμιο Ιωαννίνων 2018 Χρήστος Νομικός ( Τμήμα Μηχανικών Η/Υ Διακριτά και Πληροφορικής Μαθηματικά Πανεπιστήμιο ΙΙ Ιωαννίνων
L A P. w L A f(w) L B (10.1) u := f(w)
 Κεφάλαιο 10 NP -πληρότητα Σύνοψη Οι γλώσσες στην κλάση πολυπλοκότητας P μπορούν να αποφασίζονται σε πολωνυμικό χρόνο. Οι επιστήμονες πιστεύουν, αν και δε μπορούν να το αποδείξουν ότι η P είναι ένα γνήσιο
Κεφάλαιο 10 NP -πληρότητα Σύνοψη Οι γλώσσες στην κλάση πολυπλοκότητας P μπορούν να αποφασίζονται σε πολωνυμικό χρόνο. Οι επιστήμονες πιστεύουν, αν και δε μπορούν να το αποδείξουν ότι η P είναι ένα γνήσιο
τα βιβλία των επιτυχιών
 Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Τα βιβλία των Εκδόσεων Πουκαμισάς συμπυκνώνουν την πολύχρονη διδακτική εμπειρία των συγγραφέων μας και αποτελούν το βασικό εκπαιδευτικό υλικό που χρησιμοποιούν οι μαθητές των φροντιστηρίων μας. Μέσα από
Chapter 9: NP-Complete Problems
 Θεωρητική Πληροφορική Ι: Αλγόριθμοι και Πολυπλοκότητα Chapter 9: NP-Complete Problems 9.3 Graph-Theoretic Problems (Συνέχεια) 9.4 Sets and Numbers Γιώργος Αλεξανδρίδης gealexan@mail.ntua.gr Κεφάλαιο 9:
Θεωρητική Πληροφορική Ι: Αλγόριθμοι και Πολυπλοκότητα Chapter 9: NP-Complete Problems 9.3 Graph-Theoretic Problems (Συνέχεια) 9.4 Sets and Numbers Γιώργος Αλεξανδρίδης gealexan@mail.ntua.gr Κεφάλαιο 9:
Υπολογιστική Πολυπλοκότητα Εξέταση Ιουνίου 2017 Σελ. 1 από 5
 Υπολογιστική Πολυπλοκότητα Εξέταση Ιουνίου 2017 Σελ. 1 από 5 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις απαντήσεις
Υπολογιστική Πολυπλοκότητα Εξέταση Ιουνίου 2017 Σελ. 1 από 5 Στη σελίδα αυτή γράψτε μόνο τα στοιχεία σας. Γράψτε τις απαντήσεις σας στις επόμενες σελίδες, κάτω από τις αντίστοιχες ερωτήσεις. Στις απαντήσεις
Εξόρυξη νώσης από μέσα κοιν νικής δικτύ σης: Με έτη περίπτ σης στο Twitter.
 Πανεπιστήμιο Πατρών Τμήμα Μα ηματικών Τμήμα Μη ανικών Η/Υ & Π ηροφορικής Διατμηματικό Πρό ραμμα Μεταπτυ ιακών Σπουδών "Μα ηματικά τ ν Υπο ο ιστών και τ ν Αποφάσε ν". Εξόρυξη νώσης από μέσα κοιν νικής δικτύ
Πανεπιστήμιο Πατρών Τμήμα Μα ηματικών Τμήμα Μη ανικών Η/Υ & Π ηροφορικής Διατμηματικό Πρό ραμμα Μεταπτυ ιακών Σπουδών "Μα ηματικά τ ν Υπο ο ιστών και τ ν Αποφάσε ν". Εξόρυξη νώσης από μέσα κοιν νικής δικτύ
Τυχαίοι γράφοι Η διάμετρος του G(n, 2 ln n/n) Ioannis Giotis
 Τυχαίοι γράφοι Η διάμετρος του G(n, 2 ln n/n) Ioannis Giotis Θεώρημα για σφαίρες Θα δείξουμε ότι το γράφημα G(n, 2 ln n n 1 ) έχει μικρή διάμετρο Θα ξεκινήσουμε με ένα θεώρημα για το μέγεθος μιας σφαίρας
Τυχαίοι γράφοι Η διάμετρος του G(n, 2 ln n/n) Ioannis Giotis Θεώρημα για σφαίρες Θα δείξουμε ότι το γράφημα G(n, 2 ln n n 1 ) έχει μικρή διάμετρο Θα ξεκινήσουμε με ένα θεώρημα για το μέγεθος μιας σφαίρας
Πα κ έ τ ο Ε ρ γ α σ ί α ς 4 Α ν ά π τ υ ξ η κ α ι π ρ ο σ α ρ µ ο γ ή έ ν τ υ π ο υ κ α ι η λ ε κ τ ρ ο ν ι κ ο ύ ε κ π α ι δ ε υ τ ι κ ο ύ υ λ ι κ ο
 ΠΑΝΕΠΙΣΤΗΜΙΟ Θ ΕΣΣΑΛ ΙΑΣ ΠΟΛ Υ ΤΕΧ ΝΙΚ Η ΣΧ ΟΛ Η ΤΜΗΜΑ ΜΗΧ ΑΝΟΛ ΟΓ Ω Ν ΜΗΧ ΑΝΙΚ Ω Ν Β ΙΟΜΗΧ ΑΝΙΑΣ ΑΝΑΜΟΡΦΩΣΗ Π Π Σ ΣΥ ΝΟΠ Τ Ι Κ Η Ε Κ Θ Ε ΣΗ ΠΕ 4 Α Ν Α ΠΤ Υ Ξ Η Κ Α Ι ΠΡ Ο Σ Α Ρ Μ Ο Γ Η ΕΝ Τ Υ ΠΟ Υ Κ Α
ΠΑΝΕΠΙΣΤΗΜΙΟ Θ ΕΣΣΑΛ ΙΑΣ ΠΟΛ Υ ΤΕΧ ΝΙΚ Η ΣΧ ΟΛ Η ΤΜΗΜΑ ΜΗΧ ΑΝΟΛ ΟΓ Ω Ν ΜΗΧ ΑΝΙΚ Ω Ν Β ΙΟΜΗΧ ΑΝΙΑΣ ΑΝΑΜΟΡΦΩΣΗ Π Π Σ ΣΥ ΝΟΠ Τ Ι Κ Η Ε Κ Θ Ε ΣΗ ΠΕ 4 Α Ν Α ΠΤ Υ Ξ Η Κ Α Ι ΠΡ Ο Σ Α Ρ Μ Ο Γ Η ΕΝ Τ Υ ΠΟ Υ Κ Α
Διάλεξη 4: Απόδειξη: Για την κατεύθυνση, παρατηρούμε ότι διαγράφοντας μια κορυφή δεν μπορούμε να διαχωρίσουμε τα u και v. Αποδεικνύουμε
 Διάλεξη 4: 20.10.2016 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος 4.1 2-συνεκτικά γραφήματα (συνέχεια) Πρόταση 4.1 Δύο μπλοκ ενός γραφήματος G μοιράζονται το πολύ μία κορυφή. Απόδειξη:
Διάλεξη 4: 20.10.2016 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος 4.1 2-συνεκτικά γραφήματα (συνέχεια) Πρόταση 4.1 Δύο μπλοκ ενός γραφήματος G μοιράζονται το πολύ μία κορυφή. Απόδειξη:
ΔΥΣΚΟΛΙΑ ΣΤΗΝ ΠΡΟΣΕΓΓΙΣΙΜΟΤΗΤΑ
 ΔΥΣΚΟΛΙΑ ΣΤΗΝ ΠΡΟΣΕΓΓΙΣΙΜΟΤΗΤΑ Επιμέλεια : Γεωργίου Κωστής Παρουσίαση στα πλαίσια του μαθήματος: Δίκτυα και πολυπλοκότητα Φεβρουάριος 004 μπλ Κίνητρα για τη μελέτη της μη προσεγγισιμότητας Ο πληρέστερος
ΔΥΣΚΟΛΙΑ ΣΤΗΝ ΠΡΟΣΕΓΓΙΣΙΜΟΤΗΤΑ Επιμέλεια : Γεωργίου Κωστής Παρουσίαση στα πλαίσια του μαθήματος: Δίκτυα και πολυπλοκότητα Φεβρουάριος 004 μπλ Κίνητρα για τη μελέτη της μη προσεγγισιμότητας Ο πληρέστερος
ΑΣΚΗΣΕΙΣ ΘΕΜΑ Β. 0και 4 x 3 0.
 ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
ΚΕΦΑΛΑΙΟ ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
8. Πολλαπλές μερικές παράγωγοι
 94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
ἔστω www.esto.gr Ο...πισινός μας! American Bar το καναμε για όλους μας. * * * www.esto.gr κι από τη Σκιά τους. σε κάθε νησί;
 American Bar το καναμε * κι από τη Σκιά τους. * κι απο τις Συνιστώσες τους. * για όλους μας. * * * σε κάθε νησί; * σε κάθε υπουργείο. * έξω από το σπίτι του. * * * Ποιος είναι πίσω μας; * Ο...πισινός μας!
American Bar το καναμε * κι από τη Σκιά τους. * κι απο τις Συνιστώσες τους. * για όλους μας. * * * σε κάθε νησί; * σε κάθε υπουργείο. * έξω από το σπίτι του. * * * Ποιος είναι πίσω μας; * Ο...πισινός μας!
Αλγόριθμοι και Πολυπλοκότητα
 Αλγόριθμοι και Πολυπλοκότητα Ροή Δικτύου Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Μοντελοποίηση Δικτύων Μεταφοράς Τα γραφήματα χρησιμοποιούνται συχνά για την μοντελοποίηση
Αλγόριθμοι και Πολυπλοκότητα Ροή Δικτύου Δημήτρης Μιχαήλ Τμήμα Πληροφορικής και Τηλεματικής Χαροκόπειο Πανεπιστήμιο Μοντελοποίηση Δικτύων Μεταφοράς Τα γραφήματα χρησιμοποιούνται συχνά για την μοντελοποίηση
ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ
 ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ Οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς, τους φυσικούς και τους ακέραιους αριθμούς. Δηλαδή είναι το μεγαλύτερο σύνολο αριθμών που μπορούμε
ΜΑΘΗΜΑΤΙΚΑ Γ ΓΥΜΝΑΣΙΟΥ Οι πραγματικοί αριθμοί αποτελούνται από τους ρητούς και τους άρρητους αριθμούς, τους φυσικούς και τους ακέραιους αριθμούς. Δηλαδή είναι το μεγαλύτερο σύνολο αριθμών που μπορούμε
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΗΣ ΕΠΕΞΕΡΓΑΣΙΑΣ ΣΗΜΑΤΩΝ ΚΑΙ ΕΙΚΟΝΩΝ Ρομποτικά Εκπαιδευτικά
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΕΧΝΟΛΟΓΙΑΣ ΠΛΗΡΟΦΟΡΙΚΗΣ ΚΑΙ ΥΠΟΛΟΓΙΣΤΩΝ ΕΡΓΑΣΤΗΡΙΟ ΨΗΦΙΑΚΗΣ ΕΠΕΞΕΡΓΑΣΙΑΣ ΣΗΜΑΤΩΝ ΚΑΙ ΕΙΚΟΝΩΝ Ρομποτικά Εκπαιδευτικά
Συνέχεια συνάρτησης σε διάστημα. Η θεωρία και τι προσέχουμε. x, ισχύει: lim f (x) f ( ).
 Κεφάλαιο 4 Συνέχεια συνάρτησης σε διάστημα 411 Ερώτηση θεωρίας 1 Η θεωρία και τι προσέχουμε Πότε μια συνάρτηση f θα λέμε ότι είναι συνεχής σε ένα ανοικτό διάστημα (, ) αβ; Απάντηση Μια συνάρτηση f θα λέμε
Κεφάλαιο 4 Συνέχεια συνάρτησης σε διάστημα 411 Ερώτηση θεωρίας 1 Η θεωρία και τι προσέχουμε Πότε μια συνάρτηση f θα λέμε ότι είναι συνεχής σε ένα ανοικτό διάστημα (, ) αβ; Απάντηση Μια συνάρτηση f θα λέμε
1. ΣΤΑΤΙΚΗ ΑΡΙΣΤΟΠΟΙΗΣΗ
 . ΣΤΑΤΙΚΗ ΑΡΙΣΤΟΠΟΙΗΣΗ. Μέγιστα και Ελάχιστα Συναρτήσεων Χωρίς Περιορισμούς Συναρτήσεις μιας Μεταβλητής Εστω f ( x) είναι συνάρτηση μιας μόνο μεταβλητής. Εστω επίσης ότι x είναι ένα σημείο στο πεδίο ορισμού
. ΣΤΑΤΙΚΗ ΑΡΙΣΤΟΠΟΙΗΣΗ. Μέγιστα και Ελάχιστα Συναρτήσεων Χωρίς Περιορισμούς Συναρτήσεις μιας Μεταβλητής Εστω f ( x) είναι συνάρτηση μιας μόνο μεταβλητής. Εστω επίσης ότι x είναι ένα σημείο στο πεδίο ορισμού
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ
 ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 13: Πολυωνυμική αναγωγή Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
ΘΕΩΡΙΑ ΥΠΟΛΟΓΙΣΜΩΝ ΚΑΙ ΑΥΤΟΜΑΤΩΝ Ενότητα 13: Πολυωνυμική αναγωγή Ρεφανίδης Ιωάννης Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Ανάπτυξη συντακτικού ανα υτή φυσικής ώσσας με ρήση του φορμα ισμού LFG. Πανα ιώτης Μίνος
 Ανάπτυξη συντακτικού ανα υτή φυσικής ώσσας με ρήση του φορμα ισμού LFG Πανα ιώτης Μίνος 18 Φε ρουαρίου 2014 Περί ηψη Η παρούσα μεταπτυ ιακή διπ ματική ερ ασία αναφέρεται στον σ εδιασμό και την υ οποίηση
Ανάπτυξη συντακτικού ανα υτή φυσικής ώσσας με ρήση του φορμα ισμού LFG Πανα ιώτης Μίνος 18 Φε ρουαρίου 2014 Περί ηψη Η παρούσα μεταπτυ ιακή διπ ματική ερ ασία αναφέρεται στον σ εδιασμό και την υ οποίηση
ΚΑΝΟΝΙΣ ΜΟ Ι ΙΕΞΑΓΩΓΗΣ ΑΓΩΝΩΝ 1 / 8 SCALE IC TRA CK ΕΛ. Μ. Ε
 ΚΑΝΟΝΙΣ ΜΟ Ι ΙΕΞΑΓΩΓΗΣ ΑΓΩΝΩΝ 1 / 8 SCALE IC TRA CK ΕΛ. Μ. Ε. 2 0 1 9 Κλ ά δο ς θερ µ ι κώ ν τη λ εκα τ ευθυ νό µ εν ω ν α υ το κι νή τω ν. Υπ εύ θυνο ς Κ λ ά δ ο υ Ζωτιαδης Κωστας bo d @ e l - m e. gr
ΚΑΝΟΝΙΣ ΜΟ Ι ΙΕΞΑΓΩΓΗΣ ΑΓΩΝΩΝ 1 / 8 SCALE IC TRA CK ΕΛ. Μ. Ε. 2 0 1 9 Κλ ά δο ς θερ µ ι κώ ν τη λ εκα τ ευθυ νό µ εν ω ν α υ το κι νή τω ν. Υπ εύ θυνο ς Κ λ ά δ ο υ Ζωτιαδης Κωστας bo d @ e l - m e. gr
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ. Μαθηματικά 1. Σταύρος Παπαϊωάννου
 ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 05 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση.. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
ΤΕΧΝΟΛΟΓΙΚΟ ΕΚΠΑΙΔΕΥΤΙΚΟ ΙΔΡΥΜΑ ΚΕΝΤΡΙΚΗΣ ΜΑΚΕΔΟΝΙΑΣ ΣΧΟΛΗ ΤΜΗΜΑ Μαθηματικά Σταύρος Παπαϊωάννου Ιούνιος 05 Τίτλος Μαθήματος Περιεχόμενα Χρηματοδότηση.. Σφάλμα! Δεν έχει οριστεί σελιδοδείκτης. Σκοποί Μαθήματος
Διάλεξη 4: Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος συνεκτικά γραφήματα (συνέχεια) Πρόταση 4.1 Δύο μπλοκ ενός
 Διάλεξη 4: 20.10.2016 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος 4.1 2-συνεκτικά γραφήματα (συνέχεια) Πρόταση 4.1 Δύο μπλοκ ενός γραφήματος G μοιράζονται το πολύ μία κορυφή. Απόδειξη:
Διάλεξη 4: 20.10.2016 Θεωρία Γραφημάτων Γραφέας: Σ. Κ. Διδάσκων: Σταύρος Κολλιόπουλος 4.1 2-συνεκτικά γραφήματα (συνέχεια) Πρόταση 4.1 Δύο μπλοκ ενός γραφήματος G μοιράζονται το πολύ μία κορυφή. Απόδειξη:
Περιεχόμενα μεθόδευση του μαθήματος
 Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
Περιεχόμενα μεθόδευση του μαθήματος. Πως ορίζεται η έννοια. Το όριο. To f() f() ; f() εφόσον υπάρχει είναι μονοσήμαντα ορισμένο; εξαρτιέται από τα άκρα α, β των ( α, ) και (, β ) ;. Πως ορίζονται τα πλευρικά
Δώστε έναν επαγωγικό ορισμό για το παραπάνω σύνολο παραστάσεων.
 Εισαγωγή στη Λογική Α Τάξης Σ. Κοσμαδάκης Συντακτικό τύπων Α τάξης Α Θεωρούμε δεδομένο ένα λεξιλόγιο Λ, αποτελούμενο από (1) ένα σύνολο συμβόλων για σχέσεις, { R, S,... } (2) ένα σύνολο συμβόλων για συναρτήσεις,
Εισαγωγή στη Λογική Α Τάξης Σ. Κοσμαδάκης Συντακτικό τύπων Α τάξης Α Θεωρούμε δεδομένο ένα λεξιλόγιο Λ, αποτελούμενο από (1) ένα σύνολο συμβόλων για σχέσεις, { R, S,... } (2) ένα σύνολο συμβόλων για συναρτήσεις,
1.3 Εσωτερικό Γινόμενο
 Εσωτερικό Γινόμενο η Μορφή Ασκήσεων: Μας ζητούν να υπολοίσουμε το εσωτερικό ινόμενο δύο διανυσμάτων Έστω α, β δύο διανύσματα του επιπέδου με α =, β = π ( αβ, ) = Να υπολοισθούν τα εσωτερικά ινόμενα: i
Εσωτερικό Γινόμενο η Μορφή Ασκήσεων: Μας ζητούν να υπολοίσουμε το εσωτερικό ινόμενο δύο διανυσμάτων Έστω α, β δύο διανύσματα του επιπέδου με α =, β = π ( αβ, ) = Να υπολοισθούν τα εσωτερικά ινόμενα: i
ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ ΛΥΚΕΙΟΥ - ΠΑΠΑΔΟΠΟΥΛΟΣ ΜΑΡΙΝΟΣ ΠΕΡΙΕΧΟΜΕΝΑ. Τίτλος Θεματικές Ενότητες Σελίδες. Δυο λόγια προς τους μαθητές.
 ΠΕΡΙΕΧΟΜΕΝΑ Τίτλος Θεματικές Ενότητες Σελίδες Προλογικό Σημείωμα Δυο λόγια προς τους μαθητές. ΚΕΦΑΛΑΙΟ 1 ο Όρια Συνέχεια Συνάρτησης 1-177 Μέρος 1 ο ΣΥΝΑΡΤΗΣΕΙΣ 1-85 Μάθημα 1 Έννοια συνάρτησης Πεδίο ορισμού
ΠΕΡΙΕΧΟΜΕΝΑ Τίτλος Θεματικές Ενότητες Σελίδες Προλογικό Σημείωμα Δυο λόγια προς τους μαθητές. ΚΕΦΑΛΑΙΟ 1 ο Όρια Συνέχεια Συνάρτησης 1-177 Μέρος 1 ο ΣΥΝΑΡΤΗΣΕΙΣ 1-85 Μάθημα 1 Έννοια συνάρτησης Πεδίο ορισμού
Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός συγκρίσεων π
 Περιορισμοί Αλγοριθμικής Ισχύος Κατηγοριοποίηση πολυπλοκοτήτων Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός
Περιορισμοί Αλγοριθμικής Ισχύος Κατηγοριοποίηση πολυπλοκοτήτων Κατώτερα φράγματα Κατώτερο φράγμα: εκτίμηση της ελάχιστης εργασίας που απαιτείται για την επίλυση ενός προβλήματος. Παραδείγματα: Αριθμός
Όριο συνάρτησης στο x. 2 με εξαίρεση το σημείο A(2,4) Από τον παρακάτω πίνακα τιμών και τη γραφική παράσταση του παραπάνω σχήματος παρατηρούμε ότι:
 Όριο συνάρτησης στο Στα παρακάτω θα προσεγγίσουμε την διαισθητικά με τη βοήθεια γραφικών παραστάσεων και πινάκων τιμών. 4 4 Έστω η συνάρτηση f με τύπο f ) = και πεδίο ορισμού το σύνολο ) ) η οποία μπορεί
Όριο συνάρτησης στο Στα παρακάτω θα προσεγγίσουμε την διαισθητικά με τη βοήθεια γραφικών παραστάσεων και πινάκων τιμών. 4 4 Έστω η συνάρτηση f με τύπο f ) = και πεδίο ορισμού το σύνολο ) ) η οποία μπορεί
ΣΗΜΕΙΩΣΕΙΣ. x A αντιστοιχίζεται (συσχετίζεται) με ένα μόνο. = ονομάζεται εξίσωση της
 ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
ΚΕΦΑΛΑΙΟ 2ο: ΣΥΝΑΡΤΗΣΕΙΣ - ΟΡΙΟ - ΣΥΝΕΧΕΙΑ ΣΥΝΑΡΤΗΣΗΣ ΕΝΟΤΗΤΑ 1: ΕΝΝΟΙΑ ΠΡΑΓΜΑΤΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ - ΓΡΑΦΙΚΗ ΠΑΡΑΣΤΑΣΗ ΣΥΝΑΡΤΗΣΗΣ. IΣΟΤΗΤΑ ΣΥΝΑΡΤΗΣΕΩΝ - ΠΡΑΞΕΙΣ ΜΕ ΣΥΝΑΡΤΗΣΕΙΣ - ΣΥΝΘΕΣΗ ΣΥΝΑΡΤΗΣΕΩΝ [Ενότητα
Υ οποίηση αντα α ής κ ειδιού DH και ψηφιακών υπο ραφών ασισμένη σε ε ειπτικές καμπύ ες
 Υ οποίηση αντα α ής κ ειδιού DH και ψηφιακών υπο ραφών ασισμένη σε ε ειπτικές καμπύ ες Νίκος Γιανναράκης Ζ ή Παρασκευοπού ου Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Ε νικό Μετσό ιο Πο υτε
Υ οποίηση αντα α ής κ ειδιού DH και ψηφιακών υπο ραφών ασισμένη σε ε ειπτικές καμπύ ες Νίκος Γιανναράκης Ζ ή Παρασκευοπού ου Σ ο ή Η εκτρο ό ν Μη ανικών και Μη ανικών Υπο ο ιστών Ε νικό Μετσό ιο Πο υτε
Αριθμητική Ανάλυση και Εφαρμογές
 Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
Αριθμητική Ανάλυση και Εφαρμογές Διδάσκων: Δημήτριος Ι. Φωτιάδης Τμήμα Μηχανικών Επιστήμης Υλικών Ιωάννινα 2017-2018 Παρεμβολή και Παρεκβολή Εισαγωγή Ορισμός 6.1 Αν έχουμε στη διάθεσή μας τιμές μιας συνάρτησης
6 Συνεκτικοί τοπολογικοί χώροι
 36 6 Συνεκτικοί τοπολογικοί χώροι Έστω R διάστημα και f : R συνεχής συνάρτηση τότε, όπως γνωρίζουμε από τον Απειροστικό Λογισμό, η f έχει την ιδιότητα της ενδιάμεσου τιμής. Η ιδιότητα αυτή δεν εξαρτάται
36 6 Συνεκτικοί τοπολογικοί χώροι Έστω R διάστημα και f : R συνεχής συνάρτηση τότε, όπως γνωρίζουμε από τον Απειροστικό Λογισμό, η f έχει την ιδιότητα της ενδιάμεσου τιμής. Η ιδιότητα αυτή δεν εξαρτάται
8. Πολλαπλές μερικές παράγωγοι
 94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό ) είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
94 8 Πολλαπλές μερικές παράγωγοι Οι μερικές παράγωγοι,,, αν υπάρχουν, μιας συνάρτησης : U R R ( U ανοικτό ) είναι αυτές συναρτήσεις από το U στο R, επομένως μπορεί να ορισθεί για αυτές η έννοια της μερικής
