Maria-Liliana Bucur. MATEMATICI APLICATE în topografie
|
|
|
- Βάλιος Καζαντζής
- 6 χρόνια πριν
- Προβολές:
Transcript
1 Maria-Liliana Bucur MATEMATICI APLICATE în topografie 1
2 CUPRINS CAPITOLUL 1 Introducere CAPITOLUL Elemente de trigonometrie.1 Definiție. Funcții trigonometrice. Relații trigonometrice.3 Măsurarea unghiurilor.4 Ecuații trigonometrice.5 Geometria triunghiului.6 Aplicații în măsurători terestre.7 Folosirea transformarilor geometrice în probleme practice.8 Probleme de extrem CAPITOLUL 3 Trigonometrie sferică 3.1 Elemente de trigonometrie sferica 3. Aplicații în astronomie 3..1 Coordonate și transformări de coordonate în astronomie 3.. Timpul in astronomie
3 INTRODUCERE În multe domenii în care activează, omul îşi precizează reflecţiile cu ajutorul relaţiilor matematice. Unul din aceste domenii în care trigonometria şi geometria sunt foarte mult folosite este topografia. Multe probleme topografice (de întocmire a planurilor porţiunilor de teren) au ca model matematic rezolvarea triunghiului. În numeroase probleme practice el trebuie să cunoască distanţele dintre anumite puncte de pe suprafaţa pământului şi unghiurile dintre direcţiile determinate de câte două din aceste puncte. Măsurarea directă a acestor distanţe şi unghiuri este dificilă şi, în unele cazuri imposibilă. Folosind însă cunoştinţe matematice de trigonometrie plană sau sferică şi de geometrie, o astfel de problemă se reduce la măsurarea în teren a distanţelor între anumite puncte accesibile şi a unghiurilor dintre anumite direcţii urmând ca celelalte distanţe şi unghiuri să fie determinate prin calcul folosind teoreme ale trigonometriei şi geometriei. Distanţele în teren se măsoară cu ruleta sau cu panglica iar unghiurile cu teodolitul. Pentru vizarea obiectelor, teodolitul este prevăzut cu o lunetă care se poate roti atât în plan orizontal cât şi în planul vertical. În acest fel cu acest instrument se pot măsura unghiul dintre proiecţiile orizontale a două direcţii şi unghiul dintre o direcţie şi proiecţia sa pe planul orizontal. 3
4 CAPITOLUL Elemente de trigonometrie.1 Definitie Trigonometria (din limba greacă τρίγωνος trígonos = triunghiular si μέτρον métron = masura) e o parte a matematicii care studiaza unghiuri, triunghiuri si funcţii trigonometrice precum sinusul, cosinusul si tangenta. Unii matematicieni considera trigonometria o subdiviziune a geometriei iar altii o stiinta matematica distincta. Istorie Originea trigonometriei se considera a fi in cultura antica din Egipt, Babilon si Valea Indului, acum mai mult de 3000 de ani. Matematicienii indieni au fost pionierii calculului algebric, cu aplicatii in astronomie si in trigonometrie. Lagadha e unicul matematician cunoscut care a utilizat geometria si trigonometria pentru astronomie in cartea sa Vedanga Jyotisha, cu toate ca multe din lucrarile sale au fost distruse de catre invadatorii Indiei. Matematicianul grec Hipparchus a compilat un tabel trigonometric pentru triunghiuri in circa 150 î.hr.. Un alt matematician grec, Ptolemeu (circa 100 î.hr.) a continuat sa dezvolte calculul trigonometric. Savantul Shia Musulman Nasir al-din Tusi a fost probabil primul care a considerat trigonometria ca o disciplina matematica distincta si a fost primul care a descris sase cazuri ale unui triunghi dreptunghic in trigonometria sferica. Matematicianul de origine silesă Bartholemaeus Pitiscus a publicat o lucrare importantă în trigonometrie în anul 1595 și a introdus cuvântul în limbile franceză și engleză. O importanță specială deține tehnica de triangulaţie care este utlizată în astronomie pentru a măsura distanța până la stelele apropiate, în geografie pentru a măsura distanțele între repere terestre și în sisteme de satelit pentru navigație (maritimă, în aviație si în spațiul extraterestru). Alte domenii care 4
5 utilizează trigonometria sunt: muzica, acustica, optica, statistica, biologia, farmaceutica, chimia, oceanografia, ingineria si multe altele.. Funcții trigonometrice Definitia functiilor trigonometrice se bazeaza pe rapoarte între laturi ale unui triunghi dreptunghic plan. Intr-un astfel de triunghi, latura cea mai lungă, opusă unghiului drept, se numește ipotenuză, iar laturile care formează unghiul drept se numesc catete. În triunghiul dreptunghic, sinusul unui unghi ascutit este definit ca raportul dintre lungimea catetei opuse (c.o.) si lungimea ipotenuzei (i). Similar, cosinusul unui unghi ascutit este raportul dintre lungimea catetei alăturate și lungimea ipotenuzei: sina = cateta opusa/ipotenuza cosa = cateta alăturată/ipotenuză Acestea sunt cele mai importante funcții trigonometrice; alte funcții pot fi definite ca diferite rapoarte ale laturilor unui triunghi dreptunghic, dar pot fi exprimate în termeni de sinus și cosinus. Acestea sunt tangenta, cotangenta, secanta și cosecanta: sin A cos A tga ctga cos A sin A sec A 1 1 cos eca cos A sin A 5
6 Definitiile anterioare se aplica doar la unghiuri între 0 si 90 grade (0 si π/ radiani). Utilizând cercul unitate (un cerc cu raza de lungime 1) ele pot fi extinse la toate argumentele, pozitive și negative. Funcția sinus Funcția sinus este funcția definită pe R cu valori în R prin care α aparține lui R i se asociază un număr yα notat sinα. PROPRIETĂȚI : 1. 1 sinα 1.Formula fundamentală a trigonometriei : sin α+cos α=1 => sin 1 cos 3.Functia sinus este o functie periodica de perioada kπ unde k aparține lui Z : sin (α+kπ) = sinx pentru orice x real și orice k întreg. 4.Funcția sinus este o funcție impară adică sin(-x)= -sin(x) pentru orice x real. 5. Semnul functiei sinus Cadranul I II III IV Funcția sinus Monotonia functiei sinus Cadranul I II III IV Funcția sinus Funcția cosinus 1. Cosinusul lui α notat cosα este abscisa punctului M α..funcția cosinus este functia definita pe R cu valori în R prin care α aparține lui R i se asociază un număr xα notat cosα. 6
7 PROPRIETĂȚI : 1. 1 cosα 1.Formula fundamentala a trigonometriei : sin α+cos α=1 => cos 1 sin 3.Funcția cosinus este o funcție periodică de perioadă kπ unde k aparține lui Z : cos(α+kπ) =cosx 4. Funcția cosinus este o funcție para adică cos (-x)= cos(x) 5. Semnul funcției cosinus Cadranul I II III IV Funcția cosinus Monotonia funcției sinus Cadranul I II III IV Funcția cosinus Funcția tangentă 1. Tangenta unui unghi α notata tgα este raportul dintre sinusul unghiului α si cosinusul acestuia. tg sin cos PROPRIETĂȚI : (k 1) k Z 7
8 1. Funcția tangentă este o funcție periodică de perioada kπ : tg(α+kπ) =tgα pentru oricare α din R (k 1),k Z. Funcția tangentă este o funcție impară tg(-x) = -tg(x) 3. Semnul funcției tangentă Cadranul I II III IV Funcția tangentă 4. Funcția tangentă este strict crescătoare pe intervale de forma ; Funcția cotangentă 1. Cotangenta unui unghi α notată ctgα este raportul dintre cosinusul unghiului α și sinusul acestuia. PROPRIETĂȚI : cos sin ctg k k Z 1. Funcția cotangentă este o funcție periodică de perioadă kπ : ctg(α+kπ)=ctgα unde oricare α din R {kπ k aparține lui Z}. Functia cotangenta este o functie impara ctg(-x) = -ctg(x) 3. Semnul functiei cotangenta Cadranul I II III IV Funcția cotangentă Funcția cotangentă este strict descrescătoare pe intervale de forma (o, π). 8
9 Relații trigonometrice sin x+cos x=1 sin(x+y) = sinx cosy + siny cosx cos(x + y) = cosx cosy sinx siny sin(x- y) = sinx cosy siny cosx cos(x - y) = cosx cosy + sinx siny sinx+siny=sin sinx-siny=sin cosx+cosy=cos cosx-cosy=-sin x y x y x y x y cos cos cos sin sin( x y) tgx tgy. cos x cos y x y x y ; ; x y x y ; ; Teorema sinusurilor Dacă laturile unui triunghi oarecare sunt a, b si c ți unghiurile opuse acestor laturi sunt A, B si C, atunci teorema sinusurilor este: sin A sin B sin C a b c 1 R unde R este raza cercului circumscris triunghiului. Teorema cosinusului In orice triunghi ABC avem: a b c b a a c c b bc cos A ac cos B ab cos C 9
10 .3 Măsurarea unghiurilor Unitățile de măsură pentru unghi sunt diviziuni ale cercului. Gradul sexagesimal (1 0 ) = a 360-a parte din măsura unui cerc; Minutul sexagesimal (1 ) = 1/60* =60 ; Secunda sexagesimala (1 ) = 1/60*1 =1/3600*1 0. Gradul centesimal (1 g ) este a 400-a parte din măsura unui cerc. Radianul=măsura unui arc de cerc de raza R a cărui lungime este egală cu R. L cerc =πr (R>0,raza) 1 rad=măsura unui unghi la centru notat ABC care subîntinde un cerc AB de lungime R. Funcția de măsurare în radiani a unghiurilor și respectiv a arcurilor de cerc se notează cu µ (miu) Măsura în radiani a unui cerc este: π rad π=3, Relația de transformare a gradelor sexagesimale în radiani: (1) α=π/180 0 *n 0 (1 ) n 0 =180 0 /π*α () 1 rad= Valorile funcțiilor trigonometrice α sin α cos α tg α 0 1 / ctg α / 1 0 α rad
11 CERC TRIGONOMETRIC (circulus), cercul cu raza egala cu unitatea, pe care s-a stabilit o origine A (de la care se face masurarea arcelor) si un sens (de obicei antiorar). E: unit circle (O.M.). y B (0, 1) M(x,y) A (-1,0) O ) α N A(1,0) x B (0, - ΔONM triunghi dreptunghi y B (0, 1) M(cosα, sinα) A (-1,0) O ) α N A(1,0) x B (0, - 11
12 Punctul M se deplasează pe cerc în sens invers acelor de ceasornic, sensul numindu-se sens trigonometric sau sens direct. Pe masură ce M se mișcă pe cerc valoarea α crește, modificându-se astfel si coordonatele punctului M. M=A, α = 0 cos 0= 1 sin 0= 0 M=B, α = cos = 0 sin = 0 M = A, α = cos = -1 sin = 0 M = B, α = cos = 0 sin = -1 Cercul trigonometric este impartit de axele de coordonate in 4 regiuni numite cadrane. Cadranul I α ( ) α (0 0 ) Cadranul II α ( ) α ( ) Cadranul III α ( ) α ( ) Cadranul IV α ( ) 1
13 α ( ) Exerciții rezolvate 1.Transformați în produs: a) b) c) d) 5 sin sin sin cos ; cos cos sin sin ; sin sin sin cos ; sin tg tg cos cos 4 3.Transformați în produs: a) c) 1 cos cos 0 cos cos ;b) sin 1 tg tg tg cos cos Transformă în produs: a) sin a sin 3a sin acos a ; b) cos 3a cos5a sin 4asin a ; c) sin( a b) sin( a b) sin bsin a ; d) cos( a b) cos( a b) cos a cos b ; 1 cos cos 0 cos sin ; ;d) e) sin a sin a sin a sin 0 ; f) 4 4 a b a b cos cos cos f) tga b tga b 4 a cos a sin a cos( a b)cos( a b) 5 sin 1 tg tg tg cos cos
14 4.Transformați în produs: a) cos( x y z) cos( x y z) cos x cos( y z) z ; b) sin( x y z) sin( x y z) sin cos( x y) c) sin( x y z) sin( x y z) sin( z)cos( x y) sin z cos( x y) ; 5.Transformați în produs: a) b) cos x cos x cos 3x cos x cos x cos x cos x(1 cos x) ; 5x x cos x cos x cos3x cos 4x cos x(cos x cos3x) 4cos x cos cos c) sin x sin 3x sin 9x sin11x sin 6xcos5x sin 6xcos3x 4sin 6xcos 4xcox; d) cos cos cos cos 4cos cos cos ; e) cos x cos3x cos9x cos11x cos6x cos5x cos6x cos3x 4cos6x cos 4xcos x ; f) tgx tgx 4tg4x 8ctg8x ctgx tgx ctgx tgx 4tg4x 8ctg8x ctgx tgx 4tg4x 8ctg8x 4ctg 4x 4tg4x 8ctg8x 8ctg8x 8ctg8x 0 1 tg x 1 Am folosit : tgx ctgx tgx ctgx tgx tgx 6)Transformați în produs: a) cos x cos y sin x sin y ; x y x y cos cos sin x y x y cos 4cos x y ; b) sin x y sin x y sin x y sin x y sin x y sin x y 4sin xsin ycos y ; c) sin x sin x 8 8 sin x sin x sin x sin x sin x; 14
15 d) sin x sin x cos x sin cos x cos x cosx sin sin x 0; cosx cos.4 Ecuații trigonometrice Ecuaţiile trigonometrice sunt ecuaţii care conțin una sau mai multe necunoscute exprimate numai prin intermediul funcţiilor trigonometrice. Forma generală a unei ecuații trigonometrice de o necunoscută este F(sin, cosx, tgx, ctgx) = 0 Ecuaţii trigonometrice fundamentale Ecuaţiile cuprinse sub această titulatură sunt: 1) Dacă sin x a, a fiind real. a 1,1 a 1,ecuaţia nu are soluţii, iar dacă ecuaţiei este : ) cos x a, a fiind real. k S 1 arcsin a k, k Z,mulţimea S de soluţii a Dacă a 1,ecuaţia nu are soluţii, iar dacă a 1,1,mulţimea S de soluţii a ecuaţiei este: 3) tgx a, a fiind real. S arccos a k, Soluţiile acestei ecuaţii sunt date de mulţimea 4) ctgx a, a fiind real. S arctga k, Soluţiile acestei ecuaţii sunt date de mulţimea S arcctga k, k Z k Z k Z Dacă intervin mai multe funcţii trigonometrice, dar care au acelaşi argument, de exemplu sin xcos x 1, atunci exprimăm ambele funcţii trigonometrice prin alte funcţii, de exemplu : 15
16 x tg sin x x 1 tg, 1 tg cos x 1 tg Nu există formule generale care să rezolve ecuațiile trigonometrice, însă există diverse metode pentru anumite tipuri de ecuatii. 1. Dacă în ecuație o funcție trigonometrică apare la o putere impară, iar celelalte numai la puteri pare, atunci se ia ca necunoscută principală funcția de putere impară, celelalte expimându-se în funcție de acesta. Exemplu: Să se rezolve ecuația x x. cos x sin x ctg x 3, Soluție : Luându-se ca necunoscută cosx, avem cu x k Notând cosx=t, obținem cos x cos x 3, cos x 1 1 cos x t 4 t 3 t t 1 t 1 0 Deci, soluțiile ecuației sunt t și 1 t 6 1, de unde x k1, 4 x arccos 1 k Dacă intervine numai o funcţie trigonometrică, dar cu argumente diferite, atunci cu ajutorul formulelor trigonometrice de adunare transformăm funcţiile astfel ca să avem în expresie un argument unic. Exemplul 1. Diferite funcţii trigonometrice ale aceluiaşi argument Exprimăm sin x şi cos x în funcţie de întreg şi se obţine x x x tg 1 tg 1 tg sin xcos x 1, 16 x x x tg 1 tg 1 x x 1tg 1tg x 1 tg, pentru xk 1, k fiind număr x k, tg arctg 1
17 Deci x k, k Z. Observaţie: Întrucât numărul x tg, nu există dacă 1 x k, k Z rezultă că eventualele soluţii de această formă se pierd; prin urmare, în final, trebuie verificate in ecuaţie şi numerele respective., Ecuaţii care conţin funcţii de acelaşi nume 1) sin u x sin v x 1 k 3) tgu x tgv x ) cosu x cosv x cosu x 0, 4) ctgu x ctgv x cos v x 0 u x v x k, u x v x k, k Z. u x v x k, k Z k Z u x v x k, k Z. ; ; Exemplul. Aceeaşi funcţie trigonometrică cu argumente diferite: sin 3x sin x, x 0,. În rezolvarea acestei ecuaţii se foloseşte formula de transformare a sumei în produs: ecuaţia devine sin xcos x 0 soluţii a ecuaţiei sin 0 ecuaţiei cos x 0 este ecuaţiei este sin x S S'. a b a b sin a sin b sin cos ; sin 0 x este S k, k Z S ' k, 4 17 x sau cos x 0. Mulţimea de k Z,iar mulţimea de soluţii a. Deci mulţimea soluţiilor Exemplul 3. Diferite funcţii trigonometrice cu argumente diferite cos x, x. Utilizând formula sin x sin x cos x obţinem sin xcos x cos x 0 cos xsin x1 0 cos x 0 sau sin x 1 0.Mulţimea de soluţii a
18 ecuaţiei cos 0 x este 1 S k k,iar mulţimea de soluţii a ecuaţiei 1 sin x S S1 S. k S 1 k k 6 este.deci mulţimea soluţiilor ecuaţiei este Ecuaţiile liniare în sinx şi cosx sunt de forma asin x bcos x c, unde a, b, c sunt numere reale, de analizat). abc 0 Distingem urmatoarele metode de rezolvare : (alte cazuri conduc la ecuaţii uşor a) Metoda unghiului auxiliar. Se împarte ecuaţia prin a şi se obţinesin x b cos x a c a ; se notează b tg, deci a b arctg,, a ; după câteva calcule se ajunge la ecuaţia elementară sin x b) Metoda substitutiei. Cu ajutorul formulelor x tg sin x x 1 tg gradul al doilea cu necunoscuta x tg., 1 tg cos x 1 tg Exemplul 4. 3sin xcos x 1, x 0, (vezi ex.,b). x x c cos. a obţinem o ecuaţie de Rezolv ecuaţia utilizând metoda unghiului auxiliar ; se împarte ecuaţia prin 3 şi se obţine: 1 1 sin x cos x sin x tg cos x 6 3 sin 6 3 sin x cos x cos sin xcos sin cos x cos
19 1 sin x 6 k x 1 k k 6 6 k x 1 k k 6 6. Cum, alegem x 0, x1 3 şi x.deci x, 3. Exemplul 5. sin x cos x 1, x (vezi ex. 4, j). 6 3 Această ecuaţie se rezolvă uşor cu ajutorul cofuncţiei sin observându-se că sin x cos x 6 3 xcos x,.ecuaţia devine cos x cos x 3 1 x arccos k, k 3. Mulţimea soluţiilor ecuaţiei este k k k k 3..5 Geometria triunghiului Relaţii metrice în triunghiul dreptunghic În triunghiul dreptunghic ABC cu A unghi drept folosim notaţiile cunoscute: AB = c, AC = b, BC = a; r = raza cercului circumscris triunghiului; l a = lungimea bisectoarei dusă din vârful A; m a = lungimea medianei din A; r a = lungimea razei cercului exînscris corespunzător laturii BC; a b c p 19
20 În acest triunghi, ABC, avem: 1. a b c sin A sin B sin C. m a = R=a/ 3. cosa+cosb=cosc 4. S = p(p a)=(p - b)(p c) 5. acosc - asinc = b-c B a c ct B C B C b c tg tg b c a b c 8R cos A cos B cos C Relaţii între unghiurile şi laturile unui triunghi oarecare Avem: Într-un triunghi oarecare este adevărată relația A+B+C = π 1) ) 3) 4) 5) 6) 7) 8) Inegalităţi verificate de functiile trigonometrice ale unghiurilor unui triunghi oarecare 0
21 1) ) 3) 4) 5) 6) 7) 8) 9) Relaţii metrice în triunghiuri oarecare 1) Teorema sinusurilor: ) Teorema cosinusurilor: 3) Teorema tangentelor: 4) Formula lui Heron: 5) Teorema medianei: 1
22 Alte formule utile.6 Aplicații în măsurători terestre Ilustrăm prin câteva exemple metode de determinare a distanţelor între anumite puncte inaccesibile şi a unghiurilor dintre anumite direcţii. 1. Determinarea distanţei între două puncte accesibile A şi B între care se află un obstacol. A C B Să presupunem că avem de determinat distanţa între două puncte A şi B între care, pe direcţia lor, se află un obstacol (de exemplu un lac).
23 Pentru a calcula distanţa dintre A şi B alegem un accesibil C punct din care se văd punctele A şi B şi se pot măsura distanţele a=bc, b=ac şi unghiul ACB C. Distanţa c=ab se calculează cu ajutorul Teoremei cosinusului c =a +b -abcosα. Determinarea distanţei între două puncte A şi B aflate într-o porţiune de teren inaccesibilă. A B C D Să presupunem că avem de determinat distanţa între două puncte A şi B care sunt inaccesibile în sensul posibilităţii de măsurare efectivă a distanţei la ele din punctele în care se află instrumentele de măsură (de exemplu, acestea se află pe malul opus al unui râu faţă de punctele de măsurat). În vederea determinării distanţei între punctele A şi B se aleg două puncte C şi D din care se pot viza punctele A şi B şi se poate măsura distanţa între acestea cât şi unghiurile şi Teorema sinusurilor aplicată în triunghiul BCD, în care se cunosc o latură şi unghiurile adiacente conduce la : CD sin B BC sin D BD sin C Teorema sinusurilor conduce la, de unde deducem: 3 sin( ) BC a. sin( ) ACD în care se cunosc CD=a şi unghiurile alăturate, asin AC sin( ). Acum, în triunghiul ABC
24 în care se cunosc două laturi BA şi AC şi unghiul dintre ele AB =AC +BC - AB BC cos. Determinarea poziţiei unui unghi drept în cazul în care nu avem vizibilitate. Între localităţile D şi E se află o conductă de apă. Perpendicular pe ea va fi construită o altă conductă, pentru localitatea N. Trebuie deci să găsim distanţa x=df de unde va porni conducta spre N, F nefiind vizibil din N, şi cunoscând DE=a şi ştiind unghiurile formate de ND şi NE cu DE. Din triunghiurile DFN şi EFN rezultă că FN = xtg si iar FN = (ax)tg Deci xtg = (a-x)tg, de unde x=a tg tg tg cos sin sau, după transformarea tangentelor, x = a sin. 4
25 4. Determinarea înălţimii unui obiect (turn, copac, etc.) în ipoteza că porţiunea de teren din vecinătatea bazei sale este situată în plan orizontal. Înălţimea unui copac (turn) se poate calcula foarte uşor cunoscând înălţimea observatorului, distanţa de la punctul de unde se face măsurătoarea până la copac şi unghiul pe care îl formează direcţia orizontală cu dreapta care uneşte ochiul observatorului cu vârful copacului. B C A O O Fie AB=H înălţimea turnului şi O un punct din planul orizontal. Plasând staţia (teodolitul) în poziţia verticală O O, se vizează din punctul O punctul B- vârful turnului şi se măsoară unghiul COB= OB cu proiecţia sa pe planul orizontal. Având în vedere că distanţa AO =s se poate măsura pe teren, problema se reduce de fapt la determinarea catetei BC a triunghiului dreptunghic BCO în care se cunosc unghiul opus şi cealaltă catetă s=ao. Dacă h =O O este înălţimea teodolitului, atunci înălţimea turnului se calculează cu formula: H=AB=AC+CB=h +s tg Determinarea aproximativă a înălţimii. 1. Putem să renunţăm la determinarea unghiului dacă reuşim să situăm triunghiul dreptunghic isoscel ABC din fig. de mai jos astfel încât vârful copacului să fie pe prelungirea ipotenuzei. În acest caz ar fi de 45 o iar h=s, H=s+h. Această metodă este aplicabilă numai dacă se 5
26 dispune de spaţiu suficient pentru alegerea convenabilă a punctului de observaşie S.. Dreptunghiul ABCD este ţinut într-o astfel de poziţie încât punctul G se află pe prelungirea laturii AB a dreptunghiului din figura de mai jos. Firul de plumb suspendat în B determină pe CD un segment CL. Deoarece laturile sunt perpendiculare şi triunghiurile BCL şi BEG sunt asemenea, vor fi egale unghiurile notate cu în figură. Astfel, GE BE CL BC tg, deci înălţimea copacului va fi CL H=s +h. BC 6
27 Calculul înălţimilor cu ajutorul unghiurilor de elevaţie. Din punct de vedere practic la măsurători pe teren apar deosebiri între un unghi măsurat într-un plan orizontal și un același unghi, măsurat într-un plan vertical. Deosebirile se datorează indicilor de refracție diferiți ai aerului, funcție de densitatea locală a acestuia. Aceasta face ca o rază de lumină care se propagă cu un unghi relativ mare față de orizontală să aibă o traiectorie curbă, în locul uneia drepte. Acest fenomen se numește refracție terestră și împreună cu existența curburii pămâtului trebuie luat în considerație la determinarea înălțimilor care depășesc 00m. Tahimetria este o măsurătoare de teren rapidă; ea se utilizează la stabilirea, prin măsurători simple și rapide a poziției și înălțimii unui număr oarecare de repere, față de poziția și înălțimea, cunoscute ale unui punct P, din care se face măsurătoarea. De exemplu, se utilizează în stabilirea formei terenului, ca bază pentru un proiect de construcție. Crucea reticulară prezintă față de reperul central m, încă două repere paralele cu acesta, o și u echidistante față de m, la distanța p/. Aceste 7
28 trei repere se suprapun peste trei puncte, L m, L o și L u ale imaginii mirei plasate în punctul N. Segmentul de lungime l= L u L o de pe miră este cuprins între laturile unghiului ε, a cărui bisectoare este orizontală. Funcție de distanța focală a obiectivului f și de lungimea parcursului razei luminoase în lunetă se poate stabili distanța orizontală până la miră, a, cu o relație de forma a=cl, unde C este constanta aparatului, în cele mai multe cazuri având valoarea 100. Unghiul ε rezultă din din tgε/=(l/):a=1/(c). Dacă axa lunetei F face un unghi α cu orizontala, când reperul central al acesteia nu se suprapune peste imaginea reperului central al acesteia nu se suprapune peste iamginea reperului central al mirei Lm, atunci distanța orizontală a se poate determina prin următoarele calcule: l=h L u H L o = a [tg(α+ε/) tg(α-ε/)] a = l tg tg 8
29 sau, deoarece sin(α+ε/)cos(α-ε/) sin(α-ε/)cos(α+ε/) = sinε, rezultă: sau =l l cos cos a = = sin cos = cos sin sin sin cos l cos tg - l sin ctg l a = lc cos sin 4C În această ultimă relație al doilea termen poate fi neglijat, deoarece l și sinα sunt mult mai mici decât C=100. Rezultă deci că și h= H L m = a tgα= 1 Clsinα. a = lc cos = 1. Determinarea trigonometrică a înălţimilor cu linie de bază orizontală, cuprinsă în plan vertical. Se măsoară în direcţia reperului G o linie de bază orizontală, AB=s şi unghiurile de elevaţie şi în extremităţile acestei linii. Conform teoremei sinusurilor, rezultă înălţimea h: deci = -, u = s sin sin sin sin h = s sin şi h = usin, 9
30 . Determinarea trigonometrică a înălţimilor cu linie de bază înclinată, cuprinsă în plan vertical. Linia de bază AB=s se găseţte într-un plan vertical care trece prin G şi face cu orizontala un unghi. Unghiurile de elevaţie ale lui G sunt în A şi în B. Diferenţa de înălţime dintre A şi G se poate calcula cu ajutorul teoremei sinusurilor. Dacă AG=x rezultă h = xsin, sin unde x = s, = +180 o - şi = - sin Înlocuind se obţine sin sin h = s sin 30
31 3. Determinarea trigonometrică a înălţimilor cu linie deavând o direcţie oarecare faţă de reper. Din extremităţile A şi B ale liniei de bază AB=s, care se găseşte în acelaşi plan orizontal cu punctul de bază al reperului F, se măsoară unghiurile şi ; în plus, din punctul A se măsoară şi unghiul de elevaţie a punctului G, respectiv. Planul AFG este perpendicular pe planul orizontal FAB. Dacă AF=z se obţine unde Înlocuind se obţine z = s h=ztg sin sin = s o sin sin sin = s sin =
32 h = s sin tg sin Dacă linia de bază AB=s face un unghi 1 cu planul orizontal ce trece prin A şi în punctele A şi B se măsoară unghiurile orizontale şi respective dintre linia de bază şi punctual G ca şi unghiurile de elevaţie: 1 de la A către B; de la B către G; de la A către G, atunci problema se reduce la una cunoscută. În triunghiul AHB din planul orizontal ce trece prin A se cunosc: latura s =scos 1 şi unghiurile şi. După teorema sinusurilor sin a =s sin, b =s sin sin Din triunghiul AHG, conţinut în planul vertical se obţine 3
33 h = b tg = s sin tg sin = s cos 1 sin tg sin Pentru verificare se poate folosi relaţia h=h 1 + h unde şi h 1 =ssin 1 sin tg h =a tg = s sin = s cos 1 sin tg sin 33
34 Unghiul format de generatoarea unei grămezi de nisip în formă de con cu planul bazei. Nisipul aruncat de pe banda rulantă formează un con circular de înălţime h cu raza egală cu r. Volumul poate fi calculat după formula V= 3 r h, unde h=rtg, deci V= 3 r 3 tg, fiind unghiul format de generatoarea grămezii cu planul bazei. Dacă în loc de se ia unghiul de la vârful conului, atunci h=rctg şi V= 3 r 3 ctg 34
35 Determinarea înălţimii unui turn inaccesibil situat pe un deal. A C B D E Fie turnul marcat AB. Alegem un punct accesibil C şi lucrăm în planul determinat de punctele A,B şi C. Luăm încă un punct D pe BC şi notăm cu E punctul de intersecţie al verticalei din B cu orizontala din D. Din măsurători se obţin: ACB= ACD avem: AC a sin sin( ), deci sin AC a. sin( ) ABC avem: AB AC sin, deci AB AC. sin cos sin Aşadar, asin sin AB. sin( )cos.7 Folosirea transformarilor geometrice în probleme practice Fie mulţimea punctelor unui plan. DEFINIŢIE. O funcţie f : sau o restricţie a unei asemenea funcţii se numeşte transformarea geometrică. Atunci când utilizăm transformările geometrice în rezolvarea unor probleme de geometrie trebuie să ştim : 1) să precizăm elementele care definesc transformările geometrice. 35
36 ) să construim imaginea unui punct printr-o transformare geometrică. 3) să construim imaginea unei figuri printr-o transformare geometrică. 4) să determinăm punctele care corespund printr-o transformare geometrică. DEFINIŢIE: Fie v un vector dat. Se numeşte translaţie de vector funcţia care asociază fiecărui punct M din planul astfel încât : MM = v v, Deci T v Proprietăţi: (M) = M. MM = v ; M este imaginea lui M prin T v 1. Translaţia de vector v. Translaţia de vector v dreapta dată. 3. Translaţia de vector lor. v conservă lungimea unui segment. 4. Translaţia conservă măsura unghiurilor. duce o dreaptă într-o dreaptă paralelă cu conservă coliniaritatea unor puncte şi ordinea 5. Translaţia coservă raportul lungimilor a două segmente. 6. Translaţia transformă un poligon într-un pligon congruent cu cel dat. 7. Compunerea a două translaţii de vectori v 1 şi v este tot o translaţie de vector v 1+ v.. Aplicaţii: 1. În ce loc trebuie construit podul MN peste un râu care separă localităţile A şi B astfel încât drumul AMNB de la localităţile A şi B să fie cel mai scurt (malurile râului se consideră drepte paralele, iar podul este perpendicular pe maluri). 36
37 Soluţie : Se consideră translaţia de vector v = MN prin care Tv (A)=A. Deci A N=AM, iar drumul AMNB este egal cu A N+NB+MN. Cum lungimea segmentului MN este constantă trebuie să gasim poziţia lui N pentru care A N+NB este minimă. Se constată astfel că punctul căutat N se află la intersecţia dreptelor d şi A B.. Localităţile A şi B sunt separate de două râuri. În ce locuri trebuie construite podurile DE şi GF peste aceste râuri dacă vrem ca drumul între cele două localităţi să fie cel mai scurt (malurile râurilor se consideră drepte paralele, iar podurile sunt perpendiculare pe maluri). d d3 37
38 Soluţie: Se consideră translaţia de vector v = a translaţia de vector v =b prin care Tv (A)=A şi, prin care T v (B)=B. A, B sunt puncte fixe. Se formează paralelogramele AA DE, BB GF astfel că drumul dintre cele două localităţi devine AA DGB B. Dar AA, BB sunt constante (egale cu lăţimea râurilor, deci pentru a obţine drumul cel mai scurt trebuie ca A, D, G, B să fie coliniare. Construcţia : se construiesc punctele fixe A, B, apoi D, G se găsesc la intersecţia dreptei A B cu d, respectiv d 3. Podurile se vor obţine ducând perpendiculare din D, G pe malurile opuse. Definiţie: Punctele A şi A din planul se numesc simetrice în raport cu dreapta d din planul dacă segmentul A A este perpendiculr pe dreapta d şi o intersectează într-un punct O, astfel încât AOOA.Punctul A se numeşte simetricul punctului A în raport cu dreapta d. Definiţie: Simetria axială de axă d în planul este o transformare a planului prin care punctele dreptei d se transformă în ele însele şi orice alt punct A se transformă în simetricul său A în raport cu dreapta d. Simetria axială de axă d se notează cu S d. A Prin urmare S d : astfel încât S d (A)=A pentru orice Ad şi orice S d (A)=A pentru d 90 orice A -d, unde AA d, {O}= =AA d ;I AO = OA.(figura 9.) A =S d (A) 38
39 Aplicaţii 1. Dacă două localităţi A şi B se află de aceeaşi parte a unui drum reprezentat printr-o dreaptă d, să se afle punctul M pe d, unde trebuie construit un supermarket astfel încât suma distanţa AM + MB să fie minimă. Soluţie : Se construieşte simetricul lui A faţă de d, notat cu A. Triunghiul AA M este isoscel, deci AM + MB = A M + MB. Pentru ca distanţa AM + MB să fie minimă, trebuie ca A M + MB, ceea ce implică A, M, B coliniare. Cu alte cuvinte M se găseţte la intersecţia dreptelor A B şi d. Probleme de măsurare a distanţei pe mare Pentru măsurarea distanţei între obiective aflate pe mare trebuie luată în considerare forma sferică a pământului. Calculele se vor baza deci pe teoremele trigonometriei sferice. În cazul unor distanţe relativ reduse, se poate neglija curbura pământului şi deci, se poate utiliza trigonometria plană. Reperele care apar pe hărţile marine au precizate distanţele relative între ele, ca ţi poziţia lor. Direcţiile, în special cea de deplasare a vasului se definesc faţă de direcţia nord-sud, de exemplu N35 o E se citeşte 35 o de la nord către est. Pe un vas se goniometrează simultan farul L, sub direcţia S55,3 o E şi turla unei clădiri înalte K sub direcţia S 8,5 o V. Conform hărții de navigaţie, distanța KL=s=33,5km și are direcția N84,7 o. a) Să se afle distanțele FK=x și FL=y. b) Ce distanță trebuie să mențină vasul pentru a trece pe lângă farul L la o distanță c=4 mile marine=7,408 km? 39
40 Din α=55,3 o, β=8,5 o, γ=84,7 o, s=33,5 km se obține δ=180 o (α+γ)=40 o, ε=γ-β=56, o sin x=s sin sin y=s sin =1,49km, =7,77 km, sinφ=c/y, φ=15,47 o. Direcția vasului : S(α+φ) o E, adică S 70,77 o E..8 Probleme de extrem 1. Dintr-o placă triunghiulară ABC cu baza BC=a, AB=AC şi înălţimea AD=h, să se decupeze o placă dreptunghiulară de arie maxima, cu o latura pe baza BC. Soluţie: Vom nota cu x si y laturile dreptunghiului. Din asemănarea triunghiurilor avem relaţia: y a h x h y = a ( h x) h S(x)= yx = a ( h x) x h unde S(x) am notat aria dreptunghiului. Deci, S(x)= ax axh h S(x)= ax S(x) = h ax h +a +ax 40
41 S(x)=0 x= h Studiind semnul lui S (x) în x= pentru care S max = ah 4. h obţinem un punct de maxim local. Se dă un canal hidraulic cu secţiunea trapezoidală de arie constantă. Cunoscând că panta taluzului este constantă, tg =m=1, să se determine raportul dintre baza mică şi înălţimea secţiunii trapezoidale a canalului hidraulic, astfel încât să rezulte perimetrul minim udat. Soluţie. b Notând cu h şi respectiv cu b, înălţimea şi respectiv baza mică a secţiunii trapezoidale a canalului hidraulic, perimetrul udat este : P = b + h cos 1 Cum însă cos = (0 ) şi cum tg = m, avem 1 tg P = b+h 1 m 41
42 Notând b h = x, rezultă: P(x)=0. P = h(x+ 1 m Pe de altă parte, aria secţiunii canalului este : Sau Din care : H = A = h(b+mh), A = h (x+m) A x m ), (h0) Inlocuind ân expresia perimetrului, avem : P = A x m (x+ 1 m Deoarece A si m sunt constante, rezultă că P are un extrem când ). P(x) = A x ( 1 m ( x m) m) 3 = 0 Rezultă punctul critic x 0 = ( 1 m -m) sau x 0 0,83. Pentru a stabili natura punctului de extrem calculăm valoarea derivatei a doua şi-i studiem semnul in punctul critic obţinut. P(x) = A 4 (3 1 m ( x m) m) x 5. Inlocuind valoarea punctului de extrem in derivata secunda,avem ; P(x 0 ) = A 1 m m 0. Deci punctul critic este un minim. Valoarea minima a perimetrului udat, este : P min = A( 1 m m) P min,7 A. 4
43 3. Dintr-o arcadă plină in formă de semidisc de rază r să se decupeze o fereastră dreptunghiulară ca în figură în scopul obţinerii unei luminozităţi maxime. Soluţie: Fie x lăţimea dreptunghiului ; cealaltă latură a dreptunghiului va fi r x. Aria ferestrei va fi A= x r x, iar condiţia care trebuie pusă este ca această arie să fie maximă. Această funcţie are un singur punct critic, r /, care se dovedeşte a fi un punct de maxim. 4. Pe o scenă în formă eliptică de ecuaţie x +y = 18 se doreşte instalarea unui reflector în punctul C al elipsei, care va trimite raze pe toate direcţiile segmentelor CM, unde M se află pe segmentul BA, A(1,4) si B(3,0) fiind puncte fixe pe elipsă. Unde trebuie instalat reflectorul pentru ca suprafaţa luminată de acesta să fie maximă. Soluţie : 43
44 Semiaxele elipsei sunt : a = 3 şi b = 3. Fie C elipsei C(x, 18 x Notand cu S(x) - aria triunghilui ABC, S : 3, 3 R avem ). S(x)= 1 x x S(x)=6-x- 18 x S(x)= x 18 x 18 x S(x)=0 x= 6 Dintre cele două puncte critice obţinute - 6 este de maxim, iar S max =6+ 6. Exerciţii propuse 1. Între localităţile A şi B trebuie tras un cablu în linie dreaptă printr-o pădure. Între A şi B nu avem vizibilitate dar putem găsi un punct C din care se pot măsura distanţele b= AC = 3 1 km, a= BC = km şi unghiul 44
45 =60 o. Să se afle lungimea x a cablului şi unghiurile BAC si ABC.. Să se calculeze distanţa între două repere A şi B aflate pe acelaşi mal al unui râu ştiind că din două puncte accesibile C şi D aflate pe malul opus se pot instala instrumente care să măsoare distanţa CD =300 m şi unghiurile ADC=45 o, BDC=75 o, BCD=15 o si ACD=60 o. 3. De pe malul unui râu un arbore aflat pe malul opus se vede sub un unghi de 60 o iar de pe aceeaşi direcţie de la o depărtare de 0 m de punctul iniţial, arborele se vede sub un unghi de 30 o. Să se afle înălţimea arborelui şi lăţimea râului. 4. Două localităţi reprezentate prin două puncte A şi B se află de o parte şi de alta a unui râu cu malurile drepte şi paralele având lăţimea de 100 m. Distanţa de la localitatea A până la râu este de 1,1 km iar de la localitatea B este de 1,85 km. Dintr-un punct A aflat cu 100 m mai aproape de râu faţă de localitatea A, unghiul pe care îl face direcţia A B cu direcţia râului este de 30 o. Peste râu trebuie construit un pod MN. Să se determine la ce distanţă faţă de localitatea B trebuie să se proiecteze piciorul N al podului astfel încât drumul AMNB să fie cel mai scurt posibil şi să se calculeze lungimea acestuia. 5. Să se determine dreptunghiul de arie maximă înscris în cercul de rază r. 6. Să se determine cilindrul de arie laterală maximă înscris în sfera de rază r. 45
46 CAPITOLUL 3. Trigonometrie sferică 3.1 Elemente de trigonometrie sferică Trigonometria sferică este partea matematicii care se ocupă de rezolvarea triunghiurilor formate pe suprafața unei sfere din arce de cercuri mari. Trigonometria sferică are o mare importanță teoretică și practică și se aplică în astronomie, în geodezie, în cartografie, în cristalografie, în geometria minieră, în teoria instrumentelor și în alte științe, atunci când, pentru studiul poziției relative în spațiu a unor puncte, linii și plane, se recurge la o sferă ajutătoare. Un cerc de pe suprafaţa unei sfere se numeşte cerc mare dacă raza sa este egală cu raza sferei. Observaţie: Un cerc de pe suprafaţa unei sfere este un cerc mare dacă şi numai dacă planul determinat de el conţine centrul sferei. Partea din suprafața sferei cuprinsă între două semicercuri care au acelasi diametru, se numește fus sferic. Figura de pe suprafața sferei formată din trei arce de cerc mare care se întretaie în trei puncte se numește triunghi sferic. Elementele triunghiului sferic sunt: trei unghiuri, fiecare în parte mai mic de 180, și trei laturi; dacă laturile sunt mai mici decât d (d = 90 ), atunci triunghiul se numește triunghi al lui Euler; triunghiurile care au laturile mai mari decât d, se numesc triunghiuri Moebius Study. Triunghiurile sferice pot fi isoscele, echilaterale, dreptunghice sau oarecare. Triunghiurile sferice dreptunghice pot avea unul, două sau trei unghiuri drepte, iar triunghiurile sferice oarecare pot avea unul două sau trei unghiui obtuze. Dacă intr-un triunghi sferic, cel puțin o latură este egală cu un sfert din cerc, atunci triunghiul se numește cuadrantic. Dacă în triunghiul sferic ABC (fig. 4) considerăm vârfurile ca poli și descriem, cu raze sferice egale cu 90, polarele unui vârf, atunci aceste 46
47 polare, întretăindu-se două câte două, vor da un nou triunghi sferic A B C, numit triunghi polar sau suplimentar triunghiului dat. Evident, trei cercuri de pe suprafaţa unei sfere sunt neconcurente dacă nu există nici un punct care să fie comun tuturor celor trei cercuri. Observaţie: Trei cercuri mari determină pe suprafaţa unei sfere mai multe triunghiuri sferice. Astfel, în figură, atât ABC cât şi A'B'C' dar şi A'BC sau AB'C', sunt triunghiuri sferice. Conform definiţiei, triunghiul sferic este o figură convexă. Aceasta înseamnă că măsura nici unui unghi al triunghiului nu este mai mare de 180 (o figură concavă determinată de trei cercuri mari neconcurente pe suprafaţa unei sfere este de exemplu exteriorul triunghiului ABC din figură - aceasta nu face obiectul studiului nostru). Spre deosebire de cazul plan, pentru un triunghi sferic, suma unghiurilor este întotdeauna mai mare decât 180. Un triunghi se numeşte dreptunghic dacă are (cel puţin!) un unghi drept; el se va numi rectilater dacă are o latură cu măsura de 90. Un exemplu remarcabil de triunghi sferic este triunghiul tridreptunghic (trei unghiuri drepte) trirectilater (trei laturi de 90) - triunghiul format pe globul terestru de ecuator, meriadianele 0 si 90. Măsurile laturilor unui triunghi sferic. Se defineşte măsura unei laturi AB a triunghiului sferic ABC ca fiind măsura arcului de cerc mare AB. Evident, aceasta este egală cu unghiul la centru AOB. În mod tradiţional se notează mărimile laturilor unui triunghi ABC astfel: AB=c, AC=b, BC=c. Măsurile unghiurilor unui triunghi sferic. Măsura unghiului BAC al triunghiului sferic ABC este măsura unghiului diedru format de planele (OAB) şi (OAC). Observaţie. Cum tangenta la un cerc este perpendiculară pe raza în punctul de contact, avem că tangentele la cercurile mari AB şi AC în punctul A sunt ambele perpendiculare pe muchia diedrului format de planele OAB şi OAC. Deci, unghiul unui triunghi sferic se poate măsura şi între tangentele 47
48 la laturile triunghiului in punctul considerat. Proprietăţi Pentru orice triunghi sferic ABC avem: 0< a+b+c< 360 a< b+c, a-b< c 180 < A+B+C< 540 A+B< 180+C, A-B> 180-C Aria triunghiului sferic este dată de: S ABC = (A+B+C - 180) πr /180 La baza geometriei sferice stau următoarele teoreme: Teorema 1: Sectiunea unei sfere cu un plan oarecare este un cerc. Teorema : Cercurile mari impart sfera si suprafata ei in doua parti egale. Teorema 3: Prin doua puncte date pe suprafata unei sfere, daca acestea nu sunt asezate la extremitatile aceluiasi diametru, se poate duce un cerc mare si numai unul. Teorema 4: Intersectia planelor a doua cercuri mari este un diametru al lor si le imparte in doua parti egale. Teorema 5: Cea mai scurta distanta pe sfera intre doua puncte de pe suprafata ei este un arc de cerc mare mai mic de Formulele lui Gauss 48
49 Să considerăm un triunghi sferic oarecare ABC pe suprafaţa unei sfere de rază R şi să construim două sisteme carteziene de coordonate Oxyz şi Ox'y'z' astfel: O este centrul sferei Oz trece prin B planul Oyz este planul (OAB) Oz' trece prin A planul Oy'z' este planul (OAB) Impunând condiţia ca sistemul de coordonate să fie drept, axele Ox şi Ox' vor fi determinate. Mai mult, cum planele Oyz şi Oy'z' coincid, rezultă că Ox=Ox'. Se observă faptul că sistemul Ox'y'z' se obţine din sistemul Oxyz printr-o rotaţie în jurul axei Ox. 49
50 Pentru a găsi un set de expresii ce leagă elementele triunghiului sferic ABC, vom adopta următoarea strategie: Scriem coordonatele punctului C în sistemul Oxyz Scriem coordonatele punctului C în sistemul Ox'y'z' Scriem expresia transformării de rotaţie a sistemului Oxyz în Ox'y'z' Coordonatele punctului C în Oxyz sunt: 50
51 Raportându-ne acum la elementele triunghiului ABC avem (conform figurii): o b β = A - o şi deci obţinem: (3.1.1) Coordonatele punctului C în Ox'y'z' sunt: 51
52 În acest caz avem: o a β = o B Astfel, obţinem: (3.1.) Din nou, ne raportăm la elementele triunghiului ABC. Avem: de unde rezultă imediat: (3.1.3) 5
53 Formulele lui Gauss Din (3.1.1), (3.1.) şi (3.1.3) obţinem Simplificând cu R şi sciind în ordine inversă obţinem expresia standard a formulelor lui Gauss: Prima relaţie se numeşte teorema cosinusurilor pentru trigonometria sferică. Ultima relaţie este teorema sinusurilor, iar cea de a doua formulă se numeşte formula celor cinci elemente. Teorema sinusurilor se poate pune şi sub forma Formulele lui Gauss pentru unghiuri. Definiţie. Se numesc poli ai unui cerc mare intersecţiile cu sfera ale dreptei perpendiculare pe planul cercului în centrul sferei. Un exemplu ilustrativ este dat de polii globului terestru care reprezintă poli în sensul definiţiei de mai sus faţă de ecuatorul terestru. Formulele lui Gauss pentru unghiuri 53
54 Să considerăm un triunghi ABC şi triunghiul său polar A'B'C'. Să scriem acum formulele lui Gauss pentru A'B'C': Dar conform proprietăţilor triunghiului polar, avem: cos (180 o A) = cos (180 o B) cos (180 o C) + + sin (180 o B) sin (180 o C) cos (180 o a) sin (180 o A) cos (180 o b) = cos (180 o B) sin (180 o C) - - sin (180 o B) cos (180 o C) cos (180 o a) sin (180 o A) sin (180 o b) = sin (180 o B) sin (180 o a) Adică: cosa = - cosbcosc + sinb sinc cos a sina cosb = cosb sinc + sinb cosc cosa sina sinb = sinb sina Din nou, aplicând dualitatea unghiuri-laturi introdusă de existenţa triunghiului polar, am obţinut un nou set de ecuaţii care determină triunghiul ABC. Acestea se numesc formulele lui Gauss pentru unghiuri. În contrast cu aceasta, formulele lui Gauss în forma originală se mai numesc formulele lui Gauss pentru unghiuri. Se observă că ultima relaţie se putea deduce imediat din teorema sinusurilor pentru laturi. În schimb, demonstrarea geometrică a primelor două relaţii ar fi fost extrem de laborioasă; se observă încă o dată eleganţa prin care formalismul triunghiului polar ne aduce informaţii noi despre un triunghi sferic. 54
55 Aria triunghiului sferic Demonstrarea formulei ariei triunghiului sferic pleacă de formula ariei fusului sferic. Acesta se defineşte ca fiind zona determinată pe suprafaţa unei sfere de două cercuri mari ale căror planuri formează unghiul diedru D. Aria fusului sferic de unghi diedru D este: (pentru a reţine această formulă să observăm că întreaga sferă poate fi definită ca fiind un fus sferic de deschidere 360) Să considerăm triunghiul ABC ca în figură. Se observă pentru început că: Măsurile celor două triunghiuri sunt evident egale, datorită simetriei. Acum, să considerăm următoarele fusuri sferice: 55
56 56
57 Însumând aceste suprafeţe se observă că obţinem o semisferă plus de două ori aria triunghiului ABC (acesta aparţine fusului B cât şi fusului C, deci a fost considerat de două ori) Adunând deci aceste relaţii obţinem: S A + S B +S C = πr + S ABC = (A+B+C) πr /180 S ABC = (A+B+C - 180) πr /180 57
58 Coordonate geografice Admitem pentru început că Pământul este sferic. Axa imaginară pp, în jurul căreia el se roteşte, se numeşte axă proprie, punctele în care axa geografică proprie înţeapă sfera terestră sunt: p polul Nord geografic; p polul Sud geografic (a se vedea figura 1). Semicercul mare care trece prin polii geografici ai Pământului şi printr-un punct (loc) O de pe suprafaţa Pământului este meridianul geografic al locului. Meridianul geografic al observatorului de la Greenwich este denumit primul meridian (meridian origine / zero). Cercul mare de pe suprafaţa Pământului, care reprezintă intersecţia planului meridian zero cu sfera terestră, divizează suprafaţa Pământului în două semisfere: emisfera Est şi emisfera Vest. Putem defini coordonatele geografice ale locului O de pe suprafaţa Pământului, care sunt latitudinea geografică ( ) şi longitudinea geografică (L). Latitudinea a locului O este dată de unghiul OTB pe care îl face verticala locului O cu planul ecuatorului (dacă locul O este în emisfera Nord, 58
59 0 atunci latitudinea sa nordică este pozitivă, 0 90, iar dacă locul O este în emisfera Sud, atunci latitudinea sa sudică este negativă, ). Longitudinea L a locului O este dată de unghiul diedru G TB pe care îl face planul meridianului zero cu planul meridianului locului (dacă locul O 0 este în emisfera Est, atunci longitudinea sa estică este pozitivă, 0 L 180, iar dacă locul O este în emisfera Vest, atunci longitudinea sa vestică este negativă L 0 ). În urma studiilor efectuate în ceea ce priveşte forma Pământului, s-a constatat că ea diferă de aceea a unui elipsoid de revoluţie şi că forma geometrică a Pământului nu se poate identifica cu o formă geometrică simplă. Dacă în rezolvarea celor mai multe probleme de astronomie se admite că Pământul este o sferă omogenă, atunci când se impun evaluări mai precise ale formei şi dimensiunilor Pământului, se admite că acesta este un elipsoid de revoluţie (sferoid) neomogen. S-a stabilit că semiaxa mare, situată în planul ecuatorial, este a 6378,4 km iar semiaxa mică (a cărei direcţie coincide cu axa nord-sud) este b 6356, 86 km Măsurători efectuate prin intermediul sateliţilor au arătat că a 6375, 75 km, raza polului nord este b 6355, 36 km iar raza polului sud este b 635, 36 n km, cu 30 km mai mică decât raza polului nord, astfel încât Pamântul este un elipsoid turtit. s Probleme 1. Cât de lung este arcul unui cerc mare al globului pământesc pentru care unghiul la centru este de 60 o? (raza Pământului se consideră R=6370km). Soluție: Deoarece lungimea unui cerc de rază R este πr. Deoarece cercul corespunde unui unghi la centru de 360 o, rezultă că lungimea unui arc corespunzător unui unghi α (exprimat in grade), este: 59
60 L = (formula lungimii unui arc) Deci, în cazul nostru lungimea arcului corespunzător unghiului de 60 o va fi πr / 6, adică 6667,6km. Observație: Formula de mai sus poate fi folosită și pentru a găsi unghiul la centru atunci când se cunoaște lungimea arcului: Cât este unghiul la centru corespunzător unui arc de cerc mare al globului pământesc de lungime 0km? Din formula precedentă obținem α =, iar un calcul simplu arată că α =0,0539 o.. Doi globtroteri calatoresc intre doua meridiane, unul pe paralela de latitudine φ=56 o, iar altul pe ecuator. Știind că primul a parcurs l=100km, aflați lungimea L a drumului parcurs de cel de-al doilea. Soluție: Presupunând că unghiul dintre cele două meridiane este α, lungimea drumului parcurs de cei doi va fi: l = și L =, unde r este raza cercului paralel pe care s-a deplasat primul (cel de-al doilea s-a deplasat pe ecuator, deci raza cercului este raza Pământului R=6370). Împărțind cele două relații, obținem: 60
61 După cum se vede și din figură, unghiul OBO este egal cu φ, deci în triunghiul OBO, cos φ = r /R, așadar, R / r = 1 / cos φ, prin urmare, L = l / cos φ Deci, în urma calculului L 181,81km. 3. Un biciclist a parcurs într-o una drumul dintre două localități din Franța și Rusia, aflate la latitudinile φ 1 = 45 o, φ = 60 o, știind că longitudinile lor geografice diferă cu 90 o.câți km a parcurs biciclistul? (presupunând că a mers pe drumul cel mai scurt, adică pe cercuri mari ale Pământului). Soluție: Considerăm triunghiul sferic PAB, unde P este polul nord, iar A și B sunt cele două localități. Aplicând teorema cosinusurilor în acest triunghi, obținem: cosx = cos(90 o - φ 1 ) cos(90 o φ ) + sin(90 o - φ 1 ) sin(90 o φ ) Deci: 90 o cosx = sin φ 1 sin φ Asadar, cosx = 0,705 0,865 = 0,609, deci x = 5,4 o Folosind acum formula lungimii unui arc obținem distanța L dintre cele două localități: L = Unde R este raza Pământului. Deci L 587km 4. Prin Iași (φ = 47 o 10, L = 7 o 34 ) se duce cercul mare care atinge în cel mai nordic punct al său cercul polar de nord (φ 1 = 66 o 33 ). Sub ce unghi față de meridianul Iașilor se află acest cerc și care este longitudinea geografică a punctului de atingere? Soluție:Fie I punctul corespunzător Iașului. Prin I ducem cercul mare care este tangent în cel mai nordic punct al său cercului polar de nord, în punctul A. Meridianul acestui punct de tangență este perpendicular pe cercul polar și pe cercul mare dus. S-a construit astfel un triunghi sferic, 61
62 PAI, care are unghiul din A de 90 o. Aplicând teorema sinusurilor în triunghiul PAI, obținem: De aici rezultă că sinx =, deci sinx =, adică x = 35 o Aplicații în astronomie Datorită faptului că ochiul uman nu poate discerne distanţele pînă la obiectele cereşti (Soarele, Luna, planetele, stelele, etc.), acestea par a se afla la aceeaşi distanţă de fiecare persoană care le observă; bolta cerească apare ca o sferă pe care se deplasează corpurile cereşti. Pentru scopuri practice imediate (orientare, determinarea timpului, etc.) este necesară cunoaşterea direcţiei de vizare a unui astru, distanţa pînă la acesta fiind irelevantă. În plus, cea mai evidentă mişcare a aştrilor, mişcarea diurnă aparentă` este o mişcare de rotaţie omogenă faţă de observator (mişcare datorată rotaţiei Pământului), susţinând aparenţa cerului sferic. Din punct de vedere matematic, în măsura în care nu suntem interesaţi de distanţele reale până la aştri, vom opera doar cu direcţiile pe care aceştia se găsesc faţă de observator. În acest caz, putem construi o sferă de rază arbitrară şi putem echivala în mod trivial "direcţiile" din spaţiul tridimensional cu "punctele" acestei sfere. Astfel, formalismul calculelor ce trebuiesc efectuate pentru determinările astronomice se simplifică de la geometria tridimensională carteziană la o geometrie bidimensională sferică. Centrul unei astfel de sfere poate fi ochiul observatorului, caz în care sfera se numește sfera cerească topocentrică, sau centrul Pământului, caz în care va fi numită sferă cerească geocentrică, sau chiar centrul Soarelui, când se va numi sferă cerească heliocentrică. Verticala care trece prin centrul sferei o taie în două puncte diametral opuse : zenitul, notat Z și nadirul, notat Na. 6
63 Planul perpendicular pe verticală care trece prin centrul sferei se numește plan orizontal al locului de observație. El taie sfera după un cerc mare care se numește orizont matematic (sau adevărat al locului). Un cerc mic al sferei paralel cu orizontul matematic se numește almucantarat. Dreapta paralelă cu axa Pământului care trece prin centrul sferei se numește axa lumii. Aceasta intersectează sfera cerească în două puncte numite polul nord ceresc și polul sud ceresc. Planul care trece prin centrul sferei și este perpendicular pe axa lumii se numește plan ecuatorial ceresc, iar intersecția acestuia cu sfera cerescă se numește ecuator ceresc. Un observator terestru nu simte mișcarea de rotație a Pământului. Aceasta îi produce aparența unei mișcări de rotație a cerului întreg, în sens invers sensului de rotație al Pământului, numită mișcare diurnă aparentă. Cercurile mari care trec prin polii cerești se numesc cercuri de declinație sau orare. Punctul N al orizontului matematic cel mai apropiat de polul nord se numește punctul cardinal nord (punctul diametral opus se numește punctul cardinal sud S, iar punctele E și W egal depărtate de N și S se numesc puncte cardinal est, respectiv vest) Coordonate și transformări de coordonate în astronomie Principalele sistemele de coordonate folosite în astronomie (orizontale, ecuatoriale, ecliptice, galactice) au acelaşi reper - observatorul. O transformare de coordonate de la unul din aceste sisteme la altul este deci echivalentă cu un set de rotaţii în jurul axelor de coordonate carteziene. Dar, după cum am arătat, formulele care determină rotaţia în sistemul cartezian se reduc la formulele lui Gauss în trigonometria sferică. Astfel, determinarea direcţiilor de observare a corpurilor cereşti în diferite sisteme de coordonate se va reduce la rezolvarea unor triunghiuri pe sfera cerească, folosind fie formulele lui Gauss pentru laturi, fie formulele lui Gauss pentru unghiuri. 63
64 Sistemul coordonatelor orizontale constă în: înălţime h definită ca fiind unghiul format de raza vectoare a astrului cu planul orizontului. Aceasta se află cuprinsă între 0 o și 90 o dacă astrul se găsește deasupra orizontului și este cuprinsă între -90 o și 0 o în caz contrar; azimut A definit ca unghiul format de planul vertical al astrului cu planul meridianului locului, măsurat pe orizont de la punctul cardinal sud în sens retrograd (adică S-V-N-E). Distanţa zenitală a unui astru este complementul înălţimii z=90-h. În acest caz ca plan fundamental a fost considerat planul orizontului matematic. Sistemul coordonatelor orare constă în: 64
65 declinaţia δ definită ca fiind unghiul format de raza vectoare a astrului cu planul ecuatorului ceresc ; unghiul orar H, unghiul format de planul orar al astrului cu planul meridianului locului, măsurat pe ecuatorul ceresc al locului de la culminaţia superioară a ecuatorului Q în sens retrograd (adică Q-V-Q'- E). În mişcarea diurnă aparentă a unui astru declinaţia sa rămâne constantă (ea fiind deci o caracteristică a astrului), în timp ce unghiul orar H variază, acesta depinzând şi de locul din care este observat astrul (prin poziţia meridianului ceresc al locului de observare). De aceea, aceste coordonate orare se numesc şi coordonate semilocale. Sistemul coordonatelor ecuatoriale constă din: declinaţie δ, definită ca mai sus ascensia dreaptă α, unghiul format de planul orar al astrului cu planul orar al punctului vernal, măsurat pe ecuatorul ceresc al locului de la punctul vernal în sens direct (adică Q-E-Q'-V). 65
66 Vom începe cu transformarea coordonatelor ecuatoriale în coordonate orare. Trebuie să avem în vedere faptul că distanţa zenitală a polului ceresc este complementul latitudinii: 66
67 Se observă că pentru a face această transformare este esenţial triunghiul PZσ, numit şi triunghiul de poziţie sau triunghi paralactic al astrului. Pentru a determina latura Pσ şi unghiul alăturat acesteia σpz trebuie să aplicăm formulele lui Gauss notând triunghiul PZσ astfel: Pσ <-- a P <-- B Vom avea deci A-->Z, B-->P, C--> σ măsurile laturilor şi unghiurilor ce intervin în formulele lui Gauss vor fi: Aplicând formulele lui Gauss (1) asupra triunghiului de poziţie în aceste condiţii obţinem: 67
68 Astfel, am obţinut coordonatele orare; pentru a determina coordonatele ecuatoriale trebuie să avem în vedere că timpul sideral pentru orice astru σ. Vom avea deci: Înlocuind pe H în () obţinem: Din ecuaţiile (3) nu putem calcula direct coordonatele ecuatoriale deoarece în membrii stângi ne intervine timpul sideral s. Pentru a elimina acest inconvenient aplicăm următorul procedeu: şi obţinem: iar apoi din: 68
69 rezultă Ecuaţiile (3), (6) şi (7) ne dau transformarea coordonatelor orizontale în coordonate ecuatoriale: Sub formă matricială aceste ecuaţii se scriu: Transformarea Ecuatoriale --> Orare --> Orizonate Primul pas constă în transformarea coordonatelor orare în coordonate orizontale. În triunghiul de poziţie PZσ nu cunoaştem în acest caz latura Zσ şi unghiul din Z. Vom nota deci triunghiul de poziţie astfel: A-->P, B-->Z, C--> σ. Rezultă că: Din formulele lui Gauss obţinem: 69
70 Pentru a face legătura cu coordonatele ecuatoriale folosim din nou timpul sideral: şi obţinem: sau sub formă matricilă Transformarea Ecuatoriale --> Ecliptice Coordonatele ecliptice sunt: latitudinea ecliptică unghiul format de raza vectoare a astrului cu planul eclipticii. longitudinea ecliptică unhiul format de planul meridian ecliptic al astrului cu planul meridian ecliptic al punctului vernal, măsurat pe ecliptică de la punctul vernal în sens direct. 70
71 Triunghiul sferic ce trebuie rezolvat este în acest caz PΠσ. Trebuie determinate latura Πσ şi mărimea unghiului din Π. Vom lua deci A=P, B=Π şi C=σ şi vom avea: Formulele lui Gauss se scriu direct: Punând aceste relaţii sub formă matricială, avem: 71
72 Transformarea Ecliptice --> Ecuatoriale În acelaşi triunghi PΠσ alegem A=Π, B=P, C=σ şi deci Din formulele lui Gauss rezultă transformarea: sau sub formă matricială: 3.. Timpul în astronomie Timp sideral Definiţie. Se numeşte timp sideral, în locul de observare, corespunzător poziţiei aparente a punctului vernal într-un moment diurn oarecare, unghiul orar al punctului vernal, măsurat de-a lungul ecuatorului ceresc, în sens retrograd, de la meridianul superior al locului şi până la cercul orar al punctului vernal, exprimat în ore: ts H, unde H este unghiul orar într-un moment diurn pentru o poziţie aparentă a punctului vernal. Definiţie. Se numeşte zi siderală intervalul de timp dintre două treceri consecutive ale punctului vernal la meridianul superior al locului 7
73 (intervalul de timp dintre două culminaţii superioare succesive ale punctului vernal ). Timpul solar adevărat Centrul discului aparent al Soarelui este denumit în astronomie Soarele adevărat ( T a ). Într-un moment diurn oarecare, poziţia aparentă a Soarelui adevărat pe sfera cerească este caracterizată de unghiul orar H a. Definiţie. Se numeşte timp solar adevărat, în locul de observare, corespunzător poziţiei aparente a Soarelui adevărat într-un moment diurn oarecare, unghiul orar al Soarelui adevărat, măsurat de-a lungul ecuatorului ceresc, în sens retrograd, de la culminaţia inferioară a Soarelui adevărat până la cercul orar al Soarelui adevărat, exprimat în ore: t a 1 Definiţie. Se numeşte zi solară adevărată intervalul de timp dintre două treceri consecutive ale Soarelui adevărat la meridianul ceresc superior sau inferior al locului (intervalul de timp dintre două culminaţii de acelaşi fel consecutive). Observaţie. Într-un acelaşi loc de pe suprafaţa Pământului, durata zilei solare adevărate este variabilă şi drept urmare utilizarea acesteia nu este convenabilă pentru necesităţile vieţii cotidiene. h H a Ziua solară şi ziua siderală sunt inegale, datorită deosebirilor dintre mişcările aparente diurne şi anuale ale Soarelui şi a punctului vernal. Concluzie. Durata zilei solare adevărate este mai mare decât durata zilei siderale, diferenţa dintre ele fiind variabilă pe parcursul unui an. Timp solar mediu 73
74 Definiţie. Se numeşte timp solar mediu (timp mediu t m ), în locul de observare, corespunzător poziţiei aparente a Soarelui adevărat într-un moment diurn oarecare, unghiul orar al Soarelui mediu, măsurat de-a lungul ecuatorului ceresc, în sens retrograd, de la culminaţia inferioară a Soarelui mediu şi până la cercul orar al Soarelui mediu, exprimat în ore, aşa cum rezultă din fig. 7: t m 1 h H, m unde H m este unghiul orar al Soarelui mediu. Definiţie. Se numeşte zi solară medie (zi medie) intervalul de timp dintre două treceri (culminaţii) consecutive de acelaşi fel ale Soarelui mediu la meridianul locului. Pe baza definiţiei Soarelui mediu rezultă că durata zilei medii este egală cu media anuală a duratei zilelor solare adevărate. Timpul universal Definiţie. Se numeşte timp universal (TU) timpul solar mediu al meridianului de la Greenwich, motiv pentru care el se numeşte şi Greenwich Mean Time (GMT). Observaţie. Relaţia t, H 1 h L (unde L este longitudinea m G a geografică, este ecuaţia timpului, ea reprezentând timpul care trebuie adăugat algebric la timpul solar adevărat pentru a obţine timpul mediu, iar H a este unghiul orar al Soarelui adevărat) permite determinarea timpului mediu de la Greenwich, în orice moment, din orice loc de pe suprafaţa 74
75 Pământului. În particular, dacă determinarea o face chiar observatorul de la Greenwich (fig. 8) atunci, în relaţia anterioară, L L H a G H 0 a, G, Astfel încât t H.,, 1 h m G a G Timpul legal Definiţie. Se numeşte timp legal al unui fus orar f (timpul fusului orar f), timpul solar mediu al meridianului principal al fusului orar f, aşa cum indică fig. 9, adică t t t L TU L f m, f m, G f f, unde L f este longitudinea geografică a meridianului principal al fusului orar f, exprimată în ore L f f h ; h h h 0 m, G h h t H L 1 f, f f t TU f t f t f a ; 75
cateta alaturata, cos B= ipotenuza BC cateta alaturata AB cateta opusa AC
 .Masurarea unghiurilor intr-un triunghi dreptunghic sin B= cateta opusa ipotenuza = AC BC cateta alaturata, cos B= AB ipotenuza BC cateta opusa AC cateta alaturata AB tg B=, ctg B= cateta alaturata AB
.Masurarea unghiurilor intr-un triunghi dreptunghic sin B= cateta opusa ipotenuza = AC BC cateta alaturata, cos B= AB ipotenuza BC cateta opusa AC cateta alaturata AB tg B=, ctg B= cateta alaturata AB
Planul determinat de normală şi un punct Ecuaţia generală Plane paralele Unghi diedru Planul determinat de 3 puncte necoliniare
 1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
1 Planul în spaţiu Ecuaţia generală Plane paralele Unghi diedru 2 Ecuaţia generală Plane paralele Unghi diedru Fie reperul R(O, i, j, k ) în spaţiu. Numim normala a unui plan, un vector perpendicular pe
GEOMETRIE PLANĂ TEOREME IMPORTANTE ARII. bh lh 2. abc. abc. formula înălţimii
 GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
GEOMETRIE PLANĂ TEOREME IMPORTANTE ARII. = înălţimea triunghiului echilateral h =, R =, r = R = bh lh 2 A D ++ D. abc. abc =
 GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
GEOMETRIE PLNĂ TEOREME IMPORTNTE suma unghiurilor unui triunghi este 8º suma unghiurilor unui patrulater este 6º unghiurile de la baza unui triunghi isoscel sunt congruente într-un triunghi isoscel liniile
Profesor Blaga Mirela-Gabriela DREAPTA
 DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DREAPTA Fie punctele A ( xa, ya ), B ( xb, yb ), C ( xc, yc ) şi D ( xd, yd ) în planul xoy. 1)Distanţa AB = (x x ) + (y y ) Ex. Fie punctele A( 1, -3) şi B( -2, 5). Calculaţi distanţa AB. AB = ( 2 1)
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE
 DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
DISTANŢA DINTRE DOUĂ DREPTE NECOPLANARE ABSTRACT. Materialul prezintă o modalitate de a afla distanţa dintre două drepte necoplanare folosind volumul tetraedrului. Lecţia se adresează clasei a VIII-a Data:
Definiţia generală Cazul 1. Elipsa şi hiperbola Cercul Cazul 2. Parabola Reprezentari parametrice ale conicelor Tangente la conice
 1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
1 Conice pe ecuaţii reduse 2 Conice pe ecuaţii reduse Definiţie Numim conica locul geometric al punctelor din plan pentru care raportul distantelor la un punct fix F şi la o dreaptă fixă (D) este o constantă
(a) se numeşte derivata parţială a funcţiei f în raport cu variabila x i în punctul a.
 Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Definiţie Spunem că: i) funcţia f are derivată parţială în punctul a în raport cu variabila i dacă funcţia de o variabilă ( ) are derivată în punctul a în sens obişnuit (ca funcţie reală de o variabilă
Curs 14 Funcţii implicite. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi"
 Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
Curs 14 Funcţii implicite Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie F : D R 2 R o funcţie de două variabile şi fie ecuaţia F (x, y) = 0. (1) Problemă În ce condiţii ecuaţia
R R, f ( x) = x 7x+ 6. Determinați distanța dintre punctele de. B=, unde x și y sunt numere reale.
 5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
5p Determinați primul termen al progresiei geometrice ( b n ) n, știind că b 5 = 48 și b 8 = 84 5p Se consideră funcția f : intersecție a graficului funcției f cu aa O R R, f ( ) = 7+ 6 Determinați distanța
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate.
 Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
Curs 10 Funcţii reale de mai multe variabile reale. Limite şi continuitate. Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Fie p, q N. Fie funcţia f : D R p R q. Avem următoarele
5. FUNCŢII IMPLICITE. EXTREME CONDIŢIONATE.
 5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
5 Eerciţii reolvate 5 UNCŢII IMPLICITE EXTREME CONDIŢIONATE Eerciţiul 5 Să se determine şi dacă () este o funcţie definită implicit de ecuaţia ( + ) ( + ) + Soluţie ie ( ) ( + ) ( + ) + ( )R Evident este
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor X) functia f 1
 Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Functii definitie proprietati grafic functii elementare A. Definitii proprietatile functiilor. Fiind date doua multimi X si Y spunem ca am definit o functie (aplicatie) pe X cu valori in Y daca fiecarui
Ecuaţia generală Probleme de tangenţă Sfera prin 4 puncte necoplanare. Elipsoidul Hiperboloizi Paraboloizi Conul Cilindrul. 1 Sfera.
 pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
pe ecuaţii generale 1 Sfera Ecuaţia generală Probleme de tangenţă 2 pe ecuaţii generale Sfera pe ecuaţii generale Ecuaţia generală Probleme de tangenţă Numim sferă locul geometric al punctelor din spaţiu
Dreapta in plan. = y y 0
 Dreapta in plan 1 Dreapta in plan i) Presupunem ca planul este inzestrat cu un reper ortonormat de dreapta (O, i, j). Fiecarui punct M al planului ii corespunde vectorul OM numit vector de pozitie al punctului
Dreapta in plan 1 Dreapta in plan i) Presupunem ca planul este inzestrat cu un reper ortonormat de dreapta (O, i, j). Fiecarui punct M al planului ii corespunde vectorul OM numit vector de pozitie al punctului
2.1 Sfera. (EGS) ecuaţie care poartă denumirea de ecuaţia generală asferei. (EGS) reprezintă osferă cu centrul în punctul. 2 + p 2
 .1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
.1 Sfera Definitia 1.1 Se numeşte sferă mulţimea tuturor punctelor din spaţiu pentru care distanţa la u punct fi numit centrul sferei este egalăcuunnumăr numit raza sferei. Fie centrul sferei C (a, b,
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor
 Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
Functii definitie, proprietati, grafic, functii elementare A. Definitii, proprietatile functiilor. Fiind date doua multimi si spunem ca am definit o functie (aplicatie) pe cu valori in daca fiecarui element
TRIUNGHIUL. Profesor Alina Penciu, Școala Făgăraș, județul Brașov A. Definitii:
 TRIUNGHIUL Profesor lina Penciu, Școala Făgăraș, județul rașov Daca, si sunt trei puncte necoliniare, distincte doua câte doua, atunci ( ) [] [] [] se numeste triunghi si se noteaza cu Δ. Orice Δ determina
TRIUNGHIUL Profesor lina Penciu, Școala Făgăraș, județul rașov Daca, si sunt trei puncte necoliniare, distincte doua câte doua, atunci ( ) [] [] [] se numeste triunghi si se noteaza cu Δ. Orice Δ determina
Metode iterative pentru probleme neliniare - contractii
 Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
Metode iterative pentru probleme neliniare - contractii Problemele neliniare sunt in general rezolvate prin metode iterative si analiza convergentei acestor metode este o problema importanta. 1 Contractii
7. Fie ABCD un patrulater inscriptibil. Un cerc care trece prin A şi B intersectează
 TEMĂ 1 1. În triunghiul ABC, fie D (BC) astfel încât AB + BD = AC + CD. Demonstraţi că dacă punctele B, C şi centrele de greutate ale triunghiurilor ABD şi ACD sunt conciclice, atunci AB = AC. India 2014
TEMĂ 1 1. În triunghiul ABC, fie D (BC) astfel încât AB + BD = AC + CD. Demonstraţi că dacă punctele B, C şi centrele de greutate ale triunghiurilor ABD şi ACD sunt conciclice, atunci AB = AC. India 2014
GEOMETRIE PENTRU GIMNAZIU Partea I (cls. a V a, a VI a, a VII a) Geometrie pentru pregătirea Evaluării Naționale la Matematică
 Geometrie pentru pregătirea Evaluării Naționale la Matematică (Cls. a V a, a VI a, a VII a) UNITĂȚI DE MĂSURĂ Lungime rie Volum Capacitate DE REȚINUT! Masă 1hm 1ha 1dam 1ar 1dm 1l 1q 1kg 1t 1kg 1v 1kg
Geometrie pentru pregătirea Evaluării Naționale la Matematică (Cls. a V a, a VI a, a VII a) UNITĂȚI DE MĂSURĂ Lungime rie Volum Capacitate DE REȚINUT! Masă 1hm 1ha 1dam 1ar 1dm 1l 1q 1kg 1t 1kg 1v 1kg
V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile
 Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
Metode de Optimizare Curs V.7. Condiţii necesare de optimalitate cazul funcţiilor diferenţiabile Propoziţie 7. (Fritz-John). Fie X o submulţime deschisă a lui R n, f:x R o funcţie de clasă C şi ϕ = (ϕ,ϕ
3. Locuri geometrice Locuri geometrice uzuale
 3. Locuri geometrice 3.. Locuri geometrice uzuale oţiunea de loc geometric în plan care se găseşte şi în ELEETELE LUI EUCLID se pare că a fost folosită încă de PLATO (47-347) şi ARISTOTEL(383-3). Locurile
3. Locuri geometrice 3.. Locuri geometrice uzuale oţiunea de loc geometric în plan care se găseşte şi în ELEETELE LUI EUCLID se pare că a fost folosită încă de PLATO (47-347) şi ARISTOTEL(383-3). Locurile
Algebra si Geometrie Seminar 9
 Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Algebra si Geometrie Seminar 9 Decembrie 017 ii Equations are just the boring part of mathematics. I attempt to see things in terms of geometry. Stephen Hawking 9 Dreapta si planul in spatiu 1 Notiuni
Curs 4 Serii de numere reale
 Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
Curs 4 Serii de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Criteriul rădăcinii sau Criteriul lui Cauchy Teoremă (Criteriul rădăcinii) Fie x n o serie cu termeni
III. Serii absolut convergente. Serii semiconvergente. ii) semiconvergentă dacă este convergentă iar seria modulelor divergentă.
 III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
III. Serii absolut convergente. Serii semiconvergente. Definiţie. O serie a n se numeşte: i) absolut convergentă dacă seria modulelor a n este convergentă; ii) semiconvergentă dacă este convergentă iar
Seminariile Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reziduurilor
 Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Facultatea de Matematică Calcul Integral şi Elemente de Analiă Complexă, Semestrul I Lector dr. Lucian MATICIUC Seminariile 9 20 Capitolul X. Integrale Curbilinii: Serii Laurent şi Teorema Reiduurilor.
Subiecte Clasa a VIII-a
 Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Subiecte lasa a VIII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul
Cum folosim cazuri particulare în rezolvarea unor probleme
 Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Cum folosim cazuri particulare în rezolvarea unor probleme GHEORGHE ECKSTEIN 1 Atunci când întâlnim o problemă pe care nu ştim s-o abordăm, adesea este bine să considerăm cazuri particulare ale acesteia.
Asupra unei inegalităţi date la barajul OBMJ 2006
 Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Asupra unei inegalităţi date la barajul OBMJ 006 Mircea Lascu şi Cezar Lupu La cel de-al cincilea baraj de Juniori din data de 0 mai 006 a fost dată următoarea inegalitate: Fie x, y, z trei numere reale
Integrala nedefinită (primitive)
 nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
nedefinita nedefinită (primitive) nedefinita 2 nedefinita februarie 20 nedefinita.tabelul primitivelor Definiţia Fie f : J R, J R un interval. Funcţia F : J R se numeşte primitivă sau antiderivată a funcţiei
T R A I A N ( ) Trigonometrie. \ kπ; k. este periodică (perioada principală T * =π ), impară, nemărginită.
 Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
Trignmetrie Funcţia sinus sin : [, ] este peridică (periada principală T * = ), impară, mărginită. Funcţia arcsinus arcsin : [, ], este impară, mărginită, bijectivă. Funcţia csinus cs : [, ] este peridică
Conice - Câteva proprietǎţi elementare
 Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
Conice - Câteva proprietǎţi elementare lect.dr. Mihai Chiş Facultatea de Matematicǎ şi Informaticǎ Universitatea de Vest din Timişoara Viitori Olimpici ediţia a 5-a, etapa I, clasa a XII-a 1 Definiţii
CERCUL LUI EULER ŞI DREAPTA LUI SIMSON
 CERCUL LUI EULER ŞI DREAPTA LUI SIMSON ABSTRACT. Articolul prezintă două rezultate deosebite legate de patrulaterul inscriptibil şi câteva consecinţe ce decurg din aceste rezultate. Lecţia se adresează
CERCUL LUI EULER ŞI DREAPTA LUI SIMSON ABSTRACT. Articolul prezintă două rezultate deosebite legate de patrulaterul inscriptibil şi câteva consecinţe ce decurg din aceste rezultate. Lecţia se adresează
Ecuatii trigonometrice
 Ecuatii trigonometrice Ecuatiile ce contin necunoscute sub semnul functiilor trigonometrice se numesc ecuatii trigonometrice. Cele mai simple ecuatii trigonometrice sunt ecuatiile de tipul sin x = a, cos
Ecuatii trigonometrice Ecuatiile ce contin necunoscute sub semnul functiilor trigonometrice se numesc ecuatii trigonometrice. Cele mai simple ecuatii trigonometrice sunt ecuatiile de tipul sin x = a, cos
Vectori liberi Produs scalar Produs vectorial Produsul mixt. 1 Vectori liberi. 2 Produs scalar. 3 Produs vectorial. 4 Produsul mixt.
 liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
liberi 1 liberi 2 3 4 Segment orientat liberi Fie S spaţiul geometric tridimensional cu axiomele lui Euclid. Orice pereche de puncte din S, notată (A, B) se numeşte segment orientat. Dacă A B, atunci direcţia
Conice. Lect. dr. Constantin-Cosmin Todea. U.T. Cluj-Napoca
 Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Conice Lect. dr. Constantin-Cosmin Todea U.T. Cluj-Napoca Definiţie: Se numeşte curbă algebrică plană mulţimea punctelor din plan de ecuaţie implicită de forma (C) : F (x, y) = 0 în care funcţia F este
Sisteme diferenţiale liniare de ordinul 1
 1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1 Metoda eliminării 2 Cazul valorilor proprii reale Cazul valorilor proprii nereale 3 Catedra de Matematică 2011 Forma generală a unui sistem liniar Considerăm sistemul y 1 (x) = a 11y 1 (x) + a 12 y 2
1. Scrieti in casetele numerele log 7 8 si ln 8 astfel incat inegalitatea obtinuta sa fie adevarata. <
 Copyright c 009 NG TCV Scoala Virtuala a Tanarului Matematician 1 Ministerul Educatiei si Tineretului al Republicii Moldova Agentia de Evaluare si Examinare Examenul de bacalaureat la matematica, 17 iunie
Copyright c 009 NG TCV Scoala Virtuala a Tanarului Matematician 1 Ministerul Educatiei si Tineretului al Republicii Moldova Agentia de Evaluare si Examinare Examenul de bacalaureat la matematica, 17 iunie
3. REPREZENTAREA PLANULUI
 3.1. GENERALITĂŢI 3. REPREZENTAREA PLANULUI Un plan este definit, în general, prin trei puncte necoliniare sau prin o dreaptă şi un punct exterior, două drepte concurente sau două drepte paralele (fig.3.1).
3.1. GENERALITĂŢI 3. REPREZENTAREA PLANULUI Un plan este definit, în general, prin trei puncte necoliniare sau prin o dreaptă şi un punct exterior, două drepte concurente sau două drepte paralele (fig.3.1).
Curs 1 Şiruri de numere reale
 Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Bibliografie G. Chiorescu, Analiză matematică. Teorie şi probleme. Calcul diferenţial, Editura PIM, Iaşi, 2006. R. Luca-Tudorache, Analiză matematică, Editura Tehnopress, Iaşi, 2005. M. Nicolescu, N. Roşculeţ,
Criptosisteme cu cheie publică III
 Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Criptosisteme cu cheie publică III Anul II Aprilie 2017 Problema rucsacului ( knapsack problem ) Considerăm un număr natural V > 0 şi o mulţime finită de numere naturale pozitive {v 0, v 1,..., v k 1 }.
Să se arate că n este număr par. Dan Nedeianu
 Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
Primul test de selecție pentru juniori I. Să se determine numerele prime p, q, r cu proprietatea că 1 p + 1 q + 1 r 1. Fie ABCD un patrulater convex cu m( BCD) = 10, m( CBA) = 45, m( CBD) = 15 și m( CAB)
y y x x 1 y1 Elemente de geometrie analiticã 1. Segmente 1. DistanŃa dintre douã puncte A(x 1,y 1 ), B(x 2,y 2 ): AB = 2. Panta dreptei AB: m AB =
 Elemente de geometrie analiticã. Segmente. DistanŃa dintre douã puncte A(, ), B(, ): AB = ) + ( ) (. Panta dreptei AB: m AB = +. Coordonatele (,) ale mijlocului segmentului AB: =, =. Coordonatele punctului
Elemente de geometrie analiticã. Segmente. DistanŃa dintre douã puncte A(, ), B(, ): AB = ) + ( ) (. Panta dreptei AB: m AB = +. Coordonatele (,) ale mijlocului segmentului AB: =, =. Coordonatele punctului
a n (ζ z 0 ) n. n=1 se numeste partea principala iar seria a n (z z 0 ) n se numeste partea
 Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
Serii Laurent Definitie. Se numeste serie Laurent o serie de forma Seria n= (z z 0 ) n regulata (tayloriana) = (z z n= 0 ) + n se numeste partea principala iar seria se numeste partea Sa presupunem ca,
CURS XI XII SINTEZĂ. 1 Algebra vectorială a vectorilor liberi
 Lect. dr. Facultatea de Electronică, Telecomunicaţii şi Tehnologia Informaţiei Algebră, Semestrul I, Lector dr. Lucian MATICIUC http://math.etti.tuiasi.ro/maticiuc/ CURS XI XII SINTEZĂ 1 Algebra vectorială
Lect. dr. Facultatea de Electronică, Telecomunicaţii şi Tehnologia Informaţiei Algebră, Semestrul I, Lector dr. Lucian MATICIUC http://math.etti.tuiasi.ro/maticiuc/ CURS XI XII SINTEZĂ 1 Algebra vectorială
π } R 4. ctg:r\{kπ} R FuncŃii trigonometrice 1. DefiniŃii în triunghiul dreptunghic 2. ProprietãŃile funcńiilor trigonometrice 1.
 Trigonometrie FuncŃii trigonometrice. DefiniŃii în triunghiul dreptunghic b c b sin B, cos B, tgb c C c ctgb, sin B cosc, tgb ctgc b b. ProprietãŃile funcńiilor trigonometrice. sin:r [-,] A c B sin(-x)
Trigonometrie FuncŃii trigonometrice. DefiniŃii în triunghiul dreptunghic b c b sin B, cos B, tgb c C c ctgb, sin B cosc, tgb ctgc b b. ProprietãŃile funcńiilor trigonometrice. sin:r [-,] A c B sin(-x)
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM 1 electronica.geniu.ro
 Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
Analiza în curent continuu a schemelor electronice Eugenie Posdărăscu - DCE SEM Seminar S ANALA ÎN CUENT CONTNUU A SCHEMELO ELECTONCE S. ntroducere Pentru a analiza în curent continuu o schemă electronică,
COLEGIUL NATIONAL CONSTANTIN CARABELLA TARGOVISTE. CONCURSUL JUDETEAN DE MATEMATICA CEZAR IVANESCU Editia a VI-a 26 februarie 2005.
 SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
SUBIECTUL Editia a VI-a 6 februarie 005 CLASA a V-a Fie A = x N 005 x 007 si B = y N y 003 005 3 3 a) Specificati cel mai mic element al multimii A si cel mai mare element al multimii B. b)stabiliti care
Metode de interpolare bazate pe diferenţe divizate
 Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
Metode de interpolare bazate pe diferenţe divizate Radu Trîmbiţaş 4 octombrie 2005 1 Forma Newton a polinomului de interpolare Lagrange Algoritmul nostru se bazează pe forma Newton a polinomului de interpolare
DEFINITIVAT 1993 PROFESORI I. sinx. 0, dacă x = 0
 DEFINITIVAT 1993 TIMIŞOARA PROFESORI I 1. a) Metodica predării noţiunii de derivată a unei funcţii. b) Să se reprezinte grafic funci a sinx, dacă x (0,2π] f : [0,2π] R, f(x) = x. 0, dacă x = 0 2. Fie G
DEFINITIVAT 1993 TIMIŞOARA PROFESORI I 1. a) Metodica predării noţiunii de derivată a unei funcţii. b) Să se reprezinte grafic funci a sinx, dacă x (0,2π] f : [0,2π] R, f(x) = x. 0, dacă x = 0 2. Fie G
Subiecte Clasa a VII-a
 lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
lasa a VII Lumina Math Intrebari Subiecte lasa a VII-a (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate
Toate subiectele sunt obligatorii. Timpul de lucru efectiv este de 3 ore. Se acordă din oficiu 10 puncte. SUBIECTUL I.
 Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
Modelul 4 Se acordă din oficiu puncte.. Fie numărul complex z = i. Calculaţi (z ) 25. 2. Dacă x şi x 2 sunt rădăcinile ecuaţiei x 2 9x+8 =, atunci să se calculeze x2 +x2 2 x x 2. 3. Rezolvaţi în mulţimea
EDITURA PARALELA 45 MATEMATICĂ DE EXCELENŢĂ. Clasa a X-a Ediţia a II-a, revizuită. pentru concursuri, olimpiade şi centre de excelenţă
 Coordonatori DANA HEUBERGER NICOLAE MUŞUROIA Nicolae Muşuroia Gheorghe Boroica Vasile Pop Dana Heuberger Florin Bojor MATEMATICĂ DE EXCELENŢĂ pentru concursuri, olimpiade şi centre de excelenţă Clasa a
Coordonatori DANA HEUBERGER NICOLAE MUŞUROIA Nicolae Muşuroia Gheorghe Boroica Vasile Pop Dana Heuberger Florin Bojor MATEMATICĂ DE EXCELENŢĂ pentru concursuri, olimpiade şi centre de excelenţă Clasa a
2. Sisteme de forţe concurente...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...3
 SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
SEMINAR 2 SISTEME DE FRŢE CNCURENTE CUPRINS 2. Sisteme de forţe concurente...1 Cuprins...1 Introducere...1 2.1. Aspecte teoretice...2 2.2. Aplicaţii rezolvate...3 2. Sisteme de forţe concurente În acest
Concurs MATE-INFO UBB, 1 aprilie 2017 Proba scrisă la MATEMATICĂ
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ Concurs MATE-INFO UBB, aprilie 7 Proba scrisă la MATEMATICĂ SUBIECTUL I (3 puncte) ) (5 puncte) Fie matricele A = 3 4 9 8
SEMINAR 14. Funcţii de mai multe variabile (continuare) ( = 1 z(x,y) x = 0. x = f. x + f. y = f. = x. = 1 y. y = x ( y = = 0
 Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr. Lucian MATICIUC SEMINAR 4 Funcţii de mai multe variabile continuare). Să se arate că funcţia z,
Lectia VII Dreapta si planul
 Planul. Ecuatii, pozitii relative Dreapta. Ecuatii, pozitii relative Aplicatii Lectia VII Dreapta si planul Oana Constantinescu Oana Constantinescu Lectia VII Planul. Ecuatii, pozitii relative Dreapta.
Planul. Ecuatii, pozitii relative Dreapta. Ecuatii, pozitii relative Aplicatii Lectia VII Dreapta si planul Oana Constantinescu Oana Constantinescu Lectia VII Planul. Ecuatii, pozitii relative Dreapta.
Asemănarea triunghiurilor O selecție de probleme de geometrie elementară pentru gimnaziu Constantin Chirila Colegiul Naţional Garabet Ibrãileanu,
 Asemănarea triunghiurilor O selecție de probleme de geometrie elementară pentru gimnaziu Constantin Chirila Colegiul Naţional Garabet Ibrãileanu, Iaşi Repere metodice ale predării asemănării în gimnaziu
Asemănarea triunghiurilor O selecție de probleme de geometrie elementară pentru gimnaziu Constantin Chirila Colegiul Naţional Garabet Ibrãileanu, Iaşi Repere metodice ale predării asemănării în gimnaziu
Capitolul 9. Geometrie analitică. 9.1 Repere
 Capitolul 9 Geometrie analitică 9.1 Repere Vom considera spaţiile liniare (X, +,, R)în careelementelespaţiului X sunt vectorii de pe odreaptă, V 1, dintr-un plan, V sau din spaţiu, V 3 (adică X V 1 sau
Capitolul 9 Geometrie analitică 9.1 Repere Vom considera spaţiile liniare (X, +,, R)în careelementelespaţiului X sunt vectorii de pe odreaptă, V 1, dintr-un plan, V sau din spaţiu, V 3 (adică X V 1 sau
CONCURS DE ADMITERE, 17 iulie 2017 Proba scrisă la MATEMATICĂ
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ CONCURS DE ADMITERE, 7 iulie 207 Proba scrisă la MATEMATICĂ SUBIECTUL I (30 puncte) ) (0 puncte) Să se arate că oricare ar
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ CONCURS DE ADMITERE, 7 iulie 207 Proba scrisă la MATEMATICĂ SUBIECTUL I (30 puncte) ) (0 puncte) Să se arate că oricare ar
Lectia III Produsul scalar a doi vectori liberi
 Produsul scalar: denitie, proprietati Schimbari de repere ortonormate in plan Aplicatii Lectia III Produsul scalar a doi vectori liberi Oana Constantinescu Oana Constantinescu Lectia III Produsul scalar:
Produsul scalar: denitie, proprietati Schimbari de repere ortonormate in plan Aplicatii Lectia III Produsul scalar a doi vectori liberi Oana Constantinescu Oana Constantinescu Lectia III Produsul scalar:
z a + c 0 + c 1 (z a)
 1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
1 Serii Laurent (continuare) Teorema 1.1 Fie D C un domeniu, a D şi f : D \ {a} C o funcţie olomorfă. Punctul a este pol multiplu de ordin p al lui f dacă şi numai dacă dezvoltarea în serie Laurent a funcţiei
2. CALCULE TOPOGRAFICE
 . CALCULE TOPOGRAFICE.. CALCULAREA DISTANŢEI DINTRE DOUĂ PUNCTE... CALCULAREA DISTANŢEI DINTRE DOUĂ PUNCTE DIN COORDONATE RECTANGULARE Distanţa în linie dreaptă dintre două puncte se poate calcula dacă
. CALCULE TOPOGRAFICE.. CALCULAREA DISTANŢEI DINTRE DOUĂ PUNCTE... CALCULAREA DISTANŢEI DINTRE DOUĂ PUNCTE DIN COORDONATE RECTANGULARE Distanţa în linie dreaptă dintre două puncte se poate calcula dacă
avem V ç,, unde D = b 4ac este discriminantul ecuaţiei de gradul al doilea ax 2 + bx +
 Corina şi Cătălin Minescu 1 Determinarea funcţiei de gradul al doilea când se cunosc puncte de pe grafic, coordonatele vârfului, intersecţii cu axele de coordonate, puncte de extrem, etc. Probleme de arii.
Corina şi Cătălin Minescu 1 Determinarea funcţiei de gradul al doilea când se cunosc puncte de pe grafic, coordonatele vârfului, intersecţii cu axele de coordonate, puncte de extrem, etc. Probleme de arii.
1. Completati caseta, astfel incat propozitia obtinuta sa fie adevarata lg 4 =.
 Copyright c ONG TCV Scoala Virtuala a Tanarului Matematician Ministerul Educatiei al Republicii Moldova Agentia de Evaluare si Examinare Examenul de bacalaureat la matematica, 4 iunie Profilul real Timp
Copyright c ONG TCV Scoala Virtuala a Tanarului Matematician Ministerul Educatiei al Republicii Moldova Agentia de Evaluare si Examinare Examenul de bacalaureat la matematica, 4 iunie Profilul real Timp
2.3 Geometria analitică liniarăînspaţiu
 2.3 Geometria analitică liniarăînspaţiu Pentru început sădefinim câteva noţiuni de bază în geometria analitică. Definitia 2.3.1 Se numeşte reper în spaţiu o mulţime formată dintr-un punct O (numit originea
2.3 Geometria analitică liniarăînspaţiu Pentru început sădefinim câteva noţiuni de bază în geometria analitică. Definitia 2.3.1 Se numeşte reper în spaţiu o mulţime formată dintr-un punct O (numit originea
Aplicaţii ale numerelor complexe în geometrie, utilizând Geogebra
 ale numerelor complexe în geometrie, utilizând Geogebra Adevărul matematic, indiferent unde, la Paris sau la Toulouse, este unul şi acelaşi (Blaise Pascal) Diana-Florina Haliţă grupa 331 dianahalita@gmailcom
ale numerelor complexe în geometrie, utilizând Geogebra Adevărul matematic, indiferent unde, la Paris sau la Toulouse, este unul şi acelaşi (Blaise Pascal) Diana-Florina Haliţă grupa 331 dianahalita@gmailcom
LUCRARE DE DIPLOMĂ CENTRE REMARCABILE ÎN TRIUNGHI
 UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ SPECIALIZAREA MATEMATICI APLICATE LUCRARE DE DIPLOMĂ CENTRE REMARCABILE ÎN TRIUNGHI Conducător Ştiinţific: Lect. Dr. VĂCĂREŢU
UNIVERSITATEA BABEŞ-BOLYAI CLUJ-NAPOCA FACULTATEA DE MATEMATICĂ ŞI INFORMATICĂ SPECIALIZAREA MATEMATICI APLICATE LUCRARE DE DIPLOMĂ CENTRE REMARCABILE ÎN TRIUNGHI Conducător Ştiinţific: Lect. Dr. VĂCĂREŢU
Capitolul 4. Integrale improprii Integrale cu limite de integrare infinite
 Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Capitolul 4 Integrale improprii 7-8 În cadrul studiului integrabilităţii iemann a unei funcţii s-au evidenţiat douăcondiţii esenţiale:. funcţia :[ ] este definită peintervalînchis şi mărginit (interval
Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane
 Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Subspatii ane Lectia VI Structura de spatiu an E 3. Dreapta si planul ca subspatii ane Oana Constantinescu Oana Constantinescu Lectia VI Subspatii ane Table of Contents 1 Structura de spatiu an E 3 2 Subspatii
Timp alocat: 180 minute. In itemii 1-4 completati casetele libere, astfel incat propozitiile obtinute sa fie adevarate.
 Copyright c 009 ONG TCV Scoala Virtuala a Tanarului Matematician 1 Ministerul Educatiei si Tineretului al Republicii Moldova Agentia de Evaluare si Examinare Examenul de bacalaureat la matematica, 15 iunie
Copyright c 009 ONG TCV Scoala Virtuala a Tanarului Matematician 1 Ministerul Educatiei si Tineretului al Republicii Moldova Agentia de Evaluare si Examinare Examenul de bacalaureat la matematica, 15 iunie
Functii Breviar teoretic 8 ianuarie ianuarie 2011
 Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
Functii Breviar teoretic 8 ianuarie 011 15 ianuarie 011 I Fie I, interval si f : I 1) a) functia f este (strict) crescatoare pe I daca x, y I, x< y ( f( x) < f( y)), f( x) f( y) b) functia f este (strict)
BARAJ DE JUNIORI,,Euclid Cipru, 28 mai 2012 (barajul 3)
 BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
BARAJ DE JUNIORI,,Euclid Cipru, 8 mi 0 (brjul ) Problem Arătţi că dcă, b, c sunt numere rele cre verifică + b + c =, tunci re loc ineglitte xy + yz + zx Problem Fie şi b numere nturle nenule Dcă numărul
5.5. REZOLVAREA CIRCUITELOR CU TRANZISTOARE BIPOLARE
 5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
5.5. A CIRCUITELOR CU TRANZISTOARE BIPOLARE PROBLEMA 1. În circuitul din figura 5.54 se cunosc valorile: μa a. Valoarea intensității curentului de colector I C. b. Valoarea tensiunii bază-emitor U BE.
3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere Aspecte teoretice Aplicaţii rezolvate...4
 SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
SEMINAR 3 MMENTUL FRŢEI ÎN RAPRT CU UN PUNCT CUPRINS 3. Momentul forţei în raport cu un punct...1 Cuprins...1 Introducere...1 3.1. Aspecte teoretice...2 3.2. Aplicaţii rezolvate...4 3. Momentul forţei
Lucian Maticiuc SEMINAR Conf. dr. Lucian Maticiuc. Capitolul VI. Integrala triplă. Teoria:
 Capitolul I: Integrala triplă Conf. dr. Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Analiza Matematică II, Semestrul II Conf. dr. Lucian MATICIUC Teoria: SEMINAR 3 Capitolul I. Integrala
Capitolul I: Integrala triplă Conf. dr. Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Analiza Matematică II, Semestrul II Conf. dr. Lucian MATICIUC Teoria: SEMINAR 3 Capitolul I. Integrala
Subiecte Clasa a VIII-a
 (40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
(40 de intrebari) Puteti folosi spatiile goale ca ciorna. Nu este de ajuns sa alegeti raspunsul corect pe brosura de subiecte, ele trebuie completate pe foaia de raspuns in dreptul numarului intrebarii
CONCURSUL INTERJUDEȚEAN DE MATEMATICĂ TRAIAN LALESCU, 1998 Clasa a V-a
 CONCURSUL INTERJUDEȚEAN DE MATEMATICĂ TRAIAN LALESCU, 998 Clasa a V-a. La gara Timișoara se eliberează trei bilete de tren: unul pentru Arad, altul pentru Deva și al treilea pentru Reșița. Cel pentru Deva
CONCURSUL INTERJUDEȚEAN DE MATEMATICĂ TRAIAN LALESCU, 998 Clasa a V-a. La gara Timișoara se eliberează trei bilete de tren: unul pentru Arad, altul pentru Deva și al treilea pentru Reșița. Cel pentru Deva
6.CONUL ŞI CILINDRUL. Fig Fig. 6.2 Fig. 6.3
 6.CONUL ŞI CILINDRUL 6.1.GENERALITĂŢI Conul este corpul geometric mărginit de o suprafaţă conică şi un plan; suprafaţa conică este generată prin rotaţia unei drepte mobile, numită generatoare, concurentă
6.CONUL ŞI CILINDRUL 6.1.GENERALITĂŢI Conul este corpul geometric mărginit de o suprafaţă conică şi un plan; suprafaţa conică este generată prin rotaţia unei drepte mobile, numită generatoare, concurentă
Cercul lui Euler ( al celor nouă puncte și nu numai!)
 Cercul lui Euler ( al celor nouă puncte și nu numai!) Prof. ION CĂLINESCU,CNDG, Câmpulung Voi prezenta o abordare simplă a determinării cercului lui Euler, pe baza unei probleme de loc geometric. Preliminarii:
Cercul lui Euler ( al celor nouă puncte și nu numai!) Prof. ION CĂLINESCU,CNDG, Câmpulung Voi prezenta o abordare simplă a determinării cercului lui Euler, pe baza unei probleme de loc geometric. Preliminarii:
SEXTANTUL CUM FUNCŢIONEAZĂ UN SEXTANT?
 SEXTANTUL CUM FUNCŢIONEAZĂ UN SEXTANT? Să considerăm mai întâi (pentru a asigura o descriere fizică riguroasă) două oglinzi plane paralele M 1, M 2 (orientate după direcţia MN PQ), aparţinând spre exemplu
SEXTANTUL CUM FUNCŢIONEAZĂ UN SEXTANT? Să considerăm mai întâi (pentru a asigura o descriere fizică riguroasă) două oglinzi plane paralele M 1, M 2 (orientate după direcţia MN PQ), aparţinând spre exemplu
GRADUL II 1995 CRAIOVA PROFESORI I
 GRADUL II 1995 CRAIOVA PROFESORI I 1. Fie f : R R definită prin f(x) = x(1+e x ). a) Să se arate că f este indefinit derivabilă şi că f (n) (x) = a n e x +b n xe x, ( ) n 3, ( ) x R. Deduceţi că a n+1
GRADUL II 1995 CRAIOVA PROFESORI I 1. Fie f : R R definită prin f(x) = x(1+e x ). a) Să se arate că f este indefinit derivabilă şi că f (n) (x) = a n e x +b n xe x, ( ) n 3, ( ) x R. Deduceţi că a n+1
b = CA, c = AB, atunci concluzia rezultă din regula triunghiului de adunare a vectorilor:
 Trei vectori a, b, c formează untriunghi a + b + c = 0 (relaţia lui Chasles). Dacă a, b, c sunt laturi ale unui triunghi ABC, a = BC, b = CA, c = AB, atunci concluzia rezultă din regula triunghiului de
Trei vectori a, b, c formează untriunghi a + b + c = 0 (relaţia lui Chasles). Dacă a, b, c sunt laturi ale unui triunghi ABC, a = BC, b = CA, c = AB, atunci concluzia rezultă din regula triunghiului de
Puncte, plane si cercuri fundamentale pe sfera cereasca
 Astronomie sferica Puncte, plane si cercuri fundamentale pe sfera cereasca Aparente: Corpurile ceresti par situate pe o calota sferica; Stelele nu-si schimba pozitia relativa- gruparea in constelatii;
Astronomie sferica Puncte, plane si cercuri fundamentale pe sfera cereasca Aparente: Corpurile ceresti par situate pe o calota sferica; Stelele nu-si schimba pozitia relativa- gruparea in constelatii;
Geometrie computationala 2. Preliminarii geometrice
 Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
Platformă de e-learning și curriculă e-content pentru învățământul superior tehnic Geometrie computationala 2. Preliminarii geometrice Preliminarii geometrice Spatiu Euclidean: E d Spatiu de d-tupluri,
RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii transversale, scrisă faţă de una dintre axele de inerţie principale:,
 REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
REZISTENTA MATERIALELOR 1. Ce este modulul de rezistenţă? Exemplificaţi pentru o secţiune dreptunghiulară, respectiv dublu T. RĂSPUNS Modulul de rezistenţă este o caracteristică geometrică a secţiunii
MARCAREA REZISTOARELOR
 1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
1.2. MARCAREA REZISTOARELOR 1.2.1 MARCARE DIRECTĂ PRIN COD ALFANUMERIC. Acest cod este format din una sau mai multe cifre şi o literă. Litera poate fi plasată după grupul de cifre (situaţie în care valoarea
Varianta 1. SUBIECTUL I Pe foaia de teză se trec numai rezultatele.
 Varianta 1 1 a) Rezultatul calculului 3,7 1 6 este egal cu numărul b) Rădăcina pătrată a numărului 11 este egală cu numărul c) Media aritmetică a numerelor 3 + 7 şi 3 7 este egală cu a) Soluţia întreagă
Varianta 1 1 a) Rezultatul calculului 3,7 1 6 este egal cu numărul b) Rădăcina pătrată a numărului 11 este egală cu numărul c) Media aritmetică a numerelor 3 + 7 şi 3 7 este egală cu a) Soluţia întreagă
Seminar 5 Analiza stabilității sistemelor liniare
 Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Seminar 5 Analiza stabilității sistemelor liniare Noțiuni teoretice Criteriul Hurwitz de analiză a stabilității sistemelor liniare În cazul sistemelor liniare, stabilitatea este o condiție de localizare
Aplicaţii ale principiului I al termodinamicii la gazul ideal
 Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
Aplicaţii ale principiului I al termodinamicii la gazul ideal Principiul I al termodinamicii exprimă legea conservării şi energiei dintr-o formă în alta şi se exprimă prin relaţia: ΔUQ-L, unde: ΔU-variaţia
SERII NUMERICE. Definiţia 3.1. Fie (a n ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0
 SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
SERII NUMERICE Definiţia 3.1. Fie ( ) n n0 (n 0 IN) un şir de numere reale şi (s n ) n n0 şirul definit prin: s n0 = 0, s n0 +1 = 0 + 0 +1, s n0 +2 = 0 + 0 +1 + 0 +2,.......................................
CURS VII-IX. Capitolul IV: Funcţii derivabile. Derivate şi diferenţiale. 1 Derivata unei funcţii. Interpretarea geometrică.
 Lect dr Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr Lucian MATICIUC CURS VII-IX Capitolul IV: Funcţii derivabile Derivate şi diferenţiale 1
Lect dr Facultatea de Hidrotehnică, Geodezie şi Ingineria Mediului Matematici Superioare, Semestrul I, Lector dr Lucian MATICIUC CURS VII-IX Capitolul IV: Funcţii derivabile Derivate şi diferenţiale 1
BAC 2007 Pro Didactica
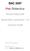 BAC 007 Pro Didactica Testare Naţională Rezolvările variantelor 1 5 versiune finală Redactia Pro Didactica Suportul pe net: http://www./ 5--007/versiune finală Cuprins Capitolul 1. Varianta 1 1. Subiectul
BAC 007 Pro Didactica Testare Naţională Rezolvările variantelor 1 5 versiune finală Redactia Pro Didactica Suportul pe net: http://www./ 5--007/versiune finală Cuprins Capitolul 1. Varianta 1 1. Subiectul
Curs 2 Şiruri de numere reale
 Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
Curs 2 Şiruri de numere reale Facultatea de Hidrotehnică Universitatea Tehnică "Gh. Asachi" Iaşi 2014 Convergenţă şi mărginire Teoremă Orice şir convergent este mărginit. Demonstraţie Fie (x n ) n 0 un
BREVIAR TEORETIC CU EXEMPLE CONCRETE, PENTRU PREGĂTIREA EXAMENULUI DE EVALUARE NAŢIONALĂ, clasa a VIII-a
 GEOMETRIE-Evaluare Naţională 010 BREVIAR TEORETIC CU EXEMPLE CONCRETE, PENTRU PREGĂTIREA EXAMENULUI DE EVALUARE NAŢIONALĂ, clasa a VIII-a - 010 Propunător: Şcoala cu clasele I-VIII Măteşti, com. Săpoca,
GEOMETRIE-Evaluare Naţională 010 BREVIAR TEORETIC CU EXEMPLE CONCRETE, PENTRU PREGĂTIREA EXAMENULUI DE EVALUARE NAŢIONALĂ, clasa a VIII-a - 010 Propunător: Şcoala cu clasele I-VIII Măteşti, com. Săpoca,
a. 11 % b. 12 % c. 13 % d. 14 %
 1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
1. Un motor termic funcţionează după ciclul termodinamic reprezentat în sistemul de coordonate V-T în figura alăturată. Motorul termic utilizează ca substanţă de lucru un mol de gaz ideal având exponentul
Miscarea oscilatorie armonica ( Fisa nr. 2 )
 Miscarea oscilatorie armonica ( Fisa nr. 2 ) In prima fisa publicata pe site-ul didactic.ro ( Miscarea armonica) am explicat parametrii ce definesc miscarea oscilatorie ( perioda, frecventa ) dar nu am
Miscarea oscilatorie armonica ( Fisa nr. 2 ) In prima fisa publicata pe site-ul didactic.ro ( Miscarea armonica) am explicat parametrii ce definesc miscarea oscilatorie ( perioda, frecventa ) dar nu am
Principiul Inductiei Matematice.
 Principiul Inductiei Matematice. Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural. Metoda inductiei
Principiul Inductiei Matematice. Principiul inductiei matematice constituie un mijloc important de demonstratie in matematica a propozitiilor (afirmatiilor) ce depind de argument natural. Metoda inductiei
EDITURA PARALELA 45. Matematică de excelenţă pentru concursuri, olimpiade şi centre de excelenţă. clasa a VIII-a. mate 2000 excelenţă
 Maranda Linţ Dorin Linţ Rozalia Marinescu Dan Ştefan Marinescu Mihai Monea Steluţa Monea Marian Stroe Matematică de excelenţă pentru concursuri, olimpiade şi centre de excelenţă clasa a VIII-a mate 000
Maranda Linţ Dorin Linţ Rozalia Marinescu Dan Ştefan Marinescu Mihai Monea Steluţa Monea Marian Stroe Matematică de excelenţă pentru concursuri, olimpiade şi centre de excelenţă clasa a VIII-a mate 000
