Оригинални научни рад UDC: 911.2:523.03(497.11) DOI: /IJGI R
|
|
|
- Ματθαίος Αναγνώστου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Доступно онлајн на Зборник радова Географског института Јован Цвијић САНУ 61(3) (1-16) Оригинални научни рад UDC: 911.2:523.03(497.11) DOI: /IJGI R АСТРОФИЗИЧКА АНАЛИЗА ЗЕМЉОТРЕСА КОД КРАЉЕВА (СРБИЈА) 03. НОВЕМБРА ГОДИНЕ Милан Радовановић* 1, Милан Стеванчевић**, Драгана Милијашевић*, Saumitra Mukherjee***, Жељко Бјељац* *Географски институт Јован Цвијић САНУ, Београд, Србија **Бивше Министарство телекомуникација, Београд, Србија ***School of Environmental Sciences, Jawaharlal Nehru University, New Delhi, India Примљено 1 августа 2011; рецензирано 3 октобра 2011; прихваћено 25 октобра 2011 Абстракт: Резултати претходних студија указали су на постојање статистички значајне везе између јоносферских, тј. атмосферских поремећаја и земљотреса. Такође, у разматрање су узета бројна досадашња истраживања која су се односила на повезаност између активности Сунца и поремећаја у атмосфери. На основу таквих показатеља покушали смо да утврдимо евентуално постојање узрочно-последичне везе између процеса на Сунцу и земљотреса који се догодио 03. новембра године у близини Краљева (Србија). На основу теоријских разматрања предложен је нов модел који сугерише настанак окидног импулса. Добијени резултати показују да би на статистички значајнијем броју узорака било неопходно утврдити потенцијалну правилност у променама параметара интерпланетарног магнетног поља (ИМП), односно компоненти Сунчевог ветра (СВ) неколико дана пре и после појаве јаких земљотреса. Кључне речи: земљотрес, интерпланетарно магнетно поље, модел, Краљево (Србија) Увод Снажни земљотреси, нарочито у односу на друге регионе у свету, нису честа појава на територији Србије. Међутим, 03. новембра године, у централном делу Србије, око 1 сат после поноћи догодио се земљотрес магнитуде 5,4 (ск. 1). Локација епицентра је 43,74 N, 20,69 E, тачно време потреса 00:56:54.4 UTC, дубина хипоцентра 2 km ( 1 Correspondence to: m.radovanovic@gi.sanu.ac.rs
2 Зборник радова Географског института Јован Цвијић САНУ 61(3) (1-16) Скица 1. Географски положај локације земљотреса 03. новембра године ( Након тога уследила је серија земљотреса знатно слабије јачине, који су се јављали до 18. новембра. На жалост двоје људи је погинуло, при чему је знатна материјална штета у великој мери отежавала нормализацију живота у хладним данима који су долазили. Као и у многим другим случајевима, не само у Србији, није било никаквих наговештаја да ће се земљотрес догодити. Односно, није нам познато да је било који од савремених модела указивао на могућност појаве подрхтавања тла, поготово не тог интензитета (Hattori, 2004). У овом раду покушаћемо да укажемо на основе модела који је заснован на интерактивној повезаности процеса на Сунцу и земљотеса који се јавио код Краљева. Основни приступ који је спроведен током истраживања односи се на каузалност, тј. временски след догађаја и то: ерупција енергије са Сунца у виду високоенергетских честица садржаних у електричном ИМП, односно СВ, намагнетисање средине (појединих делова литосфере) и појава земљотреса. Преглед досадашњих истраживања Увидом у литературу показало се да постоје бројна истраживања која указују на потенцијалну везу између процеса на Сунцу и земљотреса на неким деловима наше планете. Simpson (1967/68) истиче да се максимум фреквенције земљотреса догађа у периоду умерено високе и флуктуирајуће Сунчеве активности. Weiyu et al, (2006) закључују да код земљотреса у Индонезији 26. децембра године 1) подаци о температури ваздуха могу јасно рефлектовати топлотни знак и комплетан поступак акумулирања и ослобађања енергије земљотреса, 2) додатна структура 2
3 Астрофизичка анализа земљотреса код Краљева (Србија) 03. новембра године стреса астро-плимског окидања је важан спољни фактор окидања земљотреса и 3) анализирајући више од 40 случајева, резултати показују да се за око 60% јаких земљотреса везује абнормални раст температуре ваздуха, односно евидентна је њихова просторно-временска улога. Athanasiou et al, (2011) доказују да промене у енергији електромагнетних ултракратких (ULF) таласа Ez компоненте електричног поља јасно указују на повезаност са земљотресом на Хаитију 12. јануара године. Silva et al, (2011) су дошли до сличних закључака у случају земљотреса у Португалу године. Mukherjee, Kortvelyessy (2006) истичу да поред Сунца на подрхтавање тла могу утицати интерстеларни ветрови, односно у случају који су они разматрали, облаци врелог хелијума, са знатно већом густином честица него што је то уобичајено код СВ. Наизглед неспојива дешавања на релацији Сунце-циркулациони процеси у атмосфериземљотреси статистички су испитана у раду који су дали Odintsov et al, (2006) (ск. 2). Скица 2. Просечан број земљотреса (пуна линија) и Сунчева активност (испрекидана линија) у једанаестогодишњем Сунчевом циклусу за период године - леви графикон и годишњи број земљотреса M 7 у периоду (пуна линија) и интензитет зоналне циркулације (испрекидана линија) у истом периоду - десни графикон (Odintsov et al, 2006) Анализирајући резултате до којих су дошли, аутори споменутог рада закључују да би сценарио утицаја Сунчеве активности на сеизмичку активност могао да укључи следеће елементе: 1. надолазећи шок пулса притиска, придружен са струјама СВ високих брзина или ерупцијама честица из коронарних рупа, сабија магнетосферу, 2. јачање струјања ауроре, 3. ствoрени таласи атмосферске гравитације се трансмитују на доле, 4. јачање зоналних западних ветрова, 5. промена притиска ваздуха на површини, 3
4 Зборник радова Географског института Јован Цвијић САНУ 61(3) (1-16) 6. баланс притиска на тектонске плоче је поремећен и 7. ако је довољно тензије акумулирано, земљотрес је активиран. Radovanović et al, (2003), сматрају да јачање ауроре у поларним областима представља пропратну оптичку манифестацију спајања ИПМ и геомагнетног поља. Gomes, Radovanović (2008), Mukherjee (2008), Nikolić et al, (2010), Mukherjee, Radovanović (2011) као и многи други истичу бројне примере утицаја СВ на атмосферске процесе, као и на одређене аспекте животне средине. Gabis, Troshichev (2000) су констатовали да утицај краткотрајних промена у Сунчевој активности на поремећаје у баричком пољу (притиска) је очигледан у стратосфери (ниво на 30 mbar). Меридионални поремећаји у стратосфери у случају Форбушовог опадања и дешавања Сунчевих протона, почиње да се развија непосредно пред кључни датум, пратећи раст UV зрачења, типичан за краткотрајне промене у Сунчевој активности. Распадање меридионалног преноса догађа се након кључног дана очигледно под утицајима Сунчевог енергетског корпускуларног флукса. Флуктуације баричког поља у оквиру периода од 5±10 дана су типичне за меридионални и зонални пренос у тропосфери (ниво на 500 mbar), будући да интензитети меридионалног и зоналног трансфера имају супротне фазе. Ефекат кључног датума није изражен у овим флуктуацијама. Индекс вртложног простора карактеристичан за циклонску активност у тропосфери, одговара променама меридионалног трансфера у стратосфери. Sing et al, (2009) истичу јаку статистичку повезаност између јоносферских поремеђаја и земљотреса. Yonaiguchi, Hayakawa (2007) уочавају одређене правилности у атмосферским поремећајима и појави земљотреса током појединих делова године, наглашавајући да се њихова анализа ипак односи на податке за једну (2005) годину. Hasbi et al, (2011) констатују да у случају 4 снажна земљотреса на Суматри, у периоду године њихови резултати подржавају чињеницу да је висинска аномалија електричног поља створена у близини региона епицентра у интеракцији са источним електричним пољем, индукујући јоносферске аномалије у близини региона епицентра и дисторзије облика екваторијалне аномалије. Концентрације електрона показују позитивне и негативне аномалије од неколико часова до 6 дана пре појаве земљотреса. Имајући изнето у виду, покушали смо да утврдимо евентуалну узрочнопоследичну везу између прилива енергије са Сунца непосредно пре појаве земљотреса код Краљева. У том смислу је са теоријског аспекта предложен нов модел који би, уколико се покаже оправданим, требало да представља основу за израду прогноза. 4
5 Астрофизичка анализа земљотреса код Краљева (Србија) 03. новембра године Хелиоцентрични електромагнетни модел настанка земљотреса код Краљева Претпоставимо да је ИМП страно поље које делује на неку литосферску средину. Уколико шематски прикажемо јачину интерпланетарног поља (Н) и магнетну индукцију (В) (ск. 3) онда можемо рећи да ће са повећањем јачине ИМП, од тачке O до тачке A, намагнетисање у посматраној средини почети да расте. Криву од тачке O до A можемо назвати првобитна крива намагнетисања. Скица 3. Шематски приказ циклуса хистерезиса У тачки A долази до засићења, а ИМП достиже максималну вредност Hmax. Када се смањи јачина ИМП смањиваће се и и магнетна индукција B од тачке A до Br. Када јачина ИМП буде једнака нули, магнетна индукција не ишчезава већ задржава одређену вредност и она представља реманентну индукцију Br. При промени смера ИМП H смањиваће се магнетна индукција B и у одређеном тренутку она ће бити једнака нули. Ову тачку обележићемо са Hc и назвати је коерцитивно поље или коерцитивна сила. Да би се јавио земљотрес потребно је да ИМП промени смер, а магнетна индукција Br буде једнака нули, односно да од позитивне вредности +Br промени смер на -Br. Моменат достизања вредности Нс представља заправо тренутак појаве земљотреса. Када јачина ИМП достигне вредност 5
6 Зборник радова Географског института Јован Цвијић САНУ 61(3) (1-16) Hmin у тачки b добија се максимална негативна вредност магнетне индукције. Ако се јачина ИМП поново мења од Hmax до +Hmax и поново до Hmax добија се циклус хистерезиса за посматрану средину. Произилази да величина циклуса хистерезиса зависи од јачине ИМП и магнетних карактеристика средине која се магнетише. Ако претпоставимо да између магнетске индукције и јачине ИМП постоји линеарна зависност B = μh, добија се да је: H 0 2 ( μ / 2) H d Wm / dv = μ HdH = из чега произилази да: d Wm / dv = 1 BH 2 2 B је магнетска индукција, H јачина магнетског поља, μ- пермеабилност средине и W- енергија. Укупна енергија која се троши за време намагнетисања средине је: Wm = 1 2 v BH dv Математички израз којим би се могла описати енергија коју нека средина апсорбује приликом намагнетисања био би: dwm / dv = BdH У ситуацијама када су H и db истог знака, густина енергије HdB je позитивна, односно средина која се магнетише апсорбује енергију ИМП. У случају да су H и db различитог знака, средина која је намагнетисана ослобађа енергију. То практично значи да се расед између две тектонске плоче понаша као магнетни акумулатор енергије. Из овога можемо закључити да што је производ B и апсолутне вредности H већи за посматрану средину, то је земљотрес снажнији (Stevančević, 2011). Претпоставимо да на расед између две тектонске плоче дејствује једна од компоненти ИМП која је нормална на линију раседа. О могућности да високоенергетске честице допиру до тла писали су и Palamara, Bryant (2004) истичући да је кључно питање како се Соларна/геомагнетна 6
7 Астрофизичка анализа земљотреса код Краљева (Србија) 03. новембра године активност спаја у доњем делу атмосфере. Према мишљењу Gomes et al, (2009) тај процес се одвија на два начина: риконекцијом (у поларним областима) и продором честица СВ у областима најслабијег геомагнетног поља, тј. геомагнетних аномалија. Један од основних услова је смањена облачност, односно смањена влага у зони пропагације, која делује апсорбујуће на високоенергетске честице. Након отварања струјног поља, услед трења са све гушћим слојевима атмосфере, расипање протона се одвија лево, а електрона десно (ск. 4) у односу на главни правац продирања СВ (Radovanović, 2010). Јачина поља H и магнетска индукција B у тектонским плочама које се магнетишу имају супротне смерове. У раседу Н и В имају исте смерове. Струјно поље у атмосфери (Jet Stream) Расед Електрони Протони Тектонска плоча Тектонска плоча B и H Скица 4. Шематски приказ намагнетисања тектонских плоча високоенергетским честицама СВ На претходној скици струјно поље је означено као Jet Stream због тога што се у досадашњим анализама показало да сателитски снимци на висинама од 250 mb најчешће адекватно одсликавају процес хидродинамичког захватања ваздушних маса. Хелиоцентрична хипотеза о настанку земљотреса полази од претпоставке да је у првој фази неопходан прилив протона и електрона на одређене литосферске (тектонске) средине, између којих се налази расед. Намагнетисање средине практично може имати неограничен временски рок, због тога што у једном тренутку долази до засићења енергијом (тачка А на ск. 3). Када престане деловање ИМП, 7
8 Зборник радова Географског института Јован Цвијић САНУ 61(3) (1-16) јавиће се тзв. тиха разградња, односно тада долази до постепеног отпуштања енергије тј. размагнетисања. Са аспекта теорије, процес одавања енергије најчешће прате два карактеристична сценарија. Први се односи на постепену разградњу до тачке Нс, када се појављује окидни импулс. Временски период који обухвата размагнетисање од тачке А до тачке Нс зависи тада искључиво од геолошких одлика локалне средине. Произилази да уколико је индукција енергије била релативно слаба, при таквим условима и земљoтрес мора бити слаб. У другом случају, постоје поново два различита процеса. Први се односи на нов прилив ИМП. У зависности од његових особина зависи да ли ће доћи до земљотреса или не. У одређеним случајевима може се десити нпр. поновно враћање енергије од тачке Br према тачки А. У таквим условима локална средина опет може досегнути вредности максималног намагнетисања. Насупрот томе, карактеристике ИМП могу бити такве да процес размагнетисања убрзају, тј. да нпр. од тачке Br размагнетисање нагло спусте до вредности Нс. На основу анализе стотинак јаких земљотреса који су се десили током и почетком године, прелиминарни резултати указују да у самом раседу, приликом појаве земљотреса, магнетни флукс може имати пресудну улогу. Okubo et al, (2011) такође истичу неопходност бољег познавања промена у магнетном пољу изазваних током земљотреса. У случају земљотреса код Краљева, један дан раније запажено је кретање ваздушних маса из правца југ-југозапад ка Балканском полуострву (ск. 5). Дакле, према споменутој хелиоцентричној хипотези, током претходних дана било је неопходно да се северно и јужно од реке Западна Морава у тло индукују протони и електрони. Ова река се пружа у правцу запад-исток и протиче кроз Краљево. На ск. 5, сада можемо видети да је кретање струјног поља на 250 mb површини усмерено према централном Балкану. Самим тим задовољен је критеријум да је једна од компоненти СВ усмерена под приближно правим углом на правац пружања раседа. 8
9 Астрофизичка анализа земљотреса код Краљева (Србија) 03. новембра године Ск. 5. Струјно поље над западном Европом један дан пре појаве земљотреса код Краљева ( Да се ради о продирању високоенергетских честица не само по хоризонтали, већ и по вертикали, указује ск 6. На основу овог снимка, можемо видети да је брзина кретања ваздушних маса ка централном Балкану достизала 70 чворова (приближно 35 m/s). У овом тренутку нећемо залазити у материју која се односи на повезаност између процеса на Сунцу и хидродинамичког захватања ваздушних маса (Stevančević, 2004). Већ је било речи у уводном делу да бројни аутори, применом различитих метода, долазе до закључака да се управо то догађа и то од зоналне циркулације до најјачих облика циклоналних кретања. 9
10 Зборник радова Географског института Јован Цвијић САНУ 61(3) (1-16) Ск. 6. Географска расподела средње брзине ветра mb ниво минус mb ниво над Европом 02. новембра године ( Сагледавајући расподелу брзине ветра на претходном снимку, може се видети да млаз који се доводи у везу са земљотресом у Србији представља саставни део расподеле брзине ветра над ширим подручјем, који се у виду таласа пружа преко средњег и источног Атлантика, лучно савија према југу, тј Средоземљу, а потом поново у виду таласа скреће ка североистоку. Један од основних сегмената хелиоцентричног модела настанка земљотреса представља анализа x, y, и z компоненти СВ. Колико нам је познато, оне се сада по први пут уводе у научно сагледавање генезе потреса. За разлику од Korepanov et al, (2009) који у фокус истраживања стављају проблематику одоздо, на релацији литосфера-атмосферајоносфера-магнетосфера, у овом моделу могло би се рећи да су кључни параметри постављени обрнуто. Односно, генеза земљотреса се посматра као последица прилива и трансформације енергије која долази одозго. На основу табеле средњих часовних вредности ИМП нацртан је дијаграм (ск. 7). 10
11 Астрофизичка анализа земљотреса код Краљева (Србија) 03. новембра године nt Bx By Bz Bt date Скица 7. Компоненте СВ неколико дана пре и после појаве земљотреса код Краљева ( Анализом компоненти СВ може се видети да је током 31. октобра дошло до њиховог макисмалног распрезања. Ради се заправо о периоду најинтензивнијег регионалног намагнетисања литосфере. Да се заиста тог дана десио прилив енергије показује и ск. 8. Графикон је добијен на сличан начин, као и за претходну скицу, преузимањем табеларних података средњих часовних вредности диференцијалног флукса протона. Тренутак појаве земљотреса (на ск. 7. приказан вертикалном линијом) поклапа се са променом смера Bx у односу на Bz компоненту. У време највећег распрезања, ове две компоненте су имале исти смер кретања. Непосредно пре промене смера њиховог кретања десио се земљотрес. На ск. 9. се може запазити да је густина честица СВ од поноћи (по UTC) 03. новембра године нагло порасла, достижући максимум у релативно кратком временском интервалу. Једноставно, тешко је игнорисати чињеницу да се управо тренутак максималне густине честица СВ појавио у тренутку или непосредно пре појаве подрхтавања тла код Краљева. 11
12 Зборник радова Географског института Јован Цвијић САНУ 61(3) (1-16) 1.00E E kev kev 1.00E Nov Ск. 8. Пристизање електричне струје ка Земљи у опсегу и kev крајем октобра и почетком новембра године ( Скица 9. Густина честица СВ један дан пре, у дану појаве и један дан после земљотреса у Краљеву ( 12
13 Астрофизичка анализа земљотреса код Краљева (Србија) 03. новембра године Произилази да је земљотрес код Краљева требало заправо да се деси крајем 04. или почетком 05. новембра године када би дошло до сабијања компоненти СВ. Односно тада би се постепеним размагнетисањем вредности x, y и z компоненти међусобно приближиле до критичног нивоа. Према приказаном моделу на ск. 3, тада се могло очекивати достизање коерцитивне силе Нс. Међутим, као што се може видети на ск. 9, у међувремену је дошло до наглог прилива ИМП (ск. 5 и 6), које је нагло убрзало довођење магнетске индукције B на вредност коерцитивне силе, односно појаве земљотреса, чиме се заправо убрзао процес појаве окидног импулса. Скица 10. Н компонента геомагнетног поља крајем 02. и почетком 03. новембра године ( Пратећи даље овакав начин размишљања, било би релано очекивати да је геомагнетна активност морала одреаговати на енергетски импулс који долази споља. Претходна скица показаје да је између 01:00 и 02:00 h 03. новембра дошло до наглог пада Н компоненте геомагнетног поља. Тиме долазимо до још једног показатеља који говори у прилог приказане хипотезе. Уколико су изложена разматрања коректна, произилази да изостанак накнадног прилива ИМП заправо не би довео до појаве тако снажног земљотреса. Другим речима, постепено размагнетисање, које би требало да резултује земљотресом 04/05. новембра године, вероватно не би изазвало тако јак земљотрес, као што је то био случај два дана раније. Могло би се рећи да уколико би до потреса уопште дошло, вероватно би се радило о слабијем подрхтавању без тако тешких последица по локално становништво. 13
14 Зборник радова Географског института Јован Цвијић САНУ 61(3) (1-16) Закључак Изложени резултати могу представљати основу за хелиоцентричну хипотезу о генези земљотреса. Основа о којој је реч за циљ би требало да има стварање прогностичког модела. Међутим, разрађивањем оваквог приступа отварају се бројна нова питања међу којима треба истаћи: на који начин, кроз изложени приступ, се могу посматрати хипоцентри лоцирани на дубинама од више стотина километара, у каквом су међусобном односу релативно слаба подрхтавања тла након снажних земљотреса, да ли се према предложеном моделу могу објаснити географске закономерности локација земљотреса који су се десили истог дана на различитим деловима наше планете, уколико је наведени приступ оправдан, у каквој је функцији појава снажних земљотреса у односу на Сунчев циклус, имајући у виду начелну разлику између Космичког и Сунчевог зрачења, да ли појава земљотреса може бити изазвана енергијама пореклом изван Сунчевог система. У овом тренутку, чини се да разрада добијених резултата захтева мултидисциплинарно истраживање, као и анализу већег броја снажних земљотреса. Њихова систематизација на бази хелиоцентричног приступа може пружити основу за одговоре на постављена питања, као и нов приступ за израду прогностичких модела. Acknowledgement: Добијени резултати представљају део пројекта III47007 који финансира Министарство Просвете и науке Републике Србије Литература Athanasiou M.A, Anagnostopoulos G.C, Iliopoulos A.C, Pavlos G.P, David C.N. (2011): Enhanced ULF radiation observed by DEMETER two months around the strong 2010 Haiti earthquake. Natural Hazards and Earth System Sciences, 11, pp , doi: /nhess Gabis I.P, Troshichev O.A. (2000): Influence of short-term changes in solar activity on baric field perturbations in the stratosphere and troposphere. Journal of Atmospheric and Solar- Terrestrial Physics 62, pp Gomes J.F.P, Radovanovic M. (2008): Solar activity as a possible cause of large forest fires - а case study: Analysis of the Portuguese forest fires. Science of the total environment, Volume 394, Number 1, pp , doi: /j.scitotenv , ISSN
15 Астрофизичка анализа земљотреса код Краљева (Србија) 03. новембра године Gomes J.F.P, Radovanovic M, Ducic V, Milenkovic M, Stevancevic M. (2009): Wildfire in Deliblatska Pescara (Serbia) Case Analysis on July 24th In the book: Forest Fires: Detection, Suppression and Prevention (Chapter 3). Nova Science Publishers, New York, pp Hasbi A.M, Mohd Ali M.A, Misran N. (2011): Ionospheric variations before some large earthquakes over Sumatra. Natural Hazards and Earth System Sciences, 11, рр , doi: /nhess Hattori K. (2004): ULF Geomagnetic Changes Associated with Large Earthquakes. TAO, Vol. 15, No. 3, pp Korepanov V, Hayakawa M, Yampolski Y, Lizunov G. (2009): AGW as a seismo-ionospheric coupling responsible agent. Physics and Chemistry of the Earth, 34, рр , doi: /j.pce Mukherjee S, Kortvelyessy L. (2006): Starstorm influence on earth leads tsunami and earthquakes. In Earthquake Prediction, Brill, Leiden-Boston, pp Mukherjee S. (2008): Cosmic Influence on the Sun-Earth Environment. Sensors, 8, pp ; DOI: /s Mukherjee S, Radovanović M: (2011): Influence of the Sun in the Genesis of Tornadoes. The IUP Journal of Earth Sciences, Vol. 5, No. 1, pp Nikolić J, Radovanović M, Milijašević D. (2010). An Astrophysical Analysis of Weather Based on the Solar Wind Parameters. Nu clear Technology & Radiation Protection: Vol. 25, No. 3, pp DOI: /NTRP N. Odintsov S, Boyarchuk K, Georgieva K, Kirov B, Atanasov D. (2006): Long-period trends in global seismic and geomagnetic activity and their relation to solar activity. Physics and Chemistry of the Earth 31, pp , doi: /j.pce Okubo K, Takeuchi N, Utsugi M, Yumoto K, Sasai Y. (2011): Direct magnetic signals from earthquake rupturing: Iwate-Miyagi earthquake of M 7.2, Japan. Earth and Planetary Science Letters 305, pp , doi: /j.epsl Palamara R.D, Bryant A.E. (2004): Geomagnetic activity forcing of the Northern Annular Mode via the stratosphere. Annales Geophysicae, 22, pp Radovanović M, Stevančević M, Štrbac D. (2003): A Contibution to the Study of the Influence of the Energy of Solar Wind upon the Atmospheric Processes. Journal of the Geographical Institute Jovan Cvijić SASA, Belgrade, pp Radovanović M. (2010): Forest fires in Europe from July 22nd to 25th Archives of Biological Sciences, vol. 62, issue 2, Belgrade, pp , DOI: /ABS R. 15
16 Зборник радова Географског института Јован Цвијић САНУ 61(3) (1-16) Silva H.G, Bezzeghoud M, Reis A.H, Rosa R.N, Tlemcani M, Araujo A.A, Serrano C, Borges J.F, Caldeira B, Biagi P.F. (2011): Atmospheric electrical field decrease during the M = 4.1 Sousel earthquake (Portugal). Natural Hazards and Earth System Sciences, 11, pp , doi: /nhess Simpson J.F. ( ): Solar activity as a triggering mechanism for earthquakes. Earth and Planetary Science Letters, Volume 3, pp , doi: / x(67) Singh O.P, Chauhan V, Singh V, Singh B. (2009): Anomalous variation in total electron content (TEC) associated with earthquakes in India during September 2006 November Physics and Chemistry of the Earth 34, pp , doi: /j.pce Stevančević M. (2004): Secrets of the Solar Wind (Tajne Sunčevog vetra in serbian). Edition of the author, pp , Belgrade. Stevančević M. (2011): Theoretic Elements of Helocentric Electromagnetic Seismology. Belgrade School of Meteorology, vol. IV, pp , Edition of the authors, Belgrade. Weiyu M, Xiudeng X, Baohua X, Hangcai Z. (2006): Abnormal temperature increase and astrotidal triggering in the tsunami earthquake in Indonesiqa magnitude 9.0. In Earthquake Prediction, Brill, Leiden-Boston, pp Yonaiguchi N, Ida Y, Hayakawa M. (2007): On the statistical correlation of over-horizon VHF signals with meteorological radio ducting and seismicity. Journal of Atmospheric and Solar- Terrestrial Physics, 69, pp , doi: /j.jastp
налазе се у диелектрику, релативне диелектричне константе ε r = 2, на међусобном растојању 2 a ( a =1cm
 1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
1 Два тачкаста наелектрисања 1 400 p и 100p налазе се у диелектрику релативне диелектричне константе ε на међусобном растојању ( 1cm ) као на слици 1 Одредити силу на наелектрисање 3 100p када се оно нађе:
Слика 1. Слика 1.2 Слика 1.1
 За случај трожичног вода приказаног на слици одредити: а Вектор магнетне индукције у тачкама А ( и ( б Вектор подужне силе на проводник са струјом Систем се налази у вакууму Познато је: Слика Слика Слика
За случај трожичног вода приказаног на слици одредити: а Вектор магнетне индукције у тачкама А ( и ( б Вектор подужне силе на проводник са струјом Систем се налази у вакууму Познато је: Слика Слика Слика
Теорија електричних кола
 др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола i i i Милка Потребић др Милка Потребић, ванредни професор,
Флукс, електрична енергија, електрични потенцијал
 Флукс, електрична енергија, електрични потенцијал 1 Електрични флукс Ако линије поља пролазе кроз површину A која је нормална на њих Производ EA је флукс, Φ Генерално: Φ E = E A cos θ 2 Електрични флукс,
Флукс, електрична енергија, електрични потенцијал 1 Електрични флукс Ако линије поља пролазе кроз површину A која је нормална на њих Производ EA је флукс, Φ Генерално: Φ E = E A cos θ 2 Електрични флукс,
1.2. Сличност троуглова
 математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
математик за VIII разред основне школе.2. Сличност троуглова Учили смо и дефиницију подударности два троугла, као и четири правила (теореме) о подударности троуглова. На сличан начин наводимо (без доказа)
Tестирање хипотеза. 5.час. 30. март Боjана Тодић Статистички софтвер март / 10
 Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
Tестирање хипотеза 5.час 30. март 2016. Боjана Тодић Статистички софтвер 2 30. март 2016. 1 / 10 Монте Карло тест Монте Карло методе су методе код коjих се употребљаваjу низови случаjних броjева за извршење
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ
 7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
7. ЈЕДНОСТАВНИЈЕ КВАДРАТНЕ ДИОФАНТОВE ЈЕДНАЧИНЕ 7.1. ДИОФАНТОВА ЈЕДНАЧИНА ху = n (n N) Диофантова једначина ху = n (n N) има увек решења у скупу природних (а и целих) бројева и њено решавање није проблем,
Динамика. Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе:
 Њутнови закони 1 Динамика Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе: када су објекти довољно велики (>димензија атома) када се крећу брзином много мањом
Њутнови закони 1 Динамика Описује везу између кретања објекта и сила које делују на њега. Закони класичне динамике важе: када су објекти довољно велики (>димензија атома) када се крећу брзином много мањом
TAЧКАСТА НАЕЛЕКТРИСАЊА
 TЧКАСТА НАЕЛЕКТРИСАЊА Два тачкаста наелектрисања оптерећена количинама електрицитета и налазе се у вакууму као што је приказано на слици Одредити: а) Вектор јачине електростатичког поља у тачки А; б) Електрични
TЧКАСТА НАЕЛЕКТРИСАЊА Два тачкаста наелектрисања оптерећена количинама електрицитета и налазе се у вакууму као што је приказано на слици Одредити: а) Вектор јачине електростатичког поља у тачки А; б) Електрични
Вектори vs. скалари. Векторске величине се описују интензитетом и правцем. Примери: Померај, брзина, убрзање, сила.
 Вектори 1 Вектори vs. скалари Векторске величине се описују интензитетом и правцем Примери: Померај, брзина, убрзање, сила. Скаларне величине су комплетно описане само интензитетом Примери: Температура,
Вектори 1 Вектори vs. скалари Векторске величине се описују интензитетом и правцем Примери: Померај, брзина, убрзање, сила. Скаларне величине су комплетно описане само интензитетом Примери: Температура,
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА МАТЕМАТИКА ТЕСТ УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Разлика потенцијала није исто што и потенцијална енергија. V = V B V A = PE / q
 Разлика потенцијала Разлика потенцијала између тачака A и B се дефинише као промена потенцијалне енергије (крајња минус почетна вредност) када се наелектрисање q помера из тачке A утачку B подељена са
Разлика потенцијала Разлика потенцијала између тачака A и B се дефинише као промена потенцијалне енергије (крајња минус почетна вредност) када се наелектрисање q помера из тачке A утачку B подељена са
г) страница aa и пречник 2RR описаног круга правилног шестоугла јесте рац. бр. јесу самерљиве
 в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
в) дијагонала dd и страница aa квадрата dd = aa aa dd = aa aa = није рац. бр. нису самерљиве г) страница aa и пречник RR описаног круга правилног шестоугла RR = aa aa RR = aa aa = 1 јесте рац. бр. јесу
Положај сваке тачке кружне плоче је одређен са поларним координатама r и ϕ.
 VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
VI Савијање кружних плоча Положај сваке тачке кружне плоче је одређен са поларним координатама и ϕ слика 61 Диференцијална једначина савијања кружне плоче је: ( ϕ) 1 1 w 1 w 1 w Z, + + + + ϕ ϕ K Пресечне
Предмет: Задатак 4: Слика 1.0
 Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Лист/листова: 1/1 Задатак 4: Задатак 4.1.1. Слика 1.0 x 1 = x 0 + x x = v x t v x = v cos θ y 1 = y 0 + y y = v y t v y = v sin θ θ 1 = θ 0 + θ θ = ω t θ 1 = θ 0 + ω t x 1 = x 0 + v cos θ t y 1 = y 0 +
Анализа Петријевих мрежа
 Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
Анализа Петријевих мрежа Анализа Петријевих мрежа Мере се: Својства Петријевих мрежа: Досежљивост (Reachability) Проблем досежљивости се састоји у испитивању да ли се може достићи неко, жељено или нежељено,
2. Наставни колоквијум Задаци за вежбање ОЈЛЕРОВА МЕТОДА
 . колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
. колоквијум. Наставни колоквијум Задаци за вежбање У свим задацима се приликом рачунања добија само по једна вредност. Одступање појединачне вредности од тачне вредности је апсолутна грешка. Вредност
КРУГ. У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице.
 КРУГ У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице. Архимед (287-212 г.п.н.е.) 6.1. Централни и периферијски угао круга Круг
КРУГ У свом делу Мерење круга, Архимед је први у историји математике одрeдио приближну вред ност броја π а тиме и дужину кружнице. Архимед (287-212 г.п.н.е.) 6.1. Централни и периферијски угао круга Круг
Писмени испит из Теорије површинских носача. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама.
 Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2. За плочу
Београд, 24. јануар 2012. 1. За континуалну плочу приказану на слици одредити угиб и моменте савијања у означеним тачкама. dpl = 0.2 m P= 30 kn/m Линијско оптерећење се мења по синусном закону: 2. За плочу
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 011/01. година ТЕСТ МАТЕМАТИКА УПУТСТВО
Универзитет у Крагујевцу Факултет за машинство и грађевинарство у Краљеву Катедра за основне машинске конструкције и технологије материјала
 Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
Теоријски део: Вежба број ТЕРМИЈСКА AНАЛИЗА. Термијска анализа је поступак који је 903.год. увео G. Tamman за добијање криве хлађења(загревања). Овај поступак заснива се на принципу промене топлотног садржаја
предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА
 Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
Висока техничка школа струковних студија у Нишу предмет МЕХАНИКА 1 Студијски програми ИНДУСТРИЈСКО ИНЖЕЊЕРСТВО ДРУМСКИ САОБРАЋАЈ II ПРЕДАВАЊЕ УСЛОВИ РАВНОТЕЖЕ СИСТЕМА СУЧЕЉНИХ СИЛА Садржај предавања: Систем
ПИТАЊА ЗА КОЛОКВИЈУМ ИЗ ОБНОВЉИВИХ ИЗВОРА ЕНЕРГИЈЕ
 ПИТАЊА ЗА КОЛОКВИЈУМ ИЗ ОБНОВЉИВИХ ИЗВОРА ЕНЕРГИЈЕ 1. Удео снаге и енергије ветра у производњи електричне енергије - стање и предвиђања у свету и Европи. 2. Навести називе најмање две међународне организације
ПИТАЊА ЗА КОЛОКВИЈУМ ИЗ ОБНОВЉИВИХ ИЗВОРА ЕНЕРГИЈЕ 1. Удео снаге и енергије ветра у производњи електричне енергије - стање и предвиђања у свету и Европи. 2. Навести називе најмање две међународне организације
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 013/014. година ТЕСТ
8.2 ЛАБОРАТОРИЈСКА ВЕЖБА 2 Задатак вежбе: Израчунавање фактора појачања мотора напонским управљањем у отвореној повратној спрези
 Регулциј електромоторних погон 8 ЛАБОРАТОРИЈСКА ВЕЖБА Здтк вежбе: Изрчунвње фктор појчњ мотор нпонским упрвљњем у отвореној повртној спрези Увод Преносн функциј мотор којим се нпонски упрвљ Кд се з нулте
Регулциј електромоторних погон 8 ЛАБОРАТОРИЈСКА ВЕЖБА Здтк вежбе: Изрчунвње фктор појчњ мотор нпонским упрвљњем у отвореној повртној спрези Увод Преносн функциј мотор којим се нпонски упрвљ Кд се з нулте
b) Израз за угиб дате плоче, ако се користи само први члан реда усвојеног решења, је:
 Пример 1. III Савијање правоугаоних плоча За правоугаону плочу, приказану на слици, одредити: a) израз за угиб, b) вредност угиба и пресечних сила у тачки 1 ако се користи само први члан реда усвојеног
Пример 1. III Савијање правоугаоних плоча За правоугаону плочу, приказану на слици, одредити: a) израз за угиб, b) вредност угиба и пресечних сила у тачки 1 ако се користи само први члан реда усвојеног
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 01/01. година ТЕСТ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 01/01. година ТЕСТ
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ
 СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
СИСТЕМ ЛИНЕАРНИХ ЈЕДНАЧИНА С ДВЕ НЕПОЗНАТЕ 8.. Линеарна једначина с две непознате Упознали смо појам линеарног израза са једном непознатом. Изрази x + 4; (x 4) + 5; x; су линеарни изрази. Слично, линеарни
6.2. Симетрала дужи. Примена
 6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
6.2. Симетрала дужи. Примена Дата је дуж АВ (слика 22). Тачка О је средиште дужи АВ, а права је нормална на праву АВ(p) и садржи тачку О. p Слика 22. Права назива се симетрала дужи. Симетрала дужи је права
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Тест Математика Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 00/0. година ТЕСТ МАТЕМАТИКА
Тест Математика Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 00/0. година ТЕСТ МАТЕМАТИКА
Закони термодинамике
 Закони термодинамике Први закон термодинамике Први закон термодинамике каже да додавање енергије систему може бити утрошено на: Вршење рада Повећање унутрашње енергије Први закон термодинамике је заправо
Закони термодинамике Први закон термодинамике Први закон термодинамике каже да додавање енергије систему може бити утрошено на: Вршење рада Повећање унутрашње енергије Први закон термодинамике је заправо
ОБЛАСТИ: 1) Тачка 2) Права 3) Криве другог реда
 ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
ОБЛАСТИ: ) Тачка ) Права Jov@soft - Март 0. ) Тачка Тачка је дефинисана (одређена) у Декартовом координатном систему са своје две коодринате. Примери: М(5, ) или М(-, 7) или М(,; -5) Jov@soft - Март 0.
Осцилације система са једним степеном слободе кретања
 03-ec-18 Осцилације система са једним степеном слободе кретања Опруга Принудна сила F(t) Вискозни пригушивач ( дампер ) 1 Принудна (пертурбациона) сила опруга Реституциона сила (сила еластичног отпора)
03-ec-18 Осцилације система са једним степеном слободе кретања Опруга Принудна сила F(t) Вискозни пригушивач ( дампер ) 1 Принудна (пертурбациона) сила опруга Реституциона сила (сила еластичног отпора)
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2011/2012. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
У к у п н о :
 ГОДИШЊИ (ГЛОБАЛНИ) ПЛАН РАДА НАСТАВНИКА Наставни предмет: ФИЗИКА Разред: Седми Ред.број Н А С Т А В Н А Т Е М А / О Б Л А С Т Број часова по теми Број часова за остале обраду типове часова 1. КРЕТАЊЕ И
ГОДИШЊИ (ГЛОБАЛНИ) ПЛАН РАДА НАСТАВНИКА Наставни предмет: ФИЗИКА Разред: Седми Ред.број Н А С Т А В Н А Т Е М А / О Б Л А С Т Број часова по теми Број часова за остале обраду типове часова 1. КРЕТАЊЕ И
Аксиоме припадања. Никола Томовић 152/2011
 Аксиоме припадања Никола Томовић 152/2011 Павле Васић 104/2011 1 Шта је тачка? Шта је права? Шта је раван? Да бисмо се бавили геометријом (и не само геометријом), морамо увести основне појмове и полазна
Аксиоме припадања Никола Томовић 152/2011 Павле Васић 104/2011 1 Шта је тачка? Шта је права? Шта је раван? Да бисмо се бавили геометријом (и не само геометријом), морамо увести основне појмове и полазна
5.2. Имплицитни облик линеарне функције
 математикa за VIII разред основне школе 0 Слика 6 8. Нацртај график функције: ) =- ; ) =,5; 3) = 0. 9. Нацртај график функције и испитај њен знак: ) = - ; ) = 0,5 + ; 3) =-- ; ) = + 0,75; 5) = 0,5 +. 0.
математикa за VIII разред основне школе 0 Слика 6 8. Нацртај график функције: ) =- ; ) =,5; 3) = 0. 9. Нацртај график функције и испитај њен знак: ) = - ; ) = 0,5 + ; 3) =-- ; ) = + 0,75; 5) = 0,5 +. 0.
Теорија електричних кола
 Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
Др Милка Потребић, ванредни професор, Теорија електричних кола, вежбе, Универзитет у Београду Електротехнички факултет, 7. Теорија електричних кола Милка Потребић Др Милка Потребић, ванредни професор,
Смер: Друмски саобраћај. Висока техничка школа струковних студија у Нишу ЕЛЕКТРОТЕХНИКА СА ЕЛЕКТРОНИКОМ
 Испит из предмета Електротехника са електроником 1. Шест тачкастих наелектрисања Q 1, Q, Q, Q, Q 5 и Q налазе се у теменима правилног шестоугла, као на слици. Познато је: Q1 = Q = Q = Q = Q5 = Q ; Q 1,
Испит из предмета Електротехника са електроником 1. Шест тачкастих наелектрисања Q 1, Q, Q, Q, Q 5 и Q налазе се у теменима правилног шестоугла, као на слици. Познато је: Q1 = Q = Q = Q = Q5 = Q ; Q 1,
ТРАПЕЗ РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ. Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце
 РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
РЕГИОНАЛНИ ЦЕНТАР ИЗ ПРИРОДНИХ И ТЕХНИЧКИХ НАУКА У ВРАЊУ ТРАПЕЗ Аутор :Петар Спасић, ученик 8. разреда ОШ 8. Октобар, Власотинце Ментор :Криста Ђокић, наставник математике Власотинце, 2011. године Трапез
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 014/01. година ТЕСТ МАТЕМАТИКА
Први корак у дефинисању случајне променљиве је. дефинисање и исписивање свих могућих eлементарних догађаја.
 СЛУЧАЈНА ПРОМЕНЉИВА Једнодимензионална случајна променљива X је пресликавање у коме се сваки елементарни догађај из простора елементарних догађаја S пресликава у вредност са бројне праве Први корак у дефинисању
СЛУЧАЈНА ПРОМЕНЉИВА Једнодимензионална случајна променљива X је пресликавање у коме се сваки елементарни догађај из простора елементарних догађаја S пресликава у вредност са бројне праве Први корак у дефинисању
МАТРИЧНА АНАЛИЗА КОНСТРУКЦИЈА
 Београд, 21.06.2014. За штап приказан на слици одредити најмању вредност критичног оптерећења P cr користећи приближан поступак линеаризоване теорије другог реда и: а) и један елемент, слика 1, б) два
Београд, 21.06.2014. За штап приказан на слици одредити најмању вредност критичног оптерећења P cr користећи приближан поступак линеаризоване теорије другог реда и: а) и један елемент, слика 1, б) два
Eлектричне силе и електрична поља
 Eлектричне силе и електрична поља 1 Особине наелектрисања Постоје две врсте наелектрисања Позитивна и негативна Наелектрисања супротног знака се привлаче, а различитог знака се одбијају Основни носиоц
Eлектричне силе и електрична поља 1 Особине наелектрисања Постоје две врсте наелектрисања Позитивна и негативна Наелектрисања супротног знака се привлаче, а различитог знака се одбијају Основни носиоц
Количина топлоте и топлотна равнотежа
 Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
Количина топлоте и топлотна равнотежа Топлота и количина топлоте Топлота је један од видова енергије тела. Енергија коју тело прими или отпушта у топлотним процесима назива се количина топлоте. Количина
& 2. Брзина. (слика 3). Током кратког временског интервала Δt тачка пређе пут Δs и изврши елементарни (бесконачно мали) померај Δ r
 &. Брзина Да би се окарактерисало кретање материјалне тачке уводи се векторска величина брзина, коју одређује како интензитет кретања тако и његов правац и смер у датом моменту времена. Претпоставимо да
&. Брзина Да би се окарактерисало кретање материјалне тачке уводи се векторска величина брзина, коју одређује како интензитет кретања тако и његов правац и смер у датом моменту времена. Претпоставимо да
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 2 (13Е013ЕП2) октобар 2016.
 ЕНЕРГЕТСКИ ПРЕТВАРАЧИ (3Е03ЕП) октобар 06.. Батерија напона B = 00 пуни се преко трофазног полууправљивог мосног исправљача, који је повезан на мрежу 3x380, 50 Hz преко трансформатора у спрези y, са преносним
ЕНЕРГЕТСКИ ПРЕТВАРАЧИ (3Е03ЕП) октобар 06.. Батерија напона B = 00 пуни се преко трофазног полууправљивог мосног исправљача, који је повезан на мрежу 3x380, 50 Hz преко трансформатора у спрези y, са преносним
3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни
 ТАЧКА. ПРАВА. РАВАН Талес из Милета (624 548. пре н. е.) Еуклид (330 275. пре н. е.) Хилберт Давид (1862 1943) 3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни Настанак геометрије повезује
ТАЧКА. ПРАВА. РАВАН Талес из Милета (624 548. пре н. е.) Еуклид (330 275. пре н. е.) Хилберт Давид (1862 1943) 3.1. Однос тачке и праве, тачке и равни. Одређеност праве и равни Настанак геометрије повезује
L кплп (Калем у кплу прпстпперипдичне струје)
 L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
L кплп (Калем у кплу прпстпперипдичне струје) i L u=? За коло са слике кроз калем ппзнате позната простопериодична струја: индуктивности L претпоставићемо да протиче i=i m sin(ωt + ψ). Услед променљиве
Упутство за избор домаћих задатака
 Упутство за избор домаћих задатака Студент од изабраних задатака области Математике 2: Комбинаторика, Вероватноћа и статистика бира по 20 задатака. Студент може бирати задатке помоћу програмског пакета
Упутство за избор домаћих задатака Студент од изабраних задатака области Математике 2: Комбинаторика, Вероватноћа и статистика бира по 20 задатака. Студент може бирати задатке помоћу програмског пакета
ТАЛАСИ У МАГНЕТОСФЕРАМА ПУЛСАРА
 ТАЛАСИ У МАГНЕТОСФЕРАМА ПУЛСАРА ПУЛСАРИ Настанак, структура и својства МАГНЕТОСФЕРА ПУЛСАРА Структура електромагнетног поља МАГНЕТОСТАТИЧКО ПОЉЕ ~ ~ МАГНЕТОСФЕРА ПУЛСАРА Структура електромагнетног поља
ТАЛАСИ У МАГНЕТОСФЕРАМА ПУЛСАРА ПУЛСАРИ Настанак, структура и својства МАГНЕТОСФЕРА ПУЛСАРА Структура електромагнетног поља МАГНЕТОСТАТИЧКО ПОЉЕ ~ ~ МАГНЕТОСФЕРА ПУЛСАРА Структура електромагнетног поља
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ И НАУКЕ ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ НА КРАЈУ ОСНОВНОГ ОБРАЗОВАЊА И ВАСПИТАЊА школска 2010/2011. година ТЕСТ 3 МАТЕМАТИКА УПУТСТВО
ЛАБОРАТОРИЈСКЕ ВЕЖБЕ ИЗ ФИЗИКЕ ПРВИ КОЛОКВИЈУМ I група
 ЛАБОРАТОРИЈСКЕ ВЕЖБЕ ИЗ ФИЗИКЕ ПРВИ КОЛОКВИЈУМ 21.11.2009. I група Име и презиме студента: Број индекса: Термин у ком студент ради вежбе: Напомена: Бира се и одговара ИСКЉУЧИВО на шест питања заокруживањем
ЛАБОРАТОРИЈСКЕ ВЕЖБЕ ИЗ ФИЗИКЕ ПРВИ КОЛОКВИЈУМ 21.11.2009. I група Име и презиме студента: Број индекса: Термин у ком студент ради вежбе: Напомена: Бира се и одговара ИСКЉУЧИВО на шест питања заокруживањем
ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ
 ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ предмет: ОСНОВИ МЕХАНИКЕ студијски програм: ЗАШТИТА ЖИВОТНЕ СРЕДИНЕ И ПРОСТОРНО ПЛАНИРАЊЕ ПРЕДАВАЊЕ БРОЈ 2. Садржај предавања: Систем сучељних сила у равни
ВИСОКА ТЕХНИЧКА ШКОЛА СТРУКОВНИХ СТУДИЈА У НИШУ предмет: ОСНОВИ МЕХАНИКЕ студијски програм: ЗАШТИТА ЖИВОТНЕ СРЕДИНЕ И ПРОСТОРНО ПЛАНИРАЊЕ ПРЕДАВАЊЕ БРОЈ 2. Садржај предавања: Систем сучељних сила у равни
6.1. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре
 0 6.. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре У обичном говору се често каже да су неки предмети симетрични. Примери таквих објеката, предмета, геометријских
0 6.. Осна симетрија у равни. Симетричност двеју фигура у односу на праву. Осна симетрија фигуре У обичном говору се често каже да су неки предмети симетрични. Примери таквих објеката, предмета, геометријских
1. Функција интензитета отказа и век трајања система
 f(t). Функција интензитета отказа и век трајања система На почетку коришћења неког система јављају се откази који као узрок имају почетне слабости или пропуштене дефекте у току производње и то су рани
f(t). Функција интензитета отказа и век трајања система На почетку коришћења неког система јављају се откази који као узрок имају почетне слабости или пропуштене дефекте у току производње и то су рани
ЛИНЕАРНА ФУНКЦИЈА. k, k 0), осна и централна симетрија и сл. 2, x 0. У претходном примеру неке функције су линеарне а неке то нису.
 ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
ЛИНЕАРНА ФУНКЦИЈА 5.. Функција = a + b Функционалне зависности су веома значајне и са њиховим применама често се сусрећемо. Тако, већ су нам познате директна и обрнута пропорционалност ( = k; = k, k ),
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ЗАВРШНИ ИСПИТ У ОСНОВНОМ ОБРАЗОВАЊУ И ВАСПИТАЊУ школска 0/06. година ТЕСТ МАТЕМАТИКА
2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ
 2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ 2.1. МАТЕМАТИЧКИ РЕБУСИ Најједноставније Диофантове једначине су математички ребуси. Метод разликовања случајева код ових проблема се показује плодоносним, јер је раздвајање
2. EЛЕМЕНТАРНЕ ДИОФАНТОВЕ ЈЕДНАЧИНЕ 2.1. МАТЕМАТИЧКИ РЕБУСИ Најједноставније Диофантове једначине су математички ребуси. Метод разликовања случајева код ових проблема се показује плодоносним, јер је раздвајање
Галваномагнетни ефекти
 УНИВЕРЗИТЕТ У НОВОМ САДУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ ДЕПАРТМАН ЗА МАТЕМАТИКУ И ИНФОРМАТИКУ Владимир Голуб Миљић Јована Ивана Антић Галваномагнетни ефекти семинарски рад Нови Сад, 2010. Садржај 1 Предговор
УНИВЕРЗИТЕТ У НОВОМ САДУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ ДЕПАРТМАН ЗА МАТЕМАТИКУ И ИНФОРМАТИКУ Владимир Голуб Миљић Јована Ивана Антић Галваномагнетни ефекти семинарски рад Нови Сад, 2010. Садржај 1 Предговор
Примена првог извода функције
 Примена првог извода функције 1. Одреди дужине страница два квадрата тако да њихов збир буде 14 а збир површина тих квадрата минималан. Ре: x + y = 14, P(x, y) = x + y, P(x) = x + 14 x, P (x) = 4x 8 Први
Примена првог извода функције 1. Одреди дужине страница два квадрата тако да њихов збир буде 14 а збир површина тих квадрата минималан. Ре: x + y = 14, P(x, y) = x + y, P(x) = x + 14 x, P (x) = 4x 8 Први
АНАЛОГНА ЕЛЕКТРОНИКА ЛАБОРАТОРИЈСКЕ ВЕЖБЕ
 ЕЛЕКТРОТЕХНИЧКИ ФАКУЛТЕТ У БЕОГРАДУ КАТЕДРА ЗА ЕЛЕКТРОНИКУ АНАЛОГНА ЕЛЕКТРОНИКА ЛАБОРАТОРИЈСКЕ ВЕЖБЕ ВЕЖБА БРОЈ 2 ПОЈАЧАВАЧ СНАГЕ У КЛАСИ Б 1. 2. ИМЕ И ПРЕЗИМЕ БР. ИНДЕКСА ГРУПА ОЦЕНА ДАТУМ ВРЕМЕ ДЕЖУРНИ
ЕЛЕКТРОТЕХНИЧКИ ФАКУЛТЕТ У БЕОГРАДУ КАТЕДРА ЗА ЕЛЕКТРОНИКУ АНАЛОГНА ЕЛЕКТРОНИКА ЛАБОРАТОРИЈСКЕ ВЕЖБЕ ВЕЖБА БРОЈ 2 ПОЈАЧАВАЧ СНАГЕ У КЛАСИ Б 1. 2. ИМЕ И ПРЕЗИМЕ БР. ИНДЕКСА ГРУПА ОЦЕНА ДАТУМ ВРЕМЕ ДЕЖУРНИ
2.3. Решавање линеарних једначина с једном непознатом
 . Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
. Решимо једначину 5. ( * ) + 5 + Провера: + 5 + 0 5 + 5 +. + 0. Број је решење дате једначине... Реши једначину: ) +,5 ) + ) - ) - -.. Да ли су следеће једначине еквивалентне? Провери решавањем. ) - 0
Штампарске грешке у петом издању уџбеника Основи електротехнике, 1. део, Електростатика
 Штампарске грешке у петом издању уџбеника Основи електротехнике део Страна пасус први ред треба да гласи У четвртом делу колима променљивих струја Штампарске грешке у четвртом издању уџбеника Основи електротехнике
Штампарске грешке у петом издању уџбеника Основи електротехнике део Страна пасус први ред треба да гласи У четвртом делу колима променљивих струја Штампарске грешке у четвртом издању уџбеника Основи електротехнике
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x,
 РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
РЕШЕЊА ЗАДАТАКА - IV РАЗЕД 1. Мањи број: : x, Већи број: 1 : 4x + 1, (4 бода) Њихов збир: 1 : 5x + 1, Збир умањен за остатак: : 5x = 55, 55 : 5 = 11; 11 4 = ; + 1 = 45; : x = 11. Дакле, први број је 45
4. ЗАКОН ВЕЛИКИХ БРОЈЕВА
 4. Закон великих бројева 4. ЗАКОН ВЕЛИКИХ БРОЈЕВА Аксиоматска дефиниција вероватноће не одређује начин на који ће вероватноће случајних догађаја бити одређене у неком реалном експерименту. Зато треба наћи
4. Закон великих бројева 4. ЗАКОН ВЕЛИКИХ БРОЈЕВА Аксиоматска дефиниција вероватноће не одређује начин на који ће вероватноће случајних догађаја бити одређене у неком реалном експерименту. Зато треба наћи
У к у п н о :
 ГОДИШЊИ (ГЛОБАЛНИ) ПЛАН РАДА НАСТАВНИКА Наставни предмет: ФИЗИКА Разред: Осми Ред.број Н А С Т А В Н А Т Е М А / О Б Л А С Т Број часова по теми Број часова за остале обраду типове часова 1. ЕЛЕКТРИЧНО
ГОДИШЊИ (ГЛОБАЛНИ) ПЛАН РАДА НАСТАВНИКА Наставни предмет: ФИЗИКА Разред: Осми Ред.број Н А С Т А В Н А Т Е М А / О Б Л А С Т Број часова по теми Број часова за остале обраду типове часова 1. ЕЛЕКТРИЧНО
8. ПИТАГОРИНА ЈЕДНАЧИНА х 2 + у 2 = z 2
 8. ПИТАГОРИНА ЈЕДНАЧИНА х + у = z Један од најзанимљивијих проблема теорије бројева свакако је проблем Питагориних бројева, тј. питање решења Питагорине Диофантове једначине. Питагориним бројевима или
8. ПИТАГОРИНА ЈЕДНАЧИНА х + у = z Један од најзанимљивијих проблема теорије бројева свакако је проблем Питагориних бројева, тј. питање решења Питагорине Диофантове једначине. Питагориним бројевима или
ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
УНИВЕРЗИТЕТ У НОВОМ САДУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ ДЕПАРТМАН ЗА МАТЕМАТИКУ И ИНФОРМАТИКУ. Томсонов ефекат. семинарски рад. Нови Сад, 2010.
 УНИВЕРЗИТЕТ У НОВОМ САДУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ ДЕПАРТМАН ЗА МАТЕМАТИКУ И ИНФОРМАТИКУ Томсонов ефекат семинарски рад професор: Светлана Р. Лукић студент: Драгиња Прокић87/06 Нови Сад, 00. Термоелектричне
УНИВЕРЗИТЕТ У НОВОМ САДУ ПРИРОДНО-МАТЕМАТИЧКИ ФАКУЛТЕТ ДЕПАРТМАН ЗА МАТЕМАТИКУ И ИНФОРМАТИКУ Томсонов ефекат семинарски рад професор: Светлана Р. Лукић студент: Драгиња Прокић87/06 Нови Сад, 00. Термоелектричне
ДВАДЕСЕТПРВО РЕГИОНАЛНО ТАКМИЧЕЊЕ ЗАДАЦИ ИЗ ОСНОВА ЕЛЕКТРОТЕХНИКЕ ЗА УЧЕНИКЕ ПРВОГ РАЗРЕДА
 МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА РЕПУБЛИКЕ СРБИЈЕ ЗАЈЕДНИЦА ЕЛЕКТРОТЕХНИЧКИХ ШКОЛА РЕПУБЛИКЕ СРБИЈЕ ДВАДЕСЕТПРВО РЕГИОНАЛНО ТАКМИЧЕЊЕ ЗАДАЦИ ИЗ ОСНОВА ЕЛЕКТРОТЕХНИКЕ ЗА УЧЕНИКЕ ПРВОГ
МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА РЕПУБЛИКЕ СРБИЈЕ ЗАЈЕДНИЦА ЕЛЕКТРОТЕХНИЧКИХ ШКОЛА РЕПУБЛИКЕ СРБИЈЕ ДВАДЕСЕТПРВО РЕГИОНАЛНО ТАКМИЧЕЊЕ ЗАДАЦИ ИЗ ОСНОВА ЕЛЕКТРОТЕХНИКЕ ЗА УЧЕНИКЕ ПРВОГ
Ротационо симетрична деформација средње површи ротационе љуске
 Ротационо симетрична деформација средње површи ротационе љуске слика. У свакој тачки посматране средње површи, у општем случају, постоје два компонентална померања: v - померање у правцу тангенте на меридијалну
Ротационо симетрична деформација средње површи ротационе љуске слика. У свакој тачки посматране средње површи, у општем случају, постоје два компонентална померања: v - померање у правцу тангенте на меридијалну
Писмени испит из Метода коначних елемената
 Београд,.0.07.. За приказани билинеарни коначни елемент (Q8) одредити вектор чворног оптерећења услед задатог линијског оптерећења p. Користити природни координатни систем (ξ,η).. На слици је приказан
Београд,.0.07.. За приказани билинеарни коначни елемент (Q8) одредити вектор чворног оптерећења услед задатог линијског оптерећења p. Користити природни координатни систем (ξ,η).. На слици је приказан
Семинарски рад из линеарне алгебре
 Универзитет у Београду Машински факултет Докторске студије Милош Живановић дипл. инж. Семинарски рад из линеарне алгебре Београд, 6 Линеарна алгебра семинарски рад Дата је матрица: Задатак: a) Одредити
Универзитет у Београду Машински факултет Докторске студије Милош Живановић дипл. инж. Семинарски рад из линеарне алгебре Београд, 6 Линеарна алгебра семинарски рад Дата је матрица: Задатак: a) Одредити
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 2004
 РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 004 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор 100 VA има напон и реактансу кратког споја u 4% и x % респективно При номиналном оптерећењу
РЈЕШЕЊА ЗАДАТАКА СА ТАКМИЧЕЊА ИЗ ЕЛЕКТРИЧНИХ МАШИНА Електријада 004 ТРАНСФОРМАТОРИ Tрофазни енергетски трансформатор 100 VA има напон и реактансу кратког споја u 4% и x % респективно При номиналном оптерећењу
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ОЦЕЊИВАЊЕ ОБАВЕЗНО ПРОЧИТАТИ ОПШТА УПУТСТВА 1. Сваки
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ПРОБНИ ЗАВРШНИ ИСПИТ школска 016/017. година ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ПРОБНИ ЗАВРШНИ ИСПИТ школска 016/017. година ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
Апсорпција γ зрачења
 Универзитет у Крагујевцу Природно математички факултет Мр Владимир Марковић Предмет: Нуклеарна физика Експериментална вежба: Апсорпција γ зрачења Када сноп γ зрачења пролази кроз материју, његов интензитет
Универзитет у Крагујевцу Природно математички факултет Мр Владимир Марковић Предмет: Нуклеарна физика Експериментална вежба: Апсорпција γ зрачења Када сноп γ зрачења пролази кроз материју, његов интензитет
Хомогена диференцијална једначина је она која може да се напише у облику: = t( x)
 ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ Штa треба знати пре почетка решавања задатака? Врсте диференцијалних једначина. ДИФЕРЕНЦИЈАЛНА ЈЕДНАЧИНА КОЈА РАЗДВАЈА ПРОМЕНЉИВЕ Код ове методе поступак је следећи: раздвојити
ДИФЕРЕНЦИЈАЛНЕ ЈЕДНАЧИНЕ Штa треба знати пре почетка решавања задатака? Врсте диференцијалних једначина. ДИФЕРЕНЦИЈАЛНА ЈЕДНАЧИНА КОЈА РАЗДВАЈА ПРОМЕНЉИВЕ Код ове методе поступак је следећи: раздвојити
ГЛАСНИК СРПСКОГ ГЕОГРАФСKОГ ДРУШТВА BULLETIN OF THE SERBIAN GEOGRAPHICAL SOCIETY ГОДИНА СВЕСКА LXXXVIII- Бр. 1 YEAR 2008 TOME LXXXVIII- N о 1
 ГЛАСНИК СРПСКОГ ГЕОГРАФСKОГ ДРУШТВА BULLETIN OF THE SERBIAN GEOGRAPHICAL SOCIETY ГОДИНА 2008. СВЕСКА LXXXVIII- Бр. 1 YEAR 2008 TOME LXXXVIII- N о 1 Оригиналан научни рад UDC 911.2:551.521.11(497.11) ВЛАДАН
ГЛАСНИК СРПСКОГ ГЕОГРАФСKОГ ДРУШТВА BULLETIN OF THE SERBIAN GEOGRAPHICAL SOCIETY ГОДИНА 2008. СВЕСКА LXXXVIII- Бр. 1 YEAR 2008 TOME LXXXVIII- N о 1 Оригиналан научни рад UDC 911.2:551.521.11(497.11) ВЛАДАН
ПОГЛАВЉЕ 3: РАСПОДЕЛА РЕЗУЛТАТА МЕРЕЊА
 ПОГЛАВЉЕ 3: РАСПОДЕЛА РЕЗУЛТАТА МЕРЕЊА Стандардна девијација показује расподелу резултата мерења око средње вредности, али не указује на облик расподеле. У табели 1 су дате вредности за 50 поновљених одређивања
ПОГЛАВЉЕ 3: РАСПОДЕЛА РЕЗУЛТАТА МЕРЕЊА Стандардна девијација показује расподелу резултата мерења око средње вредности, али не указује на облик расподеле. У табели 1 су дате вредности за 50 поновљених одређивања
ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције. Diffie-Hellman размена кључева
 ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2/13 Diffie-Hellman размена кључева први алгоритам са јавним
ЗАШТИТА ПОДАТАКА Шифровање јавним кључем и хеш функције Diffie-Hellman размена кључева Преглед Биће објашњено: Diffie-Hellman размена кључева 2/13 Diffie-Hellman размена кључева први алгоритам са јавним
ФИЗИКА Час број 11 Понедељак, 8. децембар, Aвогадров закон. Увод. Авогадров закон. Гасовито агрегатно стање
 ФИЗИКА Час број Понедељак, 8. децембар, 008 Једначина стања идеалног и реалног гаса Притисак и температура гаса Молекуларно кинетичка теорија идеалног гаса Болцманова и Максвелова расподела Средњи слободни
ФИЗИКА Час број Понедељак, 8. децембар, 008 Једначина стања идеалног и реалног гаса Притисак и температура гаса Молекуларно кинетичка теорија идеалног гаса Болцманова и Максвелова расподела Средњи слободни
8. ФИЗИКА АТОМСКОГ ЈЕЗГРА. Увод
 8. ФИЗИКА АТОМСКОГ ЈЕЗГРА Увод До сада смо видели да је све што постоји сачињено од свега мање од сто различивих супстанци, које називамо хемијским елементима. Видели смо такође да је свака од тих малобројних
8. ФИЗИКА АТОМСКОГ ЈЕЗГРА Увод До сада смо видели да је све што постоји сачињено од свега мање од сто различивих супстанци, које називамо хемијским елементима. Видели смо такође да је свака од тих малобројних
2. ОСНОВЕ КОНСТРУКЦИЈЕ И ПРАЗАН ХОД ТРАНСФОРМАТОРА
 Школска година 2017 / 2018 Припремио: Проф. Зоран Радаковић октобар 2017., материјал за део градива из поглавља 2. из књиге Ђ. Калић, Р. Радосављевић: Трансформатори, Завод за уџбенике и наставна средства,
Школска година 2017 / 2018 Припремио: Проф. Зоран Радаковић октобар 2017., материјал за део градива из поглавља 2. из књиге Ђ. Калић, Р. Радосављевић: Трансформатори, Завод за уџбенике и наставна средства,
Слика 1 Ако се са RFe отпорника, онда су ова два температурно зависна отпорника везана на ред, па је укупна отпорност,
 Температурно стабилан отпорник састоји се од два једнака цилиндрична дела начињена од различитих материјала (гвожђе и графит) У ком односу стоје отпорности ова два дела отпорника ако се претпостави да
Температурно стабилан отпорник састоји се од два једнака цилиндрична дела начињена од различитих материјала (гвожђе и графит) У ком односу стоје отпорности ова два дела отпорника ако се претпостави да
T. max Т / [K] p /[ 10 Pa] 1,01 1,23 1,74 2,39 3,21 4,42 5,87 7,74 9,35 11,60
![T. max Т / [K] p /[ 10 Pa] 1,01 1,23 1,74 2,39 3,21 4,42 5,87 7,74 9,35 11,60 T. max Т / [K] p /[ 10 Pa] 1,01 1,23 1,74 2,39 3,21 4,42 5,87 7,74 9,35 11,60](/thumbs/82/84841686.jpg) II РАЗРЕД 49. РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ ФИЗИКЕ УЧЕНИКА СРЕДЊИХ ШКОЛА ШКОЛСКЕ /. ГОДИНЕ Друштво Физичара Србије Министарство просвете и науке Републике Србије ЗАДАЦИ ФИЗИЧКИ ФАКУЛТЕТ БЕОГРАД 9.4... Малу плочицу,
II РАЗРЕД 49. РЕПУБЛИЧКО ТАКМИЧЕЊЕ ИЗ ФИЗИКЕ УЧЕНИКА СРЕДЊИХ ШКОЛА ШКОЛСКЕ /. ГОДИНЕ Друштво Физичара Србије Министарство просвете и науке Републике Србије ЗАДАЦИ ФИЗИЧКИ ФАКУЛТЕТ БЕОГРАД 9.4... Малу плочицу,
MAТЕМАТИЧКОГЕОГРАФСКА АНАЛИЗА ОРИЈЕНТАЦИЈЕ СТУДЕНИЧКЕ ЦРКВЕ СВ. ЈОВАНА
 Доступно онлајн на www.gi.sanu.ac.rs Зборник радова Географског института Јован Цвијић САНУ 61(1) (1-10) Оригинални научни рад УДК:910.1:51 MAТЕМАТИЧКОГЕОГРАФСКА АНАЛИЗА ОРИЈЕНТАЦИЈЕ СТУДЕНИЧКЕ ЦРКВЕ СВ.
Доступно онлајн на www.gi.sanu.ac.rs Зборник радова Географског института Јован Цвијић САНУ 61(1) (1-10) Оригинални научни рад УДК:910.1:51 MAТЕМАТИЧКОГЕОГРАФСКА АНАЛИЗА ОРИЈЕНТАЦИЈЕ СТУДЕНИЧКЕ ЦРКВЕ СВ.
КАТЕДРА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ И ПОГОНЕ ЛАБОРАТОРИЈА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 1
 КАТЕДРА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ И ПОГОНЕ ЛАБОРАТОРИЈА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 1 Лабораторијска вежба број 1 МОНОФАЗНИ ФАЗНИ РЕГУЛАТОР СА ОТПОРНИМ И ОТПОРНО-ИНДУКТИВНИМ ОПТЕРЕЋЕЊЕМ
КАТЕДРА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ И ПОГОНЕ ЛАБОРАТОРИЈА ЗА ЕНЕРГЕТСКЕ ПРЕТВАРАЧЕ ЕНЕРГЕТСКИ ПРЕТВАРАЧИ 1 Лабораторијска вежба број 1 МОНОФАЗНИ ФАЗНИ РЕГУЛАТОР СА ОТПОРНИМ И ОТПОРНО-ИНДУКТИВНИМ ОПТЕРЕЋЕЊЕМ
Теорија одлучивања. Анализа ризика
 Теорија одлучивања Анализа ризика Циљеви предавања Упознавање са процесом анализе ризика Моделовање ризика Монте-Карло Симулација Предности и недостаци анализе ризика 2 Дефиниција ризика (квалитативни
Теорија одлучивања Анализа ризика Циљеви предавања Упознавање са процесом анализе ризика Моделовање ризика Монте-Карло Симулација Предности и недостаци анализе ризика 2 Дефиниција ризика (квалитативни
Р Ц4-07. Рачунарске провере расподеле магнетне индукције у близини енергетског трансформатора 10 kv / 0.4 kv без и са магнетним екраном
 Р Ц4-7 Рачунарске провере расподеле магнетне индукције у близини енергетског трансформатора 1 kv /.4 kv без и са магнетним екраном Марко Шоргић, Зоран Радаковић, Милан Савић, Ратко Ковачић Електротехнички
Р Ц4-7 Рачунарске провере расподеле магнетне индукције у близини енергетског трансформатора 1 kv /.4 kv без и са магнетним екраном Марко Шоргић, Зоран Радаковић, Милан Савић, Ратко Ковачић Електротехнички
4. ГУБИЦИ СНАГЕ, СТЕПЕН ИСКОРИШЋЕЊА И ПРОМЕНА НАПОНА
 Делове текста између маркера и прочитати информативно (из тог дела градива се неће постављати питања на испиту) 4. ГУБИЦИ СНАГЕ, СТЕПЕН ИСКОРИШЋЕЊА И ПРОМЕНА НАПОНА 4. 1. ГУБИЦИ У ГВОЖЂУ О губицима у гвожђу
Делове текста између маркера и прочитати информативно (из тог дела градива се неће постављати питања на испиту) 4. ГУБИЦИ СНАГЕ, СТЕПЕН ИСКОРИШЋЕЊА И ПРОМЕНА НАПОНА 4. 1. ГУБИЦИ У ГВОЖЂУ О губицима у гвожђу
Погодност за одржавање, Расположивост, Марковљеви ланци
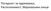 Погност за ржавање, Расположивост, Марковљеви ланци Погност за ржавање Одржавање обухвата све радње (осим рутинског сервисирања у току рада као што је замена горива или сличне мање активности) чији је
Погност за ржавање, Расположивост, Марковљеви ланци Погност за ржавање Одржавање обухвата све радње (осим рутинског сервисирања у току рада као што је замена горива или сличне мање активности) чији је
ТЕСТ МАТЕМАТИКА УПУТСТВО ЗА ПРЕГЛЕДАЊЕ
 Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
Република Србија МИНИСТАРСТВО ПРОСВЕТЕ, НАУКЕ И ТЕХНОЛОШКОГ РАЗВОЈА ЗАВОД ЗА ВРЕДНОВАЊЕ КВАЛИТЕТА ОБРАЗОВАЊА И ВАСПИТАЊА ТЕСТ МАТЕМАТИКА ПРИЈЕМНИ ИСПИТ ЗА УЧЕНИКЕ СА ПОСЕБНИМ СПОСОБНОСТИМА ЗА ИНФОРМАТИКУ
Тест за 7. разред. Шифра ученика
 Министарство просвете Републике Србије Српско хемијско друштво Окружно/градско/међуокружно такмичење из хемије 28. март 2009. године Тест за 7. разред Шифра ученика Пажљиво прочитај текстове задатака.
Министарство просвете Републике Србије Српско хемијско друштво Окружно/градско/међуокружно такмичење из хемије 28. март 2009. године Тест за 7. разред Шифра ученика Пажљиво прочитај текстове задатака.
Тангента Нека је дата крива C са једначином y = f (x)
 Dbić N Извод као појам се први пут појављује крајем XVII вијека у вези са израчунавањем неравномјерних кретања. Прецизније, помоћу извода је било могуће увести појам тренутне брзине праволинијског кретања.
Dbić N Извод као појам се први пут појављује крајем XVII вијека у вези са израчунавањем неравномјерних кретања. Прецизније, помоћу извода је било могуће увести појам тренутне брзине праволинијског кретања.
СУНЧЕВА АКТИВНОСТ И ШУМСКИ ПОЖАРИ
 ISBN 978-86-80029-40-5 СРПСКА АКАДЕМИЈА НАУКА И УМЕТНОСТИ ГЕОГРАФСКИ ИНСТИТУТ ЈОВАН ЦВИЈИЋ ПОСЕБНА ИЗДАЊА КЊИГА 71 Милан Радовановић Joao Fernando Pereira Gomes СУНЧЕВА АКТИВНОСТ И ШУМСКИ ПОЖАРИ БЕОГРАД
ISBN 978-86-80029-40-5 СРПСКА АКАДЕМИЈА НАУКА И УМЕТНОСТИ ГЕОГРАФСКИ ИНСТИТУТ ЈОВАН ЦВИЈИЋ ПОСЕБНА ИЗДАЊА КЊИГА 71 Милан Радовановић Joao Fernando Pereira Gomes СУНЧЕВА АКТИВНОСТ И ШУМСКИ ПОЖАРИ БЕОГРАД
ФИЗИКА Час број 12 Понедељак, 27. децембар 2010
 Магнетне појаве ФИЗИКА Час број 12 Понедељак, 27. децембар 2010 1 10.1. (понедељак) 2011., 2. колоквијум 21. 1.2011. ухх.хх поправни колоквијум 24.01.2011. у 09.00, испит 2 Магнети Откриће магнета-магнезија
Магнетне појаве ФИЗИКА Час број 12 Понедељак, 27. децембар 2010 1 10.1. (понедељак) 2011., 2. колоквијум 21. 1.2011. ухх.хх поправни колоквијум 24.01.2011. у 09.00, испит 2 Магнети Откриће магнета-магнезија
6.5 Површина круга и његових делова
 7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
7. Тетива је једнака полупречнику круга. Израчунај дужину мањег одговарајућег лука ако је полупречник 2,5 сm. 8. Географска ширина Београда је α = 44 47'57", а полупречник Земље 6 370 km. Израчунај удаљеност
ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ -
 ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ - ЦЕНЕ ПРОИЗВОДЊЕ И ДИСТРИБУЦИЈЕ ВОДЕ И ЦЕНЕ САКУПЉАЊА, ОДВОђЕЊА И ПРЕЧИШЋАВАЊА ОТПАДНИХ ВОДА НА НИВОУ ГРУПАЦИЈЕ ВОДОВОДА
ИЗВОД ИЗ ИЗВЕШТАЈА О ЦЕНАМА КОМУНАЛНИХ УСЛУГА - УДРУЖЕЊЕ ЗА КОМУНАЛНЕ ДЕЛАТНОСТИ - ЦЕНЕ ПРОИЗВОДЊЕ И ДИСТРИБУЦИЈЕ ВОДЕ И ЦЕНЕ САКУПЉАЊА, ОДВОђЕЊА И ПРЕЧИШЋАВАЊА ОТПАДНИХ ВОДА НА НИВОУ ГРУПАЦИЈЕ ВОДОВОДА
