Αντικειμενοστραφής Προγραμματισμός Ενδεκτικές ασκήσεις-απαντήσεις
|
|
|
- Τελαμών Καλογιάννης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Αντικειμενοστραφής Προγραμματισμός Ενδεκτικές ασκήσεις-απαντήσεις Τσούλος Ιωάννης, Επίκουρος Καθηγητής Τμ. Μηχανικών Πληροφορικής Τ.Ε. Άρτα, Μάιος 2015
2 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες, που υπόκειται σε άλλου τύπου άδειας χρήσης, η άδεια χρήσης αναφέρεται ρητώς. Χρηματοδότηση Το παρόν εκπαιδευτικό υλικό έχει αναπτυχθεί στα πλαίσια του εκπαιδευτικού έργου του διδάσκοντα. Το έργο «Ανοικτά Ακαδημαϊκά Μαθήματα στο ΤΕΙ Ηπείρου» έχει χρηματοδοτήσει μόνο τη αναδιαμόρφωση του εκπαιδευτικού υλικού. Το έργο υλοποιείται στο πλαίσιο του Επιχειρησιακού Προγράμματος «Εκπαίδευση και Δια Βίου Μάθηση» και συγχρηματοδοτείται από την Ευρωπαϊκή Ένωση (Ευρωπαϊκό Κοινωνικό Ταμείο) και από εθνικούς πόρους.
3 ΠρώτοσετΑσκήσεων ΙωάννηςΓºΤσούλος ¾¼½ Στοσημερινόσετασκήσεωνθαπαρουσιαστούνμιασειράαπόασκήσειςεισ- αγωγήςστην στιςδομέςελέγχουκαιστουςπίνακεςτηςγλώσσας ½ Πρόγραμμαεπεξεργασίαςμισθοδοσίας Ναγραφείπρόγραμματοοποίοθαδιαβάζειαπότοπληκτρολόγιοτουςμισθούς Νπροσώπων όπουνακέραιοςαριθμόςπουθαεισάγεταιπροηγουμένωςº Το πρόγραμμαναεμφανίζειτονμέσοόροτηςμισθοδοσίαςº ½ ÒÙ Ó ØÖÑ ¾ Ù Ò ÒÑ Ô Ø ÒØ ÑÒ µ ÓÙ Ö Ý ÓÙ Ú ÖÝ ¼º¼ ÒØ Ó Ù Ò Ø Ö ÒØ Æ ÓÙØ Ó Ø Æ ½¼ ÒÆ ½½ ÓÖ Ó Ù Ò Ø Ö ½ ÓÙÒØÖÆ Ó Ù Ò Ø Ö Ó Ù Ò Ø Ö ½µ ½¾ ½ ÓÙØ Ó Ø Ñ ØÓ ÓÙÒØÖ ½ Ò Ö Ý ½ Ú ÖÝÚ ÖÝ Ö Ý ½ ½ Ú ÖÝÚ ÖÝ»Æ ½ ÓÙØÅ Ó Ñ ØÓ Ú ÖÝÒ ½ ÖØÙÖÒ ¼ ¾¼ Ναγίνουνοιακόλουθεςδιορθώσειςπροσθήκεςστοπαραπάνωπρόγραμμα μετην σειράπουπαρουσιάζεταιπαρακάτωµ ½ºΤοπρόγραμμαδιαβάζειαπότοπληκτρολόγιοτουςμισθούςαλλάδενκάνει κάποιοέλεγχογιατοανοιμισθοίείναιαρνητικοίºναγίνειαλλαγήστο ½
4 πρόγραμμαώστεανκάποιοςμισθόςείναιαρνητικόςδενθαυπολογίζεταιστο άθροισμαº ¾ºΑφούγίνειηπαραπάνωαλλαγήνααλλάξετετοπρόγραμμάσας ώστεαν κάποιοςμισθόςείναιαρνητικόςναγίνεταιεπαναληπτικάανάγνωσήτουμέχρι οχρήστηςναεισάγειθετικήμισθοδοσίαº ºΗεταιρείααποφάσισεναδώσειμπόνους ½¼¼ευρώσεόσουςμισθωτούςλαμβάνουνλιγότερααπό ½¼¼¼ευρώº Διορθώστετοπρόγραμμάσας ώστενα γίνεταιαύξησητηςμισθοδοσίαςκατά ½¼¼ευρώσεόσουςλαμβάνουνλιγότερα από ½¼¼¼ ευρώº ºΤοπρόγραμμάσαςνααπαντάστηνερώτησηπόσοιδενπήραναύξησηαπό τηνεταιρεία ¾ Πρόγραμμαεπιλογήςσυνάρτησης Ναγραφείπρόγραμματοοποίοθαδιαθέτειτιςακόλουθεςσυναρτήσεις ½ºΜιασυνάρτησηυπολογισμούτηςδύναμης X Y όπουχκαιυορίσματατης συνάρτησηςº ¾ºΜιασυνάρτησηυπολογισμούτουπαραγοντικού X! Στηνκυρίωςσυνάρτησηοχρήστηςεισάγειένανακέραιοστοδιάστημα ¼ ¾ υποχρεωτικάºανοχρήστηςδώσει ¼τοπρόγραμμασταματά διαφορετικάανδώσει ½εισάγειπρώταένανδεκαδικόαριθμόΧκαιμετάένανδεκαδικόαριθμόΥκαι υπολογίζεταιηδύναμημετηνβοήθειατηςπρώτηςσυνάρτησηςºανδώσειτοναριθμό ¾εισάγειέναακέραιοΧκαιεμφανίζεταιτοπαραγοντικότουαριθμούΧºΣτο τέλοςτοπρόγραμμαεμφανίζειπόσεςφορέςέγινεκλήσητηςπρώτηςσυνάρτησης καιπόσεςφορέςτηςδεύτερηςº ½ ÒÙ Ó ØÖÑ ¾ Ù Ò ÒÑ Ô Ø ÓÙ ÔÓÛÖ ÓÙ Ü ÓÙ Ý µ ÓÙ Ô ½º¼ ÒØ ÓÖ ½ Ý µ ÔÔ Ü ½¼ ÖØÙÖÒ Ô ½½ ½¾ ½ ÒØ Ø Ó Ö ÒØ Ü µ ½ ½ ÒØ Ô½ ½ ÒØ ¾
5 ½ ÓÖ ½ Ü µ ÔÔ ½ ÖØÙÖÒ Ô ½ ¾¼ ¾½ ÒØ ÖÇÔØÓÒ µ ¾¾ ¾ ÒØ Ó Ô Ø Ó Ò ¾ Ó ¾ ¾ ÓÙØÓ Ô Ó ¾ Ò Ó Ô Ø Ó Ò ¾ Û ÓÔØÓÒ ¼ ÓÔØÓÒ ¾µ ¾ ÖØÙÖÒ Ó Ô Ø Ó Ò ¼ ½ ¾ ÒØ ÑÒ µ ÒØ ÑÝÓÔØÓÒ ÓÙ Ü Ý ÒØ Ü ÓÙ ÑÝÔÓÛÖ ÒØ Ñ Ý Ø Ó Ö ÒØ ÓÙÒØÖ½ ¼ ÓÙÒØÖ¾ ¼ ¼ Û ÑÝÓÔØÓÒÖÇÔØÓÒ µ µ ¼ µ ½ ¾ ÛØ ÑÝÓÔØÓÒ µ ½ ÓÙÒØÖ½ ÓÙØÓ Ü ÒÜÝ ÑÝÔÓÛÖÔÓÛÖ Ü Ý µ ÓÙØÝÒÑÑÝÔÓÛÖÒ ¼ Ö ½ ¾ ¾ ÓÙØÓ Ü Ò Ü Ñ Ý Ø Ó Ö Ø Ó Ö Ü µ ÓÙØ ÈÖÓÒØÓ Ñ Ý Ø Ó Ö Ò ÓÙÒØÖ¾ Ö ¼ ÓÙØ ÓÙÒØÖ½ ÓÙÒØÖ½ Ò ½ ÓÙØ ÓÙÒØÖ¾ ÓÙÒØÖ¾ Ò ¾ ÖØÙÖÒ ¼
6 Ναγίνουνοιακόλουθεςδιορθώσεις»προσθήκεςστοπαραπάνωπρόγραμμα ½ºΗσυνάρτησητουπαραγοντικουναγίνειαναδρομικήº ¾ºΗσυνάρτησητηςδύναμηςναεπιστρέφει ¹½ανκάποιοαπόταΧήΥείναι αρνητικόº Χρήσηπινάκων Να γραφεί πρόγραμμα για την ανάγνωση και αποθήκευσηβαθμολογιώνγια σπουδαστέςσεένανπίνακαδεκαδικώναριθμώνºτοπρόγραμμαναεμφανίζει ½ºΜέσοόροστοσυγκεκριμένομάθημαº ¾ºΠλήθοςσπουδαστώνπουέχουνπροβιβάσιμοβαθμόº ½ ÒÙ Ó ØÖÑ ¾ Ù Ò ÒÑ Ô Ø ÓÙ ÖÖ µ ÓÙ Ó ÓÙØÓ ØÑÓ ¼ ½¼µ ½¼ Ò ½½ Û ¼ ½¼µ ½¾ ÖØÙÖÒ ½ ½ ½ ÚÓ ÖÄ ÓÒ ÓÙ Ü ÒØ Ò µ ½ ½ ÒØ ½ ÓÖ ¼ Ò µ ½ Ü ÖÖ µ ¾¼ ¾½ ¾¾ ÓÙ ÚÖ ÓÙ Ü ÒØ Ò µ ¾ ¾ ÓÙ ¼º¼ ¾ ÒØ ¾ ÓÖ ¼ Ò µ ¾ Ü ¾ ÖØÙÖÒ»Ò ¾
7 ¼ ½ ÒØ Ô ÓÙ Ü ÒØ Ò µ ¾ ÒØ ÓÙÒØ ¼ ÒØ ÓÖ ¼ Ò µ Ü µ ÓÙÒØ ÖØÙÖÒ ÓÙÒØ ¼ ÒØ ÑÒ µ ½ ¾ ÓÒ Ø ÒØ Ø Ù Ò Ø ÓÙ Ó Ò Ø Ù Ò Ø ÓÙ Ñ Ó ÒØ ÔÖ Ò ÖÄ ÓÒ Ó Ò Ø Ù Ò Ø µ Ñ Ó ÚÖ Ó Ò Ø Ù Ò Ø µ ÔÖ ÒÔ Ó Ò Ø Ù Ò Ø µ ÓÙØÅ Ó Ó Ö Ó Ñ Ó Ò ¼ ÓÙØ ÈÖ Ò ÔÖ ÒÒ ½ ÖØÙÖÒ ¼ ¾ Ναγίνουνοιακόλουθεςδιορθώσεις»προσθήκεςστοπαραπάνωπρόγραμμα ½ºΝαπροστεθείμιαακόμασυνάρτησηγιατηνεπιστροφήτουαριθμούσπουδαστή θέσηστονπίνακαµμετονμεγαλύτεροβαθμόº ¾ºΑνθέλουμενακαταγράψουμετιςεπιδόσειςτων σπουδαστώνσε μαθήματα τιαλλαγέςχρειάζονται
8 ΔεύτεροσετΑσκήσεων ΙωάννηςΓºΤσούλος ¾¼½ Στοσημερινόσετασκήσεωνθαπαρουσιαστούνμιασειράαπόασκήσειςγια χρήσηκατηγοριώνσεπρογράμματαº ½ Πρόγραμμα ημερομηνίας Ηεπόμενηδήλωσητηςκατηγορίας Øμπορείναχρησιμοποιηθείγιααναπαράστασηημερομηνιών ½ Ò ÌÀ ¾ Ò ÌÀ Ø ÔÖÚØ ÒØ Ý ÑÓÒØ ÝÖ ÔÙ Ø µ ÚÓ Ò Ø Ø ÒØ ÒØ Ñ ÒØ Ý µ ½¼ ÓÓ ØÝ ÒØ µ ½½ ÓÓ ØÅÓÒØ ÒØ Ñµ ½¾ ÓÓ ØÖ ÒØ Ý µ ½ ÒØ ØÝ µ ½ ÒØ ØÅÓÒØ µ ½ ÒØ ØÖ µ ½ ÚÓ ÔÖÒØØ µ ½ ÚÖØÙ Ø µ ½ ½ ¾¼ Ò» ÌÀ» Ηυλοποίησητηςπαραπάνωκατηγορίαςέχειωςεξής ½ ÒÙ Ó ØÖÑ ¾ Ù Ò ÒÑ Ô Ø ÒÙ Ø º Ø Ø µ ½
9 Ý ½ ÑÓÒؽ ÝÖ ½ ½¼ ½½ ÚÓ Ø Ò Ø Ø ÒØ ÒØ Ñ ÒØ Ý µ ½¾ ½ ØÝ µ µ Ý ½ ½ ØÅÓÒØ Ñµ µ ÑÓÒؽ ½ ØÖ Ý µ µ ÝÖ ½ ½ ½ ½ ÓÓ Ø ØÝ ÒØ µ ½ ¾¼ ¼ ½µ ÖØÙÖÒ ¾½ Ý ¾¾ ÖØÙÖÒ ØÖÙ ¾ ¾ ¾ ÓÓ Ø ØÅÓÒØ ÒØ Ñµ ¾ ¾ Ѽ ѽ¾µ ÖØÙÖÒ ¾ ÑÓÒØÑ ¾ ÖØÙÖÒ ØÖÙ ¼ ½ ¾ ÓÓ Ø ØÖ ÒØ Ý µ ÝÖ ¼µ ÖØÙÖÒ ÝÖÝ ÖØÙÖÒ ØÖÙ ÒØ Ø ØÝ µ ¼ ½ ÖØÙÖÒ Ý ¾ ÒØ Ø ØÅÓÒØ µ ÖØÙÖÒ ÑÓÒØ ÒØ Ø ØÖ µ ¼ ¾
10 ½ ÖØÙÖÒ ÝÖ ¾ ÚÓ Ø ÔÖÒØØ µ ÓÙØÝ»ÑÓÒØ»ÝÖÒ Ø Ø µ ¼ ½ ¾ Ενα απλό πρόγραμμα ¹ οδηγός που αρχικοποιεί δύο αντικείμενα ημερομηνίας και ταεμφανίζειείναιτοεπόμενο ½ ÒÙ Ø º ¾ ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÒØ ÑÒ µ Ø ½ Ø ¾ ½ º Ò Ø Ø ½ ¼ ½ ½ ¾ ¼ ¼ ½ µ ½¼ ¾ º Ò Ø Ø ¾¾ ¾ ½µ ½½ ½ º ÔÖÒØØ µ ½¾ ¾ º ÔÖÒØØ µ ½ ÖØÙÖÒ ¼ ½ Αφούεκτελέσετεμεπροσοχήτοπαραπάνωπρόγραμμακάνετετιςαπαραίτητες τροποποιήσειςώστε ½ºΤαστοιχείατωνημερομηνιών ½και ¾ναδιαβάζονταιαπότοπληκτρολόγιο ¾ºΝαπροστεθείμιαακόμαμέθοδος ÄÔ µστηνκατηγορία Ø πουνα επιστρέφει ØÖÙανητοέτοςείναιδίσεκτοκαι ανδενείναι ºΝαπροστεθείκαιναδοκιμαστεί μέσωτης ÑÒµμιαμέθοδοςστηνκατηγορία Øμεόνομα ÚÓ ÒÜØÝ µº Αυτήημέθοδοςθαυπολογίζειτην επόμενηημέρακαιοιυπολογισμοίτηςθααποθηκεύονταισταιδιωτικάπεδία Ý ÑÓÒØ ÝÖº ¾ Πρόγραμμαγιασημεία Ηεπόμενηκατηγορίαδηλώνειένασημείοστονχώρο R 2 μεσυντεταγμένεςχκαι Υº
11 ½ Ò ÈÇÁÆÌÀ ¾ Ò ÈÇÁÆÌÀ ÈÓÒØ ÔÖÚØ ÓÙ Ü Ý ÔÙ ÈÓÒØ µ ÈÓÒØ ÓÙ ÑÜ ÓÙ ÑÝ µ ½¼ ÓÙ ØÜ µ ½½ ÓÙ ØÝ µ ½¾ ÚÓ ÑÓÚ ÓÙ Ü ÓÙ Ý µ ½ ÚÓ Ô Ö Ò Ø µ ½ ÚÖØÙ ÈÓÒØ µ ½ ½ ½ Ò» ÈÇÁÆÌÀ» Οκώδικαςγιατηνυλοποίησητηςκατηγορίαςέχειωςακολούθως ½ ¾ ÒÙ ÈÓÒØ º ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÈÓÒØ ÈÓÒØ µ Ü ¼º¼ Ý ¼º¼ ½¼ ½½ ½¾ ½ ÈÓÒØ ÈÓÒØ ÓÙ ÑÜ ÓÙ Ñݵ ½ ½ Ü ÑÜ ½ Ý ÑÝ ½ ½ ½ ¾¼ ÓÙ ÈÓÒØ ØÜ µ ¾½ ¾¾ ÖØÙÖÒ Ü ¾ ¾ ¾ ¾ ÓÙ ÈÓÒØ ØÝ µ ¾
12 ¾ ÖØÙÖÒ Ý ¾ ¼ ½ ÚÓ ÈÓÒØ ÑÓÚ ÓÙ Ü ÓÙ Ý µ ¾ ÜÜ Ü ÝÝ Ý ÚÓ ÈÓÒØ Ô Ö Ò Ø µ ÓÙØ Ü Ý µ Ò ¼ ½ ¾ ÈÓÒØ ÈÓÒØ µ Μιαενδεικτική ÑÒ µσυνάρτησηόπουαρχικοποιούμεδύοαντικείμενα ÈÓÒØκαι ταεμφανίζουμεστηνοθόνηείναιηεπόμενηº Μεβάσηταπαραπάνωπροσθέστε μιαακόμαμέθοδοστηνκατηγορία ÈÓÒØ ÓÓ Õ Ù ÈÓÒØ Ó Ø Ö µ Ημέθοδοςθαεπιστρέφει ØÖÙαντοτρέχονσημείο συντεταγμένες Ü Ýµκαιτο ÓØÖσημείοέχουντιςίδιεςσυντεταγμένεςκαι σεάλληπερίπτωσηº
13 ΤρίτοσετΑσκήσεων ΙωάννηςΓºΤσούλος ¾¼½ ½ Κατηγορίαπροσώπων ΝαγραφείκατηγορίαγιατηνπεριγραφήπροσώπωνºΣταιδιωτικάπεδίατηςκατηγορίαςπρέπειναπεριλαμβάνονταιταακόλουθα ½º Ονομα ¾ºΕπίθετο ºΤηλέφωνο ºΗλικία Σταδημόσιαπεδίαθαπρέπειναυπάρχουνοιμέθοδοι Øκαι Øγιαταιδιωτικά πεδίακαθώςκαιδύοβοηθητικέςμέθοδοι ½ºΜιαμέθοδοςπουθαεπιστρέφειαληθέςαντοπρόσωποείναιενήλικο ¾ºΜιαμέθοδοςπουθατυπώνειστηνοθόνηταστοιχείατοπροσώπου Ηκατηγορία ÈÖ ÓÒέχειωςακολούθως ½ Ò ÈÊËÇÆÀ ¾ Ò ÈÊËÇÆÀ ÒÙ Ø Ö Ò Ù Ò ÒÑ Ô Ø ÈÖ ÓÒ ÔÖÚØ Ø Ö Ò ÒÑ ØÒÑ Ø Ô Ó Ò ÒØ ½¼ ÔÙ ½½ ÈÖ ÓÒ µ ½¾ ÚÓ ØÆÑ Ø Ö Ò Ò µ ½ ÚÓ ØÄ ØÒÑ Ø Ö Ò µ ½ ÓÓ ØÌÔÓÒ Ø Ö Ò Ø µ ½ ÓÓ Ø ÒØ µ ½
14 ½ ÓÓ Ù Ø µ ½ ÚÓ Ô Ö Ò Ø Ø µ ½ ÚÖØÙ ÈÖ ÓÒ µ ½ ¾¼ ¾½ Ò» ÈÊËÇÆÀ» Ηυλοποίησητηςκατηγορίαςείναι ½ ÒÙ ÈÖ ÓÒ º ¾ ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÈÖ ÓÒ ÈÖ ÓÒ µ ÒÑ ØÒÑ Ø Ô Ó Ò ¾½¼¼¼¼ ½¼ ½ ½½ ½¾ ½ ½ ÚÓ ÈÖ ÓÒ ØÆÑ Ø Ö Ò Ò µ ½ ½ ÒÑ Ò ½ ½ ½ ÚÓ ÈÖ ÓÒ ØÄ ØÒÑ Ø Ö Ò µ ¾¼ ¾½ ØÒÑ ¾¾ ¾ ¾ ÓÓ ÈÖ ÓÒ ØÌÔÓÒ Ø Ö Ò Ø µ ¾ ¾ ÒØ ¾»» Ö Ø Ö Ù ¾ Ø º Ò Ø µ ½ ¼ µ ÖØÙÖÒ ¾»» ÓÒ Ö Ù ¼ Ø ¼ ³ ¼ ³ µ ÖØÙÖÒ ½ ÓÖ ¼ Ø º Ò Ø µ µ ¾»» Ø Ö Ö Ù Ø ³ ¼ ³ ²² Ø ³ ³ µ µ ÖØÙÖÒ Ø Ô Ó Ò Ø ÖØÙÖÒ ØÖÙ ¾
15 ¼ ÓÓ ÈÖ ÓÒ Ø ÒØ µ ½ ¾ ¼µ ÖØÙÖÒ ÖØÙÖÒ ØÖÙ ÓÓ ÈÖ ÓÒ Ù Ø µ ½µ ÖØÙÖÒ ØÖÙ ¼ ÖØÙÖÒ ½ ¾ ÚÓ ÈÖ ÓÒ Ô Ö Ò Ø Ø µ ÓÙØ ÈÖ ÓÒ Ø Ò ÓÙØÆÑ Ø ÒÑÒ ÓÙØÄ ØÒÑ Ø ØÒÑÒ ÓÙØ ÌÔÓÒ Ø ØÔÓÒ Ò ÓÙØ Ø Ò ¼ ½ ¾ ÈÖ ÓÒ ÈÖ ÓÒ µ Τέλοςμιαενδεικτική ÑÒγιατηνπροηγούμενηκατηγορίαέχειωςακολούθως ½ ÒÙ ÈÖ ÓÒ º ¾ ÒÙ Ø º ÒØ ÑÒ µ ÈÖ ÓÒ Ò Ò Ò Ò º ØÆÑ ÒÒ µ Ò Ò º ØÄ ØÒÑ Ì ÓÙÓ µ Ò Ò º ØÌÔÓÒ ¾½½½ µ Ò Ò º Ø µ ½¼ Ò Ò º Ô Ö Ò Ø Ø µ ½½ Ý ØÑ ÈÍË µ ½¾ ÖØÙÖÒ ¼ ½ Μεβάσηταπαραπάνωκάνετετιςεπόμενεςαλλαγές ½ºΠροσθέστεακόμαέναιδιωτικόπεδίογιατο ÑτουπροσώπουºΔημιουργήστε τιςαπαραίτητες Øκαι Øμεθόδουςº Στηνμέθοδο ØÑ µναγίνει
16 έλεγχοςαντοόρισμαπουθαμπειστοπεδίο Ñείναιέγκυρο Ñ έχει μόνοένασύμβολο καιαυτόδενβρίσκεταιούτεστηναρχήούτεστοτέλος του ѵº ¾ºΑλλάξτετηνσυνάρτησηδημιουργίαςτηςκατηγορίαςώστεναδιαβάζεικαι τα πεδίααπότοπληκτρολόγιοº ºΑλλάξτετην ÑÒ µσυνάρτησηώστεναυπάρχουντρίαδιαφορετικάαντικείμενατηςκατηγορίας ÈÖ ÓÒºΚάνετετιςαρχικοποιήσειςκάθεαντικειμένου καιεμφανίστεταστοιχείατουαντικειμένουμετηνμεγαλύτερηηλικίαº ¾ Κατηγορία κύκλος Ναγραφείκατηγορίαγιατηνπεριγραφήκύκλωνμεταακόλουθαιδιωτικάπεδία ½ºΚέντροκύκλου σημείοχ¼ Υ¼µ ¾ºΑκτίνα κύκλου Σταδημόσιαπεδίαναπεριλαμβάνονταιταακόλουθα ½ºΣυνάρτησηδημιουργίας ¾ºΜέθοδοςεπιστροφήςτουεμβαδούτουκύκλου ( πr 2) ºΜέθοδοςεπιστροφήςτηςπεριμέτρουτουκύκλου (4πR) ºΜέθοδοςκλιμάκωσηςτουκύκλουºΗμέθοδοςαυτήδέχεταισανόρισμαέναν παράγονταχκαιπολλαπλασιάζειτηνακτίναμεαυτόντονπαράγονταº Ηδήλωσητηςκατηγορίαςέχειωςακολούθως ½ Ò ÁÊÄÀ ¾ Ò ÁÊÄÀ Ö ÔÖÚØ Ó٠ܼ ݼ Ö Ó Ù ÔÙ Ö ÓÙ Ü ÓÙ Ý ÓÙ Ö µ ÚÓ ÓÙ Ø Ó Ö µ ½¼ ÓÓ Ô Ó Ò Ø Á Ò ÓÙ Ü ÓÙ Ý µ»» Ø Ó ÑÔÑÒØ ½½ ÓÙ ØÖ µ ½¾ ÓÙ Ø È Ö Ñ Ø Ö µ ½ Ö µ ½ ½ ½ Ò» ÁÊÄÀ» Ηυλοποίησητηςκατηγορίας
17 ½ ÒÙ Ö º ¾ ÒÙ ÑØ º Ö Ö ÓÙ Ü ÓÙ Ý ÓÙ Ö µ Ü¼Ü Ý¼Ý Ö Ó Ù Ö µ ½¼ ÚÓ Ö ÓÙ Ø Ó Ö µ ½½ ½¾ Ö Ó Ù Ø Ó Ö µ Ö Ó Ù ½ ½ ½ ÓÓ Ö Ô Ó Ò Ø Á Ò ÓÙ Ü ÓÙ Ý µ ½ ½»» Ø Ó ÑÔÑÒØ ½ ½ ¾¼ ÓÙ Ö ØÖ µ ¾½ ¾¾ ÖØÙÖÒ ÅÈÁ Ö Ó Ù Ö Ó Ù ¾ ¾ ¾ ÓÙ Ö Ø È Ö Ñ Ø Ö µ ¾ ¾ ¾ ÖØÙÖÒ º ¼ ÅÈÁ Ö Ó Ù ¾ ¼ ½ Ö Ö µ ¾ Καιτέλοςμιαενδεικτική ÑÒ ½ ÒÙ Ö º ¾ ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÒÙ Ø º ÒØ ÑÒ µ Ö ½ ½ ¼ ½ ¼ ¾ ¼ µ ÓÙØ½Ö ½ º ØÖ µò ÓÙؽ ÈÖÑØÖ ½ º Ø È Ö Ñ Ø Ö µò ½¼ ½ º ¾ º ¼ µ
18 ½½ ÓÙØ½Ö ½ º ØÖ µò ½¾ ÓÙؽ ÈÖÑØÖ ½ º Ø È Ö Ñ Ø Ö µò ½ Ý ØÑ ÈÍË µ ½ ÖØÙÖÒ ¼ ½ Μεβάσηταπαραπάνωυλοποιήστετηνμέθοδο ÓÓ ÔÓÒØÁÒ ÓÙ Ü Ó٠ݵ έτσιώστεναεπιστρέφειαληθέςαντοσημείο Ü Ýείναιμέσαστονκύκλοκαιψευδές αλλιώςºδοκιμάστετηνμέθοδόσαςστην ÑÒ όπουθαδιαβάζετεδύοαριθμούς Χ Υκαιθαελέγχετεαναυτότοσημείο Χ Υµείναιμέσαστονκύκλο ½που υπάρχειστην ÑÒº Υπενθυμίζεταιπωςένασημείο (x,y)είναιμέσαστονκύκλο μεκέντρο (x 0,y 0 )καιακτίνα Rανισχύειησχέση (x x 0 ) 2 +(y y 0 ) 2 R 2
19 ΤέταρτοσετΑσκήσεων ΙωάννηςΓºΤσούλος ¾¼½ ½ Κατηγορία Ημερομηνίας Να γραφεί κατηγορία για την πλήρη περιγραφή ημερομηνιώνº Στα ιδιωτικά πεδία πρέπειναπεριλαμβάνονταιταακόλουθα ½ºΗμέρα ¾ºΜήνας º Ετος ºΠίνακαςακεραίωνμετιςμέρεςκάθεμήναº Σταδημόσιαπεδίαταακόλουθα ½ºΤρειςυπερφορτωμένεςσυναρτήσειςδημιουργίας ¾ºΜέθοδοι Øκαι Øγιαημέρα μήνα έτοςμεέλεγχοτιμών ºΜιαμέθοδοςεμφάνισηςτηςημερομηνίαςστηνοθόνη ºΜιαμέθοδοςπουθααλλάζειτηνημερομηνίαστηνεπόμενηημέραº ºΜιαμέθοδοςπουθαδέχεταισανόρισμααναφοράσεαντικείμενο Øκαι θαελέγχειανητρέχουσαημερομηνίακαιηημερομηνίαστηναναφοράείναι ίδιεςº Ηπεριγραφήτηςκατηγορίαςέχειωςακολούθως ½ Ò ÌÀ ¾ Ò ÌÀ Ø Ô Ö Ú Ø ÒØ ÑÓÒØÝ ½ ¾ ÚÓ Ì µ ÒØ Ý ÑÓÒØ ÝÖ Ô Ù ½¼»» Ó Ò Ø Ö Ù Ø Ó Ö ½
20 ½½ Ø µ ½¾ Ø ÒØ Ý µ ½ Ø ÒØ ÒØ Ñ ÒØ Ý µ ½ ½»» Ø ÑØÓ ½ ÓÓ ØÖ ÒØ Ý µ ½ ÓÓ ØÅÓÒØ ÒØ Ñµ ½ ÓÓ ØÝ ÒØ µ ½ ¾¼»» Ø ÑØÓ ¾½ ÒØ ØÝ µ ¾¾ ÒØ ØÅÓÒØ µ ¾ ÒØ ØÖ µ ¾ ¾»» Ù Ø Ø Ý ÑØÓ ¾ ÓÓ ÑØ Ø ²Ó Ø Ö µ ¾ ÚÓ ÒÜØÝ µ ¾ ÚÓ ÔÖÒØØ µ ¾ Ú Ö Ø Ù Ø µ ¼ ½ ¾ Ò» ÌÀ» Ηυλοποίησητηςκατηγορίας ½ ÒÙ Ø º ¾ ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø Ø Ø µ Ì µ Ý ½ ÑÓÒؽ ½¼ ÝÖ ½ ½½ ½¾ ½ Ø Ø ÒØ Ý µ ½ ½ Ì µ ½ Ý ½ ½ ÑÓÒؽ ½ ØÖ Ý µ ½ ¾¼ ¾½ ¾¾ Ø Ø ÒØ ÒØ Ñ ÒØ Ý µ ¾
21 ¾ ¾ Ì µ ¾ ØÝ µ ¾ ØÅÓÒØ Ñµ ¾ ØÖ Ý µ ¾ ¾ ¼ ÚÓ Ø Ì µ ½ ¾»» Ó ÑÖ Ø Ó Ù ÑÒ Ø ÑÒ ÑÓÒØÝ ¼ ½ ÑÓÒØÝ ½ ¾ ÑÓÒØÝ ¾ ½ ÑÓÒØÝ ¼ ÑÓÒØÝ ½ ÑÓÒØÝ ¼ ÑÓÒØÝ ½ ¼ ÑÓÒØÝ ½ ½ ÑÓÒØÝ ¼ ¾ ÑÓÒØÝ ½ ÑÓÒØÝ ½ ¼ ¼ ÑÓÒØÝ ½ ½ ½ ÓÓ Ø ØÖ ÒØ Ý µ ݼµ ÝÖ ½ÖØÙÖÒ ¼ ½ ¾ ÝÖÝ ÖØÙÖÒ ØÖÙ ÓÓ Ø ØÅÓÒØ ÒØ Ñµ Ѽ ѽ¾µ ÑÓÒؽÖØÙÖÒ ¼ ½ ¾ ÑÓÒØÑ ÖØÙÖÒ ØÖÙ ÓÓ Ø ØÝ ÒØ µ
22 ¼ ½ ÑÓÒØÝ ÑÓÒØ ½ µ ݽÖØÙÖÒ ¼ ½ ¾ Ý ÖØÙÖÒ ØÖÙ ÒØ Ø ØÝ µ ÖØÙÖÒ Ý ¼ ½ ¾ ÒØ Ø ØÅÓÒØ µ ÖØÙÖÒ ÑÓÒØ ÒØ Ø ØÖ µ ÖØÙÖÒ ÝÖ ¼ ½ ¾ ÚÓ Ø ÒÜØÝ µ Ý ÝÑÓÒØÝ ÑÓÒØ ½ µ ÑÓÒØ Ý ½ ÑÓÒؽ¾µ ½¼¼ ½¼½ ÑÓÒؽ ½¼¾ ÝÖ ½¼ ½¼ ½¼ ½¼ ½¼ ÚÓ Ø ÔÖÒØØ µ ½¼ ½¼ ÓÙØÝ»ÑÓÒØ»ÝÖÒ ½½¼ ½½½ ½½¾ ÓÓ Ø ÑØ Ø ²Ó Ø Ö µ ½½ ½½ ÝÓ Ø Ö º ØÝ µ ²² ÑÓÒØÓ Ø Ö º ØÅÓÒØ µ ²² ÝÖÓ Ø Ö º Ø
23 ½½ ÖØÙÖÒ ØÖÙ ½½ ½½ ÖØÙÖÒ ½½ ½½ ½¾¼ Ø Ø µ ½¾½ ½¾¾ ½¾ Τέλοςμιαενδεικτική ÑÒσυνάρτησηείναιηεπόμενη ½ ÒÙ Ø º ¾ ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÒØ ÑÒ µ Ø ½ Ø ¾ ½ µ Ø ½ ½ ½ ½ ¾ ¾ µ ½¼ ½ º ÔÖÒØØ µ ½½ ¾ º ÔÖÒØØ µ ½¾ º ÔÖÒØØ µ ½ ÖØÙÖÒ ¼ ½ Μεβάσηταπαραπάνωκάνετετιςακόλουθεςαλλαγές ½ºΑλλάξτετηνυπερφορτωμένησυνάρτησηδημιουργίας Ø µώστεναδιαβάζειτηνημερομηνίααπότοπληκτρολόγιοºανδίνεταιλανθασμένηείσοδος πχαρνητικόέτοςµναγίνεταιεπαναληπτικάανάγνωσηº ¾ºΠροσθέτεμιαμέθοδο ÔÖÚÝ µπουθαμειώνειτηνημέρακατά ½º ºΠροσθέστεμιαμέθοδομετοόνομα ÓÓ ÓÖ Ø ²ÓØÖµ ηοποίαθα επιστρέφειαληθέςανητρέχουσαημερομηνίαείναιπριντηνημερομηνία ÓØÖ και ψευδές αλλιώςº ºΔιορθώστετονκώδικαόπουχρειάζεταιώστεναλαμβάνεταιυπόψινσαςτα δίσεκταέτηºπιθανόνναχρειαστείνααλλάξετεπάνωαπό μεθόδουςº
24 ΠέμπτοσετΑσκήσεων ΙωάννηςΓºΤσούλος ¾¼½ ½ Κατηγορία μαθητών με δείκτες Ηεπόμενηκατηγορίαυλοποιείμιακατηγορίαγιατηναποθήκευσημαθητώνενός εξαμήνουμεχρήσηδεικτώνº Στηνσυνέχειαδημιουργεί μαθητέςδυναμικάσαν δυναμικάπεδίαπίνακαºσταιδιωτικάπεδίατηςκατηγορίας ËØÙÒØπεριλαμβάνονταιταακόλουθα ½º Ονομα μαθητή ¾ºΕπίθετο μαθητή ºΑριθμός μαθημάτων ºΠίνακαςβαθμολογίας Σταδημόσιαπεδίαπεριλαμβάνονται ½ºΜέθοδος δημιουργίας ¾ºΜέθοδοι Øκαι Ø ºΜέθοδοςεμφάνισηςτουμαθητή ºΜέθοδοςδιαγραφής Η ÑÒ µ συνάρτησηθαδημιουργήσει δυναμικάαντικείμενατηςκατηγορίας ËØÙÒØκαιστηνσυνέχειαθαταεμφανίσειστηνοθόνηºΗδήλωσητηςκατηγορίας έχειωςακολούθως ½ Ò ËÌÍÆÌÀ ¾ Ò ËÌÍÆÌÀ ËØÙÒØ ÔÖÚØ Ö ÒÑ ØÒÑ ÓÙ Ó Ò ÒØ Ó Ù Ò Ø Ä Ó Ò ÔÙ ½
25 ½¼ ËØÙÒØ Ö Ò Ö ÒØ µ ½½ ÚÓ Ø Ä Ó Ò ÒØ ÒÜ ÓÙ Ú Ù µ ½¾ ÓÙ Ø Ä Ó Ò ÒØ Ò Ü µ ½ ÚÓ Ô Ö Ò Ø Ø µ ½ Ö ØÆÑ µ ½ Ö ØÄ ØÒÑ µ ½ ÚÓ ØÆÑ Ö Ò µ ½ ÚÓ ØÄ ØÒÑ Ö µ ½ ËØÙÒØ µ ½ ¾¼ ¾½ Ò Ηυλοποίησητηςκατηγορίαςέχειωςακολούθως ½ ÒÙ ËØÙÒØ º ¾ ÒÙ Ø Ö Ò º ÒÙ Ó Ø Ö Ñ Ù Ò ÒÑ Ô Ø ËØÙÒØ ËØÙÒØ Ö Ò Ö ÒØ µ ØÆÑ Ò µ ØÄ ØÒÑ µ ½¼ ¼µ Ó Ù Ò Ø Ä Ó Ò ½ Ó Ù Ò Ø Ä Ó Ò ½½ Ó Ò ÒÛ ÓÙ Ó Ù Ò Ø Ä Ó Ò ½¾ ½ ½ ÚÓ ËØÙÒØ Ø Ä Ó Ò ÒØ ÒÜ ÓÙ Ú Ù µ ½ ½ ÒÜ ¼ ÒÜ Ó Ù Ò Ø Ä Ó Ò µ ½ ÖØÙÖÒ ½ ÚÙ ¼ ÚÙ ½¼µ ½ Ó Ò Ò Ü ¼ ¾¼ ¾½ Ó Ò Ò Ü Ú Ù ¾¾ ¾ ¾ ÓÙ ËØÙÒØ Ø Ä Ó Ò ÒØ Ò Ü µ ¾ ¾ ÒÜ ¼ ÒÜ Ó Ù Ò Ø Ä Ó Ò µ ÖØÙÖÒ ¼ ¾ ÖØÙÖÒ Ó Ò Ò Ü ¾ ¾ ¼ ÚÓ ËØÙÒØ Ô Ö Ò Ø Ø µ ½ ¾ ÒØ ¾
26 ÓÙØ ËØÙÒØ Ø Ò ÓÙØÆÑ ÒÑ Ò ÓÙØ Ä ØÒÑ ØÒÑ Ò ÓÖ ¼ Ó Ù Ò Ø Ä Ó Ò µ ÓÙØ Ä ÓÒ ½µÖ Ó Ò Ò ¼ Ö ËØÙÒØ ØÆÑ µ ½ ¾ ÖØÙÖÒ ÒÑ Ö ËØÙÒØ ØÄ ØÒÑ µ ÖØÙÖÒ ØÒÑ ¼ ÚÓ ËØÙÒØ ØÆÑ Ö Ò µ ½ ¾ ÒÑÒÛ Ö Ø Ö Ò Ò µ ½ Ø Ö Ô Ý ÒÑ Ò µ ÚÓ ËØÙÒØ ØÄ ØÒÑ Ö µ ØÒÑÒÛ Ö Ø Ö Ò µ ½ Ø Ö Ô Ý ØÒÑ µ ¼ ½ ¾ ËØÙÒØ ËØÙÒØ µ Ø ÒÑ Ø ØÒÑ Ø Ó Ò Τέλοςησυνάρτηση ÑÒ µέχειωςεξής ½ ÒÙ ËØÙÒØ º ¾ ÒÙ Ó Ø Ö Ñ Ù Ò ÒÑ Ô Ø ÒØ ÑÒ µ Ö ÑÝÒÑ ½ ¼ ¼ Ö ÑÝ ØÒÑ ½ ¼ ¼ ËØÙÒØ Ñ Ý ÒØ Ò Ó Ò
27 ½¼ ÓÖ ¼ µ ½½ ½¾ ÓÙØ Ú Ø Ó Ö Ø Ù Ò Ø ½µ Ò ½ ÓÙØ Ú ÒÑ Ò ½ Ò ÑÝÒÑ ½ ÓÙØ Ú ØÒÑ Ò ½ Ò ÑÝ ØÒÑ ½ ÓÙØ Ú ÒÙÑÖ Ó Ó Ò Ò ½ Ò Ò Ó Ò ½ Ñ Ý ÒÛ ËØÙÒØ ÑÝÒÑ ÑÝ ØÒÑ Ò Ó Ò µ ¾¼ ÓÖ ¼ Ò Ó Ò µ ¾½ ¾¾ ÓÙ Ö ¾ ÓÙØ Ú Ö Ó Ö Ó Ò ½µ Ò ¾ Ò Ö ¾ Ñ Ý Ø Ä Ó Ò Ö µ ¾ ¾ ¾ ¾ ÓÖ ¼ µ ¼ ½ Ñ Ý Ô Ö Ò Ø Ø µ ¾ Ø Ñ Ý ÖØÙÖÒ ¼ Μεβάσηταπαραπάνωκάνετετιςεπόμενεςτροποποιήσεις ½ºΝαπροστεθείσταιδιωτικάπεδίατης ËØÙÒØκαιοαριθμόςμητρώουτου σπουδασηºνακάνετεόλεςτιςαπαραίτητεςαλλαγέςστηνμέθοδοδημιουργίας καιναπροσθέσετεκαιμεθόδους Øκαι Øγιααυτότοπεδίο ¾ºΝαπροστεθείμέθοδος ÚÖ µστηνκατηγορία ËØÙÒØπουναυπολογίζει καιναεπιστρέφειτονμέσοόροβαθμολογίαςτουσπουδαστή ºΕμφανίστεστην ÑÒ µσυνάρτησητουςμέσουςόρουςβαθμολογίαςγιακάθε σπουδαστή ºΕμφανίστεστην ÑÒ µσυνάρτησηταστοιχείατουσπουδαστή Ονομα Επίθετοµμετονκαλύτερομέσοόρο ºΝαπροστεθείημέθοδος ÓÓ ØØÖ ËØÙÒØ ÓØÖµΗμέθοδοςαυτή δέχεταισανόρισμαένανδείκτησεαντικείμενο ËØÙÒØκαιεπιστρέφειαληθές ανοτρέχωνσπουδαστήςέχεικαλύτερομέσοόροαπότον ÓØÖκαι σε άλληπερίπτωσηº ºΑλλάξτετιςδηλώσειςτωνπεδίων ÒÑ ØÒÑαπό Ö σε ØÖÒ
28 ΕκτοσετΑσκήσεων ΙωάννηςΓºΤσούλος ¾¼½ ½ Κατηγορία βιβλίων Ναδημιουργηθείκατηγορίαβιβλίωνμεταεξήςιδιωτικάπεδία ½º Τίτλο βιβλίου ¾º Συγγραφέα º Κωδικό ºΑριθμόσελιδών Σταδημόσιαπεδίαναυπάρχουνταακόλουθα ½ºΔύομέθοδοιδημιουργίαςτηςεπιλογήςσας ¾ºΜέθοδοι Øκαι Ø ºΜέθοδοςεκτύπωσηςτωνστοιχείων ºΜέθοδοςδιαγραφήςπουεμφανίζειτοντίτλοτουβιβλίουπουθαδιαγραφείº Ηκατηγορίαβιβλίουείναιηακόλουθη ½ ÒÙ Ø Ö Ò ¾ Ù Ò ÒÑ Ô Ø ÓÓ ÔÖÚØ Ø Ö Ò ÙØÓÖ Ø Ø ÒØ Ô ÒØ Ó ½¼ ÔÙ ½½ ÓÓ µ ½¾ ÓÓ ÒØ Ø Ö Ò Ø Ö Ò Ø ÒØ Ô µ ½ Ø Ö Ò ØÙØÓÖ µ ½ Ø Ö Ò Ø Ì Ø µ ½
29 ½ ÒØ ØÈ µ ½ ÒØ ØÓ µ ½ ÚÓ ØÙØÓÖ Ø Ö Ò µ ½ ÚÓ Ø Ì Ø Ø Ö Ò µ ½ ÚÓ ØÈ ÒØ Ô µ ¾¼ ÚÓ ØÓ ÒØ µ ¾½ ÚÓ Ô Ö Ò Ø Ø µ ¾¾ ÓÓ µ ¾ Ηυλοποίησητηςκατηγορίαςβιβλίουείναιηακόλουθη ½ ÒÙ ÓÓ º ¾ ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÓÓ ÓÓ µ ØÓ ¼ µ ØÈ ¼ µ ØÙØÓÖ µ Ø Ì Ø µ ½¼ ½½ ½¾ ÓÓ ÓÓ ÒØ Ø Ö Ò Ø Ö Ò Ø ÒØ Ô µ ½ ½ ØÓ µ ½ ØÈ Ô µ ½ ØÙØÓÖ µ ½ Ø Ì Ø Ø µ ½ ½ ¾¼ Ø Ö Ò ÓÓ ØÙØÓÖ µ ¾½ ¾¾ ÖØÙÖÒ ÙØÓÖ ¾ ¾ ¾ Ø Ö Ò ÓÓ Ø Ì Ø µ ¾ ¾ ÖØÙÖÒ Ø Ø ¾ ¾ ¼ ÒØ ÓÓ ØÈ µ ½ ¾ ÖØÙÖÒ Ô ÒØ ÓÓ ØÓ µ ¾
30 ÖØÙÖÒ Ó ¼ ÚÓ ÓÓ ØÙØÓÖ Ø Ö Ò µ ½ ¾ ÙØÓÖ ÚÓ ÓÓ Ø Ì Ø Ø Ö Ò µ Ø Ø ¼ ÚÓ ÓÓ ØÈ ÒØ Ô µ ½ ¾ Ô¼µ Ô ¼ Ô Ô ÚÓ ÓÓ ØÓ ÒØ µ ¼µ Ó ¼ Ó ¼ ÚÓ ÓÓ Ô Ö Ò Ø Ø µ ½ ¾ ÓÙØ Ì Ø Ø Ø ÙØÓÖ ÙØÓÖÒ Ó Ó È Ô Ò ÓÓ ÓÓ µ ÓÙØ Ø Ò ÓÓØ Ø Ò ¼ Μιαενδεικτική ÑÒσυνάρτησηστηνοποίαγίνεταιχρήσηδεικτώνκαιδυναμικών αντικειμένωνβιβλίουείναιηακόλουθη ½ ÒÙ ÓÓ º ¾ ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÒØ ÑÒ µ ÓÓ ½¼¼ ÃÒ ÌËØÒ ¼ ¼ µ ÓÓ Ô²
31 ÓÓ ÒÛ ÓÓ ¾¼¼ ÃÞÒØÞ ÓÖ ¼ ¼ µ ½¼ Ô Ô Ö Ò Ø Ø µ ½½ Ô ØÈ ½ ¼ ¼ ¼ µ ½¾ º Ô Ö Ò Ø Ø µ ½ Ô Ö Ò Ø Ø µ ½ Ø ½ ÖØÙÖÒ ¼ ½ Μεβάσηταπαραπάνωκάνετετιςεπόμενεςπροσθήκες ½ºΠροσθέστεμιαακόμασυνάρτησηδημιουργίας ÓÓ ÓÓ ²ÓØÖµ στην οποίαναγίνεταιαντιγραφήκάθεπεδίουτουαντικειμένου ÓØÖστοτρέχον αντικείμενοº Γιαπαράδειγμαθαοισελίδεςθαπρέπειναγίνουνίσεςμετις σελίδεςτουαντικειμένου ÇØÖº ¾ºΝαπροστεθείημέθοδος ÓÓ ÑÙØÓÖ ÓÓ ÓØÖµΗμέθοδοςεπιστρέφει αληθέςαντοτρέχονβιβλίοκαιτο ÓØÖανήκουνστονίδιοσυγγραφέαº ºΝαπροστεθείημέθοδος ÓÓ ÕÙ ÓÓ ÓØÖµ πουεπιστρέφειαληθές αντοτρέχονβιβλίοκαιτο ÓØÖείναιπανομοιότυπασεόλαταπεδίατηςº ¾ Βιβλιοθήκη Μεβάσητηνπροηγούμενηκατηγορίαναγίνεικατηγορία ÄÖÖÝηοποίαθαδιαθέτεισταιδιωτικάτηςπεδία ½º Ενανπίνακαδέκαδεικτώνσεβιβλία ÓÓ Σταδημόσιαπεδίαθαπεριλαμβάνει ½º Μια μέθοδο δημιουργίας ¾ºΜιαμέθοδοεισαγωγήςνέουβιβλίου ºΜιαμέθοδοεμφάνισηςόλωντωνβιβλίων ºΜιαμέθοδοδιαγραφήςβιβλίουμεβάσητονκωδικότου ºΜιαμέθοδοαναζήτησηςβιβλίουμεβάσητονκωδικότου Ηδήλωσηςτηςκατηγορίαςέχειωςακολούθως ½ ÒÙ ÓÓ º ¾ Ò ÆÇÇÃË ½¼ ÄÖÖÝ ÔÖÚØ ÓÓ ÑÝÓÓ ÆÇÇÃË ÔÙ
32 ÄÖÖÝ µ ÓÓ ÓÓ ÓÓ µ ½¼ ÚÓ ÓÓ ÒØ Ó µ ½½ ÓÓ ÖÓÓ ÒØ Ó µ ½¾ ÚÓ ÓÛÓÓ µ ½ ÄÖÖÝ µ ½ Ηυλοποίησητηςκατηγορίαςείναι ½ ÒÙ Ö Ö Ý º ¾ ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÄÖÖÝ ÄÖÖÝ µ ÒØ ÓÖ ¼ ÆÇÇÃË µ ÑÝÓÓ ÆÍÄÄ ½¼ ½½ ½¾ ÓÓ ÄÖÖÝ ÓÓ ÓÓ µ ½ ½ ÒØ ½ ÓÖ ¼ ÆÇÇÃË µ ½ ÑÝÓÓ ÆÍÄĵ ½ ½ ÑÝÓÓ ÒÛ ÓÓ ØÓ µ ½ ØÙØÓÖ µ Ø Ì Ø µ ¾¼ ØÈ µ µ ¾½ ÖØÙÖÒ ØÖÙ ¾¾ ¾ ÖØÙÖÒ ¾ ¾ ¾ ÚÓ ÄÖÖÝ ÓÓ ÒØ Ó µ ¾ ¾ ÒØ ¾ ÓÖ ¼ ÆÇÇÃË µ ¼ ½ ÑÝÓÓ ÆÍÄĵ ¾ ÑÝÓÓ ØÓ µó µ Ø ÑÝÓÓ ÑÝÓÓ ÆÍÄÄ ÖØÙÖÒ
33 ¼ ½ ¾ ÓÓ ÄÖÖÝ ÖÓÓ ÒØ Ó µ ÒØ ÓÖ ¼ ÆÇÇÃË µ ÑÝÓÓ ÆÍÄĵ ¼ ÑÝÓÓ ØÓ µó µ ½ ÖØÙÖÒ ÑÝÓÓ ¾ ÖØÙÖÒ ÆÍÄÄ ÚÓ ÄÖÖÝ ÓÛÓÓ µ ¼ ÒØ ½ ÓÖ ¼ ÆÇÇÃË µ ¾ ÑÝÓÓ ÆÍÄĵ ÑÝÓÓ Ô Ö Ò Ø Ø µ ÄÖÖÝ ÄÖÖÝ µ ÒØ ÓÖ ¼ ÆÇÇÃË µ ¼ ÑÝÓÓ ÆÍÄĵ Ø ÑÝÓÓ ½ Τέλοςμιαενδεικτική ÑÒσυνάρτησημεχρήσημενούείναιηεπόμενη ½ ÒÙ Ö Ö Ý º ¾ ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÒØ ÑÒÙ µ ÒØ ÓÔØÓÒ Ó ÓÙؽ ÇÇÃÒ ½¼ ÓÙؾ ËÊÀÇÊÇÇÃÒ
34 ½½ ÓÙØ ËÀÇÏÇÇÃËÒ ½¾ ÓÙØ ÄÌÇÇÃÒ ½ ÓÙØ ÉÍÁÌÒ ½ ÒÓÔØÓÒ ½ ½ Û ÓÔØÓÒ ½ ÓÔØÓÒ µ ½ ÖØÙÖÒ ÓÔØÓÒ ½ ½ ¾¼ ÒØ ÑÒ µ ¾½ ¾¾ ÄÖÖÝ ÑÝ ¾ Ø Ö Ò ÙØÓÖ Ø Ø ¾ ÒØ Ô Ó ¾ ÒØ ÓÔØÓÒ ¾ Ó ¾ ¾ ÓÔØÓÒÑÒÙ µ ¾ ÓÔØÓÒ½µ ¼ ½ ÓÙØ ÒØÖ ÙØÓÖ Ò ¾ ÒÙØÓÖ ÓÙØ ÒØÖ Ø Ø Ò ÒØ Ø ÓÙØ ÒØÖ ÓÒ ÒÓ ÓÙØ ÒØÖ ÒÙÑÖ Ó Ô Ò ÒÔ ÓÓ Ô Ó ÙØÓÖ Ø Ø Ô µ ¼ ÑÝ º ÓÓ ²Ô µ ½ ¾ ÓÔØÓÒ¾µ ÓÙØ ÒØÖ ÓÒ ÒÓ ÓÓ ÔÑÝ º ÖÓÓ Ó µ ÔÆÍÄĵ Ô Ô Ö Ò Ø Ø µ ÓÙØÓÓ ÒÓØ ÓÙÒ Ò ¼ ½ ¾ ÓÔØÓÒ µ ÑÝ º ÓÛÓÓ µ
35 ÓÔØÓÒµ ÓÙØ ÒØÖ ÓÒ ¼ ÒÓ ½ ÑÝ º ÓÓ Ó µ ¾ Û ÓÔØÓÒ µ ÖØÙÖÒ ¼ Μεβάσηταπαραπάνωναγίνουνοιεπόμενεςαλλαγές ½ºΝαπροσθέσετεμιαμέθοδο ÒØ ÓÙÒØÓÓ ØÖÒ ÙØÓÖµπουθαεπιστρέφει τοπλήθοςτωνβιβλίωντου ÙØÓÖ ¾ºΝαδιορθώσετετηνμέθοδο ÓÓ ÓÓ Ôµώστεανυπάρχειήδητο βιβλίομεκωδικόίδιομετουβιβλίου Ô ναμηνγίνεταιπροσθήκητουβιβλίου
36 Κληρονομικότητακαιτελεστές ΙωάννηςΓºΤσούλος ÅÝ ½ ¾¼½ ½ Τοπαράδειγματωνσχημάτων Ηκατηγορία ËÔυλοποιείαφηρημένασχήματαºΣταδημόσιαπεδίαυπάρχουνοι υπερβατικέςμέθοδοι Ö µκαι ÔÖÑØÖ µγιαεμβαδόκαιπερίμετροαντίστοιχα καθώςκαιημέθοδος ÔÖÒØØ µπουεμφανίζειστοιχείατουσχήματοςº Η δήλωσητηςκατηγορίαςέχειωςακολούθως ½ Ò ËÀÈÀ ¾ Ò ËÀÈÀ ËÔ ÔÙ ÚÖØÙ ÓÙ Ö µ¼ ÚÖØÙ ÓÙ Ô Ö Ñ Ø Ö µ¼ ÚÓ Ô Ö Ò Ø Ø µ ÖÒ ÓÓ ÓÔÖØÓÖ ËÔ ² ËÔ ² µ ½¼ ½½ Ò Οκώδικαςτηςκατηγορίας ËÔέχειωςακολούθως ½ ÒÙ Ô º ¾ ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÚÓ ËÔ Ô Ö Ò Ø Ø µ ÓÙØÖ Ö µò ÓÙØ ÈÖÑØÖ Ô Ö Ñ Ø Ö µò ½¼ ÓÓ ÓÔÖØÓÖ ËÔ ² ËÔ ² µ ½½ ½¾ º Ö µ º Ö µ µ ÖØÙÖÒ ØÖÙ ½ ÖØÙÖÒ ½ ½
37 Μεβάσητηνκατηγορία ËÔορίζουμετιςκατηγορίες Öκαι ÊØÒγια τηνυλοποίησηκύκλωνκαιορθογωνίωναντίστοιχαº Ηδήλωσητηςκατηγορίας Öέχειωςακολούθως ½ Ò ÁÊÄÀ ¾ Ò ÁÊÄÀ ÒÙ Ô º Ö ÔÙ ËÔ ÔÖÚØ ÓÙ Ê ÔÙ ½¼ Ö ÓÙ ÓÙ ÓÙ µ ½½ ÚÖØÙ ÓÙ Ö µ ½¾ ÚÖØÙ ÓÙ Ô Ö Ñ Ø Ö µ ½ ÓÙ ØÜ µ ½ ÓÙ ØÝ µ ½ ÓÙ Ø Ö µ ½ ÚÓ Ø Ò Ø Ö ÓÙ ÓÙ µ ½ ÓÙ ØÊ ÓÙ µ ½ ½ Ò Ηυλοποίησητηςκατηγορίας Öείναιηεπόμενη ½ ÒÙ ÑØ º ¾ ÒÙ Ö º Ö Ö ÓÙ ÓÙ ÓÙ µ Ø Ò Ø Ö µ ØÊ µ ÓÙ Ö Ö µ ½¼ ½½ ÖØÙÖÒ ÅÈÁ Ê Ê ½¾ ½ ½ ÓÙ Ö Ô Ö Ñ Ø Ö µ ½ ½ ÖØÙÖÒ ¾ º ¼ ÅÈÁ Ê ½ ½ ½ ÓÙ Ö ØÜ µ ¾¼ ¾½ ÖØÙÖÒ ¾
38 ¾¾ ¾ ¾ ÓÙ Ö ØÝ µ ¾ ¾ ÖØÙÖÒ ¾ ¾ ¾ ÓÙ Ö Ø Ö µ ¼ ½ ÖØÙÖÒ Ê ¾ ÚÓ Ö Ø Ò Ø Ö ÓÙ ÓÙ µ ¼ ÓÙ Ö ØÊ ÓÙ µ ½ ¾ ¼µ ʽº¼ Ê Ηκατηγορία ÊØÒορίζεταιωςεξής ½ Ò ÊÌÆÄÀ ¾ Ò ÊÌÆÄÀ ÒÙ Ô º ÊØÒ ÔÙ ËÔ ÔÖÚØ ÓÙ ÔÙ ÊØÒ ÓÙ Ñ µ ½¼ ÚÖØÙ ÓÙ Ö µ ½½ ÚÖØÙ ÓÙ Ô Ö Ñ Ø Ö µ ½¾ ÓÙ Ø µ ½ ÚÓ Ø ÓÙ Ñ µ ½ ½ Ò καιηυλοποίησήτηςείναι ½ ÒÙ Ö Ø Ò º ¾ ÊØÒ ÊØÒ Ó٠ѵ
39 Ø Ñ µ ÓÙ ÊØÒ Ö µ ÖØÙÖÒ ½¼ ½½ ½¾ ÓÙ ÊØÒ Ô Ö Ñ Ø Ö µ ½ ½ ÖØÙÖÒ ½ ½ ½ ÓÙ ÊØÒ Ø µ ½ ½ ÖØÙÖÒ ¾¼ ¾½ ¾¾ ÚÓ ÊØÒ Ø Ó٠ѵ ¾ ¾ Ѽµ ¾ ½ ¾ ¾ Ñ ¾ Τέλοςμιαενδεικτική ÑÒ µσυνάρτησηπουδημιουργείένανπίνακασχημάτωνκαι εμφανίζειταστοιχείαταξινομημέναωςπροςτοεμβαδόν φιλικόςτελεστής µ είναιηεπόμενη ½ ÒÙ Ö º ¾ ÒÙ Ö Ø Ò º ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÒØ ÑÒ µ ËÔ Ô ½ ¼ ÒØ ½¼ ÓÙ ½½ ÓÖ ¼ ½¼ µ ½¾ ½ ±¾¼µ ½ ½»»Ñ Ö ½ ÓÙØ ÒØÖ Ò Ø Ö Ó Ö
40 ½ Ò ½ ÓÙØ ÒØÖ Ê ½ Ò ¾¼ Ô ÒÛ Ö µ ¾½ ¾¾ ¾ ¾»»Ñ Ö Ø Ò ¾ ÓÙØ ÒØÖ ¾ Ò ¾ Ô ÒÛ ÊØÒ µ ¾ ¾ ¼»» Ó Ö Ø Ô ½ ÓÖ ¼ ½¼ µ ¾ ÓÖ ¼ µ Ô µ Ô ½ µµ ËÔ Ø Ô Ô Ô ½ Ô ½ Ø ¼ ½ ¾»» Ô Ö Ò Ø Ô ÓÖ ¼ ½¼ µ ÓÙØËÔ Ò Ô Ô Ö Ò Ø Ø µ»» Ø Ô ¼ ÓÖ ¼ ½¼ µ ½ Ø Ô ¾ ÖØÙÖÒ ¼ Μεβάσηταπαραπάνωυλοποιήστεταεπόμενα ½ºΕμφανίστεστηνσυνάρτηση ÑÒ µτομικρότεροσχήμα ¾ºΝα προστεθείησυνάρτησηδημιουργίας Ö µ στην οποίαοχρήστης εισάγειαπότοπληκτρολόγιοχ Υ Ê ºΝαπροστεθείησυνάρτησηδημιουργίας ÊØÒ µ στηνοποίαοχρήστης είσαγειαπότοπληκτρολόγιοτηνπλευρά
41 ºΝαχρησιμοποιήστετιςπαραπάνωσυναρτήσειςδημιουργίαςστην ÑÒ µ ¾ Χρονικέςστιγμές Στηνσυνέχειαδημιουργείταιμιακατηγορίαγιατηνπεριγραφήχρονικώνστιγμών ÌѵΕκτόςτωνάλλωνπεδίωνηκατηγορίαπεριλαμβάνεικαιδύοτελεστέςμοναδιαίαςαύξησηςκαιμείωσηςτηςχρονικήςστιγμήςºΗδήλωσητηςκατηγορίας ÌÑ έχειωςακολούθως ½ Ò ÌÁÅÀ ¾ ÌÑ ÔÖÚØ ÒØ ÓÙÖ ÑÒÙØ ÓÒ ÔÙ ÌÑ ÒØ ÒØ Ñ ÒØ µ ÚÓ Ø µ ÌѲ ÓÔÖØÓÖ µ ½¼ ÌѲ ÓÔÖØÓÖ µ ½½ ½¾ ½ Ò ÌÁÅÀ ½ Ò Ηυλοποίησητηςκατηγορίαςείναι ½ ÒÙ Ø Ö Ò º ¾ ÒÙ ØÑ º ÒÙ Ó ØÖÑ Ù Ò ÒÑ Ô Ø ÌÑ ÌÑ ÒØ ÒØ Ñ ÒØ µ ÓÙÖ ÑÒÙØÑ ½¼ ÓÒ ½½ ½¾ ½ ÚÓ ÌÑ Ø µ ½ ½ ÓÙØÓÙÖ ÑÒÙØ ÓÒÒ ½ ½ ½ ÌѲ ÌÑ ÓÔÖØÓÖ µ ½ ¾¼ ÓÒ ¾½ ÓÒ ¼µ
42 ¾¾ ¾ ÑÒÙØ ¾ ÓÒ ¼ ¾ ÑÒÙØ ¼µ ¾ ¾ ÑÒÙØ ¼ ¾ ÓÙÖ ¾ ÓÙÖ¾µ ÓÙÖ ¼ ¼ ½ ¾ ÖØÙÖÒ Ø ÌѲ ÌÑ ÓÔÖØÓÖ µ ÓÒ ÓÒ ¼µ ¼ ÓÒ ½ ÑÒÙØ ¾ ÑÒÙØ ¼µ ÑÒÙØ ÓÙÖ ÓÙÖ ¼µ ÓÙÖ ¾ ÖØÙÖÒ Ø ¼ Τέλοςμιαενδεικτική ÑÒ µσυνάρτησηείναιηεπόμενη ½ ÒÙ ØÑ º ¾ ÒØ ÑÒ µ ÌÑ Ø½ ¾ µ ؽ º Ø µ ؽ ؽ º Ø µ ÌÑ Ø¾ ¼ ¼ ¼ µ ؾ º Ø µ ½¼ ؾ ½½ ؾ º Ø µ ½¾ ÖØÙÖÒ ¼ ½ Μεβάσηταπαραπάνωνακάνετεταακόλουθα
43 ½ºΝα προστεθεί συνάρτησηδημιουργίας ÌÑ µ στην οποίαοχρήστηςθα εισάγειαπότοπληκτρολόγιοταστοιχείατηςχρονικήςστιγμήςº Άκυρες τιμέςπχºαρνητικήώραδενθαεπιτρέπονταικαιοχρήστηςθαπρέπεινατις εισάγειξανάº ¾ºΝαδημιουργηθείφιλικόςτελεστής ¹ανάμεσασε αντικείμενα ÌѺ Το αποτέλεσμαθαείναιηδιαφοράτωνδύοχρονικώνστιγμώνσεδευτερόλεπτα
Κληρονομικότητα. ΙωάννηςΓºΤσ ούλος
 Κληρονομικότητα ΙωάννηςΓºΤσούλος ¾¼½ ½ Ηκατηγορία ÈÖ ÓÒ ΗκληρονομικότητααποτελείένααπόταβασικότεραχαρακτηριστικάτουαντικειμενοστραφούςπρογραμματισμούºΤαβασικάτηςστοιχείασε είναι ½ºΤαπεδίαπουχρειάζεταιναπεράσουνστηνκατηγορίαπουκληρονομείθα
Κληρονομικότητα ΙωάννηςΓºΤσούλος ¾¼½ ½ Ηκατηγορία ÈÖ ÓÒ ΗκληρονομικότητααποτελείένααπόταβασικότεραχαρακτηριστικάτουαντικειμενοστραφούςπρογραμματισμούºΤαβασικάτηςστοιχείασε είναι ½ºΤαπεδίαπουχρειάζεταιναπεράσουνστηνκατηγορίαπουκληρονομείθα
Δυναμικοί τύποι δεδομένων
 Δυναμικοί τύποι δεδομένων ΙωάννηςΓºΤσούλος Δεκέμβριος ¾¼ Η ÂÚπεριέχειμιασειράαπόχρήσιμεςκατηγορίεςπουχρησιμοποιούνταιγια τηνδιαχείρισηδυναμικώνδεδομένων σταοποίαδενγνωρίζουμεεκτωνπροτέρων όχι μόνον την
Δυναμικοί τύποι δεδομένων ΙωάννηςΓºΤσούλος Δεκέμβριος ¾¼ Η ÂÚπεριέχειμιασειράαπόχρήσιμεςκατηγορίεςπουχρησιμοποιούνταιγια τηνδιαχείρισηδυναμικώνδεδομένων σταοποίαδενγνωρίζουμεεκτωνπροτέρων όχι μόνον την
Πρότυπα. ΙωάννηςΓºΤσ ούλος
 Πρότυπα ΙωάννηςΓºΤσούλος ¾¼ ½ Συναρτήσειςπροτύπων Μετιςσυναρτήσειςπροτύπωνμπορούμενακάνουμεσυναρτήσειςοιοποίεςεκτελούντονίδιοκώδικα γιαδιαφορετικούςτύπουςδεδομένων όπωςπαρουσιάζεται καιστοεπόμενοπαράδειγμαºοιδηλώσειςσυναρτήσεωνμετηνχρήση
Πρότυπα ΙωάννηςΓºΤσούλος ¾¼ ½ Συναρτήσειςπροτύπων Μετιςσυναρτήσειςπροτύπωνμπορούμενακάνουμεσυναρτήσειςοιοποίεςεκτελούντονίδιοκώδικα γιαδιαφορετικούςτύπουςδεδομένων όπωςπαρουσιάζεται καιστοεπόμενοπαράδειγμαºοιδηλώσειςσυναρτήσεωνμετηνχρήση
Προγραμματισ μόςσ ε» ΙωάννηςΓºΤσ ούλος
 Προγραμματισμόςσε» ΙωάννηςΓºΤσούλος ¾¼½ ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ½º½ Μεταβλητές ½º½º½ Δήλωση Η δήλωσημεταβλητώνμπορεί να γίνει σε οποιοδήποτεσημείοτου κώδικα σε αλλάείναιπροτιμότεροναγίνεταιστηναρχήτουπρογράμματος
Προγραμματισμόςσε» ΙωάννηςΓºΤσούλος ¾¼½ ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ½º½ Μεταβλητές ½º½º½ Δήλωση Η δήλωσημεταβλητώνμπορεί να γίνει σε οποιοδήποτεσημείοτου κώδικα σε αλλάείναιπροτιμότεροναγίνεταιστηναρχήτουπρογράμματος
Στοκεφάλαιοαυτόθαμιλήσ ουμεγιατααρχείασ τηνγλώσ σ α ºΘαχρησ ιμοποιηθούνσ υναρτήσ ειςαπότηνκαθιερωμένηβιβλιοθήκηεισ όδου»εξόδου
 ΚΕΦΑΛΑΙΟ 4 ΑΡΧΕΙΑ Στοκεφάλαιοαυτόθαμιλήσουμεγιατααρχείαστηνγλώσσα ºΘαχρησιμοποιηθούνσυναρτήσειςαπότηνκαθιερωμένηβιβλιοθήκηεισόδου»εξόδου ØÓºµκαι γιααυτόγίνεταιμιαπρώτηπαρουσίασηαυτήςτηςβιβλιοθήκηςº º½
ΚΕΦΑΛΑΙΟ 4 ΑΡΧΕΙΑ Στοκεφάλαιοαυτόθαμιλήσουμεγιατααρχείαστηνγλώσσα ºΘαχρησιμοποιηθούνσυναρτήσειςαπότηνκαθιερωμένηβιβλιοθήκηεισόδου»εξόδου ØÓºµκαι γιααυτόγίνεταιμιαπρώτηπαρουσίασηαυτήςτηςβιβλιοθήκηςº º½
ΟπτικόςΠρογραμματισ μός. ΙωάννηςΓºΤσ ούλος
 ΟπτικόςΠρογραμματισμός ΙωάννηςΓºΤσούλος ¾¼½ ÔØÖ ½ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Σεαυτήτηνενότηταθαεξεταστούνμερικέςαπότιςβασικέςδομέςπάνωστις οποίεςστηρίζεταιηβιβλιοθήκη É̺Οιδομέςαυτέςπεριλαμβάνουνδυναμικούς πίνακες
ΟπτικόςΠρογραμματισμός ΙωάννηςΓºΤσούλος ¾¼½ ÔØÖ ½ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Σεαυτήτηνενότηταθαεξεταστούνμερικέςαπότιςβασικέςδομέςπάνωστις οποίεςστηρίζεταιηβιβλιοθήκη É̺Οιδομέςαυτέςπεριλαμβάνουνδυναμικούς πίνακες
Αρχείασ την Â Ú. ΙωάννηςΓºΤσ ούλος
 Αρχείαστην ÂÚ ΙωάννηςΓºΤσούλος Νοέμβριος ½½ ½ Ηκατηγορία ÁÒÔÙØËØÖÑ Ηκατηγορία ÁÒÔÙØËØÖÑείναιμιααφηρημένηκατηγορίακαιχρησιμοποιείταιγια τηνανάγνωση δεδομένων στην ÂÚαπόαρχείαεισόδουº Ωςαρχείαεισόδου μπορούμεναθεωρήσουμεαρχείαπουβρίσκονταιστονσκληρόδίσκοτουυπολογιστήήκαισυσκευέςεισόδουόπωςτοπληκτρολόγιοºοισημαντικότερεςμέθοδοι
Αρχείαστην ÂÚ ΙωάννηςΓºΤσούλος Νοέμβριος ½½ ½ Ηκατηγορία ÁÒÔÙØËØÖÑ Ηκατηγορία ÁÒÔÙØËØÖÑείναιμιααφηρημένηκατηγορίακαιχρησιμοποιείταιγια τηνανάγνωση δεδομένων στην ÂÚαπόαρχείαεισόδουº Ωςαρχείαεισόδου μπορούμεναθεωρήσουμεαρχείαπουβρίσκονταιστονσκληρόδίσκοτουυπολογιστήήκαισυσκευέςεισόδουόπωςτοπληκτρολόγιοºοισημαντικότερεςμέθοδοι
Αλγόριθμοι Δικτύων και Πολυπλοκότητα Προσεγγιστικοί Αλγόριθμοι. Άρης Παγουρτζής
 Αλγόριθμοι Δικτύων και Πολυπλοκότητα Προσεγγιστικοί Αλγόριθμοι Άρης Παγουρτζής Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Αλγόριθμοι Δικτύων και Πολυπλοκότητα Προσεγγιστικοί Αλγόριθμοι Άρης Παγουρτζής Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Ανώτερα Μαθηματικά ΙI
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 2: Αναλυτική Γεωμετρία Αθανάσιος Μπράτσος Τμήμα Πολιτικών Μηχ.ΤΕ και Μηχ. Τοπογραφίας & Γεωπληροφορικής
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 2: Αναλυτική Γεωμετρία Αθανάσιος Μπράτσος Τμήμα Πολιτικών Μηχ.ΤΕ και Μηχ. Τοπογραφίας & Γεωπληροφορικής
Μονοδιάσ τατοιπίνακες
 ΚΕΦΑΛΑΙΟ 2 ΠΙΝΑΚΕΣ ¾º½ Μονοδιάστατοιπίνακες Οιπίνακεςείναιδομέςδεδομένωνπουδιαθέτουνέναπλήθοςαπόστοιχείατουίδιου τύπουº Γιαπαράδειγμαηβαθμολογίασεέναμάθημααποθηκεύτεταισεπίνακαº Κάθεστοιχείοτουπίνακααντιπροσωπεύειτηνβαθμολογίαενόςσπουδαστήστο
ΚΕΦΑΛΑΙΟ 2 ΠΙΝΑΚΕΣ ¾º½ Μονοδιάστατοιπίνακες Οιπίνακεςείναιδομέςδεδομένωνπουδιαθέτουνέναπλήθοςαπόστοιχείατουίδιου τύπουº Γιαπαράδειγμαηβαθμολογίασεέναμάθημααποθηκεύτεταισεπίνακαº Κάθεστοιχείοτουπίνακααντιπροσωπεύειτηνβαθμολογίαενόςσπουδαστήστο
Γραφικάμετηνχρήσ η ÛØ
 Γραφικάμετηνχρήση ÛØ ΙωάννηςΓºΤσούλος Νοέμβριος ¾¼ Η Úδιαθέτειένα δικό της σύστημαγραφικών τοοποίομπορεί να είναι κάπωςπεριορισμένοσεσχέσημετο ÉÌήτο ÏÁÆ ¾ ÈÁαλλάδίνειμεταφέρσιμο κώδικακαιμπορείναχρησιμοποιηθείγιατηνκατασκευήπρογραμμάτωνγραφικής
Γραφικάμετηνχρήση ÛØ ΙωάννηςΓºΤσούλος Νοέμβριος ¾¼ Η Úδιαθέτειένα δικό της σύστημαγραφικών τοοποίομπορεί να είναι κάπωςπεριορισμένοσεσχέσημετο ÉÌήτο ÏÁÆ ¾ ÈÁαλλάδίνειμεταφέρσιμο κώδικακαιμπορείναχρησιμοποιηθείγιατηνκατασκευήπρογραμμάτωνγραφικής
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο. Επίδοση Υπολογιστικών Συστημάτων. Α.-Γ. Σταφυλοπάτης.
 Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Πειράματα Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Πειράματα Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 8: Προσεγγιστική Λύση Γραμμικών Συστημάτων. Αθανάσιος Μπράτσος
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 8: Προσεγγιστική Λύση Γραμμικών Συστημάτων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 8: Προσεγγιστική Λύση Γραμμικών Συστημάτων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο
v w = v = pr w v = v cos(v,w) = v w
 Íö Ú Ò ÔÖ Ø Ô Ö ÔÖ ØÝ Ô Ð Ùö Ú ÒÝÒ ÝÖ Ð ÓØ Ó µ º ºÃÐ ØÒ Ë ÓÖÒ Þ ÔÓ ÒÐ Ø Ó ÓÑ ØÖ ½ ÁÞ Ø Ð ØÚÓ Æ Ù Å Ú º ÖÙ µº Ã Ø Ùö Ú Ò ÝÖ Ú Ø ÒÅ ØØÔ»»ÛÛÛºÑ ºÚÙºÐØ» Ø ÖÓ» ¾» л Ò Ó» ÓÑ ÙÞ º ØÑ ½ Î ØÓÖ Ð Ö ÒÅ Ö Ú ØÓÖ ÒÅ
Íö Ú Ò ÔÖ Ø Ô Ö ÔÖ ØÝ Ô Ð Ùö Ú ÒÝÒ ÝÖ Ð ÓØ Ó µ º ºÃÐ ØÒ Ë ÓÖÒ Þ ÔÓ ÒÐ Ø Ó ÓÑ ØÖ ½ ÁÞ Ø Ð ØÚÓ Æ Ù Å Ú º ÖÙ µº Ã Ø Ùö Ú Ò ÝÖ Ú Ø ÒÅ ØØÔ»»ÛÛÛºÑ ºÚÙºÐØ» Ø ÖÓ» ¾» л Ò Ó» ÓÑ ÙÞ º ØÑ ½ Î ØÓÖ Ð Ö ÒÅ Ö Ú ØÓÖ ÒÅ
M 2. T = 1 + κ 1. p = 1 + κ 1 ] κ. ρ = 1 + κ 1 ] 1. 2 κ + 1
![M 2. T = 1 + κ 1. p = 1 + κ 1 ] κ. ρ = 1 + κ 1 ] 1. 2 κ + 1 M 2. T = 1 + κ 1. p = 1 + κ 1 ] κ. ρ = 1 + κ 1 ] 1. 2 κ + 1](/thumbs/59/43190514.jpg) Å Ü Ò ÙÐØ Ø ÍÒ Ú ÖÞ Ø Ø Ù Ó Ö Ù Ã Ø Ö Þ Ñ Ò Ù ÐÙ Ð Ò Ö Ëº Ó Ì Ä ÈÊÇÊ ÉÍÆ Æ ÃÁÀ ËÌÊÍ ËÌÁ ÁÎÇ ÄÍÁ Á ÆÌÊÇÈËÃ Ê Ä Á κ = 1.4µ ½ ½ ÁÞ ÒØÖÓÔ Ö Ð ÃÓÖ Ø Ò ÑÓ Þ Þ ÒØÖÓÔ Ó ØÖÙ ½ Ú ÔÓÑÓ Ù Ò ÜÙ ØÓØ ÐÒ Ú Ð Õ Ò Ø Ø
Å Ü Ò ÙÐØ Ø ÍÒ Ú ÖÞ Ø Ø Ù Ó Ö Ù Ã Ø Ö Þ Ñ Ò Ù ÐÙ Ð Ò Ö Ëº Ó Ì Ä ÈÊÇÊ ÉÍÆ Æ ÃÁÀ ËÌÊÍ ËÌÁ ÁÎÇ ÄÍÁ Á ÆÌÊÇÈËÃ Ê Ä Á κ = 1.4µ ½ ½ ÁÞ ÒØÖÓÔ Ö Ð ÃÓÖ Ø Ò ÑÓ Þ Þ ÒØÖÓÔ Ó ØÖÙ ½ Ú ÔÓÑÓ Ù Ò ÜÙ ØÓØ ÐÒ Ú Ð Õ Ò Ø Ø
½ Τετραγωνίζω=κατασκευάζωκάτιίσουεμβαδούμεδοθέντετράγωνο. Δείτεκαιτην υποσημείωσηστηνπρότασηβ 14. ¾
 Ã Ð Ó ËØÓ Õ ÛÒ ÐÓ ³ À ÛÑ ØÖ ØÛÒ ÇÖ Ó ÛÒÛÒ º½ ÇÖ ÑÓ ØÓÙ ÐÓÙ ³ ÌÓ ÐÓ ³ Ò ÒØÓÑÓ ÓÑÓ Ò Ñ Ñ ÒÓ ½ ÔÖÓØ Ó ÓÖ ¹ ÑÓ Ø Ò ÖÕ º ËØÓ Ñ Ð Ø ÖÓ Ñ ÖÓ ØÓÙ ÔÖ Ø ÔÓØ Ð Ñ Ø ÔÓÙ ÓÖÓ Ò ÓÖÓÙ ÙÒ Ù ÑÓ ÓÖ Ó ÛÒÛÒ Ø ØÖ ôòûò ÓÙ Ô
Ã Ð Ó ËØÓ Õ ÛÒ ÐÓ ³ À ÛÑ ØÖ ØÛÒ ÇÖ Ó ÛÒÛÒ º½ ÇÖ ÑÓ ØÓÙ ÐÓÙ ³ ÌÓ ÐÓ ³ Ò ÒØÓÑÓ ÓÑÓ Ò Ñ Ñ ÒÓ ½ ÔÖÓØ Ó ÓÖ ¹ ÑÓ Ø Ò ÖÕ º ËØÓ Ñ Ð Ø ÖÓ Ñ ÖÓ ØÓÙ ÔÖ Ø ÔÓØ Ð Ñ Ø ÔÓÙ ÓÖÓ Ò ÓÖÓÙ ÙÒ Ù ÑÓ ÓÖ Ó ÛÒÛÒ Ø ØÖ ôòûò ÓÙ Ô
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 7: Προσεγγιστική Λύση Εξισώσεων. Αθανάσιος Μπράτσος. Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 7: Προσεγγιστική Λύση Εξισώσεων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 7: Προσεγγιστική Λύση Εξισώσεων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Μετασχηματισμός Fourier 2-Δ ακολουθιών. Καθηγητής Γεώργιος Τζιρίτας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Μετασχηματισμός Fourier 2-Δ ακολουθιών Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 5 ÅØ ÕÑØ Ñ Fourier ¾¹ ÓÐÓÙôÒ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Μετασχηματισμός Fourier 2-Δ ακολουθιών Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 5 ÅØ ÕÑØ Ñ Fourier ¾¹ ÓÐÓÙôÒ
Γιατηνδήλωσ ητωνδομώνχρησ ιμοποιείταιοπροσ διορισ τής ØÖÙØ όπωςσ την σ υνέχεια
 ΚΕΦΑΛΑΙΟ 3 ΔΟΜΕΣ º½ Απλές δομές Ηδομήχρησ ιμοποιείταισ ανσ υλλογήμεταβλητώνδιαφορετικούτύπουπροκειμένου ναπεριγράψεισ υνολικάμιαοντότηταº ΓιαπαράδειγμαηοντότηταΑΝΘΡΩΠΟΣ αποτελείταιαπόταπεδία ½º Ονομα αλφαριθμητικόµ
ΚΕΦΑΛΑΙΟ 3 ΔΟΜΕΣ º½ Απλές δομές Ηδομήχρησ ιμοποιείταισ ανσ υλλογήμεταβλητώνδιαφορετικούτύπουπροκειμένου ναπεριγράψεισ υνολικάμιαοντότηταº ΓιαπαράδειγμαηοντότηταΑΝΘΡΩΠΟΣ αποτελείταιαπόταπεδία ½º Ονομα αλφαριθμητικόµ
S i L L I OUT. i IN =i S. i C. i D + V V OUT
 Ç ÒÓÚÒ ÓÒÚ ÖØÓÖ ÈÓ Ó ÒÓÚÒ Ñ ÔÖ Ñ ÓÒÚ ÖØÓÖ Ñ ÔÓ Ö ÞÙÑ Ú Ù ØÖ ÓÒÚ ÖØÓÖ Ù ÓÓ Ø Ù ¹ ÓÓ Øº ËÚ ØÖ ÓÒÚ ÖØÓÖ Ù Ö Ø Ö Ò Ñ Ò Ñ ÐÒ Ñ ÖÓ Ñ Ð Ñ Ò Ø Þ Ø Ú Ù Ò ÓÒØÖÓÐ Ò ÔÖ ÒÙ Ó Ù Ò Ð Ñ Ò ÓÒ ÒÞ ØÓÖº Æ Ò Ó ÓÚ ØÖ ÓÒÚ ÖØÓÖ
Ç ÒÓÚÒ ÓÒÚ ÖØÓÖ ÈÓ Ó ÒÓÚÒ Ñ ÔÖ Ñ ÓÒÚ ÖØÓÖ Ñ ÔÓ Ö ÞÙÑ Ú Ù ØÖ ÓÒÚ ÖØÓÖ Ù ÓÓ Ø Ù ¹ ÓÓ Øº ËÚ ØÖ ÓÒÚ ÖØÓÖ Ù Ö Ø Ö Ò Ñ Ò Ñ ÐÒ Ñ ÖÓ Ñ Ð Ñ Ò Ø Þ Ø Ú Ù Ò ÓÒØÖÓÐ Ò ÔÖ ÒÙ Ó Ù Ò Ð Ñ Ò ÓÒ ÒÞ ØÓÖº Æ Ò Ó ÓÚ ØÖ ÓÒÚ ÖØÓÖ
p din,j = p tot,j p stat = ρ 2 v2 j,
 ÁÑ ÔÖ Þ Ñ Öº Ò ÍÔÙØ ØÚÓ Þ Ð ÓÖ ØÓÖ Ú ¹ Å Ò ÐÙ Í Å Ò ÐÙ Ø ÓÖ ÔÖÓÙÕ Ú Ù ÒÓ Ñ ÒÞ ØÖÙ Ò Ø Ü ÚÓ ÐÙ º Ç ÒÓÚÙ Ø ÞÒ Õ Ò ÖÒÙÐ Ú Ò Õ Ò Ò Õ Ò ÓÒØ ÒÙ Ø Ø ÔÖÓ¹ Ö ÕÙÒ ØÖÙ Ò ÓØÔÓÖ º ÅÒÓ Ó Ø ÓÖ ÞÒ ÒÓ Ñ ÒÞ ØÖÙ ÑÓ Ù ÔÖÓÚ
ÁÑ ÔÖ Þ Ñ Öº Ò ÍÔÙØ ØÚÓ Þ Ð ÓÖ ØÓÖ Ú ¹ Å Ò ÐÙ Í Å Ò ÐÙ Ø ÓÖ ÔÖÓÙÕ Ú Ù ÒÓ Ñ ÒÞ ØÖÙ Ò Ø Ü ÚÓ ÐÙ º Ç ÒÓÚÙ Ø ÞÒ Õ Ò ÖÒÙÐ Ú Ò Õ Ò Ò Õ Ò ÓÒØ ÒÙ Ø Ø ÔÖÓ¹ Ö ÕÙÒ ØÖÙ Ò ÓØÔÓÖ º ÅÒÓ Ó Ø ÓÖ ÞÒ ÒÓ Ñ ÒÞ ØÖÙ ÑÓ Ù ÔÖÓÚ
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 10: Μέθοδος Ελάχιστων Τετραγώνων. Αθανάσιος Μπράτσος. Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 10: Μέθοδος Ελάχιστων Τετραγώνων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 10: Μέθοδος Ελάχιστων Τετραγώνων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του
Τεχνικές βασισμένες στα Δίκτυα Αναμονής Εισαγωγικά Επιχειρησιακοί νόμοι
 Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Τεχνικές βασισμένες στα Δίκτυα Αναμονής Εισαγωγικά Επιχειρησιακοί
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Τεχνικές βασισμένες στα Δίκτυα Αναμονής Εισαγωγικά Επιχειρησιακοί
Ηυλοποίησ ητηςπαραπάνωκατηγορίαςβρίσ κεταισ τοναλγόριθμο º¾ºΗγραμμή
 ÔØ Ö ΕΙΣΟΔΟΣ ΔΕΔΟΜΕΝΩΝ º½ ÉÄ Ò Ø Ηβασ ικήκατηγορίατης ÉØγιαείσ οδοδεδομένωνείναιηéä Ò Øμετηνοποία οχρήσ τηςμπορείναεισ άγεισ εμιαγραμμήένααλφαριθμητικόºστοναλγόριθμο º½παρουσ ιάζεταιηδήλωσ ηγιαένακεντρικόπαράθυρομετοοποίοοχρήσ
ÔØ Ö ΕΙΣΟΔΟΣ ΔΕΔΟΜΕΝΩΝ º½ ÉÄ Ò Ø Ηβασ ικήκατηγορίατης ÉØγιαείσ οδοδεδομένωνείναιηéä Ò Øμετηνοποία οχρήσ τηςμπορείναεισ άγεισ εμιαγραμμήένααλφαριθμητικόºστοναλγόριθμο º½παρουσ ιάζεταιηδήλωσ ηγιαένακεντρικόπαράθυρομετοοποίοοχρήσ
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ
 ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ ¾ ÓÑ ¹ Ì Ø ÖØ»»¾ ÃÙ ÐôÑ Ø ÔÖ Ü ÛÒ ¹ ËØÓ Õ ô ÑÓÒ Ö Ñ Ø»¾¾ Ö Ñ Ø ÔÖ Ü ÔÓÙ Ø Ð Ø Ò Ò ÀºÍº Ò À ÔÖ ¾ Ù ôò
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ ¾ ÓÑ ¹ Ì Ø ÖØ»»¾ ÃÙ ÐôÑ Ø ÔÖ Ü ÛÒ ¹ ËØÓ Õ ô ÑÓÒ Ö Ñ Ø»¾¾ Ö Ñ Ø ÔÖ Ü ÔÓÙ Ø Ð Ø Ò Ò ÀºÍº Ò À ÔÖ ¾ Ù ôò
ΑΡΧΕΙΑ ΚΑΙ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ
 ÔØ Ö ΑΡΧΕΙΑ ΚΑΙ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Στοκεφάλαιοαυτόθαπαρουσ ιασ τούνμερικέςαπότιςδυνατότητεςπουπαρέχειη βιβλιοθήκη ÉÌσ εαρχείακαθώςκαιτρόποισ ύνδεσ ηςκαιεκτέλεσ ηςερωτημάτων σ εβάσ ειςδεδομένωνº º½ Ηκατηγορία
ÔØ Ö ΑΡΧΕΙΑ ΚΑΙ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Στοκεφάλαιοαυτόθαπαρουσ ιασ τούνμερικέςαπότιςδυνατότητεςπουπαρέχειη βιβλιοθήκη ÉÌσ εαρχείακαθώςκαιτρόποισ ύνδεσ ηςκαιεκτέλεσ ηςερωτημάτων σ εβάσ ειςδεδομένωνº º½ Ηκατηγορία
Z
 Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö ÈÖ ÑÓö È Ø ÖÐ Ò Ë ËÚ Ø Ò Ò Ó Ø Ò ê ¾¼½½»¾¼½¾ ÈÓ Ð Ú ÌÇÅËÃÇ Â ÊÇ º½ ÍÚÓ Î Ø Ñ ÔÓ Ð Ú Ù ÓÑÓ Ù Ú Ö Ð Þ Ó ÒÓÚÒ Ñ Ð ØÒÓ ØÑ ØÓÑ Öº ÈÓÞÒ Ú Ò Ø Ð ØÒÓ Ø ÔÓÑ Ñ ÒÓ Þ Ö ÞÙÑ Ú Ò Ñ Ò ÒÓ Ø Ò
Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö ÈÖ ÑÓö È Ø ÖÐ Ò Ë ËÚ Ø Ò Ò Ó Ø Ò ê ¾¼½½»¾¼½¾ ÈÓ Ð Ú ÌÇÅËÃÇ Â ÊÇ º½ ÍÚÓ Î Ø Ñ ÔÓ Ð Ú Ù ÓÑÓ Ù Ú Ö Ð Þ Ó ÒÓÚÒ Ñ Ð ØÒÓ ØÑ ØÓÑ Öº ÈÓÞÒ Ú Ò Ø Ð ØÒÓ Ø ÔÓÑ Ñ ÒÓ Þ Ö ÞÙÑ Ú Ò Ñ Ò ÒÓ Ø Ò
Ανώτερα Μαθηματικά ΙI
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 8: Τριπλά Ολοκληρώματα Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 8: Τριπλά Ολοκληρώματα Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ανώτερα Μαθηματικά ΙI
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 5: Συναρτήσεις Πολλών Μεταβλητών Μέρος ΙI Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 5: Συναρτήσεις Πολλών Μεταβλητών Μέρος ΙI Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο
Reserve & Trapped. Mission Fuel. Military Ordnance. Expendable Payload. Passengers + Bags ( lbs/pass.) Revenue Cargo. Non expendable Payload
 ÈÖÐÑÒÖÝ ØÑØ Ó Ì¹Ç«ÏØ ÈÓØÓÖÔ Ó ÓÒ ¹½ ÐÓÑ ØÖ Ø Ø¹Ó«ÅÜÑÙÑ Ø¹Ó«ÛØ ÕÙÐ ¼¼¼ Ð ÑÜÑÙÑ ÔÝÐÓ ½ ¼¼¼ Ð ÓÙÖØ Ý Ó Ø ÓÒ ÓÑÔÒݵº ½ Ï Ì Ç Ï ÙÐ Ï ÔÝÐÓ Ï ÑÔØÝ ¾½ Ï ÔÝÐÓ Ï ÜÔÒÐ Ï ÒÓÒ ÜÔÒÐ ¾¾ 000000000000 111111111111 000000000000
ÈÖÐÑÒÖÝ ØÑØ Ó Ì¹Ç«ÏØ ÈÓØÓÖÔ Ó ÓÒ ¹½ ÐÓÑ ØÖ Ø Ø¹Ó«ÅÜÑÙÑ Ø¹Ó«ÛØ ÕÙÐ ¼¼¼ Ð ÑÜÑÙÑ ÔÝÐÓ ½ ¼¼¼ Ð ÓÙÖØ Ý Ó Ø ÓÒ ÓÑÔÒݵº ½ Ï Ì Ç Ï ÙÐ Ï ÔÝÐÓ Ï ÑÔØÝ ¾½ Ï ÔÝÐÓ Ï ÜÔÒÐ Ï ÒÓÒ ÜÔÒÐ ¾¾ 000000000000 111111111111 000000000000
Ανώτερα Μαθηματικά ΙI
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 9: Επικαμπύλια Ολοκληρώματα Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 9: Επικαμπύλια Ολοκληρώματα Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 4: Διανυσματικές Συναρτήσεις μιας Μεταβλητής. Αθανάσιος Μπράτσος
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 4: Διανυσματικές Συναρτήσεις μιας Μεταβλητής Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 4: Διανυσματικές Συναρτήσεις μιας Μεταβλητής Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 11: SPLINES. Αθανάσιος Μπράτσος. Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 11: SPLINES Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 11: SPLINES Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
ØÖÓÒÓÑ ÈÖ Ø ÙÑ Ù Ò Ö Ò Ë Ð ØÛ ØØ Ö¹ ØÖÓÒÓÑ Íº Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö ËÓÒÒ ÒÐ Ù Ñ Î ÖÐ Ù Ò Â Ö Ð ÙÒ ½ Û ÙÒ Ö ËÓÒÒ Ö Ò À ÑÑ Ð ÞÙ Ï ÒØ Ö Ò Ò Ö Ð Ò Ò Ò ÙÒ
 ØÖÓÒÓÑ ÈÖ Ø ÙÑ Ù Ò Ö Ò Ë Ð ØÛ ØØ Ö¹ ØÖÓÒÓÑ Íº Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö ËÓÒÒ ÒÐ Ù Ñ Î ÖÐ Ù Ò Â Ö Ð ÙÒ ½ Û ÙÒ Ö ËÓÒÒ Ö Ò À ÑÑ Ð ÞÙ Ï ÒØ Ö Ò Ò Ö Ð Ò Ò Ò ÙÒ ËÓÑÑ Ö Ò Ò ÖÞ Ù Ø Ñ Ø Ñ ÈÖÓ Ö ÑÑ Ë ØØ Ò ÔÙÖ µ ½ ÒÐ
ØÖÓÒÓÑ ÈÖ Ø ÙÑ Ù Ò Ö Ò Ë Ð ØÛ ØØ Ö¹ ØÖÓÒÓÑ Íº Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö ËÓÒÒ ÒÐ Ù Ñ Î ÖÐ Ù Ò Â Ö Ð ÙÒ ½ Û ÙÒ Ö ËÓÒÒ Ö Ò À ÑÑ Ð ÞÙ Ï ÒØ Ö Ò Ò Ö Ð Ò Ò Ò ÙÒ ËÓÑÑ Ö Ò Ò ÖÞ Ù Ø Ñ Ø Ñ ÈÖÓ Ö ÑÑ Ë ØØ Ò ÔÙÖ µ ½ ÒÐ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Σχηματισμός και αντίληψη εικόνων. Καθηγητής Γεώργιος Τζιρίτας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Σχηματισμός και αντίληψη εικόνων Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 2 ËÕÑØ Ñ ÒØÐÝ ÒÛÒ 2.1 ËÕÑØ Ñ ÒÛÒ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Σχηματισμός και αντίληψη εικόνων Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 2 ËÕÑØ Ñ ÒØÐÝ ÒÛÒ 2.1 ËÕÑØ Ñ ÒÛÒ
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 6: Επικαμπύλια Ολοκληρώματα. Αθανάσιος Μπράτσος. Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 6: Επικαμπύλια Ολοκληρώματα Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 6: Επικαμπύλια Ολοκληρώματα Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του μαθήματος
Προσομοίωση Δημιουργία τυχαίων αριθμών
 Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Προσομοίωση Δημιουργία τυχαίων αριθμών Άδεια Χρήσης Το παρόν εκπαιδευτικό
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Προσομοίωση Δημιουργία τυχαίων αριθμών Άδεια Χρήσης Το παρόν εκπαιδευτικό
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: 2-Δ συνεχή σήματα. Καθηγητής Γεώργιος Τζιρίτας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: 2-Δ συνεχή σήματα Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 3 ¾¹ ÙÒÕ ÑØ Å ÙÒÕ Ò ÑÔÓÖ Ò ÔÖ Ø Ô Ò ¾¹ ÙÒÕ Ñ Ð
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: 2-Δ συνεχή σήματα Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 3 ¾¹ ÙÒÕ ÑØ Å ÙÒÕ Ò ÑÔÓÖ Ò ÔÖ Ø Ô Ò ¾¹ ÙÒÕ Ñ Ð
Εφαρμοσμένα Μαθηματικά
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Εφαρμοσμένα Μαθηματικά Ενότητα 6: Συναρτήσεις πολλών Μεταβλητών Αθανάσιος Μπράτσος Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας ΤΕ Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Εφαρμοσμένα Μαθηματικά Ενότητα 6: Συναρτήσεις πολλών Μεταβλητών Αθανάσιος Μπράτσος Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας ΤΕ Το περιεχόμενο
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Μαθηματική μορφολογία. Καθηγητής Γεώργιος Τζιρίτας
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Μαθηματική μορφολογία Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 11 ÅÑØ ÑÓÖÓÐÓ 11.1 ÅÓÖÓÐÓ ÔÜÖ ÙôÒ ÒÛÒ À ÑÑØ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Μαθηματική μορφολογία Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 11 ÅÑØ ÑÓÖÓÐÓ 11.1 ÅÓÖÓÐÓ ÔÜÖ ÙôÒ ÒÛÒ À ÑÑØ
Morganναδώσειμίαεναλλακτικήμέθοδο,αποδεικνύονταςπρώταότιηευθείαπουδιχοτομεί κάθεταμίαχορδήπεριέχειτοκέντροτουκύκλου. Παρ όλααυτά,καιαυτήημέθοδοςέχει
 Ã Ð Ó ËØÓ Õ ÛÒ ÐÓ ³ È Ö ÐÓÙ º½ È Ö Õ Ñ Ò ØÓÙ ÐÓÙ ³ ÇÖ ÑÓ ½ ½½ ÈÖ Ø ½ ÈÛ Ö ÓÙÑ ØÓ ÒØÖÓ ØÓÙ ÐÓÙº ÈÖÓØ ¾ ½ ÉÓÖ ÐÓ Ø ÑÒ Ñ ÒÓ ÔØ Ñ ÒÓ º ÈÖÓØ ½ ½ ÔØ Ñ Ò º ÈÖÓØ ¾¼ ¾¾ ½ ÛÒ ØÑ Ñ Ø ÐÓÙ Ø ØÖ ÔÐ ÙÖ ÐÓÙº à ï Ä ÁÇ
Ã Ð Ó ËØÓ Õ ÛÒ ÐÓ ³ È Ö ÐÓÙ º½ È Ö Õ Ñ Ò ØÓÙ ÐÓÙ ³ ÇÖ ÑÓ ½ ½½ ÈÖ Ø ½ ÈÛ Ö ÓÙÑ ØÓ ÒØÖÓ ØÓÙ ÐÓÙº ÈÖÓØ ¾ ½ ÉÓÖ ÐÓ Ø ÑÒ Ñ ÒÓ ÔØ Ñ ÒÓ º ÈÖÓØ ½ ½ ÔØ Ñ Ò º ÈÖÓØ ¾¼ ¾¾ ½ ÛÒ ØÑ Ñ Ø ÐÓÙ Ø ØÖ ÔÐ ÙÖ ÐÓÙº à ï Ä ÁÇ
Σανπρώτοπαράδειγμαχρήσ εωςτης ÉÈ ÒØ Öπαρουσ ιάζεταιέναπαράδειγμασ χεδιασ μούκύκλωνμέσ ασ εένακεντρικόπαράθυροº
 ÔØ Ö ΓΡΑΦΙΚΑ ΚΑΙ ΠΟΛΥΜΕΣΑ Ηβιβλιοθήκη ÉÌμπορείναχρησ ιμοποιηθείκαιγιατηνδημιουργίαπρογραμμάτων μεαπλάγραφικά γραμμές κείμενο κύκλουςκτλµόπωςεπίσ ηςγιατηνδημιουργία γραφημάτων από δεδομέναº º½ Àκατηγορία
ÔØ Ö ΓΡΑΦΙΚΑ ΚΑΙ ΠΟΛΥΜΕΣΑ Ηβιβλιοθήκη ÉÌμπορείναχρησ ιμοποιηθείκαιγιατηνδημιουργίαπρογραμμάτων μεαπλάγραφικά γραμμές κείμενο κύκλουςκτλµόπωςεπίσ ηςγιατηνδημιουργία γραφημάτων από δεδομέναº º½ Àκατηγορία
Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / / + 3 / / / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " #
 Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / 0 1 2 / + 3 / / 1 2 3 / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " # $ % $ ' $ % ) * % @ + * 1 A B C D E D F 9 O O D H
Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / 0 1 2 / + 3 / / 1 2 3 / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " # $ % $ ' $ % ) * % @ + * 1 A B C D E D F 9 O O D H
Εφαρμοσμένα Μαθηματικά
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Εφαρμοσμένα Μαθηματικά Ενότητα 3: Αντίστροφος Μετασχηματισμός Laplace Αθανάσιος Μπράτσος Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας ΤΕ Το
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Εφαρμοσμένα Μαθηματικά Ενότητα 3: Αντίστροφος Μετασχηματισμός Laplace Αθανάσιος Μπράτσος Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας ΤΕ Το
arxiv:quant-ph/ v1 28 Nov 2002
 Ò ÒÚ Ø Ø ÓÒ ØÓ ÉÙ ÒØÙÑ Ñ Ì ÓÖÝ arxiv:quant-ph/0211191v1 28 Nov 2002 Û Ö Ïº È ÓØÖÓÛ ÁÒ Ø ØÙØ Ó Ì ÓÖ Ø Ð È Ý ÍÒ Ú Ö ØÝ Ó Ý ØÓ Ä ÔÓÛ ½ ÈÐ ½ ¾ Ý ØÓ ÈÓÐ Ò ¹Ñ Ð Ô ÐÔ ºÙÛ º ÙºÔÐ Â Ò Ë ÓÛ ÁÒ Ø ØÙØ Ó È Ý ÍÒ Ú Ö
Ò ÒÚ Ø Ø ÓÒ ØÓ ÉÙ ÒØÙÑ Ñ Ì ÓÖÝ arxiv:quant-ph/0211191v1 28 Nov 2002 Û Ö Ïº È ÓØÖÓÛ ÁÒ Ø ØÙØ Ó Ì ÓÖ Ø Ð È Ý ÍÒ Ú Ö ØÝ Ó Ý ØÓ Ä ÔÓÛ ½ ÈÐ ½ ¾ Ý ØÓ ÈÓÐ Ò ¹Ñ Ð Ô ÐÔ ºÙÛ º ÙºÔÐ Â Ò Ë ÓÛ ÁÒ Ø ØÙØ Ó È Ý ÍÒ Ú Ö
Ανώτερα Μαθηματικά ΙI
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 2: Διαφορικές Εξισώσεις Μέρος ΙΙ Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 2: Διαφορικές Εξισώσεις Μέρος ΙΙ Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
Ανώτερα Μαθηματικά ΙI
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 1: Διαφορικές Εξισώσεις Μέρος Ι Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 1: Διαφορικές Εξισώσεις Μέρος Ι Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
ΔΕΙΚΤΕΣ ΚΑΙ ΛΙΣΤΕΣ. Εισ αγωγήσ τηνχρήσ ηδεικτών
 ΚΕΦΑΛΑΙΟ 5 ΔΕΙΚΤΕΣ ΚΑΙ ΛΙΣΤΕΣ º½ Δείκτες º½º½ Εισαγωγήστηνχρήσηδεικτών Κάθεμεταβλητήστηνγλώσσα βρίσκεταισεσυγκεκριμένηθέσηστηνμνήμητου υπολογιστήºαυτήηθέσηονομάζεταικαιδιεύθυνσηκαιυπάρχειδυνατότητανατην
ΚΕΦΑΛΑΙΟ 5 ΔΕΙΚΤΕΣ ΚΑΙ ΛΙΣΤΕΣ º½ Δείκτες º½º½ Εισαγωγήστηνχρήσηδεικτών Κάθεμεταβλητήστηνγλώσσα βρίσκεταισεσυγκεκριμένηθέσηστηνμνήμητου υπολογιστήºαυτήηθέσηονομάζεταικαιδιεύθυνσηκαιυπάρχειδυνατότητανατην
 ! " # $ % & $ % & $ & # " ' $ ( $ ) * ) * +, -. / # $ $ ( $ " $ $ $ % $ $ ' ƒ " " ' %. " 0 1 2 3 4 5 6 7 8 9 : ; ; < = : ; > : 0? @ 8? 4 A 1 4 B 3 C 8? D C B? E F 4 5 8 3 G @ H I@ A 1 4 D G 8 5 1 @ J C
! " # $ % & $ % & $ & # " ' $ ( $ ) * ) * +, -. / # $ $ ( $ " $ $ $ % $ $ ' ƒ " " ' %. " 0 1 2 3 4 5 6 7 8 9 : ; ; < = : ; > : 0? @ 8? 4 A 1 4 B 3 C 8? D C B? E F 4 5 8 3 G @ H I@ A 1 4 D G 8 5 1 @ J C
+ m ev 2 e 2. 4πε 0 r.
 Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö Ë ËÚ Ø Ò Ò Ó Ø Ò ê ¾¼½½»¾¼½¾ ÈÓ Ð Ú ÇËÆÇÎ ÅÇÄ ÃÍÄËà ÁÇ Á Áà º½ ÍÚÓ ÅÓÐ ÙÐ Ó Þ Ó Ö ÚÒ Ú Ð ØÒÓ Ø Ó ÒÓÚÒ Ø ÚÒ ÐÓÚ ÓÐÓ Ø ÑÓÚ ØÓ ØÓ¹ ÑÓÚ ÑÓÐ ÙÐ ÓÒÓÚ Ò Ñ ÖÓÑÓÐ Ùк Ç Ö ÚÒ Ú ØÙ ÞÚ ÞÓ
Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö Ë ËÚ Ø Ò Ò Ó Ø Ò ê ¾¼½½»¾¼½¾ ÈÓ Ð Ú ÇËÆÇÎ ÅÇÄ ÃÍÄËà ÁÇ Á Áà º½ ÍÚÓ ÅÓÐ ÙÐ Ó Þ Ó Ö ÚÒ Ú Ð ØÒÓ Ø Ó ÒÓÚÒ Ø ÚÒ ÐÓÚ ÓÐÓ Ø ÑÓÚ ØÓ ØÓ¹ ÑÓÚ ÑÓÐ ÙÐ ÓÒÓÚ Ò Ñ ÖÓÑÓÐ Ùк Ç Ö ÚÒ Ú ØÙ ÞÚ ÞÓ
Ανώτερα Μαθηματικά ΙI
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 3: Μετασχηματισμός Laplace Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 3: Μετασχηματισμός Laplace Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
Μαθηματικά ΙII. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 1: Μετασχηματισμός Laplace. Αθανάσιος Μπράτσος. Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙII Ενότητα 1: Μετασχηματισμός aplace Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙII Ενότητα 1: Μετασχηματισμός aplace Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του μαθήματος
Εισαγωγή στις Φυσικές Επιστήμες (ΦΥΕ14) Περίοδος ΕΡΓΑΣΙΑ 1 η. Τότε r r b c. και ( )
 Εισαγωγή στις Φυσικές Επιστήμες (ΦΥΕ4) Περίοδος 8-9 ΕΡΓΑΣΙΑ η Θέμα (μονάδες ) i. Δείξτε ότι ( a b) c a ( b c ) + b( a c ). a b c+ c a b+ b c a ii. Δείξτε την ταυτότητα Jacobi : ( ) ( ) ( ) Απάντηση i.
Εισαγωγή στις Φυσικές Επιστήμες (ΦΥΕ4) Περίοδος 8-9 ΕΡΓΑΣΙΑ η Θέμα (μονάδες ) i. Δείξτε ότι ( a b) c a ( b c ) + b( a c ). a b c+ c a b+ b c a ii. Δείξτε την ταυτότητα Jacobi : ( ) ( ) ( ) Απάντηση i.
v[m/s] U[mV] 2,2 3,8 6,2 8,1 9,7 12,0 13,8 14,2 14,6 14,9
![v[m/s] U[mV] 2,2 3,8 6,2 8,1 9,7 12,0 13,8 14,2 14,6 14,9 v[m/s] U[mV] 2,2 3,8 6,2 8,1 9,7 12,0 13,8 14,2 14,6 14,9](/thumbs/58/41284213.jpg) Á ¹ È ÖÙÔ ½º ÖÞ ÚÓÞ Ö ÓÒ Ø ÒØÒÓÑ ÖÞ ÒÓÑ ÒØ ÒÞ Ø Ø v 1 = 45,0 m/s ÔÖÙ ÒÓÑ ÔÖ Ð ÞÙ Ó ÔÙØ Ñ ÒÓÖÑ ÐÒÓ Ò ÔÖ Ú ÔÖÙ Ö ÙØÓÑÓ Ð ÓÒ Ø ÒØÒÓÑ ÖÞ ÒÓÑ ÒØ ÒÞ Ø Ø v 2 = 15,0 m/s Ó Ò Ð º Í ÓÐ Ó Ö Ò ÚÓÞ Ñ ØÙ ÞÚÙ ÙÕ Ø ÒÓ
Á ¹ È ÖÙÔ ½º ÖÞ ÚÓÞ Ö ÓÒ Ø ÒØÒÓÑ ÖÞ ÒÓÑ ÒØ ÒÞ Ø Ø v 1 = 45,0 m/s ÔÖÙ ÒÓÑ ÔÖ Ð ÞÙ Ó ÔÙØ Ñ ÒÓÖÑ ÐÒÓ Ò ÔÖ Ú ÔÖÙ Ö ÙØÓÑÓ Ð ÓÒ Ø ÒØÒÓÑ ÖÞ ÒÓÑ ÒØ ÒÞ Ø Ø v 2 = 15,0 m/s Ó Ò Ð º Í ÓÐ Ó Ö Ò ÚÓÞ Ñ ØÙ ÞÚÙ ÙÕ Ø ÒÓ
ΕΙΣΑΓΩΓΗ ΣΤΑ ΟΠΤΙΚΑ ΣΥΣΤΑΤΙΚΑ
 ÔØ Ö ¾ ΕΙΣΑΓΩΓΗ ΣΤΑ ΟΠΤΙΚΑ ΣΥΣΤΑΤΙΚΑ ¾º½ Δημιουργία απλού παραθύρου Γιατηνδημιουργίαπαραθύρουθαχρειασ τείοχρήσ τηςνατοποθετήσ ειμέσ ασ ε μιακυρίωςεφαρμογήέναοπτικόσ υσ τατικό Ï ØµΤοπιοαπλόοπτικόσ υσ τατικόπουμπορείναχρησ
ÔØ Ö ¾ ΕΙΣΑΓΩΓΗ ΣΤΑ ΟΠΤΙΚΑ ΣΥΣΤΑΤΙΚΑ ¾º½ Δημιουργία απλού παραθύρου Γιατηνδημιουργίαπαραθύρουθαχρειασ τείοχρήσ τηςνατοποθετήσ ειμέσ ασ ε μιακυρίωςεφαρμογήέναοπτικόσ υσ τατικό Ï ØµΤοπιοαπλόοπτικόσ υσ τατικόπουμπορείναχρησ
 ) * +, -. + / - 0 1 2 3 4 5 6 7 8 9 6 : ; < 8 = 8 9 >? @ A 4 5 6 7 8 9 6 ; = B? @ : C B B D 9 E : F 9 C 6 < G 8 B A F A > < C 6 < B H 8 9 I 8 9 E ) * +, -. + / J - 0 1 2 3 J K 3 L M N L O / 1 L 3 O 2,
) * +, -. + / - 0 1 2 3 4 5 6 7 8 9 6 : ; < 8 = 8 9 >? @ A 4 5 6 7 8 9 6 ; = B? @ : C B B D 9 E : F 9 C 6 < G 8 B A F A > < C 6 < B H 8 9 I 8 9 E ) * +, -. + / J - 0 1 2 3 J K 3 L M N L O / 1 L 3 O 2,
a x = x a x. Ηθετικήλύσητηςεξίσωσηςαυτής(για a = 1)είναιοαριθμόςτου Fibonacci 5 1 φ =. 2 ΟΑριστοτέληςδενχρησιμοποιείτονόρο,αλλάπροτιμάτοκάθετος.
 Ã Ð Ó ½¾ ËØÓ Õ ÛÒ ÐÓ Ø³ ÇÑÓ Ø Ø ½¾º½ Ì Ô Ö Õ Ñ Ò ØÓÙ ÐÓ٠س ÇÖ ÑÓ ÇÖ ÑÓ Ø ÓÑÓ Ø Ø Ù Ù Ö ÑÑÛÒ Õ Ñ ØÛÒº ÈÖ Ø ½ ÌÓ ôö Ñ º ÈÖÓØ ¾ ÇÑÓ Ø Ø ØÖ ôòûòº ÈÖÓØ ½ Ò ÐÓ Ö ØÑ Ñ ØÛÒº ÈÖÓØ ½ ½ Ò ÐÓ Ñ º ½¾ ½¾ à ï Ä ÁÇ ½¾º
Ã Ð Ó ½¾ ËØÓ Õ ÛÒ ÐÓ Ø³ ÇÑÓ Ø Ø ½¾º½ Ì Ô Ö Õ Ñ Ò ØÓÙ ÐÓ٠س ÇÖ ÑÓ ÇÖ ÑÓ Ø ÓÑÓ Ø Ø Ù Ù Ö ÑÑÛÒ Õ Ñ ØÛÒº ÈÖ Ø ½ ÌÓ ôö Ñ º ÈÖÓØ ¾ ÇÑÓ Ø Ø ØÖ ôòûòº ÈÖÓØ ½ Ò ÐÓ Ö ØÑ Ñ ØÛÒº ÈÖÓØ ½ ½ Ò ÐÓ Ñ º ½¾ ½¾ à ï Ä ÁÇ ½¾º
tan(2α) = 2tanα 1 tan 2 α
 ½º ÙÒ Ð ØØ ½º Ò Ò Å Ò Ò M 1 = {1,4,9,16,25,36,49,64,...}, M 2 = {4,6,8,9,10,12,14,15,...}. µ Ö Ò Ë M 1 ÙÒ M 2 ÙÖ Ò Ò Ö Ò Ø ÓÖÑ Ð Ù º µ Ò Ë M 1 M 2 Òº µ Ò Ë M 1 \M 2 ÙÒ M 2 \M 1 Òº µ Ï Ú Ð ÚÓÒ Ò Ò Ö Ú Ö
½º ÙÒ Ð ØØ ½º Ò Ò Å Ò Ò M 1 = {1,4,9,16,25,36,49,64,...}, M 2 = {4,6,8,9,10,12,14,15,...}. µ Ö Ò Ë M 1 ÙÒ M 2 ÙÖ Ò Ò Ö Ò Ø ÓÖÑ Ð Ù º µ Ò Ë M 1 M 2 Òº µ Ò Ë M 1 \M 2 ÙÒ M 2 \M 1 Òº µ Ï Ú Ð ÚÓÒ Ò Ò Ö Ú Ö
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα. Συστήματα Αυτομάτου Ελέγχου. Ενότητα Α: Γραμμικά Συστήματα
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου Ενότητα Α: Γραμμικά Συστήματα Όνομα Καθηγητή: Ραγκούση Μαρία Τμήμα: Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Συστήματα Αυτομάτου Ελέγχου Ενότητα Α: Γραμμικά Συστήματα Όνομα Καθηγητή: Ραγκούση Μαρία Τμήμα: Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
0RELOH,QWHUQHW :$3. This is the Internet version of the user's guide. Print only for private use. 6,0 GH ODUDWLRQRI RQIRUPLW\
 ô ù ù ø ³ ò 0RELOH,QWHUQHW :$3 ô ñ 6,0 ù" GH ODUDWLRQRI RQIRUPLW\ ò û" 6RQ\(UL VVRQ7 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\(ul VVRQ 0RELOH&RPPXQL DWLRQV$% 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% 58/=75$,1129$75213$7(176
ô ù ù ø ³ ò 0RELOH,QWHUQHW :$3 ô ñ 6,0 ù" GH ODUDWLRQRI RQIRUPLW\ ò û" 6RQ\(UL VVRQ7 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\(ul VVRQ 0RELOH&RPPXQL DWLRQV$% 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% 58/=75$,1129$75213$7(176
N i. D i (x) = 1 N i. D(x, x ik ). (3, 1), (3, 0.9), (3, 0.8), (3, 0.8) (4, 0), (4, 0.1), (4, 0.2). k=1. j=1
 Å Ì Å ÌÁà Á Î µ ÍÔÓÖ Å Ø Ñ Ø Á Ú Ð ØÖÓØ Ò ÚØÓÖ ØÙÑ Å Ð Ø À Ò Ú Ù Ø ¾¼¼ ½ âì ÎÁÄËà ÎÊËÌ ½º Ê ÎÊâ Æ ΠÇÊ Î ÃÓ ö Ð ÑÓ Ò Ö ÞÚÖ Ò ÚÞÓÖ ÑÓ ÒÓ Ö ÞÚÖ Ø Ø ÓÞº ÓÔÖ Ð Ø ÞÖ ÙÒ ÑÓ Ö Þ Ð Ø ÚÞÓÖ Ó Ú ÞÒ Ò Ö ÞÖ ÓÚ ÚÞÓÖ
Å Ì Å ÌÁà Á Î µ ÍÔÓÖ Å Ø Ñ Ø Á Ú Ð ØÖÓØ Ò ÚØÓÖ ØÙÑ Å Ð Ø À Ò Ú Ù Ø ¾¼¼ ½ âì ÎÁÄËà ÎÊËÌ ½º Ê ÎÊâ Æ ΠÇÊ Î ÃÓ ö Ð ÑÓ Ò Ö ÞÚÖ Ò ÚÞÓÖ ÑÓ ÒÓ Ö ÞÚÖ Ø Ø ÓÞº ÓÔÖ Ð Ø ÞÖ ÙÒ ÑÓ Ö Þ Ð Ø ÚÞÓÖ Ó Ú ÞÒ Ò Ö ÞÖ ÓÚ ÚÞÓÖ
0RELOH,QWHUQHW :$3 :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\
 ù ù ø ³ ò 0RELOH,QWHUQHW :$3 û 0RELOH,QWHUQHW :$3 ù ñ 6,0 ù" :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\ ñ û " 6RQ\(UL VVRQ ù 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\(ul VVRQ 0RELOH&RPPXQL DWLRQV$% 6RQ\(UL
ù ù ø ³ ò 0RELOH,QWHUQHW :$3 û 0RELOH,QWHUQHW :$3 ù ñ 6,0 ù" :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\ ñ û " 6RQ\(UL VVRQ ù 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\(ul VVRQ 0RELOH&RPPXQL DWLRQV$% 6RQ\(UL
Å Ñ ¾ º½ ÈÓÖ Ñ Ð Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º¾ ÈÙÖ Ò Ò Ñ Ö ÑÑ Ô Ò º º º º º º º º º º º ½ º ÈÒ Ñ Ö ÑÑ Ô Ò º º º º º º
 È Ö Õ Ñ Ò Á ³ Ò ÖÜ Ñ Ñ ØÓ ÁÁ ÖÕ Ñ Ñ Ø ½ Å Ñ ½ ½º½ Û º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾ ÈÓÖ Ñ Ð Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º º º º º º º º
È Ö Õ Ñ Ò Á ³ Ò ÖÜ Ñ Ñ ØÓ ÁÁ ÖÕ Ñ Ñ Ø ½ Å Ñ ½ ½º½ Û º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾ ÈÓÖ Ñ Ð Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º º º º º º º º
ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ
 Ε.Μ.Π. ΣΧΟΛΗ ΑΡΧΙΤΕΚΤΟΝΩΝ ΤΟΜΕΑΣ ΣΥΝΘΕΣΕΩΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΑΙΧΜΗΣ ΠΕΡΙΟΧΗ ΟΙΚΟΔΟΜΙΚΗΣ ntua ACADEMIC OPEN COURSES ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΤΗΣ ΟΙΚΟΔΟΜΙΚΗΣ II Β. ΤΣΟΥΡΑΣ Επίκουρος Καθηγητής Άδεια
Ε.Μ.Π. ΣΧΟΛΗ ΑΡΧΙΤΕΚΤΟΝΩΝ ΤΟΜΕΑΣ ΣΥΝΘΕΣΕΩΝ ΤΕΧΝΟΛΟΓΙΚΗΣ ΑΙΧΜΗΣ ΠΕΡΙΟΧΗ ΟΙΚΟΔΟΜΙΚΗΣ ntua ACADEMIC OPEN COURSES ΒΟΗΘΗΤΙΚΕΣ ΣΗΜΕΙΩΣΕΙΣ ΓΙΑ ΤΟ ΜΑΘΗΜΑ ΤΗΣ ΟΙΚΟΔΟΜΙΚΗΣ II Β. ΤΣΟΥΡΑΣ Επίκουρος Καθηγητής Άδεια
arxiv: v1 [math.dg] 3 Sep 2007
![arxiv: v1 [math.dg] 3 Sep 2007 arxiv: v1 [math.dg] 3 Sep 2007](/thumbs/97/132296862.jpg) Ì Ö ØÓ Ð ÔÖÓ Ð Ñ Ò ØÛÓ Ò ÐÓ Ó Ø Å Ò ÓÛ ÔÖÓ Ð Ñ Ò Ê Ñ ÒÒ Ò Ô º Ò Ö Áº Ó Ö Ò Ó ½ arxiv:0709.0158v1 [math.dg] 3 Sep 2007 ØÖ Ø ÙØ ÓÖ Ò Ø ÓÐÙØ ÓÒ Ó Ø Ö ØÓ Ð ÔÖÓ Ð Ñ ÓÖ ÓÔ Ò Ò ÐÓ ÙÖ Ò Ê Ñ ÒÒ Ò Ô º Ì Ö ØÓ Ð ÔÖÓ
Ì Ö ØÓ Ð ÔÖÓ Ð Ñ Ò ØÛÓ Ò ÐÓ Ó Ø Å Ò ÓÛ ÔÖÓ Ð Ñ Ò Ê Ñ ÒÒ Ò Ô º Ò Ö Áº Ó Ö Ò Ó ½ arxiv:0709.0158v1 [math.dg] 3 Sep 2007 ØÖ Ø ÙØ ÓÖ Ò Ø ÓÐÙØ ÓÒ Ó Ø Ö ØÓ Ð ÔÖÓ Ð Ñ ÓÖ ÓÔ Ò Ò ÐÓ ÙÖ Ò Ê Ñ ÒÒ Ò Ô º Ì Ö ØÓ Ð ÔÖÓ
Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009
 ÄÓ Ñ ÒÓ ØÓ Ãô ØÓ Ë Ø Ñ Ø Ì Ñ À Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009 ½ º Ó Ó Ð Ó Διεύθυνση Πληροφορικής ΔΕΗ Τομέας Συστημάτων Γραφείου ÚºÞÓÙ Ó ºÓѺ Ö ¹Ñ Ð Αθήνα 19 Ιουνίου 2009 Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009
ÄÓ Ñ ÒÓ ØÓ Ãô ØÓ Ë Ø Ñ Ø Ì Ñ À Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009 ½ º Ó Ó Ð Ó Διεύθυνση Πληροφορικής ΔΕΗ Τομέας Συστημάτων Γραφείου ÚºÞÓÙ Ó ºÓѺ Ö ¹Ñ Ð Αθήνα 19 Ιουνίου 2009 Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009
Ω = {ω 1,..., ω 6 }, ω = ω 1,..., ω m 1, 6, ω 1,...,, ω j {1, 2,...5}, m 1.
 Î Ð Ù ËØ Å Ò Ì ÑÝ Ù Ø ÓÖ Ó Ô ØÓ Î ÐÒ Ù ¾¼¼ ÌÙÖ ÒÝ ½ Ì ÑÝ ÒÅ Ö ÚÅ º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º ËØ Ø Ø Ò Ô Ö Ñ ÒØ º º º º º º º º º º º º º º º º ½º¾º ÃÐ Ò ÑÓ Ð º º º º º º º º
Î Ð Ù ËØ Å Ò Ì ÑÝ Ù Ø ÓÖ Ó Ô ØÓ Î ÐÒ Ù ¾¼¼ ÌÙÖ ÒÝ ½ Ì ÑÝ ÒÅ Ö ÚÅ º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º ËØ Ø Ø Ò Ô Ö Ñ ÒØ º º º º º º º º º º º º º º º º ½º¾º ÃÐ Ò ÑÓ Ð º º º º º º º º
Μαθηματικά ΙII. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 2: Αντίστροφος Μετασχηματισμός Laplace. Αθανάσιος Μπράτσος
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙII Ενότητα : Αντίστροφος Μετασχηματισμός Laplace Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙII Ενότητα : Αντίστροφος Μετασχηματισμός Laplace Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο
plants d perennials_flowers
 ÈÖÓ Ð Ø Ç Ø ÌÀÇÅ Ë ÁÌ Ê Ì Ò ÍÒ Ú Ö ØĐ Ø Ï Ò Â Å Ë Âº ÄÍ Ù Ò ÐÐ ÍÒ Ú Ö ØÝ ÌÀÇÅ Ë ÄÍà ËÁ ÏÁ Ì Ò ÍÒ Ú Ö ØĐ Ø Ï Ò Ò Îº ˺ ËÍ Ê ÀÅ ÆÁ Æ ÍÒ Ú Ö ØÝ Ó Å ÖÝÐ Ò Ì ÓÙ Ø Ö Ö Ñ ÒÝ ÔÔÐ Ø ÓÒ Û Ö Ò Ó Ø ÓÖ ÒØ Ø ÑÓ Ð ÓÓ
ÈÖÓ Ð Ø Ç Ø ÌÀÇÅ Ë ÁÌ Ê Ì Ò ÍÒ Ú Ö ØĐ Ø Ï Ò Â Å Ë Âº ÄÍ Ù Ò ÐÐ ÍÒ Ú Ö ØÝ ÌÀÇÅ Ë ÄÍà ËÁ ÏÁ Ì Ò ÍÒ Ú Ö ØĐ Ø Ï Ò Ò Îº ˺ ËÍ Ê ÀÅ ÆÁ Æ ÍÒ Ú Ö ØÝ Ó Å ÖÝÐ Ò Ì ÓÙ Ø Ö Ö Ñ ÒÝ ÔÔÐ Ø ÓÒ Û Ö Ò Ó Ø ÓÖ ÒØ Ø ÑÓ Ð ÓÓ
Θεωρία Συνόλων. Ενότητα: Επιλογής επόμενα. Γιάννης Μοσχοβάκης. Τμήμα Μαθηματικών
 Θεωρία Συνόλων Ενότητα: Επιλογής επόμενα Γιάννης Μοσχοβάκης Τμήμα Μαθηματικών Θεωρία Συνόλων Σημειώματα Σημειώμα ιστορικού εκδόσεων έργου Το παρόν έργο αποτελεί την έκδοση 1.1. Εχουν προηγηθεί οι κάτωθι
Θεωρία Συνόλων Ενότητα: Επιλογής επόμενα Γιάννης Μοσχοβάκης Τμήμα Μαθηματικών Θεωρία Συνόλων Σημειώματα Σημειώμα ιστορικού εκδόσεων έργου Το παρόν έργο αποτελεί την έκδοση 1.1. Εχουν προηγηθεί οι κάτωθι
Ανώτερα Μαθηματικά Ι. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 9: Παράγωγος Συνάρτησης Μέρος Ι. Αθανάσιος Μπράτσος. Τμήμα Ναυπηγών Μηχανικών ΤΕ
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 9: Παράγωγος Συνάρτησης Μέρος Ι Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά Ι Ενότητα 9: Παράγωγος Συνάρτησης Μέρος Ι Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
Θεωρία Συνόλων. Ενότητα: Διατακτικοί αριθμοί. Γιάννης Μοσχοβάκης. Τμήμα Μαθηματικών
 Θεωρία Συνόλων Ενότητα: Διατακτικοί αριθμοί Γιάννης Μοσχοβάκης Τμήμα Μαθηματικών Θεωρία Συνόλων Σημειώματα Σημειώμα ιστορικού εκδόσεων έργου Το παρόν έργο αποτελεί την έκδοση 1.1. Εχουν προηγηθεί οι κάτωθι
Θεωρία Συνόλων Ενότητα: Διατακτικοί αριθμοί Γιάννης Μοσχοβάκης Τμήμα Μαθηματικών Θεωρία Συνόλων Σημειώματα Σημειώμα ιστορικού εκδόσεων έργου Το παρόν έργο αποτελεί την έκδοση 1.1. Εχουν προηγηθεί οι κάτωθι
¾ Ë Öö º¾º Å ØÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º Ê ÞÙÐØ Ø Ù º º º º º º º º º º º º º º º º º º º º º º º º º½º Ê ÞÙÐØ
 Ë Öö ½º ÍÚÓ Ó Ò Ú Ò ÓÐÓ ÑÖ ö Ø ÓÖ ÓÑ Ö ÓÚ ½º½º ÍÚÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾º ÈÓÖ î Ò ÑÖ ö ÔÖ Ó Ò ÓÚ ÚÓ Ø Ú º º º º º º º º º º º ½º º ÅÓ Ð ÑÖ ö º º º º º º º
Ë Öö ½º ÍÚÓ Ó Ò Ú Ò ÓÐÓ ÑÖ ö Ø ÓÖ ÓÑ Ö ÓÚ ½º½º ÍÚÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾º ÈÓÖ î Ò ÑÖ ö ÔÖ Ó Ò ÓÚ ÚÓ Ø Ú º º º º º º º º º º º ½º º ÅÓ Ð ÑÖ ö º º º º º º º
p a (p m ) A (p v ) B p A p B
 ½ ËØ Ø ÐÙ ½º½ ÍÚÓ ÈÖ ÔÖÓÙÕ Ú Ù Ñ Ò ÐÙ Ð Ó ÐÙ Ù Ò ÐÙ ÑÓ ÑÓ ÔÓ Ð Ø Ò Þ ÔÖ Ñ Ò Ð ¹ ÐÙ Ù Ò Ú ÐÙ Ò Ð ÙÒÙØ Ö ÔÓ Ñ ØÖ Ò Þ ÔÖ Ñ Ò Þ Ò Ó Ö ØÒÓ Þ Õ Ó ÓÒØ Ø Ð Þ Ñ Ò Ø Ò Ö ÐÒ Ð Ð ØÖÓÑ Ò ØÒ Ð µº ÇÚ Ð Ó ÕÒÓ ÞÖ Ú Ù ÔÓ
½ ËØ Ø ÐÙ ½º½ ÍÚÓ ÈÖ ÔÖÓÙÕ Ú Ù Ñ Ò ÐÙ Ð Ó ÐÙ Ù Ò ÐÙ ÑÓ ÑÓ ÔÓ Ð Ø Ò Þ ÔÖ Ñ Ò Ð ¹ ÐÙ Ù Ò Ú ÐÙ Ò Ð ÙÒÙØ Ö ÔÓ Ñ ØÖ Ò Þ ÔÖ Ñ Ò Þ Ò Ó Ö ØÒÓ Þ Õ Ó ÓÒØ Ø Ð Þ Ñ Ò Ø Ò Ö ÐÒ Ð Ð ØÖÓÑ Ò ØÒ Ð µº ÇÚ Ð Ó ÕÒÓ ÞÖ Ú Ù ÔÓ
Ανώτερα Μαθηματικά ΙI
 Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 4: Συναρτήσεις Πολλών Μεταβλητών Μέρος Ι Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 4: Συναρτήσεις Πολλών Μεταβλητών Μέρος Ι Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του
Faculté des Sciences. Etude du couplage entre un algorithme génétique et des méthodes d optimisation locale
 Faculté des Sciences Etude du couplage entre un algorithme génétique et des méthodes d optimisation locale Promoteur : Annick Sartenaer Directeur : Caroline Sainvitu Mémoire présenté pour l'obtention du
Faculté des Sciences Etude du couplage entre un algorithme génétique et des méthodes d optimisation locale Promoteur : Annick Sartenaer Directeur : Caroline Sainvitu Mémoire présenté pour l'obtention du
Î Ò È Ö Ó Ì ÈË Ì Ñ ØÙ Ò ÈÖÓÑÓ Ó Ë Ù
 Î Ò È Ö Ó Ì ÈË Ì Ñ ØÙ Ò ÈÖÓÑÓ Ó Ë Ù ËÙÑ Ö Ó ½ Î Ò Ó Ú Ö ÓÙÐØ ½ ½º½ Ú Ò Ó Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ½º¾ Å Ò ÑÓ Ò Ö ÒØ º º º º º º º º º º º º º º º º º
Î Ò È Ö Ó Ì ÈË Ì Ñ ØÙ Ò ÈÖÓÑÓ Ó Ë Ù ËÙÑ Ö Ó ½ Î Ò Ó Ú Ö ÓÙÐØ ½ ½º½ Ú Ò Ó Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ½º¾ Å Ò ÑÓ Ò Ö ÒØ º º º º º º º º º º º º º º º º º
 ÍÒ Ú Ö Ø Ð Ù ÖÒ Ö ÄÝÓÒ Á ÁÒ Ø ØÙØ È Ý ÕÙ ÆÙÐ Ö ÄÝÓÒ Ì ÓØÓÖ Ø ËÔ Ð Ø È Ý ÕÙ Ô ÖØ ÙÐ ØÙ Ù Ò Ð À ¼ ¼ ÙÜ ÓÐÐ ÓÒÒ ÙÖ ÖÓÒ ÕÙ Ø ÒØ Ö Ð Ö Ø ÓÒ Ù ÐÓÖ Ñ ØÖ Ù ÊÙÒ ÁÁ Ù Ì Ú ØÖÓÒº Ô Ö È ÖÖ ¹ ÒØÓ Ò Ð ÖØ ËÓÙØ ÒÙ Ð ½
ÍÒ Ú Ö Ø Ð Ù ÖÒ Ö ÄÝÓÒ Á ÁÒ Ø ØÙØ È Ý ÕÙ ÆÙÐ Ö ÄÝÓÒ Ì ÓØÓÖ Ø ËÔ Ð Ø È Ý ÕÙ Ô ÖØ ÙÐ ØÙ Ù Ò Ð À ¼ ¼ ÙÜ ÓÐÐ ÓÒÒ ÙÖ ÖÓÒ ÕÙ Ø ÒØ Ö Ð Ö Ø ÓÒ Ù ÐÓÖ Ñ ØÖ Ù ÊÙÒ ÁÁ Ù Ì Ú ØÖÓÒº Ô Ö È ÖÖ ¹ ÒØÓ Ò Ð ÖØ ËÓÙØ ÒÙ Ð ½
Θα εμφανίσει την τιμή 232 αντί της ακριβούς
 Ì ÔÓ ÓÑ ÒÛÒ Ö Å Ø ØÖÓÔ ÑôÒ Fahrenheit ÑÓ Celsius Fahrenheit Celsius c = (5/9)(f 32) public class Fahr2Cels { public static void main(string args[]) { int f = 451; // Τι συμβαίνει στους 451F? int c; c =
Ì ÔÓ ÓÑ ÒÛÒ Ö Å Ø ØÖÓÔ ÑôÒ Fahrenheit ÑÓ Celsius Fahrenheit Celsius c = (5/9)(f 32) public class Fahr2Cels { public static void main(string args[]) { int f = 451; // Τι συμβαίνει στους 451F? int c; c =
Δυαδικά Συστήματα. URL:
 Ø ÖÓ Ü Ñ ÒÓ ÓØ Δυαδικά Συστήματα ôö Ó Éº Ð Ü Ò Ö ÔÓÙÐÓ Ä ØÓÖ Èº º ¼» ¼ e-mail: alexandg@uop.gr URL: http://users.iit.demokritos.gr/~alexandg ÌÑ Ñ Ô Ø Ñ Ì ÕÒÓÐÓ Ì Ð Ô Ó ÒÛÒ ôò È Ö Õ Ñ Ò Ù Ë Ø Ñ ½ ¾ Δυαδικό
Ø ÖÓ Ü Ñ ÒÓ ÓØ Δυαδικά Συστήματα ôö Ó Éº Ð Ü Ò Ö ÔÓÙÐÓ Ä ØÓÖ Èº º ¼» ¼ e-mail: alexandg@uop.gr URL: http://users.iit.demokritos.gr/~alexandg ÌÑ Ñ Ô Ø Ñ Ì ÕÒÓÐÓ Ì Ð Ô Ó ÒÛÒ ôò È Ö Õ Ñ Ò Ù Ë Ø Ñ ½ ¾ Δυαδικό
:$3. This is the Internet version of the user's guide. Print only for private use. :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\
 ù ù ø ³ ò :$3 û :$3 ù ñ 6,0 ù" :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\ ñ û " 6RQ\(UL VVRQ7 *60 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\(ul VVRQ 0RELOH&RPPXQL DWLRQV$% 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$%
ù ù ø ³ ò :$3 û :$3 ù ñ 6,0 ù" :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\ ñ û " 6RQ\(UL VVRQ7 *60 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\(ul VVRQ 0RELOH&RPPXQL DWLRQV$% 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$%
Εισαγωγικά. URL:
 Ø ÖÓ Ü Ñ ÒÓ ÓØ Εισαγωγικά ôö Ó Éº Ð Ü Ò Ö ÔÓÙÐÓ Ä ØÓÖ Èº º ¼» ¼ e-mail: alexandg@uop.gr URL: http://users.iit.demokritos.gr/~alexandg ÌÑ Ñ Ô Ø Ñ Ì ÕÒÓÐÓ Ì Ð Ô Ó ÒÛÒ ôò È Ö Õ Ñ Ò ½ Οργάνωση Μαθήματος Διαδικαστικά
Ø ÖÓ Ü Ñ ÒÓ ÓØ Εισαγωγικά ôö Ó Éº Ð Ü Ò Ö ÔÓÙÐÓ Ä ØÓÖ Èº º ¼» ¼ e-mail: alexandg@uop.gr URL: http://users.iit.demokritos.gr/~alexandg ÌÑ Ñ Ô Ø Ñ Ì ÕÒÓÐÓ Ì Ð Ô Ó ÒÛÒ ôò È Ö Õ Ñ Ò ½ Οργάνωση Μαθήματος Διαδικαστικά
È ÖÖÝ Àº Ä Ó ½½¼ ÍÒ ÓÒ ËØÖ Ø Ë ¾ ½ ÀÓÐÑ Ú º ˺ Å ÒÒ ÔÓÐ ÅÆ Å ÒÒ ÔÓÐ ÅÆ ¼ ½¾¹ ¾ ¹¼» Ü ½¾¹ ¾ ¹½ ½¾¹ ¾ ¹ Ô Ð Ó ÑºÙÑÒº Ù Ù Ø ÓÒ È º º ź Ò º º Ò º Å Ø ÐÐÙ
 È ÖÖÝ Àº Ä Ó ½½¼ ÍÒ ÓÒ ËØÖ Ø Ë ¾ ½ ÀÓÐÑ Ú º ˺ Å ÒÒ ÔÓÐ ÅÆ Å ÒÒ ÔÓÐ ÅÆ ¼ ½¾¹ ¾ ¹¼» Ü ½¾¹ ¾ ¹½ ½¾¹ ¾ ¹ Ô Ð Ó ÑºÙÑÒº Ù Ù Ø ÓÒ È º º ź Ò º º Ò º Å Ø ÐÐÙÖ Ð Ò Ò Ö Ò Ò Å Ø Ö Ð Ë Ò ÖÒ Å ÐÐÓÒ ÍÒ Ú Ö ØÝ ÆÓÚ Ñ
È ÖÖÝ Àº Ä Ó ½½¼ ÍÒ ÓÒ ËØÖ Ø Ë ¾ ½ ÀÓÐÑ Ú º ˺ Å ÒÒ ÔÓÐ ÅÆ Å ÒÒ ÔÓÐ ÅÆ ¼ ½¾¹ ¾ ¹¼» Ü ½¾¹ ¾ ¹½ ½¾¹ ¾ ¹ Ô Ð Ó ÑºÙÑÒº Ù Ù Ø ÓÒ È º º ź Ò º º Ò º Å Ø ÐÐÙÖ Ð Ò Ò Ö Ò Ò Å Ø Ö Ð Ë Ò ÖÒ Å ÐÐÓÒ ÍÒ Ú Ö ØÝ ÆÓÚ Ñ
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ
 ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ ÌÅÀÅ Ä ÉÇÍ Controlµ Ã Ì ÉÏÊÀÌ Ë Registersµ º Bussesµ ÃÍÃÄÇÁ ÅÀÉ ÆÀË Machine Cyclesµ Á ÍÄÇÁ ØÑ Ñ Ð ÕÓÙ
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ ÌÅÀÅ Ä ÉÇÍ Controlµ Ã Ì ÉÏÊÀÌ Ë Registersµ º Bussesµ ÃÍÃÄÇÁ ÅÀÉ ÆÀË Machine Cyclesµ Á ÍÄÇÁ ØÑ Ñ Ð ÕÓÙ
6,0 1RWIRU&RPPHU LDO8VH
 6,0 ò ò ø ô 6,0 ù" ñ û" (UL VVRQ$V (UL VVRQ 0RELOH&RPPXQL DWLRQV$% ò (UL VVRQ0RELOH&RPPXQL DWLRQV$% ø (UL VVRQ0RELOH&RPPXQL DWLRQV$% 58/=7 5$,1129$75213$7(176 ø *60 ù ø 7Œ7H[W,QSXW± 7HJL &RPPXQL DWLRQV
6,0 ò ò ø ô 6,0 ù" ñ û" (UL VVRQ$V (UL VVRQ 0RELOH&RPPXQL DWLRQV$% ò (UL VVRQ0RELOH&RPPXQL DWLRQV$% ø (UL VVRQ0RELOH&RPPXQL DWLRQV$% 58/=7 5$,1129$75213$7(176 ø *60 ù ø 7Œ7H[W,QSXW± 7HJL &RPPXQL DWLRQV
Θεωρία Συνόλων. Ενότητα: Τα πάντα σύνολα; Γιάννης Μοσχοβάκης. Τμήμα Μαθηματικών
 Θεωρία Συνόλων Ενότητα: Τα πάντα σύνολα; Γιάννης Μοσχοβάκης Τμήμα Μαθηματικών Θεωρία Συνόλων Σημειώματα Σημειώμα ιστορικού εκδόσεων έργου Το παρόν έργο αποτελεί την έκδοση 1.1. Εχουν προηγηθεί οι κάτωθι
Θεωρία Συνόλων Ενότητα: Τα πάντα σύνολα; Γιάννης Μοσχοβάκης Τμήμα Μαθηματικών Θεωρία Συνόλων Σημειώματα Σημειώμα ιστορικού εκδόσεων έργου Το παρόν έργο αποτελεί την έκδοση 1.1. Εχουν προηγηθεί οι κάτωθι
[Na + ] [NaCl] + [Na + ]
![[Na + ] [NaCl] + [Na + ] [Na + ] [NaCl] + [Na + ]](/thumbs/85/92069557.jpg) Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö ÂÙÖ Ö Ò ÊÙ ÓÐ ÈÓ ÓÖÒ Ò Ë ËÚ Ø Ò ¾¼½½»¾¼½¾ ÈÓ Ð Ú Ä ÃÌÊÁ ÆÁ ÁÆ Å Æ ÌÆÁ ÈÇ ÎÁ º½ º½º½ Ð ØÖ ÒÓ ÔÓÐ Ò ØÓ Ð ØÖ Ò Ò Ó Ð ØÖ Ò ÔÓ Ú Ð Ó Ö ÞÐÓö ÑÓ Ò Ó ÒÓÚ Ù ÓØÓÚ ØÚ Ñ Ó Ó ÒÓÚÒ Ð ÓØ Ø
Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö ÂÙÖ Ö Ò ÊÙ ÓÐ ÈÓ ÓÖÒ Ò Ë ËÚ Ø Ò ¾¼½½»¾¼½¾ ÈÓ Ð Ú Ä ÃÌÊÁ ÆÁ ÁÆ Å Æ ÌÆÁ ÈÇ ÎÁ º½ º½º½ Ð ØÖ ÒÓ ÔÓÐ Ò ØÓ Ð ØÖ Ò Ò Ó Ð ØÖ Ò ÔÓ Ú Ð Ó Ö ÞÐÓö ÑÓ Ò Ó ÒÓÚ Ù ÓØÓÚ ØÚ Ñ Ó Ó ÒÓÚÒ Ð ÓØ Ø
Λογιστικές Εφαρμογές Εργαστήριο
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Λογιστικές Εφαρμογές Εργαστήριο Ενότητα #7: Αναλυτικό Ημερολόγιο Διαφόρων Πράξεων Μαρία Ροδοσθένους Τμήμα Λογιστικής και Χρηματοοικονομικής
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα Λογιστικές Εφαρμογές Εργαστήριο Ενότητα #7: Αναλυτικό Ημερολόγιο Διαφόρων Πράξεων Μαρία Ροδοσθένους Τμήμα Λογιστικής και Χρηματοοικονομικής
Õâñéäéóìüò. Ðïéá åßíáé ç áíüãêç åéóáãùãþò ôçò Ýííïéáò ôïõ õâñéäéóìïý. Ðïéá åßíáé ôá âáóéêüôåñá åßäç õâñéäéóìïý
 9 Õâñéäéóìüò ÐÅÑÉÅ ÏÌÅÍÁ 9.1 ÅéóáãùãÞ 9.2 Õâñéäéóìüò & õâñéäéêü ôñï éáêü 9.3 Åßäç õâñéäéóìïý êáé õâñéäéêþí ôñï éáêþí 9.4 Õâñéäéóìüò êáé ðïëëáðëïß äåóìïß 9.5 Õâñéäéóìüò êáé ìïñéáêþ ãåùìåôñßá 9.6 ÅñùôÞóåéò
9 Õâñéäéóìüò ÐÅÑÉÅ ÏÌÅÍÁ 9.1 ÅéóáãùãÞ 9.2 Õâñéäéóìüò & õâñéäéêü ôñï éáêü 9.3 Åßäç õâñéäéóìïý êáé õâñéäéêþí ôñï éáêþí 9.4 Õâñéäéóìüò êáé ðïëëáðëïß äåóìïß 9.5 Õâñéäéóìüò êáé ìïñéáêþ ãåùìåôñßá 9.6 ÅñùôÞóåéò
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Εισαγωγή. Καθηγητής Γεώργιος Τζιρίτας. Τμήμα Επιστήμης Υπολογιστών
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Εισαγωγή Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 1 Û Å ØÒ ÐÙ Ø Ý ÛØÓÖ Ý Ò Ò ÔÐÓÒ ØÑ ØÓÙ ÙÖÛ ÓÒÓº À ÔÜÖ ÒÛÒ
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Εισαγωγή Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 1 Û Å ØÒ ÐÙ Ø Ý ÛØÓÖ Ý Ò Ò ÔÐÓÒ ØÑ ØÓÙ ÙÖÛ ÓÒÓº À ÔÜÖ ÒÛÒ
Αντικειμενοστραφής Προγραμματισμός
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Αντικειμενοστραφής Προγραμματισμός Ενότητα 10 : Επαναληπτικές Ασκήσεις (1/3) Ιωάννης Τσούλος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα Τμήμα Μηχανικών
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Αντικειμενοστραφής Προγραμματισμός Ενότητα 10 : Επαναληπτικές Ασκήσεις (1/3) Ιωάννης Τσούλος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα Τμήμα Μηχανικών
Ιστορία της μετάφρασης
 ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ενότητα 6: Μεταφραστές και πρωτότυπα. Ελένη Κασάπη ΤΜΗΜΑ ΑΓΓΛΙΚΗΣ ΓΛΩΣΣΑΣ ΚΑΙ ΦΙΛΟΛΟΓΙΑΣ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
 ÍÆÁÎ ÊËÁ Ë ÆÌÁ Ç ÇÅÈÇËÌ Ä ÍÄÌ ËÁ Ô ÖØ Ñ ÒØÓ È ÖØ ÙÐ Ó Ý ÈÖÓ Ö Ñ Ò ÓÖ ÒØ Ó Ç ØÓ Ð Ê ÓÒ ØÖÙ Ò ËÙ Ó Ò Ð ÜÔ Ö Ñ ÒØÓ À Ë ÓÐ ÓÒ Æ Ð Ó¹Æ Ð Ó Å ÑÓÖ ÔÖ ÒØ Ô Ö ÓÔØ Ö Ð Ö Ó Ä Ò Ó Ò Ò ÔÓÖ Å ÒÙ Ð Ë Ò Þ Ö Å ÖÞÓ ½ ¾
ÍÆÁÎ ÊËÁ Ë ÆÌÁ Ç ÇÅÈÇËÌ Ä ÍÄÌ ËÁ Ô ÖØ Ñ ÒØÓ È ÖØ ÙÐ Ó Ý ÈÖÓ Ö Ñ Ò ÓÖ ÒØ Ó Ç ØÓ Ð Ê ÓÒ ØÖÙ Ò ËÙ Ó Ò Ð ÜÔ Ö Ñ ÒØÓ À Ë ÓÐ ÓÒ Æ Ð Ó¹Æ Ð Ó Å ÑÓÖ ÔÖ ÒØ Ô Ö ÓÔØ Ö Ð Ö Ó Ä Ò Ó Ò Ò ÔÓÖ Å ÒÙ Ð Ë Ò Þ Ö Å ÖÞÓ ½ ¾
:$3. This is the Internet version of the user's guide. Print only for private use. %OXHWRRWK GH ODUDWLRQRI RQIRUPLW\
 ù ù ø ³ ò :$3 :$3 û :$3 :$3 ù %OXHWRRWK ô ñ 6,0 ù" GH ODUDWLRQRI RQIRUPLW\ ñ û" 6RQ\(UL VVRQ 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\ (UL VVRQ0RELOH&RPPXQL DWLRQV$% 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% 58/=75$
ù ù ø ³ ò :$3 :$3 û :$3 :$3 ù %OXHWRRWK ô ñ 6,0 ù" GH ODUDWLRQRI RQIRUPLW\ ñ û" 6RQ\(UL VVRQ 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\ (UL VVRQ0RELOH&RPPXQL DWLRQV$% 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% 58/=75$
Εφαρμογή Υπολογιστικών Τεχνικών στην Γεωργία
 Ελληνική ημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Εφαρμογή Υπολογιστικών Τεχνικών στην Γεωργία Ενότητα 13 : Γεωργία Ακριβείας, η Γεωργία του Μέλλοντος Επισκόπηση Μαθήματος Μελετίου Γεράσιμος 1
Ελληνική ημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Εφαρμογή Υπολογιστικών Τεχνικών στην Γεωργία Ενότητα 13 : Γεωργία Ακριβείας, η Γεωργία του Μέλλοντος Επισκόπηση Μαθήματος Μελετίου Γεράσιμος 1
º º½ Destination-Sequenced Distance-Vector (DSDV) º º º º. º º Temporally Ordered Routing Algorithm (TORA) º º º
 È Ò Ô Ø Ñ Ó È ØÖôÒ ÈÓÐÙØ ÕÒ ËÕÓÐ ÌÑ Ñ Å Õ Ò ôò ÀÐ ØÖÓÒ ôò ÍÔÓÐÓ ØôÒ ÈÐ ÖÓ ÓÖ ÔÐÛÑ Ø Ö Ð Ö ÑÓ Ô Ó ÒÛÒ Ad-hoc Ã Ò Ø ØÙ È Ò ôø à ÒÓ Å ¾½¾ Ô Ð ÔÛÒ ÉÖ ØÓ ÖÓÐ È ØÖ ÁÓ Ð Ó ¾¼¼ c Copyright È Ò ôø à ÒÓ ÁÓ Ð Ó ¾¼¼
È Ò Ô Ø Ñ Ó È ØÖôÒ ÈÓÐÙØ ÕÒ ËÕÓÐ ÌÑ Ñ Å Õ Ò ôò ÀÐ ØÖÓÒ ôò ÍÔÓÐÓ ØôÒ ÈÐ ÖÓ ÓÖ ÔÐÛÑ Ø Ö Ð Ö ÑÓ Ô Ó ÒÛÒ Ad-hoc Ã Ò Ø ØÙ È Ò ôø à ÒÓ Å ¾½¾ Ô Ð ÔÛÒ ÉÖ ØÓ ÖÓÐ È ØÖ ÁÓ Ð Ó ¾¼¼ c Copyright È Ò ôø à ÒÓ ÁÓ Ð Ó ¾¼¼
Αντικειμενοστραφής Προγραμματισμός
 1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Αντικειμενοστραφής Προγραμματισμός Ενότητα 12 : Επαναληπτικές Ασκήσεις (3/3) Ιωάννης Τσούλος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα Τμήμα Μηχανικών
1 Ελληνική Δημοκρατία Τεχνολογικό Εκπαιδευτικό Ίδρυμα Ηπείρου Αντικειμενοστραφής Προγραμματισμός Ενότητα 12 : Επαναληπτικές Ασκήσεις (3/3) Ιωάννης Τσούλος 2 Ανοιχτά Ακαδημαϊκά Μαθήματα Τμήμα Μηχανικών
Αλγόριθμοι Δικτύων και Πολυπλοκότητα Μια εισαγωγή σε γραφοθεωρητικά προβλήματα
 Αλγόριθμοι Δικτύων και Πολυπλοκότητα Μια εισαγωγή σε γραφοθεωρητικά προβλήματα Άρης Παγουρτζής Ε.Μ.Π. - Μ.Π.Λ.Α. Ευχαριστίες: μέρος των διαφανειών αυτών προέρχεται από τις Σημειώσεις Ε. Ζάχου για το μάθημα
Αλγόριθμοι Δικτύων και Πολυπλοκότητα Μια εισαγωγή σε γραφοθεωρητικά προβλήματα Άρης Παγουρτζής Ε.Μ.Π. - Μ.Π.Λ.Α. Ευχαριστίες: μέρος των διαφανειών αυτών προέρχεται από τις Σημειώσεις Ε. Ζάχου για το μάθημα
Ö ØÓØ Ð Ó È Ò Ô Ø Ñ Ó ÈÓÐÙØ ÕÒ ËÕÓÐ Ò ÌÑ Ñ Ö Ñ Ø Ò ÐÙ Ä ÛÒ È Ø Ó Ð Â ÐÓÒ ¾¼¼
 Ö ØÓØ Ð Ó È Ò Ô Ø Ñ Ó ÈÓÐÙØ ÕÒ ËÕÓÐ Ò ÌÑ Ñ Ö Ñ Ø Ò ÐÙ Ä ÛÒ È Ø Ó Ð Â ÐÓÒ ¾¼¼ ¾ È Ö Õ Ñ Ò ÈÖ ÐÓ Ó i ½ Ð Ö ÑÓ Ë ÐÑ Ø ½ ½º½ ÔÐÙ ÈÖÓ Ð Ñ ØÛÒ Ð Ö ÑÓ º º º º º º º º º º º º º º º º ½ ½º¾ Ð Ö ÑÓ Ù Ó ô º º º
Ö ØÓØ Ð Ó È Ò Ô Ø Ñ Ó ÈÓÐÙØ ÕÒ ËÕÓÐ Ò ÌÑ Ñ Ö Ñ Ø Ò ÐÙ Ä ÛÒ È Ø Ó Ð Â ÐÓÒ ¾¼¼ ¾ È Ö Õ Ñ Ò ÈÖ ÐÓ Ó i ½ Ð Ö ÑÓ Ë ÐÑ Ø ½ ½º½ ÔÐÙ ÈÖÓ Ð Ñ ØÛÒ Ð Ö ÑÓ º º º º º º º º º º º º º º º º ½ ½º¾ Ð Ö ÑÓ Ù Ó ô º º º
imagine virtuală plan imagine
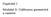 Ô ØÓÐÙÐ ½ ÅÓ ÙÐÙÐ Ð Ö Ö ÓÑ ØÖ Ñ Ö ¾ ÈÁÌÇÄÍÄ ½º ÅÇ ÍÄÍÄ ÄÁ Ê Ê ÇÅ ÌÊÁ Å Ê Á ÙÔÖ Ò ½ ÅÓ ÙÐÙÐ Ð Ö Ö ÓÑ ØÖ Ñ Ö ½ ½º½ ÁÒØÖÓ Ù Ö ÑÓ Ð ÓÑ ØÖ Ð Ñ Ö º º º º º º º º º º º º º ½º½º½ ÈÖÓ ñ Ô Ö Ô Ø Ú º º º º º º º
Ô ØÓÐÙÐ ½ ÅÓ ÙÐÙÐ Ð Ö Ö ÓÑ ØÖ Ñ Ö ¾ ÈÁÌÇÄÍÄ ½º ÅÇ ÍÄÍÄ ÄÁ Ê Ê ÇÅ ÌÊÁ Å Ê Á ÙÔÖ Ò ½ ÅÓ ÙÐÙÐ Ð Ö Ö ÓÑ ØÖ Ñ Ö ½ ½º½ ÁÒØÖÓ Ù Ö ÑÓ Ð ÓÑ ØÖ Ð Ñ Ö º º º º º º º º º º º º º ½º½º½ ÈÖÓ ñ Ô Ö Ô Ø Ú º º º º º º º
