v w = v = pr w v = v cos(v,w) = v w
|
|
|
- Φιλύρη Αβραμίδης
- 7 χρόνια πριν
- Προβολές:
Transcript
1 Íö Ú Ò ÔÖ Ø Ô Ö ÔÖ ØÝ Ô Ð Ùö Ú ÒÝÒ ÝÖ Ð ÓØ Ó µ º ºÃÐ ØÒ Ë ÓÖÒ Þ ÔÓ ÒÐ Ø Ó ÓÑ ØÖ ½ ÁÞ Ø Ð ØÚÓ Æ Ù Å Ú º ÖÙ µº Ã Ø Ùö Ú Ò ÝÖ Ú Ø ÒÅ ØØÔ»»ÛÛÛºÑ ºÚÙºÐØ» Ø ÖÓ» ¾» л Ò Ó» ÓÑ ÙÞ º ØÑ ½ Î ØÓÖ Ð Ö ÒÅ Ö Ú ØÓÖ ÒÅ Ò Ù Íö Ú Ò ÙÓ öò Ù Ù Ø Ñ Ù Ò Ð Ó Ñ Ø Ú ÑÓ Ú ØÓÖ Ò Ö Ú V = k n Ú Ö ÙÒÓ k = R,C, Ö Q Ò Ñ V ½ ¾ º Â Ñ V ½ Ø V ÙØ ÑÔ Ù Ô Ù ÙÒÙ kº Â Ñ V ¾ Ø V Ú Ò Ñ ÔÐÓ ØÙÑ º Â Ñ V Ø V Ú Ò Ñ Ô ÔÖ Ù Ö Ú º ÈÖ Ñ Ò Ñ Ð Ø Ö Ð Ò Ù Ô ÖÅ ö ÑÙ ÙÖ ÙÚÓ Ô Ø Ø Ð ÖÓ ÙÖ º Ë Ð Ö ÒÅ Ò Ù º Ì Ö Ñ ÙÓØ Ù Ú ØÓÖ v = (x 1,x,...,x n ) Ö w = (y 1,y,...,y n ) Ø Ø Ò ÖØ Ò Ð Ö Ò Ò Ù öýñå Ñ v wº È Ð Ô ÖÅ ö Ñ v w ÝÖ Ù Ô ÙÓ Ñ Ô Ð ÓÖÑÙÐ v w = n x i y i. i=1 Î ØÓÖ Ù Ð º Ä Ý Ñ Ú ØÓÖ Ù v = (x 1,...,x n ) Ð v ÝÖ Ú Ö Ø ÒÅ Ò Ð Ö ÒÅ Ò Ù Ó v v غݺ v = v v = n x i. à ÑÔ Ø ÖÔ Ú ØÓÖ Ù º à ÑÔÓ Ø ÖÔ Ú ØÓÖ Ù v,w Ó ÒÙ Ô Ð Ô ÖÅ ö Ñ ÝÖ ÐÝ Ù Ð Ö Ò Ú ØÓÖ Ù Ò Ù Ô Ð ÒØ Ù Ð Ù Ò Ù Ó i=1 cos(v,w) = v w v w.  ٠v w = 0 Ø Ý Ñ Ú ØÓÖ v Ö w ÝÖ Ø ØÑ Ò Ö öýñå Ñ v wº  ٠cos(v,w) = ±1 Ø Ý Ñ Ú ØÓÖ v Ö w ÝÖ ÓÐ Ò Ö ÐÝ Ö Ø µ Ö öýñå Ñ v w º Î ØÓÖ Ù v ÔÖÓ Ú ØÓÖ Ù w öýñå Ñ pr w vº  ÐÝ pr w v = v cos(v,w) = v w w.  ٠ÙÓØ Ù Ú ØÓÖ v,w Ø Ð Ñ ÙöÖ ÝØ ØÓ ÝÑ w = w v +w v, w v v, Ö w v v. ½
2 Æ ÙÒ Ð Ñ Ô Ø Ö ÒØ w v = (v w) (v v) v, w (v w) v = w (v v) v Î ØÓÖ Ù w Ø Ô Ò Ý v ØöÚ Ð Ù ÝÖ ÒØ Ú ØÓÖ Ù öýñ Ñ ref v (w)µ ref v (w) = w v w v = (v w) (v v) v w Î ØÓÖ ÒÅ Ò Ù ØÖ Ñ ØÅ Ö ÚÅ µº Ì Ö Ñ ÙÓØ Ù Ú ØÓÖ v 1 Ö v Ø Ú ØÓÖ Ò Ò Ù öýñå Ñ v 1 v. È Ð Ô ÖÅ ö Ñ v = v 1 v ÝÖ Ú ØÓÖ Ù Ù Ò ÓÑ ÚÝ Å Ñ ½º Î ØÓÖ Ù v Ð ÝÖ ÐÝ Ö Ø Ò Ó ÙÖ Ô ÖÅ ö Ú ØÓÖ v 1 Ö v ÔÐÓØ º ¾º v ÝÖ Ø ØÑ Ò v 1 Ö v Ú ØÓÖ Ñ º º Î ØÓÖ v,v 1,v ØÙÖ ØÓ Ô ÓÖ ÒØ Ô Ö Ý x,y,zº Ì Ö Ø ÖÑ Ò ÒØ ÙÖ Ù ÖÓ ØÖ Ù Ú ØÓÖ Ù v,v 1,v ÓÓÖ Ò ØÅ ÝÖ Ø Ñ º Î ØÓÖ Ù v = v 1 v Ð Ñ Ô ÙÓØ Ô Ð ÓÖÑÙÐ i j k ( ) v 1 v = a 1 b 1 c 1 a b c = b 1 c 1 b c, a 1 c 1 a c, a 1 b 1 a b i,j,k ÝÖ Ú Ò Ø Ò Ú ØÓÖ Ø Å Ø Ý x,y,z, v i = (a i,b i,c i ),i = 1,º Î ØÓÖ Ù v 1 v Ð Ð Ñ Ö Ø Ô Ð ÓÖÑÙÐ v 1 v = v 1 v (v 1 v ) ¾µ Å Ö Ò Ù ØÖ Ñ ØÅ Ö ÚÅ µº ÌÖ Ù Ú ØÓÖ Ù v 1,v,v 3 Ñ Ö Ò Ù ÝÖ Ù ÙÖ öýñå Ñ (v 1,v,v 3 )º È Ð Ô ÖÅ ö Ñ â Ó Ö Ò Ó Ö ÞÙÐØ Ø ÝÖ Ù (v 1,v,v 3 ) = (v 1,v,v 3 ) = (v 1 v ) v 3 = v 1 (v v 3 ). a 1 b 1 c 1 a b c a 3 b 3 c 3 ½µ, µ v i = (a i,b i,c i ),i = 1,,3º ÈÖ Ñ Ò Ñ ÓÑ ØÖ ÒÅ Ø ÖÑ Ò ÒØÓ ÔÖ ÑÅ ÝÖ ÓÖ ÒØÙÓØ Ø ÙÖ Ö Ñ Ö Ú ØÓÖ Ù Ò¹ Ù µ ÙÖ Ò ÖÙ Ò¹Ñ ØÅ Ö ÚÅ ØÚ Ù öýñå Ñ (v 1,v,...,v n )º  ÐÝ Ù (v 1,v,...,v n ) = a 1 b 1 c 1... e 1 a b c... e a n b n c n... e n, µ ¾
3 v i = (a i,b i,c i,...,e i ),i = 1,,...,nº Î Ñ Ù Ú ØÓÖ ½¹½º Î ØÓÖ a Ö b Ù ÖÓ ½¾¼ Ð Ô Ò Ù ÑÔ º Ê Ø a+b Ö a b a = 3 Ö b = 5º ¾¹ º ÙÓØ Ú ØÓÖ a = (1, 1,), b = (,0,)) Ö c = (3,,1)º Ê Ø µ ac µ (a + b)c µ a(a+3c) µ (ab)c ¹ ¼¾º Î ØÓÖ Ú Ò Ù ØÙ Ù ÖÓ ¼ Ð Ô Ò Ù ÑÔ º a = 4, b =, c = 6º Ê Ø Ú ØÓÖ Ù p = a+b+c Ð º ¹ ¼ º ÙÓØ a = 3, b = 5º Ê Ø ØÓ Ù α Ú ØÓÖ Ù a + αb ÙØÙ Ø ØÑ Ò Ú ØÓÖ Ù a αbº ¹ ¼¼º Î ØÓÖ a,b,c Ú Ò Ø Ò º a+b+c = 0º Ê Ø ab+bc+caº ¹ ¼¼³º Î ØÓÖ a,b,c ÝÖ Ò Ù Ð Ù a =, b = 3, c = 4º ØÓ a+b+c = 0º Ê Ø ab,bc,caº ¹ ¼ º Î ØÓÖ a Ö b Ù ÖÓ ÑÔ φ = π/6, a = 3, b = 1º Ê Ø ÑÔ α Ø ÖÔ Ú ØÓÖ Ù p = a+b Ö q = a bº ¹ º ÃÓ Ú ØÓÖ Ù Ø ÖÔÙ Ú Ó a,b,c Ô Å Ø Ù (a b)c = a(b c) ¹ ¾ º Î ØÓÖ b Ö a = (6; 8; 7,5) ÓÐ Ò Ö Ù º b = 50º Ê Ø Ú ØÓÖ Ù b ÓÓÖ Ò Ø º Î ØÓÖ Ù b Ù ÇÞ Ñ Ù ÖÓ Ñ ÐÙ ÑÔ º ½¼¹ º ÙÓØ ØÖÝ Ú ØÓÖ a = i+j +k,b = i+5j Ö c = 4i+4j kº Ê Ø pr c (3a b) Ú ØÓÖ Ù 3a b ÔÖÓ Ú ØÓÖ Ù c Ö ÞÙÐØ Ø ÝÖ Ù º ½½¹½ º ÙÓØ Ú ØÓÖ a = (,1,0), b = (, 1,1) Ö c = (0,1,1)º Ê Ø µ a b µ (a b) c µ pr c b (3a b) ½¾¹½ º ÙÓØ Ú ØÓÖ a = (,1,0), b = (0, 1,1) ÙÖ ÙØ ÑÔ Ù ÐÝ Ö Ø Ò Ó Ö Ø ÒÅ Ñ º Ê Ø ÐÝ Ö Ø Ò Ó ÔÐÓØ Ö ÑÔ ÙÖ Ù ÖÓ ÐÝ Ö Ø Ò Ó ØÖ ö ÒÅ Ñ º ½ ¹½ º ÙÓØ Ú ØÓÖ a = (1,0,1), b = (0,, 1), c = (1,,)º Ê Ø Ú ØÓÖ Ù m ÙÖ Ø ØÑ Ò a Ö b Ö Ó ÔÖÓ Ú ØÓÖ Ù m ÐÝ ½º ½ ¹ ½¾º ÙÓØ Ú ØÓÖ a = (4; ; 4),b= (6; 3;)º Ê Ø ½µab ¾µ a µ b µ(a 3b)(a+b) µ(a+b) µ(a b) µ a bº ½ ¹ ¼º ÙÓØ a = 10, b = Ö ab = 1º Ê Ø a b º ½ ¹ º Î ØÓÖ a Ö b Ù ÖÓ ÑÔ φ = (π)/3º a = 1 b = º Ê Ø ½µ(a b) ¾µ((a+b) (a+ b)) µ((a+3b) (3a b)) º
4 ½ ¹½º ÙÓØ Ù Ú ØÓÖ a = (1,,),b = (,6,3)º µ Ê Ø Ú ØÓÖ Ù ÙÖ Ù ÖÓ Ú ÒÓ Ù ÑÔÙ Ù ÙÓØ Ú ØÓÖ Ö ÙØÙ ØÓ Ô Ó ÔÐÓ ØÙÑÓ Ô Ö Ú ØÓÖ a,bº µ Ê Ø Ú ØÓÖ Ù c ÙÖ ÝÖ Ø Ô Ò Ý Ú ØÓÖ Ù a ØöÚ Ð Ù b غݺ c = a a,b,c ÝÖ Ú ÒÓ ÔÐÓ ØÙÑÓ ØÓ ÑÔ Ø ÖÔ b,a Ö b,c ÝÖ ÐÝ Ù º ½ ¹¾º ÙÓØ Ú ØÓÖ Ù a = (1,,3)º Ê Ø Ù Ø ØÑ ÒÙ Ú ØÓÖ Ù ÙÖ Ù ÖÓ Ø ØÙ ÑÔ Ù ÙÓØÙ Ú ØÓÖ ÙÑ º ½ ¹ º ÙÓØ ÖÓÑ Ó ØÖ ö Ò Ù Ö ÒØ Ú ØÓÖ Ù p = (,4)º Ê Ø ÖÓÑ Ù Ö Ò Ù Ö Ø Ò Ù Ú ØÓÖ Ù a,b Ù ½µ ÑÔ Ø ÖÔ a Ö p ÝÖ π 6 ¾µ ÑÔ Ø ÖÔ a Ö p ÝÖ π 4 º ¾¼¹ º ÙÓØ Ú ØÓÖ Ù a = (,1)º Ê Ø Ú ØÓÖ Ù c ÙÖ ÝÖ ÙØ Ô Ù Ù Ú ØÓÖ Ù a ¼ Ð Ô Ò Ù ÑÔÙ ÔÖ Ð ÖÓ ö Ó ÖÓ Ý Ð º ¾½¹½½½ º È Ø Ö Ò Ø Ö ÓÔÐ Ò Ö Ù ÒØÝ ØÖÝ Ú ØÓÖ ½µ a = (, 1,3), b = (1,4,), c = (3,1, 1). ¾µ l = (1,6,5), m = (3,,4), n = (7, 18,). ¾¾¹½¾ º ÌÖ ÑÔ Ó ÔÐÓØ S = 3º Î Ö ÙÒÅ A(3;1) Ö B(1; 3) ÚÓÖ Ó ÒØÖ ÝÖ Ý Çܺ Ê Ø Ú Ö ÙÒÅ C ÓÓÖ Ò Ø º ¾ ¹¼º ÙÓØ Ø A = (3,6, 1) Ö B = ( 3,9,0)º Ê Ø Ø C ÒØ Ø ÖÔ Ø Ù A Ö B ÙÖ Ø Ò ÒØÙ ÐÝ AC = CB º ¾ ¹½º ÙÓØÓ Ú Ú Ö ØÓ Ú Ö ÙÒÅ A = (3, 1) Ö B = ( 1,8) Ò Ó Ó ØÖ ö ÒÅ º Ê Ø Ø Ú Ö ØÓ Ú Ö ÙÒ º ¾ ¹½º ÙÓØ ØÖÝ ØÖ ÑÔ Ó Ö Ø Ò Ù Ú ÙÖ Ó Ø Q 1 = (1, 1,0),Q = (0,,3),Q 3 = ( 1,1,)º Ê Ø ØÖ ÑÔ Ó Ú Ö ÙÒ º ¾ ¹¾º ÙÓØÓ ØÖÝ ÐÝ Ö Ø Ò Ó Ú Ö ÙÒÅ Q 1 = (1, 1,0),Q = (0,,3),Q 3 = ( 1,1,)º ØÚ ÖØ ÐÝ Ö Ø Ò Ó Ú Ö ÙÒº Ê Ø ¾ ¹ º ÙÓØÓ ØÖÝ ØÖ ÑÔ Ó Ú Ö ÙÒÅ Q 1 = (1, 1,0),Q = (0,,3),Q 3 = ( 1,1,)º Ê Ø ØÖ ÑÔ Ó ÔÐÓØ º ¾ ¹ º ÙÓØ Ø Q 0 = (8,9, 1)),Q 1 = (1, 1,0),Q = (0,,3),Q 3 = ( 1,1,)º Ö ÔÖ Ð Ù Ó Ú Ò ÔÐÓ ØÙÑ
5 ¾ ¹ º ÙÓØ Ø A = (7,71), B = ( 1,18), C = (71,73), D = (33,37)º Ö Ø D ÝÖ ØÖ ÑÔ Ó A, B, C Ú Ù ¼¹ º ÙÓØ Ø A = (7,71), B = ( 1,18), C = (71,73), D = (33,37)º Ö Ø ÖÔÓ [A,B] Ö [C,D] ÖØ ½¹ º ÙÓØ Ø A = (7,71),B = ( 18,17),C = (33,37)º Ò ÒØ Ø Ó Ð Ò ÙÖ Ó ÔÙ Å Ù Ø Ã ÖÅ Ö ÒÅ ¾¹ º ÙÓØ ÐÙ ØÙÖ ÑÔ ÔÐÓ ØÙÑÓ ÙÖ Ó Ú Ö ÙÒÅ ÝÖ P 1,P,P 3,P 4 º Ö ÒØ Ø ÒÝ Ú Ø Ò Ã ØÙÖ ÑÔ Ó ØÖ ö ÒÅ Ù ÖØ Ø 1 4 P P P P 4. Â Ù Ò Ø Ó Ñ ØÙÖ ÑÔ Ñ Ø Ò ¹ º ÙÓØ ØÙÖ Ø Ö ÚÅ P 1,P,P 3,P 4 Ø ØÖ ÖÓ Ú Ö ÙÒÅ µº Ø ÖÔÓ Ø ÖÔ P i Ö P j Ú ÙÖ Ó Ø öýñå Ñ P ij Ø ÖÔ ÙÒ Ò Ø Ù P ij ÖP kl öýñå Ñ ij kl º Á ÖÓ ÝØ Ø ÖÔÓ 1 34, 13 4, 14 3 ÖØ Ú Ò Ñ Ø º Ê Ø º ¹½½ º Ê Ø ØÖ ÑÔ Ó ÔÐÓØ Ù Ó Ú Ö ÙÒ Ù ÓÓÖ Ò ØÅ ½µ A(; 3),B(3;) Ö C( ;5) ¾µ M 1 ( 3;),M (5; ) Ö M 3 (1;3) µ M(3; 4),N( ;3) Ö P(4;5)º ¹½½ ³º Ê Ø ØÖ ÑÔ Ó ÔÐÓØ Ù Ó Ú Ö ÙÒ Ù ÓÓÖ Ò ØÅ A(; 3;0),B(3; ;0) Ö C(; 4;) ¹½¾¾º ÌÖ ÑÔ Ó ÔÐÓØ S = 3º Î Ö ÙÒÅ A(3;1) Ö B(1; 3) Ó C ÝÖ Ý Çݺ Ê Ø Ú Ö ÙÒÅ C ÓÓÖ Ò Ø º ¹½º ÙÓØ ØÖÝ ØÖ ÑÔ Ó Ú ÙÖ Ó Ø M 1 = (1, 1,0),M = (0,,3),M 3 = ( 1,1,) Ö Ø Ó Ú Ö ÙÒ º ¹¾º Ê Ø ØÖ ÑÔ Ó M 1,M,M 3 ÔÐÓØ º ¹½¾ º ÄÝ Ö Ø Ò Ó ÔÐÓØ S = 17º Ú Ú Ö ÙÒÅ Ù ÓÓÖ Ò ØÅ Ñ A(;1) Ö B(5; 3)º Ê Ø Ú Ù ØÙ Ú Ö ÙÒ Ù ÓÓÖ Ò Ø ØÖ ö Ò Ù Ù ÖØ ÑÓ Ø ÝÖ ÒØ ÓÖ Ò Ù º ¼¹¾¾ º Ê Ø Ø Ó Q ÓÓÖ Ò Ø Ñ ØÖ Ó Ø Ù P = ( 5;13) Ø Å t : x 3y 3 = 0 ØöÚ Ð Ùº Ö Ð Ø Ö Ø ÓÖÑÙÐ ½¹¾ º ÙÓØÓ ØÖ ÑÔ Ó Ú Ö ÙÒÅ A(1; ),B(5;4) Ö C( ;0)º ËÙ ÖÝØ Ú Ò Ó Ö ÓÖ Ò Ó ÑÔÙ A ÔÙ Ù ÑÔ Ò Ù ÐÝ Ø º
6 ¾¹¾ º ÙÓØÓ ØÖ ÑÔ Ó Ú Ö ÙÒÅ A(; ),B(3; 5) Ö C(5;7)º ËÙ ÖÝØ Ø ØÑ Ò ÒÙÐ ØÓ Ú Ö ÙÒÅ C Ú Ò Ó ÑÔÓ A ÔÙ Ù ÑÔ Ò ÐÝ Ø º ¹¾ º âú Ó Ô Ò ÙÐÝ ÒÙ Ö ÔØ Ô Ð Ø t 1 : x y+5 = 0º È Ø t : 3x y+7 = 0 Ô Ò ÙÐÝ Ø Ô Ò ÒÙÓ Ó º Ê Ø Ø Å t 3 ÐÝ Ø Ô Ð ÙÖ ÒÙ Ö ÔØ Ø Ô Ò Å Ô Ò ÙÐÝ º ¹½º ÙÓØ Ø Å 4x 3y + = 0º Ê Ø Ø Ù Ú ÒÓ ÒÙØÓÐÙ Ù ÒÙÓ Ø Å Ø ØÙÑÙ ½º ÃÙÖ Ú Ù ÙØÙ Ø Ù Ù ö Ñ Ù ÒÙÖÓ ÝØÓ Ø Å ¹¾ º ËÙ ÖÝØ ØÖ ÑÔ Ó Ö Ø Ò Ù ÐÝ Ø º Î Ö ÙÒÅ B(;6) Ù Ø ÒÅ ÐÝ Ø x 7y + 15 = 0 Ö ÓÖ ÒÅ µ ÔÙ Ù ÑÔ ÒÅ ÐÝ Ø 7x + y + 5 = 0º ÈÙ Ù ÑÔ ÒÅ Ö Ù Ø ÒÅ ÒÙÐ ØÓ ØÓ Ô Ó Ú Ö ÙÒÅ º ¹¾ º ËÙ ÖÝØ ØÖ ÑÔ Ó Ö Ø Ò Ù ÐÝ º Î Ö ÙÒÅ B(; 1) Ù Ø ÒÅ ÐÝ Ø 3x 4y + 7 = 0 Ö ÔÙ Ù ÑÔ ÒÅ ÐÝ Ø x+y 5 = 0º ÈÙ Ù ÑÔ ÒÅ Ö Ù Ø ÒÅ ÒÙÐ ØÓ ÖØ Ò Ù Ú Ö ÙÒ Ù º ÈÓ Ô ØÓ ¹ ¾º¾º º Ê Ø ÔÐÓ ØÙÑÓ Ò Ó Ô Ö Ø ½ ¾ ¹½µ Ö Ø ØÑ ÒÓ ÔÐÓ ØÙÑÓÑ x+y +z = 1, x y +z = 0 ÐÝ Ø º ¹¾º¾º º Ê Ø Ø ØÙÑ Ø ÖÔ ÐÝ Ö Ù ÔÐÓ ØÙÑÙ x 3y z +3 = 0, x 3y z = 0 ¹¾º¾º½ º Ê Ø ÔÐÓ ØÙÑ ÙÖ Ð ÒØÙ ÔÙ Ù Ø Ú Ò ÑÔ Ø ÖÔ ÔÐÓ ØÙÑÙ x+y +z 1 = 0, 3x+y 6z +5 = 0 ÙÖ Ñ ÝÖ Ø ¹¾ ½ µº ¼¹¾º¾º¾¼º ÆÙ Ø ØÝØ Ö Ø ¾ µ µ ¾ µ ¹¾ ½µ ÝÖ Ú ÒÓ ÔÐÓ ØÙÑÓ º ½¹½º Ê Ø Ø Ñ ØÖ Ø Ù A(1, 1,) ÔÐÓ ØÙÑÓ p : 4x 6y+7z 7 = 0 ØöÚ Ð Ùº ¾¹½¼ º ÆÙ Ø ØÝØ Ö Ø Å ÙÐ ÔÐÓ ØÙÑÓ 4x 3y +7z 7 = 0º { 5x 3y +z 5 = 0, x y z 1 = 0.
7 ¹¾º Ê Ø Ø Ù Ú ÒÓ ÒÙØÓÐÙ Ù ÒÙÓ ØÙÖ Ù ÔÐÓ ØÙÑÙ 5x 3y +z 5 = 0, x y z 1 = 0, 4x 3y +7z 7 = 0, 6x y +3z 1 = 0. ¹½¼ ¼º Ê Ø Ø Ó (, 1,3) ÔÖÓ Ø Å x = 3t, y = 5t 7, z = t+º ¹ ¾º¾º½ Ê Ø ÔÐÓ ØÙÑÙ Ò Ö ÐÝ Ø ÙÖ Ó ÔÖ ÞÑ Ù ÖÝØ ÔÐÓ ØÙÑÙ x = 0, y = 0, x+y 1 = 0 Ö ØÙ Ô Ð ÐÝ Ö Ø ØÖ ÑÔ º ¹ º º Ê Ø ÑÔ Ø ÖÔ ÔÐÓ ØÙÑÓ x y +z + = 0 Ö Ø Å { x+y z = 0, x y 3z 1 = 0. ¹ º½¾º È Ö Ø ( 1, 1,) Ú Ø ÔÐÓ ØÙÑ Ø ØÑ Ò Ø { 4x y +z 1 = 0, x y z + = 0. ¹ º½ º È Ö Ø (1,0, 1) Ö Ø t Ú Ø ÔÐÓ ØÙÑ ¹ º½ º È Ø Ö ÒØ Ö Ø Å t : x 1 = y +1 1 = z + 7. t 1 : { x y +z +5 = 0, x 4y z +4 = 0. ir t : { 4x y z +4 = 0, x 4y +z +6 = 0. Ù ÖØ Ê Ø ÔÐÓ ØÙÑ Ò Ò Ô Ö t Ö ÐÝ Ö t 1 º ¼¹ º¾ º Ê Ø Ø ÙÖ Ö ØÙ Ø { x+y 5z +4 = 0, x y +z 5 = 0. Ö ÙØÙ Ú Ò Ù Ø ØÑ Ò º ir { 3x+y z +14 = 0, 5x+y z = 0. ½¹ ½¼ ¾ Ê Ø Ø ØÙÑ d Ø ÖÔ Ø Å t : x+3 3 = y+ = z 8 Ö Ø Ó A = (1, 1, )º
8 ¾¹ º¾ º Æ µ È Ö Ø (1,0,1) Ú Ø Ø Ø ØÑ Ò Ø Å Ñ { x+y z 3 = 0, x y 3z +1 = 0. ir { 3x+y 4z 1 = 0, x y z = 0. ¹ º Ê Ø Ô Ö Ø ÑÓ ÒØÖ Ö Ô Ò ÝÐ ÙÖ Ùö ÙÓØ ÐÝ Ø Ñ x +y +4x y +5 = 0º ¹ º Ê Ø Ô Ö Ø ÑÓ ÐÝ Ø ÙÖ ØÙ Ô Ö ÓÓÖ Ò Ù ÔÖ ö Ó Ó ÒØÖ ÙØÙ Ø C(6, 8)º ¹ ½¼µ Ê Ø Ô Ö Ø ÑÓ ÐÝ Ø ÙÖ ØÙ Ô Ö ØÖ Ø Ù ( 1,5), (, ), (5,5)º ¹ º È Ö ÝØ Ô Ö Ø ÑÙ Ð Ò Ù ØÖ Ø 4x 3y 10 = 0 3x 4y 5 = 0 3x 4y 15 = 0 ÐÝ Ø º ¹ ½ º È Ö ÝØ Ô Ö Ø ÑÓ Ò Ò Ó Ô Ö ÓÓÖ Ò Ù ÔÖ ö Ö Ú Ù Ô Ö Ø ÑÙ (x+3) +(y +1) = 5 (x ) +(y +4) = 9 Ù ÖØ ÑÓ Ø Ù ÐÝ Ø º ¹ º ÙÓØ Ð Ô Å 9x +5y = 45º Ê Ø ½µ Ó ÔÙ ¾µ ö Ò Ù µ ÒØÖ Ø Ø µ Ö ØÖ Ù ÐÝ Ø º ¹ º Ð Ô Å ÒØÖ Ø Ø e = 5 Ø ØÙÑ ÒÙÓ Ð Ô Å Ø Ó M Ö ØÖ Å ÐÝ Ù ¾¼º Ê Ø Ø ÙÑ ÒÙÓ Ø Ó M ö Ò Ó Ø Ò ÒØ Ô Ñ ÒÅ Ø Ö ØÖ º ¼¹ ¾º Ê Ø Ð Ô Å x y 36 = 1 Ø Ù ÙÖ ÝÖ ½ Ú Ò ØÙ Ø ØÙÑ ÒÙÓ Ò Ó Ó ö Ò Óº ½¹ º È Ö ÝØ Ð Ô Å ÐÝ Ø ö ÒÓ Ñ ½µ Ó ö Ó ÔÙ Å ÐÝ ½ Ö ö Ò F 1 ( 10;0),F (14;0) ¾µ Ó Ñ ö Ó ÔÙ Å ÐÝ ¾ Ö ö Ò F 1 ( 1; 1),F (1;1) µ Ó ö Ò F 1 ( ; 3 ),F (; 3 ) Ö ÒØÖ Ø Ø e = µ Ó ö Ò F 1 (1;3),F (3;1) Ö Ø ØÙÑ Ø ÖÔ Ö ØÖ Ù ÐÝ Ù 1 º ¾¹ º Æ µ È Ö ÝØ Ô Ö Ø ÑÙ Ð Ò Ù ØÖ Ø 3x+4y 35 = 0,3x 4y 35 = 0,x 1 = 0 ÐÝ Ø º ¹ º È Ö ÝØ Ð Ô Å ÐÝ Ø ö ÒÓÑ Ó ÒØÖ Ø Ø e = 3 Ö ØÖ Å ÐÝ Ø x 5 = 0º ö ÒÝ F(;1) Ö Ø Ø Ò Ó
9 ¹ ½ µº È Ö ÝØ ÐÝ Ø Ô Ö ÓÐÅ ÙÖ Ó ö Ò ÝÖ Ù Ý Ñ ØÖ ÓÓÖ Ò Ù ÔÖ ö Ó ØöÚ Ð¹ Ùº ê ÒÓ Ñ ÔÙ Å a = 8 Ö ÒØÖ Ø Ø e = 5 4 º Ê Ø ö Ò Ù Ö ØÖ ÑÔ¹ ØÓØ º ÆÙÔ Ø Ô ÒÙ º ¹ ½ µº È Ö ÝØ ÐÝ Ø Ô Ö ÓÐÅ ÙÖ Ó ö Ò ÝÖ ÓÖ Ò Ù Ý Ñ ØÖ ÓÓÖ Ò Ù ÔÖ ö Ó ØöÚ Ð Ùº ê ÒÓ Ñ ÑÔØÓ Ù ÐÝ Ø y = ± 1 5 x Ö Ø ØÙÑ Ø ÖÔ Ú Ö ÙÒ Ù º Ê Ø Ò¹ ØÖ Ø Ø Ö ØÖ Ö ö Ò Ù º ÆÙÔ Ø Ô ÒÙ º ¹ ¾ º Ê Ø Ô Ö ÓÐÅ x 64 y 36 = 1 Ø Ù ÒÙÓ ÙÖ Ù Ø ØÙÑ Ò Ó Ó ö Ò Ó ÐÝ Ù º ¹ ¾º È Ö ÝØ ÐÝ Ø Ô Ö ÓÐÅ ÙÖ Ó ö Ò ÝÖ Ù Ý Ñ ØÖ ÓÓÖ Ò Ù ÔÖ ö Ó ØöÚ Ð¹ Ù ÙÓØ ½µ Ô Ö ÓÐÅ Ø M 1 (6; 1),M ( 8; ) ¾µ Ô Ö ÓÐÅ Ø M 1 ( 5;3) Ö ÒØÖ Ø Ø e = µ Ô Ö ÓÐÅ Ø M 1 ( 9 ; 1) Ö ÑÔØÓ Ù ÐÝ ØÝ y = ± 3 x µ Ô Ö ÓÐÅ Ø M 1 ( 3; 5 ) Ö Ö ØÖ Ù ÐÝ ØÝ x = ±4 3 µ ÑÔØÓ Ù ÐÝ ØÝ y = ± 3 4 x Ö Ö ØÖ Ù ÐÝ ØÝ x = ±16 5 º ¹ º È Ö ÝØ ÐÝ Ø Ô Ö ÓÐÅ Ò Ò Ó Ô Ö ÓÓÖ Ò Ù ÔÖ ö Ö ØÙÖ Ò Ó ö Ò F(0; 3)º È Ö ÓÐÅ ÝÖ ÓÖ Ò Ù º ¹ µº ÆÙ Ø ØÝØ Ó Ó Ð Ò Ó Ö ØÓ ÐÝ Ø Ñ y = 5+ 3x 1º ÆÙ Ö öýø º ¼¹ ¼¾º È Ö ÝØ Ô Ö ÓÐÅ ÐÝ Ø ÙÓØ ö ÒÝ F(; 1) Ö Ö ØÖ Å x y 1 = 0º ½¹ ¼ º ÙÓØ Ô Ö ÓÐÅ Ú Ö ÙÒÅ A( ; 1) Ö Ö ØÖ Å ÐÝ Ø x+y 1 = 0º È Ö ÝØ Ô Ö ÓÐÅ ÐÝ Ø º ¾¹ º Æ µ ÆÙ Ø ØÝØ Ó Ó Ð Ò Ó Ö ØÓ ÐÝ Ø Ñ y = 3 x 0º ÆÙ Ö öýø º ÃÓÓÖ Ò Ù ØÖ Ò ÓÖÑ Ó ¹½¾ º ÍöÖ Ý Ø ØÖ Ò ÓÖÑ Ù ÓÖÑÙÐ Ù Ò Ù Ó ÓÓÖ Ò Ù Ø Ñ ÝÖ Ô ØÙÑØ Ø Ó Ý Ò Ô Ù ØÓ ½µ µ ¾µ ¹¾ ½µ µ ¹ µº ¹½ ½º ÍöÖ Ý Ø ØÖ Ò ÓÖÑ Ù ÓÖÑÙÐ Ù Ò Ù Ó ÓÓÖ Ò Ù Ø Ñ ÝÖ Ô Ù Ø ÑÔÙ ½µ 60 ¾µ 45 µ 90 º ¹½ º ÃÓÓÖ Ò Ù ÔÖ ö ÝÖ Ô ØÙÑØ Ø O ( 1,) Ö Ô Ù Ø ÑÔÙ α = arctan 5 1 º ê ÒÓÑÓ Ø Ù M 1 (3,),M (, 3),M 3 (13, 13) ÓÓÖ Ò ØÅ Ò Ù Ó ÓÓÖ Ò Ù Ø ÑÓ º Ê Ø ÒÙÖÓ ÝØÙ Ø Ù ÓÓÖ Ò Ø ÒÓ ÓÓÖ Ò Ù Ø ÑÓ º ¹½ º ÙÓØ ØÖÝ Ø A(5,5),B(, 1),C(1, 6)º Ê Ø Ù ÓÓÖ Ò Ø Ò Ù Ó ÓÓÖ Ò Ù Ø ¹ ÑÓ Ù ÓÓÖ Ò Ù ÔÖ ö Ô ØÙÑØ Ø B Ó Ý Ô Ù ØÓ ÑÔÙ α = arctan 3 4 º
10 ¹½ ½º ÙÓØ Ù Ø A(9, 3),B( 6,5)º ÃÓÓÖ Ò Ù ÔÖ ö Ô ØÙÑØ Ø A Ó Ò Ù Ax ÝÖ ØÓ Ô Ó ÖÝÔØ Ô Ö Ø ÖÔ ABº Ê Ø ÓÓÖ Ò Ù ØÖ Ò ÓÖÑ Ù ÓÖÑÙÐ º ¹ ½µº ÆÙ Ø ØÝØ Ó Ó Ô Ø ØÙ Ð Ò Ù ÒØÖ ÒŠغݺ ØÙÖ Ú Ò ÒØ Ð ÒØÖ µ Ó Ó Ò ØÙÖ ÒØÖÓ Ó Ó ØÙÖ ÐÓ Ù ÒØÖÙ º Ê Ø Ô ØÙÑØÓ ÒØÖ Ö ÚÅ ÐÝ Ø ½µ 3x 4xy y +3x 1y 7 = 0º ¹ º ÃÓ ØÙÖÅ ØÙ ÙØ m Ö n ÐÝ Ø mx +1xy +9y + 4x+ny 13 = 0 ÙØÙ µ ÒØÖ ÒÅ Ð Ò µ Ð Ò ÒØÖÓ µ Ð Ò ØÙÖ ÒØ ÐÓ Ù ÒØÖÙ º ¼¹ ½µº ËÙÚ Ø ÐÝ Ø 4x + 9y 40x+36y = 0 ÒÓÒ Ò Ô Ú Ð ÒÙ Ø ØÝØ Ó Ø Ô Ó Ù ÓÑ ØÖ Ò Ù Ú Þ Ù Ô ÖÅ ö Ö ÒÙ ÖÅ öø Ö Ú Ò Ù Ù Ö ÒÙ ÓÓÖ Ò Ù Ù ØöÚ Ð Ùº ½¹ ½µº ËÙÚ Ø ÐÝ Ø 3x + 5xy 7y = 0 ÒÓÒ Ò Ô Ú Ð ÒÙ Ø ØÝØ Ó Ø Ô Ó Ù ÓÑ ØÖ Ò Ù Ú Þ Ù Ô ÖÅ ö Ö ÒÙ ÖÅ öø Ö Ú Ò Ù Ù Ö ÒÙ ÓÓÖ Ò Ù Ù ØöÚ Ð Ùº ¾¹ ½µº Ê Ø ÐÝ Ø x +10xy +1y 7x+18y 15 = 0 Ø Ô Ò Ù Ó ÒØ ÒÚ Ö ÒØÙ º Æ ¹ º ËÙÚ Ø ÐÝ Ø ½µ 3x +10xy +3y x 14y 13 = 0 ¾µ 5x 14xy +5y +64x 64y 4 = 0 µ 4xy +3y +16x+1y 36 = 0 ÒÓÒ Ò Ô Ú Ð ÒÙ Ø ØÝØ Ó Ø Ô Ó Ù ÓÑ ØÖ Ò Ù Ú Þ Ù Ö Ö ÒÙ ÖÅ öø Ò Ù Ù Ö ÒÙ ÓÓÖ Ò Ù Ù ØöÚ Ð Ùº ¹ º ËÙÚ Ø ÐÝ Ø ½µ 14x +4xy +1y 4x+18y 139 = 0 ÒÓÒ Ò Ô Ú Ð ÒÙ Ø ØÝØ Ó Ø Ô Ó Ù ÓÑ ØÖ Ò Ù Ú Þ Ù Ö Ö ÒÙ ÖÅ öø Ò Ù Ù Ö ÒÙ ÓÓÖ Ò Ù Ù ØöÚ Ð Ùº ¹ º ÆÙ Ø ØÝØ Ó ÐÝ Ø ½µ x xy +y +6x 14y+9 = 0 ¾µ 9x 4xy +16y 0x+110y 50 Ô ÖÅ ö Ô Ö Óк Ê Ø Ô Ö ÓÐÅ ÒÓÒ Ò ÐÝ Ø ÒÓÒ Ò ÓÓÖ Ò Ù Ø Ñ Ö Ú Ö ÙÒº ¹ ½µº ÆÙ Ø ØÝØ Ó ÐÝ Ø 9x +4xy+16y 10x+90y = 0 ÝÖ Ô Ö ÓÐÅ Ö Ö Ø Ô Ö ÓÐÅ Ô Ö Ñ ØÖ º ¹ ½ ½µº ÆÙ Ø ØÝØ Ó ÐÝ Ø 3x +4xy+y x 1 = 0 ÝÖ Ú Ù ÖØ Ò Ó Ø Å ÑÙ Ô Ö ÓÐÅ µ Ö Ö Ø Ù Ø Ù ÐÝ Ø º ¹ ½µº ÆÙ Ø ØÝØ Ó ÐÝ Ø 4x +4xy +y 1x 6y +5 = 0 ÝÖ Ú ÐÝ Ö Ó Ø Å Ö Ö Ø Ù Ø Ù ÐÝ Ø º ½¼
11 ¹ ¼¼ ½µº ÆÙ Ø ØÝØ Ó ÐÝ Ø x 6xy +9y +4x 1y+4 = 0 ÝÖ Ú Ù Ø Å Ö Ø Ó ÐÝ Ø º ½¼¼¹ ½ º È Ö ÝØ ÐÝ Ø Ø Å ÙÖ Ð Ô Ö ÓÐ y = 8x Ö ÐÝ Ö Ø Ø x+y 3 = 0º ½¼½¹ ¾ º Á Ô Ö ÓÐÅ y = 1x ö Ò Ó Ñ ÐÙ ÑÔÙ α ÔÖ Ox ÒÙ Ö ÔØ Ú Ó Ô Ò ÙÐÝ º ê ÒÓÑ tgα = 3 4 º È Ô Ö ÓÐ Ô Ò ÙÐÝ Ø Ô Ò º È Ö ÝØ ÐÝ Ø Ø Å ÙÖ ÔÖ Ð Ù Ó Ø Ô Ò Ô Ò ÙÐÝ º ½¼¾¹ ¾º Æ µ Ê Ø ÓÑ ØÖ Ò Ù Ú Þ Ù ÙÖ Ó Ö ÐÝ ØÝ ½µ 8x 1xy +17y +16x 1y +3 = 0 ¾µ 17x 18xy 7y +34x 18y +7 = 0 µ x +3xy y +5x+10y = 0 µ 6x 6xy +9y 4x+18y+14 = 0 µ 5x xy +5y 4x+0y+0 = 0º ½¼ ¹ ¼º Ê Ø Ø Å x+y 7 = 0 Ö Ð Ô Å x 5 + 4y 5 = 1 Ù ÖØ ÑÓ Ø Ù º ½¼ ¹ ¾º Ê Ø Ø Å 3x 4y 40 = 0 Ö Ð Ô Å x 16 + y 9 = 1 Ù ÖØ ÑÓ Ø Ù º ½¼ ¹ ½º Ê Ø Ð Ô Å x 18 + y 8 = 1 Ø M 1 ÖØ Ñ Ù Ø x 3y +5 = 0 Ø ØÙÑ d ÒÙÓ M 1 Ø Å º ½¼ ¹ º Ì Å x y 5 = 0 Ð Ð Ô ÙÖ Ó ö Ò ÝÖ F 1 ( 3;0) Ö F (3;0)º È Ö ÝØ Ð Ô Å ÐÝ Ø º ½¼ ¹ ¼¼º Ê Ø Ò Ö Ð Ô Å x 45 + y 0 = 1 Ö Ô Ö ÓÐÅ y = 0 3 x Ð Ø Ò º ½¼ ¹ º ÙÓØ Ô Ö ÓÐÅ x a y b = 1 Ö Ø ÙÖ Ó Ð Ø ÒÅ P ¹ Ð Ø ÒÅ Ö Ox Ù ÖØ ÑÓ Ø Q ¹ Ð Ø ÑÓ Ø Ó ÔÖÓ Ox º Á ÖÓ ÝØ OP OQ = a º ½¼ ¹ º ÆÙ Ø ØÝ Ø Ð Ô Å x 0 +y x 5 = 1 Ö Ô Ö ÓÐÅ 1 y 3 = 1 Ù ÖØ ÑÓ Ø ÝÖ Ø ÑÔ Ó Ú Ö ÙÒÅ Ô Ö ÝØ Ó Ö Ø Ò Ù ÐÝ Ø º ½½¼¹ º Ê Ø Ô Ö ÓÐÅ ÐÝ Ø Ù Ó Ý ÙØ ÑÔ Ù ÓÓÖ Ò Ù Ñ Ö Ó Ð Ø Ò Ù ÐÝ ØÝ ÝÖ 5x 6y 16 = 0, 13x 10y 48 = 0º ½½½¹ º Æ µ À Ô Ö ÓÐÅ Ò Ô Ö Ø A( 6;3) Ö Ð Ø 9x+y 15 = 0º È Ö ÝØ ØÓ Ô Ö ÓÐÅ ÐÝ Ø Ð ÒØ ÓÓÖ Ò Ù Ô Ö ÓÐÅ Ñ º ½½¾¹½ º ÙÓØ Ø P 0 = (0,0),P 1 = (1,1),P = (0,1). Ê Ø Ø ÔÖ Ð Ù ÒØ Þ Ö Ö Ú X(t) = P i Bi(t), Ô Ö Ñ ØÖ ÝÖ t = 1/3º Ì Ô Ô Ø Ö Ø Ð Ø Ò Ø Ñ Ö Ø Ñ Ø º i=0 ½½
12 ½½ ¹¾ º Ê Ø Ò Ö Ø Ò Þ Ö Ö ÚÅ ÐÝ Ø ÙÖ ÝÖ Ô ÖÅ öø ½ Ùö Ú ÒÝ º ½½ ¹½¼ º È Ö ÝØ ÐÝ Ø ÖÓ Ù Ô Ò ÙÐ Ù r = 3 Ð Ò Ó ÔÐÓ ØÙÑ x + y + z + 3 = 0 Ø M 1 (1;1; 3)º ½½ ¹½¼ º Ê Ø ÖÓ Ð Ò Ó ÔÐÓ ØÙÑ 3x+y 6z 15 = 0,3x+y 6z +55 = 0 Ô Ò ÙÐ º ½½ ¹½¼ µº Ê Ø ØÖÙÑÔ Ù Ø ØÙÑ ÒÙÓ Ø Ó A(9; 4; 3) ÖÓ x +y +z +14x 16y 4z +41 = 0º ½½ ¹ ¾º Ê Ø Ô Ö Ø ÑÓ ÒØÖ Ö Ô Ò ÙÐ { (x 4) +(y 7) +(z +1) = 36, 3x+y z = 9. ½½ ¹½½¼ º Ê Ø ÔÐÓ ØÙÑÓ ÐÝ Ø ÙÖ Ó ÙÐ Ô Ö Ø Ñ ÔÖ Ð Ù ÒØ Ú Ñ ÖÓÑ x +y +z +3x y +z 5 = 0, x +y +z x+3y z +1 = 0. ½½ ¹½½¼ º È Ö ÝØ ÐÝ Ø ÖÓ Ò Ò Ó Ô Ö ÓÓÖ Ò Ù ÔÖ ö Ö Ô Ö Ø Ñ { x +y +z = 5, x 3y +5z 5 = 0. ½¾¼¹½½¼ º Ê Ø ÖÓ ÐÝ Ø ÙÖ Ò Ô Ö Ù Ô Ö Ø ÑÙ { x +z = 5, y = 0. { x +z = 16, y 3 = 0. ½¾½¹½ ¼º Ê Ø ÖÓ ÐÝ Ø ÙÖ Ò Ô Ö Ô Ö Ø Ñ x +y = 11,z = 0 Ö Ð ÔÐÓ ØÙÑ x+y+z = 5º ½¾¾¹ ½½¼ º Æ µ Á ÖÓ ÝØ ÔÐÓ ØÙÑ x 6y+3z 49= 0 Ð Ö x +y +z = 49º Ê Ø Ð Ø ÑÓ Ø º ½¾ ¹½½ º ÆÙ Ø ØÝØ ÔÐÓ ØÙÑ x = 0 ÖØ Ð Ô Ó x 16 + y 1 + z 4 = 1 Ð Ô Ö Ø Ó ÔÙ Ù Ö Ú Ö ÙÒ º ½¾ ¹½½ º ÆÙ Ø ØÝØ Ð Ô Ó Ó x 1 + y 4 + z 3 ÒØÖ º = 1 Ö ÔÐÓ ØÙÑÓ x 3y+4z 11 = 0 Ô ÙÚ Ó Ð Ò Ö Ø Ó ½¾ ¹½½ ½º ÆÙ Ø ØÝØ m Ö Ñ Ù ÙÖ ÓÑ ÔÐÓ ØÙÑ x+my = 0 ÖØ Ð Ô Ò Ô Ö ÓÐÓ x +z 3 = y µ Ð Ô µ Ô Ö ÓÐ º ½¾
13 ½¾ ¹½½ º ÆÙ Ø ØÝØ Ð Ô Ó x 81 + y 36 + z 9 = 1 Ö ÔÐÓ ØÙÑ 4x 3y+1z = 54 ØÙÖ Ø Ú Ò Ò Ö Ø º Ê Ø Ø Ø º ½¾ ¹½º Ã Ù Ó Ú Ö ÙÒÅ ÝÖ Ø (0,0,4) Ó Ù ÖÓÑÓ Ó ÖØ Ö Ú Ö Ø Ù Ó ÐÝ Ø º x +y = 4, x+y +z = ½¾ ¹ º Ê Ø Ù Ó ÐÝ Ø ÙÖ Ó Ú Ö ÙÒÅ ÝÖ Ø A(,0,0) Ö ÙÖ Ù Ö x +y +z = 1 غݺ Ú Ò Ù Ó Ø Å Ð Ö º ½¾ ¹½½ ¼ ¾µº Ê Ø Ø Å x 4 = y 3 = z+ 4 Ö Ô Ú Ö Ù x 16 + y 9 z 4 = 1 Ù ÖØ ÑÓ Ø Ù º ½ ¼¹½½ ½º Á ÖÓ ÝØ ÔÐÓ ØÙÑ x 1y z +16 = 0 ÖØ Ô Ö ÓÐ Ò Ô Ö ÓÐÓ x 4y = z Ô Ö Ø Ò Ù ÖÓÑ º È Ö ÝØ ØÙ Ø Ò Ù Ù ÖÓÑÙ Ù ÐÝ Ø º ½ ½¹½½ ¾º Á ÖÓ ÝØ ÔÐÓ ØÙÑ 4x 5y 10z 0 = 0 ÖØ Ú Ò Ô Ö ÓÐÓ x 5 + y 16 z 4 = 1 Ô Ö Ø Ò Ù ÖÓÑ º È Ö ÝØ ØÙ Ø Ò Ù Ù ÖÓÑÙ Ù ÐÝ Ø º ½ ¾¹½½ º Á Ø Ò Ó Ø M(1;3; 1) ÔÖ Ð Ù Ó Ô Ö ÓÐ Ò Ñ Ô Ö ÓÐÓ Ù 4x z = y Ô Ö ÝØ Ó Ø Ò Ù Ù Ö ÑÙ Ù Ò Ò Ù Ô Ö Ø M ÐÝ Ø º ½ ¹½½ ¼º È Ö ÝØ ÐÝ Ø Ù Ó ÙÖ Ó Ú Ö ÙÒÅ ÝÖ Ø ¹½ ¹¾µ Ó Ù ÖÓÑÓ ÙÓØ ÐÝ Ø Ñ { x +y z = 1, x y +z = 0. ½ ¹ º Ê Ø ÔÐÓ ØÙÑÓ ÐÝ Ø ÙÖ Ò Ô Ö Ø ¹¾ ¹¾µ Ð Ð Ô Ó x +3y +z 6 = 0 Ö Ø ØÑ Ò ÔÐÓ ØÙÑ x y +z = 0 ½ ¹¾½ Ê Ø ÐÝ Ø Ù ÑÓ Ð Ò ÖÓ ÙÖ Ñ ÙØÙ Ø Å x = y = z, x 1 = y +1 = z, x = y 1 = z +1 ÈÓ ½ Ô ØÓ ½ ¹½½ º Ê Ø ØÖÙÑÔ Ù Ö ö Ù Ø ØÙÑ Ø ÖÔ Ô Ú Ö Ù 4x + 16y + 8z = 1 Ö ÔÐÓ ØÙÑÓ x y +z +17 = 0º ½ ¹½º Ê Ø ØÖÙÑÔ Ù Ø ØÙÑ Ø ÖÔ Ø Ó (0,0,1) Ö Ô Ú Ö Ù x y = z ½ ¹¾º ÙÓØ Ø Å x 3 = y = z 7 8 Ö Ô Ú Ö Ù 7x +y z 7 = 0º Ê Ø Ð Ñ ÔÐÓ ØÙÑ Ô Ú Ö Ù ÙÖ Ó ØÙ Ô Ö Ø º ÈÓ ½ Ô ØÓ ½
14 ½ ¹½ ½º Ê Ø Ô Ú Ö Ù S Ð Ñ ÔÐÓ ØÙÑ ÙÖ ÙØÙ ÐÝ Ö Ø ÔÐÓ ØÙÑ x + y + = 0º S : 4x +6y +4z +4xz 8y 4z +3 = 0 ½ ¼¹½ º Á ÖÓ ÝØ ÔÐÓ ØÙÑ x+y +z +5 = 0 ÖØ Ô Ú Ö Ù Ú Ø º Ê Ø Ø Ø º z xy 4x y +z 3 = 0 ½
15 Ø ÝÑ ½¹½ a+b = 19, a b = 7º ¾¹ µ ac = 3 µ (a+b)c = 1 µ a(a+3c) = 13 µ (ab)c = (6,4,)º ¹ ¼¾ p = 10º ¹ ¼ α = ± 3 5 º ¹ ¼¼ ab+bc+ca = 3 º ¹ ¼¼³ ab = 3 ¹ ¼ α = arccos 7 º,ac = 11,bc = 1 º ¹ Î ØÓÖ a Ö c ÐÝ Ö Ø Ù Ö b Ø ØÑ Ò Ú ØÓÖ Ñ a Ö cº ¹ ¾ ¹¾ ¾ ¼µº ½¼¹ ¹½½º ½½¹½ µ a b = (1,, 4) µ (a b) c = (, 1,1) µ pr c b (3a b) = 3 3 ½¾¹½ ÈÐÓØ ÑÔ arccos( 1 5 )º ½ ¹½ m = ( 3, 3 4, 3 ) ½ ¹ ½¾ ½µ ¾¾ ¾µ µ µ ¹¾¼¼ µ ½¾ µ ½º ½ ¹ ¼ a b = a b (ab) = 16º ½ ¹ ½µ ¾µ ¾ µ ¼¼º ½ ¹½ µ a b+ b a = 7a+3bº µ c = ref b (a) = ( ) ab bb b a = ( 65 49, 50 49, 1 49 ), b = 49 ½ ¹¾ ¾ ½ ¼µ ¼ ¾µ ½ ¹ ½µ a = 1 p+ 1 tan(π/6)p = ( 3 3 3, ), b = 1 p 1 tan(π/6)p = ( , ), p = ( 4,)º ¾µ a = 1 p+ 1 p = ( 1,3), b = 1 p 1 p = (3,1)º ¾¼¹ c = cos(60)a+sin(60)a = ( 3, 1+ 3 ), a = ( 1,) ¾½¹½½½ ½µ Ò ÓÑÔÐ Ò Ö Ù ¾µ ÓÑÔÐ Ò Ö Ù ½
16 ¾¾¹½¾ (5;) Ö (;)º ¾ ¹¼ ½» µ ¾» µ ¹½ ¹ µº ¾ ¹½ (11,0)( 9, 4) ¾ ¹½ Q 1 +Q Q 3 = (,0,1),Q 1 +Q 3 Q = (0,, 1),Q 3 +Q Q 1 = (,4,5) ¾ ¹¾ Ð ÙØ ØÖÝ ÐÝ Ö Ø Ò Ù ØÓ ØÚ ÖØ Ú Ö ÙÒ Q 1 +Q Q 3 = (,0,1) Ö Q 1 +Q 3 Q = (0,, 1) Ö Q 3 +Q Q 1 = (,4,5)º ¾ ¹ ¾ ¹ Ò ÔÖ Ð Ù Ó ¾ ¹ D ÒÅ Ö ØÖ ÑÔ Ó Ú Ù ¼¹ º ½¹ B Ø ÒÅ ¾¹ ¹ 1 4 P P P P 4. ¹½½ ½µ ½ ¾µ ½¾ µ ¾ º ¹½½ ³ ¾º ¹½¾¾ (0; 8) Ö (0; ) ¹½ Ùö Ú ÒÝ ØÓ Ô Ø Ô ¾ ¹½ ¹¾ Ùö Ú ÒÝ ØÓ Ô Ø Ô ¾ ¹ ¹½¾ C 1 ( ;1),D 1 ( 5;16) Ö C ( ;/3),D ( 5;14/3)º ¼¹¾¾ Q = (11; 11)º Q = P ( ) t(p) n n n ½¹¾ 5x+y 3 = 0 Ú Ò Ó ÑÔÓ ÔÙ Ù ÑÔ ÒÅ ÐÝ Ø x 5y 11 = 0 ÓÖ Ò Ó ÑÔÓ ÔÙ ÑÔ ÒÅ ÐÝ Ø º ¾¹¾ x 5 = 0º ¹¾ t 3 : 9x y+33 = 0º ( ) n1 n t 3 = t t 1, t 3 = αt 1 +βt, n n ( ) n1 n n 3 = ref n (n 1 ) = n n 1 n n ¹½ ê Ñ Ù ÝÖ Ø Å 4x 3y 3 = 0 Ù Ù ÝÖ 4x 3y +7 = 0 ½
17 ¹¾ l(ac) : 4x 3y+10 = 0,l(CB) : 7x+y 0 = 0,l(AB) : 3x+4y 5 = 0º ÈÙ Ù ÑÔ ÒÅ Ö Ù Ø ÒÅ ÖØ Ø Aº ¹¾ 4x+7y 1 = 0,y 3 = 0,4x+3y 5 = 0º ¹¾º¾º x z = º ¹¾º¾º 5/ 14º ¹¾º¾º½ 4x+5y z + = 0º ¼¹¾º¾º¾¼ Ì Ôº ½¹½ B = A p(a) n n n ¾¹½¼ Ì Ô ¹¾ ¹½¼ ¼ (3,,4)º ¹¾º¾º½ x+y +z = c c¹ Ø Ó Ù º 3 3 º ¹ º π/º ¹ º½¾ x+y z +5 = 0 ¹ º½ 4x+y z 5 = 0 ¹ º½ 5x 8y+z +14 = 0 Ø Å ØÙÖ Ò Ö Ø ( 1,1,1) ¼¹ º¾ x+1 3 = y+(17/4) 5 = z 1 ½¹½¼ ¾ d = 7 d = k MA k k ¹ Ø Å ÖÝÔØ Ú ØÓÖ Ù M¹Ø Ø Å º ¾¹ º¾ x 1 1 = y 1 = z 1 1 ¹ ÒØÖ (,1) Ô Ò ÙÐÝ ÝÖ ÒÙÐ º ¹ ÄÝ Ø (x 6) +(y +8) 100 = 0º ¹ ½¼µ ÄÝ Ø (x ) +(y 1) 5 = 0º ¹ (x ) +(y ) = 1,(x 30 7 ) +(y 5 7 ) = 1º ¹ (x 5) +y = 16,(x+15) +y = 56,(x 35 3 ) +(y 40 3 ) = ( 3 3 ),(x 35 3 ) +(y ) = ½
18 ¹ ½ 13x +13y +3x+71y = 0º ¹ ½µ 5 Ö ¾µ F 1 (0; ),F (0;) µ e = 3 µ y = ± 9 º ¼¹ ½¹ ¾ ( 5;3 3) Ö( 5; 3 3) ¾¹ ½µ (x ) y 5 = 1 ¾µ x xy +y 3 = 0 µ 68x +48xy +8y 65 = 0 µ 11x +xy +11y 48x 48y 4 = 0º ¹ 5x +9y +4x 18y 55 = 0º ¹ ½ µ x 64 y 36 = 1º ¹ ½ µ x 100 y 576 = 1º ¹ ¾ (10; 9 ) Ö (10; 9 )º ¹ ¾ ½µ x 3 y 8 = 1 ¾µ x y = 16 µ x 4 y 5 µ x 18 y 8 = 1 µ x 16 y 9 = 1º = 1 Ö x 61 9 ¹ x = 1y y = 1 ¹ µô Ö ÓÐÅ (y +5) = 3(x+7) Ð ÒØ ÔÓ Ø y +5 = 0º ¼¹ ¼¾ x +xy +y 6x+y +9 = 0 ÒÓÒ ÒÅ ÐÝ Ø x = y ØÖ Ò ÓÖÑ Ó x = (x y ),y = (x+y 1) ½¹ ¼ 4x 4xy +y +3x+34y+89 = 0º ¾¹ ÃÓÓÖ Ò Ù ØÖ Ò ÓÖÑ Ó ¹½¾ ½µ x = x +3, y = y +4 ¾µ x = x, y = y +1 µ x = x 3, y = y +5 ¹½ ½ ½µ x = x y 3, y = x 3+y ¾µ x = x +y, y = x +y µ x = y, y = x ½
19 ¹½ M 1 (1,5),M (,0),M 3 (16, 5). ¹½ A(6,3),B(0,0),C(5, 10). ¹½ ½ x = x 8 17 y +9, y = 8 17 x y 3. ¹ ½µØÙÖ Ú Ò Ø Ð ÒØÖ ( 3/, 3/); 3x 4x y y 1/4 = 0º ¹ µ m 4 Ò¹ Ø ÙÖ Ù µñ n 6 µ Ñ Ò º ¼¹ ½µ Ð Ô Å x 9 + y 4 ½¹ ½µ Ô Ö ÓÐÅ x 9 y 4 cosα = 1 5 sinα = 5 º = 1 Ò Ù ÓÓÖ Ò Ù ÔÖ ö O(5; )º = 1 tgα = ¾¹ ½µ Ô Ö ÓÐ Ò Ø Ô º I 1 = 609,I = 1,I 3 = 14 ¹ ½µ Ô Ö ÓÐÅ x y 4 = 1 I 1 = 18,I = 16,I 3 = 6 Ô ÖØÚ Ö ÝÑ x = x +,y = y 1 Ö x = x y,y = x +y º ¾µ Ð Ô Å x 16 + y 9 = 1 λ 1 = 18,λ = 3,I 1 = 50,I = 4,I 3 = = ,tanα = 1 Ô ÖØÚ Ö ÝÑ x = x y 1,y = x +y +1º µ Ô Ö ÓÐÅ x 9 y 36 = 1 Ô ÖØÚ Ö ÝÑ x = x y 5 +3,y = x +y 5 4 I 1 = 3, I = 4, I 3 = 1, λ 1 = 4, λ = 1, tanα =,º ¹ º ½µ Ð Ô x 30 + y 5 = 1 ¹ º ½µ y = x,i 1 =,I = 0,I 3 = 16 Ñ ØÖ Ó x y +5 = 0 Ú Ö ÙÒÅ ¹¾ µ ÌÖ Ò ÓÖÑ Ó x = (x y )/, y = (x +y )/ +3 ¾µ Ú Ö ÙÒÅ (18/5,1/5), I 1 = 5,I 3 = 5 65 Ñ ØÖ Ó 3x 4y 10 = 0º ÌÖ Ò ÓÖÑ Ó x = 4x 3y +18 5, x = 3x +4y +1 5 º  ٠x = 4/3, y = 0 Ø x = 6,y = º Ã Ò F(6,) > 0 Ø ÐÝ Ø ÔÓ ÔÖ Ø Ò ÑÓ ÝÖ y +x = 0º ¹ ½µ p = 3, y = 6x, y = 3x+4y 5, x = 4x 3y 5,I 3 = 15 5,I 1 = 5 ¹ ½ ½µ x+y 1 = 0,3x+y +1 = 0º ¹ ½µ x+y 5 = 0,x+y 1 = 0º ¹ ¼¼ ½µ x 3y+ = 0º ½¼¼¹ ½ x+y + = 0º ½¼½¹ ¾ y 18 = 0 ÖØ ÑÓ Ø (7,18)º ½
20 ½¼¾¹ ¾ ½µ Ð Ô Å ¾µ Ô Ö ÓÐÅ µ Ù ÖØ Ò Ó Ø Å ÑÙ Ô Ö ÓÐÅ µ µ Ñ Ò Ñ Ð Ô Å µ Ø ÑÙ Ð Ô Å µº ½¼ ¹ ¼ (4; 3 ),(3;)º ½¼ ¹ ¾ ÆÅ Ö Ò ÖÙ Ø Ù º ½¼ ¹ ½ M 1 ( 3;) d = 13º ½¼ ¹ x 17 + y 8 = 1º Ä Ø ( 17 5, 8 5) º ½¼ ¹ ¼¼ Ú Ð Ø Ò x±3y+15 = 0º ½¼ ¹ ½¼ ¹ x = 4,x = 4,y = 1,y = 1º ½½¼¹ x 16 y 4 = 1 ½½½¹ x 5 y x 45 = 1, 10 y 45 = 1º ½½¾¹½ º X(1/3) = (4/9, 5/9) ½½ ¹¾ º x 4y +4xy +4y 4x = 0. ½½ ¹½¼ (x ) +(y 3) +(z +1) = 9 Ö x +(y +1) +(z +5) = 9º ½½ ¹½¼ R = 5º ½½ ¹½¼ µ ¾½º ½½ ¹ ¾ C = (1,6,0), r = 5 ½½ ¹½½¼ 5x 8y+5z 7 = 0º ½½ ¹½½¼ x +y +z 10x+15y 5z = 0º ½¾¼¹½½¼ x +(y +) +z 41 = 0º ½¾½¹½ ¼º x +y +(z +1) = 1 Ö x +y +(z +4) = 7 ½¾¾¹½½¼ º ½¾ ¹½½ 3, 3;(;3;0),(; 3;0),(;0; 3),(;0; 3) ½¾ ¹½½ Ð Ô Å ¾ ¹½ ½µ Ð Ô Å ÒØÖ º ½¾ ¹½½ ½ µ m 0 Ö m 4 1 m = 1 4 ¹ ÑÙ Ð Ô Å ¹Ø º µ m = 0º ¾¼
21 ½¾ ¹½½ º ¹¾ ¾µ ½¾ ¹½º z +xy +xz +yz 8x 8y 8z +16 = 0 ½¾ ¹ º x 3y 3z 4x+4 = 0 ½¾ ¹½½ ¼ ¾µ ¹ ¾µ ¹ Ø Å Ð Ô Ú Ö Ù º ½ ¼¹½½ ½ { x 1y z +16 = 0, x y+4 = 0. Ö { x+4y +z = 0, x y +4 = 0. { x 1y z +16 = 0, x+y 8 = 0. Ö { 4x 8y z = 0, x+y 8 = 0. ½ ½¹½½ ¾ { y +z = 0, x 5 = 0. { x 5z = 0, y +4 = 0. ½ ¾¹½½ x 1 = y+1 4 = z 1 x 1 = y+9 1 = z+3 º ½ ¹½½ ¼ 3x 5y +7z 6xy +10xz yz 4x+4y 4z +4 = 0º ½ ¹ º x+3y+z 6 = 0 ½ ¹¾½º 5x +5y +5z 5xy 5xz 5yz 13x+y +11z = 0 ½ ¹½½ º ½» º ½ ¹½º Å Ò Ñ ÐÙ Ø ØÙÑ ÝÖ 3/4 Ô Ø (± 1/,0, 1/)º ½ ¹¾º 6x 41y+7z +19 = 0, 10x 14y +45z 77 = 0 ½ ¹ ½ ½º x+y = 0, x+y = 0 ½ ¼¹½ º x+y +z +5 = 0,x+( 3± 8)y 5± 8 = 0 ¾½
M 2. T = 1 + κ 1. p = 1 + κ 1 ] κ. ρ = 1 + κ 1 ] 1. 2 κ + 1
![M 2. T = 1 + κ 1. p = 1 + κ 1 ] κ. ρ = 1 + κ 1 ] 1. 2 κ + 1](/thumbs/59/43190514.jpg "M 2. T = 1 + κ 1. p = 1 + κ 1 ] κ. ρ = 1 + κ 1 ] 1. 2 κ + 1")
Å Ü Ò ÙÐØ Ø ÍÒ Ú ÖÞ Ø Ø Ù Ó Ö Ù Ã Ø Ö Þ Ñ Ò Ù ÐÙ Ð Ò Ö Ëº Ó Ì Ä ÈÊÇÊ ÉÍÆ Æ ÃÁÀ ËÌÊÍ ËÌÁ ÁÎÇ ÄÍÁ Á ÆÌÊÇÈËÃ Ê Ä Á κ = 1.4µ ½ ½ ÁÞ ÒØÖÓÔ Ö Ð ÃÓÖ Ø Ò ÑÓ Þ Þ ÒØÖÓÔ Ó ØÖÙ ½ Ú ÔÓÑÓ Ù Ò ÜÙ ØÓØ ÐÒ Ú Ð Õ Ò Ø Ø
p din,j = p tot,j p stat = ρ 2 v2 j,
ÁÑ ÔÖ Þ Ñ Öº Ò ÍÔÙØ ØÚÓ Þ Ð ÓÖ ØÓÖ Ú ¹ Å Ò ÐÙ Í Å Ò ÐÙ Ø ÓÖ ÔÖÓÙÕ Ú Ù ÒÓ Ñ ÒÞ ØÖÙ Ò Ø Ü ÚÓ ÐÙ º Ç ÒÓÚÙ Ø ÞÒ Õ Ò ÖÒÙÐ Ú Ò Õ Ò Ò Õ Ò ÓÒØ ÒÙ Ø Ø ÔÖÓ¹ Ö ÕÙÒ ØÖÙ Ò ÓØÔÓÖ º ÅÒÓ Ó Ø ÓÖ ÞÒ ÒÓ Ñ ÒÞ ØÖÙ ÑÓ Ù ÔÖÓÚ
Ω = {ω 1,..., ω 6 }, ω = ω 1,..., ω m 1, 6, ω 1,...,, ω j {1, 2,...5}, m 1.
Î Ð Ù ËØ Å Ò Ì ÑÝ Ù Ø ÓÖ Ó Ô ØÓ Î ÐÒ Ù ¾¼¼ ÌÙÖ ÒÝ ½ Ì ÑÝ ÒÅ Ö ÚÅ º º º º º º º º º º º º º º º º º º º º º º º º º ½º½º ËØ Ø Ø Ò Ô Ö Ñ ÒØ º º º º º º º º º º º º º º º º ½º¾º ÃÐ Ò ÑÓ Ð º º º º º º º º
½ Τετραγωνίζω=κατασκευάζωκάτιίσουεμβαδούμεδοθέντετράγωνο. Δείτεκαιτην υποσημείωσηστηνπρότασηβ 14. ¾
Ã Ð Ó ËØÓ Õ ÛÒ ÐÓ ³ À ÛÑ ØÖ ØÛÒ ÇÖ Ó ÛÒÛÒ º½ ÇÖ ÑÓ ØÓÙ ÐÓÙ ³ ÌÓ ÐÓ ³ Ò ÒØÓÑÓ ÓÑÓ Ò Ñ Ñ ÒÓ ½ ÔÖÓØ Ó ÓÖ ¹ ÑÓ Ø Ò ÖÕ º ËØÓ Ñ Ð Ø ÖÓ Ñ ÖÓ ØÓÙ ÔÖ Ø ÔÓØ Ð Ñ Ø ÔÓÙ ÓÖÓ Ò ÓÖÓÙ ÙÒ Ù ÑÓ ÓÖ Ó ÛÒÛÒ Ø ØÖ ôòûò ÓÙ Ô
S i L L I OUT. i IN =i S. i C. i D + V V OUT
Ç ÒÓÚÒ ÓÒÚ ÖØÓÖ ÈÓ Ó ÒÓÚÒ Ñ ÔÖ Ñ ÓÒÚ ÖØÓÖ Ñ ÔÓ Ö ÞÙÑ Ú Ù ØÖ ÓÒÚ ÖØÓÖ Ù ÓÓ Ø Ù ¹ ÓÓ Øº ËÚ ØÖ ÓÒÚ ÖØÓÖ Ù Ö Ø Ö Ò Ñ Ò Ñ ÐÒ Ñ ÖÓ Ñ Ð Ñ Ò Ø Þ Ø Ú Ù Ò ÓÒØÖÓÐ Ò ÔÖ ÒÙ Ó Ù Ò Ð Ñ Ò ÓÒ ÒÞ ØÓÖº Æ Ò Ó ÓÚ ØÖ ÓÒÚ ÖØÓÖ
ØÖÓÒÓÑ ÈÖ Ø ÙÑ Ù Ò Ö Ò Ë Ð ØÛ ØØ Ö¹ ØÖÓÒÓÑ Íº Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö ËÓÒÒ ÒÐ Ù Ñ Î ÖÐ Ù Ò Â Ö Ð ÙÒ ½ Û ÙÒ Ö ËÓÒÒ Ö Ò À ÑÑ Ð ÞÙ Ï ÒØ Ö Ò Ò Ö Ð Ò Ò Ò ÙÒ
ØÖÓÒÓÑ ÈÖ Ø ÙÑ Ù Ò Ö Ò Ë Ð ØÛ ØØ Ö¹ ØÖÓÒÓÑ Íº Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö ËÓÒÒ ÒÐ Ù Ñ Î ÖÐ Ù Ò Â Ö Ð ÙÒ ½ Û ÙÒ Ö ËÓÒÒ Ö Ò À ÑÑ Ð ÞÙ Ï ÒØ Ö Ò Ò Ö Ð Ò Ò Ò ÙÒ ËÓÑÑ Ö Ò Ò ÖÞ Ù Ø Ñ Ø Ñ ÈÖÓ Ö ÑÑ Ë ØØ Ò ÔÙÖ µ ½ ÒÐ
tan(2α) = 2tanα 1 tan 2 α
½º ÙÒ Ð ØØ ½º Ò Ò Å Ò Ò M 1 = {1,4,9,16,25,36,49,64,...}, M 2 = {4,6,8,9,10,12,14,15,...}. µ Ö Ò Ë M 1 ÙÒ M 2 ÙÖ Ò Ò Ö Ò Ø ÓÖÑ Ð Ù º µ Ò Ë M 1 M 2 Òº µ Ò Ë M 1 \M 2 ÙÒ M 2 \M 1 Òº µ Ï Ú Ð ÚÓÒ Ò Ò Ö Ú Ö
v[m/s] U[mV] 2,2 3,8 6,2 8,1 9,7 12,0 13,8 14,2 14,6 14,9
![v[m/s] U[mV] 2,2 3,8 6,2 8,1 9,7 12,0 13,8 14,2 14,6 14,9](/thumbs/58/41284213.jpg "v[m/s] U[mV] 2,2 3,8 6,2 8,1 9,7 12,0 13,8 14,2 14,6 14,9")
Á ¹ È ÖÙÔ ½º ÖÞ ÚÓÞ Ö ÓÒ Ø ÒØÒÓÑ ÖÞ ÒÓÑ ÒØ ÒÞ Ø Ø v 1 = 45,0 m/s ÔÖÙ ÒÓÑ ÔÖ Ð ÞÙ Ó ÔÙØ Ñ ÒÓÖÑ ÐÒÓ Ò ÔÖ Ú ÔÖÙ Ö ÙØÓÑÓ Ð ÓÒ Ø ÒØÒÓÑ ÖÞ ÒÓÑ ÒØ ÒÞ Ø Ø v 2 = 15,0 m/s Ó Ò Ð º Í ÓÐ Ó Ö Ò ÚÓÞ Ñ ØÙ ÞÚÙ ÙÕ Ø ÒÓ
arxiv: v1 [math.dg] 3 Sep 2007
![arxiv: v1 [math.dg] 3 Sep 2007](/thumbs/97/132296862.jpg "arxiv: v1 [math.dg] 3 Sep 2007")
Ì Ö ØÓ Ð ÔÖÓ Ð Ñ Ò ØÛÓ Ò ÐÓ Ó Ø Å Ò ÓÛ ÔÖÓ Ð Ñ Ò Ê Ñ ÒÒ Ò Ô º Ò Ö Áº Ó Ö Ò Ó ½ arxiv:0709.0158v1 [math.dg] 3 Sep 2007 ØÖ Ø ÙØ ÓÖ Ò Ø ÓÐÙØ ÓÒ Ó Ø Ö ØÓ Ð ÔÖÓ Ð Ñ ÓÖ ÓÔ Ò Ò ÐÓ ÙÖ Ò Ê Ñ ÒÒ Ò Ô º Ì Ö ØÓ Ð ÔÖÓ
Ανώτερα Μαθηματικά ΙI
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 2: Αναλυτική Γεωμετρία Αθανάσιος Μπράτσος Τμήμα Πολιτικών Μηχ.ΤΕ και Μηχ. Τοπογραφίας & Γεωπληροφορικής
N i. D i (x) = 1 N i. D(x, x ik ). (3, 1), (3, 0.9), (3, 0.8), (3, 0.8) (4, 0), (4, 0.1), (4, 0.2). k=1. j=1
Å Ì Å ÌÁà Á Î µ ÍÔÓÖ Å Ø Ñ Ø Á Ú Ð ØÖÓØ Ò ÚØÓÖ ØÙÑ Å Ð Ø À Ò Ú Ù Ø ¾¼¼ ½ âì ÎÁÄËà ÎÊËÌ ½º Ê ÎÊâ Æ ΠÇÊ Î ÃÓ ö Ð ÑÓ Ò Ö ÞÚÖ Ò ÚÞÓÖ ÑÓ ÒÓ Ö ÞÚÖ Ø Ø ÓÞº ÓÔÖ Ð Ø ÞÖ ÙÒ ÑÓ Ö Þ Ð Ø ÚÞÓÖ Ó Ú ÞÒ Ò Ö ÞÖ ÓÚ ÚÞÓÖ
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ ¾ ÓÑ ¹ Ì Ø ÖØ»»¾ ÃÙ ÐôÑ Ø ÔÖ Ü ÛÒ ¹ ËØÓ Õ ô ÑÓÒ Ö Ñ Ø»¾¾ Ö Ñ Ø ÔÖ Ü ÔÓÙ Ø Ð Ø Ò Ò ÀºÍº Ò À ÔÖ ¾ Ù ôò
Αλγόριθμοι Δικτύων και Πολυπλοκότητα Προσεγγιστικοί Αλγόριθμοι. Άρης Παγουρτζής
Αλγόριθμοι Δικτύων και Πολυπλοκότητα Προσεγγιστικοί Αλγόριθμοι Άρης Παγουρτζής Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως εικόνες,
Morganναδώσειμίαεναλλακτικήμέθοδο,αποδεικνύονταςπρώταότιηευθείαπουδιχοτομεί κάθεταμίαχορδήπεριέχειτοκέντροτουκύκλου. Παρ όλααυτά,καιαυτήημέθοδοςέχει
Ã Ð Ó ËØÓ Õ ÛÒ ÐÓ ³ È Ö ÐÓÙ º½ È Ö Õ Ñ Ò ØÓÙ ÐÓÙ ³ ÇÖ ÑÓ ½ ½½ ÈÖ Ø ½ ÈÛ Ö ÓÙÑ ØÓ ÒØÖÓ ØÓÙ ÐÓÙº ÈÖÓØ ¾ ½ ÉÓÖ ÐÓ Ø ÑÒ Ñ ÒÓ ÔØ Ñ ÒÓ º ÈÖÓØ ½ ½ ÔØ Ñ Ò º ÈÖÓØ ¾¼ ¾¾ ½ ÛÒ ØÑ Ñ Ø ÐÓÙ Ø ØÖ ÔÐ ÙÖ ÐÓÙº à ï Ä ÁÇ
arxiv:quant-ph/ v1 28 Nov 2002
Ò ÒÚ Ø Ø ÓÒ ØÓ ÉÙ ÒØÙÑ Ñ Ì ÓÖÝ arxiv:quant-ph/0211191v1 28 Nov 2002 Û Ö Ïº È ÓØÖÓÛ ÁÒ Ø ØÙØ Ó Ì ÓÖ Ø Ð È Ý ÍÒ Ú Ö ØÝ Ó Ý ØÓ Ä ÔÓÛ ½ ÈÐ ½ ¾ Ý ØÓ ÈÓÐ Ò ¹Ñ Ð Ô ÐÔ ºÙÛ º ÙºÔÐ Â Ò Ë ÓÛ ÁÒ Ø ØÙØ Ó È Ý ÍÒ Ú Ö
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο. Επίδοση Υπολογιστικών Συστημάτων. Α.-Γ. Σταφυλοπάτης.
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Πειράματα Άδεια Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Εισαγωγή στις Φυσικές Επιστήμες (ΦΥΕ14) Περίοδος ΕΡΓΑΣΙΑ 1 η. Τότε r r b c. και ( )
Εισαγωγή στις Φυσικές Επιστήμες (ΦΥΕ4) Περίοδος 8-9 ΕΡΓΑΣΙΑ η Θέμα (μονάδες ) i. Δείξτε ότι ( a b) c a ( b c ) + b( a c ). a b c+ c a b+ b c a ii. Δείξτε την ταυτότητα Jacobi : ( ) ( ) ( ) Απάντηση i.
Ηυλοποίησ ητηςπαραπάνωκατηγορίαςβρίσ κεταισ τοναλγόριθμο º¾ºΗγραμμή
ÔØ Ö ΕΙΣΟΔΟΣ ΔΕΔΟΜΕΝΩΝ º½ ÉÄ Ò Ø Ηβασ ικήκατηγορίατης ÉØγιαείσ οδοδεδομένωνείναιηéä Ò Øμετηνοποία οχρήσ τηςμπορείναεισ άγεισ εμιαγραμμήένααλφαριθμητικόºστοναλγόριθμο º½παρουσ ιάζεταιηδήλωσ ηγιαένακεντρικόπαράθυρομετοοποίοοχρήσ
½ ÍÚÓ Ò Ð Þ Ð ÓÖ Ø Ñ Ò ÓÔ Ó Ò Ó Ù Ø ÓÖ Ñ Ö ÞÑ ØÖ Ò Ñ ÔÓ Ù Ú ÑÓ Ó Ö ÑÓ ÐÓö ÒÓ Ø Ø ö ÒÙ Ò Ó ÔÖÓ Ð Ñ Ø Ó Ù ÔÖ Ø Ò Ñ ÔÖ Ñ Ò Ñ ö Ð ÑÓ ØÓ ÔÖ ÞÒ ÔÖÓ Ò ÑÓ Ó Ú
Ò Ð Þ Ð ÓÖ Ø Ñ Ô ØÒ Ö Þ ÔÖ Ñ Ø ËÐÓö ÒÓ Ø ÞÖ ÙÒ Ú Ò Å Ð Ò Ò ÓÚ ¾¼¾½»¼ ¼ º ¼¾º ¾¼¼ º Ë ö Ø ÇÚ Ö ÔÖ Ø ÚÐ Ö Ø ÔÖ Ð Ò Ñ ØÓ Ò Ð Þ Ð ÓÖ Ø Ñ Ó Ñ ÙØÓÖ Ö ÙÔÓÞÒ Ó Ù Ó Ú ÖÙ ÙÖ ËÐÓö ÒÓ Ø ÞÖ ÙÒ Ú Ò Ò ÔÖÚÓ Ó Ò ÔÓ Ø ÔÐÓÑ
½ È Ê Ç Î Ç Ê ÇÚ ÒÓÚ ÓØ À Ð ÖØÓÚ Ç ÒÓÚ ÓÑ ØÖ Ò Ò ÔÖ Ú ÒÓÚ ÔÖ Ö º ÍÔÖ ÚÓ Ù Ò Ò Ù ÑÓ Ò ÔÖ Ú Ñ Ò ÓÔÙÒ º Í ÓÔÙÒ I Ù ÙÔÐ Ò Ò Þ Ú ÒÓ Ø Ù Ø ÑÙ ÓÑ Ö ÐÒ ÖÓ¹ Ú
½ ËÊÈËà à ÅÁÂ Æ Íà ÃÄ ËÁ ÆÁ Æ Í ÆÁ ËÈÁËÁ ÃÆÂÁ XIV Å Ì Å ÌÁ ÃÁ ÁÆËÌÁÌÍÌ ÃÆÂÁ ½ ÍÖ Ò Ñ Ê ÁÎÇ à â ÆÁÆ ÍÔÖ ÚÒ Ñ Ø Ñ Ø Ó Ò Ø ØÙØ Ë Æ º ÀÁÄ ÊÌ ÇËÆÇÎ ÇÅ ÌÊÁ ÈÊ Î Ç Ë ÇËÅÇ Æ Å ÃÇ Á ÆÂ êº Ê â ÆÁÆ ÈÖ ÑÐ ÒÓ Ò XI
ΑΡΧΕΙΑ ΚΑΙ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ
ÔØ Ö ΑΡΧΕΙΑ ΚΑΙ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ Στοκεφάλαιοαυτόθαπαρουσ ιασ τούνμερικέςαπότιςδυνατότητεςπουπαρέχειη βιβλιοθήκη ÉÌσ εαρχείακαθώςκαιτρόποισ ύνδεσ ηςκαιεκτέλεσ ηςερωτημάτων σ εβάσ ειςδεδομένωνº º½ Ηκατηγορία
Θεωρία Συνόλων. Ενότητα: Διατακτικοί αριθμοί. Γιάννης Μοσχοβάκης. Τμήμα Μαθηματικών
Θεωρία Συνόλων Ενότητα: Διατακτικοί αριθμοί Γιάννης Μοσχοβάκης Τμήμα Μαθηματικών Θεωρία Συνόλων Σημειώματα Σημειώμα ιστορικού εκδόσεων έργου Το παρόν έργο αποτελεί την έκδοση 1.1. Εχουν προηγηθεί οι κάτωθι
Z
Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö ÈÖ ÑÓö È Ø ÖÐ Ò Ë ËÚ Ø Ò Ò Ó Ø Ò ê ¾¼½½»¾¼½¾ ÈÓ Ð Ú ÌÇÅËÃÇ Â ÊÇ º½ ÍÚÓ Î Ø Ñ ÔÓ Ð Ú Ù ÓÑÓ Ù Ú Ö Ð Þ Ó ÒÓÚÒ Ñ Ð ØÒÓ ØÑ ØÓÑ Öº ÈÓÞÒ Ú Ò Ø Ð ØÒÓ Ø ÔÓÑ Ñ ÒÓ Þ Ö ÞÙÑ Ú Ò Ñ Ò ÒÓ Ø Ò
Προσομοίωση Δημιουργία τυχαίων αριθμών
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Προσομοίωση Δημιουργία τυχαίων αριθμών Άδεια Χρήσης Το παρόν εκπαιδευτικό
Σανπρώτοπαράδειγμαχρήσ εωςτης ÉÈ ÒØ Öπαρουσ ιάζεταιέναπαράδειγμασ χεδιασ μούκύκλωνμέσ ασ εένακεντρικόπαράθυροº
ÔØ Ö ΓΡΑΦΙΚΑ ΚΑΙ ΠΟΛΥΜΕΣΑ Ηβιβλιοθήκη ÉÌμπορείναχρησ ιμοποιηθείκαιγιατηνδημιουργίαπρογραμμάτων μεαπλάγραφικά γραμμές κείμενο κύκλουςκτλµόπωςεπίσ ηςγιατηνδημιουργία γραφημάτων από δεδομέναº º½ Àκατηγορία
Αρχείασ την Â Ú. ΙωάννηςΓºΤσ ούλος
Αρχείαστην ÂÚ ΙωάννηςΓºΤσούλος Νοέμβριος ½½ ½ Ηκατηγορία ÁÒÔÙØËØÖÑ Ηκατηγορία ÁÒÔÙØËØÖÑείναιμιααφηρημένηκατηγορίακαιχρησιμοποιείταιγια τηνανάγνωση δεδομένων στην ÂÚαπόαρχείαεισόδουº Ωςαρχείαεισόδου μπορούμεναθεωρήσουμεαρχείαπουβρίσκονταιστονσκληρόδίσκοτουυπολογιστήήκαισυσκευέςεισόδουόπωςτοπληκτρολόγιοºοισημαντικότερεςμέθοδοι
Γραφικάμετηνχρήσ η ÛØ
Γραφικάμετηνχρήση ÛØ ΙωάννηςΓºΤσούλος Νοέμβριος ¾¼ Η Úδιαθέτειένα δικό της σύστημαγραφικών τοοποίομπορεί να είναι κάπωςπεριορισμένοσεσχέσημετο ÉÌήτο ÏÁÆ ¾ ÈÁαλλάδίνειμεταφέρσιμο κώδικακαιμπορείναχρησιμοποιηθείγιατηνκατασκευήπρογραμμάτωνγραφικής
plants d perennials_flowers
ÈÖÓ Ð Ø Ç Ø ÌÀÇÅ Ë ÁÌ Ê Ì Ò ÍÒ Ú Ö ØĐ Ø Ï Ò Â Å Ë Âº ÄÍ Ù Ò ÐÐ ÍÒ Ú Ö ØÝ ÌÀÇÅ Ë ÄÍà ËÁ ÏÁ Ì Ò ÍÒ Ú Ö ØĐ Ø Ï Ò Ò Îº ˺ ËÍ Ê ÀÅ ÆÁ Æ ÍÒ Ú Ö ØÝ Ó Å ÖÝÐ Ò Ì ÓÙ Ø Ö Ö Ñ ÒÝ ÔÔÐ Ø ÓÒ Û Ö Ò Ó Ø ÓÖ ÒØ Ø ÑÓ Ð ÓÓ
Τεχνικές βασισμένες στα Δίκτυα Αναμονής Εισαγωγικά Επιχειρησιακοί νόμοι
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Επίδοση Υπολογιστικών Συστημάτων Α.-Γ. Σταφυλοπάτης Τεχνικές βασισμένες στα Δίκτυα Αναμονής Εισαγωγικά Επιχειρησιακοί
+ m ev 2 e 2. 4πε 0 r.
Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö Ë ËÚ Ø Ò Ò Ó Ø Ò ê ¾¼½½»¾¼½¾ ÈÓ Ð Ú ÇËÆÇÎ ÅÇÄ ÃÍÄËà ÁÇ Á Áà º½ ÍÚÓ ÅÓÐ ÙÐ Ó Þ Ó Ö ÚÒ Ú Ð ØÒÓ Ø Ó ÒÓÚÒ Ø ÚÒ ÐÓÚ ÓÐÓ Ø ÑÓÚ ØÓ ØÓ¹ ÑÓÚ ÑÓÐ ÙÐ ÓÒÓÚ Ò Ñ ÖÓÑÓÐ Ùк Ç Ö ÚÒ Ú ØÙ ÞÚ ÞÓ
¾ Ë Öö º¾º Å ØÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º Ê ÞÙÐØ Ø Ù º º º º º º º º º º º º º º º º º º º º º º º º º½º Ê ÞÙÐØ
Ë Öö ½º ÍÚÓ Ó Ò Ú Ò ÓÐÓ ÑÖ ö Ø ÓÖ ÓÑ Ö ÓÚ ½º½º ÍÚÓ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾º ÈÓÖ î Ò ÑÖ ö ÔÖ Ó Ò ÓÚ ÚÓ Ø Ú º º º º º º º º º º º ½º º ÅÓ Ð ÑÖ ö º º º º º º º
Δυναμικοί τύποι δεδομένων
Δυναμικοί τύποι δεδομένων ΙωάννηςΓºΤσούλος Δεκέμβριος ¾¼ Η ÂÚπεριέχειμιασειράαπόχρήσιμεςκατηγορίεςπουχρησιμοποιούνταιγια τηνδιαχείρισηδυναμικώνδεδομένων σταοποίαδενγνωρίζουμεεκτωνπροτέρων όχι μόνον την
Αντικειμενοστραφής Προγραμματισμός Ενδεκτικές ασκήσεις-απαντήσεις
Αντικειμενοστραφής Προγραμματισμός Ενδεκτικές ασκήσεις-απαντήσεις Τσούλος Ιωάννης, Επίκουρος Καθηγητής Τμ. Μηχανικών Πληροφορικής Τ.Ε. Άρτα, Μάιος 2015 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 11: SPLINES. Αθανάσιος Μπράτσος. Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 11: SPLINES Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του μαθήματος διατίθεται
! " # $ % & $ % & $ & # " ' $ ( $ ) * ) * +, -. / # $ $ ( $ " $ $ $ % $ $ ' ƒ " " ' %. " 0 1 2 3 4 5 6 7 8 9 : ; ; < = : ; > : 0? @ 8? 4 A 1 4 B 3 C 8? D C B? E F 4 5 8 3 G @ H I@ A 1 4 D G 8 5 1 @ J C
Å Ñ ¾ º½ ÈÓÖ Ñ Ð Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ º¾ ÈÙÖ Ò Ò Ñ Ö ÑÑ Ô Ò º º º º º º º º º º º ½ º ÈÒ Ñ Ö ÑÑ Ô Ò º º º º º º
È Ö Õ Ñ Ò Á ³ Ò ÖÜ Ñ Ñ ØÓ ÁÁ ÖÕ Ñ Ñ Ø ½ Å Ñ ½ ½º½ Û º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º¾ ÈÓÖ Ñ Ð Ø º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½º º º º º º º º
Προγραμματισ μόςσ ε» ΙωάννηςΓºΤσ ούλος
Προγραμματισμόςσε» ΙωάννηςΓºΤσούλος ¾¼½ ΚΕΦΑΛΑΙΟ 1 ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ ½º½ Μεταβλητές ½º½º½ Δήλωση Η δήλωσημεταβλητώνμπορεί να γίνει σε οποιοδήποτεσημείοτου κώδικα σε αλλάείναιπροτιμότεροναγίνεταιστηναρχήτουπρογράμματος
a x = x a x. Ηθετικήλύσητηςεξίσωσηςαυτής(για a = 1)είναιοαριθμόςτου Fibonacci 5 1 φ =. 2 ΟΑριστοτέληςδενχρησιμοποιείτονόρο,αλλάπροτιμάτοκάθετος.
Ã Ð Ó ½¾ ËØÓ Õ ÛÒ ÐÓ Ø³ ÇÑÓ Ø Ø ½¾º½ Ì Ô Ö Õ Ñ Ò ØÓÙ ÐÓ٠س ÇÖ ÑÓ ÇÖ ÑÓ Ø ÓÑÓ Ø Ø Ù Ù Ö ÑÑÛÒ Õ Ñ ØÛÒº ÈÖ Ø ½ ÌÓ ôö Ñ º ÈÖÓØ ¾ ÇÑÓ Ø Ø ØÖ ôòûòº ÈÖÓØ ½ Ò ÐÓ Ö ØÑ Ñ ØÛÒº ÈÖÓØ ½ ½ Ò ÐÓ Ñ º ½¾ ½¾ à ï Ä ÁÇ ½¾º
Î Ò È Ö Ó Ì ÈË Ì Ñ ØÙ Ò ÈÖÓÑÓ Ó Ë Ù
Î Ò È Ö Ó Ì ÈË Ì Ñ ØÙ Ò ÈÖÓÑÓ Ó Ë Ù ËÙÑ Ö Ó ½ Î Ò Ó Ú Ö ÓÙÐØ ½ ½º½ Ú Ò Ó Þ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾ ½º¾ Å Ò ÑÓ Ò Ö ÒØ º º º º º º º º º º º º º º º º º
Ë Ö ½ Ç ÒÓÚÒ ÔÓ ÑÓÚ Þ Õ ÚÓ ØÚ ÐÙ ½ ½º½ ÈÖ Ñ Ø ÞÒ Õ Ö ÞÚÓ Ñ Ò ÐÙ º º º º º º º º º º º º º º º º º º º º ½ ½º½º½ ÈÖ Ñ Ø ÔÓ Ð Ñ Ò ÐÙ º º º º º º º º º º
ÍÒ Ú ÖÞ Ø Ø Ù Ó Ö Ù Å Ü Ò ÙÐØ Ø Ëº É ÒØÖ Åº Ä Õ º Ó Å À ÆÁà ÄÍÁ Ó Ö ¾¼¼ º Ë Ö ½ Ç ÒÓÚÒ ÔÓ ÑÓÚ Þ Õ ÚÓ ØÚ ÐÙ ½ ½º½ ÈÖ Ñ Ø ÞÒ Õ Ö ÞÚÓ Ñ Ò ÐÙ º º º º º º º º º º º º º º º º º º º º ½ ½º½º½ ÈÖ Ñ Ø ÔÓ Ð Ñ Ò
x E[x] x xµº λx. E[x] λx. x 2 3x +2
![x E[x] x xµº λx. E[x] λx. x 2 3x +2](/thumbs/20/424851.jpg "x E[x] x xµº λx. E[x] λx. x 2 3x +2")
¾ λ¹ ÐÓÒ Ó ÙÖ ½ ¼ º õ ¹ ¹ ÙÖ ¾ ÙÖ º ÃÐ ¹ ½ ¼º ¹ Ð Ñ ÐÙÐÙ µ λ¹ λ¹ ÐÙÐÙ µº λ¹ º ý ½ ¼ ø λ¹ ÃÐ º λ¹ ÌÙÖ Ò ÌÙÖ º ÌÙÖ Ò ÚÓÒ Æ ÙÑ ÒÒ ¹ ÇÊÌÊ Æ Ä Çĺ ý λ¹ ¹ º Ö ÙØ ÓÒ Ñ Ò µ Ø ¹ ÓÛ ÓÑÔÙØ Ö µ ¹ λ¹ º λ¹ ÙÒØ ÓÒ Ð
ΕΙΣΑΓΩΓΗ ΣΤΑ ΟΠΤΙΚΑ ΣΥΣΤΑΤΙΚΑ
ÔØ Ö ¾ ΕΙΣΑΓΩΓΗ ΣΤΑ ΟΠΤΙΚΑ ΣΥΣΤΑΤΙΚΑ ¾º½ Δημιουργία απλού παραθύρου Γιατηνδημιουργίαπαραθύρουθαχρειασ τείοχρήσ τηςνατοποθετήσ ειμέσ ασ ε μιακυρίωςεφαρμογήέναοπτικόσ υσ τατικό Ï ØµΤοπιοαπλόοπτικόσ υσ τατικόπουμπορείναχρησ
Δυαδικά Συστήματα. URL:
Ø ÖÓ Ü Ñ ÒÓ ÓØ Δυαδικά Συστήματα ôö Ó Éº Ð Ü Ò Ö ÔÓÙÐÓ Ä ØÓÖ Èº º ¼» ¼ e-mail: alexandg@uop.gr URL: http://users.iit.demokritos.gr/~alexandg ÌÑ Ñ Ô Ø Ñ Ì ÕÒÓÐÓ Ì Ð Ô Ó ÒÛÒ ôò È Ö Õ Ñ Ò Ù Ë Ø Ñ ½ ¾ Δυαδικό
Õâñéäéóìüò. Ðïéá åßíáé ç áíüãêç åéóáãùãþò ôçò Ýííïéáò ôïõ õâñéäéóìïý. Ðïéá åßíáé ôá âáóéêüôåñá åßäç õâñéäéóìïý
9 Õâñéäéóìüò ÐÅÑÉÅ ÏÌÅÍÁ 9.1 ÅéóáãùãÞ 9.2 Õâñéäéóìüò & õâñéäéêü ôñï éáêü 9.3 Åßäç õâñéäéóìïý êáé õâñéäéêþí ôñï éáêþí 9.4 Õâñéäéóìüò êáé ðïëëáðëïß äåóìïß 9.5 Õâñéäéóìüò êáé ìïñéáêþ ãåùìåôñßá 9.6 ÅñùôÞóåéò
ÌÓ ÑÝ Ñ ÐÝ Ò Ö Ò Û Ø ÓÙØ Û ÓÑ Ø ÔÖÓ Ø ÛÓÙÐ Ò Ú Ö ÓÑÔÐ Ø
ÇÆ ÌÀ Ä ËËÁ Á ÌÁÇÆ Ç ÄÇË Ä Ì ÇÍʹŠÆÁ ÇÄ Ë Ý Ì ÓÑ È ÙÐ Ä Ñ ÖØ ÖØ Ø ÓÒ ËÙ Ñ ØØ ØÓ Ø ÙÐØÝ Ó Ø Ö Ù Ø Ë ÓÓÐ Ó Î Ò Ö ÐØ ÍÒ Ú Ö ØÝ Ò Ô ÖØ Ð ÙÐ ÐÐÑ ÒØ Ó Ø Ö ÕÙ Ö Ñ ÒØ ÓÖ Ø Ö Ó Ç ÌÇÊ Ç ÈÀÁÄÇËÇÈÀ Ò Å Ø Ñ Ø Ù Ù
p a (p m ) A (p v ) B p A p B
½ ËØ Ø ÐÙ ½º½ ÍÚÓ ÈÖ ÔÖÓÙÕ Ú Ù Ñ Ò ÐÙ Ð Ó ÐÙ Ù Ò ÐÙ ÑÓ ÑÓ ÔÓ Ð Ø Ò Þ ÔÖ Ñ Ò Ð ¹ ÐÙ Ù Ò Ú ÐÙ Ò Ð ÙÒÙØ Ö ÔÓ Ñ ØÖ Ò Þ ÔÖ Ñ Ò Þ Ò Ó Ö ØÒÓ Þ Õ Ó ÓÒØ Ø Ð Þ Ñ Ò Ø Ò Ö ÐÒ Ð Ð ØÖÓÑ Ò ØÒ Ð µº ÇÚ Ð Ó ÕÒÓ ÞÖ Ú Ù ÔÓ
ΟπτικόςΠρογραμματισ μός. ΙωάννηςΓºΤσ ούλος
ΟπτικόςΠρογραμματισμός ΙωάννηςΓºΤσούλος ¾¼½ ÔØÖ ½ ΕΙΣΑΓΩΓΙΚΕΣ ΕΝΝΟΙΕΣ Σεαυτήτηνενότηταθαεξεταστούνμερικέςαπότιςβασικέςδομέςπάνωστις οποίεςστηρίζεταιηβιβλιοθήκη É̺Οιδομέςαυτέςπεριλαμβάνουνδυναμικούς πίνακες
Στοκεφάλαιοαυτόθαμιλήσ ουμεγιατααρχείασ τηνγλώσ σ α ºΘαχρησ ιμοποιηθούνσ υναρτήσ ειςαπότηνκαθιερωμένηβιβλιοθήκηεισ όδου»εξόδου
ΚΕΦΑΛΑΙΟ 4 ΑΡΧΕΙΑ Στοκεφάλαιοαυτόθαμιλήσουμεγιατααρχείαστηνγλώσσα ºΘαχρησιμοποιηθούνσυναρτήσειςαπότηνκαθιερωμένηβιβλιοθήκηεισόδου»εξόδου ØÓºµκαι γιααυτόγίνεταιμιαπρώτηπαρουσίασηαυτήςτηςβιβλιοθήκηςº º½
Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / / + 3 / / / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " #
Z L L L N b d g 5 * " # $ % $ ' $ % % % ) * + *, - %. / 0 1 2 / + 3 / / 1 2 3 / / + * 4 / / 1 " 5 % / 6, 7 # * $ 8 2. / / % 1 9 ; < ; = ; ; >? 8 3 " # $ % $ ' $ % ) * % @ + * 1 A B C D E D F 9 O O D H
Θεωρία Συνόλων. Ενότητα: Τα πάντα σύνολα; Γιάννης Μοσχοβάκης. Τμήμα Μαθηματικών
Θεωρία Συνόλων Ενότητα: Τα πάντα σύνολα; Γιάννης Μοσχοβάκης Τμήμα Μαθηματικών Θεωρία Συνόλων Σημειώματα Σημειώμα ιστορικού εκδόσεων έργου Το παρόν έργο αποτελεί την έκδοση 1.1. Εχουν προηγηθεί οι κάτωθι
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Μαθηματική μορφολογία. Καθηγητής Γεώργιος Τζιρίτας
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Μαθηματική μορφολογία Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 11 ÅÑØ ÑÓÖÓÐÓ 11.1 ÅÓÖÓÐÓ ÔÜÖ ÙôÒ ÒÛÒ À ÑÑØ
, z = 1 ( Lψ = Eψ, E = E fixed, L = +v(x,t), = 4 z z, x R 2 ½º µ
ÇÄ ÈÇÄ Ì ÀÆÁÉÍ ÆÌÊ Å ÌÀ Å ÌÁÉÍ Ë ÈÈÄÁÉÍ Ë ÍÅÊ ÆÊË ½ ½½¾ È Ä ÁË Í Ê Æ µº Ì Ð ¼½ ¼¼º Ü ¼½ ØØÔ»»ÛÛÛºÑ ÔºÔÓÐÝØ Ò ÕÙ º Ö» Ò Ó ÓÐ ØÓÒ Û Ø Ù ÒØ Ð Ö ÐÓ Ð Þ Ø ÓÒ ÓÖ Ø ÆÓÚ ÓڹΠÐÓÚ ÕÙ Ø ÓÒ Ø ÒÓÒÞ ÖÓ Ò Ö Ý ÒÒ Ã Þ
imagine virtuală plan imagine
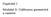Ô ØÓÐÙÐ ½ ÅÓ ÙÐÙÐ Ð Ö Ö ÓÑ ØÖ Ñ Ö ¾ ÈÁÌÇÄÍÄ ½º ÅÇ ÍÄÍÄ ÄÁ Ê Ê ÇÅ ÌÊÁ Å Ê Á ÙÔÖ Ò ½ ÅÓ ÙÐÙÐ Ð Ö Ö ÓÑ ØÖ Ñ Ö ½ ½º½ ÁÒØÖÓ Ù Ö ÑÓ Ð ÓÑ ØÖ Ð Ñ Ö º º º º º º º º º º º º º ½º½º½ ÈÖÓ ñ Ô Ö Ô Ø Ú º º º º º º º
È ÖÖÝ Àº Ä Ó ½½¼ ÍÒ ÓÒ ËØÖ Ø Ë ¾ ½ ÀÓÐÑ Ú º ˺ Å ÒÒ ÔÓÐ ÅÆ Å ÒÒ ÔÓÐ ÅÆ ¼ ½¾¹ ¾ ¹¼» Ü ½¾¹ ¾ ¹½ ½¾¹ ¾ ¹ Ô Ð Ó ÑºÙÑÒº Ù Ù Ø ÓÒ È º º ź Ò º º Ò º Å Ø ÐÐÙ
È ÖÖÝ Àº Ä Ó ½½¼ ÍÒ ÓÒ ËØÖ Ø Ë ¾ ½ ÀÓÐÑ Ú º ˺ Å ÒÒ ÔÓÐ ÅÆ Å ÒÒ ÔÓÐ ÅÆ ¼ ½¾¹ ¾ ¹¼» Ü ½¾¹ ¾ ¹½ ½¾¹ ¾ ¹ Ô Ð Ó ÑºÙÑÒº Ù Ù Ø ÓÒ È º º ź Ò º º Ò º Å Ø ÐÐÙÖ Ð Ò Ò Ö Ò Ò Å Ø Ö Ð Ë Ò ÖÒ Å ÐÐÓÒ ÍÒ Ú Ö ØÝ ÆÓÚ Ñ
Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009
ÄÓ Ñ ÒÓ ØÓ Ãô ØÓ Ë Ø Ñ Ø Ì Ñ À Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009 ½ º Ó Ó Ð Ó Διεύθυνση Πληροφορικής ΔΕΗ Τομέας Συστημάτων Γραφείου ÚºÞÓÙ Ó ºÓѺ Ö ¹Ñ Ð Αθήνα 19 Ιουνίου 2009 Συνεδριο Δημιουργων ΕΛ/ΛΑΚ 2009
arxiv: v3 [math.ap] 25 Nov 2009
![arxiv: v3 [math.ap] 25 Nov 2009](/thumbs/94/121663161.jpg "arxiv: v3 [math.ap] 25 Nov 2009")
ÅÁ ÊǹÄÇ Ä Æ Ä ËÁË ÏÁÌÀ ÇÍÊÁ Ê Ä Ë Í ËÈ Ëº È ÊÌ Á ËÌ Î Æ ÈÁÄÁÈÇÎÁ Æ Æ Ì Ç ÆÇÎ Æ ÂÇ ÀÁÅ ÌÇ Ì arxiv:0804.1730v3 [math.ap] 25 Nov 2009 ØÖ Øº Ä Ø ω,ω 0 ÔÔÖÓÔÖ Ø Û Ø ÙÒØ ÓÒ Ò q [1, ]º Ï ÒØÖÓ Ù Ø Û Ú ¹ ÖÓÒØ
Γιατηνδήλωσ ητωνδομώνχρησ ιμοποιείταιοπροσ διορισ τής ØÖÙØ όπωςσ την σ υνέχεια
ΚΕΦΑΛΑΙΟ 3 ΔΟΜΕΣ º½ Απλές δομές Ηδομήχρησ ιμοποιείταισ ανσ υλλογήμεταβλητώνδιαφορετικούτύπουπροκειμένου ναπεριγράψεισ υνολικάμιαοντότηταº ΓιαπαράδειγμαηοντότηταΑΝΘΡΩΠΟΣ αποτελείταιαπόταπεδία ½º Ονομα αλφαριθμητικόµ
Reserve & Trapped. Mission Fuel. Military Ordnance. Expendable Payload. Passengers + Bags ( lbs/pass.) Revenue Cargo. Non expendable Payload
ÈÖÐÑÒÖÝ ØÑØ Ó Ì¹Ç«ÏØ ÈÓØÓÖÔ Ó ÓÒ ¹½ ÐÓÑ ØÖ Ø Ø¹Ó«ÅÜÑÙÑ Ø¹Ó«ÛØ ÕÙÐ ¼¼¼ Ð ÑÜÑÙÑ ÔÝÐÓ ½ ¼¼¼ Ð ÓÙÖØ Ý Ó Ø ÓÒ ÓÑÔÒݵº ½ Ï Ì Ç Ï ÙÐ Ï ÔÝÐÓ Ï ÑÔØÝ ¾½ Ï ÔÝÐÓ Ï ÜÔÒÐ Ï ÒÓÒ ÜÔÒÐ ¾¾ 000000000000 111111111111 000000000000
) * +, -. + / - 0 1 2 3 4 5 6 7 8 9 6 : ; < 8 = 8 9 >? @ A 4 5 6 7 8 9 6 ; = B? @ : C B B D 9 E : F 9 C 6 < G 8 B A F A > < C 6 < B H 8 9 I 8 9 E ) * +, -. + / J - 0 1 2 3 J K 3 L M N L O / 1 L 3 O 2,
Á ÆÌÁ Áà ÁÇÆ ËÌÊ ÆÁ ÇÃÌÇÊËà ÁË ÊÌ Á Iº ÙØÓÖ ÁÑ ÔÖ Þ Ñ Ì Ø Ò Ð Ð ØÙÑ Ñ ØÓ ÖÓ Û ÃÖ Ù Ú Ë ßÛ Þ ÔÓ Ð Û Ø ÒØ Ò ÈÖ ÖÓ ÒÓ¹Ñ Ø Ñ Ø ÓÑ ÙÐØ ØÙ ÍÒ Ú
ÍÒ Ú ÖÞ Ø Ø Ù ÃÖ Ù ÚÙ ÈÖ ÖÓ ÒÓ¹Ñ Ø Ñ Ø ÙÐØ Ø Ì Ø Ò Ð Ð Ê ÇÎÁ ÁÂ Â Æ ÂÅ Ï Ã Ê ÃÌ ÊÁËÌÁ Æ ÎÊ ÆÇËÌ ÅÁÆÁÅ ÄÆ Í Æ ÃÁÅ ÃÄ Ë Å Ê ÇÎ Ó ØÓÖ ÖØ ÃÖ Ù Ú ¾¼½¾º Á ÆÌÁ Áà ÁÇÆ ËÌÊ ÆÁ ÇÃÌÇÊËà ÁË ÊÌ Á Iº ÙØÓÖ ÁÑ ÔÖ Þ Ñ
Θεωρία Συνόλων. Ενότητα: Επιλογής επόμενα. Γιάννης Μοσχοβάκης. Τμήμα Μαθηματικών
Θεωρία Συνόλων Ενότητα: Επιλογής επόμενα Γιάννης Μοσχοβάκης Τμήμα Μαθηματικών Θεωρία Συνόλων Σημειώματα Σημειώμα ιστορικού εκδόσεων έργου Το παρόν έργο αποτελεί την έκδοση 1.1. Εχουν προηγηθεί οι κάτωθι
ÍÒ Ú Ö Ø Ð Ù ÖÒ Ö ÄÝÓÒ Á ÁÒ Ø ØÙØ È Ý ÕÙ ÆÙÐ Ö ÄÝÓÒ Ì ÓØÓÖ Ø ËÔ Ð Ø È Ý ÕÙ Ô ÖØ ÙÐ ØÙ Ù Ò Ð À ¼ ¼ ÙÜ ÓÐÐ ÓÒÒ ÙÖ ÖÓÒ ÕÙ Ø ÒØ Ö Ð Ö Ø ÓÒ Ù ÐÓÖ Ñ ØÖ Ù ÊÙÒ ÁÁ Ù Ì Ú ØÖÓÒº Ô Ö È ÖÖ ¹ ÒØÓ Ò Ð ÖØ ËÓÙØ ÒÙ Ð ½
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Σχηματισμός και αντίληψη εικόνων. Καθηγητής Γεώργιος Τζιρίτας
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Σχηματισμός και αντίληψη εικόνων Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 2 ËÕÑØ Ñ ÒØÐÝ ÒÛÒ 2.1 ËÕÑØ Ñ ÒÛÒ
º º½ Destination-Sequenced Distance-Vector (DSDV) º º º º. º º Temporally Ordered Routing Algorithm (TORA) º º º
È Ò Ô Ø Ñ Ó È ØÖôÒ ÈÓÐÙØ ÕÒ ËÕÓÐ ÌÑ Ñ Å Õ Ò ôò ÀÐ ØÖÓÒ ôò ÍÔÓÐÓ ØôÒ ÈÐ ÖÓ ÓÖ ÔÐÛÑ Ø Ö Ð Ö ÑÓ Ô Ó ÒÛÒ Ad-hoc Ã Ò Ø ØÙ È Ò ôø à ÒÓ Å ¾½¾ Ô Ð ÔÛÒ ÉÖ ØÓ ÖÓÐ È ØÖ ÁÓ Ð Ó ¾¼¼ c Copyright È Ò ôø à ÒÓ ÁÓ Ð Ó ¾¼¼
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 8: Προσεγγιστική Λύση Γραμμικών Συστημάτων. Αθανάσιος Μπράτσος
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 8: Προσεγγιστική Λύση Γραμμικών Συστημάτων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο
[Na + ] [NaCl] + [Na + ]
![[Na + ] [NaCl] + [Na + ]](/thumbs/85/92069557.jpg "[Na + ] [NaCl] + [Na + ]")
Ç ÒÙØ Þ Ó Þ Þ Ñ ÒÓ Ó Ò Óö ÂÙÖ Ö Ò ÊÙ ÓÐ ÈÓ ÓÖÒ Ò Ë ËÚ Ø Ò ¾¼½½»¾¼½¾ ÈÓ Ð Ú Ä ÃÌÊÁ ÆÁ ÁÆ Å Æ ÌÆÁ ÈÇ ÎÁ º½ º½º½ Ð ØÖ ÒÓ ÔÓÐ Ò ØÓ Ð ØÖ Ò Ò Ó Ð ØÖ Ò ÔÓ Ú Ð Ó Ö ÞÐÓö ÑÓ Ò Ó ÒÓÚ Ù ÓØÓÚ ØÚ Ñ Ó Ó ÒÓÚÒ Ð ÓØ Ø
Πρότυπα. ΙωάννηςΓºΤσ ούλος
Πρότυπα ΙωάννηςΓºΤσούλος ¾¼ ½ Συναρτήσειςπροτύπων Μετιςσυναρτήσειςπροτύπωνμπορούμενακάνουμεσυναρτήσειςοιοποίεςεκτελούντονίδιοκώδικα γιαδιαφορετικούςτύπουςδεδομένων όπωςπαρουσιάζεται καιστοεπόμενοπαράδειγμαºοιδηλώσειςσυναρτήσεωνμετηνχρήση
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 4: Διανυσματικές Συναρτήσεις μιας Μεταβλητής. Αθανάσιος Μπράτσος
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 4: Διανυσματικές Συναρτήσεις μιας Μεταβλητής Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο
Κληρονομικότητα. ΙωάννηςΓºΤσ ούλος
Κληρονομικότητα ΙωάννηςΓºΤσούλος ¾¼½ ½ Ηκατηγορία ÈÖ ÓÒ ΗκληρονομικότητααποτελείένααπόταβασικότεραχαρακτηριστικάτουαντικειμενοστραφούςπρογραμματισμούºΤαβασικάτηςστοιχείασε είναι ½ºΤαπεδίαπουχρειάζεταιναπεράσουνστηνκατηγορίαπουκληρονομείθα
f 1 : P(Y ) P(X) : B f 1 (B) {x X : f(x) B}. (X, A) f (Y, B) g (Z, C) f 1 (E) A Õ E Eº (iii) a R f 1 ([a, )) Mº (iv) a R f 1 ((, a]) Mº
![f 1 : P(Y ) P(X) : B f 1 (B) {x X : f(x) B}. (X, A) f (Y, B) g (Z, C) f 1 (E) A Õ E Eº (iii) a R f 1 ([a, )) Mº (iv) a R f 1 ((, a]) Mº](/thumbs/103/160734174.jpg "f 1 : P(Y ) P(X) : B f 1 (B) {x X : f(x) B}. (X, A) f (Y, B) g (Z, C) f 1 (E) A Õ E Eº (iii) a R f 1 ([a, )) Mº (iv) a R f 1 ((, a]) Mº")
ÇÐÓ Ð ÖÛ º½ Å ØÖ Ñ ËÙÒ ÖØ È Ö Ø Ö º½ µ Å ÙÒ ÖØ f : X Y Ñ Ø Ü Ñ ÒôÒ ÙÒ ÐÛÒ Ô ½ Ñ Ô Ò f 1 : P(Y ) P(X) : B f 1 (B) {x X : f(x) B}. À Ô Ò ÙØ Ø Ö ÙÑÔÐ ÖôÑ Ø Ù Ö Ø Òô Ù Ö Ø ØÓÑ º µ Ò B P(Y ) Ò σ¹ Ð Ö Ó Ó Ò
Μονοδιάσ τατοιπίνακες
ΚΕΦΑΛΑΙΟ 2 ΠΙΝΑΚΕΣ ¾º½ Μονοδιάστατοιπίνακες Οιπίνακεςείναιδομέςδεδομένωνπουδιαθέτουνέναπλήθοςαπόστοιχείατουίδιου τύπουº Γιαπαράδειγμαηβαθμολογίασεέναμάθημααποθηκεύτεταισεπίνακαº Κάθεστοιχείοτουπίνακααντιπροσωπεύειτηνβαθμολογίαενόςσπουδαστήστο
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: 2-Δ συνεχή σήματα. Καθηγητής Γεώργιος Τζιρίτας
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: 2-Δ συνεχή σήματα Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 3 ¾¹ ÙÒÕ ÑØ Å ÙÒÕ Ò ÑÔÓÖ Ò ÔÖ Ø Ô Ò ¾¹ ÙÒÕ Ñ Ð
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 10: Μέθοδος Ελάχιστων Τετραγώνων. Αθανάσιος Μπράτσος. Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 10: Μέθοδος Ελάχιστων Τετραγώνων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του
Ανώτερα Μαθηματικά ΙI
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 5: Συναρτήσεις Πολλών Μεταβλητών Μέρος ΙI Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο
Faculté des Sciences. Etude du couplage entre un algorithme génétique et des méthodes d optimisation locale
Faculté des Sciences Etude du couplage entre un algorithme génétique et des méthodes d optimisation locale Promoteur : Annick Sartenaer Directeur : Caroline Sainvitu Mémoire présenté pour l'obtention du
6,0 1RWIRU&RPPHU LDO8VH
6,0 ò ò ø ô 6,0 ù" ñ û" (UL VVRQ$V (UL VVRQ 0RELOH&RPPXQL DWLRQV$% ò (UL VVRQ0RELOH&RPPXQL DWLRQV$% ø (UL VVRQ0RELOH&RPPXQL DWLRQV$% 58/=7 5$,1129$75213$7(176 ø *60 ù ø 7Œ7H[W,QSXW± 7HJL &RPPXQL DWLRQV
Ç ÖÚ Ø Ö Ø Ð ÒÙ Ù Ó Ø Ò ÒØ Ö Ø º È ÖÑ ÙÒ Ð Ô ÒØÖÙ Ñ Ø Ö Ð ÔÖ ÐÙ Ø ÒÙ Ù Ó Ø Ò ÖÙØ º È Ò Ø Ø Ð Ó Ö Ô ÒØÖÙ ÔÖ ÒØ Ø Ù ÓÖ Ô ÙÒ º ÔÓ Ø Ñ º
Þ ÔÓÚ Ø Ø Ö Ø Ò ÈÖ ÙÖ Ò ÐÙÖÙ ÔÖ Ð ½ ¾¼½¼ Ç ÖÚ Ø Ö Ø Ð ÒÙ Ù Ó Ø Ò ÒØ Ö Ø º È ÖÑ ÙÒ Ð Ô ÒØÖÙ Ñ Ø Ö Ð ÔÖ ÐÙ Ø ÒÙ Ù Ó Ø Ò ÖÙØ º È Ò Ø Ø Ð Ó Ö Ô ÒØÖÙ ÔÖ ÒØ Ø Ù ÓÖ Ô ÙÒ º ÔÓ Ø Ñ º ÓÒØ ÒØ ½ Å Ò ½ ½º ÄÙÑ Ñ Ø
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 7: Προσεγγιστική Λύση Εξισώσεων. Αθανάσιος Μπράτσος. Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 7: Προσεγγιστική Λύση Εξισώσεων Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ
ÈÖÓ Ö ÑÑ Ò ÑÓÖ Û ÈÖÓÔØÙÕ ÛÒ ËÔÓÙ ÛÒ ÌÑ Ñ ØÓ Å Ñ Ø ÛÒ È Ò Ô Ø Ñ Ó È ØÖÛÒ Å Ñ Û Ø Ò Ô Ø Ñ ØÛÒ ÍÔÓÐÓ ØôÒ ÌÅÀÅ Ä ÉÇÍ Controlµ Ã Ì ÉÏÊÀÌ Ë Registersµ º Bussesµ ÃÍÃÄÇÁ ÅÀÉ ÆÀË Machine Cyclesµ Á ÍÄÇÁ ØÑ Ñ Ð ÕÓÙ
Ανώτερα Μαθηματικά ΙI
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 9: Επικαμπύλια Ολοκληρώματα Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ. Ψηφιακή Επεξεργασία Εικόνων. Ενότητα: Μετασχηματισμός Fourier 2-Δ ακολουθιών. Καθηγητής Γεώργιος Τζιρίτας
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Ψηφιακή Επεξεργασία Εικόνων Ενότητα: Μετασχηματισμός Fourier 2-Δ ακολουθιών Καθηγητής Γεώργιος Τζιρίτας Τμήμα Επιστήμης Υπολογιστών ÃÐÓ 5 ÅØ ÕÑØ Ñ Fourier ¾¹ ÓÐÓÙôÒ
18.2 Sistemi sa eliptichkim krivama Sistem analogan PUKDH... 50
ÃÖ ÔØÓ Ö Å Ó Ö Ú ÓÚ ½ ÔÖ Ð ¾¼½¾ º ËÓ Ö Ò ½ ÍÚÓ ¾ Ç ÒÓÚÒ ÔÓ ÑÓÚ Á ØÓÖ ÈÖ Ð Ó ÒÓÚ Ø ÓÖ ÖÓ Ú Â ÒÓ Ø ÚÒ Ü Ö Ø Ñ ½ Ë ÚÖ Ñ Ò ÔÖÓØÓÕÒ Ü Ö ½ ÃÓÒ ÕÒ ÔÓ ½ 8 RC4 17 9 Ë ÑÓ Ò ÖÓÒ ÜÙ ÔÖÓØÓÕÒ Ü Ö ½ 10 ËÐÙÕ Ò Ü Ö ½ 11
0RELOH,QWHUQHW :$3. This is the Internet version of the user's guide. Print only for private use. 6,0 GH ODUDWLRQRI RQIRUPLW\
![0RELOH,QWHUQHW :$3. This is the Internet version of the user's guide. Print only for private use. 6,0 GH ODUDWLRQRI RQIRUPLW\](/thumbs/71/64541886.jpg "0RELOH,QWHUQHW :$3. This is the Internet version of the user's guide. Print only for private use. 6,0 GH ODUDWLRQRI RQIRUPLW\")
ô ù ù ø ³ ò 0RELOH,QWHUQHW :$3 ô ñ 6,0 ù" GH ODUDWLRQRI RQIRUPLW\ ò û" 6RQ\(UL VVRQ7 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\(ul VVRQ 0RELOH&RPPXQL DWLRQV$% 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% 58/=75$,1129$75213$7(176
Adaptive Trailing Edge Flaps for Active Load Alleviation in a Smart Rotor Configuration. DTU Wind Energy - PhD
Adaptive Trailing Edge Flaps for Active Load Alleviation in a Smart Rotor Configuration DTU Wind Energy - PhD Leonardo Bergami DTU Wind Energy PhD-0020(EN) August 2013 DTU Vindenergi Active Load Alleviation
:$3. This is the Internet version of the user's guide. Print only for private use. :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\
![:$3. This is the Internet version of the user's guide. Print only for private use. :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\](/thumbs/57/40570010.jpg ":$3. This is the Internet version of the user's guide. Print only for private use. :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\")
ù ù ø ³ ò :$3 û :$3 ù ñ 6,0 ù" :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\ ñ û " 6RQ\(UL VVRQ7 *60 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\(ul VVRQ 0RELOH&RPPXQL DWLRQV$% 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$%
Θα εμφανίσει την τιμή 232 αντί της ακριβούς
Ì ÔÓ ÓÑ ÒÛÒ Ö Å Ø ØÖÓÔ ÑôÒ Fahrenheit ÑÓ Celsius Fahrenheit Celsius c = (5/9)(f 32) public class Fahr2Cels { public static void main(string args[]) { int f = 451; // Τι συμβαίνει στους 451F? int c; c =
Μαθηματικά ΙΙΙ. Ανοικτά Ακαδημαϊκά Μαθήματα. Ενότητα 6: Επικαμπύλια Ολοκληρώματα. Αθανάσιος Μπράτσος. Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Μαθηματικά ΙΙΙ Ενότητα 6: Επικαμπύλια Ολοκληρώματα Αθανάσιος Μπράτσος Τμήμα Μηχανικών Ενεργειακής Τεχνολογίας ΤΕ Το περιεχόμενο του μαθήματος
c = a+b AC = AB + BC k res = k 1 +k 2
Ã Ô Ø Ð Á ÒÐ ØÙÒ ï ½ ÅÓ ÐÐ ÚÓÒ Î ØÓÖÖÙÑ Ò ÁÒ Ñ Ö ÅÓØ Ú Ø ÓÒ Ò Ò Òµ È Ö Ö Ô Ò Ò ÐÒ Û Ö Ô Ð ÞÙÖ Ð Ö ¹ Ò ËØÖÙ ØÙÖ Î ØÓÖÖ ÙÑ º Ò Ö ÙÒ Ò Ø Ò ØÞ Ò Û Ö Ð ÒÒØ ÚÓÖ Ù º Ò ÈÖÞ ÖÙÒ Ö ÓÐ Ø ÔØ Ö Û ÒÒ Û Ö ÙÒ ÙÑ Ò Ñ Ø
Preisdifferenzierung für Flugtickets
Ë Ñ Ø Ö Ö Ø ÏÄ ÌÀ Ö ÈÖ Ö ÒÞ ÖÙÒ Ö ÐÙ Ø Ø Ù Ò ËØÖ Ò Ö ¹ ÄÓÒ ÓÒ ÙÒ Ö Ò ÙÖØ ¹ Æ Û ÓÖ ÙØÓÖ Ò Ì ÓÑ ÖÙÒÒ Ö À ÙÖ ØÖº ¼ Ö Ñ ÐØ ÓÑ ÖÙÒÒ Öº Ö ØÓÔ Ã Ö ÐÙÑ ÒÛ ½¼ Ç ÖÛ Ð Ö ØÙ Òغ Ø Þº ØÖ Ù Ö ËØ Ò Ä Ù Ò Ø Ò ÈÖÓ ÓÖ ÖÑ
0RELOH,QWHUQHW :$3 :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\
![0RELOH,QWHUQHW :$3 :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\](/thumbs/66/56247555.jpg "0RELOH,QWHUQHW :$3 :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\")
ù ù ø ³ ò 0RELOH,QWHUQHW :$3 û 0RELOH,QWHUQHW :$3 ù ñ 6,0 ù" :HE 6RQ\(UL VVRQ GH ODUDWLRQRI RQIRUPLW\ ñ û " 6RQ\(UL VVRQ ù 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\(ul VVRQ 0RELOH&RPPXQL DWLRQV$% 6RQ\(UL
Δυναμική διαχείριση μνήμης
Σχολή Ηλεκτρολόγων Μηχανικών και Μηχανικών Υπολογιστών Τομέας Τεχνολογίας Πληροφορικής και Υπολογιστών Εθνικό Μετσόβιο Πολυτεχνείο Γλώσσες Προγραμματισμού ΙΙ Διδάσκοντες: Νικόλαος Παπασπύρου, Κωστής Σαγώνας
Εφαρμοσμένα Μαθηματικά
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Εφαρμοσμένα Μαθηματικά Ενότητα 6: Συναρτήσεις πολλών Μεταβλητών Αθανάσιος Μπράτσος Τμήμα Μηχανικών Βιοϊατρικής Τεχνολογίας ΤΕ Το περιεχόμενο
Ανώτερα Μαθηματικά ΙI
Ανοικτά Ακαδημαϊκά Μαθήματα Τεχνολογικό Εκπαιδευτικό Ίδρυμα Αθήνας Ανώτερα Μαθηματικά ΙI Ενότητα 1: Διαφορικές Εξισώσεις Μέρος Ι Αθανάσιος Μπράτσος Τμήμα Ναυπηγών Μηχανικών ΤΕ Το περιεχόμενο του μαθήματος
Ö ØÓØ Ð Ó È Ò Ô Ø Ñ Ó ÈÓÐÙØ ÕÒ ËÕÓÐ Ò ÌÑ Ñ Ö Ñ Ø Ò ÐÙ Ä ÛÒ È Ø Ó Ð Â ÐÓÒ ¾¼¼
Ö ØÓØ Ð Ó È Ò Ô Ø Ñ Ó ÈÓÐÙØ ÕÒ ËÕÓÐ Ò ÌÑ Ñ Ö Ñ Ø Ò ÐÙ Ä ÛÒ È Ø Ó Ð Â ÐÓÒ ¾¼¼ ¾ È Ö Õ Ñ Ò ÈÖ ÐÓ Ó i ½ Ð Ö ÑÓ Ë ÐÑ Ø ½ ½º½ ÔÐÙ ÈÖÓ Ð Ñ ØÛÒ Ð Ö ÑÓ º º º º º º º º º º º º º º º º ½ ½º¾ Ð Ö ÑÓ Ù Ó ô º º º
:$3. This is the Internet version of the user's guide. Print only for private use. %OXHWRRWK GH ODUDWLRQRI RQIRUPLW\
![:$3. This is the Internet version of the user's guide. Print only for private use. %OXHWRRWK GH ODUDWLRQRI RQIRUPLW\](/thumbs/57/40570217.jpg ":$3. This is the Internet version of the user's guide. Print only for private use. %OXHWRRWK GH ODUDWLRQRI RQIRUPLW\")
ù ù ø ³ ò :$3 :$3 û :$3 :$3 ù %OXHWRRWK ô ñ 6,0 ù" GH ODUDWLRQRI RQIRUPLW\ ñ û" 6RQ\(UL VVRQ 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% ô6rq\ (UL VVRQ0RELOH&RPPXQL DWLRQV$% 6RQ\(UL VVRQ0RELOH&RPPXQL DWLRQV$% 58/=75$
Άλγεβρα Boole, λογικές συναρτήσεις και κυκλώματα. URL:
Ø ÖÓ Ü Ñ ÒÓ ÓØ Άλγεβρα Boole, λογικές συναρτήσεις και κυκλώματα ôö Ó Éº Ð Ü Ò Ö ÔÓÙÐÓ Ä ØÓÖ Èº º ¼» ¼ e-mail: alexandg@uop.gr URL: http://users.iit.demokritos.gr/~alexandg ÌÑ Ñ Ô Ø Ñ Ì ÕÒÓÐÓ Ì Ð Ô Ó ÒÛÒ
Način dostopa (URL):
Bojn Kuzm ZAPISKI IZ PREDAVANJ - FOURIEROVA ANALIZA (Zbirk Izbrn poglvj iz mtemtike, št. 8 Urednic zbirke: Petruš Miholič Izdl in zložil: Knjižnic z tehniko, medicino in nrvoslovje TeMeN, Univerz n Primorskem
Απλοποίηση λογικών συναρτήσεων. URL:
Ø ÖÓ Ü Ñ ÒÓ ÓØ Απλοποίηση λογικών συναρτήσεων ôö Ó Éº Ð Ü Ò Ö ÔÓÙÐÓ Ä ØÓÖ Èº º ¼» ¼ e-mail: alexandg@uop.gr URL: http://users.iit.demokritos.gr/~alexandg ÌÑ Ñ Ô Ø Ñ Ì ÕÒÓÐÓ Ì Ð Ô Ó ÒÛÒ ôò È Ö Õ Ñ Ò É ÖØ
arxiv:math/ v2 [math.qa] 21 Sep 2009
![arxiv:math/ v2 [math.qa] 21 Sep 2009](/thumbs/70/62587598.jpg "arxiv:math/ v2 [math.qa] 21 Sep 2009")
ÍÆÁÎ ÊË Ä Ã ÉÍ ÌÁÇÆË Á ÌÀ ÄÄÁÈÌÁ Ë arxv:math/0702670v2 [math.qa] 21 Sep 2009 ÅÁ Æ Ä ÉÍ Æ ÅÁÆ ÆÊÁÉÍ Æ È Î Ä ÌÁÆ Ç ÌÓ ÙÖ ÁÚ ÒÓÚ Å Ò Ò ÓÒ ¼Ø ÖØ Ý ØÖ Øº Ï Ò ÙÒ Ú Ö Ð Ú Ö ÓÒ Ó Ø ÃÒ Þ Ò ¹ ÑÓÐÓ ÓÚ¹ ÖÒ Ö Ã µ
7in x 10in Felder appm.tex V3 - May 7, :10 A.M. Page 1
7in x 10in Felder appm.tex V3 - May 7, 2015 12:10 A.M. Page 1 APPENDIX M Ò ÛÖ ØÓ Ç¹ÆÙÑÖ ÈÖÓÐÑ ÔØÖ º Ò Ü Ó Ü º º º º ÐÐ Ó ØÑ ÛÓÖ º º º º Áº κ ÁÁº ÁÁÁº Áκ º Ü Ø = Ñ Ü Ø = Ü Ü º º º º º º º º º µ Ñ Ü Ø