ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
|
|
|
- Ἀνίκητος Αποστόλου
- 7 χρόνια πριν
- Προβολές:
Transcript
1 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ Πηγές Κατανομή χωικής d πυκνότητας φοτίου [/m 3 ] v = dv Κατανομή πιφανιακής d πυκνότητας φοτίου [/m s = ] ds Κατανομή γαμμικής πυκνότητας φοτίου [/m] Φοτία ή κατανομές ακίνητα στο χώο και αμτάβλητα στο χόνο. d = d dv: dq= v dv = ds: dq= s ds = d: dq= d = dq= dv s v = dq = ds = dq = d Σημιακό φοτίο [] N = = ΜΕΓΕΘΗ ΠΕΔΙΟΥ Οισμού df Ηλκτική πδιακή ένταση [/m] E = = φ Δύναμη ανά μονάδα φοτίου dq Διηλκτική μτατόπιση [/m ] D Ηλκτική οή ανά μονάδα πιφανίας, ή Επιφανιακή πυκνότητα δυναμικών γαμμών Διηλκτική σταθά [F/m] Χωητικότητα κύβου στοιχιωδών διαστάσων Παάγωγα Ηλκτοστατικό δυναμικό [] Ηλκτική οή [] d φ(p) Δ φ = Ed :P0 P E P : P 0 Έγο που καταναλώνται για την μταφοά μοναδιαίου φοτίου από το σημίο αναφοάς μέχι το σημίο παατήησης. N= dn= D ds P 0 ds D Ν P - - Παπαγιαννάκης Αντώνης
2 ΕΞΙΣΩΣΕΙΣ ΠΕΡΙΓΡΑΦΗΣ ΠΕΔΙΟΥ Διαφοικές σχέσις η Εξ. Mxwell E= 0 4 η Εξ. Mxwell D = v Καταστατική ξίσωση D = E (Συντηητικό πδίο) Ολοκληωτικές σχέσις Νόμος αστόβιλου : Η διαφοά δυναμικού ίναι ανξάτητη του δόμου ολοκλήωσης και ξατάται μόνο από τα δυναμικά του αχικού και του τλικού σημίου. Νόμος Guss : Η ηλκτική οή από μία κλιστή πιφάνια ισούται μ το σύνολο των φοτίων που πιέχονται μέσα στην πιφάνια. Ed 0 N = D ds = ΠΕΡ. dq d N E ds Οιακές συνθήκς Οι φαπτομνικές συνιστώσς της ηλκτικής πδιακής έντασης ίναι ίσς. ˆn Ε Ε = 0 () () E E,t E ˆn,t E Οι κάθτς συνιστώσς της διηλκτικής μτατόπισης διαφέουν κατά τα τυχόν πιφανιακά φοτία. ˆn D D = Το δυναμικό ίναι συνχές (και φ μονοσήμαντο). φ = 0 s () () D D,n D,n ˆn D - - Παπαγιαννάκης Αντώνης
3 Παάσταση πδίου Δυναμικές γαμμές Ισοδυναμικές πιφάνις E = φ E d <0 E d E= λ d >0 καμπύλη, σ κάθ σημίο της οποίας το διάνυσμα της ηλκτικής πδιακής έντασης Ε ίναι φαπτομνικό. πυκνώνουν όπου το πδίο γίνται ισχυότο και ααιώνουν όπου το πδίο γίνται ασθνέστο. ξκινούν από θτικά και καταλήγουν σ ανητικά φοτία. φ(r) = const. πιφάνια, στα σημία της οποίας το δυναμικό έχι παντού την ίδια τιμή. οι δυναμικές γαμμές ίναι καμπύλς οθογώνις πος τις ισοδυναμικές πιφάνις Παπαγιαννάκης Αντώνης
4 ΕΞΙΣΩΣΕΙΣ ΥΠΟΛΟΓΙΣΜΟΥ ΠΕΔΙΟΥ Επαλληλία Αχή της παλληλίας ή υπέθσης Σημιακά φοτία Χωικά φοτία Επιφανιακά φοτία Γαμμικά φοτία Η δάση του συνόλου των φοτίων ισούται μ το σύνολο των δάσων κάθ φοτίου ξχωιστά N N E= E = Rˆ E = = 4πR N N q D= D = R ˆ = = 4πR N N φ = = 4πR φ= = dv E = de = R ˆ v 4πR vdv ˆ 4πR D= dd= R vdv φ = dφ = 4πR sds E = ˆ de = R 4πR sds D= dd Rˆ = 4πR sds φ = dφ = 4πR d E = de Rˆ = 4πR d D= dd= Rˆ 4πR d φ = dφ = 4πR r O R R r r dv : dq= v dv = r O dv : dq= v dv = r O R R d : dq= d R r O r r r P P P E E de de de Παπαγιαννάκης Αντώνης
5 Διαφοικές ξισώσις σ χώο ισότοπο και ομογνή και μόνον για τις χωικές κατανομές φοτίων σ χώο ισότοπο και ΜΗ ομογνή και μόνον για τις χωικές κατανομές φοτίων E = φ Εξίσωση Posson v φ = D = v E = Εξίσωση Lplce φ = 0 D= 0 E= 0 v φ+ φ (ln ) = v E+ E (ln) = v Θωήματα Θ. μγίστου-λαχίστου Θ. Ernsow Θ. μονοσημάντου Σ ένα Η/Σ Πδίο, το δυναμικό παουσιάζι ακότατα μόνον πάνω σ φοτία. Ηλκτικό φοτίο που υπόκιται μόνον σ Η/Σ δυνάμις δν μποί να πααμίνι σ υσταθή ισοοπία. Ένα Η/Σ πόβλημα (: γωμτία, τλστής, πηγές και οιακές συνθήκς) πιδέχται μία και μόνον μία λύση Παπαγιαννάκης Αντώνης
6 ΜΑΚΡΟΣΚΟΠΙΚΟ ΜΟΝΤΕΛΟ ΥΛΙΚΩΝ για το Ηλκτοστατικό Πδίο. Τέλια διηλκτικά (μονωτές) Δν έχουν λύθα φοτία Δν υπάχι δυνατότητα κίνησης φοτίων στο σωτικό τους (Εκτός από το κνό) Εμφανίζονται ηλκτικά ουδέτα (αφότιστα) σ κανονική κατάσταση Χαακτηίζονται από διηλκτική σταθά ( 0 < + ) ιδική αγωγιμότητα σ = 0 χόνο χαλάωσης τ + Μποούμ να τα ποσδώσουμ φοτίο, που πααμένι όπου τοποθτίται Δν μποούν να αναπτύξουν πιφανιακά φοτία Το δυναμικό στα σωτικά και στα πιφανιακά σημία τους και το ηλκτικό πδίο στα σωτικά σημία τους ίναι μταβλητό Η ηλκτική πδιακή ένταση στα σωτικά σημία μποί, χωίς πόβλημα, να πάι οποιαδήποτ τιμή. Στην πάξη χαακτηίζονται από διηλκτική αντοχή και από τάση διάσπασης Τέλιοι αγωγοί Έχουν λύθα φοτία, πακτικά άπια Επιτέπουν την κίνηση φοτίων στο σωτικό τους (παουσιάζουν αγωγιμότητα) Εμφανίζονται ηλκτικά ουδέτοι (αφότιστοι) σ κανονική κατάσταση Χαακτηίζονται από [διηλκτική σταθά: αδιάφοη] ιδική αγωγιμότητα σ + χόνο χαλάωσης τ = 0 Μποούμ να τους ποσδώσουμ φοτίο, που ανακατανέμται και ισοοπί στην πιφάνια τους σ μηδνικό χόνο (ακαιαία) Μποούν να αναπτύξουν πιφανιακά φοτία Το δυναμικό στα σωτικά και στα πιφανιακά σημία τους ίναι σταθό και το ηλκτικό πδίο στα σωτικά σημία τους ίναι μηδνικό (ισοδυναμικός χώος) Άα: η συμπιφοά τους συνοψίζται στο να ανακατανίμουν το φοτίο έτσι, ώστ να αποκτήσουν κατάλληλη πιφανιακή κατανομή φοτίων που να τους δίνι σταθό δυναμικό και μηδνικό πδίο Σημίωση: Θώηση μη τέλιων αγωγών ( μη τέλιων διηλκτικών παγματικών αγωγών παγματικών διηλκτικών διηλκτικών μ απώλις) σημαίνι ύπαξη ππασμένης αγωγιμότητας, ισχύ του Ν. Om και άα ύμα και κίνηση φοτίων, οπότ φύγουμ πλέον από το πλαίσιο του Ηλκτοστατικού Πδίου Παπαγιαννάκης Αντώνης
7 Ροπή διπόλου [ m] p= d Διηλκτική πόλωση [/m dp ] P = dv Δέσμια ή ισοδύναμα φοτία διηλκτικής πόλωσης ΔΙΗΛΕΚΤΡΙΚΑ ΥΛΙΚΑ Χωικά [/m 3 ] v = P Επιφανιακά [/m ] s = + P nˆ Διηλκτική μτατόπιση [/m ] D = 0E+ P= E διηλκτική σταθά (για ισότοπα P = μέσα) [F/m] 0 + E σχτική διηλκτική σταθά [ ] P r = + 0 0E διηλκτική (πι)δκτικότητα [ ] P χ r = E 0 ˆn = v s Γ.Ο.Ι.Σ. Γαμμικό Ομογνές Ισότοπο Στάσιμο Χαακτηισμός υλικών Το μέτο του διανύσματος της διηλκτικής πόλωσης P ίναι ανάλογο του μέτου του διανύσματος της ηλκτικής πδιακής έντασης Ε. Οι σχέσις που πιγάφουν τα διανύσματα της διηλκτικής πόλωσης P και της ηλκτικής πδιακής έντασης Ε δν μταβάλλονται μ την θέση. Η σχέση που πιγάφι το διάνυσμα της διηλκτικής πόλωσης P (ή της ηλκτικής πδιακής έντασης Ε) πααμένι η ίδια, ανξάτητα από τον ποσανατολισμό (φοά) του Ε. Σαν συνέπια τα δύο διανύσματα ίναι παάλληλα. Οι (στοχαστικές) ιδιότητς των διανυσμάτων της διηλκτικής πόλωσης P και της ηλκτικής πδιακής έντασης Ε δν μταβάλλονται μ τον χόνο. Ισοδύναμα ποβλήματα P = 0 0 Ένα διηλκτικό μποί να πιγαφί μ έναν από τους τις, αμοιβαία αποκλιόμνους, τόπους Διηλκτική πόλωση στο κνό διηλκτικό = 0 v = 0 0 s Ισοδύναμα φοτία πόλωσης στο κνό = 0 Διηλκτική σταθά Όλα δίνουν το ίδιο (σωστό) Ε παντού Όλα δίνουν το ίδιο (σωστό) D στο κνό, έξω από το διηλκτικό. Κάθ ένα δίνι διαφοτικό D μέσα στο διηλκτικό Παπαγιαννάκης Αντώνης
8 Χωητικότητα [F] ΤΕΛΕΙΟΙ ΑΓΩΓΟΙ sds = = = const. > 0 sds 4πR Θώημα Green φ = φ ΔΥΝΑΜΕΙΣ ΚΑΙ ΕΝΕΡΓΕΙΑ Ηλκτοστατική νέγια Έγο μτακίνησης φοτίων [J] ΔW = qδφ D we = dd E Πυκνότητα νέγιας [J/m 3 ] 0 w e = D E= φ v για ομογνή και ισότοπα W = w dv = D E dv Ενέγια Η/Σ Π. Ενέγια συστήματος αγωγών ή φοτίων [J] [J] W = e πδιου = πηγων φdv φ p j j φφc j j j j = = v Ηλκτοστατικές δυνάμις Δύναμη oulom [N] F= qe Κατανομή πυκνότητας δύναμης df oulom [N/m 3 f = = ] ve = v φ dv F= W Δύναμη σ διηλκτικά F =+ W = const. φ= const. ˆ W = W = = const. ˆ W =+ W =+ φ= const. m e = const. φ= const. dw + dw = 0 υπό = const. Μταβολή νέγιας dwm + dwe = dws dw = dw s e υπό φ = const Παπαγιαννάκης Αντώνης
9 ΗΛΕΚΤΡΟΣΤΑΤΙΚΕΣ ΔΙΑΤΑΞΕΙΣ Σημιακό φοτίο [] > 0 φ(r) =, μ φ = 0 : r 4πr r E(r) = ˆ r 4πr Ισοδυναμικές: Σφαιικές πιφάνις ομόκντς r = =const., μ > 0 4π Δυναμικές γαμμές: Ακτίνς Ομοιόμοφα φοτισμένη άπιη γαμμή [/m] > 0 z 0 φ() ln 0 = π, μ φ = 0 : = 0 αυθαίτο E() = ˆ π Ισοδυναμικές: Κυλινδικές πιφάνις ομοαξονικές π = 0 exp = const. Δυναμικές γαμμές: Ακτίνς Ομοιόμοφα φοτισμένο άπιο πίπδο s [/m ] s > 0 φ(z) = s z, μ φ = 0 : z = 0 z s z E = zˆ z Ισοδυναμικές: Επίπδα παάλληλα z =± =const., μ s < 0 Δυναμικές γαμμές: Ευθίς s Παπαγιαννάκης Αντώνης
10 Ομοιόμοφα φοτισμένο υθύγαμμο τμήμα r r z z > 0 z m P(,z) =, = (z z ) z = (z + z ) m = + r (z z ) = + r (z z ) z m ( ) z zm z zm + φ(,z) = ln 4π z z + + z z ( ) μ φ = 0 : r z z z z E(,z) = ˆ + zˆ 4π r r r r Ισοδυναμικές: Ελλιψοιδή κ πιστοφής ομοστιακά 4π k = exp, μ > 0 k + = k, k = k, =, Δυναμικές γαμμές: Υπβολές ομοστιακές m z, + = Ηλκτικό δίπολο d z + θ M Ροπή διπόλου : M = d r = + z r M M cosθ M z φ(r,θ) = = = 4π r 4π 4π 3 r r φ = 0 : r E(r,θ) = ( M ) r M ˆ M = cosθ rˆ+ snθθ = (3z) ˆ+ (z )zˆ 3 5 4πr 4πr Ισοδυναμικές: πολύπλοκς Δυναμικές: πολύπλοκές Παπαγιαννάκης Αντώνης
11 ΠΥΚΝΩΤΕΣ Ιδανικός πυκνωτής Οισμός Χωητικότητα [F] (χωίς απώλις) Σύστημα δύο τλίως αγώγιμων σωμάτων μ ίσα και αντίθτα φοτία που ο μταξύ τους χώος πληούται μ τέλιο διηλκτικό. = = const. > 0 Βασικοί τύποι (αμλώντας τα φαινόμνα άκων) Σφαιικός πυκνωτής ακτίνων < = 4π [F] r + Κυλινδικός πυκνωτής Πααλλήλων πλακών ακτίνων < και μήκους π = [F] ln ( ) μβαδού σ απόσταση d = [F] d d z z Παπαγιαννάκης Αντώνης
12 ΚΑΤΟΠΤΡΙΣΜΟΣ Φοτίου ως πος αγώγιμη γιωμένη σφαία φοτίο έξω από τη σφαία (=0) φοτίο μέσα στη σφαία (=0) Ισοδύναμο πόβλημα για τον χώο έξω από τη σφαία : Ισοδύναμο πόβλημα για τον χώο μέσα στη σφαία : (φ=0) < 0 = k = > = = k Φοτίου ως πος αγώγιμο πίπδο (=0) Ισοδύναμο πόβλημα για τον χώο πάνω από το πίπδο : (κάτω από το πίπδο το πδίο ίναι μηδέν) (φ=0) = Φοτίου ως πος ημιάπιο διηλκτικό Ισοδύναμο πόβλημα για τον χώο πάνω από το πίπδο : = + Ισοδύναμο πόβλημα για τον χώο κάτω από το πίπδο : = Παπαγιαννάκης Αντώνης
III Η ΥΛΗ ΣΤΟ ΠΕ ΙΟ ΠΟΛΩΣΗ ΙΗΛΕΚΤΡΙΚΟΥ ΙΙI ΥΛΗ ΣΤΟ ΠΕ ΙΟ
 III Η ΥΛΗ ΣΤΟ ΠΕ ΙΟ ΠΟΛΩΣΗ ΙΗΛΕΚΤΡΙΚΟΥ ΙΙΙ. Συνολική οπή των διπόλων που πιέχονται στον όγκο δ V, όπου N ο αιθµός διπόλων ανά µονάδα όγκου και p η διπολική οπή του -στού διπόλου p t NV δ p ΙΙΙ. Το διάνυσµα
III Η ΥΛΗ ΣΤΟ ΠΕ ΙΟ ΠΟΛΩΣΗ ΙΗΛΕΚΤΡΙΚΟΥ ΙΙΙ. Συνολική οπή των διπόλων που πιέχονται στον όγκο δ V, όπου N ο αιθµός διπόλων ανά µονάδα όγκου και p η διπολική οπή του -στού διπόλου p t NV δ p ΙΙΙ. Το διάνυσµα
1) Ηλεκτρικό πεδίο φορτισμένου φύλλου απείρων διαστάσεων
 1) Ηλεκτικό πεδίο φοτισμένου φύλλου απείων διαστάσεων Σε αυτό το εδάφιο θα υπολογιστεί το ηλεκτικό πεδίο παντού στο χώο ενός φοτισμένου λεπτού φύλλου απείων διαστάσεων και αμελητέου πάχους όπως αυτό που
1) Ηλεκτικό πεδίο φοτισμένου φύλλου απείων διαστάσεων Σε αυτό το εδάφιο θα υπολογιστεί το ηλεκτικό πεδίο παντού στο χώο ενός φοτισμένου λεπτού φύλλου απείων διαστάσεων και αμελητέου πάχους όπως αυτό που
ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΤΗΝ ΥΛΗ ΘΕΩΡΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΤΗΝ ΥΛΗ ΘΕΩΡΙΑ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 29 - ΑΘΗΝΑ 6932 946778 www.pmoias.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΤΗΝ ΥΛΗ ΘΕΩΡΙΑ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 29 - ΑΘΗΝΑ 6932 946778 www.pmoias.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
Νόμος του Gauss 1. Ηλεκτρική Ροή ( πλήθος δυναμικών γραμμών). είναι διάνυσμα μέτρου Α και κατεύθυνσης κάθετης στην επιφάνεια. Στην γενική περίπτωση:
 Νόμος του Gauss 1. Ηλκτρική Ροή ( πλήθος δυναμικών γραμμών). ( a) cosφ ( b) ίναι διάνυσμα μέτρου Α και κατύθυνσης κάθτης στην πιφάνια. Στην γνική πρίπτωση: d d d ( ) (πιφανιακό ολοκλήρωμα) Νόμος του Gauss
Νόμος του Gauss 1. Ηλκτρική Ροή ( πλήθος δυναμικών γραμμών). ( a) cosφ ( b) ίναι διάνυσμα μέτρου Α και κατύθυνσης κάθτης στην πιφάνια. Στην γνική πρίπτωση: d d d ( ) (πιφανιακό ολοκλήρωμα) Νόμος του Gauss
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ
 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας Θέμα Ένα σημιακό φρτί Q τπθτίται στ κέντρ νός υδέτρυ σφαιρικύ αγώγιμυ κλύφυς ακτινών R και R. Να υπλγιστί τ παγόμν φρτί
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας Θέμα Ένα σημιακό φρτί Q τπθτίται στ κέντρ νός υδέτρυ σφαιρικύ αγώγιμυ κλύφυς ακτινών R και R. Να υπλγιστί τ παγόμν φρτί
6 η ΕΡΓΑΣΙΑ. Ημερομηνία Παράδοσης: 1/7/2007
 6 η ΕΡΓΑΣΙΑ Ημομηνία Παάδοσης: /7/7 Τα θέματα ίναι βαθμολογικά ισοδύναμα Άσκηση Θτικό φοτίο Q κατανέμται ομοιόμοφα κατά μήκος του θτικού άξονα y μταξύ των σημίων y και y α. Ένα ανητικό σημιακό φοτίο -
6 η ΕΡΓΑΣΙΑ Ημομηνία Παάδοσης: /7/7 Τα θέματα ίναι βαθμολογικά ισοδύναμα Άσκηση Θτικό φοτίο Q κατανέμται ομοιόμοφα κατά μήκος του θτικού άξονα y μταξύ των σημίων y και y α. Ένα ανητικό σημιακό φοτίο -
H 2 + x 2 cos ϕ. cos ϕ dϕ =
 . Άπειη γαμμική κατανομή ϕοτίου λ Θεωούμε την γαμμική κατανομή ϕοτίου στον άξονα των x και ζητάμε το ηλεκτικό πεδίο στο σημείο A που απέχει από την κατανομή. Το στοιχειώδες τμήμα dx της κατανομής στη θέση
. Άπειη γαμμική κατανομή ϕοτίου λ Θεωούμε την γαμμική κατανομή ϕοτίου στον άξονα των x και ζητάμε το ηλεκτικό πεδίο στο σημείο A που απέχει από την κατανομή. Το στοιχειώδες τμήμα dx της κατανομής στη θέση
Α ΚΙΝΗΣΗ ΦΟΡΤΙΣΜΕΝΩΝ ΣΩΜΑΤΙ ΙΩΝ ΣΤΟ ΗΛΕΚΤΡΙΚΟ ΚΑΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ
 A ΚΙΝΗΣΗ ΦΟΡΤΙΣΜΕΝΩΝ ΣΩΜΑΤΙ ΙΩΝ ΣΤΟ ΗΛΕΚΤΡΙΚΟ ΚΑΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ ΚΙΝΗΣΗ ΦΟΡΤΙΣΜΕΝΟΥ ΣΩΜΑΤΙ ΙΟΥ ΣΕ ΣΤΑΤΙΚΑ ΠΕ ΙΑ Α. Γνική ξίσωση κίνησης για µη ρλατιβιστικές πριπτώσις q( ) + B Α. Αρχή διατήρησης της νέργιας
A ΚΙΝΗΣΗ ΦΟΡΤΙΣΜΕΝΩΝ ΣΩΜΑΤΙ ΙΩΝ ΣΤΟ ΗΛΕΚΤΡΙΚΟ ΚΑΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ ΚΙΝΗΣΗ ΦΟΡΤΙΣΜΕΝΟΥ ΣΩΜΑΤΙ ΙΟΥ ΣΕ ΣΤΑΤΙΚΑ ΠΕ ΙΑ Α. Γνική ξίσωση κίνησης για µη ρλατιβιστικές πριπτώσις q( ) + B Α. Αρχή διατήρησης της νέργιας
[Ολοκληρωτική μορφή του νόμου του Gauss στο κενό ή τον αέρα]
![[Ολοκληρωτική μορφή του νόμου του Gauss στο κενό ή τον αέρα] [Ολοκληρωτική μορφή του νόμου του Gauss στο κενό ή τον αέρα]](/thumbs/26/9169893.jpg) Παν/μιο Πατρών Τμήμα Φυσικής. Μάθημα : Ηλκτρομαγνητισμός Ι (Υποχρωτικό 3 ου Εξαμήνου) ΠΝΕΠΙΣΤΗΜΙΟ ΠΤΡΩΝ - ΤΜΗΜ ΦΥΣΙΚΗΣ ΜΘΗΜ : HΛΕΚΤΡΟΜΓΝΗΤΙΣΜΟΣ Ι (Υποχρωτικό 3 ου Εξαμήνου) Διδάσκων :Δ.Σκαρλάτος, Επίκουρος
Παν/μιο Πατρών Τμήμα Φυσικής. Μάθημα : Ηλκτρομαγνητισμός Ι (Υποχρωτικό 3 ου Εξαμήνου) ΠΝΕΠΙΣΤΗΜΙΟ ΠΤΡΩΝ - ΤΜΗΜ ΦΥΣΙΚΗΣ ΜΘΗΜ : HΛΕΚΤΡΟΜΓΝΗΤΙΣΜΟΣ Ι (Υποχρωτικό 3 ου Εξαμήνου) Διδάσκων :Δ.Σκαρλάτος, Επίκουρος
C V C = 1. Πυκνωτές. Οι πυκνωτές έχουν πολλές χρήσεις λόγω του ότι αποτελούν αποθήκες ηλεκτρικού φορτίου και ηλεκτρικής δυναμικής ενέργειας.
 . Πυκνωτές Δύο αγωγοί που διαχωρίζονται από ένα μονωτή αποτλούν ένα πυκνωτή. Στην πράξη οι αγωγοί φέρουν ία και αντίθτα φορτία. Ορίζουμ αν χωρητικότητα νός πυκνωτή το ταθρό πηλίκο: ab F Οι πυκνωτές έχουν
. Πυκνωτές Δύο αγωγοί που διαχωρίζονται από ένα μονωτή αποτλούν ένα πυκνωτή. Στην πράξη οι αγωγοί φέρουν ία και αντίθτα φορτία. Ορίζουμ αν χωρητικότητα νός πυκνωτή το ταθρό πηλίκο: ab F Οι πυκνωτές έχουν
Κατοίκον Εργασία 2. (γ) το ολικό φορτίο που βρίσκεται στον κύβο. (sd p.e 4.9 p146)
 Κατοίκον Εργασία. Ένα σημιακό φορτίο (point charge) 5 mc και ένα - mc βρίσκονται στα σημία (,0,4) και (-3,0,5) αντίστοιχα. (α) Υπολογίστ την δύναμη πάνω σ ένα φορτίο (point charge) nc που βρίσκται στο
Κατοίκον Εργασία. Ένα σημιακό φορτίο (point charge) 5 mc και ένα - mc βρίσκονται στα σημία (,0,4) και (-3,0,5) αντίστοιχα. (α) Υπολογίστ την δύναμη πάνω σ ένα φορτίο (point charge) nc που βρίσκται στο
ΙV ΜΕΘΟ ΟΙ ΕΠΙΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕ ΙΟΥ
 ΜΕΘΟ Ο ΕΠΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΚΟΥ ΠΕ ΟΥ ΜΕΘΟ Ο ΕΠΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΚΟΥ ΠΕ ΟΥ ΜΕΘΟ ΟΣ ΤΟΥ ΚΑΤΟΠΤΡΣΜΟΥ Φορτίο πάνω από αγώγιµο πίπδο z o. Τιµή και θέη του κατοπτρικού φορτίου,.
ΜΕΘΟ Ο ΕΠΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΚΟΥ ΠΕ ΟΥ ΜΕΘΟ Ο ΕΠΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΚΟΥ ΠΕ ΟΥ ΜΕΘΟ ΟΣ ΤΟΥ ΚΑΤΟΠΤΡΣΜΟΥ Φορτίο πάνω από αγώγιµο πίπδο z o. Τιµή και θέη του κατοπτρικού φορτίου,.
Μάθηµα Γραµµές Μεταφοράς Κυµατοδηγοί & Οπτικές Ίνες Καθ. Θωµάς Σφηκόπουλος Κυµατοδηγοί - Μάθηµα 10o-11o
 Μάθηµα Γαµµές Μταφοάς Κυµατοδηγοί & Οπτικές Ίνς Καθ. Θωµάς Σφηκόπουος Κυµατοδηγοί - Μάθηµα o-o ΕΘΝΙΚΟ & ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τοµέας Επικοινωνιών και Επξγασίας Σήµατος Τµήµα Πηοφοικής & Τηπικοινωνιών
Μάθηµα Γαµµές Μταφοάς Κυµατοδηγοί & Οπτικές Ίνς Καθ. Θωµάς Σφηκόπουος Κυµατοδηγοί - Μάθηµα o-o ΕΘΝΙΚΟ & ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΑΘΗΝΩΝ Τοµέας Επικοινωνιών και Επξγασίας Σήµατος Τµήµα Πηοφοικής & Τηπικοινωνιών
ΡΕΥΜΑΤΑ, ΝΟΜΟΣ ΤΟΥ OHM
 Q ΡΥΜΑΤΑ, ΝΟΜΟΣ ΤΟΥ OHM Ισοοπία σε αγωγό μόνον όταν στο εσωτεικό του αγωγού είναι =0 λεύθεο Ηλεκτόνιο Πείσεια ελευθέων ηλεκτονίων ξωτεικό ηλεκτικό πεδίο εσ εξ = εσ = 0 εξ σωτεικό ηλ. πεδίο Ποσθήκη εξωτεικού
Q ΡΥΜΑΤΑ, ΝΟΜΟΣ ΤΟΥ OHM Ισοοπία σε αγωγό μόνον όταν στο εσωτεικό του αγωγού είναι =0 λεύθεο Ηλεκτόνιο Πείσεια ελευθέων ηλεκτονίων ξωτεικό ηλεκτικό πεδίο εσ εξ = εσ = 0 εξ σωτεικό ηλ. πεδίο Ποσθήκη εξωτεικού
Ο νόμος του Ampère. Διαφορική μορφή του ν.ampère. B r. Παρ : To πεδίο Β δακτυλιοειδούς πηνίου. Εντός του πηνίου
 Ο νόμος του Apèr Ο νόμος του Apèr Bis μ μ Ji Επιφάνια Bi μ π r ( π s B s r μ Η κυκλοφορία του μαγνητικού πδίου κατά μηκός μιάς κλιστής διαδρομής ισούται μ μ Ι, όπου Ι ίναι το ολικό σταθρό (χρονικά αμτάβλητο
Ο νόμος του Apèr Ο νόμος του Apèr Bis μ μ Ji Επιφάνια Bi μ π r ( π s B s r μ Η κυκλοφορία του μαγνητικού πδίου κατά μηκός μιάς κλιστής διαδρομής ισούται μ μ Ι, όπου Ι ίναι το ολικό σταθρό (χρονικά αμτάβλητο
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ Ι 10. Η μέθοδος των ειδώλων
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ Ι. Η μέθοδος των ειδώλων Περιγραφή της μεθόδου Σημειακό φορτίο και αγώγιμο επίπεδο Φορτίο μεταξύ δύο αγωγίμων ημιεπιπέδων Σημειακό φορτίο έξω από γειωμένη σφαίρα Σημειακό φορτίο
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ Ι. Η μέθοδος των ειδώλων Περιγραφή της μεθόδου Σημειακό φορτίο και αγώγιμο επίπεδο Φορτίο μεταξύ δύο αγωγίμων ημιεπιπέδων Σημειακό φορτίο έξω από γειωμένη σφαίρα Σημειακό φορτίο
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ ΤΕΛΕΙΟΥΣ ΑΓΩΓΟΥΣ
Πυκνότητα φορτίου. dq dv. Μικρή Περιοχή. φορτίου. Χωρική ρ Q V. Επιφανειακή σ. dq da Γραµµική λ Q A. σ = dq dl. Q l. Γ.
 Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
Κεφάλαιο 4: Πυροηλεκτρισμός, Πιεζο- ηλεκτρισμός, Λιαροκάπης Ευθύμιος. Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών
 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μτσόβιο Πολυτχνίο Διηλκτρικές, Οπτικές, Μαγνητικές Ιδιότητς Υλικών Κφάλαιο 4: Πυροηλκτρισμός, Πιζο- ηλκτρισμός, Σιδηροηλκτρισμός Λιαροκάπης Ευθύμιος
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μτσόβιο Πολυτχνίο Διηλκτρικές, Οπτικές, Μαγνητικές Ιδιότητς Υλικών Κφάλαιο 4: Πυροηλκτρισμός, Πιζο- ηλκτρισμός, Σιδηροηλκτρισμός Λιαροκάπης Ευθύμιος
ΚΕΝΤΡΟ ΘΕΩΡΗΤΙΚΗΣ ΦΥΣΙΚΗΣ & ΧΗΜΕΙΑΣ Ε ΟΥΑΡ ΟΥ ΛΑΓΑΝΑ Ph.D. Λεωφ. Κηφισίας 56, Αµπελόκηποι, Αθήνα Τηλ.: ,
 Ε ΟΥΑΡ ΟΥ ΛΑΓΑΝΑ Ph.D. Λωφ. Κηφισίας 56, Απλόκηποι, Αθήνα Τηλ.: 69 97 985, www.edlag.gr ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ - ΑΣΚΗΣΕΙΣ Λωφ. Κηφισίας 56, Απλόκηποι, Αθήνα Τηλ.: 69 97 985, E-mail: edlag@otenet.gr, www.edlag.gr
Ε ΟΥΑΡ ΟΥ ΛΑΓΑΝΑ Ph.D. Λωφ. Κηφισίας 56, Απλόκηποι, Αθήνα Τηλ.: 69 97 985, www.edlag.gr ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ - ΑΣΚΗΣΕΙΣ Λωφ. Κηφισίας 56, Απλόκηποι, Αθήνα Τηλ.: 69 97 985, E-mail: edlag@otenet.gr, www.edlag.gr
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΑΣΚΗΣΕΙΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΕ Γ.Ο.Ι. ΧΩΡΟΥΣ
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 18 ΙΟΥΝΙΟΥ 2001 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ
 ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 18 ΙΟΥΝΙΟΥ 1 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ 1. Σωστό το γ. Σωστό το γ. Σωστό το γ 4. Σωστό το δ
ΠΡΟΑΓΩΓΙΚΕΣ ΕΞΕΤΑΣΕΙΣ Β ΤΑΞΗΣ ΕΝΙΑΙΟΥ ΛΥΚΕΙΟΥ ΕΥΤΕΡΑ 18 ΙΟΥΝΙΟΥ 1 ΕΞΕΤΑΖΟΜΕΝΟ ΜΑΘΗΜΑ ΘΕΤΙΚΗΣ ΚΑΙ ΤΕΧΝΟΛΟΓΙΚΗΣ ΚΑΤΕΥΘΥΝΣΗΣ: ΦΥΣΙΚΗ ΑΠΑΝΤΗΣΕΙΣ ΘΕΜΑΤΩΝ 1. Σωστό το γ. Σωστό το γ. Σωστό το γ 4. Σωστό το δ
Ορίζοντας την δυναμική ενέργεια σαν: Για μετακίνηση του φορτίου ανάμεσα στις πλάκες: Ηλεκτρικό Δυναμικό 1
 Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
Ηλεκτρική Δυναμική Ενέργεια Ένα ζεύγος παράλληλων φορτισμένων μεταλλικών πλακών παράγει ομογενές ηλεκτρικό πεδίο Ε. Το έργο που παράγεται πάνω σε θετικό δοκιμαστικό φορτίο είναι: W W Fl q y q l q y Ορίζοντας
ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ
 ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ Ημερομηνία:. ΤΜΗΜΑ:.. ΟΜΑΔΑ:. Ονομ/νυμο: Α.Μ. Συνεργάτες Ονομ/νυμο: Α.Μ. Ονομ/νυμο: Α.Μ. ΠΕΡΙΛΗΨΗ ΤΗΣ ΑΣΚΗΣΗΣ (καθένας με δικά του λόγια, σε όλες τις γραμμές) ΒΑΘΜΟΣ#1: ΥΠΟΓΡΑΦΗ:
ΑΣΚΗΣΗ-1: ΗΛΕΚΤΡΙΚΑ ΠΕΔΙΑ Ημερομηνία:. ΤΜΗΜΑ:.. ΟΜΑΔΑ:. Ονομ/νυμο: Α.Μ. Συνεργάτες Ονομ/νυμο: Α.Μ. Ονομ/νυμο: Α.Μ. ΠΕΡΙΛΗΨΗ ΤΗΣ ΑΣΚΗΣΗΣ (καθένας με δικά του λόγια, σε όλες τις γραμμές) ΒΑΘΜΟΣ#1: ΥΠΟΓΡΑΦΗ:
5.6 Ενέργεια του ηλεκτρικού πεδίου παρουσία πολωμένων διηλεκτρικών. 5.6 Ενέργεια του ηλεκτρικού πεδίου παρουσία πολωμένων διηλεκτρικών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι (Υποχρωτικό 3 ου Εξαμήνου) ΔΙΔΑΣΚΩΝ : ΔΗΜΗΤΡΙΟΣ ΣΚΑΡΛΑΤΟΣ, Επίκουρος Καθηγητής ΚΕΦΑΛΑΙΟ 5 : Διηλκτρικά 5.1 Γνικές Ιδιότητς 5. Διηλκτρικά
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι (Υποχρωτικό 3 ου Εξαμήνου) ΔΙΔΑΣΚΩΝ : ΔΗΜΗΤΡΙΟΣ ΣΚΑΡΛΑΤΟΣ, Επίκουρος Καθηγητής ΚΕΦΑΛΑΙΟ 5 : Διηλκτρικά 5.1 Γνικές Ιδιότητς 5. Διηλκτρικά
ΠΕΡΙΕΧΟΜΕΝΑ ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1
 ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 - ΖΩΓΡΑΦΟΥ, 157 73 ΑΘΗΝΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 - ΖΩΓΡΑΦΟΥ, 157 73 ΑΘΗΝΑ
ΚΕΦΑΛΑΙΟ 12 ΑΝΑΚΛΑΣΗ ΚΑΙ ΙΑΘΛΑΣΗ ΕΠΙΠΕ ΟΥ ΚΥΜΑΤΟΣ
 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ ΑΝΑΚΛΑΣΗ ΚΑΙ ΙΑΘΛΑΣΗ ΕΠΙΠΕ ΟΥ ΚΥΜΑΤΟΣ. Οι βασικοί νόµοι ανάκλασης διάλασης Στο παρόν κφάλαιο ξτάζται η πρίπτωση όπου ένα πίπδο κύµα προσπίπτι σ µια πίπδη πιφάνια S που διαχωρίζι δύο µέσα
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ ΑΝΑΚΛΑΣΗ ΚΑΙ ΙΑΘΛΑΣΗ ΕΠΙΠΕ ΟΥ ΚΥΜΑΤΟΣ. Οι βασικοί νόµοι ανάκλασης διάλασης Στο παρόν κφάλαιο ξτάζται η πρίπτωση όπου ένα πίπδο κύµα προσπίπτι σ µια πίπδη πιφάνια S που διαχωρίζι δύο µέσα
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mil:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mil:
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23
 ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
ΝΟΜΟΣ ΤΟΥ GAUSS ΚΕΦ.. 23 Ροή (γενικά): Ηλεκτρική Ροή Η ποσότητα ενός μεγέθους που διέρχεται από μία επιφάνεια. Ε Ε dα dα θ Ε Ε θ Ηλεκτρική ροή dφ Ε μέσω στοιχειώδους επιφάνειας da (αφού da στοιχειώδης
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΗΛΕΚΤΡΟΣΤΑΤΙΚΗΣ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΗΛΕΚΤΡΟΣΤΑΤΙΚΗΣ Συγγφή Επιμέλι: Πνγιώτης Φ. Μίς ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΗΛΕΚΤΡΟΣΤΑΤΙΚΗΣ Συγγφή Επιμέλι: Πνγιώτης Φ. Μίς ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693
Γωνία που σχηματίζει η ε με τον άξονα. Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και ε μια ευθεία που τέμνει τον άξονα
 ΕΥΘΕΙΑ Γωνία που σχηματίζι η μ τον άξονα. Έστω O ένα σύστημα συντταγμένων στο πίπδο και μια υθία που τέμνι τον άξονα στο σημίο Α. Α ω Α ω Τη γωνία ω που διαγράφι ο άξονας όταν στραφί γύρω από το Α κατά
ΕΥΘΕΙΑ Γωνία που σχηματίζι η μ τον άξονα. Έστω O ένα σύστημα συντταγμένων στο πίπδο και μια υθία που τέμνι τον άξονα στο σημίο Α. Α ω Α ω Τη γωνία ω που διαγράφι ο άξονας όταν στραφί γύρω από το Α κατά
αριθμητή και παρονομαστή επί γ + δi. Οι γνωστές αλγεβρικές ταυτότητες ισχύουν όπως και στους πραγματικούς.
 Μθοδολογία ασκήσων ο φάλαιο Άλγβας Μιγαδικοί ιθμοί Μιγαδικοί αιθμοί Τα πόμνα σχόλια αναφέονται στις πααγάφους.1 ως και.3 σλ. 83 ως 100 του σχολικού βιβλίου των μαθηματικών θτικής τχνολογικής κατύθυνσης
Μθοδολογία ασκήσων ο φάλαιο Άλγβας Μιγαδικοί ιθμοί Μιγαδικοί αιθμοί Τα πόμνα σχόλια αναφέονται στις πααγάφους.1 ως και.3 σλ. 83 ως 100 του σχολικού βιβλίου των μαθηματικών θτικής τχνολογικής κατύθυνσης
ΚΕΦΑΛΑΙΟ 10 ΤΟ ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΟ ΠΕ ΙΟ
 ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ ΤΟ ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΟ ΠΕ ΙΟ. Εξισώσεις Maxwell Όπως έχουµε, ήδη, αναφέει, ένα ηλεκτοστατικό πεδίο E µποεί να υφίσταται ανεξάτητα από την παουσία ή όχι µαγνητικού πεδίου H, όπως για
ΚΕΦΑΛΑΙΟ ΚΕΦΑΛΑΙΟ ΤΟ ΧΡΟΝΙΚΑ ΜΕΤΑΒΑΛΛΟΜΕΝΟ ΠΕ ΙΟ. Εξισώσεις Maxwell Όπως έχουµε, ήδη, αναφέει, ένα ηλεκτοστατικό πεδίο E µποεί να υφίσταται ανεξάτητα από την παουσία ή όχι µαγνητικού πεδίου H, όπως για
Μοντέλα Ταχέως Περιστρεφόµενων Αστέρων Νετρονίων
 ιπλωµατική Εγασία Μοντέλα Ταχέως Πειστεφόµενων Αστέων Νετονίων Πασχαλίδης Βασίλειος Α.Ε.Μ.: 1188 Κατεύθυνση Αστονοµίας Αστοφυσικής Επιβλέποντες Καθηγητές: Κ. Κόκκοτας, Ν. Στεγιούλας 8 Ιουλίου 3 Πλάνο Παουσίασης
ιπλωµατική Εγασία Μοντέλα Ταχέως Πειστεφόµενων Αστέων Νετονίων Πασχαλίδης Βασίλειος Α.Ε.Μ.: 1188 Κατεύθυνση Αστονοµίας Αστοφυσικής Επιβλέποντες Καθηγητές: Κ. Κόκκοτας, Ν. Στεγιούλας 8 Ιουλίου 3 Πλάνο Παουσίασης
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ, Αγωγοί Διηλεκτρικά. Ν. Τράκας, Ι. Ράπτης Ζωγράφου 27.3.
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 8-9 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Αγωγοί Διηλεκτρικά Ν. Τράκας Ι. Ράπτης Ζωγράφου 7.3.9 Να επιστραφούν λυμένες μέχρι.4.9 οι ασκήσεις 3 4 5 [ΠΡΟΣΟΧΗ: Οι λύσεις
ΕΞΙΣΩΣΗ ΣΦΑΙΡΑΣ. είναι όλοι ίσοι και επιπλέον δεν υπάρχουν οι όροι xy, yz, zx. Γενικά µια εξίσωση της µορφής: 0 + Β + Α.
 Suies & Publishing ΣΟΛΩΜΟΥ 9 ΠΟΛΥΤΕΧΝΕΙΟ ΤΗΛ.:.38..57 www.arnοs.gr 3 Ο γωµτρικός τόπος των σηµίων που έχουν σταθρή απόσταση από το σηµίο,, του 3 ονοµάζται σφαίρα. Η σφαίρα µ κέντρο το,, και ακτίνα έχι
Suies & Publishing ΣΟΛΩΜΟΥ 9 ΠΟΛΥΤΕΧΝΕΙΟ ΤΗΛ.:.38..57 www.arnοs.gr 3 Ο γωµτρικός τόπος των σηµίων που έχουν σταθρή απόσταση από το σηµίο,, του 3 ονοµάζται σφαίρα. Η σφαίρα µ κέντρο το,, και ακτίνα έχι
Διάνυσμα μετατόπισης. Στοιχεία Διανυσματικής Ανάλυσης
 Στοιχεία Διανυσματικής νάλυσης Συστήματα Συντεταγμένων (D) Διανυσματικά και αμωτά Μεγέη Πάξεις και ιδιότητες διανυσμάτων Διανυσματικές συνατήσεις Πααγώγιση Διανυσματικών συνατήσεων Ολοκλήωση Διανυσματικών
Στοιχεία Διανυσματικής νάλυσης Συστήματα Συντεταγμένων (D) Διανυσματικά και αμωτά Μεγέη Πάξεις και ιδιότητες διανυσμάτων Διανυσματικές συνατήσεις Πααγώγιση Διανυσματικών συνατήσεων Ολοκλήωση Διανυσματικών
ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ (ΘΕΩΡΙΑ)
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ (ΘΕΩΡΙΑ) Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778.
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ (ΘΕΩΡΙΑ) Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778.
Η θεωρία στην ευθεία σε ερωτήσεις - απαντήσεις
 Η θρία στην υθία σ ρτήσις - απαντήσις Τι ονομάζουμ ξίσση γραμμής Μια ξίσση μ δύο αγνώστους λέγται ξίσση μιας γραμμής C, όταν οι συντταγμένς τν σημίν της C, και μόνο αυτές, την παληθύουν Ποιό ίναι το βασικό
Η θρία στην υθία σ ρτήσις - απαντήσις Τι ονομάζουμ ξίσση γραμμής Μια ξίσση μ δύο αγνώστους λέγται ξίσση μιας γραμμής C, όταν οι συντταγμένς τν σημίν της C, και μόνο αυτές, την παληθύουν Ποιό ίναι το βασικό
ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ
 ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ ΧΩΡΗΤΙΚΟΤΗΤΑ Ένας πυκνωτής έχει ως σκοπό να αποθηκεύει ηλεκτρική ενέργεια που μπορεί να ελευθερώνεται με ελεγχόμενο τρόπο σε βραχύ χρονικό διάστημα. Αποτελείται από 2 χωρικά
ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ ΧΩΡΗΤΙΚΟΤΗΤΑ Ένας πυκνωτής έχει ως σκοπό να αποθηκεύει ηλεκτρική ενέργεια που μπορεί να ελευθερώνεται με ελεγχόμενο τρόπο σε βραχύ χρονικό διάστημα. Αποτελείται από 2 χωρικά
Ηλεκτρική δυναμική ενέργεια
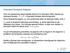 Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
Ηλεκτρική δυναμική ενέργεια Όταν ένα δοκιμαστικό φορτίο βρεθεί μέσα σε ένα ηλεκτρικό πεδίο, δέχεται μια ηλεκτρική δύναμη: F e =q o E. Η ηλεκτρική δύναμη είναι συντηρητική. Έστω δοκιμαστικό φορτίο, q 0,
(4) γενικής λύσης το x με το -x. και θα έχουμε : y ομ (x)=c 1 (-x) -1 +c 2 (-x) 3
 0 ΕΞΙΣΩΣΕΙΣ ΤΟΥ EULER Ορισμός : Οι γραμμικές διαφορικές ξισώσις, των οποίων οι συντλστές ίναι δυνάμις του βαθμού ίσου μ την τάξη της αντίστοιχης παραγώγου, ονομάζονται ξισώσις του Eule Πχ η ομογνής ξίσωση
0 ΕΞΙΣΩΣΕΙΣ ΤΟΥ EULER Ορισμός : Οι γραμμικές διαφορικές ξισώσις, των οποίων οι συντλστές ίναι δυνάμις του βαθμού ίσου μ την τάξη της αντίστοιχης παραγώγου, ονομάζονται ξισώσις του Eule Πχ η ομογνής ξίσωση
( ) y ) άγνωστη συνάρτηση, f (, )
 6. Ι ΙΑΣΑΑ ΠΡΟΒΛΗΜΑΑ ΣΥΝΟΡΙΑΚΝ ΙΜΝ 6. Πρόβληµατα πδίου σ διαστάσις Η νότητα αυτή αναφέρται σ προβλήµατα πδίου, όπου άγνωστη συνάρτηση ίναι µία βαθµωτή συνάρτηση. α προβλήµατα αυτά έχουν σηµαντικές φαρµογές
6. Ι ΙΑΣΑΑ ΠΡΟΒΛΗΜΑΑ ΣΥΝΟΡΙΑΚΝ ΙΜΝ 6. Πρόβληµατα πδίου σ διαστάσις Η νότητα αυτή αναφέρται σ προβλήµατα πδίου, όπου άγνωστη συνάρτηση ίναι µία βαθµωτή συνάρτηση. α προβλήµατα αυτά έχουν σηµαντικές φαρµογές
(α) 1. (β) Το σύστημα βρίσκεται υπό διαφορά δυναμικού 12 V: U ολ = 1 2 C ολ(δv) 2 = J.
 4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
Ηλεκτρική και Μαγνητική Πόλωση
 Ηλκτρική και Μαγνητική Πόλωση Μαγνητικά και Ηλκτρικά πδία στα υλικά Μαγνήτιση και Ηλκτρική Πόλωση Οµοιότητς και ιαφορές Συµµτρία αντιστροφής ώρου και ρόνου Μαγνητική και Σιδηροηλκτρική Υστέρηση Εξισώσις
Ηλκτρική και Μαγνητική Πόλωση Μαγνητικά και Ηλκτρικά πδία στα υλικά Μαγνήτιση και Ηλκτρική Πόλωση Οµοιότητς και ιαφορές Συµµτρία αντιστροφής ώρου και ρόνου Μαγνητική και Σιδηροηλκτρική Υστέρηση Εξισώσις
Ανάληψη αξονικού φορτίου από πάσσαλο
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΤΕΧΝΙΚΗΣ ΕΠΟΠΤΙΚΟ ΥΛΙΚΟ ΔΙΑΛΕΞΕΩΝ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «Αλληλεπίδαση Εδάφους Κατασκευής» 8 ο Εξ. ΠΟΛ. ΜΗΧ. - Ακαδ. Ετος 6 7 Διδάσκοντες : Γ. Γκαζέτας
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΟΜΕΑΣ ΓΕΩΤΕΧΝΙΚΗΣ ΕΠΟΠΤΙΚΟ ΥΛΙΚΟ ΔΙΑΛΕΞΕΩΝ ΤΟΥ ΜΑΘΗΜΑΤΟΣ «Αλληλεπίδαση Εδάφους Κατασκευής» 8 ο Εξ. ΠΟΛ. ΜΗΧ. - Ακαδ. Ετος 6 7 Διδάσκοντες : Γ. Γκαζέτας
ΦΥΣΙΚΗ ΙΙ (Θ) Χασάπης Δημήτριος ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΤΕ
 ΦΥΣΙΚΗ ΙΙ (Θ) Χασάπης Δημήτριος ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
ΦΥΣΙΚΗ ΙΙ (Θ) Χασάπης Δημήτριος ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο. Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 2014
 ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
ΔΙΑΛΕΞΗ 2 Νόμος Gauss, κίνηση σε ηλεκτρικό πεδίο Ι. Γκιάλας Χίος, 28 Φεβρουαρίου 214 Ασκηση συνολικό φορτίο λεκτρικό φορτίο Q είναι κατανεμημένο σε σφαιρικό όγκο ακτίνας R με πυκνότητα ορτίου ανάλογη του
2. ΑΡΙΘΜΗΤΙΚΗ ΕΥΡΕΣΗ ΡΙΖΩΝ ΜΗ
 . ΑΡΙΘΜΗΤΙΚΗ ΕΥΡΕΣΗ ΡΙΖΩΝ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ. Εισαγωγή Στο παόν κφάλαιο θα παουσιάσουµ αιθµητικές µθόδους για την πίλυση µη γαµµικών αλγβικών ξισώσων, ξισώσων δηλαδή της µοφής 0. όπου η συνάτηση ίναι
. ΑΡΙΘΜΗΤΙΚΗ ΕΥΡΕΣΗ ΡΙΖΩΝ ΜΗ ΓΡΑΜΜΙΚΩΝ ΕΞΙΣΩΣΕΩΝ. Εισαγωγή Στο παόν κφάλαιο θα παουσιάσουµ αιθµητικές µθόδους για την πίλυση µη γαµµικών αλγβικών ξισώσων, ξισώσων δηλαδή της µοφής 0. όπου η συνάτηση ίναι
ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Α ΒΑΘΜΟΥ
 Πριοδικό ΕΥΚΛΕΙΔΗΣ Β Ε.Μ.Ε. ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Α ΒΑΘΜΟΥ A. ΓΡΑΜΜΙΚΗ ΕΞΙΣΩΣΗ ΜΕ ΔΥΟ ΑΓΝΩΣΤΟΥΣ Γραμμική ξίσωση μ δύο αγνώστους ονομάζται κάθ ξίσωση της μορφής: α + βψ = γ (), μ α,β,γ π.χ. ψ =, =, ψ =, κλπ.
Πριοδικό ΕΥΚΛΕΙΔΗΣ Β Ε.Μ.Ε. ΓΡΑΜΜΙΚΑ ΣΥΣΤΗΜΑΤΑ Α ΒΑΘΜΟΥ A. ΓΡΑΜΜΙΚΗ ΕΞΙΣΩΣΗ ΜΕ ΔΥΟ ΑΓΝΩΣΤΟΥΣ Γραμμική ξίσωση μ δύο αγνώστους ονομάζται κάθ ξίσωση της μορφής: α + βψ = γ (), μ α,β,γ π.χ. ψ =, =, ψ =, κλπ.
Μάθηµα Γραµµές Μεταφοράς Κυµατοδηγοί & Οπτικές Ίνες Καθ. Θωµάς Σφηκόπουλος Κυµατοδηγοί - Μάθηµα 9o
 Μάθηµα Γαµµές Μταφοάς Κυµατοδηοί & Οπτικές Ίνς Καθ. Θωµάς Σφηκόπουλος Κυµατοδηοί - Μάθηµα 9o ΘΝΙΚΟ & ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΠΙΣΤΜΙΟ ΑΘΝΩΝ Τοµέας πικοινωνιών και πξασίας Σήµατος Τµήµα Πληοφοικής & Τηλπικοινωνιών
Μάθηµα Γαµµές Μταφοάς Κυµατοδηοί & Οπτικές Ίνς Καθ. Θωµάς Σφηκόπουλος Κυµατοδηοί - Μάθηµα 9o ΘΝΙΚΟ & ΚΑΠΟ ΙΣΤΡΙΑΚΟ ΠΑΝΠΙΣΤΜΙΟ ΑΘΝΩΝ Τοµέας πικοινωνιών και πξασίας Σήµατος Τµήµα Πληοφοικής & Τηλπικοινωνιών
P l+1 (cosa) P l 1 (cosa) 2δ l,0 1
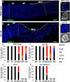 Λεοντσ ίνης Στέφανος Ηλεκτομαγνητισ μός 3 η Σειά Ασ κήσ εων 3 Tο δυναμικό λόγω αζιμουθιακής σ υμμετίας θα έχει τη μοφή φ r, θ [ Al + B l r l+] l cosθ Λόγω l Φ οιακών σ υνθηκών έχω: Φ in r R Φ out r R και
Λεοντσ ίνης Στέφανος Ηλεκτομαγνητισ μός 3 η Σειά Ασ κήσ εων 3 Tο δυναμικό λόγω αζιμουθιακής σ υμμετίας θα έχει τη μοφή φ r, θ [ Al + B l r l+] l cosθ Λόγω l Φ οιακών σ υνθηκών έχω: Φ in r R Φ out r R και
ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ ΕΝ ΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ 2 ης ΕΡΓΑΣΙΑΣ. Προθεσµία παράδοσης 22/12/09 ( )
 19/11/9 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 4 9-1 ΕΝ ΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ης ΕΡΓΑΣΙΑΣ Προθσµία παράδοσης /1/9 Άσκηση 1 Η γνική µορφή νός ΗΜ κύµατος δίνται από E E sin k r ωt (1) ( ) Α) Το µέτρο του πλάτους πλάτος
19/11/9 ΕΛΛΗΝΙΚΟ ΑΝΟΙΚΤΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΦΥΕ 4 9-1 ΕΝ ΕΙΚΤΙΚΕΣ ΛΥΣΕΙΣ ης ΕΡΓΑΣΙΑΣ Προθσµία παράδοσης /1/9 Άσκηση 1 Η γνική µορφή νός ΗΜ κύµατος δίνται από E E sin k r ωt (1) ( ) Α) Το µέτρο του πλάτους πλάτος
ΗΛΕΚΤΡΙΚΟ ΠΕ ΙΟ. HΛEKTPIKO ΦOPTIO: είναι το αίτιο των ηλεκτρικών δυνάµεων (εµπειρική αντίληψη).
 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΙΙ Ι ΑΣΚΩΝ: ΚΑΘΗΓΗΤΗΣ Μ. ΒΕΛΓΑΚΗΣ ΓΕΝΙΚΟ ΤΜΗΜΑ / ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ / ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ Στη σειρά των φροντιστηρίων αυτών καταβάλλεται µια προσπάθεια να κατανοηθούν και να εµπεδωθούν κάποιες
ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΙΙ Ι ΑΣΚΩΝ: ΚΑΘΗΓΗΤΗΣ Μ. ΒΕΛΓΑΚΗΣ ΓΕΝΙΚΟ ΤΜΗΜΑ / ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ / ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ Στη σειρά των φροντιστηρίων αυτών καταβάλλεται µια προσπάθεια να κατανοηθούν και να εµπεδωθούν κάποιες
Ηλεκτρομαγνητισμός. Ηλεκτρικό πεδίο νόμος Gauss. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Εισαγωγή Ο νόµος του Gauss: Μπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού της έντασης του ηλεκτρικού πεδίου. Βασίζεται
Ηλεκτρομαγνητισμός Ηλεκτρικό πεδίο νόμος Gauss Νίκος Ν. Αρπατζάνης Εισαγωγή Ο νόµος του Gauss: Μπορεί να χρησιµοποιηθεί ως ένας εναλλακτικός τρόπος υπολογισµού της έντασης του ηλεκτρικού πεδίου. Βασίζεται
Συμπλήρωμα 2 εδαφίου 3.3: Το γενικό μεταβολικό πρόβλημα για συναρτησιακό ολοκληρωτικού τύπου με ολοκληρωτέα συνάρτηση F κατά 2
 ΚΕΦ. 3 Η Αρχή των Ήρωνος-Fermat 3.3-8 Συμπλήρωμα 2 δαφίου 3.3: Το νικό μταβολικό πρόβλημα ια συναρτησιακό ολοκληρωτικού τύπου μ ολοκληρωτέα συνάρτηση F κατά 2 τμήματα C, ορισμένο πί καμπυλών που τέμνουν
ΚΕΦ. 3 Η Αρχή των Ήρωνος-Fermat 3.3-8 Συμπλήρωμα 2 δαφίου 3.3: Το νικό μταβολικό πρόβλημα ια συναρτησιακό ολοκληρωτικού τύπου μ ολοκληρωτέα συνάρτηση F κατά 2 τμήματα C, ορισμένο πί καμπυλών που τέμνουν
Ένα Φρένο Σε Μια Τροχαλία
 Ένα Φρένο Σ Μια Τροχαλία Η ομογνής ράβδος του σχήματος έχι μάζα ΜΡ και μήκος = και μπορί να στρέφται ως προς κάθτο άξονα που διέρχται από το σημίο μ την βοήθια άρθρωσης. Πάνω στη ράβδο και σ απόσταση /4
Ένα Φρένο Σ Μια Τροχαλία Η ομογνής ράβδος του σχήματος έχι μάζα ΜΡ και μήκος = και μπορί να στρέφται ως προς κάθτο άξονα που διέρχται από το σημίο μ την βοήθια άρθρωσης. Πάνω στη ράβδο και σ απόσταση /4
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23)
 ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
ΗΛΕΚΤΡΙΚΟ ΥΝΑΜΙΚΟ (ΚΕΦΑΛΑΙΟ 23) Υπενθύμιση/Εισαγωγή: Λέμε ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος από μία
Τίτλος Μαθήματος: Γενική Φυσική (Ηλεκτρομαγνητισμός) Διδάσκων: Επίκουρος Καθηγητής Δημήτριος Βλάχος
 Τίτλος Μαθήματος: Γενική Φυσική (Ηλεκτρομαγνητισμός) Ενότητα: ΧΩΡΗΤΙΚΟΤΗΤΑ ΚΑΙ ΔΙΗΛΕΚΤΡΙΚΑ Διδάσκων: Επίκουρος Καθηγητής Δημήτριος Βλάχος Τμήμα: Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής 1 ΚΕΦΑΛΑΙΟ
Τίτλος Μαθήματος: Γενική Φυσική (Ηλεκτρομαγνητισμός) Ενότητα: ΧΩΡΗΤΙΚΟΤΗΤΑ ΚΑΙ ΔΙΗΛΕΚΤΡΙΚΑ Διδάσκων: Επίκουρος Καθηγητής Δημήτριος Βλάχος Τμήμα: Μηχανικών Ηλεκτρονικών Υπολογιστών και Πληροφορικής 1 ΚΕΦΑΛΑΙΟ
# Κάθε σημείο που οι συντεταγμένες του. Μεθοδολογία στην ευθεία γραμμή ΜΕΘΟΔΟΛΟΓΙΑ ΓΡΑΜΜΗ
 Μθοδολογία στην υθία γραμμή Κοινά σημία δύο γραμμών. Για να βρούμ τις συντταγμένς του σημίου δύο γραμμών, λύνουμ το σύστημα των ξισώσών τους. ΓΡΑΜΜΗ Μια ξίσωση της μορφής φ(χ,ψ)= λέγται ξίσωση μιας πίπδης
Μθοδολογία στην υθία γραμμή Κοινά σημία δύο γραμμών. Για να βρούμ τις συντταγμένς του σημίου δύο γραμμών, λύνουμ το σύστημα των ξισώσών τους. ΓΡΑΜΜΗ Μια ξίσωση της μορφής φ(χ,ψ)= λέγται ξίσωση μιας πίπδης
Ηλεκτρομαγνητισμός. Ηλεκτρικό δυναμικό. Νίκος Ν. Αρπατζάνης
 Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
Ηλεκτρομαγνητισμός Ηλεκτρικό δυναμικό Νίκος Ν. Αρπατζάνης Ηλεκτρικό δυναμικό Θα συνδέσουμε τον ηλεκτρομαγνητισμό με την ενέργεια. Χρησιμοποιώντας την αρχή διατήρησης της ενέργειας μπορούμε να λύνουμε διάφορα
ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ (ΚΕΦ 24)
 ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ (ΚΕΦ 24) ΧΩΡΗΤΙΚΟΤΗΤΑ Ένας πυκνωτής έχει ως σκοπό να αποθηκεύει ηλεκτρική ενέργεια που μπορεί να ελευθερώνεται με ελεγχόμενο τρόπο σε βραχύ χρονικό διάστημα. Ένας πυκνωτής
ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ (ΚΕΦ 24) ΧΩΡΗΤΙΚΟΤΗΤΑ Ένας πυκνωτής έχει ως σκοπό να αποθηκεύει ηλεκτρική ενέργεια που μπορεί να ελευθερώνεται με ελεγχόμενο τρόπο σε βραχύ χρονικό διάστημα. Ένας πυκνωτής
Διδάσκουσα: Καθηγήτρια Εφαρμογών Σ. Πέππα
 Διδάσκουσα: Καθηγήτρια Εφαρμογών Σ. Πέππα Δυνάμις Υδροστατικές & Υδροδυναμικές δυνάμις που νργούν στα ύφαλα της γάστρας Αροδυναμικές δυνάμις που νργούν στην ιστιοφορία Ειδικές Ναυπηγικές Κατασκυές και
Διδάσκουσα: Καθηγήτρια Εφαρμογών Σ. Πέππα Δυνάμις Υδροστατικές & Υδροδυναμικές δυνάμις που νργούν στα ύφαλα της γάστρας Αροδυναμικές δυνάμις που νργούν στην ιστιοφορία Ειδικές Ναυπηγικές Κατασκυές και
2 - ΤΟ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ
 2 - ΤΟ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ 2_1. Ορισμός και ένταση ηλεκτρικού πεδίου. Ηλεκτρικό πεδίο ονομάζεται ο χώρος, όπου ασκούνται δυνάμεις σε κάθε ηλεκτρικό φορτίο που τοποθετείται σε αυτόν. Χαρακτηριστικό μέγεθος
2 - ΤΟ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ 2_1. Ορισμός και ένταση ηλεκτρικού πεδίου. Ηλεκτρικό πεδίο ονομάζεται ο χώρος, όπου ασκούνται δυνάμεις σε κάθε ηλεκτρικό φορτίο που τοποθετείται σε αυτόν. Χαρακτηριστικό μέγεθος
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 - ΖΩΓΡΑΦΟΥ, 157 73 ΑΘΗΝΑ
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΚΑΙ ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ ΚΑΙ ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ ΗΡΩΩΝ ΠΟΛΥΤΕΧΝΕΙΟΥ 9 - ΖΩΓΡΑΦΟΥ, 157 73 ΑΘΗΝΑ
Ο Νόμος του Fourier και η Εξίσωση Θερμότητας
 Ο Νόμος του Foue και η Εξίσωση Θεμότητας ΜΜΚ 3 Μεταοά Θεμότητας Τμήμα Μηχανολόγων Μηχανικών και Μηχανικών Πααγωγής ΜΜΚ 3 Μεταοά Θεμότητας Κεάλαιο ΟΝόμοςτουFoue (Foue s Law) Ο νόμος του Foue είναι μία εξίσωση
Ο Νόμος του Foue και η Εξίσωση Θεμότητας ΜΜΚ 3 Μεταοά Θεμότητας Τμήμα Μηχανολόγων Μηχανικών και Μηχανικών Πααγωγής ΜΜΚ 3 Μεταοά Θεμότητας Κεάλαιο ΟΝόμοςτουFoue (Foue s Law) Ο νόμος του Foue είναι μία εξίσωση
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
Φυσική για Μηχανικούς Ηλεκτρικό Δυναμικό Εικόνα: Οι διαδικασίες που συμβαίνουν κατά τη διάρκεια μιας καταιγίδας προκαλούν μεγάλες διαφορές ηλεκτρικού δυναμικού ανάμεσα στα σύννεφα και στο έδαφος. Το αποτέλεσμα
ΠΑΡΑΡΤΗΜΑ Γ. Επικαμπύλια και Επιφανειακά Ολοκληρώματα. Γ.1 Επικαμπύλιο Ολοκλήρωμα
 ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
ΠΑΡΑΡΤΗΜΑ Γ Επικαμπύλια και Επιφανειακά Ολοκληρώματα Η αναγκαιότητα για τον ορισμό και την περιγραφή των ολοκληρωμάτων που θα περιγράψουμε στο Παράρτημα αυτό προκύπτει από το γεγονός ότι τα μεγέθη που
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 28)
 ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
Κεφάλαιο 2 Εισαγωγή στα ροϊκά φαινόμενα
 Κεφάλαιο Εισαγωγή στα οϊκά φαινόμενα Σύνοψη Η έννοια του ανοικτού συστήματος (όγκος ελέγχου) Ρυθμός μεταβολής των ιδιοτήτων του συστήματος Νόμος της συνέχειας Νόμος της ομής (δυνάμεις) Γενικευμένη εξίσωση
Κεφάλαιο Εισαγωγή στα οϊκά φαινόμενα Σύνοψη Η έννοια του ανοικτού συστήματος (όγκος ελέγχου) Ρυθμός μεταβολής των ιδιοτήτων του συστήματος Νόμος της συνέχειας Νόμος της ομής (δυνάμεις) Γενικευμένη εξίσωση
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ. Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ.
 ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ. ΑΘΗΝΑ 9 Τιγωνοµετικοί αιθµοί Γωνία π 6 π 4 π 3 π si ϕ 3 3 os ϕ ϕ 3 3 3. Τιγωνοµετικές ταυτότητες. os ± y os os y si si y. si ± y si os y
ΣΗΜΑΤΑ ΚΑΙ ΣΥΣΤΗΜΑΤΑ ΤΥΠΟΛΟΓΙΟ Επιµέλεια. ΣΕΡΑΦΕΙΜ ΚΑΡΑΜΠΟΓΙΑΣ. ΑΘΗΝΑ 9 Τιγωνοµετικοί αιθµοί Γωνία π 6 π 4 π 3 π si ϕ 3 3 os ϕ ϕ 3 3 3. Τιγωνοµετικές ταυτότητες. os ± y os os y si si y. si ± y si os y
4.1 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
 Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ Έστω A ένα υποσύνολο του Ονομάζουμ πραγματική συνάρτηση μ πδίο ορισμού το A, μια διαδικασία f, μ την οποία, κάθ στοιχίο A αντιστοιχίζται σ ένα μόνο πραγματικό αριθμό Το
Η ΕΝΝΟΙΑ ΤΗΣ ΣΥΝΑΡΤΗΣΗΣ ΟΡΙΣΜΟΣ Έστω A ένα υποσύνολο του Ονομάζουμ πραγματική συνάρτηση μ πδίο ορισμού το A, μια διαδικασία f, μ την οποία, κάθ στοιχίο A αντιστοιχίζται σ ένα μόνο πραγματικό αριθμό Το
Hλεκτρικό. Πεδίο. Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ
 Hλεκτρικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SRWAY, Physics fo scientists nd enginees YOUNG H.D., Univesity
Hλεκτρικό Πεδίο Ζαχαριάδου Αικατερίνη Γενικό Τμήμα Φυσικής, Χημείας & Τεχνολογίας Υλικών Τομέας Φυσικής ΤΕΙ ΠΕΙΡΑΙΑ Προτεινόμενη βιβλιογραφία: SRWAY, Physics fo scientists nd enginees YOUNG H.D., Univesity
Κεφάλαιο Η4. Χωρητικότητα και διηλεκτρικά
 Κεφάλαιο Η4 Χωρητικότητα και διηλεκτρικά Κυκλώματα και στοιχεία κυκλωμάτων Τα ηλεκτρικά κυκλώματα αποτελούν τη βάση για το μεγαλύτερο μέρος των συσκευών που χρησιμοποιούνται στην κοινωνία μας. Τα ηλεκτρικά
Κεφάλαιο Η4 Χωρητικότητα και διηλεκτρικά Κυκλώματα και στοιχεία κυκλωμάτων Τα ηλεκτρικά κυκλώματα αποτελούν τη βάση για το μεγαλύτερο μέρος των συσκευών που χρησιμοποιούνται στην κοινωνία μας. Τα ηλεκτρικά
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ
 ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
ΕΡΩΤΗΣΕΙΣ ΚΑΤΑΝΟΗΣΗΣ ΦΥΣΙΚΗ ΙΙ 1. Οι δυναμικές γραμμές ηλεκτροστατικού πεδίου α Είναι κλειστές β Είναι δυνατόν να τέμνονται γ Είναι πυκνότερες σε περιοχές όπου η ένταση του πεδίου είναι μεγαλύτερη δ Ξεκινούν
Υπενθύμιση (από τη Μηχανική) /Εισαγωγή:
 ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ Υπενθύμιση (από τη Μηχανική) /Εισαγωγή: Είχαμε πει ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος
ΗΛΕΚΤΡΙΚΟ ΔΥΝΑΜΙΚΟ Υπενθύμιση (από τη Μηχανική) /Εισαγωγή: Είχαμε πει ότι ένα πεδίο δυνάμεων είναι συντηρητικό (ή διατηρητικό) όταν το έργο που παράγεται από το πεδίο δυνάμεων κατά τη μετατόπιση ενός σώματος
Ενημέρωση. Η διδασκαλία του μαθήματος, όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή
 Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
Ενημέρωση Η διδασκαλία του μαθήματος, πολλά από τα σχήματα και όλες οι ασκήσεις προέρχονται από το βιβλίο: «Πανεπιστημιακή Φυσική» του Hugh Young των Εκδόσεων Παπαζήση, οι οποίες μας επέτρεψαν τη χρήση
sin(30 o ) 4 cos(60o ) = 3200 Nm 2 /C (7)
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. (αʹ Η ηλεκτρική ϱοή διαµέσου µιας επιφάνειας A είναι
ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Τµήµα Επιστήµης Υπολογιστών HY-112: Φυσική Ι Χειµερινό Εξάµηνο 2016 ιδάσκων : Γ. Καφεντζής Πέµπτη Σειρά Ασκήσεων - Λύσεις Ασκηση 1. (αʹ Η ηλεκτρική ϱοή διαµέσου µιας επιφάνειας A είναι
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ
 ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΣΧΟΛΗ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΩΝ ΕΦΑΡΜΟΓΩΝ, ΗΛΕΚΤΡΟΟΠΤΙΚΗΣ & ΗΛΕΚΤΡΟΝΙΚΩΝ ΥΛΙΚΩΝ Καθ. Η. Ν. Γλύτσης, Tηλ.: 210-7722479 - e-mail:
Σημειώσεις IV: Μαθηματικά Υπολογιστικής Τομογραφίας
 HY 673 - Ιατική Απεικόνιση Στέλιος Οφανουδάκης Κώστας Μαιάς Σημειώσεις IV: Μαηματικά Υπολογιστικής Τομογαφίας Σεπτέμβιος 2003-Φεβουάιος 2004 Αχές Υπολογιστικής Τομογαφίας 1. Η ανάγκη απεικόνισης στις 3-Διαστάσεις
HY 673 - Ιατική Απεικόνιση Στέλιος Οφανουδάκης Κώστας Μαιάς Σημειώσεις IV: Μαηματικά Υπολογιστικής Τομογαφίας Σεπτέμβιος 2003-Φεβουάιος 2004 Αχές Υπολογιστικής Τομογαφίας 1. Η ανάγκη απεικόνισης στις 3-Διαστάσεις
ΚΥΚΛΩΜΑΤΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ (DC) Μηχανικό ανάλογο
 ΚΥΚΛΩΜΑΤΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ (DC) κατανάλωση νέργιας για την μταφορά θτικών φορτίων από το στο της μπαταρίας Υψηλό δυναμικό Χαμηλό δυναμικό κατανάλωση ηλκ.νέργιας λόγω συγκρούσων μέσα στην αντίσταση (αγωγό)
ΚΥΚΛΩΜΑΤΑ ΣΥΝΕΧΟΥΣ ΡΕΥΜΑΤΟΣ (DC) κατανάλωση νέργιας για την μταφορά θτικών φορτίων από το στο της μπαταρίας Υψηλό δυναμικό Χαμηλό δυναμικό κατανάλωση ηλκ.νέργιας λόγω συγκρούσων μέσα στην αντίσταση (αγωγό)
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΗΜ & Διάδοση ΗΜ Κυμάτων
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΗΜ & Διάδοση ΗΜ Κυμάτων Ενότητα : Κυματική Εξίσωση & Επίπεδο ΗΜ Κύμα Σαββαΐδης Στυλιανός Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ Ανώτατο Εκπαιδευτικό Ίδρυμα Πειραιά Τεχνολογικού Τομέα ΗΜ & Διάδοση ΗΜ Κυμάτων Ενότητα : Κυματική Εξίσωση & Επίπεδο ΗΜ Κύμα Σαββαΐδης Στυλιανός Τμήμα Ηλεκτρονικών Μηχανικών Τ.Ε. Άδειες
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ. 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες... 7
 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
Πρόβλημα 4.9.
 Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
Πρόβλημα 4.9. Να βρεθεί το δυναμικό V() παντού στο χώρο ενός θετικά φορτισμένου φύλλου απείρων διαστάσεων με επιφανειακή πυκνότητα φορτίου σ. Πάρτε τον άξονα κάθετα στο φύλλο και θεωρήστε ότι το φύλλο
B ρ (0, 1) = {(x, y) : x 1, y 1}
 Κεφάλαιο 3 Τοπολογία μετικών χώων 3.1 Ανοικτά και κλειστά σύνολα 3.1.1 Ανοικτά σύνολα Οισμοί 3.1.1. Εστω (X, ) μετικός χώος και έστω x 0 X. (α) Η ανοικτή -μπάλα με κέντο το x 0 και ακτίνα ε > 0 είναι το
Κεφάλαιο 3 Τοπολογία μετικών χώων 3.1 Ανοικτά και κλειστά σύνολα 3.1.1 Ανοικτά σύνολα Οισμοί 3.1.1. Εστω (X, ) μετικός χώος και έστω x 0 X. (α) Η ανοικτή -μπάλα με κέντο το x 0 και ακτίνα ε > 0 είναι το
ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ
 ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΒΙΒΛΙΟΓΡΑΦΙΑ H.D. H.D. Young Πανεπιστημιακή Φυσική Εκδόσεις Παπαζήση Alonso Alonso / Finn Θεμελιώδης Πανεπιστημιακή Φυσική Α. Φίλιππας, Λ. Ρεσβάνης (Μετ.) R. A. Seway Φυσική
ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΡΙΚΟ ΠΕΔΙΟ ΒΙΒΛΙΟΓΡΑΦΙΑ H.D. H.D. Young Πανεπιστημιακή Φυσική Εκδόσεις Παπαζήση Alonso Alonso / Finn Θεμελιώδης Πανεπιστημιακή Φυσική Α. Φίλιππας, Λ. Ρεσβάνης (Μετ.) R. A. Seway Φυσική
Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική.
 Ηλεκτρική δυναµική ενέργεια Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική. e o Έστω δοκιµαστικό φορτίο,
Ηλεκτρική δυναµική ενέργεια Όταν ένα δοκιµαστικό r φορτίο r βρεθεί µέσα σε ένα ηλεκτρικό πεδίο, δέχεται µια ηλεκτρική δύναµη: F = q E. Η ηλεκτρική δύναµη είναι συντηρητική. e o Έστω δοκιµαστικό φορτίο,
1. Ρεύμα επιπρόσθετα
 1. Ρεύμα Ρεύμα είναι οποιαδήποτε κίνηση φορτίων μεταξύ δύο περιοχών. Για να διατηρηθεί σταθερή ροή φορτίου σε αγωγό πρέπει να ασκείται μια σταθερή δύναμη στα κινούμενα φορτία. r F r qe Η δύναμη αυτή δημιουργεί
1. Ρεύμα Ρεύμα είναι οποιαδήποτε κίνηση φορτίων μεταξύ δύο περιοχών. Για να διατηρηθεί σταθερή ροή φορτίου σε αγωγό πρέπει να ασκείται μια σταθερή δύναμη στα κινούμενα φορτία. r F r qe Η δύναμη αυτή δημιουργεί
και ( n) 1 R. Αν ε > 0, επιλέγουµε για κάθε k 1 ένα καλύπτουµε τότε την ευθεία Α µε την ακολουθία των ορθογωνίων .
 80 Σύνολα µέτρου µηδέν στον και ο χαρακτηρισµός του Lebesgue των iema ολοκληρωσίµων συναρτήσων 7. Ορισµός. Έστω για κάθ 0 Α, λέµ ότι το Α έχι διάστατο µέτρο µηδέν αν, > υπάρχι ακολουθία ανοικτών διάστατων
80 Σύνολα µέτρου µηδέν στον και ο χαρακτηρισµός του Lebesgue των iema ολοκληρωσίµων συναρτήσων 7. Ορισµός. Έστω για κάθ 0 Α, λέµ ότι το Α έχι διάστατο µέτρο µηδέν αν, > υπάρχι ακολουθία ανοικτών διάστατων
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ
 ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 008 ( ΠΡΟΚΗΡΥΞΗ 5Π /008) ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος-Ειδικότητες: ΠΕ 17.03 ΗΛΕΚΤΡΟΛΟΓΩΝ, ΤΕΧΝΟΛΟΓΩΝ ΕΝΕΡΓΕΙΑΚΗΣ ΤΕΧΝΙΚΗΣ (κατεύθυνσης:
ΑΝΩΤΑΤΟ ΣΥΜΒΟΥΛΙΟ ΕΠΙΛΟΓΗΣ ΠΡΟΣΩΠΙΚΟΥ ΔΙΑΓΩΝΙΣΜΟΣ ΕΚΠΑΙΔΕΥΤΙΚΩΝ ΕΤΟΥΣ 008 ( ΠΡΟΚΗΡΥΞΗ 5Π /008) ΚΕΝΤΡΙΚΗ ΕΠΙΤΡΟΠΗ ΔΙΑΓΩΝΙΣΜΟΥ Κλάδος-Ειδικότητες: ΠΕ 17.03 ΗΛΕΚΤΡΟΛΟΓΩΝ, ΤΕΧΝΟΛΟΓΩΝ ΕΝΕΡΓΕΙΑΚΗΣ ΤΕΧΝΙΚΗΣ (κατεύθυνσης:
Φυσική για Μηχανικούς
 Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
Φυσική για Μηχανικούς Εικόνα: Μητέρα και κόρη απολαμβάνουν την επίδραση της ηλεκτρικής φόρτισης των σωμάτων τους. Κάθε μια ξεχωριστή τρίχα των μαλλιών τους φορτίζεται και προκύπτει μια απωθητική δύναμη
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ. Ν. Τράκας, Ι. Ράπτης 2/4/2018
 ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 7-8 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Ν. Τράκας Ι. Ράπτης /4/8 Παράδοση των 3 4 5 μέχρι /4/8 [Σε χειρόγραφη μορφή στο μάθημα ή σε μορφή ενιαίου αρχείου PDF στις
ΣΧΟΛΗ ΕΜΦΕ ΤΟΜΕΑΣ ΦΥΣΙΚΗΣ ΦΥΣΙΚΗ ΙΙ (ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι) 7-8 η ΣΕΙΡΑ ΑΣΚΗΣΕΩΝ Ν. Τράκας Ι. Ράπτης /4/8 Παράδοση των 3 4 5 μέχρι /4/8 [Σε χειρόγραφη μορφή στο μάθημα ή σε μορφή ενιαίου αρχείου PDF στις
x D 350 C D Co x Cm m m
 Υ ΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΘΗΓΗΤΗΣ : Ν ΚΩΤΣΟΒΙΝΟΣ ΛΕΚΤΟΡΑΣ : Π. ΑΓΓΕΛΙ ΗΣ ΛΥΣΕΙΣ B ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΚΟΡ ΟΠΟΥΛΟΣ ΗΜΗΤΡΙΟΣ ΑΜ 585 ΑΣΚΗΣΗ Θαλασσινό νεό από ένα εγοστάσιο, βεβαηµένο
Υ ΡΑΥΛΙΚΗ ΠΕΡΙΒΑΛΛΟΝΤΟΣ ΚΑΘΗΓΗΤΗΣ : Ν ΚΩΤΣΟΒΙΝΟΣ ΛΕΚΤΟΡΑΣ : Π. ΑΓΓΕΛΙ ΗΣ ΛΥΣΕΙΣ B ΣΕΙΡΑΣ ΑΣΚΗΣΕΩΝ ΤΜΗΜΑ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΣΚΟΡ ΟΠΟΥΛΟΣ ΗΜΗΤΡΙΟΣ ΑΜ 585 ΑΣΚΗΣΗ Θαλασσινό νεό από ένα εγοστάσιο, βεβαηµένο
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΗΛΕΚΤΡΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού. Ιωάννης Γκιάλας 14 Μαρτίου 2014
 Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
Δυναμική Ενέργεια σε Ηλεκτρικό πεδίο, Διαφορά ηλεκτρικού δυναμικού Ιωάννης Γκιάλας 14 Μαρτίου 2014 Έργο ηλεκτροστατικής δύναμης W F Δl W N i i1 F Δl i Η μετατόπιση Δl περιγράφεται από ένα διάνυσμα που
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ ΚΑΙ ΗΛΕΚΤΙΚΟ ΠΕΔΙΟ 1 1. ΗΛΕΚΤΡΙΚΟ ΦΟΡΤΙΟ Οι αρχαίοι Έλληνες ανακάλυψαν από το 600 π.χ. ότι, το κεχριμπάρι μπορεί να έλκει άλλα αντικείμενα όταν το τρίψουμε με μαλλί.
ΑΣΚΗΣΗ 14. έκδοση DΥΝI-EXC b
 ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΑΣΚΗΣΗ 14 έκδοση DΥΝI-EXC14-016b Copyright Ε.Μ.Π. - 016 Σχολή
ΕΡΓΑΣΤΗΡΙΟ ΔΥΝΑΜΙΚΗΣ & ΚΑΤΑΣΚΕΥΩΝ ΤΟΜΕΑΣ ΜΗΧΑΝΟΛΟΓΙΚΩΝ ΚΑΤΑΣΚΕΥΩΝ & ΑΥΤΟΜΑΤΟΥ ΕΛΕΓΧΟΥ ΣΧΟΛΗ ΜΗΧΑΝΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ ΕΘΝΙΚΟ ΜΕΤΣΟΒΙΟ ΠΟΛΥΤΕΧΝΕΙΟ ΑΣΚΗΣΗ 14 έκδοση DΥΝI-EXC14-016b Copyright Ε.Μ.Π. - 016 Σχολή
ΛΥΣΕΙΣ ΦΥΛΛΑΔΙΟΥ 3 Ευθεία - Επίπεδο ΣΧΟΛΗ ΠΟΛΙΤΙΚΩΝ ΜΗΧΑΝΙΚΩΝ/2010-11
 ΛΥΣΕΙΣ ΦΥΛΛΔΙΥ 3 Ευθία - Επίπδο ΣΧΛΗ ΠΛΙΤΙΚΩΝ ΜΗΧΝΙΚΩΝ/00-.(α) Τα διανύσματα Β = (,, ), Γ = (,, 3) ίναι μη συγγραμμικά και παράλληλα προς το πίπδο Π, νώ το σημίο (,,3) μ διάνυσμα θέσης r = (,,3) ίναι σημίο
ΛΥΣΕΙΣ ΦΥΛΛΔΙΥ 3 Ευθία - Επίπδο ΣΧΛΗ ΠΛΙΤΙΚΩΝ ΜΗΧΝΙΚΩΝ/00-.(α) Τα διανύσματα Β = (,, ), Γ = (,, 3) ίναι μη συγγραμμικά και παράλληλα προς το πίπδο Π, νώ το σημίο (,,3) μ διάνυσμα θέσης r = (,,3) ίναι σημίο
