Ηλεκτρική και Μαγνητική Πόλωση
|
|
|
- Κέρβερος Ἀβραάμ Κρεστενίτης
- 8 χρόνια πριν
- Προβολές:
Transcript
1 Ηλκτρική και Μαγνητική Πόλωση Μαγνητικά και Ηλκτρικά πδία στα υλικά Μαγνήτιση και Ηλκτρική Πόλωση Οµοιότητς και ιαφορές Συµµτρία αντιστροφής ώρου και ρόνου Μαγνητική και Σιδηροηλκτρική Υστέρηση
2 Εξισώσις Maxwell στο κνό B B µ J ρ B t µ t Νόµος Gauss Ανυπαρξία Μαγν. πόλων Νόµος Επαγωγής Faraday Νόµος Ampere Ρύµα Μτατόπισης
3 Χρονικά Σταθρά Πδία B B µ ρ J
4 Gauss ρ dv ρ dv ds Q ds Q d S Q B ds
5 Gauss>Coulomb d S Q Q 4πR 2 4π Q Q R 2 F q 4π qq 2 R
6 Ampere B µ J B L µ NI B ds B µ IN / L µ J ds B dl µ I
7 Βρόος Ρύµατος ίπολο Ν/S Ν S Ν S S Ν
8 Μαγνήτιση και Πόλωση Ν M P S Mdµ/dV Pdp/dV
9 Μαγνήτιση και Πόλωση M P µιs pqd W-µ Β W-p Mdµ/dV Pdp/dV
10 Ηλκτρική Πόλωση Υλικά που έουν µόνιµς διπολικές Στική µτατόπιση ιόντων σ ιοντικά υλικά Μτατόπιση του ηλκτρονικού νέφους σ σέση µτονπυρήνα
11 BaTiO3
12 Μαγνήτιση S < ιαµαγνητικά: Υλικά ωρίς µόνιµς µαγνητικές ροπές Παραµαγνητικά: Υλικά µ µόνιµς µαγνητικές ροπές Ασύζυκτς µταξύ τους > Σιδηροµαγνητικά, Σιδηριµαγνητικά : Υλικά µ µόνιµς µαγνητικές ροπές Ισυρά συζυγµένς µταξύ τους >>
13 ,D ( ) P D D P P P ) ( ρ ρ ρ ρ ρ ρ bound bound ( ) ( ) M B J J M B M J B M J J J B µ µ µ µ µ material material
14 Συνοριακές Συνθήκς j s B B 2,, 2,, J B 2,, 2,, A Q D D D σ ρ
15 Ισότροπα Γραµµικά µέσα ( ) D D P D P r e e ( ) ( ) B B M B M µ r µ µ µ
16 Πυκνωτής Μ ιηλκτρικό ( ) d A V Q C d V A A DA Q A Q D P D P D V Q d D A Q Q d A V Q C d V A A Q A Q r r r s s
17 Εξισώσις του Mawell µέσα στην ύλη για ρονικά σταθρά πδία D ρ B J αντί των B B ρ µ J
18 ΠΡΟΣΟΧΗ ΟΜΩΣ ΣΤΗΝ ΠΑΡΑΠΛΑΝΗΤΙΚΗ «ΑΝΑΛΟΓΙΑ» D ΚΑΙ Η Β B D ρ, M, D P J
19 Εξισώσις Maxwell σ υλικά t t J B B B µ µ ρ t t D J B B D ρ ) ( M B µ
20 Αποηλκτρίζον πδίο N d P
21 Αποµαγνητίζον Πδίο d N M B, M Οι γραµµές του Β ίναι συνίς νώ του Η πηγάζουν από τους «πόλους» στην πιφάνια νός οµογνώς µαγνητισµένου σώµατος.
22 Παράγοντς αποµαγνήτισης για απλά σήµατα Σφαίρα N x N N y z 3 Λπτός ίσκος Ζ N x N, N y z Μακρύς Κύλινδρος N x N 2, N y z Ισύι N x N y N z
23 Φαινόµνη (Εξωγνής) Επιδκτικότητα Λόγωτουπδίουαποµαγνήτισης/αποηλέκτρισης (Ηd -NM, d-np/ για µαγνητισµό/ηλκτρισµό αντίστοια) σ ισότροπα γραµµικά µέσα (όπου ισύι ΜΗ, P e Ε αντίστοια) φόσον κτός από το ξωτρικό πδίο (Ηξ, Εξ αντίστοια) υπάρουν και τα d, d oι σέσις τροποποιούνται ως ξής: ξ ξ ξ N P P N P P N P P P N e e e e e e d ( ) N N M NM M NM M M NM d φαινοµνη ξ ξ ξ
24 Πδία σ ισότροπο γραµµικό µέσο µ παράγοντα αποµαγνήτισης Ν ( ) ξ ξ ξ ξ ξ ξ ξ ξ µ µ µ N N N M B N N N N N NM N M
25 Σηµίο Λιτουργίας Μόνιµου Μαγνήτη Μόνιµος µαγνήτης µαγνητίζται και παραµένι µαγνητισµένος σ µηδέν ξωτρικό πδίο κατά µήκος διύθυνσης µ παράγοντα αποµαγνήτισης Ν Υπολογισµός των πδίων Η,Β και Μ µέσα σ ένα υλικό που αρακτηρίζται από βρόο υστέρησης Μ(Η) και έι σήµα που αντιστοιί σ παράγοντα αποµαγνήτσης Ν: Τα Μ,Η αντιστοιούν στο σηµίο P τοµής τουβρόουμ(η) µ τηνυθίαμ-η/ν (που προέρται από την σέση Η-ΝΜ)
26 Αντιστροφή Χώρου-Χρόνου r r dr d( r) υ υ dt dt 2 2 d r d ( r) a a 2 2 dt dt t t υ a dr dt 2 d r 2 dt dr d ( t) d d 2 r ( t) υ 2 a
27 Spontaneous Polarization and the ysteresis
28 rθέση tρόνος mµάζα qφορτίο Χρονικά Άρτιο Χωρικά Άρτιο m, q (αναλλοίωτα) Χωρικά Πριττό r, ad 2 r/dt 2, Fma, F/q, Χρονικά Πριττό t, Idq/dt, Lrµp,, B, M υdr/dt, pmυ, jqυ,
29 ΠΕ ΙΑ Χωρικά Άρτιο Χωρικά Πριττό Χρονικά Άρτιο Ηλκτρικό Πδίο (πολικό άνυσµα) Χρονικά Πριττό Μαγνητικό Πδίο (αξονικό άνυσµα) Fq(υxB)
30 Υλικά που µπορούν να πολωθούν Ηλκτρικά και Μαγνητικά Μαγνητικά Πολωνόµνα ΣΙδηροµαγνητικά Ηλκτρικά Πολωνόµνα ΣΙδηροηλκτρικά Πολυσιδηρικά Μαγνητοηλκτρικά
31 Υλικά που µπορούν να πολωθούν Ηλκτρικά και Μαγνητικά
32 ΥΛΙΚΑ Χωρικά Άρτιο Χωρικά Πριττό Χρονικά Άρτιο Σιδηρολαστικό Σιδηροηλκτρικό Χρονικά Πριττό Σιδηροµαγνητικό Πολυσιδηρικό
33 οµή Προβσκίτη Pb,Ba,Bi Ti,Mn,Fe,Nb,Mg Οξυγόνο Pb(Zr,Ti)O3-PZT Ba(Sr,Ti)O3-BST KNbO3 and LiNbO3 Pb(Ca,Ti)O3 -PCT Pb(Sr,Ti)O3 PST Pb(Mg/3Nb2/3)O3-PbTiO3
34 Υστέρηση P P P R C -P R -P
35 Σηµίο Curie Spontaneous Polarization (C/m 2 ) PbTiO 3 T C 49 o C Temperature [ o C]
36 Typical Ferroelectric Materials
37 Non-Volatile RAMs (memory)
38 Πιζοηλκτρισµός
39 Πιζοηλκτρισµός και κντροσυµµτρικότητα
40 32 κρυσταλλικές δοµές 2 µη κνντροσυµµτρικές 2-πιζοηλκτρικές κυβική 432 -πυροηλκτρική (αυθόρµητη πόλωση) Σιδηροηλκτρικά (αντιστρέψιµα µ πδίο) Piezoelectric crystal classes:, 2, m, 222, mm2, 4, -4, 422, 4mm, -42m, 3, 32, 3m, 6, -6, 622, 6mm, -62m, 23, -43m Pyroelectric:, 2, m, mm2, 3, 3m, 4, 4mm, 6, 6mm
ΗΛΕΚΤΡΙΚΕΣ -ΜΑΓΝΗΤΙΚΕΣ - ΟΠΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΥΛΙΚΩΝ
 KSP ΚΕΦ.8 ΗΛΕΚΤΡΙΚΕΣ -ΜΑΓΝΗΤΙΚΕΣ - ΟΠΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΥΛΙΚΩΝ Παράγραφοι 8., 8., 8.4 ΜΑΓΝΗΤΙΣΜΟΣ Παραδείγματα 8.,8.,8., 8.4,8.5, 8.6 Μαγνητική Απόκριση Στοιχείων dm d Μαγνητισμός στην ύλη Όλα τα υλικά έχουν
KSP ΚΕΦ.8 ΗΛΕΚΤΡΙΚΕΣ -ΜΑΓΝΗΤΙΚΕΣ - ΟΠΤΙΚΕΣ ΙΔΙΟΤΗΤΕΣ ΥΛΙΚΩΝ Παράγραφοι 8., 8., 8.4 ΜΑΓΝΗΤΙΣΜΟΣ Παραδείγματα 8.,8.,8., 8.4,8.5, 8.6 Μαγνητική Απόκριση Στοιχείων dm d Μαγνητισμός στην ύλη Όλα τα υλικά έχουν
Νόμος του Gauss 1. Ηλεκτρική Ροή ( πλήθος δυναμικών γραμμών). είναι διάνυσμα μέτρου Α και κατεύθυνσης κάθετης στην επιφάνεια. Στην γενική περίπτωση:
 Νόμος του Gauss 1. Ηλκτρική Ροή ( πλήθος δυναμικών γραμμών). ( a) cosφ ( b) ίναι διάνυσμα μέτρου Α και κατύθυνσης κάθτης στην πιφάνια. Στην γνική πρίπτωση: d d d ( ) (πιφανιακό ολοκλήρωμα) Νόμος του Gauss
Νόμος του Gauss 1. Ηλκτρική Ροή ( πλήθος δυναμικών γραμμών). ( a) cosφ ( b) ίναι διάνυσμα μέτρου Α και κατύθυνσης κάθτης στην πιφάνια. Στην γνική πρίπτωση: d d d ( ) (πιφανιακό ολοκλήρωμα) Νόμος του Gauss
Α ΚΙΝΗΣΗ ΦΟΡΤΙΣΜΕΝΩΝ ΣΩΜΑΤΙ ΙΩΝ ΣΤΟ ΗΛΕΚΤΡΙΚΟ ΚΑΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ
 A ΚΙΝΗΣΗ ΦΟΡΤΙΣΜΕΝΩΝ ΣΩΜΑΤΙ ΙΩΝ ΣΤΟ ΗΛΕΚΤΡΙΚΟ ΚΑΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ ΚΙΝΗΣΗ ΦΟΡΤΙΣΜΕΝΟΥ ΣΩΜΑΤΙ ΙΟΥ ΣΕ ΣΤΑΤΙΚΑ ΠΕ ΙΑ Α. Γνική ξίσωση κίνησης για µη ρλατιβιστικές πριπτώσις q( ) + B Α. Αρχή διατήρησης της νέργιας
A ΚΙΝΗΣΗ ΦΟΡΤΙΣΜΕΝΩΝ ΣΩΜΑΤΙ ΙΩΝ ΣΤΟ ΗΛΕΚΤΡΙΚΟ ΚΑΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ ΚΙΝΗΣΗ ΦΟΡΤΙΣΜΕΝΟΥ ΣΩΜΑΤΙ ΙΟΥ ΣΕ ΣΤΑΤΙΚΑ ΠΕ ΙΑ Α. Γνική ξίσωση κίνησης για µη ρλατιβιστικές πριπτώσις q( ) + B Α. Αρχή διατήρησης της νέργιας
ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΤΗΝ ΥΛΗ ΘΕΩΡΙΑ
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΤΗΝ ΥΛΗ ΘΕΩΡΙΑ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 29 - ΑΘΗΝΑ 6932 946778 www.pmoias.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 6932 946778 ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ ΣΤΗΝ ΥΛΗ ΘΕΩΡΙΑ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 29 - ΑΘΗΝΑ 6932 946778 www.pmoias.weebly.com ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ
III Η ΥΛΗ ΣΤΟ ΠΕ ΙΟ ΠΟΛΩΣΗ ΙΗΛΕΚΤΡΙΚΟΥ ΙΙI ΥΛΗ ΣΤΟ ΠΕ ΙΟ
 III Η ΥΛΗ ΣΤΟ ΠΕ ΙΟ ΠΟΛΩΣΗ ΙΗΛΕΚΤΡΙΚΟΥ ΙΙΙ. Συνολική οπή των διπόλων που πιέχονται στον όγκο δ V, όπου N ο αιθµός διπόλων ανά µονάδα όγκου και p η διπολική οπή του -στού διπόλου p t NV δ p ΙΙΙ. Το διάνυσµα
III Η ΥΛΗ ΣΤΟ ΠΕ ΙΟ ΠΟΛΩΣΗ ΙΗΛΕΚΤΡΙΚΟΥ ΙΙΙ. Συνολική οπή των διπόλων που πιέχονται στον όγκο δ V, όπου N ο αιθµός διπόλων ανά µονάδα όγκου και p η διπολική οπή του -στού διπόλου p t NV δ p ΙΙΙ. Το διάνυσµα
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ
 ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E 1 4 0 q r 2 rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: 0 qv rˆ Έχουμε εισάγει την
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E 1 4 0 q r 2 rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: 0 qv rˆ Έχουμε εισάγει την
Κλασική Ηλεκτροδυναμική
 Κλασική Ηλεκτροδυναμική Ενότητα 17: Μαγνητοστατική σε υλικά Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει τα στοιχεία θεωρίας που αφορούν
Κλασική Ηλεκτροδυναμική Ενότητα 17: Μαγνητοστατική σε υλικά Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να ολοκληρώσει τα στοιχεία θεωρίας που αφορούν
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 28)
 ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
ΠΗΓΕΣ ΜΑΓΝΗΤΙΚΟΥ ΠΕΔΙΟΥ (ΚΕΦ 8) B που παράγεται από κινούμενο φορτίο Το Ηλ. Πεδίο στο P (δεν φαίνεται) είναι E = 1 4πε 0 q r rˆ Για το Μαγνητικό Πεδίο στο P προκύπτει πειραματικά ότι: µ 0 qv rˆ B = 4π
ΙV ΜΕΘΟ ΟΙ ΕΠΙΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕ ΙΟΥ
 ΜΕΘΟ Ο ΕΠΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΚΟΥ ΠΕ ΟΥ ΜΕΘΟ Ο ΕΠΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΚΟΥ ΠΕ ΟΥ ΜΕΘΟ ΟΣ ΤΟΥ ΚΑΤΟΠΤΡΣΜΟΥ Φορτίο πάνω από αγώγιµο πίπδο z o. Τιµή και θέη του κατοπτρικού φορτίου,.
ΜΕΘΟ Ο ΕΠΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΚΟΥ ΠΕ ΟΥ ΜΕΘΟ Ο ΕΠΛΥΣΗΣ ΠΡΟΒΛΗΜΑΤΩΝ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΚΟΥ ΠΕ ΟΥ ΜΕΘΟ ΟΣ ΤΟΥ ΚΑΤΟΠΤΡΣΜΟΥ Φορτίο πάνω από αγώγιµο πίπδο z o. Τιµή και θέη του κατοπτρικού φορτίου,.
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ
 ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας Θέμα Ένα σημιακό φρτί Q τπθτίται στ κέντρ νός υδέτρυ σφαιρικύ αγώγιμυ κλύφυς ακτινών R και R. Να υπλγιστί τ παγόμν φρτί
ΛΥΜΕΝΑ ΘΕΜΑΤΑ ΕΞΕΤΑΣΕΩΝ ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας Θέμα Ένα σημιακό φρτί Q τπθτίται στ κέντρ νός υδέτρυ σφαιρικύ αγώγιμυ κλύφυς ακτινών R και R. Να υπλγιστί τ παγόμν φρτί
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΑ ΠΕΔΙΑ ΣΤΗΝ ΥΛΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
Κατοίκον Εργασία 2. (γ) το ολικό φορτίο που βρίσκεται στον κύβο. (sd p.e 4.9 p146)
 Κατοίκον Εργασία. Ένα σημιακό φορτίο (point charge) 5 mc και ένα - mc βρίσκονται στα σημία (,0,4) και (-3,0,5) αντίστοιχα. (α) Υπολογίστ την δύναμη πάνω σ ένα φορτίο (point charge) nc που βρίσκται στο
Κατοίκον Εργασία. Ένα σημιακό φορτίο (point charge) 5 mc και ένα - mc βρίσκονται στα σημία (,0,4) και (-3,0,5) αντίστοιχα. (α) Υπολογίστ την δύναμη πάνω σ ένα φορτίο (point charge) nc που βρίσκται στο
ΠΕΡΙΕΧΟΜΕΝΑ ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1
 ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
ΤΟΜΟΣ Ι ΕΙΣΑΓΩΓΗ 1 1 ΟΙ ΒΑΣΙΚΟΙ ΝΟΜΟΙ ΤΟΥ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟΥ ΠΕΔΙΟΥ 7 1.1 Μονάδες και σύμβολα φυσικών μεγεθών..................... 7 1.2 Προθέματα φυσικών μεγεθών.............................. 13 1.3 Αγωγοί,
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ. 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες... 7
 ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
ΠΕΡΙΕΧΟΜΕΝΑ 1. ΙΑΝΥΣΜΑΤΙΚΗ ΑΝΑΛΥΣΗ 1.1 Φυσικά µεγέθη... 1 1.2 ιανυσµατική άλγεβρα... 2 1.3 Μετατροπές συντεταγµένων... 6 1.3.1 Μετατροπή από καρτεσιανό σε κυλινδρικό σύστηµα... 6 1.3.2 Απειροστές ποσότητες...
3. ΚΛΑΣΣΙΚΗ ΘΕΩΡΙΑ ΤΟΥ ΠΑΡΑΜΑΓΝΗΤΙΣΜΟΥ
 . ΚΛΑΣΣΙΚΗ ΘΕΩΡΙΑ ΤΟΥ ΠΑΡΑΜΑΓΝΗΤΙΣΜΟΥ Οι πρώτες συστηματικές μετρήσεις της επιδεκτικότητας σε μεγάλο αριθμό ουσιών και σε μεγάλη περιοή θερμοκρασιών έγιναν από τον Curie το 895. Τα αποτελέσματά του έδειξαν
. ΚΛΑΣΣΙΚΗ ΘΕΩΡΙΑ ΤΟΥ ΠΑΡΑΜΑΓΝΗΤΙΣΜΟΥ Οι πρώτες συστηματικές μετρήσεις της επιδεκτικότητας σε μεγάλο αριθμό ουσιών και σε μεγάλη περιοή θερμοκρασιών έγιναν από τον Curie το 895. Τα αποτελέσματά του έδειξαν
C V C = 1. Πυκνωτές. Οι πυκνωτές έχουν πολλές χρήσεις λόγω του ότι αποτελούν αποθήκες ηλεκτρικού φορτίου και ηλεκτρικής δυναμικής ενέργειας.
 . Πυκνωτές Δύο αγωγοί που διαχωρίζονται από ένα μονωτή αποτλούν ένα πυκνωτή. Στην πράξη οι αγωγοί φέρουν ία και αντίθτα φορτία. Ορίζουμ αν χωρητικότητα νός πυκνωτή το ταθρό πηλίκο: ab F Οι πυκνωτές έχουν
. Πυκνωτές Δύο αγωγοί που διαχωρίζονται από ένα μονωτή αποτλούν ένα πυκνωτή. Στην πράξη οι αγωγοί φέρουν ία και αντίθτα φορτία. Ορίζουμ αν χωρητικότητα νός πυκνωτή το ταθρό πηλίκο: ab F Οι πυκνωτές έχουν
Πυκνότητα φορτίου. dq dv. Μικρή Περιοχή. φορτίου. Χωρική ρ Q V. Επιφανειακή σ. dq da Γραµµική λ Q A. σ = dq dl. Q l. Γ.
 Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
Πυκνότητα φορτίου Πυκνότητα φορτίου Οµοιόµορφη Μικρή Περιοχή Χωρική ρ Q V ρ= dq dv Επιφανειακή σ Q A σ = dq da Γραµµική λ Q l λ= dq dl Γ. Βούλγαρης 1 Παράσταση της έντασης Ηλεκτρικού Πεδίου. Η Εφαπτόµενη
Κεφάλαιο 4: Πυροηλεκτρισμός, Πιεζο- ηλεκτρισμός, Λιαροκάπης Ευθύμιος. Διηλεκτρικές, Οπτικές, Μαγνητικές Ιδιότητες Υλικών
 Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μτσόβιο Πολυτχνίο Διηλκτρικές, Οπτικές, Μαγνητικές Ιδιότητς Υλικών Κφάλαιο 4: Πυροηλκτρισμός, Πιζο- ηλκτρισμός, Σιδηροηλκτρισμός Λιαροκάπης Ευθύμιος
Σχολή Εφαρμοσμένων Μαθηματικών και Φυσικών Επιστημών Εθνικό Μτσόβιο Πολυτχνίο Διηλκτρικές, Οπτικές, Μαγνητικές Ιδιότητς Υλικών Κφάλαιο 4: Πυροηλκτρισμός, Πιζο- ηλκτρισμός, Σιδηροηλκτρισμός Λιαροκάπης Ευθύμιος
Ο νόμος του Ampère. Διαφορική μορφή του ν.ampère. B r. Παρ : To πεδίο Β δακτυλιοειδούς πηνίου. Εντός του πηνίου
 Ο νόμος του Apèr Ο νόμος του Apèr Bis μ μ Ji Επιφάνια Bi μ π r ( π s B s r μ Η κυκλοφορία του μαγνητικού πδίου κατά μηκός μιάς κλιστής διαδρομής ισούται μ μ Ι, όπου Ι ίναι το ολικό σταθρό (χρονικά αμτάβλητο
Ο νόμος του Apèr Ο νόμος του Apèr Bis μ μ Ji Επιφάνια Bi μ π r ( π s B s r μ Η κυκλοφορία του μαγνητικού πδίου κατά μηκός μιάς κλιστής διαδρομής ισούται μ μ Ι, όπου Ι ίναι το ολικό σταθρό (χρονικά αμτάβλητο
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ
 1 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ 1) Να αναφέρετε τις 4 παραδοχές που ισχύουν για το ηλεκτρικό φορτίο 2) Εξηγήστε πόσα είδη κατανοµών ηλεκτρικού φορτίου υπάρχουν. ιατυπώστε τους
1 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ και ΕΦΑΡΜΟΓΕΣ ΕΡΩΤΗΜΑΤΟΛΟΓΙΟ ΜΑΘΗΜΑΤΟΣ 1) Να αναφέρετε τις 4 παραδοχές που ισχύουν για το ηλεκτρικό φορτίο 2) Εξηγήστε πόσα είδη κατανοµών ηλεκτρικού φορτίου υπάρχουν. ιατυπώστε τους
Μαγνητικά Υλικά Υπεραγωγοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαγνητικά Υλικά Υπεραγωγοί ΜΑΓΝΗΤΙΚΗ ΑΝΙΣΟΤΡΟΠΙΑ Διδάσκων: Καθηγητής Ιωάννης Παναγιωτόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαγνητικά Υλικά Υπεραγωγοί ΜΑΓΝΗΤΙΚΗ ΑΝΙΣΟΤΡΟΠΙΑ Διδάσκων: Καθηγητής Ιωάννης Παναγιωτόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Το πεδίο Η στον σίδηρο εάν η μαγνήτιση είναι ομοιόμορφη είναι. Η μαγνήτιση Μ= m/v, όπου m είναι η μαγνητική ροπή και V ο όγκος του κυλίνδρου
 . Το πεδίο Β μέσα στον σίδηρο δίνεται από τη σχέση Β=μ ο (Η+Μ) Το πεδίο Η στον σίδηρο εάν η μαγνήτιση είναι ομοιόμορφη είναι Η=Η - όπου Η είναι το εξωτερικό πεδίο και Ν ο συντελεστής απομαγνήτισης. Επομένως
. Το πεδίο Β μέσα στον σίδηρο δίνεται από τη σχέση Β=μ ο (Η+Μ) Το πεδίο Η στον σίδηρο εάν η μαγνήτιση είναι ομοιόμορφη είναι Η=Η - όπου Η είναι το εξωτερικό πεδίο και Ν ο συντελεστής απομαγνήτισης. Επομένως
Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών
 Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών Το εκπαιδευτικό υλικό που ακολουθεί αναπτύχθηκε στα πλαίσια του έργου «Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών», του Μέτρου «Εισαγωγή
Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών Το εκπαιδευτικό υλικό που ακολουθεί αναπτύχθηκε στα πλαίσια του έργου «Προηγμένες Υπηρεσίες Τηλεκπαίδευσης στο Τ.Ε.Ι. Σερρών», του Μέτρου «Εισαγωγή
Experiments are the only means of knowledge. Anyother is poetry and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWELL
 ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
ΚΥΜΑΤΙΚΗ-ΟΠΤΙΚΗ 7 xpeiments ae the only means o knowledge. Anyothe is poety and imagination. M.Plank 2 ΟΙ ΕΞΙΣΩΣΕΙΣ ΤΟΥ MAXWLL Σε µια πρώτη παρουσίαση του θέµατος δίνονται οι εξισώσεις του Maxwell στο
ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ 3 ο ΜΑΘΗΜΑ ΘΕΩΡΙΑ 2017
 ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ 3 ο ΜΑΘΗΜΑ ΘΕΩΡΙΑ 2017 Χαρακτηριστικά: Γρήγορη και σχετικά εύκολη μέθοδος Χρησιμοποιεί μαγνητικά πεδία και μικρά μαγνητικά σωματίδια Προϋπόθεση το υπό-εξέταση δοκίμιο
ΤΕΧΝΟΛΟΓΙΑ ΜΗ ΚΑΤΑΣΤΡΟΦΙΚΟΥ ΕΛΕΓΧΟΥ 3 ο ΜΑΘΗΜΑ ΘΕΩΡΙΑ 2017 Χαρακτηριστικά: Γρήγορη και σχετικά εύκολη μέθοδος Χρησιμοποιεί μαγνητικά πεδία και μικρά μαγνητικά σωματίδια Προϋπόθεση το υπό-εξέταση δοκίμιο
[Ολοκληρωτική μορφή του νόμου του Gauss στο κενό ή τον αέρα]
![[Ολοκληρωτική μορφή του νόμου του Gauss στο κενό ή τον αέρα] [Ολοκληρωτική μορφή του νόμου του Gauss στο κενό ή τον αέρα]](/thumbs/26/9169893.jpg) Παν/μιο Πατρών Τμήμα Φυσικής. Μάθημα : Ηλκτρομαγνητισμός Ι (Υποχρωτικό 3 ου Εξαμήνου) ΠΝΕΠΙΣΤΗΜΙΟ ΠΤΡΩΝ - ΤΜΗΜ ΦΥΣΙΚΗΣ ΜΘΗΜ : HΛΕΚΤΡΟΜΓΝΗΤΙΣΜΟΣ Ι (Υποχρωτικό 3 ου Εξαμήνου) Διδάσκων :Δ.Σκαρλάτος, Επίκουρος
Παν/μιο Πατρών Τμήμα Φυσικής. Μάθημα : Ηλκτρομαγνητισμός Ι (Υποχρωτικό 3 ου Εξαμήνου) ΠΝΕΠΙΣΤΗΜΙΟ ΠΤΡΩΝ - ΤΜΗΜ ΦΥΣΙΚΗΣ ΜΘΗΜ : HΛΕΚΤΡΟΜΓΝΗΤΙΣΜΟΣ Ι (Υποχρωτικό 3 ου Εξαμήνου) Διδάσκων :Δ.Σκαρλάτος, Επίκουρος
3 η Εργαστηριακή Άσκηση
 3 η Εργαστηριακή Άσκηση Βρόχος υστέρησης σιδηρομαγνητικών υλικών Τα περισσότερα δείγματα του σιδήρου ή οποιουδήποτε σιδηρομαγνητικού υλικού που δεν έχουν βρεθεί ποτέ μέσα σε μαγνητικά πεδία δεν παρουσιάζουν
3 η Εργαστηριακή Άσκηση Βρόχος υστέρησης σιδηρομαγνητικών υλικών Τα περισσότερα δείγματα του σιδήρου ή οποιουδήποτε σιδηρομαγνητικού υλικού που δεν έχουν βρεθεί ποτέ μέσα σε μαγνητικά πεδία δεν παρουσιάζουν
(4) γενικής λύσης το x με το -x. και θα έχουμε : y ομ (x)=c 1 (-x) -1 +c 2 (-x) 3
 0 ΕΞΙΣΩΣΕΙΣ ΤΟΥ EULER Ορισμός : Οι γραμμικές διαφορικές ξισώσις, των οποίων οι συντλστές ίναι δυνάμις του βαθμού ίσου μ την τάξη της αντίστοιχης παραγώγου, ονομάζονται ξισώσις του Eule Πχ η ομογνής ξίσωση
0 ΕΞΙΣΩΣΕΙΣ ΤΟΥ EULER Ορισμός : Οι γραμμικές διαφορικές ξισώσις, των οποίων οι συντλστές ίναι δυνάμις του βαθμού ίσου μ την τάξη της αντίστοιχης παραγώγου, ονομάζονται ξισώσις του Eule Πχ η ομογνής ξίσωση
ΤΥΠΟΛΟΓΙΟ. q e = C Φορτίο Ηλεκτρονίου 1.1. Ηλεκτρικό Πεδίο 2.1. Ηλεκτρικό Πεδίο Σημειακού Φορτίου Q Ηλεκτρικό Πεδίο Σημειακού
 ΤΥΠΟΛΟΓΙΟ q e = 1.6 10 19 C Φορτίο Ηλεκτρονίου 1.1 F = k Q 1 Q 2 r 2 = 9 10 9 Q 1 Q 2 r 2 Νόμος Coulomb 1.2 E = F q E = k Q r 2 E = k Q r 2 e r E = 2kλ ρ E = 2kλ ρ e ρ ε 0 = 1/4πk = 8.85 10 12 S. I. Ε
ΤΥΠΟΛΟΓΙΟ q e = 1.6 10 19 C Φορτίο Ηλεκτρονίου 1.1 F = k Q 1 Q 2 r 2 = 9 10 9 Q 1 Q 2 r 2 Νόμος Coulomb 1.2 E = F q E = k Q r 2 E = k Q r 2 e r E = 2kλ ρ E = 2kλ ρ e ρ ε 0 = 1/4πk = 8.85 10 12 S. I. Ε
Ηλεκτροτεχνία Ηλ. Μηχανές & Εγκαταστάσεις πλοίου Τα στοιχεία του Πυκνωτή και του Πηνίου
 Το στοιχείο του πυκνωτή (1/2) Αποτελείται από δύο αγώγιμα σώματα (οπλισμοί)ηλεκτρικά μονωμένα μεταξύ τους μέσω κατάλληλου μονωτικού υλικού (διηλεκτρικό υλικό) Η ικανότητα του πυκνωτή να αποθηκεύει ενέργεια
Το στοιχείο του πυκνωτή (1/2) Αποτελείται από δύο αγώγιμα σώματα (οπλισμοί)ηλεκτρικά μονωμένα μεταξύ τους μέσω κατάλληλου μονωτικού υλικού (διηλεκτρικό υλικό) Η ικανότητα του πυκνωτή να αποθηκεύει ενέργεια
Πηγές μαγνητικού πεδίου Νόμος Ampere. Ιωάννης Γκιάλας 21 Μαίου 2014
 Πηγές μαγνητικού πεδίου Νόμος Ampere Ιωάννης Γκιάλας 21 Μαίου 214 Στόχοι διάλεξης Να κατανοηθεί πως προκαλείται το μαγνητικό πεδίο Νόμος Biot-Savart Μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού Μαγνητική
Πηγές μαγνητικού πεδίου Νόμος Ampere Ιωάννης Γκιάλας 21 Μαίου 214 Στόχοι διάλεξης Να κατανοηθεί πως προκαλείται το μαγνητικό πεδίο Νόμος Biot-Savart Μαγνητικό πεδίο ευθύγραμμου ρευματοφόρου αγωγού Μαγνητική
ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ
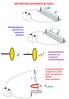 ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ =0 Αλληλεπιδράσεις μαγνητών με ηλεκτρικά ρεύματα Αλληλεπιδράσεις μαγνητών με κινούμενα ηλεκτρικά φορτία Οι αλληλεπιδράσεις συμβαίνουν μόνον όταν τα ηλεκτρικά φορτία είναι κινούμενα
ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ & ΠΕΔΙΑ =0 Αλληλεπιδράσεις μαγνητών με ηλεκτρικά ρεύματα Αλληλεπιδράσεις μαγνητών με κινούμενα ηλεκτρικά φορτία Οι αλληλεπιδράσεις συμβαίνουν μόνον όταν τα ηλεκτρικά φορτία είναι κινούμενα
4 η Εργαστηριακή Άσκηση
 4 η Εργαστηριακή Άσκηση Βρόχος υστέρησης σιδηροµαγνητικών υλικών Θεωρητικό µέρος Τα περισσότερα δείγµατα του σιδήρου ή οποιουδήποτε σιδηροµαγνητικού υλικού που δεν έχουν βρεθεί ποτέ µέσα σε µαγνητικά πεδία
4 η Εργαστηριακή Άσκηση Βρόχος υστέρησης σιδηροµαγνητικών υλικών Θεωρητικό µέρος Τα περισσότερα δείγµατα του σιδήρου ή οποιουδήποτε σιδηροµαγνητικού υλικού που δεν έχουν βρεθεί ποτέ µέσα σε µαγνητικά πεδία
ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ (ΘΕΩΡΙΑ)
 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ (ΘΕΩΡΙΑ) Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778.
ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778 ΑΓΩΓΟΙ - ΠΥΚΝΩΤΕΣ (ΘΕΩΡΙΑ) Συγγραφή Επιμέλια: Παναγιώτης Φ. Μίρας ΣΟΛΩΜΟΥ 9 - ΑΘΗΝΑ 693 946778 ΦΡΟΝΤΙΣΤΗΡΙΑΚΑ ΜΑΘΗΜΑΤΑ ΦΥΣΙΚΗΣ Π.Φ. ΜΟΙΡΑ 693 946778.
Νόμος Faraday Κανόνας Lenz Αυτεπαγωγή - Ιωάννης Γκιάλας 27 Μαίου 2014
 Νόμος Faraday Κανόνας Lenz Αυτεπαγωγή - Ιωάννης Γκιάλας 7 Μαίου 014 Στόχοι διάλεξης Πώς να: υπολογίζει την μεταβολή της μαγνητικής ροής. εφαρμόζει το νόμο του Faraday για τον υπολογισμό της επαγόμενης
Νόμος Faraday Κανόνας Lenz Αυτεπαγωγή - Ιωάννης Γκιάλας 7 Μαίου 014 Στόχοι διάλεξης Πώς να: υπολογίζει την μεταβολή της μαγνητικής ροής. εφαρμόζει το νόμο του Faraday για τον υπολογισμό της επαγόμενης
Μεταβαλλόμενα μαγνητικά πεδία
 Μεταβαλλόμενα μαγνητικά πεδία Ιστορική εισαγωγή Νόμος Faraday Πειράματα Faraday V e = dφ dt 12/11/2018 Φυσική ΙΙΙ Γ. Βούλγαρης 1 Νόμος του Lentz (1834) Πειράματα Lentz Παράδειγμα Διατήρηση Ενέργειας Helmhotz
Μεταβαλλόμενα μαγνητικά πεδία Ιστορική εισαγωγή Νόμος Faraday Πειράματα Faraday V e = dφ dt 12/11/2018 Φυσική ΙΙΙ Γ. Βούλγαρης 1 Νόμος του Lentz (1834) Πειράματα Lentz Παράδειγμα Διατήρηση Ενέργειας Helmhotz
Γωνία που σχηματίζει η ε με τον άξονα. Έστω Oxy ένα σύστημα συντεταγμένων στο επίπεδο και ε μια ευθεία που τέμνει τον άξονα
 ΕΥΘΕΙΑ Γωνία που σχηματίζι η μ τον άξονα. Έστω O ένα σύστημα συντταγμένων στο πίπδο και μια υθία που τέμνι τον άξονα στο σημίο Α. Α ω Α ω Τη γωνία ω που διαγράφι ο άξονας όταν στραφί γύρω από το Α κατά
ΕΥΘΕΙΑ Γωνία που σχηματίζι η μ τον άξονα. Έστω O ένα σύστημα συντταγμένων στο πίπδο και μια υθία που τέμνι τον άξονα στο σημίο Α. Α ω Α ω Τη γωνία ω που διαγράφι ο άξονας όταν στραφί γύρω από το Α κατά
Αστροφυσική. Ενότητα # 5: Μαγνητικά Πεδία στην Αστροφυσική. Λουκάς Βλάχος Τμήμα Φυσικής ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστροφυσική Ενότητα # 5: Μαγνητικά Πεδία στην Αστροφυσική Λουκάς Βλάχος Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΧΤΑ ΑΚΑΔΗΜΑΙΚΑ ΜΑΘΗΜΑΤΑ Αστροφυσική Ενότητα # 5: Μαγνητικά Πεδία στην Αστροφυσική Λουκάς Βλάχος Τμήμα Φυσικής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
ΜΑΘΗΜΑ. ΘΕΩΡΗΤΙΚΟΣ και ΕΦΑΡΜΟΣΜΕΝΟΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ. ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΑΣΚΗΣΕΙΣ στο ΚΕΦ. 4
 ΣΧΟΛΗ. Ν. ΟΚΙΜΩΝ ΜΑΘΗΜΑ ΘΕΩΡΗΤΙΚΟΣ κι ΕΦΑΡΜΟΣΜΕΝΟΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΑΣΚΗΣΕΙΣ στο ΚΕΦ. 4 ρ. Α. Μγουλάς Νοέµριος 5 ) Ν υπολογιστί το ηλκτρικό πδίο που δηµιουργί µι τέλι γώγιµη κοίλη σφίρ
ΣΧΟΛΗ. Ν. ΟΚΙΜΩΝ ΜΑΘΗΜΑ ΘΕΩΡΗΤΙΚΟΣ κι ΕΦΑΡΜΟΣΜΕΝΟΣ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ ΣΥΜΠΛΗΡΩΜΑΤΙΚΕΣ ΑΣΚΗΣΕΙΣ στο ΚΕΦ. 4 ρ. Α. Μγουλάς Νοέµριος 5 ) Ν υπολογιστί το ηλκτρικό πδίο που δηµιουργί µι τέλι γώγιµη κοίλη σφίρ
Andre-Marie Ampère Γάλλος φυσικός Ανακάλυψε τον ηλεκτροµαγνητισµό. Ασχολήθηκε και µε τα µαθηµατικά.
 Μαγνητικά πεδία Τα µαγνητικά πεδία δηµιουργούνται από κινούµενα ηλεκτρικά φορτία. Μπορούµε να υπολογίσουµε το µαγνητικό πεδίο που δηµιουργούν διάφορες κατανοµές ρευµάτων. Ο νόµος του Ampère χρησιµεύει
Μαγνητικά πεδία Τα µαγνητικά πεδία δηµιουργούνται από κινούµενα ηλεκτρικά φορτία. Μπορούµε να υπολογίσουµε το µαγνητικό πεδίο που δηµιουργούν διάφορες κατανοµές ρευµάτων. Ο νόµος του Ampère χρησιµεύει
Δυναμική Ηλεκτρικών Μηχανών
 Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Δυναμική Ηλεκτρικών Μηχανών Ενότητα 1: Εισαγωγή Βασικές Αρχές Επ. Καθηγήτρια Τζόγια Χ. Καππάτου Τμήμα Ηλεκτρολόγων Μηχανικών και Τεχνολογίας Υπολογιστών Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται
Κεφάλαιο 28 Πηγές Μαγνητικών Πεδίων. Copyright 2009 Pearson Education, Inc.
 Κεφάλαιο 28 Πηγές Μαγνητικών Πεδίων Περιεχόµενα Κεφαλαίου 28 Μαγνητικό πεδίου ευθύγραµµου καλωδίου Δύναµη µεταξύ παράλληλων καλωδίων Ο Νόµος του Ampère Σωληνοειδή και Πηνία Νόµος των Biot-Savart Μαγνητικά
Κεφάλαιο 28 Πηγές Μαγνητικών Πεδίων Περιεχόµενα Κεφαλαίου 28 Μαγνητικό πεδίου ευθύγραµµου καλωδίου Δύναµη µεταξύ παράλληλων καλωδίων Ο Νόµος του Ampère Σωληνοειδή και Πηνία Νόµος των Biot-Savart Μαγνητικά
y T - yy z x T + yy T + yz T + yx T + xy T + zy T - xz T - zx T - zz T - xx T + xx T + zx T + xz T + zz T - zy T - xy T - yx T - yz
 Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
Συµπληρωµατικές Σηµειώσεις στα ΗΜ Πεδία (Κ. Χιτζανίδης Μάιος 2017 ΗΜ τάσεις σε υλικές επιφάνειες T + yy T + yz T + yx T + zy T + xy T - xx T - xz T - zx T - zz T + zz T + zx T + xz T + xx T - xy T - zy
ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΗΛΕΚΤΡΟΛΟΓΙΚΑ ΥΛΙΚΑ. Ενότητα 12: ΜΑΓΝΗΤΙΚΑ ΥΛΙΚΑ ΛΙΤΣΑΡΔΑΚΗΣ ΓΕΩΡΓΙΟΣ ΤΗΜΜΥ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΛΟΓΙΚΑ ΥΛΙΚΑ Ενότητα 12: ΜΑΓΝΗΤΙΚΑ ΥΛΙΚΑ ΛΙΤΣΑΡΔΑΚΗΣ ΓΕΩΡΓΙΟΣ ΤΗΜΜΥ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ ΗΛΕΚΤΡΟΛΟΓΙΚΑ ΥΛΙΚΑ Ενότητα 12: ΜΑΓΝΗΤΙΚΑ ΥΛΙΚΑ ΛΙΤΣΑΡΔΑΚΗΣ ΓΕΩΡΓΙΟΣ ΤΗΜΜΥ Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες
Κλασική Ηλεκτροδυναμική Ι
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Κλασική Ηλεκτροδυναμική Ι ΜΑΓΝΗΤΟΣΤΑΤΙΚΗ Διδάσκων: Καθηγητής Ι. Ρίζος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
Μαγνητικά Υλικά. Κρίμπαλης Σπύρος
 Μαγνητικά Υλικά Κρίμπαλης Σπύρος Τα μαγνητικά υλικά είναι μία σπουδαία κατηγορία βιομηχανικών υλικών και χρησιμοποιούνται σε ηλεκτρονικές εφαρμογές όπως ηλεκτρομηχανολογικές εφαρμογές αλλά και σε ηλεκτρονικούς
Μαγνητικά Υλικά Κρίμπαλης Σπύρος Τα μαγνητικά υλικά είναι μία σπουδαία κατηγορία βιομηχανικών υλικών και χρησιμοποιούνται σε ηλεκτρονικές εφαρμογές όπως ηλεκτρομηχανολογικές εφαρμογές αλλά και σε ηλεκτρονικούς
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία. Ιωάννης Γκιάλας 7 Μαρτίου 2014
 Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
Εφαρμογές Νόμος Gauss, Ηλεκτρικά πεδία Ιωάννης Γκιάλας 7 Μαρτίου 14 Άσκηση: Ηλεκτρικό πεδίο διακριτών φορτίων Δύο ίσα θετικά φορτία q βρίσκονται σε απόσταση α μεταξύ τους. Να βρεθεί η ακτίνα του κύκλου,
ΚΕΦΑΛΑΙΟ 4: ΠΕΡΙΟΧΕΣ-WEISS
 ΚΕΦΑΛΑΙΟ 4: ΠΕΡΙΟΧΕΣ-WEISS Το πρώτο τμήμα της θεωρίας του Weiss εξηγεί γιατί τα σιδηρομαγνητικά υλικά έχουν αυθόρμητη μαγνήτιση Μ S και πως η μαγνήτιση Μ S μεταβάλλεται με τη θερμοκρασία. Η θεωρία υποθέτει
ΚΕΦΑΛΑΙΟ 4: ΠΕΡΙΟΧΕΣ-WEISS Το πρώτο τμήμα της θεωρίας του Weiss εξηγεί γιατί τα σιδηρομαγνητικά υλικά έχουν αυθόρμητη μαγνήτιση Μ S και πως η μαγνήτιση Μ S μεταβάλλεται με τη θερμοκρασία. Η θεωρία υποθέτει
ΤΟ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ
 VΙ TO ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ V ΤΟ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ ΒΑΣΙΚΕΣ ΕΝΕΡΓΕΙΑΚΕΣ ΣΧΕΣΕΙΣ ΤΟΥ ΠΕ ΙΟΥ VΙ. Πυκνότητα ενέργειας του ηλεκτρικού πεδίου σε γραικό και ισότροπο έσο we εe VΙ. Πυκνότητα ενέργειας του
VΙ TO ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ V ΤΟ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ ΒΑΣΙΚΕΣ ΕΝΕΡΓΕΙΑΚΕΣ ΣΧΕΣΕΙΣ ΤΟΥ ΠΕ ΙΟΥ VΙ. Πυκνότητα ενέργειας του ηλεκτρικού πεδίου σε γραικό και ισότροπο έσο we εe VΙ. Πυκνότητα ενέργειας του
div E = ρ /ε 0 ρ p = - div P, σ p = P. n div E = ρ /ε 0 = (1 /ε 0 ) (ρ l + ρ p ) div (ε 0 E + P) = ρ l /ε 0
 ιηλεκτρικά Υλικά Υλικά των µονώσεων Στερεά και ρευστά Επίδραση του Ηλεκτρικού πεδίου Η δράση του ηλεκτρικού πεδίου προσανατολίζει τα δίπολακαι δηµιουργεί το πεδίο της Πόλωσης Ρ Το προκύπτον πεδίο D της
ιηλεκτρικά Υλικά Υλικά των µονώσεων Στερεά και ρευστά Επίδραση του Ηλεκτρικού πεδίου Η δράση του ηλεκτρικού πεδίου προσανατολίζει τα δίπολακαι δηµιουργεί το πεδίο της Πόλωσης Ρ Το προκύπτον πεδίο D της
Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α
 Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
Α Ρ Χ Α Ι Α Ι Σ Τ Ο Ρ Ι Α Π Ο Λ Ι Τ Ι Κ Α Κ Α Ι Σ Τ Ρ Α Τ Ι Ω Τ Ι Κ Α Γ Ε Γ Ο Ν Ο Τ Α Σ η µ ε ί ω σ η : σ υ ν ά δ ε λ φ ο ι, ν α µ ο υ σ υ γ χ ω ρ ή σ ε τ ε τ ο γ ρ ή γ ο ρ ο κ α ι α τ η µ έ λ η τ ο ύ
(ΚΕΦ 32) f( x x f( x) x z y
 (ΚΕΦ 3) f( x x f( x) x z y ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~1860) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. Όμως, κατανόησε ότι οι εξισώσεις αυτές (όπως
(ΚΕΦ 3) f( x x f( x) x z y ΣΥΝΟΨΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΥ J. C. Maxwell (~1860) συνόψισε τη δουλειά ως τότε για το ηλεκτρικό και μαγνητικό πεδίο σε 4 εξισώσεις. Όμως, κατανόησε ότι οι εξισώσεις αυτές (όπως
T.E.I. ΣΤΕΡΕΑΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ
 T.E.I. ΣΤΕΡΕΑΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΕΡΓΑΣΤΗΡΙΟ «ΗΛΕΚΤΡΟΝΙΚΕΣ ΔΙΑΤΑΞΕΙΣ ΦΑΣΜΑΤΟΣΚΟΠΙΑΣ» ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 6: ΜΕΤΡΗΣΕΙΣ ΥΛΙΚΩΝ ΜΕ ΤΗ ΧΡΗΣΗ ΔΙΑΤΑΞΗΣ ΔΙΗΛΕΚΤΡΙΚΗΣ ΦΑΣΜΑΤΟΣΚΟΠΙΑΣ ΥΨΗΛΩΝ
T.E.I. ΣΤΕΡΕΑΣ ΕΛΛΑΔΑΣ ΤΜΗΜΑ ΗΛΕΚΤΡΟΝΙΚΩΝ ΜΗΧΑΝΙΚΩΝ ΤΕ ΕΡΓΑΣΤΗΡΙΟ «ΗΛΕΚΤΡΟΝΙΚΕΣ ΔΙΑΤΑΞΕΙΣ ΦΑΣΜΑΤΟΣΚΟΠΙΑΣ» ΕΡΓΑΣΤΗΡΙΑΚΗ ΑΣΚΗΣΗ 6: ΜΕΤΡΗΣΕΙΣ ΥΛΙΚΩΝ ΜΕ ΤΗ ΧΡΗΣΗ ΔΙΑΤΑΞΗΣ ΔΙΗΛΕΚΤΡΙΚΗΣ ΦΑΣΜΑΤΟΣΚΟΠΙΑΣ ΥΨΗΛΩΝ
Διάλεξη 2. Ηλεκτροτεχνία Ι. Κυκλώματα συνεχούς και Ηλεκτρομαγνητισμός. Α. Δροσόπουλος
 Ηλεκτροτεχνία Ι Κυκλώματα συνεχούς και Ηλεκτρομαγνητισμός Α Δροσόπουλος Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Σχολή Τεχνολογικών Εφαρμογών ΤΕΙ Δυτικής Ελλάδος Α Δροσόπουλος Ηλεκτροτεχνία Ι Θεμελιώδεις έννοιες
Ηλεκτροτεχνία Ι Κυκλώματα συνεχούς και Ηλεκτρομαγνητισμός Α Δροσόπουλος Τμήμα Ηλεκτρολόγων Μηχανικών ΤΕ Σχολή Τεχνολογικών Εφαρμογών ΤΕΙ Δυτικής Ελλάδος Α Δροσόπουλος Ηλεκτροτεχνία Ι Θεμελιώδεις έννοιες
Σχεδίαση µε τη χρήση Η/Υ
 Σχδίαση µ τη χρήση Η/Υ Ε Φ Α Λ Α Ι Ο 1 0 Ο Σ Τ Ο Ι Χ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α Σ Τ Ο Υ Χ Ω Ρ Ο Υ Ρ Λ Ε Ω Ν Ι Α Σ Α Ν Θ Ο Π Ο Υ Λ Ο Σ, Ε Π Ι Ο Υ Ρ Ο Σ Α Θ Η Γ Η Τ Η Σ Τ Μ Η Μ Α Ι Ο Ι Η Σ Η Σ Α Ι Ι Α Χ Ε Ι
Σχδίαση µ τη χρήση Η/Υ Ε Φ Α Λ Α Ι Ο 1 0 Ο Σ Τ Ο Ι Χ Ε Ι Α Γ Ε Ω Μ Ε Τ Ρ Ι Α Σ Τ Ο Υ Χ Ω Ρ Ο Υ Ρ Λ Ε Ω Ν Ι Α Σ Α Ν Θ Ο Π Ο Υ Λ Ο Σ, Ε Π Ι Ο Υ Ρ Ο Σ Α Θ Η Γ Η Τ Η Σ Τ Μ Η Μ Α Ι Ο Ι Η Σ Η Σ Α Ι Ι Α Χ Ε Ι
ΚΕΦΑΛΑΙΟ 1: ΜΑΓΝΗΤΟΣΤΑΤΙΚΗ. 1.1 Εισαγωγή στα μαγνητικά υλικά
 ΚΕΦΑΛΑΙΟ : ΜΑΓΝΗΤΟΣΤΑΤΙΚΗ. Εισαγωγή στα μαγνητικά υλικά Η ιδιότητα του μαγνητίτη να ελκύει ρινίσματα σιδήρου ήταν γνωστή στην αρχαία Ελλάδα από το 600 π.χ και αναφέρεται από τον Θαλή και τον Πλάτωνα. Το
ΚΕΦΑΛΑΙΟ : ΜΑΓΝΗΤΟΣΤΑΤΙΚΗ. Εισαγωγή στα μαγνητικά υλικά Η ιδιότητα του μαγνητίτη να ελκύει ρινίσματα σιδήρου ήταν γνωστή στην αρχαία Ελλάδα από το 600 π.χ και αναφέρεται από τον Θαλή και τον Πλάτωνα. Το
Υπεραγωγιμότητα. Βασικά Φαινόμενα: Ηλεκτροδυναμική: Επιφανειακή Ενέργεια: Κβαντικά Φαινόμενα: Μικροσκοπική Θεωρία :
 Βασικά Φαινόμενα: Ηλεκτροδυναμική: Επιφανειακή Ενέργεια: Κβαντικά Φαινόμενα: Μικροσκοπική Θεωρία : Υπεραγωγιμότητα Μηδενική Αντίσταση Missn, Κρίσιμο Πεδίο, Θερμοδυναμική Κρίσιμο Ρεύμα Εξισώσεις London,
Βασικά Φαινόμενα: Ηλεκτροδυναμική: Επιφανειακή Ενέργεια: Κβαντικά Φαινόμενα: Μικροσκοπική Θεωρία : Υπεραγωγιμότητα Μηδενική Αντίσταση Missn, Κρίσιμο Πεδίο, Θερμοδυναμική Κρίσιμο Ρεύμα Εξισώσεις London,
ΜΟΡΙΑΚΟΙ ΜΑΓΝΗΤΕΣ. Γιάννης Σανάκης, ρ ΙΝΣΤΙΤΟΥΤΟ ΕΠΙΣΤΗΜΗΣ ΥΛΙΚΩΝ ΕΚΕΦΕ «ΗΜΟΚΡΙΤΟΣ»
 ΜΟΡΙΑΚΟΙ ΜΑΓΝΗΤΕΣ Γιάννης Σανάκης, ρ ΙΝΣΤΙΤΟΥΤΟ ΕΠΙΣΤΗΜΗΣ ΥΛΙΚΩΝ ΕΚΕΦΕ «ΗΜΟΚΡΙΤΟΣ» Εισαγωγή Υλικό σε εξωτερικό µαγνητικό πεδίο, Η: Β = Η + 4πΜ Μ: Μαγνήτιση ανά µονάδα όγκου Μαγνητική επιδεκτικότητα: χ
ΜΟΡΙΑΚΟΙ ΜΑΓΝΗΤΕΣ Γιάννης Σανάκης, ρ ΙΝΣΤΙΤΟΥΤΟ ΕΠΙΣΤΗΜΗΣ ΥΛΙΚΩΝ ΕΚΕΦΕ «ΗΜΟΚΡΙΤΟΣ» Εισαγωγή Υλικό σε εξωτερικό µαγνητικό πεδίο, Η: Β = Η + 4πΜ Μ: Μαγνήτιση ανά µονάδα όγκου Μαγνητική επιδεκτικότητα: χ
5.6 Ενέργεια του ηλεκτρικού πεδίου παρουσία πολωμένων διηλεκτρικών. 5.6 Ενέργεια του ηλεκτρικού πεδίου παρουσία πολωμένων διηλεκτρικών
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι (Υποχρωτικό 3 ου Εξαμήνου) ΔΙΔΑΣΚΩΝ : ΔΗΜΗΤΡΙΟΣ ΣΚΑΡΛΑΤΟΣ, Επίκουρος Καθηγητής ΚΕΦΑΛΑΙΟ 5 : Διηλκτρικά 5.1 Γνικές Ιδιότητς 5. Διηλκτρικά
ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ ΤΜΗΜΑ ΦΥΣΙΚΗΣ ΜΑΘΗΜΑ : ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ι (Υποχρωτικό 3 ου Εξαμήνου) ΔΙΔΑΣΚΩΝ : ΔΗΜΗΤΡΙΟΣ ΣΚΑΡΛΑΤΟΣ, Επίκουρος Καθηγητής ΚΕΦΑΛΑΙΟ 5 : Διηλκτρικά 5.1 Γνικές Ιδιότητς 5. Διηλκτρικά
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ. Ενότητα 6: Πηγές μαγνητικού πεδίου. Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε.
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 6: Πηγές μαγνητικού πεδίου Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΣΜΟΣ Ενότητα 6: Πηγές μαγνητικού πεδίου Αν. Καθηγητής Πουλάκης Νικόλαος ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ Τ.Ε. Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons.
μ B = A m 2, N=
 1. Ο σίδηρος κρυσταλλώνεται σε bcc κυβική κυψελίδα με a=.866 Ǻ που περιλαμβάνει δύο άτομα Fe. Kάθε άτομο Fe έχει μαγνητική ροπή ίση με. μ Β. Υπολογίστε την πυκνότητα, την μαγνήτιση κόρου σε Α/m, και την
1. Ο σίδηρος κρυσταλλώνεται σε bcc κυβική κυψελίδα με a=.866 Ǻ που περιλαμβάνει δύο άτομα Fe. Kάθε άτομο Fe έχει μαγνητική ροπή ίση με. μ Β. Υπολογίστε την πυκνότητα, την μαγνήτιση κόρου σε Α/m, και την
T : g r i l l b a r t a s o s Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α. Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ
 Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ
Α Γ Ί Α Σ Σ Ο Φ Ί Α Σ 3, Δ Ρ Α Μ Α g r i l l b a r t a s o s Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 1 : 0 π μ Δ ι α ν ο μ έ ς κ α τ ο ί κ ο ν : 1 2 : 0 0 έ ω ς 0 1 : 0 0 π μ T ortiyas Σ ο υ
ΗΛΕΚΤΡΙΚΟ ΠΕ ΙΟ. HΛEKTPIKO ΦOPTIO: είναι το αίτιο των ηλεκτρικών δυνάµεων (εµπειρική αντίληψη).
 ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΙΙ Ι ΑΣΚΩΝ: ΚΑΘΗΓΗΤΗΣ Μ. ΒΕΛΓΑΚΗΣ ΓΕΝΙΚΟ ΤΜΗΜΑ / ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ / ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ Στη σειρά των φροντιστηρίων αυτών καταβάλλεται µια προσπάθεια να κατανοηθούν και να εµπεδωθούν κάποιες
ΜΑΘΗΜΑ: ΦΥΣΙΚΗ ΙΙ Ι ΑΣΚΩΝ: ΚΑΘΗΓΗΤΗΣ Μ. ΒΕΛΓΑΚΗΣ ΓΕΝΙΚΟ ΤΜΗΜΑ / ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ / ΠΑΝΕΠΙΣΤΗΜΙΟ ΠΑΤΡΩΝ Στη σειρά των φροντιστηρίων αυτών καταβάλλεται µια προσπάθεια να κατανοηθούν και να εµπεδωθούν κάποιες
Κεφάλαιο 1. Μαγνητικό Πεδίο & Υλικά
 Κεφάλαιο 1 Μαγνητικό Πεδίο & Υλικά Στο πρώτο κεφάλαιο γίνεται μία σύντομη ανασκόπηση της θεωρίας των μαγνητικών πεδίων και της φυσικής των μαγνητικών υλικών. Το κεφάλαιο διαιρείται σε τρείς βασικές ενότητες.
Κεφάλαιο 1 Μαγνητικό Πεδίο & Υλικά Στο πρώτο κεφάλαιο γίνεται μία σύντομη ανασκόπηση της θεωρίας των μαγνητικών πεδίων και της φυσικής των μαγνητικών υλικών. Το κεφάλαιο διαιρείται σε τρείς βασικές ενότητες.
ΦΥΣΙΚΗ ΙΙ (Θ) Χασάπης Δημήτριος ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΤΕ
 ΦΥΣΙΚΗ ΙΙ (Θ) Χασάπης Δημήτριος ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
ΦΥΣΙΚΗ ΙΙ (Θ) Χασάπης Δημήτριος ΣΧΟΛΗ ΤΕΧΝΟΛΟΓΙΚΩΝ ΕΦΑΡΜΟΓΩΝ ΤΜΗΜΑ ΜΗΧΑΝΟΛΟΓΙΑΣ ΤΕ 1 Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης Creative Commons. Για εκπαιδευτικό υλικό, όπως
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ
 ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
ΕΝΟΤΗΤΑ ΙΙΙ ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ 19 Μαγνητικό πεδίο Μαγνητικό πεδίο ονοµάζεται ο χώρος στον οποίο ασκούνται δυνάµεις σε οποιοδήποτε κινούµενο φορτίο εισάγεται σε αυτόν. Επειδή το ηλεκτρικό ρεύµα είναι διατεταγµένη
Ηλεκτρισμός & Μαγνητισμός
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρισμός & Μαγνητισμός Το ρεύμα μετατώπισης Διδάσκων : Επίκ. Καθ. Ν. Νικολής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης reative
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Ηλεκτρισμός & Μαγνητισμός Το ρεύμα μετατώπισης Διδάσκων : Επίκ. Καθ. Ν. Νικολής Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης reative
φ = ω Β=Γ Α= Β=Ε Γ=Ζ φ Ο
 1 Η Π ΕΙΞΗ ΣΤΗΝ ΕΥΚΛΕΙ ΕΙ ΕΩΜΕΤΡΙ. ΩΝΙΕΣ ΙΣΕΣ ια να αποδίξουμ ότι δύο γωνίς ίναι ίσς πρέπι να αποδίξουμ: 1. Ότι ίναι άθροισμα ή διαφορά γωνιών αντίστοια ίσων. α = β α+ γ = β + δ ν τότ γ = δ α γ = β δ.
1 Η Π ΕΙΞΗ ΣΤΗΝ ΕΥΚΛΕΙ ΕΙ ΕΩΜΕΤΡΙ. ΩΝΙΕΣ ΙΣΕΣ ια να αποδίξουμ ότι δύο γωνίς ίναι ίσς πρέπι να αποδίξουμ: 1. Ότι ίναι άθροισμα ή διαφορά γωνιών αντίστοια ίσων. α = β α+ γ = β + δ ν τότ γ = δ α γ = β δ.
ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ
 ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ ΜΑΘΗΜΑ 1 Δομή Σύγχρονης Ηλεκτρικής Μηχανής Μαγνητικά Πεδία σε ΣΗΜ Επαγόμενες Τάσεις και αλληλεπίδραση μαγνητικών Πεδίων Ουρεϊλίδης Κωνσταντίνος, Υποψ. Διδακτωρ Πρόβλημα 1. Έστω ότι
ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ Γ ΜΑΘΗΜΑ 1 Δομή Σύγχρονης Ηλεκτρικής Μηχανής Μαγνητικά Πεδία σε ΣΗΜ Επαγόμενες Τάσεις και αλληλεπίδραση μαγνητικών Πεδίων Ουρεϊλίδης Κωνσταντίνος, Υποψ. Διδακτωρ Πρόβλημα 1. Έστω ότι
ΕΙΣΑΓΩΓΗ ΣΤΑ ΜΑΓΝΗΤΙΚΑ ΥΛΙΚΑ
 ΕΙΣΑΓΩΓΗ ΣΤΑ ΜΑΓΝΗΤΙΚΑ ΥΛΙΚΑ Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γιώργος Κιοσέογλου . Η ΜΑΓΝΗΤΙΣΗ ΤΩΝ ΣΙΔΗΡΟΜΑΓΝΗΤΙΚΩΝ ΥΛΙΚΩΝ. Εισαγωγή. Περιοχές Weiss Τοιχώματα Bloch.3 Δομή των
ΕΙΣΑΓΩΓΗ ΣΤΑ ΜΑΓΝΗΤΙΚΑ ΥΛΙΚΑ Τμήμα Επιστήμης και Τεχνολογίας Υλικών Πανεπιστήμιο Κρήτης Γιώργος Κιοσέογλου . Η ΜΑΓΝΗΤΙΣΗ ΤΩΝ ΣΙΔΗΡΟΜΑΓΝΗΤΙΚΩΝ ΥΛΙΚΩΝ. Εισαγωγή. Περιοχές Weiss Τοιχώματα Bloch.3 Δομή των
ΣΤΑΤΙΚΑ ΗΜΜ ΠΕΔΙΑ. Καταναλισκόμενη ισχύς σε ωμικό αγωγό. Το έργο που παράγεται από το ηλεκτρικό πεδίο πάνω σ ένα ελεύθερο φορτίο του αγωγού είναι,
 Kεφ. 16 (Part III, pages 6-34) ΣΤΤΙΚ ΗΜΜ ΠΕΔΙ Καταναλισκόμενη ισχύς σε ωμικό αγωγό. Τ έργ πυ παράγεται από τ ηλεκτρικό πεδί πάνω σ ένα ελεύθερ φρτί τυ αγωγύ είναι, dw = f dr = qe υdt άρα Ρ = dw dt = qυ
Kεφ. 16 (Part III, pages 6-34) ΣΤΤΙΚ ΗΜΜ ΠΕΔΙ Καταναλισκόμενη ισχύς σε ωμικό αγωγό. Τ έργ πυ παράγεται από τ ηλεκτρικό πεδί πάνω σ ένα ελεύθερ φρτί τυ αγωγύ είναι, dw = f dr = qe υdt άρα Ρ = dw dt = qυ
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΜΑΓΝΗΤΙΚΑ ΠΕΔΙΑ ΚΑΙ ΜΑΓΝΗΤΙΚΕΣ ΔΥΝΑΜΕΙΣ 1 1. ΜΑΓΝΗΤΙΣΜΟΣ Μαγνητικά φαινόμενα παρατηρήθηκαν για πρώτη φορά πριν από τουλάχιστον 2500 χρόνια σε κομμάτια μαγνητισμένου σιδηρομεταλλεύματος,
Tο µαγνητικό πεδίο εντός της ύλης
 Tο µαγνητικό πεδίο εντός της ύλης Mαγνητική διαπερατότητα υλικού Θεωρούµε επίµηκες σωληνοειδές, του οποίου οι σπείρες διαρρέονται µε ηλεκτρικό ρεύµα ορισµένης έντασης Ι. Tότε στο εσωτερικό του σωληνοειδούς
Tο µαγνητικό πεδίο εντός της ύλης Mαγνητική διαπερατότητα υλικού Θεωρούµε επίµηκες σωληνοειδές, του οποίου οι σπείρες διαρρέονται µε ηλεκτρικό ρεύµα ορισµένης έντασης Ι. Tότε στο εσωτερικό του σωληνοειδούς
ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ. Παράδειγµα: Κίνηση φορτισµένου σωµατιδίου µέσα σε µαγνητικό πεδίο. z B. m υ MAΓΝΗTIKΟ ΠΕ ΙΟ
 1 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ.. Αν δοκιµαστικό φορτίο q βρεθεί κοντά σε αγωγό που διαρρέεται από ρεύµα, υφίσταται δύναµη κάθετη προς την διεύθυνση της ταχύτητάς του και µε µέτρο ανάλογο της ταχύτητάς του, F qυ Β (νόµος
1 ΜΑΓΝΗΤΙΚΟ ΠΕ ΙΟ.. Αν δοκιµαστικό φορτίο q βρεθεί κοντά σε αγωγό που διαρρέεται από ρεύµα, υφίσταται δύναµη κάθετη προς την διεύθυνση της ταχύτητάς του και µε µέτρο ανάλογο της ταχύτητάς του, F qυ Β (νόµος
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΘΕΩΡΙΑΣ
 Κ. Ι. ΠΑΠΑΧΡΗΣΤΟΥ ΕΠΙΣΚΟΠΗΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΘΕΩΡΙΑΣ ΙΑΝΥΣΜΑΤΙΚΑ ΠΕ ΙΑ Θεώρηµα tokes (Γενική Μορφή): Χωρος " Παραγωγος " Πεδιου = Οριο Πεδιο Χωρου Παραδείγµατα: 1. Θεώρηµα Newton-Leibniz (ο «χώρος» είναι
Κ. Ι. ΠΑΠΑΧΡΗΣΤΟΥ ΕΠΙΣΚΟΠΗΣΗ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗΣ ΘΕΩΡΙΑΣ ΙΑΝΥΣΜΑΤΙΚΑ ΠΕ ΙΑ Θεώρηµα tokes (Γενική Μορφή): Χωρος " Παραγωγος " Πεδιου = Οριο Πεδιο Χωρου Παραδείγµατα: 1. Θεώρηµα Newton-Leibniz (ο «χώρος» είναι
ΕΞΙΣΩΣΕΙΣ MAXWELL ΣΕ ΜΕΣΟ
 ΕΞΙΣΩΣΕΙΣ MAXWELL ΣΕ ΜΕΣΟ ΤΙ ΕΞΕΤΑΖΟΥΜΕ? ΤΟ ΦΩΣ ΙΑ Ι ΕΤΑΙ ΣΕ ΕΝΑ ΜΕΣΟ (ΓΥΑΛΙ, κα) ΑΠΑΙΤΕΙΤΑΙ ΜΕΛΕΤΗ ΤΗΣ ΙΑ ΟΣΗΣ ΣΤΟ ΜΕΣΟ ΕΦΑΡΜΟΓΗ ΣΥΝΟΡΙΑΚΩΝ ΣΥΝΘΗΚΩΝ ευθύγραµµη διάδοσητου φωτός Πυθαγόρας, ηµόκριτος, Εµπεδοκλής,
ΕΞΙΣΩΣΕΙΣ MAXWELL ΣΕ ΜΕΣΟ ΤΙ ΕΞΕΤΑΖΟΥΜΕ? ΤΟ ΦΩΣ ΙΑ Ι ΕΤΑΙ ΣΕ ΕΝΑ ΜΕΣΟ (ΓΥΑΛΙ, κα) ΑΠΑΙΤΕΙΤΑΙ ΜΕΛΕΤΗ ΤΗΣ ΙΑ ΟΣΗΣ ΣΤΟ ΜΕΣΟ ΕΦΑΡΜΟΓΗ ΣΥΝΟΡΙΑΚΩΝ ΣΥΝΘΗΚΩΝ ευθύγραµµη διάδοσητου φωτός Πυθαγόρας, ηµόκριτος, Εµπεδοκλής,
ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες)
 ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
ΑΣΚΗΣΗ 1 ΦΥΕ 14 6η ΕΡΓΑΣΙΑ Παράδοση 30-06-08 ( Οι ασκήσεις είναι ϐαθµολογικά ισοδύναµες) Α) Τρία σηµειακά ϕορτία τοποθετούνται στις κορυφές ενός τετραγώνου πλευράς α, όπως ϕαίνεται στο σχήµα 1. Υπολογίστε
Κεφάλαιο 10 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ
 Κφάλαιο 10 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ Σύνοψη Στο δέκατο τούτο κφάλαιο παρουσιάζται το φαινόμνο της ηλκτρομαγνητικής παγωγής, το οποίο πριγράφται από το νόμο του Faraday. Επξηγίται ο κανόνας του Lenz και
Κφάλαιο 10 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ Σύνοψη Στο δέκατο τούτο κφάλαιο παρουσιάζται το φαινόμνο της ηλκτρομαγνητικής παγωγής, το οποίο πριγράφται από το νόμο του Faraday. Επξηγίται ο κανόνας του Lenz και
ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ
 ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ ΧΩΡΗΤΙΚΟΤΗΤΑ Ένας πυκνωτής έχει ως σκοπό να αποθηκεύει ηλεκτρική ενέργεια που μπορεί να ελευθερώνεται με ελεγχόμενο τρόπο σε βραχύ χρονικό διάστημα. Αποτελείται από 2 χωρικά
ΧΩΡΗΤΙΚΟΤΗΤΑ και ΔΙΗΛΕΚΤΡΙΚΑ ΧΩΡΗΤΙΚΟΤΗΤΑ Ένας πυκνωτής έχει ως σκοπό να αποθηκεύει ηλεκτρική ενέργεια που μπορεί να ελευθερώνεται με ελεγχόμενο τρόπο σε βραχύ χρονικό διάστημα. Αποτελείται από 2 χωρικά
h Καλώς Ορίσατε στο μάθημα «Ηλεκτρομαγνητισμός Ι, Φ-301»!!! Τα Γενικά
 h Καλώς Ορίσατε στο μάθημα «Ηλεκτρομαγνητισμός Ι, Φ-301»!!! Τα Γενικά Διδάσκων: Ηλίας Περάκης, Καθηγητής Φυσικής Τηλέφωνο: (2810-39)4259 Γραφείο: 2.Γ27 2ος όροφος, Κτίριο Φυσικής Email : ilias@physics.uoc.gr
h Καλώς Ορίσατε στο μάθημα «Ηλεκτρομαγνητισμός Ι, Φ-301»!!! Τα Γενικά Διδάσκων: Ηλίας Περάκης, Καθηγητής Φυσικής Τηλέφωνο: (2810-39)4259 Γραφείο: 2.Γ27 2ος όροφος, Κτίριο Φυσικής Email : ilias@physics.uoc.gr
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι
 ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
ΚΕΦΑΛΑΙΟ 7: Αναπαραστάσεις Πεπερασμένων Ομάδων Ι Χρησιμοποιώντας το θεώρημα του Weddebu για ημιαπλούς δακτυλίους, αναπτύσσουμε εδώ τις πρώτες προτάσεις από τη θεωρία των αναπαραστάσεων και αρακτήρων πεπερασμένων
7η ιεθνής Μαθηµατική Εβδοµάδα Θεσσαλονίκη Μαρτίου 2015 Ολοκληρωτικές εξισώσεις: τριτοβάθµια και δευτεροβάθµια εκπαίδευση
 7η ιεθνής Μαθηµατική Εβδοµάδα Θεσσαλονίκη 18 22 Μαρτίου 215 Ολοκληρωτικές εξισώσεις: τριτοβάθµια και δευτεροβάθµια εκπαίδευση Κυριαζής Χρήστος Πρωτοπαπάς Ελευθέριος 1 Ενότητες παρουσίασης Εισαγωγικές έννοιες
7η ιεθνής Μαθηµατική Εβδοµάδα Θεσσαλονίκη 18 22 Μαρτίου 215 Ολοκληρωτικές εξισώσεις: τριτοβάθµια και δευτεροβάθµια εκπαίδευση Κυριαζής Χρήστος Πρωτοπαπάς Ελευθέριος 1 Ενότητες παρουσίασης Εισαγωγικές έννοιες
Μαγνητικά Υλικά Υπεραγωγοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαγνητικά Υλικά Υπεραγωγοί ΥΠΕΡΑΓΩΓΙΜΟΤΗΤΑ Διδάσκων: Καθηγητής Ιωάννης Παναγιωτόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαγνητικά Υλικά Υπεραγωγοί ΥΠΕΡΑΓΩΓΙΜΟΤΗΤΑ Διδάσκων: Καθηγητής Ιωάννης Παναγιωτόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό υπόκειται σε άδειες χρήσης
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ
 ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΙΣΑΓΩΓΙΚΑ Η ηλεκτρική μηχανή είναι μια διάταξη μετατροπής μηχανικής ενέργειας σε ηλεκτρική και αντίστροφα. απώλειες Μηχανική ενέργεια Γεννήτρια Κινητήρας Ηλεκτρική ενέργεια
ΕΙΣΑΓΩΓΗ ΣΤΙΣ ΗΛΕΚΤΡΙΚΕΣ ΜΗΧΑΝΕΣ ΕΙΣΑΓΩΓΙΚΑ Η ηλεκτρική μηχανή είναι μια διάταξη μετατροπής μηχανικής ενέργειας σε ηλεκτρική και αντίστροφα. απώλειες Μηχανική ενέργεια Γεννήτρια Κινητήρας Ηλεκτρική ενέργεια
Εφαρµογές στη δυναµική του κέντρου µάζας στερεού σώµατος
 Εφαρµογές στη δυναµική του κέντρου µάζας στρού σώµατος Εφαρµογή 1η Οµογνής δίσκος ακτίνας R ηρµί στην άκρη οριζόντιου τραπζιού µ το κέντρο του Κ να βρίσκται στην κατακόρυφη που διέρχται από την ία Ο του
Εφαρµογές στη δυναµική του κέντρου µάζας στρού σώµατος Εφαρµογή 1η Οµογνής δίσκος ακτίνας R ηρµί στην άκρη οριζόντιου τραπζιού µ το κέντρο του Κ να βρίσκται στην κατακόρυφη που διέρχται από την ία Ο του
Χημεία Γ Λυκείου. ΗΑ + Η 2 Ο Η 3 Ο +1 + Α -1 Αρχ: 0,05Μ Αντ: χ Μ Παρ: χ Μ χ Μ ΧΙ: 0,05 χ Μ χ + ψ Μ χ Μ
 Άσκηση 74 σολικού βιβλίου, σελίδα 90: Να βρείτε τη + σε διάλυμα που περιέει δύο ασθενή οξέα ΗΑ 0,05Μ με αηα = 4 0-5 και ΗΒ 0,Μ με αηβ = 0-5 Γράφουμε τους ιοντισμούς των δύο ασθενών οξέων ΗΑ + Η Ο Η + +
Άσκηση 74 σολικού βιβλίου, σελίδα 90: Να βρείτε τη + σε διάλυμα που περιέει δύο ασθενή οξέα ΗΑ 0,05Μ με αηα = 4 0-5 και ΗΒ 0,Μ με αηβ = 0-5 Γράφουμε τους ιοντισμούς των δύο ασθενών οξέων ΗΑ + Η Ο Η + +
ΛΥΣΕΙΣ 6 ης ΕΡΓΑΣΙΑΣ (Ημερομηνία παράδοσης 3 Ιουλίου 2005)
 Άσκηση 1. (1 μονάδες) ΛΥΣΕΙΣ 6 ης ΕΡΓΑΣΙΑΣ (Ημερομηνία παράδοσης Ιουλίου 5) Α) Δοκιμαστικό φορτίο q αφήνεται σε κάποιο σημείο μέσα σε ομογενές ηλεκτρικό πεδίο εντάσεως Ε. Να εξετάσετε πώς θα κινηθεί το
Άσκηση 1. (1 μονάδες) ΛΥΣΕΙΣ 6 ης ΕΡΓΑΣΙΑΣ (Ημερομηνία παράδοσης Ιουλίου 5) Α) Δοκιμαστικό φορτίο q αφήνεται σε κάποιο σημείο μέσα σε ομογενές ηλεκτρικό πεδίο εντάσεως Ε. Να εξετάσετε πώς θα κινηθεί το
(α) 1. (β) Το σύστημα βρίσκεται υπό διαφορά δυναμικού 12 V: U ολ = 1 2 C ολ(δv) 2 = J.
 4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
4 η Ομάδα Ασκήσεων Δύο πυκνωτές C=5 μf και C=40 μf συνδέονται παράλληλα στους ακροδέκτες πηγών τάσης VS=50 V και VS=75 V αντίστοιχα και φορτίζονται Στην συνέχεια αποσυνδέονται και συνδέονται μεταξύ τους,
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ
 ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Προχωρηµένα Εργαστήρια Φυσικής Ι Ελευθέριος Ηλιόπουλος Πείραµα ΙI Η άσκηση αποσκοπεί στην µέτρηση βασικών φυσικών µεγεθών µαγνητικών υλικών και την εξοικείωση των
ΕΛΛΗΝΙΚΗ ΔΗΜΟΚΡΑΤΙΑ ΠΑΝΕΠΙΣΤΗΜΙΟ ΚΡΗΤΗΣ Προχωρηµένα Εργαστήρια Φυσικής Ι Ελευθέριος Ηλιόπουλος Πείραµα ΙI Η άσκηση αποσκοπεί στην µέτρηση βασικών φυσικών µεγεθών µαγνητικών υλικών και την εξοικείωση των
Μαγνητισμός. Ενότητα 2. Ηλεκτρισμός & Μαγνητισμός
 Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Ηλεκτρισμός & Μαγνητισμός Ενότητα 2. Ηλεκτρισμός & Μαγνητισμός Μαγνητισμός Το φαινόμενο της μαγνήτισης είναι γνωστό από την αρχαιότητα. Παρατηρήθηκε πως
Σημειώσεις Γενικής Φυσικής - ΒΕΤ Μ. Μπενής / 2016 Ηλεκτρισμός & Μαγνητισμός Ενότητα 2. Ηλεκτρισμός & Μαγνητισμός Μαγνητισμός Το φαινόμενο της μαγνήτισης είναι γνωστό από την αρχαιότητα. Παρατηρήθηκε πως
Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας
 Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Τομέας Μηχανολογικών Κατασκευών και Αυτομάτου Ελέγχου 2.3.26.3 Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας Εξέταση 3 ου Eξαμήνου (20 Φεβρουαρίου
Εθνικό Μετσόβιο Πολυτεχνείο Σχολή Μηχανολόγων Μηχανικών Τομέας Μηχανολογικών Κατασκευών και Αυτομάτου Ελέγχου 2.3.26.3 Hλεκτρομηχανικά Συστήματα Mετατροπής Ενέργειας Εξέταση 3 ου Eξαμήνου (20 Φεβρουαρίου
ΕΞΙΣΩΣΗ ΣΦΑΙΡΑΣ. είναι όλοι ίσοι και επιπλέον δεν υπάρχουν οι όροι xy, yz, zx. Γενικά µια εξίσωση της µορφής: 0 + Β + Α.
 Suies & Publishing ΣΟΛΩΜΟΥ 9 ΠΟΛΥΤΕΧΝΕΙΟ ΤΗΛ.:.38..57 www.arnοs.gr 3 Ο γωµτρικός τόπος των σηµίων που έχουν σταθρή απόσταση από το σηµίο,, του 3 ονοµάζται σφαίρα. Η σφαίρα µ κέντρο το,, και ακτίνα έχι
Suies & Publishing ΣΟΛΩΜΟΥ 9 ΠΟΛΥΤΕΧΝΕΙΟ ΤΗΛ.:.38..57 www.arnοs.gr 3 Ο γωµτρικός τόπος των σηµίων που έχουν σταθρή απόσταση από το σηµίο,, του 3 ονοµάζται σφαίρα. Η σφαίρα µ κέντρο το,, και ακτίνα έχι
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ
 ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΕΠΑΓΩΓΗ 1 3.1 ΠΕΙΡΑΜΑΤΑ ΕΠΑΓΩΓΗΣ Το Σχ. 3.1 δείχνει μερικά από τα πειράματα που πραγματοποίησε o Michael Faraday. Στο Σχ. 3.1(α, β, γ) ένα πηνίο συνδέεται με γαλβανόμετρο.
10 ΠΡΟΣΠΤΩΣΗ Η/Μ ΚΥΜΑΤΩΝ ΣΤΗ ΙΑΧΩΡΙΣΤΙΚΗ ΕΠΙΦΑΝΕΙΑ ΥΟ ΜΕΣΩΝ
 ΚΥΜΑΤΙΚΗ - ΟΠΤΙΚΗ ΠΡΟΣΠΤΩΣΗ Η/Μ ΚΥΜΑΤΩΝ ΣΤΗ ΙΑΧΩΡΙΣΤΙΚΗ ΕΠΙΦΑΝΕΙΑ ΥΟ ΜΕΣΩΝ ΟΡΙΑΚΕΣ ΣΥΝΘΗΚΕΣ. Η φατονική συνιστώσα του ηλκτρικού δίου δύο έσα t t. Η κάθτη συνιστώσα του ανύσατος της ηλκτρικής τατόισης σταθρή
ΚΥΜΑΤΙΚΗ - ΟΠΤΙΚΗ ΠΡΟΣΠΤΩΣΗ Η/Μ ΚΥΜΑΤΩΝ ΣΤΗ ΙΑΧΩΡΙΣΤΙΚΗ ΕΠΙΦΑΝΕΙΑ ΥΟ ΜΕΣΩΝ ΟΡΙΑΚΕΣ ΣΥΝΘΗΚΕΣ. Η φατονική συνιστώσα του ηλκτρικού δίου δύο έσα t t. Η κάθτη συνιστώσα του ανύσατος της ηλκτρικής τατόισης σταθρή
Ηλεκτροτεχνικές Εφαρμογές Μαγνητικά Κυκλώματα
 Ηλεκτροτεχνικές Εφαρμογές Μαγνητικά Κυκλώματα Επισκόπηση παρουσίασης Ηλεκτροτεχνικές Εφαρμογές Μαγνητικά Κυκλώματα Μαγνητικά κυκλώματα: έννοια, ορισμοί, εφαρμογές Χαρακτηριστικά μεγέθη αντιστοιχίες με
Ηλεκτροτεχνικές Εφαρμογές Μαγνητικά Κυκλώματα Επισκόπηση παρουσίασης Ηλεκτροτεχνικές Εφαρμογές Μαγνητικά Κυκλώματα Μαγνητικά κυκλώματα: έννοια, ορισμοί, εφαρμογές Χαρακτηριστικά μεγέθη αντιστοιχίες με
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ
 ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ Πηγές Κατανομή χωικής d
ΑΡΙΣΤΟΤΕΛΕΙΟ ΠΑΝΕΠΙΣΤΗΜΙΟ ΘΕΣΣΑΛΟΝΙΚΗΣ ΠΟΛΥΤΕΧΝΙΚΗ ΣΧΟΛΗ ΤΜΗΜΑ ΗΛΕΚΤΡΟΛΟΓΩΝ ΜΗΧΑΝΙΚΩΝ & ΜΗΧΑΝΙΚΩΝ ΥΠΟΛΟΓΙΣΤΩΝ ΤΟΜΕΑΣ ΤΗΛΕΠΙΚΟΙΝΩΝΙΩΝ ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ ΗΛΕΚΤΡΟΣΤΑΤΙΚΟ ΠΕΔΙΟ Πηγές Κατανομή χωικής d
Κλασική Ηλεκτροδυναμική
 Κλασική Ηλεκτροδυναμική Ενότητα 18: Νόμοι Maxwell Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσίασει τις εξισώσεις Maxwell. 2 Περιεχόμενα ενότητας
Κλασική Ηλεκτροδυναμική Ενότητα 18: Νόμοι Maxwell Ανδρέας Τερζής Σχολή Θετικών Επιστημών Τμήμα Φυσικής Σκοποί ενότητας Σκοπός της ενότητας είναι να παρουσίασει τις εξισώσεις Maxwell. 2 Περιεχόμενα ενότητας
E = E 0 + E = E 0 P ϵ 0. = 1 + χ r. = Q E 0 l
 Πυκνωτής με διηλεκτρικό Πυκνωτής με ορθογώνιους οπλισμούς εμβαδού A και απόσταση μεταξύ των οπλισμών l έχει ϕορτίο Q. Η επιϕανειακή πυκνότητα ϕορτίου σε κάθε οπλισμό θα είνα σ = ±Q/A. Το ηλεκτρικό πεδίο
Πυκνωτής με διηλεκτρικό Πυκνωτής με ορθογώνιους οπλισμούς εμβαδού A και απόσταση μεταξύ των οπλισμών l έχει ϕορτίο Q. Η επιϕανειακή πυκνότητα ϕορτίου σε κάθε οπλισμό θα είνα σ = ±Q/A. Το ηλεκτρικό πεδίο
Μαγνητικά Υλικά Υπεραγωγοί
 ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαγνητικά Υλικά Υπεραγωγοί ΣΥΝΔΕΣΗ ΜΑΓΝΗΤΙΣΜΟΥ ΜΕ ΑΛΛΕΣ ΙΔΙΟΤΗΤΕΣ Διδάσκων: Καθηγητής Ιωάννης Παναγιωτόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΠΑΝΕΠΙΣΤΗΜΙΟ ΙΩΑΝΝΙΝΩΝ ΑΝΟΙΚΤΑ ΑΚΑΔΗΜΑΪΚΑ ΜΑΘΗΜΑΤΑ Μαγνητικά Υλικά Υπεραγωγοί ΣΥΝΔΕΣΗ ΜΑΓΝΗΤΙΣΜΟΥ ΜΕ ΑΛΛΕΣ ΙΔΙΟΤΗΤΕΣ Διδάσκων: Καθηγητής Ιωάννης Παναγιωτόπουλος Άδειες Χρήσης Το παρόν εκπαιδευτικό υλικό
ΦΥΕ14, 2009-2010-Εργασιά 6 η Ημερομηνία παράδοσης 28/6/2010
 ΦΥΕ4, 9--Εργασιά 6 η Ημερομηνία παράδοσης 8/6/ Άσκηση A) Μια ράβδος μήκους είναι ομοιόμορφα φορτισμένη θετικά με συνολικό ηλεκτρικό φορτίο Q και βρίσκεται κατά μήκος του θετικού άξονα x από το σημείο x
ΦΥΕ4, 9--Εργασιά 6 η Ημερομηνία παράδοσης 8/6/ Άσκηση A) Μια ράβδος μήκους είναι ομοιόμορφα φορτισμένη θετικά με συνολικό ηλεκτρικό φορτίο Q και βρίσκεται κατά μήκος του θετικού άξονα x από το σημείο x
